Hostname: page-component-84b7d79bbc-g78kv Total loading time: 0 Render date: 2024-07-29T09:38:28.356Z Has data issue: false hasContentIssue false
  • English
  • Français

Searching for Absolute 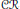$\mathcal{C}\mathcal{R}$-Epic Spaces

Published online by Cambridge University Press:  20 November 2018

Michael Barr ,
John F. Kennison  and
R. Raphael
Michael Barr
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, QC, H3A 2K6 email: barr@barrs.org
John F. Kennison
Affiliation:
Department of Mathematics and Computer Science, Clark University, Worcester, MA 01610, U.S.A. email: jkennison@clarku.edu
R. Raphael
Affiliation:
Department of Mathematics and Statistics, Concordia University, Montreal, QC, H4B 1R6 email: raphael@alcor.concordia.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In previous papers, Barr and Raphael investigated the situation of a topological space 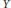$Y$ and a subspace 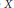$X$ such that the induced map 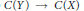$C(Y)\,\to \,C(X)$ is an epimorphism in the category 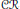$\mathcal{C}\mathcal{R}$ of commutative rings (with units). We call such an embedding a 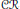$\mathcal{C}\mathcal{R}$-epic embedding and we say that 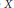$X$ is absolute 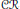$\mathcal{C}\mathcal{R}$-epic if every embedding of 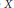$X$ is 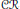$\mathcal{C}\mathcal{R}$-epic. We continue this investigation. Our most notable result shows that a Lindelöf space 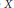$X$ is absolute 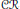$\mathcal{C}\mathcal{R}$-epic if a countable intersection of 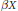$\beta X$-neighbourhoods of 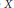$X$ is a 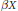$\beta X$-neighbourhood of 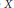$X$. This condition is stable under countable sums, the formation of closed subspaces, cozero-subspaces, and being the domain or codomain of a perfect map. A strengthening of the Lindelöf property leads to a new class with the same closure properties that is also closed under finite products. Moreover, all $\sigma $-compact spaces and all Lindelöf $P$-spaces satisfy this stronger condition. We get some results in the non-Lindelöf case that are sufficient to show that the Dieudonné plank and some closely related spaces are absolute 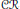$\mathcal{C}\mathcal{R}$-epic.

Keywords

18A2054C4554B30absoluteᘓℛ-epicscountable neighbourhood propertyamply LindelöfDieudonné plank
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 3 , 01 June 2007 , pp. 465 - 487
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Alster, K., On the class of all spaces of weight not greater tha. ω1 whose Cartesian product with every Lindelöf space is Lindelöf. Fund. Math. 129(1988), no. 2, 133–140.Google Scholar
[2] Barr, M., Kennison, J., and Raphael, R., On productively Lindelöf spaces. To appear in Sci. Math. Japonicae. ftp://ftp.math.mcgill.ca/pub/barr/pdffiles/alster.pdf Google Scholar
[3] Barr, M., Burgess, W., and Raphael, R., Ring epimorphisms and C(X). Theory Appl. Categories 11(2003), no. 12, 283–308.(electronic).Google Scholar
[4] Barr, M., Raphael, R., and Woods, R. G., On ᘓℛ-epic embeddings and absolute ᘓℛ-epic spaces. Canad. J. Math. 57(2005), no. 6, 1121–1138.Google Scholar
[5] Blair, R. L. and Hager, A. W., Extensions of zero-sets and real-valued functions. Math. Zeit. 136(1974), 41–52.Google Scholar
[6] Dow, A., Gubbi, A. V., and Szymanski, A., Rigid Stone spaces within ZFC. Proc. Amer. Math. Soc. 102(1988), no. 3, 745–748.Google Scholar
[7] Dugundji, J., Topology, Allyn and Bacon, Boston, MA, 1966.Google Scholar
[8] Gillman, L. and Jerison, M., Rings of Continuous Functions. D. Van Nostrand, Princeton, NJ, 1960.Google Scholar
[9] Hager, A. W. and Martinez, J., C-epic compactifications. Topology Appl. 117(2002), no. 2, 113–138.Google Scholar
[10] Henriksen, M. and Johnson, D. G., On the structure of a class of archimedean lattice-ordered algebras. Fund. Math. 50(1961/1962), 73–94.Google Scholar
[11] Isbell, J. R., Epimorphisms and dominions. In: Proc. Conf. Categorical Algebra, Springer-Verlag, New York, 1966, pp. 232–246.Google Scholar
[12] Kelley, J. L., General Topology. Van Nostrand, Toronto, 1955.Google Scholar
[13] Levy, R. and Rice, M. D., Normal P-spaces and the Gδ topology. Colloq. Math. 44(1982), no. 2, 227–240.Google Scholar
[14] van Mill, J., An introduction to βω. In: Handbook of Set-Theoretic Topology, North-Holland, Amsterdam, 1984, pp. 503–507.Google Scholar
[15] Mrówka, S., Some set-theoretic constructions in topology. Fund. Math. 94(1977), no. 2, 83–92.Google Scholar
[16] Porter, J. R. and Woods, R. G., Extensions and Absolutes of Hausdorff Spaces. Springer-Verlag, New York 1988.Google Scholar
[17] Terasawa, J., Spaces N ∪ R and their dimensions. Topology Appl. 11(1980), no. 1, 93–102.Google Scholar