Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-06-09T01:53:06.542Z Has data issue: false hasContentIssue false
  • English
  • Français

A Segal-Langevin Type Stochastic Differential Equation on a Space Of Generalized Functionals

Published online by Cambridge University Press:  20 November 2018

Gopinath Kallianpur  and
Itaru Mitoma
Gopinath Kallianpur
Affiliation:
Department of Statistics University of North Carolina Chapel Hill, NC 27599-3260 U.S.A.
Itaru Mitoma
Affiliation:
Department of Mathematics Saga University Saga840, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E′ be the dual of a nuclear Fréchet space E and L*(t) the adjoint operator of a diffusion operator L(t) of infinitely many variables, which has a formal expression:

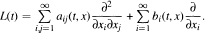
A weak form of the stochastic differential equation

dX(t) = dW(t) + L*(t)X(t)dt

is introduced and the existence of a unique solution is established. The solution process is a random linear functional (in the sense of I. E. Segal) on a space of generalized functionals on E′. The above is an appropriate model for the central limit theorem for an interacting system of spatially extended neurons. Applications to the latter problem are discussed.

Keywords

46F2560F0560H1535K22Weak solutionSDEFréchet derivativegeneralized functional spacecentral limit theoremsystem of neurons
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 3 , 01 June 1992 , pp. 524 - 552
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Billingsley, P., Convergence of Probability Measures, Wiley, New York-London-Sydney-Toronto, 1968.Google Scholar
2. Bojdecki, T. and Gorostiza, L.G., Langevin equation for S′-valued Gaussian processes and fluctuation limits of infinite particle systems, Probab. Th. Rel. Fields 73 (1986), 227–244.Google Scholar
3. Courant, R. and Hilbert, D., Methods of Mathematical Physics 1, Interscience Publishers, Inc., New York, 1966.Google Scholar
4. Dawson, D.A., Critical dynamics and fluctuations for a mean-field model of cooperative behavior, J. Statist Phys. 31 (1983), 29–85.Google Scholar
5. Deuschel, J.D., Central limit theorem for an infinite lattice system of interacting diffusion processes, Ann. Probab. 16 (1988), 700–716.Google Scholar
6. Fouque, J.P., La convergence en loi pour les processus a valeurs dans un espace nucléaire, Ann. IHP 20 (1984), 225–245.Google Scholar
7. Gelfand, I.M. and Shilov, G.E., Generalized functions 2, Academic press, New York and London, 1964.Google Scholar
8. Gikhman, J.I. and Skorokhod, A.V., Stochastic Differential Equations, Springer, Berlin, 1972.Google Scholar
9. Hitsuda, M. and Mitoma, I., Tightness problem and stochastic evolution equation arising from fluctuation phenomenafor interacting diffusions, Multivariate, J. Anal. (1986), 311–328.Google Scholar
10. Holley, R. and Stroock, D.W., Central limit phenomena of various interacting systems, Ann. Math. 110 (1979), 333–393.Google Scholar
11. Itô, K., Infinite dimensional Ornstein-Uhlenbeck processes, Taniguchi Symp. SA, Katata, Kinokuniya, Tokyo, (1984), 197–224.Google Scholar
12. Kallianpur, G. and Wolpert, R., Infinite dimensional stochastic models for spatially distributed neurons, Appl. Math. Optim 12 (1984), 125–172.Google Scholar
13. Komatsu, H., Semi-groups of operators in locally convex spaces, J. Math. Soc. Japan, 16 (1964), 232–262.Google Scholar
14. Kunita, H., Stochastic differential equations and stochastic flows of diffeomorphisms, Lect. Notes in Math. 1097, Springer 1984.Google Scholar
15. Kuo, H.H., Gaussian measures on Banach spaces, Lect. Notes in Math. 463, Springer, Berlin, 1975.Google Scholar
16. Kuo, H.H., Stochastic integrals in abstract Wiener space II, regularity properties, Nagoya Math. J. 50 (1973), 89–116.Google Scholar
17. McKean, H.P., Propagation of chaos for a class of non-linear parabolic equations, Lecture series in Differential Equations 7, Catholic Univ. (1967), 41–57.Google Scholar
18. Minlos, R.A., Generalized random processes and their extension to a measure, Selected Transi. Math. Statist. Probab. 3 (1962), 291–313.Google Scholar
19. Mitoma, I., On the sample continuity of S'-processes, J. Math. Soc. Japan, (1983), 629–636.Google Scholar
20. Mitoma, I., Tightness of probabilities on C([0,1] ; S’) andD([0,1] ; S’), Ann. Probab. 11 (1983), 989–999.Google Scholar
21. Mitoma, I., An ∞-dimensional inhomogeneousLangevin's equation, J. Functional Analysis 61 (1985), 342–359.Google Scholar
22. Mitoma, I., Generalized Ornstein-Uhlenbeck process having a characteristic operator with polynomial coefficients, Probab. Th. Rel. Fields 76 (1987), 533–555.Google Scholar
23. Martias, C., Sur les support des processus a valeurs dans des espaces nucleairs, Ann. IHP 24 (1988), 345–365.Google Scholar
24. Segal, I., Non-linear functions of weak processes, J. Funct. Anal. 4 (1969), 404–457.Google Scholar
25. Shiga, T. and Tanaka, H., Central limit theorem for a system of Markovian particles with mean-field interactions, Z. Wahrsch. verw. Gebiete 69 (1985), 439–459.Google Scholar
26. Schaefer, H.H., Topological vector spaces, Springer, Berlin, 1972.Google Scholar
27. Totoki, H., A method of construction for measures on function spaces and its applications to stochastic processes,Mem. Fac. Sci. Kyushu Univ. Ser. A, Math. 15 (1962), 178–190.Google Scholar
28. Walsh, J., An introduction to stochastic partial differential equations, École d'été de Probabilités de Saint- Flour XIV, Lect. Notes in Math. 1180, Springer, Berlin, 1984.Google Scholar
29. Watanabe, S., Lectures on stochastic differential equations and Malliavin 's calculus, Springer, Berlin, 1984.Google Scholar