Article contents
A Semimodular Imbedding of Lattices
Published online by Cambridge University Press: 20 November 2018
Extract
The study of structural or arithmetic properties of a general lattice 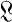 often can be facilitated by imbedding
often can be facilitated by imbedding 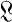 as a sublattice of a lattice
as a sublattice of a lattice  of a more restricted type whose properties are known. However, if
of a more restricted type whose properties are known. However, if  is too restricted, a general imbedding is impossible; for example,
is too restricted, a general imbedding is impossible; for example,  cannot be modular because
cannot be modular because 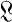 , as a sublattice of
, as a sublattice of  , would then have to be modular. One of the best results of this nature has been given by Dilworth in an unpublished work in which he shows that any finite dimensional lattice is isomorphic to a sublattice of a semi-modular point lattice (1, pp. 105 and 110). In the present paper Dilworth's imbedding process is modified to obtain a sharper result: Any finite dimensional lattice
, would then have to be modular. One of the best results of this nature has been given by Dilworth in an unpublished work in which he shows that any finite dimensional lattice is isomorphic to a sublattice of a semi-modular point lattice (1, pp. 105 and 110). In the present paper Dilworth's imbedding process is modified to obtain a sharper result: Any finite dimensional lattice 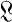 is isometrically isomorphic to a sublattice of a semi-modular lattice
is isometrically isomorphic to a sublattice of a semi-modular lattice  which has the same number of points as
which has the same number of points as 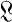 and which preserves basic properties of the join-irreducible arithmetic of
and which preserves basic properties of the join-irreducible arithmetic of 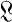 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1960
References
- 10
- Cited by


