No CrossRef data available.
Article contents
Solvable Subgroups and their Lie Algebras in Characteristic p
Published online by Cambridge University Press: 20 November 2018
Extract
1. Introduction. Throughout this paper, G is a connected linear algebraic group over an algebraically closed field whose characteristic is denoted p. For any closed subgroup H of G, 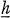 denotes the Lie algebra of H and H0 denotes the connected component of the identity of H.
denotes the Lie algebra of H and H0 denotes the connected component of the identity of H.
A Borel subalgebra of  is the Lie algebra
is the Lie algebra 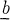 of some Borel subgroup B of G. A maximal torus of
of some Borel subgroup B of G. A maximal torus of  is the Lie algebra
is the Lie algebra 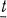 of some maximal torus T of G. In [4], it is shown that the maximal tori of
of some maximal torus T of G. In [4], it is shown that the maximal tori of  are the maximal commutative subalgebras
are the maximal commutative subalgebras 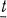 of
of  consisting of semisimple elements, and the question was raised in § 14.3 as to whether the set of Borel subalgebras of
consisting of semisimple elements, and the question was raised in § 14.3 as to whether the set of Borel subalgebras of  is the set of maximal triangulable subalgebras of
is the set of maximal triangulable subalgebras of  .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1979




