Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-08T08:06:25.400Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly Summable Ultrafilters, Union Ultrafilters, and the Trivial Sums Property

Published online by Cambridge University Press:  20 November 2018

David J. Fernández Bretón
David J. Fernández Bretón*
Affiliation:
Department of Mathematics and Statistics, York University, Toronto, ON e-mail: difernan@umich.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We answer two questions of Hindman, Steprāns, and Strauss; namely, we prove that every strongly summable ultrafilter on an abelian group is sparse and has the trivial sums property. Moreover, we show that in most cases the sparseness of the given ultrafilter is a consequence of its being isomorphic to a union ultrafilter. However, this does not happen in all cases; we also construct (assuming Martin's Axiom for countable partial orders, i.e., 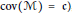$\operatorname{cov}\left( \text{M} \right)=\mathfrak{c})$, a strongly summable ultrafilter on the Boolean group that is not additively isomorphic to any union ultrafilter.

Keywords

03E7554D3554D8005D1005A1820K99ultrafilterStone–Čech compactificationsparse ultrafilterstrongly summable ultrafilterunion ultrafilterfinite sumadditive isomorphismtrivial sums propertyBoolean groupabelian group
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 1 , 01 February 2016 , pp. 44 - 66
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Blass, A., Ultrafilters related to Hindman's finite-unions theorem and its extensions. In: Logic and Combinatorics, Contemp. Math., 65, American Mathematical Society, Providence, RI, 1987, pp. 89–124.http://dx.doi.Org/10.1090/conm/065/891244 Google Scholar
[2] Blass, A.and Hindman, N., On strongly summable ultrafihers and union ultrafilters. Trans. Amer. Math. Soc. 304(1987), no. 1, 83–99.http://dx.doi.Org/10.1090/S0002-9947-1987-0906807-4 Google Scholar
[3] Eisworth, T., Forcing and stable-ordered union ultrafilters. J. Symbolic Logic 67(2002), no. 1,449–464.http://dx.doi.Org/10.2178/jsl/1190150054 Google Scholar
[4] D. Fernandez Bretón, J., Every strongly summable ultrafilter on ⊕ℤ2 is sparse. New York J. Math. 19(2013), 117–129.Google Scholar
[5] Hindman, N., The existence of certain ultrafilters on and a conjecture of Graham and Rothschild. Proc. Amer. Math. Soc. 36(1972), no. 2, 341–346.Google Scholar
[6] Hindman, N., Summable ultrafilters and finite sums. In: Logic and Combinatorics, Contemp. Math., 65, American Mathematical Society, Providence, RI, 1987, 263–274.http://dx.doi.Org/10.1090/conm/065/891252 Google Scholar
[7] Hindman, N. and Legette Jones, L., Idempotents in βS that are only products trivially. New York J. Math. 20(2014), 57–80.Google Scholar
[8] Hindman, N., Protasov, I., and Strauss, D., Strongly summable ultrafilters on Abelian groups. Mat. Stud. 10(1998), no. 2, 121–132.Google Scholar
[9] Hindman, N., Steprāns, J., and Strauss, D., Semigroups in which all strongly summable ultrafilters are sparse. New York J. Math. 18(2012), 835–848.Google Scholar
[10] Hindman, N. and Strauss, D., Algebra in the Stone-Čech compactification. Second ed., de Gruyter Textbook, Walter de Gruyter, Berlin, 2012.Google Scholar
[11] Krautzberger, P., On strongly summable ultrafilters. New York J. Math. 16(2010), 629–649.Google Scholar
[12] Krautzberger, P., On union ultrafilters. Order 29(2012), 317–343.http://dx.doi.Org/10.1007/si1083-011-9223-3 Google Scholar
[13] Protasov, I. V., Finite groups in βG. Mat. Stud. 10(1998), no. 1,17–22.Google Scholar