Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-07T15:58:28.824Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure of a Certain Class of Rings with Involution

Published online by Cambridge University Press:  20 November 2018

M. Chacron ,
I. N. Herstein  and
S. Montgomery
M. Chacron
Affiliation:
Carleton University, Ottawa, Ontario
I. N. Herstein
Affiliation:
University of Chicago, Chicago, Illinois
S. Montgomery
Affiliation:
University of Southern California, Los Angeles, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a ring with involution *, and let Z denote the center of R. In R let S = {x ∈ R|x* = x} be the set of symmetric elements of R. We shall study rings which are conditioned in the following way: given s ∈ S, then for some integer 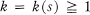and some polynomial p(t), with integer coefficients which depend on 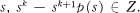. What can one hope to say about such rings? Certainly all rings in which every symmetric element is nilpotent fall into this class.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 5 , 01 October 1975 , pp. 1114 - 1126
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Amitsur, S. A., Rings with involution, Israel J. Math. 6 (1968), 99–106.Google Scholar
2. Amitsur, S. A. and Levitzki, Jacob, Minimal identities for algebras, Proc. Amer. Math. Soc. 1 (1950), 449–463.Google Scholar
3. Burgess, W. and Chacron, M., A generalization of a theorem of Herstein and Montgomery, J. Algebra (to appear).Google Scholar
4. Chacron, M., On a theorem of Herstein, Can. J. Math, (to appear).Google Scholar
5. Chacron, M., A generalization of a theorem of Kaplansky and rings with involution, Michigan Math. J. 20 (1973), 45–54.Google Scholar
6. Herstein, I. N., The structure of a certain class of rings, Amer. J. Math. 75 (1953), 864–871.Google Scholar
7. Herstein, I. N. and Montgomery, Susan, Invertible and regular elements in rings with involution, J. Algebra 25 (1973), 390–400.Google Scholar
8. Jacobson, Nathan, Lectures on quadratic Jordan algebras (Tata Institute, Bombay 1969).Google Scholar
9. Jacobson, Nathan, A structure theory for algebraic algebras of bounded degree, Ann. of Math. 4.6 (1945), 695–707.Google Scholar
10. Structure of rings (AMS Colloquium Publ. 37 ,1964).Google Scholar
11. Kaplansky, I., Linear algebra and geometry (Allyn & Bacon, Boston, 1969).Google Scholar
12. McCrimmon, K., On Herstein s theorems relating Jordan and associative algebras, J. Algebra 13 (1969), 382–392.Google Scholar
13. Montgomery, Susan, A generalization of a theorem of Jacobson, Proc. Amer. Math. Soc. 28 (1971), 366–370.Google Scholar
14. A generalization of a theorem of Jacobson II, Pacific J. Math. 44 (1973), 233–240.Google Scholar
15. Polynomial identity algebras with involution, Proc. Amer. Math. Soc. 27 (1971), 53–56.Google Scholar
16. Nagata, M., Nakayama, T. and Tuzuku, T., On an existence lemma in valuation theory, Nagoya Math. J. 6 (1953), 59–61.Google Scholar
17. Rowen, Louis, Some results on the center of a ring with polynomial identity, Bull. Amer. Math. Soc. 79 (1973), 219–223.Google Scholar