Article contents
Tail Bounds for the Stable Marriage of Poisson and Lebesgue
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $\Xi $ be a discrete set in
$\Xi $ be a discrete set in 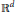 ${{\mathbb{R}}^{d}}$. Call the elements of
${{\mathbb{R}}^{d}}$. Call the elements of  $\Xi $centers. The well-known Voronoi tessellation partitions
$\Xi $centers. The well-known Voronoi tessellation partitions 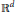 ${{\mathbb{R}}^{d}}$ into polyhedral regions (of varying volumes) by allocating each site of
${{\mathbb{R}}^{d}}$ into polyhedral regions (of varying volumes) by allocating each site of 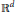 ${{\mathbb{R}}^{d}}$ to the closest center. Here we study allocations of
${{\mathbb{R}}^{d}}$ to the closest center. Here we study allocations of 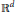 ${{\mathbb{R}}^{d}}$ to
${{\mathbb{R}}^{d}}$ to  $\Xi $ in which each center attempts to claim a region of equal volume
$\Xi $ in which each center attempts to claim a region of equal volume  $\alpha $.
$\alpha $.
We focus on the case where  $\Xi $ arises from a Poisson process of unit intensity. In an earlier paper by the authors it was proved that there is a unique allocation which is stable in the sense of the Gale–Shapley marriage problem. We study the distance
$\Xi $ arises from a Poisson process of unit intensity. In an earlier paper by the authors it was proved that there is a unique allocation which is stable in the sense of the Gale–Shapley marriage problem. We study the distance 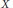 $X$ from a typical site to its allocated center in the stable allocation.
$X$ from a typical site to its allocated center in the stable allocation.
The model exhibits a phase transition in the appetite  $\alpha $. In the critical case
$\alpha $. In the critical case 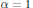 $\alpha \,=\,1$ we prove a power law upper bound on
$\alpha \,=\,1$ we prove a power law upper bound on 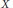 $X$ in dimension
$X$ in dimension  $d\,=\,1$. (Power law lower bounds were proved earlier for all
$d\,=\,1$. (Power law lower bounds were proved earlier for all  $d$). In the non-critical cases
$d$). In the non-critical cases 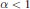 $\alpha <1$ and
$\alpha <1$ and 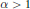 $\alpha \,>1$we prove exponential upper bounds on
$\alpha \,>1$we prove exponential upper bounds on 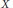 $X$.
$X$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
- 15
- Cited by




