Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-06-08T21:36:22.874Z Has data issue: false hasContentIssue false
  • English
  • Français

A Tauberian Theorem Concerning Borel-Type and Cesàro Methods of Summability

Published online by Cambridge University Press:  20 November 2018

David Borwein  and
Tom Markovich
David Borwein
Affiliation:
The University of Western Ontario, London, Ontario
Tom Markovich
Affiliation:
The University of Western Ontario, London, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose throughout that r ≧ 0, α > 0, αq + β > 0 where q is a non-negative integer. Let {sn} be a sequence of real numbers,

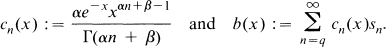
The Borel-type summability method (B, α, β) is defined as follows:

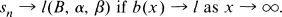
The method (B, α, β) is regular [5]; and (B, 1, 1) is the standard Borel exponential method B. For a real sequence {sn} we consider the slowly decreasing-type Tauberian condition

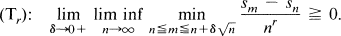
We shall also be concerned with the Cesàro summability method Cp(p > —1), the Valiron method Vα, and the Meyer-König method Sa (0 < a < 1) defined as follows:

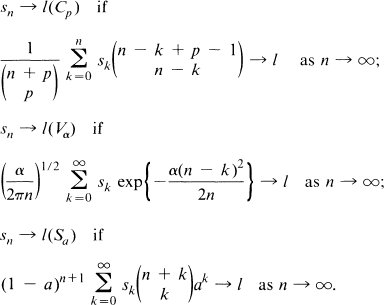
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 1 , 01 February 1988 , pp. 228 - 247
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Bateman Manuscript Project., Higher transcendental functions, vol. 1 (McGraw-Hill, 1953).Google Scholar
2. Bingham, N. H., On Valiron and circle convergence, Math Z.. 756 (1984), 273–286.Google Scholar
3. Bingham, N. H., Tauberian theorems for summability methods of random-walk type, Journal London Math. Soc, (2) 30 (1984), 281–287.Google Scholar
4. Borwein, D., Relations between Borel-type methods of summability, Journal London Math. Soc.. 35 (1960), 65–70.Google Scholar
5. Borwein, D., On methods of summability based on integral functions II, Proc. Cambridge Phil. Soc.. 56(1960), 125–131.Google Scholar
6. Borwein, D., A Tauberian theorem for Borel-type methods of summability, Canadian Journal of Math.. 21 (1969), 740–747.Google Scholar
7. Borwein, D. and Robinson, I. J. W., A Tauberian theorem for Borel-type methods of summability, Journal Reine Angew. Math. 273 (1975), 153–164.Google Scholar
8. Faulhaber, G., Aquivalenzsatze fur die Kreisverfahren der Limitierungstheorie, Math. Z.. 66 (1956), 34–52.Google Scholar
9. Hardy, G. H., Divergent series, (Oxford, 1949).Google Scholar
10. Hardy, G. H. and Littlewood, J. E., Theorems concerning the summability of series by Bore Vs exponential method, Rendiconti del Circolo Matematico di Palermo. 41 (1916), 36–53.Google Scholar
11. Hyslop, J. M., The generalisation of a theorem on Borel summability, Proc. London Math. Soc. (2) 41 (1936), 243–256.Google Scholar
12. Kwee, B., An improvement on a theorem of Hardy and Littlewood, Journal London Math. Soc. (2) 25 (1983), 93–102.Google Scholar
13. Rajagopal, C. T., On a theorem connecting Borel and Cesàro summabilities, Journal Indian Math. Soc.. 24 (1960), 433–442.Google Scholar
14. Sitaraman, Y., On Tauberian theorems for the Sα-method of summability, Math. Z.. 95 (1967), 34–49.Google Scholar