Hostname: page-component-77c89778f8-fv566 Total loading time: 0 Render date: 2024-07-19T05:43:32.110Z Has data issue: false hasContentIssue false
  • English
  • Français

A Tensor Equation of Elliptic Type

Published online by Cambridge University Press:  20 November 2018

G. F. D. Duff
G. F. D. Duff*
Affiliation:
University of Toronto
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theory of the systems of partial differential equations which arise in connection with the invariant differential operators on a Riemannian manifold may be developed by methods based on those of potential theory. It is therefore natural to consider in the same context the theory of elliptic differential equations, in particular those which are self-adjoint. Some results for a tensor equation in which appears, in addition to the operator Δ of tensor theory, a matrix or double tensor field defined on the manifold, are here presented. The equation may be written

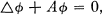
in a notation explained below.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 5 , 1953 , pp. 524 - 535
Copyright
Copyright © Canadian Mathematical Society 1953

References

1. Bergman, S. and Schiffer, M., Kernel functions in the theory of partial differential equations of elliptic type, Duke Math. J., 15 (1948), 535–566.Google Scholar
2. Bochner, S., Vector fields and Ricci curvature, Bull. Amer. Math. Soc, 52 (1946), 776–797.Google Scholar
3. Duff, G. F. D., Boundary value problems associated with the tensor Laplace equation, Can. J. Math., 5 (1953), 196–210.Google Scholar
4. Duff, G. F. D. and Spencer, D. C., Harmonic fields on Riemannian manifolds, Ann. Math., 56 (1952), 128–156.Google Scholar
5. Giraud, G., Equations et systémes d'équations oú figurent des valeurs principales d'intégrales, C. R. Acad. Sci., Paris, 204 (1937), 628–630.Google Scholar
6. Hodge, W. V. D., (a) A Dirichlet problem for harmonie functionals, Proc. London Math. Soc. (2), 35(1933), 257–303.Google Scholar
(b) Hodge, W. V. D., Theory and Applications of Harmonie Integrals (Cambridge, 1941).Google Scholar
7. Lichnerowicz, A., Courbure, nombres de Betti, et espaces symétriques, Proc. International Congress, 2 (1950), 216–223.Google Scholar
8. de Rham, G. and Kodaira, K., Harmonie integrals, mimeographed lectures, Institute for Advanced Study, Princeton, (1950).Google Scholar