Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-07T07:30:11.727Z Has data issue: false hasContentIssue false
  • English
  • Français

Tensor Products of Unitary Super-Virasoro Modules With Central Charge 7/10

Published online by Cambridge University Press:  20 November 2018

Murray R. Bremner
Murray R. Bremner*
Affiliation:
Department of Mathematics, Yale University, Box 2155 Yale Station, New HavenCT 06520 USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The two Virasoro superalgebras, known as the Neveu- Schwarz algebra and the Ramond algebra, each have two unitary irreducible lowest weight modules with central charge 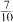. In this paper, I show how tensor products of these modules decompose into finite direct sums of irreducible modules with central charge .

Keywords

17B6517A7081E40.
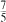Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 3 , 01 June 1990 , pp. 561 - 574
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Bremner, M.R., On tensor products of modules over the Virasoro algebra, Doctoral dissertation, Department of Mathematics, Yale University, 1989.Google Scholar
2. Bremner, M.R., Tensor products of unitarizable representations of the Virasoro algebra with centralcharge 1\2, Comm. Algebra 16 (1988), 1513–1523.Google Scholar
3. Carlitz, L., Subbarao, M.V., A simple proof of the quintuple product identity, , Proc. Amer. Math. Soc. 32 (1972)42–44.Google Scholar
4. Friedan, D., Qiu, Z., Shenker, S., Superconformai invariance in two dimensions and the tricriticalIsing model, Phys. Lett. B 151 (1986) 37–43.Google Scholar
5. Goddard, P., Kent, A., Olive, D., Unitary representations of the Virasoro and super-Virasoroalgebras, Comm. Math. Phys. 103 (1986) 105–119.Google Scholar
6. Kac, V.G., Infinite dimensional Lie algebras, second edition, Cambridge University Press, 1985.Google Scholar
7. Kac, V.G., Wakimoto, M., Unitarizable highest weight representations of the Virasoro, Neveu-Schwarz and Ramond algebras, in “Proceedings of the symposium on conformai groups and structures”, Lecture Notes in Physics 261 (1986), Springer-Verlag, New York.Google Scholar
8. Manin, Y.I., Gauge field theory and complex geometry, Springer-Verlag, New York, 1988.Google Scholar
9. Meurman, A., Rocha-Caridi, A., Highest weight representations of the Neveu-Schwarz and Ramondalgebras, Comm. Math. Phys. 107 (1987), 263–294.Google Scholar
10. Moody, R.V., Pianzola, A., Lie algebras with triangular decomposition, John Wiley & Sons, New York (to appear).Google Scholar
11. Rocha-Caridi, A., Representation theory of the Virasoro and super-Virasoro algebras: irreduciblecharacters, in “Proceedings of the 10th Johns Hopkins workshop on current problems in particle theory,” World Scientific, Singapore, 1989.Google Scholar