Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-01T22:09:30.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform Harmonic Approximation with Continuous Extension to the Boundary

Published online by Cambridge University Press:  20 November 2018

M. Goldstein  and
W. H. Ow
M. Goldstein
Affiliation:
Arizona State University, Tempe, Arizona
W. H. Ow
Affiliation:
Michigan State University, East Lansing, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a domain in the complex plane and F a nonempty subset of G such that F is the closure in G of its interior F0. We will say f ∊ C1(F) if f is continuous on F and possesses continuous first partial derivatives in F which extend continuously to F as finite-valued functions. Let G* – F be connected and locally connected, f ∊ C1(F) be harmonic in F0, and E be a subset of ∂F ∩ ∂G (here G* denotes the one-point compactification of G and the boundaries ∂F, ∂G are taken in the extended plane). Suppose there is a sequence 〈hn〉 of functions harmonic in G such that

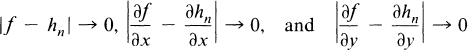
uniformly on F as n → ∞.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 6 , 01 December 1988 , pp. 1375 - 1388
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Brannan, D. A. and Clunie, J. G., Aspects of contemporary complex analysis (Academic Press, 1980).Google Scholar
2. Gauthier, P. M., Goldstein, M. and Ow, W. H., Uniform approximation on unbounded sets by harmonic functions with logarithmic singularities, Trans. Amer. Math. Soc. 261, 169–183.Google Scholar
3. Gauthier, P. M. and Hengartner, W., Approximation uniforme qualitative sur des ensembles non bornés (Les Presses de L'Université de Montréal, 1982).Google Scholar
4. Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order (Springer-Verlag, Berlin-Heidelberg-New York, 1977).CrossRefGoogle Scholar
5. Lax, P., A stability theorem for abstract differential equations and its applications to the study of the local behaviour of solutions of elliptic equations, Commun. Pure Appl. Math. 9 (1956), 747–766.Google Scholar
6. Malgrange, B., Existence et approximation des solutions des équations aux dérivées partielles et des équations de convolution, Ann. de l'Inst. Fourier 6 (1955-56), 271–355.Google Scholar
7. Narasimhan, R., Analysis on real and complex manifolds (Masson & Cie, Paris; North-Holland, Amsterdam, 1968).Google Scholar
8. Rodin, B. and Sario, L., Principal functions (D. Van Nostrand, Princeton, 1968).CrossRefGoogle Scholar
9. Roth, A., Uniform approximation by meromorphic functions on closed sets with continuous extension into the boundary, Can. J. Math. 30 (1978), 1243–1255.Google Scholar
10. Shaginyan, A. A., A boundary singularity of functions that are harmonic in a ball, Doklady Acad. Sci. Arm. SSR 78 (1984), 51–52.Google Scholar
11. Stray, A., On uniform and asymptotic approximation, Math. Ann. 234 (1978), 61–68.Google Scholar