Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-18T10:33:38.946Z Has data issue: false hasContentIssue false
  • English
  • Français

On two conjectures about the sum of element orders

Part of: Special aspects of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  26 January 2021

Morteza Baniasad Azad  and
Behrooz Khosravi
Morteza Baniasad Azad
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), 424, Hafez Avenue, Tehran15914, Iran e-mail: baniasad84@gmail.com
Behrooz Khosravi*
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), 424, Hafez Avenue, Tehran15914, Iran e-mail: baniasad84@gmail.com
*
e-mail: khosravibbb@yahoo.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite group and 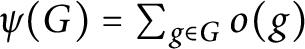$\psi (G) = \sum _{g \in G} o(g)$ , where 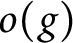$o(g)$ denotes the order of 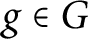$g \in G$ . There are many results on the influence of this function on the structure of a finite group G.

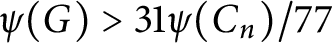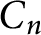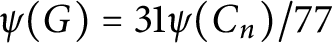In this paper, as the main result, we answer a conjecture of Tărnăuceanu. In fact, we prove that if G is a group of order n and $\psi (G)>31\psi (C_n)/77$ , where $C_n$ is the cyclic group of order n, then G is supersolvable. Also, we prove that if G is not a supersolvable group of order n and $\psi (G) = 31\psi (C_n)/77$ , then 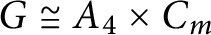$G\cong A_4 \times C_m$ , where 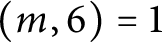$(m, 6)=1$ .

Finally, Herzog et al. in (2018, J. Algebra, 511, 215–226) posed the following conjecture: If 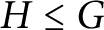$H\leq G$ , then 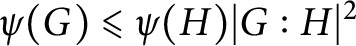$\psi (G) \unicode[stix]{x02A7D} \psi (H) |G:H|^2$ . By an example, we show that this conjecture is not satisfied in general.

Keywords

Sum of element orderssupersolvable groupelement orders

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems
Secondary: 20F16: Solvable groups, supersolvable groups
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 1 , March 2022 , pp. 30 - 38
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amiri, H. and Jafarian Amiri, S. M., Sum of element orders on finite groups of the same order . J. Algebra Appl. 10(2011), no. 2, 187–190.CrossRefGoogle Scholar
Amiri, H., Jafarian Amiri, S. M., and Isaacs, I. M., Sums of element orders in finite groups . Comm. Algebra 37(2009), no. 9, 2978–2980.10.1080/00927870802502530CrossRefGoogle Scholar
Bahri, A., Khosravi, B., and Akhlaghi, Z., A result on the sum of element orders of a finite group . Arch. Math. 114(2020), no. 1, 3–12.CrossRefGoogle Scholar
Baniasad Azad, M. and Khosravi, B., A criterion for solvability of a finite group by the sum of element orders . J. Algebra 516(2018), 115–124.CrossRefGoogle Scholar
Baniasad Azad, M. and Khosravi, B., On the sum of element orders of $PSL\left(2,p\right)$ for some p . Ital. J. Pure Appl. Math. 42(2019), 18–24.Google Scholar
Baniasad Azad, M. and Khosravi, B., A criterion for $p$ -nilpotency and $p$ -closedness by the sum of element orders . Comm. Algebra 48(2020), no. 12, 5391–5395. https://doi.org/10.1080/00927872.2020.1788571 CrossRefGoogle Scholar
Baniasad Azad, M. and Khosravi, B., Properties of finite groups determined by the product of their element orders. Bull. Aust. Math. Soc. (2020). https://doi.org/10.1017/S000497272000043X CrossRefGoogle Scholar
Baniasad Azad, M., Khosravi, B., and Jafarpour, M., An answer to a conjecture on the sum of element orders. J. Algebra Appl. https://doi.org/10.1142/S0219498822500670 CrossRefGoogle Scholar
Herzog, M., Longobardi, P., and Maj, M., An exact upper bound for sums of element orders in non-cyclic finite groups . J. Pure Appl. Algebra 222(2018), no. 7, 1628–1642.CrossRefGoogle Scholar
Herzog, M., Longobardi, P., and Maj, M., Two new criteria for solvability of finite groups . J. Algebra 511(2018), 215–226.CrossRefGoogle Scholar
Herzog, M., Longobardi, P., and Maj, M., Properties of finite and periodic groups determined by their element orders (a survey) . In: Sastry, N. and Yadav, M. (eds.), Group theory and computation, Springer, Berlin, 2018, pp. 59–90.CrossRefGoogle Scholar
Herzog, M., Longobardi, P., and Maj, M., Sums of element orders in groups of order $2m$ with $m$ odd . Comm. Algebra 47(2019), no. 5, 2035–2048.CrossRefGoogle Scholar
Herzog, M., Longobardi, P., and Maj, M., The second maximal groups with respect to the sum of element orders . J. Pure Appl. Algebra 225(2021), no. 3, 106531. https://doi.org/10.1016/j.jpaa.2020.106531 CrossRefGoogle Scholar
Jafarian Amiri, S. M. and Amiri, M., Second maximum sum of element orders on finite groups . J. Pure Appl. Algebra 218(2014), no. 3, 531–539.CrossRefGoogle Scholar
Khosravi, B. and Baniasad Azad, M., Recognition by the product element orders . Bull. Malays. Math. Sci. Soc. 43(2020), no. 2, 1183–1193.10.1007/s40840-019-00732-wCrossRefGoogle Scholar
Lazorec, M. and Tărnăuceanu, M., A density result on the sum of element orders of a finite group . Arch. Math. 114(2020), 601–607.CrossRefGoogle Scholar
Lucchini, A., On the order of transitive permutation groups with cyclic point-stabilizer . Atti Accad. Naz. Lincei, Cl. Sci. Fis. Mat. Nat., IX. Ser., Rend. Lincei, Mat. Appl. 9(1998), no. 4, 241–243.Google Scholar
Tărnăuceanu, M., Detecting structural properties of finite groups by the sum of element orders . Israel J. Math. 238(2020), no. 2, 629–637. https://doi.org/10.1007/s11856-020-2033-9 CrossRefGoogle Scholar
Tărnăuceanu, M., A criterion for nilpotency of a finite group by the sum of element orders. Comm. Algebra. https://doi.org/10.1080/00927872.2020.1840575 CrossRefGoogle Scholar