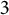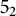1 Introduction
Let
![]() ${\mathfrak {g}}$
be the Lie algebra of a semisimple complex Lie group G, and let M be a connected compact oriented manifold. Let
${\mathfrak {g}}$
be the Lie algebra of a semisimple complex Lie group G, and let M be a connected compact oriented manifold. Let
![]() $R^{\mathrm {irr}}_G(M)$
be the (irreducible) character variety, that is, the set of conjugacy classes of irreducible representations
$R^{\mathrm {irr}}_G(M)$
be the (irreducible) character variety, that is, the set of conjugacy classes of irreducible representations
![]() $\pi _1(M) \rightarrow G$
. Given a homomorphism
$\pi _1(M) \rightarrow G$
. Given a homomorphism
![]() $ \varphi : \pi _1(M) \rightarrow G $
, we can define the adjoint (Reidemeister) torsion
$ \varphi : \pi _1(M) \rightarrow G $
, we can define the adjoint (Reidemeister) torsion
![]() $\tau _\varphi (M)$
under a mild assumption, which lies in
$\tau _\varphi (M)$
under a mild assumption, which lies in
![]() ${\Bbb C}^\times $
and is determined by the conjugacy class of
${\Bbb C}^\times $
and is determined by the conjugacy class of
![]() $\varphi $
(see [Reference Turaev15] or Section 2 for details). When
$\varphi $
(see [Reference Turaev15] or Section 2 for details). When
![]() $ \mathop {\mathrm {dim}}\nolimits M =2$
, the torsion plays an interesting role as a volume form on the space
$ \mathop {\mathrm {dim}}\nolimits M =2$
, the torsion plays an interesting role as a volume form on the space
![]() $R^{\mathrm {irr}}_G(M)$
(see [Reference Porti11, Reference Witten18]). In addition, if M is three-dimensional and
$R^{\mathrm {irr}}_G(M)$
(see [Reference Porti11, Reference Witten18]). In addition, if M is three-dimensional and
![]() $G= \mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
, some attitudes of the torsions in
$G= \mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
, some attitudes of the torsions in
![]() $R^{\mathrm {irr}}_G(M)$
are physically observed from the viewpoint of a 3D–3D correspondence, and some conjectures on the torsions are mathematically proposed in [Reference Benini, Gang and Pando Zayas1, Reference Gang, Kim and Pando Zayas4, Reference Gang, Kim and Yoon5].
$R^{\mathrm {irr}}_G(M)$
are physically observed from the viewpoint of a 3D–3D correspondence, and some conjectures on the torsions are mathematically proposed in [Reference Benini, Gang and Pando Zayas1, Reference Gang, Kim and Pando Zayas4, Reference Gang, Kim and Yoon5].
For instance, with reference to [Reference Gang, Kim and Yoon5], the conjecture can be roughly described as follows. Suppose that
![]() $\mathop {\mathrm {dim}}\nolimits M=3$
and M has a tori-boundary. For
$\mathop {\mathrm {dim}}\nolimits M=3$
and M has a tori-boundary. For
![]() $z \in {\Bbb C}$
, introduce a finite subset “
$z \in {\Bbb C}$
, introduce a finite subset “
![]() $\mathrm {tr}_{\gamma }^{-1}(z)$
” of
$\mathrm {tr}_{\gamma }^{-1}(z)$
” of
![]() $R^{\mathrm {irr}}_G(M)$
which is defined from a boundary condition, and discussed the sum of the nth powers of the twice torsions, that is,
$R^{\mathrm {irr}}_G(M)$
which is defined from a boundary condition, and discussed the sum of the nth powers of the twice torsions, that is,
![]() ${\sum _{\varphi \in \mathrm {tr}_{\gamma }^{-1}(z) }(2\tau _{\varphi }(M ))^n \in {\Bbb C}}$
for
${\sum _{\varphi \in \mathrm {tr}_{\gamma }^{-1}(z) }(2\tau _{\varphi }(M ))^n \in {\Bbb C}}$
for
![]() $n \in {\Bbb Z} $
with
$n \in {\Bbb Z} $
with
![]() $n \geq -1$
. Then, the studies in [Reference Benini, Gang and Pando Zayas1, Reference Gang, Kim and Pando Zayas4, Reference Gang, Kim and Yoon5] suggest that the sum lies in
$n \geq -1$
. Then, the studies in [Reference Benini, Gang and Pando Zayas1, Reference Gang, Kim and Pando Zayas4, Reference Gang, Kim and Yoon5] suggest that the sum lies in
![]() ${\Bbb Z}$
and, that if M is hyperbolic and
${\Bbb Z}$
and, that if M is hyperbolic and
![]() $n=-1$
, then the sum is zero. This conjecture is sometimes called the vanishing identity (see [Reference Porti and Yoon12, Reference Tran and Yamaguchi14, Reference Yoon19] and the references therein for supporting evidence of this conjecture).
$n=-1$
, then the sum is zero. This conjecture is sometimes called the vanishing identity (see [Reference Porti and Yoon12, Reference Tran and Yamaguchi14, Reference Yoon19] and the references therein for supporting evidence of this conjecture).
In this paper, we focus on the adjoint torsions in the case where
![]() $\mathop {\mathrm {dim}}\nolimits {M}=3$
and M has no boundary. According to [Reference Benini, Gang and Pando Zayas1, Reference Gang, Kim and Pando Zayas4], it is seemingly reasonable to consider the following conjecture:
$\mathop {\mathrm {dim}}\nolimits {M}=3$
and M has no boundary. According to [Reference Benini, Gang and Pando Zayas1, Reference Gang, Kim and Pando Zayas4], it is seemingly reasonable to consider the following conjecture:
Conjecture 1.1 [Reference Benini, Gang and Pando Zayas1, Reference Gang, Kim and Pando Zayas4]
Take
![]() $n \in {\Bbb Z}$
with
$n \in {\Bbb Z}$
with
![]() $n \geq -1$
. Suppose that M is a closed
$n \geq -1$
. Suppose that M is a closed
![]() $3$
-manifold, and the set
$3$
-manifold, and the set
![]() $R^{\mathrm {irr}}_G(M)$
is finite. Then, the following sum lies in the ring of integers
$R^{\mathrm {irr}}_G(M)$
is finite. Then, the following sum lies in the ring of integers
![]() ${\Bbb Z}$
:
${\Bbb Z}$
:
Furthermore, if
![]() $G=\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
, M is a hyperbolic 3-manifold, and
$G=\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
, M is a hyperbolic 3-manifold, and
![]() $n=-1$
, then the sum is zero.
$n=-1$
, then the sum is zero.
In [Reference Cui, Qiu and Wang2], when
![]() $G=\mathop {\mathrm {SL}}\nolimits _2(\mathbb {C})$
, the adjoint torsion of certain Seifert 3-manifolds and torus bundles are explicitly computed; thus, we can easily check the conjecture for the non-hyperbolic 3-manifolds.
$G=\mathop {\mathrm {SL}}\nolimits _2(\mathbb {C})$
, the adjoint torsion of certain Seifert 3-manifolds and torus bundles are explicitly computed; thus, we can easily check the conjecture for the non-hyperbolic 3-manifolds.
In contrast, this paper provides supporting evidence on Conjecture 1.1 in hyperbolic cases. For
![]() $p/q \in {\Bbb Q}$
and a knot K in
$p/q \in {\Bbb Q}$
and a knot K in
![]() $S^3$
, let
$S^3$
, let
![]() $S^3_{p/q}(K)$
be the closed
$S^3_{p/q}(K)$
be the closed
![]() $3$
-manifold obtained by
$3$
-manifold obtained by
![]() $(p/q)$
-Dehn surgery on K.
$(p/q)$
-Dehn surgery on K.
Theorem 1.2 Let G be
![]() $\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
, and let
$\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
, and let
![]() $K=4_1$
be the figure-eight knot. Let
$K=4_1$
be the figure-eight knot. Let
![]() $n=-1$
. Then, for any integers p and
$n=-1$
. Then, for any integers p and
![]() $q\neq 0$
, Conjecture 1.1 is true when
$q\neq 0$
, Conjecture 1.1 is true when
![]() $M=S^3_{p/1}(4_1)$
and
$M=S^3_{p/1}(4_1)$
and
![]() ${M=S^3_{1/q}(4_1)}$
.
${M=S^3_{1/q}(4_1)}$
.
We similarly discuss whether Conjecture 1.1 is true for
![]() $M=S^3_{1/q}{(K)}$
when the knot K is the
$M=S^3_{1/q}{(K)}$
when the knot K is the
![]() $5_2$
-knot (see Section 4).
$5_2$
-knot (see Section 4).
The outline of the proof is as follows. While some computations of the adjoint torsions of 3-manifolds with boundary are established (see, e.g., [Reference Dubois, Huynh and Yamaguchi3, Reference Tran and Yamaguchi14, Reference Yoon19]), this paper employs a procedure of computing the adjoint torsions of closed 3-manifolds, which is established in [Reference Wakijo16], and we determine all the adjoint torsion (Theorems 3.3 and 3.4). As in the previous proof of the above supporting evidence, we apply Jacobi’s residue theorem (see Lemma 3.7) to the sum (1) and demonstrate Theorem 1.2. Since it is complicated to check the condition for applying the residue theorem, we need some careful discussion (see Sections 3.2 and 3.3).Footnote
1
Finally, in Section 5, we also discuss the conjecture with
![]() $n>0$
, and see that some properties are needed to be addressed in future studies. Here, we show the
$n>0$
, and see that some properties are needed to be addressed in future studies. Here, we show the
![]() $2^{2n+1}$
-multiple of the conjecture with
$2^{2n+1}$
-multiple of the conjecture with
![]() $M=S^3_{2m/1}(4_1)$
(see Proposition 5.4).
$M=S^3_{2m/1}(4_1)$
(see Proposition 5.4).
2 Review: the adjoint Reidemeister torsion
After reviewing algebraic torsions in Section 2.1, we briefly recall the definition of the adjoint Reidemeister torsion in Section 2.2. We note that our definition of the adjoint torsion is of sign-refined type. Section 2.3 explains cellular complexes of M. Throughout this paper, we assume that any basis of a vector space is ordered.
2.1 Algebraic torsion of a cochain complex
Let
![]() $C^*$
be a bounded cochain complex consisting of finite-dimensional vector spaces over a commutative field
$C^*$
be a bounded cochain complex consisting of finite-dimensional vector spaces over a commutative field
![]() ${\Bbb F}$
, that is,
${\Bbb F}$
, that is,
Let
![]() $H^i=H^i(C^*)$
be the ith cohomology group. Choose a basis
$H^i=H^i(C^*)$
be the ith cohomology group. Choose a basis
![]() ${\mathbf {c}}^i$
of
${\mathbf {c}}^i$
of
![]() $C^i$
and a basis
$C^i$
and a basis
![]() ${\mathbf {h}}^i$
of
${\mathbf {h}}^i$
of
![]() $H^i$
. The Reidemeister torsion
$H^i$
. The Reidemeister torsion
![]() $\mathop {\mathrm {Tor}}\nolimits (C^*,{\mathbf {c}}^*,{\mathbf {h}}^*)$
is defined as follows.
$\mathop {\mathrm {Tor}}\nolimits (C^*,{\mathbf {c}}^*,{\mathbf {h}}^*)$
is defined as follows.
Let
![]() $\widetilde {{\mathbf {h}}}^i\subset C^i$
be a representative cocycle of
$\widetilde {{\mathbf {h}}}^i\subset C^i$
be a representative cocycle of
![]() ${\mathbf {h}}^i$
in
${\mathbf {h}}^i$
in
![]() $C^i$
. Let
$C^i$
. Let
![]() ${\mathbf {b}}^i$
be a tuple of vectors in
${\mathbf {b}}^i$
be a tuple of vectors in
![]() $C^i$
such that
$C^i$
such that
![]() $\delta ^i({\mathbf {b}}^i)$
is a basis of
$\delta ^i({\mathbf {b}}^i)$
is a basis of
![]() $B^{i+1}=\mathop {\mathrm {Im}}\nolimits {\delta ^i}$
. Then the union of the sequences of the vectors
$B^{i+1}=\mathop {\mathrm {Im}}\nolimits {\delta ^i}$
. Then the union of the sequences of the vectors
![]() $\delta ^{i-1}({\mathbf {b}}^{i-1})\widetilde {{\mathbf {h}}}^i {\mathbf {b}}^i$
gives a basis of
$\delta ^{i-1}({\mathbf {b}}^{i-1})\widetilde {{\mathbf {h}}}^i {\mathbf {b}}^i$
gives a basis of
![]() $C^i$
. We write
$C^i$
. We write
![]() $[\delta ^{i-1}({\mathbf {b}}^{i-1})\widetilde {{\mathbf {h}}}^i {\mathbf {b}}^i/{\mathbf {c}}^i] \in {\Bbb F}^\times ={\Bbb F}\backslash \{0\}$
for the determinant of the transition matrix that takes
$[\delta ^{i-1}({\mathbf {b}}^{i-1})\widetilde {{\mathbf {h}}}^i {\mathbf {b}}^i/{\mathbf {c}}^i] \in {\Bbb F}^\times ={\Bbb F}\backslash \{0\}$
for the determinant of the transition matrix that takes
![]() ${\mathbf {c}}^i$
to
${\mathbf {c}}^i$
to
![]() $\delta ^{i-1}({\mathbf {b}}^{i-1})\widetilde {{\mathbf {h}}}^i {\mathbf {b}}^i$
. Let
$\delta ^{i-1}({\mathbf {b}}^{i-1})\widetilde {{\mathbf {h}}}^i {\mathbf {b}}^i$
. Let
![]() $|C^*|$
be
$|C^*|$
be
![]() $\sum _{i=0}^{m}\alpha _i(C^*)\beta _i(C^*),$
where
$\sum _{i=0}^{m}\alpha _i(C^*)\beta _i(C^*),$
where ![]() and
and ![]() . Let
. Let
![]() ${\mathbf {c}}^*$
be
${\mathbf {c}}^*$
be
![]() $({\mathbf {c}}^0,\dots ,{\mathbf {c}}^{m})$
for
$({\mathbf {c}}^0,\dots ,{\mathbf {c}}^{m})$
for
![]() $C^*$
and
$C^*$
and
![]() ${\mathbf {h}}^*$
be
${\mathbf {h}}^*$
be
![]() $({\mathbf {h}}^0,\dots ,{\mathbf {h}}^{m})$
for
$({\mathbf {h}}^0,\dots ,{\mathbf {h}}^{m})$
for
![]() $H^*$
. Then, the torsion is defined to be the alternating product of the form
$H^*$
. Then, the torsion is defined to be the alternating product of the form

It is known that the torsion
![]() $\mathop {\mathrm {Tor}}\nolimits (C^*,{\mathbf {c}}^*,{\mathbf {h}}^*)$
does not depend on the choices of
$\mathop {\mathrm {Tor}}\nolimits (C^*,{\mathbf {c}}^*,{\mathbf {h}}^*)$
does not depend on the choices of
![]() $\widetilde {{\mathbf {h}}}^i$
and
$\widetilde {{\mathbf {h}}}^i$
and
![]() ${\mathbf {b}}^i$
, but depends only on
${\mathbf {b}}^i$
, but depends only on
![]() ${\mathbf {c}}^*$
and
${\mathbf {c}}^*$
and
![]() ${\mathbf {h}}^*$
. We refer to [Reference Milnor7, Reference Turaev15] for the details. Note that, if
${\mathbf {h}}^*$
. We refer to [Reference Milnor7, Reference Turaev15] for the details. Note that, if
![]() $C^*$
is acyclic (i.e.,
$C^*$
is acyclic (i.e.,
![]() $H^*(C^*)=0$
), then the torsion
$H^*(C^*)=0$
), then the torsion
![]() $\mathop {\mathrm {Tor}}\nolimits (C^*,{\mathbf {c}}^*,{\mathbf {h}}^*)$
is usually denoted by
$\mathop {\mathrm {Tor}}\nolimits (C^*,{\mathbf {c}}^*,{\mathbf {h}}^*)$
is usually denoted by
![]() $\mathop {\mathrm {Tor}}\nolimits (C^*,{\mathbf {c}}^*)$
.
$\mathop {\mathrm {Tor}}\nolimits (C^*,{\mathbf {c}}^*)$
.
Remark 2.1 In [Reference Milnor7, Reference Turaev15], the torsion was defined from a chain complex; however, for convenience of computation, we define the torsion from a cochain complex in this paper.
2.2 Adjoint Reidemeister torsion of a
 $3$
-manifold
$3$
-manifold
Let M be a connected oriented closed
![]() $3$
-manifold, and let G be a semisimple Lie group with Lie algebra
$3$
-manifold, and let G be a semisimple Lie group with Lie algebra
![]() ${\mathfrak {g}}$
. Let
${\mathfrak {g}}$
. Let
![]() $\varphi :\pi _1(M)\rightarrow G$
be a representation, that is, a group homomorphism. Suppose that G injects
$\varphi :\pi _1(M)\rightarrow G$
be a representation, that is, a group homomorphism. Suppose that G injects
![]() $\mathop {\mathrm {SL}}\nolimits _n({\Bbb C})$
for some
$\mathop {\mathrm {SL}}\nolimits _n({\Bbb C})$
for some
![]() $n\in {\Bbb N}$
.
$n\in {\Bbb N}$
.
First, we introduce the cochain complex. Choose a finite cellular decomposition of M and consider the universal covering space
![]() $\widetilde {M}$
. We can canonically obtain a cellular structure of
$\widetilde {M}$
. We can canonically obtain a cellular structure of
![]() $\widetilde {M}$
as a lift of the decomposition of M, and define the cellular complex
$\widetilde {M}$
as a lift of the decomposition of M, and define the cellular complex
![]() $(C_*(\widetilde {M};{\Bbb Z}),\partial _*)$
. We regard the covering transformation of M as a left action of
$(C_*(\widetilde {M};{\Bbb Z}),\partial _*)$
. We regard the covering transformation of M as a left action of
![]() $\pi _1(M)$
on
$\pi _1(M)$
on
![]() $\widetilde {M}$
, and naturally regard
$\widetilde {M}$
, and naturally regard
![]() $C_*(\widetilde {M};{\Bbb Z})$
as a left
$C_*(\widetilde {M};{\Bbb Z})$
as a left
![]() ${\Bbb Z}[\pi _1(M)]$
-module. Since
${\Bbb Z}[\pi _1(M)]$
-module. Since
![]() ${\mathfrak {g}}$
is a left
${\mathfrak {g}}$
is a left
![]() ${\Bbb Z}[\pi _1(M)]$
-module via the composite of
${\Bbb Z}[\pi _1(M)]$
-module via the composite of
![]() $\varphi $
and the adjoint action
$\varphi $
and the adjoint action
![]() $G\rightarrow \mathop {\mathrm {Aut}}\nolimits ({\mathfrak {g}})$
, we have the cochain complex of the form
$G\rightarrow \mathop {\mathrm {Aut}}\nolimits ({\mathfrak {g}})$
, we have the cochain complex of the form
where
![]() $\delta ^i$
is defined by
$\delta ^i$
is defined by
![]() $\delta ^i(f)=f\circ \partial _{i{+1}}$
.
$\delta ^i(f)=f\circ \partial _{i{+1}}$
.
Next, we define an ordered basis of
![]() $C^i_\varphi ({M};{\mathfrak {g}})$
. Let
$C^i_\varphi ({M};{\mathfrak {g}})$
. Let
![]() ${\mathbf {c}}_i\kern1.3pt{=}\kern1.3pt(c_{i,1},c_{i,2},\ldots ,c_{i,\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i({M};{\Bbb Z})}}\kern-1.2pt)$
be a basis of
${\mathbf {c}}_i\kern1.3pt{=}\kern1.3pt(c_{i,1},c_{i,2},\ldots ,c_{i,\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i({M};{\Bbb Z})}}\kern-1.2pt)$
be a basis of
![]() $C_i({M};{\Bbb Z})$
derived from the i-cells. Then,
$C_i({M};{\Bbb Z})$
derived from the i-cells. Then,
![]() $\widetilde {{\mathbf {c}}}_i\kern1.3pt{=}\kern1.3pt(\widetilde {c}_{i,1},\widetilde {c}_{i,2},\ldots ,\widetilde {c}_{i,\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i({M};{\Bbb Z})}}\kern-1.2pt)$
is a basis of the free
$\widetilde {{\mathbf {c}}}_i\kern1.3pt{=}\kern1.3pt(\widetilde {c}_{i,1},\widetilde {c}_{i,2},\ldots ,\widetilde {c}_{i,\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i({M};{\Bbb Z})}}\kern-1.2pt)$
is a basis of the free
![]() ${\Bbb Z}[\pi _1(M)]$
-module
${\Bbb Z}[\pi _1(M)]$
-module
![]() $C_i(\widetilde {M};{\Bbb Z})$
. Here,
$C_i(\widetilde {M};{\Bbb Z})$
. Here,
![]() $\widetilde {c}_{i,j}$
is a lift of
$\widetilde {c}_{i,j}$
is a lift of
![]() $c_{i,j}$
to
$c_{i,j}$
to
![]() $\widetilde {M}$
. Since
$\widetilde {M}$
. Since
![]() ${\mathfrak {g}}$
is semisimple, the Killing form B is nondegenerate, and we can fix an ordered basis
${\mathfrak {g}}$
is semisimple, the Killing form B is nondegenerate, and we can fix an ordered basis
![]() ${\mathcal {B}}=(e_1,e_2,\ldots ,e_{\mathop {\mathrm {dim}}\nolimits {{\mathfrak {g}}}})$
of
${\mathcal {B}}=(e_1,e_2,\ldots ,e_{\mathop {\mathrm {dim}}\nolimits {{\mathfrak {g}}}})$
of
![]() ${\mathfrak {g}}$
that is orthogonal with respect to B. Let
${\mathfrak {g}}$
that is orthogonal with respect to B. Let
![]() $c_{i,j}^k\in C^i_\varphi ({M};{\mathfrak {g}})$
be a
$c_{i,j}^k\in C^i_\varphi ({M};{\mathfrak {g}})$
be a
![]() ${\Bbb Z}[\pi _1(M)]$
-homomorphism defined by
${\Bbb Z}[\pi _1(M)]$
-homomorphism defined by
![]() $c_{i,j}^k(\widetilde {c}_{i,\ell })=\delta _{j,\ell }e_k\in {\mathfrak {g}}$
for any
$c_{i,j}^k(\widetilde {c}_{i,\ell })=\delta _{j,\ell }e_k\in {\mathfrak {g}}$
for any
![]() $i\in \{0,1,2,3\}$
,
$i\in \{0,1,2,3\}$
,
![]() $j,\ell \in \{1,2,\ldots ,\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i({M};{\Bbb Z})}\}$
, and
$j,\ell \in \{1,2,\ldots ,\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i({M};{\Bbb Z})}\}$
, and
![]() $k\in \{1,2,\ldots ,\mathop {\mathrm {dim}}\nolimits {{\mathfrak {g}}}\}$
. Here,
$k\in \{1,2,\ldots ,\mathop {\mathrm {dim}}\nolimits {{\mathfrak {g}}}\}$
. Here,
![]() $\delta _{j,\ell }$
is the Kronecker delta. Then the tuple
$\delta _{j,\ell }$
is the Kronecker delta. Then the tuple
 $$ \begin{align*}{\mathbf{c}}^i&=(c_{i,1}^1,c_{i,1}^2,\ldots,c_{i,1}^{\mathop{\mathrm{dim}}\nolimits{{\mathfrak{g}}}},c_{i,2}^1,c_{i,2}^2,\ldots,c_{i,2}^{\mathop{\mathrm{dim}}\nolimits{{\mathfrak{g}}}},\ldots,c_{i,\mathop{\mathrm{rank}}\nolimits_{\Bbb Z}{C_i(M;{\Bbb Z})}}^1,\\&\quad c_{i,\mathop{\mathrm{rank}}\nolimits_{\Bbb Z}{C_i(M;{\Bbb Z})}}^2,\ldots,c_{i,\mathop{\mathrm{rank}}\nolimits_{\Bbb Z}{C_i(M;{\Bbb Z})}}^{\mathop{\mathrm{dim}}\nolimits{{\mathfrak{g}}}})\end{align*} $$
$$ \begin{align*}{\mathbf{c}}^i&=(c_{i,1}^1,c_{i,1}^2,\ldots,c_{i,1}^{\mathop{\mathrm{dim}}\nolimits{{\mathfrak{g}}}},c_{i,2}^1,c_{i,2}^2,\ldots,c_{i,2}^{\mathop{\mathrm{dim}}\nolimits{{\mathfrak{g}}}},\ldots,c_{i,\mathop{\mathrm{rank}}\nolimits_{\Bbb Z}{C_i(M;{\Bbb Z})}}^1,\\&\quad c_{i,\mathop{\mathrm{rank}}\nolimits_{\Bbb Z}{C_i(M;{\Bbb Z})}}^2,\ldots,c_{i,\mathop{\mathrm{rank}}\nolimits_{\Bbb Z}{C_i(M;{\Bbb Z})}}^{\mathop{\mathrm{dim}}\nolimits{{\mathfrak{g}}}})\end{align*} $$
provides an ordered basis of
![]() $C^i_\varphi (M;{\mathfrak {g}})$
as desired.
$C^i_\varphi (M;{\mathfrak {g}})$
as desired.
We next consider the cellular cochain complex
![]() $C^*(M;{\Bbb R})$
with the real coefficient. Let
$C^*(M;{\Bbb R})$
with the real coefficient. Let
![]() $c^i_j:C_i(M;{\Bbb Z})\rightarrow {\Bbb R}$
be a homomorphism defined by
$c^i_j:C_i(M;{\Bbb Z})\rightarrow {\Bbb R}$
be a homomorphism defined by
![]() $c^i_j(c_{i,k})=\delta _{j,k}$
for any
$c^i_j(c_{i,k})=\delta _{j,k}$
for any
![]() ${i\in \{0,1,2,3\}}$
and
${i\in \{0,1,2,3\}}$
and
![]() $j,k\in \{1,2,\ldots ,\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i({M};{\Bbb Z})}\}$
. Then,
$j,k\in \{1,2,\ldots ,\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i({M};{\Bbb Z})}\}$
. Then,
![]() ${\mathbf {c}}^i_{\Bbb R}=(c^i_1,\ldots ,c^i_{\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i(M;{\Bbb Z})}})$
is a basis of
${\mathbf {c}}^i_{\Bbb R}=(c^i_1,\ldots ,c^i_{\mathop {\mathrm {rank}}\nolimits _{\Bbb Z}{C_i(M;{\Bbb Z})}})$
is a basis of
![]() $C^i(M;{\Bbb R})$
. By Poincaré duality, we can naturally fix a homology orientation
$C^i(M;{\Bbb R})$
. By Poincaré duality, we can naturally fix a homology orientation
![]() $\sigma _M$
of
$\sigma _M$
of
![]() $H^*(M;{\Bbb R})= \bigoplus _{i = 0}^3 H^i(M;\mathbb {R})$
. Let
$H^*(M;{\Bbb R})= \bigoplus _{i = 0}^3 H^i(M;\mathbb {R})$
. Let
![]() ${\mathbf {h}}^*_{\Bbb R} $
be a basis of
${\mathbf {h}}^*_{\Bbb R} $
be a basis of
![]() $H^*(M;{\Bbb R})$
such that the exterior product of
$H^*(M;{\Bbb R})$
such that the exterior product of
![]() ${\mathbf {h}}^*_{\Bbb R}$
coincides with
${\mathbf {h}}^*_{\Bbb R}$
coincides with
![]() $\sigma _M$
. The Reidemeister torsion of
$\sigma _M$
. The Reidemeister torsion of
![]() $C^*(M;{\Bbb R})$
associated with
$C^*(M;{\Bbb R})$
associated with
![]() ${\mathbf {c}}^*_{\Bbb R}$
and
${\mathbf {c}}^*_{\Bbb R}$
and
![]() ${\mathbf {h}}^*_{\Bbb R}$
lies in
${\mathbf {h}}^*_{\Bbb R}$
lies in
![]() ${\Bbb R}^\times $
. Therefore, we can define the sign
${\Bbb R}^\times $
. Therefore, we can define the sign
Then, the adjoint Reidemeister torsion of M associated with
![]() $\varphi $
is defined to be
$\varphi $
is defined to be
if
![]() $C^*_\varphi ({M};{\mathfrak {g}})$
is acyclic. If
$C^*_\varphi ({M};{\mathfrak {g}})$
is acyclic. If
![]() $C^*_\varphi ({M};{\mathfrak {g}})$
is not acyclic, then we define
$C^*_\varphi ({M};{\mathfrak {g}})$
is not acyclic, then we define
![]() $\tau _{\varphi }(M)=1$
. As is known [Reference Dubois, Huynh and Yamaguchi3, Reference Porti11], the definition of
$\tau _{\varphi }(M)=1$
. As is known [Reference Dubois, Huynh and Yamaguchi3, Reference Porti11], the definition of
![]() $\tau _\varphi (M)$
does not depend on the choices of the orthogonal basis
$\tau _\varphi (M)$
does not depend on the choices of the orthogonal basis
![]() ${\mathcal {B}}$
, finite cellular decompositions of M,
${\mathcal {B}}$
, finite cellular decompositions of M,
![]() $\widetilde {{\mathbf {c}}_i}$
, and
$\widetilde {{\mathbf {c}}_i}$
, and
![]() ${\mathbf {h}}^i_{\Bbb R}$
, but depends only on M and the conjugacy class of
${\mathbf {h}}^i_{\Bbb R}$
, but depends only on M and the conjugacy class of
![]() $\varphi $
.
$\varphi $
.
Finally, we give a sufficient condition for the acyclicity, which might be known.
Lemma 2.2 As in Conjecture 1.1, assume that
![]() $R^{\mathrm {irr}}_G(M)$
is of finite order. Then, for any irreducible representation
$R^{\mathrm {irr}}_G(M)$
is of finite order. Then, for any irreducible representation
![]() $ \varphi : \pi _1(M) \rightarrow G$
, the associated cohomology
$ \varphi : \pi _1(M) \rightarrow G$
, the associated cohomology
![]() $H^{*}_\varphi ( M;\mathfrak {g})$
is acyclic.
$H^{*}_\varphi ( M;\mathfrak {g})$
is acyclic.
Proof Since it is classically known [Reference Weil17] that the first cohomology
![]() $H^{1}_\varphi ( M;\mathfrak {g})$
is identified with the cotangent space of the variety
$H^{1}_\varphi ( M;\mathfrak {g})$
is identified with the cotangent space of the variety
![]() $R^{\mathrm {irr}}_G(M)$
, it vanishes by assumption; by Poincaré duality, the second one does. Meanwhile, by definition, the zeroth cohomology
$R^{\mathrm {irr}}_G(M)$
, it vanishes by assumption; by Poincaré duality, the second one does. Meanwhile, by definition, the zeroth cohomology
![]() $H^{0}_\varphi ( M;\mathfrak {g})$
equals the invariant part
$H^{0}_\varphi ( M;\mathfrak {g})$
equals the invariant part
![]() $\{ a \in \mathfrak {g} \mid a \cdot \varphi (g) = a \mathrm { \ for \ any \ } g \in \pi _1(M) \}$
, which is zero by the irreducibility. Hence, the third one also vanishes by Poincaré duality again.
$\{ a \in \mathfrak {g} \mid a \cdot \varphi (g) = a \mathrm { \ for \ any \ } g \in \pi _1(M) \}$
, which is zero by the irreducibility. Hence, the third one also vanishes by Poincaré duality again.
2.3 Presentations of the cellular complexes of M
From now on, we assume that
![]() $G=\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
and M is one of
$G=\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
and M is one of
![]() $S^3_{p/1}(4_1)$
and
$S^3_{p/1}(4_1)$
and
![]() $S^3_{1/q}(4_1)$
for some integers p and
$S^3_{1/q}(4_1)$
for some integers p and
![]() $q\neq 0$
as in Theorem 1.2. According to [Reference Nosaka8], group presentations of
$q\neq 0$
as in Theorem 1.2. According to [Reference Nosaka8], group presentations of
![]() $\pi _1(M)$
are given as follows:
$\pi _1(M)$
are given as follows:
 $$ \begin{align} \pi_1(S^3_{p/1}(4_1))&\cong\langle x_1,x_2,{\mathfrak{m}}\, |\, {\mathfrak{m}}x_1x_2{\mathfrak{m}}^{-1}x_1^{-1}, {\mathfrak{m}}x_2x_1x_2{\mathfrak{m}}^{-1}x_2^{-1}, [x_1,x_2]{\mathfrak{m}}^p \rangle, \\ \pi_1(S^3_{1/q}(4_1))&\cong\langle x_1,x_2,{\mathfrak{m}},{\mathfrak{m}}'\, |\, {\mathfrak{m}}x_1x_2{\mathfrak{m}}^{-1}x_1^{-1}, {\mathfrak{m}}x_2x_1x_2{\mathfrak{m}}^{-1}x_2^{-1}, {\mathfrak{m}}[x_1,x_2]^q, {\mathfrak{m}}'[x_1,x_2]^{-1} \rangle.\nonumber \end{align} $$
$$ \begin{align} \pi_1(S^3_{p/1}(4_1))&\cong\langle x_1,x_2,{\mathfrak{m}}\, |\, {\mathfrak{m}}x_1x_2{\mathfrak{m}}^{-1}x_1^{-1}, {\mathfrak{m}}x_2x_1x_2{\mathfrak{m}}^{-1}x_2^{-1}, [x_1,x_2]{\mathfrak{m}}^p \rangle, \\ \pi_1(S^3_{1/q}(4_1))&\cong\langle x_1,x_2,{\mathfrak{m}},{\mathfrak{m}}'\, |\, {\mathfrak{m}}x_1x_2{\mathfrak{m}}^{-1}x_1^{-1}, {\mathfrak{m}}x_2x_1x_2{\mathfrak{m}}^{-1}x_2^{-1}, {\mathfrak{m}}[x_1,x_2]^q, {\mathfrak{m}}'[x_1,x_2]^{-1} \rangle.\nonumber \end{align} $$
Here,
![]() $[x,y]$
is
$[x,y]$
is
![]() $xyx^{-1}y^{-1}$
. Let g be the number of generators of the group presentation above. Replace
$xyx^{-1}y^{-1}$
. Let g be the number of generators of the group presentation above. Replace
![]() ${\mathfrak {m}}$
by
${\mathfrak {m}}$
by
![]() $x_3$
,
$x_3$
,
![]() ${\mathfrak {m}}'$
by
${\mathfrak {m}}'$
by
![]() $x_4$
, and let
$x_4$
, and let
![]() $r_i$
denote the ith relator in (2). Under the identifications
$r_i$
denote the ith relator in (2). Under the identifications
![]() $C^i_\varphi ({M};{\mathfrak {g}})=\mathop {\mathrm {Hom}}\nolimits _{{\Bbb Z}[\pi _1(M)]}(C_i(\widetilde {M};{\Bbb Z}), {\mathfrak {g}}) = \mathop {\mathrm {Hom}}\nolimits _{{\mathfrak {g}}}({\mathfrak {g}}^{\mathop {\mathrm {rank}}\nolimits _{\Bbb Z} C_i(M;{\Bbb Z})},{\mathfrak {g}})$
, the cochain complex
$C^i_\varphi ({M};{\mathfrak {g}})=\mathop {\mathrm {Hom}}\nolimits _{{\Bbb Z}[\pi _1(M)]}(C_i(\widetilde {M};{\Bbb Z}), {\mathfrak {g}}) = \mathop {\mathrm {Hom}}\nolimits _{{\mathfrak {g}}}({\mathfrak {g}}^{\mathop {\mathrm {rank}}\nolimits _{\Bbb Z} C_i(M;{\Bbb Z})},{\mathfrak {g}})$
, the cochain complex
![]() $(C^*_\varphi ({M};{\mathfrak {g}}),\delta ^*)$
is isomorphic to the dual of the following chain complex:
$(C^*_\varphi ({M};{\mathfrak {g}}),\delta ^*)$
is isomorphic to the dual of the following chain complex:
We now describe the differentials
![]() $\delta ^*$
in detail. Let F and P be the free groups
$\delta ^*$
in detail. Let F and P be the free groups
![]() $\langle x_1, \dots , x_g\ | \ \rangle $
and
$\langle x_1, \dots , x_g\ | \ \rangle $
and
![]() $ \langle \rho _1,\ldots ,\rho _g \ | \ \rangle $
, respectively. We define the homomorphism
$ \langle \rho _1,\ldots ,\rho _g \ | \ \rangle $
, respectively. We define the homomorphism
![]() $\psi : P *F \rightarrow F$
by setting
$\psi : P *F \rightarrow F$
by setting
![]() $\psi (\rho _j)=r_j$
and
$\psi (\rho _j)=r_j$
and
![]() $\psi (x_i)=x_i.$
Let
$\psi (x_i)=x_i.$
Let
![]() $\mu $
denote the natural surjection from F to
$\mu $
denote the natural surjection from F to
![]() $\pi _1(M)$
. According to [Reference Nosaka8, Section 3.1], we can describe
$\pi _1(M)$
. According to [Reference Nosaka8, Section 3.1], we can describe
![]() $\delta ^*$
by the words of the presentations (2) as follows: let
$\delta ^*$
by the words of the presentations (2) as follows: let
![]() $W\in P*F$
be
$W\in P*F$
be
if
![]() $M=S^3_{p/1}(4_1)$
. Let
$M=S^3_{p/1}(4_1)$
. Let
![]() $W \in P*F$
be
$W \in P*F$
be
if
![]() $M=S^3_{1/q}(4_1)$
. Then, each
$M=S^3_{1/q}(4_1)$
. Then, each
![]() $\delta ^*$
can be written as the matrices
$\delta ^*$
can be written as the matrices
 $$ \begin{align} \delta^1=\left(1-x_j\right)_{j=1,\ldots,g},\,\,\, \delta^2=\left({\small \frac{\partial r_j}{\partial x_i}}\right)_{i,j=1,\ldots,g},\,\,\, \delta^3=\mu \circ \psi\left({\small \frac{\partial W}{\partial \rho_i}}\right)_{i=1,\ldots,g}, \end{align} $$
$$ \begin{align} \delta^1=\left(1-x_j\right)_{j=1,\ldots,g},\,\,\, \delta^2=\left({\small \frac{\partial r_j}{\partial x_i}}\right)_{i,j=1,\ldots,g},\,\,\, \delta^3=\mu \circ \psi\left({\small \frac{\partial W}{\partial \rho_i}}\right)_{i=1,\ldots,g}, \end{align} $$
where
![]() $\frac {\partial *}{\partial *}$
is Fox derivative (see [Reference Turaev15, Section 16] for the definition). Although each entry of the matrices is described in
$\frac {\partial *}{\partial *}$
is Fox derivative (see [Reference Turaev15, Section 16] for the definition). Although each entry of the matrices is described in
![]() ${\Bbb Z}[\pi _1(M)]$
, we regard the entry as an automorphism of
${\Bbb Z}[\pi _1(M)]$
, we regard the entry as an automorphism of
![]() ${\mathfrak {g}}$
via the adjoint action.
${\mathfrak {g}}$
via the adjoint action.
3 Proof of Theorem 1.2
The purpose of this section is to show the proof of Theorem 1.2. First, Section 3.1 determines the torsion with respect to every irreducible representation. Next, Section 3.2 establishes two key lemmas, and Section 3.3 completes the proof. Throughout this section,
![]() $E_2$
means the
$E_2$
means the
![]() $(2\times 2)$
-identity matrix, and we let G be
$(2\times 2)$
-identity matrix, and we let G be
![]() $\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
.
$\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
.
3.1 Preliminary
To state Propositions 3.1 and 3.2 and Theorems 3.3 and 3.4, let us consider a domain D in
![]() ${\Bbb C}$
of the form
${\Bbb C}$
of the form
as in Figure 1, and define the Laurent polynomial
![]() $Q_M(x)\in {\Bbb Z}[x{,x^{-1}}]$
by setting
$Q_M(x)\in {\Bbb Z}[x{,x^{-1}}]$
by setting

Let
![]() $Q_M^{-1}(0){\in {\Bbb C}}$
denote the zero set of the Laurent polynomial
$Q_M^{-1}(0){\in {\Bbb C}}$
denote the zero set of the Laurent polynomial
![]() $Q_M$
.
$Q_M$
.

Figure 1
![]() $D\subset {\Bbb C}$
.
$D\subset {\Bbb C}$
.
Proposition 3.1 Let
![]() $M=S^3_{p/1}(4_1)$
for some integer p. If
$M=S^3_{p/1}(4_1)$
for some integer p. If
![]() $p\neq 0$
, then there is a bijection
$p\neq 0$
, then there is a bijection
![]() $\Phi _{M}:R^{\mathrm {irr}}_G(M)\rightarrow Q_M^{-1}(0)\cap D$
. Here, for
$\Phi _{M}:R^{\mathrm {irr}}_G(M)\rightarrow Q_M^{-1}(0)\cap D$
. Here, for
![]() $[\varphi ]\in R^{\mathrm {irr}}_G(M)$
, we define
$[\varphi ]\in R^{\mathrm {irr}}_G(M)$
, we define
when the eigenvalues of
![]() $\varphi ({\mathfrak {m}})$
are not
$\varphi ({\mathfrak {m}})$
are not
![]() $\pm \sqrt {-1}$
. If
$\pm \sqrt {-1}$
. If
![]() $\varepsilon \sqrt {-1}\in Q_M^{-1}(0)$
for some
$\varepsilon \sqrt {-1}\in Q_M^{-1}(0)$
for some
![]() $\varepsilon \in \{\pm 1\}$
,
$\varepsilon \in \{\pm 1\}$
,
![]() $\Phi _M^{-1}(\varepsilon \sqrt {-1})$
is a conjugacy class with a representation
$\Phi _M^{-1}(\varepsilon \sqrt {-1})$
is a conjugacy class with a representation
![]() $\varphi $
defined by
$\varphi $
defined by
 $$ \begin{align}\varphi({\mathfrak{m}})=\left(\begin{array}{cc} \varepsilon \sqrt{-1} & 0 \\ 0 & -\varepsilon \sqrt{-1}\\ \end{array} \right),\,\,\,\, \varphi(x_1)=\left(\begin{array}{cc} \frac{1}{4} (-1+\varepsilon\sqrt{5}) & 1 \\ \frac{1}{8} (-5-\varepsilon\sqrt{5}) & \frac{1}{4} (-1+\varepsilon\sqrt{5}) \\ \end{array} \right). \end{align} $$
$$ \begin{align}\varphi({\mathfrak{m}})=\left(\begin{array}{cc} \varepsilon \sqrt{-1} & 0 \\ 0 & -\varepsilon \sqrt{-1}\\ \end{array} \right),\,\,\,\, \varphi(x_1)=\left(\begin{array}{cc} \frac{1}{4} (-1+\varepsilon\sqrt{5}) & 1 \\ \frac{1}{8} (-5-\varepsilon\sqrt{5}) & \frac{1}{4} (-1+\varepsilon\sqrt{5}) \\ \end{array} \right). \end{align} $$
If
![]() $p=0$
, then there is a bijection
$p=0$
, then there is a bijection
![]() $\Phi _{M}:R^{\mathrm {irr}}_{G}(M)\rightarrow \{\pm \sqrt {-1} ,\pm (1-\sqrt {5})/2\}$
.
$\Phi _{M}:R^{\mathrm {irr}}_{G}(M)\rightarrow \{\pm \sqrt {-1} ,\pm (1-\sqrt {5})/2\}$
.
Proposition 3.2 Let
![]() $M=S^3_{1/q}(4_1)$
for some integer
$M=S^3_{1/q}(4_1)$
for some integer
![]() $q\neq 0$
. Then, there is a bijection
$q\neq 0$
. Then, there is a bijection
![]() $\Phi _{M}:R^{\mathrm {irr}}_G(M)\rightarrow Q_M^{-1}(0)\cap D$
. Here,
$\Phi _{M}:R^{\mathrm {irr}}_G(M)\rightarrow Q_M^{-1}(0)\cap D$
. Here,
![]() $\Phi _M$
is defined by (5) as in Proposition 3.1. Note that, since
$\Phi _M$
is defined by (5) as in Proposition 3.1. Note that, since
![]() $\pm \sqrt {-1}\notin Q_M^{-1}(0)$
for
$\pm \sqrt {-1}\notin Q_M^{-1}(0)$
for
![]() $M=S^3_{1/q}(4_1)$
, (6) can be excluded from the definition in this case.
$M=S^3_{1/q}(4_1)$
, (6) can be excluded from the definition in this case.
Proof of Proposition 3.1
Let
![]() $p\neq 0$
. For an irreducible representation
$p\neq 0$
. For an irreducible representation
![]() $\varphi :\pi _1(M)\rightarrow \mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
, take
$\varphi :\pi _1(M)\rightarrow \mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
, take
![]() $x,y,z,w\in {\Bbb C}$
so that
$x,y,z,w\in {\Bbb C}$
so that
![]() $\varphi (x_1)=\left ( {\small \begin {array}{cc}x&y\\z&w\\ \end {array}}\right )$
and
$\varphi (x_1)=\left ( {\small \begin {array}{cc}x&y\\z&w\\ \end {array}}\right )$
and
![]() $xw-yz=1$
. We first claim that
$xw-yz=1$
. We first claim that
![]() $\varphi ({\mathfrak {m}})$
is diagonalizable. In fact, if not so, we may suppose
$\varphi ({\mathfrak {m}})$
is diagonalizable. In fact, if not so, we may suppose
![]() $\varphi ({\mathfrak {m}})=\left ({\small \begin {array}{cc}\eta &b\\0&\eta \\ \end {array}} \right )$
for some
$\varphi ({\mathfrak {m}})=\left ({\small \begin {array}{cc}\eta &b\\0&\eta \\ \end {array}} \right )$
for some
![]() $b\in {\Bbb C}^\times $
and
$b\in {\Bbb C}^\times $
and
![]() $\eta \in \{\pm 1\}$
. Since
$\eta \in \{\pm 1\}$
. Since
![]() $\varphi (r_1)=E_2$
, we have
$\varphi (r_1)=E_2$
, we have
It follows from (7) that
 $$ \begin{align} \varphi(r_3)&=\varphi(x_1)\varphi(x_2)\varphi(x_1)^{-1}\varphi(x_2)^{-1}\varphi({\mathfrak{m}})^p\nonumber\\ &=\eta^p{\small \left( \begin{array}{cc} b^4 z^4+\eta b^3 w z^3-b^2 z^2 {\left( x^2+xw-3\right)} +\eta b z (w-x)+1 & * \\ -\eta b^3 z^4-b^2 z^3 (w+x)-\eta 2 b z^2 & {*} \\ \end{array} \right).} \end{align} $$
$$ \begin{align} \varphi(r_3)&=\varphi(x_1)\varphi(x_2)\varphi(x_1)^{-1}\varphi(x_2)^{-1}\varphi({\mathfrak{m}})^p\nonumber\\ &=\eta^p{\small \left( \begin{array}{cc} b^4 z^4+\eta b^3 w z^3-b^2 z^2 {\left( x^2+xw-3\right)} +\eta b z (w-x)+1 & * \\ -\eta b^3 z^4-b^2 z^3 (w+x)-\eta 2 b z^2 & {*} \\ \end{array} \right).} \end{align} $$
Then, the condition
![]() $\varphi (r_3)=E_2$
and
$\varphi (r_3)=E_2$
and
![]() $b\neq 0$
leads to
$b\neq 0$
leads to
![]() $z=0$
. In fact, if
$z=0$
. In fact, if
![]() $z\neq 0$
, the (2,1)-entries of
$z\neq 0$
, the (2,1)-entries of
![]() $\varphi (r_3)=E_2$
yields
$\varphi (r_3)=E_2$
yields
![]() $x=-\eta 2 b^{-1}z^{-1}-w-\eta b z$
by (8). Thus, the (1,1)-entry of (8) equals
$x=-\eta 2 b^{-1}z^{-1}-w-\eta b z$
by (8). Thus, the (1,1)-entry of (8) equals
![]() $-1$
, resulting in a contradiction.
$-1$
, resulting in a contradiction.
By substituting
![]() $z=0$
into
$z=0$
into
![]() $\varphi (r_2)$
, we obtain
$\varphi (r_2)$
, we obtain
Thus,
![]() $x=w=1$
and
$x=w=1$
and
![]() $y=0$
; therefore,
$y=0$
; therefore,
![]() $\varphi (x_1)$
and
$\varphi (x_1)$
and
![]() $\varphi (x_2)$
are upper triangular matrices, which leads to a contradiction to the irreducibility.
$\varphi (x_2)$
are upper triangular matrices, which leads to a contradiction to the irreducibility.
By the above claim, we may suppose
![]() $\varphi ({\mathfrak {m}})=\left ({\small \begin {array}{cc}a & 0 \\ 0&a^{-1}\\ \end {array}}\right )$
for some
$\varphi ({\mathfrak {m}})=\left ({\small \begin {array}{cc}a & 0 \\ 0&a^{-1}\\ \end {array}}\right )$
for some
![]() $a\in D{\backslash \{0\}}$
. Since we consider
$a\in D{\backslash \{0\}}$
. Since we consider
![]() $\varphi $
up to conjugacy, we may suppose
$\varphi $
up to conjugacy, we may suppose
![]() $y=1$
. Thus,
$y=1$
. Thus,
![]() $z=xw-1$
. Since
$z=xw-1$
. Since
![]() ${\varphi (r_1)=\varphi (r_2)=\varphi (r_3)=E_2}$
, with the help of a computer program of Mathematica, we have
${\varphi (r_1)=\varphi (r_2)=\varphi (r_3)=E_2}$
, with the help of a computer program of Mathematica, we have
 $$ \begin{align} x&={\small \frac{1+a^2-a^4+\eta(1-2 a^2-a^4-2 a^6+a^8)^{1/2}}{2(1- a^2)}},\nonumber\\ z&={\small -\frac{1-3 a^2+a^4+\eta(1-2 a^2-a^4-2 a^6+a^8)^{1/2}}{2 (a^2-1)^2 }},\nonumber\\ w&={\small \frac{-1+a^2+a^4+\eta(1-2 a^2-a^4-2 a^6+a^8)^{1/2}}{2 a^2 (a^2-1)}}, \end{align} $$
$$ \begin{align} x&={\small \frac{1+a^2-a^4+\eta(1-2 a^2-a^4-2 a^6+a^8)^{1/2}}{2(1- a^2)}},\nonumber\\ z&={\small -\frac{1-3 a^2+a^4+\eta(1-2 a^2-a^4-2 a^6+a^8)^{1/2}}{2 (a^2-1)^2 }},\nonumber\\ w&={\small \frac{-1+a^2+a^4+\eta(1-2 a^2-a^4-2 a^6+a^8)^{1/2}}{2 a^2 (a^2-1)}}, \end{align} $$
and
![]() $Q_M(a)=0$
when
$Q_M(a)=0$
when
![]() $a\neq \pm \sqrt {-1}$
. Here, we fix a branch of the
$a\neq \pm \sqrt {-1}$
. Here, we fix a branch of the
![]() $1/2$
th power on
$1/2$
th power on
![]() ${\Bbb C}^\times \backslash {\Bbb R}$
, and define the signs
${\Bbb C}^\times \backslash {\Bbb R}$
, and define the signs
![]() $\eta \in \{\pm 1\}$
by setting
$\eta \in \{\pm 1\}$
by setting
 $$ \begin{align*} \eta= \begin{cases} +1, & {\mathrm{ if } }\,\, -1+a^2+2a^4+a^6-a^8+2 a^{p+4}=(a^4-1)(1-2 a^2-a^4-2 a^6+a^8)^{1/2},\\ -1, & {\mathrm{ if } } \,\,-1+a^2+2a^4+a^6-a^8+2 a^{p+4}=-(a^4-1)(1-2 a^2-a^4-2 a^6+a^8)^{1/2}.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \eta= \begin{cases} +1, & {\mathrm{ if } }\,\, -1+a^2+2a^4+a^6-a^8+2 a^{p+4}=(a^4-1)(1-2 a^2-a^4-2 a^6+a^8)^{1/2},\\ -1, & {\mathrm{ if } } \,\,-1+a^2+2a^4+a^6-a^8+2 a^{p+4}=-(a^4-1)(1-2 a^2-a^4-2 a^6+a^8)^{1/2}.\\ \end{cases} \end{align*} $$
When
![]() $a=\varepsilon \sqrt {-1}$
for some
$a=\varepsilon \sqrt {-1}$
for some
![]() $\varepsilon \in \{\pm 1\}$
, we have
$\varepsilon \in \{\pm 1\}$
, we have
by the condition
![]() $\varphi (r_1)=\varphi (r_2)=\varphi (r_3)=E_2$
. In summary, the map
$\varphi (r_1)=\varphi (r_2)=\varphi (r_3)=E_2$
. In summary, the map
![]() $\Phi _M$
is well-defined and injective. Finally, we can easily show the surjectivity of
$\Phi _M$
is well-defined and injective. Finally, we can easily show the surjectivity of
![]() $\Phi _M$
by following the reverse process of the above calculation.
$\Phi _M$
by following the reverse process of the above calculation.
In the remaining case of
![]() $p=0$
, define
$p=0$
, define
![]() $\Phi _M$
as follows: for each
$\Phi _M$
as follows: for each
![]() $\varepsilon \in \{\pm 1\}$
, let
$\varepsilon \in \{\pm 1\}$
, let
![]() $\Phi _M^{-1}(\varepsilon \sqrt {-1})$
be a representation
$\Phi _M^{-1}(\varepsilon \sqrt {-1})$
be a representation
![]() $\varphi $
defined by (6). For
$\varphi $
defined by (6). For
![]() $\varepsilon ' \in \{\pm 1\}$
, let
$\varepsilon ' \in \{\pm 1\}$
, let
![]() $\Phi _M^{-1}(\varepsilon ' (1-\sqrt {5})/2)$
has a representation
$\Phi _M^{-1}(\varepsilon ' (1-\sqrt {5})/2)$
has a representation
![]() $\varphi $
defined by
$\varphi $
defined by
 $$ \begin{align*}\varphi({\mathfrak{m}})= \left(\begin{array}{cc} \varepsilon' \frac{1-\sqrt{5}}{2} & 0 \\ 0 & \varepsilon' \frac{-1-\sqrt{5}}{2}\\ \end{array} \right),\,\,\,\, \varphi(x_1)=\left(\begin{array}{cc} 1 & 1 \\ 0 & 1\\ \end{array} \right), \end{align*} $$
$$ \begin{align*}\varphi({\mathfrak{m}})= \left(\begin{array}{cc} \varepsilon' \frac{1-\sqrt{5}}{2} & 0 \\ 0 & \varepsilon' \frac{-1-\sqrt{5}}{2}\\ \end{array} \right),\,\,\,\, \varphi(x_1)=\left(\begin{array}{cc} 1 & 1 \\ 0 & 1\\ \end{array} \right), \end{align*} $$
respectively. Then, by
![]() $\varphi (r_1)=\varphi (r_2)=\varphi (r_3)=E_2$
, we can show the well-definedness and injectivity of
$\varphi (r_1)=\varphi (r_2)=\varphi (r_3)=E_2$
, we can show the well-definedness and injectivity of
![]() $\Phi _M$
as in the case of
$\Phi _M$
as in the case of
![]() $p\neq 0$
. By following the reverse process, we can check the surjectivity of
$p\neq 0$
. By following the reverse process, we can check the surjectivity of
![]() $\Phi _M$
as well.
$\Phi _M$
as well.
Proof of Proposition 3.2
It can be proved in the same manner as Proposition 3.1. In this case, instead of (9), we have
 $$ \begin{align} &x=\frac{a^{-2 q} \left(2 a^{6 q}+2 a^{4 q+1}\right)}{2 \left(a^{2 q}-1\right)^2 \left(a^{2 q}+1\right)}, \ z=-\frac{4 a^{2 q}+2 a^{4 q}-2 a^{6 q}+2 a^{4 q+1}-2}{2 y \left(a^{2 q}-1\right)^3 \left(a^{2 q}+1\right)},\nonumber\\ &w=-\frac{4 a^{4 q}+2 a^{6 q}-2 a^{8 q}+2 a^{4 q+1}-2}{2 \left(a^{2 q}-1\right)^2 \left(a^{2 q}+1\right)}.\\[-42pt]\nonumber \end{align} $$
$$ \begin{align} &x=\frac{a^{-2 q} \left(2 a^{6 q}+2 a^{4 q+1}\right)}{2 \left(a^{2 q}-1\right)^2 \left(a^{2 q}+1\right)}, \ z=-\frac{4 a^{2 q}+2 a^{4 q}-2 a^{6 q}+2 a^{4 q+1}-2}{2 y \left(a^{2 q}-1\right)^3 \left(a^{2 q}+1\right)},\nonumber\\ &w=-\frac{4 a^{4 q}+2 a^{6 q}-2 a^{8 q}+2 a^{4 q+1}-2}{2 \left(a^{2 q}-1\right)^2 \left(a^{2 q}+1\right)}.\\[-42pt]\nonumber \end{align} $$
Theorem 3.3 Let
![]() $M=S^3_{p/1}(4_1)$
for some integer
$M=S^3_{p/1}(4_1)$
for some integer
![]() $p\neq 0$
. For
$p\neq 0$
. For
![]() $a\in Q_M^{-1}(0)\cap D$
as in Proposition 3.1, we denote the representative
$a\in Q_M^{-1}(0)\cap D$
as in Proposition 3.1, we denote the representative
![]() $\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
-representation of
$\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
-representation of
![]() $\Phi _M^{-1}(a)$
by
$\Phi _M^{-1}(a)$
by
![]() $\varphi _a$
. Then, the adjoint Reidemeister torsion of M with respect to
$\varphi _a$
. Then, the adjoint Reidemeister torsion of M with respect to
![]() $\varphi _a$
is computed as
$\varphi _a$
is computed as
 $$ \begin{align}\tau_{\varphi_a}(M)=\left\{\begin{array}{@{}l@{}ll}& -\dfrac{ 4-p+(-2+p)a^2+2pa^4+(2+p)a^6-(4+p)a^8+2pa^{4+p}}{2(a^2-1)^3(1+a^2)}, &\text{if } \,a\notin\{\pm \sqrt{-1}\},\\[4pt]& \dfrac{1}{8} (10+ a p \sqrt{-5}), &\text{if }\,a\in\{\pm \sqrt{-1}\}. \end{array}\right.\end{align} $$
$$ \begin{align}\tau_{\varphi_a}(M)=\left\{\begin{array}{@{}l@{}ll}& -\dfrac{ 4-p+(-2+p)a^2+2pa^4+(2+p)a^6-(4+p)a^8+2pa^{4+p}}{2(a^2-1)^3(1+a^2)}, &\text{if } \,a\notin\{\pm \sqrt{-1}\},\\[4pt]& \dfrac{1}{8} (10+ a p \sqrt{-5}), &\text{if }\,a\in\{\pm \sqrt{-1}\}. \end{array}\right.\end{align} $$
Theorem 3.4 Let
![]() $M=S^3_{1/q}(4_1)$
for some integer
$M=S^3_{1/q}(4_1)$
for some integer
![]() $q\neq 0$
. For
$q\neq 0$
. For
![]() $a\in Q_M^{-1}(0)\cap D$
as in Proposition 3.2, we denote the representative
$a\in Q_M^{-1}(0)\cap D$
as in Proposition 3.2, we denote the representative
![]() $\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
-representation of
$\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
-representation of
![]() $\Phi _M^{-1}(a)$
by
$\Phi _M^{-1}(a)$
by
![]() $\varphi _a$
. Then, the adjoint Reidemeister torsion of M with respect to
$\varphi _a$
. Then, the adjoint Reidemeister torsion of M with respect to
![]() $\varphi _a$
is computed as
$\varphi _a$
is computed as
 $$ \begin{align} \tau_{\varphi_a}(M)= -\frac{a^{6q}(-1+4q+(1-2q)a^{2q}+2(1+a)a^{4q}+(1+2q)a^{6q}-(1+4q)a^{8q})}{2(a^{4q}-1)^3(1-2a^{2q}-a^{4q}-2a^{6q}+a^{8q})}. \end{align} $$
$$ \begin{align} \tau_{\varphi_a}(M)= -\frac{a^{6q}(-1+4q+(1-2q)a^{2q}+2(1+a)a^{4q}+(1+2q)a^{6q}-(1+4q)a^{8q})}{2(a^{4q}-1)^3(1-2a^{2q}-a^{4q}-2a^{6q}+a^{8q})}. \end{align} $$
Proof of Theorems 3.3 and 3.4
Under the identification of
![]() ${\mathfrak {g}}\cong {\Bbb C}^3$
, we can concretely describe each
${\mathfrak {g}}\cong {\Bbb C}^3$
, we can concretely describe each
![]() $\delta ^i$
as the matrices according to (4) and the description of
$\delta ^i$
as the matrices according to (4) and the description of
![]() $\Phi _M$
in the proofs of Propositions 3.1 and 3.2. Applying the
$\Phi _M$
in the proofs of Propositions 3.1 and 3.2. Applying the
![]() $\tau $
-chain method in [Reference Turaev15, Section 2.1] to the chain complex
$\tau $
-chain method in [Reference Turaev15, Section 2.1] to the chain complex
![]() $C^*_\varphi (M;{\mathfrak {g}})$
, with the help of a computer program of Mathematica, we can directly obtain the resulting
$C^*_\varphi (M;{\mathfrak {g}})$
, with the help of a computer program of Mathematica, we can directly obtain the resulting
![]() $\tau _{\varphi _a}(M)$
.
$\tau _{\varphi _a}(M)$
.
Remark 3.5
-
(i) While this paper deals with the adjoint torsion via adjoint action, the classical Reidemeister torsion of
 $M=S^3_{p/q}(4_1)$
with respect to the
$M=S^3_{p/q}(4_1)$
with respect to the
 $\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
-representation was computed in [Reference Kitano6].
$\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
-representation was computed in [Reference Kitano6]. -
(ii) When
 $M=S^3_{p/1}(4_1)$
, the torsion
$M=S^3_{p/1}(4_1)$
, the torsion
 $\tau _{\varphi }(M)$
, up to sign, was computed in [Reference Ohtsuki and Takata10]. The advantage of Theorem 3.3 is that the sign of the torsion is recovered; thus, we can compute the sum of
$\tau _{\varphi }(M)$
, up to sign, was computed in [Reference Ohtsuki and Takata10]. The advantage of Theorem 3.3 is that the sign of the torsion is recovered; thus, we can compute the sum of
 $\tau _\varphi (M)^{n}$
’s, as is seen later.
$\tau _\varphi (M)^{n}$
’s, as is seen later. -
(iii) We can easily check that
 $\tau _{\varphi _{a^{-1}}}(M)=\tau _{\varphi _a}(M)\in {\Bbb C}^\times $
by using the relation
$\tau _{\varphi _{a^{-1}}}(M)=\tau _{\varphi _a}(M)\in {\Bbb C}^\times $
by using the relation
 $Q_M(a)=0$
when
$Q_M(a)=0$
when
 $a\neq \pm \sqrt {-1}$
, and that
$a\neq \pm \sqrt {-1}$
, and that
 $Q_M(\pm \sqrt {-1})=0$
with
$Q_M(\pm \sqrt {-1})=0$
with
 $M=S^3_{p/1}(4_1)$
if and only if p is divisible by
$M=S^3_{p/1}(4_1)$
if and only if p is divisible by
 $4$
.
$4$
. -
(iv) If
 $p=0$
, that is, if
$p=0$
, that is, if
 $M=S^3_{0/1}(4_1)$
, then we can similarly compute
$M=S^3_{0/1}(4_1)$
, then we can similarly compute
 $\tau _{\varphi _a}(M)$
as
$\tau _{\varphi _a}(M)$
as
 $5/4$
,
$5/4$
,
 $5/4$
,
$5/4$
,
 $5$
, and
$5$
, and
 $5$
with respect to
$5$
with respect to
 $a=\sqrt {-1}$
,
$a=\sqrt {-1}$
,
 $-\sqrt {-1}$
,
$-\sqrt {-1}$
,
 $(1-\sqrt {5})/2$
, and
$(1-\sqrt {5})/2$
, and
 $-(1-\sqrt {5})/2$
, respectively.
$-(1-\sqrt {5})/2$
, respectively.
3.2 Two key lemmas
As preliminaries of the proof of Theorem 1.2, we prepare two lemmas.
Lemma 3.6 Define a polynomial
![]() $\kappa _p(x) \in {\Bbb Z}[x]$
by setting
$\kappa _p(x) \in {\Bbb Z}[x]$
by setting
 $$ \begin{align*} \kappa_p(x) =\left\{ \begin{array}{ll} (1+x)^2 ,& \mathrm{if} \ \ p= 2m+1, \\ (1+x^2)^2 ,& \mathrm{if} \ \ p= 4m, \\ 1 ,& \mathrm{if} \ \ p= 4m+2, \\ \end{array} \right.\end{align*} $$
$$ \begin{align*} \kappa_p(x) =\left\{ \begin{array}{ll} (1+x)^2 ,& \mathrm{if} \ \ p= 2m+1, \\ (1+x^2)^2 ,& \mathrm{if} \ \ p= 4m, \\ 1 ,& \mathrm{if} \ \ p= 4m+2, \\ \end{array} \right.\end{align*} $$
for some
![]() $m \in {\Bbb Z}$
. Then,
$m \in {\Bbb Z}$
. Then,
![]() $Q_{M}(x)$
with
$Q_{M}(x)$
with
![]() $M=S^3_{p/1}(4_1) $
is divisible by
$M=S^3_{p/1}(4_1) $
is divisible by
![]() $\kappa _p(x) $
, and the quotient
$\kappa _p(x) $
, and the quotient
![]() $ Q_{M}(x)/\kappa _p(x)$
has no repeated roots. On the other hand,
$ Q_{M}(x)/\kappa _p(x)$
has no repeated roots. On the other hand,
![]() $Q_{M}(x)$
with
$Q_{M}(x)$
with
![]() $M=S^3_{1/q}(4_1) $
is divisible by
$M=S^3_{1/q}(4_1) $
is divisible by
![]() $(1+x)^2 $
, and the quotient
$(1+x)^2 $
, and the quotient
![]() $ Q_{M}(x)/(1+x)^2 $
also has no repeated roots.
$ Q_{M}(x)/(1+x)^2 $
also has no repeated roots.
Proof The required statement with
![]() $|p| \leq 4$
and
$|p| \leq 4$
and
![]() $|q| \leq 4$
can be directly shown, we may assume
$|q| \leq 4$
can be directly shown, we may assume
![]() $|p| \geq 5 $
and
$|p| \geq 5 $
and
![]() $|q| \geq 5.$
We first focus on the case
$|q| \geq 5.$
We first focus on the case
![]() $M=S^3_{p/1}(4_1) $
. By a computation of
$M=S^3_{p/1}(4_1) $
. By a computation of
![]() $ \frac {\mathrm {d}^n \ }{\mathrm {d}x^n} (Q_M(x))\mid _{x=b}$
with
$ \frac {\mathrm {d}^n \ }{\mathrm {d}x^n} (Q_M(x))\mid _{x=b}$
with
![]() $b= \pm 1 , \pm \sqrt {-1}$
, we can easily verify the multiplicity of
$b= \pm 1 , \pm \sqrt {-1}$
, we can easily verify the multiplicity of
![]() $Q_M(x)$
. To elaborate, if
$Q_M(x)$
. To elaborate, if
![]() $p=2m+1$
, then
$p=2m+1$
, then
are all nonzero, which implies that
![]() $1,\pm \sqrt {-1}$
are not roots of
$1,\pm \sqrt {-1}$
are not roots of
![]() $Q_M(x)$
. Furthermore,
$Q_M(x)$
. Furthermore,
indicates that
![]() $-1$
is a root of
$-1$
is a root of
![]() $Q_M(x)$
with multiplicity
$Q_M(x)$
with multiplicity
![]() $2$
. When
$2$
. When
![]() $p=4m$
or
$p=4m$
or
![]() $4m+2$
, we can analogously determine the multiplicity of
$4m+2$
, we can analogously determine the multiplicity of
![]() $Q_M(x)$
with
$Q_M(x)$
with
![]() $b=\pm 1, \pm \sqrt {-1}$
. Thus,
$b=\pm 1, \pm \sqrt {-1}$
. Thus,
![]() $Q_M(x)$
is divisible by
$Q_M(x)$
is divisible by
![]() $\kappa _p(x)$
, and
$\kappa _p(x)$
, and
![]() $Q_M(x)/\kappa _p(x)$
is not divisible by
$Q_M(x)/\kappa _p(x)$
is not divisible by
![]() $x \pm 1$
and
$x \pm 1$
and
![]() $x^2+1$
.
$x^2+1$
.
Next, suppose
![]() $Q_{M}(x) $
has a repeated root
$Q_{M}(x) $
has a repeated root
![]() $a\in {\Bbb C}$
with
$a\in {\Bbb C}$
with
![]() $a \neq \pm 1 , \pm \sqrt {-1}$
. Then,
$a \neq \pm 1 , \pm \sqrt {-1}$
. Then,
![]() $Q_{M}(a) =0$
and
$Q_{M}(a) =0$
and
![]() $ Q_{M}'(a) =0,$
which are equivalent to
$ Q_{M}'(a) =0,$
which are equivalent to
Applying (16) to (15) to kill the term
![]() $a^p$
, we equivalently have
$a^p$
, we equivalently have
Since
![]() $a^2 \neq \pm 1$
, the last quartic term equation can be solved as
$a^2 \neq \pm 1$
, the last quartic term equation can be solved as
 $$ \begin{align*}a^2 = \frac{ p^2-8 + 2 \eta p\sqrt{p^2 -15} + \varepsilon \sqrt{(40-3p^2 +2\eta p \sqrt{p^2 -15}) (p^2-24 +2\eta p \sqrt{p^2 -15})}}{2p^2 -32},\end{align*} $$
$$ \begin{align*}a^2 = \frac{ p^2-8 + 2 \eta p\sqrt{p^2 -15} + \varepsilon \sqrt{(40-3p^2 +2\eta p \sqrt{p^2 -15}) (p^2-24 +2\eta p \sqrt{p^2 -15})}}{2p^2 -32},\end{align*} $$
for some
![]() $\varepsilon , \eta \in \{ \pm 1\}.$
Let F be the field extension
$\varepsilon , \eta \in \{ \pm 1\}.$
Let F be the field extension
![]() ${\Bbb Q}(a)$
of degree 8. Let us regard (15) as a quadratic equation in F of
${\Bbb Q}(a)$
of degree 8. Let us regard (15) as a quadratic equation in F of
![]() $a^p$
. Since the discriminant is not zero and
$a^p$
. Since the discriminant is not zero and
![]() $|p|>4$
,
$|p|>4$
,
![]() $a^p $
does not lie in F. This is a contradiction. In summary,
$a^p $
does not lie in F. This is a contradiction. In summary,
![]() $Q_M(x)/\kappa _p(x)$
has no repeated roots as required.
$Q_M(x)/\kappa _p(x)$
has no repeated roots as required.
On the other hand, if
![]() $M=S^3_{1/q}(4_1) $
, we can easily show that
$M=S^3_{1/q}(4_1) $
, we can easily show that
![]() $Q_M(x)$
is divisible not by
$Q_M(x)$
is divisible not by
![]() $(1+x)^3$
but by
$(1+x)^3$
but by
![]() $(1+x)^2$
. Similarly, suppose
$(1+x)^2$
. Similarly, suppose
![]() $Q_{M}(x) $
has a repeated root
$Q_{M}(x) $
has a repeated root
![]() $a\in {\Bbb C}$
with
$a\in {\Bbb C}$
with
![]() $a \neq \pm 1 $
. Then,
$a \neq \pm 1 $
. Then,
![]() $Q_{M}(a) = Q_{M}'(a) =0$
. We can easily see
$Q_{M}(a) = Q_{M}'(a) =0$
. We can easily see
![]() $Q_{M}(1/a) = Q_{M}'(1/ a) =0$
by reciprocity of
$Q_{M}(1/a) = Q_{M}'(1/ a) =0$
by reciprocity of
![]() $Q_M$
. Thus, we obtain
$Q_M$
. Thus, we obtain
![]() $ ( x^{-4q} Q_{M})' (a) = ( x^{-4q} Q_{M})' (1/a) =0,$
which are equivalent to
$ ( x^{-4q} Q_{M})' (a) = ( x^{-4q} Q_{M})' (1/a) =0,$
which are equivalent to
Since
![]() $a^{-4q}Q_{M}(a) = 0$
is equivalent to
$a^{-4q}Q_{M}(a) = 0$
is equivalent to
the substitution of (17) and (18) into (19) gives the equation
where we replace
![]() $a^{2q}$
by b. If
$a^{2q}$
by b. If
![]() $\omega ^{2q}= \pm 1$
and
$\omega ^{2q}= \pm 1$
and
![]() $\omega \in {\Bbb C}$
, we can easily check
$\omega \in {\Bbb C}$
, we can easily check
![]() $ Q_M( \omega ) \neq 0$
by definition. Thus,
$ Q_M( \omega ) \neq 0$
by definition. Thus,
![]() $a^q$
is a solution of the quartic equation in (20) and does not lie in
$a^q$
is a solution of the quartic equation in (20) and does not lie in
![]() ${\Bbb Q}$
, for any
${\Bbb Q}$
, for any
![]() $q \in {\Bbb Z}$
. Let
$q \in {\Bbb Z}$
. Let
![]() $F /{\Bbb Q}$
be the field extension by the quartic equation. By definition, F does not contain
$F /{\Bbb Q}$
be the field extension by the quartic equation. By definition, F does not contain
![]() $ a $
and
$ a $
and
![]() $2+a+a^{-1}$
, which contradicts (19) since
$2+a+a^{-1}$
, which contradicts (19) since
![]() $|q|>4$
. In summary,
$|q|>4$
. In summary,
![]() $Q_M(x)/(1+x)^2$
has no repeated roots as required.
$Q_M(x)/(1+x)^2$
has no repeated roots as required.
Next, we should mention a slight modification of Jacobi’s residue theorem.
Lemma 3.7 Fix
![]() $ {\zeta } \in {\{ 0, 2\}}$
and
$ {\zeta } \in {\{ 0, 2\}}$
and
![]() ${\theta } \in \{ 1,2\}$
. Suppose a polynomial
${\theta } \in \{ 1,2\}$
. Suppose a polynomial
![]() $k(x) \in {\Bbb Q}[x]$
has no repeated roots and
$k(x) \in {\Bbb Q}[x]$
has no repeated roots and
![]() $k(0)\neq 0$
. Take another polynomial
$k(0)\neq 0$
. Take another polynomial
![]() $g(x)\in {\Bbb Q}[x] $
such that
$g(x)\in {\Bbb Q}[x] $
such that
![]() $\mathrm {deg}(g) \leq \mathrm {deg}(k) - {\theta } {\zeta } -2$
. Then, the following sum is zero:
$\mathrm {deg}(g) \leq \mathrm {deg}(k) - {\theta } {\zeta } -2$
. Then, the following sum is zero:
 $$ \begin{align} \sum_{a \in k^{-1}(0)} \frac{ (1 +a^{{\theta}})^{ {\zeta} } g (a)}{ \frac{\mathrm{d}}{ \mathrm{d}x }((1+x^{{\theta}})^{\zeta} k(x))|_{x=a}} =0.\end{align} $$
$$ \begin{align} \sum_{a \in k^{-1}(0)} \frac{ (1 +a^{{\theta}})^{ {\zeta} } g (a)}{ \frac{\mathrm{d}}{ \mathrm{d}x }((1+x^{{\theta}})^{\zeta} k(x))|_{x=a}} =0.\end{align} $$
Proof If
![]() $ {\zeta }=0$
, the statement is Jacobi’s residue theorem exactly (see, e.g., [Reference Tran and Yamaguchi14, Section 6]). Thus, we may suppose
$ {\zeta }=0$
, the statement is Jacobi’s residue theorem exactly (see, e.g., [Reference Tran and Yamaguchi14, Section 6]). Thus, we may suppose
![]() ${\zeta }=2 $
. Note that the derivative of
${\zeta }=2 $
. Note that the derivative of
![]() $(1+x^{{\theta }})^{\zeta } k(x) $
is
$(1+x^{{\theta }})^{\zeta } k(x) $
is
![]() $ {\zeta } {\theta } x^{\theta -1}(1+x^{{\theta }})^{{\zeta } -1} k(x)+ (1+x^{{\theta }})^{\zeta } k'(x)$
. Hence, the left-hand side of (21) is computed as
$ {\zeta } {\theta } x^{\theta -1}(1+x^{{\theta }})^{{\zeta } -1} k(x)+ (1+x^{{\theta }})^{\zeta } k'(x)$
. Hence, the left-hand side of (21) is computed as
![]() $\sum _{a \in k^{-1}(0)} g (a)/ k'(a) $
, which is equal to zero by the residue theorem.
$\sum _{a \in k^{-1}(0)} g (a)/ k'(a) $
, which is equal to zero by the residue theorem.
3.3 Proof of Theorem 1.2 with
 $n=-1$
$n=-1$
We suppose
![]() $n=-1$
and give the proof of Theorem 1.2. Recall the fact that
$n=-1$
and give the proof of Theorem 1.2. Recall the fact that
![]() $M=S^3_{p/1}(4_1)$
and
$M=S^3_{p/1}(4_1)$
and
![]() $M=S^3_{1/q}(4_1)$
are hyperbolic if and only if
$M=S^3_{1/q}(4_1)$
are hyperbolic if and only if
![]() $|p|\geq 5$
and
$|p|\geq 5$
and
![]() $|q|\geq 2$
, respectively (see, e.g., Theorem 4.7 of [Reference Thurston13]).
$|q|\geq 2$
, respectively (see, e.g., Theorem 4.7 of [Reference Thurston13]).
First, we focus on the case where
![]() $p\geq 5$
,
$p\geq 5$
,
![]() $M=S^3_{p/1}(4_1)$
, and p is not divisible by
$M=S^3_{p/1}(4_1)$
, and p is not divisible by
![]() $4$
. From the definition of
$4$
. From the definition of
![]() $Q_M(x)$
and Theorem 3.3, we can easily verify
$Q_M(x)$
and Theorem 3.3, we can easily verify
 $$ \begin{align} \frac{1}{\tau_{\varphi_a}(M)}= \frac{2(1-a^2)^3( 1+a^2)a^{p-5} }{Q_M ' (a)} \qquad \textrm{for any } a \in \left(Q_M^{-1}(0)\cap D\right)\backslash \{\pm \sqrt{-1}\}. \end{align} $$
$$ \begin{align} \frac{1}{\tau_{\varphi_a}(M)}= \frac{2(1-a^2)^3( 1+a^2)a^{p-5} }{Q_M ' (a)} \qquad \textrm{for any } a \in \left(Q_M^{-1}(0)\cap D\right)\backslash \{\pm \sqrt{-1}\}. \end{align} $$
If
![]() $p -2$
is divisible by
$p -2$
is divisible by
![]() $4$
, we replace
$4$
, we replace
![]() $g(x)$
and
$g(x)$
and
![]() $k(x)$
by
$k(x)$
by
![]() $2(1-x^2)^3( 1+x^2)x^{p-5} $
and
$2(1-x^2)^3( 1+x^2)x^{p-5} $
and
![]() $Q_M(x)$
, respectively. Then, Lemma 3.7 with
$Q_M(x)$
, respectively. Then, Lemma 3.7 with
![]() $\zeta =0$
deduces to the required conclusion as
$\zeta =0$
deduces to the required conclusion as
 $$ \begin{align} 0 = \sum_{ a \in Q_M^{-1} (0) } \frac{g(a)}{Q_M'(a)} =\sum_{ a \in Q_M^{-1} (0) } \frac{1}{\tau_{\varphi_a}(M)}= 2 \sum_{ a \in Q_M^{-1} (0) \cap D } \frac{1}{\tau_{\varphi_a}(M)} = \sum_{ \varphi \in R_{G}^{\mathrm{irr}} } \frac{2}{\tau_{\varphi}(M)}.\end{align} $$
$$ \begin{align} 0 = \sum_{ a \in Q_M^{-1} (0) } \frac{g(a)}{Q_M'(a)} =\sum_{ a \in Q_M^{-1} (0) } \frac{1}{\tau_{\varphi_a}(M)}= 2 \sum_{ a \in Q_M^{-1} (0) \cap D } \frac{1}{\tau_{\varphi_a}(M)} = \sum_{ \varphi \in R_{G}^{\mathrm{irr}} } \frac{2}{\tau_{\varphi}(M)}.\end{align} $$
Here, the second, third, and fourth equalities immediately follow from (22), Remark 3.5(iii), and Proposition 3.1, respectively. Meanwhile, when
![]() $p -1$
is divisible by
$p -1$
is divisible by
![]() $2$
, we replace
$2$
, we replace
![]() $g(x)$
and
$g(x)$
and
![]() $k(x)$
by
$k(x)$
by
![]() $2(x-1)( x^4 -1 )x^{p-5} $
and
$2(x-1)( x^4 -1 )x^{p-5} $
and
![]() $Q_M(x)/(1+x)^2$
, respectively. Then, we can readily show similar equalities to (23).
$Q_M(x)/(1+x)^2$
, respectively. Then, we can readily show similar equalities to (23).
We further discuss the case of
![]() $p/4 \in {\Bbb Z}$
. By Lemma 3.6,
$p/4 \in {\Bbb Z}$
. By Lemma 3.6,
![]() $ Q_{M}(x)/(1+x^2) $
lies in
$ Q_{M}(x)/(1+x^2) $
lies in
![]() ${\Bbb Z}[x]$
, and has no double roots. We let
${\Bbb Z}[x]$
, and has no double roots. We let
![]() $g(x)$
and
$g(x)$
and
![]() $k(x)$
be
$k(x)$
be
![]() $2(1-x^2)^3 x^{p-5} $
and
$2(1-x^2)^3 x^{p-5} $
and
![]() $Q_M(x)/(1+x^2)$
, respectively. By Lemma 3.7 with
$Q_M(x)/(1+x^2)$
, respectively. By Lemma 3.7 with
![]() $\zeta =1$
and
$\zeta =1$
and
![]() $\theta =2$
, we have
$\theta =2$
, we have
 $$ \begin{align*}0 &= \sum_{ a \in k^{-1} (0) } \frac{g(a)}{k'(a)} = \frac{g( \sqrt{-1})}{k'( \sqrt{-1})}+ \frac{g(- \sqrt{-1})}{k'(- \sqrt{-1})}+\sum_{ a \in Q_M^{-1} (0) \cap D \backslash \{ \pm \sqrt{-1}\} } \frac{2}{\tau_{\varphi_a}(M)}\\ &= \frac{32 \sqrt{-1}}{20-p^2} + \sum_{ a \in Q_M^{-1} (0) \cap D \backslash \{ \pm \sqrt{-1}\} } \frac{2}{\tau_{\varphi_a}(M)} \\ &= \frac{2}{\tau_{\varphi_{\sqrt{-1}}}(M)} +\frac{2}{\tau_{\varphi_{-\sqrt{-1}}}(M)} + \sum_{ a \in Q_M^{-1} (0) \cap D \backslash \{ \pm \sqrt{-1}\} } \frac{2}{\tau_{\varphi_a}(M)} \\ &= \sum_{ a \in Q_M^{-1} (0) \cap D } \frac{2}{\tau_{\varphi_a}(M)} = \sum_{ \varphi \in R_{G}^{\mathrm{irr}} } \frac{2}{\tau_{\varphi}(M)}, \end{align*} $$
$$ \begin{align*}0 &= \sum_{ a \in k^{-1} (0) } \frac{g(a)}{k'(a)} = \frac{g( \sqrt{-1})}{k'( \sqrt{-1})}+ \frac{g(- \sqrt{-1})}{k'(- \sqrt{-1})}+\sum_{ a \in Q_M^{-1} (0) \cap D \backslash \{ \pm \sqrt{-1}\} } \frac{2}{\tau_{\varphi_a}(M)}\\ &= \frac{32 \sqrt{-1}}{20-p^2} + \sum_{ a \in Q_M^{-1} (0) \cap D \backslash \{ \pm \sqrt{-1}\} } \frac{2}{\tau_{\varphi_a}(M)} \\ &= \frac{2}{\tau_{\varphi_{\sqrt{-1}}}(M)} +\frac{2}{\tau_{\varphi_{-\sqrt{-1}}}(M)} + \sum_{ a \in Q_M^{-1} (0) \cap D \backslash \{ \pm \sqrt{-1}\} } \frac{2}{\tau_{\varphi_a}(M)} \\ &= \sum_{ a \in Q_M^{-1} (0) \cap D } \frac{2}{\tau_{\varphi_a}(M)} = \sum_{ \varphi \in R_{G}^{\mathrm{irr}} } \frac{2}{\tau_{\varphi}(M)}, \end{align*} $$
which is the required vanishing identity. Here, the second, fourth, and sixth equalities follow from (22), Theorem 3.3, and Proposition 3.1, respectively.
Next, we focus on the case of
![]() $q\geq 2$
and
$q\geq 2$
and
![]() $M=S^3_{1/q}(4_1)$
. Similarly to (22), we can show
$M=S^3_{1/q}(4_1)$
. Similarly to (22), we can show
 $$ \begin{align} \frac{1}{\tau_{\varphi_a}(M)}= \frac{2 (a^{4 q}-1)^3 (a^{4 q}-(a^2+a+1) a^{2 q-1}+1) }{ \frac{\mathrm{d}}{\mathrm{d}x }(x^{4q+1} Q_M (x))|_{x=a}} \qquad \textrm{for any } a \in Q_M^{-1}(0)\cap D. \end{align} $$
$$ \begin{align} \frac{1}{\tau_{\varphi_a}(M)}= \frac{2 (a^{4 q}-1)^3 (a^{4 q}-(a^2+a+1) a^{2 q-1}+1) }{ \frac{\mathrm{d}}{\mathrm{d}x }(x^{4q+1} Q_M (x))|_{x=a}} \qquad \textrm{for any } a \in Q_M^{-1}(0)\cap D. \end{align} $$
By a Euclidean Algorithm, we can choose a polynomial
![]() $h(x) \in {\Bbb Q}[x]$
such that
$h(x) \in {\Bbb Q}[x]$
such that
and
![]() $\mathrm {deg}h(x ) < 8q -2$
. Recall from Lemma 3.6 that
$\mathrm {deg}h(x ) < 8q -2$
. Recall from Lemma 3.6 that
![]() $Q_M(x) $
is divisible by
$Q_M(x) $
is divisible by
![]() $(1+x)^2 $
; thus so is
$(1+x)^2 $
; thus so is
![]() $h(x)$
. In summary, we can define polynomials
$h(x)$
. In summary, we can define polynomials
![]() $g(x)$
and
$g(x)$
and
![]() $k(x)$
to be
$k(x)$
to be
![]() $h(x)/ (1+x)^2$
and
$h(x)/ (1+x)^2$
and
![]() $Q_M(x)/(1+x)^2$
, respectively. Then, Lemma 3.7 with
$Q_M(x)/(1+x)^2$
, respectively. Then, Lemma 3.7 with
![]() $\zeta =2$
and
$\zeta =2$
and
![]() $\theta =1$
readily leads to the same equalities as (23).
$\theta =1$
readily leads to the same equalities as (23).
The proof of the cases of
![]() $p\leq -5$
and
$p\leq -5$
and
![]() $q \leq -2$
can be shown in the same manner; so we here do not carry out the detailed proof.
$q \leq -2$
can be shown in the same manner; so we here do not carry out the detailed proof.
Finally, in the remaining cases of
![]() $|p|\leq 4$
for
$|p|\leq 4$
for
![]() $M=S^3_{p/1}(4_1)$
, we can obtain the following by a direct calculation:
$M=S^3_{p/1}(4_1)$
, we can obtain the following by a direct calculation:
 $$ \begin{align*} \sum_{\varphi\in R^{\mathrm{irr}}_G(M)}\frac{1}{\tau_{\varphi}(M)}&= \begin{cases} 2, & \text{ if }p\in \{0,\pm1,\pm2,\pm3\},\\ 8, & \text{ if }p\in \{\pm4\}. \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{\varphi\in R^{\mathrm{irr}}_G(M)}\frac{1}{\tau_{\varphi}(M)}&= \begin{cases} 2, & \text{ if }p\in \{0,\pm1,\pm2,\pm3\},\\ 8, & \text{ if }p\in \{\pm4\}. \end{cases} \end{align*} $$
For example, we now discuss the detail in the case
![]() $p=4$
for
$p=4$
for
![]() $M=S^3_{p/1}(4_1)$
. The roots of
$M=S^3_{p/1}(4_1)$
. The roots of
![]() $Q_M(x)=x^2 + 2 x^4 + x^6=0$
are
$Q_M(x)=x^2 + 2 x^4 + x^6=0$
are
![]() $x=\pm \sqrt {-1}$
. By Theorem 3.3, we have
$x=\pm \sqrt {-1}$
. By Theorem 3.3, we have
![]() $\tau _{\varphi _{\sqrt {-1}}}(M)= (5-2 \sqrt {5})/4$
and
$\tau _{\varphi _{\sqrt {-1}}}(M)= (5-2 \sqrt {5})/4$
and
![]() $\tau _{\varphi _{-\sqrt {-1}}}(M)=(5+2 \sqrt {5})/4$
, leading to
$\tau _{\varphi _{-\sqrt {-1}}}(M)=(5+2 \sqrt {5})/4$
, leading to
![]() $\sum _{\varphi \in R^{\mathrm {irr}}_G(M)}\tau _{\varphi }(M)^{-1}=8$
. Similarly, the computations in the other cases run well.
$\sum _{\varphi \in R^{\mathrm {irr}}_G(M)}\tau _{\varphi }(M)^{-1}=8$
. Similarly, the computations in the other cases run well.
4 Surgeries on the
 $5_2$
-knot
$5_2$
-knot
We discuss Conjecture 1.1 in the case of
![]() $M=S^3_{1/q}(K)$
, when K is the
$M=S^3_{1/q}(K)$
, when K is the
![]() $5_2$
-knot and
$5_2$
-knot and
![]() $|q|\geq 3$
. Since the outline of the discussion in this section is almost the same as that in Section 3, we now roughly describe the discussion.
$|q|\geq 3$
. Since the outline of the discussion in this section is almost the same as that in Section 3, we now roughly describe the discussion.
As in (2), according to [Reference Nosaka8], the fundamental group
![]() $\pi _1(S^3_{1/q}(5_2))$
is known to be presented as
$\pi _1(S^3_{1/q}(5_2))$
is known to be presented as
Recall the free groups F, P, and the homomorphism
![]() $\psi $
in Section 2.3. Let
$\psi $
in Section 2.3. Let
![]() $W\in P*F$
be
$W\in P*F$
be
 $$ \begin{align*}&\rho_1\cdot x_1^2\rho_2x_1^{-2} \cdot (x_1^2x_2^{-1}x_1^{-1})\rho_1^{-1}(x_1^2x_2^{-1}x_1^{-1})^{-1} \cdot (x_1^2x_2^{-1}x_1^{-2}x_2)\rho_2^{-1}(x_1^2x_2^{-1}x_1^{-2}x_2)^{-1} \cdot \rho_4^{-1}\\&\quad \cdot x_4\rho_3x_4^{-1} \cdot \rho_4 \cdot \rho_3^{-1}.\end{align*} $$
$$ \begin{align*}&\rho_1\cdot x_1^2\rho_2x_1^{-2} \cdot (x_1^2x_2^{-1}x_1^{-1})\rho_1^{-1}(x_1^2x_2^{-1}x_1^{-1})^{-1} \cdot (x_1^2x_2^{-1}x_1^{-2}x_2)\rho_2^{-1}(x_1^2x_2^{-1}x_1^{-2}x_2)^{-1} \cdot \rho_4^{-1}\\&\quad \cdot x_4\rho_3x_4^{-1} \cdot \rho_4 \cdot \rho_3^{-1}.\end{align*} $$
Then, each
![]() $\delta ^*$
can be written as in (4) according to [Reference Nosaka8, Section 3.1]. Let
$\delta ^*$
can be written as in (4) according to [Reference Nosaka8, Section 3.1]. Let
![]() $Q_M(x)$
be the polynomial of the form
$Q_M(x)$
be the polynomial of the form
The same statement in Proposition 3.2 holds for
![]() $M=S^3_{1/q}(5_2)$
and
$M=S^3_{1/q}(5_2)$
and
![]() $q\neq 0$
, namely,
$q\neq 0$
, namely,
![]() $R^{\mathrm {irr}}_G(M)$
is bijective to
$R^{\mathrm {irr}}_G(M)$
is bijective to
![]() $Q_M^{-1}(0)\cap D$
. For
$Q_M^{-1}(0)\cap D$
. For
![]() $a\in Q_M^{-1}(0)\cap D$
, let us denote the representative
$a\in Q_M^{-1}(0)\cap D$
, let us denote the representative
![]() $\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
-representation of
$\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
-representation of
![]() $\Phi _M^{-1}(a)$
by
$\Phi _M^{-1}(a)$
by
![]() $\varphi _a$
as in Theorem 3.3. Then, the adjoint torsion
$\varphi _a$
as in Theorem 3.3. Then, the adjoint torsion
![]() $\tau _{\varphi _a}(M)$
is computed as
$\tau _{\varphi _a}(M)$
is computed as
with the help of a computer program of Mathematica. Here,
![]() $P(a)\in {\Bbb Z}[a]$
is a polynomial defined by setting
$P(a)\in {\Bbb Z}[a]$
is a polynomial defined by setting
 $$ \begin{align*} P(a)=\,& 1-2 q+a (28 q+2)+a^2 (3-42 q)+a^3 (36 q-8)+a^4 (2-20 q)\\ &+a^{2q}\left((4 q-1) a^{-1}+18 q-3 +(3-32 q) a+(4-54 q) a^{2}-2 a^{3}+(8 q-1) a^{4}\right) \\ &+a^{4q}\left((1-4 q) a^{-1}-10 q +(-8 q-3) a+(38 q-4) a^{2}+(5-34 q) a^{3}+(1-10 q) a^{4}\right) \\ &+a^{6q}\left((10 q-1) a^{-1}+(18 q+2) a+(7-56 q) a+(74 q-8) a^{2}+10 q a^{3}\right)\\ &+a^{8q}\left((14 q-3) a^{-1} +18 q +(9-76 q) a-3 a^{2}+(16 q-3) a^{3}\right)\\ &+a^{10q}\left((24 q-2) a^{-1} +(1-10 q) a+(2-52 q) a+(-18 q-1) a^{2}\right)\\ &+a^{12q}\left((4 q-1) a^{-2}+8 q a^{-1}+5-62 q+(56 q-6) a+(2-6 q) a^{2}\right). \end{align*} $$
$$ \begin{align*} P(a)=\,& 1-2 q+a (28 q+2)+a^2 (3-42 q)+a^3 (36 q-8)+a^4 (2-20 q)\\ &+a^{2q}\left((4 q-1) a^{-1}+18 q-3 +(3-32 q) a+(4-54 q) a^{2}-2 a^{3}+(8 q-1) a^{4}\right) \\ &+a^{4q}\left((1-4 q) a^{-1}-10 q +(-8 q-3) a+(38 q-4) a^{2}+(5-34 q) a^{3}+(1-10 q) a^{4}\right) \\ &+a^{6q}\left((10 q-1) a^{-1}+(18 q+2) a+(7-56 q) a+(74 q-8) a^{2}+10 q a^{3}\right)\\ &+a^{8q}\left((14 q-3) a^{-1} +18 q +(9-76 q) a-3 a^{2}+(16 q-3) a^{3}\right)\\ &+a^{10q}\left((24 q-2) a^{-1} +(1-10 q) a+(2-52 q) a+(-18 q-1) a^{2}\right)\\ &+a^{12q}\left((4 q-1) a^{-2}+8 q a^{-1}+5-62 q+(56 q-6) a+(2-6 q) a^{2}\right). \end{align*} $$
In addition, when
![]() $G=\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
,
$G=\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
,
![]() $M=S^3_{1/q}(5_2)$
, and
$M=S^3_{1/q}(5_2)$
, and
![]() $n=-1$
, we can show that Conjecture 1.1 is true for any integers
$n=-1$
, we can show that Conjecture 1.1 is true for any integers
![]() $q\neq 0$
. The proof can be shown in the same fashion as Section 3.3. However, the concrete substitutions of
$q\neq 0$
. The proof can be shown in the same fashion as Section 3.3. However, the concrete substitutions of
![]() $g(x)$
and
$g(x)$
and
![]() $k(x)$
into Lemma 3.7 are slightly complicated. For this reason, we do not go into detailed proof in this paper.
$k(x)$
into Lemma 3.7 are slightly complicated. For this reason, we do not go into detailed proof in this paper.
Incidentally, we give comments on the case
![]() $M=S^3_{p/1}(5_2)$
with
$M=S^3_{p/1}(5_2)$
with
![]() $p\in {\Bbb Z}$
. With the help of a computer program, we can similarly obtain the polynomial
$p\in {\Bbb Z}$
. With the help of a computer program, we can similarly obtain the polynomial
![]() $Q_M(x)$
and determine the associated torsions
$Q_M(x)$
and determine the associated torsions
![]() $\tau _{\varphi } (M)$
. However, the resulting computation of
$\tau _{\varphi } (M)$
. However, the resulting computation of
![]() $\tau _{\varphi } (M)$
is more intricate; we do not describe the details. More generally, to show Conjecture 1.1 with
$\tau _{\varphi } (M)$
is more intricate; we do not describe the details. More generally, to show Conjecture 1.1 with
![]() $M=S^3_{p/q}(K)$
for other (twist) knots K, we might need other ideas. This is a subject for future analysis.
$M=S^3_{p/q}(K)$
for other (twist) knots K, we might need other ideas. This is a subject for future analysis.
5 The conjecture with
 $n>0$
$n>0$
We end this paper by discussing Conjecture 1.1 with
![]() $n>0$
. Hereafter, we assume that
$n>0$
. Hereafter, we assume that
![]() $G=\mathrm {SL}_2(\mathbb {C})$
, M is a closed
$G=\mathrm {SL}_2(\mathbb {C})$
, M is a closed
![]() $3$
-manifold, and
$3$
-manifold, and
![]() $R^{\mathrm {irr}}_{G}(M)$
is of finite order as above.
$R^{\mathrm {irr}}_{G}(M)$
is of finite order as above.
First, it is almost obvious that the sum (1) is a real number: precisely, the following proposition holds.
Proposition 5.1 Let
![]() $n \in {\Bbb Z}$
. The imaginary part of the sum
$n \in {\Bbb Z}$
. The imaginary part of the sum
![]() $\sum _{\varphi \in R^{\mathrm {irr}}_{G}(M) } \tau _{\varphi }{(M)}^n $
is zero.
$\sum _{\varphi \in R^{\mathrm {irr}}_{G}(M) } \tau _{\varphi }{(M)}^n $
is zero.
Proof For a homomorphism
![]() $\varphi : \pi _1(M) \rightarrow G$
, we denote by
$\varphi : \pi _1(M) \rightarrow G$
, we denote by
![]() $\bar {\varphi }$
the conjugate representation. Then,
$\bar {\varphi }$
the conjugate representation. Then,
![]() $ \tau _{ \bar {\varphi }}{(M)} = \overline {\tau _{\varphi }{(M)}} $
by definition. Since we can select representatives
$ \tau _{ \bar {\varphi }}{(M)} = \overline {\tau _{\varphi }{(M)}} $
by definition. Since we can select representatives
![]() $ \varphi _1, \dots , \varphi _m ,\overline {\varphi _1}, \dots , \overline {\varphi _m}, \eta _1 ,\dots , \eta _n $
of
$ \varphi _1, \dots , \varphi _m ,\overline {\varphi _1}, \dots , \overline {\varphi _m}, \eta _1 ,\dots , \eta _n $
of
![]() $ R^{\mathrm {irr}}_{G }(M) $
such that
$ R^{\mathrm {irr}}_{G }(M) $
such that
![]() $ [\eta _i]= [\overline {\eta _i}] \in R^{\mathrm {irr}}_{G }(M)$
, the imaginary part is zero as required.
$ [\eta _i]= [\overline {\eta _i}] \in R^{\mathrm {irr}}_{G }(M)$
, the imaginary part is zero as required.
Furthermore, we will discuss the rationality of the sum (1), with
![]() $G=\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
. For a subfield
$G=\mathop {\mathrm {SL}}\nolimits _2({\Bbb C})$
. For a subfield
![]() $F \subset {\Bbb C}$
, let
$F \subset {\Bbb C}$
, let
![]() $R_{\mathrm {SL}_2(F)}^{\mathrm {irr}}(M) $
be the set of the conjugacy classes of all irreducible representations
$R_{\mathrm {SL}_2(F)}^{\mathrm {irr}}(M) $
be the set of the conjugacy classes of all irreducible representations
![]() $\pi _1(M) \rightarrow \mathrm {SL}_2(F) .$
$\pi _1(M) \rightarrow \mathrm {SL}_2(F) .$
Proposition 5.2 Let
![]() $F/{\Bbb Q}$
be a Galois extension with embedding
$F/{\Bbb Q}$
be a Galois extension with embedding
![]() $F \hookrightarrow {\Bbb C}.$
Suppose that the inclusion
$F \hookrightarrow {\Bbb C}.$
Suppose that the inclusion
![]() $R_{\mathrm {SL}_2(F)}^{\mathrm {irr}}(M) \subset R_{\mathrm {SL}_2({\Bbb C})}^{\mathrm {irr}}(M) $
is bijective as a finite set, and is closed under the Galois action of
$R_{\mathrm {SL}_2(F)}^{\mathrm {irr}}(M) \subset R_{\mathrm {SL}_2({\Bbb C})}^{\mathrm {irr}}(M) $
is bijective as a finite set, and is closed under the Galois action of
![]() $\mathrm {Gal}(F/{\Bbb Q})$
. Then, for any
$\mathrm {Gal}(F/{\Bbb Q})$
. Then, for any
![]() $n\in {\Bbb Z}$
, the sum
$n\in {\Bbb Z}$
, the sum
![]() $\sum _{\varphi \in R^{\mathrm {irr}}_G(M)} \tau _{\varphi }{(M)}^n $
is a rational number.
$\sum _{\varphi \in R^{\mathrm {irr}}_G(M)} \tau _{\varphi }{(M)}^n $
is a rational number.
Proof By definition,
![]() $\tau _{\varphi }(M) \in F^{\times } $
, and the map
$\tau _{\varphi }(M) \in F^{\times } $
, and the map
![]() $\tau _{\bullet }(M): R_{\mathrm {SL}_2(F)}^{\mathrm {irr}}(M) \rightarrow F^{\times } $
is
$\tau _{\bullet }(M): R_{\mathrm {SL}_2(F)}^{\mathrm {irr}}(M) \rightarrow F^{\times } $
is
![]() $ \mathrm {Gal}(F/{\Bbb Q}) $
-equivariant. Thus, the sum lies in the invariant part
$ \mathrm {Gal}(F/{\Bbb Q}) $
-equivariant. Thus, the sum lies in the invariant part
![]() $F^{\mathrm {Gal}(F/{\Bbb Q})}$
. Hence, by
$F^{\mathrm {Gal}(F/{\Bbb Q})}$
. Hence, by
![]() $F^{\mathrm {Gal}(F/{\Bbb Q})}={\Bbb Q} $
, the sum (1) lies in
$F^{\mathrm {Gal}(F/{\Bbb Q})}={\Bbb Q} $
, the sum (1) lies in
![]() ${\Bbb Q}$
as desired.
${\Bbb Q}$
as desired.
Corollary 5.3 Suppose that p is even, and is relatively prime to q. Let K be a twist knot, and let M be
![]() $S^3_{p/q}(K).$
Then, for any
$S^3_{p/q}(K).$
Then, for any
![]() $n\in {\Bbb Z}$
, the sum
$n\in {\Bbb Z}$
, the sum
![]() $\sum _{\varphi \in R^{\mathrm {irr}}_G(M)} \tau _{\varphi }{(M)}^n $
is a rational number.
$\sum _{\varphi \in R^{\mathrm {irr}}_G(M)} \tau _{\varphi }{(M)}^n $
is a rational number.
Proof As is shown in [Reference Nosaka9, Section 2], there is a Galois extension
![]() $F/{\Bbb Q}$
satisfying the condition in Proposition 5.2.
$F/{\Bbb Q}$
satisfying the condition in Proposition 5.2.
Meanwhile, the integrality of the sum (1) with
![]() $ M =S^3_{p/q}(K)$
remains a future problem. When
$ M =S^3_{p/q}(K)$
remains a future problem. When
![]() $K $
is either
$K $
is either
![]() $4_1$
- or
$4_1$
- or
![]() $5_2$
-knot, we know the resulting computation of
$5_2$
-knot, we know the resulting computation of
![]() $\tau _{\varphi }(M) $
by Theorem 3.3, Theorem 3.4, and Section 4. Accordingly, it is not so hard to check numerically the conjecture from the computation of
$\tau _{\varphi }(M) $
by Theorem 3.3, Theorem 3.4, and Section 4. Accordingly, it is not so hard to check numerically the conjecture from the computation of
![]() $\tau _{\varphi }(M) $
for some small
$\tau _{\varphi }(M) $
for some small
![]() $p,q$
.
$p,q$
.
However, we give the proof of the conjecture multiplied by
![]() $2^{2n+1}$
with
$2^{2n+1}$
with
![]() $ {M =S^3_{2m/1}(4_1)}$
. Precisely, the following proposition holds.
$ {M =S^3_{2m/1}(4_1)}$
. Precisely, the following proposition holds.
Proposition 5.4 As in Theorem 1.2, let
![]() $ M =S^3_{2m/1}(4_1)$
. If
$ M =S^3_{2m/1}(4_1)$
. If
![]() $n>1$
, then the 8-fold sum
$n>1$
, then the 8-fold sum
![]() $2\sum _{\varphi \in R^{\mathrm {irr}}_G(M)} ( 8 \tau _{\varphi }(M))^{n}$
is an integer.
$2\sum _{\varphi \in R^{\mathrm {irr}}_G(M)} ( 8 \tau _{\varphi }(M))^{n}$
is an integer.
Proof Since the proof with
![]() $|2m| \leq 4$
is a direct computation, we may suppose
$|2m| \leq 4$
is a direct computation, we may suppose
![]() ${|2m|>4} $
.
${|2m|>4} $
.
We will discuss integrality. We can easily verify some integral polynomials
![]() $ h(x),k(x) \in {\Bbb Z}[x]$
such that
$ h(x),k(x) \in {\Bbb Z}[x]$
such that
 $$ \begin{align} \frac{Q_M(x)}{(1-x^2)^3 }&= h(x)+\frac{ m^2-2m+3}{1-x^2}+\frac{ 4m}{(1-x^2)^2}+\frac{ 4}{(1-x^2)^3} , \ \ \ \frac{Q_M(x)}{(1+x^2)^2 }\nonumber\\&= k(x)+\frac{ 2(1+(-1)^{m-1})}{1+x^2}. \end{align} $$
$$ \begin{align} \frac{Q_M(x)}{(1-x^2)^3 }&= h(x)+\frac{ m^2-2m+3}{1-x^2}+\frac{ 4m}{(1-x^2)^2}+\frac{ 4}{(1-x^2)^3} , \ \ \ \frac{Q_M(x)}{(1+x^2)^2 }\nonumber\\&= k(x)+\frac{ 2(1+(-1)^{m-1})}{1+x^2}. \end{align} $$
In general, as is known as Newton’s formula, the sum
![]() $\sum _{ b \in Q_M^{-1} (0) } b^n $
is an integer. Thus, the sums
$\sum _{ b \in Q_M^{-1} (0) } b^n $
is an integer. Thus, the sums
![]() $\sum _{\alpha \in Q_{M}^{-1}(0) \backslash \{\pm \sqrt {-1} \} } h(\alpha )^n$
and
$\sum _{\alpha \in Q_{M}^{-1}(0) \backslash \{\pm \sqrt {-1} \} } h(\alpha )^n$
and
![]() $\sum _{\alpha \in Q_{M}^{-1}(0) \backslash \{\pm \sqrt {-1} \} } k(\alpha )^n$
are integers; Therefore, by (25), we can easily check that
$\sum _{\alpha \in Q_{M}^{-1}(0) \backslash \{\pm \sqrt {-1} \} } k(\alpha )^n$
are integers; Therefore, by (25), we can easily check that
![]() $\sum _{\alpha \in Q_{M}^{-1}(0)} 4^n (1 - \alpha ^2)^{-n}$
and
$\sum _{\alpha \in Q_{M}^{-1}(0)} 4^n (1 - \alpha ^2)^{-n}$
and
![]() ${\sum _{\alpha \in Q_{M}^{-1}(0)} 4^n (1 + \alpha ^2)^{-n}}$
are integers by induction on n.
${\sum _{\alpha \in Q_{M}^{-1}(0)} 4^n (1 + \alpha ^2)^{-n}}$
are integers by induction on n.
Let us complete the proof. Recall from Theorem 3.3 the resulting computation of the torsion
![]() $\tau _{\varphi _a}(M) $
for
$\tau _{\varphi _a}(M) $
for
![]() $a \in Q_M^{-1} (0) \cap D$
; by the Euclidean Algorithm, we can show
$a \in Q_M^{-1} (0) \cap D$
; by the Euclidean Algorithm, we can show
 $$ \begin{align} 2 \tau_{\varphi_a}(M) =\ell(a)+ \frac{6+2m-2m^2-m^3}{1-a^2}+ \frac{-6+6m+2m^2}{(1-a^2)^2}+ \frac{-4m}{(1-a^2)^3} + \frac{m( -1+ (-1)^m ) }{2(1+a^2)}\end{align} $$
$$ \begin{align} 2 \tau_{\varphi_a}(M) =\ell(a)+ \frac{6+2m-2m^2-m^3}{1-a^2}+ \frac{-6+6m+2m^2}{(1-a^2)^2}+ \frac{-4m}{(1-a^2)^3} + \frac{m( -1+ (-1)^m ) }{2(1+a^2)}\end{align} $$
for some
![]() $ \ell (a) \in {\Bbb Z}[a]$
. Notice from by Proposition 3.1 that
$ \ell (a) \in {\Bbb Z}[a]$
. Notice from by Proposition 3.1 that
The first and second terms are integers by an elementary discussion. The last one is a sum of the above sums
![]() $ \sum _{\alpha \in Q_{M}^{-1}(0) } 8^n (1 \pm \alpha ^2)^{ s}$
, where
$ \sum _{\alpha \in Q_{M}^{-1}(0) } 8^n (1 \pm \alpha ^2)^{ s}$
, where
![]() $ s \leq 3n$
. Hence, the sum
$ s \leq 3n$
. Hence, the sum
![]() $2 \sum _{ \varphi \in R^{\mathrm {irr}}_G(M) } (8 \tau _{\varphi }(M))^n $
is an integer as required.
$2 \sum _{ \varphi \in R^{\mathrm {irr}}_G(M) } (8 \tau _{\varphi }(M))^n $
is an integer as required.
Acknowledgments
The author is deeply grateful to the referee for providing insightful comments and constructive feedback. She sincerely expresses her gratitude to Takefumi Nosaka for encouragement and useful advice. She thanks Teruaki Kitano, Yuta Nozaki, and Yoshikazu Yamaguchi for giving valuable comments. She is also greatly indebted to Seokbeom Yoon for carefully reading the paper and his insightful discussions.