Hostname: page-component-5c6d5d7d68-thh2z Total loading time: 0 Render date: 2024-08-16T11:33:59.104Z Has data issue: false hasContentIssue false
  • English
  • Français

A Bernstein–Walsh Type Inequality and Applications

Published online by Cambridge University Press:  20 November 2018

Tejinder Neelon
Tejinder Neelon*
Affiliation:
Department of Mathematics, California State University San Marcos, San Marcos, CA 92096-0001, U.S.A. e-mail: neelon@csusm.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Bernstein–Walsh type inequality for 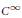${{C}^{\infty }}$ functions of several variables is derived, which then is applied to obtain analogs and generalizations of the following classical theorems: (1) Bochnak– Siciak theorem: a 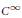${{C}^{\infty }}$ function on ${{\mathbb{R}}^{n}}$ that is real analytic on every line is real analytic; (2) Zorn–Lelong theorem: if a double power series 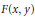$F\left( x,y \right)$ converges on a set of lines of positive capacity then 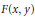$F\left( x,y \right)$ is convergent; (3) Abhyankar–Moh–Sathaye theorem: the transfinite diameter of the convergence set of a divergent series is zero.

Keywords

32A0526E05Bernstein-Walsh inequalityconvergence setsanalytic functionsultradifferentiable functionsformal power series
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 2 , 01 June 2006 , pp. 256 - 264
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Abhyankar, S., and Moh, T., A reduction theorem for divergent power series. J. Reine Angew. Math. 241(1970), 27–33.Google Scholar
[2] Bierstone, E., Milman, P. D., and Parusinski, A., A function which is arc-analytic but not continuous. Proc. Amer. Math. Soc. 113(1991), no. 2, 419–423.Google Scholar
[3] Bochnak, J., Analytic functions in Banach Spaces. Studia Math. 35(1970), 273–292.Google Scholar
[4] Constantine, G. M., and Savits, T. H., A multivariate Faá Di Bruno formula with applications. Trans. Amer. Math. Soc. 348(1996), no. 2, 503–520.Google Scholar
[5] Klimek, M., Pluripotential Theory. London Mathematical Society Monographs. New Series, 6, Oxford University Press, New York, 1991.Google Scholar
[6] Korevaar, J., Applications of ℂ n capacities. In: Several Complex Variables and Complex Geometry, Part 1. Proc. Sympos. Pure Math. 52(1991), 105–118,Google Scholar
[7] Lelong, P., On a problem of M. A. Zorn.. Proc. Amer. Math. Soc. 2(1951), 11–19.Google Scholar
[8] Levenberg, N. and Molzon, R. E., Convergence sets of a formal power series. Math. Z. 197(1988), no. 3, 411–420.Google Scholar
[9] Mouze, A., Division dans l’anneau des séries formelles á croissance contrôlée. Applications. Studia Math. 144(2001), no. 1, 63–93.Google Scholar
[10] Neelon, T. S., Ultradifferentiable functions on lines in ℝ n. Proc. Amer. Math. Soc. 127(1999), no. 7, 2099–2104. A correction to: “Ultradifferentiable functions on lines in ℝ n ”. Proc. Amer.Math. Soc. 131(2003), no. 3, 991–992 .Google Scholar
[11] Neelon, T. S., On solutions to formal equations. Bull. Belg. Math. Soc. Simon Stevin 7(2000), no. 3, 419–427.Google Scholar
[12] Neelon, T. S., Ultradifferentiable functions on smooth plane curves. J. Math. Anal. Appl. 299(2004), no. 1, 61–71.Google Scholar
[13] Sathaye, A., Convergence sets of divergent power series. J. Reine Angew. Math. 283/284(1976), 86–98.Google Scholar
[14] Siciak, J., A characterization of analytic functions of n real variables. Studia Math. 35(1970), 293–297.Google Scholar
[15] Thilliez, V., Bounds for quotients in rings of formal power series with growth constraints. Studia Math. 151(2002), no. 1, 49–65.Google Scholar