No CrossRef data available.
Article contents
Existence of Leray's Self-Similar Solutions of the Navier-Stokes Equations In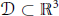 
$\mathcal{D}\,\subset \,{{\mathbb{R}}^{3}}$
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Leray's self-similar solution of the Navier-Stokes equations is defined by
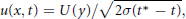$$u(x,\,t)\,=\,U(y)/\sqrt{2\sigma ({{t}^{*}}\,-\,t)},$$
where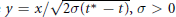 
$y\,=\,x/\sqrt{2\sigma ({{t}^{*}}\,-\,t)},\,\sigma \,>\,0$. Consider the equation for 
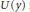$U(y)$ in a smooth bounded domain 
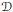$\mathcal{D}$ of 
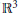${{\mathbb{R}}^{3}}$ with non-zero boundary condition:
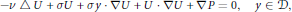$$-v\,\Delta \,U\,+\,\sigma U\,+\,\sigma y\,\cdot \,\nabla U\,+\,U\,\cdot \,\nabla U\,+\,\nabla P\,=\,0,\,\,\,y\,\in \,\mathcal{D}\,$$
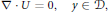$$\nabla \,\cdot \,U\,=\,0,\,\,\,y\,\in \,\mathcal{D},$$
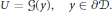$$U\,=\,\mathcal{G}(y),\,\,\,y\,\in \,\partial \mathcal{D}.$$
We prove an existence theorem for the Dirichlet problem in Sobolev space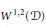 
${{W}^{1,2}}(\mathcal{D})$. This implies the local existence of a self-similar solution of the Navier-Stokes equations which blows up at 
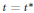$t\,=\,{{t}^{*}}$ with 
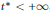${{t}^{*}}\,<\,+\infty $, provided the function 
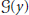$\mathcal{G}(y)$ is permissible.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
[BP]
Boratav, O. N. and Pelz, R. B., Direct numerical simulation of transition to turbulence from a high-symmetry initial condition. Phys. Fluids 6 (1994), 2757–2784.Google Scholar
[CFM]
Constantin, P., Fefferman, C. and Majda, A., Geometric constraints on potentially singular solutions for the 3d Euler equations. Comm. Partial Differential Equations 21 (1996), 559–571.Google Scholar
[CKN]
Caffarelli, L., Kohn, R. and Nirenberg, L., Partial regularity of suitable weak solutions of the Navier-Stokes equations. Comm. Pure Appl. Math. 35 (1982), 771–831.Google Scholar
[CP]
Cannone, M. and Planchon, F., Self-similar solutions for Navier-Stokes equations in R3. Comm. Partial Differential Equations 21 (1996), 179–193.Google Scholar
[G]
Galdi, G. P., An introduction to the mathematical theory of the Navier-Stokes equations. Vol I and II, Springer Tracts Nat. Philos. 39, Springer, 1994.Google Scholar
[GM]
Giga, Y. and Miyakawa, T., Navier-Stokes flow in R3 with measures as initial vorticity and Morrey spaces. Comm. Partial Differential Equations 14 (1989), 577–618.Google Scholar
[K]
Kerr, R. M., The outer regions in singular Euler. In: Fundamental Problematic Issues in Turbulence, (eds., Tsinober and Gyr), Birkh¨auser, 1998.Google Scholar
[L]
Leray, J., Sur le mouvement d'un liquide visqueux emplissant l'espace. Acta Math. 63 (1934), 193–248.Google Scholar
[LS]
Leray, J. and Schauder, J., Topologie et équations fonctionnelles. Ann. Sci. École Norm. Sup. 51 (1934), 45–78.Google Scholar
[M]
Moffatt, H. K., The interaction of skewed vortex pairs: a model for blow-up of the Navier-Stokes equations. J. Fluid Mech. 409 (2000), 51–68.Google Scholar
[NOZ]
Nagayama, M., Okamoto, H. and Zhu, J., On the blow-up of some similarity solutions of the Navier-Stokes equations. Quad. Mat. (2002), to appear.Google Scholar
[NRŠ]
Nečas, J., Råužička, M. and Šver´ak, V., On Leray's self-similar solutions of the Navier-Stokes equations. Acta Math. 176 (1996), 283–294.Google Scholar
[OG]
Ohkitani, K. and Gibbon, J. D., Numerical study of singularity formation in a class of Euler and Navier-Stokes flows. Phys. Fluids 12 (2000), 3181–3194.Google Scholar
[P]
Pelz, R. B., Locally self-similar, finite-time collapse in a high-symmetry vortex filament model. Phys. Rev. E 55 (1997), 1617–1626.Google Scholar
[SS]
Sulem, C. and Sulem, P.-L., The Nonlinear Schródinger Equation. Appl. Math. Sci. 139, Springer, 1999.Google Scholar
[T]
Tsai, T.-P., On Leray's self-similar solutions of the Navier-Stokes equations satisfying local energy estimates. Arch. Rational Mech. Anal. 143 (1998), 29–51.Google Scholar
You have
Access