Hostname: page-component-7bb8b95d7b-2h6rp Total loading time: 0 Render date: 2024-09-14T06:04:39.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of Positive Solutions for Nonlinear Noncoercive Hemivariational Inequalities

Published online by Cambridge University Press:  20 November 2018

Michael E. Filippakis  and
Nikolaos S. Papageorgiou
Michael E. Filippakis
Affiliation:
Department of Mathematics, National Technical University, Zografou Campus, Athens 15780, Greece e-mail: mfilip@math.ntua.grnpapg@math.ntua.gr
Nikolaos S. Papageorgiou
Affiliation:
Department of Mathematics, National Technical University, Zografou Campus, Athens 15780, Greece e-mail: mfilip@math.ntua.grnpapg@math.ntua.gr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we investigate the existence of positive solutions for nonlinear elliptic problems driven by the 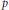$p$-Laplacian with a nonsmooth potential (hemivariational inequality). Under asymptotic conditions that make the Euler functional indefinite and incorporate in our framework the asymptotically linear problems, using a variational approach based on nonsmooth critical point theory, we obtain positive smooth solutions. Our analysis also leads naturally to multiplicity results.

Keywords

35J2035J6035J85p-Laplacianlocally Lipschitz potentialnonsmooth critical point theoryprincipal eigenvaluepositive solutionsnonsmooth Mountain Pass Theorem
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 3 , 01 September 2007 , pp. 356 - 364
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Amann, H. and Zehnder, E., Nontrivial solutions for a class of nonresonance problems and applications to nonlinear differential equations. Ann. Scuolo Norm. Sup. Pisa Cl. Sci. 7(1980), no. 4, 539–603.Google Scholar
[2] Anane, A., Simplicité et isolation de la premiere valeur propre du p-Laplacien avec poids. C. R. Acad. Sci. Paris Sér. I Math. 305(1987), no. 16, 725–728.Google Scholar
[3] Bartsch, T. amd Li, S., Critical point theory for asymptotically quadratic functionals and applications to problems with resonance. Nonlin. Anal. 28(1997), no. 3, 419–441.Google Scholar
[4] Fan, X. L., Zhao, Y. Z., and Huang, G. F., Existence of solutions for the p-Laplacian with crossing nonlinearity. Discr. Cont. Dyn. Systems 8(2002), no. 4, 1019–1024.Google Scholar
[5] Gasinski, L. and Papageorgiou, N. S., Nonsmooth Critical Point Theory and Nonlinear Boundary Value Problems. Series in Mathematical Analysis and Applications 8, Chapman and Hall/CRC, Boca Raton, FL, 2005.Google Scholar
[6] Huang, Y. S., Positive solutions of quasilinear elliptic equations. Topol. Methods Nonlin. Anal. 12(1998), no. 1, 91–107.Google Scholar
[7] Li, G. and Zhou, H.-S., Asymptotically linear Dirichlet problem for the p-Laplacian. Nonlinear Anal. 43(2001), no. 8, 1043–1055.Google Scholar
[8] Motreanu, D. and Papageorgiou, N. S., Multiple solutions for nonlinear elliptic equations at resonance with a nonsmooth potential. Nonlinear Anal. 56(2004), no. 8, 1211–1234.Google Scholar
[9] Naniewicz, Z. and Panagiotopoulos, P., Mathematical Theory of Hemivariational Inequalities and Applications. Monographs and Textbooks in Pure and Applied Mathematics 188, Marcel Dekker, New York, 1995.Google Scholar
[10] Vázquez, J. L., A strong maximum principle for some quasilinear elliptic equations. Appl. Math. Optim. 12(1984), no. 3, 191–202.Google Scholar
[11] Zhou, H.-S., Existence of asymptotically linear Dirichlet problem. Nonlin. Anal. 44(2001), no. 7, 909–918.Google Scholar