Hostname: page-component-5c6d5d7d68-wtssw Total loading time: 0 Render date: 2024-08-09T20:12:34.692Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions of Rings Having McCoy Condition

Published online by Cambridge University Press:  20 November 2018

Muhammet Tamer Koşan
Muhammet Tamer Koşan*
Affiliation:
Department of Mathematics, Gebze Institute of Technology, Çayirova Campus 41400 Gebze-Kocaeli, Turkey e-mail: mtkosan@gyte.edu.tr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $R$ be an associative ring with unity. Then $R$ is said to be a right McCoy ring when the equation 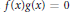$f\left( x \right)g\left( x \right)\,=\,0$ (over 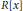$R\left[ x \right]$), where 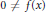$0\,\ne \,f\left( x \right)$, 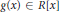$g\left( x \right)\,\in \,R\left[ x \right]$, implies that there exists a nonzero element 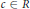$c\,\in \,R$ such that 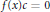$f\left( x \right)c\,=\,0$. In this paper, we characterize some basic ring extensions of right McCoy rings and we prove that if $R$ is a right McCoy ring, then 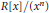$R\left[ x \right]/\left( {{x}^{n}} \right)$ is a right McCoy ring for any positive integer 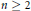$n\,\ge \,2$.

Keywords

16D1016D8016R50right McCoy ringArmendariz ringreduced ringreversible ringsemicommutative ring
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 2 , 01 June 2009 , pp. 267 - 272
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Anderson, D. D. and Camillo, V., Armendariz rings and Gaussian rings. Comm. Algebra 26(1998), no. 7, 2265–2272.Google Scholar
[2] Başer, M. and Koşan, M. T., On quasi-Armendariz modules. Taiwanese J. Math. 12(2008), no. 3, 573–582.Google Scholar
[3] Chon, P. M., Reversible rings. Bull. London Math. Soc. 31(1999), no. 6, 641–648.Google Scholar
[4] Hirano, Y., On annihilator ideals of a polynomial ring over a noncommutative ring. J. Pure Appl. Algebra 168(2002), no. 1, 45–52.Google Scholar
[5] Huh, C., Lee, Y., and Smoktunowicz, A., Armendariz rings and semicommutative rings. Comm. Algebra 30(2002), no. 2, 751–761.Google Scholar
[6] Kim, N. K. and Lee, Y., Armendariz rings and reduced rings. J. Algebra 223(2000), no. 2, 477–488.Google Scholar
[7] Kim, N. K. and Lee, Y., Extensions of reversible rings. J. Pure Appl. Algebra 185(2003), no. 1–3, 207–223.Google Scholar
[8] Lee, T.-K. and Zhou, Y., Armendariz rings and reduced rings. Comm. Algebra 32(2004), no. 6, 2287–2299.Google Scholar
[9] McCoy, N. H., Remarks on divisors of zero. Amer. Math. Monthly 49(1942), 286–295.Google Scholar
[10] Nielsen, P. P., Semicommutativity and the McCoy condition. J. Algebra 298(2006), no. 1, 134–141.Google Scholar