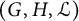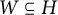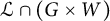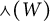1 Introduction
After the discovery of quasicrystals [Reference Shechtman, Blech, Gratias and Cahn39], it has become clear that we need to better understand the process of diffraction. Mathematically, the diffraction pattern of a solid can be viewed as the Fourier transform
![]() $\widehat {\gamma }$
of the autocorrelation measure
$\widehat {\gamma }$
of the autocorrelation measure
![]() $\gamma $
of the structure (see [Reference Hof13] for the setup and the monographs and see [Reference Baake and Grimm3, Reference Baake and Grimm4] for a general review of the theory). The measure
$\gamma $
of the structure (see [Reference Hof13] for the setup and the monographs and see [Reference Baake and Grimm3, Reference Baake and Grimm4] for a general review of the theory). The measure
![]() $\gamma $
is positive-definite, and therefore it is Fourier transformable as a measure [Reference Argabright and de Lamadrid1, Reference Berg and Forst8, Reference Moody, Strungaru, Baake and Grimm31] with positive Fourier transform
$\gamma $
is positive-definite, and therefore it is Fourier transformable as a measure [Reference Argabright and de Lamadrid1, Reference Berg and Forst8, Reference Moody, Strungaru, Baake and Grimm31] with positive Fourier transform
![]() $\widehat {\gamma }$
. It is this measure
$\widehat {\gamma }$
. It is this measure
![]() $\widehat {\gamma }$
, which models the diffraction of our solid.
$\widehat {\gamma }$
, which models the diffraction of our solid.
Structures with pure point diffraction, that is, structures for which
![]() $\widehat {\gamma }$
is a pure point measure, are now very well understood. Building on the earlier work of Gil deLamadrid–Argabright [Reference de Lamadrid and Argabright10], Solomyak [Reference Solomyak40, Reference Solomyak and Patera41], Lee–Moody–Solomyak [Reference Lee, Moody and Solomyak20], Baake–Moody [Reference Baake and Moody7], Baake–Lenz [Reference Baake and Lenz6], Gouere [Reference Gouéré11, Reference Gouéré12], Moody–Strungaru [Reference Moody and Strungaru30], and Meyer [Reference Meyer27], pure point diffraction was characterized in [Reference Lenz, Spindeler and Strungaru22, Reference Lenz, Spindeler and Strungaru23]. The focus now shifted toward models with mixed diffraction spectra, especially those with a large pure point part.
$\widehat {\gamma }$
is a pure point measure, are now very well understood. Building on the earlier work of Gil deLamadrid–Argabright [Reference de Lamadrid and Argabright10], Solomyak [Reference Solomyak40, Reference Solomyak and Patera41], Lee–Moody–Solomyak [Reference Lee, Moody and Solomyak20], Baake–Moody [Reference Baake and Moody7], Baake–Lenz [Reference Baake and Lenz6], Gouere [Reference Gouéré11, Reference Gouéré12], Moody–Strungaru [Reference Moody and Strungaru30], and Meyer [Reference Meyer27], pure point diffraction was characterized in [Reference Lenz, Spindeler and Strungaru22, Reference Lenz, Spindeler and Strungaru23]. The focus now shifted toward models with mixed diffraction spectra, especially those with a large pure point part.
The best mathematical models for Delone sets with a large pure point spectrum and (generic) positive entropy are Meyer sets. They have been introduced in the pioneering work of Meyer [Reference Meyer26], and popularized in the area of Aperiodic Order by Moody [Reference Moody and Moody28, Reference Moody, Axel, Dénoyer and Gazeau29] and Lagarias [Reference Lagarias18, Reference Lagarias, Baake and Moody19]. They are usually constructed via a cut-and-project scheme (or simply CPS) and can be characterized via harmonic analysis, discrete geometry, algebra, and almost periodicity [Reference Meyer26, Reference Moody, Axel, Dénoyer and Gazeau29, Reference Strungaru, Baake and Grimm46]. The basic idea behind a CPS is to project points from a higher-dimensional lattice, which lie within a bounded strip of the real space, into the real space (see Definition 2.8 for the exact definition). If the cross section of the strip (called the window) is regular, then the resulting model set is pure point diffractive [Reference Baake and Moody7, Reference Hof and Patera14, Reference Richard and Strungaru35, Reference Schlottmann, Baake and Moody38]. Recent work proved pure point diffractivity for a larger class of weak model sets [Reference Baake, Huck and Strungaru5, Reference Keller and Richard15–Reference Keller, Richard and Strungaru17, Reference Strungaru48].
As subsets of regular model sets, Meyer sets still exhibit a large pure point spectrum [Reference Strungaru43–Reference Strungaru47, Reference Strungaru49] and a highly ordered continuous spectrum [Reference Strungaru43, Reference Strungaru45, Reference Strungaru47, Reference Strungaru49]. The long-range order of the spectrum of Meyer sets can be traced to that of a covering regular model set [Reference Strungaru47, Reference Strungaru49], and can be derived from the Poisson summation formula for the lattice in the CPS [Reference Baake and Grimm3, Reference Lev and Olevskii25, Reference Richard and Strungaru34, Reference Richard and Strungaru35].
One would expect it to be possible to relate the diffraction of a Meyer set (or more generally a measure with Meyer set support) directly to the lattice
![]() ${\mathcal L}$
in the CPS. It is the goal of this paper to establish this connection. Let us briefly explain our approach.
${\mathcal L}$
in the CPS. It is the goal of this paper to establish this connection. Let us briefly explain our approach.
Fix a CPS
![]() $(G, H, {\mathcal L})$
and a compact set
$(G, H, {\mathcal L})$
and a compact set
![]() $W \subseteq H$
. It is easy to see that
$W \subseteq H$
. It is easy to see that
establishes a bijection between translation bounded measures supported inside
![]() ${\LARGE \curlywedge }(W)$
and translation bounded measures supported inside
${\LARGE \curlywedge }(W)$
and translation bounded measures supported inside
![]() ${\mathcal L} \cap (G \times W)$
. We first show in Proposition 3.6 that
${\mathcal L} \cap (G \times W)$
. We first show in Proposition 3.6 that
![]() $\gamma $
is positive-definite if and only if
$\gamma $
is positive-definite if and only if
![]() $\eta $
is positive-definite. Since each Fourier transformable measure supported inside a Meyer set can be written as a linear combination of positive-definite measures supported inside a common model set, we establish in Theorem 4.1 that
$\eta $
is positive-definite. Since each Fourier transformable measure supported inside a Meyer set can be written as a linear combination of positive-definite measures supported inside a common model set, we establish in Theorem 4.1 that
![]() $\gamma $
is Fourier transformable if and only if
$\gamma $
is Fourier transformable if and only if
![]() $\eta $
is Fourier transformable, and relate their Fourier transform (see (4.1)).
$\eta $
is Fourier transformable, and relate their Fourier transform (see (4.1)).
We complete the paper by discussing in Section 5 how these results can be used to re-derive the known properties of diffraction for measures with weak Meyer set support, and potentially used to prove new results.
2 Definitions and notations
Throughout the paper, G denotes a second countable locally compact Abelian group (LCAG). By
![]() $C_{\mathsf {u}}(G)$
, we denote the space of uniformly continuous and bounded functions on G. This is a Banach space with respect to the sup norm
$C_{\mathsf {u}}(G)$
, we denote the space of uniformly continuous and bounded functions on G. This is a Banach space with respect to the sup norm
![]() $\|. \|_{\infty }$
. As usual, we denote by
$\|. \|_{\infty }$
. As usual, we denote by
![]() $C^{}_{0}(G)$
the subspace of
$C^{}_{0}(G)$
the subspace of
![]() $C_{\mathsf {u}}(G)$
consisting of functions vanishing at infinity, and by
$C_{\mathsf {u}}(G)$
consisting of functions vanishing at infinity, and by
![]() $C_{\mathsf {c}}(G)$
the subspace of compactly supported continuous functions. Note that
$C_{\mathsf {c}}(G)$
the subspace of compactly supported continuous functions. Note that
![]() $C_{\mathsf {c}}(G)$
is not complete in
$C_{\mathsf {c}}(G)$
is not complete in
![]() $(C_{\mathsf {u}}(G), \|. \|_{\infty })$
.
$(C_{\mathsf {u}}(G), \|. \|_{\infty })$
.
In the spirit of [Reference de Lamadrid and Argabright10], we denote by
Given two LCAG’s G and H and two functions
![]() $g : G \to {\mathbb C}, h : H \to {\mathbb C}$
, we denote by
$g : G \to {\mathbb C}, h : H \to {\mathbb C}$
, we denote by
![]() $g \otimes h : G \times H \to {\mathbb C}$
their tensor product
$g \otimes h : G \times H \to {\mathbb C}$
their tensor product
It is obvious that whenever
![]() $\varphi \in C_{\mathsf {c}}(G), \psi \in C_{\mathsf {c}}(H)$
we have
$\varphi \in C_{\mathsf {c}}(G), \psi \in C_{\mathsf {c}}(H)$
we have
![]() $\varphi \otimes \psi \in C_{\mathsf {c}}(G \times H)$
. Moreover, if
$\varphi \otimes \psi \in C_{\mathsf {c}}(G \times H)$
. Moreover, if
![]() $\varphi \in K_2(G)$
and
$\varphi \in K_2(G)$
and
![]() $\psi \in K_2(H)$
, we have
$\psi \in K_2(H)$
, we have
![]() $\varphi \otimes \psi \in K_2(G \times H)$
.
$\varphi \otimes \psi \in K_2(G \times H)$
.
In the rest of this section, we review some of the basic concepts which are important for this paper. For a more general review of these, we recommend [Reference Baake and Grimm3, Reference Baake and Grimm4].
2.1 Measures
In the spirit of Bourbacki [Reference Bourbaki9], by a measure, we understand a linear functional on
![]() $C_{\mathsf {c}}(G)$
which is continuous with respect to the inductive topology. This notion corresponds to the classical concept of a Radon measure (see [Reference Richard and Strungaru35, Appendix]). For the case
$C_{\mathsf {c}}(G)$
which is continuous with respect to the inductive topology. This notion corresponds to the classical concept of a Radon measure (see [Reference Richard and Strungaru35, Appendix]). For the case
![]() $G={\mathbb R}^d$
, a clear exposition of this is given in [Reference Baake and Grimm3].
$G={\mathbb R}^d$
, a clear exposition of this is given in [Reference Baake and Grimm3].
Definition 2.1 A linear functional
![]() $\mu : C_{\mathsf {c}}(G) \to {\mathbb C}$
is called a Radon measure (or simply a measure) if for each compact set
$\mu : C_{\mathsf {c}}(G) \to {\mathbb C}$
is called a Radon measure (or simply a measure) if for each compact set
![]() $K \subseteq G$
there exists a constant
$K \subseteq G$
there exists a constant
![]() $C_K$
such that, for all
$C_K$
such that, for all
![]() $\varphi \in C_{\mathsf {c}}(G)$
with
$\varphi \in C_{\mathsf {c}}(G)$
with
![]() $\mbox {supp}(\varphi ) \subseteq K$
, we have
$\mbox {supp}(\varphi ) \subseteq K$
, we have
We will often write
![]() $\int _G \varphi (t) d \mu (t)$
instead of
$\int _G \varphi (t) d \mu (t)$
instead of
![]() $\mu (\varphi )$
.
$\mu (\varphi )$
.
A measure
![]() $\mu $
is called positive if for all
$\mu $
is called positive if for all
![]() $\varphi \in C_{\mathsf {c}}(G)$
with
$\varphi \in C_{\mathsf {c}}(G)$
with
![]() $\varphi \geq 0$
we have
$\varphi \geq 0$
we have
![]() $\mu (\varphi ) \geq 0$
.
$\mu (\varphi ) \geq 0$
.
By the Riesz representation theorem [Reference Rudin37], a positive Radon measure is simply a positive regular Borel measure. Moreover, each Radon measure is a linear combination of (at most four) positive Radon measures [Reference Richard and Strungaru35, Appendix].
Next, we review the total variation of a measure.
Definition 2.2 Given a measure
![]() $\mu $
, we can define [Reference Pedersen32, Reference Reiter and Stegeman33, Reference Richard and Strungaru35] a positive measure
$\mu $
, we can define [Reference Pedersen32, Reference Reiter and Stegeman33, Reference Richard and Strungaru35] a positive measure
![]() $\left | \mu \right |$
, called the total variation of
$\left | \mu \right |$
, called the total variation of
![]() $\mu $
, such that, for all
$\mu $
, such that, for all
![]() $\varphi \in C_{\mathsf {c}}(G)$
with
$\varphi \in C_{\mathsf {c}}(G)$
with
![]() $\varphi \geq 0$
, we have
$\varphi \geq 0$
, we have
We are now ready to introduce the concept of translation boundedness for measures and norm almost periodicity.
Definition 2.3 Let
![]() $A \subseteq G$
be a fixed precompact set with nonempty interior. We define the A-norm of
$A \subseteq G$
be a fixed precompact set with nonempty interior. We define the A-norm of
![]() $\mu $
via
$\mu $
via
A measure
![]() $\mu $
is called translation bounded if
$\mu $
is called translation bounded if
![]() $\| \mu \|_A <\infty $
.
$\| \mu \|_A <\infty $
.
Remark 2.4 ([Reference Baake and Moody7, Reference Spindeler and Strungaru42])
Different precompact sets
![]() $A_1, A_2$
with nonempty interior define equivalent norms. Therefore, the definition of translation boundedness does not depend on the choice of A.
$A_1, A_2$
with nonempty interior define equivalent norms. Therefore, the definition of translation boundedness does not depend on the choice of A.
This allows us to define
Then
![]() $({\mathcal M}^{\infty }(G), \|. \|_A)$
is a normed space. It is in fact a Banach space [Reference Richard and Strungaru36].
$({\mathcal M}^{\infty }(G), \|. \|_A)$
is a normed space. It is in fact a Banach space [Reference Richard and Strungaru36].
Next, we review the definition of norm almost periodicity as introduced in [Reference Baake and Moody7].
Definition 2.5 Let
![]() $ A \subseteq G$
be a fixed precompact set with nonempty interior. A measure
$ A \subseteq G$
be a fixed precompact set with nonempty interior. A measure
![]() $\mu \in {\mathcal M}^{\infty }(G)$
is called norm almost periodic if, for each
$\mu \in {\mathcal M}^{\infty }(G)$
is called norm almost periodic if, for each
![]() $\varepsilon>0$
, the set
$\varepsilon>0$
, the set
of
![]() $\varepsilon $
-norm almost periods of
$\varepsilon $
-norm almost periods of
![]() $\mu $
is relatively dense.
$\mu $
is relatively dense.
As discussed above, different precompact sets define equivalent norms. This means that while the set of
![]() $\varepsilon $
-norm almost periods on
$\varepsilon $
-norm almost periods on
![]() $\mu $
depends on the choice of A, the almost periodicity of
$\mu $
depends on the choice of A, the almost periodicity of
![]() $\mu $
is independent of this choice.
$\mu $
is independent of this choice.
Any norm almost periodic measure is strongly almost periodic [Reference Baake and Moody7], and the two concepts are equivalent for measures with Meyer set support [Reference Baake and Moody7]. In general, norm almost periodicity is an uniform version of strong almost periodicity [Reference Spindeler and Strungaru42, Theorem 4.7]. The class of norm almost periodic pure point measure was studied in detail and characterized in [Reference Strungaru, Baake and Grimm46].
Let us next recall positive-definiteness for functions and measures. For more details, we recommend [Reference Berg and Forst8, Reference Moody, Strungaru, Baake and Grimm31].
Definition 2.6 A function
![]() $f : G\longrightarrow {\mathbb C}$
is called positive-definite if, for all
$f : G\longrightarrow {\mathbb C}$
is called positive-definite if, for all
![]() $ n \in \mathbb N$
and all
$ n \in \mathbb N$
and all
![]() $x_1,\ldots , x_n\in G$
, the matrix
$x_1,\ldots , x_n\in G$
, the matrix
![]() $\left (f (x_k - x_l)\right )_{k,l=1,\ldots , n}$
is positive Hermitian. This is equivalent to
$\left (f (x_k - x_l)\right )_{k,l=1,\ldots , n}$
is positive Hermitian. This is equivalent to
 $$\begin{align*}\sum_{k,l=1}^n \overline{c_l} f (x_k - x_l) c_k \geq 0 \qquad \forall n \in \mathbb N, x_1,\ldots, x_n\in G, c_1, \ldots , c_n \in {\mathbb C} \,. \end{align*}$$
$$\begin{align*}\sum_{k,l=1}^n \overline{c_l} f (x_k - x_l) c_k \geq 0 \qquad \forall n \in \mathbb N, x_1,\ldots, x_n\in G, c_1, \ldots , c_n \in {\mathbb C} \,. \end{align*}$$
A measure
![]() $\mu $
is called positive-definite if, for all
$\mu $
is called positive-definite if, for all
![]() $ \varphi \in C_{\mathsf {c}}(G),$
we have
$ \varphi \in C_{\mathsf {c}}(G),$
we have
This is equivalent to
![]() $\mu *\varphi *\tilde {\varphi }$
being a positive-definite function for all
$\mu *\varphi *\tilde {\varphi }$
being a positive-definite function for all
![]() $\varphi \in C_{\mathsf {c}}(G)$
[Reference Berg and Forst8, Reference Moody, Strungaru, Baake and Grimm31].
$\varphi \in C_{\mathsf {c}}(G)$
[Reference Berg and Forst8, Reference Moody, Strungaru, Baake and Grimm31].
We complete the subsection by reviewing the notion of Fourier transformability for measures. For a more detailed review of the subject, we recommend [Reference Moody, Strungaru, Baake and Grimm31].
Definition 2.7 A measure
![]() $\mu $
on G is called Fourier transformable if there exists a measure
$\mu $
on G is called Fourier transformable if there exists a measure
![]() $\widehat {\mu }$
on
$\widehat {\mu }$
on
![]() $\widehat {G}$
such that, for all
$\widehat {G}$
such that, for all
![]() $\varphi \in K_2(G)$
, we have
$\varphi \in K_2(G)$
, we have
![]() $|\check {\varphi }| \in L^1( |\widehat {\mu } |)$
and
$|\check {\varphi }| \in L^1( |\widehat {\mu } |)$
and
2.2 Cut-and-project schemes and Meyer sets
In this part, we review some notions related to the cut-and-project formalism. For more details, we recommend [Reference Baake and Grimm3, Reference Moody and Moody28, Reference Moody, Axel, Dénoyer and Gazeau29].
Definition 2.8 By a CPS, we understand a triple
![]() $(G, H, {\mathcal L})$
consisting of a second countable LCAG G, an LCAG H, and a lattice
$(G, H, {\mathcal L})$
consisting of a second countable LCAG G, an LCAG H, and a lattice
![]() ${\mathcal L} \subseteq G \times H$
such that:
${\mathcal L} \subseteq G \times H$
such that:
-
(i)
 $\pi _H({\mathcal L})$
is dense in H.
$\pi _H({\mathcal L})$
is dense in H. -
(ii) The restriction
 $\pi _G|_{\mathcal L}$
of the first projection
$\pi _G|_{\mathcal L}$
of the first projection
 $\pi _G$
to
$\pi _G$
to
 ${\mathcal L}$
is one to one.
${\mathcal L}$
is one to one.
Given a CPS
![]() $(G,H, {\mathcal L})$
, we will denote by
$(G,H, {\mathcal L})$
, we will denote by
![]() $L:= \pi _G({\mathcal L})$
. Then,
$L:= \pi _G({\mathcal L})$
. Then,
![]() $\pi _G$
induces a group isomorphism between
$\pi _G$
induces a group isomorphism between
![]() ${\mathcal L}$
and L. Composing the inverse of this with the second projection
${\mathcal L}$
and L. Composing the inverse of this with the second projection
![]() $\pi _H$
, we get a mapping
$\pi _H$
, we get a mapping
which we will call the
![]() $\star $
-mapping. We then have
$\star $
-mapping. We then have
Given a CPS
![]() $(G, H, {\mathcal L})$
and a subset
$(G, H, {\mathcal L})$
and a subset
![]() $W \subseteq H$
we can define
$W \subseteq H$
we can define
When W is precompact, we will call
![]() ${\LARGE \curlywedge }(W)$
a weak model set. If furthermore W has nonempty interior
${\LARGE \curlywedge }(W)$
a weak model set. If furthermore W has nonempty interior
![]() ${\LARGE \curlywedge }(W)$
is called a model set.
${\LARGE \curlywedge }(W)$
is called a model set.
Next, let us review the concept of a Meyer set, which plays a fundamental role in this paper.
Definition 2.9 A set
![]() $\Lambda \subseteq G$
is called a Meyer set if
$\Lambda \subseteq G$
is called a Meyer set if
![]() $\Lambda $
is relatively dense and
$\Lambda $
is relatively dense and
![]() $\Lambda -\Lambda -\Lambda $
is uniformly discrete.
$\Lambda -\Lambda -\Lambda $
is uniformly discrete.
For equivalent characterizations of Meyer sets, see [Reference Lagarias18, Reference Lagarias, Baake and Moody19, Reference Meyer26, Reference Moody and Moody28, Reference Strungaru, Baake and Grimm46]. Of importance to us will be the following result.
Theorem 2.10 ([Reference Strungaru, Baake and Grimm46])
Let
![]() $\Lambda \subseteq G$
be relatively dense. Then
$\Lambda \subseteq G$
be relatively dense. Then
![]() $\Lambda $
is Meyer if and only if it is a subset of a (weak) model set.
$\Lambda $
is Meyer if and only if it is a subset of a (weak) model set.
Moreover, if
![]() $\Lambda $
is Meyer, it is a subset of a weak model set in a CPS
$\Lambda $
is Meyer, it is a subset of a weak model set in a CPS
![]() $(G,H, {\mathcal L})$
with metrizable and compactly generated H.
$(G,H, {\mathcal L})$
with metrizable and compactly generated H.
We should emphasize here that the key for all results below is that fact that a Meyer set is a subset of a model set, and relative denseness plays no role. Because of this, in the spirit of [Reference Strungaru49], we will refer to an arbitrary subset of a (weak) model set as a weak Meyer set. It is obvious that a subset of a weak Meyer set is a weak Meyer set and that a measure is supported inside a Meyer set if and only if its support is a weak Meyer set.
Given a CPS
![]() $(G,H, {\mathcal L})$
, the map
$(G,H, {\mathcal L})$
, the map
is a group isomorphism, and hence it induces an isomorphism between the spaces of (bounded) functions on L and
![]() ${\mathcal L}$
, respectively. Since
${\mathcal L}$
, respectively. Since
![]() ${\mathcal L}$
is a discrete group, the space of (translation bounded) measures on
${\mathcal L}$
is a discrete group, the space of (translation bounded) measures on
![]() ${\mathcal L}$
can be identified with the space of (bounded) functions on
${\mathcal L}$
can be identified with the space of (bounded) functions on
![]() ${\mathcal L}$
. On another hand, L is typically dense in G, and many functions on L do not induce pure point measures on G.
${\mathcal L}$
. On another hand, L is typically dense in G, and many functions on L do not induce pure point measures on G.
For us, of interest will be measures supported inside weak model sets
![]() ${\LARGE \curlywedge }(W)$
. Since
${\LARGE \curlywedge }(W)$
. Since
![]() ${\LARGE \curlywedge }(W)$
is uniformly discrete [Reference Moody and Moody28], the space of (translation bounded) measures on
${\LARGE \curlywedge }(W)$
is uniformly discrete [Reference Moody and Moody28], the space of (translation bounded) measures on
![]() ${\LARGE \curlywedge }(W)$
can be identified with the space of (bounded) functions on
${\LARGE \curlywedge }(W)$
can be identified with the space of (bounded) functions on
![]() ${\LARGE \curlywedge }(W)$
, and corresponds via the above isomorphism with the spaces of (translation bounded) measures or (bounded) functions on
${\LARGE \curlywedge }(W)$
, and corresponds via the above isomorphism with the spaces of (translation bounded) measures or (bounded) functions on
![]() ${\mathcal L}$
, respectively, that are supported inside
${\mathcal L}$
, respectively, that are supported inside
![]() $G \times W$
.
$G \times W$
.
Our focus in this paper is on these two spaces. We will study them as spaces of measures, and we will be interested in the relation between the Fourier theory of these two spaces, and the behavior of the Fourier transform with respect to the isomorphism induced by (2.1). For this reason, let us introduce the following notations.
Given a CPS
![]() $(G,H, {\mathcal L})$
and a compact set W, we denote by
$(G,H, {\mathcal L})$
and a compact set W, we denote by
 $$ \begin{align*} {\mathcal M}^{\infty}({\LARGE \curlywedge}(W)) &:= \{ \mu \in {\mathcal M}^{\infty}(G) : \mbox{supp}(\mu) \subseteq {\LARGE \curlywedge}(W)\} \,;\\ {\mathcal M}^{\infty}({\mathcal L}; W) &:=\{ \nu \in {\mathcal M}^{\infty}(G \times H) : \mbox{supp}(\nu) \subseteq \left( {\mathcal L} \cap (G \times W) \right) \} \,. \end{align*} $$
$$ \begin{align*} {\mathcal M}^{\infty}({\LARGE \curlywedge}(W)) &:= \{ \mu \in {\mathcal M}^{\infty}(G) : \mbox{supp}(\mu) \subseteq {\LARGE \curlywedge}(W)\} \,;\\ {\mathcal M}^{\infty}({\mathcal L}; W) &:=\{ \nu \in {\mathcal M}^{\infty}(G \times H) : \mbox{supp}(\nu) \subseteq \left( {\mathcal L} \cap (G \times W) \right) \} \,. \end{align*} $$
The isomorphism (2.1) induces a bijection
![]() $f: {\LARGE \curlywedge }(W) \to {\mathcal L} \cap (G \times W)$
. This induces a bijective map
$f: {\LARGE \curlywedge }(W) \to {\mathcal L} \cap (G \times W)$
. This induces a bijective map
![]() $\mathbb {L}_{G,H,{\mathcal L}, W}: {\mathcal M}^{\infty }({\LARGE \curlywedge }(W)) \to {\mathcal M}^{\infty }({\mathcal L}; W)$
, taking a measure on
$\mathbb {L}_{G,H,{\mathcal L}, W}: {\mathcal M}^{\infty }({\LARGE \curlywedge }(W)) \to {\mathcal M}^{\infty }({\mathcal L}; W)$
, taking a measure on
![]() ${\LARGE \curlywedge }(W)$
into its pushforward via f, defined by
${\LARGE \curlywedge }(W)$
into its pushforward via f, defined by
with inverse
![]() $\mathbb {P}_{G,H,{\mathcal L}, W}: {\mathcal M}^{\infty }({\mathcal L} ;W) \to {\mathcal M}^{\infty }({\LARGE \curlywedge }(W))$
$\mathbb {P}_{G,H,{\mathcal L}, W}: {\mathcal M}^{\infty }({\mathcal L} ;W) \to {\mathcal M}^{\infty }({\LARGE \curlywedge }(W))$
Let us note here in passing that
![]() $\mathbb {P}_{G,H,{\mathcal L},W}$
is simply the pushforward via
$\mathbb {P}_{G,H,{\mathcal L},W}$
is simply the pushforward via
![]() $f^{-1}$
.
$f^{-1}$
.
We will refer to these mappings as the lift operator and the projection operator, respectively. When the CPS and window are clear from the context, we will simply write
![]() $\mathbb {L}(\mu )$
and
$\mathbb {L}(\mu )$
and
![]() $\mathbb {P}(\nu )$
, respectively, instead of
$\mathbb {P}(\nu )$
, respectively, instead of
![]() $\mathbb {L}_{G,H,{\mathcal L}, W}(\mu )$
and
$\mathbb {L}_{G,H,{\mathcal L}, W}(\mu )$
and
![]() $\mathbb {P}_{G,H,{\mathcal L}, W}(\nu )$
, respectively.
$\mathbb {P}_{G,H,{\mathcal L}, W}(\nu )$
, respectively.
The main results in this paper are that these operators are bijections between the subspaces of Fourier transformable (or cones of positive-definite) measures, and relate their Fourier transforms.
To understand the connection between the Fourier transforms, let us recall the notion of dual CPS. Given a CPS
![]() $(G, H, {\mathcal L})$
, we can define
$(G, H, {\mathcal L})$
, we can define
Then,
![]() $(\widehat {G}, \widehat {H}, {\mathcal L}^0)$
is a CPS [Reference Baake, Huck and Strungaru5, Reference Moody and Moody28, Reference Moody, Axel, Dénoyer and Gazeau29, Reference Strungaru, Baake and Grimm46]. We will refer to this as the CPS dual to
$(\widehat {G}, \widehat {H}, {\mathcal L}^0)$
is a CPS [Reference Baake, Huck and Strungaru5, Reference Moody and Moody28, Reference Moody, Axel, Dénoyer and Gazeau29, Reference Strungaru, Baake and Grimm46]. We will refer to this as the CPS dual to
![]() $(G, H, {\mathcal L})$
.
$(G, H, {\mathcal L})$
.
3 Positive-definite measures with weak Meyer set support
In this section, we show that
![]() $\mathbb {L}_{G,H,{\mathcal L}, W}$
and
$\mathbb {L}_{G,H,{\mathcal L}, W}$
and
![]() $\mathbb {P}_{G,H,{\mathcal L}, W}$
take positive-definite measures to positive-definite measures.
$\mathbb {P}_{G,H,{\mathcal L}, W}$
take positive-definite measures to positive-definite measures.
Let us start with the following obvious lemma, which follows immediately from Definition 2.6 and the fact that the function from (2.1) is a group isomorphism.
Lemma 3.1 Let
![]() $(G, H, {\mathcal L})$
be a CPS, and let
$(G, H, {\mathcal L})$
be a CPS, and let
![]() $f : L \to {\mathbb C}$
be a function. Define
$f : L \to {\mathbb C}$
be a function. Define
![]() ${g :{\mathcal L} \to {\mathbb C}}$
via
${g :{\mathcal L} \to {\mathbb C}}$
via
Then f is positive-definite on L if and only if g is positive-definite on
![]() ${\mathcal L}$
.
${\mathcal L}$
.
Let us recall now the following result of [Reference Lenz and Strungaru24], which we will use often in the paper.
Proposition 3.2 ([Reference Lenz and Strungaru24, Proposition 2.4])
Let G be a LCAG, let
![]() $\mu $
be a discrete measure on G, and let
$\mu $
be a discrete measure on G, and let
Then, the following are equivalent:
-
(i) The measure
 $\mu $
is a positive-definite measure on G.
$\mu $
is a positive-definite measure on G. -
(ii) The measure
 $\mu $
is a positive-definite measure on
$\mu $
is a positive-definite measure on
 $G_{d}$
.
$G_{d}$
. -
(iii) The function f is a positive-definite function on G.
-
(iv) The function f is a positive-definite function on
 $G_{d}$
.
$G_{d}$
.
Next, we prove a slight generalization of [Reference Lenz and Strungaru24, Lemma 2.10] and [Reference Baake and Grimm3, Lemma 8.4].
Lemma 3.3 Let
![]() $\gamma $
be a positive-definite pure point measure on G, and let L be any subgroup of G. Then, the function
$\gamma $
be a positive-definite pure point measure on G, and let L be any subgroup of G. Then, the function
![]() $g : L \to {\mathbb C}$
defined via
$g : L \to {\mathbb C}$
defined via
is a positive-definite function on L.
Proof Define
![]() $f : G \to {\mathbb C}$
via
$f : G \to {\mathbb C}$
via
Then f is a positive-definite function on G Proposition 3.2. Definition 2.6 immediately gives that the restriction
![]() $g=f|_L$
to the subgroup L is a positive-definite function on L.
$g=f|_L$
to the subgroup L is a positive-definite function on L.
We will also need the following result.
Lemma 3.4 Let G be any group, and let
![]() $H \leq G$
be a subgroup. Let
$H \leq G$
be a subgroup. Let
![]() $f : H \to {\mathbb C}$
be a positive-definite functions. Then, the function
$f : H \to {\mathbb C}$
be a positive-definite functions. Then, the function
![]() $g : G \to {\mathbb C}$
defined via
$g : G \to {\mathbb C}$
defined via
 $$ \begin{align*} g(x):= \left\{ \begin{array}{l c} f(x), & \mbox{ if } x \in H, \\ 0, & \mbox{ otherwise } \end{array} \right. \end{align*} $$
$$ \begin{align*} g(x):= \left\{ \begin{array}{l c} f(x), & \mbox{ if } x \in H, \\ 0, & \mbox{ otherwise } \end{array} \right. \end{align*} $$
is positive-definite on G.
Proof Let
![]() $n \in \mathbb N, x_1,\ldots , x_n\in G$
and
$n \in \mathbb N, x_1,\ldots , x_n\in G$
and
![]() $c_1,..,c_n \in {\mathbb C}$
. Note that
$c_1,..,c_n \in {\mathbb C}$
. Note that
![]() $g(x_k-x_l) =0$
whenever
$g(x_k-x_l) =0$
whenever
![]() $x_k -x_l \notin H$
.
$x_k -x_l \notin H$
.
On G define the standard equivalence
![]() $\pmod {H}$
as
$\pmod {H}$
as
This induces an equivalence relation on the set
![]() $\{ x_1,\ldots , x_n \}$
, and hence we can partition this set in equivalence classes
$\{ x_1,\ldots , x_n \}$
, and hence we can partition this set in equivalence classes
![]() $F_1,\ldots , F_m$
.
$F_1,\ldots , F_m$
.
To make the computation clearer, define
![]() $c : G\to {\mathbb C}$
$c : G\to {\mathbb C}$
 $$\begin{align*}c(x):= \left\{ \begin{array}{cc} c_j, & \mbox{ if } x=x_j, \\ 0, & \mbox{ otherwise. } \end{array} \right.\, \end{align*}$$
$$\begin{align*}c(x):= \left\{ \begin{array}{cc} c_j, & \mbox{ if } x=x_j, \\ 0, & \mbox{ otherwise. } \end{array} \right.\, \end{align*}$$
Then,
 $$ \begin{align*} \sum_{k,l=1}^n g(x_k-x_l)c_k \overline{c_l} &=\sum_{k,l=1}^n g(x_k-x_l)c(x_k) \overline{c(x_l)} \\ &= \sum_{i=1}^m \sum_{j=1}^m \left( \sum_{x \in F_i} \sum_{y \in F_j} g(x-y) c(x) \overline{c(y)} \right)\\ &= \sum_{i=1}^m \left( \sum_{x,y \in F_i} g(x-y)c(x)\overline{c(y)} \right) \,. \end{align*} $$
$$ \begin{align*} \sum_{k,l=1}^n g(x_k-x_l)c_k \overline{c_l} &=\sum_{k,l=1}^n g(x_k-x_l)c(x_k) \overline{c(x_l)} \\ &= \sum_{i=1}^m \sum_{j=1}^m \left( \sum_{x \in F_i} \sum_{y \in F_j} g(x-y) c(x) \overline{c(y)} \right)\\ &= \sum_{i=1}^m \left( \sum_{x,y \in F_i} g(x-y)c(x)\overline{c(y)} \right) \,. \end{align*} $$
Now, fix some
![]() $1 \leq i \leq m$
, and let
$1 \leq i \leq m$
, and let
![]() $F_i:=\{ z_1,.., z_q \}$
. Then,
$F_i:=\{ z_1,.., z_q \}$
. Then,
 $$ \begin{align*} \sum_{x,y \in F_i} g(x-y)c(x)\overline{c(y)}&= \sum_{r,s=0}^q g(z_r-z_s)c(z_r)\overline{c(z_s)} \\ &= \sum_{r,s=1}^q g(z_r-z_s)c(z_r)\overline{c(z_s)} \\ &= \sum_{r,s=1}^q f\left((z_r-z_1) -(z_s-z_1)\right)c(z_r)\overline{c(z_s)} \geq 0 \end{align*} $$
$$ \begin{align*} \sum_{x,y \in F_i} g(x-y)c(x)\overline{c(y)}&= \sum_{r,s=0}^q g(z_r-z_s)c(z_r)\overline{c(z_s)} \\ &= \sum_{r,s=1}^q g(z_r-z_s)c(z_r)\overline{c(z_s)} \\ &= \sum_{r,s=1}^q f\left((z_r-z_1) -(z_s-z_1)\right)c(z_r)\overline{c(z_s)} \geq 0 \end{align*} $$
by the positive-definiteness of f applied to
![]() $m; y_1:=z_1 - z_1; y_2:=z_2 - z_1 ;\ldots; y_q:=z_q - z_1 \in H$
and
$m; y_1:=z_1 - z_1; y_2:=z_2 - z_1 ;\ldots; y_q:=z_q - z_1 \in H$
and
![]() $c^{\prime }_1=c(z_1),\ldots ,c^{\prime }_q=c(z_q)$
.
$c^{\prime }_1=c(z_1),\ldots ,c^{\prime }_q=c(z_q)$
.
Therefore, for each i, we have
![]() $\sum _{x,y \in C_i} g(x-y)c(x)\overline {c(y)} \geq 0$
, and hence
$\sum _{x,y \in C_i} g(x-y)c(x)\overline {c(y)} \geq 0$
, and hence
 $$ \begin{align*} \sum_{k,l=1}^n g(x_k-x_l)c_k \overline{c_l}=\sum_{i=1}^m \left( \sum_{x,y \in C_i} g(x-y)c(x)\overline{c(y)} \right) \geq 0.\\[-40pt] \end{align*} $$
$$ \begin{align*} \sum_{k,l=1}^n g(x_k-x_l)c_k \overline{c_l}=\sum_{i=1}^m \left( \sum_{x,y \in C_i} g(x-y)c(x)\overline{c(y)} \right) \geq 0.\\[-40pt] \end{align*} $$
Remark 3.5 One can also prove Lemma 3.4 by using Fourier analysis. Indeed, since f is positive-definite, the measure
![]() $\mu :=f \theta _{H_{\mathsf {d}}}$
is a positive-definite measure on the discrete group
$\mu :=f \theta _{H_{\mathsf {d}}}$
is a positive-definite measure on the discrete group
![]() $H_{\mathsf {d}}$
[Reference Argabright and de Lamadrid1, Corollary 4.3]. Then, it is Fourier transformable on
$H_{\mathsf {d}}$
[Reference Argabright and de Lamadrid1, Corollary 4.3]. Then, it is Fourier transformable on
![]() $H_{\mathsf {d}}$
and its Fourier transform is positive [Reference Argabright and de Lamadrid1, Reference Berg and Forst8]. As
$H_{\mathsf {d}}$
and its Fourier transform is positive [Reference Argabright and de Lamadrid1, Reference Berg and Forst8]. As
![]() $H_{\mathsf {d}}$
is closed in the discrete group
$H_{\mathsf {d}}$
is closed in the discrete group
![]() $G_{\mathsf {d}}$
, by [Reference Argabright and de Lamadrid1, Theorem 4.2], the measure
$G_{\mathsf {d}}$
, by [Reference Argabright and de Lamadrid1, Theorem 4.2], the measure
![]() $\nu :=g \theta _{G_{\mathsf {d}}}$
is Fourier transformable on
$\nu :=g \theta _{G_{\mathsf {d}}}$
is Fourier transformable on
![]() $G_{\mathsf {d}}$
and has positive Fourier transform. Then,
$G_{\mathsf {d}}$
and has positive Fourier transform. Then,
![]() $\mu $
is positive-definite [Reference Argabright and de Lamadrid1, Theorem 4.1]. Therefore, by Proposition 3.2, g is positive-definite on G.
$\mu $
is positive-definite [Reference Argabright and de Lamadrid1, Theorem 4.1]. Therefore, by Proposition 3.2, g is positive-definite on G.
We are now ready to prove the following result.
Proposition 3.6 Let
![]() $(G,H, {\mathcal L})$
be a CPS, let
$(G,H, {\mathcal L})$
be a CPS, let
![]() ${\LARGE \curlywedge }(W)$
be a weak model set, and let
${\LARGE \curlywedge }(W)$
be a weak model set, and let
![]() $f : G \to {\mathbb C}$
be a function which vanishes outside
$f : G \to {\mathbb C}$
be a function which vanishes outside
![]() ${\LARGE \curlywedge }(W)$
. Let
${\LARGE \curlywedge }(W)$
. Let
 $$ \begin{align*} \gamma &=\sum_{x \in {\LARGE \curlywedge}(W)} f(x) \delta_x, \\ \eta&= \sum_{(x,x^{\star}) \in {\mathcal L}} f(x) \delta_{(x,x^{\star})}= \mathbb{L} (\gamma) \,. \end{align*} $$
$$ \begin{align*} \gamma &=\sum_{x \in {\LARGE \curlywedge}(W)} f(x) \delta_x, \\ \eta&= \sum_{(x,x^{\star}) \in {\mathcal L}} f(x) \delta_{(x,x^{\star})}= \mathbb{L} (\gamma) \,. \end{align*} $$
Then
![]() $\gamma $
is a positive-definite measure on G if and only if
$\gamma $
is a positive-definite measure on G if and only if
![]() $\eta $
is a positive-definite measure on
$\eta $
is a positive-definite measure on
![]() $G \times H$
.
$G \times H$
.
Proof
![]() $\Rightarrow $
: Denote as usual
$\Rightarrow $
: Denote as usual
![]() $L := \pi _G({\mathcal L})$
. Define
$L := \pi _G({\mathcal L})$
. Define
![]() $g: L \to {\mathbb C}$
via
$g: L \to {\mathbb C}$
via
that is,
![]() $g= f|_{L}$
.
$g= f|_{L}$
.
Then, by Lemma 3.3, g is a positive-definite function on L and hence, by Lemma 3.1, the function
![]() $h: {\mathcal L} \to {\mathbb C}$
$h: {\mathcal L} \to {\mathbb C}$
is a positive-definite function on
![]() ${\mathcal L}$
. Therefore, by Lemma 3.4, the function
${\mathcal L}$
. Therefore, by Lemma 3.4, the function
![]() $j: G \times H \to {\mathbb C}$
$j: G \times H \to {\mathbb C}$
 $$ \begin{align*} j(z):= \left\{ \begin{array}{l c} h(z), & \mbox{ if } z \in {\mathcal L,} \\ 0, & \mbox{ otherwise } \end{array} \right. \end{align*} $$
$$ \begin{align*} j(z):= \left\{ \begin{array}{l c} h(z), & \mbox{ if } z \in {\mathcal L,} \\ 0, & \mbox{ otherwise } \end{array} \right. \end{align*} $$
is positive-definite on
![]() $G \times H$
. The claim follows from Proposition 3.2.
$G \times H$
. The claim follows from Proposition 3.2.
![]() $\Leftarrow :$
Since
$\Leftarrow :$
Since
![]() $\eta $
is positive-definite, by Lemma 3.3, the function
$\eta $
is positive-definite, by Lemma 3.3, the function
![]() $h: {\mathcal L} \to {\mathbb C}$
defined by
$h: {\mathcal L} \to {\mathbb C}$
defined by
is positive-definite on
![]() ${\mathcal L}$
and hence, by Lemma 3.1, the restriction
${\mathcal L}$
and hence, by Lemma 3.1, the restriction
![]() $g=f|_L$
is positive-definite on L. As f is zero outside
$g=f|_L$
is positive-definite on L. As f is zero outside
![]() ${\LARGE \curlywedge }(W) \subseteq L$
, it follows from Lemma 3.4 that f is a positive-definite function on G. The claim follows now from Proposition 3.2.
${\LARGE \curlywedge }(W) \subseteq L$
, it follows from Lemma 3.4 that f is a positive-definite function on G. The claim follows now from Proposition 3.2.
Remark 3.7
-
(a) In Proposition 3.6, the positive-definiteness of
 $\eta $
and
$\eta $
and
 $\gamma $
is equivalent to the positive-definiteness of the function f.
$\gamma $
is equivalent to the positive-definiteness of the function f. -
(b) Denoting by
 $$ \begin{align*} \mathcal{PD}({\LARGE \curlywedge}(W)) &:= \{ \mu \in {\mathcal M}^{\infty}({\LARGE \curlywedge}(W)) : \mu \mbox{ is positive-definite } \}, \\ \mathcal{PD}({\mathcal L}; W) &:=\{ \nu \in {\mathcal M}^{\infty}({\mathcal L}, W) : \nu \mbox{ is positive-definite } \} \,. \end{align*} $$
$$ \begin{align*} \mathcal{PD}({\LARGE \curlywedge}(W)) &:= \{ \mu \in {\mathcal M}^{\infty}({\LARGE \curlywedge}(W)) : \mu \mbox{ is positive-definite } \}, \\ \mathcal{PD}({\mathcal L}; W) &:=\{ \nu \in {\mathcal M}^{\infty}({\mathcal L}, W) : \nu \mbox{ is positive-definite } \} \,. \end{align*} $$
Proposition 3.6 says that
 $$ \begin{align*} \mathbb{L}( \mathcal{PD}({\LARGE \curlywedge}(W)) ) &=\mathcal{PD}({\mathcal L}; W), \\ \mathbb{P} (\mathcal{PD}({\mathcal L}; W) )&= \mathcal{PD}({\LARGE \curlywedge}(W)) \,.\end{align*} $$
$$ \begin{align*} \mathbb{L}( \mathcal{PD}({\LARGE \curlywedge}(W)) ) &=\mathcal{PD}({\mathcal L}; W), \\ \mathbb{P} (\mathcal{PD}({\mathcal L}; W) )&= \mathcal{PD}({\LARGE \curlywedge}(W)) \,.\end{align*} $$
4 The lift of Fourier transformable measures
We can now prove that, given a CPS
![]() $(G, H,{\mathcal L})$
and a compact set K, the lifting operator induces a bijection between the space of Fourier transformable measures supported inside
$(G, H,{\mathcal L})$
and a compact set K, the lifting operator induces a bijection between the space of Fourier transformable measures supported inside
![]() ${\LARGE \curlywedge }(W)$
and the space of Fourier transformable measures supported inside
${\LARGE \curlywedge }(W)$
and the space of Fourier transformable measures supported inside
![]() $ {\mathcal L} \cap (G \times W)$
.
$ {\mathcal L} \cap (G \times W)$
.
Theorem 4.1 Let
![]() $(G,H, {\mathcal L})$
be a CPS, and let
$(G,H, {\mathcal L})$
be a CPS, and let
![]() $W \subseteq H$
be compact. Let
$W \subseteq H$
be compact. Let
![]() $\gamma $
be a translation bounded measure supported inside
$\gamma $
be a translation bounded measure supported inside
![]() ${\LARGE \curlywedge }(W)$
, and let
${\LARGE \curlywedge }(W)$
, and let
Then
![]() $\gamma $
is Fourier transformable if and only if
$\gamma $
is Fourier transformable if and only if
![]() $\eta $
is Fourier transformable.
$\eta $
is Fourier transformable.
Moreover, if
![]() $\varphi \in K_2(H)$
is any function so that
$\varphi \in K_2(H)$
is any function so that
![]() $\varphi \equiv 1$
on W, then, for all
$\varphi \equiv 1$
on W, then, for all
![]() $\psi \in C_{\mathsf {c}}(\widehat {G})$
, we have
$\psi \in C_{\mathsf {c}}(\widehat {G})$
, we have
![]() $\psi \otimes \hat {\varphi } \in L^1(\widehat {\eta })$
and
$\psi \otimes \hat {\varphi } \in L^1(\widehat {\eta })$
and
Proof
![]() $\Longrightarrow $
By [Reference Strungaru47, Lemma 8.3], there exist a compact set
$\Longrightarrow $
By [Reference Strungaru47, Lemma 8.3], there exist a compact set
![]() $W \subseteq K$
and four positive-definite measures
$W \subseteq K$
and four positive-definite measures
![]() $\omega _{1},\omega _{2},\omega _{3},\omega _{4}$
supported inside
$\omega _{1},\omega _{2},\omega _{3},\omega _{4}$
supported inside
![]() ${\LARGE \curlywedge }(K)$
such that
${\LARGE \curlywedge }(K)$
such that
Then, we have
 $$ \begin{align*} \eta&= \mathbb{L}_{G,H,{\mathcal L}, W}(\gamma) =\mathbb{L}_{G,H,{\mathcal L}, K}(\gamma)=\mathbb{L}_{G,H,{\mathcal L}, K}(\omega_1-\omega_2+i\omega_3-i \omega_4 )\\ &= \mathbb{L}_{G,H,{\mathcal L}, K}(\omega_1)-\mathbb{L}_{G,H,{\mathcal L}, K}(\omega_2)+i\mathbb{L}_{G,H,{\mathcal L}, K}(\omega_3)-i\mathbb{L}_{G,H,{\mathcal L}, K}(\omega_4) \,. \end{align*} $$
$$ \begin{align*} \eta&= \mathbb{L}_{G,H,{\mathcal L}, W}(\gamma) =\mathbb{L}_{G,H,{\mathcal L}, K}(\gamma)=\mathbb{L}_{G,H,{\mathcal L}, K}(\omega_1-\omega_2+i\omega_3-i \omega_4 )\\ &= \mathbb{L}_{G,H,{\mathcal L}, K}(\omega_1)-\mathbb{L}_{G,H,{\mathcal L}, K}(\omega_2)+i\mathbb{L}_{G,H,{\mathcal L}, K}(\omega_3)-i\mathbb{L}_{G,H,{\mathcal L}, K}(\omega_4) \,. \end{align*} $$
Now, by Proposition 3.6, for all
![]() $1 \leq j \leq 4$
, the measure
$1 \leq j \leq 4$
, the measure
![]() $\mathbb {L}_{G,H,{\mathcal L}, K}(\omega _j)$
is positive-definite. Therefore, as a linear combination of positive-definite measures,
$\mathbb {L}_{G,H,{\mathcal L}, K}(\omega _j)$
is positive-definite. Therefore, as a linear combination of positive-definite measures,
![]() $\eta $
is Fourier transformable.
$\eta $
is Fourier transformable.
![]() $\Longleftarrow $
. Our argument is similar to [Reference Richard and Strungaru34].
$\Longleftarrow $
. Our argument is similar to [Reference Richard and Strungaru34].
First, fix an arbitrary
![]() $\varphi \in K_2(H)$
so that
$\varphi \in K_2(H)$
so that
![]() $\varphi \equiv 1$
on W. We split the rest of the argument into two steps.
$\varphi \equiv 1$
on W. We split the rest of the argument into two steps.
Step 1: We show that
![]() $(\widehat {\eta })_{\check {\varphi }}$
is a measure.
$(\widehat {\eta })_{\check {\varphi }}$
is a measure.
Let us first note that for all
![]() $\psi \in K_2(G)$
, we have
$\psi \in K_2(G)$
, we have
![]() $\psi \otimes \varphi \in K_2(G \times H)$
. Therefore, since
$\psi \otimes \varphi \in K_2(G \times H)$
. Therefore, since
![]() $\eta $
is Fourier transformable, we have
$\eta $
is Fourier transformable, we have
We now show that for all
![]() $\phi \in C_{\mathsf {c}}(\widehat {G})$
, we have
$\phi \in C_{\mathsf {c}}(\widehat {G})$
, we have
![]() $\left | \phi \otimes \check {\varphi } \right | \in L^1(|\widehat {\eta }|)$
and that
$\left | \phi \otimes \check {\varphi } \right | \in L^1(|\widehat {\eta }|)$
and that
defines a measure.
Let
![]() $K \subseteq \widehat {G}$
be a fixed compact set. Then, there exists some
$K \subseteq \widehat {G}$
be a fixed compact set. Then, there exists some
![]() $\psi \in K_2(G)$
such that
$\psi \in K_2(G)$
such that
![]() $\check {\psi } \geq 1_K$
[Reference Berg and Forst8, Reference Moody, Strungaru, Baake and Grimm31].
$\check {\psi } \geq 1_K$
[Reference Berg and Forst8, Reference Moody, Strungaru, Baake and Grimm31].
Now, for all
![]() $\phi \in C_{\mathsf {c}}(\widehat {G})$
with
$\phi \in C_{\mathsf {c}}(\widehat {G})$
with
![]() $\mbox {supp}(\phi ) \subseteq K$
, we have
$\mbox {supp}(\phi ) \subseteq K$
, we have
and hence
![]() $(\widehat {\eta })_{\check {\varphi }}$
is well defined.
$(\widehat {\eta })_{\check {\varphi }}$
is well defined.
Moreover, for all
![]() $\phi \in C_{\mathsf {c}}(\widehat {G})$
with
$\phi \in C_{\mathsf {c}}(\widehat {G})$
with
![]() $\mbox {supp}(\phi ) \subseteq K$
, it follows from (4.3) that
$\mbox {supp}(\phi ) \subseteq K$
, it follows from (4.3) that
where
This shows that
![]() $(\widehat {\eta })_{\check {\varphi }}$
is a measure.
$(\widehat {\eta })_{\check {\varphi }}$
is a measure.
Step 2: We show that for all
![]() $\phi \in K_2(G)$
, we have
$\phi \in K_2(G)$
, we have
and
Let
![]() $\phi \in K_2(G)$
be arbitrary.
$\phi \in K_2(G)$
be arbitrary.
Since G is second countable, so is
![]() $\widehat {G}$
[Reference Reiter and Stegeman33]. In particular,
$\widehat {G}$
[Reference Reiter and Stegeman33]. In particular,
![]() $\widehat {G}$
is
$\widehat {G}$
is
![]() $\sigma $
-compact [Reference Reiter and Stegeman33]. Therefore, there exists a sequence
$\sigma $
-compact [Reference Reiter and Stegeman33]. Therefore, there exists a sequence
![]() $K_n$
of compact sets with
$K_n$
of compact sets with
![]() $K_n \subseteq (K_{n+1})^{\circ }$
such that
$K_n \subseteq (K_{n+1})^{\circ }$
such that
Let
![]() $\psi _n \in C_{\mathsf {c}}(\widehat {G})$
be so that
$\psi _n \in C_{\mathsf {c}}(\widehat {G})$
be so that
![]() $1_{K_n} \leq \psi _n \leq 1_{K_{n+1}}$
.
$1_{K_n} \leq \psi _n \leq 1_{K_{n+1}}$
.
Then,
![]() $\psi _n \widehat {\phi } \in C_{\mathsf {c}}(\widehat {G})$
and by the definition of
$\psi _n \widehat {\phi } \in C_{\mathsf {c}}(\widehat {G})$
and by the definition of
, we have
Now, for all n, we have by (4.2)
Therefore, by the dominated convergence theorem [Reference Reiter and Stegeman33, Theorem 3.2.51], we have
Next, by the monotone convergence theorem [Reference Reiter and Stegeman33], we have
Note that for each n, we have

Since
, we get
This shows that
. Therefore,
is dominated by
and converges pointwise to
. Thus, by (4.4) and the dominated convergence theorem, we get
Finally, by the Fourier transformability of
![]() $\eta $
, we have
$\eta $
, we have
Therefore, we proved that for all
![]() $\phi \in K_2(G)$
, we have
$\phi \in K_2(G)$
, we have
and
This proves that
![]() $\gamma $
is Fourier transformable and
$\gamma $
is Fourier transformable and
completing the proof.
Using the fact that
![]() $\mathbb {L}$
is a bijection with inverse
$\mathbb {L}$
is a bijection with inverse
![]() $\mathbb {P}$
, we get the following corollary.
$\mathbb {P}$
, we get the following corollary.
Corollary 4.2 Let
![]() $(G,H, {\mathcal L})$
be a CPS, and let
$(G,H, {\mathcal L})$
be a CPS, and let
![]() $W \subseteq H$
be compact. Let
$W \subseteq H$
be compact. Let
![]() $\eta $
be a translation bounded measure supported inside
$\eta $
be a translation bounded measure supported inside
![]() ${\mathcal L} \cap (G \times W)$
, and let
${\mathcal L} \cap (G \times W)$
, and let
![]() $\gamma = \mathbb {P}_{G,H,{\mathcal L}, W}(\eta )$
. Then
$\gamma = \mathbb {P}_{G,H,{\mathcal L}, W}(\eta )$
. Then
![]() $\eta $
is Fourier transformable if and only if
$\eta $
is Fourier transformable if and only if
![]() $\gamma $
is Fourier transformable.
$\gamma $
is Fourier transformable.
Moreover, if
![]() $\varphi \in K_2(H)$
is any function so that
$\varphi \in K_2(H)$
is any function so that
![]() $\varphi \equiv 1$
on W, then, for all
$\varphi \equiv 1$
on W, then, for all
![]() $\psi \in C_{\mathsf {c}}(\widehat {G})$
, we have
$\psi \in C_{\mathsf {c}}(\widehat {G})$
, we have
![]() $\psi \otimes \hat {\varphi } \in L^1(\widehat {\eta })$
and (4.1) holds.
$\psi \otimes \hat {\varphi } \in L^1(\widehat {\eta })$
and (4.1) holds.
5 Applications
In this section, we will discuss the relation (4.1) and how can it be used to (re)derive some results from [Reference Strungaru47].
To make the things easier to follow, we introduce the notion of strongly admissible functions.
5.1 Strongly admissible functions for CPS
Let us start with the following definition.
Definition 5.1 Given a group H of the form
![]() $H={\mathbb R}^d \times H_0$
, with a LCAG
$H={\mathbb R}^d \times H_0$
, with a LCAG
![]() $H_0$
, a function
$H_0$
, a function
![]() $f : H \to {\mathbb C}$
is called strongly admissible if there exists
$f : H \to {\mathbb C}$
is called strongly admissible if there exists
![]() $g\in C_{\mathsf {u}}({\mathbb R}^d)$
and
$g\in C_{\mathsf {u}}({\mathbb R}^d)$
and
![]() $\varphi \in C_{\mathsf {c}}(H_0)$
such that:
$\varphi \in C_{\mathsf {c}}(H_0)$
such that:
-
•
 $\| (1+|x|^{2d}) g \|_{\infty } < \infty $
.
$\| (1+|x|^{2d}) g \|_{\infty } < \infty $
. -
•
 $f= g \otimes \varphi $
.
$f= g \otimes \varphi $
.
Next, given a CPS
![]() $(G,H,{\mathcal L})$
, we will denote by
$(G,H,{\mathcal L})$
, we will denote by
![]() ${\mathcal M}_{{\mathcal L}}(G \times H)$
, the space of
${\mathcal M}_{{\mathcal L}}(G \times H)$
, the space of
![]() ${\mathcal L}$
-periodic measures on
${\mathcal L}$
-periodic measures on
![]() $G \times H$
. Note that by [Reference Lenz and Richard21, Proposition 6.1]
$G \times H$
. Note that by [Reference Lenz and Richard21, Proposition 6.1]
We will see below that given a Fourier transformable measure
![]() $\gamma $
with weak Meyer set support, Theorem 4.1 can be used to create a CPS
$\gamma $
with weak Meyer set support, Theorem 4.1 can be used to create a CPS
![]() $(G, H={\mathbb R}^d \times H_0, {\mathcal L})$
, an
$(G, H={\mathbb R}^d \times H_0, {\mathcal L})$
, an
![]() ${\mathcal L}^0$
-periodic measure
${\mathcal L}^0$
-periodic measure
![]() $\rho (=\widehat {\eta })$
and a strongly admissible function f on
$\rho (=\widehat {\eta })$
and a strongly admissible function f on
![]() $\widehat {H} ={\mathbb R}^d \times \widehat {H_0}$
such that, equation (4.1) yields
$\widehat {H} ={\mathbb R}^d \times \widehat {H_0}$
such that, equation (4.1) yields
This motivates us to closely look at the properties of
![]() $(\rho )_f$
, for a CPS
$(\rho )_f$
, for a CPS
![]() $(G, H={\mathbb R}^d \times H_0, {\mathcal L}), \rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
and strongly admissible functions f.
$(G, H={\mathbb R}^d \times H_0, {\mathcal L}), \rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
and strongly admissible functions f.
Let us start with the following simple observation which also explains the name “strongly admissible.”
Given a CPS
![]() $(G, H={\mathbb R}^d \times H_0, {\mathcal L})$
, a measure
$(G, H={\mathbb R}^d \times H_0, {\mathcal L})$
, a measure
![]() $\rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
, and strongly admissible function f, it is obvious that the function f is admissible for
$\rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
, and strongly admissible function f, it is obvious that the function f is admissible for
![]() $(G, H, {\mathcal L},\rho )$
in the sense of [Reference Lenz and Richard21, Definition 3.1]. Therefore, by [Reference Lenz and Richard21, Proposition 6.3], we can define a translation bounded measure
$(G, H, {\mathcal L},\rho )$
in the sense of [Reference Lenz and Richard21, Definition 3.1]. Therefore, by [Reference Lenz and Richard21, Proposition 6.3], we can define a translation bounded measure
![]() $\rho _f$
on G via
$\rho _f$
on G via
This measure is strongly almost periodic by [Reference Lenz and Richard21, Theorem 3.1]. In fact, the strong admissibility of f immediately implies that
![]() $\rho _f$
is norm almost periodic.
$\rho _f$
is norm almost periodic.
Indeed, let
![]() $(G, H={\mathbb R}^d \times H_0, {\mathcal L})$
, let
$(G, H={\mathbb R}^d \times H_0, {\mathcal L})$
, let
![]() $f=g \otimes \varphi $
be strongly admissible, and let
$f=g \otimes \varphi $
be strongly admissible, and let
![]() $\rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
. Pick any compact set
$\rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
. Pick any compact set
![]() $ \mbox {supp}(\varphi ) \subseteq W \subseteq \widehat {H_0}$
, and let
$ \mbox {supp}(\varphi ) \subseteq W \subseteq \widehat {H_0}$
, and let
![]() $K, K_1 \subseteq G$
be compact sets in G with
$K, K_1 \subseteq G$
be compact sets in G with
![]() $K \subseteq K_1^{\circ }$
. Then, a standard computation similar to [Reference Strungaru47, Lemma 5.2] shows that
$K \subseteq K_1^{\circ }$
. Then, a standard computation similar to [Reference Strungaru47, Lemma 5.2] shows that
where
 $$ \begin{align*} C:= \left( \sum_{n \in {\mathbb Z}^d} \sup_{z \in n+[-\frac{1}{2},\frac{1}{2}]^d } \frac{1}{1+|z|^{2d}} \right) < \infty \,. \end{align*} $$
$$ \begin{align*} C:= \left( \sum_{n \in {\mathbb Z}^d} \sup_{z \in n+[-\frac{1}{2},\frac{1}{2}]^d } \frac{1}{1+|z|^{2d}} \right) < \infty \,. \end{align*} $$
This immediately gives the following stronger version of [Reference Strungaru47, Lemma 5.2].
Fact 5.2 Let
![]() $(G, H={\mathbb R}^d \times H_0, {\mathcal L})$
be a CPS, let
$(G, H={\mathbb R}^d \times H_0, {\mathcal L})$
be a CPS, let
![]() $\rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
, and let
$\rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
, and let
![]() $f \in C^{}_{0}(H)$
be strongly admissible. Then,
$f \in C^{}_{0}(H)$
be strongly admissible. Then,
![]() $\rho _f$
is a norm almost periodic measure.
$\rho _f$
is a norm almost periodic measure.
5.2 Fourier transform of measures with weak Meyer set support
Fix an arbitrary Meyer set
![]() $\Lambda $
and a Fourier transformable measure
$\Lambda $
and a Fourier transformable measure
![]() $\gamma $
with
$\gamma $
with
![]() $\mbox {supp}(\gamma ) \subseteq \Lambda $
.
$\mbox {supp}(\gamma ) \subseteq \Lambda $
.
By Theorem 2.10 and the structure theorem of compactly generated groups, there exists a CPS
![]() $(G, {\mathbb R}^d \times {\mathbb Z}^m \times \mathbb K, {\mathcal L})$
with compact
$(G, {\mathbb R}^d \times {\mathbb Z}^m \times \mathbb K, {\mathcal L})$
with compact
![]() $\mathbb K$
and a compact
$\mathbb K$
and a compact
![]() $W \subseteq {\mathbb R}^d \times {\mathbb Z}^m \times \mathbb K$
such that
$W \subseteq {\mathbb R}^d \times {\mathbb Z}^m \times \mathbb K$
such that
By eventually enlarging W, we can assume without loss of generality that
for compact
![]() $W_0 \subseteq {\mathbb R}^d$
and finite
$W_0 \subseteq {\mathbb R}^d$
and finite
![]() $F \subseteq {\mathbb Z}^m$
.
$F \subseteq {\mathbb Z}^m$
.
Set
![]() $H_0={\mathbb Z}^m \times \mathbb K$
. It is easy to see that we can find function
$H_0={\mathbb Z}^m \times \mathbb K$
. It is easy to see that we can find function
![]() $\varphi \in C_{\mathsf {c}}^{\infty }({\mathbb R}^d)\cap K_2({\mathbb R}^d)$
and
$\varphi \in C_{\mathsf {c}}^{\infty }({\mathbb R}^d)\cap K_2({\mathbb R}^d)$
and
![]() $\psi \in K_2(H_0)$
with the following properties:
$\psi \in K_2(H_0)$
with the following properties:
-
•
 $\phi := \varphi \otimes \psi \equiv 1$
on W.
$\phi := \varphi \otimes \psi \equiv 1$
on W. -
•
 $\widehat {\psi } \in C_{\mathsf {c}}(\widehat {H_0})$
.
$\widehat {\psi } \in C_{\mathsf {c}}(\widehat {H_0})$
.
It follows that
is a strongly admissible function of
![]() $\widehat {H} ={\mathbb R}^d \times \widehat {H_0}$
.
$\widehat {H} ={\mathbb R}^d \times \widehat {H_0}$
.
Next, define
![]() $\eta :=\mathbb {L}_{G, {\mathbb R}^d \times H,{\mathcal L}, W}(\gamma )$
. Then, by Theorem 4.1,
$\eta :=\mathbb {L}_{G, {\mathbb R}^d \times H,{\mathcal L}, W}(\gamma )$
. Then, by Theorem 4.1,
![]() $\eta $
is Fourier transformable. Moreover, since
$\eta $
is Fourier transformable. Moreover, since
![]() $\mbox {supp}(\eta ) \subseteq {\mathcal L}$
, the measure
$\mbox {supp}(\eta ) \subseteq {\mathcal L}$
, the measure
![]() $\rho =\widehat {\eta }$
is
$\rho =\widehat {\eta }$
is
![]() ${\mathcal L}^0$
-periodic by [Reference de Lamadrid and Argabright10, Proposition 6.1]. Finally, (4.1) gives
${\mathcal L}^0$
-periodic by [Reference de Lamadrid and Argabright10, Proposition 6.1]. Finally, (4.1) gives
Fact 5.2 then gives the following result.
Corollary 5.3 ([Reference Strungaru47, Theorem 7.1])
Let
![]() $\gamma $
be a measure with weak Meyer set support. Then,
$\gamma $
be a measure with weak Meyer set support. Then,
![]() $\widehat {\gamma }$
is norm almost periodic.
$\widehat {\gamma }$
is norm almost periodic.
5.3 Generalized Eberlein decomposition
In this subsection, we show a pseudo-compatibility of the mapping
![]() $\rho \to (\rho )_f$
of (5.3), for
$\rho \to (\rho )_f$
of (5.3), for
![]() ${\mathcal L}$
periodic
${\mathcal L}$
periodic
![]() $\rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
and strongly admissible f, with respect to the Lebesgue decomposition. We explain this, as well as our meaning of “pseudo-compatibility” below.
$\rho \in {\mathcal M}_{{\mathcal L}}(G \times H)$
and strongly admissible f, with respect to the Lebesgue decomposition. We explain this, as well as our meaning of “pseudo-compatibility” below.
First, it is easy to see that the map satisfies:
-
• if
 $\rho $
is pure point, then
$\rho $
is pure point, then
 $(\rho )_f$
is pure point;
$(\rho )_f$
is pure point; -
• if
 $\rho $
is absolutely continuous, then
$\rho $
is absolutely continuous, then
 $(\rho )_f$
is absolutely continuous;
$(\rho )_f$
is absolutely continuous; -
• if
 $\rho $
is singular continuous, then
$\rho $
is singular continuous, then
 $(\rho )_f$
can have all three spectral components;
$(\rho )_f$
can have all three spectral components;
and hence does not preserves the Lebesgue decomposition. On another hand, for each
![]() $\alpha \in \{\mathsf {pp}, \mathsf {ac}, \mathsf {sc}\}$
, one can defined an operator
$\alpha \in \{\mathsf {pp}, \mathsf {ac}, \mathsf {sc}\}$
, one can defined an operator
![]() $P_{\alpha }$
on the space
$P_{\alpha }$
on the space
![]() ${\mathcal M}_{{\mathcal L}}^{\infty }(G \times H)$
with the property that for all strongly admissible f and all
${\mathcal M}_{{\mathcal L}}^{\infty }(G \times H)$
with the property that for all strongly admissible f and all
![]() $\rho \in {\mathcal M}_{{\mathcal L}}^{\infty }(G \times H)$
, we have
$\rho \in {\mathcal M}_{{\mathcal L}}^{\infty }(G \times H)$
, we have
This can be done simply by first showing that
 $$\begin{align*}L_{\alpha}(\sum_{j=1}^m c_j \psi_j \otimes \phi_j) := \sum_{j=1}^m c_j \left( \rho_{\phi_j} \right)_{\alpha}(\psi_j) \end{align*}$$
$$\begin{align*}L_{\alpha}(\sum_{j=1}^m c_j \psi_j \otimes \phi_j) := \sum_{j=1}^m c_j \left( \rho_{\phi_j} \right)_{\alpha}(\psi_j) \end{align*}$$
for all
![]() $c_1,\ldots ,c_m \in {\mathbb C}, \psi _1,\ldots , \psi _m \in C_{\mathsf {c}}(\widehat {G}), \phi _1,\ldots , \phi _m \in C_{\mathsf {c}}(\widehat {H})$
is well defined, linear, and continuous with respect to the inductive topology. Therefore,
$c_1,\ldots ,c_m \in {\mathbb C}, \psi _1,\ldots , \psi _m \in C_{\mathsf {c}}(\widehat {G}), \phi _1,\ldots , \phi _m \in C_{\mathsf {c}}(\widehat {H})$
is well defined, linear, and continuous with respect to the inductive topology. Therefore,
![]() $L_{\alpha }$
can be uniquely extended to a measure
$L_{\alpha }$
can be uniquely extended to a measure
![]() $P_{\alpha } (\rho )$
, which is
$P_{\alpha } (\rho )$
, which is
![]() ${\mathcal L}$
invariant and satisfies (5.3).
${\mathcal L}$
invariant and satisfies (5.3).
Now, exactly as above, let
![]() $\gamma $
be a Fourier transformable measure supported inside a Meyer set
$\gamma $
be a Fourier transformable measure supported inside a Meyer set
![]() $\Lambda $
, and let
$\Lambda $
, and let
![]() $(G,H, {\mathcal L}), \eta , \varphi , \phi , \psi $
be as in Section 5.2. Let f be as in (5.1), and let
$(G,H, {\mathcal L}), \eta , \varphi , \phi , \psi $
be as in Section 5.2. Let f be as in (5.1), and let
![]() $\rho = \widehat {\eta }$
.
$\rho = \widehat {\eta }$
.
Then, for each
![]() $\alpha \in \{\mathsf {pp}, \mathsf {ac}, \mathsf {sc}\}$
, the measure
$\alpha \in \{\mathsf {pp}, \mathsf {ac}, \mathsf {sc}\}$
, the measure
![]() $P_{\alpha } (\rho )$
is the Fourier transform of some measure
$P_{\alpha } (\rho )$
is the Fourier transform of some measure
![]() $\mu $
supported on
$\mu $
supported on
![]() ${\mathcal L}^0$
[Reference Richard and Strungaru36].
${\mathcal L}^0$
[Reference Richard and Strungaru36].
Define
Then,
![]() $\mbox {supp}(\nu ) \subseteq {\LARGE \curlywedge }(\mbox {supp}(\phi ))$
and, exactly as in the proof of Theorem 4.1, we get
$\mbox {supp}(\nu ) \subseteq {\LARGE \curlywedge }(\mbox {supp}(\phi ))$
and, exactly as in the proof of Theorem 4.1, we get
Therefore, we get the following corollary.
Corollary 5.4 ([Reference Strungaru47, Theorem 4.1])
Let
![]() $\gamma $
be a Fourier transformable measure supported inside a Meyer set
$\gamma $
be a Fourier transformable measure supported inside a Meyer set
![]() $\Lambda $
. Then, there exist a model set
$\Lambda $
. Then, there exist a model set
![]() $\Gamma \supseteq \Lambda $
and three Fourier transformable measures
$\Gamma \supseteq \Lambda $
and three Fourier transformable measures
![]() $\gamma _{\mathsf {s}},\gamma _{\mathsf {0s}}, \gamma _{\mathsf {0a}}$
supported inside
$\gamma _{\mathsf {s}},\gamma _{\mathsf {0s}}, \gamma _{\mathsf {0a}}$
supported inside
![]() $\Gamma $
such that
$\Gamma $
such that

5.4 Discussion
We have seen in this section that the Fourier transform of a measure
![]() $\gamma $
with weak Meyer set support can be describe via (5.2) as the projection in the dual CPS of a
$\gamma $
with weak Meyer set support can be describe via (5.2) as the projection in the dual CPS of a
![]() ${\mathcal L}^0$
-periodic measure via a strongly admissible function. We used this result to (re)derive properties of
${\mathcal L}^0$
-periodic measure via a strongly admissible function. We used this result to (re)derive properties of
![]() $\widehat {\gamma }$
, and we expect that this connection will lead to some new applications in the future. Indeed, while now we know quite a few properties of the Fourier transform of measures with weak Meyer set support [Reference Aujogue2, Reference Strungaru43–Reference Strungaru49], we know much more about fully periodic measures in LCAG (see, for example, [Reference Richard and Strungaru36]). Moreover, the strong admissibility of f is likely to transfer many properties from
$\widehat {\gamma }$
, and we expect that this connection will lead to some new applications in the future. Indeed, while now we know quite a few properties of the Fourier transform of measures with weak Meyer set support [Reference Aujogue2, Reference Strungaru43–Reference Strungaru49], we know much more about fully periodic measures in LCAG (see, for example, [Reference Richard and Strungaru36]). Moreover, the strong admissibility of f is likely to transfer many properties from
![]() $\rho $
to
$\rho $
to
![]() $\rho _f$
. It is also worth pointing out that, while the strong admissibility of f was sufficient to derive the conclusions in this section, in fact f can be chosen of the form
$\rho _f$
. It is also worth pointing out that, while the strong admissibility of f was sufficient to derive the conclusions in this section, in fact f can be chosen of the form
where
![]() $g =\hat {\varphi } \in {\mathcal S}({\mathbb R}^d)$
is the Fourier transform of some
$g =\hat {\varphi } \in {\mathcal S}({\mathbb R}^d)$
is the Fourier transform of some
![]() $\varphi \in C_{\mathsf {c}}^{\infty }({\mathbb R}^d)$
; P is a trigonometric polynomial, that is, a sum of characters, that is,
$\varphi \in C_{\mathsf {c}}^{\infty }({\mathbb R}^d)$
; P is a trigonometric polynomial, that is, a sum of characters, that is,
![]() $P= \sum _{j=1}^m \chi _j$
for some
$P= \sum _{j=1}^m \chi _j$
for some
![]() $\chi _1,\ldots , \chi _j \in \widehat {\mathbb T^m}$
and
$\chi _1,\ldots , \chi _j \in \widehat {\mathbb T^m}$
and
![]() $\psi \in C_{\mathsf {c}}(\widehat {\mathbb K})$
is the characteristic function of
$\psi \in C_{\mathsf {c}}(\widehat {\mathbb K})$
is the characteristic function of
![]() $\{ 0 \}$
. These properties are much stronger than strong admissibility, and have the potential to lead to nice applications in the future.
$\{ 0 \}$
. These properties are much stronger than strong admissibility, and have the potential to lead to nice applications in the future.
Acknowledgment
We are grateful to Michael Baake and Christoph Richard for many insightful discussions which inspired this manuscript. We would like to thank the two anonymous referees for some suggestions that improved the quality of this manuscript.