Hostname: page-component-5c6d5d7d68-pkt8n Total loading time: 0 Render date: 2024-08-09T22:32:53.523Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Dirichlet Convolutions

Published online by Cambridge University Press:  20 November 2018

S. L. Segal
S. L. Segal*
Affiliation:
University of Rochester
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [3] Rubel proved that if h(n) is an arithmetic function such that 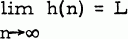, L finite, then 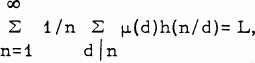where μ(n) is the Mobius function. This result was extended to functions other than μ(n) in [4]; however, (as first pointed out to the author by Benjamin Volk), the order condition imposed there is unnecessary; in fact, utilizing the result of [3], the following slightly more general theorem has an almost trivial proof.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 4 , October 1966 , pp. 457 - 462
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Landau, E., Handbuch der Lehre von der Verteilung der Primzahlen, reprinted with an appendix by Paul Bateman, Chelsea, (1953).Google Scholar
2. Prachar, K., Primzahlverteilung. Springer, Berlin, (1957)Google Scholar
3. Rubel, L.A., An Abelian Theorem for Number-Theoretic Sums. Acta Arith. 6, (1960) pages 175-177, correction Acta Arith. 6, (1961), page 523.Google Scholar
4. Segal, S. L., Dirichlet convolutions and the Silvèrman- Toeplitz conditions. Acta Arith. 10, (1964), pages 287-291.Google Scholar
5. Segal, S. L., On Ingham's Summation Method. Can. Journ. Math. 18, (1966), pages 97-105.Google Scholar
6. Segal, S. L., Summability by Dirichlet Convolutions. Submitted for publication.Google Scholar
7. Titchmarsh, E. C., The Theory of the Riemann Zeta- Function. Oxford, (1951).Google Scholar