In 2005, N. Nikolski proved among other things that for any 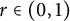$r\in (0,1)$ and any 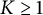$K\geq 1$, the condition number 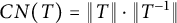$CN(T)=\Vert T\Vert \cdot \Vert T^{-1}\Vert $ of any invertible n-dimensional complex Banach space operators T satisfying the Kreiss condition, with spectrum contained in 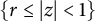$\left \{ r\leq |z|<1\right \}$, satisfies the inequality 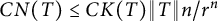$CN(T)\leq CK(T)\Vert T \Vert n/r^{n}$ where 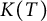$K(T)$ denotes the Kreiss constant of T and 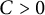$C>0$ is an absolute constant. He also proved that for 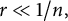$r\ll 1/n,$ the latter bound is asymptotically sharp as 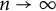$n\rightarrow \infty $. In this note, we prove that this bound is actually achieved by a family of explicit 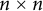$n\times n$ Toeplitz matrices with arbitrary singleton spectrum 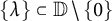$\{\lambda \}\subset \mathbb {D}\setminus \{0\}$ and uniformly bounded Kreiss constant. Independently, we exhibit a sequence of Jordan blocks with Kreiss constants tending to 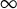$\infty $ showing that Nikolski’s inequality is still asymptotically sharp as K and n go to $\infty $.