Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-11T07:38:26.246Z Has data issue: false hasContentIssue false
  • English
  • Français

Ordering the Representations of 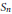${{S}_{n}}$ Using the Interchange Process

Published online by Cambridge University Press:  20 November 2018

Gil Alon  and
Gady Kozma
Gil Alon
Affiliation:
Division of Mathematics, The Open University of Israel, Raanana 43107, Israel e-mail: gilal@openu.ac.il
Gady Kozma
Affiliation:
Department of Mathematics, Weizmann Institute of Science, Rehovot 76100, Israel e-mail: gadyk@weizmann.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Inspired by Aldous' conjecture for the spectral gap of the interchange process and its recent resolution by Caputo, Liggett, and Richthammer, we define an associated order 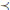$\prec $ on the irreducible representations of 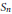${{S}_{n}}$. Aldous' conjecture is equivalent to certain representations being comparable in this order, and hence determining the “Aldous order” completely is a generalized question. We show a few additional entries for this order.

Keywords

82C2260B1543A6520B3060J2760K35Aldous' conjectureinterchange processsymmetric grouprepresentations
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 1 , 01 March 2013 , pp. 13 - 30
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Alon, G. and Kozma, G., The probability of long cycles in the interchange processes. Preprint (2010). arxiv:1009:3723v2 Google Scholar
[2] Bacher, R., Valeur propre minimale du laplacien de Coxeter pour le groupe sym´etrique. J. Algebra 167 (1994), no. 2, 460–472. http://dx.doi.org/10.1006/jabr.1994.1195 Google Scholar
[3] Caputo, P., T. M. Liggett, and Richthammer, T., Proof of Aldous’ spectral gap conjecture. J. Amer. Math. Soc. 23 (2010), no. 3, 831–851. http://dx.doi.org/10.1090/S0894-0347-10-00659-4 Google Scholar
[4] Cesi, F., On the eigenvalues of Cayley graphs on the symmetric group generated by a complete multipartite set of transpositions. J. Algebraic Combin. 32 (2010), no. 2, 155–185. http://dx.doi.org/10.1007/s10801-009-0208-x Google Scholar
[5] Diaconis, P. and Shahshahani, M., Generating a random permutation with random transpositions. Z.Wahrsch. Verw. Gebiete 57 (1981), no. 2, 159–179. http://dx.doi.org/10.1007/BF00535487 Google Scholar
[6] Dieker, A. B., Interlacings for random walks on weighted graphs and the interchange process. SIAM J. Discrete Math. 24 (2010), no. 1, 191–206. http://dx.doi.org/10.1137/090775361 Google Scholar
[7] Fulton, W. and Harris, J., Representation Theory. A First Course. Graduate Texts in Mathematics 129. Springer-Verlag, New York, 1991.Google Scholar
[8] D. M. Goldschmidt, Group Characters, Symmetric Functions, and the Hecke Algebra. University Lecture Series 4. American Mathematical Society, Providence, RI, 1993.Google Scholar
[9] Handjani, S. and Jungreis, D., Rate of convergence for shuffling cards by transpositions. J. Theoret. Probab. 9 (1996), no. 4, 983–993. http://dx.doi.org/10.1007/BF02214260 Google Scholar
[10] James, G. and Kerber, A., The representation theory of the symmetric group.. Encyclopedia of Mathematics and its Applications 16. Addison-Wesley, Reading, MA, 1981.Google Scholar
[11] Molev, A. I., Gelfand-Tsetlin bases for classical Lie algebras. In: Handbook of Algebra. Vol. 4, Elsevier/North-Holland, Amsterdam, 2006, pp. 109–170.Google Scholar
[12] Morris, B., Spectral gap for the interchange process in a box. Electron. Commun. Probab. 13 (2008), 311–318.Google Scholar
[13] Okounkov, A. and Vershik, A., A new approach to representation theory of symmetric groups. Selecta Math. 2 (1996), no. 4, 581–605. http://dx.doi.org/10.1007/BF02433451 Google Scholar
[14] Sagan, , The Symmetric Group. Representations, Combinatorial Algorithms, and Symmetric Functions. Second edition. Graduate Texts in Mathematics 203. Springer-Verlag, New York, 2001.Google Scholar
[15] Starr, S. and Conomos, M., Asymptotics of the Spectral Gap for the Interchange Process on Large Hypercubes. Preprint (2008). arxiv:0802.1368 Google Scholar