Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-28T10:36:23.344Z Has data issue: false hasContentIssue false
  • English
  • Français

Product Ranks of the 3 × 3 Determinant and Permanent

Published online by Cambridge University Press:  20 November 2018

Nathan Ilten  and
Zach Teitler
Nathan Ilten
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, BC V5A156, Canada e-mail: nilten@sfu.ca
Zach Teitler
Affiliation:
Department of Mathematics, Boise State University, 1910 University Drive, Boise, ID 83725-1555, USA e-mail: zteitler@boisestate.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

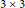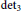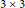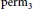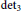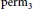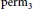We show that the product rank of the $3\,\times \,3$ determinant ${{\det }_{3}}$ is $5$ , and the product rank of the $3\,\times \,3$ permanent $\text{per}{{\text{m}}_{3}}$ is $4$ . As a corollary, we obtain that the tensor rank of ${{\det }_{3}}$ is $5$ and the tensor rank of $\text{per}{{\text{m}}_{3}}$ is $4$ . We show moreover that the border product rank of $\text{per}{{\text{m}}_{3}}$ is larger than $n$ for any 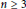$n\,\ge \,3$ .

Keywords

15A2115A6914M1214N15product ranktensor rankdeterminantpermanentFano schemes
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 311 - 319
Copyright
Copyright © Canadian Mathematical Society 2016

References

[Abol4] Abo, Hirotachi, Varieties of completely decomposable forms and their secants. J. Algebra 403(2014), 135–153. MR3166068 http://dx.doi.org/10.1016/j.jalgebra.2013.12.027 Google Scholar
[BH13] Bremner, Murray R. and Hu, Jiaxiong, On Kruskal's theorem that every 3x3x3 array has rank at most 5. Linear Algebra Appl. 439(2013), no. 2, 401–421. MR 3089693 http://dx.doi.org/10.1016/j.laa.2013.03.021 Google Scholar
[CGLM08] Comon, Pierre, Golub, Gene, Lim, Lek-Heng, and Mourrain, Bernard, Symmetric tensors and symmetric tensor rank. SIAM J. Matrix Anal. Appl. 30(2008), no. 3,1254-1279. MR 2447451 (2009i:15039) http://dx.doi.org/10.1137/060661569 Google Scholar
[CI15] Chan, Melody and Ilten, Nathan, Fano schemes of determinants and permanents. Algebra Number Theory 9(2015), no. 3, 629–679. MR 3340547 http://dx.doi.org/10.2140/ant.2015.9.629 Google Scholar
[Derl3] Derksen, Harm, On the nuclear norm and the singular value decomposition of tensors. arXiv:1308.3860[math.OC], Aug 2013.Google Scholar
[DT15] Derksen, Harm and Teitler, Zach, Lower bound for ranks of invariant forms. J. Pure Appl. Algebra 219(2015), no. 12, 5429–5441.http://dx.doi.org/10.1016/j.jpaa.2015.05.025 Google Scholar
[EHOO] Eisenbud, David and Harris, Joe, The geometry of schemes.Graduate Texts in Mathematics, 197, Springer-Verlag, New York, 2000. MR 1730819 (2001d:14002).Google Scholar
[GlylO] Glynn, David G., The permanent of a square matrix. European J. Combin. 31(2010), no. 7, 1887–1891. MR 2673027 (2011h:15010) http://dx.doi.org/10.1016/j.ejc.2O10.01.010 Google Scholar
[Gro64] Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. I, Inst. Hautes Études Sci. Publ. Math.20 (1964), p. 5–259. MR 0173675 (30 #3885).Google Scholar
[GS] Grayson, Daniel R. and Stillman, Michael E., Macaulayl, a software system for research in algebraic geometry. Available at http://www.math.uiuc.edu/Macaulay2/.Google Scholar
[Iltl4] Ilten, Nathan, Fano schemes of lines on toric surfaces. arXiv:1411.302 5[math.AG], 2014.Google Scholar
[KB09] Kolda, Tamara G. and Bader, Brett W., Tensor decompositions and applications. SIAM Rev. 51 (2009), no. 3, 455–500. MR 2535056 (2010j:15027) http://dx.doi.org/10.1137/07070111X Google Scholar
[Lanl2] Landsberg, J. M., Tensors: geometry and applications. Graduate Studies in Mathematics, 128, American Mathematical Society, Providence, RI, 2012. MR 2865915Google Scholar
[Lanl4] Landsberg, J. M., Geometric complexity theory: an introduction for geometers. Ann. Univ. Ferrara Sez. VII Sci. Mat. 61(2015), no. 1, 65–117. http://dx.doi.org/10.1007/s11565-014-0202-7 Google Scholar
[RS11] Ranestad, Kristian and Schreyer, Frank-Olaf, On the rank of a symmetric form. J. Algebra 346(2011), 340–342. MR 2842085 http://dx.doi.org/10.1016/j.jalgebra.2O11.07.032 Google Scholar
[Rys63] John Ryser, Herbert, Combinatorial mathematics. The Carus Mathematical Monographs, No. 14, The Mathematical Association of America J. Wiley, New York, 1963. MR 0150048 (27 #51)Google Scholar
[Shal5] Shafiei, SepidehMasoumeh, Apolarity for determinants and permanents of generic matrices. J. Commut. Algebra 7 (2015), no. 1, 89–123. MR 3316987 http://dx.doi.org/10.1216/JCA-2015-7-1-89 Google Scholar