Hostname: page-component-7479d7b7d-qs9v7 Total loading time: 0 Render date: 2024-07-13T16:09:22.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Remark on Zero Sets of Holomorphic Functions in Convex Domains of Finite Type

Published online by Cambridge University Press:  20 November 2018

Michał Jasiczak
Michał Jasiczak*
Affiliation:
Faculty of Mathematics and Computer Science, A. Mickiewicz University, 61-614 Poznan, Poland, and , Institute of Mathematics, Polish Academy of Sciences, 00-956 Warsaw, Poland e-mail: mjk@amu.edu.pl Institute of Mathematics, Polish Academy of Sciences, 00-956 Warsaw, Poland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that if the 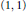$\left( 1,\,1 \right)$-current of integration on an analytic subvariety 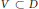$V\,\subset \,D$ satisfies the uniform Blaschke condition, then 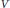$V$ is the zero set of a holomorphic function 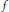$f$ such that 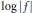$\log \,\left| f \right|$ is a function of bounded mean oscillation in 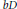$bD$. The domain 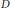$D$ is assumed to be smoothly bounded and of finite d’Angelo type. The proof amounts to non-isotropic estimates for a solution to the 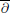$\overline{\partial }$-equation for Carleson measures.

Keywords

32A6032A3532F18
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 2 , 01 June 2010 , pp. 311 - 320
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Andersson, M. and Carlsson, H., Formulas for approximate solutions of th ∂-equation in a strictly pseudoconvex domain. Rev. Mat. Iberoamericana 11(1995), no. 1, 67–101.Google Scholar
[2] Berndtsson, B. and Andersson, M., Henkin–Ramirez formulas with weight factors. Ann. Inst. Fourier (Grenoble) 32(1982), no. 3, 91–110.Google Scholar
[3] Bruna, J., Charpentier, P., and Dupain, Y., Zero varieties for the Nevanlinna class in convex domains of finite type in ℂn . Ann. of Math. 147(1998), no. 2, 391–415. doi:10.2307/121013Google Scholar
[4] Bruna, J. and Grellier, S., Zero sets of functions in convex domains of strict finite type. Complex Variables Theory Appl. 38(1999), no. 3, 243–261.Google Scholar
[5] Christ, M., Lectures on singular integral operators. CBMS Regional Conference Series in Mathematics 77. American Mathematical Society, Providence, RI, 1990.Google Scholar
[6] Cumenge, A., Zero sets of functions in the Nevanlinna or the Nevanlinna-Djrbachian classes. Pacific J. Math. 199(2001), no. 1, 79–92. doi:10.2140/pjm.2001.199.79Google Scholar
[7] Diederich, K. and Fornaess, J. E., Support functions for convex domains of finite type. Math. Z. 230(1999), no. 1, 145–164. doi:10.1007/PL00004683Google Scholar
[8] Diederich, K. and Mazzilli, E., Zero varieties for the Nevanlinna class on all convex domains of finite type. Nagoya Math. J. 163(2001), 215–227.Google Scholar
[9] Fischer, B., Lp estimates on convex domains of finite type. Math. Z. 236(2001), no. 2, 401–418. doi:10.1007/PL00004836Google Scholar
[10] Fischer, B., Nonisotropic Hölder estimates on convex domains of finite type. Michigan Math. J. 52(2004), no. 1, 219–239 doi:10.1307/mmj/1080837745Google Scholar
[11] Henkin, G. M., H. Lewy's equation and analysis on pseudoconvex manifolds. Uspehi Mat. Nauk 32(1977), 57–118, 247.Google Scholar
[12] McNeal, J., Convex domains of finite type. J. Funct. Anal. 108(1992), 361–373. doi:10.1016/0022-1236(92)90029-IGoogle Scholar
[13] McNeal, J., Estimates on the Bergman kernels of convex domains. Adv. Math. 109(1994), no. 1, 108–139. doi:10.1006/aima.1994.1082Google Scholar
[14] Skoda, H., Valeurs au bord pour les solutions de l’opérateur d′′, et charactérisation des zéros des fonctions de la classe de Nevanlinna. Bull. Soc. Math. France 104(1976), no. 3, 225–299.Google Scholar
[15] Varopoulos, N., BMO functions and the -equation. Pacific J. Math. 71(1977), no. 1, 221–273.Google Scholar
[16] Varopoulos, N., Zeros of Hp functions in several complex variables. Pacific J. Math. 88(1980), no. 1, 189–246.Google Scholar