Hostname: page-component-77c89778f8-swr86 Total loading time: 0 Render date: 2024-07-17T16:55:15.581Z Has data issue: false hasContentIssue false
  • English
  • Français

A SAGBI Basis For 𝔽[V2 ⊕ V2 ⊕ V3]Cp

Published online by Cambridge University Press:  20 November 2018

Alexander Duncan ,
Michael LeBlanc  and
David L.Wehlau
Alexander Duncan
Affiliation:
Department of Mathematics, The University of British Columbia, Vancouver, B.C., V6T 1Z2 e-mail: duncan@math.ubc.camleblanc@math.ubc.ca
Michael LeBlanc
Affiliation:
Department of Mathematics, The University of British Columbia, Vancouver, B.C., V6T 1Z2 e-mail: duncan@math.ubc.camleblanc@math.ubc.ca
David L.Wehlau
Affiliation:
Department of Mathematics & Computer Science, Royal Military College, Kingston, Ontario, K7K 7B4 e-mail: wehlau@rmc.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 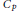${{C}_{p}}$ denote the cyclic group of order 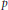$p$, where 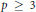$p\,\ge \,3$ is prime. We denote by 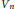${{V}_{n}}$ the indecomposable $n$ dimensional representation of 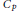${{C}_{p}}$ over a field $\mathbb{F}$ of characteristic 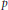$p$. We compute a set of generators, in fact a SAGBI basis, for the ring of invariants 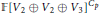$\mathbb{F}{{\left[ {{V}_{2}}\,\oplus \,{{V}_{2}}\,\oplus \,{{V}_{3}} \right]}^{{{C}_{p}}}}$.

Keywords

13A50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 1 , 01 March 2009 , pp. 72 - 83
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Bosma, W., Cannon, J., and Playoust, C., The Magma algebra system I. The user language. J. Symbolic Comput. 24(1997), no. 3–4, 235–265.Google Scholar
[2] Campbell, H. E. A., Fodden, B., and Wehlau, D. L., Invariants of the diagonal Cp-action on V 3 . J. Algebra 303(2006), no. 2, 501–513. Also see the appendix with additional details contained in the online version of this paper at the Journal of Algebra web site. Google Scholar
[3] Campbell, H. E. A. and Hughes, I. P., Vector invariants of U 2 (F p ): A proof of a conjecture of Richman. Adv. Math. 126(1997), no. 1, 1–20.Google Scholar
[4] Cox, D., Little, J., and O’Shea, D., Ideals, varieties, and algorithms. An introduction to computational algebraic geometry and commutative algebra. Undergraduate Texts in Mathematics, Springer-Verlag, New York, 1992.Google Scholar
[5] Dickson, L. E. J., On invariants and the theory of numbers. Dover Publications, Inc., New York, 1966.Google Scholar
[6] Hughes, I. and Kemper, G., Symmetric powers of modular representations, Hilbert series and degree bounds. Comm. Algebra 28(2000), no. 4, 2059–2088.Google Scholar
[7] Kapur, D. and Madlener, K., A completion procedure for computing a canonical basis of a k-subalgebra. Computers and Mathematics, Springer, New York, 1989, pp. 1–11.Google Scholar
[8] Miller, E. and Sturmfels, B., Monomial Ideals and Planar Graphs. In: Applied algebra, algebraic algorithms and error-correcting codes, Lecture Notes in Comput. Sci. 1719, Springer, Berlin, 1999, pp. 19–28.Google Scholar
[9] Richman, D., On vector invariants over finite fields. Adv. Math. 81(1990), no. 1, 30–65.Google Scholar
[10] Robbiano, L. and Sweedler, M., Subalgebra bases, In: Commutative algebra, Lecture Notes in Math. 1430, Springer, Berlin, 1990, pp. 61–87.Google Scholar
[11] Shank, R. J., S.A.G.B.I. bases for rings of formal modular seminvariants. Comment. Math. Helv. 73(1998), no. 4, 548–565.Google Scholar
[12] Shank, R. J., Classical Covariants and Modular Invariants. In: Invariant Theory in All Characteristics, CRM Proc. Lecture Notes 35, Amer. Math. Soc., Providence, RI, 2004, pp. 241–249.Google Scholar
[13] Shank, R. J. and Wehlau, D. L., Noether numbers for subrepresentations of cyclic groups of prime order. Bull. London Math. Soc. 34(2002), no. 4, 438–450.Google Scholar
[14] Sturmfels, B., Gröbner bases and convex polytopes, University Lecture Series 8, American Mathematical Society, Providence, RI, 1996.Google Scholar