Hostname: page-component-77c89778f8-gq7q9 Total loading time: 0 Render date: 2024-07-22T21:29:10.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong Extensions vs. Weak Extensions of C*-Algebras

Published online by Cambridge University Press:  20 November 2018

S. J. Cho
S. J. Cho*
Affiliation:
Dalhousde University, Halifax, Nova Scotia B3H 3J5
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 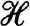be a separable complex infinite dimensional Hilbert space, 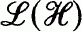the algebra of bounded operators in 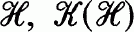the ideal of compact operators, and 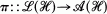the quotient map. Throughout this paper A denotes a separable nuclear C*-algebra with unit. An extension of A is a unital *-monomorphism of A into 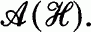. Two extensions τ1 and τ2 are strongly (weakly) equivalent if there exists a unitary (Fredholm partial isometry) U in 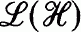such that

for all a in A.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 21 , Issue 2 , 01 June 1978 , pp. 143 - 147
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Brown, L. G., Douglas, R. G. and Fillmore, P. A., Extensions of C*-algebras, operators with compact self-commutators, and K-homology, Bull. Amer. Math. Soc. 79 (1973), 973-978 Google Scholar
1.2.Brown, L. G., Douglas, R. G. and Fillmore, P. A., Unitary equivalence modulo the compact operators and extensions of C*-algebras, in Proceedings of a Conference on Operator Theory, Lecture Notes in Mathematics, 345, Springer-Verlag, 1973. 58-128.Google Scholar
3. Brown, L. G., Douglas, R. G. and Fillmore, P. A., Extensions of C*-algebras and K-theory, Annals of Mathematics, Vol. 105 (1977), 265-324.Google Scholar
4. Choi, M. D. and Effros, E. G., The completely positive lifting problem Annals of Math., Vol. 104 (1976) 585-609.Google Scholar
5. Pimsner, M. and Popa, S., On the Ext-group of U.H.F.-algebras and a Theorem of Glimm, preprint.Google Scholar
6. Thayer, F. J., Obstructions to lifting *-morphisms into the Calkin algebra, 111, J. of Math., Vol. 20 (1976) no. 2, 322-328.Google Scholar
7. Voiculescu, D., A non commutative Weyl-von Newmann theorem, Rev. Roum. Math. Pures et Appl., Tome XXI, No. 1 (1976), 97-113.Google Scholar