Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-07-06T05:03:10.803Z Has data issue: false hasContentIssue false
  • English
  • Français

Towards the Full Mordell–Lang Conjecture for Drinfeld Modules

Published online by Cambridge University Press:  20 November 2018

Dragos Ghioca
Dragos Ghioca*
Affiliation:
Department of Mathematics and Computer Science, University of Lethbridge, Lethbridge, AB T1K 3M4 e-mail: dragos.ghioca@uleth.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 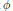$\phi$ be a Drinfeld module of generic characteristic, and let 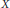$X$ be a sufficiently generic affine subvariety of 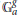$\mathbb{G}_{a}^{g}$. We show that the intersection of 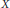$X$ with a finite rank 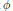$\phi$-submodule of 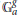$\mathbb{G}_{a}^{g}$ is finite.

Keywords

11G0911G10Drinfeld moduleMordell–Lang conjecture
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 1 , 01 March 2010 , pp. 95 - 101
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Baker, A., Transcendental Number Theory. Cambridge University Press, London, 1975.Google Scholar
[2] Bosser, V., Minorations de formes linéaires de logarithmes pour les modules de Drinfeld. J. Number Theory 75(1999), no. 2, 279–323. doi:10.1006/jnth.1998.2336Google Scholar
[3] Breuer, F., The André-Oort conjecture for products of Drinfeld modular curves. J. Reine Angew. Math. 579(2005), 115–144.Google Scholar
[4] David, S., Minorations de formes linéaires de logarithmes elliptiques. Mém. Soc. Math. France (N.S.) (1995), no. 65.Google Scholar
[5] Denis, L., Hauteurs canoniques et modules de Drinfeld. Math. Ann. 294(1992), no. 2, 213–223. doi:10.1007/BF01934322Google Scholar
[6] Denis, L., Géométrie diophantienne sur les modules de Drinfel’d. In: The Arithmetic of Function Fields. Ohio State Univ. Math. Res. Inst. Publ. 2, de Gruyter, Berlin, 1992, pp. 285–302.Google Scholar
[7] Edixhoven, B. and Yafaev, A., Subvarieties of Shimura type. Ann. of Math. 157(2003), no. 2, 621–645. doi:10.4007/annals.2003.157.621Google Scholar
[8] Faltings, G., The general case of S. Lang's conjecture. In: Barsotti Symposium in Algebraic Geometry. Perspect. Math. 15, Academic Press, San Diego, CA, 1994, pp. 175–182.Google Scholar
[9] Ghioca, D., The Mordell–Lang Theorem for Drinfeld modules. Int. Math. Res. Not. 53(2005), 3273–3307.Google Scholar
[10] Ghioca, D., Equidistribution for torsion points of a Drinfeld module. Math. Ann. 336(2006), 841–865. doi:10.1007/s00208-006-0017-7Google Scholar
[11] Ghioca, D., The Lehmer inequality and the Mordell–Weil theorem for Drinfeld modules. J. Number Theory 122(2007), 37–68. doi:10.1016/j.jnt.2006.03.004Google Scholar
[12] Ghioca, D. and Moosa, R., Division points on subvarieties of isotrivial semiabelian varieties. Int. Math. Res. Not. 2006(2006), Article ID 65437.Google Scholar
[13] Ghioca, D. and Tucker, T., Siegel's Theorem for Drinfeld modules. Math. Ann. 339(2007), no. 1, 37–60. doi:10.1007/s00208-007-0105-3Google Scholar
[14] Ghioca, D. and Tucker, T., Equidistribution and integral points for Drinfeld modules. Trans. Amer. Math. Soc. 360(2008), no. 9, 4863–4887. doi:10.1090/S0002-9947-08-04508-XGoogle Scholar
[15] Ghioca, D. and Tucker, T., A dynamical version of the Mordell–Lang conjecture for the additive group. Compositio Math. 144(2008), no. 2, 304–316.Google Scholar
[16] Goss, D., Basic structures of function field arithmetic. Ergebnisse der Mathematik und ihrer Grenzgebiete 35, Springer-Verlag, Berlin, 1996.Google Scholar
[17] Hrushovski, E., The Mordell–Lang conjecture for function fields. J. Amer. Math. Soc. 9(1996), no. 3, 667–690. doi:10.1090/S0894-0347-96-00202-0Google Scholar
[18] Hrushovski, E., The Manin–Mumford conjecture and the model theory of difference fields. Ann. Pure Appl. Logic 112(2001), 43–115. doi:10.1016/S0168-0072(01)00096-3Google Scholar
[19] McQuillan, M., Division points on semi-abelian varieties. Invent. Math. 120(1995), no. 1, 143–159. doi:10.1007/BF01241125Google Scholar
[20] Raynaud, M., Sous-variétés d’une variété abélienne et points de torsion. In: Arithmetic and Geometry, Vol. I, Prog. Math. 35, Birkhauser, Boston, MA, 1983, pp. 327–352.Google Scholar
[21] Rössler, D., An afterthought on the generalized Mordell–Lang conjecture. In Model Theory with Applications to Algebra and Analysis. London Math. Soc. Lecture Note Ser. 349, Cambridge, Cambridge University Press, 2008, pp. 63–71.Google Scholar
[22] Scanlon, T., Diophantine geometry of the torsion of a Drinfeld module. J. Number Theory 97(2002), no. 1, 10–25. doi:10.1006/jnth.2001.2751Google Scholar
[23] Scanlon, T., Automatic uniformity. Int. Math. Res. Not. (2004), no. 62, 3317–3326.Google Scholar
[24] Szpiro, L., Ullmo, E., and Zhang, S., Équirépartition des petits points. Invent. Math. 127(1997), no. 2, 337–347. doi:10.1007/s002220050123Google Scholar
[25] Vojta, P., Integral points on subvarieties of semiabelian varieties. I. Invent. Math. 126(1996), no. 1, 133–181. doi:10.1007/s002220050092Google Scholar
[26] Wang, J. T.-Y. The Mordell–Weil theorems for Drinfeld modules over finitely generated function fields. Manuscripta Math. 106(2001), 305–314. doi:10.1007/s00229-001-0207-2Google Scholar
[27] Yafaev, A., A conjecture of Yves André’s. Duke Math. J. 132(2006), no. 3, 393–407. doi:10.1215/S0012-7094-06-13231-3Google Scholar
[28] Zhang, S., Equidistribution of small points on abelian varieties. Ann. of Math. (2) 147(1998), no. 1, 159–165. doi:10.2307/120986Google Scholar