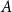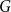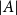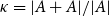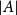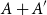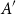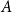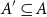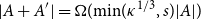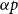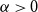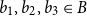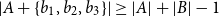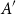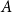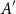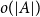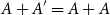1. Introduction
For finite subsets
![]() $A,B$
of an abelian group, their sumset is
$A,B$
of an abelian group, their sumset is
![]() $A+B=\{a+b\;:\;a \in A,b \in B\}$
. Estimating the sizes of sumsets is a classical topic extensively studied in additive combinatorics, and has motivated the development of a wide variety of influential tools and techniques. One of the most classical results in this area is the Cauchy–Davenport bound [Reference Cauchy7–Reference Davenport9], which says that for nonempty subsets
$A+B=\{a+b\;:\;a \in A,b \in B\}$
. Estimating the sizes of sumsets is a classical topic extensively studied in additive combinatorics, and has motivated the development of a wide variety of influential tools and techniques. One of the most classical results in this area is the Cauchy–Davenport bound [Reference Cauchy7–Reference Davenport9], which says that for nonempty subsets
![]() $A,B$
of
$A,B$
of
![]() $\mathbb{F}_p$
,
$\mathbb{F}_p$
,
![]() $|A+B|\ge \min\! (p,|A|+|B|-1)$
. This strengthens the simple observation that for nonempty subsets
$|A+B|\ge \min\! (p,|A|+|B|-1)$
. This strengthens the simple observation that for nonempty subsets
![]() $A,B\subseteq \mathbb{Z}$
,
$A,B\subseteq \mathbb{Z}$
,
![]() $|A+B|\ge |A|+|B|-1$
. The equality cases of the Cauchy–Davenport bound were later characterized by Vosper [Reference Vosper29], who showed that either
$|A+B|\ge |A|+|B|-1$
. The equality cases of the Cauchy–Davenport bound were later characterized by Vosper [Reference Vosper29], who showed that either
![]() $A,B$
must be arithmetic progressions of the same common difference, or
$A,B$
must be arithmetic progressions of the same common difference, or
![]() $\min\! (|A|,|B|)=1$
, or
$\min\! (|A|,|B|)=1$
, or
![]() $|A|+|B| \geq p-1$
.
$|A|+|B| \geq p-1$
.
Recently, in a sequence of papers, Bollobás, Leader and Tiba [Reference Bollobás, Leader and Tiba5, Reference Bollobás, Leader and Tiba6] studied several intriguing strengthenings of classical sumset estimates, including the Cauchy–Davenport bound. In particular, they showed that for nonempty subsets
![]() $A,B$
of integers with
$A,B$
of integers with
![]() $|A|\ge |B|$
, it is enough to use three elements from
$|A|\ge |B|$
, it is enough to use three elements from
![]() $B$
to achieve the sumset bound, that is, there exists a subset
$B$
to achieve the sumset bound, that is, there exists a subset
![]() $B_{(3)}$
of
$B_{(3)}$
of
![]() $B$
of size at most three such that
$B$
of size at most three such that
![]() $|A+B_{(3)}| \ge |A|+|B|-1$
. Similarly, they showed that for subsets
$|A+B_{(3)}| \ge |A|+|B|-1$
. Similarly, they showed that for subsets
![]() $A,B$
of
$A,B$
of
![]() $\mathbb{F}_p$
with
$\mathbb{F}_p$
with
![]() $|A|\ge |B|$
and
$|A|\ge |B|$
and
![]() $|A|+|B|$
bounded away from
$|A|+|B|$
bounded away from
![]() $p$
, there exists a subset
$p$
, there exists a subset
![]() $B_{(C)}$
of
$B_{(C)}$
of
![]() $B$
of constant size
$B$
of constant size
![]() $C$
for which
$C$
for which
![]() $|A+B_{(C)}|\ge \min\! (p,|A|+|B|-1)$
. (Here and throughout the paper, we use the notation
$|A+B_{(C)}|\ge \min\! (p,|A|+|B|-1)$
. (Here and throughout the paper, we use the notation
![]() $A_{(s)}$
and
$A_{(s)}$
and
![]() $B_{(s)}$
to denote subsets of
$B_{(s)}$
to denote subsets of
![]() $A$
and
$A$
and
![]() $B$
of size at most
$B$
of size at most
![]() $s$
.) The results were also later shown in the ‘medium-sized’ regime in [Reference Bollobás, Leader and Tiba6]: for subsets
$s$
.) The results were also later shown in the ‘medium-sized’ regime in [Reference Bollobás, Leader and Tiba6]: for subsets
![]() $A,B$
of
$A,B$
of
![]() $\mathbb{F}_p$
with
$\mathbb{F}_p$
with
![]() $|A|=|B|=n$
, there exist subsets
$|A|=|B|=n$
, there exist subsets
![]() $A'$
of
$A'$
of
![]() $A$
and
$A$
and
![]() $B'$
of
$B'$
of
![]() $B$
each of size at most
$B$
each of size at most
![]() $C\sqrt{n}$
for which
$C\sqrt{n}$
for which
![]() $|A'|+|B'|\ge \min\! (p,|A|+|B|-1)$
for some absolute constant
$|A'|+|B'|\ge \min\! (p,|A|+|B|-1)$
for some absolute constant
![]() $C$
. Bollobás, Leader and Tiba [Reference Bollobás, Leader and Tiba5, Reference Bollobás, Leader and Tiba6] pose several interesting conjectures motivated from their work.
$C$
. Bollobás, Leader and Tiba [Reference Bollobás, Leader and Tiba5, Reference Bollobás, Leader and Tiba6] pose several interesting conjectures motivated from their work.
Sumset estimates beyond the Cauchy–Davenport bound have been extensively studied, where the behaviour gets significantly more interesting. For example, while sets achieving the Cauchy–Davenport bound have particularly simple structure, for sets
![]() $A,B$
with
$A,B$
with
![]() $|A|=|B|=n$
and
$|A|=|B|=n$
and
![]() $|A+B|\le \lambda n$
for a constant
$|A+B|\le \lambda n$
for a constant
![]() $\lambda \gt 2$
, the structure gets considerably more complex and there is no exact characterization of
$\lambda \gt 2$
, the structure gets considerably more complex and there is no exact characterization of
![]() $A$
and
$A$
and
![]() $B$
. Nevertheless, we know from Freiman’s Theorem [Reference Freiman14, Reference Freiman15] that
$B$
. Nevertheless, we know from Freiman’s Theorem [Reference Freiman14, Reference Freiman15] that
![]() $A$
and
$A$
and
![]() $B$
are dense subsets of generalized arithmetic progressions of bounded dimension. This central result has been very influential in the further development of additive combinatorics and related areas, see for example [Reference Nathanson24, Reference Tao and Vu28]. Motivated by this theme, in this paper, we study sumset bounds beyond the Cauchy–Davenport bound that can be achieved using small subsets. We prove several positive results and present constructions which give information about the fundamental limits.
$B$
are dense subsets of generalized arithmetic progressions of bounded dimension. This central result has been very influential in the further development of additive combinatorics and related areas, see for example [Reference Nathanson24, Reference Tao and Vu28]. Motivated by this theme, in this paper, we study sumset bounds beyond the Cauchy–Davenport bound that can be achieved using small subsets. We prove several positive results and present constructions which give information about the fundamental limits.
Lower bounds beyond the Cauchy–Davenport bound. Our first main result in the paper shows that we can indeed achieve bounds much better than the Cauchy–Davenport bound using a bounded number of elements, where the size of the sumset we can guarantee using the small subset grows with the size of the sumset
![]() $A+A$
. More generally, the result holds for nonabelian groups. For subsets
$A+A$
. More generally, the result holds for nonabelian groups. For subsets
![]() $A,B$
of a group which is not necessarily abelian, we write
$A,B$
of a group which is not necessarily abelian, we write
![]() $AB=\{ab\;:\;a \in A, b \in B\}$
.
$AB=\{ab\;:\;a \in A, b \in B\}$
.
Theorem 1.1.
There exists
![]() $c\gt 0$
such that the following holds. Let
$c\gt 0$
such that the following holds. Let
![]() $G$
be a group. Let
$G$
be a group. Let
![]() $A\subseteq G$
be nonempty and let
$A\subseteq G$
be nonempty and let
![]() $\kappa =\kappa (A)\;:\!=\; |AA|/|A|$
. Then for each
$\kappa =\kappa (A)\;:\!=\; |AA|/|A|$
. Then for each
![]() $s \ge 1$
, there exists
$s \ge 1$
, there exists
![]() $A_{(s)}\subseteq A$
of size at most
$A_{(s)}\subseteq A$
of size at most
![]() $s$
such that
$s$
such that
Note that if
![]() $G$
is an abelian group, then the conclusion of Theorem 1.1 can be simplified as
$G$
is an abelian group, then the conclusion of Theorem 1.1 can be simplified as
![]() $|A+A_{(s)}| \ge c\min\! (\kappa ^{1/3},s)|A|$
. In general nonabelian group, it is necessary to consider both
$|A+A_{(s)}| \ge c\min\! (\kappa ^{1/3},s)|A|$
. In general nonabelian group, it is necessary to consider both
![]() $AA_{(s)}$
and
$AA_{(s)}$
and
![]() $A_{(s)}A$
(see Proposition 2.3). Furthermore, it is clear that
$A_{(s)}A$
(see Proposition 2.3). Furthermore, it is clear that
![]() $|AA_{(s)}|\le s|A|$
and
$|AA_{(s)}|\le s|A|$
and
![]() $|AA_{(s)}| \le \kappa |A|$
. In fact, we give a construction (see Proposition 2.5) showing that a bound better than
$|AA_{(s)}| \le \kappa |A|$
. In fact, we give a construction (see Proposition 2.5) showing that a bound better than
![]() $c\kappa ^{1/1.29}|A|$
cannot hold even in the abelian case, so the bound in Theorem 1.1 is tight up to possibly replacing
$c\kappa ^{1/1.29}|A|$
cannot hold even in the abelian case, so the bound in Theorem 1.1 is tight up to possibly replacing
![]() $\kappa ^{1/3}$
by
$\kappa ^{1/3}$
by
![]() $\kappa ^C$
for some
$\kappa ^C$
for some
![]() $C\in [1/3,1/1.29]$
.
$C\in [1/3,1/1.29]$
.
We also prove the following asymmetric version.
Theorem 1.2.
There exists
![]() $c\gt 0$
such that the following holds. Let
$c\gt 0$
such that the following holds. Let
![]() $G$
be a group. Let
$G$
be a group. Let
![]() $A,B\subseteq G$
be nonempty such that
$A,B\subseteq G$
be nonempty such that
![]() $|A|=|B|$
and let
$|A|=|B|$
and let
![]() $\kappa = \kappa (A,B)\;:\!=\;|AB|/|A|$
. Then for each
$\kappa = \kappa (A,B)\;:\!=\;|AB|/|A|$
. Then for each
![]() $s \ge 1$
, there exist
$s \ge 1$
, there exist
![]() $A_{(s)}\subseteq A$
and
$A_{(s)}\subseteq A$
and
![]() $B_{(s)}\subseteq B$
of size at most
$B_{(s)}\subseteq B$
of size at most
![]() $s$
such that
$s$
such that
Unlike the result of [Reference Bollobás, Leader and Tiba5] achieving the Cauchy–Davenport bound, in our case, it is necessary to consider
![]() $\max\! (|AB_{(s)}|,|BA_{(s)}|)$
even when the group
$\max\! (|AB_{(s)}|,|BA_{(s)}|)$
even when the group
![]() $G$
is abelian (see Proposition 2.6). In Proposition 2.4, we also derive an analogue of Theorem 1.1 for difference sets, in which the power
$G$
is abelian (see Proposition 2.6). In Proposition 2.4, we also derive an analogue of Theorem 1.1 for difference sets, in which the power
![]() $1/3$
can be replaced by
$1/3$
can be replaced by
![]() $1/2$
. We further extend these results to the medium-sized regime; however, in this setting, we can only expect to improve over the Cauchy–Davenport bound in a lower order term (see Theorem 2.8 and Proposition 2.9).
$1/2$
. We further extend these results to the medium-sized regime; however, in this setting, we can only expect to improve over the Cauchy–Davenport bound in a lower order term (see Theorem 2.8 and Proposition 2.9).
To illustrate the idea, we sketch our proof of Theorem 1.1. We first run a greedy procedure to grow
![]() $AA_{(s)}$
and
$AA_{(s)}$
and
![]() $A_{(s)}A$
, and terminate when adding any additional element does not increase
$A_{(s)}A$
, and terminate when adding any additional element does not increase
![]() $|AA_{(s)}|$
or
$|AA_{(s)}|$
or
![]() $|A_{(s)}A|$
by more than
$|A_{(s)}A|$
by more than
![]() $c|A|$
. When this happens, we show that for each element
$c|A|$
. When this happens, we show that for each element
![]() $a\in A\setminus A_{(s)}$
, all but a
$a\in A\setminus A_{(s)}$
, all but a
![]() $c$
fraction of elements
$c$
fraction of elements
![]() $a' a,a'\in A$
have to lie in
$a' a,a'\in A$
have to lie in
![]() $AA_{(s)}$
, and all but a
$AA_{(s)}$
, and all but a
![]() $c$
fraction of elements
$c$
fraction of elements
![]() $a a',a'\in A$
have to lie in
$a a',a'\in A$
have to lie in
![]() $A_{(s)}A$
. Using a path counting argument similar to the one employed in the proof of the Balog–Szemerédi–Gowers theorem [Reference Balog and Szemerédi1, Reference Gowers19], we can then upper bound
$A_{(s)}A$
. Using a path counting argument similar to the one employed in the proof of the Balog–Szemerédi–Gowers theorem [Reference Balog and Szemerédi1, Reference Gowers19], we can then upper bound
![]() $|AA|$
by
$|AA|$
by
![]() $O_c(\max\! (|AA_{(s)}|,|A_{(s)}A|)^3/n^2)$
, which yields the desired bound. The full proofs of Theorem 1.1 and Theorem 1.2 are contained in Section 2.
$O_c(\max\! (|AA_{(s)}|,|A_{(s)}A|)^3/n^2)$
, which yields the desired bound. The full proofs of Theorem 1.1 and Theorem 1.2 are contained in Section 2.
Application: The Cauchy–Davenport bound over
![]() $\mathbb{F}_p$
using three elements. The path counting argument to bound
$\mathbb{F}_p$
using three elements. The path counting argument to bound
![]() $|A+A|$
from the sum of
$|A+A|$
from the sum of
![]() $A$
and a set of bounded size is useful for other applications. In Section 3, we use this idea to resolve a conjecture of Bollobás, Leader and Tiba (Conjecture 1 of [Reference Bollobás, Leader and Tiba5]), showing that over
$A$
and a set of bounded size is useful for other applications. In Section 3, we use this idea to resolve a conjecture of Bollobás, Leader and Tiba (Conjecture 1 of [Reference Bollobás, Leader and Tiba5]), showing that over
![]() $\mathbb{F}_p$
, it suffices to use three elements to achieve the Cauchy–Davenport bound.
$\mathbb{F}_p$
, it suffices to use three elements to achieve the Cauchy–Davenport bound.
Theorem 1.3.
There exists
![]() $\alpha \gt 0$
such that the following holds. Let
$\alpha \gt 0$
such that the following holds. Let
![]() $A,B$
be nonempty subsets of
$A,B$
be nonempty subsets of
![]() $\mathbb{F}_p$
of size
$\mathbb{F}_p$
of size
![]() $n\le \alpha p$
. Then there exists a subset
$n\le \alpha p$
. Then there exists a subset
![]() $B_{(3)}$
of
$B_{(3)}$
of
![]() $B$
of size at most three such that
$B$
of size at most three such that
![]() $|A+B_{(3)}| \ge 2n-1$
.
$|A+B_{(3)}| \ge 2n-1$
.
The proof involves applying the path counting argument as in Section 2 in several iterations to bound the size of
![]() $A'+B'$
for appropriate subsets
$A'+B'$
for appropriate subsets
![]() $A'$
of
$A'$
of
![]() $A$
and
$A$
and
![]() $B'$
of
$B'$
of
![]() $B$
. When dealing with sets that have bounded sumset, one can apply appropriate rectification results to connect the problem over
$B$
. When dealing with sets that have bounded sumset, one can apply appropriate rectification results to connect the problem over
![]() $\mathbb{F}_p$
with a problem over
$\mathbb{F}_p$
with a problem over
![]() $\mathbb{Z}$
. However, the main difficulty is that sumsets are not stable under addition or removal of a small number of elements, and even controlling sums of subsets of
$\mathbb{Z}$
. However, the main difficulty is that sumsets are not stable under addition or removal of a small number of elements, and even controlling sums of subsets of
![]() $A$
and
$A$
and
![]() $B$
that contain all but at most an
$B$
that contain all but at most an
![]() $\epsilon$
fraction of elements does not yield similar control on the sum of
$\epsilon$
fraction of elements does not yield similar control on the sum of
![]() $A$
and
$A$
and
![]() $B$
. (We will later revisit this phenomenon when discussing Theorem 1.7 and Theorem 1.8.) We then need a careful argument that works directly with appropriate rectifications of subsets of
$B$
. (We will later revisit this phenomenon when discussing Theorem 1.7 and Theorem 1.8.) We then need a careful argument that works directly with appropriate rectifications of subsets of
![]() $A$
and
$A$
and
![]() $B$
and adapts the argument inspired by the argument of [Reference Bollobás, Leader and Tiba5] over
$B$
and adapts the argument inspired by the argument of [Reference Bollobás, Leader and Tiba5] over
![]() $\mathbb{Z}$
appropriately.
$\mathbb{Z}$
appropriately.
High dimensional versions. Another setting where one can expect to go beyond the Cauchy–Davenport bound is the high dimension setting, for example where we have a set
![]() $A$
in
$A$
in
![]() $\mathbb{Z}^d$
which is not close to a lower dimensional set in an appropriate sense. In particular, using the Freiman–Bilu Theorem [Reference Bilu3, Reference Green and Tao17], we can show that for every
$\mathbb{Z}^d$
which is not close to a lower dimensional set in an appropriate sense. In particular, using the Freiman–Bilu Theorem [Reference Bilu3, Reference Green and Tao17], we can show that for every
![]() $d$
and
$d$
and
![]() $\epsilon$
, there exists
$\epsilon$
, there exists
![]() $t\gt 0$
such that if
$t\gt 0$
such that if
![]() $A\subseteq \mathbb{Z}^d$
and
$A\subseteq \mathbb{Z}^d$
and
![]() $A$
cannot be covered by a union of
$A$
cannot be covered by a union of
![]() $t$
hyperplanes, then
$t$
hyperplanes, then
![]() $|A+A| \ge (2^d-\epsilon )|A|$
. In Section 4, we consider the analogue of the results of [Reference Bollobás, Leader and Tiba5] over the high dimension setting and show that the high-dimension analogue of the Cauchy–Davenport bound can be achieved using only a bounded number of elements.
$|A+A| \ge (2^d-\epsilon )|A|$
. In Section 4, we consider the analogue of the results of [Reference Bollobás, Leader and Tiba5] over the high dimension setting and show that the high-dimension analogue of the Cauchy–Davenport bound can be achieved using only a bounded number of elements.
Theorem 1.4.
Let
![]() $\epsilon \gt 0$
and let
$\epsilon \gt 0$
and let
![]() $d$
be a positive integer. There exists
$d$
be a positive integer. There exists
![]() $T$
sufficiently large in
$T$
sufficiently large in
![]() $d$
and
$d$
and
![]() $\epsilon$
such that the following holds. Let
$\epsilon$
such that the following holds. Let
![]() $A$
be a subset of
$A$
be a subset of
![]() $\mathbb{Z}^d$
such that
$\mathbb{Z}^d$
such that
![]() $A$
is not contained in the union of any
$A$
is not contained in the union of any
![]() $T$
parallel hyperplanes. Then there is a subset
$T$
parallel hyperplanes. Then there is a subset
![]() $A'$
of
$A'$
of
![]() $A$
of size
$A$
of size
![]() $O_{\epsilon,d}(1)$
for which
$O_{\epsilon,d}(1)$
for which
![]() $|A+A'| \ge (2^d-\epsilon )|A|$
.
$|A+A'| \ge (2^d-\epsilon )|A|$
.
In [Reference Bollobás, Leader and Tiba6, Question 3], it was asked if a medium-sized version holds: for a subset
![]() $A\subseteq \mathbb{Z}^d$
that is not contained in the union of any
$A\subseteq \mathbb{Z}^d$
that is not contained in the union of any
![]() $t$
parallel hyperplanes, does there exist
$t$
parallel hyperplanes, does there exist
![]() $A'\subseteq A$
with
$A'\subseteq A$
with
![]() $|A'|\le C\sqrt{|A|}$
and
$|A'|\le C\sqrt{|A|}$
and
![]() $|A'+A'|\ge (2^d-\epsilon )|A|$
? It turns out that the answer to this question is negative, as shown in Proposition 4.1. Nevertheless, the bounded size version of this, Theorem 1.4, holds.
$|A'+A'|\ge (2^d-\epsilon )|A|$
? It turns out that the answer to this question is negative, as shown in Proposition 4.1. Nevertheless, the bounded size version of this, Theorem 1.4, holds.
Saturating the entire sumset from a subset. In the following parts, we will work with subsets of general abelian groups. As discussed earlier, it is not possible to achieve a fixed positive fraction of
![]() $|A+A|$
using the sum of
$|A+A|$
using the sum of
![]() $A$
and a subset
$A$
and a subset
![]() $A_C$
of
$A_C$
of
![]() $A$
of size
$A$
of size
![]() $C$
depending only on the doubling constant
$C$
depending only on the doubling constant
![]() $\kappa =|A+A|/|A|$
(see Theorem 1.8 and Proposition 2.5). Nevertheless, it is interesting to determine how large a subset
$\kappa =|A+A|/|A|$
(see Theorem 1.8 and Proposition 2.5). Nevertheless, it is interesting to determine how large a subset
![]() $A'$
of
$A'$
of
![]() $A$
is needed in order to guarantee
$A$
is needed in order to guarantee
![]() $|A+A'|\ge (1-\epsilon )|A+A|$
. It turns out that if
$|A+A'|\ge (1-\epsilon )|A+A|$
. It turns out that if
![]() $A$
has bounded doubling,
$A$
has bounded doubling,
![]() $\kappa \le \lambda = O(1)$
, one can always guarantee the existence of a subset
$\kappa \le \lambda = O(1)$
, one can always guarantee the existence of a subset
![]() $A'$
of
$A'$
of
![]() $A$
of size
$A$
of size
![]() $o(|A|)$
with
$o(|A|)$
with
![]() $A'+A=A+A$
. Furthermore, the asymmetric version holds: for any
$A'+A=A+A$
. Furthermore, the asymmetric version holds: for any
![]() $A$
and
$A$
and
![]() $B$
with
$B$
with
![]() $|A|=|B|$
and
$|A|=|B|$
and
![]() $|A+B|\le \lambda |A|$
, one can find subsets
$|A+B|\le \lambda |A|$
, one can find subsets
![]() $A'$
of
$A'$
of
![]() $A$
and
$A$
and
![]() $B'$
of
$B'$
of
![]() $B$
each of size
$B$
each of size
![]() $o(|A|)$
such that
$o(|A|)$
such that
![]() $A+B=(A'+B)\cup (A+B')$
. In the case where
$A+B=(A'+B)\cup (A+B')$
. In the case where
![]() $A,B$
are dense subsets of
$A,B$
are dense subsets of
![]() $\mathbb{F}_p^n$
, this was earlier shown by Ellenberg [Reference Ellenberg11] with efficient bounds building on the cap-set breakthrough. In Section 5, we show that a much more general phenomenon holds for subsets of groups with bounded doubling which are not necessarily dense.
$\mathbb{F}_p^n$
, this was earlier shown by Ellenberg [Reference Ellenberg11] with efficient bounds building on the cap-set breakthrough. In Section 5, we show that a much more general phenomenon holds for subsets of groups with bounded doubling which are not necessarily dense.
Corollary 1.5.
Let
![]() $G$
be an abelian group, and let
$G$
be an abelian group, and let
![]() $S,T\subseteq G$
be nonempty subsets of equal size such that
$S,T\subseteq G$
be nonempty subsets of equal size such that
![]() $|S+T|=O(|S|)$
. Then there exist
$|S+T|=O(|S|)$
. Then there exist
![]() $S'\subseteq S$
and
$S'\subseteq S$
and
![]() $T'\subseteq T$
with
$T'\subseteq T$
with
![]() $S+T=(S'+T)\cup (S+T')$
and
$S+T=(S'+T)\cup (S+T')$
and
![]() $|S'|+|T'| = o(|S|)$
.
$|S'|+|T'| = o(|S|)$
.
Our proof also gives rise to the appropriate generalization over general groups.
Corollary 1.6.
Let
![]() $G$
be a group, and let
$G$
be a group, and let
![]() $S,T\subseteq G$
be nonempty subsets of equal size such that
$S,T\subseteq G$
be nonempty subsets of equal size such that
![]() $|S^2T|=O(|S|)$
. Then there exist
$|S^2T|=O(|S|)$
. Then there exist
![]() $S'\subseteq S$
and
$S'\subseteq S$
and
![]() $T'\subseteq T$
with
$T'\subseteq T$
with
![]() $ST=(S'T)\cup (ST')$
and
$ST=(S'T)\cup (ST')$
and
![]() $|S'|+|T'| = o(|S|)$
.
$|S'|+|T'| = o(|S|)$
.
Both corollaries follow from a more general result (Theorem 5.1) in Section 5, which is proved using the graph theoretic triangle removal lemma. A reduction from an arithmetic removal lemma to a graph removal lemma goes back to work of Král’, Serra and Vena [Reference Král’, Serra and Vena23], and our main technical result builds on and extends their argument. As applications of the graph removal lemma, our proofs of Corollaries 1.5 and 1.6 do not achieve strong quantitative bounds over general groups. By using the bounds for the arithmetic removal lemma over
![]() $\mathbb{F}_p^n$
due to Fox and Lovász [Reference Fox and Lovász13], we can achieve a polynomial saving, replacing
$\mathbb{F}_p^n$
due to Fox and Lovász [Reference Fox and Lovász13], we can achieve a polynomial saving, replacing
![]() $o(|S|)$
by an appropriate power
$o(|S|)$
by an appropriate power
![]() $|S|^{1-c_m}$
in the case where
$|S|^{1-c_m}$
in the case where
![]() $G$
is an abelian group with bounded exponent
$G$
is an abelian group with bounded exponent
![]() $m$
. Nevertheless, in the case
$m$
. Nevertheless, in the case
![]() $G=\mathbb{F}_p^n$
, the argument of Ellenberg [Reference Ellenberg11] gives a better (in fact sharp) exponent for Corollary 1.5. In Section 5, we also give constructions in the cases
$G=\mathbb{F}_p^n$
, the argument of Ellenberg [Reference Ellenberg11] gives a better (in fact sharp) exponent for Corollary 1.5. In Section 5, we also give constructions in the cases
![]() $G=\mathbb{Z}$
and
$G=\mathbb{Z}$
and
![]() $G=\mathbb{F}_p^n$
suggesting fundamental limits on quantitative bounds to the corollaries.
$G=\mathbb{F}_p^n$
suggesting fundamental limits on quantitative bounds to the corollaries.
A construction of a non-saturating set. While it is not possible to achieve almost all of
![]() $A+A$
using a bounded number of elements, one of the key results in [Reference Bollobás, Leader and Tiba5] says that this is possible upon replacing
$A+A$
using a bounded number of elements, one of the key results in [Reference Bollobás, Leader and Tiba5] says that this is possible upon replacing
![]() $A$
with a subset
$A$
with a subset
![]() $A'$
consisting of almost all elements of
$A'$
consisting of almost all elements of
![]() $A$
.
$A$
.
Theorem 1.7 ([Reference Bollobás, Leader and Tiba5]). For
![]() $\lambda,\epsilon \gt 0$
, there exists
$\lambda,\epsilon \gt 0$
, there exists
![]() $C\gt 0$
such that the following holds. Let
$C\gt 0$
such that the following holds. Let
![]() $A,B$
be nonempty subsets of an abelian group
$A,B$
be nonempty subsets of an abelian group
![]() $G$
with
$G$
with
![]() $|A|=|B|$
. Then there exist
$|A|=|B|$
. Then there exist
![]() $A'\subseteq A$
,
$A'\subseteq A$
,
![]() $B'\subseteq B$
with
$B'\subseteq B$
with
![]() $|A'|\ge (1-\epsilon )|A|$
and
$|A'|\ge (1-\epsilon )|A|$
and
![]() $|B'|\ge (1-\epsilon )|B|$
, such that if
$|B'|\ge (1-\epsilon )|B|$
, such that if
![]() $B''$
consists of
$B''$
consists of
![]() $C$
randomly chosen elements of
$C$
randomly chosen elements of
![]() $B'$
, then
$B'$
, then
In particular, if
![]() $|A+B|\le \lambda |A|$
, then there exists a subset
$|A+B|\le \lambda |A|$
, then there exists a subset
![]() $B''$
of
$B''$
of
![]() $B'$
of size at most
$B'$
of size at most
![]() $C$
such that
$C$
such that
![]() $|A'+B''| \ge (1-\epsilon )|A'+B'|$
.
$|A'+B''| \ge (1-\epsilon )|A'+B'|$
.
We remark that it is also straightforward to obtain the symmetric analogue of the above theorem, where
![]() $B=A$
and
$B=A$
and
![]() $B'=A'$
.
$B'=A'$
.
Much of the subtlety in obtaining sumset bounds growing with
![]() $|A+A|$
is that, unlike the Cauchy–Davenport bound which is stable under passing
$|A+A|$
is that, unlike the Cauchy–Davenport bound which is stable under passing
![]() $A$
to a subset
$A$
to a subset
![]() $A'$
that contains almost all elements of
$A'$
that contains almost all elements of
![]() $A$
, sumsets can generally behave unstably under addition or removal of few elements. For example, consider
$A$
, sumsets can generally behave unstably under addition or removal of few elements. For example, consider
![]() $A$
which is the union of a progression
$A$
which is the union of a progression
![]() $P$
of length
$P$
of length
![]() $n$
, and a small collection of
$n$
, and a small collection of
![]() $k$
arbitrary elements. Then
$k$
arbitrary elements. Then
![]() $|A+A|$
can be as large as
$|A+A|$
can be as large as
![]() $kn$
, whereas upon removal of
$kn$
, whereas upon removal of
![]() $k$
elements, the size of the sumset is only
$k$
elements, the size of the sumset is only
![]() $2n-1$
, matching the Cauchy–Davenport bound. This is the main reason behind stopping at the Cauchy–Davenport bound in [Reference Bollobás, Leader and Tiba5], and Theorem 1.7 suggests that this is the only obstruction.
$2n-1$
, matching the Cauchy–Davenport bound. This is the main reason behind stopping at the Cauchy–Davenport bound in [Reference Bollobás, Leader and Tiba5], and Theorem 1.7 suggests that this is the only obstruction.
The example of a progression together with few additional elements mentioned above suggests that it is impossible to replace
![]() $|A'+B'|$
with
$|A'+B'|$
with
![]() $|A+B|$
in Theorem 1.7. However, it is unclear if we can replace only one of two sets with a subset. Considering that we are allowed to make our selection of elements from
$|A+B|$
in Theorem 1.7. However, it is unclear if we can replace only one of two sets with a subset. Considering that we are allowed to make our selection of elements from
![]() $B$
, it could be the case that we only need to replace
$B$
, it could be the case that we only need to replace
![]() $A$
by a subset
$A$
by a subset
![]() $A'$
with better additive structure. Bollobás, Leader and Tiba (Question 5, [Reference Bollobás, Leader and Tiba5]) ask this explicitly: Given constants
$A'$
with better additive structure. Bollobás, Leader and Tiba (Question 5, [Reference Bollobás, Leader and Tiba5]) ask this explicitly: Given constants
![]() $\epsilon \gt 0$
and
$\epsilon \gt 0$
and
![]() $\lambda \gt 0$
, is there a constant
$\lambda \gt 0$
, is there a constant
![]() $c\gt 0$
such that the following assertion holds? If
$c\gt 0$
such that the following assertion holds? If
![]() $A,B$
are subsets of
$A,B$
are subsets of
![]() $\mathbb{F}_p$
with
$\mathbb{F}_p$
with
![]() $|A|=|B|=n$
and
$|A|=|B|=n$
and
![]() $|A+B|\le \lambda n$
, then there are sets
$|A+B|\le \lambda n$
, then there are sets
![]() $A'\subseteq A$
and
$A'\subseteq A$
and
![]() $B'\subseteq B$
such that
$B'\subseteq B$
such that
![]() $|A'|\ge (1-\epsilon )n$
and
$|A'|\ge (1-\epsilon )n$
and
![]() $|B'|\le c$
and
$|B'|\le c$
and
![]() $|A'+B'|\ge (1-\epsilon )|A'+B|$
.
$|A'+B'|\ge (1-\epsilon )|A'+B|$
.
It turns out that the answer to this question is negative. In Section 6, we give a construction showing this in a strong sense: It is not possible to achieve a fixed positive fraction of the sumset
![]() $A'+A$
using a bounded number of elements from
$A'+A$
using a bounded number of elements from
![]() $A'$
even when we are allowed to choose
$A'$
even when we are allowed to choose
![]() $A'$
which is a subset of
$A'$
which is a subset of
![]() $A$
of size at least
$A$
of size at least
![]() $(1-\epsilon )|A|$
.
$(1-\epsilon )|A|$
.
Theorem 1.8.
For any
![]() $\nu \gt 0$
, there exist
$\nu \gt 0$
, there exist
![]() $\lambda \gt 1$
and sufficiently small
$\lambda \gt 1$
and sufficiently small
![]() $\epsilon \gt 0$
such that for all
$\epsilon \gt 0$
such that for all
![]() $s\gt 0$
and
$s\gt 0$
and
![]() $p$
sufficiently large in
$p$
sufficiently large in
![]() $s$
and
$s$
and
![]() $\nu$
, there exists a subset
$\nu$
, there exists a subset
![]() $A$
of
$A$
of
![]() $\mathbb{F}_p$
of size
$\mathbb{F}_p$
of size
![]() $\Omega _{\nu }(p)$
such that
$\Omega _{\nu }(p)$
such that
![]() $|A+A| \le \lambda |A|$
, and for all
$|A+A| \le \lambda |A|$
, and for all
![]() $A'\subseteq A$
of size at least
$A'\subseteq A$
of size at least
![]() $(1-\epsilon )|A|$
and all
$(1-\epsilon )|A|$
and all
![]() $A_{(s)} \subseteq A$
of size at most
$A_{(s)} \subseteq A$
of size at most
![]() $s$
,
$s$
,
![]() $|A'+A_{(s)}| \le \nu |A'+A|$
. Furthermore, the same result holds over
$|A'+A_{(s)}| \le \nu |A'+A|$
. Furthermore, the same result holds over
![]() $\mathbb{Z}$
and
$\mathbb{Z}$
and
![]() $\mathbb{F}_2^{n}$
.
$\mathbb{F}_2^{n}$
.
In fact, in our proof, we can even let
![]() $s$
grow at some explicit rate together with the size of
$s$
grow at some explicit rate together with the size of
![]() $A$
. Note that the existence of such a set
$A$
. Note that the existence of such a set
![]() $A$
is nontrivial: Since we replace
$A$
is nontrivial: Since we replace
![]() $A$
with a subset
$A$
with a subset
![]() $A'$
which is ‘regular’ in an appropriate sense in terms of additive structure, if
$A'$
which is ‘regular’ in an appropriate sense in terms of additive structure, if
![]() $|A'+A|$
is large, it cannot be due to a small number of bad elements, and we may expect to be able to select many translates of
$|A'+A|$
is large, it cannot be due to a small number of bad elements, and we may expect to be able to select many translates of
![]() $A'$
that do not have significant overlap, leading to a large sumset. However, it turns out that this intuitive picture is not correct. Our construction involves a niveau-like set
$A'$
that do not have significant overlap, leading to a large sumset. However, it turns out that this intuitive picture is not correct. Our construction involves a niveau-like set
![]() $A$
first constructed over
$A$
first constructed over
![]() $\mathbb{F}_2^n$
, then adapted to the setting of appropriate cyclic groups and then to the integers and prime cyclic groups.
$\mathbb{F}_2^n$
, then adapted to the setting of appropriate cyclic groups and then to the integers and prime cyclic groups.
Organization of the paper. In Section 2, we consider bounds beyond the Cauchy–Davenport bound that are achievable using a bounded number of elements, and prove Theorems 1.1 and 1.2, as well as their medium-sized analogues. In Section 3, we prove Theorem 1.3, which verifies the conjecture of Bollobás, Leader and Tiba that it suffices to use three elements to achieve the Cauchy–Davenport bound over
![]() $\mathbb{F}_p$
. In Section 4, we consider the high-dimension setting and prove Theorem 1.4. In Section 5, we study the number of elements needed to saturate the entire sumset, and prove Corollaries 1.5 and 1.6. In Section 6, we give the construction proving Theorem 1.8, that it is not possible to achieve a fixed positive fraction of
$\mathbb{F}_p$
. In Section 4, we consider the high-dimension setting and prove Theorem 1.4. In Section 5, we study the number of elements needed to saturate the entire sumset, and prove Corollaries 1.5 and 1.6. In Section 6, we give the construction proving Theorem 1.8, that it is not possible to achieve a fixed positive fraction of
![]() $A'+A$
using a bounded-sized subset of
$A'+A$
using a bounded-sized subset of
![]() $A'$
, even when we are allowed to choose
$A'$
, even when we are allowed to choose
![]() $A'$
as a subset consisting of almost all elements of
$A'$
as a subset consisting of almost all elements of
![]() $A$
.
$A$
.
Notations and conventions. We use the following standard asymptotic notations. We denote
![]() $f=O_P(g)$
,
$f=O_P(g)$
,
![]() $f\ll _P g$
, or
$f\ll _P g$
, or
![]() $g=\Omega _P(f)$
when there is a constant
$g=\Omega _P(f)$
when there is a constant
![]() $C\gt 0$
depending on
$C\gt 0$
depending on
![]() $P$
so that
$P$
so that
![]() $f\le Cg$
, and we denote
$f\le Cg$
, and we denote
![]() $f=o_P(g)$
or
$f=o_P(g)$
or
![]() $g=\omega _P(f)$
if
$g=\omega _P(f)$
if
![]() $f/g\to 0$
for fixed
$f/g\to 0$
for fixed
![]() $P$
. We omit floors and ceilings when they are not essential. We denote
$P$
. We omit floors and ceilings when they are not essential. We denote
![]() $[x]=\{n\in \mathbb{Z}:1\le n \le x\}$
. For a positive integer
$[x]=\{n\in \mathbb{Z}:1\le n \le x\}$
. For a positive integer
![]() $t$
and a set
$t$
and a set
![]() $X$
(a subset of an abelian group), we use
$X$
(a subset of an abelian group), we use
![]() $tX = X + X + \cdots + X = \{x_1+\cdots + x_t:x_i\in X, i\in [t]\}$
to denote the
$tX = X + X + \cdots + X = \{x_1+\cdots + x_t:x_i\in X, i\in [t]\}$
to denote the
![]() $t$
-fold sumset. Throughout, unless otherwise stated, we use
$t$
-fold sumset. Throughout, unless otherwise stated, we use
![]() $p$
to denote a prime number.
$p$
to denote a prime number.
2. General lower bounds on product sets from small subsets
In this section, we mostly deal with general (and not necessarily abelian) groups. To signify the difference, we write the group operation in the nonabelian case multiplicatively; as such the role of the sumset is replaced by the product set
![]() $AB$
. (The additive notation for the group operation is reserved for the abelian case.) We will prove our results guaranteeing product sets with size significantly larger than the Cauchy–Davenport bound using a small number of elements, assuming that
$AB$
. (The additive notation for the group operation is reserved for the abelian case.) We will prove our results guaranteeing product sets with size significantly larger than the Cauchy–Davenport bound using a small number of elements, assuming that
![]() $|AB|$
significantly exceeds the size of the sets
$|AB|$
significantly exceeds the size of the sets
![]() $A$
and
$A$
and
![]() $B$
. In particular, we will prove Theorem 1.1 and Theorem 1.2, as well as their “medium-sized” analogues in
$B$
. In particular, we will prove Theorem 1.1 and Theorem 1.2, as well as their “medium-sized” analogues in
![]() $\mathbb{F}_p$
.
$\mathbb{F}_p$
.
Throughout this and the following sections, we use a convenient path counting argument, which we record here. A similar argument is used in Gowers’ proof of the Balog-Szemerédi-Gowers theorem (see [Reference Gowers19, Reference Tao and Vu28]). Given a set
![]() $C$
, let
$C$
, let
![]() $\Gamma _C$
be the bipartite graph on vertex sets
$\Gamma _C$
be the bipartite graph on vertex sets
![]() $A,B$
such that
$A,B$
such that
![]() $a\in A$
,
$a\in A$
,
![]() $b\in B$
are adjacent if and only if
$b\in B$
are adjacent if and only if
![]() $ab\in C$
.
$ab\in C$
.
Lemma 2.1.
Let
![]() $k$
be an odd positive integer. Let
$k$
be an odd positive integer. Let
![]() $A,B,C$
be subsets of a group. Suppose that for every pair
$A,B,C$
be subsets of a group. Suppose that for every pair
![]() $(a,b)\in A\times B$
there are at least
$(a,b)\in A\times B$
there are at least
![]() $w$
walks of length
$w$
walks of length
![]() $k$
in
$k$
in
![]() $\Gamma _C$
going from
$\Gamma _C$
going from
![]() $a$
to
$a$
to
![]() $b$
. Then
$b$
. Then
![]() $|AB|\le |C|^k/w$
.
$|AB|\le |C|^k/w$
.
Proof. For each walk
![]() $(a_0,b_1,a_2,\dots,a_{k-1},b_k)$
of length
$(a_0,b_1,a_2,\dots,a_{k-1},b_k)$
of length
![]() $k$
with
$k$
with
![]() $a_0 = a$
and
$a_0 = a$
and
![]() $b_k = b$
, we have
$b_k = b$
, we have
![]() $ab = (ab_1)(a_2b_1)^{-1}\cdots (a_{k-1}b)$
. Thus, for each
$ab = (ab_1)(a_2b_1)^{-1}\cdots (a_{k-1}b)$
. Thus, for each
![]() $x \in AB$
, fixing
$x \in AB$
, fixing
![]() $(a,b)\in A\times B$
such that
$(a,b)\in A\times B$
such that
![]() $x=ab$
, we have at least
$x=ab$
, we have at least
![]() $w$
different representations
$w$
different representations
![]() $x=c_1c_2^{-1}\cdots c_{k-1}^{-1}c_k$
where
$x=c_1c_2^{-1}\cdots c_{k-1}^{-1}c_k$
where
![]() $c_1,\dots,c_k\in C$
. Since there are at most
$c_1,\dots,c_k\in C$
. Since there are at most
![]() $|C|^k$
choices of
$|C|^k$
choices of
![]() $c_1,\dots,c_k$
, and each choice uniquely determines
$c_1,\dots,c_k$
, and each choice uniquely determines
![]() $x\in AB$
and the walk, we have that
$x\in AB$
and the walk, we have that
![]() $|AB|\cdot w\le |C|^k$
, which rearranges to the desired inequality.
$|AB|\cdot w\le |C|^k$
, which rearranges to the desired inequality.
We also have the following version of Lemma 2.1 for even values of
![]() $k$
, which follows from essentially the same proof. Note that we denote
$k$
, which follows from essentially the same proof. Note that we denote
![]() $AB^{-1} = \{ab^{-1}\; :\;a\in A, b\in B\}$
.
$AB^{-1} = \{ab^{-1}\; :\;a\in A, b\in B\}$
.
Lemma 2.2.
Let
![]() $k$
be an even positive integer. Let
$k$
be an even positive integer. Let
![]() $A,B, C$
be subsets of a group. Suppose that for every pair
$A,B, C$
be subsets of a group. Suppose that for every pair
![]() $(b,b')\in B\times B$
there are at least
$(b,b')\in B\times B$
there are at least
![]() $w$
walks of length
$w$
walks of length
![]() $k$
in
$k$
in
![]() $\Gamma _C$
going from
$\Gamma _C$
going from
![]() $b$
to
$b$
to
![]() $b'$
. Then
$b'$
. Then
![]() $|BB^{-1}|\le |C|^k/w$
.
$|BB^{-1}|\le |C|^k/w$
.
2.1. Large product sets from constant size subset
In this section, we prove Theorems 1.1 and 1.2. We recall their statements for convenience.
Theorem 1.1.
There exists
![]() $c\gt 0$
such that the following holds. Let
$c\gt 0$
such that the following holds. Let
![]() $G$
be a group. Let
$G$
be a group. Let
![]() $A\subseteq G$
be nonempty and let
$A\subseteq G$
be nonempty and let
![]() $\kappa =\kappa (A)\;:\!=\; |AA|/|A|$
. Then for each
$\kappa =\kappa (A)\;:\!=\; |AA|/|A|$
. Then for each
![]() $s \ge 1$
, there exists
$s \ge 1$
, there exists
![]() $A_{(s)}\subseteq A$
of size at most
$A_{(s)}\subseteq A$
of size at most
![]() $s$
such that
$s$
such that
As we remarked before, if
![]() $G$
is abelian, the conclusion of the above theorem can be written more simply as
$G$
is abelian, the conclusion of the above theorem can be written more simply as
![]() $|A+A_{(s)}| \ge c\min\! (\kappa ^{1/3},s)|A|$
. We give a quick construction showing that for general nonabelian groups, it is necessary to look at both
$|A+A_{(s)}| \ge c\min\! (\kappa ^{1/3},s)|A|$
. We give a quick construction showing that for general nonabelian groups, it is necessary to look at both
![]() $AA_{(s)}$
and
$AA_{(s)}$
and
![]() $A_{(s)}A$
.
$A_{(s)}A$
.
Proposition 2.3.
Let
![]() $n,t$
be integers with
$n,t$
be integers with
![]() $n\ge 4t$
. There exists a nonabelian group
$n\ge 4t$
. There exists a nonabelian group
![]() $G$
and subset
$G$
and subset
![]() $A$
such that
$A$
such that
![]() $|A|=n$
,
$|A|=n$
,
![]() $|AA|\ge tn/2$
, and for any subset
$|AA|\ge tn/2$
, and for any subset
![]() $A_{(s)}$
of
$A_{(s)}$
of
![]() $A$
of size at most
$A$
of size at most
![]() $s$
,
$s$
,
![]() $|AA_{(s)}|\le 2n+st$
.
$|AA_{(s)}|\le 2n+st$
.
Proof. Let
![]() $m=n-t$
. Consider
$m=n-t$
. Consider
![]() $G=\langle x,y \mid x^m=y^2=1\rangle$
, which is isomorphic to the free product
$G=\langle x,y \mid x^m=y^2=1\rangle$
, which is isomorphic to the free product
![]() $\mathbb{Z}_m * \mathbb{Z}_2$
. Let
$\mathbb{Z}_m * \mathbb{Z}_2$
. Let
![]() $A = \langle x\rangle \cup Ty$
for an arbitrary subset
$A = \langle x\rangle \cup Ty$
for an arbitrary subset
![]() $T$
of
$T$
of
![]() $\langle x\rangle$
of size
$\langle x\rangle$
of size
![]() $t$
. Then
$t$
. Then
![]() $|A|=n$
, and
$|A|=n$
, and
![]() $|AA|=|\langle x\rangle \cup \langle x\rangle y \cup Ty\langle x\rangle | \ge (t-1)(n-t-1) \ge tn/2$
. On the other hand, for any subset
$|AA|=|\langle x\rangle \cup \langle x\rangle y \cup Ty\langle x\rangle | \ge (t-1)(n-t-1) \ge tn/2$
. On the other hand, for any subset
![]() $A_{(s)}$
of
$A_{(s)}$
of
![]() $A$
of size at most
$A$
of size at most
![]() $s$
,
$s$
,
![]() $AA_{s} \subseteq \langle x\rangle \cup \langle x\rangle y \cup TyA_{s}$
, which has size at most
$AA_{s} \subseteq \langle x\rangle \cup \langle x\rangle y \cup TyA_{s}$
, which has size at most
![]() $2m + st \lt 2n+st$
.
$2m + st \lt 2n+st$
.
Theorem 1.2.
There exists
![]() $c\gt 0$
such that the following holds. Let
$c\gt 0$
such that the following holds. Let
![]() $G$
be a group. Let
$G$
be a group. Let
![]() $A,B\subseteq G$
be nonempty such that
$A,B\subseteq G$
be nonempty such that
![]() $|A|=|B|$
and let
$|A|=|B|$
and let
![]() $\kappa = \kappa (A,B)\;:\!=\;|AB|/|A|$
. Then for each
$\kappa = \kappa (A,B)\;:\!=\;|AB|/|A|$
. Then for each
![]() $s \ge 1$
, there exist
$s \ge 1$
, there exist
![]() $A_{(s)}\subseteq A$
and
$A_{(s)}\subseteq A$
and
![]() $B_{(s)}\subseteq B$
of size at most
$B_{(s)}\subseteq B$
of size at most
![]() $s$
such that
$s$
such that
Theorem 1.1 is a special case of Theorem 1.2. Now we present the proof of Theorem 1.2.
Proof. Fix
![]() $c=\frac{1}{14}$
. Let
$c=\frac{1}{14}$
. Let
![]() $n = |A| = |B|$
. We proceed by induction on
$n = |A| = |B|$
. We proceed by induction on
![]() $s$
to show that for every
$s$
to show that for every
![]() $s\geq 1$
there exist choices of
$s\geq 1$
there exist choices of
![]() $A_{(s)}$
and
$A_{(s)}$
and
![]() $B_{(s)}$
such that
$B_{(s)}$
such that
![]() $|AB_{(s)}|+|A_{(s)}B|\geq 2c\min\! (\kappa ^{1/3},s)n$
. For
$|AB_{(s)}|+|A_{(s)}B|\geq 2c\min\! (\kappa ^{1/3},s)n$
. For
![]() $s=1$
, we trivially have
$s=1$
, we trivially have
![]() $|AB_{(s)}|+|A_{(s)}B|\geq |A|+|B|=2sn\geq 2c\min\! (\kappa ^{1/3},s)n$
since
$|AB_{(s)}|+|A_{(s)}B|\geq |A|+|B|=2sn\geq 2c\min\! (\kappa ^{1/3},s)n$
since
![]() $c\leq 1$
. Now suppose the claim holds for
$c\leq 1$
. Now suppose the claim holds for
![]() $s-1$
, so there exist
$s-1$
, so there exist
![]() $A_{(s-1)}$
and
$A_{(s-1)}$
and
![]() $B_{(s-1)}$
such that
$B_{(s-1)}$
such that
![]() $|AB_{(s-1)}|+|A_{(s-1)}B|\geq 2c\min\! (\kappa ^{1/3},s-1)n$
. If
$|AB_{(s-1)}|+|A_{(s-1)}B|\geq 2c\min\! (\kappa ^{1/3},s-1)n$
. If
![]() $|AB_{(s-1)}|+|A_{(s-1)}B|\geq 2c\kappa ^{1/3}n$
, then we are done. So, we can assume
$|AB_{(s-1)}|+|A_{(s-1)}B|\geq 2c\kappa ^{1/3}n$
, then we are done. So, we can assume
![]() $2c(s-1)n\leq |AB_{(s-1)}|+|A_{(s-1)}B|\lt 2c\kappa ^{1/3}n$
.
$2c(s-1)n\leq |AB_{(s-1)}|+|A_{(s-1)}B|\lt 2c\kappa ^{1/3}n$
.
If there is an element
![]() $b\in B\setminus B_{(s-1)}$
such that
$b\in B\setminus B_{(s-1)}$
such that
![]() $|(Ab)\setminus (AB_{(s-1)})|\geq 2cn$
, then letting
$|(Ab)\setminus (AB_{(s-1)})|\geq 2cn$
, then letting
![]() $A_{(s)}=A_{(s-1)}$
,
$A_{(s)}=A_{(s-1)}$
,
![]() $B_{(s)}=B_{(s-1)}\cup \{b\}$
yields
$B_{(s)}=B_{(s-1)}\cup \{b\}$
yields
![]() $|AB_{(s)}|+|A_{(s)}B|\geq 2csn$
as desired. So we can assume that
$|AB_{(s)}|+|A_{(s)}B|\geq 2csn$
as desired. So we can assume that
![]() $|(Ab)\setminus (AB_{(s-1)})|\lt 2cn$
, and thus
$|(Ab)\setminus (AB_{(s-1)})|\lt 2cn$
, and thus
![]() $|(Ab)\cap (AB_{(s-1)})|\gt (1-2c)n$
, for all
$|(Ab)\cap (AB_{(s-1)})|\gt (1-2c)n$
, for all
![]() $b\in B\setminus B_{(s-1)}$
. Similarly, we can assume
$b\in B\setminus B_{(s-1)}$
. Similarly, we can assume
![]() $|(aB)\cap (A_{(s-1)}B)|\gt (1-2c)n$
for all
$|(aB)\cap (A_{(s-1)}B)|\gt (1-2c)n$
for all
![]() $a\in A\setminus A_{(s-1)}$
. The same inequalities are clearly true when
$a\in A\setminus A_{(s-1)}$
. The same inequalities are clearly true when
![]() $a\in A_{(s-1)}$
or
$a\in A_{(s-1)}$
or
![]() $b\in B_{(s-1)}$
, so we in fact have
$b\in B_{(s-1)}$
, so we in fact have
Let
![]() $C= (A_{(s-1)}B)\cup (AB_{(s-1)})$
, and consider the graph
$C= (A_{(s-1)}B)\cup (AB_{(s-1)})$
, and consider the graph
![]() $\Gamma _C$
defined as above. From (1) we know that every vertex in
$\Gamma _C$
defined as above. From (1) we know that every vertex in
![]() $A$
is adjacent to all but
$A$
is adjacent to all but
![]() $2cn$
vertices of
$2cn$
vertices of
![]() $B$
, and vice versa. In particular, given any pair
$B$
, and vice versa. In particular, given any pair
![]() $(x,y)\in A\times B$
, there are at least
$(x,y)\in A\times B$
, there are at least
![]() $(1-2c)n$
choices of
$(1-2c)n$
choices of
![]() $x'$
and
$x'$
and
![]() $(1-2c)n$
choices of
$(1-2c)n$
choices of
![]() $y'$
such that
$y'$
such that
![]() $(x,y'),(x', y)\in \Gamma _C$
. For each such choice of
$(x,y'),(x', y)\in \Gamma _C$
. For each such choice of
![]() $x'$
, all but at most
$x'$
, all but at most
![]() $2cn$
of the choices of
$2cn$
of the choices of
![]() $y'$
satisfy
$y'$
satisfy
![]() $(x',y')\in \Gamma _C$
. Thus, for every choice of
$(x',y')\in \Gamma _C$
. Thus, for every choice of
![]() $(x,y)\in A\times B$
, there are at least
$(x,y)\in A\times B$
, there are at least
![]() $(1-2c)n(1-4c)n\geq (1-6c)n^2$
paths of length three from
$(1-2c)n(1-4c)n\geq (1-6c)n^2$
paths of length three from
![]() $x$
to
$x$
to
![]() $y$
in
$y$
in
![]() $\Gamma _C$
. Applying Lemma 2.1 with
$\Gamma _C$
. Applying Lemma 2.1 with
![]() $k=3$
,
$k=3$
,
![]() $w=(1-6c)n^2$
yields
$w=(1-6c)n^2$
yields
Note that
![]() $|AB| = \kappa n$
. Simplifying the inequality above gives
$|AB| = \kappa n$
. Simplifying the inequality above gives
![]() $\frac{8c^3}{1-6c}\gt 1$
, which contradicts with
$\frac{8c^3}{1-6c}\gt 1$
, which contradicts with
![]() $c=\frac{1}{14}$
. Thus (1) is false. This means that there exist
$c=\frac{1}{14}$
. Thus (1) is false. This means that there exist
![]() $A_{(s)}$
and
$A_{(s)}$
and
![]() $B_{(s)}$
with
$B_{(s)}$
with
![]() $|AB_{(s)}|+|A_{(s)}B|\geq 2c\min\! (\kappa ^{1/3},s)n$
. By induction, this holds for all
$|AB_{(s)}|+|A_{(s)}B|\geq 2c\min\! (\kappa ^{1/3},s)n$
. By induction, this holds for all
![]() $s\geq 1$
, and we conclude that
$s\geq 1$
, and we conclude that
![]() $\max\! (|AB_{(s)}|,|A_{(s)}B|)\geq c\min\! (\kappa ^{1/3},s)n$
as desired.
$\max\! (|AB_{(s)}|,|A_{(s)}B|)\geq c\min\! (\kappa ^{1/3},s)n$
as desired.
Theorem 1.1 follows immediately by taking
![]() $B=A$
. We remark that in the case
$B=A$
. We remark that in the case
![]() $B=A^{-1} = \{a^{-1}\; :\;a\in A\}$
, a similar argument yields a better dependence on
$B=A^{-1} = \{a^{-1}\; :\;a\in A\}$
, a similar argument yields a better dependence on
![]() $\kappa$
, as follows.
$\kappa$
, as follows.
Proposition 2.4.
There exists
![]() $c\gt 0$
such that the following holds. Given
$c\gt 0$
such that the following holds. Given
![]() $A\subseteq G$
such that
$A\subseteq G$
such that
![]() $|A|=n$
and
$|A|=n$
and
![]() $|AA^{-1}|=\kappa n$
. Then for each
$|AA^{-1}|=\kappa n$
. Then for each
![]() $s \ge 1$
, there exists
$s \ge 1$
, there exists
![]() $A_{(s)}\subseteq A$
of size at most
$A_{(s)}\subseteq A$
of size at most
![]() $s$
such that
$s$
such that
The change comes from using Lemma 2.2 and counting paths of length two in
![]() $\Gamma _C$
instead of using Lemma 2.1 and counting paths of length three. In particular, if
$\Gamma _C$
instead of using Lemma 2.1 and counting paths of length three. In particular, if
![]() $G$
is an abelian group, then given
$G$
is an abelian group, then given
![]() $|A-A|=\kappa |A|$
, we can find
$|A-A|=\kappa |A|$
, we can find
![]() $A_{(s)}$
of size at most
$A_{(s)}$
of size at most
![]() $s$
such that
$s$
such that
![]() $|A-A_{(s)}| \ge c\min\! (\kappa ^{1/2},s)|A|$
.
$|A-A_{(s)}| \ge c\min\! (\kappa ^{1/2},s)|A|$
.
On the other hand, the following construction (in the abelian setting) gives an upper bound on how large of a sumset we can guarantee.
Proposition 2.5.
There exists
![]() $c\gt 0$
for arbitrarily large
$c\gt 0$
for arbitrarily large
![]() $\kappa \gt 0$
for which the following holds: For all positive integers
$\kappa \gt 0$
for which the following holds: For all positive integers
![]() $d$
, there exist infinitely many positive integers
$d$
, there exist infinitely many positive integers
![]() $n$
such that for some
$n$
such that for some
![]() $A\subset \mathbb{Z}^d$
with
$A\subset \mathbb{Z}^d$
with
![]() $|A|=n$
and
$|A|=n$
and
![]() $|A+A| = \kappa n$
, for any
$|A+A| = \kappa n$
, for any
![]() $s\le n^{c/\log \kappa }$
and any
$s\le n^{c/\log \kappa }$
and any
![]() $A_{(s)}\subseteq A$
of size at most
$A_{(s)}\subseteq A$
of size at most
![]() $s$
, we have
$s$
, we have
Proof. Note that
![]() $|A+A_{(s)}| \le s|A|$
trivially holds. Fix a small constant
$|A+A_{(s)}| \le s|A|$
trivially holds. Fix a small constant
![]() $\epsilon \in (0,1)$
. For a positive integer
$\epsilon \in (0,1)$
. For a positive integer
![]() $d$
, a perfect square
$d$
, a perfect square
![]() $m\gt 1$
, and a real number
$m\gt 1$
, and a real number
![]() $\delta \in (2\epsilon ^{-1}m^{-1/2}, 1-m^{-1/2})$
, consider
$\delta \in (2\epsilon ^{-1}m^{-1/2}, 1-m^{-1/2})$
, consider
![]() $A=([\delta m] \cup B)^d$
, where
$A=([\delta m] \cup B)^d$
, where
![]() $B = \{k\sqrt{m}\;:\; 0\leq k \lt \sqrt{m}\}\cup \{m - k\;:\;0\leq k \lt \sqrt{m}\}$
is a set of size
$B = \{k\sqrt{m}\;:\; 0\leq k \lt \sqrt{m}\}\cup \{m - k\;:\;0\leq k \lt \sqrt{m}\}$
is a set of size
![]() $2\sqrt{m}$
. In particular,
$2\sqrt{m}$
. In particular,
![]() $n=|A| \in [(\delta m + \sqrt{m})^d,(\delta m +2\sqrt{m})^d]$
. It is easy to check that for
$n=|A| \in [(\delta m + \sqrt{m})^d,(\delta m +2\sqrt{m})^d]$
. It is easy to check that for
![]() $m$
sufficiently large,
$m$
sufficiently large,
![]() $B+B \supseteq [m,2m]$
and
$B+B \supseteq [m,2m]$
and
![]() $[\delta m]+B\supseteq [m]$
. Thus, we have the inclusion
$[\delta m]+B\supseteq [m]$
. Thus, we have the inclusion
![]() ${([\delta m]\cup B)} + B{\supseteq [2m]}$
. Since
${([\delta m]\cup B)} + B{\supseteq [2m]}$
. Since
![]() $0\in B$
, we have
$0\in B$
, we have
![]() $([\delta m]\cup B)+([\delta m]\cup B)\supseteq [0,2m]$
. On the other hand,
$([\delta m]\cup B)+([\delta m]\cup B)\supseteq [0,2m]$
. On the other hand,
![]() $[\delta m]\cup B\subseteq [0,m]$
, so we conclude that
$[\delta m]\cup B\subseteq [0,m]$
, so we conclude that
![]() $([\delta m]\cup B)+([\delta m]\cup B) = [0,2m]$
. So,
$([\delta m]\cup B)+([\delta m]\cup B) = [0,2m]$
. So,
Hence,
On the other hand, for any elements
![]() $a,b\in A$
, we have
$a,b\in A$
, we have
![]() $a+b\in [(1+\delta )m]^d$
unless there is some
$a+b\in [(1+\delta )m]^d$
unless there is some
![]() $i\in [d]$
for which both
$i\in [d]$
for which both
![]() $a,b$
have their
$a,b$
have their
![]() $i$
th coordinate in
$i$
th coordinate in
![]() $B$
. Therefore, for any
$B$
. Therefore, for any
![]() $a\in A$
,
$a\in A$
,
Thus, for any
![]() $s$
and any subset
$s$
and any subset
![]() $A_{(s)}$
of
$A_{(s)}$
of
![]() $A$
of size
$A$
of size
![]() $s$
, we have that
$s$
, we have that
![]() $|(A+A_{(s)})\setminus [(1+\delta ) m]^d|\le \frac{2sd\sqrt{m}}{\delta m+\sqrt{m}}\cdot |A|{\le \frac{2sd}{\delta \sqrt{m}}|A|}\leq \frac{2s}{\sqrt{m}}\left (\frac{1+\delta }{\delta }\right )^d |A|$
. Hence,
$|(A+A_{(s)})\setminus [(1+\delta ) m]^d|\le \frac{2sd\sqrt{m}}{\delta m+\sqrt{m}}\cdot |A|{\le \frac{2sd}{\delta \sqrt{m}}|A|}\leq \frac{2s}{\sqrt{m}}\left (\frac{1+\delta }{\delta }\right )^d |A|$
. Hence,
Thus, for
![]() $s\le \epsilon \sqrt{m}/2$
, we have
$s\le \epsilon \sqrt{m}/2$
, we have
Note that
As such, there exists
![]() $\delta \in (0,1)$
such that for
$\delta \in (0,1)$
such that for
![]() $\epsilon$
sufficiently small, we have for all positive integers
$\epsilon$
sufficiently small, we have for all positive integers
![]() $d$
that
$d$
that
For
![]() $m$
sufficiently large, we have
$m$
sufficiently large, we have
![]() $\delta \in (2\epsilon ^{-1}m^{-1/2},1-m^{-1/2})$
. From (2) and (3), for
$\delta \in (2\epsilon ^{-1}m^{-1/2},1-m^{-1/2})$
. From (2) and (3), for
![]() $s\le \epsilon \sqrt{m}/2$
, we have
$s\le \epsilon \sqrt{m}/2$
, we have
Finally, recalling that
![]() $n\le (\delta m + 2\sqrt{m})^d$
,
$n\le (\delta m + 2\sqrt{m})^d$
,
![]() $\kappa \ge (2/((1+\epsilon )\delta ))^d$
, we have that
$\kappa \ge (2/((1+\epsilon )\delta ))^d$
, we have that
assuming that
![]() $c\gt 0$
is appropriately chosen. Hence,
$c\gt 0$
is appropriately chosen. Hence,
![]() $s\le \epsilon \sqrt{m}/2$
whenever
$s\le \epsilon \sqrt{m}/2$
whenever
![]() $s\le n^{c/\log \kappa }$
.
$s\le n^{c/\log \kappa }$
.
We remark that in Theorem 1.2, we cannot guarantee that there always exists
![]() $B_{(s)}\subseteq B$
such that
$B_{(s)}\subseteq B$
such that
![]() $|AB_{(s)}|$
is large, as shown by the following example in the abelian setting.
$|AB_{(s)}|$
is large, as shown by the following example in the abelian setting.
Proposition 2.6.
Given positive integers
![]() $s$
and
$s$
and
![]() $k$
and
$k$
and
![]() $\epsilon \in (0,1)$
, for
$\epsilon \in (0,1)$
, for
![]() $n$
sufficiently large, there exist
$n$
sufficiently large, there exist
![]() $A,B\subseteq \mathbb{Z}$
such that
$A,B\subseteq \mathbb{Z}$
such that
![]() $|A|=|B|=n$
,
$|A|=|B|=n$
,
![]() $|A+B| \gt kn$
, and for any subset
$|A+B| \gt kn$
, and for any subset
![]() $B_{(s)}$
of
$B_{(s)}$
of
![]() $B$
of size at most
$B$
of size at most
![]() $s$
,
$s$
,
![]() $|A+B_{(s)}| \le (2+\epsilon )n$
.
$|A+B_{(s)}| \le (2+\epsilon )n$
.
Proof. Let
![]() $A = [n{-k}] \cup \{{n,2n,\dots,kn}\}$
and
$A = [n{-k}] \cup \{{n,2n,\dots,kn}\}$
and
![]() $B = [n]$
. We have
$B = [n]$
. We have
![]() $|A+B| \gt kn$
. For any subset
$|A+B| \gt kn$
. For any subset
![]() $B_{(s)}$
of
$B_{(s)}$
of
![]() $B$
of size at most
$B$
of size at most
![]() $s$
, we have that
$s$
, we have that
![]() $|A+B_{(s)}|\le 2n + sk \le (2+\epsilon )n$
.
$|A+B_{(s)}|\le 2n + sk \le (2+\epsilon )n$
.
2.2. Large sumsets from medium-sized subsets
We now consider sumsets of medium-sized subsets, where we take subsets of both
![]() $A$
and
$A$
and
![]() $B$
while keeping the product of their sizes small. Bollobás, Leader, and Tiba [Reference Bollobás, Leader and Tiba6] proved the following result.
$B$
while keeping the product of their sizes small. Bollobás, Leader, and Tiba [Reference Bollobás, Leader and Tiba6] proved the following result.
Theorem 2.7 ([Reference Bollobás, Leader and Tiba6], Theorem 1). For all
![]() $\alpha,\beta \gt 0$
there exists
$\alpha,\beta \gt 0$
there exists
![]() $c \gt 0$
such that the following holds. Let
$c \gt 0$
such that the following holds. Let
![]() $A$
and
$A$
and
![]() $B$
be non-empty subsets of
$B$
be non-empty subsets of
![]() $\mathbb{F}_p$
with
$\mathbb{F}_p$
with
![]() $\alpha |B| \le |A| \le \alpha ^{-1}|B|$
and
$\alpha |B| \le |A| \le \alpha ^{-1}|B|$
and
![]() $|A|+|B| \le (1 - \beta )p$
. Then, for any integers
$|A|+|B| \le (1 - \beta )p$
. Then, for any integers
![]() $1 \le c_1 \le |A|$
and
$1 \le c_1 \le |A|$
and
![]() $1 \le c_2 \le |B|$
such that
$1 \le c_2 \le |B|$
such that
![]() $c_1c_2 \ge c \max\! (|A|, |B|)$
, there exist subsets
$c_1c_2 \ge c \max\! (|A|, |B|)$
, there exist subsets
![]() $A' \subset A$
and
$A' \subset A$
and
![]() $B' \subset B$
of sizes
$B' \subset B$
of sizes
![]() $c_1$
and
$c_1$
and
![]() $c_2$
such that
$c_2$
such that
![]() $|A' + B'| \ge |A| + |B| - 1$
.
$|A' + B'| \ge |A| + |B| - 1$
.
In particular, when
![]() $|A|=|B|=n$
, and we take
$|A|=|B|=n$
, and we take
![]() $c_1=c_2\ge \sqrt{cn}$
, this result again yields the Cauchy–Davenport lower bound of
$c_1=c_2\ge \sqrt{cn}$
, this result again yields the Cauchy–Davenport lower bound of
![]() $2n-1$
using only medium-sized subsets of
$2n-1$
using only medium-sized subsets of
![]() $A$
and
$A$
and
![]() $B$
. We are interested in going beyond this bound. However, in this case, unlike in the case of a constant-sized subset of
$B$
. We are interested in going beyond this bound. However, in this case, unlike in the case of a constant-sized subset of
![]() $B$
plus all of
$B$
plus all of
![]() $A$
, it turns out that only a lower-order improvement over the Cauchy–Davenport bound is possible in general.
$A$
, it turns out that only a lower-order improvement over the Cauchy–Davenport bound is possible in general.
Theorem 2.8.
For all
![]() $\beta$
there exists
$\beta$
there exists
![]() $c'\gt 0$
such that the following holds. Let
$c'\gt 0$
such that the following holds. Let
![]() $A,B$
be nonempty subsets of
$A,B$
be nonempty subsets of
![]() $\mathbb{F}_p$
with
$\mathbb{F}_p$
with
![]() $|A|=|B|=n\leq \frac{1-\beta }{2}p$
and
$|A|=|B|=n\leq \frac{1-\beta }{2}p$
and
![]() $|A+B|=\kappa n$
. Then for all
$|A+B|=\kappa n$
. Then for all
![]() $c\in (0,\sqrt{n}]$
there exist subsets
$c\in (0,\sqrt{n}]$
there exist subsets
![]() $A_{(s)} \subset A$
and
$A_{(s)} \subset A$
and
![]() $B_{(s)} \subset B$
of size
$B_{(s)} \subset B$
of size
![]() $s\leq (c'+c)\sqrt{n}$
such that
$s\leq (c'+c)\sqrt{n}$
such that
Proof. Let
![]() $c_2=\frac{1}{4}$
. By Theorem 2.7, for some
$c_2=\frac{1}{4}$
. By Theorem 2.7, for some
![]() $c_1\gt 0$
, there exist subsets
$c_1\gt 0$
, there exist subsets
![]() $A'\subset A$
and
$A'\subset A$
and
![]() $B'\subset B$
with
$B'\subset B$
with
![]() $|A'|=|B'|\le c_1\sqrt{n}$
such that
$|A'|=|B'|\le c_1\sqrt{n}$
such that
![]() $|A'+B'|\geq 2n-1$
. Fixing such a pair of subsets and letting
$|A'+B'|\geq 2n-1$
. Fixing such a pair of subsets and letting
![]() $S_0\;:\!=\;A'+B'$
, we iteratively perform the following procedure. Given
$S_0\;:\!=\;A'+B'$
, we iteratively perform the following procedure. Given
![]() $S_{i-1}$
for
$S_{i-1}$
for
![]() $1\leq i\leq \sqrt{n}$
, we form
$1\leq i\leq \sqrt{n}$
, we form
![]() $S_i\subseteq A+B$
by either taking an element
$S_i\subseteq A+B$
by either taking an element
![]() $a\in A$
such that
$a\in A$
such that
![]() $|(a+B)\setminus S_{i-1}|\geq c_2 n$
and letting
$|(a+B)\setminus S_{i-1}|\geq c_2 n$
and letting
![]() $S_i=S_{i-1}\cup (a+B)$
, or taking an element
$S_i=S_{i-1}\cup (a+B)$
, or taking an element
![]() $b\in B$
such that
$b\in B$
such that
![]() $|(b+A)\setminus S_{i-1}|\geq c_2 n$
and letting
$|(b+A)\setminus S_{i-1}|\geq c_2 n$
and letting
![]() $S_i=S_{i-1}\cup (b+A)$
. The procedure terminates when neither action is possible, or once
$S_i=S_{i-1}\cup (b+A)$
. The procedure terminates when neither action is possible, or once
![]() $S_{i}$
is formed for some
$S_{i}$
is formed for some
![]() $i\geq \sqrt{n}$
. Suppose the process terminates upon the formation of
$i\geq \sqrt{n}$
. Suppose the process terminates upon the formation of
![]() $S_\ell$
. Let
$S_\ell$
. Let
![]() $A^*$
and
$A^*$
and
![]() $B^*$
be the sets of elements chosen from
$B^*$
be the sets of elements chosen from
![]() $A$
and
$A$
and
![]() $B$
, respectively, in the course of the procedure, so
$B$
, respectively, in the course of the procedure, so
![]() $|A^*|,|B^*|\leq \ell \lt \sqrt{n}+1$
and
$|A^*|,|B^*|\leq \ell \lt \sqrt{n}+1$
and
![]() $S_\ell = S_0\cup (A^*+B) \cup (B^*+A)$
.
$S_\ell = S_0\cup (A^*+B) \cup (B^*+A)$
.
If
![]() $\ell \geq \sqrt{n}$
, then we have
$\ell \geq \sqrt{n}$
, then we have
![]() $|S_\ell |\geq |S_0|+c_2\ell n\geq |S_0|+c_2 n ^{3/2}$
. Otherwise, assume
$|S_\ell |\geq |S_0|+c_2\ell n\geq |S_0|+c_2 n ^{3/2}$
. Otherwise, assume
![]() $\ell \lt \sqrt{n}$
. Then by the termination condition, for all
$\ell \lt \sqrt{n}$
. Then by the termination condition, for all
![]() $a\in A$
and
$a\in A$
and
![]() $b\in B$
we have
$b\in B$
we have
![]() $|(b+A)\setminus S_{\ell }|,|(a+B)\setminus S_{\ell }|\lt c_2 n$
. Then in the graph
$|(b+A)\setminus S_{\ell }|,|(a+B)\setminus S_{\ell }|\lt c_2 n$
. Then in the graph
![]() $\Gamma _{S_\ell }$
, every vertex has degree at least
$\Gamma _{S_\ell }$
, every vertex has degree at least
![]() $(1-c_2)n$
, which as before means that between every pair
$(1-c_2)n$
, which as before means that between every pair
![]() $(x,y)\in A\times B$
there are at least
$(x,y)\in A\times B$
there are at least
![]() $(1-3c_2)n^2$
paths of length three. Applying Lemma 2.1 with
$(1-3c_2)n^2$
paths of length three. Applying Lemma 2.1 with
![]() $k=3$
and
$k=3$
and
![]() $w=(1-3c_2)n^2$
then yields
$w=(1-3c_2)n^2$
then yields
![]() $|A+B|\leq \frac{|S_\ell |^3}{(1-3c_2)n^2}$
, which means that
$|A+B|\leq \frac{|S_\ell |^3}{(1-3c_2)n^2}$
, which means that
![]() $|S_\ell |\geq ((1-3c_2)\kappa )^{1/3}n$
in this case.
$|S_\ell |\geq ((1-3c_2)\kappa )^{1/3}n$
in this case.
Choose subsets
![]() $\tilde{A}\subset A$
and
$\tilde{A}\subset A$
and
![]() $\tilde{B}\subset B$
of size
$\tilde{B}\subset B$
of size
![]() $\lceil c \sqrt{n}\rceil$
uniformly at random. By construction, each element of
$\lceil c \sqrt{n}\rceil$
uniformly at random. By construction, each element of
![]() $A^*+B$
appears in
$A^*+B$
appears in
![]() $A^*+\tilde{B}$
with probability at least
$A^*+\tilde{B}$
with probability at least
![]() $\frac{|\tilde B|}{B}=c n^{-1/2}$
, and likewise each element of
$\frac{|\tilde B|}{B}=c n^{-1/2}$
, and likewise each element of
![]() $A+B^*$
appears in
$A+B^*$
appears in
![]() $\tilde A+B^*$
with probability at least
$\tilde A+B^*$
with probability at least
![]() $c n^{-1/2}$
. Therefore, we have
$c n^{-1/2}$
. Therefore, we have
 \begin{align*} &\mathbb{E}_{\tilde A, \tilde B}[|(A'\cup A^*\cup \tilde A)+(B'\cup B^*\cup \tilde B)|] \\ &\geq |A'+B'|+\mathbb{E}[|((A^*\cup \tilde A)+(B^*\cup \tilde B))\setminus (A'+B')|]\\ &\geq |S_0| + \sum _{s\in ((A^*+B)\cup (A+B^*))\setminus S_0} \Pr [s\in (A^*\cup \tilde A)+(B^*\cup \tilde B)] \\ &\geq |S_0| + c n^{-1/2} |S_\ell \setminus S_0|\\ &\geq (1-c n^{-1/2})|S_0| + c n^{-1/2} \min\! (|S_0|+c_2 n^{3/2}, (1-3c_2)^{1/3} \kappa ^{1/3}n)\\ &\geq 2n-1+c \min\! (c_2 n,((1-3c_2)^{1/3} \kappa ^{1/3}-2)n^{1/2}). \end{align*}
\begin{align*} &\mathbb{E}_{\tilde A, \tilde B}[|(A'\cup A^*\cup \tilde A)+(B'\cup B^*\cup \tilde B)|] \\ &\geq |A'+B'|+\mathbb{E}[|((A^*\cup \tilde A)+(B^*\cup \tilde B))\setminus (A'+B')|]\\ &\geq |S_0| + \sum _{s\in ((A^*+B)\cup (A+B^*))\setminus S_0} \Pr [s\in (A^*\cup \tilde A)+(B^*\cup \tilde B)] \\ &\geq |S_0| + c n^{-1/2} |S_\ell \setminus S_0|\\ &\geq (1-c n^{-1/2})|S_0| + c n^{-1/2} \min\! (|S_0|+c_2 n^{3/2}, (1-3c_2)^{1/3} \kappa ^{1/3}n)\\ &\geq 2n-1+c \min\! (c_2 n,((1-3c_2)^{1/3} \kappa ^{1/3}-2)n^{1/2}). \end{align*}
Fix choices of
![]() $\tilde A,\tilde B$
such that the size of this sumset is at least its expectation, and let
$\tilde A,\tilde B$
such that the size of this sumset is at least its expectation, and let
![]() $A_{(s)}=A'\cup A^*\cup \tilde A$
and
$A_{(s)}=A'\cup A^*\cup \tilde A$
and
![]() $B_{(s)}=B'\cup B^*\cup \tilde B$
. Note that
$B_{(s)}=B'\cup B^*\cup \tilde B$
. Note that
![]() $A_{(s)},B_{(s)}$
each has size at most
$A_{(s)},B_{(s)}$
each has size at most
![]() $s\le c_1\sqrt{n}+(\sqrt{n}+1)+\lceil c\sqrt{n}\rceil \le (c'+c)\sqrt{n}$
, where
$s\le c_1\sqrt{n}+(\sqrt{n}+1)+\lceil c\sqrt{n}\rceil \le (c'+c)\sqrt{n}$
, where
![]() $c'=c_1+2$
. We then have
$c'=c_1+2$
. We then have
![]() $|A_{(s)}+B_{(s)}|\geq 2n-1+c\min\! (\frac{1}{4} n,(c'' \kappa ^{1/3}-2)\sqrt{n})$
, where
$|A_{(s)}+B_{(s)}|\geq 2n-1+c\min\! (\frac{1}{4} n,(c'' \kappa ^{1/3}-2)\sqrt{n})$
, where
![]() $c''=(1-3c_2)^{1/3}\geq \frac{1}{2}$
, as desired.
$c''=(1-3c_2)^{1/3}\geq \frac{1}{2}$
, as desired.
The matching upper bound showing that Theorem 2.8 is best possible up to the power of
![]() $\kappa$
comes from taking
$\kappa$
comes from taking
![]() $s=C\sqrt{n}$
in the following construction.
$s=C\sqrt{n}$
in the following construction.
Proposition 2.9.
For all positive integers
![]() $n,k$
with
$n,k$
with
![]() $k\leq \sqrt{n}$
, there exist a real number
$k\leq \sqrt{n}$
, there exist a real number
![]() $\kappa \in (k,k+1]$
and a set
$\kappa \in (k,k+1]$
and a set
![]() $A\subseteq \mathbb{Z}$
such that
$A\subseteq \mathbb{Z}$
such that
![]() $|A|=n$
,
$|A|=n$
,
![]() $|A+A|=\kappa n$
, and for all subsets
$|A+A|=\kappa n$
, and for all subsets
![]() $A_{(s)},B_{(s)}\subset A$
of size
$A_{(s)},B_{(s)}\subset A$
of size
![]() $s\leq n$
, we have
$s\leq n$
, we have
Proof. Let
![]() $n_0=n-k+1$
, and let
$n_0=n-k+1$
, and let
![]() $A=[n_0]\cup \{2n_0,3n_0,\dots,kn_0\}$
. Then
$A=[n_0]\cup \{2n_0,3n_0,\dots,kn_0\}$
. Then
![]() $|A|=n$
and
$|A|=n$
and
![]() $|A+A|=|{([(k+1)n_0]\setminus \{1\})}\cup \{(k+2)n_0,\dots,2kn_0\}|=(k+1)(n-k+1)+k-2$
, so indeed
$|A+A|=|{([(k+1)n_0]\setminus \{1\})}\cup \{(k+2)n_0,\dots,2kn_0\}|=(k+1)(n-k+1)+k-2$
, so indeed
![]() $(k+1)n\geq |A+A|\geq (k+1)(n-k+1)\gt (k+1)n-k^2\geq kn$
.
$(k+1)n\geq |A+A|\geq (k+1)(n-k+1)\gt (k+1)n-k^2\geq kn$
.
Fix arbitrary subsets
![]() $A_{(s)},B_{(s)}\subset A$
with
$A_{(s)},B_{(s)}\subset A$
with
![]() $|A_{(s)}|=|B_{(s)}|=s$
. Partition
$|A_{(s)}|=|B_{(s)}|=s$
. Partition
![]() $A_{(s)}$
as
$A_{(s)}$
as
![]() $A_0\sqcup A_1$
where
$A_0\sqcup A_1$
where
![]() $A_0= A_{(s)}\cap [n_0]$
, and partition
$A_0= A_{(s)}\cap [n_0]$
, and partition
![]() $B_{(s)}=B_0\sqcup B_1$
similarly. We have
$B_{(s)}=B_0\sqcup B_1$
similarly. We have
![]() $A_0+B_0\subseteq [2n_0]$
while
$A_0+B_0\subseteq [2n_0]$
while
![]() $A_1+B_1\subseteq \{2n_0,3n_0,\dots,2kn_0\}$
, and
$A_1+B_1\subseteq \{2n_0,3n_0,\dots,2kn_0\}$
, and
![]() $|A_1|,|B_1|\leq |\{2n_0,3n_0,\dots,kn_0\}|=k-1$
. Then
$|A_1|,|B_1|\leq |\{2n_0,3n_0,\dots,kn_0\}|=k-1$
. Then
 \begin{align*} |A_{(s)}+B_{(s)}| &\leq |A_0+B_0|+|A_0+B_1|+|A_1+B_0|+|A_1+B_1| \\ &\leq 2n_0 + |A_0||B_1|+|A_1||B_0| +(2k-1)\\ &\leq 2n + 1 + 2(k-1)s \leq 2n+2\kappa s, \end{align*}
\begin{align*} |A_{(s)}+B_{(s)}| &\leq |A_0+B_0|+|A_0+B_1|+|A_1+B_0|+|A_1+B_1| \\ &\leq 2n_0 + |A_0||B_1|+|A_1||B_0| +(2k-1)\\ &\leq 2n + 1 + 2(k-1)s \leq 2n+2\kappa s, \end{align*}
as desired.
3. The Cauchy–Davenport bound in
 $\mathbb{F}_p$
from three elements
$\mathbb{F}_p$
from three elements
In this section, we prove Theorem 1.3, restated below, which resolves Conjecture 1 of [Reference Bollobás, Leader and Tiba5].
Theorem 1.3.
There exists
![]() $\alpha \gt 0$
such that the following holds. Let
$\alpha \gt 0$
such that the following holds. Let
![]() $A,B$
be nonempty subsets of
$A,B$
be nonempty subsets of
![]() $\mathbb{F}_p$
of size
$\mathbb{F}_p$
of size
![]() $n\le \alpha p$
. Then there exists a subset
$n\le \alpha p$
. Then there exists a subset
![]() $B_{(3)}$
of
$B_{(3)}$
of
![]() $B$
of size at most three such that
$B$
of size at most three such that
![]() $|A+B_{(3)}| \ge 2n-1$
.
$|A+B_{(3)}| \ge 2n-1$
.
Our argument is based on an extension of the argument in Section 2, used to show that appropriate subsets of
![]() $A$
and
$A$
and
![]() $B$
have bounded doubling. We then use Freiman’s rectification principle to relate appropriate subsets of
$B$
have bounded doubling. We then use Freiman’s rectification principle to relate appropriate subsets of
![]() $\mathbb{F}_p$
and subsets of
$\mathbb{F}_p$
and subsets of
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
We will make use of the analogue of the above theorem in the integer setting that was already shown in [Reference Bollobás, Leader and Tiba5].
Theorem 3.1 ([Reference Bollobás, Leader and Tiba5], Theorem 1). Let
![]() $A,B$
be subsets of
$A,B$
be subsets of
![]() $\mathbb{Z}$
of size
$\mathbb{Z}$
of size
![]() $n$
. Then there exists a subset
$n$
. Then there exists a subset
![]() $B_{(3)}$
of
$B_{(3)}$
of
![]() $B$
of size at most three such that
$B$
of size at most three such that
![]() $|A+B_{(3)}| \ge 2n-1$
.
$|A+B_{(3)}| \ge 2n-1$
.
We will also make use of Freiman’s rectification principle [Reference Bilu, Lev and Ruzsa4, Reference Freiman14]. Recall that a Freiman
![]() $s$
-homomorphism
$s$
-homomorphism
![]() $\phi\; :\;A\to B$
is a map such that
$\phi\; :\;A\to B$
is a map such that
![]() $\sum _{i=1}^{s}\phi (a_i)=\sum _{i=1}^{s}\phi (a_i^{\prime})$
whenever
$\sum _{i=1}^{s}\phi (a_i)=\sum _{i=1}^{s}\phi (a_i^{\prime})$
whenever
![]() $\sum _{i=1}^{s}a_i=\sum _{i=1}^{s}a_i^{\prime}$
, and it is called an
$\sum _{i=1}^{s}a_i=\sum _{i=1}^{s}a_i^{\prime}$
, and it is called an
![]() $s$
-isomorphism when
$s$
-isomorphism when
![]() $\phi ^{-1}$
is also a Freiman
$\phi ^{-1}$
is also a Freiman
![]() $s$
-homomorphism.
$s$
-homomorphism.
Theorem 3.2 ([Reference Bilu, Lev and Ruzsa4, Reference Freiman14]). Let
![]() $A$
be a subset of
$A$
be a subset of
![]() $\mathbb{F}_p$
. For
$\mathbb{F}_p$
. For
![]() $\lambda \gt 0$
and
$\lambda \gt 0$
and
![]() $s\gt 0$
, there exists
$s\gt 0$
, there exists
![]() $c\gt 0$
such that if
$c\gt 0$
such that if
![]() $|A|\lt cp$
and
$|A|\lt cp$
and
![]() $|A+A|\le \lambda |A|$
, then there is a Freiman
$|A+A|\le \lambda |A|$
, then there is a Freiman
![]() $s$
-isomorphism between
$s$
-isomorphism between
![]() $A$
and a subset of
$A$
and a subset of
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
We use the following version of the Plünnecke-Ruzsa Inequality with different summands [Reference Ruzsa27].
Lemma 3.3 (The Plünnecke-Ruzsa Inequality, [Reference Ruzsa27]). Let
![]() $X,Y_1,\dots,Y_k$
be subsets of an abelian group
$X,Y_1,\dots,Y_k$
be subsets of an abelian group
![]() $G$
. Assume that
$G$
. Assume that
![]() $|X+Y_i|\le \alpha _i |X|$
for each
$|X+Y_i|\le \alpha _i |X|$
for each
![]() $i\le k$
. Then
$i\le k$
. Then
![]() $|Y_1+\dots +Y_k|\le \alpha _1\dots \alpha _k |X|$
.
$|Y_1+\dots +Y_k|\le \alpha _1\dots \alpha _k |X|$
.
Using Theorem 3.2 and Lemma 3.3, we obtain the following corollary.
Corollary 3.4.
For
![]() $\lambda,s,t\gt 0$
, there exists
$\lambda,s,t\gt 0$
, there exists
![]() $c\gt 0$
such that the following holds. Let
$c\gt 0$
such that the following holds. Let
![]() $A,B$
be subsets of
$A,B$
be subsets of
![]() $\mathbb{F}_p$
with
$\mathbb{F}_p$
with
![]() $|B|/2\le |A|\le |B|\lt cp$
. If
$|B|/2\le |A|\le |B|\lt cp$
. If
![]() $|A+B|\le \lambda |A|$
, then there is a Freiman
$|A+B|\le \lambda |A|$
, then there is a Freiman
![]() $s$
-isomorphism between
$s$
-isomorphism between
![]() $t(A\cup B)$
and a subset of
$t(A\cup B)$
and a subset of
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Proof. One application of Lemma 3.3 with
![]() $X=A,Y_1=Y_2=B$
gives
$X=A,Y_1=Y_2=B$
gives
![]() $|2B|{\le \lambda ^2} |A|$
. Another application of Lemma 3.3 with
$|2B|{\le \lambda ^2} |A|$
. Another application of Lemma 3.3 with
![]() $X = B$
and
$X = B$
and
![]() $Y_1 = \cdots = Y_k = A$
and
$Y_1 = \cdots = Y_k = A$
and
![]() $Y_{k+1}=\cdots = Y_{k+\ell } = B$
gives
$Y_{k+1}=\cdots = Y_{k+\ell } = B$
gives
![]() $|kB+\ell A|\le \lambda ^{2k+l}|B|$
and hence
$|kB+\ell A|\le \lambda ^{2k+l}|B|$
and hence
![]() $|t(A\cup B)|\le (t+1)\lambda ^{2t}|B|\lt c(t+1)\lambda ^{2t}p$
. In particular we have
$|t(A\cup B)|\le (t+1)\lambda ^{2t}|B|\lt c(t+1)\lambda ^{2t}p$
. In particular we have
![]() $|2t(A\cup B)|\le (2t+1)\lambda ^{4t}{|B| \le (2t+1)\lambda ^{4t} |t(A\cup B)|}$
, so provided that
$|2t(A\cup B)|\le (2t+1)\lambda ^{4t}{|B| \le (2t+1)\lambda ^{4t} |t(A\cup B)|}$
, so provided that
![]() $c$
is chosen sufficiently small in terms of
$c$
is chosen sufficiently small in terms of
![]() $\lambda,s,t$
, Theorem 3.2 implies that
$\lambda,s,t$
, Theorem 3.2 implies that
![]() $t(A\cup B)$
is Freiman
$t(A\cup B)$
is Freiman
![]() $s$
-isomorphic to a subset
$s$
-isomorphic to a subset
![]() $R\subseteq \mathbb{Z}$
.
$R\subseteq \mathbb{Z}$
.
The following simple lemma is a warm-up to the proof of Theorem 1.3, and suggests the general intuition behind our approach.
Lemma 3.5.
For every
![]() $\lambda \gt 0$
, there is
$\lambda \gt 0$
, there is
![]() $\alpha \gt 0$
such that the following holds. Let
$\alpha \gt 0$
such that the following holds. Let
![]() $A,B$
be subsets of
$A,B$
be subsets of
![]() $\mathbb{F}_p$
of size
$\mathbb{F}_p$
of size
![]() $n\le \alpha p$
. Assume that
$n\le \alpha p$
. Assume that
![]() $|A+B|\le \lambda n$
. Then there exists a subset
$|A+B|\le \lambda n$
. Then there exists a subset
![]() $B_{(3)}$
of
$B_{(3)}$
of
![]() $B$
of size at most three such that
$B$
of size at most three such that
![]() $|A+B_{(3)}| \ge 2n-1$
.
$|A+B_{(3)}| \ge 2n-1$
.
Proof. By Corollary 3.4, for
![]() $\alpha$
sufficiently small, there is a Freiman
$\alpha$
sufficiently small, there is a Freiman
![]() $2$
-isomorphism
$2$
-isomorphism
![]() $\psi$
from
$\psi$
from
![]() $(A\cup B)$
to a subset of
$(A\cup B)$
to a subset of
![]() $\mathbb{Z}$
. By Theorem 3.1, there exists a subset
$\mathbb{Z}$
. By Theorem 3.1, there exists a subset
![]() $B_{(3)}$
of
$B_{(3)}$
of
![]() $B$
so that
$B$
so that
![]() $|\psi (A)+\psi (B_{(3)})| \ge 2n-1$
. Noting that since
$|\psi (A)+\psi (B_{(3)})| \ge 2n-1$
. Noting that since
![]() $\psi$
is a Freiman
$\psi$
is a Freiman
![]() $2$
-isomorphism,
$2$
-isomorphism,
![]() $\psi (a)+\psi (b)=\psi (a')+\psi (b')$
if and only if
$\psi (a)+\psi (b)=\psi (a')+\psi (b')$
if and only if
![]() $a+b=a'+b'$
, this then implies
$a+b=a'+b'$
, this then implies
![]() $|A+B_{(3)}|=|\psi (A)+\psi (B_{(3)})|\ge 2n-1$
.
$|A+B_{(3)}|=|\psi (A)+\psi (B_{(3)})|\ge 2n-1$
.
The full proof of Theorem 1.3 is much more involved, due to the fact that we cannot reduce to the case
![]() $|A+B|\ll |A|$
, but can only find suitable dense subsets
$|A+B|\ll |A|$
, but can only find suitable dense subsets
![]() $\tilde{A}$
of
$\tilde{A}$
of
![]() $A$
with
$A$
with
![]() $|\tilde{A}+B|\ll |A|$
. Making the choice of elements
$|\tilde{A}+B|\ll |A|$
. Making the choice of elements
![]() $b_1,b_2,b_3$
greedily, we can find a subset
$b_1,b_2,b_3$
greedily, we can find a subset
![]() $A'$
of
$A'$
of
![]() $A$
of size at least
$A$
of size at least
![]() $|A|/2$
and a set
$|A|/2$
and a set
![]() $C$
with
$C$
with
![]() $|C|\ll |A|$
such that for each
$|C|\ll |A|$
such that for each
![]() $a\in A'$
, at least a positive fraction of
$a\in A'$
, at least a positive fraction of
![]() $b\in B$
satisfies
$b\in B$
satisfies
![]() $a'+b\in C$
. From this we obtain the bound
$a'+b\in C$
. From this we obtain the bound
![]() $|A'+B|\ll |A|$
. We then bootstrap this subset to a slightly larger subset
$|A'+B|\ll |A|$
. We then bootstrap this subset to a slightly larger subset
![]() $A''$
consisting of all
$A''$
consisting of all
![]() $a''\in A$
with
$a''\in A$
with
![]() $a''+b \in (A'+B)\cup A\cup (A+x)$
for a positive fraction of
$a''+b \in (A'+B)\cup A\cup (A+x)$
for a positive fraction of
![]() $b\in B$
. At this point, we need to employ another argument (inspired by the argument in the integer case) in order to handle the elements of
$b\in B$
. At this point, we need to employ another argument (inspired by the argument in the integer case) in order to handle the elements of
![]() $A$
that are not contained in
$A$
that are not contained in
![]() $A''$
. To proceed with the proof in full detail, we first state two useful auxiliary results.
$A''$
. To proceed with the proof in full detail, we first state two useful auxiliary results.
Lemma 3.6 (Theorem 27, [Reference Bollobás, Leader and Tiba5]). There is
![]() $c\gt 0$
such that the following holds. Let
$c\gt 0$
such that the following holds. Let
![]() $A,B$
be subsets of
$A,B$
be subsets of
![]() $\mathbb{F}_p$
of size
$\mathbb{F}_p$
of size
![]() $n\le cp$
, where
$n\le cp$
, where
![]() $B$
is contained in an interval of length at most
$B$
is contained in an interval of length at most
![]() $n(1+c)$
. Then there exists a subset
$n(1+c)$
. Then there exists a subset
![]() $B_{(3)}$
of
$B_{(3)}$
of
![]() $B$
of size at most three such that
$B$
of size at most three such that
![]() $|A+B_{(3)}| \ge 2n-1$
.
$|A+B_{(3)}| \ge 2n-1$
.
Lemma 3.7 ([Reference Grynkiewicz20]). There is
![]() $c\gt 0$
such that the following holds. Let
$c\gt 0$
such that the following holds. Let
![]() $B$
be a subset of
$B$
be a subset of
![]() $\mathbb{F}_p$
with
$\mathbb{F}_p$
with
![]() $|B-B| \lt (2+c)|B| \lt 4cp$
. Then B is contained in an interval of length at most
$|B-B| \lt (2+c)|B| \lt 4cp$
. Then B is contained in an interval of length at most
![]() $(1+c)|B|$
.
$(1+c)|B|$
.
Proof of Theorem
1.3. By Lemma 3.6, in the remaining part of the proof, we can assume that
![]() $B$
is not contained in an interval of length at most
$B$
is not contained in an interval of length at most
![]() $(1+c)n$
, and hence, by Lemma 3.7,
$(1+c)n$
, and hence, by Lemma 3.7,
![]() $|B-B|\ge (2+c)n$
.
$|B-B|\ge (2+c)n$
.
Step 1. We first show that we can assume that there exists
![]() $B_{(2)}\subseteq B$
of size at most two where
$B_{(2)}\subseteq B$
of size at most two where
![]() $|A+B_{(2)}| \ge (3/2+c_1)n$
for an appropriate constant
$|A+B_{(2)}| \ge (3/2+c_1)n$
for an appropriate constant
![]() $c_1\gt 0$
.
$c_1\gt 0$
.
If not, then for any two elements
![]() $b_1,b_2\in B$
, we have that
$b_1,b_2\in B$
, we have that
![]() $|(A+b_2-b_1)\cap A|\gt (1/2-c_1)n$
. By our assumption, we have that for any
$|(A+b_2-b_1)\cap A|\gt (1/2-c_1)n$
. By our assumption, we have that for any
![]() $b\in B-B$
, we can write
$b\in B-B$
, we can write
![]() $b=a_1-a_2$
in at least
$b=a_1-a_2$
in at least
![]() $n(1/2-c_1)$
ways. Since the number of pairs
$n(1/2-c_1)$
ways. Since the number of pairs
![]() $(a_1,a_2)$
is
$(a_1,a_2)$
is
![]() $n^2$
, we conclude that
$n^2$
, we conclude that
![]() $|B-B|\le n^2/ (n(1/2-c_1))$
. For
$|B-B|\le n^2/ (n(1/2-c_1))$
. For
![]() $c_1$
sufficiently small in
$c_1$
sufficiently small in
![]() $c$
, we then have
$c$
, we then have
![]() $|B-B|\lt (2+c)n$
, a contradiction.
$|B-B|\lt (2+c)n$
, a contradiction.
Step 2. Assume that for all
![]() $B_{(3)}\subseteq B$
of size at most three,
$B_{(3)}\subseteq B$
of size at most three,
![]() $|A+B_{(3)}| \le (2+c_1/2)n$
. From Step 1, there exists
$|A+B_{(3)}| \le (2+c_1/2)n$
. From Step 1, there exists
![]() $B_{(2)}\subseteq B$
of size at most two with
$B_{(2)}\subseteq B$
of size at most two with
![]() $|A+B_{(2)}| \geq (3/2+c_1)n$
. Then for all
$|A+B_{(2)}| \geq (3/2+c_1)n$
. Then for all
![]() $b\in B$
, we have
$b\in B$
, we have
![]() $|(A+b)\setminus (A+B_{(2)})|\le (1/2+c_1/2-c_1)n=(1/2-c_1/2)n$
.
$|(A+b)\setminus (A+B_{(2)})|\le (1/2+c_1/2-c_1)n=(1/2-c_1/2)n$
.
Recall the construction from Section 2 of a bipartite graph
![]() $\Gamma _C$
on vertex sets
$\Gamma _C$
on vertex sets
![]() $A,B$
where
$A,B$
where
![]() $a\in A$
and
$a\in A$
and
![]() $b\in B$
are connected if and only if
$b\in B$
are connected if and only if
![]() $a+b\in C$
. Let
$a+b\in C$
. Let
![]() $C=A+B_{(2)}$
. Clearly
$C=A+B_{(2)}$
. Clearly
![]() $|C|\le 2n$
. Each
$|C|\le 2n$
. Each
![]() $b\in B$
is adjacent in
$b\in B$
is adjacent in
![]() $\Gamma _C$
to at least
$\Gamma _C$
to at least
![]() $(1/2+c_1/2)n$
vertices
$(1/2+c_1/2)n$
vertices
![]() $a\in A$
. Thus, every
$a\in A$
. Thus, every
![]() $b,b'\in B$
are connected by at least
$b,b'\in B$
are connected by at least
![]() $c_1 n$
walks of length two in the graph. By Lemma 2.2, this implies that
$c_1 n$
walks of length two in the graph. By Lemma 2.2, this implies that
![]() $|B-B|\ll _{c_1}n$
.
$|B-B|\ll _{c_1}n$
.
Let
![]() $A'$
be the set of
$A'$
be the set of
![]() $a\in A$
with degree at least
$a\in A$
with degree at least
![]() $c_1n/4$
in the graph. The number of edges in the graph is at most
$c_1n/4$
in the graph. The number of edges in the graph is at most
![]() $|A'|n+(n-|A'|)c_1n/4$
and at least
$|A'|n+(n-|A'|)c_1n/4$
and at least
![]() $(1/2+c_1/2)n|B|=(1/2+c_1/2)n^2$
. Hence,
$(1/2+c_1/2)n|B|=(1/2+c_1/2)n^2$
. Hence,
Furthermore, for any
![]() $a\in A'$
and
$a\in A'$
and
![]() $b\in B$
, there exist at least
$b\in B$
, there exist at least
![]() $c_1^2n^2/4$
walks of length three between
$c_1^2n^2/4$
walks of length three between
![]() $a$
and
$a$
and
![]() $b$
. By Lemma 2.1, this implies
$b$
. By Lemma 2.1, this implies
![]() $|A'+B|\ll _{c_1} n$
.
$|A'+B|\ll _{c_1} n$
.
Let
![]() $s$
be a sufficiently large constant to be chosen later. By Corollary 3.4, provided that
$s$
be a sufficiently large constant to be chosen later. By Corollary 3.4, provided that
![]() $\alpha$
is sufficiently small in terms of
$\alpha$
is sufficiently small in terms of
![]() $s$
and
$s$
and
![]() $c_1$
, we have a Freiman
$c_1$
, we have a Freiman
![]() $(s+1)$
-isomorphism
$(s+1)$
-isomorphism
![]() $\phi$
between
$\phi$
between
![]() $A'\cup B$
and a subset
$A'\cup B$
and a subset
![]() $R$
of
$R$
of
![]() $\mathbb{Z}$
. By translation, without loss of generality, we can assume that
$\mathbb{Z}$
. By translation, without loss of generality, we can assume that
![]() $0\in A'\cup B$
and
$0\in A'\cup B$
and
![]() $0\in R$
,
$0\in R$
,
![]() $R\subset \mathbb{Z}_{\ge 0}$
, and
$R\subset \mathbb{Z}_{\ge 0}$
, and
![]() $\phi (0)=0$
. Let
$\phi (0)=0$
. Let
![]() $m=\max\! (\phi (B))$
, and let
$m=\max\! (\phi (B))$
, and let
![]() $x=\phi ^{-1}(m)\in B$
. Note that there is no solution to
$x=\phi ^{-1}(m)\in B$
. Note that there is no solution to
![]() $r_2-r_1=tm$
for
$r_2-r_1=tm$
for
![]() $r_1,r_2\in \phi (B) \setminus \{m\}$
and
$r_1,r_2\in \phi (B) \setminus \{m\}$
and
![]() $|t|\ge 1$
. Since
$|t|\ge 1$
. Since
![]() $\phi$
is a Freiman
$\phi$
is a Freiman
![]() $(s+1)$
-isomorphism on
$(s+1)$
-isomorphism on
![]() $A'\cup B$
, there is no solution to
$A'\cup B$
, there is no solution to
![]() $b_2-b_1=tx=t(x-0)$
for
$b_2-b_1=tx=t(x-0)$
for
![]() $b_1,b_2\in B \setminus \{x\}$
and
$b_1,b_2\in B \setminus \{x\}$
and
![]() $1\le |t|\le s$
, since such a solution would yield a solution to
$1\le |t|\le s$
, since such a solution would yield a solution to
![]() $\phi (b_2)-\phi (b_1)=t(m-0)$
.
$\phi (b_2)-\phi (b_1)=t(m-0)$
.
Let
![]() $S=(A'+B) \cup A\cup (A+x)$
, and consider the graph
$S=(A'+B) \cup A\cup (A+x)$
, and consider the graph
![]() $\Gamma _S$
defined as before. Let
$\Gamma _S$
defined as before. Let
![]() $c_2$
be a small constant (depending only on
$c_2$
be a small constant (depending only on
![]() $c_1$
) to be chosen later. Let
$c_1$
) to be chosen later. Let
![]() $A''$
be the set of
$A''$
be the set of
![]() $a\in A$
with degree in
$a\in A$
with degree in
![]() $\Gamma _S$
at least
$\Gamma _S$
at least
![]() $c_2n$
. We have that
$c_2n$
. We have that
![]() $|A''|\ge |A'| \ge (1/2+c_1/4)n$
provided that
$|A''|\ge |A'| \ge (1/2+c_1/4)n$
provided that
![]() $c_2\le c_1/4$
. Note that all
$c_2\le c_1/4$
. Note that all
![]() $b,b'\in B$
are connected by at least
$b,b'\in B$
are connected by at least
![]() $|A'| \ge n/2$
walks of length two in
$|A'| \ge n/2$
walks of length two in
![]() $\Gamma _S$
, and each
$\Gamma _S$
, and each
![]() $a\in A''$
is adjacent to at least
$a\in A''$
is adjacent to at least
![]() $c_2n$
vertices in
$c_2n$
vertices in
![]() $B$
in
$B$
in
![]() $\Gamma _S$
. Thus, for all
$\Gamma _S$
. Thus, for all
![]() $a\in A''$
and
$a\in A''$
and
![]() $b\in B$
, there are at least
$b\in B$
, there are at least
![]() $c_2n^2/2$
paths of length three in
$c_2n^2/2$
paths of length three in
![]() $\Gamma _S$
between
$\Gamma _S$
between
![]() $a$
and
$a$
and
![]() $b$
. As before, noting that
$b$
. As before, noting that
![]() $|S|\ll _{c_1} n$
, we can apply Lemma 2.1 to show that
$|S|\ll _{c_1} n$
, we can apply Lemma 2.1 to show that
![]() $|A''+B|\ll _{c_1,c_2} n$
(note that the implicit constant does not depend on
$|A''+B|\ll _{c_1,c_2} n$
(note that the implicit constant does not depend on
![]() $s$
). Let
$s$
). Let
![]() $k'$
be the maximum number of elements of
$k'$
be the maximum number of elements of
![]() $A''$
contained in a progression of common difference
$A''$
contained in a progression of common difference
![]() $x$
and length at most
$x$
and length at most
![]() $s$
. For any set
$s$
. For any set
![]() $\tilde{A}$
which is the intersection of
$\tilde{A}$
which is the intersection of
![]() $A''$
and a progression of common difference
$A''$
and a progression of common difference
![]() $x$
and length at most
$x$
and length at most
![]() $s$
, we have
$s$
, we have
![]() $|\tilde{A}+{(B\setminus \{x\})}|=|\tilde{A}|\cdot (|B|-1)$
since there is no solution to
$|\tilde{A}+{(B\setminus \{x\})}|=|\tilde{A}|\cdot (|B|-1)$
since there is no solution to
![]() $tx=b_1-b_2$
for
$tx=b_1-b_2$
for
![]() $b_1,b_2\in B\setminus \{x\}$
,
$b_1,b_2\in B\setminus \{x\}$
,
![]() $0\lt t\le s$
. On the other hand, we have
$0\lt t\le s$
. On the other hand, we have
![]() $|\tilde{A}+B| \ll _{c_1,c_2} n$
. Hence,
$|\tilde{A}+B| \ll _{c_1,c_2} n$
. Hence,
![]() $k'=\max |\tilde A|\leq \frac{|\tilde A+B|}{|B|-1}\ll _{c_1,c_2}1$
.
$k'=\max |\tilde A|\leq \frac{|\tilde A+B|}{|B|-1}\ll _{c_1,c_2}1$
.
Using linearity of expectation, note that
 \begin{align} \mathbb{E}_{b\in B,b\ne x}[|A+\{0,x,b\}|] &= |A+\{0,x\}|+\mathbb{E}_{b\in B,b\ne x}[|(b+A)\setminus (A+\{0,x\})|] \nonumber \\ &= |A+\{0,x\}| + \sum _{a\in A} \frac{|(a+(B\setminus \{x\}))\setminus (A+\{0,x\})|}{|B|-1}. \end{align}
\begin{align} \mathbb{E}_{b\in B,b\ne x}[|A+\{0,x,b\}|] &= |A+\{0,x\}|+\mathbb{E}_{b\in B,b\ne x}[|(b+A)\setminus (A+\{0,x\})|] \nonumber \\ &= |A+\{0,x\}| + \sum _{a\in A} \frac{|(a+(B\setminus \{x\}))\setminus (A+\{0,x\})|}{|B|-1}. \end{align}
Let
![]() $\tilde{n}$
be the minimum number of progressions of common difference
$\tilde{n}$
be the minimum number of progressions of common difference
![]() $x$
that
$x$
that
![]() $A$
can be partitioned into. Then
$A$
can be partitioned into. Then
![]() $|A\cup (A+x)|=n+\tilde{n}$
. Let
$|A\cup (A+x)|=n+\tilde{n}$
. Let
![]() $B'=B\setminus \{x\}$
. By the definition of
$B'=B\setminus \{x\}$
. By the definition of
![]() $A''$
, we have
$A''$
, we have
![]() $|(a+B')\cap (A\cup (A+x))| \le c_2n$
for
$|(a+B')\cap (A\cup (A+x))| \le c_2n$
for
![]() $a\notin A''$
. For
$a\notin A''$
. For
![]() $a\in A''$
, we will need the following claim to bound
$a\in A''$
, we will need the following claim to bound
![]() $|(a+B')\cap (A\cup (A+x))|$
.
$|(a+B')\cap (A\cup (A+x))|$
.
Claim 3.8.
If
![]() $a\in A''$
, we have
$a\in A''$
, we have
![]() $|(a+B')\cap (A\cup (A+x))|\le \tilde{n}+4(n-|A''|)/s$
.
$|(a+B')\cap (A\cup (A+x))|\le \tilde{n}+4(n-|A''|)/s$
.
Proof. Consider a fixed translate of
![]() $B'$
by
$B'$
by
![]() $a\in A$
and consider its intersection with a progression
$a\in A$
and consider its intersection with a progression
![]() $P$
with common difference
$P$
with common difference
![]() $x$
in
$x$
in
![]() $A\cup (A+x)$
. If
$A\cup (A+x)$
. If
![]() $a+b_1=p_1,a+b_2=p_2$
are in the intersection of
$a+b_1=p_1,a+b_2=p_2$
are in the intersection of
![]() $a+B'$
and
$a+B'$
and
![]() $P$
, then
$P$
, then
![]() $p_2-p_1=b_2-b_1$
. Since there is no solution to
$p_2-p_1=b_2-b_1$
. Since there is no solution to
![]() $b_2-b_1=tx$
for
$b_2-b_1=tx$
for
![]() $1\le |t|\le s$
and
$1\le |t|\le s$
and
![]() $b_1,b_2\in B'$
, it must be the case that
$b_1,b_2\in B'$
, it must be the case that
![]() $p_2-p_1=\ell x$
where either
$p_2-p_1=\ell x$
where either
![]() $\ell =0$
or
$\ell =0$
or
![]() $|\ell | \gt s$
. In particular, in every subprogression of
$|\ell | \gt s$
. In particular, in every subprogression of
![]() $P$
of length
$P$
of length
![]() $s$
, there can be at most one intersection with
$s$
, there can be at most one intersection with
![]() $a+B'$
. Hence, if there are
$a+B'$
. Hence, if there are
![]() $r\ge 2$
intersections of
$r\ge 2$
intersections of
![]() $a+B'$
and the progression
$a+B'$
and the progression
![]() $P$
, then
$P$
, then
![]() $|P|\ge (r-1)s$
. Furthermore, for
$|P|\ge (r-1)s$
. Furthermore, for
![]() $s$
chosen sufficiently large, recall that there are at most
$s$
chosen sufficiently large, recall that there are at most
![]() $k'=O_{c_1,c_2}(1)\lt s/1000$
elements in the intersection of
$k'=O_{c_1,c_2}(1)\lt s/1000$
elements in the intersection of
![]() $A''$
with any progression of length
$A''$
with any progression of length
![]() $s$
with common difference
$s$
with common difference
![]() $x$
. Similarly, there are at most
$x$
. Similarly, there are at most
![]() $s/1000$
elements in
$s/1000$
elements in
![]() $A''+x$
in a progression of common difference
$A''+x$
in a progression of common difference
![]() $x$
of length
$x$
of length
![]() $s$
. Thus,
$s$
. Thus,
![]() $P$
must contain at least
$P$
must contain at least
![]() $|P|(1-\frac{s}{500}\frac{1}{s})\ge (r-1)s/2$
elements from
$|P|(1-\frac{s}{500}\frac{1}{s})\ge (r-1)s/2$
elements from
![]() $(A\setminus A'')\cup ((A\setminus A'')+x)$
. Hence, we obtain that
$(A\setminus A'')\cup ((A\setminus A'')+x)$
. Hence, we obtain that
Summing over
![]() $P$
, we obtain
$P$
, we obtain
![]() $|(a+B')\cap (A\cup (A+x))|\le \tilde{n}+4(n-|A''|)/s.$
$|(a+B')\cap (A\cup (A+x))|\le \tilde{n}+4(n-|A''|)/s.$
Hence, if
![]() $\tilde{n}\ge 3c_2(n-1)$
, we have from (4) and Claim 3.9 that for
$\tilde{n}\ge 3c_2(n-1)$
, we have from (4) and Claim 3.9 that for
![]() $s \ge 16/c_2$
,
$s \ge 16/c_2$
,
 \begin{align*} \mathbb{E}_{b\in B,b\ne x}[|A+\{0,x,b\}|] &\ge n+\tilde{n}+ \!\left (1-c_2\frac{n}{n-1}\right )\!(n-|A''|)+\frac{|A''|}{n-1}(n-1-\tilde{n}-4(n-|A''|)/s) \\ &= 2n -\frac{\tilde{n}}{n-1}+ (n-|A''|)\left (\frac{\tilde{n}}{n-1}-1+1-c_2\frac{n}{n-1}-\frac{4|A''|}{(n-1)s}\right )\\ &\gt 2n-2. \end{align*}
\begin{align*} \mathbb{E}_{b\in B,b\ne x}[|A+\{0,x,b\}|] &\ge n+\tilde{n}+ \!\left (1-c_2\frac{n}{n-1}\right )\!(n-|A''|)+\frac{|A''|}{n-1}(n-1-\tilde{n}-4(n-|A''|)/s) \\ &= 2n -\frac{\tilde{n}}{n-1}+ (n-|A''|)\left (\frac{\tilde{n}}{n-1}-1+1-c_2\frac{n}{n-1}-\frac{4|A''|}{(n-1)s}\right )\\ &\gt 2n-2. \end{align*}
This implies the existence of
![]() $b\in B$
such that
$b\in B$
such that
![]() $|A+\{0,x,b\}|\ge 2n-1$
.
$|A+\{0,x,b\}|\ge 2n-1$
.
Next, consider the case
![]() $\tilde{n}\lt 3c_2(n-1)$
. We have the following claim.
$\tilde{n}\lt 3c_2(n-1)$
. We have the following claim.
Claim 3.9.
For
![]() $a\in A$
and
$a\in A$
and
![]() $b\in B$
, we have
$b\in B$
, we have
![]() $|(a+B)\cap (A\cup (A+b))| \le 2\tilde{n} + 2n/s + 1$
.
$|(a+B)\cap (A\cup (A+b))| \le 2\tilde{n} + 2n/s + 1$
.
Proof. Note that for any fixed
![]() $b\in B$
,
$b\in B$
,
![]() $A\cup (A+b)$
can be written as a union of at most
$A\cup (A+b)$
can be written as a union of at most
![]() $2\tilde{n}$
progressions of common difference
$2\tilde{n}$
progressions of common difference
![]() $x$
with total size at most
$x$
with total size at most
![]() $2n$
. The argument in our proof of Claim 3.9 shows that for any progression
$2n$
. The argument in our proof of Claim 3.9 shows that for any progression
![]() $P$
of common difference
$P$
of common difference
![]() $x$
and any
$x$
and any
![]() $a\in A$
,
$a\in A$
,
![]() $|(a+B')\cap P|\leq 1+|P|/s$
. Hence, summing over a partition of
$|(a+B')\cap P|\leq 1+|P|/s$
. Hence, summing over a partition of
![]() $A\cup (A+b)$
into at most
$A\cup (A+b)$
into at most
![]() $2\tilde n$
progressions, we obtain
$2\tilde n$
progressions, we obtain
We now have
 \begin{align*} \mathbb{E}_{b,b'\in B}[|A+\{0,b,b'\}|] &=|A|+\mathbb{E}_{b,b'\in B}[|(b+A)\setminus A|+|(b'+A)\setminus (A\cup (A+b))]\\ &={n + \sum _{a} \frac{|(a+B)\setminus A|}{|B|} + \mathbb{E}_{b\in B}\left [\sum _{a} \frac{|(a+B)\setminus (A\cup (A+b))|}{|B|}\right ]} \\ &\ge n + 2\frac{|A|}{|B|}\left (n-1-2\tilde{n}-2n/s\right ) \gt 2n, \end{align*}
\begin{align*} \mathbb{E}_{b,b'\in B}[|A+\{0,b,b'\}|] &=|A|+\mathbb{E}_{b,b'\in B}[|(b+A)\setminus A|+|(b'+A)\setminus (A\cup (A+b))]\\ &={n + \sum _{a} \frac{|(a+B)\setminus A|}{|B|} + \mathbb{E}_{b\in B}\left [\sum _{a} \frac{|(a+B)\setminus (A\cup (A+b))|}{|B|}\right ]} \\ &\ge n + 2\frac{|A|}{|B|}\left (n-1-2\tilde{n}-2n/s\right ) \gt 2n, \end{align*}
assuming that
![]() $s$
is sufficiently large and
$s$
is sufficiently large and
![]() $c_2$
is sufficiently small. Here, we use linearity of expectation in the second equality, and Claim 3.10 in the first inequality.
$c_2$
is sufficiently small. Here, we use linearity of expectation in the second equality, and Claim 3.10 in the first inequality.
4. Higher-dimensional versions
In this section, we consider bounds that can be shown in high dimension. In particular, we will show a negative answer to [Reference Bollobás, Leader and Tiba6, Question 3], in that we cannot expect a much better bound than the Cauchy–Davenport bound in the medium-size regime even in high dimension.
Proposition 4.1.
For all positive integers
![]() $d$
,
$d$
,
![]() $t$
, and
$t$
, and
![]() $n$
, there exists a subset
$n$
, there exists a subset
![]() $A$
of size at least
$A$
of size at least
![]() $n$
in
$n$
in
![]() $\mathbb{Z}^d$
such that
$\mathbb{Z}^d$
such that
![]() $A$
cannot be covered by a union of
$A$
cannot be covered by a union of
![]() $t$
parallel hyperplanes, and for any
$t$
parallel hyperplanes, and for any
![]() $s\leq n$
and any subset
$s\leq n$
and any subset
![]() $A'\subseteq A$
of size
$A'\subseteq A$
of size
![]() $s$
,
$s$
,
![]() $|A'+A'| \le 2|A|+O_{d,t}(s)$
.
$|A'+A'| \le 2|A|+O_{d,t}(s)$
.
Nevertheless, Theorem 1.4, restated below, shows that if, instead of the medium-sized version, one asks for a subset
![]() $A'$
of
$A'$
of
![]() $A$
of bounded size with
$A$
of bounded size with
![]() $|A'+A| \ge (2^d-\epsilon )|A|$
, then such
$|A'+A| \ge (2^d-\epsilon )|A|$
, then such
![]() $A'$
always exists.
$A'$
always exists.
Theorem 1.4.
Let
![]() $\epsilon \gt 0$
and let
$\epsilon \gt 0$
and let
![]() $d$
be a positive integer. There exists
$d$
be a positive integer. There exists
![]() $T$
sufficiently large in
$T$
sufficiently large in
![]() $d$
and
$d$
and
![]() $\epsilon$
such that the following holds. Let
$\epsilon$
such that the following holds. Let
![]() $A$
be a subset of
$A$
be a subset of
![]() $\mathbb{Z}^d$
such that
$\mathbb{Z}^d$
such that
![]() $A$
is not contained in the union of any
$A$
is not contained in the union of any
![]() $T$
parallel hyperplanes. Then there is a subset
$T$
parallel hyperplanes. Then there is a subset
![]() $A'$
of
$A'$
of
![]() $A$
of size
$A$
of size
![]() $O_{\epsilon,d}(1)$
for which
$O_{\epsilon,d}(1)$
for which
![]() $|A+A'| \ge (2^d-\epsilon )|A|$
.
$|A+A'| \ge (2^d-\epsilon )|A|$
.
Let
![]() $P(A;\,t,k,d)$
denote the property that
$P(A;\,t,k,d)$
denote the property that
![]() $A$
is not contained in the union of any
$A$
is not contained in the union of any
![]() $t$
parallel translates of a subspace of dimension
$t$
parallel translates of a subspace of dimension
![]() $k\lt d$
in
$k\lt d$
in
![]() $\mathbb{R}^d$
. The proof of both results above will make use of the following lemma.
$\mathbb{R}^d$
. The proof of both results above will make use of the following lemma.
Lemma 4.2.
For any integers
![]() $t\geq 1$
and
$t\geq 1$
and
![]() $k\in [0,d-1]$
, there exist constants
$k\in [0,d-1]$
, there exist constants
![]() $C=C(t,k,d)$
and
$C=C(t,k,d)$
and
![]() $T=T(t,k,d)$
such that any set
$T=T(t,k,d)$
such that any set
![]() $A\subseteq \mathbb{R}^d$
satisfying
$A\subseteq \mathbb{R}^d$
satisfying
![]() $P(A;\,T,k,d)$
has a subset
$P(A;\,T,k,d)$
has a subset
![]() $A_{(C)}$
of size at most
$A_{(C)}$
of size at most
![]() $C$
satisfying
$C$
satisfying
![]() $P(A_{(C)};\,t,k,d)$
.
$P(A_{(C)};\,t,k,d)$
.
Proof. We prove the result by induction on
![]() $k$
. When
$k$
. When
![]() $k=0$
, the result is immediate (with
$k=0$
, the result is immediate (with
![]() $T(t,k,d)=t$
and
$T(t,k,d)=t$
and
![]() $C(t,k,d)=t+1$
). Now assume the claim holds for all
$C(t,k,d)=t+1$
). Now assume the claim holds for all
![]() $k\lt k_0$
and consider the case
$k\lt k_0$
and consider the case
![]() $k=k_0\in [1,d-1]$
. Since
$k=k_0\in [1,d-1]$
. Since
![]() $A$
satisfies
$A$
satisfies
![]() $P(A;\,T,k,d)$
, it satisfies
$P(A;\,T,k,d)$
, it satisfies
![]() $P(A;\,T',k-1,d)$
for any
$P(A;\,T',k-1,d)$
for any
![]() $T'\le T$
, so by choosing
$T'\le T$
, so by choosing
![]() $T(t,k,d)$
appropriately we can assume that
$T(t,k,d)$
appropriately we can assume that
![]() $A$
satisfies
$A$
satisfies
![]() $P(A;\,T(t^2,k-1,d),k-1,d)$
. By the inductive hypothesis, we can select a subset
$P(A;\,T(t^2,k-1,d),k-1,d)$
. By the inductive hypothesis, we can select a subset
![]() $X$
of
$X$
of
![]() $A$
of size at most
$A$
of size at most
![]() $C(t^2,k-1,d)$
such that
$C(t^2,k-1,d)$
such that
![]() $X$
satisfies
$X$
satisfies
![]() $P(X;\,t^2,k-1,d)$
.
$P(X;\,t^2,k-1,d)$
.
Suppose there are distinct subspaces
![]() $H_1,H_2$
of dimension
$H_1,H_2$
of dimension
![]() $k$
such that
$k$
such that
![]() $X$
is contained in both a union of
$X$
is contained in both a union of
![]() $t$
translates of
$t$
translates of
![]() $H_1$
and a union of
$H_1$
and a union of
![]() $t$
translates of
$t$
translates of
![]() $H_2$
. In this case,
$H_2$
. In this case,
![]() $X$
is contained in a union of at most
$X$
is contained in a union of at most
![]() $t^2$
translates of
$t^2$
translates of
![]() $H_1\cap H_2$
, which has dimension at most
$H_1\cap H_2$
, which has dimension at most
![]() $k-1$
, violating
$k-1$
, violating
![]() $P(X;\,t^2,k-1,d)$
. Hence, there is at most one subspace
$P(X;\,t^2,k-1,d)$
. Hence, there is at most one subspace
![]() $H$
of dimension
$H$
of dimension
![]() $k$
such that
$k$
such that
![]() $X$
is contained in a union of
$X$
is contained in a union of
![]() $t$
translates of
$t$
translates of
![]() $H$
. If no such
$H$
. If no such
![]() $H$
exists, then
$H$
exists, then
![]() $X$
satisfies
$X$
satisfies
![]() $P(X;\,t,k,d)$
. Otherwise, since
$P(X;\,t,k,d)$
. Otherwise, since
![]() $A$
satisfies
$A$
satisfies
![]() $P(A;\,T,k,d)$
with
$P(A;\,T,k,d)$
with
![]() $T\geq t$
, we can find a set of
$T\geq t$
, we can find a set of
![]() $t+1$
points in
$t+1$
points in
![]() $A$
, each in a different translate of
$A$
, each in a different translate of
![]() $H$
. Taking the union of
$H$
. Taking the union of
![]() $X$
with this set of
$X$
with this set of
![]() $t+1$
points, we obtain a set
$t+1$
points, we obtain a set
![]() $\bar{X}$
satisfying
$\bar{X}$
satisfying
![]() $P(\bar{X};\,t,k,d)$
with
$P(\bar{X};\,t,k,d)$
with
![]() $|\bar{X}|\le C(t^2,k-1,d)+t+1$
. Thus the claim holds for
$|\bar{X}|\le C(t^2,k-1,d)+t+1$
. Thus the claim holds for
![]() $k=k_0$
as well with
$k=k_0$
as well with
![]() $C(t,k,d)=C(t^2,k-1,d)+t+1$
and
$C(t,k,d)=C(t^2,k-1,d)+t+1$
and
![]() $T(t,k,d)=T(t^2,k-1,d)$
, and hence by induction for all
$T(t,k,d)=T(t^2,k-1,d)$
, and hence by induction for all
![]() $k\leq d-1$
.
$k\leq d-1$
.
Using Lemma 4.2, the proofs of Proposition 4.1 and that of Theorem 1.4 directly follow.
Proof of Proposition
4.1. By Lemma 4.3 with
![]() $A = \mathbb{Z}^d$
, there exists a finite subset
$A = \mathbb{Z}^d$
, there exists a finite subset
![]() $A_{(C)} \subset \mathbb{Z}^d$
of size
$A_{(C)} \subset \mathbb{Z}^d$
of size
![]() $O_{t,d}(1)$
that cannot be covered by a union of
$O_{t,d}(1)$
that cannot be covered by a union of
![]() $t$
parallel translates of a hyperplane. Let
$t$
parallel translates of a hyperplane. Let
![]() $A$
be the union of
$A$
be the union of
![]() $A_{(C)}$
and an arithmetic progression
$A_{(C)}$
and an arithmetic progression
![]() $P$
of length
$P$
of length
![]() $n-|A_{(C)}|$
. For any subset
$n-|A_{(C)}|$
. For any subset
![]() $A' \subseteq A$
of size
$A' \subseteq A$
of size
![]() $s$
,
$s$
,
![]() $A'+A'$
is contained in
$A'+A'$
is contained in
![]() $(2P) \cup (A_{(C)}+A')$
, so
$(2P) \cup (A_{(C)}+A')$
, so
![]() $|A'+A'|\le 2|P|+|A_{(C)}||A'|\leq 2|A|+O_{d,t}(s)$
, as claimed.
$|A'+A'|\le 2|P|+|A_{(C)}||A'|\leq 2|A|+O_{d,t}(s)$
, as claimed.
Proof of Theorem
1.4. Let
![]() $\delta$
be sufficiently small in
$\delta$
be sufficiently small in
![]() $\epsilon$
. By Theorem 1.7 and the following remark, there exists
$\epsilon$
. By Theorem 1.7 and the following remark, there exists
![]() $C'$
depending on
$C'$
depending on
![]() $d$
and
$d$
and
![]() $\delta$
such that the following holds. We can find a subset
$\delta$
such that the following holds. We can find a subset
![]() $\hat{A} \subseteq A$
of size at least
$\hat{A} \subseteq A$
of size at least
![]() $(1-\delta )|A|$
such that upon choosing a random subset
$(1-\delta )|A|$
such that upon choosing a random subset
![]() $\tilde{A} \subset \hat{A}$
of size
$\tilde{A} \subset \hat{A}$
of size
![]() $C'$
, one has
$C'$
, one has
![]() $\mathbb{E}[|\tilde{A}+\hat{A}|] \ge \min\! (2^{2d}|\hat{A}|,(1-\delta )|\hat{A}+\hat{A}|)$
. In particular, there exists a subset
$\mathbb{E}[|\tilde{A}+\hat{A}|] \ge \min\! (2^{2d}|\hat{A}|,(1-\delta )|\hat{A}+\hat{A}|)$
. In particular, there exists a subset
![]() $\tilde{A}$
of
$\tilde{A}$
of
![]() $\hat{A}$
of size
$\hat{A}$
of size
![]() $C'$
for which
$C'$
for which
![]() $|\tilde{A}+\hat{A}|\ge \min\! (2^{2d}|\hat{A}|,(1-\delta )|\hat{A}+\hat{A}|)$
. If
$|\tilde{A}+\hat{A}|\ge \min\! (2^{2d}|\hat{A}|,(1-\delta )|\hat{A}+\hat{A}|)$
. If
![]() $(1-\delta )|\hat{A}+\hat{A}| \ge 2^{2d}|\hat{A}|\ge 2^{2d}(1-\delta )|A|$
, then we are done; hence, we can assume that
$(1-\delta )|\hat{A}+\hat{A}| \ge 2^{2d}|\hat{A}|\ge 2^{2d}(1-\delta )|A|$
, then we are done; hence, we can assume that
![]() $|\tilde{A}+\hat{A}|\ge (1-\delta )|\hat{A}+\hat{A}|$
.
$|\tilde{A}+\hat{A}|\ge (1-\delta )|\hat{A}+\hat{A}|$
.
Let
![]() $m$
be the smallest integer for which
$m$
be the smallest integer for which
![]() $|\hat{A}+\hat{A}|\lt (2^m-\delta )|\hat{A}|$
, and suppose
$|\hat{A}+\hat{A}|\lt (2^m-\delta )|\hat{A}|$
, and suppose
![]() $m\leq d$
. Then by the Freiman–Bilu Theorem ( [Reference Bilu3, Reference Green and Tao17]),
$m\leq d$
. Then by the Freiman–Bilu Theorem ( [Reference Bilu3, Reference Green and Tao17]),
![]() $\hat{A}$
is contained in a union of at most
$\hat{A}$
is contained in a union of at most
![]() $K(d)$
translates of a GAP in
$K(d)$
translates of a GAP in
![]() $\mathbb{Z}^d$
of dimension at most
$\mathbb{Z}^d$
of dimension at most
![]() $m-1$
and thus in a union of at most
$m-1$
and thus in a union of at most
![]() $K(d)$
translates of a subspace
$K(d)$
translates of a subspace
![]() $Q$
of dimension at most
$Q$
of dimension at most
![]() $m-1\leq d-1$
.
$m-1\leq d-1$
.
Choose
![]() $t$
sufficiently large in
$t$
sufficiently large in
![]() $K(d)$
. By Lemma 4.2, for some
$K(d)$
. By Lemma 4.2, for some
![]() $T=T(t,d)$
, assuming that
$T=T(t,d)$
, assuming that
![]() $A$
satisfies
$A$
satisfies
![]() $P(A;\,T,d-1,d)$
, we can select a subset
$P(A;\,T,d-1,d)$
, we can select a subset
![]() $A_{(C)}$
of
$A_{(C)}$
of
![]() $A$
of size at most
$A$
of size at most
![]() $C=C(t,d)$
which satisfies
$C=C(t,d)$
which satisfies
![]() $P(A_{(C)};\,t,d-1,d)$
. Let
$P(A_{(C)};\,t,d-1,d)$
. Let
![]() $A'=\tilde{A}\cup A_{(C)}$
. We have
$A'=\tilde{A}\cup A_{(C)}$
. We have
![]() $A'+A\supseteq (\tilde{A}+\hat{A})\cup (A_{(C)}+\hat{A})$
. Note that if two translates
$A'+A\supseteq (\tilde{A}+\hat{A})\cup (A_{(C)}+\hat{A})$
. Note that if two translates
![]() $a+\hat{A}$
and
$a+\hat{A}$
and
![]() $a'+\hat{A}$
intersect, then
$a'+\hat{A}$
intersect, then
![]() $a'-a \in \hat{A}-\hat{A}$
, which is contained in a set
$a'-a \in \hat{A}-\hat{A}$
, which is contained in a set
![]() $E$
which is the union of at most
$E$
which is the union of at most
![]() $K(d)^2$
translates of
$K(d)^2$
translates of
![]() $Q$
. We claim that
$Q$
. We claim that
![]() $A_{(C)}$
contains a subset
$A_{(C)}$
contains a subset
![]() $S$
such that
$S$
such that
![]() $(S-S)\cap E =\{0\}$
and
$(S-S)\cap E =\{0\}$
and
![]() $|S|\ge (t-K(d)^3)/(2K(d)^2)$
. Indeed, for a maximal subset
$|S|\ge (t-K(d)^3)/(2K(d)^2)$
. Indeed, for a maximal subset
![]() $S$
of
$S$
of
![]() $A_{(C)}$
with
$A_{(C)}$
with
![]() $S-S$
disjoint from
$S-S$
disjoint from
![]() $E\setminus \{0\}$
, we have that
$E\setminus \{0\}$
, we have that
![]() $A_{(C)}\subseteq (S+E)\cup (S-E)$
, which can be covered by
$A_{(C)}\subseteq (S+E)\cup (S-E)$
, which can be covered by
![]() $2sK(d)^2$
translates of
$2sK(d)^2$
translates of
![]() $Q$
. Since
$Q$
. Since
![]() $A_{(C)}$
satisfies
$A_{(C)}$
satisfies
![]() $P(A_{(C)};\,t,d-1,d)$
, we must have
$P(A_{(C)};\,t,d-1,d)$
, we must have
![]() $s\ge t/(2K(d)^2)$
. As such,
$s\ge t/(2K(d)^2)$
. As such,
Hence for
![]() $t$
sufficiently large, we obtain that
$t$
sufficiently large, we obtain that
![]() $|A'+A| \gt 2^d|A|$
, as desired.
$|A'+A| \gt 2^d|A|$
, as desired.
It remains to consider the case when
![]() $m\gt d$
, i.e.
$m\gt d$
, i.e.
![]() $|\hat{A}+\hat{A}|\ge (2^d-\delta )|\hat{A}|$
. In this case we have
$|\hat{A}+\hat{A}|\ge (2^d-\delta )|\hat{A}|$
. In this case we have
5. Saturating the entire sumset from a subset
In this section, we study the following question. Given a finite set
![]() $A$
contained in an abelian group with
$A$
contained in an abelian group with
![]() $|A+A| = O(|A|)$
, how large do we need
$|A+A| = O(|A|)$
, how large do we need
![]() $A'$
to be so that
$A'$
to be so that
![]() $A+A' = A+A$
? We also consider the asymmetric version: Given finite sets
$A+A' = A+A$
? We also consider the asymmetric version: Given finite sets
![]() $A,B$
contained in an abelian group with
$A,B$
contained in an abelian group with
![]() $|A|=|B|$
and
$|A|=|B|$
and
![]() $|A+B| = O(|A|)$
, how large do we need
$|A+B| = O(|A|)$
, how large do we need
![]() $A'\subseteq A,B'\subseteq B$
to be so that
$A'\subseteq A,B'\subseteq B$
to be so that
![]() $(B+A')\cup (A+B') = A+B$
? We begin first with general upper bounds that hold for arbitrary groups.
$(B+A')\cup (A+B') = A+B$
? We begin first with general upper bounds that hold for arbitrary groups.
5.1. Upper bound
The following theorem will be our main technical result.
Theorem 5.1.
Let
![]() $G$
be a group, let
$G$
be a group, let
![]() $S,T,X$
be subsets of
$S,T,X$
be subsets of
![]() $G$
, and let
$G$
, and let
![]() $Z=XST$
. Then there exist subsets
$Z=XST$
. Then there exist subsets
![]() $S'$
of
$S'$
of
![]() $S$
and
$S$
and
![]() $T'$
of
$T'$
of
![]() $T$
with
$T$
with
![]() $|S'|,|T'|=o(|Z|^2/|X|)$
, and
$|S'|,|T'|=o(|Z|^2/|X|)$
, and
![]() $(S'T)\cup (ST')=ST$
.
$(S'T)\cup (ST')=ST$
.
We will use the graph-theoretic triangle removal lemma in the proof of Theorem 5.1. The idea of using the triangle removal lemma to prove an arithmetic removal lemma in general groups goes back to work of Král’, Serra and Vena [Reference Král’, Serra and Vena23]. Here we build on and generalize their proof idea to prove a result that is potentially meaningful for sparse subsets of a group. We have stated below the triangle removal lemma, which follows from Szemerédi’s regularity lemma. The best quantitative bound known for the triangle removal lemma is by Fox [Reference Fox12], where
![]() $1/\epsilon (\delta )$
can be taken as the inverse function of an exponential tower of height
$1/\epsilon (\delta )$
can be taken as the inverse function of an exponential tower of height
![]() $O(\log \delta ^{-1})$
.
$O(\log \delta ^{-1})$
.
Lemma 5.2 (Triangle Removal Lemma [Reference Fox12]). There exists
![]() $\epsilon\; :\;\mathbb{R}_+\to \mathbb{R}_+$
such that
$\epsilon\; :\;\mathbb{R}_+\to \mathbb{R}_+$
such that
![]() $\epsilon (\delta )\to 0$
when
$\epsilon (\delta )\to 0$
when
![]() $\delta \to 0$
and the following holds. If
$\delta \to 0$
and the following holds. If
![]() $\Gamma$
is a graph with at most
$\Gamma$
is a graph with at most
![]() $\delta |V(\Gamma )|^3$
triangles, then one can remove at most
$\delta |V(\Gamma )|^3$
triangles, then one can remove at most
![]() $\epsilon (\delta )|V(\Gamma )|^2$
edges from
$\epsilon (\delta )|V(\Gamma )|^2$
edges from
![]() $\Gamma$
and obtain a triangle free graph.
$\Gamma$
and obtain a triangle free graph.
Proof of Theorem
5.1. Let
![]() $\tau \gt 0$
be a threshold to be chosen later. We consider a greedy procedure to define a subset
$\tau \gt 0$
be a threshold to be chosen later. We consider a greedy procedure to define a subset
![]() $S_*$
of
$S_*$
of
![]() $S$
. Start with
$S$
. Start with
![]() $S_*=\emptyset$
. Whenever there exists
$S_*=\emptyset$
. Whenever there exists
![]() $s\in S\setminus S_*$
such that
$s\in S\setminus S_*$
such that
![]() $|(sT)\setminus (S_*T)| \gt \tau$
, we update
$|(sT)\setminus (S_*T)| \gt \tau$
, we update
![]() $S_*$
to be
$S_*$
to be
![]() $S_*\cup \{s\}$
. The procedure terminates with a set
$S_*\cup \{s\}$
. The procedure terminates with a set
![]() $S_*$
satisfying the condition that for all
$S_*$
satisfying the condition that for all
![]() $s\in S\setminus S_*$
,
$s\in S\setminus S_*$
,
![]() $|(sT)\setminus (S_*T)| \le \tau$
. Note that
$|(sT)\setminus (S_*T)| \le \tau$
. Note that
Let
![]() $Y=XS$
and recall that
$Y=XS$
and recall that
![]() $Z=XST$
. Consider a tripartite graph
$Z=XST$
. Consider a tripartite graph
![]() $\Gamma$
with vertex sets
$\Gamma$
with vertex sets
![]() $X,Y,Z$
where
$X,Y,Z$
where
![]() $x\in X$
,
$x\in X$
,
![]() $y\in Y$
are connected if
$y\in Y$
are connected if
![]() $y=xs$
for
$y=xs$
for
![]() $s\in S\setminus S_*$
;
$s\in S\setminus S_*$
;
![]() $y\in Y$
,
$y\in Y$
,
![]() $z\in Z$
are connected if
$z\in Z$
are connected if
![]() $z=yt$
for
$z=yt$
for
![]() $t\in T$
; and
$t\in T$
; and
![]() $z\in Z$
,
$z\in Z$
,
![]() $x\in X$
are connected if
$x\in X$
are connected if
![]() $z = xu$
for
$z = xu$
for
![]() $u\in (ST)\setminus (S_*T)$
. Each triangle in
$u\in (ST)\setminus (S_*T)$
. Each triangle in
![]() $\Gamma$
corresponds to a triple
$\Gamma$
corresponds to a triple
![]() $(x,xs,xst)$
where
$(x,xs,xst)$
where
![]() $s\in S\setminus S_*$
,
$s\in S\setminus S_*$
,
![]() $t\in T$
and
$t\in T$
and
![]() $st\in (ST)\setminus (S_*T)$
. For each
$st\in (ST)\setminus (S_*T)$
. For each
![]() $x\in X$
and
$x\in X$
and
![]() $s\in S\setminus S_*$
, the number of
$s\in S\setminus S_*$
, the number of
![]() $t$
forming such a triple is at most
$t$
forming such a triple is at most
![]() $\tau$
by our choice of
$\tau$
by our choice of
![]() $S_*$
. Hence,
$S_*$
. Hence,
![]() $\Gamma$
has at most
$\Gamma$
has at most
![]() $\tau |X||S|\le (\tau/|Z|)|V(\Gamma )|^3$
triangles. By the triangle removal lemma, one can remove
$\tau |X||S|\le (\tau/|Z|)|V(\Gamma )|^3$
triangles. By the triangle removal lemma, one can remove
![]() $\epsilon (\tau/|Z|)|V(\Gamma )|^2$
edges from
$\epsilon (\tau/|Z|)|V(\Gamma )|^2$
edges from
![]() $\Gamma$
and ensure that no triangle remains. Let
$\Gamma$
and ensure that no triangle remains. Let
![]() $\hat{S}$
be the set of elements
$\hat{S}$
be the set of elements
![]() $s\in S\setminus S_*$
for which at least
$s\in S\setminus S_*$
for which at least
![]() $|X|/3$
edges
$|X|/3$
edges
![]() $(x,xs)$
of
$(x,xs)$
of
![]() $\Gamma$
are removed. Let
$\Gamma$
are removed. Let
![]() $\hat{T}$
be the set of elements
$\hat{T}$
be the set of elements
![]() $t\in T$
for which at least
$t\in T$
for which at least
![]() $|X|/3$
edges
$|X|/3$
edges
![]() $(y,yt)$
of
$(y,yt)$
of
![]() $\Gamma$
are removed. Let
$\Gamma$
are removed. Let
![]() $\hat{U}$
be the set of elements
$\hat{U}$
be the set of elements
![]() $u\in ST\setminus (S_*T)$
for which at least
$u\in ST\setminus (S_*T)$
for which at least
![]() $|X|/3$
edges
$|X|/3$
edges
![]() $(xu,x)$
are removed. For each
$(xu,x)$
are removed. For each
![]() $s \in S\setminus S_*$
and
$s \in S\setminus S_*$
and
![]() $t\in T$
with
$t\in T$
with
![]() $st\in (ST)\setminus (S_*T)$
, there are
$st\in (ST)\setminus (S_*T)$
, there are
![]() $|X|$
triangles
$|X|$
triangles
![]() $(x,xs,xst)$
in
$(x,xs,xst)$
in
![]() $\Gamma$
. Hence, in order for all such triangles to be removed, we must have that either
$\Gamma$
. Hence, in order for all such triangles to be removed, we must have that either
![]() $s\in \hat{S}$
,
$s\in \hat{S}$
,
![]() $t\in \hat{T}$
, or
$t\in \hat{T}$
, or
![]() $st\in \hat{U}$
. For each
$st\in \hat{U}$
. For each
![]() $u\in \hat{U}$
, we choose an arbitrary representation
$u\in \hat{U}$
, we choose an arbitrary representation
![]() $u=s_ut_u$
for
$u=s_ut_u$
for
![]() $s_u\in S,t_u\in T$
. Then we have
$s_u\in S,t_u\in T$
. Then we have
![]() $ST=(S'T)\cup (ST')$
for
$ST=(S'T)\cup (ST')$
for
![]() $T'=\hat{T}$
and
$T'=\hat{T}$
and
![]() $S'=S_*\cup \hat{S}\cup \{s_u:u\in \hat{U}\}$
. We also have the bound
$S'=S_*\cup \hat{S}\cup \{s_u:u\in \hat{U}\}$
. We also have the bound
Thus,
By choosing
![]() $\tau$
such that
$\tau$
such that
![]() $\tau =o(|Z|)$
and
$\tau =o(|Z|)$
and
![]() $\tau = \omega (1)$
, we obtain the desired bound
$\tau = \omega (1)$
, we obtain the desired bound
![]() $|S'|+|T'|=o(|Z|^2/|X|)$
, noting that
$|S'|+|T'|=o(|Z|^2/|X|)$
, noting that
![]() $|Z|\ge |X|$
.
$|Z|\ge |X|$
.
Applying Theorem 5.1 with
![]() $X=G$
, we obtain the following corollary.
$X=G$
, we obtain the following corollary.
Corollary 5.3.
Let
![]() $G$
be a group, and let
$G$
be a group, and let
![]() $S,T\subseteq G$
. Then there exist
$S,T\subseteq G$
. Then there exist
![]() $S'\subseteq S$
and
$S'\subseteq S$
and
![]() $T'\subseteq T$
with
$T'\subseteq T$
with
![]() $ST=(S'T)\cup (ST')$
and
$ST=(S'T)\cup (ST')$
and
![]() $|S'|+|T'|=o(|G|)$
.
$|S'|+|T'|=o(|G|)$
.
Combining with the Plünnecke-Ruzsa Inequality (Lemma 3.3), we can prove Corollary 1.5, restated here, which is a local version of Corollary 5.3 in abelian groups.
Corollary 1.5.
Let
![]() $G$
be an abelian group, and let
$G$
be an abelian group, and let
![]() $S,T\subseteq G$
be nonempty subsets of equal size such that
$S,T\subseteq G$
be nonempty subsets of equal size such that
![]() $|S+T|=O(|S|)$
. Then there exist
$|S+T|=O(|S|)$
. Then there exist
![]() $S'\subseteq S$
and
$S'\subseteq S$
and
![]() $T'\subseteq T$
with
$T'\subseteq T$
with
![]() $S+T=(S'+T)\cup (S+T')$
and
$S+T=(S'+T)\cup (S+T')$
and
![]() $|S'|+|T'| = o(|S|)$
.
$|S'|+|T'| = o(|S|)$
.
Proof. Let
![]() $X=S$
,
$X=S$
,
![]() $Y=2S$
and
$Y=2S$
and
![]() $Z=2S+T$
. By Lemma 3.3,
$Z=2S+T$
. By Lemma 3.3,
![]() $|X|,|Y|,|Z|=\Theta (|S|)$
. The result then follows from Theorem 5.1.
$|X|,|Y|,|Z|=\Theta (|S|)$
. The result then follows from Theorem 5.1.
Corollary 1.6, the nonabelian analogue of Corollary 1.5, also immediately follows from Theorem 5.1 by taking
![]() $X=S$
.
$X=S$
.
Corollary 1.6.
Let
![]() $G$
be a group, and let
$G$
be a group, and let
![]() $S,T\subseteq G$
be nonempty subsets of equal size such that
$S,T\subseteq G$
be nonempty subsets of equal size such that
![]() $|S^2T|=O(|S|)$
. Then there exist
$|S^2T|=O(|S|)$
. Then there exist
![]() $S'\subseteq S$
and
$S'\subseteq S$
and
![]() $T'\subseteq T$
with
$T'\subseteq T$
with
![]() $ST=(S'T)\cup (ST')$
and
$ST=(S'T)\cup (ST')$
and
![]() $|S'|+|T'| = o(|S|)$
.
$|S'|+|T'| = o(|S|)$
.
Due to the use of the triangle removal lemma, Theorem 5.1 does not come with good quantitative bounds. While we do not have strong quantitative bounds for the arithmetic removal lemma (the arithmetic analogue of the triangle removal lemma) for general groups, we do have them over
![]() $\mathbb{F}_p^n$
(or more generally, groups with bounded exponent). In particular, Fox and Lovász [Reference Fox and Lovász13] showed an arithmetic removal lemma with polynomial dependency over
$\mathbb{F}_p^n$
(or more generally, groups with bounded exponent). In particular, Fox and Lovász [Reference Fox and Lovász13] showed an arithmetic removal lemma with polynomial dependency over
![]() $\mathbb{F}_p^n$
, stated below. Let
$\mathbb{F}_p^n$
, stated below. Let
![]() $c_p$
be a positive constant given by
$c_p$
be a positive constant given by
![]() $p^{1-c_p} = \inf _{0\lt x\lt 1}x^{-(p-1)/3}(1+x+\dots +x^{p-1})$
, and let
$p^{1-c_p} = \inf _{0\lt x\lt 1}x^{-(p-1)/3}(1+x+\dots +x^{p-1})$
, and let
![]() $C_p = 1+1/c_p$
.
$C_p = 1+1/c_p$
.
Theorem 5.4 ([Reference Fox and Lovász13]). Let
![]() $X,Y,Z\subseteq \mathbb{F}_p^n$
be such that there are at most
$X,Y,Z\subseteq \mathbb{F}_p^n$
be such that there are at most
![]() $\delta p^{2n}$
solutions to
$\delta p^{2n}$
solutions to
![]() $x+y=z$
for
$x+y=z$
for
![]() $x\in X,y\in Y,z\in Z$
. Then we can remove
$x\in X,y\in Y,z\in Z$
. Then we can remove
![]() $\epsilon p^n$
elements from
$\epsilon p^n$
elements from
![]() $X,Y,Z$
and remove all solutions to
$X,Y,Z$
and remove all solutions to
![]() $x+y=z$
, where
$x+y=z$
, where
![]() $\epsilon =\delta ^{1/C_p-o(1)}$
.
$\epsilon =\delta ^{1/C_p-o(1)}$
.
In fact, the dependency of
![]() $\delta$
on
$\delta$
on
![]() $\epsilon$
in Theorem 5.4 is tight up to the
$\epsilon$
in Theorem 5.4 is tight up to the
![]() $o(1)$
term in the exponent.
$o(1)$
term in the exponent.
Note that in the proof of Theorem 5.1 in the case
![]() $G=X=Y=Z$
, denoting by
$G=X=Y=Z$
, denoting by
![]() $\epsilon _G(\delta )$
the bound we have for the arithmetic removal lemma over
$\epsilon _G(\delta )$
the bound we have for the arithmetic removal lemma over
![]() $G$
, we obtain a bound
$G$
, we obtain a bound
If
![]() $\epsilon (\delta )$
depends polynomially in
$\epsilon (\delta )$
depends polynomially in
![]() $\delta$
, so that
$\delta$
, so that
![]() $\epsilon (\delta ) \le \delta ^c$
for some
$\epsilon (\delta ) \le \delta ^c$
for some
![]() $c\gt 0$
, then we can optimize
$c\gt 0$
, then we can optimize
![]() $\tau$
to obtain
$\tau$
to obtain
![]() $|S'|+|T'| \le |G|^{1-c'}$
for some
$|S'|+|T'| \le |G|^{1-c'}$
for some
![]() $c'\gt 0$
depending on
$c'\gt 0$
depending on
![]() $c$
. In particular, in the case
$c$
. In particular, in the case
![]() $G=\mathbb{F}_p^n$
, we can use the arithmetic removal lemma of Fox and Lovász to obtain
$G=\mathbb{F}_p^n$
, we can use the arithmetic removal lemma of Fox and Lovász to obtain
A similar result also holds more generally over abelian groups with bounded exponent.
For
![]() $S,T\subseteq G$
of equal size with
$S,T\subseteq G$
of equal size with
![]() $|S+T|\le \lambda |S|$
, by a result of Green and Ruzsa [Reference Green and Ruzsa16], we can guarantee that
$|S+T|\le \lambda |S|$
, by a result of Green and Ruzsa [Reference Green and Ruzsa16], we can guarantee that
![]() $S$
and
$S$
and
![]() $T$
are subsets of a coset progression of size
$T$
are subsets of a coset progression of size
![]() $O_{\lambda }(|S|)$
. When
$O_{\lambda }(|S|)$
. When
![]() $G=\mathbb{F}_p^{n}$
, one can then guarantee that
$G=\mathbb{F}_p^{n}$
, one can then guarantee that
![]() $S,T$
are subsets of subgroups of
$S,T$
are subsets of subgroups of
![]() $G$
of size
$G$
of size
![]() $O_{\lambda,p}(|S|)$
. Hence, we also obtain the same result where we can guarantee
$O_{\lambda,p}(|S|)$
. Hence, we also obtain the same result where we can guarantee
![]() $|S'|+|T'|\le O_{\lambda, p}(|S|^{1-1/(2+1/c_p)+o(1)})$
. Furthermore, a power-saving bound holds in the same setting over abelian groups with bounded exponent.
$|S'|+|T'|\le O_{\lambda, p}(|S|^{1-1/(2+1/c_p)+o(1)})$
. Furthermore, a power-saving bound holds in the same setting over abelian groups with bounded exponent.
In [Reference Ellenberg11], by adapting directly the linear-algebraic method behind the cap-set result, Ellenberg obtained a power-saving bound with tight exponent for the special case
![]() $G=\mathbb{F}_p^n$
. Combining this result with the above argument, one obtains the following corollary.
$G=\mathbb{F}_p^n$
. Combining this result with the above argument, one obtains the following corollary.
Corollary 5.5.
Let
![]() $G=\mathbb{F}_p^n$
. For
$G=\mathbb{F}_p^n$
. For
![]() $S,T\subseteq G$
of equal size with
$S,T\subseteq G$
of equal size with
![]() $|S+T| = O(|S|)$
, there exist
$|S+T| = O(|S|)$
, there exist
![]() $S'\subseteq S$
and
$S'\subseteq S$
and
![]() $T'\subseteq T$
with
$T'\subseteq T$
with
![]() $S+T=(S'+T)\cup (S+T')$
and
$S+T=(S'+T)\cup (S+T')$
and
![]() $|S'|+|T'| = O(|S|^{1-c_p})$
.
$|S'|+|T'| = O(|S|^{1-c_p})$
.
5.2. Lower bound construction
In this section, we study constructions of sets
![]() $S,T$
for which
$S,T$
for which
![]() $|S+T|\ll |S|=|T|$
, and any choice of
$|S+T|\ll |S|=|T|$
, and any choice of
![]() $S'\subseteq S$
,
$S'\subseteq S$
,
![]() $T'\subseteq T$
such that
$T'\subseteq T$
such that
![]() $S+T=(S'+T)\cup (S+T')$
must necessarily have
$S+T=(S'+T)\cup (S+T')$
must necessarily have
![]() $|S'|+|T'|$
large. In fact, we will only need to focus on the symmetric case where
$|S'|+|T'|$
large. In fact, we will only need to focus on the symmetric case where
![]() $S=T=A$
.
$S=T=A$
.
First, we will show that one cannot expect a power-saving upper bound for
![]() $|S'|+|T'|$
over
$|S'|+|T'|$
over
![]() $\mathbb{Z}$
. We will make use of a construction of Behrend for progression-free sets [Reference Behrend2, Reference Elkin10, Reference Green and Wolf18].
$\mathbb{Z}$
. We will make use of a construction of Behrend for progression-free sets [Reference Behrend2, Reference Elkin10, Reference Green and Wolf18].
Proposition 5.6.
For any positive integer
![]() $t$
, the set
$t$
, the set
![]() $X_{r, n}(t) \;:\!=\; \{(x_1, \dots, x_n):1\leq x_i\leq r\;\forall \;1\leq i\leq n, \sum _{i=1}^{{n}}x_i^2 = t\}$
is progression-free in
$X_{r, n}(t) \;:\!=\; \{(x_1, \dots, x_n):1\leq x_i\leq r\;\forall \;1\leq i\leq n, \sum _{i=1}^{{n}}x_i^2 = t\}$
is progression-free in
![]() $\mathbb{Z}_m^{{n}}$
when
$\mathbb{Z}_m^{{n}}$
when
![]() $m \geq 2r$
.
$m \geq 2r$
.
Proof. Suppose that three distinct elements
![]() $x, y, z\in X_{r, n}(t)$
form a 3-term progression in
$x, y, z\in X_{r, n}(t)$
form a 3-term progression in
![]() $\mathbb{Z}_m^n$
.
$\mathbb{Z}_m^n$
.
For each
![]() $i$
, we know that
$i$
, we know that
![]() $2y_i \equiv x_i+z_i\pmod m$
. Moreover, because
$2y_i \equiv x_i+z_i\pmod m$
. Moreover, because
![]() $1\leq x_i, y_i, z_i\leq r$
, we know that
$1\leq x_i, y_i, z_i\leq r$
, we know that
![]() $2\leq 2y_i\leq 2r\leq m$
and
$2\leq 2y_i\leq 2r\leq m$
and
![]() $2\leq x_i+z_i\leq 2r\leq m$
. Therefore,
$2\leq x_i+z_i\leq 2r\leq m$
. Therefore,
![]() $2y_i = x_i+z_i$
, and hence we have
$2y_i = x_i+z_i$
, and hence we have
This is only possible when
![]() $x = z$
. Since
$x = z$
. Since
![]() $2y = x+z$
, we have
$2y = x+z$
, we have
![]() $y = (x+z)/2 = x$
, which contradicts the assumption of distinctness. Therefore we conclude that
$y = (x+z)/2 = x$
, which contradicts the assumption of distinctness. Therefore we conclude that
![]() $X_{r, n}(t)$
is progression-free in
$X_{r, n}(t)$
is progression-free in
![]() $\mathbb{Z}_m^n$
.
$\mathbb{Z}_m^n$
.
Proposition 5.7 (Construction in
![]() $\mathbb{Z}$
). For any sufficiently large positive integer
$\mathbb{Z}$
). For any sufficiently large positive integer
![]() $N$
, there exists a finite set
$N$
, there exists a finite set
![]() $A \subset \mathbb{Z}$
such that
$A \subset \mathbb{Z}$
such that
![]() $|A| \leq N$
,
$|A| \leq N$
,
![]() $|A+A| \leq 6|A|$
, and for any subset
$|A+A| \leq 6|A|$
, and for any subset
![]() $A'\subseteq A$
with
$A'\subseteq A$
with
![]() $A'+A = A+A$
, we have
$A'+A = A+A$
, we have
![]() $|A'| \geq Ne^{-c\sqrt{\log N}}$
for some absolute constant
$|A'| \geq Ne^{-c\sqrt{\log N}}$
for some absolute constant
![]() $c \gt 0$
.
$c \gt 0$
.
Proof. Let
![]() $r, n$
be determined later. We would like to use Proposition 5.6. By the Pigeonhole Principle, since
$r, n$
be determined later. We would like to use Proposition 5.6. By the Pigeonhole Principle, since
![]() $\sum _{i=1}^nx_i^2$
is in
$\sum _{i=1}^nx_i^2$
is in
![]() $[n, nr^2]$
when
$[n, nr^2]$
when
![]() $(x_1, \dots, x_n)$
is taken from
$(x_1, \dots, x_n)$
is taken from
![]() $\{1, \dots, r\}^n$
, there exists
$\{1, \dots, r\}^n$
, there exists
![]() $t$
such that
$t$
such that
![]() $X_{r, n}(t)$
contains at least
$X_{r, n}(t)$
contains at least
![]() $\frac{r^n}{nr^2}$
elements. Fix such a
$\frac{r^n}{nr^2}$
elements. Fix such a
![]() $t$
. Let
$t$
. Let
![]() $\phi \; :\;\mathbb{Z}_{2r}^n\to \{0,\dots,(2r)^n-1\}$
be a bijective map that induces a Freiman
$\phi \; :\;\mathbb{Z}_{2r}^n\to \{0,\dots,(2r)^n-1\}$
be a bijective map that induces a Freiman
![]() $2$
-isomorphism from
$2$
-isomorphism from
![]() $\{1,\dots,r\}^n$
to its image. Since
$\{1,\dots,r\}^n$
to its image. Since
![]() $X_{r,n}(t)$
is a progression-free set in
$X_{r,n}(t)$
is a progression-free set in
![]() $\mathbb{Z}^n_{2r}$
, the set
$\mathbb{Z}^n_{2r}$
, the set
![]() $A_0 \;:\!=\; \phi (X_{r, n}(t))$
is a progression-free set in
$A_0 \;:\!=\; \phi (X_{r, n}(t))$
is a progression-free set in
![]() $\mathbb{Z}$
. Thus, if
$\mathbb{Z}$
. Thus, if
![]() $2a = a_1 + a_2$
for
$2a = a_1 + a_2$
for
![]() $a, a_1, a_2\in A_0$
, then
$a, a_1, a_2\in A_0$
, then
![]() $a_1 = a_2 = a$
.
$a_1 = a_2 = a$
.
For simplicity we denote
![]() $T = (2r)^n$
. Let
$T = (2r)^n$
. Let
![]() $A_1 = [-2T, -T-1]\cap \mathbb{Z}$
and let
$A_1 = [-2T, -T-1]\cap \mathbb{Z}$
and let
![]() $A = A_0\cup A_1$
. Clearly
$A = A_0\cup A_1$
. Clearly
![]() $T= |A_1| \leq |A| = |A_0| + |A_1| \leq 2T$
. On the other hand, we have
$T= |A_1| \leq |A| = |A_0| + |A_1| \leq 2T$
. On the other hand, we have
![]() $A+A \subseteq [-4T, 2T)$
, so
$A+A \subseteq [-4T, 2T)$
, so
![]() $|A+A| \leq 6|A|$
. Suppose
$|A+A| \leq 6|A|$
. Suppose
![]() $A'\subseteq A$
satisfies that
$A'\subseteq A$
satisfies that
![]() $A' + A = A+A$
. For any
$A' + A = A+A$
. For any
![]() $a\in A_0$
, we know that
$a\in A_0$
, we know that
![]() $2a\in A+A$
. If
$2a\in A+A$
. If
![]() $2a = a_1 + a_2$
for some
$2a = a_1 + a_2$
for some
![]() $a_1, a_2\in A$
, then since
$a_1, a_2\in A$
, then since
![]() $a_1 + a_2 = 2a \gt 0$
, neither
$a_1 + a_2 = 2a \gt 0$
, neither
![]() $a_1$
nor
$a_1$
nor
![]() $a_2$
is in
$a_2$
is in
![]() $A_1$
, implying that
$A_1$
, implying that
![]() $a_1, a_2\in A_0$
. From our construction of
$a_1, a_2\in A_0$
. From our construction of
![]() $A_0$
, we must have
$A_0$
, we must have
![]() $a_1 = a_2 = a$
. Hence if
$a_1 = a_2 = a$
. Hence if
![]() $2a\in A'+A$
for some subset
$2a\in A'+A$
for some subset
![]() $A'\subseteq A$
, then we must have
$A'\subseteq A$
, then we must have
![]() $a\in A'$
. Hence,
$a\in A'$
. Hence,
![]() $A+A' = A+A$
implies that
$A+A' = A+A$
implies that
![]() $A_0\subseteq A'$
. Now if we optimize by choosing
$A_0\subseteq A'$
. Now if we optimize by choosing
![]() $N = 2T$
,
$N = 2T$
,
![]() $n = \sqrt{\log N}$
and
$n = \sqrt{\log N}$
and
![]() $r = e^{\sqrt{\log N}}/4$
, then
$r = e^{\sqrt{\log N}}/4$
, then
![]() $|A| \leq N$
and
$|A| \leq N$
and
![]() $|A'| \geq |A_0| \geq \frac{r^n}{nr^2} \geq Ne^{-c\sqrt{\log N}}$
for some positive constant
$|A'| \geq |A_0| \geq \frac{r^n}{nr^2} \geq Ne^{-c\sqrt{\log N}}$
for some positive constant
![]() $c$
.
$c$
.
As we saw in the previous subsection, the behaviour over
![]() $\mathbb{F}_p^{n}$
is different, and we can show a power-saving upper bound on
$\mathbb{F}_p^{n}$
is different, and we can show a power-saving upper bound on
![]() $|S'|+|T'|$
. For the construction over
$|S'|+|T'|$
. For the construction over
![]() $\mathbb{F}_p^n$
, we will use the result of Kleinberg, Sawin and Speyer [Reference Kleinberg, Sawin and Speyer22] (combined with a conjecture later resolved by Pebody [Reference Pebody26] and Norin [Reference Norin25]) on tricoloured sum-free sets.
$\mathbb{F}_p^n$
, we will use the result of Kleinberg, Sawin and Speyer [Reference Kleinberg, Sawin and Speyer22] (combined with a conjecture later resolved by Pebody [Reference Pebody26] and Norin [Reference Norin25]) on tricoloured sum-free sets.
Theorem 5.8 ([Reference Kleinberg, Sawin and Speyer22, Reference Norin25, Reference Pebody26]). Given a collection of ordered triples
![]() $\{(x_i, y_i, z_i)\}_{i=1}^{m}$
in
$\{(x_i, y_i, z_i)\}_{i=1}^{m}$
in
![]() $\mathbb{F}_p^n$
such that
$\mathbb{F}_p^n$
such that
![]() $x_i + y_j + z_k = 0$
holds if and only if
$x_i + y_j + z_k = 0$
holds if and only if
![]() $i = j = k$
, the size of the collection satisfies the bound
$i = j = k$
, the size of the collection satisfies the bound
![]() $m \leq p^{(1-c_p)n}$
. Furthermore, there exists such a collection with
$m \leq p^{(1-c_p)n}$
. Furthermore, there exists such a collection with
![]() $m \ge p^{(1-c_p)n-o(n)}$
.
$m \ge p^{(1-c_p)n-o(n)}$
.
Proposition 5.9 (Construction in
![]() $\mathbb{F}_p^n$
). For positive integers
$\mathbb{F}_p^n$
). For positive integers
![]() $n$
, there exists
$n$
, there exists
![]() $A\subseteq \mathbb{F}_p^n$
such that
$A\subseteq \mathbb{F}_p^n$
such that
![]() $|A+A| \leq 6|A|$
, and for any subset
$|A+A| \leq 6|A|$
, and for any subset
![]() $A'\subseteq A$
with
$A'\subseteq A$
with
![]() $A'+A = A+A$
, we have
$A'+A = A+A$
, we have
![]() $|A'|\geq p^{(1-c_p)n-o(n)}$
.
$|A'|\geq p^{(1-c_p)n-o(n)}$
.
Proof. By Theorem 5.8, there exist
![]() $m\geq p^{(1-c_p)n-o(n)}$
and
$m\geq p^{(1-c_p)n-o(n)}$
and
![]() $\{(x_i,y_i,z_i)\}_{i=1}^m$
, where
$\{(x_i,y_i,z_i)\}_{i=1}^m$
, where
![]() $x_i, y_i, z_i\in \mathbb{F}_p^{n-2}$
for each
$x_i, y_i, z_i\in \mathbb{F}_p^{n-2}$
for each
![]() $1\leq i\leq m$
, such that
$1\leq i\leq m$
, such that
![]() $x_i+y_j+z_k = 0$
if and only if
$x_i+y_j+z_k = 0$
if and only if
![]() $i = j = k$
. By this condition, if
$i = j = k$
. By this condition, if
![]() $x_i = x_j$
, then as
$x_i = x_j$
, then as
![]() $x_j+y_i+z_i = 0$
, we have
$x_j+y_i+z_i = 0$
, we have
![]() $i = j$
. Thus the
$i = j$
. Thus the
![]() $x_i$
’s are distinct, so
$x_i$
’s are distinct, so
![]() $X = \{x_i:1\leq i\leq m\}$
is of size
$X = \{x_i:1\leq i\leq m\}$
is of size
![]() $m$
. Similarly we have that
$m$
. Similarly we have that
![]() $Y = \{y_i:1\leq i\leq m\}$
is of size
$Y = \{y_i:1\leq i\leq m\}$
is of size
![]() $m$
.
$m$
.
For simplicity, for
![]() $a, b\in \mathbb{F}_p$
and
$a, b\in \mathbb{F}_p$
and
![]() $x\in \mathbb{F}_p^{n-2}$
, we write
$x\in \mathbb{F}_p^{n-2}$
, we write
![]() $(a, b, x) = (a, b, x_1, \dots, x_{n-2})$
to denote an element in
$(a, b, x) = (a, b, x_1, \dots, x_{n-2})$
to denote an element in
![]() $\mathbb{F}_p^n$
. Then we shall take
$\mathbb{F}_p^n$
. Then we shall take
![]() $A = (\{(0, 0)\}\times X)\cup (\{(0, 1)\}\times Y) \cup (\{(1, 0)\}\times \mathbb{F}_p^{n-2})$
. Clearly
$A = (\{(0, 0)\}\times X)\cup (\{(0, 1)\}\times Y) \cup (\{(1, 0)\}\times \mathbb{F}_p^{n-2})$
. Clearly
![]() $A\supset \{(1, 0)\}\times \mathbb{F}_p^{n-2}$
while
$A\supset \{(1, 0)\}\times \mathbb{F}_p^{n-2}$
while
![]() $A+A\subseteq \{(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (2, 0)\}\times \mathbb{F}_p^{n-2}$
, so
$A+A\subseteq \{(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (2, 0)\}\times \mathbb{F}_p^{n-2}$
, so
![]() $|A+A|\leq 6|A|$
.
$|A+A|\leq 6|A|$
.
We now show that for
![]() $A'\subseteq A$
, if
$A'\subseteq A$
, if
![]() $A'+A = A+A$
, then
$A'+A = A+A$
, then
![]() $|A'| \geq m$
. Note that
$|A'| \geq m$
. Note that
![]() $(0, 1, -z_i) = (0, 0, x_i) + (0, 1, y_i)\in A+A$
. We show that
$(0, 1, -z_i) = (0, 0, x_i) + (0, 1, y_i)\in A+A$
. We show that
![]() $(0, 1, -z_i)$
can only be represented in this way as a sum of two elements in
$(0, 1, -z_i)$
can only be represented in this way as a sum of two elements in
![]() $A$
. Suppose that
$A$
. Suppose that
![]() $u+v = (0, 1, -z_i)$
, where
$u+v = (0, 1, -z_i)$
, where
![]() $u,v\in A$
. If both of
$u,v\in A$
. If both of
![]() $u, v$
are in
$u, v$
are in
![]() $\{(1, 0)\}\times \mathbb{F}_p^{n-2}$
, then the second coordinate is
$\{(1, 0)\}\times \mathbb{F}_p^{n-2}$
, then the second coordinate is
![]() $0$
, which is different from
$0$
, which is different from
![]() $1$
in
$1$
in
![]() $(0, 1, -z_i)$
. If exactly one of
$(0, 1, -z_i)$
. If exactly one of
![]() $u, v$
is in
$u, v$
is in
![]() $\{(1, 0)\}\times \mathbb{F}_p^{n-2}$
, then
$\{(1, 0)\}\times \mathbb{F}_p^{n-2}$
, then
![]() $u+v$
must have the first coordinate
$u+v$
must have the first coordinate
![]() $1$
, which is different from
$1$
, which is different from
![]() $0$
in
$0$
in
![]() $(0, 1, -z_i)$
. Finally, the only possibility remaining is that
$(0, 1, -z_i)$
. Finally, the only possibility remaining is that
![]() $u, v$
are both from
$u, v$
are both from
![]() $(\{(0, 0)\}\times X)\cup (\{(0, 1)\}\times Y)$
. By considering the second coordinate in
$(\{(0, 0)\}\times X)\cup (\{(0, 1)\}\times Y)$
. By considering the second coordinate in
![]() $u+v = (0, 1, -z_i)$
, the only possible combination is that one of
$u+v = (0, 1, -z_i)$
, the only possible combination is that one of
![]() $u, v$
is from
$u, v$
is from
![]() $\{(0, 0)\}\times X$
and the other one from
$\{(0, 0)\}\times X$
and the other one from
![]() $\{(0, 1)\}\times Y$
. Without loss of generality, say that
$\{(0, 1)\}\times Y$
. Without loss of generality, say that
![]() $u = (0, 0, x_j)$
and
$u = (0, 0, x_j)$
and
![]() $v = (0, 1, y_k)$
. Then this implies that
$v = (0, 1, y_k)$
. Then this implies that
![]() $x_j+y_k = -z_i$
, which is only possible when
$x_j+y_k = -z_i$
, which is only possible when
![]() $i=j=k$
. Hence
$i=j=k$
. Hence
![]() $(0, 1, -z_i) = (0, 0, x_i) + (0, 1, y_i)$
is the only representation (up to permutation of the summands). Therefore, for each
$(0, 1, -z_i) = (0, 0, x_i) + (0, 1, y_i)$
is the only representation (up to permutation of the summands). Therefore, for each
![]() $1\leq i\leq m$
, either
$1\leq i\leq m$
, either
![]() $(0, 0, x_i)$
or
$(0, 0, x_i)$
or
![]() $(0, 1, y_i)$
is in
$(0, 1, y_i)$
is in
![]() $A'$
if
$A'$
if
![]() $A'+A \ni (0, 1, -z_i)$
. Hence
$A'+A \ni (0, 1, -z_i)$
. Hence
![]() $|A'|\geq m$
as desired.
$|A'|\geq m$
as desired.
6. Non-saturating sets
In this section, we give the construction proving Theorem 1.8, restated below for convenience.
Theorem 1.8.
For any
![]() $\nu \gt 0$
, there exist
$\nu \gt 0$
, there exist
![]() $\lambda \gt 1$
and sufficiently small
$\lambda \gt 1$
and sufficiently small
![]() $\epsilon \gt 0$
such that for all
$\epsilon \gt 0$
such that for all
![]() $s\gt 0$
and
$s\gt 0$
and
![]() $p$
sufficiently large in
$p$
sufficiently large in
![]() $s$
and
$s$
and
![]() $\nu$
, there exists a subset
$\nu$
, there exists a subset
![]() $A$
of
$A$
of
![]() $\mathbb{F}_p$
of size
$\mathbb{F}_p$
of size
![]() $\Omega _{\nu }(p)$
such that
$\Omega _{\nu }(p)$
such that
![]() $|A+A| \le \lambda |A|$
, and for all
$|A+A| \le \lambda |A|$
, and for all
![]() $A'\subseteq A$
of size at least
$A'\subseteq A$
of size at least
![]() $(1-\epsilon )|A|$
and all
$(1-\epsilon )|A|$
and all
![]() $A_{(s)} \subseteq A$
of size at most
$A_{(s)} \subseteq A$
of size at most
![]() $s$
,
$s$
,
![]() $|A'+A_{(s)}| \le \nu |A'+A|$
. Furthermore, the same result holds over
$|A'+A_{(s)}| \le \nu |A'+A|$
. Furthermore, the same result holds over
![]() $\mathbb{Z}$
and
$\mathbb{Z}$
and
![]() $\mathbb{F}_2^{n}$
.
$\mathbb{F}_2^{n}$
.
The construction is first done over
![]() $\mathbb{F}_2^n$
, and is then used to derive a construction over appropriate cyclic groups
$\mathbb{F}_2^n$
, and is then used to derive a construction over appropriate cyclic groups
![]() $\mathbb{Z}_N$
, then over the integers
$\mathbb{Z}_N$
, then over the integers
![]() $\mathbb{Z}$
and prime cyclic groups
$\mathbb{Z}$
and prime cyclic groups
![]() $\mathbb{F}_p$
.
$\mathbb{F}_p$
.
Construction over
![]() $\mathbb{F}_2^n$
. Let
$\mathbb{F}_2^n$
. Let
![]() $\theta$
be a sufficiently large constant, and
$\theta$
be a sufficiently large constant, and
![]() $\theta/4\lt \delta \lt \theta/3$
. Let
$\theta/4\lt \delta \lt \theta/3$
. Let
![]() $p,m$
be sufficiently large integers so that
$p,m$
be sufficiently large integers so that
![]() $\nu 2^p \gt 100$
and
$\nu 2^p \gt 100$
and
![]() $m\gt 2p$
, and let
$m\gt 2p$
, and let
![]() $n=p+m$
.
$n=p+m$
.
For
![]() $x\in \mathbb{F}_2^m$
, let
$x\in \mathbb{F}_2^m$
, let
![]() $|x|_1$
denote the number of coordinates of
$|x|_1$
denote the number of coordinates of
![]() $x$
that are equal to
$x$
that are equal to
![]() $1$
. Consider
$1$
. Consider
![]() $A_0\subseteq \mathbb{F}_2^m$
given by
$A_0\subseteq \mathbb{F}_2^m$
given by
![]() $A_0 = \{x\;:\;|x|_1 \le m/2-\theta \sqrt{m}\}$
. By the Central Limit Theorem, we have
$A_0 = \{x\;:\;|x|_1 \le m/2-\theta \sqrt{m}\}$
. By the Central Limit Theorem, we have
![]() $|A_0| \ge \exp\! ({-}C\theta ^2)\cdot 2^m$
for some absolute constant
$|A_0| \ge \exp\! ({-}C\theta ^2)\cdot 2^m$
for some absolute constant
![]() $C$
(provided
$C$
(provided
![]() $\theta$
is large), so
$\theta$
is large), so
![]() $A_0$
is a dense subset of
$A_0$
is a dense subset of
![]() $\mathbb{F}_2^{m}$
. Consider
$\mathbb{F}_2^{m}$
. Consider
![]() $B_0 = \{x\;:\;|x|_1 \le \theta \sqrt{m}\}$
. For
$B_0 = \{x\;:\;|x|_1 \le \theta \sqrt{m}\}$
. For
![]() $x,y\in \mathbb{F}_2^m$
, let
$x,y\in \mathbb{F}_2^m$
, let
![]() $x\otimes y = (x_1y_1,\dots,x_my_m)$
. For any
$x\otimes y = (x_1y_1,\dots,x_my_m)$
. For any
![]() $x$
with
$x$
with
![]() $|x|_1\le \theta \sqrt{m}$
, note that
$|x|_1\le \theta \sqrt{m}$
, note that
![]() $(A_0+x)\cap \{y\;:\;|y|_1\in [m/2-\delta \sqrt{m},m/2]\} \subseteq \{y\;:\;|y\otimes x|_1 \ge (\theta -\delta )\sqrt{m}\}$
.
$(A_0+x)\cap \{y\;:\;|y|_1\in [m/2-\delta \sqrt{m},m/2]\} \subseteq \{y\;:\;|y\otimes x|_1 \ge (\theta -\delta )\sqrt{m}\}$
.
Claim 6.1.
There is an absolute constant
![]() $c\gt 0$
such that the following holds. For any fixed
$c\gt 0$
such that the following holds. For any fixed
![]() $x$
with
$x$
with
![]() $|x|_1 \le \theta \sqrt{m}$
, the number of
$|x|_1 \le \theta \sqrt{m}$
, the number of
![]() $y\in \{y\;:\;|y|_1\in [m/2-\delta \sqrt{m},m/2]\}$
with
$y\in \{y\;:\;|y|_1\in [m/2-\delta \sqrt{m},m/2]\}$
with
![]() $|y\otimes x|_1\ge (\theta -\delta )\sqrt{m}$
is at most
$|y\otimes x|_1\ge (\theta -\delta )\sqrt{m}$
is at most
![]() $2^{-c\theta \sqrt{m}}\cdot 2^m$
.
$2^{-c\theta \sqrt{m}}\cdot 2^m$
.
Proof. Fix
![]() $x$
with
$x$
with
![]() $|x|_1 \le \theta \sqrt{m}$
. Consider
$|x|_1 \le \theta \sqrt{m}$
. Consider
![]() $y$
chosen uniformly at random from
$y$
chosen uniformly at random from
![]() $\{0,1\}^{m}$
. Then
$\{0,1\}^{m}$
. Then
![]() $|y\otimes x|_1$
is a binomial random variable with mean at most
$|y\otimes x|_1$
is a binomial random variable with mean at most
![]() $\theta \sqrt{m}/2$
. By the Chernoff bound, the probability that
$\theta \sqrt{m}/2$
. By the Chernoff bound, the probability that
![]() $|y\otimes x|_1 \ge (\theta -\delta )\sqrt{m}$
is at most
$|y\otimes x|_1 \ge (\theta -\delta )\sqrt{m}$
is at most
![]() $2^{-c\theta \sqrt{m}}$
for some absolute constant
$2^{-c\theta \sqrt{m}}$
for some absolute constant
![]() $c$
(assuming
$c$
(assuming
![]() $\theta$
is sufficiently large and
$\theta$
is sufficiently large and
![]() $\delta \in (\theta/4,\theta/3)$
). Thus, the number of
$\delta \in (\theta/4,\theta/3)$
). Thus, the number of
![]() $y$
with
$y$
with
![]() $|y\otimes x|_1 \ge (\theta -\delta )\sqrt{m}$
is at most
$|y\otimes x|_1 \ge (\theta -\delta )\sqrt{m}$
is at most
![]() $2^{m-c\theta \sqrt{m}}$
.
$2^{m-c\theta \sqrt{m}}$
.
By the claim, for any subset
![]() $B'$
of
$B'$
of
![]() $B_0$
,
$B_0$
,
Thus, noting that
![]() $B_0+B_0\subseteq \{y\;:\;|y|_1 \le m/2-\delta \sqrt{m}\}$
and
$B_0+B_0\subseteq \{y\;:\;|y|_1 \le m/2-\delta \sqrt{m}\}$
and
![]() $A_0+B'\subset \{y\;:\;|y|_1\le m/2\}$
, we have
$A_0+B'\subset \{y\;:\;|y|_1\le m/2\}$
, we have
for some constant
![]() $c_2\gt 0$
. For each
$c_2\gt 0$
. For each
![]() $x\in \mathbb{F}_2^{{n}}$
, write
$x\in \mathbb{F}_2^{{n}}$
, write
![]() $x=(x_1,x_2)$
where
$x=(x_1,x_2)$
where
![]() $x_1 \in \mathbb{F}_2^{p}$
and
$x_1 \in \mathbb{F}_2^{p}$
and
![]() $x_2 \in \mathbb{F}_2^{m}$
. Consider
$x_2 \in \mathbb{F}_2^{m}$
. Consider
![]() $A\subseteq \mathbb{F}_2^{{n}}$
given by
$A\subseteq \mathbb{F}_2^{{n}}$
given by
Here
![]() $\mathbb{I}$
denotes the indicator function, and for a set
$\mathbb{I}$
denotes the indicator function, and for a set
![]() $S$
,
$S$
,
![]() $S(x)\;:\!=\;\mathbb{I}[x\in S]$
. Noting that
$S(x)\;:\!=\;\mathbb{I}[x\in S]$
. Noting that
![]() $|A|\ge |A_0|\ge \exp\! ({-}C\theta ^2)\cdot 2^m$
, the doubling constant of
$|A|\ge |A_0|\ge \exp\! ({-}C\theta ^2)\cdot 2^m$
, the doubling constant of
![]() $A$
is
$A$
is
![]() $\lambda = |A+A|/|A| \le 2^{{n}}/(2^m \exp\! ({-}{C}\theta ^2)) \le 2^{p}\exp\! ({C}\theta ^2)$
.
$\lambda = |A+A|/|A| \le 2^{{n}}/(2^m \exp\! ({-}{C}\theta ^2)) \le 2^{p}\exp\! ({C}\theta ^2)$
.
By our choice of
![]() $m\gt 2p$
, if
$m\gt 2p$
, if
![]() $m$
is sufficiently large in terms of
$m$
is sufficiently large in terms of
![]() $\epsilon$
, then we have
$\epsilon$
, then we have
![]() $\epsilon |A_0|\ge (2^p-1)|B_0|$
. Then for any subset
$\epsilon |A_0|\ge (2^p-1)|B_0|$
. Then for any subset
![]() $A'$
of
$A'$
of
![]() $A$
of size at least
$A$
of size at least
![]() $(1-\epsilon )|A|$
, we have that
$(1-\epsilon )|A|$
, we have that
![]() $A_0^{\prime} \;:\!=\; \{x_2\;:\;(0,x_2)\in A'\}$
has size at least
$A_0^{\prime} \;:\!=\; \{x_2\;:\;(0,x_2)\in A'\}$
has size at least
![]() $(1-2\epsilon )|A|$
. Let
$(1-2\epsilon )|A|$
. Let
![]() $\Gamma _+=\Gamma _+^{1}(A)$
denote the set of points
$\Gamma _+=\Gamma _+^{1}(A)$
denote the set of points
![]() $y$
differing in at most one coordinate from some
$y$
differing in at most one coordinate from some
![]() $x\in A$
, and define
$x\in A$
, and define
![]() $\Gamma _+^{k+1}(A)=\Gamma _+(\Gamma _+^{k}(A))$
. Observe that
$\Gamma _+^{k+1}(A)=\Gamma _+(\Gamma _+^{k}(A))$
. Observe that
![]() $A_0^{\prime}+B_0 = \Gamma _+^{\theta \sqrt{m}}(A_0^{\prime})$
. Recall the following vertex isoperimetry inequality of Harper [Reference Harper21].
$A_0^{\prime}+B_0 = \Gamma _+^{\theta \sqrt{m}}(A_0^{\prime})$
. Recall the following vertex isoperimetry inequality of Harper [Reference Harper21].
Theorem 6.2 ([Reference Harper21]). Let
![]() $A\subseteq \{0,1\}^m$
have
$A\subseteq \{0,1\}^m$
have
![]() $|A| \ge \sum _{j=0}^{q}\binom{m}{j}$
. Then
$|A| \ge \sum _{j=0}^{q}\binom{m}{j}$
. Then
![]() $|\Gamma _+(A)| \ge \sum _{j=0}^{q+1}\binom{m}{j}$
.
$|\Gamma _+(A)| \ge \sum _{j=0}^{q+1}\binom{m}{j}$
.
Note that
 \begin{equation*} |A_0^{\prime}| \ge (1-2\epsilon )|A_0| = (1-2\epsilon )\sum _{j=0}^{m/2-\theta \sqrt {m}} \binom {m}{j} \ge \sum _{j=0}^{m/2-(\theta +\eta ) \sqrt {m}} \binom {m}{j}, \end{equation*}
\begin{equation*} |A_0^{\prime}| \ge (1-2\epsilon )|A_0| = (1-2\epsilon )\sum _{j=0}^{m/2-\theta \sqrt {m}} \binom {m}{j} \ge \sum _{j=0}^{m/2-(\theta +\eta ) \sqrt {m}} \binom {m}{j}, \end{equation*}
where
![]() $\eta \to 0$
as
$\eta \to 0$
as
![]() $\epsilon \to 0$
. By Theorem 6.2,
$\epsilon \to 0$
. By Theorem 6.2,
 \begin{equation*} |\Gamma _+^{\theta \sqrt {m}}(A_0^{\prime})| \ge \sum _{j=0}^{m/2-\eta \sqrt {m}}\binom {m}{j} \ge 2^{m-1}\exp\! ({-}C\eta ). \end{equation*}
\begin{equation*} |\Gamma _+^{\theta \sqrt {m}}(A_0^{\prime})| \ge \sum _{j=0}^{m/2-\eta \sqrt {m}}\binom {m}{j} \ge 2^{m-1}\exp\! ({-}C\eta ). \end{equation*}
Since
![]() $A'+A$
contains
$A'+A$
contains
![]() $2^{p}$
disjoint translates of
$2^{p}$
disjoint translates of
![]() $A_0^{\prime}+B_0 = \Gamma _+^{\theta \sqrt{m}}(A_0^{\prime})$
, we have for sufficiently small
$A_0^{\prime}+B_0 = \Gamma _+^{\theta \sqrt{m}}(A_0^{\prime})$
, we have for sufficiently small
![]() $\epsilon$
that
$\epsilon$
that
On the other hand, for any such
![]() $A'$
and any subset
$A'$
and any subset
![]() $A_{(s)}$
of
$A_{(s)}$
of
![]() $A$
of size at most
$A$
of size at most
![]() $s$
, let
$s$
, let
![]() $B_0^{\prime} =\{x_2\;:\;\: (x_1,x_2)\in A_{(s)}\}$
. Then
$B_0^{\prime} =\{x_2\;:\;\: (x_1,x_2)\in A_{(s)}\}$
. Then
![]() $A'+A_{(s)}$
is contained in
$A'+A_{(s)}$
is contained in
![]() $\{x\;:\;x_1=0\} \cup (\mathbb{F}_2^{p}\times ({(B_0+B_0^{\prime})\cup }(B_0+B_0)\cup (A_0^{\prime}+B_0^{\prime})))$
. By (6) and the fact that
$\{x\;:\;x_1=0\} \cup (\mathbb{F}_2^{p}\times ({(B_0+B_0^{\prime})\cup }(B_0+B_0)\cup (A_0^{\prime}+B_0^{\prime})))$
. By (6) and the fact that
![]() $|B_0^{\prime}|\le |A_{(s)}|\le s$
, we have that
$|B_0^{\prime}|\le |A_{(s)}|\le s$
, we have that
![]() $|A'+A_{(s)}|$
is bounded above by
$|A'+A_{(s)}|$
is bounded above by
We thus have that
Recall that we chose
![]() $p$
such that
$p$
such that
![]() $2^p \nu \gt 100$
. By choosing
$2^p \nu \gt 100$
. By choosing
![]() $\theta$
(and hence
$\theta$
(and hence
![]() $\delta$
) sufficiently large such that
$\delta$
) sufficiently large such that
![]() $\exp\! ({-}c_2\delta ^2)\lt \nu/25$
, as long as
$\exp\! ({-}c_2\delta ^2)\lt \nu/25$
, as long as
![]() $m$
is sufficiently large such that
$m$
is sufficiently large such that
![]() $s\lt \nu 2^{c\theta \sqrt{m}-5}$
, we conclude that
$s\lt \nu 2^{c\theta \sqrt{m}-5}$
, we conclude that
![]() $|A'+A_{(s)}|/|A'+A|\lt \nu$
as desired.
$|A'+A_{(s)}|/|A'+A|\lt \nu$
as desired.
Construction over
![]() $\mathbb{Z}_N$
. Let
$\mathbb{Z}_N$
. Let
![]() $q$
be a prime so that
$q$
be a prime so that
![]() $q\nu \gt 100$
,
$q\nu \gt 100$
,
![]() $\theta \gt 0$
sufficiently large, and
$\theta \gt 0$
sufficiently large, and
![]() $\theta/4\lt \delta \lt \theta/3$
. Consider primes
$\theta/4\lt \delta \lt \theta/3$
. Consider primes
![]() $p_1,\dots,p_m\gt q$
. Let
$p_1,\dots,p_m\gt q$
. Let
![]() $N=p_1\dots p_m$
. For each
$N=p_1\dots p_m$
. For each
![]() $i\le m$
, let
$i\le m$
, let
![]() $A_i = \{2k+1:k\le p_i/2\} \subseteq \mathbb{Z}_{p_i}$
. For each
$A_i = \{2k+1:k\le p_i/2\} \subseteq \mathbb{Z}_{p_i}$
. For each
![]() $x\in \prod _{i}\mathbb{Z}_{p_i}$
, let
$x\in \prod _{i}\mathbb{Z}_{p_i}$
, let
![]() $\pi (x) \in \{0,1\}^m$
be defined by
$\pi (x) \in \{0,1\}^m$
be defined by
![]() $\pi (x)_i = A_i(x_i)$
. Define
$\pi (x)_i = A_i(x_i)$
. Define
![]() $A_0 = \{x\;:\;|\pi (x)|_1 \le m/2-\theta \sqrt{m}\}$
, where again
$A_0 = \{x\;:\;|\pi (x)|_1 \le m/2-\theta \sqrt{m}\}$
, where again
![]() $|\pi (x)|_1$
is the number of ones in
$|\pi (x)|_1$
is the number of ones in
![]() $\pi (x)$
. Again
$\pi (x)$
. Again
![]() $|A_0|=N\exp\! ({-}c\theta ^2)$
. Let
$|A_0|=N\exp\! ({-}c\theta ^2)$
. Let
![]() $B_0 = \{x\in \{0,1\}^m:|\pi (x)|_1 \le \theta \sqrt{m}\}$
. As before, for any subset
$B_0 = \{x\in \{0,1\}^m:|\pi (x)|_1 \le \theta \sqrt{m}\}$
. As before, for any subset
![]() $B_{(s)}$
of
$B_{(s)}$
of
![]() $B_0$
of size
$B_0$
of size
![]() $s$
,
$s$
,
Consider the group
![]() $G = \mathbb{Z}_q \times \prod _i \mathbb{Z}_{p_i}$
, and denote each element
$G = \mathbb{Z}_q \times \prod _i \mathbb{Z}_{p_i}$
, and denote each element
![]() $z\in G$
by
$z\in G$
by
![]() $z=(x',x)$
with
$z=(x',x)$
with
![]() $x'\in \mathbb{Z}_q$
and
$x'\in \mathbb{Z}_q$
and
![]() $x \in \prod _i \mathbb{Z}_{p_i}$
. Define
$x \in \prod _i \mathbb{Z}_{p_i}$
. Define
![]() $A\subseteq \mathbb{Z}_q\times \prod _i \mathbb{Z}_{p_i}$
by
$A\subseteq \mathbb{Z}_q\times \prod _i \mathbb{Z}_{p_i}$
by
Then
![]() $A+A \subseteq \mathbb{Z}_q\times \{x\;:\;|\pi (x)|_1\le m/2\} \cup \{z\;:\;x'=0\}$
. For any subset
$A+A \subseteq \mathbb{Z}_q\times \{x\;:\;|\pi (x)|_1\le m/2\} \cup \{z\;:\;x'=0\}$
. For any subset
![]() $A'$
of
$A'$
of
![]() $A$
of size at least
$A$
of size at least
![]() $(1-\epsilon )|A|$
, as in the proof of the construction over
$(1-\epsilon )|A|$
, as in the proof of the construction over
![]() $\mathbb{F}_2^{N}$
, we have
$\mathbb{F}_2^{N}$
, we have
![]() $|A'+A| \ge Nq/4$
. For any such
$|A'+A| \ge Nq/4$
. For any such
![]() $A'$
and any subset
$A'$
and any subset
![]() $A_{(s)}$
of
$A_{(s)}$
of
![]() $A$
of size
$A$
of size
![]() $s$
, we can bound
$s$
, we can bound
Construction over
![]() $\mathbb{Z}$
and
$\mathbb{Z}$
and
![]() $\mathbb{F}_p$
. Let
$\mathbb{F}_p$
. Let
![]() $A$
be the set in the construction over
$A$
be the set in the construction over
![]() $\mathbb{Z}_N$
and note that upon choosing
$\mathbb{Z}_N$
and note that upon choosing
![]() $q$
depending only on
$q$
depending only on
![]() $\nu$
, we can guarantee that
$\nu$
, we can guarantee that
![]() $|A|\gg _{\nu } N$
. Let
$|A|\gg _{\nu } N$
. Let
![]() $\hat{A}$
be the set of representatives of
$\hat{A}$
be the set of representatives of
![]() $A$
in
$A$
in
![]() $[N-1]$
. Observe that
$[N-1]$
. Observe that
![]() $\hat{A}+\hat{A}\subseteq [2(N-1)]$
. We have
$\hat{A}+\hat{A}\subseteq [2(N-1)]$
. We have
![]() $|\hat{A}+\hat{A}|\le 2|A+A|\le 2\lambda |A|$
. For any
$|\hat{A}+\hat{A}|\le 2|A+A|\le 2\lambda |A|$
. For any
![]() $\hat{A}'\subseteq \hat{A}$
of size
$\hat{A}'\subseteq \hat{A}$
of size
![]() $(1-\epsilon )|\hat{A}|$
and any
$(1-\epsilon )|\hat{A}|$
and any
![]() $\hat{A}_{(s)}$
of size
$\hat{A}_{(s)}$
of size
![]() $s$
, we have that
$s$
, we have that
For any prime
![]() $p \gt 2N$
with
$p \gt 2N$
with
![]() $p\ll _{\nu } N$
, the same set
$p\ll _{\nu } N$
, the same set
![]() $\hat{A}\pmod p$
gives a construction of a subset of
$\hat{A}\pmod p$
gives a construction of a subset of
![]() $\mathbb{F}_p$
with density
$\mathbb{F}_p$
with density
![]() $\Omega _{\nu }(1)$
satisfying the required properties in Theorem 1.8.
$\Omega _{\nu }(1)$
satisfying the required properties in Theorem 1.8.
7. Concluding remarks
We believe that the following question is interesting.
Question 7.1.
Let
![]() $\lambda, \epsilon \gt 0$
be positive constants. Let
$\lambda, \epsilon \gt 0$
be positive constants. Let
![]() $A$
be a subset of an abelian group
$A$
be a subset of an abelian group
![]() $G$
with
$G$
with
![]() $|A+A|\le \lambda |A|$
. How large does a subset
$|A+A|\le \lambda |A|$
. How large does a subset
![]() $A'$
of
$A'$
of
![]() $A$
need to be to guarantee
$A$
need to be to guarantee
![]() $|A'+A|\ge (1-\epsilon )|A+A|$
?
$|A'+A|\ge (1-\epsilon )|A+A|$
?
As we saw in Section 5, even if
![]() $\epsilon =0$
, we have that
$\epsilon =0$
, we have that
![]() $|A'|=o(|A|)$
suffices (with explicit power-saving bounds over abelian groups with bounded exponent, while Behrend’s construction shows that one cannot have power-saving bounds over
$|A'|=o(|A|)$
suffices (with explicit power-saving bounds over abelian groups with bounded exponent, while Behrend’s construction shows that one cannot have power-saving bounds over
![]() $\mathbb{Z}$
or
$\mathbb{Z}$
or
![]() $\mathbb{F}_p$
). On the other hand, for some fixed positive
$\mathbb{F}_p$
). On the other hand, for some fixed positive
![]() $\epsilon$
, considering
$\epsilon$
, considering
![]() $A = [\delta n] \cup \{\sqrt{n},2\sqrt{n},\dots,n-\sqrt{n}\} \cup [n-\sqrt{n},n]$
(cf. Proposition 2.5) shows that one needs
$A = [\delta n] \cup \{\sqrt{n},2\sqrt{n},\dots,n-\sqrt{n}\} \cup [n-\sqrt{n},n]$
(cf. Proposition 2.5) shows that one needs
![]() $|A'| = \Omega (\sqrt{|A|})$
. It would be interesting to determine for
$|A'| = \Omega (\sqrt{|A|})$
. It would be interesting to determine for
![]() $\epsilon \gt 0$
if one needs
$\epsilon \gt 0$
if one needs
![]() $|A'|\ge |A|^{1-o(1)}$
when
$|A'|\ge |A|^{1-o(1)}$
when
![]() $G=\mathbb{Z}$
or
$G=\mathbb{Z}$
or
![]() $G=\mathbb{F}_p$
.
$G=\mathbb{F}_p$
.
Another interesting question is to determine the optimal exponent on the doubling constant in Theorem 1.1.
Question 7.2.
What is the largest
![]() $C$
such that the following holds? For some constant
$C$
such that the following holds? For some constant
![]() $c\gt 0$
, if
$c\gt 0$
, if
![]() $A$
is a nonempty subset of an abelian group
$A$
is a nonempty subset of an abelian group
![]() $G$
and
$G$
and
![]() $\kappa =|A+A|/|A|$
, then for each
$\kappa =|A+A|/|A|$
, then for each
![]() $s\le \kappa ^{C-o(1)}$
, there exists
$s\le \kappa ^{C-o(1)}$
, there exists
![]() $A_{(s)}\subseteq A$
of size at most
$A_{(s)}\subseteq A$
of size at most
![]() $s$
such that
$s$
such that
![]() $|A+A_{(s)}|\ge cs|A|$
.
$|A+A_{(s)}|\ge cs|A|$
.
As discussed previously, from Theorem 1.1 and Proposition 2.5 we know that
![]() $C\in [\frac{1}{3},\frac{1}{1.29}]$
, while for the setting of difference sets
$C\in [\frac{1}{3},\frac{1}{1.29}]$
, while for the setting of difference sets
![]() $A-A$
we have the better lower bound
$A-A$
we have the better lower bound
![]() $C\geq \frac{1}{2}$
.
$C\geq \frac{1}{2}$
.
Acknowledgements
The authors would like to thank the anonymous referee for their helpful comments.