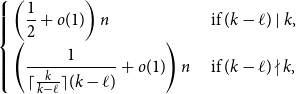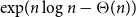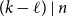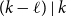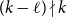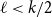1. Introduction
A central problem in extremal graph theory is to find sufficient degree conditions that force the containment of a given spanning subgraph, and here a classical result of Dirac [Reference Dirac10] from 1952 states that every graph on
![]() $n\geq 3$
vertices with minimum degree at least
$n\geq 3$
vertices with minimum degree at least
![]() $n/2$
contains a Hamilton cycle. In 1995, Bollobás [Reference Bolobás4] and Bondy [Reference Bondy5] asked for estimates of the number of distinct Hamilton cycles in graphs satisfying Dirac’s condition. Sárközy, Selkow, and Szemerédi [Reference Simonovits and Szemerédi32] used the regularity method in 2003 to show that every graph with
$n/2$
contains a Hamilton cycle. In 1995, Bollobás [Reference Bolobás4] and Bondy [Reference Bondy5] asked for estimates of the number of distinct Hamilton cycles in graphs satisfying Dirac’s condition. Sárközy, Selkow, and Szemerédi [Reference Simonovits and Szemerédi32] used the regularity method in 2003 to show that every graph with
![]() $n\geq 3$
vertices and minimum degree at least
$n\geq 3$
vertices and minimum degree at least
![]() $n/2$
contains at least
$n/2$
contains at least
![]() $c^nn!$
Hamilton cycles, for some constant
$c^nn!$
Hamilton cycles, for some constant
![]() $c\gt 0$
. This cannot be improved to any
$c\gt 0$
. This cannot be improved to any
![]() $c\gt 1/2$
, as for fixed
$c\gt 1/2$
, as for fixed
![]() $p\gt 1/2$
, the typical random graph
$p\gt 1/2$
, the typical random graph
![]() $G(n,p)$
satisfies Dirac’s condition and has
$G(n,p)$
satisfies Dirac’s condition and has
![]() $(1-o(1))^np^nn!$
distinct Hamilton cycles (see [Reference Janson16]). In 2009, Cuckler and Kahn [Reference Cuckler and Kahn8] obtained precise estimates of the number of distinct Hamilton cycles in terms of the minimum degree of the host graph. In particular, they showed that every
$(1-o(1))^np^nn!$
distinct Hamilton cycles (see [Reference Janson16]). In 2009, Cuckler and Kahn [Reference Cuckler and Kahn8] obtained precise estimates of the number of distinct Hamilton cycles in terms of the minimum degree of the host graph. In particular, they showed that every
![]() $n$
-vertex graph with minimum degree at least
$n$
-vertex graph with minimum degree at least
![]() $n/2$
contains at least
$n/2$
contains at least
![]() $(\frac 12-o(1))^nn!$
distinct Hamilton cycles, thus matching the bound given by random graphs.
$(\frac 12-o(1))^nn!$
distinct Hamilton cycles, thus matching the bound given by random graphs.
Our purpose here is to introduce a simple method to bound below the number of copies of many different spanning subgraphs in graphs and hypergraphs with a high minimum degree and apply this to give new counting results in dense hypergraphs (Theorems 1.2–1.4). However, let us already illustrate this method as it would apply to Hamilton cycles in an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree
$G$
with minimum degree
![]() $\delta (G)\geq (\frac{1}{2}+\varepsilon )n$
with
$\delta (G)\geq (\frac{1}{2}+\varepsilon )n$
with
![]() $\varepsilon \gt 0$
fixed and
$\varepsilon \gt 0$
fixed and
![]() $n$
large. Set
$n$
large. Set
![]() $r=\mu n$
with
$r=\mu n$
with
![]() $1/n\ll \mu \ll \varepsilon$
, and partition
$1/n\ll \mu \ll \varepsilon$
, and partition
![]() $V(G)=V_1\cup \ldots \cup V_r$
by choosing the location of each vertex independently and uniformly at random. With probability at least
$V(G)=V_1\cup \ldots \cup V_r$
by choosing the location of each vertex independently and uniformly at random. With probability at least
![]() $e^{-n}$
, the minimum degree of each subgraph
$e^{-n}$
, the minimum degree of each subgraph
![]() $G[V_i]$
will be at least
$G[V_i]$
will be at least
![]() $(\frac{1}{2}+\frac{\varepsilon }{2})|V_i|$
, and there will be a disjoint collection of
$(\frac{1}{2}+\frac{\varepsilon }{2})|V_i|$
, and there will be a disjoint collection of
![]() $r$
edges in
$r$
edges in
![]() $G$
connecting the sets
$G$
connecting the sets
![]() $V_1,\ldots,V_r$
in a cycle in order and connecting
$V_1,\ldots,V_r$
in a cycle in order and connecting
![]() $V_r$
to
$V_r$
to
![]() $V_1$
(see Fig. 1). Applying classical methods to find a Hamilton path through each subgraph
$V_1$
(see Fig. 1). Applying classical methods to find a Hamilton path through each subgraph
![]() $G[V_i]$
to connect these edges creates a Hamilton cycle of
$G[V_i]$
to connect these edges creates a Hamilton cycle of
![]() $G$
which passes through each of the sets
$G$
which passes through each of the sets
![]() $V_1,\ldots,V_r$
in order. As we will prove later, even though the probability of success here is small, only at least
$V_1,\ldots,V_r$
in order. As we will prove later, even though the probability of success here is small, only at least
![]() $e^{-n}$
, for this to be true, it is easy to show that
$e^{-n}$
, for this to be true, it is easy to show that
![]() $G$
must contain at least
$G$
must contain at least
![]() $c^nn!$
distinct Hamilton cycles (for some fixed
$c^nn!$
distinct Hamilton cycles (for some fixed
![]() $0\lt c\ll \varepsilon$
).
$0\lt c\ll \varepsilon$
).

Figure 1. A Hamilton cycle passing through the sets
![]() $V_1,V_2,\ldots,V_r$
in order.
$V_1,V_2,\ldots,V_r$
in order.
For each
![]() $i\in [r]$
in the above argument, we should expect
$i\in [r]$
in the above argument, we should expect
![]() $\delta (G[V_i])\geq (\frac{1}{2}+\frac{\varepsilon }{2})|V_i|$
with some constant probability close to 1 (as
$\delta (G[V_i])\geq (\frac{1}{2}+\frac{\varepsilon }{2})|V_i|$
with some constant probability close to 1 (as
![]() $\mu \ll \varepsilon$
), and so we would expect this to hold for all
$\mu \ll \varepsilon$
), and so we would expect this to hold for all
![]() $i\in [r]$
with probability at least
$i\in [r]$
with probability at least
![]() $2^{-r}\geq e^{-n}$
(say) for
$2^{-r}\geq e^{-n}$
(say) for
![]() $n$
large. Because of the dependencies here, this is not straightforward to prove, but we do this with an iterative partitioning argument inspired by a technical aspect of the iterative absorption techniques introduced by Barber, Lo, Kühn, and Osthus [Reference Barber, Kühn, Lo and Osthus2]. The result of this argument in the graph case for Hamilton cycles is much weaker than what is already known, but this argument can be used easily in hypergraphs if the subgraph sought can be constructed from pieces like the cycle in Fig. 1. This allows counting results to be inferred from the extremal minimal degree for these pieces applied to each hypergraph induced on the sets
$n$
large. Because of the dependencies here, this is not straightforward to prove, but we do this with an iterative partitioning argument inspired by a technical aspect of the iterative absorption techniques introduced by Barber, Lo, Kühn, and Osthus [Reference Barber, Kühn, Lo and Osthus2]. The result of this argument in the graph case for Hamilton cycles is much weaker than what is already known, but this argument can be used easily in hypergraphs if the subgraph sought can be constructed from pieces like the cycle in Fig. 1. This allows counting results to be inferred from the extremal minimal degree for these pieces applied to each hypergraph induced on the sets
![]() $V_i$
in the partition (with some modification to make the required connections).
$V_i$
in the partition (with some modification to make the required connections).
Dirac’s theorem has been generalised to give minimum degree conditions implying the containment of many other spanning subgraphs, including
![]() $F$
-factors [Reference Hajnal and Szemerédi15, Reference Kühn and Osthus25], trees with bounded degree [Reference Csaba, Levitt, Nagy-György and Szemeredi7, Reference Komlós, Sárközy and Szemerédi19, Reference Komlós, Sárközy and Szemerédi21], powers of Hamilton cycles [Reference Komlós, Sárközy and Szemerédi22, Reference Komlós, Sárközy and Szemerédi20], and, more generally, graphs with bounded degree and sublinear bandwidth [Reference Böttcher, Schacht and Taraz6] (see also the excellent surveys [Reference Kühn, Mycroft and Osthus24, Reference Rödl, Szemerédi and Ruciński31]). For hypergraphs, much less is known, but we will recall the progress made for Hamilton
$F$
-factors [Reference Hajnal and Szemerédi15, Reference Kühn and Osthus25], trees with bounded degree [Reference Csaba, Levitt, Nagy-György and Szemeredi7, Reference Komlós, Sárközy and Szemerédi19, Reference Komlós, Sárközy and Szemerédi21], powers of Hamilton cycles [Reference Komlós, Sárközy and Szemerédi22, Reference Komlós, Sárközy and Szemerédi20], and, more generally, graphs with bounded degree and sublinear bandwidth [Reference Böttcher, Schacht and Taraz6] (see also the excellent surveys [Reference Kühn, Mycroft and Osthus24, Reference Rödl, Szemerédi and Ruciński31]). For hypergraphs, much less is known, but we will recall the progress made for Hamilton
![]() $\ell$
-cycles, powers of tight cycles, and factors (in Section 1.1), before discussing previous counting results and our main theorems (in Section 1.2). Our technique may be applicable to other spanning subgraphs, and in particular, we note that recent work of Gupta, Hamann, Müyesser, Parczyk, and Sgueglia [Reference Gupta, Hamann, Müyesser, Parczyk and Sgueglia14] classifies some hypergraphs our techniques may apply to.
$\ell$
-cycles, powers of tight cycles, and factors (in Section 1.1), before discussing previous counting results and our main theorems (in Section 1.2). Our technique may be applicable to other spanning subgraphs, and in particular, we note that recent work of Gupta, Hamann, Müyesser, Parczyk, and Sgueglia [Reference Gupta, Hamann, Müyesser, Parczyk and Sgueglia14] classifies some hypergraphs our techniques may apply to.
1.1 Dirac-type problems in hypergraphs
A
![]() $k$
-uniform hypergraph (or
$k$
-uniform hypergraph (or
![]() $k$
-graph) is a hypergraph where every edge consists of exactly
$k$
-graph) is a hypergraph where every edge consists of exactly
![]() $k$
vertices. For a
$k$
vertices. For a
![]() $k$
-graph
$k$
-graph
![]() $H$
and a subset of vertices
$H$
and a subset of vertices
![]() $S\subset V(H)$
, the degree of
$S\subset V(H)$
, the degree of
![]() $S$
, denoted
$S$
, denoted
![]() $d_H(S)$
, is the number of edges in
$d_H(S)$
, is the number of edges in
![]() $H$
containing
$H$
containing
![]() $S$
. For
$S$
. For
![]() $1\le d\le k-1$
, the minimum
$1\le d\le k-1$
, the minimum
![]() $d$
-degree of
$d$
-degree of
![]() $H$
, denoted
$H$
, denoted
![]() $\delta _d(H)$
, is the minimum of
$\delta _d(H)$
, is the minimum of
![]() $d_H(S)$
over all subsets
$d_H(S)$
over all subsets
![]() $S\subseteq V(H)$
with
$S\subseteq V(H)$
with
![]() $|S|=d$
. When
$|S|=d$
. When
![]() $d=k-1$
, this is the minimum codegree,
$d=k-1$
, this is the minimum codegree,
![]() $\delta (H)=\delta _{k-1}(H)$
.
$\delta (H)=\delta _{k-1}(H)$
.
The first subgraphs we consider in hypergraphs are the Hamilton
![]() $\ell$
-cycles, a well-studied generalisation of Hamilton cycles to hypergraphs. For
$\ell$
-cycles, a well-studied generalisation of Hamilton cycles to hypergraphs. For
![]() $k\geq 2$
and
$k\geq 2$
and
![]() $0\le \ell \le k-1$
, say that a
$0\le \ell \le k-1$
, say that a
![]() $k$
-graph
$k$
-graph
![]() $C$
is an
$C$
is an
![]() $\ell$
-cycle if there is a cyclic ordering
$\ell$
-cycle if there is a cyclic ordering
![]() $v_1,\ldots, v_t$
of
$v_1,\ldots, v_t$
of
![]() $V(C)$
such that every edge of
$V(C)$
such that every edge of
![]() $C$
consists of
$C$
consists of
![]() $k$
consecutive vertices and every two consecutive edges intersect in exactly
$k$
consecutive vertices and every two consecutive edges intersect in exactly
![]() $\ell$
vertices. If
$\ell$
vertices. If
![]() $\ell =k-1$
, then
$\ell =k-1$
, then
![]() $C$
is called a tight cycle, and if
$C$
is called a tight cycle, and if
![]() $\ell =0$
, then
$\ell =0$
, then
![]() $C$
is a matching. A
$C$
is a matching. A
![]() $k$
-graph
$k$
-graph
![]() $H$
contains a Hamilton
$H$
contains a Hamilton
![]() $\ell$
-cycle if there is an
$\ell$
-cycle if there is an
![]() $\ell$
-cycle
$\ell$
-cycle
![]() $C\subseteq H$
with
$C\subseteq H$
with
![]() $V(C)=V(H)$
(where it can only exist if
$V(C)=V(H)$
(where it can only exist if
![]() $k-\ell$
divides
$k-\ell$
divides
![]() $|H|$
).
$|H|$
).
The asymptotic minimum codegree required to guarantee a Hamilton
![]() $\ell$
-cycle in an
$\ell$
-cycle in an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph is known due to Rödl, Ruciński, and Szemerédi [Reference Pham, Sah, Sawhney and Simkin30] if
$k$
-graph is known due to Rödl, Ruciński, and Szemerédi [Reference Pham, Sah, Sawhney and Simkin30] if
![]() $(k-\ell )|\ell$
and to Kühn, Mycroft, and Osthus [Reference Komlós, Sárközy and Szemerédi23] if
$(k-\ell )|\ell$
and to Kühn, Mycroft, and Osthus [Reference Komlós, Sárközy and Szemerédi23] if
![]() $(k-\ell )\nmid k$
, whose results together give the following theorem.
$(k-\ell )\nmid k$
, whose results together give the following theorem.
Theorem 1.1.
For each
![]() $\gamma \gt 0$
,
$\gamma \gt 0$
,
![]() $k\geq 2$
, and
$k\geq 2$
, and
![]() $1\leq \ell \lt k$
, there exists
$1\leq \ell \lt k$
, there exists
![]() $n_0$
such that the following holds for all
$n_0$
such that the following holds for all
![]() $n\geq n_0$
with
$n\geq n_0$
with
![]() $(k-\ell )\mid n$
. If
$(k-\ell )\mid n$
. If
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta (H)\geq (\delta _{k,\ell }+\gamma )n$
, where
$\delta (H)\geq (\delta _{k,\ell }+\gamma )n$
, where
 \begin{equation} \delta _{k,\ell }\;:\!=\;\left \{\begin{array}{l@{\quad}l} \dfrac{1}{2} & \text{ if }(k-\ell )\mid k, \\[5pt] \dfrac{1}{\lceil \frac{k}{k-\ell }\rceil (k-\ell )} & \text{ if }(k-\ell )\nmid k, \end{array} \right . \end{equation}
\begin{equation} \delta _{k,\ell }\;:\!=\;\left \{\begin{array}{l@{\quad}l} \dfrac{1}{2} & \text{ if }(k-\ell )\mid k, \\[5pt] \dfrac{1}{\lceil \frac{k}{k-\ell }\rceil (k-\ell )} & \text{ if }(k-\ell )\nmid k, \end{array} \right . \end{equation}
then
![]() $H$
contains a Hamilton
$H$
contains a Hamilton
![]() $\ell$
-cycle.
$\ell$
-cycle.
Due to Theorem 1.1, we say the minimum codegree threshold for a
![]() $k$
-graph to contain a Hamilton
$k$
-graph to contain a Hamilton
![]() $\ell$
-cycle is
$\ell$
-cycle is
![]() $\delta _{k,\ell }$
. Note that a Hamilton tight cycle contains a Hamilton
$\delta _{k,\ell }$
. Note that a Hamilton tight cycle contains a Hamilton
![]() $\ell$
-cycle for every
$\ell$
-cycle for every
![]() $\ell$
with
$\ell$
with
![]() $(k-\ell )\mid k$
. The results in Theorem 1.1 are tight in every case up to the ‘error term’ of
$(k-\ell )\mid k$
. The results in Theorem 1.1 are tight in every case up to the ‘error term’ of
![]() $\gamma n$
. For more discussion of this, and the seemingly much more difficult problem for other degree bounds
$\gamma n$
. For more discussion of this, and the seemingly much more difficult problem for other degree bounds
![]() $\delta _d(H)$
,
$\delta _d(H)$
,
![]() $d\lt k-1$
, see the survey by Kühn and Osthus [Reference Kühn and Osthus26].
$d\lt k-1$
, see the survey by Kühn and Osthus [Reference Kühn and Osthus26].
We will also consider the powers of Hamilton tight cycles, where for each
![]() $t\geq k\geq 2$
, a
$t\geq k\geq 2$
, a
![]() $k$
-graph
$k$
-graph
![]() $C$
is the
$C$
is the
![]() $(t-k+1)$
th power of a tight cycle if there is a cyclic ordering
$(t-k+1)$
th power of a tight cycle if there is a cyclic ordering
![]() $v_1,\ldots,v_s$
of
$v_1,\ldots,v_s$
of
![]() $V(C)$
so that
$V(C)$
so that
![]() $\{v_i,\ldots,v_{i+t-1}\}$
spans a
$\{v_i,\ldots,v_{i+t-1}\}$
spans a
![]() $k$
-uniform clique for all
$k$
-uniform clique for all
![]() $i\in [s]$
(working modulo
$i\in [s]$
(working modulo
![]() $s$
). When
$s$
). When
![]() $k=2$
, this coincides with the usual definition of powers of cycles in graphs, where for each
$k=2$
, this coincides with the usual definition of powers of cycles in graphs, where for each
![]() $t\geq 2$
, the minimum degree threshold for the containment of the
$t\geq 2$
, the minimum degree threshold for the containment of the
![]() $(t-1)$
th power of a Hamilton cycle was famously shown to be
$(t-1)$
th power of a Hamilton cycle was famously shown to be
![]() $\frac{t-1}{t}$
by Komlós, Sárközy, and Szemerédi [Reference Komlós, Sárközy and Szemerédi22, Reference Komlós, Sárközy and Szemerédi20]. In 2020, Bedenknecht and Reiher [Reference Bedenknecht and Reiher3] proved that
$\frac{t-1}{t}$
by Komlós, Sárközy, and Szemerédi [Reference Komlós, Sárközy and Szemerédi22, Reference Komlós, Sárközy and Szemerédi20]. In 2020, Bedenknecht and Reiher [Reference Bedenknecht and Reiher3] proved that
![]() $3$
-graphs with minimum codegree at least
$3$
-graphs with minimum codegree at least
![]() $(4/5+o(1))n$
contain the square of a tight Hamilton cycle (which corresponds to
$(4/5+o(1))n$
contain the square of a tight Hamilton cycle (which corresponds to
![]() $t=k+1$
and
$t=k+1$
and
![]() $k=3$
), where it is known that the constant
$k=3$
), where it is known that the constant
![]() $4/5$
cannot be reduced below
$4/5$
cannot be reduced below
![]() $3/4$
for all
$3/4$
for all
![]() $n$
. This was recently widely extended by Pavez-Signé, Sanhueza-Matamala, and Stein [Reference McDiarmid28], who showed that, with
$n$
. This was recently widely extended by Pavez-Signé, Sanhueza-Matamala, and Stein [Reference McDiarmid28], who showed that, with
![]() $\gamma \gt 0$
fixed, if an
$\gamma \gt 0$
fixed, if an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph
$k$
-graph
![]() $H$
has minimum codegree
$H$
has minimum codegree
 \begin{equation} \delta (H)\geq \left (1-\frac{1}{\binom{t-1}{k-1}+\binom{t-2}{k-2}}+\gamma \right )n, \end{equation}
\begin{equation} \delta (H)\geq \left (1-\frac{1}{\binom{t-1}{k-1}+\binom{t-2}{k-2}}+\gamma \right )n, \end{equation}
then
![]() $H$
contains the
$H$
contains the
![]() $(t-k+1)$
th power of a tight Hamilton cycle, provided that
$(t-k+1)$
th power of a tight Hamilton cycle, provided that
![]() $n$
is sufficiently large. It is not known whether the bounds given in (1.2) are tight up to
$n$
is sufficiently large. It is not known whether the bounds given in (1.2) are tight up to
![]() $\gamma n$
, though this is true for the cases
$\gamma n$
, though this is true for the cases
![]() $t\geq k=2$
and
$t\geq k=2$
and
![]() $t=k\geq 2$
which were already known [Reference Pham, Sah, Sawhney and Simkin30, Reference Komlós, Sárközy and Szemerédi22].
$t=k\geq 2$
which were already known [Reference Pham, Sah, Sawhney and Simkin30, Reference Komlós, Sárközy and Szemerédi22].
Finally, we will consider factors in hypergraphs. For a
![]() $k$
-graph
$k$
-graph
![]() $F$
, a
$F$
, a
![]() $k$
-graph
$k$
-graph
![]() $H$
contains an
$H$
contains an
![]() $F$
-factor if it contains a collection of vertex-disjoint copies of
$F$
-factor if it contains a collection of vertex-disjoint copies of
![]() $F$
covering every vertex in
$F$
covering every vertex in
![]() $H$
. Thus, a necessary condition for an
$H$
. Thus, a necessary condition for an
![]() $F$
-factor in
$F$
-factor in
![]() $H$
is that
$H$
is that
![]() $|F|$
divides
$|F|$
divides
![]() $|H|$
. For
$|H|$
. For
![]() $1\le d\le k-1$
, then, let
$1\le d\le k-1$
, then, let
![]() $\mu _{k,d}(F)$
be the smallest number such that for every
$\mu _{k,d}(F)$
be the smallest number such that for every
![]() $\gamma \gt 0$
, there is
$\gamma \gt 0$
, there is
![]() $n_0$
such that if
$n_0$
such that if
![]() $H$
is an
$H$
is an
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $n\geq n_0$
divisible by
$n\geq n_0$
divisible by
![]() $|F|$
and
$|F|$
and
![]() $\delta _d(H)\geq (\mu _{k,d}(F)+\gamma )\binom{n}{k-d}$
, then
$\delta _d(H)\geq (\mu _{k,d}(F)+\gamma )\binom{n}{k-d}$
, then
![]() $H$
contains an
$H$
contains an
![]() $F$
-factor. In contrast to the graph case, where the threshold is known (with moreover a much stronger error term) for all fixed
$F$
-factor. In contrast to the graph case, where the threshold is known (with moreover a much stronger error term) for all fixed
![]() $F$
due to Komlós, Sárközy, and Szemerédi [Reference Hajnal and Szemerédi15] and Kühn and Osthus [Reference Kühn and Osthus25], for most cases, we do not have good bounds even in the case
$F$
due to Komlós, Sárközy, and Szemerédi [Reference Hajnal and Szemerédi15] and Kühn and Osthus [Reference Kühn and Osthus25], for most cases, we do not have good bounds even in the case
![]() $d=k-1$
(see the survey by [Reference Sárközy, Selkow and Szemerédi33] and references therein).
$d=k-1$
(see the survey by [Reference Sárközy, Selkow and Szemerédi33] and references therein).
1.2 Counting spanning hypergraphs
As in Cuckler and Kahn’s work on Hamilton cycles [Reference Cuckler and Kahn8], it is reasonable to believe that an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph
$k$
-graph
![]() $H$
with
$H$
with
![]() $\delta (H)\geq \delta n$
, for
$\delta (H)\geq \delta n$
, for
![]() $(k-\ell )\mid n$
and
$(k-\ell )\mid n$
and
![]() $\delta \gt \delta _{k,\ell }$
, should contain at least
$\delta \gt \delta _{k,\ell }$
, should contain at least
distinct Hamilton
![]() $\ell$
-cycles, where
$\ell$
-cycles, where
![]() $\Psi _{k,\ell }(n,\delta )$
denotes the expected number of distinct Hamilton
$\Psi _{k,\ell }(n,\delta )$
denotes the expected number of distinct Hamilton
![]() $\ell$
-cycles in the binomial random
$\ell$
-cycles in the binomial random
![]() $k$
-graph on
$k$
-graph on
![]() $n$
vertices with edge probability
$n$
vertices with edge probability
![]() $\delta$
. In 2016, Ferber, Krivelevich, and Sudakov [Reference Ferber, Krivelevich and Sudakov12] showed that the lower bound (1.3) is correct for every
$\delta$
. In 2016, Ferber, Krivelevich, and Sudakov [Reference Ferber, Krivelevich and Sudakov12] showed that the lower bound (1.3) is correct for every
![]() $\delta \gt 1/2$
and
$\delta \gt 1/2$
and
![]() $1\le \ell \le k/2$
and asked if this can be extended to
$1\le \ell \le k/2$
and asked if this can be extended to
![]() $1\le \ell \le k-1$
and
$1\le \ell \le k-1$
and
![]() $\delta \gt \delta _{k,\ell }$
. This was partially answered by Glock, Gould, Joos, Kühn, and Osthus [Reference Glock, Gould, Joos, Kühn and Osthus13], who showed that for every
$\delta \gt \delta _{k,\ell }$
. This was partially answered by Glock, Gould, Joos, Kühn, and Osthus [Reference Glock, Gould, Joos, Kühn and Osthus13], who showed that for every
![]() $\delta \gt 1/2$
and
$\delta \gt 1/2$
and
![]() $1\le \ell \le k-1$
, the number of distinct Hamilton
$1\le \ell \le k-1$
, the number of distinct Hamilton
![]() $\ell$
-cycles is
$\ell$
-cycles is
![]() $\exp\!(n\log n-\Theta (n))$
, which is tight up to the
$\exp\!(n\log n-\Theta (n))$
, which is tight up to the
![]() $\Theta (n)$
error term in the exponent. This result was recently improved by Ferber, Hardiman, and Mond [Reference Ferber, Hardiman and Mond11], who proved that the lower bound (1.3) holds for every
$\Theta (n)$
error term in the exponent. This result was recently improved by Ferber, Hardiman, and Mond [Reference Ferber, Hardiman and Mond11], who proved that the lower bound (1.3) holds for every
![]() $\delta \gt 1/2$
and
$\delta \gt 1/2$
and
![]() $1\le \ell \le k-2$
, thus settling the problem for every
$1\le \ell \le k-2$
, thus settling the problem for every
![]() $1\le \ell \le k-2$
such that
$1\le \ell \le k-2$
such that
![]() $(k-\ell )\mid k$
. Our contribution is to use the simple method outlined above to get a bound matching that in [Reference Glock, Gould, Joos, Kühn and Osthus13] that holds for any
$(k-\ell )\mid k$
. Our contribution is to use the simple method outlined above to get a bound matching that in [Reference Glock, Gould, Joos, Kühn and Osthus13] that holds for any
![]() $\delta \gt \delta _{k,\ell }$
(with
$\delta \gt \delta _{k,\ell }$
(with
![]() $\delta _{k,\ell }$
as defined in [1.1]), thus giving a new result when
$\delta _{k,\ell }$
as defined in [1.1]), thus giving a new result when
![]() $(k-\ell )\nmid k$
and
$(k-\ell )\nmid k$
and
![]() $\ell \gt k/2$
, as follows.
$\ell \gt k/2$
, as follows.
Theorem 1.2.
For each
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $1\leq \ell \leq k-1$
, and
$1\leq \ell \leq k-1$
, and
![]() $\gamma \gt 0$
, there exist
$\gamma \gt 0$
, there exist
![]() $n_0$
and
$n_0$
and
![]() $C$
such that the following holds for any
$C$
such that the following holds for any
![]() $n\geq n_0$
with
$n\geq n_0$
with
![]() $(k-\ell )\mid n$
. Any
$(k-\ell )\mid n$
. Any
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph
$k$
-graph
![]() $H$
with
$H$
with
![]() $\delta (H)\geq (\delta _{k,\ell }+\gamma )n$
(see [1.1]) contains at least
$\delta (H)\geq (\delta _{k,\ell }+\gamma )n$
(see [1.1]) contains at least
![]() $\exp\!(n\log n-Cn)$
distinct Hamilton
$\exp\!(n\log n-Cn)$
distinct Hamilton
![]() $\ell$
-cycles.
$\ell$
-cycles.
No previous bounds on the count of powers of Hamilton tight cycles in hypergraphs with large codegree have been shown (including in graphs), and here, we use our technique to similarly get a bound tight up to
![]() $\Theta (n)$
error term in the exponent, as follows.
$\Theta (n)$
error term in the exponent, as follows.
Theorem 1.3.
For each
![]() $t\geq k\geq 2$
and
$t\geq k\geq 2$
and
![]() $\gamma \gt 0$
, there exist
$\gamma \gt 0$
, there exist
![]() $n_0$
and
$n_0$
and
![]() $C$
such that the following holds for any
$C$
such that the following holds for any
![]() $n\geq n_0$
. Any
$n\geq n_0$
. Any
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph
$k$
-graph
![]() $H$
satisfying (1.2) contains at least
$H$
satisfying (1.2) contains at least
![]() $\exp\!(n\log n-Cn)$
distinct copies of the
$\exp\!(n\log n-Cn)$
distinct copies of the
![]() $(t-k+1)$
th power of a Hamilton tight cycle.
$(t-k+1)$
th power of a Hamilton tight cycle.
Finally, we consider counting
![]() $F$
-factors in dense hypergraphs. When
$F$
-factors in dense hypergraphs. When
![]() $F$
is a single edge and
$F$
is a single edge and
![]() $k|n$
, the number of
$k|n$
, the number of
![]() $F$
-factors in a
$F$
-factors in a
![]() $k$
-graph
$k$
-graph
![]() $H$
with
$H$
with
![]() $n\geq 3k$
vertices is equal to the number of Hamilton 0-cycles multiplied by a factor of
$n\geq 3k$
vertices is equal to the number of Hamilton 0-cycles multiplied by a factor of
![]() $((n/k)-1)!/2$
. Thus, from the results of Ferber, Krivelevich, and Sudakov [Reference Ferber, Krivelevich and Sudakov12] described above, if
$((n/k)-1)!/2$
. Thus, from the results of Ferber, Krivelevich, and Sudakov [Reference Ferber, Krivelevich and Sudakov12] described above, if
![]() $k\mid n$
, then any
$k\mid n$
, then any
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph
$k$
-graph
![]() $H$
with
$H$
with
![]() $\delta (H)\geq \delta n$
has at least
$\delta (H)\geq \delta n$
has at least
![]() $(1-o(1))^n \Psi _{k,\ell }(n,\delta )/(n/k)!$
$(1-o(1))^n \Psi _{k,\ell }(n,\delta )/(n/k)!$
![]() $F$
-factors (with
$F$
-factors (with
![]() $\Psi _{k,\ell }(n,\delta )$
as defined in [1.3]). In each case as part of wider work, for
$\Psi _{k,\ell }(n,\delta )$
as defined in [1.3]). In each case as part of wider work, for
![]() $1\le d\le k-1$
, Kang, Kelly, Kühn, Osthus, and Pfenninger [Reference Kang, Kelly, Kühn, Osthus and Pfenninger18] and Pham, Sah, Sawhney, and Simkin [Reference Pavez-Signé, Sanhueza-Matamala and Stein29] showed that if
$1\le d\le k-1$
, Kang, Kelly, Kühn, Osthus, and Pfenninger [Reference Kang, Kelly, Kühn, Osthus and Pfenninger18] and Pham, Sah, Sawhney, and Simkin [Reference Pavez-Signé, Sanhueza-Matamala and Stein29] showed that if
![]() $F$
is again a single edge, and
$F$
is again a single edge, and
![]() $k\mid n$
, then any
$k\mid n$
, then any
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph
$k$
-graph
![]() $H$
with
$H$
with
![]() $\delta _d(H)\geq (\mu _{k,d}(F)+\gamma )\binom{n}{k-d}$
contains at least
$\delta _d(H)\geq (\mu _{k,d}(F)+\gamma )\binom{n}{k-d}$
contains at least
![]() $c^{-n}\exp\!((1-1/k)n\log n)$
$c^{-n}\exp\!((1-1/k)n\log n)$
![]() $F$
-factors where
$F$
-factors where
![]() $c\ll \gamma$
is fixed, and this result is tight up to the constant
$c\ll \gamma$
is fixed, and this result is tight up to the constant
![]() $c$
. When
$c$
. When
![]() $d=k-1$
, Kang, Kelly, Kühn, Osthus, and Pfenninger [Reference Kang, Kelly, Kühn, Osthus and Pfenninger18] even managed to remove the error term in the minimum degree condition.
$d=k-1$
, Kang, Kelly, Kühn, Osthus, and Pfenninger [Reference Kang, Kelly, Kühn, Osthus and Pfenninger18] even managed to remove the error term in the minimum degree condition.
In the graph case (
![]() $k=2$
), Pham, Sah, Sawhney, and Simkin [Reference Pavez-Signé, Sanhueza-Matamala and Stein29] very recently showed that if
$k=2$
), Pham, Sah, Sawhney, and Simkin [Reference Pavez-Signé, Sanhueza-Matamala and Stein29] very recently showed that if
![]() $F=K_t$
is the
$F=K_t$
is the
![]() $t$
-vertex complete graph, and
$t$
-vertex complete graph, and
![]() $t\mid n$
, then any
$t\mid n$
, then any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with
$G$
with
![]() $\delta (G)\geq (1-1/t)n$
contains
$\delta (G)\geq (1-1/t)n$
contains
![]() $c^{-n}\exp\!((1-1/t)n\log n)$
$c^{-n}\exp\!((1-1/t)n\log n)$
![]() $F$
-factors for some fixed constant
$F$
-factors for some fixed constant
![]() $c$
. The degree bound here is the famously tight Hajnal-Szemerédi bound from [Reference Hajnal and Szemerédi15], and the bound on the number of
$c$
. The degree bound here is the famously tight Hajnal-Szemerédi bound from [Reference Hajnal and Szemerédi15], and the bound on the number of
![]() $F$
-factors is tight up to the constant
$F$
-factors is tight up to the constant
![]() $c$
. This proved a recent conjecture of Allen, Böttcher, Corsten, Davies, Jenssen, Morris, Roberts, and Skokan [Reference Allen, Böttcher, Corsten, Davies, Jenssen, Morris, Roberts and Skokan1].
$c$
. This proved a recent conjecture of Allen, Böttcher, Corsten, Davies, Jenssen, Morris, Roberts, and Skokan [Reference Allen, Böttcher, Corsten, Davies, Jenssen, Morris, Roberts and Skokan1].
Here, our contribution again is to apply our methods to easily match these weaker bounds of
![]() $c^{-n}\exp\!((1-1/|F|)n\log n)$
under the stronger approximate minimum degree condition but to do this for
$c^{-n}\exp\!((1-1/|F|)n\log n)$
under the stronger approximate minimum degree condition but to do this for
![]() $F$
-factors for any fixed graph
$F$
-factors for any fixed graph
![]() $F$
and all degree bounds, as follows.
$F$
and all degree bounds, as follows.
Theorem 1.4.
For each
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $1\le d\le k-1$
, and each
$1\le d\le k-1$
, and each
![]() $k$
-graph
$k$
-graph
![]() $F$
on
$F$
on
![]() $t\geq k$
vertices, there exists
$t\geq k$
vertices, there exists
![]() $n_0$
and
$n_0$
and
![]() $C$
such that the following holds for any
$C$
such that the following holds for any
![]() $n\geq n_0$
with
$n\geq n_0$
with
![]() $t\mid n$
. Any
$t\mid n$
. Any
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph
$k$
-graph
![]() $H$
with
$H$
with
![]() $\delta _d(H)\geq (\mu _{k,d}(F)+\gamma )\binom{n}{k-d}$
contains at least
$\delta _d(H)\geq (\mu _{k,d}(F)+\gamma )\binom{n}{k-d}$
contains at least
![]() $\exp \big ((1-\frac{1}{t})n\log n-Cn\big )$
distinct
$\exp \big ((1-\frac{1}{t})n\log n-Cn\big )$
distinct
![]() $F$
-factors.
$F$
-factors.
2. Proofs
A
![]() $k$
-graph
$k$
-graph
![]() $H$
has vertex set
$H$
has vertex set
![]() $V(H)$
and edge set
$V(H)$
and edge set
![]() $E(H)$
and
$E(H)$
and
![]() $|H|=|V(H)|$
. For any
$|H|=|V(H)|$
. For any
![]() $U,S\subset V(H)$
with
$U,S\subset V(H)$
with
![]() $|U|\le k-1$
,
$|U|\le k-1$
,
![]() $d(U,S)$
is the degree of
$d(U,S)$
is the degree of
![]() $U$
in
$U$
in
![]() $S$
, that is, the number of edges of
$S$
, that is, the number of edges of
![]() $H$
containing
$H$
containing
![]() $U$
whose vertices not in
$U$
whose vertices not in
![]() $U$
are all in
$U$
are all in
![]() $S$
. The hypergraph
$S$
. The hypergraph
![]() $H[S]$
induced by
$H[S]$
induced by
![]() $S\subset V(H)$
has vertex set
$S\subset V(H)$
has vertex set
![]() $S$
and edge set consisting of all those edges in
$S$
and edge set consisting of all those edges in
![]() $H$
contained in
$H$
contained in
![]() $S$
. For a set
$S$
. For a set
![]() $X$
and
$X$
and
![]() $1\le \ell \le |X|$
, let
$1\le \ell \le |X|$
, let
![]() $\binom{X}{\ell }$
denote the collection of subsets of
$\binom{X}{\ell }$
denote the collection of subsets of
![]() $X$
of size
$X$
of size
![]() $\ell$
, and let
$\ell$
, and let
![]() $(X)_\ell$
denote the set of tuples
$(X)_\ell$
denote the set of tuples
![]() $\mathbf x=(x_1,\ldots,x_\ell )\in X^\ell$
of distinct elements in
$\mathbf x=(x_1,\ldots,x_\ell )\in X^\ell$
of distinct elements in
![]() $X$
. We will use bold letters to denote elements from
$X$
. We will use bold letters to denote elements from
![]() $(X)_{\ell }$
or
$(X)_{\ell }$
or
![]() $X^\ell$
. For
$X^\ell$
. For
![]() $a,b\in (0,1]$
, we will write
$a,b\in (0,1]$
, we will write
![]() $a\ll b$
to denote that, given
$a\ll b$
to denote that, given
![]() $b$
, we can choose
$b$
, we can choose
![]() $a$
sufficiently small so that the subsequent statements hold.
$a$
sufficiently small so that the subsequent statements hold.
2.1 Our main partitioning lemma
Here we prove our main lemma, showing that in any linear (in
![]() $|H|$
) minimum degree hypergraph
$|H|$
) minimum degree hypergraph
![]() $H$
, there are many partitions of
$H$
, there are many partitions of
![]() $V(H)$
into sets with chosen sizes whose induced subgraphs from
$V(H)$
into sets with chosen sizes whose induced subgraphs from
![]() $H$
have high minimum degree relative to their sizes (see Lemma 2.3). We need a slightly stronger condition to connect the subgraphs than found in these induced subgraphs, which motivates the following definition of a good partition.
$H$
have high minimum degree relative to their sizes (see Lemma 2.3). We need a slightly stronger condition to connect the subgraphs than found in these induced subgraphs, which motivates the following definition of a good partition.
Definition 2.1.
Let
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $\delta \in [0,1]$
, and
$\delta \in [0,1]$
, and
![]() $\mathbf{n}=(n_1,\dots, n_r)\in \mathbb N^r$
. For an
$\mathbf{n}=(n_1,\dots, n_r)\in \mathbb N^r$
. For an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph
$k$
-graph
![]() $H$
, we say that a partition
$H$
, we say that a partition
![]() $V(H)=V_1\cup \ldots \cup V_r$
is
$V(H)=V_1\cup \ldots \cup V_r$
is
![]() $(\mathbf{n},\delta )$
-good if (working modulo
$(\mathbf{n},\delta )$
-good if (working modulo
![]() $r$
in the indices) we have
$r$
in the indices) we have
-
P1
 $|V_i|=n_i$
for each
$|V_i|=n_i$
for each
 $i\in [r]$
, and
$i\in [r]$
, and
-
P2 for each
 $i\in [r]$
and
$i\in [r]$
and
 $U\subseteq V_{i-1}\cup V_i\cup V_{i+1}$
with
$U\subseteq V_{i-1}\cup V_i\cup V_{i+1}$
with
 $|U|=k-1$
,
$|U|=k-1$
,
 $d(U,V_i)\geq \delta |V_i|$
.
$d(U,V_i)\geq \delta |V_i|$
.
To find many good partitions, we will choose an appropriate distribution
![]() $\mathbf{n}$
for the size of the subsets and partition
$\mathbf{n}$
for the size of the subsets and partition
![]() $V(H)=V_1\cup \ldots \cup V_r$
uniformly at random subject to
P1
. We then show (for the parameters we use and with
$V(H)=V_1\cup \ldots \cup V_r$
uniformly at random subject to
P1
. We then show (for the parameters we use and with
![]() $n$
large) that
P2
holds with probability at least
$n$
large) that
P2
holds with probability at least
![]() $e^{-n}$
, a relatively small probability but still enough to show that many partitions are good. For any fixed
$e^{-n}$
, a relatively small probability but still enough to show that many partitions are good. For any fixed
![]() $i\in [r]$
,
P2
will hold with constant probability, and the only difficulty here is to show that (despite many dependencies) this is true for all
$i\in [r]$
,
P2
will hold with constant probability, and the only difficulty here is to show that (despite many dependencies) this is true for all
![]() $i\in [r]$
with probability at least
$i\in [r]$
with probability at least
![]() $e^{-n}$
. To do this, we form the random partition iteratively, each time dividing the subsets in two and tracking how the minimum degree condition (or more precisely something akin to
P2
) changes in the subgraphs induced on the sets. This is inspired by part of the analysis in the work by Barber, Lo, Kühn, and Osthus [Reference Barber, Kühn, Lo and Osthus2] introducing iterative absorption, and we use some similar calculations to those in [Reference Barber, Kühn, Lo and Osthus2].
$e^{-n}$
. To do this, we form the random partition iteratively, each time dividing the subsets in two and tracking how the minimum degree condition (or more precisely something akin to
P2
) changes in the subgraphs induced on the sets. This is inspired by part of the analysis in the work by Barber, Lo, Kühn, and Osthus [Reference Barber, Kühn, Lo and Osthus2] introducing iterative absorption, and we use some similar calculations to those in [Reference Barber, Kühn, Lo and Osthus2].
For our analysis, we need the following standard concentration result for hypergeometric random variables (see, e.g. [Reference Janson, uczak and Rucinski17] for the standard definition of such a variable with parameters
![]() $N$
,
$N$
,
![]() $n$
, and
$n$
, and
![]() $m$
).
$m$
).
Theorem 2.2 (see, e.g. Theorem 2.10 in [Reference Janson, uczak and Rucinski17]). Let
![]() $X$
be a hypergeometric random variable with parameters
$X$
be a hypergeometric random variable with parameters
![]() $N$
,
$N$
,
![]() $n$
, and
$n$
, and
![]() $m$
. Then, for any
$m$
. Then, for any
![]() $t\gt 0$
,
$t\gt 0$
,
We can now state and prove our key lemma (see also Lemma 2.11 for a stronger result for
![]() $\ell =0$
).
$\ell =0$
).
Lemma 2.3.
Let
![]() $1\le \ell \lt k$
and let
$1\le \ell \lt k$
and let
![]() $1/n\ll 1/m\ll \delta,\gamma,1/k$
satisfy
$1/n\ll 1/m\ll \delta,\gamma,1/k$
satisfy
![]() $(k-\ell )\mid n$
. Then, there exists a tuple
$(k-\ell )\mid n$
. Then, there exists a tuple
![]() $\mathbf{n}=(n_1,\dots,n_r)$
with
$\mathbf{n}=(n_1,\dots,n_r)$
with
![]() $\sum _{i\in [r]}n_i=n$
and, for each
$\sum _{i\in [r]}n_i=n$
and, for each
![]() $i\in [r]$
,
$i\in [r]$
,
![]() $m\le n_i\le 5m$
and
$m\le n_i\le 5m$
and
![]() $(k-\ell )\mid n_i$
, such that the following holds. If
$(k-\ell )\mid n_i$
, such that the following holds. If
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta (H)\geq (\delta +\gamma )n$
, then the number of
$\delta (H)\geq (\delta +\gamma )n$
, then the number of
![]() $(\mathbf n,\delta +\gamma/2)$
-good partitions of
$(\mathbf n,\delta +\gamma/2)$
-good partitions of
![]() $V(H)$
is at least
$V(H)$
is at least
![]() $e^{-n}\binom{n}{n_1,\ldots, n_r}$
.
$e^{-n}\binom{n}{n_1,\ldots, n_r}$
.
Proof. Let
![]() $s$
satisfy
$s$
satisfy
![]() $2m\leq n/2^s\lt 4m$
and let
$2m\leq n/2^s\lt 4m$
and let
![]() $r=2^s$
. Since
$r=2^s$
. Since
![]() $(k-\ell )\mid n$
, we can choose integers
$(k-\ell )\mid n$
, we can choose integers
![]() $n_i$
,
$n_i$
,
![]() $i\in [r]$
, so that
$i\in [r]$
, so that
![]() $m\leq n_i\leq 5m$
and
$m\leq n_i\leq 5m$
and
![]() $(k-\ell )|n_i$
, for each
$(k-\ell )|n_i$
, for each
![]() $i\in [r]$
,
$i\in [r]$
,
![]() $\sum _{i\in [r]}n_i=n$
, and
$\sum _{i\in [r]}n_i=n$
, and
![]() $|n_i-n_j|\le 2k$
for all
$|n_i-n_j|\le 2k$
for all
![]() $1\le i\lt j\le r$
. We will show that the lemma holds with
$1\le i\lt j\le r$
. We will show that the lemma holds with
![]() $\mathbf{n}\;:\!=\;(n_1,\ldots,n_r)$
, so let
$\mathbf{n}\;:\!=\;(n_1,\ldots,n_r)$
, so let
![]() $H$
be any
$H$
be any
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta (H)\geq (\delta +\gamma )n$
.
$\delta (H)\geq (\delta +\gamma )n$
.
We start by iteratively partitioning
![]() $V(H)$
in 2 at random. For each
$V(H)$
in 2 at random. For each
![]() $0\leq i\leq s$
, let
$0\leq i\leq s$
, let
![]() $r_i=2^i$
, and for each
$r_i=2^i$
, and for each
![]() $0\leq i\leq s$
and
$0\leq i\leq s$
and
![]() $j\in [r_i]$
, let
$j\in [r_i]$
, let
 \begin{equation} m_{i,j}=\sum _{i'=(j-1)\cdot 2^{s-i}+1}^{j\cdot 2^{s-i}}n_{i'}. \end{equation}
\begin{equation} m_{i,j}=\sum _{i'=(j-1)\cdot 2^{s-i}+1}^{j\cdot 2^{s-i}}n_{i'}. \end{equation}
Let
![]() $V_{0,1}=V(H)$
. Iteratively, do the following for each
$V_{0,1}=V(H)$
. Iteratively, do the following for each
![]() $i\in [s]$
. For each
$i\in [s]$
. For each
![]() $j\in [r_{i-1}]$
, uniformly at random divide
$j\in [r_{i-1}]$
, uniformly at random divide
![]() $V_{i-1,j}$
into two sets
$V_{i-1,j}$
into two sets
![]() $V_{i,2j-1}$
and
$V_{i,2j-1}$
and
![]() $V_{i,2j}$
so that
$V_{i,2j}$
so that
![]() $|V_{i,2j-1}|=m_{i,2j-1}$
and
$|V_{i,2j-1}|=m_{i,2j-1}$
and
![]() $|V_{i,2j}|=m_{i,2j}$
, noting that
$|V_{i,2j}|=m_{i,2j}$
, noting that
 \begin{align*} |V_{i-1,j}|&=m_{i-1,j}=\sum _{i'=(j-1)\cdot 2^{s-i+1}+1}^{j\cdot 2^{s-i+1}}n_{i'} =\sum _{i'=(2j-2)\cdot 2^{s-i}+1}^{(2j-1)\cdot 2^{s-i+1}}n_{i'}+\sum _{i'=(2j-1)\cdot 2^{s-i}+1}^{2j\cdot 2^{s-i+1}}n_{i'}=m_{i,{2j-1}}+m_{i,2j}. \end{align*}
\begin{align*} |V_{i-1,j}|&=m_{i-1,j}=\sum _{i'=(j-1)\cdot 2^{s-i+1}+1}^{j\cdot 2^{s-i+1}}n_{i'} =\sum _{i'=(2j-2)\cdot 2^{s-i}+1}^{(2j-1)\cdot 2^{s-i+1}}n_{i'}+\sum _{i'=(2j-1)\cdot 2^{s-i}+1}^{2j\cdot 2^{s-i+1}}n_{i'}=m_{i,{2j-1}}+m_{i,2j}. \end{align*}
Note that this process ends with the partition
![]() $V(H)=V_{s,1}\cup V_{s,2}\cup \ldots \cup V_{s,r}$
with
$V(H)=V_{s,1}\cup V_{s,2}\cup \ldots \cup V_{s,r}$
with
![]() $|V_{s,i}|=m_{s,i}=n_i$
for each
$|V_{s,i}|=m_{s,i}=n_i$
for each
![]() $i\in [r]$
, whose distribution is that of a partition of
$i\in [r]$
, whose distribution is that of a partition of
![]() $V(H)$
chosen uniformly at random subject to these set sizes.
$V(H)$
chosen uniformly at random subject to these set sizes.
Now, for each
![]() $0\leq i\leq s$
and
$0\leq i\leq s$
and
![]() $j\in [r_{i}]$
, let
$j\in [r_{i}]$
, let
![]() $E_{i,j}$
be the event where, for every
$E_{i,j}$
be the event where, for every
![]() $U\subset V_{i,j-1}\cup V_{i,j}\cup V_{i,j+1}$
(with, as in later occurrences, addition modulo
$U\subset V_{i,j-1}\cup V_{i,j}\cup V_{i,j+1}$
(with, as in later occurrences, addition modulo
![]() $r_i$
in the second subscript), if
$r_i$
in the second subscript), if
![]() $|U|=k-1$
, then
$|U|=k-1$
, then
For each
![]() $0\leq i\leq s$
, let
$0\leq i\leq s$
, let
![]() $E_i$
be the event that
$E_i$
be the event that
![]() $E_{i,j}$
holds for all
$E_{i,j}$
holds for all
![]() $j\in [r_i]$
, noting that
$j\in [r_i]$
, noting that
![]() $E_0$
holds because
$E_0$
holds because
![]() $\delta (H)\geq (\delta +\gamma )n$
. We will now show that the lemma is implied by the following claim.
$\delta (H)\geq (\delta +\gamma )n$
. We will now show that the lemma is implied by the following claim.
Claim 2.4.
For each
![]() $i\in [s]$
,
$i\in [s]$
,
![]() ${\mathbb{P}}(E_i|E_{i-1})\geq \exp\!(\!-\!r_{i-1})$
.
${\mathbb{P}}(E_i|E_{i-1})\geq \exp\!(\!-\!r_{i-1})$
.
Note that if
![]() $E_s$
holds, then
$E_s$
holds, then
![]() $(V_{s,1},\ldots,V_{s,r})$
is
$(V_{s,1},\ldots,V_{s,r})$
is
![]() $(\mathbf{n}, \delta +\gamma/2)$
-good as
$(\mathbf{n}, \delta +\gamma/2)$
-good as
![]() $m_{s,i}=n_i\geq m$
for each
$m_{s,i}=n_i\geq m$
for each
![]() $i\in [r]$
and
$i\in [r]$
and
![]() $1/m\ll \gamma$
. Thus, considering the distribution of the random partition
$1/m\ll \gamma$
. Thus, considering the distribution of the random partition
![]() $V(H)=V_{s,1}\cup V_{s,2}$
$V(H)=V_{s,1}\cup V_{s,2}$
![]() $\cup \ldots \cup V_{s,r}$
, the number of
$\cup \ldots \cup V_{s,r}$
, the number of
![]() $(\mathbf{n}, \delta +\gamma/2)$
-good partitions of
$(\mathbf{n}, \delta +\gamma/2)$
-good partitions of
![]() $V(H)$
is at least
$V(H)$
is at least
![]() ${\mathbb{P}}(E_s)\cdot \frac{n!}{n_1!\ldots n_r!}$
so that the lemma follows from the claim as
${\mathbb{P}}(E_s)\cdot \frac{n!}{n_1!\ldots n_r!}$
so that the lemma follows from the claim as
Thus, it is only left to prove the claim.
Proof of Claim
2.4. Fix
![]() $i\in [s]$
. For each
$i\in [s]$
. For each
![]() $j\in [r_{i-1}]$
, let
$j\in [r_{i-1}]$
, let
![]() $F_{i-1,j}$
be the event that, for every
$F_{i-1,j}$
be the event that, for every
![]() $U\subset V_{i-1,j-1}\cup V_{i-1,j}\cup V_{i-1,j+1}$
with
$U\subset V_{i-1,j-1}\cup V_{i-1,j}\cup V_{i-1,j+1}$
with
![]() $|U|=k-1$
, we have
$|U|=k-1$
, we have
Note that, for each
![]() $j\in [r_{i-1}]$
, as
$j\in [r_{i-1}]$
, as
![]() $V_{i-1,j}=V_{i,2j-1}\cup V_{i,2j}$
, if
$V_{i-1,j}=V_{i,2j-1}\cup V_{i,2j}$
, if
![]() $F_{i-1,j}$
holds, then both
$F_{i-1,j}$
holds, then both
![]() $E_{i,2j-1}$
and
$E_{i,2j-1}$
and
![]() $E_{i,2j}$
hold. Furthermore, once we have chosen the partition
$E_{i,2j}$
hold. Furthermore, once we have chosen the partition
![]() $V(H)=V_{i-1,1}\cup V_{i-1,2}\cup \ldots \cup V_{i-1,r_{i-1}}$
, the events
$V(H)=V_{i-1,1}\cup V_{i-1,2}\cup \ldots \cup V_{i-1,r_{i-1}}$
, the events
![]() $F_{i-1,j}$
,
$F_{i-1,j}$
,
![]() $j\in [r_{i-1}]$
, are independent. We will show that if we choose a partition
$j\in [r_{i-1}]$
, are independent. We will show that if we choose a partition
![]() $V(H)=V_{i-1,1}\cup V_{i-1,2}\cup \ldots \cup V_{i-1,r_{i-1}}$
for which
$V(H)=V_{i-1,1}\cup V_{i-1,2}\cup \ldots \cup V_{i-1,r_{i-1}}$
for which
![]() $E_{i-1}$
holds, then, for each
$E_{i-1}$
holds, then, for each
![]() $j\in [r_{i-1}]$
, the probability that
$j\in [r_{i-1}]$
, the probability that
![]() $F_{i-1,j}$
holds is at least
$F_{i-1,j}$
holds is at least
![]() $e^{-1}$
, and thus the probability that every such
$e^{-1}$
, and thus the probability that every such
![]() $F_{i-1,j}$
,
$F_{i-1,j}$
,
![]() $j\in [r_{i-1}]$
, and hence
$j\in [r_{i-1}]$
, and hence
![]() $E_{i}$
holds is at least
$E_{i}$
holds is at least
![]() $\exp\!(\!-\!r_{i-1})$
. If this holds for every partition
$\exp\!(\!-\!r_{i-1})$
. If this holds for every partition
![]() $V(H)=V_{i-1,1}\cup V_{i-1,2}\cup \ldots \cup V_{i-1,r_{i-1}}$
for which
$V(H)=V_{i-1,1}\cup V_{i-1,2}\cup \ldots \cup V_{i-1,r_{i-1}}$
for which
![]() $E_{i-1}$
holds, we then have that
$E_{i-1}$
holds, we then have that
![]() ${\mathbb{P}}(E_i|E_{i-1})\geq \exp\!(\!-\!r_{i-1})$
, as required.
${\mathbb{P}}(E_i|E_{i-1})\geq \exp\!(\!-\!r_{i-1})$
, as required.
Suppose then that we have chosen our partition
![]() $V(H)=V_{i-1,1}\cup V_{i-1,2}\cup \ldots \cup V_{i-1,r_{i-1}}$
and that
$V(H)=V_{i-1,1}\cup V_{i-1,2}\cup \ldots \cup V_{i-1,r_{i-1}}$
and that
![]() $E_{i-1}$
holds, and let
$E_{i-1}$
holds, and let
![]() $j\in [r_{i-1}]$
. Let
$j\in [r_{i-1}]$
. Let
![]() $U\subset V_{i-1,j-1}\cup V_{i-1,j}\cup V_{i-1,j+1}$
satisfy
$U\subset V_{i-1,j-1}\cup V_{i-1,j}\cup V_{i-1,j+1}$
satisfy
![]() $|U|=k-1$
. Note that
$|U|=k-1$
. Note that
![]() $d(U,V_{i,2j-1})$
has a hypergeometric distribution with parameters
$d(U,V_{i,2j-1})$
has a hypergeometric distribution with parameters
![]() $N'\;:\!=\;m_{i-1,j}$
,
$N'\;:\!=\;m_{i-1,j}$
,
![]() $n'\;:\!=\;m_{i,2j-1}$
, and
$n'\;:\!=\;m_{i,2j-1}$
, and
![]() $m'\;:\!=\;d(U,V_{i-1,j})$
. Furthermore, as
$m'\;:\!=\;d(U,V_{i-1,j})$
. Furthermore, as
![]() $E_{i-1}$
, and hence
$E_{i-1}$
, and hence
![]() $E_{i-1,j}$
holds, we have that
$E_{i-1,j}$
holds, we have that
Therefore, by Theorem 2.2, we have
Now, for each
![]() $i',j'\in [s]$
, we have
$i',j'\in [s]$
, we have
![]() $|n_{i'}-n_{j'}|\leq 2k\leq n_{i'}/10$
and hence
$|n_{i'}-n_{j'}|\leq 2k\leq n_{i'}/10$
and hence
![]() $n_{i'}\leq 11n_{j'}/10$
. Thus, by (2.1) we have
$n_{i'}\leq 11n_{j'}/10$
. Thus, by (2.1) we have
![]() $m_{i,2j-1}\leq 11 m_{i-1,j}/20$
and hence
$m_{i,2j-1}\leq 11 m_{i-1,j}/20$
and hence
as
![]() $m_{i,2j-1}\geq m$
and
$m_{i,2j-1}\geq m$
and
![]() $1/m\ll 1$
. In combination, (2.3) and (2.4) give us that
$1/m\ll 1$
. In combination, (2.3) and (2.4) give us that
Similarly, this holds with
![]() $V_{i,2j}$
and
$V_{i,2j}$
and
![]() $m_{i,2j}$
in place of
$m_{i,2j}$
in place of
![]() $V_{i,2j-1}$
and
$V_{i,2j-1}$
and
![]() $m_{i,2j-1}$
. Furthermore, from (2.1) and that
$m_{i,2j-1}$
. Furthermore, from (2.1) and that
![]() $n_{i'}\leq 11n_{j'}/10$
for all
$n_{i'}\leq 11n_{j'}/10$
for all
![]() $i',j'\in [s]$
, it follows that
$i',j'\in [s]$
, it follows that
![]() $|V_{i-1,j-1}\cup V_{i-1,j}\cup V_{i-1,j+1}|\leq 66m_{i,2j-1}/10$
and
$|V_{i-1,j-1}\cup V_{i-1,j}\cup V_{i-1,j+1}|\leq 66m_{i,2j-1}/10$
and
![]() $\leq 66m_{i,2j}/10$
. Therefore, using a union bound over all
$\leq 66m_{i,2j}/10$
. Therefore, using a union bound over all
![]() $U\subset V_{i-1,j-1}\cup V_{i-1,j}\cup V_{i-1,j+1}$
satisfying
$U\subset V_{i-1,j-1}\cup V_{i-1,j}\cup V_{i-1,j+1}$
satisfying
![]() $|U|=k-1$
, we have that
$|U|=k-1$
, we have that
![]() $F_{i-1,j}$
holds with probability at least
$F_{i-1,j}$
holds with probability at least
as required, where we have used that
![]() $m_{i,2j-1},m_{i,2j}\geq m$
and
$m_{i,2j-1},m_{i,2j}\geq m$
and
![]() $1/m\ll 1$
.
$1/m\ll 1$
.
2.2 Counting Hamilton
 $\ell$
-cycles
$\ell$
-cycles
We say that a
![]() $k$
-graph
$k$
-graph
![]() $P$
with
$P$
with
![]() $t$
vertices is an
$t$
vertices is an
![]() $\ell$
-path, where
$\ell$
-path, where
![]() $1\le \ell \lt k$
, if
$1\le \ell \lt k$
, if
![]() $(k-\ell )\mid (t-\ell )$
, and there exists an ordering
$(k-\ell )\mid (t-\ell )$
, and there exists an ordering
![]() $v_1,\ldots, v_t$
of
$v_1,\ldots, v_t$
of
![]() $V(P)$
such that every edge of
$V(P)$
such that every edge of
![]() $P$
consists of
$P$
consists of
![]() $k$
consecutive vertices and such that every two consecutive edges intersect in exactly
$k$
consecutive vertices and such that every two consecutive edges intersect in exactly
![]() $\ell$
vertices. We will usually identify an
$\ell$
vertices. We will usually identify an
![]() $\ell$
-path
$\ell$
-path
![]() $P$
with a corresponding ordering
$P$
with a corresponding ordering
![]() $v_1,\ldots, v_t$
. The ends of an
$v_1,\ldots, v_t$
. The ends of an
![]() $\ell$
-path
$\ell$
-path
![]() $P=v_1\ldots v_t$
are the tuples
$P=v_1\ldots v_t$
are the tuples
![]() $\mathbf{v}=(v_1,\ldots,v_\ell )$
and
$\mathbf{v}=(v_1,\ldots,v_\ell )$
and
![]() $\mathbf{v}'=(v_{t-\ell +1},\ldots, v_t)$
, in which case we say that
$\mathbf{v}'=(v_{t-\ell +1},\ldots, v_t)$
, in which case we say that
![]() $\mathbf{v}$
and
$\mathbf{v}$
and
![]() $\mathbf{v}'$
are
$\mathbf{v}'$
are
![]() $\ell$
-connected by
$\ell$
-connected by
![]() $P$
. We say that a
$P$
. We say that a
![]() $k$
-graph
$k$
-graph
![]() $H$
contains a Hamilton
$H$
contains a Hamilton
![]() $\ell$
-path if there is an
$\ell$
-path if there is an
![]() $\ell$
-path
$\ell$
-path
![]() $P$
in
$P$
in
![]() $H$
with
$H$
with
![]() $V(P)=V(H)$
.
$V(P)=V(H)$
.
Definition 2.5.
A
![]() $k$
-graph
$k$
-graph
![]() $H$
is Hamilton
$H$
is Hamilton
![]() $\ell$
-path connected if, for any pair of vertex-disjoint tuples
$\ell$
-path connected if, for any pair of vertex-disjoint tuples
![]() $\mathbf u,\mathbf v\in (V(H))_\ell$
, there is a Hamilton
$\mathbf u,\mathbf v\in (V(H))_\ell$
, there is a Hamilton
![]() $\ell$
-path in
$\ell$
-path in
![]() $H$
which
$H$
which
![]() $\ell$
-connects
$\ell$
-connects
![]() $\mathbf u$
with
$\mathbf u$
with
![]() $\mathbf v$
.
$\mathbf v$
.
The next lemma states that
![]() $k$
-graphs with large minimum codegree which satisfies the natural divisibility conditions are Hamilton
$k$
-graphs with large minimum codegree which satisfies the natural divisibility conditions are Hamilton
![]() $\ell$
-path connected. The proof of Lemma 2.6 is a very straightforward modification of the original argument of Kühn, Mycroft, and Osthus [Reference Komlós, Sárközy and Szemerédi23] for finding Hamilton
$\ell$
-path connected. The proof of Lemma 2.6 is a very straightforward modification of the original argument of Kühn, Mycroft, and Osthus [Reference Komlós, Sárközy and Szemerédi23] for finding Hamilton
![]() $\ell$
-cycles via the absorption method (as can be seen in the special case when
$\ell$
-cycles via the absorption method (as can be seen in the special case when
![]() $(k-\ell )\mid k$
, where this was done by Glock, Gould, Joos, Kühn, and Osthus as [Reference Glock, Gould, Joos, Kühn and Osthus13, Lemma 3.7]). For completion, however, we include a proof in an appendix.
$(k-\ell )\mid k$
, where this was done by Glock, Gould, Joos, Kühn, and Osthus as [Reference Glock, Gould, Joos, Kühn and Osthus13, Lemma 3.7]). For completion, however, we include a proof in an appendix.
Lemma 2.6.
Let
![]() $1\leq \ell \lt k$
and let
$1\leq \ell \lt k$
and let
![]() $1/n\ll \gamma,1/k$
satisfy
$1/n\ll \gamma,1/k$
satisfy
![]() $(k-\ell )\nmid (n-\ell )$
. If
$(k-\ell )\nmid (n-\ell )$
. If
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta (H)\geq (\delta _{k,\ell }+\gamma )n$
(see [1.1]), then
$\delta (H)\geq (\delta _{k,\ell }+\gamma )n$
(see [1.1]), then
![]() $H$
is Hamilton
$H$
is Hamilton
![]() $\ell$
-path connected.
$\ell$
-path connected.
Now we are ready for the proof of our first main result.
Proof of Theorem
1.2. Let
![]() $\delta =\delta _{k,\ell }$
and let
$\delta =\delta _{k,\ell }$
and let
![]() $m$
be such that every
$m$
be such that every
![]() $k$
-graph on
$k$
-graph on
![]() $m'\geq m/2$
vertices with minimum codegree at least
$m'\geq m/2$
vertices with minimum codegree at least
![]() $(\delta +\gamma/4)m'$
is Hamilton
$(\delta +\gamma/4)m'$
is Hamilton
![]() $\ell$
-path connected (using Lemma 2.6) and such that
$\ell$
-path connected (using Lemma 2.6) and such that
![]() $1/m\ll \delta,\gamma,1/k$
. Let
$1/m\ll \delta,\gamma,1/k$
. Let
![]() $n_0$
and
$n_0$
and
![]() $C$
be such that, for every
$C$
be such that, for every
![]() $n\geq n_0$
,
$n\geq n_0$
,
![]() $1/n\ll 1/C\ll 1/m$
. Let
$1/n\ll 1/C\ll 1/m$
. Let
![]() $H$
be an
$H$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta (H)\geq (\delta +\gamma )n$
. By Lemma 2.3, there exist a tuple
$\delta (H)\geq (\delta +\gamma )n$
. By Lemma 2.3, there exist a tuple
![]() $\mathbf{n}=(n_1,\dots, n_r)$
with
$\mathbf{n}=(n_1,\dots, n_r)$
with
![]() $\sum _{i\in [r]}n_i=n$
and, for each
$\sum _{i\in [r]}n_i=n$
and, for each
![]() $i\in [r]$
,
$i\in [r]$
,
![]() $m\le n_i\le 5m$
and
$m\le n_i\le 5m$
and
![]() $(k-\ell )\mid n_i$
, such that
$(k-\ell )\mid n_i$
, such that
![]() $V(H)$
has at least
$V(H)$
has at least
![]() $e^{-n}\binom{n}{n_1,\ldots,n_r}$
partitions that are
$e^{-n}\binom{n}{n_1,\ldots,n_r}$
partitions that are
![]() $(\mathbf{n},\delta +\gamma/2)$
-good.
$(\mathbf{n},\delta +\gamma/2)$
-good.
Now, given a partition
![]() $\mathcal P=(V_1,\ldots,V_r)$
of
$\mathcal P=(V_1,\ldots,V_r)$
of
![]() $V(H)$
, say that a Hamilton
$V(H)$
, say that a Hamilton
![]() $\ell$
-cycle
$\ell$
-cycle
![]() $Q$
is
$Q$
is
![]() $\mathcal P$
-respecting if, for each
$\mathcal P$
-respecting if, for each
![]() $i\in [r]$
(for some direction and working modulo
$i\in [r]$
(for some direction and working modulo
![]() $r$
in the subscript), all the vertices in
$r$
in the subscript), all the vertices in
![]() $V_i$
appear concurrently on
$V_i$
appear concurrently on
![]() $Q$
, and the interval of vertices in
$Q$
, and the interval of vertices in
![]() $V_i$
on
$V_i$
on
![]() $Q$
is just before the interval of vertices in
$Q$
is just before the interval of vertices in
![]() $V_{i+1}$
on
$V_{i+1}$
on
![]() $Q$
. (See Fig. 1 for a Hamilton cycle that is
$Q$
. (See Fig. 1 for a Hamilton cycle that is
![]() $(V_1,\ldots,V_r)$
-respecting.)
$(V_1,\ldots,V_r)$
-respecting.)
Claim 2.7.
For each
![]() $(\mathbf{n},\delta +\gamma/2)$
-good partition
$(\mathbf{n},\delta +\gamma/2)$
-good partition
![]() $\mathcal P=(V_1,\ldots,V_r)$
,
$\mathcal P=(V_1,\ldots,V_r)$
,
![]() $H$
has a
$H$
has a
![]() $\mathcal P$
-respecting Hamilton
$\mathcal P$
-respecting Hamilton
![]() $\ell$
-cycle.
$\ell$
-cycle.
Before proving Claim 2.7, let us show how to deduce the theorem from it. Note that any Hamilton
![]() $\ell$
-cycle in
$\ell$
-cycle in
![]() $H$
respects at most
$H$
respects at most
![]() $2n$
partitions
$2n$
partitions
![]() $(V_1,\ldots,V_r)$
of
$(V_1,\ldots,V_r)$
of
![]() $V(H)$
with
$V(H)$
with
![]() $|V_i|=n_i$
for each
$|V_i|=n_i$
for each
![]() $i\in [r]$
, as choosing a direction and the first vertex of
$i\in [r]$
, as choosing a direction and the first vertex of
![]() $V_1$
specifies the ordered partition. Then, by Claim 2.7 and our bound on the number of
$V_1$
specifies the ordered partition. Then, by Claim 2.7 and our bound on the number of
![]() $(\mathbf{n},\delta +\gamma/2)$
-good partitions of
$(\mathbf{n},\delta +\gamma/2)$
-good partitions of
![]() $V(H)$
, the number of Hamilton
$V(H)$
, the number of Hamilton
![]() $\ell$
-cycles in
$\ell$
-cycles in
![]() $H$
is at least
$H$
is at least
using Stirling’s formula and that
![]() $1/n\ll 1/C\ll 1/m$
.
$1/n\ll 1/C\ll 1/m$
.
Therefore, it is left only to prove Claim 2.7.
Proof of Claim
2.7. Let
![]() $\mathcal P=(V_1,\ldots,V_r)$
be an
$\mathcal P=(V_1,\ldots,V_r)$
be an
![]() $(\mathbf{n},\delta +\gamma/2)$
-good partition. For each
$(\mathbf{n},\delta +\gamma/2)$
-good partition. For each
![]() $i\in [r]$
, using that
$i\in [r]$
, using that
![]() $|V_i|\geq m\geq \ell$
, pick an arbitrary
$|V_i|\geq m\geq \ell$
, pick an arbitrary
![]() $\ell$
-tuple
$\ell$
-tuple
![]() $\mathbf v_i=(v_{i,1},v_{i,2},\ldots,v_{i,\ell })\in (V_i)_{\ell }$
. For each
$\mathbf v_i=(v_{i,1},v_{i,2},\ldots,v_{i,\ell })\in (V_i)_{\ell }$
. For each
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $H_i=H[V_i\cup \{v_{i-1,1},\ldots,v_{i-1,\ell }\}]$
(working modulo
$H_i=H[V_i\cup \{v_{i-1,1},\ldots,v_{i-1,\ell }\}]$
(working modulo
![]() $r$
in the indices) so that, as
$r$
in the indices) so that, as
![]() $\mathcal P$
is
$\mathcal P$
is
![]() $(\mathbf{n},\delta +\gamma/2)$
-good, we have that
$(\mathbf{n},\delta +\gamma/2)$
-good, we have that
![]() $\delta (H_i)\geq (\delta +\gamma/2)|V_{i}|\geq (\delta +\gamma/4)|H_i|$
. Moreover,
$\delta (H_i)\geq (\delta +\gamma/2)|V_{i}|\geq (\delta +\gamma/4)|H_i|$
. Moreover,
![]() $|H_i|-\ell =n_i$
is divisible by
$|H_i|-\ell =n_i$
is divisible by
![]() $k-\ell$
. Therefore, by Lemma 2.6, there is a Hamilton
$k-\ell$
. Therefore, by Lemma 2.6, there is a Hamilton
![]() $\ell$
-path in
$\ell$
-path in
![]() $H_i$
with vertex sequence
$H_i$
with vertex sequence
![]() $v_{i-1,1}v_{i-1,2}\ldots v_{i-1,\ell }L_i v_{i,1}\ldots v_{i,\ell }$
for some sequence
$v_{i-1,1}v_{i-1,2}\ldots v_{i-1,\ell }L_i v_{i,1}\ldots v_{i,\ell }$
for some sequence
![]() $L_i$
. Then, the ordering
$L_i$
. Then, the ordering
![]() $L_1v_{1,1}\ldots v_{1,\ell }L_2v_{2,1}\ldots v_{2,\ell }L_3\ldots v_{r-1,1}\ldots v_{r-1,\ell }L_rv_{r,1}\ldots v_{r,\ell }$
is an ordering of the vertices of
$L_1v_{1,1}\ldots v_{1,\ell }L_2v_{2,1}\ldots v_{2,\ell }L_3\ldots v_{r-1,1}\ldots v_{r-1,\ell }L_rv_{r,1}\ldots v_{r,\ell }$
is an ordering of the vertices of
![]() $H$
which gives a Hamilton
$H$
which gives a Hamilton
![]() $\ell$
-cycle respecting the partition
$\ell$
-cycle respecting the partition
![]() $(V_1,\ldots,V_r)$
, as required.
$(V_1,\ldots,V_r)$
, as required.
2.3 Counting powers of tight Hamilton cycles
For Theorem 1.3, we use the following definitions. Let
![]() $t\geq k\geq 2$
and let
$t\geq k\geq 2$
and let
![]() $H$
be a
$H$
be a
![]() $k$
-graph. The
$k$
-graph. The
![]() $t$
-clique graph of
$t$
-clique graph of
![]() $H$
, denoted
$H$
, denoted
![]() $K_t(H)$
, is the
$K_t(H)$
, is the
![]() $t$
-graph with vertex set
$t$
-graph with vertex set
![]() $V(K_t(H))=V(H)$
where
$V(K_t(H))=V(H)$
where
![]() $\{v_1,\ldots, v_t\}$
is an edge of
$\{v_1,\ldots, v_t\}$
is an edge of
![]() $K_t(H)$
if and only if
$K_t(H)$
if and only if
![]() $H[\{v_1,\ldots, v_t\}]$
is a
$H[\{v_1,\ldots, v_t\}]$
is a
![]() $k$
-uniform clique in
$k$
-uniform clique in
![]() $H$
.
$H$
.
Our proof of Theorem 1.3 is very similar to the proof of Theorem 1.2, so we do not repeat it here and only state the differences. The main thing is to note that, given
-
a partition
 $V(H)=V_1\cup \ldots \cup V_r$
and distinct vertices
$V(H)=V_1\cup \ldots \cup V_r$
and distinct vertices
 $v_{i,1},\ldots,v_{i,t-1}\in V_i$
,
$v_{i,1},\ldots,v_{i,t-1}\in V_i$
,
 $i\in [r]$
, such that, for each
$i\in [r]$
, such that, for each
 $i\in [r]$
,
$i\in [r]$
,
 $H[\{v_{i,1},\ldots,v_{i,t-1}\}]$
is a
$H[\{v_{i,1},\ldots,v_{i,t-1}\}]$
is a
 $(t-1)$
-clique, and
$(t-1)$
-clique, and -
orderings
 $L_i$
,
$L_i$
,
 $i\in [r]$
, of the vertices in
$i\in [r]$
, of the vertices in
 $V_i\setminus \{v_{i,1},\ldots,v_{i,t-1}\}$
where
$V_i\setminus \{v_{i,1},\ldots,v_{i,t-1}\}$
where
 $v_{i-1,1},\ldots,v_{i-1,t-1}L_iv_{i,1},\ldots,v_{i,t-1}$
is the ordering of a Hamilton tight path in
$v_{i-1,1},\ldots,v_{i-1,t-1}L_iv_{i,1},\ldots,v_{i,t-1}$
is the ordering of a Hamilton tight path in
 $K_t(H[V_i\cup \{v_{i-1,1},\ldots,v_{i-1,t-1}\}])$
for each
$K_t(H[V_i\cup \{v_{i-1,1},\ldots,v_{i-1,t-1}\}])$
for each
 $i\in [r]$
,
$i\in [r]$
,
the ordering
![]() $L_1v_{1,1}\ldots v_{1,t-1}L_2v_{2,1}\ldots v_{2,t-1}L_3\ldots v_{r-1,1}\ldots v_{r-1,t-1}L_rv_{r,1}\ldots v_{r,t-1}$
is an ordering of the vertices of
$L_1v_{1,1}\ldots v_{1,t-1}L_2v_{2,1}\ldots v_{2,t-1}L_3\ldots v_{r-1,1}\ldots v_{r-1,t-1}L_rv_{r,1}\ldots v_{r,t-1}$
is an ordering of the vertices of
![]() $H$
which gives a
$H$
which gives a
![]() $(t-k+1)$
th power of a Hamilton tight cycle respecting the partition
$(t-k+1)$
th power of a Hamilton tight cycle respecting the partition
![]() $(V_1,\ldots,V_r)$
. Thus, the proof of Theorem 1.3 follows identically to that of Theorem 1.2 using the following proposition to select the vertices
$(V_1,\ldots,V_r)$
. Thus, the proof of Theorem 1.3 follows identically to that of Theorem 1.2 using the following proposition to select the vertices
![]() $v_{i,1},\ldots,v_{i,t-1}\in V_i$
,
$v_{i,1},\ldots,v_{i,t-1}\in V_i$
,
![]() $i\in [r]$
, in place of the vertices
$i\in [r]$
, in place of the vertices
![]() $v_{i,1},\ldots,v_{i,\ell }\in V_i$
,
$v_{i,1},\ldots,v_{i,\ell }\in V_i$
,
![]() $i\in [r]$
, and the following lemma in place of Lemma 2.6.
$i\in [r]$
, and the following lemma in place of Lemma 2.6.
Proposition 2.8.
Let
![]() $t\geq k\geq 2$
and let
$t\geq k\geq 2$
and let
![]() $1/n\ll \gamma, 1/t$
. If
$1/n\ll \gamma, 1/t$
. If
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph satisfying (1.2), then
$k$
-graph satisfying (1.2), then
![]() $H$
contains a
$H$
contains a
![]() $t$
-vertex
$t$
-vertex
![]() $k$
-uniform clique.
$k$
-uniform clique.
Lemma 2.9.
Let
![]() $t\geq k\geq 2$
and let
$t\geq k\geq 2$
and let
![]() $1/n\ll \gamma, 1/t$
. If
$1/n\ll \gamma, 1/t$
. If
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph satisfying (1.2), then for every pair of disjoint tuples
$k$
-graph satisfying (1.2), then for every pair of disjoint tuples
![]() $\mathbf{v},\mathbf{v'}\in (V(H))_{t-1}$
whose vertices support a
$\mathbf{v},\mathbf{v'}\in (V(H))_{t-1}$
whose vertices support a
![]() $(t-1)$
-vertex
$(t-1)$
-vertex
![]() $k$
-uniform clique in
$k$
-uniform clique in
![]() $H$
, there is a Hamilton tight path in
$H$
, there is a Hamilton tight path in
![]() $K_t(H)$
with ends
$K_t(H)$
with ends
![]() $\mathbf{v}$
and
$\mathbf{v}$
and
![]() $\mathbf{v'}$
.
$\mathbf{v'}$
.
Proposition 2.8 can be proved simply by picking the vertices of the clique greedily, where the codegree bound used is comfortably sufficient for this. The proof of Lemma 2.9 follows the same ideas as the proof of Lemma 2.6 but uses the results of Pavez-Signé, Sanhueza-Matamala, and Stein [Reference McDiarmid28] in place of those by Kühn, Mycroft, and Osthus [Reference Komlós, Sárközy and Szemerédi23]. We comment further on this in the appendix.
2.4 Counting
 $F$
-factors
$F$
-factors
To count factors, we no longer need to connect the different parts of a good partition, but we do wish to have conditions for different degrees than just the codegree, motivating the following definition.
Definition 2.10.
Let
![]() $k,d\in \mathbb N$
satisfy
$k,d\in \mathbb N$
satisfy
![]() $1\le d\le k-1$
. Let
$1\le d\le k-1$
. Let
![]() $\mu \gt 0$
and
$\mu \gt 0$
and
![]() $\mathbf{n}=(n_1,\dots, n_r)\in \mathbb N^r$
. For an
$\mathbf{n}=(n_1,\dots, n_r)\in \mathbb N^r$
. For an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph
$k$
-graph
![]() $H$
, say that a partition
$H$
, say that a partition
![]() $V(H)=V_1\cup \ldots \cup V_r$
is
$V(H)=V_1\cup \ldots \cup V_r$
is
![]() $(\mathbf{n},d,\mu )$
-good if, for each
$(\mathbf{n},d,\mu )$
-good if, for each
![]() $i\in [r]$
,
$i\in [r]$
,
![]() $|V_i|=n_i$
and
$|V_i|=n_i$
and
![]() $\delta _d(H[V_i])\geq \mu \binom{n_i}{k-d}$
.
$\delta _d(H[V_i])\geq \mu \binom{n_i}{k-d}$
.
With only minor modifications, including using McDiarmid’s inequality (see Lemma 1.2 in [Reference Kühn and Osthus27]) to bound similar events to the events
![]() $E_{i,j}$
, the proof of Lemma 2.3 can be adapted to prove the following.
$E_{i,j}$
, the proof of Lemma 2.3 can be adapted to prove the following.
Lemma 2.11.
Let
![]() $1\le d\le k-1$
and let
$1\le d\le k-1$
and let
![]() $1/n\ll 1/m\ll \gamma,\mu,1/k,1/t$
satisfy
$1/n\ll 1/m\ll \gamma,\mu,1/k,1/t$
satisfy
![]() $t\mid n$
. Then, there exists a tuple
$t\mid n$
. Then, there exists a tuple
![]() $\mathbf{n} =(n_1,\ldots, n_r)\in \mathbb N^r$
, with
$\mathbf{n} =(n_1,\ldots, n_r)\in \mathbb N^r$
, with
![]() $\sum _{i\in [r]}n_i=n$
, and
$\sum _{i\in [r]}n_i=n$
, and
![]() $m\le n_i\le 5m$
and
$m\le n_i\le 5m$
and
![]() $t\mid n_i$
for each
$t\mid n_i$
for each
![]() $i\in [r]$
, such that the following holds. If
$i\in [r]$
, such that the following holds. If
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta _d(H)\geq (\mu +\gamma )\binom{n}{k-d}$
, then the number of
$\delta _d(H)\geq (\mu +\gamma )\binom{n}{k-d}$
, then the number of
![]() $(\mathbf{n},d,\mu +\gamma/2)$
-good partitions in
$(\mathbf{n},d,\mu +\gamma/2)$
-good partitions in
![]() $H$
is at least
$H$
is at least
![]() $e^{-n}\binom{n}{n_1,\ldots, n_r}$
.
$e^{-n}\binom{n}{n_1,\ldots, n_r}$
.
Recalling that
![]() $\mu _{k,d}(F)$
is defined at the end of Section 1.1, we are now ready for the proof of Theorem 1.4.
$\mu _{k,d}(F)$
is defined at the end of Section 1.1, we are now ready for the proof of Theorem 1.4.
Proof of Theorem
1.4. Let
![]() $1\le d\le k-1$
and let
$1\le d\le k-1$
and let
![]() $F$
be a fixed
$F$
be a fixed
![]() $k$
-graph on
$k$
-graph on
![]() $t$
vertices. Let
$t$
vertices. Let
![]() $m$
be such that every
$m$
be such that every
![]() $k$
-graph on
$k$
-graph on
![]() $m'\geq m$
vertices, with
$m'\geq m$
vertices, with
![]() $t\mid m'$
, and minimum
$t\mid m'$
, and minimum
![]() $d$
-degree at least
$d$
-degree at least
![]() $(\mu _{k,d}(F)+\gamma/2)\binom{m'}{k-d}$
, contains an
$(\mu _{k,d}(F)+\gamma/2)\binom{m'}{k-d}$
, contains an
![]() $F$
-factor (using the definition of
$F$
-factor (using the definition of
![]() $\mu _{k,d}(F)$
). Let
$\mu _{k,d}(F)$
). Let
![]() $n_0$
and
$n_0$
and
![]() $C$
be such that, for every
$C$
be such that, for every
![]() $n\geq n_0$
,
$n\geq n_0$
,
![]() $1/n\ll 1/C\ll 1/m$
, and let
$1/n\ll 1/C\ll 1/m$
, and let
![]() $H$
be an
$H$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta _d(H)\geq (\mu _{k,d}(F)+\gamma )n^{k-d}$
. By Lemma 2.11, there is a tuple
$\delta _d(H)\geq (\mu _{k,d}(F)+\gamma )n^{k-d}$
. By Lemma 2.11, there is a tuple
![]() $\mathbf{n}=(n_1,\ldots, n_r)$
, with
$\mathbf{n}=(n_1,\ldots, n_r)$
, with
![]() $\sum _{i\in [r]}n_i=n$
, and
$\sum _{i\in [r]}n_i=n$
, and
![]() $m\le n_i\le 5m$
and
$m\le n_i\le 5m$
and
![]() $t\mid n_i$
for each
$t\mid n_i$
for each
![]() $i\in [r]$
, such that the number of
$i\in [r]$
, such that the number of
![]() $(\mathbf{n},d,\mu _{k,d}(F)+\gamma/2)$
-good partitions of
$(\mathbf{n},d,\mu _{k,d}(F)+\gamma/2)$
-good partitions of
![]() $V(H)$
is at least
$V(H)$
is at least
![]() $e^{-n}\binom{n}{n_1,\ldots, n_r}$
.
$e^{-n}\binom{n}{n_1,\ldots, n_r}$
.
For each
![]() $(\mathbf{n},d,\mu _{k,d}(F)+\gamma/2)$
-good partition
$(\mathbf{n},d,\mu _{k,d}(F)+\gamma/2)$
-good partition
![]() $\mathcal P=(V_1,\ldots, V_r)$
, by the definition of
$\mathcal P=(V_1,\ldots, V_r)$
, by the definition of
![]() $m$
, there is an
$m$
, there is an
![]() $F$
-factor in
$F$
-factor in
![]() $H[V_i]$
for each
$H[V_i]$
for each
![]() $i\in [r]$
, and therefore,
$i\in [r]$
, and therefore,
![]() $H$
has an
$H$
has an
![]() $F$
-factor,
$F$
-factor,
![]() $G$
, say, where
$G$
, say, where
![]() $G[V_i]$
is an
$G[V_i]$
is an
![]() $F$
-factor of
$F$
-factor of
![]() $H[V_i]$
for each
$H[V_i]$
for each
![]() $i\in [r]$
. On the other hand, given an
$i\in [r]$
. On the other hand, given an
![]() $F$
-factor
$F$
-factor
![]() $G$
, the number of possible partitions
$G$
, the number of possible partitions
![]() $\mathcal P=(V_1,\ldots, V_r)$
, such that
$\mathcal P=(V_1,\ldots, V_r)$
, such that
![]() $G[V_i]$
is an
$G[V_i]$
is an
![]() $F$
-factor of
$F$
-factor of
![]() $H[V_i]$
and
$H[V_i]$
and
![]() $|V_i|=n_i$
for each
$|V_i|=n_i$
for each
![]() $i\in [r]$
, is at most
$i\in [r]$
, is at most
![]() $(n/t)^{n/t}\leq \exp\!((n\log n)/t)$
. Therefore, the number of distinct
$(n/t)^{n/t}\leq \exp\!((n\log n)/t)$
. Therefore, the number of distinct
![]() $F$
-factors in
$F$
-factors in
![]() $H$
is (similarly to [2.5]) at least
$H$
is (similarly to [2.5]) at least
 \begin{align*} &e^{-n}\cdot \exp\!(\!-\!(n/t)\log n)\cdot \binom {n}{n_1,\ldots, n_r} \geq e^{-n}\cdot \exp\!(\!-\!(n/t)\log n)\cdot \frac {n!}{(5m)!^{n/m}}\\[5pt] &\quad \geq \exp \big ((1-\tfrac {1}t)n\log n-Cn\big ),\end{align*}
\begin{align*} &e^{-n}\cdot \exp\!(\!-\!(n/t)\log n)\cdot \binom {n}{n_1,\ldots, n_r} \geq e^{-n}\cdot \exp\!(\!-\!(n/t)\log n)\cdot \frac {n!}{(5m)!^{n/m}}\\[5pt] &\quad \geq \exp \big ((1-\tfrac {1}t)n\log n-Cn\big ),\end{align*}
as required, where we have used Stirling’s formula and that
![]() $1/n\ll 1/C\ll 1/m$
.
$1/n\ll 1/C\ll 1/m$
.
Funding statement
This is supported by the European Research Council (ERC) under the European Union Horizon 2020 research and innovation programme (grant agreement no. 947978) and the Leverhulme Trust. Matías Pavez-Signé research is supportedby Agencia Nacional de Investigación y Desarrollo (ANID) Basal Grant CMM FB210005 and ANID Regular grant no. 1241398.
Appendix A. Proof of Lemmas 2.6 and 2.9
Here we provide a proof for Lemma 2.6. The proof is a straightforward modification of the original argument by Kühn, Mycroft, and Osthus [Reference Komlós, Sárközy and Szemerédi23] for finding Hamilton
![]() $\ell$
-cycles in dense hypergraphs via the absorption method.
$\ell$
-cycles in dense hypergraphs via the absorption method.
Definition A.1.
Let
![]() $1\le \ell \lt k$
and let
$1\le \ell \lt k$
and let
![]() $H$
be a
$H$
be a
![]() $k$
-graph. Say that an
$k$
-graph. Say that an
![]() $\ell$
-path
$\ell$
-path
![]() $P$
in
$P$
in
![]() $H$
, with ends
$H$
, with ends
![]() $\mathbf{a},\mathbf{b}\in (V(H))_\ell$
, can absorb a collection of pairwise disjoint
$\mathbf{a},\mathbf{b}\in (V(H))_\ell$
, can absorb a collection of pairwise disjoint
![]() $(k-\ell )$
-sets
$(k-\ell )$
-sets
![]() $S_1,\ldots, S_t$
if
$S_1,\ldots, S_t$
if
-
(i)
 $P$
contains no vertex from
$P$
contains no vertex from
 $\bigcup _{i\in [t]}S_i$
and
$\bigcup _{i\in [t]}S_i$
and
-
(ii) there is an
 $\ell$
-path
$\ell$
-path
 $Q$
with vertex set
$Q$
with vertex set
 $V(Q)=V(P)\cup \bigcup _{i\in [t]}S_i$
and with ends
$V(Q)=V(P)\cup \bigcup _{i\in [t]}S_i$
and with ends
 $\mathbf{a}$
and
$\mathbf{a}$
and
 $\mathbf{b}$
.
$\mathbf{b}$
.
In this case, we say that
![]() $P$
is an absorbing path for
$P$
is an absorbing path for
![]() $S_1,\ldots,S_t$
.
$S_1,\ldots,S_t$
.
We may use a similar definition of absorbing paths that works for powers of tight cycles (for Lemma 2.9), in which case the absorbing paths are tight paths in the
![]() $t$
-clique graph
$t$
-clique graph
![]() $K_t(H)$
that can absorb vertices rather than
$K_t(H)$
that can absorb vertices rather than
![]() $(k-\ell )$
-sets (see Definition 7.1 in [Reference McDiarmid28]).
$(k-\ell )$
-sets (see Definition 7.1 in [Reference McDiarmid28]).
Definition A.2.
Let
![]() $1\le \ell \lt k$
and let
$1\le \ell \lt k$
and let
![]() $H$
be an
$H$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph. Say that a
$k$
-graph. Say that a
![]() $(k-\ell )$
-set
$(k-\ell )$
-set
![]() $S\subset V(H)$
is
$S\subset V(H)$
is
![]() $(\beta,t)$
-good if
$(\beta,t)$
-good if
![]() $H$
contains at least
$H$
contains at least
![]() $\beta n^t$
absorbing paths for
$\beta n^t$
absorbing paths for
![]() $S$
, each with exactly
$S$
, each with exactly
![]() $t$
vertices. If
$t$
vertices. If
![]() $S$
is not
$S$
is not
![]() $(\beta,t)$
-good, we then say that
$(\beta,t)$
-good, we then say that
![]() $S$
is
$S$
is
![]() $(\beta,t)$
-bad.
$(\beta,t)$
-bad.
The following result states that most
![]() $(k-\ell )$
-sets are good in
$(k-\ell )$
-sets are good in
![]() $k$
-graphs with linear minimum codegree.
$k$
-graphs with linear minimum codegree.
Lemma A.3 (Lemma 6.2 in [Reference Komlós, Sárközy and Szemerédi23]). Let
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $1\le \ell \lt k$
satisfy
$1\le \ell \lt k$
satisfy
![]() $(k-\ell )\nmid k$
, and let
$(k-\ell )\nmid k$
, and let
![]() $1/n\ll \beta \ll \theta \ll \mu,1/k$
. There exists a constant
$1/n\ll \beta \ll \theta \ll \mu,1/k$
. There exists a constant
![]() $t=t(k,\ell )$
such that if
$t=t(k,\ell )$
such that if
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta (H)\geq \mu n$
, then the number of
$\delta (H)\geq \mu n$
, then the number of
![]() $(\beta,t)$
-bad
$(\beta,t)$
-bad
![]() $(k-\ell )$
-sets in
$(k-\ell )$
-sets in
![]() $H$
is at most
$H$
is at most
![]() $\theta n^{k-\ell }$
.
$\theta n^{k-\ell }$
.
The next lemma says that we can find a short path
![]() $P$
which can absorb any collection of
$P$
which can absorb any collection of
![]() $o(n)$
pairwise disjoint good sets and, moreover, every vertex outside
$o(n)$
pairwise disjoint good sets and, moreover, every vertex outside
![]() $P$
belongs to only a few bad sets.
$P$
belongs to only a few bad sets.
Lemma A.4 (Lemma 6.3 in [Reference Komlós, Sárközy and Szemerédi23]). Let
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $1\leq \ell \lt k$
satisfy
$1\leq \ell \lt k$
satisfy
![]() $(k-\ell )\nmid k$
, and let
$(k-\ell )\nmid k$
, and let
![]() $1/n\ll \alpha \ll \beta \ll \theta \ll \mu,1/k$
. If
$1/n\ll \alpha \ll \beta \ll \theta \ll \mu,1/k$
. If
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta (H)\geq \mu n$
and
$\delta (H)\geq \mu n$
and
![]() $t=t(k,\ell )$
from Lemma A.3
, then
$t=t(k,\ell )$
from Lemma A.3
, then
![]() $H$
contains an
$H$
contains an
![]() $\ell$
-path
$\ell$
-path
![]() $P$
on at most
$P$
on at most
![]() $\mu n$
vertices such that
$\mu n$
vertices such that
-
(i) every vertex of
 $H-V(P)$
lies in at most
$H-V(P)$
lies in at most
 $\theta n^{k-\ell -1}$
$\theta n^{k-\ell -1}$
 $(\beta,t)$
-bad
$(\beta,t)$
-bad
 $(k-\ell )$
-sets and
$(k-\ell )$
-sets and
-
(ii)
 $P$
can absorb any collection of at most
$P$
can absorb any collection of at most
 $\alpha n$
disjoint
$\alpha n$
disjoint
 $(\beta,t)$
-good
$(\beta,t)$
-good
 $(k-\ell )$
-sets of vertices of
$(k-\ell )$
-sets of vertices of
 $H-V(P)$
.
$H-V(P)$
.
For proving Lemma 2.9, we can show an analogue result in the spirit of Lemma A.4 for the
![]() $t$
-clique graph
$t$
-clique graph
![]() $K_t(H)$
using Lemma 7.3 in [Reference McDiarmid28] and Step 1 in the proof of Theorem 1.1 in [Reference McDiarmid28].
$K_t(H)$
using Lemma 7.3 in [Reference McDiarmid28] and Step 1 in the proof of Theorem 1.1 in [Reference McDiarmid28].
Next, we have a lemma for when any two disjoint ordered
![]() $\ell$
-sets can be connected by a short
$\ell$
-sets can be connected by a short
![]() $\ell$
-path, as follows.
$\ell$
-path, as follows.
Lemma A.5 (Corollary 5.4 in [Reference Komlós, Sárközy and Szemerédi23]). Let
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $1\leq \ell \leq k-1$
satisfy
$1\leq \ell \leq k-1$
satisfy
![]() $(k-\ell )\nmid k$
, and let
$(k-\ell )\nmid k$
, and let
![]() $1/n\ll \mu,1/k$
. If
$1/n\ll \mu,1/k$
. If
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta (H)\geq \mu n$
, then for any two disjoint ordered
$\delta (H)\geq \mu n$
, then for any two disjoint ordered
![]() $\ell$
-sets
$\ell$
-sets
![]() $\mathbf{a},\mathbf{b}\in (V(H))_\ell$
, there exists an
$\mathbf{a},\mathbf{b}\in (V(H))_\ell$
, there exists an
![]() $\ell$
-path
$\ell$
-path
![]() $P$
with ends
$P$
with ends
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{b}$
that contains at most
$\mathbf{b}$
that contains at most
![]() $8k^5$
vertices.
$8k^5$
vertices.
We have a similar statement in the vein of Lemma A.5 for the clique graph (see [Reference McDiarmid28, Lemma 4.1]), which states that any two disjoint
![]() $(t-1)$
-sets that support
$(t-1)$
-sets that support
![]() $(t-1)$
-cliques in
$(t-1)$
-cliques in
![]() $H$
can be connected in
$H$
can be connected in
![]() $K_t(H)$
by many short tight paths.
$K_t(H)$
by many short tight paths.
The last two ingredients we need are, first, that the degree conditions are preserved by taking random subsets and, second, that hypergraphs with large vertex degree have perfect matchings.
Lemma A.6 (Lemma 8.1 in [Reference Komlós, Sárközy and Szemerédi23]). Let
![]() $1\leq d\lt k$
and let
$1\leq d\lt k$
and let
![]() $1/n\ll \alpha,\mu,1/k$
. Let
$1/n\ll \alpha,\mu,1/k$
. Let
![]() $H$
be an
$H$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta _d(H)\geq \mu \binom{n}{k-d}$
, and let
$\delta _d(H)\geq \mu \binom{n}{k-d}$
, and let
![]() $R\subset V(H)$
be a random subset of size
$R\subset V(H)$
be a random subset of size
![]() $\alpha n$
. Then, with probability
$\alpha n$
. Then, with probability
![]() $1-o(1)$
, we have
$1-o(1)$
, we have
![]() $|N_H(S)\cap \binom{R}{k-d}|\geq \mu \binom{\alpha n}{k-d}-n^{k-d-\frac{1}{3}}$
for every
$|N_H(S)\cap \binom{R}{k-d}|\geq \mu \binom{\alpha n}{k-d}-n^{k-d-\frac{1}{3}}$
for every
![]() $S\in \binom{V(H)}{d}$
.
$S\in \binom{V(H)}{d}$
.
Theorem A.7 (Perfect matching theorem [Reference Daykin and Häggkvist9]). Let
![]() $n,k\geq 2$
such that
$n,k\geq 2$
such that
![]() $k\mid n$
. If
$k\mid n$
. If
![]() $H$
is an
$H$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
-graph with
$k$
-graph with
![]() $\delta _1(H)\geq \frac{k-1}{k}(\binom{n-1}{k-1}-1)$
, then
$\delta _1(H)\geq \frac{k-1}{k}(\binom{n-1}{k-1}-1)$
, then
![]() $H$
contains a perfect matching.
$H$
contains a perfect matching.
Now we are ready for the proof of Lemma 2.6.
Proof of Lemma 2.6. We begin by choosing constants
and let
![]() $t=t(k,\ell )$
from Lemma A.3. Given disjoint
$t=t(k,\ell )$
from Lemma A.3. Given disjoint
![]() $\ell$
-tuples
$\ell$
-tuples
![]() $\mathbf{a}=(a_1,\ldots, a_\ell )$
and
$\mathbf{a}=(a_1,\ldots, a_\ell )$
and
![]() $\mathbf{b}=(b_1,\ldots, b_\ell )$
in
$\mathbf{b}=(b_1,\ldots, b_\ell )$
in
![]() $V(H)$
, set
$V(H)$
, set
![]() $H'=H-\{a_1,\ldots,a_\ell,b_1,\ldots,b_\ell \}$
and
$H'=H-\{a_1,\ldots,a_\ell,b_1,\ldots,b_\ell \}$
and
![]() $n'=|H'|=n-2\ell$
, and note that
$n'=|H'|=n-2\ell$
, and note that
![]() $\delta (H')\geq (\delta _{k,\ell }+\gamma/2)n'$
as
$\delta (H')\geq (\delta _{k,\ell }+\gamma/2)n'$
as
![]() $1/n\ll 1/k$
. Using Lemma A.4, find an absorbing
$1/n\ll 1/k$
. Using Lemma A.4, find an absorbing
![]() $\ell$
-path
$\ell$
-path
![]() $P_0$
in
$P_0$
in
![]() $H'$
with at most
$H'$
with at most
![]() $\gamma n'/16$
vertices which can absorb any collection of at most
$\gamma n'/16$
vertices which can absorb any collection of at most
![]() $2\alpha n'$
pairwise disjoint
$2\alpha n'$
pairwise disjoint
![]() $(\beta,t)$
-good
$(\beta,t)$
-good
![]() $(k-\ell )$
-sets in
$(k-\ell )$
-sets in
![]() $V(H')$
(here we have used that
$V(H')$
(here we have used that
![]() $\delta (H')\geq \gamma n'/16$
). Let
$\delta (H')\geq \gamma n'/16$
). Let
![]() $G$
be an auxiliary
$G$
be an auxiliary
![]() $(k-\ell )$
-graph with
$(k-\ell )$
-graph with
![]() $V(G)=V(H')$
and edge set consisting of all those
$V(G)=V(H')$
and edge set consisting of all those
![]() $(k-\ell )$
-sets in
$(k-\ell )$
-sets in
![]() $H'$
which are
$H'$
which are
![]() $(\beta,t)$
-good. By Lemma A.3, for every
$(\beta,t)$
-good. By Lemma A.3, for every
![]() $v\in V(G)\setminus V(P_0)$
, we have
$v\in V(G)\setminus V(P_0)$
, we have
Let
![]() $R\subset V(H')$
be a random subset of size
$R\subset V(H')$
be a random subset of size
![]() $\alpha n'$
. Then, by Lemma A.6, with probability
$\alpha n'$
. Then, by Lemma A.6, with probability
![]() $1-o(1)$
,
$1-o(1)$
,
-
(i)
 $d_G(v,R)\geq (1-2\theta ')\binom{|R|}{k-\ell -1}$
for every
$d_G(v,R)\geq (1-2\theta ')\binom{|R|}{k-\ell -1}$
for every
 $v\in V(G)\setminus V(P_0)$
, and
$v\in V(G)\setminus V(P_0)$
, and -
(ii)
 $d_H(S,R)\geq (\delta _{k,\ell }+\gamma/4)|R|$
for every
$d_H(S,R)\geq (\delta _{k,\ell }+\gamma/4)|R|$
for every
 $S\in \binom{V(H)}{k-1}$
.
$S\in \binom{V(H)}{k-1}$
.
Moreover, as
![]() ${\mathbb{E}}[|R\cap V(P_0)|]=\alpha |P_0|$
, Lemma 2.2 implies that
${\mathbb{E}}[|R\cap V(P_0)|]=\alpha |P_0|$
, Lemma 2.2 implies that
![]() $|R\cap V(P_0)|\le 2\alpha |P_0|\le \alpha \gamma n'/8$
with probability
$|R\cap V(P_0)|\le 2\alpha |P_0|\le \alpha \gamma n'/8$
with probability
![]() $1-o(1)$
. Therefore, there is a choice of
$1-o(1)$
. Therefore, there is a choice of
![]() $R$
such that, letting
$R$
such that, letting
![]() $R'=R\setminus V(P_0)$
, we have
$R'=R\setminus V(P_0)$
, we have
-
R1
 $\alpha n'\geq |R'|\geq (1-\mu )\alpha n'$
,
$\alpha n'\geq |R'|\geq (1-\mu )\alpha n'$
, -
R2
 $d_G(v,R')\geq (1-\mu )\binom{|R'|}{k-\ell -1}$
for every
$d_G(v,R')\geq (1-\mu )\binom{|R'|}{k-\ell -1}$
for every
 $v\in V(G)\setminus V(P_0)$
, and
$v\in V(G)\setminus V(P_0)$
, and -
R3
 $d_H(S,R')\geq (\delta _{k,\ell }+\gamma/8)|R'|$
for every
$d_H(S,R')\geq (\delta _{k,\ell }+\gamma/8)|R'|$
for every
 $S\in \binom{V(H)}{k-1}$
.
$S\in \binom{V(H)}{k-1}$
.
Let
![]() $V'\subseteq V(H')\setminus (R'\cup V(P_0))$
be a subset obtained by removing at most
$V'\subseteq V(H')\setminus (R'\cup V(P_0))$
be a subset obtained by removing at most
![]() $k-\ell$
vertices so that
$k-\ell$
vertices so that
![]() $|V'|$
is divisible by
$|V'|$
is divisible by
![]() $k-\ell$
. We write
$k-\ell$
. We write
![]() $H''=H[V']$
and note that
$H''=H[V']$
and note that
![]() $\delta (H'')\geq (\delta _{k,\ell }+\gamma/16)|H''|$
. Use Theorem 1.1 to find a Hamilton
$\delta (H'')\geq (\delta _{k,\ell }+\gamma/16)|H''|$
. Use Theorem 1.1 to find a Hamilton
![]() $\ell$
-cycle in
$\ell$
-cycle in
![]() $H''$
, and hence
$H''$
, and hence
![]() $H''$
contains an
$H''$
contains an
![]() $\ell$
-path
$\ell$
-path
![]() $P$
with
$P$
with
![]() $|P|\geq |H''|-2k$
. Let
$|P|\geq |H''|-2k$
. Let
![]() $\mathbf x'=(x'_{\!\!1},\ldots,x'_{\!\!\ell})$
and
$\mathbf x'=(x'_{\!\!1},\ldots,x'_{\!\!\ell})$
and
![]() $\mathbf y'=(y'_{\!\!1},\ldots,y'_{\!\!\ell})$
be the ends of
$\mathbf y'=(y'_{\!\!1},\ldots,y'_{\!\!\ell})$
be the ends of
![]() $P_0$
, and let
$P_0$
, and let
![]() $\mathbf x=(x_1,\ldots,x_\ell )$
and
$\mathbf x=(x_1,\ldots,x_\ell )$
and
![]() $\mathbf y=(y_1,\ldots,y_\ell )$
be the ends of
$\mathbf y=(y_1,\ldots,y_\ell )$
be the ends of
![]() $P$
. Using Lemma A.5 and R3, we find sequences of vertices
$P$
. Using Lemma A.5 and R3, we find sequences of vertices
![]() $L_{\mathbf{ax'}}, L_{\mathbf{y'x}}$
, and
$L_{\mathbf{ax'}}, L_{\mathbf{y'x}}$
, and
![]() $L_{\mathbf{yb}}$
such that
$L_{\mathbf{yb}}$
such that
-
 $|L_{\mathbf{ax'}}|,|L_{\mathbf{y'x}}|, |L_{\mathbf{yb}}|\le 8k^5$
,
$|L_{\mathbf{ax'}}|,|L_{\mathbf{y'x}}|, |L_{\mathbf{yb}}|\le 8k^5$
, -
 $L_{\mathbf{ax'}}, L_{\mathbf{y'x}}$
and
$L_{\mathbf{ax'}}, L_{\mathbf{y'x}}$
and
 $L_{\mathbf{yb}}$
are pairwise disjoint and contain vertices only from
$L_{\mathbf{yb}}$
are pairwise disjoint and contain vertices only from
 $R'$
, and
$R'$
, and -
 $P_{\mathbf{ax'}}=a_1\ldots a_\ell L_{\mathbf{ax'}} x'_{\!\!1}\ldots x'_{\!\!\ell}$
,
$P_{\mathbf{ax'}}=a_1\ldots a_\ell L_{\mathbf{ax'}} x'_{\!\!1}\ldots x'_{\!\!\ell}$
,
 $P_{\mathbf{y'x}}=y'_{\!\!1}\ldots y'_{\!\!\ell} L_{\mathbf{y'x}}x_1\ldots x_\ell$
, and
$P_{\mathbf{y'x}}=y'_{\!\!1}\ldots y'_{\!\!\ell} L_{\mathbf{y'x}}x_1\ldots x_\ell$
, and
 $P_{\mathbf{yb}}=y_1\ldots y_\ell L_{\mathbf{yb}} b_1\ldots b_\ell$
are
$P_{\mathbf{yb}}=y_1\ldots y_\ell L_{\mathbf{yb}} b_1\ldots b_\ell$
are
 $\ell$
-paths.
$\ell$
-paths.
Therefore, the sequence
is an
![]() $\ell$
-path in
$\ell$
-path in
![]() $H$
connecting
$H$
connecting
![]() $\mathbf{a}$
with
$\mathbf{a}$
with
![]() $\mathbf{b}$
and using at most
$\mathbf{b}$
and using at most
![]() $24k^5$
vertices from
$24k^5$
vertices from
![]() $R'$
. Let
$R'$
. Let
![]() $X=V(H)\setminus V(Q)$
and note that, because of
R1
and
R2
, every vertex
$X=V(H)\setminus V(Q)$
and note that, because of
R1
and
R2
, every vertex
![]() $v\in X$
satisfies
$v\in X$
satisfies
where we have used that
![]() $|X\setminus R'|\le 24k^5+2k+(k-\ell )\le 25k^5$
and
$|X\setminus R'|\le 24k^5+2k+(k-\ell )\le 25k^5$
and
![]() $1/n\ll 1/k$
. Then, by (A.1) and Theorem A.7,
$1/n\ll 1/k$
. Then, by (A.1) and Theorem A.7,
![]() $G[X]$
contains a perfect matching
$G[X]$
contains a perfect matching
![]() $S_1,\dots, S_j$
, which is a collection of at most
$S_1,\dots, S_j$
, which is a collection of at most
![]() $|X|\le |R'|+2k+(k-\ell )\le 2\alpha n$
pairwise disjoint
$|X|\le |R'|+2k+(k-\ell )\le 2\alpha n$
pairwise disjoint
![]() $(\beta,t)$
-good
$(\beta,t)$
-good
![]() $(k-\ell )$
-sets. Finally, using Lemma A.4, we can absorb all the vertices from
$(k-\ell )$
-sets. Finally, using Lemma A.4, we can absorb all the vertices from
![]() $\bigcup _{i\in [j]} S_i$
which concludes the proof.
$\bigcup _{i\in [j]} S_i$
which concludes the proof.
The proof of Lemma 2.9 follows a similar strategy. Let us sketch the main steps of the proof here. Given two disjoint tuples
![]() $\mathbf{a}={(a_1,\ldots, a_{t-1})}$
and
$\mathbf{a}={(a_1,\ldots, a_{t-1})}$
and
![]() $\mathbf{b}=(b_1,\ldots, b_{t-1})$
that support
$\mathbf{b}=(b_1,\ldots, b_{t-1})$
that support
![]() $(t-1)$
-cliques in
$(t-1)$
-cliques in
![]() $H$
, set
$H$
, set
![]() $H'=H-{\{a_1,\ldots, a_{t-1}, b_1,\ldots, b_{t-1}\}}$
. The proof of Lemma 2.9 consists of the following steps:
$H'=H-{\{a_1,\ldots, a_{t-1}, b_1,\ldots, b_{t-1}\}}$
. The proof of Lemma 2.9 consists of the following steps:
-
Find a short absorbing path
 $P_0$
in
$P_0$
in
 $K_t(H')$
capable of absorbing any collection of
$K_t(H')$
capable of absorbing any collection of
 $o(n)$
vertices.
$o(n)$
vertices. -
Set aside a reservoir
 $R$
in
$R$
in
 $H'- V(P_0)$
, and find a Hamilton tight path in
$H'- V(P_0)$
, and find a Hamilton tight path in
 $K_t(H'-(V(P_0)\cup R))$
(this can be done as
$K_t(H'-(V(P_0)\cup R))$
(this can be done as
 $H'-(V(P_0)\cup R)$
satisfies (1.2) with a slightly worse error term).
$H'-(V(P_0)\cup R)$
satisfies (1.2) with a slightly worse error term). -
Using a corresponding connecting lemma ([Reference McDiarmid28, Lemma 4.1]) and the properties of the reservoir, find an almost spanning path
 $Q$
with ends
$Q$
with ends
 $\mathbf{a}$
and
$\mathbf{a}$
and
 $\mathbf{b}$
which contains
$\mathbf{b}$
which contains
 $P_0$
.
$P_0$
. -
Finish the embedding using the properties of the absorbing path.
The main difference with the proof of Lemma 2.6 is that, in this case, we do not need to use any matching result in the absorption step as
![]() $H$
contains no bad vertices (see [Reference McDiarmid28, Lemma 7.2]).
$H$
contains no bad vertices (see [Reference McDiarmid28, Lemma 7.2]).