For graphs 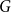$G$ and 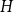$H$, the Ramsey number 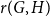$r(G,H)$ is the smallest positive integer 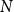$N$ such that any red/blue edge colouring of the complete graph 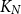$K_N$ contains either a red 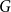$G$ or a blue 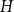$H$. A book 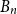$B_n$ is a graph consisting of $n$ triangles all sharing a common edge.

Recently, Conlon, Fox, and Wigderson conjectured that for any 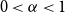$0\lt \alpha \lt 1$, the random lower bound 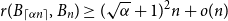$r(B_{\lceil \alpha n\rceil },B_n)\ge (\sqrt{\alpha }+1)^2n+o(n)$ is not tight. In other words, there exists some constant 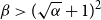$\beta \gt (\sqrt{\alpha }+1)^2$ such that 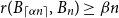$r(B_{\lceil \alpha n\rceil },B_n)\ge \beta n$ for all sufficiently large $n$. This conjecture holds for every 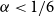$\alpha \lt 1/6$ by a result of Nikiforov and Rousseau from 2005, which says that in this range 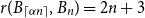$r(B_{\lceil \alpha n\rceil },B_n)=2n+3$ for all sufficiently large $n$.

We disprove the conjecture of Conlon, Fox, and Wigderson. Indeed, we show that the random lower bound is asymptotically tight for every 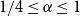$1/4\leq \alpha \leq 1$. Moreover, we show that for any 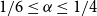$1/6\leq \alpha \le 1/4$ and large $n$, 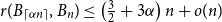$r(B_{\lceil \alpha n\rceil }, B_n)\le \left (\frac 32+3\alpha \right ) n+o(n)$, where the inequality is asymptotically tight when 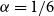$\alpha =1/6$ or 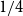$1/4$. We also give a lower bound of 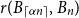$r(B_{\lceil \alpha n\rceil }, B_n)$ for 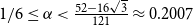$1/6\le \alpha \lt \frac{52-16\sqrt{3}}{121}\approx 0.2007$, showing that the random lower bound is not tight, i.e., the conjecture of Conlon, Fox, and Wigderson holds in this interval.