Hostname: page-component-7479d7b7d-68ccn Total loading time: 0 Render date: 2024-07-13T00:23:10.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Predecessors in Random Mappings

Published online by Cambridge University Press:  12 September 2008

Gerd Baron ,
Michael Drmota  and
Ljuben Mutafchiev
Gerd Baron
Affiliation:
Department of Discrete Mathematics, Technical University of Vienna, Wiedner Hauptstrasse 8–10/118, A-1040 Vienna, Austria
Michael Drmota
Affiliation:
Department of Discrete Mathematics, Technical University of Vienna, Wiedner Hauptstrasse 8–10/118, A-1040 Vienna, Austria
Ljuben Mutafchiev
Affiliation:
Institute of Mathematics, Bulgarian Academy of Sciences, P.O. Box 373, 1090 Sofia, Bulgaria
Get access Rights & Permissions [Opens in a new window]

Abstract

Let ℱn be the set of random mappings ϕ : {1,…,n} → {1,…,n} (such that every mapping is equally likely). For x ε {l,…,n} the elements 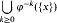are called the predecessors of x. Let Nr denote the random variable which counts the number of points x ε {l,…,n} with exactly r predecessors. In this paper we identify the limiting distribution of Nr as n → ∞. If r = r(n) = o(n⅔) then the limiting distribution is Gaussian, if r ˜ Cn⅔ then it is Poisson, and in the remaining case rn−⅔ → ∞ it is degenerate. Furthermore, it is shown that Nr is a Poisson approximation if r → ∞.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 5 , Issue 4 , December 1996 , pp. 317 - 335
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Arney, J. and Bender, E. A. (1982) Random mappings with constraints on coalescence and number of origins. Pacif. J. Math. 103 269–294.CrossRefGoogle Scholar
[2]Barbour, A. D., Holst, L. and Janson, S. (1992) Poisson Approximation, Oxford Studies in Probability 2, Clarendon Press.CrossRefGoogle Scholar
[3]Berge, C. (1968) Principes de Combinatoire, Dunod.Google Scholar
[4]Drmota, M. (1994) The height distribution of leaves in rooted trees. Discrete Math. Appl. 4 45–58. (Translation from Diskretn. Mat. 667–82.)CrossRefGoogle Scholar
[5]Drmota, M. and Soria, M.Marking in Combinatorial Constructions: Images aiid Preimages in Random Mappings. SIAM J. Discrete Math. (to appear).Google Scholar
[6]Flajolet, Ph. and Odlyzko, A. M. (1990) Singularity analysis and generating functions. SIAM J. Discrete Math. 3 216–240.CrossRefGoogle Scholar
[7]Flajolet, Ph. and Odlyzko, A. M. (1990) Random mapping statistics. In: J-J., Quisquater (ed.), Proceedings of Euroscript '89: Lecture Notes in Computer Science 434, Springer-Verlag, 329–354.Google Scholar
[8]Gittenberger, B. Local limit theorems for distributions of certain random mapping parameters. Random Structures and Algorithms. Manuscript.Google Scholar
[9]Kaup, L. and Kaup, B. (1983) Holomorphic Functions of Several Variables, de Gruyter.CrossRefGoogle Scholar
[10]Mutafchiev, L. (1985) An asymptotic distribution concerning random mappings of a finite set. Comptes rendus de l'Académie bulgare des Sciences 38 1621–1622.Google Scholar
[11]Rubin, H. and Sitgreaves, R. (1954) Probability distributions related to random transformations on a finite set. Technical Report No. 19 A, Applied Mathematics and Statistics Laboratory, Stanford University.Google Scholar