Hostname: page-component-7479d7b7d-rvbq7 Total loading time: 0 Render date: 2024-07-14T00:20:07.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Randomized Greedy Algorithms for Independent Sets and Matchings in Regular Graphs: Exact Results and Finite Girth Corrections

Published online by Cambridge University Press:  22 June 2009

DAVID GAMARNIK  and
DAVID A. GOLDBERG
DAVID GAMARNIK
Affiliation:
Operations Research Center and Sloan School of Management, MIT, Cambridge, MA 02139, USA (e-mail: gamarnik@mit.edu)
DAVID A. GOLDBERG
Affiliation:
Operations Research Center, MIT, Cambridge, MA 02139, USA (e-mail: dag3141@mit.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

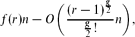We derive new results for the performance of a simple greedy algorithm for finding large independent sets and matchings in constant-degree regular graphs. We show that for r-regular graphs with n nodes and girth at least g, the algorithm finds an independent set of expected cardinality where f(r) is a function which we explicitly compute. A similar result is established for matchings. Our results imply improved bounds for the size of the largest independent set in these graphs, and provide the first results of this type for matchings. As an implication we show that the greedy algorithm returns a nearly perfect matching when both the degree r and girth g are large. Furthermore, we show that the cardinality of independent sets and matchings produced by the greedy algorithm in arbitrary bounded-degree graphs is concentrated around the mean. Finally, we analyse the performance of the greedy algorithm for the case of random i.i.d. weighted independent sets and matchings, and obtain a remarkably simple expression for the limiting expected values produced by the algorithm. In fact, all the other results are obtained as straightforward corollaries from the results for the weighted case.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 19 , Issue 1 , January 2010 , pp. 61 - 85
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ajtai, M., Erdős, P., Komlós, J. and Szemerédi, E. (1981) On Turán's theorem for sparse graphs. Combinatorica 1 313–317.CrossRefGoogle Scholar
[2]Ajtai, M., Komlós, J. and Szemerédi, E. (1980) A note on Ramsey numbers. J. Combin. Theory Ser. A 29 354–360.CrossRefGoogle Scholar
[3]Aldous, D. (2001) The ζ(2) limit in the random assignment problem. Random Struct. Alg. 18 381–418.CrossRefGoogle Scholar
[4]Aldous, D. and Steele, J. M. (2003) The objective method: Probabilistic combinatorial optimization and local weak convergence. In Discrete Combinatorial Probability (Kesten, H., ed.), Springer, pp. 1–72.Google Scholar
[5]Berman, P. and Fürer, M. (1994) Approximating maximum independent set in bounded degree graphs. In Proc. 5th Annual ACM–SIAM Symposium on Discrete Algorithms (SODA94), SIAM, Philadelphia, PA, pp. 365–371.Google Scholar
[6]Bollobás, B. (1980) A probabilistic proof of an asymptotic formula for the number of regular graphs. European J. Combin. 1 311–316.CrossRefGoogle Scholar
[7]Denley, T. (1994) The independence number of graphs with large odd girth. Electron. J. Combin. 1 #9.CrossRefGoogle Scholar
[8]Durrett, R. (1996) Probability: Theory and Examples, 2nd edn, Duxbury Press.Google Scholar
[9]Dyer, M. E. and Frieze, A. (1991) Randomized greedy matching. Random Struct. Alg. 2 29–46.CrossRefGoogle Scholar
[10]Flaxman, A. and Hoory, S. (2007) Maximum matchings in regular graphs of high girth. Electron. J. Combin. 14 #1.CrossRefGoogle Scholar
[11]Frieze, A. Personal communication.Google Scholar
[12]Gamarnik, D., Nowicki, T. and Swirscsz, G. (2006) Maximum weight independent sets and matchings in sparse random graphs: Exact results using the local weak convergence method. Random Struct. Alg. 28 76–106.CrossRefGoogle Scholar
[13]Garey, M. R., Johnson, D. S. and Stockmeyer, L. J. (1976) Some simplified NP-complete graph problems. Theoret. Comput. Sci. 1 237–267.CrossRefGoogle Scholar
[14]Griggs, J. R. (1983) An upper bound on the Ramsey numbers r(3, k). J. Combin. Theory Ser. A 35 145–153.CrossRefGoogle Scholar
[15]Halldórsson, M. and Radhakrishnan, J. (1994) Improved approximations of bounded-degree independent sets via subgraph removal. Nordic J. Comput. 1 475–492.Google Scholar
[16]Halldórsson, M. and Radhakrishnan, J. (1997) Greed is good: Approximating independent sets in sparse and bounded-degree graphs. Algorithmica 18 145–163.CrossRefGoogle Scholar
[17]Hopkins, G. W. and Staton, W. (1982) Girth and independence ratio. Canad. Math. Bull. 25 179–186.CrossRefGoogle Scholar
[18]Lauer, J. and Wormald, N. C. (2007) Large independent sets in regular graphs of large girth. J. Combin. Theory Ser. B 97 999–1009.CrossRefGoogle Scholar
[19]Miller, Z. and Pritikin, D. (1997) On randomized greedy matchings. Random Struct. Alg. 10 353–383.3.0.CO;2-V>CrossRefGoogle Scholar
[20]Monien, B. and Speckenmeyer, E. (1985) Ramsey numbers and an approximation algorithm for the vertex cover problem. Acta Informatica 22 115–123.CrossRefGoogle Scholar
[21]Murphy, O. J. (1992) Computing independent sets in graphs with large girth. Discrete Appl. Math. 35 167–170.CrossRefGoogle Scholar
[22]Rautenbach, D., Goring, F., Harant, J. and Schiermeyer, I. (2008) Locally dense independent sets in regular graphs of large girth: An example of a new approach. In Research Trends in Combinatorial Optimization (Cook, W., Lovasz, L. and Vygen, J., eds), Springer, pp. 163–183.Google Scholar
[23]Shearer, J. B. (1983) A note on the independence number of triangle-free graphs. Discrete Math. 46 83–87.CrossRefGoogle Scholar
[24]Shearer, J. (1991) A note on the independence number of triangle-free graphs 2. J. Combin. Theory Ser. B 53 300–307.CrossRefGoogle Scholar
[25]Shearer, J. (1995) The independence number of dense graphs with large odd girth. Electron. J. Combin. 2 #2.CrossRefGoogle Scholar