Hostname: page-component-77c89778f8-rkxrd Total loading time: 0 Render date: 2024-07-20T21:08:50.432Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast Solver for the Local Discontinuous Galerkin Discretization of the KdV Type Equations

Published online by Cambridge University Press:  22 January 2015

Ruihan Guo  and
Yan Xu
Ruihan Guo
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, P.R. China
Yan Xu*
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, P.R. China
*
*Email addresses: guoguo88@mail.ustc.edu.cn (R. Guo), yxu@ustc.edu.cn (Y. Xu)
Get access

Abstract

In this paper, we will develop a fast iterative solver for the system of linear equations arising from the local discontinuous Galerkin (LDG) spatial discretization and additive Runge-Kutta (ARK) time marching method for the KdV type equations. Being implicit in time, the severe time step 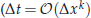, with the k-th order of the partial differential equations (PDEs)) restriction for explicit methods will be removed. The equations at the implicit time level are linear and we demonstrate an efficient, practical multigrid (MG) method for solving the equations. In particular, we numerically show the optimal or sub-optimal complexity of the MG solver and a two-level local mode analysis is used to analyze the convergence behavior of the MG method. Numerical results for one-dimensional, two-dimensional and three-dimensional cases are given to illustrate the efficiency and capability of the LDG method coupled with the multigrid method for solving the KdV type equations.

Keywords

65M6035Q53KdV type equationslocal discontinuous Galerkin methodsmultigrid algorithmadditive Runge-Kutta methodslocal mode analysis
Type
Research Article
Information
Communications in Computational Physics , Volume 17 , Issue 2 , February 2015 , pp. 424 - 457
Copyright
Copyright © Global Science Press Limited 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bassi, F.Ghidoni, A.Rebay, S. and Tesini, P.High-order accurate p-multigrid discontinuous Galerkin solution of the Euler equations, International journal for numerical methods in fluids, 60 (2008), 847–865.Google Scholar
[2]Bassi, F.Ghidoni, A. and Rebay, S.Optimal Runge-Kutta smoothers for the p-multigrid discontinuous Galerkin solution of the 1D Euler equations, J. Comput. Phys., 230 (2011), 4153–4175.Google Scholar
[3]Bona, J.L.Chen, H.Karakashian, O. and Xing, Y.Conservative, discontinuous-Galerkin methods for the generalized Korteweg-de Vries equation, Mathematics of Computation, 82 (2013), 1401–1432.Google Scholar
[4]Cockburn, B. and Shu, C.-W.The local discontinuous Galerkin method for time-dependent convection-diffusion systems, SIAM J. Numer. Anal., 35 (1998), 2440–2463.Google Scholar
[5]Guo, R. and Xu, Y.Efficient solvers of discontinuous Galerkin discretization for the Cahn-Hilliard equations, J. Sci. Comp., 58 (2014), 380–408.Google Scholar
[6]Kennedy, C.A. and Carpenter, M.H.Additive Runge-Kutta schemes for convection-diffusion-reaction equations, Appl. Num. Math., 44 (2003), 139–181.Google Scholar
[7]Klaij, C.M.van Raalte, M.H.van der Ven, H. and van der Vegt, J.J.W. , h-Multigrid for space-time discontinuous Galerkin discretizations of the compressible Navier-Stokes equations, J. Comput. Phys., 227 (2007), 1024–1045.Google Scholar
[8]Liu, H. and Yan, J.A local discontinuous Galerkin method for the KdV equation with boundary effect, J. Comput. Phys., 215 (2006), 197–218.CrossRefGoogle Scholar
[9]Liu, H. and Yan, J.The direct discontinuous Galerkin (DDG) methods for diffusion problems, SIAM J. Numer. Anal., 47(2009), 675–698.Google Scholar
[10]Reed, W. and Hill, T.Triangular mesh methods for the neutrontransport equation, La-ur-73–479, Los Alamos Scientific Laboratory, 1973.Google Scholar
[11]Shahbazi, K.Mavriplis, D. J. and Burgess, N.K.Multigrid algorithms for high-order discontinuous Galerkin discretizations of the compressible Navier-Stokes equations, J. Comput. Phys., 228 (2009), 7917–7940.CrossRefGoogle Scholar
[12]van der Vegt, J.J.W. and Rhebergen, S.hp-multigrid as smoother algorithm for higher order discontinuous Galerkin discretizations of advection dominated flows. Part I. Multilevel Analysis, J. Comput. Phys., 231 (2012), 7537–7563.Google Scholar
[13]van der Vegt, J.J.W. and Rhebergen, S.hp-multigrid as smoother algorithm for higher order discontinuous Galerkin discretizations of advection dominated flows. Part II. Optimization of the Runge-Kutta smoother, J. Comput. Phys., 231 (2012), 7564–7583.Google Scholar
[14]Xia, Y.Xu, Y. and Shu, C.-W.Efficient time discretization for local discontinuous Galerkin methods, Discrete Contin. Dyn. Syst. Ser. B., 8 (2007), 677–693.Google Scholar
[15]Xu, Y. and Shu, C.-W.Local discontinuous Galerkin methods for three classes of nonlinear wave equations, J. Comput. Math., 22 (2004), 250–274.Google Scholar
[16]Xu, Y. and Shu, C.-W.Local discontinuous Galerkin methods for two classes of two dimensional nonlinear wave equations, Physica D, 208 (2005), 21–58.Google Scholar
[17]Xu, Y. and Shu, C.-W.Local discontinuous Galerkin methods for high-order time-dependent partial differential equations, Commun. Comput. Phys., 7 (2010), 1–46.Google Scholar
[18]Yan, J. and Shu, C.-W.A local discontinuous Galerkin method for KdV type equations, SIAM J. Numer. Anal., 40 (2002), 769–791.Google Scholar
[19]Yan, J. and Shu, C.-W.Local discontinuous Galerkin methods for partial differential equations with higher order derivatives, J. Sci. Comput., 17 (2002), 27–42.CrossRefGoogle Scholar