Hostname: page-component-7479d7b7d-q6k6v Total loading time: 0 Render date: 2024-07-11T19:15:57.506Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Approach for Error Reduction in the Volume Penalization Method

Published online by Cambridge University Press:  03 June 2015

Wakana Iwakami ,
Yuzuru Yatagai ,
Nozomu Hatakeyama  and
Yuji Hattori
Wakana Iwakami*
Affiliation:
Yukawa Institute for Theoretical Physics, Kyoto University, Oiwake-cho, Kitashirakawa, Sakyo-ku, Kyoto 606-8502, Japan Advanced Research Institute for Science & Engineering, Waseda University, 3-4-1 Okubo, Shinjuku, Tokyo 169-8555, Japan
Yuzuru Yatagai*
Affiliation:
Department of Applied Information Sciences, Graduate School of Information Sciences, Tohoku University, 6-3-09 Aoba, Aramaki-aza, Aoba-ku, Sendai, Miyagi 980-8579, Japan
Nozomu Hatakeyama*
Affiliation:
NICHe, Tohoku University, 6-6-10 Aoba, Aramaki-aza, Aoba-ku, Sendai, Miyagi 980-8579, Japan
Yuji Hattori*
Affiliation:
Institute of Fluid Science, Tohoku University, 2-1-1 Katahira, Aoba-ku, Sendai, Miyagi, 980-8577, Japan
*
Corresponding author.Email:wakana@heap.phys.waseda.ac.jp
Email:yuzuru@dragon.ifs.tohoku.ac.jp
Email:hatakeyama@aki.niche.tohoku.ac.jp
Email:hattori@fmail.ifs.tohoku.ac.jp
Get access

Abstract

A new approach for reducing error of the volume penalization method is proposed. The mask function is modified by shifting the interface between solid and fluid by 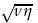toward the fluid region, where v and η are the viscosity and the permeability, respectively. The shift length 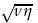is derived from the analytical solution of the one-dimensional diffusion equation with a penalization term. The effect of the error reduction is verified numerically for the one-dimensional diffusion equation, Burgers’ equation, and the two-dimensional Navier-Stokes equations. The results show that the numerical error is reduced except in the vicinity of the interface showing overall second-order accuracy, while it converges to a non-zero constant value as the number of grid points increases for the original mask function. However, the new approach is effectivewhen the grid resolution is sufficiently high so that the boundary layer,whose width is proportional to 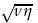, is resolved. Hence, the approach should be used when an appropriate combination of ν and η is chosen with a given numerical grid.

Keywords

60-08Volume penalization methodimmersed boundary methodcompact schemeerror reduction
Type
Research Article
Information
Communications in Computational Physics , Volume 16 , Issue 5 , November 2014 , pp. 1181 - 1200
Copyright
Copyright © Global Science Press Limited 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Angot, P., Bruneau, C.-H. and Fabrie, P., A penalization method to take into account obstacles in incompressible viscous flows, Numer. Math., 81 (1999), 497–520.Google Scholar
[2]Brinkman, H. C., A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles, Appl. Sci. Res., A1 (1949), 27–34.Google Scholar
[3]Burgers, J. M., Verh. KNAW, Afd. Natuurkunde, XVII 2 (1939), 1–53.Google Scholar
[4]Carbou, G. and Fabrie, P., Boundary layer for a penalization method for viscous incompressible flow, Adv. Differ. Equat., 8 (2003), 1453–2480.Google Scholar
[5]Cole, J. D., On a quasilinear parabolic equation occurring in aerodynamics, Q. Appl. Math., 9 (1951), 225–236.Google Scholar
[6]Hopf, E., The Partial Differential Equation, Comm. Pure Appl. Math., 3 (1950), 201–230.Google Scholar
[7]Kadoch, B., Kolomenskiy, D., Angot, P. and Schneider, K., A volume penalization method for incompressible flows and scalar advection-diffusion with moving obstacles, J. Comput. Phys., 231 (2012), 4365–4383.Google Scholar
[8]Keetels, G. H., D’Ortona, U., Kramer, W., Clercx, H. J. H., Schneider, K. and van Heijst, G. J. F., Fourier spectral and wavelet solvers for the incompressible Navier-Stokes equations with volume-penalization: Convergence of a dipole-wall collision, J. Comput. Phys., 227 (2007), 919–945.Google Scholar
[9]Kevlahan, N. K.-R. and Ghidaglia, J.-M., Computation of turbulent flow past an array of cylinders using a spectral method with Brinkman penalization, Eur. J. Mech. B - Fluids, 20 (2001), 333–350.CrossRefGoogle Scholar
[10]Kevlahan, N. K.-R. and Wadsley, J., Suppression of three-dimensional flow instabilities in tube bundles, J. Fluid. Struct., 20 (2005), 611–620.Google Scholar
[11]Kolomenskiy, D. and Schneider, K., A fourier spectral method for the Navier-Stokes equations with volume penalization for moving solid obstacles, J. Comput. Phys., 228 (2009), 5687–5709.Google Scholar
[12]Lele, S. K., Compact finite difference schemes with spectral-like resolution, J. Comput. Phys., 103 (1992), 16–42.CrossRefGoogle Scholar
[13]Mittal, R. and Iaccarino, G., Immersed boundary methods, Annu. Rev. Fluid Mech., 37 (2005), 239–261.Google Scholar
[14]Schneider, K., Numerical simulation of the transient flow behaviour in chemical reactors using a penalization method, Comput. Fluids, 34 (2005) 1223–1238.Google Scholar
[15]Schneider, K. and Farge, M., Numerical simulation of the transient flow behaviour in tube bundles using a volume penalization method, J. Fluid. Struct., 20 (2005), 555–566.CrossRefGoogle Scholar
[16]Schneider, K. and Farge, M., Decaying two-dimensional turbulence in a circular container, Phys. Rev. Lett., 95 (2005), 244502.Google Scholar
[17]Schneider, K. and Farge, M., Final states of decaying 2D turbulence in bounded domains: Influence of the geometry, Physica D, 237 (2008) 2228–2233.CrossRefGoogle Scholar
[18]Tritton, D. J., Physical Fluid Dynamics, Second Edition, Oxford University Press Inc., New York, (1988).Google Scholar