No CrossRef data available.
Article contents
Steenrod operators, the Coulomb branch and the Frobenius twist
Published online by Cambridge University Press: 04 November 2021
Abstract
We observe a fundamental relationship between Steenrod operations and the Artin–Schreier morphism. We use Steenrod's construction, together with some new geometry related to the affine Grassmannian, to prove that the quantum Coulomb branch is a Frobenius-constant quantization. We also demonstrate the corresponding result for the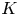 
$K$-theoretic version of the quantum Coulomb branch. At the end of the paper, we investigate what our ideas produce on the categorical level. We find that they yield, after a little fiddling, a construction which corresponds, under the geometric Satake equivalence, to the Frobenius twist functor for representations of the Langlands dual group. We also describe the unfiddled answer, conditional on a conjectural ‘modular derived Satake’, and, though it is more complicated to state, it is in our opinion just as neat and even more compelling.
MSC classification
Primary:
20G05: Representation theory
- Type
- Research Article
- Information
- Copyright
- © 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
This work was carried out at, and with the generous support of, MIT. Thanks also to AIM and the organizers of the AIM workshop on sheaves and modular representations of reductive groups, March 28 to April 1, 2016, where many of the ideas in this paper began.
References
Beĭlinson, A. A., How to glue perverse sheaves, in K-theory, arithmetic and geometry (Moscow, 1984–1986), Lecture Notes in Mathematics, vol. 1289 (Springer, Berlin, 1987), 42–51.Google Scholar
Beĭlinson, A. and Drinfeld, V., Quantization of Hitchin's integrable system and Hecke eigensheaves, Preprint (1991).Google Scholar
Bernstein, J. and Lunts, V., Equivariant sheaves and functors (Springer, New York, 2006).Google Scholar
Bezrukavnikov, R. and Finkelberg, M., Equivariant Satake category and Kostant-Whittaker reduction, Mosc. Math. J. 8 (2008), 39–72.10.17323/1609-4514-2008-8-1-39-72CrossRefGoogle Scholar
Bezrukavnikov, R. and Kaledin, D., Fedosov quantization in positive characteristic, J. Amer. Math. Soc. 21 (2008), 409–438.10.1090/S0894-0347-07-00585-1CrossRefGoogle Scholar
Braverman, A., Etingof, P. and Finkelberg, M., Cyclotomic double affine Hecke algebras (with an appendix by Hiraku Nakajima and Daisuke Yamakawa), Ann. Sci. Éc. Norm. Supér. (4) 53 (2020), 1249–1312.10.24033/asens.2446CrossRefGoogle Scholar
Braverman, A., Finkelberg, M. and Nakajima, H., Towards a mathematical definition of Coulomb branches of 
$3$-dimensional $\mathcal {N}=4$ gauge theories, II, Adv. Theor. Math. Phys. 22 (2016), 1071–1147.10.4310/ATMP.2018.v22.n5.a1CrossRefGoogle Scholar
$3$-dimensional 
$\mathcal {N}=4$ gauge theories, II, Adv. Theor. Math. Phys. 22 (2016), 1071–1147.10.4310/ATMP.2018.v22.n5.a1CrossRefGoogle ScholarBraverman, A., Finkelberg, M. and Nakajima, H., Ring objects in the equivariant derived Satake category arising from Coulomb branches (with an appendix by Gus Lonergan), Adv. Theor. Math. Phys. 23 (2017), 253–344.10.4310/ATMP.2019.v23.n2.a1CrossRefGoogle Scholar
Cartan, H. and Eilenberg, S., Homological algebra, vol. 41 (Princeton University Press, Princeton, NJ, 1999).Google Scholar
Chriss, N. and Ginzburg, V., Representation theory and complex geometry (Birkhäuser, Boston, MA, 1997).Google Scholar
Deligne, P., Beĭlinson, A. A. and Bernstein, J., Faisceaux pervers, Astérisque 100 (1983).Google Scholar
Drinfeld, V., Infinite-dimensional vector bundles in algebraic geometry, in The unity of mathematics (Springer, 2006), 263–304.10.1007/0-8176-4467-9_7CrossRefGoogle Scholar
Dyer, E. and Lashof, R. K., Homology of iterated loop spaces, Amer. J. Math. 84 (1962), 35–88.10.2307/2372804CrossRefGoogle Scholar
Kudo, T. and Araki, S., Topology of $H_n$-spaces and $H$-squaring operations, Mem. Fac. Sci. Kyushu Univ. Ser. A 10 (1956), 85–120.Google Scholar
$H_n$-spaces and 
$H$-squaring operations, Mem. Fac. Sci. Kyushu Univ. Ser. A 10 (1956), 85–120.Google ScholarMirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Ann. of Math. (2) 166 (2007), 95–143.10.4007/annals.2007.166.95CrossRefGoogle Scholar
Raskin, S., D-modules on infinite dimensional varieties, Preprint (2015).Google Scholar
Steenrod, N. E. and Epstein, D. B. A., Cohomology operations: Lectures by N. E. Steenrod. Written and revised by D. B. A. Epstein, Annals of Mathematics Studies, vol. 50 (Princeton University Press, Princeton, NJ, 1962).Google Scholar
Grothendieck, A., Raynaud, M. and Rim, D. S., Séminaire de Géométrie Algébrique du Bois Marie – 1967–69 – Groupes de monodromie en géométrie algébrique (SGA 7), vol. 1, Lecture Notes in Mathematics, vol. 288 (Springer, 1972).Google Scholar
Vezzosi, G. and Vistoli, A., Higher algebraic $K$-theory for actions of diagonalizable groups, Invent. Math. 153 (2003), 1–44.10.1007/s00222-002-0275-2CrossRefGoogle Scholar
$K$-theory for actions of diagonalizable groups, Invent. Math. 153 (2003), 1–44.10.1007/s00222-002-0275-2CrossRefGoogle ScholarWebster, B., Representation theory of the cyclotomic Cherednik algebra via the Dunkl-Opdam subalgebra, New York J. Math. 25 (2019), 1017–1047.Google Scholar