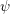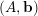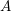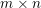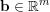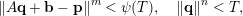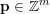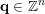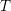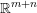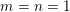1 Introduction and motivation
1.1 Homogeneous Diophantine approximation
Fix positive integers
![]() $m,n$
. Let
$m,n$
. Let
![]() $M_{m,n}$
denote the space of real
$M_{m,n}$
denote the space of real
![]() $m\times n$
matrices. The starting point for the present paper is the following theorem, proved by Dirichlet in 1842.
$m\times n$
matrices. The starting point for the present paper is the following theorem, proved by Dirichlet in 1842.
Theorem 1.1 (Dirichlet’s theorem).
For any
![]() $A\in M_{m,n}$
and
$A\in M_{m,n}$
and
![]() $T>1$
, there exist
$T>1$
, there exist
![]() $\mathbf{p}\in \mathbb{Z}^{m}$
,
$\mathbf{p}\in \mathbb{Z}^{m}$
,
![]() $\mathbf{q}\in \mathbb{Z}^{n}\smallsetminus \{0\}$
such that
$\mathbf{q}\in \mathbb{Z}^{n}\smallsetminus \{0\}$
such that
Here and hereafter
![]() $\Vert \cdot \Vert$
stands for the supremum norm on
$\Vert \cdot \Vert$
stands for the supremum norm on
![]() $\mathbb{R}^{k}$
,
$\mathbb{R}^{k}$
,
![]() $k\in \mathbb{N}$
. Informally speaking, a matrix
$k\in \mathbb{N}$
. Informally speaking, a matrix
![]() $A$
represents a vector-valued function
$A$
represents a vector-valued function
![]() $\mathbf{q}\mapsto A\mathbf{q}$
, and the above theorem asserts that one can choose a not-so-large non-zero integer vector
$\mathbf{q}\mapsto A\mathbf{q}$
, and the above theorem asserts that one can choose a not-so-large non-zero integer vector
![]() $\mathbf{q}$
so that the output of that function is close to an integer vector. In the case
$\mathbf{q}$
so that the output of that function is close to an integer vector. In the case
![]() $m=n=1$
the theorem just asserts that for any real number
$m=n=1$
the theorem just asserts that for any real number
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $T>1$
, one of the first
$T>1$
, one of the first
![]() $T$
multiples of
$T$
multiples of
![]() $\unicode[STIX]{x1D6FC}$
lies within
$\unicode[STIX]{x1D6FC}$
lies within
![]() $1/T$
of an integer. Theorem 1.1 is the archetypal uniform Diophantine approximation result, so called because it guarantees a non-trivial integer solution for all
$1/T$
of an integer. Theorem 1.1 is the archetypal uniform Diophantine approximation result, so called because it guarantees a non-trivial integer solution for all
![]() $T$
. A weaker form of approximation (sometimes called asymptotic approximation; see, for example, [Reference WaldschmidtWal12, Reference Kim and LiaoKL18]) guarantees that such a system is solvable for an unbounded set of
$T$
. A weaker form of approximation (sometimes called asymptotic approximation; see, for example, [Reference WaldschmidtWal12, Reference Kim and LiaoKL18]) guarantees that such a system is solvable for an unbounded set of
![]() $T$
. For instance, Theorem 1.1 implies that (1.1) is solvable for an unbounded set of
$T$
. For instance, Theorem 1.1 implies that (1.1) is solvable for an unbounded set of
![]() $T$
, a fortiori. The following corollary, which follows trivially from this weaker statement, is the archetypal asymptotic result.
$T$
, a fortiori. The following corollary, which follows trivially from this weaker statement, is the archetypal asymptotic result.
Corollary 1.2. For any
![]() $A\in M_{m,n}$
there exist infinitely many
$A\in M_{m,n}$
there exist infinitely many
![]() $\mathbf{q}\in \mathbb{Z}^{n}$
such that
$\mathbf{q}\in \mathbb{Z}^{n}$
such that
Together the aforementioned results initiate the metric theory of Diophantine approximation, a field concerned with understanding sets of
![]() $A\in M_{m,n}$
which admit improvements to Theorem 1.1 and Corollary 1.2. This paper has been motivated by an observation that the sensible ‘first questions’ about the asymptotic set-up were settled long ago, while the analogous questions about the uniform set-up remain open. Let us start by reviewing what is known in the asymptotic set-up.
$A\in M_{m,n}$
which admit improvements to Theorem 1.1 and Corollary 1.2. This paper has been motivated by an observation that the sensible ‘first questions’ about the asymptotic set-up were settled long ago, while the analogous questions about the uniform set-up remain open. Let us start by reviewing what is known in the asymptotic set-up.
For a function
![]() $\unicode[STIX]{x1D713}:\mathbb{R}_{+}\rightarrow \mathbb{R}_{+}$
, let us define
$\unicode[STIX]{x1D713}:\mathbb{R}_{+}\rightarrow \mathbb{R}_{+}$
, let us define
![]() $W_{m,n}(\unicode[STIX]{x1D713})$
, the set of
$W_{m,n}(\unicode[STIX]{x1D713})$
, the set of
![]() $\unicode[STIX]{x1D713}$
-approximable matrices, to be the set of
$\unicode[STIX]{x1D713}$
-approximable matrices, to be the set of
![]() $A\in M_{m,n}$
for which there exist infinitely many
$A\in M_{m,n}$
for which there exist infinitely many
![]() $\mathbf{q}\in \mathbb{Z}^{n}$
such thatFootnote
1
$\mathbf{q}\in \mathbb{Z}^{n}$
such thatFootnote
1
Throughout the paper we use the notation
![]() $\unicode[STIX]{x1D713}_{a}(x):=x^{-a}$
. Thus Corollary 1.2 asserts that
$\unicode[STIX]{x1D713}_{a}(x):=x^{-a}$
. Thus Corollary 1.2 asserts that
![]() $W_{m,n}(\unicode[STIX]{x1D713}_{1})=M_{m,n}$
, and in the above definition we have simply replaced
$W_{m,n}(\unicode[STIX]{x1D713}_{1})=M_{m,n}$
, and in the above definition we have simply replaced
![]() $\unicode[STIX]{x1D713}_{1}(\Vert \mathbf{q}\Vert ^{n})$
in (1.2) with
$\unicode[STIX]{x1D713}_{1}(\Vert \mathbf{q}\Vert ^{n})$
in (1.2) with
![]() $\unicode[STIX]{x1D713}(\Vert \mathbf{q}\Vert ^{n})$
. Precise conditions for the Lebesgue measure of
$\unicode[STIX]{x1D713}(\Vert \mathbf{q}\Vert ^{n})$
. Precise conditions for the Lebesgue measure of
![]() $W_{m,n}(\unicode[STIX]{x1D713})$
to be zero or full are given in the following theorem.
$W_{m,n}(\unicode[STIX]{x1D713})$
to be zero or full are given in the following theorem.
Theorem 1.3 (Khintchine–Groshev theorem [Reference GroshevGro38]).
Given a non-increasingFootnote
2
![]() $\unicode[STIX]{x1D713}$
, the set
$\unicode[STIX]{x1D713}$
, the set
![]() $W_{m,n}(\unicode[STIX]{x1D713})$
has zero (respectively, full) measure if and only if the series
$W_{m,n}(\unicode[STIX]{x1D713})$
has zero (respectively, full) measure if and only if the series
![]() $\sum _{k}\unicode[STIX]{x1D713}(k)$
converges (respectively, diverges).
$\sum _{k}\unicode[STIX]{x1D713}(k)$
converges (respectively, diverges).
See [Reference SprindžukSpr79] or [Reference Beresnevich, Dickinson and VelaniBDV06] for details, and also [Reference Kleinbock and MargulisKM99] for an alternative proof using dynamics on the space of lattices.
Questions related to similarly improving Theorem 1.1 were first addressed in two seminal papers [Reference Davenport and SchmidtDS70, Reference Davenport and SchmidtDS69] by Davenport and Schmidt. However no zero–one law analogous to Theorem 1.3 has yet been proved in the set-up of uniform approximation for general
![]() $m,n\in \mathbb{N}$
. Let us introduce the following definition: for a non-increasing function
$m,n\in \mathbb{N}$
. Let us introduce the following definition: for a non-increasing function
![]() $\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+}$
, where
$\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+}$
, where
![]() $T_{0}>1$
is fixed, say that
$T_{0}>1$
is fixed, say that
![]() $A\in M_{m,n}$
is
$A\in M_{m,n}$
is
![]() $\unicode[STIX]{x1D713}$
-Dirichlet, or
$\unicode[STIX]{x1D713}$
-Dirichlet, or
![]() $A\in D_{m,n}(\unicode[STIX]{x1D713})$
, if the system
$A\in D_{m,n}(\unicode[STIX]{x1D713})$
, if the system
has a non-trivial integer solution for all large enough
![]() $T$
. In other words, we have replaced
$T$
. In other words, we have replaced
![]() $\unicode[STIX]{x1D713}_{1}(T)$
in (1.1) with
$\unicode[STIX]{x1D713}_{1}(T)$
in (1.1) with
![]() $\unicode[STIX]{x1D713}(T)$
, demanded the existence of non-trivial integer solutions for all
$\unicode[STIX]{x1D713}(T)$
, demanded the existence of non-trivial integer solutions for all
![]() $T$
except those belonging to a bounded set, and sharpened one of the inequalities in (1.1). The latter change, in particular, implies the following observation: for non-increasing
$T$
except those belonging to a bounded set, and sharpened one of the inequalities in (1.1). The latter change, in particular, implies the following observation: for non-increasing
![]() $\unicode[STIX]{x1D713}$
, membership in
$\unicode[STIX]{x1D713}$
, membership in
![]() $D_{m,n}(\unicode[STIX]{x1D713})$
depends only on the solvability of the system (1.4) at integer values of
$D_{m,n}(\unicode[STIX]{x1D713})$
depends only on the solvability of the system (1.4) at integer values of
![]() $T$
. (To show this it suffices to replace
$T$
. (To show this it suffices to replace
![]() $T$
with
$T$
with
![]() $\lceil T\rceil$
and use the monotonicity of
$\lceil T\rceil$
and use the monotonicity of
![]() $\unicode[STIX]{x1D713}$
.)
$\unicode[STIX]{x1D713}$
.)
It is not difficult to see that
![]() $D_{1,1}(\unicode[STIX]{x1D713}_{1})=\mathbb{R}$
, and that for general
$D_{1,1}(\unicode[STIX]{x1D713}_{1})=\mathbb{R}$
, and that for general
![]() $m,n$
, almost every matrix is
$m,n$
, almost every matrix is
![]() $\unicode[STIX]{x1D713}_{1}$
-Dirichlet. In contrast, it was proved in [Reference Davenport and SchmidtDS69] for
$\unicode[STIX]{x1D713}_{1}$
-Dirichlet. In contrast, it was proved in [Reference Davenport and SchmidtDS69] for
![]() $\min (m,n)=1$
, and in [Reference Kleinbock and WeissKW08] for the general case, that for any
$\min (m,n)=1$
, and in [Reference Kleinbock and WeissKW08] for the general case, that for any
![]() $c<1$
, the set
$c<1$
, the set
![]() $D_{m,n}(c\unicode[STIX]{x1D713}_{1})$
of
$D_{m,n}(c\unicode[STIX]{x1D713}_{1})$
of
![]() $c\unicode[STIX]{x1D713}_{1}$
-Dirichlet matrices has Lebesgue measure zero. This naturally motivates the following question.
$c\unicode[STIX]{x1D713}_{1}$
-Dirichlet matrices has Lebesgue measure zero. This naturally motivates the following question.
Question 1.4. What is a necessary and sufficient condition on a non-increasing function
![]() $\unicode[STIX]{x1D713}$
(presumably expressed in the form of convergence/divergence of a certain series) guaranteeing that the set
$\unicode[STIX]{x1D713}$
(presumably expressed in the form of convergence/divergence of a certain series) guaranteeing that the set
![]() $D_{m,n}(\unicode[STIX]{x1D713})$
has zero or full measure?
$D_{m,n}(\unicode[STIX]{x1D713})$
has zero or full measure?
In [Reference Kleinbock and WadleighKW18] we give an answer to this question for
![]() $m=n=1$
, but in general Question 1.4 seems to be much harder than its counterpart for the sets
$m=n=1$
, but in general Question 1.4 seems to be much harder than its counterpart for the sets
![]() $W_{m,n}(\unicode[STIX]{x1D713})$
, answered by Theorem 1.3. We comment later in the paper on the reason for this difficulty, but the main subject of this paper is different: we take up an analogous inhomogeneous approximation problem, describe the analogues of the statements and concepts discussed in this section, and then show how an inhomogeneous analogue of Question 1.4 admits a complete solution based on a correspondence between Diophantine approximation and dynamics on homogeneous spaces.
$W_{m,n}(\unicode[STIX]{x1D713})$
, answered by Theorem 1.3. We comment later in the paper on the reason for this difficulty, but the main subject of this paper is different: we take up an analogous inhomogeneous approximation problem, describe the analogues of the statements and concepts discussed in this section, and then show how an inhomogeneous analogue of Question 1.4 admits a complete solution based on a correspondence between Diophantine approximation and dynamics on homogeneous spaces.
1.2 Inhomogeneous approximation: the main result
The theory of inhomogeneous Diophantine approximation starts when one replaces the values of a system of linear forms
![]() $A\mathbf{q}$
by those of a system of affine forms
$A\mathbf{q}$
by those of a system of affine forms
![]() $\mathbf{q}\mapsto A\mathbf{q}+\mathbf{b}$
, where
$\mathbf{q}\mapsto A\mathbf{q}+\mathbf{b}$
, where
![]() $A\in M_{m,n}$
and
$A\in M_{m,n}$
and
![]() $\mathbf{b}\in \mathbb{R}^{m}$
. Consider a non-increasing function
$\mathbf{b}\in \mathbb{R}^{m}$
. Consider a non-increasing function
![]() $\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+}$
and, following the definition of the set
$\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+}$
and, following the definition of the set
![]() $D_{m,n}(\unicode[STIX]{x1D713})$
, let us say that a pair
$D_{m,n}(\unicode[STIX]{x1D713})$
, let us say that a pair
![]() $(A,\mathbf{b})\in M_{m,n}\times \mathbb{R}^{m}$
is
$(A,\mathbf{b})\in M_{m,n}\times \mathbb{R}^{m}$
is
![]() $\unicode[STIX]{x1D713}$
-Dirichlet if there exist
$\unicode[STIX]{x1D713}$
-Dirichlet if there exist
![]() $\mathbf{p}\in \mathbb{Z}^{m}$
,
$\mathbf{p}\in \mathbb{Z}^{m}$
,
![]() $\mathbf{q}\in \mathbb{Z}^{n}$
such that
$\mathbf{q}\in \mathbb{Z}^{n}$
such that
whenever
![]() $T$
is large enough. (Note that in this set-up there is no need to single out the case
$T$
is large enough. (Note that in this set-up there is no need to single out the case
![]() $\mathbf{q}=0$
.) Denote the set of
$\mathbf{q}=0$
.) Denote the set of
![]() $\unicode[STIX]{x1D713}$
-Dirichlet pairs by
$\unicode[STIX]{x1D713}$
-Dirichlet pairs by
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
. Note that, as is the case with
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
. Note that, as is the case with
![]() $D_{m,n}(\unicode[STIX]{x1D713})$
, membership in
$D_{m,n}(\unicode[STIX]{x1D713})$
, membership in
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
depends only on the solubility of these inequalities at integer values of
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
depends only on the solubility of these inequalities at integer values of
![]() $T$
, provided
$T$
, provided
![]() $\unicode[STIX]{x1D713}$
is non-increasing. Hence without loss of generality one can assume
$\unicode[STIX]{x1D713}$
is non-increasing. Hence without loss of generality one can assume
![]() $\unicode[STIX]{x1D713}$
to be continuous.
$\unicode[STIX]{x1D713}$
to be continuous.
Let us start with the simplest case:
![]() $\unicode[STIX]{x1D713}\equiv c$
is a constant function, or
$\unicode[STIX]{x1D713}\equiv c$
is a constant function, or
![]() $\unicode[STIX]{x1D713}=c\unicode[STIX]{x1D713}_{0}$
in our notation. It is a trivial consequence of Dirichlet’s theorem that whenever
$\unicode[STIX]{x1D713}=c\unicode[STIX]{x1D713}_{0}$
in our notation. It is a trivial consequence of Dirichlet’s theorem that whenever
![]() $c>0$
,
$c>0$
,
is solvable in
![]() $\mathbf{p}\in \mathbb{Z}^{m}$
,
$\mathbf{p}\in \mathbb{Z}^{m}$
,
![]() $\mathbf{q}\in \mathbb{Z}^{n}\smallsetminus \{0\}$
whenever
$\mathbf{q}\in \mathbb{Z}^{n}\smallsetminus \{0\}$
whenever
![]() $T>c^{-1}$
. By contrast, it is clear that one cannot always solve
$T>c^{-1}$
. By contrast, it is clear that one cannot always solve
for
![]() $c\leqslant 1/2^{m}$
; for example, take
$c\leqslant 1/2^{m}$
; for example, take
![]() $A$
to be an integer matrix and take
$A$
to be an integer matrix and take
![]() $\mathbf{b}$
with coordinates in
$\mathbf{b}$
with coordinates in
![]() $\mathbb{Z}+\frac{1}{2}$
. However, it follows from Kronecker’s theorem [Reference CasselsCas57, § 3.5] that, for a given
$\mathbb{Z}+\frac{1}{2}$
. However, it follows from Kronecker’s theorem [Reference CasselsCas57, § 3.5] that, for a given
![]() $A\in M_{m,n}$
, there exist
$A\in M_{m,n}$
, there exist
![]() $\mathbf{b}\in \mathbb{R}^{m}$
and
$\mathbf{b}\in \mathbb{R}^{m}$
and
![]() $c>0$
such that
$c>0$
such that
![]() $(A,\mathbf{b})\notin \widehat{D}_{m,n}(c\unicode[STIX]{x1D713}_{0})$
, which amounts to saying that
$(A,\mathbf{b})\notin \widehat{D}_{m,n}(c\unicode[STIX]{x1D713}_{0})$
, which amounts to saying that
![]() $A\mathbb{Z}^{n}$
is not dense in
$A\mathbb{Z}^{n}$
is not dense in
![]() $\mathbb{R}^{m}/\mathbb{Z}^{m}$
, only if
$\mathbb{R}^{m}/\mathbb{Z}^{m}$
, only if
![]() $A^{t}(\mathbb{Z}^{m}\smallsetminus \{0\})$
contains an integer vector. The set of such
$A^{t}(\mathbb{Z}^{m}\smallsetminus \{0\})$
contains an integer vector. The set of such
![]() $A$
has measure zero since it is the union over
$A$
has measure zero since it is the union over
![]() $\mathbf{q}\in \mathbb{Z}^{n}$
,
$\mathbf{q}\in \mathbb{Z}^{n}$
,
![]() $\mathbf{p}\in \mathbb{Z}^{m}\smallsetminus \{0\}$
of the sets
$\mathbf{p}\in \mathbb{Z}^{m}\smallsetminus \{0\}$
of the sets
![]() $\{A:A^{t}\mathbf{p}=\mathbf{q}\}$
. Thus for every
$\{A:A^{t}\mathbf{p}=\mathbf{q}\}$
. Thus for every
![]() $c>0$
,
$c>0$
,
![]() $\widehat{D}_{m,n}(c\unicode[STIX]{x1D713}_{0})$
has full measure.
$\widehat{D}_{m,n}(c\unicode[STIX]{x1D713}_{0})$
has full measure.
Once
![]() $\unicode[STIX]{x1D713}$
is allowed to decay to zero, the sets
$\unicode[STIX]{x1D713}$
is allowed to decay to zero, the sets
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
become smaller. In particular, using dynamics on the space of grids in
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
become smaller. In particular, using dynamics on the space of grids in
![]() $\mathbb{R}^{m+n}$
, one can easily prove (see Proposition 2.3 below) that
$\mathbb{R}^{m+n}$
, one can easily prove (see Proposition 2.3 below) that
![]() $\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
is null for any
$\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
is null for any
![]() $C>0$
. Thus one can naturally ask the following inhomogeneous analogue of Question 1.4.
$C>0$
. Thus one can naturally ask the following inhomogeneous analogue of Question 1.4.
Question 1.5. What is a necessary and sufficient condition on a non-increasing function
![]() $\unicode[STIX]{x1D713}$
(presumably expressed in the form of convergence/divergence of a certain series) guaranteeing that the set
$\unicode[STIX]{x1D713}$
(presumably expressed in the form of convergence/divergence of a certain series) guaranteeing that the set
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has zero or full measure?
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has zero or full measure?
The remainder of this work will be given to a proof of the following answer.
Theorem 1.6. Given a non-increasing
![]() $\unicode[STIX]{x1D713}$
, the set
$\unicode[STIX]{x1D713}$
, the set
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has zero (respectively, full) measure if and only if the series
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has zero (respectively, full) measure if and only if the series
diverges (respectively, converges).
Note that this immediately gives results such as:
∙
 $\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{a})$
has zero (respectively, full) measure if
$\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{a})$
has zero (respectively, full) measure if
 $a\geqslant 1$
(respectively,
$a\geqslant 1$
(respectively,
 $a<1$
);
$a<1$
);∙ for
 $\unicode[STIX]{x1D713}(T)=C(\log T)^{b}\unicode[STIX]{x1D713}_{1}(T)$
,
$\unicode[STIX]{x1D713}(T)=C(\log T)^{b}\unicode[STIX]{x1D713}_{1}(T)$
,
 $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has zero (respectively, full) measure if
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has zero (respectively, full) measure if
 $b\leqslant 1$
(respectively,
$b\leqslant 1$
(respectively,
 $b>1$
).
$b>1$
).
Our argument is based on a correspondence between Diophantine approximation and homogeneous dynamics. In the next section we introduce the space of grids in
![]() $\mathbb{R}^{m+n}$
and reduce the aforementioned inhomogeneous approximation problem to a shrinking target phenomenon for a flow on that space. We present a warm-up problem, Proposition 2.3, that demonstrates the usefulness of the reduction to dynamics and introduces several key ideas to be used later. This is followed by the statement of the main dynamical result, Theorem 3.6, which we prove in the two subsequent sections. The last section contains some concluding remarks, in particular a discussion of Question 1.4 and other open questions.
$\mathbb{R}^{m+n}$
and reduce the aforementioned inhomogeneous approximation problem to a shrinking target phenomenon for a flow on that space. We present a warm-up problem, Proposition 2.3, that demonstrates the usefulness of the reduction to dynamics and introduces several key ideas to be used later. This is followed by the statement of the main dynamical result, Theorem 3.6, which we prove in the two subsequent sections. The last section contains some concluding remarks, in particular a discussion of Question 1.4 and other open questions.
2 Dynamics on the space of grids: a warm-up
Fix
![]() $k\in \mathbb{N}$
and let
$k\in \mathbb{N}$
and let
the latter is the group of volume-preserving affine transformations of
![]() $\mathbb{R}^{k}$
. Also put
$\mathbb{R}^{k}$
. Also put
Elements of
![]() $\widehat{G}_{k}$
will be denoted by
$\widehat{G}_{k}$
will be denoted by
![]() $\langle g,\mathbf{w}\rangle$
where
$\langle g,\mathbf{w}\rangle$
where
![]() $g\in G_{k}$
and
$g\in G_{k}$
and
![]() $\mathbf{w}\in \mathbb{R}^{k}$
; that is,
$\mathbf{w}\in \mathbb{R}^{k}$
; that is,
![]() $\langle g,\mathbf{w}\rangle$
is the affine transformation
$\langle g,\mathbf{w}\rangle$
is the affine transformation
![]() $\mathbf{x}\mapsto g\mathbf{x}+\mathbf{w}$
. Denote by
$\mathbf{x}\mapsto g\mathbf{x}+\mathbf{w}$
. Denote by
![]() $\widehat{X}_{k}$
the space of translates of unimodular lattices in
$\widehat{X}_{k}$
the space of translates of unimodular lattices in
![]() $\mathbb{R}^{k}$
; elements of
$\mathbb{R}^{k}$
; elements of
![]() $\widehat{X}_{k}$
will be referred to as unimodular grids. Clearly
$\widehat{X}_{k}$
will be referred to as unimodular grids. Clearly
![]() $\widehat{X}_{k}$
is canonically identified with
$\widehat{X}_{k}$
is canonically identified with
![]() $\widehat{G}_{k}/\widehat{\unicode[STIX]{x1D6E4}}_{k}$
via
$\widehat{G}_{k}/\widehat{\unicode[STIX]{x1D6E4}}_{k}$
via
Similarly,
![]() $X_{k}:=G_{k}/\unicode[STIX]{x1D6E4}_{k}$
is identified with the space of unimodular lattices in
$X_{k}:=G_{k}/\unicode[STIX]{x1D6E4}_{k}$
is identified with the space of unimodular lattices in
![]() $\mathbb{R}^{k}$
(i.e. unimodular grids containing the zero vector). Note that
$\mathbb{R}^{k}$
(i.e. unimodular grids containing the zero vector). Note that
![]() $\widehat{\unicode[STIX]{x1D6E4}}_{k}$
(respectively,
$\widehat{\unicode[STIX]{x1D6E4}}_{k}$
(respectively,
![]() $\unicode[STIX]{x1D6E4}_{k}$
) is a lattice in
$\unicode[STIX]{x1D6E4}_{k}$
) is a lattice in
![]() $\widehat{G}_{k}$
(respectively,
$\widehat{G}_{k}$
(respectively,
![]() $G_{k}$
). We will denote by
$G_{k}$
). We will denote by
![]() $\widehat{\unicode[STIX]{x1D707}}$
(respectively
$\widehat{\unicode[STIX]{x1D707}}$
(respectively
![]() $\unicode[STIX]{x1D707}$
) the normalized Haar measures on
$\unicode[STIX]{x1D707}$
) the normalized Haar measures on
![]() $\widehat{X}_{k}$
and
$\widehat{X}_{k}$
and
![]() $X_{k}$
, respectively.
$X_{k}$
, respectively.
Now fix
![]() $m,n\in \mathbb{N}$
with
$m,n\in \mathbb{N}$
with
![]() $m+n=k$
, and for
$m+n=k$
, and for
![]() $t\in \mathbb{R}$
let
$t\in \mathbb{R}$
let
where there are
![]() $m$
copies of
$m$
copies of
![]() $e^{t/m}$
and
$e^{t/m}$
and
![]() $n$
copies of
$n$
copies of
![]() $e^{-t/n}$
. The so-called expanding horospherical subgroup of
$e^{-t/n}$
. The so-called expanding horospherical subgroup of
![]() $\widehat{G}_{k}$
with respect to
$\widehat{G}_{k}$
with respect to
![]() $\{g_{t}:t>0\}$
is given by
$\{g_{t}:t>0\}$
is given by
On the other hand,
is a subgroup of
![]() $\widehat{G}_{k}$
complementary to
$\widehat{G}_{k}$
complementary to
![]() $H$
which is non-expanding with respect to conjugation by
$H$
which is non-expanding with respect to conjugation by
![]() $g_{t}$
,
$g_{t}$
,
![]() $t\geqslant 0$
: it is easy to see that
$t\geqslant 0$
: it is easy to see that
Let us also denote
The reduction of Diophantine properties of
![]() $(A,\mathbf{b})$
to the behavior of the
$(A,\mathbf{b})$
to the behavior of the
![]() $g_{t}$
-trajectory of
$g_{t}$
-trajectory of
![]() $\unicode[STIX]{x1D6EC}_{A,\mathbf{b}}$
described below mimics the classical Dani correspondence for homogeneous Diophantine approximation [Reference DaniDan85, Reference Kleinbock and MargulisKM99] and dates back to [Reference KleinbockKle99] (see also more recent papers [Reference ShapiraSha11, Reference Einsiedler and TsengET11, Reference Gorodnik and VisheGV18]). The crucial role is played by a function
$\unicode[STIX]{x1D6EC}_{A,\mathbf{b}}$
described below mimics the classical Dani correspondence for homogeneous Diophantine approximation [Reference DaniDan85, Reference Kleinbock and MargulisKM99] and dates back to [Reference KleinbockKle99] (see also more recent papers [Reference ShapiraSha11, Reference Einsiedler and TsengET11, Reference Gorodnik and VisheGV18]). The crucial role is played by a function
![]() $\unicode[STIX]{x1D6E5}:\widehat{X}_{k}\rightarrow [-\infty ,\infty )$
given by
$\unicode[STIX]{x1D6E5}:\widehat{X}_{k}\rightarrow [-\infty ,\infty )$
given by
Note that
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC})=-\infty$
if and only if
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC})=-\infty$
if and only if
![]() $\unicode[STIX]{x1D6EC}\ni 0$
. Also it is easy to see that
$\unicode[STIX]{x1D6EC}\ni 0$
. Also it is easy to see that
![]() $\unicode[STIX]{x1D6E5}$
is uniformly continuous outside of the set where it takes small values.
$\unicode[STIX]{x1D6E5}$
is uniformly continuous outside of the set where it takes small values.
Lemma 2.1. For any
![]() $z\in \mathbb{R}$
,
$z\in \mathbb{R}$
,
![]() $\unicode[STIX]{x1D6E5}$
is uniformly continuous on the set
$\unicode[STIX]{x1D6E5}$
is uniformly continuous on the set
![]() $\unicode[STIX]{x1D6E5}^{-1}([z,\infty ))$
. That is, for any
$\unicode[STIX]{x1D6E5}^{-1}([z,\infty ))$
. That is, for any
![]() $z\in \mathbb{R}$
and any
$z\in \mathbb{R}$
and any
![]() $\unicode[STIX]{x1D700}>0$
there exists a neighborhood
$\unicode[STIX]{x1D700}>0$
there exists a neighborhood
![]() $U$
of the identity in
$U$
of the identity in
![]() $\widehat{G}_{k}$
such that whenever
$\widehat{G}_{k}$
such that whenever
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC})\geqslant z$
and
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC})\geqslant z$
and
![]() $g\in U$
, one has
$g\in U$
, one has
![]() $|\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC})-\unicode[STIX]{x1D6E5}(g\unicode[STIX]{x1D6EC})|<\unicode[STIX]{x1D700}$
.
$|\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC})-\unicode[STIX]{x1D6E5}(g\unicode[STIX]{x1D6EC})|<\unicode[STIX]{x1D700}$
.
Proof. Let
![]() $c>1$
,
$c>1$
,
![]() $z\in \mathbb{R}$
. Choose
$z\in \mathbb{R}$
. Choose
![]() $\unicode[STIX]{x1D6FF}>0$
so that
$\unicode[STIX]{x1D6FF}>0$
so that
whenever
![]() $\Vert \mathbf{w}\Vert \leqslant \unicode[STIX]{x1D6FF}$
and
$\Vert \mathbf{w}\Vert \leqslant \unicode[STIX]{x1D6FF}$
and
![]() $\log \Vert \mathbf{v}\Vert \geqslant z-\log c$
. Then if
$\log \Vert \mathbf{v}\Vert \geqslant z-\log c$
. Then if
![]() $\log \Vert \mathbf{v}\Vert \geqslant z$
,
$\log \Vert \mathbf{v}\Vert \geqslant z$
,
![]() $\Vert \mathbf{w}\Vert <\unicode[STIX]{x1D6FF}$
and the operator norms of both
$\Vert \mathbf{w}\Vert <\unicode[STIX]{x1D6FF}$
and the operator norms of both
![]() $g$
and
$g$
and
![]() $g^{-1}$
are not greater than
$g^{-1}$
are not greater than
![]() $c$
(the latter two conditions define an open neighborhood
$c$
(the latter two conditions define an open neighborhood
![]() $U$
of the identity in
$U$
of the identity in
![]() $\widehat{G}$
such that
$\widehat{G}$
such that
![]() $\langle g,\mathbf{w}\rangle \in U$
), we have
$\langle g,\mathbf{w}\rangle \in U$
), we have
Thus if
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC})\geqslant z$
and
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC})\geqslant z$
and
![]() $\langle g,\mathbf{w}\rangle \in U$
, we have
$\langle g,\mathbf{w}\rangle \in U$
, we have
Since
![]() $c>1$
is arbitrary,
$c>1$
is arbitrary,
![]() $\unicode[STIX]{x1D6E5}$
is uniformly continuous on
$\unicode[STIX]{x1D6E5}$
is uniformly continuous on
![]() $\unicode[STIX]{x1D6E5}^{-1}([z,\infty ))$
.◻
$\unicode[STIX]{x1D6E5}^{-1}([z,\infty ))$
.◻
Another important feature of
![]() $\unicode[STIX]{x1D6E5}$
is that it is unbounded from above; indeed, the grid
$\unicode[STIX]{x1D6E5}$
is that it is unbounded from above; indeed, the grid
is disjoint from the ball centered at 0 of radius
![]() $e^{z}$
. Consequently, sets
$e^{z}$
. Consequently, sets
![]() $\unicode[STIX]{x1D6E5}^{-1}([z,\infty ))$
have non-empty interior for all
$\unicode[STIX]{x1D6E5}^{-1}([z,\infty ))$
have non-empty interior for all
![]() $z\in \mathbb{R}$
.
$z\in \mathbb{R}$
.
Let us now describe a basic special case of the correspondence between inhomogeneous improvement of Dirichlet’s theorem and dynamics on
![]() $\widehat{X}_{k}$
. The next lemma is essentially an inhomogeneous analogue of [Reference Kleinbock and WeissKW08, Proposition 2.1].
$\widehat{X}_{k}$
. The next lemma is essentially an inhomogeneous analogue of [Reference Kleinbock and WeissKW08, Proposition 2.1].
Lemma 2.2. Let
![]() $C>0$
and put
$C>0$
and put
![]() $z=(\log C)/(m+n)$
. Then
$z=(\log C)/(m+n)$
. Then
![]() $(A,\mathbf{b})\in \widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
if and only if
$(A,\mathbf{b})\in \widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
if and only if
![]() $\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})<z$
for all large enough
$\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})<z$
for all large enough
![]() $t>0$
.
$t>0$
.
Proof. For
![]() $T>1$
, put
$T>1$
, put
![]() $\unicode[STIX]{x1D713}(T)=C\unicode[STIX]{x1D713}_{1}(T)=C/T$
, and define
$\unicode[STIX]{x1D713}(T)=C\unicode[STIX]{x1D713}_{1}(T)=C/T$
, and define
Then
![]() $\unicode[STIX]{x1D713}(T)=C^{n/(m+n)}e^{-t}$
, and the system (1.5) can be written as
$\unicode[STIX]{x1D713}(T)=C^{n/(m+n)}e^{-t}$
, and the system (1.5) can be written as
which is the same as
In view of (2.1), (2.5) and (2.6), the solvability of (1.5) in
![]() $(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m+n}$
is equivalent to
$(\mathbf{p},\mathbf{q})\in \mathbb{Z}^{m+n}$
is equivalent to
and the conclusion follows. ◻
We will use the above lemma and the ergodicity of the
![]() $g_{t}$
-action on
$g_{t}$
-action on
![]() $\widehat{X}_{k}$
to compute the Lebesgue measure of
$\widehat{X}_{k}$
to compute the Lebesgue measure of
![]() $\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
. The proof contains a Fubini theorem argument (following [Reference Kleinbock and MargulisKM99, Theorem 8.7] and dating back to [Reference DaniDan85]) used to pass from an almost-everywhere statement for lattices to an almost-everywhere statement for pairs in
$\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
. The proof contains a Fubini theorem argument (following [Reference Kleinbock and MargulisKM99, Theorem 8.7] and dating back to [Reference DaniDan85]) used to pass from an almost-everywhere statement for lattices to an almost-everywhere statement for pairs in
![]() $M_{m,n}\times \mathbb{R}^{m}$
. We will refer to this argument twice more in the sequel.
$M_{m,n}\times \mathbb{R}^{m}$
. We will refer to this argument twice more in the sequel.
Proposition 2.3. For any
![]() $m,n\in \mathbb{N}$
and any
$m,n\in \mathbb{N}$
and any
![]() $C>0$
, the set
$C>0$
, the set
![]() $\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
has Lebesgue measure zero.
$\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
has Lebesgue measure zero.
Proof. Suppose
![]() $U$
is a subset of
$U$
is a subset of
![]() $M_{m,n}\times \mathbb{R}^{m}$
(
$M_{m,n}\times \mathbb{R}^{m}$
(
![]() $\cong H$
as in (2.2)) of positive Lebesgue measure such that
$\cong H$
as in (2.2)) of positive Lebesgue measure such that
![]() $\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})<(\log C)/(m+n)$
for any
$\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})<(\log C)/(m+n)$
for any
![]() $(A,\mathbf{b})\in U$
and all large enough
$(A,\mathbf{b})\in U$
and all large enough
![]() $t$
. Then there exists a neighborhood
$t$
. Then there exists a neighborhood
![]() $V$
of identity in
$V$
of identity in
![]() $\tilde{H}$
as in (2.3) such that for all
$\tilde{H}$
as in (2.3) such that for all
![]() $g\in V$
,
$g\in V$
,
![]() $(A,\mathbf{b})\in U$
and all large enough
$(A,\mathbf{b})\in U$
and all large enough
![]() $t$
,
$t$
,
Indeed, one can use Lemma 2.1 and (2.4) to choose
![]() $V$
such that if (2.7) does not hold for
$V$
such that if (2.7) does not hold for
![]() $g\in V$
, then
$g\in V$
, then
![]() $|\unicode[STIX]{x1D6E5}(g_{t}gg_{t}^{-1}g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})-\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})|<1$
. But since the product map
$|\unicode[STIX]{x1D6E5}(g_{t}gg_{t}^{-1}g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})-\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})|<1$
. But since the product map
![]() $\tilde{H}\times H\rightarrow \widehat{G}_{k}$
is a local diffeomorphism,
$\tilde{H}\times H\rightarrow \widehat{G}_{k}$
is a local diffeomorphism,
![]() $V\times U$
is mapped onto a set of positive measure. It follows that
$V\times U$
is mapped onto a set of positive measure. It follows that
![]() $\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC})<(\log C)/(m+n)+1$
for all large enough
$\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC})<(\log C)/(m+n)+1$
for all large enough
![]() $t$
and for a set of lattices
$t$
and for a set of lattices
![]() $\unicode[STIX]{x1D6EC}$
of positive Haar measure in
$\unicode[STIX]{x1D6EC}$
of positive Haar measure in
![]() $\widehat{X}_{k}$
.
$\widehat{X}_{k}$
.
On the other hand, from Moore’s ergodicity theorem [Reference MooreMoo66] together with the ergodicity criterion of Brezin and Moore (see [Reference Brezin and MooreBM81, Theorem 6.1] or [Reference MargulisMar91, Theorem 6]) it follows that every unbounded subgroup of
![]() $G_{k}$
, in particular,
$G_{k}$
, in particular,
![]() $\{g_{t}:t\in \mathbb{R}\}$
as above, acts ergodically on
$\{g_{t}:t\in \mathbb{R}\}$
as above, acts ergodically on
![]() $\widehat{X}_{k}$
. Since for any
$\widehat{X}_{k}$
. Since for any
![]() $C>0$
the set
$C>0$
the set
![]() $\unicode[STIX]{x1D6E5}^{-1}([(\log C)/(m+n)+1,\infty ))$
has a non-empty interior, it follows that
$\unicode[STIX]{x1D6E5}^{-1}([(\log C)/(m+n)+1,\infty ))$
has a non-empty interior, it follows that
![]() $\unicode[STIX]{x1D707}$
-almost every
$\unicode[STIX]{x1D707}$
-almost every
![]() $\unicode[STIX]{x1D6EC}\in \widehat{X}_{k}$
must visit any such set at unbounded times under the action of
$\unicode[STIX]{x1D6EC}\in \widehat{X}_{k}$
must visit any such set at unbounded times under the action of
![]() $g_{t}$
, a contradiction.◻
$g_{t}$
, a contradiction.◻
3 A correspondence between Dirichlet improvability and dynamics
Lemma 2.2 relates the complement of
![]() $\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{0})$
to the set of grids visiting certain ‘target’ subsets of
$\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{0})$
to the set of grids visiting certain ‘target’ subsets of
![]() $\widehat{X}_{k}$
at unbounded times under the diagonal flow
$\widehat{X}_{k}$
at unbounded times under the diagonal flow
![]() $g_{t}$
. This is the special case where the target does not change with the time parameter
$g_{t}$
. This is the special case where the target does not change with the time parameter
![]() $t$
. For general non-increasing
$t$
. For general non-increasing
![]() $\unicode[STIX]{x1D713}$
, we get a family of ‘shrinking targets’
$\unicode[STIX]{x1D713}$
, we get a family of ‘shrinking targets’
![]() $\unicode[STIX]{x1D6E5}^{-1}([z_{\unicode[STIX]{x1D713}}(t),\infty ))$
(which in fact are shrinking only in a weak sense; see Remark 3.3), where
$\unicode[STIX]{x1D6E5}^{-1}([z_{\unicode[STIX]{x1D713}}(t),\infty ))$
(which in fact are shrinking only in a weak sense; see Remark 3.3), where
![]() $z_{\unicode[STIX]{x1D713}}$
is gotten by the following change of variables, known as the Dani correspondence.
$z_{\unicode[STIX]{x1D713}}$
is gotten by the following change of variables, known as the Dani correspondence.
Lemma 3.1 (See [Reference Kleinbock and MargulisKM99, Lemma 8.3]).
Let positive integers
![]() $m,n$
and
$m,n$
and
![]() $T_{0}\in \mathbb{R}_{+}$
be given. Suppose
$T_{0}\in \mathbb{R}_{+}$
be given. Suppose
![]() $\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+}$
is a continuous, non-increasing function. Then there exists a unique continuous function
$\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+}$
is a continuous, non-increasing function. Then there exists a unique continuous function
where
![]() $t_{0}:=(m/(m+n))\log T_{0}-(n/(m+n))\log \unicode[STIX]{x1D713}(T_{0})$
, such that:
$t_{0}:=(m/(m+n))\log T_{0}-(n/(m+n))\log \unicode[STIX]{x1D713}(T_{0})$
, such that:
(i) the function
 $t\mapsto t+nz(t)$
is strictly increasing and unbounded;
$t\mapsto t+nz(t)$
is strictly increasing and unbounded;(ii) the function
 $t\mapsto t-mz(t)$
is non-decreasing;
$t\mapsto t-mz(t)$
is non-decreasing;(iii)
 $\unicode[STIX]{x1D713}(e^{t+nz(t)})=e^{-t+mz(t)}$
for all
$\unicode[STIX]{x1D713}(e^{t+nz(t)})=e^{-t+mz(t)}$
for all
 $t\geqslant t_{0}$
.
$t\geqslant t_{0}$
.
Remark 3.2. The function
![]() $z$
of Lemma 3.1 differs from the function
$z$
of Lemma 3.1 differs from the function
![]() $r$
of [Reference Kleinbock and MargulisKM99, Lemma 8.3] by a minus sign. This reflects the difference between the asymptotic and uniform approximation problems.
$r$
of [Reference Kleinbock and MargulisKM99, Lemma 8.3] by a minus sign. This reflects the difference between the asymptotic and uniform approximation problems.
Remark 3.3. For future reference, we point out that properties (1) and (2) of Lemma 3.1 imply that any
![]() $z=z_{\unicode[STIX]{x1D713}}$
does not oscillate too wildly. Namely,
$z=z_{\unicode[STIX]{x1D713}}$
does not oscillate too wildly. Namely,
Now we can state a general version of the correspondence between the improvability of the inhomogeneous Dirichlet theorem and dynamics on
![]() $\widehat{X}_{k}$
, generalizing the first paragraph of the proof of Theorem 2.3.
$\widehat{X}_{k}$
, generalizing the first paragraph of the proof of Theorem 2.3.
Lemma 3.4. Let
![]() $\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+}$
be a non-increasing continuous function, and let
$\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+}$
be a non-increasing continuous function, and let
![]() $z=z_{\unicode[STIX]{x1D713}}$
be the function associated to
$z=z_{\unicode[STIX]{x1D713}}$
be the function associated to
![]() $\unicode[STIX]{x1D713}$
by Lemma 3.1. The pair
$\unicode[STIX]{x1D713}$
by Lemma 3.1. The pair
![]() $(A,\mathbf{b})$
is in
$(A,\mathbf{b})$
is in
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
if and only if
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
if and only if
![]() $\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,b})<z_{\unicode[STIX]{x1D713}}(t)$
for all sufficiently large
$\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,b})<z_{\unicode[STIX]{x1D713}}(t)$
for all sufficiently large
![]() $t$
.
$t$
.
Proof. We argue as in the proof of Lemma 2.2. Since
![]() $t\mapsto t+nz(t)$
is increasing and unbounded,
$t\mapsto t+nz(t)$
is increasing and unbounded,
![]() $(A,\mathbf{b})\in \widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
if and only if for all large enough
$(A,\mathbf{b})\in \widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
if and only if for all large enough
![]() $t$
we have
$t$
we have
for some
![]() $\mathbf{q}\in \mathbb{Z}^{n}$
,
$\mathbf{q}\in \mathbb{Z}^{n}$
,
![]() $\mathbf{p}\in \mathbb{Z}^{m}$
. This is the same as the solvability of
$\mathbf{p}\in \mathbb{Z}^{m}$
. This is the same as the solvability of
which is the same as
![]() $\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})<z_{\unicode[STIX]{x1D713}}(t)$
.◻
$\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})<z_{\unicode[STIX]{x1D713}}(t)$
.◻
Thus a pair fails to be
![]() $\unicode[STIX]{x1D713}$
-Dirichlet if and only if the associated grid visits the ‘target’
$\unicode[STIX]{x1D713}$
-Dirichlet if and only if the associated grid visits the ‘target’
![]() $\unicode[STIX]{x1D6E5}^{-1}([z_{\unicode[STIX]{x1D713}}(t),\infty ))$
at unbounded times
$\unicode[STIX]{x1D6E5}^{-1}([z_{\unicode[STIX]{x1D713}}(t),\infty ))$
at unbounded times
![]() $t$
under the flow
$t$
under the flow
![]() $g_{t}$
. This is known as a ‘shrinking target phenomenon’. Our next goal is to recast condition (1.6) using the function
$g_{t}$
. This is known as a ‘shrinking target phenomenon’. Our next goal is to recast condition (1.6) using the function
![]() $z_{\unicode[STIX]{x1D713}}$
.
$z_{\unicode[STIX]{x1D713}}$
.
Lemma 3.5. Let
![]() $\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+},T_{0}\geqslant 0$
, be a non-increasing continuous function, and
$\unicode[STIX]{x1D713}:[T_{0},\infty )\rightarrow \mathbb{R}_{+},T_{0}\geqslant 0$
, be a non-increasing continuous function, and
![]() $z=z_{\unicode[STIX]{x1D713}}$
the function associated to
$z=z_{\unicode[STIX]{x1D713}}$
the function associated to
![]() $\unicode[STIX]{x1D713}$
by Lemma 3.1. Then we have
$\unicode[STIX]{x1D713}$
by Lemma 3.1. Then we have
Proof. We follow the lines of the proof of [Reference Kleinbock and MargulisKM99, Lemma 8.3]. Using the monotonicity of
![]() $\unicode[STIX]{x1D713}$
and Remark 3.3, we may replace the sums with integrals
$\unicode[STIX]{x1D713}$
and Remark 3.3, we may replace the sums with integrals
respectively. Define
Since
![]() $\unicode[STIX]{x1D713}(e^{\unicode[STIX]{x1D706}})=e^{-P(\unicode[STIX]{x1D706})}$
, we have
$\unicode[STIX]{x1D713}(e^{\unicode[STIX]{x1D706}})=e^{-P(\unicode[STIX]{x1D706})}$
, we have
Using
![]() $P(\unicode[STIX]{x1D706}(t))=t-mz(t)$
, we also have
$P(\unicode[STIX]{x1D706}(t))=t-mz(t)$
, we also have
 $$\begin{eqnarray}\displaystyle \int _{t_{0}}^{\infty }e^{-(m+n)z(t)}\,dt & = & \displaystyle \int _{\log T_{0}}^{\infty }e^{-(m+n)z(m\unicode[STIX]{x1D706}/(m+n)+nP(\unicode[STIX]{x1D706})/(m+n))}\,d\biggl[\frac{m}{m+n}\unicode[STIX]{x1D706}+\frac{n}{m+n}P(\unicode[STIX]{x1D706})\biggr]\nonumber\\ \displaystyle & = & \displaystyle \frac{m}{m+n}\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}+\frac{n}{m+n}\int _{\log T_{0}}^{\infty }e^{-\unicode[STIX]{x1D706}}e^{P(\unicode[STIX]{x1D706})}\,dP(\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle \frac{m}{m+n}\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}+\frac{n}{m+n}\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n}{m+n}\Bigl(\lim _{\unicode[STIX]{x1D706}\rightarrow \infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}-1\Bigr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{t_{0}}^{\infty }e^{-(m+n)z(t)}\,dt & = & \displaystyle \int _{\log T_{0}}^{\infty }e^{-(m+n)z(m\unicode[STIX]{x1D706}/(m+n)+nP(\unicode[STIX]{x1D706})/(m+n))}\,d\biggl[\frac{m}{m+n}\unicode[STIX]{x1D706}+\frac{n}{m+n}P(\unicode[STIX]{x1D706})\biggr]\nonumber\\ \displaystyle & = & \displaystyle \frac{m}{m+n}\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}+\frac{n}{m+n}\int _{\log T_{0}}^{\infty }e^{-\unicode[STIX]{x1D706}}e^{P(\unicode[STIX]{x1D706})}\,dP(\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle \frac{m}{m+n}\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}+\frac{n}{m+n}\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n}{m+n}\Bigl(\lim _{\unicode[STIX]{x1D706}\rightarrow \infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}-1\Bigr),\nonumber\end{eqnarray}$$
where we integrated by parts in the last line. Since all these quantities (aside from the constant
![]() $-1$
) are positive, the convergence of
$-1$
) are positive, the convergence of
![]() $\int _{t_{0}}^{\infty }e^{-(m+n)z(t)}\,dt$
implies the convergence of
$\int _{t_{0}}^{\infty }e^{-(m+n)z(t)}\,dt$
implies the convergence of
![]() $\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}$
. Conversely, suppose
$\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}$
. Conversely, suppose
![]() $\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}$
converges, yet
$\int _{\log T_{0}}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}$
converges, yet
![]() $\int _{t_{0}}^{\infty }e^{-(m+n)z(t)}\,dt$
diverges. Then since
$\int _{t_{0}}^{\infty }e^{-(m+n)z(t)}\,dt$
diverges. Then since
![]() $u\mapsto \int _{t_{0}}^{u}e^{(m+n)z(t)}\,dt$
is increasing in
$u\mapsto \int _{t_{0}}^{u}e^{(m+n)z(t)}\,dt$
is increasing in
![]() $u$
, and the first two terms of the sum above converge, we must have
$u$
, and the first two terms of the sum above converge, we must have
![]() $e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}$
eventually increasing in
$e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}$
eventually increasing in
![]() $\unicode[STIX]{x1D706}$
(recall that
$\unicode[STIX]{x1D706}$
(recall that
![]() $\unicode[STIX]{x1D706}$
is an increasing and unbounded function). But this contradicts the convergence of
$\unicode[STIX]{x1D706}$
is an increasing and unbounded function). But this contradicts the convergence of
![]() $\int _{\log (T_{0})}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}$
.◻
$\int _{\log (T_{0})}^{\infty }e^{P(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D706}}\,d\unicode[STIX]{x1D706}$
.◻
Now we are ready to reduce Theorem 1.6 to the following statement concerning dynamics on
![]() $\widehat{X}_{k}$
.
$\widehat{X}_{k}$
.
Theorem 3.6. Fix
![]() $k\in \mathbb{N}$
and let
$k\in \mathbb{N}$
and let
![]() $\{g_{t}:t\in \mathbb{R}\}$
be a diagonalizable unbounded one-parameter subgroup of
$\{g_{t}:t\in \mathbb{R}\}$
be a diagonalizable unbounded one-parameter subgroup of
![]() $G_{k}$
. Also take an arbitrary sequence
$G_{k}$
. Also take an arbitrary sequence
![]() $\{z(t):t\in \mathbb{N}\}$
of real numbers. Then the set
$\{z(t):t\in \mathbb{N}\}$
of real numbers. Then the set
is null (respectively, conull) if the sum
converges (respectively, diverges).
Proof of Theorem 1.6 assuming Theorem 3.6.
Suppose that the series (1.6) converges, and take
![]() $z(t)=z_{\unicode[STIX]{x1D713}}(t)$
, the function associated to
$z(t)=z_{\unicode[STIX]{x1D713}}(t)$
, the function associated to
![]() $\unicode[STIX]{x1D713}$
by Lemma 3.1. In view of Lemma 3.5, the series (3.2) converges as well. In particular, it follows that
$\unicode[STIX]{x1D713}$
by Lemma 3.1. In view of Lemma 3.5, the series (3.2) converges as well. In particular, it follows that
![]() $z(t)\geqslant 0$
for all large enough
$z(t)\geqslant 0$
for all large enough
![]() $t\in \mathbb{N}$
, and also that
$t\in \mathbb{N}$
, and also that
![]() $\sum _{t=1}^{\infty }e^{-k(z(t)-C)}<\infty$
for any
$\sum _{t=1}^{\infty }e^{-k(z(t)-C)}<\infty$
for any
![]() $C>0$
. Take
$C>0$
. Take
![]() $g_{t}$
as in (2.1); Theorem 3.6 then implies that
$g_{t}$
as in (2.1); Theorem 3.6 then implies that
Suppose that the Lebesgue measure of
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})^{c}$
is positive. Lemma 3.4 asserts that there exists a set
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})^{c}$
is positive. Lemma 3.4 asserts that there exists a set
![]() $U$
of positive measure consisting of pairs
$U$
of positive measure consisting of pairs
![]() $(A,\mathbf{b})$
for which
$(A,\mathbf{b})$
for which
![]() $\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})\geqslant z(t)$
for an unbounded set of
$\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})\geqslant z(t)$
for an unbounded set of
![]() $t\geqslant 0$
. Then, using
$t\geqslant 0$
. Then, using
![]() $z(t)\geqslant 0$
and Lemma 2.1, we can replace
$z(t)\geqslant 0$
and Lemma 2.1, we can replace
![]() $t$
with its integer part:
$t$
with its integer part:
where
![]() $c$
is a positive constant and the last inequality follows from Remark 3.3. Therefore we get
$c$
is a positive constant and the last inequality follows from Remark 3.3. Therefore we get
![]() $\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})\geqslant z(t)-c-1/m$
for an unbounded set of
$\unicode[STIX]{x1D6E5}(g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})\geqslant z(t)-c-1/m$
for an unbounded set of
![]() $t\in \mathbb{N}$
as long as
$t\in \mathbb{N}$
as long as
![]() $(A,\mathbf{b})\in U$
.
$(A,\mathbf{b})\in U$
.
Now recall the groups
![]() $H$
and
$H$
and
![]() $\tilde{H}$
from Equations (2.2) and (2.3). As in the proof of Proposition 2.3, we may identify
$\tilde{H}$
from Equations (2.2) and (2.3). As in the proof of Proposition 2.3, we may identify
![]() $U$
with a subset of
$U$
with a subset of
![]() $H$
and, using the uniform continuity of
$H$
and, using the uniform continuity of
![]() $\unicode[STIX]{x1D6E5}$
(Lemma 2.1), find a neighborhood of identity
$\unicode[STIX]{x1D6E5}$
(Lemma 2.1), find a neighborhood of identity
![]() $V\subset \tilde{H}$
such that, for all
$V\subset \tilde{H}$
such that, for all
![]() $g\in V$
and
$g\in V$
and
![]() $(A,\mathbf{b})\in U$
,
$(A,\mathbf{b})\in U$
,
for all
![]() $t\geqslant 0$
, hence
$t\geqslant 0$
, hence
![]() $\unicode[STIX]{x1D6E5}(g_{t}g\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})\geqslant z(t)-1-c-1/m$
for an unbounded set of
$\unicode[STIX]{x1D6E5}(g_{t}g\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})\geqslant z(t)-1-c-1/m$
for an unbounded set of
![]() $t\in \mathbb{N}$
. Since the product map
$t\in \mathbb{N}$
. Since the product map
![]() $\tilde{H}\times H\rightarrow \widehat{G}_{k}$
is a local diffeomorphism, the image of
$\tilde{H}\times H\rightarrow \widehat{G}_{k}$
is a local diffeomorphism, the image of
![]() $V\times U$
is a set of positive measure in
$V\times U$
is a set of positive measure in
![]() $G_{k}$
, contradicting (3.3).
$G_{k}$
, contradicting (3.3).
The proof of the divergence case proceeds along the same lines. If (1.6) diverges, by Lemma 3.5 so does (3.2). Define
![]() $z^{\prime }(t):=\max (z(t),0)$
; then we have
$z^{\prime }(t):=\max (z(t),0)$
; then we have
![]() $\sum _{t=1}^{\infty }e^{-k(z^{\prime }(t))}=\infty$
as well, therefore
$\sum _{t=1}^{\infty }e^{-k(z^{\prime }(t))}=\infty$
as well, therefore
![]() $\sum _{t=1}^{\infty }e^{-k(z^{\prime }(t)+C)}=\infty$
for any
$\sum _{t=1}^{\infty }e^{-k(z^{\prime }(t)+C)}=\infty$
for any
![]() $C>0$
. In view of Theorem 3.6,
$C>0$
. In view of Theorem 3.6,
Now assume that the set
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has positive measure. Then using Lemma 3.4, one can choose a set
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has positive measure. Then using Lemma 3.4, one can choose a set
![]() $U$
of positive measure consisting of pairs
$U$
of positive measure consisting of pairs
![]() $(A,\mathbf{b})$
for which
$(A,\mathbf{b})$
for which
for all large enough
![]() $t$
. Then, as before, using Lemma 2.1 with
$t$
. Then, as before, using Lemma 2.1 with
![]() $z=0$
and (2.4), one finds a neighborhood of identity
$z=0$
and (2.4), one finds a neighborhood of identity
![]() $V\subset \tilde{H}$
such that for all
$V\subset \tilde{H}$
such that for all
![]() $g\in V$
and
$g\in V$
and
![]() $(A,\mathbf{b})\in U$
,
$(A,\mathbf{b})\in U$
,
for all
![]() $t\geqslant 0$
; hence
$t\geqslant 0$
; hence
![]() $\unicode[STIX]{x1D6E5}(g_{t}g\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})<z^{\prime }(t)+1$
for all large enough
$\unicode[STIX]{x1D6E5}(g_{t}g\unicode[STIX]{x1D6EC}_{A,\mathbf{b}})<z^{\prime }(t)+1$
for all large enough
![]() $t$
. Again using the local product structure of
$t$
. Again using the local product structure of
![]() $\widehat{G}_{k}$
, one concludes that the image of
$\widehat{G}_{k}$
, one concludes that the image of
![]() $V\times U$
in
$V\times U$
in
![]() $\widehat{X}_{k}$
is a set of positive measure, contradicting (3.4).◻
$\widehat{X}_{k}$
is a set of positive measure, contradicting (3.4).◻
We are now left with the task of proving Theorem 3.6. The proof will have two ingredients. In the next section we will establish a dynamical Borel–Cantelli lemma (Theorem 4.4) showing that the limsup set (3.1) is null or conull according to the convergence or divergence of the series
The proof is based on the methods of [Reference Kleinbock and MargulisKM99, Reference Kleinbock and MargulisKM18]; namely, it uses the exponential mixing of the
![]() $g_{t}$
-action on
$g_{t}$
-action on
![]() $\widehat{X}_{k}$
, as well as the so-called DL property of
$\widehat{X}_{k}$
, as well as the so-called DL property of
![]() $\unicode[STIX]{x1D6E5}$
. The latter will be established in § 6. Moreover, there we will relate (3.2) and (3.5) by showing that the summands in (3.5) are equal to
$\unicode[STIX]{x1D6E5}$
. The latter will be established in § 6. Moreover, there we will relate (3.2) and (3.5) by showing that the summands in (3.5) are equal to
![]() $e^{-kz(t)}$
up to a constant (Theorem 4.6).
$e^{-kz(t)}$
up to a constant (Theorem 4.6).
4 A general dynamical Borel–Cantelli lemma and exponential mixing
In this section we let
![]() $G$
be a Lie group and
$G$
be a Lie group and
![]() $\unicode[STIX]{x1D6E4}$
a lattice in
$\unicode[STIX]{x1D6E4}$
a lattice in
![]() $G$
. Denote by
$G$
. Denote by
![]() $X$
the homogeneous space
$X$
the homogeneous space
![]() $G/\unicode[STIX]{x1D6E4}$
and by
$G/\unicode[STIX]{x1D6E4}$
and by
![]() $\unicode[STIX]{x1D707}$
the
$\unicode[STIX]{x1D707}$
the
![]() $G$
-invariant probability measure on
$G$
-invariant probability measure on
![]() $X$
. In what follows,
$X$
. In what follows,
![]() $\Vert \cdot \Vert _{p}$
will stand for the
$\Vert \cdot \Vert _{p}$
will stand for the
![]() $L^{p}$
-norm. Fix a basis
$L^{p}$
-norm. Fix a basis
![]() $\{Y_{1},\ldots ,Y_{n}\}$
for the Lie algebra
$\{Y_{1},\ldots ,Y_{n}\}$
for the Lie algebra
![]() $\mathfrak{g}$
of
$\mathfrak{g}$
of
![]() $G$
, and, given a smooth function
$G$
, and, given a smooth function
![]() $h\in C^{\infty }(X)$
and
$h\in C^{\infty }(X)$
and
![]() $\ell \in \mathbb{Z}_{+}$
, define the ‘
$\ell \in \mathbb{Z}_{+}$
, define the ‘
![]() $L^{2}$
, order
$L^{2}$
, order
![]() $\ell$
’ Sobolev norm
$\ell$
’ Sobolev norm
![]() $\Vert h\Vert _{2,\ell }$
of
$\Vert h\Vert _{2,\ell }$
of
![]() $h$
by
$h$
by
where
![]() $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
is a multi-index,
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
is a multi-index,
![]() $|\unicode[STIX]{x1D6FC}|=\sum _{i=1}^{n}\unicode[STIX]{x1D6FC}_{i}$
, and
$|\unicode[STIX]{x1D6FC}|=\sum _{i=1}^{n}\unicode[STIX]{x1D6FC}_{i}$
, and
![]() $D^{\unicode[STIX]{x1D6FC}}$
is a differential operator of order
$D^{\unicode[STIX]{x1D6FC}}$
is a differential operator of order
![]() $|\unicode[STIX]{x1D6FC}|$
which is a monomial in
$|\unicode[STIX]{x1D6FC}|$
which is a monomial in
![]() $Y_{1},\ldots ,Y_{n}$
, namely
$Y_{1},\ldots ,Y_{n}$
, namely
![]() $D^{\unicode[STIX]{x1D6FC}}=Y_{1}^{\unicode[STIX]{x1D6FC}_{1}}\cdots Y_{n}^{\unicode[STIX]{x1D6FC}_{n}}$
. This definition depends on the basis; however, a change of basis would only distort
$D^{\unicode[STIX]{x1D6FC}}=Y_{1}^{\unicode[STIX]{x1D6FC}_{1}}\cdots Y_{n}^{\unicode[STIX]{x1D6FC}_{n}}$
. This definition depends on the basis; however, a change of basis would only distort
![]() $\Vert h\Vert _{2,\ell }$
by a bounded factor. We also let
$\Vert h\Vert _{2,\ell }$
by a bounded factor. We also let
Fix a right-invariant Riemannian metric on
![]() $G$
and the corresponding metric ‘dist’ on
$G$
and the corresponding metric ‘dist’ on
![]() $X$
. For
$X$
. For
![]() $g\in G$
, let us denote by
$g\in G$
, let us denote by
![]() $\Vert g\Vert$
the distance between
$\Vert g\Vert$
the distance between
![]() $g\in G$
and the identity element of
$g\in G$
and the identity element of
![]() $G$
. Note that
$G$
. Note that
![]() $\Vert g\Vert =\Vert g^{-1}\Vert$
due to the right-invariance of the metric.
$\Vert g\Vert =\Vert g^{-1}\Vert$
due to the right-invariance of the metric.
Definition 4.1. Let
![]() $L$
be a subgroup of
$L$
be a subgroup of
![]() $G$
. Say that the
$G$
. Say that the
![]() $L$
-action on
$L$
-action on
![]() $X$
is exponentially mixing if there exist
$X$
is exponentially mixing if there exist
![]() $\unicode[STIX]{x1D6FE},E>0$
and
$\unicode[STIX]{x1D6FE},E>0$
and
![]() $\ell \in \mathbb{Z}_{+}$
such that for any
$\ell \in \mathbb{Z}_{+}$
such that for any
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in C_{2}^{\infty }(X)$
and for any
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in C_{2}^{\infty }(X)$
and for any
![]() $g\in L$
one has
$g\in L$
one has
Here
![]() $\langle \cdot ,\cdot \rangle$
stands for the inner product in
$\langle \cdot ,\cdot \rangle$
stands for the inner product in
![]() $L^{2}(X,\unicode[STIX]{x1D707})$
.
$L^{2}(X,\unicode[STIX]{x1D707})$
.
We also need two more definitions from [Reference Kleinbock and MargulisKM99, Reference Kleinbock and MargulisKM18].
Definition 4.2. A sequence of elements
![]() $\{f_{t}:t\in \mathbb{N}\}$
of elements of
$\{f_{t}:t\in \mathbb{N}\}$
of elements of
![]() $G$
is called exponentially divergent if
$G$
is called exponentially divergent if
Now let
![]() $\unicode[STIX]{x1D6E5}$
be a real-valued function on
$\unicode[STIX]{x1D6E5}$
be a real-valued function on
![]() $X$
, and for
$X$
, and for
![]() $z\in \mathbb{R}$
denote
$z\in \mathbb{R}$
denote
Definition 4.3. Say that
![]() $\unicode[STIX]{x1D6E5}$
is DL (an abbreviation for ‘distance-like’) if there exists
$\unicode[STIX]{x1D6E5}$
is DL (an abbreviation for ‘distance-like’) if there exists
![]() $z_{0}\in \mathbb{R}$
such that
$z_{0}\in \mathbb{R}$
such that
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}(z_{0})>0$
and
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}(z_{0})>0$
and
(a)
 $\unicode[STIX]{x1D6E5}$
is uniformly continuous on
$\unicode[STIX]{x1D6E5}$
is uniformly continuous on
 $\unicode[STIX]{x1D6E5}^{-1}([z_{0},\infty ))$
; that is, for all
$\unicode[STIX]{x1D6E5}^{-1}([z_{0},\infty ))$
; that is, for all
 $\unicode[STIX]{x1D700}>0$
there exists a neighborhood
$\unicode[STIX]{x1D700}>0$
there exists a neighborhood
 $U$
of identity in
$U$
of identity in
 $G$
such that for any
$G$
such that for any
 $x\in X$
with
$x\in X$
with
 $\unicode[STIX]{x1D6E5}(x)\geqslant z_{0}$
,
$\unicode[STIX]{x1D6E5}(x)\geqslant z_{0}$
,  $$\begin{eqnarray}g\in U\quad \Longrightarrow \quad |\unicode[STIX]{x1D6E5}(x)-\unicode[STIX]{x1D6E5}(gx)|<\unicode[STIX]{x1D700};\end{eqnarray}$$
$$\begin{eqnarray}g\in U\quad \Longrightarrow \quad |\unicode[STIX]{x1D6E5}(x)-\unicode[STIX]{x1D6E5}(gx)|<\unicode[STIX]{x1D700};\end{eqnarray}$$
(b) the function
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}$
does not decrease very fast; more precisely, (4.2)
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}$
does not decrease very fast; more precisely, (4.2) $$\begin{eqnarray}\exists \,c,\unicode[STIX]{x1D6FF}>0~\text{such that}~\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}(z)\geqslant c\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}(z-\unicode[STIX]{x1D6FF})\quad \forall \,z\geqslant z_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\exists \,c,\unicode[STIX]{x1D6FF}>0~\text{such that}~\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}(z)\geqslant c\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}(z-\unicode[STIX]{x1D6FF})\quad \forall \,z\geqslant z_{0}.\end{eqnarray}$$
The next theorem is a direct consequence of [Reference Kleinbock and MargulisKM18, Theorem 1.3].
Theorem 4.4. Suppose that the action of a subgroup
![]() $L\subset G$
on
$L\subset G$
on
![]() $X$
is exponentially mixing. Let
$X$
is exponentially mixing. Let
![]() $\{f_{t}:t\in \mathbb{N}\}$
be a sequence of elements of
$\{f_{t}:t\in \mathbb{N}\}$
be a sequence of elements of
![]() $L$
satisfying (4.1), and let
$L$
satisfying (4.1), and let
![]() $\unicode[STIX]{x1D6E5}$
be a DL function on
$\unicode[STIX]{x1D6E5}$
be a DL function on
![]() $X$
. Also let
$X$
. Also let
![]() $\{z(t):t\in \mathbb{N}\}$
be a sequence of real numbers. Then the set
$\{z(t):t\in \mathbb{N}\}$
be a sequence of real numbers. Then the set
is null (respectively, conull) if the sum
converges (respectively, diverges).
Proof. The convergence case is immediate from the classical Borel–Cantelli lemma. The divergence case is established in [Reference Kleinbock and MargulisKM99, Reference Kleinbock and MargulisKM18] for
![]() $L=G$
, but the argument applies verbatim if
$L=G$
, but the argument applies verbatim if
![]() $G$
is replaced by a subgroup.◻
$G$
is replaced by a subgroup.◻
From now on we will take
![]() $k\geqslant 2$
and consider the case
$k\geqslant 2$
and consider the case
![]() $G=\widehat{G}_{k}$
,
$G=\widehat{G}_{k}$
,
![]() $\unicode[STIX]{x1D6E4}=\widehat{\unicode[STIX]{x1D6E4}}_{k}$
,
$\unicode[STIX]{x1D6E4}=\widehat{\unicode[STIX]{x1D6E4}}_{k}$
,
![]() $X=\widehat{X}_{k}$
, and
$X=\widehat{X}_{k}$
, and
![]() $L=G_{k}$
, with notation as in the previous section. Then we have the following theorem.
$L=G_{k}$
, with notation as in the previous section. Then we have the following theorem.
Theorem 4.5. The
![]() $G_{k}$
-action on
$G_{k}$
-action on
![]() $\widehat{X}_{k}=\widehat{G}_{k}/\widehat{\unicode[STIX]{x1D6E4}}_{k}$
is exponentially mixing.
$\widehat{X}_{k}=\widehat{G}_{k}/\widehat{\unicode[STIX]{x1D6E4}}_{k}$
is exponentially mixing.
Proof. According to [Reference Kleinbock and MargulisKM99, Theorem 3.4], exponential mixing holds whenever the regular representation of
![]() $G_{k}$
on the space
$G_{k}$
on the space
![]() $L_{0}^{2}(\widehat{X}_{k})$
(functions in
$L_{0}^{2}(\widehat{X}_{k})$
(functions in
![]() $L^{2}(\widehat{X}_{k})$
with integral zero) is isolated in the Fell topology from the trivial representation. This is immediate if
$L^{2}(\widehat{X}_{k})$
with integral zero) is isolated in the Fell topology from the trivial representation. This is immediate if
![]() $k>2$
since in this case
$k>2$
since in this case
![]() $G_{k}$
has Property (T).
$G_{k}$
has Property (T).
If
![]() $k=2$
, let us write
$k=2$
, let us write
![]() $L_{0}^{2}(\widehat{X}_{2})$
as a direct sum of two spaces: functions invariant under the action of
$L_{0}^{2}(\widehat{X}_{2})$
as a direct sum of two spaces: functions invariant under the action of
![]() $\mathbb{R}^{2}$
by translations, and its orthogonal complement. The first representation is isomorphic to the regular representation of
$\mathbb{R}^{2}$
by translations, and its orthogonal complement. The first representation is isomorphic to the regular representation of
![]() $\operatorname{SL}_{2}(\mathbb{R})$
on
$\operatorname{SL}_{2}(\mathbb{R})$
on
![]() $L_{0}^{2}(\operatorname{SL}_{2}(\mathbb{R})/\operatorname{SL}_{2}(\mathbb{Z}))$
, which is isolated from the trivial representation by [Reference Kleinbock and MargulisKM99, Theorem 1.12]. As for the second component, one can use [Reference Howe and TanHT92, Theorem V.3.3.1] (see also [Reference Ghosh, Gorodnik and NevoGGN18, Theorem 4.3]) which asserts that for any unitary representation
$L_{0}^{2}(\operatorname{SL}_{2}(\mathbb{R})/\operatorname{SL}_{2}(\mathbb{Z}))$
, which is isolated from the trivial representation by [Reference Kleinbock and MargulisKM99, Theorem 1.12]. As for the second component, one can use [Reference Howe and TanHT92, Theorem V.3.3.1] (see also [Reference Ghosh, Gorodnik and NevoGGN18, Theorem 4.3]) which asserts that for any unitary representation
![]() $(\unicode[STIX]{x1D70C},V)$
of
$(\unicode[STIX]{x1D70C},V)$
of
![]() $\operatorname{ASL}_{2}(\mathbb{R})$
with no non-zero vectors fixed by
$\operatorname{ASL}_{2}(\mathbb{R})$
with no non-zero vectors fixed by
![]() $\mathbb{R}^{2}$
, the restriction of
$\mathbb{R}^{2}$
, the restriction of
![]() $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
![]() $\operatorname{SL}_{2}(\mathbb{R})$
is tempered, that is, there exists a dense set of vectors in
$\operatorname{SL}_{2}(\mathbb{R})$
is tempered, that is, there exists a dense set of vectors in
![]() $V$
whose matrix coefficients are in
$V$
whose matrix coefficients are in
![]() $L^{2+\unicode[STIX]{x1D700}}$
for any
$L^{2+\unicode[STIX]{x1D700}}$
for any
![]() $\unicode[STIX]{x1D700}>0$
. Exponential mixing thus follows from [Reference Katok and SpatzierKS94, Theorem 3.1], which establishes exponential decay of matrix coefficients of strongly
$\unicode[STIX]{x1D700}>0$
. Exponential mixing thus follows from [Reference Katok and SpatzierKS94, Theorem 3.1], which establishes exponential decay of matrix coefficients of strongly
![]() $L^{p}$
irreducible unitary representations of connected semisimple centerfree Lie groups. See also the preprint [Reference EdwardsEdw13] for more precise estimates.◻
$L^{p}$
irreducible unitary representations of connected semisimple centerfree Lie groups. See also the preprint [Reference EdwardsEdw13] for more precise estimates.◻
Now let
![]() $\unicode[STIX]{x1D6E5}$
be the function on
$\unicode[STIX]{x1D6E5}$
be the function on
![]() $\widehat{X}_{k}$
defined by (2.6). In the next section we will establish the following two-sided estimate for the measure of super-level sets of
$\widehat{X}_{k}$
defined by (2.6). In the next section we will establish the following two-sided estimate for the measure of super-level sets of
![]() $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
Theorem 4.6. For any
![]() $k\geqslant 2$
there exist
$k\geqslant 2$
there exist
![]() $c,C>0$
such that
$c,C>0$
such that
This is all one needs to settle Theorem 3.6.
Proof of Theorem 3.6 modulo Theorem 4.6.
Let
![]() $\{g_{t}:t\in \mathbb{R}\}$
be a diagonalizable unbounded one-parameter subgroup of
$\{g_{t}:t\in \mathbb{R}\}$
be a diagonalizable unbounded one-parameter subgroup of
![]() $G_{k}$
. By Theorem 4.5, the action of
$G_{k}$
. By Theorem 4.5, the action of
![]() $G_{k}$
on
$G_{k}$
on
![]() $\widehat{X}_{k}$
is exponentially mixing. Observe also that one has
$\widehat{X}_{k}$
is exponentially mixing. Observe also that one has
![]() $\Vert g_{t}\Vert \geqslant \unicode[STIX]{x1D6FC}t$
for some
$\Vert g_{t}\Vert \geqslant \unicode[STIX]{x1D6FC}t$
for some
![]() $\unicode[STIX]{x1D6FC}>0$
, which immediately implies (4.1). It is easy to see that (4.5) implies (4.2) with
$\unicode[STIX]{x1D6FC}>0$
, which immediately implies (4.1). It is easy to see that (4.5) implies (4.2) with
![]() $z_{0}=0$
, and part (a) of Definition 4.3 is given by Lemma 2.1. The conditions of Theorem 4.4 are therefore met, and Theorem 3.6 follows. ◻
$z_{0}=0$
, and part (a) of Definition 4.3 is given by Lemma 2.1. The conditions of Theorem 4.4 are therefore met, and Theorem 3.6 follows. ◻
5
 $\unicode[STIX]{x1D6E5}$
is distance-like: a warm-up
$\unicode[STIX]{x1D6E5}$
is distance-like: a warm-up
For the rest of the paper we keep the notation
and let
![]() $\unicode[STIX]{x1D707}$
(respectively,
$\unicode[STIX]{x1D707}$
(respectively,
![]() $\widehat{\unicode[STIX]{x1D707}}$
) be the Haar probability measure on
$\widehat{\unicode[STIX]{x1D707}}$
) be the Haar probability measure on
![]() $X$
(respectively,
$X$
(respectively,
![]() $\widehat{X}$
). We denote by
$\widehat{X}$
). We denote by
![]() $\unicode[STIX]{x1D707}_{G}$
and
$\unicode[STIX]{x1D707}_{G}$
and
![]() $\unicode[STIX]{x1D707}_{\widehat{G}}$
the left-invariant Haar measures on
$\unicode[STIX]{x1D707}_{\widehat{G}}$
the left-invariant Haar measures on
![]() $G$
and
$G$
and
![]() $\widehat{G}$
, respectively, which are locally pushed forward to
$\widehat{G}$
, respectively, which are locally pushed forward to
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $\widehat{\unicode[STIX]{x1D707}}$
.
$\widehat{\unicode[STIX]{x1D707}}$
.
Recall that
where for
![]() $\mathbf{v}\in \mathbb{R}^{k}$
and
$\mathbf{v}\in \mathbb{R}^{k}$
and
![]() $r\geqslant 0$
we let
$r\geqslant 0$
we let
![]() $B(\mathbf{v},r)$
be the open ball in
$B(\mathbf{v},r)$
be the open ball in
![]() $\mathbb{R}^{k}$
centered at
$\mathbb{R}^{k}$
centered at
![]() $\mathbf{v}$
of radius
$\mathbf{v}$
of radius
![]() $r$
with respect to the supremum norm. It will be convenient to write
$r$
with respect to the supremum norm. It will be convenient to write
Our goal is thus to prove that
where
![]() $c,C$
are constants dependent only on
$c,C$
are constants dependent only on
![]() $k$
.
$k$
.
First let us discuss the upper bound. It is in fact a special case of a recent result due to Athreya, namely a random Minkowski-type theorem for the space of grids [Reference AthreyaAth15, Theorem 1].
Proposition 5.1 (Athreya).
For a measurable
![]() $E\subset \mathbb{R}^{k}$
,
$E\subset \mathbb{R}^{k}$
,
Here and hereafter
![]() $\unicode[STIX]{x1D706}$
stands for Lebesgue measure on
$\unicode[STIX]{x1D706}$
stands for Lebesgue measure on
![]() $\mathbb{R}^{k}$
. Taking
$\mathbb{R}^{k}$
. Taking
![]() $E=B(0,r)$
shows that
$E=B(0,r)$
shows that
![]() $\widehat{\unicode[STIX]{x1D707}}(S_{r})<2^{-k}r^{-k}$
. Thus it only remains to establish a lower bound in (5.1).
$\widehat{\unicode[STIX]{x1D707}}(S_{r})<2^{-k}r^{-k}$
. Thus it only remains to establish a lower bound in (5.1).
There exists an obvious projection,
![]() $\unicode[STIX]{x1D70B}:\widehat{X}\rightarrow X$
, making
$\unicode[STIX]{x1D70B}:\widehat{X}\rightarrow X$
, making
![]() $\widehat{X}$
into a
$\widehat{X}$
into a
![]() $\mathbb{T}^{k}$
-bundle over
$\mathbb{T}^{k}$
-bundle over
![]() $X$
(
$X$
(
![]() $\unicode[STIX]{x1D70B}$
simply translates one of the vectors in a grid to the origin). It is easy to see that
$\unicode[STIX]{x1D70B}$
simply translates one of the vectors in a grid to the origin). It is easy to see that
![]() $\unicode[STIX]{x1D707}_{\widehat{G}}$
is the product of
$\unicode[STIX]{x1D707}_{\widehat{G}}$
is the product of
![]() $\unicode[STIX]{x1D707}_{G}$
and
$\unicode[STIX]{x1D707}_{G}$
and
![]() $\unicode[STIX]{x1D706}$
. Therefore one has the following Fubini formula:
$\unicode[STIX]{x1D706}$
. Therefore one has the following Fubini formula:
Here, for
![]() $\unicode[STIX]{x1D6EC}\in X$
,
$\unicode[STIX]{x1D6EC}\in X$
,
![]() $\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6EC})$
is identified with
$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6EC})$
is identified with
![]() $\mathbb{R}^{k}/\unicode[STIX]{x1D6EC}$
via
$\mathbb{R}^{k}/\unicode[STIX]{x1D6EC}$
via
and, in the hope that it will not cause any confusion, we will let
![]() $\unicode[STIX]{x1D706}$
stand for the normalized Haar measure on
$\unicode[STIX]{x1D706}$
stand for the normalized Haar measure on
![]() $\mathbb{R}^{k}/\unicode[STIX]{x1D6EC}$
for any
$\mathbb{R}^{k}/\unicode[STIX]{x1D6EC}$
for any
![]() $\unicode[STIX]{x1D6EC}\in X$
. Writing
$\unicode[STIX]{x1D6EC}\in X$
. Writing
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}}$
for the projection
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}}$
for the projection
![]() $\mathbb{R}^{k}\rightarrow \mathbb{R}^{k}/\unicode[STIX]{x1D6EC}$
, we have
$\mathbb{R}^{k}\rightarrow \mathbb{R}^{k}/\unicode[STIX]{x1D6EC}$
, we have
 $$\begin{eqnarray}\displaystyle S(r)\cap \unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6EC}) & = & \displaystyle \{[\mathbf{v}]\in \mathbb{R}^{k}/\unicode[STIX]{x1D6EC}:B(0,r)\cap (\unicode[STIX]{x1D6EC}-\mathbf{v})=\varnothing \}\nonumber\\ \displaystyle & = & \displaystyle \{[\mathbf{v}]\in \mathbb{R}^{k}/\unicode[STIX]{x1D6EC}:B(\mathbf{v},r)\cap \unicode[STIX]{x1D6EC}=\varnothing \}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}}\bigg(\mathbb{R}^{k}\smallsetminus \mathop{\bigcup }_{\mathbf{v}\in \unicode[STIX]{x1D6EC}}B(\mathbf{v},r)\bigg),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(r)\cap \unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6EC}) & = & \displaystyle \{[\mathbf{v}]\in \mathbb{R}^{k}/\unicode[STIX]{x1D6EC}:B(0,r)\cap (\unicode[STIX]{x1D6EC}-\mathbf{v})=\varnothing \}\nonumber\\ \displaystyle & = & \displaystyle \{[\mathbf{v}]\in \mathbb{R}^{k}/\unicode[STIX]{x1D6EC}:B(\mathbf{v},r)\cap \unicode[STIX]{x1D6EC}=\varnothing \}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}}\bigg(\mathbb{R}^{k}\smallsetminus \mathop{\bigcup }_{\mathbf{v}\in \unicode[STIX]{x1D6EC}}B(\mathbf{v},r)\bigg),\end{eqnarray}$$
so that
![]() $Q(\unicode[STIX]{x1D6EC},r)$
is the area of a region in a fundamental domain (parallelepiped) in
$Q(\unicode[STIX]{x1D6EC},r)$
is the area of a region in a fundamental domain (parallelepiped) in
![]() $\mathbb{R}^{k}$
for
$\mathbb{R}^{k}$
for
![]() $\unicode[STIX]{x1D6EC}$
consisting of points which are farther than
$\unicode[STIX]{x1D6EC}$
consisting of points which are farther than
![]() $r$
from its vertices, that is, from all points of
$r$
from its vertices, that is, from all points of
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Recall that
![]() $\operatorname{SL}_{2}(\mathbb{R})$
double-covers the unit tangent bundle of the hyperbolic upper-half plane,
$\operatorname{SL}_{2}(\mathbb{R})$
double-covers the unit tangent bundle of the hyperbolic upper-half plane,
![]() $\mathbb{H}^{2}$
. Since the action of
$\mathbb{H}^{2}$
. Since the action of
![]() $\operatorname{SL}_{2}(\mathbb{Z})$
on
$\operatorname{SL}_{2}(\mathbb{Z})$
on
![]() $\mathbb{H}^{2}$
has a convenient fundamental domain, there are convenient coordinates for a set of full measure in
$\mathbb{H}^{2}$
has a convenient fundamental domain, there are convenient coordinates for a set of full measure in
![]() $\operatorname{SL}_{2}(\mathbb{R})/\operatorname{SL}_{2}(\mathbb{Z})$
. This enables us to give a rather tidy proof for the two-dimensional case of (5.1), handling both bounds simultaneously without using Proposition 5.1. This proof also illustrates the main idea necessary to proving the lower bound in the general case. We therefore start with a separate, redundant proof of the two-dimensional case.
$\operatorname{SL}_{2}(\mathbb{R})/\operatorname{SL}_{2}(\mathbb{Z})$
. This enables us to give a rather tidy proof for the two-dimensional case of (5.1), handling both bounds simultaneously without using Proposition 5.1. This proof also illustrates the main idea necessary to proving the lower bound in the general case. We therefore start with a separate, redundant proof of the two-dimensional case.
Proof of (5.1) for
 $k=2$
.
$k=2$
.
For fixed
![]() $r$
, consider the map
$r$
, consider the map
![]() $(\unicode[STIX]{x1D705},n,a)\mapsto Q(\unicode[STIX]{x1D705}na\mathbb{Z}^{2},r)$
, whose domain is
$(\unicode[STIX]{x1D705},n,a)\mapsto Q(\unicode[STIX]{x1D705}na\mathbb{Z}^{2},r)$
, whose domain is
![]() $K\times N\times A$
, the Iwasawa decomposition for
$K\times N\times A$
, the Iwasawa decomposition for
![]() $G=\operatorname{SL}_{2}(\mathbb{R})$
. (Here
$G=\operatorname{SL}_{2}(\mathbb{R})$
. (Here
![]() $K$
,
$K$
,
![]() $N$
,
$N$
,
![]() $A$
are the groups of orthogonal, upper-triangular unipotent, and diagonal matrices respectively.) We first show that a change of
$A$
are the groups of orthogonal, upper-triangular unipotent, and diagonal matrices respectively.) We first show that a change of
![]() $\unicode[STIX]{x1D705}$
does not significantly change the value of
$\unicode[STIX]{x1D705}$
does not significantly change the value of
![]() $Q$
. Indeed, since rotation perturbs the sup norm by no more than a factor of
$Q$
. Indeed, since rotation perturbs the sup norm by no more than a factor of
![]() $\sqrt{2}$
, for any
$\sqrt{2}$
, for any
![]() $\unicode[STIX]{x1D705}\in K$
and
$\unicode[STIX]{x1D705}\in K$
and
![]() $\mathbf{x},\mathbf{y}\in \mathbb{R}^{2}$
we have
$\mathbf{x},\mathbf{y}\in \mathbb{R}^{2}$
we have
hence
By (5.4), this implies
Let
![]() $a=\operatorname{diag}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{-1})$
. If
$a=\operatorname{diag}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{-1})$
. If
then the lattice
![]() $na\mathbb{Z}^{2}$
consists of horizontal rows of vectors, each closer than
$na\mathbb{Z}^{2}$
consists of horizontal rows of vectors, each closer than
![]() $2r$
to its horizontal neighbors. Thus the boxes making up the union
$2r$
to its horizontal neighbors. Thus the boxes making up the union
![]() $\bigcup _{\mathbf{v}\in na\mathbb{Z}^{2}}B(\mathbf{v},r)$
overlap in the horizontal direction, creating horizontal strips. Thus, by (5.4),
$\bigcup _{\mathbf{v}\in na\mathbb{Z}^{2}}B(\mathbf{v},r)$
overlap in the horizontal direction, creating horizontal strips. Thus, by (5.4),
![]() $Q(na\mathbb{Z}^{2},r)$
is just the area of the fundamental parallelogram
$Q(na\mathbb{Z}^{2},r)$
is just the area of the fundamental parallelogram
![]() $na(I\times I)$
minus the strips on top and bottom, as in the following figure.
$na(I\times I)$
minus the strips on top and bottom, as in the following figure.

This smaller parallelogram has area
![]() $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}^{-1}-2r)$
, provided it is non-empty, that is, provided
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}^{-1}-2r)$
, provided it is non-empty, that is, provided
![]() $2r\leqslant \unicode[STIX]{x1D6FC}^{-1}$
. Thus from (5.5), if
$2r\leqslant \unicode[STIX]{x1D6FC}^{-1}$
. Thus from (5.5), if
![]() $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D705}na\mathbb{Z}^{2}$
, where
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D705}na\mathbb{Z}^{2}$
, where
![]() $a=\operatorname{diag}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{-1})$
, we have
$a=\operatorname{diag}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{-1})$
, we have
Then if
![]() $\sqrt{2}r>\unicode[STIX]{x1D6FC}$
(so that (5.6) holds for
$\sqrt{2}r>\unicode[STIX]{x1D6FC}$
(so that (5.6) holds for
![]() $na\mathbb{Z}^{2}$
, after adjusting
$na\mathbb{Z}^{2}$
, after adjusting
![]() $r$
as above), we have
$r$
as above), we have
We now identify
![]() $X_{2}$
with
$X_{2}$
with
![]() $\operatorname{SL}_{2}(\mathbb{Z})\backslash T^{1}(\mathbb{H}^{2})$
via
$\operatorname{SL}_{2}(\mathbb{Z})\backslash T^{1}(\mathbb{H}^{2})$
via
![]() $g\mathbb{Z}^{2}\mapsto g^{-1}(i,i)$
(here, the matrix
$g\mathbb{Z}^{2}\mapsto g^{-1}(i,i)$
(here, the matrix
![]() $g^{-1}$
acts on
$g^{-1}$
acts on
![]() $(i,i)$
as a fractional-linear transformation). Recall that
$(i,i)$
as a fractional-linear transformation). Recall that
is a fundamental domain for the action of
![]() $\operatorname{SL}_{2}(\mathbb{Z})$
on
$\operatorname{SL}_{2}(\mathbb{Z})$
on
![]() $T^{1}(\mathbb{H}^{2})$
. Under the correspondence
$T^{1}(\mathbb{H}^{2})$
. Under the correspondence
![]() $g^{-1}(i,i)\mapsto g\mathbb{Z}^{2}$
, a point
$g^{-1}(i,i)\mapsto g\mathbb{Z}^{2}$
, a point
![]() $(z,\unicode[STIX]{x1D703})\in F$
maps to a lattice
$(z,\unicode[STIX]{x1D703})\in F$
maps to a lattice
![]() $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D705}na\mathbb{Z}^{2}$
with
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D705}na\mathbb{Z}^{2}$
with
![]() $\sqrt{3}/2\leqslant \operatorname{Im}(z)=\unicode[STIX]{x1D6FC}^{-2}$
. Thus if
$\sqrt{3}/2\leqslant \operatorname{Im}(z)=\unicode[STIX]{x1D6FC}^{-2}$
. Thus if
(which ensures that the condition
![]() $\sqrt{2}r>\unicode[STIX]{x1D6FC}$
for (5.7) is met) then the estimates (5.7) hold with
$\sqrt{2}r>\unicode[STIX]{x1D6FC}$
for (5.7) is met) then the estimates (5.7) hold with
![]() $\operatorname{Im}(z)=\unicode[STIX]{x1D6FC}^{-2}$
for any lattice
$\operatorname{Im}(z)=\unicode[STIX]{x1D6FC}^{-2}$
for any lattice
![]() $\unicode[STIX]{x1D6EC}_{(z,\unicode[STIX]{x1D703})}$
,
$\unicode[STIX]{x1D6EC}_{(z,\unicode[STIX]{x1D703})}$
,
![]() $(z,\unicode[STIX]{x1D703})\in F$
. Writing
$(z,\unicode[STIX]{x1D703})\in F$
. Writing
![]() $y=\operatorname{Im}(z)$
, the estimates become
$y=\operatorname{Im}(z)$
, the estimates become
 $$\begin{eqnarray}\begin{array}{@{}rl@{}}\displaystyle 1-\frac{2\sqrt{2}r}{\sqrt{y}}\leqslant Q(\unicode[STIX]{x1D6EC}_{(z,\unicode[STIX]{x1D703})},r)\leqslant 1-\frac{\sqrt{2}r}{\sqrt{y}} & \text{if}~\sqrt{2}r\leqslant \sqrt{y},\\ Q(\unicode[STIX]{x1D6EC}_{(z,\unicode[STIX]{x1D703})},r)=0 & \text{if}~\sqrt{2}r\geqslant \sqrt{y}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rl@{}}\displaystyle 1-\frac{2\sqrt{2}r}{\sqrt{y}}\leqslant Q(\unicode[STIX]{x1D6EC}_{(z,\unicode[STIX]{x1D703})},r)\leqslant 1-\frac{\sqrt{2}r}{\sqrt{y}} & \text{if}~\sqrt{2}r\leqslant \sqrt{y},\\ Q(\unicode[STIX]{x1D6EC}_{(z,\unicode[STIX]{x1D703})},r)=0 & \text{if}~\sqrt{2}r\geqslant \sqrt{y}.\end{array}\end{eqnarray}$$
Since the Haar measure on
![]() $X_{2}$
corresponds to the hyperbolic measure
$X_{2}$
corresponds to the hyperbolic measure
![]() $(1/y^{2})\,dx\,dy\,d\unicode[STIX]{x1D703}$
on
$(1/y^{2})\,dx\,dy\,d\unicode[STIX]{x1D703}$
on
![]() $F$
, we have
$F$
, we have
Finally, since
![]() $r$
is large,Footnote
3
$r$
is large,Footnote
3
![]() $Q(\unicode[STIX]{x1D6EC}_{(z,\unicode[STIX]{x1D703})},r)$
vanishes in the region of
$Q(\unicode[STIX]{x1D6EC}_{(z,\unicode[STIX]{x1D703})},r)$
vanishes in the region of
![]() $F$
between the line
$F$
between the line
![]() $y=2r^{2}$
and the arc of the unit circle, permitting us to integrate over an unbounded rectangular region. The estimates (5.9) give
$y=2r^{2}$
and the arc of the unit circle, permitting us to integrate over an unbounded rectangular region. The estimates (5.9) give
where the
![]() $2\unicode[STIX]{x1D70B}$
comes from integrating a constant function over the
$2\unicode[STIX]{x1D70B}$
comes from integrating a constant function over the
![]() $\unicode[STIX]{x1D703}$
factor. Computing these integrals gives
$\unicode[STIX]{x1D703}$
factor. Computing these integrals gives
This proves (5.1). ◻
6 Completion of the proof of Theorem 4.6
We now set up the proof of the general case (
![]() $k\geqslant 2$
) with some notation and remarks on Siegel sets. Then the proof will be given following two lemmas generalizing some statements from the proof of the two-dimensional case.
$k\geqslant 2$
) with some notation and remarks on Siegel sets. Then the proof will be given following two lemmas generalizing some statements from the proof of the two-dimensional case.
As before, we wish to write
![]() $Q(\unicode[STIX]{x1D6EC},r)$
introduced in (5.2) in terms of the coordinates of the Iwasawa decomposition of a representative
$Q(\unicode[STIX]{x1D6EC},r)$
introduced in (5.2) in terms of the coordinates of the Iwasawa decomposition of a representative
![]() $g\in G$
for
$g\in G$
for
![]() $\unicode[STIX]{x1D6EC}=g\mathbb{Z}^{k}$
. We will assume
$\unicode[STIX]{x1D6EC}=g\mathbb{Z}^{k}$
. We will assume
![]() $g$
lies in a subset of a particular Siegel set. Specifically, for elements of
$g$
lies in a subset of a particular Siegel set. Specifically, for elements of
![]() $G$
of the form
$G$
of the form
 $$\begin{eqnarray}n=\left[\begin{array}{@{}ccccc@{}}1 & \unicode[STIX]{x1D708}_{1,1} & \unicode[STIX]{x1D708}_{1,2} & \cdots \, & \unicode[STIX]{x1D708}_{1,k-1}\\ 0 & 1 & \unicode[STIX]{x1D708}_{2,1} & \cdots \, & \unicode[STIX]{x1D708}_{2,k-2}\\ 0 & 0 & 1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & \unicode[STIX]{x1D708}_{k-1,1}\\ 0 & 0 & \cdots \, & 0 & 1\end{array}\right],\quad a=\left[\begin{array}{@{}ccccc@{}}a_{1} & 0 & 0 & \cdots \, & 0\\ 0 & a_{2} & 0 & \cdots \, & 0\\ 0 & 0 & a_{3} & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0\\ 0 & 0 & \cdots \, & 0 & a_{k}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}n=\left[\begin{array}{@{}ccccc@{}}1 & \unicode[STIX]{x1D708}_{1,1} & \unicode[STIX]{x1D708}_{1,2} & \cdots \, & \unicode[STIX]{x1D708}_{1,k-1}\\ 0 & 1 & \unicode[STIX]{x1D708}_{2,1} & \cdots \, & \unicode[STIX]{x1D708}_{2,k-2}\\ 0 & 0 & 1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & \unicode[STIX]{x1D708}_{k-1,1}\\ 0 & 0 & \cdots \, & 0 & 1\end{array}\right],\quad a=\left[\begin{array}{@{}ccccc@{}}a_{1} & 0 & 0 & \cdots \, & 0\\ 0 & a_{2} & 0 & \cdots \, & 0\\ 0 & 0 & a_{3} & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0\\ 0 & 0 & \cdots \, & 0 & a_{k}\end{array}\right],\end{eqnarray}$$
and for
![]() $d,e\in \mathbb{R}$
,
$d,e\in \mathbb{R}$
,
![]() $c\in \mathbb{R}_{+}$
, define
$c\in \mathbb{R}_{+}$
, define
Also write
![]() $K$
for
$K$
for
![]() $\operatorname{SO}(k)$
. It is known that
$\operatorname{SO}(k)$
. It is known that
![]() $KA_{1/2}N_{-1,0}$
is a ‘coarse fundamental domain’ for
$KA_{1/2}N_{-1,0}$
is a ‘coarse fundamental domain’ for
![]() $\unicode[STIX]{x1D6E4}_{k}$
in
$\unicode[STIX]{x1D6E4}_{k}$
in
![]() $G_{k}$
(see [Reference MorrisMor15, § 19.4(ii), following Remark 7.3.4]Footnote
4
). That is,
$G_{k}$
(see [Reference MorrisMor15, § 19.4(ii), following Remark 7.3.4]Footnote
4
). That is,
![]() $KA_{1/2}N_{-1,0}$
contains a fundamental domain for the right-action of
$KA_{1/2}N_{-1,0}$
contains a fundamental domain for the right-action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
on
$\unicode[STIX]{x1D6E4}_{k}$
on
![]() $G_{k}$
, and it is covered by finitely many
$G_{k}$
, and it is covered by finitely many
![]() $\unicode[STIX]{x1D6E4}_{k}$
-translates of that domain. Therefore
$\unicode[STIX]{x1D6E4}_{k}$
-translates of that domain. Therefore
![]() $KA_{1}N_{-1,0}$
is contained in a coarse fundamental domain, and since we are interested in a lower bound for
$KA_{1}N_{-1,0}$
is contained in a coarse fundamental domain, and since we are interested in a lower bound for
![]() $\int _{X}Q(\unicode[STIX]{x1D6EC},r)\,d\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6EC})$
, it will suffice to bound the integral
$\int _{X}Q(\unicode[STIX]{x1D6EC},r)\,d\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6EC})$
, it will suffice to bound the integral
from below.
For the purpose of the lower bound it will suffice to restrict ourselves to the subset of
![]() $KA_{1}N_{-1,0}$
with
$KA_{1}N_{-1,0}$
with
![]() $a$
satisfying
$a$
satisfying
as we will show, the integral over this set contains the highest-order term of (6.2) as a function of
![]() $r$
.
$r$
.
Lemma 6.1. Suppose
![]() $a$
and
$a$
and
![]() $n$
are as in (6.1), and assume that
$n$
are as in (6.1), and assume that
![]() $a$
satisfies (6.3). Then
$a$
satisfies (6.3). Then
Proof. The proof follows that of the two-dimensional case. Write
![]() $\unicode[STIX]{x1D6EC}=na\mathbb{Z}^{k}$
and let
$\unicode[STIX]{x1D6EC}=na\mathbb{Z}^{k}$
and let
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}}:\mathbb{R}^{k}\rightarrow \mathbb{R}^{k}/\unicode[STIX]{x1D6EC}$
be the projection. Using (5.4), one can write
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}}:\mathbb{R}^{k}\rightarrow \mathbb{R}^{k}/\unicode[STIX]{x1D6EC}$
be the projection. Using (5.4), one can write
where
![]() $I^{k}=[0,1]\times \cdots \times [0,1]$
, and
$I^{k}=[0,1]\times \cdots \times [0,1]$
, and
![]() $\unicode[STIX]{x1D706}$
, as before, stands for both the normalized volume on
$\unicode[STIX]{x1D706}$
, as before, stands for both the normalized volume on
![]() $\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6EC})$
and Lebesgue measure on
$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6EC})$
and Lebesgue measure on
![]() $\mathbb{R}^{k}$
. Equation (6.3) implies
$\mathbb{R}^{k}$
. Equation (6.3) implies
so that the measure of
![]() $naI^{k}\smallsetminus \bigcup _{\mathbf{v}\in \unicode[STIX]{x1D6EC}}B(\mathbf{v},r)$
is the measure of a parallelepiped of dimensions
$naI^{k}\smallsetminus \bigcup _{\mathbf{v}\in \unicode[STIX]{x1D6EC}}B(\mathbf{v},r)$
is the measure of a parallelepiped of dimensions
![]() $a_{1},a_{2},\ldots ,a_{k-1}$
and
$a_{1},a_{2},\ldots ,a_{k-1}$
and
![]() $a_{k}-2r$
, precisely as in the two-dimensional case. In fact the figure used in the proof of the two-dimensional case is still illustrative: just replace the squares with hypercubes, let the
$a_{k}-2r$
, precisely as in the two-dimensional case. In fact the figure used in the proof of the two-dimensional case is still illustrative: just replace the squares with hypercubes, let the
![]() $y$
-axis stand for the
$y$
-axis stand for the
![]() $a_{k}$
-axis, and let the
$a_{k}$
-axis, and let the
![]() $x$
-axis stand for the hyperplane
$x$
-axis stand for the hyperplane
![]() $a_{k}=0$
. This yields (6.4).◻
$a_{k}=0$
. This yields (6.4).◻
The next lemma will allow us to disregard the factor
![]() $K$
when estimating the integral (6.2).
$K$
when estimating the integral (6.2).
Lemma 6.2. For
![]() $\unicode[STIX]{x1D705}\in K$
and
$\unicode[STIX]{x1D705}\in K$
and
![]() $\unicode[STIX]{x1D6EC}\in X$
,
$\unicode[STIX]{x1D6EC}\in X$
,
Proof. If
![]() $P\subset \mathbb{R}^{k}$
is a fundamental parallelipiped for the action of
$P\subset \mathbb{R}^{k}$
is a fundamental parallelipiped for the action of
![]() $\unicode[STIX]{x1D6EC}$
on
$\unicode[STIX]{x1D6EC}$
on
![]() $\mathbb{R}^{k}$
, (6.5) gives
$\mathbb{R}^{k}$
, (6.5) gives
But
so the result follows from another application of (6.5). ◻
Now we are ready to write down the proof of (5.1) for the (
![]() $k>2$
)-dimensional case.
$k>2$
)-dimensional case.
Proof of (5.1) for
 $k>2$
.
$k>2$
.
Let
![]() $da,dn,d\unicode[STIX]{x1D705}$
denote Haar measures on
$da,dn,d\unicode[STIX]{x1D705}$
denote Haar measures on
![]() $A$
,
$A$
,
![]() $N$
, and
$N$
, and
![]() $K$
. Define
$K$
. Define
Then the Iwasawa decomposition identifies
![]() $\unicode[STIX]{x1D707}_{G}$
with the product measure
$\unicode[STIX]{x1D707}_{G}$
with the product measure
![]() $\unicode[STIX]{x1D702}(a)\,d\unicode[STIX]{x1D705}\,da\,dn$
(cf. [Reference Bekka and MayerBM00, V.2.4]). Recall that we aim to bound the integral (6.2) from below. Let us write
$\unicode[STIX]{x1D702}(a)\,d\unicode[STIX]{x1D705}\,da\,dn$
(cf. [Reference Bekka and MayerBM00, V.2.4]). Recall that we aim to bound the integral (6.2) from below. Let us write
![]() $n^{a}=ana^{-1}$
for
$n^{a}=ana^{-1}$
for
![]() $n\in N$
,
$n\in N$
,
![]() $a\in A$
. By decomposing
$a\in A$
. By decomposing
![]() $\unicode[STIX]{x1D707}_{G}$
as above and restricting the domain of integration, we have
$\unicode[STIX]{x1D707}_{G}$
as above and restricting the domain of integration, we have
 $$\begin{eqnarray}\displaystyle \int _{KA_{1}N_{-1,0}}Q(g\mathbb{Z}^{k},r)\,d\unicode[STIX]{x1D707}_{G}(g) & = & \displaystyle \int _{KA_{1}N_{-1,0}}Q(\unicode[STIX]{x1D705}an\mathbb{Z}^{k},r)\,d\unicode[STIX]{x1D705}\,da\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{KA_{1}N_{-1,0}}Q(\unicode[STIX]{x1D705}n^{a}a\mathbb{Z}^{k},r)\,d\unicode[STIX]{x1D705}\,da\,dn\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \int _{K}\int _{N_{-1,0}}\int _{\{a\in A_{1}:a_{k-1}\leqslant 2r\sqrt{k}\leqslant a_{k}\}}Q(\unicode[STIX]{x1D705}n^{a}a\mathbb{Z}^{k},r)\unicode[STIX]{x1D702}(a)\,da\,dn\,d\unicode[STIX]{x1D705}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{KA_{1}N_{-1,0}}Q(g\mathbb{Z}^{k},r)\,d\unicode[STIX]{x1D707}_{G}(g) & = & \displaystyle \int _{KA_{1}N_{-1,0}}Q(\unicode[STIX]{x1D705}an\mathbb{Z}^{k},r)\,d\unicode[STIX]{x1D705}\,da\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{KA_{1}N_{-1,0}}Q(\unicode[STIX]{x1D705}n^{a}a\mathbb{Z}^{k},r)\,d\unicode[STIX]{x1D705}\,da\,dn\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \int _{K}\int _{N_{-1,0}}\int _{\{a\in A_{1}:a_{k-1}\leqslant 2r\sqrt{k}\leqslant a_{k}\}}Q(\unicode[STIX]{x1D705}n^{a}a\mathbb{Z}^{k},r)\unicode[STIX]{x1D702}(a)\,da\,dn\,d\unicode[STIX]{x1D705}.\nonumber\end{eqnarray}$$
By Lemma 6.2, the latter integral is not smaller than
and by Lemma 6.1 this is the same as
Since this integrand depends only on
![]() $a$
, and the other factors have finite measure, it suffices to consider
$a$
, and the other factors have finite measure, it suffices to consider
Finally we identify
![]() $da$
with Lebesgue measure (up to a constant) on
$da$
with Lebesgue measure (up to a constant) on
![]() $\mathbb{R}^{k-1}$
via
$\mathbb{R}^{k-1}$
via
see [Reference Bekka and MayerBM00, V.2.3].Footnote 5 We are therefore left with the integral
where the
![]() $b_{k}$
occurring in the exponent of the second factor of the integrand must be understood to stand for
$b_{k}$
occurring in the exponent of the second factor of the integrand must be understood to stand for
![]() $-\sum _{i=1}^{k-1}b_{i}$
.
$-\sum _{i=1}^{k-1}b_{i}$
.
Now the challenge is not the integrand (which consists of nice exponential functions) but the domain of integration. Thankfully we only have to integrate over a piece of it, since we are interested in a lower bound. The piece we will consider is the following set:
This set is clearly contained in the domain of integration above. Reordering the variables
![]() $x_{i}:=b_{k-i}$
, and using the identity
$x_{i}:=b_{k-i}$
, and using the identity
![]() $\sum _{i<j}x_{i}-x_{j}=\sum _{i=1}^{k-1}2ix_{i}$
, we can compute the integral of
$\sum _{i<j}x_{i}-x_{j}=\sum _{i=1}^{k-1}2ix_{i}$
, we can compute the integral of
![]() $Q(a\mathbb{Z}^{k},\sqrt{k}r)$
over (6.6) as an iterated integral:
$Q(a\mathbb{Z}^{k},\sqrt{k}r)$
over (6.6) as an iterated integral:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{-\text{log}(2r\sqrt{k})/(k-1)}\int _{x_{k-1}}^{-\text{log}(2r\sqrt{k})/(k-1)}\cdots \int _{x_{2}}^{-\text{log}(2r\sqrt{k})/(k-1)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,(e^{\mathop{\sum }_{i=1}^{k-1}2ix_{i}}-2re^{\mathop{\sum }_{i=1}^{k-1}(2i+1)x_{i}})\,dx_{1}\,dx_{2}\cdots dx_{k-1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{-\text{log}(2r\sqrt{k})/(k-1)}\int _{x_{k-1}}^{-\text{log}(2r\sqrt{k})/(k-1)}\cdots \int _{x_{2}}^{-\text{log}(2r\sqrt{k})/(k-1)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,(e^{\mathop{\sum }_{i=1}^{k-1}2ix_{i}}-2re^{\mathop{\sum }_{i=1}^{k-1}(2i+1)x_{i}})\,dx_{1}\,dx_{2}\cdots dx_{k-1}.\end{eqnarray}$$
It is easily seen by induction that for
![]() $2\leqslant \ell \leqslant k-1$
,
$2\leqslant \ell \leqslant k-1$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{\ell }}^{-\text{log}(2r\sqrt{k})/(k-1)}\int _{x_{\ell -1}}^{-\text{log}(2r\sqrt{k})/(k-1)}\cdots \int _{x_{2}}^{-\text{log}(2r\sqrt{k})/(k-1)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,(e^{\mathop{\sum }_{i=1}^{k-1}2ix_{i}}-2re^{\mathop{\sum }_{i=1}^{k-1}(2i+1)x_{i}})\,dx_{1}\,dx_{2}\cdots dx_{\ell -1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{\ell }}^{-\text{log}(2r\sqrt{k})/(k-1)}\int _{x_{\ell -1}}^{-\text{log}(2r\sqrt{k})/(k-1)}\cdots \int _{x_{2}}^{-\text{log}(2r\sqrt{k})/(k-1)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,(e^{\mathop{\sum }_{i=1}^{k-1}2ix_{i}}-2re^{\mathop{\sum }_{i=1}^{k-1}(2i+1)x_{i}})\,dx_{1}\,dx_{2}\cdots dx_{\ell -1}\nonumber\end{eqnarray}$$
is a sum of terms of the form
where
![]() $c>0$
,
$c>0$
,
![]() $p_{i}$
are positive integers, and
$p_{i}$
are positive integers, and
![]() $m+\sum _{i=\ell }^{k-1}p_{i}=k(k-1)$
. Indeed,
$m+\sum _{i=\ell }^{k-1}p_{i}=k(k-1)$
. Indeed,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{\ell +1}}^{-\text{log}(2r\sqrt{k})/(k-1)}c(2r\sqrt{k})^{-m/(k-1)}e^{\mathop{\sum }_{i=\ell }^{k-1}p_{i}x_{i}}\,dx_{\ell }\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{c}{p_{\ell }}(2r\sqrt{k})^{-(m+p_{\ell })/(k-1)}\exp \biggl[\mathop{\sum }_{i=\ell +1}^{k-1}p_{i}x_{i}\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{c}{p_{\ell }}(2r\sqrt{k})^{-m/(k-1)}\exp \biggl[(p_{\ell }+p_{\ell +1})x_{\ell +1}+\mathop{\sum }_{i=\ell +2}^{k-1}p_{i}x_{i}\biggr],\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{x_{\ell +1}}^{-\text{log}(2r\sqrt{k})/(k-1)}c(2r\sqrt{k})^{-m/(k-1)}e^{\mathop{\sum }_{i=\ell }^{k-1}p_{i}x_{i}}\,dx_{\ell }\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{c}{p_{\ell }}(2r\sqrt{k})^{-(m+p_{\ell })/(k-1)}\exp \biggl[\mathop{\sum }_{i=\ell +1}^{k-1}p_{i}x_{i}\biggr]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{c}{p_{\ell }}(2r\sqrt{k})^{-m/(k-1)}\exp \biggl[(p_{\ell }+p_{\ell +1})x_{\ell +1}+\mathop{\sum }_{i=\ell +2}^{k-1}p_{i}x_{i}\biggr],\nonumber\end{eqnarray}$$
so that we have only to notice that
from the induction hypothesis. Thus (6.7) is a sum of terms of the form
 $$\begin{eqnarray}\displaystyle \int _{-\infty }^{-\text{log}(2r\sqrt{k})/(k-1)}c(2r\sqrt{k})^{-m/(k-1)}e^{p_{k-1}x_{k-1}}\,dx_{k-1} & = & \displaystyle \frac{c}{p_{k-1}}(2r\sqrt{k})^{-(m+p_{k-1})/(k-1)}\nonumber\\ \displaystyle & = & \displaystyle \frac{c}{p_{k-1}}(2r\sqrt{k})^{-k(k-1)/(k-1)}\nonumber\\ \displaystyle & = & \displaystyle \frac{c}{p_{k-1}}(2r\sqrt{k})^{-k},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{-\text{log}(2r\sqrt{k})/(k-1)}c(2r\sqrt{k})^{-m/(k-1)}e^{p_{k-1}x_{k-1}}\,dx_{k-1} & = & \displaystyle \frac{c}{p_{k-1}}(2r\sqrt{k})^{-(m+p_{k-1})/(k-1)}\nonumber\\ \displaystyle & = & \displaystyle \frac{c}{p_{k-1}}(2r\sqrt{k})^{-k(k-1)/(k-1)}\nonumber\\ \displaystyle & = & \displaystyle \frac{c}{p_{k-1}}(2r\sqrt{k})^{-k},\nonumber\end{eqnarray}$$
where we have used
![]() $m+p_{k-1}=k(k-1)$
. Since the integral is positive, the sum of the coefficients must be positive, and the integral grows no more slowly than some multiple of
$m+p_{k-1}=k(k-1)$
. Since the integral is positive, the sum of the coefficients must be positive, and the integral grows no more slowly than some multiple of
![]() $r^{-k}$
. ◻
$r^{-k}$
. ◻
7 Concluding remarks and open questions
7.1 The homogeneous problem
Here we return to the homogeneous case and discuss the approach to Question 1.4 suggested by the foregoing argument. Recall that
![]() $X=X_{k}=\operatorname{SL}_{k}(\mathbb{R})/\operatorname{SL}_{k}(\mathbb{Z})$
is the space of unimodular lattices in
$X=X_{k}=\operatorname{SL}_{k}(\mathbb{R})/\operatorname{SL}_{k}(\mathbb{Z})$
is the space of unimodular lattices in
![]() $\mathbb{R}^{k}$
. Define
$\mathbb{R}^{k}$
. Define
and for
![]() $A\in M_{m,n}$
, define
$A\in M_{m,n}$
, define
where
![]() $k=m+n$
. If we restrict the flow
$k=m+n$
. If we restrict the flow
![]() $g_{t}$
to
$g_{t}$
to
![]() $X_{k}$
, it is not difficult to showFootnote
6
the following homogeneous version of Lemma 3.4.
$X_{k}$
, it is not difficult to showFootnote
6
the following homogeneous version of Lemma 3.4.
Proposition 7.1. Fix positive integers
![]() $m,n$
, and let
$m,n$
, and let
![]() $\unicode[STIX]{x1D713}:[t_{0},\infty )\rightarrow (0,1)$
be continuous and non-increasing. Let
$\unicode[STIX]{x1D713}:[t_{0},\infty )\rightarrow (0,1)$
be continuous and non-increasing. Let
![]() $z=z_{\unicode[STIX]{x1D713}}$
be as in Lemma 3.1. Then
$z=z_{\unicode[STIX]{x1D713}}$
be as in Lemma 3.1. Then
![]() $A\in D_{m,n}(\unicode[STIX]{x1D713})$
if and only if
$A\in D_{m,n}(\unicode[STIX]{x1D713})$
if and only if
for all sufficiently large
![]() $s$
.
$s$
.
This way Question 1.4 reduces to a shrinking target problem for the flow
![]() $(X,g_{t})$
, where the targets are super-level sets
$(X,g_{t})$
, where the targets are super-level sets
![]() $\unicode[STIX]{x1D6E5}_{0}^{-1}([z,\infty ))$
. But the family of super-level sets of
$\unicode[STIX]{x1D6E5}_{0}^{-1}([z,\infty ))$
. But the family of super-level sets of
![]() $\unicode[STIX]{x1D6E5}_{0}$
differs in important ways from the family of super-level sets of
$\unicode[STIX]{x1D6E5}_{0}$
differs in important ways from the family of super-level sets of
![]() $\unicode[STIX]{x1D6E5}$
. In particular, by Minkowski’s theorem,
$\unicode[STIX]{x1D6E5}$
. In particular, by Minkowski’s theorem,
![]() $\unicode[STIX]{x1D6E5}_{0}^{-1}[z,\infty )$
is empty for
$\unicode[STIX]{x1D6E5}_{0}^{-1}[z,\infty )$
is empty for
![]() $z>0$
. Hence the problem reduces to the case where the values
$z>0$
. Hence the problem reduces to the case where the values
![]() $z_{\unicode[STIX]{x1D713}}(t)$
accumulate at 0, so that the targets shrink to the set
$z_{\unicode[STIX]{x1D713}}(t)$
accumulate at 0, so that the targets shrink to the set
![]() $\unicode[STIX]{x1D6E5}_{0}^{-1}(0)$
. The latter set is a union of finitely many compact submanifolds of
$\unicode[STIX]{x1D6E5}_{0}^{-1}(0)$
. The latter set is a union of finitely many compact submanifolds of
![]() $X$
whose structure is explicitly described by the Hajós–Minkowski theorem (see [Reference CasselsCas71, § XI.1.3] or [Reference ShahSha10, Theorem 2.3]). In particular, the function
$X$
whose structure is explicitly described by the Hajós–Minkowski theorem (see [Reference CasselsCas71, § XI.1.3] or [Reference ShahSha10, Theorem 2.3]). In particular, the function
![]() $\unicode[STIX]{x1D6E5}_{0}$
is not DL, and Theorem 4.4 is not applicable. Other approaches to shrinking target problems on homogeneous spaces [Reference KelmerKel17, Reference Kelmer and YuKY19, Reference Kleinbock and ZhaoKZ18, Reference MaucourantMau06] also do not seem to be directly applicable.
$\unicode[STIX]{x1D6E5}_{0}$
is not DL, and Theorem 4.4 is not applicable. Other approaches to shrinking target problems on homogeneous spaces [Reference KelmerKel17, Reference Kelmer and YuKY19, Reference Kleinbock and ZhaoKZ18, Reference MaucourantMau06] also do not seem to be directly applicable.
On the other hand, the one-dimensional case (
![]() $m=n=1$
) has been completely settled in [Reference Kleinbock and WadleighKW18]. In particular, the following zero–one law has been established.
$m=n=1$
) has been completely settled in [Reference Kleinbock and WadleighKW18]. In particular, the following zero–one law has been established.
Theorem 7.2 [Reference Kleinbock and WadleighKW18, Theorem 1.8].
Let
![]() $\unicode[STIX]{x1D713}:[t_{0},\infty )\rightarrow \mathbb{R}_{+}$
be non-increasing, and suppose the function
$\unicode[STIX]{x1D713}:[t_{0},\infty )\rightarrow \mathbb{R}_{+}$
be non-increasing, and suppose the function
![]() $t\mapsto t\unicode[STIX]{x1D713}(t)$
is non-decreasing and
$t\mapsto t\unicode[STIX]{x1D713}(t)$
is non-decreasing and
Then if
then the Lebesgue measure of
![]() $D_{1,1}(\unicode[STIX]{x1D713})$
(respectively, of
$D_{1,1}(\unicode[STIX]{x1D713})$
(respectively, of
![]() $D_{1,1}(\unicode[STIX]{x1D713})^{c}$
) is zero.
$D_{1,1}(\unicode[STIX]{x1D713})^{c}$
) is zero.
The proof is based on the observation that the condition
![]() $\unicode[STIX]{x1D6FC}\in D_{1,1}(\unicode[STIX]{x1D713})$
can be explicitly described in terms of the continued fraction expansion of
$\unicode[STIX]{x1D6FC}\in D_{1,1}(\unicode[STIX]{x1D713})$
can be explicitly described in terms of the continued fraction expansion of
![]() $\unicode[STIX]{x1D6FC}$
. However, this phenomenon is inherently one-dimensional, and new ideas are needed to settle the general case.
$\unicode[STIX]{x1D6FC}$
. However, this phenomenon is inherently one-dimensional, and new ideas are needed to settle the general case.
7.2 Hausdorff dimension
A sequel [Reference Hussain, Kleinbock, Wadleigh and WangHKWW18] to the paper [Reference Kleinbock and WadleighKW18] computes the Hausdorff dimension of limsup sets
![]() $D_{1,1}(\unicode[STIX]{x1D713})^{c}$
, and, more generally, establishes zero–infinity laws for the Hausdorff measure of those sets. For example, it is proved there that
$D_{1,1}(\unicode[STIX]{x1D713})^{c}$
, and, more generally, establishes zero–infinity laws for the Hausdorff measure of those sets. For example, it is proved there that
One can ask similar questions for higher-dimensional versions, both in homogeneous and inhomogeneous settings. Even the
![]() $m=n=1$
case of the inhomogeneous problem is open.
$m=n=1$
case of the inhomogeneous problem is open.
7.3 Singly versus doubly metric problems
The main result of the present paper computes Lebesgue measure of the set
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})\subset M_{m,n}\times \mathbb{R}^{m}$
. As often happens in inhomogeneous Diophantine problems, one can fix either
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})\subset M_{m,n}\times \mathbb{R}^{m}$
. As often happens in inhomogeneous Diophantine problems, one can fix either
![]() $A$
or
$A$
or
![]() $\mathbf{b}$
and ask for the Lebesgue (or Hausdorff) measure of the corresponding slices of
$\mathbf{b}$
and ask for the Lebesgue (or Hausdorff) measure of the corresponding slices of
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
. It seems plausible that the convergence/divergence of the same series (1.6) is responsible for a full/zero measure dichotomy for slices
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
. It seems plausible that the convergence/divergence of the same series (1.6) is responsible for a full/zero measure dichotomy for slices
for any fixed
![]() $\mathbf{b}\notin \mathbb{Z}^{m}$
. On the other hand, the Lebesgue measure of the set
$\mathbf{b}\notin \mathbb{Z}^{m}$
. On the other hand, the Lebesgue measure of the set
for a fixed
![]() $A\in M_{m,n}$
seems to depend heavily on Diophantine properties of
$A\in M_{m,n}$
seems to depend heavily on Diophantine properties of
![]() $A$
. For example, if
$A$
. For example, if
![]() $A$
has rational entries, then
$A$
has rational entries, then
![]() $(A,\mathbf{b})$
is not in
$(A,\mathbf{b})$
is not in
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
whenever
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
whenever
![]() $\mathbf{b}\notin \mathbb{Q}^{m}$
and
$\mathbf{b}\notin \mathbb{Q}^{m}$
and
![]() $\unicode[STIX]{x1D713}(T)\rightarrow 0$
as
$\unicode[STIX]{x1D713}(T)\rightarrow 0$
as
![]() $T\rightarrow \infty$
. And on the other end of the approximation spectrum, if
$T\rightarrow \infty$
. And on the other end of the approximation spectrum, if
![]() $A$
is badly approximable it is easy to see that there exists
$A$
is badly approximable it is easy to see that there exists
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $\mathbf{b}\in \mathbb{R}^{m}$
,
$\mathbf{b}\in \mathbb{R}^{m}$
,
![]() $(A,\mathbf{b})$
belongs to the (null) set
$(A,\mathbf{b})$
belongs to the (null) set
![]() $\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
. Indeed, by the classical Dani correspondence,
$\widehat{D}_{m,n}(C\unicode[STIX]{x1D713}_{1})$
. Indeed, by the classical Dani correspondence,
![]() $A$
is badly approximable if and only if the trajectory
$A$
is badly approximable if and only if the trajectory
![]() $\{g_{t}\unicode[STIX]{x1D6EC}_{A}:t>0\}$
is bounded in
$\{g_{t}\unicode[STIX]{x1D6EC}_{A}:t>0\}$
is bounded in
![]() $X_{k}$
, which is the case if and only if
$X_{k}$
, which is the case if and only if
![]() $\{g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}}:t>0\}$
is bounded in
$\{g_{t}\unicode[STIX]{x1D6EC}_{A,\mathbf{b}}:t>0\}$
is bounded in
![]() $\widehat{X}_{k}$
for any
$\widehat{X}_{k}$
for any
![]() $\mathbf{b}\in \mathbb{R}^{m}$
. Thus the claim follows in view of Lemma 2.2. It would be interesting to describe, for a given arbitrary non-increasing function
$\mathbf{b}\in \mathbb{R}^{m}$
. Thus the claim follows in view of Lemma 2.2. It would be interesting to describe, for a given arbitrary non-increasing function
![]() $\unicode[STIX]{x1D713}$
, explicit Diophantine conditions on
$\unicode[STIX]{x1D713}$
, explicit Diophantine conditions on
![]() $A\in M_{m,n}$
guaranteeing that
$A\in M_{m,n}$
guaranteeing that
![]() $(A,\mathbf{b})\in \widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
for all (or almost all)
$(A,\mathbf{b})\in \widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
for all (or almost all)
![]() $\mathbf{b}\in \mathbb{R}^{m}$
.
$\mathbf{b}\in \mathbb{R}^{m}$
.
7.4 Eventually always hitting
Finally, let us connect our results on improving the inhomogeneous Dirichlet theorem with a shrinking target property introduced recently by Kelmer [Reference KelmerKel17]. We start by setting some notation. Let
![]() $\unicode[STIX]{x1D6FC}$
be a measure-preserving
$\unicode[STIX]{x1D6FC}$
be a measure-preserving
![]() $\mathbb{Z}^{n}$
-action on a probability space
$\mathbb{Z}^{n}$
-action on a probability space
![]() $(Y,\unicode[STIX]{x1D708})$
. For any
$(Y,\unicode[STIX]{x1D708})$
. For any
![]() $N\in \mathbb{N}$
denote
$N\in \mathbb{N}$
denote
(here, as before,
![]() $\Vert \cdot \Vert$
stands for the supremum norm). Then, given a nested family
$\Vert \cdot \Vert$
stands for the supremum norm). Then, given a nested family
![]() ${\mathcal{B}}=\{B_{N}:N\in \mathbb{N}\}$
of subsets of
${\mathcal{B}}=\{B_{N}:N\in \mathbb{N}\}$
of subsets of
![]() $Y$
, let us say that the
$Y$
, let us say that the
![]() $\unicode[STIX]{x1D6FC}$
-orbit of a point
$\unicode[STIX]{x1D6FC}$
-orbit of a point
![]() $x\in Y$
eventually always hits
$x\in Y$
eventually always hits
![]() ${\mathcal{B}}$
if
${\mathcal{B}}$
if
![]() $\unicode[STIX]{x1D6FC}(D_{N})x\cap B_{N}\neq \varnothing$
for all sufficiently large
$\unicode[STIX]{x1D6FC}(D_{N})x\cap B_{N}\neq \varnothing$
for all sufficiently large
![]() $N\in \mathbb{N}$
. Following [Reference KelmerKel17], denote by
$N\in \mathbb{N}$
. Following [Reference KelmerKel17], denote by
![]() ${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
the set of points of
${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
the set of points of
![]() $Y$
with
$Y$
with
![]() $\unicode[STIX]{x1D6FC}$
-orbits eventually always hitting
$\unicode[STIX]{x1D6FC}$
-orbits eventually always hitting
![]() ${\mathcal{B}}$
. This is a liminf set with a rather complicated structure. In [Reference KelmerKel17] sufficient conditions for sets
${\mathcal{B}}$
. This is a liminf set with a rather complicated structure. In [Reference KelmerKel17] sufficient conditions for sets
![]() ${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
to be of full measure were found for unipotent and diagonalizable actions
${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
to be of full measure were found for unipotent and diagonalizable actions
![]() $\unicode[STIX]{x1D6FC}$
on hyperbolic manifolds. Namely, it was shownFootnote
7
(see [Reference KelmerKel17, Theorem 22 and Proposition 24]) that for rotation-invariant monotonically shrinking families
$\unicode[STIX]{x1D6FC}$
on hyperbolic manifolds. Namely, it was shownFootnote
7
(see [Reference KelmerKel17, Theorem 22 and Proposition 24]) that for rotation-invariant monotonically shrinking families
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() $\unicode[STIX]{x1D708}({\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}}))=1$
if the series
$\unicode[STIX]{x1D708}({\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}}))=1$
if the series
converges. See also [Reference Kelmer and YuKY19] for some extensions to actions on homogeneous spaces of semisimple Lie groups. However, to the best of the authors’ knowledge, there are no non-trivial examples of measure-preserving systems for which necessary and sufficient conditions for sets
![]() ${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
to be of full measure exist in the literature.
${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
to be of full measure exist in the literature.
Now, given
![]() $A\in M_{m,n}$
, take
$A\in M_{m,n}$
, take
![]() $Y=\mathbb{T}^{m}$
with normalized Lebesgue measure
$Y=\mathbb{T}^{m}$
with normalized Lebesgue measure
![]() $\unicode[STIX]{x1D708}$
and consider the
$\unicode[STIX]{x1D708}$
and consider the
![]() $\mathbb{Z}^{n}$
-action
$\mathbb{Z}^{n}$
-action
on
![]() $Y$
(generated by
$Y$
(generated by
![]() $n$
independent rotations of
$n$
independent rotations of
![]() $\mathbb{T}^{m}$
by the column vectors of
$\mathbb{T}^{m}$
by the column vectors of
![]() $A$
). Also fix
$A$
). Also fix
![]() $\mathbf{y}\in Y$
and a non-increasing sequence
$\mathbf{y}\in Y$
and a non-increasing sequence
![]() $\{r(N):N\in \mathbb{N}\}$
of positive numbers, and consider the family
$\{r(N):N\in \mathbb{N}\}$
of positive numbers, and consider the family
![]() ${\mathcal{B}}$
of open balls
${\mathcal{B}}$
of open balls
Then it is easy to see that
![]() $\mathbf{x}\in {\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
if and only if for all sufficiently large
$\mathbf{x}\in {\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
if and only if for all sufficiently large
![]() $N\in \mathbb{N}$
there exist
$N\in \mathbb{N}$
there exist
![]() $\mathbf{q}\in \mathbb{Z}^{n}$
and
$\mathbf{q}\in \mathbb{Z}^{n}$
and
![]() $\mathbf{p}\in \mathbb{Z}^{m}$
such that
$\mathbf{p}\in \mathbb{Z}^{m}$
such that
Here and hereafter
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $A$
are related via (7.4). A connection to the improvement of the inhomogeneous Dirichlet theorem is now straightforward. Indeed, from Theorem 1.6 one can derive the following corollary.
$A$
are related via (7.4). A connection to the improvement of the inhomogeneous Dirichlet theorem is now straightforward. Indeed, from Theorem 1.6 one can derive the following corollary.
Corollary 7.3. Fix
![]() $\mathbf{y}\in \mathbb{T}^{m}$
and let
$\mathbf{y}\in \mathbb{T}^{m}$
and let
![]() ${\mathcal{B}}=\{B_{N}:N\in \mathbb{N}\}$
be as in (7.5), where
${\mathcal{B}}=\{B_{N}:N\in \mathbb{N}\}$
be as in (7.5), where
![]() $\{r(N):N\in \mathbb{N}\}$
is a non-increasing sequence of positive numbers. Then for Lebesgue-almost every
$\{r(N):N\in \mathbb{N}\}$
is a non-increasing sequence of positive numbers. Then for Lebesgue-almost every
![]() $A\in M_{m,n}$
the set
$A\in M_{m,n}$
the set
![]() ${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
has zero (respectively, full) measure provided the sum (7.3) diverges (respectively, converges).
${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
has zero (respectively, full) measure provided the sum (7.3) diverges (respectively, converges).
Proof. Extend
![]() $r(\cdot )$
to a non-increasing continuous function on
$r(\cdot )$
to a non-increasing continuous function on
![]() $\mathbb{R}_{+}$
in an arbitrary way (for example, piecewise linearly). Then, similarly to the observation made after (1.4), one can notice that
$\mathbb{R}_{+}$
in an arbitrary way (for example, piecewise linearly). Then, similarly to the observation made after (1.4), one can notice that
![]() $\mathbf{x}\in {\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
if and only if the system (7.6) is solvable in integers
$\mathbf{x}\in {\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
if and only if the system (7.6) is solvable in integers
![]() $\mathbf{p},\mathbf{q}$
for all sufficiently large
$\mathbf{p},\mathbf{q}$
for all sufficiently large
![]() $N\in \mathbb{R}_{+}$
. The latter happens if and only if the pair
$N\in \mathbb{R}_{+}$
. The latter happens if and only if the pair
![]() $(A,\mathbf{x}-\mathbf{y})$
belongs to
$(A,\mathbf{x}-\mathbf{y})$
belongs to
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
, where
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
, where
In view of Theorem 1.6, the divergence of the sum
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{j}\frac{1}{\unicode[STIX]{x1D713}(j)j^{2}} & = & \displaystyle \mathop{\sum }_{j}\frac{1}{r(j^{1/n}-1)^{m}j^{2}}\asymp \int \frac{dx}{r(x^{1/n}-1)^{m}x^{2}}\asymp \int \frac{(y+1)^{n-1}\,dy}{r(y)^{m}(y+1)^{2n}}\nonumber\\ \displaystyle & \asymp & \displaystyle \int \frac{dy}{r(y)^{m}y^{n+1}}\asymp \int \frac{2^{z}\,dz}{r(2^{z})^{m}2^{z(n+1)}}\asymp \mathop{\sum }_{j}\frac{1}{r(2^{j})^{m}2^{nj}}\asymp \mathop{\sum }_{j}\frac{1}{2^{nj}\unicode[STIX]{x1D708}(B_{2^{j}})}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{j}\frac{1}{\unicode[STIX]{x1D713}(j)j^{2}} & = & \displaystyle \mathop{\sum }_{j}\frac{1}{r(j^{1/n}-1)^{m}j^{2}}\asymp \int \frac{dx}{r(x^{1/n}-1)^{m}x^{2}}\asymp \int \frac{(y+1)^{n-1}\,dy}{r(y)^{m}(y+1)^{2n}}\nonumber\\ \displaystyle & \asymp & \displaystyle \int \frac{dy}{r(y)^{m}y^{n+1}}\asymp \int \frac{2^{z}\,dz}{r(2^{z})^{m}2^{z(n+1)}}\asymp \mathop{\sum }_{j}\frac{1}{r(2^{j})^{m}2^{nj}}\asymp \mathop{\sum }_{j}\frac{1}{2^{nj}\unicode[STIX]{x1D708}(B_{2^{j}})}\nonumber\end{eqnarray}$$
implies that
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has measure zero. Hence for almost every
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
has measure zero. Hence for almost every
![]() $A$
the set
$A$
the set
![]() ${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
is null. Similarly, the convergence of (7.3) implies that
${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
is null. Similarly, the convergence of (7.3) implies that
![]() $\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
is conull. Thus for Lebesgue-generic
$\widehat{D}_{m,n}(\unicode[STIX]{x1D713})$
is conull. Thus for Lebesgue-generic
![]() $A$
the set
$A$
the set
![]() ${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
has full measure.◻
${\mathcal{A}}_{\mathbf{a}\mathbf{h}}^{\unicode[STIX]{x1D6FC}}({\mathcal{B}})$
has full measure.◻
Acknowledgements
The authors would like to thank Alexander Gorodnik, Dubi Kelmer and Shucheng Yu for helpful discussions, and the anonymous referee for useful comments.