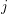1 Introduction
The Ax–Schanuel theorem [Reference AxAx71] is a result regarding the transcendence degrees of fields generated over the complex numbers by power series and their exponentials. Formulated geometrically for the uniformization maps of algebraic tori, it has inspired analogous statements for the uniformization maps of abelian varieties and Shimura varieties. The former, following from another theorem of Ax [Reference AxAx72], has recently been used by Habegger and Pila in their proof of the Zilber–Pink conjecture for curves in abelian varieties [Reference Habegger and PilaHP16].
Habegger and Pila also extended the Pila–Zannier strategy to the Zilber–Pink conjecture for products of modular curves. Their method relies on an Ax–Schanuel conjecture for the
![]() $j$
-function and is conditional on their so-called large Galois orbits conjecture. The purpose of this paper is to show that the Pila–Zannier strategy can be extended to the Zilber–Pink conjecture for general Shimura varieties.
$j$
-function and is conditional on their so-called large Galois orbits conjecture. The purpose of this paper is to show that the Pila–Zannier strategy can be extended to the Zilber–Pink conjecture for general Shimura varieties.
This conjecture can just as easily be stated in the generality of mixed Shimura varieties but, in this article, we will restrict our attention to pure Shimura varieties, though we have no explicit reason to believe that the methods presented here will not extend to the mixed setting. We begin by stating a conjecture of Pink. We note that, throughout this article, unless preceded by the word Shimura, varieties (and, indeed, subvarieties) will be assumed geometrically irreducible.
Conjecture 1.1 (Cf. [Reference PinkPin05b, Conjecture 1.3]).
Let
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
be a Shimura variety and, for any integer
$\text{Sh}_{K}(G,\mathfrak{X})$
be a Shimura variety and, for any integer
![]() $d$
, let
$d$
, let
![]() $\text{Sh}_{K}(G,\mathfrak{X})^{[d]}$
denote the union of the special subvarieties of
$\text{Sh}_{K}(G,\mathfrak{X})^{[d]}$
denote the union of the special subvarieties of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
having codimension at least
$\text{Sh}_{K}(G,\mathfrak{X})$
having codimension at least
![]() $d$
. Let
$d$
. Let
![]() $V$
be a Hodge generic subvariety of
$V$
be a Hodge generic subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
. Then
$\text{Sh}_{K}(G,\mathfrak{X})$
. Then
is not Zariski dense in
![]() $V$
.
$V$
.
The heuristics of this conjecture are as follows. For two subvarieties
![]() $V$
and
$V$
and
![]() $W$
of
$W$
of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
, such that the codimension of
$\text{Sh}_{K}(G,\mathfrak{X})$
, such that the codimension of
![]() $W$
is at least
$W$
is at least
![]() $1+\dim V$
, we expect
$1+\dim V$
, we expect
![]() $V\cap W=\emptyset$
. Even if we fix
$V\cap W=\emptyset$
. Even if we fix
![]() $V$
and take the union of
$V$
and take the union of
![]() $V\cap W$
for countably many
$V\cap W$
for countably many
![]() $W$
of codimension at least
$W$
of codimension at least
![]() $1+\dim V$
, the resulting set should still be rather small in
$1+\dim V$
, the resulting set should still be rather small in
![]() $V$
unless, of course,
$V$
unless, of course,
![]() $V$
was not sufficiently generic in
$V$
was not sufficiently generic in
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
. Pink’s conjecture turns this expectation into an explicit statement about the intersection of Hodge generic subvarieties with the special subvarieties of small dimension.
$\text{Sh}_{K}(G,\mathfrak{X})$
. Pink’s conjecture turns this expectation into an explicit statement about the intersection of Hodge generic subvarieties with the special subvarieties of small dimension.
Conjecture 1.1 can also be formulated for algebraic tori, abelian varieties, or even semiabelian varieties, though Conjecture 1.1 for mixed Shimura varieties implies all of these formulations (see [Reference PinkPin05b]). When
![]() $V$
is a curve, defined over a number field, and contained in an algebraic torus, we obtain a theorem of Maurin [Reference MaurinMau08]. We also note that Capuano, Masser, Pila, and Zannier have recently applied the Pila–Zannier method in this setting [Reference Capuano, Masser, Pila and ZannierCMPZ16]. When
$V$
is a curve, defined over a number field, and contained in an algebraic torus, we obtain a theorem of Maurin [Reference MaurinMau08]. We also note that Capuano, Masser, Pila, and Zannier have recently applied the Pila–Zannier method in this setting [Reference Capuano, Masser, Pila and ZannierCMPZ16]. When
![]() $V$
is a curve, defined over a number field, and contained in an abelian variety, we obtain the recent theorem of Habegger and Pila [Reference Habegger and PilaHP16], and it is the ideas presented there that form the basis for this article. Habegger and Pila had given some partial results when
$V$
is a curve, defined over a number field, and contained in an abelian variety, we obtain the recent theorem of Habegger and Pila [Reference Habegger and PilaHP16], and it is the ideas presented there that form the basis for this article. Habegger and Pila had given some partial results when
![]() $V$
is a curve, defined over a number field, and contained in the Shimura variety
$V$
is a curve, defined over a number field, and contained in the Shimura variety
![]() $\mathbb{C}^{n}$
[Reference Habegger and PilaHab12], and Orr has recently generalized their results to a curve contained in
$\mathbb{C}^{n}$
[Reference Habegger and PilaHab12], and Orr has recently generalized their results to a curve contained in
![]() ${\mathcal{A}}_{g}^{2}$
(see [Reference OrrOrr17] for more details).
${\mathcal{A}}_{g}^{2}$
(see [Reference OrrOrr17] for more details).
We should point out that Conjecture 1.1 implies the André–Oort conjecture.
Conjecture 1.2 (André–Oort).
Let
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
be a Shimura variety and let
$\text{Sh}_{K}(G,\mathfrak{X})$
be a Shimura variety and let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
such that the special points of
$\text{Sh}_{K}(G,\mathfrak{X})$
such that the special points of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
in
$\text{Sh}_{K}(G,\mathfrak{X})$
in
![]() $V$
are Zariski dense in
$V$
are Zariski dense in
![]() $V$
. Then
$V$
. Then
![]() $V$
is a special subvariety of
$V$
is a special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
.
$\text{Sh}_{K}(G,\mathfrak{X})$
.
To see this, we may assume that
![]() $V$
is Hodge generic in
$V$
is Hodge generic in
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
. Then, since special points have codimension
$\text{Sh}_{K}(G,\mathfrak{X})$
. Then, since special points have codimension
![]() $\dim \text{Sh}_{K}(G,\mathfrak{X})$
, Conjecture 1.1 implies that, either
$\dim \text{Sh}_{K}(G,\mathfrak{X})$
, Conjecture 1.1 implies that, either
![]() $\dim V=\dim \text{Sh}_{K}(G,\mathfrak{X})$
, in which case
$\dim V=\dim \text{Sh}_{K}(G,\mathfrak{X})$
, in which case
![]() $V$
is a connected component of
$V$
is a connected component of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
and, in particular, a special subvariety of
$\text{Sh}_{K}(G,\mathfrak{X})$
and, in particular, a special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
, or the set of special points of
$\text{Sh}_{K}(G,\mathfrak{X})$
, or the set of special points of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
in
$\text{Sh}_{K}(G,\mathfrak{X})$
in
![]() $V$
are not Zariski dense in
$V$
are not Zariski dense in
![]() $V$
.
$V$
.
In precisely the same fashion, the Zilber–Pink conjecture for abelian varieties implies the Manin–Mumford conjecture.
The André–Oort conjecture has a rich history of its own. Here, we simply recall that it was recently settled for
![]() ${\mathcal{A}}_{g}$
by Pila and Tsimerman [Reference Pila and TsimermanPT14, Reference TsimermanTsi18], thanks to recent progress on the Colmez conjecture due to Andreatta, Goren, Howard and Madapusi Pera [Reference Andreatta, Goren, Howard and Madapusi PeraAGHM18], and Yuan and Zhang [Reference Yuan and ZhangYZ18], and it is known to hold for all Shimura varieties under conjectural lower bounds for Galois orbits of special points due to the work of Orr, Klingler, Ulmo, Yafaev, and the first author [Reference Daw and OrrDO16, Reference Klingler, Ullmo and YafaevKUY16, Reference Ullmo and YafaevUY15]. Furthermore, Gao has generalized these proofs to all mixed Shimura varieties [Reference GaoGao17, Reference GaoGao16].
${\mathcal{A}}_{g}$
by Pila and Tsimerman [Reference Pila and TsimermanPT14, Reference TsimermanTsi18], thanks to recent progress on the Colmez conjecture due to Andreatta, Goren, Howard and Madapusi Pera [Reference Andreatta, Goren, Howard and Madapusi PeraAGHM18], and Yuan and Zhang [Reference Yuan and ZhangYZ18], and it is known to hold for all Shimura varieties under conjectural lower bounds for Galois orbits of special points due to the work of Orr, Klingler, Ulmo, Yafaev, and the first author [Reference Daw and OrrDO16, Reference Klingler, Ullmo and YafaevKUY16, Reference Ullmo and YafaevUY15]. Furthermore, Gao has generalized these proofs to all mixed Shimura varieties [Reference GaoGao17, Reference GaoGao16].
In his work on Schanuel’s conjecture, Zilber made his own conjecture on unlikely intersections [Reference ZilberZil02], which was closely related to the independent work of Bombieri, Masser and Zannier [Reference Bombieri, Masser and ZannierBMZ07]. To describe Zilber’s formulation, we require the following definition.
Definition 1.3. Let
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
be a Shimura variety and let
$\text{Sh}_{K}(G,\mathfrak{X})$
be a Shimura variety and let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
. A subvariety
$\text{Sh}_{K}(G,\mathfrak{X})$
. A subvariety
![]() $W$
of
$W$
of
![]() $V$
is called atypical with respect to
$V$
is called atypical with respect to
![]() $V$
if there is a special subvariety
$V$
if there is a special subvariety
![]() $T$
of
$T$
of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
such that
$\text{Sh}_{K}(G,\mathfrak{X})$
such that
![]() $W$
is an irreducible component of
$W$
is an irreducible component of
![]() $V\cap T$
and
$V\cap T$
and
We denote by
![]() $\text{Atyp}(V)$
the union of the subvarieties of
$\text{Atyp}(V)$
the union of the subvarieties of
![]() $V$
that are atypical with respect to
$V$
that are atypical with respect to
![]() $V$
.
$V$
.
Zilber’s conjecture, formulated for Shimura varieties, is then as follows.
Conjecture 1.4 (Cf. [Reference Habegger and PilaHP16, Conjecture 2.2]).
Let
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
be a Shimura variety and let
$\text{Sh}_{K}(G,\mathfrak{X})$
be a Shimura variety and let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
. Then
$\text{Sh}_{K}(G,\mathfrak{X})$
. Then
![]() $\text{Atyp}(V)$
is equal to a finite union of atypical subvarieties of
$\text{Atyp}(V)$
is equal to a finite union of atypical subvarieties of
![]() $V$
.
$V$
.
Since there are only countably many special subvarieties of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
, the conjecture is equivalent to the statement that
$\text{Sh}_{K}(G,\mathfrak{X})$
, the conjecture is equivalent to the statement that
![]() $V$
contains only finitely many subvarieties that are atypical with respect to
$V$
contains only finitely many subvarieties that are atypical with respect to
![]() $V$
and maximal with respect to this property.
$V$
and maximal with respect to this property.
We will see that Conjecture 1.4 strengthens Conjecture 1.1 and, therefore, it is Conjecture 1.4 that we refer to as the Zilber–Pink conjecture. Habegger and Pila obtained a proof of the Zilber–Pink conjecture for products of modular curves assuming the weak complex Ax conjecture and the large Galois orbits conjecture. Subsequently, Pila and Tsimerman obtained the weak complex Ax conjecture as a corollary to their proof of the Ax–Schanuel conjecture for the
![]() $j$
-function [Reference Pila and TsimermanPT16]. Habegger and Pila had previously verified the large Galois orbits conjecture for so-called asymmetric curves [Reference Habegger and PilaHab12].
$j$
-function [Reference Pila and TsimermanPT16]. Habegger and Pila had previously verified the large Galois orbits conjecture for so-called asymmetric curves [Reference Habegger and PilaHab12].
This article seeks to generalize the ideas of [Reference Habegger and PilaHP16] to general Shimura varieties. Hence, we will have to make generalizations of the previously mentioned hypotheses. The foremost of which will be the statement from functional transcendence, namely, the hyperbolic Ax–Schanuel conjecture that generalizes the Ax–Schanuel conjecture for the
![]() $j$
-function to general Shimura varieties. Our main result (Theorem 8.3) is that, under the hyperbolic Ax–Schanuel conjecture, the Zilber–Pink conjecture can be reduced to a problem of point counting. However, given that Mok, Pila, and Tsimerman have recently announced a proof of the hyperbolic Ax–Schanuel conjecture [Reference Mok, Pila and TsimermanMPT17], this result is now very likely unconditional. Besides the hyperbolic Ax–Schanuel conjecture, our main input will be the theory of o-minimality and, in particular, the fact that the uniformization map of a Shimura variety is definable in
$j$
-function to general Shimura varieties. Our main result (Theorem 8.3) is that, under the hyperbolic Ax–Schanuel conjecture, the Zilber–Pink conjecture can be reduced to a problem of point counting. However, given that Mok, Pila, and Tsimerman have recently announced a proof of the hyperbolic Ax–Schanuel conjecture [Reference Mok, Pila and TsimermanMPT17], this result is now very likely unconditional. Besides the hyperbolic Ax–Schanuel conjecture, our main input will be the theory of o-minimality and, in particular, the fact that the uniformization map of a Shimura variety is definable in
![]() $\mathbb{R}_{\text{an},\text{exp}}$
when it is restricted to an appropriate fundamental domain.
$\mathbb{R}_{\text{an},\text{exp}}$
when it is restricted to an appropriate fundamental domain.
After establishing the main result, we attempt to tackle the point counting problem using the now famous Pila–Wilkie counting theorem. To do so, we formulate several arithmetic conjectures that are inspired by previous applications of the Pila–Zannier strategy. In this vein, our paper is very much in the spirit of [Reference UllmoUll14], which, at the time, reduced the André–Oort conjecture to a point counting problem and then explained how various conjectural ingredients, namely, the hyperbolic Ax–Lindemann conjecture, lower bounds for Galois orbits of special points, upper bounds for the heights of pre-special points, and the definability of the uniformization map, could be combined to deliver a proof of the André–Oort conjecture.
Our arithmetic hypotheses are: (1) lower bounds for Galois orbits of so-called optimal points (see Definition 3.2), which we also refer to as the large Galois orbits conjecture, and (2) upper bounds for the heights of pre-special subvarieties. Hypothesis (1) generalizes the (in some cases still conjectural) lower bounds for Galois orbits of special points (when such special points are also maximal special subvarieties), and also generalizes the large Galois orbits conjecture of Habegger and Pila. Hypothesis (2) generalizes the upper bounds for heights of pre-special points, which were proved by Orr and the first author [Reference Daw and OrrDO16]. However, we also show that it is possible to replace hypothesis (2) with two other arithmetic hypotheses, namely: (3) upper bounds for the degrees of fields associated with special subvarieties, and (4) upper bounds for the heights of lattice elements. Hypothesis (3) is a replacement for the fact that, for an abelian variety, its abelian subvarieties can be defined over a fixed finite extension of the base field. Hypothesis (4) is an analogue of a known result for abelian varieties. We verify hypotheses (2), (3), and (4) for a product of modular curves.
Conventions.
⋆ Throughout this paper, definable means definable in the o-minimal structure
 $\mathbb{R}_{\text{an},\text{exp}}$
.
$\mathbb{R}_{\text{an},\text{exp}}$
.⋆ Unless preceded by the word Shimura, varieties (and, indeed, subvarieties) will be assumed geometrically irreducible.
⋆ By a subvariety, we will always mean a closed subvariety.
Index of notation. We collect here the main symbols appearing in this article.
⋆
 $\langle W\rangle$
is the smallest special subvariety containing
$\langle W\rangle$
is the smallest special subvariety containing
 $W$
.
$W$
.⋆
 $\langle W\rangle _{\text{ws}}$
is the smallest weakly special subvariety containing
$\langle W\rangle _{\text{ws}}$
is the smallest weakly special subvariety containing
 $W$
.
$W$
.⋆
 $\langle A\rangle _{\text{Zar}}$
is the smallest algebraic subvariety containing
$\langle A\rangle _{\text{Zar}}$
is the smallest algebraic subvariety containing
 $A$
.
$A$
.⋆
 $\langle A\rangle _{\text{geo}}$
is the smallest totally geodesic subvariety containing
$\langle A\rangle _{\text{geo}}$
is the smallest totally geodesic subvariety containing
 $A$
.
$A$
.⋆
 $\unicode[STIX]{x1D6FF}(W):=\dim \langle W\rangle -\dim W$
.
$\unicode[STIX]{x1D6FF}(W):=\dim \langle W\rangle -\dim W$
.⋆
 $\unicode[STIX]{x1D6FF}_{\text{ws}}(W):=\dim \langle W\rangle _{\text{ws}}-\dim W$
.
$\unicode[STIX]{x1D6FF}_{\text{ws}}(W):=\dim \langle W\rangle _{\text{ws}}-\dim W$
.⋆
 $\unicode[STIX]{x1D6FF}_{\text{Zar}}(A):=\dim \langle A\rangle _{\text{Zar}}-\dim A$
.
$\unicode[STIX]{x1D6FF}_{\text{Zar}}(A):=\dim \langle A\rangle _{\text{Zar}}-\dim A$
.⋆
 $\unicode[STIX]{x1D6FF}_{\text{geo}}(A):=\dim \langle A\rangle _{\text{geo}}-\dim A$
.
$\unicode[STIX]{x1D6FF}_{\text{geo}}(A):=\dim \langle A\rangle _{\text{geo}}-\dim A$
.⋆
 $\text{Opt}(V)$
is the set of subvarieties of
$\text{Opt}(V)$
is the set of subvarieties of
 $V$
that are optimal in
$V$
that are optimal in
 $V$
.
$V$
.⋆
 $\text{Opt}_{0}(V)$
is the set of points of
$\text{Opt}_{0}(V)$
is the set of points of
 $V$
that are optimal in
$V$
that are optimal in
 $V$
.
$V$
.⋆
 $G^{\text{ad}}$
is the adjoint group of
$G^{\text{ad}}$
is the adjoint group of
 $G$
, i.e., the quotient of
$G$
, i.e., the quotient of
 $G$
by its centre.
$G$
by its centre.⋆
 $G^{\text{der}}$
is derived group of
$G^{\text{der}}$
is derived group of
 $G$
.
$G$
.⋆
 $G^{\circ }$
is the connected component of
$G^{\circ }$
is the connected component of
 $G$
containing the identity.
$G$
containing the identity.⋆
 $G_{H}:=HZ_{G}(H)^{\circ }$
whenever
$G_{H}:=HZ_{G}(H)^{\circ }$
whenever
 $H$
is a subgroup of
$H$
is a subgroup of
 $G$
.
$G$
.
2 Special and weakly special subvarieties
Let
![]() $(G,\mathfrak{X})$
be a Shimura datum and let
$(G,\mathfrak{X})$
be a Shimura datum and let
![]() $K$
be a compact open subgroup of
$K$
be a compact open subgroup of
![]() $G(\mathbb{A}_{f})$
, where
$G(\mathbb{A}_{f})$
, where
![]() $\mathbb{A}_{f}$
will henceforth denote the finite rational adèles. Let
$\mathbb{A}_{f}$
will henceforth denote the finite rational adèles. Let
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
denote the corresponding Shimura variety. By this, we mean the complex quasi-projective algebraic variety such that
$\text{Sh}_{K}(G,\mathfrak{X})$
denote the corresponding Shimura variety. By this, we mean the complex quasi-projective algebraic variety such that
![]() $\text{Sh}_{K}(G,\mathfrak{X})(\mathbb{C})$
is equal to the image of
$\text{Sh}_{K}(G,\mathfrak{X})(\mathbb{C})$
is equal to the image of
under the canonical embedding into complex projective space given by Baily and Borel [Reference Baily and BorelBB66]. We will identify (2.0.1) with
![]() $\text{Sh}_{K}(G,\mathfrak{X})(\mathbb{C})$
. We recall that, on
$\text{Sh}_{K}(G,\mathfrak{X})(\mathbb{C})$
. We recall that, on
![]() $\mathfrak{X}\times (G(\mathbb{A}_{f})/K)$
, the action of
$\mathfrak{X}\times (G(\mathbb{A}_{f})/K)$
, the action of
![]() $G(\mathbb{Q})$
is the diagonal one.
$G(\mathbb{Q})$
is the diagonal one.
Let
![]() $X$
be a connected component of
$X$
be a connected component of
![]() $\mathfrak{X}$
and let
$\mathfrak{X}$
and let
![]() $G(\mathbb{Q})_{+}$
be the subgroup of
$G(\mathbb{Q})_{+}$
be the subgroup of
![]() $G(\mathbb{Q})$
acting on it. For any
$G(\mathbb{Q})$
acting on it. For any
![]() $g\in G(\mathbb{A}_{f})$
, we obtain a congruence subgroup
$g\in G(\mathbb{A}_{f})$
, we obtain a congruence subgroup
![]() $\unicode[STIX]{x1D6E4}_{g}$
of
$\unicode[STIX]{x1D6E4}_{g}$
of
![]() $G(\mathbb{Q})_{+}$
by intersecting it with
$G(\mathbb{Q})_{+}$
by intersecting it with
![]() $gKg^{-1}$
. Furthermore, the locally symmetric variety
$gKg^{-1}$
. Furthermore, the locally symmetric variety
![]() $\unicode[STIX]{x1D6E4}_{g}\backslash X$
is contained in (2.0.1) via the map that sends the class of
$\unicode[STIX]{x1D6E4}_{g}\backslash X$
is contained in (2.0.1) via the map that sends the class of
![]() $x$
to the class of
$x$
to the class of
![]() $(x,g)$
. If we take the disjoint union of the
$(x,g)$
. If we take the disjoint union of the
![]() $\unicode[STIX]{x1D6E4}_{g}\backslash X$
over a (finite) set of representatives for
$\unicode[STIX]{x1D6E4}_{g}\backslash X$
over a (finite) set of representatives for
the corresponding inclusion map is a bijection.
Definition 2.1. For any compact open subgroup
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $G(\mathbb{A}_{f})$
contained in
$G(\mathbb{A}_{f})$
contained in
![]() $K$
, we obtain a finite morphism
$K$
, we obtain a finite morphism
given by the natural projection. Furthermore, for any
![]() $a\in G(\mathbb{A}_{f})$
, we obtain an isomorphism
$a\in G(\mathbb{A}_{f})$
, we obtain an isomorphism
sending the class of
![]() $(x,g)$
to the class of
$(x,g)$
to the class of
![]() $(x,ga)$
. We let
$(x,ga)$
. We let
![]() $T_{K,a}$
denote the map on algebraic cycles of
$T_{K,a}$
denote the map on algebraic cycles of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
given by the algebraic correspondence
$\text{Sh}_{K}(G,\mathfrak{X})$
given by the algebraic correspondence
where the outer arrows are the natural projections and the middle arrow is the isomorphism given by
![]() $a$
. We refer to a map of this sort as a Hecke correspondence.
$a$
. We refer to a map of this sort as a Hecke correspondence.
Definition 2.2. Let
![]() $(H,\mathfrak{X}_{H})$
be a Shimura subdatum of
$(H,\mathfrak{X}_{H})$
be a Shimura subdatum of
![]() $(G,\mathfrak{X})$
and let
$(G,\mathfrak{X})$
and let
![]() $K_{H}$
denote a compact open subgroup of
$K_{H}$
denote a compact open subgroup of
![]() $H(\mathbb{A}_{f})$
contained in
$H(\mathbb{A}_{f})$
contained in
![]() $K$
. The natural map
$K$
. The natural map
yields a finite morphism of Shimura varieties
(see, for example, [Reference PinkPin05a, Facts 2.6]), and we refer to the image of any such morphism as a Shimura subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
.
$\text{Sh}_{K}(G,\mathfrak{X})$
.
For any Shimura subvariety
![]() $Z$
of
$Z$
of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
and any
$\text{Sh}_{K}(G,\mathfrak{X})$
and any
![]() $a\in G(\mathbb{A}_{f})$
, we refer to any irreducible component of
$a\in G(\mathbb{A}_{f})$
, we refer to any irreducible component of
![]() $T_{K,a}(Z)$
as a special subvariety of
$T_{K,a}(Z)$
as a special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
.
$\text{Sh}_{K}(G,\mathfrak{X})$
.
Recall that, by definition,
![]() $\mathfrak{X}$
is a
$\mathfrak{X}$
is a
![]() $G(\mathbb{R})$
conjugacy class of morphisms from
$G(\mathbb{R})$
conjugacy class of morphisms from
![]() $\mathbb{S}$
to
$\mathbb{S}$
to
![]() $G_{\mathbb{R}}$
and the Mumford-Tate group
$G_{\mathbb{R}}$
and the Mumford-Tate group
![]() $\text{MT}(x)$
of
$\text{MT}(x)$
of
![]() $x\in \mathfrak{X}$
is defined as the smallest
$x\in \mathfrak{X}$
is defined as the smallest
![]() $\mathbb{Q}$
-subgroup
$\mathbb{Q}$
-subgroup
![]() $H$
of
$H$
of
![]() $G$
such that
$G$
such that
![]() $x$
factors through
$x$
factors through
![]() $H_{\mathbb{R}}$
. If we let
$H_{\mathbb{R}}$
. If we let
![]() $\mathfrak{X}_{M}$
denote the
$\mathfrak{X}_{M}$
denote the
![]() $M(\mathbb{R})$
conjugacy class of
$M(\mathbb{R})$
conjugacy class of
![]() $x\in X$
, where
$x\in X$
, where
![]() $M:=\text{MT}(x)$
, then
$M:=\text{MT}(x)$
, then
![]() $(M,\mathfrak{X}_{M})$
is a Shimura subdatum of
$(M,\mathfrak{X}_{M})$
is a Shimura subdatum of
![]() $(G,\mathfrak{X})$
. In particular, if we let
$(G,\mathfrak{X})$
. In particular, if we let
![]() $X_{M}$
denote a connected component of
$X_{M}$
denote a connected component of
![]() $\mathfrak{X}_{M}$
contained in
$\mathfrak{X}_{M}$
contained in
![]() $X$
, then the image of
$X$
, then the image of
![]() $X_{M}$
in
$X_{M}$
in
![]() $\unicode[STIX]{x1D6E4}_{g}\backslash X$
, for any
$\unicode[STIX]{x1D6E4}_{g}\backslash X$
, for any
![]() $g\in G(\mathbb{A}_{f})$
, is a special subvariety of
$g\in G(\mathbb{A}_{f})$
, is a special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
, and it is easy to see that every special subvariety of
$\text{Sh}_{K}(G,\mathfrak{X})$
, and it is easy to see that every special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
arises this way.
$\text{Sh}_{K}(G,\mathfrak{X})$
arises this way.
Of course, if
![]() $x\in X_{M}$
, then
$x\in X_{M}$
, then
![]() $X_{M}$
is equal to the
$X_{M}$
is equal to the
![]() $M(\mathbb{R})^{+}$
conjugacy class of
$M(\mathbb{R})^{+}$
conjugacy class of
![]() $x$
. Furthermore, the action of
$x$
. Furthermore, the action of
![]() $M(\mathbb{R})$
on
$M(\mathbb{R})$
on
![]() $\mathfrak{X}_{M}$
factors through
$\mathfrak{X}_{M}$
factors through
![]() $M^{\text{ad}}(\mathbb{R})$
and the group
$M^{\text{ad}}(\mathbb{R})$
and the group
![]() $M^{\text{ad}}$
is equal to the direct product of its
$M^{\text{ad}}$
is equal to the direct product of its
![]() $\mathbb{Q}$
-simple factors. Therefore, we can write
$\mathbb{Q}$
-simple factors. Therefore, we can write
![]() $M^{\text{ad}}$
as a product
$M^{\text{ad}}$
as a product
of two normal
![]() $\mathbb{Q}$
-subgroups, either of which may (by choice or necessity) be trivial, and we thus obtain a corresponding splitting
$\mathbb{Q}$
-subgroups, either of which may (by choice or necessity) be trivial, and we thus obtain a corresponding splitting
For any such splitting, and any
![]() $x_{1}\in X_{1}$
or
$x_{1}\in X_{1}$
or
![]() $x_{2}\in X_{2}$
, we refer to the image of
$x_{2}\in X_{2}$
, we refer to the image of
![]() $\{x_{1}\}\,\times \,X_{2}$
or
$\{x_{1}\}\,\times \,X_{2}$
or
![]() $X_{1}\,\times \,\{x_{2}\}$
in
$X_{1}\,\times \,\{x_{2}\}$
in
![]() $\unicode[STIX]{x1D6E4}_{g}\backslash X$
, for any
$\unicode[STIX]{x1D6E4}_{g}\backslash X$
, for any
![]() $g\in G(\mathbb{A}_{f})$
, as a weakly special subvariety of
$g\in G(\mathbb{A}_{f})$
, as a weakly special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
. In particular, every special subvariety of
$\text{Sh}_{K}(G,\mathfrak{X})$
. In particular, every special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
is a weakly special subvariety of
$\text{Sh}_{K}(G,\mathfrak{X})$
is a weakly special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
. By [Reference MoonenMoo98, § 4], the weakly special subvarieties of
$\text{Sh}_{K}(G,\mathfrak{X})$
. By [Reference MoonenMoo98, § 4], the weakly special subvarieties of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
are precisely those subvarieties of
$\text{Sh}_{K}(G,\mathfrak{X})$
are precisely those subvarieties of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
that are totally geodesic in
$\text{Sh}_{K}(G,\mathfrak{X})$
that are totally geodesic in
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
. Furthermore, a weakly special subvariety of
$\text{Sh}_{K}(G,\mathfrak{X})$
. Furthermore, a weakly special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
is a special subvariety of
$\text{Sh}_{K}(G,\mathfrak{X})$
is a special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
if and only if it contains a special subvariety of dimension zero, henceforth known as a special point.
$\text{Sh}_{K}(G,\mathfrak{X})$
if and only if it contains a special subvariety of dimension zero, henceforth known as a special point.
Remark 2.3. The following observations will facilitate various reductions.
⋆ Let
 $K^{\prime }$
be a compact open subgroup of
$K^{\prime }$
be a compact open subgroup of
 $G(\mathbb{A}_{f})$
contained in
$G(\mathbb{A}_{f})$
contained in
 $K$
. By definition, a subvariety
$K$
. By definition, a subvariety
 $Z$
of
$Z$
of
 $\text{Sh}_{K}(G,\mathfrak{X})$
is a (weakly) special subvariety of
$\text{Sh}_{K}(G,\mathfrak{X})$
is a (weakly) special subvariety of
 $\text{Sh}_{K}(G,\mathfrak{X})$
if and only if any irreducible component of the inverse image of
$\text{Sh}_{K}(G,\mathfrak{X})$
if and only if any irreducible component of the inverse image of
 $Z$
in
$Z$
in
 $\text{Sh}_{K^{\prime }}(G,\mathfrak{X})$
is a (weakly) special subvariety of
$\text{Sh}_{K^{\prime }}(G,\mathfrak{X})$
is a (weakly) special subvariety of
 $\text{Sh}_{K^{\prime }}(G,\mathfrak{X})$
.
$\text{Sh}_{K^{\prime }}(G,\mathfrak{X})$
.⋆ For any
 $a\in G(\mathbb{A}_{f})$
, a subvariety
$a\in G(\mathbb{A}_{f})$
, a subvariety
 $Z$
of
$Z$
of
 $\text{Sh}_{K}(G,\mathfrak{X})$
is a (weakly) special subvariety of
$\text{Sh}_{K}(G,\mathfrak{X})$
is a (weakly) special subvariety of
 $\text{Sh}_{K}(G,\mathfrak{X})$
if and only if any irreducible component of
$\text{Sh}_{K}(G,\mathfrak{X})$
if and only if any irreducible component of
 $T_{K,a}(Z)$
is a (weakly) special subvariety of
$T_{K,a}(Z)$
is a (weakly) special subvariety of
 $\text{Sh}_{K^{\prime }}(G,\mathfrak{X})$
.
$\text{Sh}_{K^{\prime }}(G,\mathfrak{X})$
.⋆ If we let
 $G^{\text{ad}}$
denote the adjoint group of
$G^{\text{ad}}$
denote the adjoint group of
 $G$
, i.e., the quotient of
$G$
, i.e., the quotient of
 $G$
by its centre, we obtain another Shimura datum
$G$
by its centre, we obtain another Shimura datum
 $(G^{\text{ad}},\mathfrak{X}^{\text{ad}})$
, known as the adjoint Shimura datum associated with
$(G^{\text{ad}},\mathfrak{X}^{\text{ad}})$
, known as the adjoint Shimura datum associated with
 $(G,\mathfrak{X})$
. For any compact open subgroup
$(G,\mathfrak{X})$
. For any compact open subgroup
 $K^{\text{ad}}$
of
$K^{\text{ad}}$
of
 $G^{\text{ad}}(\mathbb{A}_{f})$
containing the image of
$G^{\text{ad}}(\mathbb{A}_{f})$
containing the image of
 $K$
, we obtain a finite morphism As in [Reference Edixhoven and YafaevEY03, Proposition 2.2], a subvariety
$K$
, we obtain a finite morphism As in [Reference Edixhoven and YafaevEY03, Proposition 2.2], a subvariety $$\begin{eqnarray}\displaystyle \text{Sh}_{K}(G,\mathfrak{X})\rightarrow \text{Sh}_{K^{\text{ad}}}(G^{\text{ad}},\mathfrak{X}^{\text{ad}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Sh}_{K}(G,\mathfrak{X})\rightarrow \text{Sh}_{K^{\text{ad}}}(G^{\text{ad}},\mathfrak{X}^{\text{ad}}). & & \displaystyle \nonumber\end{eqnarray}$$
 $Z$
of
$Z$
of
 $\text{Sh}_{K^{\text{ad}}}(G^{\text{ad}},\mathfrak{X}^{\text{ad}})$
is a special subvariety of
$\text{Sh}_{K^{\text{ad}}}(G^{\text{ad}},\mathfrak{X}^{\text{ad}})$
is a special subvariety of
 $\text{Sh}_{K^{\text{ad}}}(G^{\text{ad}},\mathfrak{X}^{\text{ad}})$
if and only if any irreducible component of its inverse image in
$\text{Sh}_{K^{\text{ad}}}(G^{\text{ad}},\mathfrak{X}^{\text{ad}})$
if and only if any irreducible component of its inverse image in
 $\text{Sh}_{K}(G,\mathfrak{X})$
is a special subvariety of
$\text{Sh}_{K}(G,\mathfrak{X})$
is a special subvariety of
 $\text{Sh}_{K}(G,\mathfrak{X})$
.
$\text{Sh}_{K}(G,\mathfrak{X})$
.
By [Reference PinkPin05a, Remark 4.9], for any subvariety
![]() $W$
of
$W$
of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
, there exists a smallest weakly special subvariety
$\text{Sh}_{K}(G,\mathfrak{X})$
, there exists a smallest weakly special subvariety
![]() $\langle W\rangle _{\text{ws}}$
of
$\langle W\rangle _{\text{ws}}$
of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
containing
$\text{Sh}_{K}(G,\mathfrak{X})$
containing
![]() $W$
and a smallest special subvariety
$W$
and a smallest special subvariety
![]() $\langle W\rangle$
of
$\langle W\rangle$
of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
containing
$\text{Sh}_{K}(G,\mathfrak{X})$
containing
![]() $W$
. We note that here, and throughout, our notations and terminology regarding subvarieties often differ from those found in [Reference Habegger and PilaHP16].
$W$
. We note that here, and throughout, our notations and terminology regarding subvarieties often differ from those found in [Reference Habegger and PilaHP16].
3 The Zilber–Pink conjecture
For the remainder of this article, we fix a Shimura datum
![]() $(G,\mathfrak{X})$
and we let
$(G,\mathfrak{X})$
and we let
![]() $X$
be a connected component of
$X$
be a connected component of
![]() $\mathfrak{X}$
. We fix a compact open subgroup
$\mathfrak{X}$
. We fix a compact open subgroup
![]() $K$
of
$K$
of
![]() $G(\mathbb{A}_{f})$
and we let
$G(\mathbb{A}_{f})$
and we let
where
![]() $G(\mathbb{Q})_{+}$
is the subgroup of
$G(\mathbb{Q})_{+}$
is the subgroup of
![]() $G(\mathbb{Q})$
acting on
$G(\mathbb{Q})$
acting on
![]() $X$
. We denote by
$X$
. We denote by
![]() $S$
the connected component
$S$
the connected component
![]() $\unicode[STIX]{x1D6E4}\backslash X$
of
$\unicode[STIX]{x1D6E4}\backslash X$
of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
.
$\text{Sh}_{K}(G,\mathfrak{X})$
.
As in [Reference Habegger and PilaHP16], we will consider an equivalent formulation of Conjecture 1.4 using the language of optimal subvarieties.
Definition 3.1. Let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $S$
. We define the defect of
$S$
. We define the defect of
![]() $W$
to be
$W$
to be
Definition 3.2. Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
and let
$S$
and let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $V$
. Then
$V$
. Then
![]() $W$
is called optimal in
$W$
is called optimal in
![]() $V$
if, for any subvariety
$V$
if, for any subvariety
![]() $Y$
of
$Y$
of
![]() $S$
,
$S$
,
We denote by
![]() $\text{Opt}(V)$
the set of all subvarieties of
$\text{Opt}(V)$
the set of all subvarieties of
![]() $V$
that are optimal in
$V$
that are optimal in
![]() $V$
.
$V$
.
Remark 3.3. Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
. First note that
$S$
. First note that
![]() $V\in \text{Opt}(V)$
. Secondly, if
$V\in \text{Opt}(V)$
. Secondly, if
![]() $W\in \text{Opt}(V)$
, then
$W\in \text{Opt}(V)$
, then
![]() $W$
is an irreducible component of
$W$
is an irreducible component of
Conjecture 3.4 (Cf. [Reference Habegger and PilaHP16, Conjecture 2.6]).
Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
. Then
$S$
. Then
![]() $\text{Opt}(V)$
is finite.
$\text{Opt}(V)$
is finite.
Observe that a maximal special subvariety of
![]() $V$
is an optimal subvariety of
$V$
is an optimal subvariety of
![]() $V$
. Therefore, Conjecture 3.4 immediately implies that
$V$
. Therefore, Conjecture 3.4 immediately implies that
![]() $V$
contains only finitely many maximal special subvarieties, which is another formulation of the André–Oort conjecture for
$V$
contains only finitely many maximal special subvarieties, which is another formulation of the André–Oort conjecture for
![]() $V$
.
$V$
.
Proof. Consider the situation described in the statement of Conjecture 1.4. By Remark 2.3, we suffer no loss in generality if we assume that
![]() $V$
is contained in
$V$
is contained in
![]() $S$
. Then the result follows from [Reference Habegger and PilaHP16, Lemma 2.7].◻
$S$
. Then the result follows from [Reference Habegger and PilaHP16, Lemma 2.7].◻
Lemma 3.6. The Zilber–Pink conjecture implies Conjecture 1.1.
Proof. By Lemma 3.5, it suffices to show that Conjecture 3.4 implies Conjecture 1.1.
Consider the situation described in Conjecture 1.1. By Remark 2.3, we suffer no loss in generality if we assume that
![]() $V$
is contained in
$V$
is contained in
![]() $S$
. Let
$S$
. Let
![]() $P$
be a point belonging to
$P$
be a point belonging to
Let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $V$
that is optimal in
$V$
that is optimal in
![]() $V$
and contains
$V$
and contains
![]() $P$
such that
$P$
such that
Since
![]() $P$
belongs to a special subvariety of codimension at least
$P$
belongs to a special subvariety of codimension at least
![]() $\dim V+1$
and
$\dim V+1$
and
![]() $V$
is Hodge generic in
$V$
is Hodge generic in
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
, we have
$\text{Sh}_{K}(G,\mathfrak{X})$
, we have
Therefore,
![]() $\unicode[STIX]{x1D6FF}(W)<\unicode[STIX]{x1D6FF}(V)$
and we conclude that
$\unicode[STIX]{x1D6FF}(W)<\unicode[STIX]{x1D6FF}(V)$
and we conclude that
![]() $W$
is not
$W$
is not
![]() $V$
. According to Conjecture 3.4, the union of the subvarieties belonging to
$V$
. According to Conjecture 3.4, the union of the subvarieties belonging to
![]() $\text{Opt}(V)\setminus V$
is not Zariski dense in
$\text{Opt}(V)\setminus V$
is not Zariski dense in
![]() $V$
.◻
$V$
.◻
4 The defect condition
In this section, we prove Habegger and Pila’s defect condition for Shimura varieties and thus show that a subvariety that is optimal is weakly optimal.
Definition 4.1. Let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $S$
. We define the weakly special defect of
$S$
. We define the weakly special defect of
![]() $W$
to be
$W$
to be
We note that, in [Reference Habegger and PilaHP16], this notion was referred to as geodesic defect.
Definition 4.2. If
![]() $V$
is a subvariety of
$V$
is a subvariety of
![]() $S$
and
$S$
and
![]() $W$
a subvariety of
$W$
a subvariety of
![]() $V$
, then
$V$
, then
![]() $W$
is called weakly optimal in
$W$
is called weakly optimal in
![]() $V$
if, for any subvariety
$V$
if, for any subvariety
![]() $Y$
of
$Y$
of
![]() $S$
,
$S$
,
Remark 4.3. Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
and
$S$
and
![]() $W$
a subvariety of
$W$
a subvariety of
![]() $V$
. If
$V$
. If
![]() $W$
is weakly optimal in
$W$
is weakly optimal in
![]() $V$
, then
$V$
, then
![]() $W$
is an irreducible component of
$W$
is an irreducible component of
Proposition 4.4 (Cf. [Reference Habegger and PilaHP16, Proposition 4.3]).
The following defect condition holds.
Let
![]() $W\subseteq Y$
be two subvarieties of
$W\subseteq Y$
be two subvarieties of
![]() $S$
. Then
$S$
. Then
Proof. We need to show that
By Remark 2.3, we can and do assume that
![]() $G$
is the generic Mumford–Tate group on
$G$
is the generic Mumford–Tate group on
![]() $X$
, that it is equal to
$X$
, that it is equal to
![]() $G^{\text{ad}}$
, and that
$G^{\text{ad}}$
, and that
![]() $Y$
is Hodge generic in
$Y$
is Hodge generic in
![]() $S$
. By definition, there exists a decomposition
$S$
. By definition, there exists a decomposition
which induces a splitting
such that
![]() $\langle Y\rangle _{\text{ws}}$
is equal to the image of
$\langle Y\rangle _{\text{ws}}$
is equal to the image of
![]() $X_{1}\times \{x_{2}\}$
in
$X_{1}\times \{x_{2}\}$
in
![]() $S$
, for some
$S$
, for some
![]() $x_{2}\in X_{2}$
.
$x_{2}\in X_{2}$
.
Let
![]() $\unicode[STIX]{x1D6E4}_{1}:=\text{p}_{1}(\unicode[STIX]{x1D6E4})$
and
$\unicode[STIX]{x1D6E4}_{1}:=\text{p}_{1}(\unicode[STIX]{x1D6E4})$
and
![]() $\unicode[STIX]{x1D6E4}_{2}:=\text{p}_{2}(\unicode[STIX]{x1D6E4})$
, where
$\unicode[STIX]{x1D6E4}_{2}:=\text{p}_{2}(\unicode[STIX]{x1D6E4})$
, where
![]() $\text{p}_{1}$
and
$\text{p}_{1}$
and
![]() $\text{p}_{2}$
are the projections from
$\text{p}_{2}$
are the projections from
![]() $G$
to
$G$
to
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
, respectively. Then
$G_{2}$
, respectively. Then
![]() $\unicode[STIX]{x1D6E4}^{\prime }:=\unicode[STIX]{x1D6E4}_{1}\,\times \,\unicode[STIX]{x1D6E4}_{2}$
is a congruence subgroup of
$\unicode[STIX]{x1D6E4}^{\prime }:=\unicode[STIX]{x1D6E4}_{1}\,\times \,\unicode[STIX]{x1D6E4}_{2}$
is a congruence subgroup of
![]() $G(\mathbb{Q})_{+}$
containing
$G(\mathbb{Q})_{+}$
containing
![]() $\unicode[STIX]{x1D6E4}$
as a finite index subgroup. Let
$\unicode[STIX]{x1D6E4}$
as a finite index subgroup. Let
![]() $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D6E4}\backslash X\rightarrow \unicode[STIX]{x1D6E4}^{\prime }\backslash X$
denote the natural (finite) morphism. Then
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D6E4}\backslash X\rightarrow \unicode[STIX]{x1D6E4}^{\prime }\backslash X$
denote the natural (finite) morphism. Then
![]() $\unicode[STIX]{x1D719}(W)\subseteq \unicode[STIX]{x1D719}(Y)\subseteq S^{\prime }:=\unicode[STIX]{x1D6E4}^{\prime }\backslash X$
, and we have
$\unicode[STIX]{x1D719}(W)\subseteq \unicode[STIX]{x1D719}(Y)\subseteq S^{\prime }:=\unicode[STIX]{x1D6E4}^{\prime }\backslash X$
, and we have
 $$\begin{eqnarray}\displaystyle & \displaystyle \dim \langle Y\rangle =\dim \langle \unicode[STIX]{x1D719}(Y)\rangle , & \displaystyle \nonumber\\ \displaystyle & \displaystyle \dim \langle W\rangle =\dim \langle \unicode[STIX]{x1D719}(W)\rangle , & \displaystyle \nonumber\\ \displaystyle & \displaystyle \dim \langle Y\rangle _{\text{ws}}=\dim \langle \unicode[STIX]{x1D719}(Y)\rangle _{\text{ws}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \dim \langle W\rangle _{\text{ws}}=\dim \langle \unicode[STIX]{x1D719}(W)\rangle _{\text{ws}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dim \langle Y\rangle =\dim \langle \unicode[STIX]{x1D719}(Y)\rangle , & \displaystyle \nonumber\\ \displaystyle & \displaystyle \dim \langle W\rangle =\dim \langle \unicode[STIX]{x1D719}(W)\rangle , & \displaystyle \nonumber\\ \displaystyle & \displaystyle \dim \langle Y\rangle _{\text{ws}}=\dim \langle \unicode[STIX]{x1D719}(Y)\rangle _{\text{ws}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \dim \langle W\rangle _{\text{ws}}=\dim \langle \unicode[STIX]{x1D719}(W)\rangle _{\text{ws}}. & \displaystyle \nonumber\end{eqnarray}$$
Therefore, after replacing
![]() $Y$
,
$Y$
,
![]() $W$
, and
$W$
, and
![]() $S$
by
$S$
by
![]() $\unicode[STIX]{x1D719}(Y)$
,
$\unicode[STIX]{x1D719}(Y)$
,
![]() $\unicode[STIX]{x1D719}(W)$
, and
$\unicode[STIX]{x1D719}(W)$
, and
![]() $S^{\prime }$
, respectively, we may assume that
$S^{\prime }$
, respectively, we may assume that
![]() $\unicode[STIX]{x1D6E4}$
is of the form
$\unicode[STIX]{x1D6E4}$
is of the form
![]() $\unicode[STIX]{x1D6E4}_{1}\times \unicode[STIX]{x1D6E4}_{2}$
, and
$\unicode[STIX]{x1D6E4}_{1}\times \unicode[STIX]{x1D6E4}_{2}$
, and
![]() $S=\unicode[STIX]{x1D6E4}_{1}\backslash X_{1}\times \unicode[STIX]{x1D6E4}_{2}\backslash X_{2}=S_{1}\times S_{2}$
.
$S=\unicode[STIX]{x1D6E4}_{1}\backslash X_{1}\times \unicode[STIX]{x1D6E4}_{2}\backslash X_{2}=S_{1}\times S_{2}$
.
Thus,
![]() $\langle Y\rangle _{\text{ws}}=S_{1}\times \{s_{2}\}$
, where
$\langle Y\rangle _{\text{ws}}=S_{1}\times \{s_{2}\}$
, where
![]() $s_{2}$
is the image of
$s_{2}$
is the image of
![]() $x_{2}$
in
$x_{2}$
in
![]() $S_{2}$
,
$S_{2}$
,
![]() $Y=Y_{1}\times \{s_{2}\}$
, where
$Y=Y_{1}\times \{s_{2}\}$
, where
![]() $Y_{1}$
is the projection of
$Y_{1}$
is the projection of
![]() $Y$
to
$Y$
to
![]() $S_{1}$
, and
$S_{1}$
, and
![]() $W=W_{1}\times \{s_{2}\}$
, where
$W=W_{1}\times \{s_{2}\}$
, where
![]() $W_{1}$
is the projection of
$W_{1}$
is the projection of
![]() $W$
to
$W$
to
![]() $S_{1}$
. In particular, we can take
$S_{1}$
. In particular, we can take
such that
![]() $\langle W\rangle$
is equal to the image in
$\langle W\rangle$
is equal to the image in
![]() $S$
of the
$S$
of the
![]() $M(\mathbb{R})^{+}$
conjugacy class
$M(\mathbb{R})^{+}$
conjugacy class
![]() $X_{M}$
of
$X_{M}$
of
![]() $x$
, where
$x$
, where
![]() $M:=\text{MT}(x)$
.
$M:=\text{MT}(x)$
.
Again, there exists a decomposition
which induces a splitting
such that
![]() $\langle W\rangle _{\text{ws}}$
is equal to the image in
$\langle W\rangle _{\text{ws}}$
is equal to the image in
![]() $S$
of
$S$
of
![]() $X_{M_{1}}\times \{y_{2}\}$
, for some
$X_{M_{1}}\times \{y_{2}\}$
, for some
![]() $y_{2}\in X_{M_{2}}$
.
$y_{2}\in X_{M_{2}}$
.
Since
![]() $\text{MT}(x_{2})$
is equal to
$\text{MT}(x_{2})$
is equal to
![]() $G_{2}$
, it follows that
$G_{2}$
, it follows that
![]() $M$
is a subgroup of
$M$
is a subgroup of
![]() $G_{1}\times G_{2}$
that surjects on to the second factor. In particular,
$G_{1}\times G_{2}$
that surjects on to the second factor. In particular,
surjects on to
![]() $X_{2}$
. Therefore, let
$X_{2}$
. Therefore, let
![]() $M_{1}^{\prime }$
and
$M_{1}^{\prime }$
and
![]() $M_{2}^{\prime }$
be two normal semisimple subgroups of
$M_{2}^{\prime }$
be two normal semisimple subgroups of
![]() $M^{\text{der}}$
corresponding to
$M^{\text{der}}$
corresponding to
![]() $M_{1}$
and
$M_{1}$
and
![]() $M_{2}$
, respectively, so that
$M_{2}$
, respectively, so that
Since
![]() $W$
is contained in
$W$
is contained in
![]() $S_{1}\times \{s_{2}\}$
, the projection of
$S_{1}\times \{s_{2}\}$
, the projection of
![]() $M_{1}^{\prime }$
to
$M_{1}^{\prime }$
to
![]() $G_{2}$
must be trivial. Hence,
$G_{2}$
must be trivial. Hence,
![]() $M_{1}^{\prime }(\mathbb{R})^{+}x$
is contained in
$M_{1}^{\prime }(\mathbb{R})^{+}x$
is contained in
![]() $X_{1}\times \{x_{2}\}$
and we conclude that
$X_{1}\times \{x_{2}\}$
and we conclude that
![]() $M_{2}^{\prime }(\mathbb{R})^{+}x$
surjects on to
$M_{2}^{\prime }(\mathbb{R})^{+}x$
surjects on to
![]() $X_{2}$
. Since
$X_{2}$
. Since
for some
![]() $y_{1}\in X_{M_{1}}$
, we have
$y_{1}\in X_{M_{1}}$
, we have
as required. ◻
Corollary 4.5 (Cf. [Reference Habegger and PilaHP16, Proposition 4.5]).
Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
. A subvariety of
$S$
. A subvariety of
![]() $V$
that is optimal in
$V$
that is optimal in
![]() $V$
is weakly optimal in
$V$
is weakly optimal in
![]() $V$
.
$V$
.
5 The hyperbolic Ax–Schanuel conjecture
In this section, we formulate various conjectures about Shimura varieties that are analogous to the original Ax–Schanuel theorem from functional transcendence theory.
Theorem 5.1 (Cf. [Reference AxAx71, Theorem 1]).
Let
![]() $f_{1},\ldots ,f_{n}\in \mathbb{C}[[t_{1},\ldots ,t_{m}]]$
be power series that are
$f_{1},\ldots ,f_{n}\in \mathbb{C}[[t_{1},\ldots ,t_{m}]]$
be power series that are
![]() $\mathbb{Q}$
-linearly independent modulo
$\mathbb{Q}$
-linearly independent modulo
![]() $\mathbb{C}$
. Then we have the following inequality
$\mathbb{C}$
. Then we have the following inequality
where
![]() $e(f)=e^{2\unicode[STIX]{x1D70B}if}\in \mathbb{C}[[t_{1},\ldots ,t_{m}]]$
.
$e(f)=e^{2\unicode[STIX]{x1D70B}if}\in \mathbb{C}[[t_{1},\ldots ,t_{m}]]$
.
The following theorem is then an immediate corollary.
Theorem 5.2. Let
![]() $f_{1},\ldots ,f_{n}\in \mathbb{C}[[t_{1},\ldots ,t_{m}]]$
as above. Then
$f_{1},\ldots ,f_{n}\in \mathbb{C}[[t_{1},\ldots ,t_{m}]]$
as above. Then
Let
![]() $\unicode[STIX]{x1D70B}$
denote the uniformization map
$\unicode[STIX]{x1D70B}$
denote the uniformization map
and let
![]() $D_{n}$
denote its graph in
$D_{n}$
denote its graph in
![]() $\mathbb{C}^{n}\times (\mathbb{C}^{\times })^{n}$
. We can rephrase Theorem 5.1 as follows.
$\mathbb{C}^{n}\times (\mathbb{C}^{\times })^{n}$
. We can rephrase Theorem 5.1 as follows.
Theorem 5.3 (Cf. [Reference Tsimerman, Jones and WilkieTsi15, Theorem 1.2]).
Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $\mathbb{C}^{n}\times (\mathbb{C}^{\times })^{n}$
and let
$\mathbb{C}^{n}\times (\mathbb{C}^{\times })^{n}$
and let
![]() $U$
be an irreducible analytic component of
$U$
be an irreducible analytic component of
![]() $V\cap D_{n}$
. Assume that the projection of
$V\cap D_{n}$
. Assume that the projection of
![]() $U$
to
$U$
to
![]() $(\mathbb{C}^{\times })^{n}$
is not contained in a coset of a proper subtorus of
$(\mathbb{C}^{\times })^{n}$
is not contained in a coset of a proper subtorus of
![]() $(\mathbb{C}^{\times })^{n}$
. Then
$(\mathbb{C}^{\times })^{n}$
. Then
Similarly, we can rephrase Theorem 5.2 as follows.
Theorem 5.4. Let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $\mathbb{C}^{n}$
and
$\mathbb{C}^{n}$
and
![]() $V$
a subvariety of
$V$
a subvariety of
![]() $(\mathbb{C}^{\times })^{n}$
. Let
$(\mathbb{C}^{\times })^{n}$
. Let
![]() $A$
be an irreducible analytic component of
$A$
be an irreducible analytic component of
![]() $W\,\cap \,\unicode[STIX]{x1D70B}^{-1}(V)$
. If
$W\,\cap \,\unicode[STIX]{x1D70B}^{-1}(V)$
. If
![]() $A$
is not contained in
$A$
is not contained in
![]() $b+L$
, for any proper
$b+L$
, for any proper
![]() $\mathbb{Q}$
-linear subspace
$\mathbb{Q}$
-linear subspace
![]() $L$
of
$L$
of
![]() $\mathbb{C}^{n}$
and any
$\mathbb{C}^{n}$
and any
![]() $b\in \mathbb{C}^{n}$
, then
$b\in \mathbb{C}^{n}$
, then
Recall that
![]() $X$
is naturally endowed with the structure of a hermitian symmetric domain. In particular, it is a complex manifold. We define an (irreducible algebraic) subvariety of
$X$
is naturally endowed with the structure of a hermitian symmetric domain. In particular, it is a complex manifold. We define an (irreducible algebraic) subvariety of
![]() $X$
as in Appendix B of [Reference Klingler, Ullmo and YafaevKUY16]. In particular, we consider the Harish-Chandra realization of
$X$
as in Appendix B of [Reference Klingler, Ullmo and YafaevKUY16]. In particular, we consider the Harish-Chandra realization of
![]() $X$
, which is a bounded domain in
$X$
, which is a bounded domain in
![]() $\mathbb{C}^{N}$
, for some
$\mathbb{C}^{N}$
, for some
![]() $N\in \mathbb{N}$
, and we define an (irreducible algebraic) subvariety of
$N\in \mathbb{N}$
, and we define an (irreducible algebraic) subvariety of
![]() $X$
to be an irreducible analytic component of the intersection of
$X$
to be an irreducible analytic component of the intersection of
![]() $X$
with an algebraic subvariety of
$X$
with an algebraic subvariety of
![]() $\mathbb{C}^{N}$
. We define an (irreducible algebraic) subvariety of
$\mathbb{C}^{N}$
. We define an (irreducible algebraic) subvariety of
![]() $X\times S$
to be an irreducible analytic component of the intersection of
$X\times S$
to be an irreducible analytic component of the intersection of
![]() $X\times S$
with an algebraic subvariety of
$X\times S$
with an algebraic subvariety of
![]() $\mathbb{C}^{N}\,\times \,S$
. We note, however, that, by [Reference Klingler, Ullmo and YafaevKUY16, Corollary B.2], the algebraic structure that we are putting on
$\mathbb{C}^{N}\,\times \,S$
. We note, however, that, by [Reference Klingler, Ullmo and YafaevKUY16, Corollary B.2], the algebraic structure that we are putting on
![]() $X$
and
$X$
and
![]() $X\times S$
does not depend on our particular choice of the Harish-Chandra realization of
$X\times S$
does not depend on our particular choice of the Harish-Chandra realization of
![]() $X$
; any realization of
$X$
; any realization of
![]() $X$
would yield the same algebraic structures.
$X$
would yield the same algebraic structures.
We are, therefore, able to formulate conjectures for Shimura varieties that are analogous to those above. Let
![]() $\unicode[STIX]{x1D70B}$
henceforth denote the uniformization map
$\unicode[STIX]{x1D70B}$
henceforth denote the uniformization map
and let
![]() $D_{S}$
denote the graph of
$D_{S}$
denote the graph of
![]() $\unicode[STIX]{x1D70B}$
in
$\unicode[STIX]{x1D70B}$
in
![]() $X\times S$
. The following conjecture generalizes [Reference Pila and TsimermanPT16, Conjecture 1.1].
$X\times S$
. The following conjecture generalizes [Reference Pila and TsimermanPT16, Conjecture 1.1].
Conjecture 5.5 (Hyperbolic Ax–Schanuel).
Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $X\times S$
and let
$X\times S$
and let
![]() $U$
be an irreducible analytic component of
$U$
be an irreducible analytic component of
![]() $V\,\cap \,D_{S}$
. Assume that the projection of
$V\,\cap \,D_{S}$
. Assume that the projection of
![]() $U$
to
$U$
to
![]() $S$
is not contained in a weakly special subvariety of
$S$
is not contained in a weakly special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
strictly contained in
$\text{Sh}_{K}(G,\mathfrak{X})$
strictly contained in
![]() $S$
. Then
$S$
. Then
For
![]() $S=\mathbb{C}^{n}$
, Conjecture 5.5 and its generalization involving derivatives were obtained in [Reference Pila and TsimermanPT16]. Mok, Pila, and Tsimerman have very recently announced a proof of Conjecture 5.5 in full [Reference Mok, Pila and TsimermanMPT17].
$S=\mathbb{C}^{n}$
, Conjecture 5.5 and its generalization involving derivatives were obtained in [Reference Pila and TsimermanPT16]. Mok, Pila, and Tsimerman have very recently announced a proof of Conjecture 5.5 in full [Reference Mok, Pila and TsimermanMPT17].
For applications to the Zilber–Pink conjecture, only the following weaker version will be needed.
Conjecture 5.6 (Cf. [Reference Habegger and PilaHP16, Conjecture 5.10]).
Let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $X$
and let
$X$
and let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
. Let
$S$
. Let
![]() $A$
be an irreducible analytic component of
$A$
be an irreducible analytic component of
![]() $W\cap \unicode[STIX]{x1D70B}^{-1}(V)$
and assume that
$W\cap \unicode[STIX]{x1D70B}^{-1}(V)$
and assume that
![]() $\unicode[STIX]{x1D70B}(A)$
is not contained in a weakly special subvariety of
$\unicode[STIX]{x1D70B}(A)$
is not contained in a weakly special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
strictly contained in
$\text{Sh}_{K}(G,\mathfrak{X})$
strictly contained in
![]() $S$
. Then
$S$
. Then
Proof that Conjecture 5.5 implies Conjecture 5.6.
Consider the situation described in the statement of Conjecture 5.6. Then
![]() $Y:=W\times V$
is an algebraic subvariety of
$Y:=W\times V$
is an algebraic subvariety of
![]() $X\times S$
and
$X\times S$
and
is an irreducible analytic component of
![]() $Y\,\cap \,D_{S}$
. Clearly, the projection of
$Y\,\cap \,D_{S}$
. Clearly, the projection of
![]() $U$
to
$U$
to
![]() $S$
is not contained in a weakly special subvariety of
$S$
is not contained in a weakly special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
strictly contained in
$\text{Sh}_{K}(G,\mathfrak{X})$
strictly contained in
![]() $S$
. Therefore, by Conjecture 5.5,
$S$
. Therefore, by Conjecture 5.5,
and the result follows since
![]() $\dim U=\dim A$
and
$\dim U=\dim A$
and
![]() $\dim Y=\dim W+\dim V$
.◻
$\dim Y=\dim W+\dim V$
.◻
In our applications, we will use a reformulation of Conjecture 5.6. For this reformulation, we will need the following definitions.
Fix a subvariety
![]() $V$
of
$V$
of
![]() $S$
.
$S$
.
Definition 5.7. An intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
is an irreducible analytic component of the intersection of
$\unicode[STIX]{x1D70B}^{-1}(V)$
is an irreducible analytic component of the intersection of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
with a subvariety of
$\unicode[STIX]{x1D70B}^{-1}(V)$
with a subvariety of
![]() $X$
.
$X$
.
Clearly, for any intersection component
![]() $A$
of
$A$
of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
, there exists a smallest subvariety
$\unicode[STIX]{x1D70B}^{-1}(V)$
, there exists a smallest subvariety
![]() $\langle A\rangle _{\text{Zar}}$
of
$\langle A\rangle _{\text{Zar}}$
of
![]() $X$
containing
$X$
containing
![]() $A$
.
$A$
.
Definition 5.8. Let
![]() $A$
be an intersection component of
$A$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. We define the Zariski defect of
$\unicode[STIX]{x1D70B}^{-1}(V)$
. We define the Zariski defect of
![]() $A$
to be
$A$
to be
Definition 5.9. We say that an intersection component
![]() $A$
of
$A$
of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
is Zariski optimal in
$\unicode[STIX]{x1D70B}^{-1}(V)$
is Zariski optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
if, for any intersection component
$\unicode[STIX]{x1D70B}^{-1}(V)$
if, for any intersection component
![]() $B$
of
$B$
of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
,
$\unicode[STIX]{x1D70B}^{-1}(V)$
,
Remark 5.10. Let
![]() $A$
be an intersection component of
$A$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. If A is Zariski optimal in
$\unicode[STIX]{x1D70B}^{-1}(V)$
. If A is Zariski optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
, then
$\unicode[STIX]{x1D70B}^{-1}(V)$
, then
![]() $A$
is an irreducible analytic component of
$A$
is an irreducible analytic component of
Definition 5.11. Let
![]() $x\in X$
and let
$x\in X$
and let
![]() $X_{M}$
denote the
$X_{M}$
denote the
![]() $M(\mathbb{R})^{+}$
conjugacy class of
$M(\mathbb{R})^{+}$
conjugacy class of
![]() $x$
in
$x$
in
![]() $X$
, where
$X$
, where
![]() $M:=\text{MT}(x)$
. Write
$M:=\text{MT}(x)$
. Write
![]() $M^{\text{ad}}$
as a product
$M^{\text{ad}}$
as a product
of two normal
![]() $\mathbb{Q}$
-subgroups, either of which may be trivial, thus inducing a splitting
$\mathbb{Q}$
-subgroups, either of which may be trivial, thus inducing a splitting
For any
![]() $x_{1}\in X_{1}$
or
$x_{1}\in X_{1}$
or
![]() $x_{2}\in X_{2}$
, we obtain a subvariety
$x_{2}\in X_{2}$
, we obtain a subvariety
![]() $\{x_{1}\}\times X_{2}$
or
$\{x_{1}\}\times X_{2}$
or
![]() $X_{1}\times \{x_{2}\}$
of
$X_{1}\times \{x_{2}\}$
of
![]() $X$
. We refer to any subvariety of
$X$
. We refer to any subvariety of
![]() $X$
taking this form as a pre-weakly special subvariety of
$X$
taking this form as a pre-weakly special subvariety of
![]() $X$
. That is, a weakly special subvariety of
$X$
. That is, a weakly special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
contained in
$\text{Sh}_{K}(G,\mathfrak{X})$
contained in
![]() $S$
is, by definition, the image in
$S$
is, by definition, the image in
![]() $S$
of a pre-weakly special subvariety of
$S$
of a pre-weakly special subvariety of
![]() $X$
.
$X$
.
Remark 5.12. Note that pre-weakly special subvarieties of
![]() $X$
are indeed subvarieties of
$X$
are indeed subvarieties of
![]() $X$
(see [Reference GaoGao17, Lemma 6.2], for example). In particular, they are irreducible analytic subsets of
$X$
(see [Reference GaoGao17, Lemma 6.2], for example). In particular, they are irreducible analytic subsets of
![]() $X$
. As explained in [Reference MoonenMoo98], pre-weakly special subvarieties of
$X$
. As explained in [Reference MoonenMoo98], pre-weakly special subvarieties of
![]() $X$
are totally geodesic subvarieties of
$X$
are totally geodesic subvarieties of
![]() $X$
.
$X$
.
Definition 5.13. An intersection component
![]() $A$
of
$A$
of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
is called pre-weakly special if it is an irreducible analytic component of
$\unicode[STIX]{x1D70B}^{-1}(V)$
is called pre-weakly special if it is an irreducible analytic component of
and
![]() $\langle A\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
$\langle A\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
![]() $X$
.
$X$
.
Conjecture 5.14 (Weak hyperbolic Ax–Schanuel).
Let
![]() $A$
be an intersection component of
$A$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
that is Zariski optimal in
$\unicode[STIX]{x1D70B}^{-1}(V)$
that is Zariski optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. Then
$\unicode[STIX]{x1D70B}^{-1}(V)$
. Then
![]() $A$
is pre-weakly special.
$A$
is pre-weakly special.
Note that, since
![]() $A$
is assumed to be Zariski optimal in
$A$
is assumed to be Zariski optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
, it is automatically an irreducible analytic component of
$\unicode[STIX]{x1D70B}^{-1}(V)$
, it is automatically an irreducible analytic component of
The content of Conjecture 5.14, therefore, is the claim that
![]() $\langle A\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
$\langle A\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
![]() $X$
.
$X$
.
Note that Conjecture 5.14 is a direct generalization of the hyperbolic Ax–Lindemann theorem.
Theorem 5.15 (Hyperbolic Ax–Lindemann).
The maximal subvarieties contained in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
are pre-weakly special.
$\unicode[STIX]{x1D70B}^{-1}(V)$
are pre-weakly special.
Proof that Conjecture 5.14 implies Theorem 5.15.
The maximal subvarieties contained in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
are precisely the intersection components of
$\unicode[STIX]{x1D70B}^{-1}(V)$
are precisely the intersection components of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
that are Zariski optimal in
$\unicode[STIX]{x1D70B}^{-1}(V)$
that are Zariski optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
and whose Zariski defect is zero.◻
$\unicode[STIX]{x1D70B}^{-1}(V)$
and whose Zariski defect is zero.◻
Although [Reference Habegger and PilaHP16, § 5.2] is dedicated to products of modular curves, the proof that Formulations A and B of Weak Complex Ax are equivalent is completely general and, when translated into our terminology, yields the following.
We conclude this section with the following consequence of the weak hyperbolic Ax–Schanuel conjecture. Here and elsewhere, we will tacitly make use of the following remark.
Remark 5.17. Let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $S$
and let
$S$
and let
![]() $A$
denote an irreducible analytic component of
$A$
denote an irreducible analytic component of
![]() $\unicode[STIX]{x1D70B}^{-1}(W)$
in
$\unicode[STIX]{x1D70B}^{-1}(W)$
in
![]() $X$
. Then, since
$X$
. Then, since
![]() $W$
is analytically irreducible, every irreducible analytic component of
$W$
is analytically irreducible, every irreducible analytic component of
![]() $\unicode[STIX]{x1D70B}^{-1}(W)$
is equal to a
$\unicode[STIX]{x1D70B}^{-1}(W)$
is equal to a
![]() $\unicode[STIX]{x1D6E4}$
-translate of
$\unicode[STIX]{x1D6E4}$
-translate of
![]() $A$
(as mentioned in [Reference Ullmo and YafaevUY11, § 4], for example). In particular,
$A$
(as mentioned in [Reference Ullmo and YafaevUY11, § 4], for example). In particular,
![]() $\unicode[STIX]{x1D70B}(A)$
is equal to
$\unicode[STIX]{x1D70B}(A)$
is equal to
![]() $W$
.
$W$
.
Lemma 5.18. Assume that the weak hyperbolic Ax–Schanuel conjecture holds for
![]() $V$
and let
$V$
and let
![]() $A$
be a Zariski optimal intersection component of
$A$
be a Zariski optimal intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. Then
$\unicode[STIX]{x1D70B}^{-1}(V)$
. Then
![]() $\unicode[STIX]{x1D70B}(A)$
is a closed irreducible subvariety of
$\unicode[STIX]{x1D70B}(A)$
is a closed irreducible subvariety of
![]() $V$
and, as such, is weakly optimal in
$V$
and, as such, is weakly optimal in
![]() $V$
.
$V$
.
Proof. Clearly, the Zariski closure
![]() $\overline{\unicode[STIX]{x1D70B}(A)}$
of
$\overline{\unicode[STIX]{x1D70B}(A)}$
of
![]() $\unicode[STIX]{x1D70B}(A)$
is irreducible. Therefore, let
$\unicode[STIX]{x1D70B}(A)$
is irreducible. Therefore, let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $V$
containing
$V$
containing
![]() $\overline{\unicode[STIX]{x1D70B}(A)}$
such that
$\overline{\unicode[STIX]{x1D70B}(A)}$
such that
![]() $\unicode[STIX]{x1D6FF}_{\text{ws}}(W)\leqslant \unicode[STIX]{x1D6FF}_{\text{ws}}(\overline{\unicode[STIX]{x1D70B}(A)})$
. We can and do assume that
$\unicode[STIX]{x1D6FF}_{\text{ws}}(W)\leqslant \unicode[STIX]{x1D6FF}_{\text{ws}}(\overline{\unicode[STIX]{x1D70B}(A)})$
. We can and do assume that
![]() $W$
is weakly optimal in
$W$
is weakly optimal in
![]() $V$
. Let
$V$
. Let
![]() $B$
be an irreducible analytic component of
$B$
be an irreducible analytic component of
![]() $\unicode[STIX]{x1D70B}^{-1}(W)$
containing
$\unicode[STIX]{x1D70B}^{-1}(W)$
containing
![]() $A$
. We have
$A$
. We have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{\text{Zar}}(B) & = & \displaystyle \dim \langle B\rangle _{\text{Zar}}-\dim B=\dim \langle B\rangle _{\text{Zar}}-\dim W\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim \langle W\rangle _{\text{ws}}-\dim W=\unicode[STIX]{x1D6FF}_{\text{ws}}(W)\leqslant \unicode[STIX]{x1D6FF}_{\text{ws}}(\overline{\unicode[STIX]{x1D70B}(A)})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim \langle A\rangle _{\text{Zar}}-\dim A=\unicode[STIX]{x1D6FF}_{\text{Zar}}(A),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{\text{Zar}}(B) & = & \displaystyle \dim \langle B\rangle _{\text{Zar}}-\dim B=\dim \langle B\rangle _{\text{Zar}}-\dim W\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim \langle W\rangle _{\text{ws}}-\dim W=\unicode[STIX]{x1D6FF}_{\text{ws}}(W)\leqslant \unicode[STIX]{x1D6FF}_{\text{ws}}(\overline{\unicode[STIX]{x1D70B}(A)})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim \langle A\rangle _{\text{Zar}}-\dim A=\unicode[STIX]{x1D6FF}_{\text{Zar}}(A),\nonumber\end{eqnarray}$$
where we use the fact that, by the weak hyperbolic Ax–Schanuel conjecture,
![]() $\langle A\rangle _{\text{Zar}}$
is pre-weakly special. Therefore, we conclude that
$\langle A\rangle _{\text{Zar}}$
is pre-weakly special. Therefore, we conclude that
![]() $B=A$
. Hence,
$B=A$
. Hence,
![]() $\unicode[STIX]{x1D70B}(A)=\unicode[STIX]{x1D70B}(B)=W$
.◻
$\unicode[STIX]{x1D70B}(A)=\unicode[STIX]{x1D70B}(B)=W$
.◻
6 A finiteness result for weakly optimal subvarieties
In this section, we deduce from the weak hyperbolic Ax–Schanuel conjecture a finiteness statement for the weakly optimal subvarieties of a given subvariety
![]() $V$
.
$V$
.
Definition 6.1. Let
![]() $x\in X$
and let
$x\in X$
and let
![]() $X_{M}$
denote the
$X_{M}$
denote the
![]() $M(\mathbb{R})^{+}$
conjugacy class of
$M(\mathbb{R})^{+}$
conjugacy class of
![]() $x$
in
$x$
in
![]() $X$
, where
$X$
, where
![]() $M:=\text{MT}(x)$
. Then
$M:=\text{MT}(x)$
. Then
![]() $X_{M}$
is a subvariety of
$X_{M}$
is a subvariety of
![]() $X$
and we refer to any subvariety of
$X$
and we refer to any subvariety of
![]() $X$
taking this form as a pre-special subvariety of
$X$
taking this form as a pre-special subvariety of
![]() $X$
. In particular, a pre-special subvariety of
$X$
. In particular, a pre-special subvariety of
![]() $X$
is a pre-weakly special subvariety of
$X$
is a pre-weakly special subvariety of
![]() $X$
. If
$X$
. If
![]() $X_{M}$
is a point, that is, if
$X_{M}$
is a point, that is, if
![]() $M$
is a torus, we refer to
$M$
is a torus, we refer to
![]() $X_{M}$
as a pre-special point of
$X_{M}$
as a pre-special point of
![]() $X$
. A special subvariety of
$X$
. A special subvariety of
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
contained in
$\text{Sh}_{K}(G,\mathfrak{X})$
contained in
![]() $S$
is, by definition, the image in
$S$
is, by definition, the image in
![]() $S$
of a pre-special subvariety of
$S$
of a pre-special subvariety of
![]() $X$
.
$X$
.
Definition 6.2. Let
![]() $x\in X$
and let
$x\in X$
and let
![]() $X_{M}$
denote the
$X_{M}$
denote the
![]() $M(\mathbb{R})^{+}$
conjugacy class of
$M(\mathbb{R})^{+}$
conjugacy class of
![]() $x$
in
$x$
in
![]() $X$
, where
$X$
, where
![]() $M:=\text{MT}(x)$
. Decomposing
$M:=\text{MT}(x)$
. Decomposing
![]() $M^{\text{ad}}$
as a product
$M^{\text{ad}}$
as a product
of two normal
![]() $\mathbb{Q}$
-subgroups, either of which may be trivial, induces a splitting
$\mathbb{Q}$
-subgroups, either of which may be trivial, induces a splitting
For any such splitting, and any
![]() $x_{1}\in X_{1}$
or
$x_{1}\in X_{1}$
or
![]() $x_{2}\in X_{2}$
, we refer to the pre-weakly special subvariety
$x_{2}\in X_{2}$
, we refer to the pre-weakly special subvariety
![]() $\{x_{1}\}\times X_{2}$
or
$\{x_{1}\}\times X_{2}$
or
![]() $X_{1}\times \{x_{2}\}$
as a fibre of (the pre-special subvariety)
$X_{1}\times \{x_{2}\}$
as a fibre of (the pre-special subvariety)
![]() $X_{M}$
. In particular, the points of
$X_{M}$
. In particular, the points of
![]() $X_{M}$
are all fibres of
$X_{M}$
are all fibres of
![]() $X_{M}$
, and so too is
$X_{M}$
, and so too is
![]() $X_{M}$
itself.
$X_{M}$
itself.
The main result of this section is the following.
Proposition 6.3 (Cf. [Reference Habegger and PilaHP16, Proposition 6.6]).
Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
and assume that the weak hyperbolic Ax–Schanuel conjecture is true for
$S$
and assume that the weak hyperbolic Ax–Schanuel conjecture is true for
![]() $V$
. Then there exists a finite set
$V$
. Then there exists a finite set
![]() $\unicode[STIX]{x1D6F4}$
of pre-special subvarieties of
$\unicode[STIX]{x1D6F4}$
of pre-special subvarieties of
![]() $X$
such that the following holds.
$X$
such that the following holds.
Let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $V$
that is weakly optimal in
$V$
that is weakly optimal in
![]() $V$
. Then there exists
$V$
. Then there exists
![]() $Y\in \unicode[STIX]{x1D6F4}$
such that
$Y\in \unicode[STIX]{x1D6F4}$
such that
![]() $\langle W\rangle _{\text{ws}}$
is equal to the image in
$\langle W\rangle _{\text{ws}}$
is equal to the image in
![]() $S$
of a fibre of
$S$
of a fibre of
![]() $Y$
.
$Y$
.
Note that similar theorems also hold for abelian varieties (see [Reference Habegger and PilaHP16, Proposition 6.1] and [Reference RémondRém09, Proposition 3.2]).
Now fix a subvariety
![]() $V$
of
$V$
of
![]() $S$
. Given an intersection component
$S$
. Given an intersection component
![]() $A$
of
$A$
of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
, there is a smallest totally geodesic subvariety
$\unicode[STIX]{x1D70B}^{-1}(V)$
, there is a smallest totally geodesic subvariety
![]() $\langle A\rangle _{\text{geo}}$
of
$\langle A\rangle _{\text{geo}}$
of
![]() $X$
that contains
$X$
that contains
![]() $A$
. In particular, we may make the following definition.
$A$
. In particular, we may make the following definition.
Definition 6.4. Let
![]() $A$
be an intersection component of
$A$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. We define the geodesic defect of
$\unicode[STIX]{x1D70B}^{-1}(V)$
. We define the geodesic defect of
![]() $A$
to be
$A$
to be
We note that, in [Reference Habegger and PilaHP16], this notion was referred to as the Möbius defect of
![]() $A$
.
$A$
.
Definition 6.5. We say that an intersection component
![]() $A$
of
$A$
of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
is geodesically optimal in
$\unicode[STIX]{x1D70B}^{-1}(V)$
is geodesically optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
if, for any intersection component
$\unicode[STIX]{x1D70B}^{-1}(V)$
if, for any intersection component
![]() $B$
of
$B$
of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
,
$\unicode[STIX]{x1D70B}^{-1}(V)$
,
We note that the terminology geodesically optimal has a different meaning in [Reference Habegger and PilaHP16].
Remark 6.6. Let
![]() $A$
be an intersection component of
$A$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. If
$\unicode[STIX]{x1D70B}^{-1}(V)$
. If
![]() $A$
is geodesically optimal in
$A$
is geodesically optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
, then
$\unicode[STIX]{x1D70B}^{-1}(V)$
, then
![]() $A$
is an irreducible analytic component of
$A$
is an irreducible analytic component of
Lemma 6.7. Assume that the weak hyperbolic Ax–Schanuel conjecture is true for
![]() $V$
and let
$V$
and let
![]() $A$
be an intersection component of
$A$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. If
$\unicode[STIX]{x1D70B}^{-1}(V)$
. If
![]() $A$
is geodesically optimal in
$A$
is geodesically optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
, then
$\unicode[STIX]{x1D70B}^{-1}(V)$
, then
![]() $A$
is Zariski optimal in
$A$
is Zariski optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
.
$\unicode[STIX]{x1D70B}^{-1}(V)$
.
Proof. Suppose that
![]() $B$
is an intersection component of
$B$
is an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
containing
$\unicode[STIX]{x1D70B}^{-1}(V)$
containing
![]() $A$
such that
$A$
such that
We can and do assume that
![]() $B$
is Zariski optimal and so, by the weak hyperbolic Ax–Schanuel conjecture, it is pre-weakly special. In particular,
$B$
is Zariski optimal and so, by the weak hyperbolic Ax–Schanuel conjecture, it is pre-weakly special. In particular,
![]() $\langle B\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
$\langle B\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
![]() $X$
and, therefore, equal to
$X$
and, therefore, equal to
![]() $\langle B\rangle _{\text{geo}}$
. Then
$\langle B\rangle _{\text{geo}}$
. Then
and, since
![]() $A$
is geodesically optimal in
$A$
is geodesically optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
, we conclude that
$\unicode[STIX]{x1D70B}^{-1}(V)$
, we conclude that
![]() $B=A$
.◻
$B=A$
.◻
Lemma 6.8. Assume that the weak hyperbolic Ax–Schanuel conjecture is true for
![]() $V$
and let
$V$
and let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $V$
that is weakly optimal in
$V$
that is weakly optimal in
![]() $V$
. Let
$V$
. Let
![]() $A$
be an irreducible analytic component of
$A$
be an irreducible analytic component of
![]() $\unicode[STIX]{x1D70B}^{-1}(W)$
. Then
$\unicode[STIX]{x1D70B}^{-1}(W)$
. Then
![]() $A$
is an intersection component of
$A$
is an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
and is geodesically optimal in
$\unicode[STIX]{x1D70B}^{-1}(V)$
and is geodesically optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
.
$\unicode[STIX]{x1D70B}^{-1}(V)$
.
Proof. Clearly,
![]() $A$
is an intersection component of
$A$
is an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
since
$\unicode[STIX]{x1D70B}^{-1}(V)$
since
![]() $W$
is an irreducible component of
$W$
is an irreducible component of
![]() $\langle W\rangle _{\text{ws}}\cap V$
and
$\langle W\rangle _{\text{ws}}\cap V$
and
![]() $\unicode[STIX]{x1D70B}^{-1}\langle W\rangle _{\text{ws}}$
is equal to the
$\unicode[STIX]{x1D70B}^{-1}\langle W\rangle _{\text{ws}}$
is equal to the
![]() $\unicode[STIX]{x1D6E4}$
-orbit of a pre-weakly special subvariety of
$\unicode[STIX]{x1D6E4}$
-orbit of a pre-weakly special subvariety of
![]() $X$
.
$X$
.
Therefore, let
![]() $B$
be an intersection component of
$B$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
containing
$\unicode[STIX]{x1D70B}^{-1}(V)$
containing
![]() $A$
such that
$A$
such that
We can and do assume that
![]() $B$
is geodesically optimal in
$B$
is geodesically optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
and so, by Lemma 6.7,
$\unicode[STIX]{x1D70B}^{-1}(V)$
and so, by Lemma 6.7,
![]() $B$
is Zariski optimal in
$B$
is Zariski optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. Therefore, by the weak hyperbolic Ax–Schanuel conjecture,
$\unicode[STIX]{x1D70B}^{-1}(V)$
. Therefore, by the weak hyperbolic Ax–Schanuel conjecture,
![]() $B$
is pre-weakly special, i.e.,
$B$
is pre-weakly special, i.e.,
![]() $\langle B\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
$\langle B\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
![]() $X$
.
$X$
.
Let
![]() $Z:=\unicode[STIX]{x1D70B}(B)$
(which is a closed irreducible subvariety of
$Z:=\unicode[STIX]{x1D70B}(B)$
(which is a closed irreducible subvariety of
![]() $V$
by Lemma 5.18). We claim that
$V$
by Lemma 5.18). We claim that
![]() $\langle Z\rangle _{\text{ws}}=\unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})$
. To see this, note that
$\langle Z\rangle _{\text{ws}}=\unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})$
. To see this, note that
![]() $Z$
is contained in
$Z$
is contained in
![]() $\unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})$
and so
$\unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})$
and so
![]() $\langle Z\rangle _{\text{ws}}$
is contained in
$\langle Z\rangle _{\text{ws}}$
is contained in
![]() $\unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})$
. On the other hand,
$\unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})$
. On the other hand,
![]() $\langle B\rangle _{\text{Zar}}$
is contained in
$\langle B\rangle _{\text{Zar}}$
is contained in
![]() $\unicode[STIX]{x1D70B}^{-1}(\langle Z\rangle _{\text{ws}})$
and so
$\unicode[STIX]{x1D70B}^{-1}(\langle Z\rangle _{\text{ws}})$
and so
![]() $\unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})$
is contained in
$\unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})$
is contained in
![]() $\langle Z\rangle _{\text{ws}}$
, which proves the claim. Therefore,
$\langle Z\rangle _{\text{ws}}$
, which proves the claim. Therefore,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{\text{ws}}(Z) & = & \displaystyle \dim \unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})-\dim Z\nonumber\\ \displaystyle & = & \displaystyle \dim \langle B\rangle _{\text{Zar}}-\dim Z\nonumber\\ \displaystyle & = & \displaystyle \dim \langle B\rangle _{\text{Zar}}-\dim B=\unicode[STIX]{x1D6FF}_{\text{geo}}(B)\leqslant \unicode[STIX]{x1D6FF}_{\text{geo}}(A)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim \langle W\rangle _{\text{ws}}-\dim W=\unicode[STIX]{x1D6FF}_{\text{ws}}(W).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{\text{ws}}(Z) & = & \displaystyle \dim \unicode[STIX]{x1D70B}(\langle B\rangle _{\text{Zar}})-\dim Z\nonumber\\ \displaystyle & = & \displaystyle \dim \langle B\rangle _{\text{Zar}}-\dim Z\nonumber\\ \displaystyle & = & \displaystyle \dim \langle B\rangle _{\text{Zar}}-\dim B=\unicode[STIX]{x1D6FF}_{\text{geo}}(B)\leqslant \unicode[STIX]{x1D6FF}_{\text{geo}}(A)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim \langle W\rangle _{\text{ws}}-\dim W=\unicode[STIX]{x1D6FF}_{\text{ws}}(W).\nonumber\end{eqnarray}$$
Since
![]() $W$
is weakly optimal in
$W$
is weakly optimal in
![]() $V$
and contained in
$V$
and contained in
![]() $Z$
, we conclude that
$Z$
, we conclude that
![]() $Z=W$
. In particular,
$Z=W$
. In particular,
![]() $B$
is contained in
$B$
is contained in
![]() $\unicode[STIX]{x1D70B}^{-1}(W)$
and, therefore,
$\unicode[STIX]{x1D70B}^{-1}(W)$
and, therefore,
![]() $B=A$
.◻
$B=A$
.◻
Let us briefly summarize the relationship between Zariski optimal and weakly optimal.
Proposition 6.9. Assume that the weak hyperbolic Ax–Schanuel conjecture is true for
![]() $V$
.
$V$
.
If
![]() $A$
is a Zariski optimal intersection component of
$A$
is a Zariski optimal intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
, then
$\unicode[STIX]{x1D70B}^{-1}(V)$
, then
![]() $\unicode[STIX]{x1D70B}(A)$
is a closed irreducible subvariety of
$\unicode[STIX]{x1D70B}(A)$
is a closed irreducible subvariety of
![]() $V$
that is weakly optimal in
$V$
that is weakly optimal in
![]() $V$
.
$V$
.
On the other hand, if
![]() $W$
is a subvariety of
$W$
is a subvariety of
![]() $V$
that is weakly optimal in
$V$
that is weakly optimal in
![]() $V$
, and
$V$
, and
![]() $A$
is an irreducible analytic component of
$A$
is an irreducible analytic component of
![]() $\unicode[STIX]{x1D70B}^{-1}(W)$
, then
$\unicode[STIX]{x1D70B}^{-1}(W)$
, then
![]() $A$
is a Zariski optimal intersection component of
$A$
is a Zariski optimal intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
.
$\unicode[STIX]{x1D70B}^{-1}(V)$
.
As explained in [Reference Klingler, Ullmo and YafaevKUY16], we can and do fix, once and for all, an open, semialgebraic fundamental set
![]() ${\mathcal{F}}$
in
${\mathcal{F}}$
in
![]() $X$
for the action of
$X$
for the action of
![]() $\unicode[STIX]{x1D6E4}$
such that the set
$\unicode[STIX]{x1D6E4}$
such that the set
![]() ${\mathcal{V}}:=\unicode[STIX]{x1D70B}^{-1}(V)\cap {\mathcal{F}}$
is definable. The key step in the proof of Proposition 6.3 is the following.
${\mathcal{V}}:=\unicode[STIX]{x1D70B}^{-1}(V)\cap {\mathcal{F}}$
is definable. The key step in the proof of Proposition 6.3 is the following.
Proposition 6.10. Assume that the weak hyperbolic Ax–Schanuel theorem is true for
![]() $V$
. There exists a finite set
$V$
. There exists a finite set
![]() $\unicode[STIX]{x1D6F4}$
of pre-special subvarieties of
$\unicode[STIX]{x1D6F4}$
of pre-special subvarieties of
![]() $X$
such that the following holds.
$X$
such that the following holds.
Let
![]() $A$
be an intersection component of
$A$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
that is pre-weakly special such that, for some
$\unicode[STIX]{x1D70B}^{-1}(V)$
that is pre-weakly special such that, for some
![]() $x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
,
$x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
,
Then there exists
![]() $Y\in \unicode[STIX]{x1D6F4}$
such that
$Y\in \unicode[STIX]{x1D6F4}$
such that
![]() $\langle A\rangle _{\text{Zar}}$
is equal to a fibre of
$\langle A\rangle _{\text{Zar}}$
is equal to a fibre of
![]() $Y$
.
$Y$
.
In order to prove Proposition 6.10, we require some further preparations.
Definition 6.11. We say that a real semisimple algebraic group
![]() $F$
is without compact factors if it is equal to an almost direct product of almost simple subgroups whose underlying real Lie groups are not compact. We allow the product to be trivial, i.e., we consider the trivial group as a real semisimple algebraic group without compact factors.
$F$
is without compact factors if it is equal to an almost direct product of almost simple subgroups whose underlying real Lie groups are not compact. We allow the product to be trivial, i.e., we consider the trivial group as a real semisimple algebraic group without compact factors.
Lemma 6.12. A subvariety of
![]() $X$
that is totally geodesic in
$X$
that is totally geodesic in
![]() $X$
is of the form
$X$
is of the form
where
![]() $F$
is a semisimple algebraic subgroup of
$F$
is a semisimple algebraic subgroup of
![]() $G_{\mathbb{R}}$
without compact factors and
$G_{\mathbb{R}}$
without compact factors and
![]() $x\in X$
factors through
$x\in X$
factors through
Conversely, if
![]() $F$
is a semisimple algebraic subgroup of
$F$
is a semisimple algebraic subgroup of
![]() $G_{\mathbb{R}}$
without compact factors and
$G_{\mathbb{R}}$
without compact factors and
![]() $x\in X$
factors through
$x\in X$
factors through
![]() $G_{F}$
, then
$G_{F}$
, then
![]() $F(\mathbb{R})^{+}x$
is a subvariety of
$F(\mathbb{R})^{+}x$
is a subvariety of
![]() $X$
that is totally geodesic in
$X$
that is totally geodesic in
![]() $X$
.
$X$
.
Proof. See [Reference Ullmo and YafaevUY18, Proposition 2.3]. ◻
We let
![]() $\unicode[STIX]{x1D6FA}$
denote a (finite) set of representatives for the
$\unicode[STIX]{x1D6FA}$
denote a (finite) set of representatives for the
![]() $G(\mathbb{R})$
-conjugacy classes of semisimple algebraic subgroups of
$G(\mathbb{R})$
-conjugacy classes of semisimple algebraic subgroups of
![]() $G_{\mathbb{R}}$
that are without compact factors. It is clear that the set
$G_{\mathbb{R}}$
that are without compact factors. It is clear that the set
parametrizing (albeit in a many-to-one fashion) the totally geodesic subvarieties of
![]() $X$
passing through
$X$
passing through
![]() ${\mathcal{V}}$
, is definable.
${\mathcal{V}}$
, is definable.
Recall from [Reference van den DriesVdD98], 1.17 that the local dimension
![]() $\dim _{x}A$
of a definable set
$\dim _{x}A$
of a definable set
![]() $A$
at a point
$A$
at a point
![]() $x\in A$
is definable. By [Reference Habegger and PilaHP16, Lemma 6.2], if
$x\in A$
is definable. By [Reference Habegger and PilaHP16, Lemma 6.2], if
![]() $A$
is also a (complex) analytic set, then this dimension is exactly twice the local analytic dimension at
$A$
is also a (complex) analytic set, then this dimension is exactly twice the local analytic dimension at
![]() $x$
. Furthermore, if
$x$
. Furthermore, if
![]() $A$
is analytically irreducible, then its local dimension at the points of
$A$
is analytically irreducible, then its local dimension at the points of
![]() $A$
is constant. For the remainder of this section, dimensions will be taken in the sense of definable sets.
$A$
is constant. For the remainder of this section, dimensions will be taken in the sense of definable sets.
Consider the two functions
and let
![]() $\unicode[STIX]{x1D6F1}_{1}$
denote the definable set
$\unicode[STIX]{x1D6F1}_{1}$
denote the definable set
Finally, let
![]() $\unicode[STIX]{x1D6F1}_{2}$
denote the definable set
$\unicode[STIX]{x1D6F1}_{2}$
denote the definable set
The proof of Proposition 6.10 will require the following three lemmas.
Lemma 6.13. Let
![]() $A$
be an intersection component of
$A$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
that is pre-weakly special such that, for some
$\unicode[STIX]{x1D70B}^{-1}(V)$
that is pre-weakly special such that, for some
![]() $x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
,
$x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
,
Then we can write
where
![]() $(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
.
$(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
.
Proof. By Lemma 6.12, we can write
for some
![]() $F\in \unicode[STIX]{x1D6FA}$
and some
$F\in \unicode[STIX]{x1D6FA}$
and some
![]() $x\in {\mathcal{V}}$
that factors through
$x\in {\mathcal{V}}$
that factors through
![]() $gG_{F}g^{-1}$
. In particular,
$gG_{F}g^{-1}$
. In particular,
![]() $(x,g,F)\in \unicode[STIX]{x1D6F1}_{0}$
. By assumption, we can and do choose
$(x,g,F)\in \unicode[STIX]{x1D6F1}_{0}$
. By assumption, we can and do choose
![]() $x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
such that
$x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
such that
Suppose that
![]() $(x,g,F)$
does not belong to
$(x,g,F)$
does not belong to
![]() $\unicode[STIX]{x1D6F1}_{1}$
, i.e., that there exists
$\unicode[STIX]{x1D6F1}_{1}$
, i.e., that there exists
![]() $(x,g_{1},F_{1})\in \unicode[STIX]{x1D6F1}_{0}$
such that
$(x,g_{1},F_{1})\in \unicode[STIX]{x1D6F1}_{0}$
such that
and
Let
![]() $B$
be an irreducible analytic component of
$B$
be an irreducible analytic component of
passing through
![]() $x$
such that
$x$
such that
From (6.13.1), we obtain
![]() $\unicode[STIX]{x1D6FF}_{\text{Zar}}(B)\leqslant \unicode[STIX]{x1D6FF}_{\text{Zar}}(A)$
.
$\unicode[STIX]{x1D6FF}_{\text{Zar}}(B)\leqslant \unicode[STIX]{x1D6FF}_{\text{Zar}}(A)$
.
On the other hand, the intersection inequality (see [Reference Grauert and RemmertGR84, ch. 5, § 3]) yields
and, from (6.13.1), we obtain
It follows that
![]() $B\,\cap \,\langle A\rangle _{\text{Zar}}$
, and hence
$B\,\cap \,\langle A\rangle _{\text{Zar}}$
, and hence
![]() $B$
itself, contains a complex neighbourhood of
$B$
itself, contains a complex neighbourhood of
![]() $x$
in
$x$
in
![]() $A$
, which implies that
$A$
, which implies that
![]() $A$
is contained in
$A$
is contained in
![]() $B$
.
$B$
.
Therefore, since
![]() $A$
is Zariski optimal, we conclude that
$A$
is Zariski optimal, we conclude that
![]() $A=B$
. However, this implies that
$A=B$
. However, this implies that
which contradicts (6.13.1).
Therefore, suppose that
![]() $(x,g,F)\in \unicode[STIX]{x1D6F1}_{1}$
does not belong to
$(x,g,F)\in \unicode[STIX]{x1D6F1}_{1}$
does not belong to
![]() $\unicode[STIX]{x1D6F1}_{2}$
, i.e., that there exists
$\unicode[STIX]{x1D6F1}_{2}$
, i.e., that there exists
![]() $(x,g_{1},F_{1})\in \unicode[STIX]{x1D6F1}_{0}$
such that
$(x,g_{1},F_{1})\in \unicode[STIX]{x1D6F1}_{0}$
such that
and
But then
![]() $A$
is contained in
$A$
is contained in
which is a contradiction. ◻
Lemma 6.14. Assume that the weak hyperbolic Ax–Schanuel conjecture is true for
![]() $V$
. Then, if
$V$
. Then, if
![]() $(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
, there exists a semisimple subgroup
$(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
, there exists a semisimple subgroup
![]() $F^{\prime }$
of
$F^{\prime }$
of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
such that
$\mathbb{Q}$
such that
![]() $gFg^{-1}$
is equal to the almost direct product of the almost simple factors of
$gFg^{-1}$
is equal to the almost direct product of the almost simple factors of
![]() $F_{\mathbb{R}}^{\prime }$
whose underlying real Lie groups are non-compact.
$F_{\mathbb{R}}^{\prime }$
whose underlying real Lie groups are non-compact.
Proof. By [Reference UllmoUll14, Proposition 3.1], it suffices to show that
![]() $gF(\mathbb{R})^{+}g^{-1}x$
is a pre-weakly special subvariety of
$gF(\mathbb{R})^{+}g^{-1}x$
is a pre-weakly special subvariety of
![]() $X$
. Therefore, let
$X$
. Therefore, let
![]() $A$
be an irreducible analytic component of
$A$
be an irreducible analytic component of
passing through
![]() $x$
such that
$x$
such that
Let
![]() $B$
be an intersection component of
$B$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
containing
$\unicode[STIX]{x1D70B}^{-1}(V)$
containing
![]() $A$
such that
$A$
such that
![]() $\unicode[STIX]{x1D6FF}_{\text{Zar}}(B)\leqslant \unicode[STIX]{x1D6FF}_{\text{Zar}}(A)$
. We can and do assume that
$\unicode[STIX]{x1D6FF}_{\text{Zar}}(B)\leqslant \unicode[STIX]{x1D6FF}_{\text{Zar}}(A)$
. We can and do assume that
![]() $B$
is Zariski optimal and, therefore, by the weak hyperbolic Ax–Schanuel conjecture, pre-weakly special, i.e.,
$B$
is Zariski optimal and, therefore, by the weak hyperbolic Ax–Schanuel conjecture, pre-weakly special, i.e.,
![]() $B$
is an irreducible component of
$B$
is an irreducible component of
and
![]() $\langle B\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
$\langle B\rangle _{\text{Zar}}$
is a pre-weakly special subvariety of
![]() $X$
.
$X$
.
Therefore,
![]() $A$
is contained in
$A$
is contained in
and we let
![]() $Y$
be an irreducible analytic component of this intersection containing
$Y$
be an irreducible analytic component of this intersection containing
![]() $A$
. Then
$A$
. Then
![]() $Y$
is a subvariety of
$Y$
is a subvariety of
![]() $X$
that is totally geodesic is
$X$
that is totally geodesic is
![]() $X$
and, hence, equal to
$X$
and, hence, equal to
![]() $g_{1}F_{1}(\mathbb{R})^{+}g_{1}^{-1}x$
for some
$g_{1}F_{1}(\mathbb{R})^{+}g_{1}^{-1}x$
for some
![]() $(x,g_{1},F_{1})\in \unicode[STIX]{x1D6F1}_{0}$
. Furthermore,
$(x,g_{1},F_{1})\in \unicode[STIX]{x1D6F1}_{0}$
. Furthermore,
and, since
![]() $(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
, we conclude that
$(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
, we conclude that
We also have
 $$\begin{eqnarray}\displaystyle \dim \langle B\rangle _{\text{Zar}}-\dim _{x}(\langle B\rangle _{\text{Zar}}\cap {\mathcal{V}}) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}_{\text{Zar}}(B)\leqslant \unicode[STIX]{x1D6FF}_{\text{Zar}}(A)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle d(x,g,F)-\dim A\nonumber\\ \displaystyle & = & \displaystyle d(x,g,F)-d_{{\mathcal{V}}}(x,g,F),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim \langle B\rangle _{\text{Zar}}-\dim _{x}(\langle B\rangle _{\text{Zar}}\cap {\mathcal{V}}) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}_{\text{Zar}}(B)\leqslant \unicode[STIX]{x1D6FF}_{\text{Zar}}(A)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle d(x,g,F)-\dim A\nonumber\\ \displaystyle & = & \displaystyle d(x,g,F)-d_{{\mathcal{V}}}(x,g,F),\nonumber\end{eqnarray}$$
and so, since
![]() $(x,g,F)\in \unicode[STIX]{x1D6F1}_{1}$
, we conclude that
$(x,g,F)\in \unicode[STIX]{x1D6F1}_{1}$
, we conclude that
Lemma 6.15. Assume that the weak hyperbolic Ax–Schanuel conjecture is true for
![]() $V$
. Then, the set
$V$
. Then, the set
is finite.
Proof. Decompose
![]() $\unicode[STIX]{x1D6F1}_{2}$
as the finite union of the
$\unicode[STIX]{x1D6F1}_{2}$
as the finite union of the
![]() $\unicode[STIX]{x1D6F1}_{F}$
, varying over the members
$\unicode[STIX]{x1D6F1}_{F}$
, varying over the members
![]() $F$
of
$F$
of
![]() $\unicode[STIX]{x1D6FA}$
, where
$\unicode[STIX]{x1D6FA}$
, where
![]() $\unicode[STIX]{x1D6F1}_{F}$
denotes the set of tuples
$\unicode[STIX]{x1D6F1}_{F}$
denotes the set of tuples
![]() $(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
. For each
$(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
. For each
![]() $F\in \unicode[STIX]{x1D6FA}$
, consider the map
$F\in \unicode[STIX]{x1D6FA}$
, consider the map
defined by
whose image, therefore, is in bijection with
![]() $\{gFg^{-1}:(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}\}$
. It is also definable and, by Lemma 6.14, it is countable. Hence, it is finite.◻
$\{gFg^{-1}:(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}\}$
. It is also definable and, by Lemma 6.14, it is countable. Hence, it is finite.◻
Proof of Proposition 6.10.
Let
![]() $A$
be an intersection component of
$A$
be an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
that is pre-weakly special such that, for some
$\unicode[STIX]{x1D70B}^{-1}(V)$
that is pre-weakly special such that, for some
![]() $x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
,
$x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
,
Then, by Lemma 6.13, we can write
where
![]() $(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
. By Lemma 6.14, there exists a semisimple subgroup
$(x,g,F)\in \unicode[STIX]{x1D6F1}_{2}$
. By Lemma 6.14, there exists a semisimple subgroup
![]() $F^{\prime }$
of
$F^{\prime }$
of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
such that
$\mathbb{Q}$
such that
![]() $gFg^{-1}$
is equal to the almost direct product of the almost simple factors of
$gFg^{-1}$
is equal to the almost direct product of the almost simple factors of
![]() $F_{\mathbb{R}}^{\prime }$
whose underlying real Lie groups are non-compact. In fact, by [Reference UllmoUll14, Proposition 3.1],
$F_{\mathbb{R}}^{\prime }$
whose underlying real Lie groups are non-compact. In fact, by [Reference UllmoUll14, Proposition 3.1],
![]() $F^{\prime }$
is the smallest subgroup of
$F^{\prime }$
is the smallest subgroup of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
containing
$\mathbb{Q}$
containing
![]() $gFg^{-1}$
. Since, by Lemma 6.15,
$gFg^{-1}$
. Since, by Lemma 6.15,
![]() $gFg^{-1}$
comes from a finite set, so too does
$gFg^{-1}$
comes from a finite set, so too does
![]() $F^{\prime }$
. Therefore, the reductive algebraic group
$F^{\prime }$
. Therefore, the reductive algebraic group
is defined over
![]() $\mathbb{Q}$
and belongs to a finite set.
$\mathbb{Q}$
and belongs to a finite set.
If we write
![]() $M^{\text{nc}}$
for the almost direct product of the almost
$M^{\text{nc}}$
for the almost direct product of the almost
![]() $\mathbb{Q}$
-simple factors of
$\mathbb{Q}$
-simple factors of
![]() $M$
whose underlying real Lie groups are not compact, then
$M$
whose underlying real Lie groups are not compact, then
![]() $x$
factors through
$x$
factors through
![]() $M_{\mathbb{R}}^{\prime }:=Z(M)_{\mathbb{R}}^{\circ }M_{\mathbb{R}}^{\text{nc}}$
and, if we write
$M_{\mathbb{R}}^{\prime }:=Z(M)_{\mathbb{R}}^{\circ }M_{\mathbb{R}}^{\text{nc}}$
and, if we write
![]() $\mathfrak{X}_{M}$
for the
$\mathfrak{X}_{M}$
for the
![]() $M^{\prime }(\mathbb{R})$
conjugacy class of
$M^{\prime }(\mathbb{R})$
conjugacy class of
![]() $x$
in
$x$
in
![]() $\mathfrak{X}$
, then, by [Reference UllmoUll07, Lemme 3.3],
$\mathfrak{X}$
, then, by [Reference UllmoUll07, Lemme 3.3],
![]() $(M^{\prime },\mathfrak{X}_{M})$
is a Shimura subdatum of
$(M^{\prime },\mathfrak{X}_{M})$
is a Shimura subdatum of
![]() $(G,\mathfrak{X})$
. Furthermore, by [Reference Ullmo and YafaevUY14, Lemma 3.7], the number of Shimura subdatum
$(G,\mathfrak{X})$
. Furthermore, by [Reference Ullmo and YafaevUY14, Lemma 3.7], the number of Shimura subdatum
![]() $(M^{\prime },\mathfrak{Y})$
is finite. Therefore, since the
$(M^{\prime },\mathfrak{Y})$
is finite. Therefore, since the
![]() $M^{\prime }(\mathbb{R})^{+}$
conjugacy class
$M^{\prime }(\mathbb{R})^{+}$
conjugacy class
![]() $X_{M}$
of
$X_{M}$
of
![]() $x$
in
$x$
in
![]() $X$
is a pre-special subvariety of
$X$
is a pre-special subvariety of
![]() $X$
and
$X$
and
![]() $\langle A\rangle _{\text{Zar}}$
is a fibre of
$\langle A\rangle _{\text{Zar}}$
is a fibre of
![]() $X_{M}$
, the proof is complete.◻
$X_{M}$
, the proof is complete.◻
Proof of Proposition 6.3.
Let
![]() $A$
be an irreducible analytic component of
$A$
be an irreducible analytic component of
![]() $\unicode[STIX]{x1D70B}^{-1}(W)$
. By Proposition 6.9,
$\unicode[STIX]{x1D70B}^{-1}(W)$
. By Proposition 6.9,
![]() $A$
is an intersection component of
$A$
is an intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
and is Zariski optimal in
$\unicode[STIX]{x1D70B}^{-1}(V)$
and is Zariski optimal in
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. Therefore, by the weak hyperbolic Ax–Schanuel conjecture,
$\unicode[STIX]{x1D70B}^{-1}(V)$
. Therefore, by the weak hyperbolic Ax–Schanuel conjecture,
![]() $A$
is pre-weakly special. It follows that the image of
$A$
is pre-weakly special. It follows that the image of
![]() $\langle A\rangle _{\text{Zar}}$
in
$\langle A\rangle _{\text{Zar}}$
in
![]() $S$
is equal to
$S$
is equal to
![]() $\langle W\rangle _{\text{ws}}$
.
$\langle W\rangle _{\text{ws}}$
.
After possibly replacing
![]() $A$
by a
$A$
by a
![]() $\unicode[STIX]{x1D6FE}A$
, for some
$\unicode[STIX]{x1D6FE}A$
, for some
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
, we can and do assume that there exists
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
, we can and do assume that there exists
![]() $x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
such that
$x\in \langle A\rangle _{\text{Zar}}\cap {\mathcal{V}}$
such that
By Proposition 6.10,
![]() $\langle A\rangle _{\text{Zar}}$
is a fibre of
$\langle A\rangle _{\text{Zar}}$
is a fibre of
![]() $Y\in \unicode[STIX]{x1D6F4}$
, where
$Y\in \unicode[STIX]{x1D6F4}$
, where
![]() $\unicode[STIX]{x1D6F4}$
is a finite set of pre-special subvarieties of
$\unicode[STIX]{x1D6F4}$
is a finite set of pre-special subvarieties of
![]() $X$
depending only on
$X$
depending only on
![]() $V$
. ◻
$V$
. ◻
7 Anomalous subvarieties
In this section, we recall the notion of an anomalous subvariety, which is defined by Bombieri, Masser and Zannier [Reference Bombieri, Masser and ZannierBMZ07] for subvarieties of algebraic tori. In fact, we give the more general notion of an
![]() $r$
-anomalous subvariety, as introduced by Rémond [Reference RémondRém09].
$r$
-anomalous subvariety, as introduced by Rémond [Reference RémondRém09].
Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
. We will use Proposition 6.3 to show that, under the weak hyperbolic Ax–Schanuel conjecture, the union of the subvarieties of
$S$
. We will use Proposition 6.3 to show that, under the weak hyperbolic Ax–Schanuel conjecture, the union of the subvarieties of
![]() $V$
that are
$V$
that are
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
constitutes a Zariski closed subset of
$V$
constitutes a Zariski closed subset of
![]() $V$
. We will then give a criterion for when it is a proper subset.
$V$
. We will then give a criterion for when it is a proper subset.
Definition 7.1. Let
![]() $r\in \mathbb{Z}$
. A subvariety
$r\in \mathbb{Z}$
. A subvariety
![]() $W$
of
$W$
of
![]() $V$
is called
$V$
is called
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
if
$V$
if
A subvariety of
![]() $V$
is maximal
$V$
is maximal
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
if it is
$V$
if it is
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
and not strictly contained in another subvariety of
$V$
and not strictly contained in another subvariety of
![]() $V$
that is also
$V$
that is also
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
.
$V$
.
We denote by
![]() $\text{an}(V,r)$
the set of subvarieties of
$\text{an}(V,r)$
the set of subvarieties of
![]() $V$
that are maximal
$V$
that are maximal
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
and by
$V$
and by
![]() $V^{\text{an},r}$
the union of the elements of
$V^{\text{an},r}$
the union of the elements of
![]() $\text{an}(V,r)$
, which is then the union of all the subvarieties of
$\text{an}(V,r)$
, which is then the union of all the subvarieties of
![]() $V$
that are
$V$
that are
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
.
$V$
.
We say that a subvariety of
![]() $V$
is anomalous if it is
$V$
is anomalous if it is
![]() $(1+\dim V)$
-anomalous. We write
$(1+\dim V)$
-anomalous. We write
![]() $\text{an}(V)$
for
$\text{an}(V)$
for
![]() $\text{an}(V,1+\dim V)$
and
$\text{an}(V,1+\dim V)$
and
![]() $V^{\text{an}}$
for
$V^{\text{an}}$
for
![]() $V^{\text{an},1+\dim V}$
.
$V^{\text{an},1+\dim V}$
.
Theorem 7.2. Assume that the weak hyperbolic Ax–Schanuel conjecture is true for
![]() $V$
and let
$V$
and let
![]() $r\in \mathbb{Z}$
. Then
$r\in \mathbb{Z}$
. Then
![]() $V^{\text{an},r}$
is a Zariski closed subset of
$V^{\text{an},r}$
is a Zariski closed subset of
![]() $V$
.
$V$
.
We refer the reader to [Reference Bombieri, Masser and ZannierBMZ07, Reference RémondRém09, Reference Habegger and PilaHP16] for similar results on algebraic tori and abelian varieties. We will require the following facts.
Proposition 7.3 (Cf. [Reference HartshorneHar77, ch. 2, Exercise 3.22(d)]).
Let
![]() $f:W\rightarrow Y$
be a dominant morphism between two integral schemes of finite type over a field and let
$f:W\rightarrow Y$
be a dominant morphism between two integral schemes of finite type over a field and let
denote the relative dimension. For
![]() $h\in \mathbb{Z}$
, let
$h\in \mathbb{Z}$
, let
![]() $E_{h}$
denote the set of points
$E_{h}$
denote the set of points
![]() $x\in W$
such that the fibre
$x\in W$
such that the fibre
![]() $f^{-1}(f(x))$
possesses an irreducible component of dimension at least
$f^{-1}(f(x))$
possesses an irreducible component of dimension at least
![]() $h$
that contains
$h$
that contains
![]() $x$
. Then we have the following.
$x$
. Then we have the following.
(1)
 $E_{h}$
is a Zariski closed subset of
$E_{h}$
is a Zariski closed subset of
 $W$
.
$W$
.(2)
 $E_{e}=W$
.
$E_{e}=W$
.(3) If
 $h>e$
,
$h>e$
,
 $E_{h}$
is not Zariski dense in
$E_{h}$
is not Zariski dense in
 $W$
.
$W$
.
Lemma 7.4. Let
![]() $W\in \text{an}(V,r)$
. Then
$W\in \text{an}(V,r)$
. Then
![]() $W$
is weakly optimal in
$W$
is weakly optimal in
![]() $V$
.
$V$
.
Proof. Let
![]() $Y$
be a subvariety of
$Y$
be a subvariety of
![]() $V$
containing
$V$
containing
![]() $W$
such that
$W$
such that
![]() $\unicode[STIX]{x1D6FF}_{\text{ws}}(Y)\leqslant \unicode[STIX]{x1D6FF}_{\text{ws}}(W)$
. We can and do assume that
$\unicode[STIX]{x1D6FF}_{\text{ws}}(Y)\leqslant \unicode[STIX]{x1D6FF}_{\text{ws}}(W)$
. We can and do assume that
![]() $Y$
is weakly optimal. Then
$Y$
is weakly optimal. Then
 $$\begin{eqnarray}\displaystyle \dim Y & = & \displaystyle \dim \langle Y\rangle _{\text{ws}}-\unicode[STIX]{x1D6FF}_{\text{ws}}(Y)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \dim \langle Y\rangle _{\text{ws}}-\unicode[STIX]{x1D6FF}_{\text{ws}}(W)\nonumber\\ \displaystyle & = & \displaystyle \dim \langle Y\rangle _{\text{ws}}-(\dim \langle W\rangle _{\text{ws}}-\dim W)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \dim \langle Y\rangle _{\text{ws}}+r-\dim S.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim Y & = & \displaystyle \dim \langle Y\rangle _{\text{ws}}-\unicode[STIX]{x1D6FF}_{\text{ws}}(Y)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \dim \langle Y\rangle _{\text{ws}}-\unicode[STIX]{x1D6FF}_{\text{ws}}(W)\nonumber\\ \displaystyle & = & \displaystyle \dim \langle Y\rangle _{\text{ws}}-(\dim \langle W\rangle _{\text{ws}}-\dim W)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \dim \langle Y\rangle _{\text{ws}}+r-\dim S.\nonumber\end{eqnarray}$$
Since
![]() $Y$
contains
$Y$
contains
![]() $W$
, we know that
$W$
, we know that
![]() $\dim Y\geqslant 1$
, and so
$\dim Y\geqslant 1$
, and so
![]() $Y$
is
$Y$
is
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
. Since
$V$
. Since
![]() $W$
is maximal
$W$
is maximal
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
, we conclude that
$V$
, we conclude that
![]() $Y$
must be equal to
$Y$
must be equal to
![]() $W$
. Therefore,
$W$
. Therefore,
![]() $W$
is weakly optimal.◻
$W$
is weakly optimal.◻
Proof of Theorem 7.2.
Let
![]() $\unicode[STIX]{x1D6F4}$
be a finite set of pre-special subvarieties of
$\unicode[STIX]{x1D6F4}$
be a finite set of pre-special subvarieties of
![]() $X$
(whose existence is ensured by Proposition 6.3) such that, if
$X$
(whose existence is ensured by Proposition 6.3) such that, if
![]() $W$
is a subvariety of
$W$
is a subvariety of
![]() $V$
that is weakly optimal in
$V$
that is weakly optimal in
![]() $V$
, then there exists
$V$
, then there exists
![]() $x\in X$
such that, if
$x\in X$
such that, if
![]() $M:=\text{MT}(x)$
, the
$M:=\text{MT}(x)$
, the
![]() $M(\mathbb{R})^{+}$
conjugacy class
$M(\mathbb{R})^{+}$
conjugacy class
![]() $X_{M}$
of
$X_{M}$
of
![]() $x$
in
$x$
in
![]() $X$
belongs to
$X$
belongs to
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\langle W\rangle _{\text{ws}}$
is equal to the image in
$\langle W\rangle _{\text{ws}}$
is equal to the image in
![]() $S$
of a fibre of
$S$
of a fibre of
![]() $X_{M}$
. That is, we may write
$X_{M}$
. That is, we may write
![]() $M^{\text{ad}}$
as a product
$M^{\text{ad}}$
as a product
![]() $M_{1}\times M_{2}$
of two normal
$M_{1}\times M_{2}$
of two normal
![]() $\mathbb{Q}$
-subgroups, which induces a splitting
$\mathbb{Q}$
-subgroups, which induces a splitting
![]() $X=X_{1}\times X_{2}$
, such that
$X=X_{1}\times X_{2}$
, such that
![]() $\langle W\rangle _{\text{ws}}$
is equal to the image in
$\langle W\rangle _{\text{ws}}$
is equal to the image in
![]() $S$
of
$S$
of
![]() $\{x_{1}\}\times X_{2}$
, for some
$\{x_{1}\}\times X_{2}$
, for some
![]() $x_{1}\in X_{1}$
.
$x_{1}\in X_{1}$
.
Let
![]() $W\in \text{an}(V,r)$
. By Lemma 7.4, there exists
$W\in \text{an}(V,r)$
. By Lemma 7.4, there exists
![]() $X_{M}\in \unicode[STIX]{x1D6F4}$
such that
$X_{M}\in \unicode[STIX]{x1D6F4}$
such that
![]() $\langle W\rangle _{\text{ws}}$
is equal to the image in
$\langle W\rangle _{\text{ws}}$
is equal to the image in
![]() $S$
of
$S$
of
![]() $\{x_{1}\}\times X_{2}$
, for some
$\{x_{1}\}\times X_{2}$
, for some
![]() $x_{1}\in X_{1}$
, where
$x_{1}\in X_{1}$
, where
![]() $X_{M}=X_{1}\times X_{2}$
, as above.
$X_{M}=X_{1}\times X_{2}$
, as above.
Let
![]() $\unicode[STIX]{x1D6E4}_{M}$
be a congruence subgroup of
$\unicode[STIX]{x1D6E4}_{M}$
be a congruence subgroup of
![]() $M(\mathbb{Q})_{+}$
contained in
$M(\mathbb{Q})_{+}$
contained in
![]() $\unicode[STIX]{x1D6E4}$
, where
$\unicode[STIX]{x1D6E4}$
, where
![]() $M(\mathbb{Q})_{+}$
denotes the subgroup of
$M(\mathbb{Q})_{+}$
denotes the subgroup of
![]() $M(\mathbb{Q})$
acting on
$M(\mathbb{Q})$
acting on
![]() $X_{M}$
, and let
$X_{M}$
, and let
![]() $\unicode[STIX]{x1D6E4}_{1}$
denote the image of
$\unicode[STIX]{x1D6E4}_{1}$
denote the image of
![]() $\unicode[STIX]{x1D6E4}$
under the natural maps
$\unicode[STIX]{x1D6E4}$
under the natural maps
We denote by
![]() $f$
the restriction of
$f$
the restriction of
to an irreducible component
![]() $\widetilde{V}$
of
$\widetilde{V}$
of
![]() $\unicode[STIX]{x1D719}^{-1}(V)$
, such that
$\unicode[STIX]{x1D719}^{-1}(V)$
, such that
![]() $\dim \widetilde{V}=\dim V$
, where
$\dim \widetilde{V}=\dim V$
, where
![]() $\unicode[STIX]{x1D719}$
denotes the natural map
$\unicode[STIX]{x1D719}$
denotes the natural map
In particular,
![]() $\unicode[STIX]{x1D719}(\widetilde{V})=V$
. Therefore, by Proposition 7.3(1), the set
$\unicode[STIX]{x1D719}(\widetilde{V})=V$
. Therefore, by Proposition 7.3(1), the set
![]() $E_{h}$
of points
$E_{h}$
of points
![]() $z$
in
$z$
in
![]() $\widetilde{V}$
such that the fibre
$\widetilde{V}$
such that the fibre
![]() $f^{-1}(f(z))$
possesses an irreducible component of dimension at least
$f^{-1}(f(z))$
possesses an irreducible component of dimension at least
![]() $h\in \mathbb{Z}$
that contains
$h\in \mathbb{Z}$
that contains
![]() $z$
is a Zariski closed subset of
$z$
is a Zariski closed subset of
![]() $\widetilde{V}$
. Since
$\widetilde{V}$
. Since
![]() $\unicode[STIX]{x1D719}$
is a closed morphism,
$\unicode[STIX]{x1D719}$
is a closed morphism,
![]() $\unicode[STIX]{x1D719}(E_{h})$
is Zariski closed in
$\unicode[STIX]{x1D719}(E_{h})$
is Zariski closed in
![]() $V$
.
$V$
.
We claim that
![]() $W$
is contained in
$W$
is contained in
![]() $\unicode[STIX]{x1D719}(E_{h})$
, where
$\unicode[STIX]{x1D719}(E_{h})$
, where
To see this, fix an irreducible component
![]() $\widetilde{W}$
of
$\widetilde{W}$
of
![]() $\unicode[STIX]{x1D719}^{-1}(W)$
contained in
$\unicode[STIX]{x1D719}^{-1}(W)$
contained in
![]() $\widetilde{V}$
such that
$\widetilde{V}$
such that
![]() $\dim \widetilde{W}=\dim W$
. Then
$\dim \widetilde{W}=\dim W$
. Then
![]() $\langle \widetilde{W}\rangle _{\text{ws}}$
is equal to the image of
$\langle \widetilde{W}\rangle _{\text{ws}}$
is equal to the image of
![]() $\{x_{1}\}\times X_{2}$
in
$\{x_{1}\}\times X_{2}$
in
![]() $\unicode[STIX]{x1D6E4}_{M}\backslash X_{M}$
and so
$\unicode[STIX]{x1D6E4}_{M}\backslash X_{M}$
and so
![]() $\widetilde{W}$
lies in a fibre of
$\widetilde{W}$
lies in a fibre of
![]() $f$
. Since
$f$
. Since
![]() $\widetilde{W}$
is contained in
$\widetilde{W}$
is contained in
![]() $E_{h}$
, which implies that
$E_{h}$
, which implies that
![]() $W$
is contained in
$W$
is contained in
![]() $\unicode[STIX]{x1D719}(E_{h})$
.
$\unicode[STIX]{x1D719}(E_{h})$
.
On the other hand, we claim that
![]() $\unicode[STIX]{x1D719}(E_{h})$
is contained in
$\unicode[STIX]{x1D719}(E_{h})$
is contained in
![]() $V^{\text{an},r}$
. To see this, let
$V^{\text{an},r}$
. To see this, let
![]() $z\in E_{h}$
and let
$z\in E_{h}$
and let
![]() $Y$
be an irreducible component of the fibre
$Y$
be an irreducible component of the fibre
![]() $f^{-1}(f(z))$
of dimension at least
$f^{-1}(f(z))$
of dimension at least
![]() $h$
containing
$h$
containing
![]() $z$
. Then
$z$
. Then
![]() $Y$
is contained in the image of
$Y$
is contained in the image of
![]() $\{x_{1}\}\times X_{2}$
in
$\{x_{1}\}\times X_{2}$
in
![]() $\unicode[STIX]{x1D6E4}_{M}\backslash X_{M}$
, where
$\unicode[STIX]{x1D6E4}_{M}\backslash X_{M}$
, where
![]() $x_{1}\in X_{1}$
lies above
$x_{1}\in X_{1}$
lies above
![]() $f(z)\in \unicode[STIX]{x1D6E4}_{1}\backslash X_{1}$
, and so
$f(z)\in \unicode[STIX]{x1D6E4}_{1}\backslash X_{1}$
, and so
Therefore,
and so
![]() $\unicode[STIX]{x1D719}(Y)$
is
$\unicode[STIX]{x1D719}(Y)$
is
![]() $r$
-anomalous in
$r$
-anomalous in
![]() $V$
.
$V$
.
Hence, if we let
![]() $E$
denote the union of the
$E$
denote the union of the
![]() $\unicode[STIX]{x1D719}(E_{h})$
as we vary over the finitely many maps
$\unicode[STIX]{x1D719}(E_{h})$
as we vary over the finitely many maps
![]() $f$
obtained from the
$f$
obtained from the
![]() $X_{M}\in \unicode[STIX]{x1D6F4}$
and their possible splittings, we conclude that
$X_{M}\in \unicode[STIX]{x1D6F4}$
and their possible splittings, we conclude that
![]() $E=V^{\text{an},r}$
, which finishes the proof.◻
$E=V^{\text{an},r}$
, which finishes the proof.◻
We denote by
![]() $V^{\text{oa}}$
the complement in
$V^{\text{oa}}$
the complement in
![]() $V$
of
$V$
of
![]() $V^{\text{an}}$
. By Theorem 7.2, this is a (possibly empty) open subset of
$V^{\text{an}}$
. By Theorem 7.2, this is a (possibly empty) open subset of
![]() $V$
. In the literature, it is sometimes referred to as the open-anomalous locus, hence the subscript. We conclude this section by showing that, when
$V$
. In the literature, it is sometimes referred to as the open-anomalous locus, hence the subscript. We conclude this section by showing that, when
![]() $V$
is sufficiently generic,
$V$
is sufficiently generic,
![]() $V^{\text{oa}}$
is not empty.
$V^{\text{oa}}$
is not empty.
Proposition 7.5. Suppose that
![]() $V$
is Hodge generic in
$V$
is Hodge generic in
![]() $S$
. Then
$S$
. Then
![]() $V^{\text{an}}=V$
if and only if we can write
$V^{\text{an}}=V$
if and only if we can write
![]() $G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
$G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
![]() $X=X_{1}\times X_{2}$
, such that
$X=X_{1}\times X_{2}$
, such that
where
![]() $f$
denotes the projection map
$f$
denotes the projection map
and
![]() $\unicode[STIX]{x1D6E4}_{1}$
denotes the image of
$\unicode[STIX]{x1D6E4}_{1}$
denotes the image of
![]() $\unicode[STIX]{x1D6E4}$
under the natural maps
$\unicode[STIX]{x1D6E4}$
under the natural maps
Proof. First suppose that
![]() $V^{\text{an}}=V$
. Then, for any set
$V^{\text{an}}=V$
. Then, for any set
![]() $\unicode[STIX]{x1D6F4}$
as in the proof of Theorem 7.2,
$\unicode[STIX]{x1D6F4}$
as in the proof of Theorem 7.2,
![]() $V$
is contained in the (finite) union of the images in
$V$
is contained in the (finite) union of the images in
![]() $S$
of the
$S$
of the
![]() $X_{M}\in \unicode[STIX]{x1D6F4}$
. Therefore, since
$X_{M}\in \unicode[STIX]{x1D6F4}$
. Therefore, since
![]() $V$
is assumed to be Hodge generic in
$V$
is assumed to be Hodge generic in
![]() $S$
, it must be that
$S$
, it must be that
![]() $X\in \unicode[STIX]{x1D6F4}$
and, furthermore, that there exists
$X\in \unicode[STIX]{x1D6F4}$
and, furthermore, that there exists
![]() $W\in \text{an}(V)$
such that
$W\in \text{an}(V)$
such that
![]() $G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
$G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
![]() $X=X_{1}\times X_{2}$
, such that
$X=X_{1}\times X_{2}$
, such that
![]() $\langle W\rangle _{\text{ws}}$
is equal to the image in
$\langle W\rangle _{\text{ws}}$
is equal to the image in
![]() $S$
of
$S$
of
![]() $\{x_{1}\}\times X_{2}$
, for some
$\{x_{1}\}\times X_{2}$
, for some
![]() $x_{1}\in X_{1}$
.
$x_{1}\in X_{1}$
.
Let
![]() $f$
denote the projection map
$f$
denote the projection map
and consider its restriction
where
![]() $\overline{f(V)}$
denotes the Zariski closure of
$\overline{f(V)}$
denotes the Zariski closure of
![]() $f(V)$
in
$f(V)$
in
![]() $\unicode[STIX]{x1D6E4}_{1}\backslash X_{1}$
. Since
$\unicode[STIX]{x1D6E4}_{1}\backslash X_{1}$
. Since
![]() $V^{\text{an}}=V$
, it follows from Proposition 7.3(3), that
$V^{\text{an}}=V$
, it follows from Proposition 7.3(3), that
Hence,
and
Conversely, suppose that
![]() $G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
$G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
![]() $X=X_{1}\times X_{2}$
, such that
$X=X_{1}\times X_{2}$
, such that
where
![]() $f$
again denotes the projection map
$f$
again denotes the projection map
Restricting
![]() $f$
to
$f$
to
as before, we see from Proposition 7.3(2) that the set
![]() $E_{h}$
of points
$E_{h}$
of points
![]() $z$
in
$z$
in
![]() $V$
such that the fibre
$V$
such that the fibre
![]() $f^{-1}(f(z))$
possesses an irreducible component of dimension at least
$f^{-1}(f(z))$
possesses an irreducible component of dimension at least
that contains
![]() $z$
is equal to
$z$
is equal to
![]() $V$
. However, from the proof of Theorem 7.2, we have seen that
$V$
. However, from the proof of Theorem 7.2, we have seen that
![]() $E_{h}$
is contained in
$E_{h}$
is contained in
![]() $V^{\text{an}}$
, so the claim follows.◻
$V^{\text{an}}$
, so the claim follows.◻
Corollary 7.6. If
![]() $G^{\text{ad}}$
is
$G^{\text{ad}}$
is
![]() $\mathbb{Q}$
-simple and
$\mathbb{Q}$
-simple and
![]() $V$
is a Hodge generic subvariety in
$V$
is a Hodge generic subvariety in
![]() $S$
, then
$S$
, then
![]() $V^{\text{an}}$
is strictly contained in
$V^{\text{an}}$
is strictly contained in
![]() $V$
. In particular,
$V$
. In particular,
![]() $V^{\text{an}}$
is strictly contained in
$V^{\text{an}}$
is strictly contained in
![]() $V$
whenever
$V$
whenever
![]() $V$
is a Hodge generic subvariety of
$V$
is a Hodge generic subvariety of
![]() ${\mathcal{A}}_{g}$
.
${\mathcal{A}}_{g}$
.
8 Main results (part 1): Reductions to point counting
In this section, we prove our main theorem: under the weak hyperbolic Ax–Schanuel conjecture, the Zilber–Pink conjecture can be reduced to a problem of point counting. We also give a reduction of Pink’s conjecture in the case when the open-anomalous locus is non-empty.
Definition 8.1. Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
. We denote by
$S$
. We denote by
![]() $\text{Opt}_{0}(V)$
the set of all points in
$\text{Opt}_{0}(V)$
the set of all points in
![]() $V$
that are optimal in
$V$
that are optimal in
![]() $V$
.
$V$
.
Consider the following corollary of the Zilber–Pink conjecture.
Conjecture 8.2. Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
. Then
$S$
. Then
![]() $\text{Opt}_{0}(V)$
is finite.
$\text{Opt}_{0}(V)$
is finite.
We will later show that, under certain arithmetic hypotheses, one can prove Conjecture 8.2 when
![]() $V$
is a curve. Our main result in this section is that (under the weak hyperbolic Ax–Schanuel conjecture), Conjecture 8.2 implies the Zilber–Pink conjecture.
$V$
is a curve. Our main result in this section is that (under the weak hyperbolic Ax–Schanuel conjecture), Conjecture 8.2 implies the Zilber–Pink conjecture.
Theorem 8.3. Assume that the weak hyperbolic Ax–Schanuel conjecture is true and assume that Conjecture 8.2 holds.
Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
. Then
$S$
. Then
![]() $\text{Opt}(V)$
is finite.
$\text{Opt}(V)$
is finite.
Proof. We prove Theorem 8.3 by induction on
![]() $\dim V$
. Of course, Theorem 8.3 is trivial when
$\dim V$
. Of course, Theorem 8.3 is trivial when
![]() $\dim V=0$
or
$\dim V=0$
or
![]() $\dim V=1$
. Therefore, we assume that
$\dim V=1$
. Therefore, we assume that
![]() $\dim V\geqslant 2$
and that Theorem 8.3 holds whenever the subvariety in question is of lower dimension.
$\dim V\geqslant 2$
and that Theorem 8.3 holds whenever the subvariety in question is of lower dimension.
We need to show that the induction hypothesis implies that there are only finitely many subvarieties of positive dimension belonging to
![]() $\text{Opt}(V)$
.
$\text{Opt}(V)$
.
Let
![]() $\unicode[STIX]{x1D6F4}$
be a finite set of pre-special subvarieties of
$\unicode[STIX]{x1D6F4}$
be a finite set of pre-special subvarieties of
![]() $X$
, as in the proof of Theorem 7.2, and let
$X$
, as in the proof of Theorem 7.2, and let
![]() $W\in \text{Opt}(V)$
be of positive dimension.
$W\in \text{Opt}(V)$
be of positive dimension.
By Corollary 4.5,
![]() $W$
is weakly optimal and, therefore, there exists
$W$
is weakly optimal and, therefore, there exists
![]() $x\in X$
such that, if
$x\in X$
such that, if
![]() $M:=\text{MT}(x)$
, the
$M:=\text{MT}(x)$
, the
![]() $M(\mathbb{R})^{+}$
conjugacy class
$M(\mathbb{R})^{+}$
conjugacy class
![]() $X_{M}$
of
$X_{M}$
of
![]() $x$
in
$x$
in
![]() $X$
belongs to
$X$
belongs to
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\langle W\rangle _{\text{ws}}$
is equal to the image in
$\langle W\rangle _{\text{ws}}$
is equal to the image in
![]() $S$
of a fibre of
$S$
of a fibre of
![]() $X_{M}$
. That is, we may write
$X_{M}$
. That is, we may write
![]() $M^{\text{ad}}$
as a product
$M^{\text{ad}}$
as a product
of two normal
![]() $\mathbb{Q}$
-subgroups, thus inducing a splitting
$\mathbb{Q}$
-subgroups, thus inducing a splitting
such that
![]() $\langle W\rangle _{\text{ws}}$
is equal to the image in
$\langle W\rangle _{\text{ws}}$
is equal to the image in
![]() $S$
of
$S$
of
![]() $\{x_{1}\}\times X_{2}$
, for some
$\{x_{1}\}\times X_{2}$
, for some
![]() $x_{1}\in X_{1}$
.
$x_{1}\in X_{1}$
.
Let
![]() $\unicode[STIX]{x1D6E4}_{M}$
be a congruence subgroup of
$\unicode[STIX]{x1D6E4}_{M}$
be a congruence subgroup of
![]() $M(\mathbb{Q})_{+}$
contained in
$M(\mathbb{Q})_{+}$
contained in
![]() $\unicode[STIX]{x1D6E4}$
, where
$\unicode[STIX]{x1D6E4}$
, where
![]() $M(\mathbb{Q})_{+}$
denotes the subgroup of
$M(\mathbb{Q})_{+}$
denotes the subgroup of
![]() $M(\mathbb{Q})$
acting on
$M(\mathbb{Q})$
acting on
![]() $X_{M}$
, such that the image of
$X_{M}$
, such that the image of
![]() $\unicode[STIX]{x1D6E4}_{M}$
under the natural map
$\unicode[STIX]{x1D6E4}_{M}$
under the natural map
is equal to a product
![]() $\unicode[STIX]{x1D6E4}_{1}\times \unicode[STIX]{x1D6E4}_{2}$
. We denote by
$\unicode[STIX]{x1D6E4}_{1}\times \unicode[STIX]{x1D6E4}_{2}$
. We denote by
![]() $f$
the natural morphism
$f$
the natural morphism
and by
![]() $\unicode[STIX]{x1D719}$
the finite morphism
$\unicode[STIX]{x1D719}$
the finite morphism
Let
![]() $\widetilde{V}$
be an irreducible component of
$\widetilde{V}$
be an irreducible component of
![]() $\unicode[STIX]{x1D719}^{-1}(V)$
such that
$\unicode[STIX]{x1D719}^{-1}(V)$
such that
![]() $\dim \widetilde{V}=\dim V$
, and let
$\dim \widetilde{V}=\dim V$
, and let
![]() $\widetilde{W}$
denote an irreducible component of
$\widetilde{W}$
denote an irreducible component of
![]() $\unicode[STIX]{x1D719}^{-1}(W)$
contained in
$\unicode[STIX]{x1D719}^{-1}(W)$
contained in
![]() $\widetilde{V}$
such that
$\widetilde{V}$
such that
![]() $\dim \widetilde{W}=\dim W$
. Then
$\dim \widetilde{W}=\dim W$
. Then
![]() $\widetilde{W}$
is optimal in
$\widetilde{W}$
is optimal in
![]() $\widetilde{V}$
. On the other hand, by the generic smoothness property, there exists a dense open subset
$\widetilde{V}$
. On the other hand, by the generic smoothness property, there exists a dense open subset
![]() $V_{0}$
of
$V_{0}$
of
![]() $\widetilde{V}$
such that the restriction
$\widetilde{V}$
such that the restriction
![]() $f_{0}$
of
$f_{0}$
of
![]() $f$
to
$f$
to
![]() $V_{0}$
is a smooth morphism of relative dimension
$V_{0}$
is a smooth morphism of relative dimension
![]() $\unicode[STIX]{x1D708}$
. We denote by
$\unicode[STIX]{x1D708}$
. We denote by
![]() $V_{1}$
the Zariski closure of
$V_{1}$
the Zariski closure of
![]() $f(V_{0})$
in
$f(V_{0})$
in
![]() $\unicode[STIX]{x1D6E4}_{1}\backslash X_{1}$
.
$\unicode[STIX]{x1D6E4}_{1}\backslash X_{1}$
.
Now suppose that
Then
![]() $\widetilde{W}$
is a subvariety of some irreducible component
$\widetilde{W}$
is a subvariety of some irreducible component
![]() $V^{0}$
of
$V^{0}$
of
![]() $\widetilde{V}\setminus V_{0}$
. Furthermore,
$\widetilde{V}\setminus V_{0}$
. Furthermore,
![]() $\widetilde{W}$
is optimal in
$\widetilde{W}$
is optimal in
![]() $V^{0}$
. However, since
$V^{0}$
. However, since
![]() $\dim V^{0}$
is strictly less than
$\dim V^{0}$
is strictly less than
![]() $\dim V$
, our induction hypothesis implies that
$\dim V$
, our induction hypothesis implies that
![]() $\text{Opt}(V^{0})$
is finite.
$\text{Opt}(V^{0})$
is finite.
Therefore, we assume that (8.3.1) does not hold. As an irreducible component of the fibre
![]() $f_{0}^{-1}(z)$
, where
$f_{0}^{-1}(z)$
, where
![]() $z$
denotes the image of
$z$
denotes the image of
![]() $x_{1}$
in
$x_{1}$
in
![]() $V_{1}$
, its dimension is equal to
$V_{1}$
, its dimension is equal to
![]() $\unicode[STIX]{x1D708}$
. In particular,
$\unicode[STIX]{x1D708}$
. In particular,
We claim that
![]() $z$
is optimal in
$z$
is optimal in
![]() $V_{1}$
. To see this, note that
$V_{1}$
. To see this, note that
![]() $f(\langle \widetilde{W}\rangle )$
contains
$f(\langle \widetilde{W}\rangle )$
contains
![]() $z$
and is a special subvariety of dimension
$z$
and is a special subvariety of dimension
Therefore, let
![]() $A$
be a subvariety of
$A$
be a subvariety of
![]() $V_{1}$
containing
$V_{1}$
containing
![]() $z$
such that
$z$
such that
and let
![]() $B$
be an irreducible component of
$B$
be an irreducible component of
![]() $f^{-1}(A)$
containing
$f^{-1}(A)$
containing
![]() $\widetilde{W}$
. Since
$\widetilde{W}$
. Since
![]() $V_{0}$
is open in
$V_{0}$
is open in
![]() $\widetilde{V}$
and
$\widetilde{V}$
and
![]() $A$
is contained in
$A$
is contained in
![]() $V_{1}$
,
$V_{1}$
,
Therefore,
and, since
![]() $\widetilde{W}$
is optimal in
$\widetilde{W}$
is optimal in
![]() $\widetilde{V}$
, we conclude that
$\widetilde{V}$
, we conclude that
![]() $B$
is equal to
$B$
is equal to
![]() $\widetilde{W}$
. In particular,
$\widetilde{W}$
. In particular,
![]() $\widetilde{W}$
is an irreducible component of
$\widetilde{W}$
is an irreducible component of
![]() $f^{-1}(A)$
but, since it is also contained in
$f^{-1}(A)$
but, since it is also contained in
![]() $f^{-1}(z)$
, it must be that
$f^{-1}(z)$
, it must be that
![]() $A$
is equal to
$A$
is equal to
![]() $z$
, proving the claim.
$z$
, proving the claim.
Since
![]() $W$
was assumed to be of positive dimension, so too must be
$W$
was assumed to be of positive dimension, so too must be
![]() $X_{2}$
. It follows that
$X_{2}$
. It follows that
![]() $\dim V_{1}$
is strictly less than
$\dim V_{1}$
is strictly less than
![]() $\dim V$
and so, by the induction hypothesis,
$\dim V$
and so, by the induction hypothesis,
![]() $\text{Opt}(V_{1})$
is finite. Since
$\text{Opt}(V_{1})$
is finite. Since
![]() $z\in \text{Opt}(V_{1})$
and since
$z\in \text{Opt}(V_{1})$
and since
![]() $\unicode[STIX]{x1D6F4}$
and the number of splittings are finite, we are done.◻
$\unicode[STIX]{x1D6F4}$
and the number of splittings are finite, we are done.◻
We will later prove that the following conjecture is a consequence of the weak hyperbolic Ax–Schanuel conjecture and our arithmetic conjectures. It is inspired by the cited theorem of Habegger and Pila.
Conjecture 8.4 (Cf. [Reference Habegger and PilaHP16, Theorem 9.15(iii)]).
Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
. Then the set
$S$
. Then the set
![]() $V^{\text{oa}}\cap S^{[1+\dim V]}$
is finite.
$V^{\text{oa}}\cap S^{[1+\dim V]}$
is finite.
The importance of Conjecture 8.4 for us is that, when
![]() $V$
is suitably generic, Conjecture 8.4 implies Pink’s conjecture (assuming the weak hyperbolic Ax–Schanuel conjecture).
$V$
is suitably generic, Conjecture 8.4 implies Pink’s conjecture (assuming the weak hyperbolic Ax–Schanuel conjecture).
Theorem 8.5. Assume that the weak hyperbolic Ax–Schanuel conjecture is true and that Conjecture 8.4 holds.
Let
![]() $V$
be a Hodge generic subvariety of
$V$
be a Hodge generic subvariety of
![]() $S$
such that (even after replacing
$S$
such that (even after replacing
![]() $\unicode[STIX]{x1D6E4}$
)
$\unicode[STIX]{x1D6E4}$
)
![]() $S$
cannot be decomposed as a product
$S$
cannot be decomposed as a product
![]() $S_{1}\times S_{2}$
such that
$S_{1}\times S_{2}$
such that
![]() $V$
is contained in
$V$
is contained in
![]() $V^{\prime }\times S_{2}$
, where
$V^{\prime }\times S_{2}$
, where
![]() $V^{\prime }$
is a proper subvariety of
$V^{\prime }$
is a proper subvariety of
![]() $S_{1}$
of dimension strictly less than the dimension of
$S_{1}$
of dimension strictly less than the dimension of
![]() $V$
. Then
$V$
. Then
is not Zariski dense in
![]() $V$
.
$V$
.
Proof. We claim that the assumptions guarantee that
![]() $V^{\text{an}}$
is strictly contained in
$V^{\text{an}}$
is strictly contained in
![]() $V$
. Otherwise, by Proposition 7.5, we can write
$V$
. Otherwise, by Proposition 7.5, we can write
![]() $G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
$G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
![]() $X=X_{1}\times X_{2}$
, such that
$X=X_{1}\times X_{2}$
, such that
where
![]() $f$
denotes the projection map
$f$
denotes the projection map
and
![]() $\unicode[STIX]{x1D6E4}_{1}$
denotes the image of
$\unicode[STIX]{x1D6E4}_{1}$
denotes the image of
![]() $\unicode[STIX]{x1D6E4}$
under the natural maps
$\unicode[STIX]{x1D6E4}$
under the natural maps
Therefore, after replacing
![]() $\unicode[STIX]{x1D6E4}$
, we can write
$\unicode[STIX]{x1D6E4}$
, we can write
![]() $S$
as a product
$S$
as a product
![]() $S_{1}\,\times \,S_{2}$
so that
$S_{1}\,\times \,S_{2}$
so that
![]() $f$
is simply the projection on to the first factor and
$f$
is simply the projection on to the first factor and
![]() $V$
is contained in
$V$
is contained in
![]() $V^{\prime }\times S_{2}$
, where
$V^{\prime }\times S_{2}$
, where
![]() $V^{\prime }$
is Zariski closure of
$V^{\prime }$
is Zariski closure of
![]() $f(V)$
in
$f(V)$
in
![]() $S_{1}$
. However, since
$S_{1}$
. However, since
this is a contradiction.
Therefore, by Theorem 7.2,
![]() $V^{\text{an}}$
is a proper Zariski closed subset of
$V^{\text{an}}$
is a proper Zariski closed subset of
![]() $V$
. On the other hand,
$V$
. On the other hand,
![]() $V\cap S^{[1+\dim V]}$
is contained in
$V\cap S^{[1+\dim V]}$
is contained in
and so the theorem follows from Conjecture 8.4. ◻
9 The counting theorem
Henceforth, we turn our attention to the counting problems themselves. We will approach these problems using a theorem of Pila and Wilkie concerned with counting points in definable sets. We first recall the notations.
Let
![]() $k\geqslant 1$
be an integer. For any real number
$k\geqslant 1$
be an integer. For any real number
![]() $y$
, we define its
$y$
, we define its
![]() $k$
-height as
$k$
-height as
where we use the convention that, if the set is empty, i.e.,
![]() $y$
is not algebraic of degree at most
$y$
is not algebraic of degree at most
![]() $k$
, then
$k$
, then
![]() $\text{H}_{k}(y)$
is
$\text{H}_{k}(y)$
is
![]() $+\infty$
. For
$+\infty$
. For
![]() $y=(y_{1},\ldots ,y_{m})\in \mathbb{R}^{m}$
, we set
$y=(y_{1},\ldots ,y_{m})\in \mathbb{R}^{m}$
, we set
For any set
![]() $A\subseteq \mathbb{R}^{m}\times \mathbb{R}^{n}$
, and for any real number
$A\subseteq \mathbb{R}^{m}\times \mathbb{R}^{n}$
, and for any real number
![]() $T\geqslant 1$
, we define
$T\geqslant 1$
, we define
The counting theorem of Pila and Wilkie is stated as follows.
Theorem 9.1 (Cf. the proof of [Reference Habegger and PilaHP16, Corollary 7.2]).
Let
![]() $D\subseteq \mathbb{R}^{l}\times \mathbb{R}^{m}\times \mathbb{R}^{n}$
be a definable family parametrized by
$D\subseteq \mathbb{R}^{l}\times \mathbb{R}^{m}\times \mathbb{R}^{n}$
be a definable family parametrized by
![]() $\mathbb{R}^{l}$
, let
$\mathbb{R}^{l}$
, let
![]() $k$
be a positive integer, and let
$k$
be a positive integer, and let
![]() $\unicode[STIX]{x1D716}>0$
. There exists a constant
$\unicode[STIX]{x1D716}>0$
. There exists a constant
![]() $c:=c(D,k,\unicode[STIX]{x1D716})>0$
with the following properties.
$c:=c(D,k,\unicode[STIX]{x1D716})>0$
with the following properties.
Let
![]() $x\in \mathbb{R}^{l}$
and let
$x\in \mathbb{R}^{l}$
and let
Let
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
denote the projections
$\unicode[STIX]{x1D70B}_{2}$
denote the projections
![]() $\mathbb{R}^{m}\times \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$
and
$\mathbb{R}^{m}\times \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$
and
![]() $\mathbb{R}^{m}\times \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$
, respectively. If
$\mathbb{R}^{m}\times \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$
, respectively. If
![]() $T\geqslant 1$
and
$T\geqslant 1$
and
![]() $\unicode[STIX]{x1D6F4}\subseteq D_{x}(k,T)$
satisfies
$\unicode[STIX]{x1D6F4}\subseteq D_{x}(k,T)$
satisfies
there exists a continuous and definable function
![]() $\unicode[STIX]{x1D6FD}:[0,1]\rightarrow D_{x}$
such that the following properties hold.
$\unicode[STIX]{x1D6FD}:[0,1]\rightarrow D_{x}$
such that the following properties hold.
(1) The composition
 $\unicode[STIX]{x1D70B}_{1}\circ \unicode[STIX]{x1D6FD}:[0,1]\rightarrow \mathbb{R}^{m}$
is semialgebraic.
$\unicode[STIX]{x1D70B}_{1}\circ \unicode[STIX]{x1D6FD}:[0,1]\rightarrow \mathbb{R}^{m}$
is semialgebraic.(2) The composition
 $\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D6FD}:[0,1]\rightarrow \mathbb{R}^{n}$
is non-constant.
$\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D6FD}:[0,1]\rightarrow \mathbb{R}^{n}$
is non-constant.(3) We have
 $\unicode[STIX]{x1D6FD}(0)\in \unicode[STIX]{x1D6F4}$
.
$\unicode[STIX]{x1D6FD}(0)\in \unicode[STIX]{x1D6F4}$
.(4) The restriction
 $\unicode[STIX]{x1D6FD}_{|(0,1)}$
is real analytic.
$\unicode[STIX]{x1D6FD}_{|(0,1)}$
is real analytic.
Note that, although the conclusion
![]() $\unicode[STIX]{x1D6FD}(0)\in \unicode[STIX]{x1D6F4}$
does not appear in the statement of [Reference Habegger and PilaHP16, Corollary 7.2], it is, indeed, established in its proof. The final property holds because
$\unicode[STIX]{x1D6FD}(0)\in \unicode[STIX]{x1D6F4}$
does not appear in the statement of [Reference Habegger and PilaHP16, Corollary 7.2], it is, indeed, established in its proof. The final property holds because
![]() $\mathbb{R}_{\text{an},\text{exp}}$
admits analytic cell decomposition (see [Reference van den Dries and MillerVdDM94]).
$\mathbb{R}_{\text{an},\text{exp}}$
admits analytic cell decomposition (see [Reference van den Dries and MillerVdDM94]).
10 Complexity
In order to apply the counting theorem, we will need a way of counting special points and, more generally, special subvarieties. Recall that
![]() $S$
is a connected component of the Shimura variety
$S$
is a connected component of the Shimura variety
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
defined by the Shimura datum
$\text{Sh}_{K}(G,\mathfrak{X})$
defined by the Shimura datum
![]() $(G,X)$
and the compact open subgroup
$(G,X)$
and the compact open subgroup
![]() $K$
of
$K$
of
![]() $G(\mathbb{A}_{f})$
.
$G(\mathbb{A}_{f})$
.
Let
![]() $P$
be a special point in
$P$
be a special point in
![]() $S$
and let
$S$
and let
![]() $x\in X$
be a pre-special point lying above
$x\in X$
be a pre-special point lying above
![]() $P$
. In particular,
$P$
. In particular,
![]() $T:=\text{MT}(x)$
is a torus and we denote by
$T:=\text{MT}(x)$
is a torus and we denote by
![]() $D_{T}$
the absolute value of the discriminant of its splitting field. We let
$D_{T}$
the absolute value of the discriminant of its splitting field. We let
![]() $K_{T}^{m}$
denote the maximal compact open subgroup of
$K_{T}^{m}$
denote the maximal compact open subgroup of
![]() $T(\mathbb{A}_{f})$
and we let
$T(\mathbb{A}_{f})$
and we let
![]() $K_{T}\subseteq K_{T}^{m}$
denote
$K_{T}\subseteq K_{T}^{m}$
denote
![]() $K\cap T(\mathbb{A}_{f})$
.
$K\cap T(\mathbb{A}_{f})$
.
Definition 10.1. The complexity of
![]() $P$
is the natural number
$P$
is the natural number
Note that this does not depend on the choice of
![]() $x$
.
$x$
.
Now let
![]() $Z$
be a special subvariety of
$Z$
be a special subvariety of
![]() $S$
. There exists a Shimura subdatum
$S$
. There exists a Shimura subdatum
![]() $(H,\mathfrak{X}_{H})$
of
$(H,\mathfrak{X}_{H})$
of
![]() $(G,\mathfrak{X})$
, such that
$(G,\mathfrak{X})$
, such that
![]() $H$
is the generic Mumford–Tate group on
$H$
is the generic Mumford–Tate group on
![]() $\mathfrak{X}_{H}$
, and a connected component
$\mathfrak{X}_{H}$
, and a connected component
![]() $X_{H}$
of
$X_{H}$
of
![]() $\mathfrak{X}_{H}$
contained in
$\mathfrak{X}_{H}$
contained in
![]() $X$
such that
$X$
such that
![]() $Z$
is the image of
$Z$
is the image of
![]() $X_{H}$
in
$X_{H}$
in
![]() $\unicode[STIX]{x1D6E4}\backslash X$
. In fact, these choices are well defined up to conjugation by
$\unicode[STIX]{x1D6E4}\backslash X$
. In fact, these choices are well defined up to conjugation by
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
By the degree
![]() $\deg (Z)$
of
$\deg (Z)$
of
![]() $Z$
, we refer to the degree of the Zariski closure of
$Z$
, we refer to the degree of the Zariski closure of
![]() $Z$
in the Baily–Borel compactification of
$Z$
in the Baily–Borel compactification of
![]() $S$
, defined in [Reference Baily and BorelBB66], which is naturally a projective variety.
$S$
, defined in [Reference Baily and BorelBB66], which is naturally a projective variety.
Definition 10.2. The complexity of
![]() $Z$
is the natural number
$Z$
is the natural number
Note that when
![]() $Z$
is a special point, this complexity coincides with the former.
$Z$
is a special point, this complexity coincides with the former.
This is a natural generalization of the complexities given in [Reference Habegger and PilaHP16, Definitions 3.4 and 3.8]. In order to count special subvarieties, however, it is crucial that the complexity of
![]() $Z$
satisfies the following property.
$Z$
satisfies the following property.
Conjecture 10.3. For any
![]() $b\geqslant 1$
, we have
$b\geqslant 1$
, we have
The obstruction to proving that this property holds for a general Shimura variety can be expressed as follows.
Conjecture 10.4. For any
![]() $b\geqslant 1$
, there exists a finite set
$b\geqslant 1$
, there exists a finite set
![]() $\unicode[STIX]{x1D6FA}$
of semisimple subgroups of
$\unicode[STIX]{x1D6FA}$
of semisimple subgroups of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
such that, if
$\mathbb{Q}$
such that, if
![]() $Z$
is a special subvariety of
$Z$
is a special subvariety of
![]() $S$
, and
$S$
, and
![]() $\deg (Z)\leqslant b$
, then
$\deg (Z)\leqslant b$
, then
for some
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
and some
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
and some
![]() $F\in \unicode[STIX]{x1D6FA}$
.
$F\in \unicode[STIX]{x1D6FA}$
.
We will later verify Conjecture 10.4 for a product of modular curves.
Proof that Conjecture 10.4 implies Conjecture 10.3.
By Conjecture 10.4, there exists a finite set
![]() $\unicode[STIX]{x1D6FA}$
of semisimple subgroups of
$\unicode[STIX]{x1D6FA}$
of semisimple subgroups of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
, independent of
$\mathbb{Q}$
, independent of
![]() $Z$
, such that
$Z$
, such that
for some
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
and some
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
and some
![]() $F\in \unicode[STIX]{x1D6FA}$
.
$F\in \unicode[STIX]{x1D6FA}$
.
Let
![]() $P\in Z$
be a special point such that
$P\in Z$
be a special point such that
![]() $\unicode[STIX]{x1D6E5}(P)$
is minimal among all special points in
$\unicode[STIX]{x1D6E5}(P)$
is minimal among all special points in
![]() $Z$
and let
$Z$
and let
![]() $x\in X$
be a point lying above
$x\in X$
be a point lying above
![]() $P$
such that
$P$
such that
![]() $\text{MT}(x)$
is contained in
$\text{MT}(x)$
is contained in
![]() $H$
. Therefore,
$H$
. Therefore,
![]() $Z$
is equal to the image of
$Z$
is equal to the image of
![]() $F(\mathbb{R})^{+}\unicode[STIX]{x1D6FE}^{-1}x$
in
$F(\mathbb{R})^{+}\unicode[STIX]{x1D6FE}^{-1}x$
in
![]() $\unicode[STIX]{x1D6E4}\backslash X$
. Furthermore,
$\unicode[STIX]{x1D6E4}\backslash X$
. Furthermore,
![]() $\text{MT}(\unicode[STIX]{x1D6FE}^{-1}x)$
is contained in
$\text{MT}(\unicode[STIX]{x1D6FE}^{-1}x)$
is contained in
and, by [Reference UllmoUll07, Lemme 3.3], if we denote by
![]() $\mathfrak{X}^{\prime }$
the
$\mathfrak{X}^{\prime }$
the
![]() $G_{F}(\mathbb{R})$
conjugacy class of
$G_{F}(\mathbb{R})$
conjugacy class of
![]() $\unicode[STIX]{x1D6FE}^{-1}x$
, we obtain a Shimura subdatum
$\unicode[STIX]{x1D6FE}^{-1}x$
, we obtain a Shimura subdatum
![]() $(G_{F},\mathfrak{X}^{\prime })$
of
$(G_{F},\mathfrak{X}^{\prime })$
of
![]() $(G,\mathfrak{X})$
.
$(G,\mathfrak{X})$
.
Therefore, let
![]() $X^{\prime }$
denote the connected component
$X^{\prime }$
denote the connected component
![]() $G_{F}(\mathbb{R})^{+}\unicode[STIX]{x1D6FE}^{-1}x$
of
$G_{F}(\mathbb{R})^{+}\unicode[STIX]{x1D6FE}^{-1}x$
of
![]() $\mathfrak{X}^{\prime }$
and let
$\mathfrak{X}^{\prime }$
and let
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
denote
$\unicode[STIX]{x1D6E4}^{\prime }$
denote
![]() $\unicode[STIX]{x1D6E4}\,\cap \,G_{F}(\mathbb{Q})_{+}$
, where
$\unicode[STIX]{x1D6E4}\,\cap \,G_{F}(\mathbb{Q})_{+}$
, where
![]() $G_{F}(\mathbb{Q})_{+}$
denotes the subgroup of
$G_{F}(\mathbb{Q})_{+}$
denotes the subgroup of
![]() $G_{F}(\mathbb{Q})$
acting on
$G_{F}(\mathbb{Q})$
acting on
![]() $X^{\prime }$
. By [Reference Ullmo and YafaevUY14, Proposition 3.21] and its proof, there exist only finitely many
$X^{\prime }$
. By [Reference Ullmo and YafaevUY14, Proposition 3.21] and its proof, there exist only finitely many
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
orbits of pre-special points in
$\unicode[STIX]{x1D6E4}^{\prime }$
orbits of pre-special points in
![]() $X^{\prime }$
whose image in
$X^{\prime }$
whose image in
![]() $\unicode[STIX]{x1D6E4}^{\prime }\backslash X^{\prime }$
has complexity at most
$\unicode[STIX]{x1D6E4}^{\prime }\backslash X^{\prime }$
has complexity at most
![]() $b$
. Therefore, there exists
$b$
. Therefore, there exists
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6E4}^{\prime }$
such that
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6E4}^{\prime }$
such that
![]() $\unicode[STIX]{x1D6FE}^{-1}x=\unicode[STIX]{x1D706}y$
, where
$\unicode[STIX]{x1D6FE}^{-1}x=\unicode[STIX]{x1D706}y$
, where
![]() $y\in X^{\prime }$
belongs to a finite set. We conclude that
$y\in X^{\prime }$
belongs to a finite set. We conclude that
![]() $Z$
is equal to the image of
$Z$
is equal to the image of
in
![]() $\unicode[STIX]{x1D6E4}\backslash X$
, which concludes the proof.◻
$\unicode[STIX]{x1D6E4}\backslash X$
, which concludes the proof.◻
11 Galois orbits
In [Reference Habegger and PilaHP16], Habegger and Pila formulated a conjecture about Galois orbits of optimal points in
![]() $\mathbb{C}^{n}$
that in [Reference Habegger and PilaHab12] they had been able to prove for so-called asymmetric curves. In [Reference OrrOrr17], Orr generalized the result to asymmetric curves in
$\mathbb{C}^{n}$
that in [Reference Habegger and PilaHab12] they had been able to prove for so-called asymmetric curves. In [Reference OrrOrr17], Orr generalized the result to asymmetric curves in
![]() ${\mathcal{A}}_{g}^{2}$
.
${\mathcal{A}}_{g}^{2}$
.
Recall that
![]() $\text{Sh}_{K}(G,\mathfrak{X})$
possesses a canonical model, defined over a number field
$\text{Sh}_{K}(G,\mathfrak{X})$
possesses a canonical model, defined over a number field
![]() $E$
, which depends only on
$E$
, which depends only on
![]() $(G,\mathfrak{X})$
. Furthermore,
$(G,\mathfrak{X})$
. Furthermore,
![]() $S$
is defined over a finite abelian extension
$S$
is defined over a finite abelian extension
![]() $F$
of
$F$
of
![]() $E$
. In particular, for any extension
$E$
. In particular, for any extension
![]() $L$
of
$L$
of
![]() $F$
contained in
$F$
contained in
![]() $\mathbb{C}$
, it makes sense to say that a subvariety
$\mathbb{C}$
, it makes sense to say that a subvariety
![]() $V$
of
$V$
of
![]() $S$
is defined over
$S$
is defined over
![]() $L$
. Moreover, if
$L$
. Moreover, if
![]() $V$
is such a subvariety, then
$V$
is such a subvariety, then
![]() $\text{Aut}(\mathbb{C}/L)$
acts on the points of
$\text{Aut}(\mathbb{C}/L)$
acts on the points of
![]() $V$
.
$V$
.
If
![]() $Z$
is a special subvariety of
$Z$
is a special subvariety of
![]() $S$
and
$S$
and
![]() $\unicode[STIX]{x1D70E}\in \text{Aut}(\mathbb{C}/F)$
, then
$\unicode[STIX]{x1D70E}\in \text{Aut}(\mathbb{C}/F)$
, then
![]() $\unicode[STIX]{x1D70E}(Z)$
is also a special subvariety of
$\unicode[STIX]{x1D70E}(Z)$
is also a special subvariety of
![]() $S$
and its complexity is also
$S$
and its complexity is also
![]() $\unicode[STIX]{x1D6E5}(Z)$
. In particular, if
$\unicode[STIX]{x1D6E5}(Z)$
. In particular, if
![]() $V$
is a subvariety of
$V$
is a subvariety of
![]() $S$
, as above, then
$S$
, as above, then
![]() $\text{Aut}(\mathbb{C}/L)$
acts on
$\text{Aut}(\mathbb{C}/L)$
acts on
![]() $\text{Opt}(V)$
and its orbits are finite.
$\text{Opt}(V)$
and its orbits are finite.
Conjecture 11.1 (Large Galois orbits).
Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
, defined over a finitely generated extension
$S$
, defined over a finitely generated extension
![]() $L$
of
$L$
of
![]() $F$
contained in
$F$
contained in
![]() $\mathbb{C}$
. There exist positive constants
$\mathbb{C}$
. There exist positive constants
![]() $c_{G}$
and
$c_{G}$
and
![]() $\unicode[STIX]{x1D6FF}_{G}$
such that the following holds.
$\unicode[STIX]{x1D6FF}_{G}$
such that the following holds.
If
![]() $P\in \text{Opt}_{0}(V)$
, then
$P\in \text{Opt}_{0}(V)$
, then
Remark 11.2. In the context of the André–Oort conjecture, there is the pioneering hypothesis that Galois orbits of special points should be large. See [Reference Edixhoven, Moonen and OortEMO01, Problem 14] for the formulation for special points in
![]() ${\mathcal{A}}_{g}$
and see [Reference YafaevYaf06, Theorem 2.1] for special points in a general Shimura variety. This hypothesis, which was verified by Tsimerman for special points of
${\mathcal{A}}_{g}$
and see [Reference YafaevYaf06, Theorem 2.1] for special points in a general Shimura variety. This hypothesis, which was verified by Tsimerman for special points of
![]() ${\mathcal{A}}_{g}$
[Reference TsimermanTsi18] via progress on the Colmez conjecture due to Andreatta, Goren, Howard and Madapusi Pera [Reference Andreatta, Goren, Howard and Madapusi PeraAGHM18], and Yuan and Zhang [Reference Yuan and ZhangYZ18], is now the only obstacle in an otherwise unconditional proof of the André–Oort conjecture. The conjecture is that there exist positive constants
${\mathcal{A}}_{g}$
[Reference TsimermanTsi18] via progress on the Colmez conjecture due to Andreatta, Goren, Howard and Madapusi Pera [Reference Andreatta, Goren, Howard and Madapusi PeraAGHM18], and Yuan and Zhang [Reference Yuan and ZhangYZ18], is now the only obstacle in an otherwise unconditional proof of the André–Oort conjecture. The conjecture is that there exist positive constants
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D6FF}$
such that, for any special point
$\unicode[STIX]{x1D6FF}$
such that, for any special point
![]() $P\in S$
,
$P\in S$
,
Of course, this conjecture does not follow from Conjecture 11.1 because special points lying in
![]() $V$
need not be optimal in
$V$
need not be optimal in
![]() $V$
. However, the proof of the André–Oort conjecture only requires the bound for special points that are not contained in the positive dimensional special subvarieties contained in
$V$
. However, the proof of the André–Oort conjecture only requires the bound for special points that are not contained in the positive dimensional special subvarieties contained in
![]() $V$
, i.e., special points contained in
$V$
, i.e., special points contained in
![]() $\text{Opt}_{0}(V)$
(see [Reference DawDaw15] for more details). Furthermore, since special points are defined over number fields, we may also assume in that case that
$\text{Opt}_{0}(V)$
(see [Reference DawDaw15] for more details). Furthermore, since special points are defined over number fields, we may also assume in that case that
![]() $V$
is defined over a finite extension of
$V$
is defined over a finite extension of
![]() $F$
. It follows that Conjecture 11.1 is sufficient to prove the André–Oort conjecture.
$F$
. It follows that Conjecture 11.1 is sufficient to prove the André–Oort conjecture.
To prove Conjecture 8.4, however, one only requires the following hypothesis.
Conjecture 11.3. Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
, defined over a finitely generated extension
$S$
, defined over a finitely generated extension
![]() $L$
of
$L$
of
![]() $F$
contained in
$F$
contained in
![]() $\mathbb{C}$
. There exist positive constants
$\mathbb{C}$
. There exist positive constants
![]() $c_{G}$
and
$c_{G}$
and
![]() $\unicode[STIX]{x1D6FF}_{G}$
such that the following holds.
$\unicode[STIX]{x1D6FF}_{G}$
such that the following holds.
If
![]() $P\in V^{\text{oa}}\cap S^{[1+\dim V]}$
, then
$P\in V^{\text{oa}}\cap S^{[1+\dim V]}$
, then
Remark 11.4. Note that, if
![]() $P\in V^{\text{oa}}\cap S^{[1+\dim V]}$
, then
$P\in V^{\text{oa}}\cap S^{[1+\dim V]}$
, then
![]() $P\in \text{Opt}_{0}(V)$
. To see this, let
$P\in \text{Opt}_{0}(V)$
. To see this, let
![]() $W$
be a subvariety of
$W$
be a subvariety of
![]() $V$
containing
$V$
containing
![]() $P$
such that
$P$
such that
![]() $\unicode[STIX]{x1D6FF}(W)\leqslant \unicode[STIX]{x1D6FF}(P)$
, i.e.,
$\unicode[STIX]{x1D6FF}(W)\leqslant \unicode[STIX]{x1D6FF}(P)$
, i.e.,
In fact, we can and do assume that
![]() $W$
is optimal. We have
$W$
is optimal. We have
and so
![]() $\dim W=0$
, as
$\dim W=0$
, as
![]() $P\notin V^{\text{an}}$
, which implies that
$P\notin V^{\text{an}}$
, which implies that
![]() $W=P$
, proving the claim. Therefore, Conjecture 11.3 follows from Conjecture 11.1, but the former may turn out to be more tractable. It is worth recalling that, when
$W=P$
, proving the claim. Therefore, Conjecture 11.3 follows from Conjecture 11.1, but the former may turn out to be more tractable. It is worth recalling that, when
![]() $S$
is an abelian variety and
$S$
is an abelian variety and
![]() $V$
is a subvariety defined over
$V$
is a subvariety defined over
![]() $\bar{\mathbb{Q}}$
, Habegger [Reference HabeggerHP09] famously showed that the Néron–Tate height is bounded on
$\bar{\mathbb{Q}}$
, Habegger [Reference HabeggerHP09] famously showed that the Néron–Tate height is bounded on
![]() $\bar{\mathbb{Q}}$
-points of
$\bar{\mathbb{Q}}$
-points of
![]() $V^{\text{oa}}\cap S^{[\dim V]}$
.
$V^{\text{oa}}\cap S^{[\dim V]}$
.
12 Further arithmetic hypotheses
The principal obstruction to applying the Pila–Wilkie counting theorems to our point counting problems (except for the availability of lower bounds for Galois orbits) is the ability to parametrize pre-special subvarieties of
![]() $S$
using points of bounded height in a definable set.
$S$
using points of bounded height in a definable set.
Definition 12.1. We say that a semisimple algebraic group defined over
![]() $\mathbb{Q}$
is of non-compact type if its almost-simple factors all have the property that their underlying real Lie group is not compact.
$\mathbb{Q}$
is of non-compact type if its almost-simple factors all have the property that their underlying real Lie group is not compact.
Let
![]() $\unicode[STIX]{x1D6FA}$
be a (finite) set of representatives for the semisimple subgroups of
$\unicode[STIX]{x1D6FA}$
be a (finite) set of representatives for the semisimple subgroups of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
of non-compact type modulo the equivalence relation
$\mathbb{Q}$
of non-compact type modulo the equivalence relation
Add the trivial group to
![]() $\unicode[STIX]{x1D6FA}$
. Our needs can be encapsulated in the following conjecture. Recall that
$\unicode[STIX]{x1D6FA}$
. Our needs can be encapsulated in the following conjecture. Recall that
![]() $X$
is realized as a bounded symmetric domain in
$X$
is realized as a bounded symmetric domain in
![]() $\mathbb{C}^{N}$
for some
$\mathbb{C}^{N}$
for some
![]() $N\in \mathbb{N}$
, which we identify with
$N\in \mathbb{N}$
, which we identify with
![]() $\mathbb{R}^{2N}$
. Henceforth, we fix an embedding of
$\mathbb{R}^{2N}$
. Henceforth, we fix an embedding of
![]() $G$
into
$G$
into
![]() $\text{GL}_{n}$
such that
$\text{GL}_{n}$
such that
![]() $\unicode[STIX]{x1D6E4}$
is contained in
$\unicode[STIX]{x1D6E4}$
is contained in
![]() $\text{GL}_{n}(\mathbb{Z})$
. We consider
$\text{GL}_{n}(\mathbb{Z})$
. We consider
![]() $\text{GL}_{n}(\mathbb{R})$
as a subset of
$\text{GL}_{n}(\mathbb{R})$
as a subset of
![]() $\mathbb{R}^{n^{2}}$
in the natural way.
$\mathbb{R}^{n^{2}}$
in the natural way.
Conjecture 12.2 (Cf. [Reference Habegger and PilaHP16, Proposition 6.7]).
There exist positive constants
![]() $d$
,
$d$
,
![]() $c_{{\mathcal{F}}}$
, and
$c_{{\mathcal{F}}}$
, and
![]() $\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
such that, if
$\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
such that, if
![]() $z\in {\mathcal{F}}$
, then the smallest pre-special subvariety of
$z\in {\mathcal{F}}$
, then the smallest pre-special subvariety of
![]() $X$
containing
$X$
containing
![]() $z$
can be written
$z$
can be written
![]() $gF(\mathbb{R})^{+}g^{-1}x$
, where
$gF(\mathbb{R})^{+}g^{-1}x$
, where
![]() $F\in \unicode[STIX]{x1D6FA}$
, and
$F\in \unicode[STIX]{x1D6FA}$
, and
![]() $g\in G(\mathbb{R})$
and
$g\in G(\mathbb{R})$
and
![]() $x\in X$
satisfy
$x\in X$
satisfy
This is seemingly a natural generalization of the following theorem due to Orr and the first author on the heights of pre-special points, which plays a crucial role in the proof of the André–Oort conjecture.
Theorem 12.3 (Cf. [Reference Daw and OrrDO16, Theorem 1.4]).
There exist positive constants
![]() $d$
,
$d$
,
![]() $c_{{\mathcal{F}}}$
and
$c_{{\mathcal{F}}}$
and
![]() $\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
such that, if
$\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
such that, if
![]() $z\in {\mathcal{F}}$
is a pre-special, then
$z\in {\mathcal{F}}$
is a pre-special, then
We remark that the problem of finding
![]() $d$
as in Conjecture 12.2 poses no obstacle in itself. Indeed a proof of the following theorem will appear in a forthcoming article of Borovoi and the authors.
$d$
as in Conjecture 12.2 poses no obstacle in itself. Indeed a proof of the following theorem will appear in a forthcoming article of Borovoi and the authors.
Theorem 12.4 (Cf. [Reference Borovoi, Daw and RenBDR18, Corollary 0.7]).
There exists a positive constant
![]() $d$
such that, for any two semisimple subgroups
$d$
such that, for any two semisimple subgroups
![]() $H_{1}$
and
$H_{1}$
and
![]() $H_{2}$
of
$H_{2}$
of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
that are conjugate by an element of
$\mathbb{Q}$
that are conjugate by an element of
![]() $G(\mathbb{R})$
, there exists a number field
$G(\mathbb{R})$
, there exists a number field
![]() $K$
contained in
$K$
contained in
![]() $\mathbb{R}$
of degree at most
$\mathbb{R}$
of degree at most
![]() $d$
, and an element
$d$
, and an element
![]() $g\in G(K)$
, such that
$g\in G(K)$
, such that
A nice feature of Conjecture 12.2 is that it implies Conjecture 10.3 that there are only finitely many special subvarieties of bounded complexity.
Proof. Let
![]() $Z$
be a special subvariety of
$Z$
be a special subvariety of
![]() $S$
such that
$S$
such that
![]() $\unicode[STIX]{x1D6E5}(Z)\leqslant b$
and let
$\unicode[STIX]{x1D6E5}(Z)\leqslant b$
and let
![]() $P\in Z$
be such that
$P\in Z$
be such that
![]() $\langle P\rangle =Z$
. Let
$\langle P\rangle =Z$
. Let
![]() $z\in {\mathcal{F}}$
be such that
$z\in {\mathcal{F}}$
be such that
![]() $\unicode[STIX]{x1D70B}(z)=P$
and let
$\unicode[STIX]{x1D70B}(z)=P$
and let
![]() $X_{H}$
be the smallest pre-special subvariety of
$X_{H}$
be the smallest pre-special subvariety of
![]() $X$
containing
$X$
containing
![]() $z$
. Then
$z$
. Then
![]() $\unicode[STIX]{x1D70B}(X_{H})=Z$
and, by Conjecture 12.2,
$\unicode[STIX]{x1D70B}(X_{H})=Z$
and, by Conjecture 12.2,
![]() $X_{H}=gFg^{-1}x$
, where
$X_{H}=gFg^{-1}x$
, where
![]() $F\in \unicode[STIX]{x1D6FA}$
, and
$F\in \unicode[STIX]{x1D6FA}$
, and
![]() $g\in G(\mathbb{R})$
and
$g\in G(\mathbb{R})$
and
![]() $x\in X$
satisfy
$x\in X$
satisfy
The claim follows, therefore, from the fact that there are only finitely many algebraic numbers of bounded degree and height, i.e., Northcott’s property. ◻
Another, albeit longer, approach to our point counting problems can be given by replacing Conjecture 12.2 with two related conjectures, although we will have to additionally assume Conjecture 10.3 in this case. We will also rely on the fact that Theorem 9.1 is uniform in families. The advantage is that the following two conjectures are seemingly more accessible.
Conjecture 12.6. For any
![]() $\unicode[STIX]{x1D705}>0$
, there exists a positive constant
$\unicode[STIX]{x1D705}>0$
, there exists a positive constant
![]() $c_{\unicode[STIX]{x1D705}}$
such that, if
$c_{\unicode[STIX]{x1D705}}$
such that, if
![]() $Z$
is a special subvariety of
$Z$
is a special subvariety of
![]() $S$
, then there exists a semisimple subgroup
$S$
, then there exists a semisimple subgroup
![]() $H$
of
$H$
of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
of non-compact type, and an extension
$\mathbb{Q}$
of non-compact type, and an extension
![]() $L$
of
$L$
of
![]() $F$
satisfying
$F$
satisfying
such that, for any
![]() $\unicode[STIX]{x1D70E}\in \text{Aut}(\mathbb{C}/L)$
,
$\unicode[STIX]{x1D70E}\in \text{Aut}(\mathbb{C}/L)$
,
where
![]() $H(\mathbb{R})^{+}x_{\unicode[STIX]{x1D70E}}$
is a pre-special subvariety of
$H(\mathbb{R})^{+}x_{\unicode[STIX]{x1D70E}}$
is a pre-special subvariety of
![]() $X$
intersecting
$X$
intersecting
![]() ${\mathcal{F}}$
.
${\mathcal{F}}$
.
Recall that, for an abelian variety
![]() $A$
, defined over a field
$A$
, defined over a field
![]() $K$
, every abelian subvariety of
$K$
, every abelian subvariety of
![]() $A$
can be defined over a fixed, finite extension of
$A$
can be defined over a fixed, finite extension of
![]() $K$
. The analogue of Conjecture 12.6 is, therefore, trivial. In a Shimura variety, one hopes that the degrees of fields of definition of strongly special subvarieties grow as in Conjecture 12.6. If this were true, Conjecture 12.6 for strongly special subvarieties would follow easily.
$K$
. The analogue of Conjecture 12.6 is, therefore, trivial. In a Shimura variety, one hopes that the degrees of fields of definition of strongly special subvarieties grow as in Conjecture 12.6. If this were true, Conjecture 12.6 for strongly special subvarieties would follow easily.
Our final conjecture is also inspired by the abelian setting.
Conjecture 12.7 (Cf. [Reference Habegger and PilaHP16, Lemma 3.2]).
There exist positive constants
![]() $c_{\unicode[STIX]{x1D6E4}}$
and
$c_{\unicode[STIX]{x1D6E4}}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}$
such that, if
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}$
such that, if
![]() $X_{H}$
is a pre-special subvariety of
$X_{H}$
is a pre-special subvariety of
![]() $X$
intersecting
$X$
intersecting
![]() ${\mathcal{F}}$
and
${\mathcal{F}}$
and
![]() $z\in {\mathcal{F}}$
belongs to
$z\in {\mathcal{F}}$
belongs to
![]() $\unicode[STIX]{x1D6E4}X_{H}$
, then
$\unicode[STIX]{x1D6E4}X_{H}$
, then
![]() $z\in \unicode[STIX]{x1D6FE}X_{H}$
, where
$z\in \unicode[STIX]{x1D6FE}X_{H}$
, where
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
satisfies
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
satisfies
Conjecture 12.7 has the following useful consequence.
Lemma 12.8. Assume that Conjecture 12.7 holds.
There exist positive constants
![]() $d$
,
$d$
,
![]() $c_{\text{H}}$
, and
$c_{\text{H}}$
, and
![]() $\unicode[STIX]{x1D6FF}_{\text{H}}$
such that, if
$\unicode[STIX]{x1D6FF}_{\text{H}}$
such that, if
![]() $H(\mathbb{R})^{+}x$
is a pre-special subvariety of
$H(\mathbb{R})^{+}x$
is a pre-special subvariety of
![]() $X$
intersecting
$X$
intersecting
![]() ${\mathcal{F}}$
, then
${\mathcal{F}}$
, then
where
![]() $\text{H}_{d}(y)\leqslant c_{\text{H}}\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70B}(H(\mathbb{R})^{+}x))^{\unicode[STIX]{x1D6FF}_{\text{H}}}$
.
$\text{H}_{d}(y)\leqslant c_{\text{H}}\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70B}(H(\mathbb{R})^{+}x))^{\unicode[STIX]{x1D6FF}_{\text{H}}}$
.
Proof. Let
![]() $d$
,
$d$
,
![]() $c_{{\mathcal{F}}}$
, and
$c_{{\mathcal{F}}}$
, and
![]() $\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
be the positive constants afforded to us by Theorem 12.3, and let
$\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
be the positive constants afforded to us by Theorem 12.3, and let
![]() $c_{\unicode[STIX]{x1D6E4}}$
and
$c_{\unicode[STIX]{x1D6E4}}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}$
be the positive constants afforded to us by Conjecture12.7.
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}$
be the positive constants afforded to us by Conjecture12.7.
Let
![]() $x^{\prime }\in \unicode[STIX]{x1D6E4}H(\mathbb{R})^{+}x\cap {\mathcal{F}}$
denote a pre-special point such that
$x^{\prime }\in \unicode[STIX]{x1D6E4}H(\mathbb{R})^{+}x\cap {\mathcal{F}}$
denote a pre-special point such that
![]() $\unicode[STIX]{x1D70B}(x^{\prime })$
is of minimal complexity among the special points of
$\unicode[STIX]{x1D70B}(x^{\prime })$
is of minimal complexity among the special points of
![]() $\unicode[STIX]{x1D70B}(H(\mathbb{R})^{+}x)$
. By Theorem 12.3, we have
$\unicode[STIX]{x1D70B}(H(\mathbb{R})^{+}x)$
. By Theorem 12.3, we have
On the other hand, by Conjecture 12.7,
![]() $x^{\prime }\in \unicode[STIX]{x1D6FE}H(\mathbb{R})^{+}x$
, where
$x^{\prime }\in \unicode[STIX]{x1D6FE}H(\mathbb{R})^{+}x$
, where
It follows easily from the properties of heights that there exist positive constants
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D6FF}$
depending only on the fixed data such that
$\unicode[STIX]{x1D6FF}$
depending only on the fixed data such that
Therefore, the previous remarks show that
satisfies the requirements of the lemma. ◻
We will now verify the arithmetic conjectures stated above in an arbitrary product of modular curves.
13 Products of modular curves
Our definition of a Shimura variety allows for the possibility that
![]() $S$
might be a product of modular curves. In that case
$S$
might be a product of modular curves. In that case
![]() $G=\text{GL}_{2}^{n}$
, where
$G=\text{GL}_{2}^{n}$
, where
![]() $n$
is the number of modular curves, and
$n$
is the number of modular curves, and
![]() $\mathfrak{X}$
is the
$\mathfrak{X}$
is the
![]() $G(\mathbb{R})$
conjugacy class of the morphism
$G(\mathbb{R})$
conjugacy class of the morphism
![]() $\mathbb{S}\rightarrow G_{\mathbb{R}}$
given by
$\mathbb{S}\rightarrow G_{\mathbb{R}}$
given by
We let
![]() $X$
denote the
$X$
denote the
![]() $G(\mathbb{R})^{+}$
conjugacy class of this morphism, which one identifies with the
$G(\mathbb{R})^{+}$
conjugacy class of this morphism, which one identifies with the
![]() $n$
th cartesian power
$n$
th cartesian power
![]() $\mathbb{H}^{n}$
of the upper half-plane
$\mathbb{H}^{n}$
of the upper half-plane
![]() $\mathbb{H}$
.
$\mathbb{H}$
.
For our purposes, we can and do suppose that
![]() $\unicode[STIX]{x1D6E4}$
is equal to
$\unicode[STIX]{x1D6E4}$
is equal to
![]() $\text{SL}_{2}(\mathbb{Z})^{n}$
and we let
$\text{SL}_{2}(\mathbb{Z})^{n}$
and we let
![]() ${\mathcal{F}}$
denote a fundamental set in
${\mathcal{F}}$
denote a fundamental set in
![]() $X$
for the action of
$X$
for the action of
![]() $\unicode[STIX]{x1D6E4}$
, equal to the
$\unicode[STIX]{x1D6E4}$
, equal to the
![]() $n$
th cartesian power of a fundamental set
$n$
th cartesian power of a fundamental set
![]() ${\mathcal{F}}_{\mathbb{H}}$
in
${\mathcal{F}}_{\mathbb{H}}$
in
![]() $\mathbb{H}$
for the action of
$\mathbb{H}$
for the action of
![]() $\text{SL}_{2}(\mathbb{Z})$
. Note that, as explained in [Reference OrrOrr18, § 1.3], we can and do choose
$\text{SL}_{2}(\mathbb{Z})$
. Note that, as explained in [Reference OrrOrr18, § 1.3], we can and do choose
![]() ${\mathcal{F}}_{\mathbb{H}}$
in the image of a Siegel set. Via the
${\mathcal{F}}_{\mathbb{H}}$
in the image of a Siegel set. Via the
![]() $j$
-function applied to each factor of
$j$
-function applied to each factor of
![]() $\mathbb{H}^{n}$
, the quotient
$\mathbb{H}^{n}$
, the quotient
![]() $\unicode[STIX]{x1D6E4}\backslash X$
is isomorphic to the algebraic variety
$\unicode[STIX]{x1D6E4}\backslash X$
is isomorphic to the algebraic variety
![]() $\mathbb{C}^{n}$
. Special subvarieties have the following well-documented description.
$\mathbb{C}^{n}$
. Special subvarieties have the following well-documented description.
Proposition 13.1 (Cf. [Reference EdixhovenEdi05, Proposition 2.1]).
Let
![]() $I=\{1,\ldots ,n\}$
. A subvariety
$I=\{1,\ldots ,n\}$
. A subvariety
![]() $Z$
of
$Z$
of
![]() $\mathbb{C}^{n}$
is a special subvariety if and only if there exists a partition
$\mathbb{C}^{n}$
is a special subvariety if and only if there exists a partition
![]() $\unicode[STIX]{x1D6FA}=(I_{1},\ldots ,I_{t})$
of
$\unicode[STIX]{x1D6FA}=(I_{1},\ldots ,I_{t})$
of
![]() $I$
, with
$I$
, with
![]() $|I_{i}|=n_{i}$
, such that
$|I_{i}|=n_{i}$
, such that
![]() $Z$
is equal to the product of subvarieties
$Z$
is equal to the product of subvarieties
![]() $Z_{i}$
of
$Z_{i}$
of
![]() $\mathbb{C}^{n_{i}}$
, where either
$\mathbb{C}^{n_{i}}$
, where either
⋆
 $I_{i}$
is a one element set and
$I_{i}$
is a one element set and
 $Z_{i}$
is a special point, or
$Z_{i}$
is a special point, or⋆
 $Z_{i}$
is the image of
$Z_{i}$
is the image of
 $\mathbb{H}$
in
$\mathbb{H}$
in
 $\mathbb{C}^{n_{i}}$
under the map sending
$\mathbb{C}^{n_{i}}$
under the map sending
 $\unicode[STIX]{x1D70F}\in \mathbb{H}$
to the image of
$\unicode[STIX]{x1D70F}\in \mathbb{H}$
to the image of
 $(g_{j}\unicode[STIX]{x1D70F})_{j\in I_{i}}$
in
$(g_{j}\unicode[STIX]{x1D70F})_{j\in I_{i}}$
in
 $\mathbb{C}^{n_{i}}$
for elements
$\mathbb{C}^{n_{i}}$
for elements
 $g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
.
$g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
.
First note that Conjecture 12.2 for
![]() $\mathbb{C}^{n}$
follows from [Reference Habegger and PilaHP16, Proposition 6.7]. Hence, we will now verify Conjectures 12.6 and 12.7 in that setting.
$\mathbb{C}^{n}$
follows from [Reference Habegger and PilaHP16, Proposition 6.7]. Hence, we will now verify Conjectures 12.6 and 12.7 in that setting.
Proof of Conjecture 12.6 for
 $\mathbb{C}^{n}$
.
$\mathbb{C}^{n}$
.
Let
![]() $Z$
be a special subvariety of
$Z$
be a special subvariety of
![]() $\mathbb{C}^{n}$
, equal to a product of special subvarieties
$\mathbb{C}^{n}$
, equal to a product of special subvarieties
![]() $Z_{i}$
of
$Z_{i}$
of
![]() $\mathbb{C}^{n_{i}}$
, as above. Without loss of generality, we may assume that the product contains only one factor and, by Theorem 12.3, we may assume that it is not a special point. Therefore,
$\mathbb{C}^{n_{i}}$
, as above. Without loss of generality, we may assume that the product contains only one factor and, by Theorem 12.3, we may assume that it is not a special point. Therefore,
![]() $Z$
is equal to the image of
$Z$
is equal to the image of
![]() $\mathbb{H}$
in
$\mathbb{H}$
in
![]() $\mathbb{C}^{n}$
under the map sending
$\mathbb{C}^{n}$
under the map sending
![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}$
to the image of
$\unicode[STIX]{x1D70F}\in \mathbb{H}$
to the image of
![]() $(g_{j}\unicode[STIX]{x1D70F})_{j=1}^{n}$
in
$(g_{j}\unicode[STIX]{x1D70F})_{j=1}^{n}$
in
![]() $\mathbb{C}^{n}$
for elements
$\mathbb{C}^{n}$
for elements
![]() $g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
.
$g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
.
In other words, we have a morphism of Shimura data from
![]() $(\text{GL}_{2},\mathbb{H}^{\pm })$
to
$(\text{GL}_{2},\mathbb{H}^{\pm })$
to
![]() $(G,\mathfrak{X})$
, where
$(G,\mathfrak{X})$
, where
![]() $\mathbb{H}^{\pm }$
is the union of the upper and lower half-planes (or, rather, the conjugacy class we associate with it, as above), induced by the morphism
$\mathbb{H}^{\pm }$
is the union of the upper and lower half-planes (or, rather, the conjugacy class we associate with it, as above), induced by the morphism
such that
![]() $Z$
is equal to the image of
$Z$
is equal to the image of
![]() $\mathbb{H}\times \{1\}$
under the corresponding morphism
$\mathbb{H}\times \{1\}$
under the corresponding morphism
where
![]() $K$
is the product of the groups
$K$
is the product of the groups
over all primes
![]() $p$
.
$p$
.
Since (13.1.1) is defined over
![]() $E(\text{GL}_{2},\mathbb{H}^{\pm })=\mathbb{Q}$
, it suffices to bound the size of
$E(\text{GL}_{2},\mathbb{H}^{\pm })=\mathbb{Q}$
, it suffices to bound the size of
which, by [Reference MilneMil05, Theorem 5.17], is in bijection with
where
![]() $\unicode[STIX]{x1D708}$
is the determinant map on
$\unicode[STIX]{x1D708}$
is the determinant map on
![]() $\text{GL}_{2}$
. However, since
$\text{GL}_{2}$
. However, since
![]() $\mathbb{A}_{f}^{\times }$
is equal to the direct product
$\mathbb{A}_{f}^{\times }$
is equal to the direct product
![]() $\mathbb{Q}_{{>}0}\hat{\mathbb{Z}}^{\times }$
, it suffices to bound the size of
$\mathbb{Q}_{{>}0}\hat{\mathbb{Z}}^{\times }$
, it suffices to bound the size of
![]() $\hat{\mathbb{Z}}^{\times }/\unicode[STIX]{x1D708}(K)$
.
$\hat{\mathbb{Z}}^{\times }/\unicode[STIX]{x1D708}(K)$
.
To that end, let
![]() $\unicode[STIX]{x1D6F4}$
denote the (finite) set of primes
$\unicode[STIX]{x1D6F4}$
denote the (finite) set of primes
![]() $p$
such that
$p$
such that
![]() $g_{j}\notin \text{GL}_{2}(\mathbb{Z}_{p})$
, for some
$g_{j}\notin \text{GL}_{2}(\mathbb{Z}_{p})$
, for some
![]() $j\in \{1,\ldots ,n\}$
. In particular,
$j\in \{1,\ldots ,n\}$
. In particular,
and, since
![]() $K_{p}$
contains the elements
$K_{p}$
contains the elements
![]() $\text{diag}(a,a)$
, where
$\text{diag}(a,a)$
, where
![]() $a\in \mathbb{Z}_{p}^{\times }$
,
$a\in \mathbb{Z}_{p}^{\times }$
,
where
![]() $\mathbb{Z}_{p}^{\times 2}$
denotes the squares in
$\mathbb{Z}_{p}^{\times 2}$
denotes the squares in
![]() $\mathbb{Z}_{p}^{\times }$
.
$\mathbb{Z}_{p}^{\times }$
.
On the other hand, by [Reference DawDaw12],
and the conjecture follows easily from the following classical fact regarding primorials.
Lemma 13.2. Let
![]() $n\in \mathbb{N}$
. The product of the first
$n\in \mathbb{N}$
. The product of the first
![]() $n$
prime numbers is equal to
$n$
prime numbers is equal to
Proof of Conjecture 12.7 for
 $\mathbb{C}^{n}$
.
$\mathbb{C}^{n}$
.
Let
![]() $X_{H}$
be a product of spaces
$X_{H}$
be a product of spaces
![]() $X_{i}\subseteq \mathbb{H}^{n_{i}}$
each equal to either a pre-special point or to the image of
$X_{i}\subseteq \mathbb{H}^{n_{i}}$
each equal to either a pre-special point or to the image of
![]() $\mathbb{H}$
given by the map sending
$\mathbb{H}$
given by the map sending
![]() $\unicode[STIX]{x1D70F}$
to
$\unicode[STIX]{x1D70F}$
to
![]() $(g_{j}\unicode[STIX]{x1D70F})_{j=1}^{n_{i}}$
for elements
$(g_{j}\unicode[STIX]{x1D70F})_{j=1}^{n_{i}}$
for elements
![]() $g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
. Without loss of generality, we may assume that the product contains only one factor. If
$g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
. Without loss of generality, we may assume that the product contains only one factor. If
![]() $X_{H}$
is a pre-special point contained in
$X_{H}$
is a pre-special point contained in
![]() ${\mathcal{F}}$
, then the claim follows from the fact that
${\mathcal{F}}$
, then the claim follows from the fact that
is finite. Therefore, assume that
![]() $X$
is equal to the image of
$X$
is equal to the image of
![]() $\mathbb{H}$
in
$\mathbb{H}$
in
![]() $\mathbb{H}^{n}$
given by the map sending
$\mathbb{H}^{n}$
given by the map sending
![]() $\unicode[STIX]{x1D70F}$
to
$\unicode[STIX]{x1D70F}$
to
![]() $(g_{j}\unicode[STIX]{x1D70F})_{j=1}^{n}$
for elements
$(g_{j}\unicode[STIX]{x1D70F})_{j=1}^{n}$
for elements
![]() $g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
. We can and do assume that
$g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
. We can and do assume that
![]() $g_{1}$
is equal to the identity element and that all of the
$g_{1}$
is equal to the identity element and that all of the
![]() $g_{j}$
have coprime integer entries.
$g_{j}$
have coprime integer entries.
As in the statement of Conjecture 12.7, we assume that
![]() $X$
intersects
$X$
intersects
![]() ${\mathcal{F}}$
, and we let
${\mathcal{F}}$
, and we let
![]() $x\in {\mathcal{F}}\,\cap \,X$
. Therefore,
$x\in {\mathcal{F}}\,\cap \,X$
. Therefore,
where
![]() $\unicode[STIX]{x1D70F}_{x}\in {\mathcal{F}}_{\mathbb{H}}$
. By [Reference OrrOrr18, Theorem 1.2] (cf. [Reference Habegger and PilaHab12, Lemma 5.2]),
$\unicode[STIX]{x1D70F}_{x}\in {\mathcal{F}}_{\mathbb{H}}$
. By [Reference OrrOrr18, Theorem 1.2] (cf. [Reference Habegger and PilaHab12, Lemma 5.2]),
![]() $\text{H}_{1}(g_{j})\leqslant c_{1}\det (g_{j})^{2}$
, for all
$\text{H}_{1}(g_{j})\leqslant c_{1}\det (g_{j})^{2}$
, for all
![]() $j\in \{1,\ldots ,n\}$
, where
$j\in \{1,\ldots ,n\}$
, where
![]() $c_{1}$
is a positive constant not depending on
$c_{1}$
is a positive constant not depending on
![]() $Z$
. In particular,
$Z$
. In particular,
for each
![]() $j\in \{1,\ldots ,n\}$
.
$j\in \{1,\ldots ,n\}$
.
Now let
![]() $z:=(z_{j})_{j=1}^{n}\in {\mathcal{F}}$
be a point belonging to
$z:=(z_{j})_{j=1}^{n}\in {\mathcal{F}}$
be a point belonging to
![]() $\unicode[STIX]{x1D6E4}X$
. For each
$\unicode[STIX]{x1D6E4}X$
. For each
![]() $j\in \{1,\ldots ,n\}$
,
$j\in \{1,\ldots ,n\}$
,
for some
![]() $g\in \text{GL}_{2}(\mathbb{R})^{+}$
and some
$g\in \text{GL}_{2}(\mathbb{R})^{+}$
and some
![]() $\unicode[STIX]{x1D6FE}_{j}\in \text{SL}_{2}(\mathbb{Z})$
. Therefore, let
$\unicode[STIX]{x1D6FE}_{j}\in \text{SL}_{2}(\mathbb{Z})$
. Therefore, let
and let
![]() ${\mathcal{C}}$
denote a set of representatives in
${\mathcal{C}}$
denote a set of representatives in
![]() $\text{SL}_{2}(\mathbb{Z})$
for
$\text{SL}_{2}(\mathbb{Z})$
for
![]() $\unicode[STIX]{x1D6EC}\backslash \text{SL}_{2}(\mathbb{Z})$
. Note that, if we define
$\unicode[STIX]{x1D6EC}\backslash \text{SL}_{2}(\mathbb{Z})$
. Note that, if we define
then, for any multiple
![]() $N$
of
$N$
of
![]() $m_{j}$
, the principal congruence subgroup
$m_{j}$
, the principal congruence subgroup
![]() $\unicode[STIX]{x1D6E4}(N)$
is contained in
$\unicode[STIX]{x1D6E4}(N)$
is contained in
![]() $g_{j}^{-1}\text{SL}_{2}(\mathbb{Z})g_{j}$
. In particular, if we define
$g_{j}^{-1}\text{SL}_{2}(\mathbb{Z})g_{j}$
. In particular, if we define
![]() $N$
to be the lowest common multiple of the
$N$
to be the lowest common multiple of the
![]() $m_{j}$
, then
$m_{j}$
, then
![]() $\unicode[STIX]{x1D6E4}(N)$
is contained in
$\unicode[STIX]{x1D6E4}(N)$
is contained in
![]() $\unicode[STIX]{x1D6EC}$
. It follows that any subset of
$\unicode[STIX]{x1D6EC}$
. It follows that any subset of
![]() $\text{SL}_{2}(\mathbb{Z})$
mapping bijectively to
$\text{SL}_{2}(\mathbb{Z})$
mapping bijectively to
![]() $\text{SL}_{2}(\mathbb{Z}/N\mathbb{Z})$
contains a set
$\text{SL}_{2}(\mathbb{Z}/N\mathbb{Z})$
contains a set
![]() ${\mathcal{C}}$
, as above. Via the procedure outlined in [Reference Diamond and ShurmanDS05, Exercise 1.2.2], it is straightforward to verify that we can (and do) choose
${\mathcal{C}}$
, as above. Via the procedure outlined in [Reference Diamond and ShurmanDS05, Exercise 1.2.2], it is straightforward to verify that we can (and do) choose
![]() ${\mathcal{C}}$
such that, for any
${\mathcal{C}}$
such that, for any
![]() $c\in {\mathcal{C}}$
,
$c\in {\mathcal{C}}$
,
(though we certainly do not claim that this is the best possible bound; any polynomial bound would suffice for our purposes).
The union
constitutes a fundamental set in
![]() $\mathbb{H}$
for the action of
$\mathbb{H}$
for the action of
![]() $\unicode[STIX]{x1D6EC}$
. Hence, there exists
$\unicode[STIX]{x1D6EC}$
. Hence, there exists
![]() $c\in {\mathcal{C}}$
and
$c\in {\mathcal{C}}$
and
![]() $\unicode[STIX]{x1D706}_{g}\in \unicode[STIX]{x1D6EC}$
such that
$\unicode[STIX]{x1D706}_{g}\in \unicode[STIX]{x1D6EC}$
such that
Furthermore, for each
![]() $j\in \{1,\ldots ,n\}$
, we can write
$j\in \{1,\ldots ,n\}$
, we can write
![]() $\unicode[STIX]{x1D706}_{g}=g_{j}^{-1}\unicode[STIX]{x1D706}_{j}g_{j}$
, for some
$\unicode[STIX]{x1D706}_{g}=g_{j}^{-1}\unicode[STIX]{x1D706}_{j}g_{j}$
, for some
![]() $\unicode[STIX]{x1D706}_{j}\in \text{SL}_{2}(\mathbb{Z})$
and, hence,
$\unicode[STIX]{x1D706}_{j}\in \text{SL}_{2}(\mathbb{Z})$
and, hence,
Therefore, by [Reference OrrOrr18, Theorem 1.2], we have
![]() $\text{H}_{1}(\unicode[STIX]{x1D6FE}_{j}\unicode[STIX]{x1D706}_{j}^{-1}g_{j}c)\leqslant c_{1}m_{j}^{2}$
, for all
$\text{H}_{1}(\unicode[STIX]{x1D6FE}_{j}\unicode[STIX]{x1D706}_{j}^{-1}g_{j}c)\leqslant c_{1}m_{j}^{2}$
, for all
![]() $j\in \{1,\ldots ,n\}$
.
$j\in \{1,\ldots ,n\}$
.
We write
where
![]() $c_{2}$
and
$c_{2}$
and
![]() $\unicode[STIX]{x1D6FF}$
are positive constants not depending on
$\unicode[STIX]{x1D6FF}$
are positive constants not depending on
![]() $Z$
, and we obtain
$Z$
, and we obtain
for each
![]() $j\in \{1,\ldots ,n\}$
, where
$j\in \{1,\ldots ,n\}$
, where
![]() $c_{3}$
is a positive constant not depending on
$c_{3}$
is a positive constant not depending on
![]() $Z$
.
$Z$
.
Conversely, by [Reference DawDaw12, § 2],
and, by writing the
![]() $g_{j}$
in Smith normal form, i.e.,
$g_{j}$
in Smith normal form, i.e.,
where
![]() $\unicode[STIX]{x1D6FE}_{j,1},\unicode[STIX]{x1D6FE}_{j,2}\in \text{SL}_{2}(\mathbb{Z})$
, we conclude that
$\unicode[STIX]{x1D6FE}_{j,1},\unicode[STIX]{x1D6FE}_{j,2}\in \text{SL}_{2}(\mathbb{Z})$
, we conclude that
whose index in
![]() $\text{SL}_{2}(\mathbb{Z})$
is the same as
$\text{SL}_{2}(\mathbb{Z})$
is the same as
![]() $\unicode[STIX]{x1D6E4}_{0}(m_{j})$
, which is
$\unicode[STIX]{x1D6E4}_{0}(m_{j})$
, which is
![]() $m_{j}\unicode[STIX]{x1D711}(m_{j})$
. It follows that
$m_{j}\unicode[STIX]{x1D711}(m_{j})$
. It follows that
and so
Therefore, we let
![]() $\unicode[STIX]{x1D6FE}:=(\unicode[STIX]{x1D6FE}_{j}\unicode[STIX]{x1D706}_{j}^{-1})_{j=1}^{n}\in \unicode[STIX]{x1D6E4}$
. By (13.2.1),
$\unicode[STIX]{x1D6FE}:=(\unicode[STIX]{x1D6FE}_{j}\unicode[STIX]{x1D706}_{j}^{-1})_{j=1}^{n}\in \unicode[STIX]{x1D6E4}$
. By (13.2.1),
![]() $z\in \unicode[STIX]{x1D6FE}X$
, and the result follows.◻
$z\in \unicode[STIX]{x1D6FE}X$
, and the result follows.◻
Finally, we will verify Conjecture 10.4 in this case.
Proof of Conjecture 10.4 for
 $\mathbb{C}^{n}$
.
$\mathbb{C}^{n}$
.
Let
![]() $Z$
be a special subvariety of
$Z$
be a special subvariety of
![]() $\mathbb{C}^{n}$
. Then
$\mathbb{C}^{n}$
. Then
![]() $Z$
is a product of special subvarieties. Since there are only finitely many partitions of
$Z$
is a product of special subvarieties. Since there are only finitely many partitions of
![]() $\{1,\ldots ,n\}$
, we may assume that the product contains only one factor. If
$\{1,\ldots ,n\}$
, we may assume that the product contains only one factor. If
![]() $Z$
is a special point,
$Z$
is a special point,
![]() $H^{\text{der}}$
is trivial. Therefore, we assume that
$H^{\text{der}}$
is trivial. Therefore, we assume that
![]() $Z$
is equal to the image of
$Z$
is equal to the image of
![]() $\mathbb{H}$
in
$\mathbb{H}$
in
![]() $\mathbb{C}^{n}$
under the map sending
$\mathbb{C}^{n}$
under the map sending
![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}$
to the image of
$\unicode[STIX]{x1D70F}\in \mathbb{H}$
to the image of
![]() $(g_{j}\cdot \unicode[STIX]{x1D70F})_{j=1}^{n}$
in
$(g_{j}\cdot \unicode[STIX]{x1D70F})_{j=1}^{n}$
in
![]() $\mathbb{C}^{n}$
for elements
$\mathbb{C}^{n}$
for elements
![]() $g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
. Then
$g_{j}\in \text{GL}_{2}(\mathbb{Q})^{+}$
. Then
![]() $H^{\text{der}}$
is the image of
$H^{\text{der}}$
is the image of
![]() $\text{SL}_{2}$
under the morphism
$\text{SL}_{2}$
under the morphism
We see from the calculations in the previous proof that the bound
![]() $\deg (Z)\leqslant b$
implies that the
$\deg (Z)\leqslant b$
implies that the
![]() $g_{j}$
come from the union of finitely many double cosets
$g_{j}$
come from the union of finitely many double cosets
![]() $\unicode[STIX]{x1D6E4}g\unicode[STIX]{x1D6E4}$
for
$\unicode[STIX]{x1D6E4}g\unicode[STIX]{x1D6E4}$
for
![]() $g\in \text{GL}_{2}(\mathbb{Q})^{+}$
. Since each such double coset is equal to a finite union of single cosets
$g\in \text{GL}_{2}(\mathbb{Q})^{+}$
. Since each such double coset is equal to a finite union of single cosets
![]() $\unicode[STIX]{x1D6E4}h$
for
$\unicode[STIX]{x1D6E4}h$
for
![]() $h\in \text{GL}_{2}(\mathbb{Q})^{+}$
, the result follows. ◻
$h\in \text{GL}_{2}(\mathbb{Q})^{+}$
, the result follows. ◻
14 Main results (part 2): Conditional solutions to the counting problems
We conclude by demonstrating how our arithmetic conjectures might be used to resolve the counting problems stated in § 8. In our applications of the counting theorem, we will need the following.
Lemma 14.1. Let
![]() $\unicode[STIX]{x1D6FD}:[0,1]\rightarrow G(\mathbb{R})\times X$
be semialgebraic. Then
$\unicode[STIX]{x1D6FD}:[0,1]\rightarrow G(\mathbb{R})\times X$
be semialgebraic. Then
![]() $\text{Im}(\unicode[STIX]{x1D6FD})$
is contained in a complex algebraic subset
$\text{Im}(\unicode[STIX]{x1D6FD})$
is contained in a complex algebraic subset
![]() $B$
of
$B$
of
![]() $G(\mathbb{C})\times \mathbb{C}^{N}$
of dimension at most
$G(\mathbb{C})\times \mathbb{C}^{N}$
of dimension at most
![]() $1$
.
$1$
.
Proof. Let
![]() $Y$
denote the real Zariski closure of
$Y$
denote the real Zariski closure of
![]() $\text{Im}(\unicode[STIX]{x1D6FD})$
in
$\text{Im}(\unicode[STIX]{x1D6FD})$
in
![]() $G(\mathbb{R})\times \mathbb{R}^{2N}$
. In particular,
$G(\mathbb{R})\times \mathbb{R}^{2N}$
. In particular,
![]() $\dim Y\leqslant 1$
. Without loss of generality, we can and do assume that
$\dim Y\leqslant 1$
. Without loss of generality, we can and do assume that
![]() $Y$
is irreducible. If
$Y$
is irreducible. If
![]() $Y$
is a point then there is nothing to prove. Therefore, we can and do assume that
$Y$
is a point then there is nothing to prove. Therefore, we can and do assume that
![]() $Y$
is an irreducible real algebraic curve. In particular, the complexification
$Y$
is an irreducible real algebraic curve. In particular, the complexification
![]() $Y_{\mathbb{C}}$
of
$Y_{\mathbb{C}}$
of
![]() $Y$
in
$Y$
in
![]() $G(\mathbb{C})\times \mathbb{C}^{2N}$
is an irreducible complex algebraic curve.
$G(\mathbb{C})\times \mathbb{C}^{2N}$
is an irreducible complex algebraic curve.
Let
![]() $g_{1},\ldots ,g_{n^{2}},x_{1},y_{1},\ldots ,x_{N},y_{N}$
denote the real coordinate functions on
$g_{1},\ldots ,g_{n^{2}},x_{1},y_{1},\ldots ,x_{N},y_{N}$
denote the real coordinate functions on
![]() $G(\mathbb{R})\times X$
and let
$G(\mathbb{R})\times X$
and let
![]() $z_{j}=x_{j}+iy_{j}$
denote the coordinate functions on
$z_{j}=x_{j}+iy_{j}$
denote the coordinate functions on
![]() $\mathbb{C}^{N}=\mathbb{R}^{2N}$
. If all of the coordinates functions on
$\mathbb{C}^{N}=\mathbb{R}^{2N}$
. If all of the coordinates functions on
![]() $\mathbb{R}^{2N}$
are constant on
$\mathbb{R}^{2N}$
are constant on
![]() $Y$
, the result is obvious. Therefore, without loss of generality, we can and do assume that
$Y$
, the result is obvious. Therefore, without loss of generality, we can and do assume that
![]() $x_{1}$
is not constant on
$x_{1}$
is not constant on
![]() $Y$
.
$Y$
.
We claim that each of the coordinate functions
![]() $x_{2},y_{2},\ldots ,x_{N},y_{N}$
on
$x_{2},y_{2},\ldots ,x_{N},y_{N}$
on
![]() $\mathbb{C}^{2N}$
is algebraic over the field
$\mathbb{C}^{2N}$
is algebraic over the field
![]() $\mathbb{C}(z_{1})$
, considered as a field of functions on
$\mathbb{C}(z_{1})$
, considered as a field of functions on
![]() $Y_{\mathbb{C}}$
. To see this, note that
$Y_{\mathbb{C}}$
. To see this, note that
![]() $z_{1}$
is non-constant on
$z_{1}$
is non-constant on
![]() $Y_{\mathbb{C}}$
, and so
$Y_{\mathbb{C}}$
, and so
![]() $\mathbb{C}(z_{1})$
has transcendence degree at least
$\mathbb{C}(z_{1})$
has transcendence degree at least
![]() $1$
. On the other hand,
$1$
. On the other hand,
![]() $\mathbb{C}(z_{1})$
is contained in
$\mathbb{C}(z_{1})$
is contained in
![]() $\mathbb{C}(x_{1},y_{1})$
, which is algebraic over
$\mathbb{C}(x_{1},y_{1})$
, which is algebraic over
![]() $\mathbb{C}(x_{1})$
.
$\mathbb{C}(x_{1})$
.
In particular, each of the functions
![]() $x_{2}+iy_{2},\ldots ,x_{N}+iy_{N}$
is algebraic over the field
$x_{2}+iy_{2},\ldots ,x_{N}+iy_{N}$
is algebraic over the field
![]() $\mathbb{C}(z_{1})$
. It follows that, for each
$\mathbb{C}(z_{1})$
. It follows that, for each
![]() $j\geqslant 2$
, there exists a polynomial
$j\geqslant 2$
, there exists a polynomial
![]() $f_{j}(z_{1},z_{j})\in \mathbb{C}[z_{1},z_{j}]$
, non-trivial in
$f_{j}(z_{1},z_{j})\in \mathbb{C}[z_{1},z_{j}]$
, non-trivial in
![]() $z_{j}$
, such that
$z_{j}$
, such that
![]() $f_{j}(z_{1},z_{j})=0$
on
$f_{j}(z_{1},z_{j})=0$
on
![]() $Y$
. Similarly, for each
$Y$
. Similarly, for each
![]() $k=1,\ldots ,n^{2}$
, there exists a polynomial
$k=1,\ldots ,n^{2}$
, there exists a polynomial
![]() $f_{j}(z_{1},g_{k})\in \mathbb{C}[z_{1},g_{k}]$
, non-trivial in
$f_{j}(z_{1},g_{k})\in \mathbb{C}[z_{1},g_{k}]$
, non-trivial in
![]() $g_{k}$
, such that
$g_{k}$
, such that
![]() $f_{k}(z_{1},g_{k})=0$
on
$f_{k}(z_{1},g_{k})=0$
on
![]() $Y$
. In particular,
$Y$
. In particular,
![]() $Y$
is contained in the vanishing locus of the
$Y$
is contained in the vanishing locus of the
![]() $f_{j}$
and the
$f_{j}$
and the
![]() $f_{k}$
, which define a complex algebraic curve in
$f_{k}$
, which define a complex algebraic curve in
![]() $G(\mathbb{C})\times \mathbb{C}^{N}$
.◻
$G(\mathbb{C})\times \mathbb{C}^{N}$
.◻
We denote by
![]() $X^{\vee }$
the compact dual of
$X^{\vee }$
the compact dual of
![]() $X$
, which is a complex algebraic variety on which
$X$
, which is a complex algebraic variety on which
![]() $G(\mathbb{C})$
acts via an algebraic morphism
$G(\mathbb{C})$
acts via an algebraic morphism
Furthermore,
![]() $X$
naturally embeds into
$X$
naturally embeds into
![]() $X^{\vee }$
and the embedding factors through an embedding of
$X^{\vee }$
and the embedding factors through an embedding of
![]() $\mathbb{C}^{N}$
, i.e., the Harish-Chandra realization, into
$\mathbb{C}^{N}$
, i.e., the Harish-Chandra realization, into
![]() $X^{\vee }$
. We could have defined subvarieties of
$X^{\vee }$
. We could have defined subvarieties of
![]() $X$
using
$X$
using
![]() $X^{\vee }$
in the place of
$X^{\vee }$
in the place of
![]() $\mathbb{C}^{N}$
but, as mentioned previously, the two notions coincide. If we have a decomposition
$\mathbb{C}^{N}$
but, as mentioned previously, the two notions coincide. If we have a decomposition
![]() $G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
$G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
![]() $X=X_{1}\times X_{2}$
, we have a natural decomposition
$X=X_{1}\times X_{2}$
, we have a natural decomposition
Furthermore, if
![]() $(H,\mathfrak{X}_{H})$
denotes a Shimura subdatum of
$(H,\mathfrak{X}_{H})$
denotes a Shimura subdatum of
![]() $(G,\mathfrak{X})$
and
$(G,\mathfrak{X})$
and
![]() $X_{H}$
is a connected component of
$X_{H}$
is a connected component of
![]() $\mathfrak{X}_{H}$
contained in
$\mathfrak{X}_{H}$
contained in
![]() $X$
, then
$X$
, then
![]() $X_{H}^{\vee }$
is naturally contained in
$X_{H}^{\vee }$
is naturally contained in
![]() $X^{\vee }$
. We refer the reader to [Reference Ullmo and YafaevUY11, § 3] for more details.
$X^{\vee }$
. We refer the reader to [Reference Ullmo and YafaevUY11, § 3] for more details.
Theorem 14.2. Assume that Conjecture 11.1 holds and assume that either
Then Conjecture 8.2 is true for curves, i.e., if
![]() $V$
is a curve contained in
$V$
is a curve contained in
![]() $S$
, then the set
$S$
, then the set
![]() $\text{Opt}_{0}(V)$
is finite.
$\text{Opt}_{0}(V)$
is finite.
Proof. We will assume that Conjecture 12.2 holds. The proof in the case that Conjectures 10.3, 12.6, and 12.7 hold is very similar, hence we omit it. To elucidate the use of Conjectures 10.3, 12.6, and 12.7 we will use them in the proof of Theorem 14.3, at the expense of making the proof longer. We suffer no loss of generality if we assume, as we will, that
![]() $V$
is Hodge generic.
$V$
is Hodge generic.
Let
![]() $\unicode[STIX]{x1D6FA}$
denote a finite set of semisimple subgroups of
$\unicode[STIX]{x1D6FA}$
denote a finite set of semisimple subgroups of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
as in § 12 and let
$\mathbb{Q}$
as in § 12 and let
![]() $d$
,
$d$
,
![]() $c_{{\mathcal{F}}}$
, and
$c_{{\mathcal{F}}}$
, and
![]() $\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
be the constants afforded to us by Conjecture 12.2. Let
$\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
be the constants afforded to us by Conjecture 12.2. Let
![]() $L$
be a finitely generated extension of
$L$
be a finitely generated extension of
![]() $F$
contained in
$F$
contained in
![]() $\mathbb{C}$
over which
$\mathbb{C}$
over which
![]() $V$
is defined and let
$V$
is defined and let
![]() $c_{G}$
and
$c_{G}$
and
![]() $\unicode[STIX]{x1D6FF}_{G}$
be the constants afforded to us by Conjecture 11.1. Let
$\unicode[STIX]{x1D6FF}_{G}$
be the constants afforded to us by Conjecture 11.1. Let
![]() $\unicode[STIX]{x1D705}:=2\unicode[STIX]{x1D6FF}_{G}/3\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
.
$\unicode[STIX]{x1D705}:=2\unicode[STIX]{x1D6FF}_{G}/3\unicode[STIX]{x1D6FF}_{{\mathcal{F}}}$
.
We claim that there exists a positive constant
![]() $c$
such that, for any
$c$
such that, for any
![]() $P\in \text{Opt}_{0}(V)$
, we have
$P\in \text{Opt}_{0}(V)$
, we have
This would be sufficient to prove Theorem 14.2 since then, by Conjecture 11.1, we obtain
and, rearranging this expression, we obtain
which is a bound independent of
![]() $P$
. We remind the reader that
$P$
. We remind the reader that
![]() $P$
is one of only finitely many irreducible components of
$P$
is one of only finitely many irreducible components of
![]() $\langle P\rangle \cap V$
. Hence, Theorem 14.2 would follow from Lemma 12.5 and, therefore, it remains only to prove the claim.
$\langle P\rangle \cap V$
. Hence, Theorem 14.2 would follow from Lemma 12.5 and, therefore, it remains only to prove the claim.
To that end, for each
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(\mathbb{C}/L)$
, let
$\unicode[STIX]{x1D70E}\in \text{Gal}(\mathbb{C}/L)$
, let
![]() $z_{\unicode[STIX]{x1D70E}}\in {\mathcal{V}}$
be a point in
$z_{\unicode[STIX]{x1D70E}}\in {\mathcal{V}}$
be a point in
![]() $\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70E}(P))$
. Therefore, by Conjecture 12.2, the smallest pre-special subvariety of
$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70E}(P))$
. Therefore, by Conjecture 12.2, the smallest pre-special subvariety of
![]() $X$
containing
$X$
containing
![]() $z_{\unicode[STIX]{x1D70E}}$
can be written
$z_{\unicode[STIX]{x1D70E}}$
can be written
![]() $g_{\unicode[STIX]{x1D70E}}F_{\unicode[STIX]{x1D70E}}(\mathbb{R})^{+}g_{\unicode[STIX]{x1D70E}}^{-1}x_{\unicode[STIX]{x1D70E}}$
, where
$g_{\unicode[STIX]{x1D70E}}F_{\unicode[STIX]{x1D70E}}(\mathbb{R})^{+}g_{\unicode[STIX]{x1D70E}}^{-1}x_{\unicode[STIX]{x1D70E}}$
, where
![]() $F_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6FA}$
, and
$F_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6FA}$
, and
![]() $g_{\unicode[STIX]{x1D70E}}\in G(\mathbb{R})$
and
$g_{\unicode[STIX]{x1D70E}}\in G(\mathbb{R})$
and
![]() $x_{\unicode[STIX]{x1D70E}}\in X$
satisfy
$x_{\unicode[STIX]{x1D70E}}\in X$
satisfy
Without loss of generality, we can and do assume that
![]() $F:=F_{\unicode[STIX]{x1D70E}}$
is fixed. Therefore, for each
$F:=F_{\unicode[STIX]{x1D70E}}$
is fixed. Therefore, for each
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(\mathbb{C}/L)$
, the tuple
$\unicode[STIX]{x1D70E}\in \text{Gal}(\mathbb{C}/L)$
, the tuple
![]() $(g_{\unicode[STIX]{x1D70E}},x_{\unicode[STIX]{x1D70E}},z_{\unicode[STIX]{x1D70E}})$
belongs to the definable set
$(g_{\unicode[STIX]{x1D70E}},x_{\unicode[STIX]{x1D70E}},z_{\unicode[STIX]{x1D70E}})$
belongs to the definable set
![]() $D$
of tuples
$D$
of tuples
such that
![]() $z\in {\mathcal{V}}\cap gF(\mathbb{R})^{+}g^{-1}x$
and
$z\in {\mathcal{V}}\cap gF(\mathbb{R})^{+}g^{-1}x$
and
![]() $x(\mathbb{S})\subseteq gG_{F}g^{-1}$
. We consider
$x(\mathbb{S})\subseteq gG_{F}g^{-1}$
. We consider
![]() $D$
as a family over a point in an omitted parameter space and choose for
$D$
as a family over a point in an omitted parameter space and choose for
![]() $c$
the constant
$c$
the constant
![]() $c(D,d,\unicode[STIX]{x1D705})$
afforded to us by Theorem 9.1 applied to
$c(D,d,\unicode[STIX]{x1D705})$
afforded to us by Theorem 9.1 applied to
![]() $D$
. Since
$D$
. Since
![]() $\unicode[STIX]{x1D6FA}$
is finite, we can and do assume that
$\unicode[STIX]{x1D6FA}$
is finite, we can and do assume that
![]() $c$
does not depend on
$c$
does not depend on
![]() $F$
. We let
$F$
. We let
![]() $\unicode[STIX]{x1D6F4}$
denote the union over
$\unicode[STIX]{x1D6F4}$
denote the union over
![]() $\text{Aut}(\mathbb{C}/L)$
of the tuples
$\text{Aut}(\mathbb{C}/L)$
of the tuples
![]() $(g_{\unicode[STIX]{x1D70E}},x_{\unicode[STIX]{x1D70E}},z_{\unicode[STIX]{x1D70E}})\in D$
. In particular,
$(g_{\unicode[STIX]{x1D70E}},x_{\unicode[STIX]{x1D70E}},z_{\unicode[STIX]{x1D70E}})\in D$
. In particular,
![]() $\unicode[STIX]{x1D6F4}$
is contained in the subset
$\unicode[STIX]{x1D6F4}$
is contained in the subset
Let
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
be the projection maps from
$\unicode[STIX]{x1D70B}_{2}$
be the projection maps from
![]() $\mathbb{R}^{n^{2}+2N}\times \mathbb{R}^{2N}$
to
$\mathbb{R}^{n^{2}+2N}\times \mathbb{R}^{2N}$
to
![]() $\mathbb{R}^{n^{2}+2N}$
and
$\mathbb{R}^{n^{2}+2N}$
and
![]() $\mathbb{R}^{2N}$
, respectively, and suppose, for the sake of obtaining a contradiction, that
$\mathbb{R}^{2N}$
, respectively, and suppose, for the sake of obtaining a contradiction, that
Then, by Theorem 9.1, there exists a continuous definable function
such that
![]() $\unicode[STIX]{x1D6FD}_{1}:=\unicode[STIX]{x1D70B}_{1}\circ \unicode[STIX]{x1D6FD}$
is semialgebraic,
$\unicode[STIX]{x1D6FD}_{1}:=\unicode[STIX]{x1D70B}_{1}\circ \unicode[STIX]{x1D6FD}$
is semialgebraic,
![]() $\unicode[STIX]{x1D6FD}_{2}:=\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D6FD}$
is non-constant,
$\unicode[STIX]{x1D6FD}_{2}:=\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D6FD}$
is non-constant,
![]() $\unicode[STIX]{x1D6FD}(0)\in \unicode[STIX]{x1D6F4}$
, and
$\unicode[STIX]{x1D6FD}(0)\in \unicode[STIX]{x1D6F4}$
, and
![]() $\unicode[STIX]{x1D6FD}_{|(0,1)}$
is real analytic. Let
$\unicode[STIX]{x1D6FD}_{|(0,1)}$
is real analytic. Let
![]() $z_{0}:=\unicode[STIX]{x1D6FD}_{2}(0)$
and let
$z_{0}:=\unicode[STIX]{x1D6FD}_{2}(0)$
and let
![]() $P_{0}:=\unicode[STIX]{x1D70B}(z_{0})$
. To obtain a contradiction, we will closely imitate arguments found in [Reference OrrOrr17].
$P_{0}:=\unicode[STIX]{x1D70B}(z_{0})$
. To obtain a contradiction, we will closely imitate arguments found in [Reference OrrOrr17].
It follows from the Global Decomposition Theorem (see [Reference Grauert and RemmertGR84, p. 172]) that there exists
![]() $0<t\leqslant 1$
such that
$0<t\leqslant 1$
such that
![]() $\unicode[STIX]{x1D6FD}_{2}([0,t))$
intersects only finitely many of the irreducible analytic components of
$\unicode[STIX]{x1D6FD}_{2}([0,t))$
intersects only finitely many of the irreducible analytic components of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. In fact, since
$\unicode[STIX]{x1D70B}^{-1}(V)$
. In fact, since
![]() $\unicode[STIX]{x1D6FD}_{2|(0,t)}$
is real analytic,
$\unicode[STIX]{x1D6FD}_{2|(0,t)}$
is real analytic,
![]() $\unicode[STIX]{x1D6FD}_{2}((0,t))$
must be wholly contained in one such component
$\unicode[STIX]{x1D6FD}_{2}((0,t))$
must be wholly contained in one such component
![]() $V_{1}$
. Since
$V_{1}$
. Since
![]() $V_{1}$
is closed, we conclude from the fact that
$V_{1}$
is closed, we conclude from the fact that
![]() $\unicode[STIX]{x1D6FD}$
is continuous that
$\unicode[STIX]{x1D6FD}$
is continuous that
![]() $V_{1}$
contains
$V_{1}$
contains
![]() $\unicode[STIX]{x1D6FD}_{2}([0,t])$
.
$\unicode[STIX]{x1D6FD}_{2}([0,t])$
.
By [Reference Ullmo and YafaevUY18, Theorem 1.3] (the inverse Ax–Lindemann conjecture),
![]() $\langle V_{1}\rangle _{\text{Zar}}$
is pre-weakly special and so, since
$\langle V_{1}\rangle _{\text{Zar}}$
is pre-weakly special and so, since
![]() $V$
is Hodge generic in
$V$
is Hodge generic in
![]() $S$
, we can decompose
$S$
, we can decompose
![]() $G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
$G^{\text{ad}}=G_{1}\times G_{2}$
, and thus
![]() $X=X_{1}\times X_{2}$
, so that
$X=X_{1}\times X_{2}$
, so that
where
![]() $x_{2}\in X_{2}$
is Hodge generic. By abuse of notation, we denote by
$x_{2}\in X_{2}$
is Hodge generic. By abuse of notation, we denote by
![]() $\unicode[STIX]{x1D70B}_{2}$
both the projection from
$\unicode[STIX]{x1D70B}_{2}$
both the projection from
![]() $G$
to
$G$
to
![]() $G_{2}$
and from
$G_{2}$
and from
![]() $X^{\vee }$
to
$X^{\vee }$
to
![]() $X_{2}^{\vee }$
.
$X_{2}^{\vee }$
.
Note that, for any
![]() $(g,x)\in \text{Im}(\unicode[STIX]{x1D6FD}_{1})$
, we have
$(g,x)\in \text{Im}(\unicode[STIX]{x1D6FD}_{1})$
, we have
![]() $(g^{-1}x)(\mathbb{S})\subseteq G_{F,\mathbb{R}}$
. If we write
$(g^{-1}x)(\mathbb{S})\subseteq G_{F,\mathbb{R}}$
. If we write
![]() $G_{F}^{\prime }$
for the largest normal subgroup of
$G_{F}^{\prime }$
for the largest normal subgroup of
![]() $G_{F}$
of non-compact type, then the properties of Shimura data imply that
$G_{F}$
of non-compact type, then the properties of Shimura data imply that
![]() $g^{-1}x$
factors through
$g^{-1}x$
factors through
![]() $G_{F,\mathbb{R}}^{\prime }$
and, if we write
$G_{F,\mathbb{R}}^{\prime }$
and, if we write
![]() $\mathfrak{X}^{\prime }$
for the
$\mathfrak{X}^{\prime }$
for the
![]() $G_{F}^{\prime }(\mathbb{R})$
conjugacy class of
$G_{F}^{\prime }(\mathbb{R})$
conjugacy class of
![]() $g^{-1}x$
in
$g^{-1}x$
in
![]() $\mathfrak{X}$
, then, by [Reference UllmoUll07, Lemme 3.3],
$\mathfrak{X}$
, then, by [Reference UllmoUll07, Lemme 3.3],
![]() $(G_{F}^{\prime },\mathfrak{X}^{\prime })$
is a Shimura subdatum of
$(G_{F}^{\prime },\mathfrak{X}^{\prime })$
is a Shimura subdatum of
![]() $(G,\mathfrak{X})$
. Furthermore, by [Reference Ullmo and YafaevUY14, Lemma 3.7], the number of Shimura subdata
$(G,\mathfrak{X})$
. Furthermore, by [Reference Ullmo and YafaevUY14, Lemma 3.7], the number of Shimura subdata
![]() $(G_{F}^{\prime },\mathfrak{Y})$
of
$(G_{F}^{\prime },\mathfrak{Y})$
of
![]() $(G,\mathfrak{X})$
is finite and, by [Reference MilneMil05, Corollary 5.3], the number of connected components
$(G,\mathfrak{X})$
is finite and, by [Reference MilneMil05, Corollary 5.3], the number of connected components
![]() $Y$
of
$Y$
of
![]() $\mathfrak{Y}$
is also finite. It follows that, after possibly replacing
$\mathfrak{Y}$
is also finite. It follows that, after possibly replacing
![]() $t$
, we can and do assume that
$t$
, we can and do assume that
![]() $g^{-1}x$
belongs to one such component
$g^{-1}x$
belongs to one such component
![]() $Y$
, which we write as
$Y$
, which we write as
![]() $Y_{1}\times Y_{2}$
, such that
$Y_{1}\times Y_{2}$
, such that
![]() $F(\mathbb{R})^{+}$
acts transitively on
$F(\mathbb{R})^{+}$
acts transitively on
![]() $Y_{1}$
. In particular,
$Y_{1}$
. In particular,
We let
![]() $p_{2}$
denote the projection from
$p_{2}$
denote the projection from
![]() $Y^{\vee }$
to
$Y^{\vee }$
to
![]() $Y_{2}^{\vee }$
.
$Y_{2}^{\vee }$
.
Let
![]() $B$
denote the complex algebraic subset of
$B$
denote the complex algebraic subset of
![]() $G(\mathbb{C})\times X^{\vee }$
of dimension at most
$G(\mathbb{C})\times X^{\vee }$
of dimension at most
![]() $1$
containing
$1$
containing
![]() $\text{Im}(\unicode[STIX]{x1D6FD}_{1})$
afforded to us by Lemma 14.1. For any
$\text{Im}(\unicode[STIX]{x1D6FD}_{1})$
afforded to us by Lemma 14.1. For any
![]() $(g,x)\in B$
, we have
$(g,x)\in B$
, we have
![]() $g^{-1}x\in Y^{\vee }$
.
$g^{-1}x\in Y^{\vee }$
.
Let
![]() $\overline{V}_{1}$
denote the Zariski closure of
$\overline{V}_{1}$
denote the Zariski closure of
![]() $V_{1}$
in
$V_{1}$
in
![]() $X^{\vee }$
and consider the complex algebraic set
$X^{\vee }$
and consider the complex algebraic set
Let
![]() $V_{B}$
denote the Zariski closure in
$V_{B}$
denote the Zariski closure in
![]() $X^{\vee }$
of the set
$X^{\vee }$
of the set
Since the latter is the image of
![]() $W_{B}$
under an algebraic morphism, we have
$W_{B}$
under an algebraic morphism, we have
![]() $\dim V_{B}\leqslant \dim W_{B}$
.
$\dim V_{B}\leqslant \dim W_{B}$
.
Since
![]() $V_{1}$
is an irreducible complex analytic curve having uncountable intersection with
$V_{1}$
is an irreducible complex analytic curve having uncountable intersection with
![]() $V_{B}$
, it follows that
$V_{B}$
, it follows that
![]() $V_{1}$
is contained in
$V_{1}$
is contained in
![]() $V_{B}$
. Therefore,
$V_{B}$
. Therefore,
![]() $\langle V_{1}\rangle _{\text{Zar}}$
is contained in
$\langle V_{1}\rangle _{\text{Zar}}$
is contained in
![]() $V_{B}$
also, and so
$V_{B}$
also, and so
Now, for each
![]() $(g,x)\in B$
, consider the fibre
$(g,x)\in B$
, consider the fibre
![]() $W_{(g,x)}$
of
$W_{(g,x)}$
of
![]() $W_{B}$
over
$W_{B}$
over
![]() $(g,x)$
, i.e., the set
$(g,x)$
, i.e., the set
Since
![]() $P_{0}\in V$
, it follows that
$P_{0}\in V$
, it follows that
![]() $\unicode[STIX]{x1D70B}_{2}(F)=G_{2}$
and so, for any
$\unicode[STIX]{x1D70B}_{2}(F)=G_{2}$
and so, for any
![]() $y\in Y_{2}^{\vee }$
, the natural projection
$y\in Y_{2}^{\vee }$
, the natural projection
is an equivariant morphism of
![]() $F(\mathbb{C})$
-homogeneous spaces. In particular, its fibres are equidimensional of dimension
$F(\mathbb{C})$
-homogeneous spaces. In particular, its fibres are equidimensional of dimension
Since
![]() $W_{(g,x)}$
is contained in such a fibre, we have
$W_{(g,x)}$
is contained in such a fibre, we have
where we use the fact that
![]() $P_{0}\in \text{Opt}_{0}(V)$
, hence,
$P_{0}\in \text{Opt}_{0}(V)$
, hence,
Since this holds for all
![]() $(g,x)\in B$
and
$(g,x)\in B$
and
![]() $\dim B\leqslant 1$
, we conclude that
$\dim B\leqslant 1$
, we conclude that
which contradicts (14.2.1). ◻
Of course, Theorem 14.2 is not really satisfactory in the sense that it only deals with curves. One would hope that, for
![]() $V$
of arbitrary dimension, a path such as
$V$
of arbitrary dimension, a path such as
![]() $\unicode[STIX]{x1D6FD}$
would yield, via the weak hyperbolic Ax–Schanuel conjecture, a positive dimensional subvariety of
$\unicode[STIX]{x1D6FD}$
would yield, via the weak hyperbolic Ax–Schanuel conjecture, a positive dimensional subvariety of
![]() $V$
, containing a conjugate of
$V$
, containing a conjugate of
![]() $P$
, having defect at most
$P$
, having defect at most
![]() $\unicode[STIX]{x1D6FF}(P)$
, thus contradicting the optimality of
$\unicode[STIX]{x1D6FF}(P)$
, thus contradicting the optimality of
![]() $P$
. However, the authors have not been able to carry out this procedure. Instead, the very same idea appears to work when one attempts to contradict the membership of a point in the open-anomalous locus. The difference is that we are only required to bound the weakly special defect, as opposed to the defect itself.
$P$
. However, the authors have not been able to carry out this procedure. Instead, the very same idea appears to work when one attempts to contradict the membership of a point in the open-anomalous locus. The difference is that we are only required to bound the weakly special defect, as opposed to the defect itself.
Theorem 14.3. Assume that Conjecture 11.3 holds and assume that the weak hyperbolic Ax–Schanuel conjecture is true. Assume also that either
Then, Conjecture 8.4 is true, i.e., if
![]() $V$
is a subvariety of
$V$
is a subvariety of
![]() $S$
, then the set
$S$
, then the set
is finite.
Proof. We will assume that Conjectures 10.3, 12.6, and 12.7 hold. The proof in the case that Conjecture 12.2 holds is very similar, hence we omit it. We used Conjecture 12.2 in the proof of Theorem 14.2.
Let
![]() $\unicode[STIX]{x1D6FA}$
denote a finite set of semisimple subgroups of
$\unicode[STIX]{x1D6FA}$
denote a finite set of semisimple subgroups of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
as in § 12. Let
$\mathbb{Q}$
as in § 12. Let
![]() $c_{\unicode[STIX]{x1D6E4}}$
and
$c_{\unicode[STIX]{x1D6E4}}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}$
be the constants afforded to us by Conjecture 12.7, let
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}$
be the constants afforded to us by Conjecture 12.7, let
![]() $d$
,
$d$
,
![]() $c_{\text{H}}$
, and
$c_{\text{H}}$
, and
![]() $\unicode[STIX]{x1D6FF}_{\text{H}}$
be the constants afforded to us by Lemma 12.8, and let
$\unicode[STIX]{x1D6FF}_{\text{H}}$
be the constants afforded to us by Lemma 12.8, and let
Let
![]() $L^{\prime }$
be a finitely generated extension of
$L^{\prime }$
be a finitely generated extension of
![]() $F$
contained in
$F$
contained in
![]() $\mathbb{C}$
over which
$\mathbb{C}$
over which
![]() $V$
is defined and let
$V$
is defined and let
![]() $c_{G}$
and
$c_{G}$
and
![]() $\unicode[STIX]{x1D6FF}_{G}$
be the constants afforded to us by Conjecture 11.1. Let
$\unicode[STIX]{x1D6FF}_{G}$
be the constants afforded to us by Conjecture 11.1. Let
![]() $\unicode[STIX]{x1D705}:=\unicode[STIX]{x1D6FF}_{G}/3$
, and let
$\unicode[STIX]{x1D705}:=\unicode[STIX]{x1D6FF}_{G}/3$
, and let
![]() $c_{\unicode[STIX]{x1D705}}$
be the constant afforded to us by Conjecture 12.6. Let
$c_{\unicode[STIX]{x1D705}}$
be the constant afforded to us by Conjecture 12.6. Let
and let
![]() $L$
and
$L$
and
![]() $H$
be, respectively, the finite field extension of
$H$
be, respectively, the finite field extension of
![]() $F$
and the semisimple subgroup of
$F$
and the semisimple subgroup of
![]() $G$
defined over
$G$
defined over
![]() $\mathbb{Q}$
of non-compact type afforded to us by Conjecture 12.6 applied to
$\mathbb{Q}$
of non-compact type afforded to us by Conjecture 12.6 applied to
![]() $\langle P\rangle$
. Replacing
$\langle P\rangle$
. Replacing
![]() $L$
by its compositum with
$L$
by its compositum with
![]() $L^{\prime }$
, we have
$L^{\prime }$
, we have
We claim that there exists a positive constant
![]() $c_{3}$
, independent of
$c_{3}$
, independent of
![]() $P$
, such that
$P$
, such that
This would be sufficient to prove Theorem 14.3 since then, by Conjecture 11.3, we obtain
and, rearranging this expression, we obtain
which is a bound independent of
![]() $P$
. We remind the reader that, as explained in Remark 11.4,
$P$
. We remind the reader that, as explained in Remark 11.4,
![]() $P\in \text{Opt}_{0}(V)$
and, therefore,
$P\in \text{Opt}_{0}(V)$
and, therefore,
![]() $P$
is one of only finitely many irreducible components of
$P$
is one of only finitely many irreducible components of
![]() $\langle P\rangle \cap V$
. Hence, Theorem 14.3 would follow from Conjecture 10.3 and it remains only, therefore, to prove the claim.
$\langle P\rangle \cap V$
. Hence, Theorem 14.3 would follow from Conjecture 10.3 and it remains only, therefore, to prove the claim.
By Conjecture 12.6, for each
![]() $\unicode[STIX]{x1D70E}\in \text{Aut}(\mathbb{C}/L)$
,
$\unicode[STIX]{x1D70E}\in \text{Aut}(\mathbb{C}/L)$
,
where
![]() $H(\mathbb{R})^{+}x_{\unicode[STIX]{x1D70E}}$
is a pre-special subvariety of
$H(\mathbb{R})^{+}x_{\unicode[STIX]{x1D70E}}$
is a pre-special subvariety of
![]() $X$
intersecting
$X$
intersecting
![]() ${\mathcal{F}}$
. By Lemma 12.8, we can and do assume that
${\mathcal{F}}$
. By Lemma 12.8, we can and do assume that
We let
![]() $z_{\unicode[STIX]{x1D70E}}\in {\mathcal{V}}$
be a point in
$z_{\unicode[STIX]{x1D70E}}\in {\mathcal{V}}$
be a point in
![]() $\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70E}(P))$
, so that
$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70E}(P))$
, so that
and so, by Conjecture 12.7, there exists
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6E4}$
satisfying
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6E4}$
satisfying
such that
![]() $z_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70E}}H(\mathbb{R})^{+}x_{\unicode[STIX]{x1D70E}}$
.
$z_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70E}}H(\mathbb{R})^{+}x_{\unicode[STIX]{x1D70E}}$
.
By definition, there exists
![]() $F\in \unicode[STIX]{x1D6FA}$
and
$F\in \unicode[STIX]{x1D6FA}$
and
![]() $g\in G(\mathbb{R})$
such that
$g\in G(\mathbb{R})$
such that
![]() $H_{\mathbb{R}}$
is equal to
$H_{\mathbb{R}}$
is equal to
![]() $gF_{\mathbb{R}}g^{-1}$
. In particular, for each
$gF_{\mathbb{R}}g^{-1}$
. In particular, for each
![]() $\unicode[STIX]{x1D70E}\in \text{Aut}(\mathbb{C}/L)$
, the tuple
$\unicode[STIX]{x1D70E}\in \text{Aut}(\mathbb{C}/L)$
, the tuple
![]() $(g,(\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70E}},x_{\unicode[STIX]{x1D70E}}),z_{\unicode[STIX]{x1D70E}})$
belongs to the definable family
$(g,(\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70E}},x_{\unicode[STIX]{x1D70E}}),z_{\unicode[STIX]{x1D70E}})$
belongs to the definable family
![]() $D$
of tuples
$D$
of tuples
parametrized by
![]() $G(\mathbb{R})$
, such that
$G(\mathbb{R})$
, such that
We choose, then, for
![]() $c_{3}$
the constant
$c_{3}$
the constant
![]() $c(D,d,\unicode[STIX]{x1D705}/\unicode[STIX]{x1D6FF})$
afforded to us by Theorem 9.1 applied to
$c(D,d,\unicode[STIX]{x1D705}/\unicode[STIX]{x1D6FF})$
afforded to us by Theorem 9.1 applied to
![]() $D$
. Since,
$D$
. Since,
![]() $\unicode[STIX]{x1D6FA}$
is finite, we can and do assume that
$\unicode[STIX]{x1D6FA}$
is finite, we can and do assume that
![]() $c_{3}$
does not depend on
$c_{3}$
does not depend on
![]() $F$
. We let
$F$
. We let
![]() $\unicode[STIX]{x1D6F4}$
denote the union over
$\unicode[STIX]{x1D6F4}$
denote the union over
![]() $\text{Aut}(\mathbb{C}/L)$
of the tuples
$\text{Aut}(\mathbb{C}/L)$
of the tuples
![]() $((\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70E}},x_{\unicode[STIX]{x1D70E}}),z_{\unicode[STIX]{x1D70E}})\in D_{g}$
(to use the notation of § 9). In particular,
$((\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70E}},x_{\unicode[STIX]{x1D70E}}),z_{\unicode[STIX]{x1D70E}})\in D_{g}$
(to use the notation of § 9). In particular,
![]() $\unicode[STIX]{x1D6F4}$
is contained in the subset
$\unicode[STIX]{x1D6F4}$
is contained in the subset
Let
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
be the projection maps from
$\unicode[STIX]{x1D70B}_{2}$
be the projection maps from
![]() $\mathbb{R}^{n^{2}+2N}\times \mathbb{R}^{2N}$
to
$\mathbb{R}^{n^{2}+2N}\times \mathbb{R}^{2N}$
to
![]() $\mathbb{R}^{n^{2}+2N}$
and
$\mathbb{R}^{n^{2}+2N}$
and
![]() $\mathbb{R}^{2N}$
, respectively, and suppose, for the sake of obtaining a contradiction, that
$\mathbb{R}^{2N}$
, respectively, and suppose, for the sake of obtaining a contradiction, that
Then, by Theorem 9.1, there exists a continuous definable function
such that
![]() $\unicode[STIX]{x1D6FD}_{1}:=\unicode[STIX]{x1D70B}_{1}\circ \unicode[STIX]{x1D6FD}$
is semialgebraic,
$\unicode[STIX]{x1D6FD}_{1}:=\unicode[STIX]{x1D70B}_{1}\circ \unicode[STIX]{x1D6FD}$
is semialgebraic,
![]() $\unicode[STIX]{x1D6FD}_{2}:=\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D6FD}$
is non-constant,
$\unicode[STIX]{x1D6FD}_{2}:=\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D6FD}$
is non-constant,
![]() $\unicode[STIX]{x1D6FD}(0)\in \unicode[STIX]{x1D6F4}$
, and
$\unicode[STIX]{x1D6FD}(0)\in \unicode[STIX]{x1D6F4}$
, and
![]() $\unicode[STIX]{x1D6FD}_{|(0,1)}$
is real analytic. Let
$\unicode[STIX]{x1D6FD}_{|(0,1)}$
is real analytic. Let
![]() $z_{0}:=\unicode[STIX]{x1D6FD}_{2}(0)$
and
$z_{0}:=\unicode[STIX]{x1D6FD}_{2}(0)$
and
![]() $(\unicode[STIX]{x1D6FE}_{0},x_{0}):=\unicode[STIX]{x1D6FD}_{1}(0)$
. Denote by
$(\unicode[STIX]{x1D6FE}_{0},x_{0}):=\unicode[STIX]{x1D6FD}_{1}(0)$
. Denote by
![]() $P_{0}$
the point
$P_{0}$
the point
![]() $\unicode[STIX]{x1D70B}(z_{0})$
and denote by
$\unicode[STIX]{x1D70B}(z_{0})$
and denote by
![]() $X_{0}$
the pre-special subvariety
$X_{0}$
the pre-special subvariety
![]() $\unicode[STIX]{x1D6FE}_{0}H(\mathbb{R})^{+}x_{0}$
.
$\unicode[STIX]{x1D6FE}_{0}H(\mathbb{R})^{+}x_{0}$
.
We claim that there exists a positive dimensional intersection component
![]() $A$
of
$A$
of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
containing
$\unicode[STIX]{x1D70B}^{-1}(V)$
containing
![]() $z_{0}$
. To see this, let
$z_{0}$
. To see this, let
![]() $W$
denote the union of the totally geodesic subvarieties
$W$
denote the union of the totally geodesic subvarieties
![]() $\unicode[STIX]{x1D6FE}H(\mathbb{R})^{+}x$
of
$\unicode[STIX]{x1D6FE}H(\mathbb{R})^{+}x$
of
![]() $X$
, where
$X$
, where
![]() $(\unicode[STIX]{x1D6FE},x)$
varies over
$(\unicode[STIX]{x1D6FE},x)$
varies over
![]() $\text{Im}(\unicode[STIX]{x1D6FD}_{1})$
, and let
$\text{Im}(\unicode[STIX]{x1D6FD}_{1})$
, and let
![]() $\overline{W}$
denote the Zariski closure of
$\overline{W}$
denote the Zariski closure of
![]() $W$
in
$W$
in
![]() $X^{\vee }$
. The irreducible analytic components of
$X^{\vee }$
. The irreducible analytic components of
![]() $\overline{W}\cap \unicode[STIX]{x1D70B}^{-1}(V)$
are, by definition, intersection components of
$\overline{W}\cap \unicode[STIX]{x1D70B}^{-1}(V)$
are, by definition, intersection components of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
. It follows from the global decomposition theorem (see [Reference Grauert and RemmertGR84, p. 172]) that there exists
$\unicode[STIX]{x1D70B}^{-1}(V)$
. It follows from the global decomposition theorem (see [Reference Grauert and RemmertGR84, p. 172]) that there exists
![]() $0<t\leqslant 1$
such that
$0<t\leqslant 1$
such that
![]() $\unicode[STIX]{x1D6FD}_{2}([0,t))$
intersects only finitely many of said components. In fact, since
$\unicode[STIX]{x1D6FD}_{2}([0,t))$
intersects only finitely many of said components. In fact, since
![]() $\unicode[STIX]{x1D6FD}_{2|(0,t)}$
is real analytic,
$\unicode[STIX]{x1D6FD}_{2|(0,t)}$
is real analytic,
![]() $\unicode[STIX]{x1D6FD}_{2}((0,t))$
must be wholly contained in one such component
$\unicode[STIX]{x1D6FD}_{2}((0,t))$
must be wholly contained in one such component
![]() $A$
. Since
$A$
. Since
![]() $A$
is closed, we conclude from the fact that
$A$
is closed, we conclude from the fact that
![]() $\unicode[STIX]{x1D6FD}$
is continuous that
$\unicode[STIX]{x1D6FD}$
is continuous that
![]() $A$
contains
$A$
contains
![]() $\unicode[STIX]{x1D6FD}_{2}([0,t])$
, which proves the claim.
$\unicode[STIX]{x1D6FD}_{2}([0,t])$
, which proves the claim.
Let
![]() $B$
denote a Zariski optimal intersection component of
$B$
denote a Zariski optimal intersection component of
![]() $\unicode[STIX]{x1D70B}^{-1}(V)$
containing
$\unicode[STIX]{x1D70B}^{-1}(V)$
containing
![]() $A$
such that
$A$
such that
and let
![]() $Z$
denote the Zariski closure of
$Z$
denote the Zariski closure of
![]() $\unicode[STIX]{x1D70B}(B)$
in
$\unicode[STIX]{x1D70B}(B)$
in
![]() $S$
. By the weak hyperbolic Ax–Schanuel conjecture,
$S$
. By the weak hyperbolic Ax–Schanuel conjecture,
![]() $\langle B\rangle _{\text{Zar}}$
is pre-weakly special and, as in the proof of Lemma 6.8,
$\langle B\rangle _{\text{Zar}}$
is pre-weakly special and, as in the proof of Lemma 6.8,
Therefore, we have
![]() $\dim Z\geqslant 1$
and, also,
$\dim Z\geqslant 1$
and, also,
where we use the fact that
![]() $\unicode[STIX]{x1D6FF}_{\text{Zar}}(A)$
is at most
$\unicode[STIX]{x1D6FF}_{\text{Zar}}(A)$
is at most
![]() $\dim \overline{W}-1$
. We claim that
$\dim \overline{W}-1$
. We claim that
![]() $\dim \overline{W}-1\leqslant \dim X_{0}$
, which would conclude the proof as
$\dim \overline{W}-1\leqslant \dim X_{0}$
, which would conclude the proof as
and this would imply that
![]() $Z\in \text{an}(V)$
, which is not allowed as
$Z\in \text{an}(V)$
, which is not allowed as
![]() $P_{0}\in Z$
.
$P_{0}\in Z$
.
Therefore, it remains to prove the claim. However, this is easy to prove working with complex duals and using the methods explained in the proof of Theorem 14.2. ◻
15 A brief note on special anomalous subvarieties
In their paper [Reference Bombieri, Masser and ZannierBMZ07], Bombieri et al. also defined what they referred to as a torsion anomalous subvariety. We will make the analogous definition in the context of Shimura varieties. Let
![]() $V$
be a subvariety of
$V$
be a subvariety of
![]() $S$
.
$S$
.
Definition 15.1. A subvariety
![]() $W$
of
$W$
of
![]() $V$
is called special anomalous in
$V$
is called special anomalous in
![]() $V$
if
$V$
if
A subvariety of
![]() $V$
is maximal special anomalous in
$V$
is maximal special anomalous in
![]() $V$
if it is special anomalous in
$V$
if it is special anomalous in
![]() $V$
and not strictly contained in another subvariety of
$V$
and not strictly contained in another subvariety of
![]() $V$
that is also special anomalous in
$V$
that is also special anomalous in
![]() $V$
.
$V$
.
The similarity with the definition of an atypical subvariety is clear. Indeed, it is immediate that a positive dimensional subvariety of
![]() $V$
that is atypical with respect to
$V$
that is atypical with respect to
![]() $V$
is special anomalous in
$V$
is special anomalous in
![]() $V$
. However, since a subvariety
$V$
. However, since a subvariety
![]() $W$
of
$W$
of
![]() $V$
that is special anomalous in
$V$
that is special anomalous in
![]() $V$
is not necessarily an irreducible component of
$V$
is not necessarily an irreducible component of
![]() $V\,\cap \,\langle W\rangle$
, it is not necessarily the case that
$V\,\cap \,\langle W\rangle$
, it is not necessarily the case that
![]() $W$
is atypical with respect to
$W$
is atypical with respect to
![]() $V$
. Nonetheless, it follows that the properties of being maximal special anomalous and atypical are equivalent for positive dimensional subvarieties of
$V$
. Nonetheless, it follows that the properties of being maximal special anomalous and atypical are equivalent for positive dimensional subvarieties of
![]() $V$
. In particular, Conjecture 1.4 implies the following analogue of the torsion openness conjecture of Bombieri, Masser, and Zannier.
$V$
. In particular, Conjecture 1.4 implies the following analogue of the torsion openness conjecture of Bombieri, Masser, and Zannier.
Conjecture 15.2. There are only finitely many subvarieties of
![]() $V$
that are maximal special anomalous in
$V$
that are maximal special anomalous in
![]() $V$
.
$V$
.
Of course, one would more naturally translate the torsion openness conjecture as follows.
Conjecture 15.3. The complement
![]() $V^{\text{sa}}$
in
$V^{\text{sa}}$
in
![]() $V$
of the subvarieties of
$V$
of the subvarieties of
![]() $V$
that are special anomalous in
$V$
that are special anomalous in
![]() $V$
is open in
$V$
is open in
![]() $V$
.
$V$
.
However, these two formulations are equivalent. Indeed, the statement that Conjecture 15.2 implies Conjecture 15.3 is obvious. On the other hand, suppose that Conjecture 15.3 were true. Then the union of all subvarieties of
![]() $V$
that are positive dimensional and atypical with respect to
$V$
that are positive dimensional and atypical with respect to
![]() $V$
would be closed in
$V$
would be closed in
![]() $V$
. In particular, we could write it as a finite union of subvarieties of
$V$
. In particular, we could write it as a finite union of subvarieties of
![]() $V$
. However, since there are only countably many subvarieties of
$V$
. However, since there are only countably many subvarieties of
![]() $V$
that are atypical with respect to
$V$
that are atypical with respect to
![]() $V$
, it follows that each member of the aforementioned union would be atypical with respect to
$V$
, it follows that each member of the aforementioned union would be atypical with respect to
![]() $V$
.
$V$
.
Of course, if one could prove Conjecture 15.2, one would reduce the Zilber–Pink conjecture to the following analogue of the torsion finiteness conjecture of Bombieri, Masser, and Zannier.
Conjecture 15.4. There are only finitely many points in
![]() $V$
that are maximal atypical with respect to
$V$
that are maximal atypical with respect to
![]() $V$
.
$V$
.
In this article, we have concerned ourselves with optimal subvarieties. Now, it is straightforward to verify that a subvariety
![]() $W$
of
$W$
of
![]() $V$
that is optimal in
$V$
that is optimal in
![]() $V$
is atypical with respect to
$V$
is atypical with respect to
![]() $V$
. However, it is not necessarily the case that
$V$
. However, it is not necessarily the case that
![]() $W$
is maximal atypical. On the other hand, a subvariety of
$W$
is maximal atypical. On the other hand, a subvariety of
![]() $V$
that is maximal atypical with respect to
$V$
that is maximal atypical with respect to
![]() $V$
is optimal. In particular, the points in
$V$
is optimal. In particular, the points in
![]() $V$
that are maximal atypical with respect to
$V$
that are maximal atypical with respect to
![]() $V$
constitute a (possibly proper) subset of
$V$
constitute a (possibly proper) subset of
![]() $\text{Opt}_{0}(V)$
.
$\text{Opt}_{0}(V)$
.
Again, it would be more natural to translate the torsion finiteness conjecture as follows.
Conjecture 15.5. For any integer
![]() $d$
, let
$d$
, let
![]() $S^{[d]}$
denote the union of the special subvarieties contained in
$S^{[d]}$
denote the union of the special subvarieties contained in
![]() $S$
having codimension at least
$S$
having codimension at least
![]() $d$
. Then
$d$
. Then
is finite. Equivalently, there are only finitely many points
![]() $P\in V^{\text{sa}}$
such that
$P\in V^{\text{sa}}$
such that
However, the two formulations are also equivalent. Indeed, Conjecture 15.5 implies Conjecture 15.4 because a point
![]() $P\in V$
that is maximal atypical with respect to
$P\in V$
that is maximal atypical with respect to
![]() $V$
is contained in
$V$
is contained in
![]() $V^{\text{sa}}$
and
$V^{\text{sa}}$
and
On the other hand, suppose that Conjecture 15.4 were true and consider a point
![]() $P\in V^{\text{sa}}$
such that
$P\in V^{\text{sa}}$
such that
Then
![]() $P$
is a component of
$P$
is a component of
![]() $\langle P\rangle \cap V$
. Otherwise, such a component
$\langle P\rangle \cap V$
. Otherwise, such a component
![]() $W$
containing
$W$
containing
![]() $P$
would be special anomalous in
$P$
would be special anomalous in
![]() $V$
, which would contradict the fact that
$V$
, which would contradict the fact that
![]() $P\in V^{\text{sa}}$
. Therefore,
$P\in V^{\text{sa}}$
. Therefore,
![]() $P$
is atypical with respect to
$P$
is atypical with respect to
![]() $V$
and, in fact, maximal atypical with respect to
$V$
and, in fact, maximal atypical with respect to
![]() $V$
.
$V$
.
In their article [Reference Bombieri, Masser and ZannierBMZ07], Bombieri et al. showed that, in fact, the torsion openness conjecture implies the torsion finiteness conjecture. We imitate their argument to show the following.
Proposition 15.6. Let
![]() $Y(1)$
denote the modular curve associated with
$Y(1)$
denote the modular curve associated with
![]() $\text{SL}_{2}(\mathbb{Z})$
. If Conjecture 15.3 is true for
$\text{SL}_{2}(\mathbb{Z})$
. If Conjecture 15.3 is true for
![]() $S\times Y(1)$
, then Conjecture 15.5 is true for
$S\times Y(1)$
, then Conjecture 15.5 is true for
![]() $S$
.
$S$
.
Proof. We denote by
![]() $U$
the complement in
$U$
the complement in
![]() $V^{\text{sa}}$
of
$V^{\text{sa}}$
of
![]() $V^{\text{sa}}\cap S^{[\dim V+1]}$
. Regarding
$V^{\text{sa}}\cap S^{[\dim V+1]}$
. Regarding
![]() $V\times Y(1)$
as a subvariety of the Shimura variety
$V\times Y(1)$
as a subvariety of the Shimura variety
![]() $S\times Y(1)$
, we claim that
$S\times Y(1)$
, we claim that
To see this, first let
![]() ${\hat{Y}}$
be a special anomalous subvariety of
${\hat{Y}}$
be a special anomalous subvariety of
![]() $V\times Y(1)$
. Then
$V\times Y(1)$
. Then
 $$\begin{eqnarray}\displaystyle \dim {\hat{Y}} & {\geqslant} & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim (V\times Y(1))-\dim (S\times Y(1))\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +(1+\dim V)-(1+\dim S)\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim V-\dim S.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim {\hat{Y}} & {\geqslant} & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim (V\times Y(1))-\dim (S\times Y(1))\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +(1+\dim V)-(1+\dim S)\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim V-\dim S.\nonumber\end{eqnarray}$$
We denote by
![]() $\unicode[STIX]{x1D70B}_{S}$
the projection
$\unicode[STIX]{x1D70B}_{S}$
the projection
![]() $\unicode[STIX]{x1D70B}_{S}:S\times Y(1)\rightarrow S$
. Then the Zariski closure
$\unicode[STIX]{x1D70B}_{S}:S\times Y(1)\rightarrow S$
. Then the Zariski closure
![]() $Y$
of
$Y$
of
![]() $\unicode[STIX]{x1D70B}_{S}({\hat{Y}})$
lies in the special subvariety
$\unicode[STIX]{x1D70B}_{S}({\hat{Y}})$
lies in the special subvariety
![]() $\unicode[STIX]{x1D70B}_{S}(\langle {\hat{Y}}\rangle )$
of
$\unicode[STIX]{x1D70B}_{S}(\langle {\hat{Y}}\rangle )$
of
![]() $S$
. If
$S$
. If
![]() $\dim Y=\dim {\hat{Y}}$
, then
$\dim Y=\dim {\hat{Y}}$
, then
 $$\begin{eqnarray}\displaystyle \dim Y & = & \displaystyle \dim {\hat{Y}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim V-\dim S\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \unicode[STIX]{x1D70B}_{S}(\langle {\hat{Y}}\rangle )+\dim V-\dim S\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \langle Y\rangle +\dim V-\dim S\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim Y & = & \displaystyle \dim {\hat{Y}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim V-\dim S\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \unicode[STIX]{x1D70B}_{S}(\langle {\hat{Y}}\rangle )+\dim V-\dim S\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \langle Y\rangle +\dim V-\dim S\nonumber\end{eqnarray}$$
and
![]() $Y$
is special anomalous in
$Y$
is special anomalous in
![]() $V$
. If
$V$
. If
![]() $1\leqslant \dim Y<\dim {\hat{Y}}$
, then
$1\leqslant \dim Y<\dim {\hat{Y}}$
, then
![]() $\dim Y=\dim {\hat{Y}}\,-\,1$
and
$\dim Y=\dim {\hat{Y}}\,-\,1$
and
![]() ${\hat{Y}}=Y\,\times \,Y(1)$
, which implies
${\hat{Y}}=Y\,\times \,Y(1)$
, which implies
![]() $\langle {\hat{Y}}\rangle =\langle Y\rangle \times Y(1)$
. Therefore,
$\langle {\hat{Y}}\rangle =\langle Y\rangle \times Y(1)$
. Therefore,
 $$\begin{eqnarray}\displaystyle \dim Y & = & \displaystyle \dim {\hat{Y}}-1\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim V-\dim S-1\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle Y\rangle +1+\dim V-\dim S-1\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle Y\rangle +\dim V-\dim S\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim Y & = & \displaystyle \dim {\hat{Y}}-1\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim V-\dim S-1\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle Y\rangle +1+\dim V-\dim S-1\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle Y\rangle +\dim V-\dim S\nonumber\end{eqnarray}$$
and
![]() $Y$
is special anomalous in
$Y$
is special anomalous in
![]() $V$
. In both cases,
$V$
. In both cases,
![]() ${\hat{Y}}$
is contained in
${\hat{Y}}$
is contained in
Finally, if
![]() $\dim Y=0$
, then
$\dim Y=0$
, then
![]() ${\hat{Y}}=\{P\}\times Y(1)$
for some
${\hat{Y}}=\{P\}\times Y(1)$
for some
![]() $P\in S$
. Since
$P\in S$
. Since
![]() ${\hat{Y}}$
is special anomalous, we have
${\hat{Y}}$
is special anomalous, we have
 $$\begin{eqnarray}\displaystyle 1 & = & \displaystyle \dim {\hat{Y}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +(1+\dim V)-(1+\dim S)\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle P\rangle +1+\dim V-\dim S\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1 & = & \displaystyle \dim {\hat{Y}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +(1+\dim V)-(1+\dim S)\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle P\rangle +1+\dim V-\dim S\nonumber\end{eqnarray}$$
and
![]() $P\in S^{[1+\dim V]}$
. Therefore,
$P\in S^{[1+\dim V]}$
. Therefore,
 $$\begin{eqnarray}\displaystyle {\hat{Y}} & \subseteq & \displaystyle V\backslash (V-S^{[1+\dim V]})\times Y(1)\nonumber\\ \displaystyle & \subseteq & \displaystyle V\backslash (V^{\text{sa}}-S^{[1+\dim V]})\times Y(1)\nonumber\\ \displaystyle & = & \displaystyle (V\backslash U)\times Y(1)\nonumber\\ \displaystyle & = & \displaystyle (V\times Y(1))\backslash (U\times Y(1)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\hat{Y}} & \subseteq & \displaystyle V\backslash (V-S^{[1+\dim V]})\times Y(1)\nonumber\\ \displaystyle & \subseteq & \displaystyle V\backslash (V^{\text{sa}}-S^{[1+\dim V]})\times Y(1)\nonumber\\ \displaystyle & = & \displaystyle (V\backslash U)\times Y(1)\nonumber\\ \displaystyle & = & \displaystyle (V\times Y(1))\backslash (U\times Y(1)).\nonumber\end{eqnarray}$$
We conclude that
![]() $(V\times Y(1))^{\text{sa}}\subseteq (U\times Y(1))$
.
$(V\times Y(1))^{\text{sa}}\subseteq (U\times Y(1))$
.
On the other hand, for any
![]() $P\in V\backslash U=V\backslash (V^{\text{sa}}-S^{[1+\dim V]})$
, we have either
$P\in V\backslash U=V\backslash (V^{\text{sa}}-S^{[1+\dim V]})$
, we have either
![]() $P\notin V^{\text{sa}}$
or
$P\notin V^{\text{sa}}$
or
![]() $P\in V^{\text{sa}}\cap S^{[1+\dim V]}$
.
$P\in V^{\text{sa}}\cap S^{[1+\dim V]}$
.
If
![]() $P\notin V^{\text{sa}}$
, then
$P\notin V^{\text{sa}}$
, then
![]() $P$
is contained in a special anomalous
$P$
is contained in a special anomalous
![]() $Y$
of
$Y$
of
![]() $V$
. Therefore,
$V$
. Therefore,
 $$\begin{eqnarray}\displaystyle \dim (Y\times Y(1)) & = & \displaystyle 1+\dim Y\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+1+\dim \langle Y\rangle +\dim V-\dim S\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle Y\times Y(1)\rangle +\dim (V\times Y(1))-\dim (S\times Y(1))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim (Y\times Y(1)) & = & \displaystyle 1+\dim Y\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+1+\dim \langle Y\rangle +\dim V-\dim S\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle Y\times Y(1)\rangle +\dim (V\times Y(1))-\dim (S\times Y(1))\nonumber\end{eqnarray}$$
and
![]() $Y\times Y(1)\subset (V\times Y(1))\backslash (U\times Y(1))$
is special anomalous.
$Y\times Y(1)\subset (V\times Y(1))\backslash (U\times Y(1))$
is special anomalous.
If
![]() $P\in V^{\text{sa}}\cap S^{[1+\dim V]}$
, we let
$P\in V^{\text{sa}}\cap S^{[1+\dim V]}$
, we let
![]() ${\hat{Y}}=\{P\}\times Y(1)$
. Then
${\hat{Y}}=\{P\}\times Y(1)$
. Then
 $$\begin{eqnarray}\displaystyle \dim {\hat{Y}} & = & \displaystyle 1\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+1+\dim \langle P\rangle +\dim V-\dim S\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim (V\times Y(1))-\dim (S\times Y(1))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim {\hat{Y}} & = & \displaystyle 1\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 1+1+\dim \langle P\rangle +\dim V-\dim S\nonumber\\ \displaystyle & = & \displaystyle 1+\dim \langle {\hat{Y}}\rangle +\dim (V\times Y(1))-\dim (S\times Y(1))\nonumber\end{eqnarray}$$
and
![]() ${\hat{Y}}\subseteq (V\,\times \,Y(1))\backslash (U\,\times \,Y(1))$
is special anomalous. We conclude that
${\hat{Y}}\subseteq (V\,\times \,Y(1))\backslash (U\,\times \,Y(1))$
is special anomalous. We conclude that
![]() $(U\,\times \,Y(1))\subseteq (V\,\times \,Y(1))^{\text{sa}}$
, which proves (15.6.1).
$(U\,\times \,Y(1))\subseteq (V\,\times \,Y(1))^{\text{sa}}$
, which proves (15.6.1).
Therefore, if Conjecture 15.3 is true for
![]() $S\times Y(1)$
, we conclude that
$S\times Y(1)$
, we conclude that
![]() $U\times Y(1)$
is open in
$U\times Y(1)$
is open in
![]() $V\times Y(1)$
. Therefore,
$V\times Y(1)$
. Therefore,
![]() $U$
is open in
$U$
is open in
![]() $V$
. On the other hand,
$V$
. On the other hand,
![]() $V^{\text{sa}}$
is also open in
$V^{\text{sa}}$
is also open in
![]() $V$
, whereas
$V$
, whereas
![]() $V^{\text{sa}}\cap S^{[1+\dim V]}$
is at most countable since there are only countably many special subvarieties and each point in
$V^{\text{sa}}\cap S^{[1+\dim V]}$
is at most countable since there are only countably many special subvarieties and each point in
![]() $V^{\text{sa}}\,\cap \,S^{[1+\dim V]}$
is an irreducible component of
$V^{\text{sa}}\,\cap \,S^{[1+\dim V]}$
is an irreducible component of
![]() $V\,\cap \,Z$
for some special subvariety
$V\,\cap \,Z$
for some special subvariety
![]() $Z$
of codimension at most
$Z$
of codimension at most
![]() $1+\dim V$
. It follows that
$1+\dim V$
. It follows that
![]() $V^{\text{sa}}\cap S^{[1+\dim V]}$
is finite.◻
$V^{\text{sa}}\cap S^{[1+\dim V]}$
is finite.◻
Acknowledgements
The first author would like to thank the EPSRC, as well as Jonathan Pila, for the opportunity to be part of the project Model Theory, Functional Transcendence, and Diophantine Geometry as a postdoctoral research assistant. He would like to thank Linacre College, Oxford, the Mathematical Institute at the University of Oxford, and the Department of Mathematics and Statistics at the University of Reading, all for providing excellent working conditions. Finally, he would like to thank Martin Orr, Jonathan Pila, Harry Schmidt, Emmanuel Ullmo, and Andrei Yafaev for several valuable discussions. The second author is grateful to the Institut des Hautes Études Scientifiques and the Université Paris Saclay for providing great environments in which to work. He would like to thank his supervisor Emmanuel Ullmo for regular discussions and constant support during the preparation of this article and he would like to thank Mikhail Borovoi, Philipp Habegger, Ziyang Gao, Martin Orr, and Jonathan Pila for several useful discussions. His work was supported by grants from Région l’Île de France. Both authors would like to thank Martin Orr, for sharing drafts of his preprint [Reference OrrOrr17], as well as the anonymous referee, for a long list of invaluable comments.