Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-06-07T01:56:20.062Z Has data issue: false hasContentIssue false
  • English
  • Français

A bimodule description of the Hecke category

Part of: Special aspects of infinite or finite groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  30 September 2021

Noriyuki Abe
Noriyuki Abe*
Affiliation:
Graduate School of Mathematical Sciences, the University of Tokyo, 3-8-1 Komaba, Meguro-ku, Tokyo153-8914, Japanabenori@ms.u-tokyo.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

For a Coxeter system and a representation 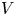$V$ of this Coxeter system, Soergel defined a category which is now called the category of Soergel bimodules and proved that this gives a categorification of the Hecke algebra when 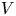$V$ is reflection faithful. Elias and Williamson defined another category when 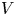$V$ is not reflection faithful and proved that this category is equivalent to the category of Soergel bimodules when 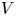$V$ is reflection faithful. Moreover, they proved the categorification theorem for their category with fewer assumptions on $V$. In this paper, we give a bimodule description of the Elias–Williamson category and re-prove the categorification theorem.

Keywords

Hecke algebraSoergel bimodules

MSC classification

Primary: 20F55: Reflection and Coxeter groups
Secondary: 20G05: Representation theory
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 10 , October 2021 , pp. 2133 - 2159
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, N., A Hecke action on G1T-modules, Preprint (2019), arXiv:1904.11350.Google Scholar
Achar, P. N., Makisumi, S., Riche, S. and Williamson, G., Koszul duality for Kac–Moody groups and characters of tilting modules, J. Amer. Math. Soc. 32 (2019), 261–310.CrossRefGoogle Scholar
Elias, B., The two-color Soergel calculus, Compos. Math. 152 (2016), 327–398.CrossRefGoogle Scholar
Elias, B. and Williamson, G., Soergel calculus, Represent. Theory 20 (2016), 295–374.CrossRefGoogle Scholar
Fiebig, P., The combinatorics of category $\mathcal {O}$ over symmetrizable Kac-Moody algebras, Transform. Groups 11 (2006), 29–49.CrossRefGoogle Scholar
Fiebig, P., The combinatorics of Coxeter categories, Trans. Amer. Math. Soc. 360 (2008), 4211–4233.CrossRefGoogle Scholar
Fiebig, P., Sheaves on moment graphs and a localization of Verma flags, Adv. Math. 217 (2008), 683–712.CrossRefGoogle Scholar
Fiebig, P., Sheaves on affine Schubert varieties, modular representations, and Lusztig's conjecture, J. Amer. Math. Soc. 24 (2011), 133–181.CrossRefGoogle Scholar
Fiebig, P. and Williamson, G., Parity sheaves, moment graphs and the $p$-smooth locus of Schubert varieties, Ann. Inst. Fourier (Grenoble) 64 (2014), 489–536.CrossRefGoogle Scholar
Libedinsky, N., Sur la catégorie des bimodules de Soergel, J. Algebra 320 (2008), 2675–2694.CrossRefGoogle Scholar
Riche, S. and Williamson, G., Tilting modules and the $p$-canonical basis, Astérisque 397 (2018).Google Scholar
Soergel, W., Kategorie $\mathcal {O}$, perverse Garben und Moduln über den Koinvarianten zur Weylgruppe, J. Amer. Math. Soc. 3 (1990), 421–445.Google Scholar
Soergel, W., Kazhdan-Lusztig-Polynome und unzerlegbare Bimoduln über Polynomringen, J. Inst. Math. Jussieu 6 (2007), 501–525.CrossRefGoogle Scholar