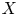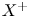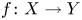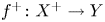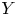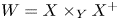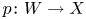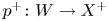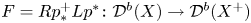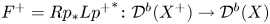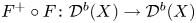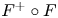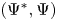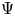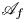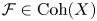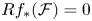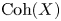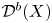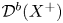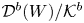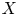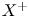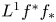1. Introduction
A homological interpretation of the minimal model program (MMP) in birational geometry was proposed in [Reference Bondal and OrlovBO95, Reference Bondal and OrlovBO02]. The basic idea is that MMP is about ‘minimisation’ of the derived category ![]() ${\mathcal {D}}^b(X)$ of coherent sheaves on a variety
${\mathcal {D}}^b(X)$ of coherent sheaves on a variety ![]() $X$ for varieties in a given birational class. More precisely, it is expected that if
$X$ for varieties in a given birational class. More precisely, it is expected that if ![]() $X$ allows a divisorial contraction or a flip
$X$ allows a divisorial contraction or a flip ![]() $X\dashrightarrow Y$, then
$X\dashrightarrow Y$, then ![]() ${\mathcal {D}}^b(X)$ has a semi-orthogonal decomposition (SOD) with one component of SOD equivalent to
${\mathcal {D}}^b(X)$ has a semi-orthogonal decomposition (SOD) with one component of SOD equivalent to ![]() ${\mathcal {D}}^b(Y)$. Thus, minimizing the birational model should have the categorical meaning of chopping off semi-orthogonal factors of the derived category. A minimal model is expected to be a representative in the birational class of a variety whose derived category does not allow semi-orthogonal factors equivalent to the derived category of a variety birationally equivalent to
${\mathcal {D}}^b(Y)$. Thus, minimizing the birational model should have the categorical meaning of chopping off semi-orthogonal factors of the derived category. A minimal model is expected to be a representative in the birational class of a variety whose derived category does not allow semi-orthogonal factors equivalent to the derived category of a variety birationally equivalent to ![]() $X$.
$X$.
As MMP in dimension greater than two deals with singular varieties, the right choice of the derived category to consider also matters. In particular, for ![]() ${\mathbb {Q}}$-Gorenstein varieties the derived category of a suitable stack is relevant (cf. [Reference KawamataKaw02, Reference KawamataKaw09]). Minimal models are not unique, and MMP considers birational maps, called flops, that link various minimal models. Conjecturally, flops induce derived equivalences [Reference Bondal and OrlovBO95, Reference KawamataKaw02, Reference Bondal and OrlovBO02].
${\mathbb {Q}}$-Gorenstein varieties the derived category of a suitable stack is relevant (cf. [Reference KawamataKaw02, Reference KawamataKaw09]). Minimal models are not unique, and MMP considers birational maps, called flops, that link various minimal models. Conjecturally, flops induce derived equivalences [Reference Bondal and OrlovBO95, Reference KawamataKaw02, Reference Bondal and OrlovBO02].
There is substantial evidence in favour of this conjectural picture, starting from the original paper [Reference Bondal and OrlovBO95], where various instances of flops were proved to induce derived equivalences, and for simple higher-dimensional flips, the required SOD was constructed.
We expect that the whole zoology of categories, functors and natural transformations relevant to MMP should be governed by interesting hidden homotopy types, maps and higher homotopies. The present work can be considered as taking steps in this direction for categories and functors invoked by flops.
It was mentioned by the authors of [Reference Bondal and OrlovBO95] that the functor that provides an equivalence ![]() ${\mathcal {D}}^b(X)\to {\mathcal {D}}^b(X^+)$, where
${\mathcal {D}}^b(X)\to {\mathcal {D}}^b(X^+)$, where ![]() $X$ and
$X$ and ![]() $X^+$ are connected by a flop, when composed with the analogous functor in the opposite direction
$X^+$ are connected by a flop, when composed with the analogous functor in the opposite direction ![]() ${\mathcal {D}}^b(X^+)\to {\mathcal {D}}^b(X)$ is not the identity but produces a non-trivial auto-equivalence of
${\mathcal {D}}^b(X^+)\to {\mathcal {D}}^b(X)$ is not the identity but produces a non-trivial auto-equivalence of ![]() ${\mathcal {D}}^b(X)$ (nowadays called a flop–flop functor). For Atiyah flop, the functor is given by what is now known as the spherical twist with respect to the spherical object
${\mathcal {D}}^b(X)$ (nowadays called a flop–flop functor). For Atiyah flop, the functor is given by what is now known as the spherical twist with respect to the spherical object ![]() ${\mathcal {O}}_C(-1)$, where
${\mathcal {O}}_C(-1)$, where ![]() $C$ is the (rational) exceptional curve. It was probably one of the first appearances of the spherical twists. (However, we should also mention here the work of Mukai [Reference MukaiMuk87] and Kuleshov [Reference KuleshovKul90] who used the action of spherical twists in their non-derived version to describe moduli of sheaves on K3 surfaces. A quick generalisation to the Calabi–Yau/derived case was understood by the authors of [Reference Bondal and OrlovBO95] in those days of sturm und drang on derived categories in Moscow in the early 1990s). Kontsevich suggested that the spherical twist of Atiyah flop should be transferred by mirror symmetry into the equivalence of the Fukaya category induced by the Dehn twist along a vanishing cycle. Properties of spherical twists with respect to spherical objects were later scrutinised by Seidel and Thomas in [Reference Seidel and ThomasST01] and for more general spherical functors by Anno and Logvinenko in [Reference Anno and LogvinenkoAL17].
$C$ is the (rational) exceptional curve. It was probably one of the first appearances of the spherical twists. (However, we should also mention here the work of Mukai [Reference MukaiMuk87] and Kuleshov [Reference KuleshovKul90] who used the action of spherical twists in their non-derived version to describe moduli of sheaves on K3 surfaces. A quick generalisation to the Calabi–Yau/derived case was understood by the authors of [Reference Bondal and OrlovBO95] in those days of sturm und drang on derived categories in Moscow in the early 1990s). Kontsevich suggested that the spherical twist of Atiyah flop should be transferred by mirror symmetry into the equivalence of the Fukaya category induced by the Dehn twist along a vanishing cycle. Properties of spherical twists with respect to spherical objects were later scrutinised by Seidel and Thomas in [Reference Seidel and ThomasST01] and for more general spherical functors by Anno and Logvinenko in [Reference Anno and LogvinenkoAL17].
Spherical (co)twist is a unification tool for various non-trivial auto-equivalences of ![]() ${\mathcal {D}}^b(X)$ (cf. [Reference AddingtonAdd16]) such as tensor products with line bundles, twists around spherical objects [Reference Seidel and ThomasST01], EZ-twists [Reference HorjaHor05] or window shifts [Reference Donovan and SegalDS14].
${\mathcal {D}}^b(X)$ (cf. [Reference AddingtonAdd16]) such as tensor products with line bundles, twists around spherical objects [Reference Seidel and ThomasST01], EZ-twists [Reference HorjaHor05] or window shifts [Reference Donovan and SegalDS14].
The homotopy meaning of spherical (co)twists can be read off from their interpretation via schobers, i.e. categorifications of perverse sheaves on stratified topological spaces, suggested by Kapranov and Schechtman [Reference Kapranov and SchechtmanKS14]. The homotopy type of the underlying stratification (the punctured disc for the case of one spherical functor) encodes the algebra of functors and natural transformations in the schober. The schober on the punctured disc has one of possible incarnations via a spherical pair, i.e. a pair of admissible subcategories in a triangulated category satisfying conditions that imply a spherical functor between them.
We study functors and natural transformations for flops with dimension of fibers of the flopping contractions bounded by one. We construct the spherical pair ![]() $({\mathcal {D}}^b(X), {\mathcal {D}}^b(X^+))$ in the appropriate quotient of the derived category of
$({\mathcal {D}}^b(X), {\mathcal {D}}^b(X^+))$ in the appropriate quotient of the derived category of ![]() $X\times _Y X^+$. The orthogonal complement to
$X\times _Y X^+$. The orthogonal complement to ![]() ${\mathcal {D}}^b(X)$ in that quotient is the bounded derived category of the abelian null category
${\mathcal {D}}^b(X)$ in that quotient is the bounded derived category of the abelian null category
By deriving the embedding ![]() ${\mathcal {A}}_f\to \mathop {{\rm Coh}}\nolimits (X)$ we obtain the spherical functor
${\mathcal {A}}_f\to \mathop {{\rm Coh}}\nolimits (X)$ we obtain the spherical functor ![]() $\Psi \colon {\mathcal {D}}^b(\mathscr {A}_f)\to {\mathcal {D}}^b(X)$. The spherical cotwist of the spherical couple (see Appendix C)
$\Psi \colon {\mathcal {D}}^b(\mathscr {A}_f)\to {\mathcal {D}}^b(X)$. The spherical cotwist of the spherical couple (see Appendix C) ![]() $(\Psi ^* ,\Psi )$ is the flop–flop functor.
$(\Psi ^* ,\Psi )$ is the flop–flop functor.
We lift our functors and natural transformations to bicategories ![]() $\mathop {\textbf {Bimod}}\nolimits$ and
$\mathop {\textbf {Bimod}}\nolimits$ and ![]() $\mathop {\textbf {FM}}\nolimits$ (see Appendix C). We systematically consider 2-categorical adjunctions instead of the usual adjunctions of functors, scrutinise the uniqueness of adjoints and of associated twists and cotwists, i.e. the cones of adjunction units and counits.
$\mathop {\textbf {FM}}\nolimits$ (see Appendix C). We systematically consider 2-categorical adjunctions instead of the usual adjunctions of functors, scrutinise the uniqueness of adjoints and of associated twists and cotwists, i.e. the cones of adjunction units and counits.
Now we describe our results in more detail.
The flop functor and Van den Bergh's functor
We consider a flopping contraction ![]() $f:X \to Y$ and its flop
$f:X \to Y$ and its flop ![]() $f^+: X^+\to Y$ with dimension of fibers bounded by one. Exceptional loci of
$f^+: X^+\to Y$ with dimension of fibers bounded by one. Exceptional loci of ![]() $f$ and
$f$ and ![]() $f^+$ are assumed to have codimension greater than one in
$f^+$ are assumed to have codimension greater than one in ![]() $X$, respectively in
$X$, respectively in ![]() $X^+$, whereas varieties
$X^+$, whereas varieties ![]() $X$,
$X$, ![]() $X^+$ and
$X^+$ and ![]() $Y$ are assumed to be Gorenstein and
$Y$ are assumed to be Gorenstein and ![]() $Y$ is assumed to have canonical hypersurface singularities of multiplicity two.
$Y$ is assumed to have canonical hypersurface singularities of multiplicity two.
Consider the diagram for the fiber product:

where ![]() $p$ and
$p$ and ![]() $p^+$ denote the projections to the factors. The flop functor is
$p^+$ denote the projections to the factors. The flop functor is
Note that this functor does not necessarily induce an equivalence if the dimension of fibers of ![]() $f$ is greater than one (see [Reference NamikawaNam04]), which means that the functor needs an adjustment for fibers of higher dimension.
$f$ is greater than one (see [Reference NamikawaNam04]), which means that the functor needs an adjustment for fibers of higher dimension.
The above assumptions on the flopping contraction are those adopted by Van den Bergh in [Reference Van den BerghVdB04]. We use also some techniques borrowed from his work. Van den Bergh constructed an equivalence ![]() ${\Sigma } \colon {\mathcal {D}}^b(X)\xrightarrow {\simeq } {\mathcal {D}}^b(X^+)$, which is given via the identification of both categories with the derived category of modules over a sheaf of non-commutative algebras on affine
${\Sigma } \colon {\mathcal {D}}^b(X)\xrightarrow {\simeq } {\mathcal {D}}^b(X^+)$, which is given via the identification of both categories with the derived category of modules over a sheaf of non-commutative algebras on affine ![]() $Y$. We first give a new interpretation for functor
$Y$. We first give a new interpretation for functor ![]() ${\Sigma }$. To this end, we identify
${\Sigma }$. To this end, we identify ![]() ${\mathcal {D}}^b(X)$ with
${\mathcal {D}}^b(X)$ with ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$, the homotopy category of complexes of projective objects
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$, the homotopy category of complexes of projective objects ![]() $\mathscr {P}_{-1}$ in the heart
$\mathscr {P}_{-1}$ in the heart ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ of the perverse
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ of the perverse ![]() $t$-structure, introduced by Bridgeland in [Reference BridgelandBri02]. We show that
$t$-structure, introduced by Bridgeland in [Reference BridgelandBri02]. We show that ![]() ${\Sigma }$ can be defined as the functor
${\Sigma }$ can be defined as the functor ![]() $(f^{+*}f_*(-))^{\vee \vee }$ applied term-wise to complexes of objects in
$(f^{+*}f_*(-))^{\vee \vee }$ applied term-wise to complexes of objects in ![]() $\mathscr {P}_{-1}$. We give an independent proof that the flop functor is an equivalence and that it can be extended to an equivalence
$\mathscr {P}_{-1}$. We give an independent proof that the flop functor is an equivalence and that it can be extended to an equivalence ![]() $\Sigma _{{\rm qc}}$ between unbounded categories of quasi-coherent sheaves (Proposition 4.6).
$\Sigma _{{\rm qc}}$ between unbounded categories of quasi-coherent sheaves (Proposition 4.6).
Then we show that the flop functor is given in the same way by the term-wise application of the functor ![]() $f^{+*}f_*(-)$. To this end, we need one of the technical innovations of our paper, the
$f^{+*}f_*(-)$. To this end, we need one of the technical innovations of our paper, the ![]() $L^1f^*f_*$-vanishing for objects in
$L^1f^*f_*$-vanishing for objects in ![]() $\mathscr {P}_{-1}$. We prove (Lemma 3.4) that if
$\mathscr {P}_{-1}$. We prove (Lemma 3.4) that if ![]() $f \colon X \to Y$ is a flopping contraction satisfying the above conditions, then
$f \colon X \to Y$ is a flopping contraction satisfying the above conditions, then ![]() $L^1f^*f_* {\mathcal {M}}$ is zero, for any
$L^1f^*f_* {\mathcal {M}}$ is zero, for any ![]() ${\mathcal {M}} \in \mathscr {P}_{-1}$. The proof of the vanishing is based on a local presentation of
${\mathcal {M}} \in \mathscr {P}_{-1}$. The proof of the vanishing is based on a local presentation of ![]() $Y$ as a divisor in a smooth variety
$Y$ as a divisor in a smooth variety ![]() ${\mathcal {Y}}$. Note that, since
${\mathcal {Y}}$. Note that, since ![]() $Y$ is singular, object
$Y$ is singular, object ![]() $Lf^*f_* {\mathcal {M}}$ in general has infinitely many non-zero cohomology sheaves, more precisely, they satisfy 2-periodicity (see § 3.5), which is reminiscent of matrix factorisations [Reference BuchweitzBuc86, Reference OrlovOrl04].
$Lf^*f_* {\mathcal {M}}$ in general has infinitely many non-zero cohomology sheaves, more precisely, they satisfy 2-periodicity (see § 3.5), which is reminiscent of matrix factorisations [Reference BuchweitzBuc86, Reference OrlovOrl04].
We consider a divisorial embedding ![]() $i \colon Y \to {\mathcal {Y}}$ into a smooth
$i \colon Y \to {\mathcal {Y}}$ into a smooth ![]() ${\mathcal {Y}}$ together with
${\mathcal {Y}}$ together with ![]() $g=i \circ f$,
$g=i \circ f$, ![]() $g^+ = i \circ f^+$. If the base
$g^+ = i \circ f^+$. If the base ![]() $Y$ of the flopping contraction is affine, then the flop functor
$Y$ of the flopping contraction is affine, then the flop functor ![]() $F$ and Van den Bergh's equivalence
$F$ and Van den Bergh's equivalence ![]() $\Sigma _{{\rm qc}}\colon {\mathcal {D}}_{{\rm qc}}(X)\to {\mathcal {D}}_{{\rm qc}}(X^+)$ fit into a functorial exact triangle (Proposition 4.13):
$\Sigma _{{\rm qc}}\colon {\mathcal {D}}_{{\rm qc}}(X)\to {\mathcal {D}}_{{\rm qc}}(X^+)$ fit into a functorial exact triangle (Proposition 4.13):
As both ![]() $Lg^{+*}Rg_*$ and
$Lg^{+*}Rg_*$ and ![]() $\Sigma _{{\rm qc}}$ take
$\Sigma _{{\rm qc}}$ take ![]() ${\mathcal {D}}^b(X)$ to
${\mathcal {D}}^b(X)$ to ![]() ${\mathcal {D}}^b(X^+)$, this allows us to conclude that the flop functor also preserves the boundedness of the derived categories.
${\mathcal {D}}^b(X^+)$, this allows us to conclude that the flop functor also preserves the boundedness of the derived categories.
Theorem 4.21 states that ![]() $\Sigma _{{\rm qc}}$ is actually the inverse of the opposite flop functor
$\Sigma _{{\rm qc}}$ is actually the inverse of the opposite flop functor
This implies that flop functors ![]() $F$ and
$F$ and ![]() $F^+$ yield (not mutually inverse) equivalences between
$F^+$ yield (not mutually inverse) equivalences between ![]() ${\mathcal {D}}^b(X)$ and
${\mathcal {D}}^b(X)$ and ![]() ${\mathcal {D}}^b(X^+)$. Following an argument of Chen [Reference ChenChe02], we generalise this statement to the case when base
${\mathcal {D}}^b(X^+)$. Following an argument of Chen [Reference ChenChe02], we generalise this statement to the case when base ![]() $Y$ is quasi-projective (see § 4.6).
$Y$ is quasi-projective (see § 4.6).
In addition, we show that the composite ![]() $F^+ F$, the ‘flop–flop’ functor, is the term-wise extension of
$F^+ F$, the ‘flop–flop’ functor, is the term-wise extension of ![]() $f^*f_*(-)|_{\mathscr {P}_{-1}}$.
$f^*f_*(-)|_{\mathscr {P}_{-1}}$.
The null category and spherical functor  $\Psi$
$\Psi$
One of the original motivations for our work was to recover the importance of the null category for ![]() $f$ as in (1). Category
$f$ as in (1). Category ![]() $\mathscr {A}_f$ admits a projective generator
$\mathscr {A}_f$ admits a projective generator ![]() ${\mathcal {P}}$, which we obtain from Van den Bergh's projective generator
${\mathcal {P}}$, which we obtain from Van den Bergh's projective generator ![]() $\mathcal {M}$ for the perverse heart
$\mathcal {M}$ for the perverse heart ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ by a projection to the null category (see Proposition 2.4). Deriving the embedding
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ by a projection to the null category (see Proposition 2.4). Deriving the embedding ![]() $\mathscr {A}_f \to \mathop {{\rm Coh}}\nolimits (X)$ gives us functor
$\mathscr {A}_f \to \mathop {{\rm Coh}}\nolimits (X)$ gives us functor
We prove that, for a flopping contraction ![]() $f \colon X \to Y$ with affine
$f \colon X \to Y$ with affine ![]() $Y$, functor
$Y$, functor ![]() $\Psi$ is spherical. The flop–flop functor
$\Psi$ is spherical. The flop–flop functor ![]() $F^+F$ is the spherical cotwist of the spherical couple
$F^+F$ is the spherical cotwist of the spherical couple ![]() $(\Psi ^*,\Psi )$, i.e. the
$(\Psi ^*,\Psi )$, i.e. the ![]() $\Psi ^* \dashv \Psi$ adjunction unit fits into a functorial exact triangle:
$\Psi ^* \dashv \Psi$ adjunction unit fits into a functorial exact triangle:
We also show that the spherical twist ![]() ${\mathcal {D}}^b(\mathscr {A}_f) \to {\mathcal {D}}^b(\mathscr {A}_f)$ of the couple
${\mathcal {D}}^b(\mathscr {A}_f) \to {\mathcal {D}}^b(\mathscr {A}_f)$ of the couple ![]() $(\Psi ^*,\Psi )$ is the shifted identity functor
$(\Psi ^*,\Psi )$ is the shifted identity functor ![]() $\mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(\mathscr {A}_f)}[4]$ (see Corollary 5.18).
$\mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(\mathscr {A}_f)}[4]$ (see Corollary 5.18).
Spherical pairs
We assume again ![]() $f \colon X\to Y$ to be a flopping contraction with affine
$f \colon X\to Y$ to be a flopping contraction with affine ![]() $Y$. Functor
$Y$. Functor ![]() $p^*$ induces an isomorphism of endomorphism algebras of a projective generator
$p^*$ induces an isomorphism of endomorphism algebras of a projective generator ![]() ${\mathcal {P}}\in \mathscr {A}_f$ and of
${\mathcal {P}}\in \mathscr {A}_f$ and of ![]() $p^* {\mathcal {P}}\in \mathop {{\rm Coh}}\nolimits (X \times _Y X^+)$. Moreover,
$p^* {\mathcal {P}}\in \mathop {{\rm Coh}}\nolimits (X \times _Y X^+)$. Moreover, ![]() $\mathop {{\rm Ext}}\nolimits ^i_{X\times _Y X^+}(p^*{\mathcal {P}}, p^* {\mathcal {P}}) = 0$, for
$\mathop {{\rm Ext}}\nolimits ^i_{X\times _Y X^+}(p^*{\mathcal {P}}, p^* {\mathcal {P}}) = 0$, for ![]() $i>0$ (see Proposition 5.3). Thus, we construct a fully faithful functor
$i>0$ (see Proposition 5.3). Thus, we construct a fully faithful functor ![]() ${\mathcal {D}}(\mathscr {A}_f) \to {\mathcal {D}}_{{\rm qc}}(X\times _Y X^+)$.
${\mathcal {D}}(\mathscr {A}_f) \to {\mathcal {D}}_{{\rm qc}}(X\times _Y X^+)$.
We consider the ‘common kernel subcategories’:
 \begin{align*} {\mathcal{K}}^b &= \{ E\in {\mathcal{D}}^b(X\times_Y X^+)\,|\, Rp_*(E) =0,\, Rp^+_*(E) =0\},\\ {\mathcal{K}}^- &= \{ E\in {\mathcal{D}}^-(X\times_Y X^+)\,|\, Rp_*(E) =0,\, Rp^+_*(E) =0\}. \end{align*}
\begin{align*} {\mathcal{K}}^b &= \{ E\in {\mathcal{D}}^b(X\times_Y X^+)\,|\, Rp_*(E) =0,\, Rp^+_*(E) =0\},\\ {\mathcal{K}}^- &= \{ E\in {\mathcal{D}}^-(X\times_Y X^+)\,|\, Rp_*(E) =0,\, Rp^+_*(E) =0\}. \end{align*}
The composite ![]() ${\mathcal {D}}^b(X) \xrightarrow {Lp^*} {\mathcal {D}}^-(X\times _Y X^+) \to {\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}^-$ (not
${\mathcal {D}}^b(X) \xrightarrow {Lp^*} {\mathcal {D}}^-(X\times _Y X^+) \to {\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}^-$ (not ![]() $Lp^*$ itself) factors via
$Lp^*$ itself) factors via ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$, thus inducing a fully faithful functor (Proposition 5.8)
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$, thus inducing a fully faithful functor (Proposition 5.8)
We prove the existence of SODs (see [Reference BondalBon89]):
As a result, we obtain a geometric description of the category ![]() ${\mathcal {D}}^b(\mathscr {A}_{f^+})$:
${\mathcal {D}}^b(\mathscr {A}_{f^+})$:
By exchanging the roles of ![]() $X$ and
$X$ and ![]() $X^+$ in (3) we obtain SODs
$X^+$ in (3) we obtain SODs
Together decompositions (3) and (4) provide us with a geometric description of 4-periodical SODs (see Proposition B.3), whose relation to spherical functors was basically discovered by Halpern-Leistner and Shipman [Reference Halpern-Leistner and ShipmanHS16] (we thank Kapranov for explanations on this). Two pairs of subcategories ![]() $({\mathcal {D}}^b(X), {\mathcal {D}}^b(X^+))$,
$({\mathcal {D}}^b(X), {\mathcal {D}}^b(X^+))$, ![]() $({\mathcal {D}}^b(\mathscr {A}_f), {\mathcal {D}}^b(\mathscr {A}_{f^+}))$ are spherical pairs [Reference Kapranov and SchechtmanKS14] (see Theorem 5.17). The corresponding spherical functor for the second spherical pair is
$({\mathcal {D}}^b(\mathscr {A}_f), {\mathcal {D}}^b(\mathscr {A}_{f^+}))$ are spherical pairs [Reference Kapranov and SchechtmanKS14] (see Theorem 5.17). The corresponding spherical functor for the second spherical pair is ![]() $\Psi$.
$\Psi$.
The contraction algebra
Assume the base ![]() $Y$ of the flopping contraction
$Y$ of the flopping contraction ![]() $f$ to be the spectrum of a complete Noetherian local ring. Then the reduced fiber of
$f$ to be the spectrum of a complete Noetherian local ring. Then the reduced fiber of ![]() $f$ over the unique closed point of
$f$ over the unique closed point of ![]() $Y$ is a union of
$Y$ is a union of ![]() $n$ smooth irreducible rational curves
$n$ smooth irreducible rational curves ![]() $C_1, \ldots, C_n$ (see Theorem D.1). The category
$C_1, \ldots, C_n$ (see Theorem D.1). The category ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ has
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ has ![]() $n+1$ irreducible projective objects
$n+1$ irreducible projective objects ![]() ${\mathcal {M}}_0, \ldots, {\mathcal {M}}_n$, with
${\mathcal {M}}_0, \ldots, {\mathcal {M}}_n$, with ![]() ${\mathcal {M}}_0 \simeq {\mathcal {O}}_X$ (see [Reference Van den BerghVdB04]).
${\mathcal {M}}_0 \simeq {\mathcal {O}}_X$ (see [Reference Van den BerghVdB04]). ![]() ${\mathcal {M}} = \bigoplus _{i=0}^n {\mathcal {M}}_i$ is a projective generator for
${\mathcal {M}} = \bigoplus _{i=0}^n {\mathcal {M}}_i$ is a projective generator for ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$.
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$.
We prove that the endomorphism algebra
of the corresponding projective generator for ![]() $\mathscr {A}_f$,
$\mathscr {A}_f$, ![]() ${\mathcal {P}}= \ker (f^*f_* {\mathcal {M}} \to {\mathcal {M}})$, is isomorphic to the contraction algebra introduced in [Reference Iyama and WemyssIW14], which is defined as the quotient of
${\mathcal {P}}= \ker (f^*f_* {\mathcal {M}} \to {\mathcal {M}})$, is isomorphic to the contraction algebra introduced in [Reference Iyama and WemyssIW14], which is defined as the quotient of ![]() $\mathop {{\rm Hom}}\nolimits _X( {\mathcal {M}}, {\mathcal {M}})$ by the ideal of morphisms that factor via direct sums of copies of
$\mathop {{\rm Hom}}\nolimits _X( {\mathcal {M}}, {\mathcal {M}})$ by the ideal of morphisms that factor via direct sums of copies of ![]() ${\mathcal {O}}_X$ (Theorem 6.2). This theorem relates our work to the results of Donovan and Wemyss [Reference Donovan and WemyssDW16, Reference Donovan and WemyssDW19], where contraction algebras appear in the context of non-commutative deformations.
${\mathcal {O}}_X$ (Theorem 6.2). This theorem relates our work to the results of Donovan and Wemyss [Reference Donovan and WemyssDW16, Reference Donovan and WemyssDW19], where contraction algebras appear in the context of non-commutative deformations.
Appendices
There are five appendices attached to the main body of the paper.
Appendix A. This appendix is an extract of some properties of the functor ![]() $f^!$, right dual to
$f^!$, right dual to ![]() $Rf_*$, and the Grothendieck duality.
$Rf_*$, and the Grothendieck duality.
Appendix B. In this appendix we introduce functorial exact triangles and use them to define spherical functors. We recall after [Reference Kapranov and SchechtmanKS14] the notion of a spherical pair and the associated spherical functor. 4-periodical SODs introduced by Halpern-Leistner and Shipman [Reference Halpern-Leistner and ShipmanHS16] produce spherical pairs.
Appendix C. In this appendix we discuss a bicategory ![]() ${\mathcal {C}}$ and a pair of 1-morphisms
${\mathcal {C}}$ and a pair of 1-morphisms ![]() $s\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,B)$,
$s\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,B)$, ![]() $r\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,A)$ that fit into a 2-categorical adjunction
$r\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,A)$ that fit into a 2-categorical adjunction ![]() $(s,r,\eta,\varepsilon )$. When
$(s,r,\eta,\varepsilon )$. When ![]() ${\mathcal {C}}$ is 1-triangulated (meaning the categories of 1-morphisms are triangulated), we define the twist
${\mathcal {C}}$ is 1-triangulated (meaning the categories of 1-morphisms are triangulated), we define the twist ![]() $t_s\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,B)$ and the cotwist
$t_s\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,B)$ and the cotwist ![]() $c_s\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,A)$ as the cones of the counit
$c_s\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,A)$ as the cones of the counit ![]() $\varepsilon \colon sr\to \mathop {{\rm Id}}\nolimits _B$ and the unit
$\varepsilon \colon sr\to \mathop {{\rm Id}}\nolimits _B$ and the unit ![]() $\eta \colon \mathop {{\rm Id}}\nolimits _A\to rs$. By using pseudo-functors and 2-categorical equivalences we show that the twist and cotwist are in a suitable sense invariant under replacing
$\eta \colon \mathop {{\rm Id}}\nolimits _A\to rs$. By using pseudo-functors and 2-categorical equivalences we show that the twist and cotwist are in a suitable sense invariant under replacing ![]() $A$ and
$A$ and ![]() $B$ by equivalent objects. If
$B$ by equivalent objects. If ![]() $t_s$ and
$t_s$ and ![]() $c_s$ are invertible in the 2-categorical sense, we say that
$c_s$ are invertible in the 2-categorical sense, we say that ![]() $(s,r,\eta, \varepsilon )$ is a spherical couple.
$(s,r,\eta, \varepsilon )$ is a spherical couple.
We lift exact functors between triangulated categories to 1-morphisms in appropriate 1-triangulated bicategories. The first bicategory is ![]() $\mathop {\textbf {Bimod}}\nolimits$ whose objects are DG algebras and categories of 1-morphisms are defined as the derived categories of DG bimodules. The second one is the Fourier–Mukai bicategory FM of schemes and the derived categories of coherent sheaves on their products as categories of 1-morphisms. Both bicategories admit 2-functors to the bicategory
$\mathop {\textbf {Bimod}}\nolimits$ whose objects are DG algebras and categories of 1-morphisms are defined as the derived categories of DG bimodules. The second one is the Fourier–Mukai bicategory FM of schemes and the derived categories of coherent sheaves on their products as categories of 1-morphisms. Both bicategories admit 2-functors to the bicategory ![]() $\textbf {Cat}$ of categories, functors and natural transformations. More precisely, we have
$\textbf {Cat}$ of categories, functors and natural transformations. More precisely, we have ![]() $\Phi \colon \mathop {\textbf {Bimod}}\nolimits \to \textbf {Cat}$,
$\Phi \colon \mathop {\textbf {Bimod}}\nolimits \to \textbf {Cat}$, ![]() $\Phi (A) = {\mathcal {D}}(A)$ and
$\Phi (A) = {\mathcal {D}}(A)$ and ![]() $\Xi \colon \mathop {\textbf {FM}}\nolimits \to \textbf {Cat}$,
$\Xi \colon \mathop {\textbf {FM}}\nolimits \to \textbf {Cat}$, ![]() $\Xi (X) = {\mathcal {D}}_{{\rm qc}}(X)$.
$\Xi (X) = {\mathcal {D}}_{{\rm qc}}(X)$.
The above theory of 2-categorical adjunctions ensures that once a lift of an exact functor ![]() ${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ to a 1-morphism in
${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ to a 1-morphism in ![]() $\mathop {\textbf {Bimod}}\nolimits$ or
$\mathop {\textbf {Bimod}}\nolimits$ or ![]() $\mathop {\textbf {FM}}\nolimits$ admitting an adjoint is fixed, we obtain essentially unique exact functors corresponding to the twist and the cotwist.
$\mathop {\textbf {FM}}\nolimits$ admitting an adjoint is fixed, we obtain essentially unique exact functors corresponding to the twist and the cotwist.
We describe 2-categorical adjunctions in ![]() $\mathop {\textbf {Bimod}}\nolimits$ using formulae for adjoint bimodules as in [Reference Anno and LogvinenkoAL21]. For
$\mathop {\textbf {Bimod}}\nolimits$ using formulae for adjoint bimodules as in [Reference Anno and LogvinenkoAL21]. For ![]() ${\mathcal {E}}\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$ we discuss functors adjoint to
${\mathcal {E}}\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$ we discuss functors adjoint to ![]() $\Xi _{\mathcal {E}}\colon {\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ and the conditions under which they are FM functors. Results of [Reference Lunts and SchnürerLS16] allow us to transfer between
$\Xi _{\mathcal {E}}\colon {\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ and the conditions under which they are FM functors. Results of [Reference Lunts and SchnürerLS16] allow us to transfer between ![]() $\mathop {\textbf {Bimod}}\nolimits$ and
$\mathop {\textbf {Bimod}}\nolimits$ and ![]() $\mathop {\textbf {FM}}\nolimits$ via fixing compact generators for
$\mathop {\textbf {FM}}\nolimits$ via fixing compact generators for ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ and
${\mathcal {D}}_{{\rm qc}}(X)$ and ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$. We use the 2-categorical adjunctions in
${\mathcal {D}}_{{\rm qc}}(Y)$. We use the 2-categorical adjunctions in ![]() $\mathop {\textbf {Bimod}}\nolimits$ to construct functorial exact triangles for
$\mathop {\textbf {Bimod}}\nolimits$ to construct functorial exact triangles for ![]() $\Xi _{\mathcal {E}}$ and its adjoints. We check that these triangles are, up to isomorphism, independent of the choice of compact generators. In particular, given a morphism
$\Xi _{\mathcal {E}}$ and its adjoints. We check that these triangles are, up to isomorphism, independent of the choice of compact generators. In particular, given a morphism ![]() $f\colon X \to Y$, we discuss the lift of
$f\colon X \to Y$, we discuss the lift of ![]() $Rf_*$, its adjoints, and the adjunction (co)units to
$Rf_*$, its adjoints, and the adjunction (co)units to ![]() $\mathop {\textbf {Bimod}}\nolimits$ and
$\mathop {\textbf {Bimod}}\nolimits$ and ![]() $\mathop {\textbf {FM}}\nolimits$. We also describe a 2-morphism in
$\mathop {\textbf {FM}}\nolimits$. We also describe a 2-morphism in ![]() $\mathop {\textbf {Bimod}}\nolimits$ whose image under
$\mathop {\textbf {Bimod}}\nolimits$ whose image under ![]() $\Phi$ is the base-change morphism.
$\Phi$ is the base-change morphism.
Appendix D. This appendix is devoted to the description of the reduced fiber of a flopping contraction ![]() $f \colon X\to Y$ with fibers of dimension bounded by one over a closed point of
$f \colon X\to Y$ with fibers of dimension bounded by one over a closed point of ![]() $Y$.
$Y$.
Appendix E. In this appendix we show that cohomology of an appropriate complex allow us to calculate morphisms in the derived category of an abelian category between bounded above complexes with bounded cohomology.
Notation
We denote by ![]() $k$ an algebraically closed field of characteristic zero. For a Noetherian
$k$ an algebraically closed field of characteristic zero. For a Noetherian ![]() $k$ scheme
$k$ scheme ![]() $X$, by
$X$, by ![]() $\mathop {{\rm Coh}}\nolimits (X)$, respectively
$\mathop {{\rm Coh}}\nolimits (X)$, respectively ![]() ${\rm QCoh}(X)$, we denote the category of coherent, respectively quasi-coherent, sheaves on
${\rm QCoh}(X)$, we denote the category of coherent, respectively quasi-coherent, sheaves on ![]() $X$.
$X$.
For an abelian category ![]() ${\mathcal {A}}$, we denote by
${\mathcal {A}}$, we denote by ![]() ${\mathcal {D}}^b({\mathcal {A}})$ and
${\mathcal {D}}^b({\mathcal {A}})$ and ![]() ${\mathcal {D}}({\mathcal {A}})$ the bounded and unbounded derived categories of
${\mathcal {D}}({\mathcal {A}})$ the bounded and unbounded derived categories of ![]() ${\mathcal {A}}$. We write
${\mathcal {A}}$. We write ![]() ${\mathcal {D}}^b(X) = {\mathcal {D}}^b(\mathop {{\rm Coh}}\nolimits (X))$,
${\mathcal {D}}^b(X) = {\mathcal {D}}^b(\mathop {{\rm Coh}}\nolimits (X))$, ![]() ${\mathcal {D}}_{{\rm qc}}(X) = {\mathcal {D}}({\rm QCoh}(X))$.
${\mathcal {D}}_{{\rm qc}}(X) = {\mathcal {D}}({\rm QCoh}(X))$.
For an abelian category ![]() ${\mathcal {A}}$, by
${\mathcal {A}}$, by ![]() ${\rm Perf}({\mathcal {A}})$ we denote the full subcategory of
${\rm Perf}({\mathcal {A}})$ we denote the full subcategory of ![]() ${\mathcal {D}}^b({\mathcal {A}})$ of objects that are quasi-isomorphic to finite complexes of projective objects in
${\mathcal {D}}^b({\mathcal {A}})$ of objects that are quasi-isomorphic to finite complexes of projective objects in ![]() ${\mathcal {A}}$. For a scheme
${\mathcal {A}}$. For a scheme ![]() $X$, by
$X$, by ![]() ${\rm Perf}(X)$ we denote the category of perfect complexes on
${\rm Perf}(X)$ we denote the category of perfect complexes on ![]() $X$, i.e. objects of
$X$, i.e. objects of ![]() ${\mathcal {D}}^b(X)$ locally quasi-isomorphic to finite complexes of locally free sheaves.
${\mathcal {D}}^b(X)$ locally quasi-isomorphic to finite complexes of locally free sheaves.
For a ![]() $k$-algebra
$k$-algebra ![]() $A$, we denote by
$A$, we denote by ![]() ${\rm Mod}\unicode{x2013}A$ the abelian category of right
${\rm Mod}\unicode{x2013}A$ the abelian category of right ![]() $A$ modules.
$A$ modules.
For a ![]() $t$-structure
$t$-structure ![]() $({\mathcal {T}}_{\leqslant 0}, {\mathcal {T}}_{\geqslant 0})$ on a triangulated category
$({\mathcal {T}}_{\leqslant 0}, {\mathcal {T}}_{\geqslant 0})$ on a triangulated category ![]() ${\mathcal {T}}$ with heart
${\mathcal {T}}$ with heart ![]() ${\mathcal {A}} = {\mathcal {T}}_{\leqslant 0 }\cap {\mathcal {T}}_{\geqslant 0}$ and an object
${\mathcal {A}} = {\mathcal {T}}_{\leqslant 0 }\cap {\mathcal {T}}_{\geqslant 0}$ and an object ![]() $T \in {\mathcal {T}}$, we denote by
$T \in {\mathcal {T}}$, we denote by ![]() ${\mathcal {H}}_{{\mathcal {A}}}^i(T)$ the
${\mathcal {H}}_{{\mathcal {A}}}^i(T)$ the ![]() $i$th cohomology of
$i$th cohomology of ![]() $T$ with respect to the
$T$ with respect to the ![]() $t$-structure
$t$-structure ![]() $({\mathcal {T}}_{\leqslant 0}, {\mathcal {T}}_{\geqslant 0})$. The truncation functors are denoted by
$({\mathcal {T}}_{\leqslant 0}, {\mathcal {T}}_{\geqslant 0})$. The truncation functors are denoted by ![]() $\tau _{\geqslant i}^{{\mathcal {A}}}$ and
$\tau _{\geqslant i}^{{\mathcal {A}}}$ and ![]() $\tau ^{{\mathcal {A}}}_{\leqslant i}$. If
$\tau ^{{\mathcal {A}}}_{\leqslant i}$. If ![]() ${\mathcal {T}} = {\mathcal {D}}_{{\rm qc}}(X)$ or
${\mathcal {T}} = {\mathcal {D}}_{{\rm qc}}(X)$ or ![]() ${\mathcal {D}}^b(X)$ with the standard
${\mathcal {D}}^b(X)$ with the standard ![]() $t$-structure with heart
$t$-structure with heart ![]() ${\rm QCoh}(X)$, respectively
${\rm QCoh}(X)$, respectively ![]() $\mathop {{\rm Coh}}\nolimits (X)$, we shorten the notation to
$\mathop {{\rm Coh}}\nolimits (X)$, we shorten the notation to ![]() ${\mathcal {H}}_X^i(T)$,
${\mathcal {H}}_X^i(T)$, ![]() $\tau _{\geqslant i}^X$ and
$\tau _{\geqslant i}^X$ and ![]() $\tau _{\leqslant i}^X$ respectively.
$\tau _{\leqslant i}^X$ respectively.
Assumptions
Throughout the paper we assume ![]() $X$ and
$X$ and ![]() $Y$ to be normal varieties over
$Y$ to be normal varieties over ![]() $k$. We usually work under one of the following assumptions on a morphism
$k$. We usually work under one of the following assumptions on a morphism ![]() $f\colon X\to Y$.
$f\colon X\to Y$.
(a) We assume
 $f\colon X\to Y$ is a proper morphism with dimension of fibers bounded by one and such that
$f\colon X\to Y$ is a proper morphism with dimension of fibers bounded by one and such that  $Rf_* {\mathcal {O}}_X \simeq {\mathcal {O}}_Y$.
$Rf_* {\mathcal {O}}_X \simeq {\mathcal {O}}_Y$.(b) We assume
 $f\colon X\to Y$ is a projective birational morphism with dimension of fibers bounded by one between quasi-projective Gorenstein varieties of dimension
$f\colon X\to Y$ is a projective birational morphism with dimension of fibers bounded by one between quasi-projective Gorenstein varieties of dimension  $n\geqslant 3$. The exceptional locus of
$n\geqslant 3$. The exceptional locus of  $f$ is of codimension greater than one in
$f$ is of codimension greater than one in  $X$. Variety
$X$. Variety  $Y$ has canonical hypersurface singularities of multiplicity two.
$Y$ has canonical hypersurface singularities of multiplicity two.(c) We assume the same as in assumption (p) and we further assume that variety
 $Y$ is affine and is embedded as a principal divisor into a smooth variety
$Y$ is affine and is embedded as a principal divisor into a smooth variety  ${\mathcal {Y}}$ of dimension
${\mathcal {Y}}$ of dimension  $n+1$.
$n+1$.(d) We assume the same as in assumption (p) with an extra assumption that
 $Y= \mathop {{\rm Spec}}\nolimits R$, where
$Y= \mathop {{\rm Spec}}\nolimits R$, where  $R$ is a complete local
$R$ is a complete local  $k$-algebra.
$k$-algebra.
Let ![]() $f$ satisfy assumption (p). As
$f$ satisfy assumption (p). As ![]() $Y$ has canonical singularities,
$Y$ has canonical singularities, ![]() $Rf_* {\mathcal {O}}_X \simeq {\mathcal {O}}_Y$ (cf. [Reference ElkikElk81]), i.e. assumption (d) is satisfied when
$Rf_* {\mathcal {O}}_X \simeq {\mathcal {O}}_Y$ (cf. [Reference ElkikElk81]), i.e. assumption (d) is satisfied when ![]() $Y$ has rational singularities and
$Y$ has rational singularities and ![]() $f\colon X\to Y$ is a smooth birational resolution.
$f\colon X\to Y$ is a smooth birational resolution.
2. The null category  $\mathscr {A}_f$
$\mathscr {A}_f$
Let ![]() $f\colon X \to Y$ be a proper morphism of Noetherian schemes. In this section we introduce the null category of
$f\colon X \to Y$ be a proper morphism of Noetherian schemes. In this section we introduce the null category of ![]() $f$:
$f$:
Under the assumption that the dimension of fibers of ![]() $f$ is bounded by one,
$f$ is bounded by one, ![]() $Y$ is affine and
$Y$ is affine and ![]() $Rf_*{\mathcal {O}}_X = {\mathcal {O}}_Y$, we construct a projective generator
$Rf_*{\mathcal {O}}_X = {\mathcal {O}}_Y$, we construct a projective generator ![]() ${\mathcal {P}}$ for
${\mathcal {P}}$ for ![]() $\mathscr {A}_f$. We also study the behaviour of the null category under decomposition
$\mathscr {A}_f$. We also study the behaviour of the null category under decomposition ![]() $f = h \circ g$ and under restriction to fibers.
$f = h \circ g$ and under restriction to fibers.
2.1 The triangulated and abelian null category of a morphism of schemes
For a proper morphism of Noetherian schemes ![]() $f \colon X \to Y$, we consider the triangulated null category
$f \colon X \to Y$, we consider the triangulated null category ![]() ${\mathcal {C}}_f$ defined as the kernel of functor
${\mathcal {C}}_f$ defined as the kernel of functor ![]() $Rf_*$ restricted to
$Rf_*$ restricted to ![]() ${\mathcal {D}}^b(X)$:
${\mathcal {D}}^b(X)$:
Similarly, we define ![]() ${\mathcal {C}}_f^- \subset {\mathcal {D}}^-(X)$ and
${\mathcal {C}}_f^- \subset {\mathcal {D}}^-(X)$ and ![]() ${{\mathcal {C}}_f}_{{\rm qc}} \subset {\mathcal {D}}_{{\rm qc}}(X)$. Denote by
${{\mathcal {C}}_f}_{{\rm qc}} \subset {\mathcal {D}}_{{\rm qc}}(X)$. Denote by ![]() ${\iota _f}_* \colon {{\mathcal {C}}_f}_{{\rm qc}} \to {\mathcal {D}}_{{\rm qc}}(X)$ the inclusion functor. As
${\iota _f}_* \colon {{\mathcal {C}}_f}_{{\rm qc}} \to {\mathcal {D}}_{{\rm qc}}(X)$ the inclusion functor. As ![]() $Lf^*\colon {\mathcal {D}}_{{\rm qc}}(Y) \to {\mathcal {D}}_{{\rm qc}}(X)$ is fully faithful with right adjoint
$Lf^*\colon {\mathcal {D}}_{{\rm qc}}(Y) \to {\mathcal {D}}_{{\rm qc}}(X)$ is fully faithful with right adjoint ![]() $Rf_*$,
$Rf_*$, ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ admits a SOD
${\mathcal {D}}_{{\rm qc}}(X)$ admits a SOD ![]() ${\mathcal {D}}_{{\rm qc}}(X) = \langle {{\mathcal {C}}_f}_{{\rm qc}}, Lf^*{\mathcal {D}}_{{\rm qc}}(Y)\rangle$, [Reference BondalBon89, Lemma 3.1]. In particular,
${\mathcal {D}}_{{\rm qc}}(X) = \langle {{\mathcal {C}}_f}_{{\rm qc}}, Lf^*{\mathcal {D}}_{{\rm qc}}(Y)\rangle$, [Reference BondalBon89, Lemma 3.1]. In particular, ![]() ${\iota _f}_*$ admits a left adjoint
${\iota _f}_*$ admits a left adjoint ![]() $\iota _f^*\colon {\mathcal {D}}_{{\rm qc}}(X)\to {{\mathcal {C}}_f}_{{\rm qc}}$, which fits into a functorial exact triangle (see (B.1)):
$\iota _f^*\colon {\mathcal {D}}_{{\rm qc}}(X)\to {{\mathcal {C}}_f}_{{\rm qc}}$, which fits into a functorial exact triangle (see (B.1)):
For the null category of ![]() $f$ as in (5), we have
$f$ as in (5), we have ![]() $\mathscr {A}_f=\mathop {{\rm Coh}}\nolimits (X)\cap {\mathcal {C}}_f$.
$\mathscr {A}_f=\mathop {{\rm Coh}}\nolimits (X)\cap {\mathcal {C}}_f$.
Lemma 2.1 Let ![]() $f \colon X \to Y$ be a proper morphism with dimension of fibers bounded by one. Then category
$f \colon X \to Y$ be a proper morphism with dimension of fibers bounded by one. Then category ![]() $\mathscr {A}_f$ is abelian. The embedding functor
$\mathscr {A}_f$ is abelian. The embedding functor ![]() $\mathscr {A}_f \to \mathop {{\rm Coh}}\nolimits (X)$ is exact and fully faithful. Its image is closed under extensions.
$\mathscr {A}_f \to \mathop {{\rm Coh}}\nolimits (X)$ is exact and fully faithful. Its image is closed under extensions.
Proof. Let ![]() $A, B$ be objects in
$A, B$ be objects in ![]() $\mathscr {A}_f$ and let
$\mathscr {A}_f$ and let ![]() $\varphi \in \mathop {{\rm Hom}}\nolimits _X(A,B)$. Consider the kernel
$\varphi \in \mathop {{\rm Hom}}\nolimits _X(A,B)$. Consider the kernel ![]() $K$, the cokernel
$K$, the cokernel ![]() $C$, and the image
$C$, and the image ![]() $I$ of
$I$ of ![]() $\varphi$. As
$\varphi$. As ![]() $Rf_*A \simeq 0 \simeq Rf_* B$, the long exact sequences of higher derived functors for
$Rf_*A \simeq 0 \simeq Rf_* B$, the long exact sequences of higher derived functors for ![]() $f_*$ applied to short exact sequences on
$f_*$ applied to short exact sequences on ![]() $X$
$X$
together with vanishing of ![]() $R^if_*$, for
$R^if_*$, for ![]() $i>1$, imply that first
$i>1$, imply that first ![]() $I$, hence
$I$, hence ![]() $K$ and
$K$ and ![]() $C$ lie in
$C$ lie in ![]() $\mathscr {A}_f$. That
$\mathscr {A}_f$. That ![]() $\mathscr {A}_f$ is closed under extensions is obvious.
$\mathscr {A}_f$ is closed under extensions is obvious.
It follows that ![]() $\mathop {{\rm Ext}}\nolimits ^1_X(A,B)=\mathop {{\rm Ext}}\nolimits ^1_{\mathscr {A}_f}(A,B)$, for
$\mathop {{\rm Ext}}\nolimits ^1_X(A,B)=\mathop {{\rm Ext}}\nolimits ^1_{\mathscr {A}_f}(A,B)$, for ![]() $A, B \in \mathscr {A}_f$.
$A, B \in \mathscr {A}_f$.
Lemma 2.2 [Reference BridgelandBri02, Lemma 3.1]
Let ![]() $X$ and
$X$ and ![]() $Y$ be Noetherian schemes and
$Y$ be Noetherian schemes and ![]() $f \colon X \to Y$ a proper morphism with fibers of dimension bounded by one. Then
$f \colon X \to Y$ a proper morphism with fibers of dimension bounded by one. Then ![]() $E\in {\mathcal {C}}_f$ if and only if
$E\in {\mathcal {C}}_f$ if and only if ![]() ${\mathcal {H}}^i_X(E)\in \mathscr {A}_f$, for all
${\mathcal {H}}^i_X(E)\in \mathscr {A}_f$, for all ![]() $i\in \mathbb {Z}$. In particular,
$i\in \mathbb {Z}$. In particular, ![]() $\mathscr {A}_f \subset {\mathcal {C}}_f$ is the heart of a bounded
$\mathscr {A}_f \subset {\mathcal {C}}_f$ is the heart of a bounded ![]() $t$-structure.
$t$-structure.
Remark 2.3 The restriction of the standard ![]() $t$-structure on
$t$-structure on ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ to
${\mathcal {D}}_{{\rm qc}}(X)$ to
was considered by Bridgeland [Reference BridgelandBri02] for a birational morphism of projective varieties satisfying assumption (d) which is easily generalised to a projective morphism ![]() $f\colon X\to Y$ satisfying assumption (d). In this case, category
$f\colon X\to Y$ satisfying assumption (d). In this case, category ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ admits a recollement [Reference Beĭlinson, Bernstein and DeligneBBD82] or, equivalently, an admissible subcategory,
${\mathcal {D}}_{{\rm qc}}(X)$ admits a recollement [Reference Beĭlinson, Bernstein and DeligneBBD82] or, equivalently, an admissible subcategory, ![]() ${{\mathcal {C}}_f}_{{\rm qc}}$ (see [Reference BondalBon89]). The Verdier quotient
${{\mathcal {C}}_f}_{{\rm qc}}$ (see [Reference BondalBon89]). The Verdier quotient ![]() ${\mathcal {D}}_{{\rm qc}}(X)/ {{\mathcal {C}}_f}_{{\rm qc}}$ is identified with
${\mathcal {D}}_{{\rm qc}}(X)/ {{\mathcal {C}}_f}_{{\rm qc}}$ is identified with ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$. The
${\mathcal {D}}_{{\rm qc}}(Y)$. The ![]() $t$-structure on
$t$-structure on ![]() ${{\mathcal {C}}_f}_{{\rm qc}}$ with heart
${{\mathcal {C}}_f}_{{\rm qc}}$ with heart ![]() $\mathscr {A}_f[-p]$ can be glued with the standard
$\mathscr {A}_f[-p]$ can be glued with the standard ![]() $t$-structure on
$t$-structure on ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$ (see [Reference Beĭlinson, Bernstein and DeligneBBD82]). As functor
${\mathcal {D}}_{{\rm qc}}(Y)$ (see [Reference Beĭlinson, Bernstein and DeligneBBD82]). As functor ![]() $f^!$ is needed for the gluing of
$f^!$ is needed for the gluing of ![]() $t$-structures, one has to consider unbounded derived categories of quasi-coherent sheaves on
$t$-structures, one has to consider unbounded derived categories of quasi-coherent sheaves on ![]() $X$ and
$X$ and ![]() $Y$. The heart of the resulting
$Y$. The heart of the resulting ![]() $t$-structure is the category
$t$-structure is the category ![]() ${}^p{\rm Per}_{{\rm qc}}(X/Y)$ of perverse sheaves. If
${}^p{\rm Per}_{{\rm qc}}(X/Y)$ of perverse sheaves. If ![]() $p=-1$ or
$p=-1$ or ![]() $p=0$, the
$p=0$, the ![]() $t$-structures with hearts
$t$-structures with hearts ![]() ${}^p{\rm Per}_{{\rm qc}}(X/Y)$ can also be obtained by the tilting in torsion pairs
${}^p{\rm Per}_{{\rm qc}}(X/Y)$ can also be obtained by the tilting in torsion pairs ![]() $({\mathcal {T}}_{-1}, {\mathcal {F}}_{-1})$,
$({\mathcal {T}}_{-1}, {\mathcal {F}}_{-1})$, ![]() $({\mathcal {T}}_{0}, {\mathcal {F}}_{0})$ in
$({\mathcal {T}}_{0}, {\mathcal {F}}_{0})$ in ![]() ${\rm QCoh(X)}$ (see [Reference Van den BerghVdB04]), where
${\rm QCoh(X)}$ (see [Reference Van den BerghVdB04]), where
By restricting the torsion pairs to ![]() $\mathop {{\rm Coh}}\nolimits (X)$ one can define abelian categories
$\mathop {{\rm Coh}}\nolimits (X)$ one can define abelian categories ![]() ${}^p{\rm Per}(X/Y)$ as subcategories of
${}^p{\rm Per}(X/Y)$ as subcategories of ![]() ${\mathcal {D}}^{b}(X)$. Thus, for
${\mathcal {D}}^{b}(X)$. Thus, for ![]() $p=-1,0$,
$p=-1,0$,
2.2 A projective generator for  $\mathscr {A}_f$
$\mathscr {A}_f$
Let ![]() $f\colon X\to Y$ satisfy assumption (d) and assume
$f\colon X\to Y$ satisfy assumption (d) and assume ![]() $Y$ is affine. By [Reference Van den BerghVdB04, Proposition 3.2.5], there exists a vector bundle
$Y$ is affine. By [Reference Van den BerghVdB04, Proposition 3.2.5], there exists a vector bundle ![]() ${\mathcal {M}}$ on
${\mathcal {M}}$ on ![]() $X$ which is a projective generator for
$X$ which is a projective generator for ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Consider
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Consider
It is an object in ![]() $\mathscr {A}_f$, which, by abuse of notation, we identify with its image under
$\mathscr {A}_f$, which, by abuse of notation, we identify with its image under ![]() $\iota _{f*}$.
$\iota _{f*}$.
Proposition 2.4 Sheaf ![]() ${\mathcal {P}}$ is a projective generator for the category
${\mathcal {P}}$ is a projective generator for the category ![]() $\mathscr {A}_f$.
$\mathscr {A}_f$.
Proof. As the ![]() $t$-structure on
$t$-structure on ![]() ${{\mathcal {C}}_f}_{{\rm qc}}$ is defined as the restriction of the standard
${{\mathcal {C}}_f}_{{\rm qc}}$ is defined as the restriction of the standard ![]() $t$-structure on
$t$-structure on ![]() ${\mathcal {D}}_{{\rm qc}}(X)$, the functor
${\mathcal {D}}_{{\rm qc}}(X)$, the functor ![]() $\iota _{f*} \colon {{\mathcal {C}}_f}_{{\rm qc}} \to {\mathcal {D}}_{\rm qc}(X)$ is exact, in particular, it commutes with the truncation functors
$\iota _{f*} \colon {{\mathcal {C}}_f}_{{\rm qc}} \to {\mathcal {D}}_{\rm qc}(X)$ is exact, in particular, it commutes with the truncation functors ![]() $\tau _{\geqslant i}$. This implies isomorphism of functors
$\tau _{\geqslant i}$. This implies isomorphism of functors
It follows that ![]() $\tau ^X_{\geqslant -1} \iota _{f*} \iota _f^* {\mathcal {M}}$ is isomorphic to
$\tau ^X_{\geqslant -1} \iota _{f*} \iota _f^* {\mathcal {M}}$ is isomorphic to ![]() $\iota _{f*}\circ {}^{-1}\iota _f^* {\mathcal {M}}$, where
$\iota _{f*}\circ {}^{-1}\iota _f^* {\mathcal {M}}$, where
is the left adjoint functor to the inclusion ![]() $\mathscr {A}_f[1] \to \mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. By Lemma 2.5,
$\mathscr {A}_f[1] \to \mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. By Lemma 2.5, ![]() ${\mathcal {P}}\in \mathscr {A}_f$ is a projective generator.
${\mathcal {P}}\in \mathscr {A}_f$ is a projective generator.
Lemma 2.5 Let ![]() ${\mathcal {D}}_0$ and
${\mathcal {D}}_0$ and ![]() ${\mathcal {D}}$ be triangulated categories with
${\mathcal {D}}$ be triangulated categories with ![]() $t$-structures with hearts
$t$-structures with hearts ![]() ${\mathcal {A}}_0\subset {\mathcal {D}}_0$ and
${\mathcal {A}}_0\subset {\mathcal {D}}_0$ and ![]() ${\mathcal {A}}\subset {\mathcal {D}}$, and
${\mathcal {A}}\subset {\mathcal {D}}$, and ![]() $i_*\colon {\mathcal {D}}_0 \to {\mathcal {D}}$ a
$i_*\colon {\mathcal {D}}_0 \to {\mathcal {D}}$ a ![]() $t$-exact functor with left adjoint
$t$-exact functor with left adjoint ![]() $i^*$. If
$i^*$. If ![]() ${\mathcal {M}} \in {\mathcal {A}}$ is projective, then
${\mathcal {M}} \in {\mathcal {A}}$ is projective, then ![]() ${\mathcal {P}}:={\mathcal {H}}^0(i^* {\mathcal {M}}) \in {\mathcal {A}}_0$ is projective. Moreover, if
${\mathcal {P}}:={\mathcal {H}}^0(i^* {\mathcal {M}}) \in {\mathcal {A}}_0$ is projective. Moreover, if ![]() ${\mathcal {M}} \in {\mathcal {A}}$ is a projective generator and
${\mathcal {M}} \in {\mathcal {A}}$ is a projective generator and ![]() $i_*$ is fully faithful, then
$i_*$ is fully faithful, then ![]() ${\mathcal {P}} \in {\mathcal {A}}_0$ is a projective generator.
${\mathcal {P}} \in {\mathcal {A}}_0$ is a projective generator.
Proof. Let ![]() $E$ be an object in
$E$ be an object in ![]() ${\mathcal {A}}_0$. Then
${\mathcal {A}}_0$. Then ![]() $i_*E \in {\mathcal {A}}$, hence
$i_*E \in {\mathcal {A}}$, hence ![]() $0=\mathop {{\rm Ext}}\nolimits ^1_{{\mathcal {D}}}({\mathcal {M}}, i_*E) \simeq \mathop {{\rm Ext}}\nolimits ^1_{{\mathcal {D}}_0}(i^*{\mathcal {M}}, E)$. As functor
$0=\mathop {{\rm Ext}}\nolimits ^1_{{\mathcal {D}}}({\mathcal {M}}, i_*E) \simeq \mathop {{\rm Ext}}\nolimits ^1_{{\mathcal {D}}_0}(i^*{\mathcal {M}}, E)$. As functor ![]() $i^*$ is left adjoint to a
$i^*$ is left adjoint to a ![]() $t$-exact functor, it is right
$t$-exact functor, it is right ![]() $t$-exact, i.e.
$t$-exact, i.e. ![]() $i^* {\mathcal {M}} \in {\mathcal {D}}_0^{\leqslant 0}$. Thus, we have an exact triangle
$i^* {\mathcal {M}} \in {\mathcal {D}}_0^{\leqslant 0}$. Thus, we have an exact triangle
As, for degree reasons, ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}(\tau _{\leqslant -1}i^*M, E) =0$, by applying
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}(\tau _{\leqslant -1}i^*M, E) =0$, by applying ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}(-,E)$ to (13), we get that
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}(-,E)$ to (13), we get that ![]() $\mathop {{\rm Ext}}\nolimits ^1_{{\mathcal {D}}_0}({\mathcal {P}}, E)=0$, i.e.
$\mathop {{\rm Ext}}\nolimits ^1_{{\mathcal {D}}_0}({\mathcal {P}}, E)=0$, i.e. ![]() ${\mathcal {P}}\in {\mathcal {A}}_0$ is projective.
${\mathcal {P}}\in {\mathcal {A}}_0$ is projective.
If ![]() ${\mathcal {M}}\in {\mathcal {A}}$ is a projective generator and
${\mathcal {M}}\in {\mathcal {A}}$ is a projective generator and ![]() $i_*$ is fully faithful, then, for any non-zero
$i_*$ is fully faithful, then, for any non-zero ![]() $E\in {\mathcal {A}}_0$, object
$E\in {\mathcal {A}}_0$, object ![]() $i_*E$ is non-zero, hence
$i_*E$ is non-zero, hence ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}}({\mathcal {M}}, i_*E) \simeq \mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}(i^*{\mathcal {M}}, E)\neq 0$. It follows from the long exact sequence obtained by applying
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}}({\mathcal {M}}, i_*E) \simeq \mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}(i^*{\mathcal {M}}, E)\neq 0$. It follows from the long exact sequence obtained by applying ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}(-,E)$ to (13) that
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}(-,E)$ to (13) that ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}({\mathcal {P}}, E) \neq 0$, i.e.
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}_0}({\mathcal {P}}, E) \neq 0$, i.e. ![]() ${\mathcal {P}}$ is a projective generator for
${\mathcal {P}}$ is a projective generator for ![]() ${\mathcal {A}}_0$.
${\mathcal {A}}_0$.
Remark 2.6 If morphism ![]() $f$ satisfies assumption (d) and
$f$ satisfies assumption (d) and ![]() $Y$ is affine, the category
$Y$ is affine, the category ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ has a projective generator
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ has a projective generator ![]() ${\mathcal {N}} = {\mathcal {M}}^{\vee }$ (see [Reference Van den BerghVdB04, Proposition 3.2.5]). An argument analogous to that in the proof of Proposition 2.4 shows that
${\mathcal {N}} = {\mathcal {M}}^{\vee }$ (see [Reference Van den BerghVdB04, Proposition 3.2.5]). An argument analogous to that in the proof of Proposition 2.4 shows that ![]() ${\mathcal {P}}_{{\mathcal {N}}} := {\mathcal {H}}_X^0 \iota _f^* {\mathcal {N}}$ is a projective generator for
${\mathcal {P}}_{{\mathcal {N}}} := {\mathcal {H}}_X^0 \iota _f^* {\mathcal {N}}$ is a projective generator for ![]() $\mathscr {A}_f$.
$\mathscr {A}_f$.
For a sheaf ![]() $F$ with
$F$ with ![]() $R^1f_*F=0$, the cohomology sequence of triangle (7) applied to
$R^1f_*F=0$, the cohomology sequence of triangle (7) applied to ![]() $F$ gives an exact sequence
$F$ gives an exact sequence
As by [Reference Van den BerghVdB04, Lemma 3.1.3] morphism ![]() $f^*f_* {\mathcal {M}} \to {\mathcal {M}}$ is surjective, sequence
$f^*f_* {\mathcal {M}} \to {\mathcal {M}}$ is surjective, sequence
is exact in ![]() $\mathop {{\rm Coh}}\nolimits (X)$.
$\mathop {{\rm Coh}}\nolimits (X)$.
Let ![]() $f\colon X\to Y$ satisfy assumption (d) and
$f\colon X\to Y$ satisfy assumption (d) and ![]() $Y = \mathop {{\rm Spec}}\nolimits R$ be a spectrum of a complete Noetherian local ring
$Y = \mathop {{\rm Spec}}\nolimits R$ be a spectrum of a complete Noetherian local ring ![]() $R$. The reduced fiber
$R$. The reduced fiber ![]() $C_{{\rm red}} = \bigcup _{i=1}^n C_i$ of
$C_{{\rm red}} = \bigcup _{i=1}^n C_i$ of ![]() $f$ over the unique closed point
$f$ over the unique closed point ![]() $y\in Y$ is a tree of rational curves (see a more precise statement in Theorem D.1).
$y\in Y$ is a tree of rational curves (see a more precise statement in Theorem D.1).
The Picard group of ![]() $X$ is isomorphic to
$X$ is isomorphic to ![]() $\mathbb {Z}^n$, where the isomorphism is given by the degrees of the restriction to irreducible components of
$\mathbb {Z}^n$, where the isomorphism is given by the degrees of the restriction to irreducible components of ![]() $C_{{\rm red}}$:
$C_{{\rm red}}$: ![]() ${\mathcal {L}} \mapsto \deg ({\mathcal {L}}|_{C_i})_{i=1,\ldots,n}$.
${\mathcal {L}} \mapsto \deg ({\mathcal {L}}|_{C_i})_{i=1,\ldots,n}$.
Remark 2.7 (Cf. [Reference Van den BerghVdB04, Lemma 3.4.4])
Let ![]() $x_i \in C_i\subset X$ be a closed point such that
$x_i \in C_i\subset X$ be a closed point such that ![]() $x_i \notin C_k$, for any
$x_i \notin C_k$, for any ![]() $k \neq i$, and
$k \neq i$, and ![]() $j_i\colon {X}_i \to \mathcal {X}_i$ a closed embedding of a neighbourhood
$j_i\colon {X}_i \to \mathcal {X}_i$ a closed embedding of a neighbourhood ![]() ${X}_i$ of
${X}_i$ of ![]() $x_i$ in
$x_i$ in ![]() $X$ into a smooth variety
$X$ into a smooth variety ![]() $\mathcal {X}_i$. There exists an effective Cartier divisor
$\mathcal {X}_i$. There exists an effective Cartier divisor ![]() $\mathcal {D}_i \subset \mathcal {X}_i$ such that scheme-theoretically
$\mathcal {D}_i \subset \mathcal {X}_i$ such that scheme-theoretically ![]() $\mathcal {D}_i \cap j_{i*} C_i = \{j_{i*} x_i\}$. By pulling back
$\mathcal {D}_i \cap j_{i*} C_i = \{j_{i*} x_i\}$. By pulling back ![]() $\mathcal {D}_i$ to
$\mathcal {D}_i$ to ![]() ${X}_i$, we obtain an effective divisor
${X}_i$, we obtain an effective divisor ![]() $D_i \subset X$ such that scheme-theoretically
$D_i \subset X$ such that scheme-theoretically ![]() $D_i.C_i = \{x_i\}$ and
$D_i.C_i = \{x_i\}$ and ![]() $D_i.C_k =0$, for
$D_i.C_k =0$, for ![]() $k\neq i$. We denote by
$k\neq i$. We denote by ![]() $\iota _{D_i} \colon D_i \to X$ the embedding of
$\iota _{D_i} \colon D_i \to X$ the embedding of ![]() $D_i$ into
$D_i$ into ![]() $X$.
$X$.
Denote by ![]() ${\mathcal {L}}_i$ the line bundle on
${\mathcal {L}}_i$ the line bundle on ![]() $X$ defined by
$X$ defined by
For every ![]() $i$, Van den Bergh defined a vector bundle
$i$, Van den Bergh defined a vector bundle ![]() ${\mathcal {M}}_i$ via the exact sequence
${\mathcal {M}}_i$ via the exact sequence
corresponding to a choice of ![]() $r_i-1$ generators of
$r_i-1$ generators of ![]() $\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {L}}_i, {\mathcal {O}}_X)$ as an
$\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {L}}_i, {\mathcal {O}}_X)$ as an ![]() $R$-module. Denote
$R$-module. Denote ![]() ${\mathcal {M}}_0:={\mathcal {O}}_X$. Then
${\mathcal {M}}_0:={\mathcal {O}}_X$. Then
 \[ {\mathcal{M}} = \bigoplus_{i=0}^n {\mathcal{M}}_i \]
\[ {\mathcal{M}} = \bigoplus_{i=0}^n {\mathcal{M}}_i \]
is a projective generator for ![]() ${}^{-1}{\rm Per}(X/Y)$ (see [Reference Van den BerghVdB04, Proposition 3.5.4]). The dual vector bundle
${}^{-1}{\rm Per}(X/Y)$ (see [Reference Van den BerghVdB04, Proposition 3.5.4]). The dual vector bundle
is a projective generator for ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ (see [Reference Van den BerghVdB04, Proposition 3.2.5]).
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ (see [Reference Van den BerghVdB04, Proposition 3.2.5]).
We put
By Proposition 2.4, sheaf ![]() ${\mathcal {P}} = \bigoplus _{i=1}^n {\mathcal {P}}_i$ is a projective generator for
${\mathcal {P}} = \bigoplus _{i=1}^n {\mathcal {P}}_i$ is a projective generator for ![]() $\mathscr {A}_f$.
$\mathscr {A}_f$.
Example Let ![]() $X$ be a smooth threefold,
$X$ be a smooth threefold, ![]() $f\colon X\to Y$ a flopping contraction. Assume
$f\colon X\to Y$ a flopping contraction. Assume ![]() $Y = \mathop {{\rm Spec}}\nolimits R$ has rational singularities and
$Y = \mathop {{\rm Spec}}\nolimits R$ has rational singularities and ![]() $C_{{\rm red}}\simeq \mathbb {P}^1\subset X$. Then the normal bundle
$C_{{\rm red}}\simeq \mathbb {P}^1\subset X$. Then the normal bundle ![]() $N_{X/C_{{\rm red}}}$ is isomorphic either to
$N_{X/C_{{\rm red}}}$ is isomorphic either to ![]() ${\mathcal {O}}(-1) \oplus {\mathcal {O}}(-1)$,
${\mathcal {O}}(-1) \oplus {\mathcal {O}}(-1)$, ![]() ${\mathcal {O}} \oplus {\mathcal {O}} (-2)$ or
${\mathcal {O}} \oplus {\mathcal {O}} (-2)$ or ![]() ${\mathcal {O}} (1) \oplus {\mathcal {O}} (-3)$. Let
${\mathcal {O}} (1) \oplus {\mathcal {O}} (-3)$. Let ![]() $D\subset X$ be a divisor such that
$D\subset X$ be a divisor such that ![]() $D.C_{{\rm red}} = 1$. For the first two cases,
$D.C_{{\rm red}} = 1$. For the first two cases, ![]() ${\mathcal {M}} \simeq {\mathcal {O}}_X \oplus {\mathcal {O}}_X(D)$, and it is of higher rank for the third case. If
${\mathcal {M}} \simeq {\mathcal {O}}_X \oplus {\mathcal {O}}_X(D)$, and it is of higher rank for the third case. If ![]() $N_{X/C_{{\rm red}}} \simeq {\mathcal {O}} (-1) \oplus {\mathcal {O}} (-1)$, the projective generator
$N_{X/C_{{\rm red}}} \simeq {\mathcal {O}} (-1) \oplus {\mathcal {O}} (-1)$, the projective generator ![]() ${\mathcal {P}}$ is
${\mathcal {P}}$ is ![]() ${\mathcal {O}} (-1)$. When
${\mathcal {O}} (-1)$. When ![]() $N_{X/C_{{\rm red}}} \simeq {\mathcal {O}} \oplus {\mathcal {O}} (-2)$,
$N_{X/C_{{\rm red}}} \simeq {\mathcal {O}} \oplus {\mathcal {O}} (-2)$, ![]() ${\mathcal {P}}$ is an
${\mathcal {P}}$ is an ![]() $n$-iterated extension of
$n$-iterated extension of ![]() ${\mathcal {O}} (-1)$ by
${\mathcal {O}} (-1)$ by ![]() ${\mathcal {O}} (-1)$, where
${\mathcal {O}} (-1)$, where ![]() $n$ is the width of
$n$ is the width of ![]() $C_{{\rm red}}$, see [Reference ReidRei83] (cf. [Reference TodaTod07]).
$C_{{\rm red}}$, see [Reference ReidRei83] (cf. [Reference TodaTod07]).
2.3 Basic properties of  $\mathscr {A}_f$
$\mathscr {A}_f$
Let ![]() $f \colon X \to Y$ satisfy assumption (d) and let
$f \colon X \to Y$ satisfy assumption (d) and let ![]() $E$ be a coherent sheaf on
$E$ be a coherent sheaf on ![]() $Y$. By the derived projection formula, we have
$Y$. By the derived projection formula, we have ![]() $Rf_*Lf^*(E) \simeq E$. As
$Rf_*Lf^*(E) \simeq E$. As ![]() $f$ has fibers of dimension bounded by one, Leray spectral sequence
$f$ has fibers of dimension bounded by one, Leray spectral sequence ![]() $R^pf_* L^qf^*(E) \Rightarrow {\mathcal {H}}_X^{p-q} E$ degenerates. Hence, an exact sequence:
$R^pf_* L^qf^*(E) \Rightarrow {\mathcal {H}}_X^{p-q} E$ degenerates. Hence, an exact sequence:
Lemma 2.8 Let ![]() $f \colon X \to Y$ and
$f \colon X \to Y$ and ![]() $E$ be as above. Then
$E$ be as above. Then ![]() $R^1f_*f^*E = 0$ and
$R^1f_*f^*E = 0$ and ![]() $Rf_*L^if^*E = 0$, for any
$Rf_*L^if^*E = 0$, for any ![]() $i >1$. Further suppose that
$i >1$. Further suppose that ![]() $E$ has no torsion supported at the image
$E$ has no torsion supported at the image ![]() $f({\rm Ex}\, f)$ of the exceptional locus of
$f({\rm Ex}\, f)$ of the exceptional locus of ![]() $f$. Then
$f$. Then ![]() $f_*f^*(E) \simeq E$ and sheaf
$f_*f^*(E) \simeq E$ and sheaf ![]() $L^1f^*E$ is in
$L^1f^*E$ is in ![]() $\mathscr {A}_f$.
$\mathscr {A}_f$.
Proof. The derived projection formula ![]() $Rf_*Lf^* E \simeq E$ and Leray spectral sequence
$Rf_*Lf^* E \simeq E$ and Leray spectral sequence ![]() $R^pf_* L^qf^*(E) \Rightarrow {\mathcal {H}}_X^{p-q} E$ imply
$R^pf_* L^qf^*(E) \Rightarrow {\mathcal {H}}_X^{p-q} E$ imply ![]() $R^1f_*f^* E \simeq 0$,
$R^1f_*f^* E \simeq 0$, ![]() $f_*L^1f^* E \simeq 0$,
$f_*L^1f^* E \simeq 0$, ![]() $Rf_* L^if^* E \simeq 0$, for any
$Rf_* L^if^* E \simeq 0$, for any ![]() $i>1$. As
$i>1$. As ![]() $R^1f_*L^1f^* E$ is supported on
$R^1f_*L^1f^* E$ is supported on ![]() $f({\rm Ex}\, f)$, the assumption that
$f({\rm Ex}\, f)$, the assumption that ![]() $E$ has no torsion supported on
$E$ has no torsion supported on ![]() $f(\mathop {{\rm Ex}}\nolimits f)$ and sequence (20) imply that
$f(\mathop {{\rm Ex}}\nolimits f)$ and sequence (20) imply that ![]() $R^1f_*L^1f^*E$ is zero and
$R^1f_*L^1f^*E$ is zero and ![]() $E \simeq f_*f^*E$.
$E \simeq f_*f^*E$.
Lemma 2.9 Let ![]() $f\colon X \to Y$ and
$f\colon X \to Y$ and ![]() $E$ be as above. If
$E$ be as above. If ![]() $E=f_* E'$, for some
$E=f_* E'$, for some ![]() $E'\in \mathop {{\rm Coh}}\nolimits (X)$, then
$E'\in \mathop {{\rm Coh}}\nolimits (X)$, then ![]() $f_*f^*(E) \simeq E$ and sheaves
$f_*f^*(E) \simeq E$ and sheaves ![]() $L^if^*E$ are in
$L^if^*E$ are in ![]() $\mathscr {A}_f$, for
$\mathscr {A}_f$, for ![]() $i>0$.
$i>0$.
Proof. Sequence (20) implies that morphism ![]() $\alpha \colon f_* E' \to f_*f^*f_* E'$ is surjective. Morphism
$\alpha \colon f_* E' \to f_*f^*f_* E'$ is surjective. Morphism ![]() $\alpha$ is the inclusion of a direct summand, because its composition with the canonical map
$\alpha$ is the inclusion of a direct summand, because its composition with the canonical map ![]() $f_*f^*f_* E'\to f_* E'$ is the identity. Hence,
$f_*f^*f_* E'\to f_* E'$ is the identity. Hence, ![]() $\alpha$ is an isomorphism. Exact sequence (20) implies that
$\alpha$ is an isomorphism. Exact sequence (20) implies that ![]() $R^1f_*L^1f^*f_* E' = 0$. The rest follows from Lemma 2.8.
$R^1f_*L^1f^*f_* E' = 0$. The rest follows from Lemma 2.8.
Proposition 2.10 Let ![]() $f\colon X\to Y$ be a proper morphism with dimension of fibers bounded by one. Consider a decomposition for
$f\colon X\to Y$ be a proper morphism with dimension of fibers bounded by one. Consider a decomposition for ![]() $f$:
$f$:

Then, for ![]() $E \in \mathop {{\rm Coh}}\nolimits (X)$ with
$E \in \mathop {{\rm Coh}}\nolimits (X)$ with ![]() $R^1f_* E =0$, we have
$R^1f_* E =0$, we have ![]() $R^1g_* E = 0$. Functor
$R^1g_* E = 0$. Functor ![]() $g_*$ restricts to an exact functor
$g_*$ restricts to an exact functor ![]() $g_*\colon \mathscr {A}_f \to \mathscr {A}_h$.
$g_*\colon \mathscr {A}_f \to \mathscr {A}_h$.
Proof. Morphism ![]() $g$ is proper by the valuative criterion. Replace
$g$ is proper by the valuative criterion. Replace ![]() $Z$ by the (closed) image of
$Z$ by the (closed) image of ![]() $g$, if necessary. Then
$g$, if necessary. Then ![]() $h$ becomes a proper morphism, cf. [Reference GrothendieckGro61, Corollaire 5.4.3]. As the dimension of fibers for
$h$ becomes a proper morphism, cf. [Reference GrothendieckGro61, Corollaire 5.4.3]. As the dimension of fibers for ![]() $f$ is bounded by one, so is the dimension of fibers for
$f$ is bounded by one, so is the dimension of fibers for ![]() $h$.
$h$.
As ![]() $Rf_*(E)$ is a sheaf on
$Rf_*(E)$ is a sheaf on ![]() $Y$, spectral sequence
$Y$, spectral sequence ![]() $R^qh_* R^sg_* E \Rightarrow R^{q+s}f_* E$ implies that
$R^qh_* R^sg_* E \Rightarrow R^{q+s}f_* E$ implies that ![]() $Rh_*R^1g_*(E) = 0$. Sheaf
$Rh_*R^1g_*(E) = 0$. Sheaf ![]() $R^1g_*(E)$ is supported in the locus of points
$R^1g_*(E)$ is supported in the locus of points ![]() $z \in Z$ such that the fiber of morphism
$z \in Z$ such that the fiber of morphism ![]() $g$ over
$g$ over ![]() $z$ is one-dimensional. As the null category of a finite morphism is zero, morphism
$z$ is one-dimensional. As the null category of a finite morphism is zero, morphism ![]() $h\colon Z\to Y$ restricted to the support of
$h\colon Z\to Y$ restricted to the support of ![]() $R^1g_*(E)$ must have fibers of dimension one. Let
$R^1g_*(E)$ must have fibers of dimension one. Let ![]() $y \in Y$ be a point in
$y \in Y$ be a point in ![]() $h({\rm Supp}\, R^1g_*(E))$. Then the fiber of
$h({\rm Supp}\, R^1g_*(E))$. Then the fiber of ![]() $f$ over
$f$ over ![]() $y$ is two-dimensional, which contradicts the assumptions. Thus,
$y$ is two-dimensional, which contradicts the assumptions. Thus, ![]() $R^1g_*(E)$ is zero.
$R^1g_*(E)$ is zero.
For any ![]() $E \in \mathscr {A}_f$, the spectral sequence
$E \in \mathscr {A}_f$, the spectral sequence ![]() $R^ph_*R^qg_* E \Rightarrow R^{p+q}f_* E = 0$ degenerates. It follows that
$R^ph_*R^qg_* E \Rightarrow R^{p+q}f_* E = 0$ degenerates. It follows that ![]() $g_* E \in \mathscr {A}_h$. As
$g_* E \in \mathscr {A}_h$. As ![]() $R^1g_*(E) = 0$, functor
$R^1g_*(E) = 0$, functor ![]() $g_* \colon \mathscr {A}_f \to \mathscr {A}_h$ is exact.
$g_* \colon \mathscr {A}_f \to \mathscr {A}_h$ is exact.
Proposition 2.11 Let ![]() $f\colon X\to Y$ be a proper morphism with dimension of fibers bounded by one and
$f\colon X\to Y$ be a proper morphism with dimension of fibers bounded by one and ![]() $g \colon Z \to Y$ a morphism of schemes over field
$g \colon Z \to Y$ a morphism of schemes over field ![]() $k$. Assume a coherent sheaf
$k$. Assume a coherent sheaf ![]() $E$ on
$E$ on ![]() $X$ satisfy
$X$ satisfy ![]() $R^lf_* E = 0$, for
$R^lf_* E = 0$, for ![]() $l\geqslant l_0$, for some
$l\geqslant l_0$, for some ![]() $l_0 \in \{0,1\}$. Then
$l_0 \in \{0,1\}$. Then ![]() $R^l\pi _{Z*} \pi _X^* E = 0$, for
$R^l\pi _{Z*} \pi _X^* E = 0$, for ![]() $l\geqslant l_0$, where
$l\geqslant l_0$, where ![]() $\pi _X \colon W \to X$ and
$\pi _X \colon W \to X$ and ![]() $\pi _Z \colon W \to Z$ are the projections for
$\pi _Z \colon W \to Z$ are the projections for ![]() $W = X\times _Y Z$:
$W = X\times _Y Z$:

Proof. The construction of ![]() $X\times _Y Z$ and the statement are local on
$X\times _Y Z$ and the statement are local on ![]() $Y$, hence we may assume that
$Y$, hence we may assume that ![]() $Y=\mathop {{\rm Spec}}\nolimits (R)$ is affine. Moreover, the statement is local on
$Y=\mathop {{\rm Spec}}\nolimits (R)$ is affine. Moreover, the statement is local on ![]() $Z$, so we may further reduce to the case when
$Z$, so we may further reduce to the case when ![]() $Z = \mathop {{\rm Spec}}\nolimits (A)$ is affine. Hence,
$Z = \mathop {{\rm Spec}}\nolimits (A)$ is affine. Hence, ![]() $g\colon Z\to Y$ is an affine morphism, which implies that
$g\colon Z\to Y$ is an affine morphism, which implies that ![]() $\pi _X$ is affine.
$\pi _X$ is affine.
The commutativity of (21) implies ![]() $R(f\pi _X)_*\pi _X^* E \simeq R(g\pi _Z)_*\pi _X^* E$. Morphisms
$R(f\pi _X)_*\pi _X^* E \simeq R(g\pi _Z)_*\pi _X^* E$. Morphisms ![]() $g$ and
$g$ and ![]() $\pi _X$ are affine, hence we have an isomorphism
$\pi _X$ are affine, hence we have an isomorphism ![]() $R^lf_* (\pi _{X*}\pi _X^* E) \simeq g_*R^l\pi _{Z*}(\pi _X^* E)$, for any
$R^lf_* (\pi _{X*}\pi _X^* E) \simeq g_*R^l\pi _{Z*}(\pi _X^* E)$, for any ![]() $l\geqslant 0$. Morphism
$l\geqslant 0$. Morphism ![]() $g$ is affine, thus
$g$ is affine, thus ![]() $g_*R^l\pi _{Z*}(\pi _X^*E)$ is zero if and only if
$g_*R^l\pi _{Z*}(\pi _X^*E)$ is zero if and only if ![]() $R^l\pi _{Z*}(\pi _X^* E)$ is also zero. Hence, we need to show that
$R^l\pi _{Z*}(\pi _X^* E)$ is also zero. Hence, we need to show that ![]() $R^lf_* (\pi _{X*}\pi _X^* E) = 0$, for
$R^lf_* (\pi _{X*}\pi _X^* E) = 0$, for ![]() $l\geqslant l_0$.
$l\geqslant l_0$.
Morphism ![]() $\pi _X$ is affine, hence
$\pi _X$ is affine, hence ![]() $\pi _{X*}\pi _X^* E \simeq E \otimes \pi _{X*}({\mathcal {O}}_{X\times _Y Z})$. The base-change morphism (cf. (47))
$\pi _{X*}\pi _X^* E \simeq E \otimes \pi _{X*}({\mathcal {O}}_{X\times _Y Z})$. The base-change morphism (cf. (47)) ![]() $f^*g_* {\mathcal {O}}_{Z}\to \pi _{X*} {\mathcal {O}}_{X\times _Y Z}$ is an isomorphism. Indeed, this can be checked locally on
$f^*g_* {\mathcal {O}}_{Z}\to \pi _{X*} {\mathcal {O}}_{X\times _Y Z}$ is an isomorphism. Indeed, this can be checked locally on ![]() $X$: if
$X$: if ![]() $X = \mathop {{\rm Spec}}\nolimits (B)$, then both sheaves
$X = \mathop {{\rm Spec}}\nolimits (B)$, then both sheaves ![]() $\pi _{X*} {\mathcal {O}}_{X\times _Y Z}$ and
$\pi _{X*} {\mathcal {O}}_{X\times _Y Z}$ and ![]() $f^*g_* {\mathcal {O}}_Z$ correspond to
$f^*g_* {\mathcal {O}}_Z$ correspond to ![]() $B$-module
$B$-module ![]() $B\otimes _R A$. Thus,
$B\otimes _R A$. Thus,
Derived projection formula ![]() $Rf_*(E \otimes ^L Lf^*g_* {\mathcal {O}}_Z) \simeq Rf_*(E) \otimes ^L g_*{\mathcal {O}}_Z$ implies that
$Rf_*(E \otimes ^L Lf^*g_* {\mathcal {O}}_Z) \simeq Rf_*(E) \otimes ^L g_*{\mathcal {O}}_Z$ implies that ![]() $Rf_* (E \otimes ^L Lf^* g_* {\mathcal {O}}_Z) \in {\mathcal {D}}(Y)^{< l_0}$. Morphism
$Rf_* (E \otimes ^L Lf^* g_* {\mathcal {O}}_Z) \in {\mathcal {D}}(Y)^{< l_0}$. Morphism ![]() $f$ is proper and with dimension of fibers bounded by one, hence
$f$ is proper and with dimension of fibers bounded by one, hence ![]() $R^pf_*(F)=0$, for
$R^pf_*(F)=0$, for ![]() $p>1$ and for any sheaf
$p>1$ and for any sheaf ![]() $F$. It follows that spectral sequence
$F$. It follows that spectral sequence
degenerates. Therefore, ![]() $R^lf_*(\pi _{X*}\pi _X^* E) \simeq R^l f_* {\mathcal {H}}_X^0(E \otimes Lf^*g_* {\mathcal {O}}_Z) = 0$, for
$R^lf_*(\pi _{X*}\pi _X^* E) \simeq R^l f_* {\mathcal {H}}_X^0(E \otimes Lf^*g_* {\mathcal {O}}_Z) = 0$, for ![]() $l\geqslant l_0$.
$l\geqslant l_0$.
Corollary 2.12 Let ![]() $f\colon X\to Y$ and
$f\colon X\to Y$ and ![]() $g \colon Z \to Y$ be as in Proposition 2.11. For
$g \colon Z \to Y$ be as in Proposition 2.11. For ![]() $E\in \mathscr {A}_f$, its pull-back
$E\in \mathscr {A}_f$, its pull-back ![]() $\pi _X^* E$ is an object in
$\pi _X^* E$ is an object in ![]() $\mathscr {A}_{\pi _Z}$.
$\mathscr {A}_{\pi _Z}$.
3.  $L^1f^*$ vanishing and 2-periodicity
$L^1f^*$ vanishing and 2-periodicity
Let ![]() $f\colon X\to Y$ satisfy assumption (d). For
$f\colon X\to Y$ satisfy assumption (d). For ![]() $p=-1,0$, we denote by
$p=-1,0$, we denote by ![]() $\mathscr {P}_p$ the category of locally projective objects in
$\mathscr {P}_p$ the category of locally projective objects in ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$. An object
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$. An object ![]() ${\mathcal {M}}$ belongs to
${\mathcal {M}}$ belongs to ![]() $\mathscr {P}_p$ if there exists an affine open covering
$\mathscr {P}_p$ if there exists an affine open covering ![]() $Y = \bigcup Y_i$, inducing
$Y = \bigcup Y_i$, inducing ![]() $X = \bigcup X_i$ with
$X = \bigcup X_i$ with ![]() $X_i = f^{-1}(Y_i)$, such that
$X_i = f^{-1}(Y_i)$, such that ![]() ${\mathcal {M}}|_{X_i}$ is projective in
${\mathcal {M}}|_{X_i}$ is projective in ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X_i/Y_i)$. By [Reference Van den BerghVdB04, Proposition 3.2.6] objects in
$\mathop {{}^{p}{\rm Per}}\nolimits (X_i/Y_i)$. By [Reference Van den BerghVdB04, Proposition 3.2.6] objects in ![]() $\mathscr {P}_{-1}$ and
$\mathscr {P}_{-1}$ and ![]() $\mathscr {P}_0$ are locally free sheaves on
$\mathscr {P}_0$ are locally free sheaves on ![]() $X$.
$X$.
In this section we discuss a spherical couple associated to a Cartier divisor. Under the assumption that ![]() $Y$ has hypersurface singularities we prove that the sheaf
$Y$ has hypersurface singularities we prove that the sheaf ![]() $L^1f^*f_* {\mathcal {M}}$ is zero, for any object
$L^1f^*f_* {\mathcal {M}}$ is zero, for any object ![]() ${\mathcal {M}} \in \mathscr {P}_{-1}$. Though technical, this result is crucial for the various description of the flop and flop–flop functors presented in the subsequent sections.
${\mathcal {M}} \in \mathscr {P}_{-1}$. Though technical, this result is crucial for the various description of the flop and flop–flop functors presented in the subsequent sections.
3.1 Cartier divisors and spherical couples
Let ![]() $X$ be a quasi-compact, quasi-separated scheme. By an effective Cartier divisor
$X$ be a quasi-compact, quasi-separated scheme. By an effective Cartier divisor ![]() $i\colon D\to X$ we mean a subscheme whose ideal sheaf
$i\colon D\to X$ we mean a subscheme whose ideal sheaf ![]() ${\mathcal {I}}_D$ is invertible. Here we discuss a 2-categorical adjunction and a spherical couple in the bicategory
${\mathcal {I}}_D$ is invertible. Here we discuss a 2-categorical adjunction and a spherical couple in the bicategory ![]() $\mathop {\textbf {FM}}\nolimits$ (see Appendix C) related to such a divisor.
$\mathop {\textbf {FM}}\nolimits$ (see Appendix C) related to such a divisor.
Denote by ![]() $\Gamma \subset D\times X$,
$\Gamma \subset D\times X$, ![]() $\Gamma ^t \subset X\times D$ the graphs of
$\Gamma ^t \subset X\times D$ the graphs of ![]() $i$. Sheaf
$i$. Sheaf ![]() ${\mathcal {O}}_\Gamma \in {\mathcal {D}}_{{\rm qc}}(D\times X)$ is an FM kernel for
${\mathcal {O}}_\Gamma \in {\mathcal {D}}_{{\rm qc}}(D\times X)$ is an FM kernel for ![]() $Ri_*\colon {\mathcal {D}}_{{\rm qc}}(D) \to {\mathcal {D}}_{{\rm qc}}(X)$, and
$Ri_*\colon {\mathcal {D}}_{{\rm qc}}(D) \to {\mathcal {D}}_{{\rm qc}}(X)$, and ![]() ${\mathcal {O}}_{\Gamma ^t}\in {\mathcal {D}}_{{\rm qc}}(X\times D)$ is an FM kernel for
${\mathcal {O}}_{\Gamma ^t}\in {\mathcal {D}}_{{\rm qc}}(X\times D)$ is an FM kernel for ![]() $Li^*\colon {\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(D)$.
$Li^*\colon {\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(D)$.
For a scheme ![]() $Y$, we denote by
$Y$, we denote by ![]() $\Delta ^Y\subset Y\times Y$ the diagonal and, for closed
$\Delta ^Y\subset Y\times Y$ the diagonal and, for closed ![]() $Z\subset Y$, by
$Z\subset Y$, by ![]() $\Delta ^{Z,Y}$ the image of
$\Delta ^{Z,Y}$ the image of ![]() $Z$ under the diagonal morphism
$Z$ under the diagonal morphism ![]() ${\rm diag}^Y\colon Y \to Y \times Y$. For
${\rm diag}^Y\colon Y \to Y \times Y$. For ![]() $F\in {\mathcal {D}}_{{\rm qc}}(D\times Y)$, we have
$F\in {\mathcal {D}}_{{\rm qc}}(D\times Y)$, we have
In particular,
Embedding ![]() $\Delta ^{D,X}\subset \Delta ^X$ gives
$\Delta ^{D,X}\subset \Delta ^X$ gives
For any scheme ![]() $Y$, and objects
$Y$, and objects ![]() $F\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$,
$F\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$, ![]() $G\in {\mathcal {D}}_{{\rm qc}}(Y \times X)$, we have
$G\in {\mathcal {D}}_{{\rm qc}}(Y \times X)$, we have
One checks locally that for ![]() $F\in {\rm QCoh}(X\times Y)$ and
$F\in {\rm QCoh}(X\times Y)$ and ![]() $G\in {\rm QCoh}(Y\times X)$ morphisms
$G\in {\rm QCoh}(Y\times X)$ morphisms
 \begin{align*} &F\simeq F\ast {\mathcal{O}}_{\Delta^X} \xrightarrow{F \ast \eta } F \ast {\mathcal{O}}_{\Gamma} \ast {\mathcal{O}}_{\Gamma^t} \simeq (i\times \mathop{{\rm Id}}\nolimits_Y)_*(i\times \mathop{{\rm Id}}\nolimits_Y)^*F \simeq F\otimes {\mathcal{O}}_{D\times Y},\\ &G \simeq {\mathcal{O}}_{\Delta^X} \ast G \xrightarrow{\eta\ast G }{\mathcal{O}}_{\Gamma} \ast {\mathcal{O}}_{\Gamma^t} \ast G \simeq (\mathop{{\rm Id}}\nolimits_Y\times i)_*(\mathop{{\rm Id}}\nolimits_Y\times i)^*G \simeq G\otimes {\mathcal{O}}_{Y\times D} \end{align*}
\begin{align*} &F\simeq F\ast {\mathcal{O}}_{\Delta^X} \xrightarrow{F \ast \eta } F \ast {\mathcal{O}}_{\Gamma} \ast {\mathcal{O}}_{\Gamma^t} \simeq (i\times \mathop{{\rm Id}}\nolimits_Y)_*(i\times \mathop{{\rm Id}}\nolimits_Y)^*F \simeq F\otimes {\mathcal{O}}_{D\times Y},\\ &G \simeq {\mathcal{O}}_{\Delta^X} \ast G \xrightarrow{\eta\ast G }{\mathcal{O}}_{\Gamma} \ast {\mathcal{O}}_{\Gamma^t} \ast G \simeq (\mathop{{\rm Id}}\nolimits_Y\times i)_*(\mathop{{\rm Id}}\nolimits_Y\times i)^*G \simeq G\otimes {\mathcal{O}}_{Y\times D} \end{align*}
are induced by restriction morphisms ![]() ${\mathcal {O}}_{X\times Y} \to {\mathcal {O}}_{D \times Y}$ and
${\mathcal {O}}_{X\times Y} \to {\mathcal {O}}_{D \times Y}$ and ![]() ${\mathcal {O}}_{Y\times X} \to {\mathcal {O}}_{Y \times D}$, respectively.
${\mathcal {O}}_{Y\times X} \to {\mathcal {O}}_{Y \times D}$, respectively.
For any scheme ![]() $Y$ and
$Y$ and ![]() $F\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$, we have
$F\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$, we have
Hence,
Subscheme ![]() $D\times D\subset X\times D$ is a Cartier divisor with ideal sheaf
$D\times D\subset X\times D$ is a Cartier divisor with ideal sheaf ![]() ${\mathcal {I}}_{D\times D}$. Therefore, object
${\mathcal {I}}_{D\times D}$. Therefore, object ![]() $(i\times \mathop {{\rm Id}}\nolimits _D)^*(i\times \mathop {{\rm Id}}\nolimits _D)_*{\mathcal {O}}_{\Delta ^D}$ has two non-zero cohomology sheaves,
$(i\times \mathop {{\rm Id}}\nolimits _D)^*(i\times \mathop {{\rm Id}}\nolimits _D)_*{\mathcal {O}}_{\Delta ^D}$ has two non-zero cohomology sheaves, ![]() ${\mathcal {O}}_{\Delta ^D}$ in degree
${\mathcal {O}}_{\Delta ^D}$ in degree ![]() $0$ and
$0$ and ![]() ${\mathcal {O}}_{\Delta ^D}\otimes {\mathcal {I}}_{D\times D}|_{D\times D}$ in degree
${\mathcal {O}}_{\Delta ^D}\otimes {\mathcal {I}}_{D\times D}|_{D\times D}$ in degree ![]() $-1$. Truncation to the zeroth cohomology gives morphism
$-1$. Truncation to the zeroth cohomology gives morphism
Formulas (22) and (24) imply that, for any scheme ![]() $Y$ and objects
$Y$ and objects ![]() $F\in {\mathcal {D}}_{{\rm qc}}(D\times Y)$ and
$F\in {\mathcal {D}}_{{\rm qc}}(D\times Y)$ and ![]() $G\in {\mathcal {D}}_{{\rm qc}}(Y\times D)$, we have
$G\in {\mathcal {D}}_{{\rm qc}}(Y\times D)$, we have
One checks locally along ![]() $D$ that for
$D$ that for ![]() $F\in {\rm QCoh}(D\times Y)$ and
$F\in {\rm QCoh}(D\times Y)$ and ![]() $G\in {\rm QCoh}(Y\times D)$ morphisms
$G\in {\rm QCoh}(Y\times D)$ morphisms
 \begin{align*} (i\times\mathop{{\rm Id}}\nolimits_Y)^*(i\times\mathop{{\rm Id}}\nolimits_Y)_*F &\simeq F \ast {\mathcal{O}}_{\Gamma^t} \ast {\mathcal{O}}_{\Gamma} \xrightarrow{F \ast \varepsilon } F \ast {\mathcal{O}}_{\Delta^D} \simeq F,\\ (\mathop{{\rm Id}}\nolimits_Y\times i)^*(\mathop{{\rm Id}}\nolimits_Y\times i)_*G &\simeq {\mathcal{O}}_{\Gamma^t} \ast {\mathcal{O}}_{\Gamma} \ast G \xrightarrow{\varepsilon\ast G}{\mathcal{O}}_{\Delta^D}\ast G \simeq G \end{align*}
\begin{align*} (i\times\mathop{{\rm Id}}\nolimits_Y)^*(i\times\mathop{{\rm Id}}\nolimits_Y)_*F &\simeq F \ast {\mathcal{O}}_{\Gamma^t} \ast {\mathcal{O}}_{\Gamma} \xrightarrow{F \ast \varepsilon } F \ast {\mathcal{O}}_{\Delta^D} \simeq F,\\ (\mathop{{\rm Id}}\nolimits_Y\times i)^*(\mathop{{\rm Id}}\nolimits_Y\times i)_*G &\simeq {\mathcal{O}}_{\Gamma^t} \ast {\mathcal{O}}_{\Gamma} \ast G \xrightarrow{\varepsilon\ast G}{\mathcal{O}}_{\Delta^D}\ast G \simeq G \end{align*}are the truncations to the zeroth cohomology.
An early version of formula (26) in the following theorem was first proven in [Reference Bondal and OrlovBO95, Lemma 3.3] under the assumption that both varieties are smooth. The result was also stated without proof in [Reference AnnoAnn07, Reference AddingtonAdd16].
Theorem 3.1 Let ![]() $i\colon D \to X$ be the embedding of an effective Cartier divisor. Then
$i\colon D \to X$ be the embedding of an effective Cartier divisor. Then ![]() $({\mathcal {O}}_{\Gamma ^t}, {\mathcal {O}}_{\Gamma }, \eta, \varepsilon )$ is a spherical couple in the bicategory
$({\mathcal {O}}_{\Gamma ^t}, {\mathcal {O}}_{\Gamma }, \eta, \varepsilon )$ is a spherical couple in the bicategory ![]() $\mathop {\textbf {FM}}\nolimits$. Object
$\mathop {\textbf {FM}}\nolimits$. Object ![]() ${\rm diag}^D_*{\mathcal {I}}_D|_D[2]$ is the spherical twist and
${\rm diag}^D_*{\mathcal {I}}_D|_D[2]$ is the spherical twist and ![]() ${\rm diag}^X_*{\mathcal {I}}_D$ the spherical cotwist. The associated functorial exact triangles read
${\rm diag}^X_*{\mathcal {I}}_D$ the spherical cotwist. The associated functorial exact triangles read
Proof. First, we check that ![]() $({\mathcal {O}}_{\Gamma ^t},{\mathcal {O}}_{\Gamma }, \eta, \varepsilon )$ is a 2-categorical adjunction, i.e. that (C.1) are equal to the identity morphisms.
$({\mathcal {O}}_{\Gamma ^t},{\mathcal {O}}_{\Gamma }, \eta, \varepsilon )$ is a 2-categorical adjunction, i.e. that (C.1) are equal to the identity morphisms.
As ![]() ${\mathcal {O}}_{\Gamma } \simeq (\mathop {{\rm Id}}\nolimits _D\times i)_*{\mathcal {O}}_{\Delta ^D}$, the composite
${\mathcal {O}}_{\Gamma } \simeq (\mathop {{\rm Id}}\nolimits _D\times i)_*{\mathcal {O}}_{\Delta ^D}$, the composite ![]() ${\mathcal {O}}_{\Gamma }\xrightarrow {\eta \ast {\mathcal {O}}_{\Gamma } } {\mathcal {O}}_{\Gamma } \ast {\mathcal {O}}_{\Gamma ^t} \ast {\mathcal {O}}_{\Gamma } \xrightarrow { {\mathcal {O}}_{\Gamma }\ast \varepsilon } {\mathcal {O}}_{\Gamma }$ reads
${\mathcal {O}}_{\Gamma }\xrightarrow {\eta \ast {\mathcal {O}}_{\Gamma } } {\mathcal {O}}_{\Gamma } \ast {\mathcal {O}}_{\Gamma ^t} \ast {\mathcal {O}}_{\Gamma } \xrightarrow { {\mathcal {O}}_{\Gamma }\ast \varepsilon } {\mathcal {O}}_{\Gamma }$ reads
Object ![]() $(\mathop {{\rm Id}}\nolimits _D\times i)_*{\mathcal {O}}_{\Delta ^D}$ is supported on
$(\mathop {{\rm Id}}\nolimits _D\times i)_*{\mathcal {O}}_{\Delta ^D}$ is supported on ![]() $D\times D$, hence the first morphism, restriction to
$D\times D$, hence the first morphism, restriction to ![]() $D\times D$, is the identity on the zeroth cohomology. The second morphism is the truncation at zeroth cohomology, hence
$D\times D$, is the identity on the zeroth cohomology. The second morphism is the truncation at zeroth cohomology, hence ![]() $({\mathcal {O}}_\Gamma \ast \varepsilon )\circ (\eta \ast {\mathcal {O}}_{\Gamma } ) = \mathop {{\rm Id}}\nolimits _{{\mathcal {O}}_{\Gamma }}$.
$({\mathcal {O}}_\Gamma \ast \varepsilon )\circ (\eta \ast {\mathcal {O}}_{\Gamma } ) = \mathop {{\rm Id}}\nolimits _{{\mathcal {O}}_{\Gamma }}$.
As ![]() ${\mathcal {O}}_{\Gamma ^t} \simeq (i\times \mathop {{\rm Id}}\nolimits _D)_*{\mathcal {O}}_{\Delta ^D}$, the composite
${\mathcal {O}}_{\Gamma ^t} \simeq (i\times \mathop {{\rm Id}}\nolimits _D)_*{\mathcal {O}}_{\Delta ^D}$, the composite ![]() ${\mathcal {O}}_{\Gamma ^t}\xrightarrow { {\mathcal {O}}_{\Gamma ^t}\ast \eta } {\mathcal {O}}_{\Gamma ^t} \ast {\mathcal {O}}_{\Gamma } \ast {\mathcal {O}}_{\Gamma ^t} \xrightarrow {\varepsilon \ast {\mathcal {O}}_{\Gamma ^t} } {\mathcal {O}}_{\Gamma ^t}$ reads
${\mathcal {O}}_{\Gamma ^t}\xrightarrow { {\mathcal {O}}_{\Gamma ^t}\ast \eta } {\mathcal {O}}_{\Gamma ^t} \ast {\mathcal {O}}_{\Gamma } \ast {\mathcal {O}}_{\Gamma ^t} \xrightarrow {\varepsilon \ast {\mathcal {O}}_{\Gamma ^t} } {\mathcal {O}}_{\Gamma ^t}$ reads
The arguments as above show that ![]() $(\varepsilon \ast {\mathcal {O}}_{\Gamma ^t} ) \circ ( {\mathcal {O}}_{\Gamma ^t}\ast \eta )$ is the identity on
$(\varepsilon \ast {\mathcal {O}}_{\Gamma ^t} ) \circ ( {\mathcal {O}}_{\Gamma ^t}\ast \eta )$ is the identity on ![]() ${\mathcal {O}}_{\Gamma ^t}$.
${\mathcal {O}}_{\Gamma ^t}$.
Now we calculate the twist and cotwist of the 2-categorical adjunction ![]() $({\mathcal {O}}_{\Gamma ^t},{\mathcal {O}}_{\Gamma }, \eta,\varepsilon )$. Morphism
$({\mathcal {O}}_{\Gamma ^t},{\mathcal {O}}_{\Gamma }, \eta,\varepsilon )$. Morphism ![]() $\eta$ in (23) is induced by the morphism
$\eta$ in (23) is induced by the morphism ![]() ${\mathcal {O}}_{X}\to {\mathcal {O}}_D$ with kernel
${\mathcal {O}}_{X}\to {\mathcal {O}}_D$ with kernel ![]() ${\mathcal {I}}_D$. Hence,
${\mathcal {I}}_D$. Hence,
is an exact triangle in ![]() ${\mathcal {D}}_{{\rm qc}}(X\times X)$. Thus, the cotwist equals
${\mathcal {D}}_{{\rm qc}}(X\times X)$. Thus, the cotwist equals ![]() ${\rm diag}_*^X{\mathcal {I}}_D$. It is an equivalence whose inverse is
${\rm diag}_*^X{\mathcal {I}}_D$. It is an equivalence whose inverse is ![]() ${\rm diag}_*^X{\mathcal {I}}_D^{-1}$. The corresponding functorial exact triangle is (26).
${\rm diag}_*^X{\mathcal {I}}_D^{-1}$. The corresponding functorial exact triangle is (26).
Morphism ![]() $\varepsilon$ in (25) is induced by the truncation to the zeroth cohomology of the object
$\varepsilon$ in (25) is induced by the truncation to the zeroth cohomology of the object ![]() $(i\times \mathop {{\rm Id}}\nolimits _D)^*(i\times \mathop {{\rm Id}}\nolimits _D)_*{\mathcal {O}}_{\Delta ^D}$. As we noted before,
$(i\times \mathop {{\rm Id}}\nolimits _D)^*(i\times \mathop {{\rm Id}}\nolimits _D)_*{\mathcal {O}}_{\Delta ^D}$. As we noted before, ![]() $(i\times \mathop {{\rm Id}}\nolimits _D)^*(i\times \mathop {{\rm Id}}\nolimits _D)_*{\mathcal {O}}_{\Delta ^D}$ has two non-zero cohomology sheaves and the truncation to the zeroth cohomology yields an exact triangle
$(i\times \mathop {{\rm Id}}\nolimits _D)^*(i\times \mathop {{\rm Id}}\nolimits _D)_*{\mathcal {O}}_{\Delta ^D}$ has two non-zero cohomology sheaves and the truncation to the zeroth cohomology yields an exact triangle
The twist
is an equivalence whose inverse is ![]() ${\rm diag}^D_*{\mathcal {I}}_D^{-1}|_D[-1]$. The corresponding functorial exact triangle is (27).
${\rm diag}^D_*{\mathcal {I}}_D^{-1}|_D[-1]$. The corresponding functorial exact triangle is (27).
3.2  $L^1f^*$ vanishing and consequences
$L^1f^*$ vanishing and consequences
Vanishing of ![]() $L^1f^*f_*(-)$ is local on
$L^1f^*f_*(-)$ is local on ![]() $Y$, therefore throughout this section we assume that
$Y$, therefore throughout this section we assume that ![]() $Y$ is affine and fix a closed embedding
$Y$ is affine and fix a closed embedding ![]() $i\colon Y \to {\mathcal {Y}}$ of
$i\colon Y \to {\mathcal {Y}}$ of ![]() $Y$ as the zero locus of a regular function on a smooth affine
$Y$ as the zero locus of a regular function on a smooth affine ![]() ${\mathcal {Y}}$. As
${\mathcal {Y}}$. As ![]() $Y\subset {\mathcal {Y}}$ is a principal Cartier divisor, the sheaf
$Y\subset {\mathcal {Y}}$ is a principal Cartier divisor, the sheaf ![]() ${\mathcal {I}}_Y$ is isomorphic to
${\mathcal {I}}_Y$ is isomorphic to ![]() ${\mathcal {O}}_{{\mathcal {Y}}}$.
${\mathcal {O}}_{{\mathcal {Y}}}$.
The following lemma is one of the key technical points of this paper.
Lemma 3.2 Let ![]() $f\colon X\to Y$ satisfy assumption (p) and let
$f\colon X\to Y$ satisfy assumption (p) and let ![]() $Y = \mathop {{\rm Spec}}\nolimits R$ be a spectrum of a complete Noetherian local ring with hypersurface singularities. Let further
$Y = \mathop {{\rm Spec}}\nolimits R$ be a spectrum of a complete Noetherian local ring with hypersurface singularities. Let further ![]() $D_i \subset X$ be as in Remark 2.7. Then
$D_i \subset X$ be as in Remark 2.7. Then ![]() $L^1f^*f_* {\mathcal {O}}_{D_i} \simeq 0$.
$L^1f^*f_* {\mathcal {O}}_{D_i} \simeq 0$.
Proof. Let ![]() $\iota _i \colon D_i \to X$ denote the embedding of
$\iota _i \colon D_i \to X$ denote the embedding of ![]() $D_i$ into
$D_i$ into ![]() $X$. We denote by
$X$. We denote by ![]() $h$ the composite
$h$ the composite ![]() $h=if\iota _i \colon D_i \to \mathcal {Y}$. Morphism
$h=if\iota _i \colon D_i \to \mathcal {Y}$. Morphism ![]() $h$ is finite, hence
$h$ is finite, hence ![]() $h_*$ is exact and, by Grothendieck duality (A.1), we have
$h_*$ is exact and, by Grothendieck duality (A.1), we have
Divisor ![]() $D_i$ is Cartier in a Gorenstein scheme, hence it is Gorenstein itself. As
$D_i$ is Cartier in a Gorenstein scheme, hence it is Gorenstein itself. As ![]() ${\mathcal {Y}}$ is smooth and it is the spectrum of a complete ring, we have
${\mathcal {Y}}$ is smooth and it is the spectrum of a complete ring, we have ![]() $\omega _{{\mathcal {Y}}}^{\boldsymbol {\cdot }} \simeq {\mathcal {O}}_{{\mathcal {Y}}}[n+1]$. It follows that
$\omega _{{\mathcal {Y}}}^{\boldsymbol {\cdot }} \simeq {\mathcal {O}}_{{\mathcal {Y}}}[n+1]$. It follows that ![]() $h^! {\mathcal {O}}_{{\mathcal {Y}}}=h^!\omega _{{\mathcal {Y}}}^{\boldsymbol {\cdot }}[-n-1]=\omega _{D_i}[-2]$ is a sheaf in homological degree
$h^! {\mathcal {O}}_{{\mathcal {Y}}}=h^!\omega _{{\mathcal {Y}}}^{\boldsymbol {\cdot }}[-n-1]=\omega _{D_i}[-2]$ is a sheaf in homological degree ![]() $2$. As
$2$. As ![]() $h_*$ is exact,
$h_*$ is exact, ![]() $Rh_* {\mathcal {H}}_{D_i}^i(h^! {\mathcal {O}}_{{\mathcal {Y}}}) \simeq h_* {\mathcal {H}}_{D_i}^i(h^! {\mathcal {O}}_{{\mathcal {Y}}})$. Hence, by (28), we have
$Rh_* {\mathcal {H}}_{D_i}^i(h^! {\mathcal {O}}_{{\mathcal {Y}}}) \simeq h_* {\mathcal {H}}_{D_i}^i(h^! {\mathcal {O}}_{{\mathcal {Y}}})$. Hence, by (28), we have
As ![]() $\mathcal {Y}$ is affine,
$\mathcal {Y}$ is affine, ![]() $\mathop {{\rm Ext}}\nolimits _{{\mathcal {Y}}}^i(h_*{\mathcal {O}}_{D_i}, {\mathcal {O}}_{\mathcal {Y}}) = 0$, for
$\mathop {{\rm Ext}}\nolimits _{{\mathcal {Y}}}^i(h_*{\mathcal {O}}_{D_i}, {\mathcal {O}}_{\mathcal {Y}}) = 0$, for ![]() $i\neq 2$. Hence, the projective dimension of
$i\neq 2$. Hence, the projective dimension of ![]() $h_* {\mathcal {O}}_{D_i}$ as an
$h_* {\mathcal {O}}_{D_i}$ as an ![]() ${\mathcal {O}}_{{\mathcal {Y}}}$ module is two. In other words,
${\mathcal {O}}_{{\mathcal {Y}}}$ module is two. In other words, ![]() $h_* {\mathcal {O}}_{D_i}$ has a locally free resolution
$h_* {\mathcal {O}}_{D_i}$ has a locally free resolution
Denote by ![]() ${\mathcal {E}}_{{\boldsymbol {\cdot }}}$ the complex
${\mathcal {E}}_{{\boldsymbol {\cdot }}}$ the complex ![]() $0 \to {\mathcal {E}}_{-2} \to {\mathcal {E}}_{-1} \to {\mathcal {E}}_0 \to 0$. The cohomology of complex
$0 \to {\mathcal {E}}_{-2} \to {\mathcal {E}}_{-1} \to {\mathcal {E}}_0 \to 0$. The cohomology of complex ![]() $i_*i^* {\mathcal {E}}_{{\boldsymbol {\cdot }}}$ is
$i_*i^* {\mathcal {E}}_{{\boldsymbol {\cdot }}}$ is ![]() ${\rm Tor}^{{\mathcal {Y}}}(h_* {\mathcal {O}}_{D_i},{\mathcal {O}}_Y)$. As
${\rm Tor}^{{\mathcal {Y}}}(h_* {\mathcal {O}}_{D_i},{\mathcal {O}}_Y)$. As ![]() $Y \subset \mathcal {Y}$ is a Cartier divisor,
$Y \subset \mathcal {Y}$ is a Cartier divisor, ![]() ${\mathcal {O}}_Y$ has a resolution of length two on
${\mathcal {O}}_Y$ has a resolution of length two on ![]() ${\mathcal {Y}}$, i.e. the zeroth and first Tor groups only can be non-zero. As functor
${\mathcal {Y}}$, i.e. the zeroth and first Tor groups only can be non-zero. As functor ![]() $i_*$ is exact, we conclude that the morphism
$i_*$ is exact, we conclude that the morphism ![]() $i^*{\mathcal {E}}_{-2} \to i^* {\mathcal {E}}_{-1}$ is injective.
$i^*{\mathcal {E}}_{-2} \to i^* {\mathcal {E}}_{-1}$ is injective.
Morphism ![]() $f$ is birational, hence the higher derived functors of
$f$ is birational, hence the higher derived functors of ![]() $f^*$ are torsion. In particular, the kernel of
$f^*$ are torsion. In particular, the kernel of ![]() $f^*i^* {\mathcal {E}}_{-2} \to f^*i^* {\mathcal {E}}_{-1}$ is torsion, meaning zero because
$f^*i^* {\mathcal {E}}_{-2} \to f^*i^* {\mathcal {E}}_{-1}$ is torsion, meaning zero because ![]() $f^*i^* {\mathcal {E}}_{-2}$ is locally free. This shows that morphism
$f^*i^* {\mathcal {E}}_{-2}$ is locally free. This shows that morphism ![]() $f^*i^* {\mathcal {E}}_{-2} \to f^*i^* {\mathcal {E}}_{-1}$ is also injective, thus complex
$f^*i^* {\mathcal {E}}_{-2} \to f^*i^* {\mathcal {E}}_{-1}$ is also injective, thus complex ![]() $\widetilde {{\mathcal {E}}}_{\boldsymbol {\cdot }} := f^*i^* {\mathcal {E}}_{{\boldsymbol {\cdot }}}$ has zero cohomology except for
$\widetilde {{\mathcal {E}}}_{\boldsymbol {\cdot }} := f^*i^* {\mathcal {E}}_{{\boldsymbol {\cdot }}}$ has zero cohomology except for ![]() ${\mathcal {H}}^{0}_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}})$ and
${\mathcal {H}}^{0}_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}})$ and ![]() ${\mathcal {H}}^{-1}_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}})$.
${\mathcal {H}}^{-1}_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}})$.
Let ![]() $E\subset X$ be the exceptional locus of
$E\subset X$ be the exceptional locus of ![]() $f$. Assume
$f$. Assume ![]() $L^1f^*f_* {\mathcal {O}}_{D_i} \neq 0$. Its support is contained in
$L^1f^*f_* {\mathcal {O}}_{D_i} \neq 0$. Its support is contained in ![]() $E$. Moreover, because
$E$. Moreover, because ![]() $L^1f^*f_* {\mathcal {O}}_{D_i} \in \mathscr {A}_f$ (see Lemma 2.9), the support of this sheaf should contain at least one component of the curve in the fiber over the closed point of
$L^1f^*f_* {\mathcal {O}}_{D_i} \in \mathscr {A}_f$ (see Lemma 2.9), the support of this sheaf should contain at least one component of the curve in the fiber over the closed point of ![]() $Y$ (see Theorem D.1 for the structure of the fiber). Therefore, there exists a closed point
$Y$ (see Theorem D.1 for the structure of the fiber). Therefore, there exists a closed point ![]() $x \in E \setminus D_i$ in the support of
$x \in E \setminus D_i$ in the support of ![]() $L^1f^*f_* {\mathcal {O}}_{D_i}$.
$L^1f^*f_* {\mathcal {O}}_{D_i}$.
By Theorem 3.1 for divisor ![]() $Y$ in
$Y$ in ![]() ${\mathcal {Y}}$, object
${\mathcal {Y}}$, object ![]() $i^* {\mathcal {E}}_{{\boldsymbol {\cdot }}} \simeq Li^*i_*f_* {\mathcal {O}}_{D_i}$ fits into an exact triangle
$i^* {\mathcal {E}}_{{\boldsymbol {\cdot }}} \simeq Li^*i_*f_* {\mathcal {O}}_{D_i}$ fits into an exact triangle
By applying functor ![]() $L f^*$ to this triangle, we obtain an exact sequence
$L f^*$ to this triangle, we obtain an exact sequence
Sheaf ![]() $f^*f_*{\mathcal {O}}_{D_i}$ is supported on the preimage of
$f^*f_*{\mathcal {O}}_{D_i}$ is supported on the preimage of ![]() $f(D_i) \subset Y$, i.e. on the set
$f(D_i) \subset Y$, i.e. on the set ![]() $E \cup D_i$. Let us restrict our attention to an open affine neighbourhood
$E \cup D_i$. Let us restrict our attention to an open affine neighbourhood ![]() $\widetilde {i} \colon \widetilde {X}\hookrightarrow X$ of point
$\widetilde {i} \colon \widetilde {X}\hookrightarrow X$ of point ![]() $x$. The support of both sheaves
$x$. The support of both sheaves ![]() $f^*f_* {\mathcal {O}}_{D_i}$ and
$f^*f_* {\mathcal {O}}_{D_i}$ and ![]() $L^1f^*f_*{\mathcal {O}}_{D_i}$ is contained in
$L^1f^*f_*{\mathcal {O}}_{D_i}$ is contained in ![]() $E$. Therefore, the assumptions on the exceptional locus for
$E$. Therefore, the assumptions on the exceptional locus for ![]() $f$ imply that
$f$ imply that ![]() ${\mathcal {H}}_X^{-1}(\widetilde {{\mathcal {E}}})$ is a non-zero sheaf with support of some codimension
${\mathcal {H}}_X^{-1}(\widetilde {{\mathcal {E}}})$ is a non-zero sheaf with support of some codimension ![]() $l>1$.
$l>1$.
Let ![]() $j\colon \widetilde {X}\to \mathcal {X}$ be a closed embedding into a smooth variety of dimension
$j\colon \widetilde {X}\to \mathcal {X}$ be a closed embedding into a smooth variety of dimension ![]() $m$. We have
$m$. We have ![]() $\omega _{\widetilde {X}} \simeq \widetilde {i}^!f^! {\mathcal {O}}_Y \simeq \widetilde {i}^! {\mathcal {O}}_X \simeq {\mathcal {O}}_{\widetilde {X}}$, hence Grothendieck duality (A.1) gives
$\omega _{\widetilde {X}} \simeq \widetilde {i}^!f^! {\mathcal {O}}_Y \simeq \widetilde {i}^! {\mathcal {O}}_X \simeq {\mathcal {O}}_{\widetilde {X}}$, hence Grothendieck duality (A.1) gives
Complex ![]() $\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}}$ consists of three locally free sheaves, thus
$\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}}$ consists of three locally free sheaves, thus ![]() ${\mathcal {E}} xt^k_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}}, {\mathcal {O}}_X)$ is zero, for
${\mathcal {E}} xt^k_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}}, {\mathcal {O}}_X)$ is zero, for ![]() $k>2$. It follows that
$k>2$. It follows that ![]() ${\mathcal {E}} xt^k_{\mathcal {X}}(j_* \widetilde {{\mathcal {E}}}_{\boldsymbol {\cdot }}, \omega _{\mathcal {X}}) = 0$, for
${\mathcal {E}} xt^k_{\mathcal {X}}(j_* \widetilde {{\mathcal {E}}}_{\boldsymbol {\cdot }}, \omega _{\mathcal {X}}) = 0$, for ![]() $k>m-n+2$. By applying functor
$k>m-n+2$. By applying functor ![]() ${\mathcal {H}} om^{{\boldsymbol {\cdot }}}_{\mathcal {X}}(-, \omega _{\mathcal {X}})$ to the exact triangle
${\mathcal {H}} om^{{\boldsymbol {\cdot }}}_{\mathcal {X}}(-, \omega _{\mathcal {X}})$ to the exact triangle
we obtain an isomorphism
for any ![]() $k\geqslant m-n+2$. Sheaf
$k\geqslant m-n+2$. Sheaf ![]() $j_* {\mathcal {H}}^{-1}_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}})$ is non-zero with support of codimension
$j_* {\mathcal {H}}^{-1}_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}})$ is non-zero with support of codimension ![]() $l+m-n \geqslant m-n+2$. It follows that sheaf
$l+m-n \geqslant m-n+2$. It follows that sheaf ![]() ${\mathcal {E}} xt^{l+m-n}_{\mathcal {X}}(j_*{\mathcal {H}}^{-1}_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}}), \omega _{\mathcal {X}})$ is non-zero with support of codimension
${\mathcal {E}} xt^{l+m-n}_{\mathcal {X}}(j_*{\mathcal {H}}^{-1}_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}}), \omega _{\mathcal {X}})$ is non-zero with support of codimension ![]() $l+m-n$, cf. [Reference Huybrechts and LehnHL10, Proposition 1.1.6].
$l+m-n$, cf. [Reference Huybrechts and LehnHL10, Proposition 1.1.6].
On the other hand, the codimension of the support of ![]() ${\mathcal {E}} xt^{l+m-n+2}_{\mathcal {X}}(j_*{\mathcal {H}}^0_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}}), \omega _{\mathcal {X}})$ is greater than or equal to
${\mathcal {E}} xt^{l+m-n+2}_{\mathcal {X}}(j_*{\mathcal {H}}^0_X(\widetilde {{\mathcal {E}}}_{{\boldsymbol {\cdot }}}), \omega _{\mathcal {X}})$ is greater than or equal to ![]() $l+m-n+2$, which contradicts (29).
$l+m-n+2$, which contradicts (29).
Lemma 3.3 Let ![]() $f\colon X \to Y$ satisfy assumption (d) and let
$f\colon X \to Y$ satisfy assumption (d) and let ![]() $Y = \mathop {{\rm Spec}}\nolimits R$ be a spectrum of a complete Noetherian local ring. Let further
$Y = \mathop {{\rm Spec}}\nolimits R$ be a spectrum of a complete Noetherian local ring. Let further ![]() ${\mathcal {M}}_i$ be the projective object in
${\mathcal {M}}_i$ be the projective object in ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ as in (17) and
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ as in (17) and ![]() ${\mathcal {N}}_i = {\mathcal {H}} om_X({\mathcal {M}}_i, {\mathcal {O}}_X)$ the projective object in
${\mathcal {N}}_i = {\mathcal {H}} om_X({\mathcal {M}}_i, {\mathcal {O}}_X)$ the projective object in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. Then there exist exact sequences
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. Then there exist exact sequences
Proof. The sheaf ![]() ${\mathcal {M}}_i$ is defined as an extension
${\mathcal {M}}_i$ is defined as an extension
For any divisor ![]() $D_i$, one can find a linearly equivalent divisor
$D_i$, one can find a linearly equivalent divisor ![]() $D'_i$ such that
$D'_i$ such that ![]() $D_i \cap D'_i$ is empty. Indeed, let
$D_i \cap D'_i$ is empty. Indeed, let ![]() $D'_i$ be a divisor as in Remark 2.7 linearly equivalent to
$D'_i$ be a divisor as in Remark 2.7 linearly equivalent to ![]() $D_i$ which intersects
$D_i$ which intersects ![]() $C_i$ in a point
$C_i$ in a point ![]() $x'_i$, not equal to
$x'_i$, not equal to ![]() $x_i = D_i \cap C_i$. Then
$x_i = D_i \cap C_i$. Then ![]() $D_i\cap D'_i$ contains no closed points (as all closed points of
$D_i\cap D'_i$ contains no closed points (as all closed points of ![]() $X$ lie on
$X$ lie on ![]() $C$), hence empty. It follows that
$C$), hence empty. It follows that ![]() ${\mathcal {O}}_{D_i}(D_i) \simeq {\mathcal {O}}_{D_i}(D'_i) \simeq {\mathcal {O}}_{D_i}$ and sequence
${\mathcal {O}}_{D_i}(D_i) \simeq {\mathcal {O}}_{D_i}(D'_i) \simeq {\mathcal {O}}_{D_i}$ and sequence
is exact. As ![]() $\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {O}}_X, {\mathcal {O}}_X) \simeq 0$, the snake lemma for the two top rows of the following diagram gives the following commutative diagram in which rows and columns are exact sequences.
$\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {O}}_X, {\mathcal {O}}_X) \simeq 0$, the snake lemma for the two top rows of the following diagram gives the following commutative diagram in which rows and columns are exact sequences.

It gives exact sequence (30). By considering local homomorphisms into the structure sheaf we obtain sequence (31).
Lemma 3.4 Let ![]() $f\colon X\to Y$ satisfy assumption (p) and assume that
$f\colon X\to Y$ satisfy assumption (p) and assume that ![]() $Y$ has hypersurface singularities. Then the sheaf
$Y$ has hypersurface singularities. Then the sheaf ![]() $L^1f^*f_* {\mathcal {M}}$ is zero, for any
$L^1f^*f_* {\mathcal {M}}$ is zero, for any ![]() ${\mathcal {M}}\in \mathscr {P}_{-1}$.
${\mathcal {M}}\in \mathscr {P}_{-1}$.
Proof. The statement is local in ![]() $Y$, therefore we might assume that
$Y$, therefore we might assume that ![]() $Y = \mathop {{\rm Spec}}\nolimits R$ is a spectrum of a complete Noetherian local ring with hypersurface singularities. Then
$Y = \mathop {{\rm Spec}}\nolimits R$ is a spectrum of a complete Noetherian local ring with hypersurface singularities. Then ![]() ${\mathcal {M}}$ is a direct sum of copies of
${\mathcal {M}}$ is a direct sum of copies of ![]() ${\mathcal {M}}_i$ and
${\mathcal {M}}_i$ and ![]() ${\mathcal {O}}_X$. Thus, it suffices to verify the lemma for
${\mathcal {O}}_X$. Thus, it suffices to verify the lemma for ![]() ${\mathcal {M}}_i$, as clearly
${\mathcal {M}}_i$, as clearly ![]() $L^1f^*{\mathcal {O}}_Y = 0$.
$L^1f^*{\mathcal {O}}_Y = 0$.
As ![]() $R^1f_* {\mathcal {O}}_X \simeq 0$, applying
$R^1f_* {\mathcal {O}}_X \simeq 0$, applying ![]() $Rf_*$ to sequence (30) gives an exact sequence
$Rf_*$ to sequence (30) gives an exact sequence
It implies an exact sequence
By Lemma 3.2, the sheaf ![]() $L^1f^*f_* {\mathcal {O}}_{D_i}$ is zero, hence the result.
$L^1f^*f_* {\mathcal {O}}_{D_i}$ is zero, hence the result.
Lemma 3.5 Let ![]() $f \colon X\to Y$ satisfy assumption (p) and let
$f \colon X\to Y$ satisfy assumption (p) and let ![]() $Y$ have hypersurface singularities. Let
$Y$ have hypersurface singularities. Let ![]() ${\mathcal {N}}$ be a locally projective object in
${\mathcal {N}}$ be a locally projective object in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. Then
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. Then ![]() $f^*f_* {\mathcal {N}}$ is torsion-free and sequence
$f^*f_* {\mathcal {N}}$ is torsion-free and sequence
is exact for the sheaf ![]() $\mathcal {Q} ={\mathcal {H}}^0_X(\iota _{f*}\iota _f^*{\mathcal {N}})$, which is locally projective in
$\mathcal {Q} ={\mathcal {H}}^0_X(\iota _{f*}\iota _f^*{\mathcal {N}})$, which is locally projective in ![]() $\mathscr {A}_f$.
$\mathscr {A}_f$.
Proof. First, we show that ![]() $f^*f_* {\mathcal {N}}$ is torsion-free. This can be done locally, i.e. we may assume that
$f^*f_* {\mathcal {N}}$ is torsion-free. This can be done locally, i.e. we may assume that ![]() $Y$ is a spectrum of a complete Noetherian local ring. By [Reference Van den BerghVdB04, Lemma 3.5.2] sheaf
$Y$ is a spectrum of a complete Noetherian local ring. By [Reference Van den BerghVdB04, Lemma 3.5.2] sheaf ![]() ${\mathcal {N}}$ is a direct sum of copies of
${\mathcal {N}}$ is a direct sum of copies of ![]() ${\mathcal {O}}_X$ and
${\mathcal {O}}_X$ and ![]() ${\mathcal {N}}_i$, where
${\mathcal {N}}_i$, where ![]() ${\mathcal {N}}_i$ are vector bundles dual to
${\mathcal {N}}_i$ are vector bundles dual to ![]() ${\mathcal {M}}_i$.
${\mathcal {M}}_i$.
By [Reference Van den BerghVdB04, Lemma 3.1.2], the sheaf ![]() $R^1f_* {\mathcal {N}}_i$ is zero. By applying
$R^1f_* {\mathcal {N}}_i$ is zero. By applying ![]() $f_*$ to sequence (31), we obtain an exact sequence on
$f_*$ to sequence (31), we obtain an exact sequence on ![]() $Y$
$Y$
As ![]() $f_*{\mathcal {O}}_{D_i}$ is a torsion sheaf,
$f_*{\mathcal {O}}_{D_i}$ is a torsion sheaf, ![]() $f_*{\mathcal {N}}_i$ is non-zero. By applying
$f_*{\mathcal {N}}_i$ is non-zero. By applying ![]() $f^*$ to sequence (33), we obtain
$f^*$ to sequence (33), we obtain
It implies that the torsion of ![]() $f^*f_* {\mathcal {N}}_i$ is
$f^*f_* {\mathcal {N}}_i$ is ![]() $L^1f^*f_* {\mathcal {O}}_{D_i}$, which is zero by Lemma 3.2. Hence, sheaf
$L^1f^*f_* {\mathcal {O}}_{D_i}$, which is zero by Lemma 3.2. Hence, sheaf ![]() $f^*f_* {\mathcal {N}}_i$ is torsion free and the counit morphism
$f^*f_* {\mathcal {N}}_i$ is torsion free and the counit morphism ![]() $\varepsilon _{{\mathcal {N}}}\colon f^*f_* {\mathcal {N}}_i \to {\mathcal {N}}_i$ is an embedding (
$\varepsilon _{{\mathcal {N}}}\colon f^*f_* {\mathcal {N}}_i \to {\mathcal {N}}_i$ is an embedding (![]() $\varepsilon _{{\mathcal {N}}}$ is non-zero as under the
$\varepsilon _{{\mathcal {N}}}$ is non-zero as under the ![]() $f^*\dashv f_*$ adjunction it corresponds to the identity endomorphism of
$f^*\dashv f_*$ adjunction it corresponds to the identity endomorphism of ![]() $f_*{\mathcal {N}}_i$).
$f_*{\mathcal {N}}_i$).
The cokernel of the morphism ![]() $f^*f_* {\mathcal {N}} \to {\mathcal {N}}$ is, by the definition of
$f^*f_* {\mathcal {N}} \to {\mathcal {N}}$ is, by the definition of ![]() $\iota _f^*$, isomorphic to
$\iota _f^*$, isomorphic to ![]() ${\mathcal {H}}_X^0(\iota _f^* {\mathcal {N}})$, hence
${\mathcal {H}}_X^0(\iota _f^* {\mathcal {N}})$, hence ![]() $\mathcal {Q}$ is an object in
$\mathcal {Q}$ is an object in ![]() $\mathscr {A}_f$. Now let
$\mathscr {A}_f$. Now let ![]() $E$ be any object in
$E$ be any object in ![]() $\mathscr {A}_f$. Then
$\mathscr {A}_f$. Then ![]() $E$, considered as an object in
$E$, considered as an object in ![]() ${\mathcal {D}}^b(X)$, lies in
${\mathcal {D}}^b(X)$, lies in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$, hence
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$, hence ![]() $\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {N}}, E) \simeq 0$. Moreover,
$\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {N}}, E) \simeq 0$. Moreover, ![]() $f^* \vdash f_*$ adjunction implies that
$f^* \vdash f_*$ adjunction implies that ![]() $\mathop {{\rm Hom}}\nolimits _X(f^*f_* {\mathcal {N}}, E) \simeq 0$. Thus, by applying higher derived functors of
$\mathop {{\rm Hom}}\nolimits _X(f^*f_* {\mathcal {N}}, E) \simeq 0$. Thus, by applying higher derived functors of ![]() $\mathop {{\rm Hom}}\nolimits _X(-,E)$ to sequence (32), we obtain
$\mathop {{\rm Hom}}\nolimits _X(-,E)$ to sequence (32), we obtain ![]() $\mathop {{\rm Ext}}\nolimits ^1_X(\mathcal {Q}, E) \simeq 0$, which proves that
$\mathop {{\rm Ext}}\nolimits ^1_X(\mathcal {Q}, E) \simeq 0$, which proves that ![]() $\mathcal {Q} \in \mathscr {A}_f$ is indeed a projective object.
$\mathcal {Q} \in \mathscr {A}_f$ is indeed a projective object.
Remark 3.6 In the complete local case, ![]() ${\mathcal {P}}$ in formula (12) is isomorphic to
${\mathcal {P}}$ in formula (12) is isomorphic to ![]() $\mathcal {Q}$ of Lemma 3.5. Indeed, applying
$\mathcal {Q}$ of Lemma 3.5. Indeed, applying ![]() $\iota _f^*$ to sequences (30) and (31) and using the fact that
$\iota _f^*$ to sequences (30) and (31) and using the fact that ![]() $\iota _f^*({\mathcal {O}}_X) \simeq 0$, we obtain an isomorphism
$\iota _f^*({\mathcal {O}}_X) \simeq 0$, we obtain an isomorphism ![]() ${\mathcal {H}}_X^0(\iota _f^* {\mathcal {N}}_i) \simeq {\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {O}}_{D_i}) \simeq {\mathcal {H}}^{-1}_X(\iota _f^* {\mathcal {M}}_i)$.
${\mathcal {H}}_X^0(\iota _f^* {\mathcal {N}}_i) \simeq {\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {O}}_{D_i}) \simeq {\mathcal {H}}^{-1}_X(\iota _f^* {\mathcal {M}}_i)$.
The ![]() $t$-structure on
$t$-structure on ![]() ${\mathcal {D}}^b(X)$ with heart
${\mathcal {D}}^b(X)$ with heart ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ is obtained from the standard
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ is obtained from the standard ![]() $t$-structure by a tilt in the torsion pair
$t$-structure by a tilt in the torsion pair ![]() $({\mathcal {T}}_{-1}, {\mathcal {F}}_{-1})$ as in (10) and (11), see [Reference Van den BerghVdB04, Lemma 3.1.2]. Hence, for any
$({\mathcal {T}}_{-1}, {\mathcal {F}}_{-1})$ as in (10) and (11), see [Reference Van den BerghVdB04, Lemma 3.1.2]. Hence, for any ![]() $F \in {\mathcal {D}}^b(X)$, sequence
$F \in {\mathcal {D}}^b(X)$, sequence
is exact in ![]() $\mathop {{\rm Coh}}\nolimits (X)$, where by
$\mathop {{\rm Coh}}\nolimits (X)$, where by ![]() ${\mathcal {T}}_{-1}(G)$ and
${\mathcal {T}}_{-1}(G)$ and ![]() ${\mathcal {F}}_{-1}(G)$ we denote the torsion and torsion-free part, respectively, of a coherent sheaf
${\mathcal {F}}_{-1}(G)$ we denote the torsion and torsion-free part, respectively, of a coherent sheaf ![]() $G$ with respect to the torsion pair
$G$ with respect to the torsion pair ![]() $({\mathcal {T}}_{-1}, {\mathcal {F}}_{-1})$.
$({\mathcal {T}}_{-1}, {\mathcal {F}}_{-1})$.
Proposition 3.7 Let ![]() $f\colon X\to Y$ satisfy assumption (p) and assume that
$f\colon X\to Y$ satisfy assumption (p) and assume that ![]() $Y$ has hypersurface singularities. Let
$Y$ has hypersurface singularities. Let ![]() ${\mathcal {M}}$ be a projective object in
${\mathcal {M}}$ be a projective object in ![]() ${}^{-1}{\rm Per}(X/Y)$. Then
${}^{-1}{\rm Per}(X/Y)$. Then
Proof. Lemma 3.8 implies that ![]() $f^*f_* {\mathcal {M}}$ is an object in
$f^*f_* {\mathcal {M}}$ is an object in ![]() $\mathop {{\rm Coh}}\nolimits (X) \cap {}^{-1}{\rm Per}(X/Y)$, hence
$\mathop {{\rm Coh}}\nolimits (X) \cap {}^{-1}{\rm Per}(X/Y)$, hence ![]() ${\mathcal {T}}_{-1}(f^*f_* {\mathcal {M}}) = f^*f_* {\mathcal {M}}$. Moreover,
${\mathcal {T}}_{-1}(f^*f_* {\mathcal {M}}) = f^*f_* {\mathcal {M}}$. Moreover, ![]() $L^1f^*f_* {\mathcal {M}} = 0$ by Lemma 3.4. We conclude by sequence (34).
$L^1f^*f_* {\mathcal {M}} = 0$ by Lemma 3.4. We conclude by sequence (34).
Lemma 3.8 Let ![]() $f \colon X\to Y$ satisfy assumption (d) and let
$f \colon X\to Y$ satisfy assumption (d) and let ![]() $E$ be a coherent sheaf on
$E$ be a coherent sheaf on ![]() $Y$. Then
$Y$. Then ![]() $f^*E$ is an object in
$f^*E$ is an object in ![]() ${}^{p}{\rm Per}(X/Y)$, for
${}^{p}{\rm Per}(X/Y)$, for ![]() $p = -1,0$. If, moreover,
$p = -1,0$. If, moreover, ![]() $E$ is locally free and
$E$ is locally free and ![]() $Y$ is affine, then
$Y$ is affine, then ![]() $f^* E$ is an object in
$f^* E$ is an object in ![]() $\mathscr {P}_p$, for
$\mathscr {P}_p$, for ![]() $p=-1,0$.
$p=-1,0$.
Proof. We have ![]() ${\rm Coh}(X) \cap {}^{0}{\rm Per}(X/Y) = {\mathcal {T}}_{0}$ and
${\rm Coh}(X) \cap {}^{0}{\rm Per}(X/Y) = {\mathcal {T}}_{0}$ and ![]() ${\rm Coh}(X) \cap {}^{-1}{\rm Per}(X/Y) = {\mathcal {T}}_{-1}$, for categories
${\rm Coh}(X) \cap {}^{-1}{\rm Per}(X/Y) = {\mathcal {T}}_{-1}$, for categories ![]() ${\mathcal {T}}_0$ and
${\mathcal {T}}_0$ and ![]() ${\mathcal {T}}_{-1}$ defined in (8) and (10), respectively.
${\mathcal {T}}_{-1}$ defined in (8) and (10), respectively.
Let ![]() $E$ be a coherent sheaf on
$E$ be a coherent sheaf on ![]() $Y$. By Lemma 2.9, sheaf
$Y$. By Lemma 2.9, sheaf ![]() $R^1f_*f^* E$ is zero, hence
$R^1f_*f^* E$ is zero, hence ![]() $f^*E$ is an object in
$f^*E$ is an object in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. From adjunction
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. From adjunction
it follows that ![]() $f^*E$ lies also in
$f^*E$ lies also in ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$.
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$.
Now we assume further that ![]() $E$ is locally free and
$E$ is locally free and ![]() $Y$ is affine. Let
$Y$ is affine. Let ![]() $E'$ be any object in
$E'$ be any object in ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$, for
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$, for ![]() $p=-1, 0$. Then
$p=-1, 0$. Then
Because ![]() $Rf_*$ is exact for the perverse
$Rf_*$ is exact for the perverse ![]() $t$-structures on
$t$-structures on ![]() ${\mathcal {D}}^b(X)$, object
${\mathcal {D}}^b(X)$, object ![]() $Rf_* E'$ is a coherent sheaf on
$Rf_* E'$ is a coherent sheaf on ![]() $Y$. As
$Y$. As ![]() $E$ is locally free and
$E$ is locally free and ![]() $Y$ is affine,
$Y$ is affine, ![]() $\mathop {{\rm Ext}}\nolimits ^1_Y(E, Rf_* E') \simeq 0$, i.e.
$\mathop {{\rm Ext}}\nolimits ^1_Y(E, Rf_* E') \simeq 0$, i.e. ![]() $f^*E$ is projective in
$f^*E$ is projective in ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$.
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$.
Remark 3.9 For any locally free sheaf ![]() ${\mathcal {E}}$ on
${\mathcal {E}}$ on ![]() $Y$, we also have an isomorphism
$Y$, we also have an isomorphism ![]() ${\mathcal {H}}^0_{\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)}(Lf^*{\mathcal {E}}) = f^*{\mathcal {E}}$. Indeed,
${\mathcal {H}}^0_{\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)}(Lf^*{\mathcal {E}}) = f^*{\mathcal {E}}$. Indeed, ![]() $Lf^* {\mathcal {E}}$ is isomorphic to
$Lf^* {\mathcal {E}}$ is isomorphic to ![]() $f^* {\mathcal {E}}$ and the latter is an object in
$f^* {\mathcal {E}}$ and the latter is an object in ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$, by Lemma 3.8.
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$, by Lemma 3.8.
3.3 The equivalence of reflexive sheaves under flopping contractions
Recall that a sheaf ![]() $F$ is normal when, for any open sets
$F$ is normal when, for any open sets ![]() $U \subset V$ such that codimension of
$U \subset V$ such that codimension of ![]() $V\setminus U$ in
$V\setminus U$ in ![]() $V$ is greater than one, the restriction morphism
$V$ is greater than one, the restriction morphism ![]() $F(V) \to F(U)$ is an isomorphism.
$F(V) \to F(U)$ is an isomorphism.
Lemma 3.10 [Reference HartshorneHar80, Proposition 1.6]
Let ![]() $X$ be a normal, integral Noetherian scheme. A sheaf
$X$ be a normal, integral Noetherian scheme. A sheaf ![]() $F$ on
$F$ on ![]() $X$ is reflexive if and only if it is torsion-free and normal.
$X$ is reflexive if and only if it is torsion-free and normal.
For a scheme ![]() $X$, denote by
$X$, denote by ![]() $\textrm{Ref}\,(X)$ the category of reflexive sheaves.
$\textrm{Ref}\,(X)$ the category of reflexive sheaves.
Lemma 3.11 (Cf. [Reference Van den BerghVdB04, Lemma 4.2.1])
Let ![]() $f \colon X\to Y$ be a projective birational morphism,
$f \colon X\to Y$ be a projective birational morphism, ![]() $X,Y$ normal Noetherian and the exceptional locus of
$X,Y$ normal Noetherian and the exceptional locus of ![]() $f$ have codimension
$f$ have codimension ![]() $>1$ in
$>1$ in ![]() $X$. Then the following functors are mutually inverse equivalences:
$X$. Then the following functors are mutually inverse equivalences:
Proof. For a torsion-free sheaf ![]() $F$ on
$F$ on ![]() $X$, its push-forward
$X$, its push-forward ![]() $f_* F$ is also torsion-free. Thus,
$f_* F$ is also torsion-free. Thus, ![]() $f_* F$ will be reflexive if we check that it is normal.
$f_* F$ will be reflexive if we check that it is normal.
Let ![]() $G$ be a torsion-free sheaf on
$G$ be a torsion-free sheaf on ![]() $Y$ which is not normal. There exist open sets
$Y$ which is not normal. There exist open sets ![]() $j \colon U \hookrightarrow V$ with the complement of
$j \colon U \hookrightarrow V$ with the complement of ![]() $U$ in codimension greater than one in
$U$ in codimension greater than one in ![]() $V$ such that canonical morphism
$V$ such that canonical morphism ![]() $G \to j_*j^* G$ is not an isomorphism. Then we have a non-trivial extension
$G \to j_*j^* G$ is not an isomorphism. Then we have a non-trivial extension
The question is local, so we can assume ![]() $Y$ to be affine. Sheaf
$Y$ to be affine. Sheaf ![]() $Q$ is supported in codimension greater than one, hence there exists a closed subscheme
$Q$ is supported in codimension greater than one, hence there exists a closed subscheme ![]() $Z \subset Y$ of codimension greater than one such that sequence
$Z \subset Y$ of codimension greater than one such that sequence
is exact. As ![]() $G$ is torsion-free,
$G$ is torsion-free, ![]() $\mathop {{\rm Hom}}\nolimits (K, G)$ is zero. Hence, vanishing of
$\mathop {{\rm Hom}}\nolimits (K, G)$ is zero. Hence, vanishing of ![]() $\mathop {{\rm Ext}}\nolimits ^1_Y({\mathcal {O}}_Z, G)$ implies that
$\mathop {{\rm Ext}}\nolimits ^1_Y({\mathcal {O}}_Z, G)$ implies that ![]() $\mathop {{\rm Ext}}\nolimits ^1_Y(Q, G)$ is also zero. Thus, in order to show that a torsion-free sheaf
$\mathop {{\rm Ext}}\nolimits ^1_Y(Q, G)$ is also zero. Thus, in order to show that a torsion-free sheaf ![]() $G$ is normal it suffices to check that
$G$ is normal it suffices to check that ![]() $\mathop {{\rm Ext}}\nolimits ^1_Y({\mathcal {O}}_Z, G)$ vanishes, for any closed
$\mathop {{\rm Ext}}\nolimits ^1_Y({\mathcal {O}}_Z, G)$ vanishes, for any closed ![]() $Z \subset Y$ of codimension greater than one.
$Z \subset Y$ of codimension greater than one.
Group ![]() $\mathop {{\rm Ext}}\nolimits ^1_Y({\mathcal {O}}_Z, f_* F)$ is zero if and only if morphism
$\mathop {{\rm Ext}}\nolimits ^1_Y({\mathcal {O}}_Z, f_* F)$ is zero if and only if morphism ![]() $\mathop {{\rm Hom}}\nolimits ({\mathcal {O}}_Y, f_* F) \to \mathop {{\rm Hom}}\nolimits (I_Z, f_* F)$ given by short exact sequence
$\mathop {{\rm Hom}}\nolimits ({\mathcal {O}}_Y, f_* F) \to \mathop {{\rm Hom}}\nolimits (I_Z, f_* F)$ given by short exact sequence
is an isomorphism. By adjunction, ![]() $\mathop {{\rm Hom}}\nolimits _Y(I_Z, f_* F)$ is isomorphic to
$\mathop {{\rm Hom}}\nolimits _Y(I_Z, f_* F)$ is isomorphic to ![]() $\mathop {{\rm Hom}}\nolimits _X(f^* I_Z, F)$. Exceptional locus of
$\mathop {{\rm Hom}}\nolimits _X(f^* I_Z, F)$. Exceptional locus of ![]() $f$ has codimension greater than one, hence
$f$ has codimension greater than one, hence ![]() $f^* I_Z$ is isomorphic to
$f^* I_Z$ is isomorphic to ![]() ${\mathcal {O}}_X$ in codimension one. As
${\mathcal {O}}_X$ in codimension one. As ![]() $F$ is reflexive, this implies
$F$ is reflexive, this implies ![]() $\mathop {{\rm Hom}}\nolimits _X(f^*I_Z, F)= \mathop {{\rm Hom}}\nolimits _X({\mathcal {O}}_X, F)$.
$\mathop {{\rm Hom}}\nolimits _X(f^*I_Z, F)= \mathop {{\rm Hom}}\nolimits _X({\mathcal {O}}_X, F)$.
Thus, functor ![]() $f_*$ maps reflexive sheaves on
$f_*$ maps reflexive sheaves on ![]() $X$ to reflexive sheaves on
$X$ to reflexive sheaves on ![]() $Y$. Clearly, the same is true about
$Y$. Clearly, the same is true about ![]() $(f^*(-))^{\vee \vee }$.
$(f^*(-))^{\vee \vee }$.
Now let ![]() $F$ be an object in
$F$ be an object in ![]() $\textrm{Ref}\,(X)$. Adjunction implies a morphism
$\textrm{Ref}\,(X)$. Adjunction implies a morphism ![]() $\alpha \colon (f^*f_*F)^{\vee \vee } \to F^{\vee \vee } \simeq F$. Both sheaves are reflexive and
$\alpha \colon (f^*f_*F)^{\vee \vee } \to F^{\vee \vee } \simeq F$. Both sheaves are reflexive and ![]() $\alpha$ is an isomorphism outside exceptional locus of
$\alpha$ is an isomorphism outside exceptional locus of ![]() $f$, which has codimension greater than one. Therefore,
$f$, which has codimension greater than one. Therefore, ![]() $\alpha$ is an isomorphism.
$\alpha$ is an isomorphism.
For ![]() $G \in \textrm{Ref}\,(Y)$, reflexification
$G \in \textrm{Ref}\,(Y)$, reflexification ![]() $f^*G \to (f^*G)^{\vee \vee }$ together with adjunction
$f^*G \to (f^*G)^{\vee \vee }$ together with adjunction ![]() $G\to f_*f^*G$ give
$G\to f_*f^*G$ give ![]() $\beta \colon G \to f_*((f^*G)^{\vee \vee })$. Again, morphism
$\beta \colon G \to f_*((f^*G)^{\vee \vee })$. Again, morphism ![]() $\beta$ is an isomorphism in codimension one between reflexive sheaves, hence an isomorphism.
$\beta$ is an isomorphism in codimension one between reflexive sheaves, hence an isomorphism.
Finally, a morphism between reflexive sheaves is determined by its restriction to any open set with the complement of codimension greater than one. Thus, functors ![]() $f_*$ and
$f_*$ and ![]() $(f^*(-))^{\vee \vee }$ give isomorphisms on the groups of morphisms between objects in
$(f^*(-))^{\vee \vee }$ give isomorphisms on the groups of morphisms between objects in ![]() $\textrm{Ref}\,(X)$ and
$\textrm{Ref}\,(X)$ and ![]() $\textrm{Ref}\,(Y)$.
$\textrm{Ref}\,(Y)$.
Let ![]() $f\colon X\to Y$ satisfy assumption (a). For
$f\colon X\to Y$ satisfy assumption (a). For ![]() ${\mathcal {M}}$ an object in
${\mathcal {M}}$ an object in ![]() $\mathscr {P}_{-1}$, put
$\mathscr {P}_{-1}$, put
By Lemma 3.11, sheaf ![]() ${\mathcal {N}}^+$ belongs to
${\mathcal {N}}^+$ belongs to ![]() $\textrm{Ref}\,(X^+)$.
$\textrm{Ref}\,(X^+)$.
Proposition 3.12 Let ![]() $f\colon X\to Y$ satisfy assumption (a) and
$f\colon X\to Y$ satisfy assumption (a) and ![]() $f^+ \colon X^+ \to Y$ its flop. Then functor
$f^+ \colon X^+ \to Y$ its flop. Then functor
restricts to equivalences ![]() $\mathscr {P}_{-1} \xrightarrow {\simeq } \mathscr {P}_0^+$ and
$\mathscr {P}_{-1} \xrightarrow {\simeq } \mathscr {P}_0^+$ and ![]() $\mathscr {P}_0 \xrightarrow {\simeq } \mathscr {P}_{-1}^+$.
$\mathscr {P}_0 \xrightarrow {\simeq } \mathscr {P}_{-1}^+$.
Proof. By [Reference Van den BerghVdB04, Proposition 3.2.6], categories ![]() $\mathscr {P}_{-1}$ and
$\mathscr {P}_{-1}$ and ![]() $\mathscr {P}_0$ are subcategories of
$\mathscr {P}_0$ are subcategories of ![]() $\textrm{Ref}\,(X)$. By [Reference Van den BerghVdB04, Proposition 4.3.1], subcategories
$\textrm{Ref}\,(X)$. By [Reference Van den BerghVdB04, Proposition 4.3.1], subcategories ![]() $f_* \mathscr {P}_{-1}$ and
$f_* \mathscr {P}_{-1}$ and ![]() $f^+_* \mathscr {P}_0^+$ of
$f^+_* \mathscr {P}_0^+$ of ![]() $\textrm{Ref}\,(Y)$ are equivalent. By Lemma 3.11, the subcategory
$\textrm{Ref}\,(Y)$ are equivalent. By Lemma 3.11, the subcategory ![]() $(f^{+*}f_* \mathscr {P}_{-1})^{\vee \vee }$ of
$(f^{+*}f_* \mathscr {P}_{-1})^{\vee \vee }$ of ![]() $\textrm{Ref}\,(X^+)$ corresponds to
$\textrm{Ref}\,(X^+)$ corresponds to ![]() $\mathscr {P}_{-1}$ under equivalences
$\mathscr {P}_{-1}$ under equivalences ![]() $\textrm{Ref}\,(X)\simeq \textrm{Ref}\,(Y) \simeq \textrm{Ref}\,(X^+)$, hence
$\textrm{Ref}\,(X)\simeq \textrm{Ref}\,(Y) \simeq \textrm{Ref}\,(X^+)$, hence ![]() $\mathscr {P}_0^+ \simeq (f^{+*}f_* \mathscr {P}_{-1})^{\vee \vee }$.
$\mathscr {P}_0^+ \simeq (f^{+*}f_* \mathscr {P}_{-1})^{\vee \vee }$.
Exchanging the roles of ![]() $f$ and
$f$ and ![]() $f^+$, we get equivalence of
$f^+$, we get equivalence of ![]() $\mathscr {P}_{-1}^+$ with
$\mathscr {P}_{-1}^+$ with ![]() $\mathscr {P}_0$.
$\mathscr {P}_0$.
3.4 A divisorial embedding into a smooth scheme and cohomology
We assume that ![]() $Y$ is affine and fix a closed embedding
$Y$ is affine and fix a closed embedding ![]() $i\colon Y \to {\mathcal {Y}}$ of
$i\colon Y \to {\mathcal {Y}}$ of ![]() $Y$ as the zero locus of a regular function on a smooth affine
$Y$ as the zero locus of a regular function on a smooth affine ![]() ${\mathcal {Y}}$. Denote
${\mathcal {Y}}$. Denote ![]() $g= i \circ f$, i.e. consider the following commutative diagram.
$g= i \circ f$, i.e. consider the following commutative diagram.

We describe objects ![]() $Lg^*g_* {\mathcal {M}}$ and
$Lg^*g_* {\mathcal {M}}$ and ![]() $Lg^*f_*{\mathcal {N}}$, for any
$Lg^*f_*{\mathcal {N}}$, for any ![]() ${\mathcal {M}}\in \mathscr {P}_{-1}$,
${\mathcal {M}}\in \mathscr {P}_{-1}$, ![]() ${\mathcal {N}} \in \mathscr {P}_0$. First, we prove that the sheaves
${\mathcal {N}} \in \mathscr {P}_0$. First, we prove that the sheaves ![]() $g_* {\mathcal {M}}$,
$g_* {\mathcal {M}}$, ![]() $g_*{\mathcal {N}}$ have short locally free resolutions.
$g_*{\mathcal {N}}$ have short locally free resolutions.
Recall that a morphism ![]() $f\colon X\to Y$ is crepant if
$f\colon X\to Y$ is crepant if ![]() $Lf^*(\omega _Y^{\boldsymbol {\cdot }})\simeq \omega _X^{\boldsymbol {\cdot }}.$
$Lf^*(\omega _Y^{\boldsymbol {\cdot }})\simeq \omega _X^{\boldsymbol {\cdot }}.$
Lemma 3.13 A proper morphism ![]() $f\colon X\to Y$ of Gorenstein varieties is crepant if and only if
$f\colon X\to Y$ of Gorenstein varieties is crepant if and only if ![]() $f^!({\mathcal {O}}_Y) \simeq {\mathcal {O}}_X$.
$f^!({\mathcal {O}}_Y) \simeq {\mathcal {O}}_X$.
Proof. As ![]() $X$ and
$X$ and ![]() $Y$ are Gorenstein,
$Y$ are Gorenstein, ![]() $\omega _X^{\boldsymbol {\cdot }}$ and
$\omega _X^{\boldsymbol {\cdot }}$ and ![]() $\omega _Y^{\boldsymbol {\cdot }}$ are, up to shift, line bundles. In particular,
$\omega _Y^{\boldsymbol {\cdot }}$ are, up to shift, line bundles. In particular, ![]() $\omega _Y^{\boldsymbol {\cdot }}$ is a perfect complex, hence, by Lemma A.1,
$\omega _Y^{\boldsymbol {\cdot }}$ is a perfect complex, hence, by Lemma A.1, ![]() $f^!(\omega _Y^{\boldsymbol {\cdot }}) \simeq f^!({\mathcal {O}}_Y) \otimes Lf^*(\omega _Y^{\boldsymbol {\cdot }})$. Isomorphism
$f^!(\omega _Y^{\boldsymbol {\cdot }}) \simeq f^!({\mathcal {O}}_Y) \otimes Lf^*(\omega _Y^{\boldsymbol {\cdot }})$. Isomorphism ![]() $\omega _X^{\boldsymbol {\cdot }} \simeq f^!(\omega _Y^{\boldsymbol {\cdot }}) \simeq f^!({\mathcal {O}}_Y)\otimes Lf^*(\omega _Y)^{\boldsymbol {\cdot }}$ implies
$\omega _X^{\boldsymbol {\cdot }} \simeq f^!(\omega _Y^{\boldsymbol {\cdot }}) \simeq f^!({\mathcal {O}}_Y)\otimes Lf^*(\omega _Y)^{\boldsymbol {\cdot }}$ implies ![]() $f^!({\mathcal {O}}_Y) \simeq \omega _X^{\boldsymbol {\cdot }} \otimes (Lf^*(\omega _Y^{\boldsymbol {\cdot }}))^{-1}$. Hence,
$f^!({\mathcal {O}}_Y) \simeq \omega _X^{\boldsymbol {\cdot }} \otimes (Lf^*(\omega _Y^{\boldsymbol {\cdot }}))^{-1}$. Hence, ![]() $Lf^*(\omega _Y^{\boldsymbol {\cdot }}) \simeq \omega _X^{\boldsymbol {\cdot }}$ if and only
$Lf^*(\omega _Y^{\boldsymbol {\cdot }}) \simeq \omega _X^{\boldsymbol {\cdot }}$ if and only ![]() $f^!({\mathcal {O}}_Y) \simeq {\mathcal {O}}_X$.
$f^!({\mathcal {O}}_Y) \simeq {\mathcal {O}}_X$.
Lemma 3.14 Let ![]() $X$,
$X$, ![]() $Y$ be Gorenstein and
$Y$ be Gorenstein and ![]() $f\colon X\to Y$ a crepant morphism satisfying assumption (d). Assume
$f\colon X\to Y$ a crepant morphism satisfying assumption (d). Assume ![]() $Y$ is affine and
$Y$ is affine and ![]() $i\colon Y \to {\mathcal {Y}}$ an embedding of
$i\colon Y \to {\mathcal {Y}}$ an embedding of ![]() $Y$ as a Cartier divisor into a smooth
$Y$ as a Cartier divisor into a smooth ![]() ${\mathcal {Y}}$. Denote
${\mathcal {Y}}$. Denote ![]() $g = i\circ f\colon X\to {\mathcal {Y}}$. Then
$g = i\circ f\colon X\to {\mathcal {Y}}$. Then ![]() $g_* {\mathcal {M}}$ and
$g_* {\mathcal {M}}$ and ![]() $g_* {\mathcal {N}}$, for
$g_* {\mathcal {N}}$, for ![]() ${\mathcal {M}} \in \mathscr {P}_{-1}$,
${\mathcal {M}} \in \mathscr {P}_{-1}$, ![]() ${\mathcal {N}} \in \mathscr {P}_0$, admit locally free resolutions of length two.
${\mathcal {N}} \in \mathscr {P}_0$, admit locally free resolutions of length two.
Proof. Let ![]() ${\mathcal {M}}$ be an object in
${\mathcal {M}}$ be an object in ![]() $\mathscr {P}_{-1}$. As
$\mathscr {P}_{-1}$. As ![]() ${\mathcal {Y}}$ is affine, the length of the locally free resolution for
${\mathcal {Y}}$ is affine, the length of the locally free resolution for ![]() $g_* {\mathcal {M}}$ is
$g_* {\mathcal {M}}$ is ![]() $l+1$, for the maximal
$l+1$, for the maximal ![]() $l$ such that
$l$ such that ![]() ${\mathcal {E}} xt^l_{{\mathcal {Y}}}(g_* {\mathcal {M}}, {\mathcal {O}}_{{\mathcal {Y}}})$ is non-zero. Thus, the question is local on
${\mathcal {E}} xt^l_{{\mathcal {Y}}}(g_* {\mathcal {M}}, {\mathcal {O}}_{{\mathcal {Y}}})$ is non-zero. Thus, the question is local on ![]() ${\mathcal {Y}}$ and, by restricting to a smaller affine open subset, we can assume that
${\mathcal {Y}}$ and, by restricting to a smaller affine open subset, we can assume that ![]() $\omega ^{{\boldsymbol {\cdot }}}_{{\mathcal {Y}}} \simeq {\mathcal {O}}_{{\mathcal {Y}}}[n+1]$ and
$\omega ^{{\boldsymbol {\cdot }}}_{{\mathcal {Y}}} \simeq {\mathcal {O}}_{{\mathcal {Y}}}[n+1]$ and ![]() $\omega ^{{\boldsymbol {\cdot }}}_{Y} \simeq {\mathcal {O}}_{Y}[n]$. Then
$\omega ^{{\boldsymbol {\cdot }}}_{Y} \simeq {\mathcal {O}}_{Y}[n]$. Then ![]() $\omega _X^{{\boldsymbol {\cdot }}} \simeq {\mathcal {O}}_X[n]$, because
$\omega _X^{{\boldsymbol {\cdot }}} \simeq {\mathcal {O}}_X[n]$, because ![]() $f$ is crepant. Let
$f$ is crepant. Let ![]() ${\mathcal {N}} = R {\mathcal {H}} om_X({\mathcal {M}}, {\mathcal {O}}_X)={\mathcal {H}} om_X({\mathcal {M}}, {\mathcal {O}}_X)$. It is an object in
${\mathcal {N}} = R {\mathcal {H}} om_X({\mathcal {M}}, {\mathcal {O}}_X)={\mathcal {H}} om_X({\mathcal {M}}, {\mathcal {O}}_X)$. It is an object in ![]() $\mathscr {P}_0$, see [Reference Van den BerghVdB04, Proposition 3.2.6]. As
$\mathscr {P}_0$, see [Reference Van den BerghVdB04, Proposition 3.2.6]. As ![]() ${\mathcal {N}}$ is an object in
${\mathcal {N}}$ is an object in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$, we have
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$, we have ![]() $Rg_* {\mathcal {N}} \simeq g_* {\mathcal {N}}$. Then we have, by Grothendieck duality (A.1),
$Rg_* {\mathcal {N}} \simeq g_* {\mathcal {N}}$. Then we have, by Grothendieck duality (A.1),
Hence, ![]() $g_* {\mathcal {M}}$ is of projective dimension one. Analogously, for
$g_* {\mathcal {M}}$ is of projective dimension one. Analogously, for ![]() ${\mathcal {N}} \in \mathscr {P}_0$, its dual
${\mathcal {N}} \in \mathscr {P}_0$, its dual ![]() ${\mathcal {M}} = R{\mathcal {H}} om_X({\mathcal {N}},{\mathcal {O}}_X)$ lies in
${\mathcal {M}} = R{\mathcal {H}} om_X({\mathcal {N}},{\mathcal {O}}_X)$ lies in ![]() $\mathscr {P}_{-1}$ and
$\mathscr {P}_{-1}$ and ![]() $R{\mathcal {H}} om(g_* {\mathcal {N}}, {\mathcal {O}}_{{\mathcal {Y}}}) \simeq g_* {\mathcal {M}}[-1]$.
$R{\mathcal {H}} om(g_* {\mathcal {N}}, {\mathcal {O}}_{{\mathcal {Y}}}) \simeq g_* {\mathcal {M}}[-1]$.
Proposition 3.15 Let ![]() $f\colon X\to Y$ be as in Lemma 3.14. Let further
$f\colon X\to Y$ be as in Lemma 3.14. Let further ![]() $p\in \{-1,0\}$ and
$p\in \{-1,0\}$ and ![]() ${\mathcal {R}} \in \mathscr {P}_p$ be a projective object in
${\mathcal {R}} \in \mathscr {P}_p$ be a projective object in ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$. Then the object
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$. Then the object ![]() $Lg^*Rg_*{\mathcal {R}}$ has cohomology
$Lg^*Rg_*{\mathcal {R}}$ has cohomology
 \[ {\mathcal{H}}^i_X(Lg^*Rg_* {\mathcal{R}}) = \begin{cases}{\mathcal{R}}, & \textrm{if }\, i=-1,\\ f^*f_* {\mathcal{R}}, & \textrm{if } i=0, \\ 0, & \textrm{otherwise.} \end{cases} \]
\[ {\mathcal{H}}^i_X(Lg^*Rg_* {\mathcal{R}}) = \begin{cases}{\mathcal{R}}, & \textrm{if }\, i=-1,\\ f^*f_* {\mathcal{R}}, & \textrm{if } i=0, \\ 0, & \textrm{otherwise.} \end{cases} \]
The same cohomology is for the ![]() $t$-structure with heart
$t$-structure with heart ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$.
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$.
Proof. As ![]() $R^1g_*{\mathcal {R}} =0$, the zero cohomology of
$R^1g_*{\mathcal {R}} =0$, the zero cohomology of ![]() $Lg^*Rg_*{\mathcal {R}}$ is the sheaf
$Lg^*Rg_*{\mathcal {R}}$ is the sheaf ![]() $g^*g_*{\mathcal {R}}$. The adjunction counit for
$g^*g_*{\mathcal {R}}$. The adjunction counit for ![]() $i\colon Y \to {\mathcal {Y}}$ gives an isomorphism
$i\colon Y \to {\mathcal {Y}}$ gives an isomorphism ![]() $g^*g_*\xrightarrow {\simeq } f^*f_*$, hence
$g^*g_*\xrightarrow {\simeq } f^*f_*$, hence ![]() ${\mathcal {H}}^0_X(Lg^*Rg_*{\mathcal {R}}) = f^*f_*{\mathcal {R}}$.
${\mathcal {H}}^0_X(Lg^*Rg_*{\mathcal {R}}) = f^*f_*{\mathcal {R}}$.
As ![]() $g_*{\mathcal {R}}$ admits a locally free resolution (see Lemma 3.14):
$g_*{\mathcal {R}}$ admits a locally free resolution (see Lemma 3.14):
the sheaves ![]() ${\mathcal {H}}^i_X(Lg^*Rg_*{\mathcal {R}})$ are zero, for
${\mathcal {H}}^i_X(Lg^*Rg_*{\mathcal {R}})$ are zero, for ![]() $i\leqslant -2$. Moreover,
$i\leqslant -2$. Moreover, ![]() $L^1g^*g_*{\mathcal {R}}$ is reflexive, as the kernel of a morphism of locally free sheaves [Reference HartshorneHar80, Proposition 1.1].
$L^1g^*g_*{\mathcal {R}}$ is reflexive, as the kernel of a morphism of locally free sheaves [Reference HartshorneHar80, Proposition 1.1].
Applying ![]() $Lf^*$ to exact triangle
$Lf^*$ to exact triangle ![]() $f_* {\mathcal {R}}[1] \to Li^*g_* {\mathcal {R}} \to f_* {\mathcal {R}} \to f_*{\mathcal {R}}[2]$ (given by Theorem 3.1 for
$f_* {\mathcal {R}}[1] \to Li^*g_* {\mathcal {R}} \to f_* {\mathcal {R}} \to f_*{\mathcal {R}}[2]$ (given by Theorem 3.1 for ![]() $Y\subset {\mathcal {Y}}$) implies the exact sequence
$Y\subset {\mathcal {Y}}$) implies the exact sequence
As ![]() $f$ is an isomorphism in codimension one, the sheaves
$f$ is an isomorphism in codimension one, the sheaves ![]() $L^2f^*f_*{\mathcal {R}}$ and
$L^2f^*f_*{\mathcal {R}}$ and ![]() $L^1f^*f_*{\mathcal {R}}$ have the support of codimension at least two. As the universal map
$L^1f^*f_*{\mathcal {R}}$ have the support of codimension at least two. As the universal map ![]() $f^*f_*{\mathcal {R}}\to (f^*f_*{\mathcal {R}})^{\vee \vee }$ is also an isomorphism in codimension one, the induced map
$f^*f_*{\mathcal {R}}\to (f^*f_*{\mathcal {R}})^{\vee \vee }$ is also an isomorphism in codimension one, the induced map ![]() $(f^*f_*{\mathcal {R}})^{\vee \vee } \to L^1g^*g_*{\mathcal {R}}$ is an isomorphism in codimension one. Hence, it is an isomorphism, see Lemma 3.10. It follows that
$(f^*f_*{\mathcal {R}})^{\vee \vee } \to L^1g^*g_*{\mathcal {R}}$ is an isomorphism in codimension one. Hence, it is an isomorphism, see Lemma 3.10. It follows that ![]() $L^1g^*g_*{\mathcal {R}} \simeq (f^*f_*{\mathcal {R}})^{\vee \vee }$. As
$L^1g^*g_*{\mathcal {R}} \simeq (f^*f_*{\mathcal {R}})^{\vee \vee }$. As ![]() ${\mathcal {R}}$ is locally free [Reference Van den BerghVdB04, Proposition 3.2.6],
${\mathcal {R}}$ is locally free [Reference Van den BerghVdB04, Proposition 3.2.6], ![]() $(f^*f_*{\mathcal {R}})^{\vee \vee }\simeq {\mathcal {R}}$ by Lemma 3.11.
$(f^*f_*{\mathcal {R}})^{\vee \vee }\simeq {\mathcal {R}}$ by Lemma 3.11.
By Lemma 3.8, ![]() $f^*f_*{\mathcal {R}}$ is an object of
$f^*f_*{\mathcal {R}}$ is an object of ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$. As the same holds for
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$. As the same holds for ![]() ${\mathcal {R}} \in \mathscr {P}_{p} \subset \mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$, the exact triangle
${\mathcal {R}} \in \mathscr {P}_{p} \subset \mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$, the exact triangle ![]() ${\mathcal {R}}[1] \to Lg^*g_*{\mathcal {R}} \to f^*f_*{\mathcal {R}}$ is also the decomposition of
${\mathcal {R}}[1] \to Lg^*g_*{\mathcal {R}} \to f^*f_*{\mathcal {R}}$ is also the decomposition of ![]() $Lg^*g_*{\mathcal {R}}$ in the
$Lg^*g_*{\mathcal {R}}$ in the ![]() $t$-structure with heart
$t$-structure with heart ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$.
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$.
Proposition 3.15 implies that triangle
is exact. By Lemma 3.14, object ![]() $Lg^*g_* {\mathcal {M}}$ is quasi-isomorphic to a complex
$Lg^*g_* {\mathcal {M}}$ is quasi-isomorphic to a complex ![]() $f^* {\mathcal {F}}_{-1} \to f^* {\mathcal {F}}_0$, for some locally free sheaves
$f^* {\mathcal {F}}_{-1} \to f^* {\mathcal {F}}_0$, for some locally free sheaves ![]() ${\mathcal {F}}_{-1}$,
${\mathcal {F}}_{-1}$, ![]() ${\mathcal {F}}_0$ on
${\mathcal {F}}_0$ on ![]() $Y$. Hence, sequence
$Y$. Hence, sequence
is a projective resolution for ![]() $f^*f_* {\mathcal {M}}$ in
$f^*f_* {\mathcal {M}}$ in ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$, see Lemma 3.8.
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$, see Lemma 3.8.
Note that short exact sequence (15) and Lemma 3.8 imply that
is a short exact sequence in ![]() ${}^{-1}{\rm Per}(X/Y)$.
${}^{-1}{\rm Per}(X/Y)$.
3.5 2-periodicity
Proposition 3.16 Let ![]() $f \colon X\to Y$ satisfy assumption (d) and assume that
$f \colon X\to Y$ satisfy assumption (d) and assume that ![]() $Y \subset {\mathcal {Y}}$ is a principal divisor in a smooth affine
$Y \subset {\mathcal {Y}}$ is a principal divisor in a smooth affine ![]() ${\mathcal {Y}}$. Then there exists a morphism
${\mathcal {Y}}$. Then there exists a morphism ![]() $Lf^* \to Lf^*[2]$ of functors
$Lf^* \to Lf^*[2]$ of functors ![]() ${\mathcal {D}}_{{\rm qc}}(Y) \to {\mathcal {D}}_{{\rm qc}}(X)$, which, for any
${\mathcal {D}}_{{\rm qc}}(Y) \to {\mathcal {D}}_{{\rm qc}}(X)$, which, for any ![]() $E$ in
$E$ in ![]() ${\mathcal {D}}^b(Y)$, is an isomorphism on almost all cohomology sheaves of
${\mathcal {D}}^b(Y)$, is an isomorphism on almost all cohomology sheaves of ![]() $Lf^*(E)$.
$Lf^*(E)$.
Proof. By applying ![]() $Lf^*$ to functorial exact triangle (27), we obtain a morphism
$Lf^*$ to functorial exact triangle (27), we obtain a morphism ![]() $Lf^*E \to Lf^*E[2]$ with cone
$Lf^*E \to Lf^*E[2]$ with cone ![]() $Lf^*Li^*i_*E[1]$. As
$Lf^*Li^*i_*E[1]$. As ![]() ${\mathcal {Y}}$ is smooth,
${\mathcal {Y}}$ is smooth, ![]() ${\mathcal {D}}^b({\mathcal {Y}})$ coincides with the category of perfect complexes on
${\mathcal {D}}^b({\mathcal {Y}})$ coincides with the category of perfect complexes on ![]() ${\mathcal {Y}}$. It follows that the functor
${\mathcal {Y}}$. It follows that the functor ![]() $Lf^*Li^*i_*$ takes
$Lf^*Li^*i_*$ takes ![]() ${\mathcal {D}}^b(Y)$ to
${\mathcal {D}}^b(Y)$ to ![]() ${\mathcal {D}}^b(X)$ (even to
${\mathcal {D}}^b(X)$ (even to ![]() $\mathop {{\rm Perf}}\nolimits (X)$), hence, for any
$\mathop {{\rm Perf}}\nolimits (X)$), hence, for any ![]() $E\in {\mathcal {D}}^b(Y)$, there exists
$E\in {\mathcal {D}}^b(Y)$, there exists ![]() $l\in \mathbb {Z}$ such that
$l\in \mathbb {Z}$ such that ![]() ${\mathcal {H}}^i(Lf^*Li^*i_*E) = 0$, for
${\mathcal {H}}^i(Lf^*Li^*i_*E) = 0$, for ![]() $i < l$. Then
$i < l$. Then ![]() ${\mathcal {H}}^i Lf^*E \simeq {\mathcal {H}}^{i-2} Lf^* E$, for any
${\mathcal {H}}^i Lf^*E \simeq {\mathcal {H}}^{i-2} Lf^* E$, for any ![]() $i< l$.
$i< l$.
Now let ![]() $f\colon X\to Y$ be a crepant morphism of Gorenstein varieties satisfying assumption (p) and assume that
$f\colon X\to Y$ be a crepant morphism of Gorenstein varieties satisfying assumption (p) and assume that ![]() $Y \subset {\mathcal {Y}}$ is a principal divisor in a smooth
$Y \subset {\mathcal {Y}}$ is a principal divisor in a smooth ![]() ${\mathcal {Y}}$. Then
${\mathcal {Y}}$. Then ![]() ${\mathcal {I}}_Y\simeq {\mathcal {O}}_{{\mathcal {Y}}}$, hence composing functorial exact triangle (27) with
${\mathcal {I}}_Y\simeq {\mathcal {O}}_{{\mathcal {Y}}}$, hence composing functorial exact triangle (27) with ![]() $Lf^*$ and precomposing with
$Lf^*$ and precomposing with ![]() $Rf_*$ gives a functorial exact triangle
$Rf_*$ gives a functorial exact triangle
Object ![]() $Lg^*g_* {\mathcal {M}}$ has only two non-zero cohomology sheaves described by Proposition 3.15, for any
$Lg^*g_* {\mathcal {M}}$ has only two non-zero cohomology sheaves described by Proposition 3.15, for any ![]() ${\mathcal {M}}\in \mathscr {P}_{-1}$. Then the long exact sequence of cohomology sheaves for triangle (39) applied to
${\mathcal {M}}\in \mathscr {P}_{-1}$. Then the long exact sequence of cohomology sheaves for triangle (39) applied to ![]() ${\mathcal {M}}$ implies short exact sequence
${\mathcal {M}}$ implies short exact sequence
and isomorphisms ![]() $L^lf^*f_* {\mathcal {M}} \simeq L^{l+2} f^*f_* {\mathcal {M}}$, for
$L^lf^*f_* {\mathcal {M}} \simeq L^{l+2} f^*f_* {\mathcal {M}}$, for ![]() $l \geqslant 1$. Hence, we have 2-periodicity
$l \geqslant 1$. Hence, we have 2-periodicity
 \begin{equation} L^lf^*f_* {\mathcal{M}} \simeq \begin{cases}{\mathcal{P}}, & \text{for even }\, l \geqslant 2,\\ 0, & \text{for odd }\, l. \end{cases} \end{equation}
\begin{equation} L^lf^*f_* {\mathcal{M}} \simeq \begin{cases}{\mathcal{P}}, & \text{for even }\, l \geqslant 2,\\ 0, & \text{for odd }\, l. \end{cases} \end{equation}Remark 3.17 From Propositions 3.16 and 3.15 it follows that
 \[ L^lf^*f_* {\mathcal{N}} \simeq \begin{cases} \mathcal{Q}, & \text{for odd }\, l\geqslant 1,\\ 0, & \text{for even }\,l\geqslant 2.\end{cases} \]
\[ L^lf^*f_* {\mathcal{N}} \simeq \begin{cases} \mathcal{Q}, & \text{for odd }\, l\geqslant 1,\\ 0, & \text{for even }\,l\geqslant 2.\end{cases} \]Remark 3.18 Let ![]() $f\colon X\to Y$ be a crepant morphism of Gorenstein varieties satisfying assumption (d) such that
$f\colon X\to Y$ be a crepant morphism of Gorenstein varieties satisfying assumption (d) such that ![]() $Y \subset {\mathcal {Y}}$ is a principal divisor in a smooth affine
$Y \subset {\mathcal {Y}}$ is a principal divisor in a smooth affine ![]() ${\mathcal {Y}}$. Using Proposition 3.15 we construct a projective resolution
${\mathcal {Y}}$. Using Proposition 3.15 we construct a projective resolution
of ![]() $f^*f_* {\mathcal {N}}$ in
$f^*f_* {\mathcal {N}}$ in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. Here,
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. Here, ![]() ${\mathcal {E}}_{-1}$ and
${\mathcal {E}}_{-1}$ and ![]() ${\mathcal {E}}_0$ are locally free sheaves on
${\mathcal {E}}_0$ are locally free sheaves on ![]() $Y$ such that
$Y$ such that ![]() $Li^*g_* {\mathcal {N}}$ is quasi-isomorphic to
$Li^*g_* {\mathcal {N}}$ is quasi-isomorphic to ![]() ${\mathcal {E}}_{-1}\to {\mathcal {E}}_0$ (see Lemma 3.14).
${\mathcal {E}}_{-1}\to {\mathcal {E}}_0$ (see Lemma 3.14).
Proposition 3.19 (Cf. [Reference Donovan and WemyssDW16, Proposition 5.6])
Let ![]() $f\colon X\to Y$ satisfy assumption (a),
$f\colon X\to Y$ satisfy assumption (a), ![]() ${\mathcal {M}}$ be in
${\mathcal {M}}$ be in ![]() $\mathscr {P}_{-1}$ and
$\mathscr {P}_{-1}$ and ![]() ${\mathcal {N}}$ in
${\mathcal {N}}$ in ![]() $\mathscr {P}_0$. Then there exist locally free sheaves
$\mathscr {P}_0$. Then there exist locally free sheaves ![]() ${\mathcal {F}}_{-1}$,
${\mathcal {F}}_{-1}$, ![]() ${\mathcal {F}}_0$,
${\mathcal {F}}_0$, ![]() ${\mathcal {E}}_{-1}$,
${\mathcal {E}}_{-1}$, ![]() ${\mathcal {E}}_0$ on
${\mathcal {E}}_0$ on ![]() $Y$ such that
$Y$ such that
are projective resolutions of ![]() ${\mathcal {P}}_{{\mathcal {M}}}[1] = {\mathcal {H}}^{-1}_X \iota _f^* {\mathcal {M}}[1]$ and
${\mathcal {P}}_{{\mathcal {M}}}[1] = {\mathcal {H}}^{-1}_X \iota _f^* {\mathcal {M}}[1]$ and ![]() ${\mathcal {P}}_{{\mathcal {N}}} = {\mathcal {H}}^0_X \iota _f^* {\mathcal {N}}$ respectively in
${\mathcal {P}}_{{\mathcal {N}}} = {\mathcal {H}}^0_X \iota _f^* {\mathcal {N}}$ respectively in ![]() ${}^{-1}{\rm Per}(X/Y)$ and
${}^{-1}{\rm Per}(X/Y)$ and ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$.
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$.
4. The flop functor and Van den Bergh's functor
Now let ![]() $X$,
$X$, ![]() $X^+$ and
$X^+$ and ![]() $Y$ be quasi-projective Gorenstein varieties of dimension
$Y$ be quasi-projective Gorenstein varieties of dimension ![]() $n$ such that
$n$ such that ![]() $X$ and
$X$ and ![]() $X^+$ are related by a flop over
$X^+$ are related by a flop over ![]() $Y$. We assume that
$Y$. We assume that ![]() $Y$ has canonical hypersurface singularities of multiplicity two. Note that this condition is satisfied if
$Y$ has canonical hypersurface singularities of multiplicity two. Note that this condition is satisfied if ![]() $Y$ has dimension three and terminal Gorenstein singularities. We assume that fibers of
$Y$ has dimension three and terminal Gorenstein singularities. We assume that fibers of ![]() $f$ have dimension bounded by one and the exceptional locus of
$f$ have dimension bounded by one and the exceptional locus of ![]() $f$ has codimension greater than one in
$f$ has codimension greater than one in ![]() $X$. Then morphism
$X$. Then morphism ![]() $f^+$ satisfies the same conditions.
$f^+$ satisfies the same conditions.
Van den Bergh in [Reference Van den BerghVdB04] proved an equivalence of ![]() ${\mathcal {D}}^b(X)$ with
${\mathcal {D}}^b(X)$ with ![]() ${\mathcal {D}}^b(X ^+)$ under these assumptions.
${\mathcal {D}}^b(X ^+)$ under these assumptions.
We consider a diagram

and the flop functor
In this section we give an alternative description of the flop functor and the functor ![]() $\Sigma$ considered in [Reference Van den BerghVdB04] under an extra assumption that
$\Sigma$ considered in [Reference Van den BerghVdB04] under an extra assumption that ![]() $Y$ is affine. We show that these are inverse to each other. Keeping the assumption that
$Y$ is affine. We show that these are inverse to each other. Keeping the assumption that ![]() $Y$ is affine we also provide an alternative description of the flop–flop functor
$Y$ is affine we also provide an alternative description of the flop–flop functor
We construct a functorial exact triangle relating ![]() $\Sigma$,
$\Sigma$, ![]() $F$ and the derived push-forward to a smooth scheme
$F$ and the derived push-forward to a smooth scheme ![]() ${\mathcal {Y}}$. We conclude that the flop functor induces an equivalence
${\mathcal {Y}}$. We conclude that the flop functor induces an equivalence ![]() ${\mathcal {D}}^b(X) \xrightarrow {\simeq }{\mathcal {D}}^b(X^+)$ and, following [Reference ChenChe02], show that
${\mathcal {D}}^b(X) \xrightarrow {\simeq }{\mathcal {D}}^b(X^+)$ and, following [Reference ChenChe02], show that ![]() $F$ is an equivalence also in the case when
$F$ is an equivalence also in the case when ![]() $Y$ is not affine.
$Y$ is not affine.
Lemma 4.1 Let ![]() $g\colon X\to Z$ be a proper surjective morphism with connected fibers. If
$g\colon X\to Z$ be a proper surjective morphism with connected fibers. If ![]() $Z$ is normal, then
$Z$ is normal, then ![]() $g_* {\mathcal {O}}_X \simeq {\mathcal {O}}_Z$.
$g_* {\mathcal {O}}_X \simeq {\mathcal {O}}_Z$.
Proof. For Stein decomposition ![]() $g \colon X\to \mathop {{\rm Spec}}\nolimits _Z g_* {\mathcal {O}}_X \xrightarrow {\varphi } Z$, morphism
$g \colon X\to \mathop {{\rm Spec}}\nolimits _Z g_* {\mathcal {O}}_X \xrightarrow {\varphi } Z$, morphism ![]() $\varphi$ is finite and has connected fibers, hence it is birational. As a finite birational morphism onto a normal variety is an isomorphism,
$\varphi$ is finite and has connected fibers, hence it is birational. As a finite birational morphism onto a normal variety is an isomorphism, ![]() $\varphi$ is an isomorphism. It follows that
$\varphi$ is an isomorphism. It follows that ![]() $g_* {\mathcal {O}}_X \simeq {\mathcal {O}}_Z$.
$g_* {\mathcal {O}}_X \simeq {\mathcal {O}}_Z$.
Remark 4.2 We assume that ![]() $X$ and
$X$ and ![]() $X^+$ are normal varieties. As morphism
$X^+$ are normal varieties. As morphism ![]() $p$ is proper, surjective and with connected fibers, Lemma 4.1 implies that
$p$ is proper, surjective and with connected fibers, Lemma 4.1 implies that ![]() $p_* {\mathcal {O}}_{X\times _Y X^+}\simeq {\mathcal {O}}_X$. Moreover, by Proposition 2.11, the sheaf
$p_* {\mathcal {O}}_{X\times _Y X^+}\simeq {\mathcal {O}}_X$. Moreover, by Proposition 2.11, the sheaf ![]() $R^1p_* {\mathcal {O}}_{X\times _Y X^+}$ vanishes. It follows that
$R^1p_* {\mathcal {O}}_{X\times _Y X^+}$ vanishes. It follows that ![]() $p$ satisfies assumption (d).
$p$ satisfies assumption (d).
4.1 An alternative description of Van den Bergh's functor
Lemma 4.3 Let ![]() $f\colon X\to Y$ satisfy assumption (d),
$f\colon X\to Y$ satisfy assumption (d), ![]() $Y$ affine and
$Y$ affine and ![]() ${\mathcal {M}}_1$,
${\mathcal {M}}_1$, ![]() ${\mathcal {M}}_2$ objects in
${\mathcal {M}}_2$ objects in ![]() $\mathscr {P}_{p}$, for
$\mathscr {P}_{p}$, for ![]() $p=-1$ or
$p=-1$ or ![]() $0$. Then
$0$. Then ![]() $\mathop {{\rm Ext}}\nolimits _X^i({\mathcal {M}}_1, {\mathcal {M}}_2) = 0$, for
$\mathop {{\rm Ext}}\nolimits _X^i({\mathcal {M}}_1, {\mathcal {M}}_2) = 0$, for ![]() $i \geqslant 1$.
$i \geqslant 1$.
Proof. By [Reference Van den BerghVdB04, Proposition 3.2.6], objects in ![]() $\mathscr {P}_{p}$ are vector bundles on
$\mathscr {P}_{p}$ are vector bundles on ![]() $X$. Hence,
$X$. Hence, ![]() ${\mathcal {E}} xt^i({\mathcal {M}}_1, {\mathcal {M}}_2) \simeq 0$, for
${\mathcal {E}} xt^i({\mathcal {M}}_1, {\mathcal {M}}_2) \simeq 0$, for ![]() $i > 0$. As morphism
$i > 0$. As morphism ![]() $f$ has fibers of dimension bounded by one, the local-to-global spectral sequence implies that
$f$ has fibers of dimension bounded by one, the local-to-global spectral sequence implies that ![]() $\mathop {{\rm Ext}}\nolimits ^i({\mathcal {M}}_1, {\mathcal {M}}_2)\simeq H^0(Y, R^if_* {\mathcal {H}} om({\mathcal {M}}_1, {\mathcal {M}}_2))$ vanishes, for
$\mathop {{\rm Ext}}\nolimits ^i({\mathcal {M}}_1, {\mathcal {M}}_2)\simeq H^0(Y, R^if_* {\mathcal {H}} om({\mathcal {M}}_1, {\mathcal {M}}_2))$ vanishes, for ![]() $i> 1$. Group
$i> 1$. Group ![]() $\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {M}}_1,{\mathcal {M}}_2)$ is isomorphic to
$\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {M}}_1,{\mathcal {M}}_2)$ is isomorphic to ![]() $\mathop {{\rm Ext}}\nolimits ^1_{\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)}({\mathcal {M}}_1, {\mathcal {M}}_2)$, hence also zero, as
$\mathop {{\rm Ext}}\nolimits ^1_{\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)}({\mathcal {M}}_1, {\mathcal {M}}_2)$, hence also zero, as ![]() ${\mathcal {M}}_1$ is an object of
${\mathcal {M}}_1$ is an object of ![]() $\mathscr {P}_p$.
$\mathscr {P}_p$.
Let ![]() $\mathscr {P} \subset {\mathcal {B}}$ be a full subcategory of an abelian category closed under extensions. Denote by
$\mathscr {P} \subset {\mathcal {B}}$ be a full subcategory of an abelian category closed under extensions. Denote by ![]() ${\rm Hot}_{{\mathcal {B}}}^{-,b}(\mathscr {P})$ the homotopy category of bounded above complexes of objects in
${\rm Hot}_{{\mathcal {B}}}^{-,b}(\mathscr {P})$ the homotopy category of bounded above complexes of objects in ![]() $\mathscr {P}$ with bounded cohomology in
$\mathscr {P}$ with bounded cohomology in ![]() ${\mathcal {B}}$. We use the notation
${\mathcal {B}}$. We use the notation ![]() ${\rm Hot}^{-,b}(\mathscr {P})$ when the category
${\rm Hot}^{-,b}(\mathscr {P})$ when the category ![]() ${\mathcal {B}}$ is clear from the context. Denote by
${\mathcal {B}}$ is clear from the context. Denote by ![]() ${\rm Hot}^{-,b}(\mathscr {P})^{\leqslant l}$ the full subcategory of complexes with non-zero cohomology in degree up to
${\rm Hot}^{-,b}(\mathscr {P})^{\leqslant l}$ the full subcategory of complexes with non-zero cohomology in degree up to ![]() $l$. Denote by
$l$. Denote by ![]() ${\rm Hot}^-(\mathscr {P})$ the category of bounded above complexes of objects in
${\rm Hot}^-(\mathscr {P})$ the category of bounded above complexes of objects in ![]() $\mathscr {P}$ without any constraint on cohomology. Finally, denote by
$\mathscr {P}$ without any constraint on cohomology. Finally, denote by ![]() ${\rm Hot}^b(\mathscr {P})$ the full subcategory of bounded complexes in
${\rm Hot}^b(\mathscr {P})$ the full subcategory of bounded complexes in ![]() ${\rm Hot}^{-,b}(\mathscr {P})$. Categories
${\rm Hot}^{-,b}(\mathscr {P})$. Categories ![]() ${\rm Hot}^{-,b}(\mathscr {P})$,
${\rm Hot}^{-,b}(\mathscr {P})$, ![]() ${\rm Hot}^-(\mathscr {P})$ and
${\rm Hot}^-(\mathscr {P})$ and ![]() ${\rm Hot}^b(\mathscr {P})$ are triangulated by [Reference NeemanNee90]. If
${\rm Hot}^b(\mathscr {P})$ are triangulated by [Reference NeemanNee90]. If ![]() $\mathscr {P}$ is the category of projective objects in
$\mathscr {P}$ is the category of projective objects in ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$, for
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$, for ![]() $p=-1,0$, then we use the above notation for the embedding
$p=-1,0$, then we use the above notation for the embedding ![]() $\mathscr {P}_p \subset \mathop {{\rm Coh}}\nolimits (X)$.
$\mathscr {P}_p \subset \mathop {{\rm Coh}}\nolimits (X)$.
Assume that morphism ![]() $f\colon X\to Y$ satisfies assumption (a). As
$f\colon X\to Y$ satisfies assumption (a). As ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ has enough projective objects, for
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ has enough projective objects, for ![]() $p=-1$ or
$p=-1$ or ![]() $0$, category
$0$, category ![]() ${\mathcal {D}}^b(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y))$ is equivalent to
${\mathcal {D}}^b(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y))$ is equivalent to ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{p})$, see [Reference Gelfand and ManinGM03, Theorem III.5.21].
${\rm Hot}^{-,b}(\mathscr {P}_{p})$, see [Reference Gelfand and ManinGM03, Theorem III.5.21].
Proposition 4.4 Let ![]() $f\colon X\to Y$ satisfy assumption (d) and
$f\colon X\to Y$ satisfy assumption (d) and ![]() $Y$ affine. Then categories
$Y$ affine. Then categories ![]() ${\mathcal {D}}^b(X)$ and
${\mathcal {D}}^b(X)$ and ![]() ${\mathcal {D}}^b(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y))$ are equivalent, for
${\mathcal {D}}^b(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y))$ are equivalent, for ![]() $p=-1$ or
$p=-1$ or ![]() $0$.
$0$.
Proof. As objects in ![]() $\mathscr {P}_{p}$ are coherent sheaves on
$\mathscr {P}_{p}$ are coherent sheaves on ![]() $X$, we have a functor
$X$, we have a functor ![]() $\Theta \colon {\rm Hot}^{-,b}(\mathscr {P}_{p})\to {\mathcal {D}}^b(X)$. There exists
$\Theta \colon {\rm Hot}^{-,b}(\mathscr {P}_{p})\to {\mathcal {D}}^b(X)$. There exists ![]() $N_0$ such that
$N_0$ such that ![]() $\mathop {{\rm Ext}}\nolimits ^q_{X}(P, C) = 0$, for any
$\mathop {{\rm Ext}}\nolimits ^q_{X}(P, C) = 0$, for any ![]() $P \in \mathscr {P}_{p}$ and
$P \in \mathscr {P}_{p}$ and ![]() $C \in \mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ and
$C \in \mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ and ![]() $q\geqslant N_0$. Indeed,
$q\geqslant N_0$. Indeed, ![]() $C$ has non-zero cohomology sheaves in degrees
$C$ has non-zero cohomology sheaves in degrees ![]() $-1$ and
$-1$ and ![]() $0$ only, and objects in
$0$ only, and objects in ![]() $\mathscr {P}_p$ are locally free sheaves on
$\mathscr {P}_p$ are locally free sheaves on ![]() $X$ (see [Reference Van den BerghVdB04, Proposition 3.2.6]). Then Proposition E.4 implies that cohomology groups of complex
$X$ (see [Reference Van den BerghVdB04, Proposition 3.2.6]). Then Proposition E.4 implies that cohomology groups of complex ![]() $\prod _{j-i = p} \mathop {{\rm Hom}}\nolimits _X(A^i, B^j)$ are isomorphic to
$\prod _{j-i = p} \mathop {{\rm Hom}}\nolimits _X(A^i, B^j)$ are isomorphic to ![]() $\mathop {{\rm Hom}}\nolimits _X(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$, for any
$\mathop {{\rm Hom}}\nolimits _X(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$, for any ![]() $A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }} \in \mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_p)$ (see Lemma 4.3). Hence,
$A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }} \in \mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_p)$ (see Lemma 4.3). Hence, ![]() $\mathop {{\rm Hom}}\nolimits ^{\boldsymbol {\cdot }}_X(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }}) \simeq \mathop {{\rm Hom}}\nolimits _{\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_p)}(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$, i.e.
$\mathop {{\rm Hom}}\nolimits ^{\boldsymbol {\cdot }}_X(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }}) \simeq \mathop {{\rm Hom}}\nolimits _{\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_p)}(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$, i.e. ![]() $\Theta$ is fully faithful. It is essentially surjective, because
$\Theta$ is fully faithful. It is essentially surjective, because ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ is the heart of a bounded
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ is the heart of a bounded ![]() $t$-structure.
$t$-structure.
By Proposition 3.12, functor
is fully faithful. Denote by
the functor obtained by applying ![]() $\Sigma _o$ term-wise to complexes of objects of
$\Sigma _o$ term-wise to complexes of objects of ![]() $\mathscr {P}_{-1}$.
$\mathscr {P}_{-1}$.
Theorem 4.5 Let ![]() $f\colon X\to Y$ satisfy assumption (a) and
$f\colon X\to Y$ satisfy assumption (a) and ![]() $f^+ \colon X^+ \to Y$ be the flop of
$f^+ \colon X^+ \to Y$ be the flop of ![]() $f$. Then functor
$f$. Then functor ![]() $\Sigma$ induces an equivalence between
$\Sigma$ induces an equivalence between ![]() ${\mathcal {D}}^b(X)$ and
${\mathcal {D}}^b(X)$ and ![]() ${\mathcal {D}}^b(X^+)$.
${\mathcal {D}}^b(X^+)$.
Proof. Lemma 3.11 implies that functor
is the inverse of ![]() $\Sigma _o$. Let us extend it term-wise to a functor
$\Sigma _o$. Let us extend it term-wise to a functor
Proposition 3.12 implies that ![]() $\Sigma$ and
$\Sigma$ and ![]() $T$ are inverse equivalences between
$T$ are inverse equivalences between ![]() $\mathscr {P}_{-1}$ and
$\mathscr {P}_{-1}$ and ![]() $\mathscr {P}_0^+$. Hence, they are also inverse equivalences between
$\mathscr {P}_0^+$. Hence, they are also inverse equivalences between ![]() $\mathop {{\rm Hot}}\nolimits ^-(\mathscr {P}_{-1})$ and
$\mathop {{\rm Hot}}\nolimits ^-(\mathscr {P}_{-1})$ and ![]() $\mathop {{\rm Hot}}\nolimits ^-(\mathscr {P}_0)$. By Proposition 4.4, we have
$\mathop {{\rm Hot}}\nolimits ^-(\mathscr {P}_0)$. By Proposition 4.4, we have ![]() ${\mathcal {D}}^b(X) \simeq {\rm Hot}^{-,b}(\mathscr {P}_{-1})$ and
${\mathcal {D}}^b(X) \simeq {\rm Hot}^{-,b}(\mathscr {P}_{-1})$ and ![]() ${\mathcal {D}}^b(X^+) \simeq {\rm Hot}^{-,b}(\mathscr {P}_0^+)$. Thus, it suffices to show that
${\mathcal {D}}^b(X^+) \simeq {\rm Hot}^{-,b}(\mathscr {P}_0^+)$. Thus, it suffices to show that ![]() $\Sigma$ takes
$\Sigma$ takes ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$ to
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$ to ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_0^+)$ and
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_0^+)$ and ![]() $T$ takes
$T$ takes ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{0}^+)$ to
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{0}^+)$ to ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$.
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$.
Let ![]() $E$ be in
$E$ be in ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$ and assume that
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$ and assume that ![]() $\Sigma (E)$ has unbounded cohomology. If cohomology of
$\Sigma (E)$ has unbounded cohomology. If cohomology of ![]() $\Sigma (E)$ is unbounded with respect to the standard
$\Sigma (E)$ is unbounded with respect to the standard ![]() $t$-structure it is also unbounded with respect to the
$t$-structure it is also unbounded with respect to the ![]() $t$-structure with heart
$t$-structure with heart ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$, because these two
$\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$, because these two ![]() $t$-structures are related by a tilt. Let
$t$-structures are related by a tilt. Let ![]() ${\mathcal {N}}^+$ be the projective generator of
${\mathcal {N}}^+$ be the projective generator of ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$. Then
$\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$. Then ![]() $\dim _k \mathop {{\rm Hom}}\nolimits _{X^+}^{\boldsymbol {\cdot }}({\mathcal {N}}^+, \Sigma (E))$ is infinite. By adjunction of inverse functors, we have that
$\dim _k \mathop {{\rm Hom}}\nolimits _{X^+}^{\boldsymbol {\cdot }}({\mathcal {N}}^+, \Sigma (E))$ is infinite. By adjunction of inverse functors, we have that ![]() $\dim _k \mathop {{\rm Hom}}\nolimits _X^{\boldsymbol {\cdot }}(T({\mathcal {N}}^+), E)$ is infinite. As
$\dim _k \mathop {{\rm Hom}}\nolimits _X^{\boldsymbol {\cdot }}(T({\mathcal {N}}^+), E)$ is infinite. As ![]() $T_o({\mathcal {N}}^+)$ is in
$T_o({\mathcal {N}}^+)$ is in ![]() $\mathscr {P}_{-1}$, it contradicts the boundedness of the cohomology of
$\mathscr {P}_{-1}$, it contradicts the boundedness of the cohomology of ![]() $E$ with respect to the
$E$ with respect to the ![]() $t$-structure with heart
$t$-structure with heart ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Analogously,
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Analogously, ![]() $T$ takes
$T$ takes ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{0}^+)$ to
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{0}^+)$ to ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$.
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$.
Let us show that Theorem 4.5 may be considered as a write-up of Van den Bergh's theorem.
Let ![]() $f\colon X\to Y$ satisfy assumption (a). As
$f\colon X\to Y$ satisfy assumption (a). As ![]() $f$ has fibers of dimension bounded by one, [Reference Van den BerghVdB04, Lemma 3.2.2] implies that for an
$f$ has fibers of dimension bounded by one, [Reference Van den BerghVdB04, Lemma 3.2.2] implies that for an ![]() $f$-ample line bundle
$f$-ample line bundle ![]() ${\mathcal {L}}$ both
${\mathcal {L}}$ both ![]() ${\mathcal {L}} \oplus {\mathcal {O}}_X$ and
${\mathcal {L}} \oplus {\mathcal {O}}_X$ and ![]() ${\mathcal {O}}_X \oplus {\mathcal {L}}^{-1}$ are compact generators of
${\mathcal {O}}_X \oplus {\mathcal {L}}^{-1}$ are compact generators of ![]() ${\mathcal {D}}_{{\rm qc}}(X)$. It follows that both the projective generator
${\mathcal {D}}_{{\rm qc}}(X)$. It follows that both the projective generator ![]() ${\mathcal {M}} = \bigoplus {\mathcal {M}}_i$ of
${\mathcal {M}} = \bigoplus {\mathcal {M}}_i$ of ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ (defined as in Remark 2.7) and
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ (defined as in Remark 2.7) and ![]() ${\mathcal {N}}= \mathop {\mathcal {H}{\rm om}}\nolimits ({\mathcal {M}}, {\mathcal {O}}_X)$ of
${\mathcal {N}}= \mathop {\mathcal {H}{\rm om}}\nolimits ({\mathcal {M}}, {\mathcal {O}}_X)$ of ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ (see Remark 2.6) are compact generators of the category
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ (see Remark 2.6) are compact generators of the category ![]() ${\mathcal {D}}_{{\rm qc}}(X)$. Analogous result holds for projective generators for
${\mathcal {D}}_{{\rm qc}}(X)$. Analogous result holds for projective generators for ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$ and
$\mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$ and ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$.
$\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$.
As ![]() $(f^{+*}f_*(-))^{\vee \vee }$ restricts to an equivalence
$(f^{+*}f_*(-))^{\vee \vee }$ restricts to an equivalence ![]() $\mathscr {P}_{-1} \to \mathscr {P}_0^+$, Proposition 3.12,
$\mathscr {P}_{-1} \to \mathscr {P}_0^+$, Proposition 3.12, ![]() ${\mathcal {N}}^+$ (as in (35)) is a projective generator for
${\mathcal {N}}^+$ (as in (35)) is a projective generator for ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$ and the endomorphisms algebras of
$\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$ and the endomorphisms algebras of ![]() ${\mathcal {M}}$ and
${\mathcal {M}}$ and ![]() ${\mathcal {N}}^+$ are isomorphic.
${\mathcal {N}}^+$ are isomorphic.
Moreover, by Lemma 4.3, both ![]() ${\mathcal {M}}$ and
${\mathcal {M}}$ and ![]() ${\mathcal {N}}^+$ have no higher self Ext groups. Hence, by the result of Keller [Reference KellerKel06] both
${\mathcal {N}}^+$ have no higher self Ext groups. Hence, by the result of Keller [Reference KellerKel06] both ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ and
${\mathcal {D}}_{{\rm qc}}(X)$ and ![]() ${\mathcal {D}}_{{\rm qc}}(X^+)$ are equivalent to the derived category of DG modules over the algebra
${\mathcal {D}}_{{\rm qc}}(X^+)$ are equivalent to the derived category of DG modules over the algebra ![]() $A = \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}},{\mathcal {M}})$, cf. [Reference Bondal and Van den BerghBVdB03]. Denote by
$A = \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}},{\mathcal {M}})$, cf. [Reference Bondal and Van den BerghBVdB03]. Denote by
the resulting equivalence.
Proposition 4.6 Let ![]() $f\colon X\to Y$ satisfy assumption (a). Functor
$f\colon X\to Y$ satisfy assumption (a). Functor ![]() $\Sigma _{{\rm qc}}|_{{\mathcal {D}}^b(X)}:{\mathcal {D}}^b(X)\to {\mathcal {D}}^b(X^+)$ is an equivalence that takes
$\Sigma _{{\rm qc}}|_{{\mathcal {D}}^b(X)}:{\mathcal {D}}^b(X)\to {\mathcal {D}}^b(X^+)$ is an equivalence that takes ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ to
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ to ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$, and it coincides with Van den Bergh's equivalence in [Reference Van den BerghVdB04, Theorem 4.4.2].
$\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$, and it coincides with Van den Bergh's equivalence in [Reference Van den BerghVdB04, Theorem 4.4.2].
Proof. Category ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$ is a subcategory of the homotopy category of complexes of projective
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$ is a subcategory of the homotopy category of complexes of projective ![]() $A$-modules; it consists of bounded above complexes. As
$A$-modules; it consists of bounded above complexes. As ![]() $\Sigma _o$ as in (45) maps projective generator for
$\Sigma _o$ as in (45) maps projective generator for ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ to the projective generator for
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ to the projective generator for ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$, we have
$\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$, we have ![]() $\Sigma _{{\rm qc}}|_{\mathscr {P}_{-1}} = \Sigma _o$. We conclude that
$\Sigma _{{\rm qc}}|_{\mathscr {P}_{-1}} = \Sigma _o$. We conclude that ![]() $\Sigma = \Sigma _{{\rm qc}}|_{\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})}$ is the equivalence defined by Van den Bergh in [Reference Van den BerghVdB04, Theorem 4.4.2].
$\Sigma = \Sigma _{{\rm qc}}|_{\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})}$ is the equivalence defined by Van den Bergh in [Reference Van den BerghVdB04, Theorem 4.4.2].
Categories ![]() $\mathscr {P}_{0}$ and
$\mathscr {P}_{0}$ and ![]() $\mathscr {P}_{-1}^+$ are also equivalent. We can thus analogously construct an equivalence
$\mathscr {P}_{-1}^+$ are also equivalent. We can thus analogously construct an equivalence ![]() $\Sigma _{{\rm qc}}^{-1} \colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^b(X^+)$ that takes
$\Sigma _{{\rm qc}}^{-1} \colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^b(X^+)$ that takes ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ to
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ to ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$.
$\mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$.
4.2 An alternative description of the flop functor
Consider diagram (42). The counit of ![]() $f^* \dashv f_*$ adjunction
$f^* \dashv f_*$ adjunction
gives a morphism
Isomorphism ![]() $p^*f^* \simeq p^{+*}f^{+*}$ and
$p^*f^* \simeq p^{+*}f^{+*}$ and ![]() $p^{+*}\dashv p^+_*$ adjunction lead to a base-change morphism
$p^{+*}\dashv p^+_*$ adjunction lead to a base-change morphism
Note that the morphism ![]() $\epsilon$ is, by definition, the composition
$\epsilon$ is, by definition, the composition
Analogous argument gives a derived base change
Lemma 4.7 Let ![]() $f$ satisfy assumption (a) and
$f$ satisfy assumption (a) and ![]() ${\mathcal {M}}$ be an object in
${\mathcal {M}}$ be an object in ![]() $\mathscr {P}_{-1}$. Then
$\mathscr {P}_{-1}$. Then ![]() $\epsilon _{{\mathcal {M}}} \colon f^{+*}f_* {\mathcal {M}} \to p^+_*p^* {\mathcal {M}}$ is an isomorphism.
$\epsilon _{{\mathcal {M}}} \colon f^{+*}f_* {\mathcal {M}} \to p^+_*p^* {\mathcal {M}}$ is an isomorphism.
Proof. As ![]() ${\mathcal {M}}$ is locally free [Reference Van den BerghVdB04, Propostion 3.2.6], applying
${\mathcal {M}}$ is locally free [Reference Van den BerghVdB04, Propostion 3.2.6], applying ![]() $p^*$ to sequence (15) we obtain an exact sequence
$p^*$ to sequence (15) we obtain an exact sequence
on ![]() $X\times _Y X^+$. Sheaf
$X\times _Y X^+$. Sheaf ![]() ${\mathcal {P}}$ is in
${\mathcal {P}}$ is in ![]() $\mathscr {A}_f$, hence Proposition 2.11 implies an isomorphism
$\mathscr {A}_f$, hence Proposition 2.11 implies an isomorphism
As diagram (42) is commutative, ![]() $p^+_*p^*f^*f_* {\mathcal {M}} \simeq p^+_*p^{+*}f^{+*}f_* {\mathcal {M}}$. Isomorphism
$p^+_*p^*f^*f_* {\mathcal {M}} \simeq p^+_*p^{+*}f^{+*}f_* {\mathcal {M}}$. Isomorphism ![]() $f^{+*}f_*{\mathcal {M}} \simeq f^{+*}f^+_* {\mathcal {N}}^+$ (see Proposition 3.12) together with Lemma 3.5 implies that
$f^{+*}f_*{\mathcal {M}} \simeq f^{+*}f^+_* {\mathcal {N}}^+$ (see Proposition 3.12) together with Lemma 3.5 implies that ![]() $f^{+*}f_*{\mathcal {M}}$ is torsion-free. Moreover, by Remark 4.2,
$f^{+*}f_*{\mathcal {M}}$ is torsion-free. Moreover, by Remark 4.2, ![]() $Rp^+_* {\mathcal {O}}_{X\times _Y X^+} = {\mathcal {O}}_{X^+}$. Thus, conditions of Lemma 2.8 are satisfied and we have an isomorphism
$Rp^+_* {\mathcal {O}}_{X\times _Y X^+} = {\mathcal {O}}_{X^+}$. Thus, conditions of Lemma 2.8 are satisfied and we have an isomorphism ![]() $f^{+*}f_* {\mathcal {M}} \xrightarrow {\simeq } p^+_*p^{+*}f^{+*}f_* {\mathcal {M}}$. Hence,
$f^{+*}f_* {\mathcal {M}} \xrightarrow {\simeq } p^+_*p^{+*}f^{+*}f_* {\mathcal {M}}$. Hence, ![]() $\epsilon _{{\mathcal {M}}}$ is a composite of two isomorphisms in (48).
$\epsilon _{{\mathcal {M}}}$ is a composite of two isomorphisms in (48).
Proposition 4.8 Let ![]() $f$ satisfy assumption (a). Then the flop functor
$f$ satisfy assumption (a). Then the flop functor ![]() $Rp^+_* Lp^*$ on
$Rp^+_* Lp^*$ on ![]() $\mathscr {P}_{-1}$ is isomorphic to the non-derived flop functor
$\mathscr {P}_{-1}$ is isomorphic to the non-derived flop functor ![]() $p^+_*p^*$.
$p^+_*p^*$.
Proof. Every object in ![]() $\mathscr {P}_{-1}$ locally free, [Reference Van den BerghVdB04, Propostion 3.2.6], hence
$\mathscr {P}_{-1}$ locally free, [Reference Van den BerghVdB04, Propostion 3.2.6], hence ![]() $Lp^*|_{ \mathscr {P}_{-1}} \simeq p^*|_{\mathscr {P}_{-1}}$. Moreover, because
$Lp^*|_{ \mathscr {P}_{-1}} \simeq p^*|_{\mathscr {P}_{-1}}$. Moreover, because ![]() $R^1f_* \mathscr {P}_{-1} \simeq 0$, [Reference Van den BerghVdB04, Lemma 3.1.2] Proposition 2.11 implies that
$R^1f_* \mathscr {P}_{-1} \simeq 0$, [Reference Van den BerghVdB04, Lemma 3.1.2] Proposition 2.11 implies that ![]() $R^1p^+_*p^* \mathscr {P}_{-1} \simeq 0$.
$R^1p^+_*p^* \mathscr {P}_{-1} \simeq 0$.
We define functor
term-wise. We use the same notation for the composite of the above functor with the canonical functor ![]() ${\rm Hot}^{-}(f^{+*}f_* \mathscr {P}_{-1}) \to {\mathcal {D}}^-(X^+)$. Also term-wise, we define a functor
${\rm Hot}^{-}(f^{+*}f_* \mathscr {P}_{-1}) \to {\mathcal {D}}^-(X^+)$. Also term-wise, we define a functor
Lemma 4.9 Let ![]() $f$ satisfy assumption (a). Then the functor
$f$ satisfy assumption (a). Then the functor ![]() $f^{+*}f_*$ maps
$f^{+*}f_*$ maps ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ to
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ to ![]() ${\mathcal {D}}^b(X^+)$. The functor
${\mathcal {D}}^b(X^+)$. The functor ![]() $f^*f_*$ maps
$f^*f_*$ maps ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ to
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ to ![]() ${\mathcal {D}}^b(X)$.
${\mathcal {D}}^b(X)$.
Proof. The ![]() $i^*\dashv i_*$ adjunction counit induces an isomorphism
$i^*\dashv i_*$ adjunction counit induces an isomorphism ![]() $g^{+*}g_*\xrightarrow {\simeq }f^{+*}f_*$. Hence, it is enough to show that the term-wise extension of
$g^{+*}g_*\xrightarrow {\simeq }f^{+*}f_*$. Hence, it is enough to show that the term-wise extension of ![]() $g^{+*}g_*$ maps
$g^{+*}g_*$ maps ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ to
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ to ![]() ${\mathcal {D}}^b(X^+)$.
${\mathcal {D}}^b(X^+)$.
Functor ![]() $Rg_*$ preserves the bounded derived category of coherent sheaves, because
$Rg_*$ preserves the bounded derived category of coherent sheaves, because ![]() $g$ is proper, and so does
$g$ is proper, and so does ![]() $Lg^{+*}$, because
$Lg^{+*}$, because ![]() ${\mathcal {Y}}$ is smooth. Hence, for
${\mathcal {Y}}$ is smooth. Hence, for ![]() $P^{\boldsymbol {\cdot }}$ in
$P^{\boldsymbol {\cdot }}$ in ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1}) \simeq {\mathcal {D}}^b(X)$ (see Proposition 4.4),
${\rm Hot}^{-,b}(\mathscr {P}_{-1}) \simeq {\mathcal {D}}^b(X)$ (see Proposition 4.4), ![]() $Lg^{+*}Rg_*(P^{\boldsymbol {\cdot }})$ is an object in
$Lg^{+*}Rg_*(P^{\boldsymbol {\cdot }})$ is an object in ![]() ${\mathcal {D}}^b(X^+)$. For
${\mathcal {D}}^b(X^+)$. For ![]() $P \in \mathscr {P}_{-1}$, we denote by
$P \in \mathscr {P}_{-1}$, we denote by ![]() $P^+ = (f^{+*}f_*P)^{\vee \vee }$ the corresponding object in
$P^+ = (f^{+*}f_*P)^{\vee \vee }$ the corresponding object in ![]() $\mathscr {P}^+_0$ (see Proposition 3.12). As
$\mathscr {P}^+_0$ (see Proposition 3.12). As ![]() $f^+_*P^+ = f_*P$ and
$f^+_*P^+ = f_*P$ and ![]() $g^+_*P^+ = g_*P$, Proposition 3.15 for
$g^+_*P^+ = g_*P$, Proposition 3.15 for ![]() $g^+$,
$g^+$, ![]() $f^+$ and
$f^+$ and ![]() $P^+$ instead of
$P^+$ instead of ![]() $g$,
$g$, ![]() $f$ and
$f$ and ![]() ${\mathcal {R}}$, implies that the first sheet of the spectral sequence
${\mathcal {R}}$, implies that the first sheet of the spectral sequence ![]() $E^{p,q}_1 = {\mathcal {H}}^q_{X^+}(Lg^{+*}g_* P^p) \Rightarrow {\mathcal {H}}^{p+q}_{X^+}(Lg^{+*}Rg_* P^{{\boldsymbol {\cdot }}})$ has two non-zero rows:
$E^{p,q}_1 = {\mathcal {H}}^q_{X^+}(Lg^{+*}g_* P^p) \Rightarrow {\mathcal {H}}^{p+q}_{X^+}(Lg^{+*}Rg_* P^{{\boldsymbol {\cdot }}})$ has two non-zero rows:
By Theorem 4.5, the complex ![]() $P^{+\bullet }$ is in
$P^{+\bullet }$ is in ![]() ${\rm Hot}^{-,b}(\mathscr {P}_0^+)$, hence cohomology of the -1st row is bounded:
${\rm Hot}^{-,b}(\mathscr {P}_0^+)$, hence cohomology of the -1st row is bounded: ![]() $E_2^{N,-1} = 0$, for
$E_2^{N,-1} = 0$, for ![]() $N\leqslant N_0$. The spectral sequence implies that, for sufficiently negative
$N\leqslant N_0$. The spectral sequence implies that, for sufficiently negative ![]() $N$,
$N$, ![]() ${\mathcal {H}}_{X^+}^{N}(g^{+*}g_*P^\bullet ) = E_2^{N,0} = E_{\infty }^{N,0} = {\mathcal {H}}_{X^+}^{N}(Lg^{+*}g_*P^\bullet )=0$, i.e.
${\mathcal {H}}_{X^+}^{N}(g^{+*}g_*P^\bullet ) = E_2^{N,0} = E_{\infty }^{N,0} = {\mathcal {H}}_{X^+}^{N}(Lg^{+*}g_*P^\bullet )=0$, i.e. ![]() $g^{+*}g_*(P^\bullet ) \in {\mathcal {D}}^b(X^+)$.
$g^{+*}g_*(P^\bullet ) \in {\mathcal {D}}^b(X^+)$.
The proof of the boundedness for ![]() $f^*f_*(P^\bullet ) = g^*g_*(P^\bullet )$ is similar with the use of Proposition 3.15 for
$f^*f_*(P^\bullet ) = g^*g_*(P^\bullet )$ is similar with the use of Proposition 3.15 for ![]() ${\mathcal {M}}$ instead of
${\mathcal {M}}$ instead of ![]() ${\mathcal {N}}^+$.
${\mathcal {N}}^+$.
Proposition 4.10 Let ![]() $f$ satisfy assumption (a). Then functors
$f$ satisfy assumption (a). Then functors ![]() $f^{+*} f_*$ and
$f^{+*} f_*$ and ![]() $p^+_*p^*$ are isomorphic on the category
$p^+_*p^*$ are isomorphic on the category ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$. They are also isomorphic to the flop functor restricted to
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$. They are also isomorphic to the flop functor restricted to ![]() ${\mathcal {D}}^b(X)$ under the equivalence
${\mathcal {D}}^b(X)$ under the equivalence ![]() ${\mathcal {D}}^b(X) \simeq {\rm Hot}^{-,b}(\mathscr {P}_{-1})$.
${\mathcal {D}}^b(X) \simeq {\rm Hot}^{-,b}(\mathscr {P}_{-1})$.
Proof. Proposition 4.8 implies that the canonical morphism ![]() $p^+_*p^*|_{\mathscr {P}_{-1}} \to Rp^+_* p^*|_{\mathscr {P}_{-1}}$ is an isomorphism. All objects in
$p^+_*p^*|_{\mathscr {P}_{-1}} \to Rp^+_* p^*|_{\mathscr {P}_{-1}}$ is an isomorphism. All objects in ![]() $\mathscr {P}_{-1}$ are locally free [Reference Van den BerghVdB04, Propostion 3.2.6], hence canonical morphism
$\mathscr {P}_{-1}$ are locally free [Reference Van den BerghVdB04, Propostion 3.2.6], hence canonical morphism ![]() $Rp^+_*Lp^*|_{\mathscr {P}_{-1}} \to Rp^+_*p^*|_{\mathscr {P}_{-1}}$ is also an isomorphism. This implies isomorphism of
$Rp^+_*Lp^*|_{\mathscr {P}_{-1}} \to Rp^+_*p^*|_{\mathscr {P}_{-1}}$ is also an isomorphism. This implies isomorphism of ![]() $p^+_*p^*|_{\mathscr {P}_{-1}}$ and
$p^+_*p^*|_{\mathscr {P}_{-1}}$ and ![]() $Rp^+_*Lp^*|_{\mathscr {P}_{-1}}$.
$Rp^+_*Lp^*|_{\mathscr {P}_{-1}}$.
Lemma 4.7 assures that the base change ![]() $\epsilon _{{\mathcal {M}}} \colon f^{+*}f_* {\mathcal {M}} \to p^+_*p^* {\mathcal {M}}$ is an isomorphism, for all
$\epsilon _{{\mathcal {M}}} \colon f^{+*}f_* {\mathcal {M}} \to p^+_*p^* {\mathcal {M}}$ is an isomorphism, for all ![]() ${\mathcal {M}}\in \mathscr {P}_{-1}$.
${\mathcal {M}}\in \mathscr {P}_{-1}$.
Thus, all three functors are isomorphic on ![]() $\mathscr {P}_{-1}$. Induction on triangles shows that the isomorphism extends to
$\mathscr {P}_{-1}$. Induction on triangles shows that the isomorphism extends to ![]() $\mathop {{\rm Hot}}\nolimits ^b(\mathscr {P}_{-1})$. By Lemmas 4.9 and 4.11, they are also isomorphic on
$\mathop {{\rm Hot}}\nolimits ^b(\mathscr {P}_{-1})$. By Lemmas 4.9 and 4.11, they are also isomorphic on ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$.
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$.
In the proof of Proposition 4.10 we use the fact that in order to check that a natural transformation gives an isomorphism of two functors defined on ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$, it suffices to check that it gives an isomorphism of the functors restricted to
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$, it suffices to check that it gives an isomorphism of the functors restricted to ![]() $\mathop {{\rm Hot}}\nolimits ^b(\mathscr {P}_{-1})$, which we prove now.
$\mathop {{\rm Hot}}\nolimits ^b(\mathscr {P}_{-1})$, which we prove now.
Lemma 4.11 Let ![]() ${\mathcal {A}}$,
${\mathcal {A}}$, ![]() ${\mathcal {B}}$ be abelian categories,
${\mathcal {B}}$ be abelian categories, ![]() $\mathscr {P}\subset {\mathcal {B}}$ a full subcategory closed under extensions and
$\mathscr {P}\subset {\mathcal {B}}$ a full subcategory closed under extensions and ![]() $F, G \colon {\rm Hot}_{{\mathcal {B}}}^{-,b}(\mathscr {P}) \to {\mathcal {D}}^-({\mathcal {A}})$ exact functors. Assume there exists
$F, G \colon {\rm Hot}_{{\mathcal {B}}}^{-,b}(\mathscr {P}) \to {\mathcal {D}}^-({\mathcal {A}})$ exact functors. Assume there exists ![]() $n_0$ such that both
$n_0$ such that both ![]() $F$ and
$F$ and ![]() $G$ map
$G$ map ![]() ${\rm Hot}_{{\mathcal {B}}}^{-,b}(\mathscr {P})^{\leqslant 0}$ to
${\rm Hot}_{{\mathcal {B}}}^{-,b}(\mathscr {P})^{\leqslant 0}$ to ![]() ${\mathcal {D}}^-({\mathcal {A}})^{\leqslant n_0}$ and that the image of either
${\mathcal {D}}^-({\mathcal {A}})^{\leqslant n_0}$ and that the image of either ![]() $F$ or
$F$ or ![]() $G$ is contained in
$G$ is contained in ![]() ${\mathcal {D}}^b({\mathcal {A}})$. Let
${\mathcal {D}}^b({\mathcal {A}})$. Let ![]() $\kappa \colon F|_{{\rm Hot}_{{\mathcal {B}}}^b(\mathscr {P})} \to G|_{{\rm Hot}_{{\mathcal {B}}}^b(\mathscr {P})}$ be an isomorphism of functors. Then
$\kappa \colon F|_{{\rm Hot}_{{\mathcal {B}}}^b(\mathscr {P})} \to G|_{{\rm Hot}_{{\mathcal {B}}}^b(\mathscr {P})}$ be an isomorphism of functors. Then ![]() $\kappa$ admits an extension to a functorial isomorphism
$\kappa$ admits an extension to a functorial isomorphism ![]() $\widetilde {\kappa } \colon F\to G$.
$\widetilde {\kappa } \colon F\to G$.
Proof. Let ![]() $E$ be an object in
$E$ be an object in ![]() ${\rm Hot}^{-,b}(\mathscr {P})$. We denote by
${\rm Hot}^{-,b}(\mathscr {P})$. We denote by ![]() $\sigma _{\geqslant k}E$ the ‘stupid’ truncation:
$\sigma _{\geqslant k}E$ the ‘stupid’ truncation:
 \[ \sigma_{\geqslant k}(E)^i = \begin{cases}E^i, & \text{if }\, i \geqslant k,\\ 0, & {\rm otherwise.} \end{cases} \]
\[ \sigma_{\geqslant k}(E)^i = \begin{cases}E^i, & \text{if }\, i \geqslant k,\\ 0, & {\rm otherwise.} \end{cases} \]
Morphism ![]() $\sigma _{\geqslant l}E \to E$ induces isomorphisms
$\sigma _{\geqslant l}E \to E$ induces isomorphisms ![]() $\tau _{\geqslant m} F(\sigma _{\geqslant l}E) \xrightarrow {\simeq } \tau _{\geqslant m} F(E)$,
$\tau _{\geqslant m} F(\sigma _{\geqslant l}E) \xrightarrow {\simeq } \tau _{\geqslant m} F(E)$, ![]() $\tau _{\geqslant m} G(\sigma _{\geqslant l}E) \xrightarrow {\simeq } \tau _{\geqslant m} G(E)$, for any
$\tau _{\geqslant m} G(\sigma _{\geqslant l}E) \xrightarrow {\simeq } \tau _{\geqslant m} G(E)$, for any ![]() $m\in \mathbb {Z}$, and
$m\in \mathbb {Z}$, and ![]() $l\leqslant m-n_0$. We have
$l\leqslant m-n_0$. We have
for any ![]() $l\leqslant m-n_0$. Let us assume that
$l\leqslant m-n_0$. Let us assume that ![]() $F(E)$ is an object in
$F(E)$ is an object in ![]() ${\mathcal {D}}^b({\mathcal {A}})$. There exists
${\mathcal {D}}^b({\mathcal {A}})$. There exists ![]() $N$ such that morphism
$N$ such that morphism ![]() $F(E) \to \tau _{\geqslant m} F(E)$ is an isomorphism, for any
$F(E) \to \tau _{\geqslant m} F(E)$ is an isomorphism, for any ![]() $m\leqslant N$. Thus, isomorphisms (50) imply that
$m\leqslant N$. Thus, isomorphisms (50) imply that ![]() $G(E)$ is also an object in
$G(E)$ is also an object in ![]() ${\mathcal {D}}^b({\mathcal {A}})$. We define
${\mathcal {D}}^b({\mathcal {A}})$. We define ![]() $\widetilde {\kappa }$ as the composite of isomorphisms
$\widetilde {\kappa }$ as the composite of isomorphisms
for any ![]() $m\leqslant N$ and
$m\leqslant N$ and ![]() $l\leqslant m-n_0$. As
$l\leqslant m-n_0$. As ![]() $\kappa$ is a natural transformation,
$\kappa$ is a natural transformation, ![]() $\tau _{\geqslant m} \kappa _{\sigma _{\geqslant l}E} \simeq \tau _{\geqslant m} \kappa _{\sigma _{\geqslant l'} E}$, for any
$\tau _{\geqslant m} \kappa _{\sigma _{\geqslant l}E} \simeq \tau _{\geqslant m} \kappa _{\sigma _{\geqslant l'} E}$, for any ![]() $l,l'\leqslant m-n_0$. Hence,
$l,l'\leqslant m-n_0$. Hence, ![]() $\widetilde {\kappa }$ does not depend on the choice of
$\widetilde {\kappa }$ does not depend on the choice of ![]() $m\leqslant N$ and
$m\leqslant N$ and ![]() $l\leqslant m-n_0$.
$l\leqslant m-n_0$.
4.3 A functorial exact triangle of functors  ${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(X^+)$
${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(X^+)$
Assume that ![]() $f\colon X\to Y$ satisfies assumption (a), i.e. there exists a closed embedding
$f\colon X\to Y$ satisfies assumption (a), i.e. there exists a closed embedding ![]() $i\colon Y \to {\mathcal {Y}}$, for a smooth
$i\colon Y \to {\mathcal {Y}}$, for a smooth ![]() ${\mathcal {Y}}$ of dimension
${\mathcal {Y}}$ of dimension ![]() $n+1$. Then,
$n+1$. Then, ![]() $X\times _Y X^+\simeq X\times _{{\mathcal {Y}}} X^+$, i.e. diagram
$X\times _Y X^+\simeq X\times _{{\mathcal {Y}}} X^+$, i.e. diagram

is fibered.
Recall, that we denote by ![]() $F= Rp^+_*Lp^*$ the flop functor and by
$F= Rp^+_*Lp^*$ the flop functor and by ![]() $\Sigma \colon \mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})\to {\mathcal {D}}^b(X^+)$ the term-wise extension of
$\Sigma \colon \mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})\to {\mathcal {D}}^b(X^+)$ the term-wise extension of ![]() $\Sigma _o = (f^{+*}f_*(-))^{\vee \vee }\colon \mathscr {P}_{-1} \to \mathscr {P}_0^+$.
$\Sigma _o = (f^{+*}f_*(-))^{\vee \vee }\colon \mathscr {P}_{-1} \to \mathscr {P}_0^+$.
Lemma 4.12 Let ![]() $f\colon X\to Y$ satisfy assumption (a). Functors
$f\colon X\to Y$ satisfy assumption (a). Functors ![]() $Rf^+_* \Sigma,Rf_*\colon \mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1}) \to {\mathcal {D}}^b(Y)$ are isomorphic.
$Rf^+_* \Sigma,Rf_*\colon \mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1}) \to {\mathcal {D}}^b(Y)$ are isomorphic.
Proof. Consider morphism ![]() $\alpha \colon f_*|_{\mathscr {P}_{-1}}\to f^+_* \Sigma _o|_{\mathscr {P}_{-1}}$ defined as the composite
$\alpha \colon f_*|_{\mathscr {P}_{-1}}\to f^+_* \Sigma _o|_{\mathscr {P}_{-1}}$ defined as the composite
for the unit ![]() $\eta$ of
$\eta$ of ![]() $f^{+*}\dashv f^+_*$ adjunction and the reflexification
$f^{+*}\dashv f^+_*$ adjunction and the reflexification ![]() $\beta \colon (-) \to (-)^{\vee \vee }$. Lemma 3.11 implies that
$\beta \colon (-) \to (-)^{\vee \vee }$. Lemma 3.11 implies that ![]() $\alpha$ is an isomorphism of functors (see Lemma 4.11).
$\alpha$ is an isomorphism of functors (see Lemma 4.11).
Morphism ![]() $\alpha$ yields morphism
$\alpha$ yields morphism ![]() $\alpha ^{-} \colon f_*^-\to (f^{+}_* \Sigma )$ of the term-wise extension of functors
$\alpha ^{-} \colon f_*^-\to (f^{+}_* \Sigma )$ of the term-wise extension of functors ![]() $f_*|_{\mathscr {P}_{-1}}$ and
$f_*|_{\mathscr {P}_{-1}}$ and ![]() $f^{+}_* \Sigma _o|_{\mathscr {P}_{-1}}$ to the category
$f^{+}_* \Sigma _o|_{\mathscr {P}_{-1}}$ to the category ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$. As
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$. As ![]() $\alpha$ is an isomorphism, the same is true about
$\alpha$ is an isomorphism, the same is true about ![]() $\alpha ^-$.
$\alpha ^-$.
Now let ![]() $E$ be an object in
$E$ be an object in ![]() ${\mathcal {D}}^b(X)$. It is isomorphic to a complex
${\mathcal {D}}^b(X)$. It is isomorphic to a complex ![]() ${\mathcal {P}}_{{\boldsymbol {\cdot }}}$ in
${\mathcal {P}}_{{\boldsymbol {\cdot }}}$ in ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$. The first layer of spectral sequence
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_{-1})$. The first layer of spectral sequence
has only one non-zero row. Hence, complex ![]() $f_* {\mathcal {P}}_{{\boldsymbol {\cdot }}}$ is isomorphic to
$f_* {\mathcal {P}}_{{\boldsymbol {\cdot }}}$ is isomorphic to ![]() $Rf_* E$. Analogously, because
$Rf_* E$. Analogously, because ![]() $\Sigma _o(\mathscr {P}_{-1}) \simeq \mathscr {P}_0^+$, complex
$\Sigma _o(\mathscr {P}_{-1}) \simeq \mathscr {P}_0^+$, complex ![]() $f^+_* \Sigma ({\mathcal {P}}_{\boldsymbol {\cdot }})$ is isomorphic to
$f^+_* \Sigma ({\mathcal {P}}_{\boldsymbol {\cdot }})$ is isomorphic to ![]() $Rf^+_* \Sigma \, E$. Thus,
$Rf^+_* \Sigma \, E$. Thus, ![]() $\alpha ^-$ induces an isomorphism of
$\alpha ^-$ induces an isomorphism of ![]() $Rf_*$ and
$Rf_*$ and ![]() $Rf^+_* \Sigma$.
$Rf^+_* \Sigma$.
Proposition 4.13 Let ![]() $f\colon X\to Y$ satisfy assumption (a) and let
$f\colon X\to Y$ satisfy assumption (a) and let ![]() $\Sigma _{{\rm qc}}$ be as in Proposition 4.6. The derived base change
$\Sigma _{{\rm qc}}$ be as in Proposition 4.6. The derived base change ![]() $\widetilde {\epsilon }$ induces a functorial exact triangle of functors
$\widetilde {\epsilon }$ induces a functorial exact triangle of functors ![]() ${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(X^+)$:
${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(X^+)$:
Proof. We have already seen in § 4.1 that there exists a choice of compact generators ![]() ${\mathcal {M}}$ and
${\mathcal {M}}$ and ![]() ${\mathcal {N}}^+$ of
${\mathcal {N}}^+$ of ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ and
${\mathcal {D}}_{{\rm qc}}(X)$ and ![]() ${\mathcal {D}}_{{\rm qc}}(X^+)$, respectively, such that
${\mathcal {D}}_{{\rm qc}}(X^+)$, respectively, such that ![]() ${\mathcal {D}}_{{\rm qc}}(X) \simeq {\mathcal {D}}(\text{Mod--}A) \simeq {\mathcal {D}}_{{\rm qc}}(X^+)$, for an algebra
${\mathcal {D}}_{{\rm qc}}(X) \simeq {\mathcal {D}}(\text{Mod--}A) \simeq {\mathcal {D}}_{{\rm qc}}(X^+)$, for an algebra ![]() $A =\mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, {\mathcal {M}})$ (see Lemma 4.3). Under these equivalences, functor
$A =\mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, {\mathcal {M}})$ (see Lemma 4.3). Under these equivalences, functor ![]() $\Sigma _{{\rm qc}}$ is given by algebra
$\Sigma _{{\rm qc}}$ is given by algebra ![]() $A$ considered as an
$A$ considered as an ![]() $A^{\mathop {{\rm op}}\nolimits }\otimes A$ bimodule.
$A^{\mathop {{\rm op}}\nolimits }\otimes A$ bimodule.
Appendix C, allows us to lift the base change ![]() $Lg^{+*}Rg_* \to Rp^+_* Lp^*$ to a 1-morphism in
$Lg^{+*}Rg_* \to Rp^+_* Lp^*$ to a 1-morphism in ![]() $\mathop {\textbf {Bimod}}\nolimits$. It induces a functorial exact triangle
$\mathop {\textbf {Bimod}}\nolimits$. It induces a functorial exact triangle
Let us show that functors ![]() $\Sigma '|_{\mathscr {P}_{-1}}$ and
$\Sigma '|_{\mathscr {P}_{-1}}$ and ![]() $\Sigma _o[1]|_{\mathscr {P}_{-1}}$ are isomorphic. To this end, we consider an object
$\Sigma _o[1]|_{\mathscr {P}_{-1}}$ are isomorphic. To this end, we consider an object ![]() ${\mathcal {M}}$ in
${\mathcal {M}}$ in ![]() $\mathscr {P}_{-1}$. By Proposition 3.12, object
$\mathscr {P}_{-1}$. By Proposition 3.12, object ![]() ${\mathcal {N}}^+ := (f^{+*}f_*({\mathcal {M}}))^{\vee \vee }$ lies in
${\mathcal {N}}^+ := (f^{+*}f_*({\mathcal {M}}))^{\vee \vee }$ lies in ![]() $\mathscr {P}_0^+$. Thus, Proposition 3.15 yields an exact triangle
$\mathscr {P}_0^+$. Thus, Proposition 3.15 yields an exact triangle
By Lemma 3.11, we have ![]() $f^+_*{\mathcal {N}}^+\simeq f_* {\mathcal {M}}$, hence
$f^+_*{\mathcal {N}}^+\simeq f_* {\mathcal {M}}$, hence ![]() $g^+_* {\mathcal {N}}^+ \simeq g_* {\mathcal {M}}$. Proposition 4.10 assures that
$g^+_* {\mathcal {N}}^+ \simeq g_* {\mathcal {M}}$. Proposition 4.10 assures that ![]() $f^{+*}f_*{\mathcal {M}} \simeq F({\mathcal {M}})$, hence triangle (53) reads
$f^{+*}f_*{\mathcal {M}} \simeq F({\mathcal {M}})$, hence triangle (53) reads
There exists a morphism from triangle (54) to triangle (52) applied to ![]() ${\mathcal {M}}$ which is equal to the identity morphism on
${\mathcal {M}}$ which is equal to the identity morphism on ![]() $Lg^{+*}g_*\, {\mathcal {M}}$ and on
$Lg^{+*}g_*\, {\mathcal {M}}$ and on ![]() $F({\mathcal {M}}) = Rp^+_*Lp^*{\mathcal {M}}$. Indeed, the map
$F({\mathcal {M}}) = Rp^+_*Lp^*{\mathcal {M}}$. Indeed, the map ![]() $Lg^{+*}Rg_*{\mathcal {M}} \to F({\mathcal {M}})$ in (54) is the composite
$Lg^{+*}Rg_*{\mathcal {M}} \to F({\mathcal {M}})$ in (54) is the composite
of the truncation ![]() $\tau _{\geqslant 0}$, which in this case is taking the zeroth cohomology, followed by the base-change isomorphism (see Proposition 4.10) and then by the isomorphism
$\tau _{\geqslant 0}$, which in this case is taking the zeroth cohomology, followed by the base-change isomorphism (see Proposition 4.10) and then by the isomorphism ![]() $p^+_*p^*{\mathcal {M}} \simeq Rp^+_*Lp^*{\mathcal {M}}$ (see Proposition 4.8). Note that, under the isomorphism
$p^+_*p^*{\mathcal {M}} \simeq Rp^+_*Lp^*{\mathcal {M}}$ (see Proposition 4.8). Note that, under the isomorphism ![]() $f^{+*}f_* \simeq g^{+*}g_*$ of functors
$f^{+*}f_* \simeq g^{+*}g_*$ of functors ![]() $\mathop {{\rm Coh}}\nolimits (X) \to \mathop {{\rm Coh}}\nolimits (X^+)$, induced by the
$\mathop {{\rm Coh}}\nolimits (X) \to \mathop {{\rm Coh}}\nolimits (X^+)$, induced by the ![]() $i^*\dashv i_*$ adjunction counit, the base change
$i^*\dashv i_*$ adjunction counit, the base change ![]() $f^{+*}f_* \to p^+_*p^*$ corresponds to the base change
$f^{+*}f_* \to p^+_*p^*$ corresponds to the base change ![]() $g^{+*}g_* \to p^+_*p^*$. On the other hand, the map
$g^{+*}g_* \to p^+_*p^*$. On the other hand, the map ![]() $Lg^{+*}Rg_* \to Rp^+_*Lp^*$ in (52) is the (derived) base change. For the degree reason (as
$Lg^{+*}Rg_* \to Rp^+_*Lp^*$ in (52) is the (derived) base change. For the degree reason (as ![]() $Rp^+_*Lp^*{\mathcal {M}}$ is a sheaf by Proposition 4.8), the derived base change for
$Rp^+_*Lp^*{\mathcal {M}}$ is a sheaf by Proposition 4.8), the derived base change for ![]() ${\mathcal {M}}$ factors via
${\mathcal {M}}$ factors via ![]() $H^0(Lg^{+*}Rg_*{\mathcal {M}})$. The existence of the desired morphism of triangles follows from the fact that the restriction of the derived base change to zeroth cohomology is the non-derived base change. Thus, for any
$H^0(Lg^{+*}Rg_*{\mathcal {M}})$. The existence of the desired morphism of triangles follows from the fact that the restriction of the derived base change to zeroth cohomology is the non-derived base change. Thus, for any ![]() ${\mathcal {M}}$ in
${\mathcal {M}}$ in ![]() $\mathscr {P}_{-1}$, there exists an isomorphism
$\mathscr {P}_{-1}$, there exists an isomorphism ![]() $\alpha _{{\mathcal {M}}} \colon \Sigma _o({\mathcal {M}})[1] \to \Sigma '({\mathcal {M}})$. It is unique, as
$\alpha _{{\mathcal {M}}} \colon \Sigma _o({\mathcal {M}})[1] \to \Sigma '({\mathcal {M}})$. It is unique, as ![]() $\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], F({\mathcal {M}})[-1]) = \mathop {{\rm Ext}}\nolimits ^{-2}_{X^+}({\mathcal {N}}^+, f^{+*}f^+_* {\mathcal {N}}^+) = 0$ (for degree reasons). Morphism
$\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], F({\mathcal {M}})[-1]) = \mathop {{\rm Ext}}\nolimits ^{-2}_{X^+}({\mathcal {N}}^+, f^{+*}f^+_* {\mathcal {N}}^+) = 0$ (for degree reasons). Morphism ![]() $\alpha _{{\mathcal {M}}}$ when composed with
$\alpha _{{\mathcal {M}}}$ when composed with ![]() $\Sigma '({\mathcal {M}}) \to Lg^{+*}Rg_*({\mathcal {M}})$ is equal to
$\Sigma '({\mathcal {M}}) \to Lg^{+*}Rg_*({\mathcal {M}})$ is equal to ![]() $\beta _{{\mathcal {M}}}$, for a morphism
$\beta _{{\mathcal {M}}}$, for a morphism ![]() $\beta = \eta \Sigma _o \colon \Sigma _o[1] \to Lg^{+*} Rg_*$. Here,
$\beta = \eta \Sigma _o \colon \Sigma _o[1] \to Lg^{+*} Rg_*$. Here, ![]() $\eta \colon \mathop {{\rm Id}}\nolimits [1] \to g^{+!}Rg^+_*[1] \simeq Lg^{+*}Rg^+_*$ is the adjunction unit (we use
$\eta \colon \mathop {{\rm Id}}\nolimits [1] \to g^{+!}Rg^+_*[1] \simeq Lg^{+*}Rg^+_*$ is the adjunction unit (we use ![]() $Rg^+_*\Sigma _o \simeq Rg_*$ which follows from Lemma 4.12).
$Rg^+_*\Sigma _o \simeq Rg_*$ which follows from Lemma 4.12).
For any ![]() ${\mathcal {M}}, {\mathcal {M}}_1 \in \mathscr {P}_{-1}$ and
${\mathcal {M}}, {\mathcal {M}}_1 \in \mathscr {P}_{-1}$ and ![]() $\varphi \colon {\mathcal {M}} \mapsto {\mathcal {M}}_1$, both compositions
$\varphi \colon {\mathcal {M}} \mapsto {\mathcal {M}}_1$, both compositions
fit into the following commuting diagram.

As both ![]() $\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], F({\mathcal {M}}_1))$ and
$\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], F({\mathcal {M}}_1))$ and ![]() $\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], F({\mathcal {M}}_1)[-1])$ vanish (also for degree reasons), we have
$\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], F({\mathcal {M}}_1)[-1])$ vanish (also for degree reasons), we have ![]() $\Sigma '(\varphi ) \circ \alpha _{{\mathcal {M}}} = \alpha _{{\mathcal {M}}_1} \circ \Sigma _o(\varphi )[1]$, i.e.
$\Sigma '(\varphi ) \circ \alpha _{{\mathcal {M}}} = \alpha _{{\mathcal {M}}_1} \circ \Sigma _o(\varphi )[1]$, i.e. ![]() $\alpha$ extends to a morphism of functors
$\alpha$ extends to a morphism of functors ![]() $\alpha \colon \Sigma _o[1]|_{\mathscr {P}_{-1}} \to \Sigma '|_{\mathscr {P}_{-1}}$. Moreover, any
$\alpha \colon \Sigma _o[1]|_{\mathscr {P}_{-1}} \to \Sigma '|_{\mathscr {P}_{-1}}$. Moreover, any ![]() $\psi$ in
$\psi$ in ![]() $\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], \Sigma _o({\mathcal {M}}_1)[1]) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, {\mathcal {M}}_1)$ uniquely determines
$\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], \Sigma _o({\mathcal {M}}_1)[1]) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, {\mathcal {M}}_1)$ uniquely determines ![]() $\widetilde {\psi } \colon \Sigma '({\mathcal {M}}) \to \Sigma '({\mathcal {M}}_1)$. Similarly, as
$\widetilde {\psi } \colon \Sigma '({\mathcal {M}}) \to \Sigma '({\mathcal {M}}_1)$. Similarly, as ![]() $\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma '({\mathcal {M}}), F({\mathcal {M}}_1)) = 0 =\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma '({\mathcal {M}}), F({\mathcal {M}}_1)[-1])$, any
$\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma '({\mathcal {M}}), F({\mathcal {M}}_1)) = 0 =\mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma '({\mathcal {M}}), F({\mathcal {M}}_1)[-1])$, any ![]() $\tau \in \mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma '({\mathcal {M}}), \Sigma '({\mathcal {M}}_1))$ determines
$\tau \in \mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma '({\mathcal {M}}), \Sigma '({\mathcal {M}}_1))$ determines ![]() $\widetilde {\tau } \colon \Sigma _o({\mathcal {M}})[1] \to \Sigma _o({\mathcal {M}}_1)[1]$. Thus, morphism
$\widetilde {\tau } \colon \Sigma _o({\mathcal {M}})[1] \to \Sigma _o({\mathcal {M}}_1)[1]$. Thus, morphism ![]() $\alpha \colon \mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], \Sigma _o({\mathcal {M}}_1)[1])\to \mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma '({\mathcal {M}}), \Sigma '({\mathcal {M}}_1))$ is a bijection. It follows that
$\alpha \colon \mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma _o({\mathcal {M}})[1], \Sigma _o({\mathcal {M}}_1)[1])\to \mathop {{\rm Hom}}\nolimits _{X^+}(\Sigma '({\mathcal {M}}), \Sigma '({\mathcal {M}}_1))$ is a bijection. It follows that ![]() $\alpha$ is an isomorphism of functors
$\alpha$ is an isomorphism of functors ![]() $\alpha \colon \Sigma _o[1]|_{\mathscr {P}_{-1}} \xrightarrow {\simeq } \Sigma '|_{\mathscr {P}_{-1}}$.
$\alpha \colon \Sigma _o[1]|_{\mathscr {P}_{-1}} \xrightarrow {\simeq } \Sigma '|_{\mathscr {P}_{-1}}$.
Lemma 4.3 implies that ![]() ${\mathcal {D}}_{qc}(X) \simeq {\mathcal {D}}(\text{Mod--}A)$, for an algebra
${\mathcal {D}}_{qc}(X) \simeq {\mathcal {D}}(\text{Mod--}A)$, for an algebra ![]() $A$. Furthermore, by definition, functor
$A$. Furthermore, by definition, functor ![]() $\Sigma _{{\rm qc}}$ is isomorphic to the bimodule functor
$\Sigma _{{\rm qc}}$ is isomorphic to the bimodule functor ![]() $\Phi _A$, for
$\Phi _A$, for ![]() $A$ considered as
$A$ considered as ![]() $A^{\mathop {{\rm op}}\nolimits }\otimes A$ bimodule. By construction (via an exact triangle),
$A^{\mathop {{\rm op}}\nolimits }\otimes A$ bimodule. By construction (via an exact triangle), ![]() $\Sigma '$ is also a bimodule functor. Thus, assumptions of Lemma C.12 are satisfied and we conclude that
$\Sigma '$ is also a bimodule functor. Thus, assumptions of Lemma C.12 are satisfied and we conclude that ![]() $\Sigma '[-1] \simeq \Sigma _{{\rm qc}}$. Hence, functorial exact triangle (52) reads
$\Sigma '[-1] \simeq \Sigma _{{\rm qc}}$. Hence, functorial exact triangle (52) reads
Corollary 4.14 Let ![]() $f\colon X\to Y$ satisfy assumption (p). The flop functor
$f\colon X\to Y$ satisfy assumption (p). The flop functor ![]() $F$ takes
$F$ takes ![]() ${\mathcal {D}}^b(X)$ to
${\mathcal {D}}^b(X)$ to ![]() ${\mathcal {D}}^b(X^+)$.
${\mathcal {D}}^b(X^+)$.
Proof. The statement is local in ![]() $Y$, therefore we can assume that morphism
$Y$, therefore we can assume that morphism ![]() $f$ satisfies assumption (a). As both
$f$ satisfies assumption (a). As both ![]() $Lg^{+*}Rg_*$ and
$Lg^{+*}Rg_*$ and ![]() $\Sigma _{{\rm qc}}$ take
$\Sigma _{{\rm qc}}$ take ![]() ${\mathcal {D}}^b(X)$ to
${\mathcal {D}}^b(X)$ to ![]() ${\mathcal {D}}^b(X^+)$ (see Theorem 4.5), the functorial exact triangle of Proposition 4.13 implies that the flop functor
${\mathcal {D}}^b(X^+)$ (see Theorem 4.5), the functorial exact triangle of Proposition 4.13 implies that the flop functor ![]() $F$ takes
$F$ takes ![]() ${\mathcal {D}}^b(X)$ to
${\mathcal {D}}^b(X)$ to ![]() ${\mathcal {D}}^b(X^+)$.
${\mathcal {D}}^b(X^+)$.
4.4 An alternative description of the flop–flop functor
We show that ![]() $F^+F$ on category
$F^+F$ on category ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ is isomorphic to
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ is isomorphic to ![]() $f^*f_*$. First, we show vanishing of higher inverse images of projective objects in
$f^*f_*$. First, we show vanishing of higher inverse images of projective objects in ![]() $\mathscr {A}_f$ and then extend Proposition 4.8 to the sheaf
$\mathscr {A}_f$ and then extend Proposition 4.8 to the sheaf ![]() $f^*f_* {\mathcal {N}}$.
$f^*f_* {\mathcal {N}}$.
Lemma 4.15 Let ![]() $f\colon X\to Y$ satisfy assumption (a) and
$f\colon X\to Y$ satisfy assumption (a) and ![]() ${\mathcal {P}}$ be projective in
${\mathcal {P}}$ be projective in ![]() $\mathscr {A}_f$. Then
$\mathscr {A}_f$. Then ![]() $L^jp^* {\mathcal {P}} = 0$, for
$L^jp^* {\mathcal {P}} = 0$, for ![]() $j\geqslant 2$.
$j\geqslant 2$.
Proof. The statement is local in ![]() $X$, in particular in
$X$, in particular in ![]() $Y$. Therefore, we can assume that
$Y$. Therefore, we can assume that ![]() $f$ satisfies assumption (c) and
$f$ satisfies assumption (c) and ![]() ${\mathcal {P}}$ is a direct sum of copies of
${\mathcal {P}}$ is a direct sum of copies of ![]() ${\mathcal {P}}_i$ as in (19).
${\mathcal {P}}_i$ as in (19).
Consider the counit ![]() $Lg^*g_* {\mathcal {M}}_i \to {\mathcal {M}}_i$ of the
$Lg^*g_* {\mathcal {M}}_i \to {\mathcal {M}}_i$ of the ![]() $Lg^* \dashv Rg_*$ adjunction. It gives an exact triangle
$Lg^* \dashv Rg_*$ adjunction. It gives an exact triangle
Applying functor ![]() $Lp^*$ to it yields an exact triangle on
$Lp^*$ to it yields an exact triangle on ![]() $X\times _Y X^+$:
$X\times _Y X^+$:
Lemma 3.14 implies that ![]() $L^j(p^*g^*)g_* {\mathcal {M}}_i = 0$, for
$L^j(p^*g^*)g_* {\mathcal {M}}_i = 0$, for ![]() $j\geqslant 2$. Thus,
$j\geqslant 2$. Thus, ![]() $L^j p^* S_{{\mathcal {M}}_i} = 0$, for
$L^j p^* S_{{\mathcal {M}}_i} = 0$, for ![]() $j>2$.
$j>2$.
Proposition 3.15, the long exact sequence of cohomology associated to triangle (55) and sequence (15) imply that ![]() $S_{{\mathcal {M}}_i}$ has two non-zero cohomology sheaves:
$S_{{\mathcal {M}}_i}$ has two non-zero cohomology sheaves:
By applying ![]() $Lp^*$ and looking at the cohomology sheaves of the obtained triangle, we obtain an isomorphism
$Lp^*$ and looking at the cohomology sheaves of the obtained triangle, we obtain an isomorphism ![]() $L^jp^*{\mathcal {P}}_i \simeq L^{j+1}p^* S_{{\mathcal {M}}_i} \simeq 0$, for
$L^jp^*{\mathcal {P}}_i \simeq L^{j+1}p^* S_{{\mathcal {M}}_i} \simeq 0$, for ![]() $j\geqslant 3$, and an exact sequence
$j\geqslant 3$, and an exact sequence
Sheaf ![]() $L^2p^* {\mathcal {P}}_i$ is supported on the exceptional divisor of
$L^2p^* {\mathcal {P}}_i$ is supported on the exceptional divisor of ![]() $p$, hence it is torsion. As
$p$, hence it is torsion. As ![]() $p^* {\mathcal {M}}_i$ is locally free,
$p^* {\mathcal {M}}_i$ is locally free, ![]() $L^2 p^* {\mathcal {P}}_i = 0$.
$L^2 p^* {\mathcal {P}}_i = 0$.
Lemma 4.16 Let ![]() $f\colon X\to Y$ satisfy assumption (a). Then, for any
$f\colon X\to Y$ satisfy assumption (a). Then, for any ![]() ${\mathcal {N}} \in \mathscr {P}_0$, the pullbacks of
${\mathcal {N}} \in \mathscr {P}_0$, the pullbacks of ![]() ${\mathcal {N}}$ and
${\mathcal {N}}$ and ![]() ${\mathcal {M}}^+ = (f^{+*}f_*{\mathcal {N}})^{\vee \vee }$ fit into the short exact sequence
${\mathcal {M}}^+ = (f^{+*}f_*{\mathcal {N}})^{\vee \vee }$ fit into the short exact sequence
on ![]() $X\times _Y X^+$.
$X\times _Y X^+$.
Proof. By Proposition 3.15, we have an exact triangle
By applying ![]() $Lp^*$ to (57), we obtain an exact triangle
$Lp^*$ to (57), we obtain an exact triangle
As ![]() $g_* {\mathcal {N}}$ has a locally free resolution of length two (see Lemma 3.14),
$g_* {\mathcal {N}}$ has a locally free resolution of length two (see Lemma 3.14), ![]() $L^2(p^*g^*)g_*{\mathcal {N}} =0$. The long exact sequence of cohomology for triangle (58) implies the exact sequence
$L^2(p^*g^*)g_*{\mathcal {N}} =0$. The long exact sequence of cohomology for triangle (58) implies the exact sequence
As ![]() ${\mathcal {N}}$ is locally free,
${\mathcal {N}}$ is locally free, ![]() $L^{>0}p^*{\mathcal {N}} =0$. Hence, by applying
$L^{>0}p^*{\mathcal {N}} =0$. Hence, by applying ![]() $Lp^*$ to sequence (32), we obtain isomorphisms
$Lp^*$ to sequence (32), we obtain isomorphisms ![]() $L^3p^*\mathcal {Q} \simeq L^2p^*(f^*f_* {\mathcal {N}})$ and
$L^3p^*\mathcal {Q} \simeq L^2p^*(f^*f_* {\mathcal {N}})$ and ![]() $L^2 p^* \mathcal {Q} \simeq L^1 p^*(f^*f_* {\mathcal {N}})$, where
$L^2 p^* \mathcal {Q} \simeq L^1 p^*(f^*f_* {\mathcal {N}})$, where ![]() $\mathcal {Q} = {\mathcal {H}}_X^0(\iota _{f*}\iota _f^* {\mathcal {N}})$ is a projective object in
$\mathcal {Q} = {\mathcal {H}}_X^0(\iota _{f*}\iota _f^* {\mathcal {N}})$ is a projective object in ![]() $\mathscr {A}_f$. In view of Lemma 4.15, sequence (59) is reduced to an isomorphism
$\mathscr {A}_f$. In view of Lemma 4.15, sequence (59) is reduced to an isomorphism ![]() $p^* {\mathcal {N}}\simeq L^1(p^*g^*)g_* {\mathcal {N}}$.
$p^* {\mathcal {N}}\simeq L^1(p^*g^*)g_* {\mathcal {N}}$.
Let ![]() ${\mathcal {M}}^+ = (f^{+*}f_* {\mathcal {N}})^{\vee \vee }$ be an object in
${\mathcal {M}}^+ = (f^{+*}f_* {\mathcal {N}})^{\vee \vee }$ be an object in ![]() $\mathscr {P}_{-1}^+$. Proposition 3.12 implies that
$\mathscr {P}_{-1}^+$. Proposition 3.12 implies that ![]() $f^+_* {\mathcal {M}}^+ \simeq f_* {\mathcal {N}}$, hence
$f^+_* {\mathcal {M}}^+ \simeq f_* {\mathcal {N}}$, hence ![]() $g^+_* {\mathcal {M}}^+ \simeq g_* {\mathcal {N}}$. As diagram (51) commutes, we have
$g^+_* {\mathcal {M}}^+ \simeq g_* {\mathcal {N}}$. As diagram (51) commutes, we have
By applying ![]() $Lp^{+*}$ to sequence (36), we obtain an exact sequence
$Lp^{+*}$ to sequence (36), we obtain an exact sequence
Now consider sequence (15) with ![]() $f^+$,
$f^+$, ![]() ${\mathcal {M}}^+$ and
${\mathcal {M}}^+$ and ![]() ${\mathcal {P}}^+$ instead of
${\mathcal {P}}^+$ instead of ![]() $f$,
$f$, ![]() ${\mathcal {M}}$ and
${\mathcal {M}}$ and ![]() ${\mathcal {P}}$. Apply functor
${\mathcal {P}}$. Apply functor ![]() $Lp^{+*}$ to it. Then Lemma 4.15 for
$Lp^{+*}$ to it. Then Lemma 4.15 for ![]() $f^+$,
$f^+$, ![]() $p^+$ and
$p^+$ and ![]() ${\mathcal {P}}^+$ instead of
${\mathcal {P}}^+$ instead of ![]() $f$,
$f$,![]() $p$ and
$p$ and ![]() ${\mathcal {P}}$, implies that
${\mathcal {P}}$, implies that ![]() $L^2p^{+*}(f^{+*}f^+_* {\mathcal {M}}^+) \simeq 0$. Hence, sequence (61) can be rewritten as
$L^2p^{+*}(f^{+*}f^+_* {\mathcal {M}}^+) \simeq 0$. Hence, sequence (61) can be rewritten as
Sequence (62) together with isomorphism (60) imply that (56) is exact.
Proposition 4.17 Let ![]() $f$ satisfy assumption (a). Then flop functor
$f$ satisfy assumption (a). Then flop functor ![]() $Rp^+_* Lp^*$ on category
$Rp^+_* Lp^*$ on category ![]() $f^*f_* \mathscr {P}_0$ is isomorphic to the non-derived flop functor
$f^*f_* \mathscr {P}_0$ is isomorphic to the non-derived flop functor ![]() $p^+_*p^*$.
$p^+_*p^*$.
Proof. In view of Lemma 4.15, ![]() $L^jp^* \mathcal {Q} \simeq 0$, for any
$L^jp^* \mathcal {Q} \simeq 0$, for any ![]() $\mathcal {Q}$ projective in
$\mathcal {Q}$ projective in ![]() $\mathscr {A}_f$ and any
$\mathscr {A}_f$ and any ![]() $j\geqslant 2$. As any object
$j\geqslant 2$. As any object ![]() ${\mathcal {N}}$ in
${\mathcal {N}}$ in ![]() $\mathscr {P}_0$ is locally free [Reference Van den BerghVdB04, Proposition 3.2.6], by applying
$\mathscr {P}_0$ is locally free [Reference Van den BerghVdB04, Proposition 3.2.6], by applying ![]() $Lp^*$ to sequence (32), we obtain an isomorphism
$Lp^*$ to sequence (32), we obtain an isomorphism ![]() $Lp^* f^*f_*{\mathcal {N}} \simeq p^*f^*f_* {\mathcal {N}}$. As diagram (42) commutes, the latter sheaf is isomorphic to
$Lp^* f^*f_*{\mathcal {N}} \simeq p^*f^*f_* {\mathcal {N}}$. As diagram (42) commutes, the latter sheaf is isomorphic to ![]() $p^{+*}f^{+*}f_* {\mathcal {N}}$. Lemma 2.8 implies that
$p^{+*}f^{+*}f_* {\mathcal {N}}$. Lemma 2.8 implies that ![]() $R^1p^+_* p^{+*}(E) \simeq 0$, for any sheaf
$R^1p^+_* p^{+*}(E) \simeq 0$, for any sheaf ![]() $E$ on
$E$ on ![]() $X^+$. Thus,
$X^+$. Thus, ![]() $Rp^+_* p^{+*}f^{+*}f_* {\mathcal {N}}\simeq p^+_* p^{+*}f^{+*}f_* {\mathcal {N}} \simeq p^+_* p^{*}f^{*}f_* {\mathcal {N}}$.
$Rp^+_* p^{+*}f^{+*}f_* {\mathcal {N}}\simeq p^+_* p^{+*}f^{+*}f_* {\mathcal {N}} \simeq p^+_* p^{*}f^{*}f_* {\mathcal {N}}$.
Base change ![]() $\epsilon$ given by (47) and an analogous
$\epsilon$ given by (47) and an analogous ![]() $\epsilon ^+ \colon f^*f^+_* \to p_* p^{+*}$ together with the adjunction unit
$\epsilon ^+ \colon f^*f^+_* \to p_* p^{+*}$ together with the adjunction unit ![]() $\eta ^{f^+}\colon \mathop {{\rm Id}}\nolimits \to f^+_*f^{+*}$ give
$\eta ^{f^+}\colon \mathop {{\rm Id}}\nolimits \to f^+_*f^{+*}$ give ![]() $\widetilde {\epsilon } \colon f^*f_* \to p_*p^{+*}p^+_*p^*$ which is the composite
$\widetilde {\epsilon } \colon f^*f_* \to p_*p^{+*}p^+_*p^*$ which is the composite
Proposition 4.18 Let ![]() $f$ satisfy assumption (a). Morphism
$f$ satisfy assumption (a). Morphism ![]() $\widetilde {\epsilon }$ is an isomorphism on the category
$\widetilde {\epsilon }$ is an isomorphism on the category ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$.
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$.
Proof. We check that, for any ![]() ${\mathcal {M}}\in \mathscr {P}_{-1}$, the map
${\mathcal {M}}\in \mathscr {P}_{-1}$, the map ![]() $\widetilde {\epsilon }_{{\mathcal {M}}}$ is a composition of three isomorphisms.
$\widetilde {\epsilon }_{{\mathcal {M}}}$ is a composition of three isomorphisms.
Take ![]() ${\mathcal {N}}^+:= (f^{+*}f_* {\mathcal {M}})^{\vee \vee }$ as in (35). In view of Lemma 3.11,
${\mathcal {N}}^+:= (f^{+*}f_* {\mathcal {M}})^{\vee \vee }$ as in (35). In view of Lemma 3.11, ![]() $f_* {\mathcal {M}} \simeq f^+_* {\mathcal {N}}^+$. Then Lemma 2.9 implies that morphism
$f_* {\mathcal {M}} \simeq f^+_* {\mathcal {N}}^+$. Then Lemma 2.9 implies that morphism ![]() $\eta ^{f^+}_{f_*{\mathcal {M}}}\colon f_* {\mathcal {M}} \to f^+_*f^{+*}f_* {\mathcal {M}}$ is an isomorphism, hence so is
$\eta ^{f^+}_{f_*{\mathcal {M}}}\colon f_* {\mathcal {M}} \to f^+_*f^{+*}f_* {\mathcal {M}}$ is an isomorphism, hence so is ![]() $f^* \eta ^{f^+}f_*$ on
$f^* \eta ^{f^+}f_*$ on ![]() ${\mathcal {M}}$.
${\mathcal {M}}$.
Natural transformation ![]() $\epsilon ^+$ is the composite of the adjunction unit
$\epsilon ^+$ is the composite of the adjunction unit ![]() $\eta ^p$ and the counit
$\eta ^p$ and the counit ![]() $\varepsilon ^{f^+}$ as in (48). We check that both maps
$\varepsilon ^{f^+}$ as in (48). We check that both maps
 \begin{align*} &f^*f^+_*f^{+*}f_*{\mathcal{M}} \xrightarrow{\eta^p_{f^*f^+_*f^{+*}f_*{\mathcal{M}}}} p_*p^*f^*f^+_*f^{+*}f_*{\mathcal{M}}, \\ &p_*p^{+*}f^{+*}f^+_*f^{+*}f_*{\mathcal{M}} \xrightarrow{p_*p^{+*}\varepsilon^{f^+}_{f^{+*}f_*{\mathcal{M}}}} p_*p^{+*}f^{+*}f_*{\mathcal{M}} \end{align*}
\begin{align*} &f^*f^+_*f^{+*}f_*{\mathcal{M}} \xrightarrow{\eta^p_{f^*f^+_*f^{+*}f_*{\mathcal{M}}}} p_*p^*f^*f^+_*f^{+*}f_*{\mathcal{M}}, \\ &p_*p^{+*}f^{+*}f^+_*f^{+*}f_*{\mathcal{M}} \xrightarrow{p_*p^{+*}\varepsilon^{f^+}_{f^{+*}f_*{\mathcal{M}}}} p_*p^{+*}f^{+*}f_*{\mathcal{M}} \end{align*}
are isomorphisms. As ![]() $f^*f^+_*f^{+*}f_* {\mathcal {M}} \simeq f^*f_* {\mathcal {M}}$, morphism
$f^*f^+_*f^{+*}f_* {\mathcal {M}} \simeq f^*f_* {\mathcal {M}}$, morphism ![]() $\eta ^p_{f^*f^+_*f^{+*}f_*{\mathcal {M}}}$ is an isomorphism if and only if
$\eta ^p_{f^*f^+_*f^{+*}f_*{\mathcal {M}}}$ is an isomorphism if and only if ![]() $\eta ^p_{f^*f_* {\mathcal {M}}}$ is also an isomorphism. Object
$\eta ^p_{f^*f_* {\mathcal {M}}}$ is also an isomorphism. Object ![]() ${\mathcal {N}}^+$ satisfies
${\mathcal {N}}^+$ satisfies ![]() $R^1f^+_*{\mathcal {N}}^+ = 0$, hence, by Proposition 2.11,
$R^1f^+_*{\mathcal {N}}^+ = 0$, hence, by Proposition 2.11, ![]() $R^1p_*p^{+*}{\mathcal {N}}^+ =0$. As, by Lemma 2.8,
$R^1p_*p^{+*}{\mathcal {N}}^+ =0$. As, by Lemma 2.8, ![]() $R^ip_*p^*{\mathcal {M}} =0$, for
$R^ip_*p^*{\mathcal {M}} =0$, for ![]() $i\geqslant 1$, applying
$i\geqslant 1$, applying ![]() $Rp_*$ to sequence (56) with the roles of
$Rp_*$ to sequence (56) with the roles of ![]() $f$ and
$f$ and ![]() $f^+$ exchanged gives
$f^+$ exchanged gives ![]() $R^1p_*L^1p^*(f^*f_*{\mathcal {M}}) \simeq R^1p_*p^{+*}{\mathcal {N}}^+ =0$. Then, short exact sequence (20), for
$R^1p_*L^1p^*(f^*f_*{\mathcal {M}}) \simeq R^1p_*p^{+*}{\mathcal {N}}^+ =0$. Then, short exact sequence (20), for ![]() $E=f^*f_*{\mathcal {M}}$ and
$E=f^*f_*{\mathcal {M}}$ and ![]() $p$ instead of
$p$ instead of ![]() $f$, implies that the adjunction unit
$f$, implies that the adjunction unit ![]() $\eta ^p_{f^*f_* {\mathcal {M}}}\colon f^*f_*{\mathcal {M}} \xrightarrow {\simeq } p_*p^*(f^*f_*{\mathcal {M}})$ is an isomorphism.
$\eta ^p_{f^*f_* {\mathcal {M}}}\colon f^*f_*{\mathcal {M}} \xrightarrow {\simeq } p_*p^*(f^*f_*{\mathcal {M}})$ is an isomorphism.
By the definition of the adjunction, morphism ![]() $\varepsilon ^{f^+}_{f^{+*}f_*{\mathcal {M}}}$ fits into the following commutative triangle.
$\varepsilon ^{f^+}_{f^{+*}f_*{\mathcal {M}}}$ fits into the following commutative triangle.

We have already seen that ![]() $\eta ^{f^+}_{f_*{\mathcal {M}}}$ is an isomorphism, hence the same is true about
$\eta ^{f^+}_{f_*{\mathcal {M}}}$ is an isomorphism, hence the same is true about ![]() $f^{+*}\eta ^{f^+}_{f_*{\mathcal {M}}}$. As, clearly,
$f^{+*}\eta ^{f^+}_{f_*{\mathcal {M}}}$. As, clearly, ![]() $\mathop {{\rm Id}}\nolimits _{f^{+*}f_*{\mathcal {M}}}$ is an isomorphism, so is the third morphism in the triangle
$\mathop {{\rm Id}}\nolimits _{f^{+*}f_*{\mathcal {M}}}$ is an isomorphism, so is the third morphism in the triangle ![]() $\varepsilon ^{f^+}_{f^{+*}f_*{\mathcal {M}}}$.
$\varepsilon ^{f^+}_{f^{+*}f_*{\mathcal {M}}}$.
Finally, by Lemma 4.7, ![]() $\epsilon _{{\mathcal {M}}} \colon f^+f_*{\mathcal {M}} \to p^+_*p^*{\mathcal {M}}$ is an isomorphism, hence so is
$\epsilon _{{\mathcal {M}}} \colon f^+f_*{\mathcal {M}} \to p^+_*p^*{\mathcal {M}}$ is an isomorphism, hence so is ![]() $p_*p^{+*}\epsilon _{{\mathcal {M}}}$.
$p_*p^{+*}\epsilon _{{\mathcal {M}}}$.
Thus, for any ![]() ${\mathcal {M}} \in \mathscr {P}_{-1}$, we have an isomorphism
${\mathcal {M}} \in \mathscr {P}_{-1}$, we have an isomorphism ![]() $f^*f_* {\mathcal {M}} \to p_*p^{+*}p^+_*p^* {\mathcal {M}}$. By induction on triangles, the isomorphism extends to
$f^*f_* {\mathcal {M}} \to p_*p^{+*}p^+_*p^* {\mathcal {M}}$. By induction on triangles, the isomorphism extends to ![]() $\mathop {{\rm Hot}}\nolimits ^b(\mathscr {P}_{-1})$. Lemmas 4.9 and 4.11 imply that base change
$\mathop {{\rm Hot}}\nolimits ^b(\mathscr {P}_{-1})$. Lemmas 4.9 and 4.11 imply that base change ![]() $\widetilde {\epsilon }$ is an isomorphism on
$\widetilde {\epsilon }$ is an isomorphism on ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$.
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$.
Proposition 4.19 Let ![]() $f\colon X \to Y$ satisfy assumption (a). The flop–flop functor
$f\colon X \to Y$ satisfy assumption (a). The flop–flop functor ![]() $F^+F$ restricted to
$F^+F$ restricted to ![]() ${\mathcal {D}}^b(X)$ is isomorphic to term-wise functor
${\mathcal {D}}^b(X)$ is isomorphic to term-wise functor ![]() $f^*f_*$ on the category
$f^*f_*$ on the category ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ under the equivalence
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$ under the equivalence ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})\simeq {\mathcal {D}}^b(X)$.
${\rm Hot}^{-,b}(\mathscr {P}_{-1})\simeq {\mathcal {D}}^b(X)$.
Proof. In view of Proposition 4.18, it suffices to check that functors ![]() $p_*p^{+*}p^+_*p^*$ and
$p_*p^{+*}p^+_*p^*$ and ![]() $Rp_*Lp^{+*}Rp^+_*Lp^*$ are isomorphic on
$Rp_*Lp^{+*}Rp^+_*Lp^*$ are isomorphic on ![]() ${\rm Hot}^{-,b}(\mathscr {P}_{-1})$. By Proposition 4.8, we have an isomorphism
${\rm Hot}^{-,b}(\mathscr {P}_{-1})$. By Proposition 4.8, we have an isomorphism ![]() $Rp^+_* Lp^* {\mathcal {M}} \simeq p^+_* p^* {\mathcal {M}}$, for any
$Rp^+_* Lp^* {\mathcal {M}} \simeq p^+_* p^* {\mathcal {M}}$, for any ![]() ${\mathcal {M}} \in \mathscr {P}_{-1}$. Proposition 4.10 implies that
${\mathcal {M}} \in \mathscr {P}_{-1}$. Proposition 4.10 implies that ![]() $p^+_*p^* {\mathcal {M}}\simeq f^{+*}f_* {\mathcal {M}}$, hence
$p^+_*p^* {\mathcal {M}}\simeq f^{+*}f_* {\mathcal {M}}$, hence ![]() $Rp_*Lp^{+*}p^+_*p^* {\mathcal {M}} \simeq p_* p^{+*}p^+_*p^* {\mathcal {M}}$ by Proposition 4.8. By induction on triangles, we have an isomorphism on
$Rp_*Lp^{+*}p^+_*p^* {\mathcal {M}} \simeq p_* p^{+*}p^+_*p^* {\mathcal {M}}$ by Proposition 4.8. By induction on triangles, we have an isomorphism on ![]() $\mathop {{\rm Hot}}\nolimits ^b(\mathscr {P}_{-1})$. We conclude by Lemma 4.11.
$\mathop {{\rm Hot}}\nolimits ^b(\mathscr {P}_{-1})$. We conclude by Lemma 4.11.
4.5 The flop functor as the inverse of Van den Bergh's functor
We show that the flop functor ![]() $F^+\colon {\mathcal {D}}^b(X^+)\to {\mathcal {D}}^b(X)$ and functor
$F^+\colon {\mathcal {D}}^b(X^+)\to {\mathcal {D}}^b(X)$ and functor ![]() $\Sigma$ are inverse to each other. In view of Theorem 4.5, this statement is equivalent to the flop functor
$\Sigma$ are inverse to each other. In view of Theorem 4.5, this statement is equivalent to the flop functor ![]() $F^+$ being isomorphic to the term-wise functor
$F^+$ being isomorphic to the term-wise functor ![]() $T = (f^*f^+_*(-))^{\vee \vee }$.
$T = (f^*f^+_*(-))^{\vee \vee }$.
Proposition 4.20 Let ![]() $f\colon X \to Y$ satisfy assumption (a). The flop functor is isomorphic to
$f\colon X \to Y$ satisfy assumption (a). The flop functor is isomorphic to ![]() $(f^{+*}f_*(-))^{\vee \vee }$ as a functor
$(f^{+*}f_*(-))^{\vee \vee }$ as a functor ![]() $\mathscr {P}_{0}\to \mathscr {P}_{-1}^+$.
$\mathscr {P}_{0}\to \mathscr {P}_{-1}^+$.
Proof. Let ![]() ${\mathcal {N}}$ be an object in
${\mathcal {N}}$ be an object in ![]() $\mathscr {P}_0$ and
$\mathscr {P}_0$ and ![]() ${\mathcal {M}}^+ =(f^{+*}f_*{\mathcal {N}})^{\vee \vee }$ its image under the equivalences of Lemma 3.11. Lemma 2.9 and Proposition 4.18 give isomorphisms
${\mathcal {M}}^+ =(f^{+*}f_*{\mathcal {N}})^{\vee \vee }$ its image under the equivalences of Lemma 3.11. Lemma 2.9 and Proposition 4.18 give isomorphisms
Thus, sequence (20) implies that ![]() $Rp^+_*(L^1p^{+*}f^{+*}f^+_* {\mathcal {M}}^+) \simeq 0$. Moreover, we have
$Rp^+_*(L^1p^{+*}f^{+*}f^+_* {\mathcal {M}}^+) \simeq 0$. Moreover, we have ![]() $Rp^+_* p^{+*}{\mathcal {M}}^+ \simeq {\mathcal {M}}^+$. Hence, by applying
$Rp^+_* p^{+*}{\mathcal {M}}^+ \simeq {\mathcal {M}}^+$. Hence, by applying ![]() $Rp^+_*$ to sequence (56), we obtain
$Rp^+_*$ to sequence (56), we obtain
Hence, the flop functor takes ![]() ${\mathcal {N}}$ to
${\mathcal {N}}$ to ![]() ${\mathcal {M}}^+$.
${\mathcal {M}}^+$.
Let ![]() $\epsilon _{{\mathcal {N}}} \colon f^{+*}f_* {\mathcal {N}} \to p^+_*p^* {\mathcal {N}}\simeq {\mathcal {M}}^+$ be the base change. As
$\epsilon _{{\mathcal {N}}} \colon f^{+*}f_* {\mathcal {N}} \to p^+_*p^* {\mathcal {N}}\simeq {\mathcal {M}}^+$ be the base change. As ![]() $f_*{\mathcal {N}} \simeq f^+_* {\mathcal {M}}^+$, we have
$f_*{\mathcal {N}} \simeq f^+_* {\mathcal {M}}^+$, we have ![]() $f^{+*}f_* {\mathcal {N}} \simeq f^{+*}f^+_* {\mathcal {M}}^+$. The kernel of reflexification
$f^{+*}f_* {\mathcal {N}} \simeq f^{+*}f^+_* {\mathcal {M}}^+$. The kernel of reflexification ![]() $f^{+*}f^+_* {\mathcal {M}}^+ \to (f^{+*}f^+_*{\mathcal {M}}^+)^{\vee \vee } \simeq {\mathcal {M}}^+$ is torsion and
$f^{+*}f^+_* {\mathcal {M}}^+ \to (f^{+*}f^+_*{\mathcal {M}}^+)^{\vee \vee } \simeq {\mathcal {M}}^+$ is torsion and ![]() $p^{+*}p_* {\mathcal {N}} \simeq {\mathcal {M}}^+$ is torsion-free, hence, by applying functor
$p^{+*}p_* {\mathcal {N}} \simeq {\mathcal {M}}^+$ is torsion-free, hence, by applying functor ![]() $\mathop {{\rm Hom}}\nolimits _{X^+}(-, p^{+*}p_* {\mathcal {N}})$ to sequence (15) with
$\mathop {{\rm Hom}}\nolimits _{X^+}(-, p^{+*}p_* {\mathcal {N}})$ to sequence (15) with ![]() $f$ and
$f$ and ![]() ${\mathcal {M}}$ replaced by
${\mathcal {M}}$ replaced by ![]() $f^+$ and
$f^+$ and ![]() ${\mathcal {M}}^+$, we obtain an isomorphism
${\mathcal {M}}^+$, we obtain an isomorphism ![]() $\mathop {{\rm Hom}}\nolimits _{X^+}({\mathcal {M}}^+, p^{+*}p_* {\mathcal {N}}) \simeq \mathop {{\rm Hom}}\nolimits _{X^+}(f^{+*}f^+_*{\mathcal {M}}^+, p^{+*}p_* {\mathcal {N}})$. It follows that
$\mathop {{\rm Hom}}\nolimits _{X^+}({\mathcal {M}}^+, p^{+*}p_* {\mathcal {N}}) \simeq \mathop {{\rm Hom}}\nolimits _{X^+}(f^{+*}f^+_*{\mathcal {M}}^+, p^{+*}p_* {\mathcal {N}})$. It follows that ![]() $\epsilon _{{\mathcal {N}}}$ factors uniquely via a morphism
$\epsilon _{{\mathcal {N}}}$ factors uniquely via a morphism ![]() $\widetilde {\epsilon }_{{\mathcal {N}}}\colon {\mathcal {M}}^+ \simeq (f^{+*}f_* {\mathcal {N}})^{\vee \vee } \to p^+_*p^*{\mathcal {N}}$ which is easily checked to be functorial. Thus, there exists a morphism
$\widetilde {\epsilon }_{{\mathcal {N}}}\colon {\mathcal {M}}^+ \simeq (f^{+*}f_* {\mathcal {N}})^{\vee \vee } \to p^+_*p^*{\mathcal {N}}$ which is easily checked to be functorial. Thus, there exists a morphism ![]() $\widetilde {\epsilon }\colon (f^{+*}f_*(-))^{\vee \vee } \to p^+_*p^*(-)$ of functors.
$\widetilde {\epsilon }\colon (f^{+*}f_*(-))^{\vee \vee } \to p^+_*p^*(-)$ of functors.
Objects of ![]() $\mathscr {P}_0$ and
$\mathscr {P}_0$ and ![]() $\mathscr {P}_{-1}^+$ are reflexive on
$\mathscr {P}_{-1}^+$ are reflexive on ![]() $X$ and
$X$ and ![]() $X^+$, hence any morphism
$X^+$, hence any morphism ![]() ${\mathcal {N}}_1 \to {\mathcal {N}}_2$ (and
${\mathcal {N}}_1 \to {\mathcal {N}}_2$ (and ![]() ${\mathcal {M}}^+_1 \to {\mathcal {M}}_2^+$) is determined by its restrictions to any open set with the complement of codimension greater than one. In particular, by its restriction to the complement
${\mathcal {M}}^+_1 \to {\mathcal {M}}_2^+$) is determined by its restrictions to any open set with the complement of codimension greater than one. In particular, by its restriction to the complement ![]() $U \subset X$ of the exceptional set of
$U \subset X$ of the exceptional set of ![]() $f$ (and
$f$ (and ![]() $f^+$). Flop functor is
$f^+$). Flop functor is ![]() $Rp^+_* Lp^*$ and the other functor is
$Rp^+_* Lp^*$ and the other functor is ![]() $(f^{+*}f_*(-))^{\vee \vee }$. Then, taking into account that maps
$(f^{+*}f_*(-))^{\vee \vee }$. Then, taking into account that maps ![]() $f$,
$f$, ![]() $f^+$,
$f^+$, ![]() $p$ and
$p$ and ![]() $p^+$ are isomorphisms outside the exceptional sets and
$p^+$ are isomorphisms outside the exceptional sets and ![]() $(f^{+})^{-1}\circ f=p^+\circ p^{-1}$ on
$(f^{+})^{-1}\circ f=p^+\circ p^{-1}$ on ![]() $U$, the morphism
$U$, the morphism ![]() $\mathop {{\rm Hom}}\nolimits _X({\mathcal {N}}_1, {\mathcal {N}}_2) \to \mathop {{\rm Hom}}\nolimits _{X^+}({\mathcal {M}}^+_1, {\mathcal {M}}^+_2)$ induced by the flop functor
$\mathop {{\rm Hom}}\nolimits _X({\mathcal {N}}_1, {\mathcal {N}}_2) \to \mathop {{\rm Hom}}\nolimits _{X^+}({\mathcal {M}}^+_1, {\mathcal {M}}^+_2)$ induced by the flop functor ![]() $F$ coincides with the morphism given by
$F$ coincides with the morphism given by ![]() $(f^{+*}f_*(-))^{\vee \vee }$. It follows that
$(f^{+*}f_*(-))^{\vee \vee }$. It follows that ![]() $\widetilde {\epsilon }$ is an isomorphism of functors.
$\widetilde {\epsilon }$ is an isomorphism of functors.
Theorem 4.21 Let ![]() $f\colon X\to Y$ satisfy assumption (a). The flop functor
$f\colon X\to Y$ satisfy assumption (a). The flop functor ![]() $F$ takes
$F$ takes ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ to
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ to ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$. It is isomorphic to
$\mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$. It is isomorphic to ![]() $\Sigma _{{\rm qc}}^{-1}$ in the category of bimodule functors
$\Sigma _{{\rm qc}}^{-1}$ in the category of bimodule functors ![]() ${\mathcal {D}}_{{\rm qc}}(X)\to {\mathcal {D}}_{{\rm qc}}(X^+)$.
${\mathcal {D}}_{{\rm qc}}(X)\to {\mathcal {D}}_{{\rm qc}}(X^+)$.
Proof. The same argument as in the proof of Proposition 4.6 shows that ![]() $\Sigma _{{\rm qc}}^{-1}$ is the term-wise extension of
$\Sigma _{{\rm qc}}^{-1}$ is the term-wise extension of ![]() $(f^{+*}f_*(-))^{\vee \vee }$ to the category
$(f^{+*}f_*(-))^{\vee \vee }$ to the category ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_0)$. Proposition 4.20 implies that
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}_0)$. Proposition 4.20 implies that ![]() $F|_{\mathscr {P}_0}\simeq \Sigma _{{\rm qc}}^{-1}|_{\mathscr {P}_0}$.
$F|_{\mathscr {P}_0}\simeq \Sigma _{{\rm qc}}^{-1}|_{\mathscr {P}_0}$.
Categories ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ and
${\mathcal {D}}_{{\rm qc}}(X)$ and ![]() ${\mathcal {D}}_{{\rm qc}}(X^+)$ have compact generators
${\mathcal {D}}_{{\rm qc}}(X^+)$ have compact generators ![]() ${\mathcal {N}}\in \mathscr {P}_0$ and
${\mathcal {N}}\in \mathscr {P}_0$ and ![]() ${\mathcal {M}}^+ = (f^{+*}f_*{\mathcal {N}})^{\vee \vee }\in \mathscr {P}_{-1}^+$. For algebras
${\mathcal {M}}^+ = (f^{+*}f_*{\mathcal {N}})^{\vee \vee }\in \mathscr {P}_{-1}^+$. For algebras ![]() $A_X = \mathop {{\rm Hom}}\nolimits _X({\mathcal {N}}, {\mathcal {N}})$ and
$A_X = \mathop {{\rm Hom}}\nolimits _X({\mathcal {N}}, {\mathcal {N}})$ and ![]() $A_{X^+} = \mathop {{\rm Hom}}\nolimits _{X^+}({\mathcal {M}}^+, {\mathcal {M}}^+)$, we have equivalences
$A_{X^+} = \mathop {{\rm Hom}}\nolimits _{X^+}({\mathcal {M}}^+, {\mathcal {M}}^+)$, we have equivalences ![]() ${\mathcal {D}}_{{\rm qc}}(X) \simeq {\mathcal {D}}(\text{Mod--}A_X)$,
${\mathcal {D}}_{{\rm qc}}(X) \simeq {\mathcal {D}}(\text{Mod--}A_X)$, ![]() ${\mathcal {D}}_{{\rm qc}}(X^+) \simeq {\mathcal {D}}(\text{Mod--}A_{X^+})$. By construction, functor
${\mathcal {D}}_{{\rm qc}}(X^+) \simeq {\mathcal {D}}(\text{Mod--}A_{X^+})$. By construction, functor ![]() $\Sigma _{{\rm qc}}^{-1}$ is isomorphic to a bimodule functor
$\Sigma _{{\rm qc}}^{-1}$ is isomorphic to a bimodule functor ![]() $\Phi _{M_1}$, for some
$\Phi _{M_1}$, for some ![]() $A_X^{\mathop {{\rm op}}\nolimits } \otimes A_{X^+}$ DG bimodule
$A_X^{\mathop {{\rm op}}\nolimits } \otimes A_{X^+}$ DG bimodule ![]() $M_1$, see Appendix C. Similarly, the flop functor
$M_1$, see Appendix C. Similarly, the flop functor ![]() $F$ is isomorphic to
$F$ is isomorphic to ![]() $\Phi _{M_2}$, for some DG bimodule
$\Phi _{M_2}$, for some DG bimodule ![]() $M_2$. Moreover, from the construction of
$M_2$. Moreover, from the construction of ![]() $\Sigma _{{\rm qc}}^{-1}$, it follows that
$\Sigma _{{\rm qc}}^{-1}$, it follows that ![]() ${\mathcal {H}}^i(M_1)= 0$, for
${\mathcal {H}}^i(M_1)= 0$, for ![]() $i \neq 0$ (see the discussion before Proposition 4.6). By Lemma C.12, isomorphism
$i \neq 0$ (see the discussion before Proposition 4.6). By Lemma C.12, isomorphism ![]() $F|_{\mathscr {P}_0} \simeq \Sigma _{{\rm qc}}^{-1}|_{\mathscr {P}_0}$ implies an isomorphism
$F|_{\mathscr {P}_0} \simeq \Sigma _{{\rm qc}}^{-1}|_{\mathscr {P}_0}$ implies an isomorphism ![]() $F\simeq \Sigma _{{\rm qc}}^{-1}$.
$F\simeq \Sigma _{{\rm qc}}^{-1}$.
As an immediate consequence of Theorems 4.5 and 4.21 we obtain the following corollary.
Corollary 4.22 Let ![]() $f\colon X\to Y$ satisfy assumption (a). Then the flop functor
$f\colon X\to Y$ satisfy assumption (a). Then the flop functor ![]() $F$ induces an equivalence of
$F$ induces an equivalence of ![]() ${\mathcal {D}}^b(X)$ with
${\mathcal {D}}^b(X)$ with ![]() ${\mathcal {D}}^b(X^+)$.
${\mathcal {D}}^b(X^+)$.
In view of Proposition 4.13 and Theorem 4.21 we have a functorial exact triangle of functors ![]() ${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(X^+)$
${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(X^+)$
Moreover, it restricts to a functorial exact triangle of functors ![]() ${\mathcal {D}}^b(X)\to {\mathcal {D}}^b(X^+)$.
${\mathcal {D}}^b(X)\to {\mathcal {D}}^b(X^+)$.
Corollary 4.23 Let ![]() $f\colon X\to Y$ satisfy assumption (a). The flop functor
$f\colon X\to Y$ satisfy assumption (a). The flop functor ![]() $F\colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^b(X^+)$ is
$F\colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^b(X^+)$ is ![]() $t$-exact when
$t$-exact when ![]() ${\mathcal {D}}^b(X)$ is endowed with the
${\mathcal {D}}^b(X)$ is endowed with the ![]() $t$-structure with heart
$t$-structure with heart ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ and
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ and ![]() ${\mathcal {D}}^b(X^+)$ with the
${\mathcal {D}}^b(X^+)$ with the ![]() $t$-structure with heart
$t$-structure with heart ![]() $\mathop {{}^{p-1}{\rm Per}}\nolimits (X^+/Y)$. Moreover,
$\mathop {{}^{p-1}{\rm Per}}\nolimits (X^+/Y)$. Moreover, ![]() $F$ induces an equivalence of
$F$ induces an equivalence of ![]() $\mathscr {A}_f$ with
$\mathscr {A}_f$ with ![]() $\mathscr {A}_{f^+}[1]$.
$\mathscr {A}_{f^+}[1]$.
Proof. As ![]() $Rf^+_* \circ F \simeq Rf_*$ and, by Theorem 4.21, functor
$Rf^+_* \circ F \simeq Rf_*$ and, by Theorem 4.21, functor ![]() $F$ takes
$F$ takes ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ to
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ to ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$, the flop
$\mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$, the flop ![]() $F$ induces an equivalence of
$F$ induces an equivalence of ![]() $\mathscr {A}_f\subset \mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ with
$\mathscr {A}_f\subset \mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ with ![]() $\mathscr {A}_{f^+}[1]\subset \mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$.
$\mathscr {A}_{f^+}[1]\subset \mathop {{}^{-1}{\rm Per}}\nolimits (X^+/Y)$.
Category ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ is defined by two conditions; we require that
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ is defined by two conditions; we require that ![]() $Rf_* E$ is a pure sheaf, for any
$Rf_* E$ is a pure sheaf, for any ![]() $E \in \mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$, and that
$E \in \mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$, and that ![]() $\mathscr {A}_f[-p] \subset \mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$. It follows from the properties of
$\mathscr {A}_f[-p] \subset \mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$. It follows from the properties of ![]() $F$ that
$F$ that ![]() $F(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)) \subset \mathop {{}^{p-1}{\rm Per}}\nolimits (X^+/Y)$. As
$F(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)) \subset \mathop {{}^{p-1}{\rm Per}}\nolimits (X^+/Y)$. As ![]() $F$ is an equivalence, both categories are hearts of bounded
$F$ is an equivalence, both categories are hearts of bounded ![]() $t$-structures on
$t$-structures on ![]() ${\mathcal {D}}^b(X^+)$. It follows that
${\mathcal {D}}^b(X^+)$. It follows that ![]() $F(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)) = \mathop {{}^{p-1}{\rm Per}}\nolimits (X^+/Y)$.
$F(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)) = \mathop {{}^{p-1}{\rm Per}}\nolimits (X^+/Y)$.
Corollary 4.24 Let morphism ![]() $f\colon X\to Y$ satisfy assumption (a). Then categories
$f\colon X\to Y$ satisfy assumption (a). Then categories ![]() ${\mathcal {D}}^b(X)$ and
${\mathcal {D}}^b(X)$ and ![]() ${\mathcal {D}}^b(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y))$ are equivalent, for
${\mathcal {D}}^b(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y))$ are equivalent, for ![]() $p\in \mathbb {Z}$.
$p\in \mathbb {Z}$.
Proof. Corollary 4.23 implies that, for any ![]() $p \in \mathbb {Z}$, category
$p \in \mathbb {Z}$, category ![]() $\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ is equivalent either to
$\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)$ is equivalent either to ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ or to
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ or to ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Hence,
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Hence, ![]() ${\mathcal {D}}^b(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)) \simeq {\mathcal {D}}^b(\mathop {{}^{q}{\rm Per}}\nolimits (X/Y))$, for
${\mathcal {D}}^b(\mathop {{}^{p}{\rm Per}}\nolimits (X/Y)) \simeq {\mathcal {D}}^b(\mathop {{}^{q}{\rm Per}}\nolimits (X/Y))$, for ![]() $q \in \{-1,0\}$,
$q \in \{-1,0\}$, ![]() $q \cong p \, \mod 2$. By Proposition 4.4, the latter category is equivalent to
$q \cong p \, \mod 2$. By Proposition 4.4, the latter category is equivalent to ![]() ${\mathcal {D}}^b(X)$, which finishes the proof.
${\mathcal {D}}^b(X)$, which finishes the proof.
Let ![]() $f\colon X\to Y$ satisfy assumption (a). Proposition 2.11 implies that
$f\colon X\to Y$ satisfy assumption (a). Proposition 2.11 implies that ![]() $Rp_* {\mathcal {O}}_{X\times _Y X^+} = {\mathcal {O}}_X$. Thus, commutativity of diagram (42) yields isomorphisms
$Rp_* {\mathcal {O}}_{X\times _Y X^+} = {\mathcal {O}}_X$. Thus, commutativity of diagram (42) yields isomorphisms ![]() $F^+ \circ Lf^{+*} \simeq Rp_*Lp^{+*}Lf^{+*} \simeq Rp_*Lp^*Lf^* \simeq Lf^*$. Hence, also
$F^+ \circ Lf^{+*} \simeq Rp_*Lp^{+*}Lf^{+*} \simeq Rp_*Lp^*Lf^* \simeq Lf^*$. Hence, also ![]() $F^+\circ Lg^{+*} \simeq Lg^*$. Composing triangle (64) with
$F^+\circ Lg^{+*} \simeq Lg^*$. Composing triangle (64) with ![]() $F^+$ leads to a functorial exact triangle of functors
$F^+$ leads to a functorial exact triangle of functors ![]() ${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(X)$:
${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(X)$:
4.6 Reduction to the affine case
We have shown with Corollary 4.22 that, if a morphism ![]() $f\colon X\to Y$ satisfies assumption (a), then the flop functor
$f\colon X\to Y$ satisfies assumption (a), then the flop functor ![]() $F$ is an equivalence of
$F$ is an equivalence of ![]() ${\mathcal {D}}^b(X)$ with
${\mathcal {D}}^b(X)$ with ![]() ${\mathcal {D}}^b(X^+)$. Now, following [Reference ChenChe02], we show that the flop functor is also an equivalence, provided morphism
${\mathcal {D}}^b(X^+)$. Now, following [Reference ChenChe02], we show that the flop functor is also an equivalence, provided morphism ![]() $f$ satisfies assumption (p).
$f$ satisfies assumption (p).
Note that the condition on ![]() $Y$ to have hypersurface singularities means that completions of the local rings at all closed points of
$Y$ to have hypersurface singularities means that completions of the local rings at all closed points of ![]() $Y$ are defined by one equation in regular complete local rings.
$Y$ are defined by one equation in regular complete local rings.
Lemma 4.25 Let ![]() $Y$ be an irreducible variety of dimension
$Y$ be an irreducible variety of dimension ![]() $n$ with hypersurface singularities. Then it has a finite open covering by affine subvarieties
$n$ with hypersurface singularities. Then it has a finite open covering by affine subvarieties ![]() $Y_i$ such that every
$Y_i$ such that every ![]() $Y_i$ admits a closed embedding as a principal divisor into a smooth affine
$Y_i$ admits a closed embedding as a principal divisor into a smooth affine ![]() ${\mathcal {Y}}_i$.
${\mathcal {Y}}_i$.
For the reader's convenience, we give the proof of this statement.
Proof. Let ![]() $y\in Y$ be a closed point. As Zariski topology is quasi-compact, it is enough to show the existence of an affine open neighbourhood of
$y\in Y$ be a closed point. As Zariski topology is quasi-compact, it is enough to show the existence of an affine open neighbourhood of ![]() $y$ which admits a closed embedding into a smooth affine
$y$ which admits a closed embedding into a smooth affine ![]() ${\mathcal {Y}}$ of dimension
${\mathcal {Y}}$ of dimension ![]() $n+1$. As the statement is local, we can assume that
$n+1$. As the statement is local, we can assume that ![]() $Y$ is affine. Then
$Y$ is affine. Then ![]() $Y$ is realised as a closed subscheme in
$Y$ is realised as a closed subscheme in ![]() ${\mathbb {A}}^m$. We can assume that
${\mathbb {A}}^m$. We can assume that ![]() $m>n+1$, because otherwise the proof is obvious. Let
$m>n+1$, because otherwise the proof is obvious. Let ![]() ${\mathbb {A}}^m\subset {\mathbb {P}}^m$ be the compactification to a projective space and
${\mathbb {A}}^m\subset {\mathbb {P}}^m$ be the compactification to a projective space and ![]() ${\bar {Y}}\subset {\mathbb {P}}^m$ the closure of
${\bar {Y}}\subset {\mathbb {P}}^m$ the closure of ![]() $Y$ in
$Y$ in ![]() ${\mathbb {P}}^m$.
${\mathbb {P}}^m$.
As ![]() $Y$ has hypersurface singularities, the Zariski tangent space at point
$Y$ has hypersurface singularities, the Zariski tangent space at point ![]() $y\in Y$ has dimension
$y\in Y$ has dimension ![]() $\leqslant n+1$. It follows that we can choose a point
$\leqslant n+1$. It follows that we can choose a point ![]() $z$ in
$z$ in ![]() ${\mathbb {P}}^m\setminus {\bar {Y}}$ such that the line
${\mathbb {P}}^m\setminus {\bar {Y}}$ such that the line ![]() $(zy)\subset {\mathbb {P}}^m$ does not contain any point of
$(zy)\subset {\mathbb {P}}^m$ does not contain any point of ![]() ${\bar {Y}}$ except for
${\bar {Y}}$ except for ![]() $y$ and is not tangent to
$y$ and is not tangent to ![]() $Y$ at
$Y$ at ![]() $y$.
$y$.
Denote by ![]() $Y_1$ the image of
$Y_1$ the image of ![]() ${\bar {Y}}$ under the projection
${\bar {Y}}$ under the projection ![]() $p:{\mathbb {P}}^m\to {\mathbb {P}}^{m-1}$ with centre in
$p:{\mathbb {P}}^m\to {\mathbb {P}}^{m-1}$ with centre in ![]() $z$. By the choice of
$z$. By the choice of ![]() $z$, the morphism
$z$, the morphism ![]() ${\bar {Y}}\to Y_1$ is an isomorphism for some Zariski neighbourhoods of
${\bar {Y}}\to Y_1$ is an isomorphism for some Zariski neighbourhoods of ![]() $y$ and
$y$ and ![]() $p(y)$. We can keep projecting in the same manner, if necessary, by replacing
$p(y)$. We can keep projecting in the same manner, if necessary, by replacing ![]() ${\bar {Y}}\subset {\mathbb {P}}^m$ with
${\bar {Y}}\subset {\mathbb {P}}^m$ with ![]() $Y_1\subset {\mathbb {P}}^{m-1}$, until we come to the projective space of dimension
$Y_1\subset {\mathbb {P}}^{m-1}$, until we come to the projective space of dimension ![]() $n+1$ and a closed irreducible subvariety
$n+1$ and a closed irreducible subvariety ![]() $Y'$ in it of dimension
$Y'$ in it of dimension ![]() $n$ together with a morphism
$n$ together with a morphism ![]() $\pi :{\bar {Y}}\to Y'$ which is an isomorphism in neighbourhoods of
$\pi :{\bar {Y}}\to Y'$ which is an isomorphism in neighbourhoods of ![]() $y$ and
$y$ and ![]() $\pi (y)$.
$\pi (y)$.
We can find an affine open neighbourhood ![]() ${\mathcal {Y}} \subset {\mathbb {P}}^{n+1}$ of
${\mathcal {Y}} \subset {\mathbb {P}}^{n+1}$ of ![]() $\pi (y)$ such that
$\pi (y)$ such that ![]() $\pi$ gives an isomorphism of
$\pi$ gives an isomorphism of ![]() $Y'\cap {\mathcal {Y}}$ with a neighbourhood of
$Y'\cap {\mathcal {Y}}$ with a neighbourhood of ![]() $y\in Y$. By choosing a smaller affine
$y\in Y$. By choosing a smaller affine ![]() ${\mathcal {Y}}$, if necessary, we can assume that
${\mathcal {Y}}$, if necessary, we can assume that ![]() $Y'\cap {\mathcal {Y}} \subset {\mathcal {Y}}$ is cut out by a single equation. Then
$Y'\cap {\mathcal {Y}} \subset {\mathcal {Y}}$ is cut out by a single equation. Then ![]() $Y'\cap {\mathcal {Y}}$ is affine and embedded as a principal divisor in
$Y'\cap {\mathcal {Y}}$ is affine and embedded as a principal divisor in ![]() ${\mathcal {Y}}$, so we are done.
${\mathcal {Y}}$, so we are done.
We consider ![]() $f\colon X\to Y$ which satisfies assumption (p). Lemma 4.25 implies the existence of a finite affine covering
$f\colon X\to Y$ which satisfies assumption (p). Lemma 4.25 implies the existence of a finite affine covering ![]() $Y = \bigcup Y_i$ such that, for every
$Y = \bigcup Y_i$ such that, for every ![]() $i$, space
$i$, space ![]() $Y_i$ admits an embedding as a principal Cartier divisor to a smooth affine
$Y_i$ admits an embedding as a principal Cartier divisor to a smooth affine ![]() ${\mathcal {Y}}_i$.
${\mathcal {Y}}_i$.
For every ![]() $i$, we pull back the whole diagram to
$i$, we pull back the whole diagram to ![]() $Y_i$ as follows.
$Y_i$ as follows.

Note that, for any ![]() $i$, morphism
$i$, morphism ![]() $f_i$ satisfies assumption (a).
$f_i$ satisfies assumption (a).
Proposition 4.26 Let ![]() $f\colon X\to Y$ and
$f\colon X\to Y$ and ![]() $f_i \colon X_i \to Y_i$ be as above. Assume that flop functors
$f_i \colon X_i \to Y_i$ be as above. Assume that flop functors ![]() $F_i \colon {\mathcal {D}}^b(X_i) \to {\mathcal {D}}^b(X_i^+)$ are equivalences, for every
$F_i \colon {\mathcal {D}}^b(X_i) \to {\mathcal {D}}^b(X_i^+)$ are equivalences, for every ![]() $i$. Then the flop functor
$i$. Then the flop functor ![]() $F \colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^b(X^+)$ is an equivalence.
$F \colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^b(X^+)$ is an equivalence.
Proof. As ![]() $X$ is Gorenstein, category
$X$ is Gorenstein, category ![]() ${\mathcal {D}}^b(X)$ has a spanning class
${\mathcal {D}}^b(X)$ has a spanning class ![]() $\Omega = \{{\mathcal {O}}_{x} \}$, where
$\Omega = \{{\mathcal {O}}_{x} \}$, where ![]() $x$ runs over all closed points in
$x$ runs over all closed points in ![]() $X$ (see [Reference Hernández Ruipérez, López Martín and de SalasHLdS07, Lemma 1.26]). With such a choice of a spanning class the same argument as in [Reference ChenChe02, Proposition 3.2] proves that
$X$ (see [Reference Hernández Ruipérez, López Martín and de SalasHLdS07, Lemma 1.26]). With such a choice of a spanning class the same argument as in [Reference ChenChe02, Proposition 3.2] proves that ![]() $F$ is an equivalence if all
$F$ is an equivalence if all ![]() $F_i$ are.
$F_i$ are.
5. Spherical pairs
With the notation of (42), we consider the category ![]() ${\mathcal {D}}^b(X\times _Y X^+)$ and its quotient by the intersection
${\mathcal {D}}^b(X\times _Y X^+)$ and its quotient by the intersection ![]() ${\mathcal {K}}^b$ of kernels of
${\mathcal {K}}^b$ of kernels of ![]() $Rp_*$ and
$Rp_*$ and ![]() $Rp^+_*$. We prove that
$Rp^+_*$. We prove that ![]() ${\mathcal {D}}^b(\mathscr {A}_f)$ is equivalent to the full subcategory of
${\mathcal {D}}^b(\mathscr {A}_f)$ is equivalent to the full subcategory of ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ defined as the kernel of
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ defined as the kernel of ![]() $Rp^+_*$. We show that
$Rp^+_*$. We show that ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ admits SODs
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ admits SODs ![]() $\langle {\mathcal {D}}^b(\mathscr {A}_f), {\mathcal {D}}^b(X^+)\rangle = \langle {\mathcal {D}}^b(X), {\mathcal {D}}^b(\mathscr {A}_f) \rangle$ and similarly for
$\langle {\mathcal {D}}^b(\mathscr {A}_f), {\mathcal {D}}^b(X^+)\rangle = \langle {\mathcal {D}}^b(X), {\mathcal {D}}^b(\mathscr {A}_f) \rangle$ and similarly for ![]() $\mathscr {A}_{f^+}$. We conclude that
$\mathscr {A}_{f^+}$. We conclude that ![]() $({\mathcal {D}}^b(X), {\mathcal {D}}^b(X^+))$ and
$({\mathcal {D}}^b(X), {\mathcal {D}}^b(X^+))$ and ![]() $({\mathcal {D}}^b(\mathscr {A}_f), {\mathcal {D}}^b(\mathscr {A}_{f^+}))$ are spherical pairs, which yields a geometric incarnation of the schober [Reference Kapranov and SchechtmanKS14] related to the flop.
$({\mathcal {D}}^b(\mathscr {A}_f), {\mathcal {D}}^b(\mathscr {A}_{f^+}))$ are spherical pairs, which yields a geometric incarnation of the schober [Reference Kapranov and SchechtmanKS14] related to the flop.
5.1 Category  ${\mathcal {D}}(\mathscr {A}_f)$ as a full subcategory of
${\mathcal {D}}(\mathscr {A}_f)$ as a full subcategory of  ${\mathcal {D}}_{{\rm qc}}(X \times _Y X^+)$
${\mathcal {D}}_{{\rm qc}}(X \times _Y X^+)$
Lemma 5.1 Let ![]() $f\colon X\to Y$ satisfy assumption (a) and let
$f\colon X\to Y$ satisfy assumption (a) and let ![]() ${\mathcal {P}}$ be a projective object in
${\mathcal {P}}$ be a projective object in ![]() $\mathscr {A}_f$. Then
$\mathscr {A}_f$. Then ![]() $p_*p^* {\mathcal {P}} \simeq {\mathcal {P}}$,
$p_*p^* {\mathcal {P}} \simeq {\mathcal {P}}$, ![]() $Rp_* L^1p^* {\mathcal {P}} = 0$ and
$Rp_* L^1p^* {\mathcal {P}} = 0$ and ![]() $Rp_* p^* {\mathcal {P}} \simeq {\mathcal {P}}$.
$Rp_* p^* {\mathcal {P}} \simeq {\mathcal {P}}$.
Proof. By Corollary 4.23, the flop functor ![]() $F^+$ induces an equivalence of
$F^+$ induces an equivalence of ![]() $\mathscr {A}_{f^+}$ and
$\mathscr {A}_{f^+}$ and ![]() $\mathscr {A}_f[1]$. Hence, there exists projective
$\mathscr {A}_f[1]$. Hence, there exists projective ![]() ${\mathcal {P}}^+\in \mathscr {A}_{f^+}$ such that
${\mathcal {P}}^+\in \mathscr {A}_{f^+}$ such that ![]() ${\mathcal {P}}[1] \simeq Rp_* Lp^{+*}{\mathcal {P}}^+$. As
${\mathcal {P}}[1] \simeq Rp_* Lp^{+*}{\mathcal {P}}^+$. As ![]() $L^ip^{+*} {\mathcal {P}}^+ = 0$, for
$L^ip^{+*} {\mathcal {P}}^+ = 0$, for ![]() $i>1$, by Lemma 4.15, and
$i>1$, by Lemma 4.15, and ![]() $Rp_*p^{+*}{\mathcal {P}}^+ = 0$, by Corollary 2.12, we have
$Rp_*p^{+*}{\mathcal {P}}^+ = 0$, by Corollary 2.12, we have ![]() ${\mathcal {P}} \simeq p_* L^1p^{+*}{\mathcal {P}}^+$. Then, according to Lemma 2.9, we have
${\mathcal {P}} \simeq p_* L^1p^{+*}{\mathcal {P}}^+$. Then, according to Lemma 2.9, we have ![]() $p_*p^* {\mathcal {P}} \simeq {\mathcal {P}}$ and
$p_*p^* {\mathcal {P}} \simeq {\mathcal {P}}$ and ![]() $Rp_* L^1p^* {\mathcal {P}} = 0$. As
$Rp_* L^1p^* {\mathcal {P}} = 0$. As ![]() $Rp_* Lp^* {\mathcal {P}} \simeq {\mathcal {P}}$, it follows that
$Rp_* Lp^* {\mathcal {P}} \simeq {\mathcal {P}}$, it follows that ![]() $Rp_* p^* {\mathcal {P}}\simeq {\mathcal {P}}$.
$Rp_* p^* {\mathcal {P}}\simeq {\mathcal {P}}$.
Lemma 5.2 Let ![]() $f\colon X \to Y$ satisfy assumption (a) and let
$f\colon X \to Y$ satisfy assumption (a) and let ![]() ${\mathcal {M}}$ be a projective object in
${\mathcal {M}}$ be a projective object in ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. There exists an exact triangle
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. There exists an exact triangle
for ![]() ${\mathcal {P}} :={\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {M}})$ projective in
${\mathcal {P}} :={\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {M}})$ projective in ![]() $\mathscr {A}_f$.
$\mathscr {A}_f$.
Proof. By Lemma 4.15, we have ![]() $L^jp^* {\mathcal {P}} = 0$, for
$L^jp^* {\mathcal {P}} = 0$, for ![]() $j>1$ and any projective object
$j>1$ and any projective object ![]() ${\mathcal {P}}$ in
${\mathcal {P}}$ in ![]() $\mathscr {A}_f$. Thus, applying
$\mathscr {A}_f$. Thus, applying ![]() $Lp^*$ to sequence (15) and using the fact that
$Lp^*$ to sequence (15) and using the fact that ![]() ${\mathcal {M}}$ is locally free, we get an isomorphism
${\mathcal {M}}$ is locally free, we get an isomorphism ![]() $L^jp^* {\mathcal {P}} \simeq L^jp^*(f^*f_* {\mathcal {M}})$, for
$L^jp^* {\mathcal {P}} \simeq L^jp^*(f^*f_* {\mathcal {M}})$, for ![]() $j>0$. Further, as
$j>0$. Further, as ![]() $Lp^*{\mathcal {M}} \simeq p^*{\mathcal {M}}$, i.e.
$Lp^*{\mathcal {M}} \simeq p^*{\mathcal {M}}$, i.e. ![]() $L^ip^*{\mathcal {M}} =0$, for
$L^ip^*{\mathcal {M}} =0$, for ![]() $i\geqslant 1$, the sequence
$i\geqslant 1$, the sequence
obtained by applying ![]() $p^*$ to sequence (15) is short exact. We also have
$p^*$ to sequence (15) is short exact. We also have
for ![]() ${\mathcal {N}}^+ \in \mathscr {P}^+_0$ given by (35). Indeed, commutativity of diagram (42) implies that
${\mathcal {N}}^+ \in \mathscr {P}^+_0$ given by (35). Indeed, commutativity of diagram (42) implies that ![]() $p^*f^*f_* {\mathcal {M}} \simeq p^{+*}f^{+*}f_* {\mathcal {M}}$. Further, Lemma 3.11 yields
$p^*f^*f_* {\mathcal {M}} \simeq p^{+*}f^{+*}f_* {\mathcal {M}}$. Further, Lemma 3.11 yields ![]() $f_* {\mathcal {M}} \simeq f^+_* {\mathcal {N}}^+$. Finally,
$f_* {\mathcal {M}} \simeq f^+_* {\mathcal {N}}^+$. Finally, ![]() ${\mathcal {P}}^+ = {\mathcal {H}}^0_X(\iota _{f^+}^*{\mathcal {N}}^+)$ is a projective object in
${\mathcal {P}}^+ = {\mathcal {H}}^0_X(\iota _{f^+}^*{\mathcal {N}}^+)$ is a projective object in ![]() $\mathscr {A}_{f^+}$, according to Lemma 3.5, hence
$\mathscr {A}_{f^+}$, according to Lemma 3.5, hence ![]() $L^jp^{+*} {\mathcal {P}}^+ = 0$, for
$L^jp^{+*} {\mathcal {P}}^+ = 0$, for ![]() $j>1$ (by Lemma 4.15). Thus, applying
$j>1$ (by Lemma 4.15). Thus, applying ![]() $p^{+*}$ to sequence (32) on
$p^{+*}$ to sequence (32) on ![]() $X^+$ yields
$X^+$ yields ![]() $L^jp^{+*}(f^{+*}f^+_* {\mathcal {N}}^+) = 0$, for
$L^jp^{+*}(f^{+*}f^+_* {\mathcal {N}}^+) = 0$, for ![]() $j>0$.
$j>0$.
It follows that the triangle given by short exact sequence (67) is isomorphic to a triangle of the form (66).
Proposition 5.3 Let ![]() $f\colon X\to Y$ satisfy assumption (a) and let
$f\colon X\to Y$ satisfy assumption (a) and let ![]() ${\mathcal {M}}$ be a projective object in
${\mathcal {M}}$ be a projective object in ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Then
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Then ![]() $p^* {\mathcal {P}}\in \mathop {{\rm Perf}}\nolimits (X\times _Y X^+)$,
$p^* {\mathcal {P}}\in \mathop {{\rm Perf}}\nolimits (X\times _Y X^+)$, ![]() $\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^* {\mathcal {P}}, p^* {\mathcal {P}}) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {P}}, {\mathcal {P}})$ and
$\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^* {\mathcal {P}}, p^* {\mathcal {P}}) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {P}}, {\mathcal {P}})$ and ![]() $\mathop {{\rm Ext}}\nolimits ^i_{X\times _Y X^+}(p^*{\mathcal {P}}, p^* {\mathcal {P}}) = 0$, for
$\mathop {{\rm Ext}}\nolimits ^i_{X\times _Y X^+}(p^*{\mathcal {P}}, p^* {\mathcal {P}}) = 0$, for ![]() $i>0$, where
$i>0$, where ![]() ${\mathcal {P}} = {\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {M}})$ is projective in
${\mathcal {P}} = {\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {M}})$ is projective in ![]() $\mathscr {A}_f$.
$\mathscr {A}_f$.
Proof. Sheaf ![]() ${\mathcal {M}}$ is locally free on
${\mathcal {M}}$ is locally free on ![]() $X$, hence
$X$, hence ![]() $Lp^* {\mathcal {M}} \in \mathop {{\rm Perf}}\nolimits (X\times _Y X^+)$. Sequence (41) implies that
$Lp^* {\mathcal {M}} \in \mathop {{\rm Perf}}\nolimits (X\times _Y X^+)$. Sequence (41) implies that ![]() $f^{+*}f^+_* {\mathcal {N}}^+ \in \mathop {{\rm Perf}}\nolimits (X^+)$, hence
$f^{+*}f^+_* {\mathcal {N}}^+ \in \mathop {{\rm Perf}}\nolimits (X^+)$, hence ![]() $Lp^{+*}f^{+*}f_* {\mathcal {N}}$ is also a perfect complex on
$Lp^{+*}f^{+*}f_* {\mathcal {N}}$ is also a perfect complex on ![]() $X\times _Y X^+$. Triangle (66) implies that
$X\times _Y X^+$. Triangle (66) implies that ![]() $p^* {\mathcal {P}} \in \mathop {{\rm Perf}}\nolimits (X\times _Y X^+)$.
$p^* {\mathcal {P}} \in \mathop {{\rm Perf}}\nolimits (X\times _Y X^+)$.
By adjunction and Lemma 5.1, we have ![]() $\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^* {\mathcal {P}},p^* {\mathcal {P}}) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {P}}, {\mathcal {P}})$. Thus, it suffices to check that
$\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^* {\mathcal {P}},p^* {\mathcal {P}}) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {P}}, {\mathcal {P}})$. Thus, it suffices to check that ![]() $\mathop {{\rm Ext}}\nolimits ^i_{X\times _Y X^+}(p^* {\mathcal {P}}, p^* {\mathcal {P}}) = 0$, for
$\mathop {{\rm Ext}}\nolimits ^i_{X\times _Y X^+}(p^* {\mathcal {P}}, p^* {\mathcal {P}}) = 0$, for ![]() $i>0$. Applying
$i>0$. Applying ![]() $\mathop {{\rm Hom}}\nolimits (-, p^* {\mathcal {P}})$ to triangle (66) yields, for any
$\mathop {{\rm Hom}}\nolimits (-, p^* {\mathcal {P}})$ to triangle (66) yields, for any ![]() $i\in \mathbb {Z}$, an isomorphism
$i\in \mathbb {Z}$, an isomorphism
because ![]() $\mathop {{\rm Ext}}\nolimits ^j_{X\times _Y X^+}(Lp^{+*}(f^{+*}f_* {\mathcal {M}}), p^* {\mathcal {P}}) \simeq \mathop {{\rm Ext}}\nolimits ^j_{X^+}(f^{+*}f_* {\mathcal {M}}, Rp^+_* p^*{\mathcal {P}})= 0$ (see Corollary 2.12). Sheaf
$\mathop {{\rm Ext}}\nolimits ^j_{X\times _Y X^+}(Lp^{+*}(f^{+*}f_* {\mathcal {M}}), p^* {\mathcal {P}}) \simeq \mathop {{\rm Ext}}\nolimits ^j_{X^+}(f^{+*}f_* {\mathcal {M}}, Rp^+_* p^*{\mathcal {P}})= 0$ (see Corollary 2.12). Sheaf ![]() ${\mathcal {M}}$ is projective in
${\mathcal {M}}$ is projective in ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ and
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ and ![]() ${\mathcal {P}}[1] \in \mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Thus, by Lemma 5.1 again, we conclude that
${\mathcal {P}}[1] \in \mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. Thus, by Lemma 5.1 again, we conclude that
for ![]() $i\neq 0$, which finishes the proof.
$i\neq 0$, which finishes the proof.
Now let ![]() ${\mathcal {M}}$ be a projective generator of
${\mathcal {M}}$ be a projective generator of ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ and
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ and ![]() ${\mathcal {P}}= {\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {M}})$. Denote by
${\mathcal {P}}= {\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {M}})$. Denote by
the endomorphism algebra of ![]() $p^* {\mathcal {P}}$. Functor
$p^* {\mathcal {P}}$. Functor ![]() $\mathop {{\rm Hom}}\nolimits _{X\times _YX^+}(p^*{\mathcal {P}}, -)\colon {\rm QCoh}(X\times _YX^+) \to \text{Mod--}A_P$ has left adjoint
$\mathop {{\rm Hom}}\nolimits _{X\times _YX^+}(p^*{\mathcal {P}}, -)\colon {\rm QCoh}(X\times _YX^+) \to \text{Mod--}A_P$ has left adjoint ![]() $(-)\otimes _{A_P}p^*P\colon \text{Mod--}A_P \to {\rm QCoh}(X\times _Y X^+)$, [Reference PopescuPop73, Theorem 3.6.3]. We denote by
$(-)\otimes _{A_P}p^*P\colon \text{Mod--}A_P \to {\rm QCoh}(X\times _Y X^+)$, [Reference PopescuPop73, Theorem 3.6.3]. We denote by ![]() $\bar {p}^* \colon {\mathcal {D}}(\mathscr {A}_f) \to {\mathcal {D}}_{{\rm qc}}(X\times _Y X^+)$ its derived functor.
$\bar {p}^* \colon {\mathcal {D}}(\mathscr {A}_f) \to {\mathcal {D}}_{{\rm qc}}(X\times _Y X^+)$ its derived functor.
As ![]() ${\mathcal {P}}$ is a projective generator of
${\mathcal {P}}$ is a projective generator of ![]() $\mathscr {A}_f$, categories
$\mathscr {A}_f$, categories ![]() ${\mathcal {D}}(\mathscr {A}_f)$ and
${\mathcal {D}}(\mathscr {A}_f)$ and ![]() ${\mathcal {D}}(\text{Mod--}A_P)$ are equivalent. We also have
${\mathcal {D}}(\text{Mod--}A_P)$ are equivalent. We also have ![]() ${\mathcal {D}}(\text{Mod--}A_P) \simeq [\textit {SF--}A_P]$, for the category
${\mathcal {D}}(\text{Mod--}A_P) \simeq [\textit {SF--}A_P]$, for the category ![]() $\textit {SF--}A_P \subset \text{DGMod--}A_P$ of semi-free
$\textit {SF--}A_P \subset \text{DGMod--}A_P$ of semi-free ![]() $A_P$ DG modules, i.e. DG modules that admit a filtration with direct sums of shifts of representable DG modules as the graded factors of the filtration [Reference DrinfeldDri04].
$A_P$ DG modules, i.e. DG modules that admit a filtration with direct sums of shifts of representable DG modules as the graded factors of the filtration [Reference DrinfeldDri04].
Proposition 5.4 Functor ![]() $\bar {p}^* \colon {\mathcal {D}}(\mathscr {A}_f) \to {\mathcal {D}}_{{\rm qc}}(X\times _Y X^+)$ is fully faithful.
$\bar {p}^* \colon {\mathcal {D}}(\mathscr {A}_f) \to {\mathcal {D}}_{{\rm qc}}(X\times _Y X^+)$ is fully faithful.
Proof. By [Reference KellerKel94, Lemma 4.2], in order to prove that functor ![]() ${\mathcal {D}}(\text{Mod--}A_P) \to {\mathcal {D}}_{qc}(X\times _Y X^+)$ is fully faithful, it suffices to show that it induces a bijection
${\mathcal {D}}(\text{Mod--}A_P) \to {\mathcal {D}}_{qc}(X\times _Y X^+)$ is fully faithful, it suffices to show that it induces a bijection ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}(A_f)}({\mathcal {P}}, {\mathcal {P}}[n]) \to \mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^*{\mathcal {P}}, p^* {\mathcal {P}}[n])$, for any
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}(A_f)}({\mathcal {P}}, {\mathcal {P}}[n]) \to \mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^*{\mathcal {P}}, p^* {\mathcal {P}}[n])$, for any ![]() $n\in \mathbb {Z}$ and that
$n\in \mathbb {Z}$ and that ![]() $p^* {\mathcal {P}} \in {\mathcal {D}}_{{\rm qc}}(X\times _Y X^+)$ is compact. Both statements follow from Proposition 5.3.
$p^* {\mathcal {P}} \in {\mathcal {D}}_{{\rm qc}}(X\times _Y X^+)$ is compact. Both statements follow from Proposition 5.3.
Functor ![]() $\overline {p}^*$ restricts to a fully faithful functor
$\overline {p}^*$ restricts to a fully faithful functor ![]() ${\mathcal {D}}^b(\mathscr {A}_f)\to {\mathcal {D}}^-(X\times _Y X^+)$. We show that
${\mathcal {D}}^b(\mathscr {A}_f)\to {\mathcal {D}}^-(X\times _Y X^+)$. We show that ![]() ${\mathcal {D}}^b(\mathscr {A}_f)$ is, in fact, a subquotient of
${\mathcal {D}}^b(\mathscr {A}_f)$ is, in fact, a subquotient of ![]() ${\mathcal {D}}^b(X\times _Y X^+)$. Following an idea of Kapranov, we show that the flop–flop functor is a spherical cotwist arising from a spherical pair.
${\mathcal {D}}^b(X\times _Y X^+)$. Following an idea of Kapranov, we show that the flop–flop functor is a spherical cotwist arising from a spherical pair.
5.2 Spherical pairs  $({\mathcal {D}}^b(X)$,
$({\mathcal {D}}^b(X)$,  ${\mathcal {D}}^b(X^+))$,
${\mathcal {D}}^b(X^+))$,  $({\mathcal {D}}^b(\mathscr {A}_f), {\mathcal {D}}^b(\mathscr {A}_{f^+}))$
$({\mathcal {D}}^b(\mathscr {A}_f), {\mathcal {D}}^b(\mathscr {A}_{f^+}))$
For a morphism ![]() $f\colon X\to Y$ satisfying (a) and its flop
$f\colon X\to Y$ satisfying (a) and its flop ![]() $f^+\colon X^+ \to Y$, we consider
$f^+\colon X^+ \to Y$, we consider
and quotient category ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$. In the above, as in diagram (42), morphisms
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$. In the above, as in diagram (42), morphisms ![]() $p$ and
$p$ and ![]() $p^+$ denote the projections for
$p^+$ denote the projections for ![]() $X\times _Y X^+$. As both
$X\times _Y X^+$. As both ![]() $p$ and
$p$ and ![]() $p^+$ have fibers of dimension bounded by one, category
$p^+$ have fibers of dimension bounded by one, category ![]() ${\mathcal {K}}$ inherits the standard
${\mathcal {K}}$ inherits the standard ![]() $t$-structure from
$t$-structure from ![]() ${\mathcal {D}}^-(X\times _Y X^+)$ (Lemma 2.2). In particular,
${\mathcal {D}}^-(X\times _Y X^+)$ (Lemma 2.2). In particular, ![]() $K\in {\mathcal {K}}$ if and only if
$K\in {\mathcal {K}}$ if and only if ![]() ${\mathcal {H}}^i(K) \in {\mathcal {K}}$, for all
${\mathcal {H}}^i(K) \in {\mathcal {K}}$, for all ![]() $i\in \mathbb {Z}$.
$i\in \mathbb {Z}$.
Let ![]() ${\rm Mor}_{{\mathcal {K}}}\subset {\mathcal {D}}^-(X\times _Y X^+)$ denote the category with objects as in
${\rm Mor}_{{\mathcal {K}}}\subset {\mathcal {D}}^-(X\times _Y X^+)$ denote the category with objects as in ![]() ${\mathcal {D}}^-(X\times _Y X^+)$ and morphisms
${\mathcal {D}}^-(X\times _Y X^+)$ and morphisms ![]() $f\colon E \to F$ such that the cone of
$f\colon E \to F$ such that the cone of ![]() $f$ lies in
$f$ lies in ![]() ${\mathcal {K}}$ (see [Reference VerdierVer77, Reference NeemanNee01]). The quotient category
${\mathcal {K}}$ (see [Reference VerdierVer77, Reference NeemanNee01]). The quotient category ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ has the same objects as
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ has the same objects as ![]() ${\mathcal {D}}^-(X\times _Y X^+)$. For any pair of objects
${\mathcal {D}}^-(X\times _Y X^+)$. For any pair of objects ![]() $E, F$, morphisms
$E, F$, morphisms ![]() $E\to F$ in
$E\to F$ in ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ are equivalence classes of triples
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ are equivalence classes of triples ![]() $(f, Z, g)$, where
$(f, Z, g)$, where ![]() $Z\xrightarrow {f} E$ is a morphism in
$Z\xrightarrow {f} E$ is a morphism in ![]() ${\rm Mor}_{{\mathcal {K}}}$ and
${\rm Mor}_{{\mathcal {K}}}$ and ![]() $Z\xrightarrow {g} F$ is a morphism in
$Z\xrightarrow {g} F$ is a morphism in ![]() ${\mathcal {D}}^-(X\times _Y X^+)$. We have
${\mathcal {D}}^-(X\times _Y X^+)$. We have ![]() $(f,Z,g) \sim (f', Z', g')$ if there exists a triple
$(f,Z,g) \sim (f', Z', g')$ if there exists a triple ![]() $(f'', Z'', g'')$ and
$(f'', Z'', g'')$ and ![]() $Z''\xrightarrow {u} Z$,
$Z''\xrightarrow {u} Z$, ![]() $Z''\xrightarrow {v} Z'$ for which diagram
$Z''\xrightarrow {v} Z'$ for which diagram

commutes, cf. [Reference NeemanNee01].
We denote by ![]() ${\mathcal {K}}^b$ the intersection
${\mathcal {K}}^b$ the intersection ![]() ${\mathcal {K}} \cap {\mathcal {D}}^b(X\times _Y X^+)$. The embedding
${\mathcal {K}} \cap {\mathcal {D}}^b(X\times _Y X^+)$. The embedding ![]() ${\mathcal {D}}^b(X\times _Y X^+) \to {\mathcal {D}}^-(X\times _Y X^+)$ induces a functor
${\mathcal {D}}^b(X\times _Y X^+) \to {\mathcal {D}}^-(X\times _Y X^+)$ induces a functor
Lemma 5.5 Functor ![]() $\chi$ is fully faithful.
$\chi$ is fully faithful.
Proof. It is clear from the above definitions that ![]() $\chi$ is well-defined. Let us check that
$\chi$ is well-defined. Let us check that ![]() $\chi$ is faithful. To this end, we assume that
$\chi$ is faithful. To this end, we assume that ![]() $(f,Z,g)$,
$(f,Z,g)$, ![]() $(f',Z',g')$ are morphisms
$(f',Z',g')$ are morphisms ![]() $E_1 \to E_2$ in
$E_1 \to E_2$ in ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ which are equivalent as morphisms in
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ which are equivalent as morphisms in ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$. Let
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$. Let ![]() $(f'', Z'', g'')$ with
$(f'', Z'', g'')$ with ![]() $Z''\in {\mathcal {D}}^-(X\times _Y X^+)$ be the triple defining the equivalence as in (70). Choose
$Z''\in {\mathcal {D}}^-(X\times _Y X^+)$ be the triple defining the equivalence as in (70). Choose ![]() $l\in \mathbb {Z}$ such that
$l\in \mathbb {Z}$ such that ![]() $E_1$,
$E_1$, ![]() $E_2$,
$E_2$, ![]() $Z$ and
$Z$ and ![]() $Z'$ belong to
$Z'$ belong to ![]() ${\mathcal {D}}^b(X\times _Y X^+)^{\geqslant l}$. Then
${\mathcal {D}}^b(X\times _Y X^+)^{\geqslant l}$. Then
 \begin{equation} {\mathcal{H}}^i({\rm Cone}(\tau_{\geqslant l} f'')) = \begin{cases} {\mathcal{H}}^i({\rm Cone}(f'')), & \textrm{for } i\geqslant l-1,\\ 0, & \textrm{for } i< l-1,\end{cases} \end{equation}
\begin{equation} {\mathcal{H}}^i({\rm Cone}(\tau_{\geqslant l} f'')) = \begin{cases} {\mathcal{H}}^i({\rm Cone}(f'')), & \textrm{for } i\geqslant l-1,\\ 0, & \textrm{for } i< l-1,\end{cases} \end{equation}
implies that all cohomology sheaves of ![]() ${\rm Cone}(\tau _{\geqslant l} f'')$ belong to
${\rm Cone}(\tau _{\geqslant l} f'')$ belong to ![]() ${\mathcal {K}}$, i.e.
${\mathcal {K}}$, i.e. ![]() ${\rm Cone}(\tau _{\geqslant l}f'')$ is an object in
${\rm Cone}(\tau _{\geqslant l}f'')$ is an object in ![]() ${\mathcal {K}}^b$. The truncation
${\mathcal {K}}^b$. The truncation ![]() $\tau _{\geqslant l}$ of diagram (70) is isomorphic to the original diagram on the boundary diamond, whereas the middle line
$\tau _{\geqslant l}$ of diagram (70) is isomorphic to the original diagram on the boundary diamond, whereas the middle line ![]() $(\tau _{\geqslant l}f'', \tau _{\geqslant l} Z'', \tau _{\geqslant l} g'')$ defines a morphism in
$(\tau _{\geqslant l}f'', \tau _{\geqslant l} Z'', \tau _{\geqslant l} g'')$ defines a morphism in ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$. Hence,
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$. Hence, ![]() $(f,Z,g) \sim (f', Z', g')$ holds in
$(f,Z,g) \sim (f', Z', g')$ holds in ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$.
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$.
Finally, let ![]() $(f, Z, g)$ be a morphism
$(f, Z, g)$ be a morphism ![]() $E_1 \to E_2$ in
$E_1 \to E_2$ in ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ and assume there exists
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ and assume there exists ![]() $l\in \mathbb {Z}$ such that both
$l\in \mathbb {Z}$ such that both ![]() ${\mathcal {H}}^i(E_1)$ and
${\mathcal {H}}^i(E_1)$ and ![]() ${\mathcal {H}}^i(E_2)$ vanish, for
${\mathcal {H}}^i(E_2)$ vanish, for ![]() $i\leqslant l$. Then (72) implies that
$i\leqslant l$. Then (72) implies that ![]() $\tau _{\geqslant l}f \in {\rm Mor}_{{\mathcal {K}}}$. Hence,
$\tau _{\geqslant l}f \in {\rm Mor}_{{\mathcal {K}}}$. Hence, ![]() $(\tau _{\geqslant l} f, \tau _{\geqslant l} Z, \tau _{\geqslant l} g)$ is a morphism
$(\tau _{\geqslant l} f, \tau _{\geqslant l} Z, \tau _{\geqslant l} g)$ is a morphism ![]() $E_1 \to E_2$ in
$E_1 \to E_2$ in ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ which functor
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ which functor ![]() $\chi$ takes to a morphism equivalent to
$\chi$ takes to a morphism equivalent to ![]() $(f,Z,g)$. Thus, functor
$(f,Z,g)$. Thus, functor ![]() $\chi$ is also full.
$\chi$ is also full.
In view of Lemma 5.5, we can regard ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ as a full subcategory of
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ as a full subcategory of ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$.
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$.
Proposition 5.6 The composite of ![]() $Lp^* \colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^-(X\times _Y X ^+)$ with the quotient functor
$Lp^* \colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^-(X\times _Y X ^+)$ with the quotient functor ![]() $Q\colon {\mathcal {D}}^-(X\times _Y X^+) \to {\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ takes
$Q\colon {\mathcal {D}}^-(X\times _Y X^+) \to {\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ takes ![]() ${\mathcal {D}}^b(X)$ to the essential image of
${\mathcal {D}}^b(X)$ to the essential image of ![]() $\chi$.
$\chi$.
Proof. Let ![]() $E\in {\mathcal {D}}^b(X)^{\geqslant l}$. As
$E\in {\mathcal {D}}^b(X)^{\geqslant l}$. As ![]() $p$ has fibers of dimension bounded by one and
$p$ has fibers of dimension bounded by one and ![]() $Rp_*Lp^*(E) \simeq E$, we have
$Rp_*Lp^*(E) \simeq E$, we have ![]() $Rp_* {\mathcal {H}}^j(Lp^* E) = 0$, for
$Rp_* {\mathcal {H}}^j(Lp^* E) = 0$, for ![]() $j< l-1$.
$j< l-1$.
As ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ is obtained from
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ is obtained from ![]() $\mathop {{\rm Coh}}\nolimits (X)$ by means of the tilt in a torsion pair, sequence (34) implies that
$\mathop {{\rm Coh}}\nolimits (X)$ by means of the tilt in a torsion pair, sequence (34) implies that ![]() ${\mathcal {H}}^j_{\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)}(E) =0$, for
${\mathcal {H}}^j_{\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)}(E) =0$, for ![]() $j< l$. By Corollary 4.23, object
$j< l$. By Corollary 4.23, object ![]() $Rp^+_* Lp^*(E)$ lies in
$Rp^+_* Lp^*(E)$ lies in ![]() ${\mathcal {D}}^b(X^+)^{\geqslant l}_{\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)}$. Category
${\mathcal {D}}^b(X^+)^{\geqslant l}_{\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)}$. Category ![]() $\mathop {{\rm Coh}}\nolimits (X^+)$ is obtained from
$\mathop {{\rm Coh}}\nolimits (X^+)$ is obtained from ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$ by the tilt in a torsion pair, hence
$\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$ by the tilt in a torsion pair, hence ![]() $Rp^+_*Lp^*E \in {\mathcal {D}}^b(X^+)_{X^+}^{\geqslant l-1}$. Finally, the dimension of fibers of
$Rp^+_*Lp^*E \in {\mathcal {D}}^b(X^+)_{X^+}^{\geqslant l-1}$. Finally, the dimension of fibers of ![]() $p^+$ being bounded by one implies that
$p^+$ being bounded by one implies that ![]() $Rp^+_* {\mathcal {H}}^j(Lp^* E) = 0$, for
$Rp^+_* {\mathcal {H}}^j(Lp^* E) = 0$, for ![]() $j< l-2$. Thus,
$j< l-2$. Thus, ![]() $\tau _{\leqslant l-3} Lp^*E$ lies in
$\tau _{\leqslant l-3} Lp^*E$ lies in ![]() ${\mathcal {K}}$, i.e. morphism
${\mathcal {K}}$, i.e. morphism ![]() $Lp^*E \to \tau _{\geqslant l-2} Lp^* E$ is an isomorphism in
$Lp^*E \to \tau _{\geqslant l-2} Lp^* E$ is an isomorphism in ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$.
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$.
We denote by
the functor invoked by Lemma 5.5 and Proposition 5.6.
In order to show existence of a right adjoint to ![]() $\widetilde {L}p^*$, we first prove the following general statement.
$\widetilde {L}p^*$, we first prove the following general statement.
Lemma 5.7 Let ![]() ${\mathcal {D}}$ be a triangulated category and
${\mathcal {D}}$ be a triangulated category and ![]() ${\mathcal {K}}$ a thick triangulated subcategory. Let further
${\mathcal {K}}$ a thick triangulated subcategory. Let further ![]() $E\in {\mathcal {D}}$ be such that
$E\in {\mathcal {D}}$ be such that ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}}(E, K) = 0$, for any
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}}(E, K) = 0$, for any ![]() $K\in {\mathcal {K}}$. Then, for any
$K\in {\mathcal {K}}$. Then, for any ![]() $F \in {\mathcal {D}}$, we have an isomorphism
$F \in {\mathcal {D}}$, we have an isomorphism
Proof. We have the map
Now let ![]() $(f, Z, g)$ be any element in
$(f, Z, g)$ be any element in ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}/{\mathcal {K}}}(E, F)$. By definition,
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}/{\mathcal {K}}}(E, F)$. By definition, ![]() $f$ is a morphism in
$f$ is a morphism in ![]() ${\rm Mor}_{{\mathcal {K}}}$. In other words we have an exact triangle
${\rm Mor}_{{\mathcal {K}}}$. In other words we have an exact triangle
with ![]() $K\in {\mathcal {K}}$. As both
$K\in {\mathcal {K}}$. As both ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}}(E,K)$ and
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}}(E,K)$ and ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}}(E,K[-1])$ vanish, object
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}}(E,K[-1])$ vanish, object ![]() $Z$ is uniquely decomposed as
$Z$ is uniquely decomposed as ![]() $Z \simeq K[-1] \oplus E$ and
$Z \simeq K[-1] \oplus E$ and ![]() $f=(0, {\rm id})$ is the projection to
$f=(0, {\rm id})$ is the projection to ![]() $E$. Accordingly, we have a decomposition
$E$. Accordingly, we have a decomposition ![]() $g=(g_K,g_E)$. Diagram
$g=(g_K,g_E)$. Diagram

commutes, i.e. ![]() $(f,Z,g) \sim ({\rm id}, E, g_E)$. Thus, map
$(f,Z,g) \sim ({\rm id}, E, g_E)$. Thus, map ![]() $\alpha$ is surjective.
$\alpha$ is surjective.
Now let ![]() $({\rm id}, E, g) \sim ({\rm id}, E, g')$ in
$({\rm id}, E, g) \sim ({\rm id}, E, g')$ in ![]() ${\mathcal {D}}/{\mathcal {K}}$. For the triple
${\mathcal {D}}/{\mathcal {K}}$. For the triple ![]() $(f'', Z'', g'')$ giving the equivalence (see diagram (70)), we have, as above, the decomposition
$(f'', Z'', g'')$ giving the equivalence (see diagram (70)), we have, as above, the decomposition ![]() $Z'' = K''[-1] \oplus E$. Commutativity of
$Z'' = K''[-1] \oplus E$. Commutativity of

yields ![]() $g = g''_E = g'$, i.e.
$g = g''_E = g'$, i.e. ![]() $\alpha$ is also a monomorphism.
$\alpha$ is also a monomorphism.
Proposition 5.8 Functor ![]() $\widetilde {L}p^*$ is fully faithful and has the right adjoint
$\widetilde {L}p^*$ is fully faithful and has the right adjoint ![]() $Rp_* \colon {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b\to {\mathcal {D}}^b(X)$.
$Rp_* \colon {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b\to {\mathcal {D}}^b(X)$.
Proof. First, note that functor ![]() $Rp_* \colon {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b \to {\mathcal {D}}^b(X)$ is well-defined, because
$Rp_* \colon {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b \to {\mathcal {D}}^b(X)$ is well-defined, because ![]() ${\mathcal {K}}^b\subset {\rm Ker} Rp_*$.
${\mathcal {K}}^b\subset {\rm Ker} Rp_*$.
For any ![]() $E\in {\mathcal {D}}^b(X)$ and
$E\in {\mathcal {D}}^b(X)$ and ![]() $F \in {\mathcal {D}}^-(X\times _Y X^+)$, we have an isomorphism
$F \in {\mathcal {D}}^-(X\times _Y X^+)$, we have an isomorphism ![]() $\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(Lp^* E, F) \simeq \mathop {{\rm Hom}}\nolimits _X(E, Rp_* F)$. As functor
$\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(Lp^* E, F) \simeq \mathop {{\rm Hom}}\nolimits _X(E, Rp_* F)$. As functor ![]() $\chi$ is fully faithful (Lemma 5.5), in order to prove that
$\chi$ is fully faithful (Lemma 5.5), in order to prove that ![]() $Rp_*$ is right adjoint to
$Rp_*$ is right adjoint to ![]() $\widetilde {L}p^*$, it suffices to show that, for any
$\widetilde {L}p^*$, it suffices to show that, for any ![]() $F \in {\mathcal {D}}^-(X\times _Y X^+)$, we have
$F \in {\mathcal {D}}^-(X\times _Y X^+)$, we have
By adjunction, ![]() $\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(Lp^*E, K) = 0$, for any
$\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(Lp^*E, K) = 0$, for any ![]() $K\in {\mathcal {K}}$, thus (73) follows from Lemma 5.7.
$K\in {\mathcal {K}}$, thus (73) follows from Lemma 5.7.
As functor ![]() $Lp^* \colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^-(X\times _Y X^+)$ is fully faithful, isomorphism (73), for
$Lp^* \colon {\mathcal {D}}^b(X) \to {\mathcal {D}}^-(X\times _Y X^+)$ is fully faithful, isomorphism (73), for ![]() $F = Lp^*(E')$, implies that functor
$F = Lp^*(E')$, implies that functor ![]() $\widetilde {L}p^*$ is fully faithful too.
$\widetilde {L}p^*$ is fully faithful too.
As ![]() $Rp_* \widetilde {L}p^* \simeq {\rm Id}_{{\mathcal {D}}^b(X)}$, we have a SOD [Reference BondalBon89, Lemma 3.1]
$Rp_* \widetilde {L}p^* \simeq {\rm Id}_{{\mathcal {D}}^b(X)}$, we have a SOD [Reference BondalBon89, Lemma 3.1]
with ![]() ${\mathcal {C}} = \{ E\in {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b\,|\, Rp_* E = 0\}$. We aim at showing that
${\mathcal {C}} = \{ E\in {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b\,|\, Rp_* E = 0\}$. We aim at showing that ![]() ${\mathcal {C}} \simeq {\mathcal {D}}^b(\mathscr {A}_{f^+})$.
${\mathcal {C}} \simeq {\mathcal {D}}^b(\mathscr {A}_{f^+})$.
By Proposition 5.3, we know that, for a projective object ![]() ${\mathcal {M}}\in \mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ and
${\mathcal {M}}\in \mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ and ![]() ${\mathcal {P}}= {\mathcal {H}}^{-1}_{X} \iota _{f}^* {\mathcal {M}}$, the endomorphisms algebras of
${\mathcal {P}}= {\mathcal {H}}^{-1}_{X} \iota _{f}^* {\mathcal {M}}$, the endomorphisms algebras of ![]() $p^{*}{\mathcal {P}}$ and
$p^{*}{\mathcal {P}}$ and ![]() ${\mathcal {P}}$ are isomorphic. Next, we show that they remain the same when we pass to the quotient category
${\mathcal {P}}$ are isomorphic. Next, we show that they remain the same when we pass to the quotient category ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$.
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$.
Lemma 5.9 Let ![]() ${\mathcal {P}}$ be as above. Then, for any
${\mathcal {P}}$ be as above. Then, for any ![]() $E\in {\mathcal {D}}^-(X\times _Y X^+)$,
$E\in {\mathcal {D}}^-(X\times _Y X^+)$,
Proof. By Lemma 5.7, it suffices to check that ![]() $\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^*{\mathcal {P}}, K) = 0$, for any
$\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^*{\mathcal {P}}, K) = 0$, for any ![]() $K \in {\mathcal {K}}$. It immediately follows from applying
$K \in {\mathcal {K}}$. It immediately follows from applying ![]() $\mathop {{\rm Hom}}\nolimits (-, K)$ to triangle (66).
$\mathop {{\rm Hom}}\nolimits (-, K)$ to triangle (66).
Consider the composite functor
where ![]() $Q$ denotes the quotient functor and
$Q$ denotes the quotient functor and ![]() $\overline {p}^*$ is as in Proposition 5.4. Recall that we assume
$\overline {p}^*$ is as in Proposition 5.4. Recall that we assume ![]() $Y= \mathop {{\rm Spec}}\nolimits R$ to be affine and Noetherian. Endomorphism algebra
$Y= \mathop {{\rm Spec}}\nolimits R$ to be affine and Noetherian. Endomorphism algebra ![]() $A_P$ of
$A_P$ of ![]() ${\mathcal {P}}$ is finite over
${\mathcal {P}}$ is finite over ![]() $R$, hence Noetherian. Thus, the category
$R$, hence Noetherian. Thus, the category ![]() $\text{mod--}A_P$ of finitely generated right
$\text{mod--}A_P$ of finitely generated right ![]() $A_P$ modules is abelian. As
$A_P$ modules is abelian. As ![]() ${\mathcal {P}}$ is a projective generator of
${\mathcal {P}}$ is a projective generator of ![]() $\mathscr {A}_f$,
$\mathscr {A}_f$, ![]() ${\mathcal {D}}^b(\mathscr {A}_f)$ is equivalent to
${\mathcal {D}}^b(\mathscr {A}_f)$ is equivalent to ![]() ${\mathcal {D}}^b(\text{mod--}A_P)$. Using this equivalence and taking into account Proposition 5.3, we can define
${\mathcal {D}}^b(\text{mod--}A_P)$. Using this equivalence and taking into account Proposition 5.3, we can define ![]() $\widetilde {p}_*$, right adjoint to
$\widetilde {p}_*$, right adjoint to ![]() $\widetilde {p}^*$, as
$\widetilde {p}^*$, as
Finally, let ![]() $\mathscr {P}$ be the category of projective objects in
$\mathscr {P}$ be the category of projective objects in ![]() $\mathscr {A}_f$ of the form
$\mathscr {A}_f$ of the form ![]() ${\mathcal {H}}^{-1}_X(\iota _f^* {\mathcal {M}})$, for
${\mathcal {H}}^{-1}_X(\iota _f^* {\mathcal {M}})$, for ![]() ${\mathcal {M}}\in \mathscr {P}_{-1}$. As there is no non-trivial extension of objects in
${\mathcal {M}}\in \mathscr {P}_{-1}$. As there is no non-trivial extension of objects in ![]() $\mathscr {P}$, it is an exact subcategory of
$\mathscr {P}$, it is an exact subcategory of ![]() $\mathscr {A}_f$. Moreover, for any
$\mathscr {A}_f$. Moreover, for any ![]() $E \in \mathscr {A}_f$, there exists
$E \in \mathscr {A}_f$, there exists ![]() ${\mathcal {M}} \in \mathscr {P}_{-1}$ and
${\mathcal {M}} \in \mathscr {P}_{-1}$ and ![]() $\varphi \colon {\mathcal {M}} \to E[1]$, surjective in
$\varphi \colon {\mathcal {M}} \to E[1]$, surjective in ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. As functor
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$. As functor ![]() $\iota _{f*}\colon \mathscr {A}_f[1] \to \mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ is
$\iota _{f*}\colon \mathscr {A}_f[1] \to \mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ is ![]() $t$-exact, its left adjoint
$t$-exact, its left adjoint ![]() $\iota _f^*$ is right exact, i.e. morphism
$\iota _f^*$ is right exact, i.e. morphism ![]() ${\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {M}}) \to {\mathcal {H}}^{-1}_X(\iota _f^* E[1]) \simeq E$ is surjective in
${\mathcal {H}}_X^{-1}(\iota _f^* {\mathcal {M}}) \to {\mathcal {H}}^{-1}_X(\iota _f^* E[1]) \simeq E$ is surjective in ![]() $\mathscr {A}_f$. This implies that
$\mathscr {A}_f$. This implies that
The last equivalence allows us to view ![]() $\widetilde {p}^*$ as a functor
$\widetilde {p}^*$ as a functor
It is the term-wise extension of the functor ![]() $p^*\colon \mathscr {P}\to {\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$.
$p^*\colon \mathscr {P}\to {\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$.
Lemma 5.1 implies that the adjunction unit ![]() $\mathop {{\rm Id}}\nolimits \to \widetilde {p}_* \widetilde {p}^*$ is an isomorphism on
$\mathop {{\rm Id}}\nolimits \to \widetilde {p}_* \widetilde {p}^*$ is an isomorphism on ![]() ${\mathcal {P}}$. By Lemma 4.11 we have an isomorphism
${\mathcal {P}}$. By Lemma 4.11 we have an isomorphism
of functors ![]() ${\mathcal {D}}^b(\mathscr {A}_f) \to {\mathcal {D}}^b(\mathscr {A}_f)$.
${\mathcal {D}}^b(\mathscr {A}_f) \to {\mathcal {D}}^b(\mathscr {A}_f)$.
The embedding ![]() $\mathscr {A}_f \to \mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ is an exact functor of abelian categories. Hence, it induces the functor
$\mathscr {A}_f \to \mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ is an exact functor of abelian categories. Hence, it induces the functor
Lemma 5.10 There exists an isomorphism ![]() $Rp_* \widetilde {p}^* \xrightarrow {\simeq } \Psi |_{{\mathcal {D}}^b(\mathscr {A}_f)}$ of functors
$Rp_* \widetilde {p}^* \xrightarrow {\simeq } \Psi |_{{\mathcal {D}}^b(\mathscr {A}_f)}$ of functors ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}) \to {\mathcal {D}}^b(X)$.
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P}) \to {\mathcal {D}}^b(X)$.
Proof. Lemma 5.1 implies that the adjunction unit gives an isomorphism ![]() $\Psi |_{\mathscr {P}} \xrightarrow {\simeq } p_*p^*|_{\mathscr {P}}$ of functors
$\Psi |_{\mathscr {P}} \xrightarrow {\simeq } p_*p^*|_{\mathscr {P}}$ of functors ![]() $\mathscr {P} \to \mathop {{\rm Coh}}\nolimits (X)$. As functor
$\mathscr {P} \to \mathop {{\rm Coh}}\nolimits (X)$. As functor ![]() $\Psi |_{{\mathcal {D}}^b(\mathscr {A}_f)}$ takes
$\Psi |_{{\mathcal {D}}^b(\mathscr {A}_f)}$ takes ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P})$ to
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P})$ to ![]() ${\mathcal {D}}^b(X)$, Lemma 4.11 implies that the term-wise extension of
${\mathcal {D}}^b(X)$, Lemma 4.11 implies that the term-wise extension of ![]() $p_*p^*$ to the category
$p_*p^*$ to the category ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P})$ is isomorphic to
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P})$ is isomorphic to ![]() $\Psi |_{{\mathcal {D}}^b(\mathscr {A}_f)}$.
$\Psi |_{{\mathcal {D}}^b(\mathscr {A}_f)}$.
Now let ![]() ${\mathcal {P}}_{{\boldsymbol {\cdot }}}$ be a complex in
${\mathcal {P}}_{{\boldsymbol {\cdot }}}$ be a complex in ![]() $\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P})$ and
$\mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P})$ and ![]() $F = \widetilde {p}^* {\mathcal {P}}_{{\boldsymbol {\cdot }}}$. Lemma 5.1 implies that the first layer of spectral sequence
$F = \widetilde {p}^* {\mathcal {P}}_{{\boldsymbol {\cdot }}}$. Lemma 5.1 implies that the first layer of spectral sequence
has one non-zero row only. Hence, ![]() $Rp_* F$ is quasi-isomorphic to
$Rp_* F$ is quasi-isomorphic to ![]() $p_* p^* {\mathcal {P}}_{{\boldsymbol {\cdot }}}$, which finishes the proof.
$p_* p^* {\mathcal {P}}_{{\boldsymbol {\cdot }}}$, which finishes the proof.
Proposition 5.11 There exists a fully faithful functor
Proof. Proposition 5.4 implies that ![]() $\widetilde {p}^* \colon {\mathcal {D}}^b(\mathscr {A}_f) \to {\mathcal {D}}^-(X\times _Y X^+)$ is fully faithful. In order to show that the composite
$\widetilde {p}^* \colon {\mathcal {D}}^b(\mathscr {A}_f) \to {\mathcal {D}}^-(X\times _Y X^+)$ is fully faithful. In order to show that the composite ![]() ${\mathcal {D}}^b(\mathscr {A}_f) \xrightarrow {\widetilde {p}^*} {\mathcal {D}}^-(X\times _Y X^+) \xrightarrow {Q} {\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ is fully faithful, we check that, for any
${\mathcal {D}}^b(\mathscr {A}_f) \xrightarrow {\widetilde {p}^*} {\mathcal {D}}^-(X\times _Y X^+) \xrightarrow {Q} {\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ is fully faithful, we check that, for any ![]() $E \in {\mathcal {D}}^b(\mathscr {A}_f)$ and
$E \in {\mathcal {D}}^b(\mathscr {A}_f)$ and ![]() $F\in {\mathcal {D}}^-(X\times _Y X^+)$, we have
$F\in {\mathcal {D}}^-(X\times _Y X^+)$, we have
By Lemma 5.7, it suffices to check that ![]() $\mathop {{\rm Hom}}\nolimits (\widetilde {p}^*E, K) = 0$, for any
$\mathop {{\rm Hom}}\nolimits (\widetilde {p}^*E, K) = 0$, for any ![]() $E \in {\mathcal {D}}^b(\mathscr {A}_f)$ and any
$E \in {\mathcal {D}}^b(\mathscr {A}_f)$ and any ![]() $K \in {\mathcal {K}}$. By induction on triangles, Lemma 5.9 implies that, for any
$K \in {\mathcal {K}}$. By induction on triangles, Lemma 5.9 implies that, for any ![]() $i\in \mathbb {Z}$,
$i\in \mathbb {Z}$, ![]() $\mathop {{\rm Hom}}\nolimits (\sigma _{\geqslant i} \widetilde {p}^*E, K) =0$. As, for any
$\mathop {{\rm Hom}}\nolimits (\sigma _{\geqslant i} \widetilde {p}^*E, K) =0$. As, for any ![]() $P\in \mathscr {P}$, the space
$P\in \mathscr {P}$, the space ![]() $\mathop {{\rm Hom}}\nolimits (p^*P, K)$ vanishes, we have
$\mathop {{\rm Hom}}\nolimits (p^*P, K)$ vanishes, we have ![]() $\mathop {{\rm Ext}}\nolimits ^j((\widetilde {p}^*E)^i,K) =0$, for any
$\mathop {{\rm Ext}}\nolimits ^j((\widetilde {p}^*E)^i,K) =0$, for any ![]() $i$ and
$i$ and ![]() $j$. It then follows from Lemma E.2 that
$j$. It then follows from Lemma E.2 that ![]() $\mathop {{\rm Hom}}\nolimits (\widetilde {p}^*E, K) = 0$.
$\mathop {{\rm Hom}}\nolimits (\widetilde {p}^*E, K) = 0$.
Thus, it suffices to show that functor ![]() $\widetilde {p}^*$ takes
$\widetilde {p}^*$ takes ![]() ${\mathcal {D}}^b(\mathscr {A}_f)$ to the image of
${\mathcal {D}}^b(\mathscr {A}_f)$ to the image of ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ in
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ in ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$, see (71). Consider
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$, see (71). Consider ![]() $E\in {\mathcal {D}}^b({\mathcal {A}}_f)$. We shall show that
$E\in {\mathcal {D}}^b({\mathcal {A}}_f)$. We shall show that ![]() $\widetilde {p}^* E$ is quasi-isomorphic in
$\widetilde {p}^* E$ is quasi-isomorphic in ![]() ${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ to a complex with bounded cohomology. To this end, we shall find
${\mathcal {D}}^-(X\times _Y X^+)/{\mathcal {K}}$ to a complex with bounded cohomology. To this end, we shall find ![]() $N$ such that
$N$ such that ![]() $\tau _{< N}\, \widetilde {p}^* E$ is an object in
$\tau _{< N}\, \widetilde {p}^* E$ is an object in ![]() ${\mathcal {K}}$.
${\mathcal {K}}$.
First, we note that ![]() $Rp^+_*(p^* {\mathcal {P}}_i) = 0$, for any
$Rp^+_*(p^* {\mathcal {P}}_i) = 0$, for any ![]() $i\in \mathbb {Z}$ (Corollary 2.12). Thus, the term-wise definition of
$i\in \mathbb {Z}$ (Corollary 2.12). Thus, the term-wise definition of ![]() $\widetilde {p}^*$ (76) implies that
$\widetilde {p}^*$ (76) implies that ![]() $Rp^+_*(\widetilde {p}^* E) = 0$ and, as
$Rp^+_*(\widetilde {p}^* E) = 0$ and, as ![]() $p^+$ has fibers of dimension bounded by one,
$p^+$ has fibers of dimension bounded by one, ![]() $Rp^+_* {\mathcal {H}}^i(\widetilde {p}^* E) =0$, for any
$Rp^+_* {\mathcal {H}}^i(\widetilde {p}^* E) =0$, for any ![]() $i\in \mathbb {Z}$ (see Lemma 2.2).
$i\in \mathbb {Z}$ (see Lemma 2.2).
By Lemma 5.10, we have ![]() $Rp_* \widetilde {p}^* E \simeq \Psi (E) \in {\mathcal {D}}^b(X)^{\geqslant k}$, for some
$Rp_* \widetilde {p}^* E \simeq \Psi (E) \in {\mathcal {D}}^b(X)^{\geqslant k}$, for some ![]() $k \in \mathbb {Z}$. As
$k \in \mathbb {Z}$. As ![]() $p$ has fibers of dimension bounded by one, it follows that
$p$ has fibers of dimension bounded by one, it follows that ![]() $Rp_* {\mathcal {H}}^i(\widetilde {p}^* E) = 0$, for
$Rp_* {\mathcal {H}}^i(\widetilde {p}^* E) = 0$, for ![]() $i< k-1$. Thus,
$i< k-1$. Thus, ![]() $\tau _{< k-1} \widetilde {p}^* E$ lies in
$\tau _{< k-1} \widetilde {p}^* E$ lies in ![]() ${\mathcal {K}}$.
${\mathcal {K}}$.
Lemma 5.12 Let ![]() ${\mathcal {M}}$ be a projective generator of
${\mathcal {M}}$ be a projective generator of ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ and put
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ and put ![]() ${\mathcal {P}} = {\mathcal {H}}^{-1}_X(\iota _f^* {\mathcal {M}})$. Further, let
${\mathcal {P}} = {\mathcal {H}}^{-1}_X(\iota _f^* {\mathcal {M}})$. Further, let ![]() $C\in {\mathcal {D}}^-(X\times _Y X^+)$ be such that
$C\in {\mathcal {D}}^-(X\times _Y X^+)$ be such that ![]() $Rp^+_* C = 0$ and
$Rp^+_* C = 0$ and ![]() $R\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^*P, C) =0$. Then
$R\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^*P, C) =0$. Then ![]() $Rp_* C = 0$.
$Rp_* C = 0$.
Proof. Applying ![]() $R\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(-,C)$ to triangle (66) yields
$R\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(-,C)$ to triangle (66) yields ![]() $R\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(Lp^*{\mathcal {M}}, C) \simeq R\mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, Rp_* C) =0$. As
$R\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(Lp^*{\mathcal {M}}, C) \simeq R\mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, Rp_* C) =0$. As ![]() ${\mathcal {M}}$ is a compact generator of
${\mathcal {M}}$ is a compact generator of ![]() ${\mathcal {D}}_{{\rm qc}}(X)$, cf. [Reference Van den BerghVdB04, Lemma 3.2.2] and the proof of Proposition 4.6, it follows that
${\mathcal {D}}_{{\rm qc}}(X)$, cf. [Reference Van den BerghVdB04, Lemma 3.2.2] and the proof of Proposition 4.6, it follows that ![]() $Rp_* C = 0$.
$Rp_* C = 0$.
Proposition 5.13 Category ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ admits a SOD
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ admits a SOD
Proof. As ![]() $\widetilde {p}^*$ is defined term-wise, Corollary 2.12 implies that
$\widetilde {p}^*$ is defined term-wise, Corollary 2.12 implies that ![]() $Rp^+_*\circ \widetilde {p}^* = 0$. In view of SOD (74) and Proposition 5.11, it suffices to show that any
$Rp^+_*\circ \widetilde {p}^* = 0$. In view of SOD (74) and Proposition 5.11, it suffices to show that any ![]() $E\in {\mathcal {D}}^b(X\times _YX^+)/{\mathcal {K}}^b$ such that
$E\in {\mathcal {D}}^b(X\times _YX^+)/{\mathcal {K}}^b$ such that ![]() $Rp^+_* E = 0$ is isomorphic to
$Rp^+_* E = 0$ is isomorphic to ![]() $\widetilde {p}^* F$, for some
$\widetilde {p}^* F$, for some ![]() $F \in {\mathcal {D}}^b(\mathscr {A}_f)$.
$F \in {\mathcal {D}}^b(\mathscr {A}_f)$.
Consider triangle
in ![]() ${\mathcal {D}}^-(X\times _Y X^+)$. As
${\mathcal {D}}^-(X\times _Y X^+)$. As ![]() $Rp^+_* E = 0$ and
$Rp^+_* E = 0$ and ![]() $Rp^+_* \widetilde {p}^*(F)=0$, for any
$Rp^+_* \widetilde {p}^*(F)=0$, for any ![]() $F \in {\mathcal {D}}^b(\mathscr {A}_f)$, by applying
$F \in {\mathcal {D}}^b(\mathscr {A}_f)$, by applying ![]() $Rp^+_*$ to triangle (78) we obtain
$Rp^+_*$ to triangle (78) we obtain ![]() $Rp^+_* C_E =0$. In view of isomorphism (77), by applying
$Rp^+_* C_E =0$. In view of isomorphism (77), by applying ![]() $\widetilde {p}_*$ to triangle (78), we obtain
$\widetilde {p}_*$ to triangle (78), we obtain ![]() $\widetilde {p}_* C_E = 0$. By formula (75),
$\widetilde {p}_* C_E = 0$. By formula (75), ![]() $R\mathop {{\rm Hom}}\nolimits (p^* {\mathcal {P}}, C_E) = 0$. By Lemma 5.12,
$R\mathop {{\rm Hom}}\nolimits (p^* {\mathcal {P}}, C_E) = 0$. By Lemma 5.12, ![]() $Rp_* C_E = 0$, i.e.
$Rp_* C_E = 0$, i.e. ![]() $C_E \in {\mathcal {K}}$. Hence,
$C_E \in {\mathcal {K}}$. Hence, ![]() $\widetilde {p}^*\widetilde {p}_*E\to E$ is an isomorphism in
$\widetilde {p}^*\widetilde {p}_*E\to E$ is an isomorphism in ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$.
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$.
The following corollary gives a geometric description for the category ![]() ${\mathcal {D}}^b(\mathscr {A}_f)$.
${\mathcal {D}}^b(\mathscr {A}_f)$.
Corollary 5.14 We have an equivalence of categories
Proposition 5.13 implies the existence of ![]() $\widetilde {p}_!\colon {\mathcal {D}}^b(X \times _Y X^+)/{\mathcal {K}}^b \to {\mathcal {D}}^b(\mathscr {A}_f)$, left adjoint to
$\widetilde {p}_!\colon {\mathcal {D}}^b(X \times _Y X^+)/{\mathcal {K}}^b \to {\mathcal {D}}^b(\mathscr {A}_f)$, left adjoint to ![]() $\widetilde {p}^{*}$, which is defined by the functorial exact triangle
$\widetilde {p}^{*}$, which is defined by the functorial exact triangle
associated to a SOD. By exchanging the role of ![]() $X$ and
$X$ and ![]() $X^+$ we also obtain
$X^+$ we also obtain ![]() $\widetilde {p}^+_! \colon {\mathcal {D}}^b(X\times _YX^+)/{\mathcal {K}}^b \to {\mathcal {D}}^b(\mathscr {A}_{f^+})$.
$\widetilde {p}^+_! \colon {\mathcal {D}}^b(X\times _YX^+)/{\mathcal {K}}^b \to {\mathcal {D}}^b(\mathscr {A}_{f^+})$.
Lemma 5.15 The composite ![]() $\widetilde {p}_!\widetilde {p}^{+*} \widetilde {p}^+_!\widetilde {p}^*\colon {\mathcal {D}}^b(\mathscr {A}_f)\to {\mathcal {D}}^b(\mathscr {A}_f)$ is isomorphic to
$\widetilde {p}_!\widetilde {p}^{+*} \widetilde {p}^+_!\widetilde {p}^*\colon {\mathcal {D}}^b(\mathscr {A}_f)\to {\mathcal {D}}^b(\mathscr {A}_f)$ is isomorphic to ![]() $\mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(\mathscr {A}_f)}[4]$.
$\mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(\mathscr {A}_f)}[4]$.
Proof. First, we check that ![]() $\widetilde {p}^+_!\widetilde {p}^*$ restricts to a functor
$\widetilde {p}^+_!\widetilde {p}^*$ restricts to a functor ![]() $\mathscr {P}\to \mathscr {P}^+$. By Lemma 5.10,
$\mathscr {P}\to \mathscr {P}^+$. By Lemma 5.10, ![]() $Rp_*\widetilde {p}^* \simeq \Psi$. Hence, for
$Rp_*\widetilde {p}^* \simeq \Psi$. Hence, for ![]() $P\in \mathscr {A}_f$ projective, triangle (79), with
$P\in \mathscr {A}_f$ projective, triangle (79), with ![]() $p$ and
$p$ and ![]() $p^+$ interchanged, applied to
$p^+$ interchanged, applied to ![]() $p^*P = \widetilde {p}^*P$ yields an exact triangle
$p^*P = \widetilde {p}^*P$ yields an exact triangle
By Lemma 4.15 object ![]() $Lp^*P$ has two non-zero cohomology sheaves,
$Lp^*P$ has two non-zero cohomology sheaves, ![]() $p^*P$ and
$p^*P$ and ![]() $L^1p^*P$. It follows that
$L^1p^*P$. It follows that ![]() $\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*P\simeq L^1p^*P[2]$. Hence, in view of Lemma 5.10,
$\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*P\simeq L^1p^*P[2]$. Hence, in view of Lemma 5.10, ![]() $\Psi \widetilde {p}^+_!\widetilde {p}^*P \simeq Rp^+_*\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*P \simeq Rp^+_*L^1p^*P[2]$. As
$\Psi \widetilde {p}^+_!\widetilde {p}^*P \simeq Rp^+_*\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*P \simeq Rp^+_*L^1p^*P[2]$. As ![]() $Rp^+_*Lp^*$ restricts to an equivalence
$Rp^+_*Lp^*$ restricts to an equivalence ![]() $\mathscr {A}_f\xrightarrow {\simeq } \mathscr {A}_{f^+}[1]$, Corollary 4.23, object
$\mathscr {A}_f\xrightarrow {\simeq } \mathscr {A}_{f^+}[1]$, Corollary 4.23, object ![]() $Rp^+_*L^1p^*P = P^+$ is projective in
$Rp^+_*L^1p^*P = P^+$ is projective in ![]() $\mathscr {A}_{f^+}$. Hence
$\mathscr {A}_{f^+}$. Hence ![]() $\widetilde {p}^+_!p^*P[-2] = P^+$ is projective in
$\widetilde {p}^+_!p^*P[-2] = P^+$ is projective in ![]() $\mathscr {A}_{f^+}$.
$\mathscr {A}_{f^+}$.
As ![]() $\widetilde {p}^+_! \widetilde {p}^*[-2]$ maps objects of
$\widetilde {p}^+_! \widetilde {p}^*[-2]$ maps objects of ![]() $\mathscr {P}$ to objects of
$\mathscr {P}$ to objects of ![]() $\mathscr {A}_{f^+}$, it maps acyclic complexes in
$\mathscr {A}_{f^+}$, it maps acyclic complexes in ![]() $\mathscr {P}$ to acyclic complexes. Hence, the class
$\mathscr {P}$ to acyclic complexes. Hence, the class ![]() $\mathscr {P}$ is adapted to
$\mathscr {P}$ is adapted to ![]() $\widetilde {p}^+_!\widetilde {p}^*[-2]$, i.e. the functor can be calculated term-wise using the equivalence
$\widetilde {p}^+_!\widetilde {p}^*[-2]$, i.e. the functor can be calculated term-wise using the equivalence ![]() ${\mathcal {D}}^b(\mathscr {A}_f) \simeq \mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P})$. The same is true for the functor
${\mathcal {D}}^b(\mathscr {A}_f) \simeq \mathop {{\rm Hot}}\nolimits ^{-,b}(\mathscr {P})$. The same is true for the functor ![]() $\widetilde {p}_!\widetilde {p}^{+*}[-2]$ in the opposite direction. Moreover, because
$\widetilde {p}_!\widetilde {p}^{+*}[-2]$ in the opposite direction. Moreover, because ![]() $\widetilde {p}^+_!\widetilde {p}^*[-2]$ maps complexes of objects of
$\widetilde {p}^+_!\widetilde {p}^*[-2]$ maps complexes of objects of ![]() $\mathscr {P}$ to complexes of objects of
$\mathscr {P}$ to complexes of objects of ![]() $\mathscr {P}^+$ also the composite
$\mathscr {P}^+$ also the composite ![]() $\widetilde {p}_!\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*[-4]$ can be calculated term-wise. Therefore, it suffices to check that
$\widetilde {p}_!\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*[-4]$ can be calculated term-wise. Therefore, it suffices to check that ![]() $\widetilde {p}_!\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*[-4]|_{\mathscr {P}}\simeq \mathop {{\rm Id}}\nolimits _{\mathscr {P}}$.
$\widetilde {p}_!\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*[-4]|_{\mathscr {P}}\simeq \mathop {{\rm Id}}\nolimits _{\mathscr {P}}$.
Precomposing triangle (79), with ![]() $p$ and
$p$ and ![]() $p^+$ interchanged, with
$p^+$ interchanged, with ![]() $\widetilde {p}^*$, composing with
$\widetilde {p}^*$, composing with ![]() $\widetilde {p}_!$ and using the isomorphism
$\widetilde {p}_!$ and using the isomorphism ![]() $\widetilde {p}_!\widetilde {p}^*\simeq \mathop {{\rm Id}}\nolimits$, we arrive at an exact triangle
$\widetilde {p}_!\widetilde {p}^*\simeq \mathop {{\rm Id}}\nolimits$, we arrive at an exact triangle
First, we calculate the image of ![]() $\widetilde {p}_!\widetilde {L}p^*Rp_*p^*P \simeq \widetilde {p}_!\widetilde {L}p^*\Psi P \simeq \widetilde {p}_!\widetilde {L}p^*P$ under
$\widetilde {p}_!\widetilde {L}p^*Rp_*p^*P \simeq \widetilde {p}_!\widetilde {L}p^*\Psi P \simeq \widetilde {p}_!\widetilde {L}p^*P$ under ![]() $\Psi = Rp_*\widetilde {p}^*$ using triangle (79) composed with
$\Psi = Rp_*\widetilde {p}^*$ using triangle (79) composed with ![]() $Rp_*$ and applied to
$Rp_*$ and applied to ![]() $\widetilde {L}p^*P$:
$\widetilde {L}p^*P$:
By Lemma 5.1 we have ![]() $Rp_*\widetilde {L}p^*P \simeq P$. As
$Rp_*\widetilde {L}p^*P \simeq P$. As ![]() $Rg_*P =0$, triangle (65) implies that
$Rg_*P =0$, triangle (65) implies that ![]() $Rp_*Lp^{+*}Rp^+_*\widetilde {L}p^*P \simeq P[2]$. It follows that
$Rp_*Lp^{+*}Rp^+_*\widetilde {L}p^*P \simeq P[2]$. It follows that ![]() $\Psi \widetilde {p}_!\widetilde {L}p^*P$ has non-zero cohomology in degrees
$\Psi \widetilde {p}_!\widetilde {L}p^*P$ has non-zero cohomology in degrees ![]() $0$ and
$0$ and ![]() $-3$ only, both isomorphic to
$-3$ only, both isomorphic to ![]() $P$. The map
$P$. The map ![]() $\widetilde {p}_!\widetilde {L}p^*Rp_*p^*P \to P$ in (80) is the composition of two adjunction counits
$\widetilde {p}_!\widetilde {L}p^*Rp_*p^*P \to P$ in (80) is the composition of two adjunction counits ![]() $\widetilde {L}p^*Rp_*\to \mathop {{\rm Id}}\nolimits$ and
$\widetilde {L}p^*Rp_*\to \mathop {{\rm Id}}\nolimits$ and ![]() $\widetilde {p}_!\widetilde {p}^* \to \mathop {{\rm Id}}\nolimits$. The first when applied to
$\widetilde {p}_!\widetilde {p}^* \to \mathop {{\rm Id}}\nolimits$. The first when applied to ![]() $p^*P$ is the truncation at the zero cohomology, the second is an isomorphism. Hence,
$p^*P$ is the truncation at the zero cohomology, the second is an isomorphism. Hence, ![]() $\widetilde {p}_!\widetilde {p}^{+*} \widetilde {p}^+_!\widetilde {p}^*P \simeq P[4]$.
$\widetilde {p}_!\widetilde {p}^{+*} \widetilde {p}^+_!\widetilde {p}^*P \simeq P[4]$.
Proposition 5.16 Category ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ admits a SOD
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ admits a SOD
Proof. Functor ![]() $\widetilde {p}_*(-) \simeq R\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b}(p^*{\mathcal {P}}, -)$ is right adjoint to the fully faithful functor
$\widetilde {p}_*(-) \simeq R\mathop {{\rm Hom}}\nolimits _{{\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b}(p^*{\mathcal {P}}, -)$ is right adjoint to the fully faithful functor ![]() $\widetilde {p}^*$ of Proposition 5.11.
$\widetilde {p}^*$ of Proposition 5.11.
First, we check that ![]() $\widetilde {p}_*\widetilde {L}p^*(E) = 0$, for any
$\widetilde {p}_*\widetilde {L}p^*(E) = 0$, for any ![]() $E \in {\mathcal {D}}^b(X)$. It follows from Lemma 5.9 that the above statement is equivalent to
$E \in {\mathcal {D}}^b(X)$. It follows from Lemma 5.9 that the above statement is equivalent to
for any ![]() $E \in {\mathcal {D}}^b(X)$.
$E \in {\mathcal {D}}^b(X)$.
By applying ![]() $\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(-, Lp^*E)$ to triangle (66), we learn that
$\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(-, Lp^*E)$ to triangle (66), we learn that ![]() $\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^* {\mathcal {P}}, Lp^* E)$ is a cone of a morphism
$\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(p^* {\mathcal {P}}, Lp^* E)$ is a cone of a morphism
As ![]() $Rp_*{\mathcal {O}}_{X\times _Y X^+} \simeq {\mathcal {O}}_X$, we have
$Rp_*{\mathcal {O}}_{X\times _Y X^+} \simeq {\mathcal {O}}_X$, we have
Moreover, in view of Proposition 4.10, we have
We check that under isomorphisms (82) and (83) morphism ![]() $\theta _E$ coincides with the morphism
$\theta _E$ coincides with the morphism ![]() $\nu _E$ induced by functor
$\nu _E$ induced by functor ![]() $F$:
$F$:
By (67) and (68), morphism ![]() $\varphi \colon Lp^{+*}f^{+*}f_*{\mathcal {M}}\to Lp^*{\mathcal {M}}$ in triangle (66) is the composite of the isomorphism
$\varphi \colon Lp^{+*}f^{+*}f_*{\mathcal {M}}\to Lp^*{\mathcal {M}}$ in triangle (66) is the composite of the isomorphism ![]() $\kappa \colon Lp^{+*}f^{+*}f_*{\mathcal {M}} \xrightarrow {\simeq } p^{+*}f^{+*}f_*{\mathcal {M}} \xrightarrow {\simeq } p^*f^*f_*{\mathcal {M}}$ with the (non-derived) pull-back
$\kappa \colon Lp^{+*}f^{+*}f_*{\mathcal {M}} \xrightarrow {\simeq } p^{+*}f^{+*}f_*{\mathcal {M}} \xrightarrow {\simeq } p^*f^*f_*{\mathcal {M}}$ with the (non-derived) pull-back ![]() $p^*$ of the
$p^*$ of the ![]() $f^*\dashv f_*$ adjunction counit
$f^*\dashv f_*$ adjunction counit ![]() $\varepsilon _{{\mathcal {M}}}\colon f^*f_*{\mathcal {M}}\to {\mathcal {M}}$. We use isomorphism (82) to identify
$\varepsilon _{{\mathcal {M}}}\colon f^*f_*{\mathcal {M}}\to {\mathcal {M}}$. We use isomorphism (82) to identify ![]() $\alpha \in \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}},E)$ with
$\alpha \in \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}},E)$ with ![]() $Lp^*(\alpha )\in \mathop {{\rm Hom}}\nolimits (Lp^*({\mathcal {M}}), Lp^*(E))$. Under isomorphism (83), the composition
$Lp^*(\alpha )\in \mathop {{\rm Hom}}\nolimits (Lp^*({\mathcal {M}}), Lp^*(E))$. Under isomorphism (83), the composition ![]() $Lp^*(\alpha ) \circ \varphi$ reads as
$Lp^*(\alpha ) \circ \varphi$ reads as ![]() $Rp^+_*Lp^*(\alpha ) \circ Rp^+_*(p^*(\varepsilon _{{\mathcal {M}}})\circ \kappa ) \circ \eta _{{\mathcal {M}}}$, for the
$Rp^+_*Lp^*(\alpha ) \circ Rp^+_*(p^*(\varepsilon _{{\mathcal {M}}})\circ \kappa ) \circ \eta _{{\mathcal {M}}}$, for the ![]() $Lp^{+*} \dashv Rp^+_*$ adjunction unit
$Lp^{+*} \dashv Rp^+_*$ adjunction unit ![]() $\eta _{{\mathcal {M}}} \colon f^{+*}f_*{\mathcal {M}} \to Rp^+_*Lp^{+*}f^{+*}f_*{\mathcal {M}}$. The composite
$\eta _{{\mathcal {M}}} \colon f^{+*}f_*{\mathcal {M}} \to Rp^+_*Lp^{+*}f^{+*}f_*{\mathcal {M}}$. The composite ![]() $f^{+*}f_*{\mathcal {M}} \xrightarrow {\eta _{{\mathcal {M}}}} Rp^+_*Lp^{+*}f^{+*}f_*{\mathcal {M}} \xrightarrow {Rp^+_*(\kappa )} Rp^+_*p^*f^*f_*{\mathcal {M}} \xrightarrow {Rp^+_*(\varepsilon _{{\mathcal {M}}})} Rp^+_*p^*{\mathcal {M}}$ is the base change (49). It follows that
$f^{+*}f_*{\mathcal {M}} \xrightarrow {\eta _{{\mathcal {M}}}} Rp^+_*Lp^{+*}f^{+*}f_*{\mathcal {M}} \xrightarrow {Rp^+_*(\kappa )} Rp^+_*p^*f^*f_*{\mathcal {M}} \xrightarrow {Rp^+_*(\varepsilon _{{\mathcal {M}}})} Rp^+_*p^*{\mathcal {M}}$ is the base change (49). It follows that ![]() $Rp^+_*Lp^*(\alpha ) \circ Rp^+_*(p^*(\varepsilon _{{\mathcal {M}}})\circ \kappa ) \circ \eta _{{\mathcal {M}}}$ is the image of
$Rp^+_*Lp^*(\alpha ) \circ Rp^+_*(p^*(\varepsilon _{{\mathcal {M}}})\circ \kappa ) \circ \eta _{{\mathcal {M}}}$ is the image of ![]() $F(\alpha ) = Rp^+_*Lp^*(\alpha ) \in \mathop {{\rm Hom}}\nolimits (F({\mathcal {M}}), F(E))$ under the isomorphism
$F(\alpha ) = Rp^+_*Lp^*(\alpha ) \in \mathop {{\rm Hom}}\nolimits (F({\mathcal {M}}), F(E))$ under the isomorphism ![]() $\mathop {{\rm Hom}}\nolimits (F({\mathcal {M}}), F(E)) \simeq \mathop {{\rm Hom}}\nolimits (f^{+*}f_*{\mathcal {M}}, F(E))$ given by Proposition 4.10.
$\mathop {{\rm Hom}}\nolimits (F({\mathcal {M}}), F(E)) \simeq \mathop {{\rm Hom}}\nolimits (f^{+*}f_*{\mathcal {M}}, F(E))$ given by Proposition 4.10.
As the flop functor is an equivalence of categories (see Corollary 4.22), ![]() $\nu _E$ is an isomorphism, i.e.
$\nu _E$ is an isomorphism, i.e. ![]() $\mathop {{\rm Hom}}\nolimits _{X \times _Y X^+}(p^*{\mathcal {P}}, Lp^*E) \simeq {\rm Cone}(\theta _E) \simeq 0$.
$\mathop {{\rm Hom}}\nolimits _{X \times _Y X^+}(p^*{\mathcal {P}}, Lp^*E) \simeq {\rm Cone}(\theta _E) \simeq 0$.
In order to prove the SOD (81) it suffices to show that, for any ![]() $E\in {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ such that
$E\in {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ such that ![]() $\widetilde {p}_*(E)\simeq 0$, we have
$\widetilde {p}_*(E)\simeq 0$, we have ![]() $E\simeq \widetilde {L}p^*(E')$, for some
$E\simeq \widetilde {L}p^*(E')$, for some ![]() $E'\in {\mathcal {D}}^b(X)$.
$E'\in {\mathcal {D}}^b(X)$.
Now let ![]() $E\in {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ satisfy
$E\in {\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$ satisfy ![]() $\widetilde {p}_*E \simeq 0$. Consider an exact triangle
$\widetilde {p}_*E \simeq 0$. Consider an exact triangle
We have ![]() $Rp_* \widetilde {C}_E =0$. Moreover, because
$Rp_* \widetilde {C}_E =0$. Moreover, because ![]() $\widetilde {p}_* \widetilde {L}p^*Rp_*E = 0$, it follows that
$\widetilde {p}_* \widetilde {L}p^*Rp_*E = 0$, it follows that ![]() $\widetilde {p}_*C_E=0$. Now, we proceed as in the proof of Lemma 5.12 to show that
$\widetilde {p}_*C_E=0$. Now, we proceed as in the proof of Lemma 5.12 to show that ![]() $Rp^+_*\widetilde {C}_E \simeq 0$.
$Rp^+_*\widetilde {C}_E \simeq 0$.
Applying ![]() $R\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(-,\widetilde {C}_E)$ to triangle (66) yields
$R\mathop {{\rm Hom}}\nolimits _{X\times _Y X^+}(-,\widetilde {C}_E)$ to triangle (66) yields
By Proposition 4.10, the sheaf ![]() $f^{+*}f_*{\mathcal {M}}$ is isomorphic to the flop
$f^{+*}f_*{\mathcal {M}}$ is isomorphic to the flop ![]() $F({\mathcal {M}})$. As the flop functor
$F({\mathcal {M}})$. As the flop functor ![]() $F$ is an equivalence (see Corollary 4.22),
$F$ is an equivalence (see Corollary 4.22), ![]() $F({\mathcal {M}})$ is a compact generator of
$F({\mathcal {M}})$ is a compact generator of ![]() ${\mathcal {D}}^b(X^+)$. Thus, vanishing of
${\mathcal {D}}^b(X^+)$. Thus, vanishing of ![]() $R\mathop {{\rm Hom}}\nolimits _{X^+}(F({\mathcal {M}}), Rp^+_*\widetilde {C}_E)$ implies that
$R\mathop {{\rm Hom}}\nolimits _{X^+}(F({\mathcal {M}}), Rp^+_*\widetilde {C}_E)$ implies that ![]() $Rp^+_*\widetilde {C}_E \simeq 0$.
$Rp^+_*\widetilde {C}_E \simeq 0$.
Hence, in triangle (84) sheaf ![]() $\widetilde {C}_E$ is an object of
$\widetilde {C}_E$ is an object of ![]() ${\mathcal {K}}^b$. Therefore,
${\mathcal {K}}^b$. Therefore, ![]() $E \simeq \widetilde {L}p^*Rp_* E$ in
$E \simeq \widetilde {L}p^*Rp_* E$ in ![]() ${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$.
${\mathcal {D}}^b(X\times _Y X^+)/{\mathcal {K}}^b$.
Theorem 5.17 Category ![]() ${\mathcal {D}}^b(X\times _YX^+)/{\mathcal {K}}^b$ admits 4-periodical SODs
${\mathcal {D}}^b(X\times _YX^+)/{\mathcal {K}}^b$ admits 4-periodical SODs
 \begin{align*} {\mathcal{D}}^b(X\times_YX^+)/{\mathcal{K}}^b &= \langle \widetilde{p}^*{\mathcal{D}}^b(\mathscr{A}_f), \widetilde{L}p^{+*}{\mathcal{D}}^b(X^+)\rangle = \langle \widetilde{L}p^{+*}{\mathcal{D}}^b(X^+), \widetilde{p}^{+*}{\mathcal{D}}^b(\mathscr{A}_{f^+})\rangle \\ &= \langle \widetilde{p}^{+*}{\mathcal{D}}^b(\mathscr{A}_{f^+}), \widetilde{L}p^{*}{\mathcal{D}}^b(X)\rangle = \langle \widetilde{L}p^{*}{\mathcal{D}}^b(X), \widetilde{p}^{*}{\mathcal{D}}^b(\mathscr{A}_{f})\rangle. \end{align*}
\begin{align*} {\mathcal{D}}^b(X\times_YX^+)/{\mathcal{K}}^b &= \langle \widetilde{p}^*{\mathcal{D}}^b(\mathscr{A}_f), \widetilde{L}p^{+*}{\mathcal{D}}^b(X^+)\rangle = \langle \widetilde{L}p^{+*}{\mathcal{D}}^b(X^+), \widetilde{p}^{+*}{\mathcal{D}}^b(\mathscr{A}_{f^+})\rangle \\ &= \langle \widetilde{p}^{+*}{\mathcal{D}}^b(\mathscr{A}_{f^+}), \widetilde{L}p^{*}{\mathcal{D}}^b(X)\rangle = \langle \widetilde{L}p^{*}{\mathcal{D}}^b(X), \widetilde{p}^{*}{\mathcal{D}}^b(\mathscr{A}_{f})\rangle. \end{align*}
In particular, ![]() $(\widetilde {p}^*{\mathcal {D}}^b(\mathscr {A}_f), \widetilde {p}^{+*}{\mathcal {D}}^b(\mathscr {A}_{f^+}))$ and
$(\widetilde {p}^*{\mathcal {D}}^b(\mathscr {A}_f), \widetilde {p}^{+*}{\mathcal {D}}^b(\mathscr {A}_{f^+}))$ and ![]() $(\widetilde {L}p^*{\mathcal {D}}^b(X), \widetilde {L}p^{*}{\mathcal {D}}^b(X^+))$ are spherical pairs.
$(\widetilde {L}p^*{\mathcal {D}}^b(X), \widetilde {L}p^{*}{\mathcal {D}}^b(X^+))$ are spherical pairs.
Proof. Propositions 5.13 and 5.16 for ![]() $X$ and
$X$ and ![]() $X^+$ imply the 4-periodical SODs. Proposition B.3 claims that
$X^+$ imply the 4-periodical SODs. Proposition B.3 claims that ![]() $(\widetilde {p}^*{\mathcal {D}}^b(\mathscr {A}_f), \widetilde {p}^{+*}{\mathcal {D}}^b(\mathscr {A}_{f^+}))$ and
$(\widetilde {p}^*{\mathcal {D}}^b(\mathscr {A}_f), \widetilde {p}^{+*}{\mathcal {D}}^b(\mathscr {A}_{f^+}))$ and ![]() $(\widetilde {L}p^*{\mathcal {D}}^b(X), \widetilde {L}p^{*}{\mathcal {D}}^b(X^+))$ are spherical pairs.
$(\widetilde {L}p^*{\mathcal {D}}^b(X), \widetilde {L}p^{*}{\mathcal {D}}^b(X^+))$ are spherical pairs.
Corollary 5.18 Functor ![]() $\Psi \colon {\mathcal {D}}^b(\mathscr {A}_f) \to {\mathcal {D}}^b(X)$ is spherical. The unit and counit for the
$\Psi \colon {\mathcal {D}}^b(\mathscr {A}_f) \to {\mathcal {D}}^b(X)$ is spherical. The unit and counit for the ![]() $\Psi ^* \dashv \Psi$ adjunction fit into functorial exact triangles:
$\Psi ^* \dashv \Psi$ adjunction fit into functorial exact triangles:
Proof. By Proposition B.3 and Theorem 5.17 ![]() $(\widetilde {p}^*{\mathcal {D}}^b(\mathscr {A}_f), \widetilde {p}^{+*}{\mathcal {D}}^b(\mathscr {A}_{f^+}))$ is a spherical pair. By Proposition B.2 the corresponding spherical functor is
$(\widetilde {p}^*{\mathcal {D}}^b(\mathscr {A}_f), \widetilde {p}^{+*}{\mathcal {D}}^b(\mathscr {A}_{f^+}))$ is a spherical pair. By Proposition B.2 the corresponding spherical functor is ![]() $Rp_*\widetilde {p}^*$. By Lemma 5.10 the latter is isomorphic to
$Rp_*\widetilde {p}^*$. By Lemma 5.10 the latter is isomorphic to ![]() $\Psi$.
$\Psi$.
By Proposition B.2 the cone of the counit ![]() $\Psi ^*\Psi \to \mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(\mathscr {A}_f)}$ is isomorphic to
$\Psi ^*\Psi \to \mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(\mathscr {A}_f)}$ is isomorphic to ![]() $\widetilde {p}_!\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*$ and the cone of the unit
$\widetilde {p}_!\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^*$ and the cone of the unit ![]() $\mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(X)} \to \Psi \Psi ^*$ is
$\mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(X)} \to \Psi \Psi ^*$ is ![]() $Rp_*\widetilde {L}p^{+*}Rp^+_*\widetilde {L}p^*\simeq Rp_*Lp^{+*}Rp^+_*Lp^*=F^+F$. We conclude by the isomorphism
$Rp_*\widetilde {L}p^{+*}Rp^+_*\widetilde {L}p^*\simeq Rp_*Lp^{+*}Rp^+_*Lp^*=F^+F$. We conclude by the isomorphism ![]() $\widetilde {p}_!\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^* \simeq \mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(\mathscr {A}_f)}[4]$, Lemma 5.15.
$\widetilde {p}_!\widetilde {p}^{+*}\widetilde {p}^+_!\widetilde {p}^* \simeq \mathop {{\rm Id}}\nolimits _{{\mathcal {D}}^b(\mathscr {A}_f)}[4]$, Lemma 5.15.
6. Contraction algebra as the endomorphism algebra of a projective generator
In [Reference Donovan and WemyssDW16] Donovan and Wemyss considered a morphism ![]() $f\colon X\to Y$ between Gorenstein varieties of dimension three that contracts a rational irreducible curve
$f\colon X\to Y$ between Gorenstein varieties of dimension three that contracts a rational irreducible curve ![]() $C$ to a point. If
$C$ to a point. If ![]() $Y$ is a spectrum of a complete local Noetherian ring, the category
$Y$ is a spectrum of a complete local Noetherian ring, the category ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ has projective generator. In [Reference Donovan and WemyssDW16] a contraction algebra
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ has projective generator. In [Reference Donovan and WemyssDW16] a contraction algebra ![]() $A_{\rm con}$ is defined as the quotient of the endomorphism algebra of the projective generator for
$A_{\rm con}$ is defined as the quotient of the endomorphism algebra of the projective generator for ![]() $\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ by morphisms which factor through
$\mathop {{}^{-1}{\rm Per}}\nolimits (X/Y)$ by morphisms which factor through ![]() ${\mathcal {O}}_X$. Algebra
${\mathcal {O}}_X$. Algebra ![]() $A_{\rm con}$ is shown to govern non-commutative deformations of
$A_{\rm con}$ is shown to govern non-commutative deformations of ![]() ${\mathcal {O}}_C(-1)$. If
${\mathcal {O}}_C(-1)$. If ![]() $N_{X/C} \simeq {\mathcal {O}}_C\oplus {\mathcal {O}}_C(-2)$, algebra
$N_{X/C} \simeq {\mathcal {O}}_C\oplus {\mathcal {O}}_C(-2)$, algebra ![]() $A_{\rm con}$ is commutative and was first considered in terms of deformation theory by Toda in [Reference TodaTod07].
$A_{\rm con}$ is commutative and was first considered in terms of deformation theory by Toda in [Reference TodaTod07].
We prove in our, more general, set-up that ![]() $A_{\rm con}$ is isomorphic to the endomorphism algebra of a projective generator for
$A_{\rm con}$ is isomorphic to the endomorphism algebra of a projective generator for ![]() $\mathscr {A}_f$.
$\mathscr {A}_f$.
Category ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ has a projective generator
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$ has a projective generator ![]() ${\mathcal {N}}$ and
${\mathcal {N}}$ and ![]() $Q = {\mathcal {H}}^0_X(\iota _f^*{\mathcal {N}})$ is a projective generator for
$Q = {\mathcal {H}}^0_X(\iota _f^*{\mathcal {N}})$ is a projective generator for ![]() $\mathscr {A}_f$, Lemma 3.5. Endomorphisms algebras
$\mathscr {A}_f$, Lemma 3.5. Endomorphisms algebras ![]() $A_Q = \mathop {{\rm End}}\nolimits _X({\mathcal {Q}})$ and
$A_Q = \mathop {{\rm End}}\nolimits _X({\mathcal {Q}})$ and ![]() $A_X = \mathop {{\rm End}}\nolimits _X({\mathcal {N}})$ are Noetherian, and we have equivalences
$A_X = \mathop {{\rm End}}\nolimits _X({\mathcal {N}})$ are Noetherian, and we have equivalences ![]() ${\mathcal {D}}(\text{Mod--}A_Q)\simeq {\mathcal {D}}(\mathscr {A}_f)$,
${\mathcal {D}}(\text{Mod--}A_Q)\simeq {\mathcal {D}}(\mathscr {A}_f)$, ![]() ${\mathcal {D}}(\text{Mod--}A_X)\simeq {\mathcal {D}}_{{\rm qc}}(X)$.
${\mathcal {D}}(\text{Mod--}A_X)\simeq {\mathcal {D}}_{{\rm qc}}(X)$.
Projective generator ![]() ${\mathcal {Q}}$ for
${\mathcal {Q}}$ for ![]() $\mathscr {A}_f$ is an object in
$\mathscr {A}_f$ is an object in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. It follows that
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. It follows that ![]() ${\mathcal {Q}}' :=R\mathop {{\rm Hom}}\nolimits _X({\mathcal {N}},{\mathcal {Q}})$ is an
${\mathcal {Q}}' :=R\mathop {{\rm Hom}}\nolimits _X({\mathcal {N}},{\mathcal {Q}})$ is an ![]() $A_Q^{\mathop {{\rm op}}\nolimits }\otimes _k A_X$ module and, under the above equivalences, functor
$A_Q^{\mathop {{\rm op}}\nolimits }\otimes _k A_X$ module and, under the above equivalences, functor ![]() $\Psi$ is isomorphic to
$\Psi$ is isomorphic to
Proposition 3.19 yields a finite projective resolution of ![]() ${\mathcal {Q}}$ in
${\mathcal {Q}}$ in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. Hence,
$\mathop {{}^{0}{\rm Per}}\nolimits (X/Y)$. Hence, ![]() ${\mathcal {Q}}'$ is a perfect
${\mathcal {Q}}'$ is a perfect ![]() $A_X$ DG module and by Proposition C.6 the right adjoint
$A_X$ DG module and by Proposition C.6 the right adjoint ![]() $\Psi ^!$ exists and is isomorphic to a bimodule functor.
$\Psi ^!$ exists and is isomorphic to a bimodule functor.
Proposition 6.1 Let ![]() $f$ satisfy assumption (a), let
$f$ satisfy assumption (a), let ![]() ${\mathcal {M}}_i$ be as in (17) and let
${\mathcal {M}}_i$ be as in (17) and let ![]() ${\mathcal {P}}_i$ be as in (19). Then
${\mathcal {P}}_i$ be as in (19). Then ![]() $\Psi \Psi ^!({\mathcal {M}}_i)\simeq \Psi {\mathcal {P}}_i[-2]$.
$\Psi \Psi ^!({\mathcal {M}}_i)\simeq \Psi {\mathcal {P}}_i[-2]$.
Proof. Considering the right adjoint to the functorial exact triangles of Corollary 5.18 yields an exact triangle:
Put ![]() ${\mathcal {K}}_i=(F^+F)^{-1}({\mathcal {M}}_i)$. As
${\mathcal {K}}_i=(F^+F)^{-1}({\mathcal {M}}_i)$. As ![]() $Rf_* F^+F = Rf_*$, we have
$Rf_* F^+F = Rf_*$, we have ![]() $Rg_*{\mathcal {K}}_i \simeq Rg_*{\mathcal {M}}_i$. Hence, by Proposition 3.15,
$Rg_*{\mathcal {K}}_i \simeq Rg_*{\mathcal {M}}_i$. Hence, by Proposition 3.15, ![]() ${\mathcal {H}}^0_X(Lg^*Rg_*{\mathcal {K}}_i)=f^*f_*{\mathcal {M}}_i$,
${\mathcal {H}}^0_X(Lg^*Rg_*{\mathcal {K}}_i)=f^*f_*{\mathcal {M}}_i$, ![]() ${\mathcal {H}}^{-1}_X(Lg^*Rg_*{\mathcal {K}}_i) = {\mathcal {M}}_i$ and the remaining cohomology sheaves vanish. Considering long exact sequence of cohomology sheaves of the exact triangle obtained by applying functorial exact triangle (65) to
${\mathcal {H}}^{-1}_X(Lg^*Rg_*{\mathcal {K}}_i) = {\mathcal {M}}_i$ and the remaining cohomology sheaves vanish. Considering long exact sequence of cohomology sheaves of the exact triangle obtained by applying functorial exact triangle (65) to ![]() ${\mathcal {K}}_i$:
${\mathcal {K}}_i$:
we get that ![]() ${\mathcal {H}}^0({\mathcal {K}}_i) \simeq {\mathcal {M}}_i$ and
${\mathcal {H}}^0({\mathcal {K}}_i) \simeq {\mathcal {M}}_i$ and ![]() ${\mathcal {H}}^1({\mathcal {K}}_i) \simeq {\mathcal {P}}_i$ (as
${\mathcal {H}}^1({\mathcal {K}}_i) \simeq {\mathcal {P}}_i$ (as ![]() ${\mathcal {P}}_i$ is the kernel of the surjective morphism
${\mathcal {P}}_i$ is the kernel of the surjective morphism ![]() $f^*f_*{\mathcal {M}}_i \to {\mathcal {M}}_i$). The long exact sequence of cohomology sheaves of (86) yields an isomorphism
$f^*f_*{\mathcal {M}}_i \to {\mathcal {M}}_i$). The long exact sequence of cohomology sheaves of (86) yields an isomorphism ![]() $\Psi \Psi ^!({\mathcal {M}}_i) \simeq {\mathcal {P}}_i[-2]\simeq \Psi {\mathcal {P}}_i[-2]$.
$\Psi \Psi ^!({\mathcal {M}}_i) \simeq {\mathcal {P}}_i[-2]\simeq \Psi {\mathcal {P}}_i[-2]$.
Theorem 6.2 Let ![]() $f$ satisfy assumption (c), let
$f$ satisfy assumption (c), let ![]() ${\mathcal {M}}_i$ be as in (17) and let
${\mathcal {M}}_i$ be as in (17) and let ![]() ${\mathcal {P}}_i$ be as in (19). The endomorphism algebra
${\mathcal {P}}_i$ be as in (19). The endomorphism algebra
 \[ A_P= \mathop{{\rm Hom}}\nolimits_{\mathscr{A}_f}\bigg(\bigoplus_{i=1}^n {\mathcal{P}}_i, \bigoplus_{i=1}^n {\mathcal{P}}_i\bigg) \]
\[ A_P= \mathop{{\rm Hom}}\nolimits_{\mathscr{A}_f}\bigg(\bigoplus_{i=1}^n {\mathcal{P}}_i, \bigoplus_{i=1}^n {\mathcal{P}}_i\bigg) \]
is isomorphic to the quotient of ![]() $\mathop {{\rm Hom}}\nolimits _X(\bigoplus _{i=1}^n{\mathcal {M}}_i, \bigoplus _{i=1}^n {\mathcal {M}}_i)$ by the subspace of morphisms that factor via direct sums of copies of the structure sheaf.
$\mathop {{\rm Hom}}\nolimits _X(\bigoplus _{i=1}^n{\mathcal {M}}_i, \bigoplus _{i=1}^n {\mathcal {M}}_i)$ by the subspace of morphisms that factor via direct sums of copies of the structure sheaf.
Proof. By Proposition 6.1 ![]() $\Psi \Psi ^!({\mathcal {M}}_i) \simeq \Psi {\mathcal {P}}_i[-2]$. As
$\Psi \Psi ^!({\mathcal {M}}_i) \simeq \Psi {\mathcal {P}}_i[-2]$. As ![]() $\Psi |_{\mathscr {A}_f}$ is fully faithful, we have
$\Psi |_{\mathscr {A}_f}$ is fully faithful, we have ![]() $\Psi ^!({\mathcal {M}}_i) \simeq {\mathcal {P}}_i[-2]$. Thus, functor
$\Psi ^!({\mathcal {M}}_i) \simeq {\mathcal {P}}_i[-2]$. Thus, functor ![]() $\Psi ^!$ gives a homomorphism of algebras
$\Psi ^!$ gives a homomorphism of algebras
where ![]() ${\mathcal {M}} = \bigoplus _{i} {\mathcal {M}}_i$. The triangle of functors right adjoint to the second triangle of (85) implies that the morphism
${\mathcal {M}} = \bigoplus _{i} {\mathcal {M}}_i$. The triangle of functors right adjoint to the second triangle of (85) implies that the morphism ![]() $\varphi$ fits into an exact sequence
$\varphi$ fits into an exact sequence
 \begin{align*} &\mathop{{\rm Hom}}\nolimits_X((F^+F)^{-1}{\mathcal{M}}, {\mathcal{M}}) \xrightarrow{\psi} \mathop{{\rm Hom}}\nolimits_X({\mathcal{M}}, {\mathcal{M}})\xrightarrow{\varphi} \mathop{{\rm Hom}}\nolimits_X(\Psi \Psi^! {\mathcal{M}}, {\mathcal{M}}) \\ &\quad \to \mathop{{\rm Hom}}\nolimits_X((F^+F)^{-1}{\mathcal{M}}[-1], {\mathcal{M}}). \end{align*}
\begin{align*} &\mathop{{\rm Hom}}\nolimits_X((F^+F)^{-1}{\mathcal{M}}, {\mathcal{M}}) \xrightarrow{\psi} \mathop{{\rm Hom}}\nolimits_X({\mathcal{M}}, {\mathcal{M}})\xrightarrow{\varphi} \mathop{{\rm Hom}}\nolimits_X(\Psi \Psi^! {\mathcal{M}}, {\mathcal{M}}) \\ &\quad \to \mathop{{\rm Hom}}\nolimits_X((F^+F)^{-1}{\mathcal{M}}[-1], {\mathcal{M}}). \end{align*}By Corollary 4.22,
Theorem 4.21 implies that ![]() ${F^+}^{-1}({\mathcal {M}}) \simeq {\mathcal {N}}^+$ is a projective object in
${F^+}^{-1}({\mathcal {M}}) \simeq {\mathcal {N}}^+$ is a projective object in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$. On the other hand,
$\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$. On the other hand, ![]() $F({\mathcal {M}}) \simeq f^{+*}f_* {\mathcal {M}}$ by Proposition 4.19. By Lemma 3.11,
$F({\mathcal {M}}) \simeq f^{+*}f_* {\mathcal {M}}$ by Proposition 4.19. By Lemma 3.11, ![]() $f^{+*}f_*{\mathcal {M}} \simeq f^{+*}f^+_*{\mathcal {N}}^+$. Then, Lemma 2.9 implies that
$f^{+*}f_*{\mathcal {M}} \simeq f^{+*}f^+_*{\mathcal {N}}^+$. Then, Lemma 2.9 implies that ![]() $R^1f^+_*(f^{+*}f_* {\mathcal {M}}) = 0$, i.e.
$R^1f^+_*(f^{+*}f_* {\mathcal {M}}) = 0$, i.e. ![]() $f^{+*}f_* {\mathcal {M}}$ is an object in
$f^{+*}f_* {\mathcal {M}}$ is an object in ![]() $\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$ (see Remark 2.3 and formula (8) therein). Thus,
$\mathop {{}^{0}{\rm Per}}\nolimits (X^+/Y)$ (see Remark 2.3 and formula (8) therein). Thus,
i.e. morphism ![]() $\varphi$ is surjective.
$\varphi$ is surjective.
Let us now describe the image of ![]() $\psi$. Triangle (64) with roles of
$\psi$. Triangle (64) with roles of ![]() $X$ and
$X$ and ![]() $X^+$ interchanged, when applied to
$X^+$ interchanged, when applied to ![]() ${\mathcal {N}}^+$, gives an exact triangle
${\mathcal {N}}^+$, gives an exact triangle
in view of ![]() $(F^+F)^{-1} {\mathcal {M}} \simeq F^{-1}({\mathcal {N}}^+)$,
$(F^+F)^{-1} {\mathcal {M}} \simeq F^{-1}({\mathcal {N}}^+)$, ![]() $Rg^+_* {\mathcal {N}}^+ \simeq Rg_* {\mathcal {M}}$, and
$Rg^+_* {\mathcal {N}}^+ \simeq Rg_* {\mathcal {M}}$, and ![]() $F^+({\mathcal {N}}^+)\simeq {\mathcal {M}}$. As
$F^+({\mathcal {N}}^+)\simeq {\mathcal {M}}$. As ![]() $\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {M}}, {\mathcal {M}})= 0 = \mathop {{\rm Ext}}\nolimits ^2_X({\mathcal {M}}, {\mathcal {M}})$, we have isomorphisms
$\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {M}}, {\mathcal {M}})= 0 = \mathop {{\rm Ext}}\nolimits ^2_X({\mathcal {M}}, {\mathcal {M}})$, we have isomorphisms ![]() $\mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, (F^+F)^{-1}{\mathcal {M}}) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, Lg^*Rg_* {\mathcal {M}}[-1])$ and
$\mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, (F^+F)^{-1}{\mathcal {M}}) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, Lg^*Rg_* {\mathcal {M}}[-1])$ and ![]() $\mathop {{\rm Hom}}\nolimits _X((F^+F)^{-1}{\mathcal {M}}, {\mathcal {M}}) \simeq \mathop {{\rm Hom}}\nolimits _X(Lg^*Rg_* {\mathcal {M}}[-1], {\mathcal {M}})$. Thus, a morphism
$\mathop {{\rm Hom}}\nolimits _X((F^+F)^{-1}{\mathcal {M}}, {\mathcal {M}}) \simeq \mathop {{\rm Hom}}\nolimits _X(Lg^*Rg_* {\mathcal {M}}[-1], {\mathcal {M}})$. Thus, a morphism ![]() ${\mathcal {M}}\to {\mathcal {M}}$ is decomposed as
${\mathcal {M}}\to {\mathcal {M}}$ is decomposed as ![]() ${\mathcal {M}} \to (F^+F)^{-1}{\mathcal {M}} \to {\mathcal {M}}$ if an only if it is decomposed as
${\mathcal {M}} \to (F^+F)^{-1}{\mathcal {M}} \to {\mathcal {M}}$ if an only if it is decomposed as ![]() ${\mathcal {M}} \to Lg^*Rg_* {\mathcal {M}}[-1] \to {\mathcal {M}}$. By Lemma 3.14, object
${\mathcal {M}} \to Lg^*Rg_* {\mathcal {M}}[-1] \to {\mathcal {M}}$. By Lemma 3.14, object ![]() $Lg^*Rg_* {\mathcal {M}}$ is quasi-isomorphic to a complex
$Lg^*Rg_* {\mathcal {M}}$ is quasi-isomorphic to a complex ![]() $\{{\mathcal {O}}_X^S \to {\mathcal {O}}_X^S\}$, for some
$\{{\mathcal {O}}_X^S \to {\mathcal {O}}_X^S\}$, for some ![]() $S\in \mathbb {Z}_+$. Thus, ‘stupid’ truncation gives an exact triangle
$S\in \mathbb {Z}_+$. Thus, ‘stupid’ truncation gives an exact triangle
As ![]() $\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {O}}_X^S, {\mathcal {M}}) = 0 = \mathop {{\rm Ext}}\nolimits ^2_X({\mathcal {O}}_X^S, {\mathcal {M}})$, we have
$\mathop {{\rm Ext}}\nolimits ^1_X({\mathcal {O}}_X^S, {\mathcal {M}}) = 0 = \mathop {{\rm Ext}}\nolimits ^2_X({\mathcal {O}}_X^S, {\mathcal {M}})$, we have ![]() $\mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, Lg^*Rg_*{\mathcal {M}}[-1]) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, {\mathcal {O}}_X^S)$ and
$\mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, Lg^*Rg_*{\mathcal {M}}[-1]) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {M}}, {\mathcal {O}}_X^S)$ and ![]() $\mathop {{\rm Hom}}\nolimits _X(Lg^*Rg_* {\mathcal {M}}[-1], {\mathcal {M}}) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {O}}_X^S, {\mathcal {M}})$. Hence, a morphism
$\mathop {{\rm Hom}}\nolimits _X(Lg^*Rg_* {\mathcal {M}}[-1], {\mathcal {M}}) \simeq \mathop {{\rm Hom}}\nolimits _X({\mathcal {O}}_X^S, {\mathcal {M}})$. Hence, a morphism ![]() ${\mathcal {M}} \to {\mathcal {M}}$ factors via
${\mathcal {M}} \to {\mathcal {M}}$ factors via ![]() $Lg^*Rg_* {\mathcal {M}}[-1]$ if and only if it factors via
$Lg^*Rg_* {\mathcal {M}}[-1]$ if and only if it factors via ![]() ${\mathcal {O}}_X^S$.
${\mathcal {O}}_X^S$.
Therefore, the image of ![]() $\psi$ is contained in the space of morphisms
$\psi$ is contained in the space of morphisms ![]() ${\mathcal {M}} \to {\mathcal {M}}$ that factor via
${\mathcal {M}} \to {\mathcal {M}}$ that factor via ![]() ${\mathcal {O}}_X^S$. Conversely, for a projective generator
${\mathcal {O}}_X^S$. Conversely, for a projective generator ![]() ${\mathcal {P}}$ of
${\mathcal {P}}$ of ![]() $\mathscr {A}_f$,
$\mathscr {A}_f$,
 \begin{align*} R\mathop{{\rm Hom}}\nolimits_{{\mathcal{D}}^b(\mathscr{A}_f)}(\Psi^!{\mathcal{M}}, \Psi^!{\mathcal{O}}_X) &\simeq R\mathop{{\rm Hom}}\nolimits_{{\mathcal{D}}^b(\mathscr{A}_f)}({\mathcal{P}}, \Psi^!{\mathcal{O}}_X[2]) \simeq R\mathop{{\rm Hom}}\nolimits_X(\Psi{\mathcal{P}}, {\mathcal{O}}_X[2]) \\ &\simeq R\mathop{{\rm Hom}}\nolimits_X(\Psi{\mathcal{P}}, f^! {\mathcal{O}}_Y[2]) \simeq R\mathop{{\rm Hom}}\nolimits_Y(Rf_* \Psi {\mathcal{P}}, {\mathcal{O}}_Y[2]) = 0, \end{align*}
\begin{align*} R\mathop{{\rm Hom}}\nolimits_{{\mathcal{D}}^b(\mathscr{A}_f)}(\Psi^!{\mathcal{M}}, \Psi^!{\mathcal{O}}_X) &\simeq R\mathop{{\rm Hom}}\nolimits_{{\mathcal{D}}^b(\mathscr{A}_f)}({\mathcal{P}}, \Psi^!{\mathcal{O}}_X[2]) \simeq R\mathop{{\rm Hom}}\nolimits_X(\Psi{\mathcal{P}}, {\mathcal{O}}_X[2]) \\ &\simeq R\mathop{{\rm Hom}}\nolimits_X(\Psi{\mathcal{P}}, f^! {\mathcal{O}}_Y[2]) \simeq R\mathop{{\rm Hom}}\nolimits_Y(Rf_* \Psi {\mathcal{P}}, {\mathcal{O}}_Y[2]) = 0, \end{align*}
which implies that the space of morphisms ![]() ${\mathcal {M}} \to {\mathcal {M}}$ that factor via direct sums of copies of
${\mathcal {M}} \to {\mathcal {M}}$ that factor via direct sums of copies of ![]() ${\mathcal {O}}_X$ is annihilated by
${\mathcal {O}}_X$ is annihilated by ![]() $\Psi ^!$, i.e. it is contained in the kernel of
$\Psi ^!$, i.e. it is contained in the kernel of ![]() $\varphi$.
$\varphi$.
Acknowledgements
We are indebted to Pieter Belmans, Chris Brav, Alexander Efimov, Mikhail Kapranov, Yujiro Kawamata, Alexander Kuznetsov, Timothy Logvinenko, Valery Lunts, Yuri Prokhorov, Łukasz Sienkiewicz, Greg Stevenson, Michel Van den Bergh and Maciej Zdanowicz for useful discussions. We also thank the anonymous referees for their comments and remarks which helped us to improve the text. The first named author would like to thank Kavli IPMU for their hospitality. The first named author was partially supported by Polish National Science Centre grants DEC-2013/11/N/ST1/03208, 2012/07/B/ST1/03343, 2018/31/D/ST1/03375, and 2018/29/B/ST1/01232. The reported study was funded by RFBR and CNRS, project number 21-51-15005. The work of A. I. Bondal was performed at the Steklov International Mathematical Center and supported by the Ministry of Science and Higher Education of the Russian Federation (agreement no. 075-15-2022-265). This research was partially supported by World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan. This work was supported by JSPS KAKENHI grant number JP20H01794.
Appendix A. Grothendieck duality and the twisted inverse image functor
Let ![]() $f\colon X \to Y$ be a proper morphism of Noetherian schemes. The direct image functor
$f\colon X \to Y$ be a proper morphism of Noetherian schemes. The direct image functor ![]() $Rf_*$, considered as a functor
$Rf_*$, considered as a functor ![]() ${\mathcal {D}}_{{\rm qc}}(X)\to {\mathcal {D}}_{{\rm qc}}(Y)$, admits the right adjoint denoted by
${\mathcal {D}}_{{\rm qc}}(X)\to {\mathcal {D}}_{{\rm qc}}(Y)$, admits the right adjoint denoted by ![]() $f^!$. Functor
$f^!$. Functor ![]() $f^!$ maps
$f^!$ maps ![]() $D^{+}_{\rm qc}(Y)$ to
$D^{+}_{\rm qc}(Y)$ to ![]() $D^{+}_{{\rm qc}}(X)$ and, for any
$D^{+}_{{\rm qc}}(X)$ and, for any ![]() $E^{\boldsymbol {\cdot }}\in {\mathcal {D}}_{{\rm qc}}(X)$ and
$E^{\boldsymbol {\cdot }}\in {\mathcal {D}}_{{\rm qc}}(X)$ and ![]() $F^{\boldsymbol {\cdot }}\in {\mathcal {D}}^{+}_{{\rm qc}}(Y)$, the sheafified Grothendieck duality
$F^{\boldsymbol {\cdot }}\in {\mathcal {D}}^{+}_{{\rm qc}}(Y)$, the sheafified Grothendieck duality
is satisfied, see [Reference Lipman and HashimotoLH09, Corollary 4.2.2].
We construct a morphism ![]() $\alpha \colon Lf^*(-) \otimes f^!({\mathcal {O}}_Y) \rightarrow f^!(-)$. In view of adjunction
$\alpha \colon Lf^*(-) \otimes f^!({\mathcal {O}}_Y) \rightarrow f^!(-)$. In view of adjunction
constructing ![]() $\alpha _{F^{\boldsymbol {\cdot }}}$ is equivalent to finding a morphism
$\alpha _{F^{\boldsymbol {\cdot }}}$ is equivalent to finding a morphism ![]() $Rf_*(Lf^*(F^{\boldsymbol {\cdot }})\otimes f^!({\mathcal {O}}_Y)) \to F^{\boldsymbol {\cdot }}$. By projection formula, we have
$Rf_*(Lf^*(F^{\boldsymbol {\cdot }})\otimes f^!({\mathcal {O}}_Y)) \to F^{\boldsymbol {\cdot }}$. By projection formula, we have
Let ![]() $\varepsilon \colon Rf_* f^!({\mathcal {O}}_Y)\to {\mathcal {O}}_Y$ be the counit of adjunction. Then morphism
$\varepsilon \colon Rf_* f^!({\mathcal {O}}_Y)\to {\mathcal {O}}_Y$ be the counit of adjunction. Then morphism
gives a morphism
Lemma A.1 Let ![]() $f\colon X \to Y$ be a proper morphism. Then
$f\colon X \to Y$ be a proper morphism. Then ![]() $\alpha _{F^{\boldsymbol {\cdot }}}$ is an isomorphism for
$\alpha _{F^{\boldsymbol {\cdot }}}$ is an isomorphism for ![]() $F^{\boldsymbol {\cdot }} \in \mathop {{\rm Perf}}\nolimits (Y)$.
$F^{\boldsymbol {\cdot }} \in \mathop {{\rm Perf}}\nolimits (Y)$.
Proof. Morphism ![]() $\alpha _{{\mathcal {O}}_Y}$ is clearly an isomorphism. By Deligne's appendix to [Reference HartshorneHar66], functor
$\alpha _{{\mathcal {O}}_Y}$ is clearly an isomorphism. By Deligne's appendix to [Reference HartshorneHar66], functor ![]() $f^!$ is defined locally on
$f^!$ is defined locally on ![]() $Y$, hence
$Y$, hence ![]() $\alpha$ is also an isomorphism for any complex
$\alpha$ is also an isomorphism for any complex ![]() $F^{\boldsymbol {\cdot }}$ which is locally quasi-isomorphic to a complex of locally free sheaves, i.e. for
$F^{\boldsymbol {\cdot }}$ which is locally quasi-isomorphic to a complex of locally free sheaves, i.e. for ![]() $F^{\boldsymbol {\cdot }}\in \mathop {{\rm Perf}}\nolimits (Y)$.
$F^{\boldsymbol {\cdot }}\in \mathop {{\rm Perf}}\nolimits (Y)$.
By [Reference Lipman and HashimotoLH09, § 4.7], morphism ![]() $Lf^*(F^{\boldsymbol {\cdot }}) \otimes f^!({\mathcal {O}}_Y) \to f^!(F^{\boldsymbol {\cdot }})$ is an isomorphism for all
$Lf^*(F^{\boldsymbol {\cdot }}) \otimes f^!({\mathcal {O}}_Y) \to f^!(F^{\boldsymbol {\cdot }})$ is an isomorphism for all ![]() $F^{\boldsymbol {\cdot }}$ in
$F^{\boldsymbol {\cdot }}$ in ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$ if and only if
${\mathcal {D}}_{{\rm qc}}(Y)$ if and only if ![]() $f$ is proper and of finite Tor dimension.
$f$ is proper and of finite Tor dimension.
Appendix B. Functorial exact triangles, spherical functors and pairs
Let ![]() ${\mathcal {C}}$ and
${\mathcal {C}}$ and ![]() ${\mathcal {D}}$ be triangulated categories. The category of exact functors
${\mathcal {D}}$ be triangulated categories. The category of exact functors ![]() ${\mathcal {C}}\to {\mathcal {D}}$ is not triangulated, thus we cannot speak about exact triangles of functors. Instead, we work with a weaker notion of a functorial exact triangle by which we mean a triple of exact functors
${\mathcal {C}}\to {\mathcal {D}}$ is not triangulated, thus we cannot speak about exact triangles of functors. Instead, we work with a weaker notion of a functorial exact triangle by which we mean a triple of exact functors ![]() ${\mathcal {C}} \to {\mathcal {D}}$ and natural transformations between them
${\mathcal {C}} \to {\mathcal {D}}$ and natural transformations between them
such that when applied to any object ![]() $C\in {\mathcal {C}}$ they give an exact triangle in
$C\in {\mathcal {C}}$ they give an exact triangle in ![]() ${\mathcal {D}}$. Note that (B.1) is not an exact triangle in any triangulated category.
${\mathcal {D}}$. Note that (B.1) is not an exact triangle in any triangulated category.
A basic example of a functorial exact triangle is given by an SOD
Denote by ![]() $i_{{\mathcal {A}}}\colon {\mathcal {A}}\to {\mathcal {D}}$ the embedding functor and by
$i_{{\mathcal {A}}}\colon {\mathcal {A}}\to {\mathcal {D}}$ the embedding functor and by ![]() $i_{{\mathcal {A}}}^*$ its left adjoint. Similarly, let
$i_{{\mathcal {A}}}^*$ its left adjoint. Similarly, let ![]() $i_{{\mathcal {B}}}\colon {\mathcal {B}} \to {\mathcal {D}}$ be the embedding and
$i_{{\mathcal {B}}}\colon {\mathcal {B}} \to {\mathcal {D}}$ be the embedding and ![]() $i_{{\mathcal {B}}}^!$ its right adjoint. Then the
$i_{{\mathcal {B}}}^!$ its right adjoint. Then the ![]() $i_{{\mathcal {A}}}^*\dashv i_{{\mathcal {A}}}$ adjunction unit
$i_{{\mathcal {A}}}^*\dashv i_{{\mathcal {A}}}$ adjunction unit ![]() $\eta$ and the
$\eta$ and the ![]() $i_{{\mathcal {B}}}^!\dashv i_{{\mathcal {B}}}$ adjunction counit
$i_{{\mathcal {B}}}^!\dashv i_{{\mathcal {B}}}$ adjunction counit ![]() $\varepsilon$ fit into a functorial exact triangle [Reference BondalBon89]:
$\varepsilon$ fit into a functorial exact triangle [Reference BondalBon89]:
Consider a general adjoint pair ![]() $F\dashv F^!$ of exact functors with
$F\dashv F^!$ of exact functors with ![]() $F\colon {\mathcal {C}}\to {\mathcal {D}}$. If the adjunction counit
$F\colon {\mathcal {C}}\to {\mathcal {D}}$. If the adjunction counit ![]() $\varepsilon$ fits into a functorial exact triangle
$\varepsilon$ fits into a functorial exact triangle
we refer to ![]() $T$ as a twist functor. If the adjunction unit
$T$ as a twist functor. If the adjunction unit ![]() $\eta$ fits into a functorial exact triangle
$\eta$ fits into a functorial exact triangle
we refer to ![]() $C$ as a cotwist functor.
$C$ as a cotwist functor.
Constructions and uniqueness of twist and cotwist functors are discussed in details in § C.4 in the framework of 2-categories. Let us briefly say that twist and cotwist are well-defined if ![]() $F$ is a functor
$F$ is a functor ![]() ${\mathcal {D}}(A)\to {\mathcal {D}}(B)$, for some DG algebras
${\mathcal {D}}(A)\to {\mathcal {D}}(B)$, for some DG algebras ![]() $A$ and
$A$ and ![]() $B$, given by the tensor product with an
$B$, given by the tensor product with an ![]() $A^{\mathop {{\rm op}}\nolimits }\otimes B$ DG bimodule and both of his adjoints are of this form too. If
$A^{\mathop {{\rm op}}\nolimits }\otimes B$ DG bimodule and both of his adjoints are of this form too. If ![]() $F$ satisfies this condition, we say that it is an
$F$ satisfies this condition, we say that it is an ![]() $A$ and
$A$ and ![]() $B$ perfect bimodule functor. Indeed, in this case the bimodule defining
$B$ perfect bimodule functor. Indeed, in this case the bimodule defining ![]() $F$ is perfect as an
$F$ is perfect as an ![]() $A$ and
$A$ and ![]() $B$ module, cf. Proposition C.6. Once the bimodule corresponding to
$B$ module, cf. Proposition C.6. Once the bimodule corresponding to ![]() $F$ is fixed, the twist
$F$ is fixed, the twist ![]() $T$ and the cotwist
$T$ and the cotwist ![]() $C$ are defined uniquely up to isomorphisms.
$C$ are defined uniquely up to isomorphisms.
Consider an ![]() $A$ and
$A$ and ![]() $B$ perfect bimodule functor
$B$ perfect bimodule functor ![]() $F\colon {\mathcal {D}}(A)\to {\mathcal {D}}(B)$. Here
$F\colon {\mathcal {D}}(A)\to {\mathcal {D}}(B)$. Here ![]() $F$ is spherical [Reference Anno and LogvinenkoAL17] if it admits both adjoints
$F$ is spherical [Reference Anno and LogvinenkoAL17] if it admits both adjoints ![]() $F^*\dashv F \dashv F^!$ and the twist
$F^*\dashv F \dashv F^!$ and the twist ![]() $T$ and the cotwist
$T$ and the cotwist ![]() $C$ are both equivalences. If this is the case we refer to
$C$ are both equivalences. If this is the case we refer to ![]() $T$ as a spherical twist and to
$T$ as a spherical twist and to ![]() $C$ as a spherical cotwist.
$C$ as a spherical cotwist.
By [Reference Anno and LogvinenkoAL17], a functor ![]() $F$ is spherical if and only if the dual twist
$F$ is spherical if and only if the dual twist ![]() $T'$ and the dual cotwist
$T'$ and the dual cotwist ![]() $C'$ are equivalences, where
$C'$ are equivalences, where ![]() $T'$ and
$T'$ and ![]() $C'$ are functors which fit into functorial exact triangles
$C'$ are functors which fit into functorial exact triangles
for the ![]() $F^*\dashv F$ adjunction unit
$F^*\dashv F$ adjunction unit ![]() $\eta '$ and counit
$\eta '$ and counit ![]() $\varepsilon '$.
$\varepsilon '$.
Spherical functors can be constructed via spherical pairs. We recall the definition following [Reference Kapranov and SchechtmanKS14]. Let ![]() ${\mathcal {E}}$ be a triangulated category and
${\mathcal {E}}$ be a triangulated category and ![]() ${\mathcal {E}}_+, {\mathcal {E}}_- \subset {\mathcal {E}}$ a pair of admissible subcategories [Reference BondalBon89]. Let
${\mathcal {E}}_+, {\mathcal {E}}_- \subset {\mathcal {E}}$ a pair of admissible subcategories [Reference BondalBon89]. Let ![]() $i_{\pm }\colon {\mathcal {E}}_{\pm } \to {\mathcal {E}}$ be the inclusions. They admit left
$i_{\pm }\colon {\mathcal {E}}_{\pm } \to {\mathcal {E}}$ be the inclusions. They admit left ![]() $i_{\pm }^*$ and right
$i_{\pm }^*$ and right ![]() $i_{\pm }^!$ adjoint functors
$i_{\pm }^!$ adjoint functors ![]() ${\mathcal {E}}\to {\mathcal {E}}_{\pm }$. By
${\mathcal {E}}\to {\mathcal {E}}_{\pm }$. By ![]() $j_{\pm } \colon {}^\perp {\mathcal {E}}_{\pm } \to {\mathcal {E}}$ we denote the inclusions of the left orthogonal complements and by
$j_{\pm } \colon {}^\perp {\mathcal {E}}_{\pm } \to {\mathcal {E}}$ we denote the inclusions of the left orthogonal complements and by ![]() $j_{\pm }^! \colon {\mathcal {E}}\to {}^\perp {\mathcal {E}}_{\pm }$ their right adjoints. We assume that all these functors are induced by appropriate DG functors.
$j_{\pm }^! \colon {\mathcal {E}}\to {}^\perp {\mathcal {E}}_{\pm }$ their right adjoints. We assume that all these functors are induced by appropriate DG functors.
Definition B.1 [Reference Kapranov and SchechtmanKS14, Definition 3.4]
The pair ![]() $({\mathcal {E}}_{+}, {\mathcal {E}}_-)$ of admissible subcategories is a spherical pair if
$({\mathcal {E}}_{+}, {\mathcal {E}}_-)$ of admissible subcategories is a spherical pair if
(i) the composites
 $i_+^* i_- \colon {\mathcal {E}}_- \to {\mathcal {E}}_+$,
$i_+^* i_- \colon {\mathcal {E}}_- \to {\mathcal {E}}_+$,  $i_-^* i_+ \colon {\mathcal {E}}_+ \to {\mathcal {E}}_-$ are equivalences;
$i_-^* i_+ \colon {\mathcal {E}}_+ \to {\mathcal {E}}_-$ are equivalences;(ii) the composites
 $j_+^!j_- \colon {}^\perp {\mathcal {E}}_- \to {}^\perp {\mathcal {E}}_+$,
$j_+^!j_- \colon {}^\perp {\mathcal {E}}_- \to {}^\perp {\mathcal {E}}_+$,  $j_-^!j_+ \colon {}^\perp {\mathcal {E}}_+ \to {}^\perp {\mathcal {E}}_-$ are equivalences.
$j_-^!j_+ \colon {}^\perp {\mathcal {E}}_+ \to {}^\perp {\mathcal {E}}_-$ are equivalences.
Proposition B.2 [Reference Kapranov and SchechtmanKS14, Propositions 3.6, 3.7]
Let ![]() $({\mathcal {E}}_{+}, {\mathcal {E}}_-) \subset {\mathcal {E}}$ be a spherical pair. Then functor
$({\mathcal {E}}_{+}, {\mathcal {E}}_-) \subset {\mathcal {E}}$ be a spherical pair. Then functor ![]() $\Psi := j_-^! i_+ \colon {\mathcal {E}}_+ \to {}^{\perp }{\mathcal {E}}_-$ is spherical. The unit and the counit for the
$\Psi := j_-^! i_+ \colon {\mathcal {E}}_+ \to {}^{\perp }{\mathcal {E}}_-$ is spherical. The unit and the counit for the ![]() $\Psi ^*\dashv \Psi$ adjunction fit into functorial exact triangles:
$\Psi ^*\dashv \Psi$ adjunction fit into functorial exact triangles:
The functorial exact triangles (B.3) are deduced from functorial exact triangles (B.2) for the SODs related to (admissible subcategories) ![]() ${\mathcal {E}}_+$ and
${\mathcal {E}}_+$ and ![]() ${\mathcal {E}}_-$. Therefore, in the presence of spherical pairs, one can define spherical functors purely in the realm of triangulated categories.
${\mathcal {E}}_-$. Therefore, in the presence of spherical pairs, one can define spherical functors purely in the realm of triangulated categories.
With the following proposition we describe spherical pairs associated to 4-periodical SODs
Proposition B.3 Let ![]() ${\mathcal {T}}$ be a triangulated category with 4-periodical SODs (B.4). Then pairs
${\mathcal {T}}$ be a triangulated category with 4-periodical SODs (B.4). Then pairs ![]() $({\mathcal {A}}, {\mathcal {C}})$,
$({\mathcal {A}}, {\mathcal {C}})$, ![]() $({\mathcal {B}}, {\mathcal {D}})$ of subcategories of
$({\mathcal {B}}, {\mathcal {D}})$ of subcategories of ![]() ${\mathcal {T}}$ are spherical.
${\mathcal {T}}$ are spherical.
Proof. We prove that ![]() $({\mathcal {A}}, {\mathcal {C}})$ is a spherical pair. Let
$({\mathcal {A}}, {\mathcal {C}})$ is a spherical pair. Let ![]() $i_{\mathcal {A}} \colon {\mathcal {A}} \to {\mathcal {T}}$ denote the inclusion functor and
$i_{\mathcal {A}} \colon {\mathcal {A}} \to {\mathcal {T}}$ denote the inclusion functor and ![]() $i_{\mathcal {A}}^*$ its left adjoint, similarly for
$i_{\mathcal {A}}^*$ its left adjoint, similarly for ![]() ${\mathcal {C}} \subset {\mathcal {T}}$. The composite
${\mathcal {C}} \subset {\mathcal {T}}$. The composite ![]() $i_{\mathcal {C}}^* i_{{\mathcal {A}}}\colon {\mathcal {A}} \to {\mathcal {C}}$ is the right mutation over
$i_{\mathcal {C}}^* i_{{\mathcal {A}}}\colon {\mathcal {A}} \to {\mathcal {C}}$ is the right mutation over ![]() ${\mathcal {B}}$, hence it is an equivalence [Reference Bondal and KapranovBK89, Lemma 1.9]. Similarly, the right mutation
${\mathcal {B}}$, hence it is an equivalence [Reference Bondal and KapranovBK89, Lemma 1.9]. Similarly, the right mutation ![]() $i_{\mathcal {A}}^* i_{\mathcal {C}}$ over
$i_{\mathcal {A}}^* i_{\mathcal {C}}$ over ![]() ${\mathcal {D}}$ is an equivalence, (i), the first condition of Definition B.1 is satisfied.
${\mathcal {D}}$ is an equivalence, (i), the first condition of Definition B.1 is satisfied.
Now let ![]() $i_{\mathcal {B}} \colon {\mathcal {B}}\to {\mathcal {T}}$ denote the inclusion functor and
$i_{\mathcal {B}} \colon {\mathcal {B}}\to {\mathcal {T}}$ denote the inclusion functor and ![]() $i_{\mathcal {B}}^! \colon {\mathcal {T}}\to {\mathcal {B}}$ its right adjoint, similarly for
$i_{\mathcal {B}}^! \colon {\mathcal {T}}\to {\mathcal {B}}$ its right adjoint, similarly for ![]() ${\mathcal {D}} \subset {\mathcal {T}}$. The composites
${\mathcal {D}} \subset {\mathcal {T}}$. The composites ![]() $i_{{\mathcal {B}}}^! i_{\mathcal {D}}$, respectively
$i_{{\mathcal {B}}}^! i_{\mathcal {D}}$, respectively ![]() $i_{\mathcal {D}}^! i_{\mathcal {B}}$, are the left mutations over
$i_{\mathcal {D}}^! i_{\mathcal {B}}$, are the left mutations over ![]() ${\mathcal {C}}$, respectively
${\mathcal {C}}$, respectively ![]() ${\mathcal {A}}$, hence they are equivalences. It follows that
${\mathcal {A}}$, hence they are equivalences. It follows that ![]() $({\mathcal {A}}, {\mathcal {C}})$ is a spherical pair in
$({\mathcal {A}}, {\mathcal {C}})$ is a spherical pair in ![]() ${\mathcal {T}}$. The proof for the pair
${\mathcal {T}}$. The proof for the pair ![]() $({\mathcal {B}}, {\mathcal {D}})$ is analogous.
$({\mathcal {B}}, {\mathcal {D}})$ is analogous.
Remark B.4 In [Reference Halpern-Leistner and ShipmanHS16, Theorem 3.11], Halpern-Leistner and Shipman proved that any spherical functor ![]() $F\colon {\mathcal {C}}\to {\mathcal {D}}$ is given by 4-periodical SODs.
$F\colon {\mathcal {C}}\to {\mathcal {D}}$ is given by 4-periodical SODs.
Appendix C. Lifting to the bicategory  ${\rm Bimod}$
${\rm Bimod}$
Let ![]() $k$ be a field. For a
$k$ be a field. For a ![]() $k$-linear DG category
$k$-linear DG category ![]() ${\mathcal {E}}$, we denote by
${\mathcal {E}}$, we denote by ![]() $[{\mathcal {E}} ]$ the homotopy category of
$[{\mathcal {E}} ]$ the homotopy category of ![]() ${\mathcal {E}}$, i.e. the category with the same objects as in
${\mathcal {E}}$, i.e. the category with the same objects as in ![]() ${\mathcal {E}}$ and morphisms the zeroth cohomology of the DG complexes of morphisms in
${\mathcal {E}}$ and morphisms the zeroth cohomology of the DG complexes of morphisms in ![]() ${\mathcal {E}}$ (see [Reference Bondal and KapranovBK90]). It is an ordinary
${\mathcal {E}}$ (see [Reference Bondal and KapranovBK90]). It is an ordinary ![]() $k$-linear category.
$k$-linear category.
By a DG enhancement of a triangulated category ![]() ${\mathcal {C}}$ we mean a choice of a pre-triangulated DG category
${\mathcal {C}}$ we mean a choice of a pre-triangulated DG category ![]() ${\mathcal {E}}$ together with an equivalence
${\mathcal {E}}$ together with an equivalence ![]() ${\mathcal {C}} \simeq [{\mathcal {E}} ]$ which is compatible with the induced triangulated structure on
${\mathcal {C}} \simeq [{\mathcal {E}} ]$ which is compatible with the induced triangulated structure on ![]() $[{\mathcal {E}} ]$ (see [Reference Bondal and KapranovBK90]). A choice of suitable DG enhancements for our categories prompts a convenient replacement for the category of functors, as well as a lift of adjunction (co)units to morphisms in this replacement. This allows us to get an interpretation for ‘cones’ of morphisms of functors that we need in the main body of the text.
$[{\mathcal {E}} ]$ (see [Reference Bondal and KapranovBK90]). A choice of suitable DG enhancements for our categories prompts a convenient replacement for the category of functors, as well as a lift of adjunction (co)units to morphisms in this replacement. This allows us to get an interpretation for ‘cones’ of morphisms of functors that we need in the main body of the text.
For the sake of simplicity, we take as DG enhancements of our categories only suitable categories of DG modules over DG algebras. The category of functors is replaced by the derived category of bimodules, and natural transformations by morphisms in the latter category. As a result we arrive at the bicategory ![]() $\mathop {\textbf {Bimod}}\nolimits$ whose objects are DG algebras and 1-morphisms are objects of the derived categories of DG bimodules. There is (after a suitable choice of universe) a bifunctor
$\mathop {\textbf {Bimod}}\nolimits$ whose objects are DG algebras and 1-morphisms are objects of the derived categories of DG bimodules. There is (after a suitable choice of universe) a bifunctor ![]() $\Phi :\mathop {\textbf {Bimod}}\nolimits \to \textbf {Cat}$ to the 2-category of categories. We are interested in lifting of adjoint pairs of functors in
$\Phi :\mathop {\textbf {Bimod}}\nolimits \to \textbf {Cat}$ to the 2-category of categories. We are interested in lifting of adjoint pairs of functors in ![]() $\textbf {Cat}$ along the functor
$\textbf {Cat}$ along the functor ![]() $\Phi$.
$\Phi$.
In the general framework of 2-categories (or bicategories), we have the uniqueness of the 2-categorical adjunction for a given 1-morphism. In addition, we show that 2-adjunctions can be transported over equivalences of objects in 2-categories, which implies an invariance of 2-categorical adjunctions in ![]() $\mathop {\textbf {Bimod}}\nolimits$ under the choice of DG enhancements.
$\mathop {\textbf {Bimod}}\nolimits$ under the choice of DG enhancements.
By fixing a lift of a functor to a 1-morphism in ![]() $\mathop {\textbf {Bimod}}\nolimits$, we get an essentially unique 2-categorical adjunction. This allows us to define a unique twist and cotwist of 2-categorical adjunctions as 1-morphisms in
$\mathop {\textbf {Bimod}}\nolimits$, we get an essentially unique 2-categorical adjunction. This allows us to define a unique twist and cotwist of 2-categorical adjunctions as 1-morphisms in ![]() $\mathop {\textbf {Bimod}}\nolimits$, thus interpreting constructions of Anno and Logvinenko [Reference Anno and LogvinenkoAL17]. In particular, we have the notion of spherical twists for spherical functors and, slightly more generally, for spherical couples.
$\mathop {\textbf {Bimod}}\nolimits$, thus interpreting constructions of Anno and Logvinenko [Reference Anno and LogvinenkoAL17]. In particular, we have the notion of spherical twists for spherical functors and, slightly more generally, for spherical couples.
Further we show how the 2-adjunction theory can be applied to functors between derived categories of (quasi-)coherent sheaves. Here another suitable 2-category is the category ![]() $\mathop {\textbf {FM}}\nolimits$ whose objects are schemes and 1-morphisms are objects of the derived category of the product of two schemes. By the results of Lunts and Schnürer [Reference Lunts and SchnürerLS16] the 2-categorical adjunctions, twists and cotwists are readily transferred to this context. We discuss uniqueness of the functorial exact triangles associated to an FM functor and its adjoints. We also construct a 2-categorical lift to
$\mathop {\textbf {FM}}\nolimits$ whose objects are schemes and 1-morphisms are objects of the derived category of the product of two schemes. By the results of Lunts and Schnürer [Reference Lunts and SchnürerLS16] the 2-categorical adjunctions, twists and cotwists are readily transferred to this context. We discuss uniqueness of the functorial exact triangles associated to an FM functor and its adjoints. We also construct a 2-categorical lift to ![]() $\mathop {\textbf {Bimod}}\nolimits$ of the base-change morphism.
$\mathop {\textbf {Bimod}}\nolimits$ of the base-change morphism.
Finally, we provide a criterion for isomorphism of functors in terms of the restriction to one (generating) object.
C.1 Abstract 2-categorical adjunctions and spherical couples
Let ![]() ${\mathcal {C}}$ be a (strict) 2-category. A quadruple
${\mathcal {C}}$ be a (strict) 2-category. A quadruple ![]() $(s,r, \eta, \varepsilon )$ of 1-morphisms
$(s,r, \eta, \varepsilon )$ of 1-morphisms ![]() $s\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,B)$,
$s\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,B)$, ![]() $r\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,A)$ and 2-morphisms
$r\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,A)$ and 2-morphisms ![]() $\eta \colon \mathop {{\rm Id}}\nolimits _A \to rs$,
$\eta \colon \mathop {{\rm Id}}\nolimits _A \to rs$, ![]() $\varepsilon \colon sr \to \mathop {{\rm Id}}\nolimits _B$ is a 2-categorical
$\varepsilon \colon sr \to \mathop {{\rm Id}}\nolimits _B$ is a 2-categorical ![]() $(A,B)$- adjunction if
$(A,B)$- adjunction if
are equal to the identity morphisms of ![]() $s$ and
$s$ and ![]() $r$, respectively. In this case,
$r$, respectively. In this case, ![]() $r$ is said to be a right 2-categorical adjoint of
$r$ is said to be a right 2-categorical adjoint of ![]() $s$,
$s$, ![]() $s$ a left 2-categorical adjoint of
$s$ a left 2-categorical adjoint of ![]() $r$ and
$r$ and ![]() $\eta$ and
$\eta$ and ![]() $\varepsilon$ the unit and counit of the adjunction. We write
$\varepsilon$ the unit and counit of the adjunction. We write ![]() $s\dashv r$ if there exist
$s\dashv r$ if there exist ![]() $\eta$ and
$\eta$ and ![]() $\varepsilon$ such that
$\varepsilon$ such that ![]() $(s,r,\eta, \varepsilon )$ is a 2-categorical adjunction. The choice of such
$(s,r,\eta, \varepsilon )$ is a 2-categorical adjunction. The choice of such ![]() $\eta$ and
$\eta$ and ![]() $\varepsilon$ is not unique.
$\varepsilon$ is not unique.
The proof of the following fact is standard.
Lemma C.1 (Cf. [Reference BénabouBén65, Reference Toën and VezzosiTV15])
Let ![]() $s$ be a 1-morphism. If
$s$ be a 1-morphism. If ![]() $s$ has a right 2-categorical adjoint, then the 2-categorical adjunction
$s$ has a right 2-categorical adjoint, then the 2-categorical adjunction ![]() $(s,r, \eta, \varepsilon )$ is unique up to a canonical 2-isomorphism. More precisely, for any other adjunction
$(s,r, \eta, \varepsilon )$ is unique up to a canonical 2-isomorphism. More precisely, for any other adjunction ![]() $(s,r', \eta ', \varepsilon ')$, the composite
$(s,r', \eta ', \varepsilon ')$, the composite ![]() $\alpha \colon r\xrightarrow {\eta 'r}r'sr \xrightarrow {r\varepsilon }r'$ is a unique 2-isomorphism commuting with the units and counits. Conversely, any 2-isomorphism
$\alpha \colon r\xrightarrow {\eta 'r}r'sr \xrightarrow {r\varepsilon }r'$ is a unique 2-isomorphism commuting with the units and counits. Conversely, any 2-isomorphism ![]() $\alpha \colon r \to r'$ yields a 2-categorical adjunction
$\alpha \colon r \to r'$ yields a 2-categorical adjunction ![]() $(s, r',\alpha s\circ \eta, \varepsilon \circ s\alpha ^{-1})$.
$(s, r',\alpha s\circ \eta, \varepsilon \circ s\alpha ^{-1})$.
An ![]() $(A,B)$-equivalence in
$(A,B)$-equivalence in ![]() ${\mathcal {C}}$ is a quadruple
${\mathcal {C}}$ is a quadruple ![]() $(f,g,\nu, \mu )$ of 1-morphisms
$(f,g,\nu, \mu )$ of 1-morphisms ![]() $f\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,B)$,
$f\in \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,B)$, ![]() $g\in \mathop {{\rm Hom}}\nolimits _{\mathcal {C}}(B,A)$ and 2-isomorphisms
$g\in \mathop {{\rm Hom}}\nolimits _{\mathcal {C}}(B,A)$ and 2-isomorphisms ![]() $\nu \colon \mathop {{\rm Id}}\nolimits _A \xrightarrow {\simeq } gf$,
$\nu \colon \mathop {{\rm Id}}\nolimits _A \xrightarrow {\simeq } gf$, ![]() $\mu \colon fg \xrightarrow {\simeq } \mathop {{\rm Id}}\nolimits _B$. It is an adjoint
$\mu \colon fg \xrightarrow {\simeq } \mathop {{\rm Id}}\nolimits _B$. It is an adjoint ![]() $(A,B)$-equivalence if
$(A,B)$-equivalence if ![]() $(f,g,\nu,\mu )$ is, in addition, a 2-categorical
$(f,g,\nu,\mu )$ is, in addition, a 2-categorical ![]() $(A,B)$-adjunction.
$(A,B)$-adjunction.
Let ![]() ${\mathcal {C}}_1$ and
${\mathcal {C}}_1$ and ![]() ${\mathcal {C}}_2$ be 2-categories. A pseudo-functor
${\mathcal {C}}_2$ be 2-categories. A pseudo-functor ![]() $\theta \colon {\mathcal {C}}_1 \to {\mathcal {C}}_2$ consists of a map
$\theta \colon {\mathcal {C}}_1 \to {\mathcal {C}}_2$ consists of a map ![]() $\theta \colon {\rm Ob}({\mathcal {C}}_1)\to {\rm Ob}({\mathcal {C}}_2)$, functors
$\theta \colon {\rm Ob}({\mathcal {C}}_1)\to {\rm Ob}({\mathcal {C}}_2)$, functors ![]() $\theta _{C,C'} \colon \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}_1}(C,C') \to \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}_2}(\theta (C), \theta (C'))$, for any pair
$\theta _{C,C'} \colon \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}_1}(C,C') \to \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}_2}(\theta (C), \theta (C'))$, for any pair ![]() $(C,C')$ of objects of
$(C,C')$ of objects of ![]() ${\mathcal {C}}_1$, and 2-isomorphisms
${\mathcal {C}}_1$, and 2-isomorphisms ![]() $u\colon \theta (\mathop {{\rm Id}}\nolimits _C) \to \mathop {{\rm Id}}\nolimits _{\theta (C)}$, for any object
$u\colon \theta (\mathop {{\rm Id}}\nolimits _C) \to \mathop {{\rm Id}}\nolimits _{\theta (C)}$, for any object ![]() $C\in {\mathcal {C}}_1$, and
$C\in {\mathcal {C}}_1$, and ![]() $a\colon \theta (g\circ f) \to \theta (g)\circ \theta (f)$, for any pair
$a\colon \theta (g\circ f) \to \theta (g)\circ \theta (f)$, for any pair ![]() $(f, g)$ of composable 1-morphisms in
$(f, g)$ of composable 1-morphisms in ![]() ${\mathcal {C}}_1$. These need to satisfy coherence conditions: for any triple
${\mathcal {C}}_1$. These need to satisfy coherence conditions: for any triple ![]() $(h, g, f)$ of composable 1-morphisms in
$(h, g, f)$ of composable 1-morphisms in ![]() ${\mathcal {C}}_1$, the two possible 2-morphisms
${\mathcal {C}}_1$, the two possible 2-morphisms ![]() $\theta (h\circ g\circ f)\to \theta (h)\circ \theta (g)\circ \theta (f)$ induced by
$\theta (h\circ g\circ f)\to \theta (h)\circ \theta (g)\circ \theta (f)$ induced by ![]() $a$ are equal, and so are the 2-morphisms
$a$ are equal, and so are the 2-morphisms ![]() $\theta (f) \to \theta (f)\circ \theta (\mathop {{\rm Id}}\nolimits )$,
$\theta (f) \to \theta (f)\circ \theta (\mathop {{\rm Id}}\nolimits )$, ![]() $\theta (g) \to \theta (\mathop {{\rm Id}}\nolimits )\circ \theta (g)$ induced by
$\theta (g) \to \theta (\mathop {{\rm Id}}\nolimits )\circ \theta (g)$ induced by ![]() $a$ and
$a$ and ![]() $u^{-1}$.
$u^{-1}$.
We say that a pseudo-functor ![]() $\theta \colon {\mathcal {C}}_1\to {\mathcal {C}}_2$ is a pseudo-equivalence if
$\theta \colon {\mathcal {C}}_1\to {\mathcal {C}}_2$ is a pseudo-equivalence if ![]() $\theta _{C_1,C_2}$ is an equivalence for all
$\theta _{C_1,C_2}$ is an equivalence for all ![]() $(C_1,C_2)\in {\mathcal {C}}_1$.
$(C_1,C_2)\in {\mathcal {C}}_1$.
Let ![]() $\alpha \colon e\to f$,
$\alpha \colon e\to f$, ![]() $\alpha '\colon e'\to f'$ be 2-morphisms in a 2-category
$\alpha '\colon e'\to f'$ be 2-morphisms in a 2-category ![]() ${\mathcal {C}}$. We say that
${\mathcal {C}}$. We say that ![]() $\alpha$ and
$\alpha$ and ![]() $\alpha '$ are isomorphic, and depict it by
$\alpha '$ are isomorphic, and depict it by ![]() $\alpha \simeq \alpha '$, if there exist isomorphisms
$\alpha \simeq \alpha '$, if there exist isomorphisms ![]() $\tau _e\colon e \xrightarrow {\simeq } e'$,
$\tau _e\colon e \xrightarrow {\simeq } e'$, ![]() $\tau _f\colon f\xrightarrow {\simeq }f'$ such that
$\tau _f\colon f\xrightarrow {\simeq }f'$ such that ![]() $\tau _f\circ \alpha = \alpha '\circ \tau _e$.
$\tau _f\circ \alpha = \alpha '\circ \tau _e$.
Lemma C.2 Let ![]() $\theta \colon {\mathcal {C}}_1 \to {\mathcal {C}}_2$ be a pseudo-functor and
$\theta \colon {\mathcal {C}}_1 \to {\mathcal {C}}_2$ be a pseudo-functor and ![]() $(s,r, \eta, \varepsilon )$ a 2-categorical
$(s,r, \eta, \varepsilon )$ a 2-categorical ![]() $(A,B)$-adjunction in
$(A,B)$-adjunction in ![]() ${\mathcal {C}}_1$. Then
${\mathcal {C}}_1$. Then ![]() $\theta (s)$ fits into a 2-categorical
$\theta (s)$ fits into a 2-categorical ![]() $(\theta (A),\theta (B))$-adjunction
$(\theta (A),\theta (B))$-adjunction ![]() $(\theta (s), \theta (r),\eta ', \varepsilon ')$ such that
$(\theta (s), \theta (r),\eta ', \varepsilon ')$ such that ![]() $\theta _{A,A}(\eta ) \simeq \eta '$,
$\theta _{A,A}(\eta ) \simeq \eta '$, ![]() $\theta _{B,B}(\varepsilon )\simeq \varepsilon '$.
$\theta _{B,B}(\varepsilon )\simeq \varepsilon '$.
Proof. A standard diagram chasing shows that for ![]() $\eta '$ and
$\eta '$ and ![]() $\varepsilon '$ defined as the composites
$\varepsilon '$ defined as the composites
 \begin{align*} & \eta'\colon \mathop{{\rm Id}}\nolimits_{\theta(A)} \xrightarrow{u^{-1}} \theta(\mathop{{\rm Id}}\nolimits_A) \xrightarrow{\theta(\eta)} \theta(rs) \xrightarrow{a} \theta(r)\theta(s),\\ &\varepsilon' \colon \theta(s)\theta(r) \xrightarrow{a^{-1}} \theta(sr)\xrightarrow{\theta(\varepsilon)} \theta(\mathop{{\rm Id}}\nolimits_B) \xrightarrow{u}\mathop{{\rm Id}}\nolimits_{\theta(B)} \end{align*}
\begin{align*} & \eta'\colon \mathop{{\rm Id}}\nolimits_{\theta(A)} \xrightarrow{u^{-1}} \theta(\mathop{{\rm Id}}\nolimits_A) \xrightarrow{\theta(\eta)} \theta(rs) \xrightarrow{a} \theta(r)\theta(s),\\ &\varepsilon' \colon \theta(s)\theta(r) \xrightarrow{a^{-1}} \theta(sr)\xrightarrow{\theta(\varepsilon)} \theta(\mathop{{\rm Id}}\nolimits_B) \xrightarrow{u}\mathop{{\rm Id}}\nolimits_{\theta(B)} \end{align*}
equalities (C.1) hold, i.e. ![]() $(\theta (s),\theta (r),\eta ', \varepsilon ')$ is a 2-categorical
$(\theta (s),\theta (r),\eta ', \varepsilon ')$ is a 2-categorical ![]() $(\theta (A), \theta (B))$-adjunction.
$(\theta (A), \theta (B))$-adjunction.
By definition of ![]() $\eta '$ and
$\eta '$ and ![]() $\varepsilon '$, diagrams
$\varepsilon '$, diagrams

commute, which proves isomorphisms ![]() $\theta _{A,A}(\eta )\simeq \eta '$ and
$\theta _{A,A}(\eta )\simeq \eta '$ and ![]() $\theta _{B,B}(\varepsilon )\simeq \varepsilon '$.
$\theta _{B,B}(\varepsilon )\simeq \varepsilon '$.
Proposition C.3 Let ![]() ${\mathcal {C}}$ be a 2-category,
${\mathcal {C}}$ be a 2-category, ![]() $(f_A,g_A, \nu _A, \mu _A)$ an
$(f_A,g_A, \nu _A, \mu _A)$ an ![]() $(A,A')$-equivalence and
$(A,A')$-equivalence and ![]() $(f_B,g_B, \nu _B, \mu _B)$ a
$(f_B,g_B, \nu _B, \mu _B)$ a ![]() $(B,B')$-equivalence in
$(B,B')$-equivalence in ![]() ${\mathcal {C}}$. Denote by
${\mathcal {C}}$. Denote by ![]() ${\mathcal {C}}_{A,B}$, respectively
${\mathcal {C}}_{A,B}$, respectively ![]() ${\mathcal {C}}_{A',B'}$, the full 2-subcategories of
${\mathcal {C}}_{A',B'}$, the full 2-subcategories of ![]() ${\mathcal {C}}$ with two objects
${\mathcal {C}}$ with two objects ![]() $A$ and
$A$ and ![]() $B$, respectively
$B$, respectively ![]() $A'$ and
$A'$ and ![]() $B'$. The four functors
$B'$. The four functors
defined for pairs ![]() $(S,T)\in \{(A,A), (A,B), (B,A), (B,B)\}$ of objects of
$(S,T)\in \{(A,A), (A,B), (B,A), (B,B)\}$ of objects of ![]() ${\mathcal {C}}_{A,B}$ and the corresponding pair
${\mathcal {C}}_{A,B}$ and the corresponding pair ![]() $(S',T')$ of objects of
$(S',T')$ of objects of ![]() ${\mathcal {C}}_{A',B'}$, can be extended to a pseudo-equivalence
${\mathcal {C}}_{A',B'}$, can be extended to a pseudo-equivalence ![]() $\theta \colon {\mathcal {C}}_{A,B} \to {\mathcal {C}}_{A',B'}$.
$\theta \colon {\mathcal {C}}_{A,B} \to {\mathcal {C}}_{A',B'}$.
Proof. By changing the 2-isomorphism ![]() $\nu _A$,
$\nu _A$, ![]() $\mu _A$,
$\mu _A$, ![]() $\nu _B$, and
$\nu _B$, and ![]() $\mu _B$ if necessary, one can assume that
$\mu _B$ if necessary, one can assume that ![]() $(f_A,g_A, \nu _A, \mu _A)$ and
$(f_A,g_A, \nu _A, \mu _A)$ and ![]() $(f_B, g_B, \nu _B, \mu _B)$ are adjoint equivalences [Reference MacLaneMac71].
$(f_B, g_B, \nu _B, \mu _B)$ are adjoint equivalences [Reference MacLaneMac71].
Functor ![]() $\theta _{S,T}$ is an equivalence with quasi-inverse
$\theta _{S,T}$ is an equivalence with quasi-inverse ![]() $g_T\circ (-)\circ f_S$. We need to define morphisms
$g_T\circ (-)\circ f_S$. We need to define morphisms ![]() $u$ and
$u$ and ![]() $a$ from the definition of pseudo-functors. The 2-isomorphisms
$a$ from the definition of pseudo-functors. The 2-isomorphisms ![]() $u$ are defined as
$u$ are defined as ![]() $\mu _A$ and
$\mu _A$ and ![]() $\mu _B$:
$\mu _B$:
For a pair ![]() $(f,g)$ of 1-morphisms such that
$(f,g)$ of 1-morphisms such that ![]() $B$ is the target of
$B$ is the target of ![]() $f$ and the source of
$f$ and the source of ![]() $g$, the 2-isomorphism
$g$, the 2-isomorphism ![]() $a$:
$a$:
where ![]() $S_f, T_g\in \{A,B\}$ are the source of
$S_f, T_g\in \{A,B\}$ are the source of ![]() $f$ and the target of
$f$ and the target of ![]() $g$, respectively. Similarly, we use
$g$, respectively. Similarly, we use ![]() $\nu _A$ if
$\nu _A$ if ![]() $A$ is the target of
$A$ is the target of ![]() $f$ and the source of
$f$ and the source of ![]() $g$.
$g$.
Equalities (C.1) for 2-adjunctions ![]() $(f_A,g_A,\nu _A,\mu _A)$ and
$(f_A,g_A,\nu _A,\mu _A)$ and ![]() $(f_B,g_B,\nu _B, \mu _B)$ imply that
$(f_B,g_B,\nu _B, \mu _B)$ imply that ![]() $u$ and
$u$ and ![]() $a$ defined in this way satisfy the required coherence conditions.
$a$ defined in this way satisfy the required coherence conditions.
We say that a 2-category ![]() ${\mathcal {C}}$ is 1-triangulated if, for any pair
${\mathcal {C}}$ is 1-triangulated if, for any pair ![]() $(B,C)$ of objects of
$(B,C)$ of objects of ![]() ${\mathcal {C}}$, the category
${\mathcal {C}}$, the category ![]() $\mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,C)$ is triangulated and, for any
$\mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,C)$ is triangulated and, for any ![]() $\varphi _A\in \mathop {{\rm Hom}}\nolimits _{\mathcal {C}}(A,B)$,
$\varphi _A\in \mathop {{\rm Hom}}\nolimits _{\mathcal {C}}(A,B)$, ![]() $\varphi _D \in \mathop {{\rm Hom}}\nolimits _{\mathcal {C}}(C,D)$, functors
$\varphi _D \in \mathop {{\rm Hom}}\nolimits _{\mathcal {C}}(C,D)$, functors ![]() $(-)\circ \varphi _A\colon \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,C) \to \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,C)$,
$(-)\circ \varphi _A\colon \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,C) \to \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(A,C)$, ![]() $\varphi _D\circ (-) \colon \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,C) \to \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,D)$ are exact.
$\varphi _D\circ (-) \colon \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,C) \to \mathop {{\rm Hom}}\nolimits _{{\mathcal {C}}}(B,D)$ are exact.
A 2-categorical ![]() $(A,B)$-adjunction
$(A,B)$-adjunction ![]() $(s,r,\eta,\varepsilon )$ in a 1-triangulated 2-category
$(s,r,\eta,\varepsilon )$ in a 1-triangulated 2-category ![]() ${\mathcal {C}}$ induces 1-endomorphisms
${\mathcal {C}}$ induces 1-endomorphisms ![]() $c_s$,
$c_s$, ![]() $t_s$ defined via exact triangles:
$t_s$ defined via exact triangles:
We say that ![]() $t_s$ is the twist and
$t_s$ is the twist and ![]() $c_s$ the cotwist for the 2-categorical adjunction
$c_s$ the cotwist for the 2-categorical adjunction ![]() $(s,r,\eta, \varepsilon )$.
$(s,r,\eta, \varepsilon )$.
Proposition C.4 Let ![]() $(s,r,\eta,\varepsilon )$ be a 2-categorical
$(s,r,\eta,\varepsilon )$ be a 2-categorical ![]() $(A,B)$ adjunction in a 1-triangulated 2-category
$(A,B)$ adjunction in a 1-triangulated 2-category ![]() ${\mathcal {C}}$. Consider a pair of
${\mathcal {C}}$. Consider a pair of ![]() $(A,A')$- and
$(A,A')$- and ![]() $(B,B')$-equivalences and the induced pseudo-equivalence
$(B,B')$-equivalences and the induced pseudo-equivalence ![]() $\theta \colon {\mathcal {C}}_{A,B}\to {\mathcal {C}}_{A',B'}$. Then the twist
$\theta \colon {\mathcal {C}}_{A,B}\to {\mathcal {C}}_{A',B'}$. Then the twist ![]() $t_{\theta (s)}$ is isomorphic to
$t_{\theta (s)}$ is isomorphic to ![]() $\theta (t_s)$ and the cotwist
$\theta (t_s)$ and the cotwist ![]() $c_{\theta (s)}$ is isomorphic to
$c_{\theta (s)}$ is isomorphic to ![]() $\theta (c_s)$.
$\theta (c_s)$.
Proof. By Proposition C.3 ![]() $(A,A')$- and
$(A,A')$- and ![]() $(B,B')$-equivalences induce a pseudo-equivalence
$(B,B')$-equivalences induce a pseudo-equivalence ![]() $\theta \colon {\mathcal {C}}_{A,B}\to {\mathcal {C}}_{A',B'}$ Lemma C.2 implies that
$\theta \colon {\mathcal {C}}_{A,B}\to {\mathcal {C}}_{A',B'}$ Lemma C.2 implies that ![]() $(\theta (s), \theta (r), \eta ', \varepsilon ')$ is an
$(\theta (s), \theta (r), \eta ', \varepsilon ')$ is an ![]() $(A',B')$-adjunction and
$(A',B')$-adjunction and ![]() $\theta (\eta ) \simeq \eta '$,
$\theta (\eta ) \simeq \eta '$, ![]() $\theta (\varepsilon ) \simeq \varepsilon '$. The isomorphism of cones follows.
$\theta (\varepsilon ) \simeq \varepsilon '$. The isomorphism of cones follows.
We say that a 2-categorical ![]() $(A,B)$-adjunction
$(A,B)$-adjunction ![]() $(s, r, \eta, \varepsilon )$ is a spherical couple if the twist
$(s, r, \eta, \varepsilon )$ is a spherical couple if the twist ![]() $t_s$, and respectively the cotwist
$t_s$, and respectively the cotwist ![]() $c_s$, defined in (C.2), is a
$c_s$, defined in (C.2), is a ![]() $(B,B)$-, respectively
$(B,B)$-, respectively ![]() $(A,A)$-equivalence.
$(A,A)$-equivalence.
Under the above assumption, octahedron

implies an isomorphism
A 1-morphism ![]() $s\colon A\to B$ is said to be spherical [Reference Anno and LogvinenkoAL17] if it has the 2-categorical left and right adjoints and
$s\colon A\to B$ is said to be spherical [Reference Anno and LogvinenkoAL17] if it has the 2-categorical left and right adjoints and ![]() $(s,r,\eta,\varepsilon )$ is a spherical couple. It is convenient to think of twist and cotwist as being assigned to a spherical couple, because their definition needs only one adjoint, not two as in the definition of the spherical functor.
$(s,r,\eta,\varepsilon )$ is a spherical couple. It is convenient to think of twist and cotwist as being assigned to a spherical couple, because their definition needs only one adjoint, not two as in the definition of the spherical functor.
C.2 The bicategory  $\mathop {\textbf {Bimod}}\nolimits$
$\mathop {\textbf {Bimod}}\nolimits$
Let ![]() $k$ be a field. We fix a universe
$k$ be a field. We fix a universe ![]() $\mathcal {U}$ and consider the bicategory
$\mathcal {U}$ and consider the bicategory ![]() $\mathop {\textbf {Bimod}}\nolimits$ whose objects are unital DG
$\mathop {\textbf {Bimod}}\nolimits$ whose objects are unital DG ![]() $k$-algebras, 1-morphisms
$k$-algebras, 1-morphisms ![]() $A \to B$ are objects in the derived category
$A \to B$ are objects in the derived category ![]() ${\mathcal {D}}_{\mathcal {U}}(A^{\rm op} \otimes _k B)$ of
${\mathcal {D}}_{\mathcal {U}}(A^{\rm op} \otimes _k B)$ of ![]() $A^{\mathop {{\rm op}}\nolimits }\otimes _k B$ DG
$A^{\mathop {{\rm op}}\nolimits }\otimes _k B$ DG ![]() $\mathcal {U}$-modules and 2-morphisms are morphisms in
$\mathcal {U}$-modules and 2-morphisms are morphisms in ![]() ${\mathcal {D}}_{\mathcal {U}}(A^{\rm op} \otimes _k B)$. Often, we drop the universe
${\mathcal {D}}_{\mathcal {U}}(A^{\rm op} \otimes _k B)$. Often, we drop the universe ![]() $\mathcal {U}$ from the notation. The derived tensor product of bimodules
$\mathcal {U}$ from the notation. The derived tensor product of bimodules ![]() $M \otimes ^L_B N$, for
$M \otimes ^L_B N$, for ![]() $M \in {\mathcal {D}}(A^{\rm op} \otimes _k B)$ and
$M \in {\mathcal {D}}(A^{\rm op} \otimes _k B)$ and ![]() $N\in {\mathcal {D}}(B^{\rm op} \otimes _k C)$, defines the composition of 1-morphisms in
$N\in {\mathcal {D}}(B^{\rm op} \otimes _k C)$, defines the composition of 1-morphisms in ![]() $\mathop {\textbf {Bimod}}\nolimits$. The derived tensor product is unique up to a canonical isomorphism, i.e. a pair of bimodule isomorphisms
$\mathop {\textbf {Bimod}}\nolimits$. The derived tensor product is unique up to a canonical isomorphism, i.e. a pair of bimodule isomorphisms ![]() $M\xrightarrow {\simeq } M'$,
$M\xrightarrow {\simeq } M'$, ![]() $N\xrightarrow {\simeq }N'$ in the derived categories induces a unique isomorphism
$N\xrightarrow {\simeq }N'$ in the derived categories induces a unique isomorphism ![]() $M\otimes ^L_B N \xrightarrow {\simeq } M' \otimes ^L_B N'$. Various choices involved in the definition of the derived tensor product are controlled by these isomorphisms. In particular, they allow to construct the associators and unitors in the bicategory
$M\otimes ^L_B N \xrightarrow {\simeq } M' \otimes ^L_B N'$. Various choices involved in the definition of the derived tensor product are controlled by these isomorphisms. In particular, they allow to construct the associators and unitors in the bicategory ![]() $\mathop {\textbf {Bimod}}\nolimits$. We write formulas as if the composition of 1-morphisms in
$\mathop {\textbf {Bimod}}\nolimits$. We write formulas as if the composition of 1-morphisms in ![]() $\mathop {\textbf {Bimod}}\nolimits$ was strictly associative and the identity morphisms were strict. If necessary, all morphisms of associativity and unitors can readily find their places in formulas. Equally, one can refer to the fact that every bicategory is biequivalent to a 2-category [Reference Mac Lane and ParéMP85].
$\mathop {\textbf {Bimod}}\nolimits$ was strictly associative and the identity morphisms were strict. If necessary, all morphisms of associativity and unitors can readily find their places in formulas. Equally, one can refer to the fact that every bicategory is biequivalent to a 2-category [Reference Mac Lane and ParéMP85].
The tensor product is an exact functor, hence the 2-category ![]() $\mathop {\textbf {Bimod}}\nolimits$ is 1-triangulated.
$\mathop {\textbf {Bimod}}\nolimits$ is 1-triangulated.
Let ![]() $\mathcal {V}$ be a universe such that
$\mathcal {V}$ be a universe such that ![]() ${\mathcal {D}}_{\mathcal {U}}(A^{{\rm op}} \otimes _k B)$ is an essentially
${\mathcal {D}}_{\mathcal {U}}(A^{{\rm op}} \otimes _k B)$ is an essentially ![]() $\mathcal {V}$-small category, for any pair
$\mathcal {V}$-small category, for any pair ![]() $A$,
$A$, ![]() $B$ of unital DG
$B$ of unital DG ![]() $k$-algebras, cf. [Reference MacLaneMac71]. Let further
$k$-algebras, cf. [Reference MacLaneMac71]. Let further ![]() $\textbf {Cat}_{\mathcal {V}}$ denote the 2-category of
$\textbf {Cat}_{\mathcal {V}}$ denote the 2-category of ![]() $\mathcal {V}$-small categories, functors and natural transformations. Consider the 2-functor
$\mathcal {V}$-small categories, functors and natural transformations. Consider the 2-functor
For ![]() $M\in {\mathcal {D}}(A^{\mathop {{\rm op}}\nolimits } \otimes _k B)$,
$M\in {\mathcal {D}}(A^{\mathop {{\rm op}}\nolimits } \otimes _k B)$, ![]() $\Phi _M \colon {\mathcal {D}}(A) \to {\mathcal {D}}(B)$ is the functor
$\Phi _M \colon {\mathcal {D}}(A) \to {\mathcal {D}}(B)$ is the functor
Finally, morphism ![]() $\alpha \colon M \to M'$ induces a natural transformation
$\alpha \colon M \to M'$ induces a natural transformation ![]() $\Phi _{\alpha }\colon \Phi _M \to \Phi _{M'}$.
$\Phi _{\alpha }\colon \Phi _M \to \Phi _{M'}$.
In particular, as ![]() $\Phi$ is a 2-functor, the tensor product of bimodules corresponds to the composition of tensor functors:
$\Phi$ is a 2-functor, the tensor product of bimodules corresponds to the composition of tensor functors:
We note that the 2-functor ![]() $\Phi$ is, in general, neither full nor faithful.
$\Phi$ is, in general, neither full nor faithful.
Note that by [Reference ToënToë07, Corollary 7.6], any DG enhanceable (i.e. admitting a lift to a functor of suitable DG enhancements) commuting with direct sums functor ![]() ${\mathcal {D}}(A)\to {\mathcal {D}}(B)$ is of the form
${\mathcal {D}}(A)\to {\mathcal {D}}(B)$ is of the form ![]() $\Phi _M$, for some bimodule
$\Phi _M$, for some bimodule ![]() $M$. We refer to functors of the form
$M$. We refer to functors of the form ![]() $\Phi _M$ as bimodule functors.
$\Phi _M$ as bimodule functors.
An exact triangle of bimodules in the category ![]() ${\mathcal {D}}(A^{\rm op}\otimes B)$:
${\mathcal {D}}(A^{\rm op}\otimes B)$:
induces via the functor ![]() $\Phi$ a functorial exact triangle
$\Phi$ a functorial exact triangle
Lemma C.5 Functor ![]() $\Phi$ is conservative on the categories of 1-morphisms in
$\Phi$ is conservative on the categories of 1-morphisms in ![]() $\mathop {\textbf {Bimod}}\nolimits$.
$\mathop {\textbf {Bimod}}\nolimits$.
Proof. Let ![]() $A$ and
$A$ and ![]() $B$ be unital DG algebras and
$B$ be unital DG algebras and ![]() $f\colon M_1\to M_2$ a morphism in
$f\colon M_1\to M_2$ a morphism in ![]() ${\mathcal {D}}(A^{\mathop {{\rm op}}\nolimits }\otimes B)$ such that
${\mathcal {D}}(A^{\mathop {{\rm op}}\nolimits }\otimes B)$ such that ![]() $\Phi _f\colon \Phi _{M_1} \to \Phi _{M_2}$ is an isomorphism. Morphism
$\Phi _f\colon \Phi _{M_1} \to \Phi _{M_2}$ is an isomorphism. Morphism ![]() $f$ fits into an exact triangle
$f$ fits into an exact triangle ![]() $M_1\xrightarrow {f} M_2\to M_3\to M_1[1]$. For any
$M_1\xrightarrow {f} M_2\to M_3\to M_1[1]$. For any ![]() $E\in {\mathcal {D}}(A)$, complex
$E\in {\mathcal {D}}(A)$, complex ![]() $\Phi _{M_1}(E)\xrightarrow {\Phi _f} \Phi _{M_2}(E)\to \Phi _{M_3}(E) \to \Phi _{M_1}(E)[1]$ is an exact triangle. As
$\Phi _{M_1}(E)\xrightarrow {\Phi _f} \Phi _{M_2}(E)\to \Phi _{M_3}(E) \to \Phi _{M_1}(E)[1]$ is an exact triangle. As ![]() $\Phi _f$ is an isomorphism,
$\Phi _f$ is an isomorphism, ![]() $\Phi _{M_3}(E) \simeq 0$. In particular,
$\Phi _{M_3}(E) \simeq 0$. In particular, ![]() $M_3\simeq \Phi _{M_3}(A) \simeq 0$, which implies that
$M_3\simeq \Phi _{M_3}(A) \simeq 0$, which implies that ![]() $f$ is an isomorphism.
$f$ is an isomorphism.
C.3 The bicategory  $\mathop {\textbf {FM}}\nolimits$
$\mathop {\textbf {FM}}\nolimits$
Let ![]() $k$ be a field. Consider the bicategory
$k$ be a field. Consider the bicategory ![]() $\mathop {\textbf {FM}}\nolimits$ whose objects are quasi-compact, quasi-separated
$\mathop {\textbf {FM}}\nolimits$ whose objects are quasi-compact, quasi-separated ![]() $k$-schemes. The category of morphisms
$k$-schemes. The category of morphisms ![]() $X\to Y$ is the derived category
$X\to Y$ is the derived category ![]() $\mathop {{\rm Hom}}\nolimits _{\mathop {\textbf {FM}}\nolimits }(X,Y) ={\mathcal {D}}_{{\rm qc}}(X\times Y)$ of
$\mathop {{\rm Hom}}\nolimits _{\mathop {\textbf {FM}}\nolimits }(X,Y) ={\mathcal {D}}_{{\rm qc}}(X\times Y)$ of ![]() $\mathcal {U}$-quasi-coherent sheaves on
$\mathcal {U}$-quasi-coherent sheaves on ![]() $X\times Y$ and the composition is given by the convolution: for schemes
$X\times Y$ and the composition is given by the convolution: for schemes ![]() $X$,
$X$, ![]() $Y$,
$Y$, ![]() $Z$,
$Z$, ![]() $K\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$ and
$K\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$ and ![]() $L\in {\mathcal {D}}_{{\rm qc}}(Y\times Z)$ their composition is
$L\in {\mathcal {D}}_{{\rm qc}}(Y\times Z)$ their composition is
where ![]() $\pi _{XY}\colon X\times Y \times Z \to X\times Y$,
$\pi _{XY}\colon X\times Y \times Z \to X\times Y$, ![]() $\pi _{YZ}\colon X\times Y \times Z \to Y\times Z$,
$\pi _{YZ}\colon X\times Y \times Z \to Y\times Z$, ![]() $\pi _{XZ}\colon X\times Y \times Z \to X\times Z$ are the projections.
$\pi _{XZ}\colon X\times Y \times Z \to X\times Z$ are the projections.
The identity in ![]() $\mathop {\textbf {FM}}\nolimits$ is given by the structure sheaf of the diagonal
$\mathop {\textbf {FM}}\nolimits$ is given by the structure sheaf of the diagonal ![]() $\Delta \subset X\times X$. For
$\Delta \subset X\times X$. For ![]() $K$ in
$K$ in ![]() ${\mathcal {D}}_{{\rm qc}}(X\times Y)$, the unitor is given by the flat base change and projection formula isomorphisms:
${\mathcal {D}}_{{\rm qc}}(X\times Y)$, the unitor is given by the flat base change and projection formula isomorphisms:
 \begin{align*} &{\pi_{13}}_*(\pi_{23}^*K \otimes \pi_{12}^*{\mathcal{O}}_\Delta ) = {\pi_{13}}_*( \pi_{23}^*K\otimes \pi_{12}^*\Delta_* {\mathcal{O}}_X ) \xrightarrow{\simeq} {\pi_{13}}_*( \pi_{23}^*K \otimes (\Delta\times \mathop{{\rm Id}}\nolimits_Y)_*\pi_1^* {\mathcal{O}}_X) \\ &\quad \xrightarrow{\simeq} {\pi_{13}}_*(\Delta\times \mathop{{\rm Id}}\nolimits_Y)_*((\Delta \times \mathop{{\rm Id}}\nolimits_Y)^*\pi_{23}^*K \otimes \pi_1^*{\mathcal{O}}_X ) \simeq {\mathop{{\rm Id}}\nolimits_X}_*( \mathop{{\rm Id}}\nolimits_X^* K)\otimes {\mathcal{O}}_{X\times Y} ) \simeq K, \end{align*}
\begin{align*} &{\pi_{13}}_*(\pi_{23}^*K \otimes \pi_{12}^*{\mathcal{O}}_\Delta ) = {\pi_{13}}_*( \pi_{23}^*K\otimes \pi_{12}^*\Delta_* {\mathcal{O}}_X ) \xrightarrow{\simeq} {\pi_{13}}_*( \pi_{23}^*K \otimes (\Delta\times \mathop{{\rm Id}}\nolimits_Y)_*\pi_1^* {\mathcal{O}}_X) \\ &\quad \xrightarrow{\simeq} {\pi_{13}}_*(\Delta\times \mathop{{\rm Id}}\nolimits_Y)_*((\Delta \times \mathop{{\rm Id}}\nolimits_Y)^*\pi_{23}^*K \otimes \pi_1^*{\mathcal{O}}_X ) \simeq {\mathop{{\rm Id}}\nolimits_X}_*( \mathop{{\rm Id}}\nolimits_X^* K)\otimes {\mathcal{O}}_{X\times Y} ) \simeq K, \end{align*}
where ![]() $\pi _{12}$,
$\pi _{12}$, ![]() $\pi _{13}$ and
$\pi _{13}$ and ![]() $\pi _{23}$ are projections from
$\pi _{23}$ are projections from ![]() $X\times X \times Y$ to the corresponding factors, similarly,
$X\times X \times Y$ to the corresponding factors, similarly, ![]() $\pi _1$ and
$\pi _1$ and ![]() $\pi _2$ are projections from
$\pi _2$ are projections from ![]() $X\times X$. We denote by
$X\times X$. We denote by ![]() $\Delta \colon X\to X\times X$ the diagonal embedding and by
$\Delta \colon X\to X\times X$ the diagonal embedding and by ![]() $\Delta \times \mathop {{\rm Id}}\nolimits _Y \colon X\times Y \to X\times X \times Y$ the map induced by
$\Delta \times \mathop {{\rm Id}}\nolimits _Y \colon X\times Y \to X\times X \times Y$ the map induced by ![]() $\Delta$ and the identity on
$\Delta$ and the identity on ![]() $Y$. The second unitor is defined analogously.
$Y$. The second unitor is defined analogously.
The associator in ![]() $\mathop {\textbf {FM}}\nolimits$ is defined analogously, using the projection formula and the flat base change isomorphism for the projections from
$\mathop {\textbf {FM}}\nolimits$ is defined analogously, using the projection formula and the flat base change isomorphism for the projections from ![]() $W\times X \times Y \times Z$ to the triple and double products.
$W\times X \times Y \times Z$ to the triple and double products.
Similarly to ![]() $\mathop {\textbf {Bimod}}\nolimits$, we consider
$\mathop {\textbf {Bimod}}\nolimits$, we consider ![]() $\mathop {\textbf {FM}}\nolimits$ as a 1-triangulated bicategory.
$\mathop {\textbf {FM}}\nolimits$ as a 1-triangulated bicategory.
Consider the bifunctor
which assigns to a 1-morphism ![]() $K\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$ the Fourier–Mukai functor with kernel
$K\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$ the Fourier–Mukai functor with kernel ![]() $K$:
$K$:
where ![]() $p_X\colon X\times Y \to X$,
$p_X\colon X\times Y \to X$, ![]() $p_Y \colon X\times Y \to Y$ are the projections. A 2-morphism
$p_Y \colon X\times Y \to Y$ are the projections. A 2-morphism ![]() $\alpha \colon K \to K'$ induces a natural transformation
$\alpha \colon K \to K'$ induces a natural transformation ![]() $\Xi _\alpha \colon \Xi _{K} \to \Xi _{K'}$.
$\Xi _\alpha \colon \Xi _{K} \to \Xi _{K'}$.
The isomorphism ![]() $\mathop {{\rm Id}}\nolimits _{{\mathcal {D}}_{{\rm qc}}(X)} \to \Xi ({\mathcal {O}}_{\Delta })$ is induced by the projection formula
$\mathop {{\rm Id}}\nolimits _{{\mathcal {D}}_{{\rm qc}}(X)} \to \Xi ({\mathcal {O}}_{\Delta })$ is induced by the projection formula
where ![]() $\pi _1, \pi _2 \colon X\times X \to X$ are the projections to the corresponding factors.
$\pi _1, \pi _2 \colon X\times X \to X$ are the projections to the corresponding factors.
For ![]() $K \in {\mathcal {D}}_{{\rm qc}}(X\times Y)$,
$K \in {\mathcal {D}}_{{\rm qc}}(X\times Y)$, ![]() $L\in {\mathcal {D}}_{{\rm qc}}(Y \times Z)$, the composition coherence isomorphism
$L\in {\mathcal {D}}_{{\rm qc}}(Y \times Z)$, the composition coherence isomorphism ![]() $\Xi (L) \otimes \Xi (K) \xrightarrow { \simeq } \Xi (L \ast K)$ is again given by the flat base change and projection formula:
$\Xi (L) \otimes \Xi (K) \xrightarrow { \simeq } \Xi (L \ast K)$ is again given by the flat base change and projection formula:
 \begin{align*} &\Xi(L) \circ \Xi(K)(-) = {q_Z}_*(L \otimes q_Y^*{r_Y}_*(K \otimes r_X^*(-))) \xrightarrow{\simeq} {q_Z}_*(L \otimes {\pi_{YZ}}_*\pi_{XY}^*(K \otimes r_X^*(-))) \\ &\quad\xrightarrow{\simeq} {q_Z}_*{\pi_{YZ}}_*(\pi_{YZ}^*L \otimes \pi_{XY}^*K \otimes \pi_{XY}^*r_X^*(-)) = {p_Z}_*{\pi_{XZ}}_*(\pi_{YZ}^*L \otimes \pi_{XY}^*K \otimes \pi_{XZ}^*p_X^*(-)) \\ &\quad\xrightarrow{\simeq} {p_Z}_*({\pi_{XZ}}_*(\pi_{YZ}^*L \otimes \pi_{XY}^*K) \otimes p_X^*(-)) = \Xi(L \ast K)(-), \end{align*}
\begin{align*} &\Xi(L) \circ \Xi(K)(-) = {q_Z}_*(L \otimes q_Y^*{r_Y}_*(K \otimes r_X^*(-))) \xrightarrow{\simeq} {q_Z}_*(L \otimes {\pi_{YZ}}_*\pi_{XY}^*(K \otimes r_X^*(-))) \\ &\quad\xrightarrow{\simeq} {q_Z}_*{\pi_{YZ}}_*(\pi_{YZ}^*L \otimes \pi_{XY}^*K \otimes \pi_{XY}^*r_X^*(-)) = {p_Z}_*{\pi_{XZ}}_*(\pi_{YZ}^*L \otimes \pi_{XY}^*K \otimes \pi_{XZ}^*p_X^*(-)) \\ &\quad\xrightarrow{\simeq} {p_Z}_*({\pi_{XZ}}_*(\pi_{YZ}^*L \otimes \pi_{XY}^*K) \otimes p_X^*(-)) = \Xi(L \ast K)(-), \end{align*}
where ![]() $\pi _{XY}$,
$\pi _{XY}$, ![]() $\pi _{XZ}$ and
$\pi _{XZ}$ and ![]() $\pi _{YZ}$ are the projections from
$\pi _{YZ}$ are the projections from ![]() $X \times Y \times Z$ to the corresponding products
$X \times Y \times Z$ to the corresponding products ![]() $X\times Y$,
$X\times Y$, ![]() $X\times Z$ and
$X\times Z$ and ![]() $Y\times Z$. We denote by
$Y\times Z$. We denote by ![]() $r_X, r_Y$ the projections from
$r_X, r_Y$ the projections from ![]() $X\times Y$, by
$X\times Y$, by ![]() $p_X, p_Z$ the projections from
$p_X, p_Z$ the projections from ![]() $X \times Z$ and by
$X \times Z$ and by ![]() $q_Y, q_Z$ the projections from
$q_Y, q_Z$ the projections from ![]() $Y \times Z$.
$Y \times Z$.
An exact triangle in the category ![]() ${\mathcal {D}}_{{\rm qc}}(X\times Y)$
${\mathcal {D}}_{{\rm qc}}(X\times Y)$
induces via the functor ![]() $\Xi$ a functorial exact triangle of FM functors:
$\Xi$ a functorial exact triangle of FM functors:
C.4 2-adjunctions, spherical couples and spherical 1-morphisms in  $\mathop {\textbf {Bimod}}\nolimits$
$\mathop {\textbf {Bimod}}\nolimits$
Any 2-functor preserves 2-adjunctions, in particular the 2-functor ![]() $\Phi$ maps a 2-categorical adjunction
$\Phi$ maps a 2-categorical adjunction ![]() $(M, R, \eta, \varepsilon )$ in
$(M, R, \eta, \varepsilon )$ in ![]() $\mathop {\textbf {Bimod}}\nolimits$ to a pair of adjoint functors
$\mathop {\textbf {Bimod}}\nolimits$ to a pair of adjoint functors ![]() $\Phi _M\dashv \Phi _R$ between the corresponding derived categories.
$\Phi _M\dashv \Phi _R$ between the corresponding derived categories.
Let ![]() $A$ and
$A$ and ![]() $B$ be unital DG algebras. We discuss when a pair of adjoint functors between
$B$ be unital DG algebras. We discuss when a pair of adjoint functors between ![]() ${\mathcal {D}}(A)$ and
${\mathcal {D}}(A)$ and ![]() ${\mathcal {D}}(B)$ can be lifted to a 2-categorical adjunction in
${\mathcal {D}}(B)$ can be lifted to a 2-categorical adjunction in ![]() $\mathop {\textbf {Bimod}}\nolimits$. For
$\mathop {\textbf {Bimod}}\nolimits$. For ![]() $M\in \,(A^{\mathop {{\rm op}}\nolimits }\otimes _k B)$, define its
$M\in \,(A^{\mathop {{\rm op}}\nolimits }\otimes _k B)$, define its ![]() $A$ and
$A$ and ![]() $B$ duals
$B$ duals ![]() $M^A, M^B\in {\mathcal {D}}(B^{\mathop {{\rm op}}\nolimits } \otimes _k A)$ (see [Reference Anno and LogvinenkoAL21]):
$M^A, M^B\in {\mathcal {D}}(B^{\mathop {{\rm op}}\nolimits } \otimes _k A)$ (see [Reference Anno and LogvinenkoAL21]):
We have several (derived) evaluation and action morphisms [Reference Anno and LogvinenkoAL21]:
 \begin{equation} \begin{aligned} & \varepsilon_R\colon M^B \otimes_A^L M \to B,\quad \varepsilon_L \colon M\otimes_B^L M^A \to A, \\ & \eta_R\colon A \to M \otimes_B^LM^B,\quad \eta_L \colon B \to M^A\otimes_A^L M. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \varepsilon_R\colon M^B \otimes_A^L M \to B,\quad \varepsilon_L \colon M\otimes_B^L M^A \to A, \\ & \eta_R\colon A \to M \otimes_B^LM^B,\quad \eta_L \colon B \to M^A\otimes_A^L M. \end{aligned} \end{equation}
Note that ![]() $\eta _R$ is defined if
$\eta _R$ is defined if ![]() $M$ is
$M$ is ![]() $B$-perfect, i.e. if its image in
$B$-perfect, i.e. if its image in ![]() ${\mathcal {D}}(B)$ lies in the full subcategory of compact objects. Respectively,
${\mathcal {D}}(B)$ lies in the full subcategory of compact objects. Respectively, ![]() $\eta _L$ is defined if
$\eta _L$ is defined if ![]() $M$ is
$M$ is ![]() $A$-perfect.
$A$-perfect.
The following proposition allows us to lift suitable pairs of adjoint functors between triangulated categories to 2-categorical adjunctions in ![]() $\mathop {\textbf {Bimod}}\nolimits$.
$\mathop {\textbf {Bimod}}\nolimits$.
Proposition C.6 Let ![]() $M$ be in
$M$ be in ![]() ${\mathcal {D}}(A^{\mathop {{\rm op}}\nolimits }\otimes _kB)$.
${\mathcal {D}}(A^{\mathop {{\rm op}}\nolimits }\otimes _kB)$.
(i) Then
 $M$ is
$M$ is  $A$-perfect if and only if the left adjoint
$A$-perfect if and only if the left adjoint  $\Phi _M^*$ to
$\Phi _M^*$ to  $\Phi _M$ exists. Under these assumptions functor
$\Phi _M$ exists. Under these assumptions functor  $\Phi _M^*$ is isomorphic to
$\Phi _M^*$ is isomorphic to  $\Phi _{M^A}$ and the evaluation and action maps yield a 2-categorical adjunction
$\Phi _{M^A}$ and the evaluation and action maps yield a 2-categorical adjunction  $(M^A, M, \eta _L, \varepsilon _L)$ in the bicategory
$(M^A, M, \eta _L, \varepsilon _L)$ in the bicategory  $\mathop {\textbf {Bimod}}\nolimits$.
$\mathop {\textbf {Bimod}}\nolimits$.(ii) Then
 $M$ is
$M$ is  $B$-perfect if and only if
$B$-perfect if and only if  $\Phi _M$ maps compact objects to compact ones if and only if the right adjoint
$\Phi _M$ maps compact objects to compact ones if and only if the right adjoint  $\Phi _M^!$ is isomorphic to
$\Phi _M^!$ is isomorphic to  $\Phi _{M^B}$. Under these assumptions the evaluation and action maps yield a 2-categorical adjunction
$\Phi _{M^B}$. Under these assumptions the evaluation and action maps yield a 2-categorical adjunction  $(M, M^B, \eta _R, \varepsilon _R)$.
$(M, M^B, \eta _R, \varepsilon _R)$.
Proof. This is basically the statement of [Reference Anno and LogvinenkoAL21, Propositions 4.2 and 4.7]. In [Reference Anno and LogvinenkoAL21] object ![]() $M$ is lifted to
$M$ is lifted to ![]() $\overline {M}$ in a suitable (weak, in the sense of Drinfeld [Reference DrinfeldDri04]) DG enhancement for
$\overline {M}$ in a suitable (weak, in the sense of Drinfeld [Reference DrinfeldDri04]) DG enhancement for ![]() ${\mathcal {D}}(A^{\mathop {{\rm op}}\nolimits }\otimes _kB)$. The
${\mathcal {D}}(A^{\mathop {{\rm op}}\nolimits }\otimes _kB)$. The ![]() $A$ and
$A$ and ![]() $B$ duals of
$B$ duals of ![]() $\overline {M}$ are defined, which lift
$\overline {M}$ are defined, which lift ![]() $M^A$ and
$M^A$ and ![]() $M^B$. Also, the evaluation and action maps are constructed on the DG level. With [Reference Anno and LogvinenkoAL21, Proposition 4.7] the authors check that the composites in (C.1) are identities of objects in the derived categories of bimodules.
$M^B$. Also, the evaluation and action maps are constructed on the DG level. With [Reference Anno and LogvinenkoAL21, Proposition 4.7] the authors check that the composites in (C.1) are identities of objects in the derived categories of bimodules.
Consider ![]() $B$-perfect
$B$-perfect ![]() $M\in {\mathcal {D}}(A^{\rm op} \otimes _k B)$. The 2-categorical adjunction
$M\in {\mathcal {D}}(A^{\rm op} \otimes _k B)$. The 2-categorical adjunction ![]() $(M,M^B, \eta _R, \varepsilon _R)$ in
$(M,M^B, \eta _R, \varepsilon _R)$ in ![]() $\mathop {\textbf {Bimod}}\nolimits$ (Proposition C.6(ii)) allows us to consider the twist
$\mathop {\textbf {Bimod}}\nolimits$ (Proposition C.6(ii)) allows us to consider the twist ![]() $T_B$ and the cotwist
$T_B$ and the cotwist ![]() $C_A$, defined with triangles (C.2). Lemma C.1 implies that
$C_A$, defined with triangles (C.2). Lemma C.1 implies that ![]() $T_B$ and
$T_B$ and ![]() $C_A$ are unique up to isomorphisms. Applying functor
$C_A$ are unique up to isomorphisms. Applying functor ![]() $\Phi$ as in (C.4) we obtain endo-functors
$\Phi$ as in (C.4) we obtain endo-functors ![]() $\Omega _{A,M}$ and
$\Omega _{A,M}$ and ![]() $\Theta _{B,M}$ of
$\Theta _{B,M}$ of ![]() ${\mathcal {D}}(A)$, respectively
${\mathcal {D}}(A)$, respectively ![]() ${\mathcal {D}}(B)$. They fit into functorial exact triangles:
${\mathcal {D}}(B)$. They fit into functorial exact triangles:
 \begin{align*} &\Omega_{A,M}\rightarrow \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}(A)} \xrightarrow{\eta_R} \Phi_M^!\Phi_M \rightarrow \Omega_{A,M}[1],\\ &\Phi_M \Phi_M^! \xrightarrow{\varepsilon_R} \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}(B)} \rightarrow \Theta_{B,M} \rightarrow \Phi \Phi^![1]. \end{align*}
\begin{align*} &\Omega_{A,M}\rightarrow \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}(A)} \xrightarrow{\eta_R} \Phi_M^!\Phi_M \rightarrow \Omega_{A,M}[1],\\ &\Phi_M \Phi_M^! \xrightarrow{\varepsilon_R} \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}(B)} \rightarrow \Theta_{B,M} \rightarrow \Phi \Phi^![1]. \end{align*}
Uniqueness of ![]() $T_A$ and
$T_A$ and ![]() $C_B$ implies that
$C_B$ implies that ![]() $\Omega _{A,M} = \Phi _{C_A}$ and
$\Omega _{A,M} = \Phi _{C_A}$ and ![]() $\Theta _{B,M} = \Phi _{T_B}$ are defined uniquely by
$\Theta _{B,M} = \Phi _{T_B}$ are defined uniquely by ![]() $M$ up to a (non-unique) functorial isomorphism. Note that we do not claim that the cotwist functor
$M$ up to a (non-unique) functorial isomorphism. Note that we do not claim that the cotwist functor ![]() $\Omega _{A,M}$ and twist functor
$\Omega _{A,M}$ and twist functor ![]() $\Theta _{B,M}$ are uniquely defined by the functor
$\Theta _{B,M}$ are uniquely defined by the functor ![]() $\Phi _M$.
$\Phi _M$.
Assume now that ![]() $M$ is
$M$ is ![]() $A$-perfect. According to Proposition C.6(i), we can consider the twist
$A$-perfect. According to Proposition C.6(i), we can consider the twist ![]() $T_A$ and the cotwist
$T_A$ and the cotwist ![]() $C_B$ for the 2-categorical adjunction
$C_B$ for the 2-categorical adjunction ![]() $(M^A,M,\eta _L,\varepsilon _L)$. By applying functor
$(M^A,M,\eta _L,\varepsilon _L)$. By applying functor ![]() $\Phi$ as in (C.4), we obtain endo-functors
$\Phi$ as in (C.4), we obtain endo-functors ![]() $\Omega _{B,M}=\Phi _{C_B}$ and
$\Omega _{B,M}=\Phi _{C_B}$ and ![]() $\Theta _{A,M}= \Phi _{T_A}$. Those fit into functorial exact triangles:
$\Theta _{A,M}= \Phi _{T_A}$. Those fit into functorial exact triangles:
 \begin{align*} & \Omega_{B,M}\rightarrow \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}(B)} \xrightarrow{\eta_L} \Phi_M\Phi_M^* \rightarrow \Omega_{B,M}[1],\\ &\Phi_M^* \Phi_M \xrightarrow{\varepsilon_L} \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}(A)} \rightarrow \Theta_{A,M} \rightarrow \Phi_M^* \Phi_M[1]. \end{align*}
\begin{align*} & \Omega_{B,M}\rightarrow \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}(B)} \xrightarrow{\eta_L} \Phi_M\Phi_M^* \rightarrow \Omega_{B,M}[1],\\ &\Phi_M^* \Phi_M \xrightarrow{\varepsilon_L} \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}(A)} \rightarrow \Theta_{A,M} \rightarrow \Phi_M^* \Phi_M[1]. \end{align*} We say that ![]() $\Phi _M$ is a spherical functor if
$\Phi _M$ is a spherical functor if ![]() $M$ is a spherical 1-morphism in
$M$ is a spherical 1-morphism in ![]() $\mathop {\textbf {Bimod}}\nolimits$.
$\mathop {\textbf {Bimod}}\nolimits$.
Theorem C.7 [Reference Anno and LogvinenkoAL17, 5.1 and 5.2]
Let ![]() $M$ be an
$M$ be an ![]() $A$ and
$A$ and ![]() $B$-perfect bimodule. Functor
$B$-perfect bimodule. Functor ![]() $\Phi _M$ is spherical if any two of the following hold:
$\Phi _M$ is spherical if any two of the following hold:
 $(S_1)\ $
$(S_1)\ $  $\Theta _{B,M}$ is an equivalence;
$\Theta _{B,M}$ is an equivalence; $(S_2)\ $
$(S_2)\ $  $\Omega _{A,M}$ is an equivalence;
$\Omega _{A,M}$ is an equivalence; $(S_3)\ $ composite
$(S_3)\ $ composite  $\Phi ^*_M \Theta _{B,M}[-1] \to \Phi _M^* \Phi _M \Phi _M^! \to \Phi _M^!$ is an isomorphism of functors;
$\Phi ^*_M \Theta _{B,M}[-1] \to \Phi _M^* \Phi _M \Phi _M^! \to \Phi _M^!$ is an isomorphism of functors; $(S_4)\ $ composite
$(S_4)\ $ composite  $\Phi _M^! \to \Phi _M^!\Phi _M \Phi _M^* \to \Omega _{A,M} \Phi _M^*[1]$ is an isomorphism of functors.
$\Phi _M^! \to \Phi _M^!\Phi _M \Phi _M^* \to \Omega _{A,M} \Phi _M^*[1]$ is an isomorphism of functors.
Then also ![]() $\Omega _{B,M}$ and
$\Omega _{B,M}$ and ![]() $\Theta _{A,M}$ are also equivalences of categories, quasi-inverse to
$\Theta _{A,M}$ are also equivalences of categories, quasi-inverse to ![]() $\Theta _{B,M}$ and
$\Theta _{B,M}$ and ![]() $\Omega _{A,M}$, respectively.
$\Omega _{A,M}$, respectively.
C.5 Lifting push-forwards, pull-backs and the base change to  $\mathop {\textbf {Bimod}}\nolimits$
$\mathop {\textbf {Bimod}}\nolimits$
We fix a DG enhancement [Reference Bondal and KapranovBK90] for the category ![]() ${\mathcal {D}}_{\rm qc}(X)$, for example, by
${\mathcal {D}}_{\rm qc}(X)$, for example, by ![]() $h$-injective complexes [Reference SpaltensteinSpa88, Reference Kashiwara and SchapiraKS06]. Let
$h$-injective complexes [Reference SpaltensteinSpa88, Reference Kashiwara and SchapiraKS06]. Let ![]() $P \in {\mathcal {D}}_{{\rm qc}}(X)$ be a compact generator (see [Reference Bondal and Van den BerghBVdB03]) and
$P \in {\mathcal {D}}_{{\rm qc}}(X)$ be a compact generator (see [Reference Bondal and Van den BerghBVdB03]) and ![]() $A$ the DG endomorphism algebra of its lift to the DG enhancement. Then
$A$ the DG endomorphism algebra of its lift to the DG enhancement. Then ![]() ${\mathcal {D}}(A)\simeq {\mathcal {D}}_{\rm qc}(X)$ by [Reference KellerKel94], which paves the way to performing the necessary constructions in the category
${\mathcal {D}}(A)\simeq {\mathcal {D}}_{\rm qc}(X)$ by [Reference KellerKel94], which paves the way to performing the necessary constructions in the category ![]() $\mathop {\textbf {Bimod}}\nolimits$. With Proposition C.9 we check that the constructed functorial exact triangles are independent of the choice of
$\mathop {\textbf {Bimod}}\nolimits$. With Proposition C.9 we check that the constructed functorial exact triangles are independent of the choice of ![]() $P$.
$P$.
Assume that ![]() $X$ and
$X$ and ![]() $Y$ are Noetherian separated schemes such that any perfect complex on both
$Y$ are Noetherian separated schemes such that any perfect complex on both ![]() $X$ and
$X$ and ![]() $Y$ is isomorphic to a bounded complex of locally free sheaves. Choose compact generators in
$Y$ is isomorphic to a bounded complex of locally free sheaves. Choose compact generators in ![]() ${\mathcal {D}}_{\rm qc}(X)$ and in
${\mathcal {D}}_{\rm qc}(X)$ and in ![]() ${\mathcal {D}}_{\rm qc}(Y)$ and fix lifts of the generators to DG enhancements of both categories. Denote by
${\mathcal {D}}_{\rm qc}(Y)$ and fix lifts of the generators to DG enhancements of both categories. Denote by ![]() $A_X$ and
$A_X$ and ![]() $A_Y$ their DG endomorphism algebras.
$A_Y$ their DG endomorphism algebras.
By [Reference Lunts and SchnürerLS16] there exists a choice of equivalences ![]() $\Upsilon _X \colon {\mathcal {D}}_{\rm qc}(X) \to {\mathcal {D}}(A_X)$,
$\Upsilon _X \colon {\mathcal {D}}_{\rm qc}(X) \to {\mathcal {D}}(A_X)$, ![]() $\Upsilon _Y \colon {\mathcal {D}}_{\rm qc}(Y) \to {\mathcal {D}}(A_Y)$ and
$\Upsilon _Y \colon {\mathcal {D}}_{\rm qc}(Y) \to {\mathcal {D}}(A_Y)$ and ![]() $\Upsilon _{X,Y}\colon {\mathcal {D}}_{{\rm qc}}(X\times Y) \simeq {\mathcal {D}}(A_X^{{\rm op}} \otimes A_Y)$ which map FM functors
$\Upsilon _{X,Y}\colon {\mathcal {D}}_{{\rm qc}}(X\times Y) \simeq {\mathcal {D}}(A_X^{{\rm op}} \otimes A_Y)$ which map FM functors ![]() ${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ to bimodule functors
${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ to bimodule functors ![]() ${\mathcal {D}}(A_X)\to {\mathcal {D}}(A_Y)$. More precisely, for any
${\mathcal {D}}(A_X)\to {\mathcal {D}}(A_Y)$. More precisely, for any ![]() ${\mathcal {E}}\in {\mathcal {D}}_{\rm qc}(X \times Y)$ the diagram
${\mathcal {E}}\in {\mathcal {D}}_{\rm qc}(X \times Y)$ the diagram

commutes up to a functorial isomorphism.
Commutativity of (C.8) implies that having fixed compact generators for ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ and
${\mathcal {D}}_{{\rm qc}}(X)$ and ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$, we can view FM functors
${\mathcal {D}}_{{\rm qc}}(Y)$, we can view FM functors ![]() ${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ as bimodule functors and vice versa.
${\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ as bimodule functors and vice versa.
Fix compact generators for ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ and
${\mathcal {D}}_{{\rm qc}}(X)$ and ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$ and consider
${\mathcal {D}}_{{\rm qc}}(Y)$ and consider ![]() ${\mathcal {E}}\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$. In view of (C.8), for
${\mathcal {E}}\in {\mathcal {D}}_{{\rm qc}}(X\times Y)$. In view of (C.8), for
functors ![]() $\Upsilon _Y\Xi _{\mathcal {E}}$ and
$\Upsilon _Y\Xi _{\mathcal {E}}$ and ![]() $\Phi _{M} \Upsilon _X$ are isomorphic.
$\Phi _{M} \Upsilon _X$ are isomorphic.
Lemma C.8 If ![]() $\Xi _{\mathcal {E}}$ has left adjoint
$\Xi _{\mathcal {E}}$ has left adjoint ![]() $\Xi _{\mathcal {E}}^*$, then
$\Xi _{\mathcal {E}}^*$, then ![]() $\Xi _{\mathcal {E}}^*\simeq \Xi _{\Upsilon _{Y,X}^{-1}(M^{A_X})}$ is an FM functor. If
$\Xi _{\mathcal {E}}^*\simeq \Xi _{\Upsilon _{Y,X}^{-1}(M^{A_X})}$ is an FM functor. If ![]() $\Xi _{\mathcal {E}}$ maps compact objects to compact objects, then the right adjoint exists and it is an FM functor,
$\Xi _{\mathcal {E}}$ maps compact objects to compact objects, then the right adjoint exists and it is an FM functor, ![]() $\Xi _{{\mathcal {E}}}^!\simeq \Xi _{\Upsilon _{Y,X}^{-1}(M^{A_Y})}$.
$\Xi _{{\mathcal {E}}}^!\simeq \Xi _{\Upsilon _{Y,X}^{-1}(M^{A_Y})}$.
Proof. If ![]() $\Xi _{{\mathcal {E}}}^*$ exists then
$\Xi _{{\mathcal {E}}}^*$ exists then ![]() $\Upsilon _X \Xi _{{\mathcal {E}}}^*\Upsilon _Y^{-1}$ is left adjoint to
$\Upsilon _X \Xi _{{\mathcal {E}}}^*\Upsilon _Y^{-1}$ is left adjoint to ![]() $\Phi _M$. Proposition C.6
$\Phi _M$. Proposition C.6![]() $(i)$ implies that
$(i)$ implies that ![]() $\Upsilon _X \Xi _{{\mathcal {E}}}^*\Upsilon _Y^{-1}\simeq \Phi _{M^{A_X}}$. Commutativity of (C.8) implies
$\Upsilon _X \Xi _{{\mathcal {E}}}^*\Upsilon _Y^{-1}\simeq \Phi _{M^{A_X}}$. Commutativity of (C.8) implies ![]() $\Xi _{{\mathcal {E}}}^*\simeq \Xi _{\Upsilon _{Y,X}^{-1}(M^{A_X})}$.
$\Xi _{{\mathcal {E}}}^*\simeq \Xi _{\Upsilon _{Y,X}^{-1}(M^{A_X})}$.
If ![]() $\Xi _{\mathcal {E}}$ maps compact objects to compact objects then so does
$\Xi _{\mathcal {E}}$ maps compact objects to compact objects then so does ![]() $\Phi _M\simeq \Upsilon _Y \Xi _{\mathcal {E}} \Upsilon _X^{-1}$. By Proposition C.6(ii),
$\Phi _M\simeq \Upsilon _Y \Xi _{\mathcal {E}} \Upsilon _X^{-1}$. By Proposition C.6(ii), ![]() $\Phi _M^!\simeq \Phi _{M^{A_Y}}$. Moreover,
$\Phi _M^!\simeq \Phi _{M^{A_Y}}$. Moreover, ![]() $\Upsilon _X^{-1}\Phi _{M^{A_Y}} \Upsilon _Y$ is right adjoint to
$\Upsilon _X^{-1}\Phi _{M^{A_Y}} \Upsilon _Y$ is right adjoint to ![]() $\Xi _{{\mathcal {E}}}$, i.e.
$\Xi _{{\mathcal {E}}}$, i.e. ![]() $\Xi _{\mathcal {E}}^!\simeq \Upsilon _X^{-1}\Phi _{M^{A_Y}} \Upsilon _Y$. As above we conclude that
$\Xi _{\mathcal {E}}^!\simeq \Upsilon _X^{-1}\Phi _{M^{A_Y}} \Upsilon _Y$. As above we conclude that ![]() $\Xi _{{\mathcal {E}}}^! \simeq \Xi _{\Upsilon _{Y,X}^{-1}(M^{A_Y})}$.
$\Xi _{{\mathcal {E}}}^! \simeq \Xi _{\Upsilon _{Y,X}^{-1}(M^{A_Y})}$.
The 2-categorical adjunctions ![]() $(M^{A_X}, M, \eta _L,\varepsilon _L )$,
$(M^{A_X}, M, \eta _L,\varepsilon _L )$, ![]() $(M, M^{A_Y}, \eta _R, \varepsilon _R)$ in
$(M, M^{A_Y}, \eta _R, \varepsilon _R)$ in ![]() $\mathop {\textbf {Bimod}}\nolimits$ define the twist and the cotwist by triangles (C.2). In view of the isomorphism
$\mathop {\textbf {Bimod}}\nolimits$ define the twist and the cotwist by triangles (C.2). In view of the isomorphism ![]() $\Xi _{{\mathcal {E}}}\simeq \Phi _{M}$ and the uniqueness of adjoint functors (see Lemma C.1), the functorial exact triangles read
$\Xi _{{\mathcal {E}}}\simeq \Phi _{M}$ and the uniqueness of adjoint functors (see Lemma C.1), the functorial exact triangles read
 \begin{equation} \begin{aligned} & \Xi_{\mathcal{E}}^*\Xi_{\mathcal{E}} \to \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(X)}\to \Theta_{X,{\mathcal{E}}}\to \Xi_{\mathcal{E}}^*\Xi_{\mathcal{E}}[1],\\ & \Omega_{Y,{\mathcal{E}}} \to\mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(Y)} \to \Xi_{\mathcal{E}} \Xi_{\mathcal{E}}^*\to \Omega_{Y,{\mathcal{E}}}[1],\\ & \Xi_{{\mathcal{E}}}\Xi_{{\mathcal{E}}}^! \to \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(Y)}\to \Theta_{Y,{\mathcal{E}}}\to \Xi_{{\mathcal{E}}}\Xi_{{\mathcal{E}}}^![1],\\ & \Omega_{X,{\mathcal{E}}}\to\mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(X)} \to \Xi_{{\mathcal{E}}}^!\Xi_{{\mathcal{E}}}\to \Omega_{X,{\mathcal{E}}}[1]. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \Xi_{\mathcal{E}}^*\Xi_{\mathcal{E}} \to \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(X)}\to \Theta_{X,{\mathcal{E}}}\to \Xi_{\mathcal{E}}^*\Xi_{\mathcal{E}}[1],\\ & \Omega_{Y,{\mathcal{E}}} \to\mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(Y)} \to \Xi_{\mathcal{E}} \Xi_{\mathcal{E}}^*\to \Omega_{Y,{\mathcal{E}}}[1],\\ & \Xi_{{\mathcal{E}}}\Xi_{{\mathcal{E}}}^! \to \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(Y)}\to \Theta_{Y,{\mathcal{E}}}\to \Xi_{{\mathcal{E}}}\Xi_{{\mathcal{E}}}^![1],\\ & \Omega_{X,{\mathcal{E}}}\to\mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(X)} \to \Xi_{{\mathcal{E}}}^!\Xi_{{\mathcal{E}}}\to \Omega_{X,{\mathcal{E}}}[1]. \end{aligned} \end{equation}
Note that we construct the triangles via the category ![]() $\mathop {\textbf {Bimod}}\nolimits$. We do not check that (C.9) are induced by morphisms between the convolutions of
$\mathop {\textbf {Bimod}}\nolimits$. We do not check that (C.9) are induced by morphisms between the convolutions of ![]() ${\mathcal {E}}$ with FM kernels of the adjoint functors and the structure sheaf of the diagonal.
${\mathcal {E}}$ with FM kernels of the adjoint functors and the structure sheaf of the diagonal.
Proposition C.9 Consider ![]() ${\mathcal {E}} \in {\mathcal {D}}_{{\rm qc}}(X\times Y)$. Then, up to an isomorphism, the functorial exact triangles of FM functors (C.9) do not depend on the choice of compact generators for
${\mathcal {E}} \in {\mathcal {D}}_{{\rm qc}}(X\times Y)$. Then, up to an isomorphism, the functorial exact triangles of FM functors (C.9) do not depend on the choice of compact generators for ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ and
${\mathcal {D}}_{{\rm qc}}(X)$ and ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$.
${\mathcal {D}}_{{\rm qc}}(Y)$.
Proof. Another choice of generators for ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ and
${\mathcal {D}}_{{\rm qc}}(X)$ and ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$ gives equivalences
${\mathcal {D}}_{{\rm qc}}(Y)$ gives equivalences ![]() $\Upsilon _X^B\colon {\mathcal {D}}_{{\rm qc}}(X)\xrightarrow {\simeq } {\mathcal {D}}(B_X)$,
$\Upsilon _X^B\colon {\mathcal {D}}_{{\rm qc}}(X)\xrightarrow {\simeq } {\mathcal {D}}(B_X)$, ![]() $\Upsilon _Y^B\colon {\mathcal {D}}_{{\rm qc}}(Y) \xrightarrow {\simeq } {\mathcal {D}}(B_Y)$, for some DG algebras
$\Upsilon _Y^B\colon {\mathcal {D}}_{{\rm qc}}(Y) \xrightarrow {\simeq } {\mathcal {D}}(B_Y)$, for some DG algebras ![]() $B_X$,
$B_X$, ![]() $B_Y$. The composite
$B_Y$. The composite ![]() $\Upsilon _X^B\circ \Upsilon _X^{-1}$, respectively
$\Upsilon _X^B\circ \Upsilon _X^{-1}$, respectively ![]() $\Upsilon _Y^B\circ \Upsilon _Y^{-1}$, is DG enhanceable and commutes with direct sums, hence it admits a lift to a bimodule functor, cf. [Reference ToënToë07]. Functor
$\Upsilon _Y^B\circ \Upsilon _Y^{-1}$, is DG enhanceable and commutes with direct sums, hence it admits a lift to a bimodule functor, cf. [Reference ToënToë07]. Functor ![]() $\Upsilon _X^B\circ \Upsilon _X^{-1}$, respectively
$\Upsilon _X^B\circ \Upsilon _X^{-1}$, respectively ![]() $\Upsilon _Y^B\circ \Upsilon _Y^{-1}$, together with its quasi-inverse yields
$\Upsilon _Y^B\circ \Upsilon _Y^{-1}$, together with its quasi-inverse yields ![]() $(A_X, B_X)$-equivalence, respectively
$(A_X, B_X)$-equivalence, respectively ![]() $(A_Y,B_Y)$-equivalence, in
$(A_Y,B_Y)$-equivalence, in ![]() $\mathop {\textbf {Bimod}}\nolimits$. By Proposition C.4, the induced pseudo-equivalence
$\mathop {\textbf {Bimod}}\nolimits$. By Proposition C.4, the induced pseudo-equivalence ![]() ${\theta \colon\!\mathop {\textbf {Bimod}}\nolimits _{A_X,A_Y} {\to} \mathop {\textbf {Bimod}}\nolimits _{B_X,B_Y}}$ preserves the twist and the cotwist of the adjunction. The image of
${\theta \colon\!\mathop {\textbf {Bimod}}\nolimits _{A_X,A_Y} {\to} \mathop {\textbf {Bimod}}\nolimits _{B_X,B_Y}}$ preserves the twist and the cotwist of the adjunction. The image of ![]() $\theta$ under functor
$\theta$ under functor ![]() $\Phi$ yields the required isomorphism of functorial triangles induced by
$\Phi$ yields the required isomorphism of functorial triangles induced by ![]() $\Upsilon$ and
$\Upsilon$ and ![]() $\Upsilon ^B$.
$\Upsilon ^B$.
Let ![]() $f\colon X\to Y$ be a proper morphism. The FM kernel of the functor
$f\colon X\to Y$ be a proper morphism. The FM kernel of the functor ![]() $Rf_*\colon {\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ is the structure sheaf of the graph of
$Rf_*\colon {\mathcal {D}}_{{\rm qc}}(X) \to {\mathcal {D}}_{{\rm qc}}(Y)$ is the structure sheaf of the graph of ![]() $f$. As functor
$f$. As functor ![]() $Lf^*$, left adjoint to
$Lf^*$, left adjoint to ![]() $Rf_*$, exists, the functorial exact triangles of endo-functors of
$Rf_*$, exists, the functorial exact triangles of endo-functors of ![]() ${\mathcal {D}}_{{\rm qc}}(X)$ and
${\mathcal {D}}_{{\rm qc}}(X)$ and ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$ are
${\mathcal {D}}_{{\rm qc}}(Y)$ are
 \begin{align*} &Lf^*Rf_* \to \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(X)}\to \Theta_{X,f}\to Lf^*Rf_*[1],\\ &\Omega_{Y,f} \to\mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(Y)} \to Rf_*Lf^*\to \Omega_{Y,f}[1]. \end{align*}
\begin{align*} &Lf^*Rf_* \to \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(X)}\to \Theta_{X,f}\to Lf^*Rf_*[1],\\ &\Omega_{Y,f} \to\mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(Y)} \to Rf_*Lf^*\to \Omega_{Y,f}[1]. \end{align*}
Assume further that ![]() $f$ is of finite Tor dimension. Then
$f$ is of finite Tor dimension. Then ![]() $Rf_*\colon {\mathcal {D}}_{{\rm qc}}(X)\to {\mathcal {D}}_{{\rm qc}}(Y)$ maps compact objects to compact objects and we have functorial exact triangles:
$Rf_*\colon {\mathcal {D}}_{{\rm qc}}(X)\to {\mathcal {D}}_{{\rm qc}}(Y)$ maps compact objects to compact objects and we have functorial exact triangles:
 \begin{align*} &Rf_*f^! \to \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(Y)}\to \Theta_{Y,f}\to Rf_*f^![1],\\ &\Omega_{X,f}\to\mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(X)} \to f^!Rf_*\to \Omega_{X,f}[1]. \end{align*}
\begin{align*} &Rf_*f^! \to \mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(Y)}\to \Theta_{Y,f}\to Rf_*f^![1],\\ &\Omega_{X,f}\to\mathop{{\rm Id}}\nolimits_{{\mathcal{D}}_{{\rm qc}}(X)} \to f^!Rf_*\to \Omega_{X,f}[1]. \end{align*}
Without the assumption on the Tor-dimension of ![]() $f$ the pair
$f$ the pair ![]() $Rf_*\dashv f^!$ admits a lift to DG functors of the categories of ind-coherent sheaves [Reference Gaitsgory and RozenblyumGR17].
$Rf_*\dashv f^!$ admits a lift to DG functors of the categories of ind-coherent sheaves [Reference Gaitsgory and RozenblyumGR17].
In the following we discuss compatibility of liftings of push-forward functors to ![]() $\mathop {\textbf {Bimod}}\nolimits$ with the composition of 1-morphisms.
$\mathop {\textbf {Bimod}}\nolimits$ with the composition of 1-morphisms.
Let ![]() $X$ be a quasi-compact quasi-separated scheme over a field
$X$ be a quasi-compact quasi-separated scheme over a field ![]() $k$. Let
$k$. Let ![]() $\mathscr {C}(X)$ denote the category of complexes of sheaves of
$\mathscr {C}(X)$ denote the category of complexes of sheaves of ![]() ${\mathcal {O}}_X$-modules with quasi-coherent cohomology and
${\mathcal {O}}_X$-modules with quasi-coherent cohomology and ![]() $\mathscr {I}(X)$ its full subcategory of
$\mathscr {I}(X)$ its full subcategory of ![]() $h$-injective objects. The category
$h$-injective objects. The category ![]() $\mathscr {I}(X)$ is a DG enhancement for
$\mathscr {I}(X)$ is a DG enhancement for ![]() ${\mathcal {D}}_{{\rm qc}}(X)$. By [Reference SchnürerSch18, Corollary 2.3] there exists a DG functor
${\mathcal {D}}_{{\rm qc}}(X)$. By [Reference SchnürerSch18, Corollary 2.3] there exists a DG functor ![]() $\iota _X\colon \mathscr {C}(X) \to \mathscr {I}(X)$ together with a natural transformation
$\iota _X\colon \mathscr {C}(X) \to \mathscr {I}(X)$ together with a natural transformation ![]() $\alpha _X \colon \mathop {{\rm Id}}\nolimits _{\mathscr {C}(X)} \to \iota _X$ whose evaluation at every object of
$\alpha _X \colon \mathop {{\rm Id}}\nolimits _{\mathscr {C}(X)} \to \iota _X$ whose evaluation at every object of ![]() $\mathscr {C}(X)$ is a quasi-isomorphism. In fact, functor
$\mathscr {C}(X)$ is a quasi-isomorphism. In fact, functor ![]() $\iota _X$ is defined in [Reference SchnürerSch18] on the bigger category of complexes of
$\iota _X$ is defined in [Reference SchnürerSch18] on the bigger category of complexes of ![]() ${\mathcal {O}}_X$-modules, here we denote by the same letter its restriction to
${\mathcal {O}}_X$-modules, here we denote by the same letter its restriction to ![]() $\mathscr {C}(X)$.
$\mathscr {C}(X)$.
Let ![]() $f\colon X\to Y$ be a morphism of quasi-compact quasi-separated schemes. The composite
$f\colon X\to Y$ be a morphism of quasi-compact quasi-separated schemes. The composite
defines a DG functor such that the induced functor on homotopy categories is isomorphic to ![]() $Rf_*$. For
$Rf_*$. For ![]() $g\colon Y \to Z$, the natural transformation
$g\colon Y \to Z$, the natural transformation ![]() $\alpha _Y \colon \mathop {{\rm Id}}\nolimits _{\mathscr {C}(Y)} \to \iota _Y$ yields a morphism
$\alpha _Y \colon \mathop {{\rm Id}}\nolimits _{\mathscr {C}(Y)} \to \iota _Y$ yields a morphism
which induces an isomorphism of the induced functors of homotopy categories.
Let ![]() $E_X\in \mathscr {I}(X)$ be an object whose image in the homotopy category is a compact generator. Denote by
$E_X\in \mathscr {I}(X)$ be an object whose image in the homotopy category is a compact generator. Denote by ![]() $A_X$ its DG endomorphism algebra. Then
$A_X$ its DG endomorphism algebra. Then
induces an equivalence
Analogously, a lift to ![]() $\mathscr {I}(Y)$ of a compact generator for
$\mathscr {I}(Y)$ of a compact generator for ![]() ${\mathcal {D}}_{{\rm qc}}(Y)$ to
${\mathcal {D}}_{{\rm qc}}(Y)$ to ![]() $\mathscr {I}(Y)$ yields an equivalence
$\mathscr {I}(Y)$ yields an equivalence ![]() $\zeta _Y\colon {\mathcal {D}}_{{\rm qc}}(Y) \to {\mathcal {D}}(A_Y)$. Consider an
$\zeta _Y\colon {\mathcal {D}}_{{\rm qc}}(Y) \to {\mathcal {D}}(A_Y)$. Consider an ![]() $A_X^{\mathop {{\rm op}}\nolimits } \otimes A_Y$-bimodule:
$A_X^{\mathop {{\rm op}}\nolimits } \otimes A_Y$-bimodule:
Then
Proposition C.10 Consider morphisms ![]() $X\xrightarrow {f} Y \xrightarrow {g}Z$ of quasi-compact separated schemes and denote by
$X\xrightarrow {f} Y \xrightarrow {g}Z$ of quasi-compact separated schemes and denote by ![]() $A_Z$ the DG endomorphism algebra of a lift
$A_Z$ the DG endomorphism algebra of a lift ![]() $E_Z$ of a compact generator for
$E_Z$ of a compact generator for ![]() ${\mathcal {D}}_{{\rm qc}}(Z)$ to
${\mathcal {D}}_{{\rm qc}}(Z)$ to ![]() $\mathscr {I}(Z)$. Then there exists a canonical isomorphism in
$\mathscr {I}(Z)$. Then there exists a canonical isomorphism in ![]() ${\mathcal {D}}(A_X^{\mathop {{\rm op}}\nolimits } \otimes A_Z)$:
${\mathcal {D}}(A_X^{\mathop {{\rm op}}\nolimits } \otimes A_Z)$:
Proof. Morphism ![]() $\beta$ (C.10) applied to
$\beta$ (C.10) applied to ![]() $E_X$ is a quasi-isomorphism of
$E_X$ is a quasi-isomorphism of ![]() $h$-injective complexes, hence it has a homotopy inverse. It follows that morphism of DG bimodules
$h$-injective complexes, hence it has a homotopy inverse. It follows that morphism of DG bimodules
has a homotopy inverse, i.e. the induced morphism ![]() $\overline {\delta }$ in
$\overline {\delta }$ in ![]() ${\mathcal {D}}(A_X^{\mathop {{\rm op}}\nolimits } \otimes A_Z)$ is an isomorphism. In particular, for equivalence
${\mathcal {D}}(A_X^{\mathop {{\rm op}}\nolimits } \otimes A_Z)$ is an isomorphism. In particular, for equivalence ![]() $\zeta _Z\colon {\mathcal {D}}_{{\rm qc}}(Z) \to {\mathcal {D}}(A_Z)$ induced by
$\zeta _Z\colon {\mathcal {D}}_{{\rm qc}}(Z) \to {\mathcal {D}}(A_Z)$ induced by ![]() $E_Z$, formula (C.12) with
$E_Z$, formula (C.12) with ![]() $f$ replaced by
$f$ replaced by ![]() $gf$,
$gf$, ![]() $\zeta _Y$ by
$\zeta _Y$ by ![]() $\zeta _Z$, and
$\zeta _Z$, and ![]() $M_f$ by
$M_f$ by ![]() $M_{gf}$ implies
$M_{gf}$ implies ![]() $\zeta _Z \circ R(gf)_*\simeq \Phi _{N_{gf}}\circ \zeta _X$.
$\zeta _Z \circ R(gf)_*\simeq \Phi _{N_{gf}}\circ \zeta _X$.
Functor ![]() $\widetilde {g}_*$ together with the composition of morphisms in
$\widetilde {g}_*$ together with the composition of morphisms in ![]() $\mathscr {I}(Z)$ defines a morphism of bimodules
$\mathscr {I}(Z)$ defines a morphism of bimodules
 \begin{align*} &\gamma \colon M_f\otimes_{A_Y} M_g = \mathop{{\rm Hom}}\nolimits_{\mathscr{I}(Y)}(E_Y, \widetilde{f}_*E_X) \otimes_{A_Y} \mathop{{\rm Hom}}\nolimits_{\mathscr{I}(Z)}(E_Z,\widetilde{g}_* E_Y) \\ &\quad \to \mathop{{\rm Hom}}\nolimits_{\mathscr{I}(Z)}(E_Z, \widetilde{g}_*\widetilde{f}_*E_X) =: N_{gf}. \end{align*}
\begin{align*} &\gamma \colon M_f\otimes_{A_Y} M_g = \mathop{{\rm Hom}}\nolimits_{\mathscr{I}(Y)}(E_Y, \widetilde{f}_*E_X) \otimes_{A_Y} \mathop{{\rm Hom}}\nolimits_{\mathscr{I}(Z)}(E_Z,\widetilde{g}_* E_Y) \\ &\quad \to \mathop{{\rm Hom}}\nolimits_{\mathscr{I}(Z)}(E_Z, \widetilde{g}_*\widetilde{f}_*E_X) =: N_{gf}. \end{align*}
Let ![]() $\overline {\gamma }$ be the induced morphism in
$\overline {\gamma }$ be the induced morphism in ![]() ${\mathcal {D}}(A_X^{\mathop {{\rm op}}\nolimits } \otimes A_Z)$.
${\mathcal {D}}(A_X^{\mathop {{\rm op}}\nolimits } \otimes A_Z)$.
Formula (C.12) and its analogue for ![]() $g\colon Y \to Z$ yields isomorphisms
$g\colon Y \to Z$ yields isomorphisms ![]() $\zeta _{Z} \circ (Rg_*\circ Rf_*)\simeq \Phi _{M_g}\circ \zeta _Y \circ Rf_*\simeq \Phi _{M_g}\circ \Phi _{M_f} \circ \zeta _X \simeq \Phi _{M_f\otimes _{A_Y}^LM_g} \circ \zeta _X$. Therefore,
$\zeta _{Z} \circ (Rg_*\circ Rf_*)\simeq \Phi _{M_g}\circ \zeta _Y \circ Rf_*\simeq \Phi _{M_g}\circ \Phi _{M_f} \circ \zeta _X \simeq \Phi _{M_f\otimes _{A_Y}^LM_g} \circ \zeta _X$. Therefore, ![]() $\Phi _{N_{gf}}$ and
$\Phi _{N_{gf}}$ and ![]() $\Phi _{M_f\otimes _{A_Y}^LM_g}$ correspond via
$\Phi _{M_f\otimes _{A_Y}^LM_g}$ correspond via ![]() $\zeta _X$ and
$\zeta _X$ and ![]() $\zeta _Z$ to
$\zeta _Z$ to ![]() $R(gf)_*$ and
$R(gf)_*$ and ![]() $Rg_*\circ Rf_*$. As these functors are isomorphic, we conclude that applying
$Rg_*\circ Rf_*$. As these functors are isomorphic, we conclude that applying ![]() $\Phi$ to
$\Phi$ to ![]() $\overline {\gamma }$ yields an isomorphism of functors. As, by Lemma C.5,
$\overline {\gamma }$ yields an isomorphism of functors. As, by Lemma C.5, ![]() $\Phi$ is conservative,
$\Phi$ is conservative, ![]() $\overline {\gamma }$ is an isomorphism. Then
$\overline {\gamma }$ is an isomorphism. Then ![]() $\overline {\delta }^{-1} \circ \overline {\gamma }$ is the sought isomorphism (C.13).
$\overline {\delta }^{-1} \circ \overline {\gamma }$ is the sought isomorphism (C.13).
Note that as functor ![]() $\Phi _{M_f} \colon {\mathcal {D}}(A_X) \to {\mathcal {D}}(A_Y)$ has left adjoint, Proposition C.6
$\Phi _{M_f} \colon {\mathcal {D}}(A_X) \to {\mathcal {D}}(A_Y)$ has left adjoint, Proposition C.6![]() $(ii)$ implies a 2-categorical adjunction
$(ii)$ implies a 2-categorical adjunction ![]() $(M_f^{A_X}, M_f, \eta _L, \varepsilon _L)$ in the category
$(M_f^{A_X}, M_f, \eta _L, \varepsilon _L)$ in the category ![]() $\mathop {\textbf {Bimod}}\nolimits$.
$\mathop {\textbf {Bimod}}\nolimits$.
Consider the following commutative diagram of morphisms of quasi-compact quasi-separated schemes.

We search for a 1-morphism in ![]() $\mathop {\textbf {Bimod}}\nolimits$ whose image under the functor
$\mathop {\textbf {Bimod}}\nolimits$ whose image under the functor ![]() $\Phi$ as in (C.4) is the base change
$\Phi$ as in (C.4) is the base change ![]() $Lg^*Rf_*\to Rq_*Lp^*$.
$Lg^*Rf_*\to Rq_*Lp^*$.
Choose ![]() $E_X\in \mathscr {I}(X)$,
$E_X\in \mathscr {I}(X)$, ![]() $E_Y\in \mathscr {I}(Y)$,
$E_Y\in \mathscr {I}(Y)$, ![]() $E_Z\in \mathscr {I}(Z)$ and
$E_Z\in \mathscr {I}(Z)$ and ![]() $E_W\in \mathscr {I}(W)$ whose images in the homotopy categories are compact generators. Denote by
$E_W\in \mathscr {I}(W)$ whose images in the homotopy categories are compact generators. Denote by ![]() $A_X$,
$A_X$, ![]() $A_Y$,
$A_Y$, ![]() $A_Z$ and
$A_Z$ and ![]() $A_W$ their DG endomorphism algebras. Let
$A_W$ their DG endomorphism algebras. Let ![]() $M_f$,
$M_f$, ![]() $M_q$,
$M_q$, ![]() $M_g$ and
$M_g$ and ![]() $M_p$ be DG bimodules as in (C.11).
$M_p$ be DG bimodules as in (C.11).
In view of Proposition C.10 equality ![]() $f\circ p = g \circ q$ implies an isomorphism
$f\circ p = g \circ q$ implies an isomorphism ![]() $\nu \colon M_p\otimes ^L_{A_X} M_f\to M_q\otimes ^L_{A_W}M_g$. Consider the composite
$\nu \colon M_p\otimes ^L_{A_X} M_f\to M_q\otimes ^L_{A_W}M_g$. Consider the composite
 \begin{align} \omega \colon M_f \otimes^L_{A_Y}M_g^{A_W} &\to M_p^{A_Z} \otimes^L_{A_Z} M_p\otimes^L_{A_X}M_f \otimes^L_{A_Y}M_g^{A_W}\nonumber\\ &\to M_p^{A_Z} \otimes^L_{A_Z}M_q\otimes^L_{A_W}M_g\otimes^L_{A_Y}M_g^{A_W}\to M_p^{A_Z} \otimes^L_{A_Z}M_q\end{align}
\begin{align} \omega \colon M_f \otimes^L_{A_Y}M_g^{A_W} &\to M_p^{A_Z} \otimes^L_{A_Z} M_p\otimes^L_{A_X}M_f \otimes^L_{A_Y}M_g^{A_W}\nonumber\\ &\to M_p^{A_Z} \otimes^L_{A_Z}M_q\otimes^L_{A_W}M_g\otimes^L_{A_Y}M_g^{A_W}\to M_p^{A_Z} \otimes^L_{A_Z}M_q\end{align}
where the first map is induced by the lift of the ![]() $Lp^*\dashv Rp_*$ adjunction unit to the unit
$Lp^*\dashv Rp_*$ adjunction unit to the unit ![]() $A_X \to M_p^{A_Z}\otimes _{A_Z}^L M_p$ of the 2-categorical
$A_X \to M_p^{A_Z}\otimes _{A_Z}^L M_p$ of the 2-categorical ![]() $(A_X,A_Z)$-adjunction, the second by
$(A_X,A_Z)$-adjunction, the second by ![]() $\nu$ and the third by the lift of the
$\nu$ and the third by the lift of the ![]() $Lg^*\dashv Rg_*$ adjunction counit to the counit
$Lg^*\dashv Rg_*$ adjunction counit to the counit ![]() $M_g\otimes _{A_Y}^LM_g^{A_W} \to A_W$ of the
$M_g\otimes _{A_Y}^LM_g^{A_W} \to A_W$ of the ![]() $(A_Y,A_W)$-adjunction. Then
$(A_Y,A_W)$-adjunction. Then ![]() $\omega$ is a lift of the ‘base change’
$\omega$ is a lift of the ‘base change’ ![]() $Lg^*Rf_* \to Rq_*Lp^*$ to a 1-morphism in
$Lg^*Rf_* \to Rq_*Lp^*$ to a 1-morphism in ![]() $\mathop {\textbf {Bimod}}\nolimits$.
$\mathop {\textbf {Bimod}}\nolimits$.
The base-change morphism ![]() $\omega$ (C.15) is the composite of appropriate adjunction units and counits. Hence, Proposition C.9 implies that
$\omega$ (C.15) is the composite of appropriate adjunction units and counits. Hence, Proposition C.9 implies that ![]() $\omega$ yields a unique up to isomorphism morphism
$\omega$ yields a unique up to isomorphism morphism ![]() $Lg^*Rf_*\to Rq_*Lp^*$ of FM functors.
$Lg^*Rf_*\to Rq_*Lp^*$ of FM functors.
C.6 Isomorphisms of functors via the restriction to one object
Throughout the paper we repeatedly use the fact that, for algebras ![]() $A$,
$A$, ![]() $B$ and functors
$B$ and functors ![]() $F,G\colon {\mathcal {D}}(A) \to {\mathcal {D}}(B)$ defined by pure modules, an isomorphism of
$F,G\colon {\mathcal {D}}(A) \to {\mathcal {D}}(B)$ defined by pure modules, an isomorphism of ![]() $F$ and
$F$ and ![]() $G$ on generators yields an isomorphism
$G$ on generators yields an isomorphism ![]() $F\xrightarrow {\simeq } G$.
$F\xrightarrow {\simeq } G$.
Lemma C.11 Let ![]() $A$,
$A$, ![]() $B$ be algebras and let
$B$ be algebras and let ![]() $M$ be a complex of
$M$ be a complex of ![]() $A-B$ bimodules such that
$A-B$ bimodules such that ![]() $H^i(M) = 0$, for
$H^i(M) = 0$, for ![]() $i\neq j$, for a fixed
$i\neq j$, for a fixed ![]() $j\in \mathbb {Z}$. Let also
$j\in \mathbb {Z}$. Let also ![]() ${\mathcal {E}} \subset {\mathcal {D}}(A)$ be the full subcategory with one object
${\mathcal {E}} \subset {\mathcal {D}}(A)$ be the full subcategory with one object ![]() $A$. Then the quasi-isomorphism class of
$A$. Then the quasi-isomorphism class of ![]() $M$ is determined by the isomorphism class of the restriction functor
$M$ is determined by the isomorphism class of the restriction functor ![]() $\Phi _{M}|_{{\mathcal {E}}} \colon {\mathcal {E}}\to {\mathcal {D}}(B)$.
$\Phi _{M}|_{{\mathcal {E}}} \colon {\mathcal {E}}\to {\mathcal {D}}(B)$.
Proof. By definition, ![]() $M \simeq \Phi _{M}(A)$ as a right
$M \simeq \Phi _{M}(A)$ as a right ![]() $B$ module. Functor
$B$ module. Functor ![]() $\Phi _{M}|_{{\mathcal {E}}}$ gives a map
$\Phi _{M}|_{{\mathcal {E}}}$ gives a map ![]() $A \simeq \mathop {{\rm Hom}}\nolimits _A(A,A) \xrightarrow {\beta } \mathop {{\rm Hom}}\nolimits _{B}(M,M)$. By assumption on
$A \simeq \mathop {{\rm Hom}}\nolimits _A(A,A) \xrightarrow {\beta } \mathop {{\rm Hom}}\nolimits _{B}(M,M)$. By assumption on ![]() $M$, we have a quasi-isomorphism
$M$, we have a quasi-isomorphism ![]() $M \simeq H^j(M)$, hence
$M \simeq H^j(M)$, hence ![]() $\mathop {{\rm Hom}}\nolimits _{B}(M,M)\simeq \mathop {{\rm Hom}}\nolimits _{B}(H^j(M), H^j(M))$. Then morphism
$\mathop {{\rm Hom}}\nolimits _{B}(M,M)\simeq \mathop {{\rm Hom}}\nolimits _{B}(H^j(M), H^j(M))$. Then morphism ![]() $\beta$ recovers the left
$\beta$ recovers the left ![]() $A$ module structure of
$A$ module structure of ![]() $H^j(M)$, hence the quasi-isomorphism class of
$H^j(M)$, hence the quasi-isomorphism class of ![]() $M$ as an
$M$ as an ![]() $A-B$ bimodule.
$A-B$ bimodule.
As an easy corollary, we obtain the following lemma.
Lemma C.12 Let ![]() $A$,
$A$, ![]() $B$ be algebras and let
$B$ be algebras and let ![]() $M_1$,
$M_1$, ![]() $M_2$ be complexes of
$M_2$ be complexes of ![]() $A-B$ bimodules such that
$A-B$ bimodules such that ![]() $H^i(M_1) =0$, for
$H^i(M_1) =0$, for ![]() $i \neq j$, for a fixed
$i \neq j$, for a fixed ![]() $j\in \mathbb {Z}$. Let
$j\in \mathbb {Z}$. Let ![]() ${\mathcal {E}} \subset {\mathcal {D}}(A)$ denote the full subcategory with one object
${\mathcal {E}} \subset {\mathcal {D}}(A)$ denote the full subcategory with one object ![]() $A$. Then functors
$A$. Then functors ![]() $\Phi _{M_1}$ and
$\Phi _{M_1}$ and ![]() $\Phi _{M_2}$ are isomorphic if and only if
$\Phi _{M_2}$ are isomorphic if and only if ![]() $\Phi _{M_1}|_{{\mathcal {E}}}$ and
$\Phi _{M_1}|_{{\mathcal {E}}}$ and ![]() $\Phi _{M_2}|_{{\mathcal {E}}}$ are.
$\Phi _{M_2}|_{{\mathcal {E}}}$ are.
Proof. As ![]() $\Phi _{M_1}(A) \simeq M_1$ and
$\Phi _{M_1}(A) \simeq M_1$ and ![]() $\Phi _{M_2}(A) \simeq M_2$, isomorphism of functors
$\Phi _{M_2}(A) \simeq M_2$, isomorphism of functors ![]() $\Phi _{M_1}|_{{\mathcal {E}}}\simeq \Phi _{M_2}|_{{\mathcal {E}}}$ implies a quasi-isomorphism of
$\Phi _{M_1}|_{{\mathcal {E}}}\simeq \Phi _{M_2}|_{{\mathcal {E}}}$ implies a quasi-isomorphism of ![]() $M_1$ and
$M_1$ and ![]() $M_2$ as complexes of right
$M_2$ as complexes of right ![]() $B$ modules. Therefore,
$B$ modules. Therefore, ![]() $H^i(M_2) = 0$, for
$H^i(M_2) = 0$, for ![]() $i\neq j$. We conclude by Lemma C.11.
$i\neq j$. We conclude by Lemma C.11.
Appendix D. The structure of the reduced fiber
Let ![]() $f\colon X \to Y$ be a proper morphism with fibers of dimension bounded by one such that
$f\colon X \to Y$ be a proper morphism with fibers of dimension bounded by one such that ![]() $Rf_*({\mathcal {O}}_X) = {\mathcal {O}}_Y$. Let
$Rf_*({\mathcal {O}}_X) = {\mathcal {O}}_Y$. Let ![]() $C$ denote the reduced fiber of
$C$ denote the reduced fiber of ![]() $f$ over a closed point of
$f$ over a closed point of ![]() $Y$.
$Y$.
Applying functor ![]() $Rf_*$ to the short exact sequence
$Rf_*$ to the short exact sequence
of sheaves on ![]() $X$, we obtain a surjective morphism
$X$, we obtain a surjective morphism ![]() $R^1f_* {\mathcal {O}}_X \to R^1f_* {\mathcal {O}}_C$, which implies
$R^1f_* {\mathcal {O}}_X \to R^1f_* {\mathcal {O}}_C$, which implies
Moreover, by [Reference HartshorneHar77, Corollary II.11.3], ![]() $C$ is connected, i.e.
$C$ is connected, i.e. ![]() $H^0({\mathcal {O}}_C) = k$.
$H^0({\mathcal {O}}_C) = k$.
Let ![]() $C = \bigcup C_i$ be a reduced curve such that all of its irreducible components
$C = \bigcup C_i$ be a reduced curve such that all of its irreducible components ![]() $C_i$ are smooth. An incidence graph is a bipartite graph whose vertices correspond to irreducible components and singular points of
$C_i$ are smooth. An incidence graph is a bipartite graph whose vertices correspond to irreducible components and singular points of ![]() $C$. An edge connects a vertex corresponding to an irreducible component
$C$. An edge connects a vertex corresponding to an irreducible component ![]() $C_i$ with a vertex corresponding to a singular point
$C_i$ with a vertex corresponding to a singular point ![]() $c \in {\rm Sing}(C)$ if and only if
$c \in {\rm Sing}(C)$ if and only if ![]() $c \in C_i$. Note that the incidence graph can be simply connected even though the dual intersection graph might be not, as the example of three curves meeting in one point shows: the incidence graph is a tree, a point connected with three other points, whereas the dual graph is a triangle.
$c \in C_i$. Note that the incidence graph can be simply connected even though the dual intersection graph might be not, as the example of three curves meeting in one point shows: the incidence graph is a tree, a point connected with three other points, whereas the dual graph is a triangle.
We say that a reduced curve has normal crossing singularities if all components of the curve are smooth and the Zariski tangent space at every singular point is the direct sum of tangent subspaces corresponding to components that meet at this point.
Theorem D.1 Let ![]() $C$ be a reduced proper algebraic curve over field
$C$ be a reduced proper algebraic curve over field ![]() $k$. Then
$k$. Then ![]() $H^1({\mathcal {O}}_C) =0$ if and only if the following conditions are satisfied:
$H^1({\mathcal {O}}_C) =0$ if and only if the following conditions are satisfied:
(i) every irreducible component
 $C_i$ of
$C_i$ of  $C$ is a smooth rational curve;
$C$ is a smooth rational curve;(ii) the incidence graph of
 $C$ has no cycles;
$C$ has no cycles;(iii) the curve has normal crossing singularities.
Proof. Assume that ![]() $H^1({\mathcal {O}}_C) =0$. Let
$H^1({\mathcal {O}}_C) =0$. Let ![]() $C_i$ be an irreducible component of
$C_i$ be an irreducible component of ![]() $C$. The restriction morphism
$C$. The restriction morphism ![]() ${\mathcal {O}}_C \to {\mathcal {O}}_{C_i}$ gives a surjection on cohomology
${\mathcal {O}}_C \to {\mathcal {O}}_{C_i}$ gives a surjection on cohomology ![]() $H^1({\mathcal {O}}_C) \to H^1({\mathcal {O}}_{C_i})$, hence
$H^1({\mathcal {O}}_C) \to H^1({\mathcal {O}}_{C_i})$, hence ![]() $H^1({\mathcal {O}}_{C_i}) =0$. Let
$H^1({\mathcal {O}}_{C_i}) =0$. Let
denote the normalisation of ![]() $C_i$. Consider a short exact sequence of sheaves on
$C_i$. Consider a short exact sequence of sheaves on ![]() $C_i$:
$C_i$:
As ![]() ${\mathcal {F}}$ is supported at singular points of
${\mathcal {F}}$ is supported at singular points of ![]() $C_i$, the group
$C_i$, the group ![]() $H^1({\mathcal {F}})$ vanishes, hence
$H^1({\mathcal {F}})$ vanishes, hence ![]() $H^1({\mathcal {O}}_{\widetilde {C_i}}) = 0$. As
$H^1({\mathcal {O}}_{\widetilde {C_i}}) = 0$. As ![]() $\widetilde {C_i}$ is smooth, it is isomorphic to
$\widetilde {C_i}$ is smooth, it is isomorphic to ![]() $\mathbb {P}^1_k$.
$\mathbb {P}^1_k$.
Sequence
is exact and the first morphism is an isomorphism. It follows that ![]() $H^0({\mathcal {F}})=0$, i.e. sheaf
$H^0({\mathcal {F}})=0$, i.e. sheaf ![]() ${\mathcal {F}}$ is trivial. This proves that
${\mathcal {F}}$ is trivial. This proves that ![]() $C_i$ is isomorphic to its normalisation
$C_i$ is isomorphic to its normalisation ![]() $\widetilde {C_i}$, which is a smooth rational curve. This proves condition (i).
$\widetilde {C_i}$, which is a smooth rational curve. This proves condition (i).
Assume that the incidence graph of ![]() $C$ has a cycle. Let
$C$ has a cycle. Let ![]() $C'\subset C$ be the corresponding (minimal) cycle of smooth rational curves, a subscheme in
$C'\subset C$ be the corresponding (minimal) cycle of smooth rational curves, a subscheme in ![]() $C$ with irreducible components
$C$ with irreducible components ![]() $C_1,\ldots,C_l$. Again, we know that
$C_1,\ldots,C_l$. Again, we know that ![]() $H^1({\mathcal {O}}_{C'}) = 0$. Then we have a short exact sequence
$H^1({\mathcal {O}}_{C'}) = 0$. Then we have a short exact sequence
 \[ 0 \to{\mathcal{O}}_{C'} \to \bigoplus_{i=1}^l {\mathcal{O}}_{C_i} \to \bigoplus_{i=1}^l {\mathcal{O}}_{c_i} \to 0, \]
\[ 0 \to{\mathcal{O}}_{C'} \to \bigoplus_{i=1}^l {\mathcal{O}}_{C_i} \to \bigoplus_{i=1}^l {\mathcal{O}}_{c_i} \to 0, \]
where ![]() $c_1, \ldots, c_l$ are singular points of
$c_1, \ldots, c_l$ are singular points of ![]() $C'$. From long exact sequence of cohomology groups it follows that
$C'$. From long exact sequence of cohomology groups it follows that ![]() $H^1({\mathcal {O}}_{C'}) = k$. This contradiction proves condition (ii).
$H^1({\mathcal {O}}_{C'}) = k$. This contradiction proves condition (ii).
Note that, for curves ![]() $C$ satisfying conditions (i) and (ii), there exists a universal curve
$C$ satisfying conditions (i) and (ii), there exists a universal curve ![]() ${\bar {C}}$ and morphism
${\bar {C}}$ and morphism
with the property that ![]() ${\bar {C}}$ has normal crossing singularities and, for every curve
${\bar {C}}$ has normal crossing singularities and, for every curve ![]() $D$ with normal crossing singularities and a map
$D$ with normal crossing singularities and a map ![]() $D\to C$, there is a unique lifting map
$D\to C$, there is a unique lifting map ![]() $D\to {\bar {C}}$.
$D\to {\bar {C}}$.
The construction of the curve ![]() ${\bar {C}}$ is simple. Consider an affine neighbourhood
${\bar {C}}$ is simple. Consider an affine neighbourhood ![]() $U\subset C$ of every point of the curve which does not contain more than one singular point. Assume there is one. The irreducible components that meet at the singular point give some affine subschemes in
$U\subset C$ of every point of the curve which does not contain more than one singular point. Assume there is one. The irreducible components that meet at the singular point give some affine subschemes in ![]() $U$. As the category of affine schemes is opposite to the category of unital commutative algebras, we can define the open chart
$U$. As the category of affine schemes is opposite to the category of unital commutative algebras, we can define the open chart ![]() ${\bar {U}}$ of the universal curve over
${\bar {U}}$ of the universal curve over ![]() $U$ as a colimit over the diagram of embedding of the singular point into all these affine subschemes (by taking the spectrum of the limit over the diagram of the corresponding commutative algebras). It has one normal crossing singularity.
$U$ as a colimit over the diagram of embedding of the singular point into all these affine subschemes (by taking the spectrum of the limit over the diagram of the corresponding commutative algebras). It has one normal crossing singularity.
If ![]() $U$ has no singular points, then we put
$U$ has no singular points, then we put ![]() ${\bar {U}}=U$. We can glue
${\bar {U}}=U$. We can glue ![]() ${\bar {U}}$ over
${\bar {U}}$ over ![]() $C$ into a curve,
$C$ into a curve, ![]() ${\bar {C}}$, with normal crossing singularities. Conditions (i) and (ii) guarantee that
${\bar {C}}$, with normal crossing singularities. Conditions (i) and (ii) guarantee that ![]() ${\bar {C}}$ has the required universal property. As we do not need this for our purpose, we skip the proof.
${\bar {C}}$ has the required universal property. As we do not need this for our purpose, we skip the proof.
Clearly, ![]() ${\bar {\pi }}$ is a set-theoretic isomorphism. We again have a short exact sequence with sheaf
${\bar {\pi }}$ is a set-theoretic isomorphism. We again have a short exact sequence with sheaf ![]() ${\mathcal {F}}$ supported at singular points of
${\mathcal {F}}$ supported at singular points of ![]() $C$:
$C$:
whose long exact sequence of cohomology shows that ![]() ${\mathcal {F}}$ is trivial sheaf. This implies that the schematic structure of
${\mathcal {F}}$ is trivial sheaf. This implies that the schematic structure of ![]() $C$ and
$C$ and ![]() ${\bar {C}}$ coincide, which proves condition (iii).
${\bar {C}}$ coincide, which proves condition (iii).
Conversely, assume that ![]() $C$ is a reduced curve satisfying conditions (i), (ii) and (iii). We can assume that the curve is connected. We proceed by induction on the number of irreducible components of
$C$ is a reduced curve satisfying conditions (i), (ii) and (iii). We can assume that the curve is connected. We proceed by induction on the number of irreducible components of ![]() $C$. The base of induction, the case of a single component, is obvious. As the incidence graph is a tree, then we can choose an irreducible component
$C$. The base of induction, the case of a single component, is obvious. As the incidence graph is a tree, then we can choose an irreducible component ![]() $C_1$ which has only one singular point,
$C_1$ which has only one singular point, ![]() $c$. The curve
$c$. The curve ![]() $C'$, the union of the other components, satisfies the same assumptions as
$C'$, the union of the other components, satisfies the same assumptions as ![]() $C$. Hence,
$C$. Hence, ![]() $H^1({\mathcal {O}}_{C'}) = 0$ by induction hypothesis. As the point
$H^1({\mathcal {O}}_{C'}) = 0$ by induction hypothesis. As the point ![]() $c$ is a normal crossing singularity, then the kernel of the restriction morphism
$c$ is a normal crossing singularity, then the kernel of the restriction morphism ![]() ${\mathcal {O}}_C\to {\mathcal {O}}_{C'}$ is easily seen to be
${\mathcal {O}}_C\to {\mathcal {O}}_{C'}$ is easily seen to be ![]() ${\mathcal {O}}_{C_1}(-1)$. Then looking at the cohomology sequence for the short exact sequence
${\mathcal {O}}_{C_1}(-1)$. Then looking at the cohomology sequence for the short exact sequence
we see that ![]() $H^1({\mathcal {O}}_C) = 0$.
$H^1({\mathcal {O}}_C) = 0$.
Appendix E. Calculation of Ext groups for bounded above complexes
Let ![]() ${\mathcal {A}}$ be an abelian category and
${\mathcal {A}}$ be an abelian category and ![]() $A^{{\boldsymbol {\cdot }}}$ a bounded above complex over
$A^{{\boldsymbol {\cdot }}}$ a bounded above complex over ![]() ${\mathcal {A}}$. Its ‘stupid’ truncations
${\mathcal {A}}$. Its ‘stupid’ truncations ![]() $\sigma _{\geqslant i}A$ define direct system
$\sigma _{\geqslant i}A$ define direct system ![]() $\sigma _{\geqslant i}A^{{\boldsymbol {\cdot }}} \to \sigma _{\geqslant i-1}A^{{\boldsymbol {\cdot }}}$. Given a complex
$\sigma _{\geqslant i}A^{{\boldsymbol {\cdot }}} \to \sigma _{\geqslant i-1}A^{{\boldsymbol {\cdot }}}$. Given a complex ![]() $B^{{\boldsymbol {\cdot }}}$, we are interested in the group
$B^{{\boldsymbol {\cdot }}}$, we are interested in the group ![]() ${\rm Hom}^{{\boldsymbol {\cdot }}}(A^{{\boldsymbol {\cdot }}}, B^{{\boldsymbol {\cdot }}})$ in terms of the stupid truncations of both complexes. There is a spectral sequence with
${\rm Hom}^{{\boldsymbol {\cdot }}}(A^{{\boldsymbol {\cdot }}}, B^{{\boldsymbol {\cdot }}})$ in terms of the stupid truncations of both complexes. There is a spectral sequence with ![]() ${\rm E}_1$-layer:
${\rm E}_1$-layer:
If both complexes ![]() $A^{{\boldsymbol {\cdot }}}$,
$A^{{\boldsymbol {\cdot }}}$, ![]() $B^{{\boldsymbol {\cdot }}}$ have finite number of non-trivial components, then it is well-known that spectral sequence (E.1) converges. If complex
$B^{{\boldsymbol {\cdot }}}$ have finite number of non-trivial components, then it is well-known that spectral sequence (E.1) converges. If complex ![]() $B^{{\boldsymbol {\cdot }}}$ is infinite then we need to put some conditions on
$B^{{\boldsymbol {\cdot }}}$ is infinite then we need to put some conditions on ![]() $A^{{\boldsymbol {\cdot }}}$ in order to guarantee the spectral sequence is converging to
$A^{{\boldsymbol {\cdot }}}$ in order to guarantee the spectral sequence is converging to ![]() ${\rm Hom}^{{\boldsymbol {\cdot }}}(A^{{\boldsymbol {\cdot }}}, B^{{\boldsymbol {\cdot }}})$. We show that if, in addition, both complexes are bounded above and
${\rm Hom}^{{\boldsymbol {\cdot }}}(A^{{\boldsymbol {\cdot }}}, B^{{\boldsymbol {\cdot }}})$. We show that if, in addition, both complexes are bounded above and ![]() $\mathop {{\rm Ext}}\nolimits ^q(A^i, B^j) =0$, for
$\mathop {{\rm Ext}}\nolimits ^q(A^i, B^j) =0$, for ![]() $q>0$ and
$q>0$ and ![]() $i,j \in \mathbb {Z}$, then we have a graded complex with terms
$i,j \in \mathbb {Z}$, then we have a graded complex with terms
whose cohomology calculate ![]() $\mathop {{\rm Ext}}\nolimits ^p(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$. Here the differentials are the limits of the relevant differentials in the sequence (E.1) when we allow the truncations of
$\mathop {{\rm Ext}}\nolimits ^p(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$. Here the differentials are the limits of the relevant differentials in the sequence (E.1) when we allow the truncations of ![]() $A^{{\boldsymbol {\cdot }}}$ and
$A^{{\boldsymbol {\cdot }}}$ and ![]() $B^{{\boldsymbol {\cdot }}}$ to go to infinity.
$B^{{\boldsymbol {\cdot }}}$ to go to infinity.
Recall the following fact about cohomology of limits. Let ![]() $(M_i)_{i \in \mathbb {Z}}$ be an inverse system of abelian groups and
$(M_i)_{i \in \mathbb {Z}}$ be an inverse system of abelian groups and ![]() $M = \varprojlim M_i$. We say that system
$M = \varprojlim M_i$. We say that system ![]() $(M_i)_{i \in \mathbb {Z}}$ satisfies
$(M_i)_{i \in \mathbb {Z}}$ satisfies ![]() $(\star )$ if morphism
$(\star )$ if morphism ![]() $M_i \to M_{i-1}$ is surjective, for any
$M_i \to M_{i-1}$ is surjective, for any ![]() $i$.
$i$.
Lemma E.1 [Reference SpaltensteinSpa88, Lemma 0.11]
Let ![]() $(A_i \xrightarrow {f_i} B_i \xrightarrow {g_i} C_i \xrightarrow {h_i} D_i)_{i \in \mathbb {Z}}$ be an inverse system of complexes of abelian groups such that systems
$(A_i \xrightarrow {f_i} B_i \xrightarrow {g_i} C_i \xrightarrow {h_i} D_i)_{i \in \mathbb {Z}}$ be an inverse system of complexes of abelian groups such that systems ![]() $(A_i)$,
$(A_i)$, ![]() $(B_i)$,
$(B_i)$, ![]() $(C_i)$,
$(C_i)$, ![]() $(D_i)$ satisfy
$(D_i)$ satisfy ![]() $(\star )$ for all
$(\star )$ for all ![]() $i$. Denote by
$i$. Denote by ![]() $(A \xrightarrow {f} B \xrightarrow {g} C \xrightarrow {h} D)$ the limit complex. Let
$(A \xrightarrow {f} B \xrightarrow {g} C \xrightarrow {h} D)$ the limit complex. Let ![]() $A_i'$,
$A_i'$, ![]() $B_i'$,
$B_i'$, ![]() $C_i'$ and
$C_i'$ and ![]() $D'_i$ be kernels of
$D'_i$ be kernels of ![]() $A_i \to A_{i-1}$,
$A_i \to A_{i-1}$, ![]() $B_i \to B_{i-1}$,
$B_i \to B_{i-1}$, ![]() $C_i \to C_{i-1}$ and
$C_i \to C_{i-1}$ and ![]() $D_i \to D_{i-1}$, respectively. Assume there is
$D_i \to D_{i-1}$, respectively. Assume there is ![]() $j\in \mathbb {Z}$ such that sequence
$j\in \mathbb {Z}$ such that sequence ![]() $A'_i \to B'_i \to C'_i \to D'_i$ is exact for all
$A'_i \to B'_i \to C'_i \to D'_i$ is exact for all ![]() $i >j$. Then the natural homomorphism
$i >j$. Then the natural homomorphism ![]() ${\rm Ker} g/ {\rm Im} f \to {\rm Ker} g_j/ {\rm Im} f_j$ is an isomorphism.
${\rm Ker} g/ {\rm Im} f \to {\rm Ker} g_j/ {\rm Im} f_j$ is an isomorphism.
Lemma E.2 Let ![]() $A^{\boldsymbol {\cdot }}$ and
$A^{\boldsymbol {\cdot }}$ and ![]() $B^{\boldsymbol {\cdot }}$ be complexes over
$B^{\boldsymbol {\cdot }}$ be complexes over ![]() ${\mathcal {A}}$,
${\mathcal {A}}$, ![]() $A^{\boldsymbol {\cdot }}$ bounded above. Assume
$A^{\boldsymbol {\cdot }}$ bounded above. Assume ![]() $l\in \mathbb {Z}$ such that
$l\in \mathbb {Z}$ such that ![]() $\mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(A^i, B^{{\boldsymbol {\cdot }}}) = 0$, for
$\mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(A^i, B^{{\boldsymbol {\cdot }}}) = 0$, for ![]() $j< l$ and all
$j< l$ and all ![]() $i$. Then the canonical morphism
$i$. Then the canonical morphism
is an isomorphism for any ![]() $j\in \mathbb {Z}$. Here
$j\in \mathbb {Z}$. Here ![]() $\sigma _{\geqslant i} A^{{\boldsymbol {\cdot }}}$ is the ‘stupid’ truncation of
$\sigma _{\geqslant i} A^{{\boldsymbol {\cdot }}}$ is the ‘stupid’ truncation of ![]() $A^{\boldsymbol {\cdot }}$.
$A^{\boldsymbol {\cdot }}$.
Proof. Fix ![]() $I^{{\boldsymbol {\cdot }}}$, an h-injective resolution of
$I^{{\boldsymbol {\cdot }}}$, an h-injective resolution of ![]() $B^{{\boldsymbol {\cdot }}}$ (see [Reference SpaltensteinSpa88]). The direct system
$B^{{\boldsymbol {\cdot }}}$ (see [Reference SpaltensteinSpa88]). The direct system ![]() $\sigma _{\geqslant i+1}A^{\boldsymbol {\cdot }} \to \sigma _{\geqslant i}A^{\boldsymbol {\cdot }}$ induces an inverse system
$\sigma _{\geqslant i+1}A^{\boldsymbol {\cdot }} \to \sigma _{\geqslant i}A^{\boldsymbol {\cdot }}$ induces an inverse system ![]() $\alpha _i \colon \mathop {{\rm Hom}}\nolimits _{{\rm Com}}(\sigma _{\geqslant i}A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }}) \to \mathop {{\rm Hom}}\nolimits _{{\rm Com}}(\sigma _{\geqslant i+1}A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }})$. Morphism
$\alpha _i \colon \mathop {{\rm Hom}}\nolimits _{{\rm Com}}(\sigma _{\geqslant i}A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }}) \to \mathop {{\rm Hom}}\nolimits _{{\rm Com}}(\sigma _{\geqslant i+1}A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }})$. Morphism ![]() $\alpha _i$ is surjective, i.e. property
$\alpha _i$ is surjective, i.e. property ![]() $(\star )$ is satisfied, and its kernel is complex
$(\star )$ is satisfied, and its kernel is complex ![]() $\mathop {{\rm Hom}}\nolimits _{{\rm Com}}(A^{i}[-i], I^{\boldsymbol {\cdot }})$. Cohomology of this complex is
$\mathop {{\rm Hom}}\nolimits _{{\rm Com}}(A^{i}[-i], I^{\boldsymbol {\cdot }})$. Cohomology of this complex is ![]() $H^j(\mathop {{\rm Hom}}\nolimits _{{\rm Com}}(A^{i}[-i], I^{\boldsymbol {\cdot }})) \simeq \mathop {{\rm Ext}}\nolimits ^{j+i}_{{\mathcal {D}}^b({\mathcal {A}})}(A^{i}, B^{\boldsymbol {\cdot }})$.
$H^j(\mathop {{\rm Hom}}\nolimits _{{\rm Com}}(A^{i}[-i], I^{\boldsymbol {\cdot }})) \simeq \mathop {{\rm Ext}}\nolimits ^{j+i}_{{\mathcal {D}}^b({\mathcal {A}})}(A^{i}, B^{\boldsymbol {\cdot }})$.
Our assumption implies that, for any ![]() $j$, there exists
$j$, there exists ![]() $N_j\in \mathbb {Z}$ such that, for
$N_j\in \mathbb {Z}$ such that, for ![]() $i< N_j$, complex
$i< N_j$, complex ![]() $\mathop {{\rm Hom}}\nolimits _{{\rm Com}}(A^{i}[-i], I^{\boldsymbol {\cdot }})$ is exact at degree
$\mathop {{\rm Hom}}\nolimits _{{\rm Com}}(A^{i}[-i], I^{\boldsymbol {\cdot }})$ is exact at degree ![]() $j$. By Lemma E.1, we conclude that
$j$. By Lemma E.1, we conclude that
In particular, the inverse system ![]() $\mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(\sigma _{\geqslant i}A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }}) \to \mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(\sigma _{\geqslant i+1} A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }})$ stabilises, hence the right-hand side of (E.3) is isomorphic to
$\mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(\sigma _{\geqslant i}A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }}) \to \mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(\sigma _{\geqslant i+1} A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }})$ stabilises, hence the right-hand side of (E.3) is isomorphic to ![]() $\varprojlim \mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(\sigma _{\geqslant i} A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$, for
$\varprojlim \mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(\sigma _{\geqslant i} A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$, for ![]() $i$ sufficiently negative. Moreover, we have
$i$ sufficiently negative. Moreover, we have ![]() $\varprojlim \mathop {{\rm Hom}}\nolimits _{{\rm Com}}(\sigma _{\geqslant i} A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }}) \simeq \mathop {{\rm Hom}}\nolimits _{{\rm Com}}(A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }})$. Hence, isomorphism (E.3) yields
$\varprojlim \mathop {{\rm Hom}}\nolimits _{{\rm Com}}(\sigma _{\geqslant i} A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }}) \simeq \mathop {{\rm Hom}}\nolimits _{{\rm Com}}(A^{\boldsymbol {\cdot }}, I^{\boldsymbol {\cdot }})$. Hence, isomorphism (E.3) yields
For the reader's convenience, we also give a proof of the following well-known fact.
Lemma E.3 Let ![]() $A^{\boldsymbol {\cdot }}$ and
$A^{\boldsymbol {\cdot }}$ and ![]() $B^{\boldsymbol {\cdot }}$ be complexes over
$B^{\boldsymbol {\cdot }}$ be complexes over ![]() ${\mathcal {A}}$ such that
${\mathcal {A}}$ such that ![]() $A^{\boldsymbol {\cdot }}$ is finite and
$A^{\boldsymbol {\cdot }}$ is finite and ![]() $B^{\boldsymbol {\cdot }}$ is bounded above and with bounded cohomology. Assume there exists
$B^{\boldsymbol {\cdot }}$ is bounded above and with bounded cohomology. Assume there exists ![]() $N\in \mathbb {Z}$ such that
$N\in \mathbb {Z}$ such that ![]() $\mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {A}}}(A^i, A) = 0$, for all
$\mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {A}}}(A^i, A) = 0$, for all ![]() $j>N$,
$j>N$, ![]() $i\in \mathbb {Z}$ and
$i\in \mathbb {Z}$ and ![]() $A\in {\mathcal {A}}$. Then, there exists a spectral sequence
$A\in {\mathcal {A}}$. Then, there exists a spectral sequence
Proof. For any ![]() $n\in \mathbb {Z}$, injective resolutions
$n\in \mathbb {Z}$, injective resolutions ![]() $I^{i,{\boldsymbol {\cdot }}}$ of
$I^{i,{\boldsymbol {\cdot }}}$ of ![]() $B^i$ give an injective resolution
$B^i$ give an injective resolution ![]() $J_n^{\boldsymbol {\cdot }}$ of
$J_n^{\boldsymbol {\cdot }}$ of ![]() $\sigma _{\geqslant n}B^{\boldsymbol {\cdot }}$ such that complex
$\sigma _{\geqslant n}B^{\boldsymbol {\cdot }}$ such that complex ![]() $J_n^{\boldsymbol {\cdot }}$ admits a filtration with graded factors
$J_n^{\boldsymbol {\cdot }}$ admits a filtration with graded factors ![]() $I^{i,{\boldsymbol {\cdot }}}$. The filtered complex
$I^{i,{\boldsymbol {\cdot }}}$. The filtered complex ![]() $J_n^{\boldsymbol {\cdot }}$ yields a spectral sequence
$J_n^{\boldsymbol {\cdot }}$ yields a spectral sequence
It follows from our assumptions that ![]() ${}^nE_1^{p,q}$ is stationary for fixed
${}^nE_1^{p,q}$ is stationary for fixed ![]() $p$,
$p$, ![]() $q$ and
$q$ and ![]() $n \rightarrow - \infty$. Moreover, the term
$n \rightarrow - \infty$. Moreover, the term ![]() ${}^nE_1^{p,q}$ is zero, for any
${}^nE_1^{p,q}$ is zero, for any ![]() $p\notin [0,N]$ or for any sufficiently positive
$p\notin [0,N]$ or for any sufficiently positive ![]() $q$. This confirms existence of the spectral sequence (E.4) and also implies that the
$q$. This confirms existence of the spectral sequence (E.4) and also implies that the ![]() $l$th layer
$l$th layer ![]() ${}^nE^{p,q}_{l}$ is stationary for fixed
${}^nE^{p,q}_{l}$ is stationary for fixed ![]() $p$,
$p$, ![]() $q$ and
$q$ and ![]() $n \rightarrow - \infty$ and
$n \rightarrow - \infty$ and ![]() $l \rightarrow \infty$.
$l \rightarrow \infty$.
As ![]() $B^{\boldsymbol {\cdot }}$ has bounded cohomology, for
$B^{\boldsymbol {\cdot }}$ has bounded cohomology, for ![]() $n$ sufficiently negative, we have
$n$ sufficiently negative, we have ![]() $\tau _{\geqslant n+1}\sigma _{\geqslant n} B^{\boldsymbol {\cdot }} \simeq B^{\boldsymbol {\cdot }}$ and
$\tau _{\geqslant n+1}\sigma _{\geqslant n} B^{\boldsymbol {\cdot }} \simeq B^{\boldsymbol {\cdot }}$ and ![]() $\tau _{\leqslant n} \sigma _{\geqslant n} B^{\boldsymbol {\cdot }} \simeq {\mathcal {H}}^n(\sigma _{\geqslant n} B^{\boldsymbol {\cdot }})[-n]$. Then triangle
$\tau _{\leqslant n} \sigma _{\geqslant n} B^{\boldsymbol {\cdot }} \simeq {\mathcal {H}}^n(\sigma _{\geqslant n} B^{\boldsymbol {\cdot }})[-n]$. Then triangle ![]() $\tau _{\leqslant n} \sigma _{\geqslant n} B^{\boldsymbol {\cdot }} \to \sigma _{\geqslant n} B^{\boldsymbol {\cdot }} \to \tau _{\geqslant n+1} \sigma _{\geqslant n} B^{\boldsymbol {\cdot }}$ reads
$\tau _{\leqslant n} \sigma _{\geqslant n} B^{\boldsymbol {\cdot }} \to \sigma _{\geqslant n} B^{\boldsymbol {\cdot }} \to \tau _{\geqslant n+1} \sigma _{\geqslant n} B^{\boldsymbol {\cdot }}$ reads
As ![]() $A^{\boldsymbol {\cdot }}$ is finite, the assumptions on
$A^{\boldsymbol {\cdot }}$ is finite, the assumptions on ![]() $A^i$ imply that there exists
$A^i$ imply that there exists ![]() $\widetilde {N}$ such that
$\widetilde {N}$ such that ![]() $\mathop {{\rm Hom}}\nolimits (A^{\boldsymbol {\cdot }}, C[k]) = 0$, for
$\mathop {{\rm Hom}}\nolimits (A^{\boldsymbol {\cdot }}, C[k]) = 0$, for ![]() $k> \widetilde {N}$ and all
$k> \widetilde {N}$ and all ![]() $C \in {\mathcal {A}}$. Thus,
$C \in {\mathcal {A}}$. Thus, ![]() $\mathop {{\rm Ext}}\nolimits ^j(A^{\boldsymbol {\cdot }}, {\mathcal {H}}^n(\sigma _{\geqslant n} B^{\boldsymbol {\cdot }})[-n]) \simeq \mathop {{\rm Hom}}\nolimits (A^{\boldsymbol {\cdot }}, {\mathcal {H}}^n(\sigma _{\geqslant n} B^{\boldsymbol {\cdot }})[j-n]) = 0$, for
$\mathop {{\rm Ext}}\nolimits ^j(A^{\boldsymbol {\cdot }}, {\mathcal {H}}^n(\sigma _{\geqslant n} B^{\boldsymbol {\cdot }})[-n]) \simeq \mathop {{\rm Hom}}\nolimits (A^{\boldsymbol {\cdot }}, {\mathcal {H}}^n(\sigma _{\geqslant n} B^{\boldsymbol {\cdot }})[j-n]) = 0$, for ![]() $n< j- \widetilde {N}$. Then, for
$n< j- \widetilde {N}$. Then, for ![]() $n< j - \widetilde {N}$, we have from the above triangle an isomorphism
$n< j - \widetilde {N}$, we have from the above triangle an isomorphism ![]() $\mathop {{\rm Ext}}\nolimits ^{j-1}_{{\mathcal {D}}^b({\mathcal {A}})}(A^{\boldsymbol {\cdot }}, \sigma _{\geqslant n} B^{\boldsymbol {\cdot }}) \simeq \mathop {{\rm Ext}}\nolimits ^{j-1}_{{\mathcal {D}}^b({\mathcal {A}})}(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$.
$\mathop {{\rm Ext}}\nolimits ^{j-1}_{{\mathcal {D}}^b({\mathcal {A}})}(A^{\boldsymbol {\cdot }}, \sigma _{\geqslant n} B^{\boldsymbol {\cdot }}) \simeq \mathop {{\rm Ext}}\nolimits ^{j-1}_{{\mathcal {D}}^b({\mathcal {A}})}(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$.
This shows that the spectral sequence in (E.4) converges to ![]() $\mathop {{\rm Hom}}\nolimits ^{\boldsymbol {\cdot }}_{{\mathcal {D}}^b({\mathcal {A}})}(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$.
$\mathop {{\rm Hom}}\nolimits ^{\boldsymbol {\cdot }}_{{\mathcal {D}}^b({\mathcal {A}})}(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$.
Proposition E.4 Let ![]() $A^{\boldsymbol {\cdot }}$,
$A^{\boldsymbol {\cdot }}$, ![]() $B^{\boldsymbol {\cdot }}$ be bounded above complexes of objects in
$B^{\boldsymbol {\cdot }}$ be bounded above complexes of objects in ![]() ${\mathcal {A}}$ with bounded cohomology. Assume that there exists
${\mathcal {A}}$ with bounded cohomology. Assume that there exists ![]() $N\in \mathbb {Z}$ such that
$N\in \mathbb {Z}$ such that ![]() $\mathop {{\rm Ext}}\nolimits ^j(A^i, A) = 0$, for all
$\mathop {{\rm Ext}}\nolimits ^j(A^i, A) = 0$, for all ![]() $j>N$,
$j>N$, ![]() $i \in \mathbb {Z}$ and
$i \in \mathbb {Z}$ and ![]() $A\in {\mathcal {A}}$. Assume further that
$A\in {\mathcal {A}}$. Assume further that ![]() $\mathop {{\rm Ext}}\nolimits ^j(A^i, B^k) = 0$, for
$\mathop {{\rm Ext}}\nolimits ^j(A^i, B^k) = 0$, for ![]() $j>0$ and all
$j>0$ and all ![]() $i, k \in \mathbb {Z}$. Then,
$i, k \in \mathbb {Z}$. Then, ![]() $\mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$ is isomorphic to the
$\mathop {{\rm Ext}}\nolimits ^j_{{\mathcal {D}}^b({\mathcal {A}})}(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$ is isomorphic to the ![]() $j$th cohomology group of complex (E.2).
$j$th cohomology group of complex (E.2).
Proof. Lemma E.3 applied to ![]() $\sigma _{\geqslant i} A^{\boldsymbol {\cdot }}$ and
$\sigma _{\geqslant i} A^{\boldsymbol {\cdot }}$ and ![]() $B^{\boldsymbol {\cdot }}$, for any
$B^{\boldsymbol {\cdot }}$, for any ![]() $i\in \mathbb {Z}$, implies that the spectral sequence (E.4) reduces to a single row. Hence, we have
$i\in \mathbb {Z}$, implies that the spectral sequence (E.4) reduces to a single row. Hence, we have ![]() $\mathop {{\rm Ext}}\nolimits ^j(\sigma _{\geqslant i}A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }}) \simeq H^j(\oplus _{k>i} \mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k}))$. The direct system
$\mathop {{\rm Ext}}\nolimits ^j(\sigma _{\geqslant i}A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }}) \simeq H^j(\oplus _{k>i} \mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k}))$. The direct system ![]() $\sigma _{\geqslant i+1} A^{\boldsymbol {\cdot }} \to \sigma _{\geqslant i} A^{\boldsymbol {\cdot }}$ induces an inverse system of complexes
$\sigma _{\geqslant i+1} A^{\boldsymbol {\cdot }} \to \sigma _{\geqslant i} A^{\boldsymbol {\cdot }}$ induces an inverse system of complexes ![]() $\bigoplus _{k>i}\mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k}) \to \bigoplus _{k>i+1} \mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k})$ satisfying condition
$\bigoplus _{k>i}\mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k}) \to \bigoplus _{k>i+1} \mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k})$ satisfying condition ![]() $(\star )$. The kernel of
$(\star )$. The kernel of ![]() $\bigoplus _{k>i}\mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k}) \to \bigoplus _{k>i+1} \mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k})$ is a complex
$\bigoplus _{k>i}\mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k}) \to \bigoplus _{k>i+1} \mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }}+k})$ is a complex ![]() $\mathop {{\rm Hom}}\nolimits (A^i, B^{\boldsymbol {\cdot }})[i]$. By Lemma E.3, we have
$\mathop {{\rm Hom}}\nolimits (A^i, B^{\boldsymbol {\cdot }})[i]$. By Lemma E.3, we have ![]() $H^j(\mathop {{\rm Hom}}\nolimits (A^i, B^{\boldsymbol {\cdot }})[i]) \simeq \mathop {{\rm Ext}}\nolimits ^{j+i}(A^i, B^{\boldsymbol {\cdot }})$, thus, for a fixed
$H^j(\mathop {{\rm Hom}}\nolimits (A^i, B^{\boldsymbol {\cdot }})[i]) \simeq \mathop {{\rm Ext}}\nolimits ^{j+i}(A^i, B^{\boldsymbol {\cdot }})$, thus, for a fixed ![]() $j$ and any sufficiently negative
$j$ and any sufficiently negative ![]() $i$, complex
$i$, complex ![]() $\mathop {{\rm Hom}}\nolimits (A^i, B^{\boldsymbol {\cdot }})[i]$ is exact at degree
$\mathop {{\rm Hom}}\nolimits (A^i, B^{\boldsymbol {\cdot }})[i]$ is exact at degree ![]() $j$. Lemma E.1 implies that, for such
$j$. Lemma E.1 implies that, for such ![]() $i$, we have
$i$, we have
 \[ H^j\bigg(\prod_k \mathop{{\rm Hom}}\nolimits(A^k, B^{{\boldsymbol{\cdot}} +k})\bigg) \simeq H^j \bigg(\bigoplus_{k>i}\mathop{{\rm Hom}}\nolimits(A^k, B^{{\boldsymbol{\cdot}}+k})\bigg) \simeq \mathop{{\rm Ext}}\nolimits^j(\sigma_{\geqslant i} A^{\boldsymbol{\cdot}}, B^{\boldsymbol{\cdot}}). \]
\[ H^j\bigg(\prod_k \mathop{{\rm Hom}}\nolimits(A^k, B^{{\boldsymbol{\cdot}} +k})\bigg) \simeq H^j \bigg(\bigoplus_{k>i}\mathop{{\rm Hom}}\nolimits(A^k, B^{{\boldsymbol{\cdot}}+k})\bigg) \simeq \mathop{{\rm Ext}}\nolimits^j(\sigma_{\geqslant i} A^{\boldsymbol{\cdot}}, B^{\boldsymbol{\cdot}}). \]
Thus, ![]() $\mathop {{\rm Ext}}\nolimits ^j(\sigma _{\geqslant i} A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$ is stationary, and
$\mathop {{\rm Ext}}\nolimits ^j(\sigma _{\geqslant i} A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$ is stationary, and ![]() $H^j(\prod _k \mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }} +k})) \simeq \varprojlim \mathop {{\rm Ext}}\nolimits ^j(\sigma _{\geqslant i}A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$. As
$H^j(\prod _k \mathop {{\rm Hom}}\nolimits (A^k, B^{{\boldsymbol {\cdot }} +k})) \simeq \varprojlim \mathop {{\rm Ext}}\nolimits ^j(\sigma _{\geqslant i}A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$. As ![]() $B^{\boldsymbol {\cdot }}$ has bounded cohomology, the assumptions of Lemma E.2 are satisfied. It follows that the latter space is isomorphic to
$B^{\boldsymbol {\cdot }}$ has bounded cohomology, the assumptions of Lemma E.2 are satisfied. It follows that the latter space is isomorphic to ![]() $\mathop {{\rm Ext}}\nolimits ^j(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$.
$\mathop {{\rm Ext}}\nolimits ^j(A^{\boldsymbol {\cdot }}, B^{\boldsymbol {\cdot }})$.