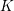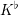Introduction
A theorem of Fontaine and Wintenberger [Reference Fontaine and WintenbergerFW79], later expanded by Scholze [Reference ScholzeSch12], states that there is an isomorphism between the Galois groups of a perfectoid field
![]() $K$
and the associated (tilted) perfect field
$K$
and the associated (tilted) perfect field
![]() $K^{\flat }$
of positive characteristic. The standard example of such a pair is formed by the completions of the fields
$K^{\flat }$
of positive characteristic. The standard example of such a pair is formed by the completions of the fields
![]() $\mathbb{Q}_{p}(p^{1/p^{\infty }})$
and
$\mathbb{Q}_{p}(p^{1/p^{\infty }})$
and
![]() $\mathbb{F}_{p}((t))(t^{1/p^{\infty }})$
. This theorem is a cornerstone of
$\mathbb{F}_{p}((t))(t^{1/p^{\infty }})$
. This theorem is a cornerstone of
![]() $p$
-adic Hodge theory, providing a striking equivalence between objects in mixed characteristic (finite étale algebras over
$p$
-adic Hodge theory, providing a striking equivalence between objects in mixed characteristic (finite étale algebras over
![]() $K$
) and objects in equal characteristic
$K$
) and objects in equal characteristic
![]() $p$
(finite étale algebras over
$p$
(finite étale algebras over
![]() $K^{\flat }$
).
$K^{\flat }$
).
In the same spirit, the ‘tilting equivalence’ of Scholze [Reference ScholzeSch12] promotes the equivalence above to a certain kind of space of higher dimension, namely the perfectoid spaces over the two fields. These objects are non-noetherian analytic spaces, which can typically be thought as certain infinite covers of classical rigid analytic varieties obtained by adding all
![]() $p$
th roots of local coordinates, and their introduction has had many different applications in arithmetic geometry (see [Reference ScholzeSch14]).
$p$
th roots of local coordinates, and their introduction has had many different applications in arithmetic geometry (see [Reference ScholzeSch14]).
The aim of this paper is to ‘descend’ Scholze’s tilting equivalence to the level of classical rigid analytic varieties defined over
![]() $K$
and
$K$
and
![]() $K^{\flat }$
, at least from a (co-)homological point of view. What we actually prove, is an equivalence between the two associated categories of (mixed, effective, with rational coefficients) rigid analytic motives
$K^{\flat }$
, at least from a (co-)homological point of view. What we actually prove, is an equivalence between the two associated categories of (mixed, effective, with rational coefficients) rigid analytic motives
![]() $\mathbf{RigDM}$
defined over the two fields, introduced by Ayoub [Reference AyoubAyo15] adapting the classic construction of
$\mathbf{RigDM}$
defined over the two fields, introduced by Ayoub [Reference AyoubAyo15] adapting the classic construction of
![]() $\mathbf{DM}$
by Voevodsky [Reference VoevodskyVoe96].
$\mathbf{DM}$
by Voevodsky [Reference VoevodskyVoe96].
Theorem 7.10
. Let
![]() $K$
be a perfectoid field with tilt
$K$
be a perfectoid field with tilt
![]() $K^{\flat }$
and let
$K^{\flat }$
and let
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $\mathbb{Q}$
-algebra. There is a monoidal triangulated equivalence of categories
$\mathbb{Q}$
-algebra. There is a monoidal triangulated equivalence of categories
We remark that, from a motivic point of view, the theorem of Fontaine and Wintenberger can be rephrased by saying that the categories of Artin motives over the two fields are equivalent. Conversely, our theorem shows that not only the absolute Galois groups of a perfectoid field and its tilt are isomorphic, but also their absolute local motivic Galois groups (in the sense of the introduction of [Reference AyoubAyo15]). By [Reference VezzaniVez17], it is also possible to state the result above with respect to motives without transfers
![]() $\mathbf{RigDA}$
defined over the two fields (the rigid analytic analog of the category
$\mathbf{RigDA}$
defined over the two fields (the rigid analytic analog of the category
![]() $\mathbf{DA}$
see [Reference AyoubAyo15]).
$\mathbf{DA}$
see [Reference AyoubAyo15]).
The statement above involves only rigid analytic varieties and its proof uses Scholze’s theory of perfectoid spaces only in an auxiliary way. Nonetheless, we can restate our main result highlighting the role of perfectoid spaces as follows.
Theorem 7.11
. Let
![]() $K$
be a perfectoid field and let
$K$
be a perfectoid field and let
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $\mathbb{Q}$
-algebra. There is a monoidal triangulated equivalence of categories
$\mathbb{Q}$
-algebra. There is a monoidal triangulated equivalence of categories
The category
![]() $\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
is built in the same way as
$\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
is built in the same way as
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
using as a starting point the big étale site of smooth, small perfectoid spaces, i.e., those that are locally étale over some perfectoid ball
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
using as a starting point the big étale site of smooth, small perfectoid spaces, i.e., those that are locally étale over some perfectoid ball
![]() $\widehat{\mathbb{B}}^{n}$
.
$\widehat{\mathbb{B}}^{n}$
.
This last theorem provides a way to ‘perfectoidify’ (and ‘de-perfectoidify’) canonically a rigid analytic variety into a perfectoid motive (and vice versa). The first theorem gives a way to ‘tilt’ (or ‘untilt’) canonically also a rigid analytic varieties over
![]() $K$
into a rigid analytic motive defined on the field
$K$
into a rigid analytic motive defined on the field
![]() $K^{\flat }$
(and vice versa).
$K^{\flat }$
(and vice versa).
We now make a rough sketch on how the motivic ‘untilting’ and ‘de-perfectoidification’ procedures work. Start from a smooth rigid variety
![]() $X$
over
$X$
over
![]() $K^{\flat }$
and associate to it a perfectoid space
$K^{\flat }$
and associate to it a perfectoid space
![]() $\widehat{X}$
obtained by taking the perfection of
$\widehat{X}$
obtained by taking the perfection of
![]() $X$
. This operation can be performed canonically since
$X$
. This operation can be performed canonically since
![]() $K^{\flat }$
has positive characteristic. We then use Scholze’s theorem to tilt
$K^{\flat }$
has positive characteristic. We then use Scholze’s theorem to tilt
![]() $\widehat{X}$
obtaining a perfectoid space
$\widehat{X}$
obtaining a perfectoid space
![]() $\widehat{Y}$
in mixed characteristic. Suppose now that
$\widehat{Y}$
in mixed characteristic. Suppose now that
![]() $\widehat{Y}$
is the limit of a tower of rigid analytic varieties
$\widehat{Y}$
is the limit of a tower of rigid analytic varieties
such that
![]() $Y_{0}$
is étale over the Tate ball
$Y_{0}$
is étale over the Tate ball
![]() $\mathbb{B}^{n}=\operatorname{Spa}K\langle \unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{n}\rangle$
and each
$\mathbb{B}^{n}=\operatorname{Spa}K\langle \unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{n}\rangle$
and each
![]() $Y_{h}$
is obtained as the pullback of
$Y_{h}$
is obtained as the pullback of
![]() $Y_{0}$
by the map
$Y_{0}$
by the map
![]() $\mathbb{B}^{n}\rightarrow \mathbb{B}^{n}$
defined by taking the
$\mathbb{B}^{n}\rightarrow \mathbb{B}^{n}$
defined by taking the
![]() $p^{h}$
-powers of the coordinates
$p^{h}$
-powers of the coordinates
![]() $\unicode[STIX]{x1D710}_{i}\mapsto \unicode[STIX]{x1D710}_{i}^{p^{h}}$
. Under such hypotheses (we will actually need slightly stronger conditions on the tower above) we then ‘de-perfectoidify’
$\unicode[STIX]{x1D710}_{i}\mapsto \unicode[STIX]{x1D710}_{i}^{p^{h}}$
. Under such hypotheses (we will actually need slightly stronger conditions on the tower above) we then ‘de-perfectoidify’
![]() $\widehat{Y}$
by associating to it
$\widehat{Y}$
by associating to it
![]() $Y_{\bar{h}}$
for a sufficiently big index
$Y_{\bar{h}}$
for a sufficiently big index
![]() $\bar{h}$
.
$\bar{h}$
.
The main technical problem of this construction is to show that it is independent of the choice of the tower, and on the index
![]() $\bar{h}$
. It is also by definition a local procedure, which is not canonically extendable to arbitrary varieties by gluing. In order to overcome these obstacles, we use in a crucial way some techniques of approximating maps between spaces up to homotopy, which are obtained by a generalization of the implicit function theorem in the non-archimedean setting.
$\bar{h}$
. It is also by definition a local procedure, which is not canonically extendable to arbitrary varieties by gluing. In order to overcome these obstacles, we use in a crucial way some techniques of approximating maps between spaces up to homotopy, which are obtained by a generalization of the implicit function theorem in the non-archimedean setting.
We point out that many deep motivic theorems are widely used throughout the article, and they are crucial to prove that the recipe sketched above gives rise to an equivalence (see the proof of 7.11) and not only for the construction of explicit homotopies. Among them, the Cancellation Theorem [Reference VoevodskyVoe10] and the dualizability of compact motives [Reference RiouRio05]. These results admit a rigid analytic version, proved by Ayoub in [Reference AyoubAyo15]. We also use the parallel between
![]() $\mathbf{DA}$
and
$\mathbf{DA}$
and
![]() $\mathbf{DM}$
and in order to do so, we introduce a finer topology in characteristic
$\mathbf{DM}$
and in order to do so, we introduce a finer topology in characteristic
![]() $p$
(the
$p$
(the
![]() $\text{Frob}\acute{\text{e}}\text{t}$
topology, also called
$\text{Frob}\acute{\text{e}}\text{t}$
topology, also called
![]() $\operatorname{quiet}$
in [Reference Fontaine and JannsenFJ13]) giving rise to transfers by means of a localization procedure (see [Reference VezzaniVez17]).
$\operatorname{quiet}$
in [Reference Fontaine and JannsenFJ13]) giving rise to transfers by means of a localization procedure (see [Reference VezzaniVez17]).
The following diagram of categories of motives summarizes the situation. The equivalence in the bottom line follows easily from the ‘tilting equivalence’ of Scholze. All notations introduced in the theorems and in the diagram will be described in later sections.

The main result also extends to the categories of non-effective motives, as follows.
Theorem 7.26
. Let
![]() $K$
be a perfectoid field with tilt
$K$
be a perfectoid field with tilt
![]() $K^{\flat }$
and let
$K^{\flat }$
and let
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $\mathbb{Q}$
-algebra. There is a monoidal triangulated equivalence of categories
$\mathbb{Q}$
-algebra. There is a monoidal triangulated equivalence of categories
Due to the intricate construction of the functor
![]() $\mathfrak{F}$
, the theorem above is not immediately obtained from the effective case and requires a little extra inspection of the categories of spectra.
$\mathfrak{F}$
, the theorem above is not immediately obtained from the effective case and requires a little extra inspection of the categories of spectra.
As for concrete applications, our theorem allows the ‘(un-)tilting’ and ‘(de-)perfectoidifying’ of any motivic cohomology theory on rigid or perfectoid spaces satisfying étale descent and homotopy invariance, having coefficients over
![]() $\mathbb{Q}$
(it is expected to extend this over
$\mathbb{Q}$
(it is expected to extend this over
![]() $\mathbb{Z}[1/p]$
as well, see Remark 7.28). Such an example is the overconvergent de Rham cohomology for rigid analytic varieties over
$\mathbb{Z}[1/p]$
as well, see Remark 7.28). Such an example is the overconvergent de Rham cohomology for rigid analytic varieties over
![]() $K$
. It gives rise to new cohomology theories ‘à la de Rham’ for (small) perfectoid spaces as well as for rigid varieties over local fields of equi-characteristic
$K$
. It gives rise to new cohomology theories ‘à la de Rham’ for (small) perfectoid spaces as well as for rigid varieties over local fields of equi-characteristic
![]() $p$
, satisfying descent, homotopy invariance, finite-dimensionality and further formal properties (see [Reference VezzaniVez18]), which are compatible with rigid cohomology [Reference VezzaniVez19]. The relation with
$p$
, satisfying descent, homotopy invariance, finite-dimensionality and further formal properties (see [Reference VezzaniVez18]), which are compatible with rigid cohomology [Reference VezzaniVez19]. The relation with
![]() $p$
-adic periods is an object of future research. Also, we underline that such realization functors might finally give rise (thanks to the derived tannakian formalism developed in [Reference AyoubAyo14b]) to the absolute local motivic Galois group of
$p$
-adic periods is an object of future research. Also, we underline that such realization functors might finally give rise (thanks to the derived tannakian formalism developed in [Reference AyoubAyo14b]) to the absolute local motivic Galois group of
![]() $K$
for any valued field
$K$
for any valued field
![]() $K$
, the case of equi-characteristic zero being described in the introduction of [Reference AyoubAyo15].
$K$
, the case of equi-characteristic zero being described in the introduction of [Reference AyoubAyo15].
It is possible to use our main theorem to answer positively to a conjecture of Ayoub [Reference AyoubAyo15, Conjecture 2.5.72] giving an explicit description of rigid analytic motives of good reduction over a local field
![]() $K$
as well as morphisms between compact rigid analytic motives over
$K$
as well as morphisms between compact rigid analytic motives over
![]() $K$
in terms of motives and morphisms defined over the residue field, extending these results from the equi-characteristic case to the mixed characteristic case (see [Reference VezzaniVez19]).
$K$
in terms of motives and morphisms defined over the residue field, extending these results from the equi-characteristic case to the mixed characteristic case (see [Reference VezzaniVez19]).
We also point out that the motivic tilting equivalence can be used to ‘replace’ the base field
![]() $K$
with another one
$K$
with another one
![]() $K^{\prime }$
having the same tilt. A classic example is formed by the completions
$K^{\prime }$
having the same tilt. A classic example is formed by the completions
![]() $K$
and
$K$
and
![]() $K^{\prime }$
of the fields
$K^{\prime }$
of the fields
![]() $\mathbb{Q}_{p}(p^{1/p^{\infty }})$
and
$\mathbb{Q}_{p}(p^{1/p^{\infty }})$
and
![]() $\mathbb{Q}_{p}(\unicode[STIX]{x1D707}_{p^{\infty }})$
, respectively. Similar techniques are exploited by Kedlaya and Liu in [Reference Kedlaya and LiuKL16].
$\mathbb{Q}_{p}(\unicode[STIX]{x1D707}_{p^{\infty }})$
, respectively. Similar techniques are exploited by Kedlaya and Liu in [Reference Kedlaya and LiuKL16].
The article is organized as follows. In § 1 we recall the basic definitions and the language of adic spaces while in § 2 we define the environment in which we will perform our construction, namely the category of semi-perfectoid spaces
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
and we define the étale topology on it. In § 3 we define the categories of motives for
$\widehat{\text{Rig}}\operatorname{Sm}$
and we define the étale topology on it. In § 3 we define the categories of motives for
![]() $\operatorname{RigSm}$
,
$\operatorname{RigSm}$
,
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
and
$\widehat{\text{Rig}}\operatorname{Sm}$
and
![]() $\operatorname{PerfSm}$
adapting the constructions of Voevodsky and Ayoub. Thanks to the general model-categorical tools introduced in this section, we give in § 4 a motivic interpretation of some approximation results of maps valid for non-archimedean Banach algebras. In §§ 5 and 6 we prove the existence of the de-perfectoidification functor
$\operatorname{PerfSm}$
adapting the constructions of Voevodsky and Ayoub. Thanks to the general model-categorical tools introduced in this section, we give in § 4 a motivic interpretation of some approximation results of maps valid for non-archimedean Banach algebras. In §§ 5 and 6 we prove the existence of the de-perfectoidification functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}$
from perfectoid motives to rigid motives in zero and positive characteristics, respectively. Finally, we give in § 7 the proof of our main result, both in its effective and stable form.
$\mathbb{L}\unicode[STIX]{x1D704}_{!}$
from perfectoid motives to rigid motives in zero and positive characteristics, respectively. Finally, we give in § 7 the proof of our main result, both in its effective and stable form.
In the appendix, we collect some technical theorems that are used in our proof. Specifically, we first present a generalization of the implicit function theorem in the rigid setting, and conclude a result about the approximation of maps modulo homotopy as well as its geometric counterpart. We also prove the existence of compatible approximations of a collection of maps
![]() $\{f_{1},\ldots ,f_{N}\}$
from a variety in
$\{f_{1},\ldots ,f_{N}\}$
from a variety in
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
of the form
$\widehat{\text{Rig}}\operatorname{Sm}$
of the form
![]() $X\,\times \,\mathbb{B}^{n}$
to a rigid variety
$X\,\times \,\mathbb{B}^{n}$
to a rigid variety
![]() $Y$
such that the compatibility conditions among the maps
$Y$
such that the compatibility conditions among the maps
![]() $f_{i}$
on the faces
$f_{i}$
on the faces
![]() $X\,\times \,\mathbb{B}^{n-1}$
are preserved. This fact has important consequences for computing maps to
$X\,\times \,\mathbb{B}^{n-1}$
are preserved. This fact has important consequences for computing maps to
![]() $\mathbb{B}^{1}$
-local complexes of presheaves in the motivic setting.
$\mathbb{B}^{1}$
-local complexes of presheaves in the motivic setting.
1 Generalities on adic spaces
We start by recalling the language of adic spaces, as introduced by Huber [Reference HuberHub93, Reference HuberHub94] and generalized by Scholze and Weinstein [Reference Scholze and WeinsteinSW13]. We will always work with adic spaces over a non-archimedean valued field
![]() $K$
in the following sense.
$K$
in the following sense.
Definition 1.1. A non-archimedean field is a topological field
![]() $K$
whose topology is induced by a non-trivial valuation of rank one. The associated norm is a multiplicative map that we denote by
$K$
whose topology is induced by a non-trivial valuation of rank one. The associated norm is a multiplicative map that we denote by
![]() $|\cdot |:K\rightarrow \mathbb{R}_{{\geqslant}0}$
and its valuation ring is denoted by
$|\cdot |:K\rightarrow \mathbb{R}_{{\geqslant}0}$
and its valuation ring is denoted by
![]() $K^{\circ }$
.
$K^{\circ }$
.
From now on, we fix a non-archimedean field
![]() $K$
and we pick a non-zero element
$K$
and we pick a non-zero element
![]() $\unicode[STIX]{x1D70B}\in K$
with
$\unicode[STIX]{x1D70B}\in K$
with
![]() $|\unicode[STIX]{x1D70B}|<1$
.
$|\unicode[STIX]{x1D70B}|<1$
.
Definition 1.2. A Tate
![]() $K$
-algebra is a topological
$K$
-algebra is a topological
![]() $K$
-algebra
$K$
-algebra
![]() $R$
for which there exists a subring
$R$
for which there exists a subring
![]() $R_{0}$
such that the set
$R_{0}$
such that the set
![]() $\{\unicode[STIX]{x1D70B}^{k}R_{0}\}$
forms a basis of neighborhoods of
$\{\unicode[STIX]{x1D70B}^{k}R_{0}\}$
forms a basis of neighborhoods of
![]() $0$
. A subring
$0$
. A subring
![]() $R_{0}$
with the above property is called a ring of definition.
$R_{0}$
with the above property is called a ring of definition.
Definition 1.3. Let
![]() $R$
be a Tate
$R$
be a Tate
![]() $K$
-algebra.
$K$
-algebra.
– A subset
 $S$
of
$S$
of
 $R$
is bounded if it is contained in the set
$R$
is bounded if it is contained in the set
 $\unicode[STIX]{x1D70B}^{-N}R_{0}$
for some integer
$\unicode[STIX]{x1D70B}^{-N}R_{0}$
for some integer
 $N$
. An element
$N$
. An element
 $x$
of
$x$
of
 $R$
is power-bounded if the set
$R$
is power-bounded if the set
 $\{x^{n}\}_{n\in \mathbb{N}}$
is bounded. The set of power-bounded elements is a subring of
$\{x^{n}\}_{n\in \mathbb{N}}$
is bounded. The set of power-bounded elements is a subring of
 $R$
that we denote by
$R$
that we denote by
 $R^{\circ }$
.
$R^{\circ }$
.– An element
 $x$
of
$x$
of
 $R$
is topologically nilpotent if
$R$
is topologically nilpotent if
 $\lim _{n\rightarrow +\infty }x^{n}=0$
. The set of topologically nilpotent elements is an ideal of
$\lim _{n\rightarrow +\infty }x^{n}=0$
. The set of topologically nilpotent elements is an ideal of
 $R^{\circ }$
that we denote by
$R^{\circ }$
that we denote by
 $R^{\circ \circ }$
.
$R^{\circ \circ }$
.
Definition 1.4. An affinoid
![]() $K$
-algebra is a pair
$K$
-algebra is a pair
![]() $(R,R^{+})$
where
$(R,R^{+})$
where
![]() $R$
is a Tate
$R$
is a Tate
![]() $K$
-algebra and
$K$
-algebra and
![]() $R^{+}$
is an open and integrally closed
$R^{+}$
is an open and integrally closed
![]() $K^{\circ }$
-subalgebra of
$K^{\circ }$
-subalgebra of
![]() $R^{\circ }$
. A morphism
$R^{\circ }$
. A morphism
![]() $(R,R^{+})\rightarrow (S,S^{+})$
of affinoid
$(R,R^{+})\rightarrow (S,S^{+})$
of affinoid
![]() $K$
-algebras is a pair of compatible
$K$
-algebras is a pair of compatible
![]() $K^{\circ }$
-linear continuous maps of rings
$K^{\circ }$
-linear continuous maps of rings
![]() $(f,f^{+})$
. An affinoid
$(f,f^{+})$
. An affinoid
![]() $K$
-algebra
$K$
-algebra
![]() $(R,R^{+})$
is called complete if
$(R,R^{+})$
is called complete if
![]() $R$
(and hence also
$R$
(and hence also
![]() $R^{+}$
) is complete.
$R^{+}$
) is complete.
Remark 1.5. By [Reference WedhornWed12, Proposition 5.30] if
![]() $R$
is a Tate
$R$
is a Tate
![]() $K$
-algebra, then
$K$
-algebra, then
![]() $(R,R^{\circ })$
is an affinoid
$(R,R^{\circ })$
is an affinoid
![]() $K$
-algebra.
$K$
-algebra.
Definition 1.6. For any complete Tate
![]() $K$
-algebra
$K$
-algebra
![]() $R$
we denote by
$R$
we denote by
![]() $R\langle \unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{n}\rangle$
the Banach algebra of strictly convergent power series in
$R\langle \unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{n}\rangle$
the Banach algebra of strictly convergent power series in
![]() $R[[\unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{n}]]$
endowed with the sup-norm (see [Reference Bosch, Güntzer and RemmertBGR84, § 1.4.1]). A topologically of finite type Tate algebra (or simply tft Tate algebra) is a Banach
$R[[\unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{n}]]$
endowed with the sup-norm (see [Reference Bosch, Güntzer and RemmertBGR84, § 1.4.1]). A topologically of finite type Tate algebra (or simply tft Tate algebra) is a Banach
![]() $K$
-algebra
$K$
-algebra
![]() $R$
isomorphic to a quotient of the normed
$R$
isomorphic to a quotient of the normed
![]() $K$
-algebra
$K$
-algebra
![]() $K\langle \unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{n}\rangle$
for some
$K\langle \unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{n}\rangle$
for some
![]() $n$
.
$n$
.
If
![]() $R$
is a tft Tate algebra, the pair
$R$
is a tft Tate algebra, the pair
![]() $(R,R^{\circ })$
is an affinoid
$(R,R^{\circ })$
is an affinoid
![]() $K$
-algebra, and
$K$
-algebra, and
![]() $R^{\circ }$
is a ring of definition whenever
$R^{\circ }$
is a ring of definition whenever
![]() $R$
is reduced (see [Reference Bosch, Güntzer and RemmertBGR84, Theorem 6.2.4/1]).
$R$
is reduced (see [Reference Bosch, Güntzer and RemmertBGR84, Theorem 6.2.4/1]).
We now recall the definition of perfectoid pairs, introduced in [Reference ScholzeSch12].
Definition 1.7. A perfectoid field
![]() $K$
is a complete non-archimedean field whose rank one valuation is non-discrete, whose residue characteristic is
$K$
is a complete non-archimedean field whose rank one valuation is non-discrete, whose residue characteristic is
![]() $p$
and such that the Frobenius is surjective on
$p$
and such that the Frobenius is surjective on
![]() $K^{\circ }/p$
. In case
$K^{\circ }/p$
. In case
![]() $\operatorname{char}K=p$
this last condition amounts to saying that
$\operatorname{char}K=p$
this last condition amounts to saying that
![]() $K$
is perfect.
$K$
is perfect.
Definition 1.8. Let
![]() $K$
be a perfectoid field.
$K$
be a perfectoid field.
– A perfectoid algebra is a Banach
 $K$
-algebra
$K$
-algebra
 $R$
such that
$R$
such that
 $R^{\circ }$
is bounded and the Frobenius map is surjective on
$R^{\circ }$
is bounded and the Frobenius map is surjective on
 $R^{\circ }/p$
.
$R^{\circ }/p$
.– A perfectoid affinoid
 $K$
-algebra is an affinoid
$K$
-algebra is an affinoid
 $K$
-algebra
$K$
-algebra
 $(R,R^{+})$
over a perfectoid field
$(R,R^{+})$
over a perfectoid field
 $K$
such that
$K$
such that
 $R$
is perfectoid.
$R$
is perfectoid.
Remark 1.9. If
![]() $R$
is a perfectoid algebra, then
$R$
is a perfectoid algebra, then
![]() $(R,R^{\circ })$
is a perfectoid affinoid
$(R,R^{\circ })$
is a perfectoid affinoid
![]() $K$
-algebra.
$K$
-algebra.
Example 1.10. Suppose that
![]() $K$
is a perfectoid field. A basic example of a perfectoid algebra is the following: let
$K$
is a perfectoid field. A basic example of a perfectoid algebra is the following: let
![]() $\text{}\underline{\unicode[STIX]{x1D710}}=(\unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{N})$
be a
$\text{}\underline{\unicode[STIX]{x1D710}}=(\unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{N})$
be a
![]() $N$
-tuple of coordinates and
$N$
-tuple of coordinates and
![]() $K^{\circ }[\text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}]$
be the ring
$K^{\circ }[\text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}]$
be the ring
![]() $\mathop{\varinjlim }\nolimits_{h}K^{\circ }[\text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}]$
endowed with the sup-norm induced by the norm on
$\mathop{\varinjlim }\nolimits_{h}K^{\circ }[\text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}]$
endowed with the sup-norm induced by the norm on
![]() $K$
. We also denote by
$K$
. We also denote by
![]() $K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle$
its
$K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle$
its
![]() $\unicode[STIX]{x1D70B}$
-adic completion. By [Reference ScholzeSch12, Proposition 5.20], the ring
$\unicode[STIX]{x1D70B}$
-adic completion. By [Reference ScholzeSch12, Proposition 5.20], the ring
![]() $K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle [\unicode[STIX]{x1D70B}^{-1}]$
is a perfectoid
$K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle [\unicode[STIX]{x1D70B}^{-1}]$
is a perfectoid
![]() $K$
-algebra, which we will denote by
$K$
-algebra, which we will denote by
![]() $K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle$
. The pair
$K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle$
. The pair
![]() $(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle )$
is a perfectoid affinoid
$(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle )$
is a perfectoid affinoid
![]() $K$
-algebra. We also define in the same way the perfectoid affinoid
$K$
-algebra. We also define in the same way the perfectoid affinoid
![]() $K$
-algebra
$K$
-algebra
![]() $(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle )$
(see [Reference ScholzeSch13, Example 4.4]).
$(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle )$
(see [Reference ScholzeSch13, Example 4.4]).
Remark 1.11.
![]() $K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle$
is isomorphic as a
$K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle$
is isomorphic as a
![]() $K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle$
-topological module to the completion
$K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle$
-topological module to the completion
![]() $\widehat{\bigoplus }K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle$
of the free module
$\widehat{\bigoplus }K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle$
of the free module
![]() $\bigoplus K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle$
with a basis indexed by the set
$\bigoplus K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle$
with a basis indexed by the set
![]() $I=(\mathbb{Z}[1/p]\cap [\!0,1\!))^{N}$
. By [Reference Bosch, Güntzer and RemmertBGR84, Proposition 2.1.5/7] there is an explicit description of this ring as the subring of
$I=(\mathbb{Z}[1/p]\cap [\!0,1\!))^{N}$
. By [Reference Bosch, Güntzer and RemmertBGR84, Proposition 2.1.5/7] there is an explicit description of this ring as the subring of
![]() $\prod _{i\in I}K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle$
whose elements are those
$\prod _{i\in I}K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle$
whose elements are those
![]() $(x_{i})_{i\in I}$
such that for any
$(x_{i})_{i\in I}$
such that for any
![]() $\unicode[STIX]{x1D700}>0$
the inequality
$\unicode[STIX]{x1D700}>0$
the inequality
![]() $\Vert x_{i}\Vert <\unicode[STIX]{x1D700}$
holds for almost all
$\Vert x_{i}\Vert <\unicode[STIX]{x1D700}$
holds for almost all
![]() $i$
(that is, for all
$i$
(that is, for all
![]() $i$
except for a finite number of them).
$i$
except for a finite number of them).
The following theorem summarizes some results of Scholze, including the tilting equivalence of perfectoid algebras, which will play a crucial role in our construction.
Theorem 1.12 [Reference ScholzeSch12].
Let
![]() $K$
be a perfectoid field.
$K$
be a perfectoid field.
(i) [Reference ScholzeSch12, Lemma 3.4] The multiplicative monoid
 $\mathop{\varprojlim }\nolimits_{x\mapsto x^{p}}K$
can be given a structure
$\mathop{\varprojlim }\nolimits_{x\mapsto x^{p}}K$
can be given a structure
 $K^{\flat }$
of perfectoid field with the norm induced by the multiplicative map
$K^{\flat }$
of perfectoid field with the norm induced by the multiplicative map
 $\sharp :K^{\flat }\rightarrow K$
. The field
$\sharp :K^{\flat }\rightarrow K$
. The field
 $K^{\flat }$
has characteristic
$K^{\flat }$
has characteristic
 $p$
and coincides with
$p$
and coincides with
 $K$
in case
$K$
in case
 $\operatorname{char}K=p$
.
$\operatorname{char}K=p$
.(ii) [Reference ScholzeSch12, Theorem 3.7] The functor
 $L\mapsto L^{\flat }$
for
$L\mapsto L^{\flat }$
for
 $L$
finite étale over
$L$
finite étale over
 $K$
induces an isomorphism
$K$
induces an isomorphism
 $\operatorname{Gal}(K)\cong \operatorname{Gal}(K^{\flat })$
.
$\operatorname{Gal}(K)\cong \operatorname{Gal}(K^{\flat })$
.(iii) [Reference ScholzeSch12, Lemma 6.2] There is an equivalence of categories, the tilting equivalence, from perfectoid affinoid
 $K$
-algebras to perfectoid affinoid
$K$
-algebras to perfectoid affinoid
 $K^{\flat }$
-algebras denoted by
$K^{\flat }$
-algebras denoted by
 $(R,R^{+})\mapsto (R^{\flat },R^{\flat +})$
such that
$(R,R^{+})\mapsto (R^{\flat },R^{\flat +})$
such that
 $R^{\flat }$
is multiplicatively isomorphic to
$R^{\flat }$
is multiplicatively isomorphic to
 $\mathop{\varprojlim }\nolimits_{x\mapsto x^{p}}R$
and
$\mathop{\varprojlim }\nolimits_{x\mapsto x^{p}}R$
and
 $R^{\flat +}$
is multiplicatively isomorphic to
$R^{\flat +}$
is multiplicatively isomorphic to
 $\mathop{\varprojlim }\nolimits_{x\mapsto x^{p}}R^{+}$
.
$\mathop{\varprojlim }\nolimits_{x\mapsto x^{p}}R^{+}$
.(iv) [Reference ScholzeSch12, Proposition 5.20 and Corollary 6.8] The tilting equivalence associates the perfectoid
 $K$
-algebra
$K$
-algebra
 $(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle )$
to
$(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle )$
to
 $(K^{\flat }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle ,K^{\flat \circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle )$
and the perfectoid
$(K^{\flat }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle ,K^{\flat \circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle )$
and the perfectoid
 $K$
-algebra
$K$
-algebra
 $(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle )$
to
$(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle )$
to
 $(K^{\flat }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle ,K^{\flat \circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle )$
.
$(K^{\flat }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle ,K^{\flat \circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle )$
.
We now recall Huber’s construction of the spectrum of a valuation ring (see [Reference HuberHub94]).
Construction 1.13. Let
![]() $(R,R^{+})$
be an affinoid
$(R,R^{+})$
be an affinoid
![]() $K$
-algebra. The set
$K$
-algebra. The set
![]() $\operatorname{Spa}(R,R^{+})$
is the set of equivalence classes of continuous multiplicative valuations
$\operatorname{Spa}(R,R^{+})$
is the set of equivalence classes of continuous multiplicative valuations
![]() $|\cdot |$
(see [Reference HuberHub93, § 3] and [Reference ScholzeSch12, Definitions 2.2, 2.5]). It is endowed with the topology generated by the basis of rational subsets
$|\cdot |$
(see [Reference HuberHub93, § 3] and [Reference ScholzeSch12, Definitions 2.2, 2.5]). It is endowed with the topology generated by the basis of rational subsets
![]() $\{U(f_{1},\ldots ,f_{n}\,\mid \,g)\}$
by letting
$\{U(f_{1},\ldots ,f_{n}\,\mid \,g)\}$
by letting
![]() $f_{1},\ldots ,f_{n},g$
vary among elements in
$f_{1},\ldots ,f_{n},g$
vary among elements in
![]() $R$
such that
$R$
such that
![]() $f_{1},\ldots ,f_{n}$
generate
$f_{1},\ldots ,f_{n}$
generate
![]() $R$
as an ideal and where the set
$R$
as an ideal and where the set
![]() $U(f_{1},\ldots ,f_{n}\,\mid \,g)$
is the set of those valuations
$U(f_{1},\ldots ,f_{n}\,\mid \,g)$
is the set of those valuations
![]() $|\cdot |$
satisfying
$|\cdot |$
satisfying
![]() $|f_{i}|\leqslant |g|$
for all
$|f_{i}|\leqslant |g|$
for all
![]() $i$
.
$i$
.
If we define maps of valuation fields over
![]() $K$
(see [Reference ScholzeSch12, Definition 2.26]) as maps of affinoid
$K$
(see [Reference ScholzeSch12, Definition 2.26]) as maps of affinoid
![]() $K$
-algebras
$K$
-algebras
![]() $(L,L^{+})\rightarrow (L^{\prime },{L^{\prime }}^{+})$
such that
$(L,L^{+})\rightarrow (L^{\prime },{L^{\prime }}^{+})$
such that
![]() ${L^{\prime }}^{+}\cap L=L^{+}$
then
${L^{\prime }}^{+}\cap L=L^{+}$
then
![]() $\operatorname{Spa}(R,R^{+})$
has the following alternative description: it is the set
$\operatorname{Spa}(R,R^{+})$
has the following alternative description: it is the set
![]() $\varinjlim \operatorname{Hom}((R,R^{+}),(L,L^{+}))$
by letting
$\varinjlim \operatorname{Hom}((R,R^{+}),(L,L^{+}))$
by letting
![]() $(L,L^{+})$
vary in the category of valuation fields over
$(L,L^{+})$
vary in the category of valuation fields over
![]() $K$
(see [Reference ScholzeSch12, Proposition 2.27]). Its topology can be defined by declaring the sets
$K$
(see [Reference ScholzeSch12, Proposition 2.27]). Its topology can be defined by declaring the sets
![]() $\{\unicode[STIX]{x1D719}:0\neq |\unicode[STIX]{x1D719}(f)|\leqslant |\unicode[STIX]{x1D719}(g)|\}$
to be open, for all pairs of elements
$\{\unicode[STIX]{x1D719}:0\neq |\unicode[STIX]{x1D719}(f)|\leqslant |\unicode[STIX]{x1D719}(g)|\}$
to be open, for all pairs of elements
![]() $f,g$
in
$f,g$
in
![]() $R$
.
$R$
.
We can associate to a rational subset
![]() $U(f_{1},\ldots ,f_{n}\,\mid \,g)$
the affinoid
$U(f_{1},\ldots ,f_{n}\,\mid \,g)$
the affinoid
![]() $K$
-algebra the affinoid
$K$
-algebra the affinoid
![]() $K$
-algebra
$K$
-algebra
defined in [Reference HuberHub94, § 1] and [Reference ScholzeSch12, Defintion 2.13]. This way, we define a presheaf of affinoid
![]() $K$
-algebras
$K$
-algebras
![]() $({\mathcal{O}}_{X},{\mathcal{O}}_{X}^{+})$
on a basis of
$({\mathcal{O}}_{X},{\mathcal{O}}_{X}^{+})$
on a basis of
![]() $X=\operatorname{Spa}(R,R^{+})$
.
$X=\operatorname{Spa}(R,R^{+})$
.
By [Reference HuberHub94, Lemma 1.5, Proposition 1.6] for any
![]() $x\in X=\operatorname{Spa}(R,R^{+})$
the valuation at
$x\in X=\operatorname{Spa}(R,R^{+})$
the valuation at
![]() $x$
extends to a valuation on
$x$
extends to a valuation on
![]() ${\mathcal{O}}_{X,x}$
and the stalk
${\mathcal{O}}_{X,x}$
and the stalk
![]() ${\mathcal{O}}_{X,x}^{+}$
is local and corresponds to
${\mathcal{O}}_{X,x}^{+}$
is local and corresponds to
![]() $\{f\in {\mathcal{O}}_{X,x}:|f(x)|\leqslant 1\}$
.
$\{f\in {\mathcal{O}}_{X,x}:|f(x)|\leqslant 1\}$
.
By [Reference HuberHub94, Proposition 1.6] there holds
![]() ${\mathcal{O}}^{+}(U)=\{f\in {\mathcal{O}}(U):|f(x)|\leqslant 1\text{ for all }x\in U\}$
for any rational subset
${\mathcal{O}}^{+}(U)=\{f\in {\mathcal{O}}(U):|f(x)|\leqslant 1\text{ for all }x\in U\}$
for any rational subset
![]() $U$
of
$U$
of
![]() $\operatorname{Spa}(R,R^{+})$
so that
$\operatorname{Spa}(R,R^{+})$
so that
![]() ${\mathcal{O}}^{+}$
is a sheaf if and only if
${\mathcal{O}}^{+}$
is a sheaf if and only if
![]() ${\mathcal{O}}$
is a sheaf.
${\mathcal{O}}$
is a sheaf.
Sadly enough,
![]() ${\mathcal{O}}$
,
${\mathcal{O}}$
,
![]() ${\mathcal{O}}^{+}$
are not sheaves in general as shown at the end of [Reference HuberHub94, § 1]. By Tate’s acyclicity theorem [Reference Bosch, Güntzer and RemmertBGR84, Theorem 8.2.1/1] and Scholze’s acyclicity theorem [Reference ScholzeSch12, Theorem 6.3], if
${\mathcal{O}}^{+}$
are not sheaves in general as shown at the end of [Reference HuberHub94, § 1]. By Tate’s acyclicity theorem [Reference Bosch, Güntzer and RemmertBGR84, Theorem 8.2.1/1] and Scholze’s acyclicity theorem [Reference ScholzeSch12, Theorem 6.3], if
![]() $(R,R^{+})$
is a tft Tate algebra or a perfectoid affinoid
$(R,R^{+})$
is a tft Tate algebra or a perfectoid affinoid
![]() $K$
-algebra, then
$K$
-algebra, then
![]() ${\mathcal{O}}$
,
${\mathcal{O}}$
,
![]() ${\mathcal{O}}^{+}$
are sheaves (see [Reference HuberHub94, § 2]). Also, if
${\mathcal{O}}^{+}$
are sheaves (see [Reference HuberHub94, § 2]). Also, if
![]() ${\mathcal{O}}^{+}(U)$
is bounded for all rational subspaces
${\mathcal{O}}^{+}(U)$
is bounded for all rational subspaces
![]() $U$
of
$U$
of
![]() $X$
(in which case we say that
$X$
(in which case we say that
![]() $X$
is stably uniform) then
$X$
is stably uniform) then
![]() ${\mathcal{O}}$
,
${\mathcal{O}}$
,
![]() ${\mathcal{O}}^{+}$
are sheaves (see [Reference Buzzard and VerberkmoesBV18]).
${\mathcal{O}}^{+}$
are sheaves (see [Reference Buzzard and VerberkmoesBV18]).
Definition 1.14. Objects of
![]() ${\mathcal{V}}$
are triples
${\mathcal{V}}$
are triples
![]() $(X,{\mathcal{O}}_{X},\{|\cdot |_{x}\}_{x\in X})$
, where
$(X,{\mathcal{O}}_{X},\{|\cdot |_{x}\}_{x\in X})$
, where
![]() $X$
is a topological space,
$X$
is a topological space,
![]() ${\mathcal{O}}_{X}$
is a sheaf of complete topological
${\mathcal{O}}_{X}$
is a sheaf of complete topological
![]() $K$
-algebras, and
$K$
-algebras, and
![]() $|\cdot |_{x}$
is a continuous valuation on
$|\cdot |_{x}$
is a continuous valuation on
![]() ${\mathcal{O}}_{X,x}$
. Maps are morphisms of ringed spaces, which induce continuous
${\mathcal{O}}_{X,x}$
. Maps are morphisms of ringed spaces, which induce continuous
![]() $K$
-algebra morphisms of sheaves and are compatible with the valuations on stalks.
$K$
-algebra morphisms of sheaves and are compatible with the valuations on stalks.
Remark 1.15. By abuse of notation, whenever
![]() $R$
is a tft Tate algebra we sometimes denote by
$R$
is a tft Tate algebra we sometimes denote by
![]() $\operatorname{Spa}R$
the object
$\operatorname{Spa}R$
the object
![]() $\operatorname{Spa}(R,R^{\circ })$
of
$\operatorname{Spa}(R,R^{\circ })$
of
![]() ${\mathcal{V}}$
.
${\mathcal{V}}$
.
Definition 1.16. Let
![]() $X$
be an object of
$X$
be an object of
![]() ${\mathcal{V}}$
.
${\mathcal{V}}$
.
– We say that
 $X$
is an affinoid adic space if it is isomorphic to
$X$
is an affinoid adic space if it is isomorphic to
 $\operatorname{Spa}(R,R^{+})$
for some affinoid
$\operatorname{Spa}(R,R^{+})$
for some affinoid
 $K$
-algebra
$K$
-algebra
 $(R,R^{+})$
.
$(R,R^{+})$
.– We say that
 $X$
is an affinoid rigid variety if it is isomorphic to
$X$
is an affinoid rigid variety if it is isomorphic to
 $\operatorname{Spa}(R,R^{\circ })$
for some tft Tate algebra
$\operatorname{Spa}(R,R^{\circ })$
for some tft Tate algebra
 $R$
.
$R$
.– We say that
 $X$
is a perfectoid affinoid space if it is isomorphic to
$X$
is a perfectoid affinoid space if it is isomorphic to
 $\operatorname{Spa}(R,R^{+})$
for some perfectoid affinoid
$\operatorname{Spa}(R,R^{+})$
for some perfectoid affinoid
 $K$
-algebra
$K$
-algebra
 $(R,R^{+})$
.
$(R,R^{+})$
.– We say that
 $X$
is an adic space if it is locally isomorphic to an affinoid adic space.
$X$
is an adic space if it is locally isomorphic to an affinoid adic space.– We say that
 $X$
is a rigid variety if it is locally isomorphic to an affinoid rigid variety.
$X$
is a rigid variety if it is locally isomorphic to an affinoid rigid variety.– We say that
 $X$
is a perfectoid space if it is locally isomorphic to a perfectoid affinoid space.
$X$
is a perfectoid space if it is locally isomorphic to a perfectoid affinoid space.
There is an apparent clash of definitions between rigid varieties as presented above, and as defined by Tate. In fact, the two categories are canonically isomorphic. We refer to [Reference HuberHub94, § 4] and [Reference ScholzeSch12, § 2] for a more detailed collection of results on the comparison between these theories.
Remark 1.17. By [Reference HuberHub94, Proposition 2.1(ii)] if
![]() $X$
is an adic space and
$X$
is an adic space and
![]() $Y=\operatorname{Spa}(R,R^{+})$
is an affinoid adic space then
$Y=\operatorname{Spa}(R,R^{+})$
is an affinoid adic space then
![]() $\operatorname{Hom}(X,Y)\cong \operatorname{Hom}((R,R^{+}),({\mathcal{O}}_{X}(X),{\mathcal{O}}_{X}^{+}(X)))$
. Moreover, as shown in [Reference HuberHub93, § 3] and [Reference HuberHub94, § 2], if
$\operatorname{Hom}(X,Y)\cong \operatorname{Hom}((R,R^{+}),({\mathcal{O}}_{X}(X),{\mathcal{O}}_{X}^{+}(X)))$
. Moreover, as shown in [Reference HuberHub93, § 3] and [Reference HuberHub94, § 2], if
![]() $(\widehat{R},\widehat{R}^{+})$
is the completion of
$(\widehat{R},\widehat{R}^{+})$
is the completion of
![]() $(R,R^{+})$
then it is an affinoid
$(R,R^{+})$
then it is an affinoid
![]() $K$
-algebra and
$K$
-algebra and
![]() $\operatorname{Spa}(\widehat{R},\widehat{R}^{+})\cong \operatorname{Spa}(R,R^{+})$
.
$\operatorname{Spa}(\widehat{R},\widehat{R}^{+})\cong \operatorname{Spa}(R,R^{+})$
.
Assumption 1.18. From now on, we will always assume that
![]() $K$
is a perfectoid field. We also make the extra assumption that the invertible element
$K$
is a perfectoid field. We also make the extra assumption that the invertible element
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $K$
satisfies
$K$
satisfies
![]() $|p|\leqslant |\unicode[STIX]{x1D70B}|<1$
and coincides with
$|p|\leqslant |\unicode[STIX]{x1D70B}|<1$
and coincides with
![]() $(\unicode[STIX]{x1D70B}^{\flat })^{\sharp }$
for a chosen
$(\unicode[STIX]{x1D70B}^{\flat })^{\sharp }$
for a chosen
![]() $\unicode[STIX]{x1D70B}^{\flat }$
in
$\unicode[STIX]{x1D70B}^{\flat }$
in
![]() $K^{\flat }$
. In particular,
$K^{\flat }$
. In particular,
![]() $\unicode[STIX]{x1D70B}$
is equipped with a compatible system of
$\unicode[STIX]{x1D70B}$
is equipped with a compatible system of
![]() $p$
-power roots
$p$
-power roots
![]() $\unicode[STIX]{x1D70B}^{1/p^{h}}$
(see [Reference ScholzeSch12, Remark 3.5]).
$\unicode[STIX]{x1D70B}^{1/p^{h}}$
(see [Reference ScholzeSch12, Remark 3.5]).
We now consider some basic examples and fix some notation.
Example 1.19. Let
![]() $\text{}\underline{\unicode[STIX]{x1D710}}=(\unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{N})$
be a
$\text{}\underline{\unicode[STIX]{x1D710}}=(\unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{N})$
be a
![]() $N$
-tuple of coordinates. The Tate
$N$
-tuple of coordinates. The Tate
![]() $N$
-ball
$N$
-ball
![]() $\operatorname{Spa}(K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle )$
will be denoted by
$\operatorname{Spa}(K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle )$
will be denoted by
![]() $\mathbb{B}^{N}$
and the
$\mathbb{B}^{N}$
and the
![]() $N$
-torus
$N$
-torus
![]() $\operatorname{Spa}(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle )$
by
$\operatorname{Spa}(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle )$
by
![]() $\mathbb{T}^{N}$
. It is the rational subspace
$\mathbb{T}^{N}$
. It is the rational subspace
![]() $U(1\,\mid \,\unicode[STIX]{x1D710}_{1}\ldots \unicode[STIX]{x1D710}_{N})$
of
$U(1\,\mid \,\unicode[STIX]{x1D710}_{1}\ldots \unicode[STIX]{x1D710}_{N})$
of
![]() $\mathbb{B}^{N}$
. The map of spaces induced by the inclusion
$\mathbb{B}^{N}$
. The map of spaces induced by the inclusion
![]() $(K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle )\rightarrow (K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle )$
will be denoted by
$(K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle )\rightarrow (K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle )$
will be denoted by
![]() $\mathbb{B}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \rightarrow \mathbb{B}^{N}$
. We use the analogous notation
$\mathbb{B}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \rightarrow \mathbb{B}^{N}$
. We use the analogous notation
![]() $\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \rightarrow \mathbb{T}^{N}$
for the torus. These maps are clearly isomorphic to the endomorphism of
$\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \rightarrow \mathbb{T}^{N}$
for the torus. These maps are clearly isomorphic to the endomorphism of
![]() $\mathbb{B}^{N}$
respectively
$\mathbb{B}^{N}$
respectively
![]() $\mathbb{T}^{N}$
induced by
$\mathbb{T}^{N}$
induced by
![]() $\unicode[STIX]{x1D710}_{i}\mapsto \unicode[STIX]{x1D710}_{i}^{p^{h}}$
.
$\unicode[STIX]{x1D710}_{i}\mapsto \unicode[STIX]{x1D710}_{i}^{p^{h}}$
.
The space defined by the perfectoid affinoid
![]() $K$
-algebra
$K$
-algebra
![]() $(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle )$
will be denoted by
$(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle )$
will be denoted by
![]() $\widehat{\mathbb{B}}^{N}$
and referred to as the perfectoid
$\widehat{\mathbb{B}}^{N}$
and referred to as the perfectoid
![]() $N$
-ball. The space defined by the perfectoid affinoid
$N$
-ball. The space defined by the perfectoid affinoid
![]() $K$
-algebra
$K$
-algebra
![]() $(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle )$
coincides with the rational subspace
$(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle )$
coincides with the rational subspace
![]() $U(1\,\mid \,\unicode[STIX]{x1D710}_{1}\ldots \unicode[STIX]{x1D710}_{N})$
of
$U(1\,\mid \,\unicode[STIX]{x1D710}_{1}\ldots \unicode[STIX]{x1D710}_{N})$
of
![]() $\widehat{\mathbb{B}}^{N}$
and will be denoted by
$\widehat{\mathbb{B}}^{N}$
and will be denoted by
![]() $\widehat{\mathbb{T}}^{N}$
and will be referred to as the perfectoid
$\widehat{\mathbb{T}}^{N}$
and will be referred to as the perfectoid
![]() $N$
-torus.
$N$
-torus.
We now recall the definition of étale maps on the category of adic spaces, taken from [Reference ScholzeSch12, § 7].
Definition 1.20. A map of affinoid adic spaces
![]() $f:\operatorname{Spa}(S,S^{+})\rightarrow \operatorname{Spa}(R,R^{+})$
is finite étale if the associated map
$f:\operatorname{Spa}(S,S^{+})\rightarrow \operatorname{Spa}(R,R^{+})$
is finite étale if the associated map
![]() $R\rightarrow S$
is a finite étale map of rings, and if
$R\rightarrow S$
is a finite étale map of rings, and if
![]() $S^{+}$
is the integral closure of
$S^{+}$
is the integral closure of
![]() $R^{+}$
in
$R^{+}$
in
![]() $S$
. A map of adic spaces
$S$
. A map of adic spaces
![]() $f:X\rightarrow Y$
is étale if for any point
$f:X\rightarrow Y$
is étale if for any point
![]() $x\in X$
there exists an open neighborhood
$x\in X$
there exists an open neighborhood
![]() $U$
of
$U$
of
![]() $x$
and an affinoid open subset
$x$
and an affinoid open subset
![]() $V$
of
$V$
of
![]() $Y$
containing
$Y$
containing
![]() $f(U)$
such that
$f(U)$
such that
![]() $f|_{U}:U\rightarrow V$
factors as an open embedding
$f|_{U}:U\rightarrow V$
factors as an open embedding
![]() $U\rightarrow W$
and a finite étale map
$U\rightarrow W$
and a finite étale map
![]() $W\rightarrow V$
for some affinoid adic space
$W\rightarrow V$
for some affinoid adic space
![]() $W$
.
$W$
.
The previous definitions, when restricted to the case of tft Tate varieties, coincide with the usual ones, as proved in [Reference Fresnel and van der PutFvdP04, Proposition 8.1.2].
Remark 1.21. Suppose we are given a diagram of affinoid
![]() $K$
-algebras.
$K$
-algebras.

In general, it is not possible to define a push-out in the category of affinoid
![]() $K$
-algebras. Nonetheless, this can be performed under some hypothesis. For example, if the affinoid
$K$
-algebras. Nonetheless, this can be performed under some hypothesis. For example, if the affinoid
![]() $K$
-algebras are tft Tate algebras then the push-out exists and it is the tft Tate algebra associated to the completion
$K$
-algebras are tft Tate algebras then the push-out exists and it is the tft Tate algebra associated to the completion
![]() $S\,\widehat{\otimes }_{R}\,T$
of
$S\,\widehat{\otimes }_{R}\,T$
of
![]() $S\,\otimes _{R}\,T$
endowed with the norm of the tensor product (see [Reference Bosch, Güntzer and RemmertBGR84, § 3.1.1]). In case the affinoid
$S\,\otimes _{R}\,T$
endowed with the norm of the tensor product (see [Reference Bosch, Güntzer and RemmertBGR84, § 3.1.1]). In case the affinoid
![]() $K$
-algebras are perfectoid affinoid, then the push-out exists and is also perfectoid affinoid. It coincides with the completion of
$K$
-algebras are perfectoid affinoid, then the push-out exists and is also perfectoid affinoid. It coincides with the completion of
![]() $(L,L^{+})$
, where
$(L,L^{+})$
, where
![]() $L$
is the ring
$L$
is the ring
![]() $S\,\otimes _{R}\,T$
endowed with the norm of the tensor product and
$S\,\otimes _{R}\,T$
endowed with the norm of the tensor product and
![]() $L^{+}$
is the integral closure of
$L^{+}$
is the integral closure of
![]() $S^{+}\,\otimes _{R^{+}}\,T^{+}$
in
$S^{+}\,\otimes _{R^{+}}\,T^{+}$
in
![]() $L$
(see [Reference ScholzeSch12, Proposition 6.18]). The same construction holds in case the map
$L$
(see [Reference ScholzeSch12, Proposition 6.18]). The same construction holds in case the map
![]() $(R,R^{+})\rightarrow (S,S^{+})$
is finite étale and
$(R,R^{+})\rightarrow (S,S^{+})$
is finite étale and
![]() $(T,T^{+})$
is a perfectoid affinoid (see [Reference ScholzeSch12, Lemma 7.3]). By Remark 1.17, the constructions above give rise to fiber products in the category of adic spaces.
$(T,T^{+})$
is a perfectoid affinoid (see [Reference ScholzeSch12, Lemma 7.3]). By Remark 1.17, the constructions above give rise to fiber products in the category of adic spaces.
2 Semi-perfectoid spaces
We can now introduce a convenient generalization of both smooth rigid varieties and smooth perfectoid spaces. We recall that our base field
![]() $K$
is a perfectoid field (see Assumption 1.18).
$K$
is a perfectoid field (see Assumption 1.18).
Proposition 2.1. Let
![]() $\text{}\underline{\unicode[STIX]{x1D710}}=\unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{N}$
and
$\text{}\underline{\unicode[STIX]{x1D710}}=\unicode[STIX]{x1D710}_{1},\ldots ,\unicode[STIX]{x1D710}_{N}$
and
![]() $\text{}\underline{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{M}$
be two systems of coordinates. Let
$\text{}\underline{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{M}$
be two systems of coordinates. Let
![]() $(R_{0},R_{0}^{\circ })$
be a tft Tate algebra and let
$(R_{0},R_{0}^{\circ })$
be a tft Tate algebra and let
![]() $f:\operatorname{Spa}(R_{0},R_{0}^{\circ })\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}=\operatorname{Spa}K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle$
be a map, which is a composition of finite étale maps and rational embeddings. Also let
$f:\operatorname{Spa}(R_{0},R_{0}^{\circ })\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}=\operatorname{Spa}K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle$
be a map, which is a composition of finite étale maps and rational embeddings. Also let
![]() $\operatorname{Spa}(R_{h},R_{h}^{\circ })$
be the affinoid rigid variety
$\operatorname{Spa}(R_{h},R_{h}^{\circ })$
be the affinoid rigid variety
![]() $\operatorname{Spa}(R_{0},R_{0}^{\circ })\,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle$
. The
$\operatorname{Spa}(R_{0},R_{0}^{\circ })\,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle$
. The
![]() $\unicode[STIX]{x1D70B}$
-adic completion
$\unicode[STIX]{x1D70B}$
-adic completion
![]() $(T,T^{+})$
of
$(T,T^{+})$
of
![]() $(\mathop{\varinjlim }\nolimits_{h}R_{h},\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ })$
represents the fiber product
$(\mathop{\varinjlim }\nolimits_{h}R_{h},\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ })$
represents the fiber product
![]() $\operatorname{Spa}(R_{0},R_{0}^{\circ })\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
and defines a bounded affinoid adic space. Moreover,
$\operatorname{Spa}(R_{0},R_{0}^{\circ })\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
and defines a bounded affinoid adic space. Moreover,
![]() $(T,T^{+})$
is isomorphic to the completion of
$(T,T^{+})$
is isomorphic to the completion of
![]() $(L,L^{+})$
, where
$(L,L^{+})$
, where
![]() $L$
is the ring
$L$
is the ring
![]() $R_{0}\,\otimes _{K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle$
endowed with the norm of the tensor product and
$R_{0}\,\otimes _{K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{\infty }}\rangle$
endowed with the norm of the tensor product and
![]() $L^{+}$
is the integral closure of
$L^{+}$
is the integral closure of
![]() $R_{0}^{\circ }$
in
$R_{0}^{\circ }$
in
![]() $L$
.
$L$
.
Proof. Let
![]() $(T,T^{+})$
be as in the last claim. We let
$(T,T^{+})$
be as in the last claim. We let
![]() $W^{\prime }$
be the fiber product of
$W^{\prime }$
be the fiber product of
![]() $\operatorname{Spa}(T,T^{+})$
and
$\operatorname{Spa}(T,T^{+})$
and
![]() $\widehat{\mathbb{T}}^{N}\,\times \,\widehat{\mathbb{T}}^{M}$
over
$\widehat{\mathbb{T}}^{N}\,\times \,\widehat{\mathbb{T}}^{M}$
over
![]() $\widehat{\mathbb{T}}^{N}\,\times \,\mathbb{T}^{M}$
. If
$\widehat{\mathbb{T}}^{N}\,\times \,\mathbb{T}^{M}$
. If
![]() $\operatorname{char}K=0$
by [Reference ScholzeSch13, Lemma 4.5(i)] it exists and is affinoid perfectoid, represented by a perfectoid pair
$\operatorname{char}K=0$
by [Reference ScholzeSch13, Lemma 4.5(i)] it exists and is affinoid perfectoid, represented by a perfectoid pair
![]() $(T^{\prime },{T^{\prime }}^{+})$
. The same is true if
$(T^{\prime },{T^{\prime }}^{+})$
. The same is true if
![]() $\operatorname{char}K=p$
as in this case it coincides with the completed perfection of
$\operatorname{char}K=p$
as in this case it coincides with the completed perfection of
![]() $X_{0}$
(indeed, the pullback of an étale map over Frobenius is isomorphic to Frobenius, see for example [Sta18, Lemma 0EBS]).
$X_{0}$
(indeed, the pullback of an étale map over Frobenius is isomorphic to Frobenius, see for example [Sta18, Lemma 0EBS]).
From the strict inclusion
![]() $(T,T^{+})\rightarrow (T^{\prime },{T^{\prime }}^{\circ })$
we deduce that
$(T,T^{+})\rightarrow (T^{\prime },{T^{\prime }}^{\circ })$
we deduce that
![]() $T^{+}$
is bounded since
$T^{+}$
is bounded since
![]() ${T^{\prime }}^{+}$
is, being
${T^{\prime }}^{+}$
is, being
![]() $T^{\prime }$
perfectoid. By considering rational subspaces of
$T^{\prime }$
perfectoid. By considering rational subspaces of
![]() $\operatorname{Spa}(T,T^{+})$
we deduce that this space is stably uniform, and hence sheafy (by [Reference Buzzard and VerberkmoesBV18]).
$\operatorname{Spa}(T,T^{+})$
we deduce that this space is stably uniform, and hence sheafy (by [Reference Buzzard and VerberkmoesBV18]).
The proof of the alternative description of
![]() $(T,T^{+})$
follows in the same way as [Reference ScholzeSch13, Lemma 4.5(i)].◻
$(T,T^{+})$
follows in the same way as [Reference ScholzeSch13, Lemma 4.5(i)].◻
Remark 2.2. The statement of the previous proposition is an instance when the second term
![]() $T^{+}$
of some affinoid
$T^{+}$
of some affinoid
![]() $K$
-algebra
$K$
-algebra
![]() $(T,T^{+})$
may not be equal to the ring
$(T,T^{+})$
may not be equal to the ring
![]() $T^{\circ }$
.
$T^{\circ }$
.
Corollary 2.3. Let
![]() $X$
be a reduced rigid variety with an étale map
$X$
be a reduced rigid variety with an étale map
Then the fiber product
![]() $X\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
exists in the category of adic spaces.
$X\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
exists in the category of adic spaces.
Proof. This follows from Proposition 2.1 and the fact that every étale map is locally (on the source) a composition of rational embeddings and finite étale maps. ◻
Definition 2.4. We denote by
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
the full subcategory of adic spaces whose objects are isomorphic to spaces
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
the full subcategory of adic spaces whose objects are isomorphic to spaces
![]() $X=X_{0}\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
with respect to a map of affinoid rigid varieties
$X=X_{0}\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
with respect to a map of affinoid rigid varieties
![]() $f:X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}$
that is a composition of rational embeddings and finite étale maps. Such spaces will be called smooth semi-perfectoid spaces with good coordinates. Because of Proposition 2.1, such fiber products
$f:X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}$
that is a composition of rational embeddings and finite étale maps. Such spaces will be called smooth semi-perfectoid spaces with good coordinates. Because of Proposition 2.1, such fiber products
![]() $X=X_{0}\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
exist and are affinoid. Whenever
$X=X_{0}\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
exist and are affinoid. Whenever
![]() $N=0$
these varieties are rigid analytic varieties and the full subcategory they form will be denoted by
$N=0$
these varieties are rigid analytic varieties and the full subcategory they form will be denoted by
![]() $\operatorname{RigSm}^{\operatorname{gc}}\!/K$
and referred to as smooth affinoid rigid varieties with good coordinates. Whenever
$\operatorname{RigSm}^{\operatorname{gc}}\!/K$
and referred to as smooth affinoid rigid varieties with good coordinates. Whenever
![]() $M=0$
these varieties are perfectoid affinoid spaces and the full subcategory they form will be denoted by
$M=0$
these varieties are perfectoid affinoid spaces and the full subcategory they form will be denoted by
![]() $\operatorname{PerfSm}^{\operatorname{gc}}\!/K$
and referred to as smooth affinoid perfectoids with good coordinates. A perfectoid space
$\operatorname{PerfSm}^{\operatorname{gc}}\!/K$
and referred to as smooth affinoid perfectoids with good coordinates. A perfectoid space
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
will be sometimes denoted with
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
will be sometimes denoted with
![]() $\widehat{X}$
.
$\widehat{X}$
.
When
![]() $X=X_{0}\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
is in
$X=X_{0}\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
is in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
we denote by
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
we denote by
![]() $X_{h}$
the fiber product
$X_{h}$
the fiber product
![]() $X_{0}\,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle$
and we will write
$X_{0}\,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle$
and we will write
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
. We say that a presentation
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
. We say that a presentation
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of an object
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of an object
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
has good reduction if the map
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
has good reduction if the map
![]() $X_{0}\rightarrow \mathbb{T}^{n}\,\times \,\mathbb{T}^{m}$
has an étale formal model
$X_{0}\rightarrow \mathbb{T}^{n}\,\times \,\mathbb{T}^{m}$
has an étale formal model
![]() $\mathfrak{X}\rightarrow \operatorname{Spf}(K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle )$
. We say that a presentation
$\mathfrak{X}\rightarrow \operatorname{Spf}(K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle )$
. We say that a presentation
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of an object
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of an object
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
has potentially good reduction if there exists a finite separable field extension
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
has potentially good reduction if there exists a finite separable field extension
![]() $L/K$
such that
$L/K$
such that
![]() $X_{L}=\mathop{\varprojlim }\nolimits_{h}(X_{h})_{L}$
has good reduction in
$X_{L}=\mathop{\varprojlim }\nolimits_{h}(X_{h})_{L}$
has good reduction in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/L$
. We warn the reader that the association
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/L$
. We warn the reader that the association
![]() $X\mapsto X_{0}$
is not functorial and the varieties
$X\mapsto X_{0}$
is not functorial and the varieties
![]() $X_{h}$
are not uniquely determined by
$X_{h}$
are not uniquely determined by
![]() $X$
in general.
$X$
in general.
We denote by
![]() $\widehat{\text{Rig}}\operatorname{Sm}/K$
the full subcategory of adic spaces which are locally isomorphic to objects in
$\widehat{\text{Rig}}\operatorname{Sm}/K$
the full subcategory of adic spaces which are locally isomorphic to objects in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
and its objects will be called smooth semi-perfectoid spaces. We denote by
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
and its objects will be called smooth semi-perfectoid spaces. We denote by
![]() $\operatorname{RigSm}/K$
the full subcategory of adic spaces, which are locally isomorphic to objects in
$\operatorname{RigSm}/K$
the full subcategory of adic spaces, which are locally isomorphic to objects in
![]() $\operatorname{RigSm}^{\operatorname{gc}}\!/K$
and by
$\operatorname{RigSm}^{\operatorname{gc}}\!/K$
and by
![]() $\operatorname{PerfSm}/K$
the one of adic spaces, which are locally isomorphic to objects in
$\operatorname{PerfSm}/K$
the one of adic spaces, which are locally isomorphic to objects in
![]() $\operatorname{PerfSm}^{\operatorname{gc}}\!/K$
. Its objects will be called smooth perfectoid spaces. Whenever the context allows it, we omit
$\operatorname{PerfSm}^{\operatorname{gc}}\!/K$
. Its objects will be called smooth perfectoid spaces. Whenever the context allows it, we omit
![]() $K$
from the notation.
$K$
from the notation.
Remark 2.5. Any smooth rigid variety (see for example [Reference AyoubAyo15, Definition 1.1.41]) has locally good coordinates over
![]() $\mathbb{T}^{N}$
by [Reference AyoubAyo15, Corollary 1.1.51]. Hence,
$\mathbb{T}^{N}$
by [Reference AyoubAyo15, Corollary 1.1.51]. Hence,
![]() $\operatorname{RigSm}$
coincides with the category of smooth rigid varieties.
$\operatorname{RigSm}$
coincides with the category of smooth rigid varieties.
We remark that the presentations defined above having good reduction are a special case of the objects considered in [Reference AndreattaAnd06].
The notation
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
is justified by the following corollary, which is inspired by [Reference Scholze and WeinsteinSW13, Proposition 2.4.5].
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
is justified by the following corollary, which is inspired by [Reference Scholze and WeinsteinSW13, Proposition 2.4.5].
Corollary 2.6. Let
![]() $Y=\operatorname{Spa}(S,S^{+})$
be an affinoid such that
$Y=\operatorname{Spa}(S,S^{+})$
be an affinoid such that
![]() $S^{+}$
is a ring of definition and let
$S^{+}$
is a ring of definition and let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Then
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Then
![]() $\operatorname{Hom}(Y,X)\cong \mathop{\varprojlim }\nolimits_{h}\operatorname{Hom}(Y,X_{h})$
.
$\operatorname{Hom}(Y,X)\cong \mathop{\varprojlim }\nolimits_{h}\operatorname{Hom}(Y,X_{h})$
.
Proof. Suppose that
![]() $X_{h}=\operatorname{Spa}(R_{h},R_{h}^{\circ })$
and
$X_{h}=\operatorname{Spa}(R_{h},R_{h}^{\circ })$
and
![]() $X=\operatorname{Spa}(R,R^{+})$
. By Proposition 2.1
$X=\operatorname{Spa}(R,R^{+})$
. By Proposition 2.1
![]() $R^{+}$
is a ring of definition and is the completion of
$R^{+}$
is a ring of definition and is the completion of
![]() $\varinjlim R_{h}^{+}$
. A map from
$\varinjlim R_{h}^{+}$
. A map from
![]() $(R,R^{+})$
to
$(R,R^{+})$
to
![]() $(S,S^{+})$
is uniquely determined by a
$(S,S^{+})$
is uniquely determined by a
![]() $K^{\circ }$
-linear map from
$K^{\circ }$
-linear map from
![]() $\varinjlim R_{h}^{\circ }$
to
$\varinjlim R_{h}^{\circ }$
to
![]() $S^{+}$
. Similarly, a map from
$S^{+}$
. Similarly, a map from
![]() $(R_{h},R_{h}^{\circ })$
to
$(R_{h},R_{h}^{\circ })$
to
![]() $(S,S^{+})$
is uniquely determined by a
$(S,S^{+})$
is uniquely determined by a
![]() $K^{\circ }$
-linear map from
$K^{\circ }$
-linear map from
![]() $R_{h}^{\circ }$
to
$R_{h}^{\circ }$
to
![]() $S^{+}$
. From the isomorphism
$S^{+}$
. From the isomorphism
![]() $\operatorname{Hom}_{K^{+}}(\varinjlim R_{h}^{\circ },S^{+})\cong \mathop{\varprojlim }\nolimits_{h}\operatorname{Hom}_{K^{+}}(R_{h}^{\circ },S^{+})$
we then deduce the claim.◻
$\operatorname{Hom}_{K^{+}}(\varinjlim R_{h}^{\circ },S^{+})\cong \mathop{\varprojlim }\nolimits_{h}\operatorname{Hom}_{K^{+}}(R_{h}^{\circ },S^{+})$
we then deduce the claim.◻
Let
![]() $\{X_{h},f_{h}\}_{h\in I}$
be a cofiltered diagram of rigid varieties and let
$\{X_{h},f_{h}\}_{h\in I}$
be a cofiltered diagram of rigid varieties and let
![]() $\{X\rightarrow X_{h}\}_{h\in I}$
be a collection of compatible maps of adic spaces. We recall that, according to [Reference HuberHub96, Remark 2.4.5], one writes
$\{X\rightarrow X_{h}\}_{h\in I}$
be a collection of compatible maps of adic spaces. We recall that, according to [Reference HuberHub96, Remark 2.4.5], one writes
![]() $X\sim \mathop{\varprojlim }\nolimits_{h}X_{h}$
when the following two conditions are satisfied.
$X\sim \mathop{\varprojlim }\nolimits_{h}X_{h}$
when the following two conditions are satisfied.
(i) The induced map on topological spaces
 $|X|\rightarrow \mathop{\varprojlim }\nolimits_{h}|X_{h}|$
is a homeomorphism.
$|X|\rightarrow \mathop{\varprojlim }\nolimits_{h}|X_{h}|$
is a homeomorphism.(ii) For any
 $x\in X$
with images
$x\in X$
with images
 $x_{h}\in X_{h}$
the map of residue fields
$x_{h}\in X_{h}$
the map of residue fields
 $\mathop{\varinjlim }\nolimits_{h}k(x_{h})\rightarrow k(x)$
has a dense image.
$\mathop{\varinjlim }\nolimits_{h}k(x_{h})\rightarrow k(x)$
has a dense image.
The apparent clash of notations is solved by the following fact.
Proposition 2.7. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Then
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Then
![]() $X\sim \mathop{\varprojlim }\nolimits_{h}X_{h}$
.
$X\sim \mathop{\varprojlim }\nolimits_{h}X_{h}$
.
Proof. This follows from
![]() $\widehat{\mathbb{T}}^{N}\sim \mathop{\varprojlim }\nolimits_{h}\operatorname{Spa}K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
and from [Reference ScholzeSch12, Proposition 7.16].◻
$\widehat{\mathbb{T}}^{N}\sim \mathop{\varprojlim }\nolimits_{h}\operatorname{Spa}K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
and from [Reference ScholzeSch12, Proposition 7.16].◻
Étale maps define a topology on
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
in the following way.
$\widehat{\text{Rig}}\operatorname{Sm}$
in the following way.
Definition 2.8. A collection of étale maps of adic spaces
![]() $\{U_{i}\rightarrow X\}_{i\in I}$
is an étale cover if the induced map
$\{U_{i}\rightarrow X\}_{i\in I}$
is an étale cover if the induced map
![]() $\bigsqcup _{i\in I}U_{i}\rightarrow X$
is surjective. These covers define a Grothendieck topology on
$\bigsqcup _{i\in I}U_{i}\rightarrow X$
is surjective. These covers define a Grothendieck topology on
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
called the étale topology.
$\widehat{\text{Rig}}\operatorname{Sm}$
called the étale topology.
We pin down the following facts on the topology of the objects
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
.
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
.
Proposition 2.9. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be an object of
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be an object of
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
.
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
.
(i) Any finite étale map
 $U\rightarrow X$
is isomorphic to
$U\rightarrow X$
is isomorphic to
 $U_{\bar{h}}\,\times _{X_{\bar{h}}}\,X$
for some integer
$U_{\bar{h}}\,\times _{X_{\bar{h}}}\,X$
for some integer
 $\bar{h}$
and some finite étale map
$\bar{h}$
and some finite étale map
 $U_{\bar{h}}\rightarrow X_{\bar{h}}$
.
$U_{\bar{h}}\rightarrow X_{\bar{h}}$
.(ii) Any rational subspace
 $U\subset X$
is isomorphic to
$U\subset X$
is isomorphic to
 $U_{\bar{h}}\,\times _{X_{\bar{h}}}\,X$
for some integer
$U_{\bar{h}}\,\times _{X_{\bar{h}}}\,X$
for some integer
 $H$
and some rational subspace
$H$
and some rational subspace
 $U_{\bar{h}}\subset X_{\bar{h}}$
.
$U_{\bar{h}}\subset X_{\bar{h}}$
.
Proof. The first statement follows from [Reference ScholzeSch12, Lemma 7.5]. For the second, we remark that according to [Reference HuberHub93, Lemma 3.10] any rational subspace
![]() $U=(f_{1},\ldots ,f_{n}|g)$
of
$U=(f_{1},\ldots ,f_{n}|g)$
of
![]() $X$
can be defined by means of elements
$X$
can be defined by means of elements
![]() $f_{i},g$
lying in
$f_{i},g$
lying in
![]() $\mathop{\varinjlim }\nolimits_{h}{\mathcal{O}}(X_{h})$
since it is dense in
$\mathop{\varinjlim }\nolimits_{h}{\mathcal{O}}(X_{h})$
since it is dense in
![]() ${\mathcal{O}}(X)$
, and hence the claim.◻
${\mathcal{O}}(X)$
, and hence the claim.◻
The proposition above can also be used to prove that a finite étale extension of an object
![]() $\operatorname{Spa}(T,T^{+})$
in
$\operatorname{Spa}(T,T^{+})$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
also lies in
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
also lies in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
, and hence arbitrary fiber products of étale maps in
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}\!/K$
, and hence arbitrary fiber products of étale maps in
![]() $\widehat{\text{Rig}}\operatorname{Sm}/K$
exist, and are étale.
$\widehat{\text{Rig}}\operatorname{Sm}/K$
exist, and are étale.
Corollary 2.10. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be an object of
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be an object of
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
and let
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
and let
![]() ${\mathcal{U}}:=\{f_{i}:U_{i}\rightarrow X\}$
be an étale covering of adic spaces. There exists an integer
${\mathcal{U}}:=\{f_{i}:U_{i}\rightarrow X\}$
be an étale covering of adic spaces. There exists an integer
![]() $\bar{h}$
and a finite affinoid refinement
$\bar{h}$
and a finite affinoid refinement
![]() $\{V_{j}\rightarrow X\}$
of
$\{V_{j}\rightarrow X\}$
of
![]() ${\mathcal{U}}$
, which is obtained by pullback of an étale covering
${\mathcal{U}}$
, which is obtained by pullback of an étale covering
![]() $\{V_{\bar{h}j}\rightarrow X_{\bar{h}}\}$
of
$\{V_{\bar{h}j}\rightarrow X_{\bar{h}}\}$
of
![]() $X_{\bar{h}}$
and such that
$X_{\bar{h}}$
and such that
![]() $V=\mathop{\varprojlim }\nolimits_{h}V_{hj}$
lies in
$V=\mathop{\varprojlim }\nolimits_{h}V_{hj}$
lies in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
by letting
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
by letting
![]() $V_{hj}$
be
$V_{hj}$
be
![]() $V_{\bar{h}j}\,\times _{X_{\bar{h}}}\,X_{h}$
for all
$V_{\bar{h}j}\,\times _{X_{\bar{h}}}\,X_{h}$
for all
![]() $h\geqslant \bar{h}$
.
$h\geqslant \bar{h}$
.
Proof. Any étale map of adic spaces is locally a composition of rational embeddings and finite étale maps and they descend because of Proposition 2.9. We, therefore, obtain an affinoid refinement
![]() $\{V_{j}\rightarrow X\}$
of
$\{V_{j}\rightarrow X\}$
of
![]() ${\mathcal{U}}$
such that each
${\mathcal{U}}$
such that each
![]() $V_{i}$
descends to some
$V_{i}$
descends to some
![]() $X_{h}$
. Since
$X_{h}$
. Since
![]() $X$
is quasi-compact, we can also refine this covering by a finite one, and choose a common index
$X$
is quasi-compact, we can also refine this covering by a finite one, and choose a common index
![]() $\bar{h}$
where each
$\bar{h}$
where each
![]() $V_{j}$
descends to.◻
$V_{j}$
descends to.◻
Corollary 2.11. A perfectoid space
![]() $X$
lies in
$X$
lies in
![]() $\operatorname{PerfSm}$
if and only if it is locally étale over
$\operatorname{PerfSm}$
if and only if it is locally étale over
![]() $\widehat{\mathbb{T}}^{N}$
.
$\widehat{\mathbb{T}}^{N}$
.
Proof. Let
![]() $X$
be locally étale over
$X$
be locally étale over
![]() $\widehat{\mathbb{T}}^{N}$
. Then it is locally open in a finite étale space over a rational subspace of
$\widehat{\mathbb{T}}^{N}$
. Then it is locally open in a finite étale space over a rational subspace of
![]() $\widehat{\mathbb{T}}^{N}=\mathop{\varprojlim }\nolimits_{h}\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
. By Proposition 2.9, we conclude it is locally of the form
$\widehat{\mathbb{T}}^{N}=\mathop{\varprojlim }\nolimits_{h}\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
. By Proposition 2.9, we conclude it is locally of the form
![]() $X_{0}\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
for some étale map
$X_{0}\,\times _{\mathbb{T}^{N}}\,\widehat{\mathbb{T}}^{N}$
for some étale map
![]() $X_{0}\rightarrow \mathbb{T}^{N}=\operatorname{Spa}(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle )$
, which is the composition of rational embeddings and finite étale maps.◻
$X_{0}\rightarrow \mathbb{T}^{N}=\operatorname{Spa}(K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle ,K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle )$
, which is the composition of rational embeddings and finite étale maps.◻
Remark 2.12. If
![]() $X$
is a smooth affinoid perfectoid space, then it has a finite number of connected components. Indeed, it is quasi-compact and locally isomorphic to a rational subspace of a perfectoid space, which is finite étale over a rational subspace of
$X$
is a smooth affinoid perfectoid space, then it has a finite number of connected components. Indeed, it is quasi-compact and locally isomorphic to a rational subspace of a perfectoid space, which is finite étale over a rational subspace of
![]() $\widehat{\mathbb{T}}^{N}$
.
$\widehat{\mathbb{T}}^{N}$
.
For later use, we record the following simple example of a space
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
for which the varieties
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
for which the varieties
![]() $X_{h}$
are easy to understand.
$X_{h}$
are easy to understand.
Proposition 2.13. Consider the smooth affinoid variety with good coordinates
One has
![]() $X_{h}\cong \mathbb{B}^{1}$
for all
$X_{h}\cong \mathbb{B}^{1}$
for all
![]() $h$
and
$h$
and
![]() $\widehat{X}=\mathop{\varprojlim }\nolimits_{h}X_{h}\cong \widehat{\mathbb{B}}^{1}$
.
$\widehat{X}=\mathop{\varprojlim }\nolimits_{h}X_{h}\cong \widehat{\mathbb{B}}^{1}$
.
Proof. By direct computation, the variety
![]() $X_{h}$
is isomorphic to
$X_{h}$
is isomorphic to
![]() $\operatorname{Spa}(K\langle \unicode[STIX]{x1D710},\unicode[STIX]{x1D714}\rangle /(\unicode[STIX]{x1D714}^{p^{h}}-(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D710}+1)))$
. Since
$\operatorname{Spa}(K\langle \unicode[STIX]{x1D710},\unicode[STIX]{x1D714}\rangle /(\unicode[STIX]{x1D714}^{p^{h}}-(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D710}+1)))$
. Since
![]() $|p|\leqslant |\unicode[STIX]{x1D70B}|$
we deduce that
$|p|\leqslant |\unicode[STIX]{x1D70B}|$
we deduce that
![]() $|\binom{p^{h}}{i}|\leqslant |\unicode[STIX]{x1D70B}|$
for all
$|\binom{p^{h}}{i}|\leqslant |\unicode[STIX]{x1D70B}|$
for all
![]() $0<i<p^{h}$
. In particular, in the ring
$0<i<p^{h}$
. In particular, in the ring
![]() $K\langle \unicode[STIX]{x1D710},\unicode[STIX]{x1D714}\rangle /(\unicode[STIX]{x1D714}^{p^{h}}-(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D710}+1))$
one has
$K\langle \unicode[STIX]{x1D710},\unicode[STIX]{x1D714}\rangle /(\unicode[STIX]{x1D714}^{p^{h}}-(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D710}+1))$
one has
Analogously, in the ring
![]() $K\langle \unicode[STIX]{x1D712}\rangle$
one has
$K\langle \unicode[STIX]{x1D712}\rangle$
one has
The following maps are, therefore, well defined and clearly mutually inverse:
 $$\begin{eqnarray}\displaystyle X_{h}=\operatorname{Spa}(K\langle \unicode[STIX]{x1D710},\unicode[STIX]{x1D714}\rangle /(\unicode[STIX]{x1D714}^{p^{h}}-(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D710}+1))) & \leftrightarrows & \displaystyle \operatorname{Spa}(K\langle \unicode[STIX]{x1D712}\rangle )=\mathbb{B}^{1}\nonumber\\ \displaystyle (\unicode[STIX]{x1D710},\unicode[STIX]{x1D714}) & \mapsto & \displaystyle ((\unicode[STIX]{x1D712}+\unicode[STIX]{x1D70B}^{-1/p^{h}})^{p^{h}}-\unicode[STIX]{x1D70B}^{-1},\unicode[STIX]{x1D70B}^{1/p^{h}}\unicode[STIX]{x1D712}+1)\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}^{-1/p^{h}}(\unicode[STIX]{x1D714}-1) & \leftarrow & \displaystyle \unicode[STIX]{x1D712}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{h}=\operatorname{Spa}(K\langle \unicode[STIX]{x1D710},\unicode[STIX]{x1D714}\rangle /(\unicode[STIX]{x1D714}^{p^{h}}-(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D710}+1))) & \leftrightarrows & \displaystyle \operatorname{Spa}(K\langle \unicode[STIX]{x1D712}\rangle )=\mathbb{B}^{1}\nonumber\\ \displaystyle (\unicode[STIX]{x1D710},\unicode[STIX]{x1D714}) & \mapsto & \displaystyle ((\unicode[STIX]{x1D712}+\unicode[STIX]{x1D70B}^{-1/p^{h}})^{p^{h}}-\unicode[STIX]{x1D70B}^{-1},\unicode[STIX]{x1D70B}^{1/p^{h}}\unicode[STIX]{x1D712}+1)\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}^{-1/p^{h}}(\unicode[STIX]{x1D714}-1) & \leftarrow & \displaystyle \unicode[STIX]{x1D712}.\nonumber\end{eqnarray}$$
Consider the multiplicative map
![]() $\sharp :K^{\flat }\langle \unicode[STIX]{x1D710}^{1/p^{\infty }}\rangle =(K\langle \unicode[STIX]{x1D710}^{1/p^{\infty }}\rangle )^{\flat }\rightarrow K\langle \unicode[STIX]{x1D710}^{1/p^{\infty }}\rangle$
defined in [Reference ScholzeSch12, Proposition 5.17]. By our assumptions on
$\sharp :K^{\flat }\langle \unicode[STIX]{x1D710}^{1/p^{\infty }}\rangle =(K\langle \unicode[STIX]{x1D710}^{1/p^{\infty }}\rangle )^{\flat }\rightarrow K\langle \unicode[STIX]{x1D710}^{1/p^{\infty }}\rangle$
defined in [Reference ScholzeSch12, Proposition 5.17]. By our assumptions on
![]() $\unicode[STIX]{x1D70B}$
the element
$\unicode[STIX]{x1D70B}$
the element
![]() $(\unicode[STIX]{x1D710}-1)^{\sharp }-(\unicode[STIX]{x1D710}-1)$
is divisible by
$(\unicode[STIX]{x1D710}-1)^{\sharp }-(\unicode[STIX]{x1D710}-1)$
is divisible by
![]() $\unicode[STIX]{x1D70B}$
in
$\unicode[STIX]{x1D70B}$
in
![]() $K^{\circ }\langle \unicode[STIX]{x1D710}^{1/p^{\infty }}\rangle$
and, therefore, the rational subspace
$K^{\circ }\langle \unicode[STIX]{x1D710}^{1/p^{\infty }}\rangle$
and, therefore, the rational subspace
![]() $\widehat{X}\cong U(\unicode[STIX]{x1D710}-1\,\mid \,\unicode[STIX]{x1D70B})$
of
$\widehat{X}\cong U(\unicode[STIX]{x1D710}-1\,\mid \,\unicode[STIX]{x1D70B})$
of
![]() $\widehat{\mathbb{T}}^{1}$
coincides with
$\widehat{\mathbb{T}}^{1}$
coincides with
![]() $U((\unicode[STIX]{x1D710}-1)^{\sharp }\,\mid \,\unicode[STIX]{x1D70B}^{\flat \sharp })$
. From [Reference ScholzeSch12, Theorem 6.3] we conclude
$U((\unicode[STIX]{x1D710}-1)^{\sharp }\,\mid \,\unicode[STIX]{x1D70B}^{\flat \sharp })$
. From [Reference ScholzeSch12, Theorem 6.3] we conclude
![]() $\widehat{X}^{\flat }\cong U(\unicode[STIX]{x1D710}-1\,\mid \,\unicode[STIX]{x1D70B}^{\flat }){\hookrightarrow}\widehat{\mathbb{T}}^{\flat 1}$
, which is isomorphic to
$\widehat{X}^{\flat }\cong U(\unicode[STIX]{x1D710}-1\,\mid \,\unicode[STIX]{x1D70B}^{\flat }){\hookrightarrow}\widehat{\mathbb{T}}^{\flat 1}$
, which is isomorphic to
![]() $\widehat{\mathbb{B}}^{\flat 1}$
, and hence the claim.◻
$\widehat{\mathbb{B}}^{\flat 1}$
, and hence the claim.◻
From the previous proposition we conclude, in particular, that the perfectoid space
![]() $\widehat{\mathbb{B}}^{1}$
lies in
$\widehat{\mathbb{B}}^{1}$
lies in
![]() $\operatorname{PerfSm}^{\operatorname{gc}}$
.
$\operatorname{PerfSm}^{\operatorname{gc}}$
.
3 Categories of adic motives
From now on, we fix a commutative ring
![]() $\unicode[STIX]{x1D6EC}$
and work with
$\unicode[STIX]{x1D6EC}$
and work with
![]() $\unicode[STIX]{x1D6EC}$
-enriched categories. In particular, the term ‘presheaf’ should be understood as ‘presheaf of
$\unicode[STIX]{x1D6EC}$
-enriched categories. In particular, the term ‘presheaf’ should be understood as ‘presheaf of
![]() $\unicode[STIX]{x1D6EC}$
-modules’ and similarly for the term ‘sheaf’. The presheaf
$\unicode[STIX]{x1D6EC}$
-modules’ and similarly for the term ‘sheaf’. The presheaf
![]() $\unicode[STIX]{x1D6EC}(X)$
represented by an object
$\unicode[STIX]{x1D6EC}(X)$
represented by an object
![]() $X$
of a category
$X$
of a category
![]() $\mathbf{C}$
sends an object
$\mathbf{C}$
sends an object
![]() $Y$
of
$Y$
of
![]() $\mathbf{C}$
to the free
$\mathbf{C}$
to the free
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() $\unicode[STIX]{x1D6EC}\operatorname{Hom}(Y,X)$
.
$\unicode[STIX]{x1D6EC}\operatorname{Hom}(Y,X)$
.
Assumption 3.1. Unless otherwise stated, we assume from now on that
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $\mathbb{Q}$
-algebra and we omit it from the notations.
$\mathbb{Q}$
-algebra and we omit it from the notations.
We make extensive use of the theory of model categories and localization, following the approach of Ayoub in [Reference AyoubAyo15, Reference AyoubAyo07]. Fix a site
![]() $(\mathbf{C},\unicode[STIX]{x1D70F})$
. In our situation, this will be the étale site of
$(\mathbf{C},\unicode[STIX]{x1D70F})$
. In our situation, this will be the étale site of
![]() $\operatorname{RigSm}$
or
$\operatorname{RigSm}$
or
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
. The category of complexes of presheaves
$\widehat{\text{Rig}}\operatorname{Sm}$
. The category of complexes of presheaves
![]() $\mathbf{Ch}(\mathbf{Psh}(\mathbf{C}))$
can be endowed with the projective model structure for which weak equivalences are quasi-isomorphisms and fibrations are maps
$\mathbf{Ch}(\mathbf{Psh}(\mathbf{C}))$
can be endowed with the projective model structure for which weak equivalences are quasi-isomorphisms and fibrations are maps
![]() ${\mathcal{F}}\rightarrow {\mathcal{F}}^{\prime }$
such that
${\mathcal{F}}\rightarrow {\mathcal{F}}^{\prime }$
such that
![]() ${\mathcal{F}}(X)\rightarrow {\mathcal{F}}^{\prime }(X)$
is a surjection for all
${\mathcal{F}}(X)\rightarrow {\mathcal{F}}^{\prime }(X)$
is a surjection for all
![]() $X$
in
$X$
in
![]() $\mathbf{C}$
(cfr [Reference HoveyHov99, § 2.3] and [Reference AyoubAyo07, Proposition 4.4.16]).
$\mathbf{C}$
(cfr [Reference HoveyHov99, § 2.3] and [Reference AyoubAyo07, Proposition 4.4.16]).
Also the category of complexes of sheaves
![]() $\mathbf{Ch}(\mathbf{Sh}_{\unicode[STIX]{x1D70F}}(\mathbf{C}))$
can be endowed with the projective model structure defined in [Reference AyoubAyo07, Definition 4.4.40]. In this structure, weak equivalences are quasi-isomorphisms of complexes of sheaves.
$\mathbf{Ch}(\mathbf{Sh}_{\unicode[STIX]{x1D70F}}(\mathbf{C}))$
can be endowed with the projective model structure defined in [Reference AyoubAyo07, Definition 4.4.40]. In this structure, weak equivalences are quasi-isomorphisms of complexes of sheaves.
Remark 3.2. Let
![]() $\mathbf{C}$
be a category. As shown in [Reference FauskFau06] any projectively cofibrant complex
$\mathbf{C}$
be a category. As shown in [Reference FauskFau06] any projectively cofibrant complex
![]() ${\mathcal{F}}$
in
${\mathcal{F}}$
in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\mathbf{C})$
is a retract of a complex that is the filtered colimit of bounded above complexes, each constituted by presheaves that are direct sums of representable ones.
$\mathbf{Ch}\,\mathbf{Psh}(\mathbf{C})$
is a retract of a complex that is the filtered colimit of bounded above complexes, each constituted by presheaves that are direct sums of representable ones.
Just like in [Reference JardineJar87, Reference Mazza, Voevodsky and WeibelMVW06, Reference Morel and VoevodskyMV99] or [Reference RiouRio07], we consider the left Bousfield localization of the model category
![]() $\mathbf{Ch}(\mathbf{Psh}(\mathbf{C}))$
with respect to the topology we select, and a chosen ‘contractible object’. We recall that left Bousfield localizations with respect to a class of maps
$\mathbf{Ch}(\mathbf{Psh}(\mathbf{C}))$
with respect to the topology we select, and a chosen ‘contractible object’. We recall that left Bousfield localizations with respect to a class of maps
![]() $S$
(see [Reference HirschhornHir03, ch. 3]) is the universal model categories in which the maps in
$S$
(see [Reference HirschhornHir03, ch. 3]) is the universal model categories in which the maps in
![]() $S$
become weak equivalences. The existence of such structures is granted only under some technical hypotheses, as shown in [Reference HirschhornHir03, Theorem 4.1.1] and [Reference AyoubAyo07, Theorem 4.2.71].
$S$
become weak equivalences. The existence of such structures is granted only under some technical hypotheses, as shown in [Reference HirschhornHir03, Theorem 4.1.1] and [Reference AyoubAyo07, Theorem 4.2.71].
Proposition 3.3. Let
![]() $(\mathbf{C},\unicode[STIX]{x1D70F})$
be a site with finite direct products and let
$(\mathbf{C},\unicode[STIX]{x1D70F})$
be a site with finite direct products and let
![]() $\mathbf{C}^{\prime }$
be a full subcategory of
$\mathbf{C}^{\prime }$
be a full subcategory of
![]() $\mathbf{C}$
such that every object of
$\mathbf{C}$
such that every object of
![]() $\mathbf{C}$
has a covering by objects of
$\mathbf{C}$
has a covering by objects of
![]() $\mathbf{C}^{\prime }$
. Also let
$\mathbf{C}^{\prime }$
. Also let
![]() $I$
be an object of
$I$
be an object of
![]() $\mathbf{C}^{\prime }$
.
$\mathbf{C}^{\prime }$
.
(i) The projective model category
 $\mathbf{Ch}\,\mathbf{Psh}(\mathbf{C})$
admits a left Bousfield localization
$\mathbf{Ch}\,\mathbf{Psh}(\mathbf{C})$
admits a left Bousfield localization
 $\mathbf{Ch}_{I}\mathbf{Psh}(\mathbf{C})$
with respect to the set
$\mathbf{Ch}_{I}\mathbf{Psh}(\mathbf{C})$
with respect to the set
 $S_{I}$
of all maps
$S_{I}$
of all maps
 $\unicode[STIX]{x1D6EC}(I\,\times \,X)[i]\rightarrow \unicode[STIX]{x1D6EC}(X)[i]$
as
$\unicode[STIX]{x1D6EC}(I\,\times \,X)[i]\rightarrow \unicode[STIX]{x1D6EC}(X)[i]$
as
 $X$
varies in
$X$
varies in
 $\mathbf{C}$
and
$\mathbf{C}$
and
 $i$
varies in
$i$
varies in
 $\mathbb{Z}$
.
$\mathbb{Z}$
.(ii) The projective model categories
 $\mathbf{Ch}\,\mathbf{Psh}(\mathbf{C})$
and
$\mathbf{Ch}\,\mathbf{Psh}(\mathbf{C})$
and
 $\mathbf{Ch}\,\mathbf{Psh}(\mathbf{C}^{\prime })$
admit left Bousfield localizations
$\mathbf{Ch}\,\mathbf{Psh}(\mathbf{C}^{\prime })$
admit left Bousfield localizations
 $\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C})$
and
$\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C})$
and
 $\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C}^{\prime })$
with respect to the class
$\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C}^{\prime })$
with respect to the class
 $S_{\unicode[STIX]{x1D70F}}$
of maps
$S_{\unicode[STIX]{x1D70F}}$
of maps
 ${\mathcal{F}}\rightarrow {\mathcal{F}}^{\prime }$
inducing isomorphisms on the
${\mathcal{F}}\rightarrow {\mathcal{F}}^{\prime }$
inducing isomorphisms on the
 $\acute{\text{e}}\text{t}$
-sheaves associated to
$\acute{\text{e}}\text{t}$
-sheaves associated to
 $H_{i}({\mathcal{F}})$
and
$H_{i}({\mathcal{F}})$
and
 $H_{i}({\mathcal{F}}^{\prime })$
for all
$H_{i}({\mathcal{F}}^{\prime })$
for all
 $i\in \mathbb{Z}$
. Moreover, the two localized model categories are Quillen equivalent and the sheafification functor induces a Quillen equivalence to the projective model category
$i\in \mathbb{Z}$
. Moreover, the two localized model categories are Quillen equivalent and the sheafification functor induces a Quillen equivalence to the projective model category
 $\mathbf{Ch}\,\mathbf{Sh}_{\unicode[STIX]{x1D70F}}(\mathbf{C})$
.
$\mathbf{Ch}\,\mathbf{Sh}_{\unicode[STIX]{x1D70F}}(\mathbf{C})$
.(iii) The model categories
 $\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C})$
and
$\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C})$
and
 $\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C}^{\prime })$
admit left Bousfield localizations
$\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C}^{\prime })$
admit left Bousfield localizations
 $\mathbf{Ch}_{\unicode[STIX]{x1D70F},I}\mathbf{Psh}(\mathbf{C})$
and
$\mathbf{Ch}_{\unicode[STIX]{x1D70F},I}\mathbf{Psh}(\mathbf{C})$
and
 $\mathbf{Ch}_{\unicode[STIX]{x1D70F},I}\mathbf{Psh}(\mathbf{C}^{\prime })$
with respect to the set
$\mathbf{Ch}_{\unicode[STIX]{x1D70F},I}\mathbf{Psh}(\mathbf{C}^{\prime })$
with respect to the set
 $S_{I}$
defined above. Moreover, the two localized model categories are Quillen equivalent.
$S_{I}$
defined above. Moreover, the two localized model categories are Quillen equivalent.
Proof. According to [Reference HirschhornHir03, Theorem 4.1.1], any model category that is left proper and cellular (some technical properties that are defined in [Reference HirschhornHir03, Definitions 12.1.1 and 13.1.1]) admits a left Boudsfield localization with respect to a set of maps. The model structure on complexes is left proper and cellular (see [Reference Schwede and ShipleySS00, p. 7]). It follows that the projective model structures in the statement are also left proper and cellular (see [Reference HirschhornHir03, Propositions 12.1.5 and 13.1.14]), and hence the first claim.
For the first part of the second claim, it suffices to apply [Reference AyoubAyo07, Proposition 4.4.31, Lemma 4.4.34] showing that the localization over
![]() $S_{\unicode[STIX]{x1D70F}}$
is equivalent to a localization over a set of maps. The second part is a restatement of [Reference AyoubAyo07, Corollary 4.4.42, Proposition 4.4.55].
$S_{\unicode[STIX]{x1D70F}}$
is equivalent to a localization over a set of maps. The second part is a restatement of [Reference AyoubAyo07, Corollary 4.4.42, Proposition 4.4.55].
Since by [Reference AyoubAyo07, Proposition 4.4.31] the
![]() $\unicode[STIX]{x1D70F}$
-localization coincides with the Bousfield localization with respect to a set, we conclude by [Reference AyoubAyo07, Theorem 4.2.71] that the model category
$\unicode[STIX]{x1D70F}$
-localization coincides with the Bousfield localization with respect to a set, we conclude by [Reference AyoubAyo07, Theorem 4.2.71] that the model category
![]() $\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C})$
is still left proper and cellular. The last statement then follows from [Reference HirschhornHir03, Theorem 4.1.1] and the second claim.◻
$\mathbf{Ch}_{\unicode[STIX]{x1D70F}}\mathbf{Psh}(\mathbf{C})$
is still left proper and cellular. The last statement then follows from [Reference HirschhornHir03, Theorem 4.1.1] and the second claim.◻
In the situation above, we will denote by
![]() $S_{(\unicode[STIX]{x1D70F},I)}$
the union of the class
$S_{(\unicode[STIX]{x1D70F},I)}$
the union of the class
![]() $S_{\unicode[STIX]{x1D70F}}$
and the set
$S_{\unicode[STIX]{x1D70F}}$
and the set
![]() $S_{I}$
.
$S_{I}$
.
Remark 3.4. A geometrically relevant situation is induced when
![]() $I$
is endowed with a multiplication map
$I$
is endowed with a multiplication map
![]() $\unicode[STIX]{x1D707}:I\,\times \,I\rightarrow I$
and maps
$\unicode[STIX]{x1D707}:I\,\times \,I\rightarrow I$
and maps
![]() $i_{0}$
and
$i_{0}$
and
![]() $i_{1}$
from the terminal object to
$i_{1}$
from the terminal object to
![]() $I$
satisfying the relations of a monoidal object with
$I$
satisfying the relations of a monoidal object with
![]() $0$
as in the definition of an interval object (see [Reference Morel and VoevodskyMV99, § 2.3]). Under these hypotheses, we say that the triple
$0$
as in the definition of an interval object (see [Reference Morel and VoevodskyMV99, § 2.3]). Under these hypotheses, we say that the triple
![]() $(\mathbf{C},\unicode[STIX]{x1D70F},I)$
is a site with an interval.
$(\mathbf{C},\unicode[STIX]{x1D70F},I)$
is a site with an interval.
Example 3.5. The affinoid rigid variety with good coordinates
![]() $\mathbb{B}^{1}=\operatorname{Spa}K\langle \unicode[STIX]{x1D712}\rangle$
is an interval object with respect to the natural multiplication
$\mathbb{B}^{1}=\operatorname{Spa}K\langle \unicode[STIX]{x1D712}\rangle$
is an interval object with respect to the natural multiplication
![]() $\unicode[STIX]{x1D707}$
and maps
$\unicode[STIX]{x1D707}$
and maps
![]() $i_{0}$
and
$i_{0}$
and
![]() $i_{1}$
induced by the substitution
$i_{1}$
induced by the substitution
![]() $\unicode[STIX]{x1D712}\mapsto 0$
and
$\unicode[STIX]{x1D712}\mapsto 0$
and
![]() $\unicode[STIX]{x1D712}\mapsto 1$
, respectively.
$\unicode[STIX]{x1D712}\mapsto 1$
, respectively.
We now apply the constructions above to the sites introduced in the previous sections. We recall that we consider adic spaces defined over a perfectoid field
![]() $K$
.
$K$
.
Corollary 3.6. The following pairs of model categories are Quillen equivalent.
–
 $\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\operatorname{RigSm})$
and
$\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\operatorname{RigSm})$
and
 $\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
.
$\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
.–
 $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm})$
and
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm})$
and
 $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
.
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
.–
 $\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
$\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
 $\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
$\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.–
 $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
 $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
Proof. It suffices to apply Proposition 3.3 to the sites with interval
![]() $(\operatorname{RigSm},\acute{\text{e}}\text{t},\mathbb{B}^{1})$
and
$(\operatorname{RigSm},\acute{\text{e}}\text{t},\mathbb{B}^{1})$
and
![]() $(\widehat{\text{Rig}}\operatorname{Sm},\acute{\text{e}}\text{t},\mathbb{B}^{1})$
, where
$(\widehat{\text{Rig}}\operatorname{Sm},\acute{\text{e}}\text{t},\mathbb{B}^{1})$
, where
![]() $\mathbf{C}^{\prime }$
is in both cases the subcategory of varieties with good coordinates.◻
$\mathbf{C}^{\prime }$
is in both cases the subcategory of varieties with good coordinates.◻
Definition 3.7. For
![]() $\unicode[STIX]{x1D702}\in \{\acute{\text{e}}\text{t},\mathbb{B}^{1},(\acute{\text{e}}\text{t},\mathbb{B}^{1})\}$
we say that a map in
$\unicode[STIX]{x1D702}\in \{\acute{\text{e}}\text{t},\mathbb{B}^{1},(\acute{\text{e}}\text{t},\mathbb{B}^{1})\}$
we say that a map in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm})$
[respectively
$\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm})$
[respectively
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] is a
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] is a
![]() $\unicode[STIX]{x1D702}$
-weak equivalence if it is a weak equivalence in the model structure
$\unicode[STIX]{x1D702}$
-weak equivalence if it is a weak equivalence in the model structure
![]() $\mathbf{Ch}_{\unicode[STIX]{x1D702}}\mathbf{Psh}(\operatorname{RigSm})$
[respectively
$\mathbf{Ch}_{\unicode[STIX]{x1D702}}\mathbf{Psh}(\operatorname{RigSm})$
[respectively
![]() $\mathbf{Ch}_{\unicode[STIX]{x1D702}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
]. The triangulated homotopy category associated to the localization
$\mathbf{Ch}_{\unicode[STIX]{x1D702}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
]. The triangulated homotopy category associated to the localization
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm})$
[respectively to the localization
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm})$
[respectively to the localization
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] is denoted by
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] is denoted by
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
[respectively
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
[respectively
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
]. We omit
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
]. We omit
![]() $\unicode[STIX]{x1D6EC}$
from the notation whenever the context allows it. The image of a variety
$\unicode[STIX]{x1D6EC}$
from the notation whenever the context allows it. The image of a variety
![]() $X$
in one of these categories is denoted by
$X$
in one of these categories is denoted by
![]() $\unicode[STIX]{x1D6EC}(X)$
. We say that an object
$\unicode[STIX]{x1D6EC}(X)$
. We say that an object
![]() ${\mathcal{F}}$
of the derived category
${\mathcal{F}}$
of the derived category
![]() $\mathbf{D}=\mathbf{D}(\mathbf{Psh}(\operatorname{RigSm}))$
[respectively
$\mathbf{D}=\mathbf{D}(\mathbf{Psh}(\operatorname{RigSm}))$
[respectively
![]() $\mathbf{D}=\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}))$
] is
$\mathbf{D}=\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}))$
] is
![]() $\unicode[STIX]{x1D702}$
-local if the functor
$\unicode[STIX]{x1D702}$
-local if the functor
![]() $\operatorname{Hom}_{\mathbf{D}}(\cdot ,{\mathcal{F}})$
sends maps in
$\operatorname{Hom}_{\mathbf{D}}(\cdot ,{\mathcal{F}})$
sends maps in
![]() $S_{\unicode[STIX]{x1D702}}$
(see Proposition 3.3) to isomorphisms. This amounts to saying that
$S_{\unicode[STIX]{x1D702}}$
(see Proposition 3.3) to isomorphisms. This amounts to saying that
![]() ${\mathcal{F}}$
is quasi-isomorphic to a
${\mathcal{F}}$
is quasi-isomorphic to a
![]() $\unicode[STIX]{x1D702}$
-fibrant object.
$\unicode[STIX]{x1D702}$
-fibrant object.
We need to keep track of
![]() $\mathbb{B}^{1}$
in the notation of
$\mathbb{B}^{1}$
in the notation of
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
since later we will perform a localization on
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
since later we will perform a localization on
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
with respect to a different interval object.
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
with respect to a different interval object.
Remark 3.8. Using the language of [Reference Beilinson and VologodskyBV08], the localizations defined above induce endofunctors
![]() $C^{\unicode[STIX]{x1D702}}$
of the derived categories
$C^{\unicode[STIX]{x1D702}}$
of the derived categories
![]() $\mathbf{D}(\mathbf{Psh}(\operatorname{RigSm}))$
,
$\mathbf{D}(\mathbf{Psh}(\operatorname{RigSm}))$
,
![]() $\mathbf{D}(\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}}))$
,
$\mathbf{D}(\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}}))$
,
![]() $\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}))$
and
$\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}))$
and
![]() $\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
such that
$\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
such that
![]() $C^{\unicode[STIX]{x1D702}}{\mathcal{F}}$
is
$C^{\unicode[STIX]{x1D702}}{\mathcal{F}}$
is
![]() $\unicode[STIX]{x1D702}$
-local for all
$\unicode[STIX]{x1D702}$
-local for all
![]() ${\mathcal{F}}$
and there is a natural transformation
${\mathcal{F}}$
and there is a natural transformation
![]() $C^{\unicode[STIX]{x1D702}}\rightarrow \operatorname{id}$
, which is a pointwise
$C^{\unicode[STIX]{x1D702}}\rightarrow \operatorname{id}$
, which is a pointwise
![]() $\unicode[STIX]{x1D702}$
-weak equivalence. The functor
$\unicode[STIX]{x1D702}$
-weak equivalence. The functor
![]() $C^{\unicode[STIX]{x1D702}}$
restricts to a triangulated equivalence on the objects
$C^{\unicode[STIX]{x1D702}}$
restricts to a triangulated equivalence on the objects
![]() ${\mathcal{F}}$
that are
${\mathcal{F}}$
that are
![]() $\unicode[STIX]{x1D702}$
-local and one can compute the Hom set
$\unicode[STIX]{x1D702}$
-local and one can compute the Hom set
![]() $\operatorname{Hom}({\mathcal{F}},{\mathcal{F}}^{\prime })$
in the homotopy category of the
$\operatorname{Hom}({\mathcal{F}},{\mathcal{F}}^{\prime })$
in the homotopy category of the
![]() $\unicode[STIX]{x1D702}$
-localization as
$\unicode[STIX]{x1D702}$
-localization as
![]() $\mathbf{D}({\mathcal{F}},C^{\unicode[STIX]{x1D702}}{\mathcal{F}}^{\prime })$
.
$\mathbf{D}({\mathcal{F}},C^{\unicode[STIX]{x1D702}}{\mathcal{F}}^{\prime })$
.
Remark 3.9. According to Proposition 3.3, for any
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
and any integer
$\widehat{\text{Rig}}\operatorname{Sm}$
and any integer
![]() $i$
, one has
$i$
, one has
![]() $\operatorname{Hom}_{\mathbf{D}}(\unicode[STIX]{x1D6EC}(X)[-i],C^{\acute{\text{e}}\text{t}}{\mathcal{F}})\cong \operatorname{Hom}_{\mathbf{D}(\mathbf{Sh}_{\acute{\text{e}}\text{t}}(\widehat{\text{Rig}}\operatorname{Sm}))}(\unicode[STIX]{x1D6EC}(X)[-i],{\mathcal{F}})$
. The latter group is the étale hypercohomology group
$\operatorname{Hom}_{\mathbf{D}}(\unicode[STIX]{x1D6EC}(X)[-i],C^{\acute{\text{e}}\text{t}}{\mathcal{F}})\cong \operatorname{Hom}_{\mathbf{D}(\mathbf{Sh}_{\acute{\text{e}}\text{t}}(\widehat{\text{Rig}}\operatorname{Sm}))}(\unicode[STIX]{x1D6EC}(X)[-i],{\mathcal{F}})$
. The latter group is the étale hypercohomology group
![]() $\mathbb{H}_{\acute{\text{e}}\text{t}}^{i}(X,{\mathcal{F}})$
, which can be computed with respect to the small étale site over
$\mathbb{H}_{\acute{\text{e}}\text{t}}^{i}(X,{\mathcal{F}})$
, which can be computed with respect to the small étale site over
![]() $X$
. The property
$X$
. The property
![]() $\operatorname{Hom}_{\mathbf{D}}(\unicode[STIX]{x1D6EC}(X)[-i],C^{\acute{\text{e}}\text{t}}{\mathcal{F}})\cong \mathbb{H}^{i}(X_{\acute{\text{e}}\text{t}},{\mathcal{F}})$
characterizes
$\operatorname{Hom}_{\mathbf{D}}(\unicode[STIX]{x1D6EC}(X)[-i],C^{\acute{\text{e}}\text{t}}{\mathcal{F}})\cong \mathbb{H}^{i}(X_{\acute{\text{e}}\text{t}},{\mathcal{F}})$
characterizes
![]() $C^{\acute{\text{e}}\text{t}}{\mathcal{F}}$
up to quasi-isomorphisms (and holds true for more general topologies, see [Reference AyoubAyo07, Proposition 4.4.58]).
$C^{\acute{\text{e}}\text{t}}{\mathcal{F}}$
up to quasi-isomorphisms (and holds true for more general topologies, see [Reference AyoubAyo07, Proposition 4.4.58]).
We now show that the étale localization can alternatively be described in terms of étale hypercoverings
![]() ${\mathcal{U}}_{\bullet }\rightarrow X$
(see for example [Reference Dugger, Hollander and IsaksenDHI04]). Any such datum defines a simplicial presheaf
${\mathcal{U}}_{\bullet }\rightarrow X$
(see for example [Reference Dugger, Hollander and IsaksenDHI04]). Any such datum defines a simplicial presheaf
![]() $n\mapsto \bigoplus _{i}\unicode[STIX]{x1D6EC}(U_{ni})$
whenever
$n\mapsto \bigoplus _{i}\unicode[STIX]{x1D6EC}(U_{ni})$
whenever
![]() ${\mathcal{U}}_{n}=\bigsqcup _{i}h_{U_{ni}}$
is the sum of the presheaves of sets
${\mathcal{U}}_{n}=\bigsqcup _{i}h_{U_{ni}}$
is the sum of the presheaves of sets
![]() $h_{U_{ni}}$
represented by
$h_{U_{ni}}$
represented by
![]() $U_{ni}$
. This simplicial presheaf can be associated to a normalized chain complex that we denote by
$U_{ni}$
. This simplicial presheaf can be associated to a normalized chain complex that we denote by
![]() $\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })$
. It is endowed with a map to
$\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })$
. It is endowed with a map to
![]() $\unicode[STIX]{x1D6EC}(X)$
.
$\unicode[STIX]{x1D6EC}(X)$
.
Proposition 3.10. The localization over
![]() $S_{\acute{\text{e}}\text{t}}$
on
$S_{\acute{\text{e}}\text{t}}$
on
![]() $\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
[respectively
$\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
[respectively
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
] coincides with the localization over the set
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
] coincides with the localization over the set
![]() $\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })[i]\rightarrow \unicode[STIX]{x1D6EC}(X)[i]$
as
$\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })[i]\rightarrow \unicode[STIX]{x1D6EC}(X)[i]$
as
![]() ${\mathcal{U}}_{\bullet }\rightarrow X$
varies among bounded étale hypercoverings of the objects
${\mathcal{U}}_{\bullet }\rightarrow X$
varies among bounded étale hypercoverings of the objects
![]() $X$
of
$X$
of
![]() $\operatorname{RigSm}^{\operatorname{gc}}$
[respectively
$\operatorname{RigSm}^{\operatorname{gc}}$
[respectively
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
] and
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
] and
![]() $i$
varies in
$i$
varies in
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Proof. Any
![]() $\acute{\text{e}}\text{t}$
-local object
$\acute{\text{e}}\text{t}$
-local object
![]() ${\mathcal{F}}$
is also local with respect to the maps of the statement. We are left to prove that a complex
${\mathcal{F}}$
is also local with respect to the maps of the statement. We are left to prove that a complex
![]() ${\mathcal{F}}$
, which is local with respect to the maps of the statement, is also
${\mathcal{F}}$
, which is local with respect to the maps of the statement, is also
![]() $\acute{\text{e}}\text{t}$
-local.
$\acute{\text{e}}\text{t}$
-local.
Since
![]() $\unicode[STIX]{x1D6EC}$
contains
$\unicode[STIX]{x1D6EC}$
contains
![]() $\mathbb{Q}$
the étale cohomology of an étale sheaf
$\mathbb{Q}$
the étale cohomology of an étale sheaf
![]() ${\mathcal{F}}$
coincides with the Nisnevich cohomology (the same proof of [Reference Mazza, Voevodsky and WeibelMVW06, Proposition 14.23] holds also here). By means of [Reference AyoubAyo15, Corollary 1.2.21] we conclude that any rigid variety
${\mathcal{F}}$
coincides with the Nisnevich cohomology (the same proof of [Reference Mazza, Voevodsky and WeibelMVW06, Proposition 14.23] holds also here). By means of [Reference AyoubAyo15, Corollary 1.2.21] we conclude that any rigid variety
![]() $X$
has a finite cohomological dimension. By [Reference Artin, Grothendieck and VerdierSGA4, Theorem V.7.4.1] and [Reference Suslin and VoevodskySV00, Theorem 0.3], we obtain for any rigid variety
$X$
has a finite cohomological dimension. By [Reference Artin, Grothendieck and VerdierSGA4, Theorem V.7.4.1] and [Reference Suslin and VoevodskySV00, Theorem 0.3], we obtain for any rigid variety
![]() $X$
and any complex of presheaves
$X$
and any complex of presheaves
![]() ${\mathcal{F}}$
an isomorphism
${\mathcal{F}}$
an isomorphism
where
![]() $\mathit{HR}_{\infty }(X)$
is the category of bounded étale hypercoverings of
$\mathit{HR}_{\infty }(X)$
is the category of bounded étale hypercoverings of
![]() $X$
(see [Reference Artin, Grothendieck and VerdierSGA4, V.7.3]) and
$X$
(see [Reference Artin, Grothendieck and VerdierSGA4, V.7.3]) and
![]() $\text{Hom}_{\bullet }$
is the
$\text{Hom}_{\bullet }$
is the
![]() $\operatorname{Hom}$
-complex computed in the unbounded derived category of presheaves. Suppose now
$\operatorname{Hom}$
-complex computed in the unbounded derived category of presheaves. Suppose now
![]() ${\mathcal{F}}$
is local with respect to the maps of the statement. Then
${\mathcal{F}}$
is local with respect to the maps of the statement. Then
![]() $\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet }),{\mathcal{F}})$
is quasi-isomorphic to
$\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet }),{\mathcal{F}})$
is quasi-isomorphic to
![]() $\text{Hom}_{\bullet }(X,{\mathcal{F}})$
for every bounded hypercovering
$\text{Hom}_{\bullet }(X,{\mathcal{F}})$
for every bounded hypercovering
![]() ${\mathcal{U}}_{\bullet }$
, and hence
${\mathcal{U}}_{\bullet }$
, and hence
![]() $H_{-n}{\mathcal{F}}(X)\cong \mathbb{H}_{\acute{\text{e}}\text{t}}^{n}(X,{\mathcal{F}})$
by the formula above. We then conclude that the map
$H_{-n}{\mathcal{F}}(X)\cong \mathbb{H}_{\acute{\text{e}}\text{t}}^{n}(X,{\mathcal{F}})$
by the formula above. We then conclude that the map
![]() ${\mathcal{F}}\rightarrow C^{\acute{\text{e}}\text{t}}{\mathcal{F}}$
is a quasi-isomorphism, proving the proposition.◻
${\mathcal{F}}\rightarrow C^{\acute{\text{e}}\text{t}}{\mathcal{F}}$
is a quasi-isomorphism, proving the proposition.◻
As the following proposition shows, there are also alternative presentations of the homotopy categories introduced so far, which we will later use.
Proposition 3.11. Let
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $\mathbb{Q}$
-algebra. The natural inclusion induces a Quillen equivalence
$\mathbb{Q}$
-algebra. The natural inclusion induces a Quillen equivalence
where
![]() $L_{S}$
denotes the Bousfield localization with respect to the set
$L_{S}$
denotes the Bousfield localization with respect to the set
![]() $S$
of shifts of the maps of complexes induced by étale Cech hypercoverings
$S$
of shifts of the maps of complexes induced by étale Cech hypercoverings
![]() ${\mathcal{U}}_{\bullet }\rightarrow X$
of objects
${\mathcal{U}}_{\bullet }\rightarrow X$
of objects
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
such that for some presentation
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
such that for some presentation
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
the covering
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
the covering
![]() ${\mathcal{U}}_{0}\rightarrow X$
descends to a covering of
${\mathcal{U}}_{0}\rightarrow X$
descends to a covering of
![]() $X_{0}$
.
$X_{0}$
.
Proof. Using Proposition 3.10, it suffices to prove that the map
![]() $\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })\rightarrow \unicode[STIX]{x1D6EC}(X)$
is an isomorphism in the homotopy category
$\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })\rightarrow \unicode[STIX]{x1D6EC}(X)$
is an isomorphism in the homotopy category
![]() $L_{S}\mathbf{Ch}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
for a fixed bounded étale hypercovering
$L_{S}\mathbf{Ch}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
for a fixed bounded étale hypercovering
![]() ${\mathcal{U}}_{\bullet }$
of an object
${\mathcal{U}}_{\bullet }$
of an object
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
.
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
.
Since the inclusion functor
![]() $\mathbf{Ch}_{{\geqslant}0}\rightarrow \mathbf{Ch}$
is a Quillen functor, it suffices to prove that
$\mathbf{Ch}_{{\geqslant}0}\rightarrow \mathbf{Ch}$
is a Quillen functor, it suffices to prove that
![]() $\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })\rightarrow \unicode[STIX]{x1D6EC}(X)$
is a weak equivalence in
$\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })\rightarrow \unicode[STIX]{x1D6EC}(X)$
is a weak equivalence in
![]() $L_{T}\mathbf{Ch}_{{\geqslant}0}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
, where
$L_{T}\mathbf{Ch}_{{\geqslant}0}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
, where
![]() $T$
is the set of shifts of the maps of complexes induced by étale Cech hypercoverings descending at finite level. Let
$T$
is the set of shifts of the maps of complexes induced by étale Cech hypercoverings descending at finite level. Let
![]() $L_{\tilde{T}}\mathbf{sPsh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
be the Bousfield localization of the projective model structure on simplicial presheaves of sets with respect to the set
$L_{\tilde{T}}\mathbf{sPsh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
be the Bousfield localization of the projective model structure on simplicial presheaves of sets with respect to the set
![]() $\tilde{T}$
formed by maps induced by étale Cech hypercoverings
$\tilde{T}$
formed by maps induced by étale Cech hypercoverings
![]() ${\mathcal{U}}_{\bullet }\rightarrow X$
descending at finite level. We remark that the Dold–Kan correspondence (see [Reference Schwede and ShipleySS03, § 4.1]) and the
${\mathcal{U}}_{\bullet }\rightarrow X$
descending at finite level. We remark that the Dold–Kan correspondence (see [Reference Schwede and ShipleySS03, § 4.1]) and the
![]() $\unicode[STIX]{x1D6EC}$
-enrichment also define a left Quillen functor from
$\unicode[STIX]{x1D6EC}$
-enrichment also define a left Quillen functor from
![]() $L_{\tilde{T}}\mathbf{sPsh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
to the category
$L_{\tilde{T}}\mathbf{sPsh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
to the category
![]() $L_{T}\mathbf{Ch}_{{\geqslant}0}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
. It, therefore, suffices to prove that
$L_{T}\mathbf{Ch}_{{\geqslant}0}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
. It, therefore, suffices to prove that
![]() ${\mathcal{U}}_{\bullet }\rightarrow X$
is a weak equivalence in
${\mathcal{U}}_{\bullet }\rightarrow X$
is a weak equivalence in
![]() $L_{\tilde{T}}\mathbf{sPsh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
and this follows from the fact that bounded hypercoverings define the same localization as Cech hypercoverings (see [Reference Dugger, Hollander and IsaksenDHI04, Theorem A.6]) together with the fact that coverings descending to finite level define the same topology (Corollary 2.10), and hence the same localization [Reference Dugger, Hollander and IsaksenDHI04, Corollary A.8]. We remark that [Reference Dugger, Hollander and IsaksenDHI04, Corollary A.8] applies in our case even if the coverings
$L_{\tilde{T}}\mathbf{sPsh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
and this follows from the fact that bounded hypercoverings define the same localization as Cech hypercoverings (see [Reference Dugger, Hollander and IsaksenDHI04, Theorem A.6]) together with the fact that coverings descending to finite level define the same topology (Corollary 2.10), and hence the same localization [Reference Dugger, Hollander and IsaksenDHI04, Corollary A.8]. We remark that [Reference Dugger, Hollander and IsaksenDHI04, Corollary A.8] applies in our case even if the coverings
![]() ${\mathcal{U}}\rightarrow X$
descending to the finite level do not form a basis of the topology, as their pullback via an arbitrary map
${\mathcal{U}}\rightarrow X$
descending to the finite level do not form a basis of the topology, as their pullback via an arbitrary map
![]() $Y\rightarrow X$
may not have the same property. However, the proof of the statement relies on [Reference Dugger, Hollander and IsaksenDHI04, Proposition A.2], where it is only used that the chosen family of coverings
$Y\rightarrow X$
may not have the same property. However, the proof of the statement relies on [Reference Dugger, Hollander and IsaksenDHI04, Proposition A.2], where it is only used that the chosen family of coverings
![]() ${\mathcal{U}}\rightarrow X$
generates the topology and that the fiber product
${\mathcal{U}}\rightarrow X$
generates the topology and that the fiber product
![]() ${\mathcal{U}}\,\times _{X}\,{\mathcal{U}}$
is defined.◻
${\mathcal{U}}\,\times _{X}\,{\mathcal{U}}$
is defined.◻
Remark 3.12. It is shown in the proof that the statements of Propositions 3.10 and 3.11 hold true without any assumptions on
![]() $\unicode[STIX]{x1D6EC}$
under the condition that all varieties
$\unicode[STIX]{x1D6EC}$
under the condition that all varieties
![]() $X$
have finite cohomological dimension with respect to the étale topology.
$X$
have finite cohomological dimension with respect to the étale topology.
As we pointed out in Remark 3.9, there is a characterization of
![]() $C^{\acute{\text{e}}\text{t}}{\mathcal{F}}$
for any complex
$C^{\acute{\text{e}}\text{t}}{\mathcal{F}}$
for any complex
![]() ${\mathcal{F}}$
. This is also true for the
${\mathcal{F}}$
. This is also true for the
![]() $\mathbb{B}^{1}$
-localization, described in the following part.
$\mathbb{B}^{1}$
-localization, described in the following part.
Definition 3.13. We denote by
![]() $\Box$
the
$\Box$
the
![]() $\unicode[STIX]{x1D6F4}$
-enriched cocubical object (see [Reference AyoubAyo14b, Appendix A]) defined by putting
$\unicode[STIX]{x1D6F4}$
-enriched cocubical object (see [Reference AyoubAyo14b, Appendix A]) defined by putting
![]() $\Box ^{n}=\mathbb{B}^{n}=\operatorname{Spa}K\langle \unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{n}\rangle$
and considering the morphisms
$\Box ^{n}=\mathbb{B}^{n}=\operatorname{Spa}K\langle \unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{n}\rangle$
and considering the morphisms
![]() $d_{r,\unicode[STIX]{x1D716}}$
induced by the maps
$d_{r,\unicode[STIX]{x1D716}}$
induced by the maps
![]() $\mathbb{B}^{n}\rightarrow \mathbb{B}^{n+1}$
corresponding to the substitution
$\mathbb{B}^{n}\rightarrow \mathbb{B}^{n+1}$
corresponding to the substitution
![]() $\unicode[STIX]{x1D70F}_{r}=\unicode[STIX]{x1D716}$
for
$\unicode[STIX]{x1D70F}_{r}=\unicode[STIX]{x1D716}$
for
![]() $\unicode[STIX]{x1D716}\in \{0,1\}$
and the morphisms
$\unicode[STIX]{x1D716}\in \{0,1\}$
and the morphisms
![]() $p_{r}$
induced by the projections
$p_{r}$
induced by the projections
![]() $\mathbb{B}^{n}\rightarrow \mathbb{B}^{n-1}$
. For any variety
$\mathbb{B}^{n}\rightarrow \mathbb{B}^{n-1}$
. For any variety
![]() $X$
and any presheaf
$X$
and any presheaf
![]() ${\mathcal{F}}$
with values in an abelian category, we can therefore consider the
${\mathcal{F}}$
with values in an abelian category, we can therefore consider the
![]() $\unicode[STIX]{x1D6F4}$
-enriched cubical object
$\unicode[STIX]{x1D6F4}$
-enriched cubical object
![]() ${\mathcal{F}}(X\,\times \,\Box )$
(see [Reference AyoubAyo14b, Appendix A]). Associated to any
${\mathcal{F}}(X\,\times \,\Box )$
(see [Reference AyoubAyo14b, Appendix A]). Associated to any
![]() $\unicode[STIX]{x1D6F4}$
-enriched cubical object
$\unicode[STIX]{x1D6F4}$
-enriched cubical object
![]() ${\mathcal{F}}$
there are the following complexes: the complex
${\mathcal{F}}$
there are the following complexes: the complex
![]() $C_{\bullet }^{\sharp }{\mathcal{F}}$
defined as
$C_{\bullet }^{\sharp }{\mathcal{F}}$
defined as
![]() $C_{n}^{\sharp }{\mathcal{F}}={\mathcal{F}}_{n}$
and with differential
$C_{n}^{\sharp }{\mathcal{F}}={\mathcal{F}}_{n}$
and with differential
![]() $\sum (-1)^{r}(d_{r,1}^{\ast }-d_{r,0}^{\ast })$
; the simple complex
$\sum (-1)^{r}(d_{r,1}^{\ast }-d_{r,0}^{\ast })$
; the simple complex
![]() $C_{\bullet }{\mathcal{F}}$
defined as
$C_{\bullet }{\mathcal{F}}$
defined as
![]() $C_{n}{\mathcal{F}}=\bigcap _{r=1}^{n}\ker d_{r,0}^{\ast }$
and with differential
$C_{n}{\mathcal{F}}=\bigcap _{r=1}^{n}\ker d_{r,0}^{\ast }$
and with differential
![]() $\sum (-1)^{r}d_{r,1}^{\ast }$
; the normalized complex
$\sum (-1)^{r}d_{r,1}^{\ast }$
; the normalized complex
![]() $N_{\bullet }{\mathcal{F}}$
defined as
$N_{\bullet }{\mathcal{F}}$
defined as
![]() $N_{n}{\mathcal{F}}=C_{n}\cap {\mathcal{F}}\bigcap _{r=2}^{n}\ker d_{r,1}^{\ast }$
and with differential
$N_{n}{\mathcal{F}}=C_{n}\cap {\mathcal{F}}\bigcap _{r=2}^{n}\ker d_{r,1}^{\ast }$
and with differential
![]() $-d_{1,1}^{\ast }$
. By [Reference AyoubAyo14c, Lemma A.3, Propositions A.8, A.11], the inclusion
$-d_{1,1}^{\ast }$
. By [Reference AyoubAyo14c, Lemma A.3, Propositions A.8, A.11], the inclusion
![]() $N_{\bullet }{\mathcal{F}}{\hookrightarrow}C_{\bullet }{\mathcal{F}}$
is a quasi-isomorphism and both inclusions
$N_{\bullet }{\mathcal{F}}{\hookrightarrow}C_{\bullet }{\mathcal{F}}$
is a quasi-isomorphism and both inclusions
![]() $C_{\bullet }{\mathcal{F}}{\hookrightarrow}C_{\bullet }^{\sharp }{\mathcal{F}}$
and
$C_{\bullet }{\mathcal{F}}{\hookrightarrow}C_{\bullet }^{\sharp }{\mathcal{F}}$
and
![]() $N_{\bullet }{\mathcal{F}}{\hookrightarrow}C_{\bullet }{\mathcal{F}}$
split.
$N_{\bullet }{\mathcal{F}}{\hookrightarrow}C_{\bullet }{\mathcal{F}}$
split.
For any complex of presheaves
![]() ${\mathcal{F}}$
we define the singular complex of
${\mathcal{F}}$
we define the singular complex of
![]() ${\mathcal{F}}$
, denoted by
${\mathcal{F}}$
, denoted by
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
, to be the total complex of the simple complex associated to the
$\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
, to be the total complex of the simple complex associated to the
![]() $\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\Box ),{\mathcal{F}})$
. It sends the object
$\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\Box ),{\mathcal{F}})$
. It sends the object
![]() $X$
to the total complex of the simple complex associated to
$X$
to the total complex of the simple complex associated to
![]() ${\mathcal{F}}(X\,\times \,\Box )$
.
${\mathcal{F}}(X\,\times \,\Box )$
.
The following lemma is the cocubical version of [Reference Mazza, Voevodsky and WeibelMVW06, Lemma 2.18].
Lemma 3.14. For any presheaf
![]() ${\mathcal{F}}$
the two maps of cubical sets
${\mathcal{F}}$
the two maps of cubical sets
![]() $i_{0}^{\ast },i_{1}^{\ast }:{\mathcal{F}}(\Box \,\times \,\mathbb{B}^{1})\rightarrow {\mathcal{F}}(\Box )$
induce chain homotopic maps on the associated simple and normalized complexes.
$i_{0}^{\ast },i_{1}^{\ast }:{\mathcal{F}}(\Box \,\times \,\mathbb{B}^{1})\rightarrow {\mathcal{F}}(\Box )$
induce chain homotopic maps on the associated simple and normalized complexes.
Proof. Consider the isomorphism
![]() $s_{n}:\mathbb{B}^{n+1}\rightarrow \mathbb{B}^{n}\,\times \,\mathbb{B}^{1}$
defined on points by separating the last coordinate and let
$s_{n}:\mathbb{B}^{n+1}\rightarrow \mathbb{B}^{n}\,\times \,\mathbb{B}^{1}$
defined on points by separating the last coordinate and let
![]() $s_{n}^{\ast }$
be the induced map
$s_{n}^{\ast }$
be the induced map
![]() ${\mathcal{F}}(\Box ^{n}\,\times \,\mathbb{B}^{1})\rightarrow {\mathcal{F}}(\Box ^{n+1})$
. We have
${\mathcal{F}}(\Box ^{n}\,\times \,\mathbb{B}^{1})\rightarrow {\mathcal{F}}(\Box ^{n+1})$
. We have
![]() $s_{n-1}^{\ast }\,\circ \,d_{r,\unicode[STIX]{x1D716}}^{\ast }=d_{r,\unicode[STIX]{x1D716}}^{\ast }\,\circ \,s_{n}^{\ast }$
for all
$s_{n-1}^{\ast }\,\circ \,d_{r,\unicode[STIX]{x1D716}}^{\ast }=d_{r,\unicode[STIX]{x1D716}}^{\ast }\,\circ \,s_{n}^{\ast }$
for all
![]() $1\leqslant r\leqslant n$
and
$1\leqslant r\leqslant n$
and
![]() $\unicode[STIX]{x1D716}\in \{0,1\}$
. We conclude that
$\unicode[STIX]{x1D716}\in \{0,1\}$
. We conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle s_{n-1}^{\ast }\,\circ \,\mathop{\sum }_{r=1}^{n}(-1)^{r}(d_{r,1}^{\ast }-d_{r,0}^{\ast })+\mathop{\sum }_{r=1}^{n+1}(-1)^{r}(d_{r,1}^{\ast }-d_{r,0}^{\ast })\,\circ \,(-s_{n}^{\ast })\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{n}(d_{n+1,1}^{\ast }\,\circ \,s_{n}^{\ast }-d_{n+1,0}^{\ast }\,\circ \,s_{n}^{\ast })=(-1)^{n}(i_{1}^{\ast }-i_{0}^{\ast }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle s_{n-1}^{\ast }\,\circ \,\mathop{\sum }_{r=1}^{n}(-1)^{r}(d_{r,1}^{\ast }-d_{r,0}^{\ast })+\mathop{\sum }_{r=1}^{n+1}(-1)^{r}(d_{r,1}^{\ast }-d_{r,0}^{\ast })\,\circ \,(-s_{n}^{\ast })\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{n}(d_{n+1,1}^{\ast }\,\circ \,s_{n}^{\ast }-d_{n+1,0}^{\ast }\,\circ \,s_{n}^{\ast })=(-1)^{n}(i_{1}^{\ast }-i_{0}^{\ast }).\nonumber\end{eqnarray}$$
Therefore, the maps
![]() $\{(-1)^{n}s_{n}^{\ast }\}$
define a chain homotopy from
$\{(-1)^{n}s_{n}^{\ast }\}$
define a chain homotopy from
![]() $i_{0}^{\ast }$
to
$i_{0}^{\ast }$
to
![]() $i_{1}^{\ast }$
as maps of complexes
$i_{1}^{\ast }$
as maps of complexes
![]() $C_{\bullet }^{\sharp }{\mathcal{F}}(\Box \,\times \,\mathbb{B}^{1})\rightarrow C_{\bullet }^{\sharp }{\mathcal{F}}(\Box )$
.
$C_{\bullet }^{\sharp }{\mathcal{F}}(\Box \,\times \,\mathbb{B}^{1})\rightarrow C_{\bullet }^{\sharp }{\mathcal{F}}(\Box )$
.
We automatically deduce that if an inclusion
![]() $C_{\bullet }^{\prime }{\mathcal{F}}\rightarrow C_{\bullet }^{\sharp }{\mathcal{F}}$
has a functorial retraction, then the maps
$C_{\bullet }^{\prime }{\mathcal{F}}\rightarrow C_{\bullet }^{\sharp }{\mathcal{F}}$
has a functorial retraction, then the maps
![]() $i_{0}^{\ast },i_{1}^{\ast }:C_{\bullet }^{\prime }{\mathcal{F}}(\Box \,\times \,\mathbb{B}^{1})\rightarrow C_{\bullet }^{\prime }{\mathcal{F}}(\Box )$
are also chain homotopic.◻
$i_{0}^{\ast },i_{1}^{\ast }:C_{\bullet }^{\prime }{\mathcal{F}}(\Box \,\times \,\mathbb{B}^{1})\rightarrow C_{\bullet }^{\prime }{\mathcal{F}}(\Box )$
are also chain homotopic.◻
The following proposition is the rigid analytic analog of [Reference AyoubAyo14b, Theorem 2.23], or the cocubical analog of [Reference AyoubAyo15, Lemma 2.5.31].
Proposition 3.15. Let
![]() ${\mathcal{F}}$
be a complex in
${\mathcal{F}}$
be a complex in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
. Then
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
. Then
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is
$\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is
![]() $\mathbb{B}^{1}$
-local and
$\mathbb{B}^{1}$
-local and
![]() $\mathbb{B}^{1}$
-weak equivalent to
$\mathbb{B}^{1}$
-weak equivalent to
![]() ${\mathcal{F}}$
in
${\mathcal{F}}$
in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
.
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
.
Proof. In order to prove that
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is
$\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is
![]() $\mathbb{B}^{1}$
-local in
$\mathbb{B}^{1}$
-local in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
we need to check that each homology presheaf
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
we need to check that each homology presheaf
![]() $H_{n}(\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}})$
is homotopy-invariant. By means of [Reference AyoubAyo15, Proposition 2.2.46] it suffices to show that the maps
$H_{n}(\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}})$
is homotopy-invariant. By means of [Reference AyoubAyo15, Proposition 2.2.46] it suffices to show that the maps
![]() $i_{0}^{\ast },i_{1}^{\ast }:N_{\bullet }{\mathcal{F}}(\Box \,\times \,\mathbb{B}^{1})\rightarrow N_{\bullet }{\mathcal{F}}(\Box )$
are chain homotopic, and this follows from Lemma 3.14.
$i_{0}^{\ast },i_{1}^{\ast }:N_{\bullet }{\mathcal{F}}(\Box \,\times \,\mathbb{B}^{1})\rightarrow N_{\bullet }{\mathcal{F}}(\Box )$
are chain homotopic, and this follows from Lemma 3.14.
We now prove that
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is
$\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is
![]() $\mathbb{B}^{1}$
-weak equivalent to
$\mathbb{B}^{1}$
-weak equivalent to
![]() ${\mathcal{F}}$
. We first prove that the canonical map
${\mathcal{F}}$
. We first prove that the canonical map
![]() $a:{\mathcal{F}}\rightarrow \text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\Box ^{n}),{\mathcal{F}})$
has an inverse up to homotopy for a fixed
$a:{\mathcal{F}}\rightarrow \text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\Box ^{n}),{\mathcal{F}})$
has an inverse up to homotopy for a fixed
![]() $n$
. Consider the map
$n$
. Consider the map
![]() $b:\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\Box ^{n}),{\mathcal{F}})\rightarrow {\mathcal{F}}$
induced by the zero section of
$b:\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\Box ^{n}),{\mathcal{F}})\rightarrow {\mathcal{F}}$
induced by the zero section of
![]() $\Box ^{n}$
. It holds that
$\Box ^{n}$
. It holds that
![]() $b\,\circ \,a=\operatorname{id}$
and
$b\,\circ \,a=\operatorname{id}$
and
![]() $a\,\circ \,b$
is homotopic to
$a\,\circ \,b$
is homotopic to
![]() $\operatorname{id}$
via the map
$\operatorname{id}$
via the map
which is deduced from the adjunction
![]() $(\unicode[STIX]{x1D6EC}(\mathbb{B}^{1})\,\otimes \,\cdot ,\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\mathbb{B}^{1}),\cdot ))$
and the map
$(\unicode[STIX]{x1D6EC}(\mathbb{B}^{1})\,\otimes \,\cdot ,\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\mathbb{B}^{1}),\cdot ))$
and the map
defined via the homothety of
![]() $\mathbb{B}^{1}$
on
$\mathbb{B}^{1}$
on
![]() $\Box ^{n}$
. As
$\Box ^{n}$
. As
![]() $\mathbb{B}^{1}$
-weak equivalences are stable under filtered colimits and cones, we also conclude that the total complex associated to the simple complex of
$\mathbb{B}^{1}$
-weak equivalences are stable under filtered colimits and cones, we also conclude that the total complex associated to the simple complex of
![]() $\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\Box ),{\mathcal{F}})$
is
$\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6EC}(\Box ),{\mathcal{F}})$
is
![]() $\mathbb{B}^{1}$
-equivalent to the one associated to the constant cubical object
$\mathbb{B}^{1}$
-equivalent to the one associated to the constant cubical object
![]() ${\mathcal{F}}$
(see, for example, the argument of [Reference AyoubAyo15, Corollary 2.5.36]), which is in turn quasi-isomorphic to
${\mathcal{F}}$
(see, for example, the argument of [Reference AyoubAyo15, Corollary 2.5.36]), which is in turn quasi-isomorphic to
![]() ${\mathcal{F}}$
.◻
${\mathcal{F}}$
.◻
Corollary 3.16. Let
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $\mathbb{Q}$
-algebra. For any
$\mathbb{Q}$
-algebra. For any
![]() ${\mathcal{F}}$
in
${\mathcal{F}}$
in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
the localization
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
the localization
![]() $C^{\mathbb{B}^{1}}{\mathcal{F}}$
is quasi-isomorphic to
$C^{\mathbb{B}^{1}}{\mathcal{F}}$
is quasi-isomorphic to
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
and the localization
$\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
and the localization
![]() $C^{\acute{\text{e}}\text{t},\mathbb{B}^{1}}{\mathcal{F}}$
is quasi-isomorphic to
$C^{\acute{\text{e}}\text{t},\mathbb{B}^{1}}{\mathcal{F}}$
is quasi-isomorphic to
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}(C^{\acute{\text{e}}\text{t}}{\mathcal{F}}^{\bullet })$
.
$\operatorname{Sing}^{\mathbb{B}^{1}}(C^{\acute{\text{e}}\text{t}}{\mathcal{F}}^{\bullet })$
.
Proof. The first claim follows from Proposition 3.15. We are left to prove that the complex
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}(C^{\acute{\text{e}}\text{t}}{\mathcal{F}}^{\bullet })$
is
$\operatorname{Sing}^{\mathbb{B}^{1}}(C^{\acute{\text{e}}\text{t}}{\mathcal{F}}^{\bullet })$
is
![]() $\acute{\text{e}}\text{t}$
-local. To this aim, we use the description given in Proposition 3.10 and we show that
$\acute{\text{e}}\text{t}$
-local. To this aim, we use the description given in Proposition 3.10 and we show that
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}(C^{\acute{\text{e}}\text{t}}{\mathcal{F}}^{\bullet })$
is local with respect to shifts of maps
$\operatorname{Sing}^{\mathbb{B}^{1}}(C^{\acute{\text{e}}\text{t}}{\mathcal{F}}^{\bullet })$
is local with respect to shifts of maps
![]() $\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })\rightarrow \unicode[STIX]{x1D6EC}(X)$
induced by bounded hypercoverings
$\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet })\rightarrow \unicode[STIX]{x1D6EC}(X)$
induced by bounded hypercoverings
![]() ${\mathcal{U}}_{\bullet }\rightarrow X$
.
${\mathcal{U}}_{\bullet }\rightarrow X$
.
Fix such a hypercovering
![]() ${\mathcal{U}}_{\bullet }\rightarrow X$
. From the isomorphisms
${\mathcal{U}}_{\bullet }\rightarrow X$
. From the isomorphisms
valid for all
![]() $p,q$
and a spectral sequence argument (see [Reference Suslin and VoevodskySV00, Theorem 0.3]) we deduce that
$p,q$
and a spectral sequence argument (see [Reference Suslin and VoevodskySV00, Theorem 0.3]) we deduce that
for all
![]() $n$
as wanted.◻
$n$
as wanted.◻
We now investigate some of the natural Quillen functors that arise between the model categories introduced so far. We start by considering the natural inclusion of categories
![]() $\operatorname{RigSm}\rightarrow \widehat{\text{Rig}}\operatorname{Sm}$
$\operatorname{RigSm}\rightarrow \widehat{\text{Rig}}\operatorname{Sm}$
Proposition 3.17. The inclusion
![]() $\operatorname{RigSm}{\hookrightarrow}\widehat{\text{Rig}}\operatorname{Sm}$
induces a Quillen adjunction
$\operatorname{RigSm}{\hookrightarrow}\widehat{\text{Rig}}\operatorname{Sm}$
induces a Quillen adjunction
Moreover, the functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }:\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
is fully faithful.
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }:\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
is fully faithful.
Proof. The first claim is a special instance of [Reference AyoubAyo07, Proposition 4.4.45].
We prove the second claim by showing that
![]() $\mathbb{R}\unicode[STIX]{x1D704}_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
is isomorphic to the identity. Let
$\mathbb{R}\unicode[STIX]{x1D704}_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
is isomorphic to the identity. Let
![]() ${\mathcal{F}}$
be a cofibrant object in
${\mathcal{F}}$
be a cofibrant object in
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm})$
. We need to prove that the map
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm})$
. We need to prove that the map
![]() ${\mathcal{F}}\rightarrow \unicode[STIX]{x1D704}_{\ast }(\operatorname{Sing}^{\mathbb{B}^{1}}C^{\acute{\text{e}}\text{t}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}))$
is an
${\mathcal{F}}\rightarrow \unicode[STIX]{x1D704}_{\ast }(\operatorname{Sing}^{\mathbb{B}^{1}}C^{\acute{\text{e}}\text{t}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}))$
is an
![]() $(\acute{\text{e}}\text{t},\mathbb{B}^{1})$
-weak equivalence. Since
$(\acute{\text{e}}\text{t},\mathbb{B}^{1})$
-weak equivalence. Since
![]() $\unicode[STIX]{x1D704}_{\ast }$
commutes with
$\unicode[STIX]{x1D704}_{\ast }$
commutes with
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}$
we are left to prove that the map
$\operatorname{Sing}^{\mathbb{B}^{1}}$
we are left to prove that the map
![]() $\unicode[STIX]{x1D704}_{\ast }\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}={\mathcal{F}}\rightarrow \unicode[STIX]{x1D704}_{\ast }C^{\acute{\text{e}}\text{t}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is an
$\unicode[STIX]{x1D704}_{\ast }\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}={\mathcal{F}}\rightarrow \unicode[STIX]{x1D704}_{\ast }C^{\acute{\text{e}}\text{t}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is an
![]() $\acute{\text{e}}\text{t}$
-weak equivalence. This follows since
$\acute{\text{e}}\text{t}$
-weak equivalence. This follows since
![]() $\unicode[STIX]{x1D704}_{\ast }$
preserves
$\unicode[STIX]{x1D704}_{\ast }$
preserves
![]() $\acute{\text{e}}\text{t}$
-weak equivalences, as it commutes with
$\acute{\text{e}}\text{t}$
-weak equivalences, as it commutes with
![]() $\acute{\text{e}}\text{t}$
-sheafification.◻
$\acute{\text{e}}\text{t}$
-sheafification.◻
We are now interested in finding a convenient set of compact objects that generate the categories above, as triangulated categories with small sums. This will simplify many definitions and proofs in what follows.
Proposition 3.18. The category
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
[respectively
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
[respectively
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
] is compactly generated (as a triangulated category with small sums) by motives
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
] is compactly generated (as a triangulated category with small sums) by motives
![]() $\unicode[STIX]{x1D6EC}(X)$
associated to rigid varieties
$\unicode[STIX]{x1D6EC}(X)$
associated to rigid varieties
![]() $X$
, which are in
$X$
, which are in
![]() $\operatorname{RigSm}^{\operatorname{gc}}$
[respectively
$\operatorname{RigSm}^{\operatorname{gc}}$
[respectively
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
].
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
].
Proof. The statements are analogous, and we only consider the case of
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
. It is clear that the set of functors
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
. It is clear that the set of functors
![]() $H_{i}\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}(X),\cdot )$
detect quasi-isomorphisms between étale local objects, by letting
$H_{i}\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}(X),\cdot )$
detect quasi-isomorphisms between étale local objects, by letting
![]() $X$
vary in
$X$
vary in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
and
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
and
![]() $i$
vary in
$i$
vary in
![]() $\mathbb{Z}$
. We are left to prove that the motives
$\mathbb{Z}$
. We are left to prove that the motives
![]() $\unicode[STIX]{x1D6EC}(X)$
with
$\unicode[STIX]{x1D6EC}(X)$
with
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
are compact. Since
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
are compact. Since
![]() $\unicode[STIX]{x1D6EC}(X)$
is compact in
$\unicode[STIX]{x1D6EC}(X)$
is compact in
![]() $\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
and
$\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}))$
and
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}$
commutes with direct sums, it suffices to prove that if
$\operatorname{Sing}^{\mathbb{B}^{1}}$
commutes with direct sums, it suffices to prove that if
![]() $\{{\mathcal{F}}_{i}\}_{i\in I}$
is a family of
$\{{\mathcal{F}}_{i}\}_{i\in I}$
is a family of
![]() $\acute{\text{e}}\text{t}$
-local complexes, then also
$\acute{\text{e}}\text{t}$
-local complexes, then also
![]() $\bigoplus _{i}{\mathcal{F}}_{i}$
is
$\bigoplus _{i}{\mathcal{F}}_{i}$
is
![]() $\acute{\text{e}}\text{t}$
-local. If
$\acute{\text{e}}\text{t}$
-local. If
![]() $I$
is finite, the claim follows from the isomorphisms
$I$
is finite, the claim follows from the isomorphisms
![]() $H_{-n}\text{Hom}_{\bullet }(X,\bigoplus _{i}{\mathcal{F}}_{i})\cong \bigoplus _{i}\mathbb{H}^{n}(X,{\mathcal{F}}_{i})\cong \mathbb{H}^{n}(X,\bigoplus _{i}{\mathcal{F}}_{i})$
. A coproduct over an arbitrary family is a filtered colimit of finite coproducts, and hence the claim follows from [Reference AyoubAyo07, Proposition 4.5.62].◻
$H_{-n}\text{Hom}_{\bullet }(X,\bigoplus _{i}{\mathcal{F}}_{i})\cong \bigoplus _{i}\mathbb{H}^{n}(X,{\mathcal{F}}_{i})\cong \mathbb{H}^{n}(X,\bigoplus _{i}{\mathcal{F}}_{i})$
. A coproduct over an arbitrary family is a filtered colimit of finite coproducts, and hence the claim follows from [Reference AyoubAyo07, Proposition 4.5.62].◻
Remark 3.19. The above proof shows that the statement of Proposition 3.18 holds true without any assumptions on
![]() $\unicode[STIX]{x1D6EC}$
under the condition that all varieties
$\unicode[STIX]{x1D6EC}$
under the condition that all varieties
![]() $X$
have finite cohomological dimension with respect to the étale topology.
$X$
have finite cohomological dimension with respect to the étale topology.
We now introduce the category of motives associated to smooth perfectoid spaces, using the same formalism as before. In this category, the canonical choice of the ‘interval object’ for defining homotopies is the perfectoid ball
![]() $\widehat{\mathbb{B}}^{1}$
.
$\widehat{\mathbb{B}}^{1}$
.
Example 3.20. The perfectoid ball
![]() $\widehat{\mathbb{B}}^{1}=\operatorname{Spa}(K\langle \unicode[STIX]{x1D712}^{1/p^{\infty }}\rangle ,K^{\circ }\langle \unicode[STIX]{x1D712}^{1/p^{\infty }}\rangle )$
is an interval object with respect to the natural multiplication
$\widehat{\mathbb{B}}^{1}=\operatorname{Spa}(K\langle \unicode[STIX]{x1D712}^{1/p^{\infty }}\rangle ,K^{\circ }\langle \unicode[STIX]{x1D712}^{1/p^{\infty }}\rangle )$
is an interval object with respect to the natural multiplication
![]() $\unicode[STIX]{x1D707}$
and maps
$\unicode[STIX]{x1D707}$
and maps
![]() $i_{0}$
and
$i_{0}$
and
![]() $i_{1}$
induced by the substitution
$i_{1}$
induced by the substitution
![]() $\unicode[STIX]{x1D712}^{1/p^{h}}\mapsto 0$
and
$\unicode[STIX]{x1D712}^{1/p^{h}}\mapsto 0$
and
![]() $\unicode[STIX]{x1D712}^{1/p^{h}}\mapsto 1$
, respectively.
$\unicode[STIX]{x1D712}^{1/p^{h}}\mapsto 1$
, respectively.
The perfectoid variety
![]() $\widehat{\mathbb{B}}^{1}$
naturally lives in
$\widehat{\mathbb{B}}^{1}$
naturally lives in
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
and has good coordinates by Proposition 2.13. It can therefore be used to define another homotopy category out of
$\widehat{\text{Rig}}\operatorname{Sm}$
and has good coordinates by Proposition 2.13. It can therefore be used to define another homotopy category out of
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
Corollary 3.21. The following pairs of model categories are Quillen equivalent.
–
 $\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\operatorname{PerfSm})$
and
$\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\operatorname{PerfSm})$
and
 $\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\operatorname{PerfSm}^{\operatorname{gc}})$
.
$\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\operatorname{PerfSm}^{\operatorname{gc}})$
.–
 $\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\operatorname{PerfSm})$
and
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\operatorname{PerfSm})$
and
 $\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\operatorname{PerfSm}^{\operatorname{gc}})$
.
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\operatorname{PerfSm}^{\operatorname{gc}})$
.–
 $\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
$\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
 $\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
$\mathbf{Ch}_{\acute{\text{e}}\text{t}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.–
 $\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
and
 $\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
Proof. It suffices to apply Proposition 3.3 to the sites with interval
![]() $(\operatorname{PerfSm},\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
and
$(\operatorname{PerfSm},\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
and
![]() $(\widehat{\text{Rig}}\operatorname{Sm},\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
, where
$(\widehat{\text{Rig}}\operatorname{Sm},\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
, where
![]() $\mathbf{C}^{\prime }$
is in both cases the subcategory of affinoid rigid varieties with good coordinates.◻
$\mathbf{C}^{\prime }$
is in both cases the subcategory of affinoid rigid varieties with good coordinates.◻
Definition 3.22. For
![]() $\unicode[STIX]{x1D702}\in \{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1},(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})\}$
we say that a map in
$\unicode[STIX]{x1D702}\in \{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1},(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})\}$
we say that a map in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\operatorname{PerfSm})$
[respectively
$\mathbf{Ch}\,\mathbf{Psh}(\operatorname{PerfSm})$
[respectively
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] is a
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] is a
![]() $\unicode[STIX]{x1D702}$
-weak equivalence if it is a weak equivalence in the model structure
$\unicode[STIX]{x1D702}$
-weak equivalence if it is a weak equivalence in the model structure
![]() $\mathbf{Ch}_{\unicode[STIX]{x1D702}}\mathbf{Psh}(\operatorname{PerfSm})$
[respectively
$\mathbf{Ch}_{\unicode[STIX]{x1D702}}\mathbf{Psh}(\operatorname{PerfSm})$
[respectively
![]() $\mathbf{Ch}_{\unicode[STIX]{x1D702}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
]. We say that an object
$\mathbf{Ch}_{\unicode[STIX]{x1D702}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
]. We say that an object
![]() ${\mathcal{F}}$
of the derived category
${\mathcal{F}}$
of the derived category
![]() $\mathbf{D}=\mathbf{D}(\mathbf{Psh}(\operatorname{PerfSm}))$
[respectively
$\mathbf{D}=\mathbf{D}(\mathbf{Psh}(\operatorname{PerfSm}))$
[respectively
![]() $\mathbf{D}=\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}))$
] is
$\mathbf{D}=\mathbf{D}(\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}))$
] is
![]() $\unicode[STIX]{x1D702}$
-local if the functor
$\unicode[STIX]{x1D702}$
-local if the functor
![]() $\operatorname{Hom}_{\mathbf{D}}(\cdot ,{\mathcal{F}})$
sends maps in
$\operatorname{Hom}_{\mathbf{D}}(\cdot ,{\mathcal{F}})$
sends maps in
![]() $S_{\unicode[STIX]{x1D702}}$
(see Proposition 3.3) to isomorphisms. This amounts to say that
$S_{\unicode[STIX]{x1D702}}$
(see Proposition 3.3) to isomorphisms. This amounts to say that
![]() ${\mathcal{F}}$
is quasi-isomorphic to a
${\mathcal{F}}$
is quasi-isomorphic to a
![]() $\unicode[STIX]{x1D702}$
-fibrant object. The triangulated homotopy category associated to the localization
$\unicode[STIX]{x1D702}$
-fibrant object. The triangulated homotopy category associated to the localization
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\operatorname{PerfSm})$
[respectively
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\operatorname{PerfSm})$
[respectively
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] will be denoted by
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] will be denoted by
![]() $\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
[respectively
$\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
[respectively
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
]. We will omit
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
]. We will omit
![]() $\unicode[STIX]{x1D6EC}$
whenever the context allows it. The image of a variety
$\unicode[STIX]{x1D6EC}$
whenever the context allows it. The image of a variety
![]() $X$
in one of these categories will be denoted by
$X$
in one of these categories will be denoted by
![]() $\unicode[STIX]{x1D6EC}(X)$
.
$\unicode[STIX]{x1D6EC}(X)$
.
We recall one of the main results of Scholze [Reference ScholzeSch12], reshaped in our derived homotopical setting. It will constitute the bridge to pass from characteristic
![]() $p$
to characteristic
$p$
to characteristic
![]() $0$
. As summarized in Theorem 1.12 there is an equivalence of categories between perfectoid affinoid
$0$
. As summarized in Theorem 1.12 there is an equivalence of categories between perfectoid affinoid
![]() $K$
-algebras and perfectoid affinoid
$K$
-algebras and perfectoid affinoid
![]() $K^{\flat }$
-algebras, extending to an equivalence between the categories of perfectoid spaces over
$K^{\flat }$
-algebras, extending to an equivalence between the categories of perfectoid spaces over
![]() $K$
and over
$K$
and over
![]() $K^{\flat }$
(see [Reference ScholzeSch12, Proposition 6.17]). We refer to this equivalence as the tilting equivalence.
$K^{\flat }$
(see [Reference ScholzeSch12, Proposition 6.17]). We refer to this equivalence as the tilting equivalence.
Proposition 3.23. There exists an equivalence of triangulated categories
induced by the tilting equivalence.
Proof. The tilting equivalence (see Theorem 1.12) induces an equivalence of the étale sites on perfectoid spaces over
![]() $K$
and over
$K$
and over
![]() $K^{\flat }$
(see [Reference ScholzeSch12, Theorem 7.12]). Moreover
$K^{\flat }$
(see [Reference ScholzeSch12, Theorem 7.12]). Moreover
![]() $(\widehat{\mathbb{T}}^{n})^{\flat }=\widehat{\mathbb{T}}^{n}$
and
$(\widehat{\mathbb{T}}^{n})^{\flat }=\widehat{\mathbb{T}}^{n}$
and
![]() $(\widehat{\mathbb{B}}^{n})^{\flat }=\widehat{\mathbb{B}}^{n}$
. It therefore induces an equivalence of sites with interval
$(\widehat{\mathbb{B}}^{n})^{\flat }=\widehat{\mathbb{B}}^{n}$
. It therefore induces an equivalence of sites with interval
![]() $(\operatorname{PerfSm}/K,\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})\cong (\operatorname{PerfSm}/K^{\flat },\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
, and hence the claim.◻
$(\operatorname{PerfSm}/K,\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})\cong (\operatorname{PerfSm}/K^{\flat },\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
, and hence the claim.◻
We now investigate the triangulated functor between the categories of motives induced by the natural embedding
![]() $\operatorname{PerfSm}\rightarrow \widehat{\text{Rig}}\operatorname{Sm}$
in the same spirit of what we did previously in Proposition 3.17.
$\operatorname{PerfSm}\rightarrow \widehat{\text{Rig}}\operatorname{Sm}$
in the same spirit of what we did previously in Proposition 3.17.
Proposition 3.24. The inclusion
![]() $\operatorname{PerfSm}{\hookrightarrow}\widehat{\text{Rig}}\operatorname{Sm}$
induces a Quillen adjunction
$\operatorname{PerfSm}{\hookrightarrow}\widehat{\text{Rig}}\operatorname{Sm}$
induces a Quillen adjunction
Moreover, the functor
![]() $\mathbb{L}j^{\ast }:\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
is fully faithful.
$\mathbb{L}j^{\ast }:\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
is fully faithful.
Proof. The result follows in the same way as Proposition 3.17. ◻
Also in this framework, the
![]() $\widehat{\mathbb{B}}^{1}$
-localization has a very explicit construction. Most proofs are straightforward analogs of those relative to the
$\widehat{\mathbb{B}}^{1}$
-localization has a very explicit construction. Most proofs are straightforward analogs of those relative to the
![]() $\mathbb{B}^{1}$
-localizations, and will therefore be omitted.
$\mathbb{B}^{1}$
-localizations, and will therefore be omitted.
Definition 3.25. We denote by
![]() $\widehat{\Box }$
the
$\widehat{\Box }$
the
![]() $\unicode[STIX]{x1D6F4}$
-enriched cocubical object (see [Reference AyoubAyo14c, Appendix A]) defined by putting
$\unicode[STIX]{x1D6F4}$
-enriched cocubical object (see [Reference AyoubAyo14c, Appendix A]) defined by putting
![]() $\widehat{\Box }^{n}=\widehat{\mathbb{B}}^{n}=\operatorname{Spa}K\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{1/\infty }}\rangle$
and considering the morphisms
$\widehat{\Box }^{n}=\widehat{\mathbb{B}}^{n}=\operatorname{Spa}K\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{1/\infty }}\rangle$
and considering the morphisms
![]() $d_{r,\unicode[STIX]{x1D716}}$
induced by the maps
$d_{r,\unicode[STIX]{x1D716}}$
induced by the maps
![]() $\widehat{\mathbb{B}}^{n}\rightarrow \widehat{\mathbb{B}}^{n+1}$
corresponding to the substitution
$\widehat{\mathbb{B}}^{n}\rightarrow \widehat{\mathbb{B}}^{n+1}$
corresponding to the substitution
![]() $\unicode[STIX]{x1D70F}_{r}^{1/p^{h}}=\unicode[STIX]{x1D716}$
for
$\unicode[STIX]{x1D70F}_{r}^{1/p^{h}}=\unicode[STIX]{x1D716}$
for
![]() $\unicode[STIX]{x1D716}\in \{0,1\}$
and the morphisms
$\unicode[STIX]{x1D716}\in \{0,1\}$
and the morphisms
![]() $p_{r}$
induced by the projections
$p_{r}$
induced by the projections
![]() $\widehat{\mathbb{B}}^{n}\rightarrow \widehat{\mathbb{B}}^{n-1}$
. For any complex of presheaves
$\widehat{\mathbb{B}}^{n}\rightarrow \widehat{\mathbb{B}}^{n-1}$
. For any complex of presheaves
![]() ${\mathcal{F}}$
we let
${\mathcal{F}}$
we let
![]() $\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
be the total complex of the simple complex associated to
$\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
be the total complex of the simple complex associated to
![]() $\text{}\underline{\text{Hom}}(\widehat{\Box },{\mathcal{F}})$
. It sends the object
$\text{}\underline{\text{Hom}}(\widehat{\Box },{\mathcal{F}})$
. It sends the object
![]() $X$
to the total complex of the simple complex associated to
$X$
to the total complex of the simple complex associated to
![]() ${\mathcal{F}}(X\,\times \,\widehat{\Box })$
.
${\mathcal{F}}(X\,\times \,\widehat{\Box })$
.
Proposition 3.26. Let
![]() ${\mathcal{F}}$
be a complex in
${\mathcal{F}}$
be a complex in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\operatorname{PerfSm})$
[respectively in
$\mathbf{Ch}\,\mathbf{Psh}(\operatorname{PerfSm})$
[respectively in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
]. Then
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
]. Then
![]() $\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
is
$\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
is
![]() $\widehat{\mathbb{B}}^{1}$
-local and
$\widehat{\mathbb{B}}^{1}$
-local and
![]() $\widehat{\mathbb{B}}^{1}$
-weak equivalent to
$\widehat{\mathbb{B}}^{1}$
-weak equivalent to
![]() ${\mathcal{F}}$
.
${\mathcal{F}}$
.
Proof. The fact that
![]() $\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
is
$\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
is
![]() $\widehat{\mathbb{B}}^{1}$
-local in
$\widehat{\mathbb{B}}^{1}$
-local in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
can be deduced by Lemmas 3.27 and 3.28. We are left to prove that
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
can be deduced by Lemmas 3.27 and 3.28. We are left to prove that
![]() $\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
is
$\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
is
![]() $\widehat{\mathbb{B}}^{1}$
-weak equivalent to
$\widehat{\mathbb{B}}^{1}$
-weak equivalent to
![]() ${\mathcal{F}}$
and this follows in the same way as in the proof of Proposition 3.15.◻
${\mathcal{F}}$
and this follows in the same way as in the proof of Proposition 3.15.◻
The following lemmas are used in the previous proof.
Lemma 3.27. A presheaf
![]() ${\mathcal{F}}$
in
${\mathcal{F}}$
in
![]() $\mathbf{Psh}(\operatorname{Sm}\operatorname{Perf})$
[respectively in
$\mathbf{Psh}(\operatorname{Sm}\operatorname{Perf})$
[respectively in
![]() $\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] is
$\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] is
![]() $\widehat{\mathbb{B}}^{1}$
-invariant if and only if
$\widehat{\mathbb{B}}^{1}$
-invariant if and only if
![]() $i_{0}^{\ast }=i_{1}^{\ast }:{\mathcal{F}}(X\,\times \,\widehat{\mathbb{B}}^{1})\rightarrow {\mathcal{F}}(X)$
for all
$i_{0}^{\ast }=i_{1}^{\ast }:{\mathcal{F}}(X\,\times \,\widehat{\mathbb{B}}^{1})\rightarrow {\mathcal{F}}(X)$
for all
![]() $X$
in
$X$
in
![]() $\operatorname{Sm}\operatorname{Perf}$
[respectively in
$\operatorname{Sm}\operatorname{Perf}$
[respectively in
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
].
$\widehat{\text{Rig}}\operatorname{Sm}$
].
Proof. This follows in the same way as [Reference Mazza, Voevodsky and WeibelMVW06, Lemma 2.16]. ◻
Lemma 3.28. For any presheaf
![]() ${\mathcal{F}}$
the two maps of cubical sets
${\mathcal{F}}$
the two maps of cubical sets
![]() $i_{0}^{\ast },i_{1}^{\ast }:{\mathcal{F}}(\widehat{\Box }\,\times \,\widehat{\mathbb{B}}^{1})\rightarrow {\mathcal{F}}(\widehat{\Box })$
induce chain homotopic maps on the associated simple and normalized complexes.
$i_{0}^{\ast },i_{1}^{\ast }:{\mathcal{F}}(\widehat{\Box }\,\times \,\widehat{\mathbb{B}}^{1})\rightarrow {\mathcal{F}}(\widehat{\Box })$
induce chain homotopic maps on the associated simple and normalized complexes.
Proof. This follows in the same way as Lemma 3.14. ◻
Corollary 3.29. Let
![]() ${\mathcal{F}}$
be in
${\mathcal{F}}$
be in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\operatorname{PerfSm})$
[respectively in
$\mathbf{Ch}\,\mathbf{Psh}(\operatorname{PerfSm})$
[respectively in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] the
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
] the
![]() $(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
-localization
$(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
-localization
![]() $C^{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
is quasi-isomorphic to
$C^{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}{\mathcal{F}}$
is quasi-isomorphic to
![]() $\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}(C^{\acute{\text{e}}\text{t}}{\mathcal{F}})$
.
$\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}(C^{\acute{\text{e}}\text{t}}{\mathcal{F}})$
.
Proof. This follows in the same way as Corollary 3.16. ◻
Proposition 3.30. The category
![]() $\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
[respectively
$\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
[respectively
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
] is compactly generated (as a triangulated category with small sums) by motives
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
] is compactly generated (as a triangulated category with small sums) by motives
![]() $\unicode[STIX]{x1D6EC}(X)$
associated to rigid varieties
$\unicode[STIX]{x1D6EC}(X)$
associated to rigid varieties
![]() $X$
, which are in
$X$
, which are in
![]() $\operatorname{PerfSm}^{\operatorname{gc}}$
[respectively
$\operatorname{PerfSm}^{\operatorname{gc}}$
[respectively
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
].
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
].
Proof. This follows in the same way as Proposition 3.18. ◻
Remark 3.31. The above proof shows that the statement of Proposition 3.30 holds true without any assumptions on
![]() $\unicode[STIX]{x1D6EC}$
under the condition that all varieties
$\unicode[STIX]{x1D6EC}$
under the condition that all varieties
![]() $X$
have finite cohomological dimension with respect to the étale topology.
$X$
have finite cohomological dimension with respect to the étale topology.
So far, we have defined two different Bousfield localizations on complexes of presheaves on
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
according to two different choices of intervals:
$\widehat{\text{Rig}}\operatorname{Sm}$
according to two different choices of intervals:
![]() $\mathbb{B}^{1}$
and
$\mathbb{B}^{1}$
and
![]() $\widehat{\mathbb{B}}^{1}$
. We remark that the second constitutes a further localization of the first, in the following sense.
$\widehat{\mathbb{B}}^{1}$
. We remark that the second constitutes a further localization of the first, in the following sense.
Proposition 3.32.
![]() $\mathbb{B}^{1}$
-weak equivalences in
$\mathbb{B}^{1}$
-weak equivalences in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
are
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
are
![]() $\widehat{\mathbb{B}}^{1}$
-weak equivalences.
$\widehat{\mathbb{B}}^{1}$
-weak equivalences.
Proof. It suffices to prove that
![]() $X\,\times \,\mathbb{B}^{1}\rightarrow X$
induces a
$X\,\times \,\mathbb{B}^{1}\rightarrow X$
induces a
![]() $\widehat{\mathbb{B}}^{1}$
-weak equivalence, for any variety
$\widehat{\mathbb{B}}^{1}$
-weak equivalence, for any variety
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
. This follows as the multiplicative homothety
$\widehat{\text{Rig}}\operatorname{Sm}$
. This follows as the multiplicative homothety
![]() $\widehat{\mathbb{B}}^{1}\,\times \,\mathbb{B}^{1}\rightarrow \mathbb{B}^{1}$
induces a homotopy between the zero map and the identity on
$\widehat{\mathbb{B}}^{1}\,\times \,\mathbb{B}^{1}\rightarrow \mathbb{B}^{1}$
induces a homotopy between the zero map and the identity on
![]() $\mathbb{B}^{1}$
.◻
$\mathbb{B}^{1}$
.◻
Corollary 3.33. The triangulated category
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
is equivalent to the full triangulated subcategory of
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
is equivalent to the full triangulated subcategory of
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
formed by
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
formed by
![]() $\widehat{\mathbb{B}}^{1}$
-local objects.
$\widehat{\mathbb{B}}^{1}$
-local objects.
Proof. Because of Proposition 3.32, the triangulated category
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
coincides with the localization of
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
coincides with the localization of
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
with respect to the set generated by the maps
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
with respect to the set generated by the maps
![]() $\unicode[STIX]{x1D6EC}(\widehat{\mathbb{B}}_{X}^{1})[n]\rightarrow \unicode[STIX]{x1D6EC}(X)[n]$
as
$\unicode[STIX]{x1D6EC}(\widehat{\mathbb{B}}_{X}^{1})[n]\rightarrow \unicode[STIX]{x1D6EC}(X)[n]$
as
![]() $X$
varies in
$X$
varies in
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
and
$\widehat{\text{Rig}}\operatorname{Sm}$
and
![]() $n$
in
$n$
in
![]() $\mathbb{Z}$
.◻
$\mathbb{Z}$
.◻
We end this section by recalling the definition of rigid motives with transfers. The notion of finite correspondence plays an important role in Voevodsky’s theory of motives. In the case of rigid varieties over a field
![]() $K$
correspondences give rise to the category
$K$
correspondences give rise to the category
![]() $\operatorname{RigCor}(K)$
as defined in [Reference AyoubAyo15, Definition 2.2.29].
$\operatorname{RigCor}(K)$
as defined in [Reference AyoubAyo15, Definition 2.2.29].
Definition 3.34. Additive presheaves over
![]() $\operatorname{RigCor}(K)$
are called presheaves with transfers, and the category they form is denoted by
$\operatorname{RigCor}(K)$
are called presheaves with transfers, and the category they form is denoted by
![]() $\mathbf{PST}(\operatorname{RigSm}/K,\unicode[STIX]{x1D6EC})$
or simply by
$\mathbf{PST}(\operatorname{RigSm}/K,\unicode[STIX]{x1D6EC})$
or simply by
![]() $\mathbf{PST}(\operatorname{RigSm})$
when the context allows it.
$\mathbf{PST}(\operatorname{RigSm})$
when the context allows it.
By [Reference AyoubAyo15, Definition 2.5.15], the projective model category
![]() $\mathbf{Ch}\,\mathbf{PST}(\operatorname{RigSm})$
admits a Bousfield localization
$\mathbf{Ch}\,\mathbf{PST}(\operatorname{RigSm})$
admits a Bousfield localization
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{PST}(\operatorname{RigSm})$
with respect to the union of the class of maps
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{PST}(\operatorname{RigSm})$
with respect to the union of the class of maps
![]() ${\mathcal{F}}\rightarrow {\mathcal{F}}^{\prime }$
inducing isomorphisms on the
${\mathcal{F}}\rightarrow {\mathcal{F}}^{\prime }$
inducing isomorphisms on the
![]() $\acute{\text{e}}\text{t}$
-sheaves associated to
$\acute{\text{e}}\text{t}$
-sheaves associated to
![]() $H_{i}({\mathcal{F}})$
and
$H_{i}({\mathcal{F}})$
and
![]() $H_{i}({\mathcal{F}}^{\prime })$
for all
$H_{i}({\mathcal{F}}^{\prime })$
for all
![]() $i\in \mathbb{Z}$
and the set of all maps
$i\in \mathbb{Z}$
and the set of all maps
![]() $\unicode[STIX]{x1D6EC}(\mathbb{B}_{X}^{1})[i]\rightarrow \unicode[STIX]{x1D6EC}(X)[i]$
as
$\unicode[STIX]{x1D6EC}(\mathbb{B}_{X}^{1})[i]\rightarrow \unicode[STIX]{x1D6EC}(X)[i]$
as
![]() $X$
varies in
$X$
varies in
![]() $\operatorname{RigSm}$
and
$\operatorname{RigSm}$
and
![]() $i$
varies in
$i$
varies in
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Definition 3.35. The triangulated homotopy category associated to
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{PST}(\operatorname{RigSm})$
will be denoted by
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{PST}(\operatorname{RigSm})$
will be denoted by
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
. We will omit
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
. We will omit
![]() $\unicode[STIX]{x1D6EC}$
from the notation whenever the context allows it. The image of a variety
$\unicode[STIX]{x1D6EC}$
from the notation whenever the context allows it. The image of a variety
![]() $X$
in will be denoted by
$X$
in will be denoted by
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X)$
.
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X)$
.
Remark 3.36. Since
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $\mathbb{Q}$
-algebra, one can equivalently consider the Nisnevich topology in the definition above and obtain a homotopy category
$\mathbb{Q}$
-algebra, one can equivalently consider the Nisnevich topology in the definition above and obtain a homotopy category
![]() $\mathbf{RigDM}_{\operatorname{Nis}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
, which is equivalent to
$\mathbf{RigDM}_{\operatorname{Nis}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
, which is equivalent to
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
.
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
.
Remark 3.37. The faithful embedding of categories
![]() $\operatorname{RigSm}\rightarrow \operatorname{RigCor}$
induces a Quillen adjunction (see [Reference AyoubAyo15, Proposition 2.5.19]):
$\operatorname{RigSm}\rightarrow \operatorname{RigCor}$
induces a Quillen adjunction (see [Reference AyoubAyo15, Proposition 2.5.19]):
such that
![]() $a_{\text{tr}}\unicode[STIX]{x1D6EC}(X)=\unicode[STIX]{x1D6EC}_{\text{tr}}(X)$
for any
$a_{\text{tr}}\unicode[STIX]{x1D6EC}(X)=\unicode[STIX]{x1D6EC}_{\text{tr}}(X)$
for any
![]() $X\in \operatorname{RigSm}$
and
$X\in \operatorname{RigSm}$
and
![]() $o_{\text{tr}}$
is the functor of forgetting transfers. These functors induce an adjoint pair:
$o_{\text{tr}}$
is the functor of forgetting transfers. These functors induce an adjoint pair:
which is investigated in [Reference VezzaniVez17].
4 Motivic interpretation of approximation results
Throughout this section,
![]() $K$
is a perfectoid field of arbitrary characteristic. We begin by presenting an approximation result whose proof is postponed to Appendix A.
$K$
is a perfectoid field of arbitrary characteristic. We begin by presenting an approximation result whose proof is postponed to Appendix A.
Proposition 4.1. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Also let
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Also let
![]() $Y$
be an affinoid rigid variety endowed with an étale map
$Y$
be an affinoid rigid variety endowed with an étale map
![]() $Y\rightarrow \mathbb{B}^{m}$
. For a given finite set of maps
$Y\rightarrow \mathbb{B}^{m}$
. For a given finite set of maps
![]() $\{f_{1},\ldots ,f_{N}\}$
in
$\{f_{1},\ldots ,f_{N}\}$
in
![]() $\operatorname{Hom}(X\,\times \,\mathbb{B}^{n},Y)$
we can find corresponding maps
$\operatorname{Hom}(X\,\times \,\mathbb{B}^{n},Y)$
we can find corresponding maps
![]() $\{H_{1},\ldots ,H_{N}\}$
in
$\{H_{1},\ldots ,H_{N}\}$
in
![]() $\operatorname{Hom}(X\,\times \,\mathbb{B}^{n}\,\times \,\mathbb{B}^{1},Y)$
and an integer
$\operatorname{Hom}(X\,\times \,\mathbb{B}^{n}\,\times \,\mathbb{B}^{1},Y)$
and an integer
![]() $\bar{h}$
such that the following are true.
$\bar{h}$
such that the following are true.
(i) For all
 $1\leqslant k\leqslant N$
it holds that
$1\leqslant k\leqslant N$
it holds that
 $i_{0}^{\ast }H_{k}=f_{k}$
and
$i_{0}^{\ast }H_{k}=f_{k}$
and
 $i_{1}^{\ast }H_{k}$
factors over the canonical map
$i_{1}^{\ast }H_{k}$
factors over the canonical map
 $X\rightarrow X_{\bar{h}}$
.
$X\rightarrow X_{\bar{h}}$
.(ii) If
 $f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=f_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
for some
$f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=f_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
for some
 $1\leqslant k,k^{\prime }\leqslant N$
and some
$1\leqslant k,k^{\prime }\leqslant N$
and some
 $(r,\unicode[STIX]{x1D716})\in \{1,\ldots ,n\}\,\times \,\{0,1\}$
then
$(r,\unicode[STIX]{x1D716})\in \{1,\ldots ,n\}\,\times \,\{0,1\}$
then
 $H_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=H_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
.
$H_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=H_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
.(iii) If for some
 $1\leqslant k\leqslant N$
and some
$1\leqslant k\leqslant N$
and some
 $h\in \mathbb{N}$
the map
$h\in \mathbb{N}$
the map
 $f_{k}\,\circ \,d_{1,1}\in \operatorname{Hom}(X\,\times \,\mathbb{B}^{n-1},Y)$
lies in
$f_{k}\,\circ \,d_{1,1}\in \operatorname{Hom}(X\,\times \,\mathbb{B}^{n-1},Y)$
lies in
 $\operatorname{Hom}(X_{h}\,\times \,\mathbb{B}^{n-1},Y)$
then the element
$\operatorname{Hom}(X_{h}\,\times \,\mathbb{B}^{n-1},Y)$
then the element
 $H_{k}\,\circ \,d_{1,1}$
of
$H_{k}\,\circ \,d_{1,1}$
of
 $\operatorname{Hom}(X\,\times \,\mathbb{B}^{n-1}\,\times \,\mathbb{B}^{1},Y)$
is constant on
$\operatorname{Hom}(X\,\times \,\mathbb{B}^{n-1}\,\times \,\mathbb{B}^{1},Y)$
is constant on
 $\mathbb{B}^{1}$
equal to
$\mathbb{B}^{1}$
equal to
 $f_{k}\,\circ \,d_{1,1}$
.
$f_{k}\,\circ \,d_{1,1}$
.
The statement above has the following interpretation in terms of complexes.
Proposition 4.2. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
and let
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
and let
![]() $Y$
be in
$Y$
be in
![]() $\operatorname{RigSm}^{\operatorname{gc}}$
. The natural map
$\operatorname{RigSm}^{\operatorname{gc}}$
. The natural map
is a quasi-isomorphism.
Proof. We need to prove that the natural map
defines bijections on homology groups.
We start by proving surjectivity. As
![]() $\Box$
is a
$\Box$
is a
![]() $\unicode[STIX]{x1D6F4}$
-enriched cocubical object, the complexes above are quasi-isomorphic to the associated normalized complexes
$\unicode[STIX]{x1D6F4}$
-enriched cocubical object, the complexes above are quasi-isomorphic to the associated normalized complexes
![]() $N_{\bullet }$
, which we consider instead. Suppose that
$N_{\bullet }$
, which we consider instead. Suppose that
![]() $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X\,\times \,\Box ^{n},Y)$
defines a cycle in
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X\,\times \,\Box ^{n},Y)$
defines a cycle in
![]() $N_{n}$
, i.e.,
$N_{n}$
, i.e.,
![]() $\unicode[STIX]{x1D6FD}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=0$
for
$\unicode[STIX]{x1D6FD}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=0$
for
![]() $1\leqslant r\leqslant n$
and
$1\leqslant r\leqslant n$
and
![]() $\unicode[STIX]{x1D716}\in \{0,1\}$
. This means that
$\unicode[STIX]{x1D716}\in \{0,1\}$
. This means that
![]() $\unicode[STIX]{x1D6FD}=\sum \unicode[STIX]{x1D706}_{k}f_{k}$
with
$\unicode[STIX]{x1D6FD}=\sum \unicode[STIX]{x1D706}_{k}f_{k}$
with
![]() $\unicode[STIX]{x1D706}_{k}\in \unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x1D706}_{k}\in \unicode[STIX]{x1D6EC}$
,
![]() $f_{k}\in \operatorname{Hom}(X\,\times \,\Box ^{n},Y)$
and
$f_{k}\in \operatorname{Hom}(X\,\times \,\Box ^{n},Y)$
and
![]() $\sum \unicode[STIX]{x1D706}_{k}f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=0$
. This amounts to saying that for every
$\sum \unicode[STIX]{x1D706}_{k}f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=0$
. This amounts to saying that for every
![]() $k,r,\unicode[STIX]{x1D716}$
the sum
$k,r,\unicode[STIX]{x1D716}$
the sum
![]() $\sum \unicode[STIX]{x1D706}_{k^{\prime }}$
over the indices
$\sum \unicode[STIX]{x1D706}_{k^{\prime }}$
over the indices
![]() $k^{\prime }$
such that
$k^{\prime }$
such that
![]() $f_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
is zero. By Proposition 4.1, we can find an integer
$f_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
is zero. By Proposition 4.1, we can find an integer
![]() $h$
and maps
$h$
and maps
![]() $H_{k}\in \operatorname{Hom}(X\,\times \,\Box ^{n}\,\times \,\mathbb{B}^{1},Y)$
such that
$H_{k}\in \operatorname{Hom}(X\,\times \,\Box ^{n}\,\times \,\mathbb{B}^{1},Y)$
such that
![]() $i_{0}^{\ast }H=f_{k}$
,
$i_{0}^{\ast }H=f_{k}$
,
![]() $i_{1}^{\ast }H=\unicode[STIX]{x1D719}(\tilde{f}_{k})$
with
$i_{1}^{\ast }H=\unicode[STIX]{x1D719}(\tilde{f}_{k})$
with
![]() $\tilde{f}_{k}\in \operatorname{Hom}(X_{h}\,\times \,\Box ^{n},Y)$
and
$\tilde{f}_{k}\in \operatorname{Hom}(X_{h}\,\times \,\Box ^{n},Y)$
and
![]() $H_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=H_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
whenever
$H_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=H_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
whenever
![]() $f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=f_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
. If we denote by
$f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=f_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
. If we denote by
![]() $H$
the cycle
$H$
the cycle
![]() $\sum \unicode[STIX]{x1D706}_{k}H_{k}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X\,\times \,\Box ^{n}\,\times \,\mathbb{B}^{1},Y)$
we therefore have
$\sum \unicode[STIX]{x1D706}_{k}H_{k}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X\,\times \,\Box ^{n}\,\times \,\mathbb{B}^{1},Y)$
we therefore have
![]() $d_{r,\unicode[STIX]{x1D716}}^{\ast }H=0$
for all
$d_{r,\unicode[STIX]{x1D716}}^{\ast }H=0$
for all
![]() $r,\unicode[STIX]{x1D716}$
.
$r,\unicode[STIX]{x1D716}$
.
By Lemma 3.14, we conclude that
![]() $i_{1}^{\ast }H$
and
$i_{1}^{\ast }H$
and
![]() $i_{0}^{\ast }H$
define the same homology class, and therefore
$i_{0}^{\ast }H$
define the same homology class, and therefore
![]() $\unicode[STIX]{x1D6FD}$
defines the same class as
$\unicode[STIX]{x1D6FD}$
defines the same class as
![]() $i_{1}^{\ast }H$
, which is the image of a class in
$i_{1}^{\ast }H$
, which is the image of a class in
![]() $\unicode[STIX]{x1D6EC}\operatorname{Hom}(X_{h}\,\times \,\Box ^{n},Y)$
, as desired.
$\unicode[STIX]{x1D6EC}\operatorname{Hom}(X_{h}\,\times \,\Box ^{n},Y)$
, as desired.
We now turn to injectivity. Consider an element
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X_{0}\,\times \,\Box ^{n},Y)$
such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X_{0}\,\times \,\Box ^{n},Y)$
such that
![]() $\unicode[STIX]{x1D6FC}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=0$
for all
$\unicode[STIX]{x1D6FC}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=0$
for all
![]() $r,\unicode[STIX]{x1D716}$
and suppose there exists an element
$r,\unicode[STIX]{x1D716}$
and suppose there exists an element
![]() $\unicode[STIX]{x1D6FD}=\sum \unicode[STIX]{x1D706}_{i}f_{i}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X\,\times \,\Box ^{n+1},Y)$
such that
$\unicode[STIX]{x1D6FD}=\sum \unicode[STIX]{x1D706}_{i}f_{i}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X\,\times \,\Box ^{n+1},Y)$
such that
![]() $\unicode[STIX]{x1D6FD}\,\circ \,d_{r,0}=0$
for
$\unicode[STIX]{x1D6FD}\,\circ \,d_{r,0}=0$
for
![]() $1\leqslant r\leqslant n+1$
,
$1\leqslant r\leqslant n+1$
,
![]() $\unicode[STIX]{x1D6FD}\,\circ \,d_{r,1}=0$
for
$\unicode[STIX]{x1D6FD}\,\circ \,d_{r,1}=0$
for
![]() $2\leqslant r\leqslant n+1$
and
$2\leqslant r\leqslant n+1$
and
![]() $\unicode[STIX]{x1D6FD}\,\circ \,d_{1,1}=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FC})$
. Again, by Proposition 4.1, we can find an integer
$\unicode[STIX]{x1D6FD}\,\circ \,d_{1,1}=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FC})$
. Again, by Proposition 4.1, we can find an integer
![]() $\bar{h}$
and maps
$\bar{h}$
and maps
![]() $H_{k}\in \operatorname{Hom}(X\,\times \,\Box ^{n+1}\,\times \,\mathbb{B}^{1},Y)$
such that
$H_{k}\in \operatorname{Hom}(X\,\times \,\Box ^{n+1}\,\times \,\mathbb{B}^{1},Y)$
such that
![]() $H:=\sum \unicode[STIX]{x1D706}_{k}H_{k}$
satisfies
$H:=\sum \unicode[STIX]{x1D706}_{k}H_{k}$
satisfies
![]() $i_{1}^{\ast }H=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})$
for some
$i_{1}^{\ast }H=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})$
for some
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X_{\bar{h}}\,\times \,\Box ^{n+1},Y)$
,
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6EC}\operatorname{Hom}(X_{\bar{h}}\,\times \,\Box ^{n+1},Y)$
,
![]() $H\,\circ \,d_{r,0}=0$
for
$H\,\circ \,d_{r,0}=0$
for
![]() $1\leqslant r\leqslant n+1$
,
$1\leqslant r\leqslant n+1$
,
![]() $H\,\circ \,d_{r,1}=0$
for
$H\,\circ \,d_{r,1}=0$
for
![]() $2\leqslant r\leqslant n+1$
and
$2\leqslant r\leqslant n+1$
and
![]() $H\,\circ \,d_{1,1}$
is constant on
$H\,\circ \,d_{1,1}$
is constant on
![]() $\mathbb{B}^{1}$
and coincides with
$\mathbb{B}^{1}$
and coincides with
![]() $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FC})$
. We conclude that
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FC})$
. We conclude that
![]() $\unicode[STIX]{x1D6FE}\in N_{n}$
and
$\unicode[STIX]{x1D6FE}\in N_{n}$
and
![]() $d\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}$
. In particular,
$d\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}$
. In particular,
![]() $\unicode[STIX]{x1D6FC}=0$
in the homology group, as desired.◻
$\unicode[STIX]{x1D6FC}=0$
in the homology group, as desired.◻
Corollary 4.3. Let
![]() ${\mathcal{F}}$
be a projectively cofibrant complex in
${\mathcal{F}}$
be a projectively cofibrant complex in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
. For any
$\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
. For any
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
the natural map
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
the natural map
is a quasi-isomorphism.
Proof. As homology commutes with filtered colimits, by means of Remark 3.2 we can assume that
![]() ${\mathcal{F}}$
is a bounded above complex formed by sums of representable presheaves. For any
${\mathcal{F}}$
is a bounded above complex formed by sums of representable presheaves. For any
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
the homology of
$\widehat{\text{Rig}}\operatorname{Sm}$
the homology of
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}(X)$
coincides with the homology of the total complex associated to
$\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}(X)$
coincides with the homology of the total complex associated to
![]() $C_{\bullet }({\mathcal{F}}(X\,\times \,\Box ))$
. The result then follows from Proposition 4.2 and the convergence of the spectral sequence associated to the double complex above, which is concentrated in one quadrant.◻
$C_{\bullet }({\mathcal{F}}(X\,\times \,\Box ))$
. The result then follows from Proposition 4.2 and the convergence of the spectral sequence associated to the double complex above, which is concentrated in one quadrant.◻
The following technical proposition is actually a crucial point of our proof, as it allows some explicit computations of morphisms in the category
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
.
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
.
Proposition 4.4. Let
![]() ${\mathcal{F}}$
be a cofibrant and
${\mathcal{F}}$
be a cofibrant and
![]() $(\mathbb{B}^{1},\acute{\text{e}}\text{t})$
-fibrant complex in
$(\mathbb{B}^{1},\acute{\text{e}}\text{t})$
-fibrant complex in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
. Then
$\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
. Then
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is
$\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is
![]() $(\mathbb{B}^{1},\acute{\text{e}}\text{t})$
-local in
$(\mathbb{B}^{1},\acute{\text{e}}\text{t})$
-local in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
.
Proof. The difficulty lies in showing that the object
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is
$\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is
![]() $\acute{\text{e}}\text{t}$
-local. By Propositions 3.11 and 3.15, it suffices to prove that
$\acute{\text{e}}\text{t}$
-local. By Propositions 3.11 and 3.15, it suffices to prove that
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is local with respect to the étale-Cech hypercoverings
$\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is local with respect to the étale-Cech hypercoverings
![]() ${\mathcal{U}}_{\bullet }\rightarrow X$
in
${\mathcal{U}}_{\bullet }\rightarrow X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
of
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
of
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
descending at finite level. Let
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
descending at finite level. Let
![]() ${\mathcal{U}}_{\bullet }\rightarrow X$
be one of them. Without loss of generality, we assume that it descends to an étale covering of
${\mathcal{U}}_{\bullet }\rightarrow X$
be one of them. Without loss of generality, we assume that it descends to an étale covering of
![]() $X_{0}$
. In particular, we conclude that
$X_{0}$
. In particular, we conclude that
![]() ${\mathcal{U}}_{n}=\mathop{\varprojlim }\nolimits_{h}{\mathcal{U}}_{nh}$
is a disjoint union of objects in
${\mathcal{U}}_{n}=\mathop{\varprojlim }\nolimits_{h}{\mathcal{U}}_{nh}$
is a disjoint union of objects in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
.
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
.
We need to show that
![]() $\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet }),\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}))$
is quasi-isomorphic to
$\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet }),\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}))$
is quasi-isomorphic to
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})(X)$
. Using Corollary 4.3, we conclude that for each
$\operatorname{Sing}^{\mathbb{B}^{1}}(\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})(X)$
. Using Corollary 4.3, we conclude that for each
![]() $n\in \mathbb{N}$
the complex
$n\in \mathbb{N}$
the complex
![]() $(\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})({\mathcal{U}}_{n})$
is quasi-isomorphic to
$(\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})({\mathcal{U}}_{n})$
is quasi-isomorphic to
![]() $\mathop{\varinjlim }\nolimits_{h}(\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})({\mathcal{U}}_{nh})$
. Passing to the homotopy limit on
$\mathop{\varinjlim }\nolimits_{h}(\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})({\mathcal{U}}_{nh})$
. Passing to the homotopy limit on
![]() $n$
on both sides, we deduce that
$n$
on both sides, we deduce that
![]() $\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet }),\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is quasi-isomorphic to
$\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet }),\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
is quasi-isomorphic to
![]() $\mathop{\varinjlim }\nolimits_{h}\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet h}),\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
. Using again Corollary 4.3, we also obtain that
$\mathop{\varinjlim }\nolimits_{h}\text{Hom}_{\bullet }(\unicode[STIX]{x1D6EC}({\mathcal{U}}_{\bullet h}),\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})$
. Using again Corollary 4.3, we also obtain that
![]() $(\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})(X)$
is quasi-isomorphic to
$(\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})(X)$
is quasi-isomorphic to
![]() $\mathop{\varinjlim }\nolimits_{h}(\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})(X_{h})$
.
$\mathop{\varinjlim }\nolimits_{h}(\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})(X_{h})$
.
From the exactness of
![]() $\varinjlim$
it suffices then to prove that the maps
$\varinjlim$
it suffices then to prove that the maps
are quasi-isomorphisms. This follows once we show that the complex
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is
$\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is
![]() $\acute{\text{e}}\text{t}$
-local.
$\acute{\text{e}}\text{t}$
-local.
We point out that since
![]() ${\mathcal{F}}$
is
${\mathcal{F}}$
is
![]() $\mathbb{B}^{1}$
-local, then the canonical map
$\mathbb{B}^{1}$
-local, then the canonical map
![]() ${\mathcal{F}}\rightarrow \operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is a quasi-isomorphism. As
${\mathcal{F}}\rightarrow \operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
is a quasi-isomorphism. As
![]() ${\mathcal{F}}$
is
${\mathcal{F}}$
is
![]() $\acute{\text{e}}\text{t}$
-local we conclude that
$\acute{\text{e}}\text{t}$
-local we conclude that
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
also is, and hence the claim.◻
$\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
also is, and hence the claim.◻
We are finally ready to state the main result of this section.
Proposition 4.5. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. For any complex of presheaves
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. For any complex of presheaves
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() $\operatorname{RigSm}^{\operatorname{gc}}$
the natural map
$\operatorname{RigSm}^{\operatorname{gc}}$
the natural map
is an isomorphism.
Proof. Since any complex
![]() ${\mathcal{F}}$
has a fibrant-cofibrant replacement in
${\mathcal{F}}$
has a fibrant-cofibrant replacement in
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
we can assume that
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}^{\operatorname{gc}})$
we can assume that
![]() ${\mathcal{F}}$
is cofibrant and
${\mathcal{F}}$
is cofibrant and
![]() $(\acute{\text{e}}\text{t},\mathbb{B}^{1})$
-fibrant. Since it is
$(\acute{\text{e}}\text{t},\mathbb{B}^{1})$
-fibrant. Since it is
![]() $\mathbb{B}^{1}$
-local, it is quasi-isomorphic to
$\mathbb{B}^{1}$
-local, it is quasi-isomorphic to
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
. By Corollary 4.3, for any integer
$\operatorname{Sing}^{\mathbb{B}^{1}}{\mathcal{F}}$
. By Corollary 4.3, for any integer
![]() $i$
one has
$i$
one has
As
![]() $\unicode[STIX]{x1D6EC}(X)$
is a cofibrant object in
$\unicode[STIX]{x1D6EC}(X)$
is a cofibrant object in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
and
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
and
![]() $\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}$
is a
$\operatorname{Sing}^{\mathbb{B}^{1}}\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}$
is a
![]() $(\mathbb{B}^{1},\acute{\text{e}}\text{t})$
-local replacement of
$(\mathbb{B}^{1},\acute{\text{e}}\text{t})$
-local replacement of
![]() ${\mathcal{F}}$
in
${\mathcal{F}}$
in
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
by Proposition 4.4, we conclude that the previous isomorphism can be rephrased in the following way:
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}})$
by Proposition 4.4, we conclude that the previous isomorphism can be rephrased in the following way:
proving the claim. ◻
5 The de-perfectoidification functor in characteristic
 $0$
$0$
The results proved in § 4 are valid both for
![]() $\operatorname{char}K=0$
and
$\operatorname{char}K=0$
and
![]() $\operatorname{char}K=p$
. In contrast, the results of this section require that
$\operatorname{char}K=p$
. In contrast, the results of this section require that
![]() $\operatorname{char}K=0$
. We will present later their variant for the case
$\operatorname{char}K=0$
. We will present later their variant for the case
![]() $\operatorname{char}K=p$
.
$\operatorname{char}K=p$
.
We start by considering the adjunction between motives with and without transfers (see Remark 3.37). Thanks to the following theorem, we are allowed to add or ignore transfers according to the situation.
Theorem 5.1 [Reference VezzaniVez17].
Suppose that
![]() $\operatorname{char}K=0$
. The functors
$\operatorname{char}K=0$
. The functors
![]() $(a_{\text{tr}},o_{\text{tr}})$
induce an equivalence:
$(a_{\text{tr}},o_{\text{tr}})$
induce an equivalence:
Remark 5.2. The proof of the statement above uses in a crucial way the fact that the ring of coefficients
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $\mathbb{Q}$
-algebra.
$\mathbb{Q}$
-algebra.
Proposition 5.3. Suppose
![]() $\operatorname{char}K=0$
. Let
$\operatorname{char}K=0$
. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. If
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. If
![]() $h$
is big enough, then the map
$h$
is big enough, then the map
![]() $\unicode[STIX]{x1D6EC}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}(X_{h})$
is an isomorphism in
$\unicode[STIX]{x1D6EC}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}(X_{h})$
is an isomorphism in
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
.
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
.
Proof. By means of Theorem 5.1, we can equally prove the statement in the category
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
. We claim that we can also make an arbitrary finite field extension
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
. We claim that we can also make an arbitrary finite field extension
![]() $L/K$
. Indeed the transpose of the natural map
$L/K$
. Indeed the transpose of the natural map
![]() $Y_{L}\rightarrow Y$
is a correspondence from
$Y_{L}\rightarrow Y$
is a correspondence from
![]() $Y$
to
$Y$
to
![]() $Y_{L}$
. Since
$Y_{L}$
. Since
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $\mathbb{Q}$
-algebra, we conclude that
$\mathbb{Q}$
-algebra, we conclude that
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(Y)$
is a direct factor of
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(Y)$
is a direct factor of
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(Y_{L})=\mathbb{L}e_{\sharp }\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(Y_{L})$
for any variety
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(Y_{L})=\mathbb{L}e_{\sharp }\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(Y_{L})$
for any variety
![]() $Y$
, where
$Y$
, where
![]() $\mathbb{L}e_{\sharp }$
is the functor
$\mathbb{L}e_{\sharp }$
is the functor
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(L)\rightarrow \mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
induced by restriction of scalars. In particular, if
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(L)\rightarrow \mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
induced by restriction of scalars. In particular, if
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}((X_{h+1})_{L})\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}((X_{h})_{L})$
is an isomorphism in
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}((X_{h+1})_{L})\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}((X_{h})_{L})$
is an isomorphism in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(L)$
then
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(L)$
then
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}((X_{h+1})_{L})\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}((X_{h})_{L})$
is an isomorphism in
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}((X_{h+1})_{L})\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}((X_{h})_{L})$
is an isomorphism in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
and therefore also
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
and therefore also
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X_{h})$
is.
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X_{h})$
is.
By lemma [Reference AyoubAyo15, 1.1.52], we can suppose that
![]() $X_{0}=\operatorname{Spa}(R_{0},R_{0}^{\circ })$
with
$X_{0}=\operatorname{Spa}(R_{0},R_{0}^{\circ })$
with
![]() $R_{0}=S\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(P(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}))$
, where
$R_{0}=S\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(P(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}))$
, where
![]() $S={\mathcal{O}}(\mathbb{T}^{M})$
,
$S={\mathcal{O}}(\mathbb{T}^{M})$
,
![]() $\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{N})$
is a
$\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{N})$
is a
![]() $N$
-tuple of coordinates,
$N$
-tuple of coordinates,
![]() $\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m})$
is a
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m})$
is a
![]() $m$
-tuple of coordinates and
$m$
-tuple of coordinates and
![]() $P$
is a set of
$P$
is a set of
![]() $m$
polynomials in
$m$
polynomials in
![]() $S[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
with
$S[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
with
![]() $\det (\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})\in R_{0}^{\times }$
. In particular,
$\det (\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})\in R_{0}^{\times }$
. In particular,
![]() $X_{1}=\operatorname{Spa}(R_{1},R_{1}^{\circ })$
with
$X_{1}=\operatorname{Spa}(R_{1},R_{1}^{\circ })$
with
![]() $R_{1}=S\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(P(\unicode[STIX]{x1D70E}^{p},\unicode[STIX]{x1D70F}))$
and the map
$R_{1}=S\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(P(\unicode[STIX]{x1D70E}^{p},\unicode[STIX]{x1D70F}))$
and the map
![]() $f:X_{1}\rightarrow X_{0}$
is induced by
$f:X_{1}\rightarrow X_{0}$
is induced by
![]() $\unicode[STIX]{x1D70E}\mapsto \unicode[STIX]{x1D70E}^{p}$
,
$\unicode[STIX]{x1D70E}\mapsto \unicode[STIX]{x1D70E}^{p}$
,
![]() $\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}$
. Since the map
$\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}$
. Since the map
![]() $f$
is finite and surjective, we can also consider the transpose correspondence
$f$
is finite and surjective, we can also consider the transpose correspondence
![]() $f^{T}\in \operatorname{RigCor}(X_{0},X_{1})$
. The composition
$f^{T}\in \operatorname{RigCor}(X_{0},X_{1})$
. The composition
![]() $f\,\circ \,f^{T}$
is associated to the correspondence
$f\,\circ \,f^{T}$
is associated to the correspondence
![]() $X_{0}\xleftarrow[{}]{\;f}X_{1}\xrightarrow[{}]{f}X_{0}$
, which is the cycle
$X_{0}\xleftarrow[{}]{\;f}X_{1}\xrightarrow[{}]{f}X_{0}$
, which is the cycle
![]() $\deg (f)X_{0}=p^{N}\,\cdot \,\operatorname{id}_{X_{0}}$
. The composition
$\deg (f)X_{0}=p^{N}\,\cdot \,\operatorname{id}_{X_{0}}$
. The composition
![]() $f^{T}\,\circ \,f$
is associated to the correspondence
$f^{T}\,\circ \,f$
is associated to the correspondence
![]() $X_{1}\xleftarrow[{}]{\;p_{1}}X_{1}\,\times _{X_{0}}\,X_{1}\xrightarrow[{}]{p_{2}}X_{1}$
. Since
$X_{1}\xleftarrow[{}]{\;p_{1}}X_{1}\,\times _{X_{0}}\,X_{1}\xrightarrow[{}]{p_{2}}X_{1}$
. Since
![]() $\mathbb{T}^{N}\langle \unicode[STIX]{x1D70E}^{1/p}\rangle \,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \unicode[STIX]{x1D70E}^{1/p}\rangle \cong \mathbb{T}^{N}\langle \unicode[STIX]{x1D70E}^{1/p}\rangle \,\times \,\unicode[STIX]{x1D707}_{p}^{N}$
we conclude that the above correspondence is
$\mathbb{T}^{N}\langle \unicode[STIX]{x1D70E}^{1/p}\rangle \,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \unicode[STIX]{x1D70E}^{1/p}\rangle \cong \mathbb{T}^{N}\langle \unicode[STIX]{x1D70E}^{1/p}\rangle \,\times \,\unicode[STIX]{x1D707}_{p}^{N}$
we conclude that the above correspondence is
![]() $X_{1}\xleftarrow[{}]{\;p_{1}}X_{1}\,\times \,(\unicode[STIX]{x1D707}_{p})^{N}\xrightarrow[{}]{\unicode[STIX]{x1D702}}X_{1}$
, where
$X_{1}\xleftarrow[{}]{\;p_{1}}X_{1}\,\times \,(\unicode[STIX]{x1D707}_{p})^{N}\xrightarrow[{}]{\unicode[STIX]{x1D702}}X_{1}$
, where
![]() $\unicode[STIX]{x1D702}$
is induced by the multiplication map
$\unicode[STIX]{x1D702}$
is induced by the multiplication map
![]() $\mathbb{T}^{N}\,\times \,\unicode[STIX]{x1D707}_{p}^{N}\rightarrow \mathbb{T}^{N}$
. Up to a finite field extension, we can assume that
$\mathbb{T}^{N}\,\times \,\unicode[STIX]{x1D707}_{p}^{N}\rightarrow \mathbb{T}^{N}$
. Up to a finite field extension, we can assume that
![]() $K$
has
$K$
has
![]() $p$
th roots of unity. The above correspondence is then equal to
$p$
th roots of unity. The above correspondence is then equal to
![]() $\sum f_{\unicode[STIX]{x1D701}}$
, where each
$\sum f_{\unicode[STIX]{x1D701}}$
, where each
![]() $f_{\unicode[STIX]{x1D701}}$
is a map
$f_{\unicode[STIX]{x1D701}}$
is a map
![]() $X_{1}\rightarrow X_{1}$
defined by
$X_{1}\rightarrow X_{1}$
defined by
![]() $\unicode[STIX]{x1D70E}_{i}\mapsto \unicode[STIX]{x1D701}_{i}\unicode[STIX]{x1D70E}_{i}$
,
$\unicode[STIX]{x1D70E}_{i}\mapsto \unicode[STIX]{x1D701}_{i}\unicode[STIX]{x1D70E}_{i}$
,
![]() $\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}$
for each
$\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}$
for each
![]() $N$
-tuple
$N$
-tuple
![]() $\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{i})$
of
$\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{i})$
of
![]() $p$
th roots of unity. If we prove that each
$p$
th roots of unity. If we prove that each
![]() $f_{\unicode[STIX]{x1D701}}$
is homotopically equivalent to
$f_{\unicode[STIX]{x1D701}}$
is homotopically equivalent to
![]() $\operatorname{id}_{X_{1}}$
then we get
$\operatorname{id}_{X_{1}}$
then we get
![]() $(1/p^{N})f^{T}\,\circ \,f=\operatorname{id}$
,
$(1/p^{N})f^{T}\,\circ \,f=\operatorname{id}$
,
![]() $f\,\circ \,(1/p^{N})f^{T}=\operatorname{id}$
in
$f\,\circ \,(1/p^{N})f^{T}=\operatorname{id}$
in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}$
, as desired.
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}$
, as desired.
We are left to find a homotopy between
![]() $\operatorname{id}$
and
$\operatorname{id}$
and
![]() $f_{\unicode[STIX]{x1D701}}$
for a fixed
$f_{\unicode[STIX]{x1D701}}$
for a fixed
![]() $\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{n})$
up to considering higher indices
$\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{n})$
up to considering higher indices
![]() $h$
. For the sake of clarity, we consider them as maps
$h$
. For the sake of clarity, we consider them as maps
![]() $\operatorname{Spa}\bar{R}_{1}\rightarrow \operatorname{Spa}R_{1}$
, where we put
$\operatorname{Spa}\bar{R}_{1}\rightarrow \operatorname{Spa}R_{1}$
, where we put
![]() $\bar{R}_{h}=S\langle \bar{\unicode[STIX]{x1D70E}},\bar{\unicode[STIX]{x1D70F}}\rangle /(P(\bar{\unicode[STIX]{x1D70E}}^{p^{h}},\bar{\unicode[STIX]{x1D70F}}))$
for any integer
$\bar{R}_{h}=S\langle \bar{\unicode[STIX]{x1D70E}},\bar{\unicode[STIX]{x1D70F}}\rangle /(P(\bar{\unicode[STIX]{x1D70E}}^{p^{h}},\bar{\unicode[STIX]{x1D70F}}))$
for any integer
![]() $h$
. The first map is induced by
$h$
. The first map is induced by
![]() $\unicode[STIX]{x1D70E}\mapsto \bar{\unicode[STIX]{x1D70E}}$
,
$\unicode[STIX]{x1D70E}\mapsto \bar{\unicode[STIX]{x1D70E}}$
,
![]() $\unicode[STIX]{x1D70F}\mapsto \bar{\unicode[STIX]{x1D70F}}$
and the second induced by
$\unicode[STIX]{x1D70F}\mapsto \bar{\unicode[STIX]{x1D70F}}$
and the second induced by
![]() $\unicode[STIX]{x1D70E}\mapsto \unicode[STIX]{x1D701}\bar{\unicode[STIX]{x1D70E}}$
,
$\unicode[STIX]{x1D70E}\mapsto \unicode[STIX]{x1D701}\bar{\unicode[STIX]{x1D70E}}$
,
![]() $\unicode[STIX]{x1D70F}\mapsto \bar{\unicode[STIX]{x1D70F}}$
. Let
$\unicode[STIX]{x1D70F}\mapsto \bar{\unicode[STIX]{x1D70F}}$
. Let
![]() $F_{h}=\sum _{n}a_{n}(\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})^{n}$
be the unique array of formal power series in
$F_{h}=\sum _{n}a_{n}(\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})^{n}$
be the unique array of formal power series in
![]() $\bar{R}_{h}[[\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}}]]$
centered in
$\bar{R}_{h}[[\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}}]]$
centered in
![]() $\bar{\unicode[STIX]{x1D70E}}$
associated to the polynomials
$\bar{\unicode[STIX]{x1D70E}}$
associated to the polynomials
![]() $P(\unicode[STIX]{x1D70E}^{p^{h}},\unicode[STIX]{x1D70F})$
in
$P(\unicode[STIX]{x1D70E}^{p^{h}},\unicode[STIX]{x1D70F})$
in
![]() $\bar{R}_{h}[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
via Corollary A.2. Also let
$\bar{R}_{h}[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
via Corollary A.2. Also let
![]() $\unicode[STIX]{x1D719}_{h}$
be the map
$\unicode[STIX]{x1D719}_{h}$
be the map
![]() $\bar{R}_{h}\rightarrow \bar{R}_{h+1}$
. From the formal equalities
$\bar{R}_{h}\rightarrow \bar{R}_{h+1}$
. From the formal equalities
![]() $P(\unicode[STIX]{x1D70E}^{p^{(h+1)}},F_{h+1}(\unicode[STIX]{x1D70E}))=0$
,
$P(\unicode[STIX]{x1D70E}^{p^{(h+1)}},F_{h+1}(\unicode[STIX]{x1D70E}))=0$
,
![]() $P(\unicode[STIX]{x1D70E}^{p^{h}},\unicode[STIX]{x1D719}(F_{h}(\unicode[STIX]{x1D70E})))=\unicode[STIX]{x1D719}_{h}(P(\unicode[STIX]{x1D70E}^{p^{h}},F_{h}(\unicode[STIX]{x1D70E})))=0$
and the uniqueness of
$P(\unicode[STIX]{x1D70E}^{p^{h}},\unicode[STIX]{x1D719}(F_{h}(\unicode[STIX]{x1D70E})))=\unicode[STIX]{x1D719}_{h}(P(\unicode[STIX]{x1D70E}^{p^{h}},F_{h}(\unicode[STIX]{x1D70E})))=0$
and the uniqueness of
![]() $F_{h+1}$
we deduce
$F_{h+1}$
we deduce
![]() $F_{h+1}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D719}_{h}(F_{h}(\unicode[STIX]{x1D70E}^{p}))$
.
$F_{h+1}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D719}_{h}(F_{h}(\unicode[STIX]{x1D70E}^{p}))$
.
We therefore have
 $$\begin{eqnarray}\displaystyle F_{h+1}(\unicode[STIX]{x1D70E}) & = & \displaystyle \mathop{\sum }_{n}\unicode[STIX]{x1D719}_{h}(a_{n})(\unicode[STIX]{x1D70E}^{p}-\bar{\unicode[STIX]{x1D70E}}^{p})^{n}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n}\unicode[STIX]{x1D719}_{h}(a_{n})\biggl((\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})^{p-1}+\mathop{\sum }_{j=1}^{p-1}\binom{p}{j}(\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})^{j-1}\bar{\unicode[STIX]{x1D70E}}^{p-j}\biggr)^{n}(\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})^{n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{h+1}(\unicode[STIX]{x1D70E}) & = & \displaystyle \mathop{\sum }_{n}\unicode[STIX]{x1D719}_{h}(a_{n})(\unicode[STIX]{x1D70E}^{p}-\bar{\unicode[STIX]{x1D70E}}^{p})^{n}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n}\unicode[STIX]{x1D719}_{h}(a_{n})\biggl((\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})^{p-1}+\mathop{\sum }_{j=1}^{p-1}\binom{p}{j}(\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})^{j-1}\bar{\unicode[STIX]{x1D70E}}^{p-j}\biggr)^{n}(\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})^{n}.\nonumber\end{eqnarray}$$
The expression
is a polynomial in
![]() $x$
and it is easy to show that the mapping
$x$
and it is easy to show that the mapping
![]() $x\mapsto Q(x)$
extends to a map
$x\mapsto Q(x)$
extends to a map
![]() $\bar{R}_{h+1}\langle x\rangle \rightarrow \bar{R}_{h+1}\langle x\rangle$
. We deduce that we can read off the convergence in the circle of radius
$\bar{R}_{h+1}\langle x\rangle \rightarrow \bar{R}_{h+1}\langle x\rangle$
. We deduce that we can read off the convergence in the circle of radius
![]() $1$
around
$1$
around
![]() $\bar{\unicode[STIX]{x1D70E}}$
and the values of
$\bar{\unicode[STIX]{x1D70E}}$
and the values of
![]() $F_{h+1}$
on its expression given above.
$F_{h+1}$
on its expression given above.
We remark that the norm of
![]() $Q(\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})$
in the circle of radius
$Q(\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}})$
in the circle of radius
![]() $\unicode[STIX]{x1D70C}\leqslant 1$
around
$\unicode[STIX]{x1D70C}\leqslant 1$
around
![]() $\bar{\unicode[STIX]{x1D70E}}$
is bounded by
$\bar{\unicode[STIX]{x1D70E}}$
is bounded by
![]() $\max \{\unicode[STIX]{x1D70C}^{p},|p|\}\leqslant \max \{\unicode[STIX]{x1D70C},|p|\}$
. Suppose that
$\max \{\unicode[STIX]{x1D70C}^{p},|p|\}\leqslant \max \{\unicode[STIX]{x1D70C},|p|\}$
. Suppose that
![]() $F_{h}$
converges in a circle of radius
$F_{h}$
converges in a circle of radius
![]() $\unicode[STIX]{x1D70C}$
with
$\unicode[STIX]{x1D70C}$
with
![]() $0<\unicode[STIX]{x1D70C}\leqslant 1$
around
$0<\unicode[STIX]{x1D70C}\leqslant 1$
around
![]() $\bar{\unicode[STIX]{x1D70E}}$
and in there it takes values in power-bounded elements. By the expression above, the same holds true for
$\bar{\unicode[STIX]{x1D70E}}$
and in there it takes values in power-bounded elements. By the expression above, the same holds true for
![]() $F_{h+1}$
in the circle of radius
$F_{h+1}$
in the circle of radius
![]() $\min \{\unicode[STIX]{x1D70C}|p|^{-1},1\}$
around
$\min \{\unicode[STIX]{x1D70C}|p|^{-1},1\}$
around
![]() $\bar{\unicode[STIX]{x1D70E}}$
. By induction we conclude that for a sufficiently big
$\bar{\unicode[STIX]{x1D70E}}$
. By induction we conclude that for a sufficiently big
![]() $h$
the power series
$h$
the power series
![]() $F_{h}$
converges in a circle of radius
$F_{h}$
converges in a circle of radius
![]() $\unicode[STIX]{x1D6FF}>|p|^{1/(p-1)}$
around
$\unicode[STIX]{x1D6FF}>|p|^{1/(p-1)}$
around
![]() $\bar{\unicode[STIX]{x1D70E}}$
and its values in it are power bounded. Up to rescaling indices, we suppose that this holds for
$\bar{\unicode[STIX]{x1D70E}}$
and its values in it are power bounded. Up to rescaling indices, we suppose that this holds for
![]() $h=1$
.
$h=1$
.
From the relation
![]() $F_{h+1}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D719}_{h}(F_{h}(\unicode[STIX]{x1D70E}^{p}))$
we also conclude
$F_{h+1}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D719}_{h}(F_{h}(\unicode[STIX]{x1D70E}^{p}))$
we also conclude
![]() $F_{1}(\unicode[STIX]{x1D701}\bar{\unicode[STIX]{x1D70E}})=F_{1}(\bar{\unicode[STIX]{x1D70E}})=\bar{\unicode[STIX]{x1D70F}}$
. Therefore, since
$F_{1}(\unicode[STIX]{x1D701}\bar{\unicode[STIX]{x1D70E}})=F_{1}(\bar{\unicode[STIX]{x1D70E}})=\bar{\unicode[STIX]{x1D70F}}$
. Therefore, since
![]() $|\unicode[STIX]{x1D701}_{i}-1|=|p|^{1/(p-1)}$
for all
$|\unicode[STIX]{x1D701}_{i}-1|=|p|^{1/(p-1)}$
for all
![]() $i$
, the map
$i$
, the map
is a well-defined map, inducing a homotopy between
![]() $\operatorname{id}_{X_{1}}$
and
$\operatorname{id}_{X_{1}}$
and
![]() $f_{\unicode[STIX]{x1D701}}$
, as claimed.◻
$f_{\unicode[STIX]{x1D701}}$
, as claimed.◻
It cannot be expected that all maps
![]() $X_{h+1}\rightarrow X_{h}$
are isomorphisms in
$X_{h+1}\rightarrow X_{h}$
are isomorphisms in
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
: consider, for example,
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
: consider, for example,
![]() $X_{0}=\mathbb{T}^{1}\langle \unicode[STIX]{x1D708}^{1/p}\rangle \rightarrow \mathbb{T}^{1}$
. Then
$X_{0}=\mathbb{T}^{1}\langle \unicode[STIX]{x1D708}^{1/p}\rangle \rightarrow \mathbb{T}^{1}$
. Then
![]() $X_{0}$
is a connected variety, while
$X_{0}$
is a connected variety, while
![]() $X_{1}$
is not. That said, there is a particular class of objects
$X_{1}$
is not. That said, there is a particular class of objects
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
for which this happens: this is the content of the following proposition, which nevertheless will not be used in the following.
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
for which this happens: this is the content of the following proposition, which nevertheless will not be used in the following.
We recall that a presentation
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of an object in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of an object in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
is of good reduction if the map
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
is of good reduction if the map
![]() $X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}$
has a formal model, which is an étale map over
$X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}$
has a formal model, which is an étale map over
![]() $\operatorname{Spf}K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle$
and is of potentially good reduction if this happens after base change by a separable finite field extension
$\operatorname{Spf}K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle$
and is of potentially good reduction if this happens after base change by a separable finite field extension
![]() $L/K$
.
$L/K$
.
Proposition 5.4. Let
![]() $\operatorname{char}K=0$
and let
$\operatorname{char}K=0$
and let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be a presentation of a variety in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be a presentation of a variety in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
of potentially good reduction. The maps
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
of potentially good reduction. The maps
![]() $\unicode[STIX]{x1D6EC}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}(X_{h})$
are isomorphisms in
$\unicode[STIX]{x1D6EC}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}(X_{h})$
are isomorphisms in
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
for all
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
for all
![]() $h$
.
$h$
.
Proof. If the map
![]() $X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}$
has an étale formal model, then also the map
$X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}$
has an étale formal model, then also the map
![]() $X_{h}\rightarrow \mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \,\times \,\mathbb{T}^{M}$
does. It is then sufficient to consider only the case
$X_{h}\rightarrow \mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \,\times \,\mathbb{T}^{M}$
does. It is then sufficient to consider only the case
![]() $h=0$
. Since
$h=0$
. Since
![]() $L/K$
is finite and
$L/K$
is finite and
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $\mathbb{Q}$
-algebra, by the same argument of the proof of Proposition 5.3 we can assume that
$\mathbb{Q}$
-algebra, by the same argument of the proof of Proposition 5.3 we can assume that
![]() $\mathop{\varprojlim }\nolimits_{h}X_{h}$
has good reduction. Also, by means of Theorem 5.1 and the Cancellation Theorem [Reference AyoubAyo15, Corollary 2.5.49], we can equally prove the statement in the stable category
$\mathop{\varprojlim }\nolimits_{h}X_{h}$
has good reduction. Also, by means of Theorem 5.1 and the Cancellation Theorem [Reference AyoubAyo15, Corollary 2.5.49], we can equally prove the statement in the stable category
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K)$
defined in [Reference AyoubAyo15, Definition 1.3.19].
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K)$
defined in [Reference AyoubAyo15, Definition 1.3.19].
Let
![]() $\mathfrak{X}_{0}\rightarrow \operatorname{Spf}K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle$
be a formal model of the map
$\mathfrak{X}_{0}\rightarrow \operatorname{Spf}K^{\circ }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle$
be a formal model of the map
![]() $X_{0}\rightarrow \mathbb{T}^{n}\,\times \,\mathbb{T}^{m}$
. We let
$X_{0}\rightarrow \mathbb{T}^{n}\,\times \,\mathbb{T}^{m}$
. We let
![]() $\bar{X}_{0}$
be the special fiber over the residue field
$\bar{X}_{0}$
be the special fiber over the residue field
![]() $k$
of
$k$
of
![]() $K$
. The variety
$K$
. The variety
![]() $X_{1}$
has also a smooth formal model
$X_{1}$
has also a smooth formal model
![]() $\mathfrak{X}_{1}$
whose special fiber is
$\mathfrak{X}_{1}$
whose special fiber is
![]() $\bar{X}_{1}$
. By definition, the natural map
$\bar{X}_{1}$
. By definition, the natural map
![]() $\bar{X}_{1}\rightarrow \bar{X}_{0}$
is the push-out of the (relative) Frobenius map
$\bar{X}_{1}\rightarrow \bar{X}_{0}$
is the push-out of the (relative) Frobenius map
![]() $\mathbb{A}_{k}^{\dim X}\rightarrow \mathbb{A}_{k}^{\dim X}$
, which is isomorphic to the relative Frobenius map, and hence an isomorphism of correspondences as
$\mathbb{A}_{k}^{\dim X}\rightarrow \mathbb{A}_{k}^{\dim X}$
, which is isomorphic to the relative Frobenius map, and hence an isomorphism of correspondences as
![]() $p$
is invertible in
$p$
is invertible in
![]() $\unicode[STIX]{x1D6EC}$
. We conclude that
$\unicode[STIX]{x1D6EC}$
. We conclude that
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(\bar{X}_{1})\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}(\bar{X}_{0})$
is an isomorphism in
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(\bar{X}_{1})\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}(\bar{X}_{0})$
is an isomorphism in
![]() $\mathbf{DM}_{\acute{\text{e}}\text{t}}(k)$
.
$\mathbf{DM}_{\acute{\text{e}}\text{t}}(k)$
.
Let
![]() $\mathbf{FormDA}_{\acute{\text{e}}\text{t}}(K^{\circ })$
be the stable category of motives of formal varieties
$\mathbf{FormDA}_{\acute{\text{e}}\text{t}}(K^{\circ })$
be the stable category of motives of formal varieties
![]() $\mathbf{FSH}_{\mathfrak{M}}(K^{\circ })$
defined in [Reference AyoubAyo15, Definition 1.4.15] associated to the model category
$\mathbf{FSH}_{\mathfrak{M}}(K^{\circ })$
defined in [Reference AyoubAyo15, Definition 1.4.15] associated to the model category
![]() $\mathfrak{M}=\mathbf{Ch}(\unicode[STIX]{x1D6EC}\boldsymbol{-Mod})$
. Using [Reference AyoubAyo14a, Theorem B.1] we deduce that the map
$\mathfrak{M}=\mathbf{Ch}(\unicode[STIX]{x1D6EC}\boldsymbol{-Mod})$
. Using [Reference AyoubAyo14a, Theorem B.1] we deduce that the map
![]() $\unicode[STIX]{x1D6EC}(\bar{X}_{1})\rightarrow \unicode[STIX]{x1D6EC}(\bar{X}_{0})$
is an isomorphism in
$\unicode[STIX]{x1D6EC}(\bar{X}_{1})\rightarrow \unicode[STIX]{x1D6EC}(\bar{X}_{0})$
is an isomorphism in
![]() $\mathbf{DA}_{\acute{\text{e}}\text{t}}(k)$
as is its image via the following functor (see [Reference AyoubAyo15, Remark 1.4.30]) induced by the special fiber functor and the generic fiber functor:
$\mathbf{DA}_{\acute{\text{e}}\text{t}}(k)$
as is its image via the following functor (see [Reference AyoubAyo15, Remark 1.4.30]) induced by the special fiber functor and the generic fiber functor:
This morphism is precisely the map
![]() $\unicode[STIX]{x1D6EC}(X_{1})\rightarrow \unicode[STIX]{x1D6EC}(X_{0})$
proving the claim.◻
$\unicode[STIX]{x1D6EC}(X_{1})\rightarrow \unicode[STIX]{x1D6EC}(X_{0})$
proving the claim.◻
We are now ready to present the main result of this section.
Theorem 5.5. Let
![]() $\operatorname{char}K=0$
. The functor
$\operatorname{char}K=0$
. The functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }:\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
has a left adjoint
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }:\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
has a left adjoint
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}$
and the counit map
$\mathbb{L}\unicode[STIX]{x1D704}_{!}$
and the counit map
![]() $\operatorname{id}\rightarrow \mathbb{L}\unicode[STIX]{x1D704}_{!}\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
is invertible. Whenever
$\operatorname{id}\rightarrow \mathbb{L}\unicode[STIX]{x1D704}_{!}\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
is invertible. Whenever
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
is an object of
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
is an object of
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
then
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
then
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X)\cong \unicode[STIX]{x1D6EC}(X_{h})$
for a sufficiently large index
$\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X)\cong \unicode[STIX]{x1D6EC}(X_{h})$
for a sufficiently large index
![]() $h$
. If moreover
$h$
. If moreover
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
is of potentially good reduction, then
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
is of potentially good reduction, then
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X)\cong \unicode[STIX]{x1D6EC}(X_{0})$
.
$\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X)\cong \unicode[STIX]{x1D6EC}(X_{0})$
.
Proof. We start by proving that the canonical map
is an isomorphism, for every
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
and for
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
and for
![]() $\bar{h}$
big enough. By Proposition 4.5, it suffices to prove that the natural map
$\bar{h}$
big enough. By Proposition 4.5, it suffices to prove that the natural map
is an isomorphism for some
![]() $\bar{h}$
. This follows from Proposition 5.3 since the maps
$\bar{h}$
. This follows from Proposition 5.3 since the maps
![]() $\unicode[STIX]{x1D6EC}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}(X_{h})$
are isomorphisms if
$\unicode[STIX]{x1D6EC}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}(X_{h})$
are isomorphisms if
![]() $h\geqslant \bar{h}$
for some big enough
$h\geqslant \bar{h}$
for some big enough
![]() $\bar{h}$
. In case
$\bar{h}$
. In case
![]() $\mathop{\varprojlim }\nolimits_{h}X_{h}$
is of potentially good reduction, then Proposition 5.4 ensures that we can choose
$\mathop{\varprojlim }\nolimits_{h}X_{h}$
is of potentially good reduction, then Proposition 5.4 ensures that we can choose
![]() $\bar{h}=0$
.
$\bar{h}=0$
.
We conclude that the subcategory
![]() $\mathbf{T}$
of
$\mathbf{T}$
of
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
formed by the objects
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
formed by the objects
![]() $M$
such that the functor
$M$
such that the functor
![]() $N\mapsto \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)(M,\mathbb{L}\unicode[STIX]{x1D704}^{\ast }N)$
is corepresentable contains all motives
$N\mapsto \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)(M,\mathbb{L}\unicode[STIX]{x1D704}^{\ast }N)$
is corepresentable contains all motives
![]() $\unicode[STIX]{x1D6EC}(X)$
with
$\unicode[STIX]{x1D6EC}(X)$
with
![]() $X$
any object of
$X$
any object of
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Since these objects form a set of compact generators of
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Since these objects form a set of compact generators of
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
by Proposition 3.18, we deduce the existence of the functor
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K)$
by Proposition 3.18, we deduce the existence of the functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}$
by Lemma 5.6.
$\mathbb{L}\unicode[STIX]{x1D704}_{!}$
by Lemma 5.6.
The formula
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\cong \operatorname{id}$
is a formal consequence of the fact that
$\mathbb{L}\unicode[STIX]{x1D704}_{!}\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\cong \operatorname{id}$
is a formal consequence of the fact that
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}$
is the left adjoint of a fully faithful functor
$\mathbb{L}\unicode[STIX]{x1D704}_{!}$
is the left adjoint of a fully faithful functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
(see Proposition 3.17).◻
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
(see Proposition 3.17).◻
Lemma 5.6. Let
![]() $\mathfrak{G}:\mathbf{T}\rightarrow \mathbf{T}^{\prime }$
be a triangulated functor of triangulated categories. The full subcategory
$\mathfrak{G}:\mathbf{T}\rightarrow \mathbf{T}^{\prime }$
be a triangulated functor of triangulated categories. The full subcategory
![]() $\mathbf{C}$
of
$\mathbf{C}$
of
![]() $\mathbf{T}^{\prime }$
of objects
$\mathbf{T}^{\prime }$
of objects
![]() $M$
such that the functor
$M$
such that the functor
![]() $a_{M}:N\mapsto \operatorname{Hom}(M,\mathfrak{G}N)$
is corepresentable is closed under cones and small direct sums.
$a_{M}:N\mapsto \operatorname{Hom}(M,\mathfrak{G}N)$
is corepresentable is closed under cones and small direct sums.
Proof. For any object
![]() $M$
in
$M$
in
![]() $\mathbf{C}$
we denote by
$\mathbf{C}$
we denote by
![]() $\mathfrak{F}M$
the object corepresenting the functor
$\mathfrak{F}M$
the object corepresenting the functor
![]() $a_{M}$
. Now let
$a_{M}$
. Now let
![]() $\{M_{i}\}_{i\in I}$
be a set of objects in
$\{M_{i}\}_{i\in I}$
be a set of objects in
![]() $\mathbf{C}$
. It is immediate to check that
$\mathbf{C}$
. It is immediate to check that
![]() $\bigoplus _{i}\mathfrak{F}M_{i}$
corepresents the functor
$\bigoplus _{i}\mathfrak{F}M_{i}$
corepresents the functor
![]() $a_{\bigoplus _{i}M_{i}}$
.
$a_{\bigoplus _{i}M_{i}}$
.
Now let
![]() $M_{1}$
,
$M_{1}$
,
![]() $M_{2}$
be two objects of
$M_{2}$
be two objects of
![]() $\mathbf{C}$
and
$\mathbf{C}$
and
![]() $f:M_{1}\rightarrow M_{2}$
be a map between them. There are canonical maps
$f:M_{1}\rightarrow M_{2}$
be a map between them. There are canonical maps
![]() $\unicode[STIX]{x1D702}_{i}:M_{i}\rightarrow \mathfrak{G}\mathfrak{F}M_{i}$
induced by the identity
$\unicode[STIX]{x1D702}_{i}:M_{i}\rightarrow \mathfrak{G}\mathfrak{F}M_{i}$
induced by the identity
![]() $\mathfrak{F}M_{i}\rightarrow \mathfrak{F}M_{i}$
and the universal property of
$\mathfrak{F}M_{i}\rightarrow \mathfrak{F}M_{i}$
and the universal property of
![]() $\mathfrak{F}M_{i}$
. By composing with
$\mathfrak{F}M_{i}$
. By composing with
![]() $\unicode[STIX]{x1D702}_{2}$
we obtain a morphism
$\unicode[STIX]{x1D702}_{2}$
we obtain a morphism
![]() $\operatorname{Hom}(M_{1},M_{2})\rightarrow \operatorname{Hom}(M_{1},\mathfrak{G}\mathfrak{F}M_{2})\cong \operatorname{Hom}(\mathfrak{F}M_{1},\mathfrak{F}M_{2})$
sending
$\operatorname{Hom}(M_{1},M_{2})\rightarrow \operatorname{Hom}(M_{1},\mathfrak{G}\mathfrak{F}M_{2})\cong \operatorname{Hom}(\mathfrak{F}M_{1},\mathfrak{F}M_{2})$
sending
![]() $f$
to a map
$f$
to a map
![]() $\mathfrak{F}f$
. Let
$\mathfrak{F}f$
. Let
![]() $C$
be the cone of
$C$
be the cone of
![]() $f$
and
$f$
and
![]() $D$
be the cone of
$D$
be the cone of
![]() $\mathfrak{F}f$
. We claim that
$\mathfrak{F}f$
. We claim that
![]() $D$
represents
$D$
represents
![]() $a_{C}$
. From the triangulated structure we obtain a map of distinguished triangles
$a_{C}$
. From the triangulated structure we obtain a map of distinguished triangles

inducing for any object
![]() $N$
of
$N$
of
![]() $\mathbf{T}$
the following maps of long exact sequences.
$\mathbf{T}$
the following maps of long exact sequences.

Since the vertical compositions are isomorphisms for
![]() $M_{1}$
and
$M_{1}$
and
![]() $M_{2}$
we deduce that they all are, proving that
$M_{2}$
we deduce that they all are, proving that
![]() $D$
corepresents
$D$
corepresents
![]() $a_{C}$
, as desired.◻
$a_{C}$
, as desired.◻
We remark that we used the fact that
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $\mathbb{Q}$
-algebra at least twice in the proof of Theorem 5.5: to allow for field extensions and correspondences using Theorem 5.1 as well as to invert the map defined by multiplication by
$\mathbb{Q}$
-algebra at least twice in the proof of Theorem 5.5: to allow for field extensions and correspondences using Theorem 5.1 as well as to invert the map defined by multiplication by
![]() $p$
.
$p$
.
The following fact is a straightforward corollary of Theorem 5.5.
Proposition 5.7. Let
![]() $\operatorname{char}K=0$
. The motive
$\operatorname{char}K=0$
. The motive
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(\widehat{\mathbb{B}}^{1})$
is isomorphic to
$\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(\widehat{\mathbb{B}}^{1})$
is isomorphic to
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Proof. In order to prove the claim, it suffices to prove that
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(\widehat{\mathbb{B}}^{1})\cong \unicode[STIX]{x1D6EC}(\mathbb{B}^{1})$
. This follows from Proposition 2.13 and the description of
$\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(\widehat{\mathbb{B}}^{1})\cong \unicode[STIX]{x1D6EC}(\mathbb{B}^{1})$
. This follows from Proposition 2.13 and the description of
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}$
given in Theorem 5.5.◻
$\mathbb{L}\unicode[STIX]{x1D704}_{!}$
given in Theorem 5.5.◻
We recall that all the homotopy categories we consider are monoidal (see [Reference AyoubAyo07, Propositions 4.2.76 and 4.4.62]), and the tensor product
![]() $\unicode[STIX]{x1D6EC}(X)\,\otimes \,\unicode[STIX]{x1D6EC}(X^{\prime })$
of two motives associated to varieties
$\unicode[STIX]{x1D6EC}(X)\,\otimes \,\unicode[STIX]{x1D6EC}(X^{\prime })$
of two motives associated to varieties
![]() $X$
and
$X$
and
![]() $Y$
coincides with
$Y$
coincides with
![]() $\unicode[STIX]{x1D6EC}(X\,\times \,X^{\prime })$
. The unit object is obviously the motive
$\unicode[STIX]{x1D6EC}(X\,\times \,X^{\prime })$
. The unit object is obviously the motive
![]() $\unicode[STIX]{x1D6EC}$
. Due to the explicit description of the functor
$\unicode[STIX]{x1D6EC}$
. Due to the explicit description of the functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}$
we constructed above, it is easy to prove that it respects the monoidal structures.
$\mathbb{L}\unicode[STIX]{x1D704}_{!}$
we constructed above, it is easy to prove that it respects the monoidal structures.
Proposition 5.8. Let
![]() $\operatorname{char}K=0$
. The functor
$\operatorname{char}K=0$
. The functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}:\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)\rightarrow \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
is a monoidal functor.
$\mathbb{L}\unicode[STIX]{x1D704}_{!}:\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)\rightarrow \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
is a monoidal functor.
Proof. Since
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}$
is the left adjoint of a monoidal functor
$\mathbb{L}\unicode[STIX]{x1D704}_{!}$
is the left adjoint of a monoidal functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
there is a canonical natural transformation of bifunctors
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
there is a canonical natural transformation of bifunctors
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}(M\,\otimes \,M^{\prime })\rightarrow \mathbb{L}\unicode[STIX]{x1D704}_{!}M\,\otimes \,\mathbb{L}\unicode[STIX]{x1D704}_{!}M^{\prime }$
. In order to prove it is an isomorphism, it suffices to check it on a set of generators of
$\mathbb{L}\unicode[STIX]{x1D704}_{!}(M\,\otimes \,M^{\prime })\rightarrow \mathbb{L}\unicode[STIX]{x1D704}_{!}M\,\otimes \,\mathbb{L}\unicode[STIX]{x1D704}_{!}M^{\prime }$
. In order to prove it is an isomorphism, it suffices to check it on a set of generators of
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}$
such as motives of semi-perfectoid varieties
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}$
such as motives of semi-perfectoid varieties
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
,
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
,
![]() $X^{\prime }=\mathop{\varprojlim }\nolimits_{h}X_{h}^{\prime }$
. Up to rescaling, we can suppose that
$X^{\prime }=\mathop{\varprojlim }\nolimits_{h}X_{h}^{\prime }$
. Up to rescaling, we can suppose that
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X)=\unicode[STIX]{x1D6EC}(X_{0})$
and
$\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X)=\unicode[STIX]{x1D6EC}(X_{0})$
and
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X^{\prime })=\unicode[STIX]{x1D6EC}(X_{0}^{\prime })$
by Theorem 5.5. In this case, by definition of the tensor product, we obtain the following isomorphisms:
$\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X^{\prime })=\unicode[STIX]{x1D6EC}(X_{0}^{\prime })$
by Theorem 5.5. In this case, by definition of the tensor product, we obtain the following isomorphisms:
proving our claim. ◻
The following proposition can be considered to be a refinement of Theorem 5.5.
Proposition 5.9. Let
![]() $\operatorname{char}K=0$
. The functor
$\operatorname{char}K=0$
. The functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}$
factors through
$\mathbb{L}\unicode[STIX]{x1D704}_{!}$
factors through
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}$
and the image of the functor
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}$
and the image of the functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }:\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
lies in the subcategory of
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }:\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)$
lies in the subcategory of
![]() $\widehat{\mathbb{B}}^{1}$
-local objects. In particular, the triangulated adjunction
$\widehat{\mathbb{B}}^{1}$
-local objects. In particular, the triangulated adjunction
restricts to a triangulated adjunction
Proof. By Propositions 5.7 and 5.8,
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}$
is a monoidal functor sending
$\mathbb{L}\unicode[STIX]{x1D704}_{!}$
is a monoidal functor sending
![]() $\unicode[STIX]{x1D6EC}(\widehat{\mathbb{B}}^{1})$
to
$\unicode[STIX]{x1D6EC}(\widehat{\mathbb{B}}^{1})$
to
![]() $\unicode[STIX]{x1D6EC}$
. This proves the first claim.
$\unicode[STIX]{x1D6EC}$
. This proves the first claim.
From the adjunction
![]() $(\mathbb{L}\unicode[STIX]{x1D704}_{!},\mathbb{L}\unicode[STIX]{x1D704}^{\ast })$
we then obtain the following isomorphisms, for any
$(\mathbb{L}\unicode[STIX]{x1D704}_{!},\mathbb{L}\unicode[STIX]{x1D704}^{\ast })$
we then obtain the following isomorphisms, for any
![]() $X$
in
$X$
in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
and any
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
and any
![]() $M$
in
$M$
in
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
:
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
:
 $$\begin{eqnarray}\displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)(\unicode[STIX]{x1D6EC}(X\,\times \,\widehat{\mathbb{B}}^{1}),\mathbb{L}\unicode[STIX]{x1D704}^{\ast }M) & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)(\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X)\,\otimes \,\unicode[STIX]{x1D6EC},M)\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)(\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X),M)\nonumber\\ \displaystyle & \cong & \displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)(\unicode[STIX]{x1D6EC}(X),\mathbb{L}\unicode[STIX]{x1D704}^{\ast }M),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)(\unicode[STIX]{x1D6EC}(X\,\times \,\widehat{\mathbb{B}}^{1}),\mathbb{L}\unicode[STIX]{x1D704}^{\ast }M) & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)(\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X)\,\otimes \,\unicode[STIX]{x1D6EC},M)\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)(\mathbb{L}\unicode[STIX]{x1D704}_{!}\unicode[STIX]{x1D6EC}(X),M)\nonumber\\ \displaystyle & \cong & \displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K)(\unicode[STIX]{x1D6EC}(X),\mathbb{L}\unicode[STIX]{x1D704}^{\ast }M),\nonumber\end{eqnarray}$$
proving the second claim. ◻
Remark 5.10. In the statement of the proposition above, we make a slight abuse of notation when denoting with
![]() $(\mathbb{L}\unicode[STIX]{x1D704}_{!},\mathbb{L}\unicode[STIX]{x1D704}^{\ast })$
both adjoint pairs. It will be clear from the context which one we consider at each instance.
$(\mathbb{L}\unicode[STIX]{x1D704}_{!},\mathbb{L}\unicode[STIX]{x1D704}^{\ast })$
both adjoint pairs. It will be clear from the context which one we consider at each instance.
6 The de-perfectoidification functor in characteristic
 $p$
$p$
We now consider the case of a perfectoid field
![]() $K^{\flat }$
of characteristic
$K^{\flat }$
of characteristic
![]() $p$
and try to generalize the results of § 5. We will need to perform an extra localization on the model structure, and in return we will prove a stronger result. In this section, we always assume that the base perfectoid field has characteristic
$p$
and try to generalize the results of § 5. We will need to perform an extra localization on the model structure, and in return we will prove a stronger result. In this section, we always assume that the base perfectoid field has characteristic
![]() $p$
. In order to emphasize this hypothesis, we denote it with
$p$
. In order to emphasize this hypothesis, we denote it with
![]() $K^{\flat }$
.
$K^{\flat }$
.
In positive characteristic, we are not able to prove Theorem 5.1 as it is stated, and it is therefore not clear that the maps
![]() $X_{h+1}\rightarrow X_{h}$
associated to an object
$X_{h+1}\rightarrow X_{h}$
associated to an object
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
are isomorphisms in
$\widehat{\text{Rig}}\operatorname{Sm}$
are isomorphisms in
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
for a sufficiently big
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
for a sufficiently big
![]() $h$
. In order to overcome this obstacle, we localize our model category further.
$h$
. In order to overcome this obstacle, we localize our model category further.
For any variety
![]() $X$
over
$X$
over
![]() $K^{\flat }$
we denote by
$K^{\flat }$
we denote by
![]() $X^{(1)}$
the pullback of
$X^{(1)}$
the pullback of
![]() $X$
over the Frobenius map
$X$
over the Frobenius map
![]() $\unicode[STIX]{x1D6F7}:K^{\flat }\rightarrow K^{\flat }$
,
$\unicode[STIX]{x1D6F7}:K^{\flat }\rightarrow K^{\flat }$
,
![]() $x\mapsto x^{p}$
. The absolute Frobenius morphism induces a
$x\mapsto x^{p}$
. The absolute Frobenius morphism induces a
![]() $K^{\flat }$
-linear map
$K^{\flat }$
-linear map
![]() $X\rightarrow X^{(1)}$
. Since
$X\rightarrow X^{(1)}$
. Since
![]() $K^{\flat }$
is perfect, we can also denote by
$K^{\flat }$
is perfect, we can also denote by
![]() $X^{(-1)}$
the pullback of
$X^{(-1)}$
the pullback of
![]() $X$
over the inverse of the Frobenius map
$X$
over the inverse of the Frobenius map
![]() $\unicode[STIX]{x1D6F7}^{-1}:K^{\flat }\rightarrow K^{\flat }$
and
$\unicode[STIX]{x1D6F7}^{-1}:K^{\flat }\rightarrow K^{\flat }$
and
![]() $X\cong (X^{(-1)})^{(1)}$
. There is, in particular, a canonical map
$X\cong (X^{(-1)})^{(1)}$
. There is, in particular, a canonical map
![]() $X^{(-1)}\rightarrow X$
, which is isomorphic to the map
$X^{(-1)}\rightarrow X$
, which is isomorphic to the map
![]() $X^{\prime }\rightarrow X$
induced by the absolute Frobenius, where we denote by
$X^{\prime }\rightarrow X$
induced by the absolute Frobenius, where we denote by
![]() $X^{\prime }$
the same variety
$X^{\prime }$
the same variety
![]() $X$
endowed with the structure map
$X$
endowed with the structure map
![]() $X\rightarrow \operatorname{Spa}K\xrightarrow[{}]{\unicode[STIX]{x1D6F7}}\operatorname{Spa}K$
.
$X\rightarrow \operatorname{Spa}K\xrightarrow[{}]{\unicode[STIX]{x1D6F7}}\operatorname{Spa}K$
.
Proposition 6.1. The model category
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K^{\flat })$
admits a left Bousfield localization denoted by
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K^{\flat })$
admits a left Bousfield localization denoted by
![]() $\mathbf{Ch}_{\text{Frob}\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K^{\flat })$
with respect to the set
$\mathbf{Ch}_{\text{Frob}\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K^{\flat })$
with respect to the set
![]() $S_{\operatorname{Frob}}$
of relative Frobenius maps
$S_{\operatorname{Frob}}$
of relative Frobenius maps
![]() $\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}(X^{(-1)})[i]\rightarrow \unicode[STIX]{x1D6EC}(X)[i]$
as
$\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}(X^{(-1)})[i]\rightarrow \unicode[STIX]{x1D6EC}(X)[i]$
as
![]() $X$
varies in
$X$
varies in
![]() $\operatorname{RigSm}$
and
$\operatorname{RigSm}$
and
![]() $i$
varies in
$i$
varies in
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Proof. Since by [Reference AyoubAyo07, Proposition 4.4.31] the
![]() $\unicode[STIX]{x1D70F}$
-localization coincides with the Bousfield localization with respect to a set, we conclude by [Reference AyoubAyo07, Theorem 4.2.71] that the model category
$\unicode[STIX]{x1D70F}$
-localization coincides with the Bousfield localization with respect to a set, we conclude by [Reference AyoubAyo07, Theorem 4.2.71] that the model category
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K^{\flat })$
is still left proper and cellular. We can then apply [Reference HirschhornHir03, Theorem 4.1.1].◻
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K^{\flat })$
is still left proper and cellular. We can then apply [Reference HirschhornHir03, Theorem 4.1.1].◻
Definition 6.2. We denote by
![]() $\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat },\unicode[STIX]{x1D6EC})$
the homotopy category associated to
$\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat },\unicode[STIX]{x1D6EC})$
the homotopy category associated to
![]() $\mathbf{Ch}_{\text{Frob}\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K^{\flat })$
. We omit
$\mathbf{Ch}_{\text{Frob}\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K^{\flat })$
. We omit
![]() $\unicode[STIX]{x1D6EC}$
whenever the context allows it. The image of a rigid variety
$\unicode[STIX]{x1D6EC}$
whenever the context allows it. The image of a rigid variety
![]() $X$
in this category is denoted by
$X$
in this category is denoted by
![]() $\unicode[STIX]{x1D6EC}(X)$
.
$\unicode[STIX]{x1D6EC}(X)$
.
The triangulated category
![]() $\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
is canonically isomorphic to the full triangulated subcategory of
$\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
is canonically isomorphic to the full triangulated subcategory of
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
formed by
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
formed by
![]() $\operatorname{Frob}$
-local objects, i.e., objects that are local with respect to the maps in
$\operatorname{Frob}$
-local objects, i.e., objects that are local with respect to the maps in
![]() $S_{\operatorname{Frob}}$
. Modulo this identification, there is an obvious functor
$S_{\operatorname{Frob}}$
. Modulo this identification, there is an obvious functor
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })\rightarrow \mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
associating to
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })\rightarrow \mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
associating to
![]() ${\mathcal{F}}$
a
${\mathcal{F}}$
a
![]() $\operatorname{Frob}$
-local object
$\operatorname{Frob}$
-local object
![]() $C^{\operatorname{Frob}}{\mathcal{F}}$
.
$C^{\operatorname{Frob}}{\mathcal{F}}$
.
Inverting Frobenius morphisms is enough to obtain an analog of Theorem 5.1 in characteristic
![]() $p$
.
$p$
.
Theorem 6.3 [Reference VezzaniVez17].
Let
![]() $\operatorname{char}K^{\flat }=p$
. The functors
$\operatorname{char}K^{\flat }=p$
. The functors
![]() $(a_{\text{tr}},o_{\text{tr}})$
induce an equivalence of triangulated categories:
$(a_{\text{tr}},o_{\text{tr}})$
induce an equivalence of triangulated categories:
Remark 6.4. The proof of the statement above uses in a crucial way the fact that the ring of coefficients
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $\mathbb{Q}$
-algebra.
$\mathbb{Q}$
-algebra.
We now investigate the relations between the category
![]() $\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
we have just defined, and the other categories of motives introduced so far.
$\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
we have just defined, and the other categories of motives introduced so far.
Proposition 6.5. Let
![]() $X_{0}$
be in
$X_{0}$
be in
![]() $\operatorname{RigSm}/K^{\flat }$
endowed with an étale map
$\operatorname{RigSm}/K^{\flat }$
endowed with an étale map
![]() $X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}=\operatorname{Spa}(K^{\flat }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle )$
. The map
$X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}=\operatorname{Spa}(K^{\flat }\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle )$
. The map
![]() $X_{1}=X_{0}\,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p}\rangle \rightarrow X_{0}$
is invertible in
$X_{1}=X_{0}\,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p}\rangle \rightarrow X_{0}$
is invertible in
![]() $\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
.
$\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
.
Proof. The map of the claim is a factor of
![]() $X_{0}\,\times _{(\mathbb{B}^{N}\times \mathbb{B}^{M})}\,(\mathbb{B}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p}\rangle \,\times \,\mathbb{B}^{M}\langle \text{}\underline{\unicode[STIX]{x1D708}}^{1/p}\rangle )\rightarrow X_{0}$
, which is isomorphic to the relative Frobenius map
$X_{0}\,\times _{(\mathbb{B}^{N}\times \mathbb{B}^{M})}\,(\mathbb{B}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p}\rangle \,\times \,\mathbb{B}^{M}\langle \text{}\underline{\unicode[STIX]{x1D708}}^{1/p}\rangle )\rightarrow X_{0}$
, which is isomorphic to the relative Frobenius map
![]() $X_{0}^{(-1)}\rightarrow X_{0}$
(see for example [Reference Gabber and RameroGR03, Theorem 3.5.13]). If we consider the diagram
$X_{0}^{(-1)}\rightarrow X_{0}$
(see for example [Reference Gabber and RameroGR03, Theorem 3.5.13]). If we consider the diagram
we conclude that the two compositions
![]() $ba$
and
$ba$
and
![]() $cb$
are isomorphisms, and hence
$cb$
are isomorphisms, and hence
![]() $c$
is also an isomorphism, as claimed.◻
$c$
is also an isomorphism, as claimed.◻
Proposition 6.6. The image via
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
of a
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
of a
![]() $\operatorname{Frob}$
-local object of
$\operatorname{Frob}$
-local object of
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
is
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
is
![]() $\widehat{\mathbb{B}}^{1}$
-local. In particular, the functor
$\widehat{\mathbb{B}}^{1}$
-local. In particular, the functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
restricts to a functor
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
restricts to a functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }:\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K^{\flat })$
.
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }:\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K^{\flat })$
.
Proof. Let
![]() $X^{\prime }=\mathop{\varprojlim }\nolimits_{h}X_{h}^{\prime }$
be in
$X^{\prime }=\mathop{\varprojlim }\nolimits_{h}X_{h}^{\prime }$
be in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. We consider the object
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. We consider the object
![]() $X^{\prime }\,\times \,\widehat{\mathbb{B}}^{1}=\mathop{\varprojlim }\nolimits_{h}(X_{h}^{\prime }\,\times \,X_{h})$
, where we use the description
$X^{\prime }\,\times \,\widehat{\mathbb{B}}^{1}=\mathop{\varprojlim }\nolimits_{h}(X_{h}^{\prime }\,\times \,X_{h})$
, where we use the description
![]() $\widehat{\mathbb{B}}^{1}=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of Proposition 2.13. Let
$\widehat{\mathbb{B}}^{1}=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of Proposition 2.13. Let
![]() $M$
be a
$M$
be a
![]() $\operatorname{Frob}$
-local object of
$\operatorname{Frob}$
-local object of
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
. From Propositions 4.5 and 6.5, we then deduce the following isomorphisms:
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
. From Propositions 4.5 and 6.5, we then deduce the following isomorphisms:
 $$\begin{eqnarray}\displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K^{\flat })(X^{\prime }\,\times \,\widehat{\mathbb{B}}^{1},\mathbb{L}\unicode[STIX]{x1D704}^{\ast }M) & \cong & \displaystyle \underset{h}{\varinjlim }\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(X_{h}^{\prime }\,\times \,X_{h},M)\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(X_{0}^{\prime }\,\times \,\mathbb{B}^{1},M)\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(X_{0}^{\prime },M)\nonumber\\ \displaystyle & \cong & \displaystyle \underset{h}{\varinjlim }\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(X_{h}^{\prime },M)\nonumber\\ \displaystyle & \cong & \displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K^{\flat })(X^{\prime },\mathbb{L}\unicode[STIX]{x1D704}^{\ast }M),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K^{\flat })(X^{\prime }\,\times \,\widehat{\mathbb{B}}^{1},\mathbb{L}\unicode[STIX]{x1D704}^{\ast }M) & \cong & \displaystyle \underset{h}{\varinjlim }\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(X_{h}^{\prime }\,\times \,X_{h},M)\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(X_{0}^{\prime }\,\times \,\mathbb{B}^{1},M)\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(X_{0}^{\prime },M)\nonumber\\ \displaystyle & \cong & \displaystyle \underset{h}{\varinjlim }\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(X_{h}^{\prime },M)\nonumber\\ \displaystyle & \cong & \displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K^{\flat })(X^{\prime },\mathbb{L}\unicode[STIX]{x1D704}^{\ast }M),\nonumber\end{eqnarray}$$
proving the claim. ◻
We remark that in positive characteristic the perfection
![]() $\operatorname{Perf}:X\mapsto \varprojlim X^{(-i)}$
is functorial. This makes the description of various functors a lot easier. We recall that we denote by
$\operatorname{Perf}:X\mapsto \varprojlim X^{(-i)}$
is functorial. This makes the description of various functors a lot easier. We recall that we denote by
the adjoint pair induced by the inclusion of categories
![]() $j:\operatorname{PerfSm}\rightarrow \widehat{\text{Rig}}\operatorname{Sm}$
.
$j:\operatorname{PerfSm}\rightarrow \widehat{\text{Rig}}\operatorname{Sm}$
.
Proposition 6.7. The perfection functor
![]() $\operatorname{Perf}:\widehat{\text{Rig}}\operatorname{Sm}\rightarrow \operatorname{PerfSm}$
induces an adjunction
$\operatorname{Perf}:\widehat{\text{Rig}}\operatorname{Sm}\rightarrow \operatorname{PerfSm}$
induces an adjunction
and
![]() $\mathbb{L}\operatorname{Perf}^{\ast }$
factors through
$\mathbb{L}\operatorname{Perf}^{\ast }$
factors through
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K^{\flat })\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K^{\flat })$
. Moreover, the functor
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K^{\flat })\rightarrow \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K^{\flat })$
. Moreover, the functor
![]() $\mathbb{L}\operatorname{Perf}^{\ast }$
coincides with
$\mathbb{L}\operatorname{Perf}^{\ast }$
coincides with
![]() $\mathbb{R}j_{\ast }$
on
$\mathbb{R}j_{\ast }$
on
![]() $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K^{\flat })$
.
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K^{\flat })$
.
Proof. The perfection functor is continuous with respect to the étale topology and maps
![]() $\mathbb{B}^{1}$
and
$\mathbb{B}^{1}$
and
![]() $\widehat{\mathbb{B}}^{1}$
to
$\widehat{\mathbb{B}}^{1}$
to
![]() $\widehat{\mathbb{B}}^{1}$
, and hence the first claim.
$\widehat{\mathbb{B}}^{1}$
, and hence the first claim.
We now consider the functors
![]() $j:\operatorname{PerfSm}\rightarrow \widehat{\text{Rig}}\operatorname{Sm}$
and
$j:\operatorname{PerfSm}\rightarrow \widehat{\text{Rig}}\operatorname{Sm}$
and
![]() $\operatorname{Perf}:\widehat{\text{Rig}}\operatorname{Sm}\rightarrow \operatorname{PerfSm}$
. They induce two Quillen pairs
$\operatorname{Perf}:\widehat{\text{Rig}}\operatorname{Sm}\rightarrow \operatorname{PerfSm}$
. They induce two Quillen pairs
![]() $(j^{\ast },j_{\ast })$
and
$(j^{\ast },j_{\ast })$
and
![]() $(\operatorname{Perf}^{\ast },\operatorname{Perf}_{\ast })$
on the associated
$(\operatorname{Perf}^{\ast },\operatorname{Perf}_{\ast })$
on the associated
![]() $(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
-localized model categories of complexes. Since
$(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
-localized model categories of complexes. Since
![]() $\operatorname{Perf}$
is a right adjoint of
$\operatorname{Perf}$
is a right adjoint of
![]() $j$
we deduce that
$j$
we deduce that
![]() $\operatorname{Perf}^{\ast }$
is a right adjoint of
$\operatorname{Perf}^{\ast }$
is a right adjoint of
![]() $j^{\ast }$
, and hence we obtain an isomorphism
$j^{\ast }$
, and hence we obtain an isomorphism
![]() $j_{\ast }\cong \operatorname{Perf}^{\ast }$
, which shows the second claim.◻
$j_{\ast }\cong \operatorname{Perf}^{\ast }$
, which shows the second claim.◻
Proposition 6.8. Let
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $\mathbb{Q}$
-algebra. The functor
$\mathbb{Q}$
-algebra. The functor
factors over
![]() $\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
and is isomorphic to
$\mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
and is isomorphic to
![]() $\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }C^{\operatorname{Frob}}$
.
$\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }C^{\operatorname{Frob}}$
.
Proof. The first claim follows as the perfection of
![]() $X^{(-1)}$
is canonically isomorphic to the perfection of
$X^{(-1)}$
is canonically isomorphic to the perfection of
![]() $X$
for any object
$X$
for any object
![]() $X$
in
$X$
in
![]() $\operatorname{RigSm}$
.
$\operatorname{RigSm}$
.
The second part of the statement follows from the first claim and the commutativity of the following diagram, which is ensured by Propositions 6.6 and 6.7.

Theorem 6.9. Let
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $\mathbb{Q}$
-algebra. The functor
$\mathbb{Q}$
-algebra. The functor
defines a monoidal, triangulated equivalence of categories.
Proof. Let
![]() $X_{0}$
and
$X_{0}$
and
![]() $Y$
be objects of
$Y$
be objects of
![]() $\operatorname{RigSm}^{\operatorname{gc}}$
. Suppose
$\operatorname{RigSm}^{\operatorname{gc}}$
. Suppose
![]() $X_{0}$
is endowed with an étale map over
$X_{0}$
is endowed with an étale map over
![]() $\mathbb{T}^{N}$
, which is a composition of finite étale maps and inclusions, and let
$\mathbb{T}^{N}$
, which is a composition of finite étale maps and inclusions, and let
![]() $\widehat{X}$
be
$\widehat{X}$
be
![]() $\mathop{\varprojlim }\nolimits_{h}X_{h}$
. We can identify
$\mathop{\varprojlim }\nolimits_{h}X_{h}$
. We can identify
![]() $\widehat{X}$
with
$\widehat{X}$
with
![]() $\operatorname{Perf}X_{0}$
. Since
$\operatorname{Perf}X_{0}$
. Since
![]() $C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)$
is
$C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)$
is
![]() $\operatorname{Frob}$
-local, by Proposition 6.5 the maps
$\operatorname{Frob}$
-local, by Proposition 6.5 the maps
are isomorphisms for all
![]() $h$
. Using Propositions 4.5 and 6.6, we obtain the following sequence of isomorphisms for any
$h$
. Using Propositions 4.5 and 6.6, we obtain the following sequence of isomorphisms for any
![]() $n\in \mathbb{Z}$
:
$n\in \mathbb{Z}$
:
 $$\begin{eqnarray}\displaystyle \mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(X_{0}),\unicode[STIX]{x1D6EC}(Y)[n]) & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(X_{0}),C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \underset{h}{\varinjlim }\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(X_{h}),C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(\widehat{X}),\mathbb{L}\unicode[STIX]{x1D704}^{\ast }C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(\widehat{X}),\mathbb{L}\unicode[STIX]{x1D704}^{\ast }C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(\widehat{X}),\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\mathbb{L}\operatorname{Perf}^{\ast }(X_{0}),\mathbb{L}\operatorname{Perf}^{\ast }(Y)[n]),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{RigDA}_{\text{Frob}\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(X_{0}),\unicode[STIX]{x1D6EC}(Y)[n]) & \cong & \displaystyle \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(X_{0}),C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \underset{h}{\varinjlim }\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(X_{h}),C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(\widehat{X}),\mathbb{L}\unicode[STIX]{x1D704}^{\ast }C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(\widehat{X}),\mathbb{L}\unicode[STIX]{x1D704}^{\ast }C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\unicode[STIX]{x1D6EC}(\widehat{X}),\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }C^{\operatorname{Frob}}\unicode[STIX]{x1D6EC}(Y)[n])\nonumber\\ \displaystyle & \cong & \displaystyle \mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(\mathbb{L}\operatorname{Perf}^{\ast }(X_{0}),\mathbb{L}\operatorname{Perf}^{\ast }(Y)[n]),\nonumber\end{eqnarray}$$
where the last isomorphism follows from the identification
![]() $\widehat{X}\cong \operatorname{Perf}X_{0}$
and Proposition 6.8. In particular, we deduce that the triangulated functor
$\widehat{X}\cong \operatorname{Perf}X_{0}$
and Proposition 6.8. In particular, we deduce that the triangulated functor
![]() $\mathbb{L}\operatorname{Perf}^{\ast }$
maps a set of compact generators to a set of compact generators (see Propositions 3.18 and 3.30) and on these objects it is fully faithful. By means of [Reference AyoubAyo15, Lemma 1.3.32], we then conclude it is a triangulated equivalence of categories, as claimed. ◻
$\mathbb{L}\operatorname{Perf}^{\ast }$
maps a set of compact generators to a set of compact generators (see Propositions 3.18 and 3.30) and on these objects it is fully faithful. By means of [Reference AyoubAyo15, Lemma 1.3.32], we then conclude it is a triangulated equivalence of categories, as claimed. ◻
Remark 6.10. From the proof of the previous claim, we also deduce that the inverse
![]() $\mathbb{R}\operatorname{Perf}_{\ast }$
of
$\mathbb{R}\operatorname{Perf}_{\ast }$
of
![]() $\mathbb{L}\operatorname{Perf}^{\ast }$
sends the motive associated to an object
$\mathbb{L}\operatorname{Perf}^{\ast }$
sends the motive associated to an object
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
to the motive of
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
to the motive of
![]() $X_{0}$
. This functor is then analogous to the de-perfectoidification functor
$X_{0}$
. This functor is then analogous to the de-perfectoidification functor
![]() $\mathbb{L}j^{\ast }\,\circ \,\mathbb{L}\unicode[STIX]{x1D704}_{!}$
of Theorem 5.5.
$\mathbb{L}j^{\ast }\,\circ \,\mathbb{L}\unicode[STIX]{x1D704}_{!}$
of Theorem 5.5.
7 The main theorem
Thanks to the results of the previous sections, we can reformulate Theorem 5.5 in terms of motives of rigid varieties. We will always assume that
![]() $\operatorname{char}K=0$
since the results of this section are tautological when
$\operatorname{char}K=0$
since the results of this section are tautological when
![]() $\operatorname{char}K=p$
.
$\operatorname{char}K=p$
.
Corollary 7.1. There exists a triangulated adjunction of categories
such that
![]() $\mathfrak{F}$
is a monoidal functor.
$\mathfrak{F}$
is a monoidal functor.
Proof. From Theorem 5.5 and Proposition 5.8, we can define an adjunction
by putting
![]() $\mathfrak{F}^{\prime }:=\mathbb{L}\unicode[STIX]{x1D704}_{!}\,\circ \,\mathbb{L}j^{\ast }\,\circ \,(-)^{\sharp }\,\circ \,\mathbb{L}\operatorname{Perf}^{\ast }$
. We remark that by Proposition 5.8,
$\mathfrak{F}^{\prime }:=\mathbb{L}\unicode[STIX]{x1D704}_{!}\,\circ \,\mathbb{L}j^{\ast }\,\circ \,(-)^{\sharp }\,\circ \,\mathbb{L}\operatorname{Perf}^{\ast }$
. We remark that by Proposition 5.8,
![]() $\mathfrak{F}^{\prime }$
is also monoidal. The claim then follows from the equivalence of motives with and without transfers (Theorems 5.1 and 6.3).◻
$\mathfrak{F}^{\prime }$
is also monoidal. The claim then follows from the equivalence of motives with and without transfers (Theorems 5.1 and 6.3).◻
Our goal is to prove that the adjunction of Corollary 7.1 is an equivalence of categories. To this aim, we recall the construction of the stable versions of the rigid motivic categories given in [Reference AyoubAyo15, Definition 2.5.27].
Definition 7.2. Let
![]() $T$
be the cokernel in
$T$
be the cokernel in
![]() $\mathbf{PST}(\operatorname{RigSm}/K)$
of the unit map
$\mathbf{PST}(\operatorname{RigSm}/K)$
of the unit map
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(K)\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}(\mathbb{T}^{1})$
. We denote by
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(K)\rightarrow \unicode[STIX]{x1D6EC}_{\operatorname{tr}}(\mathbb{T}^{1})$
. We denote by
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
or simply by
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
or simply by
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K)$
the homotopy category of the stable
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K)$
the homotopy category of the stable
![]() $(\acute{\text{e}}\text{t},\mathbb{B}^{1})$
-local model structure on symmetric spectra
$(\acute{\text{e}}\text{t},\mathbb{B}^{1})$
-local model structure on symmetric spectra
![]() $\mathbf{Spt}_{T}^{\unicode[STIX]{x1D6F4}}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{PST}(\operatorname{RigSm}/K))$
.
$\mathbf{Spt}_{T}^{\unicode[STIX]{x1D6F4}}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{PST}(\operatorname{RigSm}/K))$
.
As explained in [Reference AyoubAyo15, § 2.5],
![]() $T$
is cofibrant and the cyclic permutation induces the identity on
$T$
is cofibrant and the cyclic permutation induces the identity on
![]() $T^{\otimes 3}$
in
$T^{\otimes 3}$
in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}$
. Moreover, by [Reference HoveyHov01, Theorem 9.3],
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}$
. Moreover, by [Reference HoveyHov01, Theorem 9.3],
![]() $T\,\otimes \,-$
is a Quillen equivalence in this category, which is actually the universal model category where this holds (in some weak sense made precise by [Reference HoveyHov01, Theorem 5.1, Proposition 5.3 and Corollary 9.4]). We recall that the canonical functor
$T\,\otimes \,-$
is a Quillen equivalence in this category, which is actually the universal model category where this holds (in some weak sense made precise by [Reference HoveyHov01, Theorem 5.1, Proposition 5.3 and Corollary 9.4]). We recall that the canonical functor
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K)$
is fully faithful, as proved in [Reference AyoubAyo15, Corollary 2.5.49] as a corollary of the cancellation theorem [Reference AyoubAyo15, Theorem 2.5.38].
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K)$
is fully faithful, as proved in [Reference AyoubAyo15, Corollary 2.5.49] as a corollary of the cancellation theorem [Reference AyoubAyo15, Theorem 2.5.38].
Definition 7.3. We denote by
![]() $\unicode[STIX]{x1D6EC}(1)$
the motive
$\unicode[STIX]{x1D6EC}(1)$
the motive
![]() $T[-1]$
in
$T[-1]$
in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
. For any positive integer
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
. For any positive integer
![]() $d$
we let
$d$
we let
![]() $\unicode[STIX]{x1D6EC}(d)$
be
$\unicode[STIX]{x1D6EC}(d)$
be
![]() $\unicode[STIX]{x1D6EC}(1)^{\otimes d}$
. The functor
$\unicode[STIX]{x1D6EC}(1)^{\otimes d}$
. The functor
![]() $(\cdot )(d):=(\cdot )\,\otimes \,\unicode[STIX]{x1D6EC}(d)$
is an auto-equivalence of
$(\cdot )(d):=(\cdot )\,\otimes \,\unicode[STIX]{x1D6EC}(d)$
is an auto-equivalence of
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K)$
and its inverse will be denoted with
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K)$
and its inverse will be denoted with
![]() $(\cdot )(-d)$
.
$(\cdot )(-d)$
.
Definition 7.4. We denote by
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K,\unicode[STIX]{x1D6EC})$
or simply by
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K,\unicode[STIX]{x1D6EC})$
or simply by
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K)$
the full triangulated subcategory of
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K)$
the full triangulated subcategory of
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
whose objects are the compact ones. They are of the form
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
whose objects are the compact ones. They are of the form
![]() $M(d)$
for some compact object
$M(d)$
for some compact object
![]() $M$
in
$M$
in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
and some
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
and some
![]() $d$
in
$d$
in
![]() $\mathbb{Z}$
. This category is called the category of constructible motives.
$\mathbb{Z}$
. This category is called the category of constructible motives.
We now present an important result that is a crucial step toward the proof of our main theorem. The motivic property it induces will be given right afterwards.
Proposition 7.5. Let
![]() $\widehat{X}$
be a smooth affinoid perfectoid. The natural map of complexes
$\widehat{X}$
be a smooth affinoid perfectoid. The natural map of complexes
is a quasi-isomorphism.
Proof. We let
![]() $\widehat{X}$
be
$\widehat{X}$
be
![]() $\operatorname{Spa}(R,R^{+})$
. A map
$\operatorname{Spa}(R,R^{+})$
. A map
![]() $f$
in
$f$
in
![]() $\operatorname{Hom}(\widehat{X}\,\times \,\widehat{\mathbb{B}}^{n},\mathbb{T}^{d})$
[respectively in
$\operatorname{Hom}(\widehat{X}\,\times \,\widehat{\mathbb{B}}^{n},\mathbb{T}^{d})$
[respectively in
![]() $\operatorname{Hom}(\widehat{X}\,\times \,\widehat{\mathbb{B}}^{n},\widehat{\mathbb{T}}^{d})$
] corresponds to
$\operatorname{Hom}(\widehat{X}\,\times \,\widehat{\mathbb{B}}^{n},\widehat{\mathbb{T}}^{d})$
] corresponds to
![]() $d$
elements
$d$
elements
![]() $f_{1},\ldots ,f_{d}$
in the group
$f_{1},\ldots ,f_{d}$
in the group
![]() $(R^{+}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle )^{\times }$
[respectively in the group
$(R^{+}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle )^{\times }$
[respectively in the group
![]() $(R^{\flat +}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle )^{\times }$
] and the map between the two objects is induced by the multiplicative tilt map
$(R^{\flat +}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle )^{\times }$
] and the map between the two objects is induced by the multiplicative tilt map
![]() $R^{\flat +}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle \rightarrow R^{+}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle$
.
$R^{\flat +}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle \rightarrow R^{+}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle$
.
We now present some facts about homotopy theory for cubical objects, which mirror classical results for simplicial objects (see for example [Reference MayMay67, ch. IV]). We remark that the map of the statement is induced by a map of enriched cubical
![]() $\unicode[STIX]{x1D6EC}$
-vector spaces (see [Reference AyoubAyo14b, Definition A.6]), which is obtained by adding
$\unicode[STIX]{x1D6EC}$
-vector spaces (see [Reference AyoubAyo14b, Definition A.6]), which is obtained by adding
![]() $\unicode[STIX]{x1D6EC}$
-coefficients to a map of enriched cubical sets
$\unicode[STIX]{x1D6EC}$
-coefficients to a map of enriched cubical sets
Any enriched cubical object has connections in the sense of [Reference Brown and HigginsBH81, § 1.2], induced by the maps
![]() $m_{i}$
in [Reference AyoubAyo14b, Definition A.6]. We recall that the category of cubical sets with connections can be endowed with a model structure by which all objects are cofibrant and weak equivalences are defined through the geometric realization (see [Reference JardineJar02]). Moreover, its homotopy category is canonically equivalent to the one of simplicial sets, as cubical sets with connections form a strict test category by [Reference MaltsiniotisMal09].
$m_{i}$
in [Reference AyoubAyo14b, Definition A.6]. We recall that the category of cubical sets with connections can be endowed with a model structure by which all objects are cofibrant and weak equivalences are defined through the geometric realization (see [Reference JardineJar02]). Moreover, its homotopy category is canonically equivalent to the one of simplicial sets, as cubical sets with connections form a strict test category by [Reference MaltsiniotisMal09].
The two cubical sets appearing above are abelian groups on each level and the maps defining their cubical structure are group homomorphisms. They therefore are cubical groups. By [Reference TonksTon92], they are fibrant objects and their homotopy groups
![]() $\unicode[STIX]{x1D70B}_{i}$
coincide with the homology
$\unicode[STIX]{x1D70B}_{i}$
coincide with the homology
![]() $H_{i}N$
of the associated normalized complexes of abelian groups (see Definition 3.13). The
$H_{i}N$
of the associated normalized complexes of abelian groups (see Definition 3.13). The
![]() $\unicode[STIX]{x1D6EC}$
-enrichment functor is tensorial with respect to the monoidal structure of cubical sets introduced in [Reference Brown, Higgins and SiveraBHS11, § 11.2]. Also, the cubical Dold–Kan functor that associates to a cubical
$\unicode[STIX]{x1D6EC}$
-enrichment functor is tensorial with respect to the monoidal structure of cubical sets introduced in [Reference Brown, Higgins and SiveraBHS11, § 11.2]. Also, the cubical Dold–Kan functor that associates to a cubical
![]() $\unicode[STIX]{x1D6EC}$
-module with connections its normalized complex (see [Reference Brown, Higgins and SiveraBHS11, § 14.8]) is a left Quillen functor. We deduce that in order to prove the statement of the proposition it suffices to show that the two normalized complexes of abelian groups are quasi-isomorphic. We also remark that it suffices to consider the case
$\unicode[STIX]{x1D6EC}$
-module with connections its normalized complex (see [Reference Brown, Higgins and SiveraBHS11, § 14.8]) is a left Quillen functor. We deduce that in order to prove the statement of the proposition it suffices to show that the two normalized complexes of abelian groups are quasi-isomorphic. We also remark that it suffices to consider the case
![]() $d=1$
.
$d=1$
.
We prove the following claim: the
![]() $n$
th homology of the complex
$n$
th homology of the complex
![]() $N((R\,\widehat{\otimes }\,{\mathcal{O}}(\widehat{\Box }))^{+\times })$
is
$N((R\,\widehat{\otimes }\,{\mathcal{O}}(\widehat{\Box }))^{+\times })$
is
![]() $0$
for
$0$
for
![]() $n>0$
. Let
$n>0$
. Let
![]() $f$
be invertible in
$f$
be invertible in
![]() $R^{+}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle$
with
$R^{+}\langle \unicode[STIX]{x1D70F}_{1}^{1/p^{\infty }},\ldots ,\unicode[STIX]{x1D70F}_{n}^{1/p^{\infty }}\rangle$
with
![]() $d_{r,\unicode[STIX]{x1D716}}f=1$
for all
$d_{r,\unicode[STIX]{x1D716}}f=1$
for all
![]() $(r,\unicode[STIX]{x1D716})$
. We claim that
$(r,\unicode[STIX]{x1D716})$
. We claim that
![]() $f-1$
is topologically nilpotent. Up to adding a topological nilpotent element, we can assume that
$f-1$
is topologically nilpotent. Up to adding a topological nilpotent element, we can assume that
![]() $f\in R^{+}[\text{}\underline{\unicode[STIX]{x1D70F}}]$
. Since
$f\in R^{+}[\text{}\underline{\unicode[STIX]{x1D70F}}]$
. Since
![]() $f$
is invertible, its image in
$f$
is invertible, its image in
![]() $(R^{+}/R^{\circ \circ })[\text{}\underline{\unicode[STIX]{x1D70F}}^{1/p^{\infty }}]$
is invertible as well. Invertible elements in this ring are just the invertible constants. We deduce that all coefficients of
$(R^{+}/R^{\circ \circ })[\text{}\underline{\unicode[STIX]{x1D70F}}^{1/p^{\infty }}]$
is invertible as well. Invertible elements in this ring are just the invertible constants. We deduce that all coefficients of
![]() $f\,-\,f(0)=f-1$
are topologically nilpotent, and hence
$f\,-\,f(0)=f-1$
are topologically nilpotent, and hence
![]() $f-1$
is topologically nilpotent. In particular, the element
$f-1$
is topologically nilpotent. In particular, the element
![]() $H=f+\unicode[STIX]{x1D70F}_{n+1}(1-f)$
in
$H=f+\unicode[STIX]{x1D70F}_{n+1}(1-f)$
in
![]() $R^{+}\langle \text{}\underline{\unicode[STIX]{x1D70F}}^{1/p^{\infty }},\unicode[STIX]{x1D70F}_{n+1}^{1/p^{\infty }}\rangle$
is invertible, satisfies
$R^{+}\langle \text{}\underline{\unicode[STIX]{x1D70F}}^{1/p^{\infty }},\unicode[STIX]{x1D70F}_{n+1}^{1/p^{\infty }}\rangle$
is invertible, satisfies
![]() $d_{r,\unicode[STIX]{x1D716}}H=1$
for all
$d_{r,\unicode[STIX]{x1D716}}H=1$
for all
![]() $\unicode[STIX]{x1D716}$
and all
$\unicode[STIX]{x1D716}$
and all
![]() $1\leqslant r\leqslant n$
and determines a homotopy between
$1\leqslant r\leqslant n$
and determines a homotopy between
![]() $f$
and
$f$
and
![]() $1$
. This proves the claim.
$1$
. This proves the claim.
We can also prove that the
![]() $0$
th homology of the complex
$0$
th homology of the complex
![]() $N((R\,\widehat{\otimes }\,{\mathcal{O}}(\widehat{\Box }))^{+\times })$
coincides with
$N((R\,\widehat{\otimes }\,{\mathcal{O}}(\widehat{\Box }))^{+\times })$
coincides with
![]() $R^{+\times }/(1+R^{\circ \circ })$
. This amounts to showing that the image of the ring map
$R^{+\times }/(1+R^{\circ \circ })$
. This amounts to showing that the image of the ring map
coincides with
![]() $1+R^{\circ \circ }$
. Let
$1+R^{\circ \circ }$
. Let
![]() $f$
be invertible in
$f$
be invertible in
![]() $R^{+}\langle \unicode[STIX]{x1D70F}^{1/p^{\infty }}\rangle$
with
$R^{+}\langle \unicode[STIX]{x1D70F}^{1/p^{\infty }}\rangle$
with
![]() $f(0)=1$
. As proved above,
$f(0)=1$
. As proved above,
![]() $f-1$
is topologically nilpotent so that also
$f-1$
is topologically nilpotent so that also
![]() $f(1)-1$
is. Vice versa if
$f(1)-1$
is. Vice versa if
![]() $a\in R$
is topologically nilpotent then the element
$a\in R$
is topologically nilpotent then the element
![]() $1+a\unicode[STIX]{x1D70F}\in R^{+}\langle \unicode[STIX]{x1D70F}^{1/p^{\infty }}\rangle$
is invertible, satisfies
$1+a\unicode[STIX]{x1D70F}\in R^{+}\langle \unicode[STIX]{x1D70F}^{1/p^{\infty }}\rangle$
is invertible, satisfies
![]() $f(0)=1$
and
$f(0)=1$
and
![]() $f(1)=1+a$
, proving the claim.
$f(1)=1+a$
, proving the claim.
We are left to prove that the multiplicative map
![]() $\sharp$
induces an isomorphism
$\sharp$
induces an isomorphism
![]() $(R^{\flat +})^{\times }/(1+R^{\flat \circ \circ })\rightarrow (R^{+})^{\times }/(1+R^{\circ \circ })$
. We start by proving it is injective. Let
$(R^{\flat +})^{\times }/(1+R^{\flat \circ \circ })\rightarrow (R^{+})^{\times }/(1+R^{\circ \circ })$
. We start by proving it is injective. Let
![]() $a\in R^{\flat +}$
such that
$a\in R^{\flat +}$
such that
![]() $(a^{\sharp }-1)$
is topologically nilpotent. Since
$(a^{\sharp }-1)$
is topologically nilpotent. Since
![]() $(a^{\sharp }-1)=(a-1)^{\sharp }$
in
$(a^{\sharp }-1)=(a-1)^{\sharp }$
in
![]() $R^{+}/\unicode[STIX]{x1D70B}$
we deduce that the element
$R^{+}/\unicode[STIX]{x1D70B}$
we deduce that the element
![]() $(a-1)^{\sharp }-(a^{\sharp }-1)$
is also topologically nilpotent. We conclude that
$(a-1)^{\sharp }-(a^{\sharp }-1)$
is also topologically nilpotent. We conclude that
![]() $(a-1)^{\sharp }$
, as well as
$(a-1)^{\sharp }$
, as well as
![]() $(a-1)$
, are topologically nilpotent, as desired.
$(a-1)$
, are topologically nilpotent, as desired.
We now prove surjectivity. Let
![]() $a$
be invertible in
$a$
be invertible in
![]() $R^{+}$
. In particular, both
$R^{+}$
. In particular, both
![]() $a$
and
$a$
and
![]() $a^{-1}$
are power-bounded. From the isomorphism
$a^{-1}$
are power-bounded. From the isomorphism
![]() $R^{\flat +}/\unicode[STIX]{x1D70B}^{\flat }\cong R^{+}/\unicode[STIX]{x1D70B}$
we deduce that there exists an element
$R^{\flat +}/\unicode[STIX]{x1D70B}^{\flat }\cong R^{+}/\unicode[STIX]{x1D70B}$
we deduce that there exists an element
![]() $b\in R^{\flat +}$
such that
$b\in R^{\flat +}$
such that
![]() $b^{\sharp }=a+\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}=a(1+\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}a^{-1})$
for some (power-bounded) element
$b^{\sharp }=a+\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}=a(1+\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}a^{-1})$
for some (power-bounded) element
![]() $\unicode[STIX]{x1D6FC}\in R^{+}$
. We deduce that
$\unicode[STIX]{x1D6FC}\in R^{+}$
. We deduce that
![]() $(1\,+\,\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}a^{-1})$
lies in
$(1\,+\,\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}a^{-1})$
lies in
![]() $1\,+\,R^{\circ \circ }$
and that
$1\,+\,R^{\circ \circ }$
and that
![]() $b^{\sharp }$
is invertible. Since the multiplicative structure of
$b^{\sharp }$
is invertible. Since the multiplicative structure of
![]() $R^{\flat }$
is isomorphic to
$R^{\flat }$
is isomorphic to
![]() $\mathop{\varprojlim }\nolimits_{x\mapsto x^{p}}R$
and
$\mathop{\varprojlim }\nolimits_{x\mapsto x^{p}}R$
and
![]() $\sharp$
is given by the projection to the last component, we deduce that as
$\sharp$
is given by the projection to the last component, we deduce that as
![]() $b^{\sharp }$
is invertible, then also
$b^{\sharp }$
is invertible, then also
![]() $b$
is. In particular, the image of
$b$
is. In particular, the image of
![]() $b\in (R^{\flat +})^{\times }$
in
$b\in (R^{\flat +})^{\times }$
in
![]() $(R^{+})^{\times }/(1+R^{\circ \circ })$
is equal to
$(R^{+})^{\times }/(1+R^{\circ \circ })$
is equal to
![]() $a$
, as desired.◻
$a$
, as desired.◻
We recall that by Corollary 7.1 there is an adjunction
and our goal is to prove it is an equivalence.
Proposition 7.6. The motive
![]() $\mathfrak{G}\unicode[STIX]{x1D6EC}(d)$
is isomorphic to
$\mathfrak{G}\unicode[STIX]{x1D6EC}(d)$
is isomorphic to
![]() $\unicode[STIX]{x1D6EC}(d)$
for any positive integer
$\unicode[STIX]{x1D6EC}(d)$
for any positive integer
![]() $d$
.
$d$
.
Proof. The natural map
![]() $\unicode[STIX]{x1D6EC}(d)\rightarrow \mathfrak{G}\unicode[STIX]{x1D6EC}(d)$
is induced by the isomorphism
$\unicode[STIX]{x1D6EC}(d)\rightarrow \mathfrak{G}\unicode[STIX]{x1D6EC}(d)$
is induced by the isomorphism
![]() $\mathfrak{F}\unicode[STIX]{x1D6EC}(d)\cong \unicode[STIX]{x1D6EC}(d)$
. We need to prove it is an isomorphism. The motive
$\mathfrak{F}\unicode[STIX]{x1D6EC}(d)\cong \unicode[STIX]{x1D6EC}(d)$
. We need to prove it is an isomorphism. The motive
![]() $\unicode[STIX]{x1D6EC}(d)$
is a direct factor of the motive
$\unicode[STIX]{x1D6EC}(d)$
is a direct factor of the motive
![]() $\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})[-d]$
and the map above is induced by
$\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})[-d]$
and the map above is induced by
![]() $\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})\rightarrow \mathfrak{G}\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
. It suffices then to prove that the map
$\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})\rightarrow \mathfrak{G}\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
. It suffices then to prove that the map
![]() $\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})\rightarrow \mathfrak{G}\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
is an isomorphism.
$\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})\rightarrow \mathfrak{G}\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
is an isomorphism.
By the definition of the adjoint pair
![]() $(\mathfrak{F},\mathfrak{G})$
given in Corollary 7.1, we can equivalently consider the adjunction
$(\mathfrak{F},\mathfrak{G})$
given in Corollary 7.1, we can equivalently consider the adjunction
and prove that
![]() $\unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{d})\rightarrow (\mathbb{R}j_{\ast }\,\circ \,\mathbb{L}\unicode[STIX]{x1D704}^{\ast })\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
is an isomorphism in
$\unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{d})\rightarrow (\mathbb{R}j_{\ast }\,\circ \,\mathbb{L}\unicode[STIX]{x1D704}^{\ast })\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
is an isomorphism in
![]() $\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
.
$\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
.
From Proposition 7.5 we deduce that the complexes
![]() $\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}\unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{d})$
and
$\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}\unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{d})$
and
![]() $j_{\ast }\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
are quasi-isomorphic in
$j_{\ast }\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
are quasi-isomorphic in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\operatorname{PerfSm})$
. Since
$\mathbf{Ch}\,\mathbf{Psh}(\operatorname{PerfSm})$
. Since
![]() $j_{\ast }$
commutes with
$j_{\ast }$
commutes with
![]() $\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}$
and with
$\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}$
and with
![]() $\acute{\text{e}}\text{t}$
-sheafification, the quasi-isomorphism above can be restated as
$\acute{\text{e}}\text{t}$
-sheafification, the quasi-isomorphism above can be restated as
Due to Proposition 3.26 and the isomorphism
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})\cong \unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
this implies
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})\cong \unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
this implies
![]() $\unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{d})\cong \mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
, as desired.◻
$\unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{d})\cong \mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})$
, as desired.◻
Remark 7.7. Along the proof of the previous proposition, we showed, in particular, that
![]() $\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})\cong \unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{d})$
.
$\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(\mathbb{T}^{d})\cong \unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{d})$
.
Remark 7.8. Since
![]() $j_{\ast }$
commutes with
$j_{\ast }$
commutes with
![]() $\acute{\text{e}}\text{t}$
-sheafification, it preserves
$\acute{\text{e}}\text{t}$
-sheafification, it preserves
![]() $\acute{\text{e}}\text{t}$
-weak equivalences. It also commutes with
$\acute{\text{e}}\text{t}$
-weak equivalences. It also commutes with
![]() $\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}$
and therefore preserves
$\operatorname{Sing}^{\widehat{\mathbb{B}}^{1}}$
and therefore preserves
![]() $\mathbb{B}^{1}$
-weak equivalences. We conclude that
$\mathbb{B}^{1}$
-weak equivalences. We conclude that
![]() $\mathbb{R}j_{\ast }=j_{\ast }$
and, in particular,
$\mathbb{R}j_{\ast }=j_{\ast }$
and, in particular,
![]() $\mathbb{R}j_{\ast }$
commutes with small direct sums.
$\mathbb{R}j_{\ast }$
commutes with small direct sums.
Definition 7.9. A rigid analytic variety with good coordinates
![]() $X_{0}\rightarrow \mathbb{T}^{N}$
, such that the induced maps
$X_{0}\rightarrow \mathbb{T}^{N}$
, such that the induced maps
![]() $\unicode[STIX]{x1D6EC}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}(X_{h})$
are invertible in
$\unicode[STIX]{x1D6EC}(X_{h+1})\rightarrow \unicode[STIX]{x1D6EC}(X_{h})$
are invertible in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\mathbb{Q})$
, is called a variety with very good coordinates.
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\mathbb{Q})$
, is called a variety with very good coordinates.
We are finally ready to present the proof of our main result.
Theorem 7.10. Let
![]() $K$
be a perfectoid field and
$K$
be a perfectoid field and
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $\mathbb{Q}$
-algebra. The adjunction
$\mathbb{Q}$
-algebra. The adjunction
is a monoidal, triangulated equivalence of categories.
Before the proof, we remark that by putting Theorems 3.23 and 6.9 together, the theorem above has the following restatement.
Theorem 7.11. Let
![]() $K$
be a perfectoid field and
$K$
be a perfectoid field and
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $\mathbb{Q}$
-algebra. The adjunction
$\mathbb{Q}$
-algebra. The adjunction
is a monoidal, triangulated equivalence of categories.
Proof. By Theorem 5.5 the functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}\mathbb{L}j^{\ast }:\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
sends the motive
$\mathbb{L}\unicode[STIX]{x1D704}_{!}\mathbb{L}j^{\ast }:\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)\rightarrow \mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
sends the motive
![]() $\unicode[STIX]{x1D6EC}(\widehat{X})$
associated to a perfectoid
$\unicode[STIX]{x1D6EC}(\widehat{X})$
associated to a perfectoid
![]() $\widehat{X}=\mathop{\varprojlim }\nolimits_{h}X_{h}$
to the motive
$\widehat{X}=\mathop{\varprojlim }\nolimits_{h}X_{h}$
to the motive
![]() $\unicode[STIX]{x1D6EC}(X_{0})$
associated to
$\unicode[STIX]{x1D6EC}(X_{0})$
associated to
![]() $X_{0}$
up to rescaling indices. It is triangulated, commutes with sums, and its essential image contains motives
$X_{0}$
up to rescaling indices. It is triangulated, commutes with sums, and its essential image contains motives
![]() $\unicode[STIX]{x1D6EC}(X_{0})$
of varieties
$\unicode[STIX]{x1D6EC}(X_{0})$
of varieties
![]() $X_{0}$
having very good coordinates
$X_{0}$
having very good coordinates
![]() $X_{0}\rightarrow \mathbb{T}^{N}$
(see Definition 7.9). By Proposition 5.3, for every rigid variety with good coordinates
$X_{0}\rightarrow \mathbb{T}^{N}$
(see Definition 7.9). By Proposition 5.3, for every rigid variety with good coordinates
![]() $X_{0}\rightarrow \mathbb{T}^{N}$
there exists an index
$X_{0}\rightarrow \mathbb{T}^{N}$
there exists an index
![]() $h$
such that
$h$
such that
![]() $X_{h}=X_{0}\,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
has very good coordinates. Since
$X_{h}=X_{0}\,\times _{\mathbb{T}^{N}}\,\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
has very good coordinates. Since
![]() $\operatorname{char}K=0$
the map
$\operatorname{char}K=0$
the map
![]() $\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle \rightarrow \mathbb{T}^{N}$
is finite étale, and therefore also the map
$\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle \rightarrow \mathbb{T}^{N}$
is finite étale, and therefore also the map
![]() $X_{h}\rightarrow X_{0}$
is. We conclude that any rigid variety with good coordinates has a finite étale covering with very good coordinates, and hence the motives associated to varieties with very good coordinates generate the étale topos. In particular, the motives associated to them generate
$X_{h}\rightarrow X_{0}$
is. We conclude that any rigid variety with good coordinates has a finite étale covering with very good coordinates, and hence the motives associated to varieties with very good coordinates generate the étale topos. In particular, the motives associated to them generate
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
, and hence the functor
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
, and hence the functor
![]() $\mathbb{L}\unicode[STIX]{x1D704}_{!}\,\circ \,\mathbb{L}j^{\ast }$
maps a set of compact generators to a set of compact generators.
$\mathbb{L}\unicode[STIX]{x1D704}_{!}\,\circ \,\mathbb{L}j^{\ast }$
maps a set of compact generators to a set of compact generators.
Since
![]() $\mathfrak{F}$
is monoidal and
$\mathfrak{F}$
is monoidal and
![]() $\mathfrak{F}(\unicode[STIX]{x1D6EC}(1))=\unicode[STIX]{x1D6EC}(1)$
it extends formally to a monoidal functor from the category
$\mathfrak{F}(\unicode[STIX]{x1D6EC}(1))=\unicode[STIX]{x1D6EC}(1)$
it extends formally to a monoidal functor from the category
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat })$
to
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat })$
to
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K)$
by putting
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K)$
by putting
![]() $\mathfrak{F}(M(-d))=\mathfrak{F}(M)(-d)$
. Now let
$\mathfrak{F}(M(-d))=\mathfrak{F}(M)(-d)$
. Now let
![]() $M$
,
$M$
,
![]() $N$
in
$N$
in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K^{\flat })$
be twists of the motives associated to the analytification of smooth projective varieties
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K^{\flat })$
be twists of the motives associated to the analytification of smooth projective varieties
![]() $X$
, respectively,
$X$
, respectively,
![]() $X^{\prime }$
. They are strongly dualizable objects of
$X^{\prime }$
. They are strongly dualizable objects of
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K^{\flat })$
since
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K^{\flat })$
since
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X)$
and
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X)$
and
![]() $\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X^{\prime })$
are strongly dualizable in
$\unicode[STIX]{x1D6EC}_{\operatorname{tr}}(X^{\prime })$
are strongly dualizable in
![]() $\mathbf{DM}_{\acute{\text{e}}\text{t}}(K^{\flat })$
. Fix an integer
$\mathbf{DM}_{\acute{\text{e}}\text{t}}(K^{\flat })$
. Fix an integer
![]() $d$
such that
$d$
such that
![]() $N^{\vee }(d)$
lies in
$N^{\vee }(d)$
lies in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
. The objects
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
. The objects
![]() $M$
,
$M$
,
![]() $N$
,
$N$
,
![]() $M^{\vee }$
and
$M^{\vee }$
and
![]() $N^{\vee }$
lie in
$N^{\vee }$
lie in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat })$
and moreover
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat })$
and moreover
![]() $\mathfrak{F}(N^{\vee })=\mathfrak{F}(N)^{\vee }$
. From Lemma 7.12 we also deduce that the functor
$\mathfrak{F}(N^{\vee })=\mathfrak{F}(N)^{\vee }$
. From Lemma 7.12 we also deduce that the functor
![]() $\mathfrak{F}$
induces a bijection
$\mathfrak{F}$
induces a bijection
By means of the Cancellation Theorem [Reference AyoubAyo15, Corollary 2.5.49], the first set is isomorphic to
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(M,N)$
and the second is isomorphic to
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })(M,N)$
and the second is isomorphic to
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)(\mathfrak{F}(M),\mathfrak{F}(N))$
. We then deduce that all motives
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)(\mathfrak{F}(M),\mathfrak{F}(N))$
. We then deduce that all motives
![]() $M$
associated to the analytification of smooth projective varieties lie in the left orthogonal of the cone of the map
$M$
associated to the analytification of smooth projective varieties lie in the left orthogonal of the cone of the map
![]() $N\rightarrow \mathfrak{G}\mathfrak{F}N$
, which is closed under direct sums and cones. Since
$N\rightarrow \mathfrak{G}\mathfrak{F}N$
, which is closed under direct sums and cones. Since
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $\mathbb{Q}$
-algebra, such motives generate
$\mathbb{Q}$
-algebra, such motives generate
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
by means of [Reference AyoubAyo15, Theorem 2.5.35]. We conclude that
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
by means of [Reference AyoubAyo15, Theorem 2.5.35]. We conclude that
![]() $N\cong \mathfrak{G}\mathfrak{F}N$
. Therefore, the category
$N\cong \mathfrak{G}\mathfrak{F}N$
. Therefore, the category
![]() $\mathbf{T}$
of objects
$\mathbf{T}$
of objects
![]() $N$
such that
$N$
such that
![]() $N\cong \mathfrak{G}\mathfrak{F}N$
contains all motives associated to the analytification of smooth projective varieties. It is clear that
$N\cong \mathfrak{G}\mathfrak{F}N$
contains all motives associated to the analytification of smooth projective varieties. It is clear that
![]() $\mathbf{T}$
is closed under cones. The functors
$\mathbf{T}$
is closed under cones. The functors
![]() $\mathfrak{F}$
and
$\mathfrak{F}$
and
![]() $\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
commute with direct sums as they are left adjoint functors. As pointed out in Remark 7.8 also the functor
$\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
commute with direct sums as they are left adjoint functors. As pointed out in Remark 7.8 also the functor
![]() $\mathbb{R}j_{\ast }$
does. Since
$\mathbb{R}j_{\ast }$
does. Since
![]() $\mathfrak{G}$
is a composite of
$\mathfrak{G}$
is a composite of
![]() $\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
with equivalences of categories, it commutes with small sums as well. We conclude that
$\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
with equivalences of categories, it commutes with small sums as well. We conclude that
![]() $\mathbf{T}$
is closed under direct sums. Using again [Reference AyoubAyo15, Theorem 2.5.35] we deduce
$\mathbf{T}$
is closed under direct sums. Using again [Reference AyoubAyo15, Theorem 2.5.35] we deduce
![]() $\mathbf{T}=\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
, proving that
$\mathbf{T}=\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
, proving that
![]() $\mathfrak{F}$
is fully faithful. This is enough to prove that it is an equivalence of categories, by applying [Reference AyoubAyo15, Lemma 1.3.32].◻
$\mathfrak{F}$
is fully faithful. This is enough to prove that it is an equivalence of categories, by applying [Reference AyoubAyo15, Lemma 1.3.32].◻
Lemma 7.12. Let
![]() $M$
be an object of
$M$
be an object of
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat })$
. The functor
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat })$
. The functor
![]() $\mathfrak{F}$
induces an isomorphism
$\mathfrak{F}$
induces an isomorphism
Proof. Suppose that
![]() $d$
is an integer such that
$d$
is an integer such that
![]() $M(d)$
lies in
$M(d)$
lies in
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
. One has
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
. One has
![]() $\mathfrak{F}\unicode[STIX]{x1D6EC}(d)\cong \unicode[STIX]{x1D6EC}(d)$
and by Proposition 7.6 the unit map
$\mathfrak{F}\unicode[STIX]{x1D6EC}(d)\cong \unicode[STIX]{x1D6EC}(d)$
and by Proposition 7.6 the unit map
![]() $\unicode[STIX]{x1D702}:\unicode[STIX]{x1D6EC}(d)\rightarrow \mathfrak{G}\mathfrak{F}\unicode[STIX]{x1D6EC}(d)$
is an isomorphism. In particular, from the adjunction
$\unicode[STIX]{x1D702}:\unicode[STIX]{x1D6EC}(d)\rightarrow \mathfrak{G}\mathfrak{F}\unicode[STIX]{x1D6EC}(d)$
is an isomorphism. In particular, from the adjunction
![]() $(\mathfrak{F},\mathfrak{G})$
we obtain a commutative square
$(\mathfrak{F},\mathfrak{G})$
we obtain a commutative square

in which the top arrow is then an isomorphism. By the Cancellation Theorem [Reference AyoubAyo15, Corollary 2.5.49] we also obtain the following commutative square

and hence also the top arrow is an isomorphism. We conclude the claim from the following commutative square, whose vertical arrows are isomorphisms since the functor
![]() $(\cdot )(d)$
is invertible in
$(\cdot )(d)$
is invertible in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{}(K)$
.
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{}(K)$
.

Remark 7.13. In the proof of Theorem 7.10 we again used the hypothesis that
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $\mathbb{Q}$
-algebra in order to apply [Reference AyoubAyo15, Theorem 2.5.35], which states that the motives associated to the analytification of smooth projective varieties generate
$\mathbb{Q}$
-algebra in order to apply [Reference AyoubAyo15, Theorem 2.5.35], which states that the motives associated to the analytification of smooth projective varieties generate
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
.
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K^{\flat })$
.
Remark 7.14. In the proof, we also showed that the motives
![]() $\unicode[STIX]{x1D6EC}(X)[i]$
where
$\unicode[STIX]{x1D6EC}(X)[i]$
where
![]() $X$
has very good coordinates and
$X$
has very good coordinates and
![]() $i\in \mathbb{Z}$
generate
$i\in \mathbb{Z}$
generate
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
as a triangulated category with small sums.
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K)$
as a triangulated category with small sums.
Corollary 7.15. Let
![]() $X_{0}\rightarrow \mathbb{T}^{N}$
be a variety with very good coordinates. Then
$X_{0}\rightarrow \mathbb{T}^{N}$
be a variety with very good coordinates. Then
![]() $\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(X_{0})\cong \unicode[STIX]{x1D6EC}(\mathop{\varprojlim }\nolimits_{h}X_{h})$
.
$\mathbb{R}j_{\ast }\mathbb{L}\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(X_{0})\cong \unicode[STIX]{x1D6EC}(\mathop{\varprojlim }\nolimits_{h}X_{h})$
.
Proof. By the description given in Theorem 5.5, we conclude that
![]() $\mathbb{R}\unicode[STIX]{x1D704}_{!}\mathbb{L}j^{\ast }(\unicode[STIX]{x1D6EC}(\mathop{\varprojlim }\nolimits_{h}X_{h}))\cong \unicode[STIX]{x1D6EC}(X_{0})$
. The claim then follows from Theorem 7.10, which shows that
$\mathbb{R}\unicode[STIX]{x1D704}_{!}\mathbb{L}j^{\ast }(\unicode[STIX]{x1D6EC}(\mathop{\varprojlim }\nolimits_{h}X_{h}))\cong \unicode[STIX]{x1D6EC}(X_{0})$
. The claim then follows from Theorem 7.10, which shows that
![]() $\mathbb{R}\unicode[STIX]{x1D704}_{!}\,\circ \,\mathbb{L}j^{\ast }$
is a quasi-inverse of
$\mathbb{R}\unicode[STIX]{x1D704}_{!}\,\circ \,\mathbb{L}j^{\ast }$
is a quasi-inverse of
![]() $\mathbb{R}j_{\ast }\,\circ \,\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
.◻
$\mathbb{R}j_{\ast }\,\circ \,\mathbb{L}\unicode[STIX]{x1D704}^{\ast }$
.◻
We remark that the proof of Theorem 7.10 also induces the following result.
Corollary 7.16. The functor
is a monoidal equivalence of categories.
We can refine the previous corollary by stating the stable version of our main result (Theorem 7.26), which is based on the following intermediate results. For the definitions of spectra of model categories, we refer to [Reference AyoubAyo07, § 4.3] and [Reference HoveyHov01].
Definition 7.17. Let
![]() $T$
be the cokernel of the unit map
$T$
be the cokernel of the unit map
![]() $\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}(\mathbb{T}^{1})$
in
$\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}(\mathbb{T}^{1})$
in
![]() $\mathbf{Psh}(\operatorname{RigSm}/K)$
and let
$\mathbf{Psh}(\operatorname{RigSm}/K)$
and let
![]() $\widehat{T}$
be the cokernel of the unit map
$\widehat{T}$
be the cokernel of the unit map
![]() $\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{1})$
in
$\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{1})$
in
![]() $\mathbf{Psh}(\operatorname{PerfSm}/K)$
. They are direct factors of cofibrant objects, and hence cofibrant.
$\mathbf{Psh}(\operatorname{PerfSm}/K)$
. They are direct factors of cofibrant objects, and hence cofibrant.
(i) We denote by
 $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
the homotopy category of the stable
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
the homotopy category of the stable
 $(\acute{\text{e}}\text{t},\mathbb{B}^{1})$
-local model structure on spectra
$(\acute{\text{e}}\text{t},\mathbb{B}^{1})$
-local model structure on spectra
 $\mathbf{Spt}_{T}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K))$
. We omit
$\mathbf{Spt}_{T}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K))$
. We omit
 $\unicode[STIX]{x1D6EC}$
whenever the context allows it.
$\unicode[STIX]{x1D6EC}$
whenever the context allows it.(ii) We denote by
 $\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}^{1}}}(K,\unicode[STIX]{x1D6EC})$
the homotopy category of the stable
$\widehat{\mathbf{Rig}}\mathbf{DA}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}^{1}}}(K,\unicode[STIX]{x1D6EC})$
the homotopy category of the stable
 $(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
-local model structure on spectra
$(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
-local model structure on spectra
 $\mathbf{Spt}_{\unicode[STIX]{x1D704}^{\ast }T}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}/K))$
. We omit
$\mathbf{Spt}_{\unicode[STIX]{x1D704}^{\ast }T}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}/K))$
. We omit
 $\unicode[STIX]{x1D6EC}$
whenever the context allows it.
$\unicode[STIX]{x1D6EC}$
whenever the context allows it.(iii) We denote by
 $\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
the homotopy category of the stable
$\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
the homotopy category of the stable
 $(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
-local model structure on spectra
$(\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1})$
-local model structure on spectra
 $\mathbf{Spt}_{\widehat{T}}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{PerfSm}/K))$
. We omit
$\mathbf{Spt}_{\widehat{T}}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{PerfSm}/K))$
. We omit
 $\unicode[STIX]{x1D6EC}$
whenever the context allows it.
$\unicode[STIX]{x1D6EC}$
whenever the context allows it.(iv) For
 $\mathbf{C}$
equal to
$\mathbf{C}$
equal to
 $\operatorname{RigSm}$
,
$\operatorname{RigSm}$
,
 $\widehat{\text{Rig}}\operatorname{Sm}$
or
$\widehat{\text{Rig}}\operatorname{Sm}$
or
 $\operatorname{PerfSm}$
, we denote by
$\operatorname{PerfSm}$
, we denote by
 $\operatorname{Sus}_{k}$
the
$\operatorname{Sus}_{k}$
the
 $k$
th suspension functor from the model category of complexes of presheaves on
$k$
th suspension functor from the model category of complexes of presheaves on
 $\mathbf{C}$
to the associated spectra, which is the left adjoint of the functor
$\mathbf{C}$
to the associated spectra, which is the left adjoint of the functor  $$\begin{eqnarray}\operatorname{Ev}_{k}:(M_{n})_{n\in \mathbb{N}}\mapsto M_{k}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ev}_{k}:(M_{n})_{n\in \mathbb{N}}\mapsto M_{k}.\end{eqnarray}$$
Remark 7.18. The functor
![]() $-\,\otimes \,T$
[respectively
$-\,\otimes \,T$
[respectively
![]() $-\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T$
respectively
$-\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T$
respectively
![]() $-\,\otimes \,\widehat{T}$
] has a prolongation to a left Quillen endofunctor on the associated spectra, which is furthermore a Quillen equivalence. The category of spectra is the universal model category with this property, in a weak sense made precise by [Reference HoveyHov01, Theorem 5.1 and Proposition 5.3].
$-\,\otimes \,\widehat{T}$
] has a prolongation to a left Quillen endofunctor on the associated spectra, which is furthermore a Quillen equivalence. The category of spectra is the universal model category with this property, in a weak sense made precise by [Reference HoveyHov01, Theorem 5.1 and Proposition 5.3].
Remark 7.19. In contrast with Definition 7.2, we use above the categories of non-symmetric spectra. On the other hand, we remark that by [Reference AyoubAyo07, Proposition 4.3.47] the model categories of symmetric and non-symmetric spectra are Quillen equivalent. We then conclude by Proposition 3.23, Theorem 6.3, Proposition 6.9 and [Reference HoveyHov01, Theorem 5.5] that the canonical adjunctions
are equivalences of categories, and the prolongation of
![]() $-\,\otimes \,T$
[respectively
$-\,\otimes \,T$
[respectively
![]() $-\,\otimes \,\widehat{T}$
] corresponds to the functor
$-\,\otimes \,\widehat{T}$
] corresponds to the functor
![]() $M\mapsto M(1)$
.
$M\mapsto M(1)$
.
Remark 7.20. We point out that the functor
![]() $\operatorname{Sus}_{0}$
has an explicit description. For example, in the case of
$\operatorname{Sus}_{0}$
has an explicit description. For example, in the case of
![]() $\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K)$
it sends a complex
$\mathbf{Ch}_{\acute{\text{e}}\text{t},\mathbb{B}^{1}}\mathbf{Psh}(\operatorname{RigSm}/K)$
it sends a complex
![]() ${\mathcal{F}}$
to the spectrum
${\mathcal{F}}$
to the spectrum
![]() $({\mathcal{F}}\,\otimes \,T^{\otimes n})_{n\in \mathbb{N}}$
with the obvious transition maps. The functor
$({\mathcal{F}}\,\otimes \,T^{\otimes n})_{n\in \mathbb{N}}$
with the obvious transition maps. The functor
![]() $\operatorname{Sus}_{k}$
is the composition
$\operatorname{Sus}_{k}$
is the composition
![]() $t^{k}\operatorname{Sus}_{0}$
, where
$t^{k}\operatorname{Sus}_{0}$
, where
![]() $t$
is the shift functor such that
$t$
is the shift functor such that
![]() $\operatorname{Ev}_{0}tM=0$
and
$\operatorname{Ev}_{0}tM=0$
and
![]() $\operatorname{Ev}_{k+1}tM=\operatorname{Ev}_{k}M$
for any spectrum
$\operatorname{Ev}_{k+1}tM=\operatorname{Ev}_{k}M$
for any spectrum
![]() $M$
. The pair
$M$
. The pair
![]() $(\operatorname{Sus}_{k},\operatorname{Ev}_{k})$
is a Quillen adjunction (see [Reference AyoubAyo07, Lemma 4.3.24]) as well as the pair
$(\operatorname{Sus}_{k},\operatorname{Ev}_{k})$
is a Quillen adjunction (see [Reference AyoubAyo07, Lemma 4.3.24]) as well as the pair
![]() $(t,s)$
, where
$(t,s)$
, where
![]() $s$
is such that
$s$
is such that
![]() $\operatorname{Ev}_{k}sM=\operatorname{Ev}_{k+1}M$
for any spectrum
$\operatorname{Ev}_{k}sM=\operatorname{Ev}_{k+1}M$
for any spectrum
![]() $M$
(see [Reference HoveyHov01, Definition 3.7]).
$M$
(see [Reference HoveyHov01, Definition 3.7]).
Definition 7.21. We denote by
the Quillen adjunction induced by the pair
![]() $(\unicode[STIX]{x1D704}^{\ast },\unicode[STIX]{x1D704}_{\ast })$
by means of [Reference HoveyHov01, Proposition 5.3].
$(\unicode[STIX]{x1D704}^{\ast },\unicode[STIX]{x1D704}_{\ast })$
by means of [Reference HoveyHov01, Proposition 5.3].
The natural map
![]() $\widehat{\mathbb{T}}^{1}\rightarrow \unicode[STIX]{x1D704}^{\ast }\mathbb{T}^{1}$
induces a map
$\widehat{\mathbb{T}}^{1}\rightarrow \unicode[STIX]{x1D704}^{\ast }\mathbb{T}^{1}$
induces a map
![]() $\widehat{T}\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }T$
, which, in turn, defines a natural transformation
$\widehat{T}\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }T$
, which, in turn, defines a natural transformation
![]() $\unicode[STIX]{x1D70F}:j^{\ast }(-\,\otimes \,\widehat{T})\rightarrow (j^{\ast }-)\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T$
. Nevertheless, it is not clear that for a smooth affinoid perfectoid
$\unicode[STIX]{x1D70F}:j^{\ast }(-\,\otimes \,\widehat{T})\rightarrow (j^{\ast }-)\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T$
. Nevertheless, it is not clear that for a smooth affinoid perfectoid
![]() $\widehat{X}$
the map
$\widehat{X}$
the map
![]() $\unicode[STIX]{x1D70F}:j^{\ast }(\unicode[STIX]{x1D6EC}(\widehat{X})\,\otimes \,\widehat{T})\rightarrow (j^{\ast }\unicode[STIX]{x1D6EC}(\widehat{X}))\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T$
is a weak equivalence, so that we can not apply the criterion of [Reference HoveyHov01, Proposition 5.3] to define a Quillen adjunction between
$\unicode[STIX]{x1D70F}:j^{\ast }(\unicode[STIX]{x1D6EC}(\widehat{X})\,\otimes \,\widehat{T})\rightarrow (j^{\ast }\unicode[STIX]{x1D6EC}(\widehat{X}))\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T$
is a weak equivalence, so that we can not apply the criterion of [Reference HoveyHov01, Proposition 5.3] to define a Quillen adjunction between
![]() $\mathbf{Spt}_{\widehat{T}}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\operatorname{PerfSm}/K))$
and
$\mathbf{Spt}_{\widehat{T}}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\operatorname{PerfSm}/K))$
and
![]() $\mathbf{Spt}_{\unicode[STIX]{x1D704}^{\ast }T}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}/K))$
. Therefore, the following proposition, albeit easy to prove, has a non-trivial content.
$\mathbf{Spt}_{\unicode[STIX]{x1D704}^{\ast }T}(\mathbf{Ch}_{\acute{\text{e}}\text{t},\widehat{\mathbb{B}}^{1}}\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm}/K))$
. Therefore, the following proposition, albeit easy to prove, has a non-trivial content.
Proposition 7.22. The functor
is well defined, preserves stable weak equivalences and induces a triangulated functor
Proof. If
![]() $(M_{n})$
is a spectrum we can define the transition maps
$(M_{n})$
is a spectrum we can define the transition maps
![]() $j_{\ast }M_{n}\,\otimes \,\widehat{T}\rightarrow j_{\ast }M_{n+1}$
with the following composition
$j_{\ast }M_{n}\,\otimes \,\widehat{T}\rightarrow j_{\ast }M_{n+1}$
with the following composition
deduced by the transition maps
![]() $M_{n}\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T\rightarrow M_{n+1}$
. Moreover, as shown in the first part of the proof of [Reference HoveyHov01, Proposition 5.3]
$M_{n}\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T\rightarrow M_{n+1}$
. Moreover, as shown in the first part of the proof of [Reference HoveyHov01, Proposition 5.3]
![]() $\operatorname{Spt}j_{\ast }$
is a right Quillen functor with respect to the projective model structures on spectra, whose weak equivalences are level-wise weak equivalences. It also preserves such weak equivalences, as proved in Remark 7.8.
$\operatorname{Spt}j_{\ast }$
is a right Quillen functor with respect to the projective model structures on spectra, whose weak equivalences are level-wise weak equivalences. It also preserves such weak equivalences, as proved in Remark 7.8.
The stable model structure on spectra is obtained as a left Bousfield localization with respect to the maps
![]() $\operatorname{Sus}_{n+1}({\mathcal{F}}\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T)\rightarrow \operatorname{Sus}_{n}{\mathcal{F}}$
[respectively
$\operatorname{Sus}_{n+1}({\mathcal{F}}\,\otimes \,\unicode[STIX]{x1D704}^{\ast }T)\rightarrow \operatorname{Sus}_{n}{\mathcal{F}}$
[respectively
![]() $\operatorname{Sus}_{n+1}({\mathcal{F}}\,\otimes \,\widehat{T})\rightarrow \operatorname{Sus}_{n}{\mathcal{F}}$
] as
$\operatorname{Sus}_{n+1}({\mathcal{F}}\,\otimes \,\widehat{T})\rightarrow \operatorname{Sus}_{n}{\mathcal{F}}$
] as
![]() ${\mathcal{F}}$
runs among cofibrant objects (see for example [Reference AyoubAyo07, Definition 4.3.29]). We now prove that
${\mathcal{F}}$
runs among cofibrant objects (see for example [Reference AyoubAyo07, Definition 4.3.29]). We now prove that
![]() $\operatorname{Spt}j_{\ast }$
also preserves stable weak equivalences.
$\operatorname{Spt}j_{\ast }$
also preserves stable weak equivalences.
Consider the natural map
For
![]() $k>n$
it is an equality, and hence the map
$k>n$
it is an equality, and hence the map
is a stable weak equivalence by [Reference AyoubAyo07, Lemma 4.3.59]. We then deduce that
![]() $\operatorname{Spt}j_{\ast }$
preserves stable weak equivalences as claimed.
$\operatorname{Spt}j_{\ast }$
preserves stable weak equivalences as claimed.
The fact that
![]() $\mathbb{R}\operatorname{Spt}j_{\ast }$
is triangulated follows from the fact that it coincides with the restriction to stably local spectra of the functor induced by
$\mathbb{R}\operatorname{Spt}j_{\ast }$
is triangulated follows from the fact that it coincides with the restriction to stably local spectra of the functor induced by
![]() $\operatorname{Spt}j_{\ast }$
on the homotopy categories of the projective model structures on spectra, which is triangulated being a right derived Quillen functor.◻
$\operatorname{Spt}j_{\ast }$
on the homotopy categories of the projective model structures on spectra, which is triangulated being a right derived Quillen functor.◻
Remark 7.23. The functor
![]() $\mathbb{R}\operatorname{Spt}j_{\ast }$
commutes with small direct sums by its explicit description and Remark 7.8.
$\mathbb{R}\operatorname{Spt}j_{\ast }$
commutes with small direct sums by its explicit description and Remark 7.8.
Proposition 7.24. There is an invertible natural transformation of functors from the category
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
to
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
to
![]() $\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
:
$\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
:
Proof. For any cofibrant object
![]() ${\mathcal{F}}$
in
${\mathcal{F}}$
in
![]() $\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm})$
one has
$\mathbf{Ch}\,\mathbf{Psh}(\operatorname{RigSm})$
one has
where
![]() $Q$
is a cofibrant-replacement functor on
$Q$
is a cofibrant-replacement functor on
![]() $\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
. The natural transformation
$\mathbf{Ch}\,\mathbf{Psh}(\widehat{\text{Rig}}\operatorname{Sm})$
. The natural transformation
![]() $\unicode[STIX]{x1D702}$
of the statement is then induced by the canonical maps
$\unicode[STIX]{x1D702}$
of the statement is then induced by the canonical maps
![]() $Q(j_{\ast }\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}$
and
$Q(j_{\ast }\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}})\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }{\mathcal{F}}$
and
![]() $\widehat{T}\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }T$
.
$\widehat{T}\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }T$
.
The two functors of the statement are triangulated and commute with small direct sums by Remarks 7.8, 7.23 and Proposition 7.22. We deduce that the subcategory of
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
on which
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
on which
![]() $\unicode[STIX]{x1D702}$
is invertible is triangulated and closed under direct sums.
$\unicode[STIX]{x1D702}$
is invertible is triangulated and closed under direct sums.
By Proposition 3.18 and Remark 7.14 we conclude that it suffices to prove that
![]() $\unicode[STIX]{x1D702}$
is invertible on a fixed motive
$\unicode[STIX]{x1D702}$
is invertible on a fixed motive
![]() $\unicode[STIX]{x1D6EC}(X)[i]$
with
$\unicode[STIX]{x1D6EC}(X)[i]$
with
![]() $X$
with very good coordinates and
$X$
with very good coordinates and
![]() $i\in \mathbb{Z}$
. For such an object, using Corollary 7.15, we have an explicit description of a cofibrant replacement of
$i\in \mathbb{Z}$
. For such an object, using Corollary 7.15, we have an explicit description of a cofibrant replacement of
![]() $j_{\ast }\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(X)[i]$
namely
$j_{\ast }\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(X)[i]$
namely
![]() $\unicode[STIX]{x1D6EC}(\widehat{X})[i]$
, where
$\unicode[STIX]{x1D6EC}(\widehat{X})[i]$
, where
![]() $\widehat{X}=\mathop{\varprojlim }\nolimits_{h}X_{h}$
is built with respect to some very good coordinates
$\widehat{X}=\mathop{\varprojlim }\nolimits_{h}X_{h}$
is built with respect to some very good coordinates
![]() $X\rightarrow \mathbb{T}^{N}$
of
$X\rightarrow \mathbb{T}^{N}$
of
![]() $X$
. We are left to prove that the maps
$X$
. We are left to prove that the maps
![]() $\unicode[STIX]{x1D6EC}(\widehat{X})\,\otimes \,\widehat{T}^{\otimes k}[i]\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(X)\,\otimes \,j_{\ast }(\unicode[STIX]{x1D704}^{\ast }T)^{\otimes k}[i]$
induce a weak equivalence of spectra. We claim that each one of them is a weak equivalence.
$\unicode[STIX]{x1D6EC}(\widehat{X})\,\otimes \,\widehat{T}^{\otimes k}[i]\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6EC}(X)\,\otimes \,j_{\ast }(\unicode[STIX]{x1D704}^{\ast }T)^{\otimes k}[i]$
induce a weak equivalence of spectra. We claim that each one of them is a weak equivalence.
The object
![]() $T$
[respectively
$T$
[respectively
![]() $\widehat{T}$
] is a direct summand of
$\widehat{T}$
] is a direct summand of
![]() $\unicode[STIX]{x1D6EC}(\mathbb{T}^{1})$
[respectively
$\unicode[STIX]{x1D6EC}(\mathbb{T}^{1})$
[respectively
![]() $\unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{1})$
] and the decomposition is compatible with the map
$\unicode[STIX]{x1D6EC}(\widehat{\mathbb{T}}^{1})$
] and the decomposition is compatible with the map
![]() $\widehat{T}\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }T$
. Therefore, in order to prove the claim we can show that the maps
$\widehat{T}\rightarrow j_{\ast }\unicode[STIX]{x1D704}^{\ast }T$
. Therefore, in order to prove the claim we can show that the maps
are weak equivalences, and this follows from Corollary 7.15 and Remark 7.7. ◻
We define the following composite functor (see Remark 7.19):
which can be inserted in the diagram

whose vertical functors are fully faithful by the Cancellation Theorem [Reference AyoubAyo15, Corollary 2.5.49]. It is commutative, up to a natural transformation, by means of Proposition 7.24.
Proposition 7.25. The category
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
[respectively
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
[respectively
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
] is generated, as a triangulated category with small sums, by the objects of
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
] is generated, as a triangulated category with small sums, by the objects of
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K,\unicode[STIX]{x1D6EC})$
[respectively
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K,\unicode[STIX]{x1D6EC})$
[respectively
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat },\unicode[STIX]{x1D6EC})$
].
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat },\unicode[STIX]{x1D6EC})$
].
Proof. We prove the statement only for
![]() $K$
. From the Cancellation Theorem [Reference AyoubAyo15, Corollary 2.5.49] we deduce that any object
$K$
. From the Cancellation Theorem [Reference AyoubAyo15, Corollary 2.5.49] we deduce that any object
![]() $M$
of
$M$
of
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
is isomorphic to
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
is isomorphic to
![]() $\operatorname{hocolim}_{n}M_{n}(-n)$
with
$\operatorname{hocolim}_{n}M_{n}(-n)$
with
![]() $M_{n}$
in
$M_{n}$
in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
(see the proof of [Reference KahnKah13, Proposition 7.4.1]). In particular, it sits in a distinguished triangle
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
(see the proof of [Reference KahnKah13, Proposition 7.4.1]). In particular, it sits in a distinguished triangle
Since
![]() $\mathbf{RigDM}_{\operatorname{eff}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
is generated by compact objects by Proposition 3.18, we conclude that each
$\mathbf{RigDM}_{\operatorname{eff}}^{\operatorname{eff}}(K,\unicode[STIX]{x1D6EC})$
is generated by compact objects by Proposition 3.18, we conclude that each
![]() $M_{n}(-n)$
lies in the triangulated category with small sums generated by the objects of
$M_{n}(-n)$
lies in the triangulated category with small sums generated by the objects of
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K,\unicode[STIX]{x1D6EC})$
so that
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K,\unicode[STIX]{x1D6EC})$
so that
![]() $M$
also does.◻
$M$
also does.◻
We can finally prove the stable version of the main result of this article.
Theorem 7.26. The functor
is a monoidal triangulated equivalence of categories and, up to a natural transformation, it restricts to the equivalence
of Theorem 7.10 on the subcategories of effective motives.
Proof. By its definition, the functor
![]() $\mathbb{R}\operatorname{Spt}j_{\ast }$
commutes with the derived shift functor
$\mathbb{R}\operatorname{Spt}j_{\ast }$
commutes with the derived shift functor
![]() $\mathbb{L}t$
(see Remark 7.20). We claim that
$\mathbb{L}t$
(see Remark 7.20). We claim that
![]() $\mathbb{L}\operatorname{Spt}\unicode[STIX]{x1D704}^{\ast }$
also does. We can equivalently show that
$\mathbb{L}\operatorname{Spt}\unicode[STIX]{x1D704}^{\ast }$
also does. We can equivalently show that
![]() $\mathbb{R}\operatorname{Spt}\unicode[STIX]{x1D704}_{\ast }$
commutes with
$\mathbb{R}\operatorname{Spt}\unicode[STIX]{x1D704}_{\ast }$
commutes with
![]() $\mathbb{R}s$
and this again follows from their definitions (see Remark 7.20 and [Reference HoveyHov01, Theorem 5.3]).
$\mathbb{R}s$
and this again follows from their definitions (see Remark 7.20 and [Reference HoveyHov01, Theorem 5.3]).
By [Reference HoveyHov01, Theorem 3.8] the functor
![]() $\mathbb{L}t$
on
$\mathbb{L}t$
on
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
[respectively on
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
[respectively on
![]() $\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
] is a quasi-inverse of the prolongation of
$\mathbf{PerfDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
] is a quasi-inverse of the prolongation of
![]() $\mathbb{L}(-\,\otimes \,T)$
[respectively of
$\mathbb{L}(-\,\otimes \,T)$
[respectively of
![]() $\mathbb{L}(-\,\otimes \,\widehat{T})$
]. Therefore, we conclude that for any
$\mathbb{L}(-\,\otimes \,\widehat{T})$
]. Therefore, we conclude that for any
![]() $M$
in
$M$
in
![]() $\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
:
$\mathbf{RigDA}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
:
which implies for any
![]() $M$
in
$M$
in
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
the following canonical isomorphism:
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})$
the following canonical isomorphism:
Since we already showed in Proposition 7.24 that
![]() $\mathfrak{G}^{\operatorname{st}}$
restricts to
$\mathfrak{G}^{\operatorname{st}}$
restricts to
![]() $\mathfrak{G}$
on effective motives, we conclude that it restricts on
$\mathfrak{G}$
on effective motives, we conclude that it restricts on
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K,\unicode[STIX]{x1D6EC})$
to a quasi-inverse of the functor
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K,\unicode[STIX]{x1D6EC})$
to a quasi-inverse of the functor
![]() $\mathfrak{F}$
of Corollary 7.16. In particular, this restriction is fully faithful and its essential image contains
$\mathfrak{F}$
of Corollary 7.16. In particular, this restriction is fully faithful and its essential image contains
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat },\unicode[STIX]{x1D6EC})$
. By Remark 7.23 we also deduce that
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}^{\operatorname{ct}}(K^{\flat },\unicode[STIX]{x1D6EC})$
. By Remark 7.23 we also deduce that
![]() $\mathfrak{G}^{\operatorname{st}}$
commutes with small direct sums. The claim of the theorem then follows from Proposition 7.25 and [Reference AyoubAyo15, Lemma 1.3.32].◻
$\mathfrak{G}^{\operatorname{st}}$
commutes with small direct sums. The claim of the theorem then follows from Proposition 7.25 and [Reference AyoubAyo15, Lemma 1.3.32].◻
Remark 7.27. It is worth noticing that along the proof of our main theorem, we have not used any result on almost algebra (which nonetheless has a critical role in the theory of perfectoid spaces).
Remark 7.28. The reader may wonder if the equivalence of categories
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})\cong \mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K^{\flat },\unicode[STIX]{x1D6EC})$
still holds true for more general rings of coefficients
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})\cong \mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K^{\flat },\unicode[STIX]{x1D6EC})$
still holds true for more general rings of coefficients
![]() $\unicode[STIX]{x1D6EC}$
. The hypothesis
$\unicode[STIX]{x1D6EC}$
. The hypothesis
![]() $\mathbb{Q}\subset \unicode[STIX]{x1D6EC}$
has been used several times along the proof of the main statement, and most crucially in the following two instances. First, it was used to invoke the results of [Reference VezzaniVez17] on the equivalence of motives with and without transfers (see Remarks 5.2 and 6.4). Secondly, the hypothesis
$\mathbb{Q}\subset \unicode[STIX]{x1D6EC}$
has been used several times along the proof of the main statement, and most crucially in the following two instances. First, it was used to invoke the results of [Reference VezzaniVez17] on the equivalence of motives with and without transfers (see Remarks 5.2 and 6.4). Secondly, the hypothesis
![]() $\mathbb{Q}\subset \unicode[STIX]{x1D6EC}$
was used in order to apply the result of Ayoub [Reference AyoubAyo15, Theorem 2.5.35] about a generating set for the triangulated category
$\mathbb{Q}\subset \unicode[STIX]{x1D6EC}$
was used in order to apply the result of Ayoub [Reference AyoubAyo15, Theorem 2.5.35] about a generating set for the triangulated category
![]() $\mathbf{RigDM}(K^{\flat },\unicode[STIX]{x1D6EC})$
(see Remark 7.13).
$\mathbf{RigDM}(K^{\flat },\unicode[STIX]{x1D6EC})$
(see Remark 7.13).
On the other hand, we conjecture that the tilting equivalence
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})\cong \mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K^{\flat },\unicode[STIX]{x1D6EC})$
can be generalized to a ring of coefficients
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\unicode[STIX]{x1D6EC})\cong \mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K^{\flat },\unicode[STIX]{x1D6EC})$
can be generalized to a ring of coefficients
![]() $\unicode[STIX]{x1D6EC}$
over
$\unicode[STIX]{x1D6EC}$
over
![]() $\mathbb{Z}[1/p]$
. As a matter of fact, for any prime
$\mathbb{Z}[1/p]$
. As a matter of fact, for any prime
![]() $\ell \neq p$
we expect the category
$\ell \neq p$
we expect the category
![]() $\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\mathbb{Z}/\ell )$
to be equivalent to the derived category of Galois representations over
$\mathbf{RigDM}_{\acute{\text{e}}\text{t}}(K,\mathbb{Z}/\ell )$
to be equivalent to the derived category of Galois representations over
![]() $\mathbb{Z}/\ell$
, similarly to the case of
$\mathbb{Z}/\ell$
, similarly to the case of
![]() $\mathbf{DM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\mathbb{Z}/\ell )$
(see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 9.35]). The tilting equivalence in the case
$\mathbf{DM}_{\acute{\text{e}}\text{t}}^{\operatorname{eff}}(K,\mathbb{Z}/\ell )$
(see [Reference Mazza, Voevodsky and WeibelMVW06, Theorem 9.35]). The tilting equivalence in the case
![]() $\unicode[STIX]{x1D6EC}=\mathbb{Z}/\ell$
would then follow from the classic theorem of Fontaine and Wintenberger.
$\unicode[STIX]{x1D6EC}=\mathbb{Z}/\ell$
would then follow from the classic theorem of Fontaine and Wintenberger.
Acknowledgements
This paper is part of my PhD thesis, carried out in a co-tutelle program between the University of Milan and the University of Zurich. I am incredibly indebted to my advisor Joseph Ayoub for his suggestion of pursuing the present project, his constant and generous guidance, the outstanding amount of insight that he kindly shared with me, and his endless patience. I wish to express my gratitude to my co-advisor Luca Barbieri Viale, for his invaluable encouragement and the numerous mathematical discussions throughout the development of my thesis. I am grateful to Peter Scholze for answering many questions and also to Yves André, Fabrizio Andreatta and an anonymous referee for their remarks and suggestions. I had the opportunity to give a detailed series of talks on this work at the University of Zurich: I kindly thank Andrew Kresch for this chance and the various discussions on this topic. For the plentiful remarks on preliminary versions of this work and his precious and friendly support, I also wish to thank Simon Pepin Lehalleur.
Appendix A An implicit function theorem and approximation results
The aim of this appendix is to prove Proposition 4.1, which will be obtained as a corollary of several intermediate approximation results for maps defined from objects of
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
to rigid analytic varieties.
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
to rigid analytic varieties.
Along this section, we assume that
![]() $K$
is a complete non-archimedean field. We begin our analysis with the analog of the inverse mapping theorem, which is a variant of [Reference IgusaIgu00, Theorem 2.1.1].
$K$
is a complete non-archimedean field. We begin our analysis with the analog of the inverse mapping theorem, which is a variant of [Reference IgusaIgu00, Theorem 2.1.1].
Proposition A.1. Let
![]() $R$
be a
$R$
be a
![]() $K$
-algebra, let
$K$
-algebra, let
![]() $\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n})$
and
$\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n})$
and
![]() $\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m})$
be two systems of coordinates and let
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m})$
be two systems of coordinates and let
![]() $P=(P_{1},\ldots ,P_{m})$
be a collection of polynomials in
$P=(P_{1},\ldots ,P_{m})$
be a collection of polynomials in
![]() $R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
such that
$R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
such that
![]() $P(\unicode[STIX]{x1D70E}=0,\unicode[STIX]{x1D70F}=0)=0$
and
$P(\unicode[STIX]{x1D70E}=0,\unicode[STIX]{x1D70F}=0)=0$
and
![]() $\det (\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(\unicode[STIX]{x1D70E}=0,\unicode[STIX]{x1D70F}=0)\in R^{\times }$
. There exists a unique collection
$\det (\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(\unicode[STIX]{x1D70E}=0,\unicode[STIX]{x1D70F}=0)\in R^{\times }$
. There exists a unique collection
![]() $F=(F_{1},\ldots ,F_{m})$
of
$F=(F_{1},\ldots ,F_{m})$
of
![]() $m$
formal power series in
$m$
formal power series in
![]() $R[[\unicode[STIX]{x1D70E}]]$
such that
$R[[\unicode[STIX]{x1D70E}]]$
such that
![]() $F(\unicode[STIX]{x1D70E}=0)=0$
and
$F(\unicode[STIX]{x1D70E}=0)=0$
and
![]() $P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}))=0$
in
$P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}))=0$
in
![]() $R[[\unicode[STIX]{x1D70E}]]$
.
$R[[\unicode[STIX]{x1D70E}]]$
.
Moreover, if
![]() $R$
is a Banach
$R$
is a Banach
![]() $K$
-algebra, then
$K$
-algebra, then
![]() $F_{1},\ldots ,F_{n}$
have a positive radius of convergence.
$F_{1},\ldots ,F_{n}$
have a positive radius of convergence.
Proof. Let
![]() $f$
be the polynomial
$f$
be the polynomial
![]() $\det (\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})$
in
$\det (\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})$
in
![]() $R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
and let
$R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
and let
![]() $S$
be the ring
$S$
be the ring
![]() $R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]_{f}/(P)$
. The induced map
$R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]_{f}/(P)$
. The induced map
![]() $R[\unicode[STIX]{x1D70E}]\rightarrow S$
is étale, and from the hypothesis
$R[\unicode[STIX]{x1D70E}]\rightarrow S$
is étale, and from the hypothesis
![]() $f(0,0)\in R^{\times }$
we conclude that the map
$f(0,0)\in R^{\times }$
we conclude that the map
![]() $R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]/(P)\rightarrow R$
,
$R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]/(P)\rightarrow R$
,
![]() $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})\mapsto 0$
factors through
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})\mapsto 0$
factors through
![]() $S$
.
$S$
.
Suppose given a factorization as
![]() $R[\unicode[STIX]{x1D70E}]$
-algebras
$R[\unicode[STIX]{x1D70E}]$
-algebras
![]() $S\rightarrow R[\unicode[STIX]{x1D70E}]/(\unicode[STIX]{x1D70E})^{n}\rightarrow R$
of the map
$S\rightarrow R[\unicode[STIX]{x1D70E}]/(\unicode[STIX]{x1D70E})^{n}\rightarrow R$
of the map
![]() $S\rightarrow R$
. By the étale lifting property (see [Reference GrothendieckEGAIV, Definition IV.17.1.1 and Corollary IV.17.6.2]) applied to the square
$S\rightarrow R$
. By the étale lifting property (see [Reference GrothendieckEGAIV, Definition IV.17.1.1 and Corollary IV.17.6.2]) applied to the square

we obtain a uniquely defined
![]() $R[\unicode[STIX]{x1D70E}]$
-linear map
$R[\unicode[STIX]{x1D70E}]$
-linear map
![]() $S\rightarrow R[\unicode[STIX]{x1D70E}]/(\unicode[STIX]{x1D70E})^{n+1}$
factoring
$S\rightarrow R[\unicode[STIX]{x1D70E}]/(\unicode[STIX]{x1D70E})^{n+1}$
factoring
![]() $S\rightarrow R$
, and hence by induction a uniquely defined
$S\rightarrow R$
, and hence by induction a uniquely defined
![]() $R[\unicode[STIX]{x1D70E}]$
-linear map
$R[\unicode[STIX]{x1D70E}]$
-linear map
![]() $R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]/(P)\rightarrow R[[\unicode[STIX]{x1D70E}]]$
factoring
$R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]/(P)\rightarrow R[[\unicode[STIX]{x1D70E}]]$
factoring
![]() $R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]/(P)\rightarrow R$
, as desired. The power series
$R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]/(P)\rightarrow R$
, as desired. The power series
![]() $F_{i}$
is the image of
$F_{i}$
is the image of
![]() $\unicode[STIX]{x1D70F}_{i}$
via this map.
$\unicode[STIX]{x1D70F}_{i}$
via this map.
Assume now that
![]() $R$
is a Banach
$R$
is a Banach
![]() $K$
-algebra. We want to prove that the array
$K$
-algebra. We want to prove that the array
![]() $F=(F_{1},\ldots ,F_{m})$
of formal power series in
$F=(F_{1},\ldots ,F_{m})$
of formal power series in
![]() $R[[\unicode[STIX]{x1D70E}]]$
constructed above is convergent around
$R[[\unicode[STIX]{x1D70E}]]$
constructed above is convergent around
![]() $0$
. As
$0$
. As
![]() $R$
is complete, this amounts to proving estimates on the valuation of the coefficients of
$R$
is complete, this amounts to proving estimates on the valuation of the coefficients of
![]() $F$
. To this aim, we now try to give an explicit description of them, depending on the coefficients of
$F$
. To this aim, we now try to give an explicit description of them, depending on the coefficients of
![]() $P$
. Whenever
$P$
. Whenever
![]() $I$
is a
$I$
is a
![]() $n$
-multi-index
$n$
-multi-index
![]() $I=(i_{1},\ldots ,i_{n})$
we denote by
$I=(i_{1},\ldots ,i_{n})$
we denote by
![]() $\unicode[STIX]{x1D70E}^{I}$
the product
$\unicode[STIX]{x1D70E}^{I}$
the product
![]() $\unicode[STIX]{x1D70E}_{1}^{i_{1}}\cdot \ldots \cdot \unicode[STIX]{x1D70E}_{n}^{i_{n}}$
and we adopt the analogous notation for
$\unicode[STIX]{x1D70E}_{1}^{i_{1}}\cdot \ldots \cdot \unicode[STIX]{x1D70E}_{n}^{i_{n}}$
and we adopt the analogous notation for
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
We remark that the claim is not affected by any invertible
![]() $R$
-linear transformation of the polynomials
$R$
-linear transformation of the polynomials
![]() $P_{i}$
. Therefore, by multiplying the column vector
$P_{i}$
. Therefore, by multiplying the column vector
![]() $P$
by the matrix
$P$
by the matrix
![]() $(\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(0,0)^{-1}$
we reduce to the case in which
$(\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(0,0)^{-1}$
we reduce to the case in which
![]() $(\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(0,0)=\unicode[STIX]{x1D6FF}_{ij}$
. We can then write the polynomials
$(\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(0,0)=\unicode[STIX]{x1D6FF}_{ij}$
. We can then write the polynomials
![]() $P_{i}$
in the following form:
$P_{i}$
in the following form:
where
![]() $J$
is an
$J$
is an
![]() $n$
-multi-index,
$n$
-multi-index,
![]() $H$
is an
$H$
is an
![]() $m$
-multi-index and the coefficients
$m$
-multi-index and the coefficients
![]() $c_{iJH}$
equal
$c_{iJH}$
equal
![]() $0$
whenever
$0$
whenever
![]() $|J|=0$
and
$|J|=0$
and
![]() $|H|=1$
.
$|H|=1$
.
We will determine the functions
![]() $F_{i}(\unicode[STIX]{x1D70E})$
explicitly. We start by writing them as
$F_{i}(\unicode[STIX]{x1D70E})$
explicitly. We start by writing them as
with unknown coefficients
![]() $d_{iI}$
for any
$d_{iI}$
for any
![]() $n$
-multi-index
$n$
-multi-index
![]() $I$
. We denote their
$I$
. We denote their
![]() $q$
-homogeneous parts by
$q$
-homogeneous parts by
We need to solve the equation
![]() $P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}))=0$
, which can be rewritten as
$P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}))=0$
, which can be rewritten as
where we denote by
![]() $h_{r}$
the components of the
$h_{r}$
the components of the
![]() $m$
-multi-index
$m$
-multi-index
![]() $H$
.
$H$
.
By comparing the
![]() $q$
-homogeneous parts we get
$q$
-homogeneous parts we get
where the set
![]() $\unicode[STIX]{x1D6F4}_{iq}$
consists of triples
$\unicode[STIX]{x1D6F4}_{iq}$
consists of triples
![]() $(J,H,\unicode[STIX]{x1D6F7})$
in which
$(J,H,\unicode[STIX]{x1D6F7})$
in which
![]() $J$
is a
$J$
is a
![]() $n$
-multi-index,
$n$
-multi-index,
![]() $H$
is a
$H$
is a
![]() $m$
-multi-index and
$m$
-multi-index and
![]() $\unicode[STIX]{x1D6F7}$
is a function that associates to any element
$\unicode[STIX]{x1D6F7}$
is a function that associates to any element
![]() $(r,s)$
of the set
$(r,s)$
of the set
a positive (non-zero!) integer
![]() $\unicode[STIX]{x1D6F7}(r,s)$
such that
$\unicode[STIX]{x1D6F7}(r,s)$
such that
![]() $\sum \unicode[STIX]{x1D6F7}(r,s)=q-|J|$
.
$\sum \unicode[STIX]{x1D6F7}(r,s)=q-|J|$
.
If
![]() $\unicode[STIX]{x1D6F7}(r,s)\geqslant q$
for some
$\unicode[STIX]{x1D6F7}(r,s)\geqslant q$
for some
![]() $r$
we see by definition that
$r$
we see by definition that
![]() $|J|=0$
,
$|J|=0$
,
![]() $|H|=1$
and we know that in this case
$|H|=1$
and we know that in this case
![]() $c_{i0H}=0$
. In particular, we conclude that the right-hand side of the formula above involves only
$c_{i0H}=0$
. In particular, we conclude that the right-hand side of the formula above involves only
![]() $F_{rq^{\prime }}$
with
$F_{rq^{\prime }}$
with
![]() $q^{\prime }<q$
. Hence, we can determine the coefficients
$q^{\prime }<q$
. Hence, we can determine the coefficients
![]() $d_{iI}$
by induction on
$d_{iI}$
by induction on
![]() $|I|$
. Moreover, by construction, each coefficient
$|I|$
. Moreover, by construction, each coefficient
![]() $d_{iI}$
can be expressed as
$d_{iI}$
can be expressed as
where each
![]() $Q_{iI}$
is a polynomial in
$Q_{iI}$
is a polynomial in
![]() $c_{iJH}$
for
$c_{iJH}$
for
![]() $|J|+|H|\leqslant |I|$
with coefficients in
$|J|+|H|\leqslant |I|$
with coefficients in
![]() $\mathbb{N}$
.
$\mathbb{N}$
.
We can fix a non-zero topological nilpotent element
![]() $\unicode[STIX]{x1D70B}$
such that
$\unicode[STIX]{x1D70B}$
such that
![]() $\Vert c_{iJK}\Vert \leqslant |\unicode[STIX]{x1D70B}|^{-1}$
for all
$\Vert c_{iJK}\Vert \leqslant |\unicode[STIX]{x1D70B}|^{-1}$
for all
![]() $i,J,H$
. From the argument above, we deduce inductively that each coefficient
$i,J,H$
. From the argument above, we deduce inductively that each coefficient
![]() $d_{iI}$
is a finite sum of products of the form
$d_{iI}$
is a finite sum of products of the form
![]() $\prod c_{kJH}$
with
$\prod c_{kJH}$
with
![]() $\sum |J|\leqslant |I|$
. In particular, each product has at most
$\sum |J|\leqslant |I|$
. In particular, each product has at most
![]() $|I|$
factors, and hence
$|I|$
factors, and hence
![]() $\Vert d_{iI}\Vert \leqslant |\unicode[STIX]{x1D70B}|^{-|I|}$
. We conclude
$\Vert d_{iI}\Vert \leqslant |\unicode[STIX]{x1D70B}|^{-|I|}$
. We conclude
![]() $\Vert d_{iI}\unicode[STIX]{x1D70B}^{2|I|}\Vert \leqslant |\unicode[STIX]{x1D70B}|^{|I|}$
, which tends to
$\Vert d_{iI}\unicode[STIX]{x1D70B}^{2|I|}\Vert \leqslant |\unicode[STIX]{x1D70B}|^{|I|}$
, which tends to
![]() $0$
as
$0$
as
![]() $|I|\rightarrow \infty$
.◻
$|I|\rightarrow \infty$
.◻
The previous statement has an immediate generalization.
Corollary A.2. Let
![]() $R$
be a non-archimedean Banach
$R$
be a non-archimedean Banach
![]() $K$
-algebra, let
$K$
-algebra, let
![]() $\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n})$
and
$\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n})$
and
![]() $\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m})$
be two systems of coordinates, let
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m})$
be two systems of coordinates, let
![]() $\bar{\unicode[STIX]{x1D70E}}=(\bar{\unicode[STIX]{x1D70E}}_{1},\ldots ,\bar{\unicode[STIX]{x1D70E}}_{n})$
and
$\bar{\unicode[STIX]{x1D70E}}=(\bar{\unicode[STIX]{x1D70E}}_{1},\ldots ,\bar{\unicode[STIX]{x1D70E}}_{n})$
and
![]() $\bar{\unicode[STIX]{x1D70F}}=(\bar{\unicode[STIX]{x1D70F}}_{1},\ldots ,\bar{\unicode[STIX]{x1D70F}}_{m})$
two sequences of elements of
$\bar{\unicode[STIX]{x1D70F}}=(\bar{\unicode[STIX]{x1D70F}}_{1},\ldots ,\bar{\unicode[STIX]{x1D70F}}_{m})$
two sequences of elements of
![]() $R$
and let
$R$
and let
![]() $P=(P_{1},\ldots ,P_{m})$
be a collection of polynomials in
$P=(P_{1},\ldots ,P_{m})$
be a collection of polynomials in
![]() $R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
such that
$R[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
such that
![]() $P(\unicode[STIX]{x1D70E}=\bar{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70F}=\bar{\unicode[STIX]{x1D70F}})=0$
and
$P(\unicode[STIX]{x1D70E}=\bar{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70F}=\bar{\unicode[STIX]{x1D70F}})=0$
and
![]() $\det (\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(\unicode[STIX]{x1D70E}=\bar{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70F}=\bar{\unicode[STIX]{x1D70F}})\in R^{\times }$
. There exists a unique collection
$\det (\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(\unicode[STIX]{x1D70E}=\bar{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70F}=\bar{\unicode[STIX]{x1D70F}})\in R^{\times }$
. There exists a unique collection
![]() $F=(F_{1},\ldots ,F_{m})$
of
$F=(F_{1},\ldots ,F_{m})$
of
![]() $m$
formal power series in
$m$
formal power series in
![]() $R[[\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}}]]$
such that
$R[[\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}}]]$
such that
![]() $F(\unicode[STIX]{x1D70E}=\bar{\unicode[STIX]{x1D70E}})=\bar{\unicode[STIX]{x1D70F}}$
and
$F(\unicode[STIX]{x1D70E}=\bar{\unicode[STIX]{x1D70E}})=\bar{\unicode[STIX]{x1D70F}}$
and
![]() $P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}))=0$
in
$P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}))=0$
in
![]() $R[[\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}}]]$
and they have a positive radius of convergence around
$R[[\unicode[STIX]{x1D70E}-\bar{\unicode[STIX]{x1D70E}}]]$
and they have a positive radius of convergence around
![]() $\bar{\unicode[STIX]{x1D70E}}$
.
$\bar{\unicode[STIX]{x1D70E}}$
.
Proof. If we apply Proposition A.1 to the polynomials
![]() $P_{i}^{\prime }:=P(\bar{\unicode[STIX]{x1D70E}}+\unicode[STIX]{x1D702},\bar{\unicode[STIX]{x1D70F}}+\unicode[STIX]{x1D703})$
we obtain an array of formal power series
$P_{i}^{\prime }:=P(\bar{\unicode[STIX]{x1D70E}}+\unicode[STIX]{x1D702},\bar{\unicode[STIX]{x1D70F}}+\unicode[STIX]{x1D703})$
we obtain an array of formal power series
![]() $F^{\prime }=(F_{1},\ldots ,F_{m}^{\prime })$
in
$F^{\prime }=(F_{1},\ldots ,F_{m}^{\prime })$
in
![]() $R[[\unicode[STIX]{x1D702}]]$
with positive radius of convergence such that
$R[[\unicode[STIX]{x1D702}]]$
with positive radius of convergence such that
![]() $P^{\prime }(\unicode[STIX]{x1D702},F^{\prime }(\unicode[STIX]{x1D702}))=0$
. If we now put
$P^{\prime }(\unicode[STIX]{x1D702},F^{\prime }(\unicode[STIX]{x1D702}))=0$
. If we now put
![]() $\unicode[STIX]{x1D70E}:=\bar{\unicode[STIX]{x1D70E}}\,+\,\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D70E}:=\bar{\unicode[STIX]{x1D70E}}\,+\,\unicode[STIX]{x1D702}$
and
![]() $F:=\bar{\unicode[STIX]{x1D70F}}\,+\,F^{\prime }$
we get
$F:=\bar{\unicode[STIX]{x1D70F}}\,+\,F^{\prime }$
we get
![]() $P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}\,-\,\bar{\unicode[STIX]{x1D70E}}))=0$
in
$P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}\,-\,\bar{\unicode[STIX]{x1D70E}}))=0$
in
![]() $R[[\unicode[STIX]{x1D70E}\,-\,\bar{\unicode[STIX]{x1D70E}}]]$
, as desired.◻
$R[[\unicode[STIX]{x1D70E}\,-\,\bar{\unicode[STIX]{x1D70E}}]]$
, as desired.◻
We now assume that
![]() $K$
is perfectoid and we come back to the category
$K$
is perfectoid and we come back to the category
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
that we introduced above (see Definition 2.4). We recall that an object
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
that we introduced above (see Definition 2.4). We recall that an object
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of this category is the pullback over
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
of this category is the pullback over
![]() $\widehat{\mathbb{T}}^{N}\rightarrow \mathbb{T}^{N}$
of a map
$\widehat{\mathbb{T}}^{N}\rightarrow \mathbb{T}^{N}$
of a map
![]() $X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}$
that is a composition of rational embeddings and finite étale maps from an affinoid tft adic space
$X_{0}\rightarrow \mathbb{T}^{N}\,\times \,\mathbb{T}^{M}$
that is a composition of rational embeddings and finite étale maps from an affinoid tft adic space
![]() $X_{0}$
to a torus
$X_{0}$
to a torus
![]() $\mathbb{T}^{N}\,\times \,\mathbb{T}^{M}=\operatorname{Spa}K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle$
and
$\mathbb{T}^{N}\,\times \,\mathbb{T}^{M}=\operatorname{Spa}K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1},\text{}\underline{\unicode[STIX]{x1D708}}^{\pm 1}\rangle$
and
![]() $X_{h}$
denotes the pullback of
$X_{h}$
denotes the pullback of
![]() $X_{0}$
by
$X_{0}$
by
![]() $\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \rightarrow \mathbb{T}^{N}$
.
$\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \rightarrow \mathbb{T}^{N}$
.
Proposition A.3. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be an object of
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be an object of
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. If an element
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. If an element
![]() $\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D709}$
of
![]() ${\mathcal{O}}^{+}(X)$
is algebraic and separable over each generic point of
${\mathcal{O}}^{+}(X)$
is algebraic and separable over each generic point of
![]() $\operatorname{Spec}{\mathcal{O}}(X_{0})$
then it lies in
$\operatorname{Spec}{\mathcal{O}}(X_{0})$
then it lies in
![]() ${\mathcal{O}}^{+}(X_{\bar{h}})$
for some
${\mathcal{O}}^{+}(X_{\bar{h}})$
for some
![]() $\bar{h}$
.
$\bar{h}$
.
Proof. Let
![]() $X_{0}$
be
$X_{0}$
be
![]() $\operatorname{Spa}(R_{0},R_{0}^{\circ })$
, let
$\operatorname{Spa}(R_{0},R_{0}^{\circ })$
, let
![]() $X_{h}$
be
$X_{h}$
be
![]() $\operatorname{Spa}(R_{h},R_{h}^{\circ })$
and
$\operatorname{Spa}(R_{h},R_{h}^{\circ })$
and
![]() $X$
be
$X$
be
![]() $\operatorname{Spa}(R,R^{+})$
. For any
$\operatorname{Spa}(R,R^{+})$
. For any
![]() $h\in \mathbb{N}$
one has
$h\in \mathbb{N}$
one has
![]() $R_{h}=R_{0}\,\widehat{\otimes }_{K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
and
$R_{h}=R_{0}\,\widehat{\otimes }_{K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
and
![]() $R^{+}$
coincides with the
$R^{+}$
coincides with the
![]() $\unicode[STIX]{x1D70B}$
-adic completion of
$\unicode[STIX]{x1D70B}$
-adic completion of
![]() $\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
by Proposition 2.1. The proof is divided into several steps.
$\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
by Proposition 2.1. The proof is divided into several steps.
Step 1. We can suppose that
![]() $R$
is perfectoid. Indeed, we can consider the refined tower
$R$
is perfectoid. Indeed, we can consider the refined tower
![]() $X_{h}^{\prime }=X_{0}\,\times _{\mathbb{T}^{N}\times \mathbb{T}^{M}}\,(\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \,\times \,\mathbb{T}^{M}\langle \text{}\underline{\unicode[STIX]{x1D708}}^{1/p^{h}}\rangle )$
whose limit
$X_{h}^{\prime }=X_{0}\,\times _{\mathbb{T}^{N}\times \mathbb{T}^{M}}\,(\mathbb{T}^{N}\langle \text{}\underline{\unicode[STIX]{x1D710}}^{1/p^{h}}\rangle \,\times \,\mathbb{T}^{M}\langle \text{}\underline{\unicode[STIX]{x1D708}}^{1/p^{h}}\rangle )$
whose limit
![]() $\widehat{X}$
is perfectoid. If the claim is true for this tower, we conclude that
$\widehat{X}$
is perfectoid. If the claim is true for this tower, we conclude that
![]() $\unicode[STIX]{x1D709}$
lies in the intersection of
$\unicode[STIX]{x1D709}$
lies in the intersection of
![]() ${\mathcal{O}}(X_{h}^{\prime })$
and
${\mathcal{O}}(X_{h}^{\prime })$
and
![]() ${\mathcal{O}}(X)$
inside
${\mathcal{O}}(X)$
inside
![]() ${\mathcal{O}}(\widehat{X})$
for some
${\mathcal{O}}(\widehat{X})$
for some
![]() $h$
. By Remark 1.11 this is the intersection
$h$
. By Remark 1.11 this is the intersection
which coincides with
Step 2. We can always assume that each
![]() $R_{h}$
is an integral domain. Indeed, the number of connected components of
$R_{h}$
is an integral domain. Indeed, the number of connected components of
![]() $\operatorname{Spa}R_{h}$
may rise, but it is bounded by the number of connected components of the affinoid perfectoid
$\operatorname{Spa}R_{h}$
may rise, but it is bounded by the number of connected components of the affinoid perfectoid
![]() $X$
, which is finite by Remark 2.12.
$X$
, which is finite by Remark 2.12.
We deduce that the number of connected components of
![]() $\operatorname{Spa}R_{h}$
stabilizes for
$\operatorname{Spa}R_{h}$
stabilizes for
![]() $h$
large enough. Up to shifting indices, we can then suppose that
$h$
large enough. Up to shifting indices, we can then suppose that
![]() $\operatorname{Spa}R_{0}$
is the finite disjoint union of irreducible rigid varieties
$\operatorname{Spa}R_{0}$
is the finite disjoint union of irreducible rigid varieties
![]() $\operatorname{Spa}R_{i0}$
for
$\operatorname{Spa}R_{i0}$
for
![]() $i=1,\ldots ,k$
such that
$i=1,\ldots ,k$
such that
![]() $R_{ih}=R_{i0}\,\widehat{\otimes }_{K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
is a domain for all
$R_{ih}=R_{i0}\,\widehat{\otimes }_{K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
is a domain for all
![]() $h$
. We denote by
$h$
. We denote by
![]() $R_{i}$
the ring
$R_{i}$
the ring
![]() $R_{i0}\,\widehat{\otimes }_{K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle$
. Now let
$R_{i0}\,\widehat{\otimes }_{K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{\infty }}\rangle$
. Now let
![]() $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{i})$
be an element in
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{i})$
be an element in
![]() $R^{+}=\prod R_{i}^{+}$
that is separable over
$R^{+}=\prod R_{i}^{+}$
that is separable over
![]() $\prod \operatorname{Frac}R_{i}$
, i.e., each
$\prod \operatorname{Frac}R_{i}$
, i.e., each
![]() $\unicode[STIX]{x1D709}_{i}$
is separable over
$\unicode[STIX]{x1D709}_{i}$
is separable over
![]() $\operatorname{Frac}R_{i}$
. If the proposition holds for
$\operatorname{Frac}R_{i}$
. If the proposition holds for
![]() $R_{i}$
we then conclude that
$R_{i}$
we then conclude that
![]() $\unicode[STIX]{x1D709}_{i}$
lies in
$\unicode[STIX]{x1D709}_{i}$
lies in
![]() $R_{ih}^{\circ }$
for some large enough
$R_{ih}^{\circ }$
for some large enough
![]() $h$
so that
$h$
so that
![]() $\unicode[STIX]{x1D709}\in R_{h}^{\circ }$
as claimed.
$\unicode[STIX]{x1D709}\in R_{h}^{\circ }$
as claimed.
Step 3. We prove that we can consider a non-empty rational subspace
![]() $U_{0}=\operatorname{Spa}R_{0}\langle f_{i}/g\rangle$
of
$U_{0}=\operatorname{Spa}R_{0}\langle f_{i}/g\rangle$
of
![]() $X_{0}$
instead. Indeed, using Remark 1.11 if the result holds for
$X_{0}$
instead. Indeed, using Remark 1.11 if the result holds for
![]() $U_{0}$
assuming
$U_{0}$
assuming
![]() $\bar{h}=0$
we deduce that
$\bar{h}=0$
we deduce that
![]() $\unicode[STIX]{x1D709}$
lies in the intersection of
$\unicode[STIX]{x1D709}$
lies in the intersection of
![]() $R\cong \widehat{\bigoplus }R_{0}$
and of
$R\cong \widehat{\bigoplus }R_{0}$
and of
![]() $R_{0}\langle f_{i}/g\rangle$
inside
$R_{0}\langle f_{i}/g\rangle$
inside
![]() $R\langle f_{i}/g\rangle \cong \widehat{\bigoplus }R_{0}\langle f_{i}/g\rangle$
, which coincides with
$R\langle f_{i}/g\rangle \cong \widehat{\bigoplus }R_{0}\langle f_{i}/g\rangle$
, which coincides with
![]() $R_{0}$
.
$R_{0}$
.
Step 4. We prove that we can assume
![]() $\unicode[STIX]{x1D709}$
to be integral over
$\unicode[STIX]{x1D709}$
to be integral over
![]() $R_{0}$
. Indeed, let
$R_{0}$
. Indeed, let
![]() $P_{\unicode[STIX]{x1D709}}$
be its minimal polynomial over
$P_{\unicode[STIX]{x1D709}}$
be its minimal polynomial over
![]() $\operatorname{Frac}(R_{0})$
. We can suppose there is a common denominator
$\operatorname{Frac}(R_{0})$
. We can suppose there is a common denominator
![]() $d$
such that
$d$
such that
![]() $P_{\unicode[STIX]{x1D709}}$
has coefficients in
$P_{\unicode[STIX]{x1D709}}$
has coefficients in
![]() $R_{0}[1/d][x]$
. By [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.2.1/4(ii)] we can also assume that
$R_{0}[1/d][x]$
. By [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.2.1/4(ii)] we can also assume that
![]() $|d|=1$
. In particular, by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.2.6/3], the rational subspace associated to
$|d|=1$
. In particular, by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.2.6/3], the rational subspace associated to
![]() $R_{0}\langle 1/d\rangle$
is not empty. By step 3, we can then restrict to it and assume
$R_{0}\langle 1/d\rangle$
is not empty. By step 3, we can then restrict to it and assume
![]() $\unicode[STIX]{x1D709}$
to be integral over
$\unicode[STIX]{x1D709}$
to be integral over
![]() $R_{0}$
and
$R_{0}$
and
![]() $R_{0}[\unicode[STIX]{x1D709}]\cong R_{0}[x]/P_{\unicode[STIX]{x1D709}}(x)$
.
$R_{0}[\unicode[STIX]{x1D709}]\cong R_{0}[x]/P_{\unicode[STIX]{x1D709}}(x)$
.
Step 5. We can suppose that
![]() $P_{\unicode[STIX]{x1D709}}(x)$
is the minimal polynomial of
$P_{\unicode[STIX]{x1D709}}(x)$
is the minimal polynomial of
![]() $\unicode[STIX]{x1D709}$
with respect to all non-empty rational subspaces of
$\unicode[STIX]{x1D709}$
with respect to all non-empty rational subspaces of
![]() $X_{h}$
for all
$X_{h}$
for all
![]() $h$
. If it is not the case, from the previous steps we can rescale indices and restrict to a rational subspace with respect to which the degree of
$h$
. If it is not the case, from the previous steps we can rescale indices and restrict to a rational subspace with respect to which the degree of
![]() $P_{\unicode[STIX]{x1D709}}(x)$
is lower. Since the degree is bounded from below, we conclude the claim.
$P_{\unicode[STIX]{x1D709}}(x)$
is lower. Since the degree is bounded from below, we conclude the claim.
Step 6. We now conclude the claim. By steps 3 and 4 we may suppose that the map
![]() $R_{0}\rightarrow R_{0}[\unicode[STIX]{x1D709}]$
is finite étale. Since this map splits after tensoring with
$R_{0}\rightarrow R_{0}[\unicode[STIX]{x1D709}]$
is finite étale. Since this map splits after tensoring with
![]() $R$
, we can deduce by [Reference ScholzeSch12, Lemma 7.5] that it splits already at some level
$R$
, we can deduce by [Reference ScholzeSch12, Lemma 7.5] that it splits already at some level
![]() $h$
. By step 5, this implies that
$h$
. By step 5, this implies that
![]() $P_{\unicode[STIX]{x1D709}}(x)$
is of degree
$P_{\unicode[STIX]{x1D709}}(x)$
is of degree
![]() $1$
, and hence
$1$
, and hence
![]() $\unicode[STIX]{x1D709}\in R_{0}$
.◻
$\unicode[STIX]{x1D709}\in R_{0}$
.◻
We introduce now the geometric application of Propositions A.1 and A.3. It states that a map from
![]() $\mathop{\varprojlim }\nolimits_{h}X_{h}\in \widehat{\text{Rig}}\operatorname{Sm}$
to a rigid variety factors, up to
$\mathop{\varprojlim }\nolimits_{h}X_{h}\in \widehat{\text{Rig}}\operatorname{Sm}$
to a rigid variety factors, up to
![]() $\mathbb{B}^{1}$
-homotopy, over one of the intermediate varieties
$\mathbb{B}^{1}$
-homotopy, over one of the intermediate varieties
![]() $X_{h}$
. Analogous statements are widely used in [Reference AyoubAyo15] (see for example [Reference AyoubAyo15, Theorem 2.2.58]): there, these are obtained as corollaries of Popescu’s theorem [Reference PopescuPop85, Reference PopescuPop86], which is not available in our non-noetherian setting.
$X_{h}$
. Analogous statements are widely used in [Reference AyoubAyo15] (see for example [Reference AyoubAyo15, Theorem 2.2.58]): there, these are obtained as corollaries of Popescu’s theorem [Reference PopescuPop85, Reference PopescuPop86], which is not available in our non-noetherian setting.
Proposition A.4. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be in
![]() $\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Let
$\widehat{\text{Rig}}\operatorname{Sm}^{\operatorname{gc}}$
. Let
![]() $Y$
be an affinoid rigid variety endowed with an étale map
$Y$
be an affinoid rigid variety endowed with an étale map
![]() $Y\rightarrow \mathbb{B}^{n}$
and let
$Y\rightarrow \mathbb{B}^{n}$
and let
![]() $f:X\rightarrow Y$
be a map of adic spaces.
$f:X\rightarrow Y$
be a map of adic spaces.
(i) There exist
 $m$
polynomials
$m$
polynomials
 $Q_{1},\ldots ,Q_{m}$
in
$Q_{1},\ldots ,Q_{m}$
in
 $K[\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n},\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m}]$
such that
$K[\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n},\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m}]$
such that
 $Y\cong \operatorname{Spa}A$
with
$Y\cong \operatorname{Spa}A$
with
 $A\cong K\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(Q)$
and
$A\cong K\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(Q)$
and
 $\det (\unicode[STIX]{x2202}Q_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})\in A^{\times }$
.
$\det (\unicode[STIX]{x2202}Q_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})\in A^{\times }$
.(ii) There exists a map
 $H:X\,\times \,\mathbb{B}^{1}\rightarrow Y$
such that
$H:X\,\times \,\mathbb{B}^{1}\rightarrow Y$
such that
 $H\,\circ \,i_{0}=f$
and
$H\,\circ \,i_{0}=f$
and
 $H\,\circ \,i_{1}$
factors over the canonical map
$H\,\circ \,i_{1}$
factors over the canonical map
 $X\rightarrow X_{h}$
for some integer
$X\rightarrow X_{h}$
for some integer
 $h$
.
$h$
.
Moreover, if
![]() $f$
is induced by the map
$f$
is induced by the map
![]() $K\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle \rightarrow {\mathcal{O}}(X)$
,
$K\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle \rightarrow {\mathcal{O}}(X)$
,
![]() $\unicode[STIX]{x1D70E}\mapsto s,\unicode[STIX]{x1D70F}\mapsto t$
the map
$\unicode[STIX]{x1D70E}\mapsto s,\unicode[STIX]{x1D70F}\mapsto t$
the map
![]() $H$
can be defined via
$H$
can be defined via
where
![]() $F$
is the unique array of formal power series in
$F$
is the unique array of formal power series in
![]() ${\mathcal{O}}(X)[[\unicode[STIX]{x1D70E}-s]]$
associated to the polynomials
${\mathcal{O}}(X)[[\unicode[STIX]{x1D70E}-s]]$
associated to the polynomials
![]() $P(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})$
by Corollary A.2, and
$P(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})$
by Corollary A.2, and
![]() $\tilde{s}$
is any element in
$\tilde{s}$
is any element in
![]() $\mathop{\varinjlim }\nolimits_{h}{\mathcal{O}}^{+}(X_{h})$
such that the radius of convergence of
$\mathop{\varinjlim }\nolimits_{h}{\mathcal{O}}^{+}(X_{h})$
such that the radius of convergence of
![]() $F$
is larger than
$F$
is larger than
![]() $\Vert \tilde{s}-s\Vert$
and
$\Vert \tilde{s}-s\Vert$
and
![]() $F(\tilde{s})$
lies in
$F(\tilde{s})$
lies in
![]() ${\mathcal{O}}^{+}(X)$
.
${\mathcal{O}}^{+}(X)$
.
Proof. The first claim follows from [Reference AyoubAyo15, Lemma 1.1.52]. We turn to the second claim. Let
![]() $X_{0}$
be
$X_{0}$
be
![]() $\operatorname{Spa}(R_{0},R_{0}^{\circ })$
and
$\operatorname{Spa}(R_{0},R_{0}^{\circ })$
and
![]() $X$
be
$X$
be
![]() $\operatorname{Spa}(R,R^{+})$
. For any
$\operatorname{Spa}(R,R^{+})$
. For any
![]() $h\in \mathbb{N}$
we denote
$h\in \mathbb{N}$
we denote
![]() $R_{0}\,\widehat{\otimes }_{K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
with
$R_{0}\,\widehat{\otimes }_{K\langle \text{}\underline{\unicode[STIX]{x1D710}}\rangle }\,K\langle \text{}\underline{\unicode[STIX]{x1D710}}^{\pm 1/p^{h}}\rangle$
with
![]() $R_{h}$
so that
$R_{h}$
so that
![]() $R^{+}$
coincides with the
$R^{+}$
coincides with the
![]() $\unicode[STIX]{x1D70B}$
-adic completion of
$\unicode[STIX]{x1D70B}$
-adic completion of
![]() $\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
by Proposition 2.1.
$\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
by Proposition 2.1.
The map
![]() $f$
is determined by the choice of
$f$
is determined by the choice of
![]() $n$
elements
$n$
elements
![]() $s=(s_{1},\ldots ,s_{n})$
and
$s=(s_{1},\ldots ,s_{n})$
and
![]() $m$
elements
$m$
elements
![]() $t=(t_{1},\ldots ,t_{m})$
of
$t=(t_{1},\ldots ,t_{m})$
of
![]() $R^{+}$
such that
$R^{+}$
such that
![]() $P(s,t)=0$
. We prove that the formula for
$P(s,t)=0$
. We prove that the formula for
![]() $H$
provided in the statement defines a map
$H$
provided in the statement defines a map
![]() $H$
with the required properties.
$H$
with the required properties.
By Corollary A.2 there exists a collection
![]() $F=(F_{1},\ldots ,F_{m})$
of
$F=(F_{1},\ldots ,F_{m})$
of
![]() $m$
formal power series in
$m$
formal power series in
![]() $R[[\unicode[STIX]{x1D70E}-s]]$
with a positive radius of convergence such that
$R[[\unicode[STIX]{x1D70E}-s]]$
with a positive radius of convergence such that
![]() $F(s)=t$
and
$F(s)=t$
and
![]() $P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}))=0$
. As
$P(\unicode[STIX]{x1D70E},F(\unicode[STIX]{x1D70E}))=0$
. As
![]() $\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
is dense in
$\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
is dense in
![]() $R^{+}$
we can find an integer
$R^{+}$
we can find an integer
![]() $\bar{h}$
and elements
$\bar{h}$
and elements
![]() $\tilde{s}_{i}\in R_{\bar{h}}^{\circ }$
such that
$\tilde{s}_{i}\in R_{\bar{h}}^{\circ }$
such that
![]() $\Vert \tilde{s}-s\Vert$
is smaller than the convergence radius of
$\Vert \tilde{s}-s\Vert$
is smaller than the convergence radius of
![]() $F$
. By renaming the indices, we can assume that
$F$
. By renaming the indices, we can assume that
![]() $\bar{h}=0$
. As
$\bar{h}=0$
. As
![]() $F$
is continuous and
$F$
is continuous and
![]() $R^{+}$
is open, we can also assume that the elements
$R^{+}$
is open, we can also assume that the elements
![]() $F_{j}(\tilde{s})$
lie in
$F_{j}(\tilde{s})$
lie in
![]() $R^{+}$
. We are left to prove that they actually lie in
$R^{+}$
. We are left to prove that they actually lie in
![]() $\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
. Since the determinant of
$\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
. Since the determinant of
![]() $(\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(\tilde{s},F(\tilde{s}))$
is invertible, the field
$(\unicode[STIX]{x2202}P_{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{j})(\tilde{s},F(\tilde{s}))$
is invertible, the field
![]() $L:=\operatorname{Frac}(R_{0})(F_{1}(\tilde{s}),\ldots ,F_{m}(\tilde{s}))$
is algebraic and separable over
$L:=\operatorname{Frac}(R_{0})(F_{1}(\tilde{s}),\ldots ,F_{m}(\tilde{s}))$
is algebraic and separable over
![]() $\operatorname{Frac}(R_{0})$
. We can then apply Proposition A.3 to conclude that each element
$\operatorname{Frac}(R_{0})$
. We can then apply Proposition A.3 to conclude that each element
![]() $F_{j}(\tilde{s})$
lies in
$F_{j}(\tilde{s})$
lies in
![]() $R_{h}^{\circ }$
for a sufficiently big integer
$R_{h}^{\circ }$
for a sufficiently big integer
![]() $h$
.◻
$h$
.◻
The goal of the rest of this section is to prove Proposition 4.1. To this aim, we present a generalization of the results above for collections of maps. As before, we start with an algebraic statement and then translate it into a geometrical fact for our specific purposes.
Proposition A.5. Let
![]() $R$
be a Banach
$R$
be a Banach
![]() $K$
-algebra and let
$K$
-algebra and let
![]() $\{R_{h}\}_{h\in \mathbb{N}}$
be a collection of nested complete subrings of
$\{R_{h}\}_{h\in \mathbb{N}}$
be a collection of nested complete subrings of
![]() $R$
such that
$R$
such that
![]() $\varinjlim R_{h}$
is dense in
$\varinjlim R_{h}$
is dense in
![]() $R$
. Let
$R$
. Let
![]() $s_{1},\ldots ,s_{N}$
be elements of
$s_{1},\ldots ,s_{N}$
be elements of
![]() $R\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
. For any
$R\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
. For any
![]() $\unicode[STIX]{x1D700}>0$
there exists an integer
$\unicode[STIX]{x1D700}>0$
there exists an integer
![]() $h$
and elements
$h$
and elements
![]() $\tilde{s}_{1},\ldots ,\tilde{s}_{N}$
of
$\tilde{s}_{1},\ldots ,\tilde{s}_{N}$
of
![]() $R_{h}\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
satisfying the following conditions.
$R_{h}\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
satisfying the following conditions.
(i)
 $|s_{\unicode[STIX]{x1D6FC}}-\tilde{s}_{\unicode[STIX]{x1D6FC}}|<\unicode[STIX]{x1D700}$
for each
$|s_{\unicode[STIX]{x1D6FC}}-\tilde{s}_{\unicode[STIX]{x1D6FC}}|<\unicode[STIX]{x1D700}$
for each
 $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.(ii) For any
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \{1,\ldots ,N\}$
and any
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \{1,\ldots ,N\}$
and any
 $k\in \{1,\ldots ,n\}$
such that
$k\in \{1,\ldots ,n\}$
such that
 $s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{k}=0}=s_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D703}_{k}=0}$
we also have
$s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{k}=0}=s_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D703}_{k}=0}$
we also have
 $\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{k}=0}=\tilde{s}_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D703}_{k}=0}$
.
$\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{k}=0}=\tilde{s}_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D703}_{k}=0}$
.(iii) For any
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \{1,\ldots ,N\}$
and any
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \{1,\ldots ,N\}$
and any
 $k\in \{1,\ldots ,n\}$
such that
$k\in \{1,\ldots ,n\}$
such that
 $s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{k}=1}=s_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D703}_{k}=1}$
we also have
$s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{k}=1}=s_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D703}_{k}=1}$
we also have
 $\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{k}=1}=\tilde{s}_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D703}_{k}=1}$
.
$\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{k}=1}=\tilde{s}_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D703}_{k}=1}$
.(iv) For any
 $\unicode[STIX]{x1D6FC}\in \{1,\ldots ,N\}$
if
$\unicode[STIX]{x1D6FC}\in \{1,\ldots ,N\}$
if
 $s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{1}=1}\in R_{h^{\prime }}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
for some
$s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{1}=1}\in R_{h^{\prime }}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
for some
 $h^{\prime }$
then
$h^{\prime }$
then
 $\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{1}=1}=s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{1}=1}$
.
$\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{1}=1}=s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D703}_{1}=1}$
.
Proof. We will actually prove a stronger statement, namely that we can reinforce the previous conditions with the following.
(v) For any
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \{1,\ldots ,N\}$
any subset
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \{1,\ldots ,N\}$
any subset
 $T$
of
$T$
of
 $\{1,\ldots ,n\}$
and any map
$\{1,\ldots ,n\}$
and any map
 $\unicode[STIX]{x1D70E}:T\rightarrow \{0,1\}$
such that
$\unicode[STIX]{x1D70E}:T\rightarrow \{0,1\}$
such that
 $s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}=s_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D70E}}$
then
$s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}=s_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D70E}}$
then
 $\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}=\tilde{s}_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D70E}}$
.
$\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}=\tilde{s}_{\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D70E}}$
.
(vi) For any
 $\unicode[STIX]{x1D6FC}\in \{1,\ldots ,N\}$
any subset
$\unicode[STIX]{x1D6FC}\in \{1,\ldots ,N\}$
any subset
 $T$
of
$T$
of
 $\{1,\ldots ,n\}$
containing
$\{1,\ldots ,n\}$
containing
 $1$
and any map
$1$
and any map
 $\unicode[STIX]{x1D70E}:T\rightarrow \{0,1\}$
such that
$\unicode[STIX]{x1D70E}:T\rightarrow \{0,1\}$
such that
 $s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}\in R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
for some
$s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}\in R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
for some
 $h$
then
$h$
then
 $\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}=s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}$
.
$\tilde{s}_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}=s_{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D70E}}$
.
Above we denote by
![]() $s|_{\unicode[STIX]{x1D70E}}$
the image of
$s|_{\unicode[STIX]{x1D70E}}$
the image of
![]() $s$
via the substitution
$s$
via the substitution
![]() $(\unicode[STIX]{x1D703}_{t}=\unicode[STIX]{x1D70E}(t))_{t\in T}$
. We proceed by induction on
$(\unicode[STIX]{x1D703}_{t}=\unicode[STIX]{x1D70E}(t))_{t\in T}$
. We proceed by induction on
![]() $N$
, the case
$N$
, the case
![]() $N=0$
being trivial.
$N=0$
being trivial.
Consider the conditions we want to preserve that involve the index
![]() $N$
. They are of the form
$N$
. They are of the form
and are indexed by some pairs
![]() $(\unicode[STIX]{x1D70E},i)$
, where
$(\unicode[STIX]{x1D70E},i)$
, where
![]() $i$
is an index and
$i$
is an index and
![]() $\unicode[STIX]{x1D70E}$
varies in a set of maps
$\unicode[STIX]{x1D70E}$
varies in a set of maps
![]() $\unicode[STIX]{x1D6F4}$
. Our procedure consists in determining by induction the elements
$\unicode[STIX]{x1D6F4}$
. Our procedure consists in determining by induction the elements
![]() $\tilde{s}_{1},\ldots ,\tilde{s}_{N-1}$
first, and then deducing the existence of
$\tilde{s}_{1},\ldots ,\tilde{s}_{N-1}$
first, and then deducing the existence of
![]() $\tilde{s}_{N}$
by means of Lemma A.8 by lifting the elements
$\tilde{s}_{N}$
by means of Lemma A.8 by lifting the elements
![]() $\{\tilde{s}_{i}|_{\unicode[STIX]{x1D70E}}\}_{(\unicode[STIX]{x1D70E},i)}$
. Therefore, we first define
$\{\tilde{s}_{i}|_{\unicode[STIX]{x1D70E}}\}_{(\unicode[STIX]{x1D70E},i)}$
. Therefore, we first define
![]() $\unicode[STIX]{x1D700}^{\prime }:=(1/C)\unicode[STIX]{x1D700}$
where
$\unicode[STIX]{x1D700}^{\prime }:=(1/C)\unicode[STIX]{x1D700}$
where
![]() $C=C(\unicode[STIX]{x1D6F4})$
is the constant introduced in Lemma A.8 and then apply the induction hypothesis to the first
$C=C(\unicode[STIX]{x1D6F4})$
is the constant introduced in Lemma A.8 and then apply the induction hypothesis to the first
![]() $N-1$
elements with respect to
$N-1$
elements with respect to
![]() $\unicode[STIX]{x1D700}^{\prime }$
.
$\unicode[STIX]{x1D700}^{\prime }$
.
By the induction hypothesis, the elements
![]() $\tilde{s}_{i}|_{\unicode[STIX]{x1D70E}}$
satisfy the compatibility condition of Lemma A.8 and lie in
$\tilde{s}_{i}|_{\unicode[STIX]{x1D70E}}$
satisfy the compatibility condition of Lemma A.8 and lie in
![]() $R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
for some integer
$R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
for some integer
![]() $h$
. Without loss of generality, we assume
$h$
. Without loss of generality, we assume
![]() $h=0$
. By Lemma A.8 we can find an element
$h=0$
. By Lemma A.8 we can find an element
![]() $\tilde{s}_{N}$
of
$\tilde{s}_{N}$
of
![]() $R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
lifting them such that
$R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
lifting them such that
![]() $|\tilde{s}_{N}-s_{N}|<C\unicode[STIX]{x1D700}^{\prime }=\unicode[STIX]{x1D700}$
, as desired.◻
$|\tilde{s}_{N}-s_{N}|<C\unicode[STIX]{x1D700}^{\prime }=\unicode[STIX]{x1D700}$
, as desired.◻
The following lemmas are used in the proof of the previous proposition.
Lemma A.6. For any normed ring
![]() $R$
and any map
$R$
and any map
![]() $\unicode[STIX]{x1D70E}:T_{\unicode[STIX]{x1D70E}}\rightarrow \{0,1\}$
defined on a subset
$\unicode[STIX]{x1D70E}:T_{\unicode[STIX]{x1D70E}}\rightarrow \{0,1\}$
defined on a subset
![]() $T_{\unicode[STIX]{x1D70E}}$
of
$T_{\unicode[STIX]{x1D70E}}$
of
![]() $\{1,\ldots ,n\}$
we denote by
$\{1,\ldots ,n\}$
we denote by
![]() $I_{\unicode[STIX]{x1D70E}}$
the ideal of
$I_{\unicode[STIX]{x1D70E}}$
the ideal of
![]() $R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
generated by
$R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
generated by
![]() $\unicode[STIX]{x1D703}_{i}-\unicode[STIX]{x1D70E}(i)$
as
$\unicode[STIX]{x1D703}_{i}-\unicode[STIX]{x1D70E}(i)$
as
![]() $i$
varies in
$i$
varies in
![]() $T_{\unicode[STIX]{x1D70E}}$
. For any finite set
$T_{\unicode[STIX]{x1D70E}}$
. For any finite set
![]() $\unicode[STIX]{x1D6F4}$
of such maps and any such map
$\unicode[STIX]{x1D6F4}$
of such maps and any such map
![]() $\unicode[STIX]{x1D702}$
one has
$\unicode[STIX]{x1D702}$
one has
![]() $(\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D70E}})+I_{\unicode[STIX]{x1D702}}=\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}(I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}})$
.
$(\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D70E}})+I_{\unicode[STIX]{x1D702}}=\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}(I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}})$
.
Proof. We only need to prove the inclusion
![]() $\bigcap (I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}})\subseteq (\bigcap I_{\unicode[STIX]{x1D70E}})+I_{\unicode[STIX]{x1D702}}$
. We can make induction on the cardinality of
$\bigcap (I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}})\subseteq (\bigcap I_{\unicode[STIX]{x1D70E}})+I_{\unicode[STIX]{x1D702}}$
. We can make induction on the cardinality of
![]() $T_{\unicode[STIX]{x1D702}}$
and restrict to the case in which
$T_{\unicode[STIX]{x1D702}}$
and restrict to the case in which
![]() $T_{\unicode[STIX]{x1D702}}$
is a singleton. By changing variables, we can suppose
$T_{\unicode[STIX]{x1D702}}$
is a singleton. By changing variables, we can suppose
![]() $T_{\unicode[STIX]{x1D702}}=\{1\}$
and
$T_{\unicode[STIX]{x1D702}}=\{1\}$
and
![]() $\unicode[STIX]{x1D702}(1)=0$
so that
$\unicode[STIX]{x1D702}(1)=0$
so that
![]() $I_{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D703}_{1})$
.
$I_{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D703}_{1})$
.
We first suppose that
![]() $1\notin T_{\unicode[STIX]{x1D70E}}$
for all
$1\notin T_{\unicode[STIX]{x1D70E}}$
for all
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
. Let
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
. Let
![]() $s$
be an element of
$s$
be an element of
![]() $\bigcap (I_{\unicode[STIX]{x1D70E}}+(\unicode[STIX]{x1D703}_{1}))$
. This means we can find elements
$\bigcap (I_{\unicode[STIX]{x1D70E}}+(\unicode[STIX]{x1D703}_{1}))$
. This means we can find elements
![]() $s_{\unicode[STIX]{x1D70E}}\in I_{\unicode[STIX]{x1D70E}}$
and polynomials
$s_{\unicode[STIX]{x1D70E}}\in I_{\unicode[STIX]{x1D70E}}$
and polynomials
![]() $p_{\unicode[STIX]{x1D70E}}\in R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
such that
$p_{\unicode[STIX]{x1D70E}}\in R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
such that
![]() $s=s_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D703}_{1}$
. Since
$s=s_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D703}_{1}$
. Since
![]() $I_{\unicode[STIX]{x1D70E}}$
is generated by polynomials of the form
$I_{\unicode[STIX]{x1D70E}}$
is generated by polynomials of the form
![]() $\unicode[STIX]{x1D703}_{i}-\unicode[STIX]{x1D716}$
with
$\unicode[STIX]{x1D703}_{i}-\unicode[STIX]{x1D716}$
with
![]() $i\neq 1$
we can suppose that
$i\neq 1$
we can suppose that
![]() $s_{\unicode[STIX]{x1D70E}}$
contains no
$s_{\unicode[STIX]{x1D70E}}$
contains no
![]() $\unicode[STIX]{x1D703}_{1}$
by eventually changing
$\unicode[STIX]{x1D703}_{1}$
by eventually changing
![]() $p_{\unicode[STIX]{x1D70E}}$
. Now let
$p_{\unicode[STIX]{x1D70E}}$
. Now let
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $\unicode[STIX]{x1D70E}^{\prime }$
be in
$\unicode[STIX]{x1D70E}^{\prime }$
be in
![]() $\unicode[STIX]{x1D6F4}$
. From the equality
$\unicode[STIX]{x1D6F4}$
. From the equality
we conclude that
![]() $s_{\unicode[STIX]{x1D70E}}\in \bigcap I_{\unicode[STIX]{x1D70E}}$
. Therefore,
$s_{\unicode[STIX]{x1D70E}}\in \bigcap I_{\unicode[STIX]{x1D70E}}$
. Therefore,
![]() $s\in \bigcap I_{\unicode[STIX]{x1D70E}}+(\unicode[STIX]{x1D703}_{1})$
, as claimed.
$s\in \bigcap I_{\unicode[STIX]{x1D70E}}+(\unicode[STIX]{x1D703}_{1})$
, as claimed.
We now move to the general case. Suppose
![]() $\bar{\unicode[STIX]{x1D70E}}(1)=1$
for some
$\bar{\unicode[STIX]{x1D70E}}(1)=1$
for some
![]() $\bar{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6F4}$
. Then
$\bar{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6F4}$
. Then
![]() $I_{\bar{\unicode[STIX]{x1D70E}}}+I_{\unicode[STIX]{x1D702}}=R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
and if
$I_{\bar{\unicode[STIX]{x1D70E}}}+I_{\unicode[STIX]{x1D702}}=R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
and if
![]() $f\in \bigcap _{\unicode[STIX]{x1D70E}\neq \bar{\unicode[STIX]{x1D70E}}}I_{\unicode[STIX]{x1D70E}}$
then
$f\in \bigcap _{\unicode[STIX]{x1D70E}\neq \bar{\unicode[STIX]{x1D70E}}}I_{\unicode[STIX]{x1D70E}}$
then
![]() $f=-f(\unicode[STIX]{x1D703}_{1}-1)+f\unicode[STIX]{x1D703}_{1}\in \bigcap _{\unicode[STIX]{x1D70E}}I_{\unicode[STIX]{x1D70E}}+(\unicode[STIX]{x1D703}_{1})$
. Therefore, the contribution of
$f=-f(\unicode[STIX]{x1D703}_{1}-1)+f\unicode[STIX]{x1D703}_{1}\in \bigcap _{\unicode[STIX]{x1D70E}}I_{\unicode[STIX]{x1D70E}}+(\unicode[STIX]{x1D703}_{1})$
. Therefore, the contribution of
![]() $I_{\bar{\unicode[STIX]{x1D70E}}}$
is trivial on both sides and we can erase it from
$I_{\bar{\unicode[STIX]{x1D70E}}}$
is trivial on both sides and we can erase it from
![]() $\unicode[STIX]{x1D6F4}$
. We can, therefore, suppose that
$\unicode[STIX]{x1D6F4}$
. We can, therefore, suppose that
![]() $\unicode[STIX]{x1D70E}(1)=0$
whenever
$\unicode[STIX]{x1D70E}(1)=0$
whenever
![]() $1\in T_{\unicode[STIX]{x1D70E}}$
.
$1\in T_{\unicode[STIX]{x1D70E}}$
.
For any
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
let
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
let
![]() $\unicode[STIX]{x1D70E}^{\prime }$
be its restriction to
$\unicode[STIX]{x1D70E}^{\prime }$
be its restriction to
![]() $T_{\unicode[STIX]{x1D70E}}\setminus \{1\}$
. We have
$T_{\unicode[STIX]{x1D70E}}\setminus \{1\}$
. We have
![]() $I_{\unicode[STIX]{x1D70E}^{\prime }}\subseteq I_{\unicode[STIX]{x1D70E}}$
and
$I_{\unicode[STIX]{x1D70E}^{\prime }}\subseteq I_{\unicode[STIX]{x1D70E}}$
and
![]() $I_{\unicode[STIX]{x1D70E}^{\prime }}+(\unicode[STIX]{x1D703}_{1})=I_{\unicode[STIX]{x1D70E}}+(\unicode[STIX]{x1D703}_{1})$
for all
$I_{\unicode[STIX]{x1D70E}^{\prime }}+(\unicode[STIX]{x1D703}_{1})=I_{\unicode[STIX]{x1D70E}}+(\unicode[STIX]{x1D703}_{1})$
for all
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
. By what we already proved, the statement holds for the set
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
. By what we already proved, the statement holds for the set
![]() $\unicode[STIX]{x1D6F4}^{\prime }:=\{\unicode[STIX]{x1D70E}^{\prime }:\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}\}$
. Therefore,
$\unicode[STIX]{x1D6F4}^{\prime }:=\{\unicode[STIX]{x1D70E}^{\prime }:\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}\}$
. Therefore,
proving the claim. ◻
We recall (see [Reference Bosch, Güntzer and RemmertBGR84, Definition 1.1.9/1]) that a morphism of normed groups
![]() $\unicode[STIX]{x1D719}:G\rightarrow H$
is strict if the homomorphism
$\unicode[STIX]{x1D719}:G\rightarrow H$
is strict if the homomorphism
![]() $G/\text{ker}\,\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}(G)$
is a homeomorphism, where the former group is endowed with the quotient topology and the latter with the topology inherited from
$G/\text{ker}\,\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}(G)$
is a homeomorphism, where the former group is endowed with the quotient topology and the latter with the topology inherited from
![]() $H$
. In particular, we say that a sequence of normed
$H$
. In particular, we say that a sequence of normed
![]() $K$
-vector spaces
$K$
-vector spaces
is strict and exact at
![]() $S$
if it is exact at
$S$
if it is exact at
![]() $S$
and if
$S$
and if
![]() $f$
is strict, i.e., the quotient norm and the norm induced by
$f$
is strict, i.e., the quotient norm and the norm induced by
![]() $S$
on
$S$
on
![]() $R/\text{ker}(f)\cong \ker (g)$
are equivalent.
$R/\text{ker}(f)\cong \ker (g)$
are equivalent.
Lemma A.7. For any map
![]() $\unicode[STIX]{x1D70E}:T_{\unicode[STIX]{x1D70E}}\rightarrow \{0,1\}$
defined on a subset
$\unicode[STIX]{x1D70E}:T_{\unicode[STIX]{x1D70E}}\rightarrow \{0,1\}$
defined on a subset
![]() $T_{\unicode[STIX]{x1D70E}}$
of
$T_{\unicode[STIX]{x1D70E}}$
of
![]() $\{1,\ldots ,n\}$
we denote by
$\{1,\ldots ,n\}$
we denote by
![]() $I_{\unicode[STIX]{x1D70E}}$
the ideal of
$I_{\unicode[STIX]{x1D70E}}$
the ideal of
![]() $R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle =R\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
generated by
$R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle =R\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
generated by
![]() $\unicode[STIX]{x1D703}_{i}-\unicode[STIX]{x1D70E}(i)$
as
$\unicode[STIX]{x1D703}_{i}-\unicode[STIX]{x1D70E}(i)$
as
![]() $i$
varies in
$i$
varies in
![]() $T_{\unicode[STIX]{x1D70E}}$
. For any finite set
$T_{\unicode[STIX]{x1D70E}}$
. For any finite set
![]() $\unicode[STIX]{x1D6F4}$
of such maps and any complete normed
$\unicode[STIX]{x1D6F4}$
of such maps and any complete normed
![]() $K$
-algebra
$K$
-algebra
![]() $R$
the following sequence of Banach
$R$
the following sequence of Banach
![]() $K$
-algebras is strict and exact
$K$
-algebras is strict and exact
and the ideal
![]() $\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D70E}}$
is generated by a finite set of polynomials in the
$\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D70E}}$
is generated by a finite set of polynomials in the
![]() $\unicode[STIX]{x1D703}_{i}$
with coefficients in
$\unicode[STIX]{x1D703}_{i}$
with coefficients in
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Proof. We follow the notation and the proof of [Reference KleinertKle89]. For a collection of ideals
![]() ${\mathcal{I}}=\{I_{\unicode[STIX]{x1D70E}}\}$
we let
${\mathcal{I}}=\{I_{\unicode[STIX]{x1D70E}}\}$
we let
![]() $A({\mathcal{I}})$
be the kernel of the map
$A({\mathcal{I}})$
be the kernel of the map
![]() $\prod _{\unicode[STIX]{x1D70E}}R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}\rightarrow \prod _{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }}R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /(I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D70E}^{\prime }})$
and
$\prod _{\unicode[STIX]{x1D70E}}R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}\rightarrow \prod _{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }}R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /(I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D70E}^{\prime }})$
and
![]() $O({\mathcal{I}})$
be the cokernel of
$O({\mathcal{I}})$
be the cokernel of
![]() $R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /\bigcap _{\unicode[STIX]{x1D70E}}I_{\unicode[STIX]{x1D70E}}\rightarrow A({\mathcal{I}})$
. We make induction on the cardinality
$R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /\bigcap _{\unicode[STIX]{x1D70E}}I_{\unicode[STIX]{x1D70E}}\rightarrow A({\mathcal{I}})$
. We make induction on the cardinality
![]() $m$
of
$m$
of
![]() ${\mathcal{I}}$
. The case
${\mathcal{I}}$
. The case
![]() $m=1$
is obvious.
$m=1$
is obvious.
Let
![]() ${\mathcal{I}}^{\prime }$
be
${\mathcal{I}}^{\prime }$
be
![]() ${\mathcal{I}}\cup \{I_{\unicode[STIX]{x1D702}}\}$
. From the diagram
${\mathcal{I}}\cup \{I_{\unicode[STIX]{x1D702}}\}$
. From the diagram

we obtain by the snake lemma the exact sequence
By direct computation, it holds that
![]() $W=\bigcap (I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}})/I_{\unicode[STIX]{x1D702}}$
. By the induction hypothesis, we obtain
$W=\bigcap (I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}})/I_{\unicode[STIX]{x1D702}}$
. By the induction hypothesis, we obtain
![]() $O({\mathcal{I}})=0$
. Moreover, since
$O({\mathcal{I}})=0$
. Moreover, since
![]() $\bigcap I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}}=\bigcap (I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}})$
by Lemma A.6, we conclude that the map
$\bigcap I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}}=\bigcap (I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D702}})$
by Lemma A.6, we conclude that the map
![]() $\bigcap I_{\unicode[STIX]{x1D70E}}\rightarrow W$
is surjective, and hence
$\bigcap I_{\unicode[STIX]{x1D70E}}\rightarrow W$
is surjective, and hence
![]() $O({\mathcal{I}}^{\prime })=0$
proving the main claim.
$O({\mathcal{I}}^{\prime })=0$
proving the main claim.
We remark that the sequence of the statement is obtained from the sequence with
![]() $R=K$
, by tensoring with
$R=K$
, by tensoring with
![]() $R$
over
$R$
over
![]() $K$
and completing. The latter is a (strict) exact sequence of affinoid algebras in the sense of Tate [Reference Bosch, Güntzer and RemmertBGR84, Definition 6.1.1/1] so we deduce that the sequence is strict for any
$K$
and completing. The latter is a (strict) exact sequence of affinoid algebras in the sense of Tate [Reference Bosch, Güntzer and RemmertBGR84, Definition 6.1.1/1] so we deduce that the sequence is strict for any
![]() $R$
by means of [Reference Bosch, Güntzer and RemmertBGR84, Proposition 2.1.8/6]. We also remark that the sequence can be deduced from the analogous sequence for
$R$
by means of [Reference Bosch, Güntzer and RemmertBGR84, Proposition 2.1.8/6]. We also remark that the sequence can be deduced from the analogous sequence for
![]() $\mathbb{Z}[\text{}\underline{\unicode[STIX]{x1D703}}]$
in place of
$\mathbb{Z}[\text{}\underline{\unicode[STIX]{x1D703}}]$
in place of
![]() $R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
, by tensoring with
$R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
, by tensoring with
![]() $R$
and completing. In particular, the ideal
$R$
and completing. In particular, the ideal
![]() $\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D70E}}$
is already defined over
$\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D70E}}$
is already defined over
![]() $\mathbb{Z}[\text{}\underline{\unicode[STIX]{x1D703}}]$
, as claimed.◻
$\mathbb{Z}[\text{}\underline{\unicode[STIX]{x1D703}}]$
, as claimed.◻
Let
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}^{\prime }$
be maps defined from two subsets
$\unicode[STIX]{x1D70E}^{\prime }$
be maps defined from two subsets
![]() $T_{\unicode[STIX]{x1D70E}}$
, respectively,
$T_{\unicode[STIX]{x1D70E}}$
, respectively,
![]() $T_{\unicode[STIX]{x1D70E}^{\prime }}$
of
$T_{\unicode[STIX]{x1D70E}^{\prime }}$
of
![]() $\{1,\ldots ,n\}$
to
$\{1,\ldots ,n\}$
to
![]() $\{0,1\}$
. We say that they are compatible if
$\{0,1\}$
. We say that they are compatible if
![]() $\unicode[STIX]{x1D70E}(i)=\unicode[STIX]{x1D70E}^{\prime }(i)$
for all
$\unicode[STIX]{x1D70E}(i)=\unicode[STIX]{x1D70E}^{\prime }(i)$
for all
![]() $i\in T_{\unicode[STIX]{x1D70E}}\cap T_{\unicode[STIX]{x1D70E}^{\prime }}$
and in this case we denote by
$i\in T_{\unicode[STIX]{x1D70E}}\cap T_{\unicode[STIX]{x1D70E}^{\prime }}$
and in this case we denote by
![]() $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })$
the map from
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })$
the map from
![]() $T_{\unicode[STIX]{x1D70E}}\cup T_{\unicode[STIX]{x1D70E}^{\prime }}$
extending them.
$T_{\unicode[STIX]{x1D70E}}\cup T_{\unicode[STIX]{x1D70E}^{\prime }}$
extending them.
Lemma A.8. Let
![]() $X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be an object in
$X=\mathop{\varprojlim }\nolimits_{h}X_{h}$
be an object in
![]() $\widehat{\text{Rig}}\operatorname{Sm}$
and
$\widehat{\text{Rig}}\operatorname{Sm}$
and
![]() $\unicode[STIX]{x1D6F4}$
a set as in Lemma A.7. We denote
$\unicode[STIX]{x1D6F4}$
a set as in Lemma A.7. We denote
![]() ${\mathcal{O}}(X)$
by
${\mathcal{O}}(X)$
by
![]() $R$
and
$R$
and
![]() ${\mathcal{O}}(X_{h})$
by
${\mathcal{O}}(X_{h})$
by
![]() $R_{h}$
. For any
$R_{h}$
. For any
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
let
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
let
![]() $\bar{f}_{\unicode[STIX]{x1D70E}}$
be an element of
$\bar{f}_{\unicode[STIX]{x1D70E}}$
be an element of
![]() $R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}$
such that
$R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}$
such that
![]() $\bar{f}_{\unicode[STIX]{x1D70E}}|_{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}=\bar{f}_{\unicode[STIX]{x1D70E}^{\prime }}|_{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}$
for any couple
$\bar{f}_{\unicode[STIX]{x1D70E}}|_{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}=\bar{f}_{\unicode[STIX]{x1D70E}^{\prime }}|_{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}$
for any couple
![]() $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6F4}$
of compatible maps.
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6F4}$
of compatible maps.
(i) There exists an element
 $f\in R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
such that
$f\in R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
such that
 $f|_{\unicode[STIX]{x1D70E}}=\bar{f}_{\unicode[STIX]{x1D70E}}$
.
$f|_{\unicode[STIX]{x1D70E}}=\bar{f}_{\unicode[STIX]{x1D70E}}$
.(ii) There exists a constant
 $C=C(\unicode[STIX]{x1D6F4})$
such that if for some
$C=C(\unicode[STIX]{x1D6F4})$
such that if for some
 $g\in R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
one has
$g\in R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
one has
 $|\bar{f}_{\unicode[STIX]{x1D70E}}-g|_{\unicode[STIX]{x1D70E}}|<\unicode[STIX]{x1D700}$
for all
$|\bar{f}_{\unicode[STIX]{x1D70E}}-g|_{\unicode[STIX]{x1D70E}}|<\unicode[STIX]{x1D700}$
for all
 $\unicode[STIX]{x1D70E}$
then the element
$\unicode[STIX]{x1D70E}$
then the element
 $f$
can be chosen so that
$f$
can be chosen so that
 $|f-g|<C\unicode[STIX]{x1D700}$
. Moreover, if
$|f-g|<C\unicode[STIX]{x1D700}$
. Moreover, if
 $\bar{f}_{\unicode[STIX]{x1D70E}}\in R_{0}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}$
for all
$\bar{f}_{\unicode[STIX]{x1D70E}}\in R_{0}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}$
for all
 $\unicode[STIX]{x1D70E}$
then the element
$\unicode[STIX]{x1D70E}$
then the element
 $f$
can be chosen inside
$f$
can be chosen inside
 $R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
for some integer
$R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
for some integer
 $h$
.
$h$
.
Proof. The first claim and the first part of the second are simply a restatement of Lemma A.7, where
![]() $C=C(\unicode[STIX]{x1D6F4})$
is the constant defining the compatibility
$C=C(\unicode[STIX]{x1D6F4})$
is the constant defining the compatibility
![]() $\Vert \cdot \Vert _{1}\leqslant C\Vert \cdot \Vert _{2}$
between the norm
$\Vert \cdot \Vert _{1}\leqslant C\Vert \cdot \Vert _{2}$
between the norm
![]() $\Vert \cdot \Vert _{1}$
on
$\Vert \cdot \Vert _{1}$
on
![]() $R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /\bigcap I_{\unicode[STIX]{x1D70E}}$
induced by the quotient and the norm
$R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /\bigcap I_{\unicode[STIX]{x1D70E}}$
induced by the quotient and the norm
![]() $\Vert \cdot \Vert _{2}$
induced by the embedding in
$\Vert \cdot \Vert _{2}$
induced by the embedding in
![]() $\prod R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}$
. We now turn to the last sentence of the second claim.
$\prod R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}$
. We now turn to the last sentence of the second claim.
We apply Lemma A.7 to each
![]() $R_{h}$
and to
$R_{h}$
and to
![]() $R$
. We then obtain exact sequences of Banach spaces:
$R$
. We then obtain exact sequences of Banach spaces:
 $$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /\mathop{\bigcap }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D6FC}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6F4}}R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /(I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D70E}^{\prime }}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0\rightarrow R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /\mathop{\bigcap }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D6FC}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6F4}}R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /(I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D70E}^{\prime }}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /\mathop{\bigcap }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D6FC}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6F4}}R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /(I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D70E}^{\prime }}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0\rightarrow R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /\mathop{\bigcap }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}I_{\unicode[STIX]{x1D6FC}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /I_{\unicode[STIX]{x1D70E}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6F4}}R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle /(I_{\unicode[STIX]{x1D70E}}+I_{\unicode[STIX]{x1D70E}^{\prime }}), & \displaystyle \nonumber\end{eqnarray}$$
where all ideals that appear are finitely generated by polynomials with
![]() $\mathbb{Z}$
-coefficients, depending only on
$\mathbb{Z}$
-coefficients, depending only on
![]() $\unicode[STIX]{x1D6F4}$
.
$\unicode[STIX]{x1D6F4}$
.
In particular, there exist two lifts of
![]() $\{\bar{f}_{\unicode[STIX]{x1D70E}}\}$
: an element
$\{\bar{f}_{\unicode[STIX]{x1D70E}}\}$
: an element
![]() $f_{1}$
of
$f_{1}$
of
![]() $R_{0}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
and an element
$R_{0}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
and an element
![]() $f_{2}$
of
$f_{2}$
of
![]() $R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
such that
$R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
such that
![]() $|f_{2}-g|<C\unicode[STIX]{x1D700}$
and their difference lies in
$|f_{2}-g|<C\unicode[STIX]{x1D700}$
and their difference lies in
![]() $\bigcap I_{\unicode[STIX]{x1D70E}}$
. Hence, we can find coefficients
$\bigcap I_{\unicode[STIX]{x1D70E}}$
. Hence, we can find coefficients
![]() $\unicode[STIX]{x1D6FE}_{i}\in R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
such that
$\unicode[STIX]{x1D6FE}_{i}\in R\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
such that
![]() $f_{1}=f_{2}+\sum _{i}\unicode[STIX]{x1D6FE}_{i}p_{i}$
, where
$f_{1}=f_{2}+\sum _{i}\unicode[STIX]{x1D6FE}_{i}p_{i}$
, where
![]() $\{p_{1},\ldots ,p_{M}\}$
are generators of
$\{p_{1},\ldots ,p_{M}\}$
are generators of
![]() $\bigcap I_{\unicode[STIX]{x1D70E}}$
which have coefficients in
$\bigcap I_{\unicode[STIX]{x1D70E}}$
which have coefficients in
![]() $K$
. Now let
$K$
. Now let
![]() $\tilde{\unicode[STIX]{x1D6FE}}_{i}$
be elements of
$\tilde{\unicode[STIX]{x1D6FE}}_{i}$
be elements of
![]() $R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
with
$R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle$
with
![]() $|\tilde{\unicode[STIX]{x1D6FE}}_{i}-\unicode[STIX]{x1D6FE}_{i}|<C\unicode[STIX]{x1D700}/M|p_{i}|$
. The element
$|\tilde{\unicode[STIX]{x1D6FE}}_{i}-\unicode[STIX]{x1D6FE}_{i}|<C\unicode[STIX]{x1D700}/M|p_{i}|$
. The element
![]() $f_{3}:=f_{1}-\sum _{i}\tilde{\unicode[STIX]{x1D6FE}}_{i}p_{i}$
lies in
$f_{3}:=f_{1}-\sum _{i}\tilde{\unicode[STIX]{x1D6FE}}_{i}p_{i}$
lies in
![]() $\mathop{\varinjlim }\nolimits_{h}(R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle )$
is another lift of
$\mathop{\varinjlim }\nolimits_{h}(R_{h}\langle \text{}\underline{\unicode[STIX]{x1D703}}\rangle )$
is another lift of
![]() $\{\bar{f}_{\unicode[STIX]{x1D70E}}\}$
and satisfies
$\{\bar{f}_{\unicode[STIX]{x1D70E}}\}$
and satisfies
![]() $|f_{3}-g|\leqslant \max \{|f_{2}-g|,|f_{2}-f_{3}|\}<C\unicode[STIX]{x1D700}$
, proving the claim.◻
$|f_{3}-g|\leqslant \max \{|f_{2}-g|,|f_{2}-f_{3}|\}<C\unicode[STIX]{x1D700}$
, proving the claim.◻
We can now finally prove the approximation result that played a crucial role in § 4.
Proof of Proposition 4.1.
For any
![]() $h\in \mathbb{Z}$
we will denote
$h\in \mathbb{Z}$
we will denote
![]() ${\mathcal{O}}(X_{h})\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
by
${\mathcal{O}}(X_{h})\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
by
![]() $R_{h}$
. We also denote the
$R_{h}$
. We also denote the
![]() $\unicode[STIX]{x1D70B}$
-adic completion of
$\unicode[STIX]{x1D70B}$
-adic completion of
![]() $\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
by
$\mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
by
![]() $R^{+}$
and
$R^{+}$
and
![]() $R^{+}[\unicode[STIX]{x1D70B}^{-1}]$
by
$R^{+}[\unicode[STIX]{x1D70B}^{-1}]$
by
![]() $R$
.
$R$
.
By Proposition A.4 we conclude that there exist integers
![]() $m$
and
$m$
and
![]() $n$
and a
$n$
and a
![]() $m$
-tuple of polynomials
$m$
-tuple of polynomials
![]() $P=(P_{1},\ldots ,P_{m})$
in
$P=(P_{1},\ldots ,P_{m})$
in
![]() $K[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
, where
$K[\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}]$
, where
![]() $\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n})$
and
$\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n})$
and
![]() $\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m})$
are systems of variables such that
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{m})$
are systems of variables such that
![]() $K\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(P)\cong {\mathcal{O}}(Y)$
and each
$K\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(P)\cong {\mathcal{O}}(Y)$
and each
![]() $f_{k}$
is induced by maps
$f_{k}$
is induced by maps
![]() $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})\mapsto (s_{k},t_{k})$
from
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})\mapsto (s_{k},t_{k})$
from
![]() $K\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(P)$
to
$K\langle \unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\rangle /(P)$
to
![]() $R$
for some
$R$
for some
![]() $m$
-tuples
$m$
-tuples
![]() $s_{k}$
and
$s_{k}$
and
![]() $n$
-tuples
$n$
-tuples
![]() $t_{k}$
in
$t_{k}$
in
![]() $R$
. Moreover, there exists a sequence of power series
$R$
. Moreover, there exists a sequence of power series
![]() $F_{k}=(F_{k1},\ldots ,F_{km})$
associated to each
$F_{k}=(F_{k1},\ldots ,F_{km})$
associated to each
![]() $f_{k}$
such that
$f_{k}$
such that
defines a map
![]() $H_{k}$
satisfying the first claim, for any choice of
$H_{k}$
satisfying the first claim, for any choice of
![]() $\tilde{s}_{k}\in \mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
such that
$\tilde{s}_{k}\in \mathop{\varinjlim }\nolimits_{h}R_{h}^{\circ }$
such that
![]() $\tilde{s}_{k}$
is in the convergence radius of
$\tilde{s}_{k}$
is in the convergence radius of
![]() $F_{k}$
and
$F_{k}$
and
![]() $F_{k}(\tilde{s}_{k})$
is in
$F_{k}(\tilde{s}_{k})$
is in
![]() $R^{+}$
.
$R^{+}$
.
Now let
![]() $\unicode[STIX]{x1D700}$
be a positive real number, smaller than all radii of convergence of the series
$\unicode[STIX]{x1D700}$
be a positive real number, smaller than all radii of convergence of the series
![]() $F_{kj}$
and such that
$F_{kj}$
and such that
![]() $F(a)\in R^{+}$
for all
$F(a)\in R^{+}$
for all
![]() $|a-s|<\unicode[STIX]{x1D700}$
. Denote by
$|a-s|<\unicode[STIX]{x1D700}$
. Denote by
![]() $\tilde{s}_{ki}$
the elements associated to
$\tilde{s}_{ki}$
the elements associated to
![]() $s_{ki}$
by applying Proposition A.5 with respect to the chosen
$s_{ki}$
by applying Proposition A.5 with respect to the chosen
![]() $\unicode[STIX]{x1D700}$
. In particular, they induce a well-defined map
$\unicode[STIX]{x1D700}$
. In particular, they induce a well-defined map
![]() $H_{k}$
and the elements
$H_{k}$
and the elements
![]() $\tilde{s}_{ki}$
lie in
$\tilde{s}_{ki}$
lie in
![]() $R_{\bar{h}}^{\circ }\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
for some integer
$R_{\bar{h}}^{\circ }\langle \unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n}\rangle$
for some integer
![]() $\bar{h}$
. We show that the maps
$\bar{h}$
. We show that the maps
![]() $H_{k}$
induced by this choice also satisfy the second and third claims of the proposition.
$H_{k}$
induced by this choice also satisfy the second and third claims of the proposition.
Suppose that
![]() $f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=f_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
for some
$f_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=f_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
for some
![]() $r\in \{1,\ldots ,n\}$
and
$r\in \{1,\ldots ,n\}$
and
![]() $\unicode[STIX]{x1D716}\in \{0,1\}$
. This means that
$\unicode[STIX]{x1D716}\in \{0,1\}$
. This means that
![]() $\bar{s}:=s_{k}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}=s_{k^{\prime }}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
and
$\bar{s}:=s_{k}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}=s_{k^{\prime }}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
and
![]() $\bar{t}:=t_{k}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}=t_{k^{\prime }}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
. This implies that both
$\bar{t}:=t_{k}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}=t_{k^{\prime }}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
. This implies that both
![]() $F_{k}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
and
$F_{k}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
and
![]() $F_{k^{\prime }}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
are two
$F_{k^{\prime }}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
are two
![]() $m$
-tuples of formal power series
$m$
-tuples of formal power series
![]() $\bar{F}$
with coefficients in
$\bar{F}$
with coefficients in
![]() ${\mathcal{O}}(X\,\times \,\mathbb{B}^{n-1})$
converging around
${\mathcal{O}}(X\,\times \,\mathbb{B}^{n-1})$
converging around
![]() $\bar{s}$
and such that
$\bar{s}$
and such that
![]() $P(\unicode[STIX]{x1D70E},\bar{F}(\unicode[STIX]{x1D70E}))=0$
,
$P(\unicode[STIX]{x1D70E},\bar{F}(\unicode[STIX]{x1D70E}))=0$
,
![]() $\bar{F}(\bar{s})=\bar{t}$
. By the uniqueness of such power series stated in Corollary A.2, we conclude that they coincide.
$\bar{F}(\bar{s})=\bar{t}$
. By the uniqueness of such power series stated in Corollary A.2, we conclude that they coincide.
Moreover, by our choice of the elements
![]() $\tilde{s}_{k}$
it follows that
$\tilde{s}_{k}$
it follows that
![]() $\bar{\tilde{s}}:=\tilde{s}_{k}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}=\tilde{s}_{k^{\prime }}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
. In particular, one has
$\bar{\tilde{s}}:=\tilde{s}_{k}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}=\tilde{s}_{k^{\prime }}|_{\unicode[STIX]{x1D703}_{r}=\unicode[STIX]{x1D716}}$
. In particular, one has
and therefore
![]() $H_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=H_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
proving the second claim.
$H_{k}\,\circ \,d_{r,\unicode[STIX]{x1D716}}=H_{k^{\prime }}\,\circ \,d_{r,\unicode[STIX]{x1D716}}$
proving the second claim.
The third claim follows immediately since the elements
![]() $\tilde{s}_{ki}$
satisfy the condition (iv) of Proposition A.5.◻
$\tilde{s}_{ki}$
satisfy the condition (iv) of Proposition A.5.◻