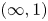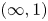1. Introduction
The Grothendieck construction, or unstraightening, is a standard procedure in category theory that associates to a diagram of categories ![]() $F\colon \mathscr {C}\longrightarrow {{\rm Cat}}$ a map of categories
$F\colon \mathscr {C}\longrightarrow {{\rm Cat}}$ a map of categories ![]() $\pi \colon \mathrm {Un}(F)\longrightarrow \mathscr {C}$ whose fibers are precisely the values of the diagram
$\pi \colon \mathrm {Un}(F)\longrightarrow \mathscr {C}$ whose fibers are precisely the values of the diagram ![]() $F$. This maneuver does not result in a loss of information: the unstraightening functor
$F$. This maneuver does not result in a loss of information: the unstraightening functor
is an embedding, whose image is the subcategory of cocartesian fibrations over ![]() $\mathscr {C}$ and maps between them that preserve cocartesian arrows [Reference Grothendieck and RaynaudGro63].
$\mathscr {C}$ and maps between them that preserve cocartesian arrows [Reference Grothendieck and RaynaudGro63].
The practical consequences of this result are twofold. On the one hand, the Grothendieck construction also provides an equivalence between cocartesian fibrations over ![]() $\mathscr {C}$ and pseudo-functors
$\mathscr {C}$ and pseudo-functors ![]() $F\colon \mathscr {C}\longrightarrow {{\rm Cat}}$. From this point of view, cocartesian fibrations provide a convenient way to encode coherent diagrams of categories, which can be rectified to strict diagrams via the inverse of unstraightening, aptly called straightening. Consequently, the language of fibrations starts to play an essential role in the homotopy coherent setting of
$F\colon \mathscr {C}\longrightarrow {{\rm Cat}}$. From this point of view, cocartesian fibrations provide a convenient way to encode coherent diagrams of categories, which can be rectified to strict diagrams via the inverse of unstraightening, aptly called straightening. Consequently, the language of fibrations starts to play an essential role in the homotopy coherent setting of ![]() $(\infty, 1)$-categories, where a version of straightening and unstraightening is available as well [Reference LurieLur09a] (see also [Reference Riehl and VerityRV18]). Indeed, many homotopy coherent diagrams of
$(\infty, 1)$-categories, where a version of straightening and unstraightening is available as well [Reference LurieLur09a] (see also [Reference Riehl and VerityRV18]). Indeed, many homotopy coherent diagrams of ![]() $(\infty, 1)$-categories are most naturally described in terms of cocartesian fibrations.
$(\infty, 1)$-categories are most naturally described in terms of cocartesian fibrations.
On the other hand, the unstraightening of a diagram ![]() $F\colon \mathscr {C}\longrightarrow {{\rm Cat}}$ is convenient to describe ‘lax constructions’ with categories, stemming from the fact that
$F\colon \mathscr {C}\longrightarrow {{\rm Cat}}$ is convenient to describe ‘lax constructions’ with categories, stemming from the fact that ![]() $\mathrm {Un}(F)$ is the oplax colimit of
$\mathrm {Un}(F)$ is the oplax colimit of ![]() $F$ (see [Reference Gepner, Haugseng and NikolausGHN17]). For example, a lax natural transformation between two diagrams
$F$ (see [Reference Gepner, Haugseng and NikolausGHN17]). For example, a lax natural transformation between two diagrams ![]() $F$ and
$F$ and ![]() $G$ can be described by a map
$G$ can be described by a map ![]() $\mathrm {Un}(F)\longrightarrow \mathrm {Un}(G)$ over
$\mathrm {Un}(F)\longrightarrow \mathrm {Un}(G)$ over ![]() $\mathscr {C}$ that need not preserve cocartesian arrows (see, e.g., [Reference Gagna, Harpaz and LanariGHL20, Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23b] for a discussion in the
$\mathscr {C}$ that need not preserve cocartesian arrows (see, e.g., [Reference Gagna, Harpaz and LanariGHL20, Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23b] for a discussion in the ![]() $\infty$-categorical setting).
$\infty$-categorical setting).
The purpose of this text is to establish a version of straightening and unstraightening for ![]() $(\infty, d)$-categories. Recall that at the moment, the theory of
$(\infty, d)$-categories. Recall that at the moment, the theory of ![]() $(\infty, d)$-categories is only in the first stages of its development, in particular when compared with
$(\infty, d)$-categories is only in the first stages of its development, in particular when compared with ![]() $(\infty, 1)$-category theory; it is already not straightforward to compare the various different homotopy-theoretic models for
$(\infty, 1)$-category theory; it is already not straightforward to compare the various different homotopy-theoretic models for ![]() $(\infty, d)$-categories (see, e.g., [Reference SimpsonSim12] for a textbook account and [Reference Barwick and Schommer-PriesBS21] for a more recent state of affairs). Nonetheless,
$(\infty, d)$-categories (see, e.g., [Reference SimpsonSim12] for a textbook account and [Reference Barwick and Schommer-PriesBS21] for a more recent state of affairs). Nonetheless, ![]() $(\infty, d)$-categories have been of interest in various areas of mathematics, also outside of the realm of category theory itself. For example, higher categories play a role in (derived) algebraic geometry via the six functor formalism (
$(\infty, d)$-categories have been of interest in various areas of mathematics, also outside of the realm of category theory itself. For example, higher categories play a role in (derived) algebraic geometry via the six functor formalism (![]() $d=2$) [Reference Gaitsgory and RozenblyumGR17, Reference MacphersonMac22] and other constructions involving correspondences [Reference Calaque, Haugseng and ScheimbauerCHS21], whereas in topology they arise in factorization homology [Reference Ayala, Francis and RozenblyumAFR18, Reference ScheimbauerSch14] and notably in topological field theories [Reference Calaque and ScheimbauerCS19, Reference LurieLur10].
$d=2$) [Reference Gaitsgory and RozenblyumGR17, Reference MacphersonMac22] and other constructions involving correspondences [Reference Calaque, Haugseng and ScheimbauerCHS21], whereas in topology they arise in factorization homology [Reference Ayala, Francis and RozenblyumAFR18, Reference ScheimbauerSch14] and notably in topological field theories [Reference Calaque and ScheimbauerCS19, Reference LurieLur10].
Given the central place of the (un)straightening correspondence in ![]() $(\infty, 1)$-category theory, it seems fair to say that the lack of a higher-categorical version of this correspondence has been one of the main problems in the theory of
$(\infty, 1)$-category theory, it seems fair to say that the lack of a higher-categorical version of this correspondence has been one of the main problems in the theory of ![]() $(\infty, d)$-categories (henceforth, simply referred to as
$(\infty, d)$-categories (henceforth, simply referred to as ![]() $d$-categories). For instance, the unstraightening procedure could be useful in the study of lax natural transformations between diagrams of
$d$-categories). For instance, the unstraightening procedure could be useful in the study of lax natural transformations between diagrams of ![]() $d$-categories and in the study of (lax) limits and colimits. Our main results establish such a procedure and show that it is essentially unique.
$d$-categories and in the study of (lax) limits and colimits. Our main results establish such a procedure and show that it is essentially unique.
To this end, we define for each ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$ two certain (non-full) subcategories
$\mathscr {C}$ two certain (non-full) subcategories
whose objects we refer to as ![]() $d$-cocartesian fibrations and
$d$-cocartesian fibrations and ![]() $d$-cartesian fibrations; the two notions are equivalent under reversing the directions of morphisms in every categorical dimension. The fibers of a
$d$-cartesian fibrations; the two notions are equivalent under reversing the directions of morphisms in every categorical dimension. The fibers of a ![]() $d$-cocartesian fibration are
$d$-cocartesian fibration are ![]() $d$-categories; in particular, a
$d$-categories; in particular, a ![]() $0$-cocartesian fibration between
$0$-cocartesian fibration between ![]() $1$-categories is simply a left fibration between
$1$-categories is simply a left fibration between ![]() $1$-categories [Reference LurieLur09a]. Furthermore, a
$1$-categories [Reference LurieLur09a]. Furthermore, a ![]() $1$-cocartesian fibration between
$1$-cocartesian fibration between ![]() $1$-categories, viewed as
$1$-categories, viewed as ![]() $2$-categories with only invertible
$2$-categories with only invertible ![]() $2$-morphisms, is simply a cocartesian fibration in the usual sense.
$2$-morphisms, is simply a cocartesian fibration in the usual sense.
More generally, a map of ![]() $(d+1)$-categories
$(d+1)$-categories ![]() $\pi \colon \mathscr {D}\longrightarrow \mathscr {C}$ is roughly said to be a
$\pi \colon \mathscr {D}\longrightarrow \mathscr {C}$ is roughly said to be a ![]() $d$-cocartesian fibration if it induces
$d$-cocartesian fibration if it induces ![]() $(d-1)$-cartesian fibrations on mapping
$(d-1)$-cartesian fibrations on mapping ![]() $d$-categories and if every
$d$-categories and if every ![]() $1$-morphism in
$1$-morphism in ![]() $\mathscr {C}$ admits enough cocartesian lifts (in an enriched sense; see § 5 for more details). For
$\mathscr {C}$ admits enough cocartesian lifts (in an enriched sense; see § 5 for more details). For ![]() $d=2$, the notion of a
$d=2$, the notion of a ![]() $2$-cocartesian fibration between
$2$-cocartesian fibration between ![]() $(2, 2)$-categories has also been considered (in a different variance) by Hermida [Reference HermidaHer99] (see also [Reference BakovićBak11, Reference BuckleyBuc14]). More recently,
$(2, 2)$-categories has also been considered (in a different variance) by Hermida [Reference HermidaHer99] (see also [Reference BakovićBak11, Reference BuckleyBuc14]). More recently, ![]() $2$-cocartesian fibrations between
$2$-cocartesian fibrations between ![]() $(\infty, 2)$-categories have been described in terms of inner cocartesian
$(\infty, 2)$-categories have been described in terms of inner cocartesian ![]() $2$-fibrations between scaled simplicial sets [Reference Gagna, Harpaz and LanariGHL21].
$2$-fibrations between scaled simplicial sets [Reference Gagna, Harpaz and LanariGHL21].
Our main result is then the following.
Theorem A (Theorem 6.1)
For each ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$, there exist equivalences of
$\mathscr {C}$, there exist equivalences of ![]() $1$-categories (here,
$1$-categories (here, ![]() $\mathfrak {c}_1$ takes the
$\mathfrak {c}_1$ takes the ![]() $1$-category underlying a
$1$-category underlying a ![]() $(d+1)$-category)
$(d+1)$-category)

between ![]() $d$-cocartesian fibrations over
$d$-cocartesian fibrations over ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $(d+1)$-functors
$(d+1)$-functors ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d$ to the
$\mathscr {C}\longrightarrow \mathbf {Cat}_d$ to the ![]() $(d+1)$-category of
$(d+1)$-category of ![]() $d$-categories, respectively, between
$d$-categories, respectively, between ![]() $d$-cartesian fibrations and
$d$-cartesian fibrations and ![]() $(d+1)$-functors
$(d+1)$-functors ![]() $\mathscr {C}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_d$.
$\mathscr {C}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_d$.
Our proof of Theorem A only relies on the straightening equivalence for left (i.e. ![]() $0$-cocartesian) fibrations, which we recall in § 4.3. In particular, it provides an independent proof of the straightening–unstraightening equivalence for cocartesian fibrations of Lurie [Reference LurieLur09a]. In fact, we will use an inductive argument to deduce Theorem A from a slight generalization of the
$0$-cocartesian) fibrations, which we recall in § 4.3. In particular, it provides an independent proof of the straightening–unstraightening equivalence for cocartesian fibrations of Lurie [Reference LurieLur09a]. In fact, we will use an inductive argument to deduce Theorem A from a slight generalization of the ![]() $1$-categorical straightening equivalence: Theorem B below.
$1$-categorical straightening equivalence: Theorem B below.
To facilitate this inductive argument, we make use of the model for ![]() $(d+1)$-categories given by iterated complete Segal spaces [Reference Barwick and Schommer-PriesBS21]. Recall that these are certain types of
$(d+1)$-categories given by iterated complete Segal spaces [Reference Barwick and Schommer-PriesBS21]. Recall that these are certain types of ![]() $(d+1)$-fold simplicial spaces
$(d+1)$-fold simplicial spaces
Here the ![]() $d$-fold simplicial space
$d$-fold simplicial space ![]() $\mathscr {C}(0)=\mathscr {C}(0, -)$ is constant and corresponds to the space of objects of
$\mathscr {C}(0)=\mathscr {C}(0, -)$ is constant and corresponds to the space of objects of ![]() $\mathscr {C}$, whereas
$\mathscr {C}$, whereas ![]() $\mathscr {C}(1)$ is itself an iterated complete Segal space, modeling the
$\mathscr {C}(1)$ is itself an iterated complete Segal space, modeling the ![]() $d$-category of arrows in
$d$-category of arrows in ![]() $\mathscr {C}$.
$\mathscr {C}$.
This Segal space model has the benefit that a diagram of ![]() $d$-categories indexed by a
$d$-categories indexed by a ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$ can be encoded explicitly by a map of
$\mathscr {C}$ can be encoded explicitly by a map of ![]() $(d+1)$-fold simplicial spaces
$(d+1)$-fold simplicial spaces ![]() $X\longrightarrow \mathscr {C}$ satisfying the following two conditions [Reference Boavida de BritoBoa18, Reference RasekhRas21]:
$X\longrightarrow \mathscr {C}$ satisfying the following two conditions [Reference Boavida de BritoBoa18, Reference RasekhRas21]:
(1)
 $X(0)$ is a
$X(0)$ is a  $d$-category;
$d$-category;(2) the Segal maps
 $X(n)\longrightarrow \mathscr {C}(n)\times _{\mathscr {C}(\{0\})} X(\{0\})$ are equivalences of
$X(n)\longrightarrow \mathscr {C}(n)\times _{\mathscr {C}(\{0\})} X(\{0\})$ are equivalences of  $d$-categories.
$d$-categories.
We will refer to such maps as Segal copresheaves, because they should be viewed as encoding a homotopy coherent action of the ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$ on the
$\mathscr {C}$ on the ![]() $d$-category
$d$-category ![]() $X(0)$. In particular, fixing the last
$X(0)$. In particular, fixing the last ![]() $d$ simplicial coordinates yields a left fibration between
$d$ simplicial coordinates yields a left fibration between ![]() $1$-categories. Work of Boavida [Reference Boavida de BritoBoa18] gives a way to straighten each of these left fibrations, resulting in an equivalence between the
$1$-categories. Work of Boavida [Reference Boavida de BritoBoa18] gives a way to straighten each of these left fibrations, resulting in an equivalence between the ![]() $1$-category of Segal copresheaves over
$1$-category of Segal copresheaves over ![]() $\mathscr {C}$ and the
$\mathscr {C}$ and the ![]() $1$-category of
$1$-category of ![]() $(d+1)$-functors
$(d+1)$-functors ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d$ (see also [Reference RasekhRas21] and § 4.3). This equivalence can be thought of as a rectification procedure relating an external (Segal-style) definition of copresheaves to their internal definition as functors
$\mathscr {C}\longrightarrow \mathbf {Cat}_d$ (see also [Reference RasekhRas21] and § 4.3). This equivalence can be thought of as a rectification procedure relating an external (Segal-style) definition of copresheaves to their internal definition as functors ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d$ (cf., in particular, Theorem 4.32).
$\mathscr {C}\longrightarrow \mathbf {Cat}_d$ (cf., in particular, Theorem 4.32).
Warning Let us emphasize that one should not think of a Segal copresheaf ![]() $X\longrightarrow \mathscr {C}$ as some sort of cocartesian fibration: its domain is typically not a
$X\longrightarrow \mathscr {C}$ as some sort of cocartesian fibration: its domain is typically not a ![]() $(d+1)$-category (unless
$(d+1)$-category (unless ![]() $d=0$) and the notion of a Segal copresheaf is therefore not defined internal to the theory of
$d=0$) and the notion of a Segal copresheaf is therefore not defined internal to the theory of ![]() $(d+1)$-categories. In particular, note that the fibers of a Segal copresheaf are constant in the first simplicial direction, whereas the fibers of a
$(d+1)$-categories. In particular, note that the fibers of a Segal copresheaf are constant in the first simplicial direction, whereas the fibers of a ![]() $d$-cocartesian fibration between
$d$-cocartesian fibration between ![]() $(d+1)$-categories are constant in the last simplicial direction. Unfortunately, the terminology employed in [Reference Boavida de BritoBoa18, Reference RasekhRas21] seems to suggest otherwise.
$(d+1)$-categories are constant in the last simplicial direction. Unfortunately, the terminology employed in [Reference Boavida de BritoBoa18, Reference RasekhRas21] seems to suggest otherwise.
The straightening–unstraightening equivalence from Theorem A is then given by a ![]() $d$-step combinatorial procedure that passes from Segal copresheaves to
$d$-step combinatorial procedure that passes from Segal copresheaves to ![]() $d$-cocartesian fibrations. In each step, we modify the behaviour of the map of
$d$-cocartesian fibrations. In each step, we modify the behaviour of the map of ![]() $(d+1)$-simplicial spaces
$(d+1)$-simplicial spaces ![]() $X\longrightarrow \mathscr {C}$ only in two consecutive simplicial directions, using the following result.
$X\longrightarrow \mathscr {C}$ only in two consecutive simplicial directions, using the following result.
Theorem B (Theorem 3.1)
Let ![]() $\mathbb {C}$ be a double category, i.e. a bisimplicial space satisfying the complete Segal conditions in the two simplicial directions (referred to as horizontal and vertical). Then there is an equivalence of categories
$\mathbb {C}$ be a double category, i.e. a bisimplicial space satisfying the complete Segal conditions in the two simplicial directions (referred to as horizontal and vertical). Then there is an equivalence of categories
between maps of double categories ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ of the following two types:
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ of the following two types:
(1)
 $p$ is a left fibration in the horizontal and a cartesian fibration in the vertical direction;
$p$ is a left fibration in the horizontal and a cartesian fibration in the vertical direction;(2)
 $p$ is a cocartesian fibration in the horizontal and a right fibration in the vertical direction.
$p$ is a cocartesian fibration in the horizontal and a right fibration in the vertical direction.
Furthermore, the fibers of ![]() $\mathbb {D}\longrightarrow \mathbb {C}$ and
$\mathbb {D}\longrightarrow \mathbb {C}$ and ![]() $\Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$ differ simply by exchanging the horizontal and vertical directions.
$\Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$ differ simply by exchanging the horizontal and vertical directions.
The definition of the equivalence ![]() $\Psi ^\perp$ uses rather simple combinatorics, inspired by the classical Grothendieck construction. Indeed, recall that for
$\Psi ^\perp$ uses rather simple combinatorics, inspired by the classical Grothendieck construction. Indeed, recall that for ![]() $F\colon \mathscr {C}\longrightarrow {{\rm Cat}}$, an object in the Grothendieck construction is a tuple
$F\colon \mathscr {C}\longrightarrow {{\rm Cat}}$, an object in the Grothendieck construction is a tuple ![]() $(c, x)$ with
$(c, x)$ with ![]() $c\in \mathscr {C}$ and
$c\in \mathscr {C}$ and ![]() $x\in F(c)$, and a morphism is given by the composite of a cocartesian (‘horizontal’) arrow
$x\in F(c)$, and a morphism is given by the composite of a cocartesian (‘horizontal’) arrow ![]() $f\colon (c, x)\longrightarrow (c', f_!x)$, followed by a ‘vertical’ arrow in the fiber
$f\colon (c, x)\longrightarrow (c', f_!x)$, followed by a ‘vertical’ arrow in the fiber ![]() $F(c')$. Likewise,
$F(c')$. Likewise, ![]() $\Psi ^\perp (\mathbb {D})$ is a double category with the same objects as
$\Psi ^\perp (\mathbb {D})$ is a double category with the same objects as ![]() $\mathbb {D}$, but with a horizontal arrow consisting of a horizontal arrow in
$\mathbb {D}$, but with a horizontal arrow consisting of a horizontal arrow in ![]() $\mathbb {D}$ followed by a fiberwise vertical arrow in
$\mathbb {D}$ followed by a fiberwise vertical arrow in ![]() $\mathbb {D}$.
$\mathbb {D}$.
Theorem A now follows from an inductive application of Theorem B. The lowest dimensional case, the straightening–unstraightening correspondence between ![]() $2$-functors
$2$-functors ![]() $\mathscr {C}\longrightarrow {{\rm Cat}}_1$ and
$\mathscr {C}\longrightarrow {{\rm Cat}}_1$ and ![]() $1$-cocartesian fibrations over a
$1$-cocartesian fibrations over a ![]() $2$-category
$2$-category ![]() $\mathscr {C}$, is simply a special case of Theorem B: when the double category
$\mathscr {C}$, is simply a special case of Theorem B: when the double category ![]() $\mathbb {C}$ is a
$\mathbb {C}$ is a ![]() $2$-category, the domain and codomain of
$2$-category, the domain and codomain of ![]() $\Psi ^\perp$ consist precisely of Segal copresheaves and
$\Psi ^\perp$ consist precisely of Segal copresheaves and ![]() $1$-cocartesian fibrations, respectively. In particular, when applied to a diagram of
$1$-cocartesian fibrations, respectively. In particular, when applied to a diagram of ![]() $(1, 1)$-categories
$(1, 1)$-categories ![]() $F\colon \mathscr {C}\longrightarrow {{\rm Cat}}_{(1, 1)}$ indexed by a
$F\colon \mathscr {C}\longrightarrow {{\rm Cat}}_{(1, 1)}$ indexed by a ![]() $(1, 1)$-category
$(1, 1)$-category ![]() $\mathscr {C}$, one obtains the following two-step process. We first associate to
$\mathscr {C}$, one obtains the following two-step process. We first associate to ![]() $F$ a Segal copresheaf over
$F$ a Segal copresheaf over ![]() $\mathscr {C}$, which corresponds informally to passing from strict to pseudo-functors, after which the functor
$\mathscr {C}$, which corresponds informally to passing from strict to pseudo-functors, after which the functor ![]() $\Psi ^\perp$ produces the classical Grothendieck construction.
$\Psi ^\perp$ produces the classical Grothendieck construction.
Note that Theorem A is not complete: both ![]() $(d+1)$-functors
$(d+1)$-functors ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d$ and
$\mathscr {C}\longrightarrow \mathbf {Cat}_d$ and ![]() $d$-cocartesian fibrations over
$d$-cocartesian fibrations over ![]() $\mathscr {C}$ can naturally be organized into
$\mathscr {C}$ can naturally be organized into ![]() $(d+1)$-categories, rather than
$(d+1)$-categories, rather than ![]() $1$-categories. In the latter case, the
$1$-categories. In the latter case, the ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathbf {Cocart}_d(\mathscr {C})$ of
$\mathbf {Cocart}_d(\mathscr {C})$ of ![]() $d$-cocartesian fibrations can be realized as a subcategory of the
$d$-cocartesian fibrations can be realized as a subcategory of the ![]() $(d+2)$-category
$(d+2)$-category ![]() $\mathbf {Cat}_{d+1}/\mathscr {C}$. Both of these (large)
$\mathbf {Cat}_{d+1}/\mathscr {C}$. Both of these (large) ![]() $(d+1)$-categories furthermore depend functorially on
$(d+1)$-categories furthermore depend functorially on ![]() $\mathscr {C}$ by restriction and base change, respectively; more precisely, they can each be organized into functors of
$\mathscr {C}$ by restriction and base change, respectively; more precisely, they can each be organized into functors of ![]() $(d+2)$-categories
$(d+2)$-categories ![]() $\mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$. We then prove the following refinement of Theorem A.
$\mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$. We then prove the following refinement of Theorem A.
Theorem C (Theorem 6.20)
There is a unique natural equivalence of ![]() $(d+2)$-functors
$(d+2)$-functors ![]() $\mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$ given at a
$\mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$ given at a ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$ by an equivalence of
$\mathscr {C}$ by an equivalence of ![]() $(d+1)$-categories
$(d+1)$-categories
The statement of Theorem C hides the following subtlety: it is not, in fact, so obvious how to write down the ![]() $(d+2)$-functor
$(d+2)$-functor
For example, note that the slice ![]() $(d+2)$-categories
$(d+2)$-categories ![]() $\mathbf {Cat}_{d+1}/\mathscr {C}$ do not depend on
$\mathbf {Cat}_{d+1}/\mathscr {C}$ do not depend on ![]() $\mathscr {C}$ in a
$\mathscr {C}$ in a ![]() $2$-functorial way in general. As one may expect, it will instead be more convenient to organize all
$2$-functorial way in general. As one may expect, it will instead be more convenient to organize all ![]() $(d+1)$-categories of
$(d+1)$-categories of ![]() $d$-cocartesian fibrations into a
$d$-cocartesian fibrations into a ![]() $(d+1)$-cartesian fibration
$(d+1)$-cartesian fibration ![]() $\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$. The above functor then arises as its straightening, using Theorem A (one categorical dimension higher).
$\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$. The above functor then arises as its straightening, using Theorem A (one categorical dimension higher).
Variants of Theorems A and C have appeared in the literature before. The straightening of ![]() $0$-cocartesian fibrations nowadays has various proofs [Reference Boavida de BritoBoa18, Reference Heuts and MoerdijkHM15, Reference LurieLur09a]. Theorem A for
$0$-cocartesian fibrations nowadays has various proofs [Reference Boavida de BritoBoa18, Reference Heuts and MoerdijkHM15, Reference LurieLur09a]. Theorem A for ![]() $1$-cocartesian fibrations over
$1$-cocartesian fibrations over ![]() $2$-categories is the content of Lurie's scaled straightening and unstraightening theorem [Reference Gagna, Harpaz and LanariGHL20, Reference LurieLur09b]. Work of Buckley [Reference BuckleyBuc14] describes the Grothendieck construction for
$2$-categories is the content of Lurie's scaled straightening and unstraightening theorem [Reference Gagna, Harpaz and LanariGHL20, Reference LurieLur09b]. Work of Buckley [Reference BuckleyBuc14] describes the Grothendieck construction for ![]() $2$-cocartesian fibrations between
$2$-cocartesian fibrations between ![]() $(2, 2)$-categories as an equivalence of
$(2, 2)$-categories as an equivalence of ![]() $3$-categories. Gaitsgory and Rozenblyum prove a strengthening of Theorem C for
$3$-categories. Gaitsgory and Rozenblyum prove a strengthening of Theorem C for ![]() $2$-cocartesian fibrations between
$2$-cocartesian fibrations between ![]() $(\infty, 2)$-categories, which also allows for lax natural transformations [Reference Gaitsgory and RozenblyumGR17, Chapter 11, Theorem 1.1.8]; this seems to rely on some unproven statements about
$(\infty, 2)$-categories, which also allows for lax natural transformations [Reference Gaitsgory and RozenblyumGR17, Chapter 11, Theorem 1.1.8]; this seems to rely on some unproven statements about ![]() $(\infty, 2)$-categories appearing in Chapter 10 of [Reference Gaitsgory and RozenblyumGR17], notably about the (conjectured) model for
$(\infty, 2)$-categories appearing in Chapter 10 of [Reference Gaitsgory and RozenblyumGR17], notably about the (conjectured) model for ![]() $(\infty, 2)$-categories in terms of lax squares. Ayala et al. have recently deduced this lax refinement of straightening for
$(\infty, 2)$-categories in terms of lax squares. Ayala et al. have recently deduced this lax refinement of straightening for ![]() $(\infty, 2)$-categories from our results and have also established a version for locally
$(\infty, 2)$-categories from our results and have also established a version for locally ![]() $2$-cocartesian fibrations [Reference Ayala, Mazel-Gee and RozenblyumAMR19]. Finally, let us mention that a version of Theorem C has been hypothesized in [Reference MacphersonMac22], where it is used to prove a universal property for the
$2$-cocartesian fibrations [Reference Ayala, Mazel-Gee and RozenblyumAMR19]. Finally, let us mention that a version of Theorem C has been hypothesized in [Reference MacphersonMac22], where it is used to prove a universal property for the ![]() $(\infty, 2)$-category of correspondences in an
$(\infty, 2)$-category of correspondences in an ![]() $(\infty, 1)$-category with fiber products.
$(\infty, 1)$-category with fiber products.
Outline
Let us give a brief overview of the contents of this paper. Sections 2 and 3 treat Theorem B and contain our main combinatorial results: § 2 discusses the fibrations of double categories appearing in Theorem B, and defines the functor ![]() $\Psi ^\perp$ on objects (§ 2.3). In § 3, we then show that
$\Psi ^\perp$ on objects (§ 2.3). In § 3, we then show that ![]() $\Psi ^\perp$ extends to an equivalence of categories (Theorem 3.1). This essentially already gives a proof of straightening and unstraightening for cocartesian fibrations of
$\Psi ^\perp$ extends to an equivalence of categories (Theorem 3.1). This essentially already gives a proof of straightening and unstraightening for cocartesian fibrations of ![]() $1$-categories (see Corollary 4.35).
$1$-categories (see Corollary 4.35).
Section 4 gives some background material on higher categories, mainly using the model of iterated complete Segal spaces. To produce examples of higher categories (e.g. of the ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathbf {Cat}_d$ of
$\mathbf {Cat}_d$ of ![]() $d$-categories), we also recall the comparison to the point-set model of (strict) enriched categories (§ 4.2). Section 4.3 reviews the results of Boavida [Reference Boavida de BritoBoa18], relating Segal copresheaves over
$d$-categories), we also recall the comparison to the point-set model of (strict) enriched categories (§ 4.2). Section 4.3 reviews the results of Boavida [Reference Boavida de BritoBoa18], relating Segal copresheaves over ![]() $\mathscr {C}$ to functors
$\mathscr {C}$ to functors ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d$. For our purposes, we will need to slightly rephrase the results from [Reference Boavida de BritoBoa18] to make them (
$\mathscr {C}\longrightarrow \mathbf {Cat}_d$. For our purposes, we will need to slightly rephrase the results from [Reference Boavida de BritoBoa18] to make them (![]() $(\infty, 1)$-)functorial in the base
$(\infty, 1)$-)functorial in the base ![]() $\mathscr {C}$; this requires some technical results about cartesian fibrations in the setting of categories of fibrant objects, discussed in Appendix A.
$\mathscr {C}$; this requires some technical results about cartesian fibrations in the setting of categories of fibrant objects, discussed in Appendix A.
In § 5, we give the definitions of ![]() $d$-cocartesian fibrations and
$d$-cocartesian fibrations and ![]() $d$-cartesian fibrations. The main result here (Proposition 5.25) asserts that
$d$-cartesian fibrations. The main result here (Proposition 5.25) asserts that ![]() $d$-cocartesian fibrations can themselves be organized into a
$d$-cocartesian fibrations can themselves be organized into a ![]() $(d+1)$-cartesian fibration
$(d+1)$-cartesian fibration ![]() $\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$.
$\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$.
Finally, § 6 contains the proofs of our main results, Theorems A and C. We first prove a version of straightening–unstraightening at the level of ![]() $1$-categories (Theorem 6.1). Using this, it follows that there is a
$1$-categories (Theorem 6.1). Using this, it follows that there is a ![]() $(d+2)$-functor
$(d+2)$-functor ![]() $\mathbf {Cocart}_d\colon \mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$ sending each
$\mathbf {Cocart}_d\colon \mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$ sending each ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$ to the large
$\mathscr {C}$ to the large ![]() $(d+1)$-category of
$(d+1)$-category of ![]() $d$-cocartesian fibrations over
$d$-cocartesian fibrations over ![]() $\mathscr {C}$. We then show that this functor is representable by
$\mathscr {C}$. We then show that this functor is representable by ![]() $\mathbf {Cat}_d$ (Theorem 6.20), providing the existence of the natural equivalence of Theorem C. The uniqueness of this natural equivalence follows from the results in § 6.2.
$\mathbf {Cat}_d$ (Theorem 6.20), providing the existence of the natural equivalence of Theorem C. The uniqueness of this natural equivalence follows from the results in § 6.2.
Conventions and notation
We phrase our results as much as possible in the language of ![]() $(\infty, 1)$-categories (with the notable exception of §§ 4.2 and 4.3, where we need to recourse to point-set models). This is mostly a matter of terminology: effectively, we only start from the
$(\infty, 1)$-categories (with the notable exception of §§ 4.2 and 4.3, where we need to recourse to point-set models). This is mostly a matter of terminology: effectively, we only start from the ![]() $(\infty, 1)$-category
$(\infty, 1)$-category ![]() $\mathscr {S}$ of spaces instead of the Kan–Quillen model structure on simplicial sets to avoid having to impose fibrancy conditions at every step. In particular, we avoid any
$\mathscr {S}$ of spaces instead of the Kan–Quillen model structure on simplicial sets to avoid having to impose fibrancy conditions at every step. In particular, we avoid any ![]() $\infty$-categorical machinery that (tacitly) relies on the straightening results of Lurie.
$\infty$-categorical machinery that (tacitly) relies on the straightening results of Lurie.
Throughout the text, we will omit all prefixes ‘![]() $\infty$-’. For instance, we abbreviate
$\infty$-’. For instance, we abbreviate ![]() $(\infty, 1)$-categories simply to categories and
$(\infty, 1)$-categories simply to categories and ![]() $(\infty, d)$-categories to
$(\infty, d)$-categories to ![]() $d$-categories, referring to ordinary categories instead as
$d$-categories, referring to ordinary categories instead as ![]() $(1, 1)$-categories. We write
$(1, 1)$-categories. We write ![]() $\mathfrak {c}_k\mathscr {C}$ for the
$\mathfrak {c}_k\mathscr {C}$ for the ![]() $k$-core of a higher category, i.e. the
$k$-core of a higher category, i.e. the ![]() $k$-category obtained by removing non-invertible morphisms in dimensions
$k$-category obtained by removing non-invertible morphisms in dimensions ![]() $>k$.
$>k$.
A subspace of a space is a ![]() $(-1)$-truncated map
$(-1)$-truncated map ![]() $S\hookrightarrow T$, i.e. an inclusion of path components. Likewise, by a subcategory of a
$S\hookrightarrow T$, i.e. an inclusion of path components. Likewise, by a subcategory of a ![]() $d$-category we will mean a
$d$-category we will mean a ![]() $(-1)$-truncated map
$(-1)$-truncated map ![]() $i\colon \mathscr {C}\hookrightarrow \mathscr {D}$; inductively, this means that
$i\colon \mathscr {C}\hookrightarrow \mathscr {D}$; inductively, this means that ![]() $i$ induces a subspace inclusion on spaces of objects and a subcategory inclusion on mapping
$i$ induces a subspace inclusion on spaces of objects and a subcategory inclusion on mapping ![]() $(d-1)$-categories. (This is, in fact, closer to the classical notion of a replete subcategory.) In particular, this means that specifying a subcategory of a
$(d-1)$-categories. (This is, in fact, closer to the classical notion of a replete subcategory.) In particular, this means that specifying a subcategory of a ![]() $d$-category comes down to specifying a subcategory of its homotopy
$d$-category comes down to specifying a subcategory of its homotopy ![]() $(d, d)$-category.
$(d, d)$-category.
Categories and ![]() $d$-categories will typically be denoted by
$d$-categories will typically be denoted by ![]() $\mathscr {C}$, whereas
$\mathscr {C}$, whereas ![]() $d$-fold categories (see § 2) will be denoted
$d$-fold categories (see § 2) will be denoted ![]() $\mathbb {C}$. We have furthermore tried to differentiate these notationally from specific point-set models by enriched categories or relative categories: for example, a
$\mathbb {C}$. We have furthermore tried to differentiate these notationally from specific point-set models by enriched categories or relative categories: for example, a ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$ can be presented by an ordinary category
$\mathscr {C}$ can be presented by an ordinary category ![]() $\mathsf {C}$ strictly enriched in the
$\mathsf {C}$ strictly enriched in the ![]() $(1, 1)$-category
$(1, 1)$-category ![]() $\mathsf {Cat}_{d}$ of fibrant objects in the
$\mathsf {Cat}_{d}$ of fibrant objects in the ![]() $d$-categorical model structure (cf. § 4.2). In particular, the
$d$-categorical model structure (cf. § 4.2). In particular, the ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathbf {Cat}_d$ of
$\mathbf {Cat}_d$ of ![]() $d$-categories is modeled by
$d$-categories is modeled by ![]() $\mathsf {Cat}_{d}$ with its canonical self-enrichment (Definition 4.22); we write
$\mathsf {Cat}_{d}$ with its canonical self-enrichment (Definition 4.22); we write ![]() ${{\rm Cat}}_d=\mathfrak {c}_1\mathbf {Cat}_d$ for its
${{\rm Cat}}_d=\mathfrak {c}_1\mathbf {Cat}_d$ for its ![]() $1$-core. Likewise, we will denote by
$1$-core. Likewise, we will denote by ![]() $\mathbf {CAT}_d$ and
$\mathbf {CAT}_d$ and ![]() $\mathrm {CAT}_d$ the (higher) categories of large
$\mathrm {CAT}_d$ the (higher) categories of large ![]() $d$-categories.
$d$-categories.
2. Fibrations of double categories
In this section, we will introduce a certain type of fibration between double categories, behaving like a left fibration in one direction and like a cartesian fibration in the other. We will show that such a fibration has a ‘reflection’, which is a cocartesian fibration in one direction and a right fibration in the other.
2.1 Recollections on double categories
Recall that a simplicial space ![]() $X\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathscr {S}$ is said to be a complete Segal space if it satisfies the following two conditions [Reference RezkRez01].
$X\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathscr {S}$ is said to be a complete Segal space if it satisfies the following two conditions [Reference RezkRez01].
(1) Segal condition: for every
 $n\geq 2$, the natural map
is an equivalence. Equivalently,
$n\geq 2$, the natural map
is an equivalence. Equivalently,
 $X(n)\simeq X(1)\times _{X(0)} \dots \times _{X(0)} X(1)$ via the inclusions of the intervals
$X(n)\simeq X(1)\times _{X(0)} \dots \times _{X(0)} X(1)$ via the inclusions of the intervals  $\{i\leq i+1\}$ into
$\{i\leq i+1\}$ into  $[n]$.
$[n]$.(2) Completeness: consider the simplicial set
 $H=\Delta [3]\big /\sim$ obtained by collapsing the
$H=\Delta [3]\big /\sim$ obtained by collapsing the  $1$-simplex
$1$-simplex  $\{0\leq 2\}$ to a point and collapsing the
$\{0\leq 2\}$ to a point and collapsing the  $1$-simplex
$1$-simplex  $\{1\leq 3\}$ to a (different) point. Then the map
$\{1\leq 3\}$ to a (different) point. Then the map  $X(0)\longrightarrow \mathrm {Map}_{s\mathscr {S}}(H, X)$ is an equivalence.
$X(0)\longrightarrow \mathrm {Map}_{s\mathscr {S}}(H, X)$ is an equivalence.
Recall that complete Segal spaces are a model for the homotopy theory of (![]() $(\infty, 1)$-)categories; we will therefore also refer to complete Segal spaces simply as (1-)categories. We will be interested in analogues of complete Segal spaces for diagrams of spaces indexed by multiple copies of the simplex category.
$(\infty, 1)$-)categories; we will therefore also refer to complete Segal spaces simply as (1-)categories. We will be interested in analogues of complete Segal spaces for diagrams of spaces indexed by multiple copies of the simplex category.
Notation 2.1 For any ![]() $k\geq 0$, we will write
$k\geq 0$, we will write ![]() $\vec {n}_k=([n_1], \dots, [n_k])\in \mathbf {\Delta }^{\times k}$ for a generic (but fixed)
$\vec {n}_k=([n_1], \dots, [n_k])\in \mathbf {\Delta }^{\times k}$ for a generic (but fixed) ![]() $k$-tuple of objects in
$k$-tuple of objects in ![]() $\mathbf {\Delta }$. Furthermore, we will abbreviate
$\mathbf {\Delta }$. Furthermore, we will abbreviate ![]() $\vec {0}_k=([0], \dots, [0])$. For example, if
$\vec {0}_k=([0], \dots, [0])$. For example, if ![]() $X\colon \mathbf {\Delta }^{\times d}\longrightarrow \mathscr {S}$ is a
$X\colon \mathbf {\Delta }^{\times d}\longrightarrow \mathscr {S}$ is a ![]() $d$-fold simplicial space, then
$d$-fold simplicial space, then
denotes the simplicial space obtained by fixing the first ![]() $k$ inputs to be
$k$ inputs to be ![]() $\vec {n}_k$ and the last
$\vec {n}_k$ and the last ![]() $d-k-1$ inputs to be
$d-k-1$ inputs to be ![]() $0$, varying only the
$0$, varying only the ![]() $(k+1)$th input. Finally, we will write
$(k+1)$th input. Finally, we will write ![]() $X(n)\colon \mathbf {\Delta }^{\times d-1}\longrightarrow \mathscr {S}$ for the
$X(n)\colon \mathbf {\Delta }^{\times d-1}\longrightarrow \mathscr {S}$ for the ![]() $(d-1)$-fold simplicial space given by
$(d-1)$-fold simplicial space given by ![]() $X(n, -, \dots, -)$.
$X(n, -, \dots, -)$.
Definition 2.2 A ![]() $d$-fold category
$d$-fold category ![]() $\mathbb {C}$ is a diagram
$\mathbb {C}$ is a diagram ![]() $\mathbb {C}\colon (\mathbf {\Delta }^{\mathrm {op}})^{\times d}\longrightarrow \mathscr {S}$ such that for each
$\mathbb {C}\colon (\mathbf {\Delta }^{\mathrm {op}})^{\times d}\longrightarrow \mathscr {S}$ such that for each ![]() $1\leq k\leq d$, all the simplicial spaces
$1\leq k\leq d$, all the simplicial spaces
are complete Segal spaces. When ![]() $d=2$, we will refer to
$d=2$, we will refer to ![]() $\mathbb {C}$ as a double category. We will denote by
$\mathbb {C}$ as a double category. We will denote by ![]() $\mathrm {Cat}^{\otimes d}\subseteq \mathrm {Fun}\big ((\mathbf {\Delta }^{\mathrm {op}})^{\times d}, \mathscr {S}\big )$ the full subcategory spanned by the
$\mathrm {Cat}^{\otimes d}\subseteq \mathrm {Fun}\big ((\mathbf {\Delta }^{\mathrm {op}})^{\times d}, \mathscr {S}\big )$ the full subcategory spanned by the ![]() $d$-fold categories.
$d$-fold categories.
Warning 2.3 Because we impose completeness conditions in all directions, this notion of a ![]() $d$-fold category is not quite the
$d$-fold category is not quite the ![]() $\infty$-categorical analogue of that of a
$\infty$-categorical analogue of that of a ![]() $d$-uple category in the sense of Ehresmann [Reference EhresmannEhr63], i.e. a (strict) category object in
$d$-uple category in the sense of Ehresmann [Reference EhresmannEhr63], i.e. a (strict) category object in ![]() $(d-1)$-uple categories. The latter type of objects (which are sometimes also called
$(d-1)$-uple categories. The latter type of objects (which are sometimes also called ![]() $d$-fold categories) corresponds instead to the more general notion of a
$d$-fold categories) corresponds instead to the more general notion of a ![]() $d$-uple Segal space [Reference HaugsengHau17].
$d$-uple Segal space [Reference HaugsengHau17].
For instance, for a double category in the sense of Definition 2.2, the completeness conditions in the horizontal and vertical direction imply that the horizontal equivalences and vertical equivalences coincide. Many examples of double (and, more generally, ![]() $d$-uple) Segal spaces do not satisfy this condition: as an example, one can take the double Segal space of associative algebras, with horizontal morphisms given by bimodules and vertical morphisms given by algebra homomorphisms [Reference HaugsengHau17].
$d$-uple) Segal spaces do not satisfy this condition: as an example, one can take the double Segal space of associative algebras, with horizontal morphisms given by bimodules and vertical morphisms given by algebra homomorphisms [Reference HaugsengHau17].
Notation 2.4 (Opposites)
Let ![]() $\mathbb {C}$ be a
$\mathbb {C}$ be a ![]() $d$-fold category and
$d$-fold category and ![]() $1\leq k\leq d$. We will write
$1\leq k\leq d$. We will write ![]() $\mathbb {C}^{k-\mathrm {op}}$ for the
$\mathbb {C}^{k-\mathrm {op}}$ for the ![]() $d$-fold category given by taking opposites in the
$d$-fold category given by taking opposites in the ![]() $k$th variable:
$k$th variable:
When ![]() $k=1$, we will simply write
$k=1$, we will simply write ![]() $\mathbb {C}^{\mathrm {op}}$. If
$\mathbb {C}^{\mathrm {op}}$. If ![]() $\mathbb {C}$ is a double category, we will furthermore write
$\mathbb {C}$ is a double category, we will furthermore write ![]() $\mathbb {C}^{\mathrm {rev}}$ for the double category with its coordinates reflected, i.e.
$\mathbb {C}^{\mathrm {rev}}$ for the double category with its coordinates reflected, i.e. ![]() $\mathbb {C}^\mathrm {rev}(m, n)=\mathbb {C}(n, m)$.
$\mathbb {C}^\mathrm {rev}(m, n)=\mathbb {C}(n, m)$.
In the case of double categories, we will employ the following conventions: we will refer to the direction of the first copy of ![]() $\mathbf {\Delta }^{\mathrm {op}}$ as the horizontal direction and to the second copy of
$\mathbf {\Delta }^{\mathrm {op}}$ as the horizontal direction and to the second copy of ![]() $\mathbf {\Delta }^{\mathrm {op}}$ as the vertical direction. Furthermore, we will use the notation
$\mathbf {\Delta }^{\mathrm {op}}$ as the vertical direction. Furthermore, we will use the notation ![]() $\longrightarrow$ for horizontal arrows and
$\longrightarrow$ for horizontal arrows and ![]() for vertical arrows.
for vertical arrows.
Example 2.5 Let ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $\mathscr {D}$ be categories. We denote by
$\mathscr {D}$ be categories. We denote by ![]() $\mathscr {C}\boxtimes \mathscr {D}$ the double category given by
$\mathscr {C}\boxtimes \mathscr {D}$ the double category given by
In particular, we write ![]() $[m, n]=[m]\boxtimes [n]$ for the (generating) double categories that look as follows.
$[m, n]=[m]\boxtimes [n]$ for the (generating) double categories that look as follows.

The squares in this picture should not be viewed as commuting squares, but rather as being filled with some type of non-invertible ![]() $2$-arrow; no confusion should arise since one cannot compose
$2$-arrow; no confusion should arise since one cannot compose ![]() $\longrightarrow$ and
$\longrightarrow$ and ![]() .
.
Example 2.6 Let ![]() $n\geq 0$ and consider the arrow double category
$n\geq 0$ and consider the arrow double category ![]() $\mathbb {A}\mathrm {r}[n]$ defined by
$\mathbb {A}\mathrm {r}[n]$ defined by
where ![]() $\star$ denotes the join. In other words, it is the double category that looks as follows.
$\star$ denotes the join. In other words, it is the double category that looks as follows.

There is an evident inclusion ![]() $\mathbb {A}\mathrm {r}[n]\longrightarrow [n, n]$, and we denote by
$\mathbb {A}\mathrm {r}[n]\longrightarrow [n, n]$, and we denote by ![]() $\pi _{\mathrm {hor}}\colon \mathbb {A}\mathrm {r}[n]\longrightarrow [n, 0]$ and
$\pi _{\mathrm {hor}}\colon \mathbb {A}\mathrm {r}[n]\longrightarrow [n, 0]$ and ![]() $\pi _{\mathrm {vert}}\colon \mathbb {A}\mathrm {r}[n]\longrightarrow [0, n]$ the obvious projections.
$\pi _{\mathrm {vert}}\colon \mathbb {A}\mathrm {r}[n]\longrightarrow [0, n]$ the obvious projections.
Example 2.7 Let ![]() $n\geq 0$ and consider the double category
$n\geq 0$ and consider the double category ![]() $\mathbb {T}\mathrm {w}[n]$ defined by
$\mathbb {T}\mathrm {w}[n]$ defined by
In other words, ![]() $\mathbb {T}\mathrm {w}[n]\simeq \mathbb {A}\mathrm {r}[n]^{2-\mathrm {op}}$ and can be depicted as follows.
$\mathbb {T}\mathrm {w}[n]\simeq \mathbb {A}\mathrm {r}[n]^{2-\mathrm {op}}$ and can be depicted as follows.

Proposition 2.8 For any ![]() $d\geq 1$, the category
$d\geq 1$, the category ![]() $\mathrm {Cat}^{\otimes d}$ is cartesian closed. In fact, the localization
$\mathrm {Cat}^{\otimes d}$ is cartesian closed. In fact, the localization
of ![]() $d$-fold simplicial spaces is monoidal for the cartesian product.
$d$-fold simplicial spaces is monoidal for the cartesian product.
We will write ![]() $Y^X$ for the internal mapping object in
$Y^X$ for the internal mapping object in ![]() $d$-fold simplicial spaces; the proposition implies that this is also the internal mapping object for
$d$-fold simplicial spaces; the proposition implies that this is also the internal mapping object for ![]() $d$-fold categories.
$d$-fold categories.
Proof. It suffices to verify that for each ![]() $d$-fold category
$d$-fold category ![]() $\mathbb {C}$ and
$\mathbb {C}$ and ![]() $m_1, \dots, m_d\geq 0$, the
$m_1, \dots, m_d\geq 0$, the ![]() $d$-fold simplicial space given by
$d$-fold simplicial space given by
remains a ![]() $d$-fold category. Using symmetry and the fact that
$d$-fold category. Using symmetry and the fact that ![]() $[m_1, \dots, m_d]=[m_1, 0, \dots, 0]\times \dots \times [0,\dots, 0, m_d]$, it suffices to verify that
$[m_1, \dots, m_d]=[m_1, 0, \dots, 0]\times \dots \times [0,\dots, 0, m_d]$, it suffices to verify that ![]() $\mathbb {C}^{[m, 0, \dots, 0]}$ is a
$\mathbb {C}^{[m, 0, \dots, 0]}$ is a ![]() $d$-fold category, i.e. satisfies the complete Segal conditions in all simplicial directions.
$d$-fold category, i.e. satisfies the complete Segal conditions in all simplicial directions.
For the first direction, note that each ![]() $\mathbb {C}^{[m, 0, \dots, 0]}(-, \vec {n}_{d-1})$ agrees with
$\mathbb {C}^{[m, 0, \dots, 0]}(-, \vec {n}_{d-1})$ agrees with ![]() $\mathbb {C}(-, \vec {n}_{d-1})^{[m]}$, which is a
$\mathbb {C}(-, \vec {n}_{d-1})^{[m]}$, which is a ![]() $1$-category by [Reference RezkRez01, Theorem 7.2]. For the remaining simplicial directions, note that the
$1$-category by [Reference RezkRez01, Theorem 7.2]. For the remaining simplicial directions, note that the ![]() $(d-1)$-fold simplicial space
$(d-1)$-fold simplicial space
sends each ![]() $(n_2, \dots, n_d)$ to the space of maps between simplicial spaces
$(n_2, \dots, n_d)$ to the space of maps between simplicial spaces
 \begin{align*} \mathrm{Map}_{s\mathscr{S}}\Big([m]\times [n], \mathbb{C}(-, n_2, \dots, n_d)\Big) &\simeq \mathrm{Map}_{s\mathscr{S}}\Big(\mathop {{\rm colim}}\limits_{_{[k]\in \mathbf{\Delta}/[m]\times [n]}} \ [k], \ \mathbb{C}(-, n_2, \dots, n_d)\Big)\\ &\simeq \lim_{[k]\in (\mathbf{\Delta}/[m]\times [n])^{\mathrm{op}}} \mathbb{C}(k, n_2, \dots, n_d). \end{align*}
\begin{align*} \mathrm{Map}_{s\mathscr{S}}\Big([m]\times [n], \mathbb{C}(-, n_2, \dots, n_d)\Big) &\simeq \mathrm{Map}_{s\mathscr{S}}\Big(\mathop {{\rm colim}}\limits_{_{[k]\in \mathbf{\Delta}/[m]\times [n]}} \ [k], \ \mathbb{C}(-, n_2, \dots, n_d)\Big)\\ &\simeq \lim_{[k]\in (\mathbf{\Delta}/[m]\times [n])^{\mathrm{op}}} \mathbb{C}(k, n_2, \dots, n_d). \end{align*}
In other words, ![]() $\mathbb {C}^{[m, 0, \dots, 0]}(n, -)$ is naturally equivalent to the limit of a certain diagram consisting of the
$\mathbb {C}^{[m, 0, \dots, 0]}(n, -)$ is naturally equivalent to the limit of a certain diagram consisting of the ![]() $(d-1)$-fold categories
$(d-1)$-fold categories ![]() $\mathbb {C}(k, -)$. Since
$\mathbb {C}(k, -)$. Since ![]() ${{\rm Cat}}^{\otimes d-1}\subseteq \mathrm {Fun}\big ((\mathbf {\Delta }^{\mathrm {op}})^{\times d-1}, \mathscr {S}\big )$ is closed under limits, each
${{\rm Cat}}^{\otimes d-1}\subseteq \mathrm {Fun}\big ((\mathbf {\Delta }^{\mathrm {op}})^{\times d-1}, \mathscr {S}\big )$ is closed under limits, each ![]() $\mathbb {C}^{[m, 0, \dots, 0]}(n, -)$ is a
$\mathbb {C}^{[m, 0, \dots, 0]}(n, -)$ is a ![]() $(d-1)$-fold category, as desired.
$(d-1)$-fold category, as desired.
2.2 Fibrations of double categories
Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of ![]() $1$-categories. Recall that an arrow
$1$-categories. Recall that an arrow ![]() $\alpha \colon d_1\longrightarrow d_2$ in
$\alpha \colon d_1\longrightarrow d_2$ in ![]() $\mathscr {D}$ is called p-cartesian (or simply cartesian, if
$\mathscr {D}$ is called p-cartesian (or simply cartesian, if ![]() $p$ is understood) if for any diagram
$p$ is understood) if for any diagram

where the restriction of ![]() $\sigma$ to
$\sigma$ to ![]() $[1<2]$ is given by
$[1<2]$ is given by ![]() $\alpha$, there is a contractible space of lifts, as indicated. Let
$\alpha$, there is a contractible space of lifts, as indicated. Let ![]() $\mathscr {D}(1)^{\mathrm {cart}}\subseteq \mathscr {D}(1)$ denote the subspace consisting of cartesian arrows. Then
$\mathscr {D}(1)^{\mathrm {cart}}\subseteq \mathscr {D}(1)$ denote the subspace consisting of cartesian arrows. Then ![]() $p$ is said to be a cartesian fibration if the map
$p$ is said to be a cartesian fibration if the map ![]() $\mathscr {D}(1)^{\mathrm {cart}}\longrightarrow \mathscr {D}(\{1\})\times _{\mathscr {C}(\{1\})} \mathscr {C}(1)$ induces a surjection on path components [Reference Ayala and FrancisAF20, Reference LurieLur09a]. It is called a right fibration if furthermore every arrow in
$\mathscr {D}(1)^{\mathrm {cart}}\longrightarrow \mathscr {D}(\{1\})\times _{\mathscr {C}(\{1\})} \mathscr {C}(1)$ induces a surjection on path components [Reference Ayala and FrancisAF20, Reference LurieLur09a]. It is called a right fibration if furthermore every arrow in ![]() $\mathscr {D}$ is cartesian. Equivalently, it is a right fibration if the map
$\mathscr {D}$ is cartesian. Equivalently, it is a right fibration if the map ![]() $\mathscr {D}(1)\longrightarrow \mathscr {D}(\{1\})\times _{\mathscr {C}(\{1\})} \mathscr {C}(1)$ is an equivalence; see, e.g., [Reference Boavida de BritoBoa18, Proposition 1.7]. Taking opposite categories, one obtains the notion of a cocartesian arrow and a cocartesian (respectively, left) fibration (some alternative characterizations also appear in § 5.1).
$\mathscr {D}(1)\longrightarrow \mathscr {D}(\{1\})\times _{\mathscr {C}(\{1\})} \mathscr {C}(1)$ is an equivalence; see, e.g., [Reference Boavida de BritoBoa18, Proposition 1.7]. Taking opposite categories, one obtains the notion of a cocartesian arrow and a cocartesian (respectively, left) fibration (some alternative characterizations also appear in § 5.1).
We will be interested in the following variant of this notion for double categories.
Definition 2.9 A map ![]() $\mathbb {D}\longrightarrow \mathbb {C}$ of double categories is called a (left, cart)-fibration if the following conditions hold.
$\mathbb {D}\longrightarrow \mathbb {C}$ of double categories is called a (left, cart)-fibration if the following conditions hold.
(1) The square of categories
is cartesian. Equivalently, each
 $\mathbb {D}(-, n)\longrightarrow \mathbb {C}(-, n)$ is a left fibration of categories.
$\mathbb {D}(-, n)\longrightarrow \mathbb {C}(-, n)$ is a left fibration of categories.(2) The map
 $\mathbb {D}(0, -)\longrightarrow \mathbb {C}(0, -)$ is a cartesian fibration of categories.
$\mathbb {D}(0, -)\longrightarrow \mathbb {C}(0, -)$ is a cartesian fibration of categories.
A strong map between (left, cart)-fibrations is a commuting square

where ![]() $f$ preserves cartesian vertical arrows. We will write
$f$ preserves cartesian vertical arrows. We will write ![]() $\mathrm {Fib}^{\mathrm {left, cart}}\subseteq \mathrm {Fun}([1], \mathrm {Cat}^{\otimes 2})$ for the subcategory of (left, cart)-fibrations and strong maps between them.
$\mathrm {Fib}^{\mathrm {left, cart}}\subseteq \mathrm {Fun}([1], \mathrm {Cat}^{\otimes 2})$ for the subcategory of (left, cart)-fibrations and strong maps between them.
Remark 2.10 By condition (1), the map ![]() $\mathscr {D}([1], -)\longrightarrow \mathscr {C}([1], -)$ is a cartesian fibration as well and
$\mathscr {D}([1], -)\longrightarrow \mathscr {C}([1], -)$ is a cartesian fibration as well and ![]() $\mathscr {D}([1], -)\longrightarrow \mathscr {D}(\{0\}, -)$ preserves cartesian arrows. The other face map
$\mathscr {D}([1], -)\longrightarrow \mathscr {D}(\{0\}, -)$ preserves cartesian arrows. The other face map ![]() $\mathscr {D}([1], -)\longrightarrow \mathscr {D}(\{1\}, -)$ is not required to preserve cartesian arrows.
$\mathscr {D}([1], -)\longrightarrow \mathscr {D}(\{1\}, -)$ is not required to preserve cartesian arrows.
Remark 2.11 The class of (left, cart)-fibrations is stable under composition and base change. Furthermore, a map ![]() $\mathbb {D}\longrightarrow \ast$ is a (left, cart)-fibration if and only if
$\mathbb {D}\longrightarrow \ast$ is a (left, cart)-fibration if and only if ![]() $\mathbb {D}$ is constant in the horizontal direction. In particular, the fibers of a (left, cart)-fibration are categories concentrated in the vertical direction (and constant in the horizontal direction).
$\mathbb {D}$ is constant in the horizontal direction. In particular, the fibers of a (left, cart)-fibration are categories concentrated in the vertical direction (and constant in the horizontal direction).
Informally, a map of double categories ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ is a (left, cart)-fibration if the following conditions hold.
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ is a (left, cart)-fibration if the following conditions hold.
(a) For every horizontal arrow
 $\alpha \colon c_0\to c_1$ in
$\alpha \colon c_0\to c_1$ in  $\mathbb {C}$ and
$\mathbb {C}$ and  $d_0\in p^{-1}(c_0)$, there exists a unique horizontal arrow
$d_0\in p^{-1}(c_0)$, there exists a unique horizontal arrow  $d_0\longrightarrow \alpha _!(d_0)$ lifting
$d_0\longrightarrow \alpha _!(d_0)$ lifting  $\alpha$. Furthermore, given any square
$\alpha$. Furthermore, given any square  $\sigma$ in
$\sigma$ in  $\mathbb {C}$ together with a lift of its left vertical arrow
there exists a unique dotted lift
$\mathbb {C}$ together with a lift of its left vertical arrow
there exists a unique dotted lift
 $\tilde {\sigma }$ as indicated (this lift includes the objects
$\tilde {\sigma }$ as indicated (this lift includes the objects  $\alpha _!(d_{00})$ and
$\alpha _!(d_{00})$ and  $\alpha '_!(d_{01})$).
$\alpha '_!(d_{01})$).(b) For every vertical arrow
 in
in  $\mathbb {D}$ and
$\mathbb {D}$ and  $d_1\in p^{-1}(c_1)$, there exists a vertically
$d_1\in p^{-1}(c_1)$, there exists a vertically  $p$-cartesian arrow
$p$-cartesian arrow  covering
covering  $\alpha$.
$\alpha$.
Now let us fix a square ![]() $\sigma$ in
$\sigma$ in ![]() $\mathbb {C}$ together with an object
$\mathbb {C}$ together with an object ![]() $d_{01}\in p^{-1}(c_{01})$. A combination of conditions (a) and (b) then implies that
$d_{01}\in p^{-1}(c_{01})$. A combination of conditions (a) and (b) then implies that ![]() $\sigma$ admits a unique lift
$\sigma$ admits a unique lift ![]() $\tilde {\sigma }$ of the form
$\tilde {\sigma }$ of the form

which is vertically ![]() $p$-cartesian, in the sense that any other square factors uniquely over
$p$-cartesian, in the sense that any other square factors uniquely over ![]() $\tilde {\sigma }$ in the vertical direction (Remark 2.10). The resulting vertical arrow
$\tilde {\sigma }$ in the vertical direction (Remark 2.10). The resulting vertical arrow ![]() $\alpha _!\beta ^*(d_{01})\longrightarrow \alpha '_!(d_{01})$ is not necessarily
$\alpha _!\beta ^*(d_{01})\longrightarrow \alpha '_!(d_{01})$ is not necessarily ![]() $p$-cartesian and decomposes as
$p$-cartesian and decomposes as
The first map ![]() $h_{\sigma }$ is contained in the fiber
$h_{\sigma }$ is contained in the fiber ![]() $p^{-1}(c_{10})$ and provides a natural comparison between the two ways to change fibers over the square
$p^{-1}(c_{10})$ and provides a natural comparison between the two ways to change fibers over the square ![]() $\sigma$, from ‘horizontally after vertically’ to ‘vertically after horizontally’.
$\sigma$, from ‘horizontally after vertically’ to ‘vertically after horizontally’.
To illustrate Definition 2.9, let us consider the following example.
Proposition 2.12 Let ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $\mathscr {D}$ be categories and let
$\mathscr {D}$ be categories and let ![]() $p=(p_1, p_2)\colon \mathscr {X}\longrightarrow \mathscr {C}\times \mathscr {D}$ be a functor such that:
$p=(p_1, p_2)\colon \mathscr {X}\longrightarrow \mathscr {C}\times \mathscr {D}$ be a functor such that:
(i)
 $p_1$ is a cocartesian fibration and all
$p_1$ is a cocartesian fibration and all  $p_1$-cocartesian arrows in
$p_1$-cocartesian arrows in  $\mathscr {X}$ map to equivalences in
$\mathscr {X}$ map to equivalences in  $\mathscr {D}$;
$\mathscr {D}$;(ii)
 $p_2$ is a cartesian fibration and all
$p_2$ is a cartesian fibration and all  $p_2$-cartesian arrows in
$p_2$-cartesian arrows in  $\mathscr {X}$ map to equivalences in
$\mathscr {X}$ map to equivalences in  $\mathscr {C}$.
$\mathscr {C}$.
Associated to ![]() $p$ is a map of double categories
$p$ is a map of double categories ![]() $p'\colon \mathbb {X}\longrightarrow \mathscr {C}\boxtimes \mathscr {D}$, where
$p'\colon \mathbb {X}\longrightarrow \mathscr {C}\boxtimes \mathscr {D}$, where ![]() $\mathbb {X}(m, n)$ is the space of diagrams
$\mathbb {X}(m, n)$ is the space of diagrams

where ![]() $\alpha \colon [m]\longrightarrow \mathscr {C}, \beta \colon [n]\longrightarrow \mathscr {D}$ and
$\alpha \colon [m]\longrightarrow \mathscr {C}, \beta \colon [n]\longrightarrow \mathscr {D}$ and ![]() $\sigma$ sends each
$\sigma$ sends each ![]() $[m]\times \{j\}$ to
$[m]\times \{j\}$ to ![]() $p_1$-cocartesian arrows in
$p_1$-cocartesian arrows in ![]() $\mathscr {X}$. Then
$\mathscr {X}$. Then ![]() $p'$ is a (left, cart)-fibration of double categories.
$p'$ is a (left, cart)-fibration of double categories.
Functors ![]() $p\colon \mathscr {X}\longrightarrow \mathscr {C}\times \mathscr {D}$ satisfying conditions (i) and (ii) have been studied in detail in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23a, Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23b], where they are called local orthofibrations. Let us point out the close analogy between the discussion preceding Proposition 2.12 and the discussion in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23b, Construction 2.3.5].
$p\colon \mathscr {X}\longrightarrow \mathscr {C}\times \mathscr {D}$ satisfying conditions (i) and (ii) have been studied in detail in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23a, Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23b], where they are called local orthofibrations. Let us point out the close analogy between the discussion preceding Proposition 2.12 and the discussion in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23b, Construction 2.3.5].
Proof. To see condition (1) of Definition 2.9, consider the pullback square of categories

where ![]() $\Delta$ takes the constant diagram and
$\Delta$ takes the constant diagram and ![]() $\iota$ is the inclusion of the space of objects. Since
$\iota$ is the inclusion of the space of objects. Since ![]() $(p_1, p_2)$ is a local orthofibration, the induced map
$(p_1, p_2)$ is a local orthofibration, the induced map ![]() $(p'_1, p'_2)\colon \mathrm {Fun}([n], \mathscr {X})\longrightarrow \mathrm {Fun}([n], \mathscr {C})\times \mathrm {Fun}([n], \mathscr {D})$ is a local orthofibration as well: a natural transformation in
$(p'_1, p'_2)\colon \mathrm {Fun}([n], \mathscr {X})\longrightarrow \mathrm {Fun}([n], \mathscr {C})\times \mathrm {Fun}([n], \mathscr {D})$ is a local orthofibration as well: a natural transformation in ![]() $\mathrm {Fun}([n], \mathscr {X})$ is
$\mathrm {Fun}([n], \mathscr {X})$ is ![]() $p'_1$-cocartesian if and only if it is given pointwise by
$p'_1$-cocartesian if and only if it is given pointwise by ![]() $p_1$-cocartesian maps in
$p_1$-cocartesian maps in ![]() $\mathscr {X}$, and similarly for
$\mathscr {X}$, and similarly for ![]() $p'_2$-cartesian natural transformations (this follows, e.g., from Lemma 5.4(3)). In particular, the base change
$p'_2$-cartesian natural transformations (this follows, e.g., from Lemma 5.4(3)). In particular, the base change ![]() $q\colon \mathrm {Fun}'([n], \mathscr {X})\longrightarrow \mathscr {C}\times \mathrm {Map}_{{{\rm Cat}}}([n], \mathscr {D})$ is a cocartesian fibration.
$q\colon \mathrm {Fun}'([n], \mathscr {X})\longrightarrow \mathscr {C}\times \mathrm {Map}_{{{\rm Cat}}}([n], \mathscr {D})$ is a cocartesian fibration.
Unraveling the definitions, one sees that the space of maps ![]() $[m]\longrightarrow \mathrm {Fun}'([n], \mathscr {X})$ is equivalent to the space of diagrams
$[m]\longrightarrow \mathrm {Fun}'([n], \mathscr {X})$ is equivalent to the space of diagrams ![]() $\sigma \colon [m]\times [n]\longrightarrow \mathscr {X}$ of the form (2.13). Furthermore,
$\sigma \colon [m]\times [n]\longrightarrow \mathscr {X}$ of the form (2.13). Furthermore, ![]() $[m]\longrightarrow \mathrm {Fun}'([n], \mathscr {X})$ sends each arrow to a
$[m]\longrightarrow \mathrm {Fun}'([n], \mathscr {X})$ sends each arrow to a ![]() $q$-cocartesian arrow if and only if
$q$-cocartesian arrow if and only if ![]() $\sigma$ sends each
$\sigma$ sends each ![]() $[m]\times \{i\}$ to
$[m]\times \{i\}$ to ![]() $p_1$-cocartesian arrows in
$p_1$-cocartesian arrows in ![]() $\mathscr {X}$. It follows that there is a factorization
$\mathscr {X}$. It follows that there is a factorization
where the first map is the inclusion of the wide subcategory spanned by the ![]() $q$-cocartesian arrows. In particular, this shows that each
$q$-cocartesian arrows. In particular, this shows that each ![]() $\mathbb {X}(-, n)\longrightarrow \big (\mathscr {C}\boxtimes \mathscr {D}\big )(-, n)$ is a left fibration, as desired.
$\mathbb {X}(-, n)\longrightarrow \big (\mathscr {C}\boxtimes \mathscr {D}\big )(-, n)$ is a left fibration, as desired.
For condition (2) of Definition 2.9, it suffices to observe that ![]() $\mathbb {X}(0, -)\longrightarrow \big (\mathscr {C}\boxtimes \mathscr {D}\big )(0, -)$ coincides with top horizontal map in the following pullback diagram.
$\mathbb {X}(0, -)\longrightarrow \big (\mathscr {C}\boxtimes \mathscr {D}\big )(0, -)$ coincides with top horizontal map in the following pullback diagram.

This map is a cartesian fibration by condition (ii) (cf. [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23b, Observation 2.3.2]).
Remark 2.14 This remark only serves to motivate Definition 2.9, and will not be used in the rest of the text (making it more precise would require a form of straightening).
Elaborating on the discussion following Definition 2.9, one can informally think of a (left, cart)-fibration ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ as a certain type of diagram of categories indexed by
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ as a certain type of diagram of categories indexed by ![]() $\mathbb {C}$. Indeed, by Remark 2.11, the fibers of
$\mathbb {C}$. Indeed, by Remark 2.11, the fibers of ![]() $p$ are all categories (in the vertical direction). Furthermore, each horizontal arrow
$p$ are all categories (in the vertical direction). Furthermore, each horizontal arrow ![]() $\alpha \colon c_0\longrightarrow c_1$ induces a map of categories
$\alpha \colon c_0\longrightarrow c_1$ induces a map of categories ![]() $\alpha _!\colon \mathbb {D}_{c_0}\longrightarrow \mathbb {D}_{c_1}$ and each vertical arrow
$\alpha _!\colon \mathbb {D}_{c_0}\longrightarrow \mathbb {D}_{c_1}$ and each vertical arrow ![]() induces a map of categories
induces a map of categories ![]() $\beta ^*\colon \mathbb {D}_{c_1}\longrightarrow \mathbb {D}_{c_0}$. Finally, each diagram
$\beta ^*\colon \mathbb {D}_{c_1}\longrightarrow \mathbb {D}_{c_0}$. Finally, each diagram ![]() $\sigma \colon [1, 1]\longrightarrow \mathbb {C}$ gives rise to a square of categories and functors commuting up to a natural transformation as follows.
$\sigma \colon [1, 1]\longrightarrow \mathbb {C}$ gives rise to a square of categories and functors commuting up to a natural transformation as follows.

In other words, a (left, cart)-fibration ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ should arise as the unstraightening of a diagram of double categories
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ should arise as the unstraightening of a diagram of double categories ![]() $\mathbb {C}^{2-\mathrm {op}}\longrightarrow \mathbb {C}\mathrm {at}^{\mathrm {oplax}}$, where
$\mathbb {C}^{2-\mathrm {op}}\longrightarrow \mathbb {C}\mathrm {at}^{\mathrm {oplax}}$, where ![]() $\mathbb {C}\mathrm {at}^{\mathrm {oplax}}$ is a certain double category whose objects are categories, horizontal and vertical morphisms are functors and squares are oplax squares as follows.
$\mathbb {C}\mathrm {at}^{\mathrm {oplax}}$ is a certain double category whose objects are categories, horizontal and vertical morphisms are functors and squares are oplax squares as follows.

Lemma 2.15 Consider the following strong map of (left, cart)-fibrations over ![]() $\mathbb {C}$.
$\mathbb {C}$.

Then ![]() $f$ is an equivalence if and only if for any object
$f$ is an equivalence if and only if for any object ![]() $c\in \mathbb {C}$, the induced map between the fibers
$c\in \mathbb {C}$, the induced map between the fibers ![]() $\mathbb {D}_c\longrightarrow \mathbb {E}_c$ is an equivalence of (vertical) categories.
$\mathbb {D}_c\longrightarrow \mathbb {E}_c$ is an equivalence of (vertical) categories.
Proof. Since ![]() $p$ and
$p$ and ![]() $q$ are left fibrations in the horizontal direction, the map
$q$ are left fibrations in the horizontal direction, the map ![]() $f$ is an equivalence if and only if the map
$f$ is an equivalence if and only if the map ![]() $f_0\colon \mathbb {D}(0, -)\longrightarrow \mathbb {E}(0, -)$ is an equivalence of cartesian fibrations over
$f_0\colon \mathbb {D}(0, -)\longrightarrow \mathbb {E}(0, -)$ is an equivalence of cartesian fibrations over ![]() $\mathbb {C}(0, -)$; in turn, the map of cartesian fibrations
$\mathbb {C}(0, -)$; in turn, the map of cartesian fibrations ![]() $f_0$ is an equivalence if and only if it induces an equivalence on fibers [Reference LurieLur09a, Corollary 2.4.4.4].
$f_0$ is an equivalence if and only if it induces an equivalence on fibers [Reference LurieLur09a, Corollary 2.4.4.4].
Variant 2.16 Taking opposites in the horizontal or vertical direction, and exchanging the vertical and horizontal direction, one obtains seven more types of fibrations. For example, a map ![]() $\mathbb {D}\longrightarrow \mathbb {C}$ is a (cocart, right)-fibration if
$\mathbb {D}\longrightarrow \mathbb {C}$ is a (cocart, right)-fibration if ![]() $\mathbb {D}(-, 0)\longrightarrow \mathbb {C}(-, 0)$ is a cocartesian fibration and each
$\mathbb {D}(-, 0)\longrightarrow \mathbb {C}(-, 0)$ is a cocartesian fibration and each ![]() $\mathbb {D}(m, -)\longrightarrow \mathbb {C}(m, -)$ is a right fibration. Strong maps between such fibrations are always required to preserve (co)cartesian arrows, either in the horizontal or vertical direction.
$\mathbb {D}(m, -)\longrightarrow \mathbb {C}(m, -)$ is a right fibration. Strong maps between such fibrations are always required to preserve (co)cartesian arrows, either in the horizontal or vertical direction.
For example, one can also associate a (cocart, right)-fibration to a two-variable fibration ![]() $(p_1, p_2)\colon \mathscr {X}\longrightarrow \mathscr {C}\times \mathscr {D}$ as in Proposition 2.12, by considering maps
$(p_1, p_2)\colon \mathscr {X}\longrightarrow \mathscr {C}\times \mathscr {D}$ as in Proposition 2.12, by considering maps ![]() $\sigma$ as in (2.13) that send each
$\sigma$ as in (2.13) that send each ![]() $\{i\}\times [n]$ to
$\{i\}\times [n]$ to ![]() $p_2$-cartesian arrows in
$p_2$-cartesian arrows in ![]() $\mathscr {X}$.
$\mathscr {X}$.
Remark 2.17 Similarly to Remark 2.14, one can informally think of a (cocart, right)-fibration ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ as a certain diagram of categories indexed by
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ as a certain diagram of categories indexed by ![]() $\mathbb {C}$. Indeed, in this case all fibers of
$\mathbb {C}$. Indeed, in this case all fibers of ![]() $p$ are categories in the horizontal direction (and constant in the vertical direction) and again each horizontal arrow
$p$ are categories in the horizontal direction (and constant in the vertical direction) and again each horizontal arrow ![]() $\alpha \colon c_0\longrightarrow c_1$ induces a map of categories
$\alpha \colon c_0\longrightarrow c_1$ induces a map of categories ![]() $\alpha _!\colon \mathbb {D}_{c_0}\longrightarrow \mathbb {D}_{c_1}$ and each vertical arrow
$\alpha _!\colon \mathbb {D}_{c_0}\longrightarrow \mathbb {D}_{c_1}$ and each vertical arrow ![]() induces a functor
induces a functor ![]() $\beta ^*\colon \mathbb {D}_{c_1}\longrightarrow \mathbb {D}_{c_0}$.
$\beta ^*\colon \mathbb {D}_{c_1}\longrightarrow \mathbb {D}_{c_0}$.
For the behaviour on a square ![]() $\sigma \colon [1, 1]\longrightarrow \mathbb {C}$, we can repeat the analysis following Definition 2.9: for each such square and a lift
$\sigma \colon [1, 1]\longrightarrow \mathbb {C}$, we can repeat the analysis following Definition 2.9: for each such square and a lift ![]() $d_{01}\in p^{-1}(c_{01})$, there exists a lift to a square
$d_{01}\in p^{-1}(c_{01})$, there exists a lift to a square

in ![]() $\mathbb {D}$ which is
$\mathbb {D}$ which is ![]() $p$-cartesian in the vertical direction. The bottom horizontal arrow is
$p$-cartesian in the vertical direction. The bottom horizontal arrow is ![]() $p$-cocartesian but the top horizontal arrow is not in general, so that one again obtains a natural map
$p$-cocartesian but the top horizontal arrow is not in general, so that one again obtains a natural map ![]() $h_\sigma \colon \alpha _!\beta ^*(d_{01})\longrightarrow \beta ^{\prime *}\alpha _!(d_{01})$.
$h_\sigma \colon \alpha _!\beta ^*(d_{01})\longrightarrow \beta ^{\prime *}\alpha _!(d_{01})$.
In other words, one can think of a (cocart, right)-fibration ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ as the unstraightening of a map of double categories
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ as the unstraightening of a map of double categories ![]() $\mathbb {C}^{2-\mathrm {op}}\longrightarrow \mathbb {C}\mathrm {at}^{\mathrm {oplax}}$, where
$\mathbb {C}^{2-\mathrm {op}}\longrightarrow \mathbb {C}\mathrm {at}^{\mathrm {oplax}}$, where ![]() $\mathbb {C}\mathrm {at}^{\mathrm {oplax}}$ is the double category described informally in Remark 2.14.
$\mathbb {C}\mathrm {at}^{\mathrm {oplax}}$ is the double category described informally in Remark 2.14.
2.3 The reflection of a (left, cart)-fibration
We will now turn to the main combinatorial construction of this text: we will associate to each (left, cart)-fibration ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ a (cocart, right)-fibration
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ a (cocart, right)-fibration ![]() $\Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$, which we will refer to as the reflection of
$\Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$, which we will refer to as the reflection of ![]() $p$. In § 3, we will study the functoriality of this construction in more detail.
$p$. In § 3, we will study the functoriality of this construction in more detail.
Before we begin, note that at a heuristic level, Remarks 2.14 and 2.17 show that (left, cart)-fibrations and (cocart, right)-fibrations over a double category ![]() $\mathbb {C}$ encode the same kind of data: both should be considered as unstraightened versions of the datum of a map of double categories
$\mathbb {C}$ encode the same kind of data: both should be considered as unstraightened versions of the datum of a map of double categories
One should therefore be able to straighten a (left, cart)-fibration to such a map of double categories and then unstraighten it to obtain a (cocart, right)-fibration. Instead of making this more precise, we will give a purely combinatorial description of (what should be) the composite functor ![]() $\Psi ^\perp$, inspired by the explicit formula for the Grothendieck construction and the combinatorics appearing in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23a]. Informally, the functor
$\Psi ^\perp$, inspired by the explicit formula for the Grothendieck construction and the combinatorics appearing in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23a]. Informally, the functor ![]() $\Psi ^\perp$ will first remove the vertical arrows in each fiber of
$\Psi ^\perp$ will first remove the vertical arrows in each fiber of ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$, so that only the cartesian vertical arrows remain, and then replaces them by fiberwise horizontal arrows instead (which can be composed with the cocartesian horizontal arrows already present in
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$, so that only the cartesian vertical arrows remain, and then replaces them by fiberwise horizontal arrows instead (which can be composed with the cocartesian horizontal arrows already present in ![]() $\mathbb {D}$).
$\mathbb {D}$).
Let us start by considering the following construction of a double category out of a (left, cart)-fibration, which will appear repeatedly in the text.
Lemma 2.18 Let ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ be a map of double categories such that each
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ be a map of double categories such that each ![]() $\mathbb {D}(-, n)\longrightarrow \mathbb {C}(-, n)$ is a left fibration. Consider the bisimplicial space
$\mathbb {D}(-, n)\longrightarrow \mathbb {C}(-, n)$ is a left fibration. Consider the bisimplicial space ![]() $X$ whose space of
$X$ whose space of ![]() $(m, n)$-simplices is given by the space of commuting squares of the following form.
$(m, n)$-simplices is given by the space of commuting squares of the following form.

Then ![]() $X$ is a double category.
$X$ is a double category.
Remark 2.20 Informally, ![]() $X$ is a double category with the same objects as
$X$ is a double category with the same objects as ![]() $\mathbb {D}$, whose squares are given by diagrams in
$\mathbb {D}$, whose squares are given by diagrams in ![]() $\mathbb {D}$ of the form
$\mathbb {D}$ of the form

where the right square is a commuting square of vertical arrows in which the top and bottom arrow are sent to degenerate arrows in ![]() $\mathbb {C}$. In other words, we keep the same vertical arrows but replace the horizontal arrows by formal composites
$\mathbb {C}$. In other words, we keep the same vertical arrows but replace the horizontal arrows by formal composites ![]() of a horizontal and a fiberwise vertical arrow. Diagrams of the above form have an evident vertical composition. For the composition of horizontal arrows, consider the following concatenation of two formal composites:
of a horizontal and a fiberwise vertical arrow. Diagrams of the above form have an evident vertical composition. For the composition of horizontal arrows, consider the following concatenation of two formal composites:
Then ![]() $\beta _1$ and
$\beta _1$ and ![]() $\alpha _2$ fit into an essentially unique
$\alpha _2$ fit into an essentially unique ![]() $(1, 1)$-cell of
$(1, 1)$-cell of ![]() $\mathbb {D}$ that covers the vertically degenerate
$\mathbb {D}$ that covers the vertically degenerate ![]() $(1, 1)$-cell
$(1, 1)$-cell ![]() $p(\alpha _2)$ in
$p(\alpha _2)$ in ![]() $\mathbb {C}$. The other two sides of this square give a formal composite
$\mathbb {C}$. The other two sides of this square give a formal composite ![]() . The composed horizontal arrow in
. The composed horizontal arrow in ![]() $X$ is then given by the formal composite
$X$ is then given by the formal composite ![]() $(\beta _2\beta '_1)\circ (\alpha '_2\alpha _1)$.
$(\beta _2\beta '_1)\circ (\alpha '_2\alpha _1)$.
Proof. To see that ![]() $X$ is a category in the vertical direction, we use that
$X$ is a category in the vertical direction, we use that ![]() $\mathrm {Cat}^{\otimes 2}$ is cartesian closed (Proposition 2.8): the simplicial space
$\mathrm {Cat}^{\otimes 2}$ is cartesian closed (Proposition 2.8): the simplicial space ![]() $X(m, -)$ can then be identified with the category
$X(m, -)$ can then be identified with the category ![]() $\big (\mathbb {D}^{\mathbb {A}\mathrm {r}[m]}\times _{\mathbb {C}^{\mathbb {A}\mathrm {r}[m]}} \mathbb {C}^{[m, 0]}\big )(0, -)$.
$\big (\mathbb {D}^{\mathbb {A}\mathrm {r}[m]}\times _{\mathbb {C}^{\mathbb {A}\mathrm {r}[m]}} \mathbb {C}^{[m, 0]}\big )(0, -)$.
To see that each ![]() $X(-, n)$ is a category, it suffices to treat the case
$X(-, n)$ is a category, it suffices to treat the case ![]() $n=0$: indeed, the general case then follows by considering the functor
$n=0$: indeed, the general case then follows by considering the functor ![]() $\mathbb {D}^{[0, n]}\longrightarrow \mathbb {C}^{[0, n]}$, which is still a left fibration in the horizontal direction. Unraveling the definitions shows that the Segal condition for
$\mathbb {D}^{[0, n]}\longrightarrow \mathbb {C}^{[0, n]}$, which is still a left fibration in the horizontal direction. Unraveling the definitions shows that the Segal condition for ![]() $X(-, 0)$ translates into the following unique lifting problem.
$X(-, 0)$ translates into the following unique lifting problem.

In other words, given a solid diagram in ![]() $\mathbb {D}$ of the form
$\mathbb {D}$ of the form

whose image in ![]() $\mathbb {C}$ has a fixed dashed extension (i.e. including the top squares), there exists a contractible space of dashed extensions as indicated. This follows immediately from the fact that each
$\mathbb {C}$ has a fixed dashed extension (i.e. including the top squares), there exists a contractible space of dashed extensions as indicated. This follows immediately from the fact that each ![]() $\mathbb {D}(-, n)\longrightarrow \mathbb {C}(-, n)$ is a left fibration of categories.
$\mathbb {D}(-, n)\longrightarrow \mathbb {C}(-, n)$ is a left fibration of categories.
For completeness of ![]() $X(-, 0)$, recall the simplicial set
$X(-, 0)$, recall the simplicial set ![]() $H=\Delta [3]/\sim$ in the definition of completeness from § 2, and note that a map
$H=\Delta [3]/\sim$ in the definition of completeness from § 2, and note that a map
corresponds to a diagram in ![]() $\mathbb {D}$ of the form
$\mathbb {D}$ of the form

in which ![]() $x_{00}\longrightarrow x_{02}$ and
$x_{00}\longrightarrow x_{02}$ and ![]() are degenerate and
are degenerate and ![]() $x_{11}\longrightarrow x_{13}$ and
$x_{11}\longrightarrow x_{13}$ and ![]() are degenerate, and whose image in
are degenerate, and whose image in ![]() $\mathbb {C}$ consists only of degenerate arrows (since
$\mathbb {C}$ consists only of degenerate arrows (since ![]() $\mathbb {C}$ is complete). We need to show that the above diagram is degenerate both in the horizontal and the vertical direction. Using that each
$\mathbb {C}$ is complete). We need to show that the above diagram is degenerate both in the horizontal and the vertical direction. Using that each ![]() $\mathbb {D}(-, n)\longrightarrow \mathbb {C}(-, n)$ is a left fibration, one sees that the above diagram is degenerate in the horizontal direction. Furthermore, the rightmost column is degenerate in the vertical direction, since both
$\mathbb {D}(-, n)\longrightarrow \mathbb {C}(-, n)$ is a left fibration, one sees that the above diagram is degenerate in the horizontal direction. Furthermore, the rightmost column is degenerate in the vertical direction, since both ![]() and
and ![]() are degenerate and
are degenerate and ![]() $\mathbb {D}(0, -)$ is a category.
$\mathbb {D}(0, -)$ is a category.
Definition 2.21 Let ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ be a (left, cart)-fibration and let
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ be a (left, cart)-fibration and let ![]() $X$ be the double category from Lemma 2.18. We will denote by
$X$ be the double category from Lemma 2.18. We will denote by ![]() $\Psi ^\perp (\mathbb {D})\subseteq X$ the bisimplicial subspace whose
$\Psi ^\perp (\mathbb {D})\subseteq X$ the bisimplicial subspace whose ![]() $(m, n)$-simplices correspond to diagrams (2.19) with the following property: the top map
$(m, n)$-simplices correspond to diagrams (2.19) with the following property: the top map ![]() $\mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow \mathbb {D}$ sends each
$\mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow \mathbb {D}$ sends each ![]() $\{ii\}\times [0, n]$ into the subspace of cartesian vertical arrows of
$\{ii\}\times [0, n]$ into the subspace of cartesian vertical arrows of ![]() $\mathbb {D}$. We will refer to the evident projection
$\mathbb {D}$. We will refer to the evident projection ![]() $\Psi ^\perp (p)\colon \Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$ as the reflection of
$\Psi ^\perp (p)\colon \Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$ as the reflection of ![]() $p$.
$p$.
In terms of the heuristic description of ![]() $X$ from Remark 2.20, one can identify
$X$ from Remark 2.20, one can identify ![]() $\Psi ^\perp (\mathbb {D})\subseteq X$ with the largest double subcategory of
$\Psi ^\perp (\mathbb {D})\subseteq X$ with the largest double subcategory of ![]() $X$ with the property that any vertical morphism
$X$ with the property that any vertical morphism ![]() $[0, 1]\to \Psi ^\perp (\mathbb {D})$ corresponds to a
$[0, 1]\to \Psi ^\perp (\mathbb {D})$ corresponds to a ![]() $p$-cartesian vertical arrow of
$p$-cartesian vertical arrow of ![]() $\mathbb {D}$. For the reason behind the terminology, see Proposition 3.15.
$\mathbb {D}$. For the reason behind the terminology, see Proposition 3.15.
Proposition 2.22 Let ![]() $p\colon \mathbb {D}\longrightarrow \mathbb {C}$ be a (left, cart)-fibration. Then the reflection
$p\colon \mathbb {D}\longrightarrow \mathbb {C}$ be a (left, cart)-fibration. Then the reflection ![]() $\Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$ is a (cocart, right)-fibration between double categories.
$\Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$ is a (cocart, right)-fibration between double categories.
Proof. We verify each of the conditions, starting with the fact that ![]() $\Psi ^\perp (\mathbb {D})$ is a double category.
$\Psi ^\perp (\mathbb {D})$ is a double category.
Segal conditions. Recall the double category ![]() $X$ from Lemma 2.18. Since each
$X$ from Lemma 2.18. Since each ![]() $\Psi ^\perp (\mathbb {D})(-, n)\subseteq X(-, n)$ is a full subcategory of the category
$\Psi ^\perp (\mathbb {D})(-, n)\subseteq X(-, n)$ is a full subcategory of the category ![]() $X(-, n)$, it follows that
$X(-, n)$, it follows that ![]() $\Psi ^\perp (\mathbb {D})(-, n)$ is a category (i.e. complete Segal space) itself. In the other direction, note that there is the following pullback square of simplicial spaces.
$\Psi ^\perp (\mathbb {D})(-, n)$ is a category (i.e. complete Segal space) itself. In the other direction, note that there is the following pullback square of simplicial spaces.

Since ![]() $X([m], -)$ is a category by Lemma 2.18, it suffices to verify that
$X([m], -)$ is a category by Lemma 2.18, it suffices to verify that ![]() $\Psi ^\perp (\mathbb {D})(0, -)\hookrightarrow X(0, -)$ is a subcategory. But this can simply be identified with the inclusion of the wide subcategory of
$\Psi ^\perp (\mathbb {D})(0, -)\hookrightarrow X(0, -)$ is a subcategory. But this can simply be identified with the inclusion of the wide subcategory of ![]() $\mathbb {D}(0, -)$ whose morphisms are cartesian morphisms.
$\mathbb {D}(0, -)$ whose morphisms are cartesian morphisms.
Vertical right fibration. Next, let us verify that each ![]() $\Psi ^\perp (\mathbb {D})(m, -)\longrightarrow \mathbb {C}(m, -)$ is a right fibration. By the horizontal Segal condition, it suffices to treat the case
$\Psi ^\perp (\mathbb {D})(m, -)\longrightarrow \mathbb {C}(m, -)$ is a right fibration. By the horizontal Segal condition, it suffices to treat the case ![]() $m=0$ and
$m=0$ and ![]() $m=1$. Unraveling the definitions, we have to verify that there are contractible spaces of diagonal lifts
$m=1$. Unraveling the definitions, we have to verify that there are contractible spaces of diagonal lifts

with the following property: the vertical arrow in ![]() $[0, 1]$, respectively the vertical arrows in
$[0, 1]$, respectively the vertical arrows in ![]() $\{00, 11\}\times [0, 1]$, are sent to cartesian vertical arrows in
$\{00, 11\}\times [0, 1]$, are sent to cartesian vertical arrows in ![]() $\mathbb {D}$. For the left square, there is a unique such lift since
$\mathbb {D}$. For the left square, there is a unique such lift since ![]() $\mathbb {D}(0, -)\longrightarrow \mathbb {C}(0, -)$ is a cartesian fibration. For the right square, we have to verify that for any solid diagram
$\mathbb {D}(0, -)\longrightarrow \mathbb {C}(0, -)$ is a cartesian fibration. For the right square, we have to verify that for any solid diagram

there exist unique objects ![]() $x_{00, 0}, x_{01, 0}, x_{11, 0}$ together with a dashed extension as indicated, such that the two arrows
$x_{00, 0}, x_{01, 0}, x_{11, 0}$ together with a dashed extension as indicated, such that the two arrows ![]() and
and ![]() are cartesian. To see this, first take these two arrows to be the (unique) cartesian lifts of their image in
are cartesian. To see this, first take these two arrows to be the (unique) cartesian lifts of their image in ![]() $\mathbb {C}$. Then the top square can be filled uniquely using that
$\mathbb {C}$. Then the top square can be filled uniquely using that ![]() $\mathbb {D}\longrightarrow \mathbb {C}$ is a left fibration in the horizontal direction. The right square (living entirely in the vertical direction) can then be filled uniquely since
$\mathbb {D}\longrightarrow \mathbb {C}$ is a left fibration in the horizontal direction. The right square (living entirely in the vertical direction) can then be filled uniquely since ![]() was cartesian.
was cartesian.
Horizontal cocartesian fibration. Note that the space ![]() $\Psi ^\perp (\mathbb {D})(1, 0)$ of horizontal arrows in
$\Psi ^\perp (\mathbb {D})(1, 0)$ of horizontal arrows in ![]() $\Psi ^\perp (\mathbb {D})$ is the space of diagrams in
$\Psi ^\perp (\mathbb {D})$ is the space of diagrams in ![]() $\mathbb {D}$ of the form
$\mathbb {D}$ of the form

covering a horizontal arrow in ![]() $\mathbb {C}$. Let us say that a horizontal arrow in
$\mathbb {C}$. Let us say that a horizontal arrow in ![]() $\Psi ^\perp (\mathbb {D})$ is marked if the corresponding vertical map
$\Psi ^\perp (\mathbb {D})$ is marked if the corresponding vertical map ![]() is an equivalence in
is an equivalence in ![]() $\mathbb {D}$. We claim that all marked horizontal arrows in
$\mathbb {D}$. We claim that all marked horizontal arrows in ![]() $\Psi ^\perp (\mathbb {D})$ are
$\Psi ^\perp (\mathbb {D})$ are ![]() $\Psi ^\perp (p)$-cocartesian. In other words, we have to find a unique diagonal lift for every diagram of categories
$\Psi ^\perp (p)$-cocartesian. In other words, we have to find a unique diagonal lift for every diagram of categories

where the top map sends ![]() $0\longrightarrow 1$ to a marked arrow. Unraveling the definitions, this corresponds to a solid diagram in
$0\longrightarrow 1$ to a marked arrow. Unraveling the definitions, this corresponds to a solid diagram in ![]() $\mathbb {D}$ covering a horizontal
$\mathbb {D}$ covering a horizontal ![]() $2$-simplex in
$2$-simplex in ![]() $\mathbb {C}$
$\mathbb {C}$

where the map ![]() is an equivalence, of which one has to find a unique dashed extension as indicated. To find the desired unique extension, using that
is an equivalence, of which one has to find a unique dashed extension as indicated. To find the desired unique extension, using that ![]() $\mathbb {D}\longrightarrow \mathbb {C}$ is a left fibration in the horizontal direction, it follows that there is a unique way to extend the square making the top triangle (living purely in the horizontal direction) commute. Since
$\mathbb {D}\longrightarrow \mathbb {C}$ is a left fibration in the horizontal direction, it follows that there is a unique way to extend the square making the top triangle (living purely in the horizontal direction) commute. Since ![]() was an equivalence, the resulting vertical arrow
was an equivalence, the resulting vertical arrow ![]() is an equivalence as well. It then follows that there is a unique vertical map
is an equivalence as well. It then follows that there is a unique vertical map ![]() with a filling of the right triangle (purely in the vertical direction). We conclude that all marked arrows in
with a filling of the right triangle (purely in the vertical direction). We conclude that all marked arrows in ![]() $\Psi ^\perp (\mathbb {D})$ are cocartesian. Finally, for every horizontal arrow
$\Psi ^\perp (\mathbb {D})$ are cocartesian. Finally, for every horizontal arrow ![]() $f\colon c\longrightarrow c'$ in
$f\colon c\longrightarrow c'$ in ![]() $\mathbb {C}$ and a lift
$\mathbb {C}$ and a lift ![]() $x\in \Psi ^\perp (\mathbb {D})_c$, there exist a marked lift
$x\in \Psi ^\perp (\mathbb {D})_c$, there exist a marked lift ![]() $\tilde {f}\colon x\longrightarrow x'$, using that
$\tilde {f}\colon x\longrightarrow x'$, using that ![]() $\mathbb {D}(-, 0)\longrightarrow \mathbb {C}(-, 0)$ was a left fibration: indeed, one can take
$\mathbb {D}(-, 0)\longrightarrow \mathbb {C}(-, 0)$ was a left fibration: indeed, one can take ![]() $\tilde {f}$ to correspond to the diagram
$\tilde {f}$ to correspond to the diagram ![]() in
in ![]() $\mathbb {D}$, where the vertical morphism is the identity.
$\mathbb {D}$, where the vertical morphism is the identity.
3. Reflecting fibrations of double categories
This section provides a more detailed analysis of the reflection of (left, cart)-fibrations between double categories (Definition 2.21). More precisely, our goal will be to prove the following theorem, which is our main technical result.
Theorem 3.1 There is an equivalence of cartesian fibrations

between the categories of (left, cart)-fibrations and (cocart, right)-fibrations. In particular, for any double category ![]() $\mathbb {C}$ this restricts to an equivalence
$\mathbb {C}$ this restricts to an equivalence ![]() $\mathrm {Fib}^{\mathrm {left, cart}}(\mathbb {C})\simeq \mathrm {Fib}^{\mathrm {cocart, right}}(\mathbb {C})$.
$\mathrm {Fib}^{\mathrm {left, cart}}(\mathbb {C})\simeq \mathrm {Fib}^{\mathrm {cocart, right}}(\mathbb {C})$.
This should not be unexpected: in light of Remarks 2.14 and 2.17, both (left, cart)-fibrations and (cocart, right)-fibrations should be equivalent to functors of double categories ![]() $\mathbb {C}^{2-\mathrm {op}}\longrightarrow \mathbb {C}\mathrm {at}^{\mathrm {oplax}}$ under some form of straightening.
$\mathbb {C}^{2-\mathrm {op}}\longrightarrow \mathbb {C}\mathrm {at}^{\mathrm {oplax}}$ under some form of straightening.
At the level of objects, the functor ![]() $\Psi ^\perp$ is given by Definition 2.21. The functor
$\Psi ^\perp$ is given by Definition 2.21. The functor ![]() $\Psi ^{\top }$ is defined analogously, taking opposites and reversing the roles of the horizontal and vertical directions. To extend
$\Psi ^{\top }$ is defined analogously, taking opposites and reversing the roles of the horizontal and vertical directions. To extend ![]() $\Psi ^\perp$ and
$\Psi ^\perp$ and ![]() $\Psi ^\top$ to functors, it will be convenient to describe the
$\Psi ^\top$ to functors, it will be convenient to describe the ![]() $\infty$-categories of (left, cart)-fibrations and (cocart, right)-fibrations in terms of marked bisimplicial spaces (§ 3.1). This allows one to describe the functor
$\infty$-categories of (left, cart)-fibrations and (cocart, right)-fibrations in terms of marked bisimplicial spaces (§ 3.1). This allows one to describe the functor ![]() $\Psi ^\perp$ very explicitly in terms of combinatorial data (§ 3.2). Finally, we will provide explicit natural equivalences exhibiting
$\Psi ^\perp$ very explicitly in terms of combinatorial data (§ 3.2). Finally, we will provide explicit natural equivalences exhibiting ![]() $\Psi ^\perp$ and
$\Psi ^\perp$ and ![]() $\Psi ^\top$ as mutual inverses (§ 3.3). We will do this by explicitly writing down a zigzag of equivalences connecting their composition to the identity.
$\Psi ^\top$ as mutual inverses (§ 3.3). We will do this by explicitly writing down a zigzag of equivalences connecting their composition to the identity.
Remark 3.2 In model categorical terms, both functors ![]() $\Psi ^\perp$ and
$\Psi ^\perp$ and ![]() $\Psi ^\top$ arise as right Quillen functors between the arrow categories of marked bisimplicial spaces. In particular, all of our arguments can be reformulated without difficulties into such model-categorical terms.
$\Psi ^\top$ arise as right Quillen functors between the arrow categories of marked bisimplicial spaces. In particular, all of our arguments can be reformulated without difficulties into such model-categorical terms.
3.1 Marked bisimplicial spaces
For technical reasons, it will be convenient to give a description of the category ![]() $\mathrm {Fib}^{\mathrm {left, cart}}$ using markings, analogous to the model for cartesian fibrations using marked simplicial sets in [Reference LurieLur09a].
$\mathrm {Fib}^{\mathrm {left, cart}}$ using markings, analogous to the model for cartesian fibrations using marked simplicial sets in [Reference LurieLur09a].
Notation 3.3 Let ![]() $\mathbf {\Delta }^{\times 2}_{\downarrow }$ denote the category obtained from
$\mathbf {\Delta }^{\times 2}_{\downarrow }$ denote the category obtained from ![]() $\mathbf {\Delta }^{\times 2}$ by freely adding a factorization of the vertical degeneracy map
$\mathbf {\Delta }^{\times 2}$ by freely adding a factorization of the vertical degeneracy map ![]() $[0, 1]\longrightarrow [0, 0]$ as follows.
$[0, 1]\longrightarrow [0, 0]$ as follows.

A presheaf ![]() $X\colon (\mathbf {\Delta }^{\times 2}_{\downarrow })^{\mathrm {op}}\longrightarrow \mathscr {S}$ is said to be a vertically marked bisimplicial space if the map
$X\colon (\mathbf {\Delta }^{\times 2}_{\downarrow })^{\mathrm {op}}\longrightarrow \mathscr {S}$ is said to be a vertically marked bisimplicial space if the map ![]() $X([0, 1]^\sharp )\longrightarrow X(0, 1)$ is a subspace inclusion. We will write
$X([0, 1]^\sharp )\longrightarrow X(0, 1)$ is a subspace inclusion. We will write ![]() $\mathrm {bis}\mathscr {S}_{\downarrow }\subseteq \mathrm {Fun}(\mathbf {\Delta }^{\times 2, \mathrm {op}}_{\downarrow }, \mathscr {S})$ for the full subcategory spanned by the vertically marked bisimplicial spaces, and typically use the same symbol for a vertically marked bisimplicial space and its underlying bisimplicial space.
$\mathrm {bis}\mathscr {S}_{\downarrow }\subseteq \mathrm {Fun}(\mathbf {\Delta }^{\times 2, \mathrm {op}}_{\downarrow }, \mathscr {S})$ for the full subcategory spanned by the vertically marked bisimplicial spaces, and typically use the same symbol for a vertically marked bisimplicial space and its underlying bisimplicial space.
Remark 3.4 The forgetful functor ![]() $\mathrm {bis}\mathscr {S}_{\downarrow }\longrightarrow \mathrm {bis}\mathscr {S}$ induces a subspace inclusion
$\mathrm {bis}\mathscr {S}_{\downarrow }\longrightarrow \mathrm {bis}\mathscr {S}$ induces a subspace inclusion
whose image consists of the path components of maps of bisimplicial spaces ![]() $f\colon X\longrightarrow Y$ with the property that
$f\colon X\longrightarrow Y$ with the property that ![]() $X(0, 1)\longrightarrow Y(0, 1)$ preserves the subspace of marked vertical arrows.
$X(0, 1)\longrightarrow Y(0, 1)$ preserves the subspace of marked vertical arrows.
Definition 3.5 A vertically marked double category is a vertically marked bisimplicial space whose underlying bisimplicial space is a double category. We will write ![]() $\mathrm {Cat}^{\otimes 2}_{\downarrow }\subseteq \mathrm {bis}\mathscr {S}_{\downarrow }$ for the full subcategory of vertically marked double categories.
$\mathrm {Cat}^{\otimes 2}_{\downarrow }\subseteq \mathrm {bis}\mathscr {S}_{\downarrow }$ for the full subcategory of vertically marked double categories.
Likewise, we write ![]() $\mathrm {Cat}^{\otimes 2}_{\to }\subseteq \mathrm {bis}\mathscr {S}_{\to }$ for the full subcategory of horizontally marked bisimplicial spaces spanned by the horizontally marked double categories.
$\mathrm {Cat}^{\otimes 2}_{\to }\subseteq \mathrm {bis}\mathscr {S}_{\to }$ for the full subcategory of horizontally marked bisimplicial spaces spanned by the horizontally marked double categories.
Notation 3.6 As usual, the forgetful functor ![]() $\mathrm {Cat}^{\otimes 2}_{\downarrow }\longrightarrow \mathrm {Cat}^{\otimes 2}$ admits a fully faithful right adjoint, sending a double category
$\mathrm {Cat}^{\otimes 2}_{\downarrow }\longrightarrow \mathrm {Cat}^{\otimes 2}$ admits a fully faithful right adjoint, sending a double category ![]() $\mathbb {C}$ to the vertically marked double category
$\mathbb {C}$ to the vertically marked double category ![]() $\mathbb {C}^{\sharp }$ where all vertical arrows are marked. We will also write
$\mathbb {C}^{\sharp }$ where all vertical arrows are marked. We will also write ![]() $\mathbb {C}^{\sharp }$ for
$\mathbb {C}^{\sharp }$ for ![]() $\mathbb {C}$ with all horizontal arrows marked; it will always be clear from the context whether we mark horizontal or vertical arrows.
$\mathbb {C}$ with all horizontal arrows marked; it will always be clear from the context whether we mark horizontal or vertical arrows.
Definition 3.7 Consider the following full subcategories of ![]() $\mathrm {Fun}\big ([1], \mathrm {bis}\mathscr {S}_{\downarrow }\big )$.
$\mathrm {Fun}\big ([1], \mathrm {bis}\mathscr {S}_{\downarrow }\big )$.
(1) Let
 $\mathrm {Fun}^\sharp \big ([1], \mathrm {bis}\mathscr {S}_{\downarrow }\big )$ be spanned by the maps
$\mathrm {Fun}^\sharp \big ([1], \mathrm {bis}\mathscr {S}_{\downarrow }\big )$ be spanned by the maps  $Y\longrightarrow X$ where
$Y\longrightarrow X$ where  $X$ is maximally marked, i.e. every
$X$ is maximally marked, i.e. every  $[0, 1]$-simplex of
$[0, 1]$-simplex of  $X$ is marked.
$X$ is marked.(2) Let
 $\mathrm {Fun}^\sharp \big ([1], \mathrm {Cat}^{\otimes 2}_{\downarrow }\big )$ be spanned by the maps
$\mathrm {Fun}^\sharp \big ([1], \mathrm {Cat}^{\otimes 2}_{\downarrow }\big )$ be spanned by the maps  $\mathbb {D}\longrightarrow \mathbb {C}^\sharp$ between marked double categories, with
$\mathbb {D}\longrightarrow \mathbb {C}^\sharp$ between marked double categories, with  $\mathbb {C}^\sharp$ maximally marked.
$\mathbb {C}^\sharp$ maximally marked.(3) Let
 $\mathrm {Fib}^{\mathrm {left, cart}}$ be spanned by the maps
$\mathrm {Fib}^{\mathrm {left, cart}}$ be spanned by the maps  $p\colon \mathbb {D}^\natural \longrightarrow \mathbb {C}^\sharp$ between marked double categories, whose underlying map of double categories is a (left, cart)-fibration and where a vertical arrow in
$p\colon \mathbb {D}^\natural \longrightarrow \mathbb {C}^\sharp$ between marked double categories, whose underlying map of double categories is a (left, cart)-fibration and where a vertical arrow in  $\mathbb {D}^\natural$ is marked if and only if it is
$\mathbb {D}^\natural$ is marked if and only if it is  $p$-cartesian.
$p$-cartesian.
The codomain projections (forgetting the maximal marking) then define the following diagram of cartesian fibrations and maps preserving cartesian arrows.

In a similar way, one can define fully faithful inclusions as follows.

Lemma 3.8 Forgetting the marking defines a functor ![]() $\mathrm {Fib}^{\mathrm {left, cart}}\longrightarrow \mathrm {Fun}\big ([1], \mathrm {Cat}^{\otimes 2})$ which is an equivalence onto the subcategory whose objects are (left, cart)-fibrations and whose morphisms are strong morphisms (Definition 2.9).
$\mathrm {Fib}^{\mathrm {left, cart}}\longrightarrow \mathrm {Fun}\big ([1], \mathrm {Cat}^{\otimes 2})$ which is an equivalence onto the subcategory whose objects are (left, cart)-fibrations and whose morphisms are strong morphisms (Definition 2.9).
Proof. By Remark 3.4, the forgetful functor ![]() $\mathrm {Fun}\big ([1], \mathrm {Cat}^{\otimes 2}_{\downarrow })\longrightarrow \mathrm {Fun}\big ([1], \mathrm {Cat}^{\otimes 2})$ induces inclusions of path components on mapping spaces, whose images consist of those commuting squares of double categories such that all maps preserve marked arrows. The result follows immediately from this.
$\mathrm {Fun}\big ([1], \mathrm {Cat}^{\otimes 2}_{\downarrow })\longrightarrow \mathrm {Fun}\big ([1], \mathrm {Cat}^{\otimes 2})$ induces inclusions of path components on mapping spaces, whose images consist of those commuting squares of double categories such that all maps preserve marked arrows. The result follows immediately from this.
Remark 3.9 The full subcategory ![]() $\mathrm {Fib}^{\mathrm {left, cart}}\hookrightarrow \mathrm {Fun}\big ([1], \mathrm {bis}\mathscr {S}_{\downarrow }\big )$ can be obtained as a left Bousfield localization (and, in particular, is a presentable category). One can also present
$\mathrm {Fib}^{\mathrm {left, cart}}\hookrightarrow \mathrm {Fun}\big ([1], \mathrm {bis}\mathscr {S}_{\downarrow }\big )$ can be obtained as a left Bousfield localization (and, in particular, is a presentable category). One can also present ![]() $\mathrm {Fib}^{\mathrm {left, cart}}$ in terms of model
$\mathrm {Fib}^{\mathrm {left, cart}}$ in terms of model ![]() $(1, 1)$-categories, as a left Bousfield localization of the injective model structure on functors
$(1, 1)$-categories, as a left Bousfield localization of the injective model structure on functors ![]() $\mathbf {\Delta }^{\times 2, \mathrm {op}}_{\downarrow }\longrightarrow \mathrm {sSet}$ (where
$\mathbf {\Delta }^{\times 2, \mathrm {op}}_{\downarrow }\longrightarrow \mathrm {sSet}$ (where ![]() $\mathrm {sSet}$ carries the Kan–Quillen model structure). All arguments appearing below can be carried out in this setting as well.
$\mathrm {sSet}$ carries the Kan–Quillen model structure). All arguments appearing below can be carried out in this setting as well.
Construction 3.10 Let us fix the following data.
(a) For each
 $m, n\geq 0$, a map of vertically marked double categories
$m, n\geq 0$, a map of vertically marked double categories  $S[m, n]\longrightarrow [m, n]^\sharp$, natural in the sense that it defines a functor fitting into the following commuting triangle.
$S[m, n]\longrightarrow [m, n]^\sharp$, natural in the sense that it defines a functor fitting into the following commuting triangle.

(b) In the vertically marked double category
 $S[1, 0]$, an additional set of path components of marked vertical edges. We will write
$S[1, 0]$, an additional set of path components of marked vertical edges. We will write  $S[1, 0]^+$ for the resulting vertically marked double category.
$S[1, 0]^+$ for the resulting vertically marked double category.
Associated to these data is the following natural map of cartesian fibrations.

To construct this diagram, observe that the codomain projection admits a left adjoint ![]() $L\colon \mathrm {bis}\mathscr {S}\longrightarrow \mathrm {Fun}^\sharp ([1], \mathrm {bis}\mathscr {S}_{\downarrow })$, sending
$L\colon \mathrm {bis}\mathscr {S}\longrightarrow \mathrm {Fun}^\sharp ([1], \mathrm {bis}\mathscr {S}_{\downarrow })$, sending ![]() $\mathbb {C}$ to
$\mathbb {C}$ to ![]() $\emptyset \longrightarrow \mathbb {C}^\sharp$; the same holds in the horizontally marked case. Now consider the following commuting squares.
$\emptyset \longrightarrow \mathbb {C}^\sharp$; the same holds in the horizontally marked case. Now consider the following commuting squares.

In the left square, ![]() $h$ is the Yoneda embedding and
$h$ is the Yoneda embedding and ![]() $\sigma$ is the functor sending
$\sigma$ is the functor sending
Furthermore, ![]() $\sigma$ sends
$\sigma$ sends ![]() $(0, [1, 0]^\sharp )$ to
$(0, [1, 0]^\sharp )$ to ![]() $S[1, 0]^+\longrightarrow [1, 0]^\sharp$ and
$S[1, 0]^+\longrightarrow [1, 0]^\sharp$ and ![]() $(1, [1, 0]^\sharp )$ to
$(1, [1, 0]^\sharp )$ to ![]() $\emptyset \longrightarrow [1, 0]^\sharp$. This induces the commuting square of left adjoint functors on the right, using that
$\emptyset \longrightarrow [1, 0]^\sharp$. This induces the commuting square of left adjoint functors on the right, using that ![]() $h$ and
$h$ and ![]() $\sigma$ induce unique colimit-preserving functors out of the corresponding presheaf categories [Reference DuggerDug01], [Reference LurieLur09a, Theorem 5.1.5.6].
$\sigma$ induce unique colimit-preserving functors out of the corresponding presheaf categories [Reference DuggerDug01], [Reference LurieLur09a, Theorem 5.1.5.6].
Let us write ![]() $\Psi _S$ for the right adjoint to
$\Psi _S$ for the right adjoint to ![]() $\Phi _S$. Explicitly, let
$\Phi _S$. Explicitly, let ![]() $p\colon Y\longrightarrow X^\sharp$ be a map of vertically marked bisimplicial spaces whose target is maximally marked. Then
$p\colon Y\longrightarrow X^\sharp$ be a map of vertically marked bisimplicial spaces whose target is maximally marked. Then ![]() $\Psi _S(p)\colon \Psi _S(Y)\longrightarrow X^\sharp$ can be described as follows: the underlying bisimplicial space of
$\Psi _S(p)\colon \Psi _S(Y)\longrightarrow X^\sharp$ can be described as follows: the underlying bisimplicial space of ![]() $\Psi _S(Y)$ has
$\Psi _S(Y)$ has ![]() $(m, n)$-simplices determined by the following.
$(m, n)$-simplices determined by the following.

Furthermore, the space of marked ![]() $[1, 0]$-simplices in
$[1, 0]$-simplices in ![]() $\Psi _S(Y)$ is the subspace consisting of those maps
$\Psi _S(Y)$ is the subspace consisting of those maps ![]() $S[1, 0]\longrightarrow Y$ that also preserve the additional marked arrows from data (b). In particular, this implies that
$S[1, 0]\longrightarrow Y$ that also preserve the additional marked arrows from data (b). In particular, this implies that ![]() $\Psi _S$ sends vertically marked bisimplicial spaces into horizontally marked bisimplicial spaces (i.e. marked edges form a subspace). We therefore obtain the desired commuting diagram (3.11). Furthermore, it follows immediately from (
$\Psi _S$ sends vertically marked bisimplicial spaces into horizontally marked bisimplicial spaces (i.e. marked edges form a subspace). We therefore obtain the desired commuting diagram (3.11). Furthermore, it follows immediately from (
) that ![]() $\Psi _K$ preserves cartesian morphisms: for every
$\Psi _K$ preserves cartesian morphisms: for every ![]() $Y\longrightarrow X^\sharp$ and
$Y\longrightarrow X^\sharp$ and ![]() $X'\longrightarrow X$, we have an equivalence
$X'\longrightarrow X$, we have an equivalence
3.2 Construction of the functors
We will use Construction 3.10 to define the functor ![]() $\Psi ^\perp$, as follows.
$\Psi ^\perp$, as follows.
Construction 3.13 For any ![]() $[m, n]\in \mathbf {\Delta }^{\times 2}$, consider the following natural map of vertically marked double categories:
$[m, n]\in \mathbf {\Delta }^{\times 2}$, consider the following natural map of vertically marked double categories:
Here ![]() $K[m, n]$ comes equipped with the marking where for each
$K[m, n]$ comes equipped with the marking where for each ![]() $ii\in \mathbb {A}\mathrm {r}[m]$ (cf. Example 2.6), all vertical arrows in
$ii\in \mathbb {A}\mathrm {r}[m]$ (cf. Example 2.6), all vertical arrows in ![]() $\{ii\}\times [0, n]$ are marked. Furthermore,
$\{ii\}\times [0, n]$ are marked. Furthermore, ![]() $K[1, 0]^+$ is the double category
$K[1, 0]^+$ is the double category ![]() $\mathbb {A}\mathrm {r}[1]$, where, in addition, the vertical arrow
$\mathbb {A}\mathrm {r}[1]$, where, in addition, the vertical arrow ![]() is marked.
is marked.
Using this, Construction 3.10 produces the following functor over ![]() $\mathrm {bis}\mathscr {S}$:
$\mathrm {bis}\mathscr {S}$:
Proposition 3.14 Let ![]() $p\colon \mathbb {D}^\natural \longrightarrow \mathbb {C}^\sharp$ be a (left, cart)-fibration with its natural marking by the
$p\colon \mathbb {D}^\natural \longrightarrow \mathbb {C}^\sharp$ be a (left, cart)-fibration with its natural marking by the ![]() $p$-cartesian vertical arrows. Then
$p$-cartesian vertical arrows. Then ![]() $\Psi _K(p)\colon \Psi _K(\mathbb {D})\longrightarrow \mathbb {C}^\sharp$ coincides with the (cocart, right)-fibration
$\Psi _K(p)\colon \Psi _K(\mathbb {D})\longrightarrow \mathbb {C}^\sharp$ coincides with the (cocart, right)-fibration ![]() $\Psi ^\perp (p)$ from Definition 2.21, with its natural horizontal marking. Consequently,
$\Psi ^\perp (p)$ from Definition 2.21, with its natural horizontal marking. Consequently, ![]() $\Psi _K$ restricts to a map of cartesian fibrations that we will denote as follows.
$\Psi _K$ restricts to a map of cartesian fibrations that we will denote as follows.

Proof. Unraveling the definition, one sees that the map of bisimplicial spaces ![]() $\Psi _K(\mathbb {D})\longrightarrow \mathbb {C}$ is precisely given by the reflection
$\Psi _K(\mathbb {D})\longrightarrow \mathbb {C}$ is precisely given by the reflection ![]() $\Psi ^\perp (p)\colon \Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$ from Definition 2.21; in particular, it is a (cocart, right)-fibration by Proposition 2.22.
$\Psi ^\perp (p)\colon \Psi ^\perp (\mathbb {D})\longrightarrow \mathbb {C}$ from Definition 2.21; in particular, it is a (cocart, right)-fibration by Proposition 2.22.
It remains to identify the marked horizontal arrows in ![]() $\Psi _K(\mathbb {D}^{\natural })$; these correspond to diagrams
$\Psi _K(\mathbb {D}^{\natural })$; these correspond to diagrams ![]() in
in ![]() $\mathbb {D}$ with the property that
$\mathbb {D}$ with the property that ![]() is a marked arrow covering an equivalence in
is a marked arrow covering an equivalence in ![]() $\mathbb {C}$. This just means that
$\mathbb {C}$. This just means that ![]() is an equivalence, so that the marked horizontal arrows coincide with the marked horizontal arrows introduced in the proof of Proposition 2.22. We have already seen there that these marked arrows are precisely the cocartesian horizontal arrows.
is an equivalence, so that the marked horizontal arrows coincide with the marked horizontal arrows introduced in the proof of Proposition 2.22. We have already seen there that these marked arrows are precisely the cocartesian horizontal arrows.
In particular, by restricting to the fibers over a double category ![]() $\mathbb {C}$ we obtain a functor
$\mathbb {C}$ we obtain a functor ![]() $\Psi ^\perp \colon \mathrm {Fib}^{\mathrm {left, cart}}(\mathbb {C})\longrightarrow \mathrm {Fib}^{\mathrm {cocart, right}}(\mathbb {C})$ that we will refer to as the reflection functor. To motivate the terminology, let us investigate more precisely the behaviour of
$\Psi ^\perp \colon \mathrm {Fib}^{\mathrm {left, cart}}(\mathbb {C})\longrightarrow \mathrm {Fib}^{\mathrm {cocart, right}}(\mathbb {C})$ that we will refer to as the reflection functor. To motivate the terminology, let us investigate more precisely the behaviour of ![]() $\Psi ^\perp$ when
$\Psi ^\perp$ when ![]() $\mathbb {C}$ is a space.
$\mathbb {C}$ is a space.
Proposition 3.15 Let ![]() $S$ be a space and let
$S$ be a space and let ![]() ${{\rm Cat}}/S$ be the category of categories over
${{\rm Cat}}/S$ be the category of categories over ![]() $S$. Consider the endofunctor of
$S$. Consider the endofunctor of ![]() ${{\rm Cat}}/S$ given by the composite
${{\rm Cat}}/S$ given by the composite
where the left equivalence sends a category ![]() $\mathscr {C}$ to the (left, cart)-fibration
$\mathscr {C}$ to the (left, cart)-fibration ![]() $[0]\boxtimes \mathscr {C}\longrightarrow [0]\boxtimes S=S$ and the right equivalence to the (cocart, right)-fibration
$[0]\boxtimes \mathscr {C}\longrightarrow [0]\boxtimes S=S$ and the right equivalence to the (cocart, right)-fibration ![]() $\mathscr {C}\boxtimes [0]\longrightarrow S\boxtimes [0]=S$ (see Example 2.5 and Remark 2.11). Then the above endofunctor of
$\mathscr {C}\boxtimes [0]\longrightarrow S\boxtimes [0]=S$ (see Example 2.5 and Remark 2.11). Then the above endofunctor of ![]() $\mathrm {Cat}/S$ is homotopic to the identity.
$\mathrm {Cat}/S$ is homotopic to the identity.
In particular, at the level of fibers the reflection functor ![]() $\Psi ^\perp$ simply exchanges the horizontal and vertical direction.
$\Psi ^\perp$ simply exchanges the horizontal and vertical direction.
Proof. Consider the natural map ![]() $K[m, n]=\mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow \mathbb {A}\mathrm {r}[m]\stackrel {\pi _\mathrm {ver}}{\longrightarrow } [0, m]$, where the second map is the vertical projection (see Example 2.6). This map sends the marked vertical arrows in
$K[m, n]=\mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow \mathbb {A}\mathrm {r}[m]\stackrel {\pi _\mathrm {ver}}{\longrightarrow } [0, m]$, where the second map is the vertical projection (see Example 2.6). This map sends the marked vertical arrows in ![]() $K[m, n]$ from Construction 3.13 to degenerate edges. For each
$K[m, n]$ from Construction 3.13 to degenerate edges. For each ![]() $\mathbb {D}\in \mathrm {Fib}^{\mathrm {left, cart}}$, we therefore obtain a natural transformation of double categories, given in degree
$\mathbb {D}\in \mathrm {Fib}^{\mathrm {left, cart}}$, we therefore obtain a natural transformation of double categories, given in degree ![]() $(m, n)$ by
$(m, n)$ by
Taking ![]() $\mathbb {D}=[0]\boxtimes \mathscr {C}$, this produces the desired map
$\mathbb {D}=[0]\boxtimes \mathscr {C}$, this produces the desired map ![]() $\mathscr {C}\boxtimes [0]\longrightarrow \Psi ^\perp ([0]\boxtimes \mathscr {C})$. To see that this is an equivalence, note that the domain and codomain are both constant in the vertical direction and complete Segal spaces in the horizontal direction. In degree
$\mathscr {C}\boxtimes [0]\longrightarrow \Psi ^\perp ([0]\boxtimes \mathscr {C})$. To see that this is an equivalence, note that the domain and codomain are both constant in the vertical direction and complete Segal spaces in the horizontal direction. In degree ![]() $(0, 0)$, the above is an equivalence since
$(0, 0)$, the above is an equivalence since ![]() $K[0, 0]\longrightarrow [0, 0]$ is an isomorphism. In degree
$K[0, 0]\longrightarrow [0, 0]$ is an isomorphism. In degree ![]() $(1, 0)$, it suffices to note that the map
$(1, 0)$, it suffices to note that the map ![]() $\pi _\mathrm {ver}\colon \mathbb {A}\mathrm {r}[1]\longrightarrow [0, 1]$ induces an equivalence on mapping spaces into a double category of the form
$\pi _\mathrm {ver}\colon \mathbb {A}\mathrm {r}[1]\longrightarrow [0, 1]$ induces an equivalence on mapping spaces into a double category of the form ![]() $[0]\boxtimes \mathscr {C}$.
$[0]\boxtimes \mathscr {C}$.
One can obtain variants of the functor ![]() $\Psi ^\perp$ for different kinds of fibrations, by taking opposites in the horizontal or vertical direction and exchanging horizontal and vertical directions.
$\Psi ^\perp$ for different kinds of fibrations, by taking opposites in the horizontal or vertical direction and exchanging horizontal and vertical directions.
Variant 3.16 Let us introduce the following two variants of the functor ![]() $\Psi ^\perp$.
$\Psi ^\perp$.
(1) There is a functor
 $\Psi ^\top \colon \mathrm {Fib}^{\mathrm {cocart, right}}\longrightarrow \mathrm {Fib}^{\mathrm {left, cart}}$, obtained by conjugating
$\Psi ^\top \colon \mathrm {Fib}^{\mathrm {cocart, right}}\longrightarrow \mathrm {Fib}^{\mathrm {left, cart}}$, obtained by conjugating  $\Psi ^\perp$ with the functor sending
$\Psi ^\perp$ with the functor sending  $\mathbb {C}\mapsto (\mathbb {C}^\mathrm {rev})^{(1, 2)-\mathrm {op}}$. Unraveling the definitions, one sees that
$\mathbb {C}\mapsto (\mathbb {C}^\mathrm {rev})^{(1, 2)-\mathrm {op}}$. Unraveling the definitions, one sees that  $\Psi ^\top =\Psi _{K'}$ is defined as in Construction 3.10 (with the roles of horizontal and vertical reversed), but this time using the maps
Here we mark the horizontal arrows in
$\Psi ^\top =\Psi _{K'}$ is defined as in Construction 3.10 (with the roles of horizontal and vertical reversed), but this time using the maps
Here we mark the horizontal arrows in
 $K'[m, n]$ contained in
$K'[m, n]$ contained in  $[m, 0]\times \{ii\}$ for each
$[m, 0]\times \{ii\}$ for each  $i\in [n]$. Furthermore,
$i\in [n]$. Furthermore,  $K'([0, 1]^\sharp )$ is given by
$K'([0, 1]^\sharp )$ is given by  $\mathbb {A}\mathrm {r}[1]$ where we mark all horizontal arrows.
$\mathbb {A}\mathrm {r}[1]$ where we mark all horizontal arrows.(2) There is another functor
 $\Psi ^{{\dagger} }\colon \mathrm {Fib}^{\mathrm {cocart, left}}\longrightarrow \mathrm {Fib}^{\mathrm {left, cocart}}$, obtained by conjugating
$\Psi ^{{\dagger} }\colon \mathrm {Fib}^{\mathrm {cocart, left}}\longrightarrow \mathrm {Fib}^{\mathrm {left, cocart}}$, obtained by conjugating  $\Psi ^\perp$ with the functor sending
$\Psi ^\perp$ with the functor sending  $\mathbb {C}\mapsto (\mathbb {C}^{\mathrm {rev}})^{1-\mathrm {op}}$. Unraveling the definitions, one sees that
$\mathbb {C}\mapsto (\mathbb {C}^{\mathrm {rev}})^{1-\mathrm {op}}$. Unraveling the definitions, one sees that  $\Psi ^{\dagger} =\Psi _L$ is defined as in Construction 3.13, but the role of the vertically marked double category
$\Psi ^{\dagger} =\Psi _L$ is defined as in Construction 3.13, but the role of the vertically marked double category  $K[m, n]$ is now played by
In
$K[m, n]$ is now played by
In
 $L[m, n]$, we mark the horizontal arrows in each
$L[m, n]$, we mark the horizontal arrows in each  $[m, 0]\times \{ii\}$. Furthermore,
$[m, 0]\times \{ii\}$. Furthermore,  $L([1, 0]^\sharp )$ is given by
$L([1, 0]^\sharp )$ is given by  $\mathbb {T}\mathrm {w}([1]^{\mathrm {op}})$ with all horizontal arrows marked.
$\mathbb {T}\mathrm {w}([1]^{\mathrm {op}})$ with all horizontal arrows marked.
Remark 3.17 Proposition 3.15 holds for the functor ![]() $\Psi ^\top$ as well: indeed, the functor
$\Psi ^\top$ as well: indeed, the functor ![]() $(-)^\mathrm {rev}$ commutes with the functor
$(-)^\mathrm {rev}$ commutes with the functor ![]() $\mathbb {C}\mapsto (\mathbb {C}^{\mathrm {rev}})^{(1, 2)-\mathrm {op}}$. In contrast, it does not apply to the functor
$\mathbb {C}\mapsto (\mathbb {C}^{\mathrm {rev}})^{(1, 2)-\mathrm {op}}$. In contrast, it does not apply to the functor ![]() $\Psi ^{\dagger}$: instead, the resulting endofunctor of
$\Psi ^{\dagger}$: instead, the resulting endofunctor of ![]() $\mathrm {Cat}$ takes opposite categories.
$\mathrm {Cat}$ takes opposite categories.
3.3 Proof of Theorem 3.1
Consider the functors from Proposition 3.14 and Variant 3.16:
We will show that these are mutually inverse, up to homotopy. More precisely, we will prove that for every (left, cart)-fibration ![]() $\mathbb {D}\longrightarrow \mathbb {C}$, there is the following natural zigzag of equivalences between (left, cart)-fibrations over
$\mathbb {D}\longrightarrow \mathbb {C}$, there is the following natural zigzag of equivalences between (left, cart)-fibrations over ![]() $\mathbb {C}$.
$\mathbb {C}$.

To motivate the precise combinatorial constructions that will follow, let us already disclose that a typical (1, 1)-cell in each of these four double categories will correspond to a diagram in ![]() $\mathbb {D}$ of the following form.
$\mathbb {D}$ of the following form.

Here ![]() denotes a
denotes a ![]() $p$-cartesian vertical arrow in
$p$-cartesian vertical arrow in ![]() $\mathbb {D}$ and
$\mathbb {D}$ and ![]() denotes a map that is sent to a degenerate arrow in
denotes a map that is sent to a degenerate arrow in ![]() $\mathbb {C}$. The rightmost diagram can be obtained by explicitly unraveling the definition of the composite functor
$\mathbb {C}$. The rightmost diagram can be obtained by explicitly unraveling the definition of the composite functor ![]() $\Psi ^{\top }\circ \Psi ^{\perp }$. The maps
$\Psi ^{\top }\circ \Psi ^{\perp }$. The maps ![]() $\zeta ^*$ and
$\zeta ^*$ and ![]() $\theta ^*$ will then be the evident equivalences which simply add degenerate squares on the right, respectively, on the top.
$\theta ^*$ will then be the evident equivalences which simply add degenerate squares on the right, respectively, on the top.
The map ![]() $\eta ^*$ takes vertical compositions and has an inverse given informally as follows (cf. the proof of Proposition 2.22). First, one decomposes the left and right vertical maps into fiberwise maps followed by
$\eta ^*$ takes vertical compositions and has an inverse given informally as follows (cf. the proof of Proposition 2.22). First, one decomposes the left and right vertical maps into fiberwise maps followed by ![]() $p$-cartesian maps. The middle column is then uniquely determined by the left column and the right half of the diagram is determined uniquely because the right vertical map was
$p$-cartesian maps. The middle column is then uniquely determined by the left column and the right half of the diagram is determined uniquely because the right vertical map was ![]() $p$-cartesian. Note that the map
$p$-cartesian. Note that the map ![]() $f$ need not be
$f$ need not be ![]() $p$-cartesian; this is why we need to add a degenerate square using
$p$-cartesian; this is why we need to add a degenerate square using ![]() $\zeta ^*$ before we can decompose the left and right vertical arrow.
$\zeta ^*$ before we can decompose the left and right vertical arrow.
Let us now start by defining the endofunctors ![]() $\Psi _A, \Psi _B\colon \mathrm {Fib}^{\mathrm {left, cart}}\longrightarrow \mathrm {Fib}^{\mathrm {left, cart}}$ more precisely, using (the vertically marked version of) Construction 3.10.
$\Psi _A, \Psi _B\colon \mathrm {Fib}^{\mathrm {left, cart}}\longrightarrow \mathrm {Fib}^{\mathrm {left, cart}}$ more precisely, using (the vertically marked version of) Construction 3.10.
Construction 3.18 For each ![]() $[m, n]\in \mathbf {\Delta }^{\times 2}$, let
$[m, n]\in \mathbf {\Delta }^{\times 2}$, let
In ![]() $A[m, n]$, we mark all vertical arrows contained in
$A[m, n]$, we mark all vertical arrows contained in ![]() $\mathbb {A}\mathrm {r}[m]\times \{i\}$, for all
$\mathbb {A}\mathrm {r}[m]\times \{i\}$, for all ![]() $i\in [n]$; in particular, note that this marking is different from Construction 3.13. In addition, define
$i\in [n]$; in particular, note that this marking is different from Construction 3.13. In addition, define ![]() $A([0, 1])^+=[0, 1]^\sharp$.
$A([0, 1])^+=[0, 1]^\sharp$.
Likewise, for each ![]() $[m, n]\in \mathbf {\Delta }^{\times 2}$, let us denote
$[m, n]\in \mathbf {\Delta }^{\times 2}$, let us denote
In ![]() $B[m, n]=\mathbb {A}\mathrm {r}[m]\times \big ([0]\boxtimes \mathrm {Fun}([1], [n])\big )$, we mark the following vertical arrows:
$B[m, n]=\mathbb {A}\mathrm {r}[m]\times \big ([0]\boxtimes \mathrm {Fun}([1], [n])\big )$, we mark the following vertical arrows:
– for each object
 $aa\in \mathbb {A}\mathrm {r}[m]$ with
$aa\in \mathbb {A}\mathrm {r}[m]$ with  $0\leq a\leq m$, we mark all edges in
$0\leq a\leq m$, we mark all edges in  $\{aa\}\boxtimes \mathrm {Fun}([1], [n])$ of the form
$\{aa\}\boxtimes \mathrm {Fun}([1], [n])$ of the form  $ik\longrightarrow jk$;
$ik\longrightarrow jk$;– for each
 $ii\in \mathrm {Fun}([1], [n])$ with
$ii\in \mathrm {Fun}([1], [n])$ with  $0\leq i\leq n$, we mark all vertical arrows in
$0\leq i\leq n$, we mark all vertical arrows in  $\mathbb {A}\mathrm {r}[m]\times \{ii\}$.
$\mathbb {A}\mathrm {r}[m]\times \{ii\}$.
In addition, define ![]() $B([0, 1])^+$ to be
$B([0, 1])^+$ to be ![]() $[0]\boxtimes \mathrm {Fun}([1], [1])$, where all vertical arrows are marked.
$[0]\boxtimes \mathrm {Fun}([1], [1])$, where all vertical arrows are marked.
Note that these vertically marked double categories are related by natural transformations as follows.

Here ![]() $\zeta \colon \mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow [m, n]$ just arises from the horizontal projection
$\zeta \colon \mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow [m, n]$ just arises from the horizontal projection ![]() $\mathbb {A}\mathrm {r}[m]\longrightarrow [m, 0]$. This sends the vertical arrows within each
$\mathbb {A}\mathrm {r}[m]\longrightarrow [m, 0]$. This sends the vertical arrows within each ![]() $\mathbb {A}\mathrm {r}[m]\times \{i\}$ to degenerate arrows and, hence, preserves markings. The map
$\mathbb {A}\mathrm {r}[m]\times \{i\}$ to degenerate arrows and, hence, preserves markings. The map ![]() $\eta \colon \mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow \mathbb {A}\mathrm {r}[m]\times \big ([0]\boxtimes \mathrm {Fun}([1], [n])\big )$ arises from the map
$\eta \colon \mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow \mathbb {A}\mathrm {r}[m]\times \big ([0]\boxtimes \mathrm {Fun}([1], [n])\big )$ arises from the map ![]() $\mathrm {cst}\colon [n]\longrightarrow \mathrm {Fun}([1], [n])$ sending each
$\mathrm {cst}\colon [n]\longrightarrow \mathrm {Fun}([1], [n])$ sending each ![]() $i\in [n]$ to the constant arrow
$i\in [n]$ to the constant arrow ![]() $i\leq i$.
$i\leq i$.
Furthermore, the maps ![]() $\zeta$ and
$\zeta$ and ![]() $\eta$ induce natural maps
$\eta$ induce natural maps ![]() $[0, 1]^\sharp \longleftarrow A[0, 1]^+\longrightarrow B[0, 1]^+$ preserving the additional marked vertical arrows. Using the naturality of Construction 3.10, we obtain a zigzag of natural transformations between functors
$[0, 1]^\sharp \longleftarrow A[0, 1]^+\longrightarrow B[0, 1]^+$ preserving the additional marked vertical arrows. Using the naturality of Construction 3.10, we obtain a zigzag of natural transformations between functors ![]() $\mathrm {Fun}^\sharp ([1], \mathrm {bis}\mathscr {S}_{\downarrow })\longrightarrow \mathrm {Fun}^\sharp ([1], \mathrm {bis}\mathscr {S}_{\downarrow })$ of the form
$\mathrm {Fun}^\sharp ([1], \mathrm {bis}\mathscr {S}_{\downarrow })\longrightarrow \mathrm {Fun}^\sharp ([1], \mathrm {bis}\mathscr {S}_{\downarrow })$ of the form
Proposition 3.19 Let ![]() $p\colon \mathbb {D}^\natural \longrightarrow \mathbb {C}^\sharp$ be a (left, cart)-fibration. Then the natural transformations
$p\colon \mathbb {D}^\natural \longrightarrow \mathbb {C}^\sharp$ be a (left, cart)-fibration. Then the natural transformations ![]() $\zeta ^*$ and
$\zeta ^*$ and ![]() $\eta ^*$ above are equivalences of marked bisimplicial spaces. In particular,
$\eta ^*$ above are equivalences of marked bisimplicial spaces. In particular, ![]() $\Psi _A(\mathbb {D}^\natural )\longrightarrow \mathbb {C}^\sharp$ and
$\Psi _A(\mathbb {D}^\natural )\longrightarrow \mathbb {C}^\sharp$ and ![]() $\Psi _B(\mathbb {D}^\natural )\longrightarrow \mathbb {C}^\sharp$ are (left, cart)-fibrations of double categories.
$\Psi _B(\mathbb {D}^\natural )\longrightarrow \mathbb {C}^\sharp$ are (left, cart)-fibrations of double categories.
Proof. Recall from the general description (3.12) that the space of ![]() $(m, n)$-simplices in
$(m, n)$-simplices in ![]() $\Psi _A(\mathbb {D}^\natural )$ is given by the space of diagrams of vertically marked double categories
$\Psi _A(\mathbb {D}^\natural )$ is given by the space of diagrams of vertically marked double categories

and likewise for ![]() $\Psi _B(\mathbb {D}^\natural )$. The maps
$\Psi _B(\mathbb {D}^\natural )$. The maps ![]() $\zeta ^*$ and
$\zeta ^*$ and ![]() $\eta ^*$ simply arise by restriction along the natural maps
$\eta ^*$ simply arise by restriction along the natural maps ![]() $\zeta \colon A[m, n]\longrightarrow [m, n]$ and
$\zeta \colon A[m, n]\longrightarrow [m, n]$ and ![]() $\eta \colon A[m, n]\longrightarrow B[m, n]$.
$\eta \colon A[m, n]\longrightarrow B[m, n]$.
![]() $\zeta ^*$ is an equivalence. Note that
$\zeta ^*$ is an equivalence. Note that ![]() $\Psi _A(\mathbb {D}^\natural )\hookrightarrow X$ is a bisimplicial subspace of the bisimplicial space
$\Psi _A(\mathbb {D}^\natural )\hookrightarrow X$ is a bisimplicial subspace of the bisimplicial space ![]() $X$ from Lemma 2.18. Indeed, the space of maps
$X$ from Lemma 2.18. Indeed, the space of maps ![]() $[m, n]\longrightarrow \Psi _A(\mathbb {D}^\natural )$ is the subspace of those diagrams (2.19) such that
$[m, n]\longrightarrow \Psi _A(\mathbb {D}^\natural )$ is the subspace of those diagrams (2.19) such that ![]() $\mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow \mathbb {D}$ sends the vertical arrows in each
$\mathbb {A}\mathrm {r}[m]\times [0, n]\longrightarrow \mathbb {D}$ sends the vertical arrows in each ![]() $\mathbb {A}\mathrm {r}[m]\times \{i\}$ with
$\mathbb {A}\mathrm {r}[m]\times \{i\}$ with ![]() $0\leq i\leq n$ to equivalences.
$0\leq i\leq n$ to equivalences.
By Lemma 2.18, ![]() $X$ is double category and one sees that each simplicial subspace
$X$ is double category and one sees that each simplicial subspace ![]() $\Psi _A(\mathbb {D}^\natural )(m, -)\hookrightarrow X(m, -)$ is the inclusion of a full subcategory. In the horizontal direction, the proof of Lemma 2.18 shows that the simplicial subspace
$\Psi _A(\mathbb {D}^\natural )(m, -)\hookrightarrow X(m, -)$ is the inclusion of a full subcategory. In the horizontal direction, the proof of Lemma 2.18 shows that the simplicial subspace ![]() $\Psi _A(\mathbb {D}^\natural )(-, n)\hookrightarrow X(-, n)$ satisfies the Segal conditions and is an equivalence on spaces of objects. This implies that
$\Psi _A(\mathbb {D}^\natural )(-, n)\hookrightarrow X(-, n)$ satisfies the Segal conditions and is an equivalence on spaces of objects. This implies that ![]() $\Psi _A(\mathbb {D}^\natural )(-, n)$ is a category, so that
$\Psi _A(\mathbb {D}^\natural )(-, n)$ is a category, so that ![]() $\Psi _A(\mathbb {D}^\natural )$ is a double category.
$\Psi _A(\mathbb {D}^\natural )$ is a double category.
Let us now show that the map of marked double categories ![]() $\zeta ^*\colon \mathbb {D}\longrightarrow \Psi _A(\mathbb {D}^\sharp )$ is an equivalence. Since
$\zeta ^*\colon \mathbb {D}\longrightarrow \Psi _A(\mathbb {D}^\sharp )$ is an equivalence. Since ![]() $\zeta$ induces an isomorphism
$\zeta$ induces an isomorphism ![]() $A[0, 1]^+\stackrel {\sim }{\longrightarrow } [0, 1]^\sharp$,
$A[0, 1]^+\stackrel {\sim }{\longrightarrow } [0, 1]^\sharp$, ![]() $\zeta ^*$ is an equivalence on marked vertical arrows. It then remains to verify that the map on
$\zeta ^*$ is an equivalence on marked vertical arrows. It then remains to verify that the map on ![]() $(1,1)$-simplices is an equivalence. Unraveling the definitions, a
$(1,1)$-simplices is an equivalence. Unraveling the definitions, a ![]() $(1,1)$-simplex in
$(1,1)$-simplex in ![]() $\Psi _A(\mathbb {D}^\natural )$ is a diagram in
$\Psi _A(\mathbb {D}^\natural )$ is a diagram in ![]() $\mathbb {D}$
$\mathbb {D}$

where the right square covers a vertical arrow in ![]() $\mathbb {C}$. The map
$\mathbb {C}$. The map ![]() $\zeta ^*\colon \mathbb {D}(1, 1)\longrightarrow \Psi _A(\mathbb {D})(1, 1)$ is simply the inclusion of the diagrams of the above form where the right square is degenerate; this is an equivalence by completeness of
$\zeta ^*\colon \mathbb {D}(1, 1)\longrightarrow \Psi _A(\mathbb {D})(1, 1)$ is simply the inclusion of the diagrams of the above form where the right square is degenerate; this is an equivalence by completeness of ![]() $\mathbb {D}$.
$\mathbb {D}$.
![]() $\eta ^*$ is an equivalence. Let us again consider the double category
$\eta ^*$ is an equivalence. Let us again consider the double category ![]() $X$ from Lemma 2.18. For each fixed
$X$ from Lemma 2.18. For each fixed ![]() $n$, consider the mapping double category
$n$, consider the mapping double category ![]() $X^{[0]\boxtimes \mathrm {Fun}([1], [n])}$ and note that there is a diagram of simplicial spaces
$X^{[0]\boxtimes \mathrm {Fun}([1], [n])}$ and note that there is a diagram of simplicial spaces

where ![]() $P$ denotes the pullback. Since the bottom map is the inclusion of a wide subcategory (as we have seen above),
$P$ denotes the pullback. Since the bottom map is the inclusion of a wide subcategory (as we have seen above), ![]() $P$ is a wide subcategory of
$P$ is a wide subcategory of ![]() $X^{[0]\boxtimes \mathrm {Fun}([1], [n])}\big (-, 0\big )$. Unraveling the definitions, we then see that the inclusion
$X^{[0]\boxtimes \mathrm {Fun}([1], [n])}\big (-, 0\big )$. Unraveling the definitions, we then see that the inclusion ![]() $\Psi _B(\mathbb {D}^\natural )(-, n)\hookrightarrow P$ is the inclusion of a full subcategory: it is the inclusion of the full subcategory on those diagrams
$\Psi _B(\mathbb {D}^\natural )(-, n)\hookrightarrow P$ is the inclusion of a full subcategory: it is the inclusion of the full subcategory on those diagrams ![]() $[0]\boxtimes \mathrm {Fun}([1], [n])\longrightarrow X$ such that each vertical arrow
$[0]\boxtimes \mathrm {Fun}([1], [n])\longrightarrow X$ such that each vertical arrow ![]() $ik\longrightarrow jk$ in
$ik\longrightarrow jk$ in ![]() $\mathrm {Fun}([1], [n])$ is sent to a cartesian arrow in
$\mathrm {Fun}([1], [n])$ is sent to a cartesian arrow in ![]() $X(0, -)\simeq \mathbb {D}(0, -)$.
$X(0, -)\simeq \mathbb {D}(0, -)$.
It follows that ![]() $\Psi _B(\mathbb {D}^\natural )$ satisfies the (complete) Segal conditions in the horizontal direction. It therefore suffices to verify that
$\Psi _B(\mathbb {D}^\natural )$ satisfies the (complete) Segal conditions in the horizontal direction. It therefore suffices to verify that ![]() $\eta ^*\colon \Psi _B(\mathbb {D}^\natural )(1, -)\longrightarrow \Psi _A(\mathbb {D})(1, -)$ is an equivalence of simplicial spaces. Unraveling the definitions, a
$\eta ^*\colon \Psi _B(\mathbb {D}^\natural )(1, -)\longrightarrow \Psi _A(\mathbb {D})(1, -)$ is an equivalence of simplicial spaces. Unraveling the definitions, a ![]() $(1, n)$-simplex in
$(1, n)$-simplex in ![]() $\Psi _B(\mathbb {D}^\natural )$ is given by the following diagram.
$\Psi _B(\mathbb {D}^\natural )$ is given by the following diagram.

Here each of the slices labeled by ![]() $x, y$ and
$x, y$ and ![]() $z$ is a diagram in
$z$ is a diagram in ![]() $\mathbb {D}(0, -)$ parametrized by
$\mathbb {D}(0, -)$ parametrized by ![]() $\mathrm {Fun}([1], [n])$, while the maps
$\mathrm {Fun}([1], [n])$, while the maps ![]() define a map
define a map ![]() $\mathbb {A}\mathrm {r}[1]\longrightarrow \mathbb {D}$. Furthermore, the condition that
$\mathbb {A}\mathrm {r}[1]\longrightarrow \mathbb {D}$. Furthermore, the condition that ![]() $B[1, n]=\mathbb {A}\mathrm {r}[1]\times \Big ([0]\boxtimes \mathrm {Fun}([1], [n])\Big )\longrightarrow \mathbb {D}$ preserves marked arrows translates into the following conditions.
$B[1, n]=\mathbb {A}\mathrm {r}[1]\times \Big ([0]\boxtimes \mathrm {Fun}([1], [n])\Big )\longrightarrow \mathbb {D}$ preserves marked arrows translates into the following conditions.
(a) The maps
 are equivalences for all
are equivalences for all  $0\leq i\leq n$, as indicated.
$0\leq i\leq n$, as indicated.(b) All downward maps in the
 $x$-slice and the
$x$-slice and the  $z$-slice are
$z$-slice are  $p$-cartesian, indicated by
$p$-cartesian, indicated by  .
.
The map ![]() $\eta ^*\colon \Psi _B(\mathbb {D}^\natural )(1, n)\longrightarrow \Psi _A(\mathbb {D}^{\natural })(1, n)$ restricts the above diagram to the diagonal face, spanned by all
$\eta ^*\colon \Psi _B(\mathbb {D}^\natural )(1, n)\longrightarrow \Psi _A(\mathbb {D}^{\natural })(1, n)$ restricts the above diagram to the diagonal face, spanned by all ![]() $x_{ii}, y_{ii}$ and
$x_{ii}, y_{ii}$ and ![]() $z_{ii}$. We have to prove that there is a unique way to extend the above diagram (with properties (a) and (b)) from this diagonal face (covering the map
$z_{ii}$. We have to prove that there is a unique way to extend the above diagram (with properties (a) and (b)) from this diagonal face (covering the map ![]() $[m, n]\longrightarrow \mathbb {C}$). Let us first look at the
$[m, n]\longrightarrow \mathbb {C}$). Let us first look at the ![]() $x$- and
$x$- and ![]() $z$-slices, both of which correspond to diagrams as follows.
$z$-slices, both of which correspond to diagrams as follows.

Let ![]() $\mathrm {cst}\colon [n]\hookrightarrow \mathrm {Fun}([1], [n])$ be the inclusion of the diagonal. For every
$\mathrm {cst}\colon [n]\hookrightarrow \mathrm {Fun}([1], [n])$ be the inclusion of the diagonal. For every ![]() $ij\in \mathrm {Fun}([1], [n])$, the comma category
$ij\in \mathrm {Fun}([1], [n])$, the comma category ![]() $ij/\mathrm {cst}$ admits an initial object, corresponding to the map
$ij/\mathrm {cst}$ admits an initial object, corresponding to the map ![]() $ij\longrightarrow jj$. Using this, one sees that condition (b) is equivalent to the assertion that the two diagrams
$ij\longrightarrow jj$. Using this, one sees that condition (b) is equivalent to the assertion that the two diagrams ![]() $x, z\colon \mathrm {Fun}([1], [n])\longrightarrow \mathbb {D}$ are relative right Kan extensions of their restriction to the diagonal.
$x, z\colon \mathrm {Fun}([1], [n])\longrightarrow \mathbb {D}$ are relative right Kan extensions of their restriction to the diagonal.
Consequently, starting from the diagonal face there is a unique way to fill the ![]() $x$- and
$x$- and ![]() $z$-slices in (3.20) so that condition (b) holds [Reference LurieLur09a, Proposition 4.3.2.1]. Using that
$z$-slices in (3.20) so that condition (b) holds [Reference LurieLur09a, Proposition 4.3.2.1]. Using that ![]() $\mathbb {D}\longrightarrow \mathbb {C}$ is a left fibration in the horizontal direction, there is then a unique extension to a horizontal transformation between the
$\mathbb {D}\longrightarrow \mathbb {C}$ is a left fibration in the horizontal direction, there is then a unique extension to a horizontal transformation between the ![]() $x$- and
$x$- and ![]() $y$-slices
$y$-slices ![]() $(x\Rightarrow y)\colon [1]\boxtimes \mathrm {Fun}([1], [n])\longrightarrow \mathbb {D}$. Finally, the natural transformation
$(x\Rightarrow y)\colon [1]\boxtimes \mathrm {Fun}([1], [n])\longrightarrow \mathbb {D}$. Finally, the natural transformation ![]() on the diagonal then extends uniquely to a natural transformation
on the diagonal then extends uniquely to a natural transformation ![]() , since the target is the relative right Kan extension of its restriction to the diagonal. We conclude that
, since the target is the relative right Kan extension of its restriction to the diagonal. We conclude that ![]() $\eta ^*\colon \Psi _B(\mathbb {D}^\sharp )\longrightarrow \Psi _A(\mathbb {D}^\sharp )$ is an equivalence on the underlying bisimplicial spaces. Finally, it identifies the marking since
$\eta ^*\colon \Psi _B(\mathbb {D}^\sharp )\longrightarrow \Psi _A(\mathbb {D}^\sharp )$ is an equivalence on the underlying bisimplicial spaces. Finally, it identifies the marking since ![]() $A[0, 1]^+\simeq B[0, 1]^+\simeq [0, 1]^\sharp$.
$A[0, 1]^+\simeq B[0, 1]^+\simeq [0, 1]^\sharp$.
Our next goal is to describe the composite functor ![]() $\Psi ^\top \circ \Psi ^\perp$ in terms of Construction 3.10.
$\Psi ^\top \circ \Psi ^\perp$ in terms of Construction 3.10.
Construction 3.21 For each ![]() $m, n\geq 0$, let
$m, n\geq 0$, let ![]() $I[m, n]$ denote the
$I[m, n]$ denote the ![]() $(1, 1)$-category whose objects are quadruples of maps of linear orders
$(1, 1)$-category whose objects are quadruples of maps of linear orders
Given two such quadruples, a map between them is given by a quadruple of maps
that intertwines ![]() $(\alpha, \beta, \gamma, \delta )$ and
$(\alpha, \beta, \gamma, \delta )$ and ![]() $(\alpha ', \beta ', \gamma ', \delta ')$. Note that
$(\alpha ', \beta ', \gamma ', \delta ')$. Note that ![]() $I[m, n]$ depends functorially on
$I[m, n]$ depends functorially on ![]() $[m, n]\in \mathbf {\Delta }^{\times 2}$, by postcomposing
$[m, n]\in \mathbf {\Delta }^{\times 2}$, by postcomposing ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$.
$\beta$.
Now consider the natural map of bisimplicial spaces (in fact, sets)
defined as follows: to each ![]() $[s, t]\longrightarrow T[m, n]$ determined by a tuple
$[s, t]\longrightarrow T[m, n]$ determined by a tuple ![]() $(\alpha, \beta, \gamma, \delta )$, we associate the map
$(\alpha, \beta, \gamma, \delta )$, we associate the map ![]() $\sigma \boxtimes \tau _0\colon [s, t]\longrightarrow [m, n]$ determined by
$\sigma \boxtimes \tau _0\colon [s, t]\longrightarrow [m, n]$ determined by
We view ![]() $T[m, n]$ as a marked bisimplicial space by marking those
$T[m, n]$ as a marked bisimplicial space by marking those ![]() $(0, 1)$-simplices corresponding to a quadruple
$(0, 1)$-simplices corresponding to a quadruple ![]() $(\alpha, \beta, \gamma, \delta )$ (with
$(\alpha, \beta, \gamma, \delta )$ (with ![]() $s=0, t=1$) such that either:
$s=0, t=1$) such that either:
(a) the map
 $\gamma \colon [1]\star [0]\longrightarrow [a]$ factors over a
$\gamma \colon [1]\star [0]\longrightarrow [a]$ factors over a  $0$-simplex of
$0$-simplex of  $[a]$;
$[a]$;(b) the map
 $\beta \colon [b]\star [a]\longrightarrow [n]$ factors over a
$\beta \colon [b]\star [a]\longrightarrow [n]$ factors over a  $0$-simplex of
$0$-simplex of  $[n]$.
$[n]$.
For every map ![]() $[m, n]\longrightarrow [m', n']$, the induced map
$[m, n]\longrightarrow [m', n']$, the induced map ![]() $T[m, n]\longrightarrow T[m', n']$ preserves such marked arrows.
$T[m, n]\longrightarrow T[m', n']$ preserves such marked arrows.
Finally, let ![]() $T[0, 1]^+$ denote
$T[0, 1]^+$ denote ![]() $T[0, 1]$, where all vertical arrows are marked.
$T[0, 1]$, where all vertical arrows are marked.
Lemma 3.23 There is a natural equivalence ![]() $\Psi _T\simeq \Psi _{K'}\circ \Psi _K$.
$\Psi _T\simeq \Psi _{K'}\circ \Psi _K$.
Proof. Recall from Construction 3.10 that ![]() $\Psi _{K'}$ arises as the right adjoint to a functor
$\Psi _{K'}$ arises as the right adjoint to a functor ![]() $\Phi _{K'}$. This functor
$\Phi _{K'}$. This functor ![]() $\Phi _{K'}\colon \mathrm {Fun}^\sharp \big ([1], \mathrm {bis}\mathscr {S}_{\downarrow }\big )\longrightarrow \mathrm {Fun}^\sharp \big ([1], \mathrm {bis}\mathscr {S}_{\to }\big )$ is uniquely determined by the fact that it preserves colimits and sends
$\Phi _{K'}\colon \mathrm {Fun}^\sharp \big ([1], \mathrm {bis}\mathscr {S}_{\downarrow }\big )\longrightarrow \mathrm {Fun}^\sharp \big ([1], \mathrm {bis}\mathscr {S}_{\to }\big )$ is uniquely determined by the fact that it preserves colimits and sends ![]() $\emptyset \longrightarrow [m, n]^\sharp$ to
$\emptyset \longrightarrow [m, n]^\sharp$ to ![]() $\emptyset \longrightarrow [m, n]^\sharp$ and
$\emptyset \longrightarrow [m, n]^\sharp$ and

Here ![]() $K'[m, n]$ was described in Variant 3.16. Using Example 2.6, we can write
$K'[m, n]$ was described in Variant 3.16. Using Example 2.6, we can write ![]() $K'[m, n]$ as a (canonical) colimit of bisimplices
$K'[m, n]$ as a (canonical) colimit of bisimplices
Unraveling the definitions, the marked ![]() $(1, 0)$-simplices of
$(1, 0)$-simplices of ![]() $K'[m, n]$ correspond precisely to tuples of
$K'[m, n]$ correspond precisely to tuples of ![]() $\alpha \colon [1]\longrightarrow [m]$ and
$\alpha \colon [1]\longrightarrow [m]$ and ![]() $\beta \colon [0]\star [1]\longrightarrow [n]$ where
$\beta \colon [0]\star [1]\longrightarrow [n]$ where ![]() $\beta$ is degenerate. Furthermore, all
$\beta$ is degenerate. Furthermore, all ![]() $(1, 0)$-simplices in
$(1, 0)$-simplices in ![]() $K'[0, 1]$ are marked.
$K'[0, 1]$ are marked.
We can apply the same reasoning to the left adjoint ![]() $\Phi _K\circ \Phi _{K'}$: this functor preserves colimits and sends
$\Phi _K\circ \Phi _{K'}$: this functor preserves colimits and sends ![]() $\emptyset \longrightarrow [m, n]^\sharp$ to
$\emptyset \longrightarrow [m, n]^\sharp$ to ![]() $\emptyset \longrightarrow [m, n]^\sharp$. It is therefore uniquely determined by its values on
$\emptyset \longrightarrow [m, n]^\sharp$. It is therefore uniquely determined by its values on ![]() $[m, n]\longrightarrow [m, n]^\sharp$ and
$[m, n]\longrightarrow [m, n]^\sharp$ and ![]() $[0, 1]^\sharp \longrightarrow [0, 1]^\sharp$. The value on
$[0, 1]^\sharp \longrightarrow [0, 1]^\sharp$. The value on ![]() $[m, n]$ is given by
$[m, n]$ is given by
 \[ \Phi_K\big(K'[m, n]\big)=\mathop {{\rm colim}}\limits_{_{\substack{\alpha\colon [a]\to [m]\\ \beta\colon [b]\star [a]\to [n]}}} K[a, b]\simeq \mathop {{\rm colim}}\limits_{_{\substack{\alpha\colon [a]\to [m]\\ \beta\colon [b]\star [a]\to [n]}}} \bigg(\mathop {{\rm colim}}\limits_{_{\substack{\gamma\colon [t]\star [s]\to [a]\\ \delta\colon [t]\to [b]}}} [s, t]\bigg). \]
\[ \Phi_K\big(K'[m, n]\big)=\mathop {{\rm colim}}\limits_{_{\substack{\alpha\colon [a]\to [m]\\ \beta\colon [b]\star [a]\to [n]}}} K[a, b]\simeq \mathop {{\rm colim}}\limits_{_{\substack{\alpha\colon [a]\to [m]\\ \beta\colon [b]\star [a]\to [n]}}} \bigg(\mathop {{\rm colim}}\limits_{_{\substack{\gamma\colon [t]\star [s]\to [a]\\ \delta\colon [t]\to [b]}}} [s, t]\bigg). \]
In other words, it is precisely given by ![]() $T[m, n]$; unraveling the definitions shows that the marking coincides with that of Construction 3.21. Likewise,
$T[m, n]$; unraveling the definitions shows that the marking coincides with that of Construction 3.21. Likewise, ![]() $\Phi _K\big (K'[0, 1]^+\big )$ can be identified with
$\Phi _K\big (K'[0, 1]^+\big )$ can be identified with ![]() $T[0, 1]$ where all vertical arrows are marked. It follows that
$T[0, 1]$ where all vertical arrows are marked. It follows that ![]() $\Phi _K\circ \Phi _{K'}\simeq \Phi _T$, so that by adjunction
$\Phi _K\circ \Phi _{K'}\simeq \Phi _T$, so that by adjunction ![]() $\Psi _{T}\simeq \Psi _{K'}\circ \Psi _K$.
$\Psi _{T}\simeq \Psi _{K'}\circ \Psi _K$.
Proof (of Theorem 3.1) By Proposition 3.14 (and Variant 3.16), we have functors
To see that they are mutually inverse, it suffices to prove that ![]() $\Psi ^{\top }\circ \Psi ^{\perp }\simeq \mathrm {id}$. Indeed, in this case, conjugating by the functor
$\Psi ^{\top }\circ \Psi ^{\perp }\simeq \mathrm {id}$. Indeed, in this case, conjugating by the functor ![]() $\mathbb {C}\mapsto (\mathbb {C}^\mathrm {rev})^{(1, 2)-\mathrm {op}}$ provides the desired equivalence
$\mathbb {C}\mapsto (\mathbb {C}^\mathrm {rev})^{(1, 2)-\mathrm {op}}$ provides the desired equivalence ![]() $\Psi ^\perp \circ \Psi ^\top \simeq \mathrm {id}$. We construct the desired natural equivalence as a zigzag
$\Psi ^\perp \circ \Psi ^\top \simeq \mathrm {id}$. We construct the desired natural equivalence as a zigzag
Here the first two equivalences follow from Proposition 3.19 and the last identification follows from Lemma 3.23. The remaining natural transformation ![]() $\theta ^*$ is induced by a natural map
$\theta ^*$ is induced by a natural map ![]() $\theta \colon T[m, n]\longrightarrow B[m, n]$ of vertically marked bisimplicial spaces over
$\theta \colon T[m, n]\longrightarrow B[m, n]$ of vertically marked bisimplicial spaces over ![]() $[m, n]$. This map is defined as follows: for every
$[m, n]$. This map is defined as follows: for every ![]() $(s, t)$-simplex of
$(s, t)$-simplex of ![]() $T[m, n]$, determined by a quadruple
$T[m, n]$, determined by a quadruple ![]() $(\alpha, \beta, \gamma, \delta )$ as in (3.22), consider the map
$(\alpha, \beta, \gamma, \delta )$ as in (3.22), consider the map
Clearly ![]() $\tau _0(i)\leq \tau _1(i)$ for all
$\tau _0(i)\leq \tau _1(i)$ for all ![]() $i$, where
$i$, where ![]() $\tau _0$ is defined in Construction 3.21. We therefore obtain a map
$\tau _0$ is defined in Construction 3.21. We therefore obtain a map ![]() $(\tau _0\leq \tau _1)\colon [s, t]\longrightarrow [0]\boxtimes \mathrm {Fun}([1], [n])$. Likewise, note that
$(\tau _0\leq \tau _1)\colon [s, t]\longrightarrow [0]\boxtimes \mathrm {Fun}([1], [n])$. Likewise, note that ![]() $\alpha \circ \gamma$ defines a map
$\alpha \circ \gamma$ defines a map ![]() $\alpha \circ \gamma \colon [s, t]\longrightarrow \mathbb {A}\mathrm {r}[m]$ (cf. Example 2.6). Combining these two, we obtain a natural map
$\alpha \circ \gamma \colon [s, t]\longrightarrow \mathbb {A}\mathrm {r}[m]$ (cf. Example 2.6). Combining these two, we obtain a natural map
for every ![]() $(s, t)$-simplex in
$(s, t)$-simplex in ![]() $T[m, n]$. This defines the desired natural map of bisimplicial spaces
$T[m, n]$. This defines the desired natural map of bisimplicial spaces ![]() $\theta \colon T[m, n]\longrightarrow B[m, n]$. Note that
$\theta \colon T[m, n]\longrightarrow B[m, n]$. Note that ![]() $\theta$ sends a marked
$\theta$ sends a marked ![]() $(0, 1)$-simplex in
$(0, 1)$-simplex in ![]() $T[m, n]$ (Construction 3.21) to a marked
$T[m, n]$ (Construction 3.21) to a marked ![]() $(0, 1)$-simplex in
$(0, 1)$-simplex in ![]() $B[m, n]$ (Construction 3.18). Finally, note that in both
$B[m, n]$ (Construction 3.18). Finally, note that in both ![]() $T[0, 1]^\sharp$ and
$T[0, 1]^\sharp$ and ![]() $B[0, 1]^\sharp$, all vertical arrows are marked, so
$B[0, 1]^\sharp$, all vertical arrows are marked, so ![]() $\theta$ induces a natural map
$\theta$ induces a natural map ![]() $T[0, 1]^\sharp \longrightarrow B[0, 1]^\sharp$ as well.
$T[0, 1]^\sharp \longrightarrow B[0, 1]^\sharp$ as well.
For any (left, cart)-fibration ![]() $p\colon \mathbb {D}^\natural \longrightarrow \mathbb {C}^\sharp$, restriction along
$p\colon \mathbb {D}^\natural \longrightarrow \mathbb {C}^\sharp$, restriction along ![]() $\theta$ therefore defines the following natural map of marked bisimplicial spaces.
$\theta$ therefore defines the following natural map of marked bisimplicial spaces.

Since both downwards-pointing maps are (left, cart)-fibrations (with marked arrows being the cartesian arrows), it suffices to verify that ![]() $\theta ^*$ induces equivalences between spaces of vertices and vertical arrows. On vertices, note that
$\theta ^*$ induces equivalences between spaces of vertices and vertical arrows. On vertices, note that ![]() $T[0, 0]\simeq B[0, 0]\simeq [0, 0]$, so that the spaces of objects of
$T[0, 0]\simeq B[0, 0]\simeq [0, 0]$, so that the spaces of objects of ![]() $\Psi _B(\mathbb {D}^\natural )$ and
$\Psi _B(\mathbb {D}^\natural )$ and ![]() $\Psi _T(\mathbb {D}^\natural )$ are both equivalent to the space of objects of
$\Psi _T(\mathbb {D}^\natural )$ are both equivalent to the space of objects of ![]() $\mathbb {D}$.
$\mathbb {D}$.
Unraveling the definitions, a vertical arrow in ![]() $\Psi _T(\mathbb {D}^\natural )\simeq \Psi ^\top \big (\Psi ^\perp (\mathbb {D}^\natural )\big )$ covering a vertical arrow
$\Psi _T(\mathbb {D}^\natural )\simeq \Psi ^\top \big (\Psi ^\perp (\mathbb {D}^\natural )\big )$ covering a vertical arrow ![]() in
in ![]() $\mathbb {C}^\sharp$ is given by a diagram in
$\mathbb {C}^\sharp$ is given by a diagram in ![]() $\mathbb {D}$ of the form
$\mathbb {D}$ of the form
Here the first two maps live in the fiber over ![]() $c$ and the vertical arrow
$c$ and the vertical arrow ![]() is a cartesian lift of
is a cartesian lift of ![]() . Since
. Since ![]() $\mathbb {D}\longrightarrow \mathbb {C}$ was a horizontal left fibration, this means that the arrow
$\mathbb {D}\longrightarrow \mathbb {C}$ was a horizontal left fibration, this means that the arrow ![]() $d_0\longrightarrow d_0'$ is an equivalence.
$d_0\longrightarrow d_0'$ is an equivalence.
On the other hand, a vertical arrow in ![]() $\Psi _B(\mathbb {D}^\natural )$ is a sequence
$\Psi _B(\mathbb {D}^\natural )$ is a sequence ![]() of vertical maps where the first map lives in the fiber over
of vertical maps where the first map lives in the fiber over ![]() $c$ and
$c$ and ![]() is cartesian. The map
is cartesian. The map ![]() $\theta ^*$ can be identified with the map sending this sequence to
$\theta ^*$ can be identified with the map sending this sequence to ![]() ; it is then an equivalence by the completeness of
; it is then an equivalence by the completeness of ![]() $\mathbb {D}$.
$\mathbb {D}$.
4. Recollections on higher categories
In the remainder of the text, we will use Theorem 3.1 to establish a version of straightening and unstraightening for cocartesian fibrations of ![]() $d$-categories. To facilitate this, we will start in this section by recalling some preliminary results on
$d$-categories. To facilitate this, we will start in this section by recalling some preliminary results on ![]() $d$-categories; our default model for
$d$-categories; our default model for ![]() $d$-categories will be in terms of iterated Segal spaces [Reference Barwick and Schommer-PriesBS21]. Section 4.2 provides a reminder on point-set models for
$d$-categories will be in terms of iterated Segal spaces [Reference Barwick and Schommer-PriesBS21]. Section 4.2 provides a reminder on point-set models for ![]() $d$-categories; its main purpose is to allow us to construct explicit examples of higher categories (such as the
$d$-categories; its main purpose is to allow us to construct explicit examples of higher categories (such as the ![]() $(d+1)$-category of
$(d+1)$-category of ![]() $d$-categories) from enriched categories.
$d$-categories) from enriched categories.
Sections 4.3 and 4.4 describe the theory of copresheaves (of ![]() $d$-categories) on
$d$-categories) on ![]() $(d+1)$-categories; this is mostly a recollection of the work of Boavida [Reference Boavida de BritoBoa18]. For our purposes, it will be convenient to reformulate the results of [Reference Boavida de BritoBoa18] as Proposition 4.40: this provides a natural equivalence between the external definition of copresheaves over a
$(d+1)$-categories; this is mostly a recollection of the work of Boavida [Reference Boavida de BritoBoa18]. For our purposes, it will be convenient to reformulate the results of [Reference Boavida de BritoBoa18] as Proposition 4.40: this provides a natural equivalence between the external definition of copresheaves over a ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$, in terms of certain fibrations of
$\mathscr {C}$, in terms of certain fibrations of ![]() $(d+1)$-fold simplicial spaces
$(d+1)$-fold simplicial spaces ![]() $X\longrightarrow \mathscr {C}$, and the internal definition of copresheaves, as maps of
$X\longrightarrow \mathscr {C}$, and the internal definition of copresheaves, as maps of ![]() $(d+1)$-categories
$(d+1)$-categories ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_{d}$.
$\mathscr {C}\longrightarrow \mathbf {Cat}_{d}$.
4.1 Higher categories via Segal spaces
Recall the iterated Segal space model for ![]() $d$-categories [Reference Barwick and Schommer-PriesBS21].
$d$-categories [Reference Barwick and Schommer-PriesBS21].
Definition 4.1 A d-category ![]() $\mathscr {C}$ is a
$\mathscr {C}$ is a ![]() $d$-fold category with the property that for each
$d$-fold category with the property that for each ![]() $\vec {n}_{k-1}$ in
$\vec {n}_{k-1}$ in ![]() $\mathbf {\Delta }^{\times k-1}$, the
$\mathbf {\Delta }^{\times k-1}$, the ![]() $(d-k)$-fold category
$(d-k)$-fold category ![]() $\mathscr {C}(\vec {n}_{k-1}, 0, -, \dots, -)$ is a space, i.e. constant. We will write
$\mathscr {C}(\vec {n}_{k-1}, 0, -, \dots, -)$ is a space, i.e. constant. We will write ![]() $\mathrm {Cat}_d\hookrightarrow \mathrm {Cat}^{\otimes d}$ for the full subcategory spanned by the
$\mathrm {Cat}_d\hookrightarrow \mathrm {Cat}^{\otimes d}$ for the full subcategory spanned by the ![]() $d$-categories.
$d$-categories.
Remark 4.2 The above definition of a ![]() $d$-category is a priori more restrictive than the usual one from [Reference Barwick and Schommer-PriesBS21]: we ask all
$d$-category is a priori more restrictive than the usual one from [Reference Barwick and Schommer-PriesBS21]: we ask all ![]() $\mathscr {C}(\vec {n}_{k-1}, -, \vec {n}_{d-k})$ to be complete, whereas this is usually only required if
$\mathscr {C}(\vec {n}_{k-1}, -, \vec {n}_{d-k})$ to be complete, whereas this is usually only required if ![]() $\vec {n}_{d-k}=\vec {0}_{d-k}$. It follows from [Reference Johnson-Freyd and ScheimbauerJS17, Lemma 2.8] that the two definitions coincide, essentially by an Eckmann–Hilton-type argument.
$\vec {n}_{d-k}=\vec {0}_{d-k}$. It follows from [Reference Johnson-Freyd and ScheimbauerJS17, Lemma 2.8] that the two definitions coincide, essentially by an Eckmann–Hilton-type argument.
If ![]() $\mathscr {C}$ is a
$\mathscr {C}$ is a ![]() $d$-category, recall that the (constant
$d$-category, recall that the (constant ![]() $(d-1)$-fold simplicial) space
$(d-1)$-fold simplicial) space ![]() $\mathscr {C}(0)$ describes the space of objects of
$\mathscr {C}(0)$ describes the space of objects of ![]() $\mathscr {C}$. Given two objects
$\mathscr {C}$. Given two objects ![]() $x_0, x_1\in \mathscr {C}$, we will write
$x_0, x_1\in \mathscr {C}$, we will write
for the mapping ![]() $(d-1)$-category between them. For any triple of objects
$(d-1)$-category between them. For any triple of objects ![]() $x_0, x_1, x_2$, there is a composition map, determined by the following commuting square.
$x_0, x_1, x_2$, there is a composition map, determined by the following commuting square.

Here the left vertical map is an equivalence by the Segal conditions.
To efficiently deal with the additional constancy conditions appearing in Definition 4.1, let us introduce the following notation.
Notation 4.3 For a category ![]() $\mathscr {I}$, let us denote by
$\mathscr {I}$, let us denote by ![]() $\lambda \colon \mathbf {\Delta }\times \mathscr {I}\longrightarrow \mathbf {\Delta }_{\mathscr {I}}$ the (
$\lambda \colon \mathbf {\Delta }\times \mathscr {I}\longrightarrow \mathbf {\Delta }_{\mathscr {I}}$ the (![]() $(\infty, 1)$-categorical) localization of
$(\infty, 1)$-categorical) localization of ![]() $\mathbf {\Delta }\times \mathscr {I}$ at the morphisms in
$\mathbf {\Delta }\times \mathscr {I}$ at the morphisms in ![]() $\{0\}\times \mathscr {I}$. Recall that restriction and Kan extension determine adjoint pairs
$\{0\}\times \mathscr {I}$. Recall that restriction and Kan extension determine adjoint pairs
that exhibit the category of presheaves on ![]() $\mathbf {\Delta }_{\mathscr {I}}$ both as a localization and a colocalization of the category of presheaves on
$\mathbf {\Delta }_{\mathscr {I}}$ both as a localization and a colocalization of the category of presheaves on ![]() $\mathbf {\Delta }\times \mathscr {I}$.
$\mathbf {\Delta }\times \mathscr {I}$.
Lemma 4.4 Let ![]() $\mathscr {I}$ be a
$\mathscr {I}$ be a ![]() $(1, 1)$-category with a terminal object
$(1, 1)$-category with a terminal object ![]() $t$ and let
$t$ and let ![]() $\lambda \colon \mathbf {\Delta }\times \mathscr {I}\longrightarrow \mathbf {\Delta }_{\mathscr {I}}$ denote the localization at the morphisms in
$\lambda \colon \mathbf {\Delta }\times \mathscr {I}\longrightarrow \mathbf {\Delta }_{\mathscr {I}}$ denote the localization at the morphisms in ![]() $\{0\}\times \mathscr {I}$. Then the following assertions hold:
$\{0\}\times \mathscr {I}$. Then the following assertions hold:
(1)
 $\mathbf {\Delta }_{\mathscr {I}}$ is a
$\mathbf {\Delta }_{\mathscr {I}}$ is a  $(1, 1)$-category with a terminal object;
$(1, 1)$-category with a terminal object;(2) for any
 $X\colon \big (\mathbf {\Delta }\times \mathscr {I}\big )^{\mathrm {op}}\longrightarrow \mathscr {S}$, consider the natural map of presheaves on
$X\colon \big (\mathbf {\Delta }\times \mathscr {I}\big )^{\mathrm {op}}\longrightarrow \mathscr {S}$, consider the natural map of presheaves on  $\mathbf {\Delta }\times \mathscr {I}$:
where
$\mathbf {\Delta }\times \mathscr {I}$:
where
 $i_*$ denote the right Kan extension along
$i_*$ denote the right Kan extension along  $i\colon \{0\}\times \mathscr {I}\hookrightarrow \mathbf {\Delta }\times \mathscr {I}$ and
$i\colon \{0\}\times \mathscr {I}\hookrightarrow \mathbf {\Delta }\times \mathscr {I}$ and  $i^*X\longrightarrow X(0, t)$ denotes the natural map from the presheaf
$i^*X\longrightarrow X(0, t)$ denotes the natural map from the presheaf  $X(0, -)$ on
$X(0, -)$ on  $\mathscr {I}$ to the constant presheaf with value
$\mathscr {I}$ to the constant presheaf with value  $X(0, t)$; this map exhibits the counit of the adjoint pair
$X(0, t)$; this map exhibits the counit of the adjoint pair  $(\lambda ^*, \lambda _*)$.
$(\lambda ^*, \lambda _*)$.
In fact, in this case ![]() $\mathbf {\Delta }_{\mathscr {I}}$ can be identified with a (non-full) subcategory of
$\mathbf {\Delta }_{\mathscr {I}}$ can be identified with a (non-full) subcategory of ![]() $\mathbf {\Delta }\wr \mathscr {I}$, given by the image of the functor
$\mathbf {\Delta }\wr \mathscr {I}$, given by the image of the functor ![]() $\delta \colon \mathbf {\Delta }\times \mathscr {I}\longrightarrow \mathbf {\Delta }\wr \mathscr {I}$ from [Reference BergerBer07].
$\delta \colon \mathbf {\Delta }\times \mathscr {I}\longrightarrow \mathbf {\Delta }\wr \mathscr {I}$ from [Reference BergerBer07].
Proof. For each ![]() $([m], i)\in \mathbf {\Delta }\times \mathscr {I}$, let
$([m], i)\in \mathbf {\Delta }\times \mathscr {I}$, let ![]() $h_{[m], i}=\mathrm {Map}\big (-, ([m], i)\big )$ be the representable presheaf. For assertion (1), consider the following (homotopy) pushout of (space-valued) presheaves.
$h_{[m], i}=\mathrm {Map}\big (-, ([m], i)\big )$ be the representable presheaf. For assertion (1), consider the following (homotopy) pushout of (space-valued) presheaves.

Here the top map is given pointwise by the inclusion of the subset of maps ![]() $([n], j)\longrightarrow ([m], i)$ such that the map
$([n], j)\longrightarrow ([m], i)$ such that the map ![]() $[n]\longrightarrow [m]$ factors over
$[n]\longrightarrow [m]$ factors over ![]() $[0]$. Using this, it follows immediately that the presheaf
$[0]$. Using this, it follows immediately that the presheaf ![]() $F$ takes values in sets and sends maps in
$F$ takes values in sets and sends maps in ![]() $\{0\}\times \mathscr {I}$ to isomorphisms. Consequently,
$\{0\}\times \mathscr {I}$ to isomorphisms. Consequently, ![]() $F\simeq \lambda ^*G$ for some set-valued presheaf
$F\simeq \lambda ^*G$ for some set-valued presheaf ![]() $G$ on
$G$ on ![]() $\mathbf {\Delta }_{\mathscr {I}}$.
$\mathbf {\Delta }_{\mathscr {I}}$.
On the other hand, the left Kan extension functor ![]() $\lambda _!$ sends the left vertical map to an equivalence, so that we find
$\lambda _!$ sends the left vertical map to an equivalence, so that we find ![]() $h_{\lambda ([m], i)}\simeq \lambda _!h_{[m], i}\simeq \lambda _!F$. We therefore find that the representable presheaf
$h_{\lambda ([m], i)}\simeq \lambda _!h_{[m], i}\simeq \lambda _!F$. We therefore find that the representable presheaf ![]() $h_{\lambda ([m], i)}$ is equivalent to the set-valued presheaf
$h_{\lambda ([m], i)}$ is equivalent to the set-valued presheaf ![]() $\lambda _!\lambda ^*G\simeq G$, so that
$\lambda _!\lambda ^*G\simeq G$, so that ![]() $\mathbf {\Delta }_{\mathscr {I}}$ is a
$\mathbf {\Delta }_{\mathscr {I}}$ is a ![]() $(1, 1)$-category. In the special case where
$(1, 1)$-category. In the special case where ![]() $[m]=0$, we see that
$[m]=0$, we see that ![]() $F$ is the terminal presheaf, so that the image of
$F$ is the terminal presheaf, so that the image of ![]() $([0], i)$ defines a terminal object in
$([0], i)$ defines a terminal object in ![]() $\mathbf {\Delta }_{\mathscr {I}}$.
$\mathbf {\Delta }_{\mathscr {I}}$.
For assertion (2), let us abbreviate ![]() $Y=X\times _{i_*i^*X} i_*\big (X(0, t)\big )$. Since
$Y=X\times _{i_*i^*X} i_*\big (X(0, t)\big )$. Since ![]() $i$ is fully faithful,
$i$ is fully faithful, ![]() $i^*i_*\simeq \mathrm {id}$ and the restriction of
$i^*i_*\simeq \mathrm {id}$ and the restriction of ![]() $Y$ along
$Y$ along ![]() $i\colon \{0\}\times \mathscr {I}\longrightarrow \mathbf {\Delta }\times \mathscr {I}$ coincides with the constant presheaf with value
$i\colon \{0\}\times \mathscr {I}\longrightarrow \mathbf {\Delta }\times \mathscr {I}$ coincides with the constant presheaf with value ![]() $X(0, t)$. This means that
$X(0, t)$. This means that ![]() $Y$ is contained in the essential image of
$Y$ is contained in the essential image of ![]() $\lambda ^*$ or, equivalently, that
$\lambda ^*$ or, equivalently, that ![]() $Y$ is a
$Y$ is a ![]() $\lambda ^*\lambda _*$-colocal object.
$\lambda ^*\lambda _*$-colocal object.
It therefore remains to verify that the projection ![]() $Y\longrightarrow X$ is a colocal equivalence, i.e. that it is sent to an equivalence by
$Y\longrightarrow X$ is a colocal equivalence, i.e. that it is sent to an equivalence by ![]() $\lambda _*$. Since
$\lambda _*$. Since ![]() $Y\longrightarrow X$ is the base change of the map
$Y\longrightarrow X$ is the base change of the map ![]() $i_*(X(0, t))\longrightarrow i_*i^*X$, it suffices to verify that
$i_*(X(0, t))\longrightarrow i_*i^*X$, it suffices to verify that ![]() $\lambda _*i_*(X(0, t))\longrightarrow \lambda _*i_*i^*X$ is an equivalence. By part (1), the functor
$\lambda _*i_*(X(0, t))\longrightarrow \lambda _*i_*i^*X$ is an equivalence. By part (1), the functor ![]() $\lambda i$ decomposes as
$\lambda i$ decomposes as ![]() $\mathscr {I}\longrightarrow \ast \longrightarrow \mathbf {\Delta }_{\mathscr {I}}$, where the second functor is the inclusion of the terminal object. The result then follows from the fact that the natural map
$\mathscr {I}\longrightarrow \ast \longrightarrow \mathbf {\Delta }_{\mathscr {I}}$, where the second functor is the inclusion of the terminal object. The result then follows from the fact that the natural map
is an equivalence since ![]() $t$ was the terminal object of
$t$ was the terminal object of ![]() $\mathscr {I}$.
$\mathscr {I}$.
Notation 4.5 We inductively define ![]() $\mathbf {\Delta }_d$ by
$\mathbf {\Delta }_d$ by ![]() $\mathbf {\Delta }_0=\ast$ and
$\mathbf {\Delta }_0=\ast$ and ![]() $\mathbf {\Delta }_{d}=\mathbf {\Delta }_{\mathbf {\Delta }_{d-1}}$, so that there is the following composition of localization functors of
$\mathbf {\Delta }_{d}=\mathbf {\Delta }_{\mathbf {\Delta }_{d-1}}$, so that there is the following composition of localization functors of ![]() $(1, 1)$-categories:
$(1, 1)$-categories:
By construction, restriction along ![]() $\delta _d$ determines a fully faithful inclusion
$\delta _d$ determines a fully faithful inclusion
whose essential image consists of ![]() $d$-fold simplicial spaces
$d$-fold simplicial spaces ![]() $X$ such that each
$X$ such that each ![]() $(d-k)$-fold simplicial space
$(d-k)$-fold simplicial space ![]() $X(\vec {n}_{k-1}, 0, -, \dots, -)$ is constant. We will systematically omit
$X(\vec {n}_{k-1}, 0, -, \dots, -)$ is constant. We will systematically omit ![]() $\delta _d^*$ and simply identify presheaves on
$\delta _d^*$ and simply identify presheaves on ![]() $\mathbf {\Delta }_d$ with
$\mathbf {\Delta }_d$ with ![]() $d$-fold simplicial spaces using this inclusion. Likewise, we can identify presheaves on
$d$-fold simplicial spaces using this inclusion. Likewise, we can identify presheaves on ![]() $\mathbf {\Delta }_d$ with simplicial object in presheaves on
$\mathbf {\Delta }_d$ with simplicial object in presheaves on ![]() $\mathbf {\Delta }_{d-1}$ which are constant in simplicial degree
$\mathbf {\Delta }_{d-1}$ which are constant in simplicial degree ![]() $0$, etc.
$0$, etc.
In these terms, we have the following pullback square of fully faithful functors.

Since the bottom and the right functors are right adjoint functors between presentable categories, the inclusion ![]() ${{\rm Cat}}_d\longrightarrow {{\rm Cat}}^{\otimes d}$ admits a left adjoint. It also admits a right adjoint, by the following observation.
${{\rm Cat}}_d\longrightarrow {{\rm Cat}}^{\otimes d}$ admits a left adjoint. It also admits a right adjoint, by the following observation.
Lemma 4.7 Let ![]() $r_d\colon \mathrm {Fun}(\mathbf {\Delta }^{\times d, \mathrm {op}}, \mathscr {S})\longrightarrow \mathrm {Fun}(\mathbf {\Delta }_d, \mathscr {S})$ be the right adjoint to
$r_d\colon \mathrm {Fun}(\mathbf {\Delta }^{\times d, \mathrm {op}}, \mathscr {S})\longrightarrow \mathrm {Fun}(\mathbf {\Delta }_d, \mathscr {S})$ be the right adjoint to ![]() $\delta _d^*$, taking right Kan extension along
$\delta _d^*$, taking right Kan extension along ![]() $\delta _d\colon \mathbf {\Delta }^{\times d, \mathrm {op}}\longrightarrow \mathbf {\Delta }_d^{\mathrm {op}}$. Then
$\delta _d\colon \mathbf {\Delta }^{\times d, \mathrm {op}}\longrightarrow \mathbf {\Delta }_d^{\mathrm {op}}$. Then ![]() $r_d$ maps the full subcategory
$r_d$ maps the full subcategory ![]() ${{\rm Cat}}^{\otimes d}$ to
${{\rm Cat}}^{\otimes d}$ to ![]() ${{\rm Cat}}_d$.
${{\rm Cat}}_d$.
Proof. We proceed by induction, the case ![]() $d=1$ being clear. Now let us take
$d=1$ being clear. Now let us take ![]() $d>1$ and assume that
$d>1$ and assume that ![]() $r_{d-1}$ sends
$r_{d-1}$ sends ![]() $(d-1)$-fold categories to
$(d-1)$-fold categories to ![]() $d$-categories. Suppose that
$d$-categories. Suppose that ![]() $X\colon \mathbf {\Delta }^{\times d, \mathrm {op}}\longrightarrow \mathscr {S}$ is a
$X\colon \mathbf {\Delta }^{\times d, \mathrm {op}}\longrightarrow \mathscr {S}$ is a ![]() $d$-fold category and factor the map
$d$-fold category and factor the map ![]() $\delta _d$ as
$\delta _d$ as
The right Kan extension along the functor ![]() $\mathrm {id}\times \delta _{d-1}$ sends
$\mathrm {id}\times \delta _{d-1}$ sends ![]() $X$ to the simplicial object
$X$ to the simplicial object ![]() $X'\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathrm {Fun}(\mathbf {\Delta }_{d-1}^{\mathrm {op}}, \mathscr {S})$ given by
$X'\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathrm {Fun}(\mathbf {\Delta }_{d-1}^{\mathrm {op}}, \mathscr {S})$ given by ![]() $X'(n)=r_{d-1}(X(n))$. Each
$X'(n)=r_{d-1}(X(n))$. Each ![]() $X'(n)$ is then a
$X'(n)$ is then a ![]() $(d-1)$-category by inductive hypothesis and the simplicial object
$(d-1)$-category by inductive hypothesis and the simplicial object ![]() $X'$ satisfies the complete Segal conditions since
$X'$ satisfies the complete Segal conditions since ![]() $r_{d-1}$ is a right adjoint.
$r_{d-1}$ is a right adjoint.
Next, we compute ![]() $r_d(X)=\lambda _*(X')$ using Lemma 4.4(2). Denoting by
$r_d(X)=\lambda _*(X')$ using Lemma 4.4(2). Denoting by ![]() $i\colon \{0\}\times \mathbf {\Delta }_{d-1}\hookrightarrow \mathbf {\Delta }\times \mathbf {\Delta }_{d-1}$ the inclusion, we have that
$i\colon \{0\}\times \mathbf {\Delta }_{d-1}\hookrightarrow \mathbf {\Delta }\times \mathbf {\Delta }_{d-1}$ the inclusion, we have that
at least after precomposing with the localization ![]() $\lambda \colon \mathbf {\Delta }\times \mathbf {\Delta }_{d-1}\longrightarrow \mathbf {\Delta }_d$. The value of this fiber product at
$\lambda \colon \mathbf {\Delta }\times \mathbf {\Delta }_{d-1}\longrightarrow \mathbf {\Delta }_d$. The value of this fiber product at ![]() $[m]\in \mathbf {\Delta }$ is given by the presheaf on
$[m]\in \mathbf {\Delta }$ is given by the presheaf on ![]() $\mathbf {\Delta }_{d-1}$ of the form
$\mathbf {\Delta }_{d-1}$ of the form
Here the map ![]() $X'(m, -)\longrightarrow X'(0, -)^{\times m+1}$ arises from the vertex inclusions
$X'(m, -)\longrightarrow X'(0, -)^{\times m+1}$ arises from the vertex inclusions ![]() $\{k\}\hookrightarrow [m]$ for all
$\{k\}\hookrightarrow [m]$ for all ![]() $k\in [m]$. This implies that
$k\in [m]$. This implies that ![]() $r_d(X)$ satisfies the Segal condition in the first simplicial direction (as the spine inclusions induce bijections on objects). Furthermore, each
$r_d(X)$ satisfies the Segal condition in the first simplicial direction (as the spine inclusions induce bijections on objects). Furthermore, each ![]() $r_d(X)(m)$ is a
$r_d(X)(m)$ is a ![]() $(d-1)$-category, since all terms in the above pullback diagram are
$(d-1)$-category, since all terms in the above pullback diagram are ![]() $(d-1)$-categories.
$(d-1)$-categories.
It remains to verify the completeness condition. By Remark 4.2, it suffices to verify the completeness condition after setting the last variables equal to ![]() $\vec {0}_{d-1}$. But in that case the above formula shows that
$\vec {0}_{d-1}$. But in that case the above formula shows that ![]() $r_d(X)(-, \vec {0}_{d-1})\simeq X'(-, \vec {0}_{d-1})$, for which we already verified that it was a complete Segal space.
$r_d(X)(-, \vec {0}_{d-1})\simeq X'(-, \vec {0}_{d-1})$, for which we already verified that it was a complete Segal space.
Remark 4.8 In fact, one sees that for any ![]() $d$-fold category
$d$-fold category ![]() $\mathbb {C}$, the counit map
$\mathbb {C}$, the counit map ![]() $r_d(\mathbb {C})\hookrightarrow \mathbb {C}$ is a
$r_d(\mathbb {C})\hookrightarrow \mathbb {C}$ is a ![]() $d$-fold simplicial subspace, given in degree
$d$-fold simplicial subspace, given in degree ![]() $(m_1, \dots, m_d)$ by the path components
$(m_1, \dots, m_d)$ by the path components ![]() $x$ satisfying (inductively) the following two conditions:
$x$ satisfying (inductively) the following two conditions:
(1)
 $x$ is contained in
$x$ is contained in  $r_{d-1}(\mathbb {C}(m_1))\hookrightarrow \mathbb {C}(m_1)$;
$r_{d-1}(\mathbb {C}(m_1))\hookrightarrow \mathbb {C}(m_1)$;(2) for each
 $i=0, \dots, m_1$, the image of
$i=0, \dots, m_1$, the image of  $x$ in
$x$ in  $\mathbb {C}(\{i\}, m_2, \dots, m_d)$ is contained in the path components
$\mathbb {C}(\{i\}, m_2, \dots, m_d)$ is contained in the path components  $\mathbb {C}(\{i\}, 0, \dots, 0)\subseteq \mathbb {C}(\{i\}, m_2, \dots, m_d)$.
$\mathbb {C}(\{i\}, 0, \dots, 0)\subseteq \mathbb {C}(\{i\}, m_2, \dots, m_d)$.
Corollary 4.9 The category ![]() ${{\rm Cat}}_d$ is cartesian closed. For any two
${{\rm Cat}}_d$ is cartesian closed. For any two ![]() $d$-categories
$d$-categories ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $\mathscr {D}$, the internal mapping object
$\mathscr {D}$, the internal mapping object ![]() $\mathrm {Fun}_d(\mathscr {C}, \mathscr {D})$ in
$\mathrm {Fun}_d(\mathscr {C}, \mathscr {D})$ in ![]() ${{\rm Cat}}_d$ is the simplicial subspace of the internal mapping object
${{\rm Cat}}_d$ is the simplicial subspace of the internal mapping object ![]() $\mathscr {D}^{\mathscr {C}}$ in
$\mathscr {D}^{\mathscr {C}}$ in ![]() $d$-fold simplicial spaces given by
$d$-fold simplicial spaces given by
Example 4.10 Let ![]() $\mathscr {A}$ be a
$\mathscr {A}$ be a ![]() $(d-1)$-category. We define
$(d-1)$-category. We define ![]() $[1]_{\mathscr {A}}$ to be the
$[1]_{\mathscr {A}}$ to be the ![]() $d$-category associated to the
$d$-category associated to the ![]() $d$-fold category
$d$-fold category ![]() $[1]\boxtimes \mathscr {A}$ by the left adjoint of Lemma 4.7. In other words, maps of
$[1]\boxtimes \mathscr {A}$ by the left adjoint of Lemma 4.7. In other words, maps of ![]() $d$-categories
$d$-categories ![]() $[1]_{\mathscr {A}}\longrightarrow \mathscr {C}$ are equivalent to maps of
$[1]_{\mathscr {A}}\longrightarrow \mathscr {C}$ are equivalent to maps of ![]() $(d-1)$-categories
$(d-1)$-categories ![]() $\mathscr {A}\longrightarrow \mathscr {C}(1)$. Explicitly,
$\mathscr {A}\longrightarrow \mathscr {C}(1)$. Explicitly, ![]() $[1]_{\mathscr {A}}$ is the
$[1]_{\mathscr {A}}$ is the ![]() $d$-fold simplicial space
$d$-fold simplicial space ![]() $[1]\boxtimes \mathscr {A}\amalg _{\{0, 1\}\boxtimes \mathscr {A}} \{0, 1\}$, i.e. it is a
$[1]\boxtimes \mathscr {A}\amalg _{\{0, 1\}\boxtimes \mathscr {A}} \{0, 1\}$, i.e. it is a ![]() $d$-category with two objects
$d$-category with two objects ![]() $0, 1$ with trivial endomorphisms and
$0, 1$ with trivial endomorphisms and ![]() $\mathrm {Map}_{[1]_{\mathscr {A}}}(0, 1)=\mathscr {A}$.
$\mathrm {Map}_{[1]_{\mathscr {A}}}(0, 1)=\mathscr {A}$.
If ![]() $\mathscr {C}$ is a
$\mathscr {C}$ is a ![]() $d$-category, then the
$d$-category, then the ![]() $d$-category
$d$-category
can be described as follows. Its space of objects is given by the space of maps ![]() $\alpha \colon [1]_{\mathscr {A}}\longrightarrow \mathscr {C}$, i.e. of tuples
$\alpha \colon [1]_{\mathscr {A}}\longrightarrow \mathscr {C}$, i.e. of tuples ![]() $\alpha _0, \alpha _1\in \mathscr {C}$ and
$\alpha _0, \alpha _1\in \mathscr {C}$ and ![]() $\alpha \colon \mathscr {A}\longrightarrow \mathrm {Map}_{\mathscr {C}}(\alpha _0, \alpha _1)$. Unraveling the definitions, one sees that the
$\alpha \colon \mathscr {A}\longrightarrow \mathrm {Map}_{\mathscr {C}}(\alpha _0, \alpha _1)$. Unraveling the definitions, one sees that the ![]() $(d-1)$-category of maps between two such
$(d-1)$-category of maps between two such ![]() $\alpha, \beta \colon [1]_{\mathscr {A}}\longrightarrow \mathscr {C}$ is given by the following pullback.
$\alpha, \beta \colon [1]_{\mathscr {A}}\longrightarrow \mathscr {C}$ is given by the following pullback.

Remark 4.11 There is a fully faithful functor ![]() $\iota \colon {{\rm Cat}}_{d-1}\hookrightarrow {{\rm Cat}}_d$, sending a
$\iota \colon {{\rm Cat}}_{d-1}\hookrightarrow {{\rm Cat}}_d$, sending a ![]() $(d-1)$-category
$(d-1)$-category ![]() $\mathscr {C}$ to the
$\mathscr {C}$ to the ![]() $d$-fold simplicial space
$d$-fold simplicial space ![]() $\iota (\mathscr {C})(m_1, \dots, m_d)=\mathscr {C}(m_1, \dots, m_{d-1})$ which is constant in the last variable. This functor has a left adjoint
$\iota (\mathscr {C})(m_1, \dots, m_d)=\mathscr {C}(m_1, \dots, m_{d-1})$ which is constant in the last variable. This functor has a left adjoint ![]() $|-|$ sending a
$|-|$ sending a ![]() $d$-fold category
$d$-fold category ![]() $\mathscr {C}$ to the
$\mathscr {C}$ to the ![]() $(d-1)$-fold category
$(d-1)$-fold category
and a right adjoint ![]() $\mathfrak {c}_{d-1}$ given by
$\mathfrak {c}_{d-1}$ given by ![]() $\mathfrak {c}_{d-1}(\mathscr {C})(m_1, \dots, m_{d-1})=\mathscr {C}(m_1, \dots, m_{d-1}, 0)$, which we will refer to as the
$\mathfrak {c}_{d-1}(\mathscr {C})(m_1, \dots, m_{d-1})=\mathscr {C}(m_1, \dots, m_{d-1}, 0)$, which we will refer to as the ![]() $(d-1)$-core.
$(d-1)$-core.
4.2 Point-set models
To produce examples of ![]() $d$-categories, it will be more useful to think of
$d$-categories, it will be more useful to think of ![]() $d$-categories as categories enriched in
$d$-categories as categories enriched in ![]() $(d-1)$-categories. This is probably best done using the theory of enriched
$(d-1)$-categories. This is probably best done using the theory of enriched ![]() $\infty$-categories [Reference Gepner and HaugsengGH15, Reference HinichHin20]. We will take a more rigid, model-categorical approach instead (which has the advantage of not relying on Lurie's (un)straightening equivalence). Recall from Notation 4.5 how we view presheaves on
$\infty$-categories [Reference Gepner and HaugsengGH15, Reference HinichHin20]. We will take a more rigid, model-categorical approach instead (which has the advantage of not relying on Lurie's (un)straightening equivalence). Recall from Notation 4.5 how we view presheaves on ![]() $\mathbf {\Delta }_d$ as
$\mathbf {\Delta }_d$ as ![]() $d$-fold simplicial spaces using the localizations
$d$-fold simplicial spaces using the localizations ![]() $\mathbf {\Delta }^{\times d}\longrightarrow \mathbf {\Delta }\times \mathbf {\Delta }_{d-1}\longrightarrow \mathbf {\Delta }_d$.
$\mathbf {\Delta }^{\times d}\longrightarrow \mathbf {\Delta }\times \mathbf {\Delta }_{d-1}\longrightarrow \mathbf {\Delta }_d$.
Definition 4.12 A functor ![]() $X\colon \mathbf {\Delta }_d\longrightarrow \mathscr {S}$ is said to be a
$X\colon \mathbf {\Delta }_d\longrightarrow \mathscr {S}$ is said to be a ![]() $d$-categorical algebra if it satisfies the following conditions:
$d$-categorical algebra if it satisfies the following conditions:
(1) each
 $X(n)\colon \mathbf {\Delta }_{d-1}\longrightarrow \mathscr {S}$ is a
$X(n)\colon \mathbf {\Delta }_{d-1}\longrightarrow \mathscr {S}$ is a  $(d-1)$-category (and
$(d-1)$-category (and  $X(0)$ is a space);
$X(0)$ is a space);(2)
 $X$ satisfies the Segal condition, i.e.
$X$ satisfies the Segal condition, i.e.  $X(n)\longrightarrow X(1)\times _{X(0)} \cdots \times _{X(0)} X(1)$ is an equivalence.
$X(n)\longrightarrow X(1)\times _{X(0)} \cdots \times _{X(0)} X(1)$ is an equivalence.
Remark 4.13 The category of ![]() $d$-categories can be identified with the full subcategory of the category of
$d$-categories can be identified with the full subcategory of the category of ![]() $d$-categorical algebras, on those
$d$-categorical algebras, on those ![]() $d$-categorical algebras that are furthermore complete [Reference Gepner and HaugsengGH15, Reference LurieLur09b]. The inclusion of
$d$-categorical algebras that are furthermore complete [Reference Gepner and HaugsengGH15, Reference LurieLur09b]. The inclusion of ![]() $d$-categories into
$d$-categories into ![]() $d$-categorical algebras admits a left adjoint
$d$-categorical algebras admits a left adjoint ![]() $L_\mathrm {DK}$, which localizes at the class of Dwyer–Kan equivalences, i.e. maps
$L_\mathrm {DK}$, which localizes at the class of Dwyer–Kan equivalences, i.e. maps ![]() $Y\longrightarrow X$ with the following two properties (see [Reference Gepner and HaugsengGH15, Reference LurieLur09b]).
$Y\longrightarrow X$ with the following two properties (see [Reference Gepner and HaugsengGH15, Reference LurieLur09b]).
(1) Fully faithfulness:
 $Y(1)\longrightarrow X(1)\times _{X(0)^{\times 2}} Y(0)^{\times 2}$ is an equivalence of
$Y(1)\longrightarrow X(1)\times _{X(0)^{\times 2}} Y(0)^{\times 2}$ is an equivalence of  $(d-1)$-categories.
$(d-1)$-categories.(2) Essential surjectivity: the induced functor on homotopy categories
 $\mathrm {ho}(Y)\longrightarrow \mathrm {ho}(X)$ is essentially surjective.
$\mathrm {ho}(Y)\longrightarrow \mathrm {ho}(X)$ is essentially surjective.
In particular, for each ![]() $d$-categorical algebra
$d$-categorical algebra ![]() $X$, the map
$X$, the map ![]() $X\longrightarrow L_\mathrm {DK}(X)$ is a Dwyer–Kan equivalence. In fact, the explicit construction shows that
$X\longrightarrow L_\mathrm {DK}(X)$ is a Dwyer–Kan equivalence. In fact, the explicit construction shows that ![]() $X\longrightarrow L_\mathrm {DK}(X)$ is not just essentially surjective, but that
$X\longrightarrow L_\mathrm {DK}(X)$ is not just essentially surjective, but that ![]() $X(0)\longrightarrow L_\mathrm {DK}(X)(0)$ is already surjective on
$X(0)\longrightarrow L_\mathrm {DK}(X)(0)$ is already surjective on ![]() $\pi _0$ (see [Reference LurieLur09b, Proposition 1.2.27]).
$\pi _0$ (see [Reference LurieLur09b, Proposition 1.2.27]).
Definition 4.14 Recall that there is a localization functor ![]() $\mathrm {sSet}\longrightarrow \mathscr {S}$ inverting the weak equivalences for the Kan–Quillen model structure. We will say that a functor
$\mathrm {sSet}\longrightarrow \mathscr {S}$ inverting the weak equivalences for the Kan–Quillen model structure. We will say that a functor ![]() $X\colon \mathbf {\Delta }_d^{\mathrm {op}}\longrightarrow \mathrm {sSet}$ is a
$X\colon \mathbf {\Delta }_d^{\mathrm {op}}\longrightarrow \mathrm {sSet}$ is a ![]() $d$-category model (respectively,
$d$-category model (respectively, ![]() $d$-categorical algebra model) if the composed functor
$d$-categorical algebra model) if the composed functor ![]() $\mathbf {\Delta }_d^{\mathrm {op}}\longrightarrow \mathrm {sSet}\longrightarrow \mathscr {S}$ is a
$\mathbf {\Delta }_d^{\mathrm {op}}\longrightarrow \mathrm {sSet}\longrightarrow \mathscr {S}$ is a ![]() $d$-category (respectively,
$d$-category (respectively, ![]() $d$-categorical algebra).
$d$-categorical algebra).
Construction 4.15 The ![]() $d$-categorical model structure on
$d$-categorical model structure on ![]() $\mathrm {sPSh}(\mathbf {\Delta }_d)=\mathrm {Fun}(\mathbf {\Delta }_d^{\mathrm {op}}, \mathrm {sSet})$ is the left proper, combinatorial model structure characterized uniquely by the following properties [Reference LurieLur09b, Proposition 1.5.4].
$\mathrm {sPSh}(\mathbf {\Delta }_d)=\mathrm {Fun}(\mathbf {\Delta }_d^{\mathrm {op}}, \mathrm {sSet})$ is the left proper, combinatorial model structure characterized uniquely by the following properties [Reference LurieLur09b, Proposition 1.5.4].
(1) The cofibrations are the monomorphisms and, in particular, every object is cofibrant.
(2) An object
 $X$ is fibrant if and only if it is fibrant in the injective model structure and it is a
$X$ is fibrant if and only if it is fibrant in the injective model structure and it is a  $d$-category model.
$d$-category model.(3) A weak equivalence between
 $d$-category models is a levelwise weak equivalence of simplicial sets (in the Kan–Quillen model structure).
$d$-category models is a levelwise weak equivalence of simplicial sets (in the Kan–Quillen model structure).
We will write ![]() $\mathsf {Cat}_d$ for the full subcategory of
$\mathsf {Cat}_d$ for the full subcategory of ![]() $\mathrm {sPSh}(\mathbf {\Delta }_d)$ on the injectively fibrant
$\mathrm {sPSh}(\mathbf {\Delta }_d)$ on the injectively fibrant ![]() $d$-category models.
$d$-category models.
Remark 4.16 The ![]() $d$-categorical model structure is a left Bousfield localization of the injective model structure on
$d$-categorical model structure is a left Bousfield localization of the injective model structure on ![]() $\mathrm {sPSh}(\mathbf {\Delta }_d)$. Since the latter is a model for the
$\mathrm {sPSh}(\mathbf {\Delta }_d)$. Since the latter is a model for the ![]() $\infty$-category of functors
$\infty$-category of functors ![]() $\mathbf {\Delta }_d^{\mathrm {op}}\longrightarrow \mathscr {S}$ (see [Reference LurieLur09a, Proposition A.3.4.13]), it follows immediately that
$\mathbf {\Delta }_d^{\mathrm {op}}\longrightarrow \mathscr {S}$ (see [Reference LurieLur09a, Proposition A.3.4.13]), it follows immediately that ![]() $\mathrm {Cat}_d$ is equivalent to the localization of
$\mathrm {Cat}_d$ is equivalent to the localization of ![]() $\mathsf {Cat}_d$ at the
$\mathsf {Cat}_d$ at the ![]() $d$-categorical (equivalently, pointwise) weak equivalences.
$d$-categorical (equivalently, pointwise) weak equivalences.
Remark 4.17 The injective model structure on ![]() $\mathrm {sPSh}(\mathbf {\Delta }_d)$ is a monoidal model structure for the cartesian product [Reference RezkRez10, Proposition 2.9], which presents the cartesian monoidal structure on
$\mathrm {sPSh}(\mathbf {\Delta }_d)$ is a monoidal model structure for the cartesian product [Reference RezkRez10, Proposition 2.9], which presents the cartesian monoidal structure on ![]() $\mathrm {Fun}(\mathbf {\Delta }_d^{\mathrm {op}}, \mathscr {S})$. Corollary 4.9 shows that
$\mathrm {Fun}(\mathbf {\Delta }_d^{\mathrm {op}}, \mathscr {S})$. Corollary 4.9 shows that ![]() $\mathrm {Fun}(\mathbf {\Delta }_d^{\mathrm {op}}, \mathscr {S})\leftrightarrows \mathrm {Cat}_d$ is a monoidal localization for the cartesian product; this implies that the
$\mathrm {Fun}(\mathbf {\Delta }_d^{\mathrm {op}}, \mathscr {S})\leftrightarrows \mathrm {Cat}_d$ is a monoidal localization for the cartesian product; this implies that the ![]() $d$-categorical model structure on
$d$-categorical model structure on ![]() $\mathrm {sPSh}(\mathbf {\Delta }_d)$ is monoidal as well. In particular, this implies that the category
$\mathrm {sPSh}(\mathbf {\Delta }_d)$ is monoidal as well. In particular, this implies that the category ![]() $\mathsf {Cat}_d$ is cartesian closed.
$\mathsf {Cat}_d$ is cartesian closed.
Construction 4.18 Let ![]() $\mathsf {CatAlg}_d\subseteq \mathrm {sPSh}(\mathbf {\Delta }_d)\subseteq \mathrm {Fun}\big (\mathbf {\Delta }^{\mathrm {op}}, \mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )$ denote the full subcategory spanned by the functors
$\mathsf {CatAlg}_d\subseteq \mathrm {sPSh}(\mathbf {\Delta }_d)\subseteq \mathrm {Fun}\big (\mathbf {\Delta }^{\mathrm {op}}, \mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )$ denote the full subcategory spanned by the functors ![]() $X\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathsf {Cat}_{d-1}$ that are
$X\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathsf {Cat}_{d-1}$ that are ![]() $d$-categorical algebra models, i.e. explicitly:
$d$-categorical algebra models, i.e. explicitly:
– each
 $X(n)\colon \mathbf {\Delta }_{d-1}^{\mathrm {op}}\longrightarrow \mathrm {sSet}$ is an injectively fibrant
$X(n)\colon \mathbf {\Delta }_{d-1}^{\mathrm {op}}\longrightarrow \mathrm {sSet}$ is an injectively fibrant  $(d-1)$-category model and
$(d-1)$-category model and  $X(0)$ is constant on a Kan complex;
$X(0)$ is constant on a Kan complex;–
 $X$ satisfies the Segal conditions in the first simplicial variable.
$X$ satisfies the Segal conditions in the first simplicial variable.
We will say that a map ![]() $Y\longrightarrow X$ is a Dwyer–Kan equivalence if the corresponding map of categorical algebras is a Dwyer–Kan equivalence as in Remark 4.13. Furthermore, we will say that a map
$Y\longrightarrow X$ is a Dwyer–Kan equivalence if the corresponding map of categorical algebras is a Dwyer–Kan equivalence as in Remark 4.13. Furthermore, we will say that a map ![]() $Y\longrightarrow X$ is an isofibration if:
$Y\longrightarrow X$ is an isofibration if:
(1) each
 $Y(n)\longrightarrow X(n)$ is a fibration in
$Y(n)\longrightarrow X(n)$ is a fibration in  $\mathsf {Cat}_{d-1}$, i.e. an injective fibration of simplicial presheaves on
$\mathsf {Cat}_{d-1}$, i.e. an injective fibration of simplicial presheaves on  $\mathbf {\Delta }_{d-1}$;
$\mathbf {\Delta }_{d-1}$;(2) the induced map on homotopy categories
 $\mathrm {ho}(Y)\longrightarrow \mathrm {ho}(X)$ is an isofibration.
$\mathrm {ho}(Y)\longrightarrow \mathrm {ho}(X)$ is an isofibration.
With these classes of maps, ![]() $\mathsf {CatAlg}_d$ becomes a category of fibrant objects as in Appendix A. A map
$\mathsf {CatAlg}_d$ becomes a category of fibrant objects as in Appendix A. A map ![]() $Y\longrightarrow X$ is an acyclic fibration if and only if each
$Y\longrightarrow X$ is an acyclic fibration if and only if each ![]() $Y(n)\longrightarrow X(n)$ is an injective fibration,
$Y(n)\longrightarrow X(n)$ is an injective fibration, ![]() $Y(0)\longrightarrow X(0)$ is surjective on
$Y(0)\longrightarrow X(0)$ is surjective on ![]() $\pi _0$ and
$\pi _0$ and ![]() $Y(1)\longrightarrow X(1)\times _{X(0)^\times 2} Y(0)^{\times 2}$ is a weak equivalence. To factor a map
$Y(1)\longrightarrow X(1)\times _{X(0)^\times 2} Y(0)^{\times 2}$ is a weak equivalence. To factor a map ![]() $Y\longrightarrow X$ in
$Y\longrightarrow X$ in ![]() $\mathsf {CatAlg}_{d}$ into a weak equivalence followed by a fibration, one can simply factor it into a weak equivalence followed by a fibration with respect to the
$\mathsf {CatAlg}_{d}$ into a weak equivalence followed by a fibration, one can simply factor it into a weak equivalence followed by a fibration with respect to the ![]() $d$-categorical model structure on
$d$-categorical model structure on ![]() $\mathrm {sPSh}(\mathbf {\Delta }_d)$; such fibrations are isofibrations by the right lifting property against
$\mathrm {sPSh}(\mathbf {\Delta }_d)$; such fibrations are isofibrations by the right lifting property against ![]() $\{0\}\longrightarrow H$, where
$\{0\}\longrightarrow H$, where ![]() $H$ is the simplicial set from § 2.
$H$ is the simplicial set from § 2.
Construction 4.19 Let us write ![]() $\mathrm {Cat}(\mathsf {Cat}_{d-1})$ for the
$\mathrm {Cat}(\mathsf {Cat}_{d-1})$ for the ![]() $(1, 1)$-category of categories (strictly) enriched over the cartesian monoidal category
$(1, 1)$-category of categories (strictly) enriched over the cartesian monoidal category ![]() $\mathsf {Cat}_{d-1}$. The nerve provides a fully faithful functor
$\mathsf {Cat}_{d-1}$. The nerve provides a fully faithful functor ![]() $\mathrm {N}\colon {{\rm Cat}}(\mathsf {Cat}_{d-1})\hookrightarrow \mathsf {CatAlg}_d$, which sends an enriched category
$\mathrm {N}\colon {{\rm Cat}}(\mathsf {Cat}_{d-1})\hookrightarrow \mathsf {CatAlg}_d$, which sends an enriched category ![]() $\mathsf {C}$ to the simplicial diagram in
$\mathsf {C}$ to the simplicial diagram in ![]() $\mathsf {Cat}_{d-1}$ given by
$\mathsf {Cat}_{d-1}$ given by
In particular, ![]() $\mathrm {N}(\mathsf {C})(0)$ is simply the set of objects of
$\mathrm {N}(\mathsf {C})(0)$ is simply the set of objects of ![]() $\mathsf {C}$. We will say that a map of enriched categories is a Dwyer–Kan equivalence, respectively, an isofibration, if its image under the nerve functor is such. This makes
$\mathsf {C}$. We will say that a map of enriched categories is a Dwyer–Kan equivalence, respectively, an isofibration, if its image under the nerve functor is such. This makes ![]() $\mathrm {Cat}(\mathsf {Cat}_{d-1})$ a category of fibrant objects.
$\mathrm {Cat}(\mathsf {Cat}_{d-1})$ a category of fibrant objects.
More precisely, the category of categories enriched in ![]() $\mathrm {sPSh}(\mathbf {\Delta }_{d-1})$ carries a model structure [Reference LurieLur09a, Proposition A.3.2.4], since the
$\mathrm {sPSh}(\mathbf {\Delta }_{d-1})$ carries a model structure [Reference LurieLur09a, Proposition A.3.2.4], since the ![]() $(d-1)$-categorical model structure on
$(d-1)$-categorical model structure on ![]() $\mathrm {sPSh}(\mathbf {\Delta }_{d-1})$ is excellent in the sense of [Reference LurieLur09a, Definition A.3.2.16]. It follows from [Reference LurieLur09a, Theorem A.3.2.24] that
$\mathrm {sPSh}(\mathbf {\Delta }_{d-1})$ is excellent in the sense of [Reference LurieLur09a, Definition A.3.2.16]. It follows from [Reference LurieLur09a, Theorem A.3.2.24] that ![]() ${{\rm Cat}}(\mathsf {Cat}_{d-1})$ (with the above classes of Dwyer–Kan equivalences and isofibrations) is the category of fibrant objects associated to this model category.
${{\rm Cat}}(\mathsf {Cat}_{d-1})$ (with the above classes of Dwyer–Kan equivalences and isofibrations) is the category of fibrant objects associated to this model category.
Proposition 4.20 The three categories of fibrant objects considered above fit into a diagram of fully faithful inclusions
that preserve fibrations and weak equivalences. The induced functors on localizations are equivalences, so that each of these relative categories is a model for ![]() $\mathrm {Cat}_d$.
$\mathrm {Cat}_d$.
Proof. The right inclusion ![]() $\mathsf {Cat}_d\longrightarrow \mathsf {CatAlg}_{d}$ has a homotopy inverse
$\mathsf {Cat}_d\longrightarrow \mathsf {CatAlg}_{d}$ has a homotopy inverse ![]() $L_\mathrm {DK}$, given by taking a fibrant replacement of a
$L_\mathrm {DK}$, given by taking a fibrant replacement of a ![]() $d$-categorical algebra model in the
$d$-categorical algebra model in the ![]() $d$-categorical model structure. The resulting objects are then related by a Dwyer–Kan equivalence.
$d$-categorical model structure. The resulting objects are then related by a Dwyer–Kan equivalence.
Furthermore, the composite functor ![]() $L_\mathrm {DK}\circ \mathrm {N}\colon \mathrm {Cat}(\mathsf {Cat}_{d-1})\longrightarrow \mathsf {Cat}_d$ can be identified with the composite
$L_\mathrm {DK}\circ \mathrm {N}\colon \mathrm {Cat}(\mathsf {Cat}_{d-1})\longrightarrow \mathsf {Cat}_d$ can be identified with the composite
where ![]() $\mathrm {Seg}_{\mathrm {sPSh}(\mathbf {\Delta }_{d-1})}$ is the category of Segal precategories from [Reference LurieLur09b, § 2]. Here the first functor
$\mathrm {Seg}_{\mathrm {sPSh}(\mathbf {\Delta }_{d-1})}$ is the category of Segal precategories from [Reference LurieLur09b, § 2]. Here the first functor ![]() $\mathrm {N}$ is a right Quillen equivalence preserving weak equivalences [Reference LurieLur09b, Theorem 2.2.16, Remark 2.2.19]. The functor
$\mathrm {N}$ is a right Quillen equivalence preserving weak equivalences [Reference LurieLur09b, Theorem 2.2.16, Remark 2.2.19]. The functor ![]() $\mathrm {UnPre}$ is a left Quillen equivalence preserving weak equivalences by [Reference LurieLur09b, Propositions 2.3.1 and 2.3.9 and Lemma 2.3.14]: this uses the fact that the inclusion
$\mathrm {UnPre}$ is a left Quillen equivalence preserving weak equivalences by [Reference LurieLur09b, Propositions 2.3.1 and 2.3.9 and Lemma 2.3.14]: this uses the fact that the inclusion ![]() $\mathrm {sPSh}(\mathbf {\Delta }_{d})\hookrightarrow \mathrm {Fun}\big (\mathbf {\Delta }^{\mathrm {op}}, \mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )$ is a Quillen equivalence between the
$\mathrm {sPSh}(\mathbf {\Delta }_{d})\hookrightarrow \mathrm {Fun}\big (\mathbf {\Delta }^{\mathrm {op}}, \mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )$ is a Quillen equivalence between the ![]() $d$-categorical model structure and the ‘complete Segal model structure’ of [Reference LurieLur09b], which detects cofibrations and weak equivalences. The last functor takes a fibrant replacement, so it follows that
$d$-categorical model structure and the ‘complete Segal model structure’ of [Reference LurieLur09b], which detects cofibrations and weak equivalences. The last functor takes a fibrant replacement, so it follows that ![]() $L_\mathrm {DK}\circ \mathrm {N}$ induces an equivalence on localizations.
$L_\mathrm {DK}\circ \mathrm {N}$ induces an equivalence on localizations.
Remark 4.21 Let us write ![]() $\widehat {\mathrm {N}}\colon \mathrm {Cat}(\mathsf {Cat}_{d-1})\longrightarrow \mathrm {Cat}_d$ for the composite functor
$\widehat {\mathrm {N}}\colon \mathrm {Cat}(\mathsf {Cat}_{d-1})\longrightarrow \mathrm {Cat}_d$ for the composite functor ![]() $L_\mathrm {DK}\circ N$. By Remark 4.13,
$L_\mathrm {DK}\circ N$. By Remark 4.13, ![]() $\widehat {\mathrm {N}}(\mathsf {C})$ is a
$\widehat {\mathrm {N}}(\mathsf {C})$ is a ![]() $d$-category which comes with a Dwyer–Kan equivalence
$d$-category which comes with a Dwyer–Kan equivalence ![]() $\mathrm {N}(\mathsf {C})\longrightarrow \widehat {\mathrm {N}}(\mathsf {C})$ from the nerve of
$\mathrm {N}(\mathsf {C})\longrightarrow \widehat {\mathrm {N}}(\mathsf {C})$ from the nerve of ![]() $\mathsf {C}$; in particular, every object of
$\mathsf {C}$; in particular, every object of ![]() $\widehat {\mathrm {N}}(\mathsf {C})$ is homotopic to an object from
$\widehat {\mathrm {N}}(\mathsf {C})$ is homotopic to an object from ![]() $\mathsf {C}$ and for any two objects in
$\mathsf {C}$ and for any two objects in ![]() $\mathsf {C}$,
$\mathsf {C}$, ![]() $\mathrm {Map}_{\mathsf {C}}(c_0, c_1)$ is a model for the
$\mathrm {Map}_{\mathsf {C}}(c_0, c_1)$ is a model for the ![]() $(d-1)$-category of maps between their images in
$(d-1)$-category of maps between their images in ![]() $\widehat {\mathrm {N}}(\mathsf {C})$.
$\widehat {\mathrm {N}}(\mathsf {C})$.
Definition 4.22 The (large) ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathbf {Cat}_{d}$ of
$\mathbf {Cat}_{d}$ of ![]() $d$-categories is given by
$d$-categories is given by ![]() $\widehat {\mathrm {N}}(\mathsf {Cat}_{d})$, where
$\widehat {\mathrm {N}}(\mathsf {Cat}_{d})$, where ![]() $\mathsf {Cat}_{d}$ is enriched over itself as in Remark 4.17.
$\mathsf {Cat}_{d}$ is enriched over itself as in Remark 4.17.
Remark 4.23 Note that the ![]() $1$-category underlying the
$1$-category underlying the ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathbf {Cat}_{d}$ arises from the simplicially enriched category of fibrant–cofibrant objects in the
$\mathbf {Cat}_{d}$ arises from the simplicially enriched category of fibrant–cofibrant objects in the ![]() $d$-categorical model structure; in particular, it is equivalent to
$d$-categorical model structure; in particular, it is equivalent to ![]() $\mathrm {Cat}_d$ (see [Reference LurieLur09a, Lemma A.3.6.17]).
$\mathrm {Cat}_d$ (see [Reference LurieLur09a, Lemma A.3.6.17]).
It follows from [Reference HaugsengHau15] that our definition of ![]() $\mathbf {Cat}_d$ (via point-set models) coincides with the definition of
$\mathbf {Cat}_d$ (via point-set models) coincides with the definition of ![]() $\mathbf {Cat}_d$ as the
$\mathbf {Cat}_d$ as the ![]() $d$-category-enriched
$d$-category-enriched ![]() $\infty$-category associated to
$\infty$-category associated to ![]() $\mathrm {Cat}_d$, viewed as enriched over itself using the cartesian closed structure.
$\mathrm {Cat}_d$, viewed as enriched over itself using the cartesian closed structure.
4.3 Copresheaves
If ![]() $\mathscr {C}$ is a
$\mathscr {C}$ is a ![]() $(d+1)$-category, we define the
$(d+1)$-category, we define the ![]() $(d+1)$-category of copresheaves (of
$(d+1)$-category of copresheaves (of ![]() $d$-categories) of
$d$-categories) of ![]() $\mathscr {C}$ to be the functor
$\mathscr {C}$ to be the functor ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_{d})$, i.e. as the internal mapping object in the category of (large)
$\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_{d})$, i.e. as the internal mapping object in the category of (large) ![]() $(d+1)$-categories. This
$(d+1)$-categories. This ![]() $(d+1)$-category can be presented explicitly in terms of the enriched categories model for
$(d+1)$-category can be presented explicitly in terms of the enriched categories model for ![]() $(d+1)$-categories.
$(d+1)$-categories.
Proposition 4.24 [Reference LurieLur09a, Proposition A.3.4.13]
Let ![]() $\mathsf {C}$ be a small
$\mathsf {C}$ be a small ![]() $\mathsf {Cat}_{d}$-enriched category and denote by
$\mathsf {Cat}_{d}$-enriched category and denote by ![]() $\mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathsf {Cat}_{d}\big )^\circ$ the
$\mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathsf {Cat}_{d}\big )^\circ$ the ![]() $\mathsf {Cat}_{d}$-enriched category of enriched functors
$\mathsf {Cat}_{d}$-enriched category of enriched functors ![]() $\mathsf {C}\longrightarrow \mathrm {sPSh}(\mathbf {\Delta }_d)$ that are fibrant–cofibrant in the projective model structure (for the
$\mathsf {C}\longrightarrow \mathrm {sPSh}(\mathbf {\Delta }_d)$ that are fibrant–cofibrant in the projective model structure (for the ![]() $d$-categorical model structure on simplicial presheaves). Then the map
$d$-categorical model structure on simplicial presheaves). Then the map
exhibits ![]() $\widehat {\mathrm {N}}(\mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathsf {Cat}_{d}\big )^\circ )$ as the internal mapping object in the category of (large)
$\widehat {\mathrm {N}}(\mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathsf {Cat}_{d}\big )^\circ )$ as the internal mapping object in the category of (large) ![]() $(d+1)$-categories.
$(d+1)$-categories.
In particular, using the point-set model of ![]() $\mathsf {Cat}_d$-enriched categories, a copresheaf
$\mathsf {Cat}_d$-enriched categories, a copresheaf ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d$ can be modeled by an enriched functor
$\mathscr {C}\longrightarrow \mathbf {Cat}_d$ can be modeled by an enriched functor ![]() $\mathsf {C}\longrightarrow \mathsf {Cat}_d$. In addition to this ‘internal’ definition of copresheaves, one can also describe copresheaves externally in terms of Segal objects, following [Reference Boavida de BritoBoa18] (see also [Reference RasekhRas21] for an in-depth discussion).
$\mathsf {C}\longrightarrow \mathsf {Cat}_d$. In addition to this ‘internal’ definition of copresheaves, one can also describe copresheaves externally in terms of Segal objects, following [Reference Boavida de BritoBoa18] (see also [Reference RasekhRas21] for an in-depth discussion).
Definition 4.25 Let ![]() $\mathscr {C}$ be a
$\mathscr {C}$ be a ![]() $(d+1)$-categorical algebra. A map of
$(d+1)$-categorical algebra. A map of ![]() $(d+1)$-fold simplicial spaces
$(d+1)$-fold simplicial spaces ![]() $X\longrightarrow \mathscr {C}$ is said to be a Segal copresheaf if the following two conditions hold.
$X\longrightarrow \mathscr {C}$ is said to be a Segal copresheaf if the following two conditions hold.
(1) The
 $d$-fold simplicial space
$d$-fold simplicial space  $X(0)$ is a
$X(0)$ is a  $d$-category.
$d$-category.(2) For each
 $[n]\in \mathbf {\Delta }$, there is the following pullback square of
$[n]\in \mathbf {\Delta }$, there is the following pullback square of  $d$-categories.
$d$-categories.

Let us write ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_{d}\subseteq \mathrm {Fun}\big ([1]\times \mathbf {\Delta }^{\times d+1, \mathrm {op}}, \mathscr {S}\big )$ for the full subcategory spanned by the Segal copresheaves
$\mathrm {coPSh}^{\mathrm {Seg}}_{d}\subseteq \mathrm {Fun}\big ([1]\times \mathbf {\Delta }^{\times d+1, \mathrm {op}}, \mathscr {S}\big )$ for the full subcategory spanned by the Segal copresheaves ![]() $X\longrightarrow \mathscr {C}$ where
$X\longrightarrow \mathscr {C}$ where ![]() $\mathscr {C}$ is a
$\mathscr {C}$ is a ![]() $(d+1)$-category. The codomain projection
$(d+1)$-category. The codomain projection ![]() $\pi \colon \mathrm {coPSh}^{\mathrm {Seg}}_{d}\longrightarrow \mathrm {Cat}_{d+1}$ is a cartesian fibration, since the pullback of a Segal copresheaf
$\pi \colon \mathrm {coPSh}^{\mathrm {Seg}}_{d}\longrightarrow \mathrm {Cat}_{d+1}$ is a cartesian fibration, since the pullback of a Segal copresheaf ![]() $X\longrightarrow \mathscr {C}$ along a map of
$X\longrightarrow \mathscr {C}$ along a map of ![]() $(d+1)$-categories
$(d+1)$-categories ![]() $\mathscr {C}'\longrightarrow \mathscr {C}$ is again a Segal copresheaf. We will write
$\mathscr {C}'\longrightarrow \mathscr {C}$ is again a Segal copresheaf. We will write ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_{d}(\mathscr {C})$ for the fiber over
$\mathrm {coPSh}^{\mathrm {Seg}}_{d}(\mathscr {C})$ for the fiber over ![]() $\mathscr {C}$.
$\mathscr {C}$.
Warning 4.26 When ![]() $d=0$, the domain of a Segal copresheaf over a
$d=0$, the domain of a Segal copresheaf over a ![]() $1$-category is itself a
$1$-category is itself a ![]() $1$-category [Reference Boavida de BritoBoa18, Corollary 1.19]; in this case, Segal copresheaves can be identified with left fibrations (or, in the terminology of § 5,
$1$-category [Reference Boavida de BritoBoa18, Corollary 1.19]; in this case, Segal copresheaves can be identified with left fibrations (or, in the terminology of § 5, ![]() $0$-cocartesian fibrations). Note that for
$0$-cocartesian fibrations). Note that for ![]() $d\geq 1$, the domain of a Segal copresheaf
$d\geq 1$, the domain of a Segal copresheaf ![]() $X\longrightarrow \mathscr {C}$ over a
$X\longrightarrow \mathscr {C}$ over a ![]() $(d+1)$-category is typically not itself a
$(d+1)$-category is typically not itself a ![]() $(d+1)$-category: if the domain were a
$(d+1)$-category: if the domain were a ![]() $(d+1)$-category, then all the fibers of the fibration would be spaces.
$(d+1)$-category, then all the fibers of the fibration would be spaces.
In the remainder of this section, we will recall the work of Boavida [Reference Boavida de BritoBoa18], which shows that the category of Segal copresheaves ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_{d}(\mathscr {C})$ coincides with the
$\mathrm {coPSh}^{\mathrm {Seg}}_{d}(\mathscr {C})$ coincides with the ![]() $1$-category underlying
$1$-category underlying ![]() $\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_{d})$. We will make use of point-set models to compare with Proposition 4.24.
$\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_{d})$. We will make use of point-set models to compare with Proposition 4.24.
Construction 4.27 Consider the functor ![]() ${{\rm Cat}}(\mathsf {Cat}_{d})^{\mathrm {op}}\longrightarrow \mathrm {FibCat}$ sending each
${{\rm Cat}}(\mathsf {Cat}_{d})^{\mathrm {op}}\longrightarrow \mathrm {FibCat}$ sending each ![]() $\mathsf {Cat}_{d}$-enriched category
$\mathsf {Cat}_{d}$-enriched category ![]() $\mathsf {C}$ to the category
$\mathsf {C}$ to the category ![]() $\mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathsf {Cat}_{d})$ of enriched functors. Note that this is the full subcategory of fibrant objects in the projective model structure on
$\mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathsf {Cat}_{d})$ of enriched functors. Note that this is the full subcategory of fibrant objects in the projective model structure on ![]() $\mathrm {Fun}\big (\mathsf {C}, \mathrm {sPSh}(\mathbf {\Delta }_{d})\big )$. We will write
$\mathrm {Fun}\big (\mathsf {C}, \mathrm {sPSh}(\mathbf {\Delta }_{d})\big )$. We will write
for its Grothendieck construction. Explicitly, an object ![]() $(\mathsf {C}, F)\in \mathsf {EnrFun}_d$ is a
$(\mathsf {C}, F)\in \mathsf {EnrFun}_d$ is a ![]() $\mathsf {Cat}_{d}$-enriched category
$\mathsf {Cat}_{d}$-enriched category ![]() $\mathsf {C}$ together with an enriched functor
$\mathsf {C}$ together with an enriched functor ![]() $F\colon \mathsf {C}\longrightarrow \mathsf {Cat}_{d}$.
$F\colon \mathsf {C}\longrightarrow \mathsf {Cat}_{d}$.
Lemma 4.28 The map ![]() $\mathsf {EnrFun}_d\longrightarrow \mathrm {Cat}(\mathsf {Cat}_{d})$ is a homotopy cartesian fibration between categories of fibrant objects, in the sense of Definition A.5.
$\mathsf {EnrFun}_d\longrightarrow \mathrm {Cat}(\mathsf {Cat}_{d})$ is a homotopy cartesian fibration between categories of fibrant objects, in the sense of Definition A.5.
Proof. We verify conditions (a) and (b) of Lemma A.2. For condition (a), note that for each weak equivalence ![]() $f\colon \mathsf {C}\longrightarrow \mathsf {D}$,
$f\colon \mathsf {C}\longrightarrow \mathsf {D}$, ![]() $f^*\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {D}, \mathsf {Cat}_{d})\longrightarrow \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathsf {Cat}_{d})$ is induced by a Quillen equivalence [Reference LurieLur09a, Proposition A.3.3.8]. For condition (b), we use Remark A.3: we can factor any
$f^*\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {D}, \mathsf {Cat}_{d})\longrightarrow \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathsf {Cat}_{d})$ is induced by a Quillen equivalence [Reference LurieLur09a, Proposition A.3.3.8]. For condition (b), we use Remark A.3: we can factor any ![]() $f\colon \mathsf {C}\longrightarrow \mathsf {D}$ into a trivial cofibration
$f\colon \mathsf {C}\longrightarrow \mathsf {D}$ into a trivial cofibration ![]() $i\colon \mathsf {C}\longrightarrow \mathsf {C}'$ (in the model structure on enriched categories) followed by a fibration
$i\colon \mathsf {C}\longrightarrow \mathsf {C}'$ (in the model structure on enriched categories) followed by a fibration ![]() $p\colon \mathsf {C}'\twoheadrightarrow \mathsf {D}$. Then
$p\colon \mathsf {C}'\twoheadrightarrow \mathsf {D}$. Then ![]() $i_!\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathrm {sPSh}(\mathbf {\Delta }_d))\leftrightarrows \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}', \mathrm {sPSh}(\mathbf {\Delta }_d))\colon i^*$ is a Quillen equivalence where
$i_!\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathrm {sPSh}(\mathbf {\Delta }_d))\leftrightarrows \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}', \mathrm {sPSh}(\mathbf {\Delta }_d))\colon i^*$ is a Quillen equivalence where ![]() $i_!$ preserves all weak equivalences. Indeed, this follows from the fact that
$i_!$ preserves all weak equivalences. Indeed, this follows from the fact that ![]() $i_!$ is left Quillen for the injective model structure as well, as a consequence of [Reference LurieLur09a, Remark A.2.9.27 and Proposition A.3.3.9].
$i_!$ is left Quillen for the injective model structure as well, as a consequence of [Reference LurieLur09a, Remark A.2.9.27 and Proposition A.3.3.9].
Construction 4.29 Let ![]() $X\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathsf {Cat}_{d}$ be an object of
$X\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathsf {Cat}_{d}$ be an object of ![]() $\mathsf {CatAlg}_{d+1}$, i.e.
$\mathsf {CatAlg}_{d+1}$, i.e. ![]() $X$ satisfies the Segal conditions and
$X$ satisfies the Segal conditions and ![]() $X(0)\in \mathrm {sPSh}(\mathbf {\Delta }_{d})$ is constant on a simplicial set. The category
$X(0)\in \mathrm {sPSh}(\mathbf {\Delta }_{d})$ is constant on a simplicial set. The category ![]() $\mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})_{/X}$ can be endowed with the projective covariant model structure, in which:
$\mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})_{/X}$ can be endowed with the projective covariant model structure, in which:
– trivial fibrations are maps
 $Y\longrightarrow Y'$ (over
$Y\longrightarrow Y'$ (over  $X$) such that each
$X$) such that each  $Y(n)\longrightarrow Y'(n)$ is an injective trivial fibration in
$Y(n)\longrightarrow Y'(n)$ is an injective trivial fibration in  $\mathrm {sPSh}(\mathbf {\Delta }_{d})$;
$\mathrm {sPSh}(\mathbf {\Delta }_{d})$;– fibrant objects are
 $Y\longrightarrow X$ such that each
$Y\longrightarrow X$ such that each  $Y(n)\longrightarrow X(n)$ is an injective fibration between injectively fibrant
$Y(n)\longrightarrow X(n)$ is an injective fibration between injectively fibrant  $(d-1)$-category models, such that
$(d-1)$-category models, such that  $Y(n)\longrightarrow X(n)\times _{X(\{0\})}^h Y(\{0\})$ is a weak equivalence.
$Y(n)\longrightarrow X(n)\times _{X(\{0\})}^h Y(\{0\})$ is a weak equivalence.
The identity functor determines a Quillen equivalence to the injective covariant model structure, defined similarly but as a left Bousfield localization of the injective model structure on ![]() $\mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_d)_{/X}$.
$\mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_d)_{/X}$.
We will write ![]() $\mathsf {coPSh}^{\mathrm {Seg, proj}}_d(X)$ for the category of fibrant objects in the projective covariant model structure. This determines a (pseudo-)functor
$\mathsf {coPSh}^{\mathrm {Seg, proj}}_d(X)$ for the category of fibrant objects in the projective covariant model structure. This determines a (pseudo-)functor ![]() $\mathsf {CatAlg}_{d+1}^{\mathrm {op}}\longrightarrow \mathrm {FibCat}$ sending
$\mathsf {CatAlg}_{d+1}^{\mathrm {op}}\longrightarrow \mathrm {FibCat}$ sending ![]() $X\mapsto \mathsf {coPSh}^{\mathrm {Seg, proj}}_d(X)$, where
$X\mapsto \mathsf {coPSh}^{\mathrm {Seg, proj}}_d(X)$, where ![]() $\mathsf {CatAlg}_{d+1}$ is a category of fibrant objects as in Construction 4.18. Let us write
$\mathsf {CatAlg}_{d+1}$ is a category of fibrant objects as in Construction 4.18. Let us write ![]() $\mathsf {coPSh}^{\mathrm {Seg, proj}}_d\longrightarrow \mathsf {CatAlg}_{d+1}$ for its Grothendieck construction.
$\mathsf {coPSh}^{\mathrm {Seg, proj}}_d\longrightarrow \mathsf {CatAlg}_{d+1}$ for its Grothendieck construction.
Lemma 4.30 The map ![]() $\mathsf {coPSh}^{\mathrm {Seg, proj}}_d\longrightarrow \mathsf {CatAlg}_{d+1}$ is a homotopy cartesian fibration between categories of fibrant objects, in the sense of Definition A.5.
$\mathsf {coPSh}^{\mathrm {Seg, proj}}_d\longrightarrow \mathsf {CatAlg}_{d+1}$ is a homotopy cartesian fibration between categories of fibrant objects, in the sense of Definition A.5.
Proof. We verify conditions (a) and (b) of Lemma A.2: for any Dwyer–Kan equivalence ![]() $f\colon X\longrightarrow X'$, there is an adjoint pair
$f\colon X\longrightarrow X'$, there is an adjoint pair ![]() $f_!\colon \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})_{/X}\leftrightarrows \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})_{/X'}\colon f^*$. This is both a Quillen pair for the projective covariant and injective covariant model structure; in particular,
$f_!\colon \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})_{/X}\leftrightarrows \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})_{/X'}\colon f^*$. This is both a Quillen pair for the projective covariant and injective covariant model structure; in particular, ![]() $f_!$ preserves all weak equivalences. It now follows from [Reference Boavida de BritoBoa18, Proposition 5.5] that
$f_!$ preserves all weak equivalences. It now follows from [Reference Boavida de BritoBoa18, Proposition 5.5] that ![]() $(f_!, f^*)$ is a Quillen equivalence: indeed, the result from [Reference Boavida de BritoBoa18] shows that the derived unit and counit are already equivalences pointwise in
$(f_!, f^*)$ is a Quillen equivalence: indeed, the result from [Reference Boavida de BritoBoa18] shows that the derived unit and counit are already equivalences pointwise in ![]() $\mathbf {\Delta }_{d}$. This immediately gives condition (a), whereas condition (b) follows from Remark A.3.
$\mathbf {\Delta }_{d}$. This immediately gives condition (a), whereas condition (b) follows from Remark A.3.
Construction 4.31 Finally, for each injectively fibrant ![]() $(d+1)$-category model
$(d+1)$-category model ![]() $X$, let us denote by
$X$, let us denote by ![]() $\mathsf {coPSh}^{\mathrm {Seg, inj}}_d(X)\subseteq \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})_{/X}$ the full subcategory of fibrant objects in the injective covariant model structure. This determines a (pseudo-)functor
$\mathsf {coPSh}^{\mathrm {Seg, inj}}_d(X)\subseteq \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})_{/X}$ the full subcategory of fibrant objects in the injective covariant model structure. This determines a (pseudo-)functor ![]() $\mathsf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathrm {FibCat}$, where
$\mathsf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathrm {FibCat}$, where ![]() $\mathsf {Cat}_{d+1}$ is a category of fibrant objects as in Construction 4.15. We will write
$\mathsf {Cat}_{d+1}$ is a category of fibrant objects as in Construction 4.15. We will write ![]() $\mathsf {coPSh}^{\mathrm {Seg, inj}}_d\longrightarrow \mathsf {Cat}_{d+1}$ for its Grothendieck construction.
$\mathsf {coPSh}^{\mathrm {Seg, inj}}_d\longrightarrow \mathsf {Cat}_{d+1}$ for its Grothendieck construction.
The same proof as in Lemma 4.30 shows that ![]() $\mathsf {coPSh}^{\mathrm {Seg, inj}}_d\longrightarrow \mathsf {Cat}_{d+1}$ is a homotopy cartesian fibration between categories of fibrant objects. In fact, unraveling the definitions shows that
$\mathsf {coPSh}^{\mathrm {Seg, inj}}_d\longrightarrow \mathsf {Cat}_{d+1}$ is a homotopy cartesian fibration between categories of fibrant objects. In fact, unraveling the definitions shows that ![]() $\mathsf {coPSh}^{\mathrm {Seg, inj}}_d$ can be identified with the category of fibrant objects for a model structure on
$\mathsf {coPSh}^{\mathrm {Seg, inj}}_d$ can be identified with the category of fibrant objects for a model structure on ![]() $\mathrm {Fun}\big ([1], \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})\big )$: indeed, one can take a left Bousfield localization of the injective model structure whose fibrant objects are injective fibrations
$\mathrm {Fun}\big ([1], \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_{d})\big )$: indeed, one can take a left Bousfield localization of the injective model structure whose fibrant objects are injective fibrations ![]() $Y\longrightarrow X$ that model Segal copresheaves in the sense of Definition 4.25. In particular, the localization of
$Y\longrightarrow X$ that model Segal copresheaves in the sense of Definition 4.25. In particular, the localization of ![]() $\mathsf {coPSh}^{\mathrm {Seg, inj}}_d\longrightarrow \mathsf {Cat}_{d+1}$ is precisely the functor
$\mathsf {coPSh}^{\mathrm {Seg, inj}}_d\longrightarrow \mathsf {Cat}_{d+1}$ is precisely the functor ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d\longrightarrow \mathrm {Cat}_{d+1}$ from Definition 4.25.
$\mathrm {coPSh}^{\mathrm {Seg}}_d\longrightarrow \mathrm {Cat}_{d+1}$ from Definition 4.25.
Theorem 4.32 (Rectification of Segal copresheaves, cf. [Reference Boavida de BritoBoa18, Theorem A])
For each ![]() $d\geq 0$, there is a commuting diagram of categories of fibrant objects
$d\geq 0$, there is a commuting diagram of categories of fibrant objects

in which the vertical functors are homotopy cartesian fibrations and the horizontal functors induce equivalences upon localization.
Proof. The bottom horizontal functors induce equivalences on localizations by Proposition 4.20. By Proposition A.7 and [Reference LurieLur09a, Corollary 2.4.4.4], the top horizontal functors induce equivalences on localizations as soon as the induced functors between fibers have this property. For the right square, this is immediate: the maps on fibers are induced by the Quillen equivalence between the injective and projective covariant model structure.
For the left square, one has to verify that for any enriched category ![]() $\mathsf {C}$, the functor between fibers
$\mathsf {C}$, the functor between fibers ![]() $\mathrm {N}\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathsf {Cat}_{d})\longrightarrow \mathsf {coPSh}^{\mathrm {Seg, proj}}_d(\mathrm {N}(\mathsf {C}))$ induces an equivalence on localizations. This functor sends an enriched functor
$\mathrm {N}\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathsf {Cat}_{d})\longrightarrow \mathsf {coPSh}^{\mathrm {Seg, proj}}_d(\mathrm {N}(\mathsf {C}))$ induces an equivalence on localizations. This functor sends an enriched functor ![]() $F\colon \mathsf {C}\longrightarrow \mathsf {Cat}_{d}$ to the obvious left fibration as follows:
$F\colon \mathsf {C}\longrightarrow \mathsf {Cat}_{d}$ to the obvious left fibration as follows:
Note that this arises from a right Quillen functor ![]() $\mathrm {N}\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathrm {sPSh}(\mathbf {\Delta }_d))\longrightarrow \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_d)_{/\mathrm {N}(\mathsf {C})}$ between the projective model structure on enriched functors and the projective covariant model structure on
$\mathrm {N}\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathrm {sPSh}(\mathbf {\Delta }_d))\longrightarrow \mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_d)_{/\mathrm {N}(\mathsf {C})}$ between the projective model structure on enriched functors and the projective covariant model structure on ![]() $\mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_d)_{/\mathrm {N}(\mathsf {C})}$. It follows from [Reference Boavida de BritoBoa18, Theorem A] that the derived unit and counit maps are pointwise weak equivalences in
$\mathrm {sPSh}(\mathbf {\Delta }\times \mathbf {\Delta }_d)_{/\mathrm {N}(\mathsf {C})}$. It follows from [Reference Boavida de BritoBoa18, Theorem A] that the derived unit and counit maps are pointwise weak equivalences in ![]() $\mathbf {\Delta }_d$. Consequently,
$\mathbf {\Delta }_d$. Consequently, ![]() $\mathrm {N}$ is a right Quillen equivalence (even when
$\mathrm {N}$ is a right Quillen equivalence (even when ![]() $\mathrm {sPSh}(\mathbf {\Delta }_d)$ is endowed with the injective, rather than
$\mathrm {sPSh}(\mathbf {\Delta }_d)$ is endowed with the injective, rather than ![]() $d$-categorical model structure) and the result follows.
$d$-categorical model structure) and the result follows.
Corollary 4.33 (Cf. [Reference Boavida de BritoBoa18, Theorem A])
For each ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$, there is an equivalence of
$\mathscr {C}$, there is an equivalence of ![]() $1$-categories
$1$-categories
Proof. It follows from Theorem 4.32 that the functor ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d\longrightarrow \mathrm {Cat}_{d+1}$ is modeled by
$\mathrm {coPSh}^{\mathrm {Seg}}_d\longrightarrow \mathrm {Cat}_{d+1}$ is modeled by ![]() $\pi \colon \mathsf {EnrFun}_d\longrightarrow \mathrm {Cat}(\mathsf {Cat}_{d})$. Proposition A.7 now implies that for any enriched category
$\pi \colon \mathsf {EnrFun}_d\longrightarrow \mathrm {Cat}(\mathsf {Cat}_{d})$. Proposition A.7 now implies that for any enriched category ![]() $\mathsf {C}$, the localization of the fiber
$\mathsf {C}$, the localization of the fiber ![]() $\pi ^{-1}(\mathsf {C})$ is a model for the fiber
$\pi ^{-1}(\mathsf {C})$ is a model for the fiber ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d(\mathscr {C})$ over the corresponding
$\mathrm {coPSh}^{\mathrm {Seg}}_d(\mathscr {C})$ over the corresponding ![]() $(d+1)$-category. The fiber
$(d+1)$-category. The fiber ![]() $\pi ^{-1}(\mathsf {C})$ is precisely the category of enriched functors
$\pi ^{-1}(\mathsf {C})$ is precisely the category of enriched functors ![]() $\mathsf {C}\longrightarrow \mathsf {Cat}_{d}$, whose localization models
$\mathsf {C}\longrightarrow \mathsf {Cat}_{d}$, whose localization models ![]() $\mathfrak {c}_1\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_{d})$ by Proposition 4.24.
$\mathfrak {c}_1\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_{d})$ by Proposition 4.24.
Remark 4.34 For ![]() $d=0$, this gives a version of (un)straightening for left fibrations over
$d=0$, this gives a version of (un)straightening for left fibrations over ![]() $1$-categories. For
$1$-categories. For ![]() $d>0$, viewing
$d>0$, viewing ![]() $\mathscr {C}$ as a presheaf on
$\mathscr {C}$ as a presheaf on ![]() $\mathbf {\Delta }\times \mathbf {\Delta }_d$, the above result essentially corresponds to (un)straightening for left fibrations, applied pointwise in
$\mathbf {\Delta }\times \mathbf {\Delta }_d$, the above result essentially corresponds to (un)straightening for left fibrations, applied pointwise in ![]() $\mathbf {\Delta }_d$.
$\mathbf {\Delta }_d$.
Corollary 4.35 Let ![]() $\mathscr {C}$ be a
$\mathscr {C}$ be a ![]() $1$-category, viewed as a
$1$-category, viewed as a ![]() $2$-category. Then there is an equivalence
$2$-category. Then there is an equivalence
to the category of cocartesian fibrations over ![]() $\mathscr {C}$ and maps preserving cocartesian morphisms.
$\mathscr {C}$ and maps preserving cocartesian morphisms.
Proof. We can combine Corollary 4.33 and Theorem 3.1, using that there are obvious equivalences ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_1(\mathscr {C})\simeq \mathrm {Fib}^{\mathrm {left, cart}}(\mathscr {C}\boxtimes [0])$ and
$\mathrm {coPSh}^{\mathrm {Seg}}_1(\mathscr {C})\simeq \mathrm {Fib}^{\mathrm {left, cart}}(\mathscr {C}\boxtimes [0])$ and ![]() ${{\rm Cocart}}_1(\mathscr {C})\simeq \mathrm {Fib}^{\mathrm {cocart, right}}(\mathscr {C}\boxtimes [0])$.
${{\rm Cocart}}_1(\mathscr {C})\simeq \mathrm {Fib}^{\mathrm {cocart, right}}(\mathscr {C}\boxtimes [0])$.
Example 4.36 Let ![]() $\mathscr {C}$ be a
$\mathscr {C}$ be a ![]() $(d+1)$-category and let
$(d+1)$-category and let ![]() $\mathrm {Tw}(\mathscr {C})\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow {{\rm Cat}}_{d}$ be the functor given by
$\mathrm {Tw}(\mathscr {C})\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow {{\rm Cat}}_{d}$ be the functor given by ![]() $\mathrm {Tw}(\mathscr {C})(n) = \mathscr {C}\big ([n]^{\mathrm {op}}\star [n]\big )$. Restriction along the inclusions
$\mathrm {Tw}(\mathscr {C})(n) = \mathscr {C}\big ([n]^{\mathrm {op}}\star [n]\big )$. Restriction along the inclusions ![]() $[n]^{\mathrm {op}}\hookrightarrow [n]^{\mathrm {op}}\star [n]\hookleftarrow [n]$ induces the following natural map of
$[n]^{\mathrm {op}}\hookrightarrow [n]^{\mathrm {op}}\star [n]\hookleftarrow [n]$ induces the following natural map of ![]() $(d+1)$-fold simplicial spaces:
$(d+1)$-fold simplicial spaces:
The Segal conditions on ![]() $\mathscr {C}$ imply that this is a Segal copresheaf. By Corollary 4.33, this corresponds to a
$\mathscr {C}$ imply that this is a Segal copresheaf. By Corollary 4.33, this corresponds to a ![]() $(d+1)$-functor that we will denote by
$(d+1)$-functor that we will denote by
This functor is easily described using point-set models: if ![]() $\mathsf {C}$ is an enriched category, then the above map of simplicial spaces is modeled by the object
$\mathsf {C}$ is an enriched category, then the above map of simplicial spaces is modeled by the object ![]() $\mathrm {Tw}(\mathrm {N}(\mathsf {C}))\longrightarrow \mathrm {N}(\mathsf {C})^{\mathrm {op}}\times \mathrm {N}(\mathsf {C})$ in
$\mathrm {Tw}(\mathrm {N}(\mathsf {C}))\longrightarrow \mathrm {N}(\mathsf {C})^{\mathrm {op}}\times \mathrm {N}(\mathsf {C})$ in ![]() $\mathsf {coPSh}^{\mathrm {Seg}, \mathrm {proj}}(\mathrm {N}(\mathsf {C}))$. Unraveling the definitions, this left fibration is exactly the image under
$\mathsf {coPSh}^{\mathrm {Seg}, \mathrm {proj}}(\mathrm {N}(\mathsf {C}))$. Unraveling the definitions, this left fibration is exactly the image under ![]() $N\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}^{\mathrm {op}}\times \mathsf {C}, \mathsf {Cat}_{d})\longrightarrow \mathrm {coPSh}^{\mathrm {Seg}, \mathrm {proj}}(\mathrm {N}(\mathsf {C}))$ of the (strict) mapping space functor
$N\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}^{\mathrm {op}}\times \mathsf {C}, \mathsf {Cat}_{d})\longrightarrow \mathrm {coPSh}^{\mathrm {Seg}, \mathrm {proj}}(\mathrm {N}(\mathsf {C}))$ of the (strict) mapping space functor ![]() $\mathrm {Map}_{\mathsf {C}}(-, -)\colon \mathsf {C}^{\mathrm {op}}\times \mathsf {C}\longrightarrow \mathsf {Cat}_{d}$.
$\mathrm {Map}_{\mathsf {C}}(-, -)\colon \mathsf {C}^{\mathrm {op}}\times \mathsf {C}\longrightarrow \mathsf {Cat}_{d}$.
Example 4.37 Consider a map in ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d$ corresponding to the following commuting square.
$\mathrm {coPSh}^{\mathrm {Seg}}_d$ corresponding to the following commuting square.

We will say that ![]() $x$ is a representation of
$x$ is a representation of ![]() $X$ if it defines a cocartesian arrow in
$X$ if it defines a cocartesian arrow in ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d$. Note that if we model
$\mathrm {coPSh}^{\mathrm {Seg}}_d$. Note that if we model ![]() $\mathscr {C}$ by an enriched category
$\mathscr {C}$ by an enriched category ![]() $\mathsf {C}$, then
$\mathsf {C}$, then ![]() $c^*\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathsf {Cat}_d)\longrightarrow \mathsf {Cat}_d$ admits a left adjoint
$c^*\colon \mathrm {Fun}_{\mathrm {enr}}(\mathsf {C}, \mathsf {Cat}_d)\longrightarrow \mathsf {Cat}_d$ admits a left adjoint ![]() $c_!$ preserving trivial fibrations. It follows from Proposition A.7(4) that the map
$c_!$ preserving trivial fibrations. It follows from Proposition A.7(4) that the map ![]() $\ast \longrightarrow \mathrm {Map}_{\mathsf {C}}(c, -)$ in
$\ast \longrightarrow \mathrm {Map}_{\mathsf {C}}(c, -)$ in ![]() $\mathsf {EnrFun}_d$ defines such a cocartesian arrow in
$\mathsf {EnrFun}_d$ defines such a cocartesian arrow in ![]() $\mathrm {coPSh}^{\mathrm {Seg}}$. Consequently, (
$\mathrm {coPSh}^{\mathrm {Seg}}$. Consequently, (
) defines a representation of ![]() $X$ if and only if it induces an equivalence
$X$ if and only if it induces an equivalence ![]() $\mathrm {Map}_{\mathscr {C}}(c, -)\simeq X$.
$\mathrm {Map}_{\mathscr {C}}(c, -)\simeq X$.
We will use the language of Example 4.37 to partially address the functoriality of Corollary 4.33.
Notation 4.39 For a regular uncountable cardinal ![]() $\kappa$, let us write
$\kappa$, let us write ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )$ for the category of Segal copresheaves
$\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )$ for the category of Segal copresheaves ![]() $X\longrightarrow \mathscr {C}$ whose fibers are essentially
$X\longrightarrow \mathscr {C}$ whose fibers are essentially ![]() $\kappa$-small. The codomain projection
$\kappa$-small. The codomain projection ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )\longrightarrow {{\rm Cat}}_{d+1}$ is a cartesian fibration. Taking the subcategory with only cartesian morphisms, we obtain a right fibration
$\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )\longrightarrow {{\rm Cat}}_{d+1}$ is a cartesian fibration. Taking the subcategory with only cartesian morphisms, we obtain a right fibration ![]() $\pi \colon \mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}\longrightarrow {{\rm Cat}}_{d+1}$.
$\pi \colon \mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}\longrightarrow {{\rm Cat}}_{d+1}$.
Note that there is a canonical element ![]() $u\in \mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}$, corresponding under the equivalence of Corollary 4.33 to the identity functor
$u\in \mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}$, corresponding under the equivalence of Corollary 4.33 to the identity functor ![]() $\mathbf {Cat}_d(\kappa )\longrightarrow \mathbf {Cat}_d(\kappa )$ on the small
$\mathbf {Cat}_d(\kappa )\longrightarrow \mathbf {Cat}_d(\kappa )$ on the small ![]() $(d+1)$-category of
$(d+1)$-category of ![]() $\kappa$-small
$\kappa$-small ![]() $d$-categories.
$d$-categories.
Proposition 4.40 The element ![]() $u\colon \ast \longrightarrow \mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )$ defines a representation of the right fibration
$u\colon \ast \longrightarrow \mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )$ defines a representation of the right fibration ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}\longrightarrow \mathrm {Cat}_{d+1}$. In other words, for every
$\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}\longrightarrow \mathrm {Cat}_{d+1}$. In other words, for every ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$, there is a
$\mathscr {C}$, there is a ![]() $1$-functorial equivalence between the space of
$1$-functorial equivalence between the space of ![]() $(d+1)$-functors
$(d+1)$-functors ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d(\kappa )$ and the space of Segal copresheaves
$\mathscr {C}\longrightarrow \mathbf {Cat}_d(\kappa )$ and the space of Segal copresheaves ![]() $X\longrightarrow \mathscr {C}$ with
$X\longrightarrow \mathscr {C}$ with ![]() $\kappa$-small fibers.
$\kappa$-small fibers.
Remark 4.41 For later purposes, we will mostly be interested in this result in the large setting, with ![]() $\kappa$ being the supremum of all small cardinals: in that case, it provides a
$\kappa$ being the supremum of all small cardinals: in that case, it provides a ![]() $1$-functorial equivalence between the spaces of
$1$-functorial equivalence between the spaces of ![]() $(d+1)$-functors
$(d+1)$-functors ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d$ and Segal copresheaves
$\mathscr {C}\longrightarrow \mathbf {Cat}_d$ and Segal copresheaves ![]() $X\longrightarrow \mathscr {C}$ with small fibers over a large
$X\longrightarrow \mathscr {C}$ with small fibers over a large ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$.
$\mathscr {C}$.
The proof uses the following well-known criterion for being a representation (cf. [Reference Boavida de BritoBoa18, Lemma 1.31], [Reference Kazhdan and VarshavskiĭKV14, Lemma 2.3.6] and [Reference RasekhRas21, Theorem 5.25]).
Lemma 4.42 Let ![]() $\mathscr {C}$ be a
$\mathscr {C}$ be a ![]() $(d+1)$-category and consider an arrow in
$(d+1)$-category and consider an arrow in ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d$ of the form (4.38). Then
$\mathrm {coPSh}^{\mathrm {Seg}}_d$ of the form (4.38). Then ![]() $x$ defines a representation of
$x$ defines a representation of ![]() $p\colon X\longrightarrow \mathscr {C}$ if and only if it determines an initial object in each
$p\colon X\longrightarrow \mathscr {C}$ if and only if it determines an initial object in each ![]() $1$-category
$1$-category ![]() $X(-, \vec {n}_{d})$.
$X(-, \vec {n}_{d})$.
Proof. Assuming ![]() $x$ defines a representation of
$x$ defines a representation of ![]() $X\longrightarrow \mathscr {C}$, we can model
$X\longrightarrow \mathscr {C}$, we can model ![]() $\mathscr {C}$ by an enriched category and identify
$\mathscr {C}$ by an enriched category and identify ![]() $x$ with the canonical map
$x$ with the canonical map ![]() $\mathrm {id}_c\colon \ast \longrightarrow N(\mathrm {Map}_{\mathsf {C}}(c, -))$. One easily verifies that
$\mathrm {id}_c\colon \ast \longrightarrow N(\mathrm {Map}_{\mathsf {C}}(c, -))$. One easily verifies that ![]() $\mathrm {id}_c$ defines an initial object in each degree
$\mathrm {id}_c$ defines an initial object in each degree ![]() $\vec {n}_{d}$.
$\vec {n}_{d}$.
Conversely, suppose that ![]() $x$ defines an initial object in each
$x$ defines an initial object in each ![]() $X(-, \vec {n}_d)$. Note that there is a fully faithful inclusion
$X(-, \vec {n}_d)$. Note that there is a fully faithful inclusion ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d\hookrightarrow \mathrm {Fun}(\mathbf {\Delta }_d, \mathrm {coPSh}^{\mathrm {Seg}}_0)$ which admits a left adjoint and preserves cartesian arrows. This implies that (4.38) defines a cocartesian arrow in
$\mathrm {coPSh}^{\mathrm {Seg}}_d\hookrightarrow \mathrm {Fun}(\mathbf {\Delta }_d, \mathrm {coPSh}^{\mathrm {Seg}}_0)$ which admits a left adjoint and preserves cartesian arrows. This implies that (4.38) defines a cocartesian arrow in ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d$ as soon as it does in
$\mathrm {coPSh}^{\mathrm {Seg}}_d$ as soon as it does in ![]() $\mathrm {Fun}(\mathbf {\Delta }_d, \mathrm {coPSh}^{\mathrm {Seg}}_0)$. It therefore suffices to verify that each
$\mathrm {Fun}(\mathbf {\Delta }_d, \mathrm {coPSh}^{\mathrm {Seg}}_0)$. It therefore suffices to verify that each ![]() $\ast \longrightarrow X(-, \vec {n}_d)$ defines a cocartesian arrow in the category of Segal copresheaves over
$\ast \longrightarrow X(-, \vec {n}_d)$ defines a cocartesian arrow in the category of Segal copresheaves over ![]() $1$-categories. This reduces everything to the case
$1$-categories. This reduces everything to the case ![]() $d=0$, where we can consider the following diagram.
$d=0$, where we can consider the following diagram.

One easily verifies that the right square defines a cocartesian arrow in the category ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_0$ of left fibrations. On the other hand, since
$\mathrm {coPSh}^{\mathrm {Seg}}_0$ of left fibrations. On the other hand, since ![]() $x\in X$ is an initial object, the left square represents the terminal copresheaf on
$x\in X$ is an initial object, the left square represents the terminal copresheaf on ![]() $X$, i.e. it also defines a cocartesian arrow in
$X$, i.e. it also defines a cocartesian arrow in ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_0$. The composite is then a cocartesian arrow as well, as desired.
$\mathrm {coPSh}^{\mathrm {Seg}}_0$. The composite is then a cocartesian arrow as well, as desired.
Proof of Proposition 4.40 By (the opposite of) Lemma 4.42, it suffices to show that ![]() $u$ defines a terminal object in
$u$ defines a terminal object in ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}$.
$\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}$.
Let us write ![]() $\mathsf {EnrFun}_d(\kappa )\subseteq \mathsf {EnrFun}_d$ for the subcategory of tuples
$\mathsf {EnrFun}_d(\kappa )\subseteq \mathsf {EnrFun}_d$ for the subcategory of tuples ![]() $(\mathsf {C}, F)$ consisting of a small
$(\mathsf {C}, F)$ consisting of a small ![]() $\mathsf {Cat}_d$-enriched category and an enriched functor
$\mathsf {Cat}_d$-enriched category and an enriched functor ![]() $F\colon \mathsf {C}\longrightarrow \mathsf {Cat}_d$ whose values are homotopy equivalent to
$F\colon \mathsf {C}\longrightarrow \mathsf {Cat}_d$ whose values are homotopy equivalent to ![]() $\kappa$-small objects. Lemma 4.28 and Theorem 4.32 imply that
$\kappa$-small objects. Lemma 4.28 and Theorem 4.32 imply that ![]() $\mathsf {EnrFun}_d(\kappa )\longrightarrow {{\rm Cat}}(\mathsf {Cat}_d)$ is a homotopically cartesian fibration between categories of fibrant objects, whose localization models
$\mathsf {EnrFun}_d(\kappa )\longrightarrow {{\rm Cat}}(\mathsf {Cat}_d)$ is a homotopically cartesian fibration between categories of fibrant objects, whose localization models ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )\longrightarrow {{\rm Cat}}_{d+1}$. The object
$\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )\longrightarrow {{\rm Cat}}_{d+1}$. The object ![]() $u\in \mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )$ simply corresponds to the tuple
$u\in \mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )$ simply corresponds to the tuple ![]() $u=(\mathsf {Cat}_d(\kappa ), \mathrm {id})$ consisting of the enriched category of
$u=(\mathsf {Cat}_d(\kappa ), \mathrm {id})$ consisting of the enriched category of ![]() $\kappa$-small
$\kappa$-small ![]() $d$-category models, together with the identity (or, more precisely, with the fully faithful inclusion
$d$-category models, together with the identity (or, more precisely, with the fully faithful inclusion ![]() $\mathsf {Cat}_d(\kappa )\hookrightarrow \mathsf {Cat}_d$).
$\mathsf {Cat}_d(\kappa )\hookrightarrow \mathsf {Cat}_d$).
Proposition A.7 now implies that ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}$ arises as the localization of the
$\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}$ arises as the localization of the ![]() $(1, 1)$-category
$(1, 1)$-category ![]() $\mathscr {H}=\mathsf {EnrFun}_d(\kappa )^{\mathrm {hocart}}$ of such tuples
$\mathscr {H}=\mathsf {EnrFun}_d(\kappa )^{\mathrm {hocart}}$ of such tuples ![]() $(\mathsf {C}, F)$, with homotopy cartesian maps between them (see Appendix A for more details). We have to show that
$(\mathsf {C}, F)$, with homotopy cartesian maps between them (see Appendix A for more details). We have to show that ![]() $\mathrm {Map}_{\mathscr {H}[W^{-1}]}(-, u)$ is the terminal (very large) presheaf. To this end, let
$\mathrm {Map}_{\mathscr {H}[W^{-1}]}(-, u)$ is the terminal (very large) presheaf. To this end, let ![]() $\psi \colon \mathscr {H}\longrightarrow \mathscr {H}[W^{-1}]$ denote the localization and consider the following adjoint pair between categories of very large presheaves:
$\psi \colon \mathscr {H}\longrightarrow \mathscr {H}[W^{-1}]$ denote the localization and consider the following adjoint pair between categories of very large presheaves:
Here ![]() $\psi ^*$ is fully faithful with essential image consisting of presheaves sending
$\psi ^*$ is fully faithful with essential image consisting of presheaves sending ![]() $W$ to equivalences. We have to show that
$W$ to equivalences. We have to show that ![]() $\psi _!(u)\simeq \ast$ (where we omit the Yoneda embedding from the notation).
$\psi _!(u)\simeq \ast$ (where we omit the Yoneda embedding from the notation).
To see this, consider for each small cardinal ![]() $\lambda \geq \kappa$ the full
$\lambda \geq \kappa$ the full ![]() $\mathsf {Cat}_{d}$-enriched subcategory
$\mathsf {Cat}_{d}$-enriched subcategory ![]() $\mathsf {U}_{\lambda, n}\subseteq \mathrm {Fun}([n], \mathsf {Cat}_d)$ spanned by sequences of trivial fibrations
$\mathsf {U}_{\lambda, n}\subseteq \mathrm {Fun}([n], \mathsf {Cat}_d)$ spanned by sequences of trivial fibrations ![]() $A_0\twoheadrightarrow \dots \twoheadrightarrow A_n$ where each
$A_0\twoheadrightarrow \dots \twoheadrightarrow A_n$ where each ![]() $A_i$ is
$A_i$ is ![]() $\lambda$-small and homotopy equivalent to a
$\lambda$-small and homotopy equivalent to a ![]() $\kappa$-small object. Each
$\kappa$-small object. Each ![]() $\mathsf {U}_{\lambda, n}$ comes with a canonical enriched functor
$\mathsf {U}_{\lambda, n}$ comes with a canonical enriched functor ![]() $p_0\colon \mathsf {U}_{\lambda, n}\longrightarrow \mathsf {Cat}_{d}$ sending
$p_0\colon \mathsf {U}_{\lambda, n}\longrightarrow \mathsf {Cat}_{d}$ sending ![]() $(A_0\longrightarrow \cdots \longrightarrow A_n)$ to
$(A_0\longrightarrow \cdots \longrightarrow A_n)$ to ![]() $A_0$. Let us write
$A_0$. Let us write ![]() $u_{\lambda, n}=(\mathsf {U}_{\lambda, n}, p_0)$ for the corresponding object in
$u_{\lambda, n}=(\mathsf {U}_{\lambda, n}, p_0)$ for the corresponding object in ![]() $\mathsf {EnrFun}_d(\kappa )$ and note that
$\mathsf {EnrFun}_d(\kappa )$ and note that ![]() $u_{\kappa, 0}$ coincides with
$u_{\kappa, 0}$ coincides with ![]() $(\mathsf {Cat}_{d}(\kappa ), \mathrm {id})$. For each
$(\mathsf {Cat}_{d}(\kappa ), \mathrm {id})$. For each ![]() $\lambda \leq \lambda '$, the evident map
$\lambda \leq \lambda '$, the evident map ![]() $u_{\lambda, n}\longrightarrow u_{\lambda ', n}$ is a weak equivalence and each
$u_{\lambda, n}\longrightarrow u_{\lambda ', n}$ is a weak equivalence and each ![]() $u_{\lambda, \bullet }\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathsf {EnrFun}_d(\kappa )$ is a simplicial object where each structure map is a weak equivalence; in particular, this defines a simplicial diagram in
$u_{\lambda, \bullet }\colon \mathbf {\Delta }^{\mathrm {op}}\longrightarrow \mathsf {EnrFun}_d(\kappa )$ is a simplicial object where each structure map is a weak equivalence; in particular, this defines a simplicial diagram in ![]() $\mathscr {H}$. Taking the (large) filtered colimit over all small cardinals
$\mathscr {H}$. Taking the (large) filtered colimit over all small cardinals ![]() $\lambda$, we then obtain a map of presheaves
$\lambda$, we then obtain a map of presheaves
which induces an equivalence upon applying ![]() $\psi _!$. It therefore remains to verify that the target is the terminal presheaf (so that its image under
$\psi _!$. It therefore remains to verify that the target is the terminal presheaf (so that its image under ![]() $\psi _!$ is terminal as well).
$\psi _!$ is terminal as well).
Now fix an object ![]() $(\mathsf {C}, F)\in \mathscr {H}$ and for each
$(\mathsf {C}, F)\in \mathscr {H}$ and for each ![]() $\lambda$ consider the space
$\lambda$ consider the space
It suffices to verify that this space is contractible for large ![]() $\lambda$; taking the (filtered) colimit over
$\lambda$; taking the (filtered) colimit over ![]() $\lambda$ then shows that the target of (4.43) is terminal.
$\lambda$ then shows that the target of (4.43) is terminal.
Unraveling the definitions, ![]() $X_\lambda$ is the classifying space of the
$X_\lambda$ is the classifying space of the ![]() $(1, 1)$-category whose objects are weak equivalences
$(1, 1)$-category whose objects are weak equivalences ![]() $F\longrightarrow F'$ of functors
$F\longrightarrow F'$ of functors ![]() $\mathsf {C}\longrightarrow \mathsf {Cat}_d$, where
$\mathsf {C}\longrightarrow \mathsf {Cat}_d$, where ![]() $F'$ takes
$F'$ takes ![]() $\lambda$-small values, and where a morphism is a (pointwise) trivial fibration
$\lambda$-small values, and where a morphism is a (pointwise) trivial fibration ![]() $F'\twoheadrightarrow F''$ of functors under
$F'\twoheadrightarrow F''$ of functors under ![]() $F$. For large enough
$F$. For large enough ![]() $\lambda$ (in particular, so that
$\lambda$ (in particular, so that ![]() $F$ takes
$F$ takes ![]() $\lambda$-small values), the under-category
$\lambda$-small values), the under-category ![]() $\mathscr {M}_\lambda = F/\mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathsf {Cat}_d(\lambda )\big )$ has the structure of a category of fibrant objects in the sense of Brown. The space
$\mathscr {M}_\lambda = F/\mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathsf {Cat}_d(\lambda )\big )$ has the structure of a category of fibrant objects in the sense of Brown. The space ![]() $X_\lambda$ is then a path component in the classifying space of the wide subcategory
$X_\lambda$ is then a path component in the classifying space of the wide subcategory ![]() $\mathrm {wf}\mathscr {M}_\lambda \subseteq \mathscr {M}_\lambda$ spanned by the trivial fibrations. By [Reference Land, Nikolaus and SzumiłoLNS17, Lemmas 14 and 15], the classifying space of
$\mathrm {wf}\mathscr {M}_\lambda \subseteq \mathscr {M}_\lambda$ spanned by the trivial fibrations. By [Reference Land, Nikolaus and SzumiłoLNS17, Lemmas 14 and 15], the classifying space of ![]() $\mathrm {wf}\mathscr {M}_\lambda$ is equivalent to that of the wide subcategory
$\mathrm {wf}\mathscr {M}_\lambda$ is equivalent to that of the wide subcategory ![]() $\mathrm {w}\mathscr {M}_\lambda \subseteq \mathscr {M}_\lambda$ spanned by the weak equivalences. Restricting to the correct path component, this implies that for large
$\mathrm {w}\mathscr {M}_\lambda \subseteq \mathscr {M}_\lambda$ spanned by the weak equivalences. Restricting to the correct path component, this implies that for large ![]() $\lambda$,
$\lambda$, ![]() $X_\lambda$ is equivalent to the classifying space of the
$X_\lambda$ is equivalent to the classifying space of the ![]() $(1, 1)$-category whose objects are weak equivalences
$(1, 1)$-category whose objects are weak equivalences ![]() $F\longrightarrow F'$ of enriched functors with
$F\longrightarrow F'$ of enriched functors with ![]() $\lambda$-small values, with weak equivalences
$\lambda$-small values, with weak equivalences ![]() $F'\longrightarrow F''$ as morphisms. This latter category has an initial object (
$F'\longrightarrow F''$ as morphisms. This latter category has an initial object (![]() $F$ itself) and is, hence, contractible.
$F$ itself) and is, hence, contractible.
Variant 4.44 Associated to the cartesian fibration ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )\longrightarrow \mathrm {Cat}_{d+1}$ is the following cartesian fibration of
$\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )\longrightarrow \mathrm {Cat}_{d+1}$ is the following cartesian fibration of ![]() $1$-categories:
$1$-categories:
The same argument as Theorem 4.32 shows that ![]() $p\colon \mathscr {X}\longrightarrow \mathrm {Cat}_{d+1}$ can be obtained as the localization of a homotopy cartesian fibration
$p\colon \mathscr {X}\longrightarrow \mathrm {Cat}_{d+1}$ can be obtained as the localization of a homotopy cartesian fibration ![]() $\mathsf {X}\longrightarrow {{\rm Cat}}(\mathsf {Cat}_{d})$ between categories of fibrant objects; here
$\mathsf {X}\longrightarrow {{\rm Cat}}(\mathsf {Cat}_{d})$ between categories of fibrant objects; here ![]() $\mathsf {X}$ is the Grothendieck construction of the functor sending a
$\mathsf {X}$ is the Grothendieck construction of the functor sending a ![]() $\mathsf {Cat}_{d}$-enriched category
$\mathsf {Cat}_{d}$-enriched category ![]() $\mathbf {C}$ to the full subcategory of
$\mathbf {C}$ to the full subcategory of ![]() $\mathrm {Fun}_{\mathrm {enr}}([1]\times \mathbf {C}, \mathsf {Cat}_{d})$ on the homotopically
$\mathrm {Fun}_{\mathrm {enr}}([1]\times \mathbf {C}, \mathsf {Cat}_{d})$ on the homotopically ![]() $\kappa$-small objects. Repeating the argument from Proposition 4.40 then shows that the underlying right fibration
$\kappa$-small objects. Repeating the argument from Proposition 4.40 then shows that the underlying right fibration ![]() $\mathscr {X}^{\mathrm {cart}}\longrightarrow \mathrm {Cat}_{d+1}$ is representable by
$\mathscr {X}^{\mathrm {cart}}\longrightarrow \mathrm {Cat}_{d+1}$ is representable by ![]() $\mathrm {Fun}_{d+1}([1], \mathbf {Cat}_{d}(\kappa ))$.
$\mathrm {Fun}_{d+1}([1], \mathbf {Cat}_{d}(\kappa ))$.
4.4 More on representability
Let ![]() $\mathscr {C}$ be a
$\mathscr {C}$ be a ![]() $(d+1)$-category and consider the
$(d+1)$-category and consider the ![]() $(d+1)$-functor
$(d+1)$-functor
adjoint to the ![]() $(d+1)$-functor
$(d+1)$-functor ![]() $\mathrm {Map}_{\mathscr {C}}\colon \mathscr {C}^{\mathrm {op}}\times \mathscr {C}\longrightarrow \mathbf {Cat}_{d}$ defined in Example 4.36. If
$\mathrm {Map}_{\mathscr {C}}\colon \mathscr {C}^{\mathrm {op}}\times \mathscr {C}\longrightarrow \mathbf {Cat}_{d}$ defined in Example 4.36. If ![]() $\mathscr {C}$ arises from an enriched category
$\mathscr {C}$ arises from an enriched category ![]() $\mathsf {C}$, then Proposition 4.24 provides an explicit model for
$\mathsf {C}$, then Proposition 4.24 provides an explicit model for ![]() $h$: it arises from the usual (strictly) enriched Yoneda embedding, i.e. the following strict functor.
$h$: it arises from the usual (strictly) enriched Yoneda embedding, i.e. the following strict functor.
Since this is (strictly) fully faithful, the functor (
4.45) is fully faithful as well. An ![]() $\infty$-categorical proof of this can also be found in [Reference HinichHin20].
$\infty$-categorical proof of this can also be found in [Reference HinichHin20].
Definition 4.46 Let ![]() $\mathscr {C}$ be a
$\mathscr {C}$ be a ![]() $(d+1)$-category. A functor
$(d+1)$-category. A functor ![]() $F\colon \mathscr {C}\longrightarrow \mathbf {Cat}_{d}$ is said to be representable if it is contained in the essential image of (4.45).
$F\colon \mathscr {C}\longrightarrow \mathbf {Cat}_{d}$ is said to be representable if it is contained in the essential image of (4.45).
Remark 4.47 Let ![]() $F\colon \mathscr {C}\longrightarrow \mathbf {Cat}_d$ be a functor and let
$F\colon \mathscr {C}\longrightarrow \mathbf {Cat}_d$ be a functor and let ![]() $p\colon X\longrightarrow \mathscr {C}$ be the corresponding Segal copresheaf. From the above presentation in terms of enriched categories, one sees that
$p\colon X\longrightarrow \mathscr {C}$ be the corresponding Segal copresheaf. From the above presentation in terms of enriched categories, one sees that ![]() $F$ is representable if and only if
$F$ is representable if and only if ![]() $p$ admits a representation in the sense of Example 4.37. By Lemma 4.42, this is equivalent to the
$p$ admits a representation in the sense of Example 4.37. By Lemma 4.42, this is equivalent to the ![]() $1$-category
$1$-category ![]() $X(-, \vec {0}_d)$ admitting an initial object and each
$X(-, \vec {0}_d)$ admitting an initial object and each ![]() $X(-, \vec {0}_d)\longrightarrow X(-, \vec {n}_{d})$ preserving the initial object. The representing object is the image of this initial object in
$X(-, \vec {0}_d)\longrightarrow X(-, \vec {n}_{d})$ preserving the initial object. The representing object is the image of this initial object in ![]() $\mathscr {C}$.
$\mathscr {C}$.
Example 4.48 For each object ![]() $c$ of a
$c$ of a ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$, consider the
$\mathscr {C}$, consider the ![]() $(d+1)$-functor
$(d+1)$-functor
given by restriction along ![]() $c\colon \ast \longrightarrow \mathscr {C}$. Then the functor
$c\colon \ast \longrightarrow \mathscr {C}$. Then the functor ![]() $\mathrm {ev}_c$ is corepresentable by an object of
$\mathrm {ev}_c$ is corepresentable by an object of ![]() $\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_d)$, which, in turn, is given by the corepresentable functor
$\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_d)$, which, in turn, is given by the corepresentable functor ![]() $h_c$. Indeed, this is a special case of the enriched Yoneda lemma, proven in the
$h_c$. Indeed, this is a special case of the enriched Yoneda lemma, proven in the ![]() $\infty$-categorical setting in [Reference HinichHin20, 6.2.7]. In terms of strict models, one can also deduce this from the strict version of the enriched Yoneda lemma: choosing a strictly enriched model
$\infty$-categorical setting in [Reference HinichHin20, 6.2.7]. In terms of strict models, one can also deduce this from the strict version of the enriched Yoneda lemma: choosing a strictly enriched model ![]() $\mathsf {C}$ for
$\mathsf {C}$ for ![]() $\mathscr {C}$, one can model
$\mathscr {C}$, one can model ![]() $\mathrm {ev}_c$ by the strictly enriched functor
$\mathrm {ev}_c$ by the strictly enriched functor ![]() $\mathrm {ev}_c\colon \mathrm {Fun}_\mathrm {enr}(\mathsf {C}, \mathsf {Cat}_d)^{\circ }\longrightarrow \mathsf {Cat}_d$ evaluating a strictly enriched functor at the object
$\mathrm {ev}_c\colon \mathrm {Fun}_\mathrm {enr}(\mathsf {C}, \mathsf {Cat}_d)^{\circ }\longrightarrow \mathsf {Cat}_d$ evaluating a strictly enriched functor at the object ![]() $c\in \mathsf {C}$. By the classical enriched Yoneda lemma, this functor is corepresented by
$c\in \mathsf {C}$. By the classical enriched Yoneda lemma, this functor is corepresented by ![]() $h_c=\mathrm {Map}_{\mathsf {C}}(c, -)$.
$h_c=\mathrm {Map}_{\mathsf {C}}(c, -)$.
Recall that ![]() $\mathbf {Cat}_{d+1}$ has a homotopy
$\mathbf {Cat}_{d+1}$ has a homotopy ![]() $(2, 2)$-category, obtained by taking the homotopy
$(2, 2)$-category, obtained by taking the homotopy ![]() $(1, 1)$-categories of all mapping
$(1, 1)$-categories of all mapping ![]() $(d+1)$-categories
$(d+1)$-categories ![]() $\mathrm {Fun}_{d+1}(\mathscr {C}, \mathscr {D})$. An adjunction between two
$\mathrm {Fun}_{d+1}(\mathscr {C}, \mathscr {D})$. An adjunction between two ![]() $(d+1)$-categories is simply an adjunction in this homotopy
$(d+1)$-categories is simply an adjunction in this homotopy ![]() $(2, 2)$-category [Reference Riehl and VerityRV16]. We then have the following standard criterion for a
$(2, 2)$-category [Reference Riehl and VerityRV16]. We then have the following standard criterion for a ![]() $(d+1)$-functor
$(d+1)$-functor ![]() $g\colon \mathscr {C}\longrightarrow \mathscr {D}$ admitting a left adjoint.
$g\colon \mathscr {C}\longrightarrow \mathscr {D}$ admitting a left adjoint.
Proposition 4.49 Let ![]() $g\colon \mathscr {C}\longrightarrow \mathscr {D}$ be a map of
$g\colon \mathscr {C}\longrightarrow \mathscr {D}$ be a map of ![]() $(d+1)$-categories. Then
$(d+1)$-categories. Then ![]() $g$ admits a left adjoint if and only if for each object
$g$ admits a left adjoint if and only if for each object ![]() $d\in \mathscr {D}$, the functor
$d\in \mathscr {D}$, the functor ![]() $\mathrm {Map}_{\mathscr {D}}(d, g(-))\colon \mathscr {C}\longrightarrow \mathbf {Cat}_{d}$ is representable.
$\mathrm {Map}_{\mathscr {D}}(d, g(-))\colon \mathscr {C}\longrightarrow \mathbf {Cat}_{d}$ is representable.
For example, the map ![]() $\mathscr {C}\longrightarrow \ast$ admits a left adjoint if and only if
$\mathscr {C}\longrightarrow \ast$ admits a left adjoint if and only if ![]() $\mathscr {C}$ admits an initial object, i.e. an object
$\mathscr {C}$ admits an initial object, i.e. an object ![]() $\emptyset$ such that
$\emptyset$ such that ![]() $\mathrm {Map}_{\mathscr {C}}(\emptyset, c)\simeq \ast$ for all
$\mathrm {Map}_{\mathscr {C}}(\emptyset, c)\simeq \ast$ for all ![]() $c\in \mathscr {C}$.
$c\in \mathscr {C}$.
Proof. As a preliminary observation, let us recall that any ![]() $2$-functor preserves adjunctions. We are going to apply this in the following two situations.
$2$-functor preserves adjunctions. We are going to apply this in the following two situations.
(a) To the
 $2$-functor
$2$-functor  $\mathrm {ho}_{(2, 2)}(\mathbf {Cat}_d)^{\mathrm {op}}\longrightarrow {{\rm Cat}}_{(1, 1)}$ sending
$\mathrm {ho}_{(2, 2)}(\mathbf {Cat}_d)^{\mathrm {op}}\longrightarrow {{\rm Cat}}_{(1, 1)}$ sending  $\mathscr {C}\longmapsto \mathrm {ho}_{(1, 1)}\mathrm {Fun}_d(\mathscr {C}, \mathbf {Cat}_{d-1})$, and (2-)morphisms to the corresponding restriction functors and natural transformations.
$\mathscr {C}\longmapsto \mathrm {ho}_{(1, 1)}\mathrm {Fun}_d(\mathscr {C}, \mathbf {Cat}_{d-1})$, and (2-)morphisms to the corresponding restriction functors and natural transformations.(b) To the localization functor
 $\mathrm {Cat}\big (\mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )\longrightarrow \mathrm {ho}_{(2, 2)}(\mathbf {Cat}_d)$ sending each
$\mathrm {Cat}\big (\mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )\longrightarrow \mathrm {ho}_{(2, 2)}(\mathbf {Cat}_d)$ sending each  $\mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )$-enriched category to the corresponding
$\mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )$-enriched category to the corresponding  $d$-category (viewed as an object in the homotopy
$d$-category (viewed as an object in the homotopy  $(2, 2)$-category of
$(2, 2)$-category of  $d$-categories). Note that this is indeed a
$d$-categories). Note that this is indeed a  $2$-functor, since it is naturally tensored over
$2$-functor, since it is naturally tensored over  ${{\rm Cat}}_{(1, 1)}$ via the cartesian product.
${{\rm Cat}}_{(1, 1)}$ via the cartesian product.
Now let us start by assuming that ![]() $g$ admits a left adjoint
$g$ admits a left adjoint ![]() $f$. Applying the 2-functor (a) to this adjoint pair, we obtain the following adjoint pair:
$f$. Applying the 2-functor (a) to this adjoint pair, we obtain the following adjoint pair:
We can model ![]() $f\colon \mathscr {D}\longrightarrow \mathscr {C}$ by a functor of
$f\colon \mathscr {D}\longrightarrow \mathscr {C}$ by a functor of ![]() $\mathsf {Cat}_{d-1}$-enriched categories
$\mathsf {Cat}_{d-1}$-enriched categories ![]() $f\colon \mathsf {D}\longrightarrow \mathsf {C}$. The functor
$f\colon \mathsf {D}\longrightarrow \mathsf {C}$. The functor ![]() $f^*$ then arises from the right Quillen functor
$f^*$ then arises from the right Quillen functor
In particular, the left adjoint ![]() $g^*$ (on homotopy
$g^*$ (on homotopy ![]() $(1, 1)$-categories) is naturally isomorphic to the left derived functor of
$(1, 1)$-categories) is naturally isomorphic to the left derived functor of ![]() $f_!\colon \mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {D}, \mathrm {sPSh}(\mathbf {\Delta }_d)\big )\longrightarrow \mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathrm {sPSh}(\mathbf {\Delta }_d)\big )$. Since the left derived functor of
$f_!\colon \mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {D}, \mathrm {sPSh}(\mathbf {\Delta }_d)\big )\longrightarrow \mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathrm {sPSh}(\mathbf {\Delta }_d)\big )$. Since the left derived functor of ![]() $f_!$ preserves representable copresheaves, it follows that
$f_!$ preserves representable copresheaves, it follows that ![]() $g^*$ preserves representable copresheaves as well; this is precisely the assertion that
$g^*$ preserves representable copresheaves as well; this is precisely the assertion that ![]() $\mathrm {Map}_{\mathscr {D}}(d, g(-))$ is representable for all
$\mathrm {Map}_{\mathscr {D}}(d, g(-))$ is representable for all ![]() $d\in \mathscr {D}$.
$d\in \mathscr {D}$.
For the converse, suppose that each ![]() $\mathrm {Map}_{\mathscr {D}}(d, g(-))\colon \mathscr {C}\longrightarrow \mathbf {Cat}_{d-1}$ is representable. To prove that
$\mathrm {Map}_{\mathscr {D}}(d, g(-))\colon \mathscr {C}\longrightarrow \mathbf {Cat}_{d-1}$ is representable. To prove that ![]() $g$ admits a left adjoint in
$g$ admits a left adjoint in ![]() $\mathrm {ho}_{(2, 2)}(\mathbf {Cat}_d)$, it will suffice to find a map
$\mathrm {ho}_{(2, 2)}(\mathbf {Cat}_d)$, it will suffice to find a map ![]() $\mathsf {C}^{\mathrm {op}}\longrightarrow \mathsf {D}^{\mathrm {op}}$ in
$\mathsf {C}^{\mathrm {op}}\longrightarrow \mathsf {D}^{\mathrm {op}}$ in ![]() $\mathrm {Cat}\big (\mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )$ which admits a (strict) right adjoint and whose image under the functor (b) is equivalent to the opposite of
$\mathrm {Cat}\big (\mathrm {sPSh}(\mathbf {\Delta }_{d-1})\big )$ which admits a (strict) right adjoint and whose image under the functor (b) is equivalent to the opposite of ![]() $g\colon \mathscr {C}\longrightarrow \mathscr {D}$.
$g\colon \mathscr {C}\longrightarrow \mathscr {D}$.
To provide the desired model for ![]() $g$, let us choose any cofibration
$g$, let us choose any cofibration ![]() $\gamma \colon \mathsf {C}_0\longrightarrow \mathsf {D}_0$ between
$\gamma \colon \mathsf {C}_0\longrightarrow \mathsf {D}_0$ between ![]() $\mathsf {Cat}_{d-1}$-enriched categories that models
$\mathsf {Cat}_{d-1}$-enriched categories that models ![]() $g\colon \mathscr {C}\longrightarrow \mathscr {D}$. This induces a Quillen pair of (in particular) simplicial model categories
$g\colon \mathscr {C}\longrightarrow \mathscr {D}$. This induces a Quillen pair of (in particular) simplicial model categories
given by restriction and left Kan extension. Now let us define
to be the full (enriched) subcategories of all enriched functors that admit a simplicial homotopy equivalence to a corepresentable functor. Since ![]() $\gamma _!$ preserves simplicial homotopy equivalences and corepresentable functors, we obtain a commuting square of categories enriched over
$\gamma _!$ preserves simplicial homotopy equivalences and corepresentable functors, we obtain a commuting square of categories enriched over ![]() $\mathrm {sPSh}(\mathbf {\Delta }_{d-1})$
$\mathrm {sPSh}(\mathbf {\Delta }_{d-1})$

where the vertical functors ![]() $h$ are the Yoneda embeddings. By construction, both of these vertical functors are Dwyer–Kan equivalences of enriched categories, so that
$h$ are the Yoneda embeddings. By construction, both of these vertical functors are Dwyer–Kan equivalences of enriched categories, so that ![]() $\gamma _!\colon \mathsf {C}^{\mathrm {op}}\longrightarrow \mathsf {D}^{\mathrm {op}}$ also maps to
$\gamma _!\colon \mathsf {C}^{\mathrm {op}}\longrightarrow \mathsf {D}^{\mathrm {op}}$ also maps to ![]() $g^{\mathrm {op}}$ under the localization functor (b). Let us point that this would not necessarily be the case if one replaced ‘simplicial homotopy equivalence’ by ‘weak equivalence’ in the definition of
$g^{\mathrm {op}}$ under the localization functor (b). Let us point that this would not necessarily be the case if one replaced ‘simplicial homotopy equivalence’ by ‘weak equivalence’ in the definition of ![]() $\mathsf {C}^{\mathrm {op}}$ (unless one imposes further fibrancy and cofibrancy conditions, which need not be preserved by both
$\mathsf {C}^{\mathrm {op}}$ (unless one imposes further fibrancy and cofibrancy conditions, which need not be preserved by both ![]() $\gamma _!$ and
$\gamma _!$ and ![]() $\gamma ^*$).
$\gamma ^*$).
We claim that the restriction functor ![]() $\gamma ^*$ also restricts to a functor
$\gamma ^*$ also restricts to a functor ![]() $\gamma ^*\colon \mathsf {D}^{\mathrm {op}}\longrightarrow \mathsf {C}^{\mathrm {op}}$. Indeed, since
$\gamma ^*\colon \mathsf {D}^{\mathrm {op}}\longrightarrow \mathsf {C}^{\mathrm {op}}$. Indeed, since ![]() $\gamma ^*$ preserves simplicial homotopy equivalences, it suffices to verify that
$\gamma ^*$ preserves simplicial homotopy equivalences, it suffices to verify that ![]() $\gamma ^*$ sends each corepresentable functor to an object in
$\gamma ^*$ sends each corepresentable functor to an object in ![]() $\mathsf {C}^{\mathrm {op}}$. In other words, we have to show that for each
$\mathsf {C}^{\mathrm {op}}$. In other words, we have to show that for each ![]() $d\in \mathsf {D}_0$, the enriched functor
$d\in \mathsf {D}_0$, the enriched functor ![]() $\mathrm {Map}_{\mathsf {D}_0}(d, \gamma (-))$ admits a simplicial homotopy equivalence to a corepresentable object. This enriched functor is a model for
$\mathrm {Map}_{\mathsf {D}_0}(d, \gamma (-))$ admits a simplicial homotopy equivalence to a corepresentable object. This enriched functor is a model for ![]() $\mathrm {Map}_{\mathscr {D}}(d, g(-))$ and is, hence, weakly equivalent to a corepresentable object. Since
$\mathrm {Map}_{\mathscr {D}}(d, g(-))$ and is, hence, weakly equivalent to a corepresentable object. Since ![]() $\mathrm {Map}_{\mathsf {D}_0}(d, \gamma (-))$ is projectively fibrant–cofibrant [Reference LurieLur09a, Proposition A.3.3.9], it then admits a simplicial homotopy equivalence to a corepresentable as well. We conclude that
$\mathrm {Map}_{\mathsf {D}_0}(d, \gamma (-))$ is projectively fibrant–cofibrant [Reference LurieLur09a, Proposition A.3.3.9], it then admits a simplicial homotopy equivalence to a corepresentable as well. We conclude that ![]() $\gamma _!\colon \mathsf {C}^{\mathrm {op}}\longrightarrow \mathsf {D}^{\mathrm {op}}$ admits a strict right adjoint
$\gamma _!\colon \mathsf {C}^{\mathrm {op}}\longrightarrow \mathsf {D}^{\mathrm {op}}$ admits a strict right adjoint ![]() $\gamma ^*$, so that its image
$\gamma ^*$, so that its image ![]() $g^{\mathrm {op}}$ in
$g^{\mathrm {op}}$ in ![]() $\mathrm {ho}_{(2, 2)}(\mathbf {Cat}_d)$ admits a right adjoint as well, as desired.
$\mathrm {ho}_{(2, 2)}(\mathbf {Cat}_d)$ admits a right adjoint as well, as desired.
Corollary 4.50 Let ![]() $g\colon \mathscr {C}\longrightarrow \mathscr {D}$ be a map of
$g\colon \mathscr {C}\longrightarrow \mathscr {D}$ be a map of ![]() $d$-categories which admits a fully faithful left adjoint. If
$d$-categories which admits a fully faithful left adjoint. If ![]() $q\colon \mathscr {D}'\longrightarrow \mathscr {D}$ is any functor, then the base change
$q\colon \mathscr {D}'\longrightarrow \mathscr {D}$ is any functor, then the base change ![]() $g'\colon \mathscr {C}\times _{\mathscr {D}} \mathscr {D}'\longrightarrow \mathscr {D}'$ admits a fully faithful left adjoint as well.
$g'\colon \mathscr {C}\times _{\mathscr {D}} \mathscr {D}'\longrightarrow \mathscr {D}'$ admits a fully faithful left adjoint as well.
Proof. For ![]() $d'\in \mathscr {D}'$, let
$d'\in \mathscr {D}'$, let ![]() $c\in \mathscr {C}$ be a representing object for
$c\in \mathscr {C}$ be a representing object for ![]() $\mathrm {Map}_{\mathscr {D}}(q(d'), g(-))$. Then
$\mathrm {Map}_{\mathscr {D}}(q(d'), g(-))$. Then ![]() $(c, d')\in \mathscr {C}\times _{\mathscr {D}} \mathscr {D}'$ provides the desired representing object for
$(c, d')\in \mathscr {C}\times _{\mathscr {D}} \mathscr {D}'$ provides the desired representing object for ![]() $\mathrm {Map}_{\mathscr {D}'}(d', g'(-))$.
$\mathrm {Map}_{\mathscr {D}'}(d', g'(-))$.
Remark 4.51 Using a similar argument, one can show the following two assertions.
(1) Consider a pullback diagram
 $\Lambda ^2[2]\longrightarrow \mathrm {Fun}([1], \mathrm {Cat}_d)$ sending each
$\Lambda ^2[2]\longrightarrow \mathrm {Fun}([1], \mathrm {Cat}_d)$ sending each  $i$ to a functor
$i$ to a functor  $g_i\colon \mathscr {C}_i\longrightarrow \mathscr {D}_i$ admitting a fully faithful left adjoint. If the functors
$g_i\colon \mathscr {C}_i\longrightarrow \mathscr {D}_i$ admitting a fully faithful left adjoint. If the functors  $\mathscr {C}_0\longrightarrow \mathscr {C}_2\longleftarrow \mathscr {C}_1$ preserve the essential images of these left adjoints, then the pullback
$\mathscr {C}_0\longrightarrow \mathscr {C}_2\longleftarrow \mathscr {C}_1$ preserve the essential images of these left adjoints, then the pullback  $g\colon \mathscr {C}_0\times _{\mathscr {C}_2}\mathscr {C}_1\longrightarrow \mathscr {D}_0\times _{\mathscr {D}_2}\mathscr {D}_1$ admits a fully faithful left adjoint as well.
$g\colon \mathscr {C}_0\times _{\mathscr {C}_2}\mathscr {C}_1\longrightarrow \mathscr {D}_0\times _{\mathscr {D}_2}\mathscr {D}_1$ admits a fully faithful left adjoint as well.(2) Consider a tower
 $\mathbb {N}^{\mathrm {op}}\longrightarrow \mathrm {Fun}([1], \mathrm {Cat}_d)$ sending each
$\mathbb {N}^{\mathrm {op}}\longrightarrow \mathrm {Fun}([1], \mathrm {Cat}_d)$ sending each  $i$ to a functor
$i$ to a functor  $g_n\colon \mathscr {C}_n\longrightarrow \mathscr {D}_n$ admitting a fully faithful left adjoint. If the functors
$g_n\colon \mathscr {C}_n\longrightarrow \mathscr {D}_n$ admitting a fully faithful left adjoint. If the functors  $\mathscr {C}_{n+1}\longrightarrow \mathscr {C}_n$ preserve the essential images of these left adjoints, then the map
$\mathscr {C}_{n+1}\longrightarrow \mathscr {C}_n$ preserve the essential images of these left adjoints, then the map  $\lim _n \mathscr {C}_n\longrightarrow \lim _n\mathscr {D}_n$ admits a fully faithful left adjoint.
$\lim _n \mathscr {C}_n\longrightarrow \lim _n\mathscr {D}_n$ admits a fully faithful left adjoint.
Indeed, in each of these cases consider an object ![]() $(d_i)\in \lim \mathscr {D}_i$ in the limit. For each
$(d_i)\in \lim \mathscr {D}_i$ in the limit. For each ![]() $i$, there exists an inverse image
$i$, there exists an inverse image ![]() $c_i\in g_i^{-1}(d_i)$ such that
$c_i\in g_i^{-1}(d_i)$ such that ![]() $\mathrm {Map}_{\mathscr {C}_i}(c_i, -)\longrightarrow \mathrm {Map}_{\mathscr {D}_i}(d_i, g_i(-))$ is an equivalence. The fact that the functors
$\mathrm {Map}_{\mathscr {C}_i}(c_i, -)\longrightarrow \mathrm {Map}_{\mathscr {D}_i}(d_i, g_i(-))$ is an equivalence. The fact that the functors ![]() $\mathscr {C}_i\longrightarrow \mathscr {C}_j$ preserve the essential images of the fully faithful left adjoints implies that we can (inductively) lift this tuple of objects
$\mathscr {C}_i\longrightarrow \mathscr {C}_j$ preserve the essential images of the fully faithful left adjoints implies that we can (inductively) lift this tuple of objects ![]() $c_i$ to an object
$c_i$ to an object ![]() $(c_i)\in \lim \mathscr {C}_i$ in the limit. This object maps to
$(c_i)\in \lim \mathscr {C}_i$ in the limit. This object maps to ![]() $(d_i)\in \lim \mathscr {D}_i$ and has the desired universal property.
$(d_i)\in \lim \mathscr {D}_i$ and has the desired universal property.
4.5 Tensoring
Let us conclude by recalling that questions about higher categories can often be reduced to questions about their underlying ![]() $1$-categories when their enriched structure arises from a (co)tensoring.
$1$-categories when their enriched structure arises from a (co)tensoring.
Definition 4.52 Let ![]() $\mathscr {C}$ be a
$\mathscr {C}$ be a ![]() $(d+1)$-category and consider the following
$(d+1)$-category and consider the following ![]() $(d+1)$-functor:
$(d+1)$-functor:
Then ![]() $\mathscr {C}$ is said to be tensored over
$\mathscr {C}$ is said to be tensored over ![]() $\mathbf {Cat}_{d}$ if this takes values in representable functors. In this case, we will write
$\mathbf {Cat}_{d}$ if this takes values in representable functors. In this case, we will write ![]() $\otimes \colon \mathbf {Cat}_{d}\times \mathscr {C}\longrightarrow \mathscr {C}$ for the induced functor.
$\otimes \colon \mathbf {Cat}_{d}\times \mathscr {C}\longrightarrow \mathscr {C}$ for the induced functor.
Remark 4.53 In other words, ![]() $K\otimes c$ is the unique object of
$K\otimes c$ is the unique object of ![]() $\mathscr {C}$ with a natural equivalence
$\mathscr {C}$ with a natural equivalence
This universal property implies that there are equivalences ![]() $K\otimes (L\otimes c)\simeq (K\times L)\otimes c$. Furthermore, note that the identity on
$K\otimes (L\otimes c)\simeq (K\times L)\otimes c$. Furthermore, note that the identity on ![]() $K\otimes c$ induces a natural map of
$K\otimes c$ induces a natural map of ![]() $d$-categories
$d$-categories ![]() $K\longrightarrow \mathrm {Map}_{\mathscr {C}}(c, K\otimes c)$.
$K\longrightarrow \mathrm {Map}_{\mathscr {C}}(c, K\otimes c)$.
Definition 4.54 Let ![]() $f\colon \mathscr {C}\longrightarrow \mathscr {D}$ be a map between two
$f\colon \mathscr {C}\longrightarrow \mathscr {D}$ be a map between two ![]() $(d+1)$-categories which are tensored over
$(d+1)$-categories which are tensored over ![]() $\mathbf {Cat}_{d}$. For each
$\mathbf {Cat}_{d}$. For each ![]() $c\in \mathscr {C}$ and
$c\in \mathscr {C}$ and ![]() $K\in \mathbf {Cat}_{d}$, the composite map
$K\in \mathbf {Cat}_{d}$, the composite map
determines a natural map ![]() $\mu \colon K\otimes f(c)\longrightarrow f(K\otimes c)$. We will say that
$\mu \colon K\otimes f(c)\longrightarrow f(K\otimes c)$. We will say that ![]() $f$ is tensored over
$f$ is tensored over ![]() ${{\rm Cat}}_{d}$ if all of these maps
${{\rm Cat}}_{d}$ if all of these maps ![]() $\mu$ are equivalences.
$\mu$ are equivalences.
Remark 4.55 Likewise, a ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$ is cotensored over
$\mathscr {C}$ is cotensored over ![]() ${{\rm Cat}}_{d}$ if
${{\rm Cat}}_{d}$ if ![]() $\mathscr {C}^{\mathrm {op}}$ is tensored over
$\mathscr {C}^{\mathrm {op}}$ is tensored over ![]() ${{\rm Cat}}_{d}$; in this case we will write
${{\rm Cat}}_{d}$; in this case we will write ![]() $c^K$ for the cotensoring of
$c^K$ for the cotensoring of ![]() $c\in \mathscr {C}$ with
$c\in \mathscr {C}$ with ![]() $K\in {{\rm Cat}}_{d}$. A functor
$K\in {{\rm Cat}}_{d}$. A functor ![]() $f\colon \mathscr {C}\longrightarrow \mathscr {D}$ is cotensored if all natural maps
$f\colon \mathscr {C}\longrightarrow \mathscr {D}$ is cotensored if all natural maps ![]() $\mu \colon f(c^K)\longrightarrow f(c)^K$ are equivalences.
$\mu \colon f(c^K)\longrightarrow f(c)^K$ are equivalences.
Example 4.56 The ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathbf {Cat}_{d}$ is evidently tensored and cotensored over
$\mathbf {Cat}_{d}$ is evidently tensored and cotensored over ![]() $\mathbf {Cat}_{d}$ itself. Likewise, every functor
$\mathbf {Cat}_{d}$ itself. Likewise, every functor ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_{d})$ is tensored and cotensored over
$\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_{d})$ is tensored and cotensored over ![]() $\mathbf {Cat}_{d}$, with (co)tensoring computed pointwise. This follows conceptually from the description of enriched functor
$\mathbf {Cat}_{d}$, with (co)tensoring computed pointwise. This follows conceptually from the description of enriched functor ![]() $\infty$-categories by Hinich [Reference HinichHin20, § 6]. Less elegantly, one can see this by working with the strict model
$\infty$-categories by Hinich [Reference HinichHin20, § 6]. Less elegantly, one can see this by working with the strict model ![]() $\mathsf {M}^\circ =\mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathsf {Cat}_{d}\big )^\circ$ provided Proposition 4.24. Indeed, for each
$\mathsf {M}^\circ =\mathrm {Fun}_{\mathrm {enr}}\big (\mathsf {C}, \mathsf {Cat}_{d}\big )^\circ$ provided Proposition 4.24. Indeed, for each ![]() $K\in \mathsf {Cat}_d$ and a fibrant–cofibrant enriched functor
$K\in \mathsf {Cat}_d$ and a fibrant–cofibrant enriched functor ![]() $F$, there is a natural isomorphism
$F$, there is a natural isomorphism
so that the pointwise product ![]() $F\times \mathrm {cst}(K)$ with the constant functor determines a (strict) tensoring on
$F\times \mathrm {cst}(K)$ with the constant functor determines a (strict) tensoring on ![]() $\mathsf {M}^{\circ }$. Dually, consider the pointwise fibrant enriched functor
$\mathsf {M}^{\circ }$. Dually, consider the pointwise fibrant enriched functor ![]() $F^K(-)=\mathrm {Map}_{\mathsf {Cat}_d}(K, F(-))$ and let
$F^K(-)=\mathrm {Map}_{\mathsf {Cat}_d}(K, F(-))$ and let ![]() $Q(F^K)\in \mathsf {M}^{\circ }$ be a projectively cofibrant replacement. Then there is a natural equivalence
$Q(F^K)\in \mathsf {M}^{\circ }$ be a projectively cofibrant replacement. Then there is a natural equivalence
which exhibits ![]() $Q(F^K)$ as a cotensoring.
$Q(F^K)$ as a cotensoring.
Lemma 4.57 Let ![]() $f\colon \mathscr {C}\longrightarrow \mathscr {D}$ be a tensored functor between
$f\colon \mathscr {C}\longrightarrow \mathscr {D}$ be a tensored functor between ![]() $(d+1)$-categories that are tensored over
$(d+1)$-categories that are tensored over ![]() $\mathbf {Cat}_{d}$. If the underlying functor of
$\mathbf {Cat}_{d}$. If the underlying functor of ![]() $1$-categories is an equivalence, then
$1$-categories is an equivalence, then ![]() $f$ is an equivalence of
$f$ is an equivalence of ![]() $(d+1)$-categories as well.
$(d+1)$-categories as well.
Proof. Note that for any ![]() $K\in {{\rm Cat}}_{d}$, the map between mapping spaces in
$K\in {{\rm Cat}}_{d}$, the map between mapping spaces in ![]() ${{\rm Cat}}_{d}$
${{\rm Cat}}_{d}$
can be identified with ![]() $\mathrm {Map}_{\mathfrak {c}_1(\mathscr {C})}(K\otimes c, d)\longrightarrow \mathrm {Map}_{\mathfrak {c}_1(\mathscr {D})}(K\otimes f(c), d)$. The latter is an equivalence since
$\mathrm {Map}_{\mathfrak {c}_1(\mathscr {C})}(K\otimes c, d)\longrightarrow \mathrm {Map}_{\mathfrak {c}_1(\mathscr {D})}(K\otimes f(c), d)$. The latter is an equivalence since ![]() $f$ is fully faithful on the underlying
$f$ is fully faithful on the underlying ![]() $1$-categories, so that
$1$-categories, so that ![]() $f$ is a fully faithful functor between
$f$ is a fully faithful functor between ![]() $(d+1)$-categories as well. It is essentially surjective since it is essentially surjective on the underlying
$(d+1)$-categories as well. It is essentially surjective since it is essentially surjective on the underlying ![]() $1$-categories.
$1$-categories.
Proposition 4.58 Let ![]() $\mathscr {C}$ be a
$\mathscr {C}$ be a ![]() $(d+1)$-category which is tensored over
$(d+1)$-category which is tensored over ![]() $\mathbf {Cat}_{d}$ and let
$\mathbf {Cat}_{d}$ and let ![]() $F\colon \mathscr {C}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_d$ be a
$F\colon \mathscr {C}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_d$ be a ![]() $(d+1)$-functor. If
$(d+1)$-functor. If ![]() $F$ is cotensored and the underlying
$F$ is cotensored and the underlying ![]() $1$-functor
$1$-functor
is representable, then ![]() $F$ is representable.
$F$ is representable.
Proof. Let ![]() $x_u\in \mathfrak {c}_0(F(c_u))$ be the element corresponding (by the Yoneda lemma) to the natural equivalence of
$x_u\in \mathfrak {c}_0(F(c_u))$ be the element corresponding (by the Yoneda lemma) to the natural equivalence of ![]() $1$-functors
$1$-functors ![]() $\mathrm {Map}_{\mathscr {C}}(-, c_u)\stackrel {\sim }{\longrightarrow } \mathfrak {c}_0(F)$. Viewing
$\mathrm {Map}_{\mathscr {C}}(-, c_u)\stackrel {\sim }{\longrightarrow } \mathfrak {c}_0(F)$. Viewing ![]() $x_u$ as an element in
$x_u$ as an element in ![]() $F(c_u)$, the enriched Yoneda lemma provides a natural transformation of
$F(c_u)$, the enriched Yoneda lemma provides a natural transformation of ![]() $(d+1)$-functors
$(d+1)$-functors ![]() $\mathrm {Map}_{\mathscr {C}}(-, c_u)\longrightarrow F$. To see that this is an equivalence, note that for any
$\mathrm {Map}_{\mathscr {C}}(-, c_u)\longrightarrow F$. To see that this is an equivalence, note that for any ![]() $K\in \mathbf {Cat}_{d}$ and
$K\in \mathbf {Cat}_{d}$ and ![]() $d\in \mathscr {C}$, there is the following commuting square.
$d\in \mathscr {C}$, there is the following commuting square.

The vertical functors are equivalences because ![]() $F$ is cotensored. Since the top map induces an equivalence on underlying spaces, it follows that the bottom map induces an equivalence on the underlying spaces for all
$F$ is cotensored. Since the top map induces an equivalence on underlying spaces, it follows that the bottom map induces an equivalence on the underlying spaces for all ![]() $K\in \mathbf {Cat}_{d}$. By the Yoneda lemma, this implies that the map
$K\in \mathbf {Cat}_{d}$. By the Yoneda lemma, this implies that the map ![]() $x_u\colon \mathrm {Map}_{\mathscr {C}}(d, c_u)\longrightarrow F(d)$ is an equivalence.
$x_u\colon \mathrm {Map}_{\mathscr {C}}(d, c_u)\longrightarrow F(d)$ is an equivalence.
5. Cocartesian fibrations of higher categories
In this section we discuss the higher categorical analogues of cocartesian fibrations whose fibers are given by ![]() $d$-categories. We will refer to such fibrations as
$d$-categories. We will refer to such fibrations as ![]() $d$-cocartesian fibrations. Most importantly, we show (§ 5.3) that
$d$-cocartesian fibrations. Most importantly, we show (§ 5.3) that ![]() $d$-cocartesian fibrations between
$d$-cocartesian fibrations between ![]() $(d+1)$-categories form the domain of a
$(d+1)$-categories form the domain of a ![]() $(d+1)$-cartesian fibration between
$(d+1)$-cartesian fibration between ![]() $(d+2)$-categories
$(d+2)$-categories ![]() $\mathbf {Cocart}_{d}\longrightarrow \mathbf {Cat}_{d+1}$.
$\mathbf {Cocart}_{d}\longrightarrow \mathbf {Cat}_{d+1}$.
5.1 Pre-cocartesian fibrations
Let us start with the following preliminary definition, which reduces to that of a cocartesian fibration when ![]() $d=0$ (see [Reference Ayala and FrancisAF20, Reference Riehl and VerityRV22]).
$d=0$ (see [Reference Ayala and FrancisAF20, Reference Riehl and VerityRV22]).
Definition 5.1 Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of ![]() $(d+1)$-categories. Then
$(d+1)$-categories. Then ![]() $p$ is said to be a pre-cocartesian fibration if the map of
$p$ is said to be a pre-cocartesian fibration if the map of ![]() $(d+1)$-categories
$(d+1)$-categories
is a right adjoint and the unit of the adjunction is an equivalence. A ![]() $1$-morphism in
$1$-morphism in ![]() $\mathscr {D}$ is called (p-)cocartesian if it is contained in the essential image of the left adjoint.
$\mathscr {D}$ is called (p-)cocartesian if it is contained in the essential image of the left adjoint.
Remark 5.3 Dually, ![]() $p$ is said to be a pre-cartesian fibration if the map
$p$ is said to be a pre-cartesian fibration if the map
is a left adjoint and the counit of the adjunction is an equivalence. A ![]() $1$-morphism in
$1$-morphism in ![]() $\mathscr {D}$ is called (p-)cartesian if it is contained in the essential image of the right adjoint.
$\mathscr {D}$ is called (p-)cartesian if it is contained in the essential image of the right adjoint.
This notion of pre-cocartesian fibration coincides with the 2-categorical notion of an abstract cocartesian fibration from Street [Reference StreetStr80] and Riehl and Verity [Reference Riehl and VerityRV22] (interpreted in the ![]() $2$-category of
$2$-category of ![]() $(d+1)$-categories). In particular, we have the following properties.
$(d+1)$-categories). In particular, we have the following properties.
Lemma 5.4 The class of pre-cocartesian fibrations has the following stability properties.
(1) If
 $q\colon \mathscr {E}\longrightarrow \mathscr {D}$ and
$q\colon \mathscr {E}\longrightarrow \mathscr {D}$ and  $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ are pre-cocartesian fibrations, then
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ are pre-cocartesian fibrations, then  $pq\colon \mathscr {E}\longrightarrow \mathscr {C}$ is a pre-cocartesian fibration as well.
$pq\colon \mathscr {E}\longrightarrow \mathscr {C}$ is a pre-cocartesian fibration as well.(2) If
 $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a pre-cocartesian fibration and
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a pre-cocartesian fibration and  $\mathscr {C}'\longrightarrow \mathscr {C}$ is any map, then the base change
$\mathscr {C}'\longrightarrow \mathscr {C}$ is any map, then the base change  $\mathscr {D}'=\mathscr {D}\times _{\mathscr {C}}\mathscr {C}'\longrightarrow \mathscr {C}'$ is a pre-cocartesian fibration.
$\mathscr {D}'=\mathscr {D}\times _{\mathscr {C}}\mathscr {C}'\longrightarrow \mathscr {C}'$ is a pre-cocartesian fibration.(3) If
 $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a pre-cocartesian fibration, then
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a pre-cocartesian fibration, then  $\mathrm {Fun}_{d+1}(\mathscr {B}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {B}, \mathscr {C})$ is a pre-cocartesian fibration for any
$\mathrm {Fun}_{d+1}(\mathscr {B}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {B}, \mathscr {C})$ is a pre-cocartesian fibration for any  $(d+1)$-category
$(d+1)$-category  $\mathscr {B}$. Furthermore, for any
$\mathscr {B}$. Furthermore, for any  $\mathscr {B}'\longrightarrow \mathscr {B}$, the restriction functor
$\mathscr {B}'\longrightarrow \mathscr {B}$, the restriction functor  $\mathrm {Fun}_{d+1}(\mathscr {B}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {B}', \mathscr {D})$ preserves cocartesian 1-morphisms.
$\mathrm {Fun}_{d+1}(\mathscr {B}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {B}', \mathscr {D})$ preserves cocartesian 1-morphisms.(4) Consider the subcategory of
 $\mathrm {Fun}([1], \mathrm {Cat}_{d+1})$ whose objects are pre-cocartesian fibrations and morphisms are squares
such that
$\mathrm {Fun}([1], \mathrm {Cat}_{d+1})$ whose objects are pre-cocartesian fibrations and morphisms are squares
such that
 $f$ preserves cocartesian
$f$ preserves cocartesian  $1$-morphisms. This subcategory is closed under limits.
$1$-morphisms. This subcategory is closed under limits.
Proof. Property (1) is easily verified. For property (2), note that the map (5.2) for ![]() $\mathscr {D}'\longrightarrow \mathscr {C}'$ is the base change of the same map for
$\mathscr {D}'\longrightarrow \mathscr {C}'$ is the base change of the same map for ![]() $\mathscr {D}\longrightarrow \mathscr {C}$. The result then follows from Corollary 4.50.
$\mathscr {D}\longrightarrow \mathscr {C}$. The result then follows from Corollary 4.50.
For property (3), note that ![]() $\mathrm {Fun}_{d+1}([1], \mathrm {Fun}_{d+1}(\mathscr {B}, \mathscr {D}))\cong \mathrm {Fun}_{d+1}(\mathscr {B}, \mathrm {Fun}_{d+1}([1], \mathscr {D}))$. Using this, the result follows from the fact that
$\mathrm {Fun}_{d+1}([1], \mathrm {Fun}_{d+1}(\mathscr {B}, \mathscr {D}))\cong \mathrm {Fun}_{d+1}(\mathscr {B}, \mathrm {Fun}_{d+1}([1], \mathscr {D}))$. Using this, the result follows from the fact that ![]() $\mathrm {Fun}_{d+1}(\mathscr {B}, -)$ preserves limits and adjunctions (with fully faithful left adjoint).
$\mathrm {Fun}_{d+1}(\mathscr {B}, -)$ preserves limits and adjunctions (with fully faithful left adjoint).
Finally, for property (4) one can directly see that the subcategory is closed under products. It then suffices to verify that it is closed under pullbacks and limits of (countable) towers. This comes down to verifying that (5.2) admitting a fully faithful left adjoint is closed under such limits, which follows from Remark 4.51. Alternatively, one can also deduce this from Corollary 5.7, using an inductive argument to find enough cocartesian lifts in the limits.
Lemma 5.5 Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of ![]() $(d+1)$-categories and
$(d+1)$-categories and ![]() $\alpha \colon d_0\longrightarrow d_1$ a
$\alpha \colon d_0\longrightarrow d_1$ a ![]() $1$-morphism in
$1$-morphism in ![]() $\mathscr {D}$. Then the following are equivalent.
$\mathscr {D}$. Then the following are equivalent.
(1) For every
 $d_2\in \mathscr {D}$, the square of mapping
$d_2\in \mathscr {D}$, the square of mapping  $d$-categories
(5.6)is cartesian.
$d$-categories
(5.6)is cartesian.
(2) For every
 $1$-morphism
$1$-morphism  $\beta \colon d'_0\longrightarrow d'_1$ in
$\beta \colon d'_0\longrightarrow d'_1$ in  $\mathscr {D}$, the map between mapping
$\mathscr {D}$, the map between mapping  $d$-categories
is an equivalence.
$d$-categories
is an equivalence.
Proof. Using the description of the mapping objects in ![]() $\mathrm {Fun}_{d+1}([1], \mathscr {D})$ from Example 4.10, the map appearing in condition (2) can be identified with
$\mathrm {Fun}_{d+1}([1], \mathscr {D})$ from Example 4.10, the map appearing in condition (2) can be identified with
In particular, condition (1) is equivalent to condition (2) in the case where ![]() $\beta$ is the identity on
$\beta$ is the identity on ![]() $d_2$. Conversely, the above map arises as the base change of
$d_2$. Conversely, the above map arises as the base change of
along the map ![]() $\beta _*\colon \mathrm {Map}_{\mathscr {D}}(d_0, d'_0)\longrightarrow \mathrm {Map}_{\mathscr {D}}(d_0, d_1')$. It follows that condition (1) implies condition (2).
$\beta _*\colon \mathrm {Map}_{\mathscr {D}}(d_0, d'_0)\longrightarrow \mathrm {Map}_{\mathscr {D}}(d_0, d_1')$. It follows that condition (1) implies condition (2).
Corollary 5.7 A map ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ of
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ of ![]() $(d+1)$-categories is a pre-cocartesian fibration if and only if the following condition holds: for every map
$(d+1)$-categories is a pre-cocartesian fibration if and only if the following condition holds: for every map ![]() $\gamma \colon c_0\longrightarrow c_1$ in
$\gamma \colon c_0\longrightarrow c_1$ in ![]() $\mathscr {C}$ and every
$\mathscr {C}$ and every ![]() $d_0\in p^{-1}(c_0)$, there exists an arrow
$d_0\in p^{-1}(c_0)$, there exists an arrow ![]() $\alpha \colon d_0\longrightarrow d_1$ in
$\alpha \colon d_0\longrightarrow d_1$ in ![]() $\mathscr {D}$ with
$\mathscr {D}$ with ![]() $p(\alpha )=\gamma$, satisfying the equivalent conditions of Lemma 5.5.
$p(\alpha )=\gamma$, satisfying the equivalent conditions of Lemma 5.5.
In this case, the ![]() $p$-cocartesian morphisms are precisely the morphisms satisfying the equivalent conditions of Lemma 5.5. For the
$p$-cocartesian morphisms are precisely the morphisms satisfying the equivalent conditions of Lemma 5.5. For the ![]() $1$-categorical case, see also [Reference Ayala and FrancisAF20].
$1$-categorical case, see also [Reference Ayala and FrancisAF20].
Proof. Using Proposition 4.49, the existence of lifts ![]() $\alpha$ satisfying the second condition of Lemma 5.5 is equivalent to
$\alpha$ satisfying the second condition of Lemma 5.5 is equivalent to ![]() $p$ being a pre-cocartesian fibration.
$p$ being a pre-cocartesian fibration.
Remark 5.8 The condition appearing in Corollary 5.7 can also be reformulated as follows: the map ![]() $\mathfrak {c}_1(\mathscr {D})\longrightarrow \mathfrak {c}_1(\mathscr {C})$ is a cocartesian fibration of
$\mathfrak {c}_1(\mathscr {D})\longrightarrow \mathfrak {c}_1(\mathscr {C})$ is a cocartesian fibration of ![]() $1$-categories and each map of
$1$-categories and each map of ![]() $1$-categories
$1$-categories ![]() $\mathscr {D}(-, \vec {0}_{d})\longrightarrow \mathscr {D}(-, \vec {n}_{d})$ preserves cocartesian arrows. Using this, a map
$\mathscr {D}(-, \vec {0}_{d})\longrightarrow \mathscr {D}(-, \vec {n}_{d})$ preserves cocartesian arrows. Using this, a map ![]() $f\colon \mathscr {D}\longrightarrow \mathscr {D}'$ preserves cocartesian
$f\colon \mathscr {D}\longrightarrow \mathscr {D}'$ preserves cocartesian ![]() $1$-morphisms if and only if the map
$1$-morphisms if and only if the map ![]() $\mathfrak {c}_1(\mathscr {D})\longrightarrow \mathfrak {c}_1(\mathscr {D}')$ preserves cocartesian arrows in the usual sense.
$\mathfrak {c}_1(\mathscr {D})\longrightarrow \mathfrak {c}_1(\mathscr {D}')$ preserves cocartesian arrows in the usual sense.
Corollary 5.9 Consider a square of ![]() $(d+1)$-categories
$(d+1)$-categories

where ![]() $T$ and
$T$ and ![]() $S$ are spaces. Then
$S$ are spaces. Then ![]() $p$ is a pre-cocartesian fibration if and only if for any
$p$ is a pre-cocartesian fibration if and only if for any ![]() $t\in T$, the map on fibers
$t\in T$, the map on fibers ![]() $p_t\colon \mathscr {D}_t\longrightarrow \mathscr {C}_{q(t)}$ is a pre-cocartesian fibration. Furthermore, a morphism in
$p_t\colon \mathscr {D}_t\longrightarrow \mathscr {C}_{q(t)}$ is a pre-cocartesian fibration. Furthermore, a morphism in ![]() $\mathscr {D}$ is
$\mathscr {D}$ is ![]() $p$-cocartesian if and only if it defines a
$p$-cocartesian if and only if it defines a ![]() $p_t$-cocartesian morphism in some fiber
$p_t$-cocartesian morphism in some fiber ![]() $\mathscr {D}_t$.
$\mathscr {D}_t$.
Proof. Suppose that ![]() $\alpha \colon d_0\longrightarrow d_1$ is an arrow in
$\alpha \colon d_0\longrightarrow d_1$ is an arrow in ![]() $\mathscr {D}$ and let
$\mathscr {D}$ and let ![]() $\tau \colon t_0\longrightarrow t_1$ be its image in
$\tau \colon t_0\longrightarrow t_1$ be its image in ![]() $T$ (which is an equivalence). For any object
$T$ (which is an equivalence). For any object ![]() $d_2\in \mathscr {D}$, the square of
$d_2\in \mathscr {D}$, the square of ![]() $d$-categories (5.6) then comes with a natural transformation to the following square of spaces.
$d$-categories (5.6) then comes with a natural transformation to the following square of spaces.

The horizontal maps in this square are equivalences. The square (5.6) of ![]() $d$-categories (i.e. specific kinds of
$d$-categories (i.e. specific kinds of ![]() $d$-fold simplicial spaces) is then cartesian if and only if for every
$d$-fold simplicial spaces) is then cartesian if and only if for every ![]() $\tau '\colon t_1\longrightarrow t_2$ in
$\tau '\colon t_1\longrightarrow t_2$ in ![]() $T$, the square of fibers over
$T$, the square of fibers over ![]() $\tau '$ is a cartesian diagram of
$\tau '$ is a cartesian diagram of ![]() $d$-categories. This means precisely that
$d$-categories. This means precisely that ![]() $\alpha$ defines a cocartesian arrow for
$\alpha$ defines a cocartesian arrow for ![]() $p_t\colon \mathscr {D}_{t}\longrightarrow \mathscr {C}_{q(t)}$, where
$p_t\colon \mathscr {D}_{t}\longrightarrow \mathscr {C}_{q(t)}$, where ![]() $\mathscr {D}_t$ is the fiber of
$\mathscr {D}_t$ is the fiber of ![]() $\mathscr {D}$ over the diagram in
$\mathscr {D}$ over the diagram in ![]() $T$ of the form
$T$ of the form
Note that such a diagram in ![]() $T$ is contractible, i.e. it is equivalent to a choice of basepoint
$T$ is contractible, i.e. it is equivalent to a choice of basepoint ![]() $t\in T$. In other words, an arrow in
$t\in T$. In other words, an arrow in ![]() $\mathscr {D}$ is
$\mathscr {D}$ is ![]() $p$-cocartesian if and only if it defines a
$p$-cocartesian if and only if it defines a ![]() $p_t$-cocartesian arrow where
$p_t$-cocartesian arrow where ![]() $p_t\colon \mathscr {D}_t\longrightarrow \mathscr {C}_{q(t)}$ is the map between fibers over
$p_t\colon \mathscr {D}_t\longrightarrow \mathscr {C}_{q(t)}$ is the map between fibers over ![]() $t\in T$. Using this and Corollary 5.7, one readily deduces that
$t\in T$. Using this and Corollary 5.7, one readily deduces that ![]() $p$ is a pre-cocartesian fibration if and only if each
$p$ is a pre-cocartesian fibration if and only if each ![]() $p_t$ is a pre-cocartesian fibration.
$p_t$ is a pre-cocartesian fibration.
5.2  $d$-cocartesian fibrations
$d$-cocartesian fibrations
We now turn to the definition of ![]() $d$-cocartesian fibrations, which proceeds by induction on
$d$-cocartesian fibrations, which proceeds by induction on ![]() $d$.
$d$.
Definition 5.10 Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of ![]() $n$-categories. We then have the following definitions, by induction on
$n$-categories. We then have the following definitions, by induction on ![]() $d$:
$d$:
(a) The map
 $p$ is said to be a
$p$ is said to be a  $0$-cocartesian fibration if
$0$-cocartesian fibration if  $\mathscr {D}(1)\longrightarrow \mathscr {C}(1)\times _{\mathscr {C}(\{0\})}\mathscr {D}(\{0\})$ is an equivalence. A strong morphism between two
$\mathscr {D}(1)\longrightarrow \mathscr {C}(1)\times _{\mathscr {C}(\{0\})}\mathscr {D}(\{0\})$ is an equivalence. A strong morphism between two  $0$-cocartesian fibrations
$0$-cocartesian fibrations  $p$ and
$p$ and  $p'$ is a commuting square of the following form.
(5.11)Dually,
$p'$ is a commuting square of the following form.
(5.11)Dually,
 $p$ is said to be a
$p$ is said to be a  $0$-cartesian fibration if
$0$-cartesian fibration if  $p^{\mathrm {op}}\colon \mathscr {D}^{\mathrm {op}}\longrightarrow \mathscr {C}^{\mathrm {op}}$ is a
$p^{\mathrm {op}}\colon \mathscr {D}^{\mathrm {op}}\longrightarrow \mathscr {C}^{\mathrm {op}}$ is a  $0$-cocartesian fibration; strong morphisms between those are commuting squares (5.11).
$0$-cocartesian fibration; strong morphisms between those are commuting squares (5.11).(b) The map
 $p$ is said to be a
$p$ is said to be a  $d$-cocartesian fibration if it satisfies the following two conditions.
$d$-cocartesian fibration if it satisfies the following two conditions.
(1) It is a homwise
 $(d-1)$-cartesian fibration: for every
$(d-1)$-cartesian fibration: for every  $x_0, x_1\in \mathscr {D}$, the induced map between mapping objects
$x_0, x_1\in \mathscr {D}$, the induced map between mapping objects  $\mathrm {Map}_{\mathscr {D}}(x_0, x_1)\longrightarrow \mathrm {Map}_{\mathscr {C}}(p(x_0), p(x_1))$ is a
$\mathrm {Map}_{\mathscr {D}}(x_0, x_1)\longrightarrow \mathrm {Map}_{\mathscr {C}}(p(x_0), p(x_1))$ is a  $(d-1)$-cartesian fibration and the composition map determines a strong map of
$(d-1)$-cartesian fibration and the composition map determines a strong map of  $(d-1)$-cartesian fibrations as follows.
(5.12)
$(d-1)$-cartesian fibrations as follows.
(5.12)
(2) It is a pre-cocartesian fibration (Definition 5.1).
(c) The map
 $p$ is said to be a
$p$ is said to be a  $d$-cartesian fibration if it satisfies the following two conditions.
$d$-cartesian fibration if it satisfies the following two conditions.
(d) A strong morphism between
 $d$-(co)cartesian fibrations is a commuting square (5.11) such that
$d$-(co)cartesian fibrations is a commuting square (5.11) such that  $f$ preserves (co)cartesian
$f$ preserves (co)cartesian  $1$-morphisms and for any
$1$-morphisms and for any  $x_0, x_1\in \mathscr {D}$, the induced square
is a strong morphism of
$x_0, x_1\in \mathscr {D}$, the induced square
is a strong morphism of
 $(d-1)$-(co)cartesian fibrations.
$(d-1)$-(co)cartesian fibrations.
Warning 5.13 A ![]() $0$-cocartesian fibration can equivalently be viewed as a Segal copresheaf (as in Definition 4.25) whose domain is an
$0$-cocartesian fibration can equivalently be viewed as a Segal copresheaf (as in Definition 4.25) whose domain is an ![]() $n$-category. Note that the Segal copresheaves that arise in this way form a very restrictive class, since their fibers are spaces (cf. Warning 4.26).
$n$-category. Note that the Segal copresheaves that arise in this way form a very restrictive class, since their fibers are spaces (cf. Warning 4.26).
Remark 5.14 As usual, there are ![]() $2^{d+1}$ variants of the notion of a
$2^{d+1}$ variants of the notion of a ![]() $d$-cocartesian fibration between
$d$-cocartesian fibration between ![]() $(d+1)$-categories, by taking opposites in the various dimensions. We will only make use of the two notions considered above, which are related by taking opposites in every dimension.
$(d+1)$-categories, by taking opposites in the various dimensions. We will only make use of the two notions considered above, which are related by taking opposites in every dimension.
Remark 5.15 The definition of a ![]() $d$-cocartesian fibration
$d$-cocartesian fibration ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ exhibits an alternating pattern: odd-dimensional cells are required to admit
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ exhibits an alternating pattern: odd-dimensional cells are required to admit ![]() $p$-cocartesian lifts and even-dimensional cells are required to admit
$p$-cocartesian lifts and even-dimensional cells are required to admit ![]() $p$-cartesian lifts. Let us explain heuristically why this should encode a fully covariant diagram of
$p$-cartesian lifts. Let us explain heuristically why this should encode a fully covariant diagram of ![]() $d$-categories indexed by
$d$-categories indexed by ![]() $\mathscr {C}$.
$\mathscr {C}$.
First, to make sure that the fiber ![]() $p^{-1}(c_0)$ over an object
$p^{-1}(c_0)$ over an object ![]() $c_0\in \mathscr {C}$ depends covariantly on
$c_0\in \mathscr {C}$ depends covariantly on ![]() $c_0$, we need to be able to associate to each
$c_0$, we need to be able to associate to each ![]() $1$-morphism
$1$-morphism ![]() $\alpha \colon c_0\longrightarrow c_1$ in
$\alpha \colon c_0\longrightarrow c_1$ in ![]() $\mathscr {C}$ and each
$\mathscr {C}$ and each ![]() $d_0\in p^{-1}(c_0)$ an object
$d_0\in p^{-1}(c_0)$ an object ![]() $\alpha _!d_0\in p^{-1}(c_1)$. Of course, this is done using the (essentially unique)
$\alpha _!d_0\in p^{-1}(c_1)$. Of course, this is done using the (essentially unique) ![]() $p$-cocartesian arrow
$p$-cocartesian arrow ![]() $\tilde {\alpha }\colon d_0\longrightarrow \alpha _!d_0$ covering
$\tilde {\alpha }\colon d_0\longrightarrow \alpha _!d_0$ covering ![]() $\alpha$.
$\alpha$.
Next, given two objects ![]() $d_0, d_1\in \mathscr {D}$ with images
$d_0, d_1\in \mathscr {D}$ with images ![]() $c_0, c_1\in \mathscr {C}$, consider the induced map
$c_0, c_1\in \mathscr {C}$, consider the induced map ![]() $p\colon \mathrm {Map}_{\mathscr {D}}(d_0, d_1)\longrightarrow \mathrm {Map}_{\mathscr {C}}(c_0, c_1)$. For each
$p\colon \mathrm {Map}_{\mathscr {D}}(d_0, d_1)\longrightarrow \mathrm {Map}_{\mathscr {C}}(c_0, c_1)$. For each ![]() $\alpha \colon c_0\longrightarrow c_1$ in
$\alpha \colon c_0\longrightarrow c_1$ in ![]() $\mathscr {C}$, its fiber is given by
$\mathscr {C}$, its fiber is given by
Consequently, if ![]() $\alpha _!d_0$ depends covariantly on the
$\alpha _!d_0$ depends covariantly on the ![]() $1$-morphism
$1$-morphism ![]() $\alpha$, then the fiber
$\alpha$, then the fiber ![]() $p^{-1}(\alpha )$ will depend contravariantly on
$p^{-1}(\alpha )$ will depend contravariantly on ![]() $\alpha$. Indeed, each
$\alpha$. Indeed, each ![]() $2$-morphism
$2$-morphism ![]() $h\colon \alpha \longrightarrow \beta$ in
$h\colon \alpha \longrightarrow \beta$ in ![]() $\mathscr {C}$ should give rise to a functor
$\mathscr {C}$ should give rise to a functor
that precomposes with the natural transformation induced by ![]() $h$. In terms of the fibration
$h$. In terms of the fibration ![]() $p$, this means that each
$p$, this means that each ![]() $2$-morphism
$2$-morphism ![]() $h\colon \alpha \to \beta$ in
$h\colon \alpha \to \beta$ in ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $g\in p^{-1}(\beta )$ should admit a
$g\in p^{-1}(\beta )$ should admit a ![]() $p$-cartesian lift
$p$-cartesian lift ![]() $\tilde {h}\colon h^*(g)\longrightarrow g$.
$\tilde {h}\colon h^*(g)\longrightarrow g$.
At the level of ![]() $2$-morphisms, we then obtain a functor of the form
$2$-morphisms, we then obtain a functor of the form
for each ![]() $f\in p^{-1}(\alpha )$ and
$f\in p^{-1}(\alpha )$ and ![]() $g\in p^{-1}(\beta )$. For a given
$g\in p^{-1}(\beta )$. For a given ![]() $2$-cell
$2$-cell ![]() $h\colon \alpha \longrightarrow \beta$ in
$h\colon \alpha \longrightarrow \beta$ in ![]() $\mathscr {C}$, postcomposition with the
$\mathscr {C}$, postcomposition with the ![]() $p$-cartesian lift
$p$-cartesian lift ![]() $\tilde {h}$ induces an equivalence
$\tilde {h}$ induces an equivalence
If the natural transformation ![]() $h(d_0)\colon \alpha _!d_0\longrightarrow \beta _!d_0$ depends covariantly on the
$h(d_0)\colon \alpha _!d_0\longrightarrow \beta _!d_0$ depends covariantly on the ![]() $2$-morphism
$2$-morphism ![]() $h$, then (5.16) shows that
$h$, then (5.16) shows that ![]() $h^*$ depends covariantly on
$h^*$ depends covariantly on ![]() $h$ as well. Consequently, the fiber
$h$ as well. Consequently, the fiber ![]() $p^{-1}(h)$ depends covariantly on
$p^{-1}(h)$ depends covariantly on ![]() $h$, so that
$h$, so that ![]() $3$-morphisms should have
$3$-morphisms should have ![]() $p$-cocartesian lifts. In higher dimensions, one can repeat the discussion from the last two paragraphs to arrive at the alternating list of cocartesian and cartesian conditions from Definition 5.10.
$p$-cocartesian lifts. In higher dimensions, one can repeat the discussion from the last two paragraphs to arrive at the alternating list of cocartesian and cartesian conditions from Definition 5.10.
Note that for any map of ![]() $n$-categories
$n$-categories ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$, the property of being a
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$, the property of being a ![]() $d$-cocartesian fibration does not depend on whether we consider
$d$-cocartesian fibration does not depend on whether we consider ![]() $p$ as a map of
$p$ as a map of ![]() $n$-categories or
$n$-categories or ![]() $(n+1)$-categories. Similarly, the difference between
$(n+1)$-categories. Similarly, the difference between ![]() $d$-cocartesian and
$d$-cocartesian and ![]() $(d+1)$-cocartesian fibrations is only fiberwise.
$(d+1)$-cocartesian fibrations is only fiberwise.
Lemma 5.17 A map ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ between
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ between ![]() $n$-categories is a
$n$-categories is a ![]() $d$-cocartesian fibration if and only if it is a
$d$-cocartesian fibration if and only if it is a ![]() $(d+1)$-cocartesian fibration and its fibers are
$(d+1)$-cocartesian fibration and its fibers are ![]() $d$-categories.
$d$-categories.
In particular, a functor between ![]() $n$-categories is a
$n$-categories is a ![]() $d$-cocartesian fibration for some
$d$-cocartesian fibration for some ![]() $d>n$ if and only if is an
$d>n$ if and only if is an ![]() $n$-cocartesian fibration.
$n$-cocartesian fibration.
Proof. An inductive argument reduces this to the case ![]() $d=0$: if
$d=0$: if ![]() $p$ is a
$p$ is a ![]() $0$-cocartesian fibration, then certainly its fibers are spaces and it is a homwise
$0$-cocartesian fibration, then certainly its fibers are spaces and it is a homwise ![]() $0$-cartesian fibration (since each
$0$-cartesian fibration (since each ![]() $\mathscr {D}(p)\longrightarrow \mathscr {C}(p)$ is the base change of a map between spaces). It is a
$\mathscr {D}(p)\longrightarrow \mathscr {C}(p)$ is the base change of a map between spaces). It is a ![]() $1$-cocartesian fibration since every arrow in
$1$-cocartesian fibration since every arrow in ![]() $\mathscr {D}$ is
$\mathscr {D}$ is ![]() $p$-cocartesian and every morphism in
$p$-cocartesian and every morphism in ![]() $\mathscr {C}$ can be lifted to an arrow in
$\mathscr {C}$ can be lifted to an arrow in ![]() $\mathscr {D}$ (since
$\mathscr {D}$ (since ![]() $p$ is a
$p$ is a ![]() $0$-cocartesian fibration).
$0$-cocartesian fibration).
Conversely, suppose that ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a ![]() $1$-cocartesian fibration whose fibers are spaces. We have to verify that the map
$1$-cocartesian fibration whose fibers are spaces. We have to verify that the map ![]() $\mathscr {D}(1)\longrightarrow \mathscr {C}(1)\times _{\mathscr {C}(\{0\})}\mathscr {D}(\{0\})$ is an equivalence of
$\mathscr {D}(1)\longrightarrow \mathscr {C}(1)\times _{\mathscr {C}(\{0\})}\mathscr {D}(\{0\})$ is an equivalence of ![]() $(n-1)$-categories. Note that this map is obtained from the map of
$(n-1)$-categories. Note that this map is obtained from the map of ![]() $n$-categories (5.2) by taking
$n$-categories (5.2) by taking ![]() $(n-1)$-cores. It particular, it admits a fully faithful left adjoint whose essential image consists of the
$(n-1)$-cores. It particular, it admits a fully faithful left adjoint whose essential image consists of the ![]() $p$-cocartesian morphisms. It therefore suffices to verify that every
$p$-cocartesian morphisms. It therefore suffices to verify that every ![]() $1$-morphism in
$1$-morphism in ![]() $\mathscr {D}$ is
$\mathscr {D}$ is ![]() $p$-cocartesian: this follows immediately from the fact that every
$p$-cocartesian: this follows immediately from the fact that every ![]() $1$-morphism
$1$-morphism ![]() $\alpha$ factors as
$\alpha$ factors as ![]() $\alpha =\alpha ''\circ \alpha '$, where
$\alpha =\alpha ''\circ \alpha '$, where ![]() $\alpha '$ is cocartesian and
$\alpha '$ is cocartesian and ![]() $\alpha ''$ is a fiberwise morphism (and, hence, an equivalence).
$\alpha ''$ is a fiberwise morphism (and, hence, an equivalence).
Remark 5.18 It will follow from straightening that the notion of a ![]() $d$-cocartesian fibration essentially stabilizes at the level of
$d$-cocartesian fibration essentially stabilizes at the level of ![]() $(d+1)$-categories: if
$(d+1)$-categories: if ![]() $p$ is a
$p$ is a ![]() $d$-cocartesian fibration between
$d$-cocartesian fibration between ![]() $(d+k)$-categories for
$(d+k)$-categories for ![]() $k\geq 2$, then
$k\geq 2$, then ![]() $p$ arises as the base change of a
$p$ arises as the base change of a ![]() $d$-cocartesian fibration
$d$-cocartesian fibration ![]() $\mathscr {D}'\longrightarrow |\mathscr {C}|_{d+1}$, where
$\mathscr {D}'\longrightarrow |\mathscr {C}|_{d+1}$, where ![]() $|\mathscr {C}|_{d+1}$ is the
$|\mathscr {C}|_{d+1}$ is the ![]() $(d+1)$-category obtained by inverting all morphisms in dimension
$(d+1)$-category obtained by inverting all morphisms in dimension ![]() $> d+1$.
$> d+1$.
Definition 5.19 (Lateral  $k$-morphisms)
$k$-morphisms)
Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a ![]() $d$-cocartesian fibration between
$d$-cocartesian fibration between ![]() $n$-categories. For any
$n$-categories. For any ![]() $1\leq k\leq d$, let
$1\leq k\leq d$, let ![]() $\alpha \in \mathscr {D}(1, \dots, 1 , \vec {0}_{n-k})$ be a
$\alpha \in \mathscr {D}(1, \dots, 1 , \vec {0}_{n-k})$ be a ![]() $k$-morphism in
$k$-morphism in ![]() $\mathscr {D}$, considered as a
$\mathscr {D}$, considered as a ![]() $1$-morphism
$1$-morphism ![]() $\alpha \colon f\longrightarrow g$ between two
$\alpha \colon f\longrightarrow g$ between two ![]() $(k-1)$-morphisms
$(k-1)$-morphisms ![]() $f, g\colon x\longrightarrow y$. Let
$f, g\colon x\longrightarrow y$. Let
be the induced map between ![]() $(n+1-k)$-categories of
$(n+1-k)$-categories of ![]() $(k-1)$-morphisms between
$(k-1)$-morphisms between ![]() $x$ and
$x$ and ![]() $y$. Then
$y$. Then ![]() $\alpha$ is said to be (
$\alpha$ is said to be (![]() $p$-)lateral if it is:
$p$-)lateral if it is:
– a
 $p_{(k-1)}$-cocartesian
$p_{(k-1)}$-cocartesian  $1$-morphism if
$1$-morphism if  $k$ is odd;
$k$ is odd;– a
 $p_{(k-1)}$-cartesian
$p_{(k-1)}$-cartesian  $1$-morphism if
$1$-morphism if  $k$ is even.
$k$ is even.
When ![]() $p$ is an
$p$ is an ![]() $d$-cartesian fibration, we define lateral
$d$-cartesian fibration, we define lateral ![]() $k$-morphisms similarly, but with the cases of
$k$-morphisms similarly, but with the cases of ![]() $k$ even and odd exchanged. In particular, the meaning depends on whether
$k$ even and odd exchanged. In particular, the meaning depends on whether ![]() $p$ is considered as a
$p$ is considered as a ![]() $d$-cocartesian or
$d$-cocartesian or ![]() $d$-cartesian fibration.
$d$-cartesian fibration.
Unraveling the definitions, a square (5.11) defines a strong morphism between two ![]() $d$-cocartesian fibrations if and only if the map
$d$-cocartesian fibrations if and only if the map ![]() $f$ preserves lateral
$f$ preserves lateral ![]() $k$-morphisms for all
$k$-morphisms for all ![]() $k\leq d$.
$k\leq d$.
Lemma 5.20 Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map of ![]() $n$-categories covering a map of spaces
$n$-categories covering a map of spaces ![]() $q\colon T\longrightarrow S$, as in Corollary 5.9. Then
$q\colon T\longrightarrow S$, as in Corollary 5.9. Then ![]() $p$ is a
$p$ is a ![]() $d$-cocartesian fibration if and only if each map on fibers
$d$-cocartesian fibration if and only if each map on fibers ![]() $p_t\colon \mathscr {D}_t\longrightarrow \mathscr {C}_{q(t)}$ is a
$p_t\colon \mathscr {D}_t\longrightarrow \mathscr {C}_{q(t)}$ is a ![]() $d$-cocartesian fibration. For each
$d$-cocartesian fibration. For each ![]() $k\leq d$, a
$k\leq d$, a ![]() $k$-morphism in
$k$-morphism in ![]() $\mathscr {D}$ covering a point
$\mathscr {D}$ covering a point ![]() $t\in T$ is
$t\in T$ is ![]() $p$-lateral if and only if it is
$p$-lateral if and only if it is ![]() $p_t$-lateral.
$p_t$-lateral.
Proof. This follows by induction, using Corollary 5.9.
Lemma 5.21 A map ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a homwise
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a homwise ![]() $(d-1)$-cartesian fibration if and only if it satisfies the following condition: for every
$(d-1)$-cartesian fibration if and only if it satisfies the following condition: for every ![]() $[m]\in \mathbf {\Delta }$, the map
$[m]\in \mathbf {\Delta }$, the map ![]() $\mathscr {D}(m)\longrightarrow \mathscr {C}(m)$ is a
$\mathscr {D}(m)\longrightarrow \mathscr {C}(m)$ is a ![]() $(d-1)$-cartesian fibration and each
$(d-1)$-cartesian fibration and each ![]() $[m]\longrightarrow [m']$ induces a strong morphism between
$[m]\longrightarrow [m']$ induces a strong morphism between ![]() $(d-1)$-cartesian fibrations.
$(d-1)$-cartesian fibrations.
Proof. Taking sources and targets defines a natural transformation from the map ![]() $\mathscr {D}(1)\longrightarrow \mathscr {C}(1)$ to the map of spaces
$\mathscr {D}(1)\longrightarrow \mathscr {C}(1)$ to the map of spaces ![]() $\mathscr {D}(0)\times \mathscr {D}(0)\longrightarrow \mathscr {C}(0)\times \mathscr {C}(0)$. By Lemma 5.20,
$\mathscr {D}(0)\times \mathscr {D}(0)\longrightarrow \mathscr {C}(0)\times \mathscr {C}(0)$. By Lemma 5.20, ![]() $\mathscr {D}(1)\longrightarrow \mathscr {C}(1)$ is then a
$\mathscr {D}(1)\longrightarrow \mathscr {C}(1)$ is then a ![]() $(d-1)$-cartesian fibration if and only if for each
$(d-1)$-cartesian fibration if and only if for each ![]() $d_0, d_1\in \mathscr {D}$, the map on fibers
$d_0, d_1\in \mathscr {D}$, the map on fibers ![]() $\mathrm {Map}_{\mathscr {D}}(d_0, d_1)\longrightarrow \mathrm {Map}_{\mathscr {C}}(pd_0, pd_1)$ is a
$\mathrm {Map}_{\mathscr {D}}(d_0, d_1)\longrightarrow \mathrm {Map}_{\mathscr {C}}(pd_0, pd_1)$ is a ![]() $(d-1)$-cartesian fibration. In turn, the Segal conditions imply that each
$(d-1)$-cartesian fibration. In turn, the Segal conditions imply that each ![]() $\mathscr {D}(m)\longrightarrow \mathscr {C}(m)$ is a
$\mathscr {D}(m)\longrightarrow \mathscr {C}(m)$ is a ![]() $(d-1)$-cartesian fibration as soon as
$(d-1)$-cartesian fibration as soon as ![]() $\mathscr {D}(1)\longrightarrow \mathscr {C}(1)$ is.
$\mathscr {D}(1)\longrightarrow \mathscr {C}(1)$ is.
In this case, the simplicial structure maps induce strong morphisms between ![]() $(d-1)$-cartesian fibrations if and only if
$(d-1)$-cartesian fibrations if and only if ![]() $d_1\colon \mathscr {D}(2)\longrightarrow \mathscr {D}(1)$ is a strong morphism. Again, Lemma 5.20 shows that this can be verified fiberwise over each triple of objects
$d_1\colon \mathscr {D}(2)\longrightarrow \mathscr {D}(1)$ is a strong morphism. Again, Lemma 5.20 shows that this can be verified fiberwise over each triple of objects ![]() $d_0, d_1, d_2\in \mathscr {D}(0)$, which means precisely that
$d_0, d_1, d_2\in \mathscr {D}(0)$, which means precisely that ![]() $\mathrm {Map}_{\mathscr {D}}(d_1, d_2)\times \mathrm {Map}_{\mathscr {D}}(d_0, d_1)\longrightarrow \mathrm {Map}_{\mathscr {D}}(d_0, d_2)$ defines a strong morphism of
$\mathrm {Map}_{\mathscr {D}}(d_1, d_2)\times \mathrm {Map}_{\mathscr {D}}(d_0, d_1)\longrightarrow \mathrm {Map}_{\mathscr {D}}(d_0, d_2)$ defines a strong morphism of ![]() $(d-1)$-cartesian fibrations.
$(d-1)$-cartesian fibrations.
Lemma 5.22 The following assertions hold.
(1) The class of
 $d$-cocartesian fibrations is closed under composition and base change.
$d$-cocartesian fibrations is closed under composition and base change.(2) If
 $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a  $d$-cocartesian fibration, then
$d$-cocartesian fibration, then  $\mathrm {Fun}_n(\mathscr {B}, \mathscr {D})\longrightarrow \mathrm {Fun}_n(\mathscr {B}, \mathscr {C})$ is a
$\mathrm {Fun}_n(\mathscr {B}, \mathscr {D})\longrightarrow \mathrm {Fun}_n(\mathscr {B}, \mathscr {C})$ is a  $d$-cocartesian fibration as well and restriction along
$d$-cocartesian fibration as well and restriction along  $\mathscr {B}'\longrightarrow \mathscr {B}$ defines a strong morphism.
$\mathscr {B}'\longrightarrow \mathscr {B}$ defines a strong morphism.(3) The subcategory of
 $\mathrm {Fun}([1], {{\rm Cat}}_{n})$ spanned by the
$\mathrm {Fun}([1], {{\rm Cat}}_{n})$ spanned by the  $d$-cocartesian fibrations and strong morphisms between them is closed under limits.
$d$-cocartesian fibrations and strong morphisms between them is closed under limits.
Proof. All properties follow from Lemma 5.4 by induction, the case ![]() $d=0$ being readily verified. The only assertion requiring extra care is part (2). Using part (3), it suffices to verify this in the case where
$d=0$ being readily verified. The only assertion requiring extra care is part (2). Using part (3), it suffices to verify this in the case where ![]() $\mathscr {B}=[1]_{\mathscr {A}}$ for an
$\mathscr {B}=[1]_{\mathscr {A}}$ for an ![]() $(n-1)$-category
$(n-1)$-category ![]() $\mathscr {A}$ (and likewise for
$\mathscr {A}$ (and likewise for ![]() $\mathscr {B}'$). By Lemma 5.4,
$\mathscr {B}'$). By Lemma 5.4, ![]() $q\colon \mathrm {Fun}_n([1]_{\mathscr {A}}, \mathscr {D})\longrightarrow \mathrm {Fun}_n([1]_{\mathscr {A}}, \mathscr {C})$ is pre-cocartesian and restriction preserves cocartesian
$q\colon \mathrm {Fun}_n([1]_{\mathscr {A}}, \mathscr {D})\longrightarrow \mathrm {Fun}_n([1]_{\mathscr {A}}, \mathscr {C})$ is pre-cocartesian and restriction preserves cocartesian ![]() $1$-morphisms. To see that it is locally
$1$-morphisms. To see that it is locally ![]() $(d-1)$-cartesian, consider the diagram of simplicial
$(d-1)$-cartesian, consider the diagram of simplicial ![]() $(n-1)$-categories, given as follows in simplicial degree
$(n-1)$-categories, given as follows in simplicial degree ![]() $m$.
$m$.

Using Lemma 5.21, it follows by inductive hypothesis that the vertical maps define simplicial diagrams of ![]() $(d-1)$-cartesian fibrations and strong morphisms between them. Furthermore, the horizontal maps define strong morphisms between these
$(d-1)$-cartesian fibrations and strong morphisms between them. Furthermore, the horizontal maps define strong morphisms between these ![]() $(d-1)$-cartesian fibrations. Taking pullbacks along the rows, we then obtain another simplicial diagram of
$(d-1)$-cartesian fibrations. Taking pullbacks along the rows, we then obtain another simplicial diagram of ![]() $(d-1)$-cartesian fibrations and strong morphisms. By Corollary 4.9, this is precisely the map
$(d-1)$-cartesian fibrations and strong morphisms. By Corollary 4.9, this is precisely the map ![]() $q\colon \mathrm {Fun}_n\big ([1]_{\mathscr {A}}, \mathscr {D}\big )\longrightarrow \mathrm {Fun}_n\big ([1]_{\mathscr {A}}, \mathscr {C}\big )$.
$q\colon \mathrm {Fun}_n\big ([1]_{\mathscr {A}}, \mathscr {D}\big )\longrightarrow \mathrm {Fun}_n\big ([1]_{\mathscr {A}}, \mathscr {C}\big )$.
We conclude by induction and Lemma 5.21 that ![]() $q$ is locally
$q$ is locally ![]() $(d-1)$-cartesian. From the above description one readily verifies that restriction along
$(d-1)$-cartesian. From the above description one readily verifies that restriction along ![]() $[1]_{\mathscr {A}'}\longrightarrow [1]_{\mathscr {A}}$ preserves lateral
$[1]_{\mathscr {A}'}\longrightarrow [1]_{\mathscr {A}}$ preserves lateral ![]() $k$-morphisms for all
$k$-morphisms for all ![]() $1\leq k\leq d$.
$1\leq k\leq d$.
5.3 The  $(d+2)$-category of
$(d+2)$-category of  $d$-cocartesian fibrations
$d$-cocartesian fibrations
Because of Remark 5.18, we will henceforth only consider ![]() $d$-cocartesian fibrations between
$d$-cocartesian fibrations between ![]() $(d+1)$-categories. In light of Lemma 5.17, this is not really restrictive, since we can always choose
$(d+1)$-categories. In light of Lemma 5.17, this is not really restrictive, since we can always choose ![]() $d$ large enough to cover
$d$ large enough to cover ![]() $n$-cocartesian fibration between
$n$-cocartesian fibration between ![]() $m$-categories for some given
$m$-categories for some given ![]() $m$ and
$m$ and ![]() $n$.
$n$.
Definition 5.23 We will write ![]() $\mathbf {Cocart}_d\subseteq \mathrm {Fun}_{d+1}\big ([1], \mathbf {Cat}_{d+1}\big )$ for the sub-
$\mathbf {Cocart}_d\subseteq \mathrm {Fun}_{d+1}\big ([1], \mathbf {Cat}_{d+1}\big )$ for the sub-![]() $(d+2)$-category whose objects are the
$(d+2)$-category whose objects are the ![]() $d$-cocartesian fibrations
$d$-cocartesian fibrations ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ and whose
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ and whose ![]() $1$-morphisms are the strong morphisms between them (and all higher morphisms between those). Let us write
$1$-morphisms are the strong morphisms between them (and all higher morphisms between those). Let us write ![]() $\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ for the codomain projection and
$\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ for the codomain projection and ![]() $\mathbf {Cocart}_d(\mathscr {C})$ for the fiber over a
$\mathbf {Cocart}_d(\mathscr {C})$ for the fiber over a ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$.
$\mathscr {C}$.
Furthermore, let us write ![]() $\pi \colon {{\rm Cocart}}_{d}\longrightarrow {{\rm Cat}}_{d+1}$ for the induced functor between
$\pi \colon {{\rm Cocart}}_{d}\longrightarrow {{\rm Cat}}_{d+1}$ for the induced functor between ![]() $1$-cores. The fiber over a
$1$-cores. The fiber over a ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$ is denoted
$\mathscr {C}$ is denoted ![]() ${{\rm Cocart}}_{d}(\mathscr {C})$.
${{\rm Cocart}}_{d}(\mathscr {C})$.
Remark 5.24 One can model ![]() $\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ by a strict functor between
$\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ by a strict functor between ![]() $\mathsf {Cat}_{d+1}$-enriched categories, where
$\mathsf {Cat}_{d+1}$-enriched categories, where ![]() $\mathbf {Cocart}_d$ is modeled by an enriched subcategory of
$\mathbf {Cocart}_d$ is modeled by an enriched subcategory of ![]() $\mathrm {Fun}_{\mathrm {enr}}([1], \mathsf {Cat}_{d+1})$ whose objects are fibrant models for
$\mathrm {Fun}_{\mathrm {enr}}([1], \mathsf {Cat}_{d+1})$ whose objects are fibrant models for ![]() $d$-cocartesian fibrations and whose mapping objects are the subobjects consisting of strong morphisms.
$d$-cocartesian fibrations and whose mapping objects are the subobjects consisting of strong morphisms.
Proposition 5.25 The projection ![]() $\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ is a
$\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ is a ![]() $(d+1)$-cartesian fibration.
$(d+1)$-cartesian fibration.
Lemma 5.26 Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a ![]() $d$-cocartesian fibration and let
$d$-cocartesian fibration and let ![]() $\mathscr {A}$ be a
$\mathscr {A}$ be a ![]() $(d+1)$-category equipped with subspaces
$(d+1)$-category equipped with subspaces ![]() $S_k\subseteq \mathscr {A}(1, \dots, 1, \vec {0}_{d+1-k})$ of ‘marked
$S_k\subseteq \mathscr {A}(1, \dots, 1, \vec {0}_{d+1-k})$ of ‘marked ![]() $k$-morphisms’ for all
$k$-morphisms’ for all ![]() $1\leq k\leq d$ (without any further condition). Let
$1\leq k\leq d$ (without any further condition). Let ![]() $\mathrm {Fun}^{\sharp }_{d+1}(\mathscr {A}, \mathscr {D})\subseteq \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {D})$ denote the full sub-
$\mathrm {Fun}^{\sharp }_{d+1}(\mathscr {A}, \mathscr {D})\subseteq \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {D})$ denote the full sub-![]() $(d+1)$-category spanned by those functors
$(d+1)$-category spanned by those functors ![]() $\mathscr {A}\longrightarrow \mathscr {D}$ sending every marked
$\mathscr {A}\longrightarrow \mathscr {D}$ sending every marked ![]() $k$-morphism in
$k$-morphism in ![]() $\mathscr {A}$ to a
$\mathscr {A}$ to a ![]() $p$-lateral
$p$-lateral ![]() $k$-morphism in
$k$-morphism in ![]() $\mathscr {D}$. Then the natural map
$\mathscr {D}$. Then the natural map ![]() $\mathrm {Fun}^{\sharp }_{d+1}(\mathscr {A}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {C})$ is a
$\mathrm {Fun}^{\sharp }_{d+1}(\mathscr {A}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {C})$ is a ![]() $d$-cocartesian fibration.
$d$-cocartesian fibration.
Proof. By Lemma 5.22, ![]() $\mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {C})$ is a
$\mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {C})$ is a ![]() $d$-cocartesian fibration. Since
$d$-cocartesian fibration. Since ![]() $\mathrm {Fun}^{\sharp }_{d+1}(\mathscr {A}, \mathscr {D})\subseteq \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {D})$ is a full sub-
$\mathrm {Fun}^{\sharp }_{d+1}(\mathscr {A}, \mathscr {D})\subseteq \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {D})$ is a full sub-![]() $(d+1)$-category,
$(d+1)$-category, ![]() $\mathrm {Fun}^{\sharp }_{d+1}(\mathscr {A}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {C})$ is a homwise
$\mathrm {Fun}^{\sharp }_{d+1}(\mathscr {A}, \mathscr {D})\longrightarrow \mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {C})$ is a homwise ![]() $(d-1)$-cartesian fibration as well. It then remains to verify the following assertion: if
$(d-1)$-cartesian fibration as well. It then remains to verify the following assertion: if ![]() $\mu \colon f\longrightarrow g$ is a cocartesian
$\mu \colon f\longrightarrow g$ is a cocartesian ![]() $1$-morphism in
$1$-morphism in ![]() $\mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {D})$ such that
$\mathrm {Fun}_{d+1}(\mathscr {A}, \mathscr {D})$ such that ![]() $f\in \mathrm {Fun}^\sharp _{d+1}(\mathscr {A}, \mathscr {D})$, then
$f\in \mathrm {Fun}^\sharp _{d+1}(\mathscr {A}, \mathscr {D})$, then ![]() $g\in \mathrm {Fun}^\sharp _{d+1}(\mathscr {A}, \mathscr {D})$ as well.
$g\in \mathrm {Fun}^\sharp _{d+1}(\mathscr {A}, \mathscr {D})$ as well.
Let us first verify that ![]() $g$ sends all marked
$g$ sends all marked ![]() $1$-morphisms in
$1$-morphisms in ![]() $\mathscr {A}$ to cocartesian morphisms in
$\mathscr {A}$ to cocartesian morphisms in ![]() $\mathscr {D}$: indeed, for every such map
$\mathscr {D}$: indeed, for every such map ![]() $\alpha \colon a_0\longrightarrow a_1$, there is a commuting square in
$\alpha \colon a_0\longrightarrow a_1$, there is a commuting square in ![]() $\mathscr {D}$ of the following form.
$\mathscr {D}$ of the following form.

The horizontal arrows are cocartesian since ![]() $\mu$ was a cocartesian natural transformation (Lemma 5.22). Since
$\mu$ was a cocartesian natural transformation (Lemma 5.22). Since ![]() $f(\alpha )$ is a cocartesian arrow, one sees that
$f(\alpha )$ is a cocartesian arrow, one sees that ![]() $g(\alpha )$ is a cocartesian arrow as well (cf. the argument in [Reference LurieLur09a, Proposition 2.4.1.7] and [Reference Riehl and VerityRV22, Lemma 5.1.5]).
$g(\alpha )$ is a cocartesian arrow as well (cf. the argument in [Reference LurieLur09a, Proposition 2.4.1.7] and [Reference Riehl and VerityRV22, Lemma 5.1.5]).
To see that ![]() $g$ preserves lateral
$g$ preserves lateral ![]() $k$-morphisms for
$k$-morphisms for ![]() $k>1$, note that for each
$k>1$, note that for each ![]() $a_0, a_1\in \mathscr {A}$ there is the following commuting square of mapping
$a_0, a_1\in \mathscr {A}$ there is the following commuting square of mapping ![]() $d$-categories.
$d$-categories.

Since ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is a ![]() $d$-cocartesian fibration, the functor
$d$-cocartesian fibration, the functor ![]() $\mu (a_1)_*$ postcomposing with
$\mu (a_1)_*$ postcomposing with ![]() $\mu (a_1)$ is strong, i.e. it preserves lateral
$\mu (a_1)$ is strong, i.e. it preserves lateral ![]() $k$-morphisms. Since
$k$-morphisms. Since ![]() $f$ sends marked
$f$ sends marked ![]() $k$-morphisms to lateral
$k$-morphisms to lateral ![]() $k$-morphisms, it follows that
$k$-morphisms, it follows that ![]() $\mu (a_1)_*\circ f$ does as well. On the other hand, since
$\mu (a_1)_*\circ f$ does as well. On the other hand, since ![]() $\mu (a_0)$ is a cocartesian
$\mu (a_0)$ is a cocartesian ![]() $1$-morphism, the map
$1$-morphism, the map ![]() $\mu (a_0)^*$ is an equivalence of
$\mu (a_0)^*$ is an equivalence of ![]() $d$-categories. This implies that
$d$-categories. This implies that ![]() $g$ sends marked
$g$ sends marked ![]() $k$-morphisms to lateral
$k$-morphisms to lateral ![]() $k$-morphisms as well.
$k$-morphisms as well.
Proof of Proposition 5.25 Let us start by verifying that ![]() $\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ is a homwise
$\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ is a homwise ![]() $d$-cocartesian fibration. Let
$d$-cocartesian fibration. Let ![]() $p_0\colon \mathscr {D}_0\longrightarrow \mathscr {C}_0$ and
$p_0\colon \mathscr {D}_0\longrightarrow \mathscr {C}_0$ and ![]() $p_1\colon \mathscr {D}_1\longrightarrow \mathscr {C}_1$ be
$p_1\colon \mathscr {D}_1\longrightarrow \mathscr {C}_1$ be ![]() $d$-cocartesian fibrations. We have to check that the induced map on mapping
$d$-cocartesian fibrations. We have to check that the induced map on mapping ![]() $(d+1)$-categories
$(d+1)$-categories
is a ![]() $d$-cocartesian fibration. To see this, note that one can identify
$d$-cocartesian fibration. To see this, note that one can identify
where ![]() $\mathrm {Fun}^{\natural }_{d+1}(\mathscr {D}_0, \mathscr {D}_1)\subseteq \mathrm {Fun}_{d+1}(\mathscr {D}_0, \mathscr {D}_1)$ is the full sub-
$\mathrm {Fun}^{\natural }_{d+1}(\mathscr {D}_0, \mathscr {D}_1)\subseteq \mathrm {Fun}_{d+1}(\mathscr {D}_0, \mathscr {D}_1)$ is the full sub-![]() $(d+1)$-category spanned by those functors
$(d+1)$-category spanned by those functors ![]() $\mathscr {D}_0\longrightarrow \mathscr {D}_1$ preserving lateral
$\mathscr {D}_0\longrightarrow \mathscr {D}_1$ preserving lateral ![]() $k$-morphisms. The result then follows from Lemma 5.26 and stability of
$k$-morphisms. The result then follows from Lemma 5.26 and stability of ![]() $d$-cocartesian fibrations under base change (Lemma 5.22).
$d$-cocartesian fibrations under base change (Lemma 5.22).
Next, given another ![]() $d$-cocartesian fibration
$d$-cocartesian fibration ![]() $p_2\colon \mathscr {D}_2\longrightarrow \mathscr {C}_2$, we have to verify that the square induced by composition
$p_2\colon \mathscr {D}_2\longrightarrow \mathscr {C}_2$, we have to verify that the square induced by composition

gives a strong morphism of ![]() $d$-cocartesian fibrations. To see this, let
$d$-cocartesian fibrations. To see this, let ![]() $f, g\in \mathrm {Map}(p_0, p_1)$ and
$f, g\in \mathrm {Map}(p_0, p_1)$ and ![]() $f', g'\in \mathrm {Map}(p_1, p_2)$. We will abuse notation and write
$f', g'\in \mathrm {Map}(p_1, p_2)$. We will abuse notation and write ![]() $f, g\colon \mathscr {D}_0\longrightarrow \mathscr {D}_1$ and
$f, g\colon \mathscr {D}_0\longrightarrow \mathscr {D}_1$ and ![]() $f', g'\colon \mathscr {D}_1\longrightarrow \mathscr {D}_2$ for the underlying functors, which all preserve lateral
$f', g'\colon \mathscr {D}_1\longrightarrow \mathscr {D}_2$ for the underlying functors, which all preserve lateral ![]() $k$-morphisms. Let
$k$-morphisms. Let ![]() $\alpha \colon f \longrightarrow g$ and
$\alpha \colon f \longrightarrow g$ and ![]() $\beta \colon f'\longrightarrow g'$ be lateral
$\beta \colon f'\longrightarrow g'$ be lateral ![]() $k$-morphisms (which we depict as 1-morphisms instead of higher cells, for simplicity). Then the image of
$k$-morphisms (which we depict as 1-morphisms instead of higher cells, for simplicity). Then the image of ![]() $(\alpha, \beta )$ under
$(\alpha, \beta )$ under ![]() $\circ$ is given by the horizontal composition
$\circ$ is given by the horizontal composition
Then ![]() $f'\alpha$ is lateral since
$f'\alpha$ is lateral since ![]() $f'$ preserves lateral
$f'$ preserves lateral ![]() $k$-morphisms and
$k$-morphisms and ![]() $\beta g$ is lateral since lateral natural transformations are detected pointwise. Consequently, their horizontal composite is a lateral
$\beta g$ is lateral since lateral natural transformations are detected pointwise. Consequently, their horizontal composite is a lateral ![]() $k$-morphism as well.
$k$-morphism as well.
It remains to check that ![]() $\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ is a pre-cartesian fibration. Given a map
$\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ is a pre-cartesian fibration. Given a map ![]() $f\colon \mathscr {C}_1\longrightarrow \mathscr {C}_2$ and a
$f\colon \mathscr {C}_1\longrightarrow \mathscr {C}_2$ and a ![]() $d$-cocartesian fibration
$d$-cocartesian fibration ![]() $p_2\colon \mathscr {D}_2\longrightarrow \mathscr {C}_2$, let
$p_2\colon \mathscr {D}_2\longrightarrow \mathscr {C}_2$, let ![]() $p_1\colon \mathscr {D}_1=\mathscr {D}_2\times _{\mathscr {C}_2}\mathscr {C}_1\longrightarrow \mathscr {C}_1$ be the base change. We have to show that the canonical (strong) map of cocartesian fibrations
$p_1\colon \mathscr {D}_1=\mathscr {D}_2\times _{\mathscr {C}_2}\mathscr {C}_1\longrightarrow \mathscr {C}_1$ be the base change. We have to show that the canonical (strong) map of cocartesian fibrations ![]() $\tilde {f}\colon \mathscr {D}_1\longrightarrow \mathscr {D}_2$ defines a cartesian lift of
$\tilde {f}\colon \mathscr {D}_1\longrightarrow \mathscr {D}_2$ defines a cartesian lift of ![]() $f$, i.e. that for any
$f$, i.e. that for any ![]() $p_0\colon \mathscr {D}_0\longrightarrow \mathscr {C}_0$, the square
$p_0\colon \mathscr {D}_0\longrightarrow \mathscr {C}_0$, the square

is cartesian. Using (5.27), one sees that this comes down to verifying that

is cartesian. This follows immediately from the fact that a functor ![]() $\mathscr {D}_0\longrightarrow \mathscr {D}_2\times _{\mathscr {C}_2}\mathscr {C}_1$ preserves lateral
$\mathscr {D}_0\longrightarrow \mathscr {D}_2\times _{\mathscr {C}_2}\mathscr {C}_1$ preserves lateral ![]() $k$-morphisms if and only if the corresponding map
$k$-morphisms if and only if the corresponding map ![]() $\mathscr {D}_0\longrightarrow \mathscr {D}_2$ does.
$\mathscr {D}_0\longrightarrow \mathscr {D}_2$ does.
6. Straightening and unstraightening
Finally, we turn to straightening and unstraightening: for a small ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$, we will establish an equivalence between
$\mathscr {C}$, we will establish an equivalence between ![]() $d$-cocartesian fibrations over
$d$-cocartesian fibrations over ![]() $\mathscr {C}$ and copresheaves
$\mathscr {C}$ and copresheaves ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d$. We will start by describing this as an equivalence of
$\mathscr {C}\longrightarrow \mathbf {Cat}_d$. We will start by describing this as an equivalence of ![]() $1$-categories (Theorem 6.1). We then use this to establish a more structured version of straightening–unstraightening that provides an equivalence of
$1$-categories (Theorem 6.1). We then use this to establish a more structured version of straightening–unstraightening that provides an equivalence of ![]() $(d+1)$-categories and is furthermore
$(d+1)$-categories and is furthermore ![]() $(d+2)$-functorial in
$(d+2)$-functorial in ![]() $\mathscr {C}$ (Theorem 6.20).
$\mathscr {C}$ (Theorem 6.20).
6.1 Straightening and unstraightening: 1-categorical version
Our first goal will be to prove the following.
Theorem 6.1 There is an equivalence of cartesian fibrations between ![]() $1$-categories as follows.
$1$-categories as follows.

In particular, for each ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$ this induces equivalences of
$\mathscr {C}$ this induces equivalences of ![]() $1$-categories
$1$-categories
between (Segal) copresheaves of ![]() $d$-categories on
$d$-categories on ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $d$-cocartesian fibrations over
$d$-cocartesian fibrations over ![]() $\mathscr {C}$.
$\mathscr {C}$.
Remark 6.2 Similarly, for every ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$, there is an equivalence of
$\mathscr {C}$, there is an equivalence of ![]() $1$-categories between cartesian fibrations and presheaves:
$1$-categories between cartesian fibrations and presheaves:
Here the first equivalence sends a functor ![]() $F\colon \mathscr {C}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_d$ to the functor
$F\colon \mathscr {C}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_d$ to the functor ![]() $c\mapsto F(c)^{(1,\dots, d)-\mathrm {op}}$ (which changes the variance with respect to higher morphisms). The second equivalence is Theorem 6.1 and the last equivalence takes
$c\mapsto F(c)^{(1,\dots, d)-\mathrm {op}}$ (which changes the variance with respect to higher morphisms). The second equivalence is Theorem 6.1 and the last equivalence takes ![]() $(1, \dots, d+1)$-opposites to obtain a cartesian fibration (Remark 5.14), whose fibers are equivalent to the values of
$(1, \dots, d+1)$-opposites to obtain a cartesian fibration (Remark 5.14), whose fibers are equivalent to the values of ![]() $F$.
$F$.
We will prove this theorem by a repeated application of Theorem 3.1 in different simplicial directions. Concretely, the above equivalence will arise as a composition of ![]() $d$ equivalences, whose intermediate categories consist of certain fibrations of
$d$ equivalences, whose intermediate categories consist of certain fibrations of ![]() $(d+1)$-fold categories.
$(d+1)$-fold categories.
Definition 6.3 Let ![]() $\mathscr {C}$ be a
$\mathscr {C}$ be a ![]() $(d+1)$-category and let
$(d+1)$-category and let ![]() $p\colon \mathbb {D}\longrightarrow \mathscr {C}$ be a map of
$p\colon \mathbb {D}\longrightarrow \mathscr {C}$ be a map of ![]() $(d+1)$-fold categories. By induction, we will say that
$(d+1)$-fold categories. By induction, we will say that ![]() $p$ is a fibration of the following type.
$p$ is a fibration of the following type.
– A
 $0$th stage fibration if
$0$th stage fibration if  $\mathbb {D}(1)\longrightarrow \mathscr {C}(1)\times _{\mathscr {C}(\{0\})} \mathbb {D}(\{0\})$ is an equivalence of
$\mathbb {D}(1)\longrightarrow \mathscr {C}(1)\times _{\mathscr {C}(\{0\})} \mathbb {D}(\{0\})$ is an equivalence of  $d$-fold categories. A strong map of
$d$-fold categories. A strong map of  $0$th stage fibrations is simply a commuting square.
$0$th stage fibrations is simply a commuting square.– A
 $k$th stage fibration, for
$k$th stage fibration, for  $1\leq k\leq d$, if it satisfies the following two conditions.
$1\leq k\leq d$, if it satisfies the following two conditions.
(a1) Each
 $\mathbb {D}(n)^{(1, \dots, d)-\mathrm {op}}\longrightarrow \mathscr {C}(n)^{(1, \dots, d)-\mathrm {op}}$ is a
$\mathbb {D}(n)^{(1, \dots, d)-\mathrm {op}}\longrightarrow \mathscr {C}(n)^{(1, \dots, d)-\mathrm {op}}$ is a  $(k-1)$th stage fibration and each
$(k-1)$th stage fibration and each  $[n]\longrightarrow [n']$ induces a strong map between
$[n]\longrightarrow [n']$ induces a strong map between  $(k-1)$th stage fibrations.
$(k-1)$th stage fibrations.(a2) The map of categories
 $\mathbb {D}(-, \vec {0}_d)\longrightarrow \mathscr {C}(-, \vec {0}_d)$ is a cocartesian fibration and each map
$\mathbb {D}(-, \vec {0}_d)\longrightarrow \mathscr {C}(-, \vec {0}_d)$ is a cocartesian fibration and each map  $\mathbb {D}(-, \vec {0}_d)\longrightarrow \mathbb {D}(-, \vec {n}_d)\times _{\mathscr {C}(-, \vec {n}_d)} \mathscr {C}(-, \vec {0}_d)$ preserves cocartesian arrows (over
$\mathbb {D}(-, \vec {0}_d)\longrightarrow \mathbb {D}(-, \vec {n}_d)\times _{\mathscr {C}(-, \vec {n}_d)} \mathscr {C}(-, \vec {0}_d)$ preserves cocartesian arrows (over  $\mathscr {C}(-, \vec {0}_d)$).
$\mathscr {C}(-, \vec {0}_d)$).
A strong map between
 $k$th stage fibrations is a commuting square such that:
$k$th stage fibrations is a commuting square such that:
(b1) evaluating at
 $[n]\in \mathbf {\Delta }$ in the first coordinate yields a strong map of
$[n]\in \mathbf {\Delta }$ in the first coordinate yields a strong map of  $(k-1)$th stage fibrations;
$(k-1)$th stage fibrations;(b2) the map
 $\mathbb {D}(-, \vec {0}_d)\longrightarrow \mathbb {D}'(-, \vec {0}_d)$ preserves cocartesian arrows.
$\mathbb {D}(-, \vec {0}_d)\longrightarrow \mathbb {D}'(-, \vec {0}_d)$ preserves cocartesian arrows.
We will write ![]() $\mathrm {Fib}_d^{(k)}\subseteq \mathrm {Fun}\big ([1], {{\rm Cat}}^{\otimes d+1}\big )$ for the subcategory whose objects are
$\mathrm {Fib}_d^{(k)}\subseteq \mathrm {Fun}\big ([1], {{\rm Cat}}^{\otimes d+1}\big )$ for the subcategory whose objects are ![]() $k$th stage fibrations (in particular, the codomain is a
$k$th stage fibrations (in particular, the codomain is a ![]() $(d+1)$-category) and whose maps are commuting squares satisfying conditions (b1) and (b2). The codomain projection defines a cartesian fibration
$(d+1)$-category) and whose maps are commuting squares satisfying conditions (b1) and (b2). The codomain projection defines a cartesian fibration
Proposition 6.4 For each ![]() $1\leq k\leq d$, there is an equivalence of categories as follows.
$1\leq k\leq d$, there is an equivalence of categories as follows.

Proof. Let us fix ![]() $k\geq 1$ and start with the following observation: if
$k\geq 1$ and start with the following observation: if ![]() $p\colon \mathbb {D}\longrightarrow \mathscr {C}$ is a
$p\colon \mathbb {D}\longrightarrow \mathscr {C}$ is a ![]() $k$th stage fibration, then each
$k$th stage fibration, then each
is a (cart, left)-fibration if ![]() $k$ is even, and a (cocart, right)-fibration if
$k$ is even, and a (cocart, right)-fibration if ![]() $k$ is odd. Furthermore, each
$k$ is odd. Furthermore, each ![]() $\vec {n}_{k-1}\longrightarrow \vec {n}_{k-1}'$ and
$\vec {n}_{k-1}\longrightarrow \vec {n}_{k-1}'$ and ![]() $\vec {n}_{d-k}\longrightarrow \vec {n}_{d-k}'$ induces a map preserving (co)cartesian morphisms. When
$\vec {n}_{d-k}\longrightarrow \vec {n}_{d-k}'$ induces a map preserving (co)cartesian morphisms. When ![]() $k=1$ this follows from condition (a2) and the fact that
$k=1$ this follows from condition (a2) and the fact that ![]() $\mathscr {C}(-, \vec {0}_d)\simeq \mathscr {C}(-, 0, \vec {n}_{d-1})$; for higher
$\mathscr {C}(-, \vec {0}_d)\simeq \mathscr {C}(-, 0, \vec {n}_{d-1})$; for higher ![]() $k$ it follows inductively, by repeatedly applying condition (a1).
$k$ it follows inductively, by repeatedly applying condition (a1).
From this point on, let us assume that ![]() $k$ is odd; when
$k$ is odd; when ![]() $k$ is even, the same argument applies up to taking opposites (in all dimensions). Note that for a
$k$ is even, the same argument applies up to taking opposites (in all dimensions). Note that for a ![]() $(k-1)$th stage fibration
$(k-1)$th stage fibration ![]() $p\colon \mathbb {D}\longrightarrow \mathscr {C}$, the map (6.5) is a (left, cart)-fibration and each
$p\colon \mathbb {D}\longrightarrow \mathscr {C}$, the map (6.5) is a (left, cart)-fibration and each ![]() $\vec {n}_{k-1}\longrightarrow \vec {n}_{k-1}'$ and
$\vec {n}_{k-1}\longrightarrow \vec {n}_{k-1}'$ and ![]() $\vec {n}_{d-k}\longrightarrow \vec {n}_{d-k}'$ induces a strong map of (left, cart)-fibrations. Indeed, the previous paragraph shows that
$\vec {n}_{d-k}\longrightarrow \vec {n}_{d-k}'$ induces a strong map of (left, cart)-fibrations. Indeed, the previous paragraph shows that ![]() $p$ is a left fibration in the
$p$ is a left fibration in the ![]() $k$th variable. Furthermore, setting the
$k$th variable. Furthermore, setting the ![]() $k$th entry equal to
$k$th entry equal to ![]() $0$ yields a map
$0$ yields a map ![]() $\mathbb {D}(\vec {n}_{k-1}, 0, -, \vec {n}_{d-k})\longrightarrow \mathscr {C}(\vec {n}_{k-1}, 0, -, \vec {n}_{d-k})$ from a
$\mathbb {D}(\vec {n}_{k-1}, 0, -, \vec {n}_{d-k})\longrightarrow \mathscr {C}(\vec {n}_{k-1}, 0, -, \vec {n}_{d-k})$ from a ![]() $1$-category to a space. In particular, each such map is a cartesian fibration and since its cartesian arrows are the equivalences, each
$1$-category to a space. In particular, each such map is a cartesian fibration and since its cartesian arrows are the equivalences, each ![]() $\vec {n}_{k-1}\longrightarrow \vec {n}_{k-1}'$ and
$\vec {n}_{k-1}\longrightarrow \vec {n}_{k-1}'$ and ![]() $\vec {n}_{d-k}\longrightarrow \vec {n}_{d-k}'$ induces a map preserving cartesian arrows.
$\vec {n}_{d-k}\longrightarrow \vec {n}_{d-k}'$ induces a map preserving cartesian arrows.
Denoting ![]() $\mathscr {I}=\big (\mathbf {\Delta }^{\times k-1}\times \mathbf {\Delta }^{\times d-k}\big )^{\mathrm {op}}$, we therefore obtain the following diagram.
$\mathscr {I}=\big (\mathbf {\Delta }^{\times k-1}\times \mathbf {\Delta }^{\times d-k}\big )^{\mathrm {op}}$, we therefore obtain the following diagram.

Here the functors from left to right are subcategory inclusions and the top right equivalence is the reflection functor from Theorem 3.1, applied to the ![]() $k$th and
$k$th and ![]() $(k+1)$th variable. We will prove by induction on
$(k+1)$th variable. We will prove by induction on ![]() $k$ that the equivalence
$k$ that the equivalence ![]() $\Psi ^\perp _{(k, k+1)}$ identifies the subcategories of
$\Psi ^\perp _{(k, k+1)}$ identifies the subcategories of ![]() $(k-1)$th stage fibrations and
$(k-1)$th stage fibrations and ![]() $k$th stage fibrations.
$k$th stage fibrations.
When ![]() $k=1$, note that the bottom and front square are pullbacks: a map
$k=1$, note that the bottom and front square are pullbacks: a map ![]() $\mathbb {D}\longrightarrow \mathscr {C}$ is a
$\mathbb {D}\longrightarrow \mathscr {C}$ is a ![]() $0$th stage fibration if and only if it is a natural (left, cart)-fibration in the first two variables, and a
$0$th stage fibration if and only if it is a natural (left, cart)-fibration in the first two variables, and a ![]() $1$st stage fibration if and only if it is a natural (cocart, right)-fibration in the first two variables. In particular,
$1$st stage fibration if and only if it is a natural (cocart, right)-fibration in the first two variables. In particular, ![]() $\Psi _{(1, 2)}^\perp$ identifies
$\Psi _{(1, 2)}^\perp$ identifies ![]() $0$th stage fibrations and
$0$th stage fibrations and ![]() $1$st stage fibrations.
$1$st stage fibrations.
For ![]() $k>1$, the inductive hypothesis implies that
$k>1$, the inductive hypothesis implies that ![]() $p\colon \mathbb {D}\longrightarrow \mathscr {C}$ satisfies condition (a1) for
$p\colon \mathbb {D}\longrightarrow \mathscr {C}$ satisfies condition (a1) for ![]() $(k-1)$th stage fibrations if and only if
$(k-1)$th stage fibrations if and only if ![]() $\Psi _{(k, k+1)}^\perp (p)\colon \Psi ^\perp (\mathbb {D})\longrightarrow \mathscr {C}$ satisfies condition (a1) for
$\Psi _{(k, k+1)}^\perp (p)\colon \Psi ^\perp (\mathbb {D})\longrightarrow \mathscr {C}$ satisfies condition (a1) for ![]() $k$th stage fibrations. For condition (a2), note that
$k$th stage fibrations. For condition (a2), note that ![]() $\mathbb {D}\times _{\mathscr {C}}\mathfrak {c}_1(\mathscr {C})\longrightarrow \mathfrak {c}_1(\mathscr {C})$ is given in the
$\mathbb {D}\times _{\mathscr {C}}\mathfrak {c}_1(\mathscr {C})\longrightarrow \mathfrak {c}_1(\mathscr {C})$ is given in the ![]() $k$th and
$k$th and ![]() $(k+1)$th variables by a (left, cart)-fibration over a space. For such (left, cart)-fibrations over spaces, the functor
$(k+1)$th variables by a (left, cart)-fibration over a space. For such (left, cart)-fibrations over spaces, the functor ![]() $\Psi ^\perp$ is equivalent to the functor that exchanges the
$\Psi ^\perp$ is equivalent to the functor that exchanges the ![]() $k$th and
$k$th and ![]() $(k+1)$th variable (Proposition 3.15). Using that
$(k+1)$th variable (Proposition 3.15). Using that ![]() $\Psi ^\perp$ is compatible with base change, we therefore find
$\Psi ^\perp$ is compatible with base change, we therefore find
 \begin{align*} \Psi_{(k, k+1)}^\perp(\mathbb{D})\big(-,\vec{n}_{k-2},m, n, \vec{n}_{d-k}\big)&\times_{\mathscr{C}(-,\vec{n}_{k-2},m, n, \vec{n}_{d-k})}\mathscr{C}(-, \vec{0}_d)\\ &\simeq \mathbb{D}\big(-,\vec{n}_{k-2},n, m, \vec{n}_{d-k}\big)\times_{\mathscr{C}(-,\vec{n}_{k-2},n, m, \vec{n}_{d-k})}\mathscr{C}(-, \vec{0}_d). \end{align*}
\begin{align*} \Psi_{(k, k+1)}^\perp(\mathbb{D})\big(-,\vec{n}_{k-2},m, n, \vec{n}_{d-k}\big)&\times_{\mathscr{C}(-,\vec{n}_{k-2},m, n, \vec{n}_{d-k})}\mathscr{C}(-, \vec{0}_d)\\ &\simeq \mathbb{D}\big(-,\vec{n}_{k-2},n, m, \vec{n}_{d-k}\big)\times_{\mathscr{C}(-,\vec{n}_{k-2},n, m, \vec{n}_{d-k})}\mathscr{C}(-, \vec{0}_d). \end{align*}
It follows that ![]() $p$ satisfies condition (a2) if and only if
$p$ satisfies condition (a2) if and only if ![]() $\Psi _{(k, k+1)}^\perp (p)$ does. A similar argument shows that
$\Psi _{(k, k+1)}^\perp (p)$ does. A similar argument shows that ![]() $\Psi _{(k, k+1)}^\perp$ identifies strong morphisms between
$\Psi _{(k, k+1)}^\perp$ identifies strong morphisms between ![]() $(k-1)$th stage fibrations and
$(k-1)$th stage fibrations and ![]() $k$th stage fibrations, so that
$k$th stage fibrations, so that ![]() $\Psi _{(k, k+1)}^\perp$ indeed restricts to an equivalence
$\Psi _{(k, k+1)}^\perp$ indeed restricts to an equivalence ![]() $\mathrm {Fib}_d^{(k-1)}\stackrel {\sim }{\longrightarrow } \mathrm {Fib}_d^{(k)}$.
$\mathrm {Fib}_d^{(k-1)}\stackrel {\sim }{\longrightarrow } \mathrm {Fib}_d^{(k)}$.
Corollary 6.6 Consider the following strong morphism of ![]() $k$th stage fibrations.
$k$th stage fibrations.

This square is cartesian if and only if the map ![]() $f$ induces equivalences on fibers
$f$ induces equivalences on fibers ![]() $\mathbb {D}_c\longrightarrow \mathbb {D}'_c$ for each object
$\mathbb {D}_c\longrightarrow \mathbb {D}'_c$ for each object ![]() $c\in \mathscr {C}$.
$c\in \mathscr {C}$.
Proof. This is evident for ![]() $k=0$. For higher
$k=0$. For higher ![]() $k$, it follows from Proposition 6.4.
$k$, it follows from Proposition 6.4.
Lemma 6.7 Let ![]() $p\colon \mathbb {D}\longrightarrow \mathscr {C}$ be a
$p\colon \mathbb {D}\longrightarrow \mathscr {C}$ be a ![]() $d$th stage fibration from a
$d$th stage fibration from a ![]() $(d+1)$-fold category to a
$(d+1)$-fold category to a ![]() $(d+1)$-category. Then the following two conditions are equivalent.
$(d+1)$-category. Then the following two conditions are equivalent.
(1) For any object
 $c\in \mathscr {C}$, the fiber
$c\in \mathscr {C}$, the fiber  $\mathbb {D}_c$ is a
$\mathbb {D}_c$ is a  $d$-category in the first
$d$-category in the first  $d$-variables, and constant in the last variable.
$d$-variables, and constant in the last variable.(2) The
 $(d+1)$-fold category
$(d+1)$-fold category  $\mathbb {D}$ is a
$\mathbb {D}$ is a  $(d+1)$-category.
$(d+1)$-category.
Proof. We proceed by induction on ![]() $d$, the case
$d$, the case ![]() $d=0$ being obvious. Note that a
$d=0$ being obvious. Note that a ![]() $d$th stage fibration is either a left or a right fibration in the last variable, so that
$d$th stage fibration is either a left or a right fibration in the last variable, so that ![]() $\mathbb {D}(\vec {n}_d, p)\simeq \mathbb {D}(\vec {n}_d, 0)\times _{\mathscr {C}(\vec {n}_d, 0)} \mathscr {C}(\vec {n}_{d}, p)$. This immediately shows that condition (2) implies condition (1). For the converse, note that condition (1) implies that the fibers of
$\mathbb {D}(\vec {n}_d, p)\simeq \mathbb {D}(\vec {n}_d, 0)\times _{\mathscr {C}(\vec {n}_d, 0)} \mathscr {C}(\vec {n}_{d}, p)$. This immediately shows that condition (2) implies condition (1). For the converse, note that condition (1) implies that the fibers of ![]() $\mathbb {D}(0)\longrightarrow \mathscr {C}(0)$ are spaces, so that
$\mathbb {D}(0)\longrightarrow \mathscr {C}(0)$ are spaces, so that ![]() $\mathbb {D}(0)$ is a space. It then remains to verify that
$\mathbb {D}(0)$ is a space. It then remains to verify that ![]() $\mathbb {D}(1)$ is a
$\mathbb {D}(1)$ is a ![]() $d$-category. Since
$d$-category. Since ![]() $\mathbb {D}(1)\longrightarrow \mathscr {C}(1)$ is the opposite of a
$\mathbb {D}(1)\longrightarrow \mathscr {C}(1)$ is the opposite of a ![]() $(d-1)$th stage fibration, the inductive hypothesis says that it suffices to verify that its fibers are
$(d-1)$th stage fibration, the inductive hypothesis says that it suffices to verify that its fibers are ![]() $(d-1)$-categories. In particular, we can reduce to the case where
$(d-1)$-categories. In particular, we can reduce to the case where ![]() $\mathscr {C}\simeq \mathfrak {c}_1(\mathscr {C})$ is a
$\mathscr {C}\simeq \mathfrak {c}_1(\mathscr {C})$ is a ![]() $1$-category.
$1$-category.
In this case, take a morphism ![]() $\gamma \colon c_0\longrightarrow c_1$ in
$\gamma \colon c_0\longrightarrow c_1$ in ![]() $\mathscr {C}$ and consider the map between fibers
$\mathscr {C}$ and consider the map between fibers ![]() $\mathbb {D}(1)_{\gamma }\longrightarrow \mathbb {D}(\{0\})_{c_0}$. Since the target is a space, it suffices to verify that the fiber over each point
$\mathbb {D}(1)_{\gamma }\longrightarrow \mathbb {D}(\{0\})_{c_0}$. Since the target is a space, it suffices to verify that the fiber over each point ![]() $d_0\in \mathbb {D}_{c_0}$ is a
$d_0\in \mathbb {D}_{c_0}$ is a ![]() $(d-1)$-category. Using condition (a2), we can take a cocartesian lift
$(d-1)$-category. Using condition (a2), we can take a cocartesian lift ![]() $\alpha \colon d_0\longrightarrow d_1$ of
$\alpha \colon d_0\longrightarrow d_1$ of ![]() $\gamma$ such that precomposition with
$\gamma$ such that precomposition with ![]() $\alpha$ determines the following equivalence of
$\alpha$ determines the following equivalence of ![]() $(d-1)$-fold categories:
$(d-1)$-fold categories:
The domain is a ![]() $(d-1)$-category since the fiber
$(d-1)$-category since the fiber ![]() $\mathbb {D}_{c_1}$ is a
$\mathbb {D}_{c_1}$ is a ![]() $d$-category by assumption.
$d$-category by assumption.
Proposition 6.8 There is a fully faithful inclusion ![]() ${{\rm Cocart}}_{d}\hookrightarrow \mathrm {Fib}_d^{(d)}$, whose essential image consists of the
${{\rm Cocart}}_{d}\hookrightarrow \mathrm {Fib}_d^{(d)}$, whose essential image consists of the ![]() $d$th stage fibrations satisfying the equivalent conditions of Lemma 6.7.
$d$th stage fibrations satisfying the equivalent conditions of Lemma 6.7.
Proof. Both ![]() ${{\rm Cocart}}_d$ and the full subcategory of
${{\rm Cocart}}_d$ and the full subcategory of ![]() $\mathrm {Fib}_d^{(d)}$ defined by Lemma 6.7 are subcategories of
$\mathrm {Fib}_d^{(d)}$ defined by Lemma 6.7 are subcategories of ![]() $\mathrm {Fun}\big ([1], {{\rm Cat}}^{\otimes d+1}\big )$. It therefore suffices to show that these two subcategories have the same objects and morphisms. We will do this by induction on
$\mathrm {Fun}\big ([1], {{\rm Cat}}^{\otimes d+1}\big )$. It therefore suffices to show that these two subcategories have the same objects and morphisms. We will do this by induction on ![]() $d$, the case
$d$, the case ![]() $d=0$ being evident.
$d=0$ being evident.
Objects. Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map between
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a map between ![]() $(d+1)$-categories. By inductive hypothesis and Lemma 5.21,
$(d+1)$-categories. By inductive hypothesis and Lemma 5.21, ![]() $p$ satisfies condition (a1) if and only if
$p$ satisfies condition (a1) if and only if ![]() $p$ is a homwise
$p$ is a homwise ![]() $(d-1)$-cartesian fibration. Assuming that
$(d-1)$-cartesian fibration. Assuming that ![]() $p$ satisfies these equivalent conditions, it remains to show that
$p$ satisfies these equivalent conditions, it remains to show that ![]() $p$ satisfies condition (a2) if and only if it is a pre-cocartesian fibration. To see this, consider the base change
$p$ satisfies condition (a2) if and only if it is a pre-cocartesian fibration. To see this, consider the base change
For any ![]() $1$-morphism
$1$-morphism ![]() $\alpha \colon d_0\longrightarrow d_1$ and object
$\alpha \colon d_0\longrightarrow d_1$ and object ![]() $d_2$ in
$d_2$ in ![]() $\mathscr {D}'$ (or, equivalently, in
$\mathscr {D}'$ (or, equivalently, in ![]() $\mathscr {D}$), we have the following commutative diagram.
$\mathscr {D}$), we have the following commutative diagram.

The left and right face of the cube are cartesian. By our assumption on ![]() $p$, the vertical arrows are
$p$, the vertical arrows are ![]() $(d-1)$-cartesian fibrations and the front and back face determine strong maps of
$(d-1)$-cartesian fibrations and the front and back face determine strong maps of ![]() $(d-1)$-cartesian fibrations. By inductive hypothesis, this means equivalently that the vertical arrows are
$(d-1)$-cartesian fibrations. By inductive hypothesis, this means equivalently that the vertical arrows are ![]() $(d-1)$th stage fibrations between
$(d-1)$th stage fibrations between ![]() $d$-categories and that the front and back face determine strong morphisms between
$d$-categories and that the front and back face determine strong morphisms between ![]() $(d-1)$th stage fibrations. Since the back and front faces are equivalent at the level of objects, Corollary 6.6 then implies that the front face is cartesian if and only if the back face is cartesian. By Corollary 5.7, this means that
$(d-1)$th stage fibrations. Since the back and front faces are equivalent at the level of objects, Corollary 6.6 then implies that the front face is cartesian if and only if the back face is cartesian. By Corollary 5.7, this means that ![]() $\alpha$ is
$\alpha$ is ![]() $p'$-cocartesian if and only if it is
$p'$-cocartesian if and only if it is ![]() $p$-cocartesian. It follows that
$p$-cocartesian. It follows that ![]() $p$ is a pre-cocartesian fibration if and only if
$p$ is a pre-cocartesian fibration if and only if ![]() $p'$ is a pre-cocartesian fibration, which, in turn, is equivalent to condition (a2), by Remark 5.8.
$p'$ is a pre-cocartesian fibration, which, in turn, is equivalent to condition (a2), by Remark 5.8.
Morphisms. A commuting square determines a strong morphism between ![]() $d$-cocartesian fibrations if and only if the induced square on
$d$-cocartesian fibrations if and only if the induced square on ![]() $d$-categories of morphisms induces a strong morphism between
$d$-categories of morphisms induces a strong morphism between ![]() $(d-1)$-cartesian fibrations and the map
$(d-1)$-cartesian fibrations and the map ![]() $\mathfrak {c}_1(\mathscr {D})\longrightarrow \mathfrak {c}_1(\mathscr {D}')$ preserves cocartesian
$\mathfrak {c}_1(\mathscr {D})\longrightarrow \mathfrak {c}_1(\mathscr {D}')$ preserves cocartesian ![]() $1$-morphisms. Comparing this with conditions (b1) and (b2) shows inductively that such strong morphisms coincide with strong morphisms of
$1$-morphisms. Comparing this with conditions (b1) and (b2) shows inductively that such strong morphisms coincide with strong morphisms of ![]() $d$th stage fibrations.
$d$th stage fibrations.
Proof (of Theorem 6.1) Composing the equivalences from Proposition 6.4 yields
that commutes with the codomain projection. Note that on both sides, the fiber over ![]() $\ast \in {{\rm Cat}}_{d+1}$ can be identified with the category
$\ast \in {{\rm Cat}}_{d+1}$ can be identified with the category ![]() ${{\rm Cat}}^{\otimes d}$ of
${{\rm Cat}}^{\otimes d}$ of ![]() $d$-fold categories: in
$d$-fold categories: in ![]() $\mathrm {Fib}^{(0)}$, a
$\mathrm {Fib}^{(0)}$, a ![]() $d$-fold category is viewed as a
$d$-fold category is viewed as a ![]() $(d+1)$-fold category which is constant in the first variable, and in
$(d+1)$-fold category which is constant in the first variable, and in ![]() $\mathrm {Fib}^{(d)}$ it is constant in the last variable. Since the above equivalence is given by repeatedly applying the functor
$\mathrm {Fib}^{(d)}$ it is constant in the last variable. Since the above equivalence is given by repeatedly applying the functor ![]() $\Psi ^\perp$, Proposition 3.15 shows that the induced equivalence on fibers over
$\Psi ^\perp$, Proposition 3.15 shows that the induced equivalence on fibers over ![]() $\ast \in {{\rm Cat}}_{d+1}$ simply sends a
$\ast \in {{\rm Cat}}_{d+1}$ simply sends a ![]() $d$-fold category to itself.
$d$-fold category to itself.
Now observe that there is a fully faithful inclusion ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_{d}\hookrightarrow \mathrm {Fib}^{(0)}$, whose essential image consists of all those
$\mathrm {coPSh}^{\mathrm {Seg}}_{d}\hookrightarrow \mathrm {Fib}^{(0)}$, whose essential image consists of all those ![]() $0$th stage fibrations
$0$th stage fibrations ![]() $p\colon \mathbb {D}\longrightarrow \mathscr {C}$ with the property that for any object
$p\colon \mathbb {D}\longrightarrow \mathscr {C}$ with the property that for any object ![]() $c\in \mathscr {C}$, the fiber
$c\in \mathscr {C}$, the fiber ![]() $\mathbb {D}_c$ is a
$\mathbb {D}_c$ is a ![]() $d$-category (rather than a
$d$-category (rather than a ![]() $d$-fold category). The essential image of
$d$-fold category). The essential image of ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d$ under (6.9) then consists of
$\mathrm {coPSh}^{\mathrm {Seg}}_d$ under (6.9) then consists of ![]() $d$th stage fibrations whose fibers are
$d$th stage fibrations whose fibers are ![]() $d$-categories. By Proposition 6.8, this means that (6.9) restricts to an equivalence
$d$-categories. By Proposition 6.8, this means that (6.9) restricts to an equivalence ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_{d}\stackrel {\sim }{\longrightarrow } {{\rm Cocart}}_{d}$, as desired. The second part of Theorem 6.1 now follows directly from Corollary 4.33.
$\mathrm {coPSh}^{\mathrm {Seg}}_{d}\stackrel {\sim }{\longrightarrow } {{\rm Cocart}}_{d}$, as desired. The second part of Theorem 6.1 now follows directly from Corollary 4.33.
6.2 Straightening and unstraightening: uniqueness and further properties
The equivalence of Theorem 6.1 arises from an iteration of explicit combinatorial maneuvers. The purpose of this intermezzo is to argue that at the level of objects, the precise construction of this equivalence is essentially irrelevant.
Proposition 6.10 There is a contractible space of equivalences of right fibrations as follows.

Combining this with Proposition 4.40 (in the large setting) and rephrasing everything in terms of presheaves rather than right fibrations (using straightening), we obtain the following.
Corollary 6.11 For any small ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$, there is a unique
$\mathscr {C}$, there is a unique ![]() $1$-natural equivalence
$1$-natural equivalence
between the spaces of copresheaves ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d$ and of
$\mathscr {C}\longrightarrow \mathbf {Cat}_d$ and of ![]() $d$-cocartesian fibrations
$d$-cocartesian fibrations ![]() $\mathscr {D}\longrightarrow \mathscr {C}$. We will refer to these functors as unstraightening and straightening.
$\mathscr {D}\longrightarrow \mathscr {C}$. We will refer to these functors as unstraightening and straightening.
Remark 6.2 also gives a unique ![]() $1$-natural equivalence
$1$-natural equivalence ![]() $\mathfrak {c}_0\mathrm {Fun}_{d+1}(\mathscr {C}^{\mathrm {op}}, \mathbf {Cat}_d)\simeq \mathfrak {c}_0{\rm Cart}_d(\mathscr {C})$.
$\mathfrak {c}_0\mathrm {Fun}_{d+1}(\mathscr {C}^{\mathrm {op}}, \mathbf {Cat}_d)\simeq \mathfrak {c}_0{\rm Cart}_d(\mathscr {C})$.
Remark 6.12 In particular, the straightening of a ![]() $d$-cocartesian fibration
$d$-cocartesian fibration ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ between
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ between ![]() $(d+1)$-categories is naturally equivalent to the straightening of
$(d+1)$-categories is naturally equivalent to the straightening of ![]() $p$, viewed as a special kind of
$p$, viewed as a special kind of ![]() $(d+1)$-cocartesian fibration between
$(d+1)$-cocartesian fibration between ![]() $(d+2)$-categories.
$(d+2)$-categories.
We will deduce Proposition 6.10 from the following (simpler) version of a result of Barwick and Schommer-Pries [Reference Barwick and Schommer-PriesBS21].
Proposition 6.13 Let ![]() $\mathbf {CAT}_{d+1}$ be the (very large)
$\mathbf {CAT}_{d+1}$ be the (very large) ![]() $(d+2)$-category of large
$(d+2)$-category of large ![]() $(d+1)$-categories and let
$(d+1)$-categories and let ![]() $\mathrm {Aut}_{\mathbf {CAT}_{d+1}}(\mathbf {Cat}_d)\subseteq \mathrm {Fun}_{d+1}(\mathbf {Cat}_d, \mathbf {Cat}_d)$ be the full sub-
$\mathrm {Aut}_{\mathbf {CAT}_{d+1}}(\mathbf {Cat}_d)\subseteq \mathrm {Fun}_{d+1}(\mathbf {Cat}_d, \mathbf {Cat}_d)$ be the full sub-![]() $(d+1)$-category on those
$(d+1)$-category on those ![]() $(d+1)$-functors that are equivalences. Then
$(d+1)$-functors that are equivalences. Then ![]() $\mathrm {Aut}_{\mathbf {CAT}_{d+1}}(\mathbf {Cat}_d)\simeq \ast$.
$\mathrm {Aut}_{\mathbf {CAT}_{d+1}}(\mathbf {Cat}_d)\simeq \ast$.
Proof. Let ![]() $\phi \colon \mathbf {Cat}_d\longrightarrow \mathbf {Cat}_d$ be an equivalence of
$\phi \colon \mathbf {Cat}_d\longrightarrow \mathbf {Cat}_d$ be an equivalence of ![]() $(d+1)$-categories. Since
$(d+1)$-categories. Since ![]() $\phi$ preserves the terminal object, we can pick a (unique) element
$\phi$ preserves the terminal object, we can pick a (unique) element ![]() $u\in \phi (\ast )$. By the enriched Yoneda lemma [Reference HinichHin20, 6.2.7] (or Example 4.48),
$u\in \phi (\ast )$. By the enriched Yoneda lemma [Reference HinichHin20, 6.2.7] (or Example 4.48), ![]() $u$ induces a natural transformation of
$u$ induces a natural transformation of ![]() $(d+1)$-functors
$(d+1)$-functors ![]() $u\colon \mathrm {Map}_{\mathbf {Cat}_d}(\ast, -)\longrightarrow \phi (-)$. Note that the domain can be identified with the identity on
$u\colon \mathrm {Map}_{\mathbf {Cat}_d}(\ast, -)\longrightarrow \phi (-)$. Note that the domain can be identified with the identity on ![]() $\mathbf {Cat}_d$, so that
$\mathbf {Cat}_d$, so that ![]() $u$ is, in particular, a natural transformation between two automorphisms of the
$u$ is, in particular, a natural transformation between two automorphisms of the ![]() $1$-category
$1$-category ![]() ${{\rm Cat}}_d$. By [Reference Barwick and Schommer-PriesBS21, Theorem 10.1],
${{\rm Cat}}_d$. By [Reference Barwick and Schommer-PriesBS21, Theorem 10.1], ![]() $u$ is a natural equivalence.
$u$ is a natural equivalence.
We conclude that ![]() $\mathrm {Aut}_{\mathbf {CAT}_{d+1}}(\mathbf {Cat}_d)$ has an essentially unique object, given by
$\mathrm {Aut}_{\mathbf {CAT}_{d+1}}(\mathbf {Cat}_d)$ has an essentially unique object, given by ![]() $\mathrm {id}_{\mathbf {Cat}_d}\simeq \mathrm {Map}_{\mathbf {Cat}_d}(\ast, -)$. Using the enriched Yoneda lemma once more, the endomorphism
$\mathrm {id}_{\mathbf {Cat}_d}\simeq \mathrm {Map}_{\mathbf {Cat}_d}(\ast, -)$. Using the enriched Yoneda lemma once more, the endomorphism ![]() $d$-category of this object can be identified with
$d$-category of this object can be identified with ![]() $\mathrm {Map}_{\mathbf {Cat}_d}(\ast, \ast )\simeq \ast$, which concludes the proof.
$\mathrm {Map}_{\mathbf {Cat}_d}(\ast, \ast )\simeq \ast$, which concludes the proof.
Proof of Proposition 6.10 By Theorem 6.1, the space of such equivalences is a nonempty torsor over the automorphism group ![]() $G$ of the right fibration
$G$ of the right fibration ![]() $\mathrm {coPSh}^{\mathrm {Seg}, \mathrm {cart}}_d\longrightarrow {{\rm Cat}}_{d+1}$. Note that this right fibration fits into a pullback square
$\mathrm {coPSh}^{\mathrm {Seg}, \mathrm {cart}}_d\longrightarrow {{\rm Cat}}_{d+1}$. Note that this right fibration fits into a pullback square

where ![]() $\mathrm {coPSH}^{\mathrm {Seg}, \mathrm {cart}}_d$ is the category of Segal copresheaves
$\mathrm {coPSH}^{\mathrm {Seg}, \mathrm {cart}}_d$ is the category of Segal copresheaves ![]() $X\longrightarrow \mathscr {C}$ over large
$X\longrightarrow \mathscr {C}$ over large ![]() $(d+1)$-categories, whose fibers are essentially small.
$(d+1)$-categories, whose fibers are essentially small.
Applying Proposition 4.40 in the large setting (with ![]() $\kappa =\kappa _{\mathrm {sm}}$ the supremum of all small cardinals), the right fibration
$\kappa =\kappa _{\mathrm {sm}}$ the supremum of all small cardinals), the right fibration ![]() $\pi '$ corresponds under (some
$\pi '$ corresponds under (some ![]() $1$-natural version of) unstraightening to the presheaf
$1$-natural version of) unstraightening to the presheaf ![]() $F\colon \mathrm {CAT}_{d+1}^{\mathrm {op}}\longrightarrow \mathscr {S}^{\mathrm {big}}$ representable by the
$F\colon \mathrm {CAT}_{d+1}^{\mathrm {op}}\longrightarrow \mathscr {S}^{\mathrm {big}}$ representable by the ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathbf {Cat}_d$. We then obtain equivalences of spaces of automorphisms as follows:
$\mathbf {Cat}_d$. We then obtain equivalences of spaces of automorphisms as follows:
Here the first equivalence is the Yoneda embedding (4.45) and the last equivalence is unstraightening. The middle equivalence uses that ![]() $\mathrm {CAT}_{d+1}$ is a (large) ind-completion of
$\mathrm {CAT}_{d+1}$ is a (large) ind-completion of ![]() ${{\rm Cat}}_{d+1}$; in particular, restriction along
${{\rm Cat}}_{d+1}$; in particular, restriction along ![]() ${{\rm Cat}}_{d+1}\longrightarrow \mathrm {CAT}_{d+1}$ is fully faithful on presheaves sending large
${{\rm Cat}}_{d+1}\longrightarrow \mathrm {CAT}_{d+1}$ is fully faithful on presheaves sending large ![]() $\kappa _\mathrm {sm}$-filtered colimits in
$\kappa _\mathrm {sm}$-filtered colimits in ![]() $\mathrm {CAT}_{d+1}$ to large limits in
$\mathrm {CAT}_{d+1}$ to large limits in ![]() $\mathscr {S}^{\mathrm {big}}$ (e.g. on representable presheaves). Finally, Proposition 6.13 implies that the left space is contractible.
$\mathscr {S}^{\mathrm {big}}$ (e.g. on representable presheaves). Finally, Proposition 6.13 implies that the left space is contractible.
Theorems 4.32 and 6.1 imply that the (un)straightening equivalence of Corollary 6.11 admits some extension to an equivalence of ![]() $1$-categories, rather than spaces. Using this, let us record some properties of the (un)straightening at the level of objects.
$1$-categories, rather than spaces. Using this, let us record some properties of the (un)straightening at the level of objects.
Example 6.14 The proof of Theorem 6.1 shows that over ![]() $\mathscr {C}=\ast$, the (un)straightening equivalence of Corollary 6.11 is homotopic to the identity on
$\mathscr {C}=\ast$, the (un)straightening equivalence of Corollary 6.11 is homotopic to the identity on ![]() ${{\rm Cat}}_d$. Since (un)straightening intertwines restriction of copresheaves with base change of
${{\rm Cat}}_d$. Since (un)straightening intertwines restriction of copresheaves with base change of ![]() $d$-cocartesian fibrations, it follows that the straightening of a cocartesian fibration
$d$-cocartesian fibrations, it follows that the straightening of a cocartesian fibration ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is given pointwise by
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ is given pointwise by ![]() $\mathrm {St}(p)_c\simeq \mathscr {D}_c$.
$\mathrm {St}(p)_c\simeq \mathscr {D}_c$.
Example 6.15 Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a ![]() $d$-cocartesian fibration and let
$d$-cocartesian fibration and let ![]() $\gamma \colon c_0\longrightarrow c_1$ be a
$\gamma \colon c_0\longrightarrow c_1$ be a ![]() $1$-morphism in
$1$-morphism in ![]() $\mathscr {C}$. The straightening of
$\mathscr {C}$. The straightening of ![]() $p$ determines a functor
$p$ determines a functor ![]() $\gamma _*\colon \mathscr {D}_{c_0}\longrightarrow \mathscr {D}_{c_1}$ that can be understood explicitly as follows. For any diagram
$\gamma _*\colon \mathscr {D}_{c_0}\longrightarrow \mathscr {D}_{c_1}$ that can be understood explicitly as follows. For any diagram ![]() $\sigma _0\colon \mathscr {K}\longrightarrow \mathscr {D}_{c_0}$, there exists a unique extension of
$\sigma _0\colon \mathscr {K}\longrightarrow \mathscr {D}_{c_0}$, there exists a unique extension of ![]() $\sigma _0$ to a map
$\sigma _0$ to a map ![]() $\sigma \colon [1]\times \mathscr {K}\longrightarrow \mathscr {D}$ that covers
$\sigma \colon [1]\times \mathscr {K}\longrightarrow \mathscr {D}$ that covers ![]() $\gamma \colon [1]\longrightarrow \mathscr {C}$ and preserves cocartesian arrows. The restriction
$\gamma \colon [1]\longrightarrow \mathscr {C}$ and preserves cocartesian arrows. The restriction ![]() $\sigma _1\colon \{1\}\times \mathscr {K}\longrightarrow \mathscr {D}_1$ to the fiber over
$\sigma _1\colon \{1\}\times \mathscr {K}\longrightarrow \mathscr {D}_1$ to the fiber over ![]() $1$ then presents the composite diagram
$1$ then presents the composite diagram ![]() $\gamma _*\circ \sigma _0$. In particular, applying this when
$\gamma _*\circ \sigma _0$. In particular, applying this when ![]() $\sigma _0=\mathrm {id}_{\mathscr {D}_{c_0}}$ gives a description of
$\sigma _0=\mathrm {id}_{\mathscr {D}_{c_0}}$ gives a description of ![]() $\gamma _*$.
$\gamma _*$.
To see this, it suffices to treat the case where ![]() $\mathscr {C}=[1]$. By naturality with respect to the projection
$\mathscr {C}=[1]$. By naturality with respect to the projection ![]() $[1]\longrightarrow \ast$, the unstraightening of a constant copresheaf
$[1]\longrightarrow \ast$, the unstraightening of a constant copresheaf ![]() $\Delta _{\mathscr {K}}\colon [1]\longrightarrow \mathbf {Cat}_d$ with value
$\Delta _{\mathscr {K}}\colon [1]\longrightarrow \mathbf {Cat}_d$ with value ![]() $\mathscr {K}$ is given by the projection
$\mathscr {K}$ is given by the projection ![]() $\pi _1\colon [1]\times \mathscr {K}\longrightarrow [1]$. Theorem 6.1 then shows that we have the following commuting diagram of mapping spaces.
$\pi _1\colon [1]\times \mathscr {K}\longrightarrow [1]$. Theorem 6.1 then shows that we have the following commuting diagram of mapping spaces.

Now note that the top zigzag is homotopic to postcomposition with ![]() $\gamma _*$, while the bottom zigzag corresponds precisely to the procedure described above.
$\gamma _*$, while the bottom zigzag corresponds precisely to the procedure described above.
Example 6.16 Let ![]() $C_2$ be the
$C_2$ be the ![]() $2$-cell and let
$2$-cell and let ![]() $[2]^\mathrm {lax}$ denote the following
$[2]^\mathrm {lax}$ denote the following ![]() $2$-category.
$2$-category.

The projection ![]() $p\colon [2]^\mathrm {lax}\longrightarrow C_2$ sending
$p\colon [2]^\mathrm {lax}\longrightarrow C_2$ sending ![]() $0\mapsto 0$ and
$0\mapsto 0$ and ![]() $1, 2\mapsto 1$ is a
$1, 2\mapsto 1$ is a ![]() $1$-cocartesian fibration. By Examples 6.14 and 6.15, the straightening
$1$-cocartesian fibration. By Examples 6.14 and 6.15, the straightening ![]() $\mathrm {St}(p)\colon C_2\longrightarrow \mathbf {Cat}_1$ is given by the diagram
$\mathrm {St}(p)\colon C_2\longrightarrow \mathbf {Cat}_1$ is given by the diagram

where the natural transformation is the only possible one. In other words, ![]() $\mathrm {St}(p)= \mathrm {Map}_{C_2}(0, -)$ is representable by
$\mathrm {St}(p)= \mathrm {Map}_{C_2}(0, -)$ is representable by ![]() $0$. Likewise, let
$0$. Likewise, let ![]() $\mathscr {K}$ be a
$\mathscr {K}$ be a ![]() $d$-category and consider the diagram
$d$-category and consider the diagram ![]() $F_{\mathscr {K}}\colon C_2\longrightarrow \mathbf {Cat}_d$ encoding the evident natural transformation from
$F_{\mathscr {K}}\colon C_2\longrightarrow \mathbf {Cat}_d$ encoding the evident natural transformation from ![]() $(0, \mathrm {id})$ to
$(0, \mathrm {id})$ to ![]() $(1, \mathrm {id})\colon \mathscr {K}\longrightarrow [1]\times \mathscr {K}$. Then
$(1, \mathrm {id})\colon \mathscr {K}\longrightarrow [1]\times \mathscr {K}$. Then ![]() $\mathrm {Un}(F_{\mathscr {K}})\simeq [2]^\mathrm {lax}\times \mathscr {K}$.
$\mathrm {Un}(F_{\mathscr {K}})\simeq [2]^\mathrm {lax}\times \mathscr {K}$.
Now let ![]() $q\colon \mathscr {D}\longrightarrow C_2$ be a general
$q\colon \mathscr {D}\longrightarrow C_2$ be a general ![]() $d$-cocartesian fibration, so that
$d$-cocartesian fibration, so that ![]() $\mathrm {St}(q)$ describes a natural transformation
$\mathrm {St}(q)$ describes a natural transformation ![]() $\mu \colon f_0\longrightarrow f_1$ between two functors
$\mu \colon f_0\longrightarrow f_1$ between two functors ![]() $f_0, f_1\colon \mathscr {D}_0\longrightarrow \mathscr {D}_1$. As in Example 6.15, one can obtain
$f_0, f_1\colon \mathscr {D}_0\longrightarrow \mathscr {D}_1$. As in Example 6.15, one can obtain ![]() $\mu$ as follows: there is a unique map
$\mu$ as follows: there is a unique map ![]() $[2]^\mathrm {lax}\times \mathscr {D}_0\longrightarrow \mathscr {D}$ over
$[2]^\mathrm {lax}\times \mathscr {D}_0\longrightarrow \mathscr {D}$ over ![]() $C_2$ restricting to the identity on
$C_2$ restricting to the identity on ![]() $\{0\}\times \mathscr {D}_0$, and
$\{0\}\times \mathscr {D}_0$, and ![]() $\mu$ is given by its restriction
$\mu$ is given by its restriction ![]() $\{1\leq 2\}\times \mathscr {D}_0\longrightarrow \mathscr {D}_1$.
$\{1\leq 2\}\times \mathscr {D}_0\longrightarrow \mathscr {D}_1$.
Example 6.17 Given a ![]() $2$-category
$2$-category ![]() $\mathscr {C}$, let us denote by
$\mathscr {C}$, let us denote by ![]() $\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})\longrightarrow \mathscr {C}^{\mathrm {op}}\times \mathscr {C}$ the
$\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})\longrightarrow \mathscr {C}^{\mathrm {op}}\times \mathscr {C}$ the ![]() $1$-cocartesian fibration arising as the unstraightening of
$1$-cocartesian fibration arising as the unstraightening of ![]() $\mathrm {Map}_{\mathscr {C}}\colon \mathscr {C}^{\mathrm {op}}\times \mathscr {C}\longrightarrow \mathbf {Cat}_1$. We will refer to
$\mathrm {Map}_{\mathscr {C}}\colon \mathscr {C}^{\mathrm {op}}\times \mathscr {C}\longrightarrow \mathbf {Cat}_1$. We will refer to ![]() $\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})$ as the lax twisted arrow
$\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})$ as the lax twisted arrow ![]() $2$-category of
$2$-category of ![]() $\mathscr {C}$.
$\mathscr {C}$.
Explicitly, ![]() $\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})$ is the image under the functor
$\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})$ is the image under the functor ![]() $\Psi ^\perp$ of the Segal copresheaf
$\Psi ^\perp$ of the Segal copresheaf ![]() $\mathrm {Tw}(\mathscr {C})\longrightarrow \mathscr {C}^{\mathrm {op}}\times \mathscr {C}$ (Example 4.36). Unraveling the definitions, one arrives at the following explicit description of
$\mathrm {Tw}(\mathscr {C})\longrightarrow \mathscr {C}^{\mathrm {op}}\times \mathscr {C}$ (Example 4.36). Unraveling the definitions, one arrives at the following explicit description of ![]() $\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})$ as a bisimplicial space. For each
$\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})$ as a bisimplicial space. For each ![]() $[m], [n]\in \mathbf {\Delta }$, consider the bisimplicial space (in fact, set)
$[m], [n]\in \mathbf {\Delta }$, consider the bisimplicial space (in fact, set)
This comes with natural inclusions ![]() $[m]^{\mathrm {op}}\boxtimes [n]\longrightarrow J[m, n]\longleftarrow [m]\boxtimes [n]$, arising as parts of the bisimplex associated to
$[m]^{\mathrm {op}}\boxtimes [n]\longrightarrow J[m, n]\longleftarrow [m]\boxtimes [n]$, arising as parts of the bisimplex associated to ![]() $(\alpha, \alpha ', \beta )=(\mathrm {cst}(0), \mathrm {id}_{[m]}, \mathrm {id}_{[n]})$. One then has that
$(\alpha, \alpha ', \beta )=(\mathrm {cst}(0), \mathrm {id}_{[m]}, \mathrm {id}_{[n]})$. One then has that
is the subspace of maps ![]() $J[m, n]\longrightarrow \mathscr {C}$ whose restriction to any bisimplex of the form
$J[m, n]\longrightarrow \mathscr {C}$ whose restriction to any bisimplex of the form ![]() $\big ([0]^{\mathrm {op}}\star [0]\big )\boxtimes [q]\longrightarrow J[m, n]$ (i.e. a summand for which
$\big ([0]^{\mathrm {op}}\star [0]\big )\boxtimes [q]\longrightarrow J[m, n]$ (i.e. a summand for which ![]() $p=0$) is degenerate in the
$p=0$) is degenerate in the ![]() $q$-direction.
$q$-direction.
Note that in the definition of ![]() $J[m, n]$, it suffices to take the colimit over the cofinal subcategory of
$J[m, n]$, it suffices to take the colimit over the cofinal subcategory of ![]() $(\alpha, \alpha ', \beta )$ such that
$(\alpha, \alpha ', \beta )$ such that ![]() $(\alpha, \alpha ')\colon [q]\longrightarrow [m]\times [n]$ is injective and
$(\alpha, \alpha ')\colon [q]\longrightarrow [m]\times [n]$ is injective and ![]() $\beta \colon [p]\longrightarrow \{\alpha (q)\leq \cdots \leq m\big \}$ is the inclusion of an upwards closed subset. Using this for low values of
$\beta \colon [p]\longrightarrow \{\alpha (q)\leq \cdots \leq m\big \}$ is the inclusion of an upwards closed subset. Using this for low values of ![]() $m$ and
$m$ and ![]() $n$, one sees that the
$n$, one sees that the ![]() $2$-category
$2$-category ![]() $\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})$ has objects given by morphisms in
$\mathrm {Tw}_{\mathrm {lax}}(\mathscr {C})$ has objects given by morphisms in ![]() $\mathscr {C}$, and
$\mathscr {C}$, and ![]() $1$- and
$1$- and ![]() $2$-morphisms can be depicted by diagrams in
$2$-morphisms can be depicted by diagrams in ![]() $\mathscr {C}$ of the following form.
$\mathscr {C}$ of the following form.

Here the left diagram defines an arrow from ![]() $c_0\longrightarrow c_1$ to
$c_0\longrightarrow c_1$ to ![]() $d_0\longrightarrow d_1$ and the right (cylindrical) diagram defines a 2-morphism from
$d_0\longrightarrow d_1$ and the right (cylindrical) diagram defines a 2-morphism from ![]() $\lambda$ to
$\lambda$ to ![]() $\mu$. The projection to
$\mu$. The projection to ![]() $\mathscr {C}^{\mathrm {op}}\times \mathscr {C}$ restricts to the left and right column.
$\mathscr {C}^{\mathrm {op}}\times \mathscr {C}$ restricts to the left and right column.
By restricting to ![]() $\mathscr {C}^{\mathrm {op}}\times \{c\}$ or
$\mathscr {C}^{\mathrm {op}}\times \{c\}$ or ![]() $\{c\}\times \mathscr {C}$, we obtain an explicit description of the unstraightening of the representable presheaf
$\{c\}\times \mathscr {C}$, we obtain an explicit description of the unstraightening of the representable presheaf ![]() $\mathrm {Map}_{\mathscr {C}}(-, c)$ and copresheaf
$\mathrm {Map}_{\mathscr {C}}(-, c)$ and copresheaf ![]() $\mathrm {Map}_{\mathscr {C}}(c, -)$ in terms of lax versions of the over- and under-category of
$\mathrm {Map}_{\mathscr {C}}(c, -)$ in terms of lax versions of the over- and under-category of ![]() $c$.
$c$.
Lemma 6.18 Let ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ be a ![]() $d$-cocartesian fibration between
$d$-cocartesian fibration between ![]() $(d+1)$-categories. Then the following assertions hold.
$(d+1)$-categories. Then the following assertions hold.
(1) The induced map
 $p'\colon \mathfrak {c}_1\mathscr {D}\longrightarrow \mathfrak {c}_1\mathscr {C}$ is a
$p'\colon \mathfrak {c}_1\mathscr {D}\longrightarrow \mathfrak {c}_1\mathscr {C}$ is a  $1$-cocartesian fibration, whose straightening
$1$-cocartesian fibration, whose straightening  $\mathrm {St}(p')$ can be identified with the 1-functor
$\mathrm {St}(p')$ can be identified with the 1-functor

(2) The restriction to cocartesian arrows
 $p''\colon (\mathfrak {c}_1\mathscr {D})^{\mathrm {cocart}}\longrightarrow \mathfrak {c}_1\mathscr {C}$ is a
$p''\colon (\mathfrak {c}_1\mathscr {D})^{\mathrm {cocart}}\longrightarrow \mathfrak {c}_1\mathscr {C}$ is a  $0$-cocartesian fibration, whose straightening
$0$-cocartesian fibration, whose straightening  $\mathrm {St}(p'')$ can be identified with the 1-functor
$\mathrm {St}(p'')$ can be identified with the 1-functor

Proof. By replacing ![]() $p$ by its base change
$p$ by its base change ![]() $\mathscr {D}\times _{\mathscr {C}}\mathfrak {c}_1\mathscr {C}\longrightarrow \mathfrak {c}_1\mathscr {C}$, we can reduce to the case where
$\mathscr {D}\times _{\mathscr {C}}\mathfrak {c}_1\mathscr {C}\longrightarrow \mathfrak {c}_1\mathscr {C}$, we can reduce to the case where ![]() $\mathscr {C}$ is a
$\mathscr {C}$ is a ![]() $1$-category. In this case, Lemma 5.17 implies that a
$1$-category. In this case, Lemma 5.17 implies that a ![]() $d$-cocartesian fibration
$d$-cocartesian fibration ![]() $q\colon \mathscr {E}\longrightarrow \mathscr {C}$ is a
$q\colon \mathscr {E}\longrightarrow \mathscr {C}$ is a ![]() $1$-cocartesian fibration if and only if
$1$-cocartesian fibration if and only if ![]() $\mathscr {E}$ is a
$\mathscr {E}$ is a ![]() $1$-category. Consequently,
$1$-category. Consequently, ![]() $p'$ is the terminal
$p'$ is the terminal ![]() $1$-cocartesian fibration over
$1$-cocartesian fibration over ![]() $\mathscr {C}$ equipped with a natural map to
$\mathscr {C}$ equipped with a natural map to ![]() $p$. Under straightening, this corresponds to the terminal
$p$. Under straightening, this corresponds to the terminal ![]() ${{\rm Cat}}_1$-valued copresheaf on
${{\rm Cat}}_1$-valued copresheaf on ![]() $\mathscr {C}$ equipped with a natural transformation to
$\mathscr {C}$ equipped with a natural transformation to ![]() $\mathrm {St}(p)$. This is precisely the composite functor given in assertion (1).
$\mathrm {St}(p)$. This is precisely the composite functor given in assertion (1).
Likewise, Lemma 5.17 implies ![]() $p''$ is the terminal
$p''$ is the terminal ![]() $0$-cocartesian fibration with a map to
$0$-cocartesian fibration with a map to ![]() $p'$. Under straightening, this corresponds to the terminal space-valued presheaf with a natural map to
$p'$. Under straightening, this corresponds to the terminal space-valued presheaf with a natural map to ![]() $\mathrm {St}(p')$, which is precisely the functor given in assertion (2).
$\mathrm {St}(p')$, which is precisely the functor given in assertion (2).
6.3 Straightening and unstraightening: higher functoriality
Theorem 6.1 shows that for every ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathscr {C}$, there is an equivalence between the
$\mathscr {C}$, there is an equivalence between the ![]() $1$-category of
$1$-category of ![]() $d$-cocartesian fibrations over
$d$-cocartesian fibrations over ![]() $\mathscr {C}$ and the
$\mathscr {C}$ and the ![]() $1$-category underlying
$1$-category underlying ![]() $\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_d)$. We will now refine this equivalence to a natural equivalence of
$\mathrm {Fun}_{d+1}(\mathscr {C}, \mathbf {Cat}_d)$. We will now refine this equivalence to a natural equivalence of ![]() $(d+2)$-functors with values in
$(d+2)$-functors with values in ![]() $(d+1)$-categories, using Theorem 6.1 one categorical dimension higher.
$(d+1)$-categories, using Theorem 6.1 one categorical dimension higher.
Definition 6.19 Consider the ![]() $(d+1)$-cartesian fibration
$(d+1)$-cartesian fibration ![]() $\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ from Proposition 5.25. We will write
$\pi \colon \mathbf {Cocart}_d\longrightarrow \mathbf {Cat}_{d+1}$ from Proposition 5.25. We will write
for the ![]() $(d+2)$-functor corresponding to
$(d+2)$-functor corresponding to ![]() $\pi$ under the (unique)
$\pi$ under the (unique) ![]() $1$-natural straightening equivalence of Corollary 6.11 (in the large setting).
$1$-natural straightening equivalence of Corollary 6.11 (in the large setting).
We now come to our main result.
Theorem 6.20 (Straightening and unstraightening)
The ![]() $(d+1)$-category of natural equivalences of
$(d+1)$-category of natural equivalences of ![]() $(d+2)$-functors
$(d+2)$-functors ![]() $\mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$,
$\mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$,
is equivalent to a single point.
Since ![]() $\mathbf {Cat}_d$ is itself a large
$\mathbf {Cat}_d$ is itself a large ![]() $(d+1)$-category, it will be convenient to first study a version of the above result where we bound the cardinality.
$(d+1)$-category, it will be convenient to first study a version of the above result where we bound the cardinality.
Notation 6.21 Let ![]() $\kappa$ be a regular uncountable cardinal and consider the
$\kappa$ be a regular uncountable cardinal and consider the ![]() $(d+2)$-functor
$(d+2)$-functor ![]() $\pi \colon \mathbf {Cocart}_d(\kappa )\longrightarrow \mathbf {Cat}_{d+1}$ whose domain is the full subcategory of
$\pi \colon \mathbf {Cocart}_d(\kappa )\longrightarrow \mathbf {Cat}_{d+1}$ whose domain is the full subcategory of ![]() $\mathbf {Cocart}_d$ on
$\mathbf {Cocart}_d$ on ![]() $d$-cocartesian fibrations with
$d$-cocartesian fibrations with ![]() $\kappa$-small fibers. This is a
$\kappa$-small fibers. This is a ![]() $(d+1)$-cartesian fibration, and we will denote its image under the (natural) straightening of Corollary 6.11 by
$(d+1)$-cartesian fibration, and we will denote its image under the (natural) straightening of Corollary 6.11 by ![]() $\mathbf {Cocart}_d^\kappa \colon \mathbf {Cat}_{d+1}^{\rm op}\longrightarrow \mathbf {Cat}_{d+1}$. Note that the values of this functor are indeed small categories: Corollary 6.11 identifies their spaces of objects with the spaces of enriched functors
$\mathbf {Cocart}_d^\kappa \colon \mathbf {Cat}_{d+1}^{\rm op}\longrightarrow \mathbf {Cat}_{d+1}$. Note that the values of this functor are indeed small categories: Corollary 6.11 identifies their spaces of objects with the spaces of enriched functors ![]() $\mathscr {C}\longrightarrow \mathbf {Cat}_d(\kappa )$.
$\mathscr {C}\longrightarrow \mathbf {Cat}_d(\kappa )$.
Let us start by recording some properties of the ![]() $(d+2)$-functor
$(d+2)$-functor ![]() $\mathbf {Cocart}^\kappa _d$.
$\mathbf {Cocart}^\kappa _d$.
Lemma 6.22 Let ![]() $f\colon \mathscr {C}\longrightarrow \mathscr {C}'$ be a functor of
$f\colon \mathscr {C}\longrightarrow \mathscr {C}'$ be a functor of ![]() $(d+1)$-categories. Then the
$(d+1)$-categories. Then the ![]() $(d+1)$-functor
$(d+1)$-functor
is tensored over ![]() $\mathbf {Cat}_{d}(\kappa )$ (in particular, so are its domain and codomain).
$\mathbf {Cat}_{d}(\kappa )$ (in particular, so are its domain and codomain).
Heuristically, this simply comes down to the fact that the tensoring of ![]() $\mathbf {Cocart}^\kappa _d(\mathscr {C})$ is given by
$\mathbf {Cocart}^\kappa _d(\mathscr {C})$ is given by ![]() $K\otimes (\mathscr {D}\to \mathscr {C}) = (K\times \mathscr {D}\longrightarrow \mathscr {C})$ and that such products are stable under base change. However, since we defined the
$K\otimes (\mathscr {D}\to \mathscr {C}) = (K\times \mathscr {D}\longrightarrow \mathscr {C})$ and that such products are stable under base change. However, since we defined the ![]() $(d+1)$-functor
$(d+1)$-functor ![]() $f^*$ somewhat abstractly, in terms of the straightening from Corollary 6.11, we will provide a more detailed argument using point-set models.
$f^*$ somewhat abstractly, in terms of the straightening from Corollary 6.11, we will provide a more detailed argument using point-set models.
Proof. The ![]() $(d+2)$-functor
$(d+2)$-functor ![]() $\pi \colon \mathbf {Cocart}_d(\kappa )\longrightarrow \mathbf {Cat}_{d+1}$ can be modeled by a strict functor of
$\pi \colon \mathbf {Cocart}_d(\kappa )\longrightarrow \mathbf {Cat}_{d+1}$ can be modeled by a strict functor of ![]() $\mathsf {Cat}_{d+1}$-enriched categories
$\mathsf {Cat}_{d+1}$-enriched categories ![]() $\underline {\pi }\colon \mathsf {Cocart}_d(\kappa )\longrightarrow \mathsf {Cat}_{d+1}$. Here
$\underline {\pi }\colon \mathsf {Cocart}_d(\kappa )\longrightarrow \mathsf {Cat}_{d+1}$. Here ![]() $\mathsf {Cocart}_d(\kappa )$ is the enriched subcategory of
$\mathsf {Cocart}_d(\kappa )$ is the enriched subcategory of ![]() $\mathrm {Fun}\big ([1], \mathsf {Cat}_d\big )$, whose objects are fibrations in
$\mathrm {Fun}\big ([1], \mathsf {Cat}_d\big )$, whose objects are fibrations in ![]() $\mathsf {Cat}_{d+1}$ that present
$\mathsf {Cat}_{d+1}$ that present ![]() $d$-cocartesian fibrations with
$d$-cocartesian fibrations with ![]() $\kappa$-small fibers and with
$\kappa$-small fibers and with
the maximal subobject in ![]() $\mathsf {Cat}_{d+1}$ that is a model for the full sub-
$\mathsf {Cat}_{d+1}$ that is a model for the full sub-![]() $d$-category of strong morphisms. Example 6.14 identifies the values of
$d$-category of strong morphisms. Example 6.14 identifies the values of ![]() $\mathbf {Cocart}^\kappa _d(-)$ with the fibers of
$\mathbf {Cocart}^\kappa _d(-)$ with the fibers of ![]() $\pi$. Since
$\pi$. Since ![]() $\underline {\pi }$ is a fibration in the model category of
$\underline {\pi }$ is a fibration in the model category of ![]() $\mathsf {Cat}_{d+1}$-enriched categories, the fibers of
$\mathsf {Cat}_{d+1}$-enriched categories, the fibers of ![]() $\pi$ can be modeled by the strict fibers of
$\pi$ can be modeled by the strict fibers of ![]() $\underline {\pi }$. Furthermore, as we already know that the fibers
$\underline {\pi }$. Furthermore, as we already know that the fibers ![]() $\mathbf {Cocart}^\kappa _d(\mathscr {C})$ are
$\mathbf {Cocart}^\kappa _d(\mathscr {C})$ are ![]() $(d+1)$-categories (instead of
$(d+1)$-categories (instead of ![]() $(d+2)$-categories), we can model each
$(d+2)$-categories), we can model each ![]() $\mathbf {Cocart}^\kappa _d(-)$ by the
$\mathbf {Cocart}^\kappa _d(-)$ by the ![]() $\mathsf {Cat}_d$-enriched category underlying
$\mathsf {Cat}_d$-enriched category underlying ![]() $\mathsf {Cocart}^\kappa _d(\mathscr {C})=\underline {\pi }^{-1}(\mathscr {C})$.
$\mathsf {Cocart}^\kappa _d(\mathscr {C})=\underline {\pi }^{-1}(\mathscr {C})$.
As a ![]() $\mathsf {Cat}_d$-enriched category (rather than a
$\mathsf {Cat}_d$-enriched category (rather than a ![]() $\mathsf {Cat}_{d+1}$-enriched category), this fiber is strictly tensored over
$\mathsf {Cat}_{d+1}$-enriched category), this fiber is strictly tensored over ![]() $\mathsf {Cat}_d(\kappa )$: the tensoring of
$\mathsf {Cat}_d(\kappa )$: the tensoring of ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ with
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ with ![]() $K\in \mathsf {Cat}_d(\kappa )$ is simply given by
$K\in \mathsf {Cat}_d(\kappa )$ is simply given by ![]() $\mathscr {D}\times K\longrightarrow \mathscr {C}$. Note that for any map
$\mathscr {D}\times K\longrightarrow \mathscr {C}$. Note that for any map ![]() $f\colon \mathscr {C}\longrightarrow \mathscr {C}'$ in
$f\colon \mathscr {C}\longrightarrow \mathscr {C}'$ in ![]() $\mathsf {Cat}_{d+1}$, taking (strict) base change along
$\mathsf {Cat}_{d+1}$, taking (strict) base change along ![]() $f$ defines an enriched functor
$f$ defines an enriched functor ![]() $f^*\colon \mathsf {Cocart}^\kappa _d(\mathscr {C}')\longrightarrow \mathsf {Cocart}^\kappa _d(\mathscr {C})$ which strictly preserves the tensoring over
$f^*\colon \mathsf {Cocart}^\kappa _d(\mathscr {C}')\longrightarrow \mathsf {Cocart}^\kappa _d(\mathscr {C})$ which strictly preserves the tensoring over ![]() $\mathsf {Cat}_d(\kappa )$. It therefore remains to verify that this
$\mathsf {Cat}_d(\kappa )$. It therefore remains to verify that this ![]() $f^*$ indeed presents the value of
$f^*$ indeed presents the value of ![]() $\mathbf {Cocart}^\kappa _d(-)$ on
$\mathbf {Cocart}^\kappa _d(-)$ on ![]() $f$.
$f$.
To see this, note that associated to ![]() $f$ is the following strict diagram of
$f$ is the following strict diagram of ![]() $\mathsf {Cat}_{d+1}$-enriched categories.
$\mathsf {Cat}_{d+1}$-enriched categories.

Here ![]() $\phi$ is given on
$\phi$ is given on ![]() $\mathsf {Cocart}^\kappa _d(\mathscr {C}')\times \{1\}$ by the fiber inclusion, and on
$\mathsf {Cocart}^\kappa _d(\mathscr {C}')\times \{1\}$ by the fiber inclusion, and on ![]() $\mathsf {Cocart}^\kappa _d(\mathscr {C}')\times \{0\}$ by the strict base change functor
$\mathsf {Cocart}^\kappa _d(\mathscr {C}')\times \{0\}$ by the strict base change functor ![]() $f^*$ (which comes with an evident natural transformation to the fiber inclusion). One easily sees that this enriched functor
$f^*$ (which comes with an evident natural transformation to the fiber inclusion). One easily sees that this enriched functor ![]() $\phi$ models a map of
$\phi$ models a map of ![]() $(d+1)$-cartesian fibrations (i.e. it preserves cartesian
$(d+1)$-cartesian fibrations (i.e. it preserves cartesian ![]() $1$-morphisms). Example 6.15 then shows that the strict functor
$1$-morphisms). Example 6.15 then shows that the strict functor ![]() $f^*$ indeed presents (up to homotopy) the value of the straightening
$f^*$ indeed presents (up to homotopy) the value of the straightening ![]() $\mathbf {Cocart}^\kappa _d(-)$ on the arrow
$\mathbf {Cocart}^\kappa _d(-)$ on the arrow ![]() $f$, so that the latter is tensored as well.
$f$, so that the latter is tensored as well.
Lemma 6.23 The underlying functor between ![]() $1$-categories
$1$-categories ![]() $\mathbf {Cocart}^\kappa _d\colon \mathrm {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathrm {Cat}_{d+1}$ preserves all small limits.
$\mathbf {Cocart}^\kappa _d\colon \mathrm {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathrm {Cat}_{d+1}$ preserves all small limits.
Proof. By Lemma 6.22, the functor of ![]() $1$-categories
$1$-categories ![]() $\mathbf {Cocart}^\kappa _d\colon \mathrm {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathrm {Cat}_{d+1}$ takes values in
$\mathbf {Cocart}^\kappa _d\colon \mathrm {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathrm {Cat}_{d+1}$ takes values in ![]() $(d+1)$-categories and functors which are tensored over
$(d+1)$-categories and functors which are tensored over ![]() $\mathbf {Cat}_d(\kappa )$. Using Lemma 4.57, Remark 4.59 and the fact that taking cores preserves limits, it then suffices to verify that the composite
$\mathbf {Cat}_d(\kappa )$. Using Lemma 4.57, Remark 4.59 and the fact that taking cores preserves limits, it then suffices to verify that the composite
preserves limits. To see this it suffices to verify that for ![]() $i=0, 1$,
$i=0, 1$,
preserves limits. By Lemma 6.18, the functor ![]() $F$ arises as the unstraightening of the cartesian fibration of
$F$ arises as the unstraightening of the cartesian fibration of ![]() $1$-categories
$1$-categories ![]() $\pi \colon {{\rm Cocart}}(\kappa )_d\longrightarrow \mathrm {CAT}_{d+1}$. Theorem 6.1 implies that this can be identified with
$\pi \colon {{\rm Cocart}}(\kappa )_d\longrightarrow \mathrm {CAT}_{d+1}$. Theorem 6.1 implies that this can be identified with ![]() $\mathrm {coPSh}^{\mathrm {Seg}}(\kappa )\longrightarrow \mathrm {Cat}_{d+1}$, where the domain consists of Segal copresheaves whose fibers are
$\mathrm {coPSh}^{\mathrm {Seg}}(\kappa )\longrightarrow \mathrm {Cat}_{d+1}$, where the domain consists of Segal copresheaves whose fibers are ![]() $\kappa$-small.
$\kappa$-small.
The two functors (6.24) therefore arise as the straightening of the right fibrations ![]() $\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}\longrightarrow \mathrm {Cat}_{d+1}$ and
$\mathrm {coPSh}^{\mathrm {Seg}}_d(\kappa )^{\mathrm {cart}}\longrightarrow \mathrm {Cat}_{d+1}$ and ![]() $\mathscr {X}^\mathrm {cart}\longrightarrow \mathrm {Cat}_{d+1}$ from Proposition 4.40 and Variant 4.44, respectively. It was shown there that the straightenings of these two right fibrations are representable, by
$\mathscr {X}^\mathrm {cart}\longrightarrow \mathrm {Cat}_{d+1}$ from Proposition 4.40 and Variant 4.44, respectively. It was shown there that the straightenings of these two right fibrations are representable, by ![]() $\mathbf {Cat}_d(\kappa )$ and
$\mathbf {Cat}_d(\kappa )$ and ![]() $\mathrm {Fun}_{d+1}\big ([1], \mathbf {Cat}_d(\kappa )\big )$, respectively. In particular, they preserve all limits, as required.
$\mathrm {Fun}_{d+1}\big ([1], \mathbf {Cat}_d(\kappa )\big )$, respectively. In particular, they preserve all limits, as required.
Theorem 6.25 The ![]() $(d+2)$-functor
$(d+2)$-functor ![]() $\mathbf {Cocart}_d^\kappa \colon \mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_{d+1}$ from Notation 6.21 is representable by
$\mathbf {Cocart}_d^\kappa \colon \mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_{d+1}$ from Notation 6.21 is representable by ![]() $\mathbf {Cat}_d(\kappa )$.
$\mathbf {Cat}_d(\kappa )$.
Proof. By Proposition 4.58, it suffices to verify that the functor of ![]() $(d+2)$-categories
$(d+2)$-categories ![]() $\mathbf {Cocart}^{\kappa }_d\colon \mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_{d+1}$ is cotensored over
$\mathbf {Cocart}^{\kappa }_d\colon \mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {Cat}_{d+1}$ is cotensored over ![]() $\mathbf {Cat}_{d+1}$ and that the functor of
$\mathbf {Cat}_{d+1}$ and that the functor of ![]() $1$-categories
$1$-categories ![]() $\mathfrak {c}_0\mathbf {Cocart}^\kappa _d\colon \mathrm {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathscr {S}$ is representable. We have already seen in the proof of Lemma 6.23 that this latter functor is representable by the
$\mathfrak {c}_0\mathbf {Cocart}^\kappa _d\colon \mathrm {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathscr {S}$ is representable. We have already seen in the proof of Lemma 6.23 that this latter functor is representable by the ![]() $(d+1)$-category
$(d+1)$-category ![]() $\mathbf {Cat}_d(\kappa )$.
$\mathbf {Cat}_d(\kappa )$.
It remains to verify that for any ![]() $K\in \mathrm {Cat}_{d+1}$ and
$K\in \mathrm {Cat}_{d+1}$ and ![]() $\mathscr {C}\in \mathrm {Cat}_{d+1}$, the comparison map
$\mathscr {C}\in \mathrm {Cat}_{d+1}$, the comparison map
from Definition 4.54 is an equivalence of ![]() $(d+1)$-categories. This will follow immediately from Lemma 4.57 once we show the following two claims:
$(d+1)$-categories. This will follow immediately from Lemma 4.57 once we show the following two claims:
(a)
 $\mu$ induces an equivalence on the underlying
$\mu$ induces an equivalence on the underlying  $1$-categories;
$1$-categories;(b) both the domain and codomain of
 $\mu$ are tensored over
$\mu$ are tensored over  $\mathbf {Cat}_d(\kappa )$ and
$\mathbf {Cat}_d(\kappa )$ and  $\mu$ is tensored over
$\mu$ is tensored over  $\mathbf {Cat}_d(\kappa )$.
$\mathbf {Cat}_d(\kappa )$.
Let us start with assertion (a). As a first reduction, note that ![]() $\mu$ depends, in particular,
$\mu$ depends, in particular, ![]() $1$-functorially on
$1$-functorially on ![]() $K$ and
$K$ and ![]() $\mathscr {C}$. Since both its domain and codomain send colimits in
$\mathscr {C}$. Since both its domain and codomain send colimits in ![]() $K$ and
$K$ and ![]() $\mathscr {C}$ to limits (Lemma 6.23 and Corollary 4.9), it suffices to verify that
$\mathscr {C}$ to limits (Lemma 6.23 and Corollary 4.9), it suffices to verify that ![]() $\mu$ is an equivalence on underlying
$\mu$ is an equivalence on underlying ![]() $1$-categories for generating objects
$1$-categories for generating objects ![]() $K$ and
$K$ and ![]() $\mathscr {C}$. We can therefore reduce to the case where
$\mathscr {C}$. We can therefore reduce to the case where ![]() $K$ and
$K$ and ![]() $\mathscr {C}$ are contained in
$\mathscr {C}$ are contained in ![]() $\Theta _{d+1}$. In particular, we may assume that
$\Theta _{d+1}$. In particular, we may assume that ![]() $K$ is
$K$ is ![]() $\kappa$-small and that for any object
$\kappa$-small and that for any object ![]() $k\in K$,
$k\in K$, ![]() $K(k, k)\simeq \ast$, and likewise for
$K(k, k)\simeq \ast$, and likewise for ![]() $\mathscr {C}$.
$\mathscr {C}$.
By Theorem 4.32, Theorem 6.1 and Lemma 6.18, the ![]() $1$-cartesian fibration between
$1$-cartesian fibration between ![]() $1$-categories
$1$-categories ![]() $\pi \colon \mathfrak {c}_1\mathbf {Cocart}_d(\kappa )\longrightarrow \mathfrak {c}_1\mathbf {Cat}_{d+1}$ arises as the localization of the homotopy cartesian fibration
$\pi \colon \mathfrak {c}_1\mathbf {Cocart}_d(\kappa )\longrightarrow \mathfrak {c}_1\mathbf {Cat}_{d+1}$ arises as the localization of the homotopy cartesian fibration ![]() $\mathsf {EnrFun}_d(\kappa )\longrightarrow {{\rm Cat}}(\mathsf {Cat}_{d})$, where
$\mathsf {EnrFun}_d(\kappa )\longrightarrow {{\rm Cat}}(\mathsf {Cat}_{d})$, where ![]() $\mathsf {EnrFun}_d(\kappa )$ consists of enriched categories
$\mathsf {EnrFun}_d(\kappa )$ consists of enriched categories ![]() $\mathsf {C}$ together with an enriched functor
$\mathsf {C}$ together with an enriched functor ![]() $\mathsf {C}\longrightarrow \mathsf {Cat}_d$ whose values are homotopically
$\mathsf {C}\longrightarrow \mathsf {Cat}_d$ whose values are homotopically ![]() $\kappa$-small, as in the proof of Proposition 4.40. In particular, this implies that there are equivalences
$\kappa$-small, as in the proof of Proposition 4.40. In particular, this implies that there are equivalences
 \begin{align*} \mathfrak{c}_1\mathbf{Cocart}_d^\kappa(K\times \mathscr{C})&\simeq \mathfrak{c}_1\mathrm{Fun}_{d+1}(K\times \mathscr{C}, \mathbf{Cat}_{d}(\kappa))\\ \mathfrak{c}_1\mathrm{Fun}_{d+1}\big(K, \mathbf{Cocart}_d^\kappa(\mathscr{C})\big)&\simeq \mathfrak{c}_1\mathrm{Fun}_{d+1}(K\times \mathscr{C}, \mathbf{Cat}_{d}(\kappa)) \end{align*}
\begin{align*} \mathfrak{c}_1\mathbf{Cocart}_d^\kappa(K\times \mathscr{C})&\simeq \mathfrak{c}_1\mathrm{Fun}_{d+1}(K\times \mathscr{C}, \mathbf{Cat}_{d}(\kappa))\\ \mathfrak{c}_1\mathrm{Fun}_{d+1}\big(K, \mathbf{Cocart}_d^\kappa(\mathscr{C})\big)&\simeq \mathfrak{c}_1\mathrm{Fun}_{d+1}(K\times \mathscr{C}, \mathbf{Cat}_{d}(\kappa)) \end{align*}
such that for any two maps ![]() $K\longrightarrow K'$ and
$K\longrightarrow K'$ and ![]() $\mathscr {C}\longrightarrow \mathscr {C}'$, the functoriality on the left-hand side is homotopic to restriction of functors on the right-hand side (we will not need any information about composition or homotopy coherence).
$\mathscr {C}\longrightarrow \mathscr {C}'$, the functoriality on the left-hand side is homotopic to restriction of functors on the right-hand side (we will not need any information about composition or homotopy coherence).
Using these identifications, the map ![]() $\mu$ therefore determines an endofunctor that fits into the following commuting diagram of
$\mu$ therefore determines an endofunctor that fits into the following commuting diagram of ![]() $1$-categories.
$1$-categories.

Here ![]() $r$ denotes the functor restricting to the sets of (isomorphism classes of) objects of
$r$ denotes the functor restricting to the sets of (isomorphism classes of) objects of ![]() $K$ and
$K$ and ![]() $\mathscr {C}$. Note that
$\mathscr {C}$. Note that ![]() $\mu$ is (by construction) homotopic to the identity when applied to monoidal unit
$\mu$ is (by construction) homotopic to the identity when applied to monoidal unit ![]() $K=\ast$. Up to homotopy, we may therefore assume that the bottom map in the square is the identity.
$K=\ast$. Up to homotopy, we may therefore assume that the bottom map in the square is the identity.
The restriction functor ![]() $r$ preserves
$r$ preserves ![]() $\kappa$-small limits and colimits and detects equivalences. By our assumption that
$\kappa$-small limits and colimits and detects equivalences. By our assumption that ![]() $K$ and
$K$ and ![]() $\mathscr {C}$ are
$\mathscr {C}$ are ![]() $\kappa$-small, it has a left adjoint
$\kappa$-small, it has a left adjoint ![]() $r_!$ sending each
$r_!$ sending each ![]() $(k, c, \mathscr {A})$ to the representable functor
$(k, c, \mathscr {A})$ to the representable functor ![]() $K(k, -)\times \mathscr {C}(c, -)\times \mathscr {A}$; this follows directly from the point-set presentation of
$K(k, -)\times \mathscr {C}(c, -)\times \mathscr {A}$; this follows directly from the point-set presentation of ![]() $r$ in terms of enriched functor categories. The above square then shows that
$r$ in terms of enriched functor categories. The above square then shows that ![]() $\mu \colon \mathfrak {c}_1\mathrm {Fun}_{d+1}(K\times \mathscr {C}, \mathbf {Cat}_{d}(\kappa ))\longrightarrow \mathfrak {c}_1\mathrm {Fun}_{d+1}(K\times \mathscr {C}, \mathbf {Cat}_{d}(\kappa ))$ preserves
$\mu \colon \mathfrak {c}_1\mathrm {Fun}_{d+1}(K\times \mathscr {C}, \mathbf {Cat}_{d}(\kappa ))\longrightarrow \mathfrak {c}_1\mathrm {Fun}_{d+1}(K\times \mathscr {C}, \mathbf {Cat}_{d}(\kappa ))$ preserves ![]() $\kappa$-small limits and colimits and detects equivalences as well, and admits a left adjoint
$\kappa$-small limits and colimits and detects equivalences as well, and admits a left adjoint ![]() $\mu _!$. It suffices to show that for any
$\mu _!$. It suffices to show that for any ![]() $G\colon K\times \mathscr {C}\longrightarrow \mathbf {Cat}_{d}(\kappa )$, the unit map
$G\colon K\times \mathscr {C}\longrightarrow \mathbf {Cat}_{d}(\kappa )$, the unit map ![]() $\eta \colon G\longrightarrow \mu \mu _!(G)$ is an equivalence. Since
$\eta \colon G\longrightarrow \mu \mu _!(G)$ is an equivalence. Since ![]() $\mu$ and
$\mu$ and ![]() $\mu _!$ both preserve
$\mu _!$ both preserve ![]() $\kappa$-small colimits, it suffices to verify this when
$\kappa$-small colimits, it suffices to verify this when ![]() $G=r_!(k, c, \mathscr {A})$ is left Kan extended from an object. By adjunction,
$G=r_!(k, c, \mathscr {A})$ is left Kan extended from an object. By adjunction, ![]() $\eta$ is then determined by a map
$\eta$ is then determined by a map
depending (![]() $1$-)naturally on
$1$-)naturally on ![]() $\mathscr {A}$. Since
$\mathscr {A}$. Since ![]() $K$ and
$K$ and ![]() $\mathscr {C}$ were assumed to have trivial endomorphisms, we therefore obtain an endomorphism
$\mathscr {C}$ were assumed to have trivial endomorphisms, we therefore obtain an endomorphism ![]() $\phi _{k, c}\colon \mathrm {id}\longrightarrow \mathrm {id}$ of the identity functor on
$\phi _{k, c}\colon \mathrm {id}\longrightarrow \mathrm {id}$ of the identity functor on ![]() $\mathrm {Cat}_{d}(\kappa )$. There is a contractible space of such natural endomorphisms by [Reference Barwick and Schommer-PriesBS21, Theorem 10.1].
$\mathrm {Cat}_{d}(\kappa )$. There is a contractible space of such natural endomorphisms by [Reference Barwick and Schommer-PriesBS21, Theorem 10.1].
The map ![]() $\phi _{k, c}$ is therefore naturally (in
$\phi _{k, c}$ is therefore naturally (in ![]() $\mathscr {A}$) homotopic to
$\mathscr {A}$) homotopic to ![]() $\{\mathrm {id}_k\}\times \{\mathrm {id}_c\}\times \mathrm {id}_{\mathscr {A}}$. This means precisely that
$\{\mathrm {id}_k\}\times \{\mathrm {id}_c\}\times \mathrm {id}_{\mathscr {A}}$. This means precisely that ![]() $\eta$ is homotopic to the identity, so in particular an equivalence. We conclude that
$\eta$ is homotopic to the identity, so in particular an equivalence. We conclude that ![]() $\mu _!$ and
$\mu _!$ and ![]() $\mu$ form an adjoint equivalence, so that
$\mu$ form an adjoint equivalence, so that ![]() $\mu$ does indeed induce an equivalence on the underlying
$\mu$ does indeed induce an equivalence on the underlying ![]() $1$-categories, as asserted.
$1$-categories, as asserted.
We now turn to assertion (b). Note that the construction of ![]() $\mu$ (Definition 4.54) implies that for any object
$\mu$ (Definition 4.54) implies that for any object ![]() $k\in K$, the composite with evaluation at
$k\in K$, the composite with evaluation at ![]() $k$
$k$
is equivalent to the value of ![]() $\mathbf {Cocart}^\kappa _d(-)$ on the inclusion
$\mathbf {Cocart}^\kappa _d(-)$ on the inclusion ![]() $\{k\}\times \mathscr {C}\hookrightarrow K\times \mathscr {C}$. By Lemma 6.22, this implies that the domain and codomain of each
$\{k\}\times \mathscr {C}\hookrightarrow K\times \mathscr {C}$. By Lemma 6.22, this implies that the domain and codomain of each ![]() $\mathrm {ev}_k\circ \mu$ are tensored over
$\mathrm {ev}_k\circ \mu$ are tensored over ![]() $\mathbf {Cat}_d(\kappa )$ and that
$\mathbf {Cat}_d(\kappa )$ and that ![]() $\mathrm {ev}_k\circ \mu$ preserves the tensoring. Claim (b) will therefore follow once we know that
$\mathrm {ev}_k\circ \mu$ preserves the tensoring. Claim (b) will therefore follow once we know that ![]() $\mathrm {Fun}_{d+1}\big (K, \mathbf {Cocart}^\kappa _d(\mathscr {C})\big )$ is tensored over
$\mathrm {Fun}_{d+1}\big (K, \mathbf {Cocart}^\kappa _d(\mathscr {C})\big )$ is tensored over ![]() $\mathbf {Cat}_d(\kappa )$ and that evaluation at each
$\mathbf {Cat}_d(\kappa )$ and that evaluation at each ![]() $k\in K$ preserves the tensoring.
$k\in K$ preserves the tensoring.
To see this, one can either use the formalism from [Reference HinichHin20] or use the following trick. We will first prove assertion (b) in the case where ![]() $\mathscr {C}=\ast$, so that the target of
$\mathscr {C}=\ast$, so that the target of ![]() $\mu$ reduces to
$\mu$ reduces to ![]() $\mathrm {Fun}_{d+1}(K, \mathbf {Cat}_d(\kappa ))$. By Example 4.56, this is indeed tensored over
$\mathrm {Fun}_{d+1}(K, \mathbf {Cat}_d(\kappa ))$. By Example 4.56, this is indeed tensored over ![]() $\mathbf {Cat}_d(\kappa )$ and restriction along
$\mathbf {Cat}_d(\kappa )$ and restriction along ![]() $\{k\}\longrightarrow K$ preserves the tensoring. Combined with assertion (a), it follows that
$\{k\}\longrightarrow K$ preserves the tensoring. Combined with assertion (a), it follows that ![]() $\mu$ yields an equivalence
$\mu$ yields an equivalence ![]() $\mathbf {Cocart}^\kappa _d(K)\simeq \mathrm {Fun}_{d+1}(K, \mathbf {Cat}_d^\kappa )$. Using this equivalence (with
$\mathbf {Cocart}^\kappa _d(K)\simeq \mathrm {Fun}_{d+1}(K, \mathbf {Cat}_d^\kappa )$. Using this equivalence (with ![]() $K$ replaced by
$K$ replaced by ![]() $\mathscr {C}$), the target of the map
$\mathscr {C}$), the target of the map ![]() $\mu$ is then equivalent to
$\mu$ is then equivalent to
Applying Example 4.56 once more then shows that this ![]() $(d+1)$-category is indeed tensored over
$(d+1)$-category is indeed tensored over ![]() $\mathbf {Cat}_d(\kappa )$ and that evaluation at
$\mathbf {Cat}_d(\kappa )$ and that evaluation at ![]() $k\in K$ preserves the tensoring. We conclude that the natural transformation
$k\in K$ preserves the tensoring. We conclude that the natural transformation ![]() $\mu$ satisfies both assertions (a) and (b), so that it is a natural equivalence as desired.
$\mu$ satisfies both assertions (a) and (b), so that it is a natural equivalence as desired.
Proof of Theorem 6.20 Let us apply Theorem 6.25 in the large setting, with ![]() $\kappa =\kappa _\mathrm {sm}$ the supremum of all small cardinals. It follows that the
$\kappa =\kappa _\mathrm {sm}$ the supremum of all small cardinals. It follows that the ![]() $(d+2)$-functor on large
$(d+2)$-functor on large ![]() $(d+1)$-categories
$(d+1)$-categories
is representable by ![]() $\mathbf {Cat}_d$. Note that the restriction of
$\mathbf {Cat}_d$. Note that the restriction of ![]() $\mathbf {Cocart}_d^{\kappa _\mathrm {sm}}$ to
$\mathbf {Cocart}_d^{\kappa _\mathrm {sm}}$ to ![]() $\mathbf {Cat}_{d+1}\subseteq \mathbf {CAT}_{d+1}$ is precisely the functor
$\mathbf {Cat}_{d+1}\subseteq \mathbf {CAT}_{d+1}$ is precisely the functor ![]() $\mathbf {Cocart}_d$ from Theorem 6.20. This proves the existence of a natural equivalence
$\mathbf {Cocart}_d$ from Theorem 6.20. This proves the existence of a natural equivalence ![]() $\mathbf {Cocart}_d(-)\simeq \mathrm {Fun}_{d+1}(-, \mathbf {Cat}_d)$ between
$\mathbf {Cocart}_d(-)\simeq \mathrm {Fun}_{d+1}(-, \mathbf {Cat}_d)$ between ![]() $(d+2)$-functors
$(d+2)$-functors ![]() $\mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$.
$\mathbf {Cat}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}_{d+1}$.
For uniqueness, let us write ![]() $F\colon \mathbf {CAT}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}$ for the
$F\colon \mathbf {CAT}_{d+1}^{\mathrm {op}}\longrightarrow \mathbf {CAT}$ for the ![]() $(d+2)$-functor represented by
$(d+2)$-functor represented by ![]() $\mathbf {Cat}_d$. Then let us write
$\mathbf {Cat}_d$. Then let us write
 \begin{align*} \mathrm{Iso}&\subseteq \mathrm{Map}_{\mathrm{Fun}_{d+2}(\mathbf{Cat}^{\mathrm{op}}_{d+1}, \mathbf{CAT}_{d+1})}\big(\mathbf{Cocart}_d, F\big|\mathbf{Cat}_{d+1}\big),\\ \mathrm{Aut}(F\big|\mathbf{Cat}_{d+1})&\subseteq \mathrm{Map}_{\mathrm{Fun}_{d+2}(\mathbf{Cat}^{\mathrm{op}}_{d+1}, \mathbf{CAT}_{d+1})}\big(F\big|\mathbf{Cat}_{d+1}, F\big|\mathbf{Cat}_{d+1}\big) \end{align*}
\begin{align*} \mathrm{Iso}&\subseteq \mathrm{Map}_{\mathrm{Fun}_{d+2}(\mathbf{Cat}^{\mathrm{op}}_{d+1}, \mathbf{CAT}_{d+1})}\big(\mathbf{Cocart}_d, F\big|\mathbf{Cat}_{d+1}\big),\\ \mathrm{Aut}(F\big|\mathbf{Cat}_{d+1})&\subseteq \mathrm{Map}_{\mathrm{Fun}_{d+2}(\mathbf{Cat}^{\mathrm{op}}_{d+1}, \mathbf{CAT}_{d+1})}\big(F\big|\mathbf{Cat}_{d+1}, F\big|\mathbf{Cat}_{d+1}\big) \end{align*}
for the full sub-![]() $(d+1)$-categories spanned by the natural equivalences between
$(d+1)$-categories spanned by the natural equivalences between ![]() $(d+2)$-functors. We have to show that
$(d+2)$-functors. We have to show that ![]() $\mathrm {Iso}\simeq \ast$. We have just verified that
$\mathrm {Iso}\simeq \ast$. We have just verified that ![]() $\mathrm {Iso}$ is nonempty, and precomposing with any element
$\mathrm {Iso}$ is nonempty, and precomposing with any element ![]() $\phi \in \mathrm {Iso}$ determines an equivalence
$\phi \in \mathrm {Iso}$ determines an equivalence ![]() $\mathrm {Iso}\simeq \mathrm {Aut}(F\big |\mathbf {Cat}_{d+1})$. It therefore remains to verify that the
$\mathrm {Iso}\simeq \mathrm {Aut}(F\big |\mathbf {Cat}_{d+1})$. It therefore remains to verify that the ![]() $(d+1)$-category of automorphisms of
$(d+1)$-category of automorphisms of ![]() $F\big |\mathbf {Cat}_{d+1}$ is equivalent to a point. As in Proposition 6.10, there are natural maps of
$F\big |\mathbf {Cat}_{d+1}$ is equivalent to a point. As in Proposition 6.10, there are natural maps of ![]() $(d+1)$-categories as follows:
$(d+1)$-categories as follows:
The first map is an equivalence by the enriched Yoneda lemma (§ 4.4). The second map arises by restricting the natural automorphisms of ![]() $F$ along
$F$ along ![]() $i\colon \mathbf {Cat}^{\mathrm {op}}_{d+1}\hookrightarrow \mathbf {CAT}^{\mathrm {op}}_{d+1}$. To see that this is an equivalence, note that together with right Kan extension, restriction along
$i\colon \mathbf {Cat}^{\mathrm {op}}_{d+1}\hookrightarrow \mathbf {CAT}^{\mathrm {op}}_{d+1}$. To see that this is an equivalence, note that together with right Kan extension, restriction along ![]() $i$ defines a coreflective localization of (very large)
$i$ defines a coreflective localization of (very large) ![]() $(d+2)$-categories as follows:
$(d+2)$-categories as follows:
The essential image of ![]() $i_*$ consists of enriched functors
$i_*$ consists of enriched functors ![]() $\mathbf {CAT}^{\mathrm {op}}_{d+1}\longrightarrow \mathbf {CAT}_{d+1}$ whose underlying
$\mathbf {CAT}^{\mathrm {op}}_{d+1}\longrightarrow \mathbf {CAT}_{d+1}$ whose underlying ![]() $1$-functor preserves large,
$1$-functor preserves large, ![]() $\kappa _{\mathrm {sm}}$-cofiltered limits; this can be verified by presenting everything by enriched (model) categories of strictly enriched functors. In particular, the representable functor
$\kappa _{\mathrm {sm}}$-cofiltered limits; this can be verified by presenting everything by enriched (model) categories of strictly enriched functors. In particular, the representable functor ![]() $F$ is contained in the essential image of
$F$ is contained in the essential image of ![]() $i_*$, so that restriction along
$i_*$, so that restriction along ![]() $i$ induces an equivalence on its automorphism
$i$ induces an equivalence on its automorphism ![]() $(d+1)$-categories. The result now follows since
$(d+1)$-categories. The result now follows since ![]() $\mathrm {Aut}_{\mathbf {CAT}_{d+1}}(\mathbf {Cat}_d)\simeq \ast$ by Proposition 6.13.
$\mathrm {Aut}_{\mathbf {CAT}_{d+1}}(\mathbf {Cat}_d)\simeq \ast$ by Proposition 6.13.
Acknowledgements
This text finds its origins (via Proposition 2.12) in joint work with Rune Haugseng, Fabian Hebestreit and Sil Linskens; I thank them for several helpful discussions, especially about constructions with spans. I would also like to thank Damien Calaque, Harry Gindi, Yonatan Harpaz, Corina Keller, Claudia Scheimbauer and Pelle Steffens for various useful conversations. Finally, I am grateful to the anonymous referee for their useful comments that helped improve the paper. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement number 768679).
Conflicts of Interest
None.
Appendix A. Technicalities on categories of fibrant objects
The purpose of this appendix is to describe a version of the Grothendieck construction for categories of fibrant objects, in the following sense.
Definition A.1 By a category of fibrant objects ![]() $\mathscr {M}$ we will mean a
$\mathscr {M}$ we will mean a ![]() $(1, 1)$-category with two classes of maps, called weak equivalences and fibrations, both containing the isomorphisms and closed under composition, such that the following conditions hold.
$(1, 1)$-category with two classes of maps, called weak equivalences and fibrations, both containing the isomorphisms and closed under composition, such that the following conditions hold.
(1) The weak equivalences have the 2-out-of-6 property.
(2) The category
 $\mathscr {M}$ admits pullbacks along fibrations and the base change of an (acyclic) fibration is again an (acyclic) fibration.
$\mathscr {M}$ admits pullbacks along fibrations and the base change of an (acyclic) fibration is again an (acyclic) fibration.(3) The category
 $\mathscr {M}$ admits a terminal object and each
$\mathscr {M}$ admits a terminal object and each  $x\longrightarrow \ast$ is a fibration.
$x\longrightarrow \ast$ is a fibration.(4) Each map in
 $\mathscr {M}$ admits a factorization into a weak equivalence, followed by a fibration.
$\mathscr {M}$ admits a factorization into a weak equivalence, followed by a fibration.
A map between categories of fibrant objects ![]() $f\colon \mathscr {M}\longrightarrow \mathscr {N}$ is a functor preserving fibrations, weak equivalences, the terminal object and pullbacks along fibrations. Let us write
$f\colon \mathscr {M}\longrightarrow \mathscr {N}$ is a functor preserving fibrations, weak equivalences, the terminal object and pullbacks along fibrations. Let us write ![]() $\mathrm {FibCat}$ for the
$\mathrm {FibCat}$ for the ![]() $(2, 1)$-category of categories of fibrant objects.
$(2, 1)$-category of categories of fibrant objects.
Our condition that weak equivalences have the 2-out-of-6 property is slightly nonstandard; it is equivalent to the assertion that a morphism in ![]() $\mathscr {M}$ is a weak equivalence if and only if its image in the localization
$\mathscr {M}$ is a weak equivalence if and only if its image in the localization ![]() $\mathscr {M}[W^{-1}]$ is an equivalence (see [Reference Radulescu-BanuRad06, Theorem 7.2.7] or use the description of
$\mathscr {M}[W^{-1}]$ is an equivalence (see [Reference Radulescu-BanuRad06, Theorem 7.2.7] or use the description of ![]() $\mathscr {M}[W^{-1}]$ from Remark A.8).
$\mathscr {M}[W^{-1}]$ from Remark A.8).
Lemma A.2 Let ![]() $\mathscr {B}\in \mathrm {FibCat}$. Consider a (pseudo-)functor
$\mathscr {B}\in \mathrm {FibCat}$. Consider a (pseudo-)functor ![]() $\mathscr {B}^{\mathrm {op}}\longrightarrow \mathrm {FibCat};\, b\longmapsto \mathscr {E}(b)$ and denote by
$\mathscr {B}^{\mathrm {op}}\longrightarrow \mathrm {FibCat};\, b\longmapsto \mathscr {E}(b)$ and denote by ![]() $p\colon \mathscr {E}\longrightarrow \mathscr {B}$ its (classical) Grothendieck construction. Suppose that the following two assertions hold.
$p\colon \mathscr {E}\longrightarrow \mathscr {B}$ its (classical) Grothendieck construction. Suppose that the following two assertions hold.
(a) For every weak equivalence
 $f\colon b_0\longrightarrow b_1$, the functor
$f\colon b_0\longrightarrow b_1$, the functor  $f^*\colon \mathscr {E}(b_1)\longrightarrow \mathscr {E}(b_0)$ induces an equivalence on localizations.
$f^*\colon \mathscr {E}(b_1)\longrightarrow \mathscr {E}(b_0)$ induces an equivalence on localizations.(b) Let
 $f\colon b_0\longrightarrow b_1$ be a morphism and
$f\colon b_0\longrightarrow b_1$ be a morphism and  $g\colon x\longrightarrow f^*y$ a morphism in
$g\colon x\longrightarrow f^*y$ a morphism in  $\mathscr {E}(b_0)$. Then there exists a factorization
$\mathscr {E}(b_0)$. Then there exists a factorization  $f=pi$ with
$f=pi$ with  $p\colon b_0'\longrightarrow b_1$ a fibration and
$p\colon b_0'\longrightarrow b_1$ a fibration and  $i\colon b_0\longrightarrow b_0'$ a weak equivalence, together with a factorization
$i\colon b_0\longrightarrow b_0'$ a weak equivalence, together with a factorization  $g=i^*(q)j$ with
$g=i^*(q)j$ with  $q\colon z\twoheadrightarrow p^*y$ a fibration in
$q\colon z\twoheadrightarrow p^*y$ a fibration in  $\mathscr {E}(b'_0)$ and
$\mathscr {E}(b'_0)$ and  $j\colon x\longrightarrow i^*z$ a weak equivalence in
$j\colon x\longrightarrow i^*z$ a weak equivalence in  $\mathscr {E}(b_0)$.
$\mathscr {E}(b_0)$.
Define a map ![]() $x_0\longrightarrow x_1$ in
$x_0\longrightarrow x_1$ in ![]() $\mathscr {E}$ to be a weak equivalence (fibration) if it factors (uniquely) as
$\mathscr {E}$ to be a weak equivalence (fibration) if it factors (uniquely) as ![]() $x_0\longrightarrow x\longrightarrow x_1$ where the second map is a
$x_0\longrightarrow x\longrightarrow x_1$ where the second map is a ![]() $p$-cartesian lift of a weak equivalence (fibration) and the first map is a weak equivalence (fibration) in
$p$-cartesian lift of a weak equivalence (fibration) and the first map is a weak equivalence (fibration) in ![]() $\mathscr {E}(px_0)$. This makes
$\mathscr {E}(px_0)$. This makes ![]() $p\colon \mathscr {E}\longrightarrow \mathscr {B}$ a map between categories of fibrant objects.
$p\colon \mathscr {E}\longrightarrow \mathscr {B}$ a map between categories of fibrant objects.
Proof. One easily verifies that pullbacks along fibrations exist and that the base change of an (acyclic) fibration remains an (acyclic) fibration. The terminal object in ![]() $\mathscr {E}$ is given by
$\mathscr {E}$ is given by ![]() $\ast \in \mathscr {E}(\ast )$ and each
$\ast \in \mathscr {E}(\ast )$ and each ![]() $x\longrightarrow \ast$ is a fibration. Condition (a) implies that for any weak equivalence
$x\longrightarrow \ast$ is a fibration. Condition (a) implies that for any weak equivalence ![]() $f\colon b_0\longrightarrow b_1$, the functor
$f\colon b_0\longrightarrow b_1$, the functor ![]() $f^*\colon \mathscr {E}(b_1)\longrightarrow \mathscr {E}(b_0)$ detects weak equivalences (which are detected in the localization). Using this, one readily verifies that the weak equivalences have the 2-out-of-6 property. Finally, the factorization condition is precisely (b).
$f^*\colon \mathscr {E}(b_1)\longrightarrow \mathscr {E}(b_0)$ detects weak equivalences (which are detected in the localization). Using this, one readily verifies that the weak equivalences have the 2-out-of-6 property. Finally, the factorization condition is precisely (b).
Remark A.3 Suppose that ![]() $\mathscr {B}^{\mathrm {op}}\longrightarrow \mathrm {FibCat}$ arises from a diagram of model categories
$\mathscr {B}^{\mathrm {op}}\longrightarrow \mathrm {FibCat}$ arises from a diagram of model categories ![]() $\mathscr {N}(b)$ and Quillen adjunctions
$\mathscr {N}(b)$ and Quillen adjunctions ![]() $f_!\colon \mathscr {N}(b_0)\leftrightarrows \mathscr {N}(b_1)\colon f^*$, by letting
$f_!\colon \mathscr {N}(b_0)\leftrightarrows \mathscr {N}(b_1)\colon f^*$, by letting ![]() $\mathscr {E}(b)\subseteq \mathscr {N}(b)$ be the full subcategory of fibrant objects. In this case, condition (b) follows from the following assertion: for every map
$\mathscr {E}(b)\subseteq \mathscr {N}(b)$ be the full subcategory of fibrant objects. In this case, condition (b) follows from the following assertion: for every map ![]() $f\colon b_0\longrightarrow b_1$ in
$f\colon b_0\longrightarrow b_1$ in ![]() $\mathscr {B}$, there exists a factorization
$\mathscr {B}$, there exists a factorization ![]() $f=pi$ with
$f=pi$ with ![]() $p\colon b'_0\longrightarrow b_1$ a fibration and
$p\colon b'_0\longrightarrow b_1$ a fibration and ![]() $i\colon b_0\longrightarrow b_0'$ a weak equivalence such that
$i\colon b_0\longrightarrow b_0'$ a weak equivalence such that ![]() $i_!\colon \mathscr {N}(b_0)\longrightarrow \mathscr {N}(b'_0)$ preserves all weak equivalences.
$i_!\colon \mathscr {N}(b_0)\longrightarrow \mathscr {N}(b'_0)$ preserves all weak equivalences.
Indeed, for a map ![]() $g\colon x\longrightarrow f^*y$ in
$g\colon x\longrightarrow f^*y$ in ![]() $\mathscr {E}(b_0)$, we can consider the adjoint map
$\mathscr {E}(b_0)$, we can consider the adjoint map ![]() $i_!x\longrightarrow p^*y$ and factor it into
$i_!x\longrightarrow p^*y$ and factor it into ![]() $i_!x\stackrel {\sim }{\longrightarrow } z$ followed by a fibration
$i_!x\stackrel {\sim }{\longrightarrow } z$ followed by a fibration ![]() $q\colon z\twoheadrightarrow p^*y$. One then obtains the desired factorization
$q\colon z\twoheadrightarrow p^*y$. One then obtains the desired factorization ![]() $g=i^*(q)j$, where
$g=i^*(q)j$, where ![]() $j\colon x\longrightarrow i^*i_!x\longrightarrow i^*z$ is a model for the derived unit map and, hence, an equivalence by condition (a).
$j\colon x\longrightarrow i^*i_!x\longrightarrow i^*z$ is a model for the derived unit map and, hence, an equivalence by condition (a).
Example A.4 Consider a model category ![]() $\mathscr {M}$ and a diagram of model categories and left Quillen functors
$\mathscr {M}$ and a diagram of model categories and left Quillen functors ![]() $\mathscr {M}\longrightarrow \mathrm {ModCat^L}$ sending
$\mathscr {M}\longrightarrow \mathrm {ModCat^L}$ sending ![]() $b\longmapsto \mathscr {N}(b)$. Let
$b\longmapsto \mathscr {N}(b)$. Let ![]() $p\colon \mathscr {N}\longrightarrow \mathscr {M}$ be the Grothendieck construction of this diagram and let us say that a map
$p\colon \mathscr {N}\longrightarrow \mathscr {M}$ be the Grothendieck construction of this diagram and let us say that a map ![]() $\alpha \colon x\longrightarrow y$ in
$\alpha \colon x\longrightarrow y$ in ![]() $\mathscr {N}$ is:
$\mathscr {N}$ is:
– a (trivial) fibration if
 $p(\alpha )\colon px\to py$ is a (trivial) fibration and the map
$p(\alpha )\colon px\to py$ is a (trivial) fibration and the map  $x\to p(\alpha )^*y$ is a (trivial) fibration in
$x\to p(\alpha )^*y$ is a (trivial) fibration in  $\mathscr {N}(px)$;
$\mathscr {N}(px)$;– a (trivial) cofibration if
 $p(\alpha )\colon px\to py$ is a (trivial) cofibration and the map
$p(\alpha )\colon px\to py$ is a (trivial) cofibration and the map  $p(\alpha )_!x\to y$ is a (trivial) fibration in
$p(\alpha )_!x\to y$ is a (trivial) fibration in  $\mathscr {N}(py)$.
$\mathscr {N}(py)$.
Harpaz and Prasma have shown that this determines a model structure on ![]() $\mathscr {N}$ if the diagram
$\mathscr {N}$ if the diagram ![]() $b\longmapsto \mathscr {N}(b)$ satisfies three conditions [Reference Harpaz and PrasmaHP15]: (a) every weak equivalence in
$b\longmapsto \mathscr {N}(b)$ satisfies three conditions [Reference Harpaz and PrasmaHP15]: (a) every weak equivalence in ![]() $\mathscr {M}$ induces a Quillen equivalence on fibers, (b) for every trivial cofibration in
$\mathscr {M}$ induces a Quillen equivalence on fibers, (b) for every trivial cofibration in ![]() $\mathscr {M}$, the associated left Quillen functor preserves weak equivalences and (c) for every trivial fibration in
$\mathscr {M}$, the associated left Quillen functor preserves weak equivalences and (c) for every trivial fibration in ![]() $\mathscr {M}$, the associated right Quillen functor preserves weak equivalences.
$\mathscr {M}$, the associated right Quillen functor preserves weak equivalences.
The diagram of model categories indexed by ![]() $\mathscr {M}$ induces a diagram of categories of fibrant objects
$\mathscr {M}$ induces a diagram of categories of fibrant objects ![]() $\mathscr {M}^{\mathrm {fib}, \mathrm {op}}\longrightarrow \mathrm {FibCat}$ sending each fibrant object
$\mathscr {M}^{\mathrm {fib}, \mathrm {op}}\longrightarrow \mathrm {FibCat}$ sending each fibrant object ![]() $b$ in
$b$ in ![]() $\mathscr {M}$ to the full subcategory of fibrant objects in
$\mathscr {M}$ to the full subcategory of fibrant objects in ![]() $\mathscr {N}(b)$. In light of Remark A.3, conditions (a) and (b) from [Reference Harpaz and PrasmaHP15] imply conditions (a) and (b) from Lemma A.2. The category of fibrant objects resulting from Lemma A.2 is then simply the category of fibrant objects associated to the model category
$\mathscr {N}(b)$. In light of Remark A.3, conditions (a) and (b) from [Reference Harpaz and PrasmaHP15] imply conditions (a) and (b) from Lemma A.2. The category of fibrant objects resulting from Lemma A.2 is then simply the category of fibrant objects associated to the model category ![]() $\mathscr {N}$ from [Reference Harpaz and PrasmaHP15].
$\mathscr {N}$ from [Reference Harpaz and PrasmaHP15].
Definition A.5 A map ![]() $p\colon \mathscr {E}\longrightarrow \mathscr {B}$ of categories of fibrant objects is said to be a homotopy cartesian fibration if it arises as in Lemma A.2. In this situation, we will say that
$p\colon \mathscr {E}\longrightarrow \mathscr {B}$ of categories of fibrant objects is said to be a homotopy cartesian fibration if it arises as in Lemma A.2. In this situation, we will say that ![]() $\alpha \colon x_0\longrightarrow x_1$ in
$\alpha \colon x_0\longrightarrow x_1$ in ![]() $\mathscr {E}$ is homotopy
$\mathscr {E}$ is homotopy ![]() $p$-cartesian if
$p$-cartesian if ![]() $x_0\longrightarrow p(\alpha )^*x_1$ is a weak equivalence in the fiber, and we will write
$x_0\longrightarrow p(\alpha )^*x_1$ is a weak equivalence in the fiber, and we will write ![]() $\mathscr {E}^{\mathrm {hocart}}\subseteq \mathscr {E}$ for the wide subcategory of homotopy cartesian arrows.
$\mathscr {E}^{\mathrm {hocart}}\subseteq \mathscr {E}$ for the wide subcategory of homotopy cartesian arrows.
Remark A.6 If ![]() $w$ is a weak equivalence in
$w$ is a weak equivalence in ![]() $\mathscr {E}$, then a composition
$\mathscr {E}$, then a composition ![]() $wf$ is homotopy cartesian if and only if
$wf$ is homotopy cartesian if and only if ![]() $f$ is homotopy cartesian, and likewise for a composition
$f$ is homotopy cartesian, and likewise for a composition ![]() $fw$. In particular,
$fw$. In particular, ![]() $\mathscr {E}^\mathrm {hocart}$ is a relative category (with the same weak equivalences as in
$\mathscr {E}^\mathrm {hocart}$ is a relative category (with the same weak equivalences as in ![]() $\mathscr {E}$) whose weak equivalences are generated under the
$\mathscr {E}$) whose weak equivalences are generated under the ![]() $2$-out-of-
$2$-out-of-![]() $3$ property by the acyclic fibrations in
$3$ property by the acyclic fibrations in ![]() $\mathscr {E}$.
$\mathscr {E}$.
Proposition A.7 Let ![]() $p\colon \mathscr {E}\longrightarrow \mathscr {B}$ be a homotopy cartesian fibration between categories of fibrant objects. Then the following assertions hold.
$p\colon \mathscr {E}\longrightarrow \mathscr {B}$ be a homotopy cartesian fibration between categories of fibrant objects. Then the following assertions hold.
(1) The pullback square of relative categories
induces a cartesian square upon localization at the weak equivalences.
(2) The functor between localizations
 $\mathscr {E}^{\mathrm {hocart}}[W^{-1}]\longrightarrow \mathscr {E}[W^{-1}]$ is a subcategory inclusion, whose image is the wide subcategory of cartesian morphisms for
$\mathscr {E}^{\mathrm {hocart}}[W^{-1}]\longrightarrow \mathscr {E}[W^{-1}]$ is a subcategory inclusion, whose image is the wide subcategory of cartesian morphisms for  $p\colon \mathscr {E}[W^{-1}]\longrightarrow \mathscr {B}[W^{-1}]$.
$p\colon \mathscr {E}[W^{-1}]\longrightarrow \mathscr {B}[W^{-1}]$.(3) The localization
 $p\colon \mathscr {E}[W^{-1}]\longrightarrow \mathscr {B}[W^{-1}]$ is a cartesian fibration.
$p\colon \mathscr {E}[W^{-1}]\longrightarrow \mathscr {B}[W^{-1}]$ is a cartesian fibration.(4) Suppose that
 $f\colon b_0\longrightarrow b_1$ is a morphism in
$f\colon b_0\longrightarrow b_1$ is a morphism in  $\mathscr {B}$ such that
$\mathscr {B}$ such that  $f^*\colon \mathscr {E}(b_1)\longrightarrow \mathscr {E}(b_0)$ admits a left adjoint
$f^*\colon \mathscr {E}(b_1)\longrightarrow \mathscr {E}(b_0)$ admits a left adjoint  $f_!$ that preserves acyclic fibrations. For every
$f_!$ that preserves acyclic fibrations. For every  $x_0\in \mathscr {E}(b_0)$, the natural arrow
$x_0\in \mathscr {E}(b_0)$, the natural arrow  $x_0\longrightarrow f_!x_0$ in
$x_0\longrightarrow f_!x_0$ in  $\mathscr {E}$ determines a
$\mathscr {E}$ determines a  $p$-cocartesian arrow in
$p$-cocartesian arrow in  $\mathscr {E}[W^{-1}]$.
$\mathscr {E}[W^{-1}]$.
This proposition is essentially a special case of a result of Hinich [Reference HinichHin16]. We have included a proof that does not rely on Lurie's (un)straightening machinery (in contrast to [Reference HinichHin16]).
Remark A.8 For ![]() $\mathscr {M}\in \mathrm {FibCat}$, its (
$\mathscr {M}\in \mathrm {FibCat}$, its (![]() $\infty$-categorical) localization can be modeled as follows [Reference HorelHor16, Reference NuitenNui16]. Let us write
$\infty$-categorical) localization can be modeled as follows [Reference HorelHor16, Reference NuitenNui16]. Let us write ![]() $\mathrm {Span}_{\mathscr {M}}$ for the
$\mathrm {Span}_{\mathscr {M}}$ for the ![]() $(2, 2)$-category whose:
$(2, 2)$-category whose:
(0) objects are the objects of
 $\mathscr {M}$;
$\mathscr {M}$;(1) mapping categories
 $\mathrm {Span}_{\mathscr {M}}(x_0, x_1)$ are the full subcategories of spans
$\mathrm {Span}_{\mathscr {M}}(x_0, x_1)$ are the full subcategories of spans  $x_0\longleftarrow x_{01}\longrightarrow x_1$ where the left morphism
$x_0\longleftarrow x_{01}\longrightarrow x_1$ where the left morphism  $\alpha \colon x_{01}\longrightarrow x_0$ is an acyclic fibration and
$\alpha \colon x_{01}\longrightarrow x_0$ is an acyclic fibration and  $\beta \colon x_{01}\longrightarrow x_1$ is any morphism (and composition by composition of spans); we will abbreviate such a span by
$\beta \colon x_{01}\longrightarrow x_1$ is any morphism (and composition by composition of spans); we will abbreviate such a span by  $(\alpha, x_{01}, \beta )\colon x_0\dashrightarrow x_1$.
$(\alpha, x_{01}, \beta )\colon x_0\dashrightarrow x_1$.
Taking classifying spaces then determines a ![]() $1$-categorical algebra (i.e. a Segal space) whose completion models the localization [Reference HorelHor16]. In fact, this description works for any relative category
$1$-categorical algebra (i.e. a Segal space) whose completion models the localization [Reference HorelHor16]. In fact, this description works for any relative category ![]() $(\mathscr {C}, W)$ where
$(\mathscr {C}, W)$ where ![]() $W$ is generated under the
$W$ is generated under the ![]() $2$-out-of-
$2$-out-of-![]() $3$ property by a class of ‘acyclic fibrations’ which is stable under base change.
$3$ property by a class of ‘acyclic fibrations’ which is stable under base change.
Proof. Let us start by considering the map of ![]() $(2, 2)$-categories
$(2, 2)$-categories ![]() $p\colon \mathrm {Span}_{\mathscr {E}}\longrightarrow \mathrm {Span}_{\mathscr {B}}$. For each
$p\colon \mathrm {Span}_{\mathscr {E}}\longrightarrow \mathrm {Span}_{\mathscr {B}}$. For each ![]() $x_0, x_1\in \mathscr {E}$, the induced functor on mapping
$x_0, x_1\in \mathscr {E}$, the induced functor on mapping ![]() $(1, 1)$-categories
$(1, 1)$-categories
is a cartesian fibration, whose fiber over a span ![]() $(\alpha, b, \beta )\colon px_0\dashrightarrow px_1$ can be identified with
$(\alpha, b, \beta )\colon px_0\dashrightarrow px_1$ can be identified with ![]() $\mathrm {Span}_{\mathscr {E}(b)}(\alpha ^*x_0, \beta ^*x_0)$. Using condition (a) and Remark A.8, it follows that for each morphism
$\mathrm {Span}_{\mathscr {E}(b)}(\alpha ^*x_0, \beta ^*x_0)$. Using condition (a) and Remark A.8, it follows that for each morphism ![]() $\gamma \colon b'\stackrel {\sim }{\longrightarrow } b$ in
$\gamma \colon b'\stackrel {\sim }{\longrightarrow } b$ in ![]() $\mathrm {Span}_{\mathscr {B}}(px_0, px_1)$, the induced map on fibers
$\mathrm {Span}_{\mathscr {B}}(px_0, px_1)$, the induced map on fibers
induces an equivalence on classifying spaces. It follows that (
A.9) satisfies the conditions of Quillen's theorem B; consequently, the classifying space functor ![]() $|-|\colon {{\rm Cat}}_{(1, 1)}\longrightarrow \mathscr {S}$ preserves all pullbacks along it.
$|-|\colon {{\rm Cat}}_{(1, 1)}\longrightarrow \mathscr {S}$ preserves all pullbacks along it.
In particular, this implies that the pullback square of ![]() $(2, 2)$-categories
$(2, 2)$-categories

induces a (homotopy) pullback square of Segal spaces upon taking classifying spaces of all mapping categories. To prove assertion (1), we have to show that this also induces a homotopy pullback square on completions. This follows as soon as ![]() $\mathrm {Span}_{\mathscr {E}}\longrightarrow \mathrm {Span}_{\mathscr {B}}$ induces an isofibration on homotopy
$\mathrm {Span}_{\mathscr {E}}\longrightarrow \mathrm {Span}_{\mathscr {B}}$ induces an isofibration on homotopy ![]() $(1, 1)$-categories (cf. [Reference Harpaz, Nuiten and PrasmaHNP20, Corollary 4.4]).
$(1, 1)$-categories (cf. [Reference Harpaz, Nuiten and PrasmaHNP20, Corollary 4.4]).
To see this, note that by the 2-out-of-6 property, any isomorphism in ![]() $\mathrm {ho}(\mathrm {Span}_{\mathscr {B}})$ arises from a span
$\mathrm {ho}(\mathrm {Span}_{\mathscr {B}})$ arises from a span ![]() $(\alpha, b, \beta )\colon b_0\dashrightarrow b_1$ in
$(\alpha, b, \beta )\colon b_0\dashrightarrow b_1$ in ![]() $\mathscr {B}$ with
$\mathscr {B}$ with ![]() $\alpha$ a trivial fibration and
$\alpha$ a trivial fibration and ![]() $\beta$ a weak equivalence. It therefore suffices to prove the following stronger assertion.
$\beta$ a weak equivalence. It therefore suffices to prove the following stronger assertion.
() For any span
 $(\alpha, b, \beta )\colon b_0\dashrightarrow b_1$ in
$(\alpha, b, \beta )\colon b_0\dashrightarrow b_1$ in  $\mathscr {B}$ with
$\mathscr {B}$ with  $\alpha$ a trivial fibration and any
$\alpha$ a trivial fibration and any  $x_1\in \mathscr {E}_{b_1}$, there exists a lift to a span
$x_1\in \mathscr {E}_{b_1}$, there exists a lift to a span  $(\tilde {\alpha }, x_{12}, \tilde {\beta })\colon x_0\dashrightarrow x_1$ with
$(\tilde {\alpha }, x_{12}, \tilde {\beta })\colon x_0\dashrightarrow x_1$ with  $\tilde {\alpha }$ a trivial fibration and
$\tilde {\alpha }$ a trivial fibration and  $\tilde {\beta }$ homotopy cartesian.
$\tilde {\beta }$ homotopy cartesian.
To see this, first take ![]() $\beta ^*x_1\in \mathscr {E}_b$ and recall that
$\beta ^*x_1\in \mathscr {E}_b$ and recall that ![]() $\alpha ^*\colon \mathscr {E}_{b_0}\longrightarrow \mathscr {E}_b$ induces an equivalence on localizations. This implies that there exists some object
$\alpha ^*\colon \mathscr {E}_{b_0}\longrightarrow \mathscr {E}_b$ induces an equivalence on localizations. This implies that there exists some object ![]() $x_0\in \mathscr {E}_{b_0}$ together with a zigzag
$x_0\in \mathscr {E}_{b_0}$ together with a zigzag ![]() $\alpha ^*(x_0)\stackrel {\sim }{\twoheadleftarrow } x\stackrel {\sim }{\longrightarrow } \beta ^*x_1$. The composite
$\alpha ^*(x_0)\stackrel {\sim }{\twoheadleftarrow } x\stackrel {\sim }{\longrightarrow } \beta ^*x_1$. The composite ![]() $x_0\stackrel {\sim }{\twoheadleftarrow } \alpha ^*(x_0) \stackrel {\sim }{\twoheadleftarrow } x\stackrel {\sim }{\longrightarrow } \beta ^*(x_1)\longrightarrow x_1$ then provides the desired lift.
$x_0\stackrel {\sim }{\twoheadleftarrow } \alpha ^*(x_0) \stackrel {\sim }{\twoheadleftarrow } x\stackrel {\sim }{\longrightarrow } \beta ^*(x_1)\longrightarrow x_1$ then provides the desired lift.
This proves assertion (1). For assertions (2) and (3), note that by Remarks A.6 and A.8, the localization of ![]() $\mathscr {E}^{\mathrm {hocart}}$ arises from the
$\mathscr {E}^{\mathrm {hocart}}$ arises from the ![]() $(2, 2)$-category
$(2, 2)$-category ![]() $\mathrm {Span}_{\mathscr {E}^\mathrm {hocart}}$. Since being a homotopy
$\mathrm {Span}_{\mathscr {E}^\mathrm {hocart}}$. Since being a homotopy ![]() $p$-cartesian morphism is invariant under weak equivalences,
$p$-cartesian morphism is invariant under weak equivalences, ![]() $\mathrm {Span}_{\mathscr {E}^\mathrm {hocart}}(x_0, x_1)\longrightarrow \mathrm {Span}_{\mathscr {E}}(x_0, x_1)$ is an inclusion of connected components, so that
$\mathrm {Span}_{\mathscr {E}^\mathrm {hocart}}(x_0, x_1)\longrightarrow \mathrm {Span}_{\mathscr {E}}(x_0, x_1)$ is an inclusion of connected components, so that ![]() $\mathscr {E}^\mathrm {hocart}[W^{-1}]\longrightarrow \mathscr {E}[W^{-1}]$ is indeed the inclusion of a wide subcategory. Assertions (2) and (3) then follow from (
$\mathscr {E}^\mathrm {hocart}[W^{-1}]\longrightarrow \mathscr {E}[W^{-1}]$ is indeed the inclusion of a wide subcategory. Assertions (2) and (3) then follow from (![]() $\ast$) as soon as every arrow in
$\ast$) as soon as every arrow in ![]() $\mathscr {E}^\mathrm {hocart}[W^{-1}]$ is a cartesian arrow.
$\mathscr {E}^\mathrm {hocart}[W^{-1}]$ is a cartesian arrow.
Let ![]() $(\tilde {\alpha }, x_{12}, \tilde {\beta })\colon x_1\dashrightarrow x_2$ be a morphism in
$(\tilde {\alpha }, x_{12}, \tilde {\beta })\colon x_1\dashrightarrow x_2$ be a morphism in ![]() $\mathrm {Span}_{\mathscr {E}^\mathrm {hocart}}$, so that
$\mathrm {Span}_{\mathscr {E}^\mathrm {hocart}}$, so that ![]() $\tilde {\beta }$ is homotopy
$\tilde {\beta }$ is homotopy ![]() $p$-cartesian, and let
$p$-cartesian, and let ![]() $(\alpha, b_{12}, \beta )\colon b_1\dashrightarrow b_2$ denote its image in
$(\alpha, b_{12}, \beta )\colon b_1\dashrightarrow b_2$ denote its image in ![]() $\mathscr {B}$. To see that this map is an equivalence, we have to show that for any
$\mathscr {B}$. To see that this map is an equivalence, we have to show that for any ![]() $x_0\in \mathscr {E}$ with image
$x_0\in \mathscr {E}$ with image ![]() $b_0=px_0$ in
$b_0=px_0$ in ![]() $\mathscr {B}$, the square of categories
$\mathscr {B}$, the square of categories

induces a homotopy cartesian square of classifying spaces. Since the vertical maps are cartesian fibrations satisfying the conditions of Quillen's Theorem B, it suffices to show that for any span ![]() $(\gamma, b_{01}, \delta )\colon b_0\dashrightarrow b_1$ in
$(\gamma, b_{01}, \delta )\colon b_0\dashrightarrow b_1$ in ![]() $\mathrm {Span}_{\mathscr {B}}(b_0, b_1)$, the induced map between fibers induces an equivalence on classifying spaces. To see this, let us denote the composite span
$\mathrm {Span}_{\mathscr {B}}(b_0, b_1)$, the induced map between fibers induces an equivalence on classifying spaces. To see this, let us denote the composite span ![]() $(\alpha, b_{12}, \beta )\circ (\gamma, b_{01}, \delta )$ by
$(\alpha, b_{12}, \beta )\circ (\gamma, b_{01}, \delta )$ by

where ![]() $b_{02}=b_{01}\times _{b_1} b_{12}$. Recall from the beginning of the proof that the fibers of the vertical maps in (
$b_{02}=b_{01}\times _{b_1} b_{12}$. Recall from the beginning of the proof that the fibers of the vertical maps in (
) are themselves given by categories of spans. Unraveling the definition, the map between the vertical fibers over ![]() $(\gamma, b_{01}, \delta )$ can then be identified with the following composite.
$(\gamma, b_{01}, \delta )$ can then be identified with the following composite.

The first map is an equivalence since ![]() $(\alpha ')^*$ induces an equivalence on localizations. The second map takes the postcomposition with the span
$(\alpha ')^*$ induces an equivalence on localizations. The second map takes the postcomposition with the span ![]() $(\delta ')^*\alpha ^*x_1\longleftarrow (\delta ')^*x_{12}\longrightarrow (\delta ')^*\beta ^*x_2$, where both maps are weak equivalences since
$(\delta ')^*\alpha ^*x_1\longleftarrow (\delta ')^*x_{12}\longrightarrow (\delta ')^*\beta ^*x_2$, where both maps are weak equivalences since ![]() $\tilde {\alpha }$ and
$\tilde {\alpha }$ and ![]() $\tilde {\beta }$ were homotopy cartesian. This map induces an equivalence on classifying spaces as well.
$\tilde {\beta }$ were homotopy cartesian. This map induces an equivalence on classifying spaces as well.
Finally, for assertion (4), let us start by recalling that for any cartesian fibration ![]() $p\colon \mathscr {D}\longrightarrow \mathscr {C}$ of
$p\colon \mathscr {D}\longrightarrow \mathscr {C}$ of ![]() $1$-categories, an arrow in
$1$-categories, an arrow in ![]() $\mathscr {D}$ is
$\mathscr {D}$ is ![]() $p$-cocartesian if and only if it is locally
$p$-cocartesian if and only if it is locally ![]() $p$-cocartesian, i.e. cocartesian in the base change of
$p$-cocartesian, i.e. cocartesian in the base change of ![]() $p$ to a
$p$ to a ![]() $1$-simplex [Reference LurieLur09a, Corollary 5.2.2.4]. In the present situation, the observations at the beginning of the proof imply that the base change of
$1$-simplex [Reference LurieLur09a, Corollary 5.2.2.4]. In the present situation, the observations at the beginning of the proof imply that the base change of ![]() $\mathscr {E}[W^{-1}]\longrightarrow \mathscr {B}[W^{-1}]$ to the
$\mathscr {E}[W^{-1}]\longrightarrow \mathscr {B}[W^{-1}]$ to the ![]() $1$-simplex
$1$-simplex ![]() $f\colon b_0\longrightarrow b_1$ can be computed at the level of
$f\colon b_0\longrightarrow b_1$ can be computed at the level of ![]() $(2, 2)$-categories. Unraveling the definitions as in the proofs of parts (2) and (3), we reduce to showing that for any
$(2, 2)$-categories. Unraveling the definitions as in the proofs of parts (2) and (3), we reduce to showing that for any ![]() $x_2\in \mathscr {E}(b_1)$,
$x_2\in \mathscr {E}(b_1)$,
induces an equivalence on classifying spaces. Here the second map precomposes spans with the unit ![]() $\eta \colon x_0\longrightarrow f^*f_!x_0$. Explicitly, the functor (
$\eta \colon x_0\longrightarrow f^*f_!x_0$. Explicitly, the functor (
) sends ![]() $f_!x_0\longleftarrow x_{12}\longrightarrow x_2$ to the span
$f_!x_0\longleftarrow x_{12}\longrightarrow x_2$ to the span ![]() $x_0\longleftarrow x_0\times _{f^*f_!x_0} f^*x_{12}\longrightarrow f^*x_2$. This induces an equivalence on classifying spaces since it admits a left adjoint, sending
$x_0\longleftarrow x_0\times _{f^*f_!x_0} f^*x_{12}\longrightarrow f^*x_2$. This induces an equivalence on classifying spaces since it admits a left adjoint, sending ![]() $x_0\longleftarrow x_{02}\longrightarrow f^*x_2$ to
$x_0\longleftarrow x_{02}\longrightarrow f^*x_2$ to ![]() $f_!x_0\longleftarrow f_!x_{02}\longrightarrow f_!f^*x_2\longrightarrow x_2$.
$f_!x_0\longleftarrow f_!x_{02}\longrightarrow f_!f^*x_2\longrightarrow x_2$.