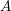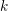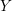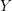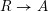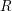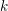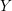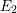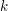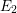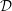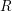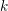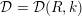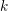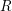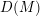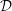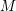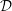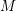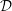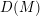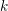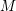1 Introduction
In [Reference HartshorneHar75], Hartshorne constructs local and global algebraic de Rham homology and cohomology theories for schemes over a field
![]() $k$
of characteristic zero. The global theories, defined for any scheme
$k$
of characteristic zero. The global theories, defined for any scheme
![]() $Y$
of finite type over
$Y$
of finite type over
![]() $k$
, are defined using a choice of embedding
$k$
, are defined using a choice of embedding
 $Y{\hookrightarrow}X$
into a smooth scheme over
$Y{\hookrightarrow}X$
into a smooth scheme over
![]() $k$
(or a local system of such embeddings if a global embedding does not exist): one computes the hypercohomology of certain complexes of sheaves on
$k$
(or a local system of such embeddings if a global embedding does not exist): one computes the hypercohomology of certain complexes of sheaves on
![]() $X$
or on the formal completion of
$X$
or on the formal completion of
![]() $Y$
in
$Y$
in
![]() $X$
. Hartshorne’s primary interest [Reference HartshorneHar75, Remark, p. 70] in constructing the local theories is the case where
$X$
. Hartshorne’s primary interest [Reference HartshorneHar75, Remark, p. 70] in constructing the local theories is the case where
![]() $Y$
is the spectrum of a complete local ring. For technical reasons, he defines the local theories for a larger class of schemes (‘category
$Y$
is the spectrum of a complete local ring. For technical reasons, he defines the local theories for a larger class of schemes (‘category
![]() ${\mathcal{C}}$
’: see [Reference HartshorneHar75, p. 65]), and proves the corresponding finiteness and duality results by reducing to the global case and using resolution of singularities.
${\mathcal{C}}$
’: see [Reference HartshorneHar75, p. 65]), and proves the corresponding finiteness and duality results by reducing to the global case and using resolution of singularities.
There is a sketch in [Reference HartshorneHar75, pp. 70–71] of a failed attempt to prove that local algebraic de Rham homology and cohomology are dual using Grothendieck’s local duality theorem. This sketch is the inspiration for the present paper, as its ideas can now be profitably pursued using Lyubeznik’s work on the
![]() ${\mathcal{D}}$
-module structure of local cohomology [Reference LyubeznikLyu93]. This structure allows us to speak of the de Rham complex of a local cohomology module, and knowledge of such complexes in turn enables us to better understand the early terms of the spectral sequences appearing in Hartshorne’s work. We are able to give a purely local proof for both the embedding-independence and the finiteness of local de Rham homology and cohomology, replacing the global methods of algebraic geometry (including resolution of singularities) with the theory of algebraic
${\mathcal{D}}$
-module structure of local cohomology [Reference LyubeznikLyu93]. This structure allows us to speak of the de Rham complex of a local cohomology module, and knowledge of such complexes in turn enables us to better understand the early terms of the spectral sequences appearing in Hartshorne’s work. We are able to give a purely local proof for both the embedding-independence and the finiteness of local de Rham homology and cohomology, replacing the global methods of algebraic geometry (including resolution of singularities) with the theory of algebraic
![]() ${\mathcal{D}}$
-modules over a formal power series ring in characteristic zero. Along the way, we will define a new set of invariants for complete local rings, analogous to the Lyubeznik numbers. Our proof shows more than is contained in [Reference HartshorneHar75], namely that the entire Hodge–de Rham spectral sequences for homology and cohomology (with the exception of the first term) are embedding-independent (up to a degree shift in the homology case) and consist of finite-dimensional
${\mathcal{D}}$
-modules over a formal power series ring in characteristic zero. Along the way, we will define a new set of invariants for complete local rings, analogous to the Lyubeznik numbers. Our proof shows more than is contained in [Reference HartshorneHar75], namely that the entire Hodge–de Rham spectral sequences for homology and cohomology (with the exception of the first term) are embedding-independent (up to a degree shift in the homology case) and consist of finite-dimensional
![]() $k$
-spaces.
$k$
-spaces.
We now give more detail, recalling Hartshorne’s results and stating ours. Let
![]() $A$
be a complete local ring with coefficient field
$A$
be a complete local ring with coefficient field
![]() $k$
of characteristic zero (that is,
$k$
of characteristic zero (that is,
![]() $k$
is the residue field of
$k$
is the residue field of
![]() $A$
, and
$A$
, and
![]() $A$
contains a field isomorphic to
$A$
contains a field isomorphic to
![]() $k$
). We view
$k$
). We view
![]() $A$
as a
$A$
as a
![]() $k$
-algebra via this coefficient field. By Cohen’s structure theorem, there exists a surjection of
$k$
-algebra via this coefficient field. By Cohen’s structure theorem, there exists a surjection of
![]() $k$
-algebras
$k$
-algebras
 $\unicode[STIX]{x1D70B}:R\rightarrow A$
where
$\unicode[STIX]{x1D70B}:R\rightarrow A$
where
![]() $R$
is a complete regular local
$R$
is a complete regular local
![]() $k$
-algebra, which must take the form
$k$
-algebra, which must take the form
 $R=k[[x_{1},\ldots ,x_{n}]]$
for some
$R=k[[x_{1},\ldots ,x_{n}]]$
for some
![]() $n$
. Let
$n$
. Let
![]() $I\subset R$
be the kernel of this surjection. We have a corresponding closed immersion
$I\subset R$
be the kernel of this surjection. We have a corresponding closed immersion
 $Y{\hookrightarrow}X$
where
$Y{\hookrightarrow}X$
where
 $Y=\operatorname{Spec}(A)$
and
$Y=\operatorname{Spec}(A)$
and
 $X=\operatorname{Spec}(R)$
. In [Reference HartshorneHar75], the de Rham homology of the local scheme
$X=\operatorname{Spec}(R)$
. In [Reference HartshorneHar75], the de Rham homology of the local scheme
![]() $Y$
is defined as
$Y$
is defined as
 $H_{i}^{\text{dR}}(Y)=\mathbf{H}_{Y}^{2n-i}(X,\unicode[STIX]{x1D6FA}_{X}^{\bullet })$
, the hypercohomology (supported at
$H_{i}^{\text{dR}}(Y)=\mathbf{H}_{Y}^{2n-i}(X,\unicode[STIX]{x1D6FA}_{X}^{\bullet })$
, the hypercohomology (supported at
![]() $Y$
) of the complex of continuous differential forms on
$Y$
) of the complex of continuous differential forms on
![]() $X$
. The differentials in this complex are merely
$X$
. The differentials in this complex are merely
![]() $k$
-linear, so the
$k$
-linear, so the
 $H_{i}^{\text{dR}}(Y)$
are
$H_{i}^{\text{dR}}(Y)$
are
![]() $k$
-spaces.
$k$
-spaces.
Now let
![]() $\widehat{X}$
be the formal completion of
$\widehat{X}$
be the formal completion of
![]() $Y$
in
$Y$
in
![]() $X$
[Reference HartshorneHar77, § II.9], that is, the topological space
$X$
[Reference HartshorneHar77, § II.9], that is, the topological space
![]() $Y$
equipped with the structure of a locally ringed space via the sheaf of rings
$Y$
equipped with the structure of a locally ringed space via the sheaf of rings
 $\varprojlim \,{\mathcal{O}}_{X}/{\mathcal{I}}^{n}$
where
$\varprojlim \,{\mathcal{O}}_{X}/{\mathcal{I}}^{n}$
where
 ${\mathcal{I}}\subset {\mathcal{O}}_{X}$
is the quasi-coherent ideal sheaf defining the chosen embedding
${\mathcal{I}}\subset {\mathcal{O}}_{X}$
is the quasi-coherent ideal sheaf defining the chosen embedding
 $Y{\hookrightarrow}X$
(every
$Y{\hookrightarrow}X$
(every
![]() ${\mathcal{O}}_{X}/{\mathcal{I}}^{n}$
is supported at
${\mathcal{O}}_{X}/{\mathcal{I}}^{n}$
is supported at
![]() $Y$
and thus can be viewed as a sheaf of rings on
$Y$
and thus can be viewed as a sheaf of rings on
![]() $Y$
). The differentials in the complex
$Y$
). The differentials in the complex
![]() $\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
are
$\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
are
![]() ${\mathcal{I}}$
-adically continuous and thus pass to
${\mathcal{I}}$
-adically continuous and thus pass to
![]() ${\mathcal{I}}$
-adic completions. We obtain in this way a complex
${\mathcal{I}}$
-adic completions. We obtain in this way a complex
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
of sheaves on
$\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
of sheaves on
![]() $\widehat{X}$
, the formal completion of
$\widehat{X}$
, the formal completion of
![]() $\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
, whose differentials are again merely
$\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
, whose differentials are again merely
![]() $k$
-linear. In [Reference HartshorneHar75], the (local) de Rham cohomology of the local scheme
$k$
-linear. In [Reference HartshorneHar75], the (local) de Rham cohomology of the local scheme
![]() $Y$
is defined as
$Y$
is defined as
 $H_{P,\text{dR}}^{i}(Y)=\mathbf{H}_{P}^{i}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet })$
, where
$H_{P,\text{dR}}^{i}(Y)=\mathbf{H}_{P}^{i}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet })$
, where
![]() $P$
is the closed point of
$P$
is the closed point of
![]() $Y$
. After making these definitions, Hartshorne establishes the following properties.
$Y$
. After making these definitions, Hartshorne establishes the following properties.
Theorem 1.1 [Reference HartshorneHar75, Theorems III.1.1 and III.2.1].
Let
![]() $A$
be a complete local ring with coefficient field
$A$
be a complete local ring with coefficient field
![]() $k$
of characteristic zero and
$k$
of characteristic zero and
 $Y=\operatorname{Spec}(A)$
.
$Y=\operatorname{Spec}(A)$
.
-
(a) The de Rham homology spaces
 $H_{i}^{\text{dR}}(Y)$
and cohomology spaces
$H_{i}^{\text{dR}}(Y)$
and cohomology spaces
 $H_{P,\text{dR}}^{i}(Y)$
as defined above are independent of the surjection of
$H_{P,\text{dR}}^{i}(Y)$
as defined above are independent of the surjection of
 $k$
-algebras
$k$
-algebras
 $R\rightarrow A$
used in their definitions.
$R\rightarrow A$
used in their definitions. -
(b) For all
 $i$
,
$i$
,
 $H_{i}^{\text{dR}}(Y)$
and
$H_{i}^{\text{dR}}(Y)$
and
 $H_{P,\text{dR}}^{i}(Y)$
are finite-dimensional
$H_{P,\text{dR}}^{i}(Y)$
are finite-dimensional
 $k$
-spaces.
$k$
-spaces. -
(c) For all
 $i$
, the
$i$
, the
 $k$
-spaces
$k$
-spaces
 $H_{i}^{\text{dR}}(Y)$
and
$H_{i}^{\text{dR}}(Y)$
and
 $H_{P,\text{dR}}^{i}(Y)$
are
$H_{P,\text{dR}}^{i}(Y)$
are
 $k$
-dual to each other.
$k$
-dual to each other.
The de Rham homology and cohomology of
 $Y=\operatorname{Spec}(A)$
are both defined using hypercohomology. As is well known, there are in general two spectral sequences converging to the hypercohomology of a complex ([Reference Grothendieck and DieudonnéGD61, 11.4.3]; also see § 2.2). If
$Y=\operatorname{Spec}(A)$
are both defined using hypercohomology. As is well known, there are in general two spectral sequences converging to the hypercohomology of a complex ([Reference Grothendieck and DieudonnéGD61, 11.4.3]; also see § 2.2). If
![]() $K^{\bullet }$
is a complex of sheaves of Abelian groups on a topological space
$K^{\bullet }$
is a complex of sheaves of Abelian groups on a topological space
![]() $Z$
, the first of these spectral sequences begins
$Z$
, the first of these spectral sequences begins
 $E_{1}^{p,q}=H^{q}(Z,K^{p})$
and has abutment
$E_{1}^{p,q}=H^{q}(Z,K^{p})$
and has abutment
 $\mathbf{H}^{p+q}(Z,K^{\bullet })$
. In our case, this takes the form of the Hodge–de Rham homology spectral sequence, which begins
$\mathbf{H}^{p+q}(Z,K^{\bullet })$
. In our case, this takes the form of the Hodge–de Rham homology spectral sequence, which begins
 $E_{1}^{n-p,n-q}=H_{Y}^{n-q}(X,\unicode[STIX]{x1D6FA}_{X}^{n-p})$
and has abutment
$E_{1}^{n-p,n-q}=H_{Y}^{n-q}(X,\unicode[STIX]{x1D6FA}_{X}^{n-p})$
and has abutment
 $H_{p+q}^{\text{dR}}(Y)$
, as well as the Hodge–de Rham cohomology spectral sequence, which begins
$H_{p+q}^{\text{dR}}(Y)$
, as well as the Hodge–de Rham cohomology spectral sequence, which begins
 $\tilde{E}_{1}^{p,q}=H_{P}^{q}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{p})$
and has abutment
$\tilde{E}_{1}^{p,q}=H_{P}^{q}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{p})$
and has abutment
 $H_{P,\text{dR}}^{p+q}(Y)$
. A priori, these spectral sequences depend on the choice of surjection
$H_{P,\text{dR}}^{p+q}(Y)$
. A priori, these spectral sequences depend on the choice of surjection
![]() $R\rightarrow A$
from a complete regular local
$R\rightarrow A$
from a complete regular local
![]() $k$
-algebra. We prove stronger versions of Hartshorne’s results for these spectral sequences. Our theorem for de Rham homology is the following.
$k$
-algebra. We prove stronger versions of Hartshorne’s results for these spectral sequences. Our theorem for de Rham homology is the following.
Theorem A. Let
![]() $A$
be a complete local ring with coefficient field
$A$
be a complete local ring with coefficient field
![]() $k$
of characteristic zero. Viewing
$k$
of characteristic zero. Viewing
![]() $A$
as a
$A$
as a
![]() $k$
-algebra via this coefficient field, let
$k$
-algebra via this coefficient field, let
![]() $R\rightarrow A$
be a choice of
$R\rightarrow A$
be a choice of
![]() $k$
-algebra surjection from a complete regular local
$k$
-algebra surjection from a complete regular local
![]() $k$
-algebra. Associated with this surjection we have a Hodge–de Rham spectral sequence for homology as above.
$k$
-algebra. Associated with this surjection we have a Hodge–de Rham spectral sequence for homology as above.
-
(a) Beginning with the
 $E_{2}$
-term, the isomorphism class of the homology spectral sequence with its abutment is independent of the choice of regular
$E_{2}$
-term, the isomorphism class of the homology spectral sequence with its abutment is independent of the choice of regular
 $k$
-algebra and surjection
$k$
-algebra and surjection
 $R\rightarrow A$
, up to a degree shift.
$R\rightarrow A$
, up to a degree shift. -
(b) The
 $k$
-spaces
$k$
-spaces
 $E_{2}^{p,q}$
appearing in the
$E_{2}^{p,q}$
appearing in the
 $E_{2}$
-term of the homology spectral sequence are finite-dimensional.
$E_{2}$
-term of the homology spectral sequence are finite-dimensional.
The meaning of ‘up to a degree shift’ in the statement of part (a) is the following: given two surjections
![]() $R\rightarrow A$
and
$R\rightarrow A$
and
 $R^{\prime }\rightarrow A$
from complete regular local
$R^{\prime }\rightarrow A$
from complete regular local
![]() $k$
-algebras, where
$k$
-algebras, where
 $\dim (R)=n$
and
$\dim (R)=n$
and
 $\dim (R^{\prime })=n^{\prime }$
, we obtain two Hodge–de Rham spectral sequences
$\dim (R^{\prime })=n^{\prime }$
, we obtain two Hodge–de Rham spectral sequences
![]() $E_{\bullet ,R}^{\bullet ,\bullet }$
and
$E_{\bullet ,R}^{\bullet ,\bullet }$
and
![]() $\mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
. Part (a) asserts that there is a morphism
$\mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
. Part (a) asserts that there is a morphism
 $E_{\bullet ,R}^{\bullet ,\bullet }\rightarrow \mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
of bidegree
$E_{\bullet ,R}^{\bullet ,\bullet }\rightarrow \mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
of bidegree
 $(n^{\prime }-n,n^{\prime }-n)$
between these spectral sequences which is an isomorphism on the objects of the
$(n^{\prime }-n,n^{\prime }-n)$
between these spectral sequences which is an isomorphism on the objects of the
![]() $E_{2}$
- (and later) terms (see § 2.2 for the precise definitions of the terms used here).
$E_{2}$
- (and later) terms (see § 2.2 for the precise definitions of the terms used here).
We also have the analogue (without a degree shift) for de Rham cohomology, as follows.
Theorem B. Let
![]() $A$
and
$A$
and
![]() $R$
be as in Theorem A. Associated with this surjection we also have a local Hodge–de Rham spectral sequence for cohomology.
$R$
be as in Theorem A. Associated with this surjection we also have a local Hodge–de Rham spectral sequence for cohomology.
-
(a) Beginning with the
 $E_{2}$
-term, the isomorphism class of the cohomology spectral sequence with its abutment is independent of the choice of regular
$E_{2}$
-term, the isomorphism class of the cohomology spectral sequence with its abutment is independent of the choice of regular
 $k$
-algebra and surjection
$k$
-algebra and surjection
 $R\rightarrow A$
.
$R\rightarrow A$
. -
(b) The
 $k$
-spaces
$k$
-spaces
 $\tilde{E}_{2}^{pq}$
appearing in the
$\tilde{E}_{2}^{pq}$
appearing in the
 $E_{2}$
-term of the cohomology spectral sequence are finite-dimensional.
$E_{2}$
-term of the cohomology spectral sequence are finite-dimensional.
Remark 1.2. In § 2.2, the notion of an isomorphism of spectral sequences is defined. As described in this subsection, the ingredients of a spectral sequence are the objects and differentials in the
![]() $E_{r}$
-term for all
$E_{r}$
-term for all
![]() $r$
, the abutment objects, and the filtrations on the abutment objects, together with the isomorphisms relating the terms with their successors and with the abutment. The assertion of Theorems A and B is that all of these ingredients (except for the
$r$
, the abutment objects, and the filtrations on the abutment objects, together with the isomorphisms relating the terms with their successors and with the abutment. The assertion of Theorems A and B is that all of these ingredients (except for the
![]() $E_{1}$
-terms) are independent of the chosen regular
$E_{1}$
-terms) are independent of the chosen regular
![]() $k$
-algebra and surjection. Therefore parts (a) and (b) of Theorem 1.1 are subsumed by Theorems A and B, which provide more information: the isomorphism classes of
$k$
-algebra and surjection. Therefore parts (a) and (b) of Theorem 1.1 are subsumed by Theorems A and B, which provide more information: the isomorphism classes of
 $H_{p+q}^{\text{dR}}(Y)$
and
$H_{p+q}^{\text{dR}}(Y)$
and
 $H_{P,\text{dR}}^{p+q}(Y)$
as filtered objects are independent of the surjection. We obtain many numerical invariants of
$H_{P,\text{dR}}^{p+q}(Y)$
as filtered objects are independent of the surjection. We obtain many numerical invariants of
![]() $(A,k)$
from the spectral sequence: the (finite) dimensions of the kernels and cokernels of the differentials
$(A,k)$
from the spectral sequence: the (finite) dimensions of the kernels and cokernels of the differentials
![]() $d_{r}$
for all
$d_{r}$
for all
![]() $r\geqslant 2$
, together with the dimensions of the filtered pieces of the abutment.
$r\geqslant 2$
, together with the dimensions of the filtered pieces of the abutment.
The proof of Theorem B requires the development of a theory of Matlis duality for
![]() ${\mathcal{D}}$
-modules. This theory is worked out in §§ 3, 4, and 5, which form a unit of independent interest. If
${\mathcal{D}}$
-modules. This theory is worked out in §§ 3, 4, and 5, which form a unit of independent interest. If
![]() $R$
is a complete local ring with coefficient field
$R$
is a complete local ring with coefficient field
![]() $k$
of characteristic zero, we can consider the ring
$k$
of characteristic zero, we can consider the ring
 ${\mathcal{D}}(R,k)$
of
${\mathcal{D}}(R,k)$
of
![]() $k$
-linear differential operators on
$k$
-linear differential operators on
![]() $R$
. Given any left module over this ring, we can define its de Rham complex and speak of its de Rham cohomology spaces. We prove that the Matlis dual of a left
$R$
. Given any left module over this ring, we can define its de Rham complex and speak of its de Rham cohomology spaces. We prove that the Matlis dual of a left
 ${\mathcal{D}}(R,k)$
-module has a natural structure of right
${\mathcal{D}}(R,k)$
-module has a natural structure of right
 ${\mathcal{D}}(R,k)$
-module. Specializing to the case of a complete regular local ring, we are able to obtain information about the de Rham cohomology of a Matlis dual. In this case, the dual of a left
${\mathcal{D}}(R,k)$
-module. Specializing to the case of a complete regular local ring, we are able to obtain information about the de Rham cohomology of a Matlis dual. In this case, the dual of a left
 ${\mathcal{D}}(R,k)$
-module can again be viewed as a left
${\mathcal{D}}(R,k)$
-module can again be viewed as a left
 ${\mathcal{D}}(R,k)$
-module. The following is the main result of our theory of Matlis duality for
${\mathcal{D}}(R,k)$
-module. The following is the main result of our theory of Matlis duality for
![]() ${\mathcal{D}}$
-modules (its two assertions are proved separately below as Proposition 4.17 and Theorem 5.1).
${\mathcal{D}}$
-modules (its two assertions are proved separately below as Proposition 4.17 and Theorem 5.1).
Theorem C. Let
![]() $k$
be a field of characteristic zero, let
$k$
be a field of characteristic zero, let
 $R=k[[x_{1},\ldots x_{n}]]$
be a formal power series ring over
$R=k[[x_{1},\ldots x_{n}]]$
be a formal power series ring over
![]() $k$
, and let
$k$
, and let
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
be the ring of
${\mathcal{D}}={\mathcal{D}}(R,k)$
be the ring of
![]() $k$
-linear differential operators on
$k$
-linear differential operators on
![]() $R$
. If
$R$
. If
![]() $M$
is a left
$M$
is a left
![]() ${\mathcal{D}}$
-module, the Matlis dual
${\mathcal{D}}$
-module, the Matlis dual
![]() $D(M)$
of
$D(M)$
of
![]() $M$
with respect to
$M$
with respect to
![]() $R$
can also be given a natural structure of left
$R$
can also be given a natural structure of left
![]() ${\mathcal{D}}$
-module. We write
${\mathcal{D}}$
-module. We write
 $H_{\text{dR}}^{\ast }(M)$
for the de Rham cohomology of a left
$H_{\text{dR}}^{\ast }(M)$
for the de Rham cohomology of a left
![]() ${\mathcal{D}}$
-module. If
${\mathcal{D}}$
-module. If
![]() $M$
is a holonomic left
$M$
is a holonomic left
![]() ${\mathcal{D}}$
-module, then for every
${\mathcal{D}}$
-module, then for every
![]() $i$
, we have an isomorphism of
$i$
, we have an isomorphism of
![]() $k$
-spaces
$k$
-spaces
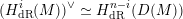 $$\begin{eqnarray}(H_{\text{dR}}^{i}(M))^{\vee }\simeq H_{\text{dR}}^{n-i}(D(M))\end{eqnarray}$$
$$\begin{eqnarray}(H_{\text{dR}}^{i}(M))^{\vee }\simeq H_{\text{dR}}^{n-i}(D(M))\end{eqnarray}$$
where
![]() $\vee$
denotes
$\vee$
denotes
![]() $k$
-linear dual.
$k$
-linear dual.
Remark 1.3. If
![]() $M$
is holonomic, its de Rham cohomology spaces are known to be finite-dimensional (see Theorem 2.2), and so it follows from Theorem C that
$M$
is holonomic, its de Rham cohomology spaces are known to be finite-dimensional (see Theorem 2.2), and so it follows from Theorem C that
![]() $D(M)$
also has finite-dimensional de Rham cohomology. Since
$D(M)$
also has finite-dimensional de Rham cohomology. Since
![]() $D(M)$
is not, in general, a holonomic
$D(M)$
is not, in general, a holonomic
![]() ${\mathcal{D}}$
-module (see Remark 1.4 below), this is not clear a priori.
${\mathcal{D}}$
-module (see Remark 1.4 below), this is not clear a priori.
When applied to the
![]() $E_{1}$
- and
$E_{1}$
- and
![]() $E_{2}$
-terms of the homology and cohomology spectral sequences, Theorem C has the following consequence.
$E_{2}$
-terms of the homology and cohomology spectral sequences, Theorem C has the following consequence.
Theorem D. Let
![]() $A$
,
$A$
,
![]() $k$
, and
$k$
, and
![]() $R$
be as in the statement of Theorem A. The objects in the
$R$
be as in the statement of Theorem A. The objects in the
![]() $E_{2}$
-terms of the homology and cohomology spectral sequences are
$E_{2}$
-terms of the homology and cohomology spectral sequences are
![]() $k$
-dual to each other: for all
$k$
-dual to each other: for all
![]() $p$
and
$p$
and
![]() $q$
,
$q$
,
 $E_{2}^{n-p,n-q}\simeq (\tilde{E}_{2}^{pq})^{\vee }$
.
$E_{2}^{n-p,n-q}\simeq (\tilde{E}_{2}^{pq})^{\vee }$
.
We conjecture that the entire spectral sequences, beginning with
![]() $E_{2}$
, should be
$E_{2}$
, should be
![]() $k$
-dual to each other (see § 8), but at present we are able only to prove the preceding statement.
$k$
-dual to each other (see § 8), but at present we are able only to prove the preceding statement.
As was already clear to Hartshorne [Reference HartshorneHar75, p. 71], the Matlis duals of the objects appearing in the
![]() $E_{1}$
-term of the homology spectral sequence are exactly the corresponding
$E_{1}$
-term of the homology spectral sequence are exactly the corresponding
![]() $E_{1}$
-objects for de Rham cohomology. What is much less clear is the relationship between the differentials. The
$E_{1}$
-objects for de Rham cohomology. What is much less clear is the relationship between the differentials. The
![]() $E_{1}$
-differentials for de Rham homology are merely
$E_{1}$
-differentials for de Rham homology are merely
![]() $k$
-linear, so the usual definition of Matlis duality over
$k$
-linear, so the usual definition of Matlis duality over
![]() $R$
cannot be applied to them. A large part of this paper is devoted to the problem of applying Matlis duality to these
$R$
cannot be applied to them. A large part of this paper is devoted to the problem of applying Matlis duality to these
![]() $k$
-linear maps and establishing that, in our setting, Matlis duality at the
$k$
-linear maps and establishing that, in our setting, Matlis duality at the
![]() $E_{1}$
-term gives rise to
$E_{1}$
-term gives rise to
![]() $k$
-duality at the
$k$
-duality at the
![]() $E_{2}$
-term.
$E_{2}$
-term.
In more detail, the outline of the paper is as follows. In § 2, after reviewing some preliminary material on differential operators, de Rham complexes, and spectral sequences, we prove Theorem A using local algebra. In the course of this proof, we define a new set of invariants for complete local rings with coefficient fields of characteristic zero. In § 3, Matlis duality for local rings containing a field
![]() $k$
is interpreted in terms of
$k$
is interpreted in terms of
![]() $k$
-linear maps, after SGA2 [Reference Grothendieck and RaynaudGR05]. This allows us to dualize continuous maps between finitely generated modules over such rings. We pass to direct limits in order to dualize
$k$
-linear maps, after SGA2 [Reference Grothendieck and RaynaudGR05]. This allows us to dualize continuous maps between finitely generated modules over such rings. We pass to direct limits in order to dualize
![]() $k$
-linear maps between arbitrary modules that satisfy certain finiteness and continuity conditions. In § 4, we consider the case of
$k$
-linear maps between arbitrary modules that satisfy certain finiteness and continuity conditions. In § 4, we consider the case of
![]() ${\mathcal{D}}$
-modules for complete local rings containing
${\mathcal{D}}$
-modules for complete local rings containing
![]() $k$
; we describe a natural right
$k$
; we describe a natural right
![]() ${\mathcal{D}}$
-module structure on the Matlis dual
${\mathcal{D}}$
-module structure on the Matlis dual
![]() $D(M)$
of a left
$D(M)$
of a left
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
. In the special case of a formal power series ring, we can regard
$M$
. In the special case of a formal power series ring, we can regard
![]() $D(M)$
as a left
$D(M)$
as a left
![]() ${\mathcal{D}}$
-module as well using a simple ‘transpose’ operation, and thus define its de Rham complex. We determine the cohomology of this complex in § 5 in the case of holonomic
${\mathcal{D}}$
-module as well using a simple ‘transpose’ operation, and thus define its de Rham complex. We determine the cohomology of this complex in § 5 in the case of holonomic
![]() $M$
, completing the proof of Theorem C. The specific case of local cohomology is considered next. In § 6, we work out precisely what happens to the action of derivations on a local cohomology module. Finally, in § 7, we give a self-contained proof of Theorem B(a) and combine the results of §§ 2, 5, and 6 to prove Theorems B(b) and D.
$M$
, completing the proof of Theorem C. The specific case of local cohomology is considered next. In § 6, we work out precisely what happens to the action of derivations on a local cohomology module. Finally, in § 7, we give a self-contained proof of Theorem B(a) and combine the results of §§ 2, 5, and 6 to prove Theorems B(b) and D.
Remark 1.4. After we identify the objects in the
![]() $E_{2}$
-term of the homology spectral sequence with de Rham cohomology spaces of local cohomology modules in § 2, part (b) of Theorem A follows from Lyubeznik’s result ([Reference LyubeznikLyu93, 2.2(d)]; cf. [Reference MebkhoutMeb77]) that local cohomology modules are holonomic
$E_{2}$
-term of the homology spectral sequence with de Rham cohomology spaces of local cohomology modules in § 2, part (b) of Theorem A follows from Lyubeznik’s result ([Reference LyubeznikLyu93, 2.2(d)]; cf. [Reference MebkhoutMeb77]) that local cohomology modules are holonomic
![]() ${\mathcal{D}}$
-modules, as it is known that holonomic
${\mathcal{D}}$
-modules, as it is known that holonomic
![]() ${\mathcal{D}}$
-modules have finite-dimensional de Rham cohomology. However, the objects in the
${\mathcal{D}}$
-modules have finite-dimensional de Rham cohomology. However, the objects in the
![]() $E_{2}$
-term of the cohomology spectral sequence are not de Rham cohomology spaces of holonomic
$E_{2}$
-term of the cohomology spectral sequence are not de Rham cohomology spaces of holonomic
![]() ${\mathcal{D}}$
-modules: as shown in § 6, they are de Rham cohomology spaces of Matlis duals of local cohomology modules. Hellus has shown [Reference HellusHel07, Corollary 2.6] that Matlis duals of local cohomology modules have, in general, infinitely many associated primes, implying that they need not be holonomic
${\mathcal{D}}$
-modules: as shown in § 6, they are de Rham cohomology spaces of Matlis duals of local cohomology modules. Hellus has shown [Reference HellusHel07, Corollary 2.6] that Matlis duals of local cohomology modules have, in general, infinitely many associated primes, implying that they need not be holonomic
![]() ${\mathcal{D}}$
-modules (which always have finitely many associated primes [Reference LyubeznikLyu93, Corollary 3.6(c)]). It is therefore surprising that the cohomology
${\mathcal{D}}$
-modules (which always have finitely many associated primes [Reference LyubeznikLyu93, Corollary 3.6(c)]). It is therefore surprising that the cohomology
![]() $E_{2}$
-objects, which are, in general, de Rham cohomology spaces of non-holonomic
$E_{2}$
-objects, which are, in general, de Rham cohomology spaces of non-holonomic
![]() ${\mathcal{D}}$
-modules, are still finite-dimensional. For this reason, the proof of Theorem B(b) is significantly more difficult than the proofs of the other parts of our main theorems.
${\mathcal{D}}$
-modules, are still finite-dimensional. For this reason, the proof of Theorem B(b) is significantly more difficult than the proofs of the other parts of our main theorems.
2 The de Rham homology of a complete local ring
In this section, after reviewing some preliminary material on modules over rings of differential operators and spectral sequences, we recall Hartshorne’s definition of algebraic de Rham homology [Reference HartshorneHar75, ch. III] in the case of the spectrum of a complete local ring in equicharacteristic zero, and examine the associated Hodge–de Rham spectral sequence. We give proofs that this de Rham homology is intrinsically defined and finite-dimensional which are purely local; in fact, we prove more, namely that up to a degree shift, the entire Hodge–de Rham spectral sequence (with the exception of the first term) is intrinsically defined and has finite-dimensional objects. As a byproduct of our proof, we obtain a new set of invariants for complete local rings analogous to the Lyubeznik numbers [Reference LyubeznikLyu93, Theorem–Definition 4.1].
2.1 Preliminaries on
 ${\mathcal{D}}$
-modules
${\mathcal{D}}$
-modules
Let
![]() $R$
be a commutative ring and
$R$
be a commutative ring and
![]() $k\subset R$
a commutative subring. The ring
$k\subset R$
a commutative subring. The ring
 ${\mathcal{D}}(R,k)$
of
${\mathcal{D}}(R,k)$
of
![]() $k$
-linear differential operators on
$k$
-linear differential operators on
![]() $R$
, a subring of
$R$
, a subring of
 $\operatorname{End}_{k}(R)$
, is defined recursively as follows [Reference Grothendieck and DieudonnéGD67, § 16]. A differential operator
$\operatorname{End}_{k}(R)$
, is defined recursively as follows [Reference Grothendieck and DieudonnéGD67, § 16]. A differential operator
![]() $R\rightarrow R$
of order zero is multiplication by an element of
$R\rightarrow R$
of order zero is multiplication by an element of
![]() $R$
. Supposing that differential operators of order less than or equal to
$R$
. Supposing that differential operators of order less than or equal to
![]() $j-1$
have been defined,
$j-1$
have been defined,
 $d\in \operatorname{End}_{k}(R)$
is said to be a differential operator of order less than or equal to
$d\in \operatorname{End}_{k}(R)$
is said to be a differential operator of order less than or equal to
![]() $j$
if, for all
$j$
if, for all
![]() $r\in R$
, the commutator
$r\in R$
, the commutator
 $[d,r]\in \operatorname{End}_{k}(R)$
is a differential operator of order less than or equal to
$[d,r]\in \operatorname{End}_{k}(R)$
is a differential operator of order less than or equal to
![]() $j-1$
, where
$j-1$
, where
 $[d,r]=dr-rd$
(the products being taken in
$[d,r]=dr-rd$
(the products being taken in
 $\operatorname{End}_{k}(R)$
). We write
$\operatorname{End}_{k}(R)$
). We write
![]() ${\mathcal{D}}^{j}(R)$
for the set of differential operators on
${\mathcal{D}}^{j}(R)$
for the set of differential operators on
![]() $R$
of order less than or equal to
$R$
of order less than or equal to
![]() $j$
and set
$j$
and set
 ${\mathcal{D}}(R,k)=\bigcup _{j}{\mathcal{D}}^{j}(R)$
. Every
${\mathcal{D}}(R,k)=\bigcup _{j}{\mathcal{D}}^{j}(R)$
. Every
![]() ${\mathcal{D}}^{j}(R)$
is naturally a left
${\mathcal{D}}^{j}(R)$
is naturally a left
![]() $R$
-module. If
$R$
-module. If
 $d\in {\mathcal{D}}^{j}(R)$
and
$d\in {\mathcal{D}}^{j}(R)$
and
 $d^{\prime }\in {\mathcal{D}}^{l}(R)$
, it is easy to prove by induction on
$d^{\prime }\in {\mathcal{D}}^{l}(R)$
, it is easy to prove by induction on
![]() $j+l$
that
$j+l$
that
 $d^{\prime }\circ d\in {\mathcal{D}}^{j+l}(R)$
, so
$d^{\prime }\circ d\in {\mathcal{D}}^{j+l}(R)$
, so
 ${\mathcal{D}}(R,k)$
is a ring.
${\mathcal{D}}(R,k)$
is a ring.
We consider now the special case in which
![]() $k$
is a field of characteristic zero and
$k$
is a field of characteristic zero and
 $R=k[[x_{1},\ldots ,x_{n}]]$
is a formal power series ring over
$R=k[[x_{1},\ldots ,x_{n}]]$
is a formal power series ring over
![]() $k$
. A standard reference for facts about the ring
$k$
. A standard reference for facts about the ring
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
and left modules over
${\mathcal{D}}={\mathcal{D}}(R,k)$
and left modules over
![]() ${\mathcal{D}}$
in this case is [Reference BjörkBjö79, ch. 3]; we summarize some of these facts now. The ring
${\mathcal{D}}$
in this case is [Reference BjörkBjö79, ch. 3]; we summarize some of these facts now. The ring
![]() ${\mathcal{D}}$
, viewed as a left
${\mathcal{D}}$
, viewed as a left
![]() $R$
-module, is freely generated by monomials in the partial differentiation operators
$R$
-module, is freely generated by monomials in the partial differentiation operators
 $\unicode[STIX]{x2202}_{1}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}_{n}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{n}$
([Reference Grothendieck and DieudonnéGD67, Theorem 16.11.2]: here the characteristic-zero assumption is necessary). This ring has an increasing filtration
$\unicode[STIX]{x2202}_{1}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}_{n}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{n}$
([Reference Grothendieck and DieudonnéGD67, Theorem 16.11.2]: here the characteristic-zero assumption is necessary). This ring has an increasing filtration
![]() $\{{\mathcal{D}}(\unicode[STIX]{x1D708})\}$
, called the order filtration, where
$\{{\mathcal{D}}(\unicode[STIX]{x1D708})\}$
, called the order filtration, where
![]() ${\mathcal{D}}(\unicode[STIX]{x1D708})$
consists of those differential operators of order less than or equal to
${\mathcal{D}}(\unicode[STIX]{x1D708})$
consists of those differential operators of order less than or equal to
![]() $\unicode[STIX]{x1D708}$
(the order of an element of
$\unicode[STIX]{x1D708}$
(the order of an element of
![]() ${\mathcal{D}}$
is the maximum of the orders of its summands, and the order of a single summand
${\mathcal{D}}$
is the maximum of the orders of its summands, and the order of a single summand
 $\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{1}^{a_{1}}\cdots \unicode[STIX]{x2202}_{n}^{a_{n}}$
with
$\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{1}^{a_{1}}\cdots \unicode[STIX]{x2202}_{n}^{a_{n}}$
with
![]() $\unicode[STIX]{x1D70C}\in R$
is
$\unicode[STIX]{x1D70C}\in R$
is
![]() $\sum a_{i}$
: this notion of order coincides with the one defined in the previous paragraph). The associated graded object
$\sum a_{i}$
: this notion of order coincides with the one defined in the previous paragraph). The associated graded object
 $\operatorname{gr}({\mathcal{D}})=\oplus {\mathcal{D}}(\unicode[STIX]{x1D708})/{\mathcal{D}}(\unicode[STIX]{x1D708}-1)$
with respect to this filtration is isomorphic to
$\operatorname{gr}({\mathcal{D}})=\oplus {\mathcal{D}}(\unicode[STIX]{x1D708})/{\mathcal{D}}(\unicode[STIX]{x1D708}-1)$
with respect to this filtration is isomorphic to
 $R[\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{n}]$
(a commutative ring), where
$R[\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{n}]$
(a commutative ring), where
![]() $\unicode[STIX]{x1D701}_{i}$
is the image of
$\unicode[STIX]{x1D701}_{i}$
is the image of
![]() $\unicode[STIX]{x2202}_{i}$
in
$\unicode[STIX]{x2202}_{i}$
in
 ${\mathcal{D}}(1)/{\mathcal{D}}(0)\subset \operatorname{gr}({\mathcal{D}})$
.
${\mathcal{D}}(1)/{\mathcal{D}}(0)\subset \operatorname{gr}({\mathcal{D}})$
.
If
![]() $M$
is a finitely generated left
$M$
is a finitely generated left
![]() ${\mathcal{D}}$
-module, there exists a good filtration
${\mathcal{D}}$
-module, there exists a good filtration
 $\{M(\unicode[STIX]{x1D708})\}$
on
$\{M(\unicode[STIX]{x1D708})\}$
on
![]() $M$
, meaning that
$M$
, meaning that
![]() $M$
becomes a filtered left
$M$
becomes a filtered left
![]() ${\mathcal{D}}$
-module with respect to the order filtration on
${\mathcal{D}}$
-module with respect to the order filtration on
![]() ${\mathcal{D}}$
and
${\mathcal{D}}$
and
 $\operatorname{gr}(M)=\oplus M(\unicode[STIX]{x1D708})/M(\unicode[STIX]{x1D708}-1)$
is a finitely generated
$\operatorname{gr}(M)=\oplus M(\unicode[STIX]{x1D708})/M(\unicode[STIX]{x1D708}-1)$
is a finitely generated
![]() $\operatorname{gr}({\mathcal{D}})$
-module. We let
$\operatorname{gr}({\mathcal{D}})$
-module. We let
![]() $J$
be the radical of
$J$
be the radical of
 $\operatorname{Ann}_{\operatorname{gr}({\mathcal{D}})}\operatorname{gr}(M)\subset \operatorname{gr}({\mathcal{D}})$
and set
$\operatorname{Ann}_{\operatorname{gr}({\mathcal{D}})}\operatorname{gr}(M)\subset \operatorname{gr}({\mathcal{D}})$
and set
 $d(M)=\dim \operatorname{gr}({\mathcal{D}})/J$
(Krull dimension). The ideal
$d(M)=\dim \operatorname{gr}({\mathcal{D}})/J$
(Krull dimension). The ideal
![]() $J$
, and hence the number
$J$
, and hence the number
![]() $d(M)$
, is independent of the choice of good filtration on
$d(M)$
, is independent of the choice of good filtration on
![]() $M$
. By Bernstein’s theorem, if
$M$
. By Bernstein’s theorem, if
![]() $M\neq 0$
is a finitely generated left
$M\neq 0$
is a finitely generated left
![]() ${\mathcal{D}}$
-module, we have
${\mathcal{D}}$
-module, we have
 $n\leqslant d(M)\leqslant 2n$
. In the case
$n\leqslant d(M)\leqslant 2n$
. In the case
 $d(M)=n$
we say that
$d(M)=n$
we say that
![]() $M$
is holonomic. It is known that submodules and quotients of holonomic
$M$
is holonomic. It is known that submodules and quotients of holonomic
![]() ${\mathcal{D}}$
-modules are holonomic, an extension of a holonomic
${\mathcal{D}}$
-modules are holonomic, an extension of a holonomic
![]() ${\mathcal{D}}$
-module by another holonomic
${\mathcal{D}}$
-module by another holonomic
![]() ${\mathcal{D}}$
-module is holonomic, holonomic
${\mathcal{D}}$
-module is holonomic, holonomic
![]() ${\mathcal{D}}$
-modules are of finite length over
${\mathcal{D}}$
-modules are of finite length over
![]() ${\mathcal{D}}$
, and holonomic
${\mathcal{D}}$
, and holonomic
![]() ${\mathcal{D}}$
-modules are cyclic (generated over
${\mathcal{D}}$
-modules are cyclic (generated over
![]() ${\mathcal{D}}$
by a single element).
${\mathcal{D}}$
by a single element).
Given any left
 ${\mathcal{D}}(R,k)$
-module
${\mathcal{D}}(R,k)$
-module
![]() $M$
, we can define its de Rham complex. This is a complex of length
$M$
, we can define its de Rham complex. This is a complex of length
![]() $n$
, denoted
$n$
, denoted
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
(or simply
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
(or simply
![]() $\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
in the case
$\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
in the case
![]() $M=R$
), whose objects are
$M=R$
), whose objects are
![]() $R$
-modules but whose differentials are merely
$R$
-modules but whose differentials are merely
![]() $k$
-linear. It is defined as follows [Reference BjörkBjö79, § 1.6]: for
$k$
-linear. It is defined as follows [Reference BjörkBjö79, § 1.6]: for
 $0\leqslant i\leqslant n$
,
$0\leqslant i\leqslant n$
,
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}$
is a direct sum of
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}$
is a direct sum of
![]() $\binom{n}{i}$
copies of
$\binom{n}{i}$
copies of
![]() $M$
, indexed by
$M$
, indexed by
![]() $i$
-tuples
$i$
-tuples
 $1\leqslant j_{1}<\cdots <j_{i}\leqslant n$
. The summand corresponding to such an
$1\leqslant j_{1}<\cdots <j_{i}\leqslant n$
. The summand corresponding to such an
![]() $i$
-tuple will be written
$i$
-tuple will be written
 $M\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}}$
.
$M\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}}$
.
Convention 2.1. The subscript
![]() $R$
in
$R$
in
![]() $\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
indicates over which ring the tensor products of objects are being taken. To simplify notation, we will follow this convention when de Rham complexes over different rings are being simultaneously considered.
$\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
indicates over which ring the tensor products of objects are being taken. To simplify notation, we will follow this convention when de Rham complexes over different rings are being simultaneously considered.
The
![]() $k$
-linear differentials
$k$
-linear differentials
 $d^{i}:M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R}^{i+1}$
are defined by
$d^{i}:M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R}^{i+1}$
are defined by
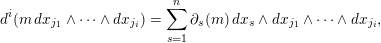 $$\begin{eqnarray}d^{i}(m\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}})=\mathop{\sum }_{s=1}^{n}\unicode[STIX]{x2202}_{s}(m)\,dx_{s}\wedge dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}},\end{eqnarray}$$
$$\begin{eqnarray}d^{i}(m\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}})=\mathop{\sum }_{s=1}^{n}\unicode[STIX]{x2202}_{s}(m)\,dx_{s}\wedge dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}},\end{eqnarray}$$
with the usual exterior algebra conventions for rearranging the wedge terms, and extended by linearity to the direct sum. The cohomology objects
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
, which are
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
, which are
![]() $k$
-spaces, are called the de Rham cohomology spaces of the left
$k$
-spaces, are called the de Rham cohomology spaces of the left
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
, and are denoted
$M$
, and are denoted
 $H_{\text{dR}}^{i}(M)$
. In the case of a holonomic module, van den Essen proved that these spaces are finite-dimensional.
$H_{\text{dR}}^{i}(M)$
. In the case of a holonomic module, van den Essen proved that these spaces are finite-dimensional.
Theorem 2.2 [Reference van den EssenvdE85, Proposition 2.2].
If
![]() $M$
is a holonomic left
$M$
is a holonomic left
![]() ${\mathcal{D}}$
-module, its de Rham cohomology
${\mathcal{D}}$
-module, its de Rham cohomology
 $H_{\text{dR}}^{i}(M)$
is a finite-dimensional
$H_{\text{dR}}^{i}(M)$
is a finite-dimensional
![]() $k$
-space for all
$k$
-space for all
![]() $i$
.
$i$
.
Remark 2.3. An important family of examples of holonomic
![]() ${\mathcal{D}}$
-modules is that of local cohomology modules. Our basic references for facts about local cohomology modules are Brodmann and Sharp [Reference Brodmann and SharpBS13] and SGA2 [Reference Grothendieck and RaynaudGR05]. If
${\mathcal{D}}$
-modules is that of local cohomology modules. Our basic references for facts about local cohomology modules are Brodmann and Sharp [Reference Brodmann and SharpBS13] and SGA2 [Reference Grothendieck and RaynaudGR05]. If
![]() $R$
is a commutative ring and
$R$
is a commutative ring and
![]() $I\subset R$
is an ideal, the functor
$I\subset R$
is an ideal, the functor
![]() $\unicode[STIX]{x1D6E4}_{I}$
of sections with support at
$\unicode[STIX]{x1D6E4}_{I}$
of sections with support at
![]() $I$
is a left-exact functor on the category of
$I$
is a left-exact functor on the category of
![]() $R$
-modules (for an
$R$
-modules (for an
![]() $R$
-module
$R$
-module
![]() $M$
,
$M$
,
![]() $\unicode[STIX]{x1D6E4}_{I}(M)$
consists of those
$\unicode[STIX]{x1D6E4}_{I}(M)$
consists of those
![]() $m\in M$
annihilated by some power of
$m\in M$
annihilated by some power of
![]() $I$
). The local cohomology modules
$I$
). The local cohomology modules
![]() $H_{I}^{i}(M)$
are the right derived functors of
$H_{I}^{i}(M)$
are the right derived functors of
 $\unicode[STIX]{x1D6E4}_{I}=H_{I}^{0}$
evaluated at
$\unicode[STIX]{x1D6E4}_{I}=H_{I}^{0}$
evaluated at
![]() $M$
. There is a more general sheaf-theoretic formulation, given in [Reference Grothendieck and RaynaudGR05]: if
$M$
. There is a more general sheaf-theoretic formulation, given in [Reference Grothendieck and RaynaudGR05]: if
![]() $X$
is a topological space,
$X$
is a topological space,
![]() $Y\subset X$
is a locally closed subset, and
$Y\subset X$
is a locally closed subset, and
![]() ${\mathcal{F}}$
is a sheaf of Abelian groups on
${\mathcal{F}}$
is a sheaf of Abelian groups on
![]() $X$
, the local cohomology groups
$X$
, the local cohomology groups
 $H_{Y}^{i}(X,{\mathcal{F}})$
are obtained by evaluating at
$H_{Y}^{i}(X,{\mathcal{F}})$
are obtained by evaluating at
![]() ${\mathcal{F}}$
the right derived functors of
${\mathcal{F}}$
the right derived functors of
![]() $\unicode[STIX]{x1D6E4}_{Y}$
, the functor of global sections supported at
$\unicode[STIX]{x1D6E4}_{Y}$
, the functor of global sections supported at
![]() $Y$
. The relationship between these two definitions in the case of an affine scheme
$Y$
. The relationship between these two definitions in the case of an affine scheme
![]() $X$
is given below in Lemma 2.16. In the case of the ring
$X$
is given below in Lemma 2.16. In the case of the ring
 $R=k[[x_{1},\ldots ,x_{n}]]$
, Lyubeznik proved that for any ideal
$R=k[[x_{1},\ldots ,x_{n}]]$
, Lyubeznik proved that for any ideal
![]() $I$
, the local cohomology modules
$I$
, the local cohomology modules
![]() $H_{I}^{i}(R)$
have a natural structure of left
$H_{I}^{i}(R)$
have a natural structure of left
![]() ${\mathcal{D}}$
-module [Reference LyubeznikLyu93]; cf. [Reference MebkhoutMeb77]. Indeed, they are holonomic
${\mathcal{D}}$
-module [Reference LyubeznikLyu93]; cf. [Reference MebkhoutMeb77]. Indeed, they are holonomic
![]() ${\mathcal{D}}$
-modules [Reference LyubeznikLyu93, 2.2(d)], a fact which will repeatedly prove crucial for us.
${\mathcal{D}}$
-modules [Reference LyubeznikLyu93, 2.2(d)], a fact which will repeatedly prove crucial for us.
In addition to the standard long exact cohomology sequence for derived functors, there is another useful long exact sequence for local cohomology: the Mayer–Vietoris sequence with respect to two ideals.
Proposition 2.4 [Reference Brodmann and SharpBS13, Theorem 3.2.3].
Let
![]() $I$
and
$I$
and
![]() $J$
be ideals of a commutative ring
$J$
be ideals of a commutative ring
![]() $R$
. There is a long exact sequence of
$R$
. There is a long exact sequence of
![]() $R$
-modules
$R$
-modules
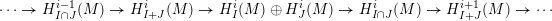 $$\begin{eqnarray}\cdots \rightarrow H_{I\cap J}^{i-1}(M)\rightarrow H_{I+J}^{i}(M)\rightarrow H_{I}^{i}(M)\oplus H_{J}^{i}(M)\rightarrow H_{I\cap J}^{i}(M)\rightarrow H_{I+J}^{i+1}(M)\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow H_{I\cap J}^{i-1}(M)\rightarrow H_{I+J}^{i}(M)\rightarrow H_{I}^{i}(M)\oplus H_{J}^{i}(M)\rightarrow H_{I\cap J}^{i}(M)\rightarrow H_{I+J}^{i+1}(M)\rightarrow \cdots\end{eqnarray}$$
for every
![]() $R$
-module
$R$
-module
![]() $M$
, functorial in
$M$
, functorial in
![]() $M$
.
$M$
.
Finally, we recall the well-known fact that the de Rham complex of a
![]() ${\mathcal{D}}$
-module is independent of the coordinates
${\mathcal{D}}$
-module is independent of the coordinates
 $x_{1},\ldots ,x_{n}$
for
$x_{1},\ldots ,x_{n}$
for
![]() $R$
. (See [Reference SwitalaSwi16, Proposition 2.5] for a proof.)
$R$
. (See [Reference SwitalaSwi16, Proposition 2.5] for a proof.)
Proposition 2.5. If
 $R=k[[x_{1},\ldots ,x_{n}]]$
and
$R=k[[x_{1},\ldots ,x_{n}]]$
and
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
, the de Rham complex of any left
${\mathcal{D}}={\mathcal{D}}(R,k)$
, the de Rham complex of any left
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
is independent of the chosen regular system of parameters
$M$
is independent of the chosen regular system of parameters
 $x_{1},\ldots ,x_{n}$
for
$x_{1},\ldots ,x_{n}$
for
![]() $R$
.
$R$
.
2.2 Preliminaries on spectral sequences
As we will be working with morphisms of spectral sequences, we collect some basic facts and definitions in this subsection concerning them. References for this material include Weibel [Reference WeibelWei94, ch. 5] and EGA [Reference Grothendieck and DieudonnéGD61, § 11]. We will not need to consider convergence issues for unbounded spectral sequences and hence make no mention of such issues here.
Definition 2.6. Let
![]() ${\mathcal{C}}$
be an Abelian category. A (cohomological) spectral sequence consists of the following data: a family
${\mathcal{C}}$
be an Abelian category. A (cohomological) spectral sequence consists of the following data: a family
![]() $\{E_{r}^{p,q}\}$
of objects of
$\{E_{r}^{p,q}\}$
of objects of
![]() ${\mathcal{C}}$
(where
${\mathcal{C}}$
(where
 $p,q\in \mathbb{Z}$
and
$p,q\in \mathbb{Z}$
and
![]() $r\geqslant 1$
or
$r\geqslant 1$
or
![]() ${\geqslant}2$
; with
${\geqslant}2$
; with
![]() $r$
fixed and
$r$
fixed and
![]() $p,q$
varying, we obtain the
$p,q$
varying, we obtain the
![]() $E_{r}$
-term of the spectral sequence), and morphisms (the differentials)
$E_{r}$
-term of the spectral sequence), and morphisms (the differentials)
 $d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}$
for all
$d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}$
for all
![]() $p,q,r$
such that
$p,q,r$
such that
 $d_{r}^{p,q}\circ d_{r}^{p-r,q+r-1}=0$
and
$d_{r}^{p,q}\circ d_{r}^{p-r,q+r-1}=0$
and
 $\ker (d_{r}^{p,q})/\text{im}(d_{r}^{p-r,q+r-1})\xrightarrow[{}]{{\sim}}E_{r+1}^{p,q}$
: a family of such isomorphisms, denoted
$\ker (d_{r}^{p,q})/\text{im}(d_{r}^{p-r,q+r-1})\xrightarrow[{}]{{\sim}}E_{r+1}^{p,q}$
: a family of such isomorphisms, denoted
![]() $\unicode[STIX]{x1D6FC}_{r}^{p,q}$
, is part of the data of the spectral sequence.
$\unicode[STIX]{x1D6FC}_{r}^{p,q}$
, is part of the data of the spectral sequence.
Let
![]() $E$
be a spectral sequence in an Abelian category
$E$
be a spectral sequence in an Abelian category
![]() ${\mathcal{C}}$
, and suppose that for all
${\mathcal{C}}$
, and suppose that for all
![]() $l$
and for all
$l$
and for all
![]() $r$
, there are only finitely many non-zero objects
$r$
, there are only finitely many non-zero objects
![]() $E_{r}^{p,q}$
with
$E_{r}^{p,q}$
with
 $p+q=l$
. Such a spectral sequence is called bounded. (For example, this occurs if
$p+q=l$
. Such a spectral sequence is called bounded. (For example, this occurs if
 $E_{r}^{p,q}=0$
whenever
$E_{r}^{p,q}=0$
whenever
![]() $p$
or
$p$
or
![]() $q$
is negative, in which case
$q$
is negative, in which case
![]() $E$
is called a first-quadrant spectral sequence.) If
$E$
is called a first-quadrant spectral sequence.) If
![]() $E$
is a bounded spectral sequence, for every pair
$E$
is a bounded spectral sequence, for every pair
![]() $(p,q)$
, there exists
$(p,q)$
, there exists
![]() $r_{0}$
such that for all
$r_{0}$
such that for all
![]() $r\geqslant r_{0}$
,
$r\geqslant r_{0}$
,
![]() $d_{r}^{p,q}$
has zero target,
$d_{r}^{p,q}$
has zero target,
 $d_{r}^{p-r,q+r-1}$
has zero source, and so
$d_{r}^{p-r,q+r-1}$
has zero source, and so
 $E_{r+1}^{p,q}\simeq E_{r}^{p,q}$
. We denote this stable object by
$E_{r+1}^{p,q}\simeq E_{r}^{p,q}$
. We denote this stable object by
![]() $E_{\infty }^{p,q}$
. We can now define the abutment of such a spectral sequence.
$E_{\infty }^{p,q}$
. We can now define the abutment of such a spectral sequence.
Definition 2.7. Let
![]() $E$
be a bounded spectral sequence in an Abelian category
$E$
be a bounded spectral sequence in an Abelian category
![]() ${\mathcal{C}}$
. Suppose we are given a family
${\mathcal{C}}$
. Suppose we are given a family
![]() $E^{m}$
of objects of
$E^{m}$
of objects of
![]() ${\mathcal{C}}$
, all endowed with a finite decreasing filtration
${\mathcal{C}}$
, all endowed with a finite decreasing filtration
 $E^{m}=E_{s}^{m}\supset E_{s+1}^{m}\supset \cdots \supset E_{t}^{m}=0$
, and for all
$E^{m}=E_{s}^{m}\supset E_{s+1}^{m}\supset \cdots \supset E_{t}^{m}=0$
, and for all
![]() $p$
, an isomorphism
$p$
, an isomorphism
 $\unicode[STIX]{x1D6FD}^{p,m-p}:E_{\infty }^{p,m-p}\xrightarrow[{}]{{\sim}}E_{p}^{m}/E_{p+1}^{m}$
. Then we say that the spectral sequence abuts or converges to
$\unicode[STIX]{x1D6FD}^{p,m-p}:E_{\infty }^{p,m-p}\xrightarrow[{}]{{\sim}}E_{p}^{m}/E_{p+1}^{m}$
. Then we say that the spectral sequence abuts or converges to
![]() $\{E^{m}\}$
(the abutment), and write
$\{E^{m}\}$
(the abutment), and write
 $E_{1}^{p,q}\Rightarrow E^{m}$
or
$E_{1}^{p,q}\Rightarrow E^{m}$
or
 $E_{2}^{p,q}\Rightarrow E^{m}$
.
$E_{2}^{p,q}\Rightarrow E^{m}$
.
For example, if
![]() $E$
is a first-quadrant spectral sequence with abutment
$E$
is a first-quadrant spectral sequence with abutment
![]() $\{E^{m}\}$
, every
$\{E^{m}\}$
, every
![]() $E^{m}$
has a filtration of length
$E^{m}$
has a filtration of length
![]() $m+1$
(we take
$m+1$
(we take
![]() $s=0$
and
$s=0$
and
 $t=m+1$
in the definition above), with
$t=m+1$
in the definition above), with
 $E^{m}/E_{1}^{m}\simeq E_{\infty }^{0,m}$
and
$E^{m}/E_{1}^{m}\simeq E_{\infty }^{0,m}$
and
 $E_{m}^{m}\simeq E_{\infty }^{m,0}$
.
$E_{m}^{m}\simeq E_{\infty }^{m,0}$
.
Given two spectral sequences, there is a natural notion of a morphism between them, which consists of morphisms between the objects in the
![]() $E_{r}$
-terms for all
$E_{r}$
-terms for all
![]() $r$
, each of which induces its successor on cohomology. There is also a natural notion of morphisms between bounded spectral sequences with given abutments.
$r$
, each of which induces its successor on cohomology. There is also a natural notion of morphisms between bounded spectral sequences with given abutments.
Definition 2.8. Let
![]() $E$
and
$E$
and
![]() $E^{\prime }$
be two spectral sequences in
$E^{\prime }$
be two spectral sequences in
![]() ${\mathcal{C}}$
with respective differentials
${\mathcal{C}}$
with respective differentials
![]() $d$
and
$d$
and
![]() $d^{\prime }$
. A morphism
$d^{\prime }$
. A morphism
 $u:E\rightarrow E^{\prime }$
is a family of morphisms
$u:E\rightarrow E^{\prime }$
is a family of morphisms
 $u_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{\prime p,q}$
such that the
$u_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{\prime p,q}$
such that the
![]() $u_{r}^{p,q}$
are compatible with the differentials (
$u_{r}^{p,q}$
are compatible with the differentials (
 $d_{r}^{\prime p,q}\circ u_{r}^{p,q}=u_{r}^{p+r,q-r+1}\circ d_{r}^{p,q}$
for all
$d_{r}^{\prime p,q}\circ u_{r}^{p,q}=u_{r}^{p+r,q-r+1}\circ d_{r}^{p,q}$
for all
![]() $p,q,r$
) and the morphisms
$p,q,r$
) and the morphisms
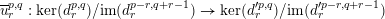 $$\begin{eqnarray}\overline{u}_{r}^{p,q}:\ker (d_{r}^{p,q})/\text{im}(d_{r}^{p-r,q+r-1})\rightarrow \ker (d_{r}^{\prime p,q})/\text{im}(d_{r}^{\prime p-r,q+r-1})\end{eqnarray}$$
$$\begin{eqnarray}\overline{u}_{r}^{p,q}:\ker (d_{r}^{p,q})/\text{im}(d_{r}^{p-r,q+r-1})\rightarrow \ker (d_{r}^{\prime p,q})/\text{im}(d_{r}^{\prime p-r,q+r-1})\end{eqnarray}$$
induced by
![]() $u_{r}^{p,q}$
commute with the given isomorphisms
$u_{r}^{p,q}$
commute with the given isomorphisms
![]() $\unicode[STIX]{x1D6FC}_{r}^{p,q}$
(that is,
$\unicode[STIX]{x1D6FC}_{r}^{p,q}$
(that is,
 $\unicode[STIX]{x1D6FC}_{r}^{\prime p,q}\circ \overline{u}_{r}^{p,q}=\overline{u}_{r+1}^{p,q}\circ \unicode[STIX]{x1D6FC}_{r}^{p,q}$
) so that, in the appropriate sense,
$\unicode[STIX]{x1D6FC}_{r}^{\prime p,q}\circ \overline{u}_{r}^{p,q}=\overline{u}_{r+1}^{p,q}\circ \unicode[STIX]{x1D6FC}_{r}^{p,q}$
) so that, in the appropriate sense,
![]() $u_{r+1}^{p,q}$
is the morphism induced by
$u_{r+1}^{p,q}$
is the morphism induced by
![]() $u_{r}^{p,q}$
. If
$u_{r}^{p,q}$
. If
![]() $E$
and
$E$
and
![]() $E^{\prime }$
are bounded spectral sequences with abutments
$E^{\prime }$
are bounded spectral sequences with abutments
![]() $\{E^{m}\}$
and
$\{E^{m}\}$
and
![]() $\{{E^{\prime }}^{m}\}$
, a morphism with abutments between the spectral sequences is a morphism
$\{{E^{\prime }}^{m}\}$
, a morphism with abutments between the spectral sequences is a morphism
 $u:E\rightarrow E^{\prime }$
as just defined together with a family of morphisms
$u:E\rightarrow E^{\prime }$
as just defined together with a family of morphisms
 $u^{m}:E^{m}\rightarrow {E^{\prime }}^{m}$
compatible with the filtrations on
$u^{m}:E^{m}\rightarrow {E^{\prime }}^{m}$
compatible with the filtrations on
![]() $E^{m}$
and
$E^{m}$
and
![]() ${E^{\prime }}^{m}$
such that, if we denote by
${E^{\prime }}^{m}$
such that, if we denote by
![]() $u_{\infty }^{p,q}$
the map induced by
$u_{\infty }^{p,q}$
the map induced by
![]() $u_{1}^{p,q}$
(or
$u_{1}^{p,q}$
(or
![]() $u_{2}^{p,q}$
) between the stable objects
$u_{2}^{p,q}$
) between the stable objects
![]() $E_{\infty }^{p,q}$
and
$E_{\infty }^{p,q}$
and
![]() $E_{\infty }^{\prime p,q}$
, this map must commute with the isomorphisms
$E_{\infty }^{\prime p,q}$
, this map must commute with the isomorphisms
![]() $\unicode[STIX]{x1D6FD}^{p,q}$
: if we denote by
$\unicode[STIX]{x1D6FD}^{p,q}$
: if we denote by
![]() $u_{p}^{m}$
the morphism
$u_{p}^{m}$
the morphism
 $E_{p}^{m}/E_{p+1}^{m}\rightarrow E_{p}^{\prime m}/E_{p+1}^{\prime m}$
induced by
$E_{p}^{m}/E_{p+1}^{m}\rightarrow E_{p}^{\prime m}/E_{p+1}^{\prime m}$
induced by
![]() $u^{m}$
, which is required to be filtration-compatible, we must have
$u^{m}$
, which is required to be filtration-compatible, we must have
 $\unicode[STIX]{x1D6FD}^{\prime p,q}\circ u_{\infty }^{p,q}=u_{p}^{p+q}\circ \unicode[STIX]{x1D6FD}^{p,q}$
.
$\unicode[STIX]{x1D6FD}^{\prime p,q}\circ u_{\infty }^{p,q}=u_{p}^{p+q}\circ \unicode[STIX]{x1D6FD}^{p,q}$
.
Convention 2.9. For the remainder of this paper, every spectral sequence will be a bounded spectral sequence with abutment, and every morphism of spectral sequences will be a morphism with abutments. Consequently, we suppress the phrase ‘with abutment’.
To show that two spectral sequences are isomorphic, it suffices to construct a morphism between them which is an isomorphism on the objects of the initial (
![]() $r=1$
or
$r=1$
or
![]() $r=2$
) terms. This result is crucial to our work in both this section and in § 7, so we record a version here.
$r=2$
) terms. This result is crucial to our work in both this section and in § 7, so we record a version here.
Proposition 2.10 [Reference WeibelWei94, Theorem 5.2.12].
Let
![]() ${\mathcal{C}}$
be an Abelian category, and let
${\mathcal{C}}$
be an Abelian category, and let
 $u=(u_{r}^{p,q},u^{n})$
be a morphism between two spectral sequences
$u=(u_{r}^{p,q},u^{n})$
be a morphism between two spectral sequences
![]() $E$
,
$E$
,
![]() $E^{\prime }$
in
$E^{\prime }$
in
![]() ${\mathcal{C}}$
. If there exists
${\mathcal{C}}$
. If there exists
![]() $r$
such that
$r$
such that
![]() $u_{r}^{p,q}$
is an isomorphism for all
$u_{r}^{p,q}$
is an isomorphism for all
![]() $p$
and
$p$
and
![]() $q$
, then
$q$
, then
![]() $u_{s}^{p,q}$
is an isomorphism for all
$u_{s}^{p,q}$
is an isomorphism for all
![]() $p$
and
$p$
and
![]() $q$
and all
$q$
and all
![]() $s\geqslant r$
, and
$s\geqslant r$
, and
![]() $u^{m}$
is an isomorphism for all
$u^{m}$
is an isomorphism for all
![]() $m$
. It follows that the abutments of
$m$
. It follows that the abutments of
![]() $E$
and
$E$
and
![]() $E^{\prime }$
are isomorphic as filtered objects.
$E^{\prime }$
are isomorphic as filtered objects.
There is also a notion of a degree-shifted morphism of spectral sequences and a degree-shifted analogue of Proposition 2.10, which we will make use of in this paper. Again, for us, all spectral sequences will be bounded and all morphisms will be morphisms with abutments.
Definition 2.11. Let
![]() $E$
and
$E$
and
![]() $E^{\prime }$
be two spectral sequences in
$E^{\prime }$
be two spectral sequences in
![]() ${\mathcal{C}}$
with respective differentials
${\mathcal{C}}$
with respective differentials
![]() $d$
and
$d$
and
![]() $d^{\prime }$
. If
$d^{\prime }$
. If
 $a,b\in \mathbb{Z}$
, a morphism
$a,b\in \mathbb{Z}$
, a morphism
 $u:E\rightarrow E^{\prime }$
of bidegree
$u:E\rightarrow E^{\prime }$
of bidegree
![]() $(a,b)$
is a family of morphisms
$(a,b)$
is a family of morphisms
 $u_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{\prime p+a,q+b}$
such that the
$u_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{\prime p+a,q+b}$
such that the
![]() $u_{r}^{p,q}$
are compatible with the differentials (
$u_{r}^{p,q}$
are compatible with the differentials (
 $d_{r}^{\prime p+a,q+b}\circ u_{r}^{p,q}=u_{r}^{p+r,q-r+1}\circ d_{r}^{p,q}$
for all
$d_{r}^{\prime p+a,q+b}\circ u_{r}^{p,q}=u_{r}^{p+r,q-r+1}\circ d_{r}^{p,q}$
for all
![]() $p,q,r$
) and
$p,q,r$
) and
![]() $u_{r+1}^{p,q}$
is induced on cohomology by
$u_{r+1}^{p,q}$
is induced on cohomology by
![]() $u_{r}^{p,q}$
. If
$u_{r}^{p,q}$
. If
![]() $E$
and
$E$
and
![]() $E^{\prime }$
are bounded spectral sequences with abutments
$E^{\prime }$
are bounded spectral sequences with abutments
![]() $\{E^{m}\}$
and
$\{E^{m}\}$
and
![]() $\{{E^{\prime }}^{m}\}$
, a morphism with abutments between the spectral sequences of bidegree
$\{{E^{\prime }}^{m}\}$
, a morphism with abutments between the spectral sequences of bidegree
![]() $(a,b)$
is a morphism
$(a,b)$
is a morphism
 $u:E\rightarrow E^{\prime }$
of bidegree
$u:E\rightarrow E^{\prime }$
of bidegree
![]() $(a,b)$
as just defined together with a family of morphisms
$(a,b)$
as just defined together with a family of morphisms
 $u^{m}:E^{m}\rightarrow E^{\prime m+a+b}$
such that
$u^{m}:E^{m}\rightarrow E^{\prime m+a+b}$
such that
 $u^{m}(E_{p}^{m})\subset E_{p+a}^{\prime m+a+b}$
for all
$u^{m}(E_{p}^{m})\subset E_{p+a}^{\prime m+a+b}$
for all
![]() $p$
and satisfying the obvious compatibility conditions analogous to those in the non-degree-shifted definition.
$p$
and satisfying the obvious compatibility conditions analogous to those in the non-degree-shifted definition.
The degree-shifted analogue of Proposition 2.10 is proved in exactly the same way, but in the conclusion (that the abutments are isomorphic as filtered objects), it is worth recording precisely which filtrations are being compared and what the corresponding degree shifts are.
Proposition 2.12. Let
![]() ${\mathcal{C}}$
be an Abelian category, and let
${\mathcal{C}}$
be an Abelian category, and let
 $u=(u_{r}^{p,q},u^{n})$
be a morphism of bidegree
$u=(u_{r}^{p,q},u^{n})$
be a morphism of bidegree
![]() $(a,b)$
between two spectral sequences
$(a,b)$
between two spectral sequences
![]() $E$
,
$E$
,
![]() $E^{\prime }$
in
$E^{\prime }$
in
![]() ${\mathcal{C}}$
. If there exists
${\mathcal{C}}$
. If there exists
![]() $r$
such that
$r$
such that
![]() $u_{r}^{p,q}$
is an isomorphism for all
$u_{r}^{p,q}$
is an isomorphism for all
![]() $p$
and
$p$
and
![]() $q$
, then
$q$
, then
![]() $u_{s}^{p,q}$
is an isomorphism for all
$u_{s}^{p,q}$
is an isomorphism for all
![]() $p$
and
$p$
and
![]() $q$
and all
$q$
and all
![]() $s\geqslant r$
, and
$s\geqslant r$
, and
![]() $u^{m}$
is an isomorphism for all
$u^{m}$
is an isomorphism for all
![]() $m$
. This has the following consequence for the abutments: for all
$m$
. This has the following consequence for the abutments: for all
![]() $m$
,
$m$
,
![]() $E^{m}$
, endowed with the filtration
$E^{m}$
, endowed with the filtration
 $\{E_{p}^{m}\}_{p=0}^{m+1}$
where
$\{E_{p}^{m}\}_{p=0}^{m+1}$
where
 $E_{p}^{m}/E_{p+1}^{m}\simeq E_{\infty }^{p,m-p}$
, is isomorphic (as a filtered object) to
$E_{p}^{m}/E_{p+1}^{m}\simeq E_{\infty }^{p,m-p}$
, is isomorphic (as a filtered object) to
 $E^{\prime m+a+b}$
, endowed with the filtration
$E^{\prime m+a+b}$
, endowed with the filtration
 $\{E_{p+a}^{\prime m+a+b}\}_{p=0}^{m+1}$
, where
$\{E_{p+a}^{\prime m+a+b}\}_{p=0}^{m+1}$
, where
 $E_{p+a}^{\prime m+a+b}/E_{p+a+1}^{\prime m+a+b}\simeq E_{\infty }^{\prime p+a,m+b-p}$
.
$E_{p+a}^{\prime m+a+b}/E_{p+a+1}^{\prime m+a+b}\simeq E_{\infty }^{\prime p+a,m+b-p}$
.
Double complexes are a common source of spectral sequences: the cohomology of the totalization of a double complex can be approximated, and in some cases even computed, by the objects in the early terms of either of two spectral sequences associated with the double complex. To be precise, let
![]() $K^{\bullet ,\bullet }$
be a double complex in an Abelian category
$K^{\bullet ,\bullet }$
be a double complex in an Abelian category
![]() ${\mathcal{C}}$
, which we think of abusively as the ‘
${\mathcal{C}}$
, which we think of abusively as the ‘
![]() $E_{0}$
-term’ of a spectral sequence, and let
$E_{0}$
-term’ of a spectral sequence, and let
![]() $T^{\bullet }$
be its totalization. Our conventions for double complexes are those of EGA: the horizontal (
$T^{\bullet }$
be its totalization. Our conventions for double complexes are those of EGA: the horizontal (
![]() $d_{h}^{\bullet ,\bullet }$
) and vertical (
$d_{h}^{\bullet ,\bullet }$
) and vertical (
![]() $d_{v}^{\bullet ,\bullet }$
) differentials of
$d_{v}^{\bullet ,\bullet }$
) differentials of
![]() $K^{\bullet ,\bullet }$
commute, we define
$K^{\bullet ,\bullet }$
commute, we define
 $T^{i}=\bigoplus _{p+q=i}K^{p,q}$
, and the differentials of
$T^{i}=\bigoplus _{p+q=i}K^{p,q}$
, and the differentials of
![]() $T^{\bullet }$
require signs, namely
$T^{\bullet }$
require signs, namely
 $d(x)=d_{h}(x)+(-1)^{p}d_{v}(x)$
for
$d(x)=d_{h}(x)+(-1)^{p}d_{v}(x)$
for
 $x\in K^{p,q}$
. The two spectral sequences associated with
$x\in K^{p,q}$
. The two spectral sequences associated with
![]() $K^{\bullet ,\bullet }$
[Reference Grothendieck and DieudonnéGD61, § 11.3] are the column-filtered (‘vertical differentials first’) spectral sequence, for which
$K^{\bullet ,\bullet }$
[Reference Grothendieck and DieudonnéGD61, § 11.3] are the column-filtered (‘vertical differentials first’) spectral sequence, for which
 $E_{1}^{p,q}=h_{v}^{q}(K^{p,\bullet })$
(and the differentials are those induced on vertical cohomology by the maps
$E_{1}^{p,q}=h_{v}^{q}(K^{p,\bullet })$
(and the differentials are those induced on vertical cohomology by the maps
![]() $d_{h}^{p,q}$
), and the row-filtered (‘horizontal differentials first’) spectral sequence, for which
$d_{h}^{p,q}$
), and the row-filtered (‘horizontal differentials first’) spectral sequence, for which
 $E_{1}^{p,q}=h_{h}^{p}(K^{\bullet ,q})$
(and the differentials are those induced on horizontal cohomology by the maps
$E_{1}^{p,q}=h_{h}^{p}(K^{\bullet ,q})$
(and the differentials are those induced on horizontal cohomology by the maps
![]() $d_{v}^{p,q}$
). Both have
$d_{v}^{p,q}$
). Both have
 $h^{p+q}(T^{\bullet })$
, the cohomology of the totalization, for their abutment. A morphism
$h^{p+q}(T^{\bullet })$
, the cohomology of the totalization, for their abutment. A morphism
 $K^{\bullet ,\bullet }\rightarrow K^{\prime \bullet ,\bullet }$
of double complexes induces morphisms between their column-filtered spectral sequences as well as between their row-filtered spectral sequences [Reference Grothendieck and DieudonnéGD61, p. 30].
$K^{\bullet ,\bullet }\rightarrow K^{\prime \bullet ,\bullet }$
of double complexes induces morphisms between their column-filtered spectral sequences as well as between their row-filtered spectral sequences [Reference Grothendieck and DieudonnéGD61, p. 30].
The spectral sequences of a double complex are useful for computing hyperderived functors of left-exact functors between Abelian categories. Suppose
![]() ${\mathcal{A}},{\mathcal{B}}$
are Abelian categories,
${\mathcal{A}},{\mathcal{B}}$
are Abelian categories,
![]() ${\mathcal{A}}$
has enough injective objects, and
${\mathcal{A}}$
has enough injective objects, and
 $F:{\mathcal{A}}\rightarrow {\mathcal{B}}$
is a left-exact additive functor. If
$F:{\mathcal{A}}\rightarrow {\mathcal{B}}$
is a left-exact additive functor. If
![]() $K^{\bullet }$
is a complex with differential
$K^{\bullet }$
is a complex with differential
![]() $d$
in
$d$
in
![]() ${\mathcal{A}}$
, the (right) hyperderived functors of
${\mathcal{A}}$
, the (right) hyperderived functors of
![]() $F$
evaluated at
$F$
evaluated at
![]() $K^{\bullet }$
are defined as follows [Reference Grothendieck and DieudonnéGD61, § 11.4]: if
$K^{\bullet }$
are defined as follows [Reference Grothendieck and DieudonnéGD61, § 11.4]: if
 $K^{\bullet }\rightarrow I^{\bullet }$
is a quasi-isomorphism and
$K^{\bullet }\rightarrow I^{\bullet }$
is a quasi-isomorphism and
![]() $I^{\bullet }$
is a complex of injective objects in
$I^{\bullet }$
is a complex of injective objects in
![]() ${\mathcal{A}}$
, then
${\mathcal{A}}$
, then
 $\mathbf{R}^{i}F(K^{\bullet })=h^{i}(F(I^{\bullet }))$
, and the objects of
$\mathbf{R}^{i}F(K^{\bullet })=h^{i}(F(I^{\bullet }))$
, and the objects of
![]() ${\mathcal{B}}$
thus obtained are independent of the choice of
${\mathcal{B}}$
thus obtained are independent of the choice of
![]() $I^{\bullet }$
. Such a complex
$I^{\bullet }$
. Such a complex
![]() $I^{\bullet }$
can be produced as the totalization of a Cartan–Eilenberg resolution of
$I^{\bullet }$
can be produced as the totalization of a Cartan–Eilenberg resolution of
![]() $K^{\bullet }$
, which is a double complex
$K^{\bullet }$
, which is a double complex
![]() $J^{\bullet ,\bullet }$
with differentials
$J^{\bullet ,\bullet }$
with differentials
![]() $d_{h},d_{v}$
such that every
$d_{h},d_{v}$
such that every
![]() $J^{p,q}$
is an injective object of
$J^{p,q}$
is an injective object of
![]() ${\mathcal{A}}$
and, for all
${\mathcal{A}}$
and, for all
![]() $p$
,
$p$
,
![]() $J^{p,\bullet }$
(respectively
$J^{p,\bullet }$
(respectively
 $\ker (d_{v}^{p,\bullet })$
,
$\ker (d_{v}^{p,\bullet })$
,
 $\operatorname{im}(d_{v}^{p,\bullet })$
,
$\operatorname{im}(d_{v}^{p,\bullet })$
,
 $h_{v}^{\bullet }(J^{p,\bullet })$
) is an injective resolution of
$h_{v}^{\bullet }(J^{p,\bullet })$
) is an injective resolution of
![]() $K^{p}$
(respectively
$K^{p}$
(respectively
![]() $\ker (d^{p})$
,
$\ker (d^{p})$
,
![]() $\operatorname{im}(d^{p})$
,
$\operatorname{im}(d^{p})$
,
![]() $h^{p}(K^{\bullet })$
). It follows that
$h^{p}(K^{\bullet })$
). It follows that
 $\mathbf{R}^{i}F(K^{\bullet })$
is the cohomology of the totalization of the double complex
$\mathbf{R}^{i}F(K^{\bullet })$
is the cohomology of the totalization of the double complex
![]() $F(J^{\bullet ,\bullet })$
, and so, by the previous paragraph, we have two spectral sequences whose abutment is this cohomology. For example, the column-filtered spectral sequence begins
$F(J^{\bullet ,\bullet })$
, and so, by the previous paragraph, we have two spectral sequences whose abutment is this cohomology. For example, the column-filtered spectral sequence begins
 $E_{1}^{p,q}=h_{v}^{q}(F(J^{p,\bullet }))$
and has abutment
$E_{1}^{p,q}=h_{v}^{q}(F(J^{p,\bullet }))$
and has abutment
 $\mathbf{R}^{p+q}F(K^{\bullet })$
. But since
$\mathbf{R}^{p+q}F(K^{\bullet })$
. But since
![]() $J^{p,\bullet }$
is an injective resolution of
$J^{p,\bullet }$
is an injective resolution of
![]() $K^{p}$
, we see that
$K^{p}$
, we see that
 $h_{v}^{q}(F(J^{p,\bullet }))=R^{q}F(K^{p})$
, the ordinary
$h_{v}^{q}(F(J^{p,\bullet }))=R^{q}F(K^{p})$
, the ordinary
![]() $q$
th right derived functor of
$q$
th right derived functor of
![]() $F$
applied to
$F$
applied to
![]() $K^{p}$
; this is the form in which the ‘first’ hyperderived functor spectral sequence is usually given [Reference Grothendieck and DieudonnéGD61, 11.4.3.1].
$K^{p}$
; this is the form in which the ‘first’ hyperderived functor spectral sequence is usually given [Reference Grothendieck and DieudonnéGD61, 11.4.3.1].
Now suppose
![]() $K^{\bullet }$
,
$K^{\bullet }$
,
![]() $K^{\prime \bullet }$
are complexes in
$K^{\prime \bullet }$
are complexes in
![]() ${\mathcal{A}}$
with respective Cartan–Eilenberg resolutions
${\mathcal{A}}$
with respective Cartan–Eilenberg resolutions
![]() $J^{\bullet ,\bullet }$
,
$J^{\bullet ,\bullet }$
,
![]() $J^{\prime \bullet ,\bullet }$
. A morphism of complexes
$J^{\prime \bullet ,\bullet }$
. A morphism of complexes
 $f:K^{\bullet }\rightarrow K^{\prime \bullet }$
induces a morphism of double complexes
$f:K^{\bullet }\rightarrow K^{\prime \bullet }$
induces a morphism of double complexes
 $J^{\bullet ,\bullet }\rightarrow J^{\prime \bullet ,\bullet }$
which is unique up to homotopy [Reference Grothendieck and DieudonnéGD61, p. 33]. This implies that
$J^{\bullet ,\bullet }\rightarrow J^{\prime \bullet ,\bullet }$
which is unique up to homotopy [Reference Grothendieck and DieudonnéGD61, p. 33]. This implies that
![]() $f$
induces a well-defined morphism between the spectral sequences for the hyperderived functors of
$f$
induces a well-defined morphism between the spectral sequences for the hyperderived functors of
![]() $F$
evaluated at
$F$
evaluated at
![]() $K^{\bullet }$
and at
$K^{\bullet }$
and at
![]() $K^{\prime \bullet }$
[Reference Grothendieck and DieudonnéGD61, p. 30], since two double complex morphisms that are chain homotopic induce the same morphisms on horizontal and vertical cohomology, hence the same spectral sequence morphisms. By taking
$K^{\prime \bullet }$
[Reference Grothendieck and DieudonnéGD61, p. 30], since two double complex morphisms that are chain homotopic induce the same morphisms on horizontal and vertical cohomology, hence the same spectral sequence morphisms. By taking
 $K^{\prime \bullet }=K^{\bullet }$
and
$K^{\prime \bullet }=K^{\bullet }$
and
![]() $f$
to be the identity, we see that the isomorphism class of the spectral sequence for
$f$
to be the identity, we see that the isomorphism class of the spectral sequence for
![]() $F$
evaluated at
$F$
evaluated at
![]() $K^{\bullet }$
is independent of the Cartan–Eilenberg resolution.
$K^{\bullet }$
is independent of the Cartan–Eilenberg resolution.
Later in this section, we will need to build a spectral sequence for hyperderived functors using a double complex that is not a Cartan–Eilenberg resolution of the original complex, and for this purpose, the following comparison lemma will be useful.
Lemma 2.13. Let
![]() ${\mathcal{A}}$
be an Abelian category with enough injective objects,
${\mathcal{A}}$
be an Abelian category with enough injective objects,
![]() ${\mathcal{B}}$
another Abelian category, and
${\mathcal{B}}$
another Abelian category, and
 $F:{\mathcal{A}}\rightarrow {\mathcal{B}}$
a left-exact additive functor. Suppose that
$F:{\mathcal{A}}\rightarrow {\mathcal{B}}$
a left-exact additive functor. Suppose that
![]() $K^{\bullet }$
is a complex in
$K^{\bullet }$
is a complex in
![]() ${\mathcal{A}}$
, concentrated in degrees
${\mathcal{A}}$
, concentrated in degrees
![]() $p\geqslant 0$
, and that
$p\geqslant 0$
, and that
![]() $L^{\bullet ,\bullet }$
is a double complex in
$L^{\bullet ,\bullet }$
is a double complex in
![]() ${\mathcal{A}}$
whose objects
${\mathcal{A}}$
whose objects
![]() $L^{p,q}$
are all
$L^{p,q}$
are all
![]() $F$
-acyclic and such that, for all
$F$
-acyclic and such that, for all
![]() $p\geqslant 0$
,
$p\geqslant 0$
,
![]() $L^{p,\bullet }$
is a resolution of
$L^{p,\bullet }$
is a resolution of
![]() $K^{p}$
. Then the first spectral sequence for the hyperderived functors of
$K^{p}$
. Then the first spectral sequence for the hyperderived functors of
![]() $F$
applied to
$F$
applied to
![]() $K^{\bullet }$
, which begins
$K^{\bullet }$
, which begins
 $E_{1}^{p,q}=R^{q}F(K^{p})$
and has
$E_{1}^{p,q}=R^{q}F(K^{p})$
and has
 $\mathbf{R}^{p+q}F(K^{\bullet })$
for its abutment, is isomorphic to the column-filtered spectral sequence of the double complex
$\mathbf{R}^{p+q}F(K^{\bullet })$
for its abutment, is isomorphic to the column-filtered spectral sequence of the double complex
![]() $F(L^{\bullet ,\bullet })$
.
$F(L^{\bullet ,\bullet })$
.
Proof. By definition, the first spectral sequence is the column-filtered spectral sequence of the double complex
![]() $F(J^{\bullet ,\bullet })$
, where
$F(J^{\bullet ,\bullet })$
, where
![]() $J^{\bullet ,\bullet }$
is a choice of Cartan–Eilenberg resolution of
$J^{\bullet ,\bullet }$
is a choice of Cartan–Eilenberg resolution of
![]() $K^{\bullet }$
in
$K^{\bullet }$
in
![]() ${\mathcal{A}}$
. The assertion of the lemma is that we can replace
${\mathcal{A}}$
. The assertion of the lemma is that we can replace
![]() $J^{\bullet ,\bullet }$
with the resolution
$J^{\bullet ,\bullet }$
with the resolution
![]() $L^{\bullet ,\bullet }$
, which is generally not a Cartan–Eilenberg resolution and whose objects may not even be injective.
$L^{\bullet ,\bullet }$
, which is generally not a Cartan–Eilenberg resolution and whose objects may not even be injective.
Our strategy will be to compare both of these double complexes to a third one. Let
![]() ${\mathcal{C}}^{+}$
denote the category of complexes in
${\mathcal{C}}^{+}$
denote the category of complexes in
![]() ${\mathcal{A}}$
that are concentrated in degrees
${\mathcal{A}}$
that are concentrated in degrees
![]() $p\geqslant 0$
. Then
$p\geqslant 0$
. Then
![]() ${\mathcal{C}}^{+}$
is an Abelian category with enough injective objects, and if
${\mathcal{C}}^{+}$
is an Abelian category with enough injective objects, and if
 $I^{\bullet }\in {\mathcal{C}}^{+}$
is injective, then
$I^{\bullet }\in {\mathcal{C}}^{+}$
is injective, then
![]() $I^{p}$
is an injective object of
$I^{p}$
is an injective object of
![]() ${\mathcal{A}}$
for all
${\mathcal{A}}$
for all
![]() $p$
[Reference RotmanRot09, Theorems 10.42, 10.43; Remark, p. 652].
$p$
[Reference RotmanRot09, Theorems 10.42, 10.43; Remark, p. 652].
We return now to the complex
![]() $K^{\bullet }$
. Choose an injective resolution
$K^{\bullet }$
. Choose an injective resolution
 $0\rightarrow K^{\bullet }\rightarrow I^{\bullet ,\bullet }$
of
$0\rightarrow K^{\bullet }\rightarrow I^{\bullet ,\bullet }$
of
![]() $K^{\bullet }$
in
$K^{\bullet }$
in
![]() ${\mathcal{C}}^{+}$
. In particular,
${\mathcal{C}}^{+}$
. In particular,
![]() $I^{\bullet ,\bullet }$
is a double complex of injective objects in
$I^{\bullet ,\bullet }$
is a double complex of injective objects in
![]() ${\mathcal{A}}$
. Now note that the two double complex resolutions
${\mathcal{A}}$
. Now note that the two double complex resolutions
![]() $J^{\bullet ,\bullet }$
and
$J^{\bullet ,\bullet }$
and
![]() $L^{\bullet ,\bullet }$
can also be regarded as resolutions of
$L^{\bullet ,\bullet }$
can also be regarded as resolutions of
![]() $K^{\bullet }$
in the category
$K^{\bullet }$
in the category
![]() ${\mathcal{C}}^{+}$
. Any resolution in
${\mathcal{C}}^{+}$
. Any resolution in
![]() ${\mathcal{C}}^{+}$
can be compared with an injective one by [Reference LangLan02, Lemma XX.5.2]: there exist morphisms
${\mathcal{C}}^{+}$
can be compared with an injective one by [Reference LangLan02, Lemma XX.5.2]: there exist morphisms
 $J^{\bullet ,\bullet }\rightarrow I^{\bullet ,\bullet }$
and
$J^{\bullet ,\bullet }\rightarrow I^{\bullet ,\bullet }$
and
 $L^{\bullet ,\bullet }\rightarrow I^{\bullet ,\bullet }$
extending the identity on
$L^{\bullet ,\bullet }\rightarrow I^{\bullet ,\bullet }$
extending the identity on
![]() $K^{\bullet }$
and unique up to homotopy as maps in
$K^{\bullet }$
and unique up to homotopy as maps in
![]() ${\mathcal{C}}^{+}$
. These morphisms of double complexes induce morphisms between the column-filtered spectral sequences corresponding to the double complexes after applying the functor
${\mathcal{C}}^{+}$
. These morphisms of double complexes induce morphisms between the column-filtered spectral sequences corresponding to the double complexes after applying the functor
![]() $F$
. To finish the proof, by Proposition 2.10, it is enough to check that these morphisms of spectral sequences are isomorphisms at the
$F$
. To finish the proof, by Proposition 2.10, it is enough to check that these morphisms of spectral sequences are isomorphisms at the
![]() $E_{1}$
-level. We first consider the morphism
$E_{1}$
-level. We first consider the morphism
 $F(J^{\bullet ,\bullet })\rightarrow F(I^{\bullet ,\bullet })$
. For all
$F(J^{\bullet ,\bullet })\rightarrow F(I^{\bullet ,\bullet })$
. For all
![]() $p$
,
$p$
,
 $J^{p,\bullet }\rightarrow I^{p,\bullet }$
is a morphism between two injective resolutions of
$J^{p,\bullet }\rightarrow I^{p,\bullet }$
is a morphism between two injective resolutions of
![]() $K^{p}$
extending the identity on
$K^{p}$
extending the identity on
![]() $K^{p}$
, which induces an isomorphism
$K^{p}$
, which induces an isomorphism
 $h^{q}(F(J^{p,\bullet }))\xrightarrow[{}]{{\sim}}h^{q}(F(I^{p,\bullet }))$
, both sides being equal to
$h^{q}(F(J^{p,\bullet }))\xrightarrow[{}]{{\sim}}h^{q}(F(I^{p,\bullet }))$
, both sides being equal to
 $R^{q}F(K^{p})$
by definition and being the
$R^{q}F(K^{p})$
by definition and being the
![]() $E_{1}^{p,q}$
-terms of the respective spectral sequences. In the case of the morphism
$E_{1}^{p,q}$
-terms of the respective spectral sequences. In the case of the morphism
 $F(L^{\bullet ,\bullet })\rightarrow F(I^{\bullet ,\bullet })$
, we do not have injective resolutions of
$F(L^{\bullet ,\bullet })\rightarrow F(I^{\bullet ,\bullet })$
, we do not have injective resolutions of
![]() $K^{p}$
(only
$K^{p}$
(only
![]() $F$
-acyclic ones) on the left-hand side, but by [Reference LangLan02, Theorem XX.6.2], this is enough: the
$F$
-acyclic ones) on the left-hand side, but by [Reference LangLan02, Theorem XX.6.2], this is enough: the
 $L^{p,\bullet }\rightarrow I^{p,\bullet }$
also give rise to isomorphisms after applying
$L^{p,\bullet }\rightarrow I^{p,\bullet }$
also give rise to isomorphisms after applying
![]() $F$
and taking cohomology. We conclude that the three column-filtered spectral sequences corresponding to the double complexes
$F$
and taking cohomology. We conclude that the three column-filtered spectral sequences corresponding to the double complexes
![]() $F(J^{\bullet ,\bullet })$
,
$F(J^{\bullet ,\bullet })$
,
![]() $F(I^{\bullet ,\bullet })$
, and
$F(I^{\bullet ,\bullet })$
, and
![]() $F(L^{\bullet ,\bullet })$
are isomorphic beginning with their
$F(L^{\bullet ,\bullet })$
are isomorphic beginning with their
![]() $E_{1}$
-terms, completing the proof.◻
$E_{1}$
-terms, completing the proof.◻
We will need one more type of spectral sequence, the Grothendieck composite-functor spectral sequence.
Proposition 2.14 [Reference WeibelWei94, Theorem 5.8.3].
Let
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() ${\mathcal{B}}$
, and
${\mathcal{B}}$
, and
![]() ${\mathcal{C}}$
be Abelian categories, and suppose
${\mathcal{C}}$
be Abelian categories, and suppose
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() ${\mathcal{B}}$
have enough injective objects. Let
${\mathcal{B}}$
have enough injective objects. Let
 $F:{\mathcal{A}}\rightarrow {\mathcal{B}}$
and
$F:{\mathcal{A}}\rightarrow {\mathcal{B}}$
and
 $G:{\mathcal{B}}\rightarrow {\mathcal{C}}$
be left-exact additive functors. Suppose that for every injective object
$G:{\mathcal{B}}\rightarrow {\mathcal{C}}$
be left-exact additive functors. Suppose that for every injective object
![]() $I$
of
$I$
of
![]() ${\mathcal{A}}$
, the object
${\mathcal{A}}$
, the object
![]() $F(I)$
of
$F(I)$
of
![]() ${\mathcal{B}}$
is acyclic for
${\mathcal{B}}$
is acyclic for
![]() $G$
. Then for every object
$G$
. Then for every object
![]() $A$
of
$A$
of
![]() ${\mathcal{A}}$
, there is a spectral sequence which begins
${\mathcal{A}}$
, there is a spectral sequence which begins
 $E_{2}^{p,q}=(R^{p}G)((R^{q}F)(A))$
and abuts to
$E_{2}^{p,q}=(R^{p}G)((R^{q}F)(A))$
and abuts to
 $R^{p+q}(G\circ F)(A)$
.
$R^{p+q}(G\circ F)(A)$
.
Example 2.15. For our purposes, the most important example of a composite-functor spectral sequence is the spectral sequence for iterated local cohomology. Let
![]() $R$
be a Noetherian ring, and let
$R$
be a Noetherian ring, and let
![]() $I$
and
$I$
and
![]() $J$
be ideals of
$J$
be ideals of
![]() $R$
. If
$R$
. If
![]() ${\mathcal{I}}$
is an injective
${\mathcal{I}}$
is an injective
![]() $R$
-module, then
$R$
-module, then
![]() $\unicode[STIX]{x1D6E4}_{J}({\mathcal{I}})$
is again injective [Reference HartshorneHar77, Lemma III.3.2], hence acyclic for the functor
$\unicode[STIX]{x1D6E4}_{J}({\mathcal{I}})$
is again injective [Reference HartshorneHar77, Lemma III.3.2], hence acyclic for the functor
![]() $\unicode[STIX]{x1D6E4}_{I}$
. It follows that the left-exact functors
$\unicode[STIX]{x1D6E4}_{I}$
. It follows that the left-exact functors
 $F=\unicode[STIX]{x1D6E4}_{J}$
and
$F=\unicode[STIX]{x1D6E4}_{J}$
and
![]() $G=\unicode[STIX]{x1D6E4}_{I}$
satisfy the conditions of Proposition 2.14. Since
$G=\unicode[STIX]{x1D6E4}_{I}$
satisfy the conditions of Proposition 2.14. Since
![]() $R$
is Noetherian,
$R$
is Noetherian,
 $\unicode[STIX]{x1D6E4}_{I}\circ \unicode[STIX]{x1D6E4}_{J}=\unicode[STIX]{x1D6E4}_{I+J}$
. For any
$\unicode[STIX]{x1D6E4}_{I}\circ \unicode[STIX]{x1D6E4}_{J}=\unicode[STIX]{x1D6E4}_{I+J}$
. For any
![]() $R$
-module
$R$
-module
![]() $M$
, the corresponding spectral sequence for the derived (local cohomology) functors begins
$M$
, the corresponding spectral sequence for the derived (local cohomology) functors begins
 $E_{2}^{p,q}=H_{I}^{p}(H_{J}^{q}(M))$
and abuts to
$E_{2}^{p,q}=H_{I}^{p}(H_{J}^{q}(M))$
and abuts to
 $H_{I+J}^{p+q}(M)$
.
$H_{I+J}^{p+q}(M)$
.
2.3 The proof of Theorem A
We now recall from [Reference HartshorneHar75] Hartshorne’s definition of de Rham homology for a complete local ring. Let
![]() $k$
be a field of characteristic zero and
$k$
be a field of characteristic zero and
![]() $A$
be a complete local ring with coefficient field
$A$
be a complete local ring with coefficient field
![]() $k$
. By Cohen’s structure theorem, there exists a surjection of
$k$
. By Cohen’s structure theorem, there exists a surjection of
![]() $k$
-algebras
$k$
-algebras
 $\unicode[STIX]{x1D70B}:R\rightarrow A$
where
$\unicode[STIX]{x1D70B}:R\rightarrow A$
where
 $R=k[[x_{1},\ldots ,x_{n}]]$
for some
$R=k[[x_{1},\ldots ,x_{n}]]$
for some
![]() $n$
. Let
$n$
. Let
![]() $I\subset R$
be the kernel of this surjection. We have a corresponding closed immersion
$I\subset R$
be the kernel of this surjection. We have a corresponding closed immersion
 $Y{\hookrightarrow}X$
where
$Y{\hookrightarrow}X$
where
 $Y=\operatorname{Spec}(A)$
and
$Y=\operatorname{Spec}(A)$
and
 $X=\operatorname{Spec}(R)$
. The de Rham homology of the local scheme
$X=\operatorname{Spec}(R)$
. The de Rham homology of the local scheme
![]() $Y$
is defined as
$Y$
is defined as
 $H_{i}^{\text{dR}}(Y)=\mathbf{H}_{Y}^{2n-i}(X,\unicode[STIX]{x1D6FA}_{X}^{\bullet })$
, the hypercohomology (with support at
$H_{i}^{\text{dR}}(Y)=\mathbf{H}_{Y}^{2n-i}(X,\unicode[STIX]{x1D6FA}_{X}^{\bullet })$
, the hypercohomology (with support at
![]() $Y$
) of the continuous de Rham complex of sheaves of
$Y$
) of the continuous de Rham complex of sheaves of
![]() $k$
-spaces on
$k$
-spaces on
![]() $X$
. Here, the sheaf
$X$
. Here, the sheaf
![]() $\unicode[STIX]{x1D6FA}_{X}^{1}$
is free of rank
$\unicode[STIX]{x1D6FA}_{X}^{1}$
is free of rank
![]() $n$
with basis
$n$
with basis
 $dx_{1},\ldots ,dx_{n}$
, and the other sheaves in the complex are its corresponding exterior powers. In fact, the complex
$dx_{1},\ldots ,dx_{n}$
, and the other sheaves in the complex are its corresponding exterior powers. In fact, the complex
![]() $\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
is the sheafified version of the de Rham complex
$\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
is the sheafified version of the de Rham complex
![]() $\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
of the left
$\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
of the left
 ${\mathcal{D}}(R,k)$
-module
${\mathcal{D}}(R,k)$
-module
![]() $R$
as defined in § 2.1.
$R$
as defined in § 2.1.
The de Rham homology spaces defined above are known to be independent of the choice of
![]() $R$
and
$R$
and
![]() $\unicode[STIX]{x1D70B}$
[Reference HartshorneHar75, Proposition III.1.1] and to be finite-dimensional
$\unicode[STIX]{x1D70B}$
[Reference HartshorneHar75, Proposition III.1.1] and to be finite-dimensional
![]() $k$
-spaces [Reference HartshorneHar75, Theorem III.2.1]. In this section we give arguments for the embedding-independence and the finiteness which are purely local and provide new information. Recall from § 1 that the Hodge–de Rham spectral sequence for homology has
$k$
-spaces [Reference HartshorneHar75, Theorem III.2.1]. In this section we give arguments for the embedding-independence and the finiteness which are purely local and provide new information. Recall from § 1 that the Hodge–de Rham spectral sequence for homology has
![]() $E_{1}$
-term given by
$E_{1}$
-term given by
 $E_{1}^{n-p,n-q}=H_{Y}^{n-q}(X,\unicode[STIX]{x1D6FA}_{X}^{n-p})$
and abuts to
$E_{1}^{n-p,n-q}=H_{Y}^{n-q}(X,\unicode[STIX]{x1D6FA}_{X}^{n-p})$
and abuts to
 $H_{p+q}^{\text{dR}}(Y)$
. (When needed, we will write
$H_{p+q}^{\text{dR}}(Y)$
. (When needed, we will write
 $\{E_{r,R}^{n-p,n-q}\}$
for this spectral sequence, recording the dependence on the base ring
$\{E_{r,R}^{n-p,n-q}\}$
for this spectral sequence, recording the dependence on the base ring
![]() $R$
.) The assertion of Theorem A is that, beginning with the
$R$
.) The assertion of Theorem A is that, beginning with the
![]() $E_{2}$
-term, this spectral sequence consists of finite-dimensional
$E_{2}$
-term, this spectral sequence consists of finite-dimensional
![]() $k$
-spaces and its isomorphism class is independent (up to a bidegree shift) of
$k$
-spaces and its isomorphism class is independent (up to a bidegree shift) of
![]() $R$
and
$R$
and
![]() $\unicode[STIX]{x1D70B}$
; this immediately recovers the embedding-independence and finiteness for the abutment
$\unicode[STIX]{x1D70B}$
; this immediately recovers the embedding-independence and finiteness for the abutment
 $H_{\ast }^{\text{dR}}(Y)$
. To make the line of argument clearer, we give the proof first for the
$H_{\ast }^{\text{dR}}(Y)$
. To make the line of argument clearer, we give the proof first for the
![]() $E_{2}$
-term only (Proposition 2.17), then explain the additional steps needed to make the basic strategy work for the rest of the spectral sequence.
$E_{2}$
-term only (Proposition 2.17), then explain the additional steps needed to make the basic strategy work for the rest of the spectral sequence.
Lemma 2.16. Let the surjection
 $\unicode[STIX]{x1D70B}:R=k[[x_{1},\ldots ,x_{n}]]\rightarrow A$
(and the associated objects
$\unicode[STIX]{x1D70B}:R=k[[x_{1},\ldots ,x_{n}]]\rightarrow A$
(and the associated objects
![]() $I,X,Y$
) be as above, and
$I,X,Y$
) be as above, and
![]() $\{E_{r}^{p,q}\}$
the corresponding Hodge–de Rham spectral sequence for homology.
$\{E_{r}^{p,q}\}$
the corresponding Hodge–de Rham spectral sequence for homology.
-
(a) For all
 $q$
,
$q$
,
 $H_{Y}^{q}(X,{\mathcal{O}}_{X})\simeq H_{I}^{q}(R)$
as
$H_{Y}^{q}(X,{\mathcal{O}}_{X})\simeq H_{I}^{q}(R)$
as
 $R$
-modules; indeed, if
$R$
-modules; indeed, if
 $M$
is any
$M$
is any
 $R$
-module and
$R$
-module and
 ${\mathcal{F}}$
the associated quasi-coherent sheaf on
${\mathcal{F}}$
the associated quasi-coherent sheaf on
 $X$
, we have
$X$
, we have
 $H_{Y}^{q}(X,{\mathcal{F}})\simeq H_{I}^{q}(M)$
.
$H_{Y}^{q}(X,{\mathcal{F}})\simeq H_{I}^{q}(M)$
. -
(b) For all
 $p$
and
$p$
and
 $q$
, we have as
$q$
, we have as $$\begin{eqnarray}E_{2}^{p,q}\simeq H_{\text{dR}}^{p}(H_{Y}^{q}(X,{\mathcal{O}}_{X}))\simeq H_{\text{dR}}^{p}(H_{I}^{q}(R))\end{eqnarray}$$
$$\begin{eqnarray}E_{2}^{p,q}\simeq H_{\text{dR}}^{p}(H_{Y}^{q}(X,{\mathcal{O}}_{X}))\simeq H_{\text{dR}}^{p}(H_{I}^{q}(R))\end{eqnarray}$$
 $k$
-spaces, where the
$k$
-spaces, where the
 ${\mathcal{D}}$
-module structure on
${\mathcal{D}}$
-module structure on
 $H_{I}^{q}(R)\simeq H_{Y}^{q}(X,{\mathcal{O}}_{X})$
is defined as in Remark 2.3.
$H_{I}^{q}(R)\simeq H_{Y}^{q}(X,{\mathcal{O}}_{X})$
is defined as in Remark 2.3.
Proof. As
![]() $X$
is affine, part (a) is well known (e.g. [Reference Grothendieck and RaynaudGR05, Exp. II, Proposition 5]). Now consider the
$X$
is affine, part (a) is well known (e.g. [Reference Grothendieck and RaynaudGR05, Exp. II, Proposition 5]). Now consider the
![]() $E_{1}$
-term of the spectral sequence. Its differentials are horizontal and so its
$E_{1}$
-term of the spectral sequence. Its differentials are horizontal and so its
![]() $E_{2}$
-objects are the cohomology objects of its rows. Fix such a row, say the
$E_{2}$
-objects are the cohomology objects of its rows. Fix such a row, say the
![]() $q$
th row, which takes the form
$q$
th row, which takes the form
 $E_{1}^{\bullet ,q}=H_{Y}^{q}(X,\unicode[STIX]{x1D6FA}_{X}^{\bullet })$
. The
$E_{1}^{\bullet ,q}=H_{Y}^{q}(X,\unicode[STIX]{x1D6FA}_{X}^{\bullet })$
. The
![]() $\unicode[STIX]{x1D6FA}_{X}^{p}$
are finite free sheaves on
$\unicode[STIX]{x1D6FA}_{X}^{p}$
are finite free sheaves on
![]() $X$
and local cohomology
$X$
and local cohomology
![]() $H_{Y}^{q}$
commutes with direct sums, so for all
$H_{Y}^{q}$
commutes with direct sums, so for all
![]() $p$
,
$p$
,
 $E_{1}^{p,q}\simeq H_{Y}^{q}(X,{\mathcal{O}}_{X})\otimes \unicode[STIX]{x1D6FA}_{R}^{p}$
. As
$E_{1}^{p,q}\simeq H_{Y}^{q}(X,{\mathcal{O}}_{X})\otimes \unicode[STIX]{x1D6FA}_{R}^{p}$
. As
![]() $p$
varies, we obtain the complex
$p$
varies, we obtain the complex
 $H_{Y}^{q}(X,{\mathcal{O}}_{X})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, whose
$H_{Y}^{q}(X,{\mathcal{O}}_{X})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, whose
![]() $k$
-linear maps are the de Rham differentials of the
$k$
-linear maps are the de Rham differentials of the
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
 $H_{Y}^{q}(X,{\mathcal{O}}_{X})$
. Therefore its cohomology objects, the
$H_{Y}^{q}(X,{\mathcal{O}}_{X})$
. Therefore its cohomology objects, the
![]() $E_{2}$
-objects of the spectral sequence, are of the stated form.◻
$E_{2}$
-objects of the spectral sequence, are of the stated form.◻
Proposition 2.17. Let the surjection
 $\unicode[STIX]{x1D70B}:R=k[[x_{1},\ldots ,x_{n}]]\rightarrow A$
(and the associated objects
$\unicode[STIX]{x1D70B}:R=k[[x_{1},\ldots ,x_{n}]]\rightarrow A$
(and the associated objects
![]() $I,X,Y$
) be as above.
$I,X,Y$
) be as above.
-
(a) For all
 $p$
and
$p$
and
 $q$
, the
$q$
, the
 $k$
-space
$k$
-space
 $E_{2}^{p,q}=H_{\text{dR}}^{p}(H_{I}^{q}(R))$
is finite-dimensional.
$E_{2}^{p,q}=H_{\text{dR}}^{p}(H_{I}^{q}(R))$
is finite-dimensional. -
(b) Suppose we have another surjection of
 $k$
-algebras
$k$
-algebras
 $\unicode[STIX]{x1D70B}^{\prime }:R^{\prime }=k[[x_{1},\ldots ,x_{n^{\prime }}]]\rightarrow A$
with kernel
$\unicode[STIX]{x1D70B}^{\prime }:R^{\prime }=k[[x_{1},\ldots ,x_{n^{\prime }}]]\rightarrow A$
with kernel
 $I^{\prime }$
. Write
$I^{\prime }$
. Write
 $\{E_{r,R}^{p,q}\}$
(respectively
$\{E_{r,R}^{p,q}\}$
(respectively
 $\{\mathbf{E}_{r,R^{\prime }}^{p,q}\}$
) for the Hodge–de Rham spectral sequence for homology defined using
$\{\mathbf{E}_{r,R^{\prime }}^{p,q}\}$
) for the Hodge–de Rham spectral sequence for homology defined using
 $\unicode[STIX]{x1D70B}$
(respectively
$\unicode[STIX]{x1D70B}$
(respectively
 $\unicode[STIX]{x1D70B}^{\prime }$
). Then for all
$\unicode[STIX]{x1D70B}^{\prime }$
). Then for all
 $p$
and
$p$
and
 $q$
, the
$q$
, the
 $k$
-spaces
$k$
-spaces
 $E_{2,R}^{p,q}$
and
$E_{2,R}^{p,q}$
and
 $\mathbf{E}_{2,R^{\prime }}^{p+n^{\prime }-n,q+n-n^{\prime }}$
are isomorphic. (That is, the
$\mathbf{E}_{2,R^{\prime }}^{p+n^{\prime }-n,q+n-n^{\prime }}$
are isomorphic. (That is, the
 $E_{2}$
-term is independent of
$E_{2}$
-term is independent of
 $R$
and
$R$
and
 $\unicode[STIX]{x1D70B}$
, up to a bidegree shift.)
$\unicode[STIX]{x1D70B}$
, up to a bidegree shift.)
Proof of part (a).
For all
![]() $q$
, the
$q$
, the
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $H_{I}^{q}(R)$
is holonomic [Reference LyubeznikLyu93, 2.2(d)], so its de Rham cohomology spaces are finite-dimensional by Theorem 2.2. This proves part (a).◻
$H_{I}^{q}(R)$
is holonomic [Reference LyubeznikLyu93, 2.2(d)], so its de Rham cohomology spaces are finite-dimensional by Theorem 2.2. This proves part (a).◻
A proof of part (b) is considerably longer. We first reduce it to Lemma 2.18 below and then prove Lemma 2.18.
Write
![]() $X^{\prime }$
for the spectrum of
$X^{\prime }$
for the spectrum of
![]() $R^{\prime }$
. The surjection
$R^{\prime }$
. The surjection
![]() $\unicode[STIX]{x1D70B}^{\prime }$
induces a closed immersion
$\unicode[STIX]{x1D70B}^{\prime }$
induces a closed immersion
 $Y{\hookrightarrow}X^{\prime }$
. Form the complete tensor product
$Y{\hookrightarrow}X^{\prime }$
. Form the complete tensor product
 $R^{\prime \prime }=R\,\widehat{\otimes }_{k}\,R^{\prime }$
[Reference SerreSer00, V.B.2], again a complete regular
$R^{\prime \prime }=R\,\widehat{\otimes }_{k}\,R^{\prime }$
[Reference SerreSer00, V.B.2], again a complete regular
![]() $k$
-algebra, and let
$k$
-algebra, and let
 $\unicode[STIX]{x1D70B}^{\prime \prime }:R^{\prime \prime }\rightarrow A$
be the induced surjection
$\unicode[STIX]{x1D70B}^{\prime \prime }:R^{\prime \prime }\rightarrow A$
be the induced surjection
![]() $\unicode[STIX]{x1D70B}\,\widehat{\otimes }_{k}\,\unicode[STIX]{x1D70B}^{\prime }$
of
$\unicode[STIX]{x1D70B}\,\widehat{\otimes }_{k}\,\unicode[STIX]{x1D70B}^{\prime }$
of
![]() $k$
-algebras, which gives rise to a third closed immersion
$k$
-algebras, which gives rise to a third closed immersion
 $Y{\hookrightarrow}X^{\prime \prime }=\operatorname{Spec}(R^{\prime \prime })$
and a third Hodge–de Rham spectral sequence
$Y{\hookrightarrow}X^{\prime \prime }=\operatorname{Spec}(R^{\prime \prime })$
and a third Hodge–de Rham spectral sequence
![]() $\{E_{r,R^{\prime \prime }}^{p,q}\}$
. It suffices to show that both
$\{E_{r,R^{\prime \prime }}^{p,q}\}$
. It suffices to show that both
![]() $E_{2,R}^{p,q}$
and
$E_{2,R}^{p,q}$
and
 $\mathbf{E}_{2,R^{\prime }}^{p+n^{\prime }-n,q+n-n^{\prime }}$
are isomorphic to
$\mathbf{E}_{2,R^{\prime }}^{p+n^{\prime }-n,q+n-n^{\prime }}$
are isomorphic to
 $E_{2,R^{\prime \prime }}^{p+n^{\prime },q+n^{\prime }}$
. Replacing
$E_{2,R^{\prime \prime }}^{p+n^{\prime },q+n^{\prime }}$
. Replacing
![]() $R^{\prime }$
with
$R^{\prime }$
with
![]() $R^{\prime \prime }$
and using symmetry, we reduce to the case in which the two surjections
$R^{\prime \prime }$
and using symmetry, we reduce to the case in which the two surjections
 $\unicode[STIX]{x1D70B}:R\rightarrow A$
and
$\unicode[STIX]{x1D70B}:R\rightarrow A$
and
 $\unicode[STIX]{x1D70B}^{\prime }:R^{\prime }\rightarrow A$
satisfy
$\unicode[STIX]{x1D70B}^{\prime }:R^{\prime }\rightarrow A$
satisfy
 $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}\circ g$
for some surjection
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}\circ g$
for some surjection
 $g:R^{\prime }\rightarrow R$
of
$g:R^{\prime }\rightarrow R$
of
![]() $k$
-algebras. Let
$k$
-algebras. Let
 $I=\ker \unicode[STIX]{x1D70B}$
,
$I=\ker \unicode[STIX]{x1D70B}$
,
 $I^{\prime }=\ker \unicode[STIX]{x1D70B}^{\prime }$
, and
$I^{\prime }=\ker \unicode[STIX]{x1D70B}^{\prime }$
, and
 $I^{\prime \prime }=\ker g$
, and suppose the dimensions of
$I^{\prime \prime }=\ker g$
, and suppose the dimensions of
![]() $R$
and
$R$
and
![]() $R^{\prime }$
are
$R^{\prime }$
are
![]() $n$
and
$n$
and
![]() $n^{\prime }$
respectively. As
$n^{\prime }$
respectively. As
 $R^{\prime }/I^{\prime \prime }\simeq R$
is regular,
$R^{\prime }/I^{\prime \prime }\simeq R$
is regular,
![]() $I^{\prime \prime }$
is generated by
$I^{\prime \prime }$
is generated by
![]() $n^{\prime }-n$
elements that form part of a regular system of parameters for
$n^{\prime }-n$
elements that form part of a regular system of parameters for
![]() $R^{\prime }$
. By induction on
$R^{\prime }$
. By induction on
![]() $n^{\prime }-n$
, we reduce further to the case
$n^{\prime }-n$
, we reduce further to the case
 $n^{\prime }-n=1$
, since we can factor the closed immersion
$n^{\prime }-n=1$
, since we can factor the closed immersion
 $X{\hookrightarrow}X^{\prime }$
into a sequence of codimension-one immersions, and the isomorphisms on
$X{\hookrightarrow}X^{\prime }$
into a sequence of codimension-one immersions, and the isomorphisms on
![]() $E_{2}$
-terms compose while the bidegree shifts add. Therefore we assume
$E_{2}$
-terms compose while the bidegree shifts add. Therefore we assume
![]() $\ker g$
is a principal ideal, of the form
$\ker g$
is a principal ideal, of the form
![]() $(f)$
where
$(f)$
where
 $x_{1},\ldots ,x_{n},f$
is a regular system of parameters for
$x_{1},\ldots ,x_{n},f$
is a regular system of parameters for
![]() $R^{\prime }$
. By Cohen’s structure theorem, the complete regular local
$R^{\prime }$
. By Cohen’s structure theorem, the complete regular local
![]() $k$
-algebra
$k$
-algebra
![]() $R^{\prime }$
takes the form
$R^{\prime }$
takes the form
 $k[[x_{1},\ldots ,x_{n},z]]$
; making a change of variables if necessary, we may assume
$k[[x_{1},\ldots ,x_{n},z]]$
; making a change of variables if necessary, we may assume
![]() $f=z$
. By Proposition 2.5, this change of variables does not affect de Rham cohomology. Thus
$f=z$
. By Proposition 2.5, this change of variables does not affect de Rham cohomology. Thus
 $R=k[[x_{1},\ldots ,x_{n}]]$
,
$R=k[[x_{1},\ldots ,x_{n}]]$
,
 $R^{\prime }=R[[z]]$
, and
$R^{\prime }=R[[z]]$
, and
![]() $g$
is the surjection carrying
$g$
is the surjection carrying
![]() $z$
to
$z$
to
![]() $0$
, so that
$0$
, so that
 $I^{\prime }=IR^{\prime }+(z)$
. We state this special case, to which we have reduced the proposition, in the form of the following lemma. Because of the amount of new notation needed to define them, we have not specified the isomorphisms in the statement of Lemma 2.18, only asserted their existence. However, the maps themselves will be needed later, and so we will refer not only to Lemma 2.18 but also to its proof.
$I^{\prime }=IR^{\prime }+(z)$
. We state this special case, to which we have reduced the proposition, in the form of the following lemma. Because of the amount of new notation needed to define them, we have not specified the isomorphisms in the statement of Lemma 2.18, only asserted their existence. However, the maps themselves will be needed later, and so we will refer not only to Lemma 2.18 but also to its proof.
Lemma 2.18. Let
 $R=k[[x_{1},\ldots ,x_{n}]]$
and let
$R=k[[x_{1},\ldots ,x_{n}]]$
and let
![]() $I$
be an ideal of
$I$
be an ideal of
![]() $R$
. Let
$R$
. Let
 $R^{\prime }=R[[z]]$
and
$R^{\prime }=R[[z]]$
and
 $I^{\prime }=IR^{\prime }+(z)$
. Then for all
$I^{\prime }=IR^{\prime }+(z)$
. Then for all
![]() $p$
and
$p$
and
![]() $q$
, we have an isomorphism
$q$
, we have an isomorphism
 $$\begin{eqnarray}H_{\text{dR}}^{p}(H_{I}^{q}(R))\simeq H_{\text{dR}}^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime }))\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{dR}}^{p}(H_{I}^{q}(R))\simeq H_{\text{dR}}^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime }))\end{eqnarray}$$
of
![]() $k$
-spaces, where the de Rham cohomology is computed by regarding
$k$
-spaces, where the de Rham cohomology is computed by regarding
![]() $H_{I}^{q}(R)$
as a
$H_{I}^{q}(R)$
as a
 ${\mathcal{D}}(R,k)$
-module and
${\mathcal{D}}(R,k)$
-module and
 $H_{I^{\prime }}^{q+1}(R^{\prime })$
as a
$H_{I^{\prime }}^{q+1}(R^{\prime })$
as a
 ${\mathcal{D}}(R^{\prime },k)$
-module.
${\mathcal{D}}(R^{\prime },k)$
-module.
We first give a definition.
Definition 2.19. Let
![]() $M$
be any
$M$
be any
![]() $k$
-space. Then
$k$
-space. Then
 $M_{+}=\bigoplus _{i>0}M\cdot z^{-i}$
, a
$M_{+}=\bigoplus _{i>0}M\cdot z^{-i}$
, a
 ${\mathcal{D}}(k[[z]],k)$
-module, whose elements are finite sums
${\mathcal{D}}(k[[z]],k)$
-module, whose elements are finite sums
 $\sum _{i}(m_{i}/z^{i})$
where
$\sum _{i}(m_{i}/z^{i})$
where
 $m_{i}\in M$
. If
$m_{i}\in M$
. If
![]() $M$
is an
$M$
is an
![]() $R$
-module (respectively a
$R$
-module (respectively a
 ${\mathcal{D}}(R,k)$
-module), then
${\mathcal{D}}(R,k)$
-module), then
![]() $M_{+}$
defined in this way is an
$M_{+}$
defined in this way is an
![]() $R^{\prime }$
-module (respectively a
$R^{\prime }$
-module (respectively a
 ${\mathcal{D}}(R^{\prime },k)$
-module), with
${\mathcal{D}}(R^{\prime },k)$
-module), with
![]() $\unicode[STIX]{x2202}_{z}$
-action defined by the quotient rule:
$\unicode[STIX]{x2202}_{z}$
-action defined by the quotient rule:
 $\unicode[STIX]{x2202}_{z}(m/z^{\unicode[STIX]{x1D6FC}})=-\unicode[STIX]{x1D6FC}m/z^{\unicode[STIX]{x1D6FC}+1}$
.
$\unicode[STIX]{x2202}_{z}(m/z^{\unicode[STIX]{x1D6FC}})=-\unicode[STIX]{x1D6FC}m/z^{\unicode[STIX]{x1D6FC}+1}$
.
We will frequently refer to this functor as the ‘
![]() $+$
-operation’ on
$+$
-operation’ on
![]() $R$
-modules or
$R$
-modules or
![]() $k$
-spaces. In the case of an
$k$
-spaces. In the case of an
![]() $R$
-module
$R$
-module
![]() $M$
, this definition coincides with the ‘key functor’
$M$
, this definition coincides with the ‘key functor’
 $G(M)=M\otimes _{R}R_{z}^{\prime }/R^{\prime }$
of Núñez–Betancourt and Witt [Reference Núñez-Betancourt and WittNBW14, § 3]. A special case of one of their results will be useful for us.
$G(M)=M\otimes _{R}R_{z}^{\prime }/R^{\prime }$
of Núñez–Betancourt and Witt [Reference Núñez-Betancourt and WittNBW14, § 3]. A special case of one of their results will be useful for us.
Proposition 2.20 [Reference Núñez-Betancourt and WittNBW14, Lemma 3.9].
With
![]() $R$
,
$R$
,
![]() $R^{\prime }$
,
$R^{\prime }$
,
![]() $I$
, and
$I$
, and
![]() $I^{\prime }$
as in the statement of Lemma 2.18, we have isomorphisms
$I^{\prime }$
as in the statement of Lemma 2.18, we have isomorphisms
 $$\begin{eqnarray}(H_{I}^{p}(R))_{+}\simeq H_{I^{\prime }}^{p+1}(R^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}(H_{I}^{p}(R))_{+}\simeq H_{I^{\prime }}^{p+1}(R^{\prime })\end{eqnarray}$$
of
![]() $R^{\prime }$
-modules, for all
$R^{\prime }$
-modules, for all
![]() $p$
(these isomorphisms are functorial in
$p$
(these isomorphisms are functorial in
![]() $R$
).
$R$
).
We need one final ingredient before giving the proof of Lemma 2.18: a short exact sequence relating the ‘full’ de Rham complex
![]() $\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }$
of
$\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }$
of
![]() $R^{\prime }$
with its ‘partial’ de Rham complex
$R^{\prime }$
with its ‘partial’ de Rham complex
 $R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
defined using the derivations
$R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
defined using the derivations
 $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
but omitting
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
but omitting
 $\unicode[STIX]{x2202}_{z}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z$
.
$\unicode[STIX]{x2202}_{z}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z$
.
Definition 2.21. With
![]() $R$
and
$R$
and
![]() $R^{\prime }$
as in the statement of Lemma 2.18, we define a short exact sequence of complexes
$R^{\prime }$
as in the statement of Lemma 2.18, we define a short exact sequence of complexes
 $$\begin{eqnarray}0\rightarrow R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}}\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}}\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\rightarrow 0,\end{eqnarray}$$
where the map
![]() $\unicode[STIX]{x1D704}$
is simply the wedge product with
$\unicode[STIX]{x1D704}$
is simply the wedge product with
![]() $dz$
, and so its image is precisely the direct sum of those summands of
$dz$
, and so its image is precisely the direct sum of those summands of
![]() $\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }$
with a
$\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }$
with a
![]() $dz$
wedge factor (thus
$dz$
wedge factor (thus
![]() $\unicode[STIX]{x1D70B}$
corresponds to setting
$\unicode[STIX]{x1D70B}$
corresponds to setting
![]() $dz=0$
). The sheaf-theoretic analogue, a short exact sequence of complexes of sheaves on
$dz=0$
). The sheaf-theoretic analogue, a short exact sequence of complexes of sheaves on
![]() $X^{\prime }$
, is constructed similarly.
$X^{\prime }$
, is constructed similarly.
This short exact sequence of complexes gives rise to a long exact sequence of cohomology:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \cdots \rightarrow h^{p-1}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{c^{p-1}}h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1])\rightarrow h^{p}(\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{c^{p}}h^{p+1}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1])\rightarrow \cdots \,,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \cdots \rightarrow h^{p-1}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{c^{p-1}}h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1])\rightarrow h^{p}(\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{c^{p}}h^{p+1}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1])\rightarrow \cdots \,,\nonumber\end{eqnarray}$$
where c denotes the connecting homomorphism. After accounting for the shift of
![]() $-1$
, we see that
$-1$
, we see that
![]() $c^{p}$
is a map from the
$c^{p}$
is a map from the
 ${\mathcal{D}}(k[[z]],k)$
-module
${\mathcal{D}}(k[[z]],k)$
-module
 $h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
to itself. We will need precisely to identify the maps
$h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
to itself. We will need precisely to identify the maps
![]() $c^{p}$
.
$c^{p}$
.
Lemma 2.22. With the notation of the previous paragraph, we have
 $c^{p}=(-1)^{p}\unicode[STIX]{x2202}_{z}$
as maps from the
$c^{p}=(-1)^{p}\unicode[STIX]{x2202}_{z}$
as maps from the
 ${\mathcal{D}}(k[[z]],k)$
-module
${\mathcal{D}}(k[[z]],k)$
-module
 $h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
to itself. (The same holds if
$h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
to itself. (The same holds if
![]() $R^{\prime }$
is replaced with any
$R^{\prime }$
is replaced with any
 ${\mathcal{D}}(R^{\prime },k)$
-module.)
${\mathcal{D}}(R^{\prime },k)$
-module.)
Proof. We use the explicit construction of the connecting homomorphism given, for example, in [Reference RotmanRot09, Proposition 6.9]. Denote by
![]() $d_{R^{\prime }}^{\bullet }$
the differentials in the de Rham complex
$d_{R^{\prime }}^{\bullet }$
the differentials in the de Rham complex
![]() $\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }$
. Given an element of
$\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }$
. Given an element of
 $h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
, which is the cohomology class of some cocycle
$h^{p}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
, which is the cohomology class of some cocycle
 $\unicode[STIX]{x1D714}\in R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p}$
, the image under
$\unicode[STIX]{x1D714}\in R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p}$
, the image under
![]() $c^{p}$
of this class is taken to be the class of the cocycle
$c^{p}$
of this class is taken to be the class of the cocycle
 $(\unicode[STIX]{x1D704}^{p+1})^{-1}(d_{R^{\prime }}^{p}((\unicode[STIX]{x1D70B}^{p})^{-1}(\unicode[STIX]{x1D714})))$
, where the superscript
$(\unicode[STIX]{x1D704}^{p+1})^{-1}(d_{R^{\prime }}^{p}((\unicode[STIX]{x1D70B}^{p})^{-1}(\unicode[STIX]{x1D714})))$
, where the superscript
![]() $-1$
means ‘choose any preimage’: this definition is independent of all choices made. We proceed to calculate this composite, making convenient choices for the preimages.
$-1$
means ‘choose any preimage’: this definition is independent of all choices made. We proceed to calculate this composite, making convenient choices for the preimages.
We can write
![]() $\unicode[STIX]{x1D714}$
as a sum
$\unicode[STIX]{x1D714}$
as a sum
 $$\begin{eqnarray}\unicode[STIX]{x1D714}=\mathop{\sum }_{i_{1},\ldots ,i_{p}}\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}}\,dx_{i_{1}}\wedge \cdots \wedge dx_{i_{p}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}=\mathop{\sum }_{i_{1},\ldots ,i_{p}}\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}}\,dx_{i_{1}}\wedge \cdots \wedge dx_{i_{p}},\end{eqnarray}$$
where all
 $\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}}\in R^{\prime }$
. One choice of preimage
$\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}}\in R^{\prime }$
. One choice of preimage
 $(\unicode[STIX]{x1D70B}^{p})^{-1}(\unicode[STIX]{x1D714})$
is
$(\unicode[STIX]{x1D70B}^{p})^{-1}(\unicode[STIX]{x1D714})$
is
![]() $\unicode[STIX]{x1D714}$
itself, since none of its terms contain
$\unicode[STIX]{x1D714}$
itself, since none of its terms contain
![]() $dz$
wedge factors and hence all are left fixed by
$dz$
wedge factors and hence all are left fixed by
![]() $\unicode[STIX]{x1D70B}^{p}$
. Therefore
$\unicode[STIX]{x1D70B}^{p}$
. Therefore
 $d_{R^{\prime }}^{p}((\unicode[STIX]{x1D70B}^{p})^{-1}(\unicode[STIX]{x1D714}))=d_{R^{\prime }}^{p}(\unicode[STIX]{x1D714})$
. Since
$d_{R^{\prime }}^{p}((\unicode[STIX]{x1D70B}^{p})^{-1}(\unicode[STIX]{x1D714}))=d_{R^{\prime }}^{p}(\unicode[STIX]{x1D714})$
. Since
![]() $\unicode[STIX]{x1D714}$
is a cocycle in
$\unicode[STIX]{x1D714}$
is a cocycle in
 $R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p}$
, its image under the
$R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p}$
, its image under the
![]() $p$
th de Rham differential with respect to
$p$
th de Rham differential with respect to
 $dx_{1},\ldots ,dx_{n}$
is zero, and so the only terms in the definition of
$dx_{1},\ldots ,dx_{n}$
is zero, and so the only terms in the definition of
![]() $d_{R^{\prime }}^{p}(\unicode[STIX]{x1D714})$
that survive are those involving
$d_{R^{\prime }}^{p}(\unicode[STIX]{x1D714})$
that survive are those involving
![]() $dz$
. That is, we have
$dz$
. That is, we have
 $$\begin{eqnarray}d_{R^{\prime }}^{p}(\unicode[STIX]{x1D714})=\mathop{\sum }_{i_{1},\ldots ,i_{p}}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}})\,dz\wedge dx_{i_{1}}\wedge \cdots \wedge dx_{i_{p}},\end{eqnarray}$$
$$\begin{eqnarray}d_{R^{\prime }}^{p}(\unicode[STIX]{x1D714})=\mathop{\sum }_{i_{1},\ldots ,i_{p}}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}})\,dz\wedge dx_{i_{1}}\wedge \cdots \wedge dx_{i_{p}},\end{eqnarray}$$
which, by rearranging the wedge terms, is equal to
 $$\begin{eqnarray}\mathop{\sum }_{i_{1},\ldots ,i_{p}}(-1)^{p}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}})\,dx_{i_{1}}\wedge \cdots \wedge dx_{i_{p}}\wedge dz.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i_{1},\ldots ,i_{p}}(-1)^{p}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}})\,dx_{i_{1}}\wedge \cdots \wedge dx_{i_{p}}\wedge dz.\end{eqnarray}$$
Finally, a choice of preimage under
![]() $\unicode[STIX]{x1D704}^{p+1}$
(which is simply the map
$\unicode[STIX]{x1D704}^{p+1}$
(which is simply the map
![]() $\wedge \,dz$
) for the above sum is
$\wedge \,dz$
) for the above sum is
 $$\begin{eqnarray}(\unicode[STIX]{x1D704}^{p+1})^{-1}(d_{R^{\prime }}^{p}((\unicode[STIX]{x1D70B}^{p})^{-1}(\unicode[STIX]{x1D714})))=\mathop{\sum }_{i_{1},\ldots ,i_{p}}(-1)^{p}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}})\,dx_{i_{1}}\wedge \cdots \wedge dx_{i_{p}}=(-1)^{p}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D714}),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D704}^{p+1})^{-1}(d_{R^{\prime }}^{p}((\unicode[STIX]{x1D70B}^{p})^{-1}(\unicode[STIX]{x1D714})))=\mathop{\sum }_{i_{1},\ldots ,i_{p}}(-1)^{p}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}})\,dx_{i_{1}}\wedge \cdots \wedge dx_{i_{p}}=(-1)^{p}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D714}),\end{eqnarray}$$
from which the lemma follows. (The same calculation works for arbitrary
 ${\mathcal{D}}(R^{\prime },k)$
-modules
${\mathcal{D}}(R^{\prime },k)$
-modules
![]() $M$
, replacing each
$M$
, replacing each
![]() $\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}}$
with an element
$\unicode[STIX]{x1D70C}_{i_{1}\cdots i_{p}}$
with an element
![]() $m_{i_{1}\cdots i_{p}}$
of
$m_{i_{1}\cdots i_{p}}$
of
![]() $M$
.)◻
$M$
.)◻
We can now prove Lemma 2.18.
Proof of Lemma 2.18.
The differentials in the complexes of Definition 2.21 are merely
![]() $k$
-linear, but in every degree
$k$
-linear, but in every degree
![]() $p$
, the short exact sequence
$p$
, the short exact sequence
 $$\begin{eqnarray}0\rightarrow R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p-1}\xrightarrow[{}]{\unicode[STIX]{x1D704}^{p}}\unicode[STIX]{x1D6FA}_{R^{\prime }}^{p}\rightarrow R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p-1}\xrightarrow[{}]{\unicode[STIX]{x1D704}^{p}}\unicode[STIX]{x1D6FA}_{R^{\prime }}^{p}\rightarrow R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\rightarrow 0\end{eqnarray}$$
is a split exact sequence of finite free
![]() $R^{\prime }$
-modules. As local cohomology commutes with direct sums, this sequence remains split exact after applying the functor
$R^{\prime }$
-modules. As local cohomology commutes with direct sums, this sequence remains split exact after applying the functor
![]() $H_{I^{\prime }}^{q}$
for any
$H_{I^{\prime }}^{q}$
for any
![]() $q$
:
$q$
:
 $$\begin{eqnarray}0\rightarrow H_{I^{\prime }}^{q}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p-1})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{q}^{p}}H_{I^{\prime }}^{q}(\unicode[STIX]{x1D6FA}_{R^{\prime }}^{p})\rightarrow H_{I^{\prime }}^{q}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H_{I^{\prime }}^{q}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p-1})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{q}^{p}}H_{I^{\prime }}^{q}(\unicode[STIX]{x1D6FA}_{R^{\prime }}^{p})\rightarrow H_{I^{\prime }}^{q}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{p})\rightarrow 0.\end{eqnarray}$$
Fixing
![]() $q$
but varying
$q$
but varying
![]() $p$
, we obtain a short exact sequence of complexes of
$p$
, we obtain a short exact sequence of complexes of
![]() $k$
-spaces
$k$
-spaces
 $$\begin{eqnarray}0\rightarrow H_{I^{\prime }}^{q}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1])\xrightarrow[{}]{\unicode[STIX]{x1D704}_{q}^{\bullet }}H_{I^{\prime }}^{q}(\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })\rightarrow H_{I^{\prime }}^{q}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H_{I^{\prime }}^{q}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1])\xrightarrow[{}]{\unicode[STIX]{x1D704}_{q}^{\bullet }}H_{I^{\prime }}^{q}(\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })\rightarrow H_{I^{\prime }}^{q}(R^{\prime }\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\rightarrow 0\end{eqnarray}$$
which we can rewrite (replacing
![]() $q$
with
$q$
with
![]() $q+1$
) as
$q+1$
) as
 $$\begin{eqnarray}0\rightarrow H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}_{q+1}^{\bullet }}H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }\rightarrow H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}_{q+1}^{\bullet }}H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }\rightarrow H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\rightarrow 0\end{eqnarray}$$
since
![]() $\unicode[STIX]{x1D6FA}_{R}^{i}$
(respectively
$\unicode[STIX]{x1D6FA}_{R}^{i}$
(respectively
![]() $\unicode[STIX]{x1D6FA}_{R^{\prime }}^{i}$
) is a finite free
$\unicode[STIX]{x1D6FA}_{R^{\prime }}^{i}$
) is a finite free
![]() $R$
- (respectively
$R$
- (respectively
![]() $R^{\prime }$
-) module. This short exact sequence of complexes gives rise to a long exact sequence of cohomology which (accounting for the shift of
$R^{\prime }$
-) module. This short exact sequence of complexes gives rise to a long exact sequence of cohomology which (accounting for the shift of
![]() $-1$
) takes the form
$-1$
) takes the form
 $$\begin{eqnarray}\displaystyle \cdots \rightarrow h^{p}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }) & \xrightarrow[{}]{\unicode[STIX]{x2202}_{z}} & \displaystyle h^{p}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{\overline{\unicode[STIX]{x1D704}}_{q+1}^{p}}h^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })\nonumber\\ \displaystyle & \rightarrow & \displaystyle h^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{z}}h^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\rightarrow \cdots \,,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \cdots \rightarrow h^{p}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }) & \xrightarrow[{}]{\unicode[STIX]{x2202}_{z}} & \displaystyle h^{p}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{\overline{\unicode[STIX]{x1D704}}_{q+1}^{p}}h^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })\nonumber\\ \displaystyle & \rightarrow & \displaystyle h^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{z}}h^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\rightarrow \cdots \,,\nonumber\end{eqnarray}$$
where we know by Lemma 2.22 that, up to a sign, the connecting homomorphism is
![]() $\unicode[STIX]{x2202}_{z}$
. Now by Lemma 2.20, we know that
$\unicode[STIX]{x2202}_{z}$
. Now by Lemma 2.20, we know that
 $H_{I^{\prime }}^{q+1}(R^{\prime })\simeq (H_{I}^{q}(R))_{+}$
as
$H_{I^{\prime }}^{q+1}(R^{\prime })\simeq (H_{I}^{q}(R))_{+}$
as
![]() $R^{\prime }$
-modules. The differentials in the complex
$R^{\prime }$
-modules. The differentials in the complex
 $H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
do not involve
$H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
do not involve
![]() $z$
or
$z$
or
![]() $dz$
, and so the
$dz$
, and so the
![]() $+$
-operation passes to its cohomology, since cohomology commutes with direct sums: we have
$+$
-operation passes to its cohomology, since cohomology commutes with direct sums: we have
 $$\begin{eqnarray}h^{p}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\simeq (h^{p}(H_{I}^{q}(R)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))_{+}\end{eqnarray}$$
$$\begin{eqnarray}h^{p}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\simeq (h^{p}(H_{I}^{q}(R)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))_{+}\end{eqnarray}$$
as
![]() $k$
-spaces for all
$k$
-spaces for all
![]() $p$
. For any
$p$
. For any
![]() $k$
-space
$k$
-space
![]() $M$
, the action of
$M$
, the action of
![]() $\unicode[STIX]{x2202}_{z}$
on
$\unicode[STIX]{x2202}_{z}$
on
![]() $M_{+}$
is given in Definition 2.19, and it is clear from this definition (since
$M_{+}$
is given in Definition 2.19, and it is clear from this definition (since
 $\operatorname{char}(k)=0$
) that
$\operatorname{char}(k)=0$
) that
 $\ker (\unicode[STIX]{x2202}_{z}:M_{+}\rightarrow M_{+})=0$
and
$\ker (\unicode[STIX]{x2202}_{z}:M_{+}\rightarrow M_{+})=0$
and
 $\operatorname{coker}(\unicode[STIX]{x2202}_{z}:M_{+}\rightarrow M_{+})\simeq M$
, the latter corresponding to the
$\operatorname{coker}(\unicode[STIX]{x2202}_{z}:M_{+}\rightarrow M_{+})\simeq M$
, the latter corresponding to the
![]() $1/z$
-component of
$1/z$
-component of
![]() $M_{+}$
. Returning to the displayed portion of the long exact sequence (with
$M_{+}$
. Returning to the displayed portion of the long exact sequence (with
 $M=h^{p}(H_{I}^{q}(R)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
), the second
$M=h^{p}(H_{I}^{q}(R)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
), the second
![]() $\unicode[STIX]{x2202}_{z}$
is injective, and so by exactness the unlabeled arrow is the zero map; this implies that
$\unicode[STIX]{x2202}_{z}$
is injective, and so by exactness the unlabeled arrow is the zero map; this implies that
![]() $\overline{\unicode[STIX]{x1D704}}_{q+1}^{p}$
is surjective, inducing an isomorphism between
$\overline{\unicode[STIX]{x1D704}}_{q+1}^{p}$
is surjective, inducing an isomorphism between
 $h^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })=H_{\text{dR}}^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime }))$
and the cokernel of the first
$h^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime })\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })=H_{\text{dR}}^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime }))$
and the cokernel of the first
![]() $\unicode[STIX]{x2202}_{z}$
. Since this cokernel is isomorphic to
$\unicode[STIX]{x2202}_{z}$
. Since this cokernel is isomorphic to
 $h^{p}(H_{I}^{q}(R)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })=H_{\text{dR}}^{p}(H_{I}^{q}(R))$
, the proof of Lemma 2.18, and hence of Proposition 2.17(b), is complete.◻
$h^{p}(H_{I}^{q}(R)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })=H_{\text{dR}}^{p}(H_{I}^{q}(R))$
, the proof of Lemma 2.18, and hence of Proposition 2.17(b), is complete.◻
Proposition 2.17 gives a new set of invariants for complete local rings in equicharacteristic zero, namely, the (finite) dimensions of the
![]() $E_{2}$
-objects, with the bidegree shift taken into account.
$E_{2}$
-objects, with the bidegree shift taken into account.
Definition 2.23. For all
 $p,q\geqslant 0$
, let
$p,q\geqslant 0$
, let
 $\unicode[STIX]{x1D70C}_{p,q}=\dim _{k}(H_{\text{dR}}^{n-p}(H_{I}^{n-q}(R)))$
.
$\unicode[STIX]{x1D70C}_{p,q}=\dim _{k}(H_{\text{dR}}^{n-p}(H_{I}^{n-q}(R)))$
.
By Proposition 2.17,
![]() $\unicode[STIX]{x1D70C}_{p,q}$
is finite and depends only on
$\unicode[STIX]{x1D70C}_{p,q}$
is finite and depends only on
![]() $A$
and a choice of coefficient field
$A$
and a choice of coefficient field
![]() $k\subset A$
. We note the similarity of the definition of the invariants
$k\subset A$
. We note the similarity of the definition of the invariants
![]() $\unicode[STIX]{x1D70C}_{p,q}$
to the Lyubeznik numbers
$\unicode[STIX]{x1D70C}_{p,q}$
to the Lyubeznik numbers
![]() $\unicode[STIX]{x1D706}_{p,q}$
[Reference LyubeznikLyu93, Theorem–Definition 4.1], although our
$\unicode[STIX]{x1D706}_{p,q}$
[Reference LyubeznikLyu93, Theorem–Definition 4.1], although our
![]() $\unicode[STIX]{x1D70C}_{p,q}$
appear to be well defined only in the characteristic zero case. One way to define
$\unicode[STIX]{x1D70C}_{p,q}$
appear to be well defined only in the characteristic zero case. One way to define
![]() $\unicode[STIX]{x1D706}_{p,q}$
is as the dimension of the socle of
$\unicode[STIX]{x1D706}_{p,q}$
is as the dimension of the socle of
 $H_{\mathfrak{m}}^{p}(H_{I}^{n-q}(R))$
, where
$H_{\mathfrak{m}}^{p}(H_{I}^{n-q}(R))$
, where
![]() $\mathfrak{m}\subset R$
is the maximal ideal [Reference LyubeznikLyu06, Lemma 2.2]. To define the
$\mathfrak{m}\subset R$
is the maximal ideal [Reference LyubeznikLyu06, Lemma 2.2]. To define the
![]() $\unicode[STIX]{x1D70C}_{p,q}$
, we use de Rham cohomology instead of iterated local cohomology; furthermore, note the difference in the indices.
$\unicode[STIX]{x1D70C}_{p,q}$
, we use de Rham cohomology instead of iterated local cohomology; furthermore, note the difference in the indices.
Remark 2.24. If
 $H_{I}^{n-q}(R)$
is supported only at
$H_{I}^{n-q}(R)$
is supported only at
![]() $\mathfrak{m}$
, so that
$\mathfrak{m}$
, so that
 $H_{I}^{n-q}(R)\simeq E^{\oplus \unicode[STIX]{x1D706}_{0,q}}$
for some
$H_{I}^{n-q}(R)\simeq E^{\oplus \unicode[STIX]{x1D706}_{0,q}}$
for some
 $\unicode[STIX]{x1D706}_{0,q}\geqslant 0$
([Reference LyubeznikLyu93, Theorem 3.4]; here
$\unicode[STIX]{x1D706}_{0,q}\geqslant 0$
([Reference LyubeznikLyu93, Theorem 3.4]; here
![]() $E$
is the Matlis dualizing module), then the de Rham cohomology of
$E$
is the Matlis dualizing module), then the de Rham cohomology of
 $H_{I}^{n-q}(R)$
is easy to calculate: we have
$H_{I}^{n-q}(R)$
is easy to calculate: we have
 $\unicode[STIX]{x1D70C}_{p,q}=\unicode[STIX]{x1D706}_{0,q}$
if
$\unicode[STIX]{x1D70C}_{p,q}=\unicode[STIX]{x1D706}_{0,q}$
if
![]() $p=0$
, and
$p=0$
, and
 $\unicode[STIX]{x1D70C}_{p,q}=0$
otherwise. Therefore, in this case,
$\unicode[STIX]{x1D70C}_{p,q}=0$
otherwise. Therefore, in this case,
 $\unicode[STIX]{x1D70C}_{p,q}=\unicode[STIX]{x1D706}_{p,q}$
for all
$\unicode[STIX]{x1D70C}_{p,q}=\unicode[STIX]{x1D706}_{p,q}$
for all
![]() $p$
and
$p$
and
![]() $q$
.
$q$
.
We now prove the full statement of Theorem A(a) (we have already proved part (b) above). Our goal is to construct a bidegree-shifted morphism between the Hodge–de Rham spectral sequences arising from two surjections
![]() $R\rightarrow A$
and
$R\rightarrow A$
and
 $R^{\prime }\rightarrow A$
of
$R^{\prime }\rightarrow A$
of
![]() $k$
-algebras which, at the level of
$k$
-algebras which, at the level of
![]() $E_{2}$
-objects, consists of the isomorphisms of Lemma 2.18: by Proposition 2.12, this is enough. The preliminary reductions given in the paragraph before Lemma 2.18 remain valid when considering the spectral sequences, so we need only address the case in which
$E_{2}$
-objects, consists of the isomorphisms of Lemma 2.18: by Proposition 2.12, this is enough. The preliminary reductions given in the paragraph before Lemma 2.18 remain valid when considering the spectral sequences, so we need only address the case in which
![]() $R$
,
$R$
,
![]() $R^{\prime }$
,
$R^{\prime }$
,
![]() $I$
, and
$I$
, and
![]() $I^{\prime }$
are as in the statement of that lemma. The basic strategy is the same: we use the short exact sequence Definition 2.21 of complexes as well as the
$I^{\prime }$
are as in the statement of that lemma. The basic strategy is the same: we use the short exact sequence Definition 2.21 of complexes as well as the
![]() $+$
-operation, which will now be applied to double complex resolutions of the de Rham complexes
$+$
-operation, which will now be applied to double complex resolutions of the de Rham complexes
![]() $\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
and
$\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
and
![]() $\unicode[STIX]{x1D6FA}_{X^{\prime }}^{\bullet }$
. Our first task is to construct these; we work first at the level of
$\unicode[STIX]{x1D6FA}_{X^{\prime }}^{\bullet }$
. Our first task is to construct these; we work first at the level of
![]() $R$
- (respectively
$R$
- (respectively
![]() $R^{\prime }$
-) modules and
$R^{\prime }$
-) modules and
![]() $k$
-linear maps, and then sheafify the results.
$k$
-linear maps, and then sheafify the results.
Lemma 2.25. Let
![]() ${\mathcal{I}}^{\bullet }$
be the minimal injective resolution of
${\mathcal{I}}^{\bullet }$
be the minimal injective resolution of
![]() $R$
as an
$R$
as an
![]() $R$
-module. For all
$R$
-module. For all
![]() $p$
,
$p$
,
![]() ${\mathcal{I}}^{p}$
has a structure of
${\mathcal{I}}^{p}$
has a structure of
 ${\mathcal{D}}(R,k)$
-module, and
${\mathcal{D}}(R,k)$
-module, and
 $R\rightarrow {\mathcal{I}}^{\bullet }$
is a complex in the category of
$R\rightarrow {\mathcal{I}}^{\bullet }$
is a complex in the category of
 ${\mathcal{D}}(R,k)$
-modules.
${\mathcal{D}}(R,k)$
-modules.
Proof. We use the Cousin complex, for which [Reference HartshorneHar66, IV.2] is the original reference. Recall that the Cousin complex
![]() $C^{\bullet }(R)$
of
$C^{\bullet }(R)$
of
![]() $R$
is constructed recursively in the following way:
$R$
is constructed recursively in the following way:
 $C^{-2}(R)=0$
,
$C^{-2}(R)=0$
,
 $C^{-1}(R)=R$
, and for
$C^{-1}(R)=R$
, and for
![]() $i\geqslant 0$
,
$i\geqslant 0$
,
 $C^{i}(R)=\oplus (\operatorname{coker}d^{i-2})_{\mathfrak{p}}$
, the direct sum extending over all
$C^{i}(R)=\oplus (\operatorname{coker}d^{i-2})_{\mathfrak{p}}$
, the direct sum extending over all
 $\mathfrak{p}\in \operatorname{Spec}(R)$
such that
$\mathfrak{p}\in \operatorname{Spec}(R)$
such that
 $\operatorname{ht}\mathfrak{p}=i$
. The differentials in the complex are simply the natural localization maps. It is immediate from the definition of the Cousin complex that it is a complex of
$\operatorname{ht}\mathfrak{p}=i$
. The differentials in the complex are simply the natural localization maps. It is immediate from the definition of the Cousin complex that it is a complex of
 ${\mathcal{D}}(R,k)$
-modules, since localizations of
${\mathcal{D}}(R,k)$
-modules, since localizations of
 ${\mathcal{D}}(R,k)$
-modules are again
${\mathcal{D}}(R,k)$
-modules are again
 ${\mathcal{D}}(R,k)$
-modules and natural localization maps are
${\mathcal{D}}(R,k)$
-modules and natural localization maps are
 ${\mathcal{D}}(R,k)$
-linear [Reference LyubeznikLyu93, Example 2.1]. However, since
${\mathcal{D}}(R,k)$
-linear [Reference LyubeznikLyu93, Example 2.1]. However, since
![]() $R$
is a Gorenstein local ring, its minimal injective resolution and its Cousin complex coincide [Reference SharpSha69, Theorem 5.4].◻
$R$
is a Gorenstein local ring, its minimal injective resolution and its Cousin complex coincide [Reference SharpSha69, Theorem 5.4].◻
Likewise, if we let
![]() ${\mathcal{J}}^{\bullet }$
be the minimal injective resolution of
${\mathcal{J}}^{\bullet }$
be the minimal injective resolution of
![]() $R^{\prime }$
as an
$R^{\prime }$
as an
![]() $R^{\prime }$
-module, Lemma 2.25 implies that
$R^{\prime }$
-module, Lemma 2.25 implies that
 $R^{\prime }\rightarrow {\mathcal{J}}^{\bullet }$
is a complex in the category of
$R^{\prime }\rightarrow {\mathcal{J}}^{\bullet }$
is a complex in the category of
 ${\mathcal{D}}(R^{\prime },k)$
-modules. By taking finite direct sums of the resolutions
${\mathcal{D}}(R^{\prime },k)$
-modules. By taking finite direct sums of the resolutions
![]() ${\mathcal{I}}^{\bullet }$
and
${\mathcal{I}}^{\bullet }$
and
![]() ${\mathcal{J}}^{\bullet }$
, we construct three double complexes.
${\mathcal{J}}^{\bullet }$
, we construct three double complexes.
Definition 2.26. Let
![]() ${\mathcal{I}}^{\bullet ,\bullet }$
be the double complex
${\mathcal{I}}^{\bullet ,\bullet }$
be the double complex
 ${\mathcal{I}}^{p,q}={\mathcal{I}}^{q}\otimes _{R}\unicode[STIX]{x1D6FA}_{R}^{p}$
whose vertical differentials are induced by the differentials in the complex
${\mathcal{I}}^{p,q}={\mathcal{I}}^{q}\otimes _{R}\unicode[STIX]{x1D6FA}_{R}^{p}$
whose vertical differentials are induced by the differentials in the complex
![]() ${\mathcal{I}}^{\bullet }$
and whose horizontal differentials are those in the de Rham complexes
${\mathcal{I}}^{\bullet }$
and whose horizontal differentials are those in the de Rham complexes
 ${\mathcal{I}}^{q}\otimes _{R}\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
of the
${\mathcal{I}}^{q}\otimes _{R}\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
of the
 ${\mathcal{D}}(R,k)$
-modules
${\mathcal{D}}(R,k)$
-modules
![]() ${\mathcal{I}}^{q}$
. Similarly, let
${\mathcal{I}}^{q}$
. Similarly, let
![]() ${\mathcal{J}}_{0}^{\bullet ,\bullet }$
be the double complex
${\mathcal{J}}_{0}^{\bullet ,\bullet }$
be the double complex
 ${\mathcal{J}}_{0}^{p,q}={\mathcal{J}}^{q}\otimes _{R}\unicode[STIX]{x1D6FA}_{R}^{p}$
and let
${\mathcal{J}}_{0}^{p,q}={\mathcal{J}}^{q}\otimes _{R}\unicode[STIX]{x1D6FA}_{R}^{p}$
and let
![]() ${\mathcal{J}}^{\bullet ,\bullet }$
be the double complex
${\mathcal{J}}^{\bullet ,\bullet }$
be the double complex
 ${\mathcal{J}}^{p,q}={\mathcal{J}}^{q}\otimes _{R^{\prime }}\unicode[STIX]{x1D6FA}_{R^{\prime }}^{p}$
.
${\mathcal{J}}^{p,q}={\mathcal{J}}^{q}\otimes _{R^{\prime }}\unicode[STIX]{x1D6FA}_{R^{\prime }}^{p}$
.
Note that these double complexes have exact sequences of
![]() $R$
- (or
$R$
- (or
![]() $R^{\prime }$
-) modules for columns, but merely complexes in the category of
$R^{\prime }$
-) modules for columns, but merely complexes in the category of
![]() $k$
-spaces for rows. In the case of
$k$
-spaces for rows. In the case of
![]() ${\mathcal{I}}^{\bullet ,\bullet }$
, the rows are the de Rham complexes of the
${\mathcal{I}}^{\bullet ,\bullet }$
, the rows are the de Rham complexes of the
 ${\mathcal{D}}(R,k)$
-modules
${\mathcal{D}}(R,k)$
-modules
![]() ${\mathcal{I}}^{q}$
; in the case of
${\mathcal{I}}^{q}$
; in the case of
![]() ${\mathcal{J}}_{0}^{\bullet ,\bullet }$
, the rows are the de Rham complexes of the
${\mathcal{J}}_{0}^{\bullet ,\bullet }$
, the rows are the de Rham complexes of the
![]() ${\mathcal{J}}^{q}$
regarded as
${\mathcal{J}}^{q}$
regarded as
 ${\mathcal{D}}(R,k)$
-modules; and in the case of
${\mathcal{D}}(R,k)$
-modules; and in the case of
![]() ${\mathcal{J}}^{\bullet ,\bullet }$
, the rows are the de Rham complexes of the
${\mathcal{J}}^{\bullet ,\bullet }$
, the rows are the de Rham complexes of the
![]() ${\mathcal{J}}^{q}$
regarded as
${\mathcal{J}}^{q}$
regarded as
 ${\mathcal{D}}(R^{\prime },k)$
-modules. (We recall again Convention 2.1: if we write
${\mathcal{D}}(R^{\prime },k)$
-modules. (We recall again Convention 2.1: if we write
![]() $\otimes \,\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, the tensor products of objects are being taken over
$\otimes \,\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, the tensor products of objects are being taken over
![]() $R$
, but if we write
$R$
, but if we write
![]() $\otimes \,\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }$
, the tensor products of objects are being taken over
$\otimes \,\unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }$
, the tensor products of objects are being taken over
![]() $R^{\prime }$
.)
$R^{\prime }$
.)
Each of these three double complexes can be sheafified. Consider first the double complex
![]() ${\mathcal{I}}^{\bullet ,\bullet }$
. For all
${\mathcal{I}}^{\bullet ,\bullet }$
. For all
![]() $p$
and
$p$
and
![]() $q$
, let
$q$
, let
![]() $\widetilde{{\mathcal{I}}^{p,q}}$
denote the associated quasi-coherent sheaf on
$\widetilde{{\mathcal{I}}^{p,q}}$
denote the associated quasi-coherent sheaf on
![]() $X$
. The vertical differentials of
$X$
. The vertical differentials of
![]() ${\mathcal{I}}^{\bullet ,\bullet }$
are
${\mathcal{I}}^{\bullet ,\bullet }$
are
![]() $R$
-linear, and so induce
$R$
-linear, and so induce
![]() ${\mathcal{O}}_{X}$
-linear morphisms between the associated sheaves, and the horizontal differentials induce
${\mathcal{O}}_{X}$
-linear morphisms between the associated sheaves, and the horizontal differentials induce
![]() $k$
-linear morphisms on the associated sheaves in the same way that the de Rham complex of
$k$
-linear morphisms on the associated sheaves in the same way that the de Rham complex of
![]() ${\mathcal{O}}_{X}$
is constructed. For all
${\mathcal{O}}_{X}$
is constructed. For all
![]() $p$
and
$p$
and
![]() $q$
,
$q$
,
![]() ${\mathcal{I}}^{p,q}$
is an injective
${\mathcal{I}}^{p,q}$
is an injective
![]() $R$
-module, and so the sheaf
$R$
-module, and so the sheaf
![]() $\widetilde{{\mathcal{I}}^{p,q}}$
is flasque [Reference HartshorneHar77, Proposition III.3.4], and hence acyclic for the functor
$\widetilde{{\mathcal{I}}^{p,q}}$
is flasque [Reference HartshorneHar77, Proposition III.3.4], and hence acyclic for the functor
![]() $\unicode[STIX]{x1D6E4}_{Y}$
on the category of sheaves of
$\unicode[STIX]{x1D6E4}_{Y}$
on the category of sheaves of
![]() $k$
-spaces on
$k$
-spaces on
![]() $X$
[Reference HartshorneHar67, Proposition 1.10]. Therefore we have a double complex
$X$
[Reference HartshorneHar67, Proposition 1.10]. Therefore we have a double complex
![]() $\widetilde{{\mathcal{I}}^{\bullet ,\bullet }}$
whose objects are all
$\widetilde{{\mathcal{I}}^{\bullet ,\bullet }}$
whose objects are all
![]() $\unicode[STIX]{x1D6E4}_{Y}$
-acyclic sheaves of
$\unicode[STIX]{x1D6E4}_{Y}$
-acyclic sheaves of
![]() $k$
-spaces on
$k$
-spaces on
![]() $X$
and whose columns are acyclic resolutions of the
$X$
and whose columns are acyclic resolutions of the
![]() $\unicode[STIX]{x1D6FA}_{X}^{p}$
(because the associated sheaf functor is exact when applied to complexes of
$\unicode[STIX]{x1D6FA}_{X}^{p}$
(because the associated sheaf functor is exact when applied to complexes of
![]() $R$
-modules). In the same way, we sheafify the double complexes
$R$
-modules). In the same way, we sheafify the double complexes
![]() ${\mathcal{J}}_{0}^{\bullet ,\bullet }$
and
${\mathcal{J}}_{0}^{\bullet ,\bullet }$
and
![]() ${\mathcal{J}}^{\bullet ,\bullet }$
, obtaining double complexes
${\mathcal{J}}^{\bullet ,\bullet }$
, obtaining double complexes
![]() $\widetilde{{\mathcal{J}}_{0}^{\bullet ,\bullet }}$
and
$\widetilde{{\mathcal{J}}_{0}^{\bullet ,\bullet }}$
and
![]() $\widetilde{{\mathcal{J}}^{\bullet ,\bullet }}$
of sheaves of
$\widetilde{{\mathcal{J}}^{\bullet ,\bullet }}$
of sheaves of
![]() $k$
-spaces on
$k$
-spaces on
![]() $X^{\prime }$
which are
$X^{\prime }$
which are
![]() $\unicode[STIX]{x1D6E4}_{Y}$
-acyclic.
$\unicode[STIX]{x1D6E4}_{Y}$
-acyclic.
Definition 2.27. Let
![]() $E_{\bullet ,R}^{\bullet ,\bullet }$
be the column-filtered spectral sequence associated with the double complex
$E_{\bullet ,R}^{\bullet ,\bullet }$
be the column-filtered spectral sequence associated with the double complex
 $\unicode[STIX]{x1D6E4}_{Y}(X,\widetilde{{\mathcal{I}}^{\bullet ,\bullet }})$
of
$\unicode[STIX]{x1D6E4}_{Y}(X,\widetilde{{\mathcal{I}}^{\bullet ,\bullet }})$
of
![]() $k$
-spaces. Similarly, let
$k$
-spaces. Similarly, let
![]() $\mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
be the column-filtered spectral sequence associated with the double complex
$\mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
be the column-filtered spectral sequence associated with the double complex
 $\unicode[STIX]{x1D6E4}_{Y}(X^{\prime },\widetilde{{\mathcal{J}}^{\bullet ,\bullet }})$
, and let
$\unicode[STIX]{x1D6E4}_{Y}(X^{\prime },\widetilde{{\mathcal{J}}^{\bullet ,\bullet }})$
, and let
![]() ${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }$
be the column-filtered spectral sequence associated with the double complex
${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }$
be the column-filtered spectral sequence associated with the double complex
 $\unicode[STIX]{x1D6E4}_{Y}(X^{\prime },\widetilde{{\mathcal{J}}_{0}^{\bullet ,\bullet }})$
.
$\unicode[STIX]{x1D6E4}_{Y}(X^{\prime },\widetilde{{\mathcal{J}}_{0}^{\bullet ,\bullet }})$
.
By Lemma 2.13, we know that
![]() $E_{\bullet ,R}^{\bullet ,\bullet }$
coincides with the Hodge–de Rham spectral sequence for the complex
$E_{\bullet ,R}^{\bullet ,\bullet }$
coincides with the Hodge–de Rham spectral sequence for the complex
![]() $\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
, and that
$\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
, and that
![]() $\mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
coincides with the Hodge–de Rham spectral sequence for the complex
$\mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
coincides with the Hodge–de Rham spectral sequence for the complex
![]() $\unicode[STIX]{x1D6FA}_{X^{\prime }}^{\bullet }$
, so there is no ambiguity of notation. The ‘intermediate’ spectral sequence
$\unicode[STIX]{x1D6FA}_{X^{\prime }}^{\bullet }$
, so there is no ambiguity of notation. The ‘intermediate’ spectral sequence
![]() ${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }$
, which by Lemma 2.13 coincides with the hypercohomology spectral sequence for the complex
${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }$
, which by Lemma 2.13 coincides with the hypercohomology spectral sequence for the complex
 ${\mathcal{O}}_{X^{\prime }}\otimes \unicode[STIX]{x1D6FA}_{X}^{\bullet }$
, will be used to relate the Hodge–de Rham spectral sequences for
${\mathcal{O}}_{X^{\prime }}\otimes \unicode[STIX]{x1D6FA}_{X}^{\bullet }$
, will be used to relate the Hodge–de Rham spectral sequences for
![]() $X$
and
$X$
and
![]() $X^{\prime }$
via the
$X^{\prime }$
via the
![]() $+$
-operation. The first step in this process is the following lemma.
$+$
-operation. The first step in this process is the following lemma.
Lemma 2.28. Let
![]() $R$
,
$R$
,
![]() $R^{\prime }$
,
$R^{\prime }$
,
![]() $I$
, and
$I$
, and
![]() $I^{\prime }$
be as in the statement of Lemma 2.18, and let
$I^{\prime }$
be as in the statement of Lemma 2.18, and let
![]() ${\mathcal{I}}^{\bullet }$
(respectively
${\mathcal{I}}^{\bullet }$
(respectively
![]() ${\mathcal{J}}^{\bullet }$
) be the minimal injective resolution of
${\mathcal{J}}^{\bullet }$
) be the minimal injective resolution of
![]() $R$
(respectively
$R$
(respectively
![]() $R^{\prime }$
) in the category of
$R^{\prime }$
) in the category of
![]() $R$
-modules (respectively
$R$
-modules (respectively
![]() $R^{\prime }$
-modules) as above. Then for all
$R^{\prime }$
-modules) as above. Then for all
![]() $q$
, we have an isomorphism
$q$
, we have an isomorphism
 $$\begin{eqnarray}(\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q-1}))_{+}\simeq \unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q})\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q-1}))_{+}\simeq \unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q})\end{eqnarray}$$
of
 ${\mathcal{D}}(R^{\prime },k)$
-modules.
${\mathcal{D}}(R^{\prime },k)$
-modules.
Proof. Fix
![]() $q\geqslant 0$
. As
$q\geqslant 0$
. As
![]() $R^{\prime }$
is a Gorenstein local ring, the structure of its minimal injective resolution
$R^{\prime }$
is a Gorenstein local ring, the structure of its minimal injective resolution
![]() ${\mathcal{J}}^{\bullet }$
is well known [Reference MatsumuraMat86, Theorem 18.8]:
${\mathcal{J}}^{\bullet }$
is well known [Reference MatsumuraMat86, Theorem 18.8]:
 ${\mathcal{J}}^{q}=\bigoplus _{\operatorname{ht}\mathfrak{p}=q}E(R^{\prime }/\mathfrak{p})$
, where
${\mathcal{J}}^{q}=\bigoplus _{\operatorname{ht}\mathfrak{p}=q}E(R^{\prime }/\mathfrak{p})$
, where
 $E(R^{\prime }/\mathfrak{p})$
is the
$E(R^{\prime }/\mathfrak{p})$
is the
![]() $R^{\prime }$
-injective hull of
$R^{\prime }$
-injective hull of
![]() $R^{\prime }/\mathfrak{p}$
. In particular,
$R^{\prime }/\mathfrak{p}$
. In particular,
![]() ${\mathcal{J}}^{q}=0$
for
${\mathcal{J}}^{q}=0$
for
 $q>n+1$
and
$q>n+1$
and
![]() ${\mathcal{J}}^{n+1}$
is the Matlis dualizing module
${\mathcal{J}}^{n+1}$
is the Matlis dualizing module
![]() $E_{R^{\prime }}$
. Applying the functor
$E_{R^{\prime }}$
. Applying the functor
![]() $\unicode[STIX]{x1D6E4}_{I^{\prime }}$
amounts to discarding those summands corresponding to prime ideals outside the closed subscheme
$\unicode[STIX]{x1D6E4}_{I^{\prime }}$
amounts to discarding those summands corresponding to prime ideals outside the closed subscheme
 $V(I^{\prime })\subset X^{\prime }$
[Reference Brodmann and SharpBS13, Example 10.1.11]: that is, we have the equality
$V(I^{\prime })\subset X^{\prime }$
[Reference Brodmann and SharpBS13, Example 10.1.11]: that is, we have the equality
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q})=\underset{\operatorname{ht}\mathfrak{p}=q,I^{\prime }\subset \mathfrak{p}}{\bigoplus }E_{R^{\prime }}(R^{\prime }/\mathfrak{p}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q})=\underset{\operatorname{ht}\mathfrak{p}=q,I^{\prime }\subset \mathfrak{p}}{\bigoplus }E_{R^{\prime }}(R^{\prime }/\mathfrak{p}),\end{eqnarray}$$
where again only prime ideals of height
![]() $q$
appear in the decomposition, since
$q$
appear in the decomposition, since
 ${\mathcal{J}}^{q}=\bigoplus _{\operatorname{ht}\mathfrak{p}=q}E(R^{\prime }/\mathfrak{p})$
. Since
${\mathcal{J}}^{q}=\bigoplus _{\operatorname{ht}\mathfrak{p}=q}E(R^{\prime }/\mathfrak{p})$
. Since
 $I^{\prime }=IR^{\prime }+(z)$
, there is a one-to-one correspondence between prime ideals
$I^{\prime }=IR^{\prime }+(z)$
, there is a one-to-one correspondence between prime ideals
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $R^{\prime }$
containing
$R^{\prime }$
containing
![]() $I^{\prime }$
and prime ideals
$I^{\prime }$
and prime ideals
![]() $\mathfrak{q}$
of
$\mathfrak{q}$
of
 $R=R^{\prime }/(z)$
containing
$R=R^{\prime }/(z)$
containing
![]() $I$
(indeed, any such
$I$
(indeed, any such
![]() $\mathfrak{p}$
takes the form
$\mathfrak{p}$
takes the form
 $\mathfrak{q}R^{\prime }+(z)$
). If
$\mathfrak{q}R^{\prime }+(z)$
). If
 $\operatorname{ht}\mathfrak{p}=q$
, then
$\operatorname{ht}\mathfrak{p}=q$
, then
 $\operatorname{ht}\mathfrak{q}=q-1$
, so we have the decomposition
$\operatorname{ht}\mathfrak{q}=q-1$
, so we have the decomposition
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q})=\underset{I\subset \mathfrak{q}\in \operatorname{Spec}(R),\operatorname{ht}\mathfrak{q}=q-1}{\bigoplus }E_{R^{\prime }}(R^{\prime }/(\mathfrak{q}R^{\prime }+(z)))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q})=\underset{I\subset \mathfrak{q}\in \operatorname{Spec}(R),\operatorname{ht}\mathfrak{q}=q-1}{\bigoplus }E_{R^{\prime }}(R^{\prime }/(\mathfrak{q}R^{\prime }+(z)))\end{eqnarray}$$
as
![]() $R^{\prime }$
-modules. Note that we have
$R^{\prime }$
-modules. Note that we have
![]() $R^{\prime }$
-module isomorphisms
$R^{\prime }$
-module isomorphisms
 $$\begin{eqnarray}R^{\prime }/(\mathfrak{q}R^{\prime }+(z))\simeq (R^{\prime }/(z))/((\mathfrak{q}R^{\prime }+(z))/(z))\simeq R/\mathfrak{q},\end{eqnarray}$$
$$\begin{eqnarray}R^{\prime }/(\mathfrak{q}R^{\prime }+(z))\simeq (R^{\prime }/(z))/((\mathfrak{q}R^{\prime }+(z))/(z))\simeq R/\mathfrak{q},\end{eqnarray}$$
where
![]() $R/\mathfrak{q}$
is viewed as an
$R/\mathfrak{q}$
is viewed as an
![]() $R$
-module upon which
$R$
-module upon which
![]() $z\in R^{\prime }$
acts trivially. But by [Reference Núñez-Betancourt and WittNBW14, Proposition 3.11], the
$z\in R^{\prime }$
acts trivially. But by [Reference Núñez-Betancourt and WittNBW14, Proposition 3.11], the
![]() $R^{\prime }$
-module
$R^{\prime }$
-module
 $E_{R^{\prime }}(R^{\prime }/(\mathfrak{q}R^{\prime }+(z)))$
is obtained from the
$E_{R^{\prime }}(R^{\prime }/(\mathfrak{q}R^{\prime }+(z)))$
is obtained from the
![]() $R$
-module
$R$
-module
 $E_{R}(R/\mathfrak{q})$
by the
$E_{R}(R/\mathfrak{q})$
by the
![]() $+$
-operation. (This identification holds at the level of
$+$
-operation. (This identification holds at the level of
 ${\mathcal{D}}(R^{\prime },k)$
-modules.) We then have isomorphisms
${\mathcal{D}}(R^{\prime },k)$
-modules.) We then have isomorphisms
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q})\simeq \underset{I\subset \mathfrak{q}\in \operatorname{Spec}(R),\operatorname{ht}\mathfrak{q}=q-1}{\bigoplus }(E_{R}(R/\mathfrak{q}))_{+}=(\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q-1}))_{+},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q})\simeq \underset{I\subset \mathfrak{q}\in \operatorname{Spec}(R),\operatorname{ht}\mathfrak{q}=q-1}{\bigoplus }(E_{R}(R/\mathfrak{q}))_{+}=(\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q-1}))_{+},\end{eqnarray}$$
of
 ${\mathcal{D}}(R^{\prime },k)$
-modules, where we have again used [Reference Brodmann and SharpBS13, Example 10.1.11].◻
${\mathcal{D}}(R^{\prime },k)$
-modules, where we have again used [Reference Brodmann and SharpBS13, Example 10.1.11].◻
Lemma 2.29. Let
![]() $E_{\bullet ,R}^{\bullet ,\bullet }$
and
$E_{\bullet ,R}^{\bullet ,\bullet }$
and
![]() ${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }$
be the spectral sequences of Definition 2.27. There is an isomorphism
${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }$
be the spectral sequences of Definition 2.27. There is an isomorphism
 $$\begin{eqnarray}(E_{\bullet ,R}^{\bullet ,\bullet })_{+}\xrightarrow[{}]{{\sim}}{\mathcal{E}}_{\bullet }^{\bullet ,\bullet }[(0,1)],\end{eqnarray}$$
$$\begin{eqnarray}(E_{\bullet ,R}^{\bullet ,\bullet })_{+}\xrightarrow[{}]{{\sim}}{\mathcal{E}}_{\bullet }^{\bullet ,\bullet }[(0,1)],\end{eqnarray}$$
where the object on the left-hand side is obtained by applying the
![]() $+$
-operation to all the objects and differentials of the spectral sequence
$+$
-operation to all the objects and differentials of the spectral sequence
![]() $E_{\bullet ,R}^{\bullet ,\bullet }$
(this notation means that the morphism of spectral sequences has bidegree
$E_{\bullet ,R}^{\bullet ,\bullet }$
(this notation means that the morphism of spectral sequences has bidegree
![]() $(0,1)$
, as in Definition 2.11).
$(0,1)$
, as in Definition 2.11).
Proof. We consider the objects of the double complexes giving rise to these spectral sequences. For all
![]() $p$
and
$p$
and
![]() $q$
, we have
$q$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{Y}(X^{\prime },\widetilde{{\mathcal{J}}_{0}^{p,q+1}})\simeq \unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}_{0}^{p,q+1})=\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q+1}\otimes \unicode[STIX]{x1D6FA}_{R}^{p})\simeq \unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q+1})\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{Y}(X^{\prime },\widetilde{{\mathcal{J}}_{0}^{p,q+1}})\simeq \unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}_{0}^{p,q+1})=\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q+1}\otimes \unicode[STIX]{x1D6FA}_{R}^{p})\simeq \unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q+1})\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\end{eqnarray}$$
and similarly
 $$\begin{eqnarray}(\unicode[STIX]{x1D6E4}_{Y}(X,\widetilde{{\mathcal{I}}^{p,q}}))_{+}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{p,q}))_{+}=(\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q}\otimes \unicode[STIX]{x1D6FA}_{R}^{p}))_{+}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q})\otimes \unicode[STIX]{x1D6FA}_{R}^{p})_{+}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6E4}_{Y}(X,\widetilde{{\mathcal{I}}^{p,q}}))_{+}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{p,q}))_{+}=(\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q}\otimes \unicode[STIX]{x1D6FA}_{R}^{p}))_{+}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q})\otimes \unicode[STIX]{x1D6FA}_{R}^{p})_{+}\end{eqnarray}$$
by Lemma 2.16 and the fact that
 $\unicode[STIX]{x1D6E4}_{I}=H_{I}^{0}$
and
$\unicode[STIX]{x1D6E4}_{I}=H_{I}^{0}$
and
 $\unicode[STIX]{x1D6E4}_{I^{\prime }}=H_{I^{\prime }}^{0}$
commute with direct sums. By Lemma 2.28, we have
$\unicode[STIX]{x1D6E4}_{I^{\prime }}=H_{I^{\prime }}^{0}$
commute with direct sums. By Lemma 2.28, we have
 $\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q+1})\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q}))_{+}$
for all
$\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q+1})\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q}))_{+}$
for all
![]() $q$
. Therefore, for all
$q$
. Therefore, for all
![]() $p$
and
$p$
and
![]() $q$
, we have
$q$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q+1})\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q}))_{+}\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q})\otimes \unicode[STIX]{x1D6FA}_{R}^{p})_{+},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{I^{\prime }}({\mathcal{J}}^{q+1})\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q}))_{+}\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q})\otimes \unicode[STIX]{x1D6FA}_{R}^{p})_{+},\end{eqnarray}$$
so the objects of the double complexes are isomorphic with the indicated bidegree shift. Finally, we observe that the differentials in the complex
![]() $\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
do not involve
$\unicode[STIX]{x1D6FA}_{R}^{\bullet }$
do not involve
![]() $z$
or
$z$
or
![]() $dz$
, so the isomorphisms
$dz$
, so the isomorphisms
 $(\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q}))_{+}\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q})\otimes \unicode[STIX]{x1D6FA}_{R}^{p})_{+}$
commute with the differentials of the double complex and thus assemble to an isomorphism of double complexes. An isomorphism of double complexes induces an isomorphism between the corresponding column-filtered spectral sequences, and the lemma follows.◻
$(\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q}))_{+}\otimes \unicode[STIX]{x1D6FA}_{R}^{p}\simeq (\unicode[STIX]{x1D6E4}_{I}({\mathcal{I}}^{q})\otimes \unicode[STIX]{x1D6FA}_{R}^{p})_{+}$
commute with the differentials of the double complex and thus assemble to an isomorphism of double complexes. An isomorphism of double complexes induces an isomorphism between the corresponding column-filtered spectral sequences, and the lemma follows.◻
We are now ready to complete the proof of Theorem A.
Proof of Theorem A(a).
As already described, we need only prove the result in the special case of Lemma 2.18. We retain the notation of that lemma. Consider again the short exact sequence of Definition 2.21 and its sheafified version
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{X^{\prime }}\otimes \unicode[STIX]{x1D6FA}_{X}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{\bullet }\rightarrow {\mathcal{O}}_{X^{\prime }}\otimes \unicode[STIX]{x1D6FA}_{X}^{\bullet }\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{X^{\prime }}\otimes \unicode[STIX]{x1D6FA}_{X}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{\bullet }\rightarrow {\mathcal{O}}_{X^{\prime }}\otimes \unicode[STIX]{x1D6FA}_{X}^{\bullet }\rightarrow 0.\end{eqnarray}$$
As described in § 2.2, the morphism of complexes
![]() $\unicode[STIX]{x1D704}$
induces a morphism between the corresponding spectral sequences for hypercohomology supported at
$\unicode[STIX]{x1D704}$
induces a morphism between the corresponding spectral sequences for hypercohomology supported at
![]() $Y$
. These spectral sequences were identified as
$Y$
. These spectral sequences were identified as
 ${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }[(-1,0)]$
(respectively,
${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }[(-1,0)]$
(respectively,
![]() $\mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
) in the paragraph following Definition 2.27. Accounting for the shift of
$\mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
) in the paragraph following Definition 2.27. Accounting for the shift of
![]() $-1$
, we see that this induced morphism has the following form:
$-1$
, we see that this induced morphism has the following form:
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\bullet }^{\bullet ,\bullet }:{\mathcal{E}}_{\bullet }^{\bullet ,\bullet }\rightarrow \mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }[(1,0)].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\bullet }^{\bullet ,\bullet }:{\mathcal{E}}_{\bullet }^{\bullet ,\bullet }\rightarrow \mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }[(1,0)].\end{eqnarray}$$
Identifying first
 ${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }[(0,1)]$
with
${\mathcal{E}}_{\bullet }^{\bullet ,\bullet }[(0,1)]$
with
 $(E_{\bullet ,R}^{\bullet ,\bullet })_{+}$
(by Lemma 2.29) and then
$(E_{\bullet ,R}^{\bullet ,\bullet })_{+}$
(by Lemma 2.29) and then
![]() $E_{\bullet ,R}^{\bullet ,\bullet }$
with the
$E_{\bullet ,R}^{\bullet ,\bullet }$
with the
![]() $1/z$
-component of
$1/z$
-component of
 $(E_{\bullet ,R}^{\bullet ,\bullet })_{+}$
, we see that this further induces a morphism
$(E_{\bullet ,R}^{\bullet ,\bullet })_{+}$
, we see that this further induces a morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\bullet }^{\bullet ,\bullet }:E_{\bullet ,R}^{\bullet ,\bullet }\rightarrow \mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }[(1,1)],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\bullet }^{\bullet ,\bullet }:E_{\bullet ,R}^{\bullet ,\bullet }\rightarrow \mathbf{E}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }[(1,1)],\end{eqnarray}$$
given in every degree by the inclusion of
![]() $E_{r,R}^{\bullet ,\bullet }$
as the
$E_{r,R}^{\bullet ,\bullet }$
as the
![]() $1/z$
-component of
$1/z$
-component of
 $(E_{r,R}^{\bullet ,\bullet })_{+}\simeq {\mathcal{E}}_{r}^{\bullet ,\bullet }[(0,1)]$
followed by
$(E_{r,R}^{\bullet ,\bullet })_{+}\simeq {\mathcal{E}}_{r}^{\bullet ,\bullet }[(0,1)]$
followed by
![]() $\unicode[STIX]{x1D704}_{\bullet }^{\bullet ,\bullet }$
. If
$\unicode[STIX]{x1D704}_{\bullet }^{\bullet ,\bullet }$
. If
![]() $r=2$
, the maps
$r=2$
, the maps
![]() $\unicode[STIX]{x1D719}_{2}^{p,q}$
are precisely the isomorphisms
$\unicode[STIX]{x1D719}_{2}^{p,q}$
are precisely the isomorphisms
 $H_{\text{dR}}^{p}(H_{I}^{q}(R))\xrightarrow[{}]{{\sim}}H_{\text{dR}}^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime }))$
appearing in the proof of Lemma 2.18, which were induced by the morphism of complexes
$H_{\text{dR}}^{p}(H_{I}^{q}(R))\xrightarrow[{}]{{\sim}}H_{\text{dR}}^{p+1}(H_{I^{\prime }}^{q+1}(R^{\prime }))$
appearing in the proof of Lemma 2.18, which were induced by the morphism of complexes
![]() $\unicode[STIX]{x1D704}$
and the inclusion of
$\unicode[STIX]{x1D704}$
and the inclusion of
 $E_{2,R}^{p,q}=H_{\text{dR}}^{p}(H_{I}^{q}(R))$
as the
$E_{2,R}^{p,q}=H_{\text{dR}}^{p}(H_{I}^{q}(R))$
as the
![]() $1/z$
-component of
$1/z$
-component of
 $(E_{2,R}^{p,q})_{+}$
. Therefore the morphism
$(E_{2,R}^{p,q})_{+}$
. Therefore the morphism
![]() $\unicode[STIX]{x1D719}_{\bullet }^{\bullet ,\bullet }$
of spectral sequences is an isomorphism at the
$\unicode[STIX]{x1D719}_{\bullet }^{\bullet ,\bullet }$
of spectral sequences is an isomorphism at the
![]() $E_{2}$
-level. By Proposition 2.12, it follows that
$E_{2}$
-level. By Proposition 2.12, it follows that
![]() $\unicode[STIX]{x1D719}$
is an isomorphism at all later levels, including the abutments. The proof is complete.◻
$\unicode[STIX]{x1D719}$
is an isomorphism at all later levels, including the abutments. The proof is complete.◻
3 Matlis duality and
 $\unicode[STIX]{x1D6F4}$
-continuous maps
$\unicode[STIX]{x1D6F4}$
-continuous maps
In this section, we describe formulations of Matlis duality for local rings containing a field
![]() $k$
in terms of continuous
$k$
in terms of continuous
![]() $k$
-linear maps to
$k$
-linear maps to
![]() $k$
. Many of these results are not new; some of them are stated without proof in SGA2 [Reference Grothendieck and RaynaudGR05, Exp. IV]. For lack of adequate references for the proofs, we provide their full details here. We also define the class of
$k$
. Many of these results are not new; some of them are stated without proof in SGA2 [Reference Grothendieck and RaynaudGR05, Exp. IV]. For lack of adequate references for the proofs, we provide their full details here. We also define the class of
![]() $k$
-linear maps (the ‘
$k$
-linear maps (the ‘
![]() $\unicode[STIX]{x1D6F4}$
-continuous’ maps) between arbitrary modules over such rings that admit Matlis duals.
$\unicode[STIX]{x1D6F4}$
-continuous’ maps) between arbitrary modules over such rings that admit Matlis duals.
Let
![]() $(R,\mathfrak{m})$
be a (Noetherian) local ring with coefficient field
$(R,\mathfrak{m})$
be a (Noetherian) local ring with coefficient field
![]() $k$
. Let
$k$
. Let
 $E=E(R/\mathfrak{m})$
denote a choice of injective hull of
$E=E(R/\mathfrak{m})$
denote a choice of injective hull of
 $R/\mathfrak{m}\simeq k$
as an
$R/\mathfrak{m}\simeq k$
as an
![]() $R$
-module. The Matlis duality functor
$R$
-module. The Matlis duality functor
![]() $D$
is defined by
$D$
is defined by
 $D(M)=\operatorname{Hom}_{R}(M,E)$
for all
$D(M)=\operatorname{Hom}_{R}(M,E)$
for all
![]() $R$
-modules
$R$
-modules
![]() $M$
. Since
$M$
. Since
![]() $E$
is injective,
$E$
is injective,
![]() $D$
is an exact, contravariant functor. (See [Reference MatsumuraMat86, § 18] for a standard treatment of this duality theory, or [Reference MatlisMat58] for its original statement by Matlis.) If
$D$
is an exact, contravariant functor. (See [Reference MatsumuraMat86, § 18] for a standard treatment of this duality theory, or [Reference MatlisMat58] for its original statement by Matlis.) If
 $f:M\rightarrow N$
is an
$f:M\rightarrow N$
is an
![]() $R$
-linear homomorphism of
$R$
-linear homomorphism of
![]() $R$
-modules, its Matlis dual is the
$R$
-modules, its Matlis dual is the
![]() $R$
-linear homomorphism
$R$
-linear homomorphism
 $f^{\ast }:D(N)\rightarrow D(M)$
defined by pre-composition with
$f^{\ast }:D(N)\rightarrow D(M)$
defined by pre-composition with
![]() $f$
:
$f$
:
 $f^{\ast }(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}\circ f$
for
$f^{\ast }(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}\circ f$
for
![]() $R$
-linear maps
$R$
-linear maps
 $\unicode[STIX]{x1D719}:N\rightarrow E$
. Using this definition, it does not make sense a priori to speak of the Matlis dual of a map
$\unicode[STIX]{x1D719}:N\rightarrow E$
. Using this definition, it does not make sense a priori to speak of the Matlis dual of a map
 $\unicode[STIX]{x1D6FF}:M\rightarrow N$
that is not
$\unicode[STIX]{x1D6FF}:M\rightarrow N$
that is not
![]() $R$
-linear. However, we will show that a more general class of maps can be dualized. We will make use of functorial identifications of the Matlis dual of a finite-length (respectively finitely generated)
$R$
-linear. However, we will show that a more general class of maps can be dualized. We will make use of functorial identifications of the Matlis dual of a finite-length (respectively finitely generated)
![]() $R$
-module with the set of
$R$
-module with the set of
![]() $k$
-linear (respectively
$k$
-linear (respectively
![]() $k$
-linear and
$k$
-linear and
![]() $\mathfrak{m}$
-adically continuous) maps from the module to
$\mathfrak{m}$
-adically continuous) maps from the module to
![]() $k$
; from these identifications, we will see that any
$k$
; from these identifications, we will see that any
![]() $k$
-linear map between finite-length
$k$
-linear map between finite-length
![]() $R$
-modules, and any
$R$
-modules, and any
![]() $\mathfrak{m}$
-adically continuous
$\mathfrak{m}$
-adically continuous
![]() $k$
-linear map between finitely generated
$k$
-linear map between finitely generated
![]() $R$
-modules, has a Matlis dual. We will also explain how this theory can be extended to the case of arbitrary modules.
$R$
-modules, has a Matlis dual. We will also explain how this theory can be extended to the case of arbitrary modules.
Remark 3.1. In [Reference Grothendieck and RaynaudGR05] the following results are stated in a slightly more general setting:
![]() $(R,\mathfrak{m})$
is a (Noetherian) local ring containing a field
$(R,\mathfrak{m})$
is a (Noetherian) local ring containing a field
![]() $k_{0}$
such that the residue field
$k_{0}$
such that the residue field
 $k=R/\mathfrak{m}$
is a finite extension of
$k=R/\mathfrak{m}$
is a finite extension of
![]() $k_{0}$
. Since we need only the case where
$k_{0}$
. Since we need only the case where
![]() $k=k_{0}$
, we make this assumption throughout to simplify the discussion. However, with only minor modifications to the arguments, all of what follows in this section is true at the level of generality of [Reference Grothendieck and RaynaudGR05].
$k=k_{0}$
, we make this assumption throughout to simplify the discussion. However, with only minor modifications to the arguments, all of what follows in this section is true at the level of generality of [Reference Grothendieck and RaynaudGR05].
Let
![]() $R$
be as above, and let
$R$
be as above, and let
![]() $N$
be any
$N$
be any
![]() $R$
-module (a fortiori,
$R$
-module (a fortiori,
![]() $N$
is a
$N$
is a
![]() $k$
-space). We can define an
$k$
-space). We can define an
![]() $R$
-module structure on the
$R$
-module structure on the
![]() $k$
-space
$k$
-space
 $\operatorname{Hom}_{k}(N,k)$
as follows. Given a
$\operatorname{Hom}_{k}(N,k)$
as follows. Given a
![]() $k$
-linear homomorphism
$k$
-linear homomorphism
 $\unicode[STIX]{x1D706}:N\rightarrow k$
, we define
$\unicode[STIX]{x1D706}:N\rightarrow k$
, we define
 $r\cdot \unicode[STIX]{x1D706}:N\rightarrow k$
by
$r\cdot \unicode[STIX]{x1D706}:N\rightarrow k$
by
 $(r\cdot \unicode[STIX]{x1D706})(n)=\unicode[STIX]{x1D706}(rn)$
, which is again
$(r\cdot \unicode[STIX]{x1D706})(n)=\unicode[STIX]{x1D706}(rn)$
, which is again
![]() $k$
-linear since, if
$k$
-linear since, if
![]() $\unicode[STIX]{x1D6FC}\in k$
, we have
$\unicode[STIX]{x1D6FC}\in k$
, we have
 $$\begin{eqnarray}(r\cdot \unicode[STIX]{x1D706})(\unicode[STIX]{x1D6FC}n)=\unicode[STIX]{x1D706}(r(\unicode[STIX]{x1D6FC}n))=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}(rn)=\unicode[STIX]{x1D6FC}(r\cdot \unicode[STIX]{x1D706})(n)\end{eqnarray}$$
$$\begin{eqnarray}(r\cdot \unicode[STIX]{x1D706})(\unicode[STIX]{x1D6FC}n)=\unicode[STIX]{x1D706}(r(\unicode[STIX]{x1D6FC}n))=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}(rn)=\unicode[STIX]{x1D6FC}(r\cdot \unicode[STIX]{x1D706})(n)\end{eqnarray}$$
by the
![]() $k$
-linearity of
$k$
-linearity of
![]() $\unicode[STIX]{x1D706}$
. (We will use the dot
$\unicode[STIX]{x1D706}$
. (We will use the dot
![]() $\cdot$
throughout this section to denote an
$\cdot$
throughout this section to denote an
![]() $R$
-action on maps which is defined by multiplication on the input of the map when multiplying the output by
$R$
-action on maps which is defined by multiplication on the input of the map when multiplying the output by
![]() $r\in R$
may not make sense.)
$r\in R$
may not make sense.)
The socle
 $\operatorname{Soc}(E)=(0:_{E}\mathfrak{m})$
of
$\operatorname{Soc}(E)=(0:_{E}\mathfrak{m})$
of
![]() $E$
is a one-dimensional
$E$
is a one-dimensional
![]() $k$
-space. We fix, once and for all, a
$k$
-space. We fix, once and for all, a
![]() $k$
-linear projection
$k$
-linear projection
 $E\rightarrow \operatorname{Soc}(E)$
which we identify with a
$E\rightarrow \operatorname{Soc}(E)$
which we identify with a
![]() $k$
-linear map
$k$
-linear map
 $\unicode[STIX]{x1D70E}:E\rightarrow k$
.
$\unicode[STIX]{x1D70E}:E\rightarrow k$
.
Remark 3.2. The various functorial identifications made throughout this section will depend on the choices of
![]() $E$
and
$E$
and
![]() $\unicode[STIX]{x1D70E}$
made here. At the end of this section, we will specify the choices of
$\unicode[STIX]{x1D70E}$
made here. At the end of this section, we will specify the choices of
![]() $E$
and
$E$
and
![]() $\unicode[STIX]{x1D70E}$
in the case where
$\unicode[STIX]{x1D70E}$
in the case where
![]() $R$
is complete and regular that will be used in the rest of the paper.
$R$
is complete and regular that will be used in the rest of the paper.
Now define, for any
![]() $R$
-module
$R$
-module
![]() $N$
, a map
$N$
, a map
 $\unicode[STIX]{x1D6F7}_{N}:\operatorname{Hom}_{R}(N,E)\rightarrow \operatorname{Hom}_{k}(N,k)$
by
$\unicode[STIX]{x1D6F7}_{N}:\operatorname{Hom}_{R}(N,E)\rightarrow \operatorname{Hom}_{k}(N,k)$
by
 $\unicode[STIX]{x1D6F7}_{N}(g)=\unicode[STIX]{x1D70E}\circ g$
. Clearly, if
$\unicode[STIX]{x1D6F7}_{N}(g)=\unicode[STIX]{x1D70E}\circ g$
. Clearly, if
![]() $g$
is
$g$
is
![]() $R$
-linear (and hence
$R$
-linear (and hence
![]() $k$
-linear), the composition
$k$
-linear), the composition
![]() $\unicode[STIX]{x1D70E}\circ g$
is
$\unicode[STIX]{x1D70E}\circ g$
is
![]() $k$
-linear.
$k$
-linear.
Lemma 3.3. The map
![]() $\unicode[STIX]{x1D6F7}_{N}$
defined above is an
$\unicode[STIX]{x1D6F7}_{N}$
defined above is an
![]() $R$
-linear homomorphism.
$R$
-linear homomorphism.
Proof. Let
 $g\in \operatorname{Hom}_{R}(N,E)$
and
$g\in \operatorname{Hom}_{R}(N,E)$
and
![]() $r\in R$
be given. Then for any
$r\in R$
be given. Then for any
![]() $n\in N$
, we have
$n\in N$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{N}(rg)(n)=\unicode[STIX]{x1D70E}((rg)(n))=\unicode[STIX]{x1D70E}(rg(n))=\unicode[STIX]{x1D70E}(g(rn))=(\unicode[STIX]{x1D70E}\circ g)(rn)=(r\cdot \unicode[STIX]{x1D6F7}_{N}(g))(n),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{N}(rg)(n)=\unicode[STIX]{x1D70E}((rg)(n))=\unicode[STIX]{x1D70E}(rg(n))=\unicode[STIX]{x1D70E}(g(rn))=(\unicode[STIX]{x1D70E}\circ g)(rn)=(r\cdot \unicode[STIX]{x1D6F7}_{N}(g))(n),\end{eqnarray}$$
so that
 $\unicode[STIX]{x1D6F7}_{N}(rg)=r\cdot \unicode[STIX]{x1D6F7}_{N}(g)$
.◻
$\unicode[STIX]{x1D6F7}_{N}(rg)=r\cdot \unicode[STIX]{x1D6F7}_{N}(g)$
.◻
We list some more elementary properties of the maps
![]() $\unicode[STIX]{x1D6F7}_{N}$
. Suppose we have an
$\unicode[STIX]{x1D6F7}_{N}$
. Suppose we have an
![]() $R$
-linear homomorphism
$R$
-linear homomorphism
 $f:M\rightarrow N$
of
$f:M\rightarrow N$
of
![]() $R$
-modules. The Matlis dual of
$R$
-modules. The Matlis dual of
![]() $f$
, which is the map
$f$
, which is the map
 $f^{\ast }:\operatorname{Hom}_{R}(N,E)\rightarrow \operatorname{Hom}_{R}(M,E)$
, is clearly
$f^{\ast }:\operatorname{Hom}_{R}(N,E)\rightarrow \operatorname{Hom}_{R}(M,E)$
, is clearly
![]() $R$
-linear.
$R$
-linear.
Lemma 3.4. The map
 $f^{\vee }:\operatorname{Hom}_{k}(N,k)\rightarrow \operatorname{Hom}_{k}(M,k)$
defined by pre-composition with
$f^{\vee }:\operatorname{Hom}_{k}(N,k)\rightarrow \operatorname{Hom}_{k}(M,k)$
defined by pre-composition with
![]() $f$
(i.e.,
$f$
(i.e.,
 $f^{\vee }(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D706}\circ f$
for a
$f^{\vee }(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D706}\circ f$
for a
![]() $k$
-linear
$k$
-linear
 $\unicode[STIX]{x1D706}:N\rightarrow k$
) is
$\unicode[STIX]{x1D706}:N\rightarrow k$
) is
![]() $R$
-linear.
$R$
-linear.
Proof. Let
![]() $r\in R$
and
$r\in R$
and
 $\unicode[STIX]{x1D706}\in \operatorname{Hom}_{k}(N,k)$
be given. Then
$\unicode[STIX]{x1D706}\in \operatorname{Hom}_{k}(N,k)$
be given. Then
 $$\begin{eqnarray}f^{\vee }(r\cdot \unicode[STIX]{x1D706})(m)=(r\cdot \unicode[STIX]{x1D706})(f(m))=\unicode[STIX]{x1D706}(rf(m))=\unicode[STIX]{x1D706}(f(rm))=f^{\vee }(\unicode[STIX]{x1D706})(rm)=(r\cdot f^{\vee }(\unicode[STIX]{x1D706}))(m)\end{eqnarray}$$
$$\begin{eqnarray}f^{\vee }(r\cdot \unicode[STIX]{x1D706})(m)=(r\cdot \unicode[STIX]{x1D706})(f(m))=\unicode[STIX]{x1D706}(rf(m))=\unicode[STIX]{x1D706}(f(rm))=f^{\vee }(\unicode[STIX]{x1D706})(rm)=(r\cdot f^{\vee }(\unicode[STIX]{x1D706}))(m)\end{eqnarray}$$
for any
![]() $m\in M$
, as desired.◻
$m\in M$
, as desired.◻
Moreover, we note that given any
 $g\in \operatorname{Hom}_{R}(N,E)$
, both
$g\in \operatorname{Hom}_{R}(N,E)$
, both
 $\unicode[STIX]{x1D6F7}_{M}(f^{\ast }(g))$
and
$\unicode[STIX]{x1D6F7}_{M}(f^{\ast }(g))$
and
 $f^{\vee }(\unicode[STIX]{x1D6F7}_{N}(g))$
are equal to the composite
$f^{\vee }(\unicode[STIX]{x1D6F7}_{N}(g))$
are equal to the composite
 $\unicode[STIX]{x1D70E}\circ g\circ f:M\rightarrow k$
. Therefore, the diagram below is commutative and all its arrows are
$\unicode[STIX]{x1D70E}\circ g\circ f:M\rightarrow k$
. Therefore, the diagram below is commutative and all its arrows are
![]() $R$
-linear maps.
$R$
-linear maps.

We have now established enough preliminaries to prove the following.
Proposition 3.5. The map
 $\unicode[STIX]{x1D6F7}_{N}:\operatorname{Hom}_{R}(N,E)\rightarrow \operatorname{Hom}_{k}(N,k)$
defined by
$\unicode[STIX]{x1D6F7}_{N}:\operatorname{Hom}_{R}(N,E)\rightarrow \operatorname{Hom}_{k}(N,k)$
defined by
 $\unicode[STIX]{x1D6F7}_{N}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}$
is an isomorphism of
$\unicode[STIX]{x1D6F7}_{N}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}$
is an isomorphism of
![]() $R$
-modules whenever
$R$
-modules whenever
![]() $N$
is of finite length.
$N$
is of finite length.
Proof. We proceed by induction on the length
![]() $l(N)$
in the category of
$l(N)$
in the category of
![]() $R$
-modules, remarking that any finite-length
$R$
-modules, remarking that any finite-length
![]() $N$
is a
$N$
is a
![]() $k$
-space of dimension
$k$
-space of dimension
![]() $l(N)$
. The base case,
$l(N)$
. The base case,
 $l(N)=1$
, is the case
$l(N)=1$
, is the case
![]() $N\simeq k$
; here
$N\simeq k$
; here
![]() $\unicode[STIX]{x1D6F7}_{N}$
is an isomorphism identifying
$\unicode[STIX]{x1D6F7}_{N}$
is an isomorphism identifying
 $\operatorname{Hom}_{k}(k,k)\simeq k$
with the socle
$\operatorname{Hom}_{k}(k,k)\simeq k$
with the socle
 $\operatorname{Soc}(E)\simeq \operatorname{Hom}_{R}(k,E)=\operatorname{Hom}_{R}(R/\mathfrak{m},E)$
of
$\operatorname{Soc}(E)\simeq \operatorname{Hom}_{R}(k,E)=\operatorname{Hom}_{R}(R/\mathfrak{m},E)$
of
![]() $E$
. Now suppose
$E$
. Now suppose
 $l(N)\geqslant 2$
, in which case there is a short exact sequence
$l(N)\geqslant 2$
, in which case there is a short exact sequence
 $0\rightarrow k\rightarrow N\rightarrow N^{\prime }\rightarrow 0$
of
$0\rightarrow k\rightarrow N\rightarrow N^{\prime }\rightarrow 0$
of
![]() $R$
-modules where
$R$
-modules where
 $l(N^{\prime })=l(N)-1$
. As
$l(N^{\prime })=l(N)-1$
. As
![]() $E$
is an injective
$E$
is an injective
![]() $R$
-module, the functor
$R$
-module, the functor
 $\operatorname{Hom}_{R}(-,E)$
is exact. Moreover,
$\operatorname{Hom}_{R}(-,E)$
is exact. Moreover,
 $\operatorname{Hom}_{k}(-,k)$
is also an exact functor on the category of
$\operatorname{Hom}_{k}(-,k)$
is also an exact functor on the category of
![]() $k$
-spaces (all
$k$
-spaces (all
![]() $k$
-spaces are injective objects). We therefore obtain a commutative diagram with exact rows.
$k$
-spaces are injective objects). We therefore obtain a commutative diagram with exact rows.

All maps in this diagram are
![]() $R$
-linear, and the bottom row is exact as a sequence of
$R$
-linear, and the bottom row is exact as a sequence of
![]() $R$
-modules, since it is exact as a sequence of
$R$
-modules, since it is exact as a sequence of
![]() $k$
-spaces. The map
$k$
-spaces. The map
![]() $\unicode[STIX]{x1D6F7}_{k}$
is an isomorphism by our base case, and
$\unicode[STIX]{x1D6F7}_{k}$
is an isomorphism by our base case, and
![]() $\unicode[STIX]{x1D6F7}_{N^{\prime }}$
is an isomorphism by the induction hypothesis, so
$\unicode[STIX]{x1D6F7}_{N^{\prime }}$
is an isomorphism by the induction hypothesis, so
![]() $\unicode[STIX]{x1D6F7}_{N}$
is an isomorphism by the five-lemma and the proof is complete.◻
$\unicode[STIX]{x1D6F7}_{N}$
is an isomorphism by the five-lemma and the proof is complete.◻
We next consider the case of
![]() $R$
-modules that are not of finite length, for which we need to restrict attention to
$R$
-modules that are not of finite length, for which we need to restrict attention to
![]() $\mathfrak{m}$
-adically continuous homomorphisms. We recall the general definition here.
$\mathfrak{m}$
-adically continuous homomorphisms. We recall the general definition here.
Definition 3.6. Let
![]() $R$
be a commutative ring,
$R$
be a commutative ring,
![]() $I\subset R$
an ideal, and
$I\subset R$
an ideal, and
![]() $M,N$
two finitely generated
$M,N$
two finitely generated
![]() $R$
-modules. The
$R$
-modules. The
![]() $I$
-adic topology on
$I$
-adic topology on
![]() $M$
(respectively
$M$
(respectively
![]() $N$
) is defined by stipulating that
$N$
) is defined by stipulating that
![]() $\{I^{n}M\}$
(respectively
$\{I^{n}M\}$
(respectively
![]() $\{I^{n}N\}$
) be a fundamental system of neighborhoods of
$\{I^{n}N\}$
) be a fundamental system of neighborhoods of
![]() $0$
. An Abelian group homomorphism
$0$
. An Abelian group homomorphism
 $f:M\rightarrow N$
is
$f:M\rightarrow N$
is
![]() $I$
-adically continuous if it is continuous with respect to these topologies on
$I$
-adically continuous if it is continuous with respect to these topologies on
![]() $M$
and
$M$
and
![]() $N$
: that is, if for all
$N$
: that is, if for all
![]() $t$
there exists an
$t$
there exists an
![]() $s$
such that
$s$
such that
 $f(I^{s}M)\subset I^{t}N$
.
$f(I^{s}M)\subset I^{t}N$
.
Remark 3.7. Note that any
![]() $R$
-linear map is automatically
$R$
-linear map is automatically
![]() $I$
-adically continuous. Also note that this definition makes sense for arbitrary
$I$
-adically continuous. Also note that this definition makes sense for arbitrary
![]() $R$
-modules, not necessarily finitely generated. We insist on finite generation here because we will make use of a different notion of continuity in the case of arbitrary modules.
$R$
-modules, not necessarily finitely generated. We insist on finite generation here because we will make use of a different notion of continuity in the case of arbitrary modules.
In the case of the local ring
![]() $(R,\mathfrak{m})$
, the only fundamental neighborhood of
$(R,\mathfrak{m})$
, the only fundamental neighborhood of
 $0\in k=R/\mathfrak{m}$
in the
$0\in k=R/\mathfrak{m}$
in the
![]() $\mathfrak{m}$
-adic topology on
$\mathfrak{m}$
-adic topology on
![]() $k$
is
$k$
is
![]() $\{0\}$
itself. Therefore, if
$\{0\}$
itself. Therefore, if
![]() $M$
is a finitely generated
$M$
is a finitely generated
![]() $R$
-module, a
$R$
-module, a
![]() $\mathfrak{m}$
-adically continuous map
$\mathfrak{m}$
-adically continuous map
 $M\rightarrow k$
is one that annihilates
$M\rightarrow k$
is one that annihilates
![]() $\mathfrak{m}^{t}M$
for some
$\mathfrak{m}^{t}M$
for some
![]() $t\geqslant 0$
. Let
$t\geqslant 0$
. Let
 $\operatorname{Hom}_{\text{cont},k}(M,k)$
be the
$\operatorname{Hom}_{\text{cont},k}(M,k)$
be the
![]() $k$
-space of
$k$
-space of
![]() $k$
-linear maps
$k$
-linear maps
 $M\rightarrow k$
that are
$M\rightarrow k$
that are
![]() $\mathfrak{m}$
-adically continuous.
$\mathfrak{m}$
-adically continuous.
Now note that if
![]() $M$
is a finitely generated
$M$
is a finitely generated
![]() $R$
-module and
$R$
-module and
 $\unicode[STIX]{x1D719}:M\rightarrow E$
is an
$\unicode[STIX]{x1D719}:M\rightarrow E$
is an
![]() $R$
-linear map,
$R$
-linear map,
![]() $\unicode[STIX]{x1D719}$
annihilates
$\unicode[STIX]{x1D719}$
annihilates
![]() $\mathfrak{m}^{t}M$
for some
$\mathfrak{m}^{t}M$
for some
![]() $t$
. Indeed, let
$t$
. Indeed, let
 $m_{1},\ldots ,m_{n}$
be generators for
$m_{1},\ldots ,m_{n}$
be generators for
![]() $M$
over
$M$
over
![]() $R$
. Since
$R$
. Since
 $E=E(R/\mathfrak{m})$
is
$E=E(R/\mathfrak{m})$
is
![]() $\mathfrak{m}$
-power torsion (every element of
$\mathfrak{m}$
-power torsion (every element of
![]() $E$
is annihilated by some power of
$E$
is annihilated by some power of
![]() $\mathfrak{m}$
[Reference MatsumuraMat86, Theorem 18.4(v)]), there exist
$\mathfrak{m}$
[Reference MatsumuraMat86, Theorem 18.4(v)]), there exist
![]() $t_{i}$
for
$t_{i}$
for
 $i=1,\ldots ,n$
such that
$i=1,\ldots ,n$
such that
![]() $\unicode[STIX]{x1D719}(m_{i})$
is annihilated by
$\unicode[STIX]{x1D719}(m_{i})$
is annihilated by
![]() $\mathfrak{m}^{t_{i}}$
; but then, setting
$\mathfrak{m}^{t_{i}}$
; but then, setting
 $t=\max \{t_{1},\ldots ,t_{n}\}$
, we have
$t=\max \{t_{1},\ldots ,t_{n}\}$
, we have
 $\unicode[STIX]{x1D719}(\mathfrak{m}^{t}M)=0$
. Therefore every such
$\unicode[STIX]{x1D719}(\mathfrak{m}^{t}M)=0$
. Therefore every such
![]() $\unicode[STIX]{x1D719}$
factors through
$\unicode[STIX]{x1D719}$
factors through
 $M/\mathfrak{m}^{t}M$
for some
$M/\mathfrak{m}^{t}M$
for some
![]() $t$
, that is,
$t$
, that is,
 $\operatorname{Hom}_{R}(M,E)=\varinjlim \operatorname{Hom}_{R}(M/\mathfrak{m}^{t}M,E)$
. The
$\operatorname{Hom}_{R}(M,E)=\varinjlim \operatorname{Hom}_{R}(M/\mathfrak{m}^{t}M,E)$
. The
![]() $R$
-module
$R$
-module
 $M/\mathfrak{m}^{t}M$
is of finite length for all
$M/\mathfrak{m}^{t}M$
is of finite length for all
![]() $t$
. Since
$t$
. Since
 $\operatorname{Hom}_{R}(M/\mathfrak{m}^{t}M,E)$
is isomorphic via
$\operatorname{Hom}_{R}(M/\mathfrak{m}^{t}M,E)$
is isomorphic via
 $\unicode[STIX]{x1D6F7}_{M/\mathfrak{m}^{t}M}$
to
$\unicode[STIX]{x1D6F7}_{M/\mathfrak{m}^{t}M}$
to
 $\operatorname{Hom}_{k}(M/\mathfrak{m}^{t}M,k)$
, and these isomorphisms form a compatible system as
$\operatorname{Hom}_{k}(M/\mathfrak{m}^{t}M,k)$
, and these isomorphisms form a compatible system as
![]() $t$
varies, we deduce the existence of an isomorphism
$t$
varies, we deduce the existence of an isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{M}:\operatorname{Hom}_{R}(M,E)\xrightarrow[{}]{{\sim}}\varinjlim \operatorname{Hom}_{k}(M/\mathfrak{m}^{t}M,k)=\operatorname{Hom}_{\text{cont},k}(M,k),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{M}:\operatorname{Hom}_{R}(M,E)\xrightarrow[{}]{{\sim}}\varinjlim \operatorname{Hom}_{k}(M/\mathfrak{m}^{t}M,k)=\operatorname{Hom}_{\text{cont},k}(M,k),\end{eqnarray}$$
again defined by
 $\unicode[STIX]{x1D6F7}_{M}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}$
. Our definition of the action of an element
$\unicode[STIX]{x1D6F7}_{M}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}$
. Our definition of the action of an element
![]() $r\in R$
on a
$r\in R$
on a
![]() $k$
-linear map
$k$
-linear map
 $\unicode[STIX]{x1D706}:M\rightarrow k$
by pre-composition by multiplication with
$\unicode[STIX]{x1D706}:M\rightarrow k$
by pre-composition by multiplication with
![]() $r$
preserves the property of
$r$
preserves the property of
![]() $\mathfrak{m}$
-adic continuity, so
$\mathfrak{m}$
-adic continuity, so
 $\operatorname{Hom}_{\text{cont},k}(M,k)$
is indeed an
$\operatorname{Hom}_{\text{cont},k}(M,k)$
is indeed an
![]() $R$
-module. As in the finite-length case, we see that
$R$
-module. As in the finite-length case, we see that
![]() $\unicode[STIX]{x1D6F7}_{M}$
is functorial in the
$\unicode[STIX]{x1D6F7}_{M}$
is functorial in the
![]() $R$
-module
$R$
-module
![]() $M$
. Note that if
$M$
. Note that if
![]() $M$
is of finite length, every
$M$
is of finite length, every
![]() $k$
-linear map
$k$
-linear map
 $M\rightarrow k$
is
$M\rightarrow k$
is
![]() $\mathfrak{m}$
-adically continuous, so that the isomorphism
$\mathfrak{m}$
-adically continuous, so that the isomorphism
![]() $\unicode[STIX]{x1D6F7}_{M}$
just defined coincides with the
$\unicode[STIX]{x1D6F7}_{M}$
just defined coincides with the
![]() $\unicode[STIX]{x1D6F7}_{M}$
defined earlier. We summarize the above discussion in the following theorem.
$\unicode[STIX]{x1D6F7}_{M}$
defined earlier. We summarize the above discussion in the following theorem.
Theorem 3.8. Let
![]() $(R,\mathfrak{m})$
be a local ring with coefficient field
$(R,\mathfrak{m})$
be a local ring with coefficient field
![]() $k$
. Let
$k$
. Let
![]() $E$
be an
$E$
be an
![]() $R$
-injective hull of
$R$
-injective hull of
![]() $k$
, and let
$k$
, and let
 $\unicode[STIX]{x1D70E}:E\rightarrow k$
be a fixed
$\unicode[STIX]{x1D70E}:E\rightarrow k$
be a fixed
![]() $k$
-linear projection of
$k$
-linear projection of
![]() $E$
onto its socle. For every finitely generated
$E$
onto its socle. For every finitely generated
![]() $R$
-module
$R$
-module
![]() $M$
, post-composition with
$M$
, post-composition with
![]() $\unicode[STIX]{x1D70E}$
defines an isomorphism
$\unicode[STIX]{x1D70E}$
defines an isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{M}:\operatorname{Hom}_{R}(M,E)\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{\text{cont},k}(M,k)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{M}:\operatorname{Hom}_{R}(M,E)\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{\text{cont},k}(M,k)\end{eqnarray}$$
of
![]() $R$
-modules, functorial in the
$R$
-modules, functorial in the
![]() $R$
-module
$R$
-module
![]() $M$
. (As a special case, if
$M$
. (As a special case, if
![]() $M$
is of finite length,
$M$
is of finite length,
 $\operatorname{Hom}_{R}(M,E)\simeq \operatorname{Hom}_{k}(M,k)$
.)
$\operatorname{Hom}_{R}(M,E)\simeq \operatorname{Hom}_{k}(M,k)$
.)
For the rest of this section, the assumptions on
![]() $R$
and
$R$
and
![]() $k$
are as in Theorem 3.8. A consequence of this theorem is that we can define the Matlis dual of a map between finitely generated (respectively finite-length)
$k$
are as in Theorem 3.8. A consequence of this theorem is that we can define the Matlis dual of a map between finitely generated (respectively finite-length)
![]() $R$
-modules as long as the map is
$R$
-modules as long as the map is
![]() $k$
-linear and
$k$
-linear and
![]() $\mathfrak{m}$
-adically continuous (respectively
$\mathfrak{m}$
-adically continuous (respectively
![]() $k$
-linear). The definition is simply pre-composition.
$k$
-linear). The definition is simply pre-composition.
Definition 3.9. Let
 $\unicode[STIX]{x1D6FF}:M\rightarrow N$
be a
$\unicode[STIX]{x1D6FF}:M\rightarrow N$
be a
![]() $k$
-linear map between finitely generated
$k$
-linear map between finitely generated
![]() $R$
-modules that is continuous with respect to the
$R$
-modules that is continuous with respect to the
![]() $\mathfrak{m}$
-adic topologies on
$\mathfrak{m}$
-adic topologies on
![]() $M$
and
$M$
and
![]() $N$
. Then pre-composition with
$N$
. Then pre-composition with
![]() $\unicode[STIX]{x1D6FF}$
is
$\unicode[STIX]{x1D6FF}$
is
![]() $k$
-linear and carries
$k$
-linear and carries
![]() $\mathfrak{m}$
-adically continuous
$\mathfrak{m}$
-adically continuous
![]() $k$
-linear maps
$k$
-linear maps
 $\unicode[STIX]{x1D706}:N\rightarrow k$
to
$\unicode[STIX]{x1D706}:N\rightarrow k$
to
![]() $\mathfrak{m}$
-adically continuous
$\mathfrak{m}$
-adically continuous
![]() $k$
-linear maps
$k$
-linear maps
 $\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D6FF}:M\rightarrow k$
, so we can define the Matlis dual
$\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D6FF}:M\rightarrow k$
, so we can define the Matlis dual
 $\unicode[STIX]{x1D6FF}^{\ast }:D(N)\rightarrow D(M)$
to be the composite
$\unicode[STIX]{x1D6FF}^{\ast }:D(N)\rightarrow D(M)$
to be the composite

Remark 3.10. If
![]() $M$
and
$M$
and
![]() $N$
are of finite length,
$N$
are of finite length,
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
can be defined in the same way as above for any
$\unicode[STIX]{x1D6FF}^{\ast }$
can be defined in the same way as above for any
![]() $k$
-linear
$k$
-linear
![]() $\unicode[STIX]{x1D6FF}$
. (More generally, we will see below that any
$\unicode[STIX]{x1D6FF}$
. (More generally, we will see below that any
![]() $k$
-linear map between Artinian modules can be dualized.)
$k$
-linear map between Artinian modules can be dualized.)
Our dual construction behaves well with respect to composition.
Proposition 3.11. If
 $M,N,P$
are finitely generated
$M,N,P$
are finitely generated
![]() $R$
-modules and
$R$
-modules and
 $\unicode[STIX]{x1D6FF}:M\rightarrow N$
,
$\unicode[STIX]{x1D6FF}:M\rightarrow N$
,
 $\unicode[STIX]{x1D6FF}^{\prime }:N\rightarrow P$
are
$\unicode[STIX]{x1D6FF}^{\prime }:N\rightarrow P$
are
![]() $\mathfrak{m}$
-adically continuous
$\mathfrak{m}$
-adically continuous
![]() $k$
-linear maps, then
$k$
-linear maps, then
 $(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ {\unicode[STIX]{x1D6FF}^{\prime }}^{\ast }$
as maps
$(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ {\unicode[STIX]{x1D6FF}^{\prime }}^{\ast }$
as maps
 $D(P)\rightarrow D(M)$
.
$D(P)\rightarrow D(M)$
.
Proof. We calculate using the definition,
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6F7}_{M}^{-1}\circ (\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\vee }\circ \unicode[STIX]{x1D6F7}_{P}=\unicode[STIX]{x1D6F7}_{M}^{-1}\circ \unicode[STIX]{x1D6FF}^{\vee }\circ \unicode[STIX]{x1D6FF}^{\prime \vee }\circ \unicode[STIX]{x1D6F7}_{P}=(\unicode[STIX]{x1D6F7}_{M}^{-1}\circ \unicode[STIX]{x1D6FF}^{\vee }\circ \unicode[STIX]{x1D6F7}_{N})\circ (\unicode[STIX]{x1D6F7}_{N}^{-1}\circ \unicode[STIX]{x1D6FF}^{\prime \vee }\circ \unicode[STIX]{x1D6F7}_{P})=\unicode[STIX]{x1D6FF}^{\ast }\circ {\unicode[STIX]{x1D6FF}^{\prime }}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6F7}_{M}^{-1}\circ (\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\vee }\circ \unicode[STIX]{x1D6F7}_{P}=\unicode[STIX]{x1D6F7}_{M}^{-1}\circ \unicode[STIX]{x1D6FF}^{\vee }\circ \unicode[STIX]{x1D6FF}^{\prime \vee }\circ \unicode[STIX]{x1D6F7}_{P}=(\unicode[STIX]{x1D6F7}_{M}^{-1}\circ \unicode[STIX]{x1D6FF}^{\vee }\circ \unicode[STIX]{x1D6F7}_{N})\circ (\unicode[STIX]{x1D6F7}_{N}^{-1}\circ \unicode[STIX]{x1D6FF}^{\prime \vee }\circ \unicode[STIX]{x1D6F7}_{P})=\unicode[STIX]{x1D6FF}^{\ast }\circ {\unicode[STIX]{x1D6FF}^{\prime }}^{\ast },\end{eqnarray}$$
as desired. ◻
In the case of an
![]() $R$
-linear map (which is automatically
$R$
-linear map (which is automatically
![]() $k$
-linear and
$k$
-linear and
![]() $\mathfrak{m}$
-adically continuous) between finitely generated
$\mathfrak{m}$
-adically continuous) between finitely generated
![]() $R$
-modules, our definition of the Matlis dual of this map agrees with the usual one, so our notation is unambiguous and our definition is in fact a generalization of the usual one. We make this precise in the following nearly tautological lemma.
$R$
-modules, our definition of the Matlis dual of this map agrees with the usual one, so our notation is unambiguous and our definition is in fact a generalization of the usual one. We make this precise in the following nearly tautological lemma.
Lemma 3.12. Let
![]() $M$
and
$M$
and
![]() $N$
be finitely generated
$N$
be finitely generated
![]() $R$
-modules. If
$R$
-modules. If
 $f:M\rightarrow N$
is an
$f:M\rightarrow N$
is an
![]() $R$
-linear homomorphism, then
$R$
-linear homomorphism, then
 $f^{\ast }=\unicode[STIX]{x1D6F7}_{M}^{-1}\circ f^{\vee }\circ \unicode[STIX]{x1D6F7}_{N}$
, so the usual definition of the Matlis dual of
$f^{\ast }=\unicode[STIX]{x1D6F7}_{M}^{-1}\circ f^{\vee }\circ \unicode[STIX]{x1D6F7}_{N}$
, so the usual definition of the Matlis dual of
![]() $f$
coincides with ours.
$f$
coincides with ours.
Proof. Suppose
 $\unicode[STIX]{x1D719}:N\rightarrow E$
is
$\unicode[STIX]{x1D719}:N\rightarrow E$
is
![]() $R$
-linear. Then
$R$
-linear. Then
 $(f^{\vee }\circ \unicode[STIX]{x1D6F7}_{N})(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}\circ f$
. As
$(f^{\vee }\circ \unicode[STIX]{x1D6F7}_{N})(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}\circ f$
. As
![]() $\unicode[STIX]{x1D6F7}_{M}$
is an isomorphism,
$\unicode[STIX]{x1D6F7}_{M}$
is an isomorphism,
 $(\unicode[STIX]{x1D6F7}_{M}^{-1}\circ f^{\vee }\circ \unicode[STIX]{x1D6F7}_{N})(\unicode[STIX]{x1D719})$
is the unique
$(\unicode[STIX]{x1D6F7}_{M}^{-1}\circ f^{\vee }\circ \unicode[STIX]{x1D6F7}_{N})(\unicode[STIX]{x1D719})$
is the unique
![]() $R$
-linear map
$R$
-linear map
 $M\rightarrow E$
which gives
$M\rightarrow E$
which gives
 $\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}\circ f$
upon post-composition with
$\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}\circ f$
upon post-composition with
![]() $\unicode[STIX]{x1D70E}$
; by the unicity, it cannot be anything but
$\unicode[STIX]{x1D70E}$
; by the unicity, it cannot be anything but
 $\unicode[STIX]{x1D719}\circ f=f^{\ast }(\unicode[STIX]{x1D719})$
. Therefore the left- and right-hand sides of the asserted equality agree upon evaluation at every
$\unicode[STIX]{x1D719}\circ f=f^{\ast }(\unicode[STIX]{x1D719})$
. Therefore the left- and right-hand sides of the asserted equality agree upon evaluation at every
 $\unicode[STIX]{x1D719}\in D(N)$
.◻
$\unicode[STIX]{x1D719}\in D(N)$
.◻
What can be said in the case of arbitrary (not necessarily finitely generated) modules? An arbitrary
![]() $R$
-module
$R$
-module
![]() $M$
can be regarded as the filtered direct limit of its finitely generated
$M$
can be regarded as the filtered direct limit of its finitely generated
![]() $R$
-submodules
$R$
-submodules
![]() $M_{\unicode[STIX]{x1D706}}$
. The Matlis dual functor (indeed, any contravariant Hom functor) converts direct limits into inverse limits [Reference RotmanRot09, Proposition 5.26], so
$M_{\unicode[STIX]{x1D706}}$
. The Matlis dual functor (indeed, any contravariant Hom functor) converts direct limits into inverse limits [Reference RotmanRot09, Proposition 5.26], so
 $D(M)=\varprojlim \,D(M_{\unicode[STIX]{x1D706}})$
. If
$D(M)=\varprojlim \,D(M_{\unicode[STIX]{x1D706}})$
. If
 $\unicode[STIX]{x1D719}:M\rightarrow E$
is
$\unicode[STIX]{x1D719}:M\rightarrow E$
is
![]() $R$
-linear (an element of
$R$
-linear (an element of
![]() $D(M)$
), the restriction of
$D(M)$
), the restriction of
![]() $\unicode[STIX]{x1D719}$
to a fixed
$\unicode[STIX]{x1D719}$
to a fixed
![]() $M_{\unicode[STIX]{x1D706}}$
corresponds by Theorem 3.8 to an
$M_{\unicode[STIX]{x1D706}}$
corresponds by Theorem 3.8 to an
![]() $\mathfrak{m}$
-adically continuous map
$\mathfrak{m}$
-adically continuous map
 $M_{\unicode[STIX]{x1D706}}\rightarrow k$
. Therefore, we will be able to repeat our earlier constructions in the case of arbitrary modules if we impose some conditions on how the maps we are studying behave under restriction to finitely generated submodules. We make this precise with the following definition.
$M_{\unicode[STIX]{x1D706}}\rightarrow k$
. Therefore, we will be able to repeat our earlier constructions in the case of arbitrary modules if we impose some conditions on how the maps we are studying behave under restriction to finitely generated submodules. We make this precise with the following definition.
Definition 3.13. Let
![]() $M$
and
$M$
and
![]() $N$
be
$N$
be
![]() $R$
-modules, and let
$R$
-modules, and let
 $\unicode[STIX]{x1D6FF}:M\rightarrow N$
be a
$\unicode[STIX]{x1D6FF}:M\rightarrow N$
be a
![]() $k$
-linear map. We say that
$k$
-linear map. We say that
![]() $\unicode[STIX]{x1D6FF}$
is
$\unicode[STIX]{x1D6FF}$
is
![]() $\unicode[STIX]{x1D6F4}$
-continuous if for every finitely generated
$\unicode[STIX]{x1D6F4}$
-continuous if for every finitely generated
![]() $R$
-submodule
$R$
-submodule
 $M_{\unicode[STIX]{x1D706}}\subset M$
, the
$M_{\unicode[STIX]{x1D706}}\subset M$
, the
![]() $R$
-submodule
$R$
-submodule
 $\langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle \subset N$
generated by the image of
$\langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle \subset N$
generated by the image of
![]() $M_{\unicode[STIX]{x1D706}}$
under
$M_{\unicode[STIX]{x1D706}}$
under
![]() $\unicode[STIX]{x1D6FF}$
is finitely generated and the restriction
$\unicode[STIX]{x1D6FF}$
is finitely generated and the restriction
 $\unicode[STIX]{x1D6FF}|_{M_{\unicode[STIX]{x1D706}}}:M_{\unicode[STIX]{x1D706}}\rightarrow \langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle$
is
$\unicode[STIX]{x1D6FF}|_{M_{\unicode[STIX]{x1D706}}}:M_{\unicode[STIX]{x1D706}}\rightarrow \langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle$
is
![]() $\mathfrak{m}$
-adically continuous in the sense of Definition 3.6. We write
$\mathfrak{m}$
-adically continuous in the sense of Definition 3.6. We write
 $\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,N)$
for the set (indeed,
$\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,N)$
for the set (indeed,
![]() $R$
-module) of
$R$
-module) of
![]() $\unicode[STIX]{x1D6F4}$
-continuous
$\unicode[STIX]{x1D6F4}$
-continuous
![]() $k$
-linear maps
$k$
-linear maps
 $M\rightarrow N$
, and refer to such maps simply as ‘
$M\rightarrow N$
, and refer to such maps simply as ‘
![]() $\unicode[STIX]{x1D6F4}$
-continuous’, the
$\unicode[STIX]{x1D6F4}$
-continuous’, the
![]() $k$
-linearity being understood.
$k$
-linearity being understood.
A
![]() $\unicode[STIX]{x1D6F4}$
-continuous map is not, in general,
$\unicode[STIX]{x1D6F4}$
-continuous map is not, in general,
![]() $\mathfrak{m}$
-adically continuous, but is built from
$\mathfrak{m}$
-adically continuous, but is built from
![]() $\mathfrak{m}$
-adically continuous maps in ‘small’ (finitely generated) stages. (The terminology ‘
$\mathfrak{m}$
-adically continuous maps in ‘small’ (finitely generated) stages. (The terminology ‘
![]() $\unicode[STIX]{x1D6F4}$
-continuous’ is meant to reflect this, by analogy with the
$\unicode[STIX]{x1D6F4}$
-continuous’ is meant to reflect this, by analogy with the
![]() $\unicode[STIX]{x1D70E}$
-finite measure spaces of real analysis and the
$\unicode[STIX]{x1D70E}$
-finite measure spaces of real analysis and the
![]() $\unicode[STIX]{x1D70E}$
-compact spaces of topology.)
$\unicode[STIX]{x1D70E}$
-compact spaces of topology.)
Lemma 3.14. Let
![]() $M$
,
$M$
,
![]() $N$
, and
$N$
, and
![]() $P$
be
$P$
be
![]() $R$
-modules.
$R$
-modules.
-
(a) Every
 $R$
-linear map
$R$
-linear map
 $\unicode[STIX]{x1D719}:M\rightarrow N$
is
$\unicode[STIX]{x1D719}:M\rightarrow N$
is
 $\unicode[STIX]{x1D6F4}$
-continuous.
$\unicode[STIX]{x1D6F4}$
-continuous. -
(b) If
 $\unicode[STIX]{x1D6FF}:M\rightarrow N$
and
$\unicode[STIX]{x1D6FF}:M\rightarrow N$
and
 $\unicode[STIX]{x1D6FF}^{\prime }:N\rightarrow P$
are
$\unicode[STIX]{x1D6FF}^{\prime }:N\rightarrow P$
are
 $\unicode[STIX]{x1D6F4}$
-continuous, then
$\unicode[STIX]{x1D6F4}$
-continuous, then
 $\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF}:M\rightarrow P$
is
$\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF}:M\rightarrow P$
is
 $\unicode[STIX]{x1D6F4}$
-continuous. In particular, for every
$\unicode[STIX]{x1D6F4}$
-continuous. In particular, for every
 $\unicode[STIX]{x1D6F4}$
-continuous map
$\unicode[STIX]{x1D6F4}$
-continuous map
 $\unicode[STIX]{x1D6FF}^{\prime }:N\rightarrow k$
, the composite
$\unicode[STIX]{x1D6FF}^{\prime }:N\rightarrow k$
, the composite
 $\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF}:M\rightarrow k$
is
$\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF}:M\rightarrow k$
is
 $\unicode[STIX]{x1D6F4}$
-continuous.
$\unicode[STIX]{x1D6F4}$
-continuous. -
(c) A
 $k$
-linear map
$k$
-linear map
 $\unicode[STIX]{x1D6FF}:M\rightarrow k$
is
$\unicode[STIX]{x1D6FF}:M\rightarrow k$
is
 $\unicode[STIX]{x1D6F4}$
-continuous if and only if, for every finitely generated
$\unicode[STIX]{x1D6F4}$
-continuous if and only if, for every finitely generated
 $R$
-submodule
$R$
-submodule
 $M_{\unicode[STIX]{x1D706}}\subset M$
, there exists
$M_{\unicode[STIX]{x1D706}}\subset M$
, there exists
 $t_{\unicode[STIX]{x1D706}}\geqslant 0$
such that
$t_{\unicode[STIX]{x1D706}}\geqslant 0$
such that
 $\unicode[STIX]{x1D6FF}(\mathfrak{m}^{t_{\unicode[STIX]{x1D706}}}M_{\unicode[STIX]{x1D706}})=0$
.
$\unicode[STIX]{x1D6FF}(\mathfrak{m}^{t_{\unicode[STIX]{x1D706}}}M_{\unicode[STIX]{x1D706}})=0$
.
Proof. Since
![]() $R$
-linear maps carry finitely generated submodules to finitely generated submodules, part (a) is immediate. Part (b) holds because both parts of the definition of
$R$
-linear maps carry finitely generated submodules to finitely generated submodules, part (a) is immediate. Part (b) holds because both parts of the definition of
![]() $\unicode[STIX]{x1D6F4}$
-continuity are preserved under composition. Finally, since
$\unicode[STIX]{x1D6F4}$
-continuity are preserved under composition. Finally, since
![]() $k$
is a finitely generated
$k$
is a finitely generated
![]() $R$
-module, the first part of the definition of
$R$
-module, the first part of the definition of
![]() $\unicode[STIX]{x1D6F4}$
-continuity is automatic when the target of the map is
$\unicode[STIX]{x1D6F4}$
-continuity is automatic when the target of the map is
![]() $k$
, and therefore a
$k$
, and therefore a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map
$\unicode[STIX]{x1D6F4}$
-continuous map
 $\unicode[STIX]{x1D6FF}:M\rightarrow k$
is a map whose restrictions to all finitely generated
$\unicode[STIX]{x1D6FF}:M\rightarrow k$
is a map whose restrictions to all finitely generated
![]() $R$
-submodules of
$R$
-submodules of
![]() $M$
are
$M$
are
![]() $\mathfrak{m}$
-adically continuous. By the paragraph following Remark 3.7, such maps are exactly those described in part (c).◻
$\mathfrak{m}$
-adically continuous. By the paragraph following Remark 3.7, such maps are exactly those described in part (c).◻
By restricting attention to
![]() $\unicode[STIX]{x1D6F4}$
-continuous maps to
$\unicode[STIX]{x1D6F4}$
-continuous maps to
![]() $k$
, we obtain a generalization of Theorem 3.8 to the case of an arbitrary module (cf. [Reference Grothendieck and RaynaudGR05, Exp. IV, Remarque 5.5]).
$k$
, we obtain a generalization of Theorem 3.8 to the case of an arbitrary module (cf. [Reference Grothendieck and RaynaudGR05, Exp. IV, Remarque 5.5]).
Theorem 3.15. Let
![]() $M$
be an
$M$
be an
![]() $R$
-module, and let
$R$
-module, and let
 $\unicode[STIX]{x1D70E}:E\rightarrow k$
be a fixed
$\unicode[STIX]{x1D70E}:E\rightarrow k$
be a fixed
![]() $k$
-linear projection of
$k$
-linear projection of
![]() $E$
onto its socle. There is an isomorphism of
$E$
onto its socle. There is an isomorphism of
![]() $R$
-modules
$R$
-modules
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{M}:D(M)=\operatorname{Hom}_{R}(M,E)\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,k)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{M}:D(M)=\operatorname{Hom}_{R}(M,E)\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,k)\end{eqnarray}$$
defined by post-composition with
![]() $\unicode[STIX]{x1D70E}$
and functorial in the
$\unicode[STIX]{x1D70E}$
and functorial in the
![]() $R$
-module
$R$
-module
![]() $M$
.
$M$
.
Proof. Consider the family
![]() $\{M_{\unicode[STIX]{x1D706}}\}$
of finitely generated
$\{M_{\unicode[STIX]{x1D706}}\}$
of finitely generated
![]() $R$
-submodules of
$R$
-submodules of
![]() $M$
. We view
$M$
. We view
![]() $M$
as the filtered direct limit of the
$M$
as the filtered direct limit of the
![]() $M_{\unicode[STIX]{x1D706}}$
. As the Matlis dual functor converts direct limits into inverse limits, we see that
$M_{\unicode[STIX]{x1D706}}$
. As the Matlis dual functor converts direct limits into inverse limits, we see that
 $D(M)=\varprojlim \,D(M_{\unicode[STIX]{x1D706}})$
, the transition maps being pre-composition with inclusions
$D(M)=\varprojlim \,D(M_{\unicode[STIX]{x1D706}})$
, the transition maps being pre-composition with inclusions
 $M_{\unicode[STIX]{x1D706}}{\hookrightarrow}M_{\unicode[STIX]{x1D706}^{\prime }}$
of finitely generated submodules. For all
$M_{\unicode[STIX]{x1D706}}{\hookrightarrow}M_{\unicode[STIX]{x1D706}^{\prime }}$
of finitely generated submodules. For all
![]() $M_{\unicode[STIX]{x1D706}}$
, post-composition with
$M_{\unicode[STIX]{x1D706}}$
, post-composition with
![]() $\unicode[STIX]{x1D70E}$
defines an isomorphism
$\unicode[STIX]{x1D70E}$
defines an isomorphism
 $\unicode[STIX]{x1D6F7}_{M_{\unicode[STIX]{x1D706}}}:D(M_{\unicode[STIX]{x1D706}})\rightarrow \operatorname{Hom}_{\text{cont},k}(M_{\unicode[STIX]{x1D706}},k)$
by Theorem 3.8. Since this isomorphism is functorial in
$\unicode[STIX]{x1D6F7}_{M_{\unicode[STIX]{x1D706}}}:D(M_{\unicode[STIX]{x1D706}})\rightarrow \operatorname{Hom}_{\text{cont},k}(M_{\unicode[STIX]{x1D706}},k)$
by Theorem 3.8. Since this isomorphism is functorial in
![]() $M_{\unicode[STIX]{x1D706}}$
, the
$M_{\unicode[STIX]{x1D706}}$
, the
![]() $\{\unicode[STIX]{x1D6F7}_{M_{\unicode[STIX]{x1D706}}}\}$
form a compatible system of
$\{\unicode[STIX]{x1D6F7}_{M_{\unicode[STIX]{x1D706}}}\}$
form a compatible system of
![]() $R$
-linear isomorphisms, inducing an
$R$
-linear isomorphisms, inducing an
![]() $R$
-linear isomorphism
$R$
-linear isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{M}^{\prime }:D(M)=\varprojlim \,D(M_{\unicode[STIX]{x1D706}})\xrightarrow[{}]{{\sim}}\varprojlim \,\operatorname{Hom}_{\text{cont},k}(M_{\unicode[STIX]{x1D706}},k);\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{M}^{\prime }:D(M)=\varprojlim \,D(M_{\unicode[STIX]{x1D706}})\xrightarrow[{}]{{\sim}}\varprojlim \,\operatorname{Hom}_{\text{cont},k}(M_{\unicode[STIX]{x1D706}},k);\end{eqnarray}$$
but the right-hand side of this isomorphism can be identified with
 $\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,k)$
, essentially by definition. The natural isomorphism
$\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,k)$
, essentially by definition. The natural isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D703}:\varprojlim \,\operatorname{Hom}_{\text{cont},k}(M_{\unicode[STIX]{x1D706}},k)\rightarrow \operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,k)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}:\varprojlim \,\operatorname{Hom}_{\text{cont},k}(M_{\unicode[STIX]{x1D706}},k)\rightarrow \operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,k)\end{eqnarray}$$
is defined on a compatible system
 $\{f_{\unicode[STIX]{x1D706}}\in \operatorname{Hom}_{\text{cont},k}(M_{\unicode[STIX]{x1D706}},k)\}$
by taking
$\{f_{\unicode[STIX]{x1D706}}\in \operatorname{Hom}_{\text{cont},k}(M_{\unicode[STIX]{x1D706}},k)\}$
by taking
![]() $\unicode[STIX]{x1D703}(\{f_{\unicode[STIX]{x1D706}}\})$
to be the unique
$\unicode[STIX]{x1D703}(\{f_{\unicode[STIX]{x1D706}}\})$
to be the unique
![]() $k$
-linear map
$k$
-linear map
 $M\rightarrow k$
whose restriction to every
$M\rightarrow k$
whose restriction to every
![]() $M_{\unicode[STIX]{x1D706}}$
is
$M_{\unicode[STIX]{x1D706}}$
is
![]() $f_{\unicode[STIX]{x1D706}}$
(this map is
$f_{\unicode[STIX]{x1D706}}$
(this map is
![]() $\unicode[STIX]{x1D6F4}$
-continuous by definition), and the composition
$\unicode[STIX]{x1D6F4}$
-continuous by definition), and the composition
 $\unicode[STIX]{x1D6F7}_{M}=\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D6F7}_{M}^{\prime }$
is nothing but post-composition with
$\unicode[STIX]{x1D6F7}_{M}=\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D6F7}_{M}^{\prime }$
is nothing but post-composition with
![]() $\unicode[STIX]{x1D70E}$
, completing the proof.◻
$\unicode[STIX]{x1D70E}$
, completing the proof.◻
Definition 3.16. Let
![]() $M$
be an
$M$
be an
![]() $R$
-module. The
$R$
-module. The
![]() $\unicode[STIX]{x1D6F4}$
-continuous dual
$\unicode[STIX]{x1D6F4}$
-continuous dual
![]() $D^{\unicode[STIX]{x1D6F4}}(M)$
of
$D^{\unicode[STIX]{x1D6F4}}(M)$
of
![]() $M$
is the
$M$
is the
![]() $R$
-module
$R$
-module
 $\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,k)$
. By Theorem 3.15, we have
$\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,k)$
. By Theorem 3.15, we have
 $D(M)\simeq D^{\unicode[STIX]{x1D6F4}}(M)$
as
$D(M)\simeq D^{\unicode[STIX]{x1D6F4}}(M)$
as
![]() $R$
-modules.
$R$
-modules.
Remark 3.17. If
![]() $M$
is a finitely generated
$M$
is a finitely generated
![]() $R$
-module, then clearly
$R$
-module, then clearly
 $$\begin{eqnarray}D^{\unicode[STIX]{x1D6F4}}(M)=\operatorname{Hom}_{\text{cont},k}(M,k),\end{eqnarray}$$
$$\begin{eqnarray}D^{\unicode[STIX]{x1D6F4}}(M)=\operatorname{Hom}_{\text{cont},k}(M,k),\end{eqnarray}$$
so in this case the
![]() $\unicode[STIX]{x1D6F7}_{M}$
of Theorem 3.15 is the same as the
$\unicode[STIX]{x1D6F7}_{M}$
of Theorem 3.15 is the same as the
![]() $\unicode[STIX]{x1D6F7}_{M}$
of Theorem 3.8.
$\unicode[STIX]{x1D6F7}_{M}$
of Theorem 3.8.
Theorem 3.15 allows us to identify the Matlis dual with the full
![]() $k$
-linear dual in the case of an Artinian module.
$k$
-linear dual in the case of an Artinian module.
Corollary 3.18. If
![]() $M$
is an
$M$
is an
![]() $R$
-module such that
$R$
-module such that
 $\operatorname{Supp}(M)=\{\mathfrak{m}\}$
(for instance if
$\operatorname{Supp}(M)=\{\mathfrak{m}\}$
(for instance if
![]() $M$
is Artinian), then
$M$
is Artinian), then
 $D(M)\simeq \operatorname{Hom}_{k}(M,k)$
as
$D(M)\simeq \operatorname{Hom}_{k}(M,k)$
as
![]() $R$
-modules.
$R$
-modules.
Proof. Let
![]() $M_{\unicode[STIX]{x1D706}}$
be a finitely generated
$M_{\unicode[STIX]{x1D706}}$
be a finitely generated
![]() $R$
-submodule of
$R$
-submodule of
![]() $M$
. The hypothesis on
$M$
. The hypothesis on
![]() $M$
implies that
$M$
implies that
![]() $M_{\unicode[STIX]{x1D706}}$
is annihilated by a power of
$M_{\unicode[STIX]{x1D706}}$
is annihilated by a power of
![]() $\mathfrak{m}$
and consequently is of finite length. Given any
$\mathfrak{m}$
and consequently is of finite length. Given any
![]() $k$
-linear map
$k$
-linear map
![]() $M\rightarrow k$
, its restriction to
$M\rightarrow k$
, its restriction to
![]() $M_{\unicode[STIX]{x1D706}}$
is therefore
$M_{\unicode[STIX]{x1D706}}$
is therefore
![]() $\mathfrak{m}$
-adically continuous. We conclude that
$\mathfrak{m}$
-adically continuous. We conclude that
 $D^{\unicode[STIX]{x1D6F4}}(M)=\operatorname{Hom}_{k}(M,k)$
: the corollary now follows from Theorem 3.15.◻
$D^{\unicode[STIX]{x1D6F4}}(M)=\operatorname{Hom}_{k}(M,k)$
: the corollary now follows from Theorem 3.15.◻
We can now extend the definition of the Matlis dual of an
![]() $\mathfrak{m}$
-adically continuous map between finitely generated
$\mathfrak{m}$
-adically continuous map between finitely generated
![]() $R$
-modules to a definition of the Matlis dual of a
$R$
-modules to a definition of the Matlis dual of a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map between arbitrary modules as follows.
$\unicode[STIX]{x1D6F4}$
-continuous map between arbitrary modules as follows.
Proposition 3.19 (Proposition–Definition).
Let
![]() $M$
and
$M$
and
![]() $N$
be
$N$
be
![]() $R$
-modules, and let
$R$
-modules, and let
 $\unicode[STIX]{x1D6FF}:M\rightarrow N$
be a
$\unicode[STIX]{x1D6FF}:M\rightarrow N$
be a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map. Define the
$\unicode[STIX]{x1D6F4}$
-continuous map. Define the
 $\text{Matlis}~\text{dual}~\unicode[STIX]{x1D6FF}^{\ast }:D(N)\rightarrow D(M)$
to be the composite
$\text{Matlis}~\text{dual}~\unicode[STIX]{x1D6FF}^{\ast }:D(N)\rightarrow D(M)$
to be the composite

where again
![]() $\unicode[STIX]{x1D6FF}^{\vee }$
is pre-composition with
$\unicode[STIX]{x1D6FF}^{\vee }$
is pre-composition with
![]() $\unicode[STIX]{x1D6FF}$
. This construction satisfies the following properties: given another
$\unicode[STIX]{x1D6FF}$
. This construction satisfies the following properties: given another
![]() $R$
-module
$R$
-module
![]() $P$
and a
$P$
and a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map
$\unicode[STIX]{x1D6F4}$
-continuous map
 $\unicode[STIX]{x1D6FF}^{\prime }:N\rightarrow P$
, we have
$\unicode[STIX]{x1D6FF}^{\prime }:N\rightarrow P$
, we have
 $(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ {\unicode[STIX]{x1D6FF}^{\prime }}^{\ast }$
as
$(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ {\unicode[STIX]{x1D6FF}^{\prime }}^{\ast }$
as
![]() $k$
-linear maps
$k$
-linear maps
 $D(P)\rightarrow D(M)$
, and
$D(P)\rightarrow D(M)$
, and
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
is the usual Matlis dual in the case in which
$\unicode[STIX]{x1D6FF}^{\ast }$
is the usual Matlis dual in the case in which
![]() $\unicode[STIX]{x1D6FF}$
is
$\unicode[STIX]{x1D6FF}$
is
![]() $R$
-linear.
$R$
-linear.
Proof. By Lemma 3.14(b),
![]() $\unicode[STIX]{x1D6FF}^{\vee }$
is a well-defined
$\unicode[STIX]{x1D6FF}^{\vee }$
is a well-defined
![]() $k$
-linear map
$k$
-linear map
 $D^{\unicode[STIX]{x1D6F4}}(N)\rightarrow D^{\unicode[STIX]{x1D6F4}}(M)$
. The final two assertions follow immediately since both Proposition 3.11 and Lemma 3.12 hold for the restriction of
$D^{\unicode[STIX]{x1D6F4}}(N)\rightarrow D^{\unicode[STIX]{x1D6F4}}(M)$
. The final two assertions follow immediately since both Proposition 3.11 and Lemma 3.12 hold for the restriction of
![]() $\unicode[STIX]{x1D6FF}$
to any finitely generated
$\unicode[STIX]{x1D6FF}$
to any finitely generated
![]() $R$
-submodule of
$R$
-submodule of
![]() $M$
.◻
$M$
.◻
Remark 3.20. Suppose
![]() $M$
,
$M$
,
![]() $N$
, and
$N$
, and
![]() $\unicode[STIX]{x1D6FF}$
are as above, and suppose we are given cofinal families
$\unicode[STIX]{x1D6FF}$
are as above, and suppose we are given cofinal families
![]() $\{M_{\unicode[STIX]{x1D706}}\}$
(respectively
$\{M_{\unicode[STIX]{x1D706}}\}$
(respectively
![]() $\{N_{\unicode[STIX]{x1D707}}\}$
) of
$\{N_{\unicode[STIX]{x1D707}}\}$
) of
![]() $R$
-submodules of
$R$
-submodules of
![]() $M$
(respectively
$M$
(respectively
![]() $N$
), meaning that every
$N$
), meaning that every
![]() $R$
-submodule of
$R$
-submodule of
![]() $M$
(respectively
$M$
(respectively
![]() $N$
) is contained in some
$N$
) is contained in some
![]() $M_{\unicode[STIX]{x1D706}}$
(respectively some
$M_{\unicode[STIX]{x1D706}}$
(respectively some
![]() $N_{\unicode[STIX]{x1D707}}$
), with the further condition that for all
$N_{\unicode[STIX]{x1D707}}$
), with the further condition that for all
![]() $\unicode[STIX]{x1D706}$
, there exists
$\unicode[STIX]{x1D706}$
, there exists
![]() $\unicode[STIX]{x1D707}$
such that
$\unicode[STIX]{x1D707}$
such that
 $\unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\subset N_{\unicode[STIX]{x1D707}}$
. Since
$\unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\subset N_{\unicode[STIX]{x1D707}}$
. Since
 $M=\varinjlim M_{\unicode[STIX]{x1D706}}$
and
$M=\varinjlim M_{\unicode[STIX]{x1D706}}$
and
 $N=\varinjlim N_{\unicode[STIX]{x1D707}}$
, it follows that
$N=\varinjlim N_{\unicode[STIX]{x1D707}}$
, it follows that
 $D(M)\simeq \varprojlim \,D(M_{\unicode[STIX]{x1D706}})$
and
$D(M)\simeq \varprojlim \,D(M_{\unicode[STIX]{x1D706}})$
and
 $D(N)\simeq \varprojlim \,D(N_{\unicode[STIX]{x1D707}})$
as
$D(N)\simeq \varprojlim \,D(N_{\unicode[STIX]{x1D707}})$
as
![]() $R$
-modules. If we write
$R$
-modules. If we write
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
for
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
for
 $\unicode[STIX]{x1D6FF}|_{M_{\unicode[STIX]{x1D706}}}:M_{\unicode[STIX]{x1D706}}\rightarrow N_{\unicode[STIX]{x1D707}}$
, then it is clear from the construction of Proposition 3.19 that
$\unicode[STIX]{x1D6FF}|_{M_{\unicode[STIX]{x1D706}}}:M_{\unicode[STIX]{x1D706}}\rightarrow N_{\unicode[STIX]{x1D707}}$
, then it is clear from the construction of Proposition 3.19 that
 $\unicode[STIX]{x1D6FF}^{\ast }:D(N)\rightarrow D(M)$
can be identified with
$\unicode[STIX]{x1D6FF}^{\ast }:D(N)\rightarrow D(M)$
can be identified with
 $\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{\ast }:D(N_{\unicode[STIX]{x1D707}})\rightarrow D(M_{\unicode[STIX]{x1D706}}))$
.
$\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{\ast }:D(N_{\unicode[STIX]{x1D707}})\rightarrow D(M_{\unicode[STIX]{x1D706}}))$
.
We next show that over a complete local ring, the Matlis dual of a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map is again
$\unicode[STIX]{x1D6F4}$
-continuous map is again
![]() $\unicode[STIX]{x1D6F4}$
-continuous in some important special cases. At present, we do not know an example of a
$\unicode[STIX]{x1D6F4}$
-continuous in some important special cases. At present, we do not know an example of a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map for which this is false. (It would be interesting to find necessary and sufficient conditions on
$\unicode[STIX]{x1D6F4}$
-continuous map for which this is false. (It would be interesting to find necessary and sufficient conditions on
![]() $M$
and
$M$
and
![]() $N$
for any
$N$
for any
![]() $\unicode[STIX]{x1D6F4}$
-continuous map
$\unicode[STIX]{x1D6F4}$
-continuous map
 $M\rightarrow N$
to have
$M\rightarrow N$
to have
![]() $\unicode[STIX]{x1D6F4}$
-continuous dual.)
$\unicode[STIX]{x1D6F4}$
-continuous dual.)
Proposition 3.21. Let
![]() $R$
be a complete local ring with coefficient field
$R$
be a complete local ring with coefficient field
![]() $k$
. Let
$k$
. Let
![]() $M$
and
$M$
and
![]() $N$
be
$N$
be
![]() $R$
-modules, and let
$R$
-modules, and let
 $\unicode[STIX]{x1D6FF}:M\rightarrow N$
be a
$\unicode[STIX]{x1D6FF}:M\rightarrow N$
be a
![]() $k$
-linear map.
$k$
-linear map.
-
(a) If
 $M$
is Artinian, then
$M$
is Artinian, then
 $\unicode[STIX]{x1D6FF}$
is
$\unicode[STIX]{x1D6FF}$
is
 $\unicode[STIX]{x1D6F4}$
-continuous.
$\unicode[STIX]{x1D6F4}$
-continuous. -
(b) If
 $M$
and
$M$
and
 $N$
are finitely generated, then
$N$
are finitely generated, then
 $\unicode[STIX]{x1D6FF}$
is
$\unicode[STIX]{x1D6FF}$
is
 $\mathfrak{m}$
-adically continuous if and only if it is
$\mathfrak{m}$
-adically continuous if and only if it is
 $\unicode[STIX]{x1D6F4}$
-continuous.
$\unicode[STIX]{x1D6F4}$
-continuous. -
(c) If
 $M$
and
$M$
and
 $N$
are Artinian, then
$N$
are Artinian, then
 $\unicode[STIX]{x1D6FF}^{\ast }$
, which is defined by part (a), is
$\unicode[STIX]{x1D6FF}^{\ast }$
, which is defined by part (a), is
 $\unicode[STIX]{x1D6F4}$
-continuous.
$\unicode[STIX]{x1D6F4}$
-continuous. -
(d) If
 $N$
is finitely generated and
$N$
is finitely generated and
 $\unicode[STIX]{x1D6FF}$
is
$\unicode[STIX]{x1D6FF}$
is
 $\unicode[STIX]{x1D6F4}$
-continuous, then
$\unicode[STIX]{x1D6F4}$
-continuous, then
 $\unicode[STIX]{x1D6FF}^{\ast }$
is
$\unicode[STIX]{x1D6FF}^{\ast }$
is
 $\unicode[STIX]{x1D6F4}$
-continuous.
$\unicode[STIX]{x1D6F4}$
-continuous.
Proof. Suppose that
![]() $M$
is Artinian. Any finitely generated
$M$
is Artinian. Any finitely generated
![]() $R$
-submodule
$R$
-submodule
 $M_{\unicode[STIX]{x1D706}}\subset M$
is of finite length and hence is annihilated by
$M_{\unicode[STIX]{x1D706}}\subset M$
is of finite length and hence is annihilated by
![]() $\mathfrak{m}^{l}$
for some
$\mathfrak{m}^{l}$
for some
![]() $l$
, so in particular
$l$
, so in particular
 $\unicode[STIX]{x1D6FF}(\mathfrak{m}^{l}M_{\unicode[STIX]{x1D706}})=0$
. Since
$\unicode[STIX]{x1D6FF}(\mathfrak{m}^{l}M_{\unicode[STIX]{x1D706}})=0$
. Since
![]() $M_{\unicode[STIX]{x1D706}}$
is of finite length (hence is a finite-dimensional
$M_{\unicode[STIX]{x1D706}}$
is of finite length (hence is a finite-dimensional
![]() $k$
-space) and
$k$
-space) and
![]() $\unicode[STIX]{x1D6FF}$
is
$\unicode[STIX]{x1D6FF}$
is
![]() $k$
-linear,
$k$
-linear,
![]() $\unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})$
is also a finite-dimensional
$\unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})$
is also a finite-dimensional
![]() $k$
-space, so the
$k$
-space, so the
![]() $R$
-submodule of
$R$
-submodule of
![]() $N$
that it generates is finitely generated over
$N$
that it generates is finitely generated over
![]() $R$
. We conclude that
$R$
. We conclude that
![]() $\unicode[STIX]{x1D6FF}$
is
$\unicode[STIX]{x1D6FF}$
is
![]() $\unicode[STIX]{x1D6F4}$
-continuous, proving part (a).
$\unicode[STIX]{x1D6F4}$
-continuous, proving part (a).
If
![]() $M$
and
$M$
and
![]() $N$
are finitely generated, the image under
$N$
are finitely generated, the image under
![]() $\unicode[STIX]{x1D6FF}$
of any submodule of
$\unicode[STIX]{x1D6FF}$
of any submodule of
![]() $M$
is contained in a finitely generated
$M$
is contained in a finitely generated
![]() $R$
-module, namely
$R$
-module, namely
![]() $N$
itself. This proves the forward direction of part (b), and the converse is obvious.
$N$
itself. This proves the forward direction of part (b), and the converse is obvious.
Suppose that
![]() $M$
and
$M$
and
![]() $N$
are Artinian. Let
$N$
are Artinian. Let
![]() $t$
be a natural number, and let
$t$
be a natural number, and let
 $M_{t}=(0:_{M}\mathfrak{m}^{t})$
, a finite-length
$M_{t}=(0:_{M}\mathfrak{m}^{t})$
, a finite-length
![]() $R$
-submodule of
$R$
-submodule of
![]() $M$
. As
$M$
. As
![]() $N$
is Artinian, every element of
$N$
is Artinian, every element of
![]() $N$
is annihilated by some power of
$N$
is annihilated by some power of
![]() $\mathfrak{m}$
, so there exists some
$\mathfrak{m}$
, so there exists some
![]() $s$
such that
$s$
such that
 $\unicode[STIX]{x1D6FF}(M_{t})\subset N_{s}=(0:_{N}\mathfrak{m}^{s})$
. Now apply Matlis duality. The containment
$\unicode[STIX]{x1D6FF}(M_{t})\subset N_{s}=(0:_{N}\mathfrak{m}^{s})$
. Now apply Matlis duality. The containment
 $\unicode[STIX]{x1D6FF}(M_{t})\subset N_{s}$
implies that the kernel of the map
$\unicode[STIX]{x1D6FF}(M_{t})\subset N_{s}$
implies that the kernel of the map
 $D(N)\rightarrow D(N_{s})$
is carried by
$D(N)\rightarrow D(N_{s})$
is carried by
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
into the kernel of
$\unicode[STIX]{x1D6FF}^{\ast }$
into the kernel of
 $D(M)\rightarrow D(M_{t})$
. This kernel (which we may identify with
$D(M)\rightarrow D(M_{t})$
. This kernel (which we may identify with
 $D(M/M_{t})$
by the exactness of
$D(M/M_{t})$
by the exactness of
![]() $D$
) is
$D$
) is
 $\mathfrak{m}^{t}D(M)$
; this means that
$\mathfrak{m}^{t}D(M)$
; this means that
 $\unicode[STIX]{x1D6FF}^{\ast }(\mathfrak{m}^{s}D(N))\subset \mathfrak{m}^{t}D(M)$
, that is, that
$\unicode[STIX]{x1D6FF}^{\ast }(\mathfrak{m}^{s}D(N))\subset \mathfrak{m}^{t}D(M)$
, that is, that
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
is continuous with respect to the
$\unicode[STIX]{x1D6FF}^{\ast }$
is continuous with respect to the
![]() $\mathfrak{m}$
-adic topologies on
$\mathfrak{m}$
-adic topologies on
![]() $D(N)$
and
$D(N)$
and
![]() $D(M)$
. Since
$D(M)$
. Since
![]() $M$
and
$M$
and
![]() $N$
are Artinian and
$N$
are Artinian and
![]() $R$
is complete,
$R$
is complete,
![]() $D(N)$
and
$D(N)$
and
![]() $D(M)$
are finitely generated [Reference MatsumuraMat86, Theorem 18.6(v)], so by part (b),
$D(M)$
are finitely generated [Reference MatsumuraMat86, Theorem 18.6(v)], so by part (b),
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
is
$\unicode[STIX]{x1D6FF}^{\ast }$
is
![]() $\unicode[STIX]{x1D6F4}$
-continuous. This proves part (c).
$\unicode[STIX]{x1D6F4}$
-continuous. This proves part (c).
If
![]() $N$
is finitely generated, then since
$N$
is finitely generated, then since
![]() $R$
is complete,
$R$
is complete,
![]() $D(N)$
is Artinian [Reference MatsumuraMat86, Theorem 18.6(v)]. The map
$D(N)$
is Artinian [Reference MatsumuraMat86, Theorem 18.6(v)]. The map
 $\unicode[STIX]{x1D6FF}^{\ast }:D(N)\rightarrow D(M)$
is
$\unicode[STIX]{x1D6FF}^{\ast }:D(N)\rightarrow D(M)$
is
![]() $k$
-linear, hence
$k$
-linear, hence
![]() $\unicode[STIX]{x1D6F4}$
-continuous by part (a). This completes the proof of part (d) and the proposition.◻
$\unicode[STIX]{x1D6F4}$
-continuous by part (a). This completes the proof of part (d) and the proposition.◻
If
![]() $M$
is any
$M$
is any
![]() $R$
-module, there is a natural map
$R$
-module, there is a natural map
 $\unicode[STIX]{x1D704}:M\rightarrow D(D(M))$
defined by evaluation: we set
$\unicode[STIX]{x1D704}:M\rightarrow D(D(M))$
defined by evaluation: we set
 $\unicode[STIX]{x1D704}(m)(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}(m)$
for all
$\unicode[STIX]{x1D704}(m)(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}(m)$
for all
![]() $m\in M$
and
$m\in M$
and
 $\unicode[STIX]{x1D719}\in D(M)$
. If
$\unicode[STIX]{x1D719}\in D(M)$
. If
![]() $R$
is complete and
$R$
is complete and
![]() $M$
is a finitely generated or Artinian
$M$
is a finitely generated or Artinian
![]() $R$
-module,
$R$
-module,
![]() $\unicode[STIX]{x1D704}$
is an isomorphism by the main theorem of classical Matlis duality [Reference MatsumuraMat86, Theorem 18.6(v)]; in fact,
$\unicode[STIX]{x1D704}$
is an isomorphism by the main theorem of classical Matlis duality [Reference MatsumuraMat86, Theorem 18.6(v)]; in fact,
![]() $\unicode[STIX]{x1D704}$
is injective even for arbitrary
$\unicode[STIX]{x1D704}$
is injective even for arbitrary
![]() $M$
[Reference MatsumuraMat86, Theorem 18.6(i)]. Moreover, if
$M$
[Reference MatsumuraMat86, Theorem 18.6(i)]. Moreover, if
 $f:M\rightarrow N$
is an
$f:M\rightarrow N$
is an
![]() $R$
-linear homomorphism between finitely generated or Artinian
$R$
-linear homomorphism between finitely generated or Artinian
![]() $R$
-modules,
$R$
-modules,
 $f^{\ast \ast }:D(D(M))\rightarrow D(D(N))$
can be naturally identified with
$f^{\ast \ast }:D(D(M))\rightarrow D(D(N))$
can be naturally identified with
![]() $f$
via the evaluation isomorphisms. Having verified that
$f$
via the evaluation isomorphisms. Having verified that
![]() $\unicode[STIX]{x1D6FF}^{\ast \ast }$
is well defined whenever
$\unicode[STIX]{x1D6FF}^{\ast \ast }$
is well defined whenever
![]() $\unicode[STIX]{x1D6FF}$
is a
$\unicode[STIX]{x1D6FF}$
is a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map between Artinian or finitely generated
$\unicode[STIX]{x1D6F4}$
-continuous map between Artinian or finitely generated
![]() $R$
-modules (Proposition 3.21(c,d)), we now show that the same is true of the double Matlis dual of a
$R$
-modules (Proposition 3.21(c,d)), we now show that the same is true of the double Matlis dual of a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map between such modules.
$\unicode[STIX]{x1D6F4}$
-continuous map between such modules.
Proposition 3.22. Let
![]() $R$
be a complete local ring with coefficient field
$R$
be a complete local ring with coefficient field
![]() $k$
.
$k$
.
-
(a) Let
 $M$
be a finitely generated or Artinian
$M$
be a finitely generated or Artinian
 $R$
-module. The evaluation map analogous to
$R$
-module. The evaluation map analogous to $$\begin{eqnarray}\unicode[STIX]{x1D704}^{\prime }:M\rightarrow D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M)),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}^{\prime }:M\rightarrow D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M)),\end{eqnarray}$$
 $\unicode[STIX]{x1D704}:M\rightarrow D(D(M))$
and defined by
$\unicode[STIX]{x1D704}:M\rightarrow D(D(M))$
and defined by
 $\unicode[STIX]{x1D704}^{\prime }(m)(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}(m)$
for all
$\unicode[STIX]{x1D704}^{\prime }(m)(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}(m)$
for all
 $m\in M$
and
$m\in M$
and
 $\unicode[STIX]{x1D6FF}\in D^{\unicode[STIX]{x1D6F4}}(M)$
, is an isomorphism of
$\unicode[STIX]{x1D6FF}\in D^{\unicode[STIX]{x1D6F4}}(M)$
, is an isomorphism of
 $R$
-modules.
$R$
-modules.
-
(b) If
 $M$
and
$M$
and
 $N$
are
$N$
are
 $R$
-modules that are either both finitely generated or both Artinian, and
$R$
-modules that are either both finitely generated or both Artinian, and
 $\unicode[STIX]{x1D6FF}:M\rightarrow N$
is a
$\unicode[STIX]{x1D6FF}:M\rightarrow N$
is a
 $\unicode[STIX]{x1D6F4}$
-continuous map, then can be naturally identified with
$\unicode[STIX]{x1D6F4}$
-continuous map, then can be naturally identified with $$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{\vee \vee }:D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\rightarrow D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(N))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{\vee \vee }:D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\rightarrow D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(N))\end{eqnarray}$$
 $\unicode[STIX]{x1D6FF}$
via the evaluation isomorphisms of part (a); consequently,
$\unicode[STIX]{x1D6FF}$
via the evaluation isomorphisms of part (a); consequently,
 $\unicode[STIX]{x1D6FF}^{\ast \ast }:D(D(M))\rightarrow D(D(N))$
can be identified with
$\unicode[STIX]{x1D6FF}^{\ast \ast }:D(D(M))\rightarrow D(D(N))$
can be identified with
 $\unicode[STIX]{x1D6FF}$
via the isomorphisms of classical Matlis duality and Theorem 3.15. (See Proposition 3.19 for the definitions of
$\unicode[STIX]{x1D6FF}$
via the isomorphisms of classical Matlis duality and Theorem 3.15. (See Proposition 3.19 for the definitions of
 $\unicode[STIX]{x1D6FF}^{\ast }$
and
$\unicode[STIX]{x1D6FF}^{\ast }$
and
 $\unicode[STIX]{x1D6FF}^{\vee }$
.)
$\unicode[STIX]{x1D6FF}^{\vee }$
.)
-
(c) With the hypotheses of part (b), the Matlis dual operation defines an isomorphism
of $$\begin{eqnarray}\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,N)\simeq \operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(D(N),D(M))\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(M,N)\simeq \operatorname{Hom}_{k}^{\unicode[STIX]{x1D6F4}}(D(N),D(M))\end{eqnarray}$$
 $k$
-spaces. (In particular, every
$k$
-spaces. (In particular, every
 $\unicode[STIX]{x1D6F4}$
-continuous map
$\unicode[STIX]{x1D6F4}$
-continuous map
 $D(N)\rightarrow D(M)$
is the Matlis dual of a
$D(N)\rightarrow D(M)$
is the Matlis dual of a
 $\unicode[STIX]{x1D6F4}$
-continuous map
$\unicode[STIX]{x1D6F4}$
-continuous map
 $M\rightarrow N$
.)
$M\rightarrow N$
.)
Proof. If
![]() $M$
is any
$M$
is any
![]() $R$
-module, we obtain an isomorphism
$R$
-module, we obtain an isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}:D(D(M))\xrightarrow[{}]{{\sim}}D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}:D(D(M))\xrightarrow[{}]{{\sim}}D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\end{eqnarray}$$
of
![]() $R$
-modules by applying Theorem 3.15 twice. This map is defined by the formula
$R$
-modules by applying Theorem 3.15 twice. This map is defined by the formula
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D713})(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6F7}_{M}^{-1}(\unicode[STIX]{x1D6FF})))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D713})(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6F7}_{M}^{-1}(\unicode[STIX]{x1D6FF})))\end{eqnarray}$$
for
 $\unicode[STIX]{x1D713}\in D(D(M))$
and
$\unicode[STIX]{x1D713}\in D(D(M))$
and
 $\unicode[STIX]{x1D6FF}\in D^{\unicode[STIX]{x1D6F4}}(M)$
. We claim that the evaluation maps
$\unicode[STIX]{x1D6FF}\in D^{\unicode[STIX]{x1D6F4}}(M)$
. We claim that the evaluation maps
![]() $\unicode[STIX]{x1D704}$
and
$\unicode[STIX]{x1D704}$
and
![]() $\unicode[STIX]{x1D704}^{\prime }$
satisfy the identity
$\unicode[STIX]{x1D704}^{\prime }$
satisfy the identity
 $\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}^{\prime }$
. If we set
$\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}^{\prime }$
. If we set
 $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D704}(m)$
for some
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D704}(m)$
for some
![]() $m\in M$
, we find
$m\in M$
, we find
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D704}(m))(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{M}^{-1}(\unicode[STIX]{x1D6FF})(m))=\unicode[STIX]{x1D6FF}(m),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D704}(m))(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{M}^{-1}(\unicode[STIX]{x1D6FF})(m))=\unicode[STIX]{x1D6FF}(m),\end{eqnarray}$$
so that
![]() $\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D704}$
agrees with
$\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D704}$
agrees with
![]() $\unicode[STIX]{x1D704}^{\prime }$
upon evaluation at every
$\unicode[STIX]{x1D704}^{\prime }$
upon evaluation at every
 $\unicode[STIX]{x1D6FF}\in D^{\unicode[STIX]{x1D6F4}}(M)$
, as claimed. If
$\unicode[STIX]{x1D6FF}\in D^{\unicode[STIX]{x1D6F4}}(M)$
, as claimed. If
![]() $M$
is finitely generated or Artinian,
$M$
is finitely generated or Artinian,
![]() $\unicode[STIX]{x1D704}$
is an isomorphism by classical Matlis duality, so
$\unicode[STIX]{x1D704}$
is an isomorphism by classical Matlis duality, so
![]() $\unicode[STIX]{x1D704}^{\prime }$
is the composite of two
$\unicode[STIX]{x1D704}^{\prime }$
is the composite of two
![]() $R$
-module isomorphisms, proving part (a).
$R$
-module isomorphisms, proving part (a).
Suppose now that
![]() $M$
and
$M$
and
![]() $N$
are finitely generated
$N$
are finitely generated
![]() $R$
-modules and
$R$
-modules and
 $\unicode[STIX]{x1D6FF}:M\rightarrow N$
is a
$\unicode[STIX]{x1D6FF}:M\rightarrow N$
is a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map (the proof of part (b) in the Artinian case is the same). Using the evaluation map
$\unicode[STIX]{x1D6F4}$
-continuous map (the proof of part (b) in the Artinian case is the same). Using the evaluation map
![]() $\unicode[STIX]{x1D704}^{\prime }$
, we identify
$\unicode[STIX]{x1D704}^{\prime }$
, we identify
![]() $M$
with
$M$
with
 $D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))$
, and likewise with
$D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))$
, and likewise with
![]() $N$
. Consider the double dual
$N$
. Consider the double dual
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{\vee \vee }:D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\rightarrow D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(N)).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{\vee \vee }:D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\rightarrow D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(N)).\end{eqnarray}$$
Every element of the source takes the form
![]() $\unicode[STIX]{x1D704}^{\prime }(m)$
for some
$\unicode[STIX]{x1D704}^{\prime }(m)$
for some
![]() $m\in M$
, and by definition we have
$m\in M$
, and by definition we have
 $\unicode[STIX]{x1D6FF}^{\vee \vee }(\unicode[STIX]{x1D704}^{\prime }(m))=\unicode[STIX]{x1D704}^{\prime }(\unicode[STIX]{x1D6FF}(m))$
; therefore
$\unicode[STIX]{x1D6FF}^{\vee \vee }(\unicode[STIX]{x1D704}^{\prime }(m))=\unicode[STIX]{x1D704}^{\prime }(\unicode[STIX]{x1D6FF}(m))$
; therefore
![]() $\unicode[STIX]{x1D6FF}^{\vee \vee }$
coincides with
$\unicode[STIX]{x1D6FF}^{\vee \vee }$
coincides with
![]() $\unicode[STIX]{x1D6FF}$
upon identifying
$\unicode[STIX]{x1D6FF}$
upon identifying
![]() $M$
and
$M$
and
![]() $N$
with their double
$N$
with their double
![]() $\unicode[STIX]{x1D6F4}$
-continuous duals. The second statement of part (b) follows from the first by Proposition 3.19.
$\unicode[STIX]{x1D6F4}$
-continuous duals. The second statement of part (b) follows from the first by Proposition 3.19.
In particular, with the hypotheses of part (b), it is clear that the map
![]() $\unicode[STIX]{x1D6FF}\mapsto \unicode[STIX]{x1D6FF}^{\ast }$
is a bijection, which already implies the parenthetical remark in part (c). It remains to show that the map
$\unicode[STIX]{x1D6FF}\mapsto \unicode[STIX]{x1D6FF}^{\ast }$
is a bijection, which already implies the parenthetical remark in part (c). It remains to show that the map
![]() $\unicode[STIX]{x1D6FF}\mapsto \unicode[STIX]{x1D6FF}^{\ast }$
is
$\unicode[STIX]{x1D6FF}\mapsto \unicode[STIX]{x1D6FF}^{\ast }$
is
![]() $k$
-linear. Let
$k$
-linear. Let
![]() $\unicode[STIX]{x1D706}\in k$
be given. Then we have
$\unicode[STIX]{x1D706}\in k$
be given. Then we have
 $$\begin{eqnarray}(\unicode[STIX]{x1D706}\cdot \unicode[STIX]{x1D6FF})^{\ast }=(\unicode[STIX]{x1D6FF}\circ \unicode[STIX]{x1D706})^{\ast }=\unicode[STIX]{x1D706}^{\ast }\circ \unicode[STIX]{x1D6FF}^{\ast }=\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D6FF}^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ \unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}\cdot \unicode[STIX]{x1D6FF}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D706}\cdot \unicode[STIX]{x1D6FF})^{\ast }=(\unicode[STIX]{x1D6FF}\circ \unicode[STIX]{x1D706})^{\ast }=\unicode[STIX]{x1D706}^{\ast }\circ \unicode[STIX]{x1D6FF}^{\ast }=\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D6FF}^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ \unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}\cdot \unicode[STIX]{x1D6FF}^{\ast },\end{eqnarray}$$
where we have used Proposition 3.11 and Lemma 3.12, as well as the
![]() $k$
-linearity of
$k$
-linearity of
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
(since
$\unicode[STIX]{x1D6FF}^{\ast }$
(since
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
need not be
$\unicode[STIX]{x1D6FF}^{\ast }$
need not be
![]() $R$
-linear, it is not true that the Matlis dual operation defines an isomorphism of
$R$
-linear, it is not true that the Matlis dual operation defines an isomorphism of
![]() $R$
-modules). This completes the proof.◻
$R$
-modules). This completes the proof.◻
Finally, consider the special case where
 $R=k[[x_{1},\ldots ,x_{n}]]$
(for
$R=k[[x_{1},\ldots ,x_{n}]]$
(for
![]() $k$
a field) and
$k$
a field) and
![]() $\mathfrak{m}$
is the maximal ideal of
$\mathfrak{m}$
is the maximal ideal of
![]() $R$
. Since
$R$
. Since
![]() $R$
is Gorenstein, the local cohomology module
$R$
is Gorenstein, the local cohomology module
![]() $H_{\mathfrak{m}}^{n}(R)$
is isomorphic to
$H_{\mathfrak{m}}^{n}(R)$
is isomorphic to
![]() $E$
[Reference Brodmann and SharpBS13, Lemma 11.2.3]. We pick one such isomorphism and think of
$E$
[Reference Brodmann and SharpBS13, Lemma 11.2.3]. We pick one such isomorphism and think of
![]() $E$
as
$E$
as
![]() $H_{\mathfrak{m}}^{n}(R)$
via this isomorphism. If we compute
$H_{\mathfrak{m}}^{n}(R)$
via this isomorphism. If we compute
![]() $H_{\mathfrak{m}}^{n}(R)$
using the Čech complex of
$H_{\mathfrak{m}}^{n}(R)$
using the Čech complex of
![]() $R$
with respect to
$R$
with respect to
 $x_{1},\ldots ,x_{n}$
[Reference Brodmann and SharpBS13, Theorem 5.1.20], the resulting
$x_{1},\ldots ,x_{n}$
[Reference Brodmann and SharpBS13, Theorem 5.1.20], the resulting
![]() $R$
-module consists of all
$R$
-module consists of all
![]() $k$
-linear combinations of ‘inverse monomials’
$k$
-linear combinations of ‘inverse monomials’
 $x_{1}^{s_{1}}\cdots x_{n}^{s_{n}}$
where
$x_{1}^{s_{1}}\cdots x_{n}^{s_{n}}$
where
 $s_{1},\ldots ,s_{n}<0$
. The
$s_{1},\ldots ,s_{n}<0$
. The
![]() $R$
-action is defined by the usual exponential rules with the caveat that non-negative powers of the variables are set equal to zero, so the product of a formal power series in
$R$
-action is defined by the usual exponential rules with the caveat that non-negative powers of the variables are set equal to zero, so the product of a formal power series in
![]() $R$
with such an ‘inverse polynomial’ has only finitely many non-zero terms. We may define a
$R$
with such an ‘inverse polynomial’ has only finitely many non-zero terms. We may define a
![]() $k$
-linear projection
$k$
-linear projection
 $\unicode[STIX]{x1D70E}:E\rightarrow k$
of
$\unicode[STIX]{x1D70E}:E\rightarrow k$
of
![]() $E$
onto its socle by the formula
$E$
onto its socle by the formula
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}\Bigl(\sum \unicode[STIX]{x1D6FC}_{s_{1},\ldots ,s_{n}}x_{1}^{s_{1}}\cdots x_{n}^{s_{n}}\Bigr)=\unicode[STIX]{x1D6FC}_{-1,\ldots ,-1}\in k,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}\Bigl(\sum \unicode[STIX]{x1D6FC}_{s_{1},\ldots ,s_{n}}x_{1}^{s_{1}}\cdots x_{n}^{s_{n}}\Bigr)=\unicode[STIX]{x1D6FC}_{-1,\ldots ,-1}\in k,\end{eqnarray}$$
which we think of as ‘taking the
 $(-1,\ldots ,-1)$
-coefficient’ of such an ‘inverse polynomial’ [Reference KunzKun08, ch. 5].
$(-1,\ldots ,-1)$
-coefficient’ of such an ‘inverse polynomial’ [Reference KunzKun08, ch. 5].
The map
![]() $\unicode[STIX]{x1D70E}$
can be thought of as a realization of the residue map in coordinates
$\unicode[STIX]{x1D70E}$
can be thought of as a realization of the residue map in coordinates
![]() $\{x_{i}\}$
, and we will sometimes abusively refer to
$\{x_{i}\}$
, and we will sometimes abusively refer to
![]() $\unicode[STIX]{x1D70E}$
as ‘the residue map’, the chosen coordinates being understood. The residue map is a canonical map
$\unicode[STIX]{x1D70E}$
as ‘the residue map’, the chosen coordinates being understood. The residue map is a canonical map
 $H_{\mathfrak{m}}^{n}(\unicode[STIX]{x1D6FA}_{R}^{n})\rightarrow k$
. The original reference for the theory of the residue map is [Reference HartshorneHar66]: see also [Reference Grothendieck and RaynaudGR05, Exp. IV, Remarque 5.5] and [Reference KunzKun08, ch. 5] for concrete descriptions in our special case. A choice of a regular system of parameters
$H_{\mathfrak{m}}^{n}(\unicode[STIX]{x1D6FA}_{R}^{n})\rightarrow k$
. The original reference for the theory of the residue map is [Reference HartshorneHar66]: see also [Reference Grothendieck and RaynaudGR05, Exp. IV, Remarque 5.5] and [Reference KunzKun08, ch. 5] for concrete descriptions in our special case. A choice of a regular system of parameters
 $x_{1},\ldots ,x_{n}$
for
$x_{1},\ldots ,x_{n}$
for
![]() $R$
induces a non-canonical
$R$
induces a non-canonical
![]() $R$
-module isomorphism
$R$
-module isomorphism
 $H_{\mathfrak{m}}^{n}(R)\simeq H_{\mathfrak{m}}^{n}(\unicode[STIX]{x1D6FA}_{R}^{n})$
(defined by
$H_{\mathfrak{m}}^{n}(R)\simeq H_{\mathfrak{m}}^{n}(\unicode[STIX]{x1D6FA}_{R}^{n})$
(defined by
 $\unicode[STIX]{x1D702}\mapsto \unicode[STIX]{x1D702}\,dx_{1}\wedge \cdots \wedge dx_{n}$
), and
$\unicode[STIX]{x1D702}\mapsto \unicode[STIX]{x1D702}\,dx_{1}\wedge \cdots \wedge dx_{n}$
), and
![]() $\unicode[STIX]{x1D70E}$
is the composite of this isomorphism with the residue map. One could instead take
$\unicode[STIX]{x1D70E}$
is the composite of this isomorphism with the residue map. One could instead take
 $E=H_{\mathfrak{m}}^{n}(\unicode[STIX]{x1D6FA}_{R}^{n})$
and the canonical residue map for
$E=H_{\mathfrak{m}}^{n}(\unicode[STIX]{x1D6FA}_{R}^{n})$
and the canonical residue map for
![]() $\unicode[STIX]{x1D70E}$
, but we will have to use coordinates in examples later in the paper.
$\unicode[STIX]{x1D70E}$
, but we will have to use coordinates in examples later in the paper.
4 Matlis duality for
 ${\mathcal{D}}$
-modules
${\mathcal{D}}$
-modules
We now specialize to the case where
![]() $(R,\mathfrak{m})$
is a complete local ring with coefficient field
$(R,\mathfrak{m})$
is a complete local ring with coefficient field
![]() $k$
. This assumption is in force throughout the section unless otherwise indicated.
$k$
. This assumption is in force throughout the section unless otherwise indicated.
We show that if
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
is the non-commutative ring of
${\mathcal{D}}={\mathcal{D}}(R,k)$
is the non-commutative ring of
![]() $k$
-linear differential operators on
$k$
-linear differential operators on
![]() $R$
and
$R$
and
![]() $M$
is a left
$M$
is a left
![]() ${\mathcal{D}}$
-module, then elements of
${\mathcal{D}}$
-module, then elements of
![]() ${\mathcal{D}}$
act on
${\mathcal{D}}$
act on
![]() $M$
via
$M$
via
![]() $\unicode[STIX]{x1D6F4}$
-continuous maps. This fact allows us immediately to apply the formalism of the previous section to define the Matlis dual of the action of an element of
$\unicode[STIX]{x1D6F4}$
-continuous maps. This fact allows us immediately to apply the formalism of the previous section to define the Matlis dual of the action of an element of
![]() ${\mathcal{D}}$
; in this way,
${\mathcal{D}}$
; in this way,
![]() $D(M)$
becomes a right
$D(M)$
becomes a right
![]() ${\mathcal{D}}$
-module. In the case of a complete regular local ring with coefficient field
${\mathcal{D}}$
-module. In the case of a complete regular local ring with coefficient field
![]() $k$
of characteristic zero, we describe a ‘transposition’ operation allowing us to regard these Matlis duals as left
$k$
of characteristic zero, we describe a ‘transposition’ operation allowing us to regard these Matlis duals as left
![]() ${\mathcal{D}}$
-modules.
${\mathcal{D}}$
-modules.
Let
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
be the ring of
${\mathcal{D}}={\mathcal{D}}(R,k)$
be the ring of
![]() $k$
-linear differential operators on
$k$
-linear differential operators on
![]() $R$
. Suppose
$R$
. Suppose
![]() $M$
is a left
$M$
is a left
![]() ${\mathcal{D}}$
-module, and let
${\mathcal{D}}$
-module, and let
 $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
be a differential operator. The map
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
be a differential operator. The map
 $\unicode[STIX]{x1D6FF}:M\rightarrow M$
defined by the action of
$\unicode[STIX]{x1D6FF}:M\rightarrow M$
defined by the action of
![]() $\unicode[STIX]{x1D6FF}$
(that is,
$\unicode[STIX]{x1D6FF}$
(that is,
 $\unicode[STIX]{x1D6FF}(m)=\unicode[STIX]{x1D6FF}\cdot m$
) is a
$\unicode[STIX]{x1D6FF}(m)=\unicode[STIX]{x1D6FF}\cdot m$
) is a
![]() $k$
-linear map (we abusively use the same letter
$k$
-linear map (we abusively use the same letter
![]() $\unicode[STIX]{x1D6FF}$
to simplify notation).
$\unicode[STIX]{x1D6FF}$
to simplify notation).
We need a lemma on the continuity of differential operators’ action.
Lemma 4.1. Let
![]() $M$
be a left
$M$
be a left
 ${\mathcal{D}}(R,k)$
-module (here
${\mathcal{D}}(R,k)$
-module (here
![]() $R$
is any commutative ring, and
$R$
is any commutative ring, and
![]() $k\subset R$
any commutative subring), and let
$k\subset R$
any commutative subring), and let
![]() $I\subset R$
be any ideal. For any
$I\subset R$
be any ideal. For any
 $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}^{j}(R)$
and
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}^{j}(R)$
and
![]() $s\geqslant 0$
, we have
$s\geqslant 0$
, we have
 $\unicode[STIX]{x1D6FF}(I^{s+j}M)\subset I^{s}M$
.
$\unicode[STIX]{x1D6FF}(I^{s+j}M)\subset I^{s}M$
.
Proof. We proceed by induction on
![]() $s+j$
. If
$s+j$
. If
 $s+j=0$
, there is nothing to prove. Now suppose
$s+j=0$
, there is nothing to prove. Now suppose
 $s+j\geqslant 0$
and the containment established for smaller values of
$s+j\geqslant 0$
and the containment established for smaller values of
![]() $s+j$
. Since
$s+j$
. Since
 $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}^{j}(R)$
, it follows that
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}^{j}(R)$
, it follows that
 $[\unicode[STIX]{x1D6FF},r]\in {\mathcal{D}}^{j-1}(R)$
for any
$[\unicode[STIX]{x1D6FF},r]\in {\mathcal{D}}^{j-1}(R)$
for any
![]() $r\in R$
, and so
$r\in R$
, and so
 $[\unicode[STIX]{x1D6FF},r](I^{s+j-1}M)\subset I^{s}M$
by the induction hypothesis for
$[\unicode[STIX]{x1D6FF},r](I^{s+j-1}M)\subset I^{s}M$
by the induction hypothesis for
![]() $s$
and
$s$
and
![]() $j-1$
. That is,
$j-1$
. That is,
 $[\unicode[STIX]{x1D6FF},r](tm)=\unicode[STIX]{x1D6FF}(rtm)-r\unicode[STIX]{x1D6FF}(tm)\in I^{s}M$
for any
$[\unicode[STIX]{x1D6FF},r](tm)=\unicode[STIX]{x1D6FF}(rtm)-r\unicode[STIX]{x1D6FF}(tm)\in I^{s}M$
for any
![]() $r\in R$
,
$r\in R$
,
 $t\in I^{s+j-1}$
and
$t\in I^{s+j-1}$
and
![]() $m\in M$
. If we further suppose that
$m\in M$
. If we further suppose that
![]() $r\in I$
and put
$r\in I$
and put
 $x=rt\in I^{s+j-1}I=I^{s+j}$
, we see that
$x=rt\in I^{s+j-1}I=I^{s+j}$
, we see that
 $\unicode[STIX]{x1D6FF}(xm)=r\unicode[STIX]{x1D6FF}(tm)+[\unicode[STIX]{x1D6FF},r](tm)$
. By the induction hypothesis for
$\unicode[STIX]{x1D6FF}(xm)=r\unicode[STIX]{x1D6FF}(tm)+[\unicode[STIX]{x1D6FF},r](tm)$
. By the induction hypothesis for
![]() $s-1$
and
$s-1$
and
![]() $j$
,
$j$
,
 $\unicode[STIX]{x1D6FF}(I^{s+j-1}M)\subset I^{s-1}M$
, so
$\unicode[STIX]{x1D6FF}(I^{s+j-1}M)\subset I^{s-1}M$
, so
 $\unicode[STIX]{x1D6FF}(tm)\in I^{s-1}M$
and
$\unicode[STIX]{x1D6FF}(tm)\in I^{s-1}M$
and
 $r\unicode[STIX]{x1D6FF}(tm)\in I^{s}M$
. Thus both terms on the right-hand side (and their sum
$r\unicode[STIX]{x1D6FF}(tm)\in I^{s}M$
. Thus both terms on the right-hand side (and their sum
![]() $\unicode[STIX]{x1D6FF}(xm)$
) belong to
$\unicode[STIX]{x1D6FF}(xm)$
) belong to
![]() $I^{s}M$
. As any element of
$I^{s}M$
. As any element of
![]() $I^{s+j}M$
can be expressed as a finite sum
$I^{s+j}M$
can be expressed as a finite sum
 $\sum _{\unicode[STIX]{x1D6FC}}r_{\unicode[STIX]{x1D6FC}}t_{\unicode[STIX]{x1D6FC}}m_{\unicode[STIX]{x1D6FC}}$
with
$\sum _{\unicode[STIX]{x1D6FC}}r_{\unicode[STIX]{x1D6FC}}t_{\unicode[STIX]{x1D6FC}}m_{\unicode[STIX]{x1D6FC}}$
with
![]() $r_{\unicode[STIX]{x1D6FC}}\in I$
and
$r_{\unicode[STIX]{x1D6FC}}\in I$
and
 $t_{\unicode[STIX]{x1D6FC}}\in I^{s+j-1}$
, the result follows.◻
$t_{\unicode[STIX]{x1D6FC}}\in I^{s+j-1}$
, the result follows.◻
If a left
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
is finitely generated as an
$M$
is finitely generated as an
![]() $R$
-module, then given any
$R$
-module, then given any
![]() $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
, the lemma shows that the corresponding map
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
, the lemma shows that the corresponding map
 $\unicode[STIX]{x1D6FF}:M\rightarrow M$
is
$\unicode[STIX]{x1D6FF}:M\rightarrow M$
is
![]() $\mathfrak{m}$
-adically continuous. Therefore the formalism of the previous section applies, and we can define the
$\mathfrak{m}$
-adically continuous. Therefore the formalism of the previous section applies, and we can define the
![]() $k$
-linear Matlis dual
$k$
-linear Matlis dual
 $\unicode[STIX]{x1D6FF}^{\ast }:D(M)\rightarrow D(M)$
in such a way that if
$\unicode[STIX]{x1D6FF}^{\ast }:D(M)\rightarrow D(M)$
in such a way that if
![]() $\unicode[STIX]{x1D6FF}^{\prime }\in {\mathcal{D}}$
is another differential operator, we have
$\unicode[STIX]{x1D6FF}^{\prime }\in {\mathcal{D}}$
is another differential operator, we have
 $(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ (\unicode[STIX]{x1D6FF}^{\prime })^{\ast }$
(note that, by Proposition 3.11, the order of composition is reversed). This allows us to define a structure of right
$(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ (\unicode[STIX]{x1D6FF}^{\prime })^{\ast }$
(note that, by Proposition 3.11, the order of composition is reversed). This allows us to define a structure of right
![]() ${\mathcal{D}}$
-module on
${\mathcal{D}}$
-module on
![]() $D(M)$
by
$D(M)$
by
 $\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D719})$
. Here is an example of this dual construction.
$\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D719})$
. Here is an example of this dual construction.
Example 4.2. Let
 $R=k[[x]]$
, where
$R=k[[x]]$
, where
![]() $k$
is a field, equipped with the
$k$
is a field, equipped with the
![]() $k$
-linear derivation
$k$
-linear derivation
 $\unicode[STIX]{x1D6FF}=d/dx$
. Denote by
$\unicode[STIX]{x1D6FF}=d/dx$
. Denote by
![]() $\mathfrak{m}$
its maximal ideal
$\mathfrak{m}$
its maximal ideal
![]() $(x)$
. Take
$(x)$
. Take
![]() $M=R$
, a finitely generated
$M=R$
, a finitely generated
![]() $R$
-module, and take for
$R$
-module, and take for
![]() $E$
the local cohomology module
$E$
the local cohomology module
 $H_{(x)}^{1}(R)$
, which is the module of finite sums
$H_{(x)}^{1}(R)$
, which is the module of finite sums
 $\sum _{s>0}(\unicode[STIX]{x1D6FC}_{s}/x^{s})$
where
$\sum _{s>0}(\unicode[STIX]{x1D6FC}_{s}/x^{s})$
where
![]() $\unicode[STIX]{x1D6FC}_{s}\in k$
. We define Matlis duals of
$\unicode[STIX]{x1D6FC}_{s}\in k$
. We define Matlis duals of
![]() $k$
-linear maps between
$k$
-linear maps between
![]() $R$
-modules using the residue map
$R$
-modules using the residue map
 $\unicode[STIX]{x1D70E}:E\rightarrow k$
given by
$\unicode[STIX]{x1D70E}:E\rightarrow k$
given by
 $\unicode[STIX]{x1D70E}(\sum _{s>0}(\unicode[STIX]{x1D6FC}_{s}/x^{s}))=\unicode[STIX]{x1D6FC}_{1}$
.
$\unicode[STIX]{x1D70E}(\sum _{s>0}(\unicode[STIX]{x1D6FC}_{s}/x^{s}))=\unicode[STIX]{x1D6FC}_{1}$
.
We determine explicitly the Matlis dual
 $\unicode[STIX]{x1D6FF}^{\ast }:D(R)\rightarrow D(R)$
. Note that
$\unicode[STIX]{x1D6FF}^{\ast }:D(R)\rightarrow D(R)$
. Note that
![]() $E$
is naturally isomorphic as
$E$
is naturally isomorphic as
![]() $R$
-module to
$R$
-module to
 $D(R)=\operatorname{Hom}_{R}(R,E)$
: an element
$D(R)=\operatorname{Hom}_{R}(R,E)$
: an element
![]() $\unicode[STIX]{x1D707}\in E$
corresponds to the map
$\unicode[STIX]{x1D707}\in E$
corresponds to the map
![]() $r\mapsto r\unicode[STIX]{x1D707}$
(and, in the other direction, a map
$r\mapsto r\unicode[STIX]{x1D707}$
(and, in the other direction, a map
![]() $R\rightarrow E$
corresponds to the image of
$R\rightarrow E$
corresponds to the image of
![]() $1$
in
$1$
in
![]() $E$
). Let
$E$
). Let
 $\unicode[STIX]{x1D707}=\sum _{s>0}(\unicode[STIX]{x1D6FC}_{s}/x^{s})$
be such an element of
$\unicode[STIX]{x1D707}=\sum _{s>0}(\unicode[STIX]{x1D6FC}_{s}/x^{s})$
be such an element of
![]() $E$
and suppose that
$E$
and suppose that
![]() $t$
is the greatest integer such that
$t$
is the greatest integer such that
![]() $\unicode[STIX]{x1D6FC}_{t}\neq 0$
. The
$\unicode[STIX]{x1D6FC}_{t}\neq 0$
. The
![]() $R$
-linear map
$R$
-linear map
![]() $R\rightarrow E$
corresponding to
$R\rightarrow E$
corresponding to
![]() $\unicode[STIX]{x1D707}$
is defined as follows: given an element
$\unicode[STIX]{x1D707}$
is defined as follows: given an element
 $\sum _{i=0}^{\infty }\unicode[STIX]{x1D6FD}_{i}x^{i}$
of
$\sum _{i=0}^{\infty }\unicode[STIX]{x1D6FD}_{i}x^{i}$
of
![]() $R$
, its image in
$R$
, its image in
![]() $E$
is the product
$E$
is the product
 $(\sum _{i=0}^{\infty }\unicode[STIX]{x1D6FD}_{i}x^{i})(\sum _{s>0}(\unicode[STIX]{x1D6FC}_{s}/x^{s}))$
, which is carried by
$(\sum _{i=0}^{\infty }\unicode[STIX]{x1D6FD}_{i}x^{i})(\sum _{s>0}(\unicode[STIX]{x1D6FC}_{s}/x^{s}))$
, which is carried by
![]() $\unicode[STIX]{x1D70E}$
to
$\unicode[STIX]{x1D70E}$
to
 $\sum _{s>0}\unicode[STIX]{x1D6FC}_{s}\unicode[STIX]{x1D6FD}_{s-1}$
. Therefore the corresponding
$\sum _{s>0}\unicode[STIX]{x1D6FC}_{s}\unicode[STIX]{x1D6FD}_{s-1}$
. Therefore the corresponding
![]() $k$
-linear map
$k$
-linear map
 $\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D707}:R\rightarrow k$
is given by
$\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D707}:R\rightarrow k$
is given by
 $\sum _{i=0}^{\infty }\unicode[STIX]{x1D6FD}_{i}x^{i}\mapsto \sum _{s>0}\unicode[STIX]{x1D6FC}_{s}\unicode[STIX]{x1D6FD}_{s-1}$
. The map
$\sum _{i=0}^{\infty }\unicode[STIX]{x1D6FD}_{i}x^{i}\mapsto \sum _{s>0}\unicode[STIX]{x1D6FC}_{s}\unicode[STIX]{x1D6FD}_{s-1}$
. The map
![]() $\unicode[STIX]{x1D707}$
annihilates
$\unicode[STIX]{x1D707}$
annihilates
![]() $\mathfrak{m}^{t}$
; write
$\mathfrak{m}^{t}$
; write
![]() $\overline{\unicode[STIX]{x1D707}}$
for the
$\overline{\unicode[STIX]{x1D707}}$
for the
![]() $R$
-linear map
$R$
-linear map
 $R/\mathfrak{m}^{t}\rightarrow E$
induced on the quotient.
$R/\mathfrak{m}^{t}\rightarrow E$
induced on the quotient.
The derivation
![]() $\unicode[STIX]{x1D6FF}$
induces a
$\unicode[STIX]{x1D6FF}$
induces a
![]() $k$
-linear map
$k$
-linear map
 $R/\mathfrak{m}^{t+1}\rightarrow R/\mathfrak{m}^{t}$
by the Leibniz rule, and the
$R/\mathfrak{m}^{t+1}\rightarrow R/\mathfrak{m}^{t}$
by the Leibniz rule, and the
![]() $k$
-linear composite
$k$
-linear composite
 $R/\mathfrak{m}^{t+1}\rightarrow R/\mathfrak{m}^{t}\xrightarrow[{}]{\unicode[STIX]{x1D70E}\circ \overline{\unicode[STIX]{x1D707}}}k$
is defined by
$R/\mathfrak{m}^{t+1}\rightarrow R/\mathfrak{m}^{t}\xrightarrow[{}]{\unicode[STIX]{x1D70E}\circ \overline{\unicode[STIX]{x1D707}}}k$
is defined by
 $$\begin{eqnarray}\mathop{\sum }_{i=0}^{t}\unicode[STIX]{x1D706}_{i}x^{i}\mapsto \mathop{\sum }_{i=0}^{t-1}(i+1)\unicode[STIX]{x1D706}_{i+1}x^{i}\mapsto \mathop{\sum }_{s>0}s\unicode[STIX]{x1D6FC}_{s}\unicode[STIX]{x1D706}_{s},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=0}^{t}\unicode[STIX]{x1D706}_{i}x^{i}\mapsto \mathop{\sum }_{i=0}^{t-1}(i+1)\unicode[STIX]{x1D706}_{i+1}x^{i}\mapsto \mathop{\sum }_{s>0}s\unicode[STIX]{x1D6FC}_{s}\unicode[STIX]{x1D706}_{s},\end{eqnarray}$$
where the scalars
![]() $\unicode[STIX]{x1D6FC}_{s}$
are the numerators in the expansion of
$\unicode[STIX]{x1D6FC}_{s}$
are the numerators in the expansion of
![]() $\unicode[STIX]{x1D707}$
. Since
$\unicode[STIX]{x1D707}$
. Since
 $R/\mathfrak{m}^{t+1}$
is of finite length as an
$R/\mathfrak{m}^{t+1}$
is of finite length as an
![]() $R$
-module, this composite corresponds to a unique
$R$
-module, this composite corresponds to a unique
![]() $R$
-linear map
$R$
-linear map
 $R/\mathfrak{m}^{t+1}\rightarrow E$
, that is, a map
$R/\mathfrak{m}^{t+1}\rightarrow E$
, that is, a map
![]() $R\rightarrow E$
defined by multiplication by an element of
$R\rightarrow E$
defined by multiplication by an element of
![]() $E$
that is annihilated by
$E$
that is annihilated by
![]() $\mathfrak{m}^{t+1}$
. This map
$\mathfrak{m}^{t+1}$
. This map
![]() $R\rightarrow E$
is the image of
$R\rightarrow E$
is the image of
![]() $\unicode[STIX]{x1D707}$
under
$\unicode[STIX]{x1D707}$
under
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
, and examining the formula above, we see that the corresponding element of
$\unicode[STIX]{x1D6FF}^{\ast }$
, and examining the formula above, we see that the corresponding element of
![]() $E$
(the image of
$E$
(the image of
![]() $1$
) cannot be anything but
$1$
) cannot be anything but
 $\sum _{s>0}(s\unicode[STIX]{x1D6FC}_{s}/x^{s+1})$
. Therefore, viewed at the level of a map
$\sum _{s>0}(s\unicode[STIX]{x1D6FC}_{s}/x^{s+1})$
. Therefore, viewed at the level of a map
![]() $E\rightarrow E$
, the map
$E\rightarrow E$
, the map
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
is defined by
$\unicode[STIX]{x1D6FF}^{\ast }$
is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{\ast }\biggl(\frac{1}{x^{s}}\biggr)=\frac{s}{x^{s+1}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{\ast }\biggl(\frac{1}{x^{s}}\biggr)=\frac{s}{x^{s+1}},\end{eqnarray}$$
which differs from the standard (‘quotient rule’) differentiation map on
![]() $E$
only by a minus sign. (Our discussion of ‘transposition’ at the end of this section will indicate the reason for this sign.) This concludes Example 4.2.
$E$
only by a minus sign. (Our discussion of ‘transposition’ at the end of this section will indicate the reason for this sign.) This concludes Example 4.2.
In order to extend this definition of Matlis dual to arbitrary
![]() ${\mathcal{D}}$
-modules, removing the finite generation hypothesis, we need to show that differential operators act on
${\mathcal{D}}$
-modules, removing the finite generation hypothesis, we need to show that differential operators act on
![]() ${\mathcal{D}}$
-modules via
${\mathcal{D}}$
-modules via
![]() $\unicode[STIX]{x1D6F4}$
-continuous maps. We prove this now using the alternate characterization of differential operators given in EGA [Reference Grothendieck and DieudonnéGD67].
$\unicode[STIX]{x1D6F4}$
-continuous maps. We prove this now using the alternate characterization of differential operators given in EGA [Reference Grothendieck and DieudonnéGD67].
Definition 4.3. Suppose that
![]() $R$
is any commutative ring and
$R$
is any commutative ring and
![]() $k\subset R$
a commutative subring. We denote by
$k\subset R$
a commutative subring. We denote by
![]() $B$
the ring
$B$
the ring
 $R\otimes _{k}R$
, by
$R\otimes _{k}R$
, by
 $\unicode[STIX]{x1D707}:B\rightarrow R$
the multiplication map
$\unicode[STIX]{x1D707}:B\rightarrow R$
the multiplication map
 $\unicode[STIX]{x1D707}(r\otimes s)=rs$
, and by
$\unicode[STIX]{x1D707}(r\otimes s)=rs$
, and by
![]() $J\subset B$
the kernel of
$J\subset B$
the kernel of
![]() $\unicode[STIX]{x1D707}$
. We identify the subring
$\unicode[STIX]{x1D707}$
. We identify the subring
 $R\otimes _{k}1=\{r\otimes 1\mid r\in R\}$
of
$R\otimes _{k}1=\{r\otimes 1\mid r\in R\}$
of
![]() $B$
with
$B$
with
![]() $R$
, and view
$R$
, and view
![]() $B$
as an
$B$
as an
![]() $R$
-algebra using this identification. In this way,
$R$
-algebra using this identification. In this way,
![]() $B$
and all ideals of
$B$
and all ideals of
![]() $B$
can be regarded as
$B$
can be regarded as
![]() $R$
-modules. Finally, for any
$R$
-modules. Finally, for any
![]() $j\geqslant 0$
, we denote by
$j\geqslant 0$
, we denote by
![]() $P_{R/k}^{j}$
(or
$P_{R/k}^{j}$
(or
![]() $P^{j}$
) the quotient
$P^{j}$
) the quotient
 $B/J^{j+1}$
.
$B/J^{j+1}$
.
In [Reference Grothendieck and DieudonnéGD67], differential operators are described in terms of
![]() $R$
-linear maps via the following correspondence.
$R$
-linear maps via the following correspondence.
Proposition 4.4 [Reference Grothendieck and DieudonnéGD67, Proposition 16.8.4].
For any commutative ring
![]() $R$
and commutative subring
$R$
and commutative subring
![]() $k\subset R$
, there is an isomorphism
$k\subset R$
, there is an isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{R}(P^{j},R)\simeq {\mathcal{D}}^{j}(R)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{R}(P^{j},R)\simeq {\mathcal{D}}^{j}(R)\end{eqnarray}$$
of
![]() $R$
-modules, where the differential operators on the right-hand side are understood to be
$R$
-modules, where the differential operators on the right-hand side are understood to be
![]() $k$
-linear.
$k$
-linear.
In our case, where
![]() $R$
is a complete local ring and
$R$
is a complete local ring and
![]() $k$
a coefficient field, both sides of the isomorphism of Proposition 4.4 are finitely generated
$k$
a coefficient field, both sides of the isomorphism of Proposition 4.4 are finitely generated
![]() $R$
-modules.
$R$
-modules.
Proposition 4.5. Let
![]() $(R,\mathfrak{m})$
be a (Noetherian) complete local ring with coefficient field
$(R,\mathfrak{m})$
be a (Noetherian) complete local ring with coefficient field
![]() $k$
. For all
$k$
. For all
![]() $j$
, the
$j$
, the
![]() $R$
-module
$R$
-module
 ${\mathcal{D}}^{j}(R)\subset {\mathcal{D}}(R,k)$
is finitely generated.
${\mathcal{D}}^{j}(R)\subset {\mathcal{D}}(R,k)$
is finitely generated.
The following definition will be used in the proof of Proposition 4.5.
Definition 4.6. Let
![]() $(R,\mathfrak{m})$
be a local ring. For any
$(R,\mathfrak{m})$
be a local ring. For any
![]() $R$
-module
$R$
-module
![]() $L$
, the maximal
$L$
, the maximal
![]() $\mathfrak{m}$
-adically separated quotient of
$\mathfrak{m}$
-adically separated quotient of
![]() $L$
is
$L$
is
 $L^{\text{sep}}=L/(\bigcap _{s}\mathfrak{m}^{s}L)$
. Note that
$L^{\text{sep}}=L/(\bigcap _{s}\mathfrak{m}^{s}L)$
. Note that
![]() $L^{\text{sep}}$
is
$L^{\text{sep}}$
is
![]() $\mathfrak{m}$
-adically separated, and
$\mathfrak{m}$
-adically separated, and
 $L/\mathfrak{m}L\simeq L^{\text{sep}}/\mathfrak{m}L^{\text{sep}}$
.
$L/\mathfrak{m}L\simeq L^{\text{sep}}/\mathfrak{m}L^{\text{sep}}$
.
Proof of Proposition 4.5.
Let
![]() $j$
be given. By Proposition 4.4, it suffices to show that
$j$
be given. By Proposition 4.4, it suffices to show that
 $\operatorname{Hom}_{R}(P^{j},R)$
is a finitely generated
$\operatorname{Hom}_{R}(P^{j},R)$
is a finitely generated
![]() $R$
-module. As
$R$
-module. As
![]() $R$
is
$R$
is
![]() $\mathfrak{m}$
-adically separated, every
$\mathfrak{m}$
-adically separated, every
 $f\in \operatorname{Hom}_{R}(P^{j},R)$
factors uniquely through
$f\in \operatorname{Hom}_{R}(P^{j},R)$
factors uniquely through
![]() $(P^{j})^{\text{sep}}$
. Therefore
$(P^{j})^{\text{sep}}$
. Therefore
 $\operatorname{Hom}_{R}((P^{j})^{\text{sep}},R)\simeq \operatorname{Hom}_{R}(P^{j},R)$
as
$\operatorname{Hom}_{R}((P^{j})^{\text{sep}},R)\simeq \operatorname{Hom}_{R}(P^{j},R)$
as
![]() $R$
-modules. We claim that
$R$
-modules. We claim that
![]() $(P^{j})^{\text{sep}}$
is itself a finitely generated
$(P^{j})^{\text{sep}}$
is itself a finitely generated
![]() $R$
-module, from which it will follow at once that
$R$
-module, from which it will follow at once that
 $$\begin{eqnarray}\operatorname{Hom}_{R}((P^{j})^{\text{sep}},R)\simeq \operatorname{Hom}_{R}(P^{j},R)\simeq {\mathcal{D}}^{j}(R)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{R}((P^{j})^{\text{sep}},R)\simeq \operatorname{Hom}_{R}(P^{j},R)\simeq {\mathcal{D}}^{j}(R)\end{eqnarray}$$
is finitely generated as well. We have
 $$\begin{eqnarray}(P^{j})^{\text{sep}}/\mathfrak{m}(P^{j})^{\text{sep}}\simeq P^{j}/\mathfrak{m}P^{j}=B/(\mathfrak{m}B+J^{j+1})\end{eqnarray}$$
$$\begin{eqnarray}(P^{j})^{\text{sep}}/\mathfrak{m}(P^{j})^{\text{sep}}\simeq P^{j}/\mathfrak{m}P^{j}=B/(\mathfrak{m}B+J^{j+1})\end{eqnarray}$$
as
![]() $k$
-spaces. Since
$k$
-spaces. Since
![]() $(P^{j})^{\text{sep}}$
is
$(P^{j})^{\text{sep}}$
is
![]() $\mathfrak{m}$
-adically separated and
$\mathfrak{m}$
-adically separated and
![]() $R$
is
$R$
is
![]() $\mathfrak{m}$
-adically complete,
$\mathfrak{m}$
-adically complete,
![]() $(P^{j})^{\text{sep}}$
is a finitely generated
$(P^{j})^{\text{sep}}$
is a finitely generated
![]() $R$
-module if
$R$
-module if
 $(P^{j})^{\text{sep}}/\mathfrak{m}(P^{j})^{\text{sep}}$
is a finite-dimensional
$(P^{j})^{\text{sep}}/\mathfrak{m}(P^{j})^{\text{sep}}$
is a finite-dimensional
![]() $k$
-space, by a form of Nakayama’s lemma [Reference EisenbudEis95, Example 7.2]. Therefore we have reduced the proof of the proposition to the proof that for all
$k$
-space, by a form of Nakayama’s lemma [Reference EisenbudEis95, Example 7.2]. Therefore we have reduced the proof of the proposition to the proof that for all
![]() $j$
, the
$j$
, the
![]() $k$
-space
$k$
-space
 $B/(\mathfrak{m}B+J^{j+1})$
is finite-dimensional, which we give now.
$B/(\mathfrak{m}B+J^{j+1})$
is finite-dimensional, which we give now.
The elements
 $r\otimes 1-1\otimes r$
with
$r\otimes 1-1\otimes r$
with
![]() $r\in R$
generate
$r\in R$
generate
![]() $J$
as an
$J$
as an
![]() $R$
-module: given
$R$
-module: given
 $b=\sum _{i}r_{i}^{\prime }\otimes r_{i}\in B$
, we have
$b=\sum _{i}r_{i}^{\prime }\otimes r_{i}\in B$
, we have
![]() $b\in J$
if and only if
$b\in J$
if and only if
 $\sum _{i}r_{i}^{\prime }r_{i}=0$
, and in this case we see that
$\sum _{i}r_{i}^{\prime }r_{i}=0$
, and in this case we see that
 $$\begin{eqnarray}b=\mathop{\sum }_{i}(r_{i}^{\prime }\otimes r_{i}-r_{i}^{\prime }r_{i}\otimes 1)=-\mathop{\sum }_{i}(r_{i}^{\prime }\otimes 1)(r_{i}\otimes 1-1\otimes r_{i})=\mathop{\sum }_{i}(-r_{i}^{\prime })\cdot (r_{i}\otimes 1-1\otimes r_{i})\end{eqnarray}$$
$$\begin{eqnarray}b=\mathop{\sum }_{i}(r_{i}^{\prime }\otimes r_{i}-r_{i}^{\prime }r_{i}\otimes 1)=-\mathop{\sum }_{i}(r_{i}^{\prime }\otimes 1)(r_{i}\otimes 1-1\otimes r_{i})=\mathop{\sum }_{i}(-r_{i}^{\prime })\cdot (r_{i}\otimes 1-1\otimes r_{i})\end{eqnarray}$$
is an
![]() $R$
-linear combination of elements of the form described. The equation
$R$
-linear combination of elements of the form described. The equation
 $$\begin{eqnarray}r\otimes r^{\prime }=rr^{\prime }\otimes 1-r\cdot (r^{\prime }\otimes 1-1\otimes r^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}r\otimes r^{\prime }=rr^{\prime }\otimes 1-r\cdot (r^{\prime }\otimes 1-1\otimes r^{\prime })\end{eqnarray}$$
for
 $r,r^{\prime }\in R$
also shows that we have an
$r,r^{\prime }\in R$
also shows that we have an
![]() $R$
-module direct sum decomposition
$R$
-module direct sum decomposition
 $B=(R\otimes _{k}1)\oplus J$
. Since
$B=(R\otimes _{k}1)\oplus J$
. Since
![]() $R$
is Noetherian, we can fix a finite set of generators
$R$
is Noetherian, we can fix a finite set of generators
 $x_{1},\ldots ,x_{s}$
for
$x_{1},\ldots ,x_{s}$
for
![]() $\mathfrak{m}$
. Moreover, since
$\mathfrak{m}$
. Moreover, since
![]() $R$
contains its residue field
$R$
contains its residue field
![]() $k$
, we have a direct sum decomposition (as
$k$
, we have a direct sum decomposition (as
![]() $k$
-spaces)
$k$
-spaces)
 $R=k\oplus \mathfrak{m}$
, so given any
$R=k\oplus \mathfrak{m}$
, so given any
![]() $r\in R$
, we can write
$r\in R$
, we can write
 $r=c+x_{1}y_{1}+\cdots +x_{s}y_{s}$
where
$r=c+x_{1}y_{1}+\cdots +x_{s}y_{s}$
where
![]() $c\in k$
and
$c\in k$
and
![]() $y_{i}\in R$
. We then have
$y_{i}\in R$
. We then have
 $r\otimes 1-1\otimes r=\sum _{i}(x_{i}y_{i}\otimes 1-1\otimes x_{i}y_{i})$
, since
$r\otimes 1-1\otimes r=\sum _{i}(x_{i}y_{i}\otimes 1-1\otimes x_{i}y_{i})$
, since
 $c\otimes 1=1\otimes c$
for
$c\otimes 1=1\otimes c$
for
![]() $c\in k$
. For all
$c\in k$
. For all
![]() $i$
, we can express
$i$
, we can express
 $x_{i}y_{i}\otimes 1-1\otimes x_{i}y_{i}$
as
$x_{i}y_{i}\otimes 1-1\otimes x_{i}y_{i}$
as
 $$\begin{eqnarray}(y_{i}\otimes 1)(x_{i}\otimes 1-1\otimes x_{i})-(x_{i}\otimes 1-1\otimes x_{i})(y_{i}\otimes 1-1\otimes y_{i})+(x_{i}\otimes 1)(y_{i}\otimes 1-1\otimes y_{i})\end{eqnarray}$$
$$\begin{eqnarray}(y_{i}\otimes 1)(x_{i}\otimes 1-1\otimes x_{i})-(x_{i}\otimes 1-1\otimes x_{i})(y_{i}\otimes 1-1\otimes y_{i})+(x_{i}\otimes 1)(y_{i}\otimes 1-1\otimes y_{i})\end{eqnarray}$$
where the second summand belongs to
![]() $J^{2}$
and the third summand belongs to
$J^{2}$
and the third summand belongs to
![]() $\mathfrak{m}J$
. We conclude that
$\mathfrak{m}J$
. We conclude that
 $r\otimes 1-1\otimes r-(\sum y_{i}\cdot (x_{i}\otimes 1-1\otimes x_{i}))\in J^{2}+\mathfrak{m}J$
. Therefore, if we write
$r\otimes 1-1\otimes r-(\sum y_{i}\cdot (x_{i}\otimes 1-1\otimes x_{i}))\in J^{2}+\mathfrak{m}J$
. Therefore, if we write
 $b_{i}=x_{i}\otimes 1-1\otimes x_{i}$
, the classes of the
$b_{i}=x_{i}\otimes 1-1\otimes x_{i}$
, the classes of the
![]() $b_{i}$
generate
$b_{i}$
generate
 $J/(J^{2}+\mathfrak{m}J)$
as an
$J/(J^{2}+\mathfrak{m}J)$
as an
![]() $R$
-module. Since
$R$
-module. Since
![]() $\mathfrak{m}$
annihilates
$\mathfrak{m}$
annihilates
 $J/(J^{2}+\mathfrak{m}J)$
, and
$J/(J^{2}+\mathfrak{m}J)$
, and
 $R=k\oplus \mathfrak{m}$
as
$R=k\oplus \mathfrak{m}$
as
![]() $k$
-spaces, we see that moreover the classes of the
$k$
-spaces, we see that moreover the classes of the
![]() $b_{i}$
span
$b_{i}$
span
 $J/(J^{2}+\mathfrak{m}J)$
as a
$J/(J^{2}+\mathfrak{m}J)$
as a
![]() $k$
-space. Let
$k$
-space. Let
![]() $L_{j}$
be the
$L_{j}$
be the
![]() $k$
-span of the monomials of degree at most
$k$
-span of the monomials of degree at most
![]() $j$
in the
$j$
in the
![]() $b_{i}$
, and let
$b_{i}$
, and let
![]() $L_{j}^{\prime }$
be the
$L_{j}^{\prime }$
be the
![]() $k$
-span of such monomials of degree precisely
$k$
-span of such monomials of degree precisely
![]() $j$
, so that
$j$
, so that
 $L_{j}=\bigcup _{l=0}^{j}L_{l}^{\prime }$
: clearly all
$L_{j}=\bigcup _{l=0}^{j}L_{l}^{\prime }$
: clearly all
![]() $L_{j}$
and
$L_{j}$
and
![]() $L_{j}^{\prime }$
are finite-dimensional
$L_{j}^{\prime }$
are finite-dimensional
![]() $k$
-spaces. With this notation, what we have just shown is that
$k$
-spaces. With this notation, what we have just shown is that
 $J=L_{1}^{\prime }+J^{2}+\mathfrak{m}J$
.
$J=L_{1}^{\prime }+J^{2}+\mathfrak{m}J$
.
Now let
![]() $b\in B$
be arbitrary. Using the
$b\in B$
be arbitrary. Using the
![]() $R$
-module direct sum decomposition
$R$
-module direct sum decomposition
 $B=(R\otimes _{k}1)\oplus J$
, we write
$B=(R\otimes _{k}1)\oplus J$
, we write
 $b=(r\otimes 1)+x$
where
$b=(r\otimes 1)+x$
where
![]() $x\in J$
. Using the
$x\in J$
. Using the
![]() $k$
-space direct sum decomposition
$k$
-space direct sum decomposition
 $R=k\oplus \mathfrak{m}$
, we write
$R=k\oplus \mathfrak{m}$
, we write
 $r=c+y$
where
$r=c+y$
where
![]() $c\in k$
and
$c\in k$
and
![]() $y\in \mathfrak{m}$
, so that
$y\in \mathfrak{m}$
, so that
 $y\otimes 1\in \mathfrak{m}B$
. Our work above shows that there exist
$y\otimes 1\in \mathfrak{m}B$
. Our work above shows that there exist
![]() $\unicode[STIX]{x1D6FD}\in J^{2}$
and
$\unicode[STIX]{x1D6FD}\in J^{2}$
and
![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{m}J$
such that
$\unicode[STIX]{x1D6FE}\in \mathfrak{m}J$
such that
 $x-\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$
lies in
$x-\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$
lies in
![]() $L_{1}^{\prime }$
. We have
$L_{1}^{\prime }$
. We have
 $(y\otimes 1)+\unicode[STIX]{x1D6FE}\in \mathfrak{m}B$
. We conclude from the decomposition
$(y\otimes 1)+\unicode[STIX]{x1D6FE}\in \mathfrak{m}B$
. We conclude from the decomposition
 $$\begin{eqnarray}b=(c\otimes 1)+(x-\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE})+\unicode[STIX]{x1D6FD}+(\unicode[STIX]{x1D6FE}+(y\otimes 1))\end{eqnarray}$$
$$\begin{eqnarray}b=(c\otimes 1)+(x-\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE})+\unicode[STIX]{x1D6FD}+(\unicode[STIX]{x1D6FE}+(y\otimes 1))\end{eqnarray}$$
that
 $B\subset L_{1}+J^{2}+\mathfrak{m}B$
(since
$B\subset L_{1}+J^{2}+\mathfrak{m}B$
(since
 $c\otimes 1=c\cdot (1\otimes 1)\in L_{0}\subset L_{1}$
), and hence that
$c\otimes 1=c\cdot (1\otimes 1)\in L_{0}\subset L_{1}$
), and hence that
 $B/(\mathfrak{m}B+J^{2})$
is spanned as a
$B/(\mathfrak{m}B+J^{2})$
is spanned as a
![]() $k$
-space by
$k$
-space by
![]() $L_{1}$
. Moreover, it follows by induction that for all
$L_{1}$
. Moreover, it follows by induction that for all
![]() $j$
,
$j$
,
 $B/(\mathfrak{m}B+J^{j+1})$
is spanned as a
$B/(\mathfrak{m}B+J^{j+1})$
is spanned as a
![]() $k$
-space by
$k$
-space by
![]() $L_{j}$
. Assume the conclusion for
$L_{j}$
. Assume the conclusion for
![]() $j-1$
, that is, that
$j-1$
, that is, that
 $B\subset L_{j-1}+\mathfrak{m}B+J^{j}$
. We have already shown
$B\subset L_{j-1}+\mathfrak{m}B+J^{j}$
. We have already shown
 $J=L_{1}^{\prime }+\mathfrak{m}J+J^{2}$
. Taking the
$J=L_{1}^{\prime }+\mathfrak{m}J+J^{2}$
. Taking the
![]() $j$
th power of both sides, we find
$j$
th power of both sides, we find
 $J^{j}\subset \mathfrak{m}J+\sum _{l=0}^{j}L_{j-l}^{\prime }J^{2l}\subset \mathfrak{m}B+L_{j}^{\prime }+J^{j+1}$
, since
$J^{j}\subset \mathfrak{m}J+\sum _{l=0}^{j}L_{j-l}^{\prime }J^{2l}\subset \mathfrak{m}B+L_{j}^{\prime }+J^{j+1}$
, since
![]() $b_{i}\in J$
and for any
$b_{i}\in J$
and for any
![]() $l>0$
,
$l>0$
,
 $2l+(j-l)\geqslant j+1$
. Therefore
$2l+(j-l)\geqslant j+1$
. Therefore
 $$\begin{eqnarray}B\subset (L_{j-1}+L_{j}^{\prime })+\mathfrak{m}B+J^{j+1}.\end{eqnarray}$$
$$\begin{eqnarray}B\subset (L_{j-1}+L_{j}^{\prime })+\mathfrak{m}B+J^{j+1}.\end{eqnarray}$$
Since
 $L_{j-1}+L_{j}^{\prime }=L_{j}$
, we have shown
$L_{j-1}+L_{j}^{\prime }=L_{j}$
, we have shown
 $B/(\mathfrak{m}B+J^{j+1})$
is spanned over
$B/(\mathfrak{m}B+J^{j+1})$
is spanned over
![]() $k$
by
$k$
by
![]() $L_{j}$
, completing the induction. It follows that every
$L_{j}$
, completing the induction. It follows that every
 $B/(\mathfrak{m}B+J^{j+1})$
is a finite-dimensional
$B/(\mathfrak{m}B+J^{j+1})$
is a finite-dimensional
![]() $k$
-space, completing the proof.◻
$k$
-space, completing the proof.◻
Remark 4.7. Our proof of Proposition 4.5 above, together with [Reference EisenbudEis95, Example 7.2], has the following consequence which we record separately for reference: if we fix generators
 $x_{1},\ldots ,x_{s}$
for the maximal ideal
$x_{1},\ldots ,x_{s}$
for the maximal ideal
![]() $\mathfrak{m}$
, then
$\mathfrak{m}$
, then
![]() $(P^{j})^{\text{sep}}$
is generated over
$(P^{j})^{\text{sep}}$
is generated over
![]() $R$
by the classes of monomials in
$R$
by the classes of monomials in
 $b_{0},b_{1},\ldots ,b_{n}$
of degree at most
$b_{0},b_{1},\ldots ,b_{n}$
of degree at most
![]() $j$
, where
$j$
, where
 $b_{0}=1\otimes 1$
and
$b_{0}=1\otimes 1$
and
 $b_{i}=x_{i}\otimes 1-1\otimes x_{i}$
for
$b_{i}=x_{i}\otimes 1-1\otimes x_{i}$
for
 $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
We have now assembled enough preliminaries to prove the
![]() $\unicode[STIX]{x1D6F4}$
-continuity of differential operators over a complete local ring.
$\unicode[STIX]{x1D6F4}$
-continuity of differential operators over a complete local ring.
Proposition 4.8. Let
![]() $(R,\mathfrak{m})$
be a (Noetherian) complete local ring with coefficient field
$(R,\mathfrak{m})$
be a (Noetherian) complete local ring with coefficient field
![]() $k$
, and let
$k$
, and let
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
. If
${\mathcal{D}}={\mathcal{D}}(R,k)$
. If
![]() $M$
is a left
$M$
is a left
![]() ${\mathcal{D}}$
-module and
${\mathcal{D}}$
-module and
 $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
, then
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
, then
 $\unicode[STIX]{x1D6FF}:M\rightarrow M$
is
$\unicode[STIX]{x1D6FF}:M\rightarrow M$
is
![]() $\unicode[STIX]{x1D6F4}$
-continuous. (The analogous statement is also true if
$\unicode[STIX]{x1D6F4}$
-continuous. (The analogous statement is also true if
![]() $M$
is a right
$M$
is a right
![]() ${\mathcal{D}}$
-module.)
${\mathcal{D}}$
-module.)
Proof. We verify the conditions of Definition 3.13. Let
![]() $M_{\unicode[STIX]{x1D706}}$
be a finitely generated
$M_{\unicode[STIX]{x1D706}}$
be a finitely generated
![]() $R$
-submodule of
$R$
-submodule of
![]() $M$
and let
$M$
and let
 $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
. We assert that the
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
. We assert that the
![]() $R$
-submodule
$R$
-submodule
 $\langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle$
of
$\langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle$
of
![]() $M$
generated by the image of
$M$
generated by the image of
![]() $M_{\unicode[STIX]{x1D706}}$
under
$M_{\unicode[STIX]{x1D706}}$
under
![]() $\unicode[STIX]{x1D6FF}$
is finitely generated over
$\unicode[STIX]{x1D6FF}$
is finitely generated over
![]() $R$
. (By Lemma 4.1, we already know the restriction of
$R$
. (By Lemma 4.1, we already know the restriction of
![]() $\unicode[STIX]{x1D6FF}$
to
$\unicode[STIX]{x1D6FF}$
to
![]() $M_{\unicode[STIX]{x1D706}}$
will be
$M_{\unicode[STIX]{x1D706}}$
will be
![]() $\mathfrak{m}$
-adically continuous, so this is all that must be proved.) With
$\mathfrak{m}$
-adically continuous, so this is all that must be proved.) With
![]() $\unicode[STIX]{x1D706}$
fixed, we proceed by induction on the order
$\unicode[STIX]{x1D706}$
fixed, we proceed by induction on the order
![]() $j$
of
$j$
of
![]() $\unicode[STIX]{x1D6FF}$
. Fix a finite set of generators
$\unicode[STIX]{x1D6FF}$
. Fix a finite set of generators
 $m_{1},\ldots ,m_{n}$
for
$m_{1},\ldots ,m_{n}$
for
![]() $M_{\unicode[STIX]{x1D706}}$
. If
$M_{\unicode[STIX]{x1D706}}$
. If
![]() $j=0$
, then
$j=0$
, then
![]() $\unicode[STIX]{x1D6FF}$
is
$\unicode[STIX]{x1D6FF}$
is
![]() $R$
-linear, so
$R$
-linear, so
 $\unicode[STIX]{x1D6FF}(m_{1}),\ldots ,\unicode[STIX]{x1D6FF}(m_{n})$
generate
$\unicode[STIX]{x1D6FF}(m_{1}),\ldots ,\unicode[STIX]{x1D6FF}(m_{n})$
generate
 $\langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle$
. Now suppose
$\langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle$
. Now suppose
![]() $j>0$
and the statement proved for smaller values of
$j>0$
and the statement proved for smaller values of
![]() $j$
. By Proposition 4.5, we can find a finite set of
$j$
. By Proposition 4.5, we can find a finite set of
![]() $R$
-module generators
$R$
-module generators
 $d_{1},\ldots ,d_{s}$
for
$d_{1},\ldots ,d_{s}$
for
 ${\mathcal{D}}^{j-1}(R)$
. Then we claim
${\mathcal{D}}^{j-1}(R)$
. Then we claim
 $$\begin{eqnarray}\{\unicode[STIX]{x1D6FF}(m_{i})\}_{i}\cup \{d_{l}(m_{i})\}_{l,i}\end{eqnarray}$$
$$\begin{eqnarray}\{\unicode[STIX]{x1D6FF}(m_{i})\}_{i}\cup \{d_{l}(m_{i})\}_{l,i}\end{eqnarray}$$
is a finite set of generators for
 $\langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle$
. Indeed, given any element
$\langle \unicode[STIX]{x1D6FF}(M_{\unicode[STIX]{x1D706}})\rangle$
. Indeed, given any element
 $m_{\unicode[STIX]{x1D706}}\in M_{\unicode[STIX]{x1D706}}$
, we can write it as a linear combination
$m_{\unicode[STIX]{x1D706}}\in M_{\unicode[STIX]{x1D706}}$
, we can write it as a linear combination
 $r_{1}m_{1}+\cdots +r_{n}m_{n}$
, and
$r_{1}m_{1}+\cdots +r_{n}m_{n}$
, and
 $\unicode[STIX]{x1D6FF}(r_{i}m_{i})=r_{i}\unicode[STIX]{x1D6FF}(m_{i})+[\unicode[STIX]{x1D6FF},r_{i}](m_{i})$
for all
$\unicode[STIX]{x1D6FF}(r_{i}m_{i})=r_{i}\unicode[STIX]{x1D6FF}(m_{i})+[\unicode[STIX]{x1D6FF},r_{i}](m_{i})$
for all
![]() $i$
. Since
$i$
. Since
 $[\unicode[STIX]{x1D6FF},r_{i}]\in {\mathcal{D}}^{j-1}(R)$
, we can write
$[\unicode[STIX]{x1D6FF},r_{i}]\in {\mathcal{D}}^{j-1}(R)$
, we can write
 $[\unicode[STIX]{x1D6FF},r_{i}]=\unicode[STIX]{x1D70C}_{1,i}d_{1}+\cdots +\unicode[STIX]{x1D70C}_{s,i}d_{s}$
for some
$[\unicode[STIX]{x1D6FF},r_{i}]=\unicode[STIX]{x1D70C}_{1,i}d_{1}+\cdots +\unicode[STIX]{x1D70C}_{s,i}d_{s}$
for some
 $\unicode[STIX]{x1D70C}_{1,i},\ldots ,\unicode[STIX]{x1D70C}_{s,i}\in R$
. Then
$\unicode[STIX]{x1D70C}_{1,i},\ldots ,\unicode[STIX]{x1D70C}_{s,i}\in R$
. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}(r_{i}m_{i})=r_{i}\unicode[STIX]{x1D6FF}(m_{i})+\unicode[STIX]{x1D70C}_{1,i}d_{1}(m_{i})+\cdots +\unicode[STIX]{x1D70C}_{s,i}d_{s}(m_{i})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}(r_{i}m_{i})=r_{i}\unicode[STIX]{x1D6FF}(m_{i})+\unicode[STIX]{x1D70C}_{1,i}d_{1}(m_{i})+\cdots +\unicode[STIX]{x1D70C}_{s,i}d_{s}(m_{i})\end{eqnarray}$$
for all
![]() $i$
. The sum
$i$
. The sum
 $\sum \unicode[STIX]{x1D6FF}(r_{i}m_{i})=\unicode[STIX]{x1D6FF}(m_{\unicode[STIX]{x1D706}})$
thus belongs to the
$\sum \unicode[STIX]{x1D6FF}(r_{i}m_{i})=\unicode[STIX]{x1D6FF}(m_{\unicode[STIX]{x1D706}})$
thus belongs to the
![]() $R$
-submodule of
$R$
-submodule of
![]() $M$
generated by the specified finite set, completing the proof.◻
$M$
generated by the specified finite set, completing the proof.◻
Remark 4.9. More generally, if
![]() $M$
and
$M$
and
![]() $N$
are any two
$N$
are any two
![]() $R$
-modules, there is a notion of
$R$
-modules, there is a notion of
![]() $k$
-linear differential operators
$k$
-linear differential operators
 $M\rightarrow N$
[Reference Grothendieck and DieudonnéGD67, Déf. 16.8.1]. We do not know under what conditions such differential operators are
$M\rightarrow N$
[Reference Grothendieck and DieudonnéGD67, Déf. 16.8.1]. We do not know under what conditions such differential operators are
![]() $\unicode[STIX]{x1D6F4}$
-continuous.
$\unicode[STIX]{x1D6F4}$
-continuous.
Corollary 4.10 (Corollary–Definition).
Let
![]() $(R,\mathfrak{m})$
be a complete local ring with coefficient field
$(R,\mathfrak{m})$
be a complete local ring with coefficient field
![]() $k$
, and let
$k$
, and let
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
. Let
${\mathcal{D}}={\mathcal{D}}(R,k)$
. Let
![]() $M$
be a left
$M$
be a left
![]() ${\mathcal{D}}$
-module. Then the Matlis dual
${\mathcal{D}}$
-module. Then the Matlis dual
 $D(M)=\,\operatorname{Hom}_{R}(M,E)$
has a natural structure of right
$D(M)=\,\operatorname{Hom}_{R}(M,E)$
has a natural structure of right
![]() ${\mathcal{D}}$
-module. If
${\mathcal{D}}$
-module. If
![]() $M$
is a right
$M$
is a right
![]() ${\mathcal{D}}$
-module,
${\mathcal{D}}$
-module,
![]() $D(M)$
has a natural structure of left
$D(M)$
has a natural structure of left
![]() ${\mathcal{D}}$
-module.
${\mathcal{D}}$
-module.
Proof. By symmetry, it suffices to prove the statement when
![]() $M$
is a left
$M$
is a left
![]() ${\mathcal{D}}$
-module. Given any
${\mathcal{D}}$
-module. Given any
 $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
, Propositions 4.8 and 3.19 imply that the Matlis dual
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
, Propositions 4.8 and 3.19 imply that the Matlis dual
 $\unicode[STIX]{x1D6FF}^{\ast }:D(M)\rightarrow D(M)$
is defined. We define a right
$\unicode[STIX]{x1D6FF}^{\ast }:D(M)\rightarrow D(M)$
is defined. We define a right
 ${\mathcal{D}}(R,k)$
-action on
${\mathcal{D}}(R,k)$
-action on
![]() $D(M)$
by
$D(M)$
by
 $\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D719})$
. This definition satisfies the axioms for a right action since, given another differential operator
$\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D719})$
. This definition satisfies the axioms for a right action since, given another differential operator
 $\unicode[STIX]{x1D6FF}^{\prime }\in {\mathcal{D}}(R,k)$
, we have
$\unicode[STIX]{x1D6FF}^{\prime }\in {\mathcal{D}}(R,k)$
, we have
 $(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ (\unicode[STIX]{x1D6FF}^{\prime })^{\ast }$
, again by Proposition 3.19.◻
$(\unicode[STIX]{x1D6FF}^{\prime }\circ \unicode[STIX]{x1D6FF})^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }\circ (\unicode[STIX]{x1D6FF}^{\prime })^{\ast }$
, again by Proposition 3.19.◻
Proposition 4.11. Let
 $\unicode[STIX]{x1D719}:M\rightarrow N$
be a homomorphism of left
$\unicode[STIX]{x1D719}:M\rightarrow N$
be a homomorphism of left
![]() ${\mathcal{D}}$
-modules. The Matlis dual
${\mathcal{D}}$
-modules. The Matlis dual
 $\unicode[STIX]{x1D719}^{\ast }:D(N)\rightarrow D(M)$
, as defined in Proposition 3.19, is a homomorphism of right
$\unicode[STIX]{x1D719}^{\ast }:D(N)\rightarrow D(M)$
, as defined in Proposition 3.19, is a homomorphism of right
![]() ${\mathcal{D}}$
-modules. The analogous statement for a homomorphism of right
${\mathcal{D}}$
-modules. The analogous statement for a homomorphism of right
![]() ${\mathcal{D}}$
-modules is true as well. Therefore, Matlis duality defines contravariant functors from the category of left
${\mathcal{D}}$
-modules is true as well. Therefore, Matlis duality defines contravariant functors from the category of left
![]() ${\mathcal{D}}$
-modules to the category of right
${\mathcal{D}}$
-modules to the category of right
![]() ${\mathcal{D}}$
-modules and vice versa.
${\mathcal{D}}$
-modules and vice versa.
Proof. Again it suffices to prove the first statement. Note first that since
![]() $\unicode[STIX]{x1D719}$
is left
$\unicode[STIX]{x1D719}$
is left
![]() ${\mathcal{D}}$
-linear, it is
${\mathcal{D}}$
-linear, it is
![]() $R$
-linear and hence
$R$
-linear and hence
![]() $\unicode[STIX]{x1D6F4}$
-continuous by Lemma 3.14(a). Let
$\unicode[STIX]{x1D6F4}$
-continuous by Lemma 3.14(a). Let
![]() $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
be given, and write
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
be given, and write
 $\unicode[STIX]{x1D6FF}_{M}:M\rightarrow M$
and
$\unicode[STIX]{x1D6FF}_{M}:M\rightarrow M$
and
 $\unicode[STIX]{x1D6FF}_{N}:N\rightarrow N$
for the actions of
$\unicode[STIX]{x1D6FF}_{N}:N\rightarrow N$
for the actions of
![]() $\unicode[STIX]{x1D6FF}$
on
$\unicode[STIX]{x1D6FF}$
on
![]() $M$
and
$M$
and
![]() $N$
. As is clear from the proof of Corollary 4.10, the right
$N$
. As is clear from the proof of Corollary 4.10, the right
![]() ${\mathcal{D}}$
-module structure on
${\mathcal{D}}$
-module structure on
![]() $D(M)$
is defined by transport of structure from that on
$D(M)$
is defined by transport of structure from that on
![]() $D^{\unicode[STIX]{x1D6F4}}(M)$
via the functorial isomorphism of Theorem 3.15. Therefore we need only check that
$D^{\unicode[STIX]{x1D6F4}}(M)$
via the functorial isomorphism of Theorem 3.15. Therefore we need only check that
 $\unicode[STIX]{x1D719}^{\vee }:D^{\unicode[STIX]{x1D6F4}}(N)\rightarrow D^{\unicode[STIX]{x1D6F4}}(M)$
is right
$\unicode[STIX]{x1D719}^{\vee }:D^{\unicode[STIX]{x1D6F4}}(N)\rightarrow D^{\unicode[STIX]{x1D6F4}}(M)$
is right
![]() ${\mathcal{D}}$
-linear. Since
${\mathcal{D}}$
-linear. Since
![]() $\unicode[STIX]{x1D719}$
is left
$\unicode[STIX]{x1D719}$
is left
![]() ${\mathcal{D}}$
-linear, we have
${\mathcal{D}}$
-linear, we have
 $\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}_{M}=\unicode[STIX]{x1D6FF}_{N}\circ \unicode[STIX]{x1D719}$
. Therefore, if
$\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}_{M}=\unicode[STIX]{x1D6FF}_{N}\circ \unicode[STIX]{x1D719}$
. Therefore, if
 $\unicode[STIX]{x1D706}\in D^{\unicode[STIX]{x1D6F4}}(N)$
, we have
$\unicode[STIX]{x1D706}\in D^{\unicode[STIX]{x1D6F4}}(N)$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D719}^{\vee }(\unicode[STIX]{x1D706}\cdot \unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D719}^{\vee }(\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D6FF}_{N})=\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D6FF}_{N}\circ \unicode[STIX]{x1D719}=\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}_{M}=\unicode[STIX]{x1D719}^{\vee }(\unicode[STIX]{x1D706})\circ \unicode[STIX]{x1D6FF}_{M}=\unicode[STIX]{x1D719}^{\vee }(\unicode[STIX]{x1D706})\cdot \unicode[STIX]{x1D6FF},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}^{\vee }(\unicode[STIX]{x1D706}\cdot \unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D719}^{\vee }(\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D6FF}_{N})=\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D6FF}_{N}\circ \unicode[STIX]{x1D719}=\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}_{M}=\unicode[STIX]{x1D719}^{\vee }(\unicode[STIX]{x1D706})\circ \unicode[STIX]{x1D6FF}_{M}=\unicode[STIX]{x1D719}^{\vee }(\unicode[STIX]{x1D706})\cdot \unicode[STIX]{x1D6FF},\end{eqnarray}$$
so that
![]() $\unicode[STIX]{x1D719}^{\vee }$
is right
$\unicode[STIX]{x1D719}^{\vee }$
is right
![]() ${\mathcal{D}}$
-linear, completing the proof.◻
${\mathcal{D}}$
-linear, completing the proof.◻
Recall from § 3 that if
![]() $M$
is an
$M$
is an
![]() $R$
-module, we have the natural evaluation map
$R$
-module, we have the natural evaluation map
 $\unicode[STIX]{x1D704}:M\rightarrow D(D(M))$
which is injective for arbitrary
$\unicode[STIX]{x1D704}:M\rightarrow D(D(M))$
which is injective for arbitrary
![]() $M$
and an isomorphism if
$M$
and an isomorphism if
![]() $M$
is finitely generated or Artinian. If
$M$
is finitely generated or Artinian. If
![]() $M$
is a left
$M$
is a left
![]() ${\mathcal{D}}$
-module, then
${\mathcal{D}}$
-module, then
 $D(D(M))$
is also a left
$D(D(M))$
is also a left
![]() ${\mathcal{D}}$
-module (apply Corollary 4.10 twice). The following proposition justifies our use of the expression ‘Matlis duality for
${\mathcal{D}}$
-module (apply Corollary 4.10 twice). The following proposition justifies our use of the expression ‘Matlis duality for
![]() ${\mathcal{D}}$
-modules’.
${\mathcal{D}}$
-modules’.
Proposition 4.12. Let
![]() $M$
be a left
$M$
be a left
![]() ${\mathcal{D}}$
-module. The evaluation map
${\mathcal{D}}$
-module. The evaluation map
 $\unicode[STIX]{x1D704}:M{\hookrightarrow}D(D(M))$
is a morphism of left
$\unicode[STIX]{x1D704}:M{\hookrightarrow}D(D(M))$
is a morphism of left
![]() ${\mathcal{D}}$
-modules. In particular, if
${\mathcal{D}}$
-modules. In particular, if
![]() $M$
is finitely generated or Artinian as an
$M$
is finitely generated or Artinian as an
![]() $R$
-module, then
$R$
-module, then
![]() $\unicode[STIX]{x1D704}$
is an isomorphism of left
$\unicode[STIX]{x1D704}$
is an isomorphism of left
![]() ${\mathcal{D}}$
-modules.
${\mathcal{D}}$
-modules.
Proof. By the proof of Proposition 3.22(a), we have an isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}:D(D(M))\xrightarrow[{}]{{\sim}}D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}:D(D(M))\xrightarrow[{}]{{\sim}}D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\end{eqnarray}$$
of
![]() $R$
-modules, and the left
$R$
-modules, and the left
![]() ${\mathcal{D}}$
-module structure on
${\mathcal{D}}$
-module structure on
 $D(D(M))$
is defined, by transport of structure, using the left
$D(D(M))$
is defined, by transport of structure, using the left
![]() ${\mathcal{D}}$
-module structure on the right-hand side. We also have an evaluation map
${\mathcal{D}}$
-module structure on the right-hand side. We also have an evaluation map
 $$\begin{eqnarray}\unicode[STIX]{x1D704}^{\prime }:M\rightarrow D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}^{\prime }:M\rightarrow D^{\unicode[STIX]{x1D6F4}}(D^{\unicode[STIX]{x1D6F4}}(M))\end{eqnarray}$$
defined by
 $\unicode[STIX]{x1D704}^{\prime }(m)(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}(m)$
for all
$\unicode[STIX]{x1D704}^{\prime }(m)(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}(m)$
for all
![]() $m\in M$
and
$m\in M$
and
 $\unicode[STIX]{x1D6FF}\in D^{\unicode[STIX]{x1D6F4}}(M)$
. The proof of Proposition 3.22(a) shows that
$\unicode[STIX]{x1D6FF}\in D^{\unicode[STIX]{x1D6F4}}(M)$
. The proof of Proposition 3.22(a) shows that
 $\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}^{\prime }$
. It therefore suffices to check that
$\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}^{\prime }$
. It therefore suffices to check that
![]() $\unicode[STIX]{x1D704}^{\prime }$
is left
$\unicode[STIX]{x1D704}^{\prime }$
is left
![]() ${\mathcal{D}}$
-linear. We must show that for any
${\mathcal{D}}$
-linear. We must show that for any
![]() $m\in M$
and
$m\in M$
and
![]() $d\in {\mathcal{D}}$
, we have
$d\in {\mathcal{D}}$
, we have
 $\unicode[STIX]{x1D704}^{\prime }(d\cdot m)=d\cdot \unicode[STIX]{x1D704}^{\prime }(m)$
. The left-hand side is the evaluation map at
$\unicode[STIX]{x1D704}^{\prime }(d\cdot m)=d\cdot \unicode[STIX]{x1D704}^{\prime }(m)$
. The left-hand side is the evaluation map at
 $d\cdot m\in M$
. The right-hand side is the same, because
$d\cdot m\in M$
. The right-hand side is the same, because
![]() $d$
acts on the evaluation map
$d$
acts on the evaluation map
![]() $\unicode[STIX]{x1D704}^{\prime }$
by precomposition with
$\unicode[STIX]{x1D704}^{\prime }$
by precomposition with
 $d:M\rightarrow M$
. This completes the proof.◻
$d:M\rightarrow M$
. This completes the proof.◻
We give some examples of Matlis duals with right
 ${\mathcal{D}}(R,k)$
-structures, mostly involving local cohomology.
${\mathcal{D}}(R,k)$
-structures, mostly involving local cohomology.
Example 4.13. Let
![]() $(R,\mathfrak{m})$
be a complete local ring with coefficient field
$(R,\mathfrak{m})$
be a complete local ring with coefficient field
![]() $k$
.
$k$
.
-
(a) Since
 $R$
is a left
$R$
is a left
 ${\mathcal{D}}(R,k)$
-module and
${\mathcal{D}}(R,k)$
-module and
 $E=D(R)$
,
$E=D(R)$
,
 $E$
has a natural structure of right
$E$
has a natural structure of right
 ${\mathcal{D}}(R,k)$
-module.
${\mathcal{D}}(R,k)$
-module. -
(b) If
 $M$
is a left
$M$
is a left
 ${\mathcal{D}}(R,k)$
-module, so is
${\mathcal{D}}(R,k)$
-module, so is
 $M_{S}$
for any multiplicatively closed subset
$M_{S}$
for any multiplicatively closed subset
 $S\subset R$
[Reference LyubeznikLyu93, Example 5.1(a)]. If
$S\subset R$
[Reference LyubeznikLyu93, Example 5.1(a)]. If
 $I\subset R$
is an ideal, the local cohomology modules
$I\subset R$
is an ideal, the local cohomology modules
 $H_{I}^{i}(R)$
supported at
$H_{I}^{i}(R)$
supported at
 $I$
have the structure of left
$I$
have the structure of left
 ${\mathcal{D}}(R,k)$
-modules, because
${\mathcal{D}}(R,k)$
-modules, because
 $H_{I}^{i}(R)$
is the
$H_{I}^{i}(R)$
is the
 $i$
th cohomology object of a complex whose objects are localizations of the left
$i$
th cohomology object of a complex whose objects are localizations of the left
 ${\mathcal{D}}(R,k)$
-module
${\mathcal{D}}(R,k)$
-module
 $R$
and whose maps, sums of natural localization maps, are
$R$
and whose maps, sums of natural localization maps, are
 ${\mathcal{D}}(R,k)$
-linear [Reference LyubeznikLyu93, Example 5.1(c)]. By the previous theorem, the Matlis duals
${\mathcal{D}}(R,k)$
-linear [Reference LyubeznikLyu93, Example 5.1(c)]. By the previous theorem, the Matlis duals
 $D(H_{I}^{i}(R))$
are right
$D(H_{I}^{i}(R))$
are right
 ${\mathcal{D}}(R,k)$
-modules.
${\mathcal{D}}(R,k)$
-modules. -
(c) Now suppose
 $I=\mathfrak{m}$
. If
$I=\mathfrak{m}$
. If
 $R$
is Cohen–Macaulay, then
$R$
is Cohen–Macaulay, then
 $H_{\mathfrak{m}}^{i}(R)$
is zero unless
$H_{\mathfrak{m}}^{i}(R)$
is zero unless
 $i=\dim (R)$
. The Matlis dual
$i=\dim (R)$
. The Matlis dual
 $D(H_{\mathfrak{m}}^{\dim (R)}(R))$
, which is the canonical module of
$D(H_{\mathfrak{m}}^{\dim (R)}(R))$
, which is the canonical module of
 $R$
, therefore has a structure of right
$R$
, therefore has a structure of right
 ${\mathcal{D}}(R,k)$
-module. If
${\mathcal{D}}(R,k)$
-module. If
 $R$
is not Cohen–Macaulay, there exists some
$R$
is not Cohen–Macaulay, there exists some
 $i<\dim (R)$
such that
$i<\dim (R)$
such that
 $H_{\mathfrak{m}}^{i}(R)$
is non-zero. For such an
$H_{\mathfrak{m}}^{i}(R)$
is non-zero. For such an
 $i$
, the Matlis dual
$i$
, the Matlis dual
 $D(H_{\mathfrak{m}}^{i}(R))$
is a right
$D(H_{\mathfrak{m}}^{i}(R))$
is a right
 ${\mathcal{D}}(R,k)$
-module that is finitely generated (since
${\mathcal{D}}(R,k)$
-module that is finitely generated (since
 $H_{\mathfrak{m}}^{i}(R)$
is Artinian) as an
$H_{\mathfrak{m}}^{i}(R)$
is Artinian) as an
 $R$
-module and whose dimension is strictly less than the dimension of
$R$
-module and whose dimension is strictly less than the dimension of
 $R$
(in fact, its dimension is bounded above by
$R$
(in fact, its dimension is bounded above by
 $i$
: [Reference Grothendieck and RaynaudGR05, Exp. V, Theorem 3.1(ii)]).
$i$
: [Reference Grothendieck and RaynaudGR05, Exp. V, Theorem 3.1(ii)]).
We give some more details related to Example 4.13(a). Since
![]() $R$
is a finitely generated
$R$
is a finitely generated
![]() $R$
-module, we know by Theorem 3.8 that
$R$
-module, we know by Theorem 3.8 that
 $E=D(R)\simeq \operatorname{Hom}_{\text{cont},k}(R,k)$
, and the right
$E=D(R)\simeq \operatorname{Hom}_{\text{cont},k}(R,k)$
, and the right
![]() ${\mathcal{D}}$
-action on
${\mathcal{D}}$
-action on
 $\operatorname{Hom}_{\text{cont},k}(R,k)$
is defined by
$\operatorname{Hom}_{\text{cont},k}(R,k)$
is defined by
 $\unicode[STIX]{x1D6FF}\cdot d=\unicode[STIX]{x1D6FF}\circ d$
for
$\unicode[STIX]{x1D6FF}\cdot d=\unicode[STIX]{x1D6FF}\circ d$
for
![]() $d\in D$
and
$d\in D$
and
 $\unicode[STIX]{x1D6FF}\in \operatorname{Hom}_{\text{cont},k}(R,k)$
. If
$\unicode[STIX]{x1D6FF}\in \operatorname{Hom}_{\text{cont},k}(R,k)$
. If
![]() $M$
is any
$M$
is any
![]() $R$
-module, we have an isomorphism
$R$
-module, we have an isomorphism
 $$\begin{eqnarray}D^{\unicode[STIX]{x1D6F4}}(M)\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{R}(M,\operatorname{Hom}_{\text{cont},k}(R,k))\end{eqnarray}$$
$$\begin{eqnarray}D^{\unicode[STIX]{x1D6F4}}(M)\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{R}(M,\operatorname{Hom}_{\text{cont},k}(R,k))\end{eqnarray}$$
by combining Theorems 3.15 and 3.8. Concretely, this isomorphism carries a
![]() $\unicode[STIX]{x1D6F4}$
-continuous map
$\unicode[STIX]{x1D6F4}$
-continuous map
 $\unicode[STIX]{x1D6FF}:M\rightarrow k$
to the
$\unicode[STIX]{x1D6FF}:M\rightarrow k$
to the
![]() $R$
-linear map
$R$
-linear map
 $M\rightarrow \operatorname{Hom}_{\text{cont},k}(R,k)$
defined by
$M\rightarrow \operatorname{Hom}_{\text{cont},k}(R,k)$
defined by
 $m\mapsto (r\mapsto \unicode[STIX]{x1D6FF}(rm))$
, and its inverse carries an
$m\mapsto (r\mapsto \unicode[STIX]{x1D6FF}(rm))$
, and its inverse carries an
![]() $R$
-linear map
$R$
-linear map
 $\unicode[STIX]{x1D713}:M\rightarrow \operatorname{Hom}_{\text{cont},k}(R,k)$
to the
$\unicode[STIX]{x1D713}:M\rightarrow \operatorname{Hom}_{\text{cont},k}(R,k)$
to the
![]() $\unicode[STIX]{x1D6F4}$
-continuous map
$\unicode[STIX]{x1D6F4}$
-continuous map
![]() $M\rightarrow k$
defined by
$M\rightarrow k$
defined by
 $m\mapsto \unicode[STIX]{x1D713}(m)(1)$
.
$m\mapsto \unicode[STIX]{x1D713}(m)(1)$
.
By identifying
![]() $E$
with
$E$
with
 $\operatorname{Hom}_{\text{cont},k}(R,k)$
endowed with the right
$\operatorname{Hom}_{\text{cont},k}(R,k)$
endowed with the right
![]() ${\mathcal{D}}$
-structure above, we can give an alternate description of the right action of derivations (differential operators of order precisely
${\mathcal{D}}$
-structure above, we can give an alternate description of the right action of derivations (differential operators of order precisely
![]() $1$
) on the Matlis dual of any left
$1$
) on the Matlis dual of any left
![]() ${\mathcal{D}}$
-module, using the formulas of [Reference Hotta, Takeuchi and TanisakiHTT08, Proposition 1.2.9]: if
${\mathcal{D}}$
-module, using the formulas of [Reference Hotta, Takeuchi and TanisakiHTT08, Proposition 1.2.9]: if
![]() $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
is a derivation and
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
is a derivation and
![]() $M$
is a left
$M$
is a left
![]() ${\mathcal{D}}$
-module, then for any
${\mathcal{D}}$
-module, then for any
![]() $R$
-linear map
$R$
-linear map
 $\unicode[STIX]{x1D719}:M\rightarrow E$
, we define an
$\unicode[STIX]{x1D719}:M\rightarrow E$
, we define an
![]() $R$
-linear map
$R$
-linear map
 $\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF}:M\rightarrow E$
by
$\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF}:M\rightarrow E$
by
 $(\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF})(m)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m)+\unicode[STIX]{x1D719}(m)\cdot \unicode[STIX]{x1D6FF}$
. This formula extends to define a right action of the
$(\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF})(m)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m)+\unicode[STIX]{x1D719}(m)\cdot \unicode[STIX]{x1D6FF}$
. This formula extends to define a right action of the
![]() $R$
-subalgebra of
$R$
-subalgebra of
![]() ${\mathcal{D}}$
generated by
${\mathcal{D}}$
generated by
![]() $R$
together with the derivations (e.g., if
$R$
together with the derivations (e.g., if
![]() $R$
is regular, this subalgebra is all of
$R$
is regular, this subalgebra is all of
![]() ${\mathcal{D}}$
). This right action coincides with the right action we have defined in Corollary 4.10, as follows.
${\mathcal{D}}$
). This right action coincides with the right action we have defined in Corollary 4.10, as follows.
Proposition 4.14. With the hypotheses of Corollary 4.10, let
![]() $M$
be a left
$M$
be a left
![]() ${\mathcal{D}}$
-module, and let
${\mathcal{D}}$
-module, and let
![]() $D(M)$
be its Matlis dual. If
$D(M)$
be its Matlis dual. If
![]() $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
is a derivation and
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
is a derivation and
 $\unicode[STIX]{x1D719}:M\rightarrow E$
is
$\unicode[STIX]{x1D719}:M\rightarrow E$
is
![]() $R$
-linear, we have
$R$
-linear, we have
 $\unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF}$
, where the right-hand side is defined as in [Reference Hotta, Takeuchi and TanisakiHTT08, Proposition 1.2.9].
$\unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF}$
, where the right-hand side is defined as in [Reference Hotta, Takeuchi and TanisakiHTT08, Proposition 1.2.9].
Proof. We use the various identifications between equivalent forms of
![]() $D(M)$
. The map
$D(M)$
. The map
![]() $\unicode[STIX]{x1D719}$
corresponds, under the isomorphism
$\unicode[STIX]{x1D719}$
corresponds, under the isomorphism
 $D(M)\xrightarrow[{}]{\unicode[STIX]{x1D6F7}_{M}}D^{\unicode[STIX]{x1D6F4}}(M)$
of Theorem 3.15, to
$D(M)\xrightarrow[{}]{\unicode[STIX]{x1D6F7}_{M}}D^{\unicode[STIX]{x1D6F4}}(M)$
of Theorem 3.15, to
![]() $\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}$
, and
$\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}$
, and
 $\unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}$
. Under the identification
$\unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}$
. Under the identification
 $D^{\unicode[STIX]{x1D6F4}}(M)\simeq \operatorname{Hom}_{R}(M,\operatorname{Hom}_{\text{cont},k}(R,k))$
given earlier,
$D^{\unicode[STIX]{x1D6F4}}(M)\simeq \operatorname{Hom}_{R}(M,\operatorname{Hom}_{\text{cont},k}(R,k))$
given earlier,
 $\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}$
corresponds to the map
$\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}$
corresponds to the map
 $$\begin{eqnarray}m\mapsto (r\mapsto \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}(rm)))).\end{eqnarray}$$
$$\begin{eqnarray}m\mapsto (r\mapsto \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}(rm)))).\end{eqnarray}$$
On the other hand, for any
![]() $m\in M$
, we have
$m\in M$
, we have
 $(\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF})(m)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m)+\unicode[STIX]{x1D719}(m)\cdot \unicode[STIX]{x1D6FF}\in E$
, where we identify
$(\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D6FF})(m)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m)+\unicode[STIX]{x1D719}(m)\cdot \unicode[STIX]{x1D6FF}\in E$
, where we identify
![]() $E$
with the right
$E$
with the right
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
 $\operatorname{Hom}_{\text{cont},k}(R,k)$
in order to define
$\operatorname{Hom}_{\text{cont},k}(R,k)$
in order to define
 $\unicode[STIX]{x1D719}(m)\cdot \unicode[STIX]{x1D6FF}$
. Under this identification,
$\unicode[STIX]{x1D719}(m)\cdot \unicode[STIX]{x1D6FF}$
. Under this identification,
 $\unicode[STIX]{x1D719}(m)\cdot \unicode[STIX]{x1D6FF}$
is the map
$\unicode[STIX]{x1D719}(m)\cdot \unicode[STIX]{x1D6FF}$
is the map
 $r\mapsto \unicode[STIX]{x1D70E}(r\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m))$
, and
$r\mapsto \unicode[STIX]{x1D70E}(r\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m))$
, and
 $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m)$
is the map
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m)$
is the map
 $r\mapsto \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}(r)\unicode[STIX]{x1D719}(m))$
. It is therefore enough to show that
$r\mapsto \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}(r)\unicode[STIX]{x1D719}(m))$
. It is therefore enough to show that
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}(rm)))=\unicode[STIX]{x1D70E}(r\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m))+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}(r)\unicode[STIX]{x1D719}(m))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}(rm)))=\unicode[STIX]{x1D70E}(r\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF}\cdot m))+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}(r)\unicode[STIX]{x1D719}(m))\end{eqnarray}$$
for all
![]() $r\in R$
and
$r\in R$
and
![]() $m\in M$
, which follows immediately from the relations
$m\in M$
, which follows immediately from the relations
 $\unicode[STIX]{x1D6FF}(rm)=\unicode[STIX]{x1D6FF}(r)m+r\unicode[STIX]{x1D6FF}(m)$
holding in any left
$\unicode[STIX]{x1D6FF}(rm)=\unicode[STIX]{x1D6FF}(r)m+r\unicode[STIX]{x1D6FF}(m)$
holding in any left
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
.◻
$M$
.◻
We now specialize further to the case in which
 $R=k[[x_{1},\ldots ,x_{n}]]$
is a formal power series ring over a field of characteristic zero. In this case, there is a transposition operation that converts left modules over
$R=k[[x_{1},\ldots ,x_{n}]]$
is a formal power series ring over a field of characteristic zero. In this case, there is a transposition operation that converts left modules over
 ${\mathcal{D}}(R,k)$
to right modules and conversely. We recall its definition (see [Reference Hotta, Takeuchi and TanisakiHTT08, p. 19 and Lemma 1.2.6] for the case of a polynomial ring, or more generally, a smooth variety over
${\mathcal{D}}(R,k)$
to right modules and conversely. We recall its definition (see [Reference Hotta, Takeuchi and TanisakiHTT08, p. 19 and Lemma 1.2.6] for the case of a polynomial ring, or more generally, a smooth variety over
![]() $k$
; the formal power series definition is essentially the same). Since
$k$
; the formal power series definition is essentially the same). Since
![]() $k$
is of characteristic zero, the ring
$k$
is of characteristic zero, the ring
 ${\mathcal{D}}(R,k)$
is a free left
${\mathcal{D}}(R,k)$
is a free left
![]() $R$
-module generated by monomials in
$R$
-module generated by monomials in
 $\unicode[STIX]{x2202}_{1}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}_{n}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{n}$
.
$\unicode[STIX]{x2202}_{1}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}_{n}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{n}$
.
Definition 4.15. Let
 $R=k[[x_{1},\ldots ,x_{n}]]$
where
$R=k[[x_{1},\ldots ,x_{n}]]$
where
![]() $k$
is a field of characteristic zero, and let
$k$
is a field of characteristic zero, and let
![]() $M$
be a left
$M$
be a left
 ${\mathcal{D}}(R,k)$
-module. Let
${\mathcal{D}}(R,k)$
-module. Let
 $\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{1}^{a_{1}}\cdots \unicode[STIX]{x2202}_{n}^{a_{n}}$
be an element of
$\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{1}^{a_{1}}\cdots \unicode[STIX]{x2202}_{n}^{a_{n}}$
be an element of
 ${\mathcal{D}}(R,k)$
, where
${\mathcal{D}}(R,k)$
, where
![]() $\unicode[STIX]{x1D70C}\in R$
. If
$\unicode[STIX]{x1D70C}\in R$
. If
![]() $\cdot$
denotes the given left action of
$\cdot$
denotes the given left action of
 ${\mathcal{D}}(R,k)$
, then for any
${\mathcal{D}}(R,k)$
, then for any
![]() $m\in M$
, the formula
$m\in M$
, the formula
 $$\begin{eqnarray}m\ast (\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{1}^{a_{1}}\cdots \unicode[STIX]{x2202}_{n}^{a_{n}})=((-1)^{a_{1}+\cdots +a_{n}}\unicode[STIX]{x2202}_{n}^{a_{n}}\cdots \unicode[STIX]{x2202}_{1}^{a_{1}}\unicode[STIX]{x1D70C})\cdot m\end{eqnarray}$$
$$\begin{eqnarray}m\ast (\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{1}^{a_{1}}\cdots \unicode[STIX]{x2202}_{n}^{a_{n}})=((-1)^{a_{1}+\cdots +a_{n}}\unicode[STIX]{x2202}_{n}^{a_{n}}\cdots \unicode[STIX]{x2202}_{1}^{a_{1}}\unicode[STIX]{x1D70C})\cdot m\end{eqnarray}$$
defines the transpose action, a right
 ${\mathcal{D}}(R,k)$
-action
${\mathcal{D}}(R,k)$
-action
![]() $\ast$
on
$\ast$
on
![]() $M$
.
$M$
.
There is, of course, a symmetric notion of the transpose of a right
![]() ${\mathcal{D}}$
-module, which is a left
${\mathcal{D}}$
-module, which is a left
![]() ${\mathcal{D}}$
-module. To see that the right action given above is well defined, we view it in the following way. Let
${\mathcal{D}}$
-module. To see that the right action given above is well defined, we view it in the following way. Let
 ${\mathcal{D}}(R,k)^{\circ }$
be the opposite algebra of
${\mathcal{D}}(R,k)^{\circ }$
be the opposite algebra of
 ${\mathcal{D}}(R,k)$
. There exists a unique isomorphism
${\mathcal{D}}(R,k)$
. There exists a unique isomorphism
 $\unicode[STIX]{x1D719}:{\mathcal{D}}(R,k)^{\circ }\rightarrow {\mathcal{D}}(R,k)$
such that
$\unicode[STIX]{x1D719}:{\mathcal{D}}(R,k)^{\circ }\rightarrow {\mathcal{D}}(R,k)$
such that
 $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70C})=\unicode[STIX]{x1D70C}$
for all
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70C})=\unicode[STIX]{x1D70C}$
for all
![]() $\unicode[STIX]{x1D70C}\in R$
and
$\unicode[STIX]{x1D70C}\in R$
and
 $\unicode[STIX]{x1D719}(\unicode[STIX]{x2202}_{i})=-\unicode[STIX]{x2202}_{i}$
for all
$\unicode[STIX]{x1D719}(\unicode[STIX]{x2202}_{i})=-\unicode[STIX]{x2202}_{i}$
for all
![]() $i$
, which when viewed as a map
$i$
, which when viewed as a map
 $\unicode[STIX]{x1D719}:{\mathcal{D}}(R,k)\rightarrow {\mathcal{D}}(R,k)$
is called the principal anti-automorphism of
$\unicode[STIX]{x1D719}:{\mathcal{D}}(R,k)\rightarrow {\mathcal{D}}(R,k)$
is called the principal anti-automorphism of
 ${\mathcal{D}}(R,k)$
. To see that this is an isomorphism, note that since all elements of
${\mathcal{D}}(R,k)$
. To see that this is an isomorphism, note that since all elements of
![]() $R$
commute with each other and all
$R$
commute with each other and all
![]() $\unicode[STIX]{x2202}_{i}$
commute with each other, the only non-trivial relations among elements of
$\unicode[STIX]{x2202}_{i}$
commute with each other, the only non-trivial relations among elements of
 ${\mathcal{D}}(R,k)$
are the relations
${\mathcal{D}}(R,k)$
are the relations
 $\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{i}+\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D70C})$
. The map
$\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{i}+\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D70C})$
. The map
![]() $\unicode[STIX]{x1D719}$
, which is clearly bijective, carries
$\unicode[STIX]{x1D719}$
, which is clearly bijective, carries
![]() $\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D70C}$
to
![]() $-\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{i}$
and
$-\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{i}$
and
 $\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{i}+\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D70C})$
to
$\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{i}+\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D70C})$
to
 $-\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D70C}+\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D70C})$
; since
$-\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D70C}+\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D70C})$
; since
 $-\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{i}=-\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D70C}+\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D70C})$
, the relations are respected. The transposed action
$-\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{i}=-\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D70C}+\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D70C})$
, the relations are respected. The transposed action
![]() $\ast$
is then simply defined by
$\ast$
is then simply defined by
 $m\ast \unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})\cdot m$
for
$m\ast \unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})\cdot m$
for
 $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
.
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}(R,k)$
.
Remark 4.16. As defined in the previous paragraph, the anti-automorphism
![]() $\unicode[STIX]{x1D719}$
(and therefore the transposition operation) depends on the choice of variables
$\unicode[STIX]{x1D719}$
(and therefore the transposition operation) depends on the choice of variables
 $x_{1},\ldots ,x_{n}$
.
$x_{1},\ldots ,x_{n}$
.
Proposition 4.17. Let
 $R=k[[x_{1},\ldots ,x_{n}]]$
with
$R=k[[x_{1},\ldots ,x_{n}]]$
with
![]() $k$
a field of characteristic zero,
$k$
a field of characteristic zero,
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
, and
${\mathcal{D}}={\mathcal{D}}(R,k)$
, and
![]() $M$
any left
$M$
any left
![]() ${\mathcal{D}}$
-module. There is a natural structure of left
${\mathcal{D}}$
-module. There is a natural structure of left
![]() ${\mathcal{D}}$
-module on the Matlis dual
${\mathcal{D}}$
-module on the Matlis dual
 $D(M)=\operatorname{Hom}_{R}(M,E)$
.
$D(M)=\operatorname{Hom}_{R}(M,E)$
.
Proof. Apply the right-to-left version of the transposition operation described above to the right
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $D(M)$
with structure defined in Corollary 4.10.◻
$D(M)$
with structure defined in Corollary 4.10.◻
Therefore, in this case, Matlis duality provides a (contravariant) functor from left
![]() ${\mathcal{D}}$
-modules to left
${\mathcal{D}}$
-modules to left
![]() ${\mathcal{D}}$
-modules. We recall here Remark 1.4: even if
${\mathcal{D}}$
-modules. We recall here Remark 1.4: even if
![]() $M$
is holonomic, the Matlis dual
$M$
is holonomic, the Matlis dual
![]() $D(M)$
need not be holonomic.
$D(M)$
need not be holonomic.
5 The de Rham complex of a Matlis dual
Let
 $R=k[[x_{1},\ldots ,x_{n}]]$
where
$R=k[[x_{1},\ldots ,x_{n}]]$
where
![]() $k$
is a field of characteristic zero, and let
$k$
is a field of characteristic zero, and let
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
. For any left
${\mathcal{D}}={\mathcal{D}}(R,k)$
. For any left
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
, we can define its de Rham complex
$M$
, we can define its de Rham complex
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
(see § 2 for definitions and notation concerning de Rham complexes). The Matlis dual
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
(see § 2 for definitions and notation concerning de Rham complexes). The Matlis dual
![]() $D(M)$
is also a left
$D(M)$
is also a left
![]() ${\mathcal{D}}$
-module by Proposition 4.17, so we can consider the de Rham complex
${\mathcal{D}}$
-module by Proposition 4.17, so we can consider the de Rham complex
 $D(M)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
. (Every
$D(M)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
. (Every
![]() ${\mathcal{D}}$
-module we consider in this section will be a left
${\mathcal{D}}$
-module we consider in this section will be a left
![]() ${\mathcal{D}}$
-module, so we no longer say so explicitly.)
${\mathcal{D}}$
-module, so we no longer say so explicitly.)
Our goal in this section is to compare the cohomology of these two complexes. Specifically, we will show the following.
Theorem 5.1. Let
![]() $R$
and
$R$
and
![]() ${\mathcal{D}}$
be as above. If
${\mathcal{D}}$
be as above. If
![]() $M$
is a holonomic
$M$
is a holonomic
![]() ${\mathcal{D}}$
-module, then for all
${\mathcal{D}}$
-module, then for all
![]() $i$
, we have isomorphisms
$i$
, we have isomorphisms
 $$\begin{eqnarray}(H_{\text{dR}}^{i}(M))^{\vee }\simeq H_{\text{dR}}^{n-i}(D(M))\end{eqnarray}$$
$$\begin{eqnarray}(H_{\text{dR}}^{i}(M))^{\vee }\simeq H_{\text{dR}}^{n-i}(D(M))\end{eqnarray}$$
where
![]() $\vee$
denotes
$\vee$
denotes
![]() $k$
-linear dual, i.e.
$k$
-linear dual, i.e.
 $\operatorname{Hom}_{k}(-,k)$
.
$\operatorname{Hom}_{k}(-,k)$
.
By Proposition 4.8, the differentials in the complex
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
are
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
are
![]() $\unicode[STIX]{x1D6F4}$
-continuous, so the entire complex can be Matlis dualized. Since the functor
$\unicode[STIX]{x1D6F4}$
-continuous, so the entire complex can be Matlis dualized. Since the functor
![]() $D$
is contravariant, the
$D$
is contravariant, the
![]() $i$
th object in this dualized complex
$i$
th object in this dualized complex
 $D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
is
$D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
is
 $D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{n-i})$
. Theorem 5.1 is a trivial consequence of the following pair of propositions.
$D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{n-i})$
. Theorem 5.1 is a trivial consequence of the following pair of propositions.
Proposition 5.2. Let
![]() $R$
and
$R$
and
![]() ${\mathcal{D}}$
be as above. If
${\mathcal{D}}$
be as above. If
![]() $M$
is a holonomic
$M$
is a holonomic
![]() ${\mathcal{D}}$
-module, then for all
${\mathcal{D}}$
-module, then for all
![]() $i$
, we have isomorphisms
$i$
, we have isomorphisms
 $$\begin{eqnarray}(h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))^{\vee }\simeq h^{n-i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })).\end{eqnarray}$$
$$\begin{eqnarray}(h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))^{\vee }\simeq h^{n-i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })).\end{eqnarray}$$
Proposition 5.3. Let
![]() $R$
and
$R$
and
![]() ${\mathcal{D}}$
be as above. If
${\mathcal{D}}$
be as above. If
![]() $M$
is any
$M$
is any
![]() ${\mathcal{D}}$
-module, then for all
${\mathcal{D}}$
-module, then for all
![]() $i$
, we have isomorphisms
$i$
, we have isomorphisms
 $$\begin{eqnarray}h^{i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))\simeq h^{i}(D(M)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}h^{i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))\simeq h^{i}(D(M)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }).\end{eqnarray}$$
Proposition 5.3 is relatively straightforward, and we prove it first. The proof of Proposition 5.2, which is the longest and most involved proof in this paper, will take up the remainder of this section.
Before giving the proof of Proposition 5.3, we recall the definition of the Koszul complex, for which a reference is [Reference WeibelWei94, § 4.5].
Definition 5.4. Let
![]() $R$
be a commutative ring, let
$R$
be a commutative ring, let
 $\mathbf{x}=(x_{1},\ldots ,x_{n})$
be a sequence of elements of
$\mathbf{x}=(x_{1},\ldots ,x_{n})$
be a sequence of elements of
![]() $R$
, and let
$R$
, and let
![]() $M$
be an
$M$
be an
![]() $R$
-module. The Koszul complex
$R$
-module. The Koszul complex
![]() $K_{\bullet }(\mathbf{x})$
of
$K_{\bullet }(\mathbf{x})$
of
![]() $R$
with respect to
$R$
with respect to
![]() $\mathbf{x}$
is the homologically indexed complex of length
$\mathbf{x}$
is the homologically indexed complex of length
![]() $n$
whose
$n$
whose
![]() $i$
th object
$i$
th object
![]() $K_{i}(\mathbf{x})$
is a direct sum of
$K_{i}(\mathbf{x})$
is a direct sum of
![]() $\binom{n}{i}$
copies of
$\binom{n}{i}$
copies of
![]() $R$
(indexed by
$R$
(indexed by
![]() $i$
-tuples
$i$
-tuples
 $e_{j_{1}}\wedge \cdots \wedge e_{j_{i}}$
where
$e_{j_{1}}\wedge \cdots \wedge e_{j_{i}}$
where
 $1\leqslant j_{1}<\cdots <j_{i}\leqslant n$
) and where the differential
$1\leqslant j_{1}<\cdots <j_{i}\leqslant n$
) and where the differential
 $d_{i}:K_{i}(\mathbf{x})\rightarrow K_{i-1}(\mathbf{x})$
carries the basis element
$d_{i}:K_{i}(\mathbf{x})\rightarrow K_{i-1}(\mathbf{x})$
carries the basis element
 $e_{j_{1}}\wedge \cdots \wedge e_{j_{i}}$
to
$e_{j_{1}}\wedge \cdots \wedge e_{j_{i}}$
to
 $$\begin{eqnarray}\mathop{\sum }_{s=1}^{i}(-1)^{s-1}x_{j_{s}}\,e_{j_{1}}\wedge \cdots \wedge \widehat{e_{j_{s}}}\wedge \cdots \wedge e_{j_{i}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{s=1}^{i}(-1)^{s-1}x_{j_{s}}\,e_{j_{1}}\wedge \cdots \wedge \widehat{e_{j_{s}}}\wedge \cdots \wedge e_{j_{i}},\end{eqnarray}$$
where the
![]() $\widehat{e_{j_{s}}}$
means that symbol is omitted. The homological Koszul complex
$\widehat{e_{j_{s}}}$
means that symbol is omitted. The homological Koszul complex
 $K_{\bullet }(M;\mathbf{x})$
of
$K_{\bullet }(M;\mathbf{x})$
of
![]() $M$
with respect to
$M$
with respect to
![]() $\mathbf{x}$
is the complex
$\mathbf{x}$
is the complex
 $K_{\bullet }(\mathbf{x})\otimes _{R}M$
, and the cohomological Koszul complex
$K_{\bullet }(\mathbf{x})\otimes _{R}M$
, and the cohomological Koszul complex
 $K^{\bullet }(M;\mathbf{x})$
of
$K^{\bullet }(M;\mathbf{x})$
of
![]() $M$
with respect to
$M$
with respect to
![]() $\mathbf{x}$
is the complex
$\mathbf{x}$
is the complex
 $\operatorname{Hom}_{R}(K_{\bullet }(\mathbf{x}),M)$
.
$\operatorname{Hom}_{R}(K_{\bullet }(\mathbf{x}),M)$
.
Proposition 5.5 [Reference WeibelWei94, Example 4.5.2].
Let
![]() $R$
be a commutative ring, let
$R$
be a commutative ring, let
 $\mathbf{x}=(x_{1},\ldots ,x_{n})$
be a sequence of elements of
$\mathbf{x}=(x_{1},\ldots ,x_{n})$
be a sequence of elements of
![]() $R$
, and let
$R$
, and let
![]() $M$
be an
$M$
be an
![]() $R$
-module. For all
$R$
-module. For all
![]() $i$
, we have
$i$
, we have
 $h_{i}(K_{\bullet }(M;\mathbf{x}))\simeq h^{n-i}(K^{\bullet }(M;\mathbf{x}))$
as
$h_{i}(K_{\bullet }(M;\mathbf{x}))\simeq h^{n-i}(K^{\bullet }(M;\mathbf{x}))$
as
![]() $R$
-modules.
$R$
-modules.
We can now prove Proposition 5.3.
Proof of Proposition 5.3.
We first compute the differentials in the complex
 $D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
. Let
$D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
. Let
![]() $i$
be given, and consider the differential
$i$
be given, and consider the differential
 $d^{i}:M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R}^{i+1}$
. An element of
$d^{i}:M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R}^{i+1}$
. An element of
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}$
is a sum of terms of the form
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}$
is a sum of terms of the form
 $m_{j_{1}\cdots j_{i}}\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}}$
where
$m_{j_{1}\cdots j_{i}}\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}}$
where
 $1\leqslant j_{1}<\cdots <j_{i}\leqslant n$
, and the formula for
$1\leqslant j_{1}<\cdots <j_{i}\leqslant n$
, and the formula for
![]() $d^{i}$
is
$d^{i}$
is
 $$\begin{eqnarray}d^{i}(m\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}})=\mathop{\sum }_{s=1}^{n}\unicode[STIX]{x2202}_{s}(m)\,dx_{s}\wedge dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}d^{i}(m\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}})=\mathop{\sum }_{s=1}^{n}\unicode[STIX]{x2202}_{s}(m)\,dx_{s}\wedge dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}}.\end{eqnarray}$$
Now consider the Matlis dual of this differential. Since the Matlis dual functor commutes with finite direct sums, we can identify
 $D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{i})$
with a direct sum of
$D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{i})$
with a direct sum of
![]() $\binom{n}{i}$
copies of
$\binom{n}{i}$
copies of
![]() $D(M)$
, again indexed by the
$D(M)$
, again indexed by the
 $dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}}$
. If
$dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i}}$
. If
 $\unicode[STIX]{x1D719}\in D(M)$
, we have the formula
$\unicode[STIX]{x1D719}\in D(M)$
, we have the formula
 $$\begin{eqnarray}(d^{i})^{\ast }(\unicode[STIX]{x1D719}\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i+1}})=\mathop{\sum }_{s=1}^{i+1}(-1)^{s-1}\unicode[STIX]{x2202}_{j_{s}}^{\ast }(\unicode[STIX]{x1D719})\,dx_{j_{1}}\wedge \cdots \wedge \widehat{dx_{j_{s}}}\wedge \cdots \wedge dx_{j_{i+1}}.\end{eqnarray}$$
$$\begin{eqnarray}(d^{i})^{\ast }(\unicode[STIX]{x1D719}\,dx_{j_{1}}\wedge \cdots \wedge dx_{j_{i+1}})=\mathop{\sum }_{s=1}^{i+1}(-1)^{s-1}\unicode[STIX]{x2202}_{j_{s}}^{\ast }(\unicode[STIX]{x1D719})\,dx_{j_{1}}\wedge \cdots \wedge \widehat{dx_{j_{s}}}\wedge \cdots \wedge dx_{j_{i+1}}.\end{eqnarray}$$
Consider the commutative subring
 $\unicode[STIX]{x1D6E5}=k[\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}]\subset {\mathcal{D}}$
. The
$\unicode[STIX]{x1D6E5}=k[\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}]\subset {\mathcal{D}}$
. The
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $D(M)$
is a fortiori a
$D(M)$
is a fortiori a
![]() $\unicode[STIX]{x1D6E5}$
-module, and the de Rham complex
$\unicode[STIX]{x1D6E5}$
-module, and the de Rham complex
 $D(M)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
is the cohomological Koszul complex
$D(M)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
is the cohomological Koszul complex
 $K^{\bullet }(D(M);\boldsymbol{\unicode[STIX]{x2202}})$
of the
$K^{\bullet }(D(M);\boldsymbol{\unicode[STIX]{x2202}})$
of the
![]() $\unicode[STIX]{x1D6E5}$
-module
$\unicode[STIX]{x1D6E5}$
-module
![]() $D(M)$
with respect to
$D(M)$
with respect to
 $\boldsymbol{\unicode[STIX]{x2202}}=(\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n})$
, where the
$\boldsymbol{\unicode[STIX]{x2202}}=(\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n})$
, where the
![]() $\unicode[STIX]{x2202}_{i}$
act on
$\unicode[STIX]{x2202}_{i}$
act on
![]() $D(M)$
via the maps
$D(M)$
via the maps
![]() $-\unicode[STIX]{x2202}_{i}^{\ast }$
(according to Definition 4.15). On the other hand, by the formula above, it is clear that
$-\unicode[STIX]{x2202}_{i}^{\ast }$
(according to Definition 4.15). On the other hand, by the formula above, it is clear that
 $D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
is the homological Koszul complex
$D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
is the homological Koszul complex
 $K_{\bullet }(D(M);\boldsymbol{\unicode[STIX]{x2202}})$
(up to a sign, which does not affect cohomology). We have
$K_{\bullet }(D(M);\boldsymbol{\unicode[STIX]{x2202}})$
(up to a sign, which does not affect cohomology). We have
 $$\begin{eqnarray}h^{i}(K^{\bullet }(D(M);\boldsymbol{\unicode[STIX]{x2202}}))\simeq h_{n-i}(K_{\bullet }(D(M);\boldsymbol{\unicode[STIX]{x2202}}))\end{eqnarray}$$
$$\begin{eqnarray}h^{i}(K^{\bullet }(D(M);\boldsymbol{\unicode[STIX]{x2202}}))\simeq h_{n-i}(K_{\bullet }(D(M);\boldsymbol{\unicode[STIX]{x2202}}))\end{eqnarray}$$
by Proposition 5.5; regarding the complex on the right as being cohomologically indexed (as we do when considering it as the Matlis dual of
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
), we see that the right-hand side is its
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
), we see that the right-hand side is its
![]() $i$
th cohomology object, completing the proof.◻
$i$
th cohomology object, completing the proof.◻
The remainder of this section is long and contains a great deal of preliminary material necessary for the proof of Proposition 5.2. Before giving this preliminary material, we first outline it for the reader’s benefit, then introduce some notation that we will use repeatedly.
-
– First, we prove some lemmas concerning direct and inverse systems of modules. The key definition here, Definition 5.10 (strong-sense stability), is a dual version of the Mittag-Leffler condition.
-
– We then introduce some definitions and results due to van den Essen, who in a series of papers studied the kernels and cokernels of differential operators. Not only his results, but also some of the ideas in his proofs, will be of necessary use to us. We discuss changes of variable and prove a technical lemma, Lemma 5.28, that relies on van den Essen’s work.
-
– We next describe how to ‘stratify’ the de Rham complex
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, writing it as a direct limit of ‘de Rham-like’ complexes whose objects are finitely generated
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, writing it as a direct limit of ‘de Rham-like’ complexes whose objects are finitely generated
 $R$
-modules. The crucial result concerning this direct system is Proposition 5.30, which asserts that the cohomology objects of these complexes satisfy strong-sense stability with finite-dimensional stable images. We also give a more general version of this result, Corollary 5.31, which will be of no use to us in this section but to which we will need to appeal in § 7.
$R$
-modules. The crucial result concerning this direct system is Proposition 5.30, which asserts that the cohomology objects of these complexes satisfy strong-sense stability with finite-dimensional stable images. We also give a more general version of this result, Corollary 5.31, which will be of no use to us in this section but to which we will need to appeal in § 7. -
– Finally, we give the proof of Proposition 5.2, using our work in § 3 on Matlis duality.
We need to work not only with the rings
![]() $R$
and
$R$
and
![]() ${\mathcal{D}}$
, but also with subrings defined using proper subsets of
${\mathcal{D}}$
, but also with subrings defined using proper subsets of
 $\{x_{1},\ldots ,x_{n}\}$
.
$\{x_{1},\ldots ,x_{n}\}$
.
Definition 5.6. Let
![]() $j\geqslant 0$
be given. We denote by
$j\geqslant 0$
be given. We denote by
![]() $R_{j}$
the subring
$R_{j}$
the subring
 $k[[x_{1},\ldots ,x_{j}]]\subset R$
, and by
$k[[x_{1},\ldots ,x_{j}]]\subset R$
, and by
![]() $R^{j}$
the subring
$R^{j}$
the subring
 $k[[x_{n-j+1},\ldots ,x_{n}]]\subset R$
. (Thus,
$k[[x_{n-j+1},\ldots ,x_{n}]]\subset R$
. (Thus,
 $R=R_{n}=R^{n}$
and
$R=R_{n}=R^{n}$
and
 $k=R_{0}=R^{0}$
.) We denote by
$k=R_{0}=R^{0}$
.) We denote by
 ${\mathcal{D}}_{j}={\mathcal{D}}(R_{j},k)$
and
${\mathcal{D}}_{j}={\mathcal{D}}(R_{j},k)$
and
 ${\mathcal{D}}^{j}={\mathcal{D}}(R^{j},k)$
the corresponding rings of differential operators, which are subrings of
${\mathcal{D}}^{j}={\mathcal{D}}(R^{j},k)$
the corresponding rings of differential operators, which are subrings of
![]() ${\mathcal{D}}$
.
${\mathcal{D}}$
.
This notation will be in force throughout the section, and will not be repeated in the statements of results.
Remark 5.7. If
![]() $M$
is any
$M$
is any
![]() ${\mathcal{D}}$
-module, it is also a module over
${\mathcal{D}}$
-module, it is also a module over
![]() ${\mathcal{D}}_{j}$
and
${\mathcal{D}}_{j}$
and
![]() ${\mathcal{D}}^{j}$
for all
${\mathcal{D}}^{j}$
for all
![]() $j$
, and we have short exact sequences relating its ‘partial’ and ‘full’ de Rham complexes analogous to the short exact sequence of Definition 2.21. These sequences take the form
$j$
, and we have short exact sequences relating its ‘partial’ and ‘full’ de Rham complexes analogous to the short exact sequence of Definition 2.21. These sequences take the form
 $$\begin{eqnarray}0\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }[-1]\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet }\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }[-1]\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet }\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }\rightarrow 0\end{eqnarray}$$
where the first map is given by
 $\wedge \,dx_{n-j}$
. The maps in the complex
$\wedge \,dx_{n-j}$
. The maps in the complex
 $M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }$
are
$M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }$
are
![]() ${\mathcal{D}}_{n-j}$
-linear, and hence its cohomology objects are
${\mathcal{D}}_{n-j}$
-linear, and hence its cohomology objects are
![]() ${\mathcal{D}}_{n-j}$
-modules; by the same argument as in Lemma 2.22, if we consider the associated long exact cohomology sequence, its connecting homomorphisms (up to a sign) are simply
${\mathcal{D}}_{n-j}$
-modules; by the same argument as in Lemma 2.22, if we consider the associated long exact cohomology sequence, its connecting homomorphisms (up to a sign) are simply
![]() $\unicode[STIX]{x2202}_{n-j}$
. Of course, there is also a version of this sequence involving de Rham complexes over
$\unicode[STIX]{x2202}_{n-j}$
. Of course, there is also a version of this sequence involving de Rham complexes over
![]() $R_{j}$
and
$R_{j}$
and
![]() $R_{j+1}$
instead of
$R_{j+1}$
instead of
![]() $R^{j}$
and
$R^{j}$
and
![]() $R^{j+1}$
.
$R^{j+1}$
.
In the proof of Proposition 5.2, we will consider various direct and inverse systems of complexes of
![]() $R$
-modules and
$R$
-modules and
![]() $k$
-spaces. (All our direct and inverse systems will be indexed by the natural numbers, but the following discussion applies to any filtered index set.) The interaction of cohomology with direct limits in these categories is not complicated: the direct limit is an exact functor [Reference WeibelWei94, Theorem 2.6.15], and so it commutes with cohomology. For inverse limits, more caution is required, as the inverse limit is, in general, only left exact. In order to ensure that cohomology commutes with inverse limits, we will need to verify the Mittag-Leffler condition for the inverse systems we consider (see Proposition 5.9 below).
$k$
-spaces. (All our direct and inverse systems will be indexed by the natural numbers, but the following discussion applies to any filtered index set.) The interaction of cohomology with direct limits in these categories is not complicated: the direct limit is an exact functor [Reference WeibelWei94, Theorem 2.6.15], and so it commutes with cohomology. For inverse limits, more caution is required, as the inverse limit is, in general, only left exact. In order to ensure that cohomology commutes with inverse limits, we will need to verify the Mittag-Leffler condition for the inverse systems we consider (see Proposition 5.9 below).
Definition 5.8 [Reference Grothendieck and DieudonnéGD61, 13.1.2].
Let
![]() $\{M_{i}\}$
be an inverse system (indexed by
$\{M_{i}\}$
be an inverse system (indexed by
![]() $\mathbb{N}$
) of modules over a commutative ring
$\mathbb{N}$
) of modules over a commutative ring
![]() $R$
, with inverse limit
$R$
, with inverse limit
 $M=\varprojlim \,M_{i}$
and transition maps
$M=\varprojlim \,M_{i}$
and transition maps
 $f_{ji}:M_{j}\rightarrow M_{i}$
for
$f_{ji}:M_{j}\rightarrow M_{i}$
for
![]() $i\leqslant j$
. We say that the system
$i\leqslant j$
. We say that the system
![]() $\{M_{i}\}$
satisfies the Mittag-Leffler condition if for all
$\{M_{i}\}$
satisfies the Mittag-Leffler condition if for all
![]() $l$
, the descending chain
$l$
, the descending chain
 $\{f_{l+s,l}(M_{l+s})\}_{s\geqslant 0}$
of submodules of
$\{f_{l+s,l}(M_{l+s})\}_{s\geqslant 0}$
of submodules of
![]() $M_{l}$
becomes stationary: there exists some
$M_{l}$
becomes stationary: there exists some
![]() $s$
such that for all
$s$
such that for all
![]() $t\geqslant s$
,
$t\geqslant s$
,
 $f_{l+s,l}(M_{l+s})=f_{l+t,l}(M_{l+t})$
.
$f_{l+s,l}(M_{l+s})=f_{l+t,l}(M_{l+t})$
.
The utility of the Mittag-Leffler condition for us is contained in the following proposition, which is an immediate consequence of [Reference Grothendieck and DieudonnéGD61, Proposition 13.2.3] (the result is stated in [Reference Grothendieck and DieudonnéGD61] only for complexes of Abelian groups, but the proof given there is valid more generally).
Proposition 5.9 [Reference Grothendieck and DieudonnéGD61, Proposition 13.2.3].
Let
![]() $\{M_{i}^{\bullet }\}$
be an inverse system (indexed by
$\{M_{i}^{\bullet }\}$
be an inverse system (indexed by
![]() $\mathbb{N}$
) of complexes of modules over a commutative ring
$\mathbb{N}$
) of complexes of modules over a commutative ring
![]() $R$
. For every
$R$
. For every
![]() $j$
, there is a canonical homomorphism
$j$
, there is a canonical homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D702}_{j}:h^{j}\Bigl(\underset{i}{\varprojlim }\,M_{i}^{\bullet }\Bigr)\rightarrow \underset{i}{\varprojlim }\,h^{j}(M_{i}^{\bullet })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{j}:h^{j}\Bigl(\underset{i}{\varprojlim }\,M_{i}^{\bullet }\Bigr)\rightarrow \underset{i}{\varprojlim }\,h^{j}(M_{i}^{\bullet })\end{eqnarray}$$
of
![]() $R$
-modules. Suppose that for every
$R$
-modules. Suppose that for every
![]() $j$
, the inverse systems
$j$
, the inverse systems
![]() $\{M_{i}^{j}\}_{i}$
and
$\{M_{i}^{j}\}_{i}$
and
 $\{h^{j}(M_{i}^{\bullet })\}_{i}$
of
$\{h^{j}(M_{i}^{\bullet })\}_{i}$
of
![]() $R$
-modules both satisfy the Mittag-Leffler condition. Then for every
$R$
-modules both satisfy the Mittag-Leffler condition. Then for every
![]() $j$
,
$j$
,
![]() $\unicode[STIX]{x1D702}_{j}$
is an isomorphism of
$\unicode[STIX]{x1D702}_{j}$
is an isomorphism of
![]() $R$
-modules.
$R$
-modules.
The following condition on direct systems can be thought of as a sort of dual to the Mittag-Leffler condition.
Definition 5.10. Let
![]() $\{M_{i}\}$
be a direct system (indexed by
$\{M_{i}\}$
be a direct system (indexed by
![]() $\mathbb{N}$
) of modules over a commutative ring
$\mathbb{N}$
) of modules over a commutative ring
![]() $R$
, with direct limit
$R$
, with direct limit
 $M=\varinjlim M_{i}$
,
$M=\varinjlim M_{i}$
,
![]() $R$
-linear transition maps
$R$
-linear transition maps
 $f_{ij}:M_{i}\rightarrow M_{j}$
for
$f_{ij}:M_{i}\rightarrow M_{j}$
for
![]() $i\leqslant j$
, and
$i\leqslant j$
, and
![]() $R$
-linear insertion maps
$R$
-linear insertion maps
 $f_{i}:M_{i}\rightarrow M$
. Fix
$f_{i}:M_{i}\rightarrow M$
. Fix
![]() $j$
and let
$j$
and let
 $N_{j}\subset M_{j}$
be an
$N_{j}\subset M_{j}$
be an
![]() $R$
-submodule. We say that the images of
$R$
-submodule. We say that the images of
![]() $N_{j}$
under the transition maps stabilize in the strong sense if there exists
$N_{j}$
under the transition maps stabilize in the strong sense if there exists
![]() $l$
such that
$l$
such that
 $f_{j+l}:M_{j+l}\rightarrow M$
induces an isomorphism
$f_{j+l}:M_{j+l}\rightarrow M$
induces an isomorphism
 $$\begin{eqnarray}f_{j,j+l}(N_{j})\xrightarrow[{}]{{\sim}}f_{j}(N_{j});\end{eqnarray}$$
$$\begin{eqnarray}f_{j,j+l}(N_{j})\xrightarrow[{}]{{\sim}}f_{j}(N_{j});\end{eqnarray}$$
equivalently,
 $f_{j,j+l}(N_{j})\cap \ker f_{j+l}=0$
. (If we say that the images of some object stabilize in the strong sense, it will be clear from context with respect to which transition maps and direct system we mean.)
$f_{j,j+l}(N_{j})\cap \ker f_{j+l}=0$
. (If we say that the images of some object stabilize in the strong sense, it will be clear from context with respect to which transition maps and direct system we mean.)
Note that since
 $\ker f_{j+l,j+l^{\prime }}\subset \ker f_{j+l}$
for any
$\ker f_{j+l,j+l^{\prime }}\subset \ker f_{j+l}$
for any
![]() $l^{\prime }\geqslant l$
, it follows at once from Definition 5.10 that there are also isomorphisms
$l^{\prime }\geqslant l$
, it follows at once from Definition 5.10 that there are also isomorphisms
 $f_{j,j+l}(N_{j})\xrightarrow[{}]{{\sim}}f_{j,j+l^{\prime }}(N_{j})$
induced by the transition maps.
$f_{j,j+l}(N_{j})\xrightarrow[{}]{{\sim}}f_{j,j+l^{\prime }}(N_{j})$
induced by the transition maps.
This condition is automatic if
![]() $R$
is Noetherian and
$R$
is Noetherian and
![]() $N_{j}$
is finitely generated.
$N_{j}$
is finitely generated.
Lemma 5.11. Let
![]() $R$
be a commutative Noetherian ring. If
$R$
be a commutative Noetherian ring. If
![]() $\{M_{i}\}$
is a direct system of
$\{M_{i}\}$
is a direct system of
![]() $R$
-modules as in Definition 5.10, and
$R$
-modules as in Definition 5.10, and
 $N_{j}\subset M_{j}$
is a finitely generated
$N_{j}\subset M_{j}$
is a finitely generated
![]() $R$
-submodule, then the images of
$R$
-submodule, then the images of
![]() $N_{j}$
stabilize in the strong sense.
$N_{j}$
stabilize in the strong sense.
Proof. Since
![]() $R$
is Noetherian,
$R$
is Noetherian,
 $\ker f_{j}\cap N_{j}$
is also a finitely generated
$\ker f_{j}\cap N_{j}$
is also a finitely generated
![]() $R$
-module. Fix
$R$
-module. Fix
![]() $R$
-generators
$R$
-generators
 $x_{1},\ldots ,x_{s}$
for
$x_{1},\ldots ,x_{s}$
for
 $\ker f_{j}\cap N_{j}$
. For all
$\ker f_{j}\cap N_{j}$
. For all
 $i\in \{1,\ldots ,s\}$
, we have
$i\in \{1,\ldots ,s\}$
, we have
 $f_{j}(x_{i})=0$
, and so there exists
$f_{j}(x_{i})=0$
, and so there exists
![]() $l_{i}\geqslant 0$
such that
$l_{i}\geqslant 0$
such that
 $f_{j,j+l_{i}}(x_{i})=0\in M_{j+l_{i}}$
. If we put
$f_{j,j+l_{i}}(x_{i})=0\in M_{j+l_{i}}$
. If we put
 $l=\max \{l_{i}\}$
, then
$l=\max \{l_{i}\}$
, then
![]() $f_{j,j+l}$
annihilates
$f_{j,j+l}$
annihilates
 $\ker f_{j}\cap N_{j}$
. We claim that
$\ker f_{j}\cap N_{j}$
. We claim that
 $$\begin{eqnarray}f_{j,j+l}(N_{j})\cap \ker f_{j+l}=0.\end{eqnarray}$$
$$\begin{eqnarray}f_{j,j+l}(N_{j})\cap \ker f_{j+l}=0.\end{eqnarray}$$
Suppose that
 $x\in M_{j+l}$
belongs to this intersection. Then we have
$x\in M_{j+l}$
belongs to this intersection. Then we have
 $f_{j+l}(x)=0$
and
$f_{j+l}(x)=0$
and
 $x=f_{j,j+l}(y)$
for some
$x=f_{j,j+l}(y)$
for some
![]() $y\in N_{j}$
. From
$y\in N_{j}$
. From
 $f_{j}(y)=f_{j+l}(f_{j,j+l}(y))=f_{j+l}(x)=0$
, we conclude
$f_{j}(y)=f_{j+l}(f_{j,j+l}(y))=f_{j+l}(x)=0$
, we conclude
 $y\in \ker f_{j}$
; but
$y\in \ker f_{j}$
; but
![]() $y\in N_{j}$
as well, and since
$y\in N_{j}$
as well, and since
![]() $f_{j,j+l}$
annihilates
$f_{j,j+l}$
annihilates
 $\ker f_{j}\cap N_{j}$
, it follows that
$\ker f_{j}\cap N_{j}$
, it follows that
 $x=f_{j,j+l}(y)=0$
, completing the proof.◻
$x=f_{j,j+l}(y)=0$
, completing the proof.◻
In the case of vector spaces over a field, the connection between the Mittag-Leffler condition and strong-sense stability can be made more precise. First, we need a basic lemma concerning the interaction of images and dual spaces. (Recall that
![]() $\vee$
denotes
$\vee$
denotes
![]() $k$
-linear dual.)
$k$
-linear dual.)
Lemma 5.12. Let
![]() $k$
be a field.
$k$
be a field.
-
(a) If
 $V$
and
$V$
and
 $W$
are vector spaces over
$W$
are vector spaces over
 $k$
, and
$k$
, and
 $f:V\rightarrow W$
is a
$f:V\rightarrow W$
is a
 $k$
-linear map, we can identify
$k$
-linear map, we can identify
 $(\operatorname{im}f)^{\vee }$
with a subspace of
$(\operatorname{im}f)^{\vee }$
with a subspace of
 $V^{\vee }$
in such a way that
$V^{\vee }$
in such a way that
 $(\operatorname{im}f)^{\vee }=\operatorname{im}(f^{\vee })$
.
$(\operatorname{im}f)^{\vee }=\operatorname{im}(f^{\vee })$
. -
(b) If
 $\{U_{i}\}_{i\in \mathbb{N}}$
is an inverse system of
$\{U_{i}\}_{i\in \mathbb{N}}$
is an inverse system of
 $k$
-spaces (with transition maps
$k$
-spaces (with transition maps
 $f_{ji}:U_{j}\rightarrow U_{i}$
for
$f_{ji}:U_{j}\rightarrow U_{i}$
for
 $i\leqslant j$
) which satisfies the Mittag-Leffler condition, then the inverse system
$i\leqslant j$
) which satisfies the Mittag-Leffler condition, then the inverse system
 $\{U_{i}^{\vee \vee }\}$
also satisfies the Mittag-Leffler condition.
$\{U_{i}^{\vee \vee }\}$
also satisfies the Mittag-Leffler condition.
Proof. Factor
![]() $f$
as
$f$
as
 $V{\twoheadrightarrow}\operatorname{im}f\subset W$
, and dualize this factorization to obtain
$V{\twoheadrightarrow}\operatorname{im}f\subset W$
, and dualize this factorization to obtain
 $W^{\vee }{\twoheadrightarrow}(\operatorname{im}f)^{\vee }{\hookrightarrow}V^{\vee }$
. The image of the last map is
$W^{\vee }{\twoheadrightarrow}(\operatorname{im}f)^{\vee }{\hookrightarrow}V^{\vee }$
. The image of the last map is
![]() $\operatorname{im}(f^{\vee })$
, and the injectivity allows us to identify this image with
$\operatorname{im}(f^{\vee })$
, and the injectivity allows us to identify this image with
![]() $(\operatorname{im}f)^{\vee }$
. This proves part (a).
$(\operatorname{im}f)^{\vee }$
. This proves part (a).
We now prove part (b). Fix
![]() $i$
. By the Mittag-Leffler condition, the descending chain
$i$
. By the Mittag-Leffler condition, the descending chain
 $\{f_{ji}(U_{j})\}_{j\geqslant i}$
of subspaces of
$\{f_{ji}(U_{j})\}_{j\geqslant i}$
of subspaces of
![]() $U_{i}$
stabilizes, say at
$U_{i}$
stabilizes, say at
![]() $j=l$
. Therefore
$j=l$
. Therefore
 $f_{li}(U_{l})=f_{si}(U_{s})$
for all
$f_{li}(U_{l})=f_{si}(U_{s})$
for all
![]() $s\geqslant l$
, and consequently
$s\geqslant l$
, and consequently
 $(f_{li}(U_{l}))^{\vee \vee }=(f_{si}(U_{s}))^{\vee \vee }$
as subspaces of
$(f_{li}(U_{l}))^{\vee \vee }=(f_{si}(U_{s}))^{\vee \vee }$
as subspaces of
![]() $U_{i}^{\vee \vee }$
for all
$U_{i}^{\vee \vee }$
for all
![]() $s\geqslant l$
. After applying part (a) twice, it follows that
$s\geqslant l$
. After applying part (a) twice, it follows that
 $f_{li}^{\vee \vee }(U_{l}^{\vee \vee })=f_{si}^{\vee \vee }(U_{s}^{\vee \vee })$
as subspaces of
$f_{li}^{\vee \vee }(U_{l}^{\vee \vee })=f_{si}^{\vee \vee }(U_{s}^{\vee \vee })$
as subspaces of
![]() $U_{i}^{\vee \vee }$
for all
$U_{i}^{\vee \vee }$
for all
![]() $s\geqslant l$
, that is, that the descending chain
$s\geqslant l$
, that is, that the descending chain
 $\{f_{ji}^{\vee \vee }(U_{j}^{\vee \vee })\}$
of subspaces of
$\{f_{ji}^{\vee \vee }(U_{j}^{\vee \vee })\}$
of subspaces of
![]() $U_{i}^{\vee \vee }$
stabilizes at
$U_{i}^{\vee \vee }$
stabilizes at
![]() $j=l$
. We conclude that
$j=l$
. We conclude that
![]() $\{U_{i}^{\vee \vee }\}$
also satisfies the Mittag-Leffler condition, completing the proof.◻
$\{U_{i}^{\vee \vee }\}$
also satisfies the Mittag-Leffler condition, completing the proof.◻
Lemma 5.13. Let
![]() $\{U_{i}\}$
be an inverse system (indexed by
$\{U_{i}\}$
be an inverse system (indexed by
![]() $\mathbb{N}$
) of vector spaces over a field
$\mathbb{N}$
) of vector spaces over a field
![]() $k$
, with transition maps
$k$
, with transition maps
![]() $f_{ji}$
. For all
$f_{ji}$
. For all
![]() $i$
, let
$i$
, let
 $V_{i}=U_{i}^{\vee }$
be the
$V_{i}=U_{i}^{\vee }$
be the
![]() $k$
-space dual of
$k$
-space dual of
![]() $U_{i}$
, and regard
$U_{i}$
, and regard
![]() $\{V_{i}\}$
as a direct system with transition maps
$\{V_{i}\}$
as a direct system with transition maps
 $\unicode[STIX]{x1D706}_{ij}=f_{ji}^{\vee }$
for
$\unicode[STIX]{x1D706}_{ij}=f_{ji}^{\vee }$
for
![]() $i\leqslant j$
. Suppose that for all
$i\leqslant j$
. Suppose that for all
![]() $l$
, the images of
$l$
, the images of
![]() $V_{l}$
under the transition maps
$V_{l}$
under the transition maps
![]() $\unicode[STIX]{x1D706}_{l,l+s}$
stabilize in the strong sense. Then
$\unicode[STIX]{x1D706}_{l,l+s}$
stabilize in the strong sense. Then
![]() $\{U_{i}\}$
satisfies the Mittag-Leffler condition.
$\{U_{i}\}$
satisfies the Mittag-Leffler condition.
Proof. We prove the contrapositive. Suppose that the system
![]() $\{U_{i}\}$
does not satisfy Mittag-Leffler. Then there is an
$\{U_{i}\}$
does not satisfy Mittag-Leffler. Then there is an
![]() $l$
such that for all
$l$
such that for all
![]() $s$
, there exists
$s$
, there exists
![]() $t\geqslant s$
such that
$t\geqslant s$
such that
 $f_{l+t,l}(U_{l+t})\subsetneq f_{l+s,l}(U_{l+s})$
. Since
$f_{l+t,l}(U_{l+t})\subsetneq f_{l+s,l}(U_{l+s})$
. Since
![]() $k$
-space dual is an exact functor, proper injections dualize to surjections with non-trivial kernels, so the surjection
$k$
-space dual is an exact functor, proper injections dualize to surjections with non-trivial kernels, so the surjection
 $(f_{l+s,l}(U_{l+s}))^{\vee }{\twoheadrightarrow}(f_{l+t,l}(U_{l+t}))^{\vee }$
is not an isomorphism. By Lemma 5.12(a), we can identify
$(f_{l+s,l}(U_{l+s}))^{\vee }{\twoheadrightarrow}(f_{l+t,l}(U_{l+t}))^{\vee }$
is not an isomorphism. By Lemma 5.12(a), we can identify
 $(f_{l+s,l}(U_{l+s}))^{\vee }$
with
$(f_{l+s,l}(U_{l+s}))^{\vee }$
with
 $\unicode[STIX]{x1D706}_{l,l+s}(V_{l})$
(respectively
$\unicode[STIX]{x1D706}_{l,l+s}(V_{l})$
(respectively
 $(f_{l+t,l}(U_{l+t}))^{\vee }$
with
$(f_{l+t,l}(U_{l+t}))^{\vee }$
with
 $\unicode[STIX]{x1D706}_{l,l+t}(V_{l})$
) as a subspace of
$\unicode[STIX]{x1D706}_{l,l+t}(V_{l})$
) as a subspace of
![]() $V_{l+s}$
(respectively
$V_{l+s}$
(respectively
![]() $V_{l+t}$
), and under these identifications, the surjection
$V_{l+t}$
), and under these identifications, the surjection
 $(f_{l+s,l}(U_{l+s}))^{\vee }{\twoheadrightarrow}(f_{l+t,l}(U_{l+t}))^{\vee }$
is nothing but
$(f_{l+s,l}(U_{l+s}))^{\vee }{\twoheadrightarrow}(f_{l+t,l}(U_{l+t}))^{\vee }$
is nothing but
![]() $\unicode[STIX]{x1D706}_{l+s,l+t}$
restricted to
$\unicode[STIX]{x1D706}_{l+s,l+t}$
restricted to
 $\unicode[STIX]{x1D706}_{l,l+s}(V_{l})$
. We conclude that the images of
$\unicode[STIX]{x1D706}_{l,l+s}(V_{l})$
. We conclude that the images of
![]() $V_{l}$
cannot stabilize in the strong sense.◻
$V_{l}$
cannot stabilize in the strong sense.◻
We will also need a technical lemma concerning double duals.
Lemma 5.14. Let
![]() $k$
be a field, and let
$k$
be a field, and let
 $\{U_{i}\}_{i\in \mathbb{N}}$
be an inverse system of
$\{U_{i}\}_{i\in \mathbb{N}}$
be an inverse system of
![]() $k$
-spaces, indexed by
$k$
-spaces, indexed by
![]() $\mathbb{N}$
, with transition maps
$\mathbb{N}$
, with transition maps
 $f_{ji}:U_{j}\rightarrow U_{i}$
for
$f_{ji}:U_{j}\rightarrow U_{i}$
for
![]() $i\leqslant j$
, and inverse limit
$i\leqslant j$
, and inverse limit
 $U=\varprojlim \,U_{i}$
. Suppose that the inverse system
$U=\varprojlim \,U_{i}$
. Suppose that the inverse system
![]() $\{U_{i}\}$
satisfies the Mittag-Leffler condition and that the inverse limit
$\{U_{i}\}$
satisfies the Mittag-Leffler condition and that the inverse limit
 $\varprojlim \,(U_{i}^{\vee \vee })$
is a finite-dimensional
$\varprojlim \,(U_{i}^{\vee \vee })$
is a finite-dimensional
![]() $k$
-space. Then
$k$
-space. Then
 $\varprojlim \,U_{i}\simeq \varprojlim \,(U_{i}^{\vee \vee })$
.
$\varprojlim \,U_{i}\simeq \varprojlim \,(U_{i}^{\vee \vee })$
.
Proof. The canonical map from a
![]() $k$
-space
$k$
-space
![]() $U_{i}$
to its double dual
$U_{i}$
to its double dual
![]() $U_{i}^{\vee \vee }$
is always injective, and the inverse limit is left exact [Reference Atiyah and MacdonaldAM69, Proposition 10.2], so there is a natural injection
$U_{i}^{\vee \vee }$
is always injective, and the inverse limit is left exact [Reference Atiyah and MacdonaldAM69, Proposition 10.2], so there is a natural injection
 $U=\varprojlim \,U_{i}{\hookrightarrow}\varprojlim \,U_{i}^{\vee \vee }$
. Therefore
$U=\varprojlim \,U_{i}{\hookrightarrow}\varprojlim \,U_{i}^{\vee \vee }$
. Therefore
![]() $U$
is also finite-dimensional. For all
$U$
is also finite-dimensional. For all
![]() $i$
, let
$i$
, let
 $U_{i}^{\prime }=\bigcap _{i\leqslant j}f_{ji}(U_{j})$
be the stable image of the transition maps inside
$U_{i}^{\prime }=\bigcap _{i\leqslant j}f_{ji}(U_{j})$
be the stable image of the transition maps inside
![]() $U_{i}$
(this descending chain stabilizes by the Mittag-Leffler hypothesis). Then [Reference HartshorneHar77, p. 191]
$U_{i}$
(this descending chain stabilizes by the Mittag-Leffler hypothesis). Then [Reference HartshorneHar77, p. 191]
![]() $\{U_{i}^{\prime }\}$
is also an inverse system, now with surjective transition maps, such that
$\{U_{i}^{\prime }\}$
is also an inverse system, now with surjective transition maps, such that
 $\varprojlim \,U_{i}^{\prime }=U$
and
$\varprojlim \,U_{i}^{\prime }=U$
and
![]() $U$
maps surjectively to all
$U$
maps surjectively to all
![]() $U_{i}^{\prime }$
. In particular, all
$U_{i}^{\prime }$
. In particular, all
![]() $U_{i}^{\prime }$
are finite-dimensional
$U_{i}^{\prime }$
are finite-dimensional
![]() $k$
-spaces and hence isomorphic to their double duals
$k$
-spaces and hence isomorphic to their double duals
![]() $(U_{i}^{\prime })^{\vee \vee }$
. By Lemma 5.12(b), the inverse system
$(U_{i}^{\prime })^{\vee \vee }$
. By Lemma 5.12(b), the inverse system
![]() $\{U_{i}^{\vee \vee }\}$
also satisfies the Mittag-Leffler condition, and moreover, we can identify the double dual of a stable image,
$\{U_{i}^{\vee \vee }\}$
also satisfies the Mittag-Leffler condition, and moreover, we can identify the double dual of a stable image,
![]() $(U_{i}^{\prime })^{\vee \vee }$
, with the stable image of the double dual,
$(U_{i}^{\prime })^{\vee \vee }$
, with the stable image of the double dual,
 $(U_{i}^{\vee \vee })^{\prime }\subset U_{i}^{\vee \vee }$
. Since for all
$(U_{i}^{\vee \vee })^{\prime }\subset U_{i}^{\vee \vee }$
. Since for all
![]() $i$
,
$i$
,
![]() $U_{i}^{\prime }$
is canonically isomorphic to its double dual, the corresponding inverse limits are also isomorphic. Thus we have isomorphisms
$U_{i}^{\prime }$
is canonically isomorphic to its double dual, the corresponding inverse limits are also isomorphic. Thus we have isomorphisms
 $$\begin{eqnarray}\varprojlim \,U_{i}\simeq \varprojlim \,U_{i}^{\prime }\simeq \varprojlim \,(U_{i}^{\prime })^{\vee \vee }\simeq \varprojlim \,(U_{i}^{\vee \vee })^{\prime }\simeq \varprojlim \,U_{i}^{\vee \vee },\end{eqnarray}$$
$$\begin{eqnarray}\varprojlim \,U_{i}\simeq \varprojlim \,U_{i}^{\prime }\simeq \varprojlim \,(U_{i}^{\prime })^{\vee \vee }\simeq \varprojlim \,(U_{i}^{\vee \vee })^{\prime }\simeq \varprojlim \,U_{i}^{\vee \vee },\end{eqnarray}$$
completing the proof. ◻
Remark 5.15. The Mittag-Leffler hypothesis in Lemma 5.14 is actually superfluous: Paul Garrett (private communication) has given a proof assuming only that
 $\varprojlim \,(U_{i}^{\vee \vee })$
is finite-dimensional. However, we will only need the statement in the Mittag-Leffler case, and the proof in general is more difficult.
$\varprojlim \,(U_{i}^{\vee \vee })$
is finite-dimensional. However, we will only need the statement in the Mittag-Leffler case, and the proof in general is more difficult.
In a series of papers [Reference van den EssenvdE79a, Reference van den EssenvdE79b, Reference van den EssenvdE82, Reference van den EssenvdE83, Reference van den EssenvdE85], van den Essen examined the effect of the operator
![]() $\unicode[STIX]{x2202}_{n}$
acting on a holonomic
$\unicode[STIX]{x2202}_{n}$
acting on a holonomic
![]() ${\mathcal{D}}$
-module, culminating in a proof of Theorem 2.2. (See also [Reference SwitalaSwi16] for an expository account of this proof.) Van den Essen’s first result was that the kernel of
${\mathcal{D}}$
-module, culminating in a proof of Theorem 2.2. (See also [Reference SwitalaSwi16] for an expository account of this proof.) Van den Essen’s first result was that the kernel of
![]() $\unicode[STIX]{x2202}_{n}$
behaves as well as we might hope.
$\unicode[STIX]{x2202}_{n}$
behaves as well as we might hope.
Theorem 5.16 [Reference van den EssenvdE79b, Theorem].
If
![]() $M$
is a holonomic
$M$
is a holonomic
![]() ${\mathcal{D}}$
-module and
${\mathcal{D}}$
-module and
![]() $M^{\ast }$
is the kernel of
$M^{\ast }$
is the kernel of
 $\unicode[STIX]{x2202}_{n}:M\rightarrow M$
, then
$\unicode[STIX]{x2202}_{n}:M\rightarrow M$
, then
![]() $M^{\ast }$
is a holonomic
$M^{\ast }$
is a holonomic
![]() ${\mathcal{D}}_{n-1}$
-module.
${\mathcal{D}}_{n-1}$
-module.
The key step in the proof of Theorem 5.16 is the following lemma, which we will use below in the proof of Lemma 5.28.
Lemma 5.17 [Reference van den EssenvdE79b, Corollary 2].
Let
![]() $M$
be a
$M$
be a
![]() ${\mathcal{D}}$
-module and let
${\mathcal{D}}$
-module and let
![]() $M^{\ast }$
be the kernel of
$M^{\ast }$
be the kernel of
 $\unicode[STIX]{x2202}_{n}:M\rightarrow M$
. If
$\unicode[STIX]{x2202}_{n}:M\rightarrow M$
. If
 $M=R\cdot M^{\ast }$
, then
$M=R\cdot M^{\ast }$
, then
 $M=M^{\ast }\oplus x_{n}M$
as
$M=M^{\ast }\oplus x_{n}M$
as
![]() ${\mathcal{D}}_{n-1}$
-modules.
${\mathcal{D}}_{n-1}$
-modules.
Without some conditions, there is no analogous result for cokernels; van den Essen gives a concrete example in [Reference van den EssenvdE82, Theorem] in which
![]() $M$
is a holonomic
$M$
is a holonomic
![]() ${\mathcal{D}}$
-module but
${\mathcal{D}}$
-module but
 $M/\unicode[STIX]{x2202}_{n}(M)$
is not holonomic.
$M/\unicode[STIX]{x2202}_{n}(M)$
is not holonomic.
Proposition 5.18 [Reference van den EssenvdE82, Proposition 1].
Let
![]() $M$
be a holonomic
$M$
be a holonomic
![]() ${\mathcal{D}}$
-module. There exists an element
${\mathcal{D}}$
-module. There exists an element
![]() $g\in R$
such that the localization
$g\in R$
such that the localization
![]() $M_{g}$
is a finitely generated
$M_{g}$
is a finitely generated
![]() $R_{g}$
-module.
$R_{g}$
-module.
Definition 5.19. Let
![]() $M$
be a
$M$
be a
![]() ${\mathcal{D}}$
-module, let
${\mathcal{D}}$
-module, let
![]() $m\in M$
, and let
$m\in M$
, and let
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{D}}$
be a derivation. We write
$\unicode[STIX]{x1D70F}\in {\mathcal{D}}$
be a derivation. We write
![]() $E_{\unicode[STIX]{x1D70F}}(m)$
for the
$E_{\unicode[STIX]{x1D70F}}(m)$
for the
![]() $R$
-submodule of
$R$
-submodule of
![]() $M$
generated by
$M$
generated by
 $\{\unicode[STIX]{x1D70F}^{i}(m)\}_{i\geqslant 0}$
.
$\{\unicode[STIX]{x1D70F}^{i}(m)\}_{i\geqslant 0}$
.
Lemma 5.20 [Reference van den EssenvdE79a, ch. II, Proposition 1.16].
Let
![]() $M$
be a
$M$
be a
![]() ${\mathcal{D}}$
-module. Suppose that there exists
${\mathcal{D}}$
-module. Suppose that there exists
![]() $g\in R$
which is
$g\in R$
which is
![]() $x_{n}$
-regular (that is, such that
$x_{n}$
-regular (that is, such that
 $g(0,0,\ldots ,0,x_{n})\neq 0$
) and such that
$g(0,0,\ldots ,0,x_{n})\neq 0$
) and such that
![]() $M_{g}$
is a finitely generated
$M_{g}$
is a finitely generated
![]() $R_{g}$
-module. Then for all
$R_{g}$
-module. Then for all
![]() $m\in M$
, there exists an
$m\in M$
, there exists an
![]() $x_{n}$
-regular
$x_{n}$
-regular
![]() $f\in R$
such that the
$f\in R$
such that the
![]() $R$
-submodule
$R$
-submodule
 $E_{f\unicode[STIX]{x2202}_{n}}(m)$
of
$E_{f\unicode[STIX]{x2202}_{n}}(m)$
of
![]() $M$
is finitely generated.
$M$
is finitely generated.
The source [Reference van den EssenvdE79a] remains unpublished; see also [Reference SwitalaSwi16, Lemma 4.2] for a proof of Lemma 5.20. The conclusion of this lemma leads us to make the following definition.
Definition 5.21. If
![]() $M$
is a
$M$
is a
![]() ${\mathcal{D}}$
-module, an element
${\mathcal{D}}$
-module, an element
![]() $m\in M$
is
$m\in M$
is
![]() $x_{n}$
-regular if there exists an
$x_{n}$
-regular if there exists an
![]() $x_{n}$
-regular element
$x_{n}$
-regular element
![]() $f\in R$
such that
$f\in R$
such that
 $E_{f\unicode[STIX]{x2202}_{n}}(m)$
is a finitely generated
$E_{f\unicode[STIX]{x2202}_{n}}(m)$
is a finitely generated
![]() $R$
-module. A holonomic
$R$
-module. A holonomic
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
is
$M$
is
![]() $x_{n}$
-regular if there exists an
$x_{n}$
-regular if there exists an
![]() $x_{n}$
-regular
$x_{n}$
-regular
![]() $m\in M$
such that
$m\in M$
such that
 $M={\mathcal{D}}\cdot m$
.
$M={\mathcal{D}}\cdot m$
.
From the following proposition, it follows immediately that if a holonomic
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
is
$M$
is
![]() $x_{n}$
-regular, then every
$x_{n}$
-regular, then every
![]() $m\in M$
such that
$m\in M$
such that
 $M={\mathcal{D}}\cdot m$
is
$M={\mathcal{D}}\cdot m$
is
![]() $x_{n}$
-regular.
$x_{n}$
-regular.
Proposition 5.22 [Reference van den EssenvdE79a, Proposition II.1.3(2)].
Let
![]() $M$
be a
$M$
be a
![]() ${\mathcal{D}}$
-module, let
${\mathcal{D}}$
-module, let
![]() $m\in M$
, and let
$m\in M$
, and let
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{D}}$
be a derivation. If the
$\unicode[STIX]{x1D70F}\in {\mathcal{D}}$
be a derivation. If the
![]() $R$
-module
$R$
-module
![]() $E_{\unicode[STIX]{x1D70F}}(m)$
is finitely generated, so is the
$E_{\unicode[STIX]{x1D70F}}(m)$
is finitely generated, so is the
![]() $R$
-module
$R$
-module
 $E_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}(m))$
for any
$E_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}(m))$
for any
![]() $\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
.
$\unicode[STIX]{x1D6FF}\in {\mathcal{D}}$
.
Since [Reference van den EssenvdE79a] remains unpublished, we reproduce for the reader the proof of Proposition 5.22 given in [Reference van den EssenvdE79a].
Proof. Since
![]() ${\mathcal{D}}$
is generated over
${\mathcal{D}}$
is generated over
![]() $R$
by finite products of the derivations
$R$
by finite products of the derivations
![]() $\unicode[STIX]{x2202}_{i}$
, it clearly suffices to check that if
$\unicode[STIX]{x2202}_{i}$
, it clearly suffices to check that if
![]() $E_{\unicode[STIX]{x1D70F}}(m)$
is finitely generated, so is
$E_{\unicode[STIX]{x1D70F}}(m)$
is finitely generated, so is
 $E_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x2202}_{i}(m))$
for all
$E_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x2202}_{i}(m))$
for all
![]() $i$
. Fix such an
$i$
. Fix such an
![]() $i$
. The hypothesis that
$i$
. The hypothesis that
![]() $E_{\unicode[STIX]{x1D70F}}(m)$
is finitely generated implies that there exists
$E_{\unicode[STIX]{x1D70F}}(m)$
is finitely generated implies that there exists
![]() $p$
such that
$p$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p}(m)\in R\cdot m+R\cdot \unicode[STIX]{x1D70F}(m)+\cdots +R\cdot \unicode[STIX]{x1D70F}^{p-1}(m).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p}(m)\in R\cdot m+R\cdot \unicode[STIX]{x1D70F}(m)+\cdots +R\cdot \unicode[STIX]{x1D70F}^{p-1}(m).\end{eqnarray}$$
For every
![]() $j$
, the commutator
$j$
, the commutator
 $[\unicode[STIX]{x1D70F},\unicode[STIX]{x2202}_{j}]=\unicode[STIX]{x1D70F}\unicode[STIX]{x2202}_{j}-\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D70F}\in {\mathcal{D}}$
is again a derivation, hence is an
$[\unicode[STIX]{x1D70F},\unicode[STIX]{x2202}_{j}]=\unicode[STIX]{x1D70F}\unicode[STIX]{x2202}_{j}-\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D70F}\in {\mathcal{D}}$
is again a derivation, hence is an
![]() $R$
-linear combination of
$R$
-linear combination of
 $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
. That is, we have
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
. That is, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}\unicode[STIX]{x2202}_{j}-\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D70F}\in R\cdot \unicode[STIX]{x2202}_{1}+\cdots +R\cdot \unicode[STIX]{x2202}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}\unicode[STIX]{x2202}_{j}-\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D70F}\in R\cdot \unicode[STIX]{x2202}_{1}+\cdots +R\cdot \unicode[STIX]{x2202}_{n}.\end{eqnarray}$$
An induction argument using the two displayed statements shows that for every
![]() $l$
, we have
$l$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{l}(\unicode[STIX]{x2202}_{i}(m))\in \mathop{\sum }_{0\leqslant q\leqslant p-1,1\leqslant j\leqslant n}R\cdot \unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D70F}^{q}(m)).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{l}(\unicode[STIX]{x2202}_{i}(m))\in \mathop{\sum }_{0\leqslant q\leqslant p-1,1\leqslant j\leqslant n}R\cdot \unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D70F}^{q}(m)).\end{eqnarray}$$
(We induce on
![]() $l$
: the second displayed statement is used to move iterates of
$l$
: the second displayed statement is used to move iterates of
![]() $\unicode[STIX]{x1D70F}$
to the right past partial derivatives, and the first displayed statement is used to limit the number of distinct powers of
$\unicode[STIX]{x1D70F}$
to the right past partial derivatives, and the first displayed statement is used to limit the number of distinct powers of
![]() $\unicode[STIX]{x1D70F}$
that appear.) It follows that
$\unicode[STIX]{x1D70F}$
that appear.) It follows that
 $E_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x2202}_{i}(m))$
is contained in the
$E_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x2202}_{i}(m))$
is contained in the
![]() $R$
-submodule of
$R$
-submodule of
![]() $M$
generated by the finite set
$M$
generated by the finite set
 $\{\unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D70F}^{q}(m))\}_{0\leqslant q\leqslant p-1,1\leqslant j\leqslant n}$
, completing the proof.◻
$\{\unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D70F}^{q}(m))\}_{0\leqslant q\leqslant p-1,1\leqslant j\leqslant n}$
, completing the proof.◻
More generally, a
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
is said to be
$M$
is said to be
![]() $x_{n}$
-regular if every
$x_{n}$
-regular if every
![]() $m\in M$
is
$m\in M$
is
![]() $x_{n}$
-regular.
$x_{n}$
-regular.
Lemma 5.23 [Reference van den EssenvdE85, Corollary 1.8].
Let
![]() $M$
be a holonomic
$M$
be a holonomic
![]() ${\mathcal{D}}$
-module. There exists a change of variables (that is, a replacement of
${\mathcal{D}}$
-module. There exists a change of variables (that is, a replacement of
 $x_{1},\ldots ,x_{n}$
with another regular system of parameters for
$x_{1},\ldots ,x_{n}$
with another regular system of parameters for
![]() $R$
) after which
$R$
) after which
![]() $M$
is
$M$
is
![]() $x_{n}$
-regular.
$x_{n}$
-regular.
Proof. We claim that, in fact, there is such a change of variables which is linear in the
![]() $x_{i}$
. By Proposition 5.18, there exists
$x_{i}$
. By Proposition 5.18, there exists
![]() $g\in R$
such that
$g\in R$
such that
![]() $M_{g}$
is finitely generated over
$M_{g}$
is finitely generated over
![]() $R_{g}$
. By Lemma 5.20, if
$R_{g}$
. By Lemma 5.20, if
![]() $g$
is
$g$
is
![]() $x_{n}$
-regular, then
$x_{n}$
-regular, then
![]() $M$
is
$M$
is
![]() $x_{n}$
-regular. Since
$x_{n}$
-regular. Since
![]() $k$
is of characteristic zero and hence infinite, there is a linear change of variables after which
$k$
is of characteristic zero and hence infinite, there is a linear change of variables after which
![]() $g$
is
$g$
is
![]() $x_{n}$
-regular, completing the proof.◻
$x_{n}$
-regular, completing the proof.◻
By Proposition 2.5, the de Rham cohomology
 $H_{\text{dR}}^{\ast }(M)$
is independent of this coordinate change. Our next observation is that the
$H_{\text{dR}}^{\ast }(M)$
is independent of this coordinate change. Our next observation is that the
![]() $x_{n}$
-regularity condition is precisely what is required for the holonomy of the cokernel of
$x_{n}$
-regularity condition is precisely what is required for the holonomy of the cokernel of
![]() $\unicode[STIX]{x2202}_{n}$
.
$\unicode[STIX]{x2202}_{n}$
.
Theorem 5.24 [Reference van den EssenvdE83, Theorem].
If
![]() $M$
is a holonomic
$M$
is a holonomic
![]() ${\mathcal{D}}$
-module that is
${\mathcal{D}}$
-module that is
![]() $x_{n}$
-regular, then
$x_{n}$
-regular, then
 $\overline{M}=M/\unicode[STIX]{x2202}_{n}(M)$
is a holonomic
$\overline{M}=M/\unicode[STIX]{x2202}_{n}(M)$
is a holonomic
![]() ${\mathcal{D}}_{n-1}$
-module.
${\mathcal{D}}_{n-1}$
-module.
The key step in the proof of Theorem 5.24 is the following lemma, which we will also use below in the proof of Lemma 5.28.
Lemma 5.25 [Reference van den EssenvdE83, Corollary 2].
Let
![]() $M$
be a
$M$
be a
![]() ${\mathcal{D}}$
-module. Suppose that
${\mathcal{D}}$
-module. Suppose that
![]() $m\in M$
is
$m\in M$
is
![]() $x_{n}$
-regular. Then there exists a finitely generated
$x_{n}$
-regular. Then there exists a finitely generated
![]() $R_{n-1}$
-submodule
$R_{n-1}$
-submodule
![]() $L$
of
$L$
of
![]() $R\cdot m$
and a natural number
$R\cdot m$
and a natural number
![]() $p$
such that
$p$
such that
 $R\cdot m\subset L+\sum _{i=1}^{p}\unicode[STIX]{x2202}_{n}^{i}(R\cdot m)\subset L+\unicode[STIX]{x2202}_{n}(\sum _{i=0}^{p-1}R\cdot \unicode[STIX]{x2202}_{n}^{i}(m))$
.
$R\cdot m\subset L+\sum _{i=1}^{p}\unicode[STIX]{x2202}_{n}^{i}(R\cdot m)\subset L+\unicode[STIX]{x2202}_{n}(\sum _{i=0}^{p-1}R\cdot \unicode[STIX]{x2202}_{n}^{i}(m))$
.
Proof. The first containment is [Reference van den EssenvdE83, Corollary 2], and the second follows from the fact (easy to check using the Leibniz rule) that for all
![]() $i\geqslant 0$
we have
$i\geqslant 0$
we have
 $\unicode[STIX]{x2202}_{n}^{i}(R\cdot m)\subset \sum _{j=0}^{i}R\cdot \unicode[STIX]{x2202}_{n}^{j}(m)$
.◻
$\unicode[STIX]{x2202}_{n}^{i}(R\cdot m)\subset \sum _{j=0}^{i}R\cdot \unicode[STIX]{x2202}_{n}^{j}(m)$
.◻
Our next two preliminary results (5.26) and (5.28) deal with the kernels and cokernels of the operators
![]() $\unicode[STIX]{x2202}_{i}$
. We are going to study the de Rham complex of a
$\unicode[STIX]{x2202}_{i}$
. We are going to study the de Rham complex of a
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
by isolating one
$M$
by isolating one
![]() $\unicode[STIX]{x2202}_{i}$
at a time, and these results guarantee that this process is well behaved.
$\unicode[STIX]{x2202}_{i}$
at a time, and these results guarantee that this process is well behaved.
Proposition 5.26. Let
![]() $M$
be a holonomic
$M$
be a holonomic
![]() ${\mathcal{D}}$
-module. There exists a change of variables (which, by Proposition 2.5, does not alter the de Rham cohomology of
${\mathcal{D}}$
-module. There exists a change of variables (which, by Proposition 2.5, does not alter the de Rham cohomology of
![]() $M$
) after which, for all
$M$
) after which, for all
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is a holonomic
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is a holonomic
![]() ${\mathcal{D}}_{n-j}$
-module which is
${\mathcal{D}}_{n-j}$
-module which is
![]() $x_{n-j}$
-regular.
$x_{n-j}$
-regular.
Proof. Let
![]() $j$
be given, and consider the short exact sequence
$j$
be given, and consider the short exact sequence
 $$\begin{eqnarray}0\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }[-1]\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet }\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }[-1]\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet }\rightarrow M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }\rightarrow 0\end{eqnarray}$$
of Remark 5.7. The corresponding long exact sequence in cohomology takes the form
 $$\begin{eqnarray}\displaystyle \cdots \rightarrow h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet }) & \rightarrow & \displaystyle h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}}h^{i+1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }[-1])(=h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }))\nonumber\\ \displaystyle & \rightarrow & \displaystyle h^{i+1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })\rightarrow h^{i+1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}}\cdots \,,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \cdots \rightarrow h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet }) & \rightarrow & \displaystyle h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}}h^{i+1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }[-1])(=h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }))\nonumber\\ \displaystyle & \rightarrow & \displaystyle h^{i+1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })\rightarrow h^{i+1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}}\cdots \,,\nonumber\end{eqnarray}$$
where the connecting homomorphisms
![]() $\unicode[STIX]{x2202}$
are given, up to a sign, by
$\unicode[STIX]{x2202}$
are given, up to a sign, by
![]() $\unicode[STIX]{x2202}_{n-j}$
. From this long sequence, we obtain short exact sequences
$\unicode[STIX]{x2202}_{n-j}$
. From this long sequence, we obtain short exact sequences
 $$\begin{eqnarray}0\rightarrow C_{n-j}^{i-1}\rightarrow h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })\rightarrow K_{n-j}^{i}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow C_{n-j}^{i-1}\rightarrow h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })\rightarrow K_{n-j}^{i}\rightarrow 0\end{eqnarray}$$
of
![]() ${\mathcal{D}}_{n-j-1}$
-modules, where
${\mathcal{D}}_{n-j-1}$
-modules, where
![]() $C_{n-j}^{i-1}$
is the cokernel of
$C_{n-j}^{i-1}$
is the cokernel of
![]() $\unicode[STIX]{x2202}_{n-j}$
acting on
$\unicode[STIX]{x2202}_{n-j}$
acting on
 $h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
and
$h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
and
![]() $K_{n-j}^{i}$
is the kernel of
$K_{n-j}^{i}$
is the kernel of
![]() $\unicode[STIX]{x2202}_{n-j}$
acting on
$\unicode[STIX]{x2202}_{n-j}$
acting on
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
. If the
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
. If the
![]() ${\mathcal{D}}_{n-j}$
-module
${\mathcal{D}}_{n-j}$
-module
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is holonomic, then the
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is holonomic, then the
![]() ${\mathcal{D}}_{n-j-1}$
-module
${\mathcal{D}}_{n-j-1}$
-module
![]() $K_{n-j}^{i}$
is holonomic by Theorem 5.16. If, moreover, the
$K_{n-j}^{i}$
is holonomic by Theorem 5.16. If, moreover, the
![]() ${\mathcal{D}}_{n-j}$
-module
${\mathcal{D}}_{n-j}$
-module
 $h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is holonomic and
$h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is holonomic and
![]() $x_{n-j}$
-regular, then the
$x_{n-j}$
-regular, then the
![]() ${\mathcal{D}}_{n-j-1}$
-module
${\mathcal{D}}_{n-j-1}$
-module
![]() $C_{n-j}^{i-1}$
is holonomic by Theorem 5.24, from which it follows from the short exact sequence displayed above that the
$C_{n-j}^{i-1}$
is holonomic by Theorem 5.24, from which it follows from the short exact sequence displayed above that the
![]() ${\mathcal{D}}_{n-j-1}$
-module
${\mathcal{D}}_{n-j-1}$
-module
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })$
is holonomic as well. Therefore, if
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })$
is holonomic as well. Therefore, if
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is holonomic and
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is holonomic and
![]() $x_{n-j}$
-regular for all
$x_{n-j}$
-regular for all
![]() $i$
, then
$i$
, then
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })$
is holonomic for all
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })$
is holonomic for all
![]() $i$
. This fact will enable us to prove the proposition by induction on
$i$
. This fact will enable us to prove the proposition by induction on
![]() $j$
.
$j$
.
By hypothesis,
 $M=h^{0}(M\otimes \unicode[STIX]{x1D6FA}_{R^{0}}^{\bullet })$
is a holonomic
$M=h^{0}(M\otimes \unicode[STIX]{x1D6FA}_{R^{0}}^{\bullet })$
is a holonomic
![]() ${\mathcal{D}}$
-module, and by Lemma 5.23, there exists a change of variables after which
${\mathcal{D}}$
-module, and by Lemma 5.23, there exists a change of variables after which
![]() $M$
is
$M$
is
![]() $x_{n}$
-regular. It follows from the previous paragraph that
$x_{n}$
-regular. It follows from the previous paragraph that
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{1}}^{\bullet })$
is a holonomic
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{1}}^{\bullet })$
is a holonomic
![]() ${\mathcal{D}}_{n-1}$
-module for
${\mathcal{D}}_{n-1}$
-module for
![]() $i=0,1$
. Now let
$i=0,1$
. Now let
 $j\in \{0,\ldots ,n-1\}$
be given, and assume that we have found a change of variables after which
$j\in \{0,\ldots ,n-1\}$
be given, and assume that we have found a change of variables after which
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet })$
is a holonomic and
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet })$
is a holonomic and
![]() $x_{n-l}$
-regular
$x_{n-l}$
-regular
![]() ${\mathcal{D}}_{n-l}$
-module for all
${\mathcal{D}}_{n-l}$
-module for all
![]() $i$
and all
$i$
and all
![]() $l\leqslant j$
(consequently,
$l\leqslant j$
(consequently,
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })$
is a holonomic
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })$
is a holonomic
![]() ${\mathcal{D}}_{n-j-1}$
-module for all
${\mathcal{D}}_{n-j-1}$
-module for all
![]() $i$
). For every
$i$
). For every
![]() $i$
, there exists (by Proposition 5.18) an element
$i$
, there exists (by Proposition 5.18) an element
![]() $g_{i}$
of
$g_{i}$
of
![]() $R_{n-j-1}$
such that the localization
$R_{n-j-1}$
such that the localization
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })[(g_{i})^{-1}]$
is a finitely generated
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })[(g_{i})^{-1}]$
is a finitely generated
 $R_{n-j-1}[(g_{i})^{-1}]$
-module. Since there are only finitely many
$R_{n-j-1}[(g_{i})^{-1}]$
-module. Since there are only finitely many
![]() $g_{i}$
, and the field
$g_{i}$
, and the field
![]() $k$
is infinite, there is a single change of variables after which every
$k$
is infinite, there is a single change of variables after which every
![]() $g_{i}$
is
$g_{i}$
is
![]() $x_{n-j-1}$
-regular. Moreover, since
$x_{n-j-1}$
-regular. Moreover, since
![]() $g_{i}$
only involves the variables
$g_{i}$
only involves the variables
 $x_{1},\ldots ,x_{n-j-1}$
, this change of variables leaves
$x_{1},\ldots ,x_{n-j-1}$
, this change of variables leaves
 $x_{n-j},\ldots ,x_{n}$
fixed.
$x_{n-j},\ldots ,x_{n}$
fixed.
The complexes
 $M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet }$
for
$M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet }$
for
![]() $l\leqslant j$
are defined using only derivations from the set
$l\leqslant j$
are defined using only derivations from the set
 $\{\unicode[STIX]{x2202}_{n-j},\ldots ,\unicode[STIX]{x2202}_{n}\}$
, and these derivations are unaffected by the change of variables; hence the isomorphism classes of the cohomology objects
$\{\unicode[STIX]{x2202}_{n-j},\ldots ,\unicode[STIX]{x2202}_{n}\}$
, and these derivations are unaffected by the change of variables; hence the isomorphism classes of the cohomology objects
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet })$
do not change. Furthermore, for every such
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet })$
do not change. Furthermore, for every such
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet })$
, there exists an
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet })$
, there exists an
![]() $x_{n-l}$
-regular element
$x_{n-l}$
-regular element
![]() $g$
of
$g$
of
![]() $R_{n-l}$
such that
$R_{n-l}$
such that
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet })[g^{-1}]$
is a finitely generated
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{l}}^{\bullet })[g^{-1}]$
is a finitely generated
 $R_{n-l}[g^{-1}]$
-module. After the given change of variables, this localization is still finitely generated, and
$R_{n-l}[g^{-1}]$
-module. After the given change of variables, this localization is still finitely generated, and
![]() $g$
is still
$g$
is still
![]() $x_{n-l}$
-regular: by the Weierstrass preparation theorem [Reference LangLan02, Theorem IV.9.2], the
$x_{n-l}$
-regular: by the Weierstrass preparation theorem [Reference LangLan02, Theorem IV.9.2], the
![]() $x_{n-l}$
-regularity of
$x_{n-l}$
-regularity of
![]() $g$
is equivalent to the existence of an expression of
$g$
is equivalent to the existence of an expression of
![]() $g$
as a monic polynomial in
$g$
as a monic polynomial in
![]() $x_{n-l}$
with coefficients in
$x_{n-l}$
with coefficients in
![]() $R_{n-l-1}$
, and after a change of variables that fixes
$R_{n-l-1}$
, and after a change of variables that fixes
 $x_{n-j},\ldots ,x_{n}$
and in which the new
$x_{n-j},\ldots ,x_{n}$
and in which the new
 $x_{1},\ldots ,x_{n-j-1}$
are linear combinations of the old
$x_{1},\ldots ,x_{n-j-1}$
are linear combinations of the old
 $x_{1},\ldots ,x_{n-j-1}$
only, such a polynomial is still monic in
$x_{1},\ldots ,x_{n-j-1}$
only, such a polynomial is still monic in
![]() $x_{n-l}$
. We conclude that the chosen change of variables does not invalidate the inductive hypothesis. After this change of variables,
$x_{n-l}$
. We conclude that the chosen change of variables does not invalidate the inductive hypothesis. After this change of variables,
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })$
is
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+1}}^{\bullet })$
is
![]() $x_{n-j-1}$
-regular for all
$x_{n-j-1}$
-regular for all
![]() $i$
by Lemma 5.20, and therefore
$i$
by Lemma 5.20, and therefore
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+2}}^{\bullet })$
is a holonomic
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j+2}}^{\bullet })$
is a holonomic
![]() ${\mathcal{D}}_{n-j-2}$
-module for all
${\mathcal{D}}_{n-j-2}$
-module for all
![]() $i$
. This induction completes the proof: beginning with
$i$
. This induction completes the proof: beginning with
![]() $M$
and repeating the inductive step
$M$
and repeating the inductive step
![]() $n$
times, we end up with a single change of variables after which, for all
$n$
times, we end up with a single change of variables after which, for all
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is a holonomic
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is a holonomic
![]() ${\mathcal{D}}_{n-j}$
-module which is
${\mathcal{D}}_{n-j}$
-module which is
![]() $x_{n-j}$
-regular.◻
$x_{n-j}$
-regular.◻
Our next technical lemma makes crucial use of van den Essen’s results. The situation we examine is that of a
![]() ${\mathcal{D}}$
-module expressible as a direct limit of
${\mathcal{D}}$
-module expressible as a direct limit of
![]() $R$
-modules, and a family of
$R$
-modules, and a family of
![]() $R_{n-1}$
-linear maps between these modules whose direct limit is the
$R_{n-1}$
-linear maps between these modules whose direct limit is the
![]() $R_{n-1}$
-linear map
$R_{n-1}$
-linear map
![]() $\unicode[STIX]{x2202}_{n}$
. We now describe the situation more precisely. Let
$\unicode[STIX]{x2202}_{n}$
. We now describe the situation more precisely. Let
![]() $M$
be a
$M$
be a
![]() ${\mathcal{D}}$
-module, and suppose that
${\mathcal{D}}$
-module, and suppose that
 $M=\varinjlim M_{i}$
as
$M=\varinjlim M_{i}$
as
![]() $R$
-modules, where
$R$
-modules, where
![]() $\{M_{i}\}$
is a direct system (indexed by
$\{M_{i}\}$
is a direct system (indexed by
![]() $\mathbb{N}$
) of
$\mathbb{N}$
) of
![]() $R$
-submodules of
$R$
-submodules of
![]() $M$
. Let
$M$
. Let
 $f_{ij}:M_{i}\rightarrow M_{j}$
(respectively
$f_{ij}:M_{i}\rightarrow M_{j}$
(respectively
 $f_{i}:M_{i}\rightarrow M$
) be the transition (respectively insertion) maps for this direct system. Suppose furthermore that there exist
$f_{i}:M_{i}\rightarrow M$
) be the transition (respectively insertion) maps for this direct system. Suppose furthermore that there exist
![]() $R_{n-1}$
-linear maps
$R_{n-1}$
-linear maps
 $\unicode[STIX]{x1D6FF}_{i}:M_{i}\rightarrow M_{i+1}$
for all
$\unicode[STIX]{x1D6FF}_{i}:M_{i}\rightarrow M_{i+1}$
for all
![]() $i$
, compatible with the transition maps, such that
$i$
, compatible with the transition maps, such that
 $\varinjlim \unicode[STIX]{x1D6FF}_{i}=\unicode[STIX]{x2202}_{n}$
. (We will write
$\varinjlim \unicode[STIX]{x1D6FF}_{i}=\unicode[STIX]{x2202}_{n}$
. (We will write
![]() $\unicode[STIX]{x2202}$
for
$\unicode[STIX]{x2202}$
for
![]() $\unicode[STIX]{x2202}_{n}$
.) Given an element
$\unicode[STIX]{x2202}_{n}$
.) Given an element
![]() $m\in M$
, there exists some
$m\in M$
, there exists some
![]() $j$
and
$j$
and
 $m_{j}\in M_{j}$
such that
$m_{j}\in M_{j}$
such that
 $m=f_{j}(m_{j})$
, and we have
$m=f_{j}(m_{j})$
, and we have
 $\unicode[STIX]{x2202}(m)=f_{j+1}(\unicode[STIX]{x1D6FF}_{j}(m_{j}))$
, independently of the choice of
$\unicode[STIX]{x2202}(m)=f_{j+1}(\unicode[STIX]{x1D6FF}_{j}(m_{j}))$
, independently of the choice of
![]() $j$
and
$j$
and
![]() $m_{j}$
.
$m_{j}$
.
Example 5.27. One example of the preceding situation, which we will consider in our proof of Proposition 5.2, is the following: let
 $M={\mathcal{D}}\cdot m$
be a holonomic
$M={\mathcal{D}}\cdot m$
be a holonomic
![]() ${\mathcal{D}}$
-module, and for each
${\mathcal{D}}$
-module, and for each
![]() $i\geqslant 0$
, let
$i\geqslant 0$
, let
 $M_{i}={\mathcal{D}}^{i}(R)\cdot m\subset M$
, where
$M_{i}={\mathcal{D}}^{i}(R)\cdot m\subset M$
, where
![]() ${\mathcal{D}}^{i}(R)$
denotes the
${\mathcal{D}}^{i}(R)$
denotes the
![]() $R$
-submodule of
$R$
-submodule of
![]() ${\mathcal{D}}$
consisting of differential operators of order at most
${\mathcal{D}}$
consisting of differential operators of order at most
![]() $i$
(so, for instance,
$i$
(so, for instance,
 $M_{0}=R\cdot m$
). Then
$M_{0}=R\cdot m$
). Then
 $M=\varinjlim M_{i}$
(the transition maps here being inclusions), and for every
$M=\varinjlim M_{i}$
(the transition maps here being inclusions), and for every
![]() $i$
, the restriction of
$i$
, the restriction of
![]() $\unicode[STIX]{x2202}$
to
$\unicode[STIX]{x2202}$
to
![]() $M_{i}$
is an
$M_{i}$
is an
![]() $R_{n-1}$
-linear map
$R_{n-1}$
-linear map
 $\unicode[STIX]{x1D6FF}_{i}:M_{i}\rightarrow M_{i+1}$
. Clearly
$\unicode[STIX]{x1D6FF}_{i}:M_{i}\rightarrow M_{i+1}$
. Clearly
 $\unicode[STIX]{x2202}=\varinjlim \unicode[STIX]{x1D6FF}_{i}$
.
$\unicode[STIX]{x2202}=\varinjlim \unicode[STIX]{x1D6FF}_{i}$
.
We return now to the general case. The transition maps
![]() $f_{ij}$
induce, by the compatibility, maps on the kernels and cokernels of the
$f_{ij}$
induce, by the compatibility, maps on the kernels and cokernels of the
![]() $\unicode[STIX]{x1D6FF}_{i}$
: for all
$\unicode[STIX]{x1D6FF}_{i}$
: for all
![]() $l$
and
$l$
and
![]() $s$
, we see that
$s$
, we see that
 $f_{l,l+s}(\ker \unicode[STIX]{x1D6FF}_{l})\subset \ker \unicode[STIX]{x1D6FF}_{l+s}$
and that
$f_{l,l+s}(\ker \unicode[STIX]{x1D6FF}_{l})\subset \ker \unicode[STIX]{x1D6FF}_{l+s}$
and that
 $f_{l}(\ker \unicode[STIX]{x1D6FF}_{l})\subset \ker \unicode[STIX]{x2202}$
. From this, it follows that
$f_{l}(\ker \unicode[STIX]{x1D6FF}_{l})\subset \ker \unicode[STIX]{x2202}$
. From this, it follows that
![]() $f_{l,l+s}$
(respectively
$f_{l,l+s}$
(respectively
![]() $f_{l}$
) induces
$f_{l}$
) induces
![]() $R_{n-1}$
-linear maps
$R_{n-1}$
-linear maps
 $f_{l,l+s}^{\ast }:\ker \unicode[STIX]{x1D6FF}_{l}\rightarrow \ker \unicode[STIX]{x1D6FF}_{l+s}$
and
$f_{l,l+s}^{\ast }:\ker \unicode[STIX]{x1D6FF}_{l}\rightarrow \ker \unicode[STIX]{x1D6FF}_{l+s}$
and
 $\overline{f}_{l,l+s}:\operatorname{coker}\unicode[STIX]{x1D6FF}_{l-1}\rightarrow \operatorname{coker}\unicode[STIX]{x1D6FF}_{l+s-1}$
(respectively
$\overline{f}_{l,l+s}:\operatorname{coker}\unicode[STIX]{x1D6FF}_{l-1}\rightarrow \operatorname{coker}\unicode[STIX]{x1D6FF}_{l+s-1}$
(respectively
 $f_{l}^{\ast }:\ker \unicode[STIX]{x1D6FF}_{l}\rightarrow \ker \unicode[STIX]{x2202}$
and
$f_{l}^{\ast }:\ker \unicode[STIX]{x1D6FF}_{l}\rightarrow \ker \unicode[STIX]{x2202}$
and
 $\overline{f}_{l}:\operatorname{coker}\unicode[STIX]{x1D6FF}_{l-1}\rightarrow \operatorname{coker}\unicode[STIX]{x2202}$
). We have, for all
$\overline{f}_{l}:\operatorname{coker}\unicode[STIX]{x1D6FF}_{l-1}\rightarrow \operatorname{coker}\unicode[STIX]{x2202}$
). We have, for all
![]() $l$
and
$l$
and
![]() $s$
,
$s$
,
 $f_{l+s}^{\ast }\circ f_{l,l+s}^{\ast }=f_{l}^{\ast }$
, and a similar compatibility for the
$f_{l+s}^{\ast }\circ f_{l,l+s}^{\ast }=f_{l}^{\ast }$
, and a similar compatibility for the
![]() $\overline{f}$
. We will use an overline to denote the class of an element modulo
$\overline{f}$
. We will use an overline to denote the class of an element modulo
![]() $\unicode[STIX]{x1D6FF}_{l-1}$
(if the element belongs to
$\unicode[STIX]{x1D6FF}_{l-1}$
(if the element belongs to
![]() $M_{l}$
) or modulo
$M_{l}$
) or modulo
![]() $\unicode[STIX]{x2202}$
(if the element belongs to
$\unicode[STIX]{x2202}$
(if the element belongs to
![]() $M$
). Since filtered direct limits are exact functors [Reference WeibelWei94, Theorem 2.6.15], the direct limit of the
$M$
). Since filtered direct limits are exact functors [Reference WeibelWei94, Theorem 2.6.15], the direct limit of the
![]() $\ker \unicode[STIX]{x1D6FF}_{l}$
with respect to the restricted transition maps
$\ker \unicode[STIX]{x1D6FF}_{l}$
with respect to the restricted transition maps
![]() $f_{l,l+s}^{\ast }$
is
$f_{l,l+s}^{\ast }$
is
 $M^{\ast }=\ker \unicode[STIX]{x2202}$
, and the direct limit of the
$M^{\ast }=\ker \unicode[STIX]{x2202}$
, and the direct limit of the
 $\operatorname{coker}\unicode[STIX]{x1D6FF}_{l-1}$
with respect to the induced transition maps
$\operatorname{coker}\unicode[STIX]{x1D6FF}_{l-1}$
with respect to the induced transition maps
![]() $\overline{f}_{l,l+s}$
is
$\overline{f}_{l,l+s}$
is
 $\overline{M}=M/\unicode[STIX]{x2202}(M)$
.
$\overline{M}=M/\unicode[STIX]{x2202}(M)$
.
If
![]() $M$
is holonomic and
$M$
is holonomic and
![]() $x_{n}$
-regular, we have a stability property for the images of these induced maps on kernels and cokernels (see Definition 5.10 for the notion of stability in the strong sense).
$x_{n}$
-regular, we have a stability property for the images of these induced maps on kernels and cokernels (see Definition 5.10 for the notion of stability in the strong sense).
Lemma 5.28. Let
![]() $M$
be a holonomic,
$M$
be a holonomic,
![]() $x_{n}$
-regular
$x_{n}$
-regular
![]() ${\mathcal{D}}$
-module. Let
${\mathcal{D}}$
-module. Let
 $\unicode[STIX]{x2202}=\unicode[STIX]{x2202}_{n}\in {\mathcal{D}}$
. Suppose that
$\unicode[STIX]{x2202}=\unicode[STIX]{x2202}_{n}\in {\mathcal{D}}$
. Suppose that
![]() $\{M_{i}\}$
is a direct system of
$\{M_{i}\}$
is a direct system of
![]() $R$
-submodules of
$R$
-submodules of
![]() $M$
with
$M$
with
 $M=\varinjlim M_{i}$
, and that
$M=\varinjlim M_{i}$
, and that
 $\{\unicode[STIX]{x1D6FF}_{i}:M_{i}\rightarrow M_{i+1}\}$
is a family of
$\{\unicode[STIX]{x1D6FF}_{i}:M_{i}\rightarrow M_{i+1}\}$
is a family of
![]() $R_{n-1}$
-linear maps, compatible with the transitions, such that
$R_{n-1}$
-linear maps, compatible with the transitions, such that
 $\unicode[STIX]{x2202}=\varinjlim \unicode[STIX]{x1D6FF}_{i}$
. Let
$\unicode[STIX]{x2202}=\varinjlim \unicode[STIX]{x1D6FF}_{i}$
. Let
 $f_{ij}:M_{i}\rightarrow M_{j}$
(respectively
$f_{ij}:M_{i}\rightarrow M_{j}$
(respectively
 $f_{i}:M_{i}\rightarrow M$
) be the transition (respectively insertion) maps for this direct system, and define the induced maps
$f_{i}:M_{i}\rightarrow M$
) be the transition (respectively insertion) maps for this direct system, and define the induced maps
![]() $f^{\ast }$
and
$f^{\ast }$
and
![]() $\overline{f}$
as in the previous paragraph. Fix
$\overline{f}$
as in the previous paragraph. Fix
![]() $l$
and let
$l$
and let
![]() $N_{l}$
be a finitely generated
$N_{l}$
be a finitely generated
![]() $R$
-submodule of
$R$
-submodule of
![]() $M_{l}$
.
$M_{l}$
.
-
(a) Let
 $N_{l}^{\ast }=N_{l}\cap \ker \unicode[STIX]{x1D6FF}_{l}$
. The images of
$N_{l}^{\ast }=N_{l}\cap \ker \unicode[STIX]{x1D6FF}_{l}$
. The images of
 $N_{l}^{\ast }$
under the
$N_{l}^{\ast }$
under the
 $f_{l,l+s}^{\ast }$
stabilize in the strong sense, and the stable image is a finitely generated
$f_{l,l+s}^{\ast }$
stabilize in the strong sense, and the stable image is a finitely generated
 $R_{n-1}$
-submodule of
$R_{n-1}$
-submodule of
 $M^{\ast }=\ker \unicode[STIX]{x2202}$
.
$M^{\ast }=\ker \unicode[STIX]{x2202}$
. -
(b) Let
 $\overline{N}_{l}$
be the image
$\overline{N}_{l}$
be the image
 $N_{l}/(N_{l}\cap \unicode[STIX]{x1D6FF}_{l-1}(M_{l-1}))$
of
$N_{l}/(N_{l}\cap \unicode[STIX]{x1D6FF}_{l-1}(M_{l-1}))$
of
 $N_{l}$
in
$N_{l}$
in
 $\operatorname{coker}\unicode[STIX]{x1D6FF}_{l-1}$
. The images of
$\operatorname{coker}\unicode[STIX]{x1D6FF}_{l-1}$
. The images of
 $\overline{N}_{l}$
under the
$\overline{N}_{l}$
under the
 $\overline{f}_{l,l+s}$
stabilize in the strong sense, and the stable image is a finitely generated
$\overline{f}_{l,l+s}$
stabilize in the strong sense, and the stable image is a finitely generated
 $R_{n-1}$
-submodule of
$R_{n-1}$
-submodule of
 $\overline{M}=\operatorname{coker}\unicode[STIX]{x2202}$
.
$\overline{M}=\operatorname{coker}\unicode[STIX]{x2202}$
.
Proof. Let
 $M^{\ast }=\ker \unicode[STIX]{x2202}$
. The Leibniz rule implies that
$M^{\ast }=\ker \unicode[STIX]{x2202}$
. The Leibniz rule implies that
![]() $R\cdot M^{\ast }$
is a
$R\cdot M^{\ast }$
is a
![]() ${\mathcal{D}}$
-submodule of
${\mathcal{D}}$
-submodule of
![]() $M$
, and it is clear that
$M$
, and it is clear that
 $M^{\ast }=(R\cdot M^{\ast })^{\ast }$
as
$M^{\ast }=(R\cdot M^{\ast })^{\ast }$
as
![]() ${\mathcal{D}}_{n-1}$
-submodules of
${\mathcal{D}}_{n-1}$
-submodules of
![]() $M$
, where
$M$
, where
 $(R\cdot M^{\ast })^{\ast }=\ker (\unicode[STIX]{x2202}:R\cdot M^{\ast }\rightarrow R\cdot M^{\ast })$
. Moreover, for all
$(R\cdot M^{\ast })^{\ast }=\ker (\unicode[STIX]{x2202}:R\cdot M^{\ast }\rightarrow R\cdot M^{\ast })$
. Moreover, for all
![]() $i$
,
$i$
,
 $\ker \unicode[STIX]{x1D6FF}_{i}\subset f_{i}^{-1}(M^{\ast })$
(since
$\ker \unicode[STIX]{x1D6FF}_{i}\subset f_{i}^{-1}(M^{\ast })$
(since
 $\unicode[STIX]{x2202}=\varinjlim \unicode[STIX]{x1D6FF}_{i}$
), so the kernels of
$\unicode[STIX]{x2202}=\varinjlim \unicode[STIX]{x1D6FF}_{i}$
), so the kernels of
![]() $\unicode[STIX]{x2202}$
and of the
$\unicode[STIX]{x2202}$
and of the
![]() $\unicode[STIX]{x1D6FF}_{i}$
, as well as the maps between them, do not change if we replace
$\unicode[STIX]{x1D6FF}_{i}$
, as well as the maps between them, do not change if we replace
![]() $M$
with
$M$
with
 $M^{\prime }=R\cdot M^{\ast }$
and all
$M^{\prime }=R\cdot M^{\ast }$
and all
![]() $M_{i}$
by
$M_{i}$
by
 $M_{i}^{\prime }=f_{i}^{-1}(M^{\prime })$
. Since
$M_{i}^{\prime }=f_{i}^{-1}(M^{\prime })$
. Since
 $M^{\prime }=\varinjlim M_{i}^{\prime }$
(the transition maps being the restrictions of
$M^{\prime }=\varinjlim M_{i}^{\prime }$
(the transition maps being the restrictions of
![]() $f_{ij}$
to
$f_{ij}$
to
![]() $M_{i}^{\prime }$
) and
$M_{i}^{\prime }$
) and
 $\unicode[STIX]{x2202}|_{M^{\prime }}=\varinjlim \unicode[STIX]{x1D6FF}_{i}|_{M_{i}^{\prime }}$
, we reduce the proof of part (a) to the case
$\unicode[STIX]{x2202}|_{M^{\prime }}=\varinjlim \unicode[STIX]{x1D6FF}_{i}|_{M_{i}^{\prime }}$
, we reduce the proof of part (a) to the case
 $M=M^{\prime }$
.
$M=M^{\prime }$
.
By Lemma 5.17, the hypothesis that
 $M=M^{\prime }$
implies that there is an
$M=M^{\prime }$
implies that there is an
![]() $R_{n-1}$
-module direct sum decomposition
$R_{n-1}$
-module direct sum decomposition
 $M=M^{\ast }\oplus x_{n}M$
. Let
$M=M^{\ast }\oplus x_{n}M$
. Let
![]() $\unicode[STIX]{x1D70B}$
be the
$\unicode[STIX]{x1D70B}$
be the
![]() $R_{n-1}$
-linear projection
$R_{n-1}$
-linear projection
 $M\rightarrow M^{\ast }$
. Since
$M\rightarrow M^{\ast }$
. Since
 $f_{l}(N_{l}^{\ast })\subset M^{\ast }$
,
$f_{l}(N_{l}^{\ast })\subset M^{\ast }$
,
![]() $\unicode[STIX]{x1D70B}$
restricts to an isomorphism
$\unicode[STIX]{x1D70B}$
restricts to an isomorphism
 $f_{l}(N_{l}^{\ast })\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D70B}(f_{l}(N_{l}^{\ast }))$
, and the composite
$f_{l}(N_{l}^{\ast })\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D70B}(f_{l}(N_{l}^{\ast }))$
, and the composite
 $$\begin{eqnarray}N_{l}^{\ast }{\hookrightarrow}N_{l}\xrightarrow[{}]{f_{l}}M\xrightarrow[{}]{\unicode[STIX]{x1D70B}}M^{\ast }\end{eqnarray}$$
$$\begin{eqnarray}N_{l}^{\ast }{\hookrightarrow}N_{l}\xrightarrow[{}]{f_{l}}M\xrightarrow[{}]{\unicode[STIX]{x1D70B}}M^{\ast }\end{eqnarray}$$
factors through the natural surjection
 $N_{l}\rightarrow N_{l}/x_{n}N_{l}$
(since
$N_{l}\rightarrow N_{l}/x_{n}N_{l}$
(since
 $\ker (\unicode[STIX]{x1D70B}\circ f_{l})$
contains
$\ker (\unicode[STIX]{x1D70B}\circ f_{l})$
contains
![]() $x_{n}N_{l}$
). Since
$x_{n}N_{l}$
). Since
![]() $N_{l}$
is a finitely generated
$N_{l}$
is a finitely generated
![]() $R$
-module,
$R$
-module,
 $N_{l}/x_{n}N_{l}$
is a finitely generated
$N_{l}/x_{n}N_{l}$
is a finitely generated
![]() $R_{n-1}$
-module. This implies that
$R_{n-1}$
-module. This implies that
 $\unicode[STIX]{x1D70B}(f_{l}(N_{l}^{\ast }))$
is contained in the
$\unicode[STIX]{x1D70B}(f_{l}(N_{l}^{\ast }))$
is contained in the
![]() $R_{n-1}$
-linear image of the finitely generated
$R_{n-1}$
-linear image of the finitely generated
![]() $R_{n-1}$
-module
$R_{n-1}$
-module
 $N_{l}/x_{n}N_{l}$
, so it is a finitely generated
$N_{l}/x_{n}N_{l}$
, so it is a finitely generated
![]() $R_{n-1}$
-module itself, and so is its isomorphic copy
$R_{n-1}$
-module itself, and so is its isomorphic copy
 $f_{l}(N_{l}^{\ast })=f_{l}^{\ast }(N_{l}^{\ast })$
. It follows that if the images of
$f_{l}(N_{l}^{\ast })=f_{l}^{\ast }(N_{l}^{\ast })$
. It follows that if the images of
![]() $N_{l}^{\ast }$
stabilize in the strong sense, the stable image is finitely generated.
$N_{l}^{\ast }$
stabilize in the strong sense, the stable image is finitely generated.
As
![]() $N_{l}$
is a finitely generated
$N_{l}$
is a finitely generated
![]() $R$
-module, its images under the
$R$
-module, its images under the
![]() $R$
-linear maps
$R$
-linear maps
![]() $f_{l,l+s}$
stabilize in the strong sense by Lemma 5.11; since
$f_{l,l+s}$
stabilize in the strong sense by Lemma 5.11; since
 $N_{l}^{\ast }\subset N_{l}$
and
$N_{l}^{\ast }\subset N_{l}$
and
![]() $f_{l,l+s}^{\ast }$
is simply a restriction of
$f_{l,l+s}^{\ast }$
is simply a restriction of
![]() $f_{l,l+s}$
for all
$f_{l,l+s}$
for all
![]() $s$
, the fact that the images of
$s$
, the fact that the images of
![]() $N_{l}^{\ast }$
under the
$N_{l}^{\ast }$
under the
![]() $f_{l,l+s}^{\ast }$
stabilize in the strong sense as well is automatic. This proves part (a).
$f_{l,l+s}^{\ast }$
stabilize in the strong sense as well is automatic. This proves part (a).
In our proof of part (b) we cannot assume (but do not need) that
 $M=M^{\prime }$
, so we drop this assumption now. We now fix a set
$M=M^{\prime }$
, so we drop this assumption now. We now fix a set
 $\{n_{1},\ldots ,n_{\unicode[STIX]{x1D6FC}_{l}}\}$
of
$\{n_{1},\ldots ,n_{\unicode[STIX]{x1D6FC}_{l}}\}$
of
![]() $R$
-generators for
$R$
-generators for
![]() $N_{l}$
. By assumption,
$N_{l}$
. By assumption,
![]() $M$
is
$M$
is
![]() $x_{n}$
-regular, so by definition all
$x_{n}$
-regular, so by definition all
 $f_{l}(n_{i})\in M$
are
$f_{l}(n_{i})\in M$
are
![]() $x_{n}$
-regular. We can therefore apply Lemma 5.25 to every
$x_{n}$
-regular. We can therefore apply Lemma 5.25 to every
![]() $f_{l}(n_{i})$
in turn. Let
$f_{l}(n_{i})$
in turn. Let
 $i\in \{1,\ldots ,\unicode[STIX]{x1D6FC}_{l}\}$
be fixed, and consider the
$i\in \{1,\ldots ,\unicode[STIX]{x1D6FC}_{l}\}$
be fixed, and consider the
![]() $R$
-submodule
$R$
-submodule
 $R\cdot f_{l}(n_{i})\subset M$
generated by
$R\cdot f_{l}(n_{i})\subset M$
generated by
![]() $f_{l}(n_{i})$
. By Lemma 5.25, there exist a positive natural number
$f_{l}(n_{i})$
. By Lemma 5.25, there exist a positive natural number
![]() $p_{i}$
and a finitely generated
$p_{i}$
and a finitely generated
![]() $R_{n-1}$
-submodule
$R_{n-1}$
-submodule
![]() $L_{i}$
of
$L_{i}$
of
 $R\cdot f_{l}(n_{i})$
such that
$R\cdot f_{l}(n_{i})$
such that
 $$\begin{eqnarray}R\cdot f_{l}(n_{i})\subset L_{i}+\unicode[STIX]{x2202}\biggl(\mathop{\sum }_{j=0}^{p_{i}-1}R\cdot \unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))\biggr).\end{eqnarray}$$
$$\begin{eqnarray}R\cdot f_{l}(n_{i})\subset L_{i}+\unicode[STIX]{x2202}\biggl(\mathop{\sum }_{j=0}^{p_{i}-1}R\cdot \unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))\biggr).\end{eqnarray}$$
If we let
![]() $L_{l}^{\prime }$
be the finitely generated
$L_{l}^{\prime }$
be the finitely generated
![]() $R_{n-1}$
-module
$R_{n-1}$
-module
 $L_{1}+\cdots +L_{\unicode[STIX]{x1D6FC}_{l}}$
and
$L_{1}+\cdots +L_{\unicode[STIX]{x1D6FC}_{l}}$
and
![]() $\unicode[STIX]{x1D6E4}_{l}$
the
$\unicode[STIX]{x1D6E4}_{l}$
the
![]() $R$
-submodule of
$R$
-submodule of
![]() $M$
generated by
$M$
generated by
 $$\begin{eqnarray}\{\unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))\}_{1\leqslant i\leqslant \unicode[STIX]{x1D6FC}_{l},0\leqslant j\leqslant p_{i}-1},\end{eqnarray}$$
$$\begin{eqnarray}\{\unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))\}_{1\leqslant i\leqslant \unicode[STIX]{x1D6FC}_{l},0\leqslant j\leqslant p_{i}-1},\end{eqnarray}$$
we see that
 $$\begin{eqnarray}f_{l}(N_{l})=\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D6FC}_{l}}R\cdot f_{l}(n_{i})\subset L_{l}^{\prime }+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l}).\end{eqnarray}$$
$$\begin{eqnarray}f_{l}(N_{l})=\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D6FC}_{l}}R\cdot f_{l}(n_{i})\subset L_{l}^{\prime }+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l}).\end{eqnarray}$$
Let
 $\{f_{l}(y_{1}),\ldots ,f_{l}(y_{\unicode[STIX]{x1D702}_{l}})\}$
be a set of
$\{f_{l}(y_{1}),\ldots ,f_{l}(y_{\unicode[STIX]{x1D702}_{l}})\}$
be a set of
![]() $R_{n-1}$
-generators for
$R_{n-1}$
-generators for
 $L_{l}^{\prime }\subset f_{l}(N_{l})$
, and write
$L_{l}^{\prime }\subset f_{l}(N_{l})$
, and write
![]() $L_{l}^{\prime \prime }$
for the
$L_{l}^{\prime \prime }$
for the
![]() $R_{n-1}$
-submodule of
$R_{n-1}$
-submodule of
![]() $N_{l}$
generated by
$N_{l}$
generated by
 $y_{1},\ldots ,y_{\unicode[STIX]{x1D702}_{l}}$
, so that
$y_{1},\ldots ,y_{\unicode[STIX]{x1D702}_{l}}$
, so that
 $f_{l}(L_{l}^{\prime \prime })=L_{l}^{\prime }$
. Then the containment
$f_{l}(L_{l}^{\prime \prime })=L_{l}^{\prime }$
. Then the containment
 $f_{l}(N_{l})\subset f_{l}(L_{l}^{\prime \prime })+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l})$
implies that
$f_{l}(N_{l})\subset f_{l}(L_{l}^{\prime \prime })+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l})$
implies that
 $$\begin{eqnarray}\overline{f}_{l}(\overline{N}_{l})\subset \overline{f}_{l}(L_{l}^{\prime \prime }/(L_{l}^{\prime \prime }\cap \unicode[STIX]{x1D6FF}_{l-1}(M_{l-1})))\end{eqnarray}$$
$$\begin{eqnarray}\overline{f}_{l}(\overline{N}_{l})\subset \overline{f}_{l}(L_{l}^{\prime \prime }/(L_{l}^{\prime \prime }\cap \unicode[STIX]{x1D6FF}_{l-1}(M_{l-1})))\end{eqnarray}$$
inside
 $M/\unicode[STIX]{x2202}(M)$
: given any class
$M/\unicode[STIX]{x2202}(M)$
: given any class
![]() $\overline{n}_{l}\in \overline{N}_{l}$
of an element
$\overline{n}_{l}\in \overline{N}_{l}$
of an element
![]() $n_{l}\in N_{l}$
, we can write
$n_{l}\in N_{l}$
, we can write
 $f_{l}(n_{l})=f_{l}(\unicode[STIX]{x1D706}_{l})+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FE}_{l})$
for some
$f_{l}(n_{l})=f_{l}(\unicode[STIX]{x1D706}_{l})+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FE}_{l})$
for some
![]() $\unicode[STIX]{x1D706}_{l}\in L_{l}^{\prime \prime }$
and
$\unicode[STIX]{x1D706}_{l}\in L_{l}^{\prime \prime }$
and
![]() $\unicode[STIX]{x1D6FE}_{l}\in \unicode[STIX]{x1D6E4}_{l}$
, so we have
$\unicode[STIX]{x1D6FE}_{l}\in \unicode[STIX]{x1D6E4}_{l}$
, so we have
 $$\begin{eqnarray}\overline{f}_{l}(\overline{n}_{l})=\overline{f_{l}(n_{l})}=\overline{f_{l}(\unicode[STIX]{x1D706}_{l})+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FE}_{l})}=\overline{f_{l}(\unicode[STIX]{x1D706}_{l})}=\overline{f}_{l}(\overline{\unicode[STIX]{x1D706}}_{l})\end{eqnarray}$$
$$\begin{eqnarray}\overline{f}_{l}(\overline{n}_{l})=\overline{f_{l}(n_{l})}=\overline{f_{l}(\unicode[STIX]{x1D706}_{l})+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FE}_{l})}=\overline{f_{l}(\unicode[STIX]{x1D706}_{l})}=\overline{f}_{l}(\overline{\unicode[STIX]{x1D706}}_{l})\end{eqnarray}$$
since the class of
![]() $\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FE}_{l})$
in
$\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FE}_{l})$
in
 $\overline{M}=M/\unicode[STIX]{x2202}(M)$
is zero (the first and last equalities are simply the definition of
$\overline{M}=M/\unicode[STIX]{x2202}(M)$
is zero (the first and last equalities are simply the definition of
![]() $\overline{f}_{l}$
). We know that
$\overline{f}_{l}$
). We know that
![]() $\overline{f}_{l}$
is
$\overline{f}_{l}$
is
![]() $R_{n-1}$
-linear and that
$R_{n-1}$
-linear and that
![]() $L_{l}^{\prime \prime }$
, and hence its quotient
$L_{l}^{\prime \prime }$
, and hence its quotient
 $L_{l}^{\prime \prime }/(L_{l}^{\prime \prime }\cap \unicode[STIX]{x1D6FF}_{l-1}(M_{l-1}))$
, is a finitely generated
$L_{l}^{\prime \prime }/(L_{l}^{\prime \prime }\cap \unicode[STIX]{x1D6FF}_{l-1}(M_{l-1}))$
, is a finitely generated
![]() $R_{n-1}$
-module, so we can conclude that
$R_{n-1}$
-module, so we can conclude that
![]() $\overline{f}_{l}(\overline{N}_{l})$
is a finitely generated
$\overline{f}_{l}(\overline{N}_{l})$
is a finitely generated
![]() $R_{n-1}$
-module. It follows that if the images of
$R_{n-1}$
-module. It follows that if the images of
![]() $\overline{N}_{l}$
stabilize in the strong sense, the stable image is finitely generated.
$\overline{N}_{l}$
stabilize in the strong sense, the stable image is finitely generated.
In order to conclude that the images of
![]() $\overline{N}_{l}$
stabilize in the strong sense, we must prove that there exists
$\overline{N}_{l}$
stabilize in the strong sense, we must prove that there exists
![]() $t$
with the property that whenever
$t$
with the property that whenever
 $f_{l}(n_{l})\in \unicode[STIX]{x2202}(M)$
for some
$f_{l}(n_{l})\in \unicode[STIX]{x2202}(M)$
for some
![]() $n_{l}\in N_{l}$
, we have
$n_{l}\in N_{l}$
, we have
 $f_{l,l+t}(n_{l})\in \unicode[STIX]{x1D6FF}_{l+t-1}(M_{l+t-1})$
; in other words, if the class of
$f_{l,l+t}(n_{l})\in \unicode[STIX]{x1D6FF}_{l+t-1}(M_{l+t-1})$
; in other words, if the class of
![]() $n_{l}$
is carried to zero in
$n_{l}$
is carried to zero in
![]() $\operatorname{coker}\unicode[STIX]{x2202}$
, it is already zero in
$\operatorname{coker}\unicode[STIX]{x2202}$
, it is already zero in
 $\operatorname{coker}\unicode[STIX]{x1D6FF}_{l+t-1}$
. (This implies that the images of
$\operatorname{coker}\unicode[STIX]{x1D6FF}_{l+t-1}$
. (This implies that the images of
![]() $\overline{N}_{l}$
stabilize at the
$\overline{N}_{l}$
stabilize at the
![]() $(l+t)$
th stage.) Choose
$(l+t)$
th stage.) Choose
![]() $t$
so large that every
$t$
so large that every
 $\unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))$
has a representative in
$\unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))$
has a representative in
![]() $M_{l+t-1}$
, as follows: for all
$M_{l+t-1}$
, as follows: for all
![]() $i$
and
$i$
and
![]() $j$
, there exists a natural number
$j$
, there exists a natural number
![]() $t_{ij}$
and an element
$t_{ij}$
and an element
 $m_{l+t_{ij}}\in M_{l+t_{ij}}$
such that
$m_{l+t_{ij}}\in M_{l+t_{ij}}$
such that
 $f_{l+t_{ij}}(m_{l+t_{ij}})=\unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))$
. Put
$f_{l+t_{ij}}(m_{l+t_{ij}})=\unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))$
. Put
 $t=\max \{t_{ij}\}+1$
. Then since the
$t=\max \{t_{ij}\}+1$
. Then since the
 $\unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))$
are
$\unicode[STIX]{x2202}^{j}(f_{l}(n_{i}))$
are
![]() $R$
-generators for
$R$
-generators for
![]() $\unicode[STIX]{x1D6E4}_{l}$
, any element of the
$\unicode[STIX]{x1D6E4}_{l}$
, any element of the
![]() $R_{n-1}$
-module
$R_{n-1}$
-module
![]() $\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l})$
can be expressed as
$\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l})$
can be expressed as
 $f_{l+t}(\unicode[STIX]{x1D6FF}_{l+t-1}(m))$
for some
$f_{l+t}(\unicode[STIX]{x1D6FF}_{l+t-1}(m))$
for some
 $m\in M_{l+t-1}$
. Consider also the
$m\in M_{l+t-1}$
. Consider also the
![]() $R_{n-1}$
-submodule
$R_{n-1}$
-submodule
 $L_{l}^{\prime }\cap \unicode[STIX]{x2202}(M)\subset M$
, which is finitely generated since
$L_{l}^{\prime }\cap \unicode[STIX]{x2202}(M)\subset M$
, which is finitely generated since
![]() $L_{l}^{\prime }$
is. Enlarging
$L_{l}^{\prime }$
is. Enlarging
![]() $t$
if necessary, we may assume (by the finite generation) that every element of
$t$
if necessary, we may assume (by the finite generation) that every element of
 $L_{l}^{\prime }\cap \unicode[STIX]{x2202}(M)$
can also be expressed as
$L_{l}^{\prime }\cap \unicode[STIX]{x2202}(M)$
can also be expressed as
 $f_{l+t}(\unicode[STIX]{x1D6FF}_{l+t-1}(m^{\prime }))$
for some
$f_{l+t}(\unicode[STIX]{x1D6FF}_{l+t-1}(m^{\prime }))$
for some
 $m^{\prime }\in M_{l+t-1}$
.
$m^{\prime }\in M_{l+t-1}$
.
Now suppose that
![]() $n_{l}\in N_{l}$
is such that
$n_{l}\in N_{l}$
is such that
 $f_{l}(n_{l})\in \unicode[STIX]{x2202}(M)$
. Since
$f_{l}(n_{l})\in \unicode[STIX]{x2202}(M)$
. Since
 $f_{l}(N_{l})\subset L_{l}^{\prime }+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l})$
, we have
$f_{l}(N_{l})\subset L_{l}^{\prime }+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l})$
, we have
 $f_{l}(n_{l})\in (L_{l}^{\prime }\cap \unicode[STIX]{x2202}(M))+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l})$
, so
$f_{l}(n_{l})\in (L_{l}^{\prime }\cap \unicode[STIX]{x2202}(M))+\unicode[STIX]{x2202}(\unicode[STIX]{x1D6E4}_{l})$
, so
 $f_{l}(n_{l})=f_{l+t}(\unicode[STIX]{x1D6FF}_{l+t-1}(m))$
for some
$f_{l}(n_{l})=f_{l+t}(\unicode[STIX]{x1D6FF}_{l+t-1}(m))$
for some
 $m\in M_{l+t-1}$
. Since
$m\in M_{l+t-1}$
. Since
 $f_{l}=f_{l+t}\circ f_{l,l+t}$
, we see that
$f_{l}=f_{l+t}\circ f_{l,l+t}$
, we see that
 $$\begin{eqnarray}f_{l,l+t}(n_{l})-\unicode[STIX]{x1D6FF}_{l+t-1}(m)\in \ker f_{l+t}.\end{eqnarray}$$
$$\begin{eqnarray}f_{l,l+t}(n_{l})-\unicode[STIX]{x1D6FF}_{l+t-1}(m)\in \ker f_{l+t}.\end{eqnarray}$$
The kernel of the restriction of
![]() $f_{l+t}$
to
$f_{l+t}$
to
 $f_{l,l+t}(N_{l})$
is a finitely generated
$f_{l,l+t}(N_{l})$
is a finitely generated
![]() $R$
-module, so by Lemma 5.11, its images stabilize in the strong sense, and the stable image is zero because the image of this kernel in
$R$
-module, so by Lemma 5.11, its images stabilize in the strong sense, and the stable image is zero because the image of this kernel in
![]() $M$
is clearly zero. Therefore, enlarging
$M$
is clearly zero. Therefore, enlarging
![]() $t$
again if necessary (so that the transition map from the old
$t$
again if necessary (so that the transition map from the old
![]() $t$
to the new
$t$
to the new
![]() $t$
annihilates this kernel; this new
$t$
annihilates this kernel; this new
![]() $t$
depends only on
$t$
depends only on
![]() $l$
, not on
$l$
, not on
![]() $n_{l}$
), we may assume that the difference
$n_{l}$
), we may assume that the difference
 $f_{l,l+t}(n_{l})-\unicode[STIX]{x1D6FF}_{l+t-1}(m)$
is zero; that is, that
$f_{l,l+t}(n_{l})-\unicode[STIX]{x1D6FF}_{l+t-1}(m)$
is zero; that is, that
 $f_{l,l+t}(n_{l})$
belongs to
$f_{l,l+t}(n_{l})$
belongs to
 $\unicode[STIX]{x1D6FF}_{l+t-1}(M_{l+t-1})$
. We conclude that the images of
$\unicode[STIX]{x1D6FF}_{l+t-1}(M_{l+t-1})$
. We conclude that the images of
![]() $\overline{N}_{l}$
stabilize in the strong sense, completing the proof of part (b) and the lemma.◻
$\overline{N}_{l}$
stabilize in the strong sense, completing the proof of part (b) and the lemma.◻
The strategy of the proof of Proposition 5.2 is to write the de Rham complex
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
of a holonomic
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
of a holonomic
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
as a direct limit of complexes whose objects are finitely generated
$M$
as a direct limit of complexes whose objects are finitely generated
![]() $R$
-modules (using the degree, or order, filtration on the ring
$R$
-modules (using the degree, or order, filtration on the ring
![]() ${\mathcal{D}}$
). Fix, once and for all, both a holonomic
${\mathcal{D}}$
). Fix, once and for all, both a holonomic
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
and an element
$M$
and an element
![]() $m\in M$
such that
$m\in M$
such that
 $M={\mathcal{D}}\cdot m$
. As in Example 5.27, let
$M={\mathcal{D}}\cdot m$
. As in Example 5.27, let
 $M_{l}={\mathcal{D}}^{l}(R)\cdot m$
for
$M_{l}={\mathcal{D}}^{l}(R)\cdot m$
for
![]() $l\geqslant 0$
. Note that
$l\geqslant 0$
. Note that
 $M=\bigcup _{l}M_{l}$
; for any
$M=\bigcup _{l}M_{l}$
; for any
![]() $i$
,
$i$
,
 $\unicode[STIX]{x2202}_{i}:M\rightarrow M$
induces
$\unicode[STIX]{x2202}_{i}:M\rightarrow M$
induces
![]() $k$
-linear maps
$k$
-linear maps
 $\unicode[STIX]{x2202}_{i}:M_{l}\rightarrow M_{l+1}$
for all
$\unicode[STIX]{x2202}_{i}:M_{l}\rightarrow M_{l+1}$
for all
![]() $l$
; and every
$l$
; and every
![]() $M_{l}$
is a finitely generated
$M_{l}$
is a finitely generated
![]() $R$
-module (a set of
$R$
-module (a set of
![]() $R$
-generators is given by
$R$
-generators is given by
![]() $\{\unicode[STIX]{x1D6FF}m\}$
where
$\{\unicode[STIX]{x1D6FF}m\}$
where
![]() $\unicode[STIX]{x1D6FF}$
runs through the monomials in
$\unicode[STIX]{x1D6FF}$
runs through the monomials in
 $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
of total degree at most
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
of total degree at most
![]() $l$
).
$l$
).
Definition 5.29. Let
![]() $M$
and
$M$
and
![]() $m$
be as above. For all
$m$
be as above. For all
 $j\in \{0,\ldots ,n\}$
and
$j\in \{0,\ldots ,n\}$
and
![]() $l\in \mathbb{N}$
, let
$l\in \mathbb{N}$
, let
![]() ${\mathcal{M}}_{l}^{j,\bullet }$
be the subcomplex
${\mathcal{M}}_{l}^{j,\bullet }$
be the subcomplex
 $$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{l}^{j,0}\rightarrow {\mathcal{M}}_{l}^{j,1}\rightarrow \cdots \rightarrow {\mathcal{M}}_{l}^{j,j}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{l}^{j,0}\rightarrow {\mathcal{M}}_{l}^{j,1}\rightarrow \cdots \rightarrow {\mathcal{M}}_{l}^{j,j}\rightarrow 0\end{eqnarray}$$
of
 $M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }$
whose
$M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }$
whose
![]() $i$
th object
$i$
th object
![]() ${\mathcal{M}}_{l}^{j,i}$
is a direct sum of
${\mathcal{M}}_{l}^{j,i}$
is a direct sum of
![]() $\binom{j}{i}$
copies of the
$\binom{j}{i}$
copies of the
![]() $R$
-submodule
$R$
-submodule
![]() $M_{l+i}$
of
$M_{l+i}$
of
![]() $M$
, indexed by
$M$
, indexed by
 $dx_{k_{1}}\wedge \cdots \wedge dx_{k_{i}}$
for
$dx_{k_{1}}\wedge \cdots \wedge dx_{k_{i}}$
for
![]() $i$
-tuples
$i$
-tuples
 $n-j+1\leqslant k_{1}<\cdots <k_{i}\leqslant n$
, and whose differentials are the restrictions of those in the complex
$n-j+1\leqslant k_{1}<\cdots <k_{i}\leqslant n$
, and whose differentials are the restrictions of those in the complex
 $M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }$
. (We simply write
$M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }$
. (We simply write
![]() ${\mathcal{M}}_{l}^{\bullet }$
for
${\mathcal{M}}_{l}^{\bullet }$
for
![]() ${\mathcal{M}}_{l}^{n,\bullet }$
.)
${\mathcal{M}}_{l}^{n,\bullet }$
.)
If we suppress the indexing wedge products, the complex
![]() ${\mathcal{M}}_{l}^{j,\bullet }$
takes the form
${\mathcal{M}}_{l}^{j,\bullet }$
takes the form
 $$\begin{eqnarray}0\rightarrow M_{l}\rightarrow \underset{1\leqslant i\leqslant n}{\bigoplus }M_{l+1}\rightarrow \cdots \rightarrow M_{l+j}\rightarrow 0;\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M_{l}\rightarrow \underset{1\leqslant i\leqslant n}{\bigoplus }M_{l+1}\rightarrow \cdots \rightarrow M_{l+j}\rightarrow 0;\end{eqnarray}$$
its objects are finitely generated
![]() $R$
-modules and its differentials are
$R$
-modules and its differentials are
![]() $k$
-linear. We have short exact sequences of complexes
$k$
-linear. We have short exact sequences of complexes
 $$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{l+1}^{j,\bullet }[-1]\rightarrow {\mathcal{M}}_{l}^{j+1,\bullet }\rightarrow {\mathcal{M}}_{l}^{j,\bullet }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{l+1}^{j,\bullet }[-1]\rightarrow {\mathcal{M}}_{l}^{j+1,\bullet }\rightarrow {\mathcal{M}}_{l}^{j,\bullet }\rightarrow 0\end{eqnarray}$$
for all
![]() $l$
, analogous to the sequence of Remark 5.7; the first non-zero morphism is given by
$l$
, analogous to the sequence of Remark 5.7; the first non-zero morphism is given by
 $\wedge \,dx_{n-j}$
and, in the induced long exact cohomology sequence, the connecting homomorphisms are given by
$\wedge \,dx_{n-j}$
and, in the induced long exact cohomology sequence, the connecting homomorphisms are given by
![]() $\unicode[STIX]{x2202}_{n-j}$
, up to a sign.
$\unicode[STIX]{x2202}_{n-j}$
, up to a sign.
The complexes
![]() ${\mathcal{M}}_{l}^{j,\bullet }$
naturally form a filtered direct system as
${\mathcal{M}}_{l}^{j,\bullet }$
naturally form a filtered direct system as
![]() $l$
varies. We have
$l$
varies. We have
 $M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }=\varinjlim {\mathcal{M}}_{l}^{j,\bullet }$
, and as filtered direct limits commute with cohomology (they are exact functors, by [Reference WeibelWei94, Theorem 2.6.15]), this implies
$M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet }=\varinjlim {\mathcal{M}}_{l}^{j,\bullet }$
, and as filtered direct limits commute with cohomology (they are exact functors, by [Reference WeibelWei94, Theorem 2.6.15]), this implies
 $$\begin{eqnarray}h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })\simeq \varinjlim h^{i}({\mathcal{M}}_{l}^{j,\bullet })\end{eqnarray}$$
$$\begin{eqnarray}h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })\simeq \varinjlim h^{i}({\mathcal{M}}_{l}^{j,\bullet })\end{eqnarray}$$
for all
![]() $i$
. In particular, taking
$i$
. In particular, taking
![]() $j=n$
, we have
$j=n$
, we have
 $H_{\text{dR}}^{i}(M)=\varinjlim h^{i}({\mathcal{M}}_{l}^{\bullet })$
as
$H_{\text{dR}}^{i}(M)=\varinjlim h^{i}({\mathcal{M}}_{l}^{\bullet })$
as
![]() $k$
-spaces. By Theorem 2.2, the left-hand side is a finite-dimensional
$k$
-spaces. By Theorem 2.2, the left-hand side is a finite-dimensional
![]() $k$
-space for all
$k$
-space for all
![]() $i$
. Thus, for all
$i$
. Thus, for all
![]() $l$
, the image of
$l$
, the image of
 $h^{i}({\mathcal{M}}_{l}^{\bullet })$
in
$h^{i}({\mathcal{M}}_{l}^{\bullet })$
in
 $H_{\text{dR}}^{i}(M)$
is a finite-dimensional
$H_{\text{dR}}^{i}(M)$
is a finite-dimensional
![]() $k$
-space. The key technical result in the proof of Proposition 5.2 is the following.
$k$
-space. The key technical result in the proof of Proposition 5.2 is the following.
Proposition 5.30. Let
 $M={\mathcal{D}}\cdot m$
be a holonomic
$M={\mathcal{D}}\cdot m$
be a holonomic
![]() ${\mathcal{D}}$
-module, and define the approximations
${\mathcal{D}}$
-module, and define the approximations
![]() ${\mathcal{M}}_{l}^{\bullet }$
to its de Rham complex as above. For all
${\mathcal{M}}_{l}^{\bullet }$
to its de Rham complex as above. For all
![]() $i$
and
$i$
and
![]() $l$
, the images of
$l$
, the images of
 $h^{i}({\mathcal{M}}_{l}^{\bullet })$
stabilize in the strong sense, with finite-dimensional stable image.
$h^{i}({\mathcal{M}}_{l}^{\bullet })$
stabilize in the strong sense, with finite-dimensional stable image.
Proof of Proposition 5.30.
We may assume, after possibly making a change of variables as in Proposition 5.26, that for all
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is a holonomic
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
is a holonomic
![]() ${\mathcal{D}}_{n-j}$
-module which is
${\mathcal{D}}_{n-j}$
-module which is
![]() $x_{n-j}$
-regular. Let
$x_{n-j}$
-regular. Let
![]() $(\ast _{j})$
be the following statement: for all
$(\ast _{j})$
be the following statement: for all
 $i\in \{0,\ldots ,j\}$
and all
$i\in \{0,\ldots ,j\}$
and all
![]() $l\geqslant 0$
, the images of
$l\geqslant 0$
, the images of
 $h^{i}({\mathcal{M}}_{l}^{j,\bullet })$
in the direct system
$h^{i}({\mathcal{M}}_{l}^{j,\bullet })$
in the direct system
 $$\begin{eqnarray}\cdots \rightarrow h^{i}({\mathcal{M}}_{l-1}^{j,\bullet })\rightarrow h^{i}({\mathcal{M}}_{l}^{j,\bullet })\rightarrow h^{i}({\mathcal{M}}_{l+1}^{j,\bullet })\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow h^{i}({\mathcal{M}}_{l-1}^{j,\bullet })\rightarrow h^{i}({\mathcal{M}}_{l}^{j,\bullet })\rightarrow h^{i}({\mathcal{M}}_{l+1}^{j,\bullet })\rightarrow \cdots\end{eqnarray}$$
stabilize in the strong sense, and the stable image is a finitely generated
![]() $R_{n-j}$
-submodule of
$R_{n-j}$
-submodule of
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
. The statement of our proposition is
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
. The statement of our proposition is
![]() $(\ast _{n})$
, and we will prove
$(\ast _{n})$
, and we will prove
![]() $(\ast _{j})$
for
$(\ast _{j})$
for
 $j=1,\ldots ,n$
by induction on
$j=1,\ldots ,n$
by induction on
![]() $j$
.
$j$
.
In the base case,
![]() $j=1$
, the complex
$j=1$
, the complex
 $M\otimes \unicode[STIX]{x1D6FA}_{R^{1}}^{\bullet }$
takes the form
$M\otimes \unicode[STIX]{x1D6FA}_{R^{1}}^{\bullet }$
takes the form
 $0\rightarrow M\xrightarrow[{}]{\unicode[STIX]{x2202}_{n}}M\rightarrow 0$
, and its
$0\rightarrow M\xrightarrow[{}]{\unicode[STIX]{x2202}_{n}}M\rightarrow 0$
, and its
![]() $l$
th approximation
$l$
th approximation
![]() ${\mathcal{M}}_{l}^{1,\bullet }$
takes the form
${\mathcal{M}}_{l}^{1,\bullet }$
takes the form
 $0\rightarrow M_{l}\xrightarrow[{}]{\unicode[STIX]{x2202}_{n}}M_{l+1}\rightarrow 0$
. By assumption,
$0\rightarrow M_{l}\xrightarrow[{}]{\unicode[STIX]{x2202}_{n}}M_{l+1}\rightarrow 0$
. By assumption,
![]() $M$
is
$M$
is
![]() $x_{n}$
-regular, so we may apply Lemma 5.28 to the direct system
$x_{n}$
-regular, so we may apply Lemma 5.28 to the direct system
![]() $\{M_{l}\}$
: every
$\{M_{l}\}$
: every
![]() $M_{l}$
is already a finitely generated
$M_{l}$
is already a finitely generated
![]() $R$
-module, so we simply take
$R$
-module, so we simply take
 $N_{l}=M_{l}$
in the statement of that lemma. The statement
$N_{l}=M_{l}$
in the statement of that lemma. The statement
![]() $(\ast _{1})$
follows at once.
$(\ast _{1})$
follows at once.
Now suppose
![]() $j\geqslant 1$
and
$j\geqslant 1$
and
![]() $(\ast _{j})$
established. By assumption, the
$(\ast _{j})$
established. By assumption, the
![]() ${\mathcal{D}}_{n-j}$
-modules
${\mathcal{D}}_{n-j}$
-modules
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
are holonomic and
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
are holonomic and
![]() $x_{n-j}$
-regular. By the inductive hypothesis
$x_{n-j}$
-regular. By the inductive hypothesis
![]() $(\ast _{j})$
, the images of
$(\ast _{j})$
, the images of
 $h^{i}({\mathcal{M}}_{l}^{j,\bullet })$
(for any
$h^{i}({\mathcal{M}}_{l}^{j,\bullet })$
(for any
![]() $i$
and
$i$
and
![]() $l$
) in the direct system (*) stabilize in the strong sense, and the stable image is a finitely generated
$l$
) in the direct system (*) stabilize in the strong sense, and the stable image is a finitely generated
![]() $R_{n-j}$
-module; applying this reasoning to all
$R_{n-j}$
-module; applying this reasoning to all
![]() $i$
at once, we see that given any
$i$
at once, we see that given any
![]() $l$
, there exists
$l$
, there exists
![]() $s$
such that, for all
$s$
such that, for all
![]() $i$
,
$i$
,
 $h^{i}({\mathcal{M}}_{l+s}^{j,\bullet })$
contains the stable image of
$h^{i}({\mathcal{M}}_{l+s}^{j,\bullet })$
contains the stable image of
 $h^{i}({\mathcal{M}}_{l}^{j,\bullet })$
. (To keep the notation as simple as possible, we will not always record the dependence on
$h^{i}({\mathcal{M}}_{l}^{j,\bullet })$
. (To keep the notation as simple as possible, we will not always record the dependence on
![]() $i$
of various objects and maps. At each stage, we assume that constructions are being carried out for all
$i$
of various objects and maps. At each stage, we assume that constructions are being carried out for all
![]() $i$
at once, and that indices large enough to work for all
$i$
at once, and that indices large enough to work for all
![]() $i$
have been chosen.) Fix
$i$
have been chosen.) Fix
![]() $l$
and let
$l$
and let
 $N\subset h^{i}({\mathcal{M}}_{l+s}^{j,\bullet })$
be this stable image, which we can identify with an
$N\subset h^{i}({\mathcal{M}}_{l+s}^{j,\bullet })$
be this stable image, which we can identify with an
![]() $R_{n-j}$
-submodule of
$R_{n-j}$
-submodule of
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
.
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
.
For all
![]() $t$
, we have
$t$
, we have
![]() $R_{n-j-1}$
-linear maps
$R_{n-j-1}$
-linear maps
 $\unicode[STIX]{x2202}_{n-j}^{t}:h^{i}({\mathcal{M}}_{t}^{j,\bullet })\rightarrow h^{i}({\mathcal{M}}_{t+1}^{j,\bullet })$
, which are (up to a sign) the connecting homomorphisms in the long exact cohomology sequence associated with the short exact sequence of complexes
$\unicode[STIX]{x2202}_{n-j}^{t}:h^{i}({\mathcal{M}}_{t}^{j,\bullet })\rightarrow h^{i}({\mathcal{M}}_{t+1}^{j,\bullet })$
, which are (up to a sign) the connecting homomorphisms in the long exact cohomology sequence associated with the short exact sequence of complexes
 $$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{t+1}^{j,\bullet }[-1]\rightarrow {\mathcal{M}}_{t}^{j+1,\bullet }\rightarrow {\mathcal{M}}_{t}^{j,\bullet }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{t+1}^{j,\bullet }[-1]\rightarrow {\mathcal{M}}_{t}^{j+1,\bullet }\rightarrow {\mathcal{M}}_{t}^{j,\bullet }\rightarrow 0\end{eqnarray}$$
described earlier. The direct limit
 $\varinjlim \unicode[STIX]{x2202}_{n-j}^{t}$
is
$\varinjlim \unicode[STIX]{x2202}_{n-j}^{t}$
is
 $\unicode[STIX]{x2202}_{n-j}:h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })\rightarrow h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
. The direct system (*) induces a direct system
$\unicode[STIX]{x2202}_{n-j}:h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })\rightarrow h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
. The direct system (*) induces a direct system
 $$\begin{eqnarray}\cdots \rightarrow \ker \unicode[STIX]{x2202}_{n-j}^{l+s-1}\rightarrow \ker \unicode[STIX]{x2202}_{n-j}^{l+s}\rightarrow \ker \unicode[STIX]{x2202}_{n-j}^{l+s+1}\rightarrow \cdots \,;\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow \ker \unicode[STIX]{x2202}_{n-j}^{l+s-1}\rightarrow \ker \unicode[STIX]{x2202}_{n-j}^{l+s}\rightarrow \ker \unicode[STIX]{x2202}_{n-j}^{l+s+1}\rightarrow \cdots \,;\end{eqnarray}$$
by Lemma 5.28, the images of
 $N\cap \ker \unicode[STIX]{x2202}_{n-j}^{l+s}$
in the direct system (**) stabilize in the strong sense, and the stable image is a finitely generated
$N\cap \ker \unicode[STIX]{x2202}_{n-j}^{l+s}$
in the direct system (**) stabilize in the strong sense, and the stable image is a finitely generated
![]() $R_{n-j-1}$
-submodule of
$R_{n-j-1}$
-submodule of
 $\ker \unicode[STIX]{x2202}_{n-j}$
. The image of
$\ker \unicode[STIX]{x2202}_{n-j}$
. The image of
 $\ker \unicode[STIX]{x2202}_{n-j}^{l}$
in
$\ker \unicode[STIX]{x2202}_{n-j}^{l}$
in
 $\ker \unicode[STIX]{x2202}_{n-j}^{l+s}$
is
$\ker \unicode[STIX]{x2202}_{n-j}^{l+s}$
is
 $N\cap \ker \unicode[STIX]{x2202}_{n-j}^{l+s}$
; consequently, the images of
$N\cap \ker \unicode[STIX]{x2202}_{n-j}^{l+s}$
; consequently, the images of
 $\ker \unicode[STIX]{x2202}_{n-j}^{l}$
in the direct system (**) also stabilize in the strong sense, and the stable image is a finitely generated
$\ker \unicode[STIX]{x2202}_{n-j}^{l}$
in the direct system (**) also stabilize in the strong sense, and the stable image is a finitely generated
![]() $R_{n-j-1}$
-module. Enlarging
$R_{n-j-1}$
-module. Enlarging
![]() $s$
if necessary, we may assume the images of
$s$
if necessary, we may assume the images of
 $\ker \unicode[STIX]{x2202}_{n-j}^{l}$
stabilize at the
$\ker \unicode[STIX]{x2202}_{n-j}^{l}$
stabilize at the
![]() $(l+s)$
th stage. We fix this
$(l+s)$
th stage. We fix this
![]() $s$
for the rest of the proof.
$s$
for the rest of the proof.
We now extract more information from the long exact cohomology sequences, which take the form
 $$\begin{eqnarray}\cdots \rightarrow h^{i-1}({\mathcal{M}}_{t}^{j,\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{n-j}^{t}}h^{i-1}({\mathcal{M}}_{t+1}^{j,\bullet })\rightarrow h^{i}({\mathcal{M}}_{t}^{j+1,\bullet })\xrightarrow[{}]{\unicode[STIX]{x1D713}_{t}}h^{i}({\mathcal{M}}_{t}^{j,\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{n-j}^{t}}h^{i}({\mathcal{M}}_{t+1}^{j,\bullet })\rightarrow \cdots \,;\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow h^{i-1}({\mathcal{M}}_{t}^{j,\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{n-j}^{t}}h^{i-1}({\mathcal{M}}_{t+1}^{j,\bullet })\rightarrow h^{i}({\mathcal{M}}_{t}^{j+1,\bullet })\xrightarrow[{}]{\unicode[STIX]{x1D713}_{t}}h^{i}({\mathcal{M}}_{t}^{j,\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{n-j}^{t}}h^{i}({\mathcal{M}}_{t+1}^{j,\bullet })\rightarrow \cdots \,;\end{eqnarray}$$
by the exactness, we have surjections
 $$\begin{eqnarray}h^{i}({\mathcal{M}}_{t}^{j+1,\bullet }){\twoheadrightarrow}\ker \unicode[STIX]{x2202}_{n-j}^{t}\end{eqnarray}$$
$$\begin{eqnarray}h^{i}({\mathcal{M}}_{t}^{j+1,\bullet }){\twoheadrightarrow}\ker \unicode[STIX]{x2202}_{n-j}^{t}\end{eqnarray}$$
for all
![]() $t$
. We also have commutative diagrams
$t$
. We also have commutative diagrams

for all
![]() $t$
(where the vertical arrow
$t$
(where the vertical arrow
![]() $\unicode[STIX]{x1D704}_{t}^{j}$
is the transition map from the
$\unicode[STIX]{x1D704}_{t}^{j}$
is the transition map from the
![]() $l$
th to the
$l$
th to the
![]() $(l+t)$
th stage in the direct system (*)), so the previous surjections induce surjections
$(l+t)$
th stage in the direct system (*)), so the previous surjections induce surjections
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{t}^{j+1}(h^{i}({\mathcal{M}}_{l}^{j+1,\bullet })){\twoheadrightarrow}\unicode[STIX]{x1D704}_{t}^{j}(\ker \unicode[STIX]{x2202}_{n-j}^{l})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{t}^{j+1}(h^{i}({\mathcal{M}}_{l}^{j+1,\bullet })){\twoheadrightarrow}\unicode[STIX]{x1D704}_{t}^{j}(\ker \unicode[STIX]{x2202}_{n-j}^{l})\end{eqnarray}$$
whose kernels we denote
![]() $K_{l+t}$
. Consider, for any
$K_{l+t}$
. Consider, for any
![]() $t\geqslant s$
, the commutative diagram
$t\geqslant s$
, the commutative diagram

with exact rows. The right vertical arrow is an isomorphism, since the images of
 $\ker \unicode[STIX]{x2202}_{n-j}^{l}$
in the direct system (**) have already stabilized at the
$\ker \unicode[STIX]{x2202}_{n-j}^{l}$
in the direct system (**) have already stabilized at the
![]() $(l+s)$
th stage, and the middle vertical arrow is a surjection, since
$(l+s)$
th stage, and the middle vertical arrow is a surjection, since
![]() $\unicode[STIX]{x1D704}_{t}^{j+1}$
factors through
$\unicode[STIX]{x1D704}_{t}^{j+1}$
factors through
![]() $\unicode[STIX]{x1D704}_{s}^{j+1}$
by the compatibility of transition and insertion maps in (*). It follows by the snake lemma that the left vertical arrow is also a surjection, so for
$\unicode[STIX]{x1D704}_{s}^{j+1}$
by the compatibility of transition and insertion maps in (*). It follows by the snake lemma that the left vertical arrow is also a surjection, so for
![]() $t\geqslant s$
the image of
$t\geqslant s$
the image of
![]() $K_{l+s}$
in
$K_{l+s}$
in
![]() $K_{l+t}$
is all of
$K_{l+t}$
is all of
![]() $K_{l+t}$
.
$K_{l+t}$
.
The direct system (*) also induces a direct system
 $$\begin{eqnarray}\cdots \rightarrow \operatorname{coker}\unicode[STIX]{x2202}_{n-j}^{l+s-1}\rightarrow \operatorname{coker}\unicode[STIX]{x2202}_{n-j}^{l+s}\rightarrow \operatorname{coker}\unicode[STIX]{x2202}_{n-j}^{l+s+1}\rightarrow \cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow \operatorname{coker}\unicode[STIX]{x2202}_{n-j}^{l+s-1}\rightarrow \operatorname{coker}\unicode[STIX]{x2202}_{n-j}^{l+s}\rightarrow \operatorname{coker}\unicode[STIX]{x2202}_{n-j}^{l+s+1}\rightarrow \cdots \,,\end{eqnarray}$$
and we claim next that the images of
 $$\begin{eqnarray}\operatorname{coker}(\unicode[STIX]{x2202}_{n-j}^{l+s}:h^{i-1}({\mathcal{M}}_{l+s}^{j,\bullet })\rightarrow h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet }))\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{coker}(\unicode[STIX]{x2202}_{n-j}^{l+s}:h^{i-1}({\mathcal{M}}_{l+s}^{j,\bullet })\rightarrow h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet }))\end{eqnarray}$$
in the direct system (***) stabilize in the strong sense. To this end, we repeat the reasoning we gave for the kernels of
![]() $\unicode[STIX]{x2202}_{n-j}$
at the beginning of the proof, this time for cokernels. We write
$\unicode[STIX]{x2202}_{n-j}$
at the beginning of the proof, this time for cokernels. We write
 $\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })}$
for the cokernel displayed above, and more generally, if
$\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })}$
for the cokernel displayed above, and more generally, if
![]() $S$
is an
$S$
is an
![]() $R_{n-j}$
-submodule of
$R_{n-j}$
-submodule of
 $h^{i-1}({\mathcal{M}}_{l+t}^{j,\bullet })$
for some
$h^{i-1}({\mathcal{M}}_{l+t}^{j,\bullet })$
for some
![]() $t$
(respectively
$t$
(respectively
 $h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
), we write
$h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
), we write
![]() $\overline{S}$
for the image of
$\overline{S}$
for the image of
![]() $S$
in the cokernel of
$S$
in the cokernel of
![]() $\unicode[STIX]{x2202}_{n-j}^{l+t}$
(respectively
$\unicode[STIX]{x2202}_{n-j}^{l+t}$
(respectively
![]() $\unicode[STIX]{x2202}_{n-j}$
). First, by the inductive hypothesis
$\unicode[STIX]{x2202}_{n-j}$
). First, by the inductive hypothesis
![]() $(\ast _{j})$
, the images of
$(\ast _{j})$
, the images of
 $h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })$
in the direct system (*) stabilize in the strong sense, and the stable image is a finitely generated
$h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })$
in the direct system (*) stabilize in the strong sense, and the stable image is a finitely generated
![]() $R_{n-j}$
-submodule
$R_{n-j}$
-submodule
![]() $L$
of
$L$
of
 $h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
, realized as a submodule of
$h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })$
, realized as a submodule of
 $h^{i-1}({\mathcal{M}}_{l+s+u+1}^{j,\bullet })$
for sufficiently large
$h^{i-1}({\mathcal{M}}_{l+s+u+1}^{j,\bullet })$
for sufficiently large
![]() $u$
. Consider the image
$u$
. Consider the image
![]() $\overline{L}$
of
$\overline{L}$
of
![]() $L$
in the quotient
$L$
in the quotient
 $\overline{h^{i-1}({\mathcal{M}}_{l+s+u+1}^{j,\bullet })}$
. Lemma 5.28 implies that the images of
$\overline{h^{i-1}({\mathcal{M}}_{l+s+u+1}^{j,\bullet })}$
. Lemma 5.28 implies that the images of
![]() $\overline{L}$
in the direct system (***) stabilize in the strong sense, and the stable image is a finitely generated
$\overline{L}$
in the direct system (***) stabilize in the strong sense, and the stable image is a finitely generated
![]() $R_{n-j-1}$
-module. The image of
$R_{n-j-1}$
-module. The image of
 $\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })}$
in
$\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })}$
in
 $\overline{h^{i-1}({\mathcal{M}}_{l+s+u+1}^{j,\bullet })}$
is
$\overline{h^{i-1}({\mathcal{M}}_{l+s+u+1}^{j,\bullet })}$
is
![]() $\overline{L}$
, so the images of
$\overline{L}$
, so the images of
 $\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })}$
in the direct system (***) also stabilize in the strong sense, and the stable image is a finitely generated
$\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })}$
in the direct system (***) also stabilize in the strong sense, and the stable image is a finitely generated
![]() $R_{n-j-1}$
-submodule of
$R_{n-j-1}$
-submodule of
 $\overline{h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })}$
. This stable image occurs at the
$\overline{h^{i-1}(M\otimes \unicode[STIX]{x1D6FA}_{R^{j}}^{\bullet })}$
. This stable image occurs at the
 $(l+s+u+1+v)$
th stage for some
$(l+s+u+1+v)$
th stage for some
![]() $v$
: for simplicity, let
$v$
: for simplicity, let
 $w=u+1+v$
.
$w=u+1+v$
.
We have
 $K_{l+s}\subset \ker \unicode[STIX]{x1D713}_{l+s}$
, and by the exactness of the long cohomology sequence,
$K_{l+s}\subset \ker \unicode[STIX]{x1D713}_{l+s}$
, and by the exactness of the long cohomology sequence,
 $$\begin{eqnarray}\ker \unicode[STIX]{x1D713}_{l+s}\simeq \operatorname{coker}\unicode[STIX]{x2202}_{n-j}^{l+s}\,(=\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })})\end{eqnarray}$$
$$\begin{eqnarray}\ker \unicode[STIX]{x1D713}_{l+s}\simeq \operatorname{coker}\unicode[STIX]{x2202}_{n-j}^{l+s}\,(=\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })})\end{eqnarray}$$
as
![]() $R_{n-j-1}$
-modules. These isomorphisms are functorial in
$R_{n-j-1}$
-modules. These isomorphisms are functorial in
![]() $s$
, so since the images of
$s$
, so since the images of
 $\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })}$
in the direct system (***) stabilize in the strong sense (with stable image a finitely generated
$\overline{h^{i-1}({\mathcal{M}}_{l+s+1}^{j,\bullet })}$
in the direct system (***) stabilize in the strong sense (with stable image a finitely generated
![]() $R_{n-j-1}$
-submodule of
$R_{n-j-1}$
-submodule of
 $\overline{h^{i-1}({\mathcal{M}}_{l+s+w}^{j,\bullet })}$
), we can conclude that the image of
$\overline{h^{i-1}({\mathcal{M}}_{l+s+w}^{j,\bullet })}$
), we can conclude that the image of
 $\ker \unicode[STIX]{x1D713}_{l+s}$
in
$\ker \unicode[STIX]{x1D713}_{l+s}$
in
 $\ker \unicode[STIX]{x1D713}_{l+s+w}$
is also a finitely generated
$\ker \unicode[STIX]{x1D713}_{l+s+w}$
is also a finitely generated
![]() $R_{n-j-1}$
-module. This module contains the image of
$R_{n-j-1}$
-module. This module contains the image of
![]() $K_{l+s}$
in
$K_{l+s}$
in
![]() $K_{l+s+w}$
; we have already seen that this image is all of
$K_{l+s+w}$
; we have already seen that this image is all of
![]() $K_{l+s+w}$
, which implies that
$K_{l+s+w}$
, which implies that
![]() $K_{l+s+w}$
is itself a finitely generated
$K_{l+s+w}$
is itself a finitely generated
![]() $R_{n-j-1}$
-module. We have a short exact sequence
$R_{n-j-1}$
-module. We have a short exact sequence
 $$\begin{eqnarray}0\rightarrow K_{l+s+w}\rightarrow \unicode[STIX]{x1D704}_{s+w}^{j+1}(h^{i}({\mathcal{M}}_{l}^{j+1,\bullet }))\rightarrow \unicode[STIX]{x1D704}_{s+w}^{j}(\ker \unicode[STIX]{x2202}_{n-j}^{l})\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow K_{l+s+w}\rightarrow \unicode[STIX]{x1D704}_{s+w}^{j+1}(h^{i}({\mathcal{M}}_{l}^{j+1,\bullet }))\rightarrow \unicode[STIX]{x1D704}_{s+w}^{j}(\ker \unicode[STIX]{x2202}_{n-j}^{l})\rightarrow 0,\end{eqnarray}$$
where the left and right terms are finitely generated
![]() $R_{n-j-1}$
-modules, so the middle term is also a finitely generated
$R_{n-j-1}$
-modules, so the middle term is also a finitely generated
![]() $R_{n-j-1}$
-module. Hence, the images of
$R_{n-j-1}$
-module. Hence, the images of
 $h^{i}({\mathcal{M}}_{l}^{j+1,\bullet })$
in the direct system (*) are eventually finitely generated
$h^{i}({\mathcal{M}}_{l}^{j+1,\bullet })$
in the direct system (*) are eventually finitely generated
![]() $R_{n-j-1}$
-modules, and it therefore follows by Lemma 5.11 that these images also stabilize in the strong sense. This completes the proof of
$R_{n-j-1}$
-modules, and it therefore follows by Lemma 5.11 that these images also stabilize in the strong sense. This completes the proof of
![]() $(\ast _{j+1})$
, and, by induction, Proposition 5.30 follows.◻
$(\ast _{j+1})$
, and, by induction, Proposition 5.30 follows.◻
By reducing to the case of Proposition 5.30, it is possible to draw the same conclusion about more general direct systems of complexes with the same limit. We record this conclusion now; the reader is warned that the following statement will not be used until § 7.
Corollary 5.31. Let
![]() $M$
be a holonomic
$M$
be a holonomic
![]() ${\mathcal{D}}$
-module. Suppose that
${\mathcal{D}}$
-module. Suppose that
![]() $\{N_{l}^{\bullet }\}$
is a direct system of complexes with the following properties: the objects of the complexes are finitely generated
$\{N_{l}^{\bullet }\}$
is a direct system of complexes with the following properties: the objects of the complexes are finitely generated
![]() $R$
-modules, the differentials are
$R$
-modules, the differentials are
![]() $k$
-linear, the transition maps
$k$
-linear, the transition maps
![]() $\unicode[STIX]{x1D706}_{l,l+s}^{\bullet }$
are
$\unicode[STIX]{x1D706}_{l,l+s}^{\bullet }$
are
![]() $R$
-linear in each degree,
$R$
-linear in each degree,
 $\varinjlim N_{l}^{\bullet }\simeq M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
in the category of complexes of
$\varinjlim N_{l}^{\bullet }\simeq M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
in the category of complexes of
![]() $k$
-spaces, and for all
$k$
-spaces, and for all
![]() $i$
, the isomorphism
$i$
, the isomorphism
 $\varinjlim N_{l}^{i}\simeq M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}$
is an isomorphism of
$\varinjlim N_{l}^{i}\simeq M\otimes \unicode[STIX]{x1D6FA}_{R}^{i}$
is an isomorphism of
![]() $R$
-modules. Then for all
$R$
-modules. Then for all
![]() $l$
and
$l$
and
![]() $i$
, the images of
$i$
, the images of
![]() $h^{i}(N_{l}^{\bullet })$
stabilize in the strong sense, with finite-dimensional stable image.
$h^{i}(N_{l}^{\bullet })$
stabilize in the strong sense, with finite-dimensional stable image.
Proof. We note first that it is harmless to assume the isomorphism
 $\varinjlim N_{l}^{\bullet }\simeq M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
is an equality, and we do so. Fix
$\varinjlim N_{l}^{\bullet }\simeq M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
is an equality, and we do so. Fix
![]() $l$
. For all
$l$
. For all
![]() $i$
, the images of
$i$
, the images of
![]() $N_{l}^{i}$
stabilize in the strong sense by Lemma 5.11, since by assumption the
$N_{l}^{i}$
stabilize in the strong sense by Lemma 5.11, since by assumption the
![]() $N_{l}^{i}$
are finitely generated and the transition maps are
$N_{l}^{i}$
are finitely generated and the transition maps are
![]() $R$
-linear. Choose
$R$
-linear. Choose
![]() $s$
large enough that the transition maps
$s$
large enough that the transition maps
![]() $\unicode[STIX]{x1D706}_{l,l+s}^{i}$
realize the stable image for all
$\unicode[STIX]{x1D706}_{l,l+s}^{i}$
realize the stable image for all
![]() $i$
at once. The stable images form a subcomplex
$i$
at once. The stable images form a subcomplex
 $\unicode[STIX]{x1D706}_{l,l+s}(N_{l}^{\bullet })$
of
$\unicode[STIX]{x1D706}_{l,l+s}(N_{l}^{\bullet })$
of
![]() $N_{l+s}^{\bullet }$
which we can identify (via the insertion map, which we denote
$N_{l+s}^{\bullet }$
which we can identify (via the insertion map, which we denote
![]() $\unicode[STIX]{x1D706}_{l+s}^{\bullet }$
) with the subcomplex
$\unicode[STIX]{x1D706}_{l+s}^{\bullet }$
) with the subcomplex
![]() $\unicode[STIX]{x1D706}_{l}(N_{l}^{\bullet })$
of
$\unicode[STIX]{x1D706}_{l}(N_{l}^{\bullet })$
of
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
. Since every
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
. Since every
![]() $N_{l}^{i}$
is a finitely generated
$N_{l}^{i}$
is a finitely generated
![]() $R$
-module and the insertion maps are
$R$
-module and the insertion maps are
![]() $R$
-linear, this is a subcomplex of
$R$
-linear, this is a subcomplex of
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
whose objects are finitely generated
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
whose objects are finitely generated
![]() $R$
-modules.
$R$
-modules.
Now define
 $M_{0}=\unicode[STIX]{x1D706}_{l}^{0}(N_{l}^{0})$
, a finitely generated
$M_{0}=\unicode[STIX]{x1D706}_{l}^{0}(N_{l}^{0})$
, a finitely generated
![]() $R$
-submodule of the holonomic
$R$
-submodule of the holonomic
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
, and for all
$M$
, and for all
![]() $j\geqslant 0$
, let
$j\geqslant 0$
, let
 $M_{j}={\mathcal{D}}^{j}(R)\cdot M_{0}$
where
$M_{j}={\mathcal{D}}^{j}(R)\cdot M_{0}$
where
![]() ${\mathcal{D}}^{j}(R)$
is the
${\mathcal{D}}^{j}(R)$
is the
![]() $R$
-submodule of
$R$
-submodule of
![]() ${\mathcal{D}}$
consisting of differential operators of order at most
${\mathcal{D}}$
consisting of differential operators of order at most
![]() $j$
. Define the complex
$j$
. Define the complex
![]() ${\mathcal{M}}_{j}^{\bullet }$
in exactly the same way as in Definition 5.29. Since
${\mathcal{M}}_{j}^{\bullet }$
in exactly the same way as in Definition 5.29. Since
![]() $\unicode[STIX]{x1D706}_{l}(N_{l}^{\bullet })$
is a subcomplex of
$\unicode[STIX]{x1D706}_{l}(N_{l}^{\bullet })$
is a subcomplex of
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, we see that in fact
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, we see that in fact
![]() $\unicode[STIX]{x1D706}_{l}(N_{l}^{\bullet })$
is a subcomplex of
$\unicode[STIX]{x1D706}_{l}(N_{l}^{\bullet })$
is a subcomplex of
![]() ${\mathcal{M}}_{0}^{\bullet }$
(and hence of
${\mathcal{M}}_{0}^{\bullet }$
(and hence of
![]() ${\mathcal{M}}_{j}^{\bullet }$
for all
${\mathcal{M}}_{j}^{\bullet }$
for all
![]() $j\geqslant 0$
). The proof of Proposition 5.30 still goes through assuming only that
$j\geqslant 0$
). The proof of Proposition 5.30 still goes through assuming only that
![]() $M_{0}$
is a finitely generated
$M_{0}$
is a finitely generated
![]() $R$
-submodule of the holonomic
$R$
-submodule of the holonomic
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
and that
$M$
and that
 $M=\bigcup _{j}M_{j}$
(we do not need
$M=\bigcup _{j}M_{j}$
(we do not need
![]() $M_{0}$
to be cyclic). In our case, since
$M_{0}$
to be cyclic). In our case, since
 $\varinjlim N_{l}^{\bullet }=M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, we also have
$\varinjlim N_{l}^{\bullet }=M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, we also have
 $\varinjlim {\mathcal{M}}_{j}^{\bullet }=M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, where this last direct limit is an ascending union of complexes. (In particular, looking at the
$\varinjlim {\mathcal{M}}_{j}^{\bullet }=M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, where this last direct limit is an ascending union of complexes. (In particular, looking at the
![]() $0$
th term of this complex, we see that the ascending union
$0$
th term of this complex, we see that the ascending union
![]() $\bigcup _{j}M_{j}$
is indeed the whole of
$\bigcup _{j}M_{j}$
is indeed the whole of
![]() $M$
.) Therefore we can invoke Proposition 5.30 (with this weaker hypothesis) to conclude that the images of
$M$
.) Therefore we can invoke Proposition 5.30 (with this weaker hypothesis) to conclude that the images of
![]() $h^{i}({\mathcal{M}}_{j}^{\bullet })$
stabilize in the strong sense. In particular, there exists
$h^{i}({\mathcal{M}}_{j}^{\bullet })$
stabilize in the strong sense. In particular, there exists
![]() $t$
large enough that for all
$t$
large enough that for all
![]() $i$
, the images of
$i$
, the images of
 $h^{i}({\mathcal{M}}_{0}^{\bullet })$
stabilize for
$h^{i}({\mathcal{M}}_{0}^{\bullet })$
stabilize for
![]() $j\geqslant t$
with a finite-dimensional stable image.
$j\geqslant t$
with a finite-dimensional stable image.
The complex
![]() ${\mathcal{M}}_{t}^{\bullet }$
is still a complex of finitely generated
${\mathcal{M}}_{t}^{\bullet }$
is still a complex of finitely generated
![]() $R$
-modules, since
$R$
-modules, since
![]() ${\mathcal{D}}^{t}(R)$
is a finitely generated
${\mathcal{D}}^{t}(R)$
is a finitely generated
![]() $R$
-submodule of
$R$
-submodule of
![]() ${\mathcal{D}}$
. We now return to the stable image of the complex
${\mathcal{D}}$
. We now return to the stable image of the complex
![]() $N_{l}^{\bullet }$
, which is
$N_{l}^{\bullet }$
, which is
 $\unicode[STIX]{x1D706}_{l,l+s}^{\bullet }(N_{l}^{\bullet })$
. Write
$\unicode[STIX]{x1D706}_{l,l+s}^{\bullet }(N_{l}^{\bullet })$
. Write
![]() $s_{l}$
for
$s_{l}$
for
![]() $s$
to display its dependence on
$s$
to display its dependence on
![]() $l$
. As this argument can be carried out for any
$l$
. As this argument can be carried out for any
![]() $l$
, we obtain a direct system
$l$
, we obtain a direct system
 $\unicode[STIX]{x1D706}_{l,l+s_{l}}^{\bullet }(N_{l}^{\bullet })$
of the stable images of
$\unicode[STIX]{x1D706}_{l,l+s_{l}}^{\bullet }(N_{l}^{\bullet })$
of the stable images of
![]() $N_{l}^{\bullet }$
as
$N_{l}^{\bullet }$
as
![]() $l$
varies. We may assume the
$l$
varies. We may assume the
![]() $s_{l}$
have been chosen so that
$s_{l}$
have been chosen so that
![]() $\{l+s_{l}\}$
is strictly increasing; then the transition maps in this direct system are the restrictions, for all pairs
$\{l+s_{l}\}$
is strictly increasing; then the transition maps in this direct system are the restrictions, for all pairs
![]() $l\leqslant l^{\prime }$
, of
$l\leqslant l^{\prime }$
, of
 $\unicode[STIX]{x1D706}_{l+s_{l},l^{\prime }+s_{l^{\prime }}}^{\bullet }$
. Because the source and target complexes are complexes of stable images under the
$\unicode[STIX]{x1D706}_{l+s_{l},l^{\prime }+s_{l^{\prime }}}^{\bullet }$
. Because the source and target complexes are complexes of stable images under the
![]() $\unicode[STIX]{x1D706}$
s, these restricted transition maps are injective, and the direct system so constructed also has
$\unicode[STIX]{x1D706}$
s, these restricted transition maps are injective, and the direct system so constructed also has
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
for its direct limit. Thus
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
for its direct limit. Thus
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
can be regarded as the ascending union of the complexes
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
can be regarded as the ascending union of the complexes
 $\unicode[STIX]{x1D706}_{l^{\prime },l^{\prime }+s_{l^{\prime }}}^{\bullet }(N_{l^{\prime }}^{\bullet })$
, all of which have finitely generated
$\unicode[STIX]{x1D706}_{l^{\prime },l^{\prime }+s_{l^{\prime }}}^{\bullet }(N_{l^{\prime }}^{\bullet })$
, all of which have finitely generated
![]() $R$
-modules as objects. Any subcomplex of
$R$
-modules as objects. Any subcomplex of
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
whose objects are all finitely generated
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
whose objects are all finitely generated
![]() $R$
-modules is thus a subcomplex of some
$R$
-modules is thus a subcomplex of some
 $\unicode[STIX]{x1D706}_{l^{\prime },l^{\prime }+s_{l^{\prime }}}^{\bullet }(N_{l^{\prime }}^{\bullet })$
. Let
$\unicode[STIX]{x1D706}_{l^{\prime },l^{\prime }+s_{l^{\prime }}}^{\bullet }(N_{l^{\prime }}^{\bullet })$
. Let
![]() $l^{\prime }$
be so large that
$l^{\prime }$
be so large that
![]() ${\mathcal{M}}_{t}^{\bullet }$
is a subcomplex of
${\mathcal{M}}_{t}^{\bullet }$
is a subcomplex of
 $\unicode[STIX]{x1D706}_{l^{\prime },l^{\prime }+s_{l^{\prime }}}^{\bullet }(N_{l^{\prime }}^{\bullet })$
, and consider the composite morphism of complexes
$\unicode[STIX]{x1D706}_{l^{\prime },l^{\prime }+s_{l^{\prime }}}^{\bullet }(N_{l^{\prime }}^{\bullet })$
, and consider the composite morphism of complexes
 $$\begin{eqnarray}N_{l}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D706}_{l,l+s_{l}}^{\bullet }}N_{l,l+s_{l}}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D706}_{l+s_{l}}^{\bullet }}{\mathcal{M}}_{0}^{\bullet }{\hookrightarrow}{\mathcal{M}}_{t}^{\bullet }{\hookrightarrow}\unicode[STIX]{x1D706}_{l^{\prime },l^{\prime }+s_{l^{\prime }}}^{\bullet }(N_{l^{\prime }}^{\bullet })\subset N_{l^{\prime }+s_{l^{\prime }}}^{\bullet },\end{eqnarray}$$
$$\begin{eqnarray}N_{l}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D706}_{l,l+s_{l}}^{\bullet }}N_{l,l+s_{l}}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D706}_{l+s_{l}}^{\bullet }}{\mathcal{M}}_{0}^{\bullet }{\hookrightarrow}{\mathcal{M}}_{t}^{\bullet }{\hookrightarrow}\unicode[STIX]{x1D706}_{l^{\prime },l^{\prime }+s_{l^{\prime }}}^{\bullet }(N_{l^{\prime }}^{\bullet })\subset N_{l^{\prime }+s_{l^{\prime }}}^{\bullet },\end{eqnarray}$$
in which all morphisms but possibly the first are injections. Every step in this composite is a morphism of complexes, hence induces a morphism on cohomology. If we choose
![]() $l^{\prime \prime }\leqslant l^{\prime }$
such that
$l^{\prime \prime }\leqslant l^{\prime }$
such that
![]() ${\mathcal{M}}_{0}^{\bullet }$
is a subcomplex of
${\mathcal{M}}_{0}^{\bullet }$
is a subcomplex of
 $\unicode[STIX]{x1D706}_{l^{\prime \prime },l^{\prime \prime }+s_{l^{\prime \prime }}}^{\bullet }(N_{l^{\prime \prime }}^{\bullet })$
, the diagram
$\unicode[STIX]{x1D706}_{l^{\prime \prime },l^{\prime \prime }+s_{l^{\prime \prime }}}^{\bullet }(N_{l^{\prime \prime }}^{\bullet })$
, the diagram

is commutative and all arrows are injections, so we can regard the vertical inclusion
 ${\mathcal{M}}_{0}^{\bullet }{\hookrightarrow}{\mathcal{M}}_{t}^{\bullet }$
as a restriction of
${\mathcal{M}}_{0}^{\bullet }{\hookrightarrow}{\mathcal{M}}_{t}^{\bullet }$
as a restriction of
 $\unicode[STIX]{x1D706}_{l^{\prime \prime }+s_{l^{\prime \prime }},l^{\prime }+s_{l^{\prime }}}$
. This compatibility implies that the composite morphism above induces morphisms on cohomology through which the morphisms induced by
$\unicode[STIX]{x1D706}_{l^{\prime \prime }+s_{l^{\prime \prime }},l^{\prime }+s_{l^{\prime }}}$
. This compatibility implies that the composite morphism above induces morphisms on cohomology through which the morphisms induced by
![]() $\unicode[STIX]{x1D706}_{l,l^{\prime }+s_{l^{\prime }}}^{i}$
factor for all
$\unicode[STIX]{x1D706}_{l,l^{\prime }+s_{l^{\prime }}}^{i}$
factor for all
![]() $i$
. But we have seen already that partway through this composite morphism (at the
$i$
. But we have seen already that partway through this composite morphism (at the
 ${\mathcal{M}}_{0}^{\bullet }{\hookrightarrow}{\mathcal{M}}_{t}^{\bullet }$
stage) the cohomology has attained a finite-dimensional stable image. Therefore, for all
${\mathcal{M}}_{0}^{\bullet }{\hookrightarrow}{\mathcal{M}}_{t}^{\bullet }$
stage) the cohomology has attained a finite-dimensional stable image. Therefore, for all
![]() $i$
, the images of
$i$
, the images of
![]() $h^{i}(N_{l}^{\bullet })$
stabilize, with finite-dimensional stable image, at the
$h^{i}(N_{l}^{\bullet })$
stabilize, with finite-dimensional stable image, at the
 $(l^{\prime }+s_{l^{\prime }})$
th stage.◻
$(l^{\prime }+s_{l^{\prime }})$
th stage.◻
We now return to our original case, and prove Proposition 5.2 (and hence Theorem 5.1).
Proof of Proposition 5.2.
For all
![]() $l$
, the differentials in the complex
$l$
, the differentials in the complex
![]() ${\mathcal{M}}_{l}^{\bullet }$
are
${\mathcal{M}}_{l}^{\bullet }$
are
![]() $\unicode[STIX]{x1D6F4}$
-continuous, and therefore we can consider the Matlis dual
$\unicode[STIX]{x1D6F4}$
-continuous, and therefore we can consider the Matlis dual
![]() $D({\mathcal{M}}_{l}^{\bullet })$
, a complex whose
$D({\mathcal{M}}_{l}^{\bullet })$
, a complex whose
![]() $i$
th object is the
$i$
th object is the
![]() $R$
-module
$R$
-module
 $D({\mathcal{M}}_{l}^{n-i})$
(which is Artinian, since
$D({\mathcal{M}}_{l}^{n-i})$
(which is Artinian, since
![]() ${\mathcal{M}}_{l}^{n-i}$
is finitely generated [Reference MatsumuraMat86, Theorem 18.6(v)]) and whose differentials are
${\mathcal{M}}_{l}^{n-i}$
is finitely generated [Reference MatsumuraMat86, Theorem 18.6(v)]) and whose differentials are
![]() $k$
-linear. By Propositions 3.18 and 3.21(a), the Matlis dual of this complex coincides with its
$k$
-linear. By Propositions 3.18 and 3.21(a), the Matlis dual of this complex coincides with its
![]() $k$
-linear dual. Together with Proposition 3.22, this implies that for all
$k$
-linear dual. Together with Proposition 3.22, this implies that for all
![]() $l$
, the complexes
$l$
, the complexes
![]() ${\mathcal{M}}_{l}^{\bullet }$
and
${\mathcal{M}}_{l}^{\bullet }$
and
 $(D({\mathcal{M}}_{l}^{\bullet }))^{\vee }$
are naturally isomorphic as complexes of
$(D({\mathcal{M}}_{l}^{\bullet }))^{\vee }$
are naturally isomorphic as complexes of
![]() $k$
-spaces, where
$k$
-spaces, where
![]() $\vee$
denotes
$\vee$
denotes
![]() $k$
-linear dual. Note that
$k$
-linear dual. Note that
 $\varprojlim \,D({\mathcal{M}}_{l}^{\bullet })\simeq D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
as complexes of
$\varprojlim \,D({\mathcal{M}}_{l}^{\bullet })\simeq D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
as complexes of
![]() $k$
-spaces, by Remark 3.20.
$k$
-spaces, by Remark 3.20.
For every
![]() $i$
, the inverse system
$i$
, the inverse system
 $\{D({\mathcal{M}}_{l}^{i})\}_{l}$
of
$\{D({\mathcal{M}}_{l}^{i})\}_{l}$
of
![]() $R$
-modules (a fortiori, of
$R$
-modules (a fortiori, of
![]() $k$
-spaces) satisfies the Mittag-Leffler condition, since the transition maps are surjective (they are the Matlis duals of the
$k$
-spaces) satisfies the Mittag-Leffler condition, since the transition maps are surjective (they are the Matlis duals of the
![]() $R$
-linear inclusions
$R$
-linear inclusions
 ${\mathcal{M}}_{l}^{i}{\hookrightarrow}{\mathcal{M}}_{l+1}^{i}$
). Furthermore, the inverse system
${\mathcal{M}}_{l}^{i}{\hookrightarrow}{\mathcal{M}}_{l+1}^{i}$
). Furthermore, the inverse system
 $\{h^{i}(D({\mathcal{M}}_{l}^{\bullet }))\}_{l}$
of
$\{h^{i}(D({\mathcal{M}}_{l}^{\bullet }))\}_{l}$
of
![]() $k$
-spaces also satisfies the Mittag-Leffler condition. To see this, note that for all
$k$
-spaces also satisfies the Mittag-Leffler condition. To see this, note that for all
![]() $i$
, we have
$i$
, we have
 $$\begin{eqnarray}h^{n-i}({\mathcal{M}}_{l}^{\bullet })\simeq h^{n-i}(D({\mathcal{M}}_{l}^{\bullet })^{\vee })\simeq (h^{i}(D({\mathcal{M}}_{l}^{\bullet })))^{\vee };\end{eqnarray}$$
$$\begin{eqnarray}h^{n-i}({\mathcal{M}}_{l}^{\bullet })\simeq h^{n-i}(D({\mathcal{M}}_{l}^{\bullet })^{\vee })\simeq (h^{i}(D({\mathcal{M}}_{l}^{\bullet })))^{\vee };\end{eqnarray}$$
the first isomorphism holds because
 ${\mathcal{M}}_{l}^{\bullet }\simeq (D({\mathcal{M}}_{l}^{\bullet }))^{\vee }$
as complexes of
${\mathcal{M}}_{l}^{\bullet }\simeq (D({\mathcal{M}}_{l}^{\bullet }))^{\vee }$
as complexes of
![]() $k$
-spaces, and the second holds because
$k$
-spaces, and the second holds because
![]() $k$
-linear dual is an exact contravariant functor. By Proposition 5.30, the images of
$k$
-linear dual is an exact contravariant functor. By Proposition 5.30, the images of
 $h^{n-i}({\mathcal{M}}_{l}^{\bullet })\simeq (h^{i}(D({\mathcal{M}}_{l}^{\bullet })))^{\vee }$
stabilize in the strong sense, so by Lemma 5.13, the original system
$h^{n-i}({\mathcal{M}}_{l}^{\bullet })\simeq (h^{i}(D({\mathcal{M}}_{l}^{\bullet })))^{\vee }$
stabilize in the strong sense, so by Lemma 5.13, the original system
 $\{h^{i}(D({\mathcal{M}}_{l}^{\bullet }))\}$
satisfies Mittag-Leffler. The Mittag-Leffler conditions for
$\{h^{i}(D({\mathcal{M}}_{l}^{\bullet }))\}$
satisfies Mittag-Leffler. The Mittag-Leffler conditions for
 $\{D({\mathcal{M}}_{l}^{i})\}$
and
$\{D({\mathcal{M}}_{l}^{i})\}$
and
 $\{h^{i}(D({\mathcal{M}}_{l}^{\bullet }))\}$
allow us to apply Proposition 5.9, which implies that there are isomorphisms
$\{h^{i}(D({\mathcal{M}}_{l}^{\bullet }))\}$
allow us to apply Proposition 5.9, which implies that there are isomorphisms
 $$\begin{eqnarray}h^{i}(\varprojlim \,D({\mathcal{M}}_{l}^{\bullet }))\xrightarrow[{}]{{\sim}}\varprojlim \,h^{i}(D({\mathcal{M}}_{l}^{\bullet })).\end{eqnarray}$$
$$\begin{eqnarray}h^{i}(\varprojlim \,D({\mathcal{M}}_{l}^{\bullet }))\xrightarrow[{}]{{\sim}}\varprojlim \,h^{i}(D({\mathcal{M}}_{l}^{\bullet })).\end{eqnarray}$$
of
![]() $k$
-spaces. Therefore, we have a chain of isomorphisms
$k$
-spaces. Therefore, we have a chain of isomorphisms
 $$\begin{eqnarray}\displaystyle h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }) & \simeq & \displaystyle (h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))^{\vee \vee }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }) & \simeq & \displaystyle (h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))^{\vee \vee }\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (h^{i}(\varinjlim {\mathcal{M}}_{l}^{\bullet }))^{\vee \vee }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (h^{i}(\varinjlim {\mathcal{M}}_{l}^{\bullet }))^{\vee \vee }\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varinjlim h^{i}({\mathcal{M}}_{l}^{\bullet }))^{\vee \vee }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varinjlim h^{i}({\mathcal{M}}_{l}^{\bullet }))^{\vee \vee }\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varprojlim \,(h^{i}({\mathcal{M}}_{l}^{\bullet }))^{\vee })^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varprojlim \,(h^{i}({\mathcal{M}}_{l}^{\bullet }))^{\vee })^{\vee }\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varprojlim \,(h^{i}((D({\mathcal{M}}_{l}^{\bullet }))^{\vee }))^{\vee })^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varprojlim \,(h^{i}((D({\mathcal{M}}_{l}^{\bullet }))^{\vee }))^{\vee })^{\vee }\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varprojlim \,(h^{n-i}(D({\mathcal{M}}_{l}^{\bullet })))^{\vee \vee })^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varprojlim \,(h^{n-i}(D({\mathcal{M}}_{l}^{\bullet })))^{\vee \vee })^{\vee }\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varprojlim \,h^{n-i}(D({\mathcal{M}}_{l}^{\bullet })))^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (\varprojlim \,h^{n-i}(D({\mathcal{M}}_{l}^{\bullet })))^{\vee }\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (h^{n-i}(\varprojlim \,D({\mathcal{M}}_{l}^{\bullet })))^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (h^{n-i}(\varprojlim \,D({\mathcal{M}}_{l}^{\bullet })))^{\vee }\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (h^{n-i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })))^{\vee },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \simeq & \displaystyle (h^{n-i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })))^{\vee },\end{eqnarray}$$
where (1) holds because
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
is a finite-dimensional
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
is a finite-dimensional
![]() $k$
-space, (3) since
$k$
-space, (3) since
![]() $\varinjlim$
is exact and thus commutes with cohomology, (4) because taking
$\varinjlim$
is exact and thus commutes with cohomology, (4) because taking
![]() $k$
-dual converts direct limits into inverse limits [Reference RotmanRot09, Proposition 5.26], (5) since
$k$
-dual converts direct limits into inverse limits [Reference RotmanRot09, Proposition 5.26], (5) since
![]() ${\mathcal{M}}_{l}^{\bullet }$
and
${\mathcal{M}}_{l}^{\bullet }$
and
 $(D({\mathcal{M}}_{l}^{\bullet }))^{\vee }$
are isomorphic complexes of
$(D({\mathcal{M}}_{l}^{\bullet }))^{\vee }$
are isomorphic complexes of
![]() $k$
-spaces, (6) since
$k$
-spaces, (6) since
![]() $k$
-dual is an exact contravariant functor, (7) by Lemma 5.14 applied to the inverse system
$k$
-dual is an exact contravariant functor, (7) by Lemma 5.14 applied to the inverse system
 $\{h^{i}(D({\mathcal{M}}_{l}^{\bullet }))\}$
, (8) by Proposition 5.9, and (9) by Remark 3.20. Since
$\{h^{i}(D({\mathcal{M}}_{l}^{\bullet }))\}$
, (8) by Proposition 5.9, and (9) by Remark 3.20. Since
 $h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
is a finite-dimensional
$h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
is a finite-dimensional
![]() $k$
-space, all of the
$k$
-space, all of the
![]() $k$
-spaces appearing in the chain of isomorphisms are finite-dimensional as well. Therefore
$k$
-spaces appearing in the chain of isomorphisms are finite-dimensional as well. Therefore
 $h^{n-i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))$
is canonically isomorphic to its own double dual, so we can dualize the isomorphism obtained above to find
$h^{n-i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))$
is canonically isomorphic to its own double dual, so we can dualize the isomorphism obtained above to find
 $h^{n-i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))\simeq (h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))^{\vee }$
, as desired.◻
$h^{n-i}(D(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))\simeq (h^{i}(M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))^{\vee }$
, as desired.◻
6 Local cohomology of formal schemes
In this section, we recall the description of the Matlis duals of local cohomology modules (over any local Gorenstein ring) in terms of local cohomology on a formal scheme. (A reference for this description is Ogus’s thesis [Reference OgusOgu73].) Specializing to the case of a complete local ring with a coefficient field, we obtain a right
![]() ${\mathcal{D}}$
-module structure on the local cohomology of a formal scheme by applying the results of § 4 to dualize the left
${\mathcal{D}}$
-module structure on the local cohomology of a formal scheme by applying the results of § 4 to dualize the left
![]() ${\mathcal{D}}$
-module structure on ordinary local cohomology. We then recall a natural left
${\mathcal{D}}$
-module structure on ordinary local cohomology. We then recall a natural left
![]() ${\mathcal{D}}$
-module structure on the local cohomology of the formal scheme: the structure implicitly used to define its de Rham complex in [Reference HartshorneHar75]. The main result of this section is that in the case where the complete local ring is regular and of characteristic zero, these left and right
${\mathcal{D}}$
-module structure on the local cohomology of the formal scheme: the structure implicitly used to define its de Rham complex in [Reference HartshorneHar75]. The main result of this section is that in the case where the complete local ring is regular and of characteristic zero, these left and right
![]() ${\mathcal{D}}$
-module structures are transposes of each other, so our theory and that of [Reference HartshorneHar75] are compatible.
${\mathcal{D}}$
-module structures are transposes of each other, so our theory and that of [Reference HartshorneHar75] are compatible.
Let
![]() $(R,\mathfrak{m})$
be a Gorenstein local ring. The key ingredient in the identification of the Matlis duals of local cohomology modules over
$(R,\mathfrak{m})$
be a Gorenstein local ring. The key ingredient in the identification of the Matlis duals of local cohomology modules over
![]() $R$
with local cohomology of a formal scheme is the local duality theorem of Grothendieck.
$R$
with local cohomology of a formal scheme is the local duality theorem of Grothendieck.
Theorem 6.1 [Reference HartshorneHar67, Theorem 6.3].
Let
![]() $(R,\mathfrak{m})$
be a Gorenstein local ring of dimension
$(R,\mathfrak{m})$
be a Gorenstein local ring of dimension
![]() $n$
,
$n$
,
![]() $E$
an injective hull of its residue field, and
$E$
an injective hull of its residue field, and
 $D(-)=\operatorname{Hom}_{R}(-,E)$
the Matlis dual functor for
$D(-)=\operatorname{Hom}_{R}(-,E)$
the Matlis dual functor for
![]() $R$
-modules. If
$R$
-modules. If
![]() $M$
is a finitely generated
$M$
is a finitely generated
![]() $R$
-module, there are isomorphisms
$R$
-module, there are isomorphisms
 $H_{\mathfrak{m}}^{n-i}(M)\simeq D(\operatorname{Ext}_{R}^{i}(M,R))$
, for all
$H_{\mathfrak{m}}^{n-i}(M)\simeq D(\operatorname{Ext}_{R}^{i}(M,R))$
, for all
![]() $i$
, that are functorial in
$i$
, that are functorial in
![]() $M$
.
$M$
.
Remark 6.2. If moreover
![]() $R$
is complete, we also have
$R$
is complete, we also have
 $\operatorname{Ext}_{R}^{n-i}(M,R)\simeq D(H_{\mathfrak{m}}^{i}(M))$
, since the double Matlis dual and the identity functor are naturally isomorphic when restricted to the full subcategories of finitely generated or Artinian
$\operatorname{Ext}_{R}^{n-i}(M,R)\simeq D(H_{\mathfrak{m}}^{i}(M))$
, since the double Matlis dual and the identity functor are naturally isomorphic when restricted to the full subcategories of finitely generated or Artinian
![]() $R$
-modules [Reference MatsumuraMat86, Theorem 18.6(v)].
$R$
-modules [Reference MatsumuraMat86, Theorem 18.6(v)].
Now recall the definition of local cohomology as a direct limit of Ext modules: for any module
![]() $M$
over any commutative Noetherian ring
$M$
over any commutative Noetherian ring
![]() $R$
, and any ideal
$R$
, and any ideal
![]() $I\subset R$
, we have isomorphisms
$I\subset R$
, we have isomorphisms
 $H_{I}^{i}(M)\simeq \varinjlim \operatorname{Ext}_{R}^{i}(R/I^{t},M)$
[Reference Brodmann and SharpBS13, Theorem 1.3.8]. Now put
$H_{I}^{i}(M)\simeq \varinjlim \operatorname{Ext}_{R}^{i}(R/I^{t},M)$
[Reference Brodmann and SharpBS13, Theorem 1.3.8]. Now put
![]() $M=R$
, a Gorenstein local ring of dimension
$M=R$
, a Gorenstein local ring of dimension
![]() $n$
with maximal ideal
$n$
with maximal ideal
![]() $\mathfrak{m}$
. Taking Matlis duals (and using the fact that any contravariant Hom functor converts direct limits into inverse limits) we have isomorphisms
$\mathfrak{m}$
. Taking Matlis duals (and using the fact that any contravariant Hom functor converts direct limits into inverse limits) we have isomorphisms
 $$\begin{eqnarray}D(H_{I}^{i}(R))\simeq D(\varinjlim \operatorname{Ext}_{R}^{i}(R/I^{t},R))\simeq \varprojlim \,D(\operatorname{Ext}_{R}^{i}(R/I^{t},R))\simeq \varprojlim \,H_{\mathfrak{ m}}^{n-i}(R/I^{t}),\end{eqnarray}$$
$$\begin{eqnarray}D(H_{I}^{i}(R))\simeq D(\varinjlim \operatorname{Ext}_{R}^{i}(R/I^{t},R))\simeq \varprojlim \,D(\operatorname{Ext}_{R}^{i}(R/I^{t},R))\simeq \varprojlim \,H_{\mathfrak{ m}}^{n-i}(R/I^{t}),\end{eqnarray}$$
where in the last step we have used local duality for every
![]() $t$
and passed to the inverse limit. If we let
$t$
and passed to the inverse limit. If we let
 $X=\operatorname{Spec}(R)$
and
$X=\operatorname{Spec}(R)$
and
![]() $Y$
the closed subscheme
$Y$
the closed subscheme
 $V(I)\subset X$
defined by
$V(I)\subset X$
defined by
![]() $I$
, and if we write
$I$
, and if we write
![]() $\widehat{X}$
for the formal completion of
$\widehat{X}$
for the formal completion of
![]() $Y$
in
$Y$
in
![]() $X$
(see §§ 1 and 7 for the definition of formal completion),
$X$
(see §§ 1 and 7 for the definition of formal completion),
![]() $P$
for its closed point, and
$P$
for its closed point, and
![]() ${\mathcal{O}}_{\widehat{X}}$
for its structure sheaf, then the last object in the sequence of isomorphisms above is precisely the local cohomology
${\mathcal{O}}_{\widehat{X}}$
for its structure sheaf, then the last object in the sequence of isomorphisms above is precisely the local cohomology
 $H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
supported at the closed point [Reference OgusOgu73, Proposition 2.2]. (We may also write
$H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
supported at the closed point [Reference OgusOgu73, Proposition 2.2]. (We may also write
![]() $X_{/Y}$
and
$X_{/Y}$
and
![]() ${\mathcal{O}}_{X_{/Y}}$
for
${\mathcal{O}}_{X_{/Y}}$
for
![]() $\widehat{X}$
and
$\widehat{X}$
and
![]() ${\mathcal{O}}_{\widehat{X}}$
when we need to record explicitly the dependence on
${\mathcal{O}}_{\widehat{X}}$
when we need to record explicitly the dependence on
![]() $Y$
.) It follows that for all
$Y$
.) It follows that for all
![]() $i$
, the
$i$
, the
![]() $R$
-modules
$R$
-modules
 $D(H_{I}^{i}(R))$
and
$D(H_{I}^{i}(R))$
and
 $H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
are isomorphic. We record this conclusion separately for future reference.
$H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
are isomorphic. We record this conclusion separately for future reference.
Proposition 6.3 [Reference OgusOgu73, Proposition 2.2].
Let
![]() $R$
be a Gorenstein local ring of dimension
$R$
be a Gorenstein local ring of dimension
![]() $n$
with maximal ideal
$n$
with maximal ideal
![]() $\mathfrak{m}$
. For all
$\mathfrak{m}$
. For all
![]() $i$
, we have isomorphisms
$i$
, we have isomorphisms
 $$\begin{eqnarray}D(H_{I}^{i}(R))\simeq \varprojlim \,H_{\mathfrak{ m}}^{n-i}(R/I^{t})\simeq H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\end{eqnarray}$$
$$\begin{eqnarray}D(H_{I}^{i}(R))\simeq \varprojlim \,H_{\mathfrak{ m}}^{n-i}(R/I^{t})\simeq H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\end{eqnarray}$$
of
![]() $R$
-modules, where the rightmost object is the formal local cohomology defined in the previous paragraph.
$R$
-modules, where the rightmost object is the formal local cohomology defined in the previous paragraph.
For the remainder of the section, we identify the
![]() $R$
-modules
$R$
-modules
 $D(H_{I}^{i}(R))$
and
$D(H_{I}^{i}(R))$
and
 $H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
using the proposition above, suppressing any explicit mention of this isomorphism.
$H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
using the proposition above, suppressing any explicit mention of this isomorphism.
Now suppose that
![]() $(R,\mathfrak{m})$
is a complete local ring with coefficient field
$(R,\mathfrak{m})$
is a complete local ring with coefficient field
![]() $k$
. By Example 4.13, we know that if
$k$
. By Example 4.13, we know that if
![]() $I\subset R$
is an ideal, every
$I\subset R$
is an ideal, every
![]() $H_{I}^{i}(R)$
is a left
$H_{I}^{i}(R)$
is a left
 ${\mathcal{D}}(R,k)$
-module, and since
${\mathcal{D}}(R,k)$
-module, and since
![]() $R$
is complete,
$R$
is complete,
 $D(H_{I}^{i}(R))$
is a right
$D(H_{I}^{i}(R))$
is a right
 ${\mathcal{D}}(R,k)$
-module by Corollary 4.10. If moreover
${\mathcal{D}}(R,k)$
-module by Corollary 4.10. If moreover
![]() $R$
is Gorenstein, we have
$R$
is Gorenstein, we have
 $D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
by Proposition 6.3, defining by transport of structure a right
$D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
by Proposition 6.3, defining by transport of structure a right
 ${\mathcal{D}}(R,k)$
-module structure on
${\mathcal{D}}(R,k)$
-module structure on
 $H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
.
$H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
.
There is also a natural left
 ${\mathcal{D}}(R,k)$
-module structure on
${\mathcal{D}}(R,k)$
-module structure on
 $H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
, defined without Matlis duality: see [Reference HartshorneHar75, §§ I.7 and III.2] and [Reference HellusHel07, § 7.2]. Let
$H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
, defined without Matlis duality: see [Reference HartshorneHar75, §§ I.7 and III.2] and [Reference HellusHel07, § 7.2]. Let
 $d\in {\mathcal{D}}(R,k)$
be a differential operator of order
$d\in {\mathcal{D}}(R,k)$
be a differential operator of order
![]() $j$
. For all
$j$
. For all
![]() $t\geqslant 0$
,
$t\geqslant 0$
,
 $d(I^{t+j})\subset I^{t}$
, and so
$d(I^{t+j})\subset I^{t}$
, and so
![]() $d$
induces a
$d$
induces a
![]() $k$
-linear map
$k$
-linear map
 $d_{t}:R/I^{t+j}\rightarrow R/I^{t}$
. If
$d_{t}:R/I^{t+j}\rightarrow R/I^{t}$
. If
 ${\mathcal{I}}\subset {\mathcal{O}}_{X}$
is the sheaf of ideals on
${\mathcal{I}}\subset {\mathcal{O}}_{X}$
is the sheaf of ideals on
 $X=\operatorname{Spec}(R)$
corresponding to
$X=\operatorname{Spec}(R)$
corresponding to
![]() $I$
, the map
$I$
, the map
![]() $d_{t}$
induces a sheafified map
$d_{t}$
induces a sheafified map
 $\tilde{d}_{t}:{\mathcal{O}}_{X}/{\mathcal{I}}^{t+j}\rightarrow {\mathcal{O}}_{X}/{\mathcal{I}}^{t}$
of sheaves of
$\tilde{d}_{t}:{\mathcal{O}}_{X}/{\mathcal{I}}^{t+j}\rightarrow {\mathcal{O}}_{X}/{\mathcal{I}}^{t}$
of sheaves of
![]() $k$
-spaces on
$k$
-spaces on
![]() $X$
; taking local cohomology, we obtain
$X$
; taking local cohomology, we obtain
![]() $k$
-linear maps
$k$
-linear maps
 $\overline{d}_{t}:H_{\mathfrak{m}}^{n-i}(R/I^{t+j})\rightarrow H_{\mathfrak{m}}^{n-i}(R/I^{t})$
, where we have identified
$\overline{d}_{t}:H_{\mathfrak{m}}^{n-i}(R/I^{t+j})\rightarrow H_{\mathfrak{m}}^{n-i}(R/I^{t})$
, where we have identified
 $H_{\mathfrak{m}}^{n-i}(R/I^{l})$
with
$H_{\mathfrak{m}}^{n-i}(R/I^{l})$
with
 $H_{P}^{n-i}(X,{\mathcal{O}}_{X}/{\mathcal{I}}^{l})$
as
$H_{P}^{n-i}(X,{\mathcal{O}}_{X}/{\mathcal{I}}^{l})$
as
![]() $R$
-modules for all
$R$
-modules for all
![]() $l$
[Reference Grothendieck and RaynaudGR05, Exp. II, Corollary 4]. The reason that sheaves were introduced here is to make clear that merely
$l$
[Reference Grothendieck and RaynaudGR05, Exp. II, Corollary 4]. The reason that sheaves were introduced here is to make clear that merely
![]() $k$
-linear (or even additive) maps between
$k$
-linear (or even additive) maps between
![]() $R$
-modules still induce maps on local cohomology, because local cohomology, in its most general form, is a functor on sheaves of Abelian groups on a topological space [Reference Grothendieck and RaynaudGR05, Exp. I, Déf. 2.1].
$R$
-modules still induce maps on local cohomology, because local cohomology, in its most general form, is a functor on sheaves of Abelian groups on a topological space [Reference Grothendieck and RaynaudGR05, Exp. I, Déf. 2.1].
These maps
![]() $\overline{d}_{t}$
are compatible with the natural surjections
$\overline{d}_{t}$
are compatible with the natural surjections
 $R/I^{t+l}\rightarrow R/I^{t}$
, in the sense that we have commutative diagrams
$R/I^{t+l}\rightarrow R/I^{t}$
, in the sense that we have commutative diagrams

for all
![]() $t$
,
$t$
,
![]() $j$
, and
$j$
, and
![]() $l$
, where the vertical arrows are the
$l$
, where the vertical arrows are the
![]() $R$
-linear maps induced by the natural surjections. Therefore, upon passing to inverse limits, the
$R$
-linear maps induced by the natural surjections. Therefore, upon passing to inverse limits, the
![]() $\overline{d}_{t}$
define a
$\overline{d}_{t}$
define a
![]() $k$
-linear map
$k$
-linear map
 $\overline{d}:\varprojlim \,H_{\mathfrak{m}}^{n-i}(R/I^{t})\rightarrow \varprojlim \,H_{\mathfrak{m}}^{n-i}(R/I^{t})$
. If
$\overline{d}:\varprojlim \,H_{\mathfrak{m}}^{n-i}(R/I^{t})\rightarrow \varprojlim \,H_{\mathfrak{m}}^{n-i}(R/I^{t})$
. If
 $\unicode[STIX]{x1D6FE}\in \varprojlim \,H_{\mathfrak{m}}^{n-i}(R/I^{t})=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
, we set
$\unicode[STIX]{x1D6FE}\in \varprojlim \,H_{\mathfrak{m}}^{n-i}(R/I^{t})=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
, we set
 $d\cdot \unicode[STIX]{x1D6FE}=\overline{d}(\unicode[STIX]{x1D6FE})$
, and in this way define a left action of
$d\cdot \unicode[STIX]{x1D6FE}=\overline{d}(\unicode[STIX]{x1D6FE})$
, and in this way define a left action of
 ${\mathcal{D}}(R,k)$
on
${\mathcal{D}}(R,k)$
on
 $H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
.
$H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
.
Definition 6.4. If
![]() $(R,\mathfrak{m})$
is a complete Gorenstein local ring of dimension
$(R,\mathfrak{m})$
is a complete Gorenstein local ring of dimension
![]() $n$
with coefficient field
$n$
with coefficient field
![]() $k$
and
$k$
and
![]() $I\subset R$
is an ideal, the Matlis dual action of
$I\subset R$
is an ideal, the Matlis dual action of
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
on
${\mathcal{D}}={\mathcal{D}}(R,k)$
on
 $D(H_{I}^{i}(R))$
for any
$D(H_{I}^{i}(R))$
for any
![]() $i$
is the right action defined by dualizing the natural structure of left
$i$
is the right action defined by dualizing the natural structure of left
![]() ${\mathcal{D}}$
-module on
${\mathcal{D}}$
-module on
![]() $H_{I}^{i}(R)$
, and the inverse limit action of
$H_{I}^{i}(R)$
, and the inverse limit action of
![]() ${\mathcal{D}}$
on
${\mathcal{D}}$
on
 $D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
is the left action defined in the previous paragraph.
$D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
is the left action defined in the previous paragraph.
In the case of a characteristic-zero complete regular local ring
![]() $(R,\mathfrak{m})$
containing its residue field
$(R,\mathfrak{m})$
containing its residue field
![]() $k$
, we can state precisely how these two
$k$
, we can state precisely how these two
![]() ${\mathcal{D}}$
-module structures are related: they are transposes of each other, as in Definition 4.15. This is the main result of this section.
${\mathcal{D}}$
-module structures are related: they are transposes of each other, as in Definition 4.15. This is the main result of this section.
Theorem 6.5. Let
![]() $k$
be a field of characteristic zero, let
$k$
be a field of characteristic zero, let
 $R=k[[x_{1},\ldots ,x_{n}]]$
, and let
$R=k[[x_{1},\ldots ,x_{n}]]$
, and let
![]() $I\subset R$
be an ideal. Denote by
$I\subset R$
be an ideal. Denote by
![]() $\mathfrak{m}$
the maximal ideal of
$\mathfrak{m}$
the maximal ideal of
![]() $R$
, and by
$R$
, and by
 ${\mathcal{D}}={\mathcal{D}}(R,k)$
the ring of
${\mathcal{D}}={\mathcal{D}}(R,k)$
the ring of
![]() $k$
-linear differential operators on
$k$
-linear differential operators on
![]() $R$
. Then for all
$R$
. Then for all
![]() $i$
, the Matlis dual action of
$i$
, the Matlis dual action of
![]() ${\mathcal{D}}$
on
${\mathcal{D}}$
on
 $D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
is the transpose of the inverse limit action.
$D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
is the transpose of the inverse limit action.
Remark 6.6. It follows from Theorem 6.5 that the identification of Proposition 6.3 can be extended to an identification of left
![]() ${\mathcal{D}}$
-modules, regarding
${\mathcal{D}}$
-modules, regarding
 $D(H_{I}^{i}(R))$
as a left
$D(H_{I}^{i}(R))$
as a left
![]() ${\mathcal{D}}$
-module by transposing the Matlis dual action as in Proposition 4.17. We can therefore identify the de Rham complexes of both sides as well.
${\mathcal{D}}$
-module by transposing the Matlis dual action as in Proposition 4.17. We can therefore identify the de Rham complexes of both sides as well.
Proof. Every element of
![]() ${\mathcal{D}}$
is a finite sum of terms of the form
${\mathcal{D}}$
is a finite sum of terms of the form
 $\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{1}^{a_{1}}\cdots \unicode[STIX]{x2202}_{n}^{a_{n}}$
where
$\unicode[STIX]{x1D70C}\unicode[STIX]{x2202}_{1}^{a_{1}}\cdots \unicode[STIX]{x2202}_{n}^{a_{n}}$
where
![]() $\unicode[STIX]{x1D70C}\in R$
, and Matlis duality respects composition of operators (reversing the order), so we need only check the statement of the theorem for the action of a single
$\unicode[STIX]{x1D70C}\in R$
, and Matlis duality respects composition of operators (reversing the order), so we need only check the statement of the theorem for the action of a single
![]() $\unicode[STIX]{x1D70C}$
or
$\unicode[STIX]{x1D70C}$
or
![]() $\unicode[STIX]{x2202}_{i}$
. There is nothing to prove in the case of an element
$\unicode[STIX]{x2202}_{i}$
. There is nothing to prove in the case of an element
![]() $\unicode[STIX]{x1D70C}\in R$
, since the Matlis dual of the
$\unicode[STIX]{x1D70C}\in R$
, since the Matlis dual of the
![]() $R$
-linear multiplication by such an element
$R$
-linear multiplication by such an element
![]() $\unicode[STIX]{x1D70C}$
is again multiplication by
$\unicode[STIX]{x1D70C}$
is again multiplication by
![]() $\unicode[STIX]{x1D70C}$
. Therefore, to prove Theorem 6.5, we need only to show that if
$\unicode[STIX]{x1D70C}$
. Therefore, to prove Theorem 6.5, we need only to show that if
![]() $i$
is fixed (
$i$
is fixed (
 $1\leqslant i\leqslant n$
), the Matlis dual and inverse limit actions of the partial derivative
$1\leqslant i\leqslant n$
), the Matlis dual and inverse limit actions of the partial derivative
![]() $\unicode[STIX]{x2202}_{i}\in {\mathcal{D}}$
on
$\unicode[STIX]{x2202}_{i}\in {\mathcal{D}}$
on
 $D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
differ by a sign (transposing the action of
$D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
differ by a sign (transposing the action of
![]() $\unicode[STIX]{x2202}_{i}$
introduces a sign change, by Definition 4.15). Without loss of generality, we may assume
$\unicode[STIX]{x2202}_{i}$
introduces a sign change, by Definition 4.15). Without loss of generality, we may assume
![]() $i=1$
and write
$i=1$
and write
![]() $x$
for
$x$
for
![]() $x_{1}$
, so that
$x_{1}$
, so that
 $R=k[[x,x_{2},\ldots ,x_{n}]]$
and
$R=k[[x,x_{2},\ldots ,x_{n}]]$
and
![]() $\unicode[STIX]{x2202}=\unicode[STIX]{x2202}_{1}$
. We denote the inverse limit action of
$\unicode[STIX]{x2202}=\unicode[STIX]{x2202}_{1}$
. We denote the inverse limit action of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
by
$D(H_{I}^{i}(R))=H_{P}^{n-i}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
by
![]() $\overline{\unicode[STIX]{x1D6FF}}$
and the Matlis dual action by
$\overline{\unicode[STIX]{x1D6FF}}$
and the Matlis dual action by
![]() $\unicode[STIX]{x2202}^{\ast }$
. In order to prove the theorem, it is enough to prove the equality
$\unicode[STIX]{x2202}^{\ast }$
. In order to prove the theorem, it is enough to prove the equality
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}=-\unicode[STIX]{x2202}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}=-\unicode[STIX]{x2202}^{\ast }.\end{eqnarray}$$
We will prove this equality first for a complete intersection ideal
![]() $I$
and then in general. We prove the complete intersection case by induction on the number of generators of
$I$
and then in general. We prove the complete intersection case by induction on the number of generators of
![]() $I$
. Suppose that
$I$
. Suppose that
 $f_{1},\ldots ,f_{s}$
is a regular sequence in
$f_{1},\ldots ,f_{s}$
is a regular sequence in
![]() $R$
, and assume the theorem has been proved for complete intersection ideals with
$R$
, and assume the theorem has been proved for complete intersection ideals with
![]() $s-1$
generators: the base case,
$s-1$
generators: the base case,
![]() $s=0$
, has already been established as Example 4.2, since
$s=0$
, has already been established as Example 4.2, since
 $H_{(0)}^{0}(R)=R$
and
$H_{(0)}^{0}(R)=R$
and
 $H_{(0)}^{i}(R)=0$
for
$H_{(0)}^{i}(R)=0$
for
![]() $i>0$
. We write
$i>0$
. We write
![]() $f$
for
$f$
for
![]() $f_{s}$
. Let
$f_{s}$
. Let
![]() $I$
be the ideal
$I$
be the ideal
 $(f_{1},\ldots ,f_{s})$
and
$(f_{1},\ldots ,f_{s})$
and
![]() $J\subset I$
the ideal
$J\subset I$
the ideal
 $(f_{1},\ldots ,f_{s-1})$
, so that
$(f_{1},\ldots ,f_{s-1})$
, so that
 $I=J+(f)$
. Let
$I=J+(f)$
. Let
![]() $Y$
(respectively
$Y$
(respectively
![]() $Z$
) be the closed subscheme of
$Z$
) be the closed subscheme of
 $X=\operatorname{Spec}(R)$
defined by
$X=\operatorname{Spec}(R)$
defined by
![]() $I$
(respectively
$I$
(respectively
![]() $J$
), and let
$J$
), and let
 $X_{t}=\operatorname{Spec}(R/(f^{t}))$
for all
$X_{t}=\operatorname{Spec}(R/(f^{t}))$
for all
![]() $t\geqslant 1$
. We claim that the Matlis dual and inverse limit actions of
$t\geqslant 1$
. We claim that the Matlis dual and inverse limit actions of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{I}^{i}(R))=H_{P}^{n-i}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
differ by a sign for all
$D(H_{I}^{i}(R))=H_{P}^{n-i}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
differ by a sign for all
![]() $i$
. Since
$i$
. Since
![]() $I$
is a complete intersection ideal,
$I$
is a complete intersection ideal,
 $H_{I}^{i}(R)=0$
unless
$H_{I}^{i}(R)=0$
unless
![]() $i=s$
, so this is the only case we need to consider.
$i=s$
, so this is the only case we need to consider.
Let
 $M=H_{J}^{s-1}(R)$
. Since
$M=H_{J}^{s-1}(R)$
. Since
 $f_{1},\ldots ,f_{s}$
is a regular sequence, the composite local cohomology spectral sequence of Example 2.15 (with respect to the ideals
$f_{1},\ldots ,f_{s}$
is a regular sequence, the composite local cohomology spectral sequence of Example 2.15 (with respect to the ideals
![]() $J$
and
$J$
and
![]() $(f)$
) degenerates at
$(f)$
) degenerates at
![]() $E_{2}$
, and consequently we have
$E_{2}$
, and consequently we have
 $H_{I}^{s}(R)\simeq H_{(f)}^{1}(M)$
as
$H_{I}^{s}(R)\simeq H_{(f)}^{1}(M)$
as
![]() $R$
-modules (indeed, as left
$R$
-modules (indeed, as left
![]() ${\mathcal{D}}$
-modules). We write
${\mathcal{D}}$
-modules). We write
![]() $\unicode[STIX]{x2202}_{M}$
for the action of
$\unicode[STIX]{x2202}_{M}$
for the action of
![]() $\unicode[STIX]{x2202}$
on the left
$\unicode[STIX]{x2202}$
on the left
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
,
$M$
,
![]() $\unicode[STIX]{x2202}_{M}^{\ast }$
for the corresponding Matlis dual action on
$\unicode[STIX]{x2202}_{M}^{\ast }$
for the corresponding Matlis dual action on
![]() $D(M)$
, and
$D(M)$
, and
![]() $\overline{\unicode[STIX]{x1D6FF}}_{Z}$
for the inverse limit action of
$\overline{\unicode[STIX]{x1D6FF}}_{Z}$
for the inverse limit action of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(M)=H_{P}^{n-s+1}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
(note that our induction hypothesis is that
$D(M)=H_{P}^{n-s+1}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
(note that our induction hypothesis is that
 $\overline{\unicode[STIX]{x1D6FF}}_{Z}=-\unicode[STIX]{x2202}_{M}^{\ast }$
).
$\overline{\unicode[STIX]{x1D6FF}}_{Z}=-\unicode[STIX]{x2202}_{M}^{\ast }$
).
By the Čech complex definition of local cohomology,
 $H_{(f)}^{1}(M)$
is the cokernel of the localization map
$H_{(f)}^{1}(M)$
is the cokernel of the localization map
 $M\rightarrow M_{f}$
. Since
$M\rightarrow M_{f}$
. Since
 $f_{1},\ldots ,f_{s}$
is a regular sequence, this localization map is injective: identifying
$f_{1},\ldots ,f_{s}$
is a regular sequence, this localization map is injective: identifying
![]() $M$
with its image, we view
$M$
with its image, we view
![]() $M$
as a submodule of
$M$
as a submodule of
![]() $M_{f}$
and write
$M_{f}$
and write
![]() $M_{f}/M$
for the cokernel, which we can express as the direct limit
$M_{f}/M$
for the cokernel, which we can express as the direct limit
 $\varinjlim M/f^{t}M$
. Here, the transition map
$\varinjlim M/f^{t}M$
. Here, the transition map
 $M/f^{t}M\rightarrow M/f^{t+1}M$
carries the class of
$M/f^{t}M\rightarrow M/f^{t+1}M$
carries the class of
![]() $m\in M$
to the class of
$m\in M$
to the class of
![]() $fm$
, and the
$fm$
, and the
![]() $R$
-linear isomorphism
$R$
-linear isomorphism
 $M_{f}/M\rightarrow \varinjlim M/f^{t}M$
carries the class of
$M_{f}/M\rightarrow \varinjlim M/f^{t}M$
carries the class of
 $(m/f^{t})\in M_{f}$
to the class of
$(m/f^{t})\in M_{f}$
to the class of
![]() $m\in M$
modulo
$m\in M$
modulo
![]() $f^{t}M$
. The action of
$f^{t}M$
. The action of
![]() $\unicode[STIX]{x2202}$
on the left
$\unicode[STIX]{x2202}$
on the left
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
induces an action of
$M$
induces an action of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
![]() $M_{f}/M$
, defined by the quotient rule: we have a
$M_{f}/M$
, defined by the quotient rule: we have a
![]() $k$
-linear map
$k$
-linear map
 $(\unicode[STIX]{x2202}_{M})_{f}:M_{f}\rightarrow M_{f}$
given by
$(\unicode[STIX]{x2202}_{M})_{f}:M_{f}\rightarrow M_{f}$
given by
 $(\unicode[STIX]{x2202}_{M})_{f}(m/f^{t})=(f\unicode[STIX]{x2202}_{M}(m)-t\unicode[STIX]{x2202}(f)m)/f^{t+1}$
that carries
$(\unicode[STIX]{x2202}_{M})_{f}(m/f^{t})=(f\unicode[STIX]{x2202}_{M}(m)-t\unicode[STIX]{x2202}(f)m)/f^{t+1}$
that carries
 $M\subset M_{f}$
into itself and therefore descends to the quotient
$M\subset M_{f}$
into itself and therefore descends to the quotient
![]() $M_{f}/M$
. In terms of the description of
$M_{f}/M$
. In terms of the description of
![]() $M_{f}/M$
as the direct limit
$M_{f}/M$
as the direct limit
 $\varinjlim M/f^{t}M$
, the map
$\varinjlim M/f^{t}M$
, the map
![]() $(\unicode[STIX]{x2202}_{M})_{f}$
is defined by the direct limit of the
$(\unicode[STIX]{x2202}_{M})_{f}$
is defined by the direct limit of the
![]() $k$
-linear maps
$k$
-linear maps
 $\unicode[STIX]{x2202}_{t}:M/f^{t}M\rightarrow M/f^{t+1}M$
where
$\unicode[STIX]{x2202}_{t}:M/f^{t}M\rightarrow M/f^{t+1}M$
where
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D707})=(f\unicode[STIX]{x2202}_{M}(m)-t\unicode[STIX]{x2202}(f)m)+f^{t+1}M\in M/f^{t+1}M\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D707})=(f\unicode[STIX]{x2202}_{M}(m)-t\unicode[STIX]{x2202}(f)m)+f^{t+1}M\in M/f^{t+1}M\end{eqnarray}$$
if
![]() $\unicode[STIX]{x1D707}$
is the class of
$\unicode[STIX]{x1D707}$
is the class of
![]() $m\in M$
in
$m\in M$
in
 $M/f^{t}M$
. It is straightforward to check that
$M/f^{t}M$
. It is straightforward to check that
![]() $\unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D707})$
is well defined (that is, depends only on
$\unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D707})$
is well defined (that is, depends only on
![]() $\unicode[STIX]{x1D707}$
and not on
$\unicode[STIX]{x1D707}$
and not on
![]() $m$
) and that
$m$
) and that
![]() $\unicode[STIX]{x2202}_{t}$
satisfies the Leibniz rule:
$\unicode[STIX]{x2202}_{t}$
satisfies the Leibniz rule:
 $\unicode[STIX]{x2202}_{t}(r\unicode[STIX]{x1D707})=\unicode[STIX]{x2202}(r)\overline{\unicode[STIX]{x1D707}}+r\unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D707})$
for
$\unicode[STIX]{x2202}_{t}(r\unicode[STIX]{x1D707})=\unicode[STIX]{x2202}(r)\overline{\unicode[STIX]{x1D707}}+r\unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D707})$
for
![]() $r\in R$
, where
$r\in R$
, where
![]() $\overline{\unicode[STIX]{x1D707}}$
is the image of
$\overline{\unicode[STIX]{x1D707}}$
is the image of
![]() $\unicode[STIX]{x1D707}$
under the transition map
$\unicode[STIX]{x1D707}$
under the transition map
 $M/f^{t}M\rightarrow M/f^{t+1}M$
.
$M/f^{t}M\rightarrow M/f^{t+1}M$
.
The maps
![]() $\unicode[STIX]{x2202}_{t}$
defined in the previous paragraph fit into commutative diagrams
$\unicode[STIX]{x2202}_{t}$
defined in the previous paragraph fit into commutative diagrams

for all
![]() $t$
, where the rows are exact sequences of
$t$
, where the rows are exact sequences of
![]() $R$
-modules and the vertical arrows are
$R$
-modules and the vertical arrows are
![]() $k$
-linear. The commutativity of the right square is clear, while the calculation
$k$
-linear. The commutativity of the right square is clear, while the calculation
 $$\begin{eqnarray}\displaystyle (f\unicode[STIX]{x2202}_{M}-t\unicode[STIX]{x2202}(f))(f^{t}m)=f\unicode[STIX]{x2202}_{M}(f^{t}m)-t\unicode[STIX]{x2202}(f)f^{t}m & = & \displaystyle f(tf^{t-1}\unicode[STIX]{x2202}(f)m+f^{t}\unicode[STIX]{x2202}_{M}(m))-t\unicode[STIX]{x2202}(f)f^{t}m\nonumber\\ \displaystyle & = & \displaystyle f^{t+1}\unicode[STIX]{x2202}_{M}(m)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (f\unicode[STIX]{x2202}_{M}-t\unicode[STIX]{x2202}(f))(f^{t}m)=f\unicode[STIX]{x2202}_{M}(f^{t}m)-t\unicode[STIX]{x2202}(f)f^{t}m & = & \displaystyle f(tf^{t-1}\unicode[STIX]{x2202}(f)m+f^{t}\unicode[STIX]{x2202}_{M}(m))-t\unicode[STIX]{x2202}(f)f^{t}m\nonumber\\ \displaystyle & = & \displaystyle f^{t+1}\unicode[STIX]{x2202}_{M}(m)\nonumber\end{eqnarray}$$
for
![]() $m\in M$
shows that the left square is commutative. Fix
$m\in M$
shows that the left square is commutative. Fix
![]() $t$
and consider the Matlis dual of the above diagram, which takes the following form.
$t$
and consider the Matlis dual of the above diagram, which takes the following form.

Since
 $H_{(f)}^{1}(M)$
is the direct limit
$H_{(f)}^{1}(M)$
is the direct limit
 $\varinjlim M/f^{t}M$
, the Matlis dual
$\varinjlim M/f^{t}M$
, the Matlis dual
 $D(H_{(f)}^{1}(M))$
is the inverse limit
$D(H_{(f)}^{1}(M))$
is the inverse limit
 $\varprojlim \,D(M/f^{t}M)$
, and by Remark 3.20, the Matlis dual action of
$\varprojlim \,D(M/f^{t}M)$
, and by Remark 3.20, the Matlis dual action of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{(f)}^{1}(M))$
is defined by
$D(H_{(f)}^{1}(M))$
is defined by
![]() $\varprojlim \,\unicode[STIX]{x2202}_{t}^{\ast }$
(the Leibniz rule implies that all
$\varprojlim \,\unicode[STIX]{x2202}_{t}^{\ast }$
(the Leibniz rule implies that all
![]() $\unicode[STIX]{x2202}_{t}$
are
$\unicode[STIX]{x2202}_{t}$
are
![]() $\unicode[STIX]{x1D6F4}$
-continuous).
$\unicode[STIX]{x1D6F4}$
-continuous).
We turn next to the inverse limit action of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{I}^{s}(R))=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
. Again we let
$D(H_{I}^{s}(R))=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
. Again we let
 $M=H_{J}^{s-1}(R)$
. From the long exact sequence of local cohomology supported at
$M=H_{J}^{s-1}(R)$
. From the long exact sequence of local cohomology supported at
![]() $J$
applied to the short exact sequence
$J$
applied to the short exact sequence
 $$\begin{eqnarray}0\rightarrow R\xrightarrow[{}]{f^{t}}R\rightarrow R/(f^{t})\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow R\xrightarrow[{}]{f^{t}}R\rightarrow R/(f^{t})\rightarrow 0\end{eqnarray}$$
of
![]() $R$
-modules, it follows at once that
$R$
-modules, it follows at once that
 $M/f^{t}M\simeq H_{J}^{s-1}(R/(f^{t}))$
as
$M/f^{t}M\simeq H_{J}^{s-1}(R/(f^{t}))$
as
![]() $R$
-modules. By the change of ring principle [Reference Brodmann and SharpBS13, Theorem 4.2.1], we have
$R$
-modules. By the change of ring principle [Reference Brodmann and SharpBS13, Theorem 4.2.1], we have
 $H_{J}^{s-1}(R/(f^{t}))\simeq H_{\overline{J}}^{s-1}(R/(f^{t}))$
as
$H_{J}^{s-1}(R/(f^{t}))\simeq H_{\overline{J}}^{s-1}(R/(f^{t}))$
as
![]() $R$
-modules, where
$R$
-modules, where
 $\overline{J}=(J+(f^{t}))/(f^{t})\subset R/(f^{t})$
, the local cohomology module on the right-hand side is computed in the category of
$\overline{J}=(J+(f^{t}))/(f^{t})\subset R/(f^{t})$
, the local cohomology module on the right-hand side is computed in the category of
![]() $R/(f^{t})$
-modules, and its
$R/(f^{t})$
-modules, and its
![]() $R$
-module structure is defined using the natural surjection
$R$
-module structure is defined using the natural surjection
 $R\rightarrow R/(f^{t})$
. Therefore
$R\rightarrow R/(f^{t})$
. Therefore
 $D(M/f^{t}M)\simeq D(H_{\overline{J}}^{s-1}(R/(f^{t})))$
as
$D(M/f^{t}M)\simeq D(H_{\overline{J}}^{s-1}(R/(f^{t})))$
as
![]() $R$
-modules. Since
$R$
-modules. Since
 $M/f^{t}M$
(and hence
$M/f^{t}M$
(and hence
 $H_{\overline{J}}^{s-1}(R/(f^{t}))$
) is annihilated by
$H_{\overline{J}}^{s-1}(R/(f^{t}))$
) is annihilated by
![]() $f^{t}$
, it does not matter whether the Matlis dual on the right-hand side is computed over the ring
$f^{t}$
, it does not matter whether the Matlis dual on the right-hand side is computed over the ring
![]() $R$
or
$R$
or
![]() $R/(f^{t})$
. Taking the second point of view, we can apply Proposition 6.3 to the
$R/(f^{t})$
. Taking the second point of view, we can apply Proposition 6.3 to the
![]() $(n-1)$
-dimensional Gorenstein local ring
$(n-1)$
-dimensional Gorenstein local ring
![]() $R/(f^{t})$
, obtaining an isomorphism
$R/(f^{t})$
, obtaining an isomorphism
 $$\begin{eqnarray}D(M/f^{t}M)\simeq D(H_{\overline{J}}^{s-1}(R/(f^{t})))\simeq H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\end{eqnarray}$$
$$\begin{eqnarray}D(M/f^{t}M)\simeq D(H_{\overline{J}}^{s-1}(R/(f^{t})))\simeq H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\end{eqnarray}$$
of
![]() $R$
-modules (the cohomological degree is
$R$
-modules (the cohomological degree is
 $n-s=(n-1)-(s-1)=\dim (R/(f^{t}))-(s-1)$
). Here, we have abusively written
$n-s=(n-1)-(s-1)=\dim (R/(f^{t}))-(s-1)$
). Here, we have abusively written
![]() $Z$
for the closed subscheme of
$Z$
for the closed subscheme of
![]() $X_{t}$
defined by
$X_{t}$
defined by
 $\overline{J}=(J+(f^{t}))/(f^{t})$
. We already know the inverse limit
$\overline{J}=(J+(f^{t}))/(f^{t})$
. We already know the inverse limit
 $\varprojlim \,D(M/f^{t}M)$
is isomorphic as an
$\varprojlim \,D(M/f^{t}M)$
is isomorphic as an
![]() $R$
-module to
$R$
-module to
 $$\begin{eqnarray}D(H_{(f)}^{1}(M))\simeq D(H_{I}^{s}(R))=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}}),\end{eqnarray}$$
$$\begin{eqnarray}D(H_{(f)}^{1}(M))\simeq D(H_{I}^{s}(R))=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}}),\end{eqnarray}$$
from which it follows (by passing to the inverse limit in
![]() $t$
) that we must have
$t$
) that we must have
 $$\begin{eqnarray}\varprojlim \,H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\simeq H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})\end{eqnarray}$$
$$\begin{eqnarray}\varprojlim \,H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\simeq H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})\end{eqnarray}$$
as
![]() $R$
-modules. In order to see how this last isomorphism interacts with the inverse limit action of
$R$
-modules. In order to see how this last isomorphism interacts with the inverse limit action of
![]() $\unicode[STIX]{x2202}$
, we describe it more explicitly. For all
$\unicode[STIX]{x2202}$
, we describe it more explicitly. For all
![]() $t$
, we have
$t$
, we have
 $$\begin{eqnarray}H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\simeq \underset{l}{\varprojlim }\,H_{\mathfrak{m}}^{n-s}((R/(f^{t}))/\overline{J}^{l})\simeq \underset{l}{\varprojlim }\,H_{\mathfrak{ m}}^{n-s}(R/(J^{l}+(f^{t})))\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\simeq \underset{l}{\varprojlim }\,H_{\mathfrak{m}}^{n-s}((R/(f^{t}))/\overline{J}^{l})\simeq \underset{l}{\varprojlim }\,H_{\mathfrak{ m}}^{n-s}(R/(J^{l}+(f^{t})))\end{eqnarray}$$
as
![]() $R$
-modules. Passing to the inverse limit in
$R$
-modules. Passing to the inverse limit in
![]() $t$
, we obtain
$t$
, we obtain
 $$\begin{eqnarray}\underset{t}{\varprojlim }\,H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\simeq \underset{t}{\varprojlim }\,\underset{l}{\varprojlim }\,H_{\mathfrak{m}}^{n-s}(R/(J^{l}+(f^{t}))).\end{eqnarray}$$
$$\begin{eqnarray}\underset{t}{\varprojlim }\,H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\simeq \underset{t}{\varprojlim }\,\underset{l}{\varprojlim }\,H_{\mathfrak{m}}^{n-s}(R/(J^{l}+(f^{t}))).\end{eqnarray}$$
As the family
 $\{I^{l}\}=\{(J+(f))^{l}\}$
of ideals of
$\{I^{l}\}=\{(J+(f))^{l}\}$
of ideals of
![]() $R$
is cofinal with the family
$R$
is cofinal with the family
 $\{J^{l}+(f^{t})\}_{(l,t)}$
, this last inverse limit is isomorphic to
$\{J^{l}+(f^{t})\}_{(l,t)}$
, this last inverse limit is isomorphic to
 $$\begin{eqnarray}\underset{l}{\varprojlim }\,H_{\mathfrak{m}}^{n-s}(R/(J+(f))^{l})=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}}),\end{eqnarray}$$
$$\begin{eqnarray}\underset{l}{\varprojlim }\,H_{\mathfrak{m}}^{n-s}(R/(J+(f))^{l})=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}}),\end{eqnarray}$$
as claimed. For all
![]() $t$
and
$t$
and
![]() $l$
, there are
$l$
, there are
![]() $k$
-linear maps
$k$
-linear maps
 $\unicode[STIX]{x1D6FF}_{l,t}:R/(J^{l+1}+(f^{t+1}))\rightarrow R/(J^{l}+(f^{t}))$
and
$\unicode[STIX]{x1D6FF}_{l,t}:R/(J^{l+1}+(f^{t+1}))\rightarrow R/(J^{l}+(f^{t}))$
and
 $\unicode[STIX]{x1D6FF}_{l}:R/J^{l+1}\rightarrow R/J^{l}$
, induced on the quotients by
$\unicode[STIX]{x1D6FF}_{l}:R/J^{l+1}\rightarrow R/J^{l}$
, induced on the quotients by
 $\unicode[STIX]{x2202}:R\rightarrow R$
, that induce
$\unicode[STIX]{x2202}:R\rightarrow R$
, that induce
![]() $k$
-linear maps
$k$
-linear maps
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}_{l,t}:H_{\mathfrak{m}}^{n-s}(R/(J^{l+1}+(f^{t+1})))\rightarrow H_{\mathfrak{ m}}^{n-s}(R/(J^{l}+(f^{t})))\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}_{l,t}:H_{\mathfrak{m}}^{n-s}(R/(J^{l+1}+(f^{t+1})))\rightarrow H_{\mathfrak{ m}}^{n-s}(R/(J^{l}+(f^{t})))\end{eqnarray}$$
and
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}_{l}:H_{\mathfrak{m}}^{n-s}(R/J^{l+1})\rightarrow H_{\mathfrak{ m}}^{n-s}(R/J^{l})\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}_{l}:H_{\mathfrak{m}}^{n-s}(R/J^{l+1})\rightarrow H_{\mathfrak{ m}}^{n-s}(R/J^{l})\end{eqnarray}$$
on local cohomology, by viewing local cohomology as a functor on sheaves of
![]() $k$
-spaces on the topological space
$k$
-spaces on the topological space
 $\operatorname{Spec}(R)$
. (Here we write, for instance,
$\operatorname{Spec}(R)$
. (Here we write, for instance,
![]() $\unicode[STIX]{x1D6FF}_{l}$
rather than
$\unicode[STIX]{x1D6FF}_{l}$
rather than
![]() $\unicode[STIX]{x2202}_{l}$
to avoid confusion with the maps
$\unicode[STIX]{x2202}_{l}$
to avoid confusion with the maps
![]() $\unicode[STIX]{x2202}_{l}$
defined earlier in the proof.) The inverse limit action of
$\unicode[STIX]{x2202}_{l}$
defined earlier in the proof.) The inverse limit action of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
, which we have denoted
$H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
, which we have denoted
![]() $\overline{\unicode[STIX]{x1D6FF}}$
, is defined by
$\overline{\unicode[STIX]{x1D6FF}}$
, is defined by
 $\mathop{\varprojlim }\nolimits_{(l,t)}\overline{\unicode[STIX]{x1D6FF}}_{l,t}$
. If we pass to the inverse limit in
$\mathop{\varprojlim }\nolimits_{(l,t)}\overline{\unicode[STIX]{x1D6FF}}_{l,t}$
. If we pass to the inverse limit in
![]() $l$
first, we find that
$l$
first, we find that
 $\overline{\unicode[STIX]{x1D6FF}}=\mathop{\varprojlim }\nolimits_{t}\overline{\unicode[STIX]{x1D6FF}}_{Z,t}$
, where for all
$\overline{\unicode[STIX]{x1D6FF}}=\mathop{\varprojlim }\nolimits_{t}\overline{\unicode[STIX]{x1D6FF}}_{Z,t}$
, where for all
![]() $t$
, the map
$t$
, the map
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}_{Z,t}:H_{P}^{n-s}((X_{t+1})_{/Z},{\mathcal{O}}_{(X_{t+1})_{/Z}})\rightarrow H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}_{Z,t}:H_{P}^{n-s}((X_{t+1})_{/Z},{\mathcal{O}}_{(X_{t+1})_{/Z}})\rightarrow H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\end{eqnarray}$$
is simply
![]() $\mathop{\varprojlim }\nolimits_{l}\overline{\unicode[STIX]{x1D6FF}}_{l,t}$
.
$\mathop{\varprojlim }\nolimits_{l}\overline{\unicode[STIX]{x1D6FF}}_{l,t}$
.
The maps
![]() $\unicode[STIX]{x1D6FF}_{l,t}$
and
$\unicode[STIX]{x1D6FF}_{l,t}$
and
![]() $\unicode[STIX]{x1D6FF}_{l}$
defined in the previous paragraph fit into commutative diagrams
$\unicode[STIX]{x1D6FF}_{l}$
defined in the previous paragraph fit into commutative diagrams

for all
![]() $l$
and
$l$
and
![]() $t$
, where the rows are exact sequences of
$t$
, where the rows are exact sequences of
![]() $R$
-modules and the vertical arrows are
$R$
-modules and the vertical arrows are
![]() $k$
-linear. It is clear that the map
$k$
-linear. It is clear that the map
 $\unicode[STIX]{x2202}f+t\unicode[STIX]{x2202}(f):R\rightarrow R$
carries
$\unicode[STIX]{x2202}f+t\unicode[STIX]{x2202}(f):R\rightarrow R$
carries
![]() $J^{l+1}$
into
$J^{l+1}$
into
![]() $J^{l}$
(the left vertical arrow is the
$J^{l}$
(the left vertical arrow is the
![]() $k$
-linear map that this map induces on the quotients), and the calculation (at the level of elements of
$k$
-linear map that this map induces on the quotients), and the calculation (at the level of elements of
![]() $R$
)
$R$
)
 $$\begin{eqnarray}\displaystyle f^{t}((\unicode[STIX]{x2202}f+t\unicode[STIX]{x2202}(f))(r))=f^{t}(\unicode[STIX]{x2202}(fr)+t\unicode[STIX]{x2202}(f)(r)) & = & \displaystyle f^{t}(\unicode[STIX]{x2202}(f)r+f\unicode[STIX]{x2202}(r)+t\unicode[STIX]{x2202}(f)(r))\nonumber\\ \displaystyle & = & \displaystyle f^{t+1}\unicode[STIX]{x2202}(r)+(t+1)f^{t}\unicode[STIX]{x2202}(f)r\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}(f^{t+1}r)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f^{t}((\unicode[STIX]{x2202}f+t\unicode[STIX]{x2202}(f))(r))=f^{t}(\unicode[STIX]{x2202}(fr)+t\unicode[STIX]{x2202}(f)(r)) & = & \displaystyle f^{t}(\unicode[STIX]{x2202}(f)r+f\unicode[STIX]{x2202}(r)+t\unicode[STIX]{x2202}(f)(r))\nonumber\\ \displaystyle & = & \displaystyle f^{t+1}\unicode[STIX]{x2202}(r)+(t+1)f^{t}\unicode[STIX]{x2202}(f)r\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}(f^{t+1}r)\nonumber\end{eqnarray}$$
for
![]() $r\in R$
shows that the left square is commutative (the commutativity of the right square is clear). Fix
$r\in R$
shows that the left square is commutative (the commutativity of the right square is clear). Fix
![]() $l$
and
$l$
and
![]() $t$
. Since the rows of the above diagram are short exact sequences of
$t$
. Since the rows of the above diagram are short exact sequences of
![]() $R$
-modules, both induce long exact sequences of local cohomology supported at
$R$
-modules, both induce long exact sequences of local cohomology supported at
![]() $\mathfrak{m}$
, and the vertical arrows, which are
$\mathfrak{m}$
, and the vertical arrows, which are
![]() $k$
-linear, induce
$k$
-linear, induce
![]() $k$
-linear maps on local cohomology as defined in the previous paragraph. Since
$k$
-linear maps on local cohomology as defined in the previous paragraph. Since
![]() $J$
is a complete intersection ideal,
$J$
is a complete intersection ideal,
![]() $R/J^{l}$
is a Cohen–Macaulay ring (of dimension
$R/J^{l}$
is a Cohen–Macaulay ring (of dimension
 $n-s+1$
) for all
$n-s+1$
) for all
![]() $l$
by [Reference MatsumuraMat86, Example 17.4], so
$l$
by [Reference MatsumuraMat86, Example 17.4], so
 $H_{\mathfrak{m}}^{i}(R/J^{l})=0$
unless
$H_{\mathfrak{m}}^{i}(R/J^{l})=0$
unless
 $i=n-s+1$
. It follows that
$i=n-s+1$
. It follows that
 $H_{\mathfrak{m}}^{i}(R/(J^{l}+(f^{t})))=0$
unless
$H_{\mathfrak{m}}^{i}(R/(J^{l}+(f^{t})))=0$
unless
 $i=n-s$
, since
$i=n-s$
, since
![]() $f^{t}$
is a non-zero divisor on
$f^{t}$
is a non-zero divisor on
![]() $R/J^{l}$
for all
$R/J^{l}$
for all
![]() $l$
and
$l$
and
![]() $t$
. Therefore, the only non-zero portion of the resulting diagram is
$t$
. Therefore, the only non-zero portion of the resulting diagram is

where the middle arrow is the map induced by
 $\overline{\unicode[STIX]{x2202}f+t\unicode[STIX]{x2202}(f)}$
on local cohomology. We now pass to the inverse limit in
$\overline{\unicode[STIX]{x2202}f+t\unicode[STIX]{x2202}(f)}$
on local cohomology. We now pass to the inverse limit in
![]() $l$
while keeping
$l$
while keeping
![]() $t$
fixed. By [Reference Brodmann and SharpBS13, Theorem 7.1.3], the local cohomology modules appearing in the above diagram are all Artinian, and if
$t$
fixed. By [Reference Brodmann and SharpBS13, Theorem 7.1.3], the local cohomology modules appearing in the above diagram are all Artinian, and if
![]() $t$
is fixed, the transition maps in the inverse systems
$t$
is fixed, the transition maps in the inverse systems
 $\{H_{\mathfrak{m}}^{n-s+1}(R/J^{l})\}_{l}$
and
$\{H_{\mathfrak{m}}^{n-s+1}(R/J^{l})\}_{l}$
and
 $\{H_{\mathfrak{m}}^{n-s}(R/(J^{l}+(f^{t})))\}_{l}$
are
$\{H_{\mathfrak{m}}^{n-s}(R/(J^{l}+(f^{t})))\}_{l}$
are
![]() $R$
-linear. Consequently, the Mittag-Leffler hypotheses of Proposition 5.9 are satisfied, and so the rows in the above diagram remain exact after passing to the inverse limit in
$R$
-linear. Consequently, the Mittag-Leffler hypotheses of Proposition 5.9 are satisfied, and so the rows in the above diagram remain exact after passing to the inverse limit in
![]() $l$
. The result is a commutative diagram
$l$
. The result is a commutative diagram

where the rows are short exact sequences of
![]() $R$
-modules. Recall that
$R$
-modules. Recall that
![]() $\overline{\unicode[STIX]{x1D6FF}}_{Z}$
defines the inverse limit action of
$\overline{\unicode[STIX]{x1D6FF}}_{Z}$
defines the inverse limit action of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $H_{P}^{n-s+1}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
. We have already established that the inverse limit action of
$H_{P}^{n-s+1}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
. We have already established that the inverse limit action of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $$\begin{eqnarray}H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})\simeq \varprojlim \,H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})\simeq \varprojlim \,H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})\end{eqnarray}$$
is given by
![]() $\varprojlim \,\overline{\unicode[STIX]{x1D6FF}}_{Z,t}$
. We now have a diagram
$\varprojlim \,\overline{\unicode[STIX]{x1D6FF}}_{Z,t}$
. We now have a diagram

in which the front face is the left square of diagram (*), and the back face is the left square of diagram (**), so these two faces commute. Consider next the arrows from the front face to the back face. The arrows on the right are the isomorphisms of Proposition 6.3. These are inverse limits of the local duality isomorphisms of Theorem 6.1, which are functorial. The arrows on the left are composites of the isomorphisms of Proposition 6.3 with inverse limits of the change-of-ring isomorphisms
 $H_{J}^{s-1}(R/(f^{t}))\simeq H_{\overline{J}}^{s-1}(R/(f^{t}))$
[Reference Brodmann and SharpBS13, Theorem 4.2.1], which are also functorial. Therefore the top and bottom faces also commute.
$H_{J}^{s-1}(R/(f^{t}))\simeq H_{\overline{J}}^{s-1}(R/(f^{t}))$
[Reference Brodmann and SharpBS13, Theorem 4.2.1], which are also functorial. Therefore the top and bottom faces also commute.
By the induction hypothesis, the Matlis dual and inverse limit actions of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $$\begin{eqnarray}D(M)=H_{P}^{n-s+1}(X_{/Z},{\mathcal{O}}_{X_{/Z}})\end{eqnarray}$$
$$\begin{eqnarray}D(M)=H_{P}^{n-s+1}(X_{/Z},{\mathcal{O}}_{X_{/Z}})\end{eqnarray}$$
differ by a sign, that is,
 $\overline{\unicode[STIX]{x1D6FF}}_{Z}=-\unicode[STIX]{x2202}_{M}^{\ast }$
. Therefore, the right vertical arrow in the front face is
$\overline{\unicode[STIX]{x1D6FF}}_{Z}=-\unicode[STIX]{x2202}_{M}^{\ast }$
. Therefore, the right vertical arrow in the front face is
 $$\begin{eqnarray}(f\unicode[STIX]{x2202}_{M}-t\unicode[STIX]{x2202}(f))^{\ast }=(f\unicode[STIX]{x2202}_{M})^{\ast }-t\unicode[STIX]{x2202}(f)=\unicode[STIX]{x2202}_{M}^{\ast }f-t\unicode[STIX]{x2202}(f)=-\overline{\unicode[STIX]{x1D6FF}}_{Z}f-t\unicode[STIX]{x2202}(f)\end{eqnarray}$$
$$\begin{eqnarray}(f\unicode[STIX]{x2202}_{M}-t\unicode[STIX]{x2202}(f))^{\ast }=(f\unicode[STIX]{x2202}_{M})^{\ast }-t\unicode[STIX]{x2202}(f)=\unicode[STIX]{x2202}_{M}^{\ast }f-t\unicode[STIX]{x2202}(f)=-\overline{\unicode[STIX]{x1D6FF}}_{Z}f-t\unicode[STIX]{x2202}(f)\end{eqnarray}$$
under the identification
 $D(M)=H_{P}^{n-s+1}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
(here we have used the fact that the Matlis dual of multiplication by an element of
$D(M)=H_{P}^{n-s+1}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
(here we have used the fact that the Matlis dual of multiplication by an element of
![]() $R$
is again multiplication by that element). We conclude that the right face of the diagram anticommutes. Since the horizontal arrows of the front and back faces are injective, the left face must also anticommute. Consequently, under the identification
$R$
is again multiplication by that element). We conclude that the right face of the diagram anticommutes. Since the horizontal arrows of the front and back faces are injective, the left face must also anticommute. Consequently, under the identification
 $D(H_{I}^{s}(R))=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
and isomorphisms
$D(H_{I}^{s}(R))=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
and isomorphisms
 $D(H_{I}^{s}(R))\simeq \varprojlim \,D(M/f^{t}M)$
and
$D(H_{I}^{s}(R))\simeq \varprojlim \,D(M/f^{t}M)$
and
 $H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})\simeq \varprojlim \,H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})$
, we have
$H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})\simeq \varprojlim \,H_{P}^{n-s}((X_{t})_{/Z},{\mathcal{O}}_{(X_{t})_{/Z}})$
, we have
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}=\varprojlim \,\overline{\unicode[STIX]{x1D6FF}}_{Z,t}=\varprojlim \,(-\unicode[STIX]{x2202}_{t}^{\ast })=-\varprojlim \,\unicode[STIX]{x2202}_{t}^{\ast }=-\unicode[STIX]{x2202}^{\ast };\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6FF}}=\varprojlim \,\overline{\unicode[STIX]{x1D6FF}}_{Z,t}=\varprojlim \,(-\unicode[STIX]{x2202}_{t}^{\ast })=-\varprojlim \,\unicode[STIX]{x2202}_{t}^{\ast }=-\unicode[STIX]{x2202}^{\ast };\end{eqnarray}$$
that is, the Matlis dual and inverse limit actions on
 $D(H_{I}^{s}(R))=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
also differ by a sign, completing the proof by induction for complete intersection ideals
$D(H_{I}^{s}(R))=H_{P}^{n-s}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
also differ by a sign, completing the proof by induction for complete intersection ideals
![]() $I$
.◻
$I$
.◻
Before beginning the proof for arbitrary ideals
![]() $I$
, we need a lemma.
$I$
, we need a lemma.
Lemma 6.7. Let
![]() $J\subset I$
be ideals of
$J\subset I$
be ideals of
![]() $R$
, and let
$R$
, and let
![]() $Y$
(respectively
$Y$
(respectively
![]() $Z$
) be the closed subscheme of
$Z$
) be the closed subscheme of
 $X=\operatorname{Spec}(R)$
defined by
$X=\operatorname{Spec}(R)$
defined by
![]() $I$
(respectively
$I$
(respectively
![]() $J$
).
$J$
).
-
(a) If the natural map
 $H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is surjective, and the Matlis dual and inverse limit actions of
$H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is surjective, and the Matlis dual and inverse limit actions of
 $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{I}^{j}(R))=H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
differ by a sign, then the Matlis dual and inverse limit actions of
$D(H_{I}^{j}(R))=H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
differ by a sign, then the Matlis dual and inverse limit actions of
 $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{J}^{j}(R))=H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
also differ by a sign.
$D(H_{J}^{j}(R))=H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
also differ by a sign. -
(b) If the natural map
 $H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is injective, and the Matlis dual and inverse limit actions of
$H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is injective, and the Matlis dual and inverse limit actions of
 $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{J}^{j}(R))=H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
differ by a sign, then the Matlis dual and inverse limit actions of
$D(H_{J}^{j}(R))=H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
differ by a sign, then the Matlis dual and inverse limit actions of
 $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{I}^{j}(R))=H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
also differ by a sign.
$D(H_{I}^{j}(R))=H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
also differ by a sign.
Proof of Lemma 6.7.
There are canonical surjections
 $R/J^{l}\rightarrow R/I^{l}$
for all
$R/J^{l}\rightarrow R/I^{l}$
for all
![]() $l$
which induce
$l$
which induce
![]() $R$
-linear maps
$R$
-linear maps
 $H_{\mathfrak{m}}^{n-j}(R/J^{l})\rightarrow H_{\mathfrak{m}}^{n-j}(R/I^{l})$
and
$H_{\mathfrak{m}}^{n-j}(R/J^{l})\rightarrow H_{\mathfrak{m}}^{n-j}(R/I^{l})$
and
 $\operatorname{Ext}_{R}^{j}(R/I^{l},R)\rightarrow \operatorname{Ext}_{R}^{j}(R/J^{l},R)$
. The first of these maps and the Matlis dual of the second are the horizontal arrows in the diagram
$\operatorname{Ext}_{R}^{j}(R/I^{l},R)\rightarrow \operatorname{Ext}_{R}^{j}(R/J^{l},R)$
. The first of these maps and the Matlis dual of the second are the horizontal arrows in the diagram

whose vertical arrows are the isomorphisms of Theorem 6.1: the diagram commutes because the isomorphisms of Theorem 6.1 are functorial. By Proposition 6.3, the inverse limit in
![]() $l$
of these commutative diagrams is the commutative diagram
$l$
of these commutative diagrams is the commutative diagram

of
![]() $R$
-modules. If the natural map
$R$
-modules. If the natural map
 $H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is surjective (respectively injective), then the top horizontal arrow of this diagram is injective (respectively surjective), as is the bottom horizontal arrow (because the vertical maps are isomorphisms).
$H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is surjective (respectively injective), then the top horizontal arrow of this diagram is injective (respectively surjective), as is the bottom horizontal arrow (because the vertical maps are isomorphisms).
Both parts of the lemma will follow if we can show that the top (respectively bottom) horizontal arrow commutes with the Matlis dual (respectively inverse limit) action on both sides; for then in the case that the map
 $H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is surjective (so both horizontal maps in the preceding commutative diagram are injective), the Matlis dual (respectively inverse limit) action on
$H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is surjective (so both horizontal maps in the preceding commutative diagram are injective), the Matlis dual (respectively inverse limit) action on
 $D(H_{J}^{j}(R))=H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
is induced by the Matlis dual (respectively inverse limit) action on
$D(H_{J}^{j}(R))=H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
is induced by the Matlis dual (respectively inverse limit) action on
 $D(H_{I}^{j}(R))=H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
, and in the case that the map
$D(H_{I}^{j}(R))=H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
, and in the case that the map
 $H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is injective (so both horizontal maps in the preceding commutative diagram are surjective), the Matlis dual (respectively inverse limit) action on
$H_{I}^{j}(R)\rightarrow H_{J}^{j}(R)$
is injective (so both horizontal maps in the preceding commutative diagram are surjective), the Matlis dual (respectively inverse limit) action on
 $D(H_{I}^{j}(R))=H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
is induced by the Matlis dual (respectively inverse limit) action on
$D(H_{I}^{j}(R))=H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
is induced by the Matlis dual (respectively inverse limit) action on
 $D(H_{J}^{j}(R))=H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
.
$D(H_{J}^{j}(R))=H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
.
The top arrow commutes with the Matlis dual action of
![]() ${\mathcal{D}}$
on both sides because it is the Matlis dual of an
${\mathcal{D}}$
on both sides because it is the Matlis dual of an
![]() ${\mathcal{D}}$
-linear map. Finally, the bottom arrow
${\mathcal{D}}$
-linear map. Finally, the bottom arrow
 $$\begin{eqnarray}H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})\rightarrow H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{n-j}(X_{/Z},{\mathcal{O}}_{X_{/Z}})\rightarrow H_{P}^{n-j}(X_{/Y},{\mathcal{O}}_{X_{/Y}})\end{eqnarray}$$
commutes with the inverse limit action of
![]() ${\mathcal{D}}$
on both sides, because if
${\mathcal{D}}$
on both sides, because if
![]() $d\in {\mathcal{D}}$
is a differential operator of order
$d\in {\mathcal{D}}$
is a differential operator of order
![]() $j$
, we have commutative diagrams
$j$
, we have commutative diagrams

for all
![]() $t$
where the vertical arrows are induced by
$t$
where the vertical arrows are induced by
![]() $d$
, and these diagrams remain commutative after applying the functor
$d$
, and these diagrams remain commutative after applying the functor
![]() $H_{\mathfrak{m}}^{j}$
to all of their objects and maps (viewing local cohomology as a functor on sheaves of
$H_{\mathfrak{m}}^{j}$
to all of their objects and maps (viewing local cohomology as a functor on sheaves of
![]() $k$
-spaces on the topological space
$k$
-spaces on the topological space
 $\operatorname{Spec}(R)$
).◻
$\operatorname{Spec}(R)$
).◻
Now let
![]() $I\subset R$
be an arbitrary ideal, and let
$I\subset R$
be an arbitrary ideal, and let
 $h=\operatorname{ht}(I)$
. Choose a regular sequence
$h=\operatorname{ht}(I)$
. Choose a regular sequence
 $f_{1},\ldots ,f_{h}\in I$
and denote by
$f_{1},\ldots ,f_{h}\in I$
and denote by
![]() $J$
the ideal generated by
$J$
the ideal generated by
 $f_{1},\ldots ,f_{h}$
, so that
$f_{1},\ldots ,f_{h}$
, so that
![]() $J\subset I$
and
$J\subset I$
and
![]() $J$
is a complete intersection ideal. Let
$J$
is a complete intersection ideal. Let
 $J=\mathfrak{q}_{1}\cap \cdots \cap \mathfrak{q}_{r}$
be a primary decomposition of
$J=\mathfrak{q}_{1}\cap \cdots \cap \mathfrak{q}_{r}$
be a primary decomposition of
![]() $J$
. Reindexing if necessary, we may assume
$J$
. Reindexing if necessary, we may assume
 $I\subset \sqrt{\mathfrak{q}_{1}},\ldots ,I\subset \sqrt{\mathfrak{q}_{s}},I\not \subset \sqrt{\mathfrak{q}_{s+1}},\ldots ,I\not \subset \sqrt{\mathfrak{q}_{r}}$
. We may assume
$I\subset \sqrt{\mathfrak{q}_{1}},\ldots ,I\subset \sqrt{\mathfrak{q}_{s}},I\not \subset \sqrt{\mathfrak{q}_{s+1}},\ldots ,I\not \subset \sqrt{\mathfrak{q}_{r}}$
. We may assume
![]() $s<r$
, as otherwise
$s<r$
, as otherwise
 $\sqrt{I}=\sqrt{J}$
and there is nothing left to prove. Put
$\sqrt{I}=\sqrt{J}$
and there is nothing left to prove. Put
 $I^{\prime }=\mathfrak{q}_{1}\cap \cdots \cap \mathfrak{q}_{s}$
and
$I^{\prime }=\mathfrak{q}_{1}\cap \cdots \cap \mathfrak{q}_{s}$
and
 $I^{\prime \prime }=\mathfrak{q}_{s+1}\cap \cdots \cap \mathfrak{q}_{r}$
; then we have
$I^{\prime \prime }=\mathfrak{q}_{s+1}\cap \cdots \cap \mathfrak{q}_{r}$
; then we have
 $\operatorname{ht}(I^{\prime })=h,\operatorname{ht}(I^{\prime }+I^{\prime \prime })=h+1$
,
$\operatorname{ht}(I^{\prime })=h,\operatorname{ht}(I^{\prime }+I^{\prime \prime })=h+1$
,
 $J=I^{\prime }\cap I^{\prime \prime }$
, and
$J=I^{\prime }\cap I^{\prime \prime }$
, and
 $\sqrt{I}=\sqrt{I^{\prime }}$
.
$\sqrt{I}=\sqrt{I^{\prime }}$
.
The ideals
![]() $I^{\prime }$
and
$I^{\prime }$
and
![]() $I^{\prime \prime }$
give rise to a Mayer–Vietoris sequence of local cohomology (Proposition 2.4)
$I^{\prime \prime }$
give rise to a Mayer–Vietoris sequence of local cohomology (Proposition 2.4)
 $$\begin{eqnarray}\cdots \rightarrow H_{J}^{h-1}(R)\rightarrow H_{I^{\prime }+I^{\prime \prime }}^{h}(R)\rightarrow H_{I}^{h}(R)\oplus H_{I^{\prime \prime }}^{h}(R)\rightarrow H_{J}^{h}(R)\rightarrow H_{I^{\prime }+I^{\prime \prime }}^{h+1}(R)\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow H_{J}^{h-1}(R)\rightarrow H_{I^{\prime }+I^{\prime \prime }}^{h}(R)\rightarrow H_{I}^{h}(R)\oplus H_{I^{\prime \prime }}^{h}(R)\rightarrow H_{J}^{h}(R)\rightarrow H_{I^{\prime }+I^{\prime \prime }}^{h+1}(R)\rightarrow \cdots\end{eqnarray}$$
where we identify
![]() $H_{I}^{i}(R)$
with
$H_{I}^{i}(R)$
with
![]() $H_{I^{\prime }}^{i}(R)$
for all
$H_{I^{\prime }}^{i}(R)$
for all
![]() $i$
because the ideals
$i$
because the ideals
![]() $I$
and
$I$
and
![]() $I^{\prime }$
have the same radical [Reference Brodmann and SharpBS13, Remark 1.2.3]. Since
$I^{\prime }$
have the same radical [Reference Brodmann and SharpBS13, Remark 1.2.3]. Since
 $\operatorname{ht}(I^{\prime }+I^{\prime \prime })>h$
, we have
$\operatorname{ht}(I^{\prime }+I^{\prime \prime })>h$
, we have
 $H_{I^{\prime }+I^{\prime \prime }}^{h}(R)=0$
, so there is an injection
$H_{I^{\prime }+I^{\prime \prime }}^{h}(R)=0$
, so there is an injection
 $H_{I}^{h}(R)\oplus H_{I^{\prime \prime }}^{h}(R){\hookrightarrow}H_{J}^{h}(R)$
; composing with the inclusion of the first summand, we obtain an injection
$H_{I}^{h}(R)\oplus H_{I^{\prime \prime }}^{h}(R){\hookrightarrow}H_{J}^{h}(R)$
; composing with the inclusion of the first summand, we obtain an injection
 $H_{I}^{h}(R){\hookrightarrow}H_{J}^{h}(R)$
, which is just the natural map induced by the inclusion
$H_{I}^{h}(R){\hookrightarrow}H_{J}^{h}(R)$
, which is just the natural map induced by the inclusion
![]() $J\subset I$
of ideals. By the previous step of the proof, since
$J\subset I$
of ideals. By the previous step of the proof, since
![]() $J$
is a complete intersection ideal, the Matlis dual and inverse limit actions of
$J$
is a complete intersection ideal, the Matlis dual and inverse limit actions of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{J}^{h}(R))=H_{P}^{n-h}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
differ by a sign. We conclude from Lemma 6.7(b) that the Matlis dual and inverse limit actions of
$D(H_{J}^{h}(R))=H_{P}^{n-h}(X_{/Z},{\mathcal{O}}_{X_{/Z}})$
differ by a sign. We conclude from Lemma 6.7(b) that the Matlis dual and inverse limit actions of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{I}^{h}(R))=H_{P}^{n-h}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
also differ by a sign. This proves the theorem for an arbitrary ideal
$D(H_{I}^{h}(R))=H_{P}^{n-h}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
also differ by a sign. This proves the theorem for an arbitrary ideal
![]() $I$
in cohomological degree equal to the height of
$I$
in cohomological degree equal to the height of
![]() $I$
.
$I$
.
Finally, we prove the theorem in arbitrary cohomological degree
![]() $i$
by induction on
$i$
by induction on
 $i-\operatorname{ht}(I)$
; the base case, where
$i-\operatorname{ht}(I)$
; the base case, where
 $i=\operatorname{ht}(I)$
, was proved in the previous paragraph. Let
$i=\operatorname{ht}(I)$
, was proved in the previous paragraph. Let
 $i>h=\operatorname{ht}(I)$
be given. Since
$i>h=\operatorname{ht}(I)$
be given. Since
![]() $J$
is a complete intersection ideal of height
$J$
is a complete intersection ideal of height
![]() $h$
,
$h$
,
 $H_{J}^{i}(R)=0$
unless
$H_{J}^{i}(R)=0$
unless
![]() $i=h$
, so from the Mayer–Vietoris sequence we also conclude that
$i=h$
, so from the Mayer–Vietoris sequence we also conclude that
 $H_{I^{\prime }+I^{\prime \prime }}^{i}(R)$
maps surjectively to
$H_{I^{\prime }+I^{\prime \prime }}^{i}(R)$
maps surjectively to
 $H_{I}^{i}(R)\oplus H_{I^{\prime \prime }}^{i}(R)$
; composing with the projection onto the first summand, we obtain a surjection
$H_{I}^{i}(R)\oplus H_{I^{\prime \prime }}^{i}(R)$
; composing with the projection onto the first summand, we obtain a surjection
 $H_{I^{\prime }+I^{\prime \prime }}^{i}(R)\rightarrow H_{I}^{i}(R)$
, which is just the natural map induced by the inclusion
$H_{I^{\prime }+I^{\prime \prime }}^{i}(R)\rightarrow H_{I}^{i}(R)$
, which is just the natural map induced by the inclusion
 $I\subset I^{\prime }+I^{\prime \prime }$
of ideals. We have
$I\subset I^{\prime }+I^{\prime \prime }$
of ideals. We have
 $\operatorname{ht}(I^{\prime }+I^{\prime \prime })>\operatorname{ht}(I)$
, so
$\operatorname{ht}(I^{\prime }+I^{\prime \prime })>\operatorname{ht}(I)$
, so
 $i-\operatorname{ht}(I^{\prime }+I^{\prime \prime })<i-\operatorname{ht}(I)$
. By the induction hypothesis, the Matlis dual and inverse limit actions of
$i-\operatorname{ht}(I^{\prime }+I^{\prime \prime })<i-\operatorname{ht}(I)$
. By the induction hypothesis, the Matlis dual and inverse limit actions of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{I^{\prime }+I^{\prime \prime }}^{i}(R))=H_{P}^{n-i}(X_{/Z^{\prime }},{\mathcal{O}}_{X_{/Z^{\prime }}})$
differ by a sign, where
$D(H_{I^{\prime }+I^{\prime \prime }}^{i}(R))=H_{P}^{n-i}(X_{/Z^{\prime }},{\mathcal{O}}_{X_{/Z^{\prime }}})$
differ by a sign, where
![]() $Z^{\prime }$
is the closed subscheme of
$Z^{\prime }$
is the closed subscheme of
 $X=\operatorname{Spec}(R)$
defined by
$X=\operatorname{Spec}(R)$
defined by
![]() $I^{\prime }+I^{\prime \prime }$
. We conclude from Lemma 6.7(a) that the Matlis dual and inverse limit actions of
$I^{\prime }+I^{\prime \prime }$
. We conclude from Lemma 6.7(a) that the Matlis dual and inverse limit actions of
![]() $\unicode[STIX]{x2202}$
on
$\unicode[STIX]{x2202}$
on
 $D(H_{I}^{i}(R))=H_{P}^{n-i}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
also differ by a sign.◻
$D(H_{I}^{i}(R))=H_{P}^{n-i}(X_{/Y},{\mathcal{O}}_{X_{/Y}})$
also differ by a sign.◻
7 The de Rham cohomology of a complete local ring
In this section, we turn our attention to de Rham cohomology, and prove Theorems B and D. We prove the latter theorem (and Theorem B(b) as an immediate corollary) first, by synthesizing our results from the previous sections on Matlis duality and local cohomology of formal schemes. The proof of Theorem B(a), which we give next, proceeds similarly to that of Theorem A(a). As in § 2, we will first give the proof of Theorem B(a) for the
![]() $E_{2}$
-terms of the spectral sequences, to bring out the main ideas of the proof. There is a technical complication that will make the
$E_{2}$
-terms of the spectral sequences, to bring out the main ideas of the proof. There is a technical complication that will make the
![]() $E_{2}$
case more difficult than the
$E_{2}$
case more difficult than the
![]() $E_{2}$
case of Theorem A(a). (We will need to verify various Mittag-Leffler hypotheses for inverse systems, for which Corollary 5.31 will be necessary.)
$E_{2}$
case of Theorem A(a). (We will need to verify various Mittag-Leffler hypotheses for inverse systems, for which Corollary 5.31 will be necessary.)
We begin by recalling notation used in § 2 and giving Hartshorne’s definition of de Rham cohomology. Thus
![]() $A$
is again a complete local ring with a coefficient field
$A$
is again a complete local ring with a coefficient field
![]() $k$
of characteristic zero and
$k$
of characteristic zero and
 $\unicode[STIX]{x1D70B}:R\rightarrow A$
is a surjection of
$\unicode[STIX]{x1D70B}:R\rightarrow A$
is a surjection of
![]() $k$
-algebras with
$k$
-algebras with
 $R=k[[x_{1},\ldots ,x_{n}]]$
for some
$R=k[[x_{1},\ldots ,x_{n}]]$
for some
![]() $n$
. The surjection
$n$
. The surjection
![]() $\unicode[STIX]{x1D70B}$
induces a closed immersion of spectra
$\unicode[STIX]{x1D70B}$
induces a closed immersion of spectra
 $\operatorname{Spec}(A)=Y{\hookrightarrow}X=\operatorname{Spec}(R)$
, defined by the coherent sheaf of ideals
$\operatorname{Spec}(A)=Y{\hookrightarrow}X=\operatorname{Spec}(R)$
, defined by the coherent sheaf of ideals
 ${\mathcal{I}}\subset {\mathcal{O}}_{X}$
associated with the ideal
${\mathcal{I}}\subset {\mathcal{O}}_{X}$
associated with the ideal
 $I=\ker \unicode[STIX]{x1D70B}\subset R$
. Let
$I=\ker \unicode[STIX]{x1D70B}\subset R$
. Let
![]() $\widehat{X}$
be the formal completion of
$\widehat{X}$
be the formal completion of
![]() $Y$
in
$Y$
in
![]() $X$
, that is, the topological space
$X$
, that is, the topological space
![]() $Y$
equipped with the structure of a locally ringed space via the sheaf of rings
$Y$
equipped with the structure of a locally ringed space via the sheaf of rings
 ${\mathcal{O}}_{\widehat{X}}=\varprojlim \,{\mathcal{O}}_{X}/{\mathcal{I}}^{l}$
, an inverse limit of sheaves of rings supported at
${\mathcal{O}}_{\widehat{X}}=\varprojlim \,{\mathcal{O}}_{X}/{\mathcal{I}}^{l}$
, an inverse limit of sheaves of rings supported at
![]() $Y$
. For any coherent sheaf
$Y$
. For any coherent sheaf
![]() ${\mathcal{F}}$
of
${\mathcal{F}}$
of
![]() ${\mathcal{O}}_{X}$
-modules, we can define its
${\mathcal{O}}_{X}$
-modules, we can define its
![]() ${\mathcal{I}}$
-adic completion
${\mathcal{I}}$
-adic completion
 $\widehat{{\mathcal{F}}}=\varprojlim \,{\mathcal{F}}/{\mathcal{I}}^{l}{\mathcal{F}}$
, which is a sheaf of
$\widehat{{\mathcal{F}}}=\varprojlim \,{\mathcal{F}}/{\mathcal{I}}^{l}{\mathcal{F}}$
, which is a sheaf of
![]() ${\mathcal{O}}_{\widehat{X}}$
-modules.
${\mathcal{O}}_{\widehat{X}}$
-modules.
Now consider again the (continuous) de Rham complex
![]() $\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
. By the Leibniz rule, the
$\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
. By the Leibniz rule, the
![]() $k$
-linear differentials in this complex of sheaves on
$k$
-linear differentials in this complex of sheaves on
![]() $X$
are
$X$
are
![]() ${\mathcal{I}}$
-adically continuous, and therefore pass to the
${\mathcal{I}}$
-adically continuous, and therefore pass to the
![]() ${\mathcal{I}}$
-adic completions of the coherent
${\mathcal{I}}$
-adic completions of the coherent
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
![]() $\unicode[STIX]{x1D6FA}_{X}^{i}$
. We obtain, therefore, a complex
$\unicode[STIX]{x1D6FA}_{X}^{i}$
. We obtain, therefore, a complex
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
, whose objects are sheaves of
$\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
, whose objects are sheaves of
![]() ${\mathcal{O}}_{\widehat{X}}$
-modules but whose differentials are merely
${\mathcal{O}}_{\widehat{X}}$
-modules but whose differentials are merely
![]() $k$
-linear. Since
$k$
-linear. Since
![]() $X$
is the spectrum of a complete regular local ring and so the sheaves
$X$
is the spectrum of a complete regular local ring and so the sheaves
![]() $\unicode[STIX]{x1D6FA}_{X}^{i}$
are finite free
$\unicode[STIX]{x1D6FA}_{X}^{i}$
are finite free
![]() ${\mathcal{O}}_{X}$
-modules, there is a simpler description of the complex
${\mathcal{O}}_{X}$
-modules, there is a simpler description of the complex
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
. As formal completion commutes with finite direct sums, the sheaf
$\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
. As formal completion commutes with finite direct sums, the sheaf
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{X}^{i}$
is a direct sum of copies of
$\widehat{\unicode[STIX]{x1D6FA}}_{X}^{i}$
is a direct sum of copies of
![]() ${\mathcal{O}}_{\widehat{X}}$
. All of the derivations
${\mathcal{O}}_{\widehat{X}}$
. All of the derivations
 $\unicode[STIX]{x2202}_{x_{j}}:R\rightarrow R$
induce
$\unicode[STIX]{x2202}_{x_{j}}:R\rightarrow R$
induce
![]() ${\mathcal{I}}$
-adically continuous maps
${\mathcal{I}}$
-adically continuous maps
 ${\mathcal{O}}_{\widehat{X}}\rightarrow {\mathcal{O}}_{\widehat{X}}$
, and if we form the de Rham complex of
${\mathcal{O}}_{\widehat{X}}\rightarrow {\mathcal{O}}_{\widehat{X}}$
, and if we form the de Rham complex of
![]() ${\mathcal{O}}_{\widehat{X}}$
with respect to these derivations, we recover precisely the complex
${\mathcal{O}}_{\widehat{X}}$
with respect to these derivations, we recover precisely the complex
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
.
$\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
.
In [Reference HartshorneHar75], the (local) de Rham cohomology of the local scheme
![]() $Y$
is defined as
$Y$
is defined as
 $H_{P,\text{dR}}^{i}(Y)=\mathbf{H}_{P}^{i}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet })$
, the hypercohomology (supported at the closed point
$H_{P,\text{dR}}^{i}(Y)=\mathbf{H}_{P}^{i}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet })$
, the hypercohomology (supported at the closed point
![]() $P$
of
$P$
of
![]() $Y$
) of the completed de Rham complex. These
$Y$
) of the completed de Rham complex. These
![]() $k$
-spaces are known to be independent of the choice of
$k$
-spaces are known to be independent of the choice of
![]() $R$
and
$R$
and
![]() $\unicode[STIX]{x1D70B}$
[Reference HartshorneHar75, Proposition III.1.1] and finite-dimensional [Reference HartshorneHar75, Theorem III.2.1]. Since the local de Rham cohomology is defined as the hypercohomology of a complex, we have, as in the case of homology, a Hodge–de Rham spectral sequence that begins
$\unicode[STIX]{x1D70B}$
[Reference HartshorneHar75, Proposition III.1.1] and finite-dimensional [Reference HartshorneHar75, Theorem III.2.1]. Since the local de Rham cohomology is defined as the hypercohomology of a complex, we have, as in the case of homology, a Hodge–de Rham spectral sequence that begins
 $\tilde{E}_{1}^{p,q}=H_{P}^{q}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{p})$
and abuts to
$\tilde{E}_{1}^{p,q}=H_{P}^{q}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{p})$
and abuts to
 $H_{P,\text{dR}}^{p+q}(Y)$
.
$H_{P,\text{dR}}^{p+q}(Y)$
.
We also recall from § 2 that the Hodge–de Rham spectral sequence for homology has
![]() $E_{1}$
-term given by
$E_{1}$
-term given by
 $E_{1}^{n-p,n-q}=H_{Y}^{n-q}(X,\unicode[STIX]{x1D6FA}_{X}^{n-p})$
and abuts to
$E_{1}^{n-p,n-q}=H_{Y}^{n-q}(X,\unicode[STIX]{x1D6FA}_{X}^{n-p})$
and abuts to
 $H_{p+q}^{\text{dR}}(Y)$
. The assertion of Theorem D is that, for all
$H_{p+q}^{\text{dR}}(Y)$
. The assertion of Theorem D is that, for all
![]() $p$
and
$p$
and
![]() $q$
, the
$q$
, the
![]() $k$
-spaces
$k$
-spaces
 $E_{2}^{n-p,n-q}$
and
$E_{2}^{n-p,n-q}$
and
![]() $\tilde{E}_{2}^{p,q}$
are dual to each other. Since we know by Theorem A(b) that the former
$\tilde{E}_{2}^{p,q}$
are dual to each other. Since we know by Theorem A(b) that the former
![]() $k$
-space is finite-dimensional, this duality implies that the latter is as well, which will prove Theorem B(b). Our work in §§ 5 and 6 is nearly enough to establish this duality; all that remains is to identify the rows of the
$k$
-space is finite-dimensional, this duality implies that the latter is as well, which will prove Theorem B(b). Our work in §§ 5 and 6 is nearly enough to establish this duality; all that remains is to identify the rows of the
![]() $E_{1}$
-term of the cohomology spectral sequence with de Rham complexes of
$E_{1}$
-term of the cohomology spectral sequence with de Rham complexes of
![]() ${\mathcal{D}}$
-modules.
${\mathcal{D}}$
-modules.
We recall again Convention 2.1, which remains in force in this section: if
![]() $M$
is a left
$M$
is a left
 ${\mathcal{D}}(R,k)$
-module, we write
${\mathcal{D}}(R,k)$
-module, we write
 $M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
for its de Rham complex, where the subscript
$M\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
for its de Rham complex, where the subscript
![]() $R$
indicates the ring over which the complex is being computed: the objects of this complex are tensor products of
$R$
indicates the ring over which the complex is being computed: the objects of this complex are tensor products of
![]() $R$
-modules taken over
$R$
-modules taken over
![]() $R$
, but the maps are not
$R$
, but the maps are not
![]() $R$
-linear.
$R$
-linear.
Lemma 7.1. Let the surjection
 $\unicode[STIX]{x1D70B}:R=k[[x_{1},\ldots ,x_{n}]]\rightarrow A$
(and the associated objects
$\unicode[STIX]{x1D70B}:R=k[[x_{1},\ldots ,x_{n}]]\rightarrow A$
(and the associated objects
 $I,X,\widehat{X},Y$
) be as above, and
$I,X,\widehat{X},Y$
) be as above, and
![]() $\{\tilde{E}_{\bullet }^{\bullet ,\bullet }\}$
the corresponding Hodge–de Rham spectral sequence for cohomology. For all
$\{\tilde{E}_{\bullet }^{\bullet ,\bullet }\}$
the corresponding Hodge–de Rham spectral sequence for cohomology. For all
![]() $q$
, the
$q$
, the
![]() $q$
th row
$q$
th row
![]() $\{\tilde{E}_{1}^{\bullet ,q}\}$
of the
$\{\tilde{E}_{1}^{\bullet ,q}\}$
of the
![]() $E_{1}$
-term
$E_{1}$
-term
![]() $\{\tilde{E}_{1}^{\bullet ,\bullet }\}$
is isomorphic, as a complex of
$\{\tilde{E}_{1}^{\bullet ,\bullet }\}$
is isomorphic, as a complex of
![]() $k$
-spaces, to the de Rham complex
$k$
-spaces, to the de Rham complex
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, where the left
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
, where the left
 ${\mathcal{D}}(R,k)$
-structure on
${\mathcal{D}}(R,k)$
-structure on
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
is given by the inverse limit action of Definition 6.4.
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
is given by the inverse limit action of Definition 6.4.
Proof. Let
![]() $q$
be fixed. Both formal completion along
$q$
be fixed. Both formal completion along
![]() $Y$
and local cohomology
$Y$
and local cohomology
![]() $H_{P}^{q}$
commute with finite direct sums, so for all
$H_{P}^{q}$
commute with finite direct sums, so for all
![]() $p$
,
$p$
,
 $\tilde{E}_{1}^{p,q}=H_{P}^{q}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{p})$
is a direct sum of copies of the
$\tilde{E}_{1}^{p,q}=H_{P}^{q}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{p})$
is a direct sum of copies of the
![]() $R$
-module
$R$
-module
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
, and the complex
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
, and the complex
![]() $\{\tilde{E}_{1}^{\bullet ,q}\}$
has differentials induced by the differentials in the complex
$\{\tilde{E}_{1}^{\bullet ,q}\}$
has differentials induced by the differentials in the complex
![]() $\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
by first passing to
$\unicode[STIX]{x1D6FA}_{X}^{\bullet }$
by first passing to
![]() ${\mathcal{I}}$
-adic completions and then applying the functor
${\mathcal{I}}$
-adic completions and then applying the functor
![]() $H_{P}^{q}$
. This is exactly the de Rham complex of
$H_{P}^{q}$
. This is exactly the de Rham complex of
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
with respect to the inverse limit action, since by Proposition 6.3 we have an isomorphism
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
with respect to the inverse limit action, since by Proposition 6.3 we have an isomorphism
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\simeq \varprojlim \,H_{P}^{q}(\widehat{X},{\mathcal{O}}_{X}/{\mathcal{I}}^{l})$
.◻
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\simeq \varprojlim \,H_{P}^{q}(\widehat{X},{\mathcal{O}}_{X}/{\mathcal{I}}^{l})$
.◻
Proof of Theorems D and B(b).
Fix
![]() $q$
. By Lemma 7.1, the
$q$
. By Lemma 7.1, the
![]() $q$
th row of the
$q$
th row of the
![]() $E_{1}$
-term of the cohomology spectral sequence,
$E_{1}$
-term of the cohomology spectral sequence,
![]() $\tilde{E}_{1}^{\bullet ,q}$
, is the de Rham complex of the left
$\tilde{E}_{1}^{\bullet ,q}$
, is the de Rham complex of the left
 ${\mathcal{D}}(R,k)$
-module
${\mathcal{D}}(R,k)$
-module
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
. By Theorem 6.5 and Remark 6.6, this complex is isomorphic (as a complex of
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
. By Theorem 6.5 and Remark 6.6, this complex is isomorphic (as a complex of
![]() $k$
-spaces) to the de Rham complex of the left
$k$
-spaces) to the de Rham complex of the left
 ${\mathcal{D}}(R,k)$
-module
${\mathcal{D}}(R,k)$
-module
 $D(H_{I}^{n-q}(R))$
. We obtain the
$D(H_{I}^{n-q}(R))$
. We obtain the
![]() $E_{2}$
-term by taking cohomology, so for all
$E_{2}$
-term by taking cohomology, so for all
![]() $p$
,
$p$
,
 $\tilde{E}_{2}^{p,q}=H_{\text{dR}}^{p}(D(H_{I}^{n-q}(R)))$
. Since
$\tilde{E}_{2}^{p,q}=H_{\text{dR}}^{p}(D(H_{I}^{n-q}(R)))$
. Since
 $H_{I}^{n-q}(R)$
is a holonomic
$H_{I}^{n-q}(R)$
is a holonomic
 ${\mathcal{D}}(R,k)$
-module, Theorem 5.1 applies: we have an isomorphism
${\mathcal{D}}(R,k)$
-module, Theorem 5.1 applies: we have an isomorphism
 $$\begin{eqnarray}H_{\text{dR}}^{p}(D(H_{I}^{n-q}(R)))\simeq (H_{\text{dR}}^{n-p}(H_{I}^{n-q}(R)))^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{dR}}^{p}(D(H_{I}^{n-q}(R)))\simeq (H_{\text{dR}}^{n-p}(H_{I}^{n-q}(R)))^{\vee }.\end{eqnarray}$$
The right-hand side of this isomorphism is nothing but
 $(E_{2}^{n-p,n-q})^{\vee }$
(by Lemma 2.16), completing the proof.◻
$(E_{2}^{n-p,n-q})^{\vee }$
(by Lemma 2.16), completing the proof.◻
We will now begin working toward the proof of Theorem B(a). The reductions immediately preceding Lemma 2.18 are equally valid here, so for the remainder of the section, we assume that
 $R=k[[x_{1},\ldots ,x_{n}]]$
and
$R=k[[x_{1},\ldots ,x_{n}]]$
and
 $R^{\prime }=R[[z]]$
, and it suffices to compare the Hodge–de Rham spectral sequences for cohomology corresponding to an arbitrary ideal
$R^{\prime }=R[[z]]$
, and it suffices to compare the Hodge–de Rham spectral sequences for cohomology corresponding to an arbitrary ideal
![]() $I\subset R$
(defining a closed immersion
$I\subset R$
(defining a closed immersion
 $Y=\operatorname{Spec}(R/I){\hookrightarrow}X=\operatorname{Spec}(R)$
) and the ideal
$Y=\operatorname{Spec}(R/I){\hookrightarrow}X=\operatorname{Spec}(R)$
) and the ideal
 $I^{\prime }=IR^{\prime }+(z)\subset R^{\prime }$
(defining a closed immersion
$I^{\prime }=IR^{\prime }+(z)\subset R^{\prime }$
(defining a closed immersion
 $Y{\hookrightarrow}X^{\prime }=\operatorname{Spec}(R^{\prime })$
).
$Y{\hookrightarrow}X^{\prime }=\operatorname{Spec}(R^{\prime })$
).
In the proof of Theorem A(a), we made use of an operation (Definition 2.19) on
![]() $k$
-spaces. Its replacement in this section is the following operation.
$k$
-spaces. Its replacement in this section is the following operation.
Definition 7.2. Let
![]() $M$
be any
$M$
be any
![]() $k$
-space. We define
$k$
-space. We define
 $M^{+}=M[[z]]$
, the
$M^{+}=M[[z]]$
, the
 ${\mathcal{D}}(k[[z]],k)$
-module of formal power series with coefficients in
${\mathcal{D}}(k[[z]],k)$
-module of formal power series with coefficients in
![]() $M$
. If
$M$
. If
![]() $M$
is an
$M$
is an
![]() $R$
-module (respectively a
$R$
-module (respectively a
 ${\mathcal{D}}(R,k)$
-module), then
${\mathcal{D}}(R,k)$
-module), then
![]() $M^{+}$
defined in this way is an
$M^{+}$
defined in this way is an
![]() $R^{\prime }$
-module (respectively a
$R^{\prime }$
-module (respectively a
 ${\mathcal{D}}(R^{\prime },k)$
-module), with
${\mathcal{D}}(R^{\prime },k)$
-module), with
![]() $\unicode[STIX]{x2202}_{z}$
-action defined by
$\unicode[STIX]{x2202}_{z}$
-action defined by
 $\unicode[STIX]{x2202}_{z}(\sum m_{l}z^{l})=\sum (l+1)m_{l+1}z^{l}$
.
$\unicode[STIX]{x2202}_{z}(\sum m_{l}z^{l})=\sum (l+1)m_{l+1}z^{l}$
.
If
![]() $M$
is an
$M$
is an
![]() $R$
-module, the
$R$
-module, the
![]() $R^{\prime }$
-module
$R^{\prime }$
-module
![]() $M^{+}$
is always
$M^{+}$
is always
![]() $z$
-adically complete. What is more,
$z$
-adically complete. What is more,
![]() $k$
-linear maps between
$k$
-linear maps between
![]() $k$
-spaces and
$k$
-spaces and
![]() $R$
-linear maps between
$R$
-linear maps between
![]() $R$
-modules extend to the corresponding formal power series objects: if
$R$
-modules extend to the corresponding formal power series objects: if
 $f:M\rightarrow N$
is a
$f:M\rightarrow N$
is a
![]() $k$
-linear map between
$k$
-linear map between
![]() $k$
-spaces (or an
$k$
-spaces (or an
![]() $R$
-linear map between
$R$
-linear map between
![]() $R$
-modules),
$R$
-modules),
 $f^{+}:M^{+}\rightarrow N^{+}$
is defined by
$f^{+}:M^{+}\rightarrow N^{+}$
is defined by
 $f^{+}(\sum m_{l}z^{l})=\sum f(m_{l})z^{l}$
.
$f^{+}(\sum m_{l}z^{l})=\sum f(m_{l})z^{l}$
.
Remark 7.3. If
![]() $M$
is an
$M$
is an
![]() $R$
-module, the
$R$
-module, the
![]() $R^{\prime }$
-module
$R^{\prime }$
-module
 $M^{+}=M[[z]]$
is usually not isomorphic to
$M^{+}=M[[z]]$
is usually not isomorphic to
 $M\otimes _{R}R^{\prime }$
. This is an example of the failure of inverse limits to commute with tensor products. We do have
$M\otimes _{R}R^{\prime }$
. This is an example of the failure of inverse limits to commute with tensor products. We do have
 $$\begin{eqnarray}M^{+}\simeq \varprojlim \,M[[z]]/z^{l}\simeq \varprojlim \,(M\otimes _{R}R^{\prime }/z^{l}),\end{eqnarray}$$
$$\begin{eqnarray}M^{+}\simeq \varprojlim \,M[[z]]/z^{l}\simeq \varprojlim \,(M\otimes _{R}R^{\prime }/z^{l}),\end{eqnarray}$$
where every
 $M\otimes _{R}R^{\prime }/z^{l}$
is regarded as an
$M\otimes _{R}R^{\prime }/z^{l}$
is regarded as an
![]() $R^{\prime }$
-module via the natural surjection
$R^{\prime }$
-module via the natural surjection
 $R^{\prime }\rightarrow R^{\prime }/z^{l}$
, but this inverse limit need not be isomorphic to
$R^{\prime }\rightarrow R^{\prime }/z^{l}$
, but this inverse limit need not be isomorphic to
 $M\otimes _{R}(\varprojlim \,R^{\prime }/z^{l})$
.
$M\otimes _{R}(\varprojlim \,R^{\prime }/z^{l})$
.
In the proofs below, we will often take two inverse limits simultaneously in the process of forming the module
![]() $M^{+}$
. The general principle is the following.
$M^{+}$
. The general principle is the following.
Lemma 7.4. Let
![]() $\{M_{l}\}$
be an inverse system of
$\{M_{l}\}$
be an inverse system of
![]() $R$
-modules, indexed by
$R$
-modules, indexed by
![]() $\mathbb{N}$
, and let
$\mathbb{N}$
, and let
 $M=\varprojlim \,M_{l}$
. Then
$M=\varprojlim \,M_{l}$
. Then
 $\varprojlim \,(M_{l}\otimes _{R}R^{\prime }/z^{l})\simeq M^{+}$
as
$\varprojlim \,(M_{l}\otimes _{R}R^{\prime }/z^{l})\simeq M^{+}$
as
![]() $R^{\prime }$
-modules.
$R^{\prime }$
-modules.
Proof. As an
![]() $R^{\prime }$
-module,
$R^{\prime }$
-module,
 $M^{+}\simeq \mathop{\varprojlim }\nolimits_{l}((\mathop{\varprojlim }\nolimits_{s}M_{s})\otimes _{R}R^{\prime }/z^{l})$
. Consider the inverse system
$M^{+}\simeq \mathop{\varprojlim }\nolimits_{l}((\mathop{\varprojlim }\nolimits_{s}M_{s})\otimes _{R}R^{\prime }/z^{l})$
. Consider the inverse system
 $\{M_{s}\otimes _{R}R^{\prime }/z^{l}\}$
, indexed by
$\{M_{s}\otimes _{R}R^{\prime }/z^{l}\}$
, indexed by
![]() $\mathbb{N}\times \mathbb{N}$
where
$\mathbb{N}\times \mathbb{N}$
where
 $(s,l)\leqslant (s^{\prime },l^{\prime })$
if and only if
$(s,l)\leqslant (s^{\prime },l^{\prime })$
if and only if
![]() $s\leqslant s^{\prime }$
and
$s\leqslant s^{\prime }$
and
![]() $l\leqslant l^{\prime }$
. Then
$l\leqslant l^{\prime }$
. Then
 $$\begin{eqnarray}\underset{l}{\varprojlim }\,\Bigl(\Bigl(\underset{s}{\varprojlim }\,M_{s}\Bigr)\otimes _{R}R^{\prime }/z^{l}\Bigr)\simeq \underset{(s,l)}{\varprojlim }\,M_{s}\otimes _{R}R^{\prime }/z^{l}.\end{eqnarray}$$
$$\begin{eqnarray}\underset{l}{\varprojlim }\,\Bigl(\Bigl(\underset{s}{\varprojlim }\,M_{s}\Bigr)\otimes _{R}R^{\prime }/z^{l}\Bigr)\simeq \underset{(s,l)}{\varprojlim }\,M_{s}\otimes _{R}R^{\prime }/z^{l}.\end{eqnarray}$$
As the ‘diagonal’ inverse system
 $\{M_{l}\otimes _{R}R^{\prime }/z^{l}\}_{l}$
is cofinal with
$\{M_{l}\otimes _{R}R^{\prime }/z^{l}\}_{l}$
is cofinal with
 $\{M_{s}\otimes _{R}R^{\prime }/z^{l}\}_{(s,l)}$
, their inverse limits are isomorphic, as desired.◻
$\{M_{s}\otimes _{R}R^{\prime }/z^{l}\}_{(s,l)}$
, their inverse limits are isomorphic, as desired.◻
We have defined the formal power series operation both for
![]() $k$
-spaces and for
$k$
-spaces and for
![]() $R$
-modules. In what follows, we will frequently apply the operation to an entire complex whose objects are
$R$
-modules. In what follows, we will frequently apply the operation to an entire complex whose objects are
![]() $R$
-modules but whose differentials are merely
$R$
-modules but whose differentials are merely
![]() $k$
-linear. We will still (abusively) use the notation
$k$
-linear. We will still (abusively) use the notation
![]() $\otimes \,R^{\prime }/z^{l}$
for the
$\otimes \,R^{\prime }/z^{l}$
for the
![]() $l$
th truncation of the formal power series operation, a convention which we record here.
$l$
th truncation of the formal power series operation, a convention which we record here.
Definition 7.5. Let
![]() $C^{\bullet }$
be a complex whose objects are
$C^{\bullet }$
be a complex whose objects are
![]() $R$
-modules and whose differentials are merely
$R$
-modules and whose differentials are merely
![]() $k$
-linear. The complex
$k$
-linear. The complex
 $C^{\bullet }\otimes R^{\prime }/z^{l}$
is the direct sum of
$C^{\bullet }\otimes R^{\prime }/z^{l}$
is the direct sum of
![]() $l$
copies of
$l$
copies of
![]() $C^{\bullet }$
, indexed by
$C^{\bullet }$
, indexed by
![]() $z^{i}$
for
$z^{i}$
for
 $i=0,\ldots ,l-1$
.
$i=0,\ldots ,l-1$
.
Note that the complex
![]() $(C^{\bullet })^{+}$
, obtained by applying the formal power series operation to all objects and differentials of
$(C^{\bullet })^{+}$
, obtained by applying the formal power series operation to all objects and differentials of
![]() $C^{\bullet }$
, is the inverse limit (in the category of complexes of
$C^{\bullet }$
, is the inverse limit (in the category of complexes of
![]() $k$
-spaces) of
$k$
-spaces) of
 $C^{\bullet }\otimes R^{\prime }/z^{l}$
.
$C^{\bullet }\otimes R^{\prime }/z^{l}$
.
Remark 7.6. We note one important difference between the formal power series operation defined above and the operation of Definition 2.19. The latter operation is defined using an infinite direct sum. Therefore, the question of whether it commutes with cohomology reduces to the question of whether the underlying category satisfies Grothendieck’s axiom
![]() $AB4$
[Reference GrothendieckGro57], that is, whether direct sums are exact. This is true for the categories of
$AB4$
[Reference GrothendieckGro57], that is, whether direct sums are exact. This is true for the categories of
![]() $R$
-modules, of
$R$
-modules, of
![]() $k$
-spaces, and of sheaves of Abelian groups on a topological space [Reference WeibelWei94, p. 80]. By contrast, the formal power series operation is defined using an infinite direct product, which commutes with cohomology if the underlying category satisfies axiom
$k$
-spaces, and of sheaves of Abelian groups on a topological space [Reference WeibelWei94, p. 80]. By contrast, the formal power series operation is defined using an infinite direct product, which commutes with cohomology if the underlying category satisfies axiom
![]() $AB4^{\ast }$
. This is true for the categories of
$AB4^{\ast }$
. This is true for the categories of
![]() $R$
-modules and
$R$
-modules and
![]() $k$
-spaces but not sheaves [Reference WeibelWei94, p. 80].
$k$
-spaces but not sheaves [Reference WeibelWei94, p. 80].
The main technical preliminary result we need concerns the interaction of the formal power series operation with the de Rham complexes of local cohomology modules on formal schemes. For reference, we repeat in the statement of this proposition the notation we will use for the remainder of this section.
Lemma 7.7. Let
 $R=k[[x_{1},\ldots ,x_{n}]]$
and let
$R=k[[x_{1},\ldots ,x_{n}]]$
and let
![]() $I$
be an ideal of
$I$
be an ideal of
![]() $R$
. Let
$R$
. Let
 $R^{\prime }=R[[z]]$
and
$R^{\prime }=R[[z]]$
and
 $I^{\prime }=IR^{\prime }+(z)$
. Let
$I^{\prime }=IR^{\prime }+(z)$
. Let
![]() ${\mathcal{I}}$
(respectively
${\mathcal{I}}$
(respectively
![]() ${\mathcal{I}}^{\prime }$
) be the associated sheaf of ideals of
${\mathcal{I}}^{\prime }$
) be the associated sheaf of ideals of
![]() ${\mathcal{O}}_{X}$
(respectively
${\mathcal{O}}_{X}$
(respectively
![]() ${\mathcal{O}}_{X^{\prime }}$
) where
${\mathcal{O}}_{X^{\prime }}$
) where
 $X=\operatorname{Spec}(R)$
and
$X=\operatorname{Spec}(R)$
and
 $X^{\prime }=\operatorname{Spec}(R^{\prime })$
. Let
$X^{\prime }=\operatorname{Spec}(R^{\prime })$
. Let
![]() $Y$
be the closed subscheme of
$Y$
be the closed subscheme of
![]() $X$
defined by
$X$
defined by
![]() ${\mathcal{I}}$
; via the natural closed immersion
${\mathcal{I}}$
; via the natural closed immersion
 $X{\hookrightarrow}X^{\prime }$
, we identify
$X{\hookrightarrow}X^{\prime }$
, we identify
![]() $Y$
with the closed subscheme of
$Y$
with the closed subscheme of
![]() $X^{\prime }$
defined by
$X^{\prime }$
defined by
![]() ${\mathcal{I}}^{\prime }$
, which we also denote
${\mathcal{I}}^{\prime }$
, which we also denote
![]() $Y$
. Let
$Y$
. Let
![]() $P\in Y$
be the closed point. Then for all
$P\in Y$
be the closed point. Then for all
![]() $q$
, we have
$q$
, we have
 $$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\simeq (H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })^{+}\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\simeq (H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })^{+}\end{eqnarray}$$
as complexes of
![]() $k$
-spaces, where the
$k$
-spaces, where the
 ${\mathcal{D}}(R,k)$
-structure on both local cohomology modules is given by the inverse limit action of Definition 6.4.
${\mathcal{D}}(R,k)$
-structure on both local cohomology modules is given by the inverse limit action of Definition 6.4.
The proof of Lemma 7.7 involves several ideas, so we begin with a lemma focusing on a single local cohomology module, with no reference to its de Rham complex. We will appeal below not only to this lemma but also to its proof.
Lemma 7.8. All notation is the same as in Lemma 7.7. For all
![]() $q$
, we have
$q$
, we have
 $$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\simeq (H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))^{+}\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\simeq (H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))^{+}\end{eqnarray}$$
as
![]() $R^{\prime }$
-modules.
$R^{\prime }$
-modules.
Proof. For all
![]() $l$
, let
$l$
, let
![]() $J_{l}$
be the ideal
$J_{l}$
be the ideal
 $I^{l}R^{\prime }+(z^{l})$
. The families
$I^{l}R^{\prime }+(z^{l})$
. The families
![]() $\{J_{l}\}$
and
$\{J_{l}\}$
and
![]() $\{(I^{\prime })^{l}\}$
of ideals of
$\{(I^{\prime })^{l}\}$
of ideals of
![]() $R^{\prime }$
are cofinal, and we have isomorphisms
$R^{\prime }$
are cofinal, and we have isomorphisms
 $$\begin{eqnarray}R^{\prime }/J_{l}=R^{\prime }/(I^{l}R^{\prime }+(z^{l}))\simeq R/I^{l}\otimes _{R}R^{\prime }/z^{l}\end{eqnarray}$$
$$\begin{eqnarray}R^{\prime }/J_{l}=R^{\prime }/(I^{l}R^{\prime }+(z^{l}))\simeq R/I^{l}\otimes _{R}R^{\prime }/z^{l}\end{eqnarray}$$
as
![]() $R^{\prime }$
-modules for all
$R^{\prime }$
-modules for all
![]() $l$
(the
$l$
(the
![]() $R^{\prime }$
-module structure on
$R^{\prime }$
-module structure on
 $R/I^{l}\otimes _{R}R^{\prime }/z^{l}$
being defined via the natural surjection
$R/I^{l}\otimes _{R}R^{\prime }/z^{l}$
being defined via the natural surjection
 $R^{\prime }\rightarrow R^{\prime }/z^{l}$
).
$R^{\prime }\rightarrow R^{\prime }/z^{l}$
).
Denote by
![]() $\mathfrak{n}$
(respectively
$\mathfrak{n}$
(respectively
![]() $\mathfrak{m}$
) the maximal ideal of
$\mathfrak{m}$
) the maximal ideal of
![]() $R^{\prime }$
(respectively
$R^{\prime }$
(respectively
![]() $R$
). For all
$R$
). For all
![]() $q$
, we have isomorphisms
$q$
, we have isomorphisms
 $$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\simeq \varprojlim \,H_{\mathfrak{n}}^{q}(R^{\prime }/(I^{\prime })^{l})\simeq \varprojlim \,H_{\mathfrak{ n}}^{q}(R^{\prime }/J_{l}),\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\simeq \varprojlim \,H_{\mathfrak{n}}^{q}(R^{\prime }/(I^{\prime })^{l})\simeq \varprojlim \,H_{\mathfrak{ n}}^{q}(R^{\prime }/J_{l}),\end{eqnarray}$$
the first isomorphism by Proposition 6.3 and the second by the cofinality of
![]() $\{J_{l}\}$
and
$\{J_{l}\}$
and
![]() $\{(I^{\prime })^{l}\}$
. We saw above that
$\{(I^{\prime })^{l}\}$
. We saw above that
 $R^{\prime }/J_{l}\simeq R/I^{l}\otimes _{R}R^{\prime }/z^{l}$
as
$R^{\prime }/J_{l}\simeq R/I^{l}\otimes _{R}R^{\prime }/z^{l}$
as
![]() $R^{\prime }$
-modules, and therefore
$R^{\prime }$
-modules, and therefore
 $$\begin{eqnarray}H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l})\simeq H_{\mathfrak{n}}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l})\simeq H_{\mathfrak{n}}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\end{eqnarray}$$
as
![]() $R^{\prime }$
-modules. We claim that the right-hand side is isomorphic to
$R^{\prime }$
-modules. We claim that the right-hand side is isomorphic to
 $H_{\mathfrak{m}}^{q}(R/I^{l})\otimes _{R}R^{\prime }/z^{l}$
as an
$H_{\mathfrak{m}}^{q}(R/I^{l})\otimes _{R}R^{\prime }/z^{l}$
as an
![]() $R^{\prime }$
-module.
$R^{\prime }$
-module.
The
![]() $R^{\prime }$
-module
$R^{\prime }$
-module
 $R/I^{l}\otimes _{R}R^{\prime }/z^{l}$
is annihilated by a power of
$R/I^{l}\otimes _{R}R^{\prime }/z^{l}$
is annihilated by a power of
![]() $z$
, and so
$z$
, and so
 $$\begin{eqnarray}H_{(z)}^{i}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})=R/I^{l}\otimes _{R}R^{\prime }/z^{l}\end{eqnarray}$$
$$\begin{eqnarray}H_{(z)}^{i}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})=R/I^{l}\otimes _{R}R^{\prime }/z^{l}\end{eqnarray}$$
if
![]() $i=0$
, and is zero otherwise. The spectral sequence of Example 2.15 corresponding to the composite functor
$i=0$
, and is zero otherwise. The spectral sequence of Example 2.15 corresponding to the composite functor
 $\unicode[STIX]{x1D6E4}_{\mathfrak{n}}=\unicode[STIX]{x1D6E4}_{\mathfrak{m}R^{\prime }}\circ \unicode[STIX]{x1D6E4}_{(z)}$
therefore degenerates at
$\unicode[STIX]{x1D6E4}_{\mathfrak{n}}=\unicode[STIX]{x1D6E4}_{\mathfrak{m}R^{\prime }}\circ \unicode[STIX]{x1D6E4}_{(z)}$
therefore degenerates at
![]() $E_{2}$
, and we have isomorphisms
$E_{2}$
, and we have isomorphisms
 $$\begin{eqnarray}H_{\mathfrak{n}}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\simeq H_{\mathfrak{ m}R^{\prime }}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathfrak{n}}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\simeq H_{\mathfrak{ m}R^{\prime }}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\end{eqnarray}$$
as
![]() $R^{\prime }$
-modules. By the change of ring principle [Reference Brodmann and SharpBS13, Theorem 4.2.1], it does not matter whether we compute this last local cohomology module over
$R^{\prime }$
-modules. By the change of ring principle [Reference Brodmann and SharpBS13, Theorem 4.2.1], it does not matter whether we compute this last local cohomology module over
![]() $R^{\prime }$
or over
$R^{\prime }$
or over
![]() $R^{\prime }/z^{l}$
, so in fact
$R^{\prime }/z^{l}$
, so in fact
 $$\begin{eqnarray}H_{\mathfrak{m}R^{\prime }}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\simeq H_{\mathfrak{ m}(R^{\prime }/z^{l})}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathfrak{m}R^{\prime }}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\simeq H_{\mathfrak{ m}(R^{\prime }/z^{l})}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\end{eqnarray}$$
as
![]() $R^{\prime }/z^{l}$
-modules. Finally, since
$R^{\prime }/z^{l}$
-modules. Finally, since
![]() $R^{\prime }/z^{l}$
is flat over
$R^{\prime }/z^{l}$
is flat over
![]() $R$
, the flat base change theorem [Reference Brodmann and SharpBS13, Theorem 4.3.2] implies that
$R$
, the flat base change theorem [Reference Brodmann and SharpBS13, Theorem 4.3.2] implies that
 $$\begin{eqnarray}H_{\mathfrak{m}(R^{\prime }/z^{l})}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\simeq H_{\mathfrak{ m}}^{q}(R/I^{l})\otimes _{R}R^{\prime }/z^{l}\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathfrak{m}(R^{\prime }/z^{l})}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\simeq H_{\mathfrak{ m}}^{q}(R/I^{l})\otimes _{R}R^{\prime }/z^{l}\end{eqnarray}$$
as
![]() $R^{\prime }/z^{l}$
-modules. The previous two isomorphisms of
$R^{\prime }/z^{l}$
-modules. The previous two isomorphisms of
![]() $R^{\prime }/z^{l}$
-modules are isomorphisms of
$R^{\prime }/z^{l}$
-modules are isomorphisms of
![]() $R^{\prime }$
-modules, as well, since the
$R^{\prime }$
-modules, as well, since the
![]() $R^{\prime }$
-structures are defined using the natural surjection
$R^{\prime }$
-structures are defined using the natural surjection
 $R^{\prime }\rightarrow R^{\prime }/z^{l}$
. Putting these isomorphisms together, we see that
$R^{\prime }\rightarrow R^{\prime }/z^{l}$
. Putting these isomorphisms together, we see that
 $$\begin{eqnarray}H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l})\simeq H_{\mathfrak{n}}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\simeq H_{\mathfrak{ m}}^{q}(R/I^{l})\otimes _{R}R^{\prime }/z^{l}\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l})\simeq H_{\mathfrak{n}}^{q}(R/I^{l}\otimes _{R}R^{\prime }/z^{l})\simeq H_{\mathfrak{ m}}^{q}(R/I^{l})\otimes _{R}R^{\prime }/z^{l}\end{eqnarray}$$
as
![]() $R^{\prime }$
-modules, for all
$R^{\prime }$
-modules, for all
![]() $l$
. As the isomorphisms of [Reference Brodmann and SharpBS13, Theorem 4.2.1, Theorem 4.3.2] are functorial, the isomorphisms above form a compatible system, and passing to the inverse limit, we have
$l$
. As the isomorphisms of [Reference Brodmann and SharpBS13, Theorem 4.2.1, Theorem 4.3.2] are functorial, the isomorphisms above form a compatible system, and passing to the inverse limit, we have
 $$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\simeq \varprojlim \,H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l})\simeq \varprojlim \,H_{\mathfrak{m}}^{q}(R/I^{l})\otimes _{R}R^{\prime }/z^{l},\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\simeq \varprojlim \,H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l})\simeq \varprojlim \,H_{\mathfrak{m}}^{q}(R/I^{l})\otimes _{R}R^{\prime }/z^{l},\end{eqnarray}$$
and since
 $\varprojlim \,H_{\mathfrak{m}}^{q}(R/I^{l})\simeq H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
(again by Proposition 6.3), the rightmost module above is isomorphic as an
$\varprojlim \,H_{\mathfrak{m}}^{q}(R/I^{l})\simeq H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
(again by Proposition 6.3), the rightmost module above is isomorphic as an
![]() $R^{\prime }$
-module to
$R^{\prime }$
-module to
 $(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))^{+}$
by Lemma 7.4, as desired.◻
$(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))^{+}$
by Lemma 7.4, as desired.◻
We now consider the de Rham complexes as well, and prove Lemma 7.7.
Proof of Lemma 7.7.
We retain the notation introduced in the proof of Lemma 7.8. For all
![]() $l$
and
$l$
and
![]() $s$
, let
$s$
, let
 $J_{l,s}=I^{l+s}R^{\prime }+(z^{l})$
. (Note that
$J_{l,s}=I^{l+s}R^{\prime }+(z^{l})$
. (Note that
 $J_{l,0}=J_{l}$
.) The families
$J_{l,0}=J_{l}$
.) The families
![]() $\{J_{l,s}\}$
(with
$\{J_{l,s}\}$
(with
![]() $s$
fixed) and
$s$
fixed) and
![]() $\{(I^{\prime })^{l}\}$
of ideals of
$\{(I^{\prime })^{l}\}$
of ideals of
![]() $R^{\prime }$
are cofinal. For all
$R^{\prime }$
are cofinal. For all
![]() $l$
and
$l$
and
![]() $s$
, the derivations
$s$
, the derivations
 $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
induce (by the Leibniz rule)
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
induce (by the Leibniz rule)
![]() $k$
-linear maps
$k$
-linear maps
 $R^{\prime }/J_{l,s}\rightarrow R^{\prime }/J_{l,s-1}$
, as all of these derivations are
$R^{\prime }/J_{l,s}\rightarrow R^{\prime }/J_{l,s-1}$
, as all of these derivations are
![]() $z$
-linear. In turn, these maps induce
$z$
-linear. In turn, these maps induce
![]() $k$
-linear maps on local cohomology as described in § 6. We can therefore construct, for every
$k$
-linear maps on local cohomology as described in § 6. We can therefore construct, for every
![]() $l$
, a ‘de Rham-like’ complex
$l$
, a ‘de Rham-like’ complex
 $$\begin{eqnarray}0\rightarrow H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l,n})\rightarrow \underset{1\leqslant i\leqslant n}{\bigoplus }H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l,n-1})\rightarrow \cdots \rightarrow H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l,0})\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l,n})\rightarrow \underset{1\leqslant i\leqslant n}{\bigoplus }H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l,n-1})\rightarrow \cdots \rightarrow H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l,0})\rightarrow 0\end{eqnarray}$$
using the derivations
 $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
. We write
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
. We write
![]() $H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })$
for this complex (cf. Definition 7.10 below). The argument in the proof of Lemma 7.8 applies to all terms of this complex, and using the fact that the differentials in this complex do not involve
$H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })$
for this complex (cf. Definition 7.10 below). The argument in the proof of Lemma 7.8 applies to all terms of this complex, and using the fact that the differentials in this complex do not involve
![]() $z$
or
$z$
or
![]() $dz$
, we see that this complex is isomorphic to the complex
$dz$
, we see that this complex is isomorphic to the complex
 $$\begin{eqnarray}\biggl(0\rightarrow H_{\mathfrak{m}}^{q}(R/I^{l+n})\rightarrow \underset{1\leqslant i\leqslant n}{\bigoplus }H_{\mathfrak{ m}}^{q}(R/I^{l+n-1})\rightarrow \cdots \rightarrow H_{\mathfrak{ m}}^{q}(R/I^{l})\rightarrow 0\biggr)\otimes R^{\prime }/z^{l},\end{eqnarray}$$
$$\begin{eqnarray}\biggl(0\rightarrow H_{\mathfrak{m}}^{q}(R/I^{l+n})\rightarrow \underset{1\leqslant i\leqslant n}{\bigoplus }H_{\mathfrak{ m}}^{q}(R/I^{l+n-1})\rightarrow \cdots \rightarrow H_{\mathfrak{ m}}^{q}(R/I^{l})\rightarrow 0\biggr)\otimes R^{\prime }/z^{l},\end{eqnarray}$$
which we write
 $H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l}$
, again anticipating Definition 7.10. We now pass to the inverse limit in
$H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l}$
, again anticipating Definition 7.10. We now pass to the inverse limit in
![]() $l$
of both systems of complexes. For all
$l$
of both systems of complexes. For all
![]() $s$
, we have
$s$
, we have
 $$\begin{eqnarray}\underset{l}{\varprojlim }\,H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l,s})\simeq H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\end{eqnarray}$$
$$\begin{eqnarray}\underset{l}{\varprojlim }\,H_{\mathfrak{n}}^{q}(R^{\prime }/J_{l,s})\simeq H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\end{eqnarray}$$
as
![]() $R^{\prime }$
-modules, by Proposition 6.3 and the cofinality of
$R^{\prime }$
-modules, by Proposition 6.3 and the cofinality of
![]() $\{J_{l,s}\}$
and
$\{J_{l,s}\}$
and
![]() $\{(I^{\prime })^{l}\}$
. Moreover, by the definition of the inverse limit action, the differentials in the complex
$\{(I^{\prime })^{l}\}$
. Moreover, by the definition of the inverse limit action, the differentials in the complex
 $H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
are given by taking the inverse limit of the differentials in the complexes
$H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
are given by taking the inverse limit of the differentials in the complexes
![]() $H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })$
. That is, we have
$H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })$
. That is, we have
 $$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\simeq \varprojlim \,H_{\mathfrak{ n}}^{q}({\mathcal{C}}_{l}^{\bullet }),\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\simeq \varprojlim \,H_{\mathfrak{ n}}^{q}({\mathcal{C}}_{l}^{\bullet }),\end{eqnarray}$$
for all
![]() $l$
, as complexes of
$l$
, as complexes of
![]() $k$
-spaces. On the other hand, again using Proposition 6.3, we have
$k$
-spaces. On the other hand, again using Proposition 6.3, we have
 $$\begin{eqnarray}\varprojlim \,H_{\mathfrak{m}}^{q}(R/I^{l})\simeq H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\end{eqnarray}$$
$$\begin{eqnarray}\varprojlim \,H_{\mathfrak{m}}^{q}(R/I^{l})\simeq H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\end{eqnarray}$$
as
![]() $R$
-modules, and, by the definition of the inverse limit action,
$R$
-modules, and, by the definition of the inverse limit action,
 $$\begin{eqnarray}H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\simeq \varprojlim \,H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet }),\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\simeq \varprojlim \,H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet }),\end{eqnarray}$$
for all
![]() $l$
, as complexes of
$l$
, as complexes of
![]() $k$
-spaces. To conclude the lemma, it suffices to show that
$k$
-spaces. To conclude the lemma, it suffices to show that
 $$\begin{eqnarray}\varprojlim \,H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })\simeq (\varprojlim \,H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet }))^{+}\end{eqnarray}$$
$$\begin{eqnarray}\varprojlim \,H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })\simeq (\varprojlim \,H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet }))^{+}\end{eqnarray}$$
as complexes of
![]() $k$
-spaces. We have already shown that we have isomorphisms
$k$
-spaces. We have already shown that we have isomorphisms
 $H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })\simeq H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l}$
that clearly form a compatible system, which implies
$H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })\simeq H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l}$
that clearly form a compatible system, which implies
 $$\begin{eqnarray}\varprojlim \,H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })\simeq \varprojlim \,H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l},\end{eqnarray}$$
$$\begin{eqnarray}\varprojlim \,H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })\simeq \varprojlim \,H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l},\end{eqnarray}$$
and since
 $\varprojlim \,H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l}\simeq (\varprojlim \,H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))^{+}$
(by applying Lemma 7.4 to all objects in the complex) the lemma follows.◻
$\varprojlim \,H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l}\simeq (\varprojlim \,H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))^{+}$
(by applying Lemma 7.4 to all objects in the complex) the lemma follows.◻
We can now begin the proof of Theorem B(a). We have already reduced ourselves to the case where
![]() $R$
and
$R$
and
![]() $R^{\prime }$
are as in the statement of Lemma 7.7. With
$R^{\prime }$
are as in the statement of Lemma 7.7. With
![]() $R$
and
$R$
and
![]() $R^{\prime }$
as in the statement of that lemma, our goal is to compare the spectral sequence
$R^{\prime }$
as in the statement of that lemma, our goal is to compare the spectral sequence
![]() $\{\tilde{E}_{r,R}^{p,q}\}$
arising from the surjection
$\{\tilde{E}_{r,R}^{p,q}\}$
arising from the surjection
![]() $R\rightarrow A$
, to the spectral sequence
$R\rightarrow A$
, to the spectral sequence
![]() $\{\tilde{\mathbf{E}}_{r,R^{\prime }}^{p,q}\}$
arising from the surjection
$\{\tilde{\mathbf{E}}_{r,R^{\prime }}^{p,q}\}$
arising from the surjection
 $R^{\prime }\rightarrow A$
. We will first prove that the
$R^{\prime }\rightarrow A$
. We will first prove that the
![]() $E_{2}$
-objects of these spectral sequences are isomorphic. As we have identified these
$E_{2}$
-objects of these spectral sequences are isomorphic. As we have identified these
![]() $E_{2}$
-objects in Lemma 7.1, this claim is equivalent to the following proposition. As with Lemma 2.18, we will later need not only the statement of this proposition, but the specific isomorphisms appearing in its proof.
$E_{2}$
-objects in Lemma 7.1, this claim is equivalent to the following proposition. As with Lemma 2.18, we will later need not only the statement of this proposition, but the specific isomorphisms appearing in its proof.
Proposition 7.9. All notation is the same as in Lemma 7.7. For all
![]() $p$
and
$p$
and
![]() $q$
, we have
$q$
, we have
 $$\begin{eqnarray}\tilde{E}_{2,R}^{p,q}=H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))\simeq H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}}))=\tilde{\mathbf{E}}_{2,R^{\prime }}^{p,q}\end{eqnarray}$$
$$\begin{eqnarray}\tilde{E}_{2,R}^{p,q}=H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))\simeq H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}}))=\tilde{\mathbf{E}}_{2,R^{\prime }}^{p,q}\end{eqnarray}$$
as
![]() $k$
-spaces, where the de Rham cohomology is computed by regarding
$k$
-spaces, where the de Rham cohomology is computed by regarding
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
as a
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
as a
 ${\mathcal{D}}(R,k)$
-module and
${\mathcal{D}}(R,k)$
-module and
 $H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})$
as a
$H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})$
as a
 ${\mathcal{D}}(R^{\prime },k)$
-module.
${\mathcal{D}}(R^{\prime },k)$
-module.
Proof. The argument closely parallels that of Lemma 2.18. Consider the short exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}}\widehat{\unicode[STIX]{x1D6FA}}_{X^{\prime }}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}{\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}}\widehat{\unicode[STIX]{x1D6FA}}_{X^{\prime }}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}{\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\rightarrow 0\end{eqnarray}$$
of complexes of sheaves of
![]() $k$
-spaces on
$k$
-spaces on
![]() $\widehat{X^{\prime }}$
, where
$\widehat{X^{\prime }}$
, where
![]() $\unicode[STIX]{x1D704}$
is simply
$\unicode[STIX]{x1D704}$
is simply
![]() $\wedge \,dz$
. This sequence is the analogue, for completed sheaves, of the short exact sequence given in Definition 2.21, and consists of split exact sequences of finite free
$\wedge \,dz$
. This sequence is the analogue, for completed sheaves, of the short exact sequence given in Definition 2.21, and consists of split exact sequences of finite free
![]() ${\mathcal{O}}_{\widehat{X^{\prime }}}$
-modules. Apply
${\mathcal{O}}_{\widehat{X^{\prime }}}$
-modules. Apply
![]() $H_{P}^{q}$
to the entire sequence of complexes: as formal completion and local cohomology commute with finite direct sums, we obtain a short exact sequence
$H_{P}^{q}$
to the entire sequence of complexes: as formal completion and local cohomology commute with finite direct sums, we obtain a short exact sequence
 $$\begin{eqnarray}0\rightarrow H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1]\rightarrow H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{q}^{\bullet }}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }[-1]\rightarrow H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{q}^{\bullet }}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\rightarrow 0\end{eqnarray}$$
of complexes of
![]() $k$
-spaces. The corresponding long exact sequence in cohomology (accounting for the shift of
$k$
-spaces. The corresponding long exact sequence in cohomology (accounting for the shift of
![]() $-1$
) is
$-1$
) is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \cdots \rightarrow h^{p-1}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{z}}h^{p-1}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })\xrightarrow[{}]{\overline{\unicode[STIX]{x1D70B}}_{q}^{p}}h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{z}}h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\rightarrow \cdots \,,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \cdots \rightarrow h^{p-1}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{z}}h^{p-1}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })\xrightarrow[{}]{\overline{\unicode[STIX]{x1D70B}}_{q}^{p}}h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\xrightarrow[{}]{\unicode[STIX]{x2202}_{z}}h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\rightarrow \cdots \,,\nonumber\end{eqnarray}$$
where we know by Lemma 2.22 that, up to a sign, the connecting homomorphism is
![]() $\unicode[STIX]{x2202}_{z}$
. By Lemma 7.7, we have
$\unicode[STIX]{x2202}_{z}$
. By Lemma 7.7, we have
 $$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\simeq (H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })^{+}\end{eqnarray}$$
$$\begin{eqnarray}H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }\simeq (H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })^{+}\end{eqnarray}$$
as complexes of
![]() $k$
-spaces. By Remark 7.6, the formal power series operation on the right-hand side commutes with cohomology (since we are now applying this operation to
$k$
-spaces. By Remark 7.6, the formal power series operation on the right-hand side commutes with cohomology (since we are now applying this operation to
![]() $k$
-spaces, not sheaves). Taking the cohomology of both sides, we find
$k$
-spaces, not sheaves). Taking the cohomology of both sides, we find
 $$\begin{eqnarray}h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\simeq (h^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))^{+}\end{eqnarray}$$
$$\begin{eqnarray}h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })\simeq (h^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }))^{+}\end{eqnarray}$$
as
![]() $k$
-spaces for all
$k$
-spaces for all
![]() $p$
. For any
$p$
. For any
![]() $k$
-space
$k$
-space
![]() $M$
, the action of
$M$
, the action of
![]() $\unicode[STIX]{x2202}_{z}$
on
$\unicode[STIX]{x2202}_{z}$
on
![]() $M^{+}$
is given in Definition 7.2, and it is clear from this definition (since
$M^{+}$
is given in Definition 7.2, and it is clear from this definition (since
 $\operatorname{char}(k)=0$
) that
$\operatorname{char}(k)=0$
) that
 $\operatorname{coker}(\unicode[STIX]{x2202}_{z}:M^{+}\rightarrow M^{+})=0$
and
$\operatorname{coker}(\unicode[STIX]{x2202}_{z}:M^{+}\rightarrow M^{+})=0$
and
 $\ker (\unicode[STIX]{x2202}_{z}:M^{+}\rightarrow M^{+})\simeq M$
, the latter corresponding to the ‘constant term’ component of
$\ker (\unicode[STIX]{x2202}_{z}:M^{+}\rightarrow M^{+})\simeq M$
, the latter corresponding to the ‘constant term’ component of
![]() $M^{+}$
. Returning to the displayed portion of the long exact sequence (with
$M^{+}$
. Returning to the displayed portion of the long exact sequence (with
 $M=h^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
), the first
$M=h^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })$
), the first
![]() $\unicode[STIX]{x2202}_{z}$
is surjective, and so by exactness the unlabeled arrow is the zero map; this implies that
$\unicode[STIX]{x2202}_{z}$
is surjective, and so by exactness the unlabeled arrow is the zero map; this implies that
![]() $\overline{\unicode[STIX]{x1D70B}}_{q}^{p}$
is injective, inducing an isomorphism between the kernel of the second
$\overline{\unicode[STIX]{x1D70B}}_{q}^{p}$
is injective, inducing an isomorphism between the kernel of the second
![]() $\unicode[STIX]{x2202}_{z}$
and
$\unicode[STIX]{x2202}_{z}$
and
 $$\begin{eqnarray}h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })=H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})).\end{eqnarray}$$
$$\begin{eqnarray}h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})\otimes \unicode[STIX]{x1D6FA}_{R^{\prime }}^{\bullet })=H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}})).\end{eqnarray}$$
Since this kernel is isomorphic to
 $h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })=H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))$
, the proof is complete.◻
$h^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X}})\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet })=H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))$
, the proof is complete.◻
We next work toward the general case of Theorem B(a). Our goal is to construct a morphism between the Hodge–de Rham spectral sequences
![]() $\{\tilde{E}_{r,R}^{p,q}\}$
and
$\{\tilde{E}_{r,R}^{p,q}\}$
and
![]() $\{\tilde{\mathbf{E}}_{r,R^{\prime }}^{p,q}\}$
arising from the two surjections
$\{\tilde{\mathbf{E}}_{r,R^{\prime }}^{p,q}\}$
arising from the two surjections
![]() $R\rightarrow A$
and
$R\rightarrow A$
and
 $R^{\prime }\rightarrow A$
which, at the level of
$R^{\prime }\rightarrow A$
which, at the level of
![]() $E_{2}$
-objects, consists of the isomorphisms of Proposition 7.9 : by Proposition 2.10, this is enough. As in the proof of Theorem A(a), we will construct an ‘intermediate’ spectral sequence
$E_{2}$
-objects, consists of the isomorphisms of Proposition 7.9 : by Proposition 2.10, this is enough. As in the proof of Theorem A(a), we will construct an ‘intermediate’ spectral sequence
![]() $\{\tilde{{\mathcal{E}}}_{r}^{p,q}\}$
. The analogue of Lemma 2.29, however, will be significantly harder to prove, since we are working with inverse limits and must therefore check various Mittag-Leffler conditions.
$\{\tilde{{\mathcal{E}}}_{r}^{p,q}\}$
. The analogue of Lemma 2.29, however, will be significantly harder to prove, since we are working with inverse limits and must therefore check various Mittag-Leffler conditions.
We begin with definitions of several complexes, collecting pieces of notation introduced in the course of the preceding proofs together with some obvious variations.
Definition 7.10. All notation is the same as in Lemma 7.7.
(a) Let
![]() $C_{l}^{\bullet }$
be the complex
$C_{l}^{\bullet }$
be the complex
 $$\begin{eqnarray}0\rightarrow R/I^{l+n}\rightarrow \underset{1\leqslant 1\leqslant n}{\bigoplus }R/I^{l+n-1}\rightarrow \cdots \rightarrow R/I^{l}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow R/I^{l+n}\rightarrow \underset{1\leqslant 1\leqslant n}{\bigoplus }R/I^{l+n-1}\rightarrow \cdots \rightarrow R/I^{l}\rightarrow 0\end{eqnarray}$$
defined using the derivations
 $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
. Note that this is a complex of
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
. Note that this is a complex of
![]() $R$
-modules with
$R$
-modules with
![]() $k$
-linear differentials.
$k$
-linear differentials.
(b) Let
![]() ${\mathcal{C}}_{l}^{\bullet }$
be the complex
${\mathcal{C}}_{l}^{\bullet }$
be the complex
 $$\begin{eqnarray}0\rightarrow R^{\prime }/J_{l,n}\rightarrow \underset{1\leqslant 1\leqslant n}{\bigoplus }R^{\prime }/J_{l,n-1}\rightarrow \cdots \rightarrow R^{\prime }/J_{l,0}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow R^{\prime }/J_{l,n}\rightarrow \underset{1\leqslant 1\leqslant n}{\bigoplus }R^{\prime }/J_{l,n-1}\rightarrow \cdots \rightarrow R^{\prime }/J_{l,0}\rightarrow 0\end{eqnarray}$$
defined using the derivations
 $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
, where for all
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{n}$
, where for all
![]() $l$
and
$l$
and
![]() $s$
,
$s$
,
 $J_{l,s}=I^{l+s}R^{\prime }+(z^{l})$
. This is a complex of
$J_{l,s}=I^{l+s}R^{\prime }+(z^{l})$
. This is a complex of
![]() $R^{\prime }$
-modules with
$R^{\prime }$
-modules with
![]() $k$
-linear differentials, and we have
$k$
-linear differentials, and we have
 ${\mathcal{C}}_{l}^{\bullet }\simeq C_{l}^{\bullet }\otimes R^{\prime }/z^{l}$
.
${\mathcal{C}}_{l}^{\bullet }\simeq C_{l}^{\bullet }\otimes R^{\prime }/z^{l}$
.
(c) Let
 $H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })$
(respectively
$H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })$
(respectively
![]() $H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })$
) be the complex obtained by applying local cohomology functors to the previous two complexes. In the course of the proof of Lemma 7.7, we remarked that
$H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })$
) be the complex obtained by applying local cohomology functors to the previous two complexes. In the course of the proof of Lemma 7.7, we remarked that
 $H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })\simeq H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l}$
.
$H_{\mathfrak{n}}^{q}({\mathcal{C}}_{l}^{\bullet })\simeq H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\otimes R^{\prime }/z^{l}$
.
(d) Let
 $$\begin{eqnarray}\widetilde{C_{l}}^{\bullet }=\biggl(0\rightarrow {\mathcal{O}}_{X}/{\mathcal{I}}^{l+n}\rightarrow \underset{1\leqslant 1\leqslant n}{\bigoplus }{\mathcal{O}}_{X}/{\mathcal{I}}^{l+n-1}\rightarrow \cdots \rightarrow {\mathcal{O}}_{X}/{\mathcal{I}}^{l}\rightarrow 0\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{C_{l}}^{\bullet }=\biggl(0\rightarrow {\mathcal{O}}_{X}/{\mathcal{I}}^{l+n}\rightarrow \underset{1\leqslant 1\leqslant n}{\bigoplus }{\mathcal{O}}_{X}/{\mathcal{I}}^{l+n-1}\rightarrow \cdots \rightarrow {\mathcal{O}}_{X}/{\mathcal{I}}^{l}\rightarrow 0\biggr)\end{eqnarray}$$
and
 $$\begin{eqnarray}\widetilde{{\mathcal{C}}}_{l}^{\bullet }=\biggl(0\rightarrow {\mathcal{O}}_{X^{\prime }}/{\mathcal{J}}_{l,n}\rightarrow \underset{1\leqslant 1\leqslant n}{\bigoplus }{\mathcal{O}}_{X^{\prime }}/{\mathcal{J}}_{l,n-1}\rightarrow \cdots \rightarrow {\mathcal{O}}_{X^{\prime }}/{\mathcal{J}}_{l,0}\rightarrow 0\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\mathcal{C}}}_{l}^{\bullet }=\biggl(0\rightarrow {\mathcal{O}}_{X^{\prime }}/{\mathcal{J}}_{l,n}\rightarrow \underset{1\leqslant 1\leqslant n}{\bigoplus }{\mathcal{O}}_{X^{\prime }}/{\mathcal{J}}_{l,n-1}\rightarrow \cdots \rightarrow {\mathcal{O}}_{X^{\prime }}/{\mathcal{J}}_{l,0}\rightarrow 0\biggr)\end{eqnarray}$$
be the sheafified versions of the first two complexes, where
 ${\mathcal{J}}_{l,s}=\widetilde{J_{l,s}}$
for all
${\mathcal{J}}_{l,s}=\widetilde{J_{l,s}}$
for all
![]() $l$
and
$l$
and
![]() $s$
. These can be viewed as complexes of sheaves of
$s$
. These can be viewed as complexes of sheaves of
![]() $k$
-spaces on
$k$
-spaces on
![]() $\widehat{X}$
(respectively
$\widehat{X}$
(respectively
![]() $\widehat{X^{\prime }}$
). We have
$\widehat{X^{\prime }}$
). We have
 $\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\simeq \varprojlim \,\widetilde{C_{l}^{\bullet }}$
and
$\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\simeq \varprojlim \,\widetilde{C_{l}^{\bullet }}$
and
 ${\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\simeq \varprojlim \,\widetilde{{\mathcal{C}}_{l}^{\bullet }}$
in the respective categories of complexes of sheaves.
${\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\simeq \varprojlim \,\widetilde{{\mathcal{C}}_{l}^{\bullet }}$
in the respective categories of complexes of sheaves.
(e) Finally, we consider a sheaf-theoretic variant of Definition 7.5. If
![]() ${\mathcal{F}}^{\bullet }$
is a complex whose objects are sheaves of
${\mathcal{F}}^{\bullet }$
is a complex whose objects are sheaves of
![]() ${\mathcal{O}}_{X}$
-modules and whose differentials are merely
${\mathcal{O}}_{X}$
-modules and whose differentials are merely
![]() $k$
-linear, the complex
$k$
-linear, the complex
 ${\mathcal{F}}^{\bullet }\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}$
is the direct sum of
${\mathcal{F}}^{\bullet }\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}$
is the direct sum of
![]() $l$
copies of
$l$
copies of
![]() ${\mathcal{F}}^{\bullet }$
, indexed by
${\mathcal{F}}^{\bullet }$
, indexed by
![]() $z^{i}$
for
$z^{i}$
for
 $i=0,\ldots ,l-1$
. (At the level of objects,
$i=0,\ldots ,l-1$
. (At the level of objects,
 ${\mathcal{F}}\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}$
is shorthand for the
${\mathcal{F}}\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}$
is shorthand for the
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
 ${\mathcal{F}}\otimes _{{\mathcal{O}}_{X}}i^{\ast }({\mathcal{O}}_{X^{\prime }}/{\mathcal{Z}}^{l})$
, where
${\mathcal{F}}\otimes _{{\mathcal{O}}_{X}}i^{\ast }({\mathcal{O}}_{X^{\prime }}/{\mathcal{Z}}^{l})$
, where
![]() $i$
is the closed immersion
$i$
is the closed immersion
 $X{\hookrightarrow}X^{\prime }$
and
$X{\hookrightarrow}X^{\prime }$
and
![]() ${\mathcal{Z}}$
is the sheaf of ideals defining this immersion.) As an example, we have
${\mathcal{Z}}$
is the sheaf of ideals defining this immersion.) As an example, we have
 $\widetilde{{\mathcal{C}}_{l}^{\bullet }}\simeq \widetilde{C_{l}^{\bullet }}\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}$
.
$\widetilde{{\mathcal{C}}_{l}^{\bullet }}\simeq \widetilde{C_{l}^{\bullet }}\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}$
.
For the complexes of sheaves in Definition 7.10, we have corresponding spectral sequences for local hypercohomology, and we will need to work with all of these.
Definition 7.11. If
![]() ${\mathcal{F}}^{\bullet }$
is a complex of sheaves of
${\mathcal{F}}^{\bullet }$
is a complex of sheaves of
![]() $k$
-spaces on
$k$
-spaces on
![]() $\widehat{X}$
(or
$\widehat{X}$
(or
![]() $\widehat{X^{\prime }}$
, which has the same underlying space), the local hypercohomology spectral sequence for
$\widehat{X^{\prime }}$
, which has the same underlying space), the local hypercohomology spectral sequence for
![]() ${\mathcal{F}}^{\bullet }$
is the spectral sequence defined in § 2.2 with respect to the functor
${\mathcal{F}}^{\bullet }$
is the spectral sequence defined in § 2.2 with respect to the functor
![]() $\unicode[STIX]{x1D6E4}_{P}$
of sections supported at the closed point. If
$\unicode[STIX]{x1D6E4}_{P}$
of sections supported at the closed point. If
![]() ${\mathcal{L}}^{\bullet ,\bullet }$
is any Cartan–Eilenberg resolution of
${\mathcal{L}}^{\bullet ,\bullet }$
is any Cartan–Eilenberg resolution of
![]() ${\mathcal{F}}^{\bullet }$
(or, more generally, a double complex resolution satisfying the conditions of Lemma 2.13), this spectral sequence is the column-filtered spectral sequence associated with the double complex
${\mathcal{F}}^{\bullet }$
(or, more generally, a double complex resolution satisfying the conditions of Lemma 2.13), this spectral sequence is the column-filtered spectral sequence associated with the double complex
 $\unicode[STIX]{x1D6E4}_{P}(\widehat{X},{\mathcal{L}}^{\bullet ,\bullet })$
. It begins
$\unicode[STIX]{x1D6E4}_{P}(\widehat{X},{\mathcal{L}}^{\bullet ,\bullet })$
. It begins
 $E_{1}^{p,q}=H_{P}^{q}(\widehat{X},{\mathcal{F}}^{p})$
and has abutment
$E_{1}^{p,q}=H_{P}^{q}(\widehat{X},{\mathcal{F}}^{p})$
and has abutment
 $\mathbf{H}_{P}^{p+q}(\widehat{X},{\mathcal{F}}^{\bullet })$
. We introduce the following notation for the specific hypercohomology spectral sequences we will consider below.
$\mathbf{H}_{P}^{p+q}(\widehat{X},{\mathcal{F}}^{\bullet })$
. We introduce the following notation for the specific hypercohomology spectral sequences we will consider below.
-
(a) The local hypercohomology spectral sequence for
 $\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
will be denoted
$\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
will be denoted
 $\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
. (This is precisely the Hodge–de Rham spectral sequence arising from the surjection
$\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
. (This is precisely the Hodge–de Rham spectral sequence arising from the surjection
 $R\rightarrow A$
.)
$R\rightarrow A$
.) -
(b) The local hypercohomology spectral sequence for
 $\widehat{\unicode[STIX]{x1D6FA}}_{X^{\prime }}^{\bullet }$
will be denoted
$\widehat{\unicode[STIX]{x1D6FA}}_{X^{\prime }}^{\bullet }$
will be denoted
 $\tilde{\mathbf{E}}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
. (This is precisely the Hodge–de Rham spectral sequence arising from the surjection
$\tilde{\mathbf{E}}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }$
. (This is precisely the Hodge–de Rham spectral sequence arising from the surjection
 $R^{\prime }\rightarrow A$
.)
$R^{\prime }\rightarrow A$
.) -
(c) The local hypercohomology spectral sequence for
 ${\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
will be denoted
${\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }$
will be denoted
 $\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
.
$\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
. -
(d) For all
 $l$
, the local hypercohomology spectral sequence for
$l$
, the local hypercohomology spectral sequence for
 $\widetilde{C_{l}^{\bullet }}$
will be denoted
$\widetilde{C_{l}^{\bullet }}$
will be denoted
 $(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
.
$(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
. -
(e) For all
 $l$
, the local hypercohomology spectral sequence for
$l$
, the local hypercohomology spectral sequence for
 $\widetilde{{\mathcal{C}}_{l}^{\bullet }}$
will be denoted
$\widetilde{{\mathcal{C}}_{l}^{\bullet }}$
will be denoted
 $(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
.
$(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
.
The key to the proof of Theorem B(a) is the following analogue of Lemma 2.29. Once this lemma is established, the rest of the proof will closely parallel our work in § 2.
Lemma 7.12. Let
![]() $\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
and
$\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
and
![]() $\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
be the spectral sequences of Definition 7.11. There is an isomorphism
$\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
be the spectral sequences of Definition 7.11. There is an isomorphism
 $$\begin{eqnarray}(\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}\xrightarrow[{}]{{\sim}}\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet },\end{eqnarray}$$
$$\begin{eqnarray}(\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}\xrightarrow[{}]{{\sim}}\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet },\end{eqnarray}$$
where the object on the left-hand side is obtained by applying the formal power series operation to all the objects and differentials of the spectral sequence
![]() $\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
.
$\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
.
Lemma 2.29 was a consequence of the fact that the double complexes giving rise to the two spectral sequences considered there were related by the
![]() $+$
-operation of Definition 2.19. We were therefore able to prove that lemma by working entirely at the level of double complexes. The analogous reasoning fails here for reasons alluded to in Remark 7.6: the formal power series operation is an infinite direct product. The obvious extension of this operation to sheaves need not commute with the functor
$+$
-operation of Definition 2.19. We were therefore able to prove that lemma by working entirely at the level of double complexes. The analogous reasoning fails here for reasons alluded to in Remark 7.6: the formal power series operation is an infinite direct product. The obvious extension of this operation to sheaves need not commute with the functor
![]() $\unicode[STIX]{x1D6E4}_{P}$
, because taking stalks of sheaves (a direct limit) and direct products of sheaves (an inverse limit) need not commute. The proof of Lemma 7.12 will take place at the level of spectral sequences, not merely double complexes.
$\unicode[STIX]{x1D6E4}_{P}$
, because taking stalks of sheaves (a direct limit) and direct products of sheaves (an inverse limit) need not commute. The proof of Lemma 7.12 will take place at the level of spectral sequences, not merely double complexes.
We will give the proof of Lemma 7.12 in steps, as follows.
-
(1)
 $\varprojlim \,(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
, defined by taking the ‘term-by-term’ inverse limit of all objects and differentials in the spectral sequences, is again a spectral sequence: each term is derived from its predecessor by taking cohomology. (An identical proof shows that
$\varprojlim \,(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
, defined by taking the ‘term-by-term’ inverse limit of all objects and differentials in the spectral sequences, is again a spectral sequence: each term is derived from its predecessor by taking cohomology. (An identical proof shows that
 $\varprojlim \,(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
is a spectral sequence.)
$\varprojlim \,(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
is a spectral sequence.) -
(2) The spectral sequences
 $\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
and
$\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
and
 $\varprojlim \,(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
are isomorphic. (An identical proof works for
$\varprojlim \,(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
are isomorphic. (An identical proof works for
 $\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
and
$\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
and
 $\varprojlim \,(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
.)
$\varprojlim \,(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
.) -
(3) For all
 $l$
, the spectral sequences
$l$
, the spectral sequences
 $(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
and
$(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
and
 $(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }\otimes R^{\prime }/z^{l}$
are isomorphic, via isomorphisms compatible with the transition maps for varying
$(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }\otimes R^{\prime }/z^{l}$
are isomorphic, via isomorphisms compatible with the transition maps for varying
 $l$
(the latter spectral sequence, defined by the natural extension of Definition 7.5 to spectral sequences, is a direct sum of
$l$
(the latter spectral sequence, defined by the natural extension of Definition 7.5 to spectral sequences, is a direct sum of
 $l$
copies of
$l$
copies of
 $(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
).
$(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
). -
(4) There is an isomorphism
 $(\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}\xrightarrow[{}]{{\sim}}\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
of spectral sequences (the general statement).
$(\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}\xrightarrow[{}]{{\sim}}\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
of spectral sequences (the general statement).
Step (4) follows immediately from step (3) by applying Lemma 7.4 to all objects of the spectral sequences, so we will not give it a separate proof below. Steps (2) and (3) are not difficult. Step (1), which is necessary in order for the later steps to make sense, is more difficult and depends crucially on our work in § 5.
Proof of step (1).
We show first that the
![]() $E_{2}$
-term
$E_{2}$
-term
 $\varprojlim \,(\tilde{E_{l}})_{2,R}^{\bullet ,\bullet }$
of the ‘term-by-term’ inverse limit is obtained from the
$\varprojlim \,(\tilde{E_{l}})_{2,R}^{\bullet ,\bullet }$
of the ‘term-by-term’ inverse limit is obtained from the
![]() $E_{1}$
-term by taking cohomology: that is, we show that for all
$E_{1}$
-term by taking cohomology: that is, we show that for all
![]() $p$
and
$p$
and
![]() $q$
, we have isomorphisms
$q$
, we have isomorphisms
 $$\begin{eqnarray}\varprojlim \,(\tilde{E_{l}})_{2,R}^{p,q}=\varprojlim \,h^{p}(H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet }))\simeq h^{p}(\varprojlim \,H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet }))=h^{p}(\varprojlim \,(\tilde{E_{l}})_{1,R}^{\bullet ,q})\end{eqnarray}$$
$$\begin{eqnarray}\varprojlim \,(\tilde{E_{l}})_{2,R}^{p,q}=\varprojlim \,h^{p}(H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet }))\simeq h^{p}(\varprojlim \,H_{\mathfrak{ m}}^{q}(C_{l}^{\bullet }))=h^{p}(\varprojlim \,(\tilde{E_{l}})_{1,R}^{\bullet ,q})\end{eqnarray}$$
of
![]() $k$
-spaces. This is the assertion that for the inverse system
$k$
-spaces. This is the assertion that for the inverse system
 $\{H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\}$
of complexes of
$\{H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })\}$
of complexes of
![]() $k$
-spaces, taking cohomology commutes with inverse limits. By Proposition 5.9, it suffices to check that for all
$k$
-spaces, taking cohomology commutes with inverse limits. By Proposition 5.9, it suffices to check that for all
![]() $p$
and
$p$
and
![]() $q$
the inverse systems
$q$
the inverse systems
 $\{H_{\mathfrak{m}}^{q}(C_{l}^{p})\}$
and
$\{H_{\mathfrak{m}}^{q}(C_{l}^{p})\}$
and
 $\{h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
both satisfy the Mittag-Leffler condition. By [Reference Brodmann and SharpBS13, Theorem 7.1.3], each
$\{h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
both satisfy the Mittag-Leffler condition. By [Reference Brodmann and SharpBS13, Theorem 7.1.3], each
 $H_{\mathfrak{m}}^{q}(C_{l}^{p})$
is an Artinian
$H_{\mathfrak{m}}^{q}(C_{l}^{p})$
is an Artinian
![]() $R$
-module; as the transition maps in this inverse system are
$R$
-module; as the transition maps in this inverse system are
![]() $R$
-linear, induced by the canonical
$R$
-linear, induced by the canonical
![]() $R$
-linear maps
$R$
-linear maps
 $C_{l+1}^{p}\rightarrow C_{l}^{p}$
, the Mittag-Leffler condition for this first system is immediate.
$C_{l+1}^{p}\rightarrow C_{l}^{p}$
, the Mittag-Leffler condition for this first system is immediate.
In order to verify the Mittag-Leffler condition for the second system, we consider the Matlis dual of the first system. For all
![]() $q$
and
$q$
and
![]() $l$
, the differentials in the complex
$l$
, the differentials in the complex
 $H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })$
have Matlis duals by Proposition 3.21(a), since they are
$H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })$
have Matlis duals by Proposition 3.21(a), since they are
![]() $k$
-linear maps between Artinian
$k$
-linear maps between Artinian
![]() $R$
-modules. The transition maps in the direct system
$R$
-modules. The transition maps in the direct system
 $\{D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
of complexes are
$\{D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
of complexes are
![]() $R$
-linear in each degree, and each
$R$
-linear in each degree, and each
 $D(H_{\mathfrak{m}}^{q}(C_{l}^{p}))$
is a finitely generated
$D(H_{\mathfrak{m}}^{q}(C_{l}^{p}))$
is a finitely generated
![]() $R$
-module (since it is the Matlis dual of an Artinian
$R$
-module (since it is the Matlis dual of an Artinian
![]() $R$
-module). In fact, by Theorem 6.1,
$R$
-module). In fact, by Theorem 6.1,
 $D(H_{\mathfrak{m}}^{q}(C_{l}^{p}))$
is a direct sum of
$D(H_{\mathfrak{m}}^{q}(C_{l}^{p}))$
is a direct sum of
![]() $\binom{n}{p}$
copies of the
$\binom{n}{p}$
copies of the
![]() $R$
-module
$R$
-module
 $\operatorname{Ext}_{R}^{n-q}(R/I^{l+n-p},R)$
, and so
$\operatorname{Ext}_{R}^{n-q}(R/I^{l+n-p},R)$
, and so
 $\varinjlim D(H_{\mathfrak{m}}^{q}(C_{l}^{p}))$
is a direct sum of
$\varinjlim D(H_{\mathfrak{m}}^{q}(C_{l}^{p}))$
is a direct sum of
![]() $\binom{n}{p}$
copies of
$\binom{n}{p}$
copies of
 $$\begin{eqnarray}\varinjlim \operatorname{Ext}_{R}^{n-q}(R/I^{l+n-p},R)\simeq H_{I}^{n-q}(R).\end{eqnarray}$$
$$\begin{eqnarray}\varinjlim \operatorname{Ext}_{R}^{n-q}(R/I^{l+n-p},R)\simeq H_{I}^{n-q}(R).\end{eqnarray}$$
Finally, the de Rham complex of the
 ${\mathcal{D}}(R,k)$
-module
${\mathcal{D}}(R,k)$
-module
 $H_{I}^{n-q}(R)$
is the direct limit of the Matlis dual complexes
$H_{I}^{n-q}(R)$
is the direct limit of the Matlis dual complexes
 $D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))$
, since the inverse limit of their Matlis duals is the de Rham complex of
$D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))$
, since the inverse limit of their Matlis duals is the de Rham complex of
 $D(H_{I}^{n-q}(R))=H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
by Theorem 6.5 and the definition of the inverse limit action on
$D(H_{I}^{n-q}(R))=H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
by Theorem 6.5 and the definition of the inverse limit action on
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
.
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
.
The direct system
 $\{D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
thus satisfies the hypotheses of Corollary 5.31: it is a direct system of complexes with
$\{D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
thus satisfies the hypotheses of Corollary 5.31: it is a direct system of complexes with
![]() $k$
-linear differentials whose objects are finitely generated
$k$
-linear differentials whose objects are finitely generated
![]() $R$
-modules, the transition maps are
$R$
-modules, the transition maps are
![]() $R$
-linear in each degree, and the direct limit is the de Rham complex
$R$
-linear in each degree, and the direct limit is the de Rham complex
 $H_{I}^{n-q}(R)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
of a holonomic
$H_{I}^{n-q}(R)\otimes \unicode[STIX]{x1D6FA}_{R}^{\bullet }$
of a holonomic
 ${\mathcal{D}}(R,k)$
-module. We conclude from that corollary that for all
${\mathcal{D}}(R,k)$
-module. We conclude from that corollary that for all
![]() $p$
and
$p$
and
![]() $l$
the images of
$l$
the images of
 $h^{n-p}(D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })))$
in
$h^{n-p}(D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })))$
in
 $h^{n-p}(D(H_{\mathfrak{m}}^{q}(C_{l+s}^{\bullet })))$
stabilize in the strong sense as
$h^{n-p}(D(H_{\mathfrak{m}}^{q}(C_{l+s}^{\bullet })))$
stabilize in the strong sense as
![]() $s$
varies, with finite-dimensional stable image. By Corollary 3.18 and Proposition 3.21, all the Matlis duals (of objects and differentials) in the direct system
$s$
varies, with finite-dimensional stable image. By Corollary 3.18 and Proposition 3.21, all the Matlis duals (of objects and differentials) in the direct system
 $\{D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
coincide with
$\{D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
coincide with
![]() $k$
-linear duals. Since
$k$
-linear duals. Since
![]() $k$
-linear dual is a contravariant, exact functor, we thus have
$k$
-linear dual is a contravariant, exact functor, we thus have
 $h^{n-p}(D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })))\simeq (h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })))^{\vee }$
, and by Lemma 5.13, the inverse system
$h^{n-p}(D(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })))\simeq (h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet })))^{\vee }$
, and by Lemma 5.13, the inverse system
 $\{h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
satisfies the Mittag-Leffler condition, as desired.
$\{h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
satisfies the Mittag-Leffler condition, as desired.
Examining the proof of Lemma 5.13, we see that in fact we can conclude something stronger than the Mittag-Leffler condition, namely the following: for all
![]() $p$
and
$p$
and
![]() $q$
, given
$q$
, given
![]() $l$
, there exists
$l$
, there exists
![]() $s$
such that the image of
$s$
such that the image of
 $h^{p}(H_{\mathfrak{m}}^{q}(C_{l+s}^{\bullet }))$
in
$h^{p}(H_{\mathfrak{m}}^{q}(C_{l+s}^{\bullet }))$
in
 $h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))$
is a finite-dimensional
$h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))$
is a finite-dimensional
![]() $k$
-space. That is, the inverse system
$k$
-space. That is, the inverse system
 $\{h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
is eventually finite. Since any descending chain of
$\{h^{p}(H_{\mathfrak{m}}^{q}(C_{l}^{\bullet }))\}$
is eventually finite. Since any descending chain of
![]() $k$
-subspaces of a finite-dimensional
$k$
-subspaces of a finite-dimensional
![]() $k$
-space must terminate, it is clear that eventual finiteness implies the Mittag-Leffler condition. But what is more, eventual finiteness is inherited by cohomology: if, for any
$k$
-space must terminate, it is clear that eventual finiteness implies the Mittag-Leffler condition. But what is more, eventual finiteness is inherited by cohomology: if, for any
![]() $r$
, the inverse system
$r$
, the inverse system
 $\{(\tilde{E_{l}})_{r,R}^{p,q}\}$
is eventually finite, so is the inverse system
$\{(\tilde{E_{l}})_{r,R}^{p,q}\}$
is eventually finite, so is the inverse system
 $\{(\tilde{E_{l}})_{r+1,R}^{p,q}\}$
, since the objects
$\{(\tilde{E_{l}})_{r+1,R}^{p,q}\}$
, since the objects
 $(\tilde{E_{l}})_{r+1,R}^{p,q}$
are subquotients of the objects
$(\tilde{E_{l}})_{r+1,R}^{p,q}$
are subquotients of the objects
![]() $(\tilde{E_{l}})_{r,R}^{p,q}$
. By induction on
$(\tilde{E_{l}})_{r,R}^{p,q}$
. By induction on
![]() $r$
, we conclude that the
$r$
, we conclude that the
![]() $E_{r+1}$
-term of the ‘term-by-term’ inverse limit,
$E_{r+1}$
-term of the ‘term-by-term’ inverse limit,
 $\varprojlim \,(\tilde{E_{l}})_{r+1,R}^{\bullet ,\bullet }$
, is obtained from the
$\varprojlim \,(\tilde{E_{l}})_{r+1,R}^{\bullet ,\bullet }$
, is obtained from the
![]() $E_{r}$
-term by taking cohomology, and so
$E_{r}$
-term by taking cohomology, and so
 $\varprojlim \,(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
is a well-defined spectral sequence.◻
$\varprojlim \,(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
is a well-defined spectral sequence.◻
Proof of step (2).
Since
 $\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\simeq \varprojlim \,\widetilde{C_{l}^{\bullet }}$
as complexes of sheaves on
$\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\simeq \varprojlim \,\widetilde{C_{l}^{\bullet }}$
as complexes of sheaves on
![]() $\widehat{X}$
, we have projection maps
$\widehat{X}$
, we have projection maps
 $\unicode[STIX]{x1D70B}_{l}:\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\rightarrow \widetilde{C_{l}^{\bullet }}$
for all
$\unicode[STIX]{x1D70B}_{l}:\widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\rightarrow \widetilde{C_{l}^{\bullet }}$
for all
![]() $l$
. As described in § 2.2, each such projection map induces a morphism between the corresponding local hypercohomology spectral sequences. By the universal property of inverse limits, this family of projection maps induces a morphism of spectral sequences
$l$
. As described in § 2.2, each such projection map induces a morphism between the corresponding local hypercohomology spectral sequences. By the universal property of inverse limits, this family of projection maps induces a morphism of spectral sequences
 $\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }\rightarrow \varprojlim \,(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
(where the right-hand side is a well-defined spectral sequence by step (1)). We claim this is an isomorphism; by Proposition 2.10, it suffices to check this on the
$\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }\rightarrow \varprojlim \,(\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }$
(where the right-hand side is a well-defined spectral sequence by step (1)). We claim this is an isomorphism; by Proposition 2.10, it suffices to check this on the
![]() $E_{1}$
-objects of both sides. By definition, for all
$E_{1}$
-objects of both sides. By definition, for all
![]() $p$
and
$p$
and
![]() $q$
, we have
$q$
, we have
 $\tilde{E}_{1,R}^{p,q}=H_{P}^{q}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{p})$
, a direct sum of
$\tilde{E}_{1,R}^{p,q}=H_{P}^{q}(\widehat{X},\widehat{\unicode[STIX]{x1D6FA}}_{X}^{p})$
, a direct sum of
![]() $\binom{n}{p}$
copies of
$\binom{n}{p}$
copies of
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
, and for all
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})$
, and for all
![]() $l$
, we have
$l$
, we have
 $(\tilde{E}_{l})_{1,R}^{p,q}=H_{P}^{q}(\widehat{X},\widetilde{C_{l}^{p}})$
, a direct sum of
$(\tilde{E}_{l})_{1,R}^{p,q}=H_{P}^{q}(\widehat{X},\widetilde{C_{l}^{p}})$
, a direct sum of
![]() $\binom{n}{p}$
copies of
$\binom{n}{p}$
copies of
 $H_{\mathfrak{m}}^{q}(R/I^{l+n-p})$
. The induced map
$H_{\mathfrak{m}}^{q}(R/I^{l+n-p})$
. The induced map
 $\tilde{E}_{1,R}^{p,q}\rightarrow \varprojlim \,(\tilde{E}_{l})_{1,R}^{p,q}$
is therefore a finite direct sum of copies of the canonical map
$\tilde{E}_{1,R}^{p,q}\rightarrow \varprojlim \,(\tilde{E}_{l})_{1,R}^{p,q}$
is therefore a finite direct sum of copies of the canonical map
 $H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\rightarrow \varprojlim \,H_{\mathfrak{m}}^{q}(R/I^{l+n-p})$
, which we already know to be an isomorphism by Proposition 6.3.◻
$H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})\rightarrow \varprojlim \,H_{\mathfrak{m}}^{q}(R/I^{l+n-p})$
, which we already know to be an isomorphism by Proposition 6.3.◻
Proof of step (3).
This is the only step in the proof where we can work entirely at the level of the double complexes giving rise to the spectral sequences. Let
![]() $l$
be given. Choose a Cartan–Eilenberg resolution
$l$
be given. Choose a Cartan–Eilenberg resolution
 $\widetilde{C_{l}^{\bullet }}\rightarrow {\mathcal{L}}_{l}^{\bullet ,\bullet }$
in the category of sheaves of
$\widetilde{C_{l}^{\bullet }}\rightarrow {\mathcal{L}}_{l}^{\bullet ,\bullet }$
in the category of sheaves of
![]() $k$
-spaces on
$k$
-spaces on
![]() $\widehat{X}$
. By Remark 7.6, this category satisfies axiom
$\widehat{X}$
. By Remark 7.6, this category satisfies axiom
![]() $AB4$
, and so direct sums are exact; furthermore, direct sums of injective sheaves are again injective, and the functor
$AB4$
, and so direct sums are exact; furthermore, direct sums of injective sheaves are again injective, and the functor
![]() $\unicode[STIX]{x1D6E4}_{P}$
commutes with direct sums. We conclude that the double complex
$\unicode[STIX]{x1D6E4}_{P}$
commutes with direct sums. We conclude that the double complex
 ${\mathcal{L}}_{l}^{\bullet ,\bullet }\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}$
(which is simply a finite direct sum of copies of
${\mathcal{L}}_{l}^{\bullet ,\bullet }\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}$
(which is simply a finite direct sum of copies of
![]() ${\mathcal{L}}_{l}^{\bullet ,\bullet }$
) satisfies the conditions of Lemma 2.13, and so the double complex
${\mathcal{L}}_{l}^{\bullet ,\bullet }$
) satisfies the conditions of Lemma 2.13, and so the double complex
 $\unicode[STIX]{x1D6E4}_{P}(\widehat{X},{\mathcal{L}}_{l}^{\bullet ,\bullet }\otimes {\mathcal{O}}_{X^{\prime }}/z^{l})$
gives rise to the local hypercohomology spectral sequence for the complex
$\unicode[STIX]{x1D6E4}_{P}(\widehat{X},{\mathcal{L}}_{l}^{\bullet ,\bullet }\otimes {\mathcal{O}}_{X^{\prime }}/z^{l})$
gives rise to the local hypercohomology spectral sequence for the complex
 $\widetilde{C_{l}^{\bullet }}\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}\simeq \widetilde{{\mathcal{C}}_{l}^{\bullet }}$
. On the one hand, this spectral sequence is
$\widetilde{C_{l}^{\bullet }}\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}\simeq \widetilde{{\mathcal{C}}_{l}^{\bullet }}$
. On the one hand, this spectral sequence is
![]() $(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
by definition. On the other hand, since
$(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }$
by definition. On the other hand, since
![]() $\unicode[STIX]{x1D6E4}_{P}$
commutes with direct sums, we have
$\unicode[STIX]{x1D6E4}_{P}$
commutes with direct sums, we have
 $\unicode[STIX]{x1D6E4}_{P}(\widehat{X},{\mathcal{L}}_{l}^{\bullet ,\bullet }\otimes {\mathcal{O}}_{X^{\prime }}/z^{l})\simeq \unicode[STIX]{x1D6E4}_{P}(\widehat{X},{\mathcal{L}}_{l}^{\bullet ,\bullet })\otimes R^{\prime }/z^{l}$
as double complexes of
$\unicode[STIX]{x1D6E4}_{P}(\widehat{X},{\mathcal{L}}_{l}^{\bullet ,\bullet }\otimes {\mathcal{O}}_{X^{\prime }}/z^{l})\simeq \unicode[STIX]{x1D6E4}_{P}(\widehat{X},{\mathcal{L}}_{l}^{\bullet ,\bullet })\otimes R^{\prime }/z^{l}$
as double complexes of
![]() $k$
-spaces, and since cohomology of
$k$
-spaces, and since cohomology of
![]() $k$
-spaces commutes with direct sums, this isomorphism induces an isomorphism
$k$
-spaces commutes with direct sums, this isomorphism induces an isomorphism
 $(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }\simeq (\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }\otimes R^{\prime }/z^{l}$
at the level of spectral sequences, as desired. The fact that these isomorphisms are compatible with the transition maps for varying
$(\tilde{{\mathcal{E}}_{l}})_{\bullet }^{\bullet ,\bullet }\simeq (\tilde{E_{l}})_{\bullet ,R}^{\bullet ,\bullet }\otimes R^{\prime }/z^{l}$
at the level of spectral sequences, as desired. The fact that these isomorphisms are compatible with the transition maps for varying
![]() $l$
follows from the fact that the same is true for the isomorphisms
$l$
follows from the fact that the same is true for the isomorphisms
 $\widetilde{C_{l}^{\bullet }}\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}\simeq \widetilde{{\mathcal{C}}_{l}^{\bullet }}$
, since as discussed in § 2.2, the association of a local hypercohomology spectral sequence with a complex of sheaves is functorial in the complex. This completes the proof of Lemma 7.12.◻
$\widetilde{C_{l}^{\bullet }}\otimes {\mathcal{O}}_{X^{\prime }}/z^{l}\simeq \widetilde{{\mathcal{C}}_{l}^{\bullet }}$
, since as discussed in § 2.2, the association of a local hypercohomology spectral sequence with a complex of sheaves is functorial in the complex. This completes the proof of Lemma 7.12.◻
We are now ready to complete the proof of Theorem B.
Proof of Theorem B(a).
Consider again the short exact sequence from the proof of Proposition 7.9:
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}}\widehat{\unicode[STIX]{x1D6FA}}_{X^{\prime }}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}{\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }[-1]\xrightarrow[{}]{\unicode[STIX]{x1D704}}\widehat{\unicode[STIX]{x1D6FA}}_{X^{\prime }}^{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}{\mathcal{O}}_{\widehat{X^{\prime }}}\otimes \widehat{\unicode[STIX]{x1D6FA}}_{X}^{\bullet }\rightarrow 0.\end{eqnarray}$$
As described in § 2.2, the morphism of complexes
![]() $\unicode[STIX]{x1D70B}$
induces a morphism between the corresponding spectral sequences for local hypercohomology, given in Definition 7.11. That is, there is an induced morphism
$\unicode[STIX]{x1D70B}$
induces a morphism between the corresponding spectral sequences for local hypercohomology, given in Definition 7.11. That is, there is an induced morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\bullet }^{\bullet ,\bullet }:\tilde{\mathbf{E}}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }\rightarrow \tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\bullet }^{\bullet ,\bullet }:\tilde{\mathbf{E}}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }\rightarrow \tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }.\end{eqnarray}$$
Identifying first
![]() $\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
with
$\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }$
with
 $(\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}$
(by Lemma 7.12) and then
$(\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}$
(by Lemma 7.12) and then
![]() $\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
with the ‘constant term’ component of
$\tilde{E}_{\bullet ,R}^{\bullet ,\bullet }$
with the ‘constant term’ component of
 $(\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}$
, we see that this further induces a morphism
$(\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}$
, we see that this further induces a morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{\bullet }^{\bullet ,\bullet }:\tilde{\mathbf{E}}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }\rightarrow \tilde{E}_{\bullet ,R}^{\bullet ,\bullet }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{\bullet }^{\bullet ,\bullet }:\tilde{\mathbf{E}}_{\bullet ,R^{\prime }}^{\bullet ,\bullet }\rightarrow \tilde{E}_{\bullet ,R}^{\bullet ,\bullet }\end{eqnarray}$$
given in every degree by
![]() $\unicode[STIX]{x1D70B}_{\bullet }^{\bullet ,\bullet }$
followed by the projection of
$\unicode[STIX]{x1D70B}_{\bullet }^{\bullet ,\bullet }$
followed by the projection of
 $\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }\simeq (\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}$
on its constant term component. If
$\tilde{{\mathcal{E}}}_{\bullet }^{\bullet ,\bullet }\simeq (\tilde{E}_{\bullet ,R}^{\bullet ,\bullet })^{+}$
on its constant term component. If
![]() $r=2$
, the maps
$r=2$
, the maps
![]() $\unicode[STIX]{x1D713}_{2}^{p,q}$
are precisely the inverses of the isomorphisms
$\unicode[STIX]{x1D713}_{2}^{p,q}$
are precisely the inverses of the isomorphisms
 $$\begin{eqnarray}H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))\simeq H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}}))\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}}))\simeq H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X^{\prime }},{\mathcal{O}}_{\widehat{X^{\prime }}}))\end{eqnarray}$$
appearing in the proof of Proposition 7.9, which were induced by the morphism of complexes
![]() $\unicode[STIX]{x1D70B}$
and the projection of
$\unicode[STIX]{x1D70B}$
and the projection of
 $(\tilde{E}_{2,R}^{p,q})^{+}=(H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})))^{+}$
on its constant term component. Therefore the morphism
$(\tilde{E}_{2,R}^{p,q})^{+}=(H_{\text{dR}}^{p}(H_{P}^{q}(\widehat{X},{\mathcal{O}}_{\widehat{X}})))^{+}$
on its constant term component. Therefore the morphism
![]() $\unicode[STIX]{x1D713}_{\bullet }^{\bullet ,\bullet }$
of spectral sequences is an isomorphism at the
$\unicode[STIX]{x1D713}_{\bullet }^{\bullet ,\bullet }$
of spectral sequences is an isomorphism at the
![]() $E_{2}$
-level. By Proposition 2.10, it follows that
$E_{2}$
-level. By Proposition 2.10, it follows that
![]() $\unicode[STIX]{x1D713}$
is an isomorphism at all later levels, including the abutments. The proof is complete.◻
$\unicode[STIX]{x1D713}$
is an isomorphism at all later levels, including the abutments. The proof is complete.◻
8 Some open questions
In this final section, we pose two questions and state a conjecture left open by our work above.
Our first question concerns coefficient fields. A priori, the isomorphism classes of the spectral sequences
![]() $\{E_{r,R}^{p,q}\}$
and
$\{E_{r,R}^{p,q}\}$
and
![]() $\{\tilde{E}_{r,R}^{p,q}\}$
, as well as the integers
$\{\tilde{E}_{r,R}^{p,q}\}$
, as well as the integers
![]() $\unicode[STIX]{x1D70C}_{p,q}$
of Definition 2.23, depend on the choice of coefficient field
$\unicode[STIX]{x1D70C}_{p,q}$
of Definition 2.23, depend on the choice of coefficient field
![]() $k\subset A$
.
$k\subset A$
.
Question 8.1. Are the isomorphism classes of the spectral sequences
![]() $\{E_{r,R}^{p,q}\}$
and
$\{E_{r,R}^{p,q}\}$
and
![]() $\{\tilde{E}_{r,R}^{p,q}\}$
, as well as the integers
$\{\tilde{E}_{r,R}^{p,q}\}$
, as well as the integers
![]() $\unicode[STIX]{x1D70C}_{p,q}$
of Definition 2.23, independent of the choice of coefficient field
$\unicode[STIX]{x1D70C}_{p,q}$
of Definition 2.23, independent of the choice of coefficient field
![]() $k\subset A$
?
$k\subset A$
?
In the case where the local cohomology modules
![]() $H_{I}^{q}(R)$
are supported only at the maximal ideal
$H_{I}^{q}(R)$
are supported only at the maximal ideal
![]() $\mathfrak{m}$
, the
$\mathfrak{m}$
, the
![]() $\unicode[STIX]{x1D70C}_{p,q}$
are indeed independent of this choice by Remark 2.24 (since the
$\unicode[STIX]{x1D70C}_{p,q}$
are indeed independent of this choice by Remark 2.24 (since the
![]() $\unicode[STIX]{x1D706}_{p,q}$
are known to be independent), which provides supporting evidence for a positive answer to Question 8.1.
$\unicode[STIX]{x1D706}_{p,q}$
are known to be independent), which provides supporting evidence for a positive answer to Question 8.1.
Our second question concerns degeneration of the spectral sequences. In general, the
![]() $E_{1}$
-objects
$E_{1}$
-objects
 $E_{1}^{p,q}=H_{Y}^{q}(X,\unicode[STIX]{x1D6FA}_{X}^{p})$
in the local Hodge–de Rham homology spectral sequence (for a complete local ring
$E_{1}^{p,q}=H_{Y}^{q}(X,\unicode[STIX]{x1D6FA}_{X}^{p})$
in the local Hodge–de Rham homology spectral sequence (for a complete local ring
![]() $A$
with coefficient field
$A$
with coefficient field
![]() $k$
of characteristic zero) are not even finitely generated as
$k$
of characteristic zero) are not even finitely generated as
![]() $R$
-modules (where
$R$
-modules (where
![]() $R{\twoheadrightarrow}A$
is as in § 2), so the spectral sequence need not degenerate at
$R{\twoheadrightarrow}A$
is as in § 2), so the spectral sequence need not degenerate at
![]() $E_{1}$
. However, this obstruction does not exist for the
$E_{1}$
. However, this obstruction does not exist for the
![]() $E_{2}$
-term since, by Theorem A(b), the
$E_{2}$
-term since, by Theorem A(b), the
![]() $E_{2}$
-objects are finite-dimensional
$E_{2}$
-objects are finite-dimensional
![]() $k$
-spaces. Therefore, the question of possible degeneration at
$k$
-spaces. Therefore, the question of possible degeneration at
![]() $E_{2}$
reduces to a comparison of dimensions: do we have equalities
$E_{2}$
reduces to a comparison of dimensions: do we have equalities
 $\dim _{k}\mathbf{H}_{Y}^{l}(X,\unicode[STIX]{x1D6FA}_{X}^{\bullet })=\sum _{p+q=l}\dim _{k}E_{2}^{p,q}=\sum _{p+q=l}\dim _{k}H_{\text{dR}}^{p}(H_{I}^{q}(R))$
for all
$\dim _{k}\mathbf{H}_{Y}^{l}(X,\unicode[STIX]{x1D6FA}_{X}^{\bullet })=\sum _{p+q=l}\dim _{k}E_{2}^{p,q}=\sum _{p+q=l}\dim _{k}H_{\text{dR}}^{p}(H_{I}^{q}(R))$
for all
![]() $l$
?
$l$
?
Question 8.2. Does the local Hodge–de Rham homology spectral sequence (for a complete local ring
![]() $A$
with coefficient field
$A$
with coefficient field
![]() $k$
of characteristic zero) degenerate at
$k$
of characteristic zero) degenerate at
![]() $E_{2}$
?
$E_{2}$
?
Note that by Theorems 1.1(c) and D, degeneration of the homology spectral sequence at
![]() $E_{2}$
is equivalent to degeneration of the cohomology spectral sequence at
$E_{2}$
is equivalent to degeneration of the cohomology spectral sequence at
![]() $E_{2}$
, so it is enough to answer the question for the homology sequence. Even if the answer to Question 8.2 is negative in general, it would be interesting to find conditions on the complete local ring
$E_{2}$
, so it is enough to answer the question for the homology sequence. Even if the answer to Question 8.2 is negative in general, it would be interesting to find conditions on the complete local ring
![]() $A$
under which such degeneration occurs.
$A$
under which such degeneration occurs.
Finally, we restate a conjecture which appeared already in § 1.
Conjecture 8.3. Let
![]() $A$
,
$A$
,
![]() $k$
, and
$k$
, and
![]() $R$
be as in the statement of Theorem A. Beginning with the
$R$
be as in the statement of Theorem A. Beginning with the
![]() $E_{2}$
-terms, the homology and cohomology spectral sequences are
$E_{2}$
-terms, the homology and cohomology spectral sequences are
![]() $k$
-dual to each other: for all
$k$
-dual to each other: for all
![]() $r\geqslant 2$
, and for all
$r\geqslant 2$
, and for all
![]() $p$
and
$p$
and
![]() $q$
,
$q$
,
 $E_{r}^{n-p,n-q}\simeq (\tilde{E}_{r}^{pq})^{\vee }$
, and similarly for the differentials.
$E_{r}^{n-p,n-q}\simeq (\tilde{E}_{r}^{pq})^{\vee }$
, and similarly for the differentials.
So far, we have only proved the
![]() $k$
-duality asserted in Conjecture 8.3 for the
$k$
-duality asserted in Conjecture 8.3 for the
![]() $E_{2}$
-objects. We remark that although our proof of Theorem B(a) is independent of Theorem A, the former becomes an immediate corollary of the latter if Conjecture 8.3 is known.
$E_{2}$
-objects. We remark that although our proof of Theorem B(a) is independent of Theorem A, the former becomes an immediate corollary of the latter if Conjecture 8.3 is known.
Acknowledgements
The results in this paper are from the author’s thesis, supervised by Gennady Lyubeznik. We would like to thank Lyubeznik, not only for suggesting this topic, but also for providing constant guidance and insight. We also thank William Messing for profitable conversations on algebraic de Rham cohomology and Lemma 2.13, as well as an exchange concerning the lemmas in § 5; Joel Gomez for asking a question that led to Proposition 4.12; and Paul Garrett for an exchange concerning Lemma 5.14. Finally, we thank Robin Hartshorne, for reading a preliminary version of this paper and making numerous suggestions that improved the exposition.