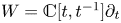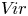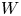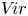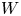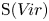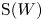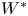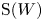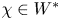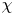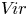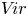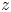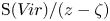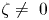1. Introduction
Let ![]() $G$ be a connected algebraic group over
$G$ be a connected algebraic group over ![]() $\mathbb {C}$ with Lie algebra
$\mathbb {C}$ with Lie algebra ![]() $\mathfrak g$, and consider the coadjoint action of
$\mathfrak g$, and consider the coadjoint action of ![]() $G$ on
$G$ on ![]() $\mathfrak g^*$. This is a beautiful classical topic, with profound connections to areas from geometric representation theory to combinatorics to physics. Algebraic geometry tells us that coadjoint orbits in
$\mathfrak g^*$. This is a beautiful classical topic, with profound connections to areas from geometric representation theory to combinatorics to physics. Algebraic geometry tells us that coadjoint orbits in ![]() $\mathfrak g^*$ correspond to
$\mathfrak g^*$ correspond to ![]() $G$-invariant radical ideals in the symmetric algebra
$G$-invariant radical ideals in the symmetric algebra ![]() $\operatorname {S}(\mathfrak g)$.
$\operatorname {S}(\mathfrak g)$.
These can also be defined using the Kostant–Kirillov Poisson bracket on ![]() $\operatorname {S}(\mathfrak g)$:
$\operatorname {S}(\mathfrak g)$:
 \[ \{f, g\}=\sum_{i,j}\frac{\partial f}{\partial e_i}\frac{\partial f}{\partial e_j}[e_i, e_j], \]
\[ \{f, g\}=\sum_{i,j}\frac{\partial f}{\partial e_i}\frac{\partial f}{\partial e_j}[e_i, e_j], \]
where ![]() $\{e_i\}$ is a basis of
$\{e_i\}$ is a basis of ![]() $\mathfrak g$. Recall that an ideal
$\mathfrak g$. Recall that an ideal ![]() $I$ of
$I$ of ![]() $\operatorname {S}(\mathfrak g)$ is a Poisson ideal if
$\operatorname {S}(\mathfrak g)$ is a Poisson ideal if ![]() $I$ is also a Lie ideal for the Poisson bracket. A basic fact is that
$I$ is also a Lie ideal for the Poisson bracket. A basic fact is that ![]() $I$ is
$I$ is ![]() $G$-invariant if and only if
$G$-invariant if and only if ![]() $I$ is Poisson.
$I$ is Poisson.
Thus, to compute the closure of the coadjoint orbit of ![]() $\chi \in \mathfrak g^*$, let
$\chi \in \mathfrak g^*$, let ![]() $\mathfrak m_\chi$ be the kernel of the evaluation morphism
$\mathfrak m_\chi$ be the kernel of the evaluation morphism
and let ![]() $\operatorname {P}(\chi )$ be the Poisson core of
$\operatorname {P}(\chi )$ be the Poisson core of ![]() $\mathfrak m_\chi$: the maximal Poisson ideal contained in
$\mathfrak m_\chi$: the maximal Poisson ideal contained in ![]() $\mathfrak m_\chi$. By definition, an ideal of the form
$\mathfrak m_\chi$. By definition, an ideal of the form ![]() $\operatorname {P}(\chi )$ is called a Poisson primitive; by a slight abuse of notation, we refer to
$\operatorname {P}(\chi )$ is called a Poisson primitive; by a slight abuse of notation, we refer to ![]() $\operatorname {P}(\chi )$ as the Poisson core of
$\operatorname {P}(\chi )$ as the Poisson core of ![]() $\chi$. The closure of the coadjoint orbit of
$\chi$. The closure of the coadjoint orbit of ![]() $\chi$ is defined by
$\chi$ is defined by ![]() $\operatorname {P}(\chi )$:
$\operatorname {P}(\chi )$:
and so ![]() $\chi, \nu \in \mathfrak g^*$ are in the same
$\chi, \nu \in \mathfrak g^*$ are in the same ![]() $G$-orbit if and only if
$G$-orbit if and only if ![]() $\operatorname {P}(\chi ) = \operatorname {P}(\nu )$. In the case of algebraic Lie algebras over
$\operatorname {P}(\chi ) = \operatorname {P}(\nu )$. In the case of algebraic Lie algebras over ![]() $\mathbb {C}$ or
$\mathbb {C}$ or ![]() $\mathbb {R}$, coadjoint orbits are symplectic leaves for the respective Poisson structure.
$\mathbb {R}$, coadjoint orbits are symplectic leaves for the respective Poisson structure.
In this paper, we investigate how this theory extends to the Witt algebra ![]() $W= \mathbb {C}[t, t^{-1}]\partial _t$ of algebraic vector fields on
$W= \mathbb {C}[t, t^{-1}]\partial _t$ of algebraic vector fields on ![]() $\mathbb {C}^\times$, and to its central extension the Virasoro algebra
$\mathbb {C}^\times$, and to its central extension the Virasoro algebra ![]() $V\!ir = \mathbb {C}[t, t^{-1}] \partial _t \oplus \mathbb {C} z$, with Lie bracket given by
$V\!ir = \mathbb {C}[t, t^{-1}] \partial _t \oplus \mathbb {C} z$, with Lie bracket given by
(We also consider some important Lie subalgebras of ![]() $W$.) These infinite-dimensional Lie algebras, of fundamental importance in representation theory and in physics, have no adjoint group [Reference LempertLem97], but one can still study the Poisson cores of maximal ideals and, more generally, the Poisson ideal structure of
$W$.) These infinite-dimensional Lie algebras, of fundamental importance in representation theory and in physics, have no adjoint group [Reference LempertLem97], but one can still study the Poisson cores of maximal ideals and, more generally, the Poisson ideal structure of ![]() $\operatorname {S}(W)$ and
$\operatorname {S}(W)$ and ![]() $\operatorname {S}(V\!ir)$. Motivated by (1.0.1), we say that functions
$\operatorname {S}(V\!ir)$. Motivated by (1.0.1), we say that functions ![]() $\chi, \nu \in V\!ir^*$ or in
$\chi, \nu \in V\!ir^*$ or in ![]() $W^*$ are in the same pseudo-orbit if
$W^*$ are in the same pseudo-orbit if ![]() $\operatorname {P}(\chi ) = \operatorname {P}(\nu )$. These (coadjoint) pseudo-orbits can be considered as algebraic symplectic leaves in
$\operatorname {P}(\chi ) = \operatorname {P}(\nu )$. These (coadjoint) pseudo-orbits can be considered as algebraic symplectic leaves in ![]() $V\!ir^*$ or
$V\!ir^*$ or ![]() $W^*$.
$W^*$.
Taking the previous discussion as our guide, we focus on prime Poisson ideals and Poisson primitive ideals of ![]() $\operatorname {S}(V\!ir)$ and
$\operatorname {S}(V\!ir)$ and ![]() $\operatorname {S}(W)$. Important questions here, which for brevity we ask in the introduction only for
$\operatorname {S}(W)$. Important questions here, which for brevity we ask in the introduction only for ![]() $V\!ir$, include the following.
$V\!ir$, include the following.
(i) Given
 $\chi \in V\!ir^*$, can we compute the Poisson core
$\chi \in V\!ir^*$, can we compute the Poisson core  $\operatorname {P}(\chi )$ and the pseudo-orbit of
$\operatorname {P}(\chi )$ and the pseudo-orbit of  $\chi$? When is
$\chi$? When is  $\operatorname {P}(\chi )$ nontrivial?
$\operatorname {P}(\chi )$ nontrivial?(ii) How can we understand prime Poisson ideals of
 $\operatorname {S}(V\!ir)$? Can we parameterise them in a reasonable fashion, ideally in a way which gives us further information about the ideal? How does one distinguish Poisson primitive ideals from other prime Poisson ideals?
$\operatorname {S}(V\!ir)$? Can we parameterise them in a reasonable fashion, ideally in a way which gives us further information about the ideal? How does one distinguish Poisson primitive ideals from other prime Poisson ideals?(iii) It is known, see [Reference León Sánchez and SierraLS08, Corollary 5.1], that
 $\operatorname {S}(V\!ir)$ satisfies the ascending chain condition on prime Poisson ideals. The augmentation ideal of
$\operatorname {S}(V\!ir)$ satisfies the ascending chain condition on prime Poisson ideals. The augmentation ideal of  $\operatorname {S}(V\!ir)$, that is, the ideal generated by
$\operatorname {S}(V\!ir)$, that is, the ideal generated by  $V\!ir \subset \operatorname {S}(V\!ir)$, is clearly a maximal Poisson ideal. What are the others? Conversely, does any nontrivial prime Poisson ideal have finite height?
$V\!ir \subset \operatorname {S}(V\!ir)$, is clearly a maximal Poisson ideal. What are the others? Conversely, does any nontrivial prime Poisson ideal have finite height?(iv) Do prime Poisson ideals induce any reasonable algebraic geometry on the uncountable-dimensional vector space
 $V\!ir^*$?
$V\!ir^*$?
We answer all of these questions, almost completely working out the structure of the Poisson spectra of ![]() $\operatorname {S}(V\!ir)$ and
$\operatorname {S}(V\!ir)$ and ![]() $\operatorname {S}(W)$.
$\operatorname {S}(W)$.
Let us begin by discussing the idea of algebraic geometry on ![]() $V\!ir^*$. A priori, this seems completely intractable as
$V\!ir^*$. A priori, this seems completely intractable as ![]() $V\!ir^*$ is an uncountable-dimensional affine space; little interesting can be said about
$V\!ir^*$ is an uncountable-dimensional affine space; little interesting can be said about ![]() $\operatorname {S}(\mathfrak a)$ where
$\operatorname {S}(\mathfrak a)$ where ![]() $\mathfrak a$ is a countable-dimensional abelian Lie algebra. However,
$\mathfrak a$ is a countable-dimensional abelian Lie algebra. However, ![]() $V\!ir$ and
$V\!ir$ and ![]() $W$ are extremely noncommutative and so Poisson ideals in their symmetric algebras are very large: in particular, by a result of Iyudu and the second author [Reference Iyudu and SierraIS20, Theorem 1.3], if
$W$ are extremely noncommutative and so Poisson ideals in their symmetric algebras are very large: in particular, by a result of Iyudu and the second author [Reference Iyudu and SierraIS20, Theorem 1.3], if ![]() $I$ is a nontrivial Poisson ideal of
$I$ is a nontrivial Poisson ideal of ![]() $\operatorname {S}(W)$ (respectively, a noncentrally generated Poisson ideal of
$\operatorname {S}(W)$ (respectively, a noncentrally generated Poisson ideal of ![]() $\operatorname {S}(V\!ir)$), then
$\operatorname {S}(V\!ir)$), then ![]() $\operatorname {S}(W)/I$ (respectively,
$\operatorname {S}(W)/I$ (respectively, ![]() $\operatorname {S}(V\!ir)/I$) has polynomial growth. This suggests that we might hope that a Poisson primitive ideal, and, more generally, a prime Poisson ideal, would correspond to a finite-dimensional algebraic subvariety of
$\operatorname {S}(V\!ir)/I$) has polynomial growth. This suggests that we might hope that a Poisson primitive ideal, and, more generally, a prime Poisson ideal, would correspond to a finite-dimensional algebraic subvariety of ![]() $V\!ir^*$, which we might be able to investigate using tools from affine algebraic geometry. We show that this is indeed the case.
$V\!ir^*$, which we might be able to investigate using tools from affine algebraic geometry. We show that this is indeed the case.
From the discussion, it is important to characterise which functions ![]() $\chi \in V\!ir^*$ have nontrivial Poisson cores. One striking result, proved in this paper, is that such
$\chi \in V\!ir^*$ have nontrivial Poisson cores. One striking result, proved in this paper, is that such ![]() $\chi$ must vanish on the central element
$\chi$ must vanish on the central element ![]() $z$. Further, the induced function
$z$. Further, the induced function ![]() $\overline \chi \in W^*$ is given by evaluating local behaviour on a proper (that is, finite) subscheme of
$\overline \chi \in W^*$ is given by evaluating local behaviour on a proper (that is, finite) subscheme of ![]() $\mathbb {C}^\times$. We have the following result.
$\mathbb {C}^\times$. We have the following result.
Theorem 1.1 (Theorem 3.3.1)
Let ![]() $\chi \in V\!ir^*$. The following are equivalent.
$\chi \in V\!ir^*$. The following are equivalent.
(1) The Poisson core of
 $\chi$ is nontrivial: that is,
$\chi$ is nontrivial: that is,  $\operatorname {P}(\chi ) \supsetneqq (z - \chi (z))$.
$\operatorname {P}(\chi ) \supsetneqq (z - \chi (z))$.(2) We have
 $\chi (z) = 0$ and the induced function
$\chi (z) = 0$ and the induced function  $\overline {\chi } \in W^*$ is a linear combination of functions of the form
where
$\overline {\chi } \in W^*$ is a linear combination of functions of the form
where \[ f\partial_t\mapsto \alpha_0f(x)+\cdots+\alpha_nf^{(n)}(x), \]
\[ f\partial_t\mapsto \alpha_0f(x)+\cdots+\alpha_nf^{(n)}(x), \]
 $x \in \mathbb {C}^\times$ and
$x \in \mathbb {C}^\times$ and  $\alpha _0, \ldots, \alpha _n \in \mathbb {C}$.
$\alpha _0, \ldots, \alpha _n \in \mathbb {C}$.(3) The isotropy subalgebra
 $V\!ir^\chi$ of
$V\!ir^\chi$ of  $\chi$ has finite codimension in
$\chi$ has finite codimension in  $V\!ir$.
$V\!ir$.
We call functions ![]() $\chi \in V\!ir^*$ satisfying the equivalent conditions of Theorem 1.1 local functions as by condition
$\chi \in V\!ir^*$ satisfying the equivalent conditions of Theorem 1.1 local functions as by condition ![]() $(2)$ they are defined by local data.
$(2)$ they are defined by local data.
Motivated by condition ![]() $(3)$ of Theorem 1.1, we investigate subalgebras of
$(3)$ of Theorem 1.1, we investigate subalgebras of ![]() $V\!ir$ of finite codimension. We prove the following.
$V\!ir$ of finite codimension. We prove the following.
Theorem 1.2 (Proposition 3.3.3)
Let ![]() $\mathfrak k \subseteq V\!ir$ be a subalgebra of finite codimension. Then there is
$\mathfrak k \subseteq V\!ir$ be a subalgebra of finite codimension. Then there is ![]() $f \in \mathbb {C}[t, t^{-1}] \setminus \{0\}$ so that
$f \in \mathbb {C}[t, t^{-1}] \setminus \{0\}$ so that ![]() $\mathfrak k \supseteq \mathbb {C} z + f \mathbb {C}[t, t^{-1}] \partial _t$. In particular, any finite codimension subalgebra of
$\mathfrak k \supseteq \mathbb {C} z + f \mathbb {C}[t, t^{-1}] \partial _t$. In particular, any finite codimension subalgebra of ![]() $V\!ir$ contains
$V\!ir$ contains ![]() $z$.
$z$.
As an immediate corollary of Theorem 1.2, we show the following result.
Corollary 1.3 (Corollary 3.3.5)
If ![]() $0 \neq \zeta \in \mathbb {C}$, then
$0 \neq \zeta \in \mathbb {C}$, then ![]() $\operatorname {S}(V\!ir)/(z-\zeta )$ is Poisson simple : it has no nontrivial Poisson ideals.
$\operatorname {S}(V\!ir)/(z-\zeta )$ is Poisson simple : it has no nontrivial Poisson ideals.
We then study the pseudo-orbits of local functions on ![]() $V\!ir$,
$V\!ir$, ![]() $W$ and related Lie algebras; we describe our results for
$W$ and related Lie algebras; we describe our results for ![]() $V\!ir$ in the introduction. If
$V\!ir$ in the introduction. If ![]() $\chi \in V\!ir^*$ is local, then by combining Theorem 1.1 and [Reference Iyudu and SierraIS20, Theorem 1.3],
$\chi \in V\!ir^*$ is local, then by combining Theorem 1.1 and [Reference Iyudu and SierraIS20, Theorem 1.3], ![]() $\operatorname {S}(V\!ir)/\operatorname {P}(\chi )$ has polynomial growth and we thus expect the pseudo-orbit of
$\operatorname {S}(V\!ir)/\operatorname {P}(\chi )$ has polynomial growth and we thus expect the pseudo-orbit of ![]() $\chi$ to be finite-dimensional. We show that pseudo-orbits of local functions in
$\chi$ to be finite-dimensional. We show that pseudo-orbits of local functions in ![]() $V\!ir^*$ are, in fact, orbits of a finite-dimensional solvable algebraic (Lie) group acting on an affine variety which maps injectively to
$V\!ir^*$ are, in fact, orbits of a finite-dimensional solvable algebraic (Lie) group acting on an affine variety which maps injectively to ![]() $V\!ir^*$, and we describe these orbits explicitly (Section 4.2). This allows us to completely determine the pseudo-orbit of an arbitrary local function in
$V\!ir^*$, and we describe these orbits explicitly (Section 4.2). This allows us to completely determine the pseudo-orbit of an arbitrary local function in ![]() $V\!ir^*$ (Theorem 4.3.1) and thus also determine the Poisson primitive ideals of
$V\!ir^*$ (Theorem 4.3.1) and thus also determine the Poisson primitive ideals of ![]() $\operatorname {S}(V\!ir)$ (Remark 4.3.9). We also classify maximal Poisson ideals in
$\operatorname {S}(V\!ir)$ (Remark 4.3.9). We also classify maximal Poisson ideals in ![]() $\operatorname {S}(V\!ir)$ (Corollary 4.3.18): they are the augmentation ideal, the ideals
$\operatorname {S}(V\!ir)$ (Corollary 4.3.18): they are the augmentation ideal, the ideals ![]() $(z-\zeta )$ for
$(z-\zeta )$ for ![]() $\zeta \in \mathbb {C}^\times$, and the defining ideals of all but one of the two-dimensional pseudo-orbits.
$\zeta \in \mathbb {C}^\times$, and the defining ideals of all but one of the two-dimensional pseudo-orbits.
Through this analysis, we obtain a nice combinatorial description of pseudo-orbits in ![]() $W^*$: pseudo-orbits of local functions on
$W^*$: pseudo-orbits of local functions on ![]() $W$ and, thus, Poisson primitive ideals of
$W$ and, thus, Poisson primitive ideals of ![]() $\operatorname {S}(W)$, correspond to a choice of a partition
$\operatorname {S}(W)$, correspond to a choice of a partition ![]() $\lambda$ and a point in an open subvariety of a finite-dimensional affine space
$\lambda$ and a point in an open subvariety of a finite-dimensional affine space ![]() $\mathbb {A}^k$, where
$\mathbb {A}^k$, where ![]() $k$ can be calculated from
$k$ can be calculated from ![]() $\lambda$. (See Remark 4.3.3.) In Theorem 5.2.8 and Remark 5.2.13, we expand this correspondence to obtain a parameterisation of all prime Poisson ideals of
$\lambda$. (See Remark 4.3.3.) In Theorem 5.2.8 and Remark 5.2.13, we expand this correspondence to obtain a parameterisation of all prime Poisson ideals of ![]() $\operatorname {S}(W)$ and
$\operatorname {S}(W)$ and ![]() $\operatorname {S}(V\!ir)$. We also study the related Lie algebra
$\operatorname {S}(V\!ir)$. We also study the related Lie algebra ![]() $W_{\geqslant -1} = \mathbb {C}[t]\partial _t$, and prove (Corollary 5.2.14) that Poisson primitive and prime Poisson ideals of
$W_{\geqslant -1} = \mathbb {C}[t]\partial _t$, and prove (Corollary 5.2.14) that Poisson primitive and prime Poisson ideals of ![]() $\operatorname {S}(W_{\geqslant -1})$ are induced by restriction from
$\operatorname {S}(W_{\geqslant -1})$ are induced by restriction from ![]() $\operatorname {S}(W)$.
$\operatorname {S}(W)$.
Our understanding of prime Poisson ideals allows us to determine exactly which prime Poisson ideals of ![]() $\operatorname {S}(V\!ir)$ obey the Poisson Dixmier–Moeglin equivalence (PDME), which generalises the characterisation of primitive ideals in enveloping algebras of finite-dimensional Lie algebras due to Dixmier and Moeglin. The central question is when a Poisson primitive ideal of
$\operatorname {S}(V\!ir)$ obey the Poisson Dixmier–Moeglin equivalence (PDME), which generalises the characterisation of primitive ideals in enveloping algebras of finite-dimensional Lie algebras due to Dixmier and Moeglin. The central question is when a Poisson primitive ideal of ![]() $\operatorname {S}(V\!ir)$ is Poisson locally closed: that is, locally closed in the Zariski topology on Poisson primitive ideals. (If
$\operatorname {S}(V\!ir)$ is Poisson locally closed: that is, locally closed in the Zariski topology on Poisson primitive ideals. (If ![]() $\dim \mathfrak g < \infty$, then a prime Poisson ideal of
$\dim \mathfrak g < \infty$, then a prime Poisson ideal of ![]() $\operatorname {S}(\mathfrak g)$ is Poisson primitive if and only if it is Poisson locally closed [Reference Launois and León SánchezLL19, Theorem 2].) We show (Theorem 5.3.1) that
$\operatorname {S}(\mathfrak g)$ is Poisson primitive if and only if it is Poisson locally closed [Reference Launois and León SánchezLL19, Theorem 2].) We show (Theorem 5.3.1) that ![]() $(z)$ is the only Poisson primitive ideal of
$(z)$ is the only Poisson primitive ideal of ![]() $\operatorname {S}(V\!ir)$ which is not Poisson locally closed. We further prove (Corollary 5.4.2) that
$\operatorname {S}(V\!ir)$ which is not Poisson locally closed. We further prove (Corollary 5.4.2) that ![]() $\operatorname {S}(W)$ has no nonzero prime Poisson ideals of finite height.
$\operatorname {S}(W)$ has no nonzero prime Poisson ideals of finite height.
One part of the proof of Theorem 1.2 is to show that, given a subalgebra ![]() $\mathfrak k$ of finite codimension in
$\mathfrak k$ of finite codimension in ![]() $W$, there are a finite collection of points
$W$, there are a finite collection of points ![]() $S$ (the ‘support’ of
$S$ (the ‘support’ of ![]() $\mathfrak k$) and
$\mathfrak k$) and ![]() $n\in \mathbb {Z}_{\geqslant 0}$ such that all vector fields in
$n\in \mathbb {Z}_{\geqslant 0}$ such that all vector fields in ![]() $\mathfrak k$ vanish at all points of
$\mathfrak k$ vanish at all points of ![]() $S$ and so that
$S$ and so that ![]() $\mathfrak k$ contains all vector fields vanishing to order
$\mathfrak k$ contains all vector fields vanishing to order ![]() $\geqslant n$ at every point of
$\geqslant n$ at every point of ![]() $S$. Based on this result, we classify subalgebras of
$S$. Based on this result, we classify subalgebras of ![]() $V\!ir$ of codimension
$V\!ir$ of codimension ![]() $\leqslant 3$ in § 6.
$\leqslant 3$ in § 6.
Our original motivation for studying Poisson ideals of ![]() $\operatorname {S}(V\!ir)$ was to study two-sided ideals in the universal enveloping algebra
$\operatorname {S}(V\!ir)$ was to study two-sided ideals in the universal enveloping algebra ![]() $\operatorname {U}(V\!ir)$, and we turn to enveloping algebras in § 7. In the finite-dimensional setting, Kirillov's orbit method gives a correspondence between primitive ideals of
$\operatorname {U}(V\!ir)$, and we turn to enveloping algebras in § 7. In the finite-dimensional setting, Kirillov's orbit method gives a correspondence between primitive ideals of ![]() $\operatorname {U}(\mathfrak g)$ and coadjoint orbits in
$\operatorname {U}(\mathfrak g)$ and coadjoint orbits in ![]() $\mathfrak g^*$. We conjecture that a similar correspondence exists for
$\mathfrak g^*$. We conjecture that a similar correspondence exists for ![]() $V\!ir$ and related Lie algebras, and in § 7.1 we show that pseudo-orbits of dimension two in
$V\!ir$ and related Lie algebras, and in § 7.1 we show that pseudo-orbits of dimension two in ![]() $V\!ir^*$ quantise to give a family of primitive ideals, kernels of well-known maps from
$V\!ir^*$ quantise to give a family of primitive ideals, kernels of well-known maps from ![]() $\operatorname {U}(V\!ir)$ through
$\operatorname {U}(V\!ir)$ through ![]() $\operatorname {U}(W)$ to the localised Weyl algebra. We end the paper with some conjectures about (two-sided) ideals of the universal enveloping algebra
$\operatorname {U}(W)$ to the localised Weyl algebra. We end the paper with some conjectures about (two-sided) ideals of the universal enveloping algebra ![]() $\operatorname {U}(V\!ir)$ which are motivated by our work on
$\operatorname {U}(V\!ir)$ which are motivated by our work on ![]() $\operatorname {S}(V\!ir)$; these are the subject of further research.
$\operatorname {S}(V\!ir)$; these are the subject of further research.
To end the introduction, let us briefly discuss the classical (continuous) version of the theory of coadjoint orbits of the Virasoro algebra. If one considers the real Lie algebra of continuous vector fields on the circle and its central extension the real Virasoro algebra ![]() $V\!ir_{\mathbb {R}}$, then the group of diffeomorphisms of the circle acts on
$V\!ir_{\mathbb {R}}$, then the group of diffeomorphisms of the circle acts on ![]() $V\!ir_{\mathbb {R}}$ and its continuous dual. There are, of course, notions of coadjoint orbits in this context, see [Reference KirillovKir81, Reference WittenWit88]. However, it happens that the corresponding orbits do not define an interesting (Poisson) ideal in the symmetric algebra
$V\!ir_{\mathbb {R}}$ and its continuous dual. There are, of course, notions of coadjoint orbits in this context, see [Reference KirillovKir81, Reference WittenWit88]. However, it happens that the corresponding orbits do not define an interesting (Poisson) ideal in the symmetric algebra ![]() $\operatorname {S}(V\!ir_{\mathbb {R}})$; in fact, this can be viewed as a somewhat informal result of our paper. Note that the local functions which appear in Theorem 1.1 and which we study in this paper can be thought of as a product of a point-based distribution with a vector field and, hence, are very far from being continuous.
$\operatorname {S}(V\!ir_{\mathbb {R}})$; in fact, this can be viewed as a somewhat informal result of our paper. Note that the local functions which appear in Theorem 1.1 and which we study in this paper can be thought of as a product of a point-based distribution with a vector field and, hence, are very far from being continuous.
2. Poisson ideals and pseudo-orbits
In this section, we recall the general notions of Poisson algebra, Poisson ideal and Poisson primitive ideal. We then consider how these concepts behave for the symmetric algebras of the infinite-dimensional Lie algebras in which we are interested.
Throughout, let ![]() $\Bbbk$ be an uncountable algebraically closed field of characteristic zero. Let us define the Lie algebras of interest in this paper. The Witt algebra
$\Bbbk$ be an uncountable algebraically closed field of characteristic zero. Let us define the Lie algebras of interest in this paper. The Witt algebra ![]() $W =\Bbbk [t, t^{-1}]\partial$ is the Lie algebra of vector fields on
$W =\Bbbk [t, t^{-1}]\partial$ is the Lie algebra of vector fields on ![]() $\Bbbk ^\times :=\Bbbk \setminus \{0\}$; here
$\Bbbk ^\times :=\Bbbk \setminus \{0\}$; here ![]() $\partial = \partial _t = {d}/{dt}$. It is graded by setting
$\partial = \partial _t = {d}/{dt}$. It is graded by setting ![]() $\deg t^n \partial = n-1$. Then
$\deg t^n \partial = n-1$. Then ![]() $W_{\geqslant -1}$ is the subalgebra
$W_{\geqslant -1}$ is the subalgebra ![]() $\Bbbk [t]\partial$ of
$\Bbbk [t]\partial$ of ![]() $W$ and
$W$ and ![]() $W_{\geqslant 1}$, sometimes called the positive Witt algebra, is the subalgebra
$W_{\geqslant 1}$, sometimes called the positive Witt algebra, is the subalgebra ![]() $t^2\Bbbk [t]\partial$;
$t^2\Bbbk [t]\partial$; ![]() $W_{\geqslant 0}$ stands for
$W_{\geqslant 0}$ stands for ![]() $t\Bbbk [t]\partial$.
$t\Bbbk [t]\partial$.
The Virasoro algebra ![]() $V\!ir$ is isomorphic as a vector space to
$V\!ir$ is isomorphic as a vector space to ![]() $\Bbbk [t, t^{-1}]\partial \oplus \Bbbk z$. It is endowed with a Lie algebra structure by the formula
$\Bbbk [t, t^{-1}]\partial \oplus \Bbbk z$. It is endowed with a Lie algebra structure by the formula
(Here ![]() $\operatorname {Res}_0(f)$ denotes the algebraic residue of
$\operatorname {Res}_0(f)$ denotes the algebraic residue of ![]() $f$ at 0, i.e. the coefficient of
$f$ at 0, i.e. the coefficient of ![]() $t^{-1}$ in the Laurent expansion of
$t^{-1}$ in the Laurent expansion of ![]() $f$ at 0.) It is well-known that
$f$ at 0.) It is well-known that ![]() $V\!ir$ is the unique nontrivial one-dimensional central extension of
$V\!ir$ is the unique nontrivial one-dimensional central extension of ![]() $W$. There is a canonical Lie algebra homomorphism
$W$. There is a canonical Lie algebra homomorphism ![]() $V\!ir\to W$ given by factoring out
$V\!ir\to W$ given by factoring out ![]() $z$.
$z$.
Let ![]() $V$ be a
$V$ be a ![]() $\Bbbk$-vector space. We use
$\Bbbk$-vector space. We use ![]() $\operatorname {S}(V)$ to denote the symmetric algebra of
$\operatorname {S}(V)$ to denote the symmetric algebra of ![]() $V$; that is, polynomial functions on
$V$; that is, polynomial functions on ![]() $V^*$. For
$V^*$. For ![]() $\chi \in V^*$ we denote by
$\chi \in V^*$ we denote by ![]() $\operatorname {ev}_\chi$ the induced homomorphism
$\operatorname {ev}_\chi$ the induced homomorphism ![]() $\operatorname {S}(V)\to \Bbbk$ defined by
$\operatorname {S}(V)\to \Bbbk$ defined by ![]() $\operatorname {ev}_\chi (f) = f(\chi )$.
$\operatorname {ev}_\chi (f) = f(\chi )$.
Let ![]() $\mathfrak g$ be one of the Lie algebras
$\mathfrak g$ be one of the Lie algebras ![]() $V\!ir$,
$V\!ir$, ![]() $W$,
$W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$. Our assumption on the cardinality of the field
$W_{\geqslant 1}$. Our assumption on the cardinality of the field ![]() $\Bbbk$ means that the following extended Nullstellensatz applies to
$\Bbbk$ means that the following extended Nullstellensatz applies to ![]() $\operatorname {S}(\mathfrak g)$; see [Reference McConnell and RobsonMR87, Corollary 9.1.8, Lemma 9.1.2].
$\operatorname {S}(\mathfrak g)$; see [Reference McConnell and RobsonMR87, Corollary 9.1.8, Lemma 9.1.2].
Theorem 2.0.1 (Extended Nullstellensatz)
Let ![]() $A$ be a commutative
$A$ be a commutative ![]() $\Bbbk$-algebra such that
$\Bbbk$-algebra such that ![]() $\dim _\Bbbk A<|\Bbbk |$. Then:
$\dim _\Bbbk A<|\Bbbk |$. Then:
•
 $A$ is a Jacobson ring: every radical ideal is an intersection of a family of maximal ideals;
$A$ is a Jacobson ring: every radical ideal is an intersection of a family of maximal ideals;• if
 $\mathfrak m\subseteq A$ is a maximal ideal, then the canonical map
$\mathfrak m\subseteq A$ is a maximal ideal, then the canonical map  $\Bbbk \to A/\mathfrak m$ is an isomorphism;
$\Bbbk \to A/\mathfrak m$ is an isomorphism;• if
 $A = \operatorname {S}(V)$ for a vector space
$A = \operatorname {S}(V)$ for a vector space  $V$ with
$V$ with  $\dim V<|\Bbbk |$, then the maximal ideals of
$\dim V<|\Bbbk |$, then the maximal ideals of  $A$ are all of the form
$A$ are all of the form  $\mathfrak m_\chi =\operatorname {\ker } {\rm ev}_\chi$ for some
$\mathfrak m_\chi =\operatorname {\ker } {\rm ev}_\chi$ for some  $\chi \in V^*$.
$\chi \in V^*$.
Let ![]() $A$ be a commutative
$A$ be a commutative ![]() $\Bbbk$-algebra. (Note that we make no noetherianity or finiteness assumption on
$\Bbbk$-algebra. (Note that we make no noetherianity or finiteness assumption on ![]() $A$.) Denote by
$A$.) Denote by ![]() $\operatorname {MSpec} A$ the set of maximal ideals of
$\operatorname {MSpec} A$ the set of maximal ideals of ![]() $A$, which we consider as a (potentially infinite-dimensional) variety. We denote by
$A$, which we consider as a (potentially infinite-dimensional) variety. We denote by ![]() $\mathfrak {m}_x$ the maximal ideal corresponding to a point
$\mathfrak {m}_x$ the maximal ideal corresponding to a point ![]() $x \in {\rm MSpec}A$. As usual,
$x \in {\rm MSpec}A$. As usual, ![]() $\operatorname {MSpec} A$ is a topological space under the Zariski topology. Given an ideal
$\operatorname {MSpec} A$ is a topological space under the Zariski topology. Given an ideal ![]() $N$ of
$N$ of ![]() $A$, we denote the corresponding closed subset of
$A$, we denote the corresponding closed subset of ![]() $\operatorname {MSpec} A$ by
$\operatorname {MSpec} A$ by
Given ![]() $X \subseteq \operatorname {MSpec} A$, we denote the corresponding radical ideal of
$X \subseteq \operatorname {MSpec} A$, we denote the corresponding radical ideal of ![]() $A$ by
$A$ by
As we have enlarged the class of varieties somewhat beyond the usual, we make the convention that for us an algebraic variety is a classical variety: a (nonempty) integral separated scheme of finite type over ![]() $\Bbbk$, as in [Reference HartshorneHar77, p. 105]. If
$\Bbbk$, as in [Reference HartshorneHar77, p. 105]. If ![]() $A, B$ are commutative
$A, B$ are commutative ![]() $\Bbbk$-algebras which are domains, an algebraic map or morphism of varieties
$\Bbbk$-algebras which are domains, an algebraic map or morphism of varieties ![]() $\phi : \operatorname {MSpec} A \to \operatorname {MSpec} B$ has the usual meaning: a function so that the pullback
$\phi : \operatorname {MSpec} A \to \operatorname {MSpec} B$ has the usual meaning: a function so that the pullback ![]() $\phi ^*$ defines an algebra homomorphism
$\phi ^*$ defines an algebra homomorphism ![]() $B \to A$.
$B \to A$.
Let ![]() $\{\cdot, \cdot \}: A\times A\to A$ be a skew-symmetric
$\{\cdot, \cdot \}: A\times A\to A$ be a skew-symmetric ![]() $\Bbbk$-bilinear map. We say that
$\Bbbk$-bilinear map. We say that ![]() $(A, \{\cdot, \cdot \})$ is a Poisson algebra if
$(A, \{\cdot, \cdot \})$ is a Poisson algebra if ![]() $\{\cdot, \cdot \}$ satisfies the Leibniz rule on each input and the Jacobi identity. An ideal
$\{\cdot, \cdot \}$ satisfies the Leibniz rule on each input and the Jacobi identity. An ideal ![]() $I$ of
$I$ of ![]() $A$ is Poisson if
$A$ is Poisson if ![]() $\{I, A\}\subseteq I$. It is clear that the sum of all Poisson subideals of any ideal
$\{I, A\}\subseteq I$. It is clear that the sum of all Poisson subideals of any ideal ![]() $I$ of
$I$ of ![]() $A$ is the maximal Poisson ideal inside
$A$ is the maximal Poisson ideal inside ![]() $I$; we denote this ideal by
$I$; we denote this ideal by ![]() ${\rm Core}(I)$ and refer to it as the Poisson core of
${\rm Core}(I)$ and refer to it as the Poisson core of ![]() $I$. Note that if
$I$. Note that if ![]() $I$ is radical, respectively prime, then
$I$ is radical, respectively prime, then ![]() ${\rm Core}(I)$ inherits this property; see [Reference Petukhov and SierraPS20, Lemmata 2.6 and 2.8].
${\rm Core}(I)$ inherits this property; see [Reference Petukhov and SierraPS20, Lemmata 2.6 and 2.8].
A Poisson ideal ![]() $I$ is called Poisson primitive if
$I$ is called Poisson primitive if ![]() $I={\rm Core}(\mathfrak m)$ for a maximal ideal
$I={\rm Core}(\mathfrak m)$ for a maximal ideal ![]() $\mathfrak m$ of
$\mathfrak m$ of ![]() $A$; Poisson primitive ideals are prime. We denote the set of Poisson primitive ideals of
$A$; Poisson primitive ideals are prime. We denote the set of Poisson primitive ideals of ![]() $A$ by
$A$ by ![]() $\operatorname {PSpec}_{\rm prim}A$, and the set of prime Poisson ideals by
$\operatorname {PSpec}_{\rm prim}A$, and the set of prime Poisson ideals by ![]() $\operatorname {PSpec} A$. Both are given the Zariski topology, where the closed subsets are defined by Poisson ideals of
$\operatorname {PSpec} A$. Both are given the Zariski topology, where the closed subsets are defined by Poisson ideals of ![]() $A$.
$A$.
Consider a Lie algebra ![]() $\mathfrak g$ with
$\mathfrak g$ with ![]() $\dim \mathfrak g < |\Bbbk |$. It is well-known that
$\dim \mathfrak g < |\Bbbk |$. It is well-known that ![]() $\operatorname {S}(\mathfrak g)$ possesses a canonical Poisson algebra structure, induced by defining
$\operatorname {S}(\mathfrak g)$ possesses a canonical Poisson algebra structure, induced by defining ![]() $\{u, v\} = [u, v]$ for any
$\{u, v\} = [u, v]$ for any ![]() $u, v \in \mathfrak g$. As
$u, v \in \mathfrak g$. As ![]() $\dim \mathfrak g<|\Bbbk |$, then by the Nullstellensatz
$\dim \mathfrak g<|\Bbbk |$, then by the Nullstellensatz ![]() $\operatorname {MSpec}(\operatorname {S}(\mathfrak g))$ can be canonically identified with
$\operatorname {MSpec}(\operatorname {S}(\mathfrak g))$ can be canonically identified with ![]() $\mathfrak g^*:$
$\mathfrak g^*:$
Thus, any Poisson primitive ideal of ![]() $\operatorname {S}(\mathfrak g)$ is equal to
$\operatorname {S}(\mathfrak g)$ is equal to ![]() $\operatorname {Core}(\mathfrak {m}_\chi )$ for some
$\operatorname {Core}(\mathfrak {m}_\chi )$ for some ![]() $\chi \in \mathfrak g^*$. Set
$\chi \in \mathfrak g^*$. Set ![]() $\operatorname {P} (\chi ):=\operatorname {Core}(\mathfrak {m}_\chi )$. For any Lie algebra
$\operatorname {P} (\chi ):=\operatorname {Core}(\mathfrak {m}_\chi )$. For any Lie algebra ![]() $\mathfrak g$, the ideal
$\mathfrak g$, the ideal ![]() $\mathfrak m_0 = \operatorname {Core}(\mathfrak {m}_0)=\operatorname {P}(0)$ (the augmentation ideal) is the Poisson core of
$\mathfrak m_0 = \operatorname {Core}(\mathfrak {m}_0)=\operatorname {P}(0)$ (the augmentation ideal) is the Poisson core of ![]() $0 \in \mathfrak g^*$ and so is Poisson primitive.
$0 \in \mathfrak g^*$ and so is Poisson primitive.
Even in the absence of an adjoint group to ![]() $\mathfrak g$, the Poisson primitives
$\mathfrak g$, the Poisson primitives ![]() $\operatorname {P}(\chi )$ give analogues of coadjoint orbits.
$\operatorname {P}(\chi )$ give analogues of coadjoint orbits.
Definition 2.0.2 Let ![]() $\mathfrak g$ be any Lie algebra. The pseudo-orbit of
$\mathfrak g$ be any Lie algebra. The pseudo-orbit of ![]() $\chi \in \mathfrak g^*$ is
$\chi \in \mathfrak g^*$ is
The dimension of ![]() $\mathbb {O}(\chi )$ is defined to be
$\mathbb {O}(\chi )$ is defined to be ![]() $\operatorname {GKdim} \operatorname {S}(\mathfrak g)/\operatorname {P}(\chi )$. (Here if
$\operatorname {GKdim} \operatorname {S}(\mathfrak g)/\operatorname {P}(\chi )$. (Here if ![]() $R$ is a
$R$ is a ![]() $\Bbbk$-algebra, then
$\Bbbk$-algebra, then ![]() $\operatorname {GKdim} R$ denotes the Gelfand–Kirillov dimension of
$\operatorname {GKdim} R$ denotes the Gelfand–Kirillov dimension of ![]() $R$; see [Reference Krause and LenaganKL00].)
$R$; see [Reference Krause and LenaganKL00].)
Remark 2.0.3 If ![]() $\mathfrak g = {\rm Lie}\, G$ is the Lie algebra of a connected algebraic group and
$\mathfrak g = {\rm Lie}\, G$ is the Lie algebra of a connected algebraic group and ![]() $\chi \in \mathfrak g^*$, then
$\chi \in \mathfrak g^*$, then ![]() $\mathbb {O}(\chi )$ is the coadjoint orbit of
$\mathbb {O}(\chi )$ is the coadjoint orbit of ![]() $\chi$. In our setting,
$\chi$. In our setting, ![]() $\mathfrak g$ is not the Lie algebra of any algebraic group. However, we show that we can still define algebraic group actions on pieces of
$\mathfrak g$ is not the Lie algebra of any algebraic group. However, we show that we can still define algebraic group actions on pieces of ![]() $\mathfrak g^*$ that allow us to recover pseudo-orbits as actual orbits.
$\mathfrak g^*$ that allow us to recover pseudo-orbits as actual orbits.
Part (b) of the next result is an analogue of (1.0.1) for pseudo-orbits.
Lemma 2.0.4 Let ![]() $\mathfrak g$ be a Lie algebra with
$\mathfrak g$ be a Lie algebra with ![]() $\dim \mathfrak g < | \Bbbk |$.
$\dim \mathfrak g < | \Bbbk |$.
(a) Any radical Poisson ideal in
 $\operatorname {S}(\mathfrak g)$ is equal to an intersection of Poisson primitive ideals. Explicitly, given a radical Poisson ideal
$\operatorname {S}(\mathfrak g)$ is equal to an intersection of Poisson primitive ideals. Explicitly, given a radical Poisson ideal  $I$ we have
$I$ we have
 \[ I = \bigcap \{\operatorname{P}(\chi) \,|\, \chi \in \mathfrak g^*,~\operatorname{ev}_\chi(I) = 0\} . \]
\[ I = \bigcap \{\operatorname{P}(\chi) \,|\, \chi \in \mathfrak g^*,~\operatorname{ev}_\chi(I) = 0\} . \]
(b) Assume now that
 $\dim \mathfrak g$ is countable and let
$\dim \mathfrak g$ is countable and let  $\chi \in \mathfrak g^*$ be nonzero. Then
$\chi \in \mathfrak g^*$ be nonzero. Then
 \[ \operatorname{P}(\chi) = \bigcap_{\nu \in \mathbb{O}(\chi)} \mathfrak m_\nu. \]
\[ \operatorname{P}(\chi) = \bigcap_{\nu \in \mathbb{O}(\chi)} \mathfrak m_\nu. \]
Proof. Part (a) is well-known, but we give a proof for completeness. As ![]() $I$ is radical and Poisson,
$I$ is radical and Poisson,
and this is contained, by definition, in ![]() $\bigcap _{\chi \in \mathfrak g^*,\ \operatorname {ev}_\chi (I) = 0} \mathfrak m_\chi$. By the Nullstellensatz, this last part is equal to
$\bigcap _{\chi \in \mathfrak g^*,\ \operatorname {ev}_\chi (I) = 0} \mathfrak m_\chi$. By the Nullstellensatz, this last part is equal to ![]() $I$.
$I$.
For part (b), set ![]() $R:=\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi )$. Thanks to the proof of [Reference León Sánchez and SierraLS08, Theorem 6.3], which uses only that
$R:=\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi )$. Thanks to the proof of [Reference León Sánchez and SierraLS08, Theorem 6.3], which uses only that ![]() $\mathfrak g$ is countably generated (see also [Reference Bell, Launois, León Sánchez and MoosaBLLM17, Theorem 3.2]), there is a sequence of nonzero Poisson ideals
$\mathfrak g$ is countably generated (see also [Reference Bell, Launois, León Sánchez and MoosaBLLM17, Theorem 3.2]), there is a sequence of nonzero Poisson ideals ![]() $L_1, L_2, \ldots$ of
$L_1, L_2, \ldots$ of ![]() $R$ such that if
$R$ such that if ![]() $\mu \in \mathfrak g^*$ with
$\mu \in \mathfrak g^*$ with ![]() $\operatorname {P}(\mu )$ strictly containing
$\operatorname {P}(\mu )$ strictly containing ![]() $\operatorname {P}(\chi )$, then
$\operatorname {P}(\chi )$, then ![]() $\operatorname {P}(\mu )/\operatorname {P}(\chi )$ contains
$\operatorname {P}(\mu )/\operatorname {P}(\chi )$ contains ![]() $L_i$ for at least one
$L_i$ for at least one ![]() $i$.
$i$.
This is equivalent to the following statement: there is a sequence ![]() $f_1, f_2, \ldots \in R \setminus \{0\}$ such that if
$f_1, f_2, \ldots \in R \setminus \{0\}$ such that if ![]() $\operatorname {P}(\mu )$ strictly contains
$\operatorname {P}(\mu )$ strictly contains ![]() $\operatorname {P}(\chi )$ then
$\operatorname {P}(\chi )$ then ![]() $f_i(\mu )=0$ for at least one
$f_i(\mu )=0$ for at least one ![]() $i$. Therefore,
$i$. Therefore, ![]() $R'=(\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi ))[f_1^{-1}, f_2^{-1},\ldots ]$ is Poisson simple. On the other hand,
$R'=(\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi ))[f_1^{-1}, f_2^{-1},\ldots ]$ is Poisson simple. On the other hand, ![]() $R'$ is clearly at most countable-dimensional and, hence,
$R'$ is clearly at most countable-dimensional and, hence, ![]() $(0)\subset R'$ is an intersection of a family of maximal ideals of
$(0)\subset R'$ is an intersection of a family of maximal ideals of ![]() $R'$ by the Nullstellensatz. The definition of
$R'$ by the Nullstellensatz. The definition of ![]() $R'$ and
$R'$ and ![]() $f_i'$ guarantees that
$f_i'$ guarantees that ![]() $\operatorname {P}(\mu )=\operatorname {P}(\chi )$ for each
$\operatorname {P}(\mu )=\operatorname {P}(\chi )$ for each ![]() $\mu \in \mathfrak g^*$ defining such an ideal. We thus obtain a family of maximal ideals of
$\mu \in \mathfrak g^*$ defining such an ideal. We thus obtain a family of maximal ideals of ![]() $\operatorname {S}(\mathfrak g)$ contained in the pseudo-orbit of
$\operatorname {S}(\mathfrak g)$ contained in the pseudo-orbit of ![]() $\chi$ whose intersection is
$\chi$ whose intersection is ![]() $\operatorname {P}(\chi )$. This implies the desired result.
$\operatorname {P}(\chi )$. This implies the desired result.
2.1 Some results on pseudo-orbits
We now give several results which are well-known for finite-dimensional algebraic Lie algebras, but require proof in our setting. Throughout this subsection, let ![]() $\mathfrak g$ be a Lie algebra with
$\mathfrak g$ be a Lie algebra with ![]() $\dim \mathfrak g < |\Bbbk |$.
$\dim \mathfrak g < |\Bbbk |$.
For every ![]() $\chi \in \mathfrak g^*$ define the skew-symmetric bilinear form
$\chi \in \mathfrak g^*$ define the skew-symmetric bilinear form ![]() $B_\chi (x, y):=\chi ([x, y])$. The kernel of
$B_\chi (x, y):=\chi ([x, y])$. The kernel of ![]() $B_\chi$ is a Lie subalgebra of
$B_\chi$ is a Lie subalgebra of ![]() $\mathfrak g$, which we denote by
$\mathfrak g$, which we denote by ![]() $\mathfrak g^\chi$. Observe that
$\mathfrak g^\chi$. Observe that ![]() $\mathfrak g^\chi$ is precisely
$\mathfrak g^\chi$ is precisely ![]() $\{v \in \mathfrak g \,|\, v \cdot \chi = 0\}$; that is,
$\{v \in \mathfrak g \,|\, v \cdot \chi = 0\}$; that is, ![]() $\mathfrak g^\chi$ is the isotropy subalgebra of
$\mathfrak g^\chi$ is the isotropy subalgebra of ![]() $\chi$ under the (coadjoint) action of
$\chi$ under the (coadjoint) action of ![]() $\mathfrak g$ on
$\mathfrak g$ on ![]() $\mathfrak g^*$. As
$\mathfrak g^*$. As ![]() $B_\chi$ induces a nondegenerate skew-symmetric form on
$B_\chi$ induces a nondegenerate skew-symmetric form on ![]() $\mathfrak g / \mathfrak g^\chi$, we have
$\mathfrak g / \mathfrak g^\chi$, we have ![]() $\operatorname {rk} B_\chi = \dim \mathfrak g/\mathfrak g^\chi$.
$\operatorname {rk} B_\chi = \dim \mathfrak g/\mathfrak g^\chi$.
Lemma 2.1.1 The dimension of ![]() $\mathbb {O}(\chi )$ is at least
$\mathbb {O}(\chi )$ is at least ![]() $\operatorname {rk} B_\chi$, i.e.
$\operatorname {rk} B_\chi$, i.e.
Before proving Lemma 2.1.1, we establish some notation, which we need for several results. For ![]() $u_1,\ldots, u_n,$
$u_1,\ldots, u_n,$ ![]() $v_1, \ldots, v_n\in \mathfrak g$ set
$v_1, \ldots, v_n\in \mathfrak g$ set ![]() $D(u_1, \ldots, u_n; v_1, \ldots, v_n)\in \operatorname {S}(\mathfrak g)$ to be the determinant
$D(u_1, \ldots, u_n; v_1, \ldots, v_n)\in \operatorname {S}(\mathfrak g)$ to be the determinant
 \begin{equation} \begin{vmatrix} [u_1, v_1] & \cdots & [u_1, v_{n}]\\ \cdots & \cdots & \cdots\\ {[u_{n}, v_1]} & \cdots & {[u_{n}, v_{n}]} \end{vmatrix}.\end{equation}
\begin{equation} \begin{vmatrix} [u_1, v_1] & \cdots & [u_1, v_{n}]\\ \cdots & \cdots & \cdots\\ {[u_{n}, v_1]} & \cdots & {[u_{n}, v_{n}]} \end{vmatrix}.\end{equation}Proof of Lemma 2.1.1 Pick ![]() $r\in \mathbb {Z}_{\geqslant 0}$ such that
$r\in \mathbb {Z}_{\geqslant 0}$ such that ![]() $r\leqslant \operatorname {rk} B_\chi$. Then there is an
$r\leqslant \operatorname {rk} B_\chi$. Then there is an ![]() $r$-dimensional subspace
$r$-dimensional subspace ![]() $V$ of
$V$ of ![]() $\mathfrak g$ so that
$\mathfrak g$ so that ![]() $\operatorname {rk} ( B_\chi |_{V})=r$; that is, if
$\operatorname {rk} ( B_\chi |_{V})=r$; that is, if ![]() $u_1, \ldots, u_r$ is a basis of
$u_1, \ldots, u_r$ is a basis of ![]() $V$, then
$V$, then ![]() $\operatorname {ev}_{\chi }(D(u_1, \ldots, u_r, u_1, \ldots, u_r)) \neq 0$. We show that
$\operatorname {ev}_{\chi }(D(u_1, \ldots, u_r, u_1, \ldots, u_r)) \neq 0$. We show that ![]() $u_1, \ldots, u_r$ are algebraically independent in
$u_1, \ldots, u_r$ are algebraically independent in ![]() ${\rm S}(\mathfrak g)/\operatorname {P}(\chi )$; that is, that
${\rm S}(\mathfrak g)/\operatorname {P}(\chi )$; that is, that ![]() $\operatorname {GKdim} (\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi ) ) \geqslant r$.
$\operatorname {GKdim} (\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi ) ) \geqslant r$.
Assume to the contrary that the ![]() $u_i$ are not algebraically independent modulo
$u_i$ are not algebraically independent modulo ![]() $\operatorname {P}(\chi )$. This means that there is some nonzero
$\operatorname {P}(\chi )$. This means that there is some nonzero ![]() $P \in \Bbbk [u_1, \ldots, u_r] \cap \operatorname {P}(\chi )$, and we may assume
$P \in \Bbbk [u_1, \ldots, u_r] \cap \operatorname {P}(\chi )$, and we may assume ![]() $P$ is of minimal degree among such elements. As
$P$ is of minimal degree among such elements. As ![]() $\operatorname {P}(\chi )$ is Poisson,
$\operatorname {P}(\chi )$ is Poisson,
where ![]() $\partial _j P = {\partial P}/{\partial u_j}$.
$\partial _j P = {\partial P}/{\partial u_j}$.
Let ![]() $Q$ be the field of fractions of
$Q$ be the field of fractions of ![]() $\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi )$ (recall that
$\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi )$ (recall that ![]() $\operatorname {P}(\chi )$ is prime). We may rewrite (2.1.3) as the matrix equation
$\operatorname {P}(\chi )$ is prime). We may rewrite (2.1.3) as the matrix equation
 \[ (\{u_i, u_j\})_{ij} \begin{pmatrix} \partial_1 P \\ \vdots \\ \partial_r P \end{pmatrix} = \vec{0} \]
\[ (\{u_i, u_j\})_{ij} \begin{pmatrix} \partial_1 P \\ \vdots \\ \partial_r P \end{pmatrix} = \vec{0} \]
over ![]() $Q$. By minimality of
$Q$. By minimality of ![]() $\deg P$, the vector
$\deg P$, the vector  $\left(\begin{smallmatrix}\partial _1 P \\ \vdots \\ \partial _r P \end {smallmatrix}\right) \in Q^r$ is nonzero. Thus,
$\left(\begin{smallmatrix}\partial _1 P \\ \vdots \\ \partial _r P \end {smallmatrix}\right) \in Q^r$ is nonzero. Thus, ![]() $(\{u_i, u_j\})_{ij} \in M_{r\times r}(Q)$ is singular, so
$(\{u_i, u_j\})_{ij} \in M_{r\times r}(Q)$ is singular, so ![]() $D(u_1, \ldots, u_r; u_1, \ldots, u_r) \in \operatorname {P}(\chi ) \subseteq \mathfrak {m}_\chi$. This contradicts the first paragraph of the proof.
$D(u_1, \ldots, u_r; u_1, \ldots, u_r) \in \operatorname {P}(\chi ) \subseteq \mathfrak {m}_\chi$. This contradicts the first paragraph of the proof.
It is not necessarily easy to calculate ![]() $\operatorname {P}(\chi )$, but we can sometimes use GK dimension to show that a Poisson ideal contained in
$\operatorname {P}(\chi )$, but we can sometimes use GK dimension to show that a Poisson ideal contained in ![]() $\mathfrak {m}_\chi$ is, in fact, equal to
$\mathfrak {m}_\chi$ is, in fact, equal to ![]() $\operatorname {P}(\chi )$. This is given by the following lemma.
$\operatorname {P}(\chi )$. This is given by the following lemma.
Lemma 2.1.4 Let ![]() $\mathfrak g$ be a Lie algebra and
$\mathfrak g$ be a Lie algebra and ![]() $A$ a commutative
$A$ a commutative ![]() $\Bbbk$-algebra that is a domain. Let
$\Bbbk$-algebra that is a domain. Let ![]() ${\phi }: \operatorname {S}(\mathfrak g) \to A$ be an algebra homomorphism so that
${\phi }: \operatorname {S}(\mathfrak g) \to A$ be an algebra homomorphism so that ![]() $\ker {\phi }$ is Poisson. Let
$\ker {\phi }$ is Poisson. Let ![]() $\chi \in \mathfrak g^*$ be such that
$\chi \in \mathfrak g^*$ be such that
Then ![]() $\operatorname {\ker }\phi = \operatorname {P}(\chi )$ and, thus, is Poisson primitive; further,
$\operatorname {\ker }\phi = \operatorname {P}(\chi )$ and, thus, is Poisson primitive; further, ![]() $\operatorname {rk} B_\chi = \operatorname {GKdim} A = \dim \mathbb {O}(\chi )$.
$\operatorname {rk} B_\chi = \operatorname {GKdim} A = \dim \mathbb {O}(\chi )$.
Proof. Certainly ![]() $\ker {\phi } \subseteq \operatorname {P}(\chi )$. If the containment is strict, then as
$\ker {\phi } \subseteq \operatorname {P}(\chi )$. If the containment is strict, then as ![]() $A$ is a domain,
$A$ is a domain,
contradicting Lemma 2.1.1. The final equality is direct from Lemma 2.1.1.
Corollary 2.1.6 If both ![]() $\chi _1, \chi _2$ satisfy (2.1.5) for the same
$\chi _1, \chi _2$ satisfy (2.1.5) for the same ![]() ${\phi }$, then
${\phi }$, then ![]() $\operatorname {P}(\chi _1)=\operatorname {P}(\chi _2)$.
$\operatorname {P}(\chi _1)=\operatorname {P}(\chi _2)$.
We use Lemma 2.1.4 and Corollary 2.1.6 to describe primitive ideals in ![]() $\operatorname {S}(\mathfrak g)$ and the corresponding pseudo-orbits in
$\operatorname {S}(\mathfrak g)$ and the corresponding pseudo-orbits in ![]() $\mathfrak g^*$ explicitly. In the situation of Lemma 2.1.4,
$\mathfrak g^*$ explicitly. In the situation of Lemma 2.1.4, ![]() $A$ may not necessarily be a Poisson algebra. We abuse notation slightly, however, and say that if
$A$ may not necessarily be a Poisson algebra. We abuse notation slightly, however, and say that if ![]() $\ker {\phi }$ is a Poisson ideal, then
$\ker {\phi }$ is a Poisson ideal, then ![]() ${\phi }$ is a Poisson morphism. Further, given a morphism of varieties
${\phi }$ is a Poisson morphism. Further, given a morphism of varieties
we say that ![]() $\psi$ is Poisson if
$\psi$ is Poisson if ![]() $\psi ^*: \operatorname {S}(\mathfrak g) \to A$ is Poisson.
$\psi ^*: \operatorname {S}(\mathfrak g) \to A$ is Poisson.
It is important to know under which conditions maps are Poisson and the answer is given in Proposition 2.1.7. To explain the setup we need to use some concepts from (affine) algebraic geometry. As mentioned, we, somewhat loosely, refer to infinite-dimensional vector spaces such as ![]() $\mathfrak g^*$ as varieties, enlarging the class from standard usage. For any variety
$\mathfrak g^*$ as varieties, enlarging the class from standard usage. For any variety ![]() $X$ and any point
$X$ and any point ![]() $x\in X$ let
$x\in X$ let ![]() ${\rm T}_xX = (\mathfrak {m}_x/\mathfrak {m}_x^2)^*$ denote the tangent space to
${\rm T}_xX = (\mathfrak {m}_x/\mathfrak {m}_x^2)^*$ denote the tangent space to ![]() $X$ at
$X$ at ![]() $x$; this definition makes sense for
$x$; this definition makes sense for ![]() $X= \mathfrak g^*$ as well. Without further comment, we identify
$X= \mathfrak g^*$ as well. Without further comment, we identify ![]() ${\rm T}_x X$ with elements of
${\rm T}_x X$ with elements of ![]() $\mathfrak {m}_x^*$ which vanish on
$\mathfrak {m}_x^*$ which vanish on ![]() $\mathfrak {m}_x^2$. If there is a map
$\mathfrak {m}_x^2$. If there is a map ![]() $\psi : X\to Y$ between algebraic varieties
$\psi : X\to Y$ between algebraic varieties ![]() $X$ and
$X$ and ![]() $Y$, then, for all
$Y$, then, for all ![]() $x\in X$, there is an induced map
$x\in X$, there is an induced map ![]() $\psi _x: {\rm T}_xX\to {\rm T}_{\psi (x)}Y$.
$\psi _x: {\rm T}_xX\to {\rm T}_{\psi (x)}Y$.
We canonically identify the tangent space to ![]() $\mathfrak g^*$ at
$\mathfrak g^*$ at ![]() $\chi \in \mathfrak g^*$ with
$\chi \in \mathfrak g^*$ with ![]() $\mathfrak g^*$. For any derivation
$\mathfrak g^*$. For any derivation ![]() $D$ of
$D$ of ![]() $\operatorname {S}(\mathfrak g)$ and any
$\operatorname {S}(\mathfrak g)$ and any ![]() $\chi \in \mathfrak g^*$ we denote by
$\chi \in \mathfrak g^*$ we denote by ![]() $D_{\chi }$ the tangent vector defined by
$D_{\chi }$ the tangent vector defined by ![]() $D$ at
$D$ at ![]() $\chi$; that is,
$\chi$; that is, ![]() $D_\chi (f) = \chi (Df)$ for any
$D_\chi (f) = \chi (Df)$ for any ![]() $f \in \mathfrak {m}_\chi$. Now,
$f \in \mathfrak {m}_\chi$. Now, ![]() $\mathfrak g$ acts by derivations on
$\mathfrak g$ acts by derivations on ![]() $\operatorname {S}(\mathfrak g)$. For
$\operatorname {S}(\mathfrak g)$. For ![]() $u \in \mathfrak g$ and
$u \in \mathfrak g$ and ![]() $\chi \in \mathfrak g^*$ let
$\chi \in \mathfrak g^*$ let ![]() $u_\chi$ be the tangent vector defined by
$u_\chi$ be the tangent vector defined by ![]() $u$ at
$u$ at ![]() $\chi$. If
$\chi$. If ![]() $v \in \mathfrak g$, then
$v \in \mathfrak g$, then ![]() $u_\chi (v) = \chi ([u, v])$ and, thus,
$u_\chi (v) = \chi ([u, v])$ and, thus, ![]() $u_\chi \in {\rm T}_\chi (\mathfrak g^*) = \mathfrak g^*$ is identified with
$u_\chi \in {\rm T}_\chi (\mathfrak g^*) = \mathfrak g^*$ is identified with ![]() $u \cdot \chi$. If
$u \cdot \chi$. If ![]() $\mathfrak u \subseteq \mathfrak g$ let
$\mathfrak u \subseteq \mathfrak g$ let ![]() $\mathfrak u_\chi = \{ u_\chi \,|\, u \in \mathfrak u\}$. Thus,
$\mathfrak u_\chi = \{ u_\chi \,|\, u \in \mathfrak u\}$. Thus, ![]() $\mathfrak g_\chi \cong \mathfrak g \cdot \chi \cong \mathfrak g/ \mathfrak g^\chi$ and
$\mathfrak g_\chi \cong \mathfrak g \cdot \chi \cong \mathfrak g/ \mathfrak g^\chi$ and ![]() $\operatorname {rk} B_\chi = \dim \mathfrak g_\chi$.
$\operatorname {rk} B_\chi = \dim \mathfrak g_\chi$.
Proposition 2.1.7 Let ![]() $\mathfrak g$ be a Lie algebra with
$\mathfrak g$ be a Lie algebra with ![]() $\dim \mathfrak g < |\Bbbk |$. Let
$\dim \mathfrak g < |\Bbbk |$. Let ![]() $X$ be an affine variety and let
$X$ be an affine variety and let ![]() $\phi : X \to \mathfrak g^*$ be a morphism of varieties. Then
$\phi : X \to \mathfrak g^*$ be a morphism of varieties. Then ![]() $\phi$ is Poisson if and only if
$\phi$ is Poisson if and only if ![]() $\mathfrak g_{\phi (x)}\subseteq \phi _x({\rm T}_xX)$ for all
$\mathfrak g_{\phi (x)}\subseteq \phi _x({\rm T}_xX)$ for all ![]() $x\in X$.
$x\in X$.
Proposition 2.1.7 is a direct consequence of the following lemma.
Lemma 2.1.8 Let ![]() $\mathfrak g, X, \phi$ be as in the statement of Proposition 2.1.7 and let
$\mathfrak g, X, \phi$ be as in the statement of Proposition 2.1.7 and let ![]() $D$ be a derivation of
$D$ be a derivation of ![]() $\operatorname {S}(\mathfrak g)$. Then
$\operatorname {S}(\mathfrak g)$. Then ![]() $\ker \phi ^*$ is
$\ker \phi ^*$ is ![]() $D$-stable if and only if
$D$-stable if and only if ![]() $D_{\phi (x)}\in \phi _x({\rm T}_xX)$ for all
$D_{\phi (x)}\in \phi _x({\rm T}_xX)$ for all ![]() $x\in X$.
$x\in X$.
Proof. Suppose that ![]() $D_{\phi (x)} \in \phi _x({\rm T}_xX)$ for all
$D_{\phi (x)} \in \phi _x({\rm T}_xX)$ for all ![]() $x\in X$. Let
$x\in X$. Let ![]() $f \in \ker \phi ^*$. We show that
$f \in \ker \phi ^*$. We show that ![]() $\phi ^*(Df) = 0$ or, equivalently, that
$\phi ^*(Df) = 0$ or, equivalently, that ![]() $Df \in \mathfrak {m}_{\phi (x)}$ for all
$Df \in \mathfrak {m}_{\phi (x)}$ for all ![]() $x \in X$. Fix
$x \in X$. Fix ![]() $x$ and let
$x$ and let ![]() $\ell \in {\rm T}_x X$ be such that
$\ell \in {\rm T}_x X$ be such that ![]() $D_{\phi (x)} = \phi _x(\ell )$. Then
$D_{\phi (x)} = \phi _x(\ell )$. Then
as needed.
Conversely, let ![]() $x \in X$ and let
$x \in X$ and let ![]() $\mathfrak n_x := \mathfrak {m}_x \cap \phi ^*(\operatorname {S}(\mathfrak g))$. If
$\mathfrak n_x := \mathfrak {m}_x \cap \phi ^*(\operatorname {S}(\mathfrak g))$. If ![]() $\ker \phi ^*$ is
$\ker \phi ^*$ is ![]() $D$-stable, then
$D$-stable, then ![]() $D$ induces a derivation
$D$ induces a derivation ![]() $\overline {D}$ on
$\overline {D}$ on ![]() $\phi ^*(\operatorname {S}(\mathfrak g))$, defined by
$\phi ^*(\operatorname {S}(\mathfrak g))$, defined by
and, thus, defines an element ![]() $\overline D_x \in (\mathfrak n_x/\mathfrak n_x^2)^*$. Let
$\overline D_x \in (\mathfrak n_x/\mathfrak n_x^2)^*$. Let ![]() $\ell \in {\rm T}_xX$ be any extension of
$\ell \in {\rm T}_xX$ be any extension of ![]() $\overline D_x$ to
$\overline D_x$ to ![]() $\mathfrak {m}_x/\mathfrak {m}_x^2$. Then for
$\mathfrak {m}_x/\mathfrak {m}_x^2$. Then for ![]() $f \in \mathfrak {m}_{\phi (x)}$ we have
$f \in \mathfrak {m}_{\phi (x)}$ we have
showing that ![]() $D_{\phi (x)} \in \phi _x({\rm T}_xX)$.
$D_{\phi (x)} \in \phi _x({\rm T}_xX)$.
2.2 Some pseudo-orbits in  $W^*$ and
$W^*$ and  $W_{\geqslant -1}^*$
$W_{\geqslant -1}^*$
This subsection is effectively an extended example, where we use the methods of the previous subsection, particularly Lemma 2.1.4, to compute the Poisson cores of some particular functions in ![]() $W^*$ and
$W^*$ and ![]() $W_{\geqslant -1}^*$. We show later (Proposition 4.3.14) that these give all of the prime Poisson ideals of
$W_{\geqslant -1}^*$. We show later (Proposition 4.3.14) that these give all of the prime Poisson ideals of ![]() $\operatorname {S}(W)$ and
$\operatorname {S}(W)$ and ![]() $\operatorname {S}(W_{\geqslant -1})$ of co-GK-dimension two.
$\operatorname {S}(W_{\geqslant -1})$ of co-GK-dimension two.
Throughout the subsection fix ![]() $x,\alpha, \gamma \in \Bbbk$ with
$x,\alpha, \gamma \in \Bbbk$ with ![]() $x \neq 0$ and
$x \neq 0$ and ![]() $\alpha, \gamma$ not both zero. Let
$\alpha, \gamma$ not both zero. Let ![]() $\chi := \chi _{x;\alpha,\gamma } \in W^*$ be defined by
$\chi := \chi _{x;\alpha,\gamma } \in W^*$ be defined by
Further, given ![]() $g\in \Bbbk [t,t^{-1}]$ let
$g\in \Bbbk [t,t^{-1}]$ let ![]() $W(g) := \Bbbk [t,t^{-1}] g \partial \subseteq W$. Both sets of notation are generalised and used more extensively in § 3.
$W(g) := \Bbbk [t,t^{-1}] g \partial \subseteq W$. Both sets of notation are generalised and used more extensively in § 3.
We first compute the isotropy subalgebra of ![]() $\chi$.
$\chi$.
Lemma 2.2.1 We have
 \[ W^\chi = \begin{cases} W((t-x)^2) & \gamma = 0 ,\\ \{ g \partial \,|\, g(x) = \alpha g'(x) + \gamma g''(x) = 0 \} & \gamma \neq 0. \end{cases} \]
\[ W^\chi = \begin{cases} W((t-x)^2) & \gamma = 0 ,\\ \{ g \partial \,|\, g(x) = \alpha g'(x) + \gamma g''(x) = 0 \} & \gamma \neq 0. \end{cases} \]
Proof. Recall that ![]() $\chi$ defines a bilinear form
$\chi$ defines a bilinear form ![]() $B_\chi$ on
$B_\chi$ on ![]() $W$ by
$W$ by ![]() $B_\chi (v, w) = \chi ([v, w])$, and that
$B_\chi (v, w) = \chi ([v, w])$, and that ![]() $W^\chi = \ker B_\chi$. For all
$W^\chi = \ker B_\chi$. For all ![]() $\chi$, that is, for all choices of
$\chi$, that is, for all choices of ![]() $x, \alpha, \gamma$, therefore,
$x, \alpha, \gamma$, therefore, ![]() $W^\chi \neq W$.
$W^\chi \neq W$.
First assume that ![]() $\gamma = 0$. If
$\gamma = 0$. If ![]() $g\partial \in W((t-x)^2)$, then
$g\partial \in W((t-x)^2)$, then
so ![]() $W((t-x)^2) \subseteq W^\chi$. However,
$W((t-x)^2) \subseteq W^\chi$. However, ![]() $B_\chi$ defines a nondegenerate bilinear form on
$B_\chi$ defines a nondegenerate bilinear form on ![]() $W/W^\chi$, so
$W/W^\chi$, so ![]() $\dim W/W^\chi \geqslant 2$ and, thus,
$\dim W/W^\chi \geqslant 2$ and, thus, ![]() $W((t-x)^2) = W^\chi$.
$W((t-x)^2) = W^\chi$.
Now suppose ![]() $\gamma \neq 0$. Let
$\gamma \neq 0$. Let
which is a codimension-two subspace of ![]() $\Bbbk [t,t^{-1}]$ and let
$\Bbbk [t,t^{-1}]$ and let ![]() $g \in V$,
$g \in V$, ![]() $f\in \Bbbk [t,t^{-1}]$. Then
$f\in \Bbbk [t,t^{-1}]$. Then
which is zero by assumption on ![]() $g$. Thus,
$g$. Thus, ![]() $W^\chi \supseteq V\partial$ and, as before, the two must be equal.
$W^\chi \supseteq V\partial$ and, as before, the two must be equal.
Note that in all cases ![]() $W^\chi \supseteq W((t-x)^3)$ and that if
$W^\chi \supseteq W((t-x)^3)$ and that if ![]() $\lambda \neq 0$, then
$\lambda \neq 0$, then ![]() $W^{\chi } = W^{\chi _{x; \lambda \alpha, \lambda \gamma }}$.
$W^{\chi } = W^{\chi _{x; \lambda \alpha, \lambda \gamma }}$.
We now compute ![]() $\operatorname {P}(\chi )$. Let
$\operatorname {P}(\chi )$. Let ![]() $B = \Bbbk [t,t^{-1}, y]$, and define a Poisson bracket on
$B = \Bbbk [t,t^{-1}, y]$, and define a Poisson bracket on ![]() $B$ induced from defining
$B$ induced from defining ![]() $\{y, t\} = 1$.
$\{y, t\} = 1$.
Define ![]() $p_\gamma : \operatorname {S}(W) \to B$ as the algebra homomorphism induced by defining
$p_\gamma : \operatorname {S}(W) \to B$ as the algebra homomorphism induced by defining
We verify
Thus, ![]() $p_\gamma$ respects Poisson brackets, so
$p_\gamma$ respects Poisson brackets, so ![]() $\ker p_\gamma$ is a Poisson ideal of
$\ker p_\gamma$ is a Poisson ideal of ![]() $\operatorname {S}(W)$.
$\operatorname {S}(W)$.
Lemma 2.2.3 The Poisson core of ![]() $\chi$ is equal to
$\chi$ is equal to ![]() $\ker p_\gamma$ and, in particular, depends only on
$\ker p_\gamma$ and, in particular, depends only on ![]() $\gamma$ as long as
$\gamma$ as long as ![]() $(\alpha, \gamma ) \neq (0,0)$.
$(\alpha, \gamma ) \neq (0,0)$.
Proof. First, ![]() $\chi (f\partial ) = p_\gamma (f \partial )|_{t=x,y=\alpha }$, and it follows immediately that if we extend
$\chi (f\partial ) = p_\gamma (f \partial )|_{t=x,y=\alpha }$, and it follows immediately that if we extend ![]() $\chi$ to a homomorphism
$\chi$ to a homomorphism ![]() $\operatorname {ev}_\chi : \operatorname {S}(W) \to \Bbbk$, it factors through
$\operatorname {ev}_\chi : \operatorname {S}(W) \to \Bbbk$, it factors through ![]() $p_\gamma$. As a result,
$p_\gamma$. As a result, ![]() $\operatorname {ev}_\chi (\ker p_\gamma ) = 0.$ As, in all cases,
$\operatorname {ev}_\chi (\ker p_\gamma ) = 0.$ As, in all cases, ![]() $W^\chi$ has codimension
$W^\chi$ has codimension ![]() $2 = \operatorname {GKdim}(B)$ by Lemma 2.2.1, the result is a direct consequence of Lemma 2.1.4.
$2 = \operatorname {GKdim}(B)$ by Lemma 2.2.1, the result is a direct consequence of Lemma 2.1.4.
Remark 2.2.4 Let ![]() $x, \alpha, \gamma \in \Bbbk$ with
$x, \alpha, \gamma \in \Bbbk$ with ![]() $\alpha, \gamma$ not both zero, and define
$\alpha, \gamma$ not both zero, and define ![]() $\nu \in W_{\geqslant -1}^*$ analogously to
$\nu \in W_{\geqslant -1}^*$ analogously to ![]() $\chi$: that is,
$\chi$: that is, ![]() $\nu (f\partial ) = \alpha f(x) + \gamma f'(x)$. One may similarly prove that
$\nu (f\partial ) = \alpha f(x) + \gamma f'(x)$. One may similarly prove that ![]() $\operatorname {P}(\nu ) = \operatorname {S}(W_{\geqslant -1}) \cap \ker p_\gamma$ and, in particular, that
$\operatorname {P}(\nu ) = \operatorname {S}(W_{\geqslant -1}) \cap \ker p_\gamma$ and, in particular, that
We show in Proposition 4.3.6 that this is true for all elements of ![]() $W^*$. Likewise,
$W^*$. Likewise, ![]() $\operatorname {P}(\chi |_{W_{\geqslant 1}}) = \operatorname {P}(\chi ) \cap \operatorname {S}(W_{\geqslant 1})$.
$\operatorname {P}(\chi |_{W_{\geqslant 1}}) = \operatorname {P}(\chi ) \cap \operatorname {S}(W_{\geqslant 1})$.
2.3 Pseudo-orbits versus orbits
We wish to relate the pseudo-orbits from § 2.1 to orbits of an algebraic group acting on an appropriate algebraic variety ![]() $X$. The next result gives us a general technique to do this.
$X$. The next result gives us a general technique to do this.
Proposition 2.3.1 Let ![]() $\mathfrak g$ be a Lie algebra with
$\mathfrak g$ be a Lie algebra with ![]() $\dim \mathfrak g < | \Bbbk |$. Let
$\dim \mathfrak g < | \Bbbk |$. Let ![]() $X$ be an irreducible affine algebraic variety acted on by a connected algebraic group
$X$ be an irreducible affine algebraic variety acted on by a connected algebraic group ![]() $H$ with Lie algebra
$H$ with Lie algebra ![]() $\mathfrak h$ and let
$\mathfrak h$ and let ![]() $U\subseteq X$ be an open affine subset. Fix a morphism of varieties
$U\subseteq X$ be an open affine subset. Fix a morphism of varieties ![]() $\phi : U \to \mathfrak g^*$. Assume that for every
$\phi : U \to \mathfrak g^*$. Assume that for every ![]() $x\in U$ we have
$x\in U$ we have ![]() $\mathfrak g_{\phi (x)}\subseteq \phi _x(\mathfrak h_x)$.
$\mathfrak g_{\phi (x)}\subseteq \phi _x(\mathfrak h_x)$.
(a) For all
 $x\in U$ the pseudo-orbit of
$x\in U$ the pseudo-orbit of  $\phi (x)$ is contained in
$\phi (x)$ is contained in  $\overline {\phi (Hx\cap U)}$, recalling that the topology on
$\overline {\phi (Hx\cap U)}$, recalling that the topology on  $\mathfrak g^*$ is the Zariski topology.
$\mathfrak g^*$ is the Zariski topology.(b) For
 $x\in U$, let
$x\in U$, let  $I^U(Hx)$ be the defining ideal in
$I^U(Hx)$ be the defining ideal in  $\Bbbk [U]$ of
$\Bbbk [U]$ of  $\overline {Hx} \cap U$. Let
$\overline {Hx} \cap U$. Let  $x\in U$ be such that
$x\in U$ be such that  $\dim \mathfrak g_{\phi (x)}=\dim \mathfrak h_x$. Then
$\dim \mathfrak g_{\phi (x)}=\dim \mathfrak h_x$. Then  $\operatorname {P}(\phi (x))$ is equal to the kernel of the induced homomorphism
(2.3.2)and
$\operatorname {P}(\phi (x))$ is equal to the kernel of the induced homomorphism
(2.3.2)and \begin{equation} \operatorname{S}(\mathfrak g) \to \Bbbk[U]/I^U(Hx) = \Bbbk[\overline{Hx} \cap U], \end{equation}(2.3.3)In particular, if
\begin{equation} \operatorname{S}(\mathfrak g) \to \Bbbk[U]/I^U(Hx) = \Bbbk[\overline{Hx} \cap U], \end{equation}(2.3.3)In particular, if \begin{equation} \dim \mathbb{O}(\phi(x)) = \operatorname{GKdim} \operatorname{S}(\mathfrak g)/\operatorname{P}(\phi(x)) = \dim \mathfrak g_{\phi(x)}. \end{equation}
\begin{equation} \dim \mathbb{O}(\phi(x)) = \operatorname{GKdim} \operatorname{S}(\mathfrak g)/\operatorname{P}(\phi(x)) = \dim \mathfrak g_{\phi(x)}. \end{equation} $y \in U$ is such that
$y \in U$ is such that  $Hx = Hy$ and
$Hx = Hy$ and  $\dim \mathfrak g_{\phi (y)}=\dim \mathfrak h_y$, then
$\dim \mathfrak g_{\phi (y)}=\dim \mathfrak h_y$, then  $\operatorname {P}(\phi (x))=\operatorname {P}(\phi (y))$.
$\operatorname {P}(\phi (x))=\operatorname {P}(\phi (y))$.(c) Let
 $x, y\in U$ be such that
$x, y\in U$ be such that  $\dim \mathfrak g_{\phi (x)}=\dim \mathfrak h_x$ and
$\dim \mathfrak g_{\phi (x)}=\dim \mathfrak h_x$ and  $\dim \mathfrak g_{\phi (y)}=\dim \mathfrak h_y$. Then
$\dim \mathfrak g_{\phi (y)}=\dim \mathfrak h_y$. Then  $\operatorname {P}(\phi (x))=\operatorname {P}(\phi (y))$ if and only if there are open subsets
$\operatorname {P}(\phi (x))=\operatorname {P}(\phi (y))$ if and only if there are open subsets  $U_x\subseteq Hx\cap U$ and
$U_x\subseteq Hx\cap U$ and  $U_y\subseteq Hy\cap U$ such that
$U_y\subseteq Hy\cap U$ such that  $\phi (U_x)=\phi (U_y)$.
$\phi (U_x)=\phi (U_y)$.
Proof. (a) The kernel of (2.3.2) is Poisson by Proposition 2.1.7 and is contained in ![]() $\mathfrak {m}_{\phi (x)}$ by definition. Thus, it is contained in
$\mathfrak {m}_{\phi (x)}$ by definition. Thus, it is contained in ![]() $\operatorname {P}(\phi (x))$, which is what we need. Note also that this statement is completely trivial if
$\operatorname {P}(\phi (x))$, which is what we need. Note also that this statement is completely trivial if ![]() $\mathfrak g$ is the Lie algebra of a finite-dimensional algebraic group.
$\mathfrak g$ is the Lie algebra of a finite-dimensional algebraic group.
(b) Let ![]() $K$ be the kernel of (2.3.2). Then
$K$ be the kernel of (2.3.2). Then ![]() $K$ is Poisson by part (a). We have
$K$ is Poisson by part (a). We have
so ![]() $K = \operatorname {P}(\phi (x))$ by Lemma 2.1.4. Certainly
$K = \operatorname {P}(\phi (x))$ by Lemma 2.1.4. Certainly
and the two are equal by Lemma 2.1.4. The final statement follows from Corollary 2.1.6.
(c) For any dense subset ![]() $U_x \subseteq Hx \cap U$, by part (b)
$U_x \subseteq Hx \cap U$, by part (b) ![]() $\operatorname {P}(\phi (x))$ is equal to the kernel of the induced map
$\operatorname {P}(\phi (x))$ is equal to the kernel of the induced map ![]() $\operatorname {S}(\mathfrak g) \to \Bbbk [U_x]$. This is determined by
$\operatorname {S}(\mathfrak g) \to \Bbbk [U_x]$. This is determined by ![]() $\phi (U_x)$, so if
$\phi (U_x)$, so if ![]() $\phi (U_x) = \phi (U_y)$, then
$\phi (U_x) = \phi (U_y)$, then ![]() $\operatorname {P}(\phi (x)) = \operatorname {P}(\phi (y))$.
$\operatorname {P}(\phi (x)) = \operatorname {P}(\phi (y))$.
Suppose now that ![]() $\operatorname {P}(\phi (x)) = \operatorname {P}(\phi (y))$. Consider the induced maps
$\operatorname {P}(\phi (x)) = \operatorname {P}(\phi (y))$. Consider the induced maps ![]() $Hx\to \mathfrak g^*, Hy\to \mathfrak g^*$ and the respective fibre product
$Hx\to \mathfrak g^*, Hy\to \mathfrak g^*$ and the respective fibre product ![]() $(Hx)\times _{\mathfrak g^*}(Hy)$. Note that
$(Hx)\times _{\mathfrak g^*}(Hy)$. Note that ![]() $(Hx)\times _{\mathfrak g^*}(Hy)$ is a closed subset of
$(Hx)\times _{\mathfrak g^*}(Hy)$ is a closed subset of ![]() $(Hx)\times (Hy)$ and, hence, the ideal defining
$(Hx)\times (Hy)$ and, hence, the ideal defining ![]() $(Hx)\times _{\mathfrak g^*}(Hy)$ is generated by a finite collection of elements. This implies that there is a finite-dimensional subspace
$(Hx)\times _{\mathfrak g^*}(Hy)$ is generated by a finite collection of elements. This implies that there is a finite-dimensional subspace ![]() $V\subset \mathfrak g$ such that
$V\subset \mathfrak g$ such that
As ![]() $\operatorname {P}(\phi (x)) =\operatorname {P}(\phi (y))$, the images of
$\operatorname {P}(\phi (x)) =\operatorname {P}(\phi (y))$, the images of ![]() $Hx$ and
$Hx$ and ![]() $Hy$ in
$Hy$ in ![]() $V^*$ have the same closure in
$V^*$ have the same closure in ![]() $V^*$; call it
$V^*$; call it ![]() $Z$. The image of
$Z$. The image of ![]() $Hx$ in
$Hx$ in ![]() $V^*$ may not be open in
$V^*$ may not be open in ![]() $Z$, but it is constructible and, thus, contains an open subset
$Z$, but it is constructible and, thus, contains an open subset ![]() $U(x)$ of
$U(x)$ of ![]() $Z$. Likewise the image of
$Z$. Likewise the image of ![]() $Hy$ in
$Hy$ in ![]() $V^*$ contains an open subset
$V^*$ contains an open subset ![]() $U(y)$ of
$U(y)$ of ![]() $Z$. We pick
$Z$. We pick ![]() $U_x$ to be the preimage of
$U_x$ to be the preimage of ![]() $U(x) \cap U(y)$ in
$U(x) \cap U(y)$ in ![]() $Hx$ and let
$Hx$ and let ![]() $U_y$ be the preimage of
$U_y$ be the preimage of ![]() $U(x) \cap U(y)$ in
$U(x) \cap U(y)$ in ![]() $Hy$; then they satisfy the desired property.
$Hy$; then they satisfy the desired property.
3. Primitive ideals and local functions
We now specialise to let ![]() $\mathfrak g$ be one of
$\mathfrak g$ be one of ![]() $W$,
$W$, ![]() $W_{\geqslant 1}$,
$W_{\geqslant 1}$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $V\!ir$. The main goal of this section is to determine which functions
$V\!ir$. The main goal of this section is to determine which functions ![]() $\chi \in \mathfrak g^*$ have nontrivial Poisson core
$\chi \in \mathfrak g^*$ have nontrivial Poisson core ![]() $\operatorname {P}(\chi )$. We show that these
$\operatorname {P}(\chi )$. We show that these ![]() $\chi$ are precisely those
$\chi$ are precisely those ![]() $\chi$ which measure the local behaviour of
$\chi$ which measure the local behaviour of ![]() $f\partial \in \mathfrak g$ at a finite collection of points; we call these functions local. (For example, the functions
$f\partial \in \mathfrak g$ at a finite collection of points; we call these functions local. (For example, the functions ![]() $\chi \in W^*$ of § 2.2 are local.) We provide several equivalent characterisations of local functions and apply these to classify subalgebras of
$\chi \in W^*$ of § 2.2 are local.) We provide several equivalent characterisations of local functions and apply these to classify subalgebras of ![]() $\mathfrak g$ of finite codimension. As a consequence, we show that
$\mathfrak g$ of finite codimension. As a consequence, we show that ![]() $\operatorname {S}(V\!ir)/(z-\zeta )$ is Poisson simple for
$\operatorname {S}(V\!ir)/(z-\zeta )$ is Poisson simple for ![]() $\zeta \neq 0$.
$\zeta \neq 0$.
More formally, consider ![]() $\mathfrak g = W_{\geqslant -1}$. Let
$\mathfrak g = W_{\geqslant -1}$. Let ![]() $x, \alpha _0, \ldots,\alpha _n \in \Bbbk$ with
$x, \alpha _0, \ldots,\alpha _n \in \Bbbk$ with ![]() $(\alpha _0, \ldots, \alpha _n) \neq \vec {\hspace {2pt}0}$. Define a linear function
$(\alpha _0, \ldots, \alpha _n) \neq \vec {\hspace {2pt}0}$. Define a linear function ![]() $\chi _{x; \alpha _0, \ldots, \alpha _n} \in W_{\geqslant -1}^*$ by
$\chi _{x; \alpha _0, \ldots, \alpha _n} \in W_{\geqslant -1}^*$ by
The same formula defines elements of ![]() $W_{\geqslant 1}^*$ and
$W_{\geqslant 1}^*$ and ![]() $W^*$, although in the last case we need to require that
$W^*$, although in the last case we need to require that ![]() $x\ne 0$.
$x\ne 0$.
We now formally define local functions.
Definition 3.0.2
(a) A local function on
 $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or  $W_{\geqslant 1}$ is a sum of finitely many functions of the form (3.0.1) with (possibly) distinct
$W_{\geqslant 1}$ is a sum of finitely many functions of the form (3.0.1) with (possibly) distinct  $x$.
$x$.(b) A local function on
 $W$ is a sum of finitely many functions of the form (3.0.1) with (possibly) distinct
$W$ is a sum of finitely many functions of the form (3.0.1) with (possibly) distinct  $x\ne 0$.
$x\ne 0$.(c) A local function on
 $V\!ir$ is the pullback of a local function on
$V\!ir$ is the pullback of a local function on  $W\!$ via the canonical map
$W\!$ via the canonical map  $V\!ir \to W$.
$V\!ir \to W$.
A local function of the form (3.0.1) is called a one-point local function. Let ![]() $\chi = \chi _{x; \alpha _0,\ldots, \alpha _n}$ be a one-point local function. We say that
$\chi = \chi _{x; \alpha _0,\ldots, \alpha _n}$ be a one-point local function. We say that ![]() $\{x\}$ is the support of
$\{x\}$ is the support of ![]() $\chi$ and that
$\chi$ and that ![]() $x$ is the base point of
$x$ is the base point of ![]() $\chi$. If
$\chi$. If ![]() $\alpha _n \neq 0$, we say that
$\alpha _n \neq 0$, we say that ![]() $n$ is the order of
$n$ is the order of ![]() $\chi$.
$\chi$.
Let ![]() $\chi$ be an arbitrary local function. The support of
$\chi$ be an arbitrary local function. The support of ![]() $\chi$ is the union of the supports of the component one-point local functions. Further, the orders of the component one-point local functions give rise to a partition
$\chi$ is the union of the supports of the component one-point local functions. Further, the orders of the component one-point local functions give rise to a partition ![]() $\lambda (\chi )$. More explicitly, write
$\lambda (\chi )$. More explicitly, write ![]() $\chi = \chi _1 + \cdots + \chi _{r}$, where the
$\chi = \chi _1 + \cdots + \chi _{r}$, where the ![]() $\chi _i$ are one-point local functions based at distinct points. Let
$\chi _i$ are one-point local functions based at distinct points. Let ![]() $m_i$ be the order of
$m_i$ be the order of ![]() $\chi _i$. By reordering the
$\chi _i$. By reordering the ![]() $\chi _i$ if necessary, we may assume that
$\chi _i$ if necessary, we may assume that ![]() $m_1 \geqslant m_2 \geqslant \cdots \geqslant m_r$. The partition
$m_1 \geqslant m_2 \geqslant \cdots \geqslant m_r$. The partition
is called the order partition of ![]() $\chi$. (We add 1 here so that the partition
$\chi$. (We add 1 here so that the partition ![]() $(0)$ corresponds to the zero function.) We call
$(0)$ corresponds to the zero function.) We call ![]() $m_1$ the order of
$m_1$ the order of ![]() $\chi$.
$\chi$.
It follows from the Chinese remainder theorem that a local function is zero if and only if it is zero pointwise and, thus, any local function ![]() $\chi$ on
$\chi$ on ![]() $W$,
$W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $V\!ir$ has a unique presentation as a sum of nonzero one-point local functions with distinct base points. This also shows that the partition
$V\!ir$ has a unique presentation as a sum of nonzero one-point local functions with distinct base points. This also shows that the partition ![]() $\lambda (\chi )$ and the order of
$\lambda (\chi )$ and the order of ![]() $\chi$ are well-defined. For
$\chi$ are well-defined. For ![]() $W_{\geqslant 1}$ it is easy to see that
$W_{\geqslant 1}$ it is easy to see that ![]() $\chi _{0; 1}=\chi _{0;0, 1}=0$ and the presentation is unique under the assumption that the coefficients of
$\chi _{0; 1}=\chi _{0;0, 1}=0$ and the presentation is unique under the assumption that the coefficients of ![]() $f(0)$ and
$f(0)$ and ![]() $f'(0)$ are zero.
$f'(0)$ are zero.
Remark 3.0.3 Let ![]() $\mathfrak g$ be
$\mathfrak g$ be ![]() $V\!ir$,
$V\!ir$, ![]() $W$,
$W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$. Then
$W_{\geqslant 1}$. Then ![]() $\mathfrak g^*$ and the subspace of local functions are both uncountable-dimensional vector spaces; for local functions observe that any set of one-point local functions with distinct base points is linearly independent. On the other hand, clearly ‘most’ elements of
$\mathfrak g^*$ and the subspace of local functions are both uncountable-dimensional vector spaces; for local functions observe that any set of one-point local functions with distinct base points is linearly independent. On the other hand, clearly ‘most’ elements of ![]() $\mathfrak g^*$ are not local. In fact, we show in Remark 5.2.3 that local functions are parameterised by a countable union of algebraic varieties.
$\mathfrak g^*$ are not local. In fact, we show in Remark 5.2.3 that local functions are parameterised by a countable union of algebraic varieties.
For a specific example of a nonlocal function, let ![]() $\alpha _0, \alpha _1, \ldots \in \Bbbk$ be algebraically independent over
$\alpha _0, \alpha _1, \ldots \in \Bbbk$ be algebraically independent over ![]() $\mathbb {Q}$, and define
$\mathbb {Q}$, and define ![]() $\varkappa \in W_{\geqslant -1}^*$ by
$\varkappa \in W_{\geqslant -1}^*$ by ![]() $\varkappa (t^i\partial ) = \alpha _i$.
$\varkappa (t^i\partial ) = \alpha _i$.
As local functions are defined similarly for ![]() $W$,
$W$, ![]() $W_{\geqslant 1}$,
$W_{\geqslant 1}$, ![]() $W_{\geqslant -1}$ and
$W_{\geqslant -1}$ and ![]() $V\!ir$ we sometimes discuss all of them simultaneously. When we do so, we assume without comment whenever we talk about a one-point local function on
$V\!ir$ we sometimes discuss all of them simultaneously. When we do so, we assume without comment whenever we talk about a one-point local function on ![]() $W$ or
$W$ or ![]() $V\!ir$ that
$V\!ir$ that ![]() $x\ne 0$.
$x\ne 0$.
Pick ![]() $\chi \in W^*$ or
$\chi \in W^*$ or ![]() $W_{\geqslant 1}^*$ or
$W_{\geqslant 1}^*$ or ![]() $W_{\geqslant -1}^*$. In this section, we show that
$W_{\geqslant -1}^*$. In this section, we show that ![]() $\operatorname {P}(\chi )$ is nonzero if and only if
$\operatorname {P}(\chi )$ is nonzero if and only if ![]() $\chi$ is local and prove a similar statement for
$\chi$ is local and prove a similar statement for ![]() $V\!ir^*$. The starting point here is the following result, due in its strongest form to Iyudu and the second author.
$V\!ir^*$. The starting point here is the following result, due in its strongest form to Iyudu and the second author.
Theorem 3.0.4 Let ![]() $\mathfrak g$ be
$\mathfrak g$ be ![]() $W$,
$W$, ![]() $W_{\geqslant 1}$ or
$W_{\geqslant 1}$ or ![]() $W_{\geqslant -1}$ and let
$W_{\geqslant -1}$ and let ![]() $I$ be a nonzero Poisson ideal of
$I$ be a nonzero Poisson ideal of ![]() $\operatorname {S}(\mathfrak g)$. Then
$\operatorname {S}(\mathfrak g)$. Then
In particular, if ![]() $\chi \in \mathfrak g^*$ is such that
$\chi \in \mathfrak g^*$ is such that ![]() $(0) \neq \operatorname {P}(\chi )$, then
$(0) \neq \operatorname {P}(\chi )$, then ![]() $\operatorname {GKdim} (\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi ))<\infty$.
$\operatorname {GKdim} (\operatorname {S}(\mathfrak g)/\operatorname {P}(\chi ))<\infty$.
Further, if ![]() $\chi \in V\!ir^*$ is such that
$\chi \in V\!ir^*$ is such that ![]() $\operatorname {P}(\chi ) \neq (z - \chi (z))$, then
$\operatorname {P}(\chi ) \neq (z - \chi (z))$, then
Proof. See [Reference Petukhov and SierraPS20, Theorem 1.4] for ![]() $W_{\geqslant 1}$ and [Reference Iyudu and SierraIS20, Theorem 1.3] for all other
$W_{\geqslant 1}$ and [Reference Iyudu and SierraIS20, Theorem 1.3] for all other ![]() $\mathfrak g$.
$\mathfrak g$.
Theorem 3.0.4 has the following extremely useful consequence.
Corollary 3.0.5 Let ![]() $\mathfrak g$ be as before and let
$\mathfrak g$ be as before and let ![]() $\chi \in \mathfrak g^*$. If
$\chi \in \mathfrak g^*$. If ![]() $\mathfrak g = W$,
$\mathfrak g = W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$, assume that
$W_{\geqslant 1}$, assume that ![]() $\operatorname {P}(\chi ) \neq (0)$, and if
$\operatorname {P}(\chi ) \neq (0)$, and if ![]() $\mathfrak g = V\!ir$, assume that
$\mathfrak g = V\!ir$, assume that ![]() $\operatorname {P}(\chi ) \neq (z - \chi (z))$. Then
$\operatorname {P}(\chi ) \neq (z - \chi (z))$. Then ![]() $\dim \mathfrak g\cdot \chi <\infty$.
$\dim \mathfrak g\cdot \chi <\infty$.
We also recall the following result.
Proposition 3.0.6 [Reference León Sánchez and SierraLS08, Corollary 5.1] Let ![]() $\mathfrak g$ be
$\mathfrak g$ be ![]() $V\!ir$,
$V\!ir$, ![]() $W$,
$W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$. Then
$W_{\geqslant 1}$. Then ![]() $\operatorname {S}(\mathfrak g)$ satisfies the ascending chain condition on radical Poisson ideals and every Poisson ideal has finitely many minimal primes above it, each of which is Poisson.
$\operatorname {S}(\mathfrak g)$ satisfies the ascending chain condition on radical Poisson ideals and every Poisson ideal has finitely many minimal primes above it, each of which is Poisson.
It is not known for any of these Lie algebras whether ![]() $\operatorname {S}(\mathfrak g)$ satisfies the ascending chain condition on arbitrary Poisson ideals.
$\operatorname {S}(\mathfrak g)$ satisfies the ascending chain condition on arbitrary Poisson ideals.
Although we use similar notation for ![]() $W_{\geqslant -1}$,
$W_{\geqslant -1}$, ![]() $W_{\geqslant 1}$,
$W_{\geqslant 1}$, ![]() $W$ and
$W$ and ![]() $V\!ir$, the details are slightly different, so we analyse local functions in each of these cases separately.
$V\!ir$, the details are slightly different, so we analyse local functions in each of these cases separately.
3.1 Local functions on  $W_{\geqslant -1}$ and
$W_{\geqslant -1}$ and  $W_{\geqslant 1}$
$W_{\geqslant 1}$
In this subsection we set ![]() $\mathfrak g=W_{\geqslant -1}=\Bbbk [t]\partial$. It is useful to consider Lie subalgebras of
$\mathfrak g=W_{\geqslant -1}=\Bbbk [t]\partial$. It is useful to consider Lie subalgebras of ![]() $W_{\geqslant -1}$ of a particular form. For any
$W_{\geqslant -1}$ of a particular form. For any ![]() $f\in \Bbbk [x] \setminus \{0\}$ denote by
$f\in \Bbbk [x] \setminus \{0\}$ denote by ![]() $W_{\geqslant -1}(f)$ the space of vector fields of the form
$W_{\geqslant -1}(f)$ the space of vector fields of the form
In other words, ![]() $W_{\geqslant -1}(f) = f W_{\geqslant -1}$ under the obvious notation. It is clear that
$W_{\geqslant -1}(f) = f W_{\geqslant -1}$ under the obvious notation. It is clear that ![]() $W_{\geqslant -1}(f)$ is a Lie subalgebra of
$W_{\geqslant -1}(f)$ is a Lie subalgebra of ![]() $W_{\geqslant -1}=W_{\geqslant -1}(1)$.
$W_{\geqslant -1}=W_{\geqslant -1}(1)$.
We give five equivalent conditions for local functions. Similar conditions will hold for the other Lie algebras we consider, see Theorems 3.2.1 and 3.3.1.
Theorem 3.1.1 Let ![]() $f\in \Bbbk [t] \setminus \{0\}$ and
$f\in \Bbbk [t] \setminus \{0\}$ and ![]() $\chi \in W_{\geqslant -1}(f)^*$. Then the following conditions are equivalent:
$\chi \in W_{\geqslant -1}(f)^*$. Then the following conditions are equivalent:
(1)
 $\chi$ is the restriction of a local function on
$\chi$ is the restriction of a local function on  $W_{\geqslant -1}$;
$W_{\geqslant -1}$;(2)
 $\operatorname {P}(\chi )\ne (0)$;
$\operatorname {P}(\chi )\ne (0)$;(3)
 $\dim W_{\geqslant -1}(f)/W_{\geqslant -1}(f)^\chi =\dim W_{\geqslant -1}(f) \cdot \chi <\infty$;
$\dim W_{\geqslant -1}(f)/W_{\geqslant -1}(f)^\chi =\dim W_{\geqslant -1}(f) \cdot \chi <\infty$;(4) there exists
 $h\in \Bbbk [t]$ such that
$h\in \Bbbk [t]$ such that  $\chi |_{W_{\geqslant -1}(fh)}=0$;
$\chi |_{W_{\geqslant -1}(fh)}=0$;(5)
 $W_{\geqslant -1}(f)^\chi \ne (0)$.
$W_{\geqslant -1}(f)^\chi \ne (0)$.
Remark 3.1.2 Fix a basis ![]() $\{ ft^i\partial \,|\, i\geqslant -1 \}$ of
$\{ ft^i\partial \,|\, i\geqslant -1 \}$ of ![]() $W_{\geqslant -1}(f)$ and consider a local function
$W_{\geqslant -1}(f)$ and consider a local function ![]() $\chi \in W_{\geqslant -1}(f)^*$. Then
$\chi \in W_{\geqslant -1}(f)^*$. Then ![]() $\chi$ can be identified with a sequence
$\chi$ can be identified with a sequence
Condition ![]() $(3)$ can be restated as follows:
$(3)$ can be restated as follows:
for all ![]() $m\geqslant 0$, where
$m\geqslant 0$, where ![]() $h=a_nt^n+\cdots +a_0$. Therefore, local functions on
$h=a_nt^n+\cdots +a_0$. Therefore, local functions on ![]() $W_{\geqslant -1}(f)$ can be identified with sequences (3.1.3) obeying a linear recurrence relation. This shows, in particular, that the function
$W_{\geqslant -1}(f)$ can be identified with sequences (3.1.3) obeying a linear recurrence relation. This shows, in particular, that the function ![]() $\varkappa$ defined in Remark 3.0.3 is not local.
$\varkappa$ defined in Remark 3.0.3 is not local.
Part of the proof of Theorem 3.1.1 is a general technique that can allow us to show that Poisson cores of elements of ![]() $\mathfrak g^*$ are nontrivial for any Lie algebra
$\mathfrak g^*$ are nontrivial for any Lie algebra ![]() $\mathfrak g$.
$\mathfrak g$.
Lemma 3.1.4 Let ![]() $\mathfrak g$ be an arbitrary Lie algebra and let
$\mathfrak g$ be an arbitrary Lie algebra and let ![]() $n \in \mathbb {Z}_{\geqslant 0}$. There is a Poisson ideal
$n \in \mathbb {Z}_{\geqslant 0}$. There is a Poisson ideal ![]() $I(n)$ with the property that
$I(n)$ with the property that
for any ![]() $\chi \in \mathfrak g^*$.
$\chi \in \mathfrak g^*$.
Proof. Recall the determinant ![]() $D(u_1, \ldots, u_n; v_1, \ldots, v_n)$ from (2.1.2), and note that
$D(u_1, \ldots, u_n; v_1, \ldots, v_n)$ from (2.1.2), and note that ![]() $\dim \mathfrak g \cdot \chi \leqslant ~n-1$ if and only if for all
$\dim \mathfrak g \cdot \chi \leqslant ~n-1$ if and only if for all ![]() $u_1,\ldots, u_{n}, v_1, \ldots, v_{n}\in \mathfrak g$, (2.1.2) evaluated at
$u_1,\ldots, u_{n}, v_1, \ldots, v_{n}\in \mathfrak g$, (2.1.2) evaluated at ![]() $\chi$ is degenerate, i.e.
$\chi$ is degenerate, i.e.
Let ![]() $I(n)$ be the ideal generated by the
$I(n)$ be the ideal generated by the ![]() $D(u_1, u_2, \ldots, u_{n+1}; v_1, v_2, \ldots, v_{n+1})$ for all possible tuples
$D(u_1, u_2, \ldots, u_{n+1}; v_1, v_2, \ldots, v_{n+1})$ for all possible tuples
By the previous paragraph,
Let ![]() $w \in \mathfrak g$. It is easy to check that
$w \in \mathfrak g$. It is easy to check that
 \begin{align*} & \{D(u_1, u_2, \ldots; v_1, v_2, \ldots), w\}\\ &\quad =D([u_1, w], u_2, u_3, \ldots; v_1, v_2, \ldots)+D(u_1, [u_2, w], u_3, \ldots; v_1, v_2, \ldots)+\cdots\\ &\qquad + D(u_1, u_2, \ldots; [v_1, w], v_2, v_3, \ldots)+D(u_1, u_2, \ldots; v_1, [v_2, w], v_3, \ldots)+\cdots \in I(n). \end{align*}
\begin{align*} & \{D(u_1, u_2, \ldots; v_1, v_2, \ldots), w\}\\ &\quad =D([u_1, w], u_2, u_3, \ldots; v_1, v_2, \ldots)+D(u_1, [u_2, w], u_3, \ldots; v_1, v_2, \ldots)+\cdots\\ &\qquad + D(u_1, u_2, \ldots; [v_1, w], v_2, v_3, \ldots)+D(u_1, u_2, \ldots; v_1, [v_2, w], v_3, \ldots)+\cdots \in I(n). \end{align*}
It follows that ![]() $I(n)$ is Poisson.
$I(n)$ is Poisson.
Proof of Theorem 3.1.1 That ![]() $(0)$
$(0)$ ![]() $\iff$
$\iff$ ![]() $(3)$ is a straightforward application of the Chinese remainder theorem. It is clear that
$(3)$ is a straightforward application of the Chinese remainder theorem. It is clear that ![]() $(2)$
$(2)$ ![]() $\Rightarrow$
$\Rightarrow$ ![]() $(4)$; Corollary 3.0.5 gives that
$(4)$; Corollary 3.0.5 gives that ![]() $(1) \Rightarrow (2)$. We show that
$(1) \Rightarrow (2)$. We show that ![]() $(4)\Rightarrow (3) \Rightarrow (2) \Rightarrow (1)$. This will complete the proof.
$(4)\Rightarrow (3) \Rightarrow (2) \Rightarrow (1)$. This will complete the proof.
We first show that condition ![]() $(4)$ implies condition
$(4)$ implies condition ![]() $(3)$. Let
$(3)$. Let ![]() $hf\partial \in W_{\geqslant -1}(f)^\chi \setminus \{0\}$ with
$hf\partial \in W_{\geqslant -1}(f)^\chi \setminus \{0\}$ with ![]() $h\in \Bbbk [t]$. Then
$h\in \Bbbk [t]$. Then
for all ![]() $r\in \Bbbk [t]$. This is equivalent to
$r\in \Bbbk [t]$. This is equivalent to ![]() $\chi |_{W_{\geqslant -1}(h^2f^2)}=0$ as needed.
$\chi |_{W_{\geqslant -1}(h^2f^2)}=0$ as needed.
Next, we show that condition ![]() $(3)$ implies condition
$(3)$ implies condition ![]() $(2)$. Let
$(2)$. Let ![]() $h$ satisfy condition
$h$ satisfy condition ![]() $(3)$. As
$(3)$. As
we have ![]() $W_{\geqslant -1}(h^2f^2)\subseteq W_{\geqslant -1}(f)^\chi$ and, thus,
$W_{\geqslant -1}(h^2f^2)\subseteq W_{\geqslant -1}(f)^\chi$ and, thus, ![]() $\dim W(f)/W(f)^\chi < \infty$ as needed.
$\dim W(f)/W(f)^\chi < \infty$ as needed.
Finally we show that condition ![]() $(2)$ implies condition
$(2)$ implies condition ![]() $(1)$. Suppose that
$(1)$. Suppose that ![]() $\chi \in W_{\geqslant -1}(f)$ satisfies condition
$\chi \in W_{\geqslant -1}(f)$ satisfies condition ![]() $(2)$. Let
$(2)$. Let ![]() $n = \dim W_{\geqslant -1}(f)/W_{\geqslant -1}(f)^\chi = \dim W_{\geqslant -1}(f) \cdot \chi$ and let
$n = \dim W_{\geqslant -1}(f)/W_{\geqslant -1}(f)^\chi = \dim W_{\geqslant -1}(f) \cdot \chi$ and let ![]() $I(n)$ be the ideal defined in Lemma 3.1.4. By that lemma,
$I(n)$ be the ideal defined in Lemma 3.1.4. By that lemma, ![]() $I(n)$ is Poisson and
$I(n)$ is Poisson and ![]() $I(n) \subseteq \mathfrak m_\chi$, so
$I(n) \subseteq \mathfrak m_\chi$, so ![]() $I(n)\subseteq \operatorname {P}(\chi )$.
$I(n)\subseteq \operatorname {P}(\chi )$.
Therefore, if ![]() $I(n)\ne 0$, then
$I(n)\ne 0$, then ![]() $\operatorname {P}(\chi )\ne 0$. To show that
$\operatorname {P}(\chi )\ne 0$. To show that ![]() $I(n)\ne 0$ it suffices to find
$I(n)\ne 0$ it suffices to find ![]() $\omega \in W_{\geqslant -1}(f)^*$ with
$\omega \in W_{\geqslant -1}(f)^*$ with ![]() $\dim W_{\geqslant -1}(f) \cdot \omega >n$. In fact, we find
$\dim W_{\geqslant -1}(f) \cdot \omega >n$. In fact, we find ![]() $\omega \in W_{\geqslant -1}^*$ with
$\omega \in W_{\geqslant -1}^*$ with
Indeed, as ![]() $(2)$
$(2)$ ![]() $\Rightarrow$
$\Rightarrow$ ![]() $(3)$, if
$(3)$, if ![]() $\dim W_{\geqslant -1}(f)\cdot \omega < \infty$, then
$\dim W_{\geqslant -1}(f)\cdot \omega < \infty$, then ![]() $\omega$ can be represented by a linearly recurrent sequence by Remark 3.1.2. On the other hand, the sequence
$\omega$ can be represented by a linearly recurrent sequence by Remark 3.1.2. On the other hand, the sequence ![]() $1, \frac 12, \frac 13, \ldots$ is clearly not linearly recurrent.
$1, \frac 12, \frac 13, \ldots$ is clearly not linearly recurrent.
Remark 3.1.7 Similarly to Remarks 3.0.3 and 5.2.3, we should expect that ‘most’ sequences are not linearly recurrent and that the linearly recurrent sequences are parameterised by a countable union of affine varieties, although we do not formalise these notions here.
Note that ![]() $W_{\geqslant -1}(t^2)=W_{\geqslant 1}$ and that
$W_{\geqslant -1}(t^2)=W_{\geqslant 1}$ and that ![]() $W_{\geqslant -1}(t)$ is equal to the nonnegative Witt algebra
$W_{\geqslant -1}(t)$ is equal to the nonnegative Witt algebra ![]() $W_{\geqslant 0}$. Therefore, Theorem 3.1.1 gives a complete characterisation of local functions on
$W_{\geqslant 0}$. Therefore, Theorem 3.1.1 gives a complete characterisation of local functions on ![]() $W_{\geqslant 1}$ and
$W_{\geqslant 1}$ and ![]() $W_{\geqslant 0}$.
$W_{\geqslant 0}$.
3.2 Local functions on  $W$ and applications
$W$ and applications
In this subsection we set ![]() $\mathfrak g=\Bbbk [t, t^{-1}]\partial$ and define
$\mathfrak g=\Bbbk [t, t^{-1}]\partial$ and define ![]() $W(f)$ similarly to
$W(f)$ similarly to ![]() $W_{\geqslant 1}(f)$. A partial analogue of Theorem 3.1.1 holds for
$W_{\geqslant 1}(f)$. A partial analogue of Theorem 3.1.1 holds for ![]() $W$.
$W$.
Theorem 3.2.1 For any ![]() $f\in \Bbbk [t] \setminus \{0\}$ and
$f\in \Bbbk [t] \setminus \{0\}$ and ![]() $\chi \in W(f)^*$ the following conditions are equivalent:
$\chi \in W(f)^*$ the following conditions are equivalent:
(1)
 $\chi$ is the restriction of a local function on
$\chi$ is the restriction of a local function on  $W$;
$W$;(2)
 $\operatorname {P}(\chi )\ne (0)$;
$\operatorname {P}(\chi )\ne (0)$;(3)
 $\dim W(f)/W(f)^\chi <\infty$;
$\dim W(f)/W(f)^\chi <\infty$;(4) there exists
 $h\in \Bbbk [x]$ such that
$h\in \Bbbk [x]$ such that  $\chi |_{W(fh)}=0$.
$\chi |_{W(fh)}=0$.
Remark 3.2.2 The reason that Theorem 3.2.1 differs slightly from Theorem 3.1.1 is that the function ![]() $\operatorname {Res}_0(\cdot ) \in W^*$ satisfies condition (4) of Theorem 3.1.1 but does not satisfy the other conditions (0), (1), (2), and (3).
$\operatorname {Res}_0(\cdot ) \in W^*$ satisfies condition (4) of Theorem 3.1.1 but does not satisfy the other conditions (0), (1), (2), and (3).
Before proving Theorem 3.2.1 we give two lemmata on functions defined by residues. Denote by ![]() $\Bbbk ((t))$ the field of formal Laurent power series in
$\Bbbk ((t))$ the field of formal Laurent power series in ![]() $t$. Fix
$t$. Fix ![]() $f\in \Bbbk ((t))$ and consider the map
$f\in \Bbbk ((t))$ and consider the map
which defines a skew-symmetric bilinear form on ![]() $\Bbbk ((t))$.
$\Bbbk ((t))$.
Lemma 3.2.4 The kernel of ![]() $(a, b)_f$ is one-dimensional if
$(a, b)_f$ is one-dimensional if ![]() $f$ is a perfect square in
$f$ is a perfect square in ![]() $\Bbbk ((t))$ and is trivial otherwise. In the first case, the kernel is generated by
$\Bbbk ((t))$ and is trivial otherwise. In the first case, the kernel is generated by ![]() $1/{\sqrt {f}}$.
$1/{\sqrt {f}}$.
Proof. Let ![]() $a$ be in the kernel of
$a$ be in the kernel of ![]() $(\cdot, \cdot )_f$. Then
$(\cdot, \cdot )_f$. Then
for all ![]() $r \in \Bbbk ((t))$. This implies that
$r \in \Bbbk ((t))$. This implies that ![]() $fa^2$ is constant. Thus,
$fa^2$ is constant. Thus, ![]() $f$ is a perfect square in
$f$ is a perfect square in ![]() $\Bbbk ((t))$ and
$\Bbbk ((t))$ and ![]() $a$ is proportional to
$a$ is proportional to ![]() $1/{\sqrt {f}}$. Equation (3.2.5) also gives that if
$1/{\sqrt {f}}$. Equation (3.2.5) also gives that if ![]() $f$ is a perfect square, then
$f$ is a perfect square, then ![]() $1/{\sqrt f}$ belongs to the kernel of
$1/{\sqrt f}$ belongs to the kernel of ![]() $(\cdot, \cdot )_f$.
$(\cdot, \cdot )_f$.
The second lemma proves part of (a more general version of) Remark 3.2.2.
Lemma 3.2.6 Let ![]() $g \in \Bbbk [t,t^{-1}] \setminus \{0\}$ and define
$g \in \Bbbk [t,t^{-1}] \setminus \{0\}$ and define ![]() $\omega \in W(g^2)^*$ by
$\omega \in W(g^2)^*$ by
Then ![]() $\dim W(g^2)\cdot \omega = \infty$.
$\dim W(g^2)\cdot \omega = \infty$.
Proof. For ![]() $a,b \in \Bbbk [t, t^{-1}]$ we have
$a,b \in \Bbbk [t, t^{-1}]$ we have
Suppose that ![]() $a \not \in \Bbbk \cdot {1}/{g}$. Then by Lemma 3.2.4 there is a formal Laurent series
$a \not \in \Bbbk \cdot {1}/{g}$. Then by Lemma 3.2.4 there is a formal Laurent series ![]() $\hat {b}$ so that
$\hat {b}$ so that
However, the computation of ![]() $\operatorname {Res}_0(g^2(a \hat {b}'-a'\hat {b}))$ needs only finitely many terms in the Laurent expansion of
$\operatorname {Res}_0(g^2(a \hat {b}'-a'\hat {b}))$ needs only finitely many terms in the Laurent expansion of ![]() $\hat {b}$ and so we may replace
$\hat {b}$ and so we may replace ![]() $\hat {b}$ by
$\hat {b}$ by ![]() $b \in \Bbbk [t, t^{-1}]$ so that
$b \in \Bbbk [t, t^{-1}]$ so that ![]() $\operatorname {Res}_0(g^2(ab'-a'b)) \neq 0$. Thus
$\operatorname {Res}_0(g^2(ab'-a'b)) \neq 0$. Thus ![]() $a g^2\partial \not \in \ker B_\omega = W(g^2)^\omega$. This means that
$a g^2\partial \not \in \ker B_\omega = W(g^2)^\omega$. This means that ![]() $W(g^2)^\omega \subseteq \Bbbk \cdot g \partial$ and
$W(g^2)^\omega \subseteq \Bbbk \cdot g \partial$ and ![]() $\dim W(g^2)\cdot \omega = \infty$.
$\dim W(g^2)\cdot \omega = \infty$.
Proof of Theorem 3.2.1 The proofs of ![]() $(0)\iff (3)$,
$(0)\iff (3)$, ![]() $(1) \Rightarrow (2)$ and
$(1) \Rightarrow (2)$ and ![]() $(3)\Rightarrow (2)\Rightarrow (1)$ are very similar to the corresponding steps of the proof of Theorem 3.1.1. The only part which is significantly different is
$(3)\Rightarrow (2)\Rightarrow (1)$ are very similar to the corresponding steps of the proof of Theorem 3.1.1. The only part which is significantly different is ![]() $(2)\Rightarrow (3)$.
$(2)\Rightarrow (3)$.
Pick ![]() $\chi$ satisfying condition
$\chi$ satisfying condition ![]() $(2)$ and
$(2)$ and ![]() $h \in W(f)^\chi \setminus \{0\}$. Then (3.1.6) holds for all
$h \in W(f)^\chi \setminus \{0\}$. Then (3.1.6) holds for all ![]() $r\in \Bbbk [t, t^{-1}]$. Unfortunately, this is not enough to show that
$r\in \Bbbk [t, t^{-1}]$. Unfortunately, this is not enough to show that ![]() $\chi$ vanishes on
$\chi$ vanishes on ![]() $W(h^2f^2)$, as the map
$W(h^2f^2)$, as the map ![]() $r\mapsto r'$ is not surjective on
$r\mapsto r'$ is not surjective on ![]() $\Bbbk [t, t^{-1}]$.
$\Bbbk [t, t^{-1}]$.
Consider ![]() $\chi |_{W(f^2h^2)}$: we have
$\chi |_{W(f^2h^2)}$: we have
for all ![]() $p \in \Bbbk [t, t^{-1}]$. Suppose that
$p \in \Bbbk [t, t^{-1}]$. Suppose that ![]() $\chi ( {f^2h^2}{t}\partial ) \neq 0$. Then
$\chi ( {f^2h^2}{t}\partial ) \neq 0$. Then ![]() $\dim W(f^2h^2)\cdot \chi |_{W(f^2h^2)} = \infty$ by Lemma 3.2.6. Thus,
$\dim W(f^2h^2)\cdot \chi |_{W(f^2h^2)} = \infty$ by Lemma 3.2.6. Thus, ![]() $\dim W(h^2f^2) \cdot \chi = \infty$, as
$\dim W(h^2f^2) \cdot \chi = \infty$, as ![]() $\dim W(f)/W(f^2h^2) < \infty$. This contradicts our assumption that
$\dim W(f)/W(f^2h^2) < \infty$. This contradicts our assumption that ![]() $\chi$ satisfies condition
$\chi$ satisfies condition ![]() $(2)$ and so
$(2)$ and so ![]() $\chi ( ({f^2h^2}/{t})\partial ) = 0$, i.e.
$\chi ( ({f^2h^2}/{t})\partial ) = 0$, i.e. ![]() $\chi |_{W(f^2h^2)} = 0$.
$\chi |_{W(f^2h^2)} = 0$.
To end the subsection, we apply Theorem 3.2.1 to obtain a structure result on finite codimension subalgebras of ![]() $W$. For a polynomial
$W$. For a polynomial ![]() $f\in \Bbbk [t, t^{-1}]$ set
$f\in \Bbbk [t, t^{-1}]$ set
Proposition 3.2.7 Let ![]() $\mathfrak k$ be a subalgebra of
$\mathfrak k$ be a subalgebra of ![]() $W\!$ of finite codimension. Then:
$W\!$ of finite codimension. Then:
(a) there exists
 $f\in \Bbbk [t, t^{-1}]$ so that
$f\in \Bbbk [t, t^{-1}]$ so that  $W({\rm rad}(f)) \supseteq \mathfrak k \supseteq W(f)$;
$W({\rm rad}(f)) \supseteq \mathfrak k \supseteq W(f)$;(b) we can choose
 $f$ satisfying
$f$ satisfying  $\mathrm {(a)}$ so that
$\mathrm {(a)}$ so that  $f\in \Bbbk [t]$,
$f\in \Bbbk [t]$,  $f$ is monic and
$f$ is monic and  $f(0) \neq 0$;
$f(0) \neq 0$;(c) if we assume that
 $f$ is of minimal degree then such a choice of
$f$ is of minimal degree then such a choice of  $f$ is unique.
$f$ is unique.
Proof. The inclusion ![]() $\mathfrak k \subseteq W$ induces the dual map
$\mathfrak k \subseteq W$ induces the dual map ![]() $W^*\to \mathfrak k^*$. We identify
$W^*\to \mathfrak k^*$. We identify ![]() $(W/\mathfrak k)^*$ with the kernel of this map; that is, with elements of
$(W/\mathfrak k)^*$ with the kernel of this map; that is, with elements of ![]() $W^*$ which vanish on
$W^*$ which vanish on ![]() $\mathfrak k$, so
$\mathfrak k$, so ![]() $\mathfrak k$ is the set of common zeros of
$\mathfrak k$ is the set of common zeros of ![]() $(W/\mathfrak k)^* \subseteq W^*$. Let
$(W/\mathfrak k)^* \subseteq W^*$. Let ![]() $\chi _1, \ldots, \chi _s$ be a basis of
$\chi _1, \ldots, \chi _s$ be a basis of ![]() $(W/\mathfrak k)^*$. Fix
$(W/\mathfrak k)^*$. Fix ![]() $i\in \{1, \ldots, s\}$; by definition, we have
$i\in \{1, \ldots, s\}$; by definition, we have ![]() $B_{\chi _i}(\mathfrak k, \mathfrak k)=0$, so
$B_{\chi _i}(\mathfrak k, \mathfrak k)=0$, so ![]() $\mathfrak k$ is an isotropic subspace of
$\mathfrak k$ is an isotropic subspace of ![]() $W\!$ with respect to
$W\!$ with respect to ![]() $B_{\chi _i}$. Hence, the rank of
$B_{\chi _i}$. Hence, the rank of ![]() $B_{\chi _i}$ is at most
$B_{\chi _i}$ is at most ![]() $2\dim (W/\mathfrak k)$ and, thus, is finite. By Theorem 3.2.1,
$2\dim (W/\mathfrak k)$ and, thus, is finite. By Theorem 3.2.1, ![]() $\chi _i$ is local.
$\chi _i$ is local.
Theorem 3.2.1 implies that for all ![]() $i$ there is
$i$ there is ![]() $h_i\in \Bbbk [t, t^{-1}]\setminus \{0\}$ with
$h_i\in \Bbbk [t, t^{-1}]\setminus \{0\}$ with ![]() $\chi _i(W(h_i))=0$. Therefore
$\chi _i(W(h_i))=0$. Therefore ![]() $W(h_1\cdots h_s)$ is annihilated by all
$W(h_1\cdots h_s)$ is annihilated by all ![]() $\chi _i$ and therefore
$\chi _i$ and therefore ![]() $W(h_1\cdots h_s)\subseteq \mathfrak k$ as desired.
$W(h_1\cdots h_s)\subseteq \mathfrak k$ as desired.
Let ![]() $f \in \Bbbk [t,t^{-1}] \setminus \{0\}$ with
$f \in \Bbbk [t,t^{-1}] \setminus \{0\}$ with ![]() $\mathfrak k \supseteq W(f)$; we may assume without loss of generality that
$\mathfrak k \supseteq W(f)$; we may assume without loss of generality that ![]() $f \in \Bbbk [t]$,
$f \in \Bbbk [t]$, ![]() $f$ is monic and
$f$ is monic and ![]() $f(0) \neq 0$ as
$f(0) \neq 0$ as ![]() $W(f)$ corresponds to an ideal of
$W(f)$ corresponds to an ideal of ![]() $\Bbbk [t, t^{-1}]$. Suppose, in addition, that
$\Bbbk [t, t^{-1}]$. Suppose, in addition, that ![]() $f$ has minimal degree among all such polynomials with
$f$ has minimal degree among all such polynomials with ![]() $\mathfrak k \supseteq W(f)$. Thus, if
$\mathfrak k \supseteq W(f)$. Thus, if ![]() $\mathfrak k \supseteq W(h)$, then by the Euclidean algorithm
$\mathfrak k \supseteq W(h)$, then by the Euclidean algorithm ![]() $f | h$. This justifies uniqueness of
$f | h$. This justifies uniqueness of ![]() $f$.
$f$.
Write ![]() $f = \prod _{i=1}^n (t-x_i)^{a_i}$ with the
$f = \prod _{i=1}^n (t-x_i)^{a_i}$ with the ![]() $x_i\ne 0$ distinct and
$x_i\ne 0$ distinct and ![]() $a_i > 0$; set
$a_i > 0$; set ![]() $h:={\rm rad}(f)=(t-x_1)\cdots (t-x_n)$. It is clear that
$h:={\rm rad}(f)=(t-x_1)\cdots (t-x_n)$. It is clear that ![]() $h\mid f\mid h^{\max (a_i)}$. Let
$h\mid f\mid h^{\max (a_i)}$. Let ![]() $k\partial \in \mathfrak k$. We wish to show that
$k\partial \in \mathfrak k$. We wish to show that ![]() $h\,|\, k$. Indeed, for all
$h\,|\, k$. Indeed, for all ![]() $r \in \Bbbk [t,t^{-1}]$ the element
$r \in \Bbbk [t,t^{-1}]$ the element ![]() $[k\partial, fr\partial ] = (k(fr'+ f'r)-frk')\partial$ is in
$[k\partial, fr\partial ] = (k(fr'+ f'r)-frk')\partial$ is in ![]() $\mathfrak k$. As
$\mathfrak k$. As ![]() $\mathfrak k \supseteq W(f)$, thus
$\mathfrak k \supseteq W(f)$, thus ![]() $kf'r \in \mathfrak k$ for all
$kf'r \in \mathfrak k$ for all ![]() $r\in \Bbbk [t, t^{-1}]$. Thus,
$r\in \Bbbk [t, t^{-1}]$. Thus, ![]() $\mathfrak k \supseteq W(kf')$ and so
$\mathfrak k \supseteq W(kf')$ and so ![]() $f \,|\, f'k$. This forces
$f \,|\, f'k$. This forces ![]() $k$ to vanish at all roots of
$k$ to vanish at all roots of ![]() $f$, which is equivalent to
$f$, which is equivalent to ![]() $h \,|\, k$.
$h \,|\, k$.
3.3 Local functions on  $V\!ir$
$V\!ir$
In this subsection we set ![]() $\mathfrak g=V\!ir$.
$\mathfrak g=V\!ir$.
The natural map ![]() $V\!ir\to W$ extends to the morphism
$V\!ir\to W$ extends to the morphism ![]() $\operatorname {S}(V\!ir)\to \operatorname {S}(W)$; the kernel is the Poisson ideal
$\operatorname {S}(V\!ir)\to \operatorname {S}(W)$; the kernel is the Poisson ideal ![]() $(z)$ of
$(z)$ of ![]() $\operatorname {S}(V\!ir)$. The main goal of the subsection is to prove the following analogue of Theorem 3.2.1 for
$\operatorname {S}(V\!ir)$. The main goal of the subsection is to prove the following analogue of Theorem 3.2.1 for ![]() $V\!ir$.
$V\!ir$.
Theorem 3.3.1 For ![]() $\chi \in V\!ir^*$ we have
$\chi \in V\!ir^*$ we have
In particular, if ![]() $\operatorname {P}(\chi ) \neq (z-\chi (z))$, then
$\operatorname {P}(\chi ) \neq (z-\chi (z))$, then ![]() $\chi (z) = 0$.
$\chi (z) = 0$.
Remark 3.3.2 It follows from Theorems 3.2.1 and 3.3.1 that ![]() $\chi \in V\!ir^*$ is local if and only if there is some
$\chi \in V\!ir^*$ is local if and only if there is some ![]() $f \in \Bbbk [t, t^{-1}]$ such that
$f \in \Bbbk [t, t^{-1}]$ such that ![]() $\chi$ vanishes on
$\chi$ vanishes on ![]() $W(f) + \Bbbk \cdot z \subseteq V\!ir$.
$W(f) + \Bbbk \cdot z \subseteq V\!ir$.
Before proving Theorem 3.3.1, we consider arbitrary subalgebras of ![]() $V\!ir$ of finite codimension and show they are strongly constrained.
$V\!ir$ of finite codimension and show they are strongly constrained.
Proposition 3.3.3 If ![]() $\mathfrak k$ is a subalgebra of
$\mathfrak k$ is a subalgebra of ![]() $V\!ir$ of finite codimension, then
$V\!ir$ of finite codimension, then ![]() $z \in [\mathfrak k, \mathfrak k]$. Thus,
$z \in [\mathfrak k, \mathfrak k]$. Thus, ![]() $\dim V\!ir/\mathfrak k < \infty$ if and only if
$\dim V\!ir/\mathfrak k < \infty$ if and only if ![]() $\mathfrak k$ contains some
$\mathfrak k$ contains some ![]() $W(f) + \Bbbk \cdot z$, where
$W(f) + \Bbbk \cdot z$, where ![]() $f \in \Bbbk [t,t^{-1}] \setminus \{0\}$.
$f \in \Bbbk [t,t^{-1}] \setminus \{0\}$.
This result generalises [Reference Ondrus and WiesnerOW18, Proposition 2.3], which considered subalgebras of ![]() $V\!ir$ of codimension one. We also note that [Reference Ondrus and WiesnerOW18] refers to subalgebras of
$V\!ir$ of codimension one. We also note that [Reference Ondrus and WiesnerOW18] refers to subalgebras of ![]() $V\!ir$ of the form
$V\!ir$ of the form ![]() $W(f)+\Bbbk \cdot z$ as polynomial subalgebras.
$W(f)+\Bbbk \cdot z$ as polynomial subalgebras.
Proof of Proposition 3.3.3 Let ![]() $\bar {\mathfrak k}$ be the image of
$\bar {\mathfrak k}$ be the image of ![]() $\mathfrak k$ in
$\mathfrak k$ in ![]() $W$. By Proposition 3.2.7 there is some
$W$. By Proposition 3.2.7 there is some ![]() $f \in \Bbbk [t, t^{-1}] \setminus \{0\}$ so that
$f \in \Bbbk [t, t^{-1}] \setminus \{0\}$ so that ![]() $\bar {\mathfrak k} \supseteq W(f)$. Thus, for all
$\bar {\mathfrak k} \supseteq W(f)$. Thus, for all ![]() $p \in \mathbb {Z}$, there is
$p \in \mathbb {Z}$, there is ![]() $\zeta _p \in \Bbbk$ so that the element
$\zeta _p \in \Bbbk$ so that the element
is in ![]() $\mathfrak k$. Therefore,
$\mathfrak k$. Therefore, ![]() $[\mathfrak k, \mathfrak k]$ contains the elements
$[\mathfrak k, \mathfrak k]$ contains the elements
for all ![]() $p,q \in \mathbb {Z}$. Fix
$p,q \in \mathbb {Z}$. Fix ![]() $d=p+q$ and consider
$d=p+q$ and consider ![]() $p = d-q$ as a function of
$p = d-q$ as a function of ![]() $q$. The only part of (3.3.4) that varies with
$q$. The only part of (3.3.4) that varies with ![]() $q$ is
$q$ is ![]() $q(d-q) \operatorname {Res}_0(t^{d-3} f^2)$.
$q(d-q) \operatorname {Res}_0(t^{d-3} f^2)$.
If ![]() $\operatorname {Res}_0(t^{d-3} f^2)$ is not zero, then
$\operatorname {Res}_0(t^{d-3} f^2)$ is not zero, then
is a nonzero scalar multiple of ![]() $z$ for almost all
$z$ for almost all ![]() $q_1, q_2$. If
$q_1, q_2$. If ![]() $z\not \in [ \mathfrak k, \mathfrak k]$, we therefore have
$z\not \in [ \mathfrak k, \mathfrak k]$, we therefore have ![]() $\operatorname {Res}_0(t^d f^2)=0$ for all
$\operatorname {Res}_0(t^d f^2)=0$ for all ![]() $d\in \mathbb {Z}$. This implies that
$d\in \mathbb {Z}$. This implies that ![]() $f^2=0$, contradicting our assumption on
$f^2=0$, contradicting our assumption on ![]() $f$.
$f$.
The final sentence is an immediate consequence of Proposition 3.2.7.
Proof of Theorem 3.3.1 Let ![]() $\chi \in V\!ir^*$. If
$\chi \in V\!ir^*$. If ![]() $\chi$ is local, then by definition
$\chi$ is local, then by definition ![]() $\chi$ descends to a local function
$\chi$ descends to a local function ![]() $\overline {\chi }$ on
$\overline {\chi }$ on ![]() $V\!ir/(z) \cong W$. By Theorem 3.2.1,
$V\!ir/(z) \cong W$. By Theorem 3.2.1, ![]() $\operatorname {P}(\chi ) \supsetneqq (z)$ and
$\operatorname {P}(\chi ) \supsetneqq (z)$ and ![]() $\dim V\!ir/V\!ir^\chi = \dim W/W^{\overline \chi } < \infty$.
$\dim V\!ir/V\!ir^\chi = \dim W/W^{\overline \chi } < \infty$.
If ![]() $\dim V\!ir/V\!ir^\chi < \infty$, then by Proposition 3.3.3,
$\dim V\!ir/V\!ir^\chi < \infty$, then by Proposition 3.3.3, ![]() $z \in [V\!ir^\chi, V\!ir^\chi ]$ and so
$z \in [V\!ir^\chi, V\!ir^\chi ]$ and so ![]() $\chi (z) = 0$, as
$\chi (z) = 0$, as ![]() $\chi$ vanishes, by definition, on
$\chi$ vanishes, by definition, on ![]() $[V\!ir^\chi, V\!ir^\chi ]$. We may, thus, factor out
$[V\!ir^\chi, V\!ir^\chi ]$. We may, thus, factor out ![]() $z$ and apply Theorem 3.2.1 again to conclude that
$z$ and apply Theorem 3.2.1 again to conclude that ![]() $\chi$ is local.
$\chi$ is local.
Finally, suppose that ![]() $\operatorname {P}(\chi ) \neq (z-\chi (z))$. Then by Corollary 3.0.5
$\operatorname {P}(\chi ) \neq (z-\chi (z))$. Then by Corollary 3.0.5 ![]() $\dim V\!ir \cdot \chi = \dim V\!ir/V\!ir^\chi < \infty$.
$\dim V\!ir \cdot \chi = \dim V\!ir/V\!ir^\chi < \infty$.
As an immediate corollary of Theorem 3.3.1, we obtain a powerful result on Poisson ideals of ![]() $\operatorname {S}(V\!ir)$.
$\operatorname {S}(V\!ir)$.
Corollary 3.3.5 If ![]() $\zeta \in \Bbbk ^\times$, then
$\zeta \in \Bbbk ^\times$, then ![]() $\operatorname {S}(V\!ir)/(z-\zeta )$ is Poisson simple, i.e. contains no nontrivial Poisson ideals.
$\operatorname {S}(V\!ir)/(z-\zeta )$ is Poisson simple, i.e. contains no nontrivial Poisson ideals.
Proof. Let ![]() $\zeta \in \Bbbk$. If
$\zeta \in \Bbbk$. If ![]() $\operatorname {S}(V\!ir)/(z-\zeta )$ is not Poisson simple, then
$\operatorname {S}(V\!ir)/(z-\zeta )$ is not Poisson simple, then ![]() $(z-\zeta )$ is strictly contained in some proper Poisson ideal
$(z-\zeta )$ is strictly contained in some proper Poisson ideal ![]() $J$ of
$J$ of ![]() $\operatorname {S}(V\!ir)$. By the Nullstellensatz there is some
$\operatorname {S}(V\!ir)$. By the Nullstellensatz there is some ![]() $\chi \in V\!ir^*$ with
$\chi \in V\!ir^*$ with ![]() $J \subseteq \mathfrak {m}_\chi$; thus,
$J \subseteq \mathfrak {m}_\chi$; thus, ![]() $\chi (z) = \zeta$ as
$\chi (z) = \zeta$ as ![]() $z -\zeta \in \mathfrak m_\chi$. Further
$z -\zeta \in \mathfrak m_\chi$. Further ![]() $\operatorname {P}(\chi ) \supseteq J \supsetneqq (z-\zeta )$ and so by Theorem 3.3.1 we have
$\operatorname {P}(\chi ) \supseteq J \supsetneqq (z-\zeta )$ and so by Theorem 3.3.1 we have ![]() $\zeta = 0$.
$\zeta = 0$.
We thus show that almost all prime Poisson ideals of ![]() $\operatorname {S}(V\!ir)$ contain
$\operatorname {S}(V\!ir)$ contain ![]() $z$.
$z$.
Corollary 3.3.6 Let ![]() $Q$ be a prime Poisson ideal of
$Q$ be a prime Poisson ideal of ![]() $\operatorname {S}(V\!ir)$. Then either:
$\operatorname {S}(V\!ir)$. Then either:
(i)
 $Q = (0)$;
$Q = (0)$;(ii)
 $Q = (z-\zeta )$ for some
$Q = (z-\zeta )$ for some  $\zeta \in \Bbbk ^\times$;
$\zeta \in \Bbbk ^\times$;(iii)
 $Q \supseteq (z)$.
$Q \supseteq (z)$.
Proof. By Corollary 3.3.5 and primeness of ![]() $Q$, it suffices to prove that if
$Q$, it suffices to prove that if ![]() $Q \neq (0)$, then
$Q \neq (0)$, then ![]() $Q$ contains a nonzero element of
$Q$ contains a nonzero element of ![]() $\Bbbk [z]$. Let
$\Bbbk [z]$. Let ![]() $h \in Q \setminus \{0\}$; using primeness of
$h \in Q \setminus \{0\}$; using primeness of ![]() $Q$ we may assume that
$Q$ we may assume that ![]() $h$ is not a multiple of any element of
$h$ is not a multiple of any element of ![]() $\Bbbk [z] \setminus \Bbbk$. Let
$\Bbbk [z] \setminus \Bbbk$. Let ![]() $\chi \in V\!ir^*$ so that
$\chi \in V\!ir^*$ so that ![]() $Q \subseteq \mathfrak m_\chi$. As
$Q \subseteq \mathfrak m_\chi$. As ![]() $h \in \operatorname {P}(\chi )$, we see that
$h \in \operatorname {P}(\chi )$, we see that ![]() $\operatorname {P}(\chi ) \neq (z-\chi (z))$. By Theorem 3.3.1
$\operatorname {P}(\chi ) \neq (z-\chi (z))$. By Theorem 3.3.1 ![]() $\operatorname {P}(\chi ) \supseteq (z)$. Thus, applying Lemma 2.0.4(a),
$\operatorname {P}(\chi ) \supseteq (z)$. Thus, applying Lemma 2.0.4(a),
Given Corollary 3.3.5 it is natural to conjecture as follows.
Conjecture 3.3.7 If ![]() $\zeta \neq 0$, then
$\zeta \neq 0$, then ![]() $\operatorname {U}(V\!ir)/(z-\zeta )$ is simple.
$\operatorname {U}(V\!ir)/(z-\zeta )$ is simple.
However, we as yet have no proof of Conjecture 3.3.7. Note that the obvious strategy of proof by taking the associated graded of an ideal ![]() $(z-\zeta ) \subsetneqq J \triangleleft \operatorname {U}(V\!ir)$ does not work, because in this case
$(z-\zeta ) \subsetneqq J \triangleleft \operatorname {U}(V\!ir)$ does not work, because in this case ![]() $\operatorname {gr} J \ni z$ and Corollary 3.3.5 is not directly relevant.
$\operatorname {gr} J \ni z$ and Corollary 3.3.5 is not directly relevant.
4. Pseudo-orbits and Poisson primitive ideals for the algebras of interest
Let ![]() $\mathfrak g$ be one of
$\mathfrak g$ be one of ![]() $V\!ir$,
$V\!ir$, ![]() $W$,
$W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$. In this section, we describe the pseudo-orbits for
$W_{\geqslant 1}$. In this section, we describe the pseudo-orbits for ![]() $\mathfrak g$, using the results on local functions from the previous section and the general strategy of Proposition 2.3.1, and derive some consequences for the Poisson primitive spectrum of
$\mathfrak g$, using the results on local functions from the previous section and the general strategy of Proposition 2.3.1, and derive some consequences for the Poisson primitive spectrum of ![]() $\operatorname {S}(\mathfrak g)$.
$\operatorname {S}(\mathfrak g)$.
We begin by describing the pseudo-orbits of non-local functions, where the results of § 3 quickly give the answer.
Proposition 4.0.1 For ![]() $\mathfrak g = W$,
$\mathfrak g = W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$, the nonlocal functions in
$W_{\geqslant 1}$, the nonlocal functions in ![]() $\mathfrak g^*$ form a pseudo-orbit. If
$\mathfrak g^*$ form a pseudo-orbit. If ![]() $\mathfrak g = V\!ir$, then for any
$\mathfrak g = V\!ir$, then for any ![]() $\zeta \in \Bbbk$ the nonlocal functions
$\zeta \in \Bbbk$ the nonlocal functions ![]() $\chi$ with
$\chi$ with ![]() $\chi (z) = \zeta$ form a pseudo-orbit.
$\chi (z) = \zeta$ form a pseudo-orbit.
Proof. This is immediate from Theorems 3.1.1 (![]() $\mathfrak g = W_{\geqslant -1}$ or
$\mathfrak g = W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$), 3.2.1 (
$W_{\geqslant 1}$), 3.2.1 (![]() $\mathfrak g= W$) or 3.3.1 (
$\mathfrak g= W$) or 3.3.1 (![]() $\mathfrak g = V\!ir$). By those results, if
$\mathfrak g = V\!ir$). By those results, if ![]() $\mathfrak g = W$,
$\mathfrak g = W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$, then
$W_{\geqslant 1}$, then ![]() $\chi \in \mathfrak g^*$ is not local if and only if
$\chi \in \mathfrak g^*$ is not local if and only if ![]() $\operatorname {P}(\chi ) = 0$; and if
$\operatorname {P}(\chi ) = 0$; and if ![]() $\mathfrak g = V\!ir$, then
$\mathfrak g = V\!ir$, then ![]() $\chi$ is not local if and only if
$\chi$ is not local if and only if ![]() $\operatorname {P}(\chi ) = (z - \chi (z))$.
$\operatorname {P}(\chi ) = (z - \chi (z))$.
We may thus restrict to considering pseudo-orbits of local functions. By Proposition 4.0.1 if ![]() $\chi \in \mathfrak g^*$ is local and
$\chi \in \mathfrak g^*$ is local and ![]() $\omega \in \mathbb {O}(\chi )$, then
$\omega \in \mathbb {O}(\chi )$, then ![]() $\omega$ is also local. As, by definition, local functions on
$\omega$ is also local. As, by definition, local functions on ![]() $V\!ir$ vanish on
$V\!ir$ vanish on ![]() $z$, the pseudo-orbits for
$z$, the pseudo-orbits for ![]() $W$ directly determine those for
$W$ directly determine those for ![]() $V\!ir$.
$V\!ir$.
Thus, for the rest of the section we let ![]() $\mathfrak g$ be
$\mathfrak g$ be ![]() $W$,
$W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$. In § 4.1 we introduce a finite-dimensional action which determines the pseudo-orbits of one-point local functions on
$W_{\geqslant 1}$. In § 4.1 we introduce a finite-dimensional action which determines the pseudo-orbits of one-point local functions on ![]() $\mathfrak g$, in § 4.2 we describe the orbits of this action explicitly and in § 4.3 we use this action to describe pseudo-orbits of arbitrary local functions.
$\mathfrak g$, in § 4.2 we describe the orbits of this action explicitly and in § 4.3 we use this action to describe pseudo-orbits of arbitrary local functions.
4.1 An algebraic group acting on local functions
Set ![]() $\mathfrak g$ to be
$\mathfrak g$ to be ![]() $W$,
$W$, ![]() $W_{\geqslant -1}$, or
$W_{\geqslant -1}$, or ![]() $W_{\geqslant 1}$. We fix notation for the subsection.
$W_{\geqslant 1}$. We fix notation for the subsection.
Definition 4.1.1 For ![]() $x \in \Bbbk$,
$x \in \Bbbk$, ![]() $n \in \mathbb {Z}_{\geqslant 0}$, let
$n \in \mathbb {Z}_{\geqslant 0}$, let ![]() $\textit {Loc}_x^{\leqslant n}$ denote the subspace of
$\textit {Loc}_x^{\leqslant n}$ denote the subspace of ![]() $\mathfrak g^*$ consisting of one-point local functions based at
$\mathfrak g^*$ consisting of one-point local functions based at ![]() $x$ and of order
$x$ and of order ![]() $\leqslant n$. Let
$\leqslant n$. Let ![]() $\textit {Loc}_x:=\bigcup _{n\geqslant 0}\textit {Loc}_x^{\leqslant n}.$ Define
$\textit {Loc}_x:=\bigcup _{n\geqslant 0}\textit {Loc}_x^{\leqslant n}.$ Define ![]() $\textit {Loc}^{\leqslant n}_{\mathfrak g}=\bigcup _{x\in \Bbbk ^\times }\textit {Loc}_x^{\leqslant n}$ if
$\textit {Loc}^{\leqslant n}_{\mathfrak g}=\bigcup _{x\in \Bbbk ^\times }\textit {Loc}_x^{\leqslant n}$ if ![]() $\mathfrak g=W$, and
$\mathfrak g=W$, and ![]() $\textit {Loc}^{\leqslant n}_{\mathfrak g}=\bigcup _{x\in \Bbbk }\textit {Loc}_x^{\leqslant n}$ if
$\textit {Loc}^{\leqslant n}_{\mathfrak g}=\bigcup _{x\in \Bbbk }\textit {Loc}_x^{\leqslant n}$ if ![]() $\mathfrak g=W_{\geqslant -1}$ or
$\mathfrak g=W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$. Let
$W_{\geqslant 1}$. Let
 \[ \widetilde{\textit{Loc}}_{\mathfrak g}^{\leqslant n} =\begin{cases} \Bbbk^\times \times \Bbbk^{n+1} & \mathfrak g = W \\ \Bbbk \times \Bbbk^{n+1} & \mathfrak g= W_{\geqslant -1} \\ \Bbbk \times \Bbbk^{n+1} & \mathfrak g = W_{\geqslant 1}. \end{cases} \]
\[ \widetilde{\textit{Loc}}_{\mathfrak g}^{\leqslant n} =\begin{cases} \Bbbk^\times \times \Bbbk^{n+1} & \mathfrak g = W \\ \Bbbk \times \Bbbk^{n+1} & \mathfrak g= W_{\geqslant -1} \\ \Bbbk \times \Bbbk^{n+1} & \mathfrak g = W_{\geqslant 1}. \end{cases} \]
For all ![]() $\mathfrak g$ there is a canonical map
$\mathfrak g$ there is a canonical map ![]() $\pi _{\mathfrak g}^{\leqslant n}: \widetilde {\textit {Loc}}_{\mathfrak g}^{\leqslant n} \to \textit {Loc}_{\mathfrak g}^{\leqslant n}$ (this is, in fact, birational, cf. Proposition 5.1.1). If
$\pi _{\mathfrak g}^{\leqslant n}: \widetilde {\textit {Loc}}_{\mathfrak g}^{\leqslant n} \to \textit {Loc}_{\mathfrak g}^{\leqslant n}$ (this is, in fact, birational, cf. Proposition 5.1.1). If ![]() $\mathfrak g=W, W_{\geqslant -1}$, then
$\mathfrak g=W, W_{\geqslant -1}$, then ![]() $\pi _{\mathfrak g}^{\leqslant n}$ is an isomorphism away from
$\pi _{\mathfrak g}^{\leqslant n}$ is an isomorphism away from ![]() $\chi = 0$. If
$\chi = 0$. If ![]() $\mathfrak g=W_{\geqslant 1}$ it is an isomorphism away from
$\mathfrak g=W_{\geqslant 1}$ it is an isomorphism away from ![]() $\chi = 0$ and
$\chi = 0$ and ![]() $x=0$, due to the fact that
$x=0$, due to the fact that ![]() $\chi _{0; \beta _0, \beta _1}=0$ for all
$\chi _{0; \beta _0, \beta _1}=0$ for all ![]() $\beta _0, \beta _1\in \Bbbk$ in this case. Formally, we let
$\beta _0, \beta _1\in \Bbbk$ in this case. Formally, we let ![]() $\phi _{\mathfrak g }^{\leqslant n}: \widetilde {\textit {Loc}}_{\mathfrak g}^{\leqslant n} \to \mathfrak g^*$ be the composition of
$\phi _{\mathfrak g }^{\leqslant n}: \widetilde {\textit {Loc}}_{\mathfrak g}^{\leqslant n} \to \mathfrak g^*$ be the composition of ![]() $\pi _{\mathfrak g}^{\leqslant n}$ with the inclusion
$\pi _{\mathfrak g}^{\leqslant n}$ with the inclusion ![]() $\textit {Loc}_{\mathfrak g}^{\leqslant n} \subseteq \mathfrak g^*$. There is an induced pullback morphism
$\textit {Loc}_{\mathfrak g}^{\leqslant n} \subseteq \mathfrak g^*$. There is an induced pullback morphism ![]() $(\phi ^{\leqslant n}_{\mathfrak g})^*:\operatorname {S}(\mathfrak g)\to \Bbbk [\widetilde {\textit {Loc}}_{\mathfrak g}^{\leqslant n}]$.
$(\phi ^{\leqslant n}_{\mathfrak g})^*:\operatorname {S}(\mathfrak g)\to \Bbbk [\widetilde {\textit {Loc}}_{\mathfrak g}^{\leqslant n}]$.
If ![]() $\chi$ is a local function on
$\chi$ is a local function on ![]() $\mathfrak g$ and
$\mathfrak g$ and ![]() $v \in \mathfrak g$, then
$v \in \mathfrak g$, then ![]() $v\cdot \chi$ is local and, in fact, the coadjoint action of
$v\cdot \chi$ is local and, in fact, the coadjoint action of ![]() $\mathfrak g$ preserves
$\mathfrak g$ preserves ![]() $\textit {Loc}_x$ for all
$\textit {Loc}_x$ for all ![]() $x$. We now study the action of
$x$. We now study the action of ![]() $\mathfrak g$ on
$\mathfrak g$ on ![]() $\textit {Loc}_x$, and relate it to a finite-dimensional action using Proposition 2.3.1.
$\textit {Loc}_x$, and relate it to a finite-dimensional action using Proposition 2.3.1.
We begin by defining a group action. Fix ![]() $x\in \Bbbk$ (if
$x\in \Bbbk$ (if ![]() $\mathfrak g = W$ we assume that
$\mathfrak g = W$ we assume that ![]() $x \neq 0$). Let
$x \neq 0$). Let ![]() $\tilde t:= t-x$. Clearly, (3.0.1) makes sense for every formal power series
$\tilde t:= t-x$. Clearly, (3.0.1) makes sense for every formal power series ![]() $f\partial \in \Bbbk [[\tilde t]]\partial$, and so
$f\partial \in \Bbbk [[\tilde t]]\partial$, and so ![]() $\textit {Loc}_{x}^{\leqslant n}$ also gives elements of
$\textit {Loc}_{x}^{\leqslant n}$ also gives elements of ![]() $(\Bbbk [[\tilde t]]\partial )^*$. For every
$(\Bbbk [[\tilde t]]\partial )^*$. For every ![]() $s\in \Bbbk [[\tilde t]]$ with
$s\in \Bbbk [[\tilde t]]$ with ![]() $s(x)=x$ we introduce a local change of coordinates endomorphism
$s(x)=x$ we introduce a local change of coordinates endomorphism ![]() $\operatorname {End}_{t\to s}(\cdot )$ of
$\operatorname {End}_{t\to s}(\cdot )$ of ![]() $\Bbbk [[\tilde t]]$ through the formula
$\Bbbk [[\tilde t]]$ through the formula ![]() $t\to s$. Note that
$t\to s$. Note that ![]() $\operatorname {End}_{t \to s}$ is invertible if
$\operatorname {End}_{t \to s}$ is invertible if ![]() $s'(x)\ne 0$. Let
$s'(x)\ne 0$. Let ![]() $\textit {DLoc}_x$, the group of formal local diffeomorphisms at
$\textit {DLoc}_x$, the group of formal local diffeomorphisms at ![]() $x$, denote the group of all
$x$, denote the group of all ![]() $\operatorname {End}_{t \to s}$ with
$\operatorname {End}_{t \to s}$ with ![]() $s(x) = x$ and
$s(x) = x$ and ![]() $s'(x) \neq 0$. The group
$s'(x) \neq 0$. The group ![]() $\textit {DLoc}_x$ has a subgroup of transformations of the form
$\textit {DLoc}_x$ has a subgroup of transformations of the form ![]() $t \to \zeta t + (1-\zeta ) x$, for
$t \to \zeta t + (1-\zeta ) x$, for ![]() $\zeta \in \Bbbk ^\times$; we also write this transformation as
$\zeta \in \Bbbk ^\times$; we also write this transformation as ![]() $\tilde t\to \zeta \tilde t$ and let
$\tilde t\to \zeta \tilde t$ and let ![]() $\textit {Dil}_x$ denote the group of such transformations, which we term dilations at
$\textit {Dil}_x$ denote the group of such transformations, which we term dilations at ![]() $x$.
$x$.
Pick ![]() $s\in \Bbbk [[\tilde t]]$ with
$s\in \Bbbk [[\tilde t]]$ with ![]() $s(x)=x$ and
$s(x)=x$ and ![]() $s'(x) \neq 0$. We extend
$s'(x) \neq 0$. We extend ![]() $\operatorname {End}_{t\to s}$ to an automorphism of
$\operatorname {End}_{t\to s}$ to an automorphism of ![]() $\Bbbk [[\tilde t]]\partial$ via the formulae
$\Bbbk [[\tilde t]]\partial$ via the formulae
This gives actions of ![]() $\textit {DLoc}_x$ on
$\textit {DLoc}_x$ on ![]() $\Bbbk [[\tilde t]]\partial$ and on
$\Bbbk [[\tilde t]]\partial$ and on ![]() $(\Bbbk [[\tilde t]]\partial )^*$. We may consider
$(\Bbbk [[\tilde t]]\partial )^*$. We may consider ![]() $\textit {Loc}_x^{\leqslant n}$ as a subset of
$\textit {Loc}_x^{\leqslant n}$ as a subset of ![]() $(\Bbbk [[\tilde t]]\partial )^*$, and this subset is preserved by the
$(\Bbbk [[\tilde t]]\partial )^*$, and this subset is preserved by the ![]() $\textit {DLoc}_x$-action.
$\textit {DLoc}_x$-action.
Denote by ![]() $\textit {DLoc}_x^{\leqslant n}$ the image of
$\textit {DLoc}_x^{\leqslant n}$ the image of ![]() $\textit {DLoc}_x$ in the group
$\textit {DLoc}_x$ in the group ![]() $\operatorname {Aut}(\textit {Loc}_x^{\leqslant n})$ of linear automorphisms of
$\operatorname {Aut}(\textit {Loc}_x^{\leqslant n})$ of linear automorphisms of ![]() $\textit {Loc}_x^{\leqslant n}$. Although
$\textit {Loc}_x^{\leqslant n}$. Although ![]() $\textit {DLoc}_x$ is infinite-dimensional, its image in
$\textit {DLoc}_x$ is infinite-dimensional, its image in ![]() $\operatorname {Aut}(\textit {Loc}_x^{\leqslant n})$ is a finite-dimensional solvable algebraic group. Let us consider the action of the corresponding (finite-dimensional) Lie algebra, which we denote by
$\operatorname {Aut}(\textit {Loc}_x^{\leqslant n})$ is a finite-dimensional solvable algebraic group. Let us consider the action of the corresponding (finite-dimensional) Lie algebra, which we denote by ![]() $\operatorname {lie}_x^{\leqslant n}$.
$\operatorname {lie}_x^{\leqslant n}$.
Lemma 4.1.3 Identify ![]() $\operatorname {lie}_x^{\leqslant n}$ with the tangent space to
$\operatorname {lie}_x^{\leqslant n}$ with the tangent space to ![]() $\textit {DLoc}_x^{\leqslant n}$ at the identity. Let
$\textit {DLoc}_x^{\leqslant n}$ at the identity. Let ![]() $s \in \Bbbk [[t]]$ with
$s \in \Bbbk [[t]]$ with ![]() $s(x)=0$ and denote by
$s(x)=0$ and denote by ![]() $\xi _s$ the tangent direction at the identity defined by the line
$\xi _s$ the tangent direction at the identity defined by the line ![]() $h\to \operatorname {End}_{t\to t+hs}(\cdot )$ for
$h\to \operatorname {End}_{t\to t+hs}(\cdot )$ for ![]() $h\in \Bbbk$. The action of
$h\in \Bbbk$. The action of ![]() $\textit {DLoc}_x^{\leqslant n}$ derives to an action of
$\textit {DLoc}_x^{\leqslant n}$ derives to an action of ![]() $\xi _s$ on
$\xi _s$ on ![]() $\textit {Loc}_x^{\leqslant n}$. Then:
$\textit {Loc}_x^{\leqslant n}$. Then:
(a)
 $\operatorname {lie}_x^{\leqslant n}$ consists of vectors of the form
$\operatorname {lie}_x^{\leqslant n}$ consists of vectors of the form  $\xi _s$ with
$\xi _s$ with  $s(x)=0$;
$s(x)=0$;(b)
 $\xi _s\cdot \chi =s\partial \cdot \chi$ for all
$\xi _s\cdot \chi =s\partial \cdot \chi$ for all  $\chi \in \textit {Loc}_x$.
$\chi \in \textit {Loc}_x$.
Proof. Part (a) is clear from the definition of ![]() $\textit {DLoc}_x^{\leqslant n}$. For part (b), as the action of
$\textit {DLoc}_x^{\leqslant n}$. For part (b), as the action of ![]() $\xi _s$ on
$\xi _s$ on ![]() $\textit {Loc}_x$ is induced by the action (4.1.2) on
$\textit {Loc}_x$ is induced by the action (4.1.2) on ![]() $\Bbbk [[\tilde t]] \partial$, it is enough to check that
$\Bbbk [[\tilde t]] \partial$, it is enough to check that ![]() $\xi _s \cdot f \partial = [s \partial, f\partial ]$ for all
$\xi _s \cdot f \partial = [s \partial, f\partial ]$ for all ![]() $f \partial \in \mathfrak g$. However,
$f \partial \in \mathfrak g$. However,
 \begin{align*} \xi_s \cdot f\partial &= (\xi_s \cdot f) \partial + f (\xi_s \cdot \partial) \\ &= (\partial_h f(t+hs))|_{h = 0}\partial + f (\partial_h(\operatorname{End}_{t \to t+hs}\partial))|_{h=0} \\ &= (f'(t+hs) s)|_{h = 0} \partial + f \bigg(\partial_h\bigg(\frac{1}{1+hs'}\partial\bigg)\bigg)\bigg|_{h = 0} \\ &= f's \partial - f s'\partial = [s\partial, f \partial], \end{align*}
\begin{align*} \xi_s \cdot f\partial &= (\xi_s \cdot f) \partial + f (\xi_s \cdot \partial) \\ &= (\partial_h f(t+hs))|_{h = 0}\partial + f (\partial_h(\operatorname{End}_{t \to t+hs}\partial))|_{h=0} \\ &= (f'(t+hs) s)|_{h = 0} \partial + f \bigg(\partial_h\bigg(\frac{1}{1+hs'}\partial\bigg)\bigg)\bigg|_{h = 0} \\ &= f's \partial - f s'\partial = [s\partial, f \partial], \end{align*}
as needed.
We now let ![]() $\mathfrak g=W_{\geqslant -1}$. For all
$\mathfrak g=W_{\geqslant -1}$. For all ![]() $x, n$, the coadjoint action of
$x, n$, the coadjoint action of ![]() $W_{\geqslant -1}(t-x)$ preserves
$W_{\geqslant -1}(t-x)$ preserves ![]() $\textit {Loc}_x^{\leqslant n}$, and Lemma 4.1.3 shows that
$\textit {Loc}_x^{\leqslant n}$, and Lemma 4.1.3 shows that
for ![]() $\chi \in \textit {Loc}_x^{\leqslant n}$. For
$\chi \in \textit {Loc}_x^{\leqslant n}$. For ![]() $z \in \Bbbk$ define
$z \in \Bbbk$ define
The set ![]() $\{\textit {Shift}_z \,|\, z\in \Bbbk \}$ forms a one-dimensional algebraic group, which we denote by
$\{\textit {Shift}_z \,|\, z\in \Bbbk \}$ forms a one-dimensional algebraic group, which we denote by ![]() $\textit {Shifts}$; clearly
$\textit {Shifts}$; clearly ![]() $\textit {Shifts} \cong \Bbbk ^+$. Deriving the action of
$\textit {Shifts} \cong \Bbbk ^+$. Deriving the action of ![]() $\textit {Shifts}$ on
$\textit {Shifts}$ on ![]() $\textit {Loc}_{W_{\geqslant -1}}$ and on
$\textit {Loc}_{W_{\geqslant -1}}$ and on ![]() $\textit {Loc}_{W_{\geqslant -1}}^{\leqslant n}$, we have
$\textit {Loc}_{W_{\geqslant -1}}^{\leqslant n}$, we have
 \begin{align} &\partial_h \textit{Shift}_h(\chi_{x; \alpha_0, \ldots, \alpha_n}(f\partial))|_{h=0} \nonumber\\ &\quad = \partial_h(\alpha_0 f(x+h) + \alpha_1 f'(x+h) + \cdots + \alpha_n f^{(n)}(x+h)) |_{h=0} \nonumber\\ &\quad= \alpha_0 f'(x) + \cdots + \alpha_n f^{(n+1)}(x) = (\partial \cdot \chi_{x; \alpha_0, \ldots, \alpha_n})(f\partial) \end{align}
\begin{align} &\partial_h \textit{Shift}_h(\chi_{x; \alpha_0, \ldots, \alpha_n}(f\partial))|_{h=0} \nonumber\\ &\quad = \partial_h(\alpha_0 f(x+h) + \alpha_1 f'(x+h) + \cdots + \alpha_n f^{(n)}(x+h)) |_{h=0} \nonumber\\ &\quad= \alpha_0 f'(x) + \cdots + \alpha_n f^{(n+1)}(x) = (\partial \cdot \chi_{x; \alpha_0, \ldots, \alpha_n})(f\partial) \end{align}
and, thus, we may without ambiguity identify the Lie algebra of ![]() $\textit {Shifts}$ with
$\textit {Shifts}$ with ![]() $\Bbbk \cdot \partial$.
$\Bbbk \cdot \partial$.
For all ![]() $x, z\in \Bbbk$,
$x, z\in \Bbbk$, ![]() $\textit {Shift}_z$ gives a continuous homomorphism
$\textit {Shift}_z$ gives a continuous homomorphism ![]() $\Bbbk [[t-x]]\to \Bbbk [[t-x-z]]$ and, hence, induces an isomorphism
$\Bbbk [[t-x]]\to \Bbbk [[t-x-z]]$ and, hence, induces an isomorphism
In particular, we can take ![]() $x = 1$, and then for
$x = 1$, and then for ![]() $\mathfrak g = W_{\geqslant -1}$ and for all
$\mathfrak g = W_{\geqslant -1}$ and for all ![]() $n$ the action map
$n$ the action map ![]() $\textit {Shifts}\times \textit {Loc}^{\leqslant n}_1\to \textit {Loc}_{W_{\geqslant -1}}^{\leqslant n}$ is clearly bijective. This allows us to introduce the action of
$\textit {Shifts}\times \textit {Loc}^{\leqslant n}_1\to \textit {Loc}_{W_{\geqslant -1}}^{\leqslant n}$ is clearly bijective. This allows us to introduce the action of ![]() $\widehat {\textit {DLoc}}^{\leqslant n}:=\textit {Shifts} \times \textit {DLoc}_1^{\leqslant n}$ and
$\widehat {\textit {DLoc}}^{\leqslant n}:=\textit {Shifts} \times \textit {DLoc}_1^{\leqslant n}$ and ![]() $\widehat {\textit {DLoc}} := \textit {Shifts} \times \textit {DLoc}_1$ on
$\widehat {\textit {DLoc}} := \textit {Shifts} \times \textit {DLoc}_1$ on
componentwise. Note that ![]() $\widehat {\textit {DLoc}}$ and
$\widehat {\textit {DLoc}}$ and ![]() $\widehat {\textit {DLoc}}^{\leqslant n}$ also act on
$\widehat {\textit {DLoc}}^{\leqslant n}$ also act on ![]() $\widetilde {\textit {Loc}}_{W_{\geqslant -1}}^{\leqslant n}$ in such a way that
$\widetilde {\textit {Loc}}_{W_{\geqslant -1}}^{\leqslant n}$ in such a way that ![]() $\pi _{W_{\geqslant -1}}^{\leqslant n}$ is equivariant.
$\pi _{W_{\geqslant -1}}^{\leqslant n}$ is equivariant.
Let ![]() $\widehat {\operatorname {lie}}^{\leqslant n}$ denote the Lie algebra of
$\widehat {\operatorname {lie}}^{\leqslant n}$ denote the Lie algebra of ![]() $\widehat {\textit {DLoc}}^{\leqslant n}$. From Lemma 4.1.3 we have the following result.
$\widehat {\textit {DLoc}}^{\leqslant n}$. From Lemma 4.1.3 we have the following result.
Lemma 4.1.6 Let ![]() $\mathfrak g = W$,
$\mathfrak g = W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$ and fix
$W_{\geqslant 1}$ and fix ![]() $x$,
$x$, ![]() $n$ and
$n$ and ![]() $\chi \in \textit {Loc}_x^{\leqslant n}$ (recall that
$\chi \in \textit {Loc}_x^{\leqslant n}$ (recall that ![]() $x\ne 0$ if
$x\ne 0$ if ![]() $\mathfrak g=W$).
$\mathfrak g=W$).
(a) If
 $\mathfrak g=W_{\geqslant -1}$, then
$\mathfrak g=W_{\geqslant -1}$, then
 \[ \mathfrak g \cdot\chi=\operatorname{lie}_x^{\leqslant n}\cdot\chi + \Bbbk \partial_x\cdot\chi. \]
\[ \mathfrak g \cdot\chi=\operatorname{lie}_x^{\leqslant n}\cdot\chi + \Bbbk \partial_x\cdot\chi. \]
(b) If
 $\mathfrak g=W_{\geqslant -1}$, then
$\mathfrak g=W_{\geqslant -1}$, then  $\mathfrak g\cdot \chi =\widehat {\rm lie}^{\leqslant n}\cdot \chi$ for all
$\mathfrak g\cdot \chi =\widehat {\rm lie}^{\leqslant n}\cdot \chi$ for all  $\chi \in \textit {Loc}_{\mathfrak g}^{\leqslant n}$.
$\chi \in \textit {Loc}_{\mathfrak g}^{\leqslant n}$.(c) If
 $x\ne 0$, then we can identify
$x\ne 0$, then we can identify  $\textit {Loc}_x^{\leqslant n}$ for
$\textit {Loc}_x^{\leqslant n}$ for  $W$,
$W$,  $W_{\geqslant -1}$ and
$W_{\geqslant -1}$ and  $W_{\geqslant 1}$. If
$W_{\geqslant 1}$. If  $\mathfrak g = W$ or
$\mathfrak g = W$ or  $\mathfrak g = W_{\geqslant 1}$, under this identification we have
$\mathfrak g = W_{\geqslant 1}$, under this identification we have  $\mathfrak g\cdot \chi =W_{\geqslant -1}\cdot \chi$.
$\mathfrak g\cdot \chi =W_{\geqslant -1}\cdot \chi$.(d) If
 $\mathfrak g=W_{\geqslant 1}$ and
$\mathfrak g=W_{\geqslant 1}$ and  $x=0$, then
$x=0$, then  $\mathfrak g\cdot \chi =\operatorname {lie}_x^{\leqslant n}\cdot \chi$.
$\mathfrak g\cdot \chi =\operatorname {lie}_x^{\leqslant n}\cdot \chi$.
Proof. Parts (a), (b) and (d) are straightforward from the previous discussion. For part (c) note that the image of ![]() $f \partial$ in
$f \partial$ in ![]() $\textit {Loc}_x^{\leqslant n}$ depends only on the Taylor series expansion of
$\textit {Loc}_x^{\leqslant n}$ depends only on the Taylor series expansion of ![]() $f$ around
$f$ around ![]() $x$ up to degree
$x$ up to degree ![]() $n+1$, which is not affected by the behaviour of
$n+1$, which is not affected by the behaviour of ![]() $f$ at
$f$ at ![]() $0$.
$0$.
It is useful to have a more detailed description of ![]() $\textit {DLoc}_x$ and
$\textit {DLoc}_x$ and ![]() $\textit {DLoc}_x^{\leqslant n}$. The main point here is that
$\textit {DLoc}_x^{\leqslant n}$. The main point here is that ![]() $\textit {DLoc}_x^{\leqslant n}$ is a connected solvable algebraic group which has a filtration by normal subgroups with one-dimensional quotients.
$\textit {DLoc}_x^{\leqslant n}$ is a connected solvable algebraic group which has a filtration by normal subgroups with one-dimensional quotients.
Pick ![]() $k\geqslant 2$. Let
$k\geqslant 2$. Let ![]() $x \in \Bbbk$ (or
$x \in \Bbbk$ (or ![]() $x \in \Bbbk ^\times$ if
$x \in \Bbbk ^\times$ if ![]() $\mathfrak g = W$), and recall that
$\mathfrak g = W$), and recall that ![]() $\tilde t$ denotes
$\tilde t$ denotes ![]() $t-x$. Elements of the form
$t-x$. Elements of the form
constitute a subgroup of ![]() $\textit {DLoc}_x$ and we denote this subgroup by
$\textit {DLoc}_x$ and we denote this subgroup by ![]() $\textit {DLoc}_x^{k+}$. We use the notation
$\textit {DLoc}_x^{k+}$. We use the notation ![]() $\textit {DLoc}_x^{\leqslant n, k+}$ for the image of
$\textit {DLoc}_x^{\leqslant n, k+}$ for the image of ![]() $\textit {DLoc}_x^{k+}$ in
$\textit {DLoc}_x^{k+}$ in ![]() $\textit {DLoc}_x^{\leqslant n}$. The following lemma is straightforward.
$\textit {DLoc}_x^{\leqslant n}$. The following lemma is straightforward.
Lemma 4.1.7 Let ![]() $x\in \Bbbk$ and let
$x\in \Bbbk$ and let ![]() $\mathfrak g=W$,
$\mathfrak g=W$, ![]() $W_{\geqslant 1}$ or
$W_{\geqslant 1}$ or ![]() $W_{\geqslant -1}$ with
$W_{\geqslant -1}$ with ![]() $x\ne 0$ for
$x\ne 0$ for ![]() $\mathfrak g=W$.
$\mathfrak g=W$.
(a) The group
 $\textit {DLoc}_x^{2+, \leqslant n}$ is the unipotent radical of
$\textit {DLoc}_x^{2+, \leqslant n}$ is the unipotent radical of  $\textit {DLoc}_x^{\leqslant n}$ and
$\textit {DLoc}_x^{\leqslant n}$ and  $\textit {Dil}_x$ is a maximal reductive subgroup of
$\textit {Dil}_x$ is a maximal reductive subgroup of  $\textit {DLoc}_x^{\leqslant n}$. In particular, the natural map
is an isomorphism.
$\textit {DLoc}_x^{\leqslant n}$. In particular, the natural map
is an isomorphism. \[ \textit{Dil}_x\to \textit{DLoc}_x^{\leqslant n}/\textit{DLoc}_x^{2+, \leqslant n} \]
\[ \textit{Dil}_x\to \textit{DLoc}_x^{\leqslant n}/\textit{DLoc}_x^{2+, \leqslant n} \]
(b) The group
 $\textit {DLoc}_x^{k+, \leqslant n}/\textit {DLoc}_x^{k+1+, \leqslant n}$ is either isomorphic to
$\textit {DLoc}_x^{k+, \leqslant n}/\textit {DLoc}_x^{k+1+, \leqslant n}$ is either isomorphic to  $\Bbbk$ or
$\Bbbk$ or  $\{0\}$ if
$\{0\}$ if  $2\leqslant k\leqslant n$. Moreover, the natural map
induced by sending
$2\leqslant k\leqslant n$. Moreover, the natural map
induced by sending \[ \Bbbk \to \textit{DLoc}_x^{k+, \leqslant n}/\textit{DLoc}_x^{k+1+, \leqslant n} \]
\[ \Bbbk \to \textit{DLoc}_x^{k+, \leqslant n}/\textit{DLoc}_x^{k+1+, \leqslant n} \]
 $h \mapsto \operatorname {End}_{\tilde t\to \tilde t+ h\tilde t^n}(\cdot )$ is surjective.
$h \mapsto \operatorname {End}_{\tilde t\to \tilde t+ h\tilde t^n}(\cdot )$ is surjective.(c) The group
 $\textit {DLoc}_x^{k+, \leqslant n}$ is trivial for
$\textit {DLoc}_x^{k+, \leqslant n}$ is trivial for  $k\geqslant n$.
$k\geqslant n$.
4.2 Explicit description of  $\textit {DLoc}_x^{\leqslant n}$-orbits
$\textit {DLoc}_x^{\leqslant n}$-orbits
We now compute the ![]() $\textit {DLoc}_x$-orbits of one-point local functions; in the next subsection we see that this allows us to compute the pseudo-orbit of an arbitrary local function. If
$\textit {DLoc}_x$-orbits of one-point local functions; in the next subsection we see that this allows us to compute the pseudo-orbit of an arbitrary local function. If ![]() $\mathfrak g = W_{\geqslant -1}$, then the action of
$\mathfrak g = W_{\geqslant -1}$, then the action of ![]() $\textit {DLoc}_x$ is clearly homogeneous in
$\textit {DLoc}_x$ is clearly homogeneous in ![]() $x$ for all
$x$ for all ![]() $x\in \Bbbk$, and similarly for
$x\in \Bbbk$, and similarly for ![]() $W$ for
$W$ for ![]() $x \neq 0$. If
$x \neq 0$. If ![]() $x=0$ and
$x=0$ and ![]() $\mathfrak g=W_{\geqslant 1}$, the story is a bit more delicate.
$\mathfrak g=W_{\geqslant 1}$, the story is a bit more delicate.
Let ![]() $\mathfrak g$ be
$\mathfrak g$ be ![]() $W_{\geqslant -1}$,
$W_{\geqslant -1}$, ![]() $W$ or
$W$ or ![]() $W_{\geqslant 1}$ and let
$W_{\geqslant 1}$ and let ![]() $x \in \Bbbk$. If
$x \in \Bbbk$. If ![]() $\mathfrak g= W$ or
$\mathfrak g= W$ or ![]() $W_{\geqslant -1}$, we additionally assume that
$W_{\geqslant -1}$, we additionally assume that ![]() $x \neq 0$. For
$x \neq 0$. For ![]() $i \in \mathbb {Z}_{\geqslant 0}$ we set
$i \in \mathbb {Z}_{\geqslant 0}$ we set ![]() $e_i(x)=(t-x)^{i+1}\partial$ and define
$e_i(x)=(t-x)^{i+1}\partial$ and define ![]() $e_i(x)^*$ by the formula
$e_i(x)^*$ by the formula
so that ![]() $e_i(x)^*(e_j(x))=\delta _{ij}$. (We view the
$e_i(x)^*(e_j(x))=\delta _{ij}$. (We view the ![]() $e_i(x)^*$ as elements either of
$e_i(x)^*$ as elements either of ![]() $(\Bbbk [[t-x]]\partial )^*$ or
$(\Bbbk [[t-x]]\partial )^*$ or ![]() $\mathfrak g^*$, depending on context.) The main goal of this subsection is to prove the following theorem, and to consider its consequences.
$\mathfrak g^*$, depending on context.) The main goal of this subsection is to prove the following theorem, and to consider its consequences.
Theorem 4.2.1 Assume ![]() $\mathfrak g=W_{\geqslant -1}$,
$\mathfrak g=W_{\geqslant -1}$, ![]() $W$ or
$W$ or ![]() $W_{\geqslant 1}$ and let
$W_{\geqslant 1}$ and let ![]() $x \in \Bbbk$. If
$x \in \Bbbk$. If ![]() $\mathfrak g= W$ or
$\mathfrak g= W$ or ![]() $W_{\geqslant 1}$ we additionally assume that
$W_{\geqslant 1}$ we additionally assume that ![]() $x \neq 0$. Fix
$x \neq 0$. Fix ![]() $n, \beta _0, \ldots, \beta _n$ with
$n, \beta _0, \ldots, \beta _n$ with ![]() $\beta _n\ne 0$ and set
$\beta _n\ne 0$ and set ![]() $\chi =\chi _{x; \beta _0,\ldots, \beta _n}$. Let
$\chi =\chi _{x; \beta _0,\ldots, \beta _n}$. Let ![]() $e_i := e_i(x)$ and
$e_i := e_i(x)$ and ![]() $e_i^*:= e_i(x)^*$ for all
$e_i^*:= e_i(x)^*$ for all ![]() $i \in \mathbb {Z}_{\geqslant 0}$.
$i \in \mathbb {Z}_{\geqslant 0}$.
(a) If
 $n$ is even, then
$n$ is even, then  $\textit {DLoc}_x^{\leqslant n}\chi =\textit {DLoc}_x^{\leqslant n}e_{n-1}^*$ and
$\textit {DLoc}_x^{\leqslant n}\chi =\textit {DLoc}_x^{\leqslant n}e_{n-1}^*$ and  $\dim \textit {DLoc}_x^{\leqslant n}\chi =n+1$.
$\dim \textit {DLoc}_x^{\leqslant n}\chi =n+1$.(b) If
 $n$ is odd and
$n$ is odd and  $n>1$, then there is
$n>1$, then there is  $\beta$ such that
$\beta$ such that  $\textit {DLoc}_x^{\leqslant n}\chi =\textit {DLoc}_x^{\leqslant n} (e_{n-1}^*+\beta e_k^*)$ where
$\textit {DLoc}_x^{\leqslant n}\chi =\textit {DLoc}_x^{\leqslant n} (e_{n-1}^*+\beta e_k^*)$ where  $k= ({n-1})/2$. We have
$k= ({n-1})/2$. We have  $\dim \textit {DLoc}_x^{\leqslant n}\chi =n$.
$\dim \textit {DLoc}_x^{\leqslant n}\chi =n$.(b′) If
 $n=1$, then
$n=1$, then  $\textit {DLoc}_0^{\leqslant n}\chi =\textit {DLoc}_x^{\leqslant n} (\beta _1 e_0^*)$ and
$\textit {DLoc}_0^{\leqslant n}\chi =\textit {DLoc}_x^{\leqslant n} (\beta _1 e_0^*)$ and  $\dim \textit {DLoc}_x^{\leqslant n}\chi =1$.
$\dim \textit {DLoc}_x^{\leqslant n}\chi =1$.(c) Pick
 $\beta _1, \beta _2\in \Bbbk$ and
$\beta _1, \beta _2\in \Bbbk$ and  $k\in \mathbb {Z}_{\geqslant 1}$. Then
$k\in \mathbb {Z}_{\geqslant 1}$. Then  $\textit {DLoc}_x^{\leqslant n}(e_{2k}^*+\beta _1 e_k^*)= \textit {DLoc}_x^{\leqslant n}(e_{2k}^*+\beta _2 e_k^*)$ if and only if
$\textit {DLoc}_x^{\leqslant n}(e_{2k}^*+\beta _1 e_k^*)= \textit {DLoc}_x^{\leqslant n}(e_{2k}^*+\beta _2 e_k^*)$ if and only if  $\beta _1=\pm \beta _2$.
$\beta _1=\pm \beta _2$.(c′) Pick
 $\beta _1, \beta _2\in \Bbbk$. Then
$\beta _1, \beta _2\in \Bbbk$. Then  $\textit {DLoc}_x^{\leqslant 1}(\beta _1e_{0}^*)= \textit {DLoc}_x^{\leqslant 1}(\beta _2e_{0}^*)$ if and only if
$\textit {DLoc}_x^{\leqslant 1}(\beta _1e_{0}^*)= \textit {DLoc}_x^{\leqslant 1}(\beta _2e_{0}^*)$ if and only if  $\beta _1=\beta _2$.
$\beta _1=\beta _2$.
Proof. The proof is the same for any base point; to reduce notation we give the proof for ![]() $\mathfrak g= W_{\geqslant -1}$ and
$\mathfrak g= W_{\geqslant -1}$ and ![]() $x =0$.
$x =0$.
First we compute the dimensions of the corresponding orbits. Note that
see (4.1.4). Moreover, (4.1.5) implies that ![]() $W_{\geqslant -1}\cdot \chi \not \subseteq \textit {Loc}_0^{\leqslant n}$. Thus,
$W_{\geqslant -1}\cdot \chi \not \subseteq \textit {Loc}_0^{\leqslant n}$. Thus, ![]() $\dim W_{\geqslant -1}\cdot \chi =\dim W_{\geqslant 0}\cdot \chi +1$. Further
$\dim W_{\geqslant -1}\cdot \chi =\dim W_{\geqslant 0}\cdot \chi +1$. Further ![]() $\dim W_{\geqslant -1}\cdot \chi =\operatorname {rk} B_{\chi }$. The rank of this form can be evaluated explicitly. Indeed,
$\dim W_{\geqslant -1}\cdot \chi =\operatorname {rk} B_{\chi }$. The rank of this form can be evaluated explicitly. Indeed,
 \[ \chi_{0; \beta_0, \ldots, \beta_n}([e_i, e_j])= \begin{cases} 0 & {\rm if}\ i+j>n-1,\\ (j-i)(i+j+1)!\beta_{i+j+1} & {\rm if}\ i+j\leqslant n-1. \end{cases} \]
\[ \chi_{0; \beta_0, \ldots, \beta_n}([e_i, e_j])= \begin{cases} 0 & {\rm if}\ i+j>n-1,\\ (j-i)(i+j+1)!\beta_{i+j+1} & {\rm if}\ i+j\leqslant n-1. \end{cases} \]
From this formula it is clear that ![]() $B_\chi (e_i, e_j)=0$ if
$B_\chi (e_i, e_j)=0$ if ![]() $i\geqslant n+1$ or
$i\geqslant n+1$ or ![]() $j\geqslant n+1$. Thus, the rank of this form can be evaluated on the first
$j\geqslant n+1$. Thus, the rank of this form can be evaluated on the first ![]() $(n+2)\times (n+2)$ entries corresponding to
$(n+2)\times (n+2)$ entries corresponding to ![]() $-1\leqslant i$,
$-1\leqslant i$, ![]() $j\leqslant n$. This block is skew-upper-triangular. If
$j\leqslant n$. This block is skew-upper-triangular. If ![]() $n$ is even, then all values on the skew-diagonal line are nonzero (because
$n$ is even, then all values on the skew-diagonal line are nonzero (because ![]() $\beta _n\ne 0$); hence, the rank is
$\beta _n\ne 0$); hence, the rank is ![]() $n+2$ in this case. If
$n+2$ in this case. If ![]() $n$ is odd, then this skew-diagonal line contains zero only in the position corresponding to
$n$ is odd, then this skew-diagonal line contains zero only in the position corresponding to ![]() $i=j = ({n-1})/2$; hence the rank is
$i=j = ({n-1})/2$; hence the rank is ![]() $n+1$ in this case. This provides the desired dimensions.
$n+1$ in this case. This provides the desired dimensions.
The idea of the rest of the proof is to use the subnormal series in Lemma 4.1.7 to reduce the number of coefficients which we have to consider step by step.
Let ![]() $i \in \mathbb {Z}_{\geqslant 0}$. For
$i \in \mathbb {Z}_{\geqslant 0}$. For ![]() $j \geqslant 1$ we have
$j \geqslant 1$ we have
 \begin{align*} \operatorname{End}_{t \to t + \alpha t^{j+1}}(e_i) = \frac{(t + \alpha t^{j+1})^{i+1}}{1 + \alpha(j+1) t^j} \partial &=(t^{i+1} + \alpha(i-j) t^{i+j+1} + \mbox{higher}) \partial\\ &= e_i + \alpha(i-j) e_{i+j} + \mbox{higher}. \end{align*}
\begin{align*} \operatorname{End}_{t \to t + \alpha t^{j+1}}(e_i) = \frac{(t + \alpha t^{j+1})^{i+1}}{1 + \alpha(j+1) t^j} \partial &=(t^{i+1} + \alpha(i-j) t^{i+j+1} + \mbox{higher}) \partial\\ &= e_i + \alpha(i-j) e_{i+j} + \mbox{higher}. \end{align*}
Thus,
Likewise
We apply these transformations to
noting that the coefficient of ![]() $e_{n-1}^*$ in (4.2.4) is nonzero.
$e_{n-1}^*$ in (4.2.4) is nonzero.
By applying ![]() $\operatorname {End}_{t \to t+ \alpha _1 t^2}$ with appropriate
$\operatorname {End}_{t \to t+ \alpha _1 t^2}$ with appropriate ![]() $\alpha _1$ we may cancel the coefficient of
$\alpha _1$ we may cancel the coefficient of ![]() $e_{n-2}^*$, using (4.2.2). This does not affect the coefficient of
$e_{n-2}^*$, using (4.2.2). This does not affect the coefficient of ![]() $e_{n-1}^*$. Then by applying the appropriate
$e_{n-1}^*$. Then by applying the appropriate ![]() $\operatorname {End}_{t \to t+\alpha _2 t^3}$ we can cancel the coefficient of
$\operatorname {End}_{t \to t+\alpha _2 t^3}$ we can cancel the coefficient of ![]() $e_{n-3}^*$ without changing the coefficient of
$e_{n-3}^*$ without changing the coefficient of ![]() $e_{n-2}^*$ or
$e_{n-2}^*$ or ![]() $e_{n-1}^*$. Repeating, we may cancel the coefficients of all
$e_{n-1}^*$. Repeating, we may cancel the coefficients of all ![]() $e_{n-1-k}^*$ with
$e_{n-1-k}^*$ with ![]() $1 \leqslant k \leqslant n$, unless
$1 \leqslant k \leqslant n$, unless ![]() $k = ({n-1})/{2}$.
$k = ({n-1})/{2}$.
Thus, in cases (a) or (b![]() $'$) we obtain that
$'$) we obtain that ![]() $\omega = \beta _n e_{n-1}^* \in \textit {DLoc}_0^{\leqslant n}(\chi )$. In case (b) we obtain some
$\omega = \beta _n e_{n-1}^* \in \textit {DLoc}_0^{\leqslant n}(\chi )$. In case (b) we obtain some
Now applying (4.2.3) to ![]() $\omega$ we may rescale the coefficient of
$\omega$ we may rescale the coefficient of ![]() $e_{n-1}^*$ by any
$e_{n-1}^*$ by any ![]() $\zeta ^{n-1}$, so if
$\zeta ^{n-1}$, so if ![]() $n \neq 1$ we may set the coefficient of
$n \neq 1$ we may set the coefficient of ![]() $e_{n-1}^*$ to be
$e_{n-1}^*$ to be ![]() $1$. This proves the rest of the cases (a), (b) and (b
$1$. This proves the rest of the cases (a), (b) and (b![]() $'$).
$'$).
We now prove case (c![]() $'$). It follows from (4.2.2) that applying any nontrivial element of the unipotent radical of
$'$). It follows from (4.2.2) that applying any nontrivial element of the unipotent radical of ![]() $\textit {DLoc}_0^{\leqslant 1}$ to
$\textit {DLoc}_0^{\leqslant 1}$ to ![]() $e_0^*$ will give a nonzero
$e_0^*$ will give a nonzero ![]() $e_{-1}^*$ term. Thus, we must simply consider acting by
$e_{-1}^*$ term. Thus, we must simply consider acting by ![]() $\textit {Dil}_0$, and rescaling as in (4.2.3) does not affect the coefficient of
$\textit {Dil}_0$, and rescaling as in (4.2.3) does not affect the coefficient of ![]() $e_0^*$.
$e_0^*$.
Finally, we prove case (c). Formula (4.2.3) implies that if ![]() $\beta _1=\pm \beta _2$, then
$\beta _1=\pm \beta _2$, then
Pick ![]() $\beta _1, \beta _2\in \Bbbk$ and set
$\beta _1, \beta _2\in \Bbbk$ and set ![]() $\chi _1=e_{2k}^*+\beta _1e_{k}^*, \chi _2=e_{2k}^*+\beta _2e_{k}^*$. Assume that
$\chi _1=e_{2k}^*+\beta _1e_{k}^*, \chi _2=e_{2k}^*+\beta _2e_{k}^*$. Assume that ![]() $\textit {DLoc}_0^{\leqslant n}(\chi _1)=\textit {DLoc}_0^{\leqslant n}(\chi _2)$, so there exists
$\textit {DLoc}_0^{\leqslant n}(\chi _1)=\textit {DLoc}_0^{\leqslant n}(\chi _2)$, so there exists ![]() $s\in \Bbbk [[t]]$ with
$s\in \Bbbk [[t]]$ with ![]() $\operatorname {End}_{t\to s}(\chi _1)=\chi _2$,
$\operatorname {End}_{t\to s}(\chi _1)=\chi _2$, ![]() $s(0)=0$ and
$s(0)=0$ and ![]() $s'(0)\ne 0$.
$s'(0)\ne 0$.
If
then the statement of case (c) is straightforward. Assume to the contrary that ![]() $s\ne s'(0)t$. Then
$s\ne s'(0)t$. Then
for some ![]() $d$, and we choose
$d$, and we choose ![]() $d$ to be minimal.
$d$ to be minimal.
If ![]() $d\geqslant 2k+2$, then linear operators
$d\geqslant 2k+2$, then linear operators ![]() $\operatorname {End}_{t\to s}$ and
$\operatorname {End}_{t\to s}$ and ![]() $\operatorname {End}_{t\to s'(0)t}$ coincide after the restriction to
$\operatorname {End}_{t\to s'(0)t}$ coincide after the restriction to ![]() $\textit {Loc}_0^{\leqslant n}$, i.e. we can replace
$\textit {Loc}_0^{\leqslant n}$, i.e. we can replace ![]() $s$ by
$s$ by ![]() $s'(0)t$, which is case (4.2.5).
$s'(0)t$, which is case (4.2.5).
If ![]() $d\leqslant 2k+1$, then
$d\leqslant 2k+1$, then
with ![]() $s^{(d)}(0)\ne 0$; set
$s^{(d)}(0)\ne 0$; set ![]() $\gamma =s'(0)$,
$\gamma =s'(0)$, ![]() $\tau ={s^{(d)}(0)}/{d!}$. Further (4.2.2) and (4.2.3) imply
$\tau ={s^{(d)}(0)}/{d!}$. Further (4.2.2) and (4.2.3) imply
This cannot give ![]() $\chi _2$ unless
$\chi _2$ unless ![]() $d =k$.
$d =k$.
Thus, suppose ![]() $d=k$ and note that
$d=k$ and note that
for every ![]() $\alpha \in \Bbbk$. Thus, we can replace
$\alpha \in \Bbbk$. Thus, we can replace ![]() $s$ by
$s$ by
for an arbitrary ![]() $\alpha$. Pick
$\alpha$. Pick ![]() $\alpha =-{s^{(d+1)}(0)}/{(d+1)!(s'(0))^{d+1}}$. Then (4.2.6) is equal to
$\alpha =-{s^{(d+1)}(0)}/{(d+1)!(s'(0))^{d+1}}$. Then (4.2.6) is equal to ![]() $s'(0)t \mod t^{d+1}$ and we have reduced this case to the previous one.
$s'(0)t \mod t^{d+1}$ and we have reduced this case to the previous one.
Remark 4.2.7 If ![]() $\chi \in W^*$ is a one-point local function, the beginning of the proof of Theorem 4.2.1 provides an explicit description of
$\chi \in W^*$ is a one-point local function, the beginning of the proof of Theorem 4.2.1 provides an explicit description of ![]() $W^\chi$. Indeed, if
$W^\chi$. Indeed, if ![]() $\chi =\chi _{x; \beta _0, \beta _1, \ldots, \beta _n}$ with
$\chi =\chi _{x; \beta _0, \beta _1, \ldots, \beta _n}$ with ![]() $\beta _n\ne 0$, then
$\beta _n\ne 0$, then ![]() $W^\chi =W((t-x)^{n+1})$ if
$W^\chi =W((t-x)^{n+1})$ if ![]() $n$ is even, and
$n$ is even, and ![]() $W^\chi$ is the sum of
$W^\chi$ is the sum of ![]() $W((t-x)^{n+1})$ with a one-dimensional subspace if
$W((t-x)^{n+1})$ with a one-dimensional subspace if ![]() $n$ is odd.
$n$ is odd.
A modification of Theorem 4.2.1 holds for ![]() $\mathfrak g = W_{\geqslant 1}$ and
$\mathfrak g = W_{\geqslant 1}$ and ![]() $x=0$ with a very similar proof, which we leave to the reader.
$x=0$ with a very similar proof, which we leave to the reader.
Theorem 4.2.8 Assume ![]() $\mathfrak g=W_{\geqslant 1}$. Fix
$\mathfrak g=W_{\geqslant 1}$. Fix ![]() $n \geqslant 2$ and
$n \geqslant 2$ and ![]() $\beta _2, \ldots, \beta _n$ with
$\beta _2, \ldots, \beta _n$ with ![]() $\beta _n\ne 0$ and set
$\beta _n\ne 0$ and set ![]() $\chi =\chi _{0; 0, 0, \beta _2,\ldots, \beta _n}$.
$\chi =\chi _{0; 0, 0, \beta _2,\ldots, \beta _n}$.
(a) If
 $n$ is even, then
$n$ is even, then  $\textit {DLoc}_0^{\leqslant n}\chi =\textit {DLoc}_0^{\leqslant n}e_{n-1}^*$. We have
$\textit {DLoc}_0^{\leqslant n}\chi =\textit {DLoc}_0^{\leqslant n}e_{n-1}^*$. We have  $\dim \textit {DLoc}_0^{\leqslant n}\chi =n-1.$
$\dim \textit {DLoc}_0^{\leqslant n}\chi =n-1.$(b) If
 $n$ is odd and
$n$ is odd and  $n>1$, then there is
$n>1$, then there is  $\beta$ such that
$\beta$ such that  $\textit {DLoc}_0^{\leqslant n}\chi =\textit {DLoc}_0^{\leqslant n} (e_{n-1}^*+\beta e_k^*)$ where
$\textit {DLoc}_0^{\leqslant n}\chi =\textit {DLoc}_0^{\leqslant n} (e_{n-1}^*+\beta e_k^*)$ where  $k= ({n-1})/2$. We have
$k= ({n-1})/2$. We have  $\dim \textit {DLoc}_0^{\leqslant n} \chi =n-2$.
$\dim \textit {DLoc}_0^{\leqslant n} \chi =n-2$.(c) Pick
 $\beta _1, \beta _2\in \Bbbk$ and
$\beta _1, \beta _2\in \Bbbk$ and  $k\in \mathbb {Z}_{\geqslant 1}$. Then
$k\in \mathbb {Z}_{\geqslant 1}$. Then  $\textit {DLoc}_0^{\leqslant n}(e_{2k}^*+\beta _1 e_k^*)= \textit {DLoc}_0^{\leqslant n}(e_{2k}^*+\beta _2 e_k^*)$ if and only if
$\textit {DLoc}_0^{\leqslant n}(e_{2k}^*+\beta _1 e_k^*)= \textit {DLoc}_0^{\leqslant n}(e_{2k}^*+\beta _2 e_k^*)$ if and only if  $\beta _1=\pm \beta _2$.
$\beta _1=\pm \beta _2$.
We next describe the ‘Bruhat order’ on ![]() $\textit {DLoc}_x^{\leqslant n}$ orbits (that is, the inclusions of orbit closures): it turns out that it can almost be computed just from the dimension of the orbit.
$\textit {DLoc}_x^{\leqslant n}$ orbits (that is, the inclusions of orbit closures): it turns out that it can almost be computed just from the dimension of the orbit.
Corollary 4.2.9 Let ![]() $\mathfrak g, x$ be as in the statement of Theorem 4.2.1. Let
$\mathfrak g, x$ be as in the statement of Theorem 4.2.1. Let ![]() $\chi ^-, \chi ^+\!$ be local functions on
$\chi ^-, \chi ^+\!$ be local functions on ![]() $\mathfrak g$ based at
$\mathfrak g$ based at ![]() $x$ and of order
$x$ and of order ![]() $\leqslant n$.
$\leqslant n$.
Then the following conditions are equivalent:
(1)
 $\textit {DLoc}_x^{\leqslant n}\cdot \chi ^-$ is contained in the closure of
$\textit {DLoc}_x^{\leqslant n}\cdot \chi ^-$ is contained in the closure of  $\textit {DLoc}_x^{\leqslant n}\cdot \chi ^+$ and
$\textit {DLoc}_x^{\leqslant n}\cdot \chi ^+$ and  $\textit {DLoc}_x^{\leqslant n}\cdot \chi ^-\ne \textit {DLoc}_x^{\leqslant n}\cdot \chi ^+$;
$\textit {DLoc}_x^{\leqslant n}\cdot \chi ^-\ne \textit {DLoc}_x^{\leqslant n}\cdot \chi ^+$;(2)
 $\operatorname {P}(\chi ^+)\subsetneqq \operatorname {P}(\chi ^-)$;
$\operatorname {P}(\chi ^+)\subsetneqq \operatorname {P}(\chi ^-)$;(3)
 $\dim \textit {DLoc}_x^{\leqslant n}\cdot \chi ^-<\dim \textit {DLoc}_x^{\leqslant n}\cdot \chi ^+$ and
$\dim \textit {DLoc}_x^{\leqslant n}\cdot \chi ^-<\dim \textit {DLoc}_x^{\leqslant n}\cdot \chi ^+$ and  $\chi ^+$ is not of order one.
$\chi ^+$ is not of order one.
Proof. We again give the proof for ![]() $\mathfrak g = W_{\geqslant -1}$ and
$\mathfrak g = W_{\geqslant -1}$ and ![]() $x=0$. We show that
$x=0$. We show that ![]() $(2)\Rightarrow (3) \Leftrightarrow (1) \Rightarrow (2)$. Next, without loss of generality we assume that
$(2)\Rightarrow (3) \Leftrightarrow (1) \Rightarrow (2)$. Next, without loss of generality we assume that ![]() $n$ is the order of
$n$ is the order of ![]() $\chi ^+$.
$\chi ^+$.
We first show that ![]() $(3)$ implies
$(3)$ implies ![]() $(1)$. As in Theorem 4.2.1, pick the related presentation
$(1)$. As in Theorem 4.2.1, pick the related presentation ![]() $\chi _{0; \beta _0^+, \beta _1^+, \ldots, \beta _n^+}$ for
$\chi _{0; \beta _0^+, \beta _1^+, \ldots, \beta _n^+}$ for ![]() $\chi ^+$, with
$\chi ^+$, with ![]() $\beta _n^+ \neq 0$. If
$\beta _n^+ \neq 0$. If ![]() $n$ is even, then the closure of
$n$ is even, then the closure of ![]() $\textit {DLoc}_0^{\leqslant n}\cdot \chi ^+$ equals
$\textit {DLoc}_0^{\leqslant n}\cdot \chi ^+$ equals ![]() $\textit {Loc}_0^{\leqslant n}$. On the other hand, all orbits of strictly smaller dimension belong to
$\textit {Loc}_0^{\leqslant n}$. On the other hand, all orbits of strictly smaller dimension belong to ![]() $\textit {Loc}_0^{\leqslant n}$, so this completes the proof in this case.
$\textit {Loc}_0^{\leqslant n}$, so this completes the proof in this case.
If ![]() $n=2k+1$ is odd, then
$n=2k+1$ is odd, then ![]() $k\geqslant 1$ by the assumptions of condition (3). The closure of
$k\geqslant 1$ by the assumptions of condition (3). The closure of ![]() $\textit {DLoc}_0^{\leqslant n}\cdot \chi ^+$ is an irreducible subvariety of
$\textit {DLoc}_0^{\leqslant n}\cdot \chi ^+$ is an irreducible subvariety of ![]() $\textit {Loc}_0^{\leqslant n}$ of codimension one, i.e. a hypersurface defined by some function
$\textit {Loc}_0^{\leqslant n}$ of codimension one, i.e. a hypersurface defined by some function ![]() $F_+$. We claim that this function is semi-invariant with respect to
$F_+$. We claim that this function is semi-invariant with respect to ![]() $\textit {DLoc}_0^{\leqslant n}$.
$\textit {DLoc}_0^{\leqslant n}$.
To prove that ![]() $F_+$ is semi-invariant, we describe it in more detail. Let
$F_+$ is semi-invariant, we describe it in more detail. Let ![]() $R=\Bbbk [\beta _0, \beta _1,\ldots, \beta _{n-1}, \beta _n^{\pm 1}]$, where
$R=\Bbbk [\beta _0, \beta _1,\ldots, \beta _{n-1}, \beta _n^{\pm 1}]$, where ![]() $\beta _0, \beta _1, \ldots, \beta _n$ are free variables. Denote by
$\beta _0, \beta _1, \ldots, \beta _n$ are free variables. Denote by ![]() $(\cdot )_{\Bbbk \to R}$ the base change from
$(\cdot )_{\Bbbk \to R}$ the base change from ![]() $\Bbbk$ to
$\Bbbk$ to ![]() $R$. The arguments of Theorem 4.2.1(b) imply that there exists a group element
$R$. The arguments of Theorem 4.2.1(b) imply that there exists a group element ![]() $g\in (\textit {DLoc}_0^{\leqslant n})_{\Bbbk \to R}$ and
$g\in (\textit {DLoc}_0^{\leqslant n})_{\Bbbk \to R}$ and ![]() $h\in R$ such that
$h\in R$ such that
Recall that ![]() $k = ({n-1})/{2}\geqslant 1$. By replacing each
$k = ({n-1})/{2}\geqslant 1$. By replacing each ![]() $\beta _i$ by
$\beta _i$ by ![]() ${e_{i-1}}/{i!}$ (cf. (4.2.4)) we may identify
${e_{i-1}}/{i!}$ (cf. (4.2.4)) we may identify ![]() $R$ with
$R$ with ![]() $\Bbbk [\textit {Loc}_0^{\leqslant n}][e_{2k}^{-1}]$. (Here we regard the
$\Bbbk [\textit {Loc}_0^{\leqslant n}][e_{2k}^{-1}]$. (Here we regard the ![]() $e_i$ as functions on
$e_i$ as functions on ![]() $\textit {Loc}_0^{\leqslant n}$ in the obvious way.) Then
$\textit {Loc}_0^{\leqslant n}$ in the obvious way.) Then ![]() $h=f/e_{2k}^\ell$ for some
$h=f/e_{2k}^\ell$ for some ![]() $f\in \Bbbk [\textit {Loc}_0^{\leqslant n}]$ and
$f\in \Bbbk [\textit {Loc}_0^{\leqslant n}]$ and ![]() $\ell \in \mathbb {Z}_{\geqslant 0}$.
$\ell \in \mathbb {Z}_{\geqslant 0}$.
Let ![]() $\chi, \chi ' \in \textit {Loc}_0^{\leqslant n}$ with
$\chi, \chi ' \in \textit {Loc}_0^{\leqslant n}$ with ![]() $e_{2k}(\chi ), e_{2k}(\chi ') \neq 0$. As in the proof of Theorem 4.2.1(c),
$e_{2k}(\chi ), e_{2k}(\chi ') \neq 0$. As in the proof of Theorem 4.2.1(c), ![]() $\textit {DLoc}_0^{\leqslant n} \cdot \chi = \textit {DLoc}_0^{\leqslant n} \cdot \chi '$ if and only if
$\textit {DLoc}_0^{\leqslant n} \cdot \chi = \textit {DLoc}_0^{\leqslant n} \cdot \chi '$ if and only if
The rational function
is, thus, ![]() $\textit {DLoc}_0^{\leqslant n}$-invariant and separates orbits. Therefore,
$\textit {DLoc}_0^{\leqslant n}$-invariant and separates orbits. Therefore, ![]() $\textit {DLoc}_0^{\leqslant n} \cdot \chi ^+$ is the hypersurface in
$\textit {DLoc}_0^{\leqslant n} \cdot \chi ^+$ is the hypersurface in ![]() $\textit {Loc}_0^{\leqslant n} \setminus \textit {Loc}_0^{\leqslant n-1}$ defined by
$\textit {Loc}_0^{\leqslant n} \setminus \textit {Loc}_0^{\leqslant n-1}$ defined by
Note that ![]() $F_+$ is semi-invariant, as claimed.
$F_+$ is semi-invariant, as claimed.
All orbits of dimension more than ![]() $n$ belong to
$n$ belong to ![]() $\textit {Loc}_0^{\leqslant n-2}$. We check that the closure of
$\textit {Loc}_0^{\leqslant n-2}$. We check that the closure of ![]() $\textit {DLoc}_0^{\leqslant n}\cdot \chi ^+$ contains
$\textit {DLoc}_0^{\leqslant n}\cdot \chi ^+$ contains ![]() $\textit {Loc}_0^{\leqslant n-2}$. The orbit closure
$\textit {Loc}_0^{\leqslant n-2}$. The orbit closure ![]() $\overline {\textit {DLoc}_0^{\leqslant n} \chi ^+}$ is defined in
$\overline {\textit {DLoc}_0^{\leqslant n} \chi ^+}$ is defined in ![]() $\textit {Loc}_0^{\leqslant n}$ by
$\textit {Loc}_0^{\leqslant n}$ by ![]() $F_+$, so we must show that
$F_+$, so we must show that ![]() $F_+|_{\textit {Loc}_0^{\leqslant n-2}}=0.$ The restriction of
$F_+|_{\textit {Loc}_0^{\leqslant n-2}}=0.$ The restriction of ![]() $F_+$ to
$F_+$ to ![]() $\textit {Loc}^{\leqslant n-1}_{0}$ is also a semi-invariant function; in particular, this restriction is invariant with respect to
$\textit {Loc}^{\leqslant n-1}_{0}$ is also a semi-invariant function; in particular, this restriction is invariant with respect to ![]() $\textit {DLoc}_0^{1+, \leqslant n}$, see Lemma 4.1.7. The arguments of Theorem 4.2.1 imply that all
$\textit {DLoc}_0^{1+, \leqslant n}$, see Lemma 4.1.7. The arguments of Theorem 4.2.1 imply that all ![]() $n$-dimensional
$n$-dimensional ![]() $\textit {DLoc}_0^{1+, \leqslant n}$-invariant hypersurfaces of
$\textit {DLoc}_0^{1+, \leqslant n}$-invariant hypersurfaces of ![]() $\textit {Loc}_0^{\leqslant n-1}$ are defined by the equality
$\textit {Loc}_0^{\leqslant n-1}$ are defined by the equality ![]() $e_{n-1}=\beta _{n-1}$ for some
$e_{n-1}=\beta _{n-1}$ for some ![]() $\beta _{n-1}\in \Bbbk$. This implies that the restriction of
$\beta _{n-1}\in \Bbbk$. This implies that the restriction of ![]() $F_+$ is a polynomial in
$F_+$ is a polynomial in ![]() $e_{n-1}$. The fact that
$e_{n-1}$. The fact that ![]() $F_+$ is
$F_+$ is ![]() $\textit {DLoc}_0^{\leqslant n}$-semi-invariant implies that
$\textit {DLoc}_0^{\leqslant n}$-semi-invariant implies that ![]() $F_+|_{\textit {Loc}^{\leqslant n-1}_{0}}=c (e_{n-1})^m$ for some
$F_+|_{\textit {Loc}^{\leqslant n-1}_{0}}=c (e_{n-1})^m$ for some ![]() $m \geqslant 0$ and
$m \geqslant 0$ and ![]() $c\in \Bbbk$. This implies the desired condition that
$c\in \Bbbk$. This implies the desired condition that ![]() $F_+|_{\textit {Loc}^{\leqslant n-2}_{0}}=0$.
$F_+|_{\textit {Loc}^{\leqslant n-2}_{0}}=0$.
We now show that condition ![]() $(1)$ implies condition
$(1)$ implies condition ![]() $(3)$, so suppose that condition
$(3)$, so suppose that condition ![]() $(1)$ holds. The dimension inequality in condition
$(1)$ holds. The dimension inequality in condition ![]() $(3)$ is clear. Thus, we are left to deal with the case when
$(3)$ is clear. Thus, we are left to deal with the case when ![]() $\chi ^+$ has order one; we want to show this cannot happen.
$\chi ^+$ has order one; we want to show this cannot happen.
Suppose now that ![]() $\chi ^+= \chi _{x;\alpha, \beta }$ has order one, so
$\chi ^+= \chi _{x;\alpha, \beta }$ has order one, so ![]() $\beta \neq 0$. By the dimension inequality,
$\beta \neq 0$. By the dimension inequality, ![]() $\chi ^- = 0$. Now, Theorem 4.2.1(b
$\chi ^- = 0$. Now, Theorem 4.2.1(b![]() $'$) shows that
$'$) shows that ![]() $\textit {DLoc}_0^{\leqslant 1} \cdot \chi ^+ = \textit {DLoc}_0^{\leqslant 1} \cdot (\beta e_0^*)$ consists of all
$\textit {DLoc}_0^{\leqslant 1} \cdot \chi ^+ = \textit {DLoc}_0^{\leqslant 1} \cdot (\beta e_0^*)$ consists of all ![]() $\chi _{0; \alpha ', \beta }$ for
$\chi _{0; \alpha ', \beta }$ for ![]() $\alpha ' \in \Bbbk$, and so is defined in
$\alpha ' \in \Bbbk$, and so is defined in ![]() $\textit {Loc}_0^{\leqslant 1} \setminus \textit {Loc}_0^{\leqslant 0} = \operatorname {Spec} \Bbbk [\beta _0, \beta _1, \beta _1^{-1}]$ by
$\textit {Loc}_0^{\leqslant 1} \setminus \textit {Loc}_0^{\leqslant 0} = \operatorname {Spec} \Bbbk [\beta _0, \beta _1, \beta _1^{-1}]$ by ![]() $\beta _1 = \beta$. Thus,
$\beta _1 = \beta$. Thus, ![]() $\overline {\textit {DLoc}_0^{\leqslant 1} \cdot \chi ^+}$ is defined in
$\overline {\textit {DLoc}_0^{\leqslant 1} \cdot \chi ^+}$ is defined in ![]() $\textit {Loc}_0^{\leqslant 1} \cong \operatorname {Spec} \Bbbk [\beta _0, \beta _1]$ by
$\textit {Loc}_0^{\leqslant 1} \cong \operatorname {Spec} \Bbbk [\beta _0, \beta _1]$ by ![]() $\beta _1= \beta$ and does not contain
$\beta _1= \beta$ and does not contain ![]() $0 = \chi _{0; 0, 0}$, a contradiction.
$0 = \chi _{0; 0, 0}$, a contradiction.
We now show that ![]() $(1) \Rightarrow (2)$. This is an application of Proposition 2.3.1. Let
$(1) \Rightarrow (2)$. This is an application of Proposition 2.3.1. Let ![]() $X = \widetilde {\textit {Loc}}^{\leqslant n}_{\mathfrak g}$ (recall that
$X = \widetilde {\textit {Loc}}^{\leqslant n}_{\mathfrak g}$ (recall that ![]() $\mathfrak g = W_{\geqslant -1}$) and let
$\mathfrak g = W_{\geqslant -1}$) and let ![]() $H = \widehat {\textit {DLoc}}^{\leqslant n}$. Let
$H = \widehat {\textit {DLoc}}^{\leqslant n}$. Let ![]() $\mathfrak h = \widehat {\operatorname {lie}}^{\leqslant n} = \operatorname {Lie}(H)$. Let
$\mathfrak h = \widehat {\operatorname {lie}}^{\leqslant n} = \operatorname {Lie}(H)$. Let ![]() $\phi = \phi ^{\leqslant n}_{\mathfrak g}: X \to \mathfrak g^*$. Choose
$\phi = \phi ^{\leqslant n}_{\mathfrak g}: X \to \mathfrak g^*$. Choose ![]() $x^+ \in \phi ^{-1}(\chi ^+)$ and
$x^+ \in \phi ^{-1}(\chi ^+)$ and ![]() $x^- \in \phi ^{-1}(\chi ^-)$; note here that
$x^- \in \phi ^{-1}(\chi ^-)$; note here that ![]() $\phi$ is bijective onto
$\phi$ is bijective onto ![]() $\textit {Loc}^{\leqslant n}_{\mathfrak g} \setminus \{0\}$ so
$\textit {Loc}^{\leqslant n}_{\mathfrak g} \setminus \{0\}$ so ![]() $x^{\pm }$ may be uniquely determined. By Lemma 4.1.6,
$x^{\pm }$ may be uniquely determined. By Lemma 4.1.6, ![]() $\dim \mathfrak h_{x^\pm } = \dim \mathfrak g_{\chi ^\pm }$. Thus, by Proposition 2.3.1,
$\dim \mathfrak h_{x^\pm } = \dim \mathfrak g_{\chi ^\pm }$. Thus, by Proposition 2.3.1, ![]() $\operatorname {P}(\chi ^+)$ is the kernel of the map
$\operatorname {P}(\chi ^+)$ is the kernel of the map ![]() $\phi ^+:\operatorname {S}(\mathfrak g) \to \Bbbk [\overline {H \cdot x^+}]$ induced from
$\phi ^+:\operatorname {S}(\mathfrak g) \to \Bbbk [\overline {H \cdot x^+}]$ induced from ![]() $\phi ^*: \operatorname {S}(\mathfrak g) \to \Bbbk [X]$ and
$\phi ^*: \operatorname {S}(\mathfrak g) \to \Bbbk [X]$ and ![]() $\operatorname {P}(\chi ^-)$ is the kernel of
$\operatorname {P}(\chi ^-)$ is the kernel of ![]() $\phi ^-:\operatorname {S}(\mathfrak g) \to \Bbbk [\overline {H \cdot x^-}]$. However, by assumption,
$\phi ^-:\operatorname {S}(\mathfrak g) \to \Bbbk [\overline {H \cdot x^-}]$. However, by assumption, ![]() $H \cdot x^- \subseteq \overline {H \cdot x^+} \subseteq X$, giving the following commutative diagram.
$H \cdot x^- \subseteq \overline {H \cdot x^+} \subseteq X$, giving the following commutative diagram.

Thus, ![]() $\operatorname {P}(\chi ^-) = \ker \phi ^- \supseteq \ker \phi ^+ = \operatorname {P}(\chi ^+)$. The two are clearly distinct.
$\operatorname {P}(\chi ^-) = \ker \phi ^- \supseteq \ker \phi ^+ = \operatorname {P}(\chi ^+)$. The two are clearly distinct.
We still must show condition (2) implies condition (3). If condition ![]() $(2)$ holds, then
$(2)$ holds, then ![]() $\dim \mathbb {O}(\chi ^-)<\dim \mathbb {O}(\chi ^+)$. By the previous discussion and (2.3.3),
$\dim \mathbb {O}(\chi ^-)<\dim \mathbb {O}(\chi ^+)$. By the previous discussion and (2.3.3),
Finally, note that if ![]() $\chi ^+ = \chi _{x;\alpha,\gamma }$ has order zero or one, by the dimension inequality we must have
$\chi ^+ = \chi _{x;\alpha,\gamma }$ has order zero or one, by the dimension inequality we must have ![]() $\chi ^- = 0$. We have seen in Lemma 2.2.3 that
$\chi ^- = 0$. We have seen in Lemma 2.2.3 that ![]() $\operatorname {P}(\chi ^+)$ is the kernel of
$\operatorname {P}(\chi ^+)$ is the kernel of
We compute
and so ![]() $[(t-x)\partial ]^2 - \partial [(t-x)^2 \partial ]-\gamma ^2 \in \ker p_\gamma$. This element is contained in
$[(t-x)\partial ]^2 - \partial [(t-x)^2 \partial ]-\gamma ^2 \in \ker p_\gamma$. This element is contained in ![]() $\mathfrak m_0 = \operatorname {P}(0)$ if and only if
$\mathfrak m_0 = \operatorname {P}(0)$ if and only if ![]() $\gamma =0$, so
$\gamma =0$, so ![]() $\chi ^+$ cannot have order one.
$\chi ^+$ cannot have order one.
For future reference, we record that Corollary 4.2.9 also gives information about ![]() $\widehat {\textit {DLoc}}^{\leqslant n}$ orbits. Let
$\widehat {\textit {DLoc}}^{\leqslant n}$ orbits. Let
and similarly define ![]() $\textit {Loc}_W^n$. We identify
$\textit {Loc}_W^n$. We identify ![]() $\Bbbk [\textit {Loc}_{W_{\geqslant -1}}^n]$ with
$\Bbbk [\textit {Loc}_{W_{\geqslant -1}}^n]$ with ![]() $\Bbbk [x, \beta _0, \ldots, \beta _n, \beta _n^{-1}]$. Note that each
$\Bbbk [x, \beta _0, \ldots, \beta _n, \beta _n^{-1}]$. Note that each ![]() $\textit {Loc}_{W_{\geqslant -1}}^n$ is
$\textit {Loc}_{W_{\geqslant -1}}^n$ is ![]() $\widehat {\textit {DLoc}}^{\leqslant n}$-stable.
$\widehat {\textit {DLoc}}^{\leqslant n}$-stable.
The action of ![]() $\textit {Shifts}$ and, thus, the action of
$\textit {Shifts}$ and, thus, the action of ![]() $\widehat {DLoc}$ on
$\widehat {DLoc}$ on ![]() $\textit {Loc}_W$ is only partially defined, as we cannot shift the base point to
$\textit {Loc}_W$ is only partially defined, as we cannot shift the base point to ![]() $0$. We refer to orbits of this partial action with the obvious meaning: the intersection of an orbit in
$0$. We refer to orbits of this partial action with the obvious meaning: the intersection of an orbit in ![]() $\textit {Loc}_{W_{\geqslant -1}}$ with
$\textit {Loc}_{W_{\geqslant -1}}$ with ![]() $W^*$.
$W^*$.
Corollary 4.2.11 Let ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $W_{\geqslant -1}$.
$W_{\geqslant -1}$.
(a) If
 $n$ is even, then
$n$ is even, then  $\textit {Loc}_{\mathfrak g}^n$ is a single
$\textit {Loc}_{\mathfrak g}^n$ is a single  $\widehat {\textit {DLoc}}^{\leqslant n}$-orbit.
$\widehat {\textit {DLoc}}^{\leqslant n}$-orbit.(b) If
 $n\geqslant 3$ is odd, there is
$n\geqslant 3$ is odd, there is  $F_n \in \Bbbk [x, x^{-1}, \beta _0, \ldots, \beta _n, \beta _n^{-1}]$ (if
$F_n \in \Bbbk [x, x^{-1}, \beta _0, \ldots, \beta _n, \beta _n^{-1}]$ (if  $\mathfrak g = W$) or in
$\mathfrak g = W$) or in  $\Bbbk [x, \beta _0, \ldots, \beta _n, \beta _n^{-1}]$ (if
$\Bbbk [x, \beta _0, \ldots, \beta _n, \beta _n^{-1}]$ (if  $\mathfrak g = W_{\geqslant -1})$ so that the
$\mathfrak g = W_{\geqslant -1})$ so that the  $\widehat {\textit {DLoc}}^{\leqslant n}$-orbits are precisely the fibres of the morphism
$\widehat {\textit {DLoc}}^{\leqslant n}$-orbits are precisely the fibres of the morphism  $F_n: \textit {Loc}_{\mathfrak g}^n \to \mathbb {A}^1.$
$F_n: \textit {Loc}_{\mathfrak g}^n \to \mathbb {A}^1.$(c) Define
 $F_1: \textit {Loc}_{\mathfrak g}^1 \to \mathbb {A}^1\setminus \{0\}$ by
$F_1: \textit {Loc}_{\mathfrak g}^1 \to \mathbb {A}^1\setminus \{0\}$ by  $\chi _{x; \alpha, \gamma }\mapsto \gamma$. Then the fibres of
$\chi _{x; \alpha, \gamma }\mapsto \gamma$. Then the fibres of  $F_1$ are exactly the orbits of
$F_1$ are exactly the orbits of  $\widehat {\textit {DLoc}}^{\leqslant 1}$ on
$\widehat {\textit {DLoc}}^{\leqslant 1}$ on  $\textit {Loc}_{\mathfrak g}^1$.
$\textit {Loc}_{\mathfrak g}^1$.
Proof. This result is a consequence of Theorem 4.2.1 and the proof of Corollary 4.2.9. If ![]() $n\geqslant 3$ is odd, note that, by definition, applying an element of
$n\geqslant 3$ is odd, note that, by definition, applying an element of ![]() $\textit {Shifts}$ changes
$\textit {Shifts}$ changes ![]() $x$ but not any of the
$x$ but not any of the ![]() $\beta _i$. Thus, we may take
$\beta _i$. Thus, we may take ![]() $F_n$ to be the polynomial
$F_n$ to be the polynomial ![]() $F$ defined in (4.2.10), regarded as an element of
$F$ defined in (4.2.10), regarded as an element of ![]() $\Bbbk [x, \beta _0, \ldots, \beta _n, \beta _n^{-1}]$. The proof for
$\Bbbk [x, \beta _0, \ldots, \beta _n, \beta _n^{-1}]$. The proof for ![]() $n=1$ is similar.
$n=1$ is similar.
It is instructive to compute that for ![]() $n=3$, the polynomial
$n=3$, the polynomial ![]() $F_3$ given by Corollary 4.2.11 is a scalar multiple of
$F_3$ given by Corollary 4.2.11 is a scalar multiple of ![]() $\beta _2^2/\beta _3$. In particular,
$\beta _2^2/\beta _3$. In particular, ![]() $x$ does not occur.
$x$ does not occur.
Remark 4.2.12 The dimension of a ![]() $\widehat {DLoc}^{\leqslant n}$-orbit in Corollary 4.2.11 is
$\widehat {DLoc}^{\leqslant n}$-orbit in Corollary 4.2.11 is
 \[ 2 \bigg\lfloor \frac{n+2}2 \bigg\rfloor = \begin{cases} n+2 & \mbox{n even} , \\ n+1 & n \mbox{ odd}. \end{cases} \]
\[ 2 \bigg\lfloor \frac{n+2}2 \bigg\rfloor = \begin{cases} n+2 & \mbox{n even} , \\ n+1 & n \mbox{ odd}. \end{cases} \]
4.3 Implicit description of pseudo-orbits
Let ![]() $\mathfrak g = W$,
$\mathfrak g = W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$. We now consider arbitrary local functions on
$W_{\geqslant 1}$. We now consider arbitrary local functions on ![]() $\mathfrak g$. We provide every pair of local functions
$\mathfrak g$. We provide every pair of local functions ![]() $\chi, \nu \in \mathfrak g^*$ with an affine variety
$\chi, \nu \in \mathfrak g^*$ with an affine variety ![]() $X$ acted on by an algebraic group
$X$ acted on by an algebraic group ![]() $H$, an open subset
$H$, an open subset ![]() $U\subseteq X$, a Poisson map
$U\subseteq X$, a Poisson map ![]() $\phi :U \to \mathfrak g^*$ and a pair of points
$\phi :U \to \mathfrak g^*$ and a pair of points ![]() $x, y\in X$ which will satisfy the conditions of Proposition 2.3.1. Thus, we reduce the mysterious infinite-dimensional case to the more easily comprehensible action of an algebraic group on an affine variety. We use this to determine the pseudo-orbits in
$x, y\in X$ which will satisfy the conditions of Proposition 2.3.1. Thus, we reduce the mysterious infinite-dimensional case to the more easily comprehensible action of an algebraic group on an affine variety. We use this to determine the pseudo-orbits in ![]() $\mathfrak g^*$.
$\mathfrak g^*$.
Theorem 4.3.1 Let ![]() $\mathfrak g = V\!ir$,
$\mathfrak g = V\!ir$, ![]() $\mathfrak g=W$ or
$\mathfrak g=W$ or ![]() $W_{\geqslant -1}$. Let
$W_{\geqslant -1}$. Let ![]() $\chi ^{I}$ and
$\chi ^{I}$ and ![]() $\chi ^{II}$ be local functions in
$\chi ^{II}$ be local functions in ![]() $\mathfrak g^*$ represented by sums
$\mathfrak g^*$ represented by sums
 \[ \chi^{I}=\sum_{i=1}^{\ell}\chi_i^{I},\quad \chi^{II}=\sum_{i=1}^{\ell}\chi_i^{II},\quad \chi_i^{I}\in \textit{Loc}_{x_i^{I}},\quad \chi_i^{II}\in \textit{Loc}_{x_i^{II}}, \]
\[ \chi^{I}=\sum_{i=1}^{\ell}\chi_i^{I},\quad \chi^{II}=\sum_{i=1}^{\ell}\chi_i^{II},\quad \chi_i^{I}\in \textit{Loc}_{x_i^{I}},\quad \chi_i^{II}\in \textit{Loc}_{x_i^{II}}, \]
such that ![]() $x^{I}_i\ne x^{I}_j$ and
$x^{I}_i\ne x^{I}_j$ and ![]() $x^{II}_i\ne x^{II}_j$ for
$x^{II}_i\ne x^{II}_j$ for ![]() $i\ne j$. Then
$i\ne j$. Then ![]() $\chi ^{I}$ and
$\chi ^{I}$ and ![]() $\chi ^{II}$ are in the same pseudo-orbit if and only if it is possible to reorder
$\chi ^{II}$ are in the same pseudo-orbit if and only if it is possible to reorder ![]() $x^{I}_i$ and
$x^{I}_i$ and ![]() $x^{II}_i$ in such a way that
$x^{II}_i$ in such a way that
that is,
In particular, if ![]() $\mathbb {O}(\chi ^{I})=\mathbb {O}(\chi ^{II})$, then
$\mathbb {O}(\chi ^{I})=\mathbb {O}(\chi ^{II})$, then ![]() $\lambda (\chi ^{I})=\lambda (\chi ^{II})$ and, hence, the supports of
$\lambda (\chi ^{I})=\lambda (\chi ^{II})$ and, hence, the supports of ![]() $\chi ^{I}$ and
$\chi ^{I}$ and ![]() $\chi ^{II}$ have the same cardinality.
$\chi ^{II}$ have the same cardinality.
Remark 4.3.3 Let ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $W_{\geqslant -1}$. Fix a partition
$W_{\geqslant -1}$. Fix a partition ![]() $\lambda = (m_1, \ldots, m_r)$ and consider the set
$\lambda = (m_1, \ldots, m_r)$ and consider the set ![]() $V^\lambda _{\mathfrak g}$ of all local functions
$V^\lambda _{\mathfrak g}$ of all local functions ![]() $\chi \in {\mathfrak g}^*$ with
$\chi \in {\mathfrak g}^*$ with ![]() $\lambda (\chi ) = \lambda$. Let
$\lambda (\chi ) = \lambda$. Let ![]() $\chi = \chi _1 + \cdots + \chi _r, \nu = \nu _1 + \cdots + \nu _r \in V^\lambda _{\mathfrak g}$, where each
$\chi = \chi _1 + \cdots + \chi _r, \nu = \nu _1 + \cdots + \nu _r \in V^\lambda _{\mathfrak g}$, where each ![]() $\chi _i$ (respectively,
$\chi _i$ (respectively, ![]() $\nu _i$) is a one-point local function of order
$\nu _i$) is a one-point local function of order ![]() $m_i-1$. By Theorem 4.3.1,
$m_i-1$. By Theorem 4.3.1, ![]() $\mathbb {O}(\chi ) = \mathbb {O}(\nu )$
$\mathbb {O}(\chi ) = \mathbb {O}(\nu )$ ![]() $\iff$
$\iff$ ![]() $\mathbb {O}(\chi _i) = \mathbb {O}(\nu _i)$ for
$\mathbb {O}(\chi _i) = \mathbb {O}(\nu _i)$ for ![]() $1 \leqslant i \leqslant r$ (up to permutation of indices). Combining Corollary 4.2.11 and Theorem 4.3.1 applied to one-point local functions we have
$1 \leqslant i \leqslant r$ (up to permutation of indices). Combining Corollary 4.2.11 and Theorem 4.3.1 applied to one-point local functions we have
(a) if
 $m_i$ is odd, then
$m_i$ is odd, then  $\textit {Loc}^{m_i-1}_{\mathfrak g}$ is a single pseudo-orbit;
$\textit {Loc}^{m_i-1}_{\mathfrak g}$ is a single pseudo-orbit;(b) if
 $m_i$ is even and
$m_i$ is even and  $m_i\ne 2$, then the pseudo-orbits in
$m_i\ne 2$, then the pseudo-orbits in  $\textit {Loc}_{\mathfrak g}^{m_i-1}$ are parameterised by
$\textit {Loc}_{\mathfrak g}^{m_i-1}$ are parameterised by  $\mathbb {A}^1$;
$\mathbb {A}^1$;(c) the pseudo-orbits in
 $\textit {Loc}_{\mathfrak g}^{1}$ are parameterised by
$\textit {Loc}_{\mathfrak g}^{1}$ are parameterised by  $\mathbb {A}^1\setminus \{0\}$.
$\mathbb {A}^1\setminus \{0\}$.
Thus, pseudo-orbits in ![]() $V^\lambda _{\mathfrak g}$ (and the corresponding Poisson primitive ideals of
$V^\lambda _{\mathfrak g}$ (and the corresponding Poisson primitive ideals of ![]() $\operatorname {S}({\mathfrak g})$) are parameterised by a symmetric product
$\operatorname {S}({\mathfrak g})$) are parameterised by a symmetric product ![]() $(\mathbb {A}^1)^{\times (k-k_2)}\times (\mathbb {A}^1\setminus \{0\})^{\times k_2}$, where
$(\mathbb {A}^1)^{\times (k-k_2)}\times (\mathbb {A}^1\setminus \{0\})^{\times k_2}$, where ![]() $k$ is the total number of even parts of
$k$ is the total number of even parts of ![]() $\lambda$ and
$\lambda$ and ![]() $k_2:=|\{i\mid m_i=2\}|.$
$k_2:=|\{i\mid m_i=2\}|.$
More specifically, let
 \[ \mathbb{A}(\lambda) := \begin{cases} \mathbb{A}^k & \text{if}\ k_2=0,\\ \mathbb{A}^{k-1} \times (\mathbb{A}^1\setminus\{0\}) & \text{if}\ k_2\ne0. \end{cases} \]
\[ \mathbb{A}(\lambda) := \begin{cases} \mathbb{A}^k & \text{if}\ k_2=0,\\ \mathbb{A}^{k-1} \times (\mathbb{A}^1\setminus\{0\}) & \text{if}\ k_2\ne0. \end{cases} \]
Let ![]() $\mathfrak S_{\lambda } = \{ \sigma \in \mathfrak S_k \,|\, m_i = m_{\sigma (i)} \mbox { for all } i\}$. The pseudo-orbits in
$\mathfrak S_{\lambda } = \{ \sigma \in \mathfrak S_k \,|\, m_i = m_{\sigma (i)} \mbox { for all } i\}$. The pseudo-orbits in ![]() $V^\lambda _{\mathfrak g}$ are parameterised by
$V^\lambda _{\mathfrak g}$ are parameterised by
In § 5.2 we refine this parameterisation to apply to arbitrary prime Poisson ideals of ![]() $\operatorname {S}(\mathfrak g)$.
$\operatorname {S}(\mathfrak g)$.
To prove Theorem 4.3.1 we need two preparatory results.
Lemma 4.3.4 Let ![]() $\chi \in W^*$ be a local function with
$\chi \in W^*$ be a local function with ![]() $\chi =\chi _1+\cdots +\chi _s$ and
$\chi =\chi _1+\cdots +\chi _s$ and ![]() $\chi _i\in \textit {Loc}_{x_i}$ such that
$\chi _i\in \textit {Loc}_{x_i}$ such that ![]() $x_i\ne x_j$ if
$x_i\ne x_j$ if ![]() $i\ne j$. Then
$i\ne j$. Then ![]() $W\cdot \chi =\bigoplus _i W\cdot \chi _i$. Likewise, if
$W\cdot \chi =\bigoplus _i W\cdot \chi _i$. Likewise, if ![]() $\chi \in W_{\geqslant -1}^*$, then
$\chi \in W_{\geqslant -1}^*$, then ![]() $W_{\geqslant -1} \cdot \chi = \bigoplus _i W_{\geqslant -1}\cdot \chi _i$.
$W_{\geqslant -1} \cdot \chi = \bigoplus _i W_{\geqslant -1}\cdot \chi _i$.
Proof. This statement is basically implied by the Chinese remainder theorem, but we give the details for ![]() $W$. It is easy to verify that
$W$. It is easy to verify that ![]() $W\cdot \chi =\{B_\chi (u, \cdot )\mid u\in W\}$. As
$W\cdot \chi =\{B_\chi (u, \cdot )\mid u\in W\}$. As ![]() $\chi$ is local, there are
$\chi$ is local, there are ![]() $d_1, \ldots, d_s \in \mathbb {Z}_{\geqslant 1}$ so that
$d_1, \ldots, d_s \in \mathbb {Z}_{\geqslant 1}$ so that ![]() $\chi |_{W(\prod _i(t-x_i)^{d_i})}=0$. Let
$\chi |_{W(\prod _i(t-x_i)^{d_i})}=0$. Let ![]() $f:=\prod _i(t-x_i)^{d_i+1}$. Then
$f:=\prod _i(t-x_i)^{d_i+1}$. Then ![]() $B_\chi |_{W(f)}=0$. By the Chinese remainder theorem,
$B_\chi |_{W(f)}=0$. By the Chinese remainder theorem,
This leads to the decomposition
It is straightforward to verify that the partial restriction ![]() $B_{\chi _i}(W(f_j), \cdot )$ is nonzero only if
$B_{\chi _i}(W(f_j), \cdot )$ is nonzero only if ![]() $i=j$. Hence,
$i=j$. Hence,
This implies the desired result.
We next apply the general results from § 2 and the group action from § 4.1 to the Poisson cores of local functions and deduce some consequences.
Proposition 4.3.6
(a) Let
 $\chi \in W^*$. Then
$\chi \in W^*$. Then
 \[ \operatorname{P}(\chi) \cap \operatorname{S}(W_{\geqslant -1}) = \operatorname{P}(\chi|_{W_{\geqslant -1}}). \]
\[ \operatorname{P}(\chi) \cap \operatorname{S}(W_{\geqslant -1}) = \operatorname{P}(\chi|_{W_{\geqslant -1}}). \]
(b) Let
 $\mathfrak g$ be
$\mathfrak g$ be  $W$,
$W$,  $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or  $W_{\geqslant 1}$ and pick
$W_{\geqslant 1}$ and pick  $\chi \in \mathfrak g^*$. Then
$\chi \in \mathfrak g^*$. Then
 \[ \dim \mathbb{O}(\chi) = \operatorname{GKdim} \operatorname{S}(\mathfrak g)/\operatorname{P}(\chi) = \dim \mathfrak g \cdot \chi. \]
\[ \dim \mathbb{O}(\chi) = \operatorname{GKdim} \operatorname{S}(\mathfrak g)/\operatorname{P}(\chi) = \dim \mathfrak g \cdot \chi. \]
We alert the reader that the proof of Proposition 4.3.6 establishes notation that is also used in the proof of Theorem 4.3.1. (This notation generalises that used in the proof of the last part of Corollary 4.2.9.)
Proof. (a) If ![]() $\chi$ is not local, then by Theorems 3.2.1 and 3.1.1
$\chi$ is not local, then by Theorems 3.2.1 and 3.1.1 ![]() $\operatorname {P}(\chi )$ and
$\operatorname {P}(\chi )$ and ![]() $\operatorname {P}(\chi |_{W_{\geqslant -1}})$ are the zero ideals, respectively, of
$\operatorname {P}(\chi |_{W_{\geqslant -1}})$ are the zero ideals, respectively, of ![]() $\operatorname {S}(W)$ and
$\operatorname {S}(W)$ and ![]() $\operatorname {S}(W_{\geqslant -1})$.
$\operatorname {S}(W_{\geqslant -1})$.
Thus, we may assume that ![]() $\chi$ is local. Write
$\chi$ is local. Write ![]() $\chi = \sum _{i=1}^\ell \chi _i$ with
$\chi = \sum _{i=1}^\ell \chi _i$ with ![]() $\chi _i \in \textit {Loc}_{x_i}$ and
$\chi _i \in \textit {Loc}_{x_i}$ and ![]() $x_i \neq x_j$ if
$x_i \neq x_j$ if ![]() $i\neq j$; further, assume that no
$i\neq j$; further, assume that no ![]() $\chi _i =0$. Let
$\chi _i =0$. Let ![]() $n$ be the order of
$n$ be the order of ![]() $\chi$.
$\chi$.
Let ![]() $X := (\widetilde {\textit {Loc}}^{\leqslant n}_{W_{\geqslant -1}})^{\times \ell }$, let
$X := (\widetilde {\textit {Loc}}^{\leqslant n}_{W_{\geqslant -1}})^{\times \ell }$, let ![]() $Y :=(\widetilde {\textit {Loc}}^{\leqslant n}_{W})^{\times \ell }$ and let
$Y :=(\widetilde {\textit {Loc}}^{\leqslant n}_{W})^{\times \ell }$ and let ![]() $U \subseteq Y$ be the complement of all the diagonals
$U \subseteq Y$ be the complement of all the diagonals ![]() $\Delta _{ij}$ in
$\Delta _{ij}$ in ![]() $Y$, where for
$Y$, where for ![]() $i \neq j$ we define
$i \neq j$ we define
where ![]() $\underline {\alpha }^i$ stands for the sequence
$\underline {\alpha }^i$ stands for the sequence ![]() $\underline {\alpha }^i_0, \underline {\alpha }^i_1, \ldots\, $. That is,
$\underline {\alpha }^i_0, \underline {\alpha }^i_1, \ldots\, $. That is, ![]() $U$ gives representations of local functions as sums of one-point local functions based at distinct points. Note that
$U$ gives representations of local functions as sums of one-point local functions based at distinct points. Note that ![]() $U, Y$ are open subsets of
$U, Y$ are open subsets of ![]() $X$, and
$X$, and ![]() $H:= (\widehat {\textit {DLoc}}^{\leqslant n})^{\times \ell }$ acts on
$H:= (\widehat {\textit {DLoc}}^{\leqslant n})^{\times \ell }$ acts on ![]() $X$. Let
$X$. Let ![]() $\Sigma _W: (W^*)^{\times \ell } \to W^*$ be the summation map, and likewise define
$\Sigma _W: (W^*)^{\times \ell } \to W^*$ be the summation map, and likewise define ![]() $\Sigma _{W_{\geqslant -1}}$. Let
$\Sigma _{W_{\geqslant -1}}$. Let ![]() $\phi _W: U \to W^*$ be
$\phi _W: U \to W^*$ be ![]() $\Sigma _W \circ (\phi _W^{\leqslant n})^{\times \ell }$ and let
$\Sigma _W \circ (\phi _W^{\leqslant n})^{\times \ell }$ and let ![]() $\phi _{W_{\geqslant -1}}: X \to W_{\geqslant -1}^*$ be
$\phi _{W_{\geqslant -1}}: X \to W_{\geqslant -1}^*$ be ![]() $\Sigma _{W_{\geqslant -1}} \circ (\phi _{W_{\geqslant -1}}^{\leqslant n})^{\times \ell }$. There is a commutative diagram
$\Sigma _{W_{\geqslant -1}} \circ (\phi _{W_{\geqslant -1}}^{\leqslant n})^{\times \ell }$. There is a commutative diagram

where the right vertical arrow is restriction. This induces maps

By Lemma 4.3.4, ![]() $\dim W \cdot \chi = \oplus _i \dim W \cdot \chi _i$, which is
$\dim W \cdot \chi = \oplus _i \dim W \cdot \chi _i$, which is ![]() $\dim ((\widehat {\operatorname {lie}}^{\leqslant n})^{\times \ell }) \cdot \chi$ by Lemma 4.1.6. Let
$\dim ((\widehat {\operatorname {lie}}^{\leqslant n})^{\times \ell }) \cdot \chi$ by Lemma 4.1.6. Let ![]() $y \in \phi _W^{-1}(\chi )$. By Proposition 2.3.1,
$y \in \phi _W^{-1}(\chi )$. By Proposition 2.3.1, ![]() $\operatorname {P}(\chi )$ is the full preimage under
$\operatorname {P}(\chi )$ is the full preimage under ![]() $\phi _W^*$ of
$\phi _W^*$ of ![]() $I^U(Hy)$ and, likewise,
$I^U(Hy)$ and, likewise, ![]() $\operatorname {P}(\chi |_{W_{\geqslant -1}})$ is the full preimage under
$\operatorname {P}(\chi |_{W_{\geqslant -1}})$ is the full preimage under ![]() $\phi _{W_{\geqslant -1}}^*$ of
$\phi _{W_{\geqslant -1}}^*$ of ![]() $I^U(Hy)$. By commutativity of (
$I^U(Hy)$. By commutativity of (
), this is ![]() $\operatorname {P}(\chi ) \cap \operatorname {S}(W_{\geqslant -1})$.
$\operatorname {P}(\chi ) \cap \operatorname {S}(W_{\geqslant -1})$.
(b) If ![]() $\dim \mathfrak g\cdot \chi =\infty$, then the result follows from Lemma 2.1.1. Thus, we can assume
$\dim \mathfrak g\cdot \chi =\infty$, then the result follows from Lemma 2.1.1. Thus, we can assume ![]() $\mathfrak g\cdot \chi <\infty$. For
$\mathfrak g\cdot \chi <\infty$. For ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $W_{\geqslant -1}$ this follows from the previous discussion and Proposition 2.3.1; see, in particular, (2.3.3). The proof for
$W_{\geqslant -1}$ this follows from the previous discussion and Proposition 2.3.1; see, in particular, (2.3.3). The proof for ![]() $\mathfrak g = W_{\geqslant 1}$ is similar.
$\mathfrak g = W_{\geqslant 1}$ is similar.
We now give the proof of Theorem 4.3.1.
Proof of Theorem 4.3.1 We give the proof for the case ![]() $\mathfrak g=W$.
$\mathfrak g=W$.
By definition, ![]() $\mathbb {O}(\chi ^{I}) = \mathbb {O}(\chi ^{II})$ if and only if
$\mathbb {O}(\chi ^{I}) = \mathbb {O}(\chi ^{II})$ if and only if ![]() $\operatorname {P}(\chi ^{I}) = \operatorname {P}(\chi ^{II})$. Thus, we compute the Poisson cores of
$\operatorname {P}(\chi ^{I}) = \operatorname {P}(\chi ^{II})$. Thus, we compute the Poisson cores of ![]() $\chi ^{I}$ and
$\chi ^{I}$ and ![]() $\chi ^{II}$.
$\chi ^{II}$.
First, by changing ![]() $\ell$ and switching
$\ell$ and switching ![]() $\chi ^{I}$ and
$\chi ^{I}$ and ![]() $\chi ^{II}$ if necessary, we may assume that none of the
$\chi ^{II}$ if necessary, we may assume that none of the ![]() $\chi _i^{I}$ are zero. Let
$\chi _i^{I}$ are zero. Let ![]() $n$ be the maximum of the orders of
$n$ be the maximum of the orders of ![]() $\chi ^{I}$ and of
$\chi ^{I}$ and of ![]() $\chi ^{II}$; thus, both are in the image of
$\chi ^{II}$; thus, both are in the image of ![]() $(\textit {Loc}_W^{\leqslant n})^{\times \ell }$.
$(\textit {Loc}_W^{\leqslant n})^{\times \ell }$.
Define ![]() $U, V, X, H$ as in the proof of Proposition 4.3.6, and set up maps as in (4.3.7) and (4.3.8). Let
$U, V, X, H$ as in the proof of Proposition 4.3.6, and set up maps as in (4.3.7) and (4.3.8). Let ![]() $\phi = \phi _W$. Then
$\phi = \phi _W$. Then ![]() $\chi ^{I} = \phi (y^{I})$,
$\chi ^{I} = \phi (y^{I})$, ![]() $\chi ^{II} = \phi (y^{II})$ for some
$\chi ^{II} = \phi (y^{II})$ for some ![]() $y^{I}, y^{II}\in U$. As in the proof of Proposition 4.3.6,
$y^{I}, y^{II}\in U$. As in the proof of Proposition 4.3.6, ![]() $\operatorname {P}(\chi ^{I})$ is the full preimage under
$\operatorname {P}(\chi ^{I})$ is the full preimage under ![]() ${\phi }^*$ of the defining ideal of
${\phi }^*$ of the defining ideal of ![]() $I^U(Hy^{I})$. Likewise,
$I^U(Hy^{I})$. Likewise, ![]() $\operatorname {P}(\chi ^{II})$ is the full preimage under
$\operatorname {P}(\chi ^{II})$ is the full preimage under ![]() ${\phi }^*$ of the defining ideal of
${\phi }^*$ of the defining ideal of ![]() $I^U(Hy^{II})$.
$I^U(Hy^{II})$.
Note that ![]() $\phi$ factors through the dominant map
$\phi$ factors through the dominant map ![]() $U \to U/{\mathfrak S}_{\ell }$, where
$U \to U/{\mathfrak S}_{\ell }$, where ![]() $\mathfrak S_\ell$ is the symmetric group. It is clear that if we can reorder the
$\mathfrak S_\ell$ is the symmetric group. It is clear that if we can reorder the ![]() $\chi _i^{I}$ and
$\chi _i^{I}$ and ![]() $\chi _i^{II}$ as described, then
$\chi _i^{II}$ as described, then ![]() $\operatorname {P}(\chi ^{I}) = \operatorname {P}(\chi ^{II})$.
$\operatorname {P}(\chi ^{I}) = \operatorname {P}(\chi ^{II})$.
Suppose now that ![]() $\operatorname {P}(\chi ^{I}) = \operatorname {P}(\chi ^{II})$. Then by Proposition 2.3.1(c), there are open sets
$\operatorname {P}(\chi ^{I}) = \operatorname {P}(\chi ^{II})$. Then by Proposition 2.3.1(c), there are open sets ![]() $U^{I}\subseteq Hy^{I}\cap U$ and
$U^{I}\subseteq Hy^{I}\cap U$ and ![]() $U^{II}\subseteq Hy^{II}\cap U$ such that their images in
$U^{II}\subseteq Hy^{II}\cap U$ such that their images in ![]() $W^*$ are the same. In particular, there are
$W^*$ are the same. In particular, there are ![]() $h_1^{I}, h_1^{II}, \ldots, h_\ell ^{I}, h_\ell ^{II} \in \widehat {\textit {DLoc}}^{\leqslant n}$, with
$h_1^{I}, h_1^{II}, \ldots, h_\ell ^{I}, h_\ell ^{II} \in \widehat {\textit {DLoc}}^{\leqslant n}$, with ![]() $(h_1^{I}\chi _1^{I}, \ldots, h_\ell ^{I}\chi _\ell ^{I}) \in U$ and so that
$(h_1^{I}\chi _1^{I}, \ldots, h_\ell ^{I}\chi _\ell ^{I}) \in U$ and so that ![]() $\sum h_i^{I} \chi _i^{I} - \sum h_i^{II} \chi _i^{II} = 0$. Now, a set of one-point local functions with distinct base points is linearly independent. As, by the definition of
$\sum h_i^{I} \chi _i^{I} - \sum h_i^{II} \chi _i^{II} = 0$. Now, a set of one-point local functions with distinct base points is linearly independent. As, by the definition of ![]() $U$, the base points of the one-point local functions
$U$, the base points of the one-point local functions ![]() $h_i^{I} \chi _i^{I}$ are distinct, the only option is that the supports of
$h_i^{I} \chi _i^{I}$ are distinct, the only option is that the supports of ![]() $\sum h_i^{I} \chi _i^{I}$ and
$\sum h_i^{I} \chi _i^{I}$ and ![]() $\sum h_i^{II} \chi _i^{II}$ are equal and we can reorder
$\sum h_i^{II} \chi _i^{II}$ are equal and we can reorder ![]() $\chi _1^{II}, \ldots, \chi _\ell ^{II}$ so that
$\chi _1^{II}, \ldots, \chi _\ell ^{II}$ so that ![]() $h_i^{I} \chi _i^{I} = h_i^{II} \chi _i^{II}$ for all
$h_i^{I} \chi _i^{I} = h_i^{II} \chi _i^{II}$ for all ![]() $i$. This is clearly equivalent to (4.3.2).
$i$. This is clearly equivalent to (4.3.2).
Remark 4.3.9 Let ![]() $\mathfrak g = V\!ir$,
$\mathfrak g = V\!ir$, ![]() $W$ or
$W$ or ![]() $W_{\geqslant -1}$ and let
$W_{\geqslant -1}$ and let ![]() $\chi \in \mathfrak g^*$. If
$\chi \in \mathfrak g^*$. If ![]() $\chi$ is not local, then
$\chi$ is not local, then ![]() $\operatorname {P}(\chi ) = (0)$ (if
$\operatorname {P}(\chi ) = (0)$ (if ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $W_{\geqslant -1}$) or
$W_{\geqslant -1}$) or ![]() $\operatorname {P}(\chi ) = (z- \chi (z))$ (if
$\operatorname {P}(\chi ) = (z- \chi (z))$ (if ![]() $\mathfrak g = V\!ir$). If
$\mathfrak g = V\!ir$). If ![]() $\chi$ is local, then by Lemma 2.0.4(a) we may construct
$\chi$ is local, then by Lemma 2.0.4(a) we may construct ![]() $\operatorname {P}(\chi ) = \bigcap \{ \mathfrak m_\nu \,|\, \nu \in \mathbb {O}(\chi )\}$ from Theorem 4.3.1.
$\operatorname {P}(\chi ) = \bigcap \{ \mathfrak m_\nu \,|\, \nu \in \mathbb {O}(\chi )\}$ from Theorem 4.3.1.
Further combining Corollary 4.2.11 with Theorem 4.3.1 one may, in principle, compute all the Poisson primitive ideals of ![]() $\operatorname {S}(W)$ or
$\operatorname {S}(W)$ or ![]() $\operatorname {S}(W_{\geqslant -1})$; the function
$\operatorname {S}(W_{\geqslant -1})$; the function ![]() $F_{2k+1}$ whose fibres by Corollary 4.2.11 give the pseudo-orbits of a one-point local function of order
$F_{2k+1}$ whose fibres by Corollary 4.2.11 give the pseudo-orbits of a one-point local function of order ![]() $2k+1$ may be worked out using Lemma 4.1.7 for any
$2k+1$ may be worked out using Lemma 4.1.7 for any ![]() $k$. There is an example of this in § 2.2, although we have not given a fully general formula.
$k$. There is an example of this in § 2.2, although we have not given a fully general formula.
Note also that we have not studied generators (in any sense) for the Poisson prime ideals ![]() $\operatorname {P}(\chi )$, and this might be an interesting subject of research.
$\operatorname {P}(\chi )$, and this might be an interesting subject of research.
A version of Theorem 4.3.1 holds for ![]() $W_{\geqslant 1}$ and
$W_{\geqslant 1}$ and ![]() $W_{\geqslant 0}$ with almost the same proof. We state it as follows.
$W_{\geqslant 0}$ with almost the same proof. We state it as follows.
Theorem 4.3.10 Let ![]() $\mathfrak g=W_{\geqslant 0}$ or
$\mathfrak g=W_{\geqslant 0}$ or ![]() $W_{\geqslant 1}$. Let
$W_{\geqslant 1}$. Let ![]() $\chi ^{I}, \chi ^{II}\in \mathfrak g^*$ be local functions. Then there are unique local functions
$\chi ^{I}, \chi ^{II}\in \mathfrak g^*$ be local functions. Then there are unique local functions ![]() $\chi _W^{I}, \chi _W^{II}\in W^*$ and
$\chi _W^{I}, \chi _W^{II}\in W^*$ and ![]() $\chi ^{I}_{[0]}, \chi ^{II}_{[0]}\in \textit {Loc}_0$ such that
$\chi ^{I}_{[0]}, \chi ^{II}_{[0]}\in \textit {Loc}_0$ such that
Moreover, ![]() $\operatorname {P}(\chi ^{I})=\operatorname {P}(\chi ^{II} )$ if and only if
$\operatorname {P}(\chi ^{I})=\operatorname {P}(\chi ^{II} )$ if and only if ![]() $\operatorname {P}(\chi ^{I}_{W})=\operatorname {P}(\chi ^{II}_{W} )$ and
$\operatorname {P}(\chi ^{I}_{W})=\operatorname {P}(\chi ^{II}_{W} )$ and ![]() $\textit {DLoc}_0(\chi ^{I}_{[0]})=\textit {DLoc}_0(\chi ^{II}_{[0]})$.
$\textit {DLoc}_0(\chi ^{I}_{[0]})=\textit {DLoc}_0(\chi ^{II}_{[0]})$.
The description of pseudo-orbits in Theorem 4.3.1 has several immediate applications. We start by comparing pseudo-orbits in ![]() $W^*$ and
$W^*$ and ![]() $W^*_{\geqslant -1}$.
$W^*_{\geqslant -1}$.
Corollary 4.3.11 Let ![]() $\chi ^{I}, \chi ^{II}\in W^*$ be local functions. Then
$\chi ^{I}, \chi ^{II}\in W^*$ be local functions. Then
Further, restriction induces a bijection
In Corollary 5.2.14 we show that restriction also provides a bijection between Poisson prime ideals of ![]() $\operatorname {S}(W)$ and
$\operatorname {S}(W)$ and ![]() $\operatorname {S}(W_{\geqslant -1})$.
$\operatorname {S}(W_{\geqslant -1})$.
Proof. The first statement is immediate from Theorem 4.3.1. By that result, if ![]() $\chi \in W_{\geqslant -1}^*$ is a local function, then there is
$\chi \in W_{\geqslant -1}^*$ is a local function, then there is ![]() $\nu \in \mathbb {O}(\chi )$ so that
$\nu \in \mathbb {O}(\chi )$ so that ![]() $0$ is not in the support of
$0$ is not in the support of ![]() $\nu$. Thus, restriction of local functions induces a bijection on pseudo-orbits.
$\nu$. Thus, restriction of local functions induces a bijection on pseudo-orbits.
By Lemma 2.0.4 there are bijections
 \begin{align*} {\rm nonzero}\ & \text{Poisson primitive ideals of}\ \text{S}(W) \leftrightarrow \text{pseudo-orbits in}\ W^{\ast}\\ &\quad \leftrightarrow \text{pseudo-orbits in}\ W^{\ast}_{\geqslant\, -1} \leftrightarrow \text{nonzero Poisson primitive ideals of}\ {\rm S}(W_{\geqslant\, -1}), \end{align*}
\begin{align*} {\rm nonzero}\ & \text{Poisson primitive ideals of}\ \text{S}(W) \leftrightarrow \text{pseudo-orbits in}\ W^{\ast}\\ &\quad \leftrightarrow \text{pseudo-orbits in}\ W^{\ast}_{\geqslant\, -1} \leftrightarrow \text{nonzero Poisson primitive ideals of}\ {\rm S}(W_{\geqslant\, -1}), \end{align*}
where the middle bijection comes from restriction of local functions as in the first paragraph of the proof. By Proposition 4.3.6(a) ![]() $\operatorname {P}(\chi ) \cap \operatorname {S}(W_{\geqslant -1}) = \operatorname {P}(\chi |_{W_{\geqslant -1}})$. Thus, the bijection from left to right above agrees with restriction of ideals from
$\operatorname {P}(\chi ) \cap \operatorname {S}(W_{\geqslant -1}) = \operatorname {P}(\chi |_{W_{\geqslant -1}})$. Thus, the bijection from left to right above agrees with restriction of ideals from ![]() $\operatorname {S}(W)$ to
$\operatorname {S}(W)$ to ![]() $\operatorname {S}(W_{\geqslant -1})$.
$\operatorname {S}(W_{\geqslant -1})$.
Remark 4.3.13 Let ![]() $P = \operatorname {P}(\chi )$ be a Poisson primitive ideal of
$P = \operatorname {P}(\chi )$ be a Poisson primitive ideal of ![]() $\operatorname {S}(W_{\geqslant -1})$, where
$\operatorname {S}(W_{\geqslant -1})$, where ![]() $\chi \in (W_{\geqslant -1})^*$ is local. As we may apply elements of
$\chi \in (W_{\geqslant -1})^*$ is local. As we may apply elements of ![]() $\textit {Shifts}$ to
$\textit {Shifts}$ to ![]() $\chi$ without affecting
$\chi$ without affecting ![]() $\operatorname {P}(\chi )$, we may assume that
$\operatorname {P}(\chi )$, we may assume that ![]() $\chi$ does not involve any element of
$\chi$ does not involve any element of ![]() $\textit {Loc}_0$. Then
$\textit {Loc}_0$. Then ![]() $\chi$ extends uniquely to a local function
$\chi$ extends uniquely to a local function ![]() $\widetilde {\chi }$ on
$\widetilde {\chi }$ on ![]() $W$, and we have seen that
$W$, and we have seen that ![]() $\operatorname {P}(\chi ) = \operatorname {P}(\widetilde {\chi }) \cap \operatorname {S}(W_{\geqslant -1})$.
$\operatorname {P}(\chi ) = \operatorname {P}(\widetilde {\chi }) \cap \operatorname {S}(W_{\geqslant -1})$.
Let ![]() $\gamma \in \Bbbk$ and recall the definition of the map
$\gamma \in \Bbbk$ and recall the definition of the map ![]() $p_\gamma$ of (2.2.2) and the fact, proved in Lemma 2.2.3 that
$p_\gamma$ of (2.2.2) and the fact, proved in Lemma 2.2.3 that ![]() $\ker p_\gamma = \operatorname {P}(\chi _{x;\alpha, \gamma })$.
$\ker p_\gamma = \operatorname {P}(\chi _{x;\alpha, \gamma })$.
Proposition 4.3.14 The ideals ![]() $\ker p_\gamma$ are all of the Poisson prime ideals of
$\ker p_\gamma$ are all of the Poisson prime ideals of ![]() $\operatorname {S}(W)$ of co-GK 2.
$\operatorname {S}(W)$ of co-GK 2.
Proof. Let ![]() $J(\gamma ) = \ker p_\gamma$ for all
$J(\gamma ) = \ker p_\gamma$ for all ![]() $\gamma \in \Bbbk$. Let
$\gamma \in \Bbbk$. Let ![]() $J$ be a prime Poisson ideal of
$J$ be a prime Poisson ideal of ![]() $\operatorname {S}(W)$ with
$\operatorname {S}(W)$ with ![]() $\operatorname {GKdim} \operatorname {S}(W)/J = 2$. By Lemma 2.0.4
$\operatorname {GKdim} \operatorname {S}(W)/J = 2$. By Lemma 2.0.4
Fix such ![]() $\chi$. By Lemma 2.1.1
$\chi$. By Lemma 2.1.1 ![]() $\operatorname {rk} B_\chi$, which must be even as
$\operatorname {rk} B_\chi$, which must be even as ![]() $B_\chi$ is an alternating form, is zero or two. The only
$B_\chi$ is an alternating form, is zero or two. The only ![]() $\chi \in W^*$ with
$\chi \in W^*$ with ![]() $\operatorname {rk} B_\chi = 0$ is
$\operatorname {rk} B_\chi = 0$ is ![]() $\chi = 0$; as
$\chi = 0$; as ![]() $J \neq \operatorname {P}(0) = \mathfrak m_0$ there is some
$J \neq \operatorname {P}(0) = \mathfrak m_0$ there is some ![]() $\nu \in W^*$ with
$\nu \in W^*$ with ![]() $\operatorname {ev}_\nu (J) = 0$ and
$\operatorname {ev}_\nu (J) = 0$ and ![]() $\operatorname {rk} B_\nu = 2$.
$\operatorname {rk} B_\nu = 2$.
If ![]() $J \subsetneqq \operatorname {P}(\nu )$, then
$J \subsetneqq \operatorname {P}(\nu )$, then ![]() $2 = \operatorname {GKdim} \operatorname {S}(W)/J > \operatorname {GKdim}\operatorname {S}(W)/\operatorname {P}(\nu )$, but this last is
$2 = \operatorname {GKdim} \operatorname {S}(W)/J > \operatorname {GKdim}\operatorname {S}(W)/\operatorname {P}(\nu )$, but this last is ![]() $\dim W \cdot \nu$ by Proposition 4.3.6, which must be an even positive integer. Thus,
$\dim W \cdot \nu$ by Proposition 4.3.6, which must be an even positive integer. Thus, ![]() $J = \operatorname {P}(\nu )$ and
$J = \operatorname {P}(\nu )$ and ![]() $\dim W\cdot \nu = 2$.
$\dim W\cdot \nu = 2$.
Lemma 4.3.4 implies that ![]() $\nu$ is a one-point local function, and by Theorem 4.2.1 we must have
$\nu$ is a one-point local function, and by Theorem 4.2.1 we must have ![]() $\nu = \chi _{x; \alpha, \gamma }$ for some
$\nu = \chi _{x; \alpha, \gamma }$ for some ![]() $x \in \Bbbk ^\times, \alpha, \gamma \in \Bbbk$. Thus,
$x \in \Bbbk ^\times, \alpha, \gamma \in \Bbbk$. Thus, ![]() $J = \operatorname {P}(\nu ) = J(\gamma )$.
$J = \operatorname {P}(\nu ) = J(\gamma )$.
Remark 4.3.15 The codomain of the maps ![]() $p_\gamma$ of (2.2.2) is the localised Poisson–Weyl algebra
$p_\gamma$ of (2.2.2) is the localised Poisson–Weyl algebra ![]() $B = \Bbbk [t, t^{-1}, y]$ with
$B = \Bbbk [t, t^{-1}, y]$ with ![]() $\{ y, t \}= 1$. Define a Poisson bracket on
$\{ y, t \}= 1$. Define a Poisson bracket on ![]() $B[s]$ by setting
$B[s]$ by setting ![]() $s$ to be Poisson central, and define
$s$ to be Poisson central, and define
As in § 2.2, it is easy to check that ![]() $\Phi$ is a Poisson map. One can show using the methods of the proof of Proposition 4.3.14 that
$\Phi$ is a Poisson map. One can show using the methods of the proof of Proposition 4.3.14 that ![]() $\ker \Phi$ is the unique prime Poisson ideal of
$\ker \Phi$ is the unique prime Poisson ideal of ![]() $\operatorname {S}(W)$ of co-GK 3. This is proved in Remark 5.2.11 with a different argument, so we do not give a proof here.
$\operatorname {S}(W)$ of co-GK 3. This is proved in Remark 5.2.11 with a different argument, so we do not give a proof here.
Let ![]() $\mathfrak g$ be a Lie algebra and let
$\mathfrak g$ be a Lie algebra and let ![]() $\chi \in \mathfrak g^*$. The closure of
$\chi \in \mathfrak g^*$. The closure of ![]() $\mathbb {O}(\chi )$ is, by definition,
$\mathbb {O}(\chi )$ is, by definition, ![]() $V(\operatorname {P}(\chi ))$. We call
$V(\operatorname {P}(\chi ))$. We call ![]() $V(\operatorname {P}(\chi )) =\overline {\mathbb {O}(\chi )}$ the orbit closure of
$V(\operatorname {P}(\chi )) =\overline {\mathbb {O}(\chi )}$ the orbit closure of ![]() $\chi$. (Technically, this term should probably be ‘pseudo-orbit closure’; we have used wording which we find more pleasant at the cost of a slight abuse of terminology.) Note that
$\chi$. (Technically, this term should probably be ‘pseudo-orbit closure’; we have used wording which we find more pleasant at the cost of a slight abuse of terminology.) Note that ![]() $\mu$ is in the orbit closure of
$\mu$ is in the orbit closure of ![]() $\chi$ if and only if
$\chi$ if and only if ![]() $\operatorname {P}(\mu )\supseteq \operatorname {P}(\chi )$.
$\operatorname {P}(\mu )\supseteq \operatorname {P}(\chi )$.
The orbit closure relations for one-point local functions are essentially given by Corollary 4.2.9, but for arbitrary local functions they are quite complex. Consider the following example, which for simplicity we give for ![]() $W_{\geqslant -1}$ only.
$W_{\geqslant -1}$ only.
Example 4.3.16 Let ![]() $\Bbbk = \mathbb {C}$, let
$\Bbbk = \mathbb {C}$, let ![]() $x \neq y \in \mathbb {C}$ and let
$x \neq y \in \mathbb {C}$ and let ![]() $a,b,c,d \in \mathbb {C}$ with
$a,b,c,d \in \mathbb {C}$ with ![]() $(a,b)$ not both zero and likewise for
$(a,b)$ not both zero and likewise for ![]() $(c,d)$. Let
$(c,d)$. Let ![]() $\chi = \chi _{x;a,b} + \chi _{y; c, d}$. We claim that
$\chi = \chi _{x;a,b} + \chi _{y; c, d}$. We claim that ![]() $Loc_{W_{\geqslant -1}}^{\leqslant 1} \subseteq \overline {\mathbb {O}(\chi )}$ and, in particular,
$Loc_{W_{\geqslant -1}}^{\leqslant 1} \subseteq \overline {\mathbb {O}(\chi )}$ and, in particular, ![]() $\overline {\mathbb {O}(\chi )}$ contains the functions
$\overline {\mathbb {O}(\chi )}$ contains the functions ![]() $0$,
$0$, ![]() $\chi _{x;a,b}$ and
$\chi _{x;a,b}$ and ![]() $\chi _{y;c,d}$.
$\chi _{y;c,d}$.
To see this, let ![]() $\gamma,s \in \mathbb {C}^\times$. Consider the local function
$\gamma,s \in \mathbb {C}^\times$. Consider the local function
By Theorems 4.3.1 and 4.2.1, the ![]() $\chi (\gamma,s)$ are all in
$\chi (\gamma,s)$ are all in ![]() $\mathbb {O}(\chi )$. For
$\mathbb {O}(\chi )$. For ![]() $f \in \Bbbk [t]$, we have
$f \in \Bbbk [t]$, we have
As Zariski closed sets are closed in the complex analytic topology,
for any ![]() $\gamma$. Applying Corollary 4.2.9,
$\gamma$. Applying Corollary 4.2.9, ![]() $\overline {\mathbb {O}(\chi )}$ contains all of
$\overline {\mathbb {O}(\chi )}$ contains all of ![]() $\textit {Loc}_{W_{\geqslant -1}}^{\leqslant 1}$.
$\textit {Loc}_{W_{\geqslant -1}}^{\leqslant 1}$.
The same statement holds for arbitrary ![]() $\Bbbk$ by the Lefschetz principle.
$\Bbbk$ by the Lefschetz principle.
Although arbitrary orbit closures are complicated, we are able to give a partial description of orbit closures of general local functions in the next corollary.
Corollary 4.3.17 Let ![]() $\mathfrak g = V\!ir$,
$\mathfrak g = V\!ir$, ![]() $W$,
$W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$.
$W_{\geqslant 1}$.
(a) Let
 $\mu, \chi \in \mathfrak g^*$ be local functions with disjoint support and let
$\mu, \chi \in \mathfrak g^*$ be local functions with disjoint support and let  $\nu$ be in the orbit closure of
$\nu$ be in the orbit closure of  $\mu$. Then
$\mu$. Then  $\nu + \chi$ is in the orbit closure of
$\nu + \chi$ is in the orbit closure of  $\mu + \chi$.
$\mu + \chi$.(b) Let
 $\chi$ be a local function. Then
$\chi$ be a local function. Then  $0$ is not in the orbit closure of
$0$ is not in the orbit closure of  $\chi$ if and only if
$\chi$ if and only if  $\lambda (\chi ) = (2)$, i.e.
$\lambda (\chi ) = (2)$, i.e.  $\chi = \chi _{x;\alpha, \beta }$ for some
$\chi = \chi _{x;\alpha, \beta }$ for some  $\beta \in \Bbbk ^\times$.
$\beta \in \Bbbk ^\times$.
Proof. For part (a), by Theorem 4.3.1, the pseudo-orbit of ![]() $\mu +\chi$ consists of all local functions of the form
$\mu +\chi$ consists of all local functions of the form ![]() $\mu '+\chi '$ where
$\mu '+\chi '$ where ![]() $\mu ' \in \mathbb {O}(\mu )$,
$\mu ' \in \mathbb {O}(\mu )$, ![]() $\chi ' \in \mathbb {O}(\chi )$ and the supports of
$\chi ' \in \mathbb {O}(\chi )$ and the supports of ![]() $\mu '$ and
$\mu '$ and ![]() $\chi '$ are disjoint. A modification of Corollary 4.2.9 for the multipoint case implies that the orbit closure
$\chi '$ are disjoint. A modification of Corollary 4.2.9 for the multipoint case implies that the orbit closure ![]() $\overline {\mathbb {O}(\mu +\chi )}$ contains
$\overline {\mathbb {O}(\mu +\chi )}$ contains ![]() $\nu +\chi$.
$\nu +\chi$.
For part (b), Corollary 4.2.9 gives that if ![]() $\lambda (\chi ) = (2)$, then
$\lambda (\chi ) = (2)$, then ![]() $0 \not \in \overline {\mathbb {O}(\chi )}$.
$0 \not \in \overline {\mathbb {O}(\chi )}$.
Assume now that ![]() $0 \not \in \overline {\mathbb {O}(\chi )}$. Write
$0 \not \in \overline {\mathbb {O}(\chi )}$. Write
where the ![]() $\mu _i, \nu _j$ are 1-point local functions supported at distinct points, the
$\mu _i, \nu _j$ are 1-point local functions supported at distinct points, the ![]() $\mu _i$ have order zero or one and the
$\mu _i$ have order zero or one and the ![]() $\nu _j$ have order
$\nu _j$ have order ![]() $n_j > 1$. By part (a),
$n_j > 1$. By part (a), ![]() $0$ must not be in the orbit closure of at least one of the component 1-point local functions of
$0$ must not be in the orbit closure of at least one of the component 1-point local functions of ![]() $\chi$, so
$\chi$, so ![]() $\ell \geqslant 1$ by Corollary 4.2.9.
$\ell \geqslant 1$ by Corollary 4.2.9.
Write ![]() $\mu _i = \chi _{x_i;\beta _i, \gamma _i}$ and
$\mu _i = \chi _{x_i;\beta _i, \gamma _i}$ and ![]() $\nu _j = \chi _{y_j; \alpha ^j_0, \ldots, \alpha ^j_{n_j}}$, where
$\nu _j = \chi _{y_j; \alpha ^j_0, \ldots, \alpha ^j_{n_j}}$, where ![]() $\alpha ^j_{n_j} \neq 0$. If
$\alpha ^j_{n_j} \neq 0$. If ![]() $r \geqslant 1$, then let
$r \geqslant 1$, then let ![]() $\mu _i' = \chi _{y_1;\beta _i,\gamma _i}$. As we may move points within an orbit,
$\mu _i' = \chi _{y_1;\beta _i,\gamma _i}$. As we may move points within an orbit,
which is a 1-point local function of order ![]() $n_1 > 1$, is in the orbit closure of
$n_1 > 1$, is in the orbit closure of ![]() $\mu _1 + \cdots +\mu _\ell + \nu _1$. By part (a) and the previous paragraph, then 0 is in the orbit closure of
$\mu _1 + \cdots +\mu _\ell + \nu _1$. By part (a) and the previous paragraph, then 0 is in the orbit closure of ![]() $\chi$, a contradiction. Thus,
$\chi$, a contradiction. Thus, ![]() $r=0$.
$r=0$.
If ![]() $\ell \geqslant 2$, then, applying Example 4.3.16 and part (a) repeatedly, we have
$\ell \geqslant 2$, then, applying Example 4.3.16 and part (a) repeatedly, we have ![]() $0 \in \overline {\mathbb {O}(\chi )}$. Thus,
$0 \in \overline {\mathbb {O}(\chi )}$. Thus, ![]() $\ell =1$, and by Corollary 4.2.9
$\ell =1$, and by Corollary 4.2.9 ![]() $\chi = \mu _1$ must have order 1.
$\chi = \mu _1$ must have order 1.
We now apply our results to classify maximal Poisson ideals of ![]() $\operatorname {S}(V\!ir)$.
$\operatorname {S}(V\!ir)$.
Corollary 4.3.18 The maximal Poisson ideals of ![]() $\operatorname {S}(V\!ir)$ are the ideals
$\operatorname {S}(V\!ir)$ are the ideals ![]() $(z-\zeta )$ for
$(z-\zeta )$ for ![]() $\zeta \in \Bbbk ^\times$, the ideals
$\zeta \in \Bbbk ^\times$, the ideals ![]() $\operatorname {P}(\chi _{1;0, \gamma })$ for
$\operatorname {P}(\chi _{1;0, \gamma })$ for ![]() $\gamma \in \Bbbk ^\times$, and the augmentation ideal
$\gamma \in \Bbbk ^\times$, and the augmentation ideal ![]() $\operatorname {P}(0)$.
$\operatorname {P}(0)$.
Proof. That ![]() $(z-\zeta )$ is a maximal Poisson ideal if
$(z-\zeta )$ is a maximal Poisson ideal if ![]() $\zeta \in \Bbbk ^\times$ is Corollary 3.3.5. If
$\zeta \in \Bbbk ^\times$ is Corollary 3.3.5. If ![]() $Q$ is any other maximal Poisson ideal, then we must have
$Q$ is any other maximal Poisson ideal, then we must have ![]() $z \in Q$; it follows from the Nullstellensatz and Theorem 3.2.1 that there is a local function
$z \in Q$; it follows from the Nullstellensatz and Theorem 3.2.1 that there is a local function ![]() $\chi$ with
$\chi$ with ![]() $Q = \operatorname {P}(\chi )$. If
$Q = \operatorname {P}(\chi )$. If ![]() $\lambda (\chi ) \neq (2)$, then by Corollary 4.3.17 we have
$\lambda (\chi ) \neq (2)$, then by Corollary 4.3.17 we have ![]() $\operatorname {P}(\chi ) \subseteq \operatorname {P}(0)$, so we must have
$\operatorname {P}(\chi ) \subseteq \operatorname {P}(0)$, so we must have ![]() $\chi = 0$ and
$\chi = 0$ and ![]() $Q$ must be the augmentation ideal
$Q$ must be the augmentation ideal ![]() $\operatorname {P}(0)$.
$\operatorname {P}(0)$.
If ![]() $\lambda (\chi ) = (2)$, then
$\lambda (\chi ) = (2)$, then ![]() $\operatorname {P}(\chi )$ is maximal among Poisson primitive ideals by Corollaries 4.2.9 and 4.3.17, and thus maximal among Poisson ideals.
$\operatorname {P}(\chi )$ is maximal among Poisson primitive ideals by Corollaries 4.2.9 and 4.3.17, and thus maximal among Poisson ideals.
5. Prime Poisson ideals
In this section we apply our results on Poisson primitive ideals to the structure of arbitrary Poisson prime ideals of ![]() $\operatorname {S}(\mathfrak g)$, where
$\operatorname {S}(\mathfrak g)$, where ![]() $\mathfrak g$ is one of our Lie algebras of interest. After a preliminary subsection on birational maps in our context, we show that the partition data associated to local functions may be used to parameterise Poisson primes of
$\mathfrak g$ is one of our Lie algebras of interest. After a preliminary subsection on birational maps in our context, we show that the partition data associated to local functions may be used to parameterise Poisson primes of ![]() $\operatorname {S}(W)$ and
$\operatorname {S}(W)$ and ![]() $\operatorname {S}(W_{\geqslant 1})$. This will allow us to show that the bijection
$\operatorname {S}(W_{\geqslant 1})$. This will allow us to show that the bijection ![]() $\operatorname {PSpec}_{\rm prim}\operatorname {S}(W) \to \operatorname {PSpec}_{\rm prim}\operatorname {S}(W_{\geqslant -1})$ of Corollary 4.3.11 extends to prime Poisson ideals. We then investigate when the Poisson analogue of the Dixmier–Moeglin equivalence holds for
$\operatorname {PSpec}_{\rm prim}\operatorname {S}(W) \to \operatorname {PSpec}_{\rm prim}\operatorname {S}(W_{\geqslant -1})$ of Corollary 4.3.11 extends to prime Poisson ideals. We then investigate when the Poisson analogue of the Dixmier–Moeglin equivalence holds for ![]() $\operatorname {S}(\mathfrak g)$ and, in particular, when Poisson primitive ideals are locally closed in
$\operatorname {S}(\mathfrak g)$ and, in particular, when Poisson primitive ideals are locally closed in ![]() $\operatorname {PSpec} \operatorname {S}(\mathfrak g)$; we show that this is almost always, but not always, the case. Finally, we answer a question of León Sánchez and the second author [Reference León Sánchez and SierraLS08] on heights of Poisson prime ideals, and in the process show that
$\operatorname {PSpec} \operatorname {S}(\mathfrak g)$; we show that this is almost always, but not always, the case. Finally, we answer a question of León Sánchez and the second author [Reference León Sánchez and SierraLS08] on heights of Poisson prime ideals, and in the process show that ![]() $\operatorname {PSpec} \operatorname {S}(W)$ has the somewhat counterintuitive property that every proper radical Poisson ideal contains a proper Poisson primitive ideal.
$\operatorname {PSpec} \operatorname {S}(W)$ has the somewhat counterintuitive property that every proper radical Poisson ideal contains a proper Poisson primitive ideal.
5.1 Birational maps
Chevalley's fundamental result that images of algebraic maps are constructible holds for morphisms of finite presentation [SP22, Theorem 10.29.10, Tag 00FE] and, thus, applies to any homomorphism from ![]() $\operatorname {S}(\mathfrak g)$ to an affine algebra. The main result of this subsection is related to Chevalley's theorem, and allows us to conclude that two domains are birational, even in our non-noetherian context.
$\operatorname {S}(\mathfrak g)$ to an affine algebra. The main result of this subsection is related to Chevalley's theorem, and allows us to conclude that two domains are birational, even in our non-noetherian context.
Proposition 5.1.1 Let ![]() $A$,
$A$, ![]() $B$ be commutative
$B$ be commutative ![]() $\Bbbk$-algebras which are domains, and let
$\Bbbk$-algebras which are domains, and let ![]() $\phi : A\to B$ be an injective homomorphism. Assume also that
$\phi : A\to B$ be an injective homomorphism. Assume also that ![]() $B$ is affine, (we make no additional assumption on
$B$ is affine, (we make no additional assumption on ![]() $A$) and that the map
$A$) and that the map ![]() $\operatorname {MSpec} B\to \operatorname {MSpec} A$ is also injective. Then there is
$\operatorname {MSpec} B\to \operatorname {MSpec} A$ is also injective. Then there is ![]() $f\in A \setminus \{ 0\}$ so that the natural map
$f\in A \setminus \{ 0\}$ so that the natural map ![]() $A[f^{-1}]\to B[f^{-1}]$ is an isomorphism.
$A[f^{-1}]\to B[f^{-1}]$ is an isomorphism.
Before proving Proposition 5.1.1 we provide a preliminary lemma.
Lemma 5.1.2 Let ![]() $A$,
$A$, ![]() $B$ be commutative
$B$ be commutative ![]() $\Bbbk$-algebras which are domains, and let
$\Bbbk$-algebras which are domains, and let ![]() $\phi : A\to B$ be an injective homomorphism. Assume also that
$\phi : A\to B$ be an injective homomorphism. Assume also that ![]() $B$ is affine (we make no additional assumption on
$B$ is affine (we make no additional assumption on ![]() $A$). Let
$A$). Let ![]() $b \in B \setminus \{ 0\}$. There is
$b \in B \setminus \{ 0\}$. There is ![]() $a\in A \setminus \{ 0\}$ so that if
$a\in A \setminus \{ 0\}$ so that if ![]() $\chi : A\to \Bbbk$ is a homomorphism with
$\chi : A\to \Bbbk$ is a homomorphism with ![]() $\chi (a) \neq 0$, then there is some
$\chi (a) \neq 0$, then there is some ![]() $\chi ':B \to \Bbbk$ with
$\chi ':B \to \Bbbk$ with ![]() $\chi ' \phi = \chi$ and
$\chi ' \phi = \chi$ and ![]() $\chi '(b) \neq 0$.
$\chi '(b) \neq 0$.
Proof. Without loss of generality ![]() $A \subseteq B$ and
$A \subseteq B$ and ![]() $\phi$ is the inclusion. Denote by
$\phi$ is the inclusion. Denote by ![]() $B[b^{-1}]$ the localisation of
$B[b^{-1}]$ the localisation of ![]() $B$ by
$B$ by ![]() $b$. As
$b$. As ![]() $B$ is affine,
$B$ is affine, ![]() $B[b^{-1}]$ is finitely generated over
$B[b^{-1}]$ is finitely generated over ![]() $A$. By Chevalley's theorem the image of
$A$. By Chevalley's theorem the image of ![]() $\operatorname {MSpec} B[b^{-1}]$ contains an open subset
$\operatorname {MSpec} B[b^{-1}]$ contains an open subset ![]() $\{\mathfrak m\in \operatorname {MSpec} A\mid a\notin \mathfrak m\}$ of
$\{\mathfrak m\in \operatorname {MSpec} A\mid a\notin \mathfrak m\}$ of ![]() $\operatorname {MSpec} A$ defined by some element
$\operatorname {MSpec} A$ defined by some element ![]() $a\in A\setminus \{0\}$. This implies that
$a\in A\setminus \{0\}$. This implies that ![]() $a\in A$ satisfies the desired property.
$a\in A$ satisfies the desired property.
Proof of Proposition 5.1.1 As ![]() $\dim _\Bbbk A \leqslant \dim _\Bbbk B \leqslant \aleph _0 < |\Bbbk |$,
$\dim _\Bbbk A \leqslant \dim _\Bbbk B \leqslant \aleph _0 < |\Bbbk |$, ![]() $A$ is a Jacobson ring and the Nullstellensatz applies. In particular, if
$A$ is a Jacobson ring and the Nullstellensatz applies. In particular, if ![]() $\mathfrak m \in \operatorname {MSpec} A$, then the natural map
$\mathfrak m \in \operatorname {MSpec} A$, then the natural map ![]() $\Bbbk \to A/\mathfrak m$ is an isomorphism.
$\Bbbk \to A/\mathfrak m$ is an isomorphism.
Without loss of generality ![]() $A \subseteq B$ and
$A \subseteq B$ and ![]() $\phi$ is the inclusion. Let
$\phi$ is the inclusion. Let ![]() $Q(A)$ and
$Q(A)$ and ![]() $Q(B)$ be the quotient fields of
$Q(B)$ be the quotient fields of ![]() $A$ and
$A$ and ![]() $B$, respectively. Assume that
$B$, respectively. Assume that ![]() $Q(B)$ is not algebraic over
$Q(B)$ is not algebraic over ![]() $Q(A)$. Then there exists
$Q(A)$. Then there exists ![]() $x\in B$ so that
$x\in B$ so that ![]() $x$ is not algebraic over
$x$ is not algebraic over ![]() $Q(A)$, i.e. the natural map
$Q(A)$, i.e. the natural map ![]() $A[t]\to B, t\mapsto x$ is injective; we denote the image of this map by
$A[t]\to B, t\mapsto x$ is injective; we denote the image of this map by ![]() $A[x]$.
$A[x]$.
Choose ![]() $p\in A[x]\setminus \{0\}$ to be the element defined by Lemma 5.1.2 for
$p\in A[x]\setminus \{0\}$ to be the element defined by Lemma 5.1.2 for ![]() $A=A[x]$,
$A=A[x]$, ![]() $B=B$ and
$B=B$ and ![]() $b=1$. Let
$b=1$. Let ![]() $p_0\in A$ be a nonzero coefficient of
$p_0\in A$ be a nonzero coefficient of ![]() $p$. Then, for every
$p$. Then, for every ![]() $\mathfrak m\in \operatorname {MSpec} A$ with
$\mathfrak m\in \operatorname {MSpec} A$ with ![]() $p_0\not \in \mathfrak m$ there are at most finitely many
$p_0\not \in \mathfrak m$ there are at most finitely many ![]() $x_0\in \Bbbk$ such that
$x_0\in \Bbbk$ such that ![]() $p(x_0)\in \mathfrak m$. Every other
$p(x_0)\in \mathfrak m$. Every other ![]() $x_0$ provides a maximal ideal
$x_0$ provides a maximal ideal ![]() $(\mathfrak m, x-x_0)$ of
$(\mathfrak m, x-x_0)$ of ![]() $A[x]$ which extends to a maximal ideal of
$A[x]$ which extends to a maximal ideal of ![]() $B$ thanks to Lemma 5.1.2. Thus, every such
$B$ thanks to Lemma 5.1.2. Thus, every such ![]() $\mathfrak m$ has uncountably many preimages in
$\mathfrak m$ has uncountably many preimages in ![]() $\operatorname {MSpec} B$, contradicting our assumption.
$\operatorname {MSpec} B$, contradicting our assumption.
Thus, we can assume that ![]() $Q(B)$ is algebraic over
$Q(B)$ is algebraic over ![]() $Q(A)$. Let
$Q(A)$. Let ![]() $B$ be generated as a
$B$ be generated as a ![]() $\Bbbk$-algebra by
$\Bbbk$-algebra by ![]() $b_1, \ldots, b_k$. If
$b_1, \ldots, b_k$. If ![]() $Q(A)=Q(B)$, then every
$Q(A)=Q(B)$, then every ![]() $b_i$ can be written
$b_i$ can be written ![]() ${a^+_i}/{a^-_i}$ with
${a^+_i}/{a^-_i}$ with ![]() $a_i^\pm \in A\setminus \{0\}$; further, we have that
$a_i^\pm \in A\setminus \{0\}$; further, we have that ![]() $A[f^{-1}]= B[f^{-1}]$ for
$A[f^{-1}]= B[f^{-1}]$ for ![]() $f=a_1^-\cdots a_k^-$. Thus, we can assume that
$f=a_1^-\cdots a_k^-$. Thus, we can assume that ![]() $Q(A)\ne Q(B)$ and, hence, there exists
$Q(A)\ne Q(B)$ and, hence, there exists ![]() $x\in B\setminus Q(A)$.
$x\in B\setminus Q(A)$.
As ![]() $x$ is algebraic over
$x$ is algebraic over ![]() $Q(A)$ there are
$Q(A)$ there are ![]() $a_0, a_1, \ldots, a_n\in A$ with
$a_0, a_1, \ldots, a_n\in A$ with ![]() $a_0\ne 0, a_n\ne 0$ such that
$a_0\ne 0, a_n\ne 0$ such that
with ![]() $n\geqslant 2$. Let
$n\geqslant 2$. Let ![]() $p={p^+}/{a_n^d}$ with
$p={p^+}/{a_n^d}$ with ![]() $p^+\in A\setminus \{0\},\ d\in \mathbb {Z}_{\geqslant 0}$ be the resultant of
$p^+\in A\setminus \{0\},\ d\in \mathbb {Z}_{\geqslant 0}$ be the resultant of ![]() $F$. Consider
$F$. Consider ![]() $\mathfrak m\in \operatorname {MSpec} A$ with
$\mathfrak m\in \operatorname {MSpec} A$ with ![]() $a_n, p^+\not \in \mathfrak m$. Then it is well-known that there are exactly
$a_n, p^+\not \in \mathfrak m$. Then it is well-known that there are exactly ![]() $n$ maximal ideals
$n$ maximal ideals ![]() $\mathfrak m'$ of
$\mathfrak m'$ of ![]() $A[x]$ with
$A[x]$ with ![]() $\mathfrak m=\mathfrak m' \cap A$. Pick
$\mathfrak m=\mathfrak m' \cap A$. Pick ![]() $y\in A[x]$ to be the element defined by Lemma 5.1.2 for
$y\in A[x]$ to be the element defined by Lemma 5.1.2 for ![]() $A=A[x]$,
$A=A[x]$, ![]() $B=B$ and
$B=B$ and ![]() $b=1$. This element
$b=1$. This element ![]() $y$ is algebraic over
$y$ is algebraic over ![]() $A$ and thus there are
$A$ and thus there are ![]() $a_0', a_1', \ldots \in A$ with
$a_0', a_1', \ldots \in A$ with ![]() $a_0'\ne 0$ such that
$a_0'\ne 0$ such that
If ![]() $\mathfrak m'$ is a maximal ideal of
$\mathfrak m'$ is a maximal ideal of ![]() $A[x]$ such that
$A[x]$ such that ![]() $a_0'\not \in \mathfrak m=\mathfrak m'\cap A$, then we have
$a_0'\not \in \mathfrak m=\mathfrak m'\cap A$, then we have ![]() $y\notin \mathfrak m'$.
$y\notin \mathfrak m'$.
Pick ![]() $\mathfrak m\in \operatorname {MSpec} A$ such that
$\mathfrak m\in \operatorname {MSpec} A$ such that ![]() $a_np^+a_0'\notin \mathfrak m$. Then there are at least
$a_np^+a_0'\notin \mathfrak m$. Then there are at least ![]() $n$ maximal ideals
$n$ maximal ideals ![]() $\mathfrak m''$ of
$\mathfrak m''$ of ![]() $B$ such that
$B$ such that ![]() $\mathfrak m''\cap A=\mathfrak m$. This contradicts the injectivity of
$\mathfrak m''\cap A=\mathfrak m$. This contradicts the injectivity of ![]() $\operatorname {MSpec} B\to \operatorname {MSpec} A$.
$\operatorname {MSpec} B\to \operatorname {MSpec} A$.
5.2 Parameterising Poisson primes
Throughout this subsection, let ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $W_{\geqslant -1}$. We refine Remark 4.3.3 to a parameterisation of Poisson primes of
$W_{\geqslant -1}$. We refine Remark 4.3.3 to a parameterisation of Poisson primes of ![]() $\operatorname {S}(\mathfrak g)$; we use this to show in Corollary 5.2.14 that the bijection of Corollary 4.3.11 extends to prime Poisson ideals.
$\operatorname {S}(\mathfrak g)$; we use this to show in Corollary 5.2.14 that the bijection of Corollary 4.3.11 extends to prime Poisson ideals.
Given a local function ![]() $\chi$, recall the definition of the partition
$\chi$, recall the definition of the partition ![]() $\lambda (\chi )$ from § 3. Write
$\lambda (\chi )$ from § 3. Write ![]() $\lambda (\chi ) = (m_i)$ and define
$\lambda (\chi ) = (m_i)$ and define
By Proposition 4.3.6 and Remark 4.2.12,
and, in particular, ![]() $\dim \mathbb {O}(\chi )$ depends only on
$\dim \mathbb {O}(\chi )$ depends only on ![]() $\lambda (\chi )$.
$\lambda (\chi )$.
Fix a partition ![]() $\lambda = (m_1 \geqslant m_2 \geqslant \cdots \geqslant m_r)$, where
$\lambda = (m_1 \geqslant m_2 \geqslant \cdots \geqslant m_r)$, where ![]() $m_i \in \mathbb {Z}_{\geqslant 1}$, and let
$m_i \in \mathbb {Z}_{\geqslant 1}$, and let
Let
 \[ \textit{Loc}^\lambda_{\mathfrak g}:= \prod_{i=1}^r \textit{Loc}^{m_i-1}_{\mathfrak g}, \]
\[ \textit{Loc}^\lambda_{\mathfrak g}:= \prod_{i=1}^r \textit{Loc}^{m_i-1}_{\mathfrak g}, \]
where recall that ![]() $\textit {Loc}^{m}_{\mathfrak g} = \{ \chi _{x; \alpha _0, \ldots, \alpha _m} \in \mathfrak g^* \,|\, \alpha _{m} \neq 0\}.$ There is a natural summation map
$\textit {Loc}^{m}_{\mathfrak g} = \{ \chi _{x; \alpha _0, \ldots, \alpha _m} \in \mathfrak g^* \,|\, \alpha _{m} \neq 0\}.$ There is a natural summation map ![]() $\Sigma ^\lambda _{\mathfrak g}: \textit {Loc}^\lambda _{\mathfrak g} \to \mathfrak g^*$ defined by
$\Sigma ^\lambda _{\mathfrak g}: \textit {Loc}^\lambda _{\mathfrak g} \to \mathfrak g^*$ defined by ![]() $\Sigma ^\lambda _{\mathfrak g}(\chi _1, \ldots, \chi _r) = \sum \chi _i$. As in the proof of Proposition 4.3.6, let
$\Sigma ^\lambda _{\mathfrak g}(\chi _1, \ldots, \chi _r) = \sum \chi _i$. As in the proof of Proposition 4.3.6, let
(here ![]() $\underline {\alpha }^i$ stands for a sequence
$\underline {\alpha }^i$ stands for a sequence ![]() $\underline {\alpha }^i_0, \underline {\alpha }^i_1, \ldots$). Note that
$\underline {\alpha }^i_0, \underline {\alpha }^i_1, \ldots$). Note that ![]() $\Sigma ^\lambda _{\mathfrak g}(U^\lambda _{\mathfrak g})$ is precisely
$\Sigma ^\lambda _{\mathfrak g}(U^\lambda _{\mathfrak g})$ is precisely ![]() $V^\lambda _{\mathfrak g}$, whereas
$V^\lambda _{\mathfrak g}$, whereas ![]() $\Sigma ^\lambda _{\mathfrak g}(\textit {Loc}^\lambda _{\mathfrak g})$ usually includes other local functions.
$\Sigma ^\lambda _{\mathfrak g}(\textit {Loc}^\lambda _{\mathfrak g})$ usually includes other local functions.
Let the partition
consist of the even parts occurring in ![]() $\lambda$ (with the same multiplicity); set
$\lambda$ (with the same multiplicity); set ![]() $k:= \operatorname {len}(\lambda ^{\rm e})$,
$k:= \operatorname {len}(\lambda ^{\rm e})$, ![]() $k_2:=|\{i\mid m_i=2\}|$. For any
$k_2:=|\{i\mid m_i=2\}|$. For any ![]() $m_i \in \lambda ^{\rm e}$ let
$m_i \in \lambda ^{\rm e}$ let
 \[ \pi_i: \textit{Loc}^{m_i-1}_{\mathfrak g} \to \begin{cases} \mathbb{A}^1 & \mbox{ if } m_i > 2 \\ \mathbb{A}^1 \setminus \{0\} & \mbox{ if } m_i=2 \end{cases} \]
\[ \pi_i: \textit{Loc}^{m_i-1}_{\mathfrak g} \to \begin{cases} \mathbb{A}^1 & \mbox{ if } m_i > 2 \\ \mathbb{A}^1 \setminus \{0\} & \mbox{ if } m_i=2 \end{cases} \]
be the morphism ![]() $F_{m_i-1}$ defined in Corollary 4.2.11. The fibres of
$F_{m_i-1}$ defined in Corollary 4.2.11. The fibres of ![]() $\pi _i$ are pseudo-orbits (that is,
$\pi _i$ are pseudo-orbits (that is, ![]() $\widehat {\textit {DLoc}}^{\leqslant m_i-1}$-orbits) in
$\widehat {\textit {DLoc}}^{\leqslant m_i-1}$-orbits) in ![]() $\textit {Loc}^{m_i-1}_{\mathfrak g}$.
$\textit {Loc}^{m_i-1}_{\mathfrak g}$.
Let
be the composition
where ![]() ${\rm pr}$ denotes projection.
${\rm pr}$ denotes projection.
Now, ![]() $\widehat {\textit {DLoc}}^{\leqslant m_i-1}$-orbits in
$\widehat {\textit {DLoc}}^{\leqslant m_i-1}$-orbits in ![]() $\textit {Loc}^{m_i-1}_{\mathfrak g}$ are nonsingular and all are of dimension
$\textit {Loc}^{m_i-1}_{\mathfrak g}$ are nonsingular and all are of dimension ![]() $2 \lfloor ({m_i+1})/2 \rfloor$. Further,
$2 \lfloor ({m_i+1})/2 \rfloor$. Further, ![]() $\pi _i$ is flat: any torsion-free module over
$\pi _i$ is flat: any torsion-free module over ![]() $\Bbbk [x]$ or
$\Bbbk [x]$ or ![]() $\Bbbk [x, x^{-1}]$ is flat. Thus, by [Reference HartshorneHar77, Theorem III.10.2],
$\Bbbk [x, x^{-1}]$ is flat. Thus, by [Reference HartshorneHar77, Theorem III.10.2], ![]() $\pi _i$ is smooth, and so
$\pi _i$ is smooth, and so ![]() $\pi ^\lambda _{\mathfrak g}$ is also smooth.
$\pi ^\lambda _{\mathfrak g}$ is also smooth.
Given a partition ![]() $\lambda = (m_i)$ as before, we also write
$\lambda = (m_i)$ as before, we also write
where ![]() $n_1 > n_2 > \cdots > n_\ell$. Note that
$n_1 > n_2 > \cdots > n_\ell$. Note that ![]() $m_1= \cdots = m_{j_1} = n_1$,
$m_1= \cdots = m_{j_1} = n_1$, ![]() $m_{j_1+1} = m_{j_1+2} = \cdots = m_{j_1+j_2} = n_2$, etc., and
$m_{j_1+1} = m_{j_1+2} = \cdots = m_{j_1+j_2} = n_2$, etc., and ![]() $r =\operatorname {len}(\lambda )= \sum _{i=1}^\ell j_i$. The multisymmetric group
$r =\operatorname {len}(\lambda )= \sum _{i=1}^\ell j_i$. The multisymmetric group ![]() $\mathfrak S_\lambda := \mathfrak S_{j_1} \times \cdots \times \mathfrak S_{j_\ell }$ acts on
$\mathfrak S_\lambda := \mathfrak S_{j_1} \times \cdots \times \mathfrak S_{j_\ell }$ acts on ![]() $\textit {Loc}^\lambda _{\mathfrak g}$ and on
$\textit {Loc}^\lambda _{\mathfrak g}$ and on ![]() $U^\lambda _{\mathfrak g}$ by permuting the factors. Further,
$U^\lambda _{\mathfrak g}$ by permuting the factors. Further, ![]() $\mathfrak S_\lambda$ also acts on
$\mathfrak S_\lambda$ also acts on ![]() $\mathbb {A}^{k-k_2}\times (\mathbb {A}^1\setminus 0)^{\times {}k_2}$ by permutations (if
$\mathbb {A}^{k-k_2}\times (\mathbb {A}^1\setminus 0)^{\times {}k_2}$ by permutations (if ![]() $n_i$ is odd, the factor
$n_i$ is odd, the factor ![]() $\mathfrak S_{j_i}$ acts trivially). We name the action map
$\mathfrak S_{j_i}$ acts trivially). We name the action map
because we need to refer to it later. As in Remark 4.3.3, denote the quotient ![]() $[(\mathbb {A}^1)^{\times (k-k_2)}\times (\mathbb {A}^1\setminus \{0\})^{\times k_2}] / \mathfrak S_\lambda$ by
$[(\mathbb {A}^1)^{\times (k-k_2)}\times (\mathbb {A}^1\setminus \{0\})^{\times k_2}] / \mathfrak S_\lambda$ by ![]() $\mathbb {A}(\lambda )$.
$\mathbb {A}(\lambda )$.
Note that ![]() $\pi ^\lambda _{\mathfrak g}$ is
$\pi ^\lambda _{\mathfrak g}$ is ![]() $\mathfrak S_\lambda$-equivariant. There is thus an induced map
$\mathfrak S_\lambda$-equivariant. There is thus an induced map
We remark that ![]() $U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$ and
$U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$ and ![]() $\mathbb {A}(\lambda )$ are affine. Further,
$\mathbb {A}(\lambda )$ are affine. Further, ![]() $\mathbb {A}(\lambda )$ is nonsingular (in fact, isomorphic to
$\mathbb {A}(\lambda )$ is nonsingular (in fact, isomorphic to ![]() $\mathbb {A}^k$ or
$\mathbb {A}^k$ or ![]() $\mathbb {A}^{k-1}\times (\mathbb {A}^1\setminus \{0\})$) because
$\mathbb {A}^{k-1}\times (\mathbb {A}^1\setminus \{0\})$) because ![]() $\mathfrak S_\lambda$ is a reflection group, see also Remark 4.3.3. The fibres of
$\mathfrak S_\lambda$ is a reflection group, see also Remark 4.3.3. The fibres of ![]() $\overline {\pi ^\lambda _{\mathfrak g} }$ are isomorphic to fibres of the smooth morphism
$\overline {\pi ^\lambda _{\mathfrak g} }$ are isomorphic to fibres of the smooth morphism ![]() $\pi ^\lambda _{\mathfrak g}$ and are thus nonsingular. Therefore,
$\pi ^\lambda _{\mathfrak g}$ and are thus nonsingular. Therefore, ![]() $U^\lambda _{\mathfrak g}/ \mathfrak S_\lambda$ is also nonsingular.
$U^\lambda _{\mathfrak g}/ \mathfrak S_\lambda$ is also nonsingular.
The summation map ![]() $\Sigma ^\lambda _\mathfrak g$ factors through
$\Sigma ^\lambda _\mathfrak g$ factors through ![]() $\textit {Loc}^\lambda _\mathfrak g/\mathfrak S_\lambda$. This induces a morphism of varieties
$\textit {Loc}^\lambda _\mathfrak g/\mathfrak S_\lambda$. This induces a morphism of varieties
which is injective, as any collection of one-point functions with distinct supports is linearly independent. The image of ![]() $\psi ^\lambda _{\mathfrak g}$ is precisely the set
$\psi ^\lambda _{\mathfrak g}$ is precisely the set ![]() $V^\lambda _{\mathfrak g}$ of local functions with order partition
$V^\lambda _{\mathfrak g}$ of local functions with order partition ![]() $\lambda$. Further note that
$\lambda$. Further note that ![]() $\psi _\mathfrak g^\lambda$ maps the tangent space to a
$\psi _\mathfrak g^\lambda$ maps the tangent space to a ![]() $\widehat {\textit {DLoc}}$-orbit of
$\widehat {\textit {DLoc}}$-orbit of ![]() $\chi \in \mathfrak g^*$ at
$\chi \in \mathfrak g^*$ at ![]() $\chi ^*$ to
$\chi ^*$ to ![]() $\mathfrak g_{\psi ^\lambda _\mathfrak g(\chi )}$ (see Lemma 4.1.6 and 4.3.4), i.e. it satisfies the conditions of Propositions 2.1.7 and 2.3.1.
$\mathfrak g_{\psi ^\lambda _\mathfrak g(\chi )}$ (see Lemma 4.1.6 and 4.3.4), i.e. it satisfies the conditions of Propositions 2.1.7 and 2.3.1.
Remark 5.2.3 We may identify ![]() $V^\lambda _{\mathfrak g}$ with
$V^\lambda _{\mathfrak g}$ with ![]() $U^\lambda _{\mathfrak g}/\mathfrak S_{\lambda }$ as a set. This construction allows us to write the set of local functions on
$U^\lambda _{\mathfrak g}/\mathfrak S_{\lambda }$ as a set. This construction allows us to write the set of local functions on ![]() $\mathfrak g$ as a countable union of the affine varieties
$\mathfrak g$ as a countable union of the affine varieties ![]() $U^\lambda _{\mathfrak g}/\mathfrak S_{\lambda }$, further justifying the statement in Remark 3.0.3 that most elements of
$U^\lambda _{\mathfrak g}/\mathfrak S_{\lambda }$, further justifying the statement in Remark 3.0.3 that most elements of ![]() $\mathfrak g^*$ are not local.
$\mathfrak g^*$ are not local.
We abuse notation slightly, and identify ![]() $\textit {Loc}^\lambda _W$, via restriction, with the subset of
$\textit {Loc}^\lambda _W$, via restriction, with the subset of ![]() $\textit {Loc}^\lambda _{W_{\geqslant -1}}$ consisting of functions whose support does not contain
$\textit {Loc}^\lambda _{W_{\geqslant -1}}$ consisting of functions whose support does not contain ![]() $0$. The diagram
$0$. The diagram

commutes, and both maps to ![]() $\mathbb {A}(\lambda )$ are surjective.
$\mathbb {A}(\lambda )$ are surjective.
Let ![]() $\widehat {\textit {DLoc}}^\lambda := \widehat {\textit {DLoc}}^{\leqslant m_1-1} \times \cdots \times \widehat {\textit {DLoc}}^{\leqslant m_r-1}$. The group
$\widehat {\textit {DLoc}}^\lambda := \widehat {\textit {DLoc}}^{\leqslant m_1-1} \times \cdots \times \widehat {\textit {DLoc}}^{\leqslant m_r-1}$. The group ![]() $\widehat {\textit {DLoc}}^\lambda$ acts on
$\widehat {\textit {DLoc}}^\lambda$ acts on ![]() $\textit {Loc}^\lambda _{W_{\geqslant -1}}$, and there are partial
$\textit {Loc}^\lambda _{W_{\geqslant -1}}$, and there are partial ![]() $\widehat {\textit {DLoc}}^\lambda$-actions on
$\widehat {\textit {DLoc}}^\lambda$-actions on ![]() $\textit {Loc}^\lambda _W$, on
$\textit {Loc}^\lambda _W$, on ![]() $U^\lambda _W$, and on
$U^\lambda _W$, and on ![]() $U^\lambda _{W_{\geqslant -1}}$; as usual, we speak of
$U^\lambda _{W_{\geqslant -1}}$; as usual, we speak of ![]() $\widehat {\textit {DLoc}}^\lambda$-orbits on these varieties to mean the intersections with full orbits in
$\widehat {\textit {DLoc}}^\lambda$-orbits on these varieties to mean the intersections with full orbits in ![]() $\textit {Loc}^\lambda _{W_{\geqslant -1}}$. This (partial) action does not commute with the
$\textit {Loc}^\lambda _{W_{\geqslant -1}}$. This (partial) action does not commute with the ![]() $\mathfrak S_\lambda$-action. Nevertheless, it is compatible with the natural action of
$\mathfrak S_\lambda$-action. Nevertheless, it is compatible with the natural action of ![]() $\mathfrak S_\lambda$ on
$\mathfrak S_\lambda$ on ![]() $\widehat {\textit {DLoc}}^\lambda$ and together these provide an action of the semidirect product
$\widehat {\textit {DLoc}}^\lambda$ and together these provide an action of the semidirect product ![]() $\widehat {\textit {DLoc}}^\lambda \rtimes \mathfrak S_\lambda$. Further, by Corollary 4.2.11 the fibres of
$\widehat {\textit {DLoc}}^\lambda \rtimes \mathfrak S_\lambda$. Further, by Corollary 4.2.11 the fibres of ![]() $\overline {\pi ^\lambda _{\mathfrak g}}$ are precisely the images in
$\overline {\pi ^\lambda _{\mathfrak g}}$ are precisely the images in ![]() $U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$ of
$U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$ of ![]() $\widehat {\textit {DLoc}}^\lambda \rtimes \mathfrak S_\lambda$-orbits in
$\widehat {\textit {DLoc}}^\lambda \rtimes \mathfrak S_\lambda$-orbits in ![]() $U^\lambda _{\mathfrak g}$. (In particular, they all have dimension
$U^\lambda _{\mathfrak g}$. (In particular, they all have dimension ![]() $D(\lambda )$.) It follows from Theorem 4.3.1 that these fibres correspond under
$D(\lambda )$.) It follows from Theorem 4.3.1 that these fibres correspond under ![]() $\psi ^\lambda _{\mathfrak g}$ precisely with pseudo-orbits of local functions with partition
$\psi ^\lambda _{\mathfrak g}$ precisely with pseudo-orbits of local functions with partition ![]() $\lambda$. We refer to the image in
$\lambda$. We refer to the image in ![]() $U^\lambda /\mathfrak S_\lambda$ of a
$U^\lambda /\mathfrak S_\lambda$ of a ![]() $\widehat {\textit {DLoc}}^\lambda \rtimes \mathfrak S_\lambda$-orbit in
$\widehat {\textit {DLoc}}^\lambda \rtimes \mathfrak S_\lambda$-orbit in ![]() $U^\lambda _{\mathfrak g}$ as simply a
$U^\lambda _{\mathfrak g}$ as simply a ![]() $\widehat {\textit {DLoc}}^\lambda$-orbit quotient. We abuse terminology and say a subset or subvariety of
$\widehat {\textit {DLoc}}^\lambda$-orbit quotient. We abuse terminology and say a subset or subvariety of ![]() $U^\lambda /\mathfrak S_\lambda$ is
$U^\lambda /\mathfrak S_\lambda$ is ![]() $\widehat {\textit {DLoc}}^\lambda$-invariant if it is a union of
$\widehat {\textit {DLoc}}^\lambda$-invariant if it is a union of ![]() $\widehat {\textit {DLoc}}^\lambda$-orbit quotients.
$\widehat {\textit {DLoc}}^\lambda$-orbit quotients.
We can use the maps ![]() $\psi ^\lambda _{\mathfrak g}$ defined previously to strengthen Proposition 2.1.7 in our setting.
$\psi ^\lambda _{\mathfrak g}$ defined previously to strengthen Proposition 2.1.7 in our setting.
Proposition 5.2.5 Let ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $\mathfrak g = W_{\geqslant -1}$. Let
$\mathfrak g = W_{\geqslant -1}$. Let ![]() $Q$ be a proper radical ideal of
$Q$ be a proper radical ideal of ![]() $\operatorname {S}(\mathfrak g)$ and let
$\operatorname {S}(\mathfrak g)$ and let ![]() $Z := V(Q)$. Suppose also that for some
$Z := V(Q)$. Suppose also that for some ![]() $\lambda$ the set
$\lambda$ the set ![]() $V^\lambda _{\mathfrak g} \cap Z$ is (Zariski) dense in
$V^\lambda _{\mathfrak g} \cap Z$ is (Zariski) dense in ![]() $Z$. Then
$Z$. Then ![]() $Q$ is Poisson if and only if
$Q$ is Poisson if and only if ![]() $(\psi ^\lambda _{\mathfrak g})^{-1}(Z \cap V^\lambda _{\mathfrak g})$ is
$(\psi ^\lambda _{\mathfrak g})^{-1}(Z \cap V^\lambda _{\mathfrak g})$ is ![]() $\widehat {\textit {DLoc}}^\lambda$-invariant.
$\widehat {\textit {DLoc}}^\lambda$-invariant.
Proof. Let ![]() $\psi := \psi ^\lambda _{\mathfrak g}$, let
$\psi := \psi ^\lambda _{\mathfrak g}$, let ![]() $U := U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$, let
$U := U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$, let ![]() $X := \overline {\psi ^{-1}(Z)} \subseteq U$ and let
$X := \overline {\psi ^{-1}(Z)} \subseteq U$ and let ![]() $\widetilde X$ be the preimage of
$\widetilde X$ be the preimage of ![]() $X$ in
$X$ in ![]() $U^\lambda _W$. As
$U^\lambda _W$. As ![]() $Z \cap V^\lambda$ is dense in
$Z \cap V^\lambda$ is dense in ![]() $Z$, thus
$Z$, thus ![]() $Q$ is the kernel of the composition
$Q$ is the kernel of the composition
and by Proposition 2.1.7, ![]() $Q$ is Poisson if and only if
$Q$ is Poisson if and only if ![]() $\mathfrak g_{\psi (x)} \subseteq \psi _x(T_xX)$ for all
$\mathfrak g_{\psi (x)} \subseteq \psi _x(T_xX)$ for all ![]() $x \in X$.
$x \in X$.
Denote by ![]() $A$ the image of
$A$ the image of ![]() $\operatorname {S}(\mathfrak g)$ in
$\operatorname {S}(\mathfrak g)$ in ![]() $\Bbbk [X]$. The map
$\Bbbk [X]$. The map ![]() $U\to \mathfrak g^*$ is injective and therefore the map
$U\to \mathfrak g^*$ is injective and therefore the map ![]() $X\to \operatorname {MSpec} A$ is also injective. Let
$X\to \operatorname {MSpec} A$ is also injective. Let ![]() $f\in A$ be the element given by Proposition 5.1.1. Then the open subsets
$f\in A$ be the element given by Proposition 5.1.1. Then the open subsets ![]() $\operatorname {MSpec}(A[f^{-1}])$ and
$\operatorname {MSpec}(A[f^{-1}])$ and ![]() $\operatorname {MSpec}(\Bbbk [X][f^{-1}])$ of
$\operatorname {MSpec}(\Bbbk [X][f^{-1}])$ of ![]() $\operatorname {MSpec}(A)$ and
$\operatorname {MSpec}(A)$ and ![]() $X$, respectively, are isomorphic to each other. This implies that
$X$, respectively, are isomorphic to each other. This implies that ![]() $\psi _x$ identifies the tangent spaces
$\psi _x$ identifies the tangent spaces ![]() $T_xX$ and
$T_xX$ and ![]() $T_{\psi (x)}Z$ for every
$T_{\psi (x)}Z$ for every ![]() $x \in \operatorname {MSpec}(\Bbbk [X][f^{-1}])$.
$x \in \operatorname {MSpec}(\Bbbk [X][f^{-1}])$.
Moreover, ![]() $\widetilde {X}\to X$ is finite and so by generic smoothness there are dense open affine subsets
$\widetilde {X}\to X$ is finite and so by generic smoothness there are dense open affine subsets ![]() $X' \subseteq X$,
$X' \subseteq X$, ![]() $\widetilde {X'} \subseteq \widetilde {X}$ so that
$\widetilde {X'} \subseteq \widetilde {X}$ so that ![]() $\widetilde {X'} \to X'$ is étale and so identifies tangent spaces.
$\widetilde {X'} \to X'$ is étale and so identifies tangent spaces.
Let ![]() $X'' = X' \cap \operatorname {MSpec}(\Bbbk [X][f^{-1}])$ and let
$X'' = X' \cap \operatorname {MSpec}(\Bbbk [X][f^{-1}])$ and let ![]() $\widetilde {X''} \subseteq \widetilde X$ be the preimage of
$\widetilde {X''} \subseteq \widetilde X$ be the preimage of ![]() $X''$, which is also affine. For every
$X''$, which is also affine. For every ![]() $x\in X''$ and every preimage
$x\in X''$ and every preimage ![]() $\widetilde x \in \widetilde {X''}$ of
$\widetilde x \in \widetilde {X''}$ of ![]() $x$, the map
$x$, the map ![]() $\widetilde X\to \mathfrak g^*$ gives an isomorphism of the tangent spaces
$\widetilde X\to \mathfrak g^*$ gives an isomorphism of the tangent spaces ![]() $T_{\widetilde x} \widetilde X$ and
$T_{\widetilde x} \widetilde X$ and ![]() $T_{\psi (x)}Z$.
$T_{\psi (x)}Z$.
Let ![]() $\mathfrak h$ be the Lie algebra of
$\mathfrak h$ be the Lie algebra of ![]() $\widehat {\textit {DLoc}}^\lambda$. The proofs of Lemma 4.1.6 and Lemma 4.3.4 show that
$\widehat {\textit {DLoc}}^\lambda$. The proofs of Lemma 4.1.6 and Lemma 4.3.4 show that ![]() $\psi _x( \mathfrak h_x) = \mathfrak g_{\psi (x)}$ for any
$\psi _x( \mathfrak h_x) = \mathfrak g_{\psi (x)}$ for any ![]() $x\in U$. By Proposition 2.1.7 applied to the morphism
$x\in U$. By Proposition 2.1.7 applied to the morphism ![]() $X'' \to \mathfrak g^*$ and the previous discussion, the ideal
$X'' \to \mathfrak g^*$ and the previous discussion, the ideal ![]() $Q$ is Poisson if and only if
$Q$ is Poisson if and only if ![]() $\mathfrak h_x \subseteq T_x\widetilde X$ for all
$\mathfrak h_x \subseteq T_x\widetilde X$ for all ![]() $x\in \widetilde {X''}$. To finish the proof we note that the following conditions are equivalent:
$x\in \widetilde {X''}$. To finish the proof we note that the following conditions are equivalent:
(a)
 $\mathfrak h_x \subseteq T_x\widetilde {X}$ for all
$\mathfrak h_x \subseteq T_x\widetilde {X}$ for all  $x\in \widetilde {X''}$ (that is, tangent spaces to
$x\in \widetilde {X''}$ (that is, tangent spaces to  $\widehat {\textit {DLoc}}^\lambda$-orbits of points of
$\widehat {\textit {DLoc}}^\lambda$-orbits of points of  $\widetilde {X''}$ are tangent to
$\widetilde {X''}$ are tangent to  $\widetilde {X}$);
$\widetilde {X}$);(b)
 $\widetilde X=\overline {\widetilde {X''}}$ is
$\widetilde X=\overline {\widetilde {X''}}$ is  $\widehat {\textit {DLoc}}^\lambda$-invariant; that is, a union of
$\widehat {\textit {DLoc}}^\lambda$-invariant; that is, a union of  $\widehat {DLoc}^\lambda$-orbits;
$\widehat {DLoc}^\lambda$-orbits;(c) the defining ideal of
 $X = \overline {X''}$ is
$X = \overline {X''}$ is  $\widehat {\textit {DLoc}}^\lambda$-invariant.
$\widehat {\textit {DLoc}}^\lambda$-invariant.
Let ![]() $J^\lambda _{\mathfrak g} := I(V^\lambda _{\mathfrak g})$. We immediately obtain the following.
$J^\lambda _{\mathfrak g} := I(V^\lambda _{\mathfrak g})$. We immediately obtain the following.
Corollary 5.2.6 The ideal ![]() $J^\lambda _{\mathfrak g}$ is a prime Poisson ideal.
$J^\lambda _{\mathfrak g}$ is a prime Poisson ideal.
Proof. That ![]() $J^\lambda _{\mathfrak g}$ is Poisson is an immediate application of Proposition 5.2.5. To see that it is prime, note that
$J^\lambda _{\mathfrak g}$ is Poisson is an immediate application of Proposition 5.2.5. To see that it is prime, note that ![]() $U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$ is irreducible and that
$U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$ is irreducible and that ![]() $J^\lambda _{\mathfrak g}$ is the kernel of
$J^\lambda _{\mathfrak g}$ is the kernel of ![]() $(\psi ^\lambda _{\mathfrak g})^*: \operatorname {S}(\mathfrak g) \to \Bbbk [U^\lambda _{\mathfrak g}/\mathfrak S_\lambda ]$.
$(\psi ^\lambda _{\mathfrak g})^*: \operatorname {S}(\mathfrak g) \to \Bbbk [U^\lambda _{\mathfrak g}/\mathfrak S_\lambda ]$.
Remark 5.2.7 Recall that ![]() $V^\lambda _{\mathfrak g} \subset \mathfrak g^*$ is the image of the affine variety
$V^\lambda _{\mathfrak g} \subset \mathfrak g^*$ is the image of the affine variety ![]() $U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$. Thus, by Chevalley's theorem
$U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$. Thus, by Chevalley's theorem ![]() $V^\lambda _{\mathfrak g}$ contains a nonempty open subset of
$V^\lambda _{\mathfrak g}$ contains a nonempty open subset of ![]() $\overline {V^\lambda _{\mathfrak g}}$. Let
$\overline {V^\lambda _{\mathfrak g}}$. Let ![]() $U$ be the union of all open subsets of
$U$ be the union of all open subsets of ![]() $\overline {V^\lambda _{\mathfrak g}}$ contained in
$\overline {V^\lambda _{\mathfrak g}}$ contained in ![]() $V^\lambda _{\mathfrak g}$. It is surely true that
$V^\lambda _{\mathfrak g}$. It is surely true that ![]() $U$ is Poisson, in the sense that the defining ideal of
$U$ is Poisson, in the sense that the defining ideal of ![]() $\overline {V^\lambda _{\mathfrak g}} \setminus U$ is a Poisson ideal. However, we cannot prove this at this point.
$\overline {V^\lambda _{\mathfrak g}} \setminus U$ is a Poisson ideal. However, we cannot prove this at this point.
We next show how to parameterise Poisson primes of ![]() $\operatorname {S}(\mathfrak g)$.
$\operatorname {S}(\mathfrak g)$.
Theorem 5.2.8 Let ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $\mathfrak g = W_{\geqslant -1}$.
$\mathfrak g = W_{\geqslant -1}$.
(a) Let
 $Q$ be a nonzero proper prime Poisson ideal of
$Q$ be a nonzero proper prime Poisson ideal of  $\operatorname {S}(\mathfrak g)$. There is a unique
$\operatorname {S}(\mathfrak g)$. There is a unique  $\lambda := \lambda (Q)$ so that
$\lambda := \lambda (Q)$ so that  $V(Q) \cap V^\lambda _{\mathfrak g}$ contains a nonempty open subset of
$V(Q) \cap V^\lambda _{\mathfrak g}$ contains a nonempty open subset of  $V(Q)$. Further,
$V(Q)$. Further,  $Y(Q) := \overline {\pi ^\lambda _{\mathfrak g}}(\psi ^\lambda _{\mathfrak g})^{-1}(V(Q))$ is a (nonempty) irreducible closed subvariety of
$Y(Q) := \overline {\pi ^\lambda _{\mathfrak g}}(\psi ^\lambda _{\mathfrak g})^{-1}(V(Q))$ is a (nonempty) irreducible closed subvariety of  $\mathbb {A}(\lambda )$, and
$\mathbb {A}(\lambda )$, and
 \[ \operatorname{GKdim} \operatorname{S}(\mathfrak g)/Q = \dim Y(Q) + D(\lambda(Q)). \]
\[ \operatorname{GKdim} \operatorname{S}(\mathfrak g)/Q = \dim Y(Q) + D(\lambda(Q)). \]
(b) The function
 $Q \mapsto (\lambda (Q), Y(Q))$ defines a bijection
$Q \mapsto (\lambda (Q), Y(Q))$ defines a bijection
 \[ \Psi_{\mathfrak g}: \operatorname{PSpec} \operatorname{S}(\mathfrak g) \to \{ (\lambda, Y) \,|\, Y \mbox{ is an irreducible subvariety of } Var_{\lambda(Q)} \} . \]
\[ \Psi_{\mathfrak g}: \operatorname{PSpec} \operatorname{S}(\mathfrak g) \to \{ (\lambda, Y) \,|\, Y \mbox{ is an irreducible subvariety of } Var_{\lambda(Q)} \} . \]
(c) If
 $Q, Q'$ are Poisson primes of
$Q, Q'$ are Poisson primes of  $\operatorname {S}(\mathfrak g)$ with
$\operatorname {S}(\mathfrak g)$ with  $\lambda (Q) = \lambda (Q')$, then
$\lambda (Q) = \lambda (Q')$, then  $Q\subseteq Q'$ if and only if
$Q\subseteq Q'$ if and only if  $Y(Q) \supseteq Y(Q')$.
$Y(Q) \supseteq Y(Q')$.
We call the partition ![]() $\lambda (Q)$ defined in Theorem 5.2.8 the generic order partition of
$\lambda (Q)$ defined in Theorem 5.2.8 the generic order partition of ![]() $Q$, in other words the partition of a generic orbit in the associated variety. It is easy to check that the construction of Theorem 5.2.8(a) guarantees that a Poisson prime
$Q$, in other words the partition of a generic orbit in the associated variety. It is easy to check that the construction of Theorem 5.2.8(a) guarantees that a Poisson prime ![]() $Q$ is the kernel of the map
$Q$ is the kernel of the map
where ![]() $\lambda = \lambda (Q)$. This provides the explicit inverse to the map
$\lambda = \lambda (Q)$. This provides the explicit inverse to the map ![]() $\Psi _\mathfrak g$ of Theorem 5.2.8(b).
$\Psi _\mathfrak g$ of Theorem 5.2.8(b).
Proof. Let ![]() $Q$ be a nonzero proper prime Poisson ideal of
$Q$ be a nonzero proper prime Poisson ideal of ![]() $\operatorname {S}(\mathfrak g)$ and let
$\operatorname {S}(\mathfrak g)$ and let ![]() $Z:= V(Q)$. As
$Z:= V(Q)$. As ![]() $Q$ is prime, there can be at most one
$Q$ is prime, there can be at most one ![]() $\lambda$ so that
$\lambda$ so that ![]() $Z \cap V^\lambda _{\mathfrak g}$ contains a nonempty open subset of
$Z \cap V^\lambda _{\mathfrak g}$ contains a nonempty open subset of ![]() $Z$; it remains to establish existence of some such
$Z$; it remains to establish existence of some such ![]() $\lambda$.
$\lambda$.
By Theorem 3.0.4 ![]() $d:=\operatorname {GKdim}(\operatorname {S}(\mathfrak g)/Q) < \infty$. By (5.2.1) there are thus only finitely many partitions
$d:=\operatorname {GKdim}(\operatorname {S}(\mathfrak g)/Q) < \infty$. By (5.2.1) there are thus only finitely many partitions ![]() $\lambda$ such that
$\lambda$ such that ![]() $\dim \mathbb {O}(\chi ) \leqslant d$ for any
$\dim \mathbb {O}(\chi ) \leqslant d$ for any ![]() $\chi$ with order partition
$\chi$ with order partition ![]() $\lambda$, and so for some
$\lambda$, and so for some ![]() $\lambda ^1, \ldots, \lambda ^n$ we have
$\lambda ^1, \ldots, \lambda ^n$ we have
Fix ![]() $i$ and let
$i$ and let ![]() $\lambda = \lambda ^i$. Let
$\lambda = \lambda ^i$. Let ![]() $Q'$ be a minimal prime of
$Q'$ be a minimal prime of ![]() $Q + J^\lambda _{\mathfrak g}$, which exists by Proposition 3.0.6, and let
$Q + J^\lambda _{\mathfrak g}$, which exists by Proposition 3.0.6, and let ![]() $Z'= V(Q')$, which is an irreducible component of
$Z'= V(Q')$, which is an irreducible component of ![]() $Z \cap \overline {V^\lambda _{\mathfrak g}}$. Let
$Z \cap \overline {V^\lambda _{\mathfrak g}}$. Let ![]() $X' = (\psi ^\lambda _{\mathfrak g})^{-1}(Z')$. By Chevalley's theorem
$X' = (\psi ^\lambda _{\mathfrak g})^{-1}(Z')$. By Chevalley's theorem ![]() $V^{\lambda }_{\mathfrak g} \cap Z$ contains a dense subset
$V^{\lambda }_{\mathfrak g} \cap Z$ contains a dense subset ![]() $U_i$ which is locally closed in
$U_i$ which is locally closed in ![]() $Z$. As
$Z$. As ![]() $\overline { \bigcup U_i } = Z$, by primeness of
$\overline { \bigcup U_i } = Z$, by primeness of ![]() $Q$ some
$Q$ some ![]() $U_j$ has
$U_j$ has ![]() $\overline {U_j} =Z$: in other words,
$\overline {U_j} =Z$: in other words, ![]() $U_j$ is open in its closure
$U_j$ is open in its closure ![]() $Z$. Thus,
$Z$. Thus, ![]() $\lambda (Q) = \lambda _j$.
$\lambda (Q) = \lambda _j$.
Let ![]() $\lambda := \lambda (Q) = \lambda _j$, and let
$\lambda := \lambda (Q) = \lambda _j$, and let ![]() $X := (\psi ^{\lambda }_{\mathfrak g})^{-1}(Z)$. This is an irreducible closed subvariety of
$X := (\psi ^{\lambda }_{\mathfrak g})^{-1}(Z)$. This is an irreducible closed subvariety of ![]() $U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$, and by Proposition 5.2.5 it is a union of
$U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$, and by Proposition 5.2.5 it is a union of ![]() $\widehat {\textit {DLoc}}^\lambda$-orbits. It therefore follows that
$\widehat {\textit {DLoc}}^\lambda$-orbits. It therefore follows that ![]() $Y(Q):= \overline {\pi ^\lambda _{\mathfrak g}}(X)$ is closed in
$Y(Q):= \overline {\pi ^\lambda _{\mathfrak g}}(X)$ is closed in ![]() $\mathbb {A}(\lambda )$. This proves all but the last statement of part (a).
$\mathbb {A}(\lambda )$. This proves all but the last statement of part (a).
We now prove part (b). Fix a partition ![]() $\lambda$ and let
$\lambda$ and let ![]() $k := \operatorname {len}(\lambda ^{\rm e})$. Let
$k := \operatorname {len}(\lambda ^{\rm e})$. Let ![]() $\mathfrak S_\lambda$ acts as in (5.2.2). Let
$\mathfrak S_\lambda$ acts as in (5.2.2). Let ![]() $Y$ be an irreducible closed subvariety of
$Y$ be an irreducible closed subvariety of ![]() $\mathbb {A}(\lambda )$. Let
$\mathbb {A}(\lambda )$. Let ![]() $X:= (\overline {\pi ^\lambda _{\mathfrak g}})^{-1}(Y)$. As the fibres of
$X:= (\overline {\pi ^\lambda _{\mathfrak g}})^{-1}(Y)$. As the fibres of ![]() $\overline {\pi ^\lambda _{\mathfrak g}}$ are
$\overline {\pi ^\lambda _{\mathfrak g}}$ are ![]() $\widehat {\textit {DLoc}}^\lambda$-orbit quotients and are therefore irreducible (note that
$\widehat {\textit {DLoc}}^\lambda$-orbit quotients and are therefore irreducible (note that ![]() $\widehat {\textit {DLoc}}^\lambda$ is a connected algebraic group),
$\widehat {\textit {DLoc}}^\lambda$ is a connected algebraic group), ![]() $X$ is an irreducible
$X$ is an irreducible ![]() $\widehat {\textit {DLoc}}^\lambda$-invariant closed subvariety of
$\widehat {\textit {DLoc}}^\lambda$-invariant closed subvariety of ![]() $U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$ with
$U^\lambda _{\mathfrak g}/\mathfrak S_\lambda$ with ![]() $Y = \pi ^\lambda _{\mathfrak g}(X)$. Let
$Y = \pi ^\lambda _{\mathfrak g}(X)$. Let ![]() $Q$ be the kernel of
$Q$ be the kernel of ![]() $\operatorname {S}(\mathfrak g) \to \Bbbk [X]$; clearly
$\operatorname {S}(\mathfrak g) \to \Bbbk [X]$; clearly ![]() $Q$ is prime, and by Proposition 5.2.5
$Q$ is prime, and by Proposition 5.2.5 ![]() $Q$ is a Poisson ideal of
$Q$ is a Poisson ideal of ![]() $\operatorname {S}(\mathfrak g)$. Let
$\operatorname {S}(\mathfrak g)$. Let ![]() $Z:= V(Q)$. By applying Chevalley's theorem to the morphism
$Z:= V(Q)$. By applying Chevalley's theorem to the morphism ![]() $\psi ^\lambda _{\mathfrak g}: X \to Z$ we see that
$\psi ^\lambda _{\mathfrak g}: X \to Z$ we see that ![]() $\psi ^\lambda _{\mathfrak g}(X)$ contains a nonempty open subset of
$\psi ^\lambda _{\mathfrak g}(X)$ contains a nonempty open subset of ![]() $Z$. This shows, in particular, that
$Z$. This shows, in particular, that ![]() $\lambda = \lambda (Q)$, and it is clear that
$\lambda = \lambda (Q)$, and it is clear that ![]() $Y = Y(Q)$.
$Y = Y(Q)$.
Conversely, given ![]() $Q$ apply the procedure in the previous paragraph to
$Q$ apply the procedure in the previous paragraph to ![]() $\lambda (Q)$ and
$\lambda (Q)$ and ![]() $Y(Q)$; one recovers
$Y(Q)$; one recovers ![]() $Q$, see also (5.2.9). This shows that
$Q$, see also (5.2.9). This shows that ![]() $\Psi _{\mathfrak g}$ is bijective, completing the proof of part (b).
$\Psi _{\mathfrak g}$ is bijective, completing the proof of part (b).
Given a nonzero proper Poisson prime ![]() $Q$ of
$Q$ of ![]() $\operatorname {S}(\mathfrak g)$ let
$\operatorname {S}(\mathfrak g)$ let ![]() $\lambda := \lambda (Q)$ and
$\lambda := \lambda (Q)$ and ![]() $Y := Y(Q)$. Let
$Y := Y(Q)$. Let ![]() $X:= (\overline {\pi ^\lambda _{\mathfrak g}})^{-1}(Y)$. We have seen that the fibres of
$X:= (\overline {\pi ^\lambda _{\mathfrak g}})^{-1}(Y)$. We have seen that the fibres of ![]() $\overline {\pi ^\lambda _{\mathfrak g}}$ have dimension
$\overline {\pi ^\lambda _{\mathfrak g}}$ have dimension ![]() $D(\lambda )$ and so
$D(\lambda )$ and so ![]() $\dim X = \dim Y + D(\lambda )$. It is shown in the proof of Proposition 5.2.5 that
$\dim X = \dim Y + D(\lambda )$. It is shown in the proof of Proposition 5.2.5 that ![]() $\operatorname {S}(\mathfrak g)$ and
$\operatorname {S}(\mathfrak g)$ and ![]() $\Bbbk [X]$ are birational, so
$\Bbbk [X]$ are birational, so ![]() $\dim X = \operatorname {GKdim} \operatorname {S}(\mathfrak g)/Q$. This completes part (a).
$\dim X = \operatorname {GKdim} \operatorname {S}(\mathfrak g)/Q$. This completes part (a).
For part (c), let ![]() $\lambda = \lambda (Q)=\lambda (Q')$ and let
$\lambda = \lambda (Q)=\lambda (Q')$ and let ![]() $\psi = \psi ^\lambda _{\mathfrak g}$ and
$\psi = \psi ^\lambda _{\mathfrak g}$ and ![]() $\pi = \overline {\pi ^\lambda _{\mathfrak g}}$. Now let
$\pi = \overline {\pi ^\lambda _{\mathfrak g}}$. Now let ![]() $Z = V(Q)$,
$Z = V(Q)$, ![]() $X = \psi ^{-1}(Z) = \psi ^{-1}(Z \cap V^\lambda _{\mathfrak g})$ and
$X = \psi ^{-1}(Z) = \psi ^{-1}(Z \cap V^\lambda _{\mathfrak g})$ and ![]() $Y = Y(Q) = \pi (X)$. Likewise define
$Y = Y(Q) = \pi (X)$. Likewise define ![]() $Z'=V(Q')$,
$Z'=V(Q')$, ![]() $X' = \psi ^{-1}(Z')$ and
$X' = \psi ^{-1}(Z')$ and ![]() $Y' = Y(Q')$.
$Y' = Y(Q')$.
By the Nullstellensatz,
Thus, if ![]() $Q \subseteq Q'$ we have
$Q \subseteq Q'$ we have ![]() $Z \cap V^\lambda _{\mathfrak g} \supseteq Z' \cap V^\lambda _{\mathfrak g}$ and we see immediately that
$Z \cap V^\lambda _{\mathfrak g} \supseteq Z' \cap V^\lambda _{\mathfrak g}$ and we see immediately that ![]() $Y\supseteq Y'$. Conversely, if
$Y\supseteq Y'$. Conversely, if ![]() $Y \supseteq Y'$, then
$Y \supseteq Y'$, then ![]() $\psi (X) = Z \cap V^\lambda _{\mathfrak g} \supseteq \psi (X') = Z' \cap V^\lambda _{\mathfrak g}$. The proof of part (b) showed that
$\psi (X) = Z \cap V^\lambda _{\mathfrak g} \supseteq \psi (X') = Z' \cap V^\lambda _{\mathfrak g}$. The proof of part (b) showed that ![]() $Z = \overline {Z \cap V^\lambda _{\mathfrak g}}$, which clearly contains
$Z = \overline {Z \cap V^\lambda _{\mathfrak g}}$, which clearly contains ![]() $\overline {Z' \cap V^\lambda _{\mathfrak g}} = Z'$.
$\overline {Z' \cap V^\lambda _{\mathfrak g}} = Z'$.
It follows from Theorem 5.2.8 that ![]() $\operatorname {PSpec}(W)$ and
$\operatorname {PSpec}(W)$ and ![]() $\operatorname {PSpec}(W_{\geqslant -1})$ are partitioned into countably many affine strata, corresponding to partitions. Given a partition
$\operatorname {PSpec}(W_{\geqslant -1})$ are partitioned into countably many affine strata, corresponding to partitions. Given a partition ![]() $\lambda$, the corresponding stratum consists of prime Poisson ideals
$\lambda$, the corresponding stratum consists of prime Poisson ideals ![]() $Q$ with
$Q$ with ![]() $\lambda (Q)=\lambda$ and is homeomorphic to the affine variety
$\lambda (Q)=\lambda$ and is homeomorphic to the affine variety ![]() $\mathbb {A}(\lambda )$, an open subset of a finite-dimensional affine space. However, we do not know how to tell in terms of the parameterisation
$\mathbb {A}(\lambda )$, an open subset of a finite-dimensional affine space. However, we do not know how to tell in terms of the parameterisation ![]() $Q \leftrightarrow (\lambda, Y)$ when
$Q \leftrightarrow (\lambda, Y)$ when ![]() $Q \subseteq Q'$ for arbitrary
$Q \subseteq Q'$ for arbitrary ![]() $Q, Q'$. In fact, we cannot answer this question completely even when
$Q, Q'$. In fact, we cannot answer this question completely even when ![]() $Q, Q'$ are Poisson primitive; see Corollary 4.3.17 and Example 4.3.16 for some discussion of the complexities.
$Q, Q'$ are Poisson primitive; see Corollary 4.3.17 and Example 4.3.16 for some discussion of the complexities.
Corollary 5.2.10 (Cf. [Reference Petukhov and SierraPS20, Lemma 2.9])
Let ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $\mathfrak g = W_{\geqslant -1}$ and let
$\mathfrak g = W_{\geqslant -1}$ and let ![]() $Q$ be a prime Poisson ideal of
$Q$ be a prime Poisson ideal of ![]() $\operatorname {S}(\mathfrak g)$. Then there exists
$\operatorname {S}(\mathfrak g)$. Then there exists ![]() $f\in \operatorname {S}(\mathfrak g)\setminus Q$ such that
$f\in \operatorname {S}(\mathfrak g)\setminus Q$ such that ![]() $(\operatorname {S}(\mathfrak g)/Q)[f^{-1}]$ is a finitely generated Poisson algebra.
$(\operatorname {S}(\mathfrak g)/Q)[f^{-1}]$ is a finitely generated Poisson algebra.
Proof. It is clear that ![]() $(\operatorname {S}(\mathfrak g)/Q)[f^{-1}]$ is a Poisson algebra for every such
$(\operatorname {S}(\mathfrak g)/Q)[f^{-1}]$ is a Poisson algebra for every such ![]() $f$ and, thus, we need to choose
$f$ and, thus, we need to choose ![]() $f$ in such a way that
$f$ in such a way that ![]() $(\operatorname {S}(\mathfrak g)/Q)[f^{-1}]$ is finitely generated. Set
$(\operatorname {S}(\mathfrak g)/Q)[f^{-1}]$ is finitely generated. Set ![]() $A=\operatorname {S}(\mathfrak g)/Q$,
$A=\operatorname {S}(\mathfrak g)/Q$, ![]() $\lambda = \lambda (Q)$ and
$\lambda = \lambda (Q)$ and ![]() $B=\Bbbk [\overline {(\pi _\mathfrak g^{\lambda })}^{-1}(Y(Q))]$; note that
$B=\Bbbk [\overline {(\pi _\mathfrak g^{\lambda })}^{-1}(Y(Q))]$; note that ![]() $B$ is finitely generated as it is easy to check that
$B$ is finitely generated as it is easy to check that ![]() $\overline {(\pi _\mathfrak g^\lambda )}^{-1}(Y(Q))$ is affine. By (5.2.9) we have an injective map
$\overline {(\pi _\mathfrak g^\lambda )}^{-1}(Y(Q))$ is affine. By (5.2.9) we have an injective map ![]() $A\to B$ and the induced map
$A\to B$ and the induced map ![]() $\operatorname {MSpec} B\to \operatorname {MSpec} A$ is injective as well because it is a restriction of an injective map
$\operatorname {MSpec} B\to \operatorname {MSpec} A$ is injective as well because it is a restriction of an injective map ![]() $U^\lambda _\mathfrak g/\mathfrak S_\lambda \to \mathfrak g^*$. This together with Proposition 5.1.1 guarantees the existence of
$U^\lambda _\mathfrak g/\mathfrak S_\lambda \to \mathfrak g^*$. This together with Proposition 5.1.1 guarantees the existence of ![]() $f$.
$f$.
Remark 5.2.11 Let ![]() $Q$ be a prime Poisson ideal of
$Q$ be a prime Poisson ideal of ![]() $\operatorname {S}(W)$ of co-GK 3. By Theorem 5.2.8 we have
$\operatorname {S}(W)$ of co-GK 3. By Theorem 5.2.8 we have
and, recalling that ![]() $D(\lambda (Q))$ is even by definition, we must have
$D(\lambda (Q))$ is even by definition, we must have ![]() $\dim Y(Q) = 1$ and
$\dim Y(Q) = 1$ and ![]() $D(\lambda (Q)) = 2$. (The case
$D(\lambda (Q)) = 2$. (The case ![]() $\dim Y(Q) = 3$,
$\dim Y(Q) = 3$, ![]() $D(\lambda (Q)) = 0$ cannot occur.) Thus,
$D(\lambda (Q)) = 0$ cannot occur.) Thus, ![]() $\lambda (Q) = (2)$ and
$\lambda (Q) = (2)$ and ![]() $\mathbb {A}(\lambda ) = \mathbb {A}^1 \setminus \{0\} = Y(Q)$.
$\mathbb {A}(\lambda ) = \mathbb {A}^1 \setminus \{0\} = Y(Q)$.
Now, if ![]() $\chi \in W^*$, then
$\chi \in W^*$, then ![]() $\lambda (\chi ) = (2)$ if and only if
$\lambda (\chi ) = (2)$ if and only if ![]() $\chi = \chi _{x; \alpha, \gamma }$ for some
$\chi = \chi _{x; \alpha, \gamma }$ for some ![]() $x, \gamma \in \Bbbk ^*$,
$x, \gamma \in \Bbbk ^*$, ![]() $\alpha \in \Bbbk$, and so
$\alpha \in \Bbbk$, and so
 \[ Q= \bigcap_{\substack{x, \gamma \in \Bbbk^* \\ \alpha \in \Bbbk}} \operatorname{P} (\chi_{x;\alpha, \gamma}) = \bigcap_\gamma \ker p_\gamma, \]
\[ Q= \bigcap_{\substack{x, \gamma \in \Bbbk^* \\ \alpha \in \Bbbk}} \operatorname{P} (\chi_{x;\alpha, \gamma}) = \bigcap_\gamma \ker p_\gamma, \]
using Lemma 2.2.3. However, from the definition of ![]() $p_\gamma$ in (2.2.2) we see that
$p_\gamma$ in (2.2.2) we see that ![]() $\bigcap \ker p_\gamma$ is precisely the kernel of the map
$\bigcap \ker p_\gamma$ is precisely the kernel of the map ![]() $\Phi$ from Remark 4.3.15. Thus,
$\Phi$ from Remark 4.3.15. Thus, ![]() $\ker \Phi$ is the only prime Poisson ideal of
$\ker \Phi$ is the only prime Poisson ideal of ![]() $\operatorname {S}(W)$ of co-GK 3.
$\operatorname {S}(W)$ of co-GK 3.
We thank the anonymous referee for drawing our attention to this fact.
Remark 5.2.12 Fix a partition ![]() $\lambda$. Taking
$\lambda$. Taking ![]() $Y = \mathbb {A}(\lambda )$ in Theorem 5.2.8 we see that the pair
$Y = \mathbb {A}(\lambda )$ in Theorem 5.2.8 we see that the pair ![]() $(\lambda, Y)$ corresponds to the ideal
$(\lambda, Y)$ corresponds to the ideal ![]() $J^\lambda _{\mathfrak g}$. This is another way to see that
$J^\lambda _{\mathfrak g}$. This is another way to see that ![]() $J^\lambda _{\mathfrak g}$ is prime.
$J^\lambda _{\mathfrak g}$ is prime.
Remark 5.2.13 By Corollary 3.3.6 any noncentrally generated prime Poisson ideal of ![]() $\operatorname {S}(V\!ir)$ strictly contains
$\operatorname {S}(V\!ir)$ strictly contains ![]() $(z)$ and thus corresponds to a nontrivial prime Poisson ideal of
$(z)$ and thus corresponds to a nontrivial prime Poisson ideal of ![]() $\operatorname {S}(W)$ as given in Theorem 5.2.8. On the other hand, centrally generated prime Poisson ideals of course correspond to prime ideals of
$\operatorname {S}(W)$ as given in Theorem 5.2.8. On the other hand, centrally generated prime Poisson ideals of course correspond to prime ideals of ![]() $\Bbbk [z]$. Thus,
$\Bbbk [z]$. Thus, ![]() $\operatorname {PSpec} \operatorname {S}(V\!ir)$ is also partitioned into countably many strata, each homeomorphic either to a finite-dimensional affine space or to some
$\operatorname {PSpec} \operatorname {S}(V\!ir)$ is also partitioned into countably many strata, each homeomorphic either to a finite-dimensional affine space or to some ![]() $\mathbb {A}^k \times (\mathbb {A}^1\setminus \{0\})$.
$\mathbb {A}^k \times (\mathbb {A}^1\setminus \{0\})$.
We now prove that restriction from ![]() $\operatorname {S}(W)$ to
$\operatorname {S}(W)$ to ![]() $\operatorname {S}(W_{\geqslant -1})$ induces a bijection on arbitrary prime Poisson ideals, not just Poisson primitive ideals. We conjecture that this bijection is, in fact, a homeomorphism between
$\operatorname {S}(W_{\geqslant -1})$ induces a bijection on arbitrary prime Poisson ideals, not just Poisson primitive ideals. We conjecture that this bijection is, in fact, a homeomorphism between ![]() ${\rm PSpec_{prim}}(\operatorname {S}(W))$ and
${\rm PSpec_{prim}}(\operatorname {S}(W))$ and ![]() ${\rm PSpec_{prim}}(\operatorname {S}(W_{\geqslant -1}))$, but at this point we cannot prove it.
${\rm PSpec_{prim}}(\operatorname {S}(W_{\geqslant -1}))$, but at this point we cannot prove it.
Corollary 5.2.14 Restriction induces a bijection between prime Poisson ![]() $\operatorname {S}(W)$ and prime Poisson ideals of
$\operatorname {S}(W)$ and prime Poisson ideals of ![]() $\operatorname {S}(W_{\geqslant -1})$, and a bijection between irreducible closed subsets of
$\operatorname {S}(W_{\geqslant -1})$, and a bijection between irreducible closed subsets of
Proof. We must show that restriction gives a bijection
Certainly, if ![]() $J$ is a prime Poisson ideal of
$J$ is a prime Poisson ideal of ![]() $\operatorname {S}(W)$, then
$\operatorname {S}(W)$, then ![]() $J$ is closed under all
$J$ is closed under all ![]() $\{v, -\}$ for
$\{v, -\}$ for ![]() $v \in W_{\geqslant -1}$ and so
$v \in W_{\geqslant -1}$ and so ![]() $J \cap \operatorname {S}(W_{\geqslant -1})$ is a prime Poisson ideal. Thus,
$J \cap \operatorname {S}(W_{\geqslant -1})$ is a prime Poisson ideal. Thus, ![]() $\operatorname {res}$ is well-defined.
$\operatorname {res}$ is well-defined.
Let ![]() $P \in \operatorname {PSpec} \operatorname {S}(W)$. Let
$P \in \operatorname {PSpec} \operatorname {S}(W)$. Let ![]() $(\lambda, Y) := \Psi _W(P)$ and let
$(\lambda, Y) := \Psi _W(P)$ and let ![]() $Q := \Psi _{W_{\geqslant -1}}^{-1}(\lambda, Y)$. We claim that
$Q := \Psi _{W_{\geqslant -1}}^{-1}(\lambda, Y)$. We claim that ![]() $Q = \operatorname {res}(P)$.
$Q = \operatorname {res}(P)$.
For each ![]() $y \in Y$ choose a representative
$y \in Y$ choose a representative ![]() $\chi _y \in W^*$ lying in the pseudo-orbit corresponding via
$\chi _y \in W^*$ lying in the pseudo-orbit corresponding via ![]() $\overline {\pi ^\lambda _W}$ to
$\overline {\pi ^\lambda _W}$ to ![]() $y$. Then Theorem 5.2.8 gives that
$y$. Then Theorem 5.2.8 gives that
By Lemma 2.0.4, this is ![]() $\bigcap _{y\in Y} \operatorname {P}(\chi _y)$. Likewise,
$\bigcap _{y\in Y} \operatorname {P}(\chi _y)$. Likewise, ![]() $Q$ is equal to
$Q$ is equal to
By Proposition 4.3.6(a), this is
As ![]() $\operatorname {res}$ acts on nonzero Poisson prime ideals as the composition of the bijections
$\operatorname {res}$ acts on nonzero Poisson prime ideals as the composition of the bijections ![]() $\Psi _W$ and
$\Psi _W$ and ![]() $\Psi _{W_{\geqslant -1}}^{-1}$, it is a bijection.
$\Psi _{W_{\geqslant -1}}^{-1}$, it is a bijection.
5.3 The PDME
We next consider which Poisson prime ideals satisfy the PDME. This is the Poisson version of the equivalent conditions for primitive ideals in enveloping algebras of finite-dimensional Lie algebras, which are due to Dixmier and Moeglin. We describe the conditions here.
Let ![]() $Q$ be a Poisson prime ideal in a Poisson algebra
$Q$ be a Poisson prime ideal in a Poisson algebra ![]() $A$, which we assume to be a domain. Then
$A$, which we assume to be a domain. Then ![]() $Q$ is Poisson locally closed if it is locally closed in the Zariski topology on
$Q$ is Poisson locally closed if it is locally closed in the Zariski topology on ![]() $\operatorname {PSpec}(A)$. We say
$\operatorname {PSpec}(A)$. We say ![]() $Q$ is Poisson rational if the Poisson centre of the field of fractions of
$Q$ is Poisson rational if the Poisson centre of the field of fractions of ![]() $A/Q$ is algebraic over
$A/Q$ is algebraic over ![]() $\Bbbk$. We say the PDME holds for
$\Bbbk$. We say the PDME holds for ![]() $A$ if for any prime Poisson ideal
$A$ if for any prime Poisson ideal ![]() $Q$ of
$Q$ of ![]() $A$, the conditions
$A$, the conditions
 \[ \begin{array}{l} Q \mbox{ is Poisson
locally closed,}\\ Q \mbox{ is Poisson primitive,}\\ Q
\mbox{ is Poisson rational,} \end{array}
\]
\[ \begin{array}{l} Q \mbox{ is Poisson
locally closed,}\\ Q \mbox{ is Poisson primitive,}\\ Q
\mbox{ is Poisson rational,} \end{array}
\]
are equivalent. If ![]() $\mathfrak g$ is a finite-dimensional Lie algebra, then the PDME holds for
$\mathfrak g$ is a finite-dimensional Lie algebra, then the PDME holds for ![]() $\operatorname {S}(\mathfrak g)$ (see [Reference Launois and León SánchezLL19, Theorem 2]).
$\operatorname {S}(\mathfrak g)$ (see [Reference Launois and León SánchezLL19, Theorem 2]).
On the other hand, the next result shows that the PDME fails for ![]() $\operatorname {S}(V\!ir)$,
$\operatorname {S}(V\!ir)$, ![]() $\operatorname {S}(W)$ and
$\operatorname {S}(W)$ and ![]() $\operatorname {S}(W_{\geqslant -1})$. However, it almost holds: for all these algebras, there is only one Poisson prime for which the PDME fails.
$\operatorname {S}(W_{\geqslant -1})$. However, it almost holds: for all these algebras, there is only one Poisson prime for which the PDME fails.
Theorem 5.3.1 The PDME holds for all prime Poisson ideals of ![]() $\operatorname {S}(V\!ir)$ except for
$\operatorname {S}(V\!ir)$ except for ![]() $(z)$: that is, if
$(z)$: that is, if ![]() $Q \neq (z)$ is a prime Poisson ideal of
$Q \neq (z)$ is a prime Poisson ideal of ![]() $\operatorname {S}(V\!ir)$, then
$\operatorname {S}(V\!ir)$, then ![]() $Q$ is locally closed in the Poisson spectrum if and only if
$Q$ is locally closed in the Poisson spectrum if and only if ![]() $Q$ is Poisson primitive, if and only if
$Q$ is Poisson primitive, if and only if ![]() $Q$ is Poisson rational. However,
$Q$ is Poisson rational. However, ![]() $(z)$ is Poisson primitive and Poisson rational but not Poisson locally closed. Thus, the PDME for
$(z)$ is Poisson primitive and Poisson rational but not Poisson locally closed. Thus, the PDME for ![]() $\operatorname {S}(W)$ fails but holds for all prime Poisson ideals except for
$\operatorname {S}(W)$ fails but holds for all prime Poisson ideals except for ![]() $(0)$. Likewise, the PDME for
$(0)$. Likewise, the PDME for ![]() $\operatorname {S}(W_{\geqslant -1})$ fails but holds for all prime Poisson ideals except for
$\operatorname {S}(W_{\geqslant -1})$ fails but holds for all prime Poisson ideals except for ![]() $(0)$.
$(0)$.
Remark 5.3.2 By Corollary 3.3.5, the Poisson spectrum of ![]() $\operatorname {S}(V\!ir)[z^{-1}]$, which is in natural bijection with the set of prime Poisson ideals of
$\operatorname {S}(V\!ir)[z^{-1}]$, which is in natural bijection with the set of prime Poisson ideals of ![]() $\operatorname {S}(V\!ir)$ that do not contain
$\operatorname {S}(V\!ir)$ that do not contain ![]() $z$, consists of
$z$, consists of ![]() $(0)$ and the ideals
$(0)$ and the ideals ![]() $(z-\lambda )$ for
$(z-\lambda )$ for ![]() $\lambda \in \Bbbk ^*$: in other words,
$\lambda \in \Bbbk ^*$: in other words, ![]() $\operatorname {PSpec}(\operatorname {S}(V\!ir)[z^{-1}]) \cong \mathbb {A}^1 \setminus \{0\}$. Therefore, the most interesting structure of
$\operatorname {PSpec}(\operatorname {S}(V\!ir)[z^{-1}]) \cong \mathbb {A}^1 \setminus \{0\}$. Therefore, the most interesting structure of ![]() $\operatorname {S}(V\!ir)$ is concentrated above the ideal
$\operatorname {S}(V\!ir)$ is concentrated above the ideal ![]() $(z)$, which Theorem 5.3.1 shows to be pathological in some sense.
$(z)$, which Theorem 5.3.1 shows to be pathological in some sense.
To prove Theorem 5.3.1, we need notation for the Zariski topology on ![]() $\operatorname {PSpec} \operatorname {S}(\mathfrak g)$. If
$\operatorname {PSpec} \operatorname {S}(\mathfrak g)$. If ![]() $A$ is a Poisson algebra and
$A$ is a Poisson algebra and ![]() $N$ is a Poisson ideal of
$N$ is a Poisson ideal of ![]() $A$, we denote the corresponding closed subset of
$A$, we denote the corresponding closed subset of ![]() $\operatorname {PSpec} A$ by
$\operatorname {PSpec} A$ by
We caution the reader that although ![]() $V(N) \subseteq \operatorname {MSpec} A$ consists of maximal ideals,
$V(N) \subseteq \operatorname {MSpec} A$ consists of maximal ideals, ![]() $V_P(N) \subseteq \operatorname {PSpec} A$ consists of prime (Poisson) ideals.
$V_P(N) \subseteq \operatorname {PSpec} A$ consists of prime (Poisson) ideals.
Before proving Theorem 5.3.1, we note that the standard equivalent condition for a Poisson prime to be locally closed also holds in this infinite-dimensional setting.
Lemma 5.3.3 Let ![]() $A$ be a (possibly non-noetherian) Poisson algebra, and let
$A$ be a (possibly non-noetherian) Poisson algebra, and let ![]() $Q$ be a prime Poisson ideal of
$Q$ be a prime Poisson ideal of ![]() $A$. Then
$A$. Then ![]() $Q$ is locally closed in
$Q$ is locally closed in ![]() $\operatorname {PSpec} A$ if and only if there is some
$\operatorname {PSpec} A$ if and only if there is some ![]() $f \in A \setminus Q$ so that
$f \in A \setminus Q$ so that ![]() $(A/Q)[f^{-1}]$ is Poisson simple.
$(A/Q)[f^{-1}]$ is Poisson simple.
We leave the proof to the reader.
Proof of Theorem 5.3.1 Let ![]() $\mathfrak g$ be any countable-dimensional Lie algebra. By [Reference León Sánchez and SierraLS08, Theorem 6.3], for prime Poisson ideals of
$\mathfrak g$ be any countable-dimensional Lie algebra. By [Reference León Sánchez and SierraLS08, Theorem 6.3], for prime Poisson ideals of ![]() $\operatorname {S}(\mathfrak g)$, Poisson locally closed implies Poisson primitive and Poisson primitive is equivalent to Poisson rational. Thus, to prove the theorem for
$\operatorname {S}(\mathfrak g)$, Poisson locally closed implies Poisson primitive and Poisson primitive is equivalent to Poisson rational. Thus, to prove the theorem for ![]() $\operatorname {S}(V\!ir)$ and
$\operatorname {S}(V\!ir)$ and ![]() $\operatorname {S}(W)$, it suffices to prove the following.
$\operatorname {S}(W)$, it suffices to prove the following.
(a) Let
 $Q$ be a prime Poisson ideal of
$Q$ be a prime Poisson ideal of  $\operatorname {S}(V\!ir)$ with
$\operatorname {S}(V\!ir)$ with  $Q \neq (z)$. If
$Q \neq (z)$. If  $Q$ is Poisson primitive, then
$Q$ is Poisson primitive, then  $Q$ is Poisson locally closed.
$Q$ is Poisson locally closed.(b) The ideal
 $(z)$ is Poisson primitive but not Poisson locally closed.
$(z)$ is Poisson primitive but not Poisson locally closed.
We first prove part (b). Let ![]() $\nu \in V\!ir^*$ be any nonlocal function with
$\nu \in V\!ir^*$ be any nonlocal function with ![]() $\nu (z) = 0$ (for example, we can take
$\nu (z) = 0$ (for example, we can take ![]() $\nu$ to induce the nonlocal function
$\nu$ to induce the nonlocal function ![]() $\varkappa$ on
$\varkappa$ on ![]() $W$ given in Remark 3.0.3). By Theorem 3.3.1,
$W$ given in Remark 3.0.3). By Theorem 3.3.1, ![]() $\operatorname {P}(\nu ) = (z)$ and so
$\operatorname {P}(\nu ) = (z)$ and so ![]() $(z)$ is Poisson primitive.
$(z)$ is Poisson primitive.
To prove that ![]() $(z)$ is not Poisson locally closed, by Lemma 5.3.3 it is enough to prove that
$(z)$ is not Poisson locally closed, by Lemma 5.3.3 it is enough to prove that ![]() $\operatorname {S}(W)[f^{-1}]$ is not Poisson simple for any
$\operatorname {S}(W)[f^{-1}]$ is not Poisson simple for any ![]() $f\in \operatorname {S}(W) \setminus \{0\}$. Suppose that
$f\in \operatorname {S}(W) \setminus \{0\}$. Suppose that ![]() $\operatorname {S}(W)[f^{-1}]$ is Poisson simple. Then
$\operatorname {S}(W)[f^{-1}]$ is Poisson simple. Then ![]() $f$ is contained in all proper Poisson ideals of
$f$ is contained in all proper Poisson ideals of ![]() $\operatorname {S}(W)$. Let
$\operatorname {S}(W)$. Let ![]() $\chi \in W^*$ be a local function. The Poisson core
$\chi \in W^*$ be a local function. The Poisson core ![]() $\operatorname {P}(\chi )$ of
$\operatorname {P}(\chi )$ of ![]() $\chi$ is nontrivial, so
$\chi$ is nontrivial, so ![]() $f \in \operatorname {P}(\chi ) \subseteq \mathfrak m_\chi$. In other words, for any local function
$f \in \operatorname {P}(\chi ) \subseteq \mathfrak m_\chi$. In other words, for any local function ![]() $\chi \in W^*$, we have
$\chi \in W^*$, we have ![]() $\operatorname {ev}_\chi (f) = 0$, which is ridiculous.
$\operatorname {ev}_\chi (f) = 0$, which is ridiculous.
We now prove part (a). Let ![]() $\chi \in V\!ir^*$ with
$\chi \in V\!ir^*$ with ![]() $\operatorname {P}(\chi ) \neq (z)$. We show that
$\operatorname {P}(\chi ) \neq (z)$. We show that ![]() $\operatorname {P}(\chi )$ is Poisson locally closed.
$\operatorname {P}(\chi )$ is Poisson locally closed.
The ideals ![]() $(z-\zeta )$ with
$(z-\zeta )$ with ![]() $\zeta \neq 0$ are maximal in
$\zeta \neq 0$ are maximal in ![]() $\operatorname {PSpec} \operatorname {S}(V\!ir)$ by Corollary 3.3.5 and are, thus, closed points of
$\operatorname {PSpec} \operatorname {S}(V\!ir)$ by Corollary 3.3.5 and are, thus, closed points of ![]() $\operatorname {PSpec} \operatorname {S}(V\!ir)$. Thus, we may assume that
$\operatorname {PSpec} \operatorname {S}(V\!ir)$. Thus, we may assume that ![]() $\operatorname {P}(\chi ) \neq (z-\chi (z))$. By Theorem 3.3.1
$\operatorname {P}(\chi ) \neq (z-\chi (z))$. By Theorem 3.3.1 ![]() $\chi$ is therefore local and
$\chi$ is therefore local and ![]() $d:= \dim V\!ir/V\!ir^\chi < \infty$.
$d:= \dim V\!ir/V\!ir^\chi < \infty$.
Let ![]() $I(d-1)$ be the Poisson ideal of
$I(d-1)$ be the Poisson ideal of ![]() $\operatorname {S}(V\!ir)$ defined in Lemma 3.1.4. We claim that
$\operatorname {S}(V\!ir)$ defined in Lemma 3.1.4. We claim that
so ![]() $\operatorname {P}(\chi )$ is Poisson locally closed.
$\operatorname {P}(\chi )$ is Poisson locally closed.
First, by (3.1.5) ![]() $I(d-1) \not \subseteq \mathfrak m_\chi$ so
$I(d-1) \not \subseteq \mathfrak m_\chi$ so ![]() $\operatorname {P}(\chi ) \not \in V_P(I(d-1))$. By Proposition 4.3.6
$\operatorname {P}(\chi ) \not \in V_P(I(d-1))$. By Proposition 4.3.6 ![]() $d = \operatorname {GKdim} \operatorname {S}(V\!ir)/ \operatorname {P}(\chi )$. Thus, if
$d = \operatorname {GKdim} \operatorname {S}(V\!ir)/ \operatorname {P}(\chi )$. Thus, if ![]() $\nu \in \overline {\mathbb {O}(\chi )} \setminus \mathbb {O}(\chi )$, we have
$\nu \in \overline {\mathbb {O}(\chi )} \setminus \mathbb {O}(\chi )$, we have
where we have used Proposition 4.3.6 again for the last equality. Thus, ![]() $I(d-1) \subseteq \mathfrak m_\nu$ by (3.1.5), so
$I(d-1) \subseteq \mathfrak m_\nu$ by (3.1.5), so ![]() $I(d-1) \subseteq \operatorname {P}(\nu )$. It follows that if
$I(d-1) \subseteq \operatorname {P}(\nu )$. It follows that if ![]() $P$ is a Poisson prime ideal of
$P$ is a Poisson prime ideal of ![]() $\operatorname {S}(V\!ir)$ with
$\operatorname {S}(V\!ir)$ with ![]() $P \supsetneqq \operatorname {P}(\chi )$, then writing
$P \supsetneqq \operatorname {P}(\chi )$, then writing
we have ![]() $P \supseteq I(d-1)$, establishing the claim.
$P \supseteq I(d-1)$, establishing the claim.
The proof for ![]() $\operatorname {S}(W_{\geqslant -1})$ is almost identical.
$\operatorname {S}(W_{\geqslant -1})$ is almost identical.
We remark that we have used relatively few pieces of structure theory of ![]() $V\!ir$,
$V\!ir$, ![]() $W$ and
$W$ and ![]() $W_{\geqslant -1}$ in the proof of Theorem 5.3.1 (the inputs are essentially that
$W_{\geqslant -1}$ in the proof of Theorem 5.3.1 (the inputs are essentially that ![]() $\dim \mathbb {O}(\chi )=\dim \mathfrak g\cdot \chi$ and that
$\dim \mathbb {O}(\chi )=\dim \mathfrak g\cdot \chi$ and that ![]() $\dim \mathfrak g\cdot \chi <\infty$ for all
$\dim \mathfrak g\cdot \chi <\infty$ for all ![]() $\chi$ in which we are interested). Thus, similar results may hold for a wider class of Lie algebras.
$\chi$ in which we are interested). Thus, similar results may hold for a wider class of Lie algebras.
5.4 Radical Poisson ideals contain Poisson primitive ideals
Let ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $W_{\geqslant -1}$. From the bijection in Theorem 5.2.8 it is tempting to think of Poisson primitive ideals of
$W_{\geqslant -1}$. From the bijection in Theorem 5.2.8 it is tempting to think of Poisson primitive ideals of ![]() $\operatorname {S}(\mathfrak g)$ as analogous to closed points: by that result, a prime Poisson ideal
$\operatorname {S}(\mathfrak g)$ as analogous to closed points: by that result, a prime Poisson ideal ![]() $Q$ is Poisson primitive if and only if
$Q$ is Poisson primitive if and only if ![]() $Y(Q)$ is a single point. Note, however, that Theorem 5.3.1 also tells how to distinguish Poisson primitive ideals in
$Y(Q)$ is a single point. Note, however, that Theorem 5.3.1 also tells how to distinguish Poisson primitive ideals in ![]() $\operatorname {PSpec} \operatorname {S}(W)$, and we saw there that, in general, they are only locally closed. The next result shows how far most of the Poisson primitive ideals are from being maximal in
$\operatorname {PSpec} \operatorname {S}(W)$, and we saw there that, in general, they are only locally closed. The next result shows how far most of the Poisson primitive ideals are from being maximal in ![]() $\operatorname {PSpec} \operatorname {S}(\mathfrak g)$; see also Corollary 4.3.18.
$\operatorname {PSpec} \operatorname {S}(\mathfrak g)$; see also Corollary 4.3.18.
Proposition 5.4.1 Let ![]() $\mathfrak g=W$,
$\mathfrak g=W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$ and let
$W_{\geqslant 1}$ and let ![]() $I$ be a nonzero radical Poisson ideal of
$I$ be a nonzero radical Poisson ideal of ![]() $\operatorname {S}(\mathfrak g)$. Then there is some local function
$\operatorname {S}(\mathfrak g)$. Then there is some local function ![]() $\nu \in \mathfrak g^*$ with
$\nu \in \mathfrak g^*$ with ![]() $\operatorname {P}(\nu )\subseteq I$.
$\operatorname {P}(\nu )\subseteq I$.
If ![]() $I$ is prime and
$I$ is prime and ![]() $\mathfrak g = W$ or
$\mathfrak g = W$ or ![]() $W_{\geqslant -1}$ this may be deduced from the bijection
$W_{\geqslant -1}$ this may be deduced from the bijection ![]() $\Psi$ of Subsection 5.2. We provide a direct proof, however.
$\Psi$ of Subsection 5.2. We provide a direct proof, however.
Proof. Thanks to Theorem 3.0.4 we have that ![]() $\operatorname {GKdim}(\operatorname {S}(\mathfrak g)/I)<\infty$; pick
$\operatorname {GKdim}(\operatorname {S}(\mathfrak g)/I)<\infty$; pick ![]() $d\in \mathbb {Z}_{\geqslant 1}$ with
$d\in \mathbb {Z}_{\geqslant 1}$ with ![]() $2d>\operatorname {GKdim}(\operatorname {S}(\mathfrak g)/I)$. By Lemma 2.0.4
$2d>\operatorname {GKdim}(\operatorname {S}(\mathfrak g)/I)$. By Lemma 2.0.4 ![]() $I$ is an intersection of a family of primitive ideals
$I$ is an intersection of a family of primitive ideals ![]() $\operatorname {P}(\mu )$, and
$\operatorname {P}(\mu )$, and
for each ![]() $\mu$ with
$\mu$ with ![]() $\mathfrak m_\mu \supseteq I$. We show that there exists
$\mathfrak m_\mu \supseteq I$. We show that there exists ![]() $\nu = \nu _{d} \in \mathfrak g^*$ such that if
$\nu = \nu _{d} \in \mathfrak g^*$ such that if ![]() $\mu \in \mathfrak g^*$ with
$\mu \in \mathfrak g^*$ with
then ![]() $\operatorname {P}(\nu )\subseteq \operatorname {P}(\mu )$.
$\operatorname {P}(\nu )\subseteq \operatorname {P}(\mu )$.
Pick ![]() $\mu \in \mathfrak g^*$ with
$\mu \in \mathfrak g^*$ with ![]() $\dim \mathfrak g\cdot \mu =\operatorname {GKdim}(\operatorname {S}(\mathfrak g)/\operatorname {P}(\mu ))<2d$, see Proposition 4.3.6(b). Then
$\dim \mathfrak g\cdot \mu =\operatorname {GKdim}(\operatorname {S}(\mathfrak g)/\operatorname {P}(\mu ))<2d$, see Proposition 4.3.6(b). Then ![]() $\mu$ is local and, thus, is a sum of several (say
$\mu$ is local and, thus, is a sum of several (say ![]() $\ell$) nonzero one-point local functions
$\ell$) nonzero one-point local functions ![]() $\mu _i\in \mathfrak g^*$ with distinct supports
$\mu _i\in \mathfrak g^*$ with distinct supports ![]() $x_i$. Recall that
$x_i$. Recall that ![]() $\dim \mathfrak g\cdot \mu =\sum _{i=1}^\ell \dim \mathfrak g\cdot \mu _i$ by Lemma 4.3.4 and therefore
$\dim \mathfrak g\cdot \mu =\sum _{i=1}^\ell \dim \mathfrak g\cdot \mu _i$ by Lemma 4.3.4 and therefore ![]() $\dim \mathfrak g\cdot \mu _i<2d$ together with
$\dim \mathfrak g\cdot \mu _i<2d$ together with ![]() $\ell < 2d$. Pick
$\ell < 2d$. Pick ![]() $n\in \mathbb {Z}_{\geqslant 0}$ such that
$n\in \mathbb {Z}_{\geqslant 0}$ such that ![]() $n\geqslant 2d$ and
$n\geqslant 2d$ and ![]() $\mu _i\in \textit {Loc}_{x_i}^{\leqslant n}$ for all
$\mu _i\in \textit {Loc}_{x_i}^{\leqslant n}$ for all ![]() $i$. Thanks to Lemmata 4.1.3 and 4.1.6 we have
$i$. Thanks to Lemmata 4.1.3 and 4.1.6 we have ![]() $\dim \textit {DLoc}_{x_i}^{\leqslant n}\mu _i<2d$ for all
$\dim \textit {DLoc}_{x_i}^{\leqslant n}\mu _i<2d$ for all ![]() $i$.
$i$.
Let ![]() $\widetilde \chi _i:=\chi _{x_i; \small {\underbrace {0, 0, \ldots,0,}_{2d\text {~times}}} \mbox {1}}$. Thanks to Theorem 4.2.1 we have
$\widetilde \chi _i:=\chi _{x_i; \small {\underbrace {0, 0, \ldots,0,}_{2d\text {~times}}} \mbox {1}}$. Thanks to Theorem 4.2.1 we have ![]() $\dim \textit {DLoc}_{x_i}^{\leqslant n}\widetilde \chi _i=2d+1>\dim \textit {DLoc}_{x_i}^{\leqslant n}\mu _i$. This together with Corollary 4.2.9 implies that
$\dim \textit {DLoc}_{x_i}^{\leqslant n}\widetilde \chi _i=2d+1>\dim \textit {DLoc}_{x_i}^{\leqslant n}\mu _i$. This together with Corollary 4.2.9 implies that ![]() $\operatorname {P}(\widetilde \chi _i)\subseteq \operatorname {P}(\chi _i)$.
$\operatorname {P}(\widetilde \chi _i)\subseteq \operatorname {P}(\chi _i)$.
By Corollary 4.3.17, ![]() $\operatorname {P}(\sum _{i=1}^{\ell }\widetilde {\chi _i})\subseteq \operatorname {P}(\mu )$.
$\operatorname {P}(\sum _{i=1}^{\ell }\widetilde {\chi _i})\subseteq \operatorname {P}(\mu )$.
Set ![]() $\widetilde {\chi _i}':=\chi _{{\it {i}}; \underbrace {\scriptsize {0, 0, \ldots,0,}}_{2d\text {~times}} \mbox {1}}$. By Theorem 4.3.1,
$\widetilde {\chi _i}':=\chi _{{\it {i}}; \underbrace {\scriptsize {0, 0, \ldots,0,}}_{2d\text {~times}} \mbox {1}}$. By Theorem 4.3.1, ![]() $\operatorname {P}(\sum _{i=1}^{\ell }\widetilde {\chi _i})=\operatorname {P}(\sum _{i=1}^\ell \widetilde {\chi _i}')$ and hence, applying Corollary 4.3.17,
$\operatorname {P}(\sum _{i=1}^{\ell }\widetilde {\chi _i})=\operatorname {P}(\sum _{i=1}^\ell \widetilde {\chi _i}')$ and hence, applying Corollary 4.3.17, ![]() $\nu =\sum _{i=1}^{2d}\widetilde {\chi _i}'$ satisfies the desired properties.
$\nu =\sum _{i=1}^{2d}\widetilde {\chi _i}'$ satisfies the desired properties.
By Lemma 2.0.4, ![]() $\operatorname {P}(\nu ) \subseteq I$.
$\operatorname {P}(\nu ) \subseteq I$.
The statement of the above corollary can be rephrased as follows: every proper algebraic collection of pseudo-orbits is (strictly) contained in the closure of a single finite-dimensional pseudo-orbit. If ![]() $\dim \mathfrak g < \infty$, this means that
$\dim \mathfrak g < \infty$, this means that ![]() $\mathfrak g^*$ contains a dense coadjoint orbit; such Lie algebras are called Frobenius Lie algebras and there are very few of them. For infinite-dimensional Lie algebras this statement seems quite counterintuitive. We expect that only a few Lie algebras satisfy it.
$\mathfrak g^*$ contains a dense coadjoint orbit; such Lie algebras are called Frobenius Lie algebras and there are very few of them. For infinite-dimensional Lie algebras this statement seems quite counterintuitive. We expect that only a few Lie algebras satisfy it.
The next corollary answers Question 6.8 of [Reference León Sánchez and SierraLS08].
Corollary 5.4.2 Let ![]() $\mathfrak g = W$,
$\mathfrak g = W$, ![]() $W_{\geqslant -1}$ or
$W_{\geqslant -1}$ or ![]() $W_{\geqslant 1}$. Then
$W_{\geqslant 1}$. Then ![]() $\operatorname {S}(\mathfrak g)$ has no nonzero prime Poisson ideals of finite height.
$\operatorname {S}(\mathfrak g)$ has no nonzero prime Poisson ideals of finite height.
Proof. For ![]() $d \in \mathbb {Z}_{\geqslant 0}$ let
$d \in \mathbb {Z}_{\geqslant 0}$ let ![]() $\nu _d \in \mathfrak g^*$ be the local function defined in the proof of Proposition 5.4.1. The crucial property of
$\nu _d \in \mathfrak g^*$ be the local function defined in the proof of Proposition 5.4.1. The crucial property of ![]() $\nu _d$, established in that proof, is that
$\nu _d$, established in that proof, is that
Let ![]() $Q$ be a nonzero Poisson prime ideal of
$Q$ be a nonzero Poisson prime ideal of ![]() $\operatorname {S}(\mathfrak g)$ and let
$\operatorname {S}(\mathfrak g)$ and let ![]() $d_1 := \operatorname {GKdim} \operatorname {S}(\mathfrak g)/Q$, which is finite by Theorem 3.0.4. By the proof of Proposition 5.4.1,
$d_1 := \operatorname {GKdim} \operatorname {S}(\mathfrak g)/Q$, which is finite by Theorem 3.0.4. By the proof of Proposition 5.4.1, ![]() $\operatorname {P}(\nu _{d_1}) \subseteq Q$. Then define
$\operatorname {P}(\nu _{d_1}) \subseteq Q$. Then define ![]() $d_i$ by induction: let
$d_i$ by induction: let ![]() $d_{i+1} := \operatorname {GKdim}(\operatorname {S}(\mathfrak g)/\operatorname {P}(\nu _{d_i}))+2$. By (5.4.3), each
$d_{i+1} := \operatorname {GKdim}(\operatorname {S}(\mathfrak g)/\operatorname {P}(\nu _{d_i}))+2$. By (5.4.3), each ![]() $\operatorname {P}(\nu _{d_{i+1}}) \subsetneqq \operatorname {P}(\nu _{d_i})$.
$\operatorname {P}(\nu _{d_{i+1}}) \subsetneqq \operatorname {P}(\nu _{d_i})$.
By Corollary 3.3.5, if ![]() $\zeta \in \Bbbk ^\times$, then
$\zeta \in \Bbbk ^\times$, then ![]() $(0)$ is the only prime Poisson ideal of
$(0)$ is the only prime Poisson ideal of ![]() $\operatorname {S}(V\!ir)$ which is contained in
$\operatorname {S}(V\!ir)$ which is contained in ![]() $(z-\zeta )$; thus, the maximal Poisson ideal
$(z-\zeta )$; thus, the maximal Poisson ideal ![]() $(z-\zeta )$ has height 1 as a prime Poisson ideal.
$(z-\zeta )$ has height 1 as a prime Poisson ideal.
6. Subalgebras of finite codimension
In this section we sharpen earlier results to classify subalgebras of ![]() $V\!ir$ of small codimension. By Proposition 3.3.3 we know any such subalgebra contains
$V\!ir$ of small codimension. By Proposition 3.3.3 we know any such subalgebra contains ![]() $z$, so we may reduce to considering the corresponding subalgebra of
$z$, so we may reduce to considering the corresponding subalgebra of ![]() $W$; by Proposition 3.2.7 this contains some
$W$; by Proposition 3.2.7 this contains some ![]() $W(f)$ with
$W(f)$ with ![]() $f \neq 0$. We refine these results and provide more precise statements on subalgebras of
$f \neq 0$. We refine these results and provide more precise statements on subalgebras of ![]() $V\!ir$ and of
$V\!ir$ and of ![]() $W$ of codimensions one, two and three.
$W$ of codimensions one, two and three.
Throughout this section we assume that ![]() $\mathfrak k$ is a subalgebra of
$\mathfrak k$ is a subalgebra of ![]() $W\!$ of finite codimension. Let
$W\!$ of finite codimension. Let ![]() $f_{\mathfrak k} \in \Bbbk [t]$ be the lowest-degree monic polynomial with
$f_{\mathfrak k} \in \Bbbk [t]$ be the lowest-degree monic polynomial with ![]() $\mathfrak k\supset W(f)$, which exists by Proposition 3.2.7. Proposition 3.2.7, in fact, gives us that
$\mathfrak k\supset W(f)$, which exists by Proposition 3.2.7. Proposition 3.2.7, in fact, gives us that
where recall that ![]() ${\rm rad}(f)=\prod \{ (t-x) \,|\, f(x) = 0\}$. Thus,
${\rm rad}(f)=\prod \{ (t-x) \,|\, f(x) = 0\}$. Thus,
By the Euclidean algorithm, ![]() $W(h)\subseteq \mathfrak k$ if and only if
$W(h)\subseteq \mathfrak k$ if and only if ![]() $f_{\mathfrak k} \mid h$.
$f_{\mathfrak k} \mid h$.
We immediately obtain a classification of subalgebras of codimension one, a more conceptual proof of a result originally due to Ondrus and Wiesner [Reference Ondrus and WiesnerOW18, Proposition 2.3].
Corollary 6.0.3 Let ![]() $\mathfrak h$ be a subalgebra of
$\mathfrak h$ be a subalgebra of ![]() $V\!ir$ of codimension one. Then there is
$V\!ir$ of codimension one. Then there is ![]() $x \in \Bbbk ^\times$ so that
$x \in \Bbbk ^\times$ so that
Proof. As remarked previously, by Proposition 3.3.3 ![]() $z \in \mathfrak h$ so it suffices to prove that
$z \in \mathfrak h$ so it suffices to prove that ![]() $\mathfrak k := \mathfrak h /(z)$, which is a subalgebra of
$\mathfrak k := \mathfrak h /(z)$, which is a subalgebra of ![]() $W\!$ of codimension one, is equal to some
$W\!$ of codimension one, is equal to some ![]() $W(t-x)$. By (6.0.2)
$W(t-x)$. By (6.0.2) ![]() $f_{\mathfrak k}$ must be equal to some
$f_{\mathfrak k}$ must be equal to some ![]() $(t-x)^a$ and by (6.0.1)
$(t-x)^a$ and by (6.0.1) ![]() $\mathfrak k \subseteq W(t-x)$. However,
$\mathfrak k \subseteq W(t-x)$. However, ![]() $W(t-x)$ already has codimension one.
$W(t-x)$ already has codimension one.
The problem of classifying general cofinite-dimensional subalgebras of ![]() $V\!ir$ is equivalent, by Proposition 3.3.3 and (6.0.1), to the problem of classifying subalgebras of an arbitrary Lie algebra of the form
$V\!ir$ is equivalent, by Proposition 3.3.3 and (6.0.1), to the problem of classifying subalgebras of an arbitrary Lie algebra of the form ![]() $W({\rm rad}(f))/W(f)$; note that
$W({\rm rad}(f))/W(f)$; note that ![]() $W(f)$ is a Lie ideal of
$W(f)$ is a Lie ideal of ![]() $W({\rm rad}(f))$ and that
$W({\rm rad}(f))$ and that ![]() $W({\rm rad}(f))/W(f)$ is finite-dimensional and nilpotent. In §§ 6.2 and 6.3 we give a complete classification of Lie subalgebras
$W({\rm rad}(f))/W(f)$ is finite-dimensional and nilpotent. In §§ 6.2 and 6.3 we give a complete classification of Lie subalgebras ![]() $\mathfrak k\subseteq W$ of codimension two and three, illustrating the complexity of the problem.
$\mathfrak k\subseteq W$ of codimension two and three, illustrating the complexity of the problem.
6.1 Notation and concepts
We begin by establishing some needed notation. We call the full list of subalgebras of ![]() $W$ of codimension one the spectrum of
$W$ of codimension one the spectrum of ![]() $W$. Corollary 6.0.3 implies that every such subalgebra is of the form
$W$. Corollary 6.0.3 implies that every such subalgebra is of the form ![]() $W(t-x)$ for an appropriate
$W(t-x)$ for an appropriate ![]() $x\in \Bbbk ^\times$ and, thus, we can identify the spectrum of
$x\in \Bbbk ^\times$ and, thus, we can identify the spectrum of ![]() $W$ with
$W$ with ![]() $\Bbbk ^\times$. Pick a subalgebra
$\Bbbk ^\times$. Pick a subalgebra ![]() $\mathfrak k$ of
$\mathfrak k$ of ![]() $W$ of finite codimension. Denote by
$W$ of finite codimension. Denote by ![]() $\operatorname {supp}(\mathfrak k)$ the list of
$\operatorname {supp}(\mathfrak k)$ the list of ![]() $x\in \Bbbk ^\times$ so that
$x\in \Bbbk ^\times$ so that ![]() $\mathfrak k\subseteq W(t-x)$. By (6.0.1)
$\mathfrak k\subseteq W(t-x)$. By (6.0.1) ![]() $\operatorname {supp}(\mathfrak k)$ is nonempty and finite. The picture is parallel to that of ideals in a commutative
$\operatorname {supp}(\mathfrak k)$ is nonempty and finite. The picture is parallel to that of ideals in a commutative ![]() $\Bbbk$-algebra, where subalgebras of codimension one (maximal subalgebras) are the natural analogues of ideals of codimension one (maximal ideals).
$\Bbbk$-algebra, where subalgebras of codimension one (maximal subalgebras) are the natural analogues of ideals of codimension one (maximal ideals).
It will be useful below to carry out a more detailed analysis of subalgebras with ![]() $|\operatorname {supp}(\mathfrak k)|=1$. We establish notation for various invariants of such
$|\operatorname {supp}(\mathfrak k)|=1$. We establish notation for various invariants of such ![]() $\mathfrak k$.
$\mathfrak k$.
Notation 6.1.1 Let ![]() $\mathfrak k$ be a finite-codimension subalgebra of
$\mathfrak k$ be a finite-codimension subalgebra of ![]() $W$ with
$W$ with ![]() $|\operatorname {supp}(\mathfrak k)|=1$. We define the following invariants of
$|\operatorname {supp}(\mathfrak k)|=1$. We define the following invariants of ![]() $\mathfrak k$.
$\mathfrak k$.
Let ![]() $d:= d(\mathfrak k) := \operatorname {codim}_W\mathfrak k$. As
$d:= d(\mathfrak k) := \operatorname {codim}_W\mathfrak k$. As ![]() $\operatorname {supp}(\mathfrak k)=\{x\}$ for some
$\operatorname {supp}(\mathfrak k)=\{x\}$ for some ![]() $x\in \Bbbk ^\times$ we have
$x\in \Bbbk ^\times$ we have ![]() $f_{\mathfrak k} = (t-x)^a$ for some
$f_{\mathfrak k} = (t-x)^a$ for some ![]() $a \geqslant d$. Let
$a \geqslant d$. Let ![]() $a(\mathfrak k) := a$. If
$a(\mathfrak k) := a$. If ![]() $a= d$, then
$a= d$, then ![]() $\mathfrak k = W((t-x)^{d})$. By the definition of
$\mathfrak k = W((t-x)^{d})$. By the definition of ![]() $f_{\mathfrak k}$, if
$f_{\mathfrak k}$, if ![]() $a \neq d$, then
$a \neq d$, then
Assume that ![]() $a \neq d$. Set
$a \neq d$. Set ![]() $\tilde t:=t-x$. Let
$\tilde t:=t-x$. Let ![]() $f_1, f_2, \ldots, f_{a-d}$ be elements of
$f_1, f_2, \ldots, f_{a-d}$ be elements of ![]() $\Bbbk [t, t^{-1}]$ so that the images of the
$\Bbbk [t, t^{-1}]$ so that the images of the ![]() $f_i \partial$ give a basis for
$f_i \partial$ give a basis for ![]() $\mathfrak k / W(f)$. We may write each
$\mathfrak k / W(f)$. We may write each ![]() $f_i$ as
$f_i$ as ![]() $\tilde t^{n_i} k_i$ where
$\tilde t^{n_i} k_i$ where ![]() $k_i(x) = 1$. By cancelling leading terms in the Taylor expansion of
$k_i(x) = 1$. By cancelling leading terms in the Taylor expansion of ![]() $f_i$ around
$f_i$ around ![]() $\tilde t=0$ we may assume that
$\tilde t=0$ we may assume that
where we used (6.1.2) for the last inequality. Write ![]() $\{ 1, \ldots, a-1\} \setminus \{ n_1, \ldots, n_{a-d}\} = \{ g_1, \ldots, g_{d-1}\}$ where
$\{ 1, \ldots, a-1\} \setminus \{ n_1, \ldots, n_{a-d}\} = \{ g_1, \ldots, g_{d-1}\}$ where ![]() $g_1 < g_2< \cdots$. We say that
$g_1 < g_2< \cdots$. We say that
are the leading degrees of ![]() $\mathfrak k$. We say that
$\mathfrak k$. We say that ![]() $\operatorname {gaps}(\mathfrak k):=\{g_1-1, \ldots, g_d-1\}$ are gaps of
$\operatorname {gaps}(\mathfrak k):=\{g_1-1, \ldots, g_d-1\}$ are gaps of ![]() $\mathfrak k$.
$\mathfrak k$.
Note that we do not allow ![]() $\operatorname {gaps}(\mathfrak k) = \{0, \ldots, a-2\}$ as this would mean that
$\operatorname {gaps}(\mathfrak k) = \{0, \ldots, a-2\}$ as this would mean that ![]() $\operatorname {ldeg} (\mathfrak k) = \emptyset$, contradicting the assumption that
$\operatorname {ldeg} (\mathfrak k) = \emptyset$, contradicting the assumption that ![]() $a(\mathfrak k) \neq d(\mathfrak k)$.
$a(\mathfrak k) \neq d(\mathfrak k)$.
Lemma 6.1.3
(a) Let
 $\mathfrak k$ satisfy
$\mathfrak k$ satisfy  $|\operatorname {supp}(\mathfrak k) | = 1$ with
$|\operatorname {supp}(\mathfrak k) | = 1$ with  $a := a(\mathfrak k) > d:= d(\mathfrak k)$. Pick
$a := a(\mathfrak k) > d:= d(\mathfrak k)$. Pick  $1\leqslant i\ne j\leqslant a-d$. Then either
$1\leqslant i\ne j\leqslant a-d$. Then either  $(n_i-1)+(n_j-1)\geqslant (a-1)$ or
$(n_i-1)+(n_j-1)\geqslant (a-1)$ or  $(n_i-1)+(n_j-1)\in \operatorname {ldeg}(\mathfrak k)$.
$(n_i-1)+(n_j-1)\in \operatorname {ldeg}(\mathfrak k)$.(b) Let
 $S = \{ n_1, \ldots, n_\ell \}$ be a subset of
$S = \{ n_1, \ldots, n_\ell \}$ be a subset of  $\{1,\ldots, a-2\}$ satisfying the conclusion of part (a). Then there exists a subalgebra
$\{1,\ldots, a-2\}$ satisfying the conclusion of part (a). Then there exists a subalgebra  $\tilde {\mathfrak k}$ of
$\tilde {\mathfrak k}$ of  $W\!$ with
$W\!$ with  $a(\tilde {\mathfrak k})=a$ and
$a(\tilde {\mathfrak k})=a$ and  $\operatorname {ldeg}(\tilde {\mathfrak k})=S$.
$\operatorname {ldeg}(\tilde {\mathfrak k})=S$.
Proof. For part (a), consider
It is easy to verify that ![]() $k_{i, j}=\tilde {f}_{i, j}/\tilde t^{n_i+n_j-1} \in \Bbbk [t, t^{-1}]$ and
$k_{i, j}=\tilde {f}_{i, j}/\tilde t^{n_i+n_j-1} \in \Bbbk [t, t^{-1}]$ and ![]() $k_{i, j}(x)\ne 0$. This implies part (a).
$k_{i, j}(x)\ne 0$. This implies part (a).
For part (b), it is clear that the space ![]() $\tilde {\mathfrak k}$ defined as the span of
$\tilde {\mathfrak k}$ defined as the span of ![]() $W(\tilde t^a)$ and
$W(\tilde t^a)$ and ![]() $\tilde t^i\partial$ with
$\tilde t^i\partial$ with ![]() $i\in S$ is a Lie subalgebra of
$i\in S$ is a Lie subalgebra of ![]() $W$.
$W$.
The reason for subtracting 1 in the definition of the leading degrees of ![]() $\mathfrak k$ is that Lemma 6.1.3 shows that
$\mathfrak k$ is that Lemma 6.1.3 shows that ![]() $\operatorname {ldeg}(\mathfrak k)$ has the structure of a partial semigroup under addition.
$\operatorname {ldeg}(\mathfrak k)$ has the structure of a partial semigroup under addition.
We deduce from Lemma 6.1.3 the following fact.
Lemma 6.1.4 Let ![]() $\mathfrak k$ satisfy
$\mathfrak k$ satisfy ![]() $|\operatorname {supp}(\mathfrak k) | = 1$ with
$|\operatorname {supp}(\mathfrak k) | = 1$ with ![]() $a := a(\mathfrak k) > d:= d(\mathfrak k)$. If
$a := a(\mathfrak k) > d:= d(\mathfrak k)$. If ![]() $g_1=1$, then
$g_1=1$, then ![]() $g_i\leqslant 2i-1$ for all
$g_i\leqslant 2i-1$ for all ![]() $i, 1\leqslant i\leqslant d-1$. If
$i, 1\leqslant i\leqslant d-1$. If ![]() $g_1\ne 1$, then
$g_1\ne 1$, then ![]() $g_i\leqslant 2i+1$ for all
$g_i\leqslant 2i+1$ for all ![]() $i, 1\leqslant i\leqslant d$.
$i, 1\leqslant i\leqslant d$.
Proof. First assume that ![]() $g_1=1$. Next, assume to the contrary that
$g_1=1$. Next, assume to the contrary that ![]() $g_i=2i-1+\delta$ with
$g_i=2i-1+\delta$ with ![]() $\delta >0$. Consider the list of pairs
$\delta >0$. Consider the list of pairs
For each pair ![]() $(p,q)$ in (6.1.5) we have
$(p,q)$ in (6.1.5) we have ![]() $p+q-1=g_i$; further, Lemma 6.1.3 implies that either
$p+q-1=g_i$; further, Lemma 6.1.3 implies that either ![]() $p-1$ or
$p-1$ or ![]() $q-1$ belongs to
$q-1$ belongs to ![]() $\operatorname {gaps}(\mathfrak k)$ for each pair
$\operatorname {gaps}(\mathfrak k)$ for each pair ![]() $(p, q)$ from (6.1.5), it must be in
$(p, q)$ from (6.1.5), it must be in ![]() $\{g_2, \ldots, g_{i-1}\}$ as
$\{g_2, \ldots, g_{i-1}\}$ as ![]() $g_1 = 1< p, q$. There are
$g_1 = 1< p, q$. There are ![]() $i-1$ pairs in (6.1.5) but only
$i-1$ pairs in (6.1.5) but only ![]() $i-2$ gaps from
$i-2$ gaps from ![]() $g_2$ to
$g_2$ to ![]() $g_{i-1}$. This contradiction completes the case
$g_{i-1}$. This contradiction completes the case ![]() $g_1=1$. In the case
$g_1=1$. In the case ![]() $g_1>1$ we have to do the same thing with a minor modification: we have to add
$g_1>1$ we have to do the same thing with a minor modification: we have to add ![]() $g_1$ to the list
$g_1$ to the list ![]() $\{g_2, \ldots, g_{i-1}\}$.
$\{g_2, \ldots, g_{i-1}\}$.
Remark 6.1.6 Note that ![]() $g_d=a-1\leqslant 2d+1$ and, hence, one can enumerate all the pairs
$g_d=a-1\leqslant 2d+1$ and, hence, one can enumerate all the pairs ![]() $(S, a)$ satisfying the conclusion of condition (a) of Lemma 6.1.3 for a given codimension
$(S, a)$ satisfying the conclusion of condition (a) of Lemma 6.1.3 for a given codimension ![]() $d$. We believe that such pairs
$d$. We believe that such pairs ![]() $(S, a)$ are in bijection with irreducible components of the moduli space of subalgebras
$(S, a)$ are in bijection with irreducible components of the moduli space of subalgebras ![]() $\mathfrak k$ of codimension
$\mathfrak k$ of codimension ![]() $d$ with
$d$ with ![]() $|\operatorname {supp}(\mathfrak k)|=1$.
$|\operatorname {supp}(\mathfrak k)|=1$.
6.2 Subalgebras of codimension two
The goal of this subsection is to show that all subalgebras of ![]() $W\!$ of codimension two are listed in Table 1.
$W\!$ of codimension two are listed in Table 1.
Table 1. Subalgebras of ![]() $W\!$ of codimension two.
$W\!$ of codimension two.

Here ![]() $x, y, \alpha$ are parameters taking values in
$x, y, \alpha$ are parameters taking values in ![]() $\Bbbk$ with
$\Bbbk$ with ![]() $x, y\ne 0$.
$x, y\ne 0$.
The proof consists of the following two statements.
Proposition 6.2.1
(a) If
 $\operatorname {codim}_W \mathfrak k=2$, then
$\operatorname {codim}_W \mathfrak k=2$, then  $|\operatorname {supp}(\mathfrak k)|\in \{1, 2\}$.
$|\operatorname {supp}(\mathfrak k)|\in \{1, 2\}$.(b) If
 $|\operatorname {supp}(\mathfrak k)|=2$, then
$|\operatorname {supp}(\mathfrak k)|=2$, then  $\mathfrak k=W((t-x)(t-y))$ and
$\mathfrak k=W((t-x)(t-y))$ and  $\operatorname {supp}(\mathfrak k)=\{x, y\}$ for some
$\operatorname {supp}(\mathfrak k)=\{x, y\}$ for some  $x \neq y\in \Bbbk ^\times$.
$x \neq y\in \Bbbk ^\times$.
Proposition 6.2.2
(a) If
 $\operatorname {codim}_W\mathfrak k=2$ and
$\operatorname {codim}_W\mathfrak k=2$ and  $| \operatorname {supp}(\mathfrak k)| = 1$ (so
$| \operatorname {supp}(\mathfrak k)| = 1$ (so  $\operatorname {supp}(\mathfrak k)=\{x\}$ for some
$\operatorname {supp}(\mathfrak k)=\{x\}$ for some  $x \in \Bbbk ^\times$), then either
$x \in \Bbbk ^\times$), then either  $\mathfrak k = W((t-x)^2)$ or
$\mathfrak k = W((t-x)^2)$ or  $\operatorname {gaps}(\mathfrak k)$ is
$\operatorname {gaps}(\mathfrak k)$ is  $\{1\}$ or
$\{1\}$ or  $\{2\}$.
$\{2\}$.(b) If
 $\operatorname {gaps}(\mathfrak k)=\{1\}$, then
$\operatorname {gaps}(\mathfrak k)=\{1\}$, then  $\mathfrak k=W_{x; \alpha }^{2; 1}$ for a unique
$\mathfrak k=W_{x; \alpha }^{2; 1}$ for a unique  $\alpha \in \Bbbk$.
$\alpha \in \Bbbk$.(c) If
 $\operatorname {gaps}(\mathfrak k)=\{2\}$, then
$\operatorname {gaps}(\mathfrak k)=\{2\}$, then  $\mathfrak k=W_{x; \alpha }^{2; 2}$ for a unique
$\mathfrak k=W_{x; \alpha }^{2; 2}$ for a unique  $\alpha \in \Bbbk$.
$\alpha \in \Bbbk$.
Proof of Proposition 6.2.1 Theorem 3.2.7 implies ![]() $|\operatorname {supp}(\mathfrak k)|\geqslant 1$, and (6.0.2) implies that
$|\operatorname {supp}(\mathfrak k)|\geqslant 1$, and (6.0.2) implies that ![]() $|\operatorname {supp}(\mathfrak k)|\leqslant 2$. This proves part (a).
$|\operatorname {supp}(\mathfrak k)|\leqslant 2$. This proves part (a).
Assume ![]() $\operatorname {supp}(\mathfrak k)=\{x, y\}$ for some distinct
$\operatorname {supp}(\mathfrak k)=\{x, y\}$ for some distinct ![]() $x, y\in \Bbbk ^\times$. We have
$x, y\in \Bbbk ^\times$. We have ![]() $\mathfrak k\subseteq W((t-x)(t-y))$ and
$\mathfrak k\subseteq W((t-x)(t-y))$ and
Hence, ![]() $\mathfrak k=W((t-x)(t-y))$ and part (b) is complete.
$\mathfrak k=W((t-x)(t-y))$ and part (b) is complete.
Proof of Proposition 6.2.2 We may assume that ![]() $\mathfrak k \neq W((t-x)^2)$. Adopt the terminology of Notation 6.1.1. We have
$\mathfrak k \neq W((t-x)^2)$. Adopt the terminology of Notation 6.1.1. We have ![]() $|\operatorname {gaps}(\mathfrak k)|=\operatorname {codim}(\mathfrak k)-1$ and, hence,
$|\operatorname {gaps}(\mathfrak k)|=\operatorname {codim}(\mathfrak k)-1$ and, hence, ![]() $|\operatorname {gaps}(\mathfrak k)|=\{g_1-1\}$ for a certain positive integer
$|\operatorname {gaps}(\mathfrak k)|=\{g_1-1\}$ for a certain positive integer ![]() $g_1$. Note that
$g_1$. Note that ![]() $g_1 = a(\mathfrak k) - 1$ by (6.1.2). Thanks to Lemma 6.1.3 we have
$g_1 = a(\mathfrak k) - 1$ by (6.1.2). Thanks to Lemma 6.1.3 we have ![]() $g_1\leqslant 3$. This proves part (a).
$g_1\leqslant 3$. This proves part (a).
Note that ![]() $g_1 \neq 1$ as by convention
$g_1 \neq 1$ as by convention ![]() $\operatorname {gaps}(\mathfrak k)$ cannot be equal to
$\operatorname {gaps}(\mathfrak k)$ cannot be equal to ![]() $\{0, \ldots, a-2\}$. Assume
$\{0, \ldots, a-2\}$. Assume ![]() $g_1=2$, so
$g_1=2$, so ![]() $a(\mathfrak k)=3$. Recall that
$a(\mathfrak k)=3$. Recall that ![]() $\tilde t=t-x$. Let
$\tilde t=t-x$. Let ![]() $f_1 = \tilde {t}k_1$ be as in Notation 6.1.1; as
$f_1 = \tilde {t}k_1$ be as in Notation 6.1.1; as ![]() $a(\mathfrak k) - d(\mathfrak k) = 1$, the image of
$a(\mathfrak k) - d(\mathfrak k) = 1$, the image of ![]() $f_1\partial$ in
$f_1\partial$ in ![]() $\mathfrak k / W(\tilde t^3)$ provides a generator of this one-dimensional vector space. We can assume that
$\mathfrak k / W(\tilde t^3)$ provides a generator of this one-dimensional vector space. We can assume that ![]() $f_1$ is monic in
$f_1$ is monic in ![]() $\tilde t$ and contains no terms in
$\tilde t$ and contains no terms in ![]() $\tilde t$ of degree three or more. Thus,
$\tilde t$ of degree three or more. Thus, ![]() $f_1=\tilde t+\alpha \tilde t^2$ for some
$f_1=\tilde t+\alpha \tilde t^2$ for some ![]() $\alpha \in \Bbbk$ and
$\alpha \in \Bbbk$ and ![]() $\mathfrak k=W_{x; \alpha }^{2; 1}$. Further,
$\mathfrak k=W_{x; \alpha }^{2; 1}$. Further, ![]() $\alpha$ is unique as
$\alpha$ is unique as ![]() $\dim \mathfrak k /W(\tilde t^3) = 1$.
$\dim \mathfrak k /W(\tilde t^3) = 1$.
Assume ![]() $g_1=3$, so
$g_1=3$, so ![]() $a(\mathfrak k)=4$. Let
$a(\mathfrak k)=4$. Let ![]() $f_1 = \tilde t k_1$,
$f_1 = \tilde t k_1$, ![]() $f_2 = \tilde t^2 k_2 \in \Bbbk [t]=\Bbbk [\tilde t]$ be as in Notation 6.1.1, so the images of
$f_2 = \tilde t^2 k_2 \in \Bbbk [t]=\Bbbk [\tilde t]$ be as in Notation 6.1.1, so the images of ![]() $f_1\partial, f_2\partial$ in
$f_1\partial, f_2\partial$ in ![]() $\mathfrak k / W((t-x)^3)$ give a basis. We can assume that
$\mathfrak k / W((t-x)^3)$ give a basis. We can assume that ![]() $f_1, f_2$ contain no terms in
$f_1, f_2$ contain no terms in ![]() $\tilde t$ of degree four or more and
$\tilde t$ of degree four or more and ![]() $f_1$ contains no terms in
$f_1$ contains no terms in ![]() $\tilde t$ of degree two. Thus,
$\tilde t$ of degree two. Thus, ![]() $f_1=\tilde {t}+\alpha \tilde {t}^3, f_2=\tilde {t}^2+\beta \tilde t^3$ for some
$f_1=\tilde {t}+\alpha \tilde {t}^3, f_2=\tilde {t}^2+\beta \tilde t^3$ for some ![]() $\alpha, \beta \in \Bbbk$. We have
$\alpha, \beta \in \Bbbk$. We have
Hence, ![]() $[f_1\partial, f_2\partial ]=f_2\partial$ modulo
$[f_1\partial, f_2\partial ]=f_2\partial$ modulo ![]() $W(\tilde t^4)$. This implies
$W(\tilde t^4)$. This implies ![]() $\beta =0$ and, therefore,
$\beta =0$ and, therefore, ![]() $\mathfrak k= W_{x; \alpha }^{2; 2}$. Again
$\mathfrak k= W_{x; \alpha }^{2; 2}$. Again ![]() $\alpha$ is unique.
$\alpha$ is unique.
Remark 6.2.3 Similar proofs give a classification of subalgebras of ![]() $W_{\geqslant -1}$ of codimension two: these are either of the form
$W_{\geqslant -1}$ of codimension two: these are either of the form ![]() $W_{\geqslant -1}((t-x)(t-y))$ or may be written
$W_{\geqslant -1}((t-x)(t-y))$ or may be written ![]() $(W_{\geqslant -1})^{2;1}_{x;\alpha }$ or
$(W_{\geqslant -1})^{2;1}_{x;\alpha }$ or ![]() $(W_{\geqslant -1})^{2;2}_{x;\alpha }$, where these last two are defined similarly to the analogous subalgebras of
$(W_{\geqslant -1})^{2;2}_{x;\alpha }$, where these last two are defined similarly to the analogous subalgebras of ![]() $W$. (Here, of course, we allow
$W$. (Here, of course, we allow ![]() $x,y$ to be zero.) These subalgebras are all deformations of
$x,y$ to be zero.) These subalgebras are all deformations of ![]() $W_{\geqslant -1}(t^2) = W_{\geqslant 1}$.
$W_{\geqslant -1}(t^2) = W_{\geqslant 1}$.
Deformations of ![]() $W_{\geqslant 1}$ are classified in [Reference FialowskiFia83] (see also [Reference Fialowski and FuchsFF97]). These papers show that up to isomorphism there are three such deformations, denoted in [Reference FialowskiFia83] by
$W_{\geqslant 1}$ are classified in [Reference FialowskiFia83] (see also [Reference Fialowski and FuchsFF97]). These papers show that up to isomorphism there are three such deformations, denoted in [Reference FialowskiFia83] by ![]() $L_1^{(1)}$,
$L_1^{(1)}$, ![]() $L_1^{(2)}$,
$L_1^{(2)}$, ![]() $L_1^{(3)}$. It can be shown that
$L_1^{(3)}$. It can be shown that
for appropriate ![]() $y, \alpha$. We thank Lucas Buzaglo for explaining this to us.
$y, \alpha$. We thank Lucas Buzaglo for explaining this to us.
6.3 Subalgebras of codimension three
It can also be shown that all subalgebras of ![]() $W$ of codimension three are listed in Table 2. Because the methods are similar to those in § 6.2 we omit the proof.
$W$ of codimension three are listed in Table 2. Because the methods are similar to those in § 6.2 we omit the proof.
Table 2. Subalgebras of ![]() $W\!$ of codimension three.
$W\!$ of codimension three.

The notation here is as follows:
•
 $\mathfrak k$ is given in the final column as either an intersection of two explicitly given subalgebras or is spanned by
$\mathfrak k$ is given in the final column as either an intersection of two explicitly given subalgebras or is spanned by  $W(f_\mathfrak k)$ and a few more explicit generators;
$W(f_\mathfrak k)$ and a few more explicit generators;•
 $\alpha, \beta$ are parameters taking arbitrary values in
$\alpha, \beta$ are parameters taking arbitrary values in  $\Bbbk$ for all cases but
$\Bbbk$ for all cases but  $W^{3A}_{x, y; \alpha, \beta }$ (for this case the required restrictions on
$W^{3A}_{x, y; \alpha, \beta }$ (for this case the required restrictions on  $\alpha, \beta$ are given in the table);
$\alpha, \beta$ are given in the table);•
 $x, y$ are parameters taking arbitrary values in
$x, y$ are parameters taking arbitrary values in  $\Bbbk ^\times$ except when restrictions are given in the table.
$\Bbbk ^\times$ except when restrictions are given in the table.
It is easy to verify that a subalgebra ![]() $\mathfrak k$ of
$\mathfrak k$ of ![]() $W$ of codimension three belongs to only one type and, moreover, the parameters defining
$W$ of codimension three belongs to only one type and, moreover, the parameters defining ![]() $\mathfrak k$ are unique if
$\mathfrak k$ are unique if ![]() $\mathfrak k\ne W_{x, y; \alpha, \beta }^{3A}$ and unique up to scaling
$\mathfrak k\ne W_{x, y; \alpha, \beta }^{3A}$ and unique up to scaling ![]() $(\alpha, \beta )\to (\lambda \alpha, \lambda \beta )$ in the case
$(\alpha, \beta )\to (\lambda \alpha, \lambda \beta )$ in the case ![]() $\mathfrak k = W_{x, y; \alpha, \beta }^{3A}$.
$\mathfrak k = W_{x, y; \alpha, \beta }^{3A}$.
Remark 6.3.1 ![]() $(1)$ Recall the analogy between subalgebras of
$(1)$ Recall the analogy between subalgebras of ![]() $W$ of codimension one and maximal ideals. It is natural to ask whether or not an analogue of the Lasker–Noether primary decomposition theorem holds in this setting. However, this statement fails as we can easily see that the Lie algebra
$W$ of codimension one and maximal ideals. It is natural to ask whether or not an analogue of the Lasker–Noether primary decomposition theorem holds in this setting. However, this statement fails as we can easily see that the Lie algebra ![]() $W^{3A}_{x, y; \alpha, \beta }$ is not an intersection of subalgebras
$W^{3A}_{x, y; \alpha, \beta }$ is not an intersection of subalgebras ![]() $\mathfrak k_x$ and
$\mathfrak k_x$ and ![]() $\mathfrak k_y$ with
$\mathfrak k_y$ with ![]() $\operatorname {supp}(\mathfrak k_x)=\{x\}$ and
$\operatorname {supp}(\mathfrak k_x)=\{x\}$ and ![]() $\operatorname {supp}(\mathfrak k_y)=\{y\}$.
$\operatorname {supp}(\mathfrak k_y)=\{y\}$.
![]() $(2)$ Recall that every subalgebra
$(2)$ Recall that every subalgebra ![]() $\mathfrak k$ of finite codimension in
$\mathfrak k$ of finite codimension in ![]() $W$ lies between
$W$ lies between ![]() $W(f_\mathfrak k)$ and
$W(f_\mathfrak k)$ and ![]() $W({\rm rad}(f_\mathfrak k))$. One can construct a sequence of polynomials
$W({\rm rad}(f_\mathfrak k))$. One can construct a sequence of polynomials
with ![]() $\deg h_{i+1}=\deg h_i+1$ and
$\deg h_{i+1}=\deg h_i+1$ and ![]() $h_i\mid h_{i+1}$ and consider the filtration of
$h_i\mid h_{i+1}$ and consider the filtration of ![]() $W({\rm rad}f_\mathfrak k)$ by the Lie ideals
$W({\rm rad}f_\mathfrak k)$ by the Lie ideals ![]() $W(h_i)$. The associated graded algebra
$W(h_i)$. The associated graded algebra
is isomorphic to a graded algebra ![]() $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\mathfrak k}$ with
$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\mathfrak k}$ with
The subalgebras ![]() $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\mathfrak k}$ can be described in purely combinatorial terms and, thus, they give a collection of discrete invariants for
$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\mathfrak k}$ can be described in purely combinatorial terms and, thus, they give a collection of discrete invariants for ![]() $\mathfrak k$. This generalises the notation of gaps and leading degrees for subalgebras with one-point support.
$\mathfrak k$. This generalises the notation of gaps and leading degrees for subalgebras with one-point support.
6.4 Some general comments on finite codimension subalgebras of  $W$
$W$
The lattice of subalgebras ![]() $\mathfrak k$ with
$\mathfrak k$ with ![]() $\operatorname {supp}(\mathfrak k) = \{x\}$ and
$\operatorname {supp}(\mathfrak k) = \{x\}$ and ![]() $a(\mathfrak k)\leqslant a$ can be naturally identified with the subalgebras of
$a(\mathfrak k)\leqslant a$ can be naturally identified with the subalgebras of
in particular, the isomorphism class of this lattice is independent of ![]() $x$.
$x$.
A similar result holds true in a greater generality. Pick ![]() $s\geqslant 0$,
$s\geqslant 0$, ![]() $a\geqslant 1$ and distinct
$a\geqslant 1$ and distinct ![]() $x_1, \ldots, x_s\in \Bbbk ^\times$; set
$x_1, \ldots, x_s\in \Bbbk ^\times$; set ![]() $h:=(t-x_1)\cdots (t-x_s)$. Consider subalgebras
$h:=(t-x_1)\cdots (t-x_s)$. Consider subalgebras ![]() $\mathfrak k$ satisfying
$\mathfrak k$ satisfying ![]() $W(h)\supset \mathfrak k\supset W(h^a)$. It is clear that
$W(h)\supset \mathfrak k\supset W(h^a)$. It is clear that ![]() $W(h^a)$ is a Lie ideal of
$W(h^a)$ is a Lie ideal of ![]() $W(h)$ and the quotient
$W(h)$ and the quotient ![]() $W(h)/W(h^a)$ is a finite-dimensional solvable Lie algebra. A version of the Chinese remainder theorem implies that
$W(h)/W(h^a)$ is a finite-dimensional solvable Lie algebra. A version of the Chinese remainder theorem implies that
In particular, the isomorphism class of ![]() $W(h)/W(h^a)$ depends only on
$W(h)/W(h^a)$ depends only on ![]() $a$ and
$a$ and ![]() $s$ but not on the particular choice of the
$s$ but not on the particular choice of the ![]() $x_i$. This immediately gives the following corollaries.
$x_i$. This immediately gives the following corollaries.
Corollary 6.4.2 Let ![]() $\mathfrak k$ be a subalgebra of finite codimension of
$\mathfrak k$ be a subalgebra of finite codimension of ![]() $\mathfrak g=W$,
$\mathfrak g=W$, ![]() $W_{\geqslant -1}$,
$W_{\geqslant -1}$, ![]() $W_{\geqslant 1}$ or
$W_{\geqslant 1}$ or ![]() $V\!ir$. Then there are subalgebras
$V\!ir$. Then there are subalgebras ![]() $\mathfrak k^+, \mathfrak k^-$ with
$\mathfrak k^+, \mathfrak k^-$ with
Proof. A similar statement is well-known for subalgebras of solvable Lie algebras so (6.4.1) implies the desired result if ![]() $\mathfrak k\ne W(f_\mathfrak k)$. If
$\mathfrak k\ne W(f_\mathfrak k)$. If ![]() $\mathfrak k=W(f_\mathfrak k)$ the result follows from a similar fact on ideals in
$\mathfrak k=W(f_\mathfrak k)$ the result follows from a similar fact on ideals in ![]() $\Bbbk [t, t^{-1}]$.
$\Bbbk [t, t^{-1}]$.
Corollary 6.4.3 The lattices of subalgebras of finite codimension of ![]() $V\!ir$, of
$V\!ir$, of ![]() $W\!$ and of
$W\!$ and of ![]() $W_{\geqslant -1}$ are all isomorphic.
$W_{\geqslant -1}$ are all isomorphic.
Proof. Lemma 3.3.3 implies that the lattices of subalgebras of finite codimension are isomorphic for ![]() $W$ and
$W$ and ![]() $V\!ir$; hence, we left to show that the lattices are isomorphic for
$V\!ir$; hence, we left to show that the lattices are isomorphic for ![]() $W$ and
$W$ and ![]() $W_{\geqslant -1}$.
$W_{\geqslant -1}$.
Theorem 3.2.7 implies that the lattices of subalgebras of finite codimension for both ![]() $W$ and
$W$ and ![]() $W_{\geqslant -1}$ are direct limits of the sublattices of subalgebras
$W_{\geqslant -1}$ are direct limits of the sublattices of subalgebras ![]() $\mathfrak k$ containing
$\mathfrak k$ containing ![]() $W((t-x_1)^a\cdots (t-x_s)^a)$ for all tuples
$W((t-x_1)^a\cdots (t-x_s)^a)$ for all tuples ![]() $( a; x_1, \ldots, x_s)$; the only difference between
$( a; x_1, \ldots, x_s)$; the only difference between ![]() $W\!$ and
$W\!$ and ![]() $W_{\geqslant -1}$ here is that in the first case
$W_{\geqslant -1}$ here is that in the first case ![]() $x_i\ne 0$. These lattices are isomorphic for
$x_i\ne 0$. These lattices are isomorphic for ![]() $W\!$ and
$W\!$ and ![]() $W_{\geqslant -1}$ and the embeddings between them are the same for
$W_{\geqslant -1}$ and the embeddings between them are the same for ![]() $W$ and
$W$ and ![]() $W_{\geqslant -1}$ (they essentially depend only on the integer-valued parameters
$W_{\geqslant -1}$ (they essentially depend only on the integer-valued parameters ![]() $s$ and
$s$ and ![]() $a$ and on the cardinality of
$a$ and on the cardinality of ![]() $\Bbbk$).
$\Bbbk$).
7. Implications of our results for  $\operatorname {U}(\mathfrak g)$
$\operatorname {U}(\mathfrak g)$
In this final section, we shift, for the first time in this paper, to considering the universal enveloping algebra ![]() $\operatorname {U}(\mathfrak g)$ of one of our Lie algebras of interest. We apply a version of the orbit method to relate the Poisson primitive ideals
$\operatorname {U}(\mathfrak g)$ of one of our Lie algebras of interest. We apply a version of the orbit method to relate the Poisson primitive ideals ![]() $\ker p_\gamma = \operatorname {P}(\chi _{x;\alpha, \gamma })$ of
$\ker p_\gamma = \operatorname {P}(\chi _{x;\alpha, \gamma })$ of ![]() $\operatorname {S}(\mathfrak g)$ to primitive ideals of
$\operatorname {S}(\mathfrak g)$ to primitive ideals of ![]() $\operatorname {U}(W)$ obtained as kernels of maps to the (localised) Weyl algebra. We end with some conjectures about ideals in
$\operatorname {U}(W)$ obtained as kernels of maps to the (localised) Weyl algebra. We end with some conjectures about ideals in ![]() $\operatorname {U}(V\!ir)$,
$\operatorname {U}(V\!ir)$, ![]() $\operatorname {U}(W)$, and
$\operatorname {U}(W)$, and ![]() $\operatorname {U}(W_{\geqslant -1})$.
$\operatorname {U}(W_{\geqslant -1})$.
7.1 Constructing primitive ideals through the orbit method
Kirillov's orbit method for nilpotent and solvable Lie algebras attaches to ![]() $\chi \in \mathfrak g^*$ the annihilator in
$\chi \in \mathfrak g^*$ the annihilator in ![]() $\operatorname {U}(\mathfrak g)$ of the module induced from a polarisation of
$\operatorname {U}(\mathfrak g)$ of the module induced from a polarisation of ![]() $\chi$ and the induced character. We apply the same construction to
$\chi$ and the induced character. We apply the same construction to ![]() $\mathfrak g=W$ and
$\mathfrak g=W$ and ![]() $\chi =\chi _{x; \alpha, \gamma }$. We denote the corresponding induced
$\chi =\chi _{x; \alpha, \gamma }$. We denote the corresponding induced ![]() $W$-modules by
$W$-modules by ![]() $M_{x; \gamma }$.
$M_{x; \gamma }$.
A description of the annihilators of ![]() $M_{x, \gamma }$ is given in Proposition 7.1.5. The main result here is that
$M_{x, \gamma }$ is given in Proposition 7.1.5. The main result here is that
depends only on ![]() $\gamma$; thanks to Theorem 4.2.1 (or Lemma 2.2.3) the same holds for
$\gamma$; thanks to Theorem 4.2.1 (or Lemma 2.2.3) the same holds for ![]() $\operatorname {P}(\chi _{x; \alpha ; \gamma })$. This shows that the constructions of Kirillov's orbit method give rise to a map from a certain class of Poisson primitive ideals of
$\operatorname {P}(\chi _{x; \alpha ; \gamma })$. This shows that the constructions of Kirillov's orbit method give rise to a map from a certain class of Poisson primitive ideals of ![]() $\operatorname {S}(W)$ to a certain class of primitive ideals of
$\operatorname {S}(W)$ to a certain class of primitive ideals of ![]() $\operatorname {U}(W)$, which are known in the literature [Reference Conley and MartinCM07, Reference Sierra and WaltonSW16] as kernels of maps to the localised Weyl algebra. We believe this map extends to a surjection from Poisson primitive ideals of
$\operatorname {U}(W)$, which are known in the literature [Reference Conley and MartinCM07, Reference Sierra and WaltonSW16] as kernels of maps to the localised Weyl algebra. We believe this map extends to a surjection from Poisson primitive ideals of ![]() $\operatorname {S}(\mathfrak g)$ to primitive ideals of
$\operatorname {S}(\mathfrak g)$ to primitive ideals of ![]() $\operatorname {U}(\mathfrak g)$; this is the subject of ongoing research.
$\operatorname {U}(\mathfrak g)$; this is the subject of ongoing research.
Throughout this section, we write the localised Weyl algebra as ![]() $A = \Bbbk [t,t^{-1}, \partial ]$, with
$A = \Bbbk [t,t^{-1}, \partial ]$, with ![]() $\partial t = t \partial + 1$.
$\partial t = t \partial + 1$.
We first describe a polarisation for ![]() $\chi _{x; \alpha, \gamma }$. Let
$\chi _{x; \alpha, \gamma }$. Let ![]() $x, \alpha, \gamma \in \Bbbk$ with
$x, \alpha, \gamma \in \Bbbk$ with ![]() $x \neq 0, (\alpha, \gamma ) \neq (0,0)$ and let
$x \neq 0, (\alpha, \gamma ) \neq (0,0)$ and let ![]() $\chi = \chi _{x;\alpha, \gamma }$. Recall the computation of
$\chi = \chi _{x;\alpha, \gamma }$. Recall the computation of ![]() $W^\chi$ in Lemma 2.2.1, and consider the Lie subalgebra
$W^\chi$ in Lemma 2.2.1, and consider the Lie subalgebra ![]() $W(t-x)$ of
$W(t-x)$ of ![]() $W$, which contains
$W$, which contains ![]() $W^{\chi }$. We have
$W^{\chi }$. We have
As ![]() $B_\chi ((t-x) \partial, (t-x)\partial ) = 0$, thus
$B_\chi ((t-x) \partial, (t-x)\partial ) = 0$, thus ![]() $W(t-x)$ is a totally isotropic subspace of
$W(t-x)$ is a totally isotropic subspace of ![]() $(W, B_\chi )$; by dimension count it is maximal totally isotropic. Thus,
$(W, B_\chi )$; by dimension count it is maximal totally isotropic. Thus, ![]() $W(t-x)$ is a polarisation of
$W(t-x)$ is a polarisation of ![]() $W$ at
$W$ at ![]() $\chi$, as in [Reference DixmierDix96, 1.12.8]. Further,
$\chi$, as in [Reference DixmierDix96, 1.12.8]. Further, ![]() $W(t-x)$ is the unique polarisation of
$W(t-x)$ is the unique polarisation of ![]() $W$ at
$W$ at ![]() $\chi$: because any polarisation of
$\chi$: because any polarisation of ![]() $W$ at
$W$ at ![]() $\chi$ must be a codimension-one subalgebra of
$\chi$ must be a codimension-one subalgebra of ![]() $W$, by Corollary 6.0.3 it must be equal to some
$W$, by Corollary 6.0.3 it must be equal to some ![]() $W(t-y)$ and it is easy to see that we must have
$W(t-y)$ and it is easy to see that we must have ![]() $y=x$.
$y=x$.
Note that ![]() $\chi$ is a character of
$\chi$ is a character of ![]() $W(t-x)$; let
$W(t-x)$; let ![]() $\Bbbk m_{x;\gamma }$ be the corresponding one-dimensional representation of
$\Bbbk m_{x;\gamma }$ be the corresponding one-dimensional representation of ![]() $W(t-x)$, with basis element
$W(t-x)$, with basis element ![]() $m_{x; \gamma }$. (The restriction
$m_{x; \gamma }$. (The restriction ![]() $\chi |_{W(t-x)}$, which sends
$\chi |_{W(t-x)}$, which sends ![]() $p \partial \mapsto \gamma p'(x)$, depends only on
$p \partial \mapsto \gamma p'(x)$, depends only on ![]() $x$ and
$x$ and ![]() $\gamma$: this is the reason to omit
$\gamma$: this is the reason to omit ![]() $\alpha$ in the notation
$\alpha$ in the notation ![]() $\Bbbk m_{x; \gamma }$.) Put
$\Bbbk m_{x; \gamma }$.) Put
As ![]() $e_{-1} = \partial \not \in W(t-x)$, thus
$e_{-1} = \partial \not \in W(t-x)$, thus ![]() $W = \Bbbk e_{-1} \oplus W(t-x)$ and by the Poincaré–Birkhoff–Witt theorem the set
$W = \Bbbk e_{-1} \oplus W(t-x)$ and by the Poincaré–Birkhoff–Witt theorem the set ![]() $\{e_{-1}^k m_{x;\gamma } | k \in \mathbb {Z}_{\geqslant 0}\}$ is a basis for
$\{e_{-1}^k m_{x;\gamma } | k \in \mathbb {Z}_{\geqslant 0}\}$ is a basis for ![]() $M_{x; \gamma }$.
$M_{x; \gamma }$.
We now give an alternative construction of ![]() $M_{x; \gamma }$. Set
$M_{x; \gamma }$. Set
For every ![]() $x$,
$x$, ![]() $N_x$ is a simple (faithful) left
$N_x$ is a simple (faithful) left ![]() $A$-module.
$A$-module.
Remark 7.1.1 The space ![]() $N_x$ can be thought of as a space of distributions on
$N_x$ can be thought of as a space of distributions on ![]() $\Bbbk ^\times$; for, setting
$\Bbbk ^\times$; for, setting ![]() $\delta _x = (t-x)^{-1} \in N_x$ we have
$\delta _x = (t-x)^{-1} \in N_x$ we have ![]() $(t-x) \delta _x = 0$ so
$(t-x) \delta _x = 0$ so ![]() $\delta _x$ behaves like a
$\delta _x$ behaves like a ![]() $\delta$-function at
$\delta$-function at ![]() $x$. The elements
$x$. The elements ![]() $\partial ^k \delta _x$ form a basis of
$\partial ^k \delta _x$ form a basis of ![]() $N_x$.
$N_x$.
Recall that, for any ![]() $\gamma \in \Bbbk$, the map
$\gamma \in \Bbbk$, the map
is a Lie algebra homomorphism; see [Reference Conley and MartinCM07]. Thus, ![]() $\pi _\gamma$ extends to define a ring homomorphism
$\pi _\gamma$ extends to define a ring homomorphism ![]() $\operatorname {U}(W) \to A$. Note that the map
$\operatorname {U}(W) \to A$. Note that the map ![]() $p_\gamma$ defined in (2.2.2) is not the associated graded map attached to
$p_\gamma$ defined in (2.2.2) is not the associated graded map attached to ![]() $\pi _\gamma$ even though they are clearly analogous.
$\pi _\gamma$ even though they are clearly analogous.
The images of ![]() $\pi _\gamma$ have been computed in [Reference Conley and MartinCM07, Lemma 2.1], and we give them here.
$\pi _\gamma$ have been computed in [Reference Conley and MartinCM07, Lemma 2.1], and we give them here.
Lemma 7.1.3 We have:
(a)
 $\operatorname {im}(\pi _0) = \Bbbk \oplus A \partial$, and
$\operatorname {im}(\pi _0) = \Bbbk \oplus A \partial$, and  $\operatorname {im} \pi _1 = \Bbbk \oplus \partial A$;
$\operatorname {im} \pi _1 = \Bbbk \oplus \partial A$;(b)
 $\operatorname {im}(\pi _\gamma ) = A$ if
$\operatorname {im}(\pi _\gamma ) = A$ if  $\gamma \ne 0, 1$.
$\gamma \ne 0, 1$.
Remark 7.1.4 The restriction of ![]() $\pi _\gamma$ to
$\pi _\gamma$ to ![]() $\operatorname {U}(W_{\geqslant 1})$ was considered, under slightly different notation, in [Reference Sierra and WaltonSW16]; see [Reference Sierra and WaltonSW16, Remark 3.14]. It was shown there that the ideal
$\operatorname {U}(W_{\geqslant 1})$ was considered, under slightly different notation, in [Reference Sierra and WaltonSW16]; see [Reference Sierra and WaltonSW16, Remark 3.14]. It was shown there that the ideal ![]() $\ker \pi _0|_{W_{\geqslant 1}} = \ker \pi _1|_{W_{\geqslant 1}}$ is not finitely generated as a left or right ideal of
$\ker \pi _0|_{W_{\geqslant 1}} = \ker \pi _1|_{W_{\geqslant 1}}$ is not finitely generated as a left or right ideal of ![]() $\operatorname {U}(W_{\geqslant 1})$.
$\operatorname {U}(W_{\geqslant 1})$.
For every ![]() $\gamma \in \Bbbk$ the map
$\gamma \in \Bbbk$ the map ![]() $\pi _\gamma$ from (7.1.2) induces the structure of a
$\pi _\gamma$ from (7.1.2) induces the structure of a ![]() $W$-module on
$W$-module on ![]() $N_x$; we denote the space
$N_x$; we denote the space ![]() $N_x$ with the corresponding
$N_x$ with the corresponding ![]() $W$-module structure
$W$-module structure ![]() $\cdot _\gamma$ by
$\cdot _\gamma$ by ![]() $N_x^\gamma$.
$N_x^\gamma$.
Proposition 7.1.5 Let ![]() $x\neq 0, \alpha, \gamma \in \Bbbk$. Then
$x\neq 0, \alpha, \gamma \in \Bbbk$. Then ![]() $N_x^\gamma \cong M_{x; \gamma -1}$. Moreover,
$N_x^\gamma \cong M_{x; \gamma -1}$. Moreover, ![]() $N_x^\gamma$ is a simple
$N_x^\gamma$ is a simple ![]() $W$-module if and only if
$W$-module if and only if ![]() $\gamma \ne 1$. There is an exact sequence
$\gamma \ne 1$. There is an exact sequence
For all ![]() $\gamma$ the annihilator of
$\gamma$ the annihilator of ![]() $N_x^\gamma$ is equal to
$N_x^\gamma$ is equal to ![]() $\ker \pi _\gamma$, which is primitive.
$\ker \pi _\gamma$, which is primitive.
Proof. Let ![]() $p\in \Bbbk [t, t^{-1}]$ with
$p\in \Bbbk [t, t^{-1}]$ with ![]() $(t-x)|p$. By taking the Taylor expansion of
$(t-x)|p$. By taking the Taylor expansion of ![]() $p$ about
$p$ about ![]() $x$ one may verify that
$x$ one may verify that
This immediately implies that there exists a surjective module homomorphism ![]() $M_{x; \gamma -1}\to N_x^{\gamma }$ which sends
$M_{x; \gamma -1}\to N_x^{\gamma }$ which sends ![]() $m_{x; \gamma -1}\mapsto \delta _x$. The basis element
$m_{x; \gamma -1}\mapsto \delta _x$. The basis element ![]() $e_{-1}^k m_{x; \gamma -1}$ maps to
$e_{-1}^k m_{x; \gamma -1}$ maps to ![]() $\partial ^k \delta _x$, so this map is an isomorphism.
$\partial ^k \delta _x$, so this map is an isomorphism.
Assume ![]() $\gamma \neq 0,1$. In this case
$\gamma \neq 0,1$. In this case ![]() $\pi _\gamma$ is surjective by Lemma 7.1.3, so simplicity of
$\pi _\gamma$ is surjective by Lemma 7.1.3, so simplicity of ![]() $N_x^\gamma$ follows from simplicity of
$N_x^\gamma$ follows from simplicity of ![]() $N_x$ as an
$N_x$ as an ![]() $A$-module.
$A$-module.
We claim that ![]() $N_x^0$ is simple. To see this, let
$N_x^0$ is simple. To see this, let ![]() $0\neq n \in N_x$, which we recall is a simple
$0\neq n \in N_x$, which we recall is a simple ![]() $A$-module. By construction of
$A$-module. By construction of ![]() $N_x$ there is some
$N_x$ there is some ![]() $0 \neq f(t) \in \Bbbk [t, t^{-1}]$ so that
$0 \neq f(t) \in \Bbbk [t, t^{-1}]$ so that ![]() $fn =0$ and, thus,
$fn =0$ and, thus, ![]() $\partial n \neq 0$ as
$\partial n \neq 0$ as ![]() $A\partial + Af(t) = A$. Thus,
$A\partial + Af(t) = A$. Thus, ![]() $A \partial n = N_x$, proving the claim because by Lemma 7.1.3
$A \partial n = N_x$, proving the claim because by Lemma 7.1.3 ![]() $A\partial \subseteq \pi _0(\operatorname {U}(W))$.
$A\partial \subseteq \pi _0(\operatorname {U}(W))$.
Finally, we consider ![]() $N_x^1$. Lemma 7.1.3 implies
$N_x^1$. Lemma 7.1.3 implies ![]() $\partial A \triangleleft \operatorname {im} \pi _1 = \Bbbk \oplus \partial A$ and, thus,
$\partial A \triangleleft \operatorname {im} \pi _1 = \Bbbk \oplus \partial A$ and, thus, ![]() $\tilde {N} := \partial A N_x = \partial N_x$ is a submodule of
$\tilde {N} := \partial A N_x = \partial N_x$ is a submodule of ![]() $N_x^1$, with
$N_x^1$, with ![]() $N_x^1/\tilde {N} \cong \Bbbk$. We claim that
$N_x^1/\tilde {N} \cong \Bbbk$. We claim that ![]() $\tilde {N}$ is simple. Let
$\tilde {N}$ is simple. Let ![]() $0 \neq n \in \tilde {N}$. As
$0 \neq n \in \tilde {N}$. As ![]() $N_x$ is a simple
$N_x$ is a simple ![]() $A$-module,
$A$-module, ![]() $\partial A n = \tilde {N}$ and so
$\partial A n = \tilde {N}$ and so ![]() $\operatorname {U}(W) \cdot _1 n = (\Bbbk \oplus \partial A) n = \tilde {N}$, as needed. The reader may verify that as in (7.1.6)
$\operatorname {U}(W) \cdot _1 n = (\Bbbk \oplus \partial A) n = \tilde {N}$, as needed. The reader may verify that as in (7.1.6)
and so ![]() $\tilde {N} \cong M_{x; -1} \cong N_x^0$. The claim about annihilators follows from the fact that
$\tilde {N} \cong M_{x; -1} \cong N_x^0$. The claim about annihilators follows from the fact that ![]() $N_x$ is a faithful module over the (simple) ring
$N_x$ is a faithful module over the (simple) ring ![]() $A$. That
$A$. That ![]() $\ker \pi _\gamma$ is primitive is immediate for
$\ker \pi _\gamma$ is primitive is immediate for ![]() $\gamma \neq 1$; for
$\gamma \neq 1$; for ![]() $\gamma =1$ it follows from the fact that
$\gamma =1$ it follows from the fact that ![]() $\ker \pi _1 = \ker \pi _0$.
$\ker \pi _1 = \ker \pi _0$.
Remark 7.1.7 (a) Note that the primitive ideal ![]() $\ker \pi _\gamma$ is completely prime. We do not know of a primitive (or prime) ideal of
$\ker \pi _\gamma$ is completely prime. We do not know of a primitive (or prime) ideal of ![]() $\operatorname {U}(W)$ which is not completely prime.
$\operatorname {U}(W)$ which is not completely prime.
(b) We believe that the ideals ![]() $\ker \pi _\gamma$ above are all of the primitive ideals of
$\ker \pi _\gamma$ above are all of the primitive ideals of ![]() $\operatorname {U}(W)$ of Gelfand–Kirillov codimension two.
$\operatorname {U}(W)$ of Gelfand–Kirillov codimension two.
(c) By Remark 7.1.4, ![]() $\ker \pi _0 = \ker \pi _1$. However,
$\ker \pi _0 = \ker \pi _1$. However, ![]() $\ker p_0 \neq \ker p_1$. To see this, note that if
$\ker p_0 \neq \ker p_1$. To see this, note that if ![]() $\ker p_0 = \ker p_1$ then
$\ker p_0 = \ker p_1$ then ![]() $\chi _{1;1,0} \in V(\ker p_1) = \overline {\mathbb {O}(\chi _{1;1,1})}$. Thus, either
$\chi _{1;1,0} \in V(\ker p_1) = \overline {\mathbb {O}(\chi _{1;1,1})}$. Thus, either ![]() $\mathbb {O}(\chi _{1;1,0} ) = \mathbb {O}(\chi _{1;1,1})$ or
$\mathbb {O}(\chi _{1;1,0} ) = \mathbb {O}(\chi _{1;1,1})$ or ![]() $\dim \mathbb {O}(\chi _{1;1,0}) < \dim \mathbb {O}(\chi _{1;1,1})$. Neither is true.
$\dim \mathbb {O}(\chi _{1;1,0}) < \dim \mathbb {O}(\chi _{1;1,1})$. Neither is true.
Thus, the orbit method does not give a bijection from Poisson primitive ideals of ![]() $\operatorname {S}(W)$ to primitive ideals of
$\operatorname {S}(W)$ to primitive ideals of ![]() $\operatorname {U}(W)$.
$\operatorname {U}(W)$.
7.2 Conjectures for  $\operatorname {U}(\mathfrak g)$
$\operatorname {U}(\mathfrak g)$
We have focused almost entirely on the symmetric algebra of ![]() $\mathfrak g$, where
$\mathfrak g$, where ![]() $\mathfrak g$ is one of
$\mathfrak g$ is one of ![]() $V\!ir$,
$V\!ir$, ![]() $W$ or several related Lie algebras. However, our results are at a minimum suggestive for the enveloping algebras of these Lie algebras. In this final subsection, we make several conjectures for
$W$ or several related Lie algebras. However, our results are at a minimum suggestive for the enveloping algebras of these Lie algebras. In this final subsection, we make several conjectures for ![]() $\operatorname {U}(\mathfrak g)$. Broadly speaking, these are instances of the meta-conjecture.
$\operatorname {U}(\mathfrak g)$. Broadly speaking, these are instances of the meta-conjecture.
The ideal structure of ![]() $\operatorname {U}(\mathfrak g)$ is closely analogous to the Poisson structure of
$\operatorname {U}(\mathfrak g)$ is closely analogous to the Poisson structure of ![]() $\operatorname {S}(\mathfrak g)$.
$\operatorname {S}(\mathfrak g)$.
For each conjecture, we give the Poisson result which suggested it to us.
Conjecture 7.2.1 (Cf. Corollary 3.3.5)
If ![]() $\zeta \neq 0$, then
$\zeta \neq 0$, then ![]() $\operatorname {U}(V\!ir)/(z-\zeta )$ is simple.
$\operatorname {U}(V\!ir)/(z-\zeta )$ is simple.
Conjecture 7.2.2 (Cf. Corollaries 4.3.11 and 5.2.14)
Restriction gives a bijection between primitive (respectively, prime) ideals of ![]() $\operatorname {U}(W)$ and
$\operatorname {U}(W)$ and ![]() $\operatorname {U}(W_{\geqslant -1})$, and a homeomorphism
$\operatorname {U}(W_{\geqslant -1})$, and a homeomorphism
Conjecture 7.2.3 (Cf. Proposition 5.4.1)
Every proper prime ideal of ![]() $\operatorname {U}(W)$ contains a proper primitive ideal.
$\operatorname {U}(W)$ contains a proper primitive ideal.
Conjecture 7.2.4 (Cf. Proposition 4.3.14)
The ![]() $\operatorname {\ker } \pi _\gamma$ are all of the prime ideals of
$\operatorname {\ker } \pi _\gamma$ are all of the prime ideals of ![]() $\operatorname {U}(W)$ of co-GK-dimension two.
$\operatorname {U}(W)$ of co-GK-dimension two.
Conjecture 7.2.5 (cf. § 7.1)
Kirillov's orbit method, i.e. the assignment
always produces a primitive ideal, is independent of polarisation, and depends only on ![]() $\mathbb {O}(\chi )$. There is thus an induced map
$\mathbb {O}(\chi )$. There is thus an induced map ![]() ${\rm PSpec}_{prim}\operatorname {S}(\mathfrak g) \to \operatorname {Spec}_{\rm prim}\operatorname {U}(\mathfrak g)$ for
${\rm PSpec}_{prim}\operatorname {S}(\mathfrak g) \to \operatorname {Spec}_{\rm prim}\operatorname {U}(\mathfrak g)$ for ![]() $\mathfrak g=V\!ir, W, W_{\geqslant -1}$. This map is surjective onto
$\mathfrak g=V\!ir, W, W_{\geqslant -1}$. This map is surjective onto ![]() $\operatorname {Spec}_{\rm prim} \operatorname {U}(\mathfrak g)$.
$\operatorname {Spec}_{\rm prim} \operatorname {U}(\mathfrak g)$.
These conjectures are the subject of ongoing research.
Index of notation
![]() $(a, b)_f$
$(a, b)_f$
![]() $a(\mathfrak k)$
$a(\mathfrak k)$
![]() $\mathbb {A}(\lambda )$
$\mathbb {A}(\lambda )$
![]() $B_\chi (x,y)$
$B_\chi (x,y)$
![]() $\chi _{x; \alpha _0,\ldots, \alpha _n}$
$\chi _{x; \alpha _0,\ldots, \alpha _n}$
![]() $d(\mathfrak k)$
$d(\mathfrak k)$
![]() $D_\chi$
$D_\chi$
![]() $D(\lambda (\chi ))$
$D(\lambda (\chi ))$
![]() $\textit {Dil}_x$
$\textit {Dil}_x$
![]() $\textit {DLoc}_x$
$\textit {DLoc}_x$
![]() $\textit {DLoc}_x^{\leqslant n}$
$\textit {DLoc}_x^{\leqslant n}$
![]() $\textit {DLoc}_x^{k+}$,
$\textit {DLoc}_x^{k+}$, ![]() $\textit {DLoc}_x^{\leqslant n, k+}$
$\textit {DLoc}_x^{\leqslant n, k+}$
![]() $\widehat {\textit {DLoc}}^\lambda$
$\widehat {\textit {DLoc}}^\lambda$
![]() $\widehat {\textit {DLoc}}^{\leqslant n}$,
$\widehat {\textit {DLoc}}^{\leqslant n}$, ![]() $\widehat {\textit {DLoc}}$
$\widehat {\textit {DLoc}}$
![]() $\widehat {\textit {DLoc}}^\lambda$-orbit quotient
$\widehat {\textit {DLoc}}^\lambda$-orbit quotient
![]() $D(u_1, \ldots, u_n; v_1, \ldots, v_n)$
$D(u_1, \ldots, u_n; v_1, \ldots, v_n)$
![]() $e_i(x)$,
$e_i(x)$, ![]() $e_i(x)^*$
$e_i(x)^*$
![]() $\operatorname {End}_{t\to s}(\cdot )$
$\operatorname {End}_{t\to s}(\cdot )$
![]() $\operatorname {ev}_\chi$
$\operatorname {ev}_\chi$
![]() $f_{\mathfrak k}$
$f_{\mathfrak k}$
![]() $\operatorname {gaps}(\mathfrak k)$, gaps of a subalgebra
$\operatorname {gaps}(\mathfrak k)$, gaps of a subalgebra
![]() $\mathfrak g^\chi$
$\mathfrak g^\chi$
![]() $I(n)$
$I(n)$
![]() $I(X) \subseteq A$
$I(X) \subseteq A$
![]() $J^\lambda _{\mathfrak g} := I(V^\lambda _{\mathfrak g})$
$J^\lambda _{\mathfrak g} := I(V^\lambda _{\mathfrak g})$
![]() $\lambda (\chi )$, order partition of
$\lambda (\chi )$, order partition of ![]() $\chi$
$\chi$
![]() $\lambda (Q)$, generic order partition of
$\lambda (Q)$, generic order partition of ![]() $Q$
$Q$
![]() $\operatorname {ldeg}(\mathfrak k)$, leading degrees of a subalgebra
$\operatorname {ldeg}(\mathfrak k)$, leading degrees of a subalgebra
![]() $\operatorname {lie}_x^{\leqslant n}$
$\operatorname {lie}_x^{\leqslant n}$
![]() $\widehat {\operatorname {lie}}^{\leqslant n}$
$\widehat {\operatorname {lie}}^{\leqslant n}$
![]() $\textit {Loc}^\lambda _{\mathfrak g}$
$\textit {Loc}^\lambda _{\mathfrak g}$
![]() $\textit {Loc}^{\leqslant n}_{\mathfrak g}$,
$\textit {Loc}^{\leqslant n}_{\mathfrak g}$, ![]() $\widetilde {\textit {Loc}}_{\mathfrak g}^{\leqslant n}$,
$\widetilde {\textit {Loc}}_{\mathfrak g}^{\leqslant n}$, ![]() $\textit {Loc}_x$,
$\textit {Loc}_x$, ![]() $\textit {Loc}_x^{\leqslant n}$
$\textit {Loc}_x^{\leqslant n}$
Local function
![]() $\mathfrak {m}_\chi$
$\mathfrak {m}_\chi$
![]() $\operatorname {MSpec} A$
$\operatorname {MSpec} A$
![]() $\overline {\mathbb {O}(\chi )}$, orbit closure of
$\overline {\mathbb {O}(\chi )}$, orbit closure of ![]() $\chi$
$\chi$
Order of a local function
![]() $p_\gamma : \operatorname {S}(W) \to \Bbbk [t, t^{-1}, y]$
$p_\gamma : \operatorname {S}(W) \to \Bbbk [t, t^{-1}, y]$
![]() $\pi _{\mathfrak g}^{\leqslant n}$,
$\pi _{\mathfrak g}^{\leqslant n}$, ![]() $\phi _{\mathfrak g }^{\leqslant n}$
$\phi _{\mathfrak g }^{\leqslant n}$
![]() $\operatorname {P}(\chi )$, Poisson core
$\operatorname {P}(\chi )$, Poisson core
Poisson morphism
![]() $\operatorname {PSpec}_{\rm prim}A$,
$\operatorname {PSpec}_{\rm prim}A$, ![]() $\operatorname {PSpec} A$
$\operatorname {PSpec} A$
Pseudo-orbit, ![]() $\mathbb {O}(\chi )$
$\mathbb {O}(\chi )$
![]() ${\rm rad}(f)$
${\rm rad}(f)$
![]() $\mathfrak S_\lambda$
$\mathfrak S_\lambda$
![]() $\Sigma ^\lambda _{\mathfrak g}$
$\Sigma ^\lambda _{\mathfrak g}$
![]() $\textit {Shift}_z$,
$\textit {Shift}_z$, ![]() $\textit {Shifts}$
$\textit {Shifts}$
Support of a local function
Support of a subalgebra, ![]() $\operatorname {supp}(\mathfrak k)$
$\operatorname {supp}(\mathfrak k)$
![]() $u_\chi, \mathfrak u_\chi$
$u_\chi, \mathfrak u_\chi$
![]() $V\!ir$
$V\!ir$
![]() $V^\lambda _{\mathfrak g}$
$V^\lambda _{\mathfrak g}$
![]() $V(N) \subseteq \operatorname {MSpec}(A)$
$V(N) \subseteq \operatorname {MSpec}(A)$
![]() $V_P(N) \subseteq \operatorname {PSpec} A$
$V_P(N) \subseteq \operatorname {PSpec} A$
![]() $W$
$W$
![]() $W(g)$
$W(g)$
![]() $W_{\geqslant -1}$
$W_{\geqslant -1}$
![]() $W_{\geqslant -1}(f)$
$W_{\geqslant -1}(f)$
![]() $W_{\geqslant 1}$
$W_{\geqslant 1}$
![]() $W_{x; \alpha }^{2; 1}$,
$W_{x; \alpha }^{2; 1}$, ![]() $W_{x; \alpha }^{2; 2}$
$W_{x; \alpha }^{2; 2}$
![]() $W_{x, y; \alpha, \beta }^{3A}$,
$W_{x, y; \alpha, \beta }^{3A}$, ![]() $W_{x, y; \alpha }^{3B1}$, etc.
$W_{x, y; \alpha }^{3B1}$, etc.
![]() $Y(Q)$
$Y(Q)$
Acknowledgements
We thank Jason Bell, Ken Brown, Lucas Buzaglo, Iain Gordon, Ivan Frolov, Omar León Sánchez and Toby Stafford for interesting discussion and questions. We would also like to thank the anonymous referee for their comments and, in particular, for suggesting Remark 5.2.11 to us.
The second author is partially supported by EPSRC grants EP/M008460/1 and EP/T018844/1. Section 6 was done with the support of grant 22-41-02028 of the first author from the Russian Science Foundation. Section 7 was done with the support of grant 20-01-00091-a of the first author from the Russian Foundation for Basic Research.
In addition, we are grateful to the Edinburgh Mathematical Society and the University of Edinburgh School of Mathematics for supporting a 2019 mini-workshop on enveloping algebras of infinite-dimensional Lie algebras.