Hostname: page-component-7bb8b95d7b-dtkg6 Total loading time: 0 Render date: 2024-09-14T01:08:09.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur le rang des courbes elliptiques sur les corps de classes de Hilbert

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  10 February 2011

Nicolas Templier
Nicolas Templier*
Affiliation:
Institute for Advanced Study, Princeton, NJ 08540, USA (email: nicolas.templier@normalesup.org)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E/ℚ be an elliptic curve and let D<0 be a sufficiently large fundamental discriminant. If 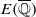contains Heegner points of discriminant D, those points generate a subgroup of rank at least |D|δ, where δ>0 is an absolute constant. This result is compatible with the Birch and Swinnerton-Dyer conjecture.

Résumé

Soit E/ℚ une courbe elliptique. Soit D<0 un discriminant fondamental suffisamment grand. Si 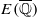contient des points de Heegner de discriminant D, ces points engendrent un sous-groupe dont le rang est supérieur à |D|δ, où δ>0 est une constante absolue. Ce résultat est en accord avec la conjecture de Birch et Swinnerton-Dyer.

Keywords

automorphic formsequidistributionL-functionsHeegner pointselliptic curves

MSC classification

Secondary: 11G05: Elliptic curves over global fields 14G40: Arithmetic varieties and schemes; Arakelov theory; heights 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture 11G15: Complex multiplication and moduli of abelian varieties
Type
Research Article
Information
Compositio Mathematica , Volume 147 , Issue 4 , July 2011 , pp. 1087 - 1104
Copyright
Copyright © Foundation Compositio Mathematica 2011

References

[AN10]Aflalo, E. and Nekovář, J., Non-triviality of CM points in ring class field towers, Israel J. Math. 175 (2010), 225–284.CrossRefGoogle Scholar
[BCHIS66]Borel, A., Chowla, S., Herz, C. S., Iwasawa, K. and Serre, J.-P., Seminar on complex multiplication, in Seminar held at the Institute for Advanced Study, Princeton, NJ, 1957–1958, Lecture Notes in Mathematics, vol. 21 (Springer, Berlin, 1966).Google Scholar
[BCDT01]Breuil, C., Conrad, B., Diamond, F. and Taylor, R., On the modularity of elliptic curves over Q: wild 3-adic exercises, J. Amer. Math. Soc. 14 (2001), 843–939.CrossRefGoogle Scholar
[BP09]Buium, A. and Poonen, B., Independence of points on elliptic curves arising from special points on modular and Shimura curves. I. Global results, Duke Math. J. 147 (2009), 181–191.CrossRefGoogle Scholar
[BFH90]Bump, D., Friedberg, S. and Hoffstein, J., Nonvanishing theorems for L-functions of modular forms and their derivatives, Invent. Math. 102 (1990), 543–618.CrossRefGoogle Scholar
[Cor02a]Cornut, C., Mazur’s conjecture on higher Heegner points, Invent. Math. 148 (2002), 495–523.CrossRefGoogle Scholar
[Cor02b]Cornut, C., Non-trivialité des points de Heegner, C. R. Math. Acad. Sci. Paris 334 (2002), 1039–1042.Google Scholar
[CV05]Cornut, C. and Vatsal, V., CM points and quaternion algebras, Doc. Math. 10 (2005), 263–309 (electronic).CrossRefGoogle Scholar
[CV07]Cornut, C. and Vatsal, V., Nontriviality of Rankin–Selberg L-functions and CM points, in L-functions and Galois representations, London Mathematical Society Lecture Note Series, vol. 320 (Cambridge University Press, Cambridge, 2007), 121–186.CrossRefGoogle Scholar
[Dar01]Darmon, H., Integration on ℋp×ℋ and arithmetic applications, Ann. of Math. (2) 154 (2001), 589–639.CrossRefGoogle Scholar
[Dar04]Darmon, H., Rational points on modular elliptic curves, CBMS Regional Conference Series in Mathematics, vol. 101 (Published for the Conference Board of the Mathematical Sciences, Washington, DC, 2004).Google Scholar
[Dar06]Darmon, H., Heegner points, Stark–Heegner points, and values of L-series, in International congress of mathematicians, Vol. II (Eur. Math. Soc. Zürich, 2006), 313–345.Google Scholar
[Duk88]Duke, W., Hyperbolic distribution problems and half-integral weight Maass forms, Invent. Math. 92 (1988), 73–90.CrossRefGoogle Scholar
[DFI95]Duke, W., Friedlander, J. and Iwaniec, H., Class group L-functions, Duke Math. J. 79 (1995), 1–56.CrossRefGoogle Scholar
[Gro88]Gross, B., Local orders, root numbers, and modular curves, Amer. J. Math. 110 (1988), 1153–1182.CrossRefGoogle Scholar
[GP91]Gross, B. and Prasad, D., Test vectors for linear forms, Math. Ann. 291 (1991), 343–355.CrossRefGoogle Scholar
[GZ86]Gross, B. and Zagier, D., Heegner points and derivatives of L-series, Invent. Math. 84 (1986), 225–320.CrossRefGoogle Scholar
[HPS89]Hijikata, H., Pizer, A. and Shemanske, T., Orders in quaternion algebras, J. Reine Angew. Math. 394 (1989), 59–106.Google Scholar
[Iwa90]Iwaniec, H., On the order of vanishing of modular L-functions at the critical point, Sém. Théor. Nombres Bordeaux (2) 2 (1990), 365–376.CrossRefGoogle Scholar
[Jac72]Jacquet, H., Automorphic forms on GL(2). Part II, Lecture Notes in Mathematics, vol. 278 (Springer, Berlin, 1972).CrossRefGoogle Scholar
[JL70]Jacquet, H. and Langlands, R., Automorphic forms on GL(2) (Springer, Berlin, 1970).CrossRefGoogle Scholar
[KS99]Katz, N. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy, American Mathematical Society Colloquium Publications, vol. 45 (American Mathematical Society, Providence, RI, 1999).Google Scholar
[Kol88a]Kolyvagin, V., Finiteness of E(Q) and SH(E,Q) for a subclass of Weil curves, Izv. Akad. Nauk SSSR Ser. Mat. 52 (1988), 522–540, 670–671.Google Scholar
[Kol88b]Kolyvagin, V., The Mordell–Weil and Shafarevich–Tate groups for Weil elliptic curves, Izv. Akad. Nauk SSSR Ser. Mat. 52 (1988), 1154–1180, 1327.Google Scholar
[Maz84]Mazur, B., Modular curves and arithmetic, in Proceedings of the International Congress of Mathematicians (Warsaw 1983), Vol. 1, 2 (PWN, Warsaw, 1984), 185–211.Google Scholar
[MS74]Mazur, B. and Swinnerton-Dyer, P., Arithmetic of Weil curves, Invent. Math. 25 (1974), 1–61.CrossRefGoogle Scholar
[Mic04]Michel, Ph., The subconvexity problem for Rankin–Selberg L-functions and equidistribution of Heegner points, Ann. of Math. (2) 160 (2004), 185–236.CrossRefGoogle Scholar
[MV06]Michel, Ph. and Venkatesh, A., Equidistribution, L-functions and ergodic theory: on some problems of Yu. Linnik, in International congress of mathematicians, Vol. II (Eur. Math. Soc. Zürich, 2006), 421–457.Google Scholar
[MV07]Michel, Ph. and Venkatesh, A., Heegner points and non-vanishing of Rankin/SelbergL-functions, in Analytic number theory, Clay Mathematics Proceedings, vol. 7 (American Mathematical Society, Providence, RI, 2007), 169–183.Google Scholar
[MR82]Montgomery, H. and Rohrlich, D., On the L-functions of canonical Hecke characters of imaginary quadratic fields. II, Duke Math. J. 49 (1982), 937–942.CrossRefGoogle Scholar
[MM91]Murty, M. and Murty, V., Mean values of derivatives of modular L-series, Ann. of Math. (2) 133 (1991), 447–475.CrossRefGoogle Scholar
[Nek07]Nekovář, J., The Euler system method for CM points on Shimura curves, in L-functions and Galois representations, London Mathematical Society Lecture Note Series, vol. 320 (Cambridge University Press, Cambridge, 2007), 471–547.CrossRefGoogle Scholar
[NS99]Nekovář, J. and Schappacher, N., On the asymptotic behaviour of Heegner points, Turkish J. Math. 23 (1999), 549–556.Google Scholar
[PR94]Platonov, V. and Rapinchuk, A., Algebraic groups and number theory, Pure and Applied Mathematics, vol. 139 (Academic Press, Boston, MA, 1994), Translated from the 1991 Russian original by Rachel Rowen.Google Scholar
[Pra07]Prasad, D., Relating invariant linear form and local epsilon factors via global methods, Duke Math. J. 138 (2007), 233–261.CrossRefGoogle Scholar
[Rib92]Ribet, K., Abelian varieties over Q and modular forms, in Algebra and topology 1992 (Taejŏn) (Korea Advanced Institute of Science and Technology, Taejŏn, 1992), 53–79.Google Scholar
[RT09]Ricotta, G. and Templier, N., Comportement asymptotique des hauteurs des points de Heegner, J. Théor. Nombres Bordeaux 21 (2009), 741–753.CrossRefGoogle Scholar
[RV08]Ricotta, G. and Vidick, T., Hauteur asymptotique des points de Heegner, Canad. J. Math. 60 (2008), 1406–1436 (in French, with English summary).CrossRefGoogle Scholar
[Roh80a]Rohrlich, D., Galois conjugacy of unramified twists of Hecke characters, Duke Math. J. 47 (1980), 695–703.CrossRefGoogle Scholar
[Roh80b]Rohrlich, D., The nonvanishing of certain Hecke L-functions at the center of the critical strip, Duke Math. J. 47 (1980), 223–232.CrossRefGoogle Scholar
[Roh80c]Rohrlich, D., On the L-functions of canonical Hecke characters of imaginary quadratic fields, Duke Math. J. 47 (1980), 547–557.CrossRefGoogle Scholar
[RS07]Rosen, M. and Silverman, J., On the independence of Heegner points associated to distinct quadratic imaginary fields, J. Number Theory 127 (2007), 10–36.CrossRefGoogle Scholar
[Sie35]Siegel, C.-L., Über die Classenzahl quadratischer Zahlkörper, Acta Arith. 1 (1935), 83–86 (reprinted in Ges. Abh. I, 406–409, Springer, Berlin, 1966).CrossRefGoogle Scholar
[Sil09]Silverman, J., The arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 106, second edition (Springer, New York, 2009), corrected reprint of the 1986 original.CrossRefGoogle Scholar
[SUZ97]Szpiro, L., Ullmo, E. and Zhang, S., Équirépartition des petits points, Invent. Math. 127 (1997), 337–347.CrossRefGoogle Scholar
[TW95]Taylor, R. and Wiles, A., Ring-theoretic properties of certain Hecke algebras, Ann. of Math. (2) 141 (1995), 553–572.CrossRefGoogle Scholar
[Tem07]Templier, N., Heegner points and Eisenstein series, Preprint (2007), available at http://arxiv.org/abs/0808.1476, Forum Math., to appear.Google Scholar
[Tem08a]Templier, N., Minoration de rangs de courbes elliptiques, C. R. Math. Acad. Sci. Paris 346 (2008), 1225–1230 (in French, with English and French summaries).Google Scholar
[Tem08b]Templier, N., A non-split sum of coefficients of modular forms, Preprint (2008), available at arXiv:0902.2496, Duke Math. J., to appear.Google Scholar
[Tun83]Tunnell, J., Local ϵ-factors and characters of GL(2), Amer. J. Math. 105 (1983), 1277–1307.CrossRefGoogle Scholar
[Ull98]Ullmo, E., Positivité et discrétion des points algébriques des courbes, Ann. of Math. (2) 147 (1998), 167–179.CrossRefGoogle Scholar
[Vat03]Vatsal, V., Special values of anticyclotomic L-functions, Duke Math. J. 116 (2003), 219–261.CrossRefGoogle Scholar
[Wal85]Waldspurger, J.-L., Sur les valeurs de certaines fonctions L automorphes en leur centre de symétrie, Compositio Math. 54 (1985), 173–242.Google Scholar
[Wil95]Wiles, A., Modular elliptic curves and Fermat’s last theorem, Ann. of Math. (2) 141 (1995), 443–551.CrossRefGoogle Scholar
[Win07]Wintenberger, J.-P., La conjecture de modularité de Serre : le cas de conducteur (d’après C. Khare), Astérisque (2007), Exp. No. 956, viii, 99–121, Sém. Bourbaki. Vol. 2005–2006.Google Scholar
[YZZ]Yuan, X., Zhang, S.-W. and Zhang, W., Gross–Zagier formula, Ann. of Math. Stud., to appear.Google Scholar
[Zha98]Zhang, S.-W., Equidistribution of small points on abelian varieties, Ann. of Math. (2) 147 (1998), 159–165.CrossRefGoogle Scholar
[Zha01a]Zhang, S.-W., Heights of Heegner points on Shimura curves, Ann. of Math. (2) 153 (2001), 27–147.CrossRefGoogle Scholar
[Zha01b]Zhang, S.-W., Gross–Zagier formula for GL 2, Asian J. Math. 5 (2001), 183–290.CrossRefGoogle Scholar
[Zha05]Zhang, S.-W., Equidistribution of CM-points on quaternion Shimura varieties, Int. Math. Res. Not. (2005), 3657–3689.CrossRefGoogle Scholar