Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T19:27:59.006Z Has data issue: false hasContentIssue false
  • English
  • Français

BIAS REDUCTION AND LIKELIHOOD-BASED ALMOST EXACTLY SIZED HYPOTHESIS TESTING IN PREDICTIVE REGRESSIONS USING THE RESTRICTED LIKELIHOOD

Published online by Cambridge University Press:  01 October 2009

Willa W. Chen  and
Rohit S. Deo
Willa W. Chen
Affiliation:
Texas A & M University
Rohit S. Deo*
Affiliation:
New York University
*
*Address correspondence to Rohit S. Deo, 8-57 KMC, New York University, West 4th Street New York, NY 10012, USA; e-mail: rdeo@stern.nyu.edu.
Get access Rights & Permissions [Opens in a new window]

Abstract

Difficulties with inference in predictive regressions are generally attributed to strong persistence in the predictor series. We show that the major source of the problem is actually the nuisance intercept parameter, and we propose basing inference on the restricted likelihood, which is free of such nuisance location parameters and also possesses small curvature, making it suitable for inference. The bias of the restricted maximum likelihood (REML) estimates is shown to be approximately 50% less than that of the ordinary least squares (OLS) estimates near the unit root, without loss of efficiency. The error in the chi-square approximation to the distribution of the REML-based likelihood ratio test (RLRT) for no predictability is shown to be 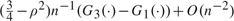where |ρ| < 1 is the correlation of the innovation series and Gs(·) is the cumulative distribution function (c.d.f.) of a 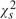random variable. This very small error, free of the autoregressive (AR) parameter, suggests that the RLRT for predictability has very good size properties even when the regressor has strong persistence. The Bartlett-corrected RLRT achieves an O(n−2) error. Power under local alternatives is obtained, and extensions to more general univariate regressors and vector AR(1) regressors, where OLS may no longer be asymptotically efficient, are provided. In simulations the RLRT maintains size well, is robust to nonnormal errors, and has uniformly higher power than the Jansson and Moreira (2006, Econometrica 74, 681–714) test with gains that can be substantial. The Campbell and Yogo (2006, Journal of Financial Econometrics 81, 27–60) Bonferroni Q test is found to have size distortions and can be significantly oversized.

Type
ARTICLES
Information
Econometric Theory , Volume 25 , Issue 5 , October 2009 , pp. 1143 - 1179
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Amihud, Y. & Hurvich, C. (2004) Predictive regressions: A reduced-bias estimation method. Journal of Financial and Quantitative Analysis 39, 813–841.CrossRefGoogle Scholar
Baker, M., Taliaferro, R., & Wurgler, J. (2006) Predicting returns with managerial decision variables: Is there a small sample bias? Journal of Finance 61, 1711–1730.CrossRefGoogle Scholar
Barndorff-Nielsen, O.E. & Hall, P. (1988) On the level-error after Bartlett adjustment of the likelihood ratio statistic. Biometrika 75, 374–378.CrossRefGoogle Scholar
Bartlett, M. (1953) Approximate confidence intervals III. More than one unknown parameter. Biometrika 40, 306–317.CrossRefGoogle Scholar
Campbell, J. & Yogo, M. (2005) Implementing the Econometric Methods in “Efficient Tests of Stock Return Predictability.” Available at http://finance.wharton.upenn.edu/~yogo/.Google Scholar
Campbell, J. & Yogo, M. (2006) Efficient tests of stock return predictability. Journal of Financial Economics 81, 27–60.CrossRefGoogle Scholar
Chandra, T.K. & Ghosh, J.K. (1979) Valid asymptotic expansions for the likelihood ratio statistic and other perturbed chi-square variables. Sankhya, Series A. 41, 22–47.Google Scholar
Cheang, W.K. & Reinsel, G. (2000) Bias reduction of autoregressive estimates in time series regression model through restricted maximum likelihood. Journal of the American Statistical Association 95, 1173–1184.CrossRefGoogle Scholar
Chen, W. & Deo, R. (2006) A Smooth Transition to the Unit Root Distribution via the Chi-Square Distribution with Interval Estimation for Nearly Integrated Autoregressive Processes. Working paper, Texas A & M and New York University.Google Scholar
Chen, W. & Deo, R. (2007) The Chi-Square Approximation of the Restricted Likelihood Ratio Test for the Sum of Autoregressive Coefficients with Interval Estimation. Working paper, Texas A & M and New York University.Google Scholar
Chesher, A. & Smith, R. (1995) Bartlett corrections to likelihood ratio tests. Biometrika 82, 433–436.CrossRefGoogle Scholar
Cordeiro, G. (1987) On the corrections to the likelihood ratio statistics. Biometrika 74, 265–274.CrossRefGoogle Scholar
Cordeiro, G., Botter, D., & Ferrari, S.L. (1994) Nonnull asymptotic distributions of three classic criteria in generalised linear models. Biometrika 81, 709–720.CrossRefGoogle Scholar
Cribari-Neto, F. & Cordeiro, G. (1996) On Bartlett and Bartlett-type corrections. Econometric Reviews 15, 339–367.CrossRefGoogle Scholar
Dufour, J.-M. & King, M.L. (1991) Optimal invariant tests for the autocorrelation coefficient in linear regressions with stationary or non-stationary AR(1) errors. Journal of Econometrics 47, 115–143.CrossRefGoogle Scholar
Efron, B. (1975) Defining the curvature of a statistical problem (with applications to second order efficiency). Annals of Statistics 3, 1189–1242.CrossRefGoogle Scholar
Fisher, R. (1973) Statistical Methods and Scientific Inference. Haffner.Google Scholar
Francke, M. & de Vos, A. (2006) Marginal likelihood and unit roots. Journal of Econometrics 137, 708–728.CrossRefGoogle Scholar
Giraitis, L. & Phillips, P.C.B. (2006) Uniform limit theory for stationary autoregression. Journal of Time Series Analysis 27, 51–60.CrossRefGoogle Scholar
Harris, P. & Peers, H.W. (1980) The local power of the efficient scores test statistic. Biometrika 67, 525–529.CrossRefGoogle Scholar
Harville, D. (1974) Bayesian inference of variance components using only error contrasts. Biometrika 61, 383–385.CrossRefGoogle Scholar
Harville, D. (1977) Maximum likelihood approaches to variance component estimation and to related problems. Journal of the American Statistical Association 72, 320–338.CrossRefGoogle Scholar
Hayakawa, T. (1975) The likelihood ratio criterion for a composite hypothesis under a local alternative. Biometrika 62, 451–460.CrossRefGoogle Scholar
Hayakawa, T. (1977) The likelihood ratio criterion and the asymptotic expansion of its distribution. Annals of the Institute of Statistical Mathematics 29, 359–378.CrossRefGoogle Scholar
Hayakawa, T. (1987) Correction. Annals of the Institute of Statistical Mathematics 39, 681.CrossRefGoogle Scholar
Jansson, M. & Moreira, M. (2006) Optimal inference in regression models with nearly integrated regressors. Econometrica 74, 681–714.CrossRefGoogle Scholar
Kalbfleisch, J. & Sprott, D. (1970) Application of likelihood methods to models involving large numbers of parameters. Journal of the Royal Statistical Society, Series B 32, 175–194.Google Scholar
Kang, W., Shin, D., & Lee, Y. (2003) Biases of the restricted maximum likelihood estimators for ARMA processes with polynomial time trend. Journal of Statistical Planning and Inference 116, 163–176.CrossRefGoogle Scholar
Kass, R.E. & Slate, E.H. (1994) Some diagnostics of maximum likelihood and posterior nonnormality. Annals of Statistics 22, 668–695.CrossRefGoogle Scholar
Lewellen, J. (2004) Predicting returns with financial ratios. Journal of Financial Economics 74, 209–235.CrossRefGoogle Scholar
Lehmann, E. & Romano, J. (2005) Testing Statistical Hypotheses, 3rd ed. Springer-Verlag.Google Scholar
Marriott, F. & Pope, J. (1954) Bias in the estimation of autocorrelations. Biometrika 41, 390–402.CrossRefGoogle Scholar
McCullagh, P. & Cox, D.R. (1986) Invariants and likelihood ratio statistics. Annals of Statistics 14, 1419–1430.CrossRefGoogle Scholar
Phillips, P.C.B. & Magdalinos, T. (2007) Limit theory for moderate deviations from a unit root. Journal of Econometrics 136, 115–130.CrossRefGoogle Scholar
Rahman, S. & King, M. (1997) Marginal-likelihood score-based tests of regression disturbances in the presence of nuisance parameters. Journal of Econometrics 82, 81–106.CrossRefGoogle Scholar
Smyth, G. & Verbyla, A. (1996) A conditional likelihood approach to residual maximum likelihood estimation in generalized linear models. Journal of the Royal Statistical Society, Series B 58, 565–572.Google Scholar
Sprott, D. (1973) Normal likelihoods and their relation to large sample theory of estimation. Biometrika 60, 457–465.CrossRefGoogle Scholar
Sprott, D. (1975) Application of maximum likelihood methods to finite samples. Sankhya, Series B 37, 259–270.Google Scholar
Sprott, D. (1980) Maximum likelihood in small samples: Estimation in the presence of nuisance parameters. Biometrika 67, 515–523.CrossRefGoogle Scholar
Sprott, D. (1990) Inferential estimation, likelihood, and linear pivotals. Canadian Journal of Statistics 18, 1–10.CrossRefGoogle Scholar
Sprott, D. & Viveros-Aguilera, R. (1984) The interpretation of maximum-likelihood estimation. Canadian Journal of Statistics 12, 27–38.CrossRefGoogle Scholar
Stambaugh, R. (1999) Predictive regressions. Journal of Financial Economics 54, 375–421.CrossRefGoogle Scholar
Tunnicliffe Wilson, G. (1989) On the use of marginal likelihood in time series model estimation. Journal of the Royal Statistical Society, Series B 51, 15–27.Google Scholar
van Garderen, K. (1999) Exact geometry of autoregressive models. Journal of Time Series Analysis 20, 1–21.CrossRefGoogle Scholar
van Giersbergen, N. (2006) Bartlett Correction in the Stable AR(1) Model with Intercept and Trend. Working paper, Universiteit van Amsterdam.Google Scholar