1. Introduction
In A Treatise of Human Nature (Hume Reference Hume, Norton and Norton2007 [1740]; henceforth Treatise), Hume presents a rather remarkable theory of how people regard an action as being either moral or immoral: the inference we draw (through the associated pleasure or uneasiness we feel), upon observing the action, of the character of the person who chose it. On first glance, there seems nothing terribly remarkable about that view. But, in fact, at times Hume states that that inference is the sole source of the morality or immorality of the action; if the action doesn’t act as a sign of character, it is meaningless to call it moral or immoral. Morality pertains primarily to character, and the morality of an action consists solely in its role in signalling good character. In contrast to (for example) consequentialist theories of morality, doing a good deed is not virtuous because of, say, the beneficial effects it has for others (giving to charity, for example), but because it (typically) indicates the benevolence of the person doing the deed.
Game theory aficionados will recognize that Hume is implicitly arguing that actions acquire their virtuous/vicious labels due entirely to what they signal about the type of the person who chose the action, where for simplicity we can consider the type to be either good or bad. To that end, I construct and analyse a variety of simple game-theoretic models to try to get a better handle on what Hume’s signalling theory of virtuous/vicious actions entails, as well as some additional implications that seem to follow from that theory.
To briefly preview the analysis, I argue that Hume presents two distinct, although possibly related, criteria for what causes an action to be regarded by observers as moral: (i) there exist at least some people (I will call these the good character types) who are naturally inclined to choose the action, regardless of any possible rewards, punishments, and/or sense of duty associated with it (this criterion is also the fundamental one that distinguishes what Hume calls natural virtues from artificial ones), and (ii) the action acts as a credible signal of the agent’s good character. In a game-theoretic signalling model, criterion (i) is a structural choice that the analyst makes, namely whether there exist good types in the model, or instead all types are bad (in Hume’s terms, whether we are dealing with a natural or artificial virtue). Criterion (ii) is an equilibrium phenomenon, i.e. the answer to the question of whether a signalling (separating) equilibrium exists (as well as what other equilibria exist, if any) is endogenously determined by solving the model.
The first signalling model I construct adopts criterion (i), i.e. assumes that there are two types of agent A (she), a good type and a bad type. The good type is naturally inclined (as specified by her utilities) to choose a certain action that I label the moral action, whereas the bad type is naturally inclined to choose a different action that I label the immoral action (this may simply involve doing nothing, i.e. not choosing the moral action). There is an observer, B (he), who doesn’t know A’s type but does observe A’s action, and then chooses whether to punish (impose a cost on) or not punish A for her action. Consistent with Hume’s notion of character-based informal social punishments imposed by observers (discussed in detail later), I assume that B is inclined to punish the bad type of A, but not punish the good type.
It turns out that this Hume-inspired signalling model does indeed have a separating equilibrium, in which the good type chooses the moral action and the bad type chooses the immoral action, and hence the action is completely informative to B about A’s type: Hume’s criterion (ii) for moral actions is satisfied (the first criterion is satisfied by construction in this first version of the model). However, this is only an equilibrium (in which case it is also the unique one) if the moral action is so distasteful (i.e. costly) to the bad type (in terms of her utilities) that she prefers the immoral action with punishment to the moral action without punishment. If (and only if) this is the case, then the moral action acts as a credible signal of good character because it is too costly (distasteful) for the bad type to choose to try to mimic the good type and avoid social punishment.
This is of course consistent with modern signalling theory’s core insight that when the actors’ interests are too divergent (as here) for costless messages (‘cheap talk’) to allow for credible signalling (Crawford and Sobel Reference Crawford and Sobel1982), then a costly signal may allow for information transmission (Spence Reference Spence1974), but only if it is sufficiently costly for the type that would bluff with costless messages (the bad type here, who would verbally claim to be the good type to try to avoid punishment), and sufficiently low-cost for the other type (for whom it may not be costly at all, as here). Footnote 1 Hume hints at a credibility requirement when he writes that ‘Actions are, indeed, better indications of a character than words, or even wishes and sentiments …’ (T 3.3.1.5), Footnote 2 but doesn’t develop this in a costly signalling direction. But that a straightforward formalization of his theory easily and naturally pushes in that direction suggests that the rudiments of costly signalling theory can be found in Treatise, Footnote 3 and that his theory can be reasonably extended to state that an action that good character types are naturally inclined to choose will only be informative of character, and hence be regarded by observers as a moral action, if it is sufficiently costly (distasteful) for bad types so as to deter them from also choosing it to try to appear as good types. Not any action will do.
If the moral action is not too costly (distasteful) for the bad type, then the equilibrium is either (depending on how prevalent good types are in the population) a completely uninformative pooling one or a partially informative semi-separating one. If good types are highly prevalent in the population, then the unique equilibrium is a pooling one, in which both types choose the moral action (hence, criterion ii fails), upon which B chooses to not punish because A is probably a good type. Consistent with an intuition by Hume, under certain conditions a bad type may choose to ‘disguise’ (T 3.2.1.8) herself by choosing the moral action against her natural inclination. Hume doesn’t identify the ‘not too costly/distasteful for the bad type’ condition for pooling behaviour to occur, but remarkably does state that this disguising behaviour is especially likely to occur when good types are highly prevalent.
The existence of a pooling equilibrium, in addition to the separating equilibrium, also reveals a tension between Hume’s signalling theory of moral actions, and the consequentialist goal of getting everyone to choose beneficial actions. In Hume’s theory, morality pertains primarily to character (and hence he is generally regarded as being part of the virtue ethics tradition; e.g. Swanton Reference Swanton2015), and actions serve mainly to reveal character, which is what an observer is really interested in. However, moral actions presumably have beneficial effects for others (indeed, Hume himself states numerous times that one of the main reasons we admire good character is because such people tend to do things that help others), in which case from a consequentialist perspective we want everyone to choose moral actions (regardless of character). This is precisely what happens in the pooling equilibrium. Although good from a consequentialist viewpoint, the downside is that the moral action entirely loses its signalling value. In the separating equilibrium, on the other hand, actions are fully informative of character type, but the consequentialist downside is that bad types don’t choose moral actions.
The analysis suggests that if our priority is to get everyone to choose moral actions, then the social punishment costs for not doing so need to be sufficiently high. If, on the other hand, we mainly care about gleaning peoples’ characters, then those costs need to be low enough that bad types are willing to reveal themselves through their actions. When the parameters are such that neither the separating nor the pooling equilibrium exists, then the unique equilibrium is a semi-separating one that embodies a ‘compromise’ to this signalling-versus-consequentialism tradeoff, in that the moral action is partially informative, and even bad types choose the moral action with positive probability. Footnote 4
The rest of the paper is organized as follows. In the next section, I discuss how criteria (i) and (ii) regarding moral actions can be gleaned from Hume’s statements in Treatise. Following that, I set up and analyse a variety of simple game-theoretic models that culminate in the main signalling model I have been discussing. Along the way, to justify the models, I discuss Hume’s statements about informal social punishments imposed by observers, and the observer utilities that they seem to suggest. Finally, I analyse a variant in which both types of A are bad, but to differing degrees, to examine whether artificial virtues can occur in the model, whereby no type is naturally inclined to choose the moral action, but may be incentivized to do so. It turns out that artificial virtues can occur, but only under a punishment condition on which Hume’s stance is unclear. Footnote 5
2. Actions as signals of character
Early in Book III of Treatise, in setting up his famous argument that justice (with regard to property rights) is an artificial virtue, Hume makes some rather astonishing statements about the moral status of actions. Footnote 6
(A) ’Tis evident, that when we praise any actions, we regard only the motives that produced them, and consider the actions as signs or indications of certain principles in the mind and temper. The external performance has no merit. We must look within to find the moral quality. This we cannot do directly; and therefore fix our attention on actions, as on external signs. But these actions are still considered as signs; and the ultimate object of our praise and approbation is the motive, that produc’d them. (T 3.2.1.2)
(B) It appears, therefore, that all virtuous actions derive their merit only from virtuous motives, and are consider’d merely as signs of those motives. (T 3.2.1.4)
Much later in Book III, he makes similar statements.
(C) If any action be either virtuous or vicious, ’tis only as a sign of some quality or character. It must depend upon durable principles of the mind, which extend over the whole conduct, and enter into the personal character. Actions themselves, not proceeding from any constant principle, have no influence on love or hatred, pride or humility; and consequently are never consider’d in morality. (T 3.3.1.4)
(D) We are never to consider any single action in our enquiries concerning the origin of morals; but only the quality or character from which the action proceeded. These alone are durable enough to affect our sentiments concerning the person. Actions are, indeed, better indications of a character than words, or even wishes and sentiments; but ’tis only so far as they are such indications, that they are attended with love or hatred, praise or blame. (T 3.3.1.5)
These statements form the basis of my claim that, at least at times, Hume regards actions as having moral or immoral (‘virtuous or vicious’) status only in-so-far as they act as signals of the agent’s good or bad character, which is what an observer is really interested in knowing about the agent. Footnote 7
Implicit here are two ideas. First, that people differ in their character, i.e. there is variation in character types, and hence in general an observer is uncertain about any given individual’s character. Second, that actions may serve as credible signals of a person’s character, and generally carry more credibility than words alone.
Another relevant Humean point to make here, captured in his ‘to reason in a circle’ argument (and more generally, in his distinction between natural and artificial virtues), is that a given action can only be designated as moral if there are some character types that are naturally inclined to choose that action, independent of any possible punishment (social, legal, and/or divine) for not performing it, reward for performing it, and/or sense of duty to perform it. That is, I interpret his circle argument as implying that (a) if no character type would choose the action absent punishment/reward/duty, but (b) we then label the action moral and as a result a punishment/reward/duty is created, as a result of which (c) at least some character types now choose the action, then (d) it is meaningless to call the action moral. In Hume’s own words:
(E) A virtuous motive is requisite to render an action virtuous. An action must be virtuous, before we can have a regard to its virtue. Some virtuous motive, therefore, must be antecedent to that regard. (T 3.2.1.4)
(F) In short, it may be establish’d as an undoubted maxim, that no action can be virtuous, or morally good, unless there be in human nature some motive to produce it, distinct from the sense of its morality. (T 3.2.1.7)
On the basis of all these statements, it seems to me that Hume presents two distinct (although possibly related) criteria for what makes an action moral: (i) there has to be at least some character types who would choose the action even if there were no rewards, punishments, and/or sense of duty associated with it, and (ii) it acts as a credible signal of the agent’s good character. Criterion (i), in addition to being a requirement for a moral action, is what distinguishes natural from artificial virtues. In a game-theoretic model, whether or not (i) holds is a structural feature of the model, specified by the analyst. For most of the paper, the model will be such that (i) does hold, but later I consider a variant in which it doesn’t. After constructing a model which attempts to capture Hume’s core arguments, we can solve the model to determine whether there exist equilibria in which (ii) holds, as well as what other types of equilibria exist, if any.
3. A model of moral choice: no reward, punishment, and/or duty considerations
Before presenting the signalling models, I set up some simple complete information games to distinguish between good types and bad types, and the incentives (or lack thereof) of either type to act against her natural inclination.
I designate the agent who makes a choice between two actions, which I label as moral and immoral, as agent A, and use female pronouns to refer to her. So suppose that A chooses between two actions, a moral action (labelled MA) and an immoral action (IA). IA need not be an action that we regard as immoral on its own terms; instead, it may simply involve not choosing the moral action. But for convenience I will simply refer to it as the immoral action.
First consider the choice of a ‘good’ type of A, whose decision-tree is shown in Figure 1. This is a simple decision-theoretic model since there is not yet another actor. If the good type chooses MA, then her utility is
![]() ${a_1}$
, whereas it is the lower
${a_1}$
, whereas it is the lower
![]() ${a_2}$
if she chooses IA. That is, I assume that
${a_2}$
if she chooses IA. That is, I assume that
![]() ${a_1} \gt {a_2}$
; even absent any reward/punishment/duty considerations, she would choose MA, which is what makes her the good type. She is naturally inclined to choose MA; in Hume’s terms (passages B and E above), she has a ‘virtuous motive’ for doing so. Given her utilities, she of course chooses MA.
Footnote 8
${a_1} \gt {a_2}$
; even absent any reward/punishment/duty considerations, she would choose MA, which is what makes her the good type. She is naturally inclined to choose MA; in Hume’s terms (passages B and E above), she has a ‘virtuous motive’ for doing so. Given her utilities, she of course chooses MA.
Footnote 8

Figure 1. Decision-theoretic model with good type of
![]() $A.$
$A.$
Figure 2 shows the analogous decision-tree of a ‘bad’ type of A. For this type, I assume that
![]() ${a_4} \gt {a_3}$
: absent any reward/punishment/duty considerations, she would choose IA, which is thus her natural inclination. When I later introduce such considerations, she may end up choosing MA, but she doesn’t have a ‘virtuous motive’ for doing so. Making a choice without any reward/punishment/duty considerations, which is the situation captured in Figure 2, she of course chooses IA.
${a_4} \gt {a_3}$
: absent any reward/punishment/duty considerations, she would choose IA, which is thus her natural inclination. When I later introduce such considerations, she may end up choosing MA, but she doesn’t have a ‘virtuous motive’ for doing so. Making a choice without any reward/punishment/duty considerations, which is the situation captured in Figure 2, she of course chooses IA.

Figure 2. Decision-theoretic model with bad type of
![]() $A$
.
$A$
.
To model Hume’s theory that actions may serve as signals of character (here, A’s type, either good or bad), I now introduce a second player B, for whom I use male pronouns. In the initial signalling game, B is simply an observer who takes no action of his own, and we thus don’t yet have to specify his utilities for the various outcomes that can result from A’s choice. But based on that choice, B may make inferences about A’s type.
The signalling model that captures B’s ability to make such an inference is shown in Figure 3. This is still essentially a decision-theoretic model as there is only one actor that chooses actions, and the other actor’s only role is to possibly make inferences about the first actor’s type (and the game ends at information-sets, which is certainly unusual). But this model is the appropriate one to capture Hume’s theory of actions as signals of character, without any reward/punishment/duty considerations. Later I will introduce such considerations, and use a more standard signalling model to capture them.

Figure 3. Decision-theoretic signalling model.
The model begins with a fictional player labelled ‘nature’ or ‘chance’ probabilistically choosing A’s type, either good or bad. Suppose that nature chooses A’s type to be good with some probability
![]() $0 \lt p \lt 1$
, and bad with probability
$0 \lt p \lt 1$
, and bad with probability
![]() $1 - p$
. B does not observe this move and hence begins the interaction uncertain of A’s type, but does know the probabilities. Thus, these probabilities essentially represent B’s prior belief that A is the good type (Harsanyi Reference Harsanyi1967–68). For example, if B generally believes that most people are of the good type on the character trait under consideration, then p would be high, but low if B believes that good types are rare. Alternatively, if A is a specific person that B knows, then B may begin the interaction with certain prior beliefs (possibly based on past interactions) about the likelihood of her being the good type.
$1 - p$
. B does not observe this move and hence begins the interaction uncertain of A’s type, but does know the probabilities. Thus, these probabilities essentially represent B’s prior belief that A is the good type (Harsanyi Reference Harsanyi1967–68). For example, if B generally believes that most people are of the good type on the character trait under consideration, then p would be high, but low if B believes that good types are rare. Alternatively, if A is a specific person that B knows, then B may begin the interaction with certain prior beliefs (possibly based on past interactions) about the likelihood of her being the good type.
A knows her own type (i.e. observes nature’s move) and chooses between MA and IA. If B observes that MA was chosen, then he is at an information-set labelled
![]() ${I_1}$
. If B observes that IA was chosen, then he is at an information-set labelled
${I_1}$
. If B observes that IA was chosen, then he is at an information-set labelled
![]() ${I_2}$
. The information-sets capture the idea that B observes the action chosen, but didn’t observe nature’s move.
${I_2}$
. The information-sets capture the idea that B observes the action chosen, but didn’t observe nature’s move.
![]() ${I_1}$
is represented by a dashed line connecting the histories (good A, MA) and (bad A, MA), capturing the idea that B doesn’t know for sure (if that information-set is reached) which of these two histories occurred, in particular whether it was the good type who chose MA, or the bad type. But he has beliefs, with
${I_1}$
is represented by a dashed line connecting the histories (good A, MA) and (bad A, MA), capturing the idea that B doesn’t know for sure (if that information-set is reached) which of these two histories occurred, in particular whether it was the good type who chose MA, or the bad type. But he has beliefs, with
![]() $0 \le x \le 1$
being the probability he assigns (conditional on
$0 \le x \le 1$
being the probability he assigns (conditional on
![]() ${I_1}$
being reached) to history (good A, MA) having occurred, and
${I_1}$
being reached) to history (good A, MA) having occurred, and
![]() $1 - x$
being the probability he assigns to history (bad A, MA) having occurred. Similarly, he has beliefs y and
$1 - x$
being the probability he assigns to history (bad A, MA) having occurred. Similarly, he has beliefs y and
![]() $1 - y$
at
$1 - y$
at
![]() ${I_2}$
. For solving the model, I use perfect Bayesian equilibrium (PBE), the standard solution concept for sequential-move games of imperfect information (i.e. those containing at least one non-singleton information-set), a category that includes signalling games (e.g. Gibbons Reference Gibbons1992: Ch. 4).
${I_2}$
. For solving the model, I use perfect Bayesian equilibrium (PBE), the standard solution concept for sequential-move games of imperfect information (i.e. those containing at least one non-singleton information-set), a category that includes signalling games (e.g. Gibbons Reference Gibbons1992: Ch. 4).
In Figure 3, the good type of A chooses MA since
![]() ${a_1} \gt {a_2}$
, and the bad type chooses IA since
${a_1} \gt {a_2}$
, and the bad type chooses IA since
![]() ${a_4} \gt {a_3}$
. Thus, both information-sets are on the equilibrium path (i.e. reached with positive probability given the strategy profile), and Bayes’ rule gives that
${a_4} \gt {a_3}$
. Thus, both information-sets are on the equilibrium path (i.e. reached with positive probability given the strategy profile), and Bayes’ rule gives that
![]() $x = 1$
and
$x = 1$
and
![]() $y = 0$
.
$y = 0$
.
Proposition 1 The model of Figure 3 has a unique PBE, as follows:
-
(a) The good type of A chooses MA, and the bad type chooses IA.
-
(b) By Bayes’ rule,
 $x = 1$
and
$x = 1$
and
 $y = 0$
.
$y = 0$
.
The model has a unique PBE, of a type that the signalling literature calls a ‘separating’ PBE: the two types choose different actions, i.e. ‘separate’ themselves through their messages or actions, and hence the action is perfectly informative to the uninformed actor about the other actor’s type. Footnote 9 This PBE is consistent with Hume’s theory of actions serving as credible signals of character. Moreover, in Hume’s framework MA would seem to qualify as a genuinely moral action, because both of his criteria are satisfied: (i) there exists a type naturally inclined to choose the action, and (ii) it acts as a credible signal of good character. Footnote 10
4. A model of moral choice: introducing reward, punishment and/or duty considerations
That the model of Figure 3 has a separating PBE, which is in fact the unique PBE, is not at all surprising: because the observer B’s only role is to form beliefs about A’s type based on her action, and he takes no action of his own that could cause A to reconsider her choice, each type of A simply chooses the action she is naturally inclined to take. Thus, the unique equilibrium is a separating one.
But immediately upon presenting his signalling theory of virtuous action early in Book III of Treatise, Hume recognizes and addresses a possible objection to it: what if some people choose the moral action not because they have a natural inclination (‘virtuous motive’) to do so, but for some alternative reason.
(G) But may not the sense of morality or duty produce an action, without any other motive? I answer, It may: But this is no objection to the present doctrine. When any virtuous motive or principle is common in human nature, a person, who feels his heart devoid of that principle, may hate himself upon that account, and may perform the action without the motive, from a certain sense of duty, in order to acquire by practice, that virtuous principle, or at least, to disguise to himself, as much as possible, his want of it. (T 3.2.1.8)
Hume states that if some people perform a moral action for one of these alternative reasons, ‘this is no objection to the present doctrine’. While it is certainly not an objection to the claim that others perform it due to a genuine ‘virtuous motive’ (criterion i), which is what he seems to have in mind by ‘the present doctrine’, it would dilute the signalling value of the moral action (criterion ii), which Hume also seems to consider vital for an action to be considered moral.
To examine this possibility in the game-theoretic model, we need to modify the model so that even the bad type of A may have some incentive to choose the moral action. Some of the above reasons that Hume gives for why an individual lacking the ‘virtuous motive’ may nevertheless choose the action seem to imply a possible reward/benefit for performing the action, and/or a possible punishment/cost for not performing it. These punishments and/or rewards seem to be primarily informal social ones, e.g. holding one in low regard for not choosing the action, and high regard for choosing it. Moreover, throughout Book III Hume uses language implying social rewards and/or punishments, such as ‘when we require any action, or blame a person for not performing it’, ‘we esteem it vicious in him to be regardless of it’, ‘we retract our blame, and have the same esteem for him’ (all from T 3.2.1.3), ‘We blame a father for neglecting his child’ (T 3.2.1.5), etc. He also explicitly refers to punishments/rewards by individuals:
(H) As to the good or ill desert of virtue or vice, ’tis an evident consequence of the sentiments of pleasure or uneasiness. These sentiments produce love or hatred; and love or hatred, by the original constitution of human passion, is attended with benevolence or anger; that is, with a desire of making happy the person we love, and miserable the person we hate. (T 3.3.1.31)
In Book III Hume refers mainly to social rewards/punishments, but in Book II (especially T 2.3.2.5-7) he briefly refers to legal punishments and rewards, as well as religious beliefs about divine punishments and rewards. He suggests that existing legal punishment schemes, as well as peoples’ beliefs about divine ones, are based on the idea that our actions largely proceed from our characters, and hence that we implicitly believe that only bad character is worthy of punishment, not a one-time bad action by an otherwise good person. Footnote 11 Indeed, he suggests that any punishment scheme imagined by ‘any reasonable being’ must be based on this idea. I will return to this point shortly, and at the moment just point out that in addition to the social punishments/rewards mentioned in Book III, in Book II Hume also talks briefly about legal and divine punishment/reward schemes, that presumably create incentives to choose moral actions even for someone who lacks the ‘virtuous motive’ (inherent inclination) to do so. Footnote 12
So I modify the signalling model of Figure 3 to suppose that the observer B not only observes A’s action and forms beliefs about A’s type (character), but also chooses between punishing A or not, depending on A’s action. Presumably this is an informal social punishment imposed by an observer, but B could also represent the state, in which case this might be a legal punishment. If we are willing to be a bit liberal with the model, B may even represent A’s conscience, with the punishment being associated with a sense of duty (a person ‘may hate himself upon that account’; passage G above) and/or a fear of divine punishment.
But before analysing signalling when B can punish, we need to characterize B’s preference for punishing or not, depending on A’s type, and A’s action. This is best examined in a complete-information setting in which B knows A’s type.
4.1. Complete information: A is the good type
First consider the situation where B faces the good type of A. The game-tree is shown in Figure 4. The good type of A chooses between MA and IA, and in each case, B chooses whether to punish A (this action is labelled P) or not (NP). Recall from Figure 1 that the good type of A gets utility
![]() ${a_1}$
for choosing MA, and the smaller
${a_1}$
for choosing MA, and the smaller
![]() ${a_2}$
for choosing IA. In Figure 4, it makes sense to assign these same utilities for the respective outcome where A chooses MA and B chooses NP, and where A chooses IA and B chooses NP.
${a_2}$
for choosing IA. In Figure 4, it makes sense to assign these same utilities for the respective outcome where A chooses MA and B chooses NP, and where A chooses IA and B chooses NP.

Figure 4. Game-theoretic model with good type of
![]() $A.$
$A.$
What if B punishes? I assume that this imposes a punishment cost of
![]() $c \gt 0$
on A. Thus, the good type’s utility is
$c \gt 0$
on A. Thus, the good type’s utility is
![]() ${a_1} - c$
for the outcome (MA, P), and
${a_1} - c$
for the outcome (MA, P), and
![]() ${a_2} - c$
for the outcome (IA, P). With this specification of payoffs, it is always the case that the good type of A most prefers the outcome (
${a_2} - c$
for the outcome (IA, P). With this specification of payoffs, it is always the case that the good type of A most prefers the outcome (
![]() $MA,NP$
), and least prefers the outcome (
$MA,NP$
), and least prefers the outcome (
![]() $IA,P$
). In between these two extremes, if the punishment cost is small enough that
$IA,P$
). In between these two extremes, if the punishment cost is small enough that
![]() ${a_1} - c \gt {a_2}$
, i.e.
${a_1} - c \gt {a_2}$
, i.e.
![]() $c \lt {a_1} - {a_2}$
, then she prefers (
$c \lt {a_1} - {a_2}$
, then she prefers (
![]() $MA,P$
) to (
$MA,P$
) to (
![]() $IA,NP$
). But if
$IA,NP$
). But if
![]() $c \gt {a_1} - {a_2}$
, then she has the opposite preference ordering. A sufficiently high punishment cost can induce her to choose IA, if B’s strategy is P/NP, i.e. choose P at his left decision-node, and NP at his right decision-node (but it is not clear why B would ever choose such a strategy; see below).
$c \gt {a_1} - {a_2}$
, then she has the opposite preference ordering. A sufficiently high punishment cost can induce her to choose IA, if B’s strategy is P/NP, i.e. choose P at his left decision-node, and NP at his right decision-node (but it is not clear why B would ever choose such a strategy; see below).
What about B’s utilities? Going from left to right in Figure 4, I label B’s utilities
![]() ${b_1}$
-
${b_1}$
-
![]() ${b_4}$
. In Hume’s framework, it is certainly the case that
${b_4}$
. In Hume’s framework, it is certainly the case that
![]() ${b_2} \gt {b_1}$
: if a good character chooses a moral action, an observer certainly would not want to punish her. In fact,
${b_2} \gt {b_1}$
: if a good character chooses a moral action, an observer certainly would not want to punish her. In fact,
![]() ${b_2}$
is probably best regarded as the highest possible utility that B can get in the interaction (including the larger game that contains both types of A; see Figure 6), with a very high value consistent with the pleasure Hume refers to an observer feeling upon observing an action that convinces him of the high character of the person.
Footnote 13
${b_2}$
is probably best regarded as the highest possible utility that B can get in the interaction (including the larger game that contains both types of A; see Figure 6), with a very high value consistent with the pleasure Hume refers to an observer feeling upon observing an action that convinces him of the high character of the person.
Footnote 13
What about
![]() ${b_3}$
versus
${b_3}$
versus
![]() ${b_4}$
? Would B punish the good type for choosing the immoral action? As mentioned earlier, in Book II Hume suggests that existing legal punishment schemes, as well as our beliefs about divine ones, are implicitly based on punishing bad character, and not occasional bad actions by a good person. And he suggests that any reasonable punishment scheme must be based on this principle. Moreover, at various points in Treatise, he indicates that people forgive bad actions taken by a good person under difficult circumstances.
Footnote 14
${b_4}$
? Would B punish the good type for choosing the immoral action? As mentioned earlier, in Book II Hume suggests that existing legal punishment schemes, as well as our beliefs about divine ones, are implicitly based on punishing bad character, and not occasional bad actions by a good person. And he suggests that any reasonable punishment scheme must be based on this principle. Moreover, at various points in Treatise, he indicates that people forgive bad actions taken by a good person under difficult circumstances.
Footnote 14
(I) After the same manner, when we require any action, or blame a person for not performing it, we always suppose, that one in that situation shou’d be influenc’d by the proper motive of that action, and we esteem it vicious in him to be regardless of it. If we find, upon enquiry, that the virtuous motive was still powerful over his breast, tho’ check’d in its operation by some circumstances unknown to us, we retract our blame, and have the same esteem for him, as if he had actually perform’d the action, which we require of him. (T 3.2.1.3)
This suggests that in Hume’s framework,
![]() ${b_4}{ \gt b_3}$
: if B knows that A is the good type, then he prefers to not punish even if A chooses IA.
Footnote 15
While I believe that this is the assumption most faithful to Hume’s account of morality and punishment, nevertheless in the analyses below, we will consider both possibilities.
${b_4}{ \gt b_3}$
: if B knows that A is the good type, then he prefers to not punish even if A chooses IA.
Footnote 15
While I believe that this is the assumption most faithful to Hume’s account of morality and punishment, nevertheless in the analyses below, we will consider both possibilities.
Now we can do backwards induction to determine the subgame-perfect equilibria (SPE). First suppose that
![]() ${b_4} \gt {b_3}$
. Then at each of his decision-nodes, B chooses NP. Therefore, A chooses MA (since
${b_4} \gt {b_3}$
. Then at each of his decision-nodes, B chooses NP. Therefore, A chooses MA (since
![]() ${a_1} \gt {a_2}$
).
${a_1} \gt {a_2}$
).
Proposition 2
If
![]() ${b_4} \gt {b_3}$
, then (MA, NP/NP) is the unique SPE of the model of Figure 4
. The SPE outcome is that A chooses MA, followed by B choosing NP.
${b_4} \gt {b_3}$
, then (MA, NP/NP) is the unique SPE of the model of Figure 4
. The SPE outcome is that A chooses MA, followed by B choosing NP.
Now suppose that
![]() ${b_4} \lt {b_3}$
. Then if A chooses MA, B chooses NP, but chooses P if A chooses IA. Because
${b_4} \lt {b_3}$
. Then if A chooses MA, B chooses NP, but chooses P if A chooses IA. Because
![]() ${a_1} \gt {a_2} - c$
(in fact,
${a_1} \gt {a_2} - c$
(in fact,
![]() ${a_1} \gt {a_2}$
), A chooses MA.
${a_1} \gt {a_2}$
), A chooses MA.
Proposition 3
If
![]() ${b_4} \lt {b_3}$
, then (MA, NP/P) is the unique SPE of the model of Figure 4
. The SPE outcome is that A chooses MA, followed by B choosing NP.
${b_4} \lt {b_3}$
, then (MA, NP/P) is the unique SPE of the model of Figure 4
. The SPE outcome is that A chooses MA, followed by B choosing NP.
Thus, the predicted outcome does not depend on whether or not
![]() ${b_4} \gt {b_3}$
holds, i.e. whether or not B would punish the good type for choosing IA. Because B would certainly not punish the good type for choosing the moral action, and this type is naturally inclined to choose the moral action anyway, she does so in every SPE, regardless of what B would do (off the equilibrium path) upon observing IA.
${b_4} \gt {b_3}$
holds, i.e. whether or not B would punish the good type for choosing IA. Because B would certainly not punish the good type for choosing the moral action, and this type is naturally inclined to choose the moral action anyway, she does so in every SPE, regardless of what B would do (off the equilibrium path) upon observing IA.
4.2. Complete information: A is the bad type
Now suppose that A is the bad type. The game-tree is shown in Figure 5. As with the good type, I simply import the bad type’s utilities from Figure 2 for the outcomes where B chooses NP (and recall that
![]() ${a_4} \gt {a_3}$
), and subtract the punishment cost from those utilities if B chooses P. Thus, the bad type’s utility is
${a_4} \gt {a_3}$
), and subtract the punishment cost from those utilities if B chooses P. Thus, the bad type’s utility is
![]() ${a_3} - c$
for the outcome (MA, P), and
${a_3} - c$
for the outcome (MA, P), and
![]() ${a_4} - c$
for the outcome (IA, P). With this specification of utilities, it is always the case that the bad type of A most prefers the outcome (
${a_4} - c$
for the outcome (IA, P). With this specification of utilities, it is always the case that the bad type of A most prefers the outcome (
![]() $IA,NP$
), and least prefers the outcome (
$IA,NP$
), and least prefers the outcome (
![]() $MA,P$
). In between these two extremes, if the punishment cost is small enough that
$MA,P$
). In between these two extremes, if the punishment cost is small enough that
![]() ${a_4} - c \gt {a_3}$
, i.e.
${a_4} - c \gt {a_3}$
, i.e.
![]() $c \lt {a_4} - {a_3}$
, then she prefers (
$c \lt {a_4} - {a_3}$
, then she prefers (
![]() $IA,P$
) to (
$IA,P$
) to (
![]() $MA,NP$
). But if
$MA,NP$
). But if
![]() $c \gt {a_4} - {a_3}$
, then she has the opposite preference ordering. A sufficiently high punishment cost can induce the bad type of A to choose MA, if B’s strategy is NP/P (which is a very plausible strategy; see below).
$c \gt {a_4} - {a_3}$
, then she has the opposite preference ordering. A sufficiently high punishment cost can induce the bad type of A to choose MA, if B’s strategy is NP/P (which is a very plausible strategy; see below).
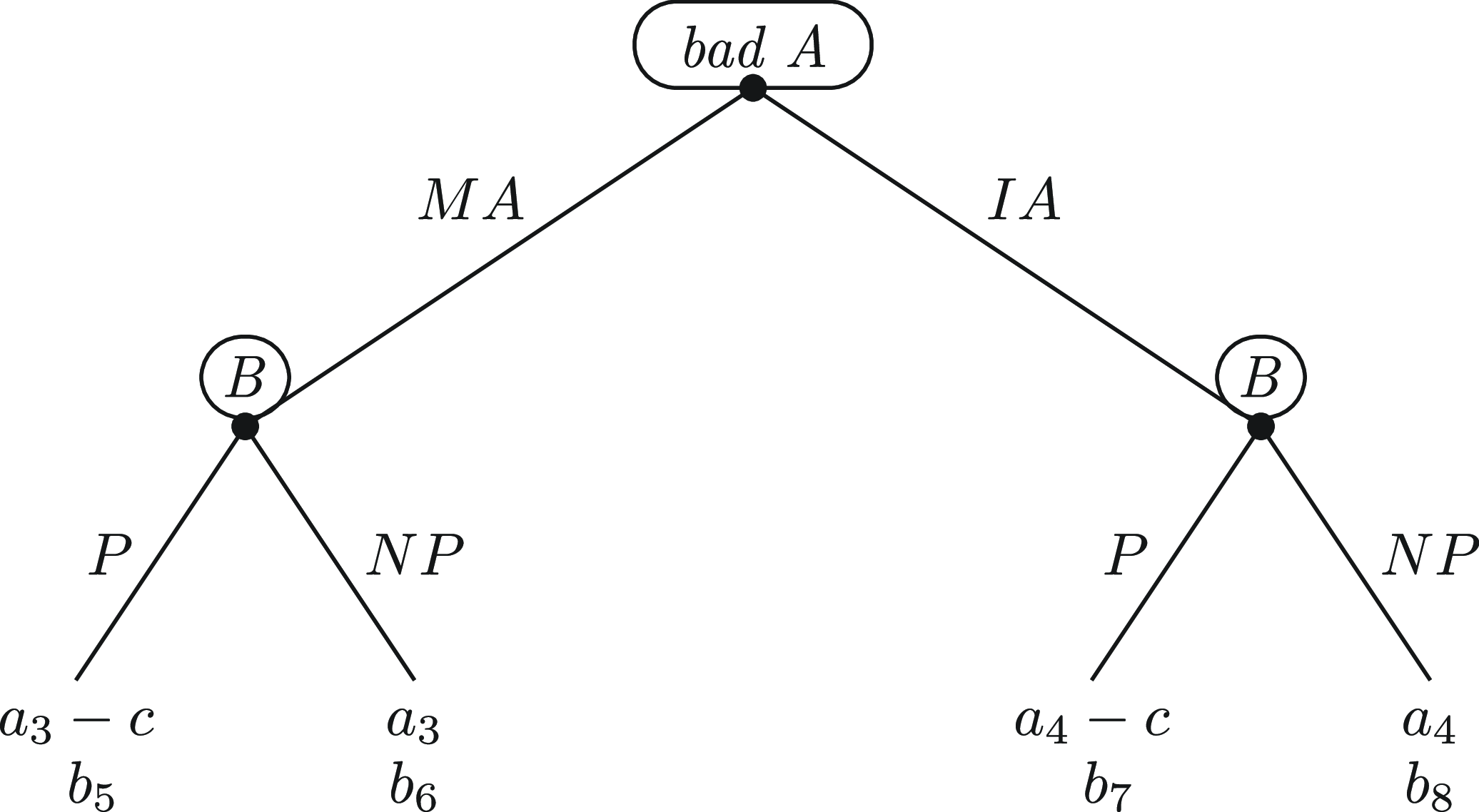
Figure 5. Game-theoretic model with bad type of
![]() $A$
.
$A$
.

Figure 6. Game-theoretic signalling model.
What about B’s utilities? In Hume’s framework, it is certainly the case that
![]() ${b_7} \gt {b_8}$
: if a bad character chooses an immoral action, an observer would certainly punish her. What about
${b_7} \gt {b_8}$
: if a bad character chooses an immoral action, an observer would certainly punish her. What about
![]() ${b_5}$
versus
${b_5}$
versus
![]() ${b_6}$
? Whereas Hume clearly states a number of times that an observer would forgive a good character for committing an immoral action (presumably under difficult circumstances), he at best vaguely hints at the analogous action of punishing a bad character even for choosing a moral action. For example, in passage I above, Hume seems to say that even if one performs a moral action, ‘we esteem it vicious in him to be regardless of’ the virtuous motive for choosing it. But this is not really clear, and I wasn’t able to find any other passage where Hume indicates this type of punishment. Therefore, in the analyses below, we will consider both possibilities. One could argue that Hume’s overall view is that people are inclined to esteem good characters, and punish bad characters, regardless of the action (which acts merely as a signal) chosen, in which case
${b_6}$
? Whereas Hume clearly states a number of times that an observer would forgive a good character for committing an immoral action (presumably under difficult circumstances), he at best vaguely hints at the analogous action of punishing a bad character even for choosing a moral action. For example, in passage I above, Hume seems to say that even if one performs a moral action, ‘we esteem it vicious in him to be regardless of’ the virtuous motive for choosing it. But this is not really clear, and I wasn’t able to find any other passage where Hume indicates this type of punishment. Therefore, in the analyses below, we will consider both possibilities. One could argue that Hume’s overall view is that people are inclined to esteem good characters, and punish bad characters, regardless of the action (which acts merely as a signal) chosen, in which case
![]() ${b_5} \gt {b_6}$
, i.e. B would punish a bad character even for choosing the moral action. But this strikes us as a bit unfair even for merely social punishments, and is certainly unacceptable for legal punishments.
Footnote 16
Therefore, we will consider the
${b_5} \gt {b_6}$
, i.e. B would punish a bad character even for choosing the moral action. But this strikes us as a bit unfair even for merely social punishments, and is certainly unacceptable for legal punishments.
Footnote 16
Therefore, we will consider the
![]() ${b_5} \lt {b_6}$
case as well.
${b_5} \lt {b_6}$
case as well.
Now we can do backwards induction to determine the SPE. First suppose that
![]() ${b_5} \gt {b_6}$
. Then at each of his decision-nodes, B chooses P. Therefore, A chooses IA. If B is going to punish either way, then the bad type chooses IA, as that is her natural inclination.
${b_5} \gt {b_6}$
. Then at each of his decision-nodes, B chooses P. Therefore, A chooses IA. If B is going to punish either way, then the bad type chooses IA, as that is her natural inclination.
Proposition 4
If
![]() ${b_5} \gt {b_6}$
, then (IA, P/P) is the unique SPE of the model of Figure 5
. The SPE outcome is that A chooses IA, followed by B choosing P.
${b_5} \gt {b_6}$
, then (IA, P/P) is the unique SPE of the model of Figure 5
. The SPE outcome is that A chooses IA, followed by B choosing P.
Now suppose that
![]() ${b_5} \lt {b_6}$
. Then if A chooses IA, B chooses P, but chooses NP if A chooses MA. Then A’s optimal choice comes down to whether
${b_5} \lt {b_6}$
. Then if A chooses IA, B chooses P, but chooses NP if A chooses MA. Then A’s optimal choice comes down to whether
![]() ${a_3}$
or
${a_3}$
or
![]() ${a_4} - c$
is larger. If
${a_4} - c$
is larger. If
![]() ${a_4} - c \gt {a_3}$
, i.e.
${a_4} - c \gt {a_3}$
, i.e.
![]() $c \lt {a_4} - {a_3}$
, then A chooses IA. But if
$c \lt {a_4} - {a_3}$
, then A chooses IA. But if
![]() $c \gt {a_4} - {a_3}$
, then she chooses MA.
$c \gt {a_4} - {a_3}$
, then she chooses MA.
Proposition 5
If
![]() ${b_5} \lt {b_6}$
and
${b_5} \lt {b_6}$
and
![]() $c \lt {a_4} - {a_3}$
, then (IA, NP/P) is the unique SPE of the model of Figure 5
. The SPE outcome is that A chooses IA, followed by B choosing P.
$c \lt {a_4} - {a_3}$
, then (IA, NP/P) is the unique SPE of the model of Figure 5
. The SPE outcome is that A chooses IA, followed by B choosing P.
Proposition 6
If
![]() ${b_5} \lt {b_6}$
and
${b_5} \lt {b_6}$
and
![]() $c \gt {a_4} - {a_3}$
, then (MA, NP/P) is the unique SPE of the model of Figure 5
. The SPE outcome is that A chooses MA, followed by B choosing NP.
$c \gt {a_4} - {a_3}$
, then (MA, NP/P) is the unique SPE of the model of Figure 5
. The SPE outcome is that A chooses MA, followed by B choosing NP.
Recall from the previous section that if A is the good type, then there is a unique SPE outcome (regardless of whether or not B would punish her for choosing the immoral action): she chooses the moral action, followed by B choosing to not punish. In equilibrium, the good type always chooses the action she is naturally inclined to take. But if A is the bad type, then there exist conditions under which she is induced to act against her natural inclination and choose the moral action: when B would not punish her for doing so despite her lacking the ‘virtuous motive’, and the punishment cost that she would incur for choosing the immoral action is sufficiently large. Note that the punishment-cost threshold is
![]() ${a_4} - {a_3}$
, which can be thought of as a measure of her distaste for choosing the moral action: the larger that distaste, the larger the punishment cost has to be to induce her to choose the moral action.
${a_4} - {a_3}$
, which can be thought of as a measure of her distaste for choosing the moral action: the larger that distaste, the larger the punishment cost has to be to induce her to choose the moral action.
4.3. Actions as signals: B is uncertain of A’s type
The complete-information results are somewhat interesting, but the main goal of that analysis was to establish B’s possible preference orderings (in Hume’s framework) once we modify the signalling model of Figure 3 to allow B the option of punishing A for her action. The new signalling model is shown in Figure 6. It is similar to that of Figure 3, but allows B to choose whether or not to punish A for her action, and imports the utilities from Figures 4 and 5.
Recall from the previous two sections that I am certainly assuming that
![]() ${b_2} \gt {b_1}$
and
${b_2} \gt {b_1}$
and
![]() ${b_7} \gt {b_8}$
: B would not punish the good type of A for choosing the moral action, and would punish the bad type for choosing the immoral action. The ambiguous situations are whether he would punish the good type for choosing the immoral action, and the bad type even for choosing the moral action. I argued that Hume gives a number of clear statements to the effect that, at least in social punishments, people forgive good types for occasionally choosing immoral actions. Thus, I think that
${b_7} \gt {b_8}$
: B would not punish the good type of A for choosing the moral action, and would punish the bad type for choosing the immoral action. The ambiguous situations are whether he would punish the good type for choosing the immoral action, and the bad type even for choosing the moral action. I argued that Hume gives a number of clear statements to the effect that, at least in social punishments, people forgive good types for occasionally choosing immoral actions. Thus, I think that
![]() ${b_4} \gt {b_3}$
best represents the Humean perspective on social punishments (also see Kauppinen Reference Kauppinen and Fileva2017), and I will assume this for the rest of the paper. Hume is much less clear about how people respond to moral actions by bad types. The overall theme of Hume’s theory of morality seems to be that character is the root of our moral evaluations, and that actions are secondary and primarily serve as signals of character. Thus, I would venture that regarding bad types, the assumption that fits best with Hume’s overall framework is that
${b_4} \gt {b_3}$
best represents the Humean perspective on social punishments (also see Kauppinen Reference Kauppinen and Fileva2017), and I will assume this for the rest of the paper. Hume is much less clear about how people respond to moral actions by bad types. The overall theme of Hume’s theory of morality seems to be that character is the root of our moral evaluations, and that actions are secondary and primarily serve as signals of character. Thus, I would venture that regarding bad types, the assumption that fits best with Hume’s overall framework is that
![]() ${b_5} \gt {b_6}$
: if B knows that A is the bad type, he would punish her even if she chooses the moral action. Nevertheless, in the analyses below, I consider both cases. It turns out that in both cases, depending on parameter conditions, there is a separating PBE analogous to the one in the signalling model of Figure 3, as well as a pooling PBE in which both types choose the moral action. The only difference is that when
${b_5} \gt {b_6}$
: if B knows that A is the bad type, he would punish her even if she chooses the moral action. Nevertheless, in the analyses below, I consider both cases. It turns out that in both cases, depending on parameter conditions, there is a separating PBE analogous to the one in the signalling model of Figure 3, as well as a pooling PBE in which both types choose the moral action. The only difference is that when
![]() ${b_5} \gt {b_6}$
(arguably the best fit with Hume), then there is a semi-separating PBE as well, in which the good type chooses MA, whereas the bad type mixes between MA and IA, and upon observing MA, B mixes between P and NP.
${b_5} \gt {b_6}$
(arguably the best fit with Hume), then there is a semi-separating PBE as well, in which the good type chooses MA, whereas the bad type mixes between MA and IA, and upon observing MA, B mixes between P and NP.
4.3.1.
 ${b_4} \gt {b_3}$
and
${b_4} \gt {b_3}$
and
 ${b_5} \gt {b_6}$
${b_5} \gt {b_6}$
First suppose that
![]() ${b_4} \gt {b_3}$
and
${b_4} \gt {b_3}$
and
![]() ${b_5} \gt {b_6}$
: B would not punish the good type for choosing IA, and would punish the bad type even for choosing MA. Then at information-set
${b_5} \gt {b_6}$
: B would not punish the good type for choosing IA, and would punish the bad type even for choosing MA. Then at information-set
![]() ${I_1}$
, where B has observed the moral action chosen and assigns probability
${I_1}$
, where B has observed the moral action chosen and assigns probability
![]() $x \in \left[ {0,1} \right]$
to A being the good type, he chooses NP if this probability is sufficiently high, in particular if
$x \in \left[ {0,1} \right]$
to A being the good type, he chooses NP if this probability is sufficiently high, in particular if
![]() $x \gt {x_{crit}} \equiv {{{b_5} - {b_6}} \over {\left( {{b_5} - {b_6}} \right) + \left( {{b_2} - {b_1}} \right)}} \in \left( {0,1} \right)$
.
Footnote 17
Similarly, at
$x \gt {x_{crit}} \equiv {{{b_5} - {b_6}} \over {\left( {{b_5} - {b_6}} \right) + \left( {{b_2} - {b_1}} \right)}} \in \left( {0,1} \right)$
.
Footnote 17
Similarly, at
![]() ${I_2}$
, where B has observed the immoral action chosen and assigns probability
${I_2}$
, where B has observed the immoral action chosen and assigns probability
![]() $y \in \left[ {0,1} \right]$
to A being the good type, he chooses NP if this probability is sufficiently high, in particular if
$y \in \left[ {0,1} \right]$
to A being the good type, he chooses NP if this probability is sufficiently high, in particular if
![]() $y \gt {y_{crit}} \equiv {{{b_7} - {b_8}} \over {\left( {{b_7} - {b_8}} \right) + \left( {{b_4} - {b_3}} \right)}} \in \left( {0,1} \right)$
.
Footnote 18
$y \gt {y_{crit}} \equiv {{{b_7} - {b_8}} \over {\left( {{b_7} - {b_8}} \right) + \left( {{b_4} - {b_3}} \right)}} \in \left( {0,1} \right)$
.
Footnote 18
Separating Equilibrium
Now that we have determined what B would do at each of his information-sets depending on his beliefs there, our first question of interest is whether there exists a separating PBE in which the good type of A chooses MA, and the bad type chooses IA. If there exists a PBE like this, then in it, by Bayes’ rule
![]() $x = 1$
and
$x = 1$
and
![]() $y = 0$
. Because
$y = 0$
. Because
![]() $x \gt {x_{crit}}$
, B chooses NP at
$x \gt {x_{crit}}$
, B chooses NP at
![]() ${I_1}$
. And because
${I_1}$
. And because
![]() $y \lt {y_{crit}}$
, B chooses P at
$y \lt {y_{crit}}$
, B chooses P at
![]() ${I_2}$
. Thus, this is a PBE if and only if neither type benefits by deviating to the other action. The good type gets a utility of
${I_2}$
. Thus, this is a PBE if and only if neither type benefits by deviating to the other action. The good type gets a utility of
![]() ${a_1}$
by sticking to MA, and would get the lower utility of
${a_1}$
by sticking to MA, and would get the lower utility of
![]() ${a_2} - c$
by deviating to IA (in fact,
${a_2} - c$
by deviating to IA (in fact,
![]() ${a_1}$
is her highest possible utility in the entire game). Therefore, the good type certainly doesn’t benefit by deviating. What about the bad type? She gets
${a_1}$
is her highest possible utility in the entire game). Therefore, the good type certainly doesn’t benefit by deviating. What about the bad type? She gets
![]() ${a_4} - c$
by sticking to IA, and would get
${a_4} - c$
by sticking to IA, and would get
![]() ${a_3}$
by deviating to MA. Thus, she doesn’t benefit by deviating if and only if
${a_3}$
by deviating to MA. Thus, she doesn’t benefit by deviating if and only if
![]() ${a_4} - c \ge {a_3}$
, i.e.
${a_4} - c \ge {a_3}$
, i.e.
![]() $c \le {a_4} - {a_3}$
.
$c \le {a_4} - {a_3}$
.
Proposition 7
A separating PBE in which the good type of A chooses MA and the bad type chooses IA exists if and only if
![]() $c \le {a_4} - {a_3}$
, and has the following form.
$c \le {a_4} - {a_3}$
, and has the following form.
-
(a) The good type chooses MA, and the bad type chooses IA.
-
(b) By Bayes’ rule,
 $x = 1$
and
$x = 1$
and
 $y = 0$
.
$y = 0$
. -
(c) B chooses NP at
 ${I_1}$
, and P at
${I_1}$
, and P at
 ${I_2}$
.
${I_2}$
.
Thus, just as in the simpler signalling model of Figure 3, a separating PBE exists. However, over there that is the unique PBE, and it exists for all parameter values. Over here, this is a PBE if and only if
![]() $c \le {a_4} - {a_3}$
holds (in which case it is also the unique one, as shown in the Appendix; and if this doesn’t hold, then other PBE exist, as discussed below). This condition is that the punishment cost that the bad type incurs for choosing the immoral action is not too large. Alternatively, holding c fixed, it is that the difference
$c \le {a_4} - {a_3}$
holds (in which case it is also the unique one, as shown in the Appendix; and if this doesn’t hold, then other PBE exist, as discussed below). This condition is that the punishment cost that the bad type incurs for choosing the immoral action is not too large. Alternatively, holding c fixed, it is that the difference
![]() ${a_4} - {a_3}$
is sufficiently large, i.e. the bad type finds the moral action sufficiently distasteful relative to the immoral action. If this holds, then the bad type is willing to choose the immoral action, the action that she is naturally inclined to choose, even though she is (not too severely) punished for it. And therefore actions serve the role that Hume attributes to them when they actually have moral content, namely signalling the character of the agent.
${a_4} - {a_3}$
is sufficiently large, i.e. the bad type finds the moral action sufficiently distasteful relative to the immoral action. If this holds, then the bad type is willing to choose the immoral action, the action that she is naturally inclined to choose, even though she is (not too severely) punished for it. And therefore actions serve the role that Hume attributes to them when they actually have moral content, namely signalling the character of the agent.
In fact, both of Hume’s criteria (i) and (ii) for moral actions are satisfied, and hence MA would seem to qualify as a genuinely moral action (associated with a natural virtue) in his framework. Moreover, as mentioned in the Introduction, although Hume hints at a credible signalling aspect to his moral theory when he writes that ‘Actions are, indeed, better indications of a character than words, or even wishes and sentiments …’ (passage D above), he doesn’t explicitly develop this in a costly signalling direction. But that a straightforward formalization of his signalling theory of moral actions pushes in that direction (namely, the required condition for the separating PBE that the bad type finds the moral action sufficiently distasteful, i.e. costly) suggests that the rudiments of costly signalling theory are contained in Treatise, and that Hume’s moral theory can reasonably be extended to state that an action that good types are naturally inclined to choose will only be informative of good character (and thus be regarded as a moral action) if it is sufficiently distasteful/costly for bad character types so as to deter them from also choosing it to try to appear as good types and avoid punishment.
Pooling Equilibrium
What if
![]() $c \le {a_4} - {a_3}$
doesn’t hold? When
$c \le {a_4} - {a_3}$
doesn’t hold? When
![]() $c \ge {a_4} - {a_3}$
and B’s prior belief that A is the good type satisfies
$c \ge {a_4} - {a_3}$
and B’s prior belief that A is the good type satisfies
![]() $p \ge {x_{crit}}$
, then there is a pooling PBE (that is the unique PBE) in which both types choose MA.
$p \ge {x_{crit}}$
, then there is a pooling PBE (that is the unique PBE) in which both types choose MA.
Proposition 8
A pooling PBE in which both types of A choose MA exists if and only if
![]() $c \ge {a_4} - {a_3}$
and
$c \ge {a_4} - {a_3}$
and
![]() $p \ge {x_{crit}}$
, and has the following form.
$p \ge {x_{crit}}$
, and has the following form.
-
(a) Both types choose MA.
-
(b) By Bayes’ rule,
 $x = p$
. B chooses NP at
$x = p$
. B chooses NP at
 ${I_1}$
.
${I_1}$
. -
(c) The off-the-equilibrium-path belief must satisfy
 $y \le {y_{crit}}$
. B chooses P at
$y \le {y_{crit}}$
. B chooses P at
 ${I_2}$
.
${I_2}$
.
In a pooling PBE, both types choose the same action (they ‘pool’ their behaviour), and hence the action is completely uninformative about the agent’s type. Therefore, upon observing that action, the uninformed actor’s belief remains at the prior (i.e. is not updated), and he chooses the expected-utility maximizing action given this belief. This is why the condition
![]() $p \ge {x_{crit}}$
is needed. For the bad type to be willing to choose MA against her natural inclination, B must be choosing NP upon observing MA; if B is choosing P instead, then the bad type is better off deviating to IA regardless of what B chooses upon observing IA. B only chooses NP upon observing MA if
$p \ge {x_{crit}}$
is needed. For the bad type to be willing to choose MA against her natural inclination, B must be choosing NP upon observing MA; if B is choosing P instead, then the bad type is better off deviating to IA regardless of what B chooses upon observing IA. B only chooses NP upon observing MA if
![]() $x \ge {x_{crit}}$
, and since
$x \ge {x_{crit}}$
, and since
![]() $x = p$
(by Bayes’ rule) in a pooling-on-MA PBE, we have the requirement that
$x = p$
(by Bayes’ rule) in a pooling-on-MA PBE, we have the requirement that
![]() $p \ge {x_{crit}}$
needs to hold.
$p \ge {x_{crit}}$
needs to hold.
In addition, the off-the-equilibrium-path belief y, if B unexpectedly observes IA, must satisfy
![]() $y \le {y_{crit}}$
, so that B chooses P upon observing IA; if B is instead choosing NP there, then the bad type is better off deviating to IA. And this is a very reasonable off-the-equilibrium-path belief (e.g. Cho and Kreps Reference Cho and Kreps1987), namely that if B unexpectedly observes IA, he assigns sufficiently high probability to A being the bad type, since it is this type whose natural inclination is to choose IA (in fact, one could argue that the only reasonable off-the-equilibrium-path belief in a pooling-on-MA PBE is
$y \le {y_{crit}}$
, so that B chooses P upon observing IA; if B is instead choosing NP there, then the bad type is better off deviating to IA. And this is a very reasonable off-the-equilibrium-path belief (e.g. Cho and Kreps Reference Cho and Kreps1987), namely that if B unexpectedly observes IA, he assigns sufficiently high probability to A being the bad type, since it is this type whose natural inclination is to choose IA (in fact, one could argue that the only reasonable off-the-equilibrium-path belief in a pooling-on-MA PBE is
![]() $y = 0$
).
$y = 0$
).
So B is choosing NP upon observing MA and P upon observing IA, and we know from the separating PBE analysis that when
![]() $c \ge {a_4} - {a_3}$
, then the bad type prefers MA with no punishment to IA with punishment, and hence doesn’t benefit by deviating to IA. And the good type certainly doesn’t benefit by deviating to IA, and hence this is a PBE.
$c \ge {a_4} - {a_3}$
, then the bad type prefers MA with no punishment to IA with punishment, and hence doesn’t benefit by deviating to IA. And the good type certainly doesn’t benefit by deviating to IA, and hence this is a PBE.
Thus, if the punishment cost the bad type incurs for choosing IA is sufficiently high (alternatively, the bad type doesn’t find the moral action too distasteful), then there exists a pooling PBE in which the bad type mimics the good type to avoid punishment. This PBE is consistent with Hume’s intuition (passage G above) that even types not naturally inclined to choose a moral action may nevertheless choose it to ‘disguise’ themselves. Hume doesn’t identify the ‘not too distasteful/costly for the bad type’ condition, but remarkably does state that this disguising behaviour is especially likely when the ‘virtuous motive or principle is common in human nature’, which is exactly what the condition
![]() $p \ge {x_{crit}}$
implies: B begins the interaction assigning sufficiently high probability to A being the good type.
$p \ge {x_{crit}}$
implies: B begins the interaction assigning sufficiently high probability to A being the good type.
This is a PBE in which Hume’s criterion (i) for moral actions is satisfied, but not criterion (ii). There exist individuals naturally inclined to choose the action (and hence it pertains to a natural rather than artificial virtue), but it does not act as a credible signal of character because it is not distasteful/costly enough for bad types to deter them from also choosing it to avoid punishment. Although Hume recognizes that bad types may sometimes choose moral actions to ‘disguise’ themselves, he apparently doesn’t recognize that in the extreme this may cause the action to entirely lose its signalling value; but the pooling PBE suggests that this is entirely possible.
As mentioned in the Introduction, a comparison between the separating and pooling PBE also reveals a tension between consequentialist theories of morality and Hume’s signalling theory of moral actions. Presumably moral actions are regarded as moral at least in part because they have beneficial effects for others (i.e. positive consequences), and indeed Hume himself states numerous times that one of the reasons we admire good character is because such individuals tend to do things that help others. Thus, from a consequentialist perspective we should want to incentivize such actions by everyone, even those not naturally inclined to choose them. This is precisely what happens in the pooling PBE (as well as in the semi-separating PBE below, to a more limited extent), where the large social punishment cost incurred for choosing the immoral action gets even the bad type to choose the moral action. But a downside is that actions lose their signalling value (which requires the social punishment cost to be low), which Hume thinks is also very important, and is indeed for him a crucial criterion for an action to be regarded as genuinely moral. In the separating PBE, the social punishment cost is low enough that actions are informative of character, but a consequentialist downside is that only good types choose moral actions.
Hume doesn’t discuss this tradeoff, and I imagine he would come down on the side of incentivizing moral actions by everyone (via large social punishment costs), but this seems to be an unresolved issue in his moral theory. Perhaps his naturalistic theory of morality implies simply that social punishment costs are what they are, and we can’t influence their size, but merely analyse their origins and effects.
Semi-Separating Equilibrium
Finally, if the punishment cost is high enough that
![]() $c \gt {a_4} - {a_3}$
holds as before (but the pooling PBE just requires this to hold weakly), but now B begins the interaction assigning relatively low probability to A being the good type, in particular
$c \gt {a_4} - {a_3}$
holds as before (but the pooling PBE just requires this to hold weakly), but now B begins the interaction assigning relatively low probability to A being the good type, in particular
![]() $p \lt {x_{crit}}$
, then there is a semi-separating PBE (which is also the unique PBE) in which the good type chooses MA, whereas the bad type mixes (probabilistically chooses) between MA and IA. She mixes with exactly probability such that upon observing MA, B’s updated (via Bayes’ rule) belief that A is the good type satisfies
$p \lt {x_{crit}}$
, then there is a semi-separating PBE (which is also the unique PBE) in which the good type chooses MA, whereas the bad type mixes (probabilistically chooses) between MA and IA. She mixes with exactly probability such that upon observing MA, B’s updated (via Bayes’ rule) belief that A is the good type satisfies
![]() $x = {x_{crit}}$
, and (thus being indifferent) he mixes between P and NP with exact probability such that the bad type is indifferent between MA and IA (given that B chooses P upon observing IA).
Footnote 19
$x = {x_{crit}}$
, and (thus being indifferent) he mixes between P and NP with exact probability such that the bad type is indifferent between MA and IA (given that B chooses P upon observing IA).
Footnote 19
Proposition 9
A semi-separating PBE in which the good type of A chooses MA and the bad type mixes between MA and IA, exists if and only if
![]() $c \gt {a_4} - {a_3}$
and
$c \gt {a_4} - {a_3}$
and
![]() $p \lt {x_{crit}}$
, and has the following form.
$p \lt {x_{crit}}$
, and has the following form.
-
(a) The good type chooses MA, and the bad type chooses MA with probability
 ${a^*} \equiv {{p\left( {{b_2} - {b_1}} \right)} \over {\left( {1 - p} \right)\left( {{b_5} - {b_6}} \right)}} \in \left( {0,1} \right)$
and IA with probability
${a^*} \equiv {{p\left( {{b_2} - {b_1}} \right)} \over {\left( {1 - p} \right)\left( {{b_5} - {b_6}} \right)}} \in \left( {0,1} \right)$
and IA with probability
 $1 - {a^*}$
.
$1 - {a^*}$
. -
(b) By Bayes’ rule,
 $x = {x_{crit}}$
. At
$x = {x_{crit}}$
. At
 ${I_1}$
, B chooses P with probability
${I_1}$
, B chooses P with probability
 ${b^*} \equiv {{{a_3} - \left( {{a_4} - c} \right)} \over c} \in \left( {0,1} \right)$
and NP with probability
${b^*} \equiv {{{a_3} - \left( {{a_4} - c} \right)} \over c} \in \left( {0,1} \right)$
and NP with probability
 $1 - {b^*}$
.
$1 - {b^*}$
. -
(c) By Bayes’ rule,
 $y = 0$
. B chooses P at
$y = 0$
. B chooses P at
 ${I_2}$
.
${I_2}$
.
In this PBE (the proposition is proven in the Appendix), the moral action is partially informative to B about A’s type (unlike the pooling PBE), but not fully informative (unlike the separating PBE). In particular, B begins the interaction assigning relatively low probability to A being the good type (
![]() $p \lt {x_{crit}}$
), and hence would punish A if no belief-updating occurs. But because the good type chooses MA with certainty whereas the bad type only chooses it with positive probability less than one, upon observing MA, B becomes more confident that A is the good type (since the updated belief is
$p \lt {x_{crit}}$
), and hence would punish A if no belief-updating occurs. But because the good type chooses MA with certainty whereas the bad type only chooses it with positive probability less than one, upon observing MA, B becomes more confident that A is the good type (since the updated belief is
![]() $x = {x_{crit}} \gt p$
), confident enough to now be willing to choose NP with positive probability.
$x = {x_{crit}} \gt p$
), confident enough to now be willing to choose NP with positive probability.
In this PBE, both of Hume’s criteria for moral actions are satisfied (criterion ii only partially, since the moral action is only partially informative about A’s character), and hence MA would seem to count as a genuinely moral action (associated with a natural virtue). This PBE also illustrates that an action that good types are naturally inclined to choose can be partially informative of good character even if it is not too distasteful (i.e. costly) for bad types to mimic to try to avoid punishment. But this requires good types to not be too prevalent in the population (i.e.
![]() $p \lt {x_{crit}}$
), for otherwise the PBE is the completely uninformative pooling one. When this condition holds, then in Hume’s framework the action would presumably be regarded by observers as moral in that it partially signals good character, but perhaps not as moral as actions that bad types find so distasteful that they are fully informative of good character. That is, a comparison between the separating and semi-separating PBE suggests that Hume’s theory can be reasonably extended to state that observers will perceive actions as moral to differing degrees based on how informative they are of good character, and that this ultimately comes down to how distasteful and difficult bad types find those actions.
$p \lt {x_{crit}}$
), for otherwise the PBE is the completely uninformative pooling one. When this condition holds, then in Hume’s framework the action would presumably be regarded by observers as moral in that it partially signals good character, but perhaps not as moral as actions that bad types find so distasteful that they are fully informative of good character. That is, a comparison between the separating and semi-separating PBE suggests that Hume’s theory can be reasonably extended to state that observers will perceive actions as moral to differing degrees based on how informative they are of good character, and that this ultimately comes down to how distasteful and difficult bad types find those actions.
The semi-separating PBE captures a natural intuition that upon observing a moral action, an observer typically becomes more confident that the agent has good character, but not certain because it may be a bad type mimicking a good type to try to avoid social punishment. Finally, this PBE embodies a compromise regarding the consequentialism-versus-signalling tradeoff identified earlier: the bad type is partially incentivized to choose the moral action (good from a consequentialist perspective), and the moral action is partially informative (good from Hume’s signalling perspective). In contrast, the pooling PBE fully embodies the consequentialist position, whereas the separating PBE fully embodies the signalling viewpoint. Footnote 20
4.3.2.
 ${b_{4}} \gt {b_3}$
and
${b_{4}} \gt {b_3}$
and
 ${b_5} \lt {b_6}$
${b_5} \lt {b_6}$
I argued earlier that Hume seems to clearly say that people do not punish good types (if the type is known) even for choosing an immoral action (presumably under difficult circumstances), but is less clear about whether bad types are punished even for choosing a moral action. The previous section assumed that they are (which is arguably more consistent with Hume’s overall view that moral evaluations ultimately pertain to character), but now suppose that they aren’t, i.e. suppose that
![]() ${b_5} \lt {b_6}$
holds. Then upon observing MA (i.e. at
${b_5} \lt {b_6}$
holds. Then upon observing MA (i.e. at
![]() ${I_1}$
), B chooses NP regardless of his belief x there about A being the good type (i.e. there is no longer a relevant threshold
${I_1}$
), B chooses NP regardless of his belief x there about A being the good type (i.e. there is no longer a relevant threshold
![]() ${x_{crit}}$
). This means that the semi-separating PBE no longer exists, and only the separating and pooling PBE exist. Proposition 7 holds exactly as is, and Proposition 8 drops the requirement that
${x_{crit}}$
). This means that the semi-separating PBE no longer exists, and only the separating and pooling PBE exist. Proposition 7 holds exactly as is, and Proposition 8 drops the requirement that
![]() $p \ge {x_{crit}}$
; now the pooling PBE exists as long as
$p \ge {x_{crit}}$
; now the pooling PBE exists as long as
![]() $c \ge {a_4} - {a_3}$
, regardless of the value of the prior p. Because B certainly chooses NP upon observing MA, the bad type’s choice of whether to choose MA or IA simply comes down to whether the punishment cost incurred for choosing IA exceeds a certain threshold (alternatively, holding c fixed, whether she finds the moral action sufficiently distasteful); if it does, then the PBE is the pooling one, and if it doesn’t, then the PBE is the separating one. The overall results are robust to whether or not
$c \ge {a_4} - {a_3}$
, regardless of the value of the prior p. Because B certainly chooses NP upon observing MA, the bad type’s choice of whether to choose MA or IA simply comes down to whether the punishment cost incurred for choosing IA exceeds a certain threshold (alternatively, holding c fixed, whether she finds the moral action sufficiently distasteful); if it does, then the PBE is the pooling one, and if it doesn’t, then the PBE is the separating one. The overall results are robust to whether or not
![]() ${b_5} \gt {b_6}$
holds, and this assumption only matters for the existence of the semi-separating PBE.
Footnote 21
${b_5} \gt {b_6}$
holds, and this assumption only matters for the existence of the semi-separating PBE.
Footnote 21
4.3.3. Both types are bad
All of the previous analyses have assumed that there is a good type who is naturally inclined to choose the moral action, and hence Hume’s criterion (i) is satisfied (by construction), and thus the moral action pertains to a natural virtue. Now suppose that both types are bad, but to differing degrees. Recall from Figures 2 and 5 that the bad type is characterized by
![]() ${a_4} \gt {a_3}$
: her underlying (i.e. without punishment) utility for choosing the immoral action is higher than her underlying utility for choosing the moral action. Now suppose that there are two bad types, who differ only in their underlying utility for choosing the moral action,
${a_4} \gt {a_3}$
: her underlying (i.e. without punishment) utility for choosing the immoral action is higher than her underlying utility for choosing the moral action. Now suppose that there are two bad types, who differ only in their underlying utility for choosing the moral action,
![]() ${a_3}$
. One type is ‘very bad’, with underlying utility
${a_3}$
. One type is ‘very bad’, with underlying utility
![]() ${a_{3l}}$
(l standing for ‘low’), and the other type is only ‘somewhat bad’, with higher underlying utility
${a_{3l}}$
(l standing for ‘low’), and the other type is only ‘somewhat bad’, with higher underlying utility
![]() ${a_{3h}}$
(‘high’). Suppose that
${a_{3h}}$
(‘high’). Suppose that
![]() ${a_4} \gt {a_{3h}} \gt {a_{3l}}$
: the ‘somewhat bad’ type has a higher underlying utility for choosing MA than does the ‘very bad’ type, but still prefers IA. The ‘very bad’ type finds the moral action more distasteful than does the ‘somewhat bad’ type.
${a_4} \gt {a_{3h}} \gt {a_{3l}}$
: the ‘somewhat bad’ type has a higher underlying utility for choosing MA than does the ‘very bad’ type, but still prefers IA. The ‘very bad’ type finds the moral action more distasteful than does the ‘somewhat bad’ type.
Suppose that nature chooses the ‘somewhat bad’ type with probability
![]() $p \in \left( {0,1} \right)$
, and the ‘very bad’ type with probability
$p \in \left( {0,1} \right)$
, and the ‘very bad’ type with probability
![]() $1 - p$
. The game-tree is shown in Figure 7. It is very similar to that of Figure 6, but with the utilities adjusted to reflect that both types are bad. In particular, note that B’s utilities are all imported from Figure 5, since both types are bad.
$1 - p$
. The game-tree is shown in Figure 7. It is very similar to that of Figure 6, but with the utilities adjusted to reflect that both types are bad. In particular, note that B’s utilities are all imported from Figure 5, since both types are bad.

Figure 7. Signalling model when both types of
![]() $A$
are bad.
$A$
are bad.
Upon observing A (i.e. at
![]() ${I_2}$
), B certainly (i.e. regardless of the value of y) chooses P, as
${I_2}$
), B certainly (i.e. regardless of the value of y) chooses P, as
![]() ${b_7} \gt {b_8}$
is an assumption we have been maintaining throughout (B certainly punishes a bad type for choosing an immoral action). If
${b_7} \gt {b_8}$
is an assumption we have been maintaining throughout (B certainly punishes a bad type for choosing an immoral action). If
![]() ${b_5} \gt {b_6}$
, i.e. B punishes a bad type even for choosing a moral action (which I have suggested is arguably more consistent with Hume’s framework, although he is not clear about this), then B certainly chooses P upon observing MA as well (i.e. at
${b_5} \gt {b_6}$
, i.e. B punishes a bad type even for choosing a moral action (which I have suggested is arguably more consistent with Hume’s framework, although he is not clear about this), then B certainly chooses P upon observing MA as well (i.e. at
![]() ${I_1}$
). In this case there is a unique PBE, that is a pooling one in which both types choose IA (by Bayes’ rule
${I_1}$
). In this case there is a unique PBE, that is a pooling one in which both types choose IA (by Bayes’ rule
![]() $y = p$
, and the off-the-equilibrium-path belief x can be anything). If B punishes a bad type even for choosing a moral action, then each type simply chooses the immoral action, as she will be punished either way, and she is naturally inclined to choose IA. This is a situation where neither of Hume’s criteria (i) or (ii) hold.
$y = p$
, and the off-the-equilibrium-path belief x can be anything). If B punishes a bad type even for choosing a moral action, then each type simply chooses the immoral action, as she will be punished either way, and she is naturally inclined to choose IA. This is a situation where neither of Hume’s criteria (i) or (ii) hold.
Now suppose that
![]() ${b_5} \lt {b_6}$
instead. Then B certainly chooses NP upon observing MA. Now each type weighs her utility for choosing MA and not getting punished, versus choosing IA and getting punished. The ‘very bad’ type chooses MA if
${b_5} \lt {b_6}$
instead. Then B certainly chooses NP upon observing MA. Now each type weighs her utility for choosing MA and not getting punished, versus choosing IA and getting punished. The ‘very bad’ type chooses MA if
![]() ${a_{3l}} \gt {a_4} - c$
, i.e.
${a_{3l}} \gt {a_4} - c$
, i.e.
![]() $c \gt {a_4} - {a_3}$
. The ‘somewhat bad’ type chooses MA if
$c \gt {a_4} - {a_3}$
. The ‘somewhat bad’ type chooses MA if
![]() ${a_{3h}} \gt {a_4} - c$
, i.e.
${a_{3h}} \gt {a_4} - c$
, i.e.
![]() $c \gt {a_4} - {a_{3h}}$
. This leads to the following result.
$c \gt {a_4} - {a_{3h}}$
. This leads to the following result.
Proposition 10
In the model of Figure 7, suppose that
![]() ${b_5} \lt {b_6}$
.
${b_5} \lt {b_6}$
.
-
(a) If
 $c \lt {a_4} - {a_{3h}}$
, then there is a unique PBE, that is a pooling one in which both types choose IA. B chooses NP at
$c \lt {a_4} - {a_{3h}}$
, then there is a unique PBE, that is a pooling one in which both types choose IA. B chooses NP at
 ${I_1}$
, and P at
${I_1}$
, and P at
 ${I_2}$
. By Bayes’ rule,
${I_2}$
. By Bayes’ rule,
 $y = p$
, and the off-the-equilibrium-path belief x can be anything.
$y = p$
, and the off-the-equilibrium-path belief x can be anything.
-
(b) If
 ${a_4}{ - _{3h}} \lt c \lt {a_4} - {a_{3l}}$
, then there is a unique PBE, that is a separating one in which the ‘somewhat bad’ type chooses MA, and the ‘very bad’ type chooses IA. B chooses NP at
${a_4}{ - _{3h}} \lt c \lt {a_4} - {a_{3l}}$
, then there is a unique PBE, that is a separating one in which the ‘somewhat bad’ type chooses MA, and the ‘very bad’ type chooses IA. B chooses NP at
 ${I_1}$
, and P at
${I_1}$
, and P at
 ${I_2}$
. By Bayes’ rule,
${I_2}$
. By Bayes’ rule,
 $x = 1$
and
$x = 1$
and
 $y = 0$
.
$y = 0$
. -
(c) If
 ${a_4} - {a_{3l}} \lt c$
, then there is a unique PBE, that is a pooling one in which both types choose MA. B chooses NP at
${a_4} - {a_{3l}} \lt c$
, then there is a unique PBE, that is a pooling one in which both types choose MA. B chooses NP at
 ${I_1}$
, and P at
${I_1}$
, and P at
 ${I_2}$
. By Bayes’ rule,
${I_2}$
. By Bayes’ rule,
 $x = p$
, and the off-the-equilibrium-path belief y can be anything.
$x = p$
, and the off-the-equilibrium-path belief y can be anything.
If the punishment cost c is low (case a), then the PBE is a pooling one in which both types choose IA according to their natural inclination. If it is medium (case b), then the PBE is a separating one in which the ‘somewhat bad’ type chooses the moral action, whereas the ‘very bad’ type chooses the immoral action. The cost is large enough to get the ‘somewhat bad’ type, who doesn’t find the moral action too distasteful, to choose it, but is too low to get the ‘very bad’ type, who finds MA very distasteful, to choose it as well. Finally, if the cost is large (case c), then even the ‘very bad’ type chooses the moral action, and we are back to a pooling PBE.
Cases (b) and (c) are consistent with Hume’s account of artificial virtues, where no one is naturally inclined to choose the ‘moral’ action (quotation marks to represent Hume’s scepticism that such an action can be regarded as a genuinely moral one), but other factors such as social conventions (that are presumably costly to violate), can get some or all to do so. It is interesting that to get artificial virtues to occur in the signalling model, we have to assume that an observer would not punish a bad type for acting according to the virtue, i.e. that the observer would not hold it against her that she is only doing it to avoid punishment, and lacks the ‘virtuous motive’.
Finally, note that because both types are bad, in none of the three equilibria is Hume’s criterion (i) for moral actions satisfied (i.e. at best we are dealing with artificial rather than natural virtues). But in case (b), criterion (ii) is satisfied, in that the action chosen is informative about the person’s type. Even if no type is naturally inclined to choose the ‘moral’ action, medium-level social punishment costs can lead to actions separating ‘somewhat bad’ types from ‘very bad’ types. If the ‘moral’ action has benefits for others, then from a consequentialist perspective we want social punishment costs to be large enough that case (c) occurs. With artificial virtues, we have the same tradeoff between signalling (albeit among all ‘bad’ types, but bad to differing degrees) and incentivizing everyone to choose the ‘moral’ action that we had for natural virtues, but now the social punishment cost can’t be too low or else not even signalling will occur, as both types will choose the ‘immoral’ action (thus defeating both signalling and consequentialist goals).
5. Conclusion
In Treatise, Hume makes the remarkable claim that actions have moral status only in-so-far as they signal something about the agent’s character, which is what an observer is really interested in. I construct a game-theoretic signalling model that attempts to capture the core features of Hume’s theory of moral actions. Consistent with modern costly signalling theory, the analysis indicates that an action that good character types are naturally inclined to choose will only credibly signal good character if bad character types find the action distasteful (i.e. costly) enough that they are deterred from also choosing it to try to appear as good types and thus avoid social punishment. Although Hume hints at a credibility requirement when he states that actions carry more credibility than words, he doesn’t develop his theory in a costly signalling direction. But that a straightforward formalization of his theory easily pushes in that direction suggests that the rudiments of costly signalling theory can be found in Treatise, and that his theory can reasonably be extended to include the ‘moral actions must be sufficiently costly for bad types’ condition.
The analysis identifies a tension between Hume’s theory that actions are regarded as moral only if they credibly signal good character (implicitly, a separating equilibrium), and the consequentialist goal of getting everyone to choose beneficial actions (implicitly, a pooling equilibrium). The analysis suggests that if we primarily want to know an agent’s character, then actions can be informative of that, but only if social punishment costs for not choosing moral actions are kept low enough to actually allow for separation: don’t punish bad types too severely for acting according to their natural inclination – let them be themselves! Alternatively, we may not care primarily about gleaning character and instead mainly want to incentivize good behaviour by everyone (regardless of character), in which case we want social punishment costs to be high. Footnote 22 Under certain conditions, a semi-separating equilibrium exists that embodies a compromise between these two goals, in that moral actions are partially informative of character, and even bad types choose beneficial actions with positive probability.
Finally, the analysis shows that behaviour consistent with Hume’s artificial virtues can occur in the model, whereby no type is naturally inclined to choose the moral action, but may be induced to do so by sufficiently high social punishment costs for not choosing it. Interestingly, this requires observers to not require that the agent have a ‘virtuous motive’ for choosing the moral action, i.e. to not hold it against her that she is only doing so to avoid social punishment. Thus, the analysis suggests that Hume’s theory of artificial virtues requires that observers not punish a bad character type for choosing a moral action, an issue on which Hume’s stance is unclear despite being very clear (regarding an analogous situation) that an observer would not punish a good character type for choosing an immoral action.
Acknowledgements
My thanks to two anonymous reviewers and the editor for their insightful comments that improved the paper considerably.
Appendix
PROPOSITION 9: I just provide a proof of Proposition 9 (the semi-separating PBE), as the other results are essentially proven in the main text. We want to explore the existence of a PBE in which the good type chooses MA, and the bad type mixes between MA and IA. If a PBE like this exists, then in it, by Bayes’ rule
![]() $y = 0$
, and hence B chooses P at
$y = 0$
, and hence B chooses P at
![]() ${I_2}$
. For the bad type to be mixing between MA and IA, he has to be indifferent between these two actions. Therefore, if a PBE of this form exists, it can’t involve B choosing P at
${I_2}$
. For the bad type to be mixing between MA and IA, he has to be indifferent between these two actions. Therefore, if a PBE of this form exists, it can’t involve B choosing P at
![]() ${I_1}$
as well, because then the bad type is not indifferent (and optimally chooses IA). And if B is choosing NP at
${I_1}$
as well, because then the bad type is not indifferent (and optimally chooses IA). And if B is choosing NP at
![]() ${I_1}$
, then the bad type is only indifferent if the knife-edge parameter condition
${I_1}$
, then the bad type is only indifferent if the knife-edge parameter condition
![]() ${a_3} = {a_4} - c$
holds, and PBE reliant on knife-edge parameter conditions are substantively uninteresting. Therefore, any substantively interesting PBE of this form requires B to be mixing at
${a_3} = {a_4} - c$
holds, and PBE reliant on knife-edge parameter conditions are substantively uninteresting. Therefore, any substantively interesting PBE of this form requires B to be mixing at
![]() ${I_1}$
. B can only be doing so if
${I_1}$
. B can only be doing so if
![]() $x = {x_{crit}}$
. Suppose that the bad type chooses MA with probability
$x = {x_{crit}}$
. Suppose that the bad type chooses MA with probability
![]() $a \in \left( {0,1} \right)$
, and B chooses P with probability
$a \in \left( {0,1} \right)$
, and B chooses P with probability
![]() $b \in \left( {0,1} \right)$
at
$b \in \left( {0,1} \right)$
at
![]() ${I_1}$
. Then by Bayes’ rule
${I_1}$
. Then by Bayes’ rule
![]() $x = {{\left( p \right)\left( 1 \right)} \over {\left( p \right)\left( 1 \right) + \left( {1 - p} \right)\left( a \right)}}$
, and
$x = {{\left( p \right)\left( 1 \right)} \over {\left( p \right)\left( 1 \right) + \left( {1 - p} \right)\left( a \right)}}$
, and
![]() $x = {x_{crit}}$
can be solved for a to give
$x = {x_{crit}}$
can be solved for a to give
![]() ${a^{\rm{*}}} = {{p\left( {{b_2} - {b_1}} \right)} \over {\left( {1 - p} \right)\left( {{b_5} - {b_6}} \right)}}$
. Note that
${a^{\rm{*}}} = {{p\left( {{b_2} - {b_1}} \right)} \over {\left( {1 - p} \right)\left( {{b_5} - {b_6}} \right)}}$
. Note that
![]() ${a^{\rm{*}}} \gt 0$
is always true, and
${a^{\rm{*}}} \gt 0$
is always true, and
![]() ${a^{\rm{*}}} \lt 1$
can be re-written as
${a^{\rm{*}}} \lt 1$
can be re-written as
![]() $p \lt {x_{crit}}$
, which is thus a necessary condition for a PBE of this form. For the bad type,
$p \lt {x_{crit}}$
, which is thus a necessary condition for a PBE of this form. For the bad type,
![]() $E{U_A}\left( {MA} \right) = \left( b \right)\left( {{a_3} - c} \right) + \left( {1 - b} \right)\left( {{a_3}} \right)$
and
$E{U_A}\left( {MA} \right) = \left( b \right)\left( {{a_3} - c} \right) + \left( {1 - b} \right)\left( {{a_3}} \right)$
and
![]() $E{U_A}\left( {IA} \right) = {a_4} - c$
, and
$E{U_A}\left( {IA} \right) = {a_4} - c$
, and
![]() $E{U_A}\left( {MA} \right) = E{U_A}\left( {IA} \right)$
can be solved for b to give
$E{U_A}\left( {MA} \right) = E{U_A}\left( {IA} \right)$
can be solved for b to give
![]() ${b^{\rm{*}}} = {{{a_3} - \left( {{a_4} - c} \right)} \over c}$
. Note that
${b^{\rm{*}}} = {{{a_3} - \left( {{a_4} - c} \right)} \over c}$
. Note that
![]() ${b^{\rm{*}}} \lt 1$
is always true, and
${b^{\rm{*}}} \lt 1$
is always true, and
![]() ${b^{\rm{*}}} \gt 0$
can be re-written as
${b^{\rm{*}}} \gt 0$
can be re-written as
![]() $c \gt {a_4} - {a_3}$
, which is thus another necessary condition for a PBE of this form. Finally, note that the good type is strictly worse off deviating to IA (since B is choosing P at
$c \gt {a_4} - {a_3}$
, which is thus another necessary condition for a PBE of this form. Finally, note that the good type is strictly worse off deviating to IA (since B is choosing P at
![]() ${I_2}$
), and this proves Proposition 9. Q.E.D.
${I_2}$
), and this proves Proposition 9. Q.E.D.
UNIQUENESS OF EQUILIBRIA IN SECTION 4.3.1: The three propositions of section 4.3.1 just establish the existence of the pooling, separating, and semi-separating PBE, whereas the other propositions establish (because it is easy to do so) uniqueness as well. I now establish (a little more challenging) the essential uniqueness of those three PBE. The method will be to exhaustively consider every possibility for A’s strategy.
-
(a) Pooling-on-MA: Proposition 8.
-
(b) Pooling-on-IA: By Bayes’ rule,
 $y = p$
. If
$y = p$
. If
 $p \lt {y_{crit}}$
, then this can’t be a PBE because B chooses P at
$p \lt {y_{crit}}$
, then this can’t be a PBE because B chooses P at
 ${I_2}$
, in which case the good type is strictly better off deviating to MA regardless of what B chooses at
${I_2}$
, in which case the good type is strictly better off deviating to MA regardless of what B chooses at
 ${I_1}$
. Thus, this can possibly be a PBE only if
${I_1}$
. Thus, this can possibly be a PBE only if
 $p \gt {y_{crit}}$
and so B chooses NP at
$p \gt {y_{crit}}$
and so B chooses NP at
 ${I_2}$
. And the off-the-equilibrium-path belief x must satisfy
${I_2}$
. And the off-the-equilibrium-path belief x must satisfy
 $x \lt {x_{crit}}$
so that B chooses P at
$x \lt {x_{crit}}$
so that B chooses P at
 ${I_1}$
, for if B is instead choosing NP there, then the good type is strictly better off deviating to MA. So although we can construct a PBE here (if
${I_1}$
, for if B is instead choosing NP there, then the good type is strictly better off deviating to MA. So although we can construct a PBE here (if
 $c \ge {a_1} - {a_2}$
so that the good type doesn’t benefit by deviating to MA), it is an implausible one, as it relies on the implausible off-the-equilibrium-path belief that if he unexpectedly observes MA, B is sufficiently confident that he faces the bad type so as to choose P. This is why I say ‘essentially’ unique: there is one additional pooling PBE, but it is a very implausible one.
$c \ge {a_1} - {a_2}$
so that the good type doesn’t benefit by deviating to MA), it is an implausible one, as it relies on the implausible off-the-equilibrium-path belief that if he unexpectedly observes MA, B is sufficiently confident that he faces the bad type so as to choose P. This is why I say ‘essentially’ unique: there is one additional pooling PBE, but it is a very implausible one. -
(c) Separating with the good type choosing MA and the bad type choosing IA: Proposition 7.
-
(d) Separating with the good type choosing IA and the bad type choosing MA: Upon observing IA, B would choose NP, and hence this can’t be a PBE as the bad type optimally deviates to IA.
-
That exhausts all possibilities where A is adopting a pure strategy. Now we consider mixed strategies.
-
(e) Good type chooses MA, bad type mixes: Proposition 9.
-
(f) Good type chooses IA, bad type mixes: Upon observing MA, B would choose P, and hence this can’t be a PBE as the bad type optimally deviates to IA.
-
(g) Good type mixes, bad type chooses MA: Upon observing IA, B would choose NP, and hence this can’t be a PBE as the bad type optimally deviates to IA.
-
(h) Good type mixes, bad type chooses IA: Upon observing MA, B would choose NP, and hence this can’t be a PBE as the good type optimally deviates to MA.
-
(i) Both types are mixing, B adopts a pure strategy at
 ${I_1}$
and
${I_1}$
and
 ${I_2}$
: Because B is adopting a pure strategy at both information-sets, the two types can only be indifferent between MA and IA if knife-edge parameter conditions hold, and thus even if such PBE can be constructed, they are of no substantive interest.
${I_2}$
: Because B is adopting a pure strategy at both information-sets, the two types can only be indifferent between MA and IA if knife-edge parameter conditions hold, and thus even if such PBE can be constructed, they are of no substantive interest. -
(j) Both types are mixing, B mixes at
 ${I_1}$
, chooses P at
${I_1}$
, chooses P at
 ${I_2}$
: No PBE here, as the good type optimally deviates to MA.
${I_2}$
: No PBE here, as the good type optimally deviates to MA. -
(k) Both types are mixing, B mixes at
 ${I_1}$
, chooses NP at
${I_1}$
, chooses NP at
 ${I_2}$
: No PBE here, as the bad type optimally deviates to IA.
${I_2}$
: No PBE here, as the bad type optimally deviates to IA. -
(l) Both types are mixing, B mixes at
 ${I_2}$
, chooses P at
${I_2}$
, chooses P at
 ${I_1}$
: No PBE here, as the bad type optimally deviates to IA.
${I_1}$
: No PBE here, as the bad type optimally deviates to IA. -
(m) Both types are mixing, B mixes at
 ${I_2}$
, chooses NP at
${I_2}$
, chooses NP at
 ${I_1}$
: No PBE here, as the good type optimally deviates to MA.
${I_1}$
: No PBE here, as the good type optimally deviates to MA. -
(n) Both types are mixing, B mixes at
 ${I_1}$
and
${I_1}$
and
 ${I_2}$
: Suppose that B chooses P with probability
${I_2}$
: Suppose that B chooses P with probability
 $m \in \left( {0,1} \right)$
at
$m \in \left( {0,1} \right)$
at
 ${I_1}$
, and with probability
${I_1}$
, and with probability
 $n \in \left( {0,1} \right)$
at
$n \in \left( {0,1} \right)$
at
 ${I_2}$
. If
${I_2}$
. If
 $m \ge n$
, then the bad type optimally deviates to IA. If
$m \ge n$
, then the bad type optimally deviates to IA. If
 $m \le n$
, then the good type optimally deviates to MA. Thus, there is no PBE here. Q.E.D.
$m \le n$
, then the good type optimally deviates to MA. Thus, there is no PBE here. Q.E.D.
Ahmer Tarar is an associate professor in the Department of Political Science at Texas A&M University. His research applies game theory to a variety of topics in the social sciences and the humanities. URL: http://people.tamu.edu/∼ahmertarar/















