INTRODUCTION
Influenza is a common infectious disease, which has an important impact on society each year [Reference Simonsen1]. The typical clinical features of influenza disease include fever, respiratory symptoms, headache, muscle ache and fatigue [Reference Nicholson2]. In most cases, the influenza disease is self-limiting but it can evolve to life-threatening medical complications [Reference Rothberg, Haessler and Brown3]. Recently, influenza has been identified as one of the three infectious diseases causing the highest burden in Europe, along with HIV infection and tuberculosis [Reference van Lier, Havelaar and Nanda4]. Moreover, genetic reassortments and mutations of influenza viruses might lead to the emergence of pandemics during which the rates of morbidity and mortality increase further.
Influenza surveillance is implemented by many national and international authorities throughout the world [5, 6]. The World Health Organization (WHO) stresses the importance of influenza surveillance activities for the annual determination of influenza vaccine content and as an indispensable tool for pandemic preparedness [7]. A standard tool for monitoring influenza activity is the combination of virological and clinical surveillance by a network of sentinel practitioners [5, 6]. As a tool for detection of the first circulating viruses, virological surveillance allows the characterization of strains by monitoring the rates of influenza virus positivity. Clinical surveillance is based on consultations for influenza-like illness (ILI), which is a clinical diagnosis of a set of common aspecific symptoms. These symptoms include typical clinical features of influenza, although heterogeneous case definitions are used [Reference Aguilera8]. The combination of virological and clinical surveillance is generally considered to be the most accurate tool for monitoring influenza activity [Reference Mikanatha9].
Respiratory pathogens other than influenza are generally not monitored by combined influenza surveillance [5, 6]. However, such pathogens might also cause ILI, resulting in poor to moderate positive predictive values of ILI diagnoses of laboratory-confirmed influenza infections [Reference Navarro-Mari10–Reference Zambon12]. In particular, along with influenza viruses A and B, parainfluenza virus, respiratory syncytial virus (RSV), adenovirus and Mycoplasma pneumoniae are regarded as other important respiratory pathogens with the potential to cause ILI. For most of these respiratory pathogens seasonality has been consistently observed, although the driving mechanisms are still poorly understood [Reference Altizer13]. A typical example of a seasonal infectious disease is influenza. Annual influenza epidemics commonly occur during the winter season in temperate regions of the world with varying onset, duration and severity [Reference Paget14]. Moreover, the incidence of RSV varies conspicuously by season, showing distinct seasonal patterns in different countries [Reference Terletskaia-Ladwig15, Reference White16]. Such seasonality in pathogen activity naturally implies seasonality in ILI consultations.
In this study, the pathogens’ contribution to seasonal variation in ILI was statistically modelled, using data from two independent surveillance systems in Belgium. Data from both clinical sentinel surveillance [Reference Van Casteren17], and laboratory sentinel surveillance were used in monitoring trends of different respiratory pathogens [Reference Ducoffre, Quoilin and Wuillaume18]. The pathogens’ contribution to the seasonality of ILI was estimated using smooth modulation models for seasonal time series [Reference Eilers19] and Poisson models regressing the number of ILI consultations in the number of laboratory reports for various respiratory pathogens. Epidemiological interpretations in terms of relative measures of underreported pathogens were obtained by using ratios of estimated Poisson regression parameters.
METHODOLOGY
Data
Clinical surveillance
The clinical data on ILI consultations from January 2004 to December 2008 were extracted from the General Practitioners (GPs) influenza surveillance database, which is obtained through a weekly registration network of GPs coordinated by the Belgian Scientific Institute of Public Health (WIV-ISP) [Reference Van Casteren17]. This database contains, among others, weekly information on the number of ILI consultations with the case definition for ILI being sudden onset of illness, associated with fever, respiratory and general symptoms. Since October 2007, data have been collected by the Belgian sentinel GPs network, in which about 180 GPs participate. The participating GPs cover 1.75% of the total Belgian patient population and are representative of the profile of family physicians in Belgium in terms of age, sex and geographical location [Reference Boffin, Bossuyt and Van Casteren20]. Before October 2007, data were collected by a smaller network of 40–80 GPs.
The counts of ILI consultations were extrapolated to the whole Belgian population to adjust for changes in the size of the represented patient population as a result of changes in the number of GPs reporting over time. In total, data for 214 measurements were available. For the years preceding 2007, ILI consultations were not monitored outside the influenza season, resulting in incomplete time series.
Laboratory surveillance
The sentinel laboratory network, coordinated by WIV-ISP, has collected data on about 40 infectious diseases since 1983 [Reference Ducoffre, Quoilin and Wuillaume18]. In 2009, 100 laboratories, representing 58% of all Belgian laboratories, participated to the surveillance system on a voluntary basis. The participating private or hospital laboratories are evenly distributed over 33 out of 43 administrative districts in Belgium. These laboratories receive biological samples from routine diagnostic testing at GP practices, hospitals, care homes, etc. On a weekly basis, the laboratories send anonymized data to WIV-ISP using an electronic system (Epi-Lab), internet application or registration form. The incidence of different infections, which includes respiratory infections, is monitored using this surveillance system, allowing for the detection of changes in time or geographical trends.
Data on all pathogens available that potentially cause ILI were extracted from the Belgian sentinel laboratory surveillance database. In particular, data on the weekly number of samples that tested positive for influenza virus A, influenza virus B, parainfluenza, RSV and M. pneumoniae were obtained for the period from January 2004 to December 2008, resulting in 260 measurement points for each of the five pathogens as the time series are complete.
Data analysis
Modulation models for seasonal time series
The clinical and five virological time series were first smoothed, with the aim of revealing the essential (non-parametric) patterns while suppressing excessive variations. Smoothing techniques are increasingly popular because they provide a statistical tool to graphically explore the data and allow modelling of the data when classical parametric models fail [Reference Ruppert, Wand and Carroll21]. Because the virological and clinical time series exhibit irregular seasonal variation, the time trends were smoothed using modulation models for seasonal time series [Reference Eilers19]. In these models, the overall time trend is modelled using an intercept and the periodicity is modelled using sine and cosine regressors. The coefficients of the intercept, sine and cosine regressors are allowed to vary smoothly over time. This permits the modelling of global time trends and varying onset, duration and severity of incidence peaks over time (for details, see Eilers et al. [Reference Eilers19]). Because the clinical data X is a time series of counts exhibiting overdispersion, the Poisson quasi-likelihood with log-link and deviance-based correction for overdispersion was used [Reference Eilers19]. In particular, the Poisson expectation 
$\tilde{X}$ was modelled as a smooth function of time t using a basis of 30 B splines of third degree for the intercept, sine and cosine regressors and second-order smoothness penalties. The optimal smoothness parameters were selected using quasi-Akaike's Information Criteria [Reference Eilers19]. For each of the five respiratory pathogens, smooth functions Yi with i = 1, 2, …, 5 were obtained similarly.
Multiple Poisson regression
Second, the ILI consultation counts X were linearly regressed on the smoothed predictions of the five respiratory pathogens, Y 1, Y 2, …, Y 5, to assess the pathogens’ contribution to the seasonal variation in ILI. To this end, the Poisson quasi-likelihood with deviance-based correction for overdispersion and identity link was used, as it had the expected ILI counts
$$g\lpar E\lpar X\rpar \rpar \equals E\lpar X\rpar \equals \sum\limits_{i \equals \setnum{1}}^{\setnum{5}} \alpha _{i} \mathop {\tilde{Y}}\nolimits_{i} .$$Although the log-link is the natural link for Poisson regression [Reference Agresti22], the identity link g was used to obtain epidemiological interpretations of the estimated Poisson parameters 
$\mathop {\hat{\alpha }}\nolimits_{i} $, which is explained below.
Epidemiological interpretation of parameters
Introducing some notation, we allow N(t)ILI to denote the total number of ILI cases in a given population as a function of time t. Similarly, we denote the total number of illness cases due to influenza virus A, influenza virus B, parainfluenza virus, RSV and M. pneumoniae as N(t)inflA, N(t)inflB, N(t)para, N(t)RSV and N(t)myco, respectively. Then, assuming that no other pathogens are causing ILI, it immediately follows that
$$\eqalign{N\lpar t\rpar _{{\rm ILI}} \equals\tab N\lpar t\rpar _{{\rm inflA}} \plus N\lpar t\rpar _{{\rm inflB}} \plus N\lpar t\rpar _{{\rm para}}\cr\tab \plus N\lpar t\rpar _{{\rm RSV}} \plus N\lpar t\rpar _{{\rm myco}}.$$However, the total number of cases N(t) in a given population is typically unknown as a result of underreporting. Instead, the number of reported cases R(t) is observed. Assuming that the reporting probability π is constant over time, it follows that R(t) = πN(t). Hence, rewriting equation (2) in terms of the number of reported cases R(t) assuming disease- or pathogen-specific reporting probabilities gives
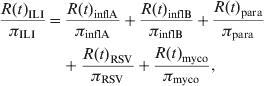$$\eqalign{ {{R\lpar t\rpar _{{\rm ILI}} } \over {\pi _{{\rm ILI}} }} \equals \tab {{R\lpar t\rpar _{{\rm inflA}} } \over {\pi _{{\rm inflA}} }} \plus {{R\lpar t\rpar _{{\rm inflB}} } \over {\pi _{{\rm inflB}} }} \plus {{R\lpar t\rpar _{{\rm para}} } \over {\pi _{{\rm para}} }} \cr \tab \plus {{R\lpar t\rpar _{{\rm RSV}} } \over {\pi _{{\rm RSV}} }} \plus {{R\lpar t\rpar _{{\rm myco}} } \over {\pi _{{\rm myco}} }}\comma \cr} $$with, e.g. R(t)ILI being the number of reported ILI cases at time t and πILI being the probability of reporting an ILI case. Rewriting again and subsequently simplifying, it follows that
$$\eqalign{ R\lpar t\rpar _{{\rm ILI}} \equals \tab \alpha _{{\rm inflA}} R\lpar t\rpar _{{\rm inlfA}} \plus \alpha _{{\rm inflB}} R\lpar t\rpar _{{\rm inflB}} \plus \alpha _{{\rm para}} R\lpar t\rpar _{{\rm para}}\cr \tab \plus \alpha _{{\rm RSV}} R\lpar t\rpar _{{\rm RSV}} \plus \alpha _{{\rm myco}} R\lpar t\rpar _{{\rm myco}} \comma \cr} $$where, πILI/πinflA ≡ αinflA, πILI/πinflB ≡ αinflB, etc. It should be noted that equation (4) is of the same form as equation (1), implying that the parameters α can be estimated as explained above. The additivity of the model given in equation (4) also explains the choice of the identity link. Indeed, using the identity link in Poisson regression gives rise to an additive interpretation of the parameters α whereas the commonly used log-link gives rise to a multiplicative interpretation [Reference Agresti22].
Finally, by using ratios of the parameters α, interesting epidemiological interpretations were obtained. For instance, take (arbitrarily) the parameter αRSV as reference and construct, for the remaining parameters, ratios relative to that reference. For instance, construct ΦinflA = αinflA/αRSV, which is straightforwardly rewritten using the definitions in expression (4) as
$$\rmPhi _{{\rm inflA}} \equals {{\alpha _{{\rm inflA}} } \over {\alpha _{{\rm RSV}} }} \equals {{\pi _{{\rm ILI}} \sol \pi _{{\rm inflA}} } \over {\pi _{{\rm ILI}} \sol \pi _{{\rm RSV}} }} \equals {{1\sol \pi _{{\rm inflA}} } \over {1\sol \pi _{{\rm RSV}} }} \equiv {{\phi _{{\rm inflA}} } \over {\phi _{{\rm RSV}} }}\comma $$where 1/πinflA ≡ ϕinflA is the factor needed to correct for underreporting of diseases due to influenza A and similarly, 1/πRSV ≡ ϕRSV is the factor needed to correct for underreporting of diseases due to RSV. Hence, ΦinflA should be interpreted as the factor needed to correct for underreporting of influenza A diseases relative to the factor needed to correct for underreporting of RSV.
RESULTS
Data smoothing
From the laboratory reports, RSV (54·42%) was the most commonly reported pathogen during 2004–2008, consecutively followed by M. pneumoniae (31·52%), influenza virus A (7·10%), parainfluenza virus (4·79%) and influenza virus B (2·20%). Figure 1(a–e) presents the weekly number of laboratory reports of influenza virus A, influenza virus B, parainfluenza virus, RSV, and M. pneumoniae, respectively, together with the smoothed time series and 95% confidence intervals. Clearly, strong seasonality can be observed for influenza virus A, influenza virus B and RSV with the RSV peaks preceding those of influenza viruses A and B. Weaker seasonality can be observed for parainfluenza and M. pneumoniae with the latter showing a clearly decreasing trend over time. Figure 1f presents the weekly number of ILI consultations, also showing strong seasonality, that most closely coincides with the seasonal patterns of the influenza viruses.
Fig. 1. Weekly number of laboratory reports of (a) influenza virus A, (b) influenza virus B, (c) parainfluenza, (d) RSV, (e) Mycoplasma pneumoniae and (f) weekly numbers of influenza-like illness (ILI) with corresponding smoothed time series.
Multiple Poisson regression
The results of the multiple Poisson model regressing the ILI consultation counts on the smoothed time series of influenza virus A, influenza virus B, parainfluenza, RSV and M. pneumoniae are given in Table 1. As can be seen, all respiratory pathogens except M. pneumoniae, significantly contribute in explaining the seasonal variation in ILI consultations. The results for the ratios Φ of factors correcting for underreporting with RSV as reference are given in the last two columns Table 1. The 95% confidence intervals are obtained using Fieller's method [Reference Herson23]. The ratios Φ indicate that diseases due to RSV were the least underreported by Belgian laboratory surveillance whereas diseases due to influenza viruses A and B were the most underreported.
Table 1. Results of the multiple Poisson regression: regression parameters α and ratios Φ of factors to correct for underreporting with respiratory syncytial virus as reference
Figure 2 gives a graphical representation of the Poisson regression model given in equation (4). The smoothed time series of the respiratory pathogens, Yi (i = 1, 2, …, 5), are jointly presented in Figure 2 a. To predict the ILI consultations, the smoothed time series are first rescaled using regression weights αi (Fig. 2 b). Then these rescaled time series αiYi are summed to predict the ILI consultation counts. The predicted curve and its 95% confidence interval are presented by the dark grey area in Figure 2 c. As can be seen from Figure 2(b, c), the peaks in ILI consultations are mainly explained by influenza virus A and, to a lesser extent, by influenza virus B. Furthermore, Figure 2(b, c) suggests that the excess in ILI consultations before the onset of the influenza epidemic is mainly explained by RSV. By means of comparison, the smoothed time series of ILI consultations $\tilde{X}$ is also presented in Figure 2 c (light grey area). As can be seen, both the smoothed ILI curve as well as the ILI curve, as predicted based on the smoothed time series of the respiratory pathogens, are nicely overlapping. This observation is well in line with the obtained pseudo-R 2 value for the overdispersed Poisson regression model [Reference Heinzl and Mittlböck24], i.e. R 2 = 0·82, indicating that ILI seasonality is well predicted by the seasonality of the respiratory pathogens.
Fig. 2. Graphical presentation of the multiple Poisson regression: (a) smoothed time series of respiratory pathogens, (b) rescaled time series of respiratory pathogens, (c) smoothed and predicted time series of influenza-like illness. RSV, Respiratory syncytial virus.
DISCUSSION
In this study, the contribution of respiratory pathogens to the seasonal variation in ILI consultations was statistically modelled using data from the Belgian clinical and laboratory sentinel surveillance systems, which are two independent surveillance systems. The statistical methods were smooth modulation models for seasonal time series and Poisson regression with correction for overdispersion.
Methods regressing syndromic incidence data on the number of laboratory reports have been used previously. Linear regression methods have been used, among others, to assess the burden of influenza in terms of general practice consultations, hospital admissions and deaths [Reference Pitman25], in order to estimate the contribution of different respiratory pathogens to the seasonality of NHS Direct respiratory calls [Reference Cooper26] and to validate other syndromic surveillance systems (e.g. absenteeism, pharmacy sales, laboratory submissions) for their capability of capturing respiratory pathogen activity [Reference Van den Wijngaard27]. More evolved regression methods have been used recently by Yang et al. [Reference Yang28], who used wavelet analysis to investigate the synchrony of clinical and laboratory surveillance in Hong Kong. The method we propose has the advantage of providing solid epidemiological interpretations. By using ratios of the estimated regression parameters, relative factors of disease underreporting by laboratory surveillance were obtained. Furthermore, the method allows interesting and interpretable visualizations of the model results.
The model results indicate that, in line with previous research, significant contributions were found for influenza viruses A and B, parainfluenza virus and RSV [Reference Zambon12]. The contribution of M. pneumoniae was not found to be significant. The peaks of ILI consultations were mainly explained by influenza virus A and, to a lesser extent, by influenza virus B, whereas the excess in ILI consultations prior to the onset of the influenza epidemic was explained by RSV. A significant year round contribution was found for parainfluenza. By using ratios of the estimated regression parameters, we found that diseases due to RSV and M. pneumoniae were the least underreported by Belgian laboratory surveillance whereas diseases due to influenza viruses A and B were the most underreported. These large differences in relative measures of underreporting are due to case ascertainment bias and can be interpreted as a reflection of medical practice in Belgium. For instance, causes of childhood diseases are frequently tested, as a cautious principle of sampling is often adopted for young patients. RSV is such a childhood disease. Furthermore, the costs of RSV testing for children aged <2 years are reimbursed by compulsory Belgian medical insurance, explaining the (relatively) small amount of RSV underreporting. On the other hand, as ILI is a clinically based diagnosis with a symptom-related treatment, its causes are rarely tested during the influenza season, which explains the (relatively) large amount of underreporting for influenza viruses A and B. Causes of respiratory infections outside the influenza season could be more frequently tested, explaining the (relatively) small amount of underreporting for M. pneumoniae, being a non-seasonal virus circulating throughout the year.
The proposed regression model provides a good fit, indicating that ILI seasonality is well predicted by the seasonality of respiratory pathogens. This can also be regarded as a mutual validation of the independent clinical and laboratory surveillance systems. The model relies on two important assumptions. First, it is assumed that the pathogen-specific reporting probabilities are constant over time. This assumption seems epidemiologically plausible and, moreover, is hard to relax as it could lead to non-identifiable regression models. The second assumption that all ILI cases are caused by a limited set of respiratory pathogens (i.e. influenza virus A, influenza virus B, parainfluenza virus, RSV, M. pneumoniae) is obviously not correct. However, other pathogens with the potential to cause ILI are not monitored by Belgian laboratory surveillance and hence, could not be included in the regression model. Instead, an intercept might be included to implicitly account for the pathogens for which no or only limited information is available. However, this assumes that the contribution of these unknown or missing pathogens to ILI consultations is constant over time, which is clearly not the case. By excluding the intercept, as done in the current study, the model predictions are likely to locally underestimate the observed number of ILI consultations. These underestimations are informative, suggesting the activity of an unknown or missing pathogen. Future research might attempt to discover an explanation for the observed underestimation using other databases or published studies. For the Belgian data, such an underestimation was observed prior to the influenza epidemic of 2008 (see Fig. 2 c), but could not be explained.
To conclude, the seasonality of ILI is well predicted by the seasonality of influenza viruses A and B, parainfluenza and RSV. In addition, relative factors of underreporting of respiratory pathogens in laboratory surveillance have been obtained indicating that RSV is the least and influenza A is the most underreported pathogen in Belgian laboratory surveillance. The results of this study are helpful in interpreting the data of clinical and laboratory surveillance, which are the essential parts of influenza sentinel surveillance. The proposed methods provide interesting epidemiological interpretations and are versatile. Future research might include an extension of the current analysis by including additional covariate information such as age and geographical location. Furthermore, although not explicitly investigated in this paper, the smooth modulation models for seasonal time series [Reference Eilers19] allow the modelling of varying onset, duration and severity of the incidence peaks over time. Such an approach would yield interesting insights into the temporal variation in viral agents [Reference Laguna-Torres29] and disease dynamics.
ACKNOWLEDGEMENTS
We thank all the GPs and laboratories participating in our surveillance networks for their important contribution to surveillance.
DECLARATION OF INTEREST
None.
Open access
