Hostname: page-component-7bb8b95d7b-2h6rp Total loading time: 0 Render date: 2024-09-13T19:13:11.968Z Has data issue: false hasContentIssue false
  • English
  • Français

Codimension one compact center foliations are uniformly compact

Part of: Dynamical systems with hyperbolic behavior Differential topology

Published online by Cambridge University Press:  13 March 2019

VERÓNICA DE MARTINO  and
SANTIAGO MARTINCHICH
VERÓNICA DE MARTINO
Affiliation:
CMAT, Facultad de Ciencias, Universidad de la República, Uruguay email vdemartino@cmat.edu.uy, smartinchich@cmat.edu.uy
SANTIAGO MARTINCHICH
Affiliation:
CMAT, Facultad de Ciencias, Universidad de la República, Uruguay email vdemartino@cmat.edu.uy, smartinchich@cmat.edu.uy
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 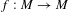$f:M\rightarrow M$ be a dynamically coherent partially hyperbolic diffeomorphism whose center foliation has all its leaves compact. We prove that if the unstable bundle of 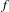$f$ is one-dimensional, then the volume of center leaves must be bounded in 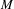$M$.

Keywords

partial hyperbolicitycompact foliationsskew productsclassification

MSC classification

Primary: 37D30: Partially hyperbolic systems and dominated splittings
Secondary: 57R30: Foliations; geometric theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2349 - 2367
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bohnet, D.. Codimension-1 partially hyperbolic diffeomorphisms with a uniformly compact center foliation. J. Mod. Dyn. 7(4) (2013), 565–604.Google Scholar
Bohnet, D. and Bonatti, C.. Partially hyperbolic diffeomorphisms with a uniformly compact center foliation: the quotient dynamics. Ergod. Th. & Dynam. Sys. 36(4) (2016), 1067–1105.Google Scholar
Bonatti, C. and Wilkinson, A.. Transitive partially hyperbolic diffeomorphisms on 3-manifolds. Topology 44(3) (2005), 475–508.Google Scholar
Camacho, C. and Lins Neto, A.. Geometric Theory of Foliations. Birkhäuser, Boston, 1985.Google Scholar
Candel, A. and Conlon, L.. Foliations I (Graduate Studies in Mathematics, 23). American Mathematical Society, Providence, RI, 2000.Google Scholar
Carrasco, P.. Compact dynamical foliations. Ergod. Th. & Dynam. Sys. 35(8) (2015), 2474–2498.Google Scholar
Edwards, R., Millett, K. and Sullivan, D.. Foliations with all leaves compact. Topology 16(1) (1977), 13–32.Google Scholar
Epstein, D. B. A.. Foliations with all leaves compact. Ann. Inst. Fourier (Grenoble) 26(1) (1976), 265–282.Google Scholar
Epstein, D. B. A. and Vogt, E.. A counterexample to the periodic orbit conjecture in codimension 3. Ann. of Math. (2) 108(3) (1978), 539–552.Google Scholar
Gogolev, A.. Partially hyperbolic diffeomorphisms with compact center foliations. J. Mod. Dyn. 5(4) (2012), 747–769.Google Scholar
Hector, G. and Hirsch, U.. Introduction to the Geometry of Foliations, Part B (Aspects of Mathematics, E3), 2nd edn. Vieweg, Braunschweig, 1987.Google Scholar
Hiraide, K.. A simple proof of the Franks-Newhouse theorem on codimension-one Anosov diffeomorphisms. Ergod. Th. & Dynam. Sys. 21(3) (2001), 801–806.Google Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Springer Lecture Notes in Mathematics, 583). Springer, Berlin, 1977.Google Scholar
Lessa, P.. Reeb stability and the Gromov–Hausdorff limits of leaves in compact foliations. Asian J. Math. 19(3) (2015), 433–464.Google Scholar
Newhouse, S. E.. On codimension one Anosov diffeomorphisms. Amer. J. Math. 92(3) (1970), 761–770.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A. and Ures, R.. A Survey of Partially Hyperbolic Dynamics, Partially Hyperbolic Dynamics, Laminations, and Teichmüler Flow (Fields Institute Communications, 51). American Mathematical Society, Providence, RI, 2007, pp. 35–87.Google Scholar
Sullivan, D.. A counterexample to the periodic orbit conjecture. Publ. Math. Inst. Hautes Études Sci. 46 (1976), 5–14.Google Scholar
Vogt, E.. A periodic flow with infinite Epstein hierarchy. Manuscripta Math. 22(4) (1977), 403–412.Google Scholar