Hostname: page-component-84b7d79bbc-x5cpj Total loading time: 0 Render date: 2024-07-27T14:31:42.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast and slow points of Birkhoff sums

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Ergodic theory Classical measure theory Limit theorems

Published online by Cambridge University Press:  11 July 2019

FRÉDÉRIC BAYART ,
ZOLTÁN BUCZOLICH  and
YANICK HEURTEAUX
FRÉDÉRIC BAYART
Affiliation:
Université Clermont Auvergne, LMBP, UMR 6620 – CNRS, Campus des Cézeaux, 3 place Vasarely, TSA 60026, CS 60026 F-63178 Aubière Cedex, France Department of Analysis, ELTE Eötvös Loránd University, Pázmány Péter Sétány 1/c, 1117Budapest, Hungary email Frederic.Bayart@uca.fr, buczo@cs.elte.hu, Yanick.Heurteaux@uca.fr
ZOLTÁN BUCZOLICH
Affiliation:
Department of Analysis, ELTE Eötvös Loránd University, Pázmány Péter Sétány 1/c, 1117Budapest, Hungary email Frederic.Bayart@uca.fr, buczo@cs.elte.hu, Yanick.Heurteaux@uca.fr
YANICK HEURTEAUX
Affiliation:
Université Clermont Auvergne, LMBP, UMR 6620 – CNRS, Campus des Cézeaux, 3 place Vasarely, TSA 60026, CS 60026 F-63178 Aubière Cedex, France Department of Analysis, ELTE Eötvös Loránd University, Pázmány Péter Sétány 1/c, 1117Budapest, Hungary email Frederic.Bayart@uca.fr, buczo@cs.elte.hu, Yanick.Heurteaux@uca.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the growth rate of the Birkhoff sums 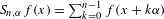$S_{n,\unicode[STIX]{x1D6FC}}f(x)=\sum _{k=0}^{n-1}f(x+k\unicode[STIX]{x1D6FC})$, where 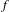$f$ is a continuous function with zero mean defined on the unit circle $\mathbb{T}$ and 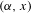$(\unicode[STIX]{x1D6FC},x)$ is a ‘typical’ element of 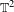$\mathbb{T}^{2}$. The answer depends on the meaning given to the word ‘typical’. Part of the work will be done in a more general context.

Keywords

Birkhoff sumtypical/generic propertiesgroup rotationcoboundarylaw of iterated logarithm

MSC classification

Primary: 37A05: Measure-preserving transformations
Secondary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension 28A78: Hausdorff and packing measures 60F15: Strong theorems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 12 , December 2020 , pp. 3236 - 3256
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atkinson, G.. Recurrence of co-cycles and random walks. J. Lond. Math. Soc. (2) 13(3) (1976), 486–488.Google Scholar
Beck, J.. Randomness of the square root of 2 and the giant leap, Part 1. Period. Math. Hungar. 60(2) (2010), 137–242.Google Scholar
Beck, J.. Randomness of the square root of 2 and the giant leap, Part 2. Period. Math. Hungar. 62(2) (2011), 127–246.Google Scholar
Billingsley, P.. Probability and Measure (Wiley Series in Probability and Statistics). Wiley, New York, 1995.Google Scholar
Bromberg, M. and Ulcigrai, C.. A temporal central limit theorem for real-valued cocycles over rotations. Ann. Inst. Henri Poincaré Probab. Stat. 54(4) (2018), 2304–2334.Google Scholar
Doob, J. L.. Stochastic Processes (Wiley Publications in Statistics). John Wiley & Sons Inc., New York; Chapman & Hall, Limited, London, 1953.Google Scholar
Eisner, T., Farkas, B., Haase, M. and Nagel, R.. Operator Theoretic Aspects of Ergodic Theory (Graduate Texts in Mathematics). Springer International Publishing, Cham, 2015.Google Scholar
Fan, A. and Schmeling, J.. On fast Birkhoff averaging. Math. Proc. Cambridge Philos. Soc. 135 (2003), 443–467.Google Scholar
Fan, A. and Schmeling, J.. Everywhere divergence of one-sided ergodic Hilbert transform. Ann. Inst. Fourier (Grenoble) 68(6) (2018), 2477–2500.Google Scholar
Herman, M.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–233.Google Scholar
Huveneers, F.. Subdiffusive behavior generated by irrational rotations. Ergod. Th. & Dynam. Sys. 29(4) (2009), 1217–1233.Google Scholar
Kahane, J.-P.. Séries de Fourier Absolument Convergentes (Ergebnisse der Mathematik und Ihrer Grenzgebiete). Springer, Berlin, 1970.Google Scholar
Kesten, H.. Uniform distribution mod 1. Ann. of Math. (2) 71 (1960), 445–471.Google Scholar
Kesten, H.. Uniform distribution mod 1. II. Acta Arith. 7 (1961/1962), 355–380.Google Scholar
Krengel, U.. On the speed of convergence in the ergodic theorem. Monatsh. Math. 86 (1978), 3–6.Google Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences (Dover Books on Mathematics). Dover Publications, Mineola, NY, 2006.Google Scholar
Liardet, P. and Volný, D.. Continuous and differentiable functions in dynamical systems. Israel J. Math. 98 (1997), 29–60.Google Scholar
Rudin, W.. Fourier Analysis on Groups (Interscience Tracts in Pure and Applied Mathematics, 12). Interscience Publishers, New York, 1962.Google Scholar
Sinai, Y.. Topics in Ergodic Theory (Princeton Mathematical Series, 44). Princeton University Press, Princeton, NY, 1994.Google Scholar
Zajiček, L.. Porosity and 𝜎-porosity. Real Anal. Exchange 13 (1987–1988), 314–350.Google Scholar