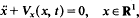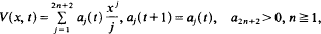Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Levi, Mark
1991.
Quasiperiodic motions in superquadratic time-periodic potentials.
Communications in Mathematical Physics,
Vol. 143,
Issue. 1,
p.
43.
Levi, M.
and
Zehnder, E.
1995.
Boundedness of Solutions for Quasiperiodic Potentials.
SIAM Journal on Mathematical Analysis,
Vol. 26,
Issue. 5,
p.
1233.
Chow, Shui-Nee
and
Pei, Ming-Liang
1995.
Aubry-mather theorem and quasiperiodic orbits for time dependent reversible systems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 25,
Issue. 9-10,
p.
905.
Kruger, T
Pustyl'nikov, L D
and
Troubetzkoy, S E
1995.
Acceleration of bouncing balls in external fields.
Nonlinearity,
Vol. 8,
Issue. 3,
p.
397.
Lamba, H.
1995.
Chaotic, regular and unbounded behaviour in the elastic impact oscillator.
Physica D: Nonlinear Phenomena,
Vol. 82,
Issue. 1-2,
p.
117.
Koiller, J
Markarian, R
Kamphorst, S O
and
Carvalho, S P de
1995.
Time-dependent billiards.
Nonlinearity,
Vol. 8,
Issue. 6,
p.
983.
Wang, Yiqian
and
You, Jiangong
1996.
Boundedness of solutions for polynomial potentials withC 2 time dependent coefficients.
ZAMP Zeitschrift f�r angewandte Mathematik und Physik,
Vol. 47,
Issue. 6,
p.
943.
Koiller, Jair
Markarian, Roberto
Oliffson Kamphorst, Sylvie
and
Pinto de Carvalho, Sônia
1996.
Static and time-dependent perturbations of the classical elliptical billiard.
Journal of Statistical Physics,
Vol. 83,
Issue. 1-2,
p.
127.
Huang, Hai
and
Yuan, Rong
1997.
Boundedness of solutions and existence of invariant tori for generalized pendulum type equation.
Chinese Science Bulletin,
Vol. 42,
Issue. 20,
p.
1673.
Kunze, M.
Küpper, T.
and
You, J.
1997.
On the Application of KAM Theory to Discontinuous Dynamical Systems.
Journal of Differential Equations,
Vol. 139,
Issue. 1,
p.
1.
Levi, Mark
and
You, Jiangong
1997.
Oscillatory Escape in a Duffing Equation with a Polynomial Potential.
Journal of Differential Equations,
Vol. 140,
Issue. 2,
p.
415.
Yuan, Xiaoping
1998.
Invariant Tori of Duffing-Type Equations.
Journal of Differential Equations,
Vol. 142,
Issue. 2,
p.
231.
Liu, B.
and
You, J.
1998.
Quasiperiodic solutions of Duffing’s equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 33,
Issue. 6,
p.
645.
Carminati, Carlo
1998.
Forced systems with almost periodic and quasiperiodic forcing term.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 32,
Issue. 6,
p.
727.
Liu, Bin
and
Zanolin, Fabio
1998.
Boundedness of Solutions of Nonlinear Differential Equations.
Journal of Differential Equations,
Vol. 144,
Issue. 1,
p.
66.
Zharnitsky, Vadim
1998.
Quasiperiodic Motion in the Hamiltonian Systems of the Billiard Type.
Physical Review Letters,
Vol. 81,
Issue. 22,
p.
4839.
Yuan, Xiaoping
1998.
Boundedness of solutions for Duffing-type equation.
Science in China Series A: Mathematics,
Vol. 41,
Issue. 6,
p.
595.
Liu, Bin
1998.
Boundedness of Solutions for Semilinear Duffing Equations.
Journal of Differential Equations,
Vol. 145,
Issue. 1,
p.
119.
Rong Yuan
1998.
Quasiperiodic solutions and boundedness of solutions for a class of nonlinear differential equations of second order.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 31,
Issue. 5-6,
p.
649.
Zharnitsky, Vadim
1998.
Instability in Fermi-Ulam `ping-pong' problem.
Nonlinearity,
Vol. 11,
Issue. 6,
p.
1481.