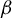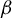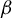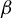1 Introduction
1.1 Expansions in base
 $\beta $
$\beta $
Throughout the paper, we fix a real number
![]() $\beta $
,
$\beta $
,
![]() $1 < \beta < 2$
. For
$1 < \beta < 2$
. For
![]() $x \in [0,1)$
, an expansion of x in base
$x \in [0,1)$
, an expansion of x in base
![]() $\beta $
is a sequence
$\beta $
is a sequence
![]() $(x_n)_{n \geqslant 1}$
of
$(x_n)_{n \geqslant 1}$
of
![]() $\{0,1\}$
such that
$\{0,1\}$
such that
 $$ \begin{align*} x = \sum_{n=1}^{+\infty} \dfrac{x_n}{\beta^n}. \end{align*} $$
$$ \begin{align*} x = \sum_{n=1}^{+\infty} \dfrac{x_n}{\beta^n}. \end{align*} $$
Rényi [Reference Rényi13] introduced the greedy map
![]() $T_{\beta }$
defined on
$T_{\beta }$
defined on
![]() $[0,1)$
by
$[0,1)$
by
![]() $T_{\beta }(x) = \beta x \ \text {mod} \ 1$
, which provides a particular expansion of any real number in
$T_{\beta }(x) = \beta x \ \text {mod} \ 1$
, which provides a particular expansion of any real number in
![]() $[0,1)$
, given by the sequence
$[0,1)$
, given by the sequence
![]() , for all
, for all
![]() $n \geqslant 1$
. This expansion is called the greedy expansion of x. In fact, almost every
$n \geqslant 1$
. This expansion is called the greedy expansion of x. In fact, almost every
![]() $x \in [0,1)$
has an infinite number of expansions in base
$x \in [0,1)$
has an infinite number of expansions in base
![]() $\beta $
, and the greedy expansion is the greatest in the lexicographic order [Reference Erdős, Joó and Komornik7].
$\beta $
, and the greedy expansion is the greatest in the lexicographic order [Reference Erdős, Joó and Komornik7].
Rényi proved that
![]() $T_{\beta }$
has a unique absolutely continuous invariant probability measure
$T_{\beta }$
has a unique absolutely continuous invariant probability measure
![]() $\nu _{\beta }$
, and Parry [Reference Parry12] proved that its density is proportional to the function
$\nu _{\beta }$
, and Parry [Reference Parry12] proved that its density is proportional to the function

and that the associated measure-preserving system is weakly mixing.
Smorodinsky then showed in [Reference Smorodinsky15] that the natural extension of this system is a Bernoulli automorphism. This result was also obtained by Dajani, Kraaikamp, and Solomyak in [Reference Dajani, Kraaikamp and Solomyak6] through a geometric construction of this natural extension, in the form of a tower.
The greedy map can be extended to a map
![]() $T_g$
defined on the interval
$T_g$
defined on the interval
![]() ${I_{\beta }\kern1.3pt{:=}\kern1.3pt[0,{1}/({\beta \kern1.3pt{-}\kern1.3pt 1})]}$
by setting
${I_{\beta }\kern1.3pt{:=}\kern1.3pt[0,{1}/({\beta \kern1.3pt{-}\kern1.3pt 1})]}$
by setting
 $$\begin{align*}T_g(x) :=\begin{cases}T_{\beta }(x) &\text{for} \ x \in [0,1[ ,\\ \beta x -1 &\text {for} \ x \in [1,{1}/({\beta - 1})]. \end{cases}\end{align*}$$
$$\begin{align*}T_g(x) :=\begin{cases}T_{\beta }(x) &\text{for} \ x \in [0,1[ ,\\ \beta x -1 &\text {for} \ x \in [1,{1}/({\beta - 1})]. \end{cases}\end{align*}$$
We will still refer to this extended map as the greedy map. The measure
![]() $\nu _{\beta }$
extended to
$\nu _{\beta }$
extended to
![]() $I_{\beta }$
by setting
$I_{\beta }$
by setting
![]() $\nu _{\beta }([1,{1}/({\,\beta - 1})]) = 0$
is still the unique absolutely continuous invariant probability measure of
$\nu _{\beta }([1,{1}/({\,\beta - 1})]) = 0$
is still the unique absolutely continuous invariant probability measure of
![]() $T_g$
on
$T_g$
on
![]() $I_{\beta }$
.
$I_{\beta }$
.
We can obtain the smallest expansion of any real number of the interval
![]() $I_{\beta }$
with the lazy map
$I_{\beta }$
with the lazy map
![]() $T_{\ell }$
[Reference Erdős, Joó and Komornik7], defined by
$T_{\ell }$
[Reference Erdős, Joó and Komornik7], defined by
 $$ \begin{align*} \begin{array}{l l c l} T_{\ell}:\!\!\!\! & I_{\beta} & \!\!\!\to\!\!\!\! & I_{\beta} \\ & x & \!\!\!\mapsto\!\!\!\! & \begin{cases} \beta x & \text{if } x \leqslant \dfrac{1}{\beta(\beta-1)},\\ \beta x -1 & \text{otherwise}. \end{cases} \\ \end{array}\!\! \end{align*} $$
$$ \begin{align*} \begin{array}{l l c l} T_{\ell}:\!\!\!\! & I_{\beta} & \!\!\!\to\!\!\!\! & I_{\beta} \\ & x & \!\!\!\mapsto\!\!\!\! & \begin{cases} \beta x & \text{if } x \leqslant \dfrac{1}{\beta(\beta-1)},\\ \beta x -1 & \text{otherwise}. \end{cases} \\ \end{array}\!\! \end{align*} $$
For
![]() $x \in I_{\beta }$
, the lazy expansion of x is given by the sequence
$x \in I_{\beta }$
, the lazy expansion of x is given by the sequence
![]() $(x^{\prime }_n)$
defined for all
$(x^{\prime }_n)$
defined for all
![]() $n \geqslant 1$
by
$n \geqslant 1$
by
![]() .
.
Let s be the symmetry on
![]() $I_{\beta }$
, defined by
$I_{\beta }$
, defined by
![]() $s(x) = {1}/({\,\beta - 1}) - x$
. The pushforward measure
$s(x) = {1}/({\,\beta - 1}) - x$
. The pushforward measure
![]() $\tilde {\nu }_{\beta } := \nu _{\beta } \circ s^{-1}$
is the unique absolutely continuous invariant measure for
$\tilde {\nu }_{\beta } := \nu _{\beta } \circ s^{-1}$
is the unique absolutely continuous invariant measure for
![]() $T_{\ell }$
, and s conjugates
$T_{\ell }$
, and s conjugates
![]() $T_g$
and
$T_g$
and
![]() $T_{\ell }$
; hence the systems
$T_{\ell }$
; hence the systems
![]() $(I_{\beta },\mathcal {B},\nu _{\beta },T_g)$
and
$(I_{\beta },\mathcal {B},\nu _{\beta },T_g)$
and
![]() $(I_{\beta },\mathcal {B},\tilde {\nu }_{\beta },T_{\ell })$
are isomorphic [Reference Dajani and Kraaikamp4].
$(I_{\beta },\mathcal {B},\tilde {\nu }_{\beta },T_{\ell })$
are isomorphic [Reference Dajani and Kraaikamp4].
In 2003, Dajani and Kraaikamp [Reference Dajani and Kraaikamp5] introduced the random
![]() $\beta $
transformation. We set
$\beta $
transformation. We set
![]() $\Omega := \{g,\ell \}^{\mathbb {N} \cup \{0\}}$
, the set of sequences of g and
$\Omega := \{g,\ell \}^{\mathbb {N} \cup \{0\}}$
, the set of sequences of g and
![]() $\ell $
. We then define the transformation
$\ell $
. We then define the transformation
![]() $K_{\beta }$
on
$K_{\beta }$
on
![]() $\Omega \times I_{\beta }$
by
$\Omega \times I_{\beta }$
by
where
![]() $\sigma $
is the left shift on
$\sigma $
is the left shift on
![]() $\Omega $
. The sequence
$\Omega $
. The sequence
![]() $\omega \in \Omega $
describes the successive transformations that will be applied to the real
$\omega \in \Omega $
describes the successive transformations that will be applied to the real
![]() $x \in I_{\beta }$
: once
$x \in I_{\beta }$
: once
![]() $T_{\omega _0}$
is applied to x, we shift the sequence
$T_{\omega _0}$
is applied to x, we shift the sequence
![]() $\omega $
to the left and then apply
$\omega $
to the left and then apply
![]() $T_{\omega _1}$
, and so on. If we fix
$T_{\omega _1}$
, and so on. If we fix
![]() $\omega \in \Omega $
, we obtain a particular expansion of x in base
$\omega \in \Omega $
, we obtain a particular expansion of x in base
![]() $\beta $
, by setting, for any
$\beta $
, by setting, for any
![]() $n \geqslant 1$
:
$n \geqslant 1$
:

where
![]() $\pi $
is the projection on
$\pi $
is the projection on
![]() $I_{\beta }$
. Any expansion of x can be obtain with a sequence
$I_{\beta }$
. Any expansion of x can be obtain with a sequence
![]() $\omega \in \Omega $
[Reference Dajani and de Vries3].
$\omega \in \Omega $
[Reference Dajani and de Vries3].
In the model we consider, the sequence
![]() $\omega $
will be drawn with the product Bernoulli measure
$\omega $
will be drawn with the product Bernoulli measure
![]() $m_p$
, where
$m_p$
, where
![]() $p \in (0,1)$
is a fixed parameter. In other words, we draw each transformation independently with probability p for
$p \in (0,1)$
is a fixed parameter. In other words, we draw each transformation independently with probability p for
![]() $T_g$
and
$T_g$
and
![]() $1-p$
for
$1-p$
for
![]() $T_{\ell }$
. Dajani and De Vries proved in [Reference Dajani and de Vries3] that there is a unique absolutely continuous probability measure
$T_{\ell }$
. Dajani and De Vries proved in [Reference Dajani and de Vries3] that there is a unique absolutely continuous probability measure
![]() $\mu _p$
on
$\mu _p$
on
![]() $I_{\beta }$
such that
$I_{\beta }$
such that
![]() $m_p \otimes \mu _p$
is
$m_p \otimes \mu _p$
is
![]() $K_{\beta }$
-invariant. Kempton [Reference Kempton11] obtained an expression of the density
$K_{\beta }$
-invariant. Kempton [Reference Kempton11] obtained an expression of the density
![]() $\rho _{1/2}$
of
$\rho _{1/2}$
of
![]() $\mu _{1/2}$
with the construction of a natural extension of
$\mu _{1/2}$
with the construction of a natural extension of
![]() $(\Omega \times I_{\beta },m_{1/2} \otimes \mu _{1/2},\mathcal {K}_{\beta })$
, using two symmetric towers. Suzuki [Reference Suzuki16] then generalized this expression for any p with the use of the Perron–Frobenius operators.
$(\Omega \times I_{\beta },m_{1/2} \otimes \mu _{1/2},\mathcal {K}_{\beta })$
, using two symmetric towers. Suzuki [Reference Suzuki16] then generalized this expression for any p with the use of the Perron–Frobenius operators.
1.2 Roadmap of this paper
In this paper, we consider several extensions of the random
![]() $\beta $
-transformation. See Figure 1. In §2, we construct a first geometrico-symbolic extension
$\beta $
-transformation. See Figure 1. In §2, we construct a first geometrico-symbolic extension
![]() $\mathcal {K}$
of the random transformation. This extension is defined on two towers (the greedy tower and the lazy tower), each tower having a ‘base’. By providing a simple invariant measure on this extension and projecting it on
$\mathcal {K}$
of the random transformation. This extension is defined on two towers (the greedy tower and the lazy tower), each tower having a ‘base’. By providing a simple invariant measure on this extension and projecting it on
![]() $I_{\beta }$
, we obtain the expression of the density of
$I_{\beta }$
, we obtain the expression of the density of
![]() $\mu _p$
for any
$\mu _p$
for any
![]() $p \in (0,1)$
(formula (8)). We then study the transformation
$p \in (0,1)$
(formula (8)). We then study the transformation
![]() $\mathcal {K}_g$
induced by
$\mathcal {K}_g$
induced by
![]() $\mathcal {K}$
on the base of the greedy tower, and define a particular partition of this base. We prove that this partition is an independent generator of the induced system (Proposition 10), and thus prove that this induced system is isomorphic to a unilateral Bernoulli shift. This provides a new proof of the ergodicity of the random system and of the uniqueness of
$\mathcal {K}$
on the base of the greedy tower, and define a particular partition of this base. We prove that this partition is an independent generator of the induced system (Proposition 10), and thus prove that this induced system is isomorphic to a unilateral Bernoulli shift. This provides a new proof of the ergodicity of the random system and of the uniqueness of
![]() $\mu _p$
. This first extension is not yet invertible. In §3, we construct a geometrico-symbolic version of the natural extension of this first extension. With the use of the relatively independent joining above a factor, we prove that this new extension is in fact the natural extension of the random
$\mu _p$
. This first extension is not yet invertible. In §3, we construct a geometrico-symbolic version of the natural extension of this first extension. With the use of the relatively independent joining above a factor, we prove that this new extension is in fact the natural extension of the random
![]() $\beta $
-transformation (Theorem 21). We then prove that this extension is isomorphic to a bilateral Bernoulli shift (Theorem 26), by ‘unfolding’ the previous partition on the two towers.
$\beta $
-transformation (Theorem 21). We then prove that this extension is isomorphic to a bilateral Bernoulli shift (Theorem 26), by ‘unfolding’ the previous partition on the two towers.

Figure 1 Extensions involved in this paper.
2 The first extension
In this section, we extend the dynamics
![]() $K_{\beta }$
on two towers. Kempton [Reference Kempton11] implemented the same type of strategy in the case
$K_{\beta }$
on two towers. Kempton [Reference Kempton11] implemented the same type of strategy in the case
![]() $p = \tfrac 12$
, but his construction does not generalize to any p. We construct a different extension, valid for any
$p = \tfrac 12$
, but his construction does not generalize to any p. We construct a different extension, valid for any
![]() $p \in (0,1)$
.
$p \in (0,1)$
.
2.1 The domain of the extension: the greedy and lazy towers
As in [Reference Kempton11], the towers are made of floors. We first define the ‘base’ of each tower. Let
![]() $E_g$
be the base of the greedy tower
$E_g$
be the base of the greedy tower
![]() $\mathcal {G}$
, defined by
$\mathcal {G}$
, defined by
The label of the greedy base is
![]() $(g)$
, telling us that it is the first floor of the greedy tower
$(g)$
, telling us that it is the first floor of the greedy tower
![]() $\mathcal {G}$
. Likewise,
$\mathcal {G}$
. Likewise,
![]() $E_{\ell }$
is the base of the lazy tower
$E_{\ell }$
is the base of the lazy tower
![]() $\mathcal {L}$
, defined by
$\mathcal {L}$
, defined by
 $$ \begin{align*}E_{\ell} := \Omega \times \{\ell\} \times \bigg[s(1),\dfrac{1}{\beta - 1}\bigg]. \end{align*} $$
$$ \begin{align*}E_{\ell} := \Omega \times \{\ell\} \times \bigg[s(1),\dfrac{1}{\beta - 1}\bigg]. \end{align*} $$
A floor in one of the towers is denoted by
![]() $E_e$
, where e is the label of the floor. This floor is of the form
$E_e$
, where e is the label of the floor. This floor is of the form
where
![]() $I_e$
is a sub-interval of
$I_e$
is a sub-interval of
![]() $I_{\beta }$
that will be specified later. Thus, a point in one of the two towers is of the form
$I_{\beta }$
that will be specified later. Thus, a point in one of the two towers is of the form
![]() $c = (\omega , e,x)$
, where the following hold.
$c = (\omega , e,x)$
, where the following hold.
-
• The sequence
 $\omega \in \{g,\ell \}^{\mathbb {N} \cup \{0\}}$
describes the successive transformations
$\omega \in \{g,\ell \}^{\mathbb {N} \cup \{0\}}$
describes the successive transformations
 $T_g$
and
$T_g$
and
 $T_{\ell }$
to be applied to x.
$T_{\ell }$
to be applied to x. -
• The label e is of the form
and characterizes the floor containing the point c. The letter h indicates the tower in which: if $$ \begin{align*} e = (h, \omega_{-n}, \omega_{-n+1}, \ldots, \omega_{-1}) \end{align*} $$
$$ \begin{align*} e = (h, \omega_{-n}, \omega_{-n+1}, \ldots, \omega_{-1}) \end{align*} $$
 $h =g$
, the floor is from the greedy tower; and if
$h =g$
, the floor is from the greedy tower; and if
 $h = \ell $
, the floor is from the lazy tower. The integer n is the level of the floor
$h = \ell $
, the floor is from the lazy tower. The integer n is the level of the floor
 $E_e$
. Therefore, there are
$E_e$
. Therefore, there are
 $2^n$
floors of level n in each tower, the bases being at level
$2^n$
floors of level n in each tower, the bases being at level
 $0$
. Finally, the symbols
$0$
. Finally, the symbols
 $\omega _{-n},\ldots ,\omega _{-1}$
indicate the applied transformations since the last passage in one of the two bases; in other words, the maps
$\omega _{-n},\ldots ,\omega _{-1}$
indicate the applied transformations since the last passage in one of the two bases; in other words, the maps
 $T_{\omega _{-n}}$
to
$T_{\omega _{-n}}$
to
 $T_{\omega _{-1}}$
were applied to the real component of a point in
$T_{\omega _{-1}}$
were applied to the real component of a point in
 $E_e$
since the base
$E_e$
since the base
 $E_h$
.
$E_h$
.
-
• x represents the real component of the point c, on which will be applied the transformation
 $T_{\omega _0}$
. We have
$T_{\omega _0}$
. We have
 $x \in I_e$
, where where the
$x \in I_e$
, where where the $$ \begin{align*} \begin{cases} I_e := [0,T_{\omega_{-n}, \omega_{-n+1}, \ldots, \omega_{-1}}(1^+)] & \text{if } h = g, \\ I_e := \bigg[T_{\omega_{-n}, \omega_{-n+1}, \ldots, \omega_{-1}}(s(1)^-),\dfrac{1}{\beta - 1}\bigg] & \text{if } h = \ell, \end{cases}\! \end{align*} $$
$$ \begin{align*} \begin{cases} I_e := [0,T_{\omega_{-n}, \omega_{-n+1}, \ldots, \omega_{-1}}(1^+)] & \text{if } h = g, \\ I_e := \bigg[T_{\omega_{-n}, \omega_{-n+1}, \ldots, \omega_{-1}}(s(1)^-),\dfrac{1}{\beta - 1}\bigg] & \text{if } h = \ell, \end{cases}\! \end{align*} $$
 $+$
and
$+$
and
 $-$
signs respectively refer to the right and left limit at the considered points, and
$-$
signs respectively refer to the right and left limit at the considered points, and
 $T_{\omega _{-n}, \omega _{-n+1}, \ldots , \omega _{-1}}$
is the composition
$T_{\omega _{-n}, \omega _{-n+1}, \ldots , \omega _{-1}}$
is the composition
 $T_{\omega _{-1}} \circ \cdots \circ T_{\omega _{-n}}$
. For simplification, we will often denote
$T_{\omega _{-1}} \circ \cdots \circ T_{\omega _{-n}}$
. For simplification, we will often denote
 $T_v$
with
$T_v$
with
 $v \in \{g,\ell \}^n$
to refer to this type of composition.
$v \in \{g,\ell \}^n$
to refer to this type of composition.
We then define the greedy tower as the disjoint union of all floors whose label starts with a g, and the lazy tower as the disjoint union of all floors whose label starts with an
![]() $\ell $
:
$\ell $
:
 $$ \begin{align*} \mathcal{G} := \bigsqcup_{e' \in \{g,\ell\}^*}E_{g \cdot e'}, \end{align*} $$
$$ \begin{align*} \mathcal{G} := \bigsqcup_{e' \in \{g,\ell\}^*}E_{g \cdot e'}, \end{align*} $$
 $$ \begin{align*}\mathcal{L} := \bigsqcup_{e' \in \{g,\ell\}^*}E_{\ell \cdot e'}, \end{align*} $$
$$ \begin{align*}\mathcal{L} := \bigsqcup_{e' \in \{g,\ell\}^*}E_{\ell \cdot e'}, \end{align*} $$
where the point
![]() $\cdot $
represents the concatenation, and the set
$\cdot $
represents the concatenation, and the set
![]() $\{g,\ell \}^*$
is the set of finite sequences (including the empty sequence) of g and
$\{g,\ell \}^*$
is the set of finite sequences (including the empty sequence) of g and
![]() $\ell $
. We then denote by
$\ell $
. We then denote by
![]() $X:= \mathcal {G} \sqcup \mathcal {L}$
the disjoint union of the two towers, on which will be defined
$X:= \mathcal {G} \sqcup \mathcal {L}$
the disjoint union of the two towers, on which will be defined
![]() $\mathcal {K}$
. Finally, given a floor of X, we call the length of this floor the Lebesgue measure of the associated interval.
$\mathcal {K}$
. Finally, given a floor of X, we call the length of this floor the Lebesgue measure of the associated interval.
Applying the dynamics
![]() $\mathcal {K}$
to a point in a tower consists in going up a level in the tower, or going back to the base of the tower, or going to the base of the other tower, depending on certain conditions that we will detail in the next section.
$\mathcal {K}$
to a point in a tower consists in going up a level in the tower, or going back to the base of the tower, or going to the base of the other tower, depending on certain conditions that we will detail in the next section.
We represent the two towers in Figure 2, one above the other (the lazy tower is represented upside down). The
![]() $\omega $
-component is represented vertically. Two points on a same vertical line have the same real coordinate x.
$\omega $
-component is represented vertically. Two points on a same vertical line have the same real coordinate x.

Figure 2 Greedy and lazy towers.
2.2 The dynamics on the two towers
We define the dynamics
![]() $\mathcal {K}$
on the greedy tower first. We consider a floor of
$\mathcal {K}$
on the greedy tower first. We consider a floor of
![]() $\mathcal {G}$
, with label
$\mathcal {G}$
, with label
![]() $e := (g,\omega _{-n},\ldots , \omega _{-1})$
. The floor
$e := (g,\omega _{-n},\ldots , \omega _{-1})$
. The floor
![]() $E_e$
is split into two parts, depending on
$E_e$
is split into two parts, depending on
![]() $\omega _0$
:
$\omega _0$
:
where
![]() $E_e \cap [g]_0$
abusively refers to the set of points
$E_e \cap [g]_0$
abusively refers to the set of points
![]() $(\omega ,e,x)$
of
$(\omega ,e,x)$
of
![]() $E_e$
such that
$E_e$
such that
![]() $\omega _0 = g$
(and in the same way for
$\omega _0 = g$
(and in the same way for
![]() $\ell $
). The dynamics
$\ell $
). The dynamics
![]() $\mathcal {K}$
is different on each of these parts. In the following, we denote by t the upper bound of
$\mathcal {K}$
is different on each of these parts. In the following, we denote by t the upper bound of
![]() $I_e$
.
$I_e$
.
-
(1) If
 $\omega _0 = g$
and if
$\omega _0 = g$
and if
 $t <{1}/{\beta }$
(see Figure 3): Here,
$t <{1}/{\beta }$
(see Figure 3): Here, $$ \begin{align*}\mathcal{K}:\!\! \begin{array}{l c l} E_{e} \cap [g]_0 & \!\!\!\to\!\!\!\! & E_{e \cdot g} \\ (\omega,e,x) & \!\!\!\mapsto\!\!\!\! & (\sigma(\omega),e \cdot g,\beta x). \end{array}\end{align*} $$
$$ \begin{align*}\mathcal{K}:\!\! \begin{array}{l c l} E_{e} \cap [g]_0 & \!\!\!\to\!\!\!\! & E_{e \cdot g} \\ (\omega,e,x) & \!\!\!\mapsto\!\!\!\! & (\sigma(\omega),e \cdot g,\beta x). \end{array}\end{align*} $$
 $\mathcal {K}$
sends
$\mathcal {K}$
sends
 $E_e \cap [g]_0$
onto the floor
$E_e \cap [g]_0$
onto the floor
 $E_{e \cdot g}$
.
$E_{e \cdot g}$
.
Figure 3
 $\omega _0 = g$
and
$\omega _0 = g$
and
 $t < {1}/{\beta }$
.
$t < {1}/{\beta }$
. -
(2) If
 $\omega _0 = g$
and if
$\omega _0 = g$
and if
 $t \geqslant {1}/{\beta }$
, the left part of the floor is sent back onto the base
$t \geqslant {1}/{\beta }$
, the left part of the floor is sent back onto the base
 $E_g$
(see Figure 4):
$E_g$
(see Figure 4):  $$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = g, x < \dfrac{1}{\beta}\bigg\} &\to E_g \\ (\omega,e,x)&\mapsto(\sigma(\omega),g,\beta x); \end{array} \end{align*} $$
$$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = g, x < \dfrac{1}{\beta}\bigg\} &\to E_g \\ (\omega,e,x)&\mapsto(\sigma(\omega),g,\beta x); \end{array} \end{align*} $$

Figure 4
 $\omega _0 = g$
and
$\omega _0 = g$
and
 $t \geqslant {1}/{\beta }$
.
$t \geqslant {1}/{\beta }$
.and the right part goes up onto
 $E_{e \cdot g}$
:
$E_{e \cdot g}$
:  $$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = g, x \geqslant \dfrac{1}{\beta}\bigg\} &\to E_{e \cdot g} \\ (\omega,e,x) &\mapsto (\sigma(\omega),e \cdot g,\beta x - 1) .\end{array}\end{align*} $$
$$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = g, x \geqslant \dfrac{1}{\beta}\bigg\} &\to E_{e \cdot g} \\ (\omega,e,x) &\mapsto (\sigma(\omega),e \cdot g,\beta x - 1) .\end{array}\end{align*} $$
-
(3) If
 $\omega _0 = \ell $
and if
$\omega _0 = \ell $
and if
 $t < {1}/{\beta (\beta - 1)}$
(see Figure 5): The part
$t < {1}/{\beta (\beta - 1)}$
(see Figure 5): The part $$ \begin{align*} \mathcal{K}:\!\! \begin{array}{l c l} E_e \cap [\ell]_0 & \!\!\!\to\!\!\!\! & E_{e \cdot \ell} \\ (\omega,e,x) & \!\!\!\mapsto\!\!\!\! & (\sigma(\omega),e \cdot \ell,\beta x). \end{array} \end{align*} $$
$$ \begin{align*} \mathcal{K}:\!\! \begin{array}{l c l} E_e \cap [\ell]_0 & \!\!\!\to\!\!\!\! & E_{e \cdot \ell} \\ (\omega,e,x) & \!\!\!\mapsto\!\!\!\! & (\sigma(\omega),e \cdot \ell,\beta x). \end{array} \end{align*} $$
 $E_e \cap [\ell ]_0 $
is sent onto the floor
$E_e \cap [\ell ]_0 $
is sent onto the floor
 $E_{e \cdot \ell }$
.
$E_{e \cdot \ell }$
.
Figure 5
 $\omega _0 = \ell $
and
$\omega _0 = \ell $
and
 $t < {1}/{\beta (\beta - 1)}$
.
$t < {1}/{\beta (\beta - 1)}$
. -
(4) If
 $\omega _0 = \ell $
and if
$\omega _0 = \ell $
and if
 $t \geqslant {1}/{\beta (\beta - 1)}$
(see Figure 6), the central part of the floor is sent onto the base
$t \geqslant {1}/{\beta (\beta - 1)}$
(see Figure 6), the central part of the floor is sent onto the base
 $E_{\ell }$
:
$E_{\ell }$
:  $$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = \ell, \dfrac{s(1)}{\beta} < x \leqslant \dfrac{1}{\beta(\beta - 1)}\bigg\} & \to E_{\ell} \\ (\omega,e,x) & \mapsto (\sigma(\omega),\ell,\beta x) ;\end{array} \end{align*} $$
$$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = \ell, \dfrac{s(1)}{\beta} < x \leqslant \dfrac{1}{\beta(\beta - 1)}\bigg\} & \to E_{\ell} \\ (\omega,e,x) & \mapsto (\sigma(\omega),\ell,\beta x) ;\end{array} \end{align*} $$

Figure 6
 $\omega _0 = \ell $
and
$\omega _0 = \ell $
and
 $t \geqslant {1}/{\beta (\beta - 1)}$
.
$t \geqslant {1}/{\beta (\beta - 1)}$
.and the left and right parts go up onto
 $E_{e \cdot \ell }$
:
$E_{e \cdot \ell }$
:  $$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = \ell, x \leqslant \dfrac{s(1)}{\beta}\bigg\} &\to E_{e \cdot \ell} \\ (\omega,e,x) &\mapsto (\sigma(\omega),e \cdot \ell,\beta x) ;\end{array} \end{align*} $$
$$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = \ell, x \leqslant \dfrac{s(1)}{\beta}\bigg\} &\to E_{e \cdot \ell} \\ (\omega,e,x) &\mapsto (\sigma(\omega),e \cdot \ell,\beta x) ;\end{array} \end{align*} $$
 $$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = \ell, x> \dfrac{1}{\beta(\beta - 1)}\bigg\} & \to E_{e \cdot \ell} \\ (\omega,e,x) &\mapsto (\sigma(\omega),e \cdot \omega_0,\beta x - 1). \end{array} \end{align*} $$
$$ \begin{align*} \mathcal{K}:\!\! \begin{array}{r@{\ }l} E_e \cap \bigg\{\omega_0 = \ell, x> \dfrac{1}{\beta(\beta - 1)}\bigg\} & \to E_{e \cdot \ell} \\ (\omega,e,x) &\mapsto (\sigma(\omega),e \cdot \omega_0,\beta x - 1). \end{array} \end{align*} $$
On the lazy tower, the dynamics
![]() $\mathcal {K}$
is defined in the same way by symmetry (see Figures 7 and 8).
$\mathcal {K}$
is defined in the same way by symmetry (see Figures 7 and 8).

Figure 7 Overview of the dynamics on a floor
![]() $E_e$
of the greedy tower, depending on the length of the floor.
$E_e$
of the greedy tower, depending on the length of the floor.

Figure 8 Overview of the dynamics on a floor
![]() $E_e$
of the lazy tower (reversed), depending on the length of the floor.
$E_e$
of the lazy tower (reversed), depending on the length of the floor.
We denote by
![]() $\pi : X \to \Omega \times I_{\beta }$
the projection onto
$\pi : X \to \Omega \times I_{\beta }$
the projection onto
![]() $\Omega \times I_{\beta }$
. By construction, we have
$\Omega \times I_{\beta }$
. By construction, we have
2.3 Construction of an invariant measure
The goal of this section is to define a
![]() $\mathcal {K}$
-invariant measure
$\mathcal {K}$
-invariant measure
![]() $\mu $
on X, such that the projection of this measure on
$\mu $
on X, such that the projection of this measure on
![]() $I_{\beta }$
is absolutely continuous. We denote the Lebesgue measure by
$I_{\beta }$
is absolutely continuous. We denote the Lebesgue measure by
![]() $\unicode{x3bb} $
, regardless of the interval on which we consider it. We recall that
$\unicode{x3bb} $
, regardless of the interval on which we consider it. We recall that
![]() $m_p$
is the product Bernoulli measure of parameter p on
$m_p$
is the product Bernoulli measure of parameter p on
![]() $\Omega $
(we draw g with probability p and
$\Omega $
(we draw g with probability p and
![]() $\ell $
with probability
$\ell $
with probability
![]() $1-p$
, independently at each step).
$1-p$
, independently at each step).
We first define the measures
![]() $\mu _g$
and
$\mu _g$
and
![]() $\mu _{\ell }$
with respective support
$\mu _{\ell }$
with respective support
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {L}$
as follows.
$\mathcal {L}$
as follows.
On the bases, we set:
On the floor
![]() $E_{g,\omega _{-n},\ldots ,\omega _{-1}}$
, the measure
$E_{g,\omega _{-n},\ldots ,\omega _{-1}}$
, the measure
![]() $\mu _g$
is defined by
$\mu _g$
is defined by
where
![]() $[\omega _{-n},\ldots ,\omega _{-1}]_0^{n-1}$
is the cylinder of
$[\omega _{-n},\ldots ,\omega _{-1}]_0^{n-1}$
is the cylinder of
![]() $\Omega $
containing the sequences
$\Omega $
containing the sequences
![]() $\omega $
whose n first terms are
$\omega $
whose n first terms are
![]() $(\omega _{-n},\ldots ,\omega _{-1})$
.
$(\omega _{-n},\ldots ,\omega _{-1})$
.
Likewise on the floor
![]() $E_{\ell ,\omega _{-n},\ldots ,\omega _{-1}}$
, the measure
$E_{\ell ,\omega _{-n},\ldots ,\omega _{-1}}$
, the measure
![]() $\mu _{\ell }$
is defined by
$\mu _{\ell }$
is defined by
On their respective tower, the measure
![]() $\mu _g$
and
$\mu _g$
and
![]() $\mu _{\ell }$
are preserved by
$\mu _{\ell }$
are preserved by
![]() $\mathcal {K}$
when it goes up in the tower, but we look for a measure
$\mathcal {K}$
when it goes up in the tower, but we look for a measure
![]() $\mu $
on X, globally preserved by
$\mu $
on X, globally preserved by
![]() $\mathcal {K}$
. The following theorem describes the situation in a more abstract framework, and shows the existence of the measure
$\mathcal {K}$
. The following theorem describes the situation in a more abstract framework, and shows the existence of the measure
![]() $\mu $
.
$\mu $
.
Theorem 1. Let
![]() $(X,\mathcal {B})$
be a standard Borel space,
$(X,\mathcal {B})$
be a standard Borel space,
![]() $\mathcal {K}$
a transformation on X, and
$\mathcal {K}$
a transformation on X, and
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {L}$
two disjoint subsets of X such that the following hold.
$\mathcal {L}$
two disjoint subsets of X such that the following hold.
-
(1)
 $X = \mathcal {G} \sqcup \mathcal {L}$
.
$X = \mathcal {G} \sqcup \mathcal {L}$
. -
(2) There exist two sets
 $E_g \subset \mathcal {G}$
and
$E_g \subset \mathcal {G}$
and
 $E_{\ell } \subset \mathcal {L}$
such that (1)and
$E_{\ell } \subset \mathcal {L}$
such that (1)and $$ \begin{align} \mathcal{K}(\mathcal{G}) \subset \mathcal{G} \cup E_{\ell} \end{align} $$
$$ \begin{align} \mathcal{K}(\mathcal{G}) \subset \mathcal{G} \cup E_{\ell} \end{align} $$
 $$ \begin{align*} \mathcal{K}(\mathcal{L}) \subset \mathcal{L} \cup E_g. \end{align*} $$
$$ \begin{align*} \mathcal{K}(\mathcal{L}) \subset \mathcal{L} \cup E_g. \end{align*} $$
-
(3) There exist two finite measures
 $\mu _g$
and
$\mu _g$
and
 $\mu _{\ell }$
with respective support in
$\mu _{\ell }$
with respective support in
 $\mathcal {G}$
and
$\mathcal {G}$
and
 $\mathcal {L}$
such that and for any measurable A of
$\mathcal {L}$
such that and for any measurable A of $$ \begin{align*} \mu_g(E_g) = \mu_{\ell}(E_{\ell}) = 1 \end{align*} $$
$$ \begin{align*} \mu_g(E_g) = \mu_{\ell}(E_{\ell}) = 1 \end{align*} $$
 $\mathcal {G} \setminus E_g$
, we have (2)
$\mathcal {G} \setminus E_g$
, we have (2) $$ \begin{align} \mu_g(\mathcal{K}^{\,-1}(A)) = \mu_g(A), \end{align} $$
$$ \begin{align} \mu_g(\mathcal{K}^{\,-1}(A)) = \mu_g(A), \end{align} $$
and for any measurable A of
 $\mathcal {L} \setminus E_{\ell }$
, we have
$\mathcal {L} \setminus E_{\ell }$
, we have  $$ \begin{align*} \mu_{\ell}(\mathcal{K}^{\,-1}(A)) = \mu_{\ell}(A). \end{align*} $$
$$ \begin{align*} \mu_{\ell}(\mathcal{K}^{\,-1}(A)) = \mu_{\ell}(A). \end{align*} $$
-
(4) There exists positive constants
 $g_0, \ell _0, g_1, \ell _1$
such that for any measurable A of X included in
$g_0, \ell _0, g_1, \ell _1$
such that for any measurable A of X included in
 $E_g$
, we have (3)and
$E_g$
, we have (3)and $$ \begin{align} \mu_g(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) = g_0 \mu_g(A) \end{align} $$
(4)
$$ \begin{align} \mu_g(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) = g_0 \mu_g(A) \end{align} $$
(4) $$ \begin{align} \mu_{\ell}(\mathcal{K}^{\,-1}(A) \cap \mathcal{L})) = \ell_0 \mu_g(A), \end{align} $$
$$ \begin{align} \mu_{\ell}(\mathcal{K}^{\,-1}(A) \cap \mathcal{L})) = \ell_0 \mu_g(A), \end{align} $$
and for any measurable A of X included in
 $E_{\ell }$
, we have and
$E_{\ell }$
, we have and $$ \begin{align*} \mu_g(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) = g_1 \mu_{\ell}(A) \end{align*} $$
$$ \begin{align*} \mu_g(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) = g_1 \mu_{\ell}(A) \end{align*} $$
 $$ \begin{align*} \mu_{\ell}(\mathcal{K}^{\,-1}(A) \cap \mathcal{L})) = \ell_1 \mu_{\ell}(A). \end{align*} $$
$$ \begin{align*} \mu_{\ell}(\mathcal{K}^{\,-1}(A) \cap \mathcal{L})) = \ell_1 \mu_{\ell}(A). \end{align*} $$
Then there exist a unique probability measure
![]() $\mu $
on X, linear combination of
$\mu $
on X, linear combination of
![]() $\mu _g$
and
$\mu _g$
and
![]() $\mu _{\ell }$
, such that
$\mu _{\ell }$
, such that
![]() $\mu $
is
$\mu $
is
![]() $\mathcal {K}$
-invariant.
$\mathcal {K}$
-invariant.
Proof. Let
![]() $\mu $
be a measure of the form
$\mu $
be a measure of the form
with
![]() $\Gamma _g$
and
$\Gamma _g$
and
![]() $\Gamma _{\ell }$
two positive constants. We wish to determine the values of
$\Gamma _{\ell }$
two positive constants. We wish to determine the values of
![]() $\Gamma _g$
and
$\Gamma _g$
and
![]() $\Gamma _{\ell }$
such that
$\Gamma _{\ell }$
such that
![]() $\mu $
is a
$\mu $
is a
![]() $\mathcal {K}$
-invariant probability measure on X.
$\mathcal {K}$
-invariant probability measure on X.
Let A be a measurable subset of X included in
![]() $\mathcal {G} \setminus E_g$
. We have
$\mathcal {G} \setminus E_g$
. We have
![]() $\mu (A) = \Gamma _g\mu _g(A)$
. Then, by the assumptions in equations (1) and (2), we have
$\mu (A) = \Gamma _g\mu _g(A)$
. Then, by the assumptions in equations (1) and (2), we have
Similarly, for any measurable A of X included in
![]() $\mathcal {L} \setminus E_{\ell }$
:
$\mathcal {L} \setminus E_{\ell }$
:
Let A be a measurable subset of X included in
![]() $E_g$
. We have, by the assumptions in equations (3) and (4):
$E_g$
. We have, by the assumptions in equations (3) and (4):
 $$ \begin{align*} \mu(\mathcal{K}^{\,-1}(A)) =& \ \mu(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) + \mu(\mathcal{K}^{\,-1}(A) \cap \mathcal{L}) \\ =& \ \Gamma_g\mu_g(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) + \Gamma_{\ell} \mu_{\ell}(\mathcal{K}^{\,-1}(A) \cap \mathcal{L}) \\ =& \ g_0 \Gamma_g \mu_g(A) + \ell_0 \Gamma_{\ell} \mu_g(A) \\ =& \ (g_0 \Gamma_g + \ell_0 \Gamma_{\ell})\mu_g(A). \end{align*} $$
$$ \begin{align*} \mu(\mathcal{K}^{\,-1}(A)) =& \ \mu(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) + \mu(\mathcal{K}^{\,-1}(A) \cap \mathcal{L}) \\ =& \ \Gamma_g\mu_g(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) + \Gamma_{\ell} \mu_{\ell}(\mathcal{K}^{\,-1}(A) \cap \mathcal{L}) \\ =& \ g_0 \Gamma_g \mu_g(A) + \ell_0 \Gamma_{\ell} \mu_g(A) \\ =& \ (g_0 \Gamma_g + \ell_0 \Gamma_{\ell})\mu_g(A). \end{align*} $$
Therefore,
![]() $\mu (\mathcal {K}^{\,-1}(A)) = \mu (A)$
if and only if
$\mu (\mathcal {K}^{\,-1}(A)) = \mu (A)$
if and only if
Likewise, if A is a measurable subset of X included in
![]() $E_{\ell }$
,
$E_{\ell }$
,
![]() $\mu (\mathcal {K}^{\,-1}(A)) = \mu (A)$
if and only if
$\mu (\mathcal {K}^{\,-1}(A)) = \mu (A)$
if and only if
We need both the equations (5) and (6) to be satisfied. In other words, we solve the system:
 $$ \begin{align} \begin{cases} (g_0-1)\Gamma_g + \ell_0 \Gamma_{\ell}=0, \\ g_1 \Gamma_g + (\ell_1 -1)\Gamma_{\ell}=0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} (g_0-1)\Gamma_g + \ell_0 \Gamma_{\ell}=0, \\ g_1 \Gamma_g + (\ell_1 -1)\Gamma_{\ell}=0. \end{cases} \end{align} $$
From the assumption in equation (1), we have
and since
![]() $\mu _g(\mathcal {K}^{\,-1}(\mathcal {G} \setminus E_g)) = \mu _g(\mathcal {G} \setminus E_g)$
, we get
$\mu _g(\mathcal {K}^{\,-1}(\mathcal {G} \setminus E_g)) = \mu _g(\mathcal {G} \setminus E_g)$
, we get
Since
![]() $\mu _g(E_g) = 1$
, we deduce that
$\mu _g(E_g) = 1$
, we deduce that
Similarly,
Therefore, the system in equation (7) can be reduced to
For
![]() $\mu $
to be a probability measure, we must also have
$\mu $
to be a probability measure, we must also have
We finally obtain the (positive) values
 $$ \begin{align*} \Gamma_g = \dfrac{\ell_0}{\ell_0 \mu_g(\mathcal{G}) + g_1 \mu_{\ell}(\mathcal{L})} \end{align*} $$
$$ \begin{align*} \Gamma_g = \dfrac{\ell_0}{\ell_0 \mu_g(\mathcal{G}) + g_1 \mu_{\ell}(\mathcal{L})} \end{align*} $$
and
With this choice of constants, the measure
![]() $\mu $
is a
$\mu $
is a
![]() $\mathcal {K}$
-invariant probability measure on X.
$\mathcal {K}$
-invariant probability measure on X.
Let us prove that the extension built in the previous section satisfies the assumptions of Theorem 1.
-
(1) The greedy and lazy towers are disjoint.
-
(2) Under the action of
 $\mathcal {K}$
, any element of
$\mathcal {K}$
, any element of
 $\mathcal {G}$
can go up in the tower
$\mathcal {G}$
can go up in the tower
 $\mathcal {G}$
, or go back to the base
$\mathcal {G}$
, or go back to the base
 $E_g$
, or be sent in the lazy base
$E_g$
, or be sent in the lazy base
 $E_{\ell }$
, and the situation is symmetric for the elements of the lazy tower.
$E_{\ell }$
, and the situation is symmetric for the elements of the lazy tower. -
(3) The measures
 $\mu _g$
and
$\mu _g$
and
 $\mu _{\ell }$
have their respective support in
$\mu _{\ell }$
have their respective support in
 $\mathcal {G}$
and
$\mathcal {G}$
and
 $\mathcal {L}$
, and
$\mathcal {L}$
, and
 $\mu _g(E_g) = \mu _{\ell }(E_{\ell }) = 1$
. Let A be a measurable subset of
$\mu _g(E_g) = \mu _{\ell }(E_{\ell }) = 1$
. Let A be a measurable subset of
 $E_{g,\omega _{-n},\ldots ,\omega _{-1}}$
of the form
$E_{g,\omega _{-n},\ldots ,\omega _{-1}}$
of the form
 $A := [u]_0^{|u|-1} \times \{(g,\omega _{-n},\ldots ,\omega _{-1})\} \times [a,b]$
, where u is a finite sequence of elements of
$A := [u]_0^{|u|-1} \times \{(g,\omega _{-n},\ldots ,\omega _{-1})\} \times [a,b]$
, where u is a finite sequence of elements of
 $\{g,\ell \}$
, and
$\{g,\ell \}$
, and
 $|u|$
denotes the length of this sequence. Let us prove that A and
$|u|$
denotes the length of this sequence. Let us prove that A and
 $\mathcal {K}^{\,-1}(A)$
have the same measure. We have
$\mathcal {K}^{\,-1}(A)$
have the same measure. We have  $$ \begin{align*} \mu_g(\mathcal{K}^{\,-1}(A)) & = \dfrac{1}{\beta^{n-1}} m_p([\omega_{-n},\ldots,\omega_{-2}]_0^{n-2}) m_p([\omega_{-1} \cdot u]_0^{|u|}) \dfrac{1}{\beta}(b-a) \\ & = \dfrac{1}{\beta^n} m_p([\omega_{-n},\ldots,\omega_{-1}]_0^{n-1})m_p([u]_0^{|u|-1}) (b-a). \end{align*} $$
$$ \begin{align*} \mu_g(\mathcal{K}^{\,-1}(A)) & = \dfrac{1}{\beta^{n-1}} m_p([\omega_{-n},\ldots,\omega_{-2}]_0^{n-2}) m_p([\omega_{-1} \cdot u]_0^{|u|}) \dfrac{1}{\beta}(b-a) \\ & = \dfrac{1}{\beta^n} m_p([\omega_{-n},\ldots,\omega_{-1}]_0^{n-1})m_p([u]_0^{|u|-1}) (b-a). \end{align*} $$
We then deduce that for any measurable set A of
 $\mathcal {G} \setminus E_g$
, we have
$\mathcal {G} \setminus E_g$
, we have
 $\mu _g(\mathcal {K}^{\,-1}(A)) \,{=}\, \mu _g(A)$
. Similarly, for any measurable set A of
$\mu _g(\mathcal {K}^{\,-1}(A)) \,{=}\, \mu _g(A)$
. Similarly, for any measurable set A of
 $\mathcal {L} \setminus E_{\ell }$
, we have
$\mathcal {L} \setminus E_{\ell }$
, we have
 $\mu _{\ell }(\mathcal {K}^{\,-1}(A)) = \mu _{\ell }(A)$
.
$\mu _{\ell }(\mathcal {K}^{\,-1}(A)) = \mu _{\ell }(A)$
. -
(4) We set
Let $$ \begin{align*} g_0 := & \ \mu_g(\mathcal{K}^{\,-1}(E_g) \cap \mathcal{G}) = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{\substack{v \in \{g,\ell\}^n \\T_v(1^+) \geqslant {1}/{\beta}}} m_p([v \cdot g]_0^n), \\ \ell_0 := & \ \mu_{\ell}(\mathcal{K}^{\,-1}(E_g) \cap \mathcal{L}) = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{\substack{w \in \{g,\ell\}^n \\ T_w(s(1)^-) \leqslant {1}/{\beta}}} m_p([w \cdot g]_0^n), \\g_1 := & \ \mu_g(\mathcal{K}^{\,-1}(E_{\ell}) \cap \mathcal{G}) = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{\substack{v \in \{g,\ell\}^n \\ T_v(1^+) \geqslant {1}/{\beta(\beta-1)}}} m_p([v \cdot \ell]_0^n), \\ l_1 := & \ \mu_{\ell}(\mathcal{K}^{\,-1}(E_{\ell}) \cap \mathcal{L}) = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{\substack{w \in \{g,\ell\}^n \\ T_w(s(1)^-) \leqslant {1}/{\beta(\beta-1)}}} m_p([w \cdot \ell]_0^n). \end{align*} $$
$$ \begin{align*} g_0 := & \ \mu_g(\mathcal{K}^{\,-1}(E_g) \cap \mathcal{G}) = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{\substack{v \in \{g,\ell\}^n \\T_v(1^+) \geqslant {1}/{\beta}}} m_p([v \cdot g]_0^n), \\ \ell_0 := & \ \mu_{\ell}(\mathcal{K}^{\,-1}(E_g) \cap \mathcal{L}) = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{\substack{w \in \{g,\ell\}^n \\ T_w(s(1)^-) \leqslant {1}/{\beta}}} m_p([w \cdot g]_0^n), \\g_1 := & \ \mu_g(\mathcal{K}^{\,-1}(E_{\ell}) \cap \mathcal{G}) = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{\substack{v \in \{g,\ell\}^n \\ T_v(1^+) \geqslant {1}/{\beta(\beta-1)}}} m_p([v \cdot \ell]_0^n), \\ l_1 := & \ \mu_{\ell}(\mathcal{K}^{\,-1}(E_{\ell}) \cap \mathcal{L}) = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{\substack{w \in \{g,\ell\}^n \\ T_w(s(1)^-) \leqslant {1}/{\beta(\beta-1)}}} m_p([w \cdot \ell]_0^n). \end{align*} $$
 $A \subset E_g$
of the form
$A \subset E_g$
of the form
 $A = [u]_0^{|u|-1} \times \{g\} \times ]a;b[$
, with
$A = [u]_0^{|u|-1} \times \{g\} \times ]a;b[$
, with
 $0 \leqslant a \leqslant b \leqslant 1$
. Then, Therefore,
$0 \leqslant a \leqslant b \leqslant 1$
. Then, Therefore, $$ \begin{align*}\mathcal{K}^{\,-1}(A) \cap \mathcal{G} = \bigsqcup_{n \geqslant 0} \bigsqcup_{\substack{v \in \{g,\ell\}^n \\ T_v(1^+) \geqslant {1}/{\beta}}} E_{g \cdot v} \cap \bigg\{x \in \bigg]\dfrac{a}{\beta};\dfrac{b}{\beta}\bigg[; \omega \in [g \cdot u]_0^{|u|}\bigg\}. \end{align*} $$
We obtain the three other formulas with a similar computation.
$$ \begin{align*}\mathcal{K}^{\,-1}(A) \cap \mathcal{G} = \bigsqcup_{n \geqslant 0} \bigsqcup_{\substack{v \in \{g,\ell\}^n \\ T_v(1^+) \geqslant {1}/{\beta}}} E_{g \cdot v} \cap \bigg\{x \in \bigg]\dfrac{a}{\beta};\dfrac{b}{\beta}\bigg[; \omega \in [g \cdot u]_0^{|u|}\bigg\}. \end{align*} $$
We obtain the three other formulas with a similar computation. $$ \begin{align*} \mu_g(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) = & \ \sum_{n \geqslant 0} \sum_{\substack{v \in \{g,\ell\}^n \\ T_v(1^+) \geqslant {1}/{\beta}}} \!\dfrac{1}{\beta^n} \times m_p([v]_0^{n-1}) \times m_p([g \cdot u]_0^{|u|}) \times \dfrac{1}{\beta}(b-a) \\ = & \ g_0 \mu_g(A). \end{align*} $$
$$ \begin{align*} \mu_g(\mathcal{K}^{\,-1}(A) \cap \mathcal{G}) = & \ \sum_{n \geqslant 0} \sum_{\substack{v \in \{g,\ell\}^n \\ T_v(1^+) \geqslant {1}/{\beta}}} \!\dfrac{1}{\beta^n} \times m_p([v]_0^{n-1}) \times m_p([g \cdot u]_0^{|u|}) \times \dfrac{1}{\beta}(b-a) \\ = & \ g_0 \mu_g(A). \end{align*} $$
Therefore, by setting
![]() $\Gamma _g := {\ell _0}/({\ell _0 \mu _g(\mathcal {G}) + g_1 \mu _{\ell }(\mathcal {L})})$
and
$\Gamma _g := {\ell _0}/({\ell _0 \mu _g(\mathcal {G}) + g_1 \mu _{\ell }(\mathcal {L})})$
and
![]() $\Gamma _{\ell } := {g_1}/(\ell _0 \mu _g(\mathcal {G})+ g_1 \mu _{\ell } (\mathcal {L}))$
, the measure
$\Gamma _{\ell } := {g_1}/(\ell _0 \mu _g(\mathcal {G})+ g_1 \mu _{\ell } (\mathcal {L}))$
, the measure
![]() $\mu := \Gamma _g\mu _g + \Gamma _{\ell } \mu _{\ell }$
is a
$\mu := \Gamma _g\mu _g + \Gamma _{\ell } \mu _{\ell }$
is a
![]() $\mathcal {K}$
-invariant probability measure on X.
$\mathcal {K}$
-invariant probability measure on X.
On each floor of the two towers, the measure
![]() $\mu $
can be represented as the product of
$\mu $
can be represented as the product of
![]() $m_p$
on
$m_p$
on
![]() $\Omega $
and a multiple of
$\Omega $
and a multiple of
![]() $\unicode{x3bb} $
. Thus, we get the following proposition.
$\unicode{x3bb} $
. Thus, we get the following proposition.
Proposition 2. By projecting the measure
![]() $\mu $
on
$\mu $
on
![]() $\Omega \times I_{\beta }$
, we obtain the measure
$\Omega \times I_{\beta }$
, we obtain the measure
![]() ${m_p \otimes \mu _p}$
, where
${m_p \otimes \mu _p}$
, where
![]() $\mu _p$
has for density
$\mu _p$
has for density

As a consequence, the natural projection
![]() $\pi : X \to \Omega \times I_{\beta }$
is a factor map from the system
$\pi : X \to \Omega \times I_{\beta }$
is a factor map from the system
![]() $(X,\mu ,\mathcal {K})$
to
$(X,\mu ,\mathcal {K})$
to
![]() $(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
.
$(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
.
2.4 Properties of the extension
The aim of this section is to prove that the system
![]() $(X,\mu ,\mathcal {K})$
is ergodic. For that, we first study the properties of
$(X,\mu ,\mathcal {K})$
is ergodic. For that, we first study the properties of
![]() $\mathcal {K}$
when following paths on the towers. We then study the induced transformation of
$\mathcal {K}$
when following paths on the towers. We then study the induced transformation of
![]() $\mathcal {K}$
on the greedy base
$\mathcal {K}$
on the greedy base
![]() $E_g$
, and prove that the induced system is Bernoulli. From this, we derive the ergodicity of the system
$E_g$
, and prove that the induced system is Bernoulli. From this, we derive the ergodicity of the system
![]() $(X,\mu ,\mathcal {K})$
, which implies the ergodicity of the initial random system and the uniqueness of
$(X,\mu ,\mathcal {K})$
, which implies the ergodicity of the initial random system and the uniqueness of
![]() $\mu _p$
(as an absolutely continuous probability measure on
$\mu _p$
(as an absolutely continuous probability measure on
![]() $I_{\beta }$
such that
$I_{\beta }$
such that
![]() ${m_p \otimes \mu _p}$
is
${m_p \otimes \mu _p}$
is
![]() $K_{\beta }$
-invariant).
$K_{\beta }$
-invariant).
To study the behavior of the dynamics along paths in the towers we first define a class of functions that will be useful in the following definition.
Definition 3. Let
![]() $n \in \mathbb {N}$
. We define the class of functions
$n \in \mathbb {N}$
. We define the class of functions
![]() $\mathfrak {F}_n$
(see Figure 9) as the set of functions f satisfying, up to a set of zero measure:
$\mathfrak {F}_n$
(see Figure 9) as the set of functions f satisfying, up to a set of zero measure:
-
• there exists a finite number of disjoint intervals
 $I_1, \ldots , I_r$
and a sub-interval J of
$I_1, \ldots , I_r$
and a sub-interval J of
 $I_{\beta }$
such that
$I_{\beta }$
such that
 $f: I_1 \sqcup \cdots \sqcup I_r \to J$
;
$f: I_1 \sqcup \cdots \sqcup I_r \to J$
; -
• the function f is non-decreasing on its definition domain;
-
• on each interval
 $I_i$
, f is a linear map with slope
$I_i$
, f is a linear map with slope
 $\beta ^n$
;
$\beta ^n$
; -
•
 $f(\bigsqcup _{i=1}^r I_i) = \bigsqcup _{i = 1}^r f(I_i) = J$
.
$f(\bigsqcup _{i=1}^r I_i) = \bigsqcup _{i = 1}^r f(I_i) = J$
.

Figure 9 Function from the class
![]() $\mathfrak {F}_n$
.
$\mathfrak {F}_n$
.
In particular, the intervals
![]() $(I_i)$
are in the same order as the intervals
$(I_i)$
are in the same order as the intervals
![]() $(f(I_i))$
, and we have
$(f(I_i))$
, and we have
Lemma 4. Let
![]() $n_1,n_2 \in \mathbb {N}$
and
$n_1,n_2 \in \mathbb {N}$
and
![]() $f \in \mathfrak {F}_{n_1}$
,
$f \in \mathfrak {F}_{n_1}$
,
![]() $g \in \mathfrak {F}_{n_2}$
such that the definition domain
$g \in \mathfrak {F}_{n_2}$
such that the definition domain
![]() $D_f$
of f is included in the image of g. Then,
$D_f$
of f is included in the image of g. Then,
![]() $f \circ g_{|g^{-1}(D_f)} \in \mathfrak {F}_{n_1+n_2}$
.
$f \circ g_{|g^{-1}(D_f)} \in \mathfrak {F}_{n_1+n_2}$
.
Proof. We denote
![]() $g: I_1 \sqcup \cdots \sqcup I_{r_1} \to J$
and
$g: I_1 \sqcup \cdots \sqcup I_{r_1} \to J$
and
![]() $f: J_1 \sqcup \cdots \sqcup J_{r_2} \to L$
and
$f: J_1 \sqcup \cdots \sqcup J_{r_2} \to L$
and
![]() $h = f \circ g_{|g^{-1}(D_f)}$
. Then,
$h = f \circ g_{|g^{-1}(D_f)}$
. Then,
![]() $g^{-1}(D_f)$
is the disjoint union of the intervals
$g^{-1}(D_f)$
is the disjoint union of the intervals
![]() $g^{-1}(J_i) \cap I_j$
(when this set is not empty). Therefore, h is defined on
$g^{-1}(J_i) \cap I_j$
(when this set is not empty). Therefore, h is defined on
![]() $\bigsqcup _{i,j} g^{-1}(J_i) \cap I_j$
with values in L. As the composition of non-decreasing functions, h is non-decreasing on its definition domain. Moreover, h is the composition of two linear maps of slope
$\bigsqcup _{i,j} g^{-1}(J_i) \cap I_j$
with values in L. As the composition of non-decreasing functions, h is non-decreasing on its definition domain. Moreover, h is the composition of two linear maps of slope
![]() $\beta ^{n_1}$
and
$\beta ^{n_1}$
and
![]() $\beta ^{n_2}$
on each non-empty
$\beta ^{n_2}$
on each non-empty
![]() $g^{-1}(J_i) \cap I_j$
, so it is a linear map of slope
$g^{-1}(J_i) \cap I_j$
, so it is a linear map of slope
![]() $\beta ^{n_1+n_2}$
. Finally, for all
$\beta ^{n_1+n_2}$
. Finally, for all
![]() $i \in \{1,\ldots ,r_2\}$
, we have
$i \in \{1,\ldots ,r_2\}$
, we have
 $$ \begin{align*} \bigsqcup_{j}g(g^{-1}(J_i) \cap I_j) = J_i, \end{align*} $$
$$ \begin{align*} \bigsqcup_{j}g(g^{-1}(J_i) \cap I_j) = J_i, \end{align*} $$
and thus
 $$ \begin{align*} \bigsqcup_{i,j}h(g^{-1}(J_i) \cap I_j) = L.\\[-50pt] \end{align*} $$
$$ \begin{align*} \bigsqcup_{i,j}h(g^{-1}(J_i) \cap I_j) = L.\\[-50pt] \end{align*} $$
We denote by
![]() $\mathcal {E}: = \{g,\ell \}^* \setminus \{\varnothing \} $
the set of non-empty finite sequences of
$\mathcal {E}: = \{g,\ell \}^* \setminus \{\varnothing \} $
the set of non-empty finite sequences of
![]() $\{g,\ell \}$
, in other words, the set of labels. For
$\{g,\ell \}$
, in other words, the set of labels. For
![]() $e \in \mathcal {E}$
, we denote by
$e \in \mathcal {E}$
, we denote by
![]() $e(0)$
the first term of e and
$e(0)$
the first term of e and
![]() $e(-1)$
its last term.
$e(-1)$
its last term.
We define the oriented graph
![]() $G $
on
$G $
on
![]() $\mathcal {E}$
describing the set of admissible sequences of labels. A label
$\mathcal {E}$
describing the set of admissible sequences of labels. A label
![]() $e \in \mathcal {E}$
can be followed by the label
$e \in \mathcal {E}$
can be followed by the label
![]() $e' \in \mathcal {E}$
(we then denote
$e' \in \mathcal {E}$
(we then denote
![]() $e \to e'$
) if
$e \to e'$
) if
![]() $\mu (\mathcal {K}^{\,-1}(E_{e'}) \cap E_e)> 0$
. In other words, we have
$\mu (\mathcal {K}^{\,-1}(E_{e'}) \cap E_e)> 0$
. In other words, we have
![]() $e \to e'$
if the map
$e \to e'$
if the map
![]() $\mathcal {K}$
sends a subset of positive measure of the floor
$\mathcal {K}$
sends a subset of positive measure of the floor
![]() $E_e$
onto the floor
$E_e$
onto the floor
![]() $E_{e'}$
.
$E_{e'}$
.
We use the new class of functions
![]() $\mathfrak {F}_n$
to describe the dynamics along paths in the two towers.
$\mathfrak {F}_n$
to describe the dynamics along paths in the two towers.
Proposition 5. Let
![]() $C = (e_0 =e,e_1,\ldots ,e_n = e') $
(
$C = (e_0 =e,e_1,\ldots ,e_n = e') $
(
![]() $n \geqslant 1$
) be a finite sequence of labels of
$n \geqslant 1$
) be a finite sequence of labels of
![]() $\mathcal {E}$
corresponding to a path in the graph G. We have
$\mathcal {E}$
corresponding to a path in the graph G. We have
 $$ \begin{align*} E_C :=\bigcap_{k = 0}^n \mathcal{K}^{-k}E_{e_k} = [e_1(-1),\ldots,e_n(-1)]^{n-1}_0 \times \{e\} \times J_C \end{align*} $$
$$ \begin{align*} E_C :=\bigcap_{k = 0}^n \mathcal{K}^{-k}E_{e_k} = [e_1(-1),\ldots,e_n(-1)]^{n-1}_0 \times \{e\} \times J_C \end{align*} $$
with:
-
(1)
 $J_C $
is a finite union of disjoint intervals
$J_C $
is a finite union of disjoint intervals
 $I_1,\ldots ,I_r$
;
$I_1,\ldots ,I_r$
; -
(2)
 ${T_{e_1(-1),\ldots ,e_n(-1)}}_{|J_C} \in \mathfrak {F}_n$
.
${T_{e_1(-1),\ldots ,e_n(-1)}}_{|J_C} \in \mathfrak {F}_n$
.
In particular, the intervals
![]() $(I_i)$
are in the same order as the intervals
$(I_i)$
are in the same order as the intervals
![]() $(T_{e_1(-1),\ldots ,e_n(-1)} (I_i))$
,
$(T_{e_1(-1),\ldots ,e_n(-1)} (I_i))$
,
![]() $\unicode{x3bb} (J_C) = {1}/{\beta ^n} \unicode{x3bb} (I_{e'})$
and the mapping
$\unicode{x3bb} (J_C) = {1}/{\beta ^n} \unicode{x3bb} (I_{e'})$
and the mapping
![]() $\mathcal {K}^n: E_C \to E_{e'}$
is a bijection.
$\mathcal {K}^n: E_C \to E_{e'}$
is a bijection.
Proof. We prove each point by induction on the length of the path C. Suppose that
![]() $C \,{=}\, (e,e')$
is an edge in the graph of transitions of
$C \,{=}\, (e,e')$
is an edge in the graph of transitions of
![]() $\mathcal {E}$
. Set
$\mathcal {E}$
. Set
![]() $\omega _0 = e'(-1)$
. Without loss of generality, we can suppose that
$\omega _0 = e'(-1)$
. Without loss of generality, we can suppose that
![]() $e(0) = g$
. Finally, set
$e(0) = g$
. Finally, set
![]() $I_e = [0,t]$
, with
$I_e = [0,t]$
, with
![]() ${t \in [0,{1}/({\beta -1})[}$
.
${t \in [0,{1}/({\beta -1})[}$
.
-
• If
 $\omega _0 = g$
, then
$\omega _0 = g$
, then
 $E_C = [g]_0 \times \{e\} \times J_C$
with
$E_C = [g]_0 \times \{e\} \times J_C$
with-
– if
 $t < {1}/{\beta }$
, then
$t < {1}/{\beta }$
, then
 $J_C = I_e$
,
$J_C = I_e$
, -
– if
 $t \geqslant {1}/{\beta }$
, either
$t \geqslant {1}/{\beta }$
, either
 $e' = (g)$
, then
$e' = (g)$
, then
 $J_C = [0,{1}/{\beta }[$
, or
$J_C = [0,{1}/{\beta }[$
, or
 $e' = e \cdot g$
then
$e' = e \cdot g$
then
 $J_C = [{1}/{\beta },t]$
.
$J_C = [{1}/{\beta },t]$
.
-
-
• If
 $\omega _0 = \ell $
, then
$\omega _0 = \ell $
, then
 $E_C = [\ell ]_0 \times \{e\} \times J_C$
with
$E_C = [\ell ]_0 \times \{e\} \times J_C$
with-
– if
 $t < {1}/{\beta (\beta - 1)}$
, then
$t < {1}/{\beta (\beta - 1)}$
, then
 $J_C = I_e$
,
$J_C = I_e$
, -
– if
 $t \geqslant {1}/{\beta (\beta - 1)}$
, either
$t \geqslant {1}/{\beta (\beta - 1)}$
, either
 $e' = (\ell )$
then
$e' = (\ell )$
then
 $J_C = ]{s(1)}/{\beta };{1}/{\beta (\beta - 1)}]$
, or
$J_C = ]{s(1)}/{\beta };{1}/{\beta (\beta - 1)}]$
, or
 $e' = e \cdot \ell $
then
$e' = e \cdot \ell $
then
 $J_C = [0,{s(1)}/{\beta }] \sqcup ]{1}/{\beta (\beta - 1)},t]$
.
$J_C = [0,{s(1)}/{\beta }] \sqcup ]{1}/{\beta (\beta - 1)},t]$
.
-
In each case,
![]() $J_C$
is a finite union of disjoint intervals. Moreover,
$J_C$
is a finite union of disjoint intervals. Moreover,
![]() $T_{\omega _0}: J_C \to I_{e'}$
is a function of
$T_{\omega _0}: J_C \to I_{e'}$
is a function of
![]() $\mathfrak {F}_1$
.
$\mathfrak {F}_1$
.
Suppose now that
![]() $C = (e = e_0,e_1,\ldots , e_{n+1} = e')$
. Set
$C = (e = e_0,e_1,\ldots , e_{n+1} = e')$
. Set
![]() $C' = (e_1,\ldots ,e_{n+1})$
. The path
$C' = (e_1,\ldots ,e_{n+1})$
. The path
![]() $C'$
is a path of length n in the graph of transitions of
$C'$
is a path of length n in the graph of transitions of
![]() $\mathcal {E}$
, such that
$\mathcal {E}$
, such that
![]() $E_{C'}$
satisfies the conclusions of the proposition.
$E_{C'}$
satisfies the conclusions of the proposition.
-
•
 $E_{C'} = [e_2(-1),\ldots ,e_{n+1}(-1)]_0^{n-1} \times \{e_1\} \times J_{C'}$
where
$E_{C'} = [e_2(-1),\ldots ,e_{n+1}(-1)]_0^{n-1} \times \{e_1\} \times J_{C'}$
where
 $J_{C'}$
is a finite union of disjoint intervals.
$J_{C'}$
is a finite union of disjoint intervals. -
•
 ${T_{e_2(-1),\ldots ,e_{n+1}(-1)}}_{|J_{C'}}\! \in \mathfrak {F}_n$
.
${T_{e_2(-1),\ldots ,e_{n+1}(-1)}}_{|J_{C'}}\! \in \mathfrak {F}_n$
.
We then have
![]() $E_C = E_e \cap \mathcal {K}^{\,-1}(E_{C'})$
.
$E_C = E_e \cap \mathcal {K}^{\,-1}(E_{C'})$
.
The component in
![]() $\Omega $
is indeed
$\Omega $
is indeed
![]() $[e_1(-1),e_2(-1),\ldots ,e_{n+1}(-1)]_0^n$
.
$[e_1(-1),e_2(-1),\ldots ,e_{n+1}(-1)]_0^n$
.
Set
![]() $g = {T_{e_1(-1)}}_{|J_{e_0,e_1}}$
and
$g = {T_{e_1(-1)}}_{|J_{e_0,e_1}}$
and
![]() $f = {T_{e_2(-1),\ldots ,e_{n+1}(-1)}}_{|J_{C'}}$
. We have
$f = {T_{e_2(-1),\ldots ,e_{n+1}(-1)}}_{|J_{C'}}$
. We have
![]() $g \in \mathfrak {F}_1$
and
$g \in \mathfrak {F}_1$
and
![]() $f \in \mathfrak {F}_n$
. By setting
$f \in \mathfrak {F}_n$
. By setting
![]() $J_C := g^{-1}(J_{C'})$
, we do have that
$J_C := g^{-1}(J_{C'})$
, we do have that
![]() $J_C$
is a finite union of disjoint intervals and
$J_C$
is a finite union of disjoint intervals and
Furthermore,
![]() ${T_{e_1(-1),e_2(-1),\ldots ,e_{n+1}(-1)}}_{|J_C} = f \circ g_{|J_C}$
. Applying Lemma 4, the function
${T_{e_1(-1),e_2(-1),\ldots ,e_{n+1}(-1)}}_{|J_C} = f \circ g_{|J_C}$
. Applying Lemma 4, the function
![]() ${T_{e_1(-1),e_2(-1),\ldots ,e_{n+1}(-1)}}_{|J_C}$
is in
${T_{e_1(-1),e_2(-1),\ldots ,e_{n+1}(-1)}}_{|J_C}$
is in
![]() $\mathfrak {F}_{n+1}$
.
$\mathfrak {F}_{n+1}$
.
We now study the induced transformation of
![]() $\mathcal {K}$
on the base
$\mathcal {K}$
on the base
![]() $E_g$
. We denote by
$E_g$
. We denote by
![]() $\mathcal {K}_g$
this induced transformation. The measure
$\mathcal {K}_g$
this induced transformation. The measure
![]() $\mu (.|E_g)$
is the measure
$\mu (.|E_g)$
is the measure
![]() $\mu _g$
, and is preserved by the induced map
$\mu _g$
, and is preserved by the induced map
![]() $\mathcal {K}_g$
[Reference Boyarsky and Góra1, Proposition 3.6.1, pp. 58]. In the following, we identify the base
$\mathcal {K}_g$
[Reference Boyarsky and Góra1, Proposition 3.6.1, pp. 58]. In the following, we identify the base
![]() $E_g$
with
$E_g$
with
![]() $\Omega \times [0,1]$
.
$\Omega \times [0,1]$
.
We consider the set
![]() $\mathscr {C}$
of possible paths for a first return to the base
$\mathscr {C}$
of possible paths for a first return to the base
![]() $E_g$
. In other words,
$E_g$
. In other words,
![]() $\mathscr {C}$
is the set of paths of the form
$\mathscr {C}$
is the set of paths of the form
![]() $C = (e_0 = (g),e_1,\ldots ,e_n = (g))$
(where
$C = (e_0 = (g),e_1,\ldots ,e_n = (g))$
(where
![]() $|C|:= n$
is the length of the path C), with
$|C|:= n$
is the length of the path C), with
![]() $e_k \neq (g)$
for
$e_k \neq (g)$
for
![]() $1 \leqslant k \leqslant n-1$
such that
$1 \leqslant k \leqslant n-1$
such that
 $$ \begin{align*} \mu\bigg(\bigcap_{k = 0}^n \mathcal{K}^{-k}(E_{e_k})\bigg)> 0. \end{align*} $$
$$ \begin{align*} \mu\bigg(\bigcap_{k = 0}^n \mathcal{K}^{-k}(E_{e_k})\bigg)> 0. \end{align*} $$
We then define the set
![]() $\mathcal {P} $
of subsets of
$\mathcal {P} $
of subsets of
![]() $E_g$
by
$E_g$
by
Lemma 6. The set
![]() $\mathcal {P}$
is a countable partition of
$\mathcal {P}$
is a countable partition of
![]() $E_g$
, up to a set of zero measure.
$E_g$
, up to a set of zero measure.
Proof. If we consider two distinct paths
![]() $C,C' \in \mathscr {C}$
, then it is clear that
$C,C' \in \mathscr {C}$
, then it is clear that
![]() $E_C$
and
$E_C$
and
![]() $E_{C'}$
are disjoint. Additionally, since
$E_{C'}$
are disjoint. Additionally, since
![]() $\mu _g$
-almost every a in
$\mu _g$
-almost every a in
![]() $E_g$
has a finite return time, there exists
$E_g$
has a finite return time, there exists
![]() $C \in \mathscr {C}$
such that
$C \in \mathscr {C}$
such that
![]() $a \in E_C$
.
$a \in E_C$
.
For almost every
![]() $a \in E_g$
, we call
$a \in E_g$
, we call
![]() $\mathcal {P}$
-name of a the unique sequence
$\mathcal {P}$
-name of a the unique sequence
![]() $(P_n)_{n \geqslant 0}$
of atoms of
$(P_n)_{n \geqslant 0}$
of atoms of
![]() $\mathcal {P}$
such that for any
$\mathcal {P}$
such that for any
![]() $n \geqslant 0$
,
$n \geqslant 0$
,
![]() $K_g^n(a) \in P_n$
.
$K_g^n(a) \in P_n$
.
Proposition 7. The sequence of partitions
![]() $(\mathcal {K}_g^{-n}(\mathcal {P}))_{n \geqslant 0}$
is independent for the measure
$(\mathcal {K}_g^{-n}(\mathcal {P}))_{n \geqslant 0}$
is independent for the measure
![]() $\mu _g$
, that is, for any integer
$\mu _g$
, that is, for any integer
![]() $n \in \mathbb {N}$
, the partitions
$n \in \mathbb {N}$
, the partitions
![]() $\mathcal {K}_g^{-n}\mathcal {P}$
and
$\mathcal {K}_g^{-n}\mathcal {P}$
and
![]() $\bigvee _{0 \leqslant k \leqslant n-1} \mathcal {K}_g^{-k}\mathcal {P}$
are independent.
$\bigvee _{0 \leqslant k \leqslant n-1} \mathcal {K}_g^{-k}\mathcal {P}$
are independent.
Proof. Consider a path
starting and ending with the label of the greedy base
![]() $E_g$
. Then, this path is a unique concatenation of paths
$E_g$
. Then, this path is a unique concatenation of paths
![]() $C_0,\ldots ,C_k \in \mathscr {C}$
, and
$C_0,\ldots ,C_k \in \mathscr {C}$
, and
 $$ \begin{align*} E_C = \bigcap_{i = 0}^k \mathcal{K}_g^{-i} E_{C_i} = \bigcap_{i = 0}^N \mathcal{K}^{-i}(E_{e_i}) = [e_1(-1),\ldots,e_N(-1)]_0^{N-1} \times J_C \end{align*} $$
$$ \begin{align*} E_C = \bigcap_{i = 0}^k \mathcal{K}_g^{-i} E_{C_i} = \bigcap_{i = 0}^N \mathcal{K}^{-i}(E_{e_i}) = [e_1(-1),\ldots,e_N(-1)]_0^{N-1} \times J_C \end{align*} $$
with
![]() $\unicode{x3bb} (J_C) = ({1}/{\beta ^N})\unicode{x3bb} (I_{(g)}) = {1}/{\beta ^N}$
, from Proposition 5. Then, we have
$\unicode{x3bb} (J_C) = ({1}/{\beta ^N})\unicode{x3bb} (I_{(g)}) = {1}/{\beta ^N}$
, from Proposition 5. Then, we have
and we have a similar equality for all
![]() $C_j$
,
$C_j$
,
![]() $0 \leqslant j \leqslant k$
. Therefore, it is clear that
$0 \leqslant j \leqslant k$
. Therefore, it is clear that
 $$ \begin{align*}\mu_g(E_C) = \prod_{j = 0}^k \mu_g(E_{C_j}).\\[-50pt] \end{align*} $$
$$ \begin{align*}\mu_g(E_C) = \prod_{j = 0}^k \mu_g(E_{C_j}).\\[-50pt] \end{align*} $$
From Proposition 5, each atom of
![]() $\mathcal {P}$
is of the form
$\mathcal {P}$
is of the form
![]() $[\omega _0,\ldots ,\omega _{r-1}] \times J_C$
. Likewise, for each
$[\omega _0,\ldots ,\omega _{r-1}] \times J_C$
. Likewise, for each
![]() $ N \geqslant 0$
, each atom of
$ N \geqslant 0$
, each atom of
![]() $\bigvee _{j=0}^N \mathcal {K}_g^{-j}\mathcal {P}$
is again of this form.
$\bigvee _{j=0}^N \mathcal {K}_g^{-j}\mathcal {P}$
is again of this form.
Definition 8. Let
![]() $N \in \mathbb {N} \cup \{0\}$
and
$N \in \mathbb {N} \cup \{0\}$
and
![]() $(\omega ,x) \in E_g$
such that there exists an atom of
$(\omega ,x) \in E_g$
such that there exists an atom of
![]() $\bigvee _{j=0}^N \mathcal {K}_g^{-j}\mathcal {P}$
containing
$\bigvee _{j=0}^N \mathcal {K}_g^{-j}\mathcal {P}$
containing
![]() $(\omega ,x)$
. We denote C the associated path. Then, we define the set
$(\omega ,x)$
. We denote C the associated path. Then, we define the set
![]() $A_N(\omega ,x)$
included in the interval
$A_N(\omega ,x)$
included in the interval
![]() $[0,1]$
by
$[0,1]$
by
Lemma 9. For almost every
![]() $(\omega ,x) \in E_g$
, for all
$(\omega ,x) \in E_g$
, for all
![]() $n \in \mathbb {N} \cup \{0\}$
and
$n \in \mathbb {N} \cup \{0\}$
and
![]() $m \in \mathbb {N}$
, there exists
$m \in \mathbb {N}$
, there exists
![]() $N \geqslant n$
and
$N \geqslant n$
and
![]() $t \in [0,1]$
such that
$t \in [0,1]$
such that
Proof. Let
![]() $P_0 = [g]_0 \times [0,{1}/{\beta }[$
. The set
$P_0 = [g]_0 \times [0,{1}/{\beta }[$
. The set
![]() $P_0$
is an atom of the partition
$P_0$
is an atom of the partition
![]() $\mathcal {P}$
, of positive measure, corresponding to the set of points returning to the base
$\mathcal {P}$
, of positive measure, corresponding to the set of points returning to the base
![]() $E_g$
in one step. The process that maps a point in
$E_g$
in one step. The process that maps a point in
![]() $E_g$
to its
$E_g$
to its
![]() $\mathcal {P}$
-name (defined for almost every
$\mathcal {P}$
-name (defined for almost every
![]() $(\omega ,x) \in E_g$
) is a Bernoulli process. Therefore, for almost every
$(\omega ,x) \in E_g$
) is a Bernoulli process. Therefore, for almost every
![]() $(\omega ,x) \in E_g$
, the orbit of
$(\omega ,x) \in E_g$
, the orbit of
![]() $(\omega ,x)$
under
$(\omega ,x)$
under
![]() $\mathcal {K}_g$
meets infinitely often the atom
$\mathcal {K}_g$
meets infinitely often the atom
![]() $P_0$
. Even better, for any
$P_0$
. Even better, for any
![]() $m \in \mathbb {N}$
, the orbit of
$m \in \mathbb {N}$
, the orbit of
![]() $(\omega ,x)$
meets the atom
$(\omega ,x)$
meets the atom
![]() $P_0\ m$
times in a row, infinitely often.
$P_0\ m$
times in a row, infinitely often.
Let
![]() $n \in \mathbb {N} \cup \{0\}$
. For such a point
$n \in \mathbb {N} \cup \{0\}$
. For such a point
![]() $(\omega ,x)$
, let
$(\omega ,x)$
, let
![]() $N \geqslant n$
be an integer such that
$N \geqslant n$
be an integer such that
Observe that the atom of
![]() $\bigvee _{j=0}^N K_g^{-j}\mathcal {P}$
containing
$\bigvee _{j=0}^N K_g^{-j}\mathcal {P}$
containing
![]() $(\omega ,x)$
is of the form
$(\omega ,x)$
is of the form
If we note
![]() $A_N(\omega ,x) = I_1 \sqcup \cdots \sqcup I_m$
, Proposition 5 implies
$A_N(\omega ,x) = I_1 \sqcup \cdots \sqcup I_m$
, Proposition 5 implies
where
![]() $T_{\omega _0,\ldots ,\omega _{r-1}}I_i$
is an interval for every
$T_{\omega _0,\ldots ,\omega _{r-1}}I_i$
is an interval for every
![]() $1 \leqslant i \leqslant m$
, and the order of the intervals
$1 \leqslant i \leqslant m$
, and the order of the intervals
![]() $(T_{\omega _0,\ldots ,\omega _{r-1}}I_i)$
is the same as the order of the intervals
$(T_{\omega _0,\ldots ,\omega _{r-1}}I_i)$
is the same as the order of the intervals
![]() $(I_i)$
.
$(I_i)$
.
Since
![]() $ \mathcal {K}_g^N(\omega ,x) \in P_0$
, we have
$ \mathcal {K}_g^N(\omega ,x) \in P_0$
, we have
 $$ \begin{align*} A_{N+1}(\omega,x) = \bigg\{y \in A_N(\omega,x), T_{\omega_0,\ldots,\omega_{r-1}}(y) \in \bigg[0,\dfrac{1}{\beta}\bigg[\bigg\}. \end{align*} $$
$$ \begin{align*} A_{N+1}(\omega,x) = \bigg\{y \in A_N(\omega,x), T_{\omega_0,\ldots,\omega_{r-1}}(y) \in \bigg[0,\dfrac{1}{\beta}\bigg[\bigg\}. \end{align*} $$
Then, there exists
![]() $t_1 \in [0,1]$
such that
$t_1 \in [0,1]$
such that
![]() $T_{\omega _0,\ldots ,\omega _{r-1}}(A_N(\omega ,x) \cap [0,t_1]) = [0,{1}/{\beta }[$
. See Figure 10. Hence,
$T_{\omega _0,\ldots ,\omega _{r-1}}(A_N(\omega ,x) \cap [0,t_1]) = [0,{1}/{\beta }[$
. See Figure 10. Hence,
Finally, since
![]() $\mathcal {K}_g^N(\omega ,x),\ldots ,\mathcal {K}_g^{N+m-1}(\omega ,x) \in P_0$
, we can apply the same reasoning m times, which implies the existence of
$\mathcal {K}_g^N(\omega ,x),\ldots ,\mathcal {K}_g^{N+m-1}(\omega ,x) \in P_0$
, we can apply the same reasoning m times, which implies the existence of
![]() $t \in [0,1]$
such that
$t \in [0,1]$
such that
This real number t is such that
![]() $\unicode{x3bb} (A_N(\omega ,x) \cap [0,t]) = ({1}/{\beta ^m}) \unicode{x3bb} (A_N(\omega ,x))$
.
$\unicode{x3bb} (A_N(\omega ,x) \cap [0,t]) = ({1}/{\beta ^m}) \unicode{x3bb} (A_N(\omega ,x))$
.
Let
![]() $\mathcal {F}$
be the factor
$\mathcal {F}$
be the factor
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {F} := \bigvee _{j=0}^{+\infty } \mathcal {K}_g^{-j}\mathcal {P}$
. The partition
$\mathcal {F} := \bigvee _{j=0}^{+\infty } \mathcal {K}_g^{-j}\mathcal {P}$
. The partition
![]() $\mathcal {P}$
provides a Bernoulli process, and we want to show that this process generates the induced system by proving the following proposition.
$\mathcal {P}$
provides a Bernoulli process, and we want to show that this process generates the induced system by proving the following proposition.

Figure 10 Passage from
![]() $A_N(\omega ,x)$
to
$A_N(\omega ,x)$
to
![]() $A_{N+1}(\omega ,x)$
.
$A_{N+1}(\omega ,x)$
.
Proposition 10. The
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {F}$
is (up to zero measure sets) the Borel
$\mathcal {F}$
is (up to zero measure sets) the Borel
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $E_g$
. In other words, the partition
$E_g$
. In other words, the partition
![]() $\mathcal {P}$
is a generator of the induced system, which is isomorphic to a one-sided Bernoulli shift.
$\mathcal {P}$
is a generator of the induced system, which is isomorphic to a one-sided Bernoulli shift.
Lemma 11.
![]() $\mathcal {F}$
contains the
$\mathcal {F}$
contains the
![]() $\sigma $
-algebra generated by the
$\sigma $
-algebra generated by the
![]() $\omega $
-component.
$\omega $
-component.
Proof. Let
![]() $N \in \mathbb {N}$
. As said earlier, every atom of
$N \in \mathbb {N}$
. As said earlier, every atom of
![]() $\bigvee _{j=0}^{N} \mathcal {K}_g^{-j}\mathcal {P}$
is of the form
$\bigvee _{j=0}^{N} \mathcal {K}_g^{-j}\mathcal {P}$
is of the form
![]() $[\omega _0,\ldots ,\omega _{r-1}]_0^{r-1} \times J_C$
, with
$[\omega _0,\ldots ,\omega _{r-1}]_0^{r-1} \times J_C$
, with
![]() $r \geqslant N$
. Therefore, for any
$r \geqslant N$
. Therefore, for any
![]() $N \in \mathbb {N}$
,
$N \in \mathbb {N}$
,
![]() $(\omega _0,\ldots ,\omega _{N-1})$
is
$(\omega _0,\ldots ,\omega _{N-1})$
is
![]() $\mathcal {F}$
-measurable.
$\mathcal {F}$
-measurable.
To prove Proposition 10, it suffices to show that for any continuous function
![]() $\varphi : E_g\to \mathbb {R}_+$
, the conditional expectation
$\varphi : E_g\to \mathbb {R}_+$
, the conditional expectation
![]() $E[\varphi | \mathcal {F}]$
satisfies
$E[\varphi | \mathcal {F}]$
satisfies
The existence of the regular conditional probability implies that for almost every
![]() $(\omega ,x) \in E_g$
, there exists a measure
$(\omega ,x) \in E_g$
, there exists a measure
![]() $\mu _{(\omega ,x)}$
on
$\mu _{(\omega ,x)}$
on
![]() $E_g$
such that for any positive continuous function
$E_g$
such that for any positive continuous function
![]() $\varphi : E_g \to \mathbb {R}_+$
,
$\varphi : E_g \to \mathbb {R}_+$
,
We want to prove that for almost every
![]() $(\omega ,x) \in E_g$
, the measure
$(\omega ,x) \in E_g$
, the measure
![]() $\mu _{(\omega ,x)}$
equals the Dirac measure on
$\mu _{(\omega ,x)}$
equals the Dirac measure on
![]() $(\omega ,x)$
, which leads to the announced result. Lemma 11 implies that, for almost every
$(\omega ,x)$
, which leads to the announced result. Lemma 11 implies that, for almost every
![]() $(\omega ,x) \in E_g$
, the measure
$(\omega ,x) \in E_g$
, the measure
![]() $\mu _{(\omega ,x)}$
is of the form
$\mu _{(\omega ,x)}$
is of the form
![]() $\delta _{\omega } \otimes \tilde {\mu }_{(\omega ,x)}$
, where
$\delta _{\omega } \otimes \tilde {\mu }_{(\omega ,x)}$
, where
![]() $\tilde {\mu }_{(\omega ,x)}$
is a measure on
$\tilde {\mu }_{(\omega ,x)}$
is a measure on
![]() $[0,1]$
. In the following, we identify the measures
$[0,1]$
. In the following, we identify the measures
![]() $\mu _{(\omega ,x)}$
and
$\mu _{(\omega ,x)}$
and
![]() $\tilde {\mu }_{(\omega ,x)}$
. Therefore, it remains to prove that
$\tilde {\mu }_{(\omega ,x)}$
. Therefore, it remains to prove that
![]() $\mu _{(\omega ,x)}$
is the Dirac measure on x.
$\mu _{(\omega ,x)}$
is the Dirac measure on x.
Let
![]() $\varphi : E_g \to \mathbb {R}_+$
be a continuous function depending only on the real variable x, that is,
$\varphi : E_g \to \mathbb {R}_+$
be a continuous function depending only on the real variable x, that is,
![]() $\varphi (\omega ,x) = f(x)$
, where f is a continuous function from
$\varphi (\omega ,x) = f(x)$
, where f is a continuous function from
![]() $[0,1]$
into
$[0,1]$
into
![]() $\mathbb {R}^+$
.
$\mathbb {R}^+$
.
By the martingale convergence theorem, we have the almost sure convergence:
 $$ \begin{align*} E\bigg[\varphi \bigg \rvert \bigvee_{j=0}^{N} \mathcal{K}_g^{-j}\mathcal{P}\bigg] \to E[\varphi | \mathcal{F}]. \end{align*} $$
$$ \begin{align*} E\bigg[\varphi \bigg \rvert \bigvee_{j=0}^{N} \mathcal{K}_g^{-j}\mathcal{P}\bigg] \to E[\varphi | \mathcal{F}]. \end{align*} $$
Thus, for almost every
![]() $(\omega ,x) \in E_g$
, we have the convergence
$(\omega ,x) \in E_g$
, we have the convergence
 $$ \begin{align*} E\bigg[\varphi \bigg \rvert\bigvee_{j=0}^{N} \mathcal{K}_g^{-j}\mathcal{P}\bigg](\omega,x) \to \int f(y) \,d\mu_{(\omega,x)}(y). \end{align*} $$
$$ \begin{align*} E\bigg[\varphi \bigg \rvert\bigvee_{j=0}^{N} \mathcal{K}_g^{-j}\mathcal{P}\bigg](\omega,x) \to \int f(y) \,d\mu_{(\omega,x)}(y). \end{align*} $$
With N fixed, and for almost every
![]() $(\omega ,x) \in E_g$
, we have
$(\omega ,x) \in E_g$
, we have
 $$ \begin{align*} E\bigg[\varphi \bigg \rvert \bigvee_{j=0}^{N} \mathcal{K}_g^{-j}\mathcal{P}](\omega,x) = \dfrac{1}{\unicode{x3bb}(A_N(\omega,x))} \int_{A_N(\omega,x)}f(y)\,dy. \end{align*} $$
$$ \begin{align*} E\bigg[\varphi \bigg \rvert \bigvee_{j=0}^{N} \mathcal{K}_g^{-j}\mathcal{P}](\omega,x) = \dfrac{1}{\unicode{x3bb}(A_N(\omega,x))} \int_{A_N(\omega,x)}f(y)\,dy. \end{align*} $$
Set
![]() $\mu _{A_N(\omega ,x)}:=({1}/{\unicode{x3bb} (A_N(\omega ,x))})\unicode{x3bb} _{|A_N(\omega ,x)}$
as the normalized Lebesgue measure on
$\mu _{A_N(\omega ,x)}:=({1}/{\unicode{x3bb} (A_N(\omega ,x))})\unicode{x3bb} _{|A_N(\omega ,x)}$
as the normalized Lebesgue measure on
![]() $A_N(\omega ,x)$
. For almost every
$A_N(\omega ,x)$
. For almost every
![]() $(\omega ,x) \in E_g$
, the sequence of measures
$(\omega ,x) \in E_g$
, the sequence of measures
![]() $(\mu _{A_N(\omega ,x)})_N$
converges weakly to the measure
$(\mu _{A_N(\omega ,x)})_N$
converges weakly to the measure
![]() $\mu _{\omega ,x}$
.
$\mu _{\omega ,x}$
.
We define the set
![]() $\bar {E}_g$
of full measure as the set of points
$\bar {E}_g$
of full measure as the set of points
![]() $(\omega ,x) \in E_g$
satisfying the following conditions.
$(\omega ,x) \in E_g$
satisfying the following conditions.
-
• There exists a probability measure
 $\mu _{(\omega ,x)}$
on
$\mu _{(\omega ,x)}$
on
 $E_g$
such that for any continuous function
$E_g$
such that for any continuous function
 $\varphi :E_g \to \mathbb {R}_+$
, we have
$\varphi :E_g \to \mathbb {R}_+$
, we have  $$ \begin{align*}E[\varphi | \mathcal{F}](\omega,x) = \int \varphi \,d\mu_{(\omega,x)}.\end{align*} $$
$$ \begin{align*}E[\varphi | \mathcal{F}](\omega,x) = \int \varphi \,d\mu_{(\omega,x)}.\end{align*} $$
-
• For any continuous function
 $\varphi : E_g \to \mathbb {R}_+$
,
$\varphi : E_g \to \mathbb {R}_+$
,
 $E[\varphi | \bigvee _{j = 0}^n \mathcal {K}_g^{-j}\mathcal {P}](\omega ,x)$
tends to
$E[\varphi | \bigvee _{j = 0}^n \mathcal {K}_g^{-j}\mathcal {P}](\omega ,x)$
tends to
 $E[\varphi | \mathcal {F}](\omega ,x)$
.
$E[\varphi | \mathcal {F}](\omega ,x)$
. -
• For any integer N, the point
 $(\omega ,x)$
belongs to an atom of the partition
$(\omega ,x)$
belongs to an atom of the partition
 $\bigvee _{j = 0}^N \mathcal {K}_g^{-j}\mathcal {P}$
and satisfies Lemma 9.
$\bigvee _{j = 0}^N \mathcal {K}_g^{-j}\mathcal {P}$
and satisfies Lemma 9. -
• For any integer N and for any continuous function
 $\varphi : E_g \to \mathbb {R}_+$
such that there exists a continuous function
$\varphi : E_g \to \mathbb {R}_+$
such that there exists a continuous function
 $f:\mathbb {R} \to \mathbb {R}_+$
such that
$f:\mathbb {R} \to \mathbb {R}_+$
such that
 $\varphi (\omega ,x) = f(x)$
for any
$\varphi (\omega ,x) = f(x)$
for any
 $(\omega ,x) \in E_g$
, we have
$(\omega ,x) \in E_g$
, we have $$ \begin{align*} E\bigg[\varphi \bigg \rvert \bigvee_{j = 0}^N \mathcal{K}_g^{-j}\mathcal{P}\bigg](\omega,x) = \int f(y) \,d\mu_{A_N(\omega,x)}(y). \end{align*} $$
$$ \begin{align*} E\bigg[\varphi \bigg \rvert \bigvee_{j = 0}^N \mathcal{K}_g^{-j}\mathcal{P}\bigg](\omega,x) = \int f(y) \,d\mu_{A_N(\omega,x)}(y). \end{align*} $$
Lemma 12. Let
![]() $(\omega ,x) \in \bar {E}_g$
. Let
$(\omega ,x) \in \bar {E}_g$
. Let
![]() $[a,b] \subset [0,1]$
such that
$[a,b] \subset [0,1]$
such that
![]() $\mu _{(\omega ,x)}[a,b] = 1$
. Then one of these two propositions is true:
$\mu _{(\omega ,x)}[a,b] = 1$
. Then one of these two propositions is true:
-
(i)
 $\mu _{(\omega ,x)}[a,({a+b})/{2}] = 1$
;
$\mu _{(\omega ,x)}[a,({a+b})/{2}] = 1$
; -
(ii)
 $\mu _{(\omega ,x)}]({a+b})/{2},b] = 1$
.
$\mu _{(\omega ,x)}]({a+b})/{2},b] = 1$
.
Proof. Suppose that proposition (ii) does not hold. Set
![]() $\eta := \mu _{(\omega ,x)}([a,({a+b})/{2}])>0$
. Let m be a large enough integer so that
$\eta := \mu _{(\omega ,x)}([a,({a+b})/{2}])>0$
. Let m be a large enough integer so that
![]() ${1}/{\beta ^m} < {\eta }/{2}$
. Let
${1}/{\beta ^m} < {\eta }/{2}$
. Let
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $f_{\varepsilon }$
be the continuous function defined on
$f_{\varepsilon }$
be the continuous function defined on
![]() $[0,1]$
by
$[0,1]$
by
![]() $f_{\varepsilon } = 0$
on
$f_{\varepsilon } = 0$
on
![]() $[a,({a+b})/{2}]$
,
$[a,({a+b})/{2}]$
,
![]() $f_{\varepsilon }= 1$
on
$f_{\varepsilon }= 1$
on
![]() $[({a+b})/{2}+\varepsilon ,b]$
, and
$[({a+b})/{2}+\varepsilon ,b]$
, and
![]() $f_{\varepsilon }$
is a linear map on
$f_{\varepsilon }$
is a linear map on
![]() $[({a+b})/{2},({a+b})/{2}+ \varepsilon ]$
. See Figure 11.
$[({a+b})/{2},({a+b})/{2}+ \varepsilon ]$
. See Figure 11.

Figure 11 Graph of the function
![]() $f_{\varepsilon }$
.
$f_{\varepsilon }$
.
Then,
Therefore, since the sequence
![]() $(\mu _{A_n(\omega ,x)})_n$
converges weakly to
$(\mu _{A_n(\omega ,x)})_n$
converges weakly to
![]() $\mu _{(\omega ,x)}$
, there exists
$\mu _{(\omega ,x)}$
, there exists
![]() $N_0 \in \mathbb {N}$
, such that for any
$N_0 \in \mathbb {N}$
, such that for any
![]() $ n \geqslant N_0$
,
$ n \geqslant N_0$
,
Thus, for any
![]() $n \geqslant N_0$
,
$n \geqslant N_0$
,
 $$ \begin{align*} \mu_{A_n(\omega,x)}\bigg(\bigg[\dfrac{a+b}{2}+\varepsilon,b\bigg]\bigg) \leqslant 1 - \dfrac{\eta}{2} \leqslant 1 - \dfrac{1}{\beta^m}. \end{align*} $$
$$ \begin{align*} \mu_{A_n(\omega,x)}\bigg(\bigg[\dfrac{a+b}{2}+\varepsilon,b\bigg]\bigg) \leqslant 1 - \dfrac{\eta}{2} \leqslant 1 - \dfrac{1}{\beta^m}. \end{align*} $$
It then implies that
 $$ \begin{align*} \mu_{A_n(\omega,x)}\bigg(\bigg[a,\dfrac{a+b}{2}+\varepsilon\bigg[\bigg)> \dfrac{1}{\beta^m}. \end{align*} $$
$$ \begin{align*} \mu_{A_n(\omega,x)}\bigg(\bigg[a,\dfrac{a+b}{2}+\varepsilon\bigg[\bigg)> \dfrac{1}{\beta^m}. \end{align*} $$
Let
![]() $n \geqslant N_0$
such that
$n \geqslant N_0$
such that
![]() $K_g^n(\omega ,x),\ldots ,K_g^{n+m-1}(\omega ,x) \in P_0$
. Then from Lemma 9, there exists a real number
$K_g^n(\omega ,x),\ldots ,K_g^{n+m-1}(\omega ,x) \in P_0$
. Then from Lemma 9, there exists a real number
![]() $t \in [0,1]$
such that
$t \in [0,1]$
such that
![]() $A_{n+m}(\omega ,x) = A_n(\omega ,x) \cap [0,t]$
. Moreover,
$A_{n+m}(\omega ,x) = A_n(\omega ,x) \cap [0,t]$
. Moreover,
![]() $\unicode{x3bb} (A_{n+m}(\omega ,x)) = ({1}/{\beta ^m})\unicode{x3bb} (A_n(\omega ,x))$
. It implies that
$\unicode{x3bb} (A_{n+m}(\omega ,x)) = ({1}/{\beta ^m})\unicode{x3bb} (A_n(\omega ,x))$
. It implies that
![]() $A_{n+m}(\omega ,x) \subset [a,({a+b})/{2} + \varepsilon [$
, and hence, for any
$A_{n+m}(\omega ,x) \subset [a,({a+b})/{2} + \varepsilon [$
, and hence, for any
![]() $n' \geqslant n+m$
,
$n' \geqslant n+m$
,
 $$ \begin{align*} \mu_{A_{n'}(\omega,x)}\bigg(\bigg[\dfrac{a+b}{2}+\varepsilon,b\bigg]\bigg) = 0. \end{align*} $$
$$ \begin{align*} \mu_{A_{n'}(\omega,x)}\bigg(\bigg[\dfrac{a+b}{2}+\varepsilon,b\bigg]\bigg) = 0. \end{align*} $$
Furthermore, we have
We then get that for any
![]() $\varepsilon\kern1.2pt{>}\kern1.2pt0$
,
$\varepsilon\kern1.2pt{>}\kern1.2pt0$
,
![]() $\mu _{(\omega ,x)}([({a+b})/{2} + 2\varepsilon ,b]) \kern1.2pt{=}\kern1.2pt 0$
, and hence
$\mu _{(\omega ,x)}([({a+b})/{2} + 2\varepsilon ,b]) \kern1.2pt{=}\kern1.2pt 0$
, and hence
![]() $\mu _{(\omega ,x)}(]({a\kern1.2pt{+}\kern1.2ptb})/ {2},b]) = 0$
.
$\mu _{(\omega ,x)}(]({a\kern1.2pt{+}\kern1.2ptb})/ {2},b]) = 0$
.
By dichotomy, we deduce that for any
![]() $(\omega ,x) \in E_g$
, the measure
$(\omega ,x) \in E_g$
, the measure
![]() $\mu _{(\omega ,x)}$
is the Dirac measure on x, which proves Proposition 10. In particular, the induced transformation
$\mu _{(\omega ,x)}$
is the Dirac measure on x, which proves Proposition 10. In particular, the induced transformation
![]() $\mathcal {K}_g$
is isomorphic to a one-sided Bernoulli shift.
$\mathcal {K}_g$
is isomorphic to a one-sided Bernoulli shift.
Lemma 13. There exists a floor of the greedy tower with length greater than or equal to
![]() ${1}/{\beta (\beta - 1)}$
. In particular, it is always possible to go from the tower
${1}/{\beta (\beta - 1)}$
. In particular, it is always possible to go from the tower
![]() $\mathcal {G}$
to the tower
$\mathcal {G}$
to the tower
![]() $\mathcal {L}$
under
$\mathcal {L}$
under
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Proof. We set
 $$ \begin{align*} n_0 = \min\bigg\{n \in \mathbb{N} \cup \{0\},T_{\ell}^n(1) \geqslant \dfrac{1}{\beta(\beta - 1)}\bigg\}. \end{align*} $$
$$ \begin{align*} n_0 = \min\bigg\{n \in \mathbb{N} \cup \{0\},T_{\ell}^n(1) \geqslant \dfrac{1}{\beta(\beta - 1)}\bigg\}. \end{align*} $$
Such an integer
![]() $n_0$
exists for any
$n_0$
exists for any
![]() $\beta> 1$
: if
$\beta> 1$
: if
![]() $1 < {1}/{\beta (\beta - 1)}$
, then
$1 < {1}/{\beta (\beta - 1)}$
, then
![]() $T_{\ell }(1) = \beta \times 1$
. Iterating
$T_{\ell }(1) = \beta \times 1$
. Iterating
![]() $T_{\ell }$
from
$T_{\ell }$
from
![]() $1$
is just a multiplication by
$1$
is just a multiplication by
![]() $\beta $
, as long as the images are less than
$\beta $
, as long as the images are less than
![]() ${1}/{\beta (\beta - 1)}$
. Thus, the length of the floor
${1}/{\beta (\beta - 1)}$
. Thus, the length of the floor
![]() $E_{g\ell ^{n_0}}$
is greater than or equal to
$E_{g\ell ^{n_0}}$
is greater than or equal to
![]() ${1}/{\beta (\beta - 1)}$
. Then we have
${1}/{\beta (\beta - 1)}$
. Then we have
 $$ \begin{align*} \mathcal{K}\bigg(E_{g\ell^{n_0}} \cap \bigg\{\omega_0 = \ell, x \in \bigg]\dfrac{s(1)}{\beta},\dfrac{1}{\beta(\beta - 1)}\bigg]\bigg\}\bigg) = E_{\ell}.\\[-44pt] \end{align*} $$
$$ \begin{align*} \mathcal{K}\bigg(E_{g\ell^{n_0}} \cap \bigg\{\omega_0 = \ell, x \in \bigg]\dfrac{s(1)}{\beta},\dfrac{1}{\beta(\beta - 1)}\bigg]\bigg\}\bigg) = E_{\ell}.\\[-44pt] \end{align*} $$
Theorem 14. The system
![]() $(X,\mu ,\mathcal {K})$
is ergodic.
$(X,\mu ,\mathcal {K})$
is ergodic.
Proof. The induced transformation of
![]() $\mathcal {K}$
on
$\mathcal {K}$
on
![]() $E_g$
is Bernoulli, and hence ergodic. Therefore, it suffices to prove that, up to a zero measure set,
$E_g$
is Bernoulli, and hence ergodic. Therefore, it suffices to prove that, up to a zero measure set,
In other words, we want to prove that almost every point in X reaches the base
![]() $E_g$
in a finite number of iterations of
$E_g$
in a finite number of iterations of
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
We first prove that almost every point in X can be reached from the base
![]() $E_g$
. By construction of
$E_g$
. By construction of
![]() $\mathcal {K}$
, every floor of the greedy tower is the image of a part of
$\mathcal {K}$
, every floor of the greedy tower is the image of a part of
![]() $E_g$
by a power of
$E_g$
by a power of
![]() $\mathcal {K}$
. More precisely, for any
$\mathcal {K}$
. More precisely, for any
![]() $e \in \mathcal {E}$
such that
$e \in \mathcal {E}$
such that
![]() $e(0) = g$
, we have
$e(0) = g$
, we have
 $$ \begin{align*} E_e = \mathcal{K}^{|e|-1}\bigg(\bigcap_{k=0}^{|e| - 1} \mathcal{K}^{-k}(E_{e(0),\ldots,e(k)})\bigg). \end{align*} $$
$$ \begin{align*} E_e = \mathcal{K}^{|e|-1}\bigg(\bigcap_{k=0}^{|e| - 1} \mathcal{K}^{-k}(E_{e(0),\ldots,e(k)})\bigg). \end{align*} $$
Similarly, every floor of the lazy tower is the image by a power of
![]() $\mathcal {K}$
of a part of the base
$\mathcal {K}$
of a part of the base
![]() $E_{\ell }$
. Finally, from Lemma 13, we can pass from the greedy tower to the lazy tower.
$E_{\ell }$
. Finally, from Lemma 13, we can pass from the greedy tower to the lazy tower.
Additionally, almost every point in the base
![]() $E_g$
returns to
$E_g$
returns to
![]() $E_g$
in a finite number of iterations of
$E_g$
in a finite number of iterations of
![]() $\mathcal {K}$
(from Poincaré recurrence theorem). Denote by
$\mathcal {K}$
(from Poincaré recurrence theorem). Denote by
![]() $\mathcal {N}_g$
the set of points of
$\mathcal {N}_g$
the set of points of
![]() $E_g$
which do not return to
$E_g$
which do not return to
![]() $E_g$
. Then
$E_g$
. Then
![]() $\mathcal {N}_g$
is a zero measure set. Therefore, the set
$\mathcal {N}_g$
is a zero measure set. Therefore, the set
![]() $\bigcup _{n \geqslant 0}\mathcal {K}^n(\mathcal {N}_g)$
is measurable, and of measure zero. Indeed, let
$\bigcup _{n \geqslant 0}\mathcal {K}^n(\mathcal {N}_g)$
is measurable, and of measure zero. Indeed, let
![]() $n \in \mathbb {N} \cup \{0\}$
. Then
$n \in \mathbb {N} \cup \{0\}$
. Then
For any path C of length n, the transformation
![]() $\mathcal {K}^n$
is invertible on
$\mathcal {K}^n$
is invertible on
![]() $\mathcal {N}_g \cap E_C$
from Proposition 5. Therefore,
$\mathcal {N}_g \cap E_C$
from Proposition 5. Therefore,
![]() $\mu (K^n(\mathcal {N}_g \cap E_C)) = 0$
and
$\mu (K^n(\mathcal {N}_g \cap E_C)) = 0$
and
![]() $\mu (\mathcal {K}^n(\mathcal {N}_g)) = 0$
.
$\mu (\mathcal {K}^n(\mathcal {N}_g)) = 0$
.
Let
![]() $a \in X \setminus \bigcup _{n \geqslant 0}\mathcal {K}^n(\mathcal {N}_g)$
. There exist
$a \in X \setminus \bigcup _{n \geqslant 0}\mathcal {K}^n(\mathcal {N}_g)$
. There exist
![]() $a_0 \in E_g$
and
$a_0 \in E_g$
and
![]() $n \in \mathbb {N} \cup \{0\}$
such that
$n \in \mathbb {N} \cup \{0\}$
such that
![]() ${\mathcal {K}^n(a_0) = a}$
. Moreover,
${\mathcal {K}^n(a_0) = a}$
. Moreover,
![]() $a_0 \notin \bigcup _{n \geqslant 0}\mathcal {K}^n(\mathcal {N}_g)$
so there exists a path
$a_0 \notin \bigcup _{n \geqslant 0}\mathcal {K}^n(\mathcal {N}_g)$
so there exists a path
![]() $C_0^a \in \mathscr {C}$
such that
$C_0^a \in \mathscr {C}$
such that
![]() $a_0 \in P_{C_0^a}$
. It implies that a will return to the greedy base in a finite number of iterations of
$a_0 \in P_{C_0^a}$
. It implies that a will return to the greedy base in a finite number of iterations of
![]() $\mathcal {K}$
(following the path
$\mathcal {K}$
(following the path
![]() $C_0^a$
).
$C_0^a$
).
Since the system
![]() $(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
is a factor of the system
$(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
is a factor of the system
![]() $(X,\mu ,\mathcal {K})$
, we have the following corollary.
$(X,\mu ,\mathcal {K})$
, we have the following corollary.
Corollary 15. The system
![]() $(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
is ergodic.
$(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
is ergodic.
Corollary 16. The measure
![]() $\mu _p$
is the unique absolutely continuous probability measure on
$\mu _p$
is the unique absolutely continuous probability measure on
![]() $I_{\beta }$
such that
$I_{\beta }$
such that
![]() $m_p \otimes \mu _p$
is
$m_p \otimes \mu _p$
is
![]() $K_{\beta }$
-invariant.
$K_{\beta }$
-invariant.
Proof. From Lemma 13, for any
![]() $1 < \beta < 2$
, there exists a floor of the greedy tower whose length is greater than or equal to
$1 < \beta < 2$
, there exists a floor of the greedy tower whose length is greater than or equal to
![]() ${1}/{\beta (\beta - 1)}$
. Symmetrically, there exists a floor of the lazy tower whose left limit is less than or equal to
${1}/{\beta (\beta - 1)}$
. Symmetrically, there exists a floor of the lazy tower whose left limit is less than or equal to
![]() ${1}/{\beta }$
. It implies that the support of
${1}/{\beta }$
. It implies that the support of
![]() $\mu _p$
is the full interval
$\mu _p$
is the full interval
![]() $I_{\beta }$
, and that
$I_{\beta }$
, and that
![]() $m_p \otimes \mu _p$
is equivalent to
$m_p \otimes \mu _p$
is equivalent to
![]() $m_p \otimes \unicode{x3bb} $
.
$m_p \otimes \unicode{x3bb} $
.
Let
![]() $\nu $
be an absolutely continuous probability measure (with respect to
$\nu $
be an absolutely continuous probability measure (with respect to
![]() $\unicode{x3bb} $
, and so with respect to
$\unicode{x3bb} $
, and so with respect to
![]() $\mu _p$
) such that
$\mu _p$
) such that
![]() $m_p \otimes \nu $
is
$m_p \otimes \nu $
is
![]() $K_{\beta }$
-invariant. Then the measure
$K_{\beta }$
-invariant. Then the measure
![]() $m_p \otimes \nu $
is absolutely continuous with respect to the ergodic measure
$m_p \otimes \nu $
is absolutely continuous with respect to the ergodic measure
![]() $m_p \otimes \mu _p$
, and hence
$m_p \otimes \mu _p$
, and hence
![]() $m_p \otimes \nu = m_p \otimes \mu _p$
and
$m_p \otimes \nu = m_p \otimes \mu _p$
and
![]() $\nu = \mu _p$
.
$\nu = \mu _p$
.
In [Reference Suzuki16], Suzuki proves that the density of
![]() $\mu _p$
is proportional to the function
$\mu _p$
is proportional to the function

where

By uniqueness of
![]() $\mu _p$
, we know that the density in equation (8) and the expression obtained by Suzuki (10) are equal. This result can be easily proved in the case where
$\mu _p$
, we know that the density in equation (8) and the expression obtained by Suzuki (10) are equal. This result can be easily proved in the case where
![]() $\beta $
is not a root of a polynomial of the form
$\beta $
is not a root of a polynomial of the form
![]() $X^{n_0} - X^{n_1} - \cdots - X^{n_k} - 1$
with
$X^{n_0} - X^{n_1} - \cdots - X^{n_k} - 1$
with
![]() $n_0> n_1 > \cdots > n_k$
(which is equivalent to say that
$n_0> n_1 > \cdots > n_k$
(which is equivalent to say that
![]() $1$
has no finite expansion in base
$1$
has no finite expansion in base
![]() $\beta $
).
$\beta $
).
Indeed, we prove that, in this case,
![]() $\ell _0 = B^0(\beta ,p)$
. On one hand, we recall that
$\ell _0 = B^0(\beta ,p)$
. On one hand, we recall that
 $$ \begin{align*} \ell_0 = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{w \in \{g,\ell\}^n, T_w(s(1)^-) \leqslant {1}/{\beta}} m_p([w \cdot g]_0^n). \end{align*} $$
$$ \begin{align*} \ell_0 = \sum_{n = 0}^{+\infty} \dfrac{1}{\beta^{n+1}} \sum_{w \in \{g,\ell\}^n, T_w(s(1)^-) \leqslant {1}/{\beta}} m_p([w \cdot g]_0^n). \end{align*} $$
Since
![]() $\beta $
is not a root of a polynomial of the form
$\beta $
is not a root of a polynomial of the form
![]() $X^{n_0} - X^{n_1} - \cdots - X^{n_k} - 1$
, then
$X^{n_0} - X^{n_1} - \cdots - X^{n_k} - 1$
, then
![]() $T_w(s(1)^-) = T_w(s(1))$
for any
$T_w(s(1)^-) = T_w(s(1))$
for any
![]() $w \in \{g,\ell \}^n$
. Moreover,
$w \in \{g,\ell \}^n$
. Moreover,
![]() $T_w(s(1)^-) \leqslant {1}/{\beta }$
is equivalent to
$T_w(s(1)^-) \leqslant {1}/{\beta }$
is equivalent to
![]() $T_w(s(1)) < {1}/{\beta }$
. Therefore, after adjusting the index of summation, we have
$T_w(s(1)) < {1}/{\beta }$
. Therefore, after adjusting the index of summation, we have

On the other hand, after a new reindexing in
![]() $\ell _1$
, we have
$\ell _1$
, we have

Thus,

By symmetry, we also obtain that
![]() $g_1 = B^0(\beta ,1-p)$
, and the equality of the two densities follows.
$g_1 = B^0(\beta ,1-p)$
, and the equality of the two densities follows.
In the case where
![]() $1$
has a finite expansion in base
$1$
has a finite expansion in base
![]() $\beta $
, there exists
$\beta $
, there exists
![]() $n \in \mathbb {N}$
and a sequence
$n \in \mathbb {N}$
and a sequence
![]() $w \in \{g,\ell \}^n$
such that
$w \in \{g,\ell \}^n$
such that
![]() $T_w(1) = 0$
, and the right limit
$T_w(1) = 0$
, and the right limit
![]() $T_v(1^+)$
and the value
$T_v(1^+)$
and the value
![]() $T_v(1)$
can differ, thus complicating the identification of the two formulas. For the simple case where
$T_v(1)$
can differ, thus complicating the identification of the two formulas. For the simple case where
![]() ${\beta = ({1+\sqrt {5}})/{2}}$
, we refer to the computations in the appendix of [Reference Tierce17].
${\beta = ({1+\sqrt {5}})/{2}}$
, we refer to the computations in the appendix of [Reference Tierce17].
3 The natural extension
3.1 Construction of the new extension
Any point in X which is not in a base has a unique preimage by
![]() $\mathcal {K}$
. However, a point in one of the two bases can come from several floors. Indeed, at each return to a base, the map
$\mathcal {K}$
. However, a point in one of the two bases can come from several floors. Indeed, at each return to a base, the map
![]() $\mathcal {K}$
‘forgets’ from where it comes. This lack of information prevents
$\mathcal {K}$
‘forgets’ from where it comes. This lack of information prevents
![]() $\mathcal {K}$
from being invertible.
$\mathcal {K}$
from being invertible.
We wish to construct a natural extension of
![]() $\mathcal {K}$
, denoted by
$\mathcal {K}$
, denoted by
![]() $\tilde {\mathcal {K}}$
. In some sense, it is the smallest invertible extension of
$\tilde {\mathcal {K}}$
. In some sense, it is the smallest invertible extension of
![]() $\mathcal {K}$
. Therefore, to construct
$\mathcal {K}$
. Therefore, to construct
![]() $\tilde {\mathcal {K}}$
, we need to extend the set X such that the information of the past floors is available. We recall the definition of a natural extension of a system (see for example [Reference Bruin and Kalle2]).
$\tilde {\mathcal {K}}$
, we need to extend the set X such that the information of the past floors is available. We recall the definition of a natural extension of a system (see for example [Reference Bruin and Kalle2]).
Definition 17. The system
![]() $(Y,\mathcal {C},\nu ,F)$
is a natural extension of the system
$(Y,\mathcal {C},\nu ,F)$
is a natural extension of the system
![]() $(X,\mathcal {B},\mu ,T)$
if there exist two sets
$(X,\mathcal {B},\mu ,T)$
if there exist two sets
![]() $X^* \in \mathcal {B}$
and
$X^* \in \mathcal {B}$
and
![]() $Y^* \in \mathcal {C}$
such that
$Y^* \in \mathcal {C}$
such that
![]() $\mu (X^*) = \nu (Y^*) = 1$
and a measurable mapping
$\mu (X^*) = \nu (Y^*) = 1$
and a measurable mapping
![]() $\pi : Y^* \to X^*$
such that:
$\pi : Y^* \to X^*$
such that:
-
(1) F is a bijection of
 $Y^*$
;
$Y^*$
; -
(2)
 $\mu = \nu \circ \pi ^{-1}$
;
$\mu = \nu \circ \pi ^{-1}$
; -
(3)
 $\pi \circ F = T \circ \pi $
; and
$\pi \circ F = T \circ \pi $
; and -
(4)
 $ \mathcal {C} = \bigvee _{n \geqslant 0} F^n (\pi ^{-1}(\mathcal {B}))$
.
$ \mathcal {C} = \bigvee _{n \geqslant 0} F^n (\pi ^{-1}(\mathcal {B}))$
.
Moreover, all natural extensions of a system are isomorphic [Reference Rokhlin14]. We now construct the extension
![]() $\tilde {\mathcal {K}}$
of
$\tilde {\mathcal {K}}$
of
![]() $\mathcal {K}$
, and then prove that it is one of its natural extensions. In the initial definition of the towers
$\mathcal {K}$
, and then prove that it is one of its natural extensions. In the initial definition of the towers
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {L}$
, each floor has a label e. More precisely, a label e is a finite sequence of g and
$\mathcal {L}$
, each floor has a label e. More precisely, a label e is a finite sequence of g and
![]() $\ell $
, where the first term of e describes the present tower and the following terms of e (when there are) describe which transformations have been applied since the base: the label describes the recent past of a point in the floor. Therefore, instead of ‘erasing’ the label at each return to a base, we will keep track of every past label, so that we can uniquely determine the past orbit of almost any point in the two towers.
$\ell $
, where the first term of e describes the present tower and the following terms of e (when there are) describe which transformations have been applied since the base: the label describes the recent past of a point in the floor. Therefore, instead of ‘erasing’ the label at each return to a base, we will keep track of every past label, so that we can uniquely determine the past orbit of almost any point in the two towers.
We denote by Z the set of left-infinite sequences generated by the graph G, that is,
A sequence of labels in Z contains in particular the information of the sequence of past transformations. Given a sequence
![]() $\mathbf {e}$
in Z, we will denote
$\mathbf {e}$
in Z, we will denote
![]() $e_0$
its term of index
$e_0$
its term of index
![]() $0$
.
$0$
.
For
![]() $e \in \mathcal {E}$
, we set
$e \in \mathcal {E}$
, we set
We then define the base of the two towers by
and
 $$ \begin{align*}\tilde{E}_{\ell} := \Omega \times Z_{(\ell)} \times \bigg[s(1),\dfrac{1}{\beta - 1}\bigg].\end{align*} $$
$$ \begin{align*}\tilde{E}_{\ell} := \Omega \times Z_{(\ell)} \times \bigg[s(1),\dfrac{1}{\beta - 1}\bigg].\end{align*} $$
If
![]() $e = (g,\omega _{-n},\ldots ,\omega _{-1})$
,
$e = (g,\omega _{-n},\ldots ,\omega _{-1})$
,
![]() $n \in \mathbb {N}$
, we set
$n \in \mathbb {N}$
, we set
If
![]() $e = (\ell ,\omega _{-n},\ldots ,\omega _{-1})$
,
$e = (\ell ,\omega _{-n},\ldots ,\omega _{-1})$
,
![]() $n \in \mathbb {N}$
, we set
$n \in \mathbb {N}$
, we set
 $$ \begin{align*} \tilde{E}_e := \Omega \times Z_e \times \bigg[T_{\omega_{-n},\ldots,\omega_{-1}}(s(1)^-),\dfrac{1}{\beta - 1}\bigg]. \end{align*} $$
$$ \begin{align*} \tilde{E}_e := \Omega \times Z_e \times \bigg[T_{\omega_{-n},\ldots,\omega_{-1}}(s(1)^-),\dfrac{1}{\beta - 1}\bigg]. \end{align*} $$
We note
 $$ \begin{align*} \tilde{\mathcal{G}} := \bigsqcup_{e \in \mathcal{E}, e(0) = g} \tilde{E}_e \end{align*} $$
$$ \begin{align*} \tilde{\mathcal{G}} := \bigsqcup_{e \in \mathcal{E}, e(0) = g} \tilde{E}_e \end{align*} $$
and
 $$ \begin{align*} \tilde{\mathcal{L}} := \bigsqcup_{e \in \mathcal{E}, e(0) = \ell} \tilde{E}_e. \end{align*} $$
$$ \begin{align*} \tilde{\mathcal{L}} := \bigsqcup_{e \in \mathcal{E}, e(0) = \ell} \tilde{E}_e. \end{align*} $$
We finally note
![]() $\tilde {X} := \tilde {\mathcal {G}} \sqcup \tilde {\mathcal {L}}$
. We set
$\tilde {X} := \tilde {\mathcal {G}} \sqcup \tilde {\mathcal {L}}$
. We set
 $$ \begin{align*} \pi_{\tilde{X},X}:\!\! \begin{array}{l c l} \tilde{X} & \!\!\!\to\!\!\!\! & X \\ (\omega,\mathbf{e},x) & \!\!\!\mapsto\!\!\!\! &(\omega,e_0,x) \end{array} \end{align*} $$
$$ \begin{align*} \pi_{\tilde{X},X}:\!\! \begin{array}{l c l} \tilde{X} & \!\!\!\to\!\!\!\! & X \\ (\omega,\mathbf{e},x) & \!\!\!\mapsto\!\!\!\! &(\omega,e_0,x) \end{array} \end{align*} $$
as the projection from
![]() $\tilde {X}$
onto X.
$\tilde {X}$
onto X.
Let
![]() $a = (\omega ,\mathbf {e},x) \in \tilde {X}$
. Then
$a = (\omega ,\mathbf {e},x) \in \tilde {X}$
. Then
![]() $\pi _{\tilde {X},X}(a) = (\omega ,e_0,x)$
. We have
$\pi _{\tilde {X},X}(a) = (\omega ,e_0,x)$
. We have
![]() $\mathcal {K}(\omega ,e_0,x) = (\sigma (\omega ),e', T_{\omega _0}(x))$
, where the label
$\mathcal {K}(\omega ,e_0,x) = (\sigma (\omega ),e', T_{\omega _0}(x))$
, where the label
![]() $e'$
depends on
$e'$
depends on
![]() $e_0$
,
$e_0$
,
![]() $\omega _0$
, and x, according to the previous construction. By construction of
$\omega _0$
, and x, according to the previous construction. By construction of
![]() $\mathcal {K}$
, we obviously have
$\mathcal {K}$
, we obviously have
![]() $e_0 \to e'$
in the graph G.
$e_0 \to e'$
in the graph G.
Applying the new dynamics
![]() $\tilde {\mathcal {K}}$
on a consists in concatenating the new label
$\tilde {\mathcal {K}}$
on a consists in concatenating the new label
![]() $e'$
to the sequence
$e'$
to the sequence
![]() $\mathbf {e}$
(we denote by
$\mathbf {e}$
(we denote by
![]() $\mathbf {e} \cdot e'$
this new sequence), in addition to shifting the sequence
$\mathbf {e} \cdot e'$
this new sequence), in addition to shifting the sequence
![]() $\omega $
and applying
$\omega $
and applying
![]() $T_{\omega _0}$
to x: we retain every past labels in memory.
$T_{\omega _0}$
to x: we retain every past labels in memory.
In other words, the dynamics
![]() $\tilde {\mathcal {K}}$
is defined on
$\tilde {\mathcal {K}}$
is defined on
![]() $\tilde {X}$
by
$\tilde {X}$
by
 $$ \begin{align*}\tilde{\mathcal{K}}:\!\! \begin{array}{l l l} \tilde{X} & \!\!\!\to\!\!\!\! & \tilde{X} \\ (\omega, \mathbf{e},x) & \!\!\!\mapsto\!\!\!\! & (\sigma(\omega),\mathbf{e} \cdot e',T_{\omega_0}(x)), \end{array} \end{align*} $$
$$ \begin{align*}\tilde{\mathcal{K}}:\!\! \begin{array}{l l l} \tilde{X} & \!\!\!\to\!\!\!\! & \tilde{X} \\ (\omega, \mathbf{e},x) & \!\!\!\mapsto\!\!\!\! & (\sigma(\omega),\mathbf{e} \cdot e',T_{\omega_0}(x)), \end{array} \end{align*} $$
where
![]() $e'$
is the label associated with the point
$e'$
is the label associated with the point
![]() $\mathcal {K}(\omega ,e_0,x) \in X$
.
$\mathcal {K}(\omega ,e_0,x) \in X$
.
The projection
![]() $\pi _{\tilde {X},X}$
is measurable and we have by construction
$\pi _{\tilde {X},X}$
is measurable and we have by construction
Denote by
![]() $\mathcal {B}$
the Borel
$\mathcal {B}$
the Borel
![]() $\sigma $
-algebra on X and by
$\sigma $
-algebra on X and by
![]() $\tilde {\mathcal {B}}$
the Borel
$\tilde {\mathcal {B}}$
the Borel
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $\tilde {X}$
. Let us prove that
$\tilde {X}$
. Let us prove that
The inclusion
![]() $\bigvee _{n \geqslant 0} \tilde {\mathcal {K}}^n(\pi _{\tilde {X},X}^{-1}(\mathcal {B})) \subset \tilde {\mathcal {B}}$
is clear.
$\bigvee _{n \geqslant 0} \tilde {\mathcal {K}}^n(\pi _{\tilde {X},X}^{-1}(\mathcal {B})) \subset \tilde {\mathcal {B}}$
is clear.
Let k and n be two non-negative integers. We consider a set A of
![]() $\tilde {\mathcal {B}}$
of the form
$\tilde {\mathcal {B}}$
of the form
![]() ${A = [\omega _0,\omega _1,\ldots , \omega _n]_0^n \times [e_{-k},\ldots ,e_0]_{-k}^{0} \times [a,b]}$
. We then have
${A = [\omega _0,\omega _1,\ldots , \omega _n]_0^n \times [e_{-k},\ldots ,e_0]_{-k}^{0} \times [a,b]}$
. We then have
Set
![]() $A_- = \Omega \times [e_{-k},\ldots ,e_{-1}]_{-k}^{-1} \times [a,b]$
and
$A_- = \Omega \times [e_{-k},\ldots ,e_{-1}]_{-k}^{-1} \times [a,b]$
and
![]() $A_+ = [\omega _0,\omega _1,\ldots , \omega _n]_0^n \times [e_0]_0 \times [a,b]$
.
$A_+ = [\omega _0,\omega _1,\ldots , \omega _n]_0^n \times [e_0]_0 \times [a,b]$
.
Then,
![]() $A_- \in \tilde {\mathcal {K}}^k(\pi _{\tilde {X},X}^{-1}(\mathcal {B})) $
and
$A_- \in \tilde {\mathcal {K}}^k(\pi _{\tilde {X},X}^{-1}(\mathcal {B})) $
and
![]() $A_+ \in \pi _{\tilde {X},X}^{-1}(\mathcal {B})$
, which implies that
$A_+ \in \pi _{\tilde {X},X}^{-1}(\mathcal {B})$
, which implies that
![]() $A \in \bigvee _{n \geqslant 0} \tilde {\mathcal {K}}^n(\pi _{\tilde {X},X}^{-1} (\mathcal {B}))$
, and proves equation (11).
$A \in \bigvee _{n \geqslant 0} \tilde {\mathcal {K}}^n(\pi _{\tilde {X},X}^{-1} (\mathcal {B}))$
, and proves equation (11).
We can now define the measure
![]() $\tilde {\mu }$
on
$\tilde {\mu }$
on
![]() $\tilde {X}$
. For
$\tilde {X}$
. For
![]() $ A \in \bigvee _{n = 0}^N \tilde {\mathcal {K}}^n(\pi _{\tilde {X},X}^{-1}(\mathcal {B}))$
, we set
$ A \in \bigvee _{n = 0}^N \tilde {\mathcal {K}}^n(\pi _{\tilde {X},X}^{-1}(\mathcal {B}))$
, we set
In some sense, the measure
![]() $\tilde {\mu }$
of this set A is obtained by ‘shifting’ the set A to the future, so that it can be viewed as a set in the first extension X. No information is lost by projecting it on X, allowing us to use the measure
$\tilde {\mu }$
of this set A is obtained by ‘shifting’ the set A to the future, so that it can be viewed as a set in the first extension X. No information is lost by projecting it on X, allowing us to use the measure
![]() $\mu $
. The measure
$\mu $
. The measure
![]() $\tilde {\mu }$
is well defined: if
$\tilde {\mu }$
is well defined: if
![]() $ A \in \bigvee _{n = 0}^N \tilde {\mathcal {K}}^n(\pi _{\tilde {X},X}^{-1}(\mathcal {B}))$
, then for any integer
$ A \in \bigvee _{n = 0}^N \tilde {\mathcal {K}}^n(\pi _{\tilde {X},X}^{-1}(\mathcal {B}))$
, then for any integer
![]() $k \in \mathbb {N}$
, we have
$k \in \mathbb {N}$
, we have
since
![]() $\mu $
is
$\mu $
is
![]() $\mathcal {K}$
-invariant. For any
$\mathcal {K}$
-invariant. For any
![]() $B \in \mathcal {B}$
, we have
$B \in \mathcal {B}$
, we have
![]() $\tilde {\mu } \circ \pi ^{-1}_{\tilde {X},X}(B) = \mu (B)$
, and the measure
$\tilde {\mu } \circ \pi ^{-1}_{\tilde {X},X}(B) = \mu (B)$
, and the measure
![]() $\tilde {\mu }$
is
$\tilde {\mu }$
is
![]() $\tilde {\mathcal {K}}$
-invariant.
$\tilde {\mathcal {K}}$
-invariant.
Finally, by construction,
![]() $\tilde {\mathcal {K}}$
is one to one on
$\tilde {\mathcal {K}}$
is one to one on
![]() $\tilde {X}$
. It implies that
$\tilde {X}$
. It implies that
![]() $(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
is a natural extension of
$(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
is a natural extension of
![]() $(X,\mu ,\mathcal {K})$
. Moreover, the natural extension of an ergodic system is ergodic, which provides the following result, as a direct consequence of Theorem 14.
$(X,\mu ,\mathcal {K})$
. Moreover, the natural extension of an ergodic system is ergodic, which provides the following result, as a direct consequence of Theorem 14.
Corollary 18. The system
![]() $(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
is ergodic.
$(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
is ergodic.
3.2 Natural extension of the initial system
The goal of this section is to prove that the previous extension is in fact a natural extension of the initial system
![]() $(\Omega \times I_{\beta },m_p \otimes \mu _p, K_{\beta })$
. To do so, we first introduce a canonic way to construct a natural extension of the initial system, then prove that the two extensions are isomorphic.
$(\Omega \times I_{\beta },m_p \otimes \mu _p, K_{\beta })$
. To do so, we first introduce a canonic way to construct a natural extension of the initial system, then prove that the two extensions are isomorphic.
We adapt the construction described in [Reference Boyarsky and Góra1, pp. 62], which provides a natural extension of
![]() $K_{\beta }$
. We set
$K_{\beta }$
. We set
Let
![]() $\underline {\mathcal {B}}$
be the
$\underline {\mathcal {B}}$
be the
![]() $\sigma $
-algebra generated by the cylinders of
$\sigma $
-algebra generated by the cylinders of
![]() $\underline {X}$
. We define the measure
$\underline {X}$
. We define the measure
![]() $\underline {\mu }$
on every set of the form
$\underline {\mu }$
on every set of the form
![]() $A = [\omega _k,\ldots ,\omega _{n+k}]_k^{n+k} \times [I_k,\ldots , I_{n+k}]_k^{n+k}$
, with
$A = [\omega _k,\ldots ,\omega _{n+k}]_k^{n+k} \times [I_k,\ldots , I_{n+k}]_k^{n+k}$
, with
![]() $k \in \mathbb {Z}, n \in \mathbb {N}$
, and for any
$k \in \mathbb {Z}, n \in \mathbb {N}$
, and for any
![]() $k \leqslant i \leqslant n+k$
,
$k \leqslant i \leqslant n+k$
,
![]() $\omega _i \in \{g,\ell \}$
, and
$\omega _i \in \{g,\ell \}$
, and
![]() $I_i$
sub-interval of
$I_i$
sub-interval of
![]() $I_{\beta }$
by
$I_{\beta }$
by
 $$ \begin{align*} \underline{\mu}(A) = m_p \otimes \mu_p\bigg([\omega_k,\ldots,\omega_{n+k}]_0^n \times \bigcap_{i =0}^n T_{\omega_{k+i}}^{-i}(I_{k+i})\bigg). \end{align*} $$
$$ \begin{align*} \underline{\mu}(A) = m_p \otimes \mu_p\bigg([\omega_k,\ldots,\omega_{n+k}]_0^n \times \bigcap_{i =0}^n T_{\omega_{k+i}}^{-i}(I_{k+i})\bigg). \end{align*} $$
We denote by
![]() $\underline {K}$
the shift on
$\underline {K}$
the shift on
![]() $\underline {X}$
.
$\underline {X}$
.
Proposition 19. [Reference Boyarsky and Góra1]
The dynamical system
![]() $(\underline {X},\underline {\mu },\underline {K})$
is a natural extension of the system
$(\underline {X},\underline {\mu },\underline {K})$
is a natural extension of the system
![]() $(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
.
$(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
.
Let
![]() $(\omega ,\mathbf {e},x) \in \tilde {X}$
. We denote by
$(\omega ,\mathbf {e},x) \in \tilde {X}$
. We denote by
![]() $\underline {\omega } = \underline {\omega }(\omega ,\mathbf {e})$
the sequence of
$\underline {\omega } = \underline {\omega }(\omega ,\mathbf {e})$
the sequence of
![]() $\{g,\ell \}^{\mathbb {Z}}$
defined by
$\{g,\ell \}^{\mathbb {Z}}$
defined by
![]() ${\underline {\omega }(k) = \omega _k}$
if
${\underline {\omega }(k) = \omega _k}$
if
![]() $k \geqslant 0$
and
$k \geqslant 0$
and
![]() $\underline {\omega }(k) = \mathbf {e}_{k+1}(-1)$
if
$\underline {\omega }(k) = \mathbf {e}_{k+1}(-1)$
if
![]() $k\leqslant -1$
. The sequence
$k\leqslant -1$
. The sequence
![]() $\underline {\omega }$
is the bi-infinite sequence of applied transformations in the past, and transformations to be applied in the future. For any
$\underline {\omega }$
is the bi-infinite sequence of applied transformations in the past, and transformations to be applied in the future. For any
![]() $k \in \mathbb {Z}$
, we denote by
$k \in \mathbb {Z}$
, we denote by
![]() $x_k$
the real component of
$x_k$
the real component of
![]() $\tilde {\mathcal {K}}^{k}(\omega ,\mathbf {e},x)$
, and
$\tilde {\mathcal {K}}^{k}(\omega ,\mathbf {e},x)$
, and
![]() $\underline {x} := (x_k)_{k \in \mathbb {Z}}$
. We define the application
$\underline {x} := (x_k)_{k \in \mathbb {Z}}$
. We define the application
 $$ \begin{align*}\phi:\!\! \begin{array}{l l l} \tilde{X} & \!\!\!\to\!\!\!\! & \underline{X} \\ (\omega,\mathbf{e},x) & \!\!\!\to\!\!\!\! & (\underline{\omega},\underline{x}). \end{array}\end{align*} $$
$$ \begin{align*}\phi:\!\! \begin{array}{l l l} \tilde{X} & \!\!\!\to\!\!\!\! & \underline{X} \\ (\omega,\mathbf{e},x) & \!\!\!\to\!\!\!\! & (\underline{\omega},\underline{x}). \end{array}\end{align*} $$
One easily checks the following lemma.
Lemma 20. The application
![]() $\phi $
is a factor map from
$\phi $
is a factor map from
![]() $(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
to
$(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
to
![]() $(\underline {X},\underline {\mu },\underline {K})$
.
$(\underline {X},\underline {\mu },\underline {K})$
.
Theorem 21. The factor map
![]() $\phi $
is an isomorphism. Therefore, the system
$\phi $
is an isomorphism. Therefore, the system
![]() $(\tilde {X},\tilde {\mu }, \tilde {\mathcal {K}})$
is a natural extension of
$(\tilde {X},\tilde {\mu }, \tilde {\mathcal {K}})$
is a natural extension of
![]() $(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
.
$(\Omega \times I_{\beta },m_p \otimes \mu _p,K_{\beta })$
.
To prove this theorem, we use the notion of relatively independent joinings above a factor (see for example [Reference Glasner8, pp. 126–127]).
Let
![]() $\mathbb {P}$
be the relatively independent self-joining of the system
$\mathbb {P}$
be the relatively independent self-joining of the system
![]() $(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
above its factor
$(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
above its factor
![]() $\underline {X}$
, that is, the measure on
$\underline {X}$
, that is, the measure on
![]() $\tilde {X} \times \tilde {X}$
such that for two measurable sets
$\tilde {X} \times \tilde {X}$
such that for two measurable sets
![]() $A,B \in \tilde {X}$
,
$A,B \in \tilde {X}$
,
where
![]() $\mathcal {F} = \phi ^{-1}(\mathcal {B}(\underline {X}))$
is the factor
$\mathcal {F} = \phi ^{-1}(\mathcal {B}(\underline {X}))$
is the factor
![]() $\sigma $
-algebra associated to the factor
$\sigma $
-algebra associated to the factor
![]() $(\underline {X},\underline {\mu },\underline {K})$
. We have the following properties:
$(\underline {X},\underline {\mu },\underline {K})$
. We have the following properties:
-
•
 $\mathbb {P}$
is a self-joining so its marginals on the first and second coordinate are
$\mathbb {P}$
is a self-joining so its marginals on the first and second coordinate are
 $\tilde {\mu }$
, and
$\tilde {\mu }$
, and
 $\mathbb {P}$
is
$\mathbb {P}$
is
 $\tilde {\mathcal {K}} \times \tilde {\mathcal {K}}$
-invariant;
$\tilde {\mathcal {K}} \times \tilde {\mathcal {K}}$
-invariant; -
• the measure
 $\mathbb {P}$
is supported on the set
$\mathbb {P}$
is supported on the set
 $\{(a,b) \in \tilde {X} \times \tilde {X}: \phi (a) = \phi (b)\}$
;
$\{(a,b) \in \tilde {X} \times \tilde {X}: \phi (a) = \phi (b)\}$
; -
•
 $\mathbb {P}$
is supported on the diagonal of
$\mathbb {P}$
is supported on the diagonal of
 $\tilde {X} \times \tilde {X}$
if and only if the factor map
$\tilde {X} \times \tilde {X}$
if and only if the factor map
 $\phi $
is an isomorphism.
$\phi $
is an isomorphism.
Let
![]() $a = (\omega ,\mathbf {e},x)$
and
$a = (\omega ,\mathbf {e},x)$
and
![]() $b = (\omega ',\mathbf {e}',x')$
be two elements of
$b = (\omega ',\mathbf {e}',x')$
be two elements of
![]() $\tilde {X}$
such that
$\tilde {X}$
such that
![]() $\phi (a) = \phi (b)$
. We then have
$\phi (a) = \phi (b)$
. We then have
![]() $\underline {\omega }(\omega ,\mathbf {e}) = \underline {\omega }(\omega ',\mathbf {e}')$
and
$\underline {\omega }(\omega ,\mathbf {e}) = \underline {\omega }(\omega ',\mathbf {e}')$
and
![]() $\underline {x} = \underline {x}'$
. In other words, a and b describe two trajectories in the towers, starting from the same real number x and with the same transformations
$\underline {x} = \underline {x}'$
. In other words, a and b describe two trajectories in the towers, starting from the same real number x and with the same transformations
![]() $\underline {\omega }$
, but possibly following different floors
$\underline {\omega }$
, but possibly following different floors
![]() $\mathbf {e}$
and
$\mathbf {e}$
and
![]() $\mathbf {e}'$
. Proving that
$\mathbf {e}'$
. Proving that
![]() $\mathbb {P}$
is supported by the diagonal of
$\mathbb {P}$
is supported by the diagonal of
![]() $\tilde {X} \times \tilde {X}$
consists in proving that for
$\tilde {X} \times \tilde {X}$
consists in proving that for
![]() $\mathbb {P}$
-almost every
$\mathbb {P}$
-almost every
![]() $(a,b) \in \tilde {X} \times \tilde {X}$
, the two sequences of floors
$(a,b) \in \tilde {X} \times \tilde {X}$
, the two sequences of floors
![]() $\mathbf {e}$
and
$\mathbf {e}$
and
![]() $\mathbf {e}'$
are actually equal.
$\mathbf {e}'$
are actually equal.
The idea of the proof consists in taking two trajectories in
![]() $\tilde {X}$
starting from the same real number x, with the same transformations, and proving that they end up in the same floor. Once these trajectories come at the same time in the same floor, they coincide in the future and in the past by injectivity.
$\tilde {X}$
starting from the same real number x, with the same transformations, and proving that they end up in the same floor. Once these trajectories come at the same time in the same floor, they coincide in the future and in the past by injectivity.
We first work on the extension X. Let
![]() $k \in \mathbb {N}$
and consider the set of positive measure
$k \in \mathbb {N}$
and consider the set of positive measure
 $$ \begin{align*} C_k : = \bigg\{(\omega,e,x) \in X: x < \dfrac{1}{\beta^k}, \omega_0 = \omega_1 = \cdots = \omega_{k-1} = g \bigg\}. \end{align*} $$
$$ \begin{align*} C_k : = \bigg\{(\omega,e,x) \in X: x < \dfrac{1}{\beta^k}, \omega_0 = \omega_1 = \cdots = \omega_{k-1} = g \bigg\}. \end{align*} $$
The set
![]() $C_k$
describes the points of X whose real component is close to
$C_k$
describes the points of X whose real component is close to
![]() $0$
, and on which the greedy transformation will be applied k times in a row. The label e does not take part in the definition of
$0$
, and on which the greedy transformation will be applied k times in a row. The label e does not take part in the definition of
![]() $C_k$
, which means that the event
$C_k$
, which means that the event
![]() $C_k$
is measurable with respect to the factor
$C_k$
is measurable with respect to the factor
![]() $\underline {X}$
: given two trajectories with the same real component and the same sequence of transformations, the event
$\underline {X}$
: given two trajectories with the same real component and the same sequence of transformations, the event
![]() $C_k$
happens almost surely (by ergodicity of
$C_k$
happens almost surely (by ergodicity of
![]() $\tilde {\mathcal {K}}$
and because
$\tilde {\mathcal {K}}$
and because
![]() $C_k$
is of positive measure) and at the same time for both trajectories. Knowing that
$C_k$
is of positive measure) and at the same time for both trajectories. Knowing that
![]() $C_k$
is realized actually gives some information about the label. We will prove that for large k and conditionally to
$C_k$
is realized actually gives some information about the label. We will prove that for large k and conditionally to
![]() $C_k$
, both trajectories are in a floor of the greedy tower whose interval is large, with high probability.
$C_k$
, both trajectories are in a floor of the greedy tower whose interval is large, with high probability.
Let
![]() $A_k$
be the union of the floors of
$A_k$
be the union of the floors of
![]() $\mathcal {G}$
whose length is less than
$\mathcal {G}$
whose length is less than
![]() ${1}/{\beta ^k}$
. Let
${1}/{\beta ^k}$
. Let
![]() $B_k$
be the complementary set of
$B_k$
be the complementary set of
![]() $A_k$
in
$A_k$
in
![]() $\mathcal {G}$
. Then the set
$\mathcal {G}$
. Then the set
![]() $C_k$
can be divided into three parts:
$C_k$
can be divided into three parts:
![]() $C_k \cap \mathcal {L}$
,
$C_k \cap \mathcal {L}$
,
![]() $C_k \cap A_k$
, and
$C_k \cap A_k$
, and
![]() $C_k \cap B_k$
. The set
$C_k \cap B_k$
. The set
![]() $C_k \cap B_k$
is particularly interesting since a point in this set will end up in the greedy base
$C_k \cap B_k$
is particularly interesting since a point in this set will end up in the greedy base
![]() $E_g$
in at most k iterations: such a point will remain in the left part of its floor under the action of
$E_g$
in at most k iterations: such a point will remain in the left part of its floor under the action of
![]() $\mathcal {K}$
, and the length of the floor will eventually be larger than
$\mathcal {K}$
, and the length of the floor will eventually be larger than
![]() ${1}/{\beta }$
, allowing the point to go to
${1}/{\beta }$
, allowing the point to go to
![]() $E_g$
in less than k iterations (see Figures 3 and 4). In the following, we prove that for large k and knowing
$E_g$
in less than k iterations (see Figures 3 and 4). In the following, we prove that for large k and knowing
![]() $C_k$
, the event
$C_k$
, the event
![]() $C_k \cap B_k$
happens with high probability.
$C_k \cap B_k$
happens with high probability.
We first introduce the following technical lemma.
Lemma 22. The intervals of the lazy tower
![]() $\mathcal {L}$
never contain
$\mathcal {L}$
never contain
![]() $0$
.
$0$
.
Proof. This property holds by construction of the extension
![]() $\mathcal {K}$
. Indeed, if an interval of a floor of
$\mathcal {K}$
. Indeed, if an interval of a floor of
![]() $\mathcal {L}$
contained
$\mathcal {L}$
contained
![]() $0$
, it would have to be the image by
$0$
, it would have to be the image by
![]() $T_g$
of an interval whose lower bound is
$T_g$
of an interval whose lower bound is
![]() ${1}/{\beta }$
. However, if the lower bound of an interval of
${1}/{\beta }$
. However, if the lower bound of an interval of
![]() $\mathcal {L}$
equals
$\mathcal {L}$
equals
![]() ${1}/{\beta }$
, we are in the case where the part of the floor satisfying
${1}/{\beta }$
, we are in the case where the part of the floor satisfying
![]() $x \in [{1}/{\beta },{2}/{\beta }[$
is sent to the greedy base when applying
$x \in [{1}/{\beta },{2}/{\beta }[$
is sent to the greedy base when applying
![]() $T_g$
.
$T_g$
.
For any label
![]() $e \in \mathcal {E}$
, we set
$e \in \mathcal {E}$
, we set
![]() $Y_e := \Omega \times \{e\}$
, and we have
$Y_e := \Omega \times \{e\}$
, and we have
![]() $E_e = Y_e \times I_e$
. We then set
$E_e = Y_e \times I_e$
. We then set
![]() $Y := \bigsqcup _{e \in \mathcal {E}} Y_e$
, which is represented vertically in Figure 2. Let us define the measure
$Y := \bigsqcup _{e \in \mathcal {E}} Y_e$
, which is represented vertically in Figure 2. Let us define the measure
![]() $\nu $
on Y by, for any
$\nu $
on Y by, for any
![]() $e \in \mathcal {E}$
with
$e \in \mathcal {E}$
with
![]() $e = (h,\omega _{-n},\ldots , \omega _{-1})$
,
$e = (h,\omega _{-n},\ldots , \omega _{-1})$
,
where
![]() $\Gamma _h$
is one of the two constants
$\Gamma _h$
is one of the two constants
![]() $\Gamma _g$
and
$\Gamma _g$
and
![]() $\Gamma _{\ell }$
defined in Theorem 1. In this way, we have
$\Gamma _{\ell }$
defined in Theorem 1. In this way, we have
Finally, we denote
![]() $\pi _{X,Y}$
the projection from X onto Y.
$\pi _{X,Y}$
the projection from X onto Y.
Let
![]() $\varepsilon> 0$
be small enough, so that
$\varepsilon> 0$
be small enough, so that
![]() $1 - ({1+2(\beta -1)})/{(\beta - 1)\mu (\mathcal {G})}\varepsilon> 0.5$
. Let
$1 - ({1+2(\beta -1)})/{(\beta - 1)\mu (\mathcal {G})}\varepsilon> 0.5$
. Let
![]() $N \in ~\mathbb {N}$
be such that the measure
$N \in ~\mathbb {N}$
be such that the measure
![]() $\mu $
of the floors beyond the level N in
$\mu $
of the floors beyond the level N in
![]() $\mathcal {L}$
is less than
$\mathcal {L}$
is less than
![]() $\varepsilon $
. By the previous lemma, there exists
$\varepsilon $
. By the previous lemma, there exists
![]() $k_0 \in \mathbb {N}$
such that no floor of
$k_0 \in \mathbb {N}$
such that no floor of
![]() $\mathcal {L}$
up to the level N has an interval whose lower bound is less than
$\mathcal {L}$
up to the level N has an interval whose lower bound is less than
![]() ${1}/{\beta ^k}$
.
${1}/{\beta ^k}$
.
As previously said, we have
We want to estimate each term of the right-hand side of equation (12). We will prove that for large k,
![]() $C_k \cap \mathcal {L}$
and
$C_k \cap \mathcal {L}$
and
![]() $C_k \cap A_k$
have a small measure, and that
$C_k \cap A_k$
have a small measure, and that
![]() $C_k \cap B_k$
represents more than half of the measure of
$C_k \cap B_k$
represents more than half of the measure of
![]() $C_k$
.
$C_k$
.
Lemma 23. For k large enough, we have
Proof. Let
![]() $k \geqslant k_0$
. A floor of
$k \geqslant k_0$
. A floor of
![]() $\mathcal {L}$
can intersect
$\mathcal {L}$
can intersect
![]() $C_k$
only if the lower bound of its interval is less than
$C_k$
only if the lower bound of its interval is less than
![]() ${1}/{\beta ^k}$
. The integer N is fixed such that every floor below the level N does not contain
${1}/{\beta ^k}$
. The integer N is fixed such that every floor below the level N does not contain
![]() ${1}/{\beta ^k}$
. Therefore, only the floors beyond the level N can intersect
${1}/{\beta ^k}$
. Therefore, only the floors beyond the level N can intersect
![]() $C_k$
. Additionally, for any
$C_k$
. Additionally, for any
![]() $e \in \mathcal {E}$
, we have, by definition of the measure
$e \in \mathcal {E}$
, we have, by definition of the measure
![]() $\mu $
on each floor,
$\mu $
on each floor,
 $$ \begin{align*}\mu\bigg(\bigg\{(\omega,e,x) \in E_e: \omega_0 = \cdots = \omega_{k-1} = g, x < \dfrac{1}{\beta^k}\bigg\}\bigg) = p^k \mu\bigg(E_e \cap \bigg\{x < \dfrac{1}{\beta^k}\bigg\}\bigg).\end{align*} $$
$$ \begin{align*}\mu\bigg(\bigg\{(\omega,e,x) \in E_e: \omega_0 = \cdots = \omega_{k-1} = g, x < \dfrac{1}{\beta^k}\bigg\}\bigg) = p^k \mu\bigg(E_e \cap \bigg\{x < \dfrac{1}{\beta^k}\bigg\}\bigg).\end{align*} $$
We then have
 $$ \begin{align*}\mu(C_k \cap \mathcal{L}) = p^k \sum_{e \in \mathcal{E}, e(0) = \ell, |e| \geqslant N+1} \nu(Y_e) \unicode{x3bb}\bigg(I_e \cap \bigg[0;\dfrac{1}{\beta^k}\bigg]\bigg). \end{align*} $$
$$ \begin{align*}\mu(C_k \cap \mathcal{L}) = p^k \sum_{e \in \mathcal{E}, e(0) = \ell, |e| \geqslant N+1} \nu(Y_e) \unicode{x3bb}\bigg(I_e \cap \bigg[0;\dfrac{1}{\beta^k}\bigg]\bigg). \end{align*} $$
For a floor
![]() $E_e$
of the lazy tower such that
$E_e$
of the lazy tower such that
![]() $I_e \cap [0;{1}/{\beta ^k}] \neq \varnothing $
, we have
$I_e \cap [0;{1}/{\beta ^k}] \neq \varnothing $
, we have
For k large enough, we then have
It implies that
 $$ \begin{align*}\unicode{x3bb}\bigg(I_e \cap \bigg[0;\dfrac{1}{\beta^k}\bigg]\bigg) \leqslant \dfrac{1}{\beta^k} \leqslant 2 \dfrac{\beta - 1}{\beta^k} \unicode{x3bb}(I_e)\end{align*} $$
$$ \begin{align*}\unicode{x3bb}\bigg(I_e \cap \bigg[0;\dfrac{1}{\beta^k}\bigg]\bigg) \leqslant \dfrac{1}{\beta^k} \leqslant 2 \dfrac{\beta - 1}{\beta^k} \unicode{x3bb}(I_e)\end{align*} $$
and hence
Lemma 24. For k large enough, we have
 $$ \begin{align*}\mu(C_k \cap A_k) \leqslant \dfrac{p^k}{\beta^k} \varepsilon. \end{align*} $$
$$ \begin{align*}\mu(C_k \cap A_k) \leqslant \dfrac{p^k}{\beta^k} \varepsilon. \end{align*} $$
Proof. Let
![]() $k \in \mathbb {N}$
.
$k \in \mathbb {N}$
.
 $$ \begin{align*} \mu(C_k \cap A_k) = p^k \sum_{e \in \mathcal{E}, E_e \subset A_k} \nu(Y_e) \unicode{x3bb}\bigg(I_e \cap \bigg[0;\dfrac{1}{\beta^k}\bigg]\bigg). \end{align*} $$
$$ \begin{align*} \mu(C_k \cap A_k) = p^k \sum_{e \in \mathcal{E}, E_e \subset A_k} \nu(Y_e) \unicode{x3bb}\bigg(I_e \cap \bigg[0;\dfrac{1}{\beta^k}\bigg]\bigg). \end{align*} $$
If
![]() $E_e$
is a floor of
$E_e$
is a floor of
![]() $A_k$
, then
$A_k$
, then
![]() $\unicode{x3bb} (I_e \cap [0;{1}/{\beta ^k}]) \leqslant {1}/{\beta ^k}$
. Therefore,
$\unicode{x3bb} (I_e \cap [0;{1}/{\beta ^k}]) \leqslant {1}/{\beta ^k}$
. Therefore,
 $$ \begin{align*} \mu(C_k \cap A_k) \leqslant \dfrac{p^k}{\beta^k}\nu(\pi_{X,Y}(A_k)). \end{align*} $$
$$ \begin{align*} \mu(C_k \cap A_k) \leqslant \dfrac{p^k}{\beta^k}\nu(\pi_{X,Y}(A_k)). \end{align*} $$
We have
and hence
 $$ \begin{align*} \pi_{X,Y} \bigg(\bigcap_{k \geqslant 1} A_k\bigg) = \varnothing. \end{align*} $$
$$ \begin{align*} \pi_{X,Y} \bigg(\bigcap_{k \geqslant 1} A_k\bigg) = \varnothing. \end{align*} $$
Since the intersection of the
![]() $A_k$
is decreasing, we have
$A_k$
is decreasing, we have
It implies that
We can choose k large enough, so that
![]() $\nu (\pi _{X,Y}(A_k)) < \varepsilon $
. Therefore,
$\nu (\pi _{X,Y}(A_k)) < \varepsilon $
. Therefore,
 $$ \begin{align*} \mu(C_k \cap A_k) \leqslant \dfrac{p^k}{\beta^k} \varepsilon.\\[-42pt] \end{align*} $$
$$ \begin{align*} \mu(C_k \cap A_k) \leqslant \dfrac{p^k}{\beta^k} \varepsilon.\\[-42pt] \end{align*} $$
Proposition 25. For k large enough, we have
Proof. Let
![]() $k \in \mathbb {N}$
be large enough such that Lemmas 23 and 24 are both satisfied. We have
$k \in \mathbb {N}$
be large enough such that Lemmas 23 and 24 are both satisfied. We have
From Lemmas 23 and 24, we then have
 $$ \begin{align*}\dfrac{\mu(C_k \cap B_k)}{\mu(C_k)} &\geqslant 1 - \dfrac{({p^k}/{\beta^k})\varepsilon + 2p^k (({\,\beta - 1})/{\beta^k})\varepsilon}{\mu(C_k)}\\ &\geqslant 1 - \dfrac{({p^k}/{\beta^k})\varepsilon + 2p^k (({\,\beta - 1})/{\beta^k})\varepsilon}{\mu(C_k \cap \mathcal{G})}. \end{align*} $$
$$ \begin{align*}\dfrac{\mu(C_k \cap B_k)}{\mu(C_k)} &\geqslant 1 - \dfrac{({p^k}/{\beta^k})\varepsilon + 2p^k (({\,\beta - 1})/{\beta^k})\varepsilon}{\mu(C_k)}\\ &\geqslant 1 - \dfrac{({p^k}/{\beta^k})\varepsilon + 2p^k (({\,\beta - 1})/{\beta^k})\varepsilon}{\mu(C_k \cap \mathcal{G})}. \end{align*} $$
However,
 $$ \begin{align*} \mu(C_k \cap \mathcal{G}) = p^k \sum_{e \in \mathcal{E}, e(0) = g} \nu(Y_e) \unicode{x3bb}\bigg(I_e \cap \bigg[0;\dfrac{1}{\beta^k}\bigg]\bigg). \end{align*} $$
$$ \begin{align*} \mu(C_k \cap \mathcal{G}) = p^k \sum_{e \in \mathcal{E}, e(0) = g} \nu(Y_e) \unicode{x3bb}\bigg(I_e \cap \bigg[0;\dfrac{1}{\beta^k}\bigg]\bigg). \end{align*} $$
For any floor
![]() $E_e$
of
$E_e$
of
![]() $\mathcal {G}$
, we have the minoration
$\mathcal {G}$
, we have the minoration
![]() $\unicode{x3bb} (I_e \cap [0,{1}/{\beta ^k}]) \geqslant \unicode{x3bb} (I_e)({\beta -1})/{\beta ^k}$
and hence
$\unicode{x3bb} (I_e \cap [0,{1}/{\beta ^k}]) \geqslant \unicode{x3bb} (I_e)({\beta -1})/{\beta ^k}$
and hence
 $$ \begin{align*}\dfrac{\mu(C_k \cap B_k)}{\mu(C_k)} \geqslant 1 - \dfrac{({p^k}/{\beta^k})\varepsilon + 2p^k (({\beta - 1})/{\beta^k})\varepsilon}{p^k (({\beta - 1})/{\beta^k})\mu(\mathcal{G})} = 1 - \dfrac{1+2(\beta-1)}{(\beta - 1)\mu(\mathcal{G})}\varepsilon.\end{align*} $$
$$ \begin{align*}\dfrac{\mu(C_k \cap B_k)}{\mu(C_k)} \geqslant 1 - \dfrac{({p^k}/{\beta^k})\varepsilon + 2p^k (({\beta - 1})/{\beta^k})\varepsilon}{p^k (({\beta - 1})/{\beta^k})\mu(\mathcal{G})} = 1 - \dfrac{1+2(\beta-1)}{(\beta - 1)\mu(\mathcal{G})}\varepsilon.\end{align*} $$
The real
![]() $\varepsilon $
is such that
$\varepsilon $
is such that
![]() $1 - ({1+2(\beta -1)})/{(\beta - 1)\mu (\mathcal {G})}\varepsilon> 0.5$
, which gives the result.
$1 - ({1+2(\beta -1)})/{(\beta - 1)\mu (\mathcal {G})}\varepsilon> 0.5$
, which gives the result.
All these computations are also valid on the extension
![]() $\tilde {X}$
. Indeed,
$\tilde {X}$
. Indeed,
![]() $\pi _{\tilde {X},X}^{-1}(C_k) \in \pi _{\tilde {X},X}^{-1}(\mathcal {B})$
, which implies
$\pi _{\tilde {X},X}^{-1}(C_k) \in \pi _{\tilde {X},X}^{-1}(\mathcal {B})$
, which implies
![]() $\tilde {\mu }(\pi _{\tilde {X},X}^{-1}(C_k)) = \mu (C_k)$
. In the following, we will still denote
$\tilde {\mu }(\pi _{\tilde {X},X}^{-1}(C_k)) = \mu (C_k)$
. In the following, we will still denote
![]() $C_k$
instead of
$C_k$
instead of
![]() $\pi _{\tilde {X},X}^{-1}(C_k)$
.
$\pi _{\tilde {X},X}^{-1}(C_k)$
.
Since
![]() $\tilde {\mathcal {K}}$
is ergodic and
$\tilde {\mathcal {K}}$
is ergodic and
![]() $\mu (C_k)> 0$
, almost every trajectory in
$\mu (C_k)> 0$
, almost every trajectory in
![]() $\tilde {X}$
encounters
$\tilde {X}$
encounters
![]() $C_k$
with frequency
$C_k$
with frequency
![]() $\mu (C_k)$
. Therefore, for
$\mu (C_k)$
. Therefore, for
![]() $\mathbb {P}$
-almost every couple of trajectories in
$\mathbb {P}$
-almost every couple of trajectories in
![]() $\tilde {X}$
, both trajectories simultaneously encounter
$\tilde {X}$
, both trajectories simultaneously encounter
![]() $C_k$
(since
$C_k$
(since
![]() $C_k$
is measurable with respect to the factor
$C_k$
is measurable with respect to the factor
![]() $\underline {X}$
) with frequency
$\underline {X}$
) with frequency
![]() $\mu (C_k)$
(since
$\mu (C_k)$
(since
![]() $\mathbb {P}$
is a self-joining of
$\mathbb {P}$
is a self-joining of
![]() $\mu $
). In other words, we have, for
$\mu $
). In other words, we have, for
![]() $\mathbb {P}$
-almost every
$\mathbb {P}$
-almost every
![]() $(a,b) \in \tilde {X} \times \tilde {X}$
, for any
$(a,b) \in \tilde {X} \times \tilde {X}$
, for any
![]() $n \in \mathbb {N} \cup \{0\}$
:
$n \in \mathbb {N} \cup \{0\}$
:
-
•
 $\tilde {\mathcal {K}}^n(a) \in C_k$
if and only if
$\tilde {\mathcal {K}}^n(a) \in C_k$
if and only if
 $\tilde {\mathcal {K}}^n(b) \in C_k$
;
$\tilde {\mathcal {K}}^n(b) \in C_k$
; -
•
 .
.
The ergodicity of
![]() $\tilde {\mathcal {K}}$
and Proposition 25 also imply that among the occurrences of
$\tilde {\mathcal {K}}$
and Proposition 25 also imply that among the occurrences of
![]() $C_k$
, the event
$C_k$
, the event
![]() $C_k \cap B_k$
occurs with a frequency greater that
$C_k \cap B_k$
occurs with a frequency greater that
![]() $0.5$
for the orbits of
$0.5$
for the orbits of
![]() $\mathbb {P}$
-almost every
$\mathbb {P}$
-almost every
![]() $(a,b) \in \tilde {X} \times \tilde {X}$
under
$(a,b) \in \tilde {X} \times \tilde {X}$
under
![]() $\tilde {\mathcal {K}}$
. Therefore, for
$\tilde {\mathcal {K}}$
. Therefore, for
![]() $\mathbb {P}$
-almost every
$\mathbb {P}$
-almost every
![]() $(a,b) \in \tilde {X} \times \tilde {X}$
, there exists
$(a,b) \in \tilde {X} \times \tilde {X}$
, there exists
![]() ${n_0 \in \mathbb {N} \cup \{0\}}$
such that
${n_0 \in \mathbb {N} \cup \{0\}}$
such that
![]() $\tilde {\mathcal {K}}^{n_0}(a) \in C_k \cap B_k$
and
$\tilde {\mathcal {K}}^{n_0}(a) \in C_k \cap B_k$
and
![]() $\tilde {\mathcal {K}}^{n_0}(b) \in C_k \cap B_k$
. Once the two trajectories are in
$\tilde {\mathcal {K}}^{n_0}(b) \in C_k \cap B_k$
. Once the two trajectories are in
![]() $C_k \cap B_k$
simultaneously, they will end up in the greedy base in at most k iterations (note that even if one of the two points goes in the base before the other, it will ‘wait’ for the second one to join it. Since its real component is small enough, the point is in the atom
$C_k \cap B_k$
simultaneously, they will end up in the greedy base in at most k iterations (note that even if one of the two points goes in the base before the other, it will ‘wait’ for the second one to join it. Since its real component is small enough, the point is in the atom
![]() $P_0$
). In conclusion, for
$P_0$
). In conclusion, for
![]() $\mathbb {P}$
-almost every
$\mathbb {P}$
-almost every
![]() $(a,b) \in \tilde {X} \times \tilde {X}$
, if we note
$(a,b) \in \tilde {X} \times \tilde {X}$
, if we note
![]() $a = (\omega ,\mathbf {e},x)$
and
$a = (\omega ,\mathbf {e},x)$
and
![]() $b = (\omega ,\mathbf {e}',x)$
, there exists an integer
$b = (\omega ,\mathbf {e}',x)$
, there exists an integer
![]() $M = M(\underline {\omega },\underline {x},\mathbf {e},\mathbf {e}')$
such that
$M = M(\underline {\omega },\underline {x},\mathbf {e},\mathbf {e}')$
such that
![]() $e_M = e^{\prime }_M = (g)$
.
$e_M = e^{\prime }_M = (g)$
.
Let
![]() $\delta>0$
. There exists an integer
$\delta>0$
. There exists an integer
![]() $M_{\delta }$
such that
$M_{\delta }$
such that
Therefore, we have
![]() $\mathbb {P}( e_{M_{\delta }} = e^{\prime }_{M_{\delta }}) \geqslant 1 - \delta $
. Since
$\mathbb {P}( e_{M_{\delta }} = e^{\prime }_{M_{\delta }}) \geqslant 1 - \delta $
. Since
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\tilde {\mathcal {K}} \times \tilde {\mathcal {K}}$
-invariant, we deduce that for any integer
$\tilde {\mathcal {K}} \times \tilde {\mathcal {K}}$
-invariant, we deduce that for any integer
![]() $k \in \mathbb {Z}$
and any
$k \in \mathbb {Z}$
and any
![]() $\delta>0$
,
$\delta>0$
,
and hence
![]() $\mathbf {e} = \mathbf {e}'$
. We proved that
$\mathbf {e} = \mathbf {e}'$
. We proved that
![]() $\mathbb {P}$
is supported by the diagonal of
$\mathbb {P}$
is supported by the diagonal of
![]() $\tilde {X} \times \tilde {X}$
, which implies that
$\tilde {X} \times \tilde {X}$
, which implies that
![]() $\phi $
is an isomorphism. Therefore,
$\phi $
is an isomorphism. Therefore,
![]() $(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
is a natural extension of the initial system, which concludes the proof of Theorem 21.
$(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
is a natural extension of the initial system, which concludes the proof of Theorem 21.
3.3 Bernoullicity
We know that the natural extension of the initial random system is ergodic. In fact, we have the following stronger result.
Theorem 26. The natural extension of the random
![]() $\beta $
-transformation is isomorphic to a Bernoulli shift.
$\beta $
-transformation is isomorphic to a Bernoulli shift.
To prove this theorem, we introduce a generating partition of the two towers. We then prove that this partition is weak-Bernoulli, by an argument on countable state space Markov chains of Ito, Murata, and Totoki [Reference Ito, Murata and Totoki9], which implies the theorem. In the following, we denote
![]() $\tilde {\mu }_g := \tilde {\mu }(\cdot | \tilde {E}_g)$
, and by
$\tilde {\mu }_g := \tilde {\mu }(\cdot | \tilde {E}_g)$
, and by
![]() $\tilde {\mathcal {K}}_g$
the induced transformation of
$\tilde {\mathcal {K}}_g$
the induced transformation of
![]() $\tilde {\mathcal {K}}$
on the base
$\tilde {\mathcal {K}}$
on the base
![]() $\tilde {E}_g$
.
$\tilde {E}_g$
.
Lemma 27. Let
![]() $(X,\mu ,T)$
be an ergodic dynamical system, and A a measurable set of X with positive measure. Denote by
$(X,\mu ,T)$
be an ergodic dynamical system, and A a measurable set of X with positive measure. Denote by
![]() $(\tilde {X},\tilde {\mu },\tilde {T})$
a natural extension of the system, and by
$(\tilde {X},\tilde {\mu },\tilde {T})$
a natural extension of the system, and by
![]() $\pi $
a factor map from
$\pi $
a factor map from
![]() $\tilde {X}$
onto X. Then the system induced by
$\tilde {X}$
onto X. Then the system induced by
![]() $\tilde {T}$
on
$\tilde {T}$
on
![]() $\pi ^{-1}(A)$
is a natural extension of the system induced by T on A.
$\pi ^{-1}(A)$
is a natural extension of the system induced by T on A.
Proof. We start by introducing the necessary notation. The natural extension of the system
![]() $(X,\mu ,T)$
can be described by a two-sided shift
$(X,\mu ,T)$
can be described by a two-sided shift
![]() $\tilde {T}$
on the set
$\tilde {T}$
on the set
with the factor map
![]() $\pi $
given by
$\pi $
given by
![]() $\pi ((x_n)_{n \in \mathbb {Z}}) = x_0$
, and the measure
$\pi ((x_n)_{n \in \mathbb {Z}}) = x_0$
, and the measure
![]() $\tilde {\mu }$
defined by
$\tilde {\mu }$
defined by
 $$ \begin{align*} \tilde{\mu}([A_{k},A_{k+1},\ldots,A_{n+k}]_k^{n+k}) = \mu\bigg(\bigcap_{i = 0}^n T^{-i}(A_{k+i})\bigg), \end{align*} $$
$$ \begin{align*} \tilde{\mu}([A_{k},A_{k+1},\ldots,A_{n+k}]_k^{n+k}) = \mu\bigg(\bigcap_{i = 0}^n T^{-i}(A_{k+i})\bigg), \end{align*} $$
where
![]() $A_k,\ldots ,A_{n+k}$
are measurable sets of X and
$A_k,\ldots ,A_{n+k}$
are measurable sets of X and
![]() $[A_{k},A_{k+1},\ldots ,A_{n+k}]_k^{n+k} := \{\mathbf {x} \in \tilde {X}: \text {for} \ k \leqslant i \leqslant n+k, x_i \in A_i\}$
.
$[A_{k},A_{k+1},\ldots ,A_{n+k}]_k^{n+k} := \{\mathbf {x} \in \tilde {X}: \text {for} \ k \leqslant i \leqslant n+k, x_i \in A_i\}$
.
Denote by
![]() $\tilde {A}:= \pi ^{-1}(A) = \{(x_n) \in \tilde {X}, x_0 \in A\}$
and
$\tilde {A}:= \pi ^{-1}(A) = \{(x_n) \in \tilde {X}, x_0 \in A\}$
and
![]() $(\tilde {A},\tilde {\mu }_{\tilde {A}},\tilde {T}_{\tilde {A}})$
the system induced by
$(\tilde {A},\tilde {\mu }_{\tilde {A}},\tilde {T}_{\tilde {A}})$
the system induced by
![]() $\tilde {T}$
on
$\tilde {T}$
on
![]() $\tilde {A}$
. The transformation
$\tilde {A}$
. The transformation
![]() $\tilde {T}_{\tilde {A}}$
is defined by
$\tilde {T}_{\tilde {A}}$
is defined by
![]() $\tilde {T}_{\tilde {A}}(\mathbf {x}) = \tilde {T}^{r_A(x_0)}(\mathbf {x})$
for every
$\tilde {T}_{\tilde {A}}(\mathbf {x}) = \tilde {T}^{r_A(x_0)}(\mathbf {x})$
for every
![]() $\mathbf {x} \in \tilde {A}$
, where
$\mathbf {x} \in \tilde {A}$
, where
![]() $r_A(x_0)$
is the return time of
$r_A(x_0)$
is the return time of
![]() $x_0$
in A, which is the same as the return time of
$x_0$
in A, which is the same as the return time of
![]() $\mathbf {x}$
in
$\mathbf {x}$
in
![]() $\tilde {A}$
.
$\tilde {A}$
.
We denote by
![]() $(A,\mu (\cdot |A),T_A)$
the system induced by T on A. The natural extension of this induced system can also be described by a two-sided shift
$(A,\mu (\cdot |A),T_A)$
the system induced by T on A. The natural extension of this induced system can also be described by a two-sided shift
![]() $\underline {T}$
on the set
$\underline {T}$
on the set
![]() $\underline {A} = \{\mathbf {x} = (x_n)_{n \in \mathbb {Z}} \in A^{\mathbb {Z}}, \text { for all } n \in \mathbb {Z}, T_A (x_n) = x_{n+1}\}$
, with the measure
$\underline {A} = \{\mathbf {x} = (x_n)_{n \in \mathbb {Z}} \in A^{\mathbb {Z}}, \text { for all } n \in \mathbb {Z}, T_A (x_n) = x_{n+1}\}$
, with the measure
![]() $\underline {\mu }$
defined in the same way as
$\underline {\mu }$
defined in the same way as
![]() $\tilde {\mu }$
.
$\tilde {\mu }$
.
We want to prove that the two systems
![]() $(\tilde {A},\tilde {\mu }_{\tilde {A}},\tilde {T}_{\tilde {A}})$
and
$(\tilde {A},\tilde {\mu }_{\tilde {A}},\tilde {T}_{\tilde {A}})$
and
![]() $(\underline {A},\underline {\mu },\underline {T})$
are isomorphic. We define the map
$(\underline {A},\underline {\mu },\underline {T})$
are isomorphic. We define the map
![]() $\varphi $
as
$\varphi $
as
 $$ \begin{align*}\varphi:\!\! \begin{array}{lcl} \tilde{A} & \!\!\!\to\!\!\!\! & \underline{A} \\ \mathbf{x} &\!\!\!\mapsto\!\!\!\!& ((\tilde{T}_{\tilde{A}}^n(\mathbf{x}))_0)_{n \in \mathbb{Z}}. \end{array} \end{align*} $$
$$ \begin{align*}\varphi:\!\! \begin{array}{lcl} \tilde{A} & \!\!\!\to\!\!\!\! & \underline{A} \\ \mathbf{x} &\!\!\!\mapsto\!\!\!\!& ((\tilde{T}_{\tilde{A}}^n(\mathbf{x}))_0)_{n \in \mathbb{Z}}. \end{array} \end{align*} $$
The map
![]() $\varphi $
consists in keeping only the terms of the sequence x that belong to A.
$\varphi $
consists in keeping only the terms of the sequence x that belong to A.
We clearly have that
![]() $\varphi \circ \tilde {T}_{\tilde {A}} = \underline {T} \circ \varphi $
and that
$\varphi \circ \tilde {T}_{\tilde {A}} = \underline {T} \circ \varphi $
and that
![]() $\underline {\mu }$
is the pushforward measure
$\underline {\mu }$
is the pushforward measure
![]() $\tilde {\mu }_{\tilde {A}} \circ \varphi ^{-1}$
: the map
$\tilde {\mu }_{\tilde {A}} \circ \varphi ^{-1}$
: the map
![]() $\varphi $
is a factor map from
$\varphi $
is a factor map from
![]() $(\tilde {A},\tilde {\mu }_{\tilde {A}},\tilde {T}_{\tilde {A}})$
to
$(\tilde {A},\tilde {\mu }_{\tilde {A}},\tilde {T}_{\tilde {A}})$
to
![]() $(\underline {A},\underline {\mu },\underline {T})$
.
$(\underline {A},\underline {\mu },\underline {T})$
.
We now prove that
![]() $\varphi $
is an isomorphism. Let
$\varphi $
is an isomorphism. Let
![]() $\mathbf {y} = (y_n)_{n \in \mathbb {Z}} \in \underline {A}$
. Let
$\mathbf {y} = (y_n)_{n \in \mathbb {Z}} \in \underline {A}$
. Let
![]() $n \in \mathbb {Z}$
. From
$n \in \mathbb {Z}$
. From
![]() $y_n$
, we can construct the finite sequence of the iterates of
$y_n$
, we can construct the finite sequence of the iterates of
![]() $y_n$
:
$y_n$
:
stopping just before
![]() $y_{n+1} = T^{r_A(y_n)}(y_n)$
. Then the sequence
$y_{n+1} = T^{r_A(y_n)}(y_n)$
. Then the sequence
![]() $\mathbf {x}$
obtained by concatenating the sequences
$\mathbf {x}$
obtained by concatenating the sequences
![]() $s(y_n)$
for all
$s(y_n)$
for all
![]() $n \in \mathbb {Z}$
is, by construction, a sequence of
$n \in \mathbb {Z}$
is, by construction, a sequence of
![]() $\tilde {A}$
such that
$\tilde {A}$
such that
![]() $\varphi (\mathbf {x}) = \mathbf {y}$
.
$\varphi (\mathbf {x}) = \mathbf {y}$
.
Let us prove that
![]() $\varphi $
is one-to-one. Let
$\varphi $
is one-to-one. Let
![]() $\mathbf {w},\mathbf {x} \in \tilde {A}$
such that
$\mathbf {w},\mathbf {x} \in \tilde {A}$
such that
![]() $\varphi (\mathbf {w}) = \varphi (\mathbf {x})$
. Then
$\varphi (\mathbf {w}) = \varphi (\mathbf {x})$
. Then
![]() ${w_0 = x_0}$
, which implies that for any
${w_0 = x_0}$
, which implies that for any
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $T^n(w_0) = T^n(x_0)$
, that is,
$T^n(w_0) = T^n(x_0)$
, that is,
![]() $x_n = w_n$
. Let
$x_n = w_n$
. Let
![]() $j_0:= \max \{\kern0.5pt j \,{<}\, 0, \tilde {T}^j(\mathbf {w}) \in \tilde {A}\}$
and
$j_0:= \max \{\kern0.5pt j \,{<}\, 0, \tilde {T}^j(\mathbf {w}) \in \tilde {A}\}$
and
![]() $j_1:= \max \{\,j < 0, \tilde {T}^j(\mathbf {x}) \in \tilde {A}\}$
. The existence of the integers
$j_1:= \max \{\,j < 0, \tilde {T}^j(\mathbf {x}) \in \tilde {A}\}$
. The existence of the integers
![]() $j_0$
and
$j_0$
and
![]() $j_1$
is assured by Poincaré’s recurrence theorem applied to
$j_1$
is assured by Poincaré’s recurrence theorem applied to
![]() $\tilde {T}^{-1}$
. Note that
$\tilde {T}^{-1}$
. Note that
![]() $\tilde {T}^{j_0}(\mathbf {w}) = \tilde {T}_{\tilde {A}}^{-1}(\mathbf {w})$
and
$\tilde {T}^{j_0}(\mathbf {w}) = \tilde {T}_{\tilde {A}}^{-1}(\mathbf {w})$
and
![]() $\tilde {T}^{j_1}(\mathbf {x}) = \tilde {T}_{\tilde {A}}^{-1}(\mathbf {x})$
. Since
$\tilde {T}^{j_1}(\mathbf {x}) = \tilde {T}_{\tilde {A}}^{-1}(\mathbf {x})$
. Since
![]() $\varphi (\mathbf {w}) = \varphi (\mathbf {x})$
, we get that
$\varphi (\mathbf {w}) = \varphi (\mathbf {x})$
, we get that
![]() $\tilde {T}^{j_0}(\mathbf {w}) = \tilde {T}^{j_1}(\mathbf {x})$
, that is,
$\tilde {T}^{j_0}(\mathbf {w}) = \tilde {T}^{j_1}(\mathbf {x})$
, that is,
![]() ${w_{j_0} = x_{j_1}}$
. The integer
${w_{j_0} = x_{j_1}}$
. The integer
![]() $-j_0$
is the return time of
$-j_0$
is the return time of
![]() $w_{j_0}$
in A, which implies that
$w_{j_0}$
in A, which implies that
![]() $j_0 = j_1$
, and
$j_0 = j_1$
, and
![]() $w_n = x_n$
for
$w_n = x_n$
for
![]() $n \geqslant j_0$
. By induction, we prove that
$n \geqslant j_0$
. By induction, we prove that
![]() $\mathbf {w} = \mathbf {x}$
, and
$\mathbf {w} = \mathbf {x}$
, and
![]() $\varphi $
is an isomorphism, which concludes the proof.
$\varphi $
is an isomorphism, which concludes the proof.
Corollary 28. The system
![]() $(\tilde {E}_g,\tilde {\mu }_g,\tilde {\mathcal {K}}_g)$
is a natural extension of the system
$(\tilde {E}_g,\tilde {\mu }_g,\tilde {\mathcal {K}}_g)$
is a natural extension of the system
![]() $(E_g,\mu _g,\mathcal {K}_g)$
.
$(E_g,\mu _g,\mathcal {K}_g)$
.
Proposition 29. The partition
![]() $\tilde {\mathcal {P}} := \pi ^{-1}(\mathcal {P}) $
is a generator of the system
$\tilde {\mathcal {P}} := \pi ^{-1}(\mathcal {P}) $
is a generator of the system
Proof.
![]() $\mu _g$
-almost every point
$\mu _g$
-almost every point
![]() $a \in E_g$
is associated to a unique sequence
$a \in E_g$
is associated to a unique sequence
![]() $(C_n^a)_{n \geqslant 0}$
of
$(C_n^a)_{n \geqslant 0}$
of
![]() $\mathscr {C}^{\kern2pt\mathbb {N} \cup \{0\}}$
such that for any
$\mathscr {C}^{\kern2pt\mathbb {N} \cup \{0\}}$
such that for any
![]() $n \in \mathbb {N} \cup \{0\}$
,
$n \in \mathbb {N} \cup \{0\}$
,
![]() $\mathcal {K}_g^n(a) \in E_{C_n^a}$
: the sequence
$\mathcal {K}_g^n(a) \in E_{C_n^a}$
: the sequence
![]() $(C_n^a)_{n \geqslant 0}$
can be viewed as the
$(C_n^a)_{n \geqslant 0}$
can be viewed as the
![]() $\mathcal {P}$
-name of the point a. Denote by
$\mathcal {P}$
-name of the point a. Denote by
![]() $\phi _{\mathcal {P}}$
the application defined almost everywhere on
$\phi _{\mathcal {P}}$
the application defined almost everywhere on
![]() $E_g$
by
$E_g$
by
![]() $\phi _{\mathcal {P}}(a) = (C_n^a)_{n \geqslant 0}$
. Denote by
$\phi _{\mathcal {P}}(a) = (C_n^a)_{n \geqslant 0}$
. Denote by
![]() $\nu $
the image measure of
$\nu $
the image measure of
![]() $\mu _g$
by
$\mu _g$
by
![]() $\phi _{\mathcal {P}}$
and by
$\phi _{\mathcal {P}}$
and by
![]() $\sigma $
the left shift on
$\sigma $
the left shift on
![]() $\mathscr {C}^{\kern2pt\mathbb {N} \cup \{0\}}$
. The application
$\mathscr {C}^{\kern2pt\mathbb {N} \cup \{0\}}$
. The application
![]() $\phi _{\mathcal {P}}$
is a factor map from the system
$\phi _{\mathcal {P}}$
is a factor map from the system
![]() $(E_g,\mu _g,\mathcal {K}_g)$
to the one-sided Bernoulli shift
$(E_g,\mu _g,\mathcal {K}_g)$
to the one-sided Bernoulli shift
![]() $(\mathscr {C}^{\kern2pt\mathbb {N} \cup \{0\}},\nu ,\sigma )$
. From Proposition 10, the partition
$(\mathscr {C}^{\kern2pt\mathbb {N} \cup \{0\}},\nu ,\sigma )$
. From Proposition 10, the partition
![]() $\mathcal {P}$
is a generator of the system
$\mathcal {P}$
is a generator of the system
![]() $(E_g,\mu _g,\mathcal {K}_g)$
. Therefore, the application
$(E_g,\mu _g,\mathcal {K}_g)$
. Therefore, the application
![]() $\phi _{\mathcal {P}}$
is an isomorphism.
$\phi _{\mathcal {P}}$
is an isomorphism.
We can construct a natural extension of the system
![]() $(\mathscr {C}^{\kern2pt\mathbb {N} \cup \{0\}},\nu ,\sigma )$
the same way we did for
$(\mathscr {C}^{\kern2pt\mathbb {N} \cup \{0\}},\nu ,\sigma )$
the same way we did for
![]() $\underline {K}$
. Doing so, we construct the system
$\underline {K}$
. Doing so, we construct the system
![]() $(\mathscr {C}^{\kern2pt\mathbb {Z}},\tilde {\nu },\sigma )$
, which is a two-sided Bernoulli shift on
$(\mathscr {C}^{\kern2pt\mathbb {Z}},\tilde {\nu },\sigma )$
, which is a two-sided Bernoulli shift on
![]() $\mathscr {C}^{\kern2pt\mathbb {Z}}$
. Since the natural extensions of a system are isomorphic to one another, we deduce from the previous lemma that the systems
$\mathscr {C}^{\kern2pt\mathbb {Z}}$
. Since the natural extensions of a system are isomorphic to one another, we deduce from the previous lemma that the systems
![]() $(\mathscr {C}^{\kern2pt\mathbb {Z}},\tilde {\nu },\sigma )$
and
$(\mathscr {C}^{\kern2pt\mathbb {Z}},\tilde {\nu },\sigma )$
and
![]() $(\tilde {E}_g,\tilde {\mu }_G,\tilde {\mathcal {K}}_g)$
are isomorphic, and thus conclude the proof.
$(\tilde {E}_g,\tilde {\mu }_G,\tilde {\mathcal {K}}_g)$
are isomorphic, and thus conclude the proof.
From this partition
![]() $\tilde {\mathcal {P}}$
, we construct the set
$\tilde {\mathcal {P}}$
, we construct the set
This family is obtained by ‘unfolding’ the partition
![]() $\tilde {\mathcal {P}}$
on the two towers: each path C of
$\tilde {\mathcal {P}}$
on the two towers: each path C of
![]() $\mathscr {C}$
is not only described by the first atom
$\mathscr {C}$
is not only described by the first atom
![]() $\tilde {E}_C$
, but by the sequence of successive images of this atom by
$\tilde {E}_C$
, but by the sequence of successive images of this atom by
![]() $\tilde {\mathcal {K}}$
.
$\tilde {\mathcal {K}}$
.
Lemma 30. The set
![]() $\mathcal {P}_{\tilde {X}}$
is a partition of
$\mathcal {P}_{\tilde {X}}$
is a partition of
![]() $\tilde {X}$
.
$\tilde {X}$
.
Proof. Two distinct sets of
![]() $\mathcal {P}_{\tilde {X}}$
are clearly disjoint.
$\mathcal {P}_{\tilde {X}}$
are clearly disjoint.
However, let
![]() $(\omega ,\mathbf {e},x) \in \tilde {X}$
. Almost surely, there exists
$(\omega ,\mathbf {e},x) \in \tilde {X}$
. Almost surely, there exists
![]() $k \in \mathbb {N} \cup \{0\}$
such that
$k \in \mathbb {N} \cup \{0\}$
such that
![]() ${\mathbf {e}_{-k} = (g)}$
(applying Poincaré recurrence theorem to
${\mathbf {e}_{-k} = (g)}$
(applying Poincaré recurrence theorem to
![]() $\tilde {\mathcal {K}}^{-1}$
). Let
$\tilde {\mathcal {K}}^{-1}$
). Let
![]() $k_0 := \min \{k \in \mathbb {N} \cup \{0\}, \mathbf {e}_{-k} = (g)\}$
. The integer
$k_0 := \min \{k \in \mathbb {N} \cup \{0\}, \mathbf {e}_{-k} = (g)\}$
. The integer
![]() $-k_0$
corresponds to the last visit of the greedy base in the past orbit of
$-k_0$
corresponds to the last visit of the greedy base in the past orbit of
![]() $(\omega ,\mathbf {e},x)$
. Almost surely, there exists a unique
$(\omega ,\mathbf {e},x)$
. Almost surely, there exists a unique
![]() $C \in \mathscr {C}$
such that
$C \in \mathscr {C}$
such that
![]() $\tilde {\mathcal {K}}^{-k_0}(\omega ,\mathbf {e},x) \in \tilde {E}_C$
. Since
$\tilde {\mathcal {K}}^{-k_0}(\omega ,\mathbf {e},x) \in \tilde {E}_C$
. Since
![]() $k_0$
is minimal, we have
$k_0$
is minimal, we have
![]() $0 \leqslant k_0 \leqslant |C|-1$
, and
$0 \leqslant k_0 \leqslant |C|-1$
, and
![]() $(\omega ,\mathbf {e},x) \in \tilde {\mathcal {K}}^{k_0}(\tilde {E}_C)$
.
$(\omega ,\mathbf {e},x) \in \tilde {\mathcal {K}}^{k_0}(\tilde {E}_C)$
.
Proposition 31. The partition
![]() $\mathcal {P}_{\tilde {X}}$
is a generator of the system
$\mathcal {P}_{\tilde {X}}$
is a generator of the system
![]() $(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
.
$(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
.
Proof. The goal is to prove that almost every point in
![]() $\tilde {X}$
is uniquely determined by its
$\tilde {X}$
is uniquely determined by its
![]() $\mathcal {P}_{\tilde {X}}$
-name.
$\mathcal {P}_{\tilde {X}}$
-name.
Let
![]() $(\omega ,\mathbf {e},x) \in \tilde {X}$
. Almost surely, we can define the integer
$(\omega ,\mathbf {e},x) \in \tilde {X}$
. Almost surely, we can define the integer
![]() $k_0$
as in the previous proof:
$k_0$
as in the previous proof:
We note
![]() $a := \tilde {\mathcal {K}}^{-k_0}(e,x) \in \tilde {E}_g$
. Almost surely, a is characterized by its
$a := \tilde {\mathcal {K}}^{-k_0}(e,x) \in \tilde {E}_g$
. Almost surely, a is characterized by its
![]() $\tilde {\mathcal {P}}$
-name
$\tilde {\mathcal {P}}$
-name
![]() $(C_n)_{n \in \mathbb {Z}}$
. To each path,
$(C_n)_{n \in \mathbb {Z}}$
. To each path,
![]() $C_n$
corresponds to a unique sequence of length
$C_n$
corresponds to a unique sequence of length
![]() $|C_n|$
of atoms of
$|C_n|$
of atoms of
![]() $\mathcal {P}_{\tilde {X}}$
: the sequence
$\mathcal {P}_{\tilde {X}}$
: the sequence
![]() $(\tilde {\mathcal {K}}^k(\tilde {E}_{C_n}), 0 \leqslant k \leqslant |C_n|-1)$
. Therefore, a is characterized by the unique sequence
$(\tilde {\mathcal {K}}^k(\tilde {E}_{C_n}), 0 \leqslant k \leqslant |C_n|-1)$
. Therefore, a is characterized by the unique sequence
![]() $(P_n)_{n \in \mathbb {Z}}$
of elements of
$(P_n)_{n \in \mathbb {Z}}$
of elements of
![]() $\mathcal {P}_{\tilde {X}}$
such that for any
$\mathcal {P}_{\tilde {X}}$
such that for any
![]() $n \in \mathbb {Z}$
,
$n \in \mathbb {Z}$
,
We deduce that the point
![]() $(\omega ,\mathbf {e},x)$
is uniquely determined by the sequence
$(\omega ,\mathbf {e},x)$
is uniquely determined by the sequence
![]() $(P_{n+k})_{n \in \mathbb {Z}}$
.
$(P_{n+k})_{n \in \mathbb {Z}}$
.
We then define the isomorphism
![]() $\varphi $
, which associates to almost every point in
$\varphi $
, which associates to almost every point in
![]() $\tilde {X}$
its
$\tilde {X}$
its
![]() $\mathcal {P}_{\tilde {X}}$
-name. We denote by
$\mathcal {P}_{\tilde {X}}$
-name. We denote by
![]() $\eta $
the image measure of
$\eta $
the image measure of
![]() $\tilde {\mu }$
by
$\tilde {\mu }$
by
![]() $\varphi $
and by
$\varphi $
and by
![]() $\sigma $
the left shift on
$\sigma $
the left shift on
![]() $\mathcal {P}_{\tilde {X}}^{\mathbb {Z}}$
. Then
$\mathcal {P}_{\tilde {X}}^{\mathbb {Z}}$
. Then
![]() $\varphi $
is a factor map from
$\varphi $
is a factor map from
![]() $(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
to
$(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
to
![]() $(\mathcal {P}_{\tilde {X}}^{\mathbb {Z}},\eta ,\sigma )$
.
$(\mathcal {P}_{\tilde {X}}^{\mathbb {Z}},\eta ,\sigma )$
.
The measure
![]() $\eta $
is the Markov measure generated by the invariant distribution
$\eta $
is the Markov measure generated by the invariant distribution
![]() $(\tilde {\mu }(P))_{P \in \mathcal {P}_{\tilde {X}}}$
and the following transition probabilities.
$(\tilde {\mu }(P))_{P \in \mathcal {P}_{\tilde {X}}}$
and the following transition probabilities.
-
• From an atom
 $\tilde {\mathcal {K}}^k(\tilde {E}_C)$
with
$\tilde {\mathcal {K}}^k(\tilde {E}_C)$
with
 $C \in \mathscr {C}$
and
$C \in \mathscr {C}$
and
 $0 \leqslant k \leqslant |C|-2$
, the process goes to the atom
$0 \leqslant k \leqslant |C|-2$
, the process goes to the atom
 $\tilde {\mathcal {K}}^{k+1}(\tilde {E}_C)$
with probability
$\tilde {\mathcal {K}}^{k+1}(\tilde {E}_C)$
with probability
 $1$
.
$1$
. -
• From an atom
 $\tilde {\mathcal {K}}^{|C|-1}(\tilde {E}_C)$
with
$\tilde {\mathcal {K}}^{|C|-1}(\tilde {E}_C)$
with
 $C \in \mathscr {C}$
, the process can go to
$C \in \mathscr {C}$
, the process can go to
 $\tilde {E}_{C'}$
for any
$\tilde {E}_{C'}$
for any
 $C' \in \mathscr {C}$
with probability
$C' \in \mathscr {C}$
with probability
 $\mu _g(E_{C'})$
.
$\mu _g(E_{C'})$
.
Therefore, we can identify the natural extension
![]() $(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
with a Markov shift on
$(\tilde {X},\tilde {\mu },\tilde {\mathcal {K}})$
with a Markov shift on
![]() $\mathcal {P}_{\tilde {X}}^{\mathbb {Z}}$
. This Markov shift is irreducible and recurrent, since
$\mathcal {P}_{\tilde {X}}^{\mathbb {Z}}$
. This Markov shift is irreducible and recurrent, since
![]() $\tilde {\mathcal {K}}$
is ergodic. Moreover, it is aperiodic (the atom
$\tilde {\mathcal {K}}$
is ergodic. Moreover, it is aperiodic (the atom
![]() $[g]_0 \times \{(g)\} \times [0,{1}/{\beta }[$
can appear twice in a row, for example). Proposition
$[g]_0 \times \{(g)\} \times [0,{1}/{\beta }[$
can appear twice in a row, for example). Proposition
![]() $2$
on pp. 579 of [Reference Ito, Murata and Totoki9] implies that the partition
$2$
on pp. 579 of [Reference Ito, Murata and Totoki9] implies that the partition
![]() $\mathcal {P}_{\tilde {X}}$
is weak-Bernoulli, and the system
$\mathcal {P}_{\tilde {X}}$
is weak-Bernoulli, and the system
![]() $(\tilde {X}, \tilde {\mu },\tilde {\mathcal {K}})$
is isomorphic to a Bernoulli shift. This concludes the proof of Theorem 26.
$(\tilde {X}, \tilde {\mu },\tilde {\mathcal {K}})$
is isomorphic to a Bernoulli shift. This concludes the proof of Theorem 26.
3.4 Open questions
-
(1) Can we generalize the extensions of this paper to any
 $\beta>2$
? We must take into account the different branches of the greedy and lazy transformations in the construction of the natural extension, especially the branches that induce a return to a base.
$\beta>2$
? We must take into account the different branches of the greedy and lazy transformations in the construction of the natural extension, especially the branches that induce a return to a base. -
(2) It seems natural to apply this kind of construction to other dynamical systems, either deterministic or random ones. It seems that it can be generalized to random systems with piecewise linear maps, even when the branches have different slopes. Indeed, with the construction of the towers, we can keep track of the exact branch that is being applied at each step.
However, systems based on continued fraction expansions should pose many more difficulties. In [Reference Janvresse, Rittaud and de la Rue10], the authors highlight a bijection between the
 $\beta $
parameter of the non-integer base expansions and the
$\beta $
parameter of the non-integer base expansions and the
 $\unicode{x3bb} $
parameter of
$\unicode{x3bb} $
parameter of
 $\unicode{x3bb} $
-continued fractions. The first question would be to identify the analog of the greedy and lazy transformations in this case, and then to closely study this bijection.
$\unicode{x3bb} $
-continued fractions. The first question would be to identify the analog of the greedy and lazy transformations in this case, and then to closely study this bijection. -
(3) The description of the extension
 $(X,\mu ,\mathcal {K})$
provides a better understanding of the random
$(X,\mu ,\mathcal {K})$
provides a better understanding of the random
 $\beta $
-transformation. The extension shows off some nice renewal times at each passage to the greedy base, which provided a proof of the Bernoullicity of the natural extension. We can hope to get limit theorems as well thanks to this property. Indeed, in [Reference Young18], Young describes a certain class of dynamical systems with renewal properties on reference sets. Young shows that the tail distribution of the return time to this reference set is directly linked to the convergence to equilibrium and limit theorems. In our setup, an estimation of the length of paths of
$\beta $
-transformation. The extension shows off some nice renewal times at each passage to the greedy base, which provided a proof of the Bernoullicity of the natural extension. We can hope to get limit theorems as well thanks to this property. Indeed, in [Reference Young18], Young describes a certain class of dynamical systems with renewal properties on reference sets. Young shows that the tail distribution of the return time to this reference set is directly linked to the convergence to equilibrium and limit theorems. In our setup, an estimation of the length of paths of
 $\mathscr {C}$
should help in this direction. Could we then obtain a central limit theorem for the digit sequences in base
$\mathscr {C}$
should help in this direction. Could we then obtain a central limit theorem for the digit sequences in base
 $\beta $
following a fixed sequence
$\beta $
following a fixed sequence
 $\omega $
? Or an average on
$\omega $
? Or an average on
 $\omega $
?
$\omega $
? -
(4) Our construction heavily relies on the independent choice of the transformations at each step. Could we adapt some of these constructions to more general stationary measures on
 $\Omega $
? For example, Markov measures?
$\Omega $
? For example, Markov measures?
Acknowledgements
Many thanks go to Karma Dajani for her inspiring suggestions and the interest she showed in my work. Thanks also go to Thierry de la Rue and Jean-Baptiste Bardet as well for the numerous discussions we had during my PhD candidature, and for their continuous support. Finally, thanks go to the anonymous referee who helped to improve the paper.